Top 50 câu trắc nghiệm về hàm số mũ và logarit – Trần Thanh Minh

Tài liệu 50 câu trắc nghiệm về hàm số mũ và logarit do thầy Trần Thanh Minh biên soạn gồm 5 trang, có đáp án.

103 52 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

89 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 01
C©u 1 :
Hàm số
22
ln( 1 ) 1y x x x x
. Mệnh đề nào sau đây sai ?
A.
Hàm số có đạo hàm
2
' ln( 1 )y x x
B.
Hàm số tăng trên khoảng
C.
Tập xác định của hàm số là
D
D.
Hàm số giảm trên khoảng
C©u 2 :
Hàm số
2
.
x
y x e
nghịch biến trên khoảng :
A.
( ; 2)
B.
( 2;0)
C.
(1; )
D.
( ;1)
C©u 3 :
Giá trị của biểu thức
3 1 3 4
3 2 0
2 .2 5 .5
10 :10 (0,1)
P
là:
A.
9
B.
9
C.
10
D.
10
C©u 4 :
Phương trình
12
5 5.0,2 26
xx
có tổng các nghiệm là:
A.
4
B.
2
C.
1
D.
3
C©u 5 :
Nghiệm của bất phương trình
32.4 18.2 1 0
xx
là:
A.
14x
B.
11
16 2
x
C.
24x
D.
41x
C©u 6 :
Tìm m để phương trình sau có đúng 3 nghiệm:
22
2
4 2 6
xx
m
A.
23m
B.
3m
C.
2m
D.
3m
C©u 7 :
Phương trình
1 x 1 x
3 3 10
A.
Có hai nghiệm âm.
B.
Vô nghiệm
C.
Có hai nghiệm dương
D.
Có một nghiệm âm và một nghiệm
dương
C©u 8 :
Tập nghiệm của phương trình
x1
2x
1
125
25
bằng
2
A.
1
B.
4
C.
1
4
D.
1
8
C©u 9 :
Nghiệm của phương trình
4 2 2 4
log (log ) log (log ) 2xx
là:
A.
2x
B.
4x
C.
8x
D.
16x
C©u 10 :
Nếu
30
log 3a
và
30
log 5b
thì:
A.
30
log 1350 2 2ab
B.
30
log 1350 2 1ab
C.
30
log 1350 2 1ab
D.
30
log 1350 2 2ab
C©u 11 :
Tìm tập xác định hàm số sau:
2
1
2
3 2x
( ) log
1
x
fx
x

A.
3 13 3 13
; 3 ;1
22
D



B.
; 3 1;D
C.
3 13 3 13
; 3 ;1
22
D
D.
3 13 3 13
;;
22
D
 



C©u 12 :
Phương trình
22
1
4 2 3
x x x x

có nghiệm:
A.
1
2
x
x
B.
1
1
x
x

C.
0
1
x
x
D.
1
0
x
x

C©u 13 :
Tính đạo hàm của hàm số sau:
()
x
f x x
A.
1
'( ) ( lnx)
x
f x x x

B.
'( ) (lnx 1)
x
f x x
C.
'( )
x
f x x
D.
'( ) lnxf x x
C©u 14 :
Phương trình:
3
log (3x 2) 3
có nghiệm là:
A.
11
3
B.
25
3
C.
29
3
D.
87
C©u 15 :
T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A.
Hµm sè y =
a
log x
víi a > 1 lµ mét hµm sè nghÞch biÕn trªn kho¶ng (0 ; +)
B.
Hµm sè y =
a
log x
víi 0 < a < 1 lµ mét hµm sè ®ång biÕn trªn kho¶ng (0 ; +)
C.
Hµm sè y =
a
log x
(0 < a 1) cã tËp x¸c ®Þnh lµ R
3
D.
§å thÞ c¸c hµm sè y =
a
log x
vµ y =
1
a
log x
(0 < a 1) th× ®èi xøng víi nhau qua trôc hoµnh
C©u 16 :
Giả sử các số logarit đều có nghĩa, điều nào sau đây là đúng?
A.
Cả 3 đáp án trên đều sai
B.
log log
aa
b c b c
C.
log log
aa
b c b c
D.
log log
aa
b c b c
C©u 17 :
Hàm số
lny x x
đồng biến trên khoảng :
A.
(0; )
B.
1
;
e
C.
(0;1)
D.
1
0;
e
C©u 18 :
Tính đạo hàm của hàm số sau:
()
xx
xx
ee
fx
ee
A.
2
4
'( )
()
xx
fx
ee
B.
'( )
xx
f x e e

C.
2
'( )
()
x
xx
e
fx
ee
D.
2
5
'( )
()
xx
fx
ee
C©u 19 :
Nếu
15
log 3a
thì:
A.
25
3
log 15
5(1 )a
B.
25
5
log 15
3(1 )a
C.
25
1
log 15
2(1 )a
D.
25
1
log 15
5(1 )a
C©u 20 :
Cho
( 2 1) ( 2 1)
mn
. Khi đó
A.
mn
B.
mn
C.
mn
D.
mn
C©u 21 :
Nghiệm của phương trình
21
7
1
8 0,25. 2
x
x
x
là:
A.
2
1,
7
xx
B.
2
1,
7
xx
C.
2
1,
7
xx
D.
2
1,
7
xx
C©u 22 :
Tập xác định của hàm số
3
( 2)yx
là:
A.
\ {2}
B.
C.
( ;2)
D.
(2; )
C©u 23 :
Nghiệm của phương trình
22
3 3 30
xx
là:
A.
0x
B.
Phương trình vô
nghiệm
C.
3x
D.
1x
4
C©u 24 :
Tập xác định của hàm số
3
2
10
log
3x 2
x
y
x

là:
A.
(1; )
B.
( ;10)
C.
( ;1) (2;10)
D.
(2;10)
C©u 25 :
Giá trị của
2
a
8log 7
a 0 a 1
bằng
A.
2
7
B.
8
7
C.
16
7
D.
4
7
C©u 26 :
Cho f(x) =
ln sin 2x
. §¹o hµm f’
8



b»ng:
A.
1
B.
3
C.
4
D.
2
C©u 27 :
Phương trình
21
3 4.3 1 0
xx
có hai nghiệm
12
,xx
trong đó
12
xx
, chọn phát biểu
đúng?
A.
12
20xx
B.
12
21xx
C.
12
2xx
D.
12
.1xx
C©u 28 :
Tập xác định của hàm số
3
18
2
2
log 1 log 3 log 1f x x x x
là:
A.
1x
B.
13x
C.
3x
D.
11x
C©u 29 :
Nghiệm của phương trình
2x 2
1
3 .5 15
x
x
là:
A.
1x
B.
2
2, log 5xx
C.
4x
D.
3
3, log 5xx
C©u 30 :
Giá trị của biểu thức
57
9 125
2
log 6 log 8
1 log 4 log 27
2 log 3
25 49 3
3 4 5
P
là:
A.
8
B.
10
C.
9
D.
12
C©u 31 :
Cho
2
logam
với
0; 1mm
và
log 8
m
Am
. Khi đó mối quan hệ giữa
A
và
a
là:
A.
3A a a
B.
3 a
A
a
C.
3 a
A
a
D.
3A a a
C©u 32 :
Hµm sè y =
2
ln x 5x 6
cã tËp x¸c ®Þnh lµ:
A.
(-; 2) (3; +)
B.
(0; +)
C.
(-; 0)
D.
(2; 3)
C©u 33 :
Tập các số x thỏa mãn
0,4
log ( 4) 1 0x
là:
A.
13
4;
2


B.
13
;
2




C.
13
;
2



D.
(4; )
5
C©u 34 :
Cho hàm số
.
x
y x e
, với
0;x
. Mệnh đề nào sau đây là mệnh đề đúng ?
A.
0;
0;
11
; min
x
x
max y y
ee
B.
0;
0;
1
; min 0
x
x
max y y
e
C.
0;
1
min ;
x
y
e
không tồn tại
D.
0;
1
;
x
max y
e
không tồn tại
0;
min
x
y
C©u 35 :
Tập nghiệm của bất phương trình
32.4 18.2 1 0
xx
là tập con của tập :
A.
( 5; 2)
B.
( 4;0)
C.
(1;4)
D.
( 3;1)
C©u 36 :
T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A.
Hµm sè y = a
x
víi 0 < a < 1 lµ mét hµm sè ®ång biÕn trªn (-: +)
B.
Hµm sè y = a
x
víi a > 1 lµ mét hµm sè nghÞch biÕn trªn (-: +)
C.
§å thÞ hµm sè y = a
x
(0 < a 1) lu«n ®i qua ®iÓm (a ; 1)
D.
§å thÞ c¸c hµm sè y = a
x
vµ y =
x
1
a



(0 < a 1) th× ®èi xøng víi nhau qua trôc tung
C©u 37 :
Trong các khẳng định sau, khẳng định nào sai ?
A.
3
log 5 0
B.
22
x 3 x 3
log 2007 log 2008
C.
34
1
log 4 log
3
D.
0,3
log 0,8 0
C©u 38 :
Dùng định nghĩa, tính đạo hàm của hàm số sau:
gxxxf cot.)(
A.
x
x
gxxf
2
sin
cot)('
B.
gxxxf cot.)('
C.
1cot)(' gxf
D.
x
x
tgxxf
2
cos
)('
C©u 39 :
Cho
log 3
a
b
. Khi đó giá trị của biểu thức
log
b
a
b
a
là
A.
31
32
B.
31
C.
31
D.
31
32
C©u 40 :
Cho
21
33
( 1) ( 1)aa
. Khi đó ta có thể kết luận về a là:
A.
2a
B.
1a
C.
12a
D.
01a
6
C©u 41 :
Hµm sè y =
5
1
log
6x
cã tËp x¸c ®Þnh lµ:
A.
(0; +)
B.
R
C.
(6; +)
D.
(-; 6)
C©u 42 :
Đạo hàm của hàm số
2
( ) sin2 .ln (1 )f x x x
là:
A.
2
2sin2 .ln(1 )
'( ) 2 os2 .ln (1 )
1
xx
f x c x x
x
B.
2
2sin2
'( ) 2 os2 .ln (1 )
1
x
f x c x x
x
C.
2
'( ) 2 os2 .ln (1 ) 2sin2 .ln(1 )f x c x x x x
D.
'( ) 2 os2 2ln(1 )f x c x x
C©u 43 :
Cho hàm số
1
x
e
y
x
. Mệnh đề nào sau đây là mệnh đề đúng ?
A.
Đạo hàm
2
'
( 1)
x
e
y
x
B.
Hàm số đạt cực đại tại
(0;1)
C.
Hàm số đạt cực tiểu tại
(0;1)
D.
Hàm số tăng trên
\1
C©u 44 :
Nghiệm của bất phương trình
41
4
3 1 3
log 3 1 .log
16 4
x
x
là:
A.
;1 2;x
B.
1;2x
C.
1;2x
D.
0;1 2;x
C©u 45 :
Giải phương trình
2
5.2 8
log 3
22
x
x
x
với
x
là nghiệm của phương trình trên. Vậy giá
trị
2
log 4 x
Px
là:
A.
4P
B.
8P
C.
2P
D.
1P
C©u 46 :
Bất phương trình
23
log (2 1) log (4 2) 2
xx
có tập nghiệm:
A.
( ;0)
B.
[0; )
C.
( ;0]
D.
0;
C©u 47 :
Phương trình
22
3 .5 15
x
x
x
có một nghiệm dạng
log
a
xb
, với a và b là các số nguyên
dương lớn hơn 1 và nhỏ hơn 8. Khi đó
2ab
bằng:
A.
13
B.
8
C.
3
D.
5
C©u 48 :
Cho phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
12
,xx
. Tổng
12
xx
là:
A.
2
log 6 4 2
B.
2
C.
4
D.
6 4 2
7
C©u 49 :
Giải bất phương trình:
ln( 1)xx
A.
Vô nghiệm
B.
0x
C.
01x
D.
2x
C©u 50 :
Nghiệm của phương trình:
2
2 2 2
log 2x log 6 log 4x
4 2.3 .x
A.
1
0,
4
xx
B.
1
4
x
C.
2
3
x 
D.
Vô nghiệm
C©u 51 :
Điều nào sau đây là đúng?
A.
mn
a a m n
B.
mn
a a m n
C.
Cả 3 câu đáp án trên đều sai.
D.
Nếu
ab
thì
0
mm
a b m
C©u 52 :
Nếu
2
log 3a
và
2
log 5b
thì:
A.
6
2
1 1 1
log 360
3 4 6
ab
B.
6
2
1 1 1
log 360
2 6 3
ab
C.
6
2
1 1 1
log 360
2 3 6
ab
D.
6
2
1 1 1
log 360
6 2 3
ab
C©u 53 :
Phương trình
12
1
5 lg 1 lgxx
có số nghiệm là
A.
2
B.
1
C.
3
D.
4
C©u 54 :
Tập giá trị của hàm số
( 0, 1)
x
y a a a
là:
A.
[0; )
B.
\{0}
C.
(0; )
D.
C©u 55 :
Bất phương trình:
2
log 4
32
x
x
có tập nghiệm:
A.
1
;2
10



B.
1
;4
32



C.
1
;2
32



D.
1
;4
10



C©u 56 :
Tìm giá trị nhỏ nhất của hàm số:
13
( ) 2 2
xx
fx


A.
4
B.
6
C.
-4
D.
Đáp án khác
C©u 57 :
Hệ phương trình
30
logx log 3log6
xy
y


có nghiệm:
A.
14
16
x
y
và
16
14
x
y
B.
15
15
x
y
và
14
16
x
y
8
C.
12
18
x
y
và
18
12
x
y
D.
15
15
x
y
C©u 58 :
Hµm sè y =
2x
x 2x 2 e
cã ®¹o hµm lµ :
A.
KÕt qu¶ kh¸c
B.
y’ = -2xe
x
C.
y’ = (2x - 2)e
x
D.
y’ = x
2
e
x
C©u 59 :
Tập giá trị của hàm số
log ( 0, 0, 1)
a
y x x a a
là:
A.
(0; )
B.
[0; )
C.
D.
Cả 3 đáp án trên
đều sai
C©u 60 :
Cho biểu thức
1
2
4a b ab
, với
0ba
. Khi đó biểu thức có thể rút gọn là
A.
ba
B.
a
C.
ab
D.
ab
9
ĐÁP ÁN
01
28
{ ) } ~
55
{ | ) ~
02
{ ) } ~
29
{ ) } ~
56
) | } ~
03
{ | ) ~
30
{ | ) ~
57
{ | ) ~
04
) | } ~
31
{ ) } ~
58
{ | } )
05
{ | } )
32
{ | } )
59
{ | ) ~
06
{ ) } ~
33
) | } ~
60
) | } ~
07
{ | } )
34
{ ) } ~
08
{ | } )
35
) | } ~
09
{ | } )
36
{ | } )
10
{ | ) ~
37
{ | } )
11
) | } ~
38
) | } ~
12
{ | ) ~
39
) | } ~
13
{ ) } ~
40
) | } ~
14
{ | ) ~
41
{ | } )
15
{ | } )
42
) | } ~
16
{ | ) ~
43
{ ) } ~
17
{ ) } ~
44
{ | } )
18
) | } ~
45
{ ) } ~
19
{ | ) ~
46
{ | ) ~
20
) | } ~
47
) | } ~
21
{ | } )
48
{ ) } ~
22
) | } ~
49
{ ) } ~
23
{ | } )
50
{ ) } ~
24
{ | ) ~
51
{ | ) ~
25
{ | } )
52
{ | ) ~
26
{ | } )
53
) | } ~
27
{ ) } ~
54
{ | ) ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 02
C©u 1 :
Số nghiệm của phương trình:

1
3 3 2
xx
là
A.
0
B.
3
C.
1
D.
2
C©u 2 :
(x; y) l nghiệm của hệ
23
23
log 3 1 log
log 3 1 log
xy
yx
. Tng
2xy
bng
A.
6
B.
9
C.
39
D.
3
C©u 3 :
Số nghiệm của phương trình
1
3 3 2
xx

A.
Vô nghiệm
B.
3
C.
2
D.
1
C©u 4 :
Số nghiệm của phương trình
2
x+ 2x+5
- 2
1+ 2x+5
+ 2
6-x
- 32 = 0 là :
A.
4
B.
2
C.
1
D.
3
C©u 5 :
Hàm số y = ln(x
2
-2mx + 4) có tập xác định D = R khi:
A.
m < 2
B.
-2 < m < 2
C.
m = 2
D.
m > 2 hoặc m < -2
C©u 6 :
Tập xác định của hàm số
2
2
1
2 5 2 ln
1
xx
x
là:
A.
1;2
B.
1;2
C.
1;2
D.
1;2
C©u 7 :
Phương trình
3
2
1
2.4 3.( 2) 0
2
x
xx



A.
-1
B.
2
log 5
C.
0
D.
2
log 3
C©u 8 :
Số nghiệm của phương trình
2
31
3
log ( 4 ) log (2 3) 0x x x
l:
A.
3
B.
2
C.
Vô nghiệm.
D.
1
C©u 9 :
Số nghiệm của hệ phương trình
012
84
1
2
y
y
x
x
l:
2
A.
Vô nghiệm
B.
2
C.
3
D.
1
C©u 10 :
Tập xác định của hàm số
2
( 3 2)
e
y x x
là:
A.
( ; 2)
B.
( 1; )
C.
( 2; 1)
D.



2; 1
C©u 11 :
Nếu
3
2
3
2
34
và log log
45
bb
aa
thì:
A.
0 < a < 1, 0 < b < 1
B.
0 < a < 1, b > 1
C.
a > 1, 0 < b < 1
D.
a > 1, b > 1
C©u 12 :
Cho a>0, b >0 tha mn
22
7a b ab
. Chn mệnh đ đng trong các mệnh đ sau:
A.
1
3log( ) (log log )
2
a b a b
B.
3
log( ) (log log )
2
a b a b
C.
2(log log ) log(7ab)ab
D.
1
log (log log )
32
ab
ab

C©u 13 :
Tập nghiệm của bất phương trình
21
3 10.3 3 0
xx
là :
A.
1;1
B.
1;0
C.
0;1
D.
1;1
C©u 14 :
Phương trình
1
4 .2 2 0
xx
mm
có hai nghiệm
12
,xx
tha
12
3xx
khi
A.
4m
B.
2m
C.
1m
D.
3m
C©u 15 :
Tập nghiệm của bất phương trình log
3
x < log
3
(12-x) là :
A.
(0;12)
B.
(0;9)
C.
(9;16)
D.
(0;16)
C©u 16 :
Hàm số y = x.lnx có đạo hàm là :
A.
1
x
B.
lnx + 1
C.
lnx
D.
1
C©u 17 :
Đạo hàm của hàm số
21
5
x
x
y
là :
3
A.
22
ln 5 ln5
55
x
x



B.
2 2 1
ln ln5
5 5 5
xx
C.
11
21
.
55
xx
xx

D.
11
21
..
55
xx
xx

C©u 18 :
Cho phương trình:
3
3( 1)
1 12
2 6.2 1
22
xx
xx
(*). Số nghiệm của phương trình (*) l:
A.
Vô nghiệm.
B.
2
C.
1
D.
3
C©u 19 :
Tính
36
log 24
theo
12
log 27 a
là
A.
9
62
a
a
B.
9
62
a
a
C.
9
62
a
a
D.
9
62
a
a
C©u 20 :
Số nghiệm của phương trình log
2
5
(5x) - log
25
(5x) - 3 = 0 là :
A.
1
B.
2
C.
4
D.
3
C©u 21 :
Tính
30
log 1350
theo a, b với
30
log 3 a
và
30
log 5 b
là
A.
21ab
B.
21ab
C.
21ab
D.
21ab
C©u 22 :
Rút gn biểu thức
55
44
4
4
(x,y 0)
x y xy
xy
được kết quả là:
A.
2xy
B.
xy
C.
xy
D.
2
xy
C©u 23 :
Tích hai nghiệm của phương trình
4 2 4 2
2 4 6 2 3
2 2.2 1 0
x x x x
là:
A.
-9
B.
-1
C.
1
D.
9
C©u 24 :
Tập nghiệm của bất phương trình (2- 3 )
x
> (2 + 3)
x+2
là :
A.
(-2;+ )
B.
(- ;-1)
C.
(-1;+ )
D.
(- ;-2)
C©u 25 :
Nghiệm của phương trình
31
4
1
3
9
x
x



là
A.
1
3
B.
1
C.
6
7
D.
7
6
4
C©u 26 :
Tập nghiệm của bất phương trình log
2
2
(2x) - 2log
2
(4x
2
) - 8 0 là :
A.
[2;+ )
B.
[
1
4
;2]
C.
[-2;1]
D.
(- ;
1
4
]
C©u 27 :
Biểu thức A = 4
log
2
3
có giá trị là :
A.
16
B.
9
C.
12
D.
3
C©u 28 :
Rút gn biểu thức
7 1 2 7
2 2 2 2
.
(a 0)
()
aa
a


được kết quả là
A.
a
4
B.
a
C.
a
5
D.
a
3
C©u 29 :
10.Đạo hàm của hàm số:
2
(x )yx

là:
A.
21
2 (x )x
B.
21
(x ) (2x 1)x

C.
21
(x ) (2x 1)x

D.
21
(x )x
C©u 30 :
Hàm số
ln x
y
x
A.
Có một cực tiểu
B.
Có một cực đại
C.
Không có cực trị
D.
Có một cực đại và một cực tiểu
C©u 31 :
Nghiệm của phương trình
2
3 5 3 5 3.
xx
x
l:
A.
x = 2 hoc x = -3
B.
Đáp án khác
C.
x = 0 hoc x = -1
D.
x = 1 hoc x=-1
C©u 32 :
Số nghiệm của phương trình ln
3
x – 3ln
2
x – 4lnx+ 12 = 0 là
A.
1
B.
3
C.
2
D.
0
C©u 33 :
Trong các điu kiện của biểu thức tồn tại, kết quả rút gn của
32
log 2log log log log log
b b b a ab b
A a a a b b a
là
A.
1
B.
2
C.
0
D.
3
5
C©u 34 :
32
2 2 2
log ( 1) log ( 1) 2log 0
x x x x
A.
1
x

B.
0
x
C.
x
D.
x > 0
C©u 35 :
Tập nghiệm của bất phương trình
2
22
55
xx
là:
A.
12x
B.
x < -2 hoặc x > 1
C.
x > 1
D.
Đáp án khác
C©u 36 :
.Nếu
3
2
3
2
aa
và
34
log log
45
bb
thì :
A.
0<a<1,0<b<1
B.
C.a>1,b>1
C.
0<a<1,b>1
D.
a>1,0<b<1
C©u 37 :
Số nghiệm của phương trình
3
log ( 2) 1
x

l
A.
3
B.
2
C.
0
D.
1
C©u 38 :
Tch các nghiệm của phương trình:
6 5 2 3
x x x x
bng:
A.
4
B.
3
C.
0
D.
1
C©u 39 :
Nghiệm của bất phương trình
2
12
2
log log (2 ) 0
x



l:
A.
( 1;1) (2; )
B.
(-1;1)
C.
Đáp án khác
D.
( 1;0) (0;1)
C©u 40 :
Phương trình
9 3.3 2 0
xx
c hai nghiêm
1 2 1 2
, ( )
x x x x
Giá trị của
12
23
A x x

A.
0
B.
2
4 log 3
C.
2
D.
3
3log 2
C©u 41 :
Phương trình:
9 3.3 2 0
xx
có hai nghiệm
1 2 1 2
, ( )x x x x
.Giá trị của
12
23A x x
là:
A.
0
B.
2
4log 3
C.
3
3log 2
D.
2
C©u 42 :
Tập xác định của hàm số
2
32
log 1 1 4
x
x

là
A.
21
; \ ;0
33



B.
21
;\
33



C.
2
; \ 0
3




D.
2
;
3




C©u 43 :
Giá trị rút gọn của biểu thức
19
44
15
44
aa
A
aa
là:
A.
1 + a
B.
1 - a
C.
2a
D.
a
C©u 44 :
Số nghiệm của phương trình
2 3 2
log .log (2 1) 2log
x x x

l:
6
A.
0
B.
1
C.
3
D.
2
C©u 45 :
Rút gn biểu thức
1 1 1 1
3 3 3 3
3 2 3 2
(a,b 0, )
a b a b
ab
ab

được kết quả là:
A.
2
3
1
()ab
B.
2
3
()ab
C.
C.
3
1
ab
D.
3
ab
C©u 46 :
Chọn khẳng định sai trong các khẳng định sau
A.
11
33
log log 0a b a b
B.
ln 0 1xx
C.
3
log 0 0 1xx
D.
11
22
log log 0a b a b
C©u 47 :
Phương trình
22
33
log log 1 2 1 0x x m
có nghiệm trên
3
1;3


khi :
A.
3
0;
2
m



B.
3
;0 ;
2
m

 

C.
0;
D.
3
;
2



C©u 48 :
Giá trị nhỏ nhất , giá trị lớn nhất của hàm số y = x - lnx trên
1
2
;e
theo thứ tự là :
A.
1
2
+ ln2 và e-1
B.
1 và e-1
C.
1 và
1
2
+ ln2
D.
1
2
và e
C©u 49 :
Nghiệm của bất phương trình
2.2 3.3 6 1 0
x x x
l:
A.
3x
B.
2x
C.
Mi x
D.
x < 2
C©u 50 :
Số nghiệm của phương trình
2
2 7 5
21
xx
là:
A.
2
B.
1
C.
0
D.
3
C©u 51 :
Tập nghiệm của bất phương trình
2
4.3 9.2 5.6
x
xx

là
A.
;4
B.
4;
C.
;5
D.
5;
C©u 52 :
Nghiệm của phương trình
63
3 2 0
xx
ee
là:
A.
1
0, ln2
3
xx
B.
x = -1,
1
ln2
3
x
C.
Đáp án khác
D.
x = 0, x = -1
7
C©u 53 :
Bất phương trình
21
11
12 0
33
xx
c tập nghiệm l
A.
(0; )
B.
( ; 1)
C.
(-1;0)
D.
\0R
.
C©u 54 :
Phương trình:
22
2(x 1) x 2
( 2).2 ( 1).2 2 6m m m

c nghiệm khi
A.
29m
B.
29m
C.
29m
.
D.
29m
C©u 55 :
Đạo hàm của hàm số y = x(lnx – 1) là:
A.
lnx -1
B.
lnx
C.
1
D.
1
1
x
C©u 56 :
Nghiệm của bất phương trình
2 2 2
log ( 1) 2 log (5 ) 1 log ( 2)
x x x
A.
2 < x < 5
B.
-4 < x < 3
C.
1 < x < 2
D.
2 < x < 3
C©u 57 :
Giá trị nh nhất của hm số
( ) (2 ln )
f x x x

trên
2;3
A.
e
B.
2 2 ln2
C.
4 2ln2
D.
1
C©u 58 :
Giá trị nhỏ nhất , giá trị lớn nhất của hàm số y =
x
2
e
x
trên đoạn
[ ]
-1;1
theo thứ tự là :
A.
0 và
1
e
B.
0 và e
C.
1
e
và e
D.
1 và e
C©u 59 :
Tập nghiệm của bất phương trình:
2
2
12
0
2
2
x
xx

l
A.
;0
B.
;1
C.
2;
D.
0;2
.
8
ĐÁP ÁN
01
{ | ) ~
28
{ | ) ~
55
{ ) } ~
02
{ | } )
29
{ | ) ~
56
{ | } )
03
{ | } )
30
{ ) } ~
57
{ | } )
04
{ ) } ~
31
{ | } )
58
{ ) } ~
05
{ ) } ~
32
{ ) } ~
59
{ | ) ~
06
) | } ~
33
) | } ~
07
{ | } )
34
{ | } )
08
{ | ) ~
35
) | } ~
09
{ | } )
36
{ | ) ~
10
{ | ) ~
37
{ | } )
11
{ ) } ~
38
{ | ) ~
12
{ | } )
39
{ | } )
13
) | } ~
40
{ | } )
14
) | } ~
41
{ | ) ~
15
{ ) } ~
42
) | } ~
16
{ ) } ~
43
) | } ~
17
) | } ~
44
{ | } )
18
{ | ) ~
45
{ | ) ~
19
) | } ~
46
) | } ~
20
{ ) } ~
47
) | } ~
21
) | } ~
48
{ ) } ~
22
{ ) } ~
49
{ | } )
23
{ | ) ~
50
) | } ~
24
{ ) } ~
51
) | } ~
25
{ | ) ~
52
) | } ~
26
{ ) } ~
53
{ | ) ~
27
{ ) } ~
54
{ | ) ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 03
C©u 1 :
Tập xác định của hàm số
2
3
y log x x 12
:
A.
( 4;3)
B.
( ; 4) (3; ) 
C.
( 4;3]
D.
R \ 4
C©u 2 :
Tập nghiệm của phương trình
2
2
2
log 4log 0xx
A.
1;16S
B.
1;2S
C.
1;4S
D.
4S
C©u 3 :
Cho hàm số
x
y ex e

. Nghiệm của phương trình
y' 0
là:
A.
x ln3
B.
x1
C.
x0
D.
x ln2
C©u 4 :
Nếu
log3 a
thì
81
1
log 100
bằng
A.
4
a
B.
16a
C.
8
a
D.
2a
C©u 5 :
Các kết luận sau , kết luận nào sai
I.
3
17 28
II.
32
11
32
III.
57
44
IV.
45
13 23
A.
I
B.
II và III
C.
III
D.
II và IV
C©u 6 :
Hàm số nào sau đây có tập xác định là R?
A.
0,1
2
4yx
B.
1/2
4yx
C.
3
2x
y
x



D.
2
2
23y x x
C©u 7 :
Nếu
12
log 6 a
và
12
log 7 b
thì
A.
12
log 7
1
a
b
B.
12
log 7
1
a
b
C.
12
log 7
1
a
a
D.
12
log 7
1
b
a
C©u 8 :
Tìm m để phương trình
2
22
log log 0x x m
có nghiệm
(0;1)x
2
A.
1m
B.
1
4
m
C.
1
4
m
D.
1m
C©u 9 :
Số giá trị nguyên âm của m để
.9 2 1 6 .4 0
x x x
m m m
với
0;1x
là
A.
6
B.
4
C.
5
D.
3
C©u 10 :
Tập xác định của hàm số
1
2
21yx
là:
A.
1
;
2




B.
1
2



C.
1
;
2



D.
C©u 11 :
Phát biểu nào sau đây không đúng?
A.
Hai hàm số
x
ya
và
log
a
yx
có cùng tập giá trị.
B.
Hai đồ thị hàm số
x
ya
và
log
a
yx
đối xứng nhau qua đường thẳng
yx
C.
Hai hàm số
x
ya
và
log
a
yx
có cùng tính đơn điệu.
D.
Hai đồ thị hàm số
x
ya
và
log
a
yx
đều có đường tiệm cận.
C©u 12 :
Tìm giá trị nhỏ nhất của hàm số:
22
sin os
44
x c x
y 
A.
2
B.
C.
2
D.
4
C©u 13 :
Cho
0; 0ab
và
22
7a b ab
. Đẳng thức nào sau đây là đúng?
A.
7 7 7
1
log log log
32
ab
ab

B.
3 3 3
1
log log log
27
ab
ab

C.
3 3 3
1
log log log
72
ab
ab

D.
7 7 7
1
log log log
23
ab
ab

C©u 14 :
Số nghiệm của phương trình
00
cos36 cos72 3.2
xx
x

là:
A.
3
B.
2
C.
1
D.
4
C©u 15 :
Giá trị của
2
4log 5
a
a
(
0a
và
1a
) bằng
A.
8
5
B.
4
5
C.
5
D.
2
5
C©u 16 :
Cho hàm số
x
ya
, Các mệnh đề sau , mệnh đề nào sai
A.
Đố thị hàm số luon đi qua điểm
0;1M
và
B.
Đồ thị hàm số có đường tiệm cận là
0y
3
1;Na
C.
Đồ thị hàm số không có điểm uốn
D.
Đồ thị hàm số luôn tăng
C©u 17 :
Hệ phương trình
2
2
8
16 2 2
2 2 2
4 3 1 4 3 4 8 17
ln( 3 3) 1 4 3 8
yy
x
x x y y y
x x x y x x
có 1 cặp nghiệm
;xy
. Giá trị của
3xy
là:
A.
-1
B.
-3
C.
0
D.
-2
C©u 18 :
Phương trình
22
log log 1 1xx
có tập nghiệm là:
A.
1S
B.
1; 2S 
C.
15
2
S






D.
15
2
S






C©u 19 :
Tính giá trị biểu thức:
35
2 2 4
3
. . .
log
a
a a a a
A
a
A.
67
5
B.
62
15
C.
22
5
D.
16
5
C©u 20 :
Đạo hàm của hàm số
23
2
x
y
là:
A.
23
2.2 ln2
x
B.
23
2 ln2
x
C.
23
2.2
x
D.
22
2 3 2
x
x
C©u 21 :
Tập nghiệm của bất phương trình
22
log log 2 1xx
là:
A.
S 
B.
1;3S
C.
;1S 
D.
1
;0
2
S




C©u 22 :
Cho hàm số
x 1 x
y 2 3

. Giá trị của đạo hàm của hàm số tại
x0
:
A.
2
3
B.
ln54
C.
3ln3
D.
2ln6
C©u 23 :
Bất phương trình
2
22
33
xx
có tập nghiệm là:
A.
;1
B.
1;
C.
1;2
D.
1;2
C©u 24 :
Cho hàm số
yx
4
, Các kết luận sau , kết luận nào sai
A.
Tập xác định
0;D
B.
Hàm số luôn luôn đồng biến với mọi
x
thuộc tập xác định
4
C.
Hàm số luôn đi qua điểm
1;1M
D.
Hàm số không có tiệm cận
C©u 25 :
Cho
a 0 ; a 1
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
Tập xác định của hàm số
x
ya
là khoảng
0;
B.
Tập giá trị của hàm số
a
y log x
là tập
C.
Tập xác định của hàm số
a
y log x
là tập
D.
Tập giá trị của hàm số
x
ya
là tập
C©u 26 :
Cho hàm số
2
y ln(x 1)
. Nghiệm của phương trình
y' 0
:
A.
x1
B.
x0
C.
x1
D.
x 0 v x 1
C©u 27 :
Cho hàm số
2
f(x) ln x x
. Giá trị của đạo hàm cấp hai của hàm số tại
x2
:
A.
36
B.
13
36
C.
2ln6
D.
13
C©u 28 :
Nếu
17 15
38
aa
và
log 2 5 log 2 3
bb
thì
A.
1a
,
1b
B.
01a
,
1b
C.
1a
,
01b
D.
01a
,
01b
C©u 29 :
Cho
0; 0; 1; 1;a b a b n R
, một học sinh tính biểu thức
2
1 1 1
......
log log log
an
aa
P
b b b
theo các bước sau
I .
2
log log ... log
n
b b b
P a a a
II.
2
log . ...
n
b
P a a a
III.
1 2 3 ...
log
n
b
Pa
IV.
1 log
b
P n n a
Bạn học sinh trên đã giải sai ở bước nào
A.
I
B.
II
C.
III
D.
IV
C©u 30 :
Khẳng định nào sau đây sai ?
A.
2 1 3
22
B.
2016 2017
2 1 2 1
5
C.
2018 2017
22
11
22
D.
2017 2016
3 1 3 1
C©u 31 :
Cho hàm số
yx
1
3
, Các mệnh đề sau , mệnh đề nào sai
A.
1
3
lim
x
fx
B.
Hàm số có đồ thị nhận trục tung làm trục
đối xứng
C.
Hàm số không có đạo hàm tại
0x
D.
Hàm số đồng biến trên
;0
và nghịch
biến
0;
C©u 32 :
Nếu
4
3
5
4
aa
và
12
log log
23
bb
thì
A.
1a
,
1b
B.
01a
,
01b
C.
01a
,
1b
D.
1a
,
01b
C©u 33 :
Đạo hàm của hàm số
2
2
log 2 1yx
là:
A.
2
2log 2 1
2 1 ln2
x
x
B.
2
4log 2 1
2 1 ln2
x
x
C.
2
4log 2 1
21
x
x
D.
2
2 1 ln2x
C©u 34 :
Cho:
2k
a
aa
1 1 1
...
log log log
M
x x x
M thỏa mãn biểu thức nào trong các biểu thức sau:
A.
a
( 1)
log
kk
M
x
B.
a
4 ( 1)
log
kk
M
x
C.
a
( 1)
2log
kk
M
x
D.
a
( 1)
3log
kk
M
x
C©u 35 :
Rút gọn biểu thức
11
16
x x x x : x
, ta được :
A.
6
x
B.
4
x
C.
8
x
D.
x
C©u 36 :
Cho hàm số
yx
1
3
, Trong các mệnh đề sau , mệnh đề nào sai
A.
Hàm số đồng biến trên tập xác định
B.
Hàm số nhận
0; 0O
làm tâm đối xứng
C.
Hàm số lõm
;0
và lồi
0;
D.
Hàm số có đồ thị nhận trục tung làm trục
đối xứng
6
C©u 37 :
Hàm số
2
x3
y log
2x
có nghĩa khi :
A.
x2
B.
3 x 2
C.
x 3 x 2
D.
3 x 2
C©u 38 :
Cho hàm số
yx
2
2
32

, tập xác định của hàm số là
A.
22
;;
33
D
B.
22
;;
33
D
C.
22
;
33
D
D.
2
\
3
DR
C©u 39 :
Cho hàm số
yx
5
31

, tập xác định của hàm số là
A.
DR
B.
;1D
C.
1;D
D.
\1DR
C©u 40 :
Đạo hàm của hàm số
2
2
log 2 1f x x
là
A.
2
4
'( )
2 1 ln2
x
fx
x
B.
2
1
'( )
2 1 ln2
fx
x
C.
2
4
'( )
2 1 ln2
x
fx
x

D.
Kết quả khác
C©u 41 :
Rút gọn
41
1
2
33
3
3
22
3
33
8
. 1 2
24
a a b b
Aa
a
a ab b





được kết quả:
A.
1
B.
a + b
C.
0
D.
2a - b
C©u 42 :
Cho
15
log 3 a
, giá trị của
25
log 15
là:
A.
1 a
a
B.
1
1
a
a
C.
1 a
a
D.
1
1
a
a
C©u 43 :
Nếu
6 5 6 5
x
thì
A.
1x 
B.
1x
C.
1x 
D.
1x
C©u 44 :
Số nghiệm nguyên của bất phương trình
31
13
10 3 10 3
xx
xx


là
A.
1
B.
3
C.
0
D.
2
C©u 45 :
Giá trị của
log 4
a
a
(
0a
và
1a
) bằng
7
A.
4
B.
2
C.
16
D.
1
2
C©u 46 :
Số nghiệm dương của phương trình là:
2 2 1
2
log 2 log 5 log 8 0.xx
A.
0
B.
3
C.
2
D.
1
C©u 47 :
Nếu
log3 a
thì
log9000
bằng
A.
2
3a
B.
2
a
C.
2
3a
D.
32a
C©u 48 :
Cho hàm số
y xlnx
. Giá trị của
y''(e)
A.
3
B.
1
e
C.
2
D.
e
C©u 49 :
Đạo hàm của hàm số
1
2
x
fx



là:
A.
1
'( ) ln2
2
x
fx




B.
1
'( ) lg2
2
x
fx




C.
1
'( ) ln2
2
x
fx



D.
1
'( ) lg2
2
x
fx



C©u 50 :
Bất phương trình
31
3
2log 4 3 log 2 3 2xx
là
A.
3
;
4



B.
3
;
4




C.
3
;3
4


D.
3
;3
4



C©u 51 :
Giá trị lớn nhất , nhỏ nhất của hàm số
2
x
y
trên
2;2
là
A.
GTLN = 4 ; GTNN =
1
4
B.
GTLN = 4 ; GTNN =
1
4
C.
GTLN = 1 ; GTNN =
1
4
D.
GTLN = 4 ; GTNN = 1
C©u 52 :
Đạo hàm của hàm số
2
ln 1y x x
là:
A.
2
1
ln 1xx
B.
2
21
1
x
xx

C.
2
21
ln 1
x
xx

D.
2
1
1xx
C©u 53 :
Cho
ab
33
log 15; log 10
vậy
3
log 50 ?
A.
31ab
B.
41ab
C.
1ab
D.
21ab
C©u 54 :
Cho phương trình
22
2 2 2 4 2 2
5 5 2 0
x mx x mx
x mx m
. Tìm m để phương trình vô nghiệm?
8
A.
1
0
m
m

B.
1m
C.
01m
D.
0m
C©u 55 :
Cho các nhận định sau (giả sử các biểu thức đều có nghĩa:
1)
1
log 2 2 log 2 log log
2
a a a a
x y x y
với
22
4 12 .x y xy
2) Phương trình
f x g x
aa
tương đương với
f x g x
3)
3a
lg lg lg
4
b
ab

với
22
9 10 .a b ab
4) Hàm số
3



x
y
e
luôn nghịch biến.
5)
( ) ( ) ( ) ( )
log log 2log log
b c c b c b c b
a a a a
với
2 2 2
.a b c
6)
2 2 2
21x y x y

với
1 ln
(1 ln )
x
y
xx

Số nhận định đúng là:
A.
1
B.
2
C.
3
D.
4
C©u 56 :
4
4
log 8
bằng bao nhiêu ?
A.
1
2
B.
3
8
C.
5
4
D.
2
C©u 57 :
Đạo hàm của hàm số
5
yx
là:
A.
5
1
5 x
B.
5
4
1
5 x
C.
4
5
1
5
x
D.
5
4
5
x
C©u 58 :
Tập nghiệm của bất phương trình
0,2 0,2
log 1 log 3xx
là:
A.
1;3S
B.
1;3S
C.
1;S 
D.
;3S 
C©u 59 :
Cho đường cong
2
1
: y 3 3 2 3
xx
C m m m
và
2
: y 3 1
x
C 
. Tìm m để
1
C
và
2
C
tiếp xúc nhau?
A.
5 40
3
B.
5 3 2
3
C.
5 40
3
D.
5 3 2
3
C©u 60 :
Giá trị của
3
log
a
a
(
0a
và
1a
) bằng
9
A.
3
B.
1
3
C.
1
3
D.
3
10
ĐÁP ÁN
01
{ ) } ~
28
{ | ) ~
55
{ | ) ~
02
{ ) } ~
29
{ | } )
56
{ ) } ~
03
{ ) } ~
30
{ | } )
57
{ ) } ~
04
{ | } )
31
{ | } )
58
) | } ~
05
{ | } )
32
{ | ) ~
59
{ | ) ~
06
) | } ~
33
{ ) } ~
60
{ | ) ~
07
{ | } )
34
{ | ) ~
08
{ | ) ~
35
{ ) } ~
09
) | } ~
36
{ | } )
10
) | } ~
37
{ ) } ~
11
) | } ~
38
{ | } )
12
{ | ) ~
39
{ | } )
13
) | } ~
40
) | } ~
14
{ | ) ~
41
{ | ) ~
15
{ | } )
42
) | } ~
16
{ | } )
43
{ | ) ~
17
{ | ) ~
44
) | } ~
18
) | } ~
45
{ | ) ~
19
{ ) } ~
46
{ | ) ~
20
) | } ~
47
{ | } )
21
) | } ~
48
{ ) } ~
22
{ ) } ~
49
) | } ~
23
) | } ~
50
) | } ~
24
{ | } )
51
{ | } )
25
{ ) } ~
52
{ ) } ~
26
{ ) } ~
53
{ | } )
27
{ ) } ~
54
{ | ) ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 04
C©u 1 :
Nghiệm của bất phương trình :
1
2
log 2 3 0
x

A.
2
log 3 2x
B.
2x
C.
2x
D.
02x
C©u 2 :
Nếu
12 12
log 6, log 7ab
thì
2
log 7
bằng:
A.
1
a
b
B.
1
b
a
C.
1
a
b
D.
1
a
a
C©u 3 :
Phương trình
󰉪
A.
 󰇛 󰇜
B.
󰇛 󰇠
C.
 󰇛󰇜
D.
󰇟󰇜
C©u 4 :
Cho lgx=a , ln10=b
Tính
10
()log
e
x
A.
1
a
b
B.
1
b
b
C.
1
ab
b
D.
2
1
ab
b
C©u 5 :
Đạo hàm của hàm số
2
( 1)
x
y x e
bằng
A.
22
( 1)
x
xe
B.
( 1)
x
xe
C.
2
( 1)
x
xe
D.
2 x
xe
C©u 6 :
Cho hàm
s
ố
.siny x x
. Biểu thức nào sau đây biểu diễn đúng?
A.
'' 2 ' 2xy y xy sinx
B.
' '' ' 2xy yy xy sinx
C.
' ' ' 2sinxy yy xy x
D.
'' ' 2cos sinxy y xy x x
C©u 7 :
Nghiệm của phương trình
24
log log 1x
là :
A.
16
B.
2
C.
4
D.
8
C©u 8 :
Tìm đạo hàm của hàm số:
2
x
y
tại x =2
A.
2ln2
B.
2
C.
4
D.
ln2
C©u 9 :
Nghiệm của phương trình 
󰇛
󰇜

󰇛
󰇜
là:
2
A.
9
B.
-1
C.
1
D.
0
C©u 10 :
Hàm số
2
()
x
f x x e
có giá trị lớn nhất trên đoạn
1;1
là
A.
1
e
B.
e
C.
0
D.
2e
C©u 11 :
Tập xác định của phương trình
23
42
log 1 log 1 25xx
là:
A.
1x
B.
1x
C.
1x
D.
x
C©u 12 :
Tập xác định của phương trình
log
2
(x
3
+ 󰇜log
2
(x
2
x + 󰇜2log
2
x = 0 là?
A.
0x
B.
13
2
x
C.
1x 
D.
10x
C©u 13 :
Cho hàm số
yx
4
, Các kết luận sau , kết luận nào sai
A.
Tập xác định
0;D
B.
Hàm số luôn đi qua điểm
1;1M
C.
Hàm số luôn luôn đồng biến với mọi
x
thuộc tập xác định
D.
Hàm số không có tiệm cận
C©u 14 :
Cho a, b > 0 thỏa mãn:
12
13
33
24
,a a b b
Khi đó:
A.
1, 1ab
B.
a > 1, 0 < b < 1
C.
0 1, 1ab
D.
0 1, 0 1ab
C©u 15 :
Giá trị lớn nhất , nhỏ nhất của hàm số
2
x
y
trên
2;2
là
A.
GTLN = 1 ; GTNN =
1
4
B.
GTLN = 4 ; GTNN =
1
4
C.
GTLN = 4 ; GTNN =
1
4
D.
GTLN = 4 ; GTNN = 1
C©u 16 :
Hàm số sau
2
()
x
f x x e
tăng trên khoảng nào
A.
0;2
B.
2;
C.
; 
D.
;0
C©u 17 :
Cho hàm số
x
ya
, Các mệnh đề sau , mệnh đề nào sai
A.
Đố thị hàm số luon đi qua điểm
0;1M
và
1;Na
B.
Đồ thị hàm số có đường tiệm cận là
0y
3
C.
Đồ thị hàm số không có điểm uốn
D.
Đồ thị hàm số luôn tăng
C©u 18 :
Với 0<x<1 , ta có
4
2
1
(1 )
1
x
x
bằng
A.
3
4
(1 )
1
x
x
B.
4
1
1
x
x
C.
3
4
(1 )
1
x
x
D.
4
1
1
x
x
C©u 19 :
Với biểu thức
5
3
6
4
aa
cơ số a phải thỏa điều kiện
A.
1a
B.
0a
C.
01a
D.
1a
C©u 20 :
Cho hàm số

. Khẳng định nào sau đây sai:
A.
Hàm số nghịch biến trên khoảng
󰇛

󰇜
B.
Hàm số nghịch biến trên R
C.
Giá trị gần đúng ( với 3 chữ số thập phân ) của hàm số tại x=3 là 0,932
D.
Giá trị gần đúng ( với 3 chữ số thập phân ) của hàm số tại
 là 0,928
C©u 21 :
Cho hàm số
yx
1
3
, Trong các mệnh đề sau , mệnh đề nào sai
A.
Hàm số đồng biến trên tập xác định
B.
Hàm số nhận
0; 0O
làm tâm đối xứng
C.
Hàm số lõm
;0
và lồi
0;
D.
Hàm số có đồ thị nhận trục tung làm trục
đối xứng
C©u 22 :
Cho
0; 0; 1; 1;a b a b n R
, một học sinh tính biểu thức
2
1 1 1
......
log log log
an
aa
P
b b b
theo các bước sau
I .
2
log log ... log
n
b b b
P a a a
II.
2
log . ...
n
b
P a a a
III.
1 2 3 ...
log
n
b
Pa
IV.
1 log
b
P n n a
Bạn học sinh trên đã giải sai ở bước nào
A.
III
B.
II
C.
I
D.
IV
4
C©u 23 :
Nếu
11
53
aa
và
11
log log
32
bb
thì
A.
0 1, 1ab
B.
1, 1ab
C.
1,0 1ab
D.
0 1,0 1ab
C©u 24 :
Cho hàm số
yx
5
31

, tập xác định của hàm số là
A.
1;D
B.
DR
C.
;1D
D.
\1DR
C©u 25 :
Hàm số
2
ln 2 1x x m
có tập xác định là khi
A.
0m
B.
03m
C.
0
1
m
m

D.
0m
C©u 26 :
Phương trình
2
2
log 4 log 2 3
x
x 
có bao nhiêu nghiệm?
A.
2 nghiệm
B.
3 nghiệm
C.
1 nghiệm
D.
4 nghiệm
C©u 27 :
Đạo hàm của hàm số
( ) lnf x x x
là:
A.
1
x
B.
ln x
C.
1
D.
ln 1x
C©u 28 :
Giải phương trình
9 2.3 3 0
xx
:
A.
x = 1
B.
x = 0
C.
x = -1
D.
x = 1 hay x = 0
C©u 29 :
Tìm cơ số a biết 
A.
a = 2
B.
a = 6
C.
a = 8
D.
a = 4
C©u 30 :
Hàm số
2
( ) ln xf x x
có giá trị nhỏ nhất trên đoạn
3;5
là
A.
25ln5
B.
9ln3
C.
8ln2
D.
32ln2
C©u 31 :
Cho hàm số
yx
1
3
, Các mệnh đề sau , mệnh đề nào sai
A.
Hàm số có đồ thị nhận trục tung làm trục
đối xứng
B.
1
3
lim
x
fx
C.
Hàm số không có đạo hàm tại
0x
D.
Hàm số đồng biến trên
;0
và nghịch
biến
0;
C©u 32 :
Theo hình thức lãi kép một người gửi 100 triệu đồng vào ngân hàng theo kỳ hạn một năm
với lãi suất 1,75% (giả sử lãi suất hàng năm không thay đổi) thì sau hai năm người đó thu
5
được một số tiền là
A.
103,351 triệu đồng
B.
103,530 triệu đồng
C.
103,531 triệu đồng
D.
103,500 triệu đồng
C©u 33 :
Giá trị
2
log 4
a
a
bằng:
A.
4
B.
2
C.
8
D.
16.
C©u 34 :
Đạo hàm của hàm số
cos2x
ye
tại
6
x
A.
3
2
e
B.
3e
C.
3
2
e
D.
3e
C©u 35 :
Số nghiệm của phương trình
4 2 2 4
log log log log 2xx
là
A.
2
B.
1
C.
3
D.
0
C©u 36 :
Cho hai số dương a và b. Xét các mệnh đề sau mệnh đề nào đúng
(I).
lg lgba
ab
(II)
ln lnba
ab
(III)
10
()
lg
1
log b
b
aa
(IV)
1
log ( )
ln
b
e
b
aa
A.
Chỉ có (III) đúng
B.
Chỉ có (I) đúng
C.
Tất cả các mệnh đề đều đúng
D.
Chỉ có (II) đúng
C©u 37 :
Số nghiệm của phương trình
2
2+s
2
2s
=
15
là:
A.
2
B.
0
C.
1
D.
3
C©u 38 :
Nghiệm của bất phương trình 

󰇛

󰇜

󰇛
󰇜

A.
x>4
B.
x<2
C.
Vô nghiệm
D.
0<x<1
C©u 39 :
Giá trị của biểu thức 









là:
A.


B.


C.


D.
28
C©u 40 :
Nghiệm của phương trình 
󰇛

󰇜

󰇛
 
󰇜


6
A.
0 và -3
B.
-4 và -3
C.
-5 và -4
D.
0 và -5
C©u 41 :
Hàm số
( ) lnf x x x
A.
Không có cực trị
B.
Có một cực tiểu
C.
Có một cực đại
D.
Có một cực đại và một cực tiểu
C©u 42 :
Nghiệm của bất phương trình


là:
A.
B.
C.

D.
C©u 43 :
Đối với hàm số
1
ln
1
y
x
, ta có
A.
'1
y
xy e
B.
'1
y
xy e
C.
'1
y
xy e
D.
'1
y
xy e
C©u 44 :
Nghiệm của
32.4 18.2 1 0
xx
đồng biến trên (0; 2)
A.
14x
B.
41x
C.
24x
D.
11
16 2
x
C©u 45 :
Đạo hàm của hàm số




là:
A.


󰇛

󰇜
B.

󰇛

󰇜
C.


󰇛

󰇜
D.


󰇛

󰇜
C©u 46 :
Cho hàm số
yx
2
2
32

, tập xác định của hàm số là
A.
22
;
33
D
B.
22
;;
33
D
C.
22
;;
33
D
D.
2
\
3
DR
C©u 47 :
Các kết luận sau , kết luận nào sai
I.
3
17 28
II.
32
11
32
III.
57
44
IV.
45
13 23
A.
II và III
B.
III
C.
I
D.
II và IV
C©u 48 :
Tập nghiệm của phương trình
22
sin os
2.2 2 3
x c x

là
7
A.
(2 1) ,x k k Z
B.
2,
2
x k k Z
C.
,
2
x k k Z
D.
,x k k Z

C©u 49 :
Cho phương trình
22
3 7 2 3
log 9 12 4 log 6 23 21 4
xx
x x x x

. Chọn phát biểu đúng?
A.
Tập xác định của phương trình là
3
;
2




.
B.
Phương trình có duy nhất một nghiệm.
C.
Phương trình có 2 nghiệm trái dấu.
D.
Phương trình có một nghiệm là
1
4
x
C©u 50 :
Phương trình
9
s
3
.
3
s
+
2
=
0
có hai nghiệm
x
1
,
x
2
(
x
1
<
x
2
)
. Giá trị của A
=
2
x
1
+
3
x
2
là:
A.
3 log
2
3
B.
4 log
2
3
C.
2
D.
0
C©u 51 :
Tìm tập xác định của hàm số sau:
2
1
log (1 2 )
x
xx
A.
(0; )D
B.
0;D 
C.
(0; ) / 1D 
D.
1;D 
C©u 52 :
Số nghiệm của phương trình: log
3
(x
2
󰇜
3
󰇛󰇜là:
A, 0 B. 1 C. 2 D. 3
A.
1
B.
2
C.
0
D.
3
C©u 53 :
Đạo hàm của hàm số
()
x
f x xe
là
A.
'( ) 1
x
f x e
B.
'( ) 1
x
f x x e
C.
'( ) 1
x
f x x e
D.
'( )
x
f x e
C©u 54 :
Với
1x
và
,,abc
là các số dương khác 1 và
log log 0 log
a b c
x x x
. So sánh các số
,,abc
là
A.
bac
B.
c a b
C.
c b a
D.
abc
C©u 55 :
Hàm số
2
1
8 6 3 ln2
xx
yx


là đạo hàm của hàm số nào sau đây:
A.
2
1
2
xx
y

.
B.
2
1
8
xx
y

.
C.
2
3 3 1
2
xx
y

.
D.
2
3 3 1
8
xx
y

.
C©u 56 :
Cho
ab
33
log 15; log 10
vậy
3
log 50 ?
8
A.
1ab
B.
31ab
C.
41ab
D.
21ab
C©u 57 :
Tập nghiệm của bất phương trình
23
x
x
A.
;3
B.
1; 
C.
;1
D.
1; 
C©u 58 :
Giá trị của biểu thức







󰇛


󰇜
sau khi rút gọn là:
A.

B.

C.

D.
C©u 59 :
Với giá trị nào của m, phương trình
9 3 0
xx
m
có nghiệm
A.
1
4
m
B.
0m
C.
1
4
m
D.
0m
C©u 60 :
Phương trình
1
31
3
x
x

có bao nhiêu nghiệm
A.
2
B.
0
C.
1
D.
Vô số nghiệm
9
ĐÁP ÁN
01
) | } ~
28
{ ) } ~
55
{ ) } ~
02
{ ) } ~
29
{ | } )
56
{ | } )
03
{ | ) ~
30
{ ) } ~
57
{ ) } ~
04
{ | ) ~
31
{ | } )
58
{ | ) ~
05
{ | ) ~
32
{ | ) ~
59
{ | ) ~
06
) | } ~
33
{ ) } ~
60
{ | ) ~
07
) | } ~
34
) | } ~
08
) | } ~
35
{ ) } ~
09
{ | } )
36
{ | ) ~
10
{ ) } ~
37
) | } ~
11
{ ) } ~
38
{ | ) ~
12
) | } ~
39
{ | ) ~
13
{ | } )
40
{ | } )
14
{ ) } ~
41
{ ) } ~
15
{ | } )
42
{ | } )
16
) | } ~
43
) | } ~
17
{ | } )
44
{ ) } ~
18
{ | ) ~
45
{ | ) ~
19
{ | ) ~
46
{ | } )
20
{ | } )
47
{ | } )
21
{ | } )
48
{ | ) ~
22
{ | } )
49
{ ) } ~
23
) | } ~
50
) | } ~
24
{ | } )
51
{ | ) ~
25
) | } ~
52
) | } ~
26
) | } ~
53
{ ) } ~
27
{ ) } ~
54
) | } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 05
C©u 1 :
Giá trị nhỏ nhất của hàm số:
2
( 3)
x
y e x
trên đoạn
[ 2;2]
là:
A.
2
e
B.
2e
C.
3
6
e
D.
2
1
e
C©u 2 :
Logarit cơ số 3 của số nào
1
3
:
A.
3
3
B.
3
1
3
C.
1
27
D.
1
33
C©u 3 :
S nghim ca phương trnh
22
2
log (9 4) log 3 log 3
x
x
l
A.
2
B.
0
C.
1
D.
Đp s khc
C©u 4 :
Đạo hàm của hàm số
2
( 2 2)
x
y x x e
là:
A.
x
xe
B.
2 x
xe
C.
2
( 4 )
x
x x e
D.
(2 2)
x
xe
C©u 5 :
Phương trnh
9 3.3 2 0
xx
c hai nghim
1 2 1 2
, ( )x x x x
. Gi tr A=
12
23xx
l
A.
3
4log 2
B.
1
C.
3
3log 2
D.
Đp s khc
C©u 6 :
S nghim ca phương trnh
22
2log 1 2 log ( 2)xx
l
A.
2
B.
0
C.
1
D.
Đp s khc
C©u 7 :
Cho hàm số
1
ln
1
y
x
. Hệ thức nào sau đây là đúng?
A.
'1
x
yy e
B.
'1
y
xy e
C.
'1
x
xy e
D.
'1
y
xy e
C©u 8 :
Tập xác định của hàm số
2
ln( 4)yx
là:
A.
( ; 2) (2; ) 
B.
(2; )
C.
( 2;2)
D.
( 2; ) 
C©u 9 :
Tìm để phương trnh


có 4 nghim phân bit trong đ c 3 nghim
lớn hơn 
2
A.
B.
C.
Đp n khc
D.
C©u 10 :
S nghim ca phương trnh
22
2 2 15
xx

l
A.
3
B.
2
C.
1
D.
0
C©u 11 :
Chọn khẳng định đúng trong các khẳng định sau
A.
Cơ số của logarit là một số dương khác 1
B.
Cơ số của logarit là một số nguyên
C.
Cơ số của logarit là một số thực bất kỳ
D.
Cơ số của logarit là một số nguyên dương
C©u 12 :
Gọi x
1
; x
2
là hai nghiệm của phương trình:
2
59
7 343
xx
. Tổng x
1
+ x
2
là:
A.
5
B.
3
C.
4
D.
2
C©u 13 :
Số nghiệm của pt
2
33
log 6 log 2 1
xx
là
A.
1
B.
0
C.
2
D.
3
C©u 14 :
Tập xác định của hàm
ln(ln )yx
là:
A.
(0;1)
B.
(1; )
C.
(0; )
D.
0;
C©u 15 :
Hãy tìm logarit của
1
33
theo cơ số 3
A.
3
2
B.
3
2
C.
2
3
D.
2
3
C©u 16 :
tính đạo hàm ca hàm s sau:
󰇛
󰇜


A.
󰆒
󰇛
󰇜


B.
󰆒
󰇛
󰇜
󰇛󰇜


C.
󰆒
󰇛
󰇜




D.
󰆒
󰇛
󰇜

󰇛󰇜


C©u 17 :
Cho hàm số
x
f x xe
Gọi
''
fx
là đạo hàm cấp 2. Ta có
'' 1
f
bằng
A.
3e
B.
2e
C.
0
D.
1
C©u 18 :
Chọn câu sai:
A.
Hàm s
không chẵn cũng không lẻ
B.
Hàm s 󰇛
󰇜 là hàm s lẻ
C.
Hàm s
có tập giá tr là 󰇛 󰇜
3
D.
Hàm s 󰇛
󰇜 không chẵn cũng không lẻ
C©u 19 :
Phương trnh sau c bao nhiêu nghim thực phân bit:

󰇛
󰇜

󰇛 󰇜

󰇛󰇜
A.
0
B.
1
C.
3
D.
2
C©u 20 :
S nghim ca phương trnh
4 6 25 2
xx
x
l
A.
3
B.
1
C.
0
D.
2
C©u 21 :
Cho hàm số
( ) 2
x
fx
. Biểu thức
( 1) ( )f a f a
bằng:
A.
2
a
B.
1
C.
21
a
D.
2
C©u 22 :
Giá trị nhỏ nhất của hàm số:
2
4ln(1 )y x x
trên đoạn
[ 2;0]
A.
1
B.
1 4ln2
C.
0
D.
4 4ln3
C©u 23 :
Biết
log2 ;log3ab
thì
log45
tính theo a và b bằng:
A.
21ba
B.
21ba
C.
15b
D.
21ab
C©u 24 :
Cho m > 0. Biểu thức
32
3
1
m
m



bằng:
A.
2
m
B.
2 3 3
m
C.
2
m
D.
2 3 2
m
C©u 25 :
Tập xác định của hàm số
51
5
log (log ( 1))yx
là:
A.
( 1;0]
B.
( 1;0)
C.
( 1; ) 
D.
(0; )
C©u 26 :
Đạo hàm của hàm số
5
ln7yx
bằng:
A.
5
4
1
5 ln 7xx
B.
5
4
7
5 ln 7xx
C.
5
4
1
5 ln 7x
D.
5
4
1
35 ln 7xx
C©u 27 :
Chọn khẳng định đúng trong các khẳng định sau
A.
Chỉ có logarit của một số thực dương
B.
Có logarit của một số thực bất kỳ
C.
Chỉ có logarit của một số thực dương khác
1
D.
Chỉ có logarit của một số thực lớn hơn 1
C©u 28 :
Tập nghiệm của phương trình
2x
48
mx
(m là tham số) là
A.
2m
B.
−m
C.
m
D.
−2m
4
C©u 29 :
Giá trị nhỏ nhất của hàm số:
22
( 4 1).
x
g x x x e
trên
2; 3
A.
22e
B.
4
3
e
C.
3
2
e
D.
7
6
e
C©u 30 :
Giá trị lớn nhất của hàm số:
21
x
e
y
x
trên đoạn [0;2] là:
A.
1
B.
2
5
e
C.
2
D.
2
e
C©u 31 :
Đạo hàm của hàm số

2
( 2 )
x
y x x e
là:
A.
2 x
xe
B.
2
( 2)
x
xe
C.
x
xe
D.
(2 2)
x
xe
C©u 32 :
Giá trị của biểu thức
5
7
1
log
5
bằng:
A.
-7
B.
1
7
C.
7
D.
1
7
C©u 33 :
S nghim ca phương trnh
4 6 25 2
xx
x
l
A.
0
B.
1
C.
2
D.
3
C©u 34 :
Viết dưới dạng lũy thừa thì số:
5
3
222
bằng:
A.
3
10
2
B.
7
10
2
C.
17
10
2
D.
7
30
2
C©u 35 :
Phương trnh sau c bao nhiêu nghim thực phân bit:



A.
2
B.
3
C.
1
D.
4
C©u 36 :
S nghim ca phương trnh
9 2.3 3 0
xx
l
A.
0
B.
2
C.
1
D.
3
C©u 37 :
Dùng đnh nghĩa, tính đạo hàm ca hàm s sau:
)1(log)(
2
xxf
A.
1
1
)('
x
xf
B.
0)(' xf
C.
)1(log)('
2
xxf
D.
2ln)1(
1
)('
x
xf
C©u 38 :
Giá trị nhỏ nhất của hàm số:
2
( 5)
x
y e x x
trên đoạn [1;3] là:
A.
- 5e
B.
-3e
2
C.
e
3
D.
-5e
2
5
C©u 39 :
Tìm để phương trnh:


có 4 nghim thực phân bit:
A.

B.

C.
D.
C©u 40 :
Hàm số
sin
x
ye
gọi
'
y
là đạo hà của hàm số. Khẳng định nào sau đây đúng
A.
sinx
' cosx
ye
B.
sin
' cosx.e
x
y

C.
cosx
'
ye
D.
cosx
' sin .
y x e
C©u 41 :
Cho phương trnh
1
1
3 9( ) 4 0
3
xx
. Tng cc nghim ca phương trnh l:
A.
-1
B.
0
C.
1
D.
2
C©u 42 :
Nghim ca bt phương trnh
2 4 2
log ( 1) 2log (5 ) 1 log ( 2)x x x
l
A.
2<x<5
B.
1<x<2
C.
Đp s khc
D.
2<x<3
C©u 43 :
S nghim ca phương trnh
22
2
log (9 4) log 3 log 3
x
x
l
A.
0
B.
Đp s khc
C.
2
D.
1
C©u 44 :
Giá trị của biểu thức
33
2 2 5 5
4 :16
bằng:
A.
16
B.
8
C.
1
D.
3
5
16
C©u 45 :
Nghiệm của phương trình
log4 logx
4 32
x

là
A.
100
B.
10;100
C.
20;100
D.
10
C©u 46 :
Đạo hàm của hàm số

2
( 1)
x
y x e
là:
A.
2
(2 1)
x
xe
B.
2
(2 3)
x
xe
C.
2
( 2)
x
xe
D.
2x
e
C©u 47 :
Cho phương trnh
1
1
3 9( ) 4 0
3
xx
. Tng cc nghim ca phương trnh l:
A.
-1
B.
2
C.
0
D.
1
C©u 48 :
Phương trnh
9 3.3 2 0
xx
c hai nghim
1 2 1 2
, ( )x x x x
. Gi tr A=
12
23xx
l
A.
1
B.
3
4log 2
C.
3
3log 2
D.
Đp s khc
C©u 49 :
Tìm giá tr lớn nht M và nhỏ nht m ca hàm s


A.
Đp n khc
B.

C.

D.

C©u 50 :
Giá trị lớn nhất của hàm số:
2
(2 8)
x
y e x x
trên đoạn
2;2
6
A.
2
2
e
B.
5e
C.
2
2e
D.
5e
C©u 51 :
Bất phương trình
5.4 2.25 7.10 0
x x x
có nghiệm là
A.
01
x

B.
12
x

C.
21
x
D.
10
x
C©u 52 :
Nghim ca bt phương trnh
2 4 2
log ( 1) 2log (5 ) 1 log ( 2)x x x
l
A.
1<x<2
B.
2<x<5
C.
2<x<3
D.
Đp s khc
C©u 53 :
S nghim ca phương trnh
2
33
log ( 6) log ( 2) 1xx
A.
3
B.
2
C.
1
D.
0
C©u 54 :
Giải bt phương trnh:

 

󰇛 󰇜
A.
B.
C.
D.

C©u 55 :
S nghim ca phương trnh
2
33
log ( 6) log ( 2) 1xx
A.
0
B.
2
C.
1
D.
3
C©u 56 :
S nghim ca phương trnh
22
2 2 15
xx

l
A.
2
B.
3
C.
1
D.
0
C©u 57 :
Tìm để phương trnh


có 8 nghim phân bit:
A.
Không có giá tr m
B.
C.
D.
C©u 58 :
S nghim ca phương trnh
22
2log 1 2 log ( 2)xx
l
A.
2
B.
0
C.
Đp s khc
D.
1
C©u 59 :
Tm gi tr nhỏ nht ca hm s
( ) (2 ln )f x x x
trên [ 2; 3] l
A.
Đp s khc
B.
e
C.
1
D.
4-2ln2
C©u 60 :
Giá trị nhỏ nhất của hàm số:
2
( 2)
x
y e x
trên đoạn
1;3
là:
A.
e
B.
0
C.
e
3
D.
e
2
C©u 61 :
S nghim ca phương trnh
9 2.3 3 0
xx
l
A.
0
B.
2
C.
1
D.
3
7
C©u 62 :
Tm gi tr nhỏ nht ca hm s
( ) (2 ln )f x x x
trên [ 2; 3] l
A.
Đp s khc
B.
e
C.
4-2ln2
D.
1
C©u 63 :
Đạo hàm của hàm số
4
lnyx
là:
A.
3
4ln x
B.
3
4
ln x
x
C.
3
4ln( )x
D.
3
4
ln( )x
x
C©u 64 :
Phương trình
3
log 1 log
2
x
x

có nghiệm là kết quả nào sau đây
A.
Vô nghiệm
B.
2
C.
1
2
D.
3
8
ĐÁP ÁN
01
{ ) } ~
28
) | } ~
55
{ | ) ~
02
{ ) } ~
29
{ | ) ~
56
{ | ) ~
03
{ | ) ~
30
{ ) } ~
57
{ | } )
04
{ ) } ~
31
{ ) } ~
58
{ | } )
05
{ | ) ~
32
{ ) } ~
59
{ | } )
06
{ | ) ~
33
{ | ) ~
60
{ ) } ~
07
{ ) } ~
34
) | } ~
61
{ | ) ~
08
) | } ~
35
{ | } )
62
{ | ) ~
09
{ | } )
36
{ | ) ~
63
{ ) } ~
10
{ | ) ~
37
{ | } )
64
) | } ~
11
) | } ~
38
{ ) } ~
12
) | } ~
39
{ | } )
13
) | } ~
40
) | } ~
14
{ ) } ~
41
{ | ) ~
15
) | } ~
42
{ | } )
16
{ | } )
43
{ | } )
17
) | } ~
44
) | } ~
18
{ | } )
45
) | } ~
19
{ | } )
46
{ ) } ~
20
{ | } )
47
{ | } )
21
) | } ~
48
{ | ) ~
22
{ ) } ~
49
{ | } )
23
{ ) } ~
50
{ | ) ~
24
) | } ~
51
) | } ~
25
{ ) } ~
52
{ | ) ~
26
{ ) } ~
53
{ | ) ~
27
) | } ~
54
{ | } )
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 06
C©u 1 :
Phương trình
1
2 2 4
xx

có nghiệm là
A.
2
1 log 3
B.
2
log 3 2
C.
2
log 3 1
D.
2
3 log 3
C©u 2 :
Cho
log 2,log 5
aa
bc
.Giá trị của
3
log
a
ab
c
là
A.
5
3
B.
4
3
C.
2
3
D.
5
3
C©u 3 :
Biến đổi
5
3
4
( 0)x x x
thành dạng lũy thừa với số mũ hữu tỉ ta được:
A.
21
12
x
B.
23
12
x
.
C.
3
20
x
D.
12
5
x
.
C©u 4 :
Giá trị nhỏ nhất của hàm số
2
2
1
log
m
m
yx
( m là tham số) trên [1;2] lớn hơn -1 khi
A.
10
01
m
m

B.
1
1
m
m

C.
1
m
D.
11
m
C©u 5 :
Nếu
1 1 1
2 2 2
21
log log log
35
x a b
thì x bằng
A.
3
2
5
a
b
B.
1
3
5
2
ab
C.
3
2
1
5
a
b
D.
3
1
5
a
b
C©u 6 :
Cho hàm số
23
ln
f x x x
thì
3'
f
bằng
A.
93ln
B.
9 6 3ln
C.
9 18 3ln
D.
9 9 3ln
C©u 7 :
Cho a>0, b> 0. Giá trị của x bằng bao nhiêu biết
2 2 2
3 3 3
14
log log log
47
x a b
2
A.
47
ab
B.
4
1
7
4
ab
C.
4
7
a
b
D.
7
4
4
.ab
C©u 8 :
Hàm số
ln
x
y
x
đồng biến trên khoảng
A.
0;
B.
;
e

C.
0;
e
D.
1
0;
e



C©u 9 :
Tất cả các giá trị của m để phương trình
2 1 2
2 0
x
m m

có nghiệm là
A.
0m
.
B.
01m
.
C.
1m
.
D.
; 10m m
.
C©u 10 :
Tập xác định của hàm số
( 1)
e
yx

là
A.
(1; )
B.
\ {1}
C.
R
D.
[1; )
C©u 11 :
Xác định m để phương trình
2 1 2
3 2 3 0
x
mm
có nghiệm:
A.
0;1m
B.
3
1;
2
m




C.
1
;0
2
m




D.
0;m 
C©u 12 :
Đạo hàm của hàm số
(3x 1)
y

là
A.
1
3 (3x 1)
B.
3(3x 1) ln(3x 1)

C.
(3x 1) ln(3x 1)

D.
1
(3x 1)
C©u 13 :
Cho a,b,c là các số thực dương và
,1
ab
. Khẳng định nào sau đây sai
A.
1
log
log
a
c
c
a
B.
log
log
log
b
a
b
c
c
a
C.
log log .log
a a b
c b c
D.
log .log 1
ab
ba
C©u 14 :
Hình bên dưới là đồ thị của hàm số nào ?
3
A.
2
x
y

B.
1
2
x
y
C.
2
x
y
D.
1
2
x
y

C©u 15 :
Giá trị của
log 3
(0 1)
a
a a
bằng:
A.
12
B.
9.
C.
3
D.
6
C©u 16 :
Nếu
3
3 3 3 3
log 4log 7log logt x y x
thì t bằng
A.
11
3
7
x
y
B.
3
11
7
x
y
C.
11
3
7
x
y
D.
11
7
3
xy
C©u 17 :
Với điều kiện nào của a thì
2
1 3 4
x
y a a
là mọt hàm số mũ?
A.
1
;1 1;
4
a




B.
3 3 1
1; ;0 0;
4 4 4
a
C.
13
1; 0;
44
a
D.
1 3 3
;;
4 4 4
a

C©u 18 :
Tập nghiệm của bpt
2
2
3
log 2 1 0xx
là:
A.
3
1;
2



B.
3
0;
2



C.
1
;0 ;
2

 


D.
3
; 1 ;
2

 


C©u 19 :
Tập xác định của hàm số
1
x
x
e
y
e
là tập nào sau đây?
A.
1\{ }
B.
C.
0\ { }
D.
\{ }
e
C©u 20 :
Tập xác định của hàm số
1
1
2
ln
yx
x
là
A.
0;

B.
2\
C.
12;
D.
12;;
C©u 21 :
Bất dẳng thức nào sau đáy sai?
A.
10 5
22
11
22
B.
2008 2009
1 2 1 2
22

4
C.
56
3 1 3 1
D.
300 301
33
33
C©u 22 :
Phương trình
42
log 12 .log 1xx
có nghiệm là:
A.
3x 
B.
4x
C.
4
3
x
x

D.
Đáp án khác
C©u 23 :
Cho
01a
và
0, 0xy
. Khi đó ta có:
log .
a
xy
bằng:
A.
log log
aa
xy
B.
log log
aa
xy
C.
log .log
ay
x
D.
log
log
a
a
x
y
C©u 24 :
Cho hàm số
x
y xe
. Hệ thức nào sau đây đúng?
A.
2 1 0'' '
yy
B.
2 3 0'' '
y y y
C.
20'' '
y y y
D.
2 3 0'' '
y y y
C©u 25 :
Đồ thị dưới đây là của hàm số nào?
A.
2
y log 1x
B.
2
(1og )ly x
C.
3
logy x
D.
3
(1y log )x
C©u 26 :
Cho
x
e
fx
x
, nghiệm của phương trình
0'
fx
là
A.
2
B.
0
C.
1
D.
e
C©u 27 :
Nếu
log4 a
thì
log4000
bằng:
A.
42a
B.
3 a
C.
32a
D.
4 a
C©u 28 :
Hàm số nào sau đây là đạo hàm của hàm số
2
sin
x
ye
A.
2
2sin
.cos
x
ex
B.
2
2
sin
.cos
x
ex
C.
2
2
sin
.sin
x
ex
D.
2
2sin
.sin
x
ex
5
C©u 29 :
Đạo hàm của hàm số
7
cosy x
là:
A.
7
6
sin
7 cos
x
x
B.
7
6
sin
7 cos x
x
C.
7
6
1
7 cos x
D.
7
8
sin
7 cos
x
x
C©u 30 :
Phương trình
2 1 1
3 3 3 9
x x x
có nghiệm là:
A.
1
3
x 
B.
2x 
C.
1
2
x
D.
1x
C©u 31 :
Cho mệnh đề “ với mọi
,,
a b x
, nếu
0
ab

thì
xx
ab
. Mệnh đề đúng khi
A.
x<0
B.
0<x<1
C.
x>1
D.
x>0
C©u 32 :
Đặt
2
log 3a
. Khi đó giá trị của biểu thức
2 2 2
log 18 log 21 log 63P
là:
A.
2a
B.
1 a
C.
1 a
D.
2 a
C©u 33 :
Tập xác định của hàm số
1
log
x
yx
là
A.
(1; ) \ {2}
B.
(2; )
C.
(1; )
D.
(0; )
C©u 34 :
Giá trị của biểu thức
3
1 1 1
3 3 3
1
2log 6 log 400 3log 45
2
A
là
A.
4
B.
-3
C.
5
D.
-4
C©u 35 :
Hàm số
ln
y x x
đồng biến trên khoảng
A.
1
;
e




B.
1;
C.
1
1;
e



D.
1
;
e




C©u 36 :
Hàm số
xx
y e e

có bao nhiêu cực trị
A.
0
B.
3
C.
2
D.
1
C©u 37 :
Cho hàm số
x
y x e

. Khẳng định nào sau đây đúng?
A.
Hàm số đạt cực tiểu tại
0
x
B.
Hàm số không xác định tại
0
x
C.
Hàm số đạt cực đại tại
0
x
D.
Hàm số không đạt cực trị tại
0
x
C©u 38 :
Nếu
12
log 18 x
và
3
log 10 b
thì
3
log 50
bằng
A.
2 2 4ab
B.
2 2 4ab
C.
21ab
D.
21ab
6
C©u 39 :
Bất phương trình
2
3
22
x
x
có tập nghiệm là:
A.
1; 
B.
;0
C.
;8
D.
6; 
C©u 40 :
Cho hàm số
2
ln 2 5y x x
. Mệnh đề nào sau đây sai?
A.
' 0 1yx
B.
ln5 0yx
C.
Hàm số đạt GTNN bẳng 2ln2 khi x = 1
D.
Hàm số có tập xác định
DR
C©u 41 :
Một người đi mua chiếc xe máy với giá 90 triệu. Biết rằng sau một năm giá trị chiếc xe chỉ
còn 60%. Hỏi sau bao nhiệm năm thì giá trị chiếc xe chỉ còn 10 triệu?
A.
1
2
3
năm
B.
2 năm
C.
3 năm
D.
1
3
3
C©u 42 :
Đạo hàm của hàm số
3
y x
là:
A.
3
2
1
3 x
B.
3
2
1
x
C.
3
1
2 x
D.
4
3
1
3
x
C©u 43 :
Nếu
2
log 5 a
thì
4
log 1250
bằng:
A.
1+4a
B.
4a-1
C.
1
2
a
D.
1
2
2
a
C©u 44 :
Cho các khẳng định
1
3
1)( 27) 3;
5
2)( 2) 32
;
0
3) 1
a
với mọi
a
;
5
2
5
2
4)
aa
với mọi
a
.
Khẳng định đúng là
A.
2
B.
1và 2
C.
1,2 và 4.
D.
1,2,3 và 4
C©u 45 :
Cho hàm số
2
2
1
()
2
xx
y
. Tìm khẳng định đúng
A.
Nghịch biến trên nửa khoảng
[1; )
B.
Đồng biến trên R
C.
Nghịch biến trên R
D.
Đồng biến ttrên khoảng
(1; )
C©u 46 :
Giá trị của biểu thức
3
7 7 7
2log 36 log 14 3log 21B
là
A.
3
B.
2
C.
-3
D.
-2
7
C©u 47 :
Đạo hàm của hàm số
ln
y x x x

là
A.
ln
xx
B.
1
1
x
C.
ln
x
D.
1ln
x
C©u 48 :
Cho hàm số
1ln
y x x
. Khẳng định nào sau đây đúng?
A.
Hàm số có tập xác định là
1\
B.
Hàm số giảm trên
1; 
C.
Hàm số tăng trên
1; 
D.
Hàm số giảm trên
10;
và tăng trên
0;
C©u 49 :
Đạo hàm của hàm số
1
1
ln
x
y
x
bằng
A.
1
1
x
x
B.
2
1
1
x
C.
2
2
1
x
D.
2
1
21
x
C©u 50 :
Nếu
12
log 18 a
thì
2
log 3
bằng
A.
21
2
a
a
B.
1
2
a
a
C.
1
22
a
a
D.
12
2
a
a
C©u 51 :
Cho
27 8 2
l log 7og 3.5 g, ,lobca 
Tính
12
log 35
bằng:
A.
32
2
b ac
c
.
B.
33
2
b ac
c
C.
32
3
b ac
c
.
D.
33
1
b ac
c
.
C©u 52 :
Tập xác định của hàm số
5
ln
36
x
y
x
là:
A.
D =
;0) 2; )( ( 
B.
D =
(0;2)
.
C.
D =
[0;2]
.
D.
D =
(2; )
.
C©u 53 :
Hàm số nào có đồ thị như hình vẽ dưới đây:
8
A.
3
1
x
y



B.
1
3
x
y



C.
3
x
y
D.
3)(
x
y
C©u 54 :
Tập nghiệm của bất phương trình
22
2 1 5 1log log
xx
là
A.
15;
B.
33;


C.
35;


D.
13;
C©u 55 :
Tập xác định của hàm số
2ln
yx

là
A.
2
;
e

B.
0;
C.
2
1
;
e



D.
;
9
ĐÁP ÁN
01
{ | } )
28
{ | ) ~
55
{ | ) ~
02
{ | } )
29
) | } ~
03
) | } ~
30
{ ) } ~
04
) | } ~
31
) | } ~
05
{ | } )
32
{ ) } ~
06
{ | ) ~
33
) | } ~
07
{ | } )
34
{ | } )
08
{ | ) ~
35
{ | } )
09
{ ) } ~
36
{ | } )
10
) | } ~
37
{ | ) ~
11
{ ) } ~
38
{ | } )
12
) | } ~
39
{ | ) ~
13
) | } ~
40
{ ) } ~
14
) | } ~
41
) | } ~
15
{ ) } ~
42
) | } ~
16
{ | } )
43
{ | } )
17
{ ) } ~
44
) | } ~
18
{ | ) ~
45
) | } ~
19
{ | ) ~
46
{ | } )
20
{ | ) ~
47
{ | ) ~
21
{ ) } ~
48
{ | ) ~
22
{ ) } ~
49
{ | ) ~
23
{ ) } ~
50
{ | } )
24
{ | ) ~
51
{ ) } ~
25
{ ) } ~
52
) | } ~
26
{ | ) ~
53
{ ) } ~
27
{ ) } ~
54
{ | } )
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 07
C©u 1 :
Tìm giá trị của biểu thức sau:
69
log 5 log 36
1 lg2
36 10 3

A.
15
B.
40
C.
24
D.
30
C©u 2 :
Giải bất phương trình
2
log 1xx
A.
x > 0
B.
0 < x <2
C.
x > 2
D.
x > 1
C©u 3 :
Giá trị của
2
4log 5
0, 1
a
a a a
bằng
A.
5
8
B.
5
4
C.
5
2
D.
5
C©u 4 :
Phương trình
lg 3 lg 2 1 lg5xx
có bao nhiêu nghiệm?
A.
0
B.
3
C.
2
D.
1
C©u 5 :
Với x
0, đơn giản biểu thức :
5
6 12 2
35
x y xy



ta được kết quả:
A.
-2xy
2
B.
0
C.
-xy
2
D.
2xy
2
C©u 6 :
Tập các số x thỏa mãn
0,4
log 4 1 0x
A.
;6,5
B.
6,5;
C.
4;
D.
4;6,5
C©u 7 :
Tìm giá trị của biểu thức sau:
3
1 1 1
3 3 3
1
2log 6 log 400 3log 45
2
B
A.
3
B.
-3
C.
-4
D.
4
C©u 8 :
Để phương trình: (m+1).16
x
-2(2m-3)4
x
+6m+5=0 có hai nghiệm trái dấu thì m phải thõa mãn
điều kiện:
A.
Không tồn tại m
B.
-4<m<-1
C.
3
1
2
m
D.
5
1
6
m
C©u 9 :
Bất phương trình
2
lg x mlgx m 3 0
có nghiệm x > 1 khi giá trị của m là:
A.
( ; 3)
B.
; 3 6;
C.
6;
D.
3;6
2
C©u 10 :
Tìm giá trị của biểu thức sau:
22
log 2sin log os
12 12
Ac





A.
3
B.
2
C.
-1
D.
-2
C©u 11 :
Tìm giá trị của biểu thức sau:
77
5
1
log 9 log 6
log 4
2
72 49 5A




A.
22
B.
19
C.
22,5
D.
30
C©u 12 :
Hệ
3 .3 27
3 3 12
xy
xy

có nghiệm
00
;xy
. Khi đó
00
2xy
thuộc về tập hợp:
A.
2;1;3
B.
1;0;2
C.
0;1;2
D.
0;1;2;3
C©u 13 :
Cho
2
log 5 a
. Khi đó
4
log 1250
bằng:
A.
1
14
2
a
B.
2 1 4a
C.
14a
D.
24a
C©u 14 :
Bất phương trình:
2
1
6
2
0
4
log log
xx
x



có nghiệm là
A.
Vô nghiệm
B.
4 3;x 8x
C.
4;x 8x
D.
4; 3 x 8x
C©u 15 :
Cường độ một trận động đất M (richter) được cho bởi công thức
0
log log
M A A

, với A là
biên độ rung chấn tối đa và
0
A
là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động
đất ở San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác
Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ là
A.
11
B.
2.075
C.
33.2
D.
8.9
C©u 16 :
Các số thực x thỏa mãn
1
1
2
xx
aa

A.
x = 1
B.
x > 0
C.
Không có x nào
D.
x = 0
C©u 17 :
Tập hợp các số x thỏa mãn
42
23
32
xx
A.
2
;
5



B.
2
;
5



C.
2
;
3



D.
2
;
3



C©u 18 :
Nếu
6 5 6 5
x
thì
3
A.
x < 1
B.
x > - 1
C.
x > 1
D.
x < - 1
C©u 19 :
Xét các mệnh đề:
(I)
5
3 2 1
27
2
log 5.log 7.log 4.log 41 0
(II)
23
3
a
aa
log 12.log 16.log 1 0
(với 0 < a
1)
Mệnh đề nào đúng?
A.
(I) đúng, (II) sai
B.
Cả (I) và (II) đều đúng
C.
Cả (I) và (II) đều sai
D.
(I) sai, (II) đúng
C©u 20 :
Hàm số
lnx
y
x
A.
Có một cực tiểu
B.
Có một cực đại
C.
Không có cực trị
D.
Có một cực đại và một cực tiểu.
C©u 21 :
Nghiệm của phương trình
9
log x
2
9.x x
là:
A.
12
B.
9
C.
6
D.
3
C©u 22 :
Cho bất phương trình
3 10
log 2 1 1x
có tập nghiệm S. \S bằng:
A.
17
;;
2 20
 


B.
13 7
;;
20 20
 


C.
13 7
;;
20 20
 
D.
Đáp số khác
C©u 23 :
Tìm giá trị của biểu thức sau:
3
3 3 3 3
44
log 7 3 log 49 21 9B
A.
-2
B.
2
C.
1
D.
-1
C©u 24 :
Cho
2
log 14a
. Tính
49
log 32
theo a
A.
5
1a
B.
1
2( 1)a
C.
5
21a
D.
10 1a
C©u 25 :
Nếu
12 12
log 6 ;log 7ab
thì
2
log 7
bằng
A.
1
a
b
B.
1
a
a
C.
1
a
b
D.
1
b
a
C©u 26 :
Một lon nước soda 80
0
F được đưa vào một máy làm lạnh chứa đá tại 32
0
F. Nhiệt độ
4
của soda ở phút thứ t được tính theo định luật Newton bởi công thức
( ) 32 48.( 0.9)
t
Tt

. Phải làm mát soda trong bao lâu để nhiệt độ là 50
0
F?
A.
4
B.
1,56
C.
2
D.
9,3
C©u 27 :
Xét các mệnh đề:
(I)
3 1,7
11
55
(II)
5 2,23
44
Mệnh đề nào đúng?
A.
(I) đúng, (II) sai
B.
(I) sai, (II) đúng
C.
Cả (I) và (II) đều đúng
D.
Cả (I) và (II) đều sai
C©u 28 :
Cho hàm số
2
3
5
xx
y
. Tính
'y
A.
2
3
' 2 3 5 ln5
xx
yx

B.
2
3
' 5 ln5
xx
y
C.
2
3
' 2 3 5
xx
yx

D.
2
23
' 3 5 ln5
xx
y x x

C©u 29 :
Biết
6
log 2a
thì
6
log a
bằng
A.
36
B.
6
C.
4
D.
1
C©u 30 :
Đạo hàm của hàm số
2
3
y ln(x 1 x ) log (sin2x)
là:
A.
2
1 2cot 2x
ln3
x 1 x

B.
2
1 2cot 2x
ln3
1x
C.
2
2x 2cot 2x
ln3
x 1 x

D.
2
1 2tan2x
ln3
1x
C©u 31 :
Phương trình:
64.9 84.12 27.16 0
x x x
có nghiệm là
A.
X=1; x=2
B.
Vô nghiệm
C.
93
;
16 4
x
D.
X=-1; -2
C©u 32 :
Bất Phương trình:
64.9 84.12 27.16 0
x x x
có nghiệm là
A.
1<x<2
B.
93
16 4
x
C.
X<1 hoặc x>2
D.
Vô nghiệm
C©u 33 :
Tập nghiệm của hệ phương trình
22
x1
3x 2 2x x 4
33
0,2 0,2
là:
5
A.
3
;
2



B.
2
C.
2;3
D.
C©u 34 :
Số nghiệm nguyên của bất phương trình:
1 5 1 5
log 3 5 log 1xx
là:
A.
0
B.
2
C.
1
D.
Vô số
C©u 35 :
Cho hàm số
1 cos
ln
sin
x
y
x
. Tìm
'y
A.
1
'
sin
y
x

B.
1
'
cos
y
x
C.
1
'
sin
y
x
D.
1
'
cos
y
x

C©u 36 :
Trên đoạn
1;25
bất phương trình
4
3
log log 4
2
x
x 
có mấy nghiệm nguyên?
A.
15
B.
8
C.
0
D.
16
C©u 37 :
Tập nghiệm của bất phương trình
33
log 3 log 5 1xx
là:
A.
5;6
B.
5;
C.
6;
D.
2;6
C©u 38 :
7.Tìm giá trị của biểu thức sau:
36 1
6
1
log 2 log 3
2
C 
A.
1
2
B.
3
2
C.
1
2
D.
5
2
C©u 39 :
Bất Phương trình:
25
53
4log log
x
x 
có nghiệm là:
A.
0 5; 5xx
B.
55x
C.
5; 5xx
D.
1
0 ; 1
2
xx
C©u 40 :
Phương trình: 4
x
- 3.2
x
-4=0 có nghiệm là
A.
X=2
B.
X=-1; 4
C.
X= 1; 4
D.
Vô nghiệm
C©u 41 :
Phương trình:
57
( 2)
log log
xx
có nghiệm là
A.
X=1
B.
X=5
C.
Vô nghiệm
D.
X=7
C©u 42 :
Tập xác định của hàm số
x2
y (3 9)

là:
A.
B.
\2
C.
(2; )
D.
( ;2)
C©u 43 :
Tập nghiệm của bất phương trình
4 2 2 0
xx
là:
6
A.
;1
B.
2;
C.
1; 
D.
;2
C©u 44 :
Giá trị của biểu thức :
0,75
1
0,5
4
1
81 36
16




bằng:
A.
7
B.
5
C.
6
D.
8
C©u 45 :
Tập nghiệm của bất phương trình
12
2
lg (x 1) lg (2 x)
A.
1 5;1 5



B.
1 5 1 5
;
22




C.
15
;
2



D.
1;2
C©u 46 :
Cho
3
log 15a
. Khi đó
25
log 15
bằng:
A.
21
a
a
B.
1
a
a
C.
21
a
a
D.
1
a
a
C©u 47 :
Tìm giá trị của biểu thức sau:
9
125 7
11
log 4
log 8 log 2
42
81 25 .49A




A.
20
B.
Đáp án khác
C.
19
D.
18
C©u 48 :
Tìm giá trị của biểu thức sau:
25
4
1
log 3 3log 5
1 log 5
2
16 4A

A.
192
B.
529
C.
592
D.
Đáp án khác
C©u 49 :
Số lượng của một số loài vi khuẩn sau t (giờ) được xấp xỉ bởi đẳng thức
0.195
0
t
Q Q e
, trong
đó
0
Q
là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn ban đầu là 5000 con thì sau bao
lâu có 100.000 con.
A.
20
B.
3.55
C.
24
D.
15,36
C©u 50 :
8.Tìm giá trị của biểu thức sau:
1
33
5
3
4
1
3
3
27
log 27 log
9
11
log log
81 3
C



A.
1
2
B.
3
2
C.
4
5
D.
Đáp án khác
C©u 51 :
Tìm giá trị của biểu thức sau:
9 9 9
log 15 log 18 log 10A
A.
4
B.
2
3
C.
3
2
D.
3
7
C©u 52 :
Phương trình
22
12
1
5 log 1 logxx


có tổng các nghiệm là:
A.
5
B.
33
64
C.
66
D.
12
C©u 53 :
Bất Phương trình: 4
x
- 3.2
x
-4<0 có nghiệm là
A.
X<2
B.
0<x<2
C.
X=2
D.
-1<x<4
C©u 54 :
Cường độ một trận động đất M được cho bởi công thức
0
log log
M A A

, với A là biên độ
rung chấn tối đa và
0
A
là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở
San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó
đo được 7.1 độ Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu trận
động đất này.
A.
4
B.
1,17
C.
2,2
D.
15,8
C©u 55 :
Phương trình:
4 2 2 4
log (log ) log (log ) 2xx
có nghiệm là
A.
X=8
B.
X=16
C.
X=2
D.
X=4
C©u 56 :
Nghiệm của phương trình
1
5 5 2.2 8.2
x x x x
là
A.
5
2
log 4x
B.
5
2
8
log
3
x
C.
1x
D.
5
2
5
log
3
x
C©u 57 :
Số nghiệm âm của phương trình
x 2 5
1 2log 5 log (x 2)
là:
A.
0
B.
1
C.
2
D.
Đáp số khác
C©u 58 :
Tìm nghiệm của phương trình
12
3.2 5.2 2 21
x x x
A.
2
log 3x
B.
16x
C.
8x
D.
3x
C©u 59 :
Phương trình:
25
53
4log log
x
x 
có nghiệm là:
A.
5; 5xx
B.
X=1; 1/2
C.
X=1/5; 5
D.
1/ 5; 5xx
C©u 60 :
Tập xác định của hàm số
log 3 3
x
y

là:
A.
1; 
B.
Một đáp số khác
C.
3; 
D.
1; 
C©u 61 :
Phương trình
22
6.2 13.6 6.3 0
x x x
có tập nghiệm là tập con của tập
8
A.
3
; 1;4;5
2




B.
21
; 1; ;2
33




C.
4; 3;1;0
D.
2; 1;1;3
C©u 62 :
Tập nghiệm của phương trình
22
11
9 3 6 0
xx
là:
A.
0
B.
1;0;1
C.
2;0;2
D.
1;1
9
ĐÁP ÁN
01
{ | ) ~
28
) | } ~
55
{ ) } ~
02
{ | } )
29
{ | ) ~
56
{ | ) ~
03
{ | ) ~
30
{ ) } ~
57
{ ) } ~
04
{ | } )
31
) | } ~
58
) | } ~
05
{ ) } ~
32
) | } ~
59
) | } ~
06
{ | } )
33
{ ) } ~
60
) | } ~
07
{ | ) ~
34
{ | } )
61
{ | } )
08
{ ) } ~
35
) | } ~
62
) | } ~
09
{ ) } ~
36
) | } ~
10
{ | ) ~
37
) | } ~
11
{ | ) ~
38
{ | ) ~
12
{ | } )
39
) | } ~
13
) | } ~
40
) | } ~
14
{ ) } ~
41
{ ) } ~
15
{ | } )
42
{ ) } ~
16
{ | } )
43
) | } ~
17
{ | ) ~
44
{ ) } ~
18
{ | } )
45
{ ) } ~
19
{ ) } ~
46
) | } ~
20
{ ) } ~
47
{ | ) ~
21
{ ) } ~
48
{ | ) ~
22
{ | } )
49
{ | } )
23
{ | ) ~
50
{ | ) ~
24
{ | ) ~
51
{ | ) ~
25
{ | } )
52
{ | } )
26
{ | } )
53
) | } ~
27
{ ) } ~
54
{ | } )
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 08
C©u 1 :
Phương trnh
3 2 3 4
2 1 2 1
.2 2 .2 2
xx
xx
xx

c nghim l:
A.
1
,3
2
xx
B.
1, 3xx
C.
1
,3
4
xx
D.
Mt kt qu khc.
C©u 2 :
Phương trnh
1 2 4 3
7.3 5 3 5
x x x x
c nghim l:
A.
1x 
B.
1x
C.
2x 
D.
2x
C©u 3 :
Cho phương trình
2 3 3
1 1 1
4 4 4
3
log 2 3 log 4 log 6 (1)
2
x x x
.
Trong các mệnh đề sau:
(I). Điều kiện phương trình:
64x
và
2x
;
(II).
1 1 1
4 4 4
(1) 3log 2 3 3log 4 3log 6x x x
;
(III).


11
44
(1) log 4 2 log (4 )( 6)x x x
,
Mệnh đề nào đúng ?
A.
C I, II, III
B.
Chỉ III, I.
C.
Chỉ II, III.
D.
Chỉ I, II.
C©u 4 :
Số nghim nguyên của bất phương trnh (x-3).(1+lgx) <0 là
A.
0
B.
2
C.
1
D.
Vô số
C©u 5 :
Cho phương trình
2
2
22
log 1 log 2 1 9 (1)x x x
.Trong các mệnh đề:
(I).
22
(1) 2log 1 log 1 9,xx
với điều kiện
1.x
(II).
(1) 1 8,x
II).
2
(1) 2x 63 0,x
2
mệnh đề nào đúng?
A.
Chỉ III, I.
B.
C I, II, III.
C.
Chỉ I, II.
D.
Chỉ II, III.
C©u 6 :
Tập nghim của bất phương trnh
2
5
0
log 4 1
x
x
là
A.
4 2;S
B.
5;S
C.
4 2;S
D.
4;S
C©u 7 :
Bất phương trnh 
󰇛
󰇜

󰇛
󰇜
có tập nghim là:
A.
󰇛
󰇠
B.
󰇛

󰇠
C.
󰇟
󰇠
D.
󰇛

󰇠
C©u 8 :
Giá trị nhỏ nhất của hàm số
2
x
fx
trên
2;2
là
A.
1
2
B.
2
2
C.
1
D.
2
C©u 9 :
Cho hàm số
yx
1
3
, Các mệnh đề sau , mệnh đề nào sai
A.
Hàm số có đồ thị nhận trục tung làm trục
đối xứng
B.
1
3
lim
x
fx
C.
Hàm số không có đạo hàm tại
0x
D.
Hàm số đồng biến trên
;0
và nghịch
biến
0;
C©u 10 :
Đặt
5
x
t
thì bất phương trình
22
5 3.5 32 0
xx
trở thành bất phương trình nào
sau đây?
A.
2
75 32 0
tt
B.
2
6 32 0
tt
C.
2
3 32 0
tt
D.
2
16 32 0
tt
C©u 11 :
Hàm số

đồng bin trên
A.
󰇛󰇜
B.
󰇛
󰇜
C.
󰇛󰇜
D.
󰇛󰇜
C©u 12 :
Phương trnh
57
log log 2xx
c nghim l
A.
5x
B.
1
7
x
C.
1
5
x
D.
7x
C©u 13 :
Cho hàm số
2
ln(1 2 )y x x
. Kết luận nào sau đây về cực trị hàm số này là đúng?
3
A.
1 4ln 2
4
CT
y
tại
1
x
B.
1 4ln 2
4
CT
y
tại
1
2
x
C.
1 4ln 2
4
CÑ
y
tại
1
2
x
D.
1 4 ln2
4
CT
y
tại
1
x
C©u 14 :
Các kết luận sau , kết luận nào sai
I.
3
17 28
II.
32
11
32
III.
57
44
IV.
45
13 23
A.
I
B.
III
C.
II và III
D.
II và IV
C©u 15 :
Tm m để phương trnh c 2 nghim phân bit 9
x
–m.3
x
+1=0
A.
m>2 hoặc m<-2
B.
m>2
C.
-2<m<2
D.
m<-2
C©u 16 :
Tìm tập xác định của hàm số

1
log 2
x
yx
.
A.
1;2
D
B.
1;2
D


C.
;2
D

D.
1;
D

C©u 17 :
Cho hàm số
󰇛
󰇜

,khi đ
󰆒
󰇛
󰇜
.
Giá trị của a bằng:
A.
B.
2
C.
1
D.
C©u 18 :
Phương trnh
1 1 1
4 6 9
x x x

c nghim l:
A.
51
2
3
log
2
x
B.
2
3
51
log
2
x



C.
51
2
2
log
3
x
D.
3
2
51
log
2
x



C©u 19 :
󰉼󰉴
2
3 2 2 3 2 2
log 1 log 0.x m mx x

󰈨󰉴󰈨 󰈖 󰈜
󰉼󰉴 󰈨󰈘
A.
3m 
B.
1m 
C.
3m
D.
1m
C©u 20 :
Phương trnh
lg lg 1 lg 1 lg 1
7 5 3.5 13.7
x x x x
c nghim l
A.
100x
B.
1x
C.
10x
D.
1
10
x
C©u 21 :
Cho hàm số
yx
1
3
, Trong các mệnh đề sau , mệnh đề nào sai
4
A.
Hàm số nhận
0; 0O
làm tâm đối xứng
B.
Hàm số đồng biến trên tập xác định
C.
Hàm số lõm
;0
và lồi
0;
D.
Hàm số có đồ thị nhận trục tung làm trục
đối xứng
C©u 22 :
Số nghim của phương trnh:

󰇛

󰇜

󰇛

󰇜
à:
A.
0
B.
2
C.
1
D.
3
C©u 23 :
Cho
0; 0; 1; 1;a b a b n R
, một học sinh tính biểu thức
2
1 1 1
......
log log log
an
aa
P
b b b
theo các bước sau
I .
2
log log ... log
n
b b b
P a a a
II.
2
log . ...
n
b
P a a a
III.
1 2 3 ...
log
n
b
Pa
IV.
1 log
b
P n n a
Bạn học sinh trên đã giải sai ở bước nào
A.
I
B.
II
C.
III
D.
IV
C©u 24 :
Cho hàm số
yx
4
, Các kết luận sau , kết luận nào sai
A.
Tập xác định
0;D
B.
Hàm số luôn luôn đồng biến với mọi
x
thuộc tập xác định
C.
Hàm số luôn đi qua điểm
1;1M
D.
Hàm số không có tiệm cận
C©u 25 :
Tìm khẳng định đúng
A.
20172016
3232
B.
20172016
3232
C.
20172016
3232
D.
20172016
3232
C©u 26 :
Cho
ab
33
log 15; log 10
vậy
3
log 50 ?
A.
1ab
B.
41ab
C.
31ab
D.
21ab
5
C©u 27 :
Cho hàm số
2
sin x
f x e
. Tập nghim của phương trnh
'0fx
là
A.
S
B.
;S k k
C.
,
2
k
Sk
D.
2,S k k
C©u 28 :
Cho hàm số
yx
2
2
32

, tập xác định của hàm số là
A.
22
;
33
D
B.
22
;;
33
D
C.
22
;;
33
D
D.
2
\
3
DR
C©u 29 :
Với mọi số
;0ab
thỏa mãn
22
9 10a b ab
th đẳng thức đúng l
A.
lg 3 lg lga b a b
B.
lg 1 lg 1ab
C.
3 lg lg
lg
42
a b a b
D.
2lg 3 lg lga b a b
C©u 30 :
Tính đạo hàm cấp hai
''y
của hàm số
ln(3 2)yx
.
A.
2
9
''
(3 2)
y
x
B.
9
''
32
y
x
C.
2
3
''
(3 2)
y
x
D.
2
'' 3ln (3 2)
yx

C©u 31 :
Tm m để phương trnh
01loglog
3
3
2
xmx
có nghim duy nhất nhỏ hơn 1.
A.
m=2
B.
m= -2
C.
2m
D.
Không tồn tại m
C©u 32 :
Cho hàm số
yx
5
31

, tập xác định của hàm số là
A.
DR
B.
1;D
C.
;1D
D.
\1DR
C©u 33 :
Phương trnh
2 1 1
2 33.2 4 0
xx
c nghim l:
A.
2, 3xx
B.
1, 4xx
C.
2, 3xx
D.
1, 4xx
C©u 34 :
Số nghim của phương trnh
󰇛
󰇜


là:
A.
0
B.
3
C.
2
D.
1
C©u 35 :
Trong các khẳng định sau thì khẳng định nào sai?
6
A.
xx
20172016
3232
B.
xx
20172016
3232
C.
20172016
3232
xx
D.
xx
20162016
3232
C©u 36 :
Hàm số đồng bin trên từng khong xc định của nó là
A.
4
21f x x
B.
1
fx
x
C.
1
x
f x e
x
D.
lnf x x
C©u 37 :
Tập nghim của bất phương trnh
3lg4 x
là
A.
4;3
B.
10000;1000
C.
;100001000;0
D.
Vô nghiệm
C©u 38 :
Nghim của phương trnh
33
3 log log 3 1 0xx
.
A.
9; 27xx
B.
3; 27xx
C.
3; 81xx
D.
9; 81xx
C©u 39 :
Tm m để phương trnh c 1 nghim 9
x
–m.3
x
+1=0
A.
2m
B.
2m
C.
2m
D.
2m
C©u 40 :
Tập nghim của bất phương trnh
255
22
x
là
A.
x>2
B.
x>2 hoặc x<0
C.
x<0
D.
0<x<2
C©u 41 :
Cho hàm số
2
()
x
e
fx
x
. Tính
'(1)f
.
A.
4
'(1)
5
fe
B.
'(1) e
f

C.
'(1) 3
fe
D.
4
'(1)
3
fe
C©u 42 :
Phương trnh
5 24 5 24 10
xx
c nghim l
A.
2x 
B.
1x 
C.
4x 
D.
1
2
x 
C©u 43 :
Bất phương trnh:
21
2
log 2 1 log 2 1xx
có tập nghim là:
A.
󰇛󰇜
B.
󰇣
󰇤
C.
(2 ;
󰇠
D.
󰇛󰇠
C©u 44 :
Cho
2
log 14 m
, tính
49
log 32P
theo m.
A.
5
22
P
m
B.
31
Pm

C.
32
Pm

D.
1
1
P
m
7
C©u 45 :
Hàm số

󰇛
󰇜 có tập xc định là:
A.
󰇛󰇜 󰇛󰇜
B.
󰇝
󰇞
C.
󰇛󰇜
󰇛󰇜
D.
󰇛󰇜
C©u 46 :
Hàm số
x
f x x e
đồng bin trên
A.
0;
B.
0;
C.
;0
D.
C©u 47 :
Tập nghim của phương trnh
21log
3
x
là
A.
3
B.
2;4
C.
2;10
D.
2;3
C©u 48 :
Tập xc định của hàm số
2
2
1
lg 3 2
45
f x x x
xx
là
A.
1;1 2;5
B.
1;1 2;5
C.
1;1 2;5
D.
1;1 2;5
C©u 49 :
Tất c các giá trị của
x
thỏa mãn
3
log 1
13
x
x
là
A.
1x
B.
x
C.
1x
D.
0x
C©u 50 :
Giá trị của
223
4.2
bằng
A.
8
B.
23
2
C.
426
4
D.
32
C©u 51 :
Cho hàm số
x
ya
, Các mệnh đề sau , mệnh đề nào sai
A.
Đồ thị hàm số không có điểm uốn
B.
Đố thị hàm số luon đi qua điểm
0;1M
và
1;Na
C.
Đồ thị hàm số có đường tiệm cận là
0y
D.
Đồ thị hàm số luôn tăng
C©u 52 :
Giá trị lớn nhất , nhỏ nhất của hàm số
2
x
y
trên
2;2
là
A.
GTLN = 1 ; GTNN =
1
4
B.
GTLN = 4 ; GTNN =
1
4
C.
GTLN = 4 ; GTNN =
1
4
D.
GTLN = 4 ; GTNN = 1
C©u 53 :
Bất phương trnh 
󰇛
󰇜

󰇛
 
󰇜
có tập nghim là:
A.
󰇛


󰇜
B.
󰇛

󰇠
󰇟
󰇜
8
C.
󰇛

󰇠
󰇟

󰇜
D.
󰇛

󰇠
󰇟
󰇜
C©u 54 :
Giải bất phương trình

21
1
11
3 12
33
xx
.
A.
3
x
B.
10
x
C.
2
x
D.
24
x

C©u 55 :
Cho phương trnh
3
2
2
2
log 2 5
33
x
m x x
, với m là tham số.
Tất c các giá trị của m để phương trnh trên c mt nghim là
A.
34 2
22m
B.
4m
hoặc
34
02m
C.
4m
hoặc
34
02m
.
D.
2;
C©u 56 :
Giá trị nhỏ nhất của hàm số


󰇛
󰇜


󰇛
󰇜
bằng:
A.
8
B.
4
C.
6
D.
2
C©u 57 :
Cho hàm số
ln(4 3)yx
. Đẳng thức nào sau đây đúng?
A.
4 ' 3 '' 0
yy

B.
4 ' (4 3) '' 0
y x y
C.
' 4 '' 0
yy

D.
4 ' (4 3) '' 0
y y x y
C©u 58 :
󰉼󰉴
4 2 2 4
log log log log 2xx
 󰈨 
A.
16x
B.
8x
C.
4x
D.
2x
C©u 59 :
Phương trnh
xxx
4.369
11
có bao nhiêu nghim:
A.
4
B.
3
C.
2
D.
1
C©u 60 :
Cho phương trnh
39
log 1 log 4 3 4 1 .x x x x
Trong cc pht biểu sau,
pht biểu no l sai.
A.
Phương trnh c nghim l
9x
B.
Phương trnh c nghim l
0x
C.
Phương trnh c nghim l
4x
D.
Phương trnh c nghim l
1x
9
ĐÁP ÁN
01
) | } ~
28
{ | } )
55
{ | ) ~
02
) | } ~
29
{ | ) ~
56
{ | } )
03
) | } ~
30
) | } ~
57
{ ) } ~
04
{ ) } ~
31
{ ) } ~
58
) | } ~
05
{ ) } ~
32
{ | } )
59
{ | } )
06
{ | ) ~
33
) | } ~
60
) | } ~
07
{ | } )
34
{ | ) ~
08
{ | ) ~
35
{ ) } ~
09
{ | } )
36
{ | ) ~
10
) | } ~
37
{ ) } ~
11
{ | ) ~
38
{ | ) ~
12
) | } ~
39
{ ) } ~
13
{ ) } ~
40
{ ) } ~
14
{ | } )
41
{ ) } ~
15
{ ) } ~
42
) | } ~
16
) | } ~
43
{ | ) ~
17
{ | } )
44
) | } ~
18
) | } ~
45
{ | ) ~
19
) | } ~
46
{ | ) ~
20
) | } ~
47
{ ) } ~
21
{ | } )
48
{ | ) ~
22
{ | ) ~
49
{ | ) ~
23
{ | } )
50
{ ) } ~
24
{ | } )
51
{ | } )
25
{ ) } ~
52
{ | } )
26
{ | } )
53
{ | } )
27
{ | ) ~
54
{ ) } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 09
C©u 1 :
Số
3
3
222
333
bằng:
A.
5
18
3
2



B.
7
2
3
2



C.
3
27
3
2



D.
5
18
3
2



C©u 2 :
Phương trình
2
22
2 2 3
x x x x

có tổng các nghiệm bằng:
A.
1
B.
0
C.
-1
D.
-2
C©u 3 :
Hàm số f(x) =
2
x ln x
đạt cực trị tại điểm:
A.
x =
1
e
B.
x =
1
e
C.
x =
e
D.
x = e
C©u 4 :
Phát biểu nào sau đây là sai:
A.
Hàm số lôgarit
log 0, 1
a
y x a a
có tập xác định là
0; 
.
B.
Hàm số mũ
x
ya
nhận trục Ox làm tiệm cận ngang.
C.
Hàm số mũ
x
ya
có tập xác định là
0; 
.
D.
Hàm số
x
ya
và
log
a
yx
đồng biến khi a > 1.
C©u 5 :
Cho hàm số
2
1
4
y log x
và
8
2
y log x
. Tổng các hoành độ giao điểm của hai đồ thị hàm số
đã cho là:
A.
2
B.
3
C.
5
D.
-1
C©u 6 :
Phương trình
2 1 2 1 2 2 0
xx
có tích các nghiệm là:
A.
-1
B.
1
C.
0
D.
2
2
C©u 7 :
Hàm số y =
1-x
3
x
2.
5



A.
Đồng biến trên
0; 
B.
Nghịch biến trên tập R
C.
Đồng biến trên tập R
D.
Đồng biến trên
1;
, nghịch biến trên
;1
C©u 8 :
Giả sử ta có hệ thức a
2
+ b
2
= 7ab (a, b > 0). Hệ thức nào sau đây là đúng?
A.
2 2 2
2log a b log a log b
B.
2 2 2
ab
2 log log a log b
3

C.
2 2 2
ab
log 2 log a log b
3

D.
2 2 2
ab
log log a log b
6

C©u 9 :
Cho hàm số
2
8ln x
y f x
x
. Chọn câu đúng nhất.
A.
Hàm số nghịch biến trên
0;1
và đồng biến trên
1; 
.
B.
Đồ thị hàm số có một điểm cực đại và một điểm cực tiểu.
C.
Đồ thị hàm số nhận điểm
M 1;0
làm điểm cực tiểu.
D.
Hàm số đồng biến trên
0;1
và nghịch biến trên
1; 
C©u 10 :
Tổng các nghiệm của phương trình:
2x 4 1
2 5.2 1 0
x
A.
4
B.
5
C.
-4
D.
5
8
C©u 11 :
Nghiệm của bất phương trình
23
11
23
log ( 3) log ( 3)
0
1
xx
x
là:
A.
1x 
B.
0x
C.
2x 
D.
21x
C©u 12 :
Tập nghiệm của bất phương trình
1
2 2 6
xx

là:
A.
( ;0)
B.
( ;2)
C.
( ;3)
D.
( ;1)
C©u 13 :
Tập nghiệm của phương trình
2x x 2x
2.2 9.14 7.7 0
là :
A.
S 0;1
B.
S 1;0
C.
S0
D.
S 1;0
3
C©u 14 :
Giá trị lớn nhất của hàm số
2
y lnx ln x 1
trên đoạn
1
;2
2



đạt tại :
A.
x1
B.
1
x
2
C.
3
x
2
D.
3
x
4
C©u 15 :
Để giải bất phương trình: ln
2x
x1
> 0 (*), một học sinh lập luận qua ba bước như sau:
Bước 1: Điều kiện:
2x
0
x1
x0
x1
(1)
Bước 2: Ta có ln
2x
x1
> 0 ln
2x
x1
> ln1
2x
1
x1
(2)
Bước3: (2) 2x > x - 1 x > -1 (3)
Kết hợp (3) và (1) ta được
1 x 0
x1
Vậy tập nghiệm của bất phương trình là: (-1; 0) (1; +)
Hỏi lập luận trên đúng hay sai? Nếu sai thì sai từ bước nào?
A.
Lập luận hoàn
toàn đúng
B.
Sai từ bước 3
C.
Sai từ bước 1
D.
Sai từ bước 2
C©u 16 :
Hàm số nào đồng biến trên khoảng
;0
?
A.
2
y x 1
B.
x
1
ye
x

C.
x2
y e x

D.
2
y ln x x 2
C©u 17 :
Cho hai hàm số
a
y f x log x
và
x
y g x a
. Mệnh đề nào sau đây là sai?
I. Đồ thị hai hai hàm số f và g luôn cắt nhau tại một điểm.
II. Chiều biến thiên của hai hàm số f và g là giống nhau.
III. Đồ thị hàm số f nhận trục Oy làm tiệm cận.
IV. Chỉ có đồ thị hàm số f có tiệm cận.
A.
I, IV.
B.
I, II.
C.
III, IV.
D.
II, III.
C©u 18 :
Bất phương trình
21
3 ( 3)3 2( 3) 0
xx
mm
khi:
A.
3m 
B.
3m 
C.
0m
D.
21m
C©u 19 :
Phương trình
2
22
log ( 1) 6log 1 2 0xx
có tập nghiệm là:
4
A.
3;15
B.
1;2
C.
D.
1;3
C©u 20 :
Hàm số y =x.lnx đồng biến trên khoảng nào
A.
(0; )
B.
1
(0; )
e
C.
1
( ; )
e

D.
1
( ; )
e

C©u 21 :
Nghiệm của phương trình
1 1 2
2
2 2 3 2
xx

là
A.
3x 
B.
2x
C.
3
2x
D.
3
2x 
C©u 22 :
Phương trình
8.3 3.2 24 6
x x x
có tổng các nghiệm bằng:
A.
4
B.
6
C.
2
D.
3
C©u 23 :
Phương trình
21
2
2log 2 2 log 9 1 1xx
có tổng các nghiệm bằng:
A.
5/2
B.
0
C.
3/2
D.
-3/2
C©u 24 :
Tập nghiệm của bất phương trình
21
32
23
xx
là:
A.
3
1
;
B.
1;
C.
;
3
1
D.
 ;1
C©u 25 :
Cho hệ phương trình
22
ln ln
6 2 6 0
x y y x
x y x y
. Nghiệm (x;y) của hệ là
A.
(1;3);(3;3)
B.
(1;3);(3;1)
C.
(1;1);(3;3)
D.
(1;1);(3;1)
C©u 26 :
Phương trình

x 16
log 2 log x 0
có tích các nghiệm bằng:
A.
1
B.
-1
C.
0
D.
-4
C©u 27 :
Điều kiện cần và đủ của a và b để cho
log 0
a
b
là :
A.
a 0, 0b
B.
a 0, 0b
C.
a 0, 0b
và
a-1 . 1 0b 
D.
a 1, 1b
C©u 28 :
Trong các hàm số sau, hàm nào luôn đồng biến
A.
(0,99)
x
B.
0,5
log ( 1)yx
C.
2
1yx
D.
2
logyx
C©u 29 :
Tập nghiệm của bất phương trình
41
4
3 1 3
log (3 1)log
16 4
x
x

là:
5
A.
(0;1]
B.
[1;2]
C.
[2; )
D.
(0;1] [2; ) 
C©u 30 :
Giá trị lớn nhất của hàm số
2
y ln x 2lnx 2
trên đoạn
3
1;e


là :
A.
1
.
B.
0
..
C.
2
.
D.
Không tồn tại giá
trị lớn nhất.
C©u 31 :
Bất phương trình:
x x 1
4 2 3

có tập nghiệm là:
A.
1; 3
B.
2
;log 3
C.
2; 4
D.
2
log 3; 5
C©u 32 :
Cho hệ phương trình
22
ln ln
6 2 6 0
x y y x
x y mx my
. Giá trị của m để hệ có 2 cặp nghiệm phân
biệt là
A.
01m
B.
1
2
m
C.
1
2
2
m
D.
3
2
m
C©u 33 :
Phát biểu nào sau đây là sai:
A.
log log
,(a,b,c 0; 1)
bb
ca
a c b
B.
log log , 0; 0; 1;
a
a
b b a b a R
C.
2
log 2log , 0, 1
aa
b b a a
D.
ln
log , 0; 0; 1
ln
a
b
b a b a
a
C©u 34 :
Đơn giản biểu thức:
1
2
1
1,5
2
11
:
1
1
x
x
xx

A.
1
B.
1x
C.
1
2
1x
D.
1x
C©u 35 :
Số nghiệm nguyên của phương trình
22
x x 5 x 1 x 5
4 12.2 8
là:
A.
2
B.
1
C.
0
D.
3
C©u 36 :
Đạo hàm của hàn số y=
2 .3
xx
là
A.
11
23
xx
B.
23
xx
C.
6 .ln6
x
D.
6
x
C©u 37 :
Đạo hàm của hàm số
x1
y ln
x2
là :
A.
x2
x1
B.
2
3
x x 2

C.
2
x1
x2
D.
x2
x1
x 1 ln
x2



6
C©u 38 :
Phương trình
22
22
4 2.4 4 0
x x x x
có tích các nghiệm bằng:
A.
0
B.
1
C.
-1
D.
2
C©u 39 :
Phương trình:

12
4 log x 2 logx
= 1 có tập nghiệm là:
A.
1; 20
B.
10; 100
C.
1
; 10
10



D.
C©u 40 :
Phương trình
3
2
log 4 2
x
kx
có 2 nghiệm phân biệt khi:
A.
1
2
k
B.
1
2
k
C.
0k
D.
1
0
2
k
C©u 41 :
Tập xác định của hàm y=
2
0,5
log ( 2 )xx
là
A.
( ;0)
B.
(0;2)
C.
(2; )
D.
\[0;2]R
C©u 42 :
Cho hàm số y=
sinx
e
. Khi đó y’.cosx-y” =?
A.
.cosxy
B.
.sinxy
C.
.sinxy
D.
.cosxy
C©u 43 :
Cho hàm số
2
3
(2x 1)y 
, Tập xác định của hàm số là:
A.
1
;
2



B.
R
C.
1
;
2




D.
0; 
C©u 44 :
Cho
12 24
a log 18,b log 54
. Tính giá trị của biểu thức
E ab 5 a b
A.
1
B.
- 1.
C.
2
D.
- 2
C©u 45 :
Phương trình
3.8 4.12 18 2.27 0
x x x x
có tập nghiệm là:
A.
1
B.
1;1
C.
0;1
D.
C©u 46 :
So sánh
2 3 4 2 2 3 2 4
M a a b b a b
với
3
3 2 3 2
N a b
:
A.
MN
B.
0MN
C.
MN
D.
MN
C©u 47 :
Tập nghiệm của phương trình:
x 1 3 x
5 5 26


là:
A.
3; 5
B.
1; 3
C.
2; 4
D.
C©u 48 :
Phương trình:
2
log x x 6
có tập nghiệm là:
7
A.
4
B.
C.
3
D.
2; 5
C©u 49 :
Phương trình
2
33
log x x 5 log 2x 5
có tổng các nghiệm bằng:
A.
3
B.
5
C.
2
D.
-10
C©u 50 :
Cho
,0ab
và
,1ab
;
x
và
y
là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log ( ) log log
a a a
x y x y
B.
log .log log
b a b
a x x
C.
11
log
log
a
a
xx
D.
log
log
log
a
a
a
x
x
yy
C©u 51 :
Tính giới hạn sau :
x0
ln 1 2x
lim
3x
A.
2
3
B.
0
C.
1
D.
2
C©u 52 :
Tập nghiệm của bất phương trình
0,5
log 2x 5 0
A.
;3
B.
3;
C.
5
;3
2


D.
11
;
4



C©u 53 :
Cho hàm số
x
sin
n2
2
l
y



. Đạo hàm của hàm số đã cho là:
A.
x
sin 1
n2
x
' sin 1 .2
n2
l
y
l










B.
x
sin
n2
xx
' cos .2 .
n2 n2
l
y
ll






C.
x
sin
n2
x
' cos .2
n2
l
y
l






D.
Tất cả đều sai.
C©u 54 :
Bất phương trình
12
4 ( 2)2 2 2 0
xx
m m m
có tập nghiệm là khi:
A.
1m
B.
2m 
C.
2m
D.
1m 
C©u 55 :
Cho hệ bất phương trình
22
22
3
2
log log 0
3 5 9 0
3
xx
x
xx

Nghiệm hệ bất phương trình là:
A.
01x
B.
4x
C.
0x
D.
14x
8
C©u 56 :
Cho log
23
5 a; log 5 b
. Khi đó
6
log 5
tính theo a và b là:
A.
a + b
B.
ab
ab
C.
1
ab
D.
22
ab
C©u 57 :
Nghiệm của bất phương trình
2
3 3 2
0
42
x
x
x

là
A.
0x
B.
1
0
2
x
C.
2x
D.
1
2
2
x
C©u 58 :
Phương trình
2
cos2 cos
4 4 3
xx

có tổng các nghiệm bằng:
A.
B.
2
C.
4
D.
0
C©u 59 :
Phương trình
12
4 2 0
xx
m

có nghiệm khi:
A.
0m
B.
1m
C.
0m
D.
1m
C©u 60 :
Cho
0a
và
1a
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
log 1
a
a
và
log 0
a
a
B.
log log
aa
xx
, với
0, 0x

C.
log ( ) log .log
a a a
xy x y
D.
log
a
x
có nghĩa với mọi
x
9
ĐÁP ÁN
01
{ | } )
28
{ | } )
55
{ | } )
02
) | } ~
29
{ | } )
56
{ ) } ~
03
{ ) } ~
30
) | } ~
57
{ | } )
04
{ | ) ~
31
{ ) } ~
58
) | } ~
05
{ | ) ~
32
{ | } )
59
{ | } )
06
) | } ~
33
{ | ) ~
60
{ ) } ~
07
{ | ) ~
34
{ | } )
08
{ ) } ~
35
{ ) } ~
09
{ ) } ~
36
{ | ) ~
10
{ | ) ~
37
{ ) } ~
11
{ | } )
38
) | } ~
12
{ | } )
39
{ ) } ~
13
{ ) } ~
40
{ | } )
14
) | } ~
41
{ | } )
15
{ ) } ~
42
{ | ) ~
16
{ ) } ~
43
{ | ) ~
17
) | } ~
44
) | } ~
18
{ | } )
45
) | } ~
19
) | } ~
46
{ | } )
20
{ | ) ~
47
{ ) } ~
21
{ | ) ~
48
{ ) } ~
22
) | } ~
49
) | } ~
23
) | } ~
50
{ ) } ~
24
{ | ) ~
51
) | } ~
25
{ | ) ~
52
{ | ) ~
26
) | } ~
53
{ | ) ~
27
{ | ) ~
54
{ | } )
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT
ĐỀ 010
C©u 1 :
Giả sử phương trình
13
21
22
9 2 2 3
xx
xx


có nghiệm là
a
. Khi đó giá trị biểu thức
9
2
1
log 2
2
a
là:
A.
9
2
1
1 log 2
2
B.
1
C.
9
2
1 log 2
D.
9
2
1
log 2
2
C©u 2 :
Phương trình
2
log 9 2 3
x
x
tương đương với phương trình nào dưới đây
A.
9 2 3
x
x
B.
2
30xx
C.
2
30xx
D.
9 2 3 2
xx
C©u 3 :
Cho phương trình :
21
81 4.3 27 0
xx
.Tổng các nghiệm của phương trình là bao nhiêu ?
A.
1
2
B.
1
C.
2
D.
3
2
C©u 4 :
Tìm miền xác định của hàm số sau:
3
log ( 2) 3yx
A.
29;
B.
2; 
C.
29;
D.
2;29
C©u 5 :
Đạo hàm của hàm số
( ) lnf x x x x
bằng
A.
'( ) lnf x x
B.
1
'( ) 1fx
x

C.
'( ) ln 1f x x
D.
'( ) lnf x x x
C©u 6 :
Biểu thức
49 7
11
log 5 log 5
P
bằng
A.
7
log 5
B.
1
2
C.
2
D.
5
log 7
C©u 7 :
Số giá trị nguyên của
n
thỏa mãn bất đẳng thức
1
log 1 log 2
nn
nn
là:
A.
0
B.
Vô số
C.
2
D.
1
C©u 8 :
Cho phương trình :
log 2
1000
x
xx
.Tích các nghiệm của phương trình là bao nhiêu
A.
10
B.
100
C.
1
D.
100
C©u 9 :
Cho bất phương trình
log 2
x
xa
, khẳng định nào sau đây là sai:
2
A.
Với
1a
thì phương trình đã cho vô
nghiệm.
B.
Nếu
1
0
4
a
thì
1 1 4
2
a
ax


.
C.
Nếu
0a
thì
14
1
2
a
x

.
D.
Nếu
0a
thì bất phương trình đã cho tồn
tại ngiệm.
C©u 10 :
Cho
log 5;log 3
aa
bc
.Giá trị biểu thức
3
log log . .
1
.
9
ca
a b c
M c


là:
A.
9
B.
1
9
C.
81
D.
1
81
C©u 11 :
Cho hàm số sau:
1
1 ln
y
xx

. Hãy chọn hệ thức đúng”
A.
' ln 1xy y x y
B.
'ln 1xy y x y
C.
ln 1 'xy y x y
D.
' ln 1xy y x y
C©u 12 :
Giá trị của
2
log (0 1)
a
aa
bằng
A.
2
B.
2
C.
1
2
D.
1
2
C©u 13 :
Nghiệm của bất phương trình
3
2
log
2
51
x
là:
A.
2x
B.
0x
C.
0x
D.
0x
C©u 14 :
Cho phương trình :
2
33
2log 3 log 4 0xx
.Một học sinh giải bài toán như sau :
Bước 1: Điều kiện :
30
3
40
4
x
x
x
x



Bước 2: Ta có :
33
2log ( 3) 2log ( 4) 0xx
3
log 3 4 0xx
Bước 3:
2
3 4 1
7 11 0
75
2
75
2
xx
xx
x
x
Vậy phương trình có nghiệm :
75
2
x
3
Học sinh đó giải sai ở bước nào ?
A.
Tất cả các Bước
đều đúng
B.
Bước 3
C.
Bước 2
D.
Bước 1
C©u 15 :
Đạo hàm của hàm số sau:
2
( ) ln 1f x x x
bằng
A.
2
1
'( )
1
fx
x
B.
2
1
'( )
1
x
fx
x
C.
2
2
'( )
1
x
fx
x
D.
2
'( )
1
x
fx
x
C©u 16 :
Phương trình
1
2
log log 0;( 0, 1)
a
a
ax
x a a
a
có nghiệm là:
A.
21xa
.
B.
1xa
.
C.
2xa
.
D.
xa
.
C©u 17 :
Cho bất phương trình :
33
log log
2
10 1 10 1
3
xx
x
.Tập nghiệm của bất phương trình là
?
A.
2x
B.
4x
C.
24x
D.
3x
C©u 18 :
Tìm m để bất phương trình
.9 (2 1).6 .4 0
x x x
m m m
có nghiệm với mọi
0,1x
A.
6m 
B.
4m 
C.
64m
D.
6m 
C©u 19 :
Nhận xét nào dưới đây là đúng
A.
Hàm số
2017x
e
đồng biến trên
.
B.
log .log .log 1, , ,
a b c
b c a a b c
C.
2 2 2
log log log , , , 0a b a b a b c
D.
Hàm số
ln x
là hàm số nghịch biến trên
0;
.
C©u 20 :
Cho
12 24
log 18, log 54.ab
Hệ thức nào dưới đây là đúng.
A.
51ab a b
B.
51ab a b
C.
51ab a b
D.
51ab a b
C©u 21 :
Cho hàm số sau:
2
( ) 5
x
f x e
và biểu thức
1
' 2 0 ' 0
5
A f x xf x f f
.
Đâu là hệ thức đúng của biểu thức A?
A.
1A
B.
2A
C.
3A
D.
5A
C©u 22 :
Phương trình
22
2
log (( ) 1) 1;( 1, 2)
ax
ax a a
có:
A.
Vô nghiệm.
B.
3 nghiệm.
C.
1 nghiệm.
D.
2 nghiệm.
4
C©u 23 :
Cho
27 8 2
log 5 ;log 7 ;log 3a b c
. Khi đó biểu thức
6
log 35
được biểu diễn là:
A.
2( )
1
b ac
c
.
B.
2(1 )
b ac
c
.
C.
3( )
1
b ac
c
.
D.
1
b ac
c
.
C©u 24 :
Số tiệm cận của đồ thị hàm số
x
y xe
là
A.
0
B.
1
C.
2
D.
3
C©u 25 :
Đạo hàm của hàm số
2
2
log (2 1)y x x
là:
A.
2
2
' (4 1).log (2 1)y x x x
.
B.
2
41
'
(2 1).ln 2
x
y
xx

.
C.
2
2(4 1)
'
(2 1).ln 2
x
y
xx

.
D.
2
2
' 2(4 1)log (2 1)y x x x
.
C©u 26 :
Phương trình
2
log ( 1) 2 1
x
x x x
có 2 nghiệm
12
;.xx
Tổng
22
1 2 1 2
x x x x
có giá trị là:
A.
0
B.
1
C.
2
D.
3
C©u 27 :
Cho phương trình :
33
3 log log 3 1 0xx
.Bình phương một tổng của các nghiệm của
phương trình là bao nhiêu ?
A.
90
B.
6570
C.
144
D.
7056
C©u 28 :
Tích các nghiệm của phương trình
22
3 3 30


xx
là
A.
1
B.
2
C.
1
D.
2
C©u 29 :
Cho hàm số
2
( ) .
2
x
y f x x e

. Trong các hệ thức sau đậy, hệ thức nào đúng?
A.
2
'1xy x y
B.
2
1'xy x y
C.
2
1'xy x y
D.
2
' 1 'xy x y
C©u 30 :
Phương trình
22
sin cos
2 5.2 7
xx

có nghiệm là:
A.
2
2
3
xk

.
B.
3xk

.
C.
2
xk

.
D.
x
.
C©u 31 :
Cho hàm số
cos
( ) .sin
x
f x e x
. Tính
'
2
f
A.
1
B.
2
C.
1
D.
2
C©u 32 :
Cho
12 24
log 18, log 54.ab
Hệ thức nào dưới đây là đúng.
5
A.
51ab a b
B.
51ab a b
C.
51ab a b
D.
51ab a b
C©u 33 :
Phương trình
2
log ( 1) 2 1
x
x x x
có 2 nghiệm
12
;.xx
Tổng
22
1 2 1 2
x x x x
có giá trị là:
A.
0
B.
1
C.
2
D.
3
C©u 34 :
Phương trình
2
log 9 2 3
x
x
tương đương với phương trình nào dưới đây
A.
2
30xx
B.
2
30xx
C.
9 2 3
x
x
D.
9 2 3 2
xx
C©u 35 :
Cho hàm số
22
sin cos
55
xx
y 
.Tổng giá trị lớn nhất và nhỏ nhất của hàm số là bao nhiêu ?
A.
75
B.
7 3 5
C.
6 4 5
D.
6 2 5
C©u 36 :
Giả sử bất đẳng thức
21
log 2 1 log 3 0
aa
xx
đúng với
1x
và
4x
. Khi đó giá trị
của a là:
A.
01a
B.
1a
C.
1a
D.
0 , 1aa
C©u 37 :
Tập nghiệm của bất phương trình
1
3
31
log 1
2
x
x
là:
A.
1
2;
3
S




.
B.
5
2;2 ;
8
S




.
C.
;2S 
.
D.
5
;2 ;
8
S

 


.
C©u 38 :
Giả sử phương trình
13
21
22
9 2 2 3
xx
xx


có nghiệm là
a
. Khi đó giá trị biểu thức
9
2
1
log 2
2
a
là:
A.
9
2
1
1 log 2
2
B.
1
C.
9
2
1
log 2
2
D.
9
2
1 log 2
C©u 39 :
Cho phương trình :
2
82
2 2 8 2
x x x
xx

có hai nghiệm
12
,xx
.Tính
33
12
xx
A.
28
B.
65
C.
9
D.
72
C©u 40 :
Biết
log 3 0, 1, 0
b
a b b a
. Giá trị của
3
log
a
b
a
P
b
là:
A.
3
.
B.
3
2
.
C.
3
3
.
D.
1
3
.
6
C©u 41 :
Cho hàm số
2
( ) 4ln 4 4f x x x x x
.
Biểu thức
2
4 ' 8 .ln2ff


bằng số nào trong các số sau:
A.
2ln2
B.
6ln2
C.
8ln2
D.
4ln2
C©u 42 :
Nhận xét nào dưới đây là đúng
A.
log .log .log 1, , ,
a b c
b c a a b c
B.
Hàm số
2017x
e
đồng biến trên
.
C.
Hàm số
ln x
là hàm số nghịch biến trên
0;
.
D.
2 2 2
log log log , , , 0a b a b a b c
C©u 43 :
Giả sử bất đẳng thức
21
log 2 1 log 3 0
aa
xx
đúng với
1x
và
4x
. Khi đó giá trị
của a là:
A.
1a
B.
01a
C.
1a
D.
0 , 1aa
C©u 44 :
Cho
log 5;log 3
aa
bc
.Giá trị biểu thức
3
log log . .
1
.
9
ca
a b c
M c


là:
A.
1
9
B.
9
C.
81
D.
1
81
C©u 45 :
Cho hàm số :
2
3 lny x x x
trên đoạn
1,2
.Tích của giá trị lớn nhất và giá trị nhỏ nhất
là bao nhiêu ?
A.
4ln2 4 7
B.
7 4ln2
C.
4ln2 3 7
D.
2 7 4ln2
C©u 46 :
Nghiệm của bất phương trình
2
7 12
51

xx
là:
A.
3
5
x
x
B.
2
4
x
x
C.
3
4
x
x
D.
34x
C©u 47 :
Phương trình
2
88
4
2log 2 log ( 1)
3
xx
có :
A.
Phương trình đã
cho vô nghiệm.
B.
2 nghiệm.
C.
1 nghiệm.
D.
3 nghiệm.
C©u 48 :
Cho hàm số sau:
cos
()
x
f x e
.
Biểu thức
' " '"f f f f
bằng số nào trong các số sau:
A.
2
e
B.
e
C.
1
e
D.
2
e
7
C©u 49 :
Phương trình
2
22
4 4 1 1
4 log ( 1) 2log ( 1) ( 4) log 4.log 16
xx
x x x x

có:
A.
Vô nghiệm.
B.
1 nghiệm.
C.
2 nghiệm.
D.
3 nghiệm.
C©u 50 :
Tính đạo hàm của hàm số
2
()
sin
x
e
fx
x
A.
2
(sin cos ) cos
'( )
sin
x
e x x x
fx
x

B.
2
(sin cos ) 2cos
'( )
sin
x
e x x x
fx
x

C.
2
(sin cos ) 2cos
'( )
sin
x
e x x x
fx
x

D.
2
(sin cos ) 2 cos
'( )
sin
x
e x x x
fx
x

C©u 51 :
Nhận xét nào dưới đây là đúng khi nói về biểu thức
2
2
2
log
2
3
log 9 2 ln
x
A e x
A.
Biểu thức A luôn luôn tồn tại và giá trị của A không phụ thuộc vào giá trị của
.x
B.
Biểu thức A chỉ xác định khi
0x
và giá trị của A không phụ thuộc vào giá trị của
.x
C.
Biểu thức A chỉ xác định khi
0x
và giá trị của A phụ thuộc vào giá trị của
.x
D.
Biểu thức A chỉ xác định khi
0, 1xx
và giá trị của A phụ thuộc vào giá trị của
.x
C©u 52 :
Đạo hàm của hàm số
1
( ) ln
1
x
fx
x
bằng
A.
2
2
'( )
1
fx
x
B.
1
'( )
1
x
fx
x
C.
2
1
'( )
1
fx
x
D.
1
'( )
1
fx
x
C©u 53 :
Cho hàm số
x
y xe
có đạo hàm y’ và y”. Hệ thức nào sau đây đúng?
A.
" 2 ' 0y y y
B.
" 2 ' 1 0yy
C.
" 2 ' 3 0yy
D.
" 2 ' 3 0y y y
C©u 54 :
Cho
2 2 4
xy
, giá trị nhỏ nhất của
xy
là
A.
1
B.
3
C.
2
D.
4
C©u 55 :
Số giá trị nguyên của
n
thỏa mãn bất đẳng thức
1
log 1 log 2
nn
nn
là:
A.
Vô số
B.
0
C.
1
D.
2
C©u 56 :
Giá trị
a
thỏa mãn
15 7 5 2
aa
là
A.
1a
B.
0a
C.
1a
D.
01a
C©u 57 :
Đạo hàm của hàm số
2
sin
()
x
f x e
bằng
8
A.
2
sin
'( ) .sin2
x
f x e x
B.
2
2 sin
'( ) cos
x
f x xe
C.
2
sin
'( ) cos2
x
f x e x
D.
2
sin
'( ) 2 cos
x
f x e x
C©u 58 :
Số tiệm cận của đồ thị hàm số
x
y xe
là
A.
0
B.
1
C.
2
D.
3
C©u 59 :
Nhận xét nào dưới đây là đúng khi nói về biểu thức
2
2
2
log
2
3
log 9 2 ln
x
A e x
A.
Biểu thức A chỉ xác định khi
0x
và giá trị của A không phụ thuộc vào giá trị của
.x
B.
Biểu thức A luôn luôn tồn tại và giá trị của A không phụ thuộc vào giá trị của
.x
C.
Biểu thức A chỉ xác định khi
0, 1xx
và giá trị của A phụ thuộc vào giá trị của
.x
D.
Biểu thức A chỉ xác định khi
0x
và giá trị của A phụ thuộc vào giá trị của
.x
C©u 60 :
Cho phương trình :
2
22
1
1
4 2 1 2
x
x x x

.Tổng bình phương các nghiệm của phương trình là
bao nhiêu ?
A.
0
B.
1
C.
4
D.
2
9
ĐÁP ÁN
01
{ ) } ~
28
{ | ) ~
55
) | } ~
02
{ ) } ~
29
) | } ~
56
{ | ) ~
03
{ | } )
30
{ | ) ~
57
) | } ~
04
{ | ) ~
31
{ | ) ~
58
{ ) } ~
05
) | } ~
32
{ ) } ~
59
) | } ~
06
{ | ) ~
33
{ ) } ~
60
{ | } )
07
{ ) } ~
34
{ ) } ~
08
{ | } )
35
{ | } )
09
{ | } )
36
{ ) } ~
10
) | } ~
37
{ | } )
11
) | } ~
38
{ ) } ~
12
{ | ) ~
39
{ | } )
13
{ | ) ~
40
{ | ) ~
14
{ | } )
41
) | } ~
15
) | } ~
42
{ ) } ~
16
{ | } )
43
) | } ~
17
{ | } )
44
{ ) } ~
18
{ | } )
45
{ | } )
19
) | } ~
46
{ | ) ~
20
{ ) } ~
47
{ | ) ~
21
) | } ~
48
) | } ~
22
{ | } )
49
{ | } )
23
{ | ) ~
50
{ | ) ~
24
{ ) } ~
51
{ ) } ~
25
{ | ) ~
52
) | } ~
26
{ ) } ~
53
) | } ~
27
{ | } )
54
{ | ) ~
| 1/89
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 01 C©u 1 : Hàm số 2 2 y xln(x 1 x ) 1
x . Mệnh đề nào sau đây sai ?
A. Hàm số có đạo hàm 2 y' ln(x 1 x )
B. Hàm số tăng trên khoảng (0; )
C. Tập xác định của hàm số là D
D. Hàm số giảm trên khoảng (0; ) C©u 2 : Hàm số 2 . x y
x e nghịch biến trên khoảng : A. ( ; 2) B. ( 2;0) C. (1; ) D. ( ;1) C©u 3 : 3 1 3 4 2 .2 5 .5
Giá trị của biểu thức P là: 3 2 0 10 :10 (0,1) A. 9 B. 9 C. 10 D. 10
C©u 4 : Phương trình x 1 x 2 5 5.0,2
26 có tổng các nghiệm là: A. 4 B. 2 C. 1 D. 3 C©u 5 : 32.4x 18.2x 1 0
Nghiệm của bất phương trình là: 1 1 A. 1 x 4 B. x x x 16 2 C. 2 4 D. 4 1 C©u 6 : Tìm m để 2 2
phương trình sau có đúng 3 nghiệm: x x 2 4  2  6  m
A. 2  m  3 B. m  3 C. m  2 D. m  3 C©u 7 : Phương trình 1 x 1 x 3 3 10
A. Có hai nghiệm âm. B. Vô nghiệm
C. Có hai nghiệm dương
D. Có một nghiệm âm và một nghiệm dương C©u 8 : x 1 1
Tập nghiệm của phương trình 2x 125 bằng 25 1 1 1 A. 1 B. 4 C. 4 D. 8
C©u 9 : Nghiệm của phương trình log (log x) log (log x) 2 4 2 2 4 là: A. x 2 B. x 4 C. x 8 D. x 16 C©u 10 : Nếu a log 3 b log 5 30 và 30 thì: A. log 1350 2a b 2 log 1350 a 2b 1 30 B. 30 C. log 1350 2a b 1 log 1350 a 2b 2 30 D. 30 C©u 11 : 2 3  2x  x
Tìm tập xác định hàm số sau: f (x)  log 1 x 1 2  3   13   3   13  A. D   ; 3     ;1  
B. D   ;    3  1;  2 2      3   13   3   13   3   13   3   13  C. D   ; 3    ;1    
D. D    ;     ;     2 2     2 2     C©u 12 : Phương trình 2 2 x x x x 1 4 2    3 có nghiệm: x  1 x  1  x  0 x  1  A. B. C. D.  x  2 x 1 x  1 x  0
C©u 13 : Tính đạo hàm của hàm số sau: ( ) x f x x x 1 f '(x) x   (x  ln x) '( ) x
f x x (ln x 1) A. B. C. '( ) x f x x
D. f '(x)  x ln x
C©u 14 : Phương trình: log (3x  2)  3 có nghiệm là: 3 11 25 29 A. B. C. D. 87 3 3 3
C©u 15 : T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A. Hµm sè y = log x víi a > 1 lµ mét hµm sè nghÞch biÕn trªn kho¶ng (0 ; +) a
B. Hµm sè y = log x víi 0 < a < 1 lµ mét hµm sè ®ång biÕn trªn kho¶ng (0 ; +) a
C. Hµm sè y = log x (0 < a  1) cã tËp x¸c ®Þnh lµ R a 2
D. §å thÞ c¸c hµm sè y = log x vµ y = log x (0 < a  1) th× ®èi xøng víi nhau qua trôc hoµnh a 1 a
C©u 16 : Giả sử các số logarit đều có nghĩa, điều nào sau đây là đúng?
A. Cả 3 đáp án trên đều sai
B. log b  log c b c a a
C. log b  log c b c b
c b c a a D. log log a a
C©u 17 : Hàm số y xlnx đồng biến trên khoảng : 1 1 A. (0; ) B. ; C. (0;1) D. 0; e e C©u 18 : xx  Tính đạ e e
o hàm của hàm số sau: f (x)  xx e e 4 
A. f '(x)  B. '( ) x x f x e e   x x 2 (e e ) x e 5 
C. f '(x) 
D. f '(x)  x x 2 (e e ) x x 2 (e e ) C©u 19 : Nếu a log 3 15 thì: 3 5 A. log 15 log 15 25 5(1 a) B. 25 3(1 a) 1 1 C. log 15 log 15 25 2(1 a) D. 25 5(1 a) C©u 20 : Cho ( 2 1)m ( 2 1)n . Khi đó A. m n B. m n C. m n D. m n C©u 21 : 2x 1 7x
Nghiệm của phương trình x 1 8 0,25. 2 là: 2 2 2 2 A. x 1, x B. x 1, x C. x 1, x D. x 1, x 7 7 7 7
C©u 22 : Tập xác định của hàm số 3 y (x 2) là: A. \ {2} B. C. ( ;2) D. (2; )
C©u 23 : Nghiệm của phương trình 2 x 2 3 3 x 30 là: Phương trình vô A. x 0 B. C. x 3 D. x 1 nghiệm 3 C©u 24 : 10  x
Tập xác định của hàm số y log3 2 x  3x  2 là: A. (1; )  B. ( ;  10) C. ( ;  1) (2;10) D. (2;10) C©u 25 : 8 log 7 Giá trị của 2 a a 0 a 1 bằng A. 2 7 B. 8 7 C. 16 7 D. 4 7 C©u 26 :   
Cho f(x) = ln sin 2x . §¹o hµm f’   b»ng:  8  A. 1 B. 3 C. 4 D. 2
C©u 27 : Phương trình 2x 1 3 4.3x
1 0 có hai nghiệm x , x trong đó x
x , chọn phát biểu 1 2 1 2 đúng? A. 2x x 0 x 2x 1 x x 2 x .x 1 1 2 B. 1 2 C. 1 2 D. 1 2
C©u 28 : Tập xác định của hàm số 3 f x log x 1 log 3 x log x 1 là: 2 1 8 2 A. x 1 B. 1 x 3 C. x 3 D. 1 x 1 C©u 29 : 2x2
Nghiệm của phương trình x 1 3  .5 x 15 là: A. x  1
B. x  2, x  log 5
x  3, x  log 5 2 C. x  4 D. 3 C©u 30 : log5 6 log7 8 25 49 3
Giá trị của biểu thức P là: 1 log9 4 2 log2 3 lo 1 g 25 27 3 4 5 A. 8 B. 10 C. 9 D. 12
C©u 31 : Cho a log m với m 0; m 1 và A log 8m . Khi đó mối quan hệ giữa A và a là: 2 m 3 a 3 a A. A 3 a a B. A C. A D. A 3 a a a a C©u 32 : Hµm sè y =  2
ln x  5x  6 cã tËp x¸c ®Þnh lµ:
A. (-; 2)  (3; +) B. (0; +) C. (-; 0) D. (2; 3)
C©u 33 : Tập các số x thỏa mãn log (x  4) 1 0 0,4 là:  13  13  13  A. 4;   ;    ;        B. C. D. (4; ) 2   2   2  4 C©u 34 : Cho hàm số . x y x e , với x 0;
. Mệnh đề nào sau đây là mệnh đề đúng ? 1 1 1 A. max y ; min y B. max y ; min y 0 x 0; x 0; e e x 0; x 0; e 1 1 C. min y
; không tồn tại max y D. max y
; không tồn tại min y x 0; e x 0; x 0; e x 0;
C©u 35 : Tập nghiệm của bất phương trình 32.4x 18.2x 1 0 là tập con của tập : A. ( 5; 2) B. ( 4; 0) C. (1; 4) D. ( 3;1)
C©u 36 : T×m mÖnh ®Ò ®óng trong c¸c mÖnh ®Ò sau:
A. Hµm sè y = ax víi 0 < a < 1 lµ mét hµm sè ®ång biÕn trªn (-: +)
B. Hµm sè y = ax víi a > 1 lµ mét hµm sè nghÞch biÕn trªn (-: +)
C. §å thÞ hµm sè y = ax (0 < a  1) lu«n ®i qua ®iÓm (a ; 1) x  1 
D. §å thÞ c¸c hµm sè y = ax vµ y =   (0 < a  1) th× ®èi xøng víi nhau qua trôc tung  a 
C©u 37 : Trong các khẳng định sau, khẳng định nào sai ? A. log 5 0 log 2007 log 2008 3 B. 2 2 x 3 x 3 1 C. log 4 log log 0, 8 0 3 4 3 D. 0,3
C©u 38 : Dùng định nghĩa, tính đạo hàm của hàm số sau: f (x)  x.cot gx x A.
f '(x)  cot gx B.
f '(x)  x.cot gx 2 sin x x
C. f '(x)  cot 1 g
D. f '(x)  tgx  2 cos x C©u 39 : b Cho log b
3 . Khi đó giá trị của biểu thức log a b a là a 3 1 3 1 A. B. 3 1 C. 3 1 D. 3 2 3 2 C©u 40 : 2 1 Cho 3 3 (a 1) (a
1) . Khi đó ta có thể kết luận về a là: A. a 2 B. a 1 C. 1 a 2 D. 0 a 1 5 C©u 41 : 1 Hµm sè y = log cã tËp x¸c ®Þnh lµ: 5 6  x A. (0; +) B. R C. (6; +) D. (-; 6)
C©u 42 : Đạo hàm của hàm số 2 f (x)
sin2x.ln (1 x) là: 2 sin 2x.ln(1 x) 2 f '(x) 2 o
c s2x.ln (1 x) 2 sin 2x A. 1 x B. 2 f '(x) 2 o
c s2x.ln (1 x) 1 x 2 f '(x) 2 o
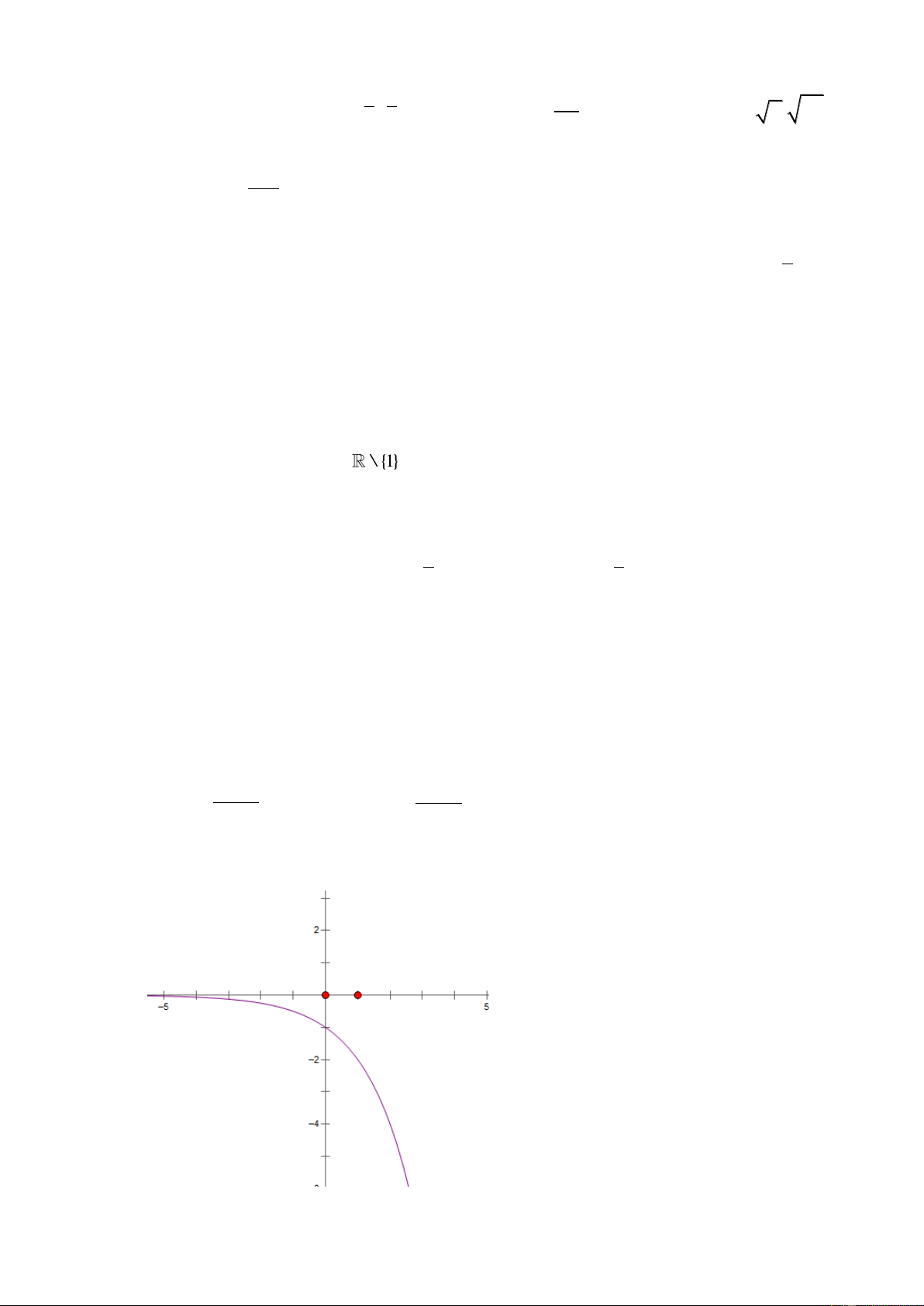
c s2x.ln (1 x) 2 sin2x.ln(1 x) C. D. f '(x) 2 o c s2x 2 ln(1 x) C©u 43 : x Cho hàm số e y
. Mệnh đề nào sau đây là mệnh đề đúng ? x 1 x e
A. Đạo hàm y' 2
B. Hàm số đạt cực đại tại (0;1) (x 1)
C. Hàm số đạt cực tiểu tại (0;1)
D. Hàm số tăng trên \ 1 C©u 44 : 3x x 1 3
Nghiệm của bất phương trình log 3 1 .log 4 1 là: 16 4 4 x ;1 2; A. B. x 1;2 C. x 1;2 D. x 0;1 2; C©u 45 : 5.2x 8 Giải phương trình log
3 x với x là nghiệm của phương trình trên. Vậy giá 2 2x 2 trị log2 4x P x là: A. P 4 B. P 8 C. P 2 D. P 1
C©u 46 : Bất phương trình log (2x 1) log (4x  
 2)  2 có tập nghiệm: 2 3 A. ( ;  0) B. [0; )  C. ( ;  0] D. 0;  C©u 47 : 2x 2
Phương trình 3x.5 x
15 có một nghiệm dạng x
log b , với a và b là các số nguyên a
dương lớn hơn 1 và nhỏ hơn 8. Khi đó a 2b bằng: A. 13 B. 8 C. 3 D. 5
C©u 48 : Cho phương trình log 3.2x 1
x 1 có hai nghiệm x , x . Tổng x x là: 4 1 2 1 2 A. log 6 4 2 2 B. 2 C. 4 D. 6 4 2 6
C©u 49 : Giải bất phương trình: ln(x 1)  x A. Vô nghiệm B. x  0 C. 0  x 1 D. x  2
C©u 50 : Nghiệm của phương trình: 2 log 2x log 6 log 4x 2 2 2 4  x  2.3 . 1 1 2
A. x  0, x B. x C. x   D. Vô nghiệm 4 4 3
C©u 51 : Điều nào sau đây là đúng? A. m n
a a m n B. m n
a a m n
C. Cả 3 câu đáp án trên đều sai. a b m m    D. a b m 0 Nếu thì C©u 52 : Nếu a log 3 b log 5 2 và 2 thì: 1 1 1 1 1 1 A. 6 log 360 a b log 360 a b 2 B. 6 3 4 6 2 2 6 3 1 1 1 1 1 1 C. 6 log 360 a b log 360 a b 2 D. 6 2 3 6 2 6 2 3 C©u 53 : 1 2 Phương trình 1có số nghiệm là 5 lg x 1 lg x A. 2 B. 1 C. 3 D. 4
C©u 54 : Tập giá trị của hàm số x
y a (a  0, a  1) là: A. [0; )  B. \{0} C. (0; )  D.
C©u 55 : Bất phương trình: log x4 2 x  32 có tập nghiệm:  1   1   1   1  A. ; 2   ; 4 ; 2 D. ; 4        10  B. 32  C. 32  10 
C©u 56 : Tìm giá trị nhỏ nhất của hàm số: x 1 3 ( ) 2 2 x f x     A. 4 B. 6 C. -4 D. Đáp án khác C©u 57 :
x y  30 Hệ phương trình  có nghiệm:
log x  log y  3log 6 x  14 x 16 x 15 x 14 A.  và  B.   y  16 y 14
y 15và y 16 7 x 12 x 18 x 15 C.   D.
y 18và y 12 y 15
C©u 58 : Hµm sè y =  2    x x 2x 2 e cã ®¹o hµm lµ : A. KÕt qu¶ kh¸c B. y’ = -2xex C. y’ = (2x - 2)ex D. y’ = x2ex
C©u 59 : Tập giá trị của hàm số y  log x(x  0, a  0, a  1) là: a Cả 3 đáp án trên A. (0; )  B. [0; )  C. D. đều sai C©u 60 : 1 2 Cho biểu thức a b 4 ab , với b a
0 . Khi đó biểu thức có thể rút gọn là A. b a B. a C. a b D. a b 8 ĐÁP ÁN 01 28 { ) } ~ 55 { | ) ~ 02 { ) } ~ 29 { ) } ~ 56 ) | } ~ 03 { | ) ~ 30 { | ) ~ 57 { | ) ~ 04 ) | } ~ 31 { ) } ~ 58 { | } ) 05 { | } ) 32 { | } ) 59 { | ) ~ 06 { ) } ~ 33 ) | } ~ 60 ) | } ~ 07 { | } ) 34 { ) } ~ 08 { | } ) 35 ) | } ~ 09 { | } ) 36 { | } ) 10 { | ) ~ 37 { | } ) 11 ) | } ~ 38 ) | } ~ 12 { | ) ~ 39 ) | } ~ 13 { ) } ~ 40 ) | } ~ 14 { | ) ~ 41 { | } ) 15 { | } ) 42 ) | } ~ 16 { | ) ~ 43 { ) } ~ 17 { ) } ~ 44 { | } ) 18 ) | } ~ 45 { ) } ~ 19 { | ) ~ 46 { | ) ~ 20 ) | } ~ 47 ) | } ~ 21 { | } ) 48 { ) } ~ 22 ) | } ~ 49 { ) } ~ 23 { | } ) 50 { ) } ~ 24 { | ) ~ 51 { | ) ~ 25 { | } ) 52 { | ) ~ 26 { | } ) 53 ) | } ~ 27 { ) } ~ 54 { | ) ~ 9 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 02
C©u 1 : Số nghiệm của phương trình: x   1 3 3 x  2 là A. 0 B. 3 C. 1 D. 2 C©u 2 :
log x 3 1 log y
(x; y) là nghiệm của hệ 2 3 
. Tổng x  2y bằng log
y  3  1 log x  2 3 A. 6 B. 9 C. 39 D. 3
C©u 3 : Số nghiệm của phương trình x 1 3  3 x  2 A. Vô nghiệm B. 3 C. 2 D. 1
C©u 4 : Số nghiệm của phương trình x+ 2x+5 1+ 2x+5 2 - 2 + 26-x - 32 = 0 là : A. 4 B. 2 C. 1 D. 3
C©u 5 : Hàm số y = ln(x2 -2mx + 4) có tập xác định D = R khi: A. m < 2 B. -2 < m < 2 C. m = 2
D. m > 2 hoặc m < -2 C©u 6 : 1
Tập xác định của hàm số 2 2
x  5x  2  ln là: 2 x 1 A. 1; 2 B. 1; 2 C. 1; 2 D. 1; 2 C©u 7 : 3  x Phương trình  1  x 2  2.4  3.( 2) x  0    2  A. -1 B. log 5 log 3 2 C. 0 D. 2
C©u 8 : Số nghiệm của phương trình 2
log (x  4x)  log (2x  3)  0 là: 3 1 3 A. 3 B. 2 C. Vô nghiệm. D. 1 C©u 9 :  2 y  4x
Số nghiệm của hệ phương trình 8  là:  x 2 1  y 1  0 1 A. Vô nghiệm B. 2 C. 3 D. 1
C©u 10 : Tập xác định của hàm số 2   (  3  2) e y x x là: A. (;2) B. (1;) C. (2;1) D. 2;     1 C©u 11 : 3 2 3 4 Nếu 3 2 aa và log  log thì: b 4 b 5
A. 0 < a < 1, 0 < b < 1
B. 0 < a < 1, b > 1
C. a > 1, 0 < b < 1 D. a > 1, b > 1
C©u 12 : Cho a>0, b >0 thỏa mãn 2 2
a b  7ab . Chọn mệnh đề đúng trong các mệnh đề sau: 1 3
A. 3log(a b) 
(log a  log b)
B. log(a b) 
(log a  log b) 2 2 a b 1
C. 2(log a  log ) b  log(7 ab)   D. log (log a log b) 3 2
C©u 13 : Tập nghiệm của bất phương trình 2x 1
3  10.3x  3  0 là : A.  1   ;1 B.  1  ;0 C. 0  ;1 D.  1   ;1
C©u 14 : Phương trình x x 1 4 . m 2  
 2m  0 có hai nghiệm x , x thỏa x x  3 1 2 1 2 khi A. m  4 B. m  2 C. m  1 D. m  3 C©u 15 :
Tập nghiệm của bất phương trình log3 x < log (12-x) là : 3 A. (0;12) B. (0;9) C. (9;16) D. (0;16)
C©u 16 : Hàm số y = x.lnx có đạo hàm là : 1 A. B. lnx + 1 C. lnx D. 1 x C©u 17 : x  Đạ 2 1
o hàm của hàm số y  là : 5x 2 xx x 2  2  2  2  1  A. ln  5x ln 5   B. ln  ln 5      5  5  5  5  5  x 1  x 1   x 1  x 1  2   1   2   1  C. . xx     D. . x  . x      5   5   5   5 
C©u 18 : Cho phương trình: x x 1 12 3 2  6.2   1 3( x 1  )
(*). Số nghiệm của phương trình (*) là: 2 2x A. Vô nghiệm. B. 2 C. 1 D. 3
C©u 19 : Tính log 24 theo log 27  a là 36 12 9  a 9  a 9  a 9  a A. B. C. D. 6  2a 6  2a 6  2a 6  2a
C©u 20 : Số nghiệm của phương trình log2 5(5x) - log25 (5x) - 3 = 0 là : A. 1 B. 2 C. 4 D. 3
C©u 21 : Tính log 1350 theo a, b với log 3  a và log 5  b là 30 30 30
A. 2a b 1
B. 2a b 1
C. a  2b 1
D. 2a b 1 C©u 22 : 5 5 4 4 x y xy Rút gọn biểu thức
(x, y  0) được kết quả là: 4 4 x y A. 2xy B. xy C. xy D. 2 xy
C©u 23 : Tích hai nghiệm của phương trình 4 2 4 2 2 x 4 x 6 x 2 x 3 2 2.2   1 0 là: A. -9 B. -1 C. 1 D. 9
C©u 24 : Tập nghiệm của bất phương trình (2- 3 )x > (2 + 3)x+2 là : A. (-2;+ ) B. (- ;-1) C. (-1;+ ) D. (- ;-2) C©u 25 : 3 x 1 
Nghiệm của phương trình x   4 1 3   là 9    1 6 7 A. B. 1 C. D. 3 7 6 3 C©u 26 :
Tập nghiệm của bất phương trình log2 (2x) - 2log 2 2 (4x2 ) - 8  0 là : A. [2;+ ) B. 1 [ ;2] 4 C. [-2;1] D. 1 (- ; ] 4 C©u 27 : log 23 Biểu thức A = 4 có giá trị là : 9 A. 16 B. C. 12 D. 3 C©u 28 : 7 1  2 7 a .a Rút gọn biểu thức
(a  0) được kết quả là 2 2 2 2 (a ) A. a4 B. a C. a5 D. a3
C©u 29 : 10.Đạo hàm của hàm số: 2 
y  (x  x) là:   A. 2 1 2(x x)   B. 2 1 (x x)   (2 x1)    C. 2 1 (x x)   (2 x1) D. 2 1 (x  x) C©u 30 : ln x Hàm số y x
A. Có một cực tiểu
B. Có một cực đại
C. Không có cực trị
D. Có một cực đại và một cực tiểu C©u 31 : x x
Nghiệm của phương trình       2 3 5 3 5  3.x là:
A. x = 2 hoặc x = -3 B. Đáp án khác
C. x = 0 hoặc x = -1 D. x = 1 hoặc x=-1
C©u 32 : Số nghiệm của phương trình ln3x – 3ln2x – 4lnx+ 12 = 0 là A. 1 B. 3 C. 2 D. 0
C©u 33 : Trong các điều kiện của biểu thức tồn tại, kết quả rút gọn của A   3 2
log a  2log a  log alog b  log b  log a là b b b a ab b A. 1 B. 2 C. 0 D. 3 4 C©u 34 : 3 2
log (x 1)  log (x  x 1)  2 log x  0 2 2 2 A. x  1  B. x  0 C. x D. x > 0 C©u 35 : 2 x x  2   2 
Tập nghiệm của bất phương trình      là:  5   5 
A. 1  x  2
B. x < -2 hoặc x > 1 C. x > 1 D. Đáp án khác C©u 36 : 3 2 3 4 .Nếu 3 2 aa và log  log thì : b 4 b 5
A. 0B. C.a>1,b>1 C. 01
D. a>1,0C©u 37 : Số nghiệm của phương trình log (x  2) 1 là 3 A. 3 B. 2 C. 0 D. 1
C©u 38 : Tích các nghiệm của phương trình: 6x 5x 2x 3x    bằng: A. 4 B. 3 C. 0 D. 1
C©u 39 : Nghiệm của bất phương trình 2 log log (2  x )  0 1  2  là: 2 A. ( 1  ;1)(2; )  B. (-1;1) C. Đáp án khác D. ( 1  ;0)(0;1)
C©u 40 : Phương trình 9x 3.3x 
 2  0 có hai nghiêm x , x (x  x ) Giá trị của A 2x  3x 1 2 1 2 1 2 A. 0 B. 4 log 3 3log 2 2 C. 2 D. 3
C©u 41 : Phương trình: 9x  3.3x  2  0 có hai nghiệm x , x (x x ) .Giá trị của A  2x  3x là: 1 2 1 2 1 2 A. 0 B. 4log 3 3log 2 2 C. 3 D. 2
C©u 42 : Tập xác định của hàm số log   x là x  2 1 1 4 3 2   2   1   ; \    ;0  2   1  2   2  A.  3   3  B.  ; \     C.  ; \     0 D.  ;    3   3  3   3  C©u 43 : 1 9 4 4 a a
Giá trị rút gọn của biểu thức A  là: 1 5 4 4 a a A. 1 + a B. 1 - a C. 2a D. a
C©u 44 : Số nghiệm của phương trình log .
x log (2x 1)  2 log x là: 2 3 2 5 A. 0 B. 1 C. 3 D. 2 C©u 45 : 1 1  1 1  3 3 3 3 a ba b
Rút gọn biểu thức
(a, b  0, a b) được kết quả là: 3 2 3 2 a b 1 1 A. B. 2 3 (ab) C. C. D. 3 2 ab 3 (ab) 3 ab
C©u 46 : Chọn khẳng định sai trong các khẳng định sau
log a  log b a b  0 A. 1 1
B. ln x  0  x 1 3 3
log a  log b a b  0
C. log x  0  0  x 1 3 D. 1 1 2 2 C©u 47 : Phương trình 2 2
log x  log x 1  2m 1  0 có nghiệm trên 3 1  ;3  3 3   khi :    3 m   3 ; 0  ;     3  A. m  0;   B.  C. 0; D. ;    2  2   2  C©u 48 : 1 
Giá trị nhỏ nhất , giá trị lớn nhất của hàm số y = x - lnx trên   ;e
2  theo thứ tự là : A. 1 B. 1 và e-1 + ln2 và e-1 2 C. 1 D. 1 1 và + ln2 và e 2 2
C©u 49 : Nghiệm của bất phương trình 2.2x 3.3x 6x   1 0 là: A. x  3 B. x  2 C. Mọi x D. x < 2 C©u 50 : 2
Số nghiệm của phương trình 2x 7x5 2 1 là: A. 2 B. 1 C. 0 D. 3 C©u 51 : x
Tập nghiệm của bất phương trình x x 2 4.3  9.2  5.6 là A.  ;  4 B. 4;  C.  ;5   D. 5; 
C©u 52 : Nghiệm của phương trình 6x 3 3 x e e  2  0 là: 1 1
A. x  0, x  ln 2 B. x  ln 2 C. Đáp án khác D. x = 0, x = -1 3 x = -1, 3 6 C©u 53 : 2 1
Bất phương trình 1 x 1 x      12  0     có tập nghiệm là  3   3  A. (0; )  B. ( ;  1  ) C. (-1;0) D. R \   0 . C©u 54 : Phương trình 2 2 : 2(x 1  ) x 2 (m  2).2  (m 1).2  2m  6 có nghiệm khi
A. 2  m  9
B. 2  m  9
C. 2  m  9 .
D. 2  m  9
C©u 55 : Đạo hàm của hàm số y = x(lnx – 1) là: 1 A. lnx -1 B. lnx C. 1 D. 1 x
C©u 56 : Nghiệm của bất phương trình log (x 1)  2 log (5  ) x  1 log (x  2) 2 2 2 A. 2 < x < 5 B. -4 < x < 3 C. 1 < x < 2 D. 2 < x < 3
C©u 57 : Giá trị nhỏ nhất của hàm số f( ) x  ( x 2  ln ) x trên 2;  3 A. e B. 2   2ln2 C. 4  2 ln 2 D. 1 C©u 58 : x2
Giá trị nhỏ nhất , giá trị lớn nhất của hàm số y = trên đoạn [-1;1] theo thứ tự là : ex A. 1 B. 0 và e 0 và e C. 1 D. 1 và e và e e C©u 59 : x
Tập nghiệm của bất phương trình 1 2 :   0 là 2 x 2 x 2 2 0;2 A.  ;  0 B.   ;1  C. 2;  D. . 7 ĐÁP ÁN 01 { | ) ~ 28 { | ) ~ 55 { ) } ~ 02 { | } ) 29 { | ) ~ 56 { | } ) 03 { | } ) 30 { ) } ~ 57 { | } ) 04 { ) } ~ 31 { | } ) 58 { ) } ~ 05 { ) } ~ 32 { ) } ~ 59 { | ) ~ 06 ) | } ~ 33 ) | } ~ 07 { | } ) 34 { | } ) 08 { | ) ~ 35 ) | } ~ 09 { | } ) 36 { | ) ~ 10 { | ) ~ 37 { | } ) 11 { ) } ~ 38 { | ) ~ 12 { | } ) 39 { | } ) 13 ) | } ~ 40 { | } ) 14 ) | } ~ 41 { | ) ~ 15 { ) } ~ 42 ) | } ~ 16 { ) } ~ 43 ) | } ~ 17 ) | } ~ 44 { | } ) 18 { | ) ~ 45 { | ) ~ 19 ) | } ~ 46 ) | } ~ 20 { ) } ~ 47 ) | } ~ 21 ) | } ~ 48 { ) } ~ 22 { ) } ~ 49 { | } ) 23 { | ) ~ 50 ) | } ~ 24 { ) } ~ 51 ) | } ~ 25 { | ) ~ 52 ) | } ~ 26 { ) } ~ 53 { | ) ~ 27 { ) } ~ 54 { | ) ~ 8 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 03
C©u 1 : Tập xác định của hàm số 2 y  log x  x 12 : 3 A. ( 4  ;3) B. ( ;  4  ) (3; )  C. ( 4  ;3] D. R \   4 
C©u 2 : Tập nghiệm của phương trình 2 log x  4log  2 x 0 2
A. S  1;1  6
B. S  1;  2
C. S  1;  4 D. S    4 C©u 3 : Cho hàm số x y ex e  
. Nghiệm của phương trình y'  0 là: A. x  ln 3 B. x  1  C. x  0 D. x  ln 2 C©u 4 : 1 Nếu log3  a thì bằng log 100 81 a A. 4 a B. 16a C. D. 2a 8
C©u 5 : Các kết luận sau , kết luận nào sai 3 2 1 1 I. 3 17 28 II. III. 5 7 4 4 IV. 4 5 13 23 3 2 A. I B. II và III C. III D. II và IV
C©u 6 : Hàm số nào sau đây có tập xác định là R? 3  x  2  
A. y  x  0,1 2 4
B. y   x  1/2 4 C. y   
D. y  x x   2 2 2 3  x
C©u 7 : Nếu log 6  a và log 7  b thì 12 12 a a a b A. log 7  B. log 7  C. log 7  D. log 7  12 1 b 12 1 b 12 a 1 12 1 a
C©u 8 : Tìm m để phương trình 2
log x  log x m  0 có nghiệm x (0;1) 2 2 1 1 1 A. m  1 B. m C. m D. m  1 4 4
C©u 9 : Số giá trị nguyên âm của m để .9x  2   1 6x  .4x m m m  0 với x  0;  1 là A. 6 B. 4 C. 5 D. 3
C©u 10 : Tập xác định của hàm số y   x  12 2 1 là:  1  1  1  A. ;    B.   C. ;    D.  2  2 2 
C©u 11 : Phát biểu nào sau đây không đúng? A. Hai hàm số x
y a và y  log x có cùng tập giá trị. a
B. Hai đồ thị hàm số x
y a và y  log x đối xứng nhau qua đường thẳng y x a C. Hai hàm số x
y a và y  log x có cùng tính đơn điệu. a Hai đồ thị hàm số x
y a và y  log x đều có đường tiệm cận. a D. C©u 12 : 2 2
Tìm giá trị nhỏ nhất của hàm số: sin x o c s 4 4 x y   A. 2 B. C. 2 D. 4
C©u 13 : Cho a  0;b  0 và 2 2
a b  7ab . Đẳng thức nào sau đây là đúng? a b 1 a b 1 A. log 
log a  log b B. log 
log a  log b 3  3 3  7  7 7  3 2 2 7 a b 1 a b 1 C. log 
log a  log b D. log 
log a  log b 7  7 7  3  3 3  7 2 2 3 C©u 14 : x x
Số nghiệm của phương trình  0   0 cos36
cos72   3.2x là: A. 3 B. 2 C. 1 D. 4
C©u 15 : Giá trị của 4log 25 a a
( a  0 và a  1) bằng A. 8 5 B. 4 5 C. 5 D. 2 5 C©u 16 : Cho hàm số x
y a , Các mệnh đề sau , mệnh đề nào sai
A. Đố thị hàm số luon đi qua điểm M 0;1 và B. Đồ thị hàm số có đường tiệm cận là y 0 2 N 1;a
C. Đồ thị hàm số không có điểm uốn
D. Đồ thị hàm số luôn tăng C©u 17 : 2 2  x 16 2 y 8 y 2 4
 3 x x  1  4
 3 y  4  y  8y  17 Hệ phương trình  có 1 cặp nghiệm 2
ln(x  3x  3)    2x   2
1 y  4x  3x  8
x;y. Giá trị của 3xy là: A. -1 B. -3 C. 0 D. -2 C©u 18 : Phương trình log    2 x log2  x  1 1 có tập nghiệm là:  1   5   1   5  A. S    1
B. S  1;   2 C. S    D. S     2    2   C©u 19 : 2 3 2 5 4 a . a . . a a
Tính giá trị biểu thức: A  log a 3 a 67 62 22 16 A. B. C. D. 5 15 5 5 C©u 20 : Đạ  o hàm của hàm số 2 3  2 x y là:  A. 2x 3   2.2 ln 2 B. 2x 3 2 ln 2 C. 2 3 2.2 xD.    2 2 2 3 2 x x
C©u 21 : Tập nghiệm của bất phương trình log   2 x log2 2x  1 là:  1  A. S  
B. S  1;3
C. S   ;    1 D. S   ;0    2  C©u 22 : Cho hàm số x 1 x y 2 3   
. Giá trị của đạo hàm của hàm số tại x  0 : 2 A. B. ln 54 C. 3ln 3 D. 2ln 6 3 C©u 23 : 2 x x  2   2  Bất phương trình   
  có tập nghiệm là:  3   3  A.   ;1  B. 1; C. 1;2 D. 1;2 C©u 24 : 
Cho hàm số y x 4 , Các kết luận sau , kết luận nào sai
Hàm số luôn luôn đồng biến với mọi x
A. Tập xác định D 0;
B. thuộc tập xác định 3
C. Hàm số luôn đi qua điểm M 1;1
D. Hàm số không có tiệm cận
C©u 25 : Cho a  0 ; a  1 . Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tập xác định của hàm số x
y  a là khoảng 0; 
B. Tập giá trị của hàm số y  log x là tập a
C. Tập xác định của hàm số y  log x là tập a
D. Tập giá trị của hàm số x y  a là tập C©u 26 : Cho hàm số 2
y  ln(x 1) . Nghiệm của phương trình y'  0 : A. x  1  B. x  0 C. x 1 D. x  0 v x 1 C©u 27 : Cho hàm số   2 f (x)
ln x  x  . Giá trị của đạo hàm cấp hai của hàm số tại x  2: 13 A. 36 B. C. 2ln 6 D. 13  36 C©u 28 : 17 15 Nếu 3 8 a
a và log  2  5  log  2  3 thì b b
A. a  1, b  1
B. 0  a 1, b 1
C. a  1, 0  b 1
D. 0  a 1, 0  b 1
C©u 29 : Cho a 0;b 0;a 1;b 1;n R , một học sinh tính biểu thức 1 1 1 P ...... theo các bước sau log b log b log b a 2 n a a I . 2 P log a log a ... log n a b b b II. 2 P
log a.a ... n a b III. 1 2 3 ... P log n a b IV. P n n 1 log a b
Bạn học sinh trên đã giải sai ở bước nào A. I B. II C. III D. IV
C©u 30 : Khẳng định nào sau đây sai ? 2016 2017 A. 2 1  3 2  2 B.  2   1   2   1 4 2018 2017  2   2  2017 2016 C. 1   1      D.  3   1   3   1 2 2     C©u 31 : 1
Cho hàm số y x 3 , Các mệnh đề sau , mệnh đề nào sai 1
B. Hàm số có đồ thị nhận trục tung làm trục A. lim f x 3 đối xứng x
Hàm số đồng biến trên ; 0 và nghịch
C. Hàm số không có đạo hàm tại x 0 D. biến 0; C©u 32 : 3 4 1 2 Nếu 4 5 a a và log  log thì b 2 b 3
A. a  1, b  1
B. 0  a 1, 0  b 1 C. 0  a 1, b 1
D. a 1, 0  b 1
C©u 33 : Đạo hàm của hàm số 2 y  log  là: 2  2x  1 2 log  4 log  4 log  2 2  2x  2  2x  2  2x  1 1 1 A. B. C. D. 2x   1 ln 2 2x   1 ln 2 2x   2x 1 1 ln 2 C©u 34 : 1 1 1 Cho:   . . .   M log x log x log x 2 k a a a
M thỏa mãn biểu thức nào trong các biểu thức sau: ( 1) 4 ( 1) A. k k M M k k B. log x log x a a ( 1) ( 1) C. k k M M k k D. 2 log x 3log x a a C©u 35 : 11 Rút gọn biểu thức 16 x x x x : x , ta được : A. 6 x B. 4 x C. 8 x D. x C©u 36 : 1 Cho hàm số y x3 
, Trong các mệnh đề sau , mệnh đề nào sai
A. Hàm số đồng biến trên tập xác định
B. Hàm số nhận O 0; 0 làm tâm đối xứng
D. Hàm số có đồ thị nhận trục tung làm trục C. Hàm số lõm ; 0 và lồi 0; đối xứng 5 C©u 37 : x  3 Hàm số y  log có nghĩa khi : 2 2  x A. x  2 B. 3   x  2 C. x  3   x  2 D. 3   x  2 C©u 38 : 2 
Cho hàm số y   x2 3
 2 , tập xác định của hàm số là 2 2 2 2 A. D ; ; B. D ; ; 3 3 3 3 2 2 2 C. D ; D. D R \ 3 3 3 C©u 39 :  Cho hàm số 5
y  3x   1
, tập xác định của hàm số là A. D R B. D ;1 C. D 1; D. D R \ 1
C©u 40 : Đạo hàm của hàm số f x  log  2 2x 1 là 2  4x 1
A. f '(x)   f '(x)  2 B. 2x   1 ln 2  2 2x   1 ln 2 4x D. Kết quả khác
C. f '(x)    2 2x   1 ln 2 C©u 41 : 4 1 1  2 3 3 a  8a bb  Rút gọn 3 3 A  .1 2
  a được kết quả: 2 2   a   3 3 3
a  2 ab  4b A. 1 B. a + b C. 0 D. 2a - b
C©u 42 : Cho log 3  a , giá trị của log 15 là: 15 25 1  a 1  a 1  a a  1 A. B. C. D. a a  1 a 1  a C©u 43 : x
Nếu  6  5  6  5 thì A. x  1  B. x 1 C. x  1  D. x 1 C©u 44 : 3 x x 1 
Số nghiệm nguyên của bất phương trình   x 1    x3 10 3 10 3 là A. 1 B. 3 C. 0 D. 2
C©u 45 : Giá trị của log 4 a a
( a  0 và a  1) bằng 6 1 A. 4 B. 2 C. 16 D. 2
C©u 46 : Số nghiệm dương của phương trình là: log x  2  log x  5  log 8  0. 2 2 1 2 A. 0 B. 3 C. 2 D. 1
C©u 47 : Nếu log3  a thì log9000 bằng A. 2 a  3 B. 2 a C. 2 3a D. 3 2a
C©u 48 : Cho hàm số y  x ln x . Giá trị của y'(e) 1 A. 3 B. C. 2 D. e e C©u 49 : x Đạ  
o hàm của hàm số f x 1    là:  2  xx x x 1   1   1   1 
A. f '(x)   ln 2  
B. f '(x)   lg 2  
C. f '(x)  ln 2  
D. f '(x)  lg 2    2   2   2   2 
C©u 50 : Bất phương trình 2log 4x  3  log 2x  3  2 là 3   1   3 3   3   3   3  A. ;    B. ;    C. ;3  D. ;3     4   4   4   4 
C©u 51 : Giá trị lớn nhất , nhỏ nhất của hàm số 2x y trên 2;2 là 1 1 A. GTLN = 4 ; GTNN = B. GTLN = 4 ; GTNN = 4 4 1 D. GTLN = 4 ; GTNN = 1 C. GTLN = 1 ; GTNN = 4
C©u 52 : Đạo hàm của hàm số y   2
ln x x   1 là: 1 2x 1 2x 1 1 A. B. C. D. ln  2 x x   1 2 ln  2 x x   x x 1 1 2 x x 1
C©u 53 : Cho a  log 15;b  log 10 vậy log 50 ? 3 3 3 A. 3 a b 1 B. 4 a b 1 C. a b 1 D. 2 a b 1 C©u 54 : 2 2
Cho phương trình x 2mx2 2x 4mx2 2 5  5
x  2mx m  0. Tìm m để phương trình vô nghiệm? 7 m  1 A. B. m  1
C. 0  m  1 D. m  0 m   0
C©u 55 : Cho các nhận định sau (giả sử các biểu thức đều có nghĩa: 1
1) log x y    x y với 2 2
x  4y  12x . y a  2  2log 2 a log log a a  2 f xgx 2) Phương trình aa
tương đương với f x  g x 3a  b 3) lg
 lg a  lgb với 2 2
9a b  10a . b 4  x 3 
4) Hàm số y     luôn nghịch biến. e  5) log a  log a  2log alog a với 2 2 2
a b c . (bc) (cb) (cb) (cb) 1 ln x 6) 2 2 2
2x y  x y  1 với y   ( x 1 ln x)
Số nhận định đúng là: A. 1 B. 2 C. 3 D. 4 C©u 56 : 4 log 8 bằng bao nhiêu ? 4 1 3 5 A. B. C. D. 2 2 8 4
C©u 57 : Đạo hàm của hàm số 5 y x là: 1 1 4  5 A. B. C. 1 5 5 x D. 5 x 5 4 5 x 5 4 5 x
C©u 58 : Tập nghiệm của bất phương trình log    0,2  x  1 log0,2 3 x là:
A. S  1;3
B. S  1;  3
C. S  1; 
D. S   ;3  
C©u 59 : Cho đường cong   : y  3x 3x Cm 2 2
m  3m và  : y 3x C
1. Tìm m để C và C2  1  2  1 tiếp xúc nhau? 5  40  5  40  A. B. 5 3 2 C. D. 5 3 2 3 3 3 3
C©u 60 : Giá trị của log a ( a  0 và a  1) bằng 3 a 8 1 1 A. 3 B. C. D. 3 3 3 9 ĐÁP ÁN 01 { ) } ~ 28 { | ) ~ 55 { | ) ~ 02 { ) } ~ 29 { | } ) 56 { ) } ~ 03 { ) } ~ 30 { | } ) 57 { ) } ~ 04 { | } ) 31 { | } ) 58 ) | } ~ 05 { | } ) 32 { | ) ~ 59 { | ) ~ 06 ) | } ~ 33 { ) } ~ 60 { | ) ~ 07 { | } ) 34 { | ) ~ 08 { | ) ~ 35 { ) } ~ 09 ) | } ~ 36 { | } ) 10 ) | } ~ 37 { ) } ~ 11 ) | } ~ 38 { | } ) 12 { | ) ~ 39 { | } ) 13 ) | } ~ 40 ) | } ~ 14 { | ) ~ 41 { | ) ~ 15 { | } ) 42 ) | } ~ 16 { | } ) 43 { | ) ~ 17 { | ) ~ 44 ) | } ~ 18 ) | } ~ 45 { | ) ~ 19 { ) } ~ 46 { | ) ~ 20 ) | } ~ 47 { | } ) 21 ) | } ~ 48 { ) } ~ 22 { ) } ~ 49 ) | } ~ 23 ) | } ~ 50 ) | } ~ 24 { | } ) 51 { | } ) 25 { ) } ~ 52 { ) } ~ 26 { ) } ~ 53 { | } ) 27 { ) } ~ 54 { | ) ~ 10 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 04
C©u 1 : Nghiệm của bất phương trình : log 2x  3  0 1   2
A. log 3  x  2   2 B. x  2 C. x  2 D. 0 x 2 C©u 2 : Nếu a  lo  thì 1 g 2 6, b lo 1 g 2 7 log2 7 bằng: a b a a A. B. C. D. b 1 1 a b 1 a 1 C©u 3 : 𝑥 𝑥
Phương trình (2 + √3) + (2 − √3) = 𝑚 𝑐ó 𝑛𝑔ℎ𝑖ệ𝑚 𝑘ℎ𝑖: A. 𝑚 ∈ (−∞; 5) B. 𝑚 ∈ (−∞; 5] C. 𝑚 ∈ (2; +∞) D. 𝑚 ∈ [2; +∞) C©u 4 : Cho lgx=a , ln10=b Tính log (x) 10e a b ab 2ab A. B. C. D. 1 b 1 b 1 b 1 b
C©u 5 : Đạo hàm của hàm số 2  ( 1) x y x e bằng A. 2 2 ( 1) x x e B. ( 1) x x e C. 2 ( 1) x x e D. 2 x x e
C©u 6 : Cho hàm số y  .
x sin x . Biểu thức nào sau đây biểu diễn đúng?
A. xy '  2y ' xy  2  sinx
B. xy '  yy '  xy '  2sinx
C. xy '  yy '  xy '  2sin x
D. xy '  y ' xy  2cos x  sin x
C©u 7 : Nghiệm của phương trình log log x 1 là : 2  4  A. 16 B. 2 C. 4 D. 8
C©u 8 : Tìm đạo hàm của hàm số: 2x y  tại x =2 A. 2ln 2 B. 2 C. 4 D. ln 2
C©u 9 : Nghiệm của phương trình 𝑙𝑜𝑔2(𝑥 − 1)2 = 2𝑙𝑜𝑔2(𝑥3 + 𝑥 + 1) là: 1 A. 9 B. -1 C. 1 D. 0 C©u 10 : Hàm số 2 ( ) x
f x x e có giá trị lớn nhất trên đoạn  1   ;1 là 1 A. B. e C. 0 D. 2e e C©u 11 : 4 2 2 3
Tập xác định của phương trình log  x   1  log x   1  25 là: A. x  1 B. x  1 C. x  1 D. x  C©u 12 :
Tập xác định của phương trình
log2(x3 + 1)− log2(x2 − x + 1)− 2log2 x = 0 là? 1 3 A. x  0 B. x C. x  1  D. 1   x  0 2 C©u 13 : 
Cho hàm số y x 4 , Các kết luận sau , kết luận nào sai
A. Tập xác định D 0;
B. Hàm số luôn đi qua điểm M 1;1
Hàm số luôn luôn đồng biến với mọi x
D. Hàm số không có tiệm cận
C. thuộc tập xác định C©u 14 : 1 1 2 3 Cho a, b > 0 thỏa mãn: 2 3 3 4
a a , b b Khi đó:
A. a 1, b 1
B. a > 1, 0 < b < 1
C. 0  a 1, b 1
D. 0  a 1, 0  b 1
C©u 15 : Giá trị lớn nhất , nhỏ nhất của hàm số 2x y trên 2;2 là 1 1 A. GTLN = 1 ; GTNN = B. GTLN = 4 ; GTNN = 4 4 1 D. GTLN = 4 ; GTNN = 1 C. GTLN = 4 ; GTNN = 4 C©u 16 : Hàm số sau 2 ( ) x f x x e  tăng trên khoảng nào A. 0; 2 B. 2;  C.  ;   D.  ;  0 C©u 17 : Cho hàm số x
y a , Các mệnh đề sau , mệnh đề nào sai
Đố thị hàm số luon đi qua điểm M 0;1 và A.
B. Đồ thị hàm số có đường tiệm cận là y 0 N 1;a 2
C. Đồ thị hàm số không có điểm uốn
D. Đồ thị hàm số luôn tăng C©u 18 : 1  Với 04 (1 x) 2 1 x bằng 3 (1 x) 1 x 3 (1 x) 1 x A. 4  B. 4  C. 4 D. 4 1 x 1 x 1 x 1 x C©u 19 : 3 5 Với biểu thức 4 6
a a cơ số a phải thỏa điều kiện A. a  1 B. a  0 C. 0  a 1 D. a  1 C©u 20 : 𝑥
Cho hàm số 𝑦 = (√17 − √3 − √2) . Khẳng định nào sau đây sai:
A. Hàm số nghịch biến trên khoảng (0; +∞)
B. Hàm số nghịch biến trên R
C. Giá trị gần đúng ( với 3 chữ số thập phân ) của hàm số tại x=3 là 0,932
D. Giá trị gần đúng ( với 3 chữ số thập phân ) của hàm số tại 𝑥 = √10 là 0,928 C©u 21 : 1 Cho hàm số y x3 
, Trong các mệnh đề sau , mệnh đề nào sai
A. Hàm số đồng biến trên tập xác định
B. Hàm số nhận O 0; 0 làm tâm đối xứng
D. Hàm số có đồ thị nhận trục tung làm trục C. Hàm số lõm ; 0 và lồi 0; đối xứng
C©u 22 : Cho a 0;b 0;a 1;b 1;n R , một học sinh tính biểu thức 1 1 1 P ...... theo các bước sau log b log b log b a 2 n a a I . 2 P log a log a ... log n a b b b II. 2 P
log a.a ... n a b III. 1 2 3 ... P log n a b IV. P n n 1 log a b
Bạn học sinh trên đã giải sai ở bước nào A. III B. II C. I D. IV 3 C©u 23 : 1 1 1 1 Nếu 5 3 a a và log  log thì b 3 b 2
A. 0  a 1,b 1
B. a  1,b 1
C. a 1,0  b 1
D. 0  a 1,0  b 1 C©u 24 :  Cho hàm số 5
y  3x   1
, tập xác định của hàm số là A. D 1; B. D R C. D ;1 D. D R \ 1 C©u 25 : Hàm số  2
ln x  2x m   1 có tập xác định là khi m  0 A. m  0
B. 0  m  3 C. D. m  0 m  1 
C©u 26 : Phương trình log 4x  log 2  3 có bao nhiêu nghiệm? 2 x 2 A. 2 nghiệm B. 3 nghiệm C. 1 nghiệm D. 4 nghiệm
C©u 27 : Đạo hàm của hàm số f (x)  x ln x là: 1 A. B. ln x C. 1 D. ln x 1 x
C©u 28 : Giải phương trình 9x 2.3x  3  0: A. x = 1 B. x = 0 C. x = -1 D. x = 1 hay x = 0 C©u 29 : Tìm cơ số 3
a biết 𝑙𝑜𝑔𝑎4√2 = 7 6 A. a = 2 B. a = 6 C. a = 8 D. a = 4 C©u 30 : Hàm số 2
f (x)  x ln x có giá trị nhỏ nhất trên đoạn 3;  5 là A. 25ln 5 B. 9ln 3 C. 8ln 2 D. 32ln 2 C©u 31 : 1
Cho hàm số y x 3 , Các mệnh đề sau , mệnh đề nào sai
A. Hàm số có đồ thị nhận trục tung làm trục 1 lim f x 3 đối xứng B. x
Hàm số đồng biến trên ; 0 và nghịch
C. Hàm số không có đạo hàm tại x 0 D. biến 0;
C©u 32 : Theo hình thức lãi kép một người gửi 100 triệu đồng vào ngân hàng theo kỳ hạn một năm
với lãi suất 1,75% (giả sử lãi suất hàng năm không thay đổi) thì sau hai năm người đó thu 4
được một số tiền là
A. 103,351 triệu đồng
B. 103,530 triệu đồng
C. 103,531 triệu đồng
D. 103,500 triệu đồng C©u 33 : log 4 Giá trị 2 a a bằng: A. 4 B. 2 C. 8 D. 16. C©u 34 :  Đạo hàm của hàm số cos 2 x y e tại x  6 3 3 A.  2 e B. 3e C. 2 e D. 3e
C©u 35 : Số nghiệm của phương trình log   4 log2 x
log2 log4 x 2 là A. 2 B. 1 C. 3 D. 0
C©u 36 : Cho hai số dương a và b. Xét các mệnh đề sau mệnh đề nào đúng (I). lgb lg a ab (II) ln b ln a ab 1 log10 (b) lg b aa (III) 1 (IV) log ( ) ln b e b aa
A. Chỉ có (III) đúng
B. Chỉ có (I) đúng
C. Tất cả các mệnh đề đều đúng
D. Chỉ có (II) đúng
C©u 37 : Số nghiệm của phương trình 22+s − 22–s = 15 là: A. 2 B. 0 C. 1 D. 3
C©u 38 : Nghiệm của bất phương trình 𝑙𝑜𝑔1/5(𝑥2 − 6𝑥 + 8) + 2𝑙𝑜𝑔5(𝑥 − 4) > 0 𝑙à: A. x>4 B. x<2 C. Vô nghiệm D. 0C©u 39 : √ 3 4
Giá trị của biểu thức 𝐵 = 15𝑙𝑜𝑔1/√2 2 √5 + 81𝑙𝑜𝑔35 8
27𝑙𝑜𝑔936+ 3𝑙𝑜𝑔92401 là: 125 16 1609 A. 53 B. 35 C. 53 D. 28
C©u 40 : Nghiệm của phương trình 𝑙𝑜𝑔2(𝑥2 + 3𝑥 + 2) + 𝑙𝑜𝑔2(𝑥2 + 7𝑥 + 12) = 3 + 𝑙𝑜𝑔23 5 A. 0 và -3 B. -4 và -3 C. -5 và -4 D. 0 và -5
C©u 41 : Hàm số f (x)  x ln x
A. Không có cực trị
B. Có một cực tiểu
C. Có một cực đại
D. Có một cực đại và một cực tiểu
C©u 42 : Nghiệm của bất phương trình 1 ≤ 2𝑥−1 là: 2√𝑥2−2𝑥 A. 𝑥 ≤ 0 B. 0 ≤ 𝑥 ≤ 2 C. 𝑥 ≤ −1 D. 𝑥 ≥ 2 C©u 43 : Đố 1
i với hàm số y  ln , ta có x 1 A. '1 y xye B. '1 y xyeC. '1 y xyeD. '1 y xye
C©u 44 : Nghiệm của 32.4x 18.2x
1 0 đồng biến trên (0; 2) 1 1
A. 1  x  4 B. 4   x  1 
C. 2  x  4 D. x  16 2
C©u 45 : Đạo hàm của hàm số 𝑦 = 𝑒𝑥− 𝑒−𝑥 𝑒𝑥+ 𝑒−𝑥 là: A. 2𝑒2𝑥 B. 𝑒2𝑥 (𝑒2𝑥 + 1)2 (𝑒2𝑥 + 1)2 C. 4𝑒2𝑥 D. 3𝑒2𝑥 (𝑒2𝑥 + 1)2 (𝑒2𝑥 + 1)2 C©u 46 : 2 
Cho hàm số y   x2 3
 2 , tập xác định của hàm số là 2 2 2 2 A. D ; B. D ; ; 3 3 3 3 2 2 2 C. D ; ; D. D R \ 3 3 3
C©u 47 : Các kết luận sau , kết luận nào sai 3 2 1 1 I. 3 17 28 II. III. 5 7 4 4 IV. 4 5 13 23 3 2 A. II và III B. III C. I D. II và IV
C©u 48 : Tập nghiệm của phương trình 2 2 sin x o c s 2.2 2 x   3 là 6 
A. x  (2k 1) , k Z B. x
k2 ,k Z 2  C. x
k ,k Z
D. x k , k Z 2 C©u 49 : Cho phương trình 2 2 log 9 12x  4x  log
6x  23x  21  4 . Chọn phát biểu đúng? 3x7   2x 3 
Tập xác định của phương trình là
B. Phương trình có duy nhất một nghiệm. A.  3   ;    .  2 
C. Phương trình có 2 nghiệm trái dấu. 1
D. Phương trình có một nghiệm là x  4
C©u 50 : Phương trình 9s − 3.3s + 2 = 0 có hai nghiệm x1,x2 (x1 < x2). Giá trị của A = 2x1 + 3x2 là: A. 3 log2 3 B. 4 log2 3 C. 2 D. 0
C©u 51 : Tìm tập xác định của hàm số sau: 2
log (1 2x x ) 1 x
A. D  (0;  ) 
B. D  0; 
C. D  (0;  )  /  1
D. D  1;  C©u 52 :
Số nghiệm của phương trình: log3(x2 − 6)= log3(x − 2)+ 1 là: A, 0 B. 1 C. 2 D. 3 A. 1 B. 2 C. 0 D. 3
C©u 53 : Đạo hàm của hàm số ( ) x f x xe là A. '( ) x f x e 1    x   B. '( )   1 x f x x e C. f '(x) x e 1 D. '( ) x f x e
C©u 54 : Với x  1 và a, ,
b c là các số dương khác 1 và log x  log x  0  log x . So sánh các số a, , b c a b c là
A. b a c
B. c a b
C. c b a
D. a b c C©u 55 : 2 Hàm số x x 1  y  8
6x 3ln2 là đạo hàm của hàm số nào sau đây: 2 2 2 2 A.  1         2x x y . B. 1  8x x y . C. 3 3 1  2 x x y . D. 3 3 1  8 x x y .
C©u 56 : Cho a  log 15;b  log 10 vậy log 50 ? 3 3 3 7 A. a b 1 B. 3 a b 1 C. 4 a b 1 D. 2 a b 1
C©u 57 : Tập nghiệm của bất phương trình 2x  3  x A.  ;3   B. 1;  C.   ;1  D. 1;  C©u 58 : 2(𝑎−1𝑏2)
Giá trị của biểu thức 𝐴 = 𝑎𝑏−2(𝑎𝑏−1)
𝑎−2𝑏(𝑎−2𝑏−1)3 sau khi rút gọn là: A. 𝑎10𝑏2 B. 𝑎2𝑏10 C. 𝑎10 D. 𝑎2
C©u 59 : Với giá trị nào của m, phương trình 9x  3x m  0 có nghiệm 1 1 A. m B. m  0 C. m D. m  0 4 4
C©u 60 : Phương trình x 1 3
x 1 có bao nhiêu nghiệm 3 A. 2 B. 0 C. 1 D. Vô số nghiệm 8 ĐÁP ÁN 01 ) | } ~ 28 { ) } ~ 55 { ) } ~ 02 { ) } ~ 29 { | } ) 56 { | } ) 03 { | ) ~ 30 { ) } ~ 57 { ) } ~ 04 { | ) ~ 31 { | } ) 58 { | ) ~ 05 { | ) ~ 32 { | ) ~ 59 { | ) ~ 06 ) | } ~ 33 { ) } ~ 60 { | ) ~ 07 ) | } ~ 34 ) | } ~ 08 ) | } ~ 35 { ) } ~ 09 { | } ) 36 { | ) ~ 10 { ) } ~ 37 ) | } ~ 11 { ) } ~ 38 { | ) ~ 12 ) | } ~ 39 { | ) ~ 13 { | } ) 40 { | } ) 14 { ) } ~ 41 { ) } ~ 15 { | } ) 42 { | } ) 16 ) | } ~ 43 ) | } ~ 17 { | } ) 44 { ) } ~ 18 { | ) ~ 45 { | ) ~ 19 { | ) ~ 46 { | } ) 20 { | } ) 47 { | } ) 21 { | } ) 48 { | ) ~ 22 { | } ) 49 { ) } ~ 23 ) | } ~ 50 ) | } ~ 24 { | } ) 51 { | ) ~ 25 ) | } ~ 52 ) | } ~ 26 ) | } ~ 53 { ) } ~ 27 { ) } ~ 54 ) | } ~ 9 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 05
C©u 1 : Giá trị nhỏ nhất của hàm số: x 2
y e (x  3) trên đoạn [  2; 2] là: 6 1 A. 2 e B. 2  e C. D. 3 e 2 e C©u 2 : 1
Logarit cơ số 3 của số nào  : 3 1 1 1 A. 3 3 B. C. D. 3 3 27 3 3
C©u 3 : Số nghiệm của phương trình log (9x  4)  x log 3 log 3 là 2 2 2 A. 2 B. 0 C. 1 D. Đáp số khác
C©u 4 : Đạo hàm của hàm số  2 (  2  2) x y x x e là: A. x xe B. 2 x x e C. 2 (  4 ) x x x e D. (2  2) x x e
C©u 5 : Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x ( x x ) . Giá trị A= 2x  3x là 1 2 1 2 1 2 A. 4 log 2 3log 2 3 B. 1 C. 3 D. Đáp số khác
C©u 6 : Số nghiệm của phương trình 2log
x 1  2  log (x  2) là 2 2 A. 2 B. 0 C. 1 D. Đáp số khác C©u 7 : 1 Cho hàm số y  ln
. Hệ thức nào sau đây là đúng? 1 x A. '1 x yye B. '1 y xye C. '1 x xye D. '1 y xye
C©u 8 : Tập xác định của hàm số 2
y  ln(x  4) là: A. ( ;  2  ) (2; )  B. (2; )  C. ( 2  ;2) D. ( 2  ; ) 
C©u 9 : Tìm 𝑚 để phương trình 𝑥4 − 6𝑥2 − log2 𝑚 = 0 có 4 nghiệm phân biệt trong đó có 3 nghiệm lớn hơn −1 1 1 1 1 A. < 𝑚 < 1 B. ≤ 𝑚 < 1 C. Đáp án khác D. < 𝑚 < 1 29 29 25
C©u 10 : Số nghiệm của phương trình 2x 2 2  2 x 15 là A. 3 B. 2 C. 1 D. 0
C©u 11 : Chọn khẳng định đúng trong các khẳng định sau
A. Cơ số của logarit là một số dương khác 1
B. Cơ số của logarit là một số nguyên
C. Cơ số của logarit là một số thực bất kỳ
D. Cơ số của logarit là một số nguyên dương C©u 12 : Gọi x x x 
1; x2 là hai nghiệm của phương trình: 2 5 9 7 343. Tổng x1 + x2 là: A. 5 B. 3 C. 4 D. 2
C©u 13 : Số nghiệm của pt log  2
x  6  log x  2 1 là 3  3   A. 1 B. 0 C. 2 D. 3
C©u 14 : Tập xác định của hàm y  ln(ln x) là: A. (0;1) B. (1; )  C. (0; )  D. 0; C©u 15 : 1 Hãy tìm logarit của theo cơ số 3 3 3 3 3 2 2 A. B. C. D. 2 2 3 3 C©u 16 : 𝑥+1
tính đạo hàm của hàm số sau: 𝑓(𝑥) = 𝑒3𝑥−2 A. 𝑥+1 𝑥+1 𝑓′(𝑥) = 𝑒3𝑥−2 B. 𝑓′(𝑥) = 5 . 𝑒3𝑥−2 (3𝑥−2)2 C. 𝑥+1 𝑥+1
𝑓′(𝑥) = 𝑥+1 𝑒3𝑥−2
D. 𝑓′(𝑥) = −5 . 𝑒3𝑥−2 3𝑥−2 (3𝑥−2)2
C©u 17 : Cho hàm số   x
f x  xe Gọi f '' x là đạo hàm cấp 2. Ta có f ''  1 bằng A. 3e B. 2e C. 0 D. 1 C©u 18 : Chọn câu sai:
A. Hàm số 𝑦 = 𝑒𝑥 không chẵn cũng không lẻ
B. Hàm số 𝑦 = ln(𝑥 + √𝑥2 + 1) là hàm số lẻ
C. Hàm số 𝑦 = 𝑒𝑥 có tập giá trị là (0; +∞) 2
D. Hàm số 𝑦 = ln(𝑥 + √𝑥2 + 1) không chẵn cũng không lẻ
C©u 19 : Phương trình sau có bao nhiêu nghiệm thực phân biệt: 1 log (𝑥 + 3) + 1 log 2 √2 4
4(𝑥 − 1)8 = 3 log8(4𝑥) A. 0 B. 1 C. 3 D. 2
C©u 20 : Số nghiệm của phương trình 4x  6x  25x  2 là A. 3 B. 1 C. 0 D. 2
C©u 21 : Cho hàm số ( ) 2x f x
. Biểu thức f (a 1)  f (a) bằng: A. 2a B. 1 C. 2a 1 D. 2
C©u 22 : Giá trị nhỏ nhất của hàm số: 2
y x  4ln(1 x) trên đoạn [  2;0] A. 1 B. 1 4ln 2 C. 0 D. 4  4ln 3 C©u 23 : Biết log 2  ;
a log 3  b thì log 45 tính theo a và b bằng:
A. 2b a 1
B. 2b a 1 C. 15b
D. a  2b 1 C©u 24 : 32  1  Cho m > 0. Biểu thức 3 m   bằng:  m A. 2 m B. 2 3 3 mC. 2 mD. 2 3 2 m
C©u 25 : Tập xác định của hàm số y  log (log (x 1)) là: 5 1 5 A. ( 1  ;0] B. ( 1  ;0) C. ( 1  ; )  D. (0; ) 
C©u 26 : Đạo hàm của hàm số 5
y  ln 7x bằng: 1 7 1 1 A. B. C. D. 5 4 5x ln 7x 5 4 5x ln 7x 5 4 5 ln 7x 5 4 35x ln 7x
C©u 27 : Chọn khẳng định đúng trong các khẳng định sau
A. Chỉ có logarit của một số thực dương
B. Có logarit của một số thực bất kỳ
C. Chỉ có logarit của một số thực dương khác D. Chỉ có logarit của một số thực lớn hơn 1 1
C©u 28 : Tập nghiệm của phương trình 2x
4 m  8x (m là tham số) là A. 2m B. −m C. m D. −2m 3
C©u 29 : Giá trị nhỏ nhất của hàm số: 2 2 ( 4 1). x g x x x e trên 2;3 3 2 6 A. 22e B. C. D. 4 e 3 e 7 e C©u 30 : x e
Giá trị lớn nhất của hàm số: y  trên đoạn [0;2] là: 2x 1 2 e e A. 1 B. C. 2 D. 5 2
C©u 31 : Đạo hàm của hàm số 2   (  2 ) x y x x e là: A. 2 x x e B. 2 ( 2) x x e  C. x xe D. (2  2) x x e C©u 32 : 1
Giá trị của biểu thức log bằng: 5 7 5 1 1 A. -7 B. C. 7 D. 7 7
C©u 33 : Số nghiệm của phương trình 4x  6x  25x  2 là A. 0 B. 1 C. 2 D. 3
C©u 34 : Viết dưới dạng lũy thừa thì số: 5 3 2 2 2 bằng: 3 7 17 7 A. 10 2 B. 10 2 C. 10 2 D. 30 2
C©u 35 : Phương trình sau có bao nhiêu nghiệm thực phân biệt:
log2|𝑥 − 2| − log1|𝑥 + 5| − log2 8 = 0 2 A. 2 B. 3 C. 1 D. 4
C©u 36 : Số nghiệm của phương trình 9x 2.3x  3  0 là A. 0 B. 2 C. 1 D. 3
C©u 37 : Dùng định nghĩa, tính đạo hàm của hàm số sau: f (x)  log (x  ) 1 2 1 1 A. f '(x)  B. f '(x)  0
C. f '(x)  log (x  )
1 D. f '(x)  x 1 2 (x  ) 1 ln 2
C©u 38 : Giá trị nhỏ nhất của hàm số: x 2
y e (x x  5) trên đoạn [1;3] là: A. - 5e B. -3e2 C. e3 D. -5e2 4
C©u 39 : Tìm 𝑎 để phương trình: 𝑥4 − 4𝑥2 + |log3 𝑎| + 3 = 0 có 4 nghiệm thực phân biệt: 1 1 A. < 𝑎 < 3 B. ≤ 𝑎 < 3 C. 1 < 𝑎 < 3 D. 1 ≤ 𝑎 < 3 27 27 C©u 40 : Hàm số sin x y  e
gọi y' là đạo hà của hàm số. Khẳng định nào sau đây đúng A. sinx y'  e cosx B. sin ' cosx.e x y   C. cosx y'  e D. cosx y'  sin . x e
C©u 41 : Cho phương trình x 1 x 1 3 9( )  
 4  0 . Tổng các nghiệm của phương trình là: 3 A. -1 B. 0 C. 1 D. 2
C©u 42 : Nghiệm của bất phương trình log (x 1)  2log (5  )
x  1 log (x  2) là 2 4 2
A. 2B. 1C. Đáp số khác
D. 2C©u 43 : Số nghiệm của phương trình log (9x  4)  x log 3 log 3 là 2 2 2 A. 0 B. Đáp số khác C. 2 D. 1
C©u 44 : Giá trị của biểu thức 3 3 22 5 5 4 :16 bằng: A. 16 B. 8 C. 1 D. 3 5 16
C©u 45 : Nghiệm của phương trình log4 logx x  4  32 là A. 100 B. 10;100 C. 20;100 D. 10
C©u 46 : Đạo hàm của hàm số   2 ( 1) x y x e là: A. 2 (2 1) x x e B. 2 (2  3) x x e C. 2 (  2) x x e D. 2 x e
C©u 47 : Cho phương trình x 1 x 1 3 9( )  
 4  0 . Tổng các nghiệm của phương trình là: 3 A. -1 B. 2 C. 0 D. 1
C©u 48 : Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x ( x x ) . Giá trị A= 2x  3x là 1 2 1 2 1 2 A. 1 B. 4 log 2 3log 2 3 C. 3 D. Đáp số khác
C©u 49 : Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số 𝑦 = 4𝑠𝑖𝑛2𝑥 + 4𝑐𝑜𝑠2𝑥 A. Đáp án khác B. 𝑀 = 5; 𝑚 = 2 C. 𝑀 = 4; 𝑚 = 2 D. 𝑀 = 5; 𝑚 = 4
C©u 50 : Giá trị lớn nhất của hàm số: x 2     y e (2x
x 8) trên đoạn  2;2 5 2 A. B. 5e C. 2 2e D. 5  e 2 e
C©u 51 : Bất phương trình 5.4x 2.25x 7.10x    0 có nghiệm là A. 0  x  1 B. 1 x  2 C. 2   x  1  D. 1   x  0
C©u 52 : Nghiệm của bất phương trình log (x 1)  2log (5  )
x  1 log (x  2) là 2 4 2
A. 1B. 2C. 2D. Đáp số khác
C©u 53 : Số nghiệm của phương trình 2
log (x  6)  log (x  2) 1 3 3 A. 3 B. 2 C. 1 D. 0
C©u 54 : Giải bất phương trình:
log3 √𝑥2 − 5𝑥 + 6 + log1 √𝑥 − 2 > 1 log1(𝑥 + 3) 3 2 3 A. 𝑥 > 5 B. 𝑥 > 3 C. 3 < 𝑥 < 5 D. 𝑥 > √10
C©u 55 : Số nghiệm của phương trình 2
log (x  6)  log (x  2) 1 3 3 A. 0 B. 2 C. 1 D. 3
C©u 56 : Số nghiệm của phương trình 2x 2 2  2 x 15 là A. 2 B. 3 C. 1 D. 0
C©u 57 : Tìm 𝑚 để phương trình |𝑥4 − 5𝑥2 + 4| = log2 𝑚 có 8 nghiệm phân biệt:
A. Không có giá trị m B. −√ 4 29 < 𝑚 < √ 4 29 C. 0 < 𝑚 < √ 4 29 4
D. 1 < 𝑚 < √29
C©u 58 : Số nghiệm của phương trình 2log
x 1  2  log (x  2) là 2 2 A. 2 B. 0 C. Đáp số khác D. 1
C©u 59 : Tìm giá trị nhỏ nhất của hàm số f (x)  x(2  ln ) x trên [ 2; 3] là A. Đáp số khác B. e C. 1 D. 4-2ln2
C©u 60 : Giá trị nhỏ nhất của hàm số: x 2
y e (x  2) trên đoạn 1;  3 là: A. e B. 0 C. e3 D. e2
C©u 61 : Số nghiệm của phương trình 9x 2.3x  3  0 là A. 0 B. 2 C. 1 D. 3 6
C©u 62 : Tìm giá trị nhỏ nhất của hàm số f (x)  x(2  ln ) x trên [ 2; 3] là A. Đáp số khác B. e C. 4-2ln2 D. 1
C©u 63 : Đạo hàm của hàm số 4
y  ln x là: 4 4 A. 3 4 ln x B. 3 ln x C. 3 4 ln(x ) D. 3 ln(x ) x x C©u 64 : Phương trình x  
có nghiệm là kết quả nào sau đây x   3 log 1 log 2 1 A. Vô nghiệm B. 2 C. D. 3 2 7 ĐÁP ÁN 01 { ) } ~ 28 ) | } ~ 55 { | ) ~ 02 { ) } ~ 29 { | ) ~ 56 { | ) ~ 03 { | ) ~ 30 { ) } ~ 57 { | } ) 04 { ) } ~ 31 { ) } ~ 58 { | } ) 05 { | ) ~ 32 { ) } ~ 59 { | } ) 06 { | ) ~ 33 { | ) ~ 60 { ) } ~ 07 { ) } ~ 34 ) | } ~ 61 { | ) ~ 08 ) | } ~ 35 { | } ) 62 { | ) ~ 09 { | } ) 36 { | ) ~ 63 { ) } ~ 10 { | ) ~ 37 { | } ) 64 ) | } ~ 11 ) | } ~ 38 { ) } ~ 12 ) | } ~ 39 { | } ) 13 ) | } ~ 40 ) | } ~ 14 { ) } ~ 41 { | ) ~ 15 ) | } ~ 42 { | } ) 16 { | } ) 43 { | } ) 17 ) | } ~ 44 ) | } ~ 18 { | } ) 45 ) | } ~ 19 { | } ) 46 { ) } ~ 20 { | } ) 47 { | } ) 21 ) | } ~ 48 { | ) ~ 22 { ) } ~ 49 { | } ) 23 { ) } ~ 50 { | ) ~ 24 ) | } ~ 51 ) | } ~ 25 { ) } ~ 52 { | ) ~ 26 { ) } ~ 53 { | ) ~ 27 ) | } ~ 54 { | } ) 8 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 06
C©u 1 : Phương trình x x 1  2  2  4 có nghiệm là A. 1  log    2 3 B. log2 3 2 C. log2 3 1 D. 3 log2 3 C©u 2 : a b Cho log b  2  ,log c  5 log a a .Giá trị của a là 3 c 5 4 2 5 A. B. C. D.  3 3 3 3 C©u 3 : Biến đổi 3 5 4 x
x (x  0) thành dạng lũy thừa với số mũ hữu tỉ ta được: 21 23 20 12 A. 12 x B. 12 x . C. 3 x D. 5 x .
C©u 4 : Giá trị nhỏ nhất của hàm số y  log x
( m là tham số) trên [1;2] lớn hơn -1 khi 2 m 2 m 1   1   m  0 m  1 A. B. C. m  1 D. 1   m 1 0  m  1 m  1  C©u 5 : 2 1 Nếu log   1 x log1 a log1 b thì x bằng 3 5 2 2 2 3 3 3 1 2 a 3 a A. 2 a B. C. D. 2 5 a b 1 1 5 b 5 b 5 b
C©u 6 : Cho hàm số f x 2  x  3
ln x  thì f '3 bằng A. 9  ln3 B. 9  6ln3 C. 9 18ln3 D. 9  9ln3 C©u 7 : 1 4
Cho a>0, b> 0. Giá trị của x bằng bao nhiêu biết log   2 x log 2 a log 2 b 4 7 3 3 3 1 4 1 4 a A. 4 7 a b B. C. 4 7 4 D. 7 4 a b 7 a. b b C©u 8 : ln x
Hàm số y  x đồng biến trên khoảng  1  A. 0; B.  ; e  C. 0;  e D. 0;  e  
C©u 9 : Tất cả các giá trị của m để phương trình 2x 1  2 2
m m  0 có nghiệm là A. m  0 .
B. 0  m 1 . C. m  1 . D. m  ; 0 m  1 .
C©u 10 : Tập xác định của hàm số  ( 1)e y x là A. (1; )  B. \ {1} C. R D. [1; ) 
C©u 11 : Xác định m để phương trình 2x 1  2 3
 2m m  3  0 có nghiệm:  3   1 
A. m  0;  1 m   1  ; m   ;0 m  0;  B.   2   C. 2   D.  
C©u 12 : Đạo hàm của hàm số y   (3x 1) là  3(3x 1) ln(3x 1) A.  1   3 (3x 1)   B.
C. (3x 1) ln(3x 1) D. 1 (3x 1)  
C©u 13 : Cho a,b,c là các số thực dương và a,b  1. Khẳng định nào sau đây sai 1 log c log c  log . b log c A. log c  log b c  a a b b a  a B. C. D. log . log 1 log a a log a a b c b
C©u 14 : Hình bên dưới là đồ thị của hàm số nào ? 2 1 1 A. 2x y   B. y  C. 2x y  y   2x D. 2x
C©u 15 : Giá trị của log 3 a a
(0  a  1) bằng: A. 12 B. 9. C. 3 D. 6 C©u 16 : Nếu 3 log    3 t
4log3 x 7log3 y log3 x thì t bằng 11 3 11  3 11 3 11 A. x x x B. C. D. 7 3 x y 7 y 7 y 7 y C©u 17 : x
Với điều kiện nào của a thì y   2
1  3a  4a  là mọt hàm số mũ?  3   3   1    a   1
 ;    ;0  0;  4 4 4
A. a    1 ;1   1  ;  B.       4    1   3   1 3   3  C. a   1  ;   0; 
D. a    ;    ;   4 4     4 4 4    
C©u 18 : Tập nghiệm của bpt log  2
2x x  1  0 là: 2  3      3   3    1 ;0   ;    3 ; 1   ; A.  1  ;  0;  C. 2 2 2 B. D.       2   C©u 19 : x e
Tập xác định của hàm số y  x e là tập nào sau đây? 1 A. \ 1 { } B. C. \ 0 { } D. \ { } e C©u 20 : 1
Tập xác định của hàm số y   lnx   1 là 2  x A. 0;    B. \   2 C. 1;2 D.  ;   1  2;
C©u 21 : Bất dẳng thức nào sau đáy sai? 10 5  2008 2009 2   2   1 2   1 2    A. 1    1         2   2  B.         2 2     3 300 301 5 6  3   3  C.  3   1   3   1      D.  3   3     
C©u 22 : Phương trình log x  12 .log x  1 có nghiệm là: 4   2 x   4 A. x  3  B. x  4 C. x  3  D. Đáp án khác 
C©u 23 : Cho 0  a  1 và x  0,y  0. Khi đó ta có: log x.y bằng: a  log x
A. log x  log y x y x a a a B. log log a a C. log .log a y D. log y a C©u 24 : Cho hàm số x
y  xe . Hệ thức nào sau đây đúng?
A. y'' 2y'1  0
B. y'' 2y' 3y  0
C. y'' 2y' y  0
D. y'' 2y' 3y  0
C©u 25 : Đồ thị dưới đây là của hàm số nào?
A. y  log x 1 y  og l (x 1) y  log x y  log (x 1) 2 B. 2 C. 3 D. 3 C©u 26 : Cho   x e f x 
, nghiệm của phương trình f 'x  0 là x A. 2 B. 0 C. 1 D. e
C©u 27 : Nếu log 4  a thì log 4000 bằng: A. 4  2a B. 3  a C. 3  2a D. 4  a C©u 28 : 2
Hàm số nào sau đây là đạo hàm của hàm số sin x y  e A. 2 sin x 2 e .cos x B. 2 sin x e .cos sin x sin x 2x C. 2 e .sin2x D. 2 2 e .sin x 4
C©u 29 : Đạo hàm của hàm số 7
y  cos x là: sin x sin x  sin x 7 6 1 7 8 A. B. 7 cos x C. D. 7 cos x 7 6 7 cos x 7 6 7 cos x
C©u 30 : Phương trình x 2x 1  x 1 3 3 3     9 có nghiệm là: 1 1 A. x   B. x   2 x D. x  1 3 C. 2
C©u 31 : Cho mệnh đề “ với mọi a, , b x , nếu 0  a  b thì x x
a  b . Mệnh đề đúng khi A. x<0 B. 0C. x>1 D. x>0
C©u 32 : Đặt a  log 3 . Khi đó giá trị của biểu thức P  log 18  log 21  log 63 là: 2 2 2 2 A. 2a B. 1  a   C. 1 a D. 2 a
C©u 33 : Tập xác định của hàm số y  log x là x 1  A. (1; )  \ {2} B. (2; )  C. (1; )  D. (0; )  C©u 34 : 1
Giá trị của biểu thức 3 A  2log   1 6 log1 400 3log1 45 là 2 3 3 3 A. 4 B. -3 C. 5 D. -4
C©u 35 : Hàm số y  xln x đồng biến trên khoảng  1   1   1  A. ;   ; e B. 1; C. 1 ;   D.      e   e  C©u 36 : Hàm số x x y e e   có bao nhiêu cực trị A. 0 B. 3 C. 2 D. 1 C©u 37 : Cho hàm số x
y  x  e . Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x  0
B. Hàm số không xác định tại x  0
C. Hàm số đạt cực đại tại x  0
D. Hàm số không đạt cực trị tại x  0 C©u 38 : Nếu lo   12 g 18
x và log310 b thì log 50 bằng 3
A. 2a  2b  4
B. 2a  2b  4
C. 2a b   1
D. 2a b   1 5 C©u 39 : x
Bất phương trình   2 x 3 2  2 có tập nghiệm là: A. 1;  ;0   ;  8  6;  B.   C.   D.  
C©u 40 : Cho hàm số y   2
ln x  2x  5 . Mệnh đề nào sau đây sai?
A. y '  0  x  1
B. y  ln 5  x  0
C. Hàm số đạt GTNN bẳng 2ln2 khi x = 1 D R
D. Hàm số có tập xác định
C©u 41 : Một người đi mua chiếc xe máy với giá 90 triệu. Biết rằng sau một năm giá trị chiếc xe chỉ
còn 60%. Hỏi sau bao nhiệm năm thì giá trị chiếc xe chỉ còn 10 triệu? 1 1 A. 2 năm B. 2 năm C. 3 năm D. 3 3 3
C©u 42 : Đạo hàm của hàm số 3 y x là: 1 1 1 4 1 A. B. C. D. 3 x 3 2 3 x 3 2 x 3 2 x 3 C©u 43 : Nếu log  2 5
a thì log41250 bằng: 1 1 A. 1+4a B. 4a-1 C. a D.  2a 2 2 C©u 44 : 1 Cho các khẳng định 3 1)( 2  7)  3  ; 5 2)( 2)   3  2 ; 5 0 3)a  1 với mọi a  ; 5 2 2 4) a  a với mọi a  . Khẳng định đúng là A. 2 B. 1và 2 C. 1,2 và 4. D. 1,2,3 và 4 C©u 45 : 2 1 Cho hàm số x 2 ( ) x y   . Tìm khẳng định đúng 2
A. Nghịch biến trên nửa khoảng [1; ) 
B. Đồng biến trên R
C. Nghịch biến trên R
D. Đồng biến ttrên khoảng (1; ) 
C©u 46 : Giá trị của biểu thức 3 B  2log   7 36 log714 3log7 21 là A. 3 B. 2 C. -3 D. -2 6
C©u 47 : Đạo hàm của hàm số y  xln x  x là 1 A. ln x  x B. 1 ln x  x C. ln x D. 1
C©u 48 : Cho hàm số y  x  ln1 x. Khẳng định nào sau đây đúng?
A. Hàm số có tập xác định là \   1
B. Hàm số giảm trên  1  ; Hàm số giảm trên  1  ;0 và tăng trên
C. Hàm số tăng trên  1  ; D. 0; C©u 49 : x 1
Đạo hàm của hàm số y  ln x bằng 1 x 1 1 2 1 A. x B. D. C. 1 2 x 1 2 x 1 2 x  2 1 C©u 50 : Nếu lo  12 g 18 a thì log2 3 bằng 2a 1 1  a a 1 1  2a A. a B. 2 a C. 2 2a D. 2 a  2 C©u 51 : Cho log 5  , a log 7  , b l g o 3  .
c Tính log 35 bằng: 27 8 2 12 3b  2ac 3b  3ac 3b  2ac 3b  3ac A. . B. C. . D. . c  2 c  2 c  3 c 1 C©u 52 : 5x
Tập xác định của hàm số y  ln là: 3x  6 D = A. B. D = (0; 2) . C. D = [0; 2] . D. D = (2;  )  . ( ;  0) (2; ) 
C©u 53 : Hàm số nào có đồ thị như hình vẽ dưới đây: 7 x  1  x  1  A. y   
B. y    C. 3x y D. ( 3)x y   3   3 
C©u 54 : Tập nghiệm của bất phương trình 2log x 1  log 5  x 1 là 2   2   A. 1;5 B.  3  ;3   C. 3;5   D. 1;3
C©u 55 : Tập xác định của hàm số y  ln x  2 là  1  2 A. e ;    B. 0; C. ;   D.  ;   2 e  8 ĐÁP ÁN 01 { | } ) 28 { | ) ~ 55 { | ) ~ 02 { | } ) 29 ) | } ~ 03 ) | } ~ 30 { ) } ~ 04 ) | } ~ 31 ) | } ~ 05 { | } ) 32 { ) } ~ 06 { | ) ~ 33 ) | } ~ 07 { | } ) 34 { | } ) 08 { | ) ~ 35 { | } ) 09 { ) } ~ 36 { | } ) 10 ) | } ~ 37 { | ) ~ 11 { ) } ~ 38 { | } ) 12 ) | } ~ 39 { | ) ~ 13 ) | } ~ 40 { ) } ~ 14 ) | } ~ 41 ) | } ~ 15 { ) } ~ 42 ) | } ~ 16 { | } ) 43 { | } ) 17 { ) } ~ 44 ) | } ~ 18 { | ) ~ 45 ) | } ~ 19 { | ) ~ 46 { | } ) 20 { | ) ~ 47 { | ) ~ 21 { ) } ~ 48 { | ) ~ 22 { ) } ~ 49 { | ) ~ 23 { ) } ~ 50 { | } ) 24 { | ) ~ 51 { ) } ~ 25 { ) } ~ 52 ) | } ~ 26 { | ) ~ 53 { ) } ~ 27 { ) } ~ 54 { | } ) 9 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 07 C©u 1 : log 5 1lg2 log 36
Tìm giá trị của biểu thức sau: 6 9 36 10 3 A. 15 B. 40 C. 24 D. 30
C©u 2 : Giải bất phương trình x  log x 1 2 A. x > 0 B. 0 < x <2 C. x > 2 D. x > 1 C©u 3 : 4log 5 2 Giá trị của a a
a  0,a  1 bằng A. 58 B. 54 C. 52 D. 5
C©u 4 : Phương trình lgx  3  lgx  2  1 lg5 có bao nhiêu nghiệm? A. 0 B. 3 C. 2 D. 1 C©u 5 : 5  
Với x  0, đơn giản biểu thức : 3 6 12 5 2 x y  
xy  ta được kết quả:   A. -2xy2 B. 0 C. -xy2 D. 2xy2
C©u 6 : Tập các số x thỏa mãn log x  4 1  0 0,4   A.  ;  6,5 B. 6,5;  C. 4;  D. 4;6,  5 C©u 7 : 1
Tìm giá trị của biểu thức sau: 3 B  2 log 6  log 400  3log 45 1 1 1 2 3 3 3 A. 3 B. -3 C. -4 D. 4
C©u 8 : Để phương trình: (m+1).16x-2(2m-3)4x+6m+5=0 có hai nghiệm trái dấu thì m phải thõa mãn điều kiện: 3 5 
A. Không tồn tại m B. -4C. 1   m D. 1   m  2 6
C©u 9 : Bất phương trình 2
lg x  m lg x  m  3  0 có nghiệm x > 1 khi giá trị của m là: A. ( ;  3  ) B.  ;  3  6; C. 6; D. 3;6 1 C©u 10 :    
Tìm giá trị của biểu thức sau: A  log 2sin  log o c s 2   2  12  12 A. 3 B. 2 C. -1 D. -2 C©u 11 : 1  log 9log 6  7 7 log 4 2 5   
Tìm giá trị của biểu thức sau: A 72 49 5    A. 22 B. 19 C. 22,5 D. 30 C©u 12 : 3x  .3y  27 Hệ 
có nghiệm  x ; y . Khi đó 2x y thuộc về tập hợp: 0 0  0 0 3x   3y  12 A.  2  ;1;  3 B.  1  ;0;  2 C. 0;1;  2 D. 0;1;2;  3 C©u 13 : Cho log  . Khi đó 2 5 a log41250 bằng: 1 A. 1 4a
B. 21 4aC. 1 4a D. 2  4a 2 C©u 14 : 2  x x  Bất phương trình: log  có nghiệm là 1 log 0  6 x  4 2   A. Vô nghiệm B. 4   x  3
 ;x  8 C. x  4  ;x  8 D. x  4  ; 3   x  8
C©u 15 : Cường độ một trận động đất M (richter) được cho bởi công thức M  logA logA0 , với A là
biên độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động
đất ở San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác
Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ là A. 11 B. 2.075 C. 33.2 D. 8.9 C©u 16 : 1
Các số thực x thỏa mãn  x x a a   1 2 A. x = 1 B. x > 0 C. Không có x nào D. x = 0 C©u 17 : 4 x 2 x  2   3 
Tập hợp các số x thỏa mãn       3   2   2   2   2   2  A. ;    B. ;    C.  ;   D. ;     5  5   3   3  C©u 18 : x
Nếu  6  5  6  5 thì 2 A. x < 1 B. x > - 1 C. x > 1 D. x < - 1
C©u 19 : Xét các mệnh đề: (I) 5 log 5.log 7.log 4.log 41  0 3 2 1 27 2 (II) 3 log 12.log
16.log 1  0 (với 0 < a  1) 2 3 a a a Mệnh đề nào đúng?
A. (I) đúng, (II) sai
B. Cả (I) và (II) đều đúng
C. Cả (I) và (II) đều sai
D. (I) sai, (II) đúng C©u 20 : ln x Hàm số y  x
A. Có một cực tiểu
B. Có một cực đại
C. Không có cực trị
D. Có một cực đại và một cực tiểu.
C©u 21 : Nghiệm của phương trình log x 9 2 9.x  x là: A. 12 B. 9 C. 6 D. 3
C©u 22 : Cho bất phương trình log
2x 1  1 có tập nghiệm S. \S bằng: 3 10  1   7   13   7  A.  ;     ;      B.  ;     ;       2   20   20   20   13   7  D. Đáp số khác C.  ;     ;       20   20 
C©u 23 : Tìm giá trị của biểu thức sau: B  log 3 3 7  3  log  3 3 3 49  21  9 4 4  A. -2 B. 2 C. 1 D. -1
C©u 24 : Cho a  log 14 . Tính log 32 theo a 2 49 5 1 5 A. B. C.
D. 10a   1 a 1 2(a 1) 2a   1 C©u 25 : Nếu log 6  ;
a log 7  b thì log 7 bằng 12 12 2 a a a b A. B. C. D.  1 b a 1 b 1 a 1
C©u 26 : Một lon nước soda 800F được đưa vào một máy làm lạnh chứa đá tại 320F. Nhiệt độ 3
của soda ở phút thứ t được tính theo định luật Newton bởi công thức ( ) 32 48.( 0.9)t T t  
. Phải làm mát soda trong bao lâu để nhiệt độ là 500F? A. 4 B. 1,56 C. 2 D. 9,3
C©u 27 : Xét các mệnh đề: 3 1,7  1   1  (I)      (II) 5 2,23 4  4  5   5  Mệnh đề nào đúng?
A. (I) đúng, (II) sai
B. (I) sai, (II) đúng
C. Cả (I) và (II) đều đúng
D. Cả (I) và (II) đều sai C©u 28 : 2  Cho hàm số 3  5x x y . Tính y '  2 A.     2x 3 ' 2 3 5 x y x ln 5 B. x 3 '  5 x y ln 5  x x C.     2 3 ' 2 3 5x x y x
D. y  x x 2 2 3 ' 3 5 ln 5 C©u 29 : Biết log
a  2 thì log a bằng 6 6 A. 36 B. 6 C. 4 D. 1
C©u 30 : Đạo hàm của hàm số 2
y  ln(x 1 x )  log (sin 2x) là: 3 1 2co t 2x 1 2 cot 2x A. B.  2   ln 3 x 1 x 2  ln 3 1 x 2x 2co t 2x 1 2 tan 2x C. D.  2   ln 3 x 1 x 2  ln 3 1 x
C©u 31 : Phương trình: 64.9x 84.12x 27.16x    0 có nghiệm là 9 3 A. X=1; x=2 B. Vô nghiệm C. x  ; D. X=-1; -2 16 4
C©u 32 : Bất Phương trình: 64.9x 84.12x 27.16x    0 có nghiệm là 9 3 A. 1B. x
C. X<1 hoặc x>2 D. Vô nghiệm 16 4 C©u 33 : x 1 3    3
Tập nghiệm của hệ phương trình  là: 2 2 3x 2 2x x 4 0,2  0,2 4  3  A. ;    B.   2  C.  2  ;  3 D.   2 
C©u 34 : Số nghiệm nguyên của bất phương trình: log 3x  5  log x 1 là: 1 5   1 5   A. 0 B. 2 C. 1 D. Vô số C©u 35 : 1 cos x Cho hàm số y  ln . Tìm y ' sin x 1 1 1 1 A. y '   B. y '  C. y '  D. y '   sin x cos x sin x cos x C©u 36 : Trên đoạ 3 n 1;2  5 bất phương trình log  4 x  log 4 x có mấy nghiệm nguyên? 2 A. 15 B. 8 C. 0 D. 16
C©u 37 : Tập nghiệm của bất phương trình log     3  x  3 log3  x 5 1 là: A. 5;6 B. 5;  C. 6;  D. 2;6 C©u 38 : 1
7.Tìm giá trị của biểu thức sau: C  log 2  log 3 36 1 2 6 1 3 1 5 A. B. C. D. 2 2 2 2
C©u 39 : Bất Phương trình: x  5  3 4log log có nghiệm là: 25 x 1
A. 0  x  5; x  5 B. 5  x  5
C. x  5; x  5 D. 0  x  ; x  1 2
C©u 40 : Phương trình: 4x- 3.2x-4=0 có nghiệm là A. X=2 B. X=-1; 4 C. X= 1; 4 D. Vô nghiệm C©u 41 : Phương trình: x  (x  2) log log có nghiệm là 5 7 A. X=1 B. X=5 C. Vô nghiệm D. X=7
C©u 42 : Tập xác định của hàm số x 2 y (3 9)   là: A. B. \   2 C. (2; )  D. ( ;  2)
C©u 43 : Tập nghiệm của bất phương trình 4x 2x   2  0 là: 5 A.   ;1  B. 2;  C. 1; D.  ;  2 C©u 44 : 0  ,75 1  1 
Giá trị của biểu thức : 0,5 4 81   36   bằng: 16  A. 7 B. 5 C. 6 D. 8
C©u 45 : Tập nghiệm của bất phương trình lg (x 1)  lg (2  x) 1 2 2 1 5 1 5   1 5  A. 1   5;1 5   B.  ;  C.  ;    D.  1  ;2 2 2   2   C©u 46 : Cho a  log . Khi đó 315 log2515 bằng: a a a a A. B. C. D. 2a   1 a 1 2a   1 a  1 C©u 47 : 1 1   log 4  9 log 8 log 2 4 2 125 7   
Tìm giá trị của biểu thức sau: A 81 25 .49   A. 20 B. Đáp án khác C. 19 D. 18 C©u 48 : 1 log 33log 5 2 5 1log 5
Tìm giá trị của biểu thức sau: 4 2 A 16  4 A. 192 B. 529 C. 592 D. Đáp án khác
C©u 49 : Số lượng của một số loài vi khuẩn sau t (giờ) được xấp xỉ bởi đẳng thức 0.195t Q Q e 0 , trong
đó Q0 là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn ban đầu là 5000 con thì sau bao lâu có 100.000 con. A. 20 B. 3.55 C. 24 D. 15,36 C©u 50 : 27 log 27  log 1 3 3 5 9
8.Tìm giá trị của biểu thức sau: 3 C  4 1  1  log  log   1 3 81  3  3 1 3 4 A. B. C. D. Đáp án khác 2 2 5
C©u 51 : Tìm giá trị của biểu thức sau: A  log 15  log 18  log 10 9 9 9 2 3 A. 4 B. C. D. 3 3 2 6 C©u 52 : 1 2 Phương trình   1 5  log x 1 
có tổng các nghiệm là: log x 2 2 33 A. 5 B. C. 66 D. 12 64
C©u 53 : Bất Phương trình: 4x- 3.2x-4<0 có nghiệm là A. X<2 B. 0C. X=2
D. -1C©u 54 : Cường độ một trận động đất M được cho bởi công thức M  logA logA0 , với A là biên độ
rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở
San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó
đo được 7.1 độ Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu trận động đất này. A. 4 B. 1,17 C. 2,2 D. 15,8
C©u 55 : Phương trình: log (log x)  log (log x)  2 có nghiệm là 4 2 2 4 A. X=8 B. X=16 C. X=2 D. X=4
C©u 56 : Nghiệm của phương trình x 1
5   5x  2.2x  8.2x là x  log 4 8 5 A. 5 B. x  log x  log 5 C. x  1 D. 5 2 3 3 2 2
C©u 57 : Số nghiệm âm của phương trình 1 2log 5  log (x  2) là: x2 5 A. 0 B. 1 C. 2 D. Đáp số khác C©u 58 :  
Tìm nghiệm của phương trình x 1 x x 2 3.2  5.2  2  21 A. x  log 2 3 B. x  16 C. x  8 D. x  3 C©u 59 : Phương trình: x  5  3 4log log có nghiệm là: 25 x
A. x  5; x  5 B. X=1; 1/2 C. X=1/5; 5
D. x  1 / 5; x  5
C©u 60 : Tập xác định của hàm số  log 3x y  3 là: A. 1; 
B. Một đáp số khác C. 3;  D. 1; C©u 61 : Phương trình 2x x 2 6.2 13.6 6.3 x  
 0 có tập nghiệm là tập con của tập 7  3   2 1  A.  ; 1  ;4;5 B.  ; 1  ; ;2 C.  4  ; 3  ;1;  0 D.  2  ; 1  ;1;  3  2   3 3  C©u 62 : 2 2  
Tập nghiệm của phương trình x 1 x 1 9  3  6  0 là: A.   0 B.  1  ;0;  1 C.  2  ;0;  2 D.  1  ;  1 8 ĐÁP ÁN 01 { | ) ~ 28 ) | } ~ 55 { ) } ~ 02 { | } ) 29 { | ) ~ 56 { | ) ~ 03 { | ) ~ 30 { ) } ~ 57 { ) } ~ 04 { | } ) 31 ) | } ~ 58 ) | } ~ 05 { ) } ~ 32 ) | } ~ 59 ) | } ~ 06 { | } ) 33 { ) } ~ 60 ) | } ~ 07 { | ) ~ 34 { | } ) 61 { | } ) 08 { ) } ~ 35 ) | } ~ 62 ) | } ~ 09 { ) } ~ 36 ) | } ~ 10 { | ) ~ 37 ) | } ~ 11 { | ) ~ 38 { | ) ~ 12 { | } ) 39 ) | } ~ 13 ) | } ~ 40 ) | } ~ 14 { ) } ~ 41 { ) } ~ 15 { | } ) 42 { ) } ~ 16 { | } ) 43 ) | } ~ 17 { | ) ~ 44 { ) } ~ 18 { | } ) 45 { ) } ~ 19 { ) } ~ 46 ) | } ~ 20 { ) } ~ 47 { | ) ~ 21 { ) } ~ 48 { | ) ~ 22 { | } ) 49 { | } ) 23 { | ) ~ 50 { | ) ~ 24 { | ) ~ 51 { | ) ~ 25 { | } ) 52 { | } ) 26 { | } ) 53 ) | } ~ 27 { ) } ~ 54 { | } ) 9 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 08
C©u 1 : Phương trình 2 x 1  x 3  2 2 x 3  4 x 1 x .2 2 x .2 2     có nghiệm là: 1 1
A. x   , x  3 B. x  1  , x  3
C. x   , x  3
D. Một kết quả khác. 2 4 C©u 2 : Phương trình x 1  x2 x4 x3 7.3 5
 3 5 có nghiệm là: A. x  1  B. x  1 C. x  2  D. x  2 C©u 3 : 3 2 3 3 Cho phương trình log x 2 3 log 4 x log x 6 (1) 1      1     1    . 2 4 4 4 Trong các mệnh đề sau:
(I). Điều kiện phương trình: 6  x  4 và x  2 ;
(II). (1)  3log x  2  3  3log 4  x  3log x  6 1 1 1 ; 4 4 4
(III). (1)  log 4 x 2 log (4 ) x (x 6) 1         1   , 4 4 Mệnh đề nào đúng ? A. Cả I, II, III B. Chỉ III, I. C. Chỉ II, III. D. Chỉ I, II.
C©u 4 : Số nghiệm nguyên của bất phương trình (x-3).(1+lgx) <0 là A. 0 B. 2 C. 1 D. Vô số C©u 5 : 2
Cho phương trình log x 1 log x
2x 1 9 (1) .Trong các mệnh đề: 2     2    2
(I). (1)  2log x  1  log x  1  9, với điều kiện x  1. 2 2
(II). (1)  x  1  8, II).  2 (1) x  2x 63  0, 1 mệnh đề nào đúng? A. Chỉ III, I. B. Cả I, II, III. C. Chỉ I, II. D. Chỉ II, III. C©u 6 : x 5
Tập nghiệm của bất phương trình 0 là log x 4 1 2 S 4 2; A. S 4 2; B. S 5; C. D. S 4;
C©u 7 : Bất phương trình 𝑙𝑜𝑔2(𝑥 − 3) + 𝑙𝑜𝑔2(𝑥 − 1) ≤ 3 có tập nghiệm là: (3; 5] A. (3; 9] B. (3; 11] C. [9 ; 5] D. 2 2 2
C©u 8 : Giá trị nhỏ nhất của hàm số 2x f x trên 2;2 là 1 A. B. 2 2 2 C. 1 D. 2 C©u 9 : 1
Cho hàm số y x 3 , Các mệnh đề sau , mệnh đề nào sai
A. Hàm số có đồ thị nhận trục tung làm trục 1 lim f x 3 đối xứng B. x
Hàm số đồng biến trên ; 0 và nghịch
C. Hàm số không có đạo hàm tại x 0 D. biến 0; C©u 10 : Đặt  5x t
thì bất phương trình 2x x  2 5 3.5
 32  0 trở thành bất phương trình nào sau đây? A. 2 t  75t 32  0 B. 2 t 6t 32  0 C. 2 t 3t 32  0 D. 2 t 16t 32  0
C©u 11 : Hàm số 𝑦 = ln𝑥 đồng biến trên 𝑥 A. (0; +∞) B. (1 ; +∞) C. (0; 𝑒) D. (𝑒; +∞) 𝑒
C©u 12 : Phương trình log x  log x  2 có nghiệm là 5 7   1 1 A. x  5 B. x C. x D. x  7 7 5
C©u 13 : Cho hàm số y  2 x  ln(1  2 )
x . Kết luận nào sau đây về cực trị hàm số này là đúng? 2 1 4 ln 2 1 4 ln 2 1 A. y   x  y   x  CT 4 tại 1 B. CT 4 tại 2 1 4 ln 2 1 1 4 ln 2 C. y   x  y   x  CÑ 4 tại 2 D. CT 4 tại 1
C©u 14 : Các kết luận sau , kết luận nào sai 3 2 1 1 I. 3 17 28 II. III. 5 7 4 4 IV. 4 5 13 23 3 2 A. I B. III C. II và III D. II và IV
C©u 15 : Tìm m để phương trình có 2 nghiệm phân biệt 9x –m.3x+1=0
A. m>2 hoặc m<-2 B. m>2 C. -2D. m<-2
C©u 16 : Tìm tập xác định của hàm số y  log 2  x . x1   A. D  1;2 B. D  1  ;2   C. D   ;2  
D. D  1;
C©u 17 : Cho hàm số 𝑦 = 𝑓(𝑥) = ln √𝑥2 + 1 ,khi đó 𝑓′(1) = 𝑎. Giá trị của a bằng: 1 1 A. B. 2 C. 1 D. 4 2 C©u 18 : 1 1 1   
Phương trình 4 x  6 x  9 x có nghiệm là:  5 1  5 1 3 x  log   2 x  log   A. x  log x  log 5 1  B. 2 2 C. D. 3 2 2  3   5 1 3 2   2 2
C©u 19 : Cho phương trình log
x m  1  log 
 Giá trị thích hợp của m để    2 mx x 0. 3 2 2 3 2 2 
phương trình có nghiê ̣m duy nhát là: A. m  3  B. m  1  C. m  3 D. m 1
C©u 20 : Phương trình lgx lg x 1  lg x 1  lg x 1 7 5 3.5 13.7     có nghiệm là 1 A. x  100 B. x  1 C. x  10 D. x  10 C©u 21 : 1 Cho hàm số y x3 
, Trong các mệnh đề sau , mệnh đề nào sai 3
A. Hàm số nhận O 0; 0 làm tâm đối xứng
B. Hàm số đồng biến trên tập xác định
D. Hàm số có đồ thị nhận trục tung làm trục C. Hàm số lõm ; 0 và lồi 0; đối xứng C©u 22 :
Số nghiệm của phương trình:
2𝑙𝑜𝑔8(2𝑥) + 𝑙𝑜𝑔8(𝑥2 − 2𝑥 + 1) = 4 3 𝑙à: A. 0 B. 2 C. 1 D. 3
C©u 23 : Cho a 0;b 0;a 1;b 1;n R , một học sinh tính biểu thức 1 1 1 P ...... theo các bước sau log b log b log b a 2 n a a I . 2 P log a log a ... log n a b b b II. 2 P
log a.a ... n a b III. 1 2 3 ... P log n a b IV. P n n 1 log a b
Bạn học sinh trên đã giải sai ở bước nào A. I B. II C. III D. IV C©u 24 : 
Cho hàm số y x 4 , Các kết luận sau , kết luận nào sai
Hàm số luôn luôn đồng biến với mọi x
A. Tập xác định D 0;
B. thuộc tập xác định
C. Hàm số luôn đi qua điểm M 1;1
D. Hàm số không có tiệm cận
C©u 25 : Tìm khẳng định đúng 2016 2016 A. 2  3  2  32017 B. 2  3  2  32017 2016   2016  C.  2  3    2  3 2017 D. 2  3  2  3 2017
C©u 26 : Cho a  log 15;b  log 10 vậy log 50 ? 3 3 3 A. a b 1 B. 4 a b 1 C. 3 a b 1 D. 2 a b 1 4 C©u 27 : 2 Cho hàm số sin x f x e
. Tập nghiệm của phương trình f ' x 0 là k S k2 , k A. S B. S k ; k C. S , k D. 2 C©u 28 : 2 
Cho hàm số y   x2 3
 2 , tập xác định của hàm số là 2 2 2 2 A. D ; B. D ; ; 3 3 3 3 2 2 2 C. D ; ; D. D R \ 3 3 3
C©u 29 : Với mọi số a;b 0 thỏa mãn 2 2 a 9b
10ab thì đẳng thức đúng là A. lg a 3b lga lgb B. lg a 1 lgb 1 a 3b lga lgb C. lg D. 2 lg a 3b lga lgb 4 2
C©u 30 : Tính đạo hàm cấp hai y'' của hàm số y  ln(3x  2) . 9  9  3 A. y''  y''  y''  y  x  2 (3x  2) B. 3x C. D. 2 '' 3ln (3 2)  2 2 (3x  2)
C©u 31 : Tìm m để phương trình log2 x m x   3 log 1
0 có nghiệm duy nhất nhỏ hơn 1. 3 A. m=2 B. m= -2 C. m  2 
D. Không tồn tại m C©u 32 :  Cho hàm số 5
y  3x   1
, tập xác định của hàm số là A. D R B. D 1; C. D ;1 D. D R \ 1
C©u 33 : Phương trình 2x 1  x 1 2 33.2  
 4  0 có nghiệm là: A. x  2  , x  3
B. x  1, x  4 
C. x  2, x  3  D. x  1  , x  4 C©u 34 :
Số nghiệm của phương trình
(𝑙𝑜𝑔24𝑥)2 − 3𝑙𝑜𝑔√2 𝑥 − 7 = 0 là: A. 0 B. 3 C. 2 D. 1
C©u 35 : Trong các khẳng định sau thì khẳng định nào sai? 5  2016 x  2017  2016 x  2017 A. 2  3  2  3 x B. 2  3  2  3 x x2016   2016 x  2016 C. 2  x 3  2  3 2017 D. 2  3  2  3 x
C©u 36 : Hàm số đồng biến trên từng khoảng xác định của nó là 4 1 x 1 A. f x 2x 1 B. f x C. f x e D. f x lnx x x
C©u 37 : Tập nghiệm của bất phương trình  4  lg x  3  là  1000 ; 0    ; 10000 A.  4 ; 3  B.  10000 ; 1000  C. D. Vô nghiệm
C©u 38 : Nghiệm của phương trình 3 log x log 3x 1 0 . 3 3 A. x 9;x 27 B. x 3; x 27 C. x 3;x 81 D. x 9;x 81
C©u 39 : Tìm m để phương trình có 1 nghiệm 9x –m.3x+1=0 A. m  2  B. m  2 C. m  2  D. m  2 C©u 40 : x
Tập nghiệm của bất phương trình 5 2 2  25 là A. x>2
B. x>2 hoặc x<0 C. x<0 D. 0C©u 41 : x e
Cho hàm số f (x)  . Tính f '(1) . 2 x 4 4 A. f '(1)  e f   f  e f '(1)  e 5 B. '(1) e C. '(1) 3 D. 3 C©u 42 : x x
Phương trình  5 24   5 24  10 có nghiệm là 1 A. x  2  B. x  1  C. x  4  D. x   2
C©u 43 : Bất phương trình: log 2x 1  log x  2 1 có tập nghiệm là: 2   1   2 5 A. (2; +∞) B. [5 ; 3] C. (2 ; ] D. (2; 3] 2 2
C©u 44 : Cho log 14  m , tính P  log 32 theo m. 2 49 5 1 A. P  P  m P  m P  2m  2 B. 3 1 C. 3 2 D. m1 6
C©u 45 : Hàm số 𝑦 = 1 − ln (𝑥2 − 1) có tập xác định là: √2−𝑥 (−∞; −1) ∪
A. (−∞; 1) ∪ (1; 2) B. 𝑅\{2} C. (1; 2) D. (1; 2) C©u 46 : Hàm số x f x x
e đồng biến trên A. 0; B. 0; C. ;0 D.
C©u 47 : Tập nghiệm của phương trình log x 1  2 là 3 A.   3 B.   2 ; 4 C.   2 ; 10 D.   2 ; 3 C©u 48 : 1
Tập xác định của hàm số 2 f x lg x 3x 2 là 2 x 4x 5 A. 1;1 2;5 B. 1;1 2;5 C. 1;1 2;5 D. 1;1 2;5 C©u 49 : log 1
Tất cả các giá trị của x thỏa mãn 3 1 3 x x là A. x 1 B. x C. x 1 D. x 0 C©u 50 : Giá trị của 3 2 2 2  4 . bằng A. 8 B. 3 2 2  C. 6 2 4 4  D. 32 C©u 51 : Cho hàm số x
y a , Các mệnh đề sau , mệnh đề nào sai
A. Đồ thị hàm số không có điểm uốn
Đố thị hàm số luon đi qua điểm M 0;1 và
B. N 1;a
C. Đồ thị hàm số có đường tiệm cận là y
0 D. Đồ thị hàm số luôn tăng
C©u 52 : Giá trị lớn nhất , nhỏ nhất của hàm số 2x y trên 2;2 là 1 1 A. GTLN = 1 ; GTNN = B. GTLN = 4 ; GTNN = 4 4 1 D. GTLN = 4 ; GTNN = 1 C. GTLN = 4 ; GTNN = 4
C©u 53 : Bất phương trình 2𝑙𝑜𝑔9(9𝑥 + 9) + 𝑙𝑜𝑔1(28 − 2. 3𝑥) ≥ 𝑥 có tập nghiệm là: 3
A. (−∞; 𝑙𝑜𝑔314)
B. (−∞; 1] ∪ [2; 𝑙𝑜𝑔314) 7
C. (−∞; −1] ∪ [2; 12)
D. (−∞; −1] ∪ [2; 𝑙𝑜𝑔314) 5 C©u 54 : 2 1   x   1 1 1 x Giải bất phương trình  3      12 .  3   3  A. x  3 B. 1   x  0 C. x  2 D. 2  x  4 C©u 55 : 3 Cho phương trình x 2 2 log m 2x 5x , với m là tham số. 2 3 3
Tất cả các giá trị của m để phương trình trên có một nghiệm là A. 34 2 2 m 2 B. m 4 hoặc 34 0 m 2 m 4 hoặc 34 0 m 2 . C. D. 2;
C©u 56 : Giá trị nhỏ nhất của hàm số 𝑦 = |𝑙𝑜𝑔𝑥2+1(4 − 𝑥2) + 𝑙𝑜𝑔4−𝑥2(𝑥2 + 1)| bằng: A. 8 B. 4 C. 6 D. 2
C©u 57 : Cho hàm số y  ln(4x  3) . Đẳng thức nào sau đây đúng? 4y'(4x3)y''  0 y 4y'(4x3)y''  0 A. 4y' 3y''  0 B. C. y' 4y''  0 D. C©u 58 : Phương trình
log log x  log log x  2 có nghiê ̣m là: 4  2  2  4  A. x  16 B. x  8 C. x  4 D. x  2
C©u 59 : Phương trình x 1  x 1  x 9  6  4 . 3 có bao nhiêu nghiệm: A. 4 B. 3 C. 2 D. 1
C©u 60 : Cho phương trình log x x 1  log 4 x  3  4
x 1 . Trong các phát biểu sau, 3   9  phát biểu nào là sai.
A. Phương trình có nghiệm là x  9
B. Phương trình có nghiệm là x  0
C. Phương trình có nghiệm là x  4
D. Phương trình có nghiệm là x  1 8 ĐÁP ÁN 01 ) | } ~ 28 { | } ) 55 { | ) ~ 02 ) | } ~ 29 { | ) ~ 56 { | } ) 03 ) | } ~ 30 ) | } ~ 57 { ) } ~ 04 { ) } ~ 31 { ) } ~ 58 ) | } ~ 05 { ) } ~ 32 { | } ) 59 { | } ) 06 { | ) ~ 33 ) | } ~ 60 ) | } ~ 07 { | } ) 34 { | ) ~ 08 { | ) ~ 35 { ) } ~ 09 { | } ) 36 { | ) ~ 10 ) | } ~ 37 { ) } ~ 11 { | ) ~ 38 { | ) ~ 12 ) | } ~ 39 { ) } ~ 13 { ) } ~ 40 { ) } ~ 14 { | } ) 41 { ) } ~ 15 { ) } ~ 42 ) | } ~ 16 ) | } ~ 43 { | ) ~ 17 { | } ) 44 ) | } ~ 18 ) | } ~ 45 { | ) ~ 19 ) | } ~ 46 { | ) ~ 20 ) | } ~ 47 { ) } ~ 21 { | } ) 48 { | ) ~ 22 { | ) ~ 49 { | ) ~ 23 { | } ) 50 { ) } ~ 24 { | } ) 51 { | } ) 25 { ) } ~ 52 { | } ) 26 { | } ) 53 { | } ) 27 { | ) ~ 54 { ) } ~ 9 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 09 C©u 1 : 2 2 2 Số 3 3 bằng: 3 3 3 5 7 3 5  18   2   27   18   A. 3 3 3 3   B.   C.   D.    2   2   2   2 
C©u 2 : Phương trình 2 2 x x 2 2
 2 xx  3 có tổng các nghiệm bằng: A. 1 B. 0 C. -1 D. -2 C©u 3 : Hàm số f(x) = 2
x ln x đạt cực trị tại điểm: 1 1 A. x = B. x = C. x = e D. x = e e e
C©u 4 : Phát biểu nào sau đây là sai: A.
y  log xa  0,a   Hàm số lôgarit 1 0;  a có tập xác định là  . B. Hàm số mũ x
y a nhận trục Ox làm tiệm cận ngang. C. Hàm số mũ x
y a có tập xác định là 0;  . D. x
Hàm số y a và y  log x đồng biến khi a > 1. a C©u 5 : Cho hàm số 2 y  log x và 8
y  log x . Tổng các hoành độ giao điểm của hai đồ thị hàm số 1 2 4 đã cho là: A. 2 B. 3 C. 5 D. -1 C©u 6 : x x
Phương trình  2   1   2   1
 2 2  0 có tích các nghiệm là: A. -1 B. 1 C. 0 D. 2 1 C©u 7 : 1-x x  3  Hàm số y = 2 .   5 
A. Đồng biến trên 0; 
B. Nghịch biến trên tập R
C. Đồng biến trên tập R Đồng biến trên  1 ;  , nghịch biến trên D.    ; 1
C©u 8 : Giả sử ta có hệ thức a2 + b2 = 7ab (a, b > 0). Hệ thức nào sau đây là đúng? a  b
A. 2 log a  b  log a  log b B. 2 log  log a  log b 2   2 2 2 2 2 3 a  b a  b C. log  2 log a  log b D. log  log a  log b 2  2 2  3 2 2 2 6
C©u 9 : Cho hàm số    2 8ln x y f x   . Chọn câu đúng nhất. x
A. Hàm số nghịch biến trên 0 
;1 và đồng biến trên 1;  .
B. Đồ thị hàm số có một điểm cực đại và một điểm cực tiểu.
C. Đồ thị hàm số nhận điểm M 1;0 làm điểm cực tiểu.
D. Hàm số đồng biến trên 0 
;1 và nghịch biến trên 1;  C©u 10 :  
Tổng các nghiệm của phương trình: 2x 4 x 1 2  5.2 1  0 5 A. 4 B. 5 D. C. -4 8 C©u 11 : 2 3
log (x  3)  log (x  3) 1 1
Nghiệm của bất phương trình 2 3  0 là: x 1 A. x  1  B. x  0 C. x  2  D. 2   x  1 
C©u 12 : Tập nghiệm của bất phương trình x x 1 2 2    6 là: A. ( ;  0) B. ( ;  2) C. ( ;  3) D. ( ;  1)
C©u 13 : Tập nghiệm của phương trình 2x x 2x 2.2 9.14  7.7  0 là : A. S  0;  1 B. S   1  ;  0 C. S    0 D. S   1  ;  0 2 C©u 14 : 1 
Giá trị lớn nhất của hàm số    2 y ln x ln x   1 trên đoạn ; 2   đạt tại : 2  1 3 3 A. x 1 B. x  C. x  D. x  2 2 4
C©u 15 : Để giải bất phương trình: ln 2x > 0 (*), một học sinh lập luận qua ba bước như sau: x  1   Bước 1: Điề 2x x 0 u kiện:  0   (1) x  1 x  1 Bướ 2x 2x 2x c 2: Ta có ln > 0  ln > ln1   1 (2) x  1 x  1 x  1
Bước3: (2)  2x > x - 1  x > -1 (3)  1   x  0
Kết hợp (3) và (1) ta được  x  1
Vậy tập nghiệm của bất phương trình là: (-1; 0)  (1; +)
Hỏi lập luận trên đúng hay sai? Nếu sai thì sai từ bước nào? Lập luận hoàn A. toàn đúng B. Sai từ bước 3 C. Sai từ bước 1 D. Sai từ bước 2
C©u 16 : Hàm số nào đồng biến trên khoảng  ;  0 ? 1   2 y ln x  x  2 A. 2 y  x 1 B. x y  e  C. x 2 y  e  x D. x C©u 17 :
Cho hai hàm số y  f x  log x và    x y
g x  a . Mệnh đề nào sau đây là sai? a I.
Đồ thị hai hai hàm số f và g luôn cắt nhau tại một điểm. II.
Chiều biến thiên của hai hàm số f và g là giống nhau. III.
Đồ thị hàm số f nhận trục Oy làm tiệm cận. IV.
Chỉ có đồ thị hàm số f có tiệm cận. A. I, IV. B. I, II. C. III, IV. D. II, III.
C©u 18 : Bất phương trình 2x 1 3   (  3)3x m
 2(m  3)  0 khi: A. m  3  B. m  3  C. m  0 D. m  21 C©u 19 : Phương trình 2 log (x 1)  6log
x 1  2  0 có tập nghiệm là: 2 2 3 A. 3;1 5 B. 1; 2 C. D. 1; 3
C©u 20 : Hàm số y =x.lnx đồng biến trên khoảng nào 1 1 1 A. (0; )  B. (0; ) C. ( ; ) D. ( ; ) e e e
C©u 21 : Nghiệm của phương trình x 1  12 x 2 2  2  3 2 là A. x   3 B. x  2 C. 3 x  2 D. 3 x   2
C©u 22 : Phương trình 8.3x 3.2x 24 6x  
có tổng các nghiệm bằng: A. 4 B. 6 C. 2 D. 3
C©u 23 : Phương trình 2log 2x  2  log 9x 1  1có tổng các nghiệm bằng: 2   1   2 A. 5/2 B. 0 C. 3/2 D. -3/2 C©u 24 : 2x x 1   3   2 
Tập nghiệm của bất phương trình      là:  2   3   1 1  A.   ;  B.  ;    1 C. ; D.  ; 1     3 3  C©u 25 :
ln x  ln y y x Cho hệ phương trình 
. Nghiệm (x;y) của hệ là 2 2
x y  6x  2y  6  0 A. (1;3);(3;3) B. (1;3);(3;1) C. (1;1);(3;3) D. (1;1);(3;1)
C©u 26 : Phương trình log 2  log x  0 có tích các nghiệm bằng: x 16 A. 1 B. -1 C. 0 D. -4
C©u 27 : Điều kiện cần và đủ của a và b để cho log b  0 là : a
A. a  0,b  0
B. a  0,b  0
C. a  0,b  0 và a-  1 .b   1  0
D. a  1,b  1
C©u 28 : Trong các hàm số sau, hàm nào luôn đồng biến A. (0,99)x
B. y  log (x 1)   y  log x 0,5 C. 2 y x 1 D. 2 C©u 29 : 3x x 1 3
Tập nghiệm của bất phương trình log (3 1) log  là: 4 1 16 4 4 4 A. (0;1] B. [1;2] C. [2; )  D. (0;1][2; ) 
C©u 30 : Giá trị lớn nhất của hàm số 2
y  ln x  2ln x  2 trên đoạn 3 1  ;e    là : Không tồn tại giá A. 1. B. 0 .. C. 2  . D. trị lớn nhất.
C©u 31 : Bất phương trình: x x 1 4 2    3 có tập nghiệm là: A. 1; 3 B.  ;  log 3 2; 4 log 3; 5 2  C.   D.  2  C©u 32 :
ln x  ln y y x Cho hệ phương trình 
. Giá trị của m để hệ có 2 cặp nghiệm phân 2 2
x y  6mx  2my  6  0 biệt là 1 1 3 A. 0  m 1 B. m C. m  2 D. m  2 2 2
C©u 33 : Phát biểu nào sau đây là sai: log b  log         b , a 0; b 0; a 1; R a  log c log a A. b b ac
,(a, b,c  0; b  1) a B. 2 ln b
C. log b  2 log b,a  0, a   1 log b
, a  0; b  0; a  1 a a D. a   ln a C©u 34 : 1 2  Đơn giả x 1 1 n biểu thức: : 1 1,5 x 1 2 x x 1 1 A. 1 B. x 1 C. 2 x 1 D. x 1
C©u 35 : Số nghiệm nguyên của phương trình 2 2 x x 5  x 1   x 5 4 12.2    8  là: A. 2 B. 1 C. 0 D. 3
C©u 36 : Đạo hàm của hàn số y= 2 .x3x là A. x 1  x 1 2 3   B. 2x 3xC. 6 . x ln 6 D. 6x C©u 37 :  Đạ x 1
o hàm của hàm số y  ln là : x  2 x  2 x  2 3 x 1 A. B. C. D.  x 1  x 1 2 x  x  2 x  22 x   1 ln    x  2  5
C©u 38 : Phương trình 2 2 2 x x x 2 4  2.4
 4 x  0 có tích các nghiệm bằng: A. 0 B. 1 C. -1 D. 2 C©u 39 : Phương trình: 1  2 = 1 có tập nghiệm là: 4  log x 2  log x  1  A. 1; 2  0 B. 10; 10  0 C.  ; 10 D.   10 
C©u 40 : Phương trình log  x 3 4  2k
x có 2 nghiệm phân biệt khi: 2  1 1 1 A. k B. k C. k  0 D. 0  k  2 2 2
C©u 41 : Tập xác định của hàm y= 2 log (x  2x) 0,5 là A. ( ;  0) B. (0; 2) C. (2; )  D. R \ [0; 2]
C©u 42 : Cho hàm số y= sinx e . Khi đó y’.cosx-y” =? A. . y cosx B.  . y s inx C. . y s inx D.  . y cosx C©u 43 : 2 Cho hàm số 3
y  (2x  1) , Tập xác định của hàm số là:  1   1  A. ;    B. R C. ;    D. 0;  2   2 
C©u 44 : Cho a  log 18,b  log 54 . Tính giá trị của biểu thức E  ab  5a  b 12 24 A. 1 B. - 1. C. 2 D. - 2
C©u 45 : Phương trình 3.8x 4.12x 18x 2.27x   
 0 có tập nghiệm là: A.   1 B. 1; 1 C. 0; 1 D.  C©u 46 : So sánh 2 3 4 2 2 3 2 4
M a a b b a b với    3 3 2 3 2 N a b :
A. M N
B. M N  0
C. M N
D. M N
C©u 47 : Tập nghiệm của phương trình: x 1  3x 5  5  26 là: A. 3;  5 B. 1;  3 C. 2;  4 D.
C©u 48 : Phương trình: log x  x  6 có tập nghiệm là: 2 6 A.   4 B. C.   3 D. 2;  5
C©u 49 : Phương trình log  2
x  x  5  log 2x  5 có tổng các nghiệm bằng: 3  3   A. 3 B. 5 C. 2 D. -10
C©u 50 : Cho a,b  0 và a,b  1 ; x và y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau:
A. log (x y)  log x  log y B. log .
a log x  log x a a a b a b 1 1 x log x C. log  log aa D. x log x a y log y a a C©u 51 : ln 1 2x Tính giới hạn sau : lim x0 3x 2 A. B. 0 C. 1 D. 2 3
C©u 52 : Tập nghiệm của bất phương trình log 2x  5  0 0,5    5  11  A. ; 3    B. 3;   C.  ; 3 D. ;    2   4  C©u 53 :  x  sin   n2  Cho hàm số  2 l y
. Đạo hàm của hàm số đã cho là:  x   x  sin      1 x sin  x     l  x A.  n2 '  s in     1.2 l y  n2
B. y '  cos  .2 .   n2 l    n l 2  n l 2  x 
D. Tất cả đều sai. sin  x    C.  n2 '  cos  .2 l y   n2 l
C©u 54 : Bất phương trình x x 1  2 4  (m  2)2
m  2m  2  0 có tập nghiệm là khi: A. m  1 B. m  2  C. m  2 D. m  1  C©u 55 : 2 2
log x  log x  0 2 2 
Cho hệ bất phương trình 3  x 2 
 3x  5x  9  0  3
Nghiệm hệ bất phương trình là: A. 0  x 1 B. x  4 C. x  0 D. 1 x  4 7
C©u 56 : Cho log 5  a; log 5  b . Khi đó log 5 tính theo a và b là: 2 3 6 ab 1 A. a + b B. C. D. 2 2 a  b a  b a  b C©u 57 : 2
3 x  3  2x
Nghiệm của bất phương trình  0 4x  2 là 1 1 A. x  0 B. 0  x C. x  2 D. x  2 2 2
C©u 58 : Phương trình 2 cos 2 x cos 4 4 x
 3 có tổng các nghiệm bằng: A. B. 2C. 4D. 0
C©u 59 : Phương trình x 1  x2 4  2
m  0 có nghiệm khi: A. m  0 B. m 1 C. m  0 D. m 1
C©u 60 : Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau: 
A. log 1  a và log a  0
B. log x   log x , với x  0,  0 a a a a
C. log (xy)  log . x log y
D. log x có nghĩa với mọi x a a a a 8 ĐÁP ÁN 01 { | } ) 28 { | } ) 55 { | } ) 02 ) | } ~ 29 { | } ) 56 { ) } ~ 03 { ) } ~ 30 ) | } ~ 57 { | } ) 04 { | ) ~ 31 { ) } ~ 58 ) | } ~ 05 { | ) ~ 32 { | } ) 59 { | } ) 06 ) | } ~ 33 { | ) ~ 60 { ) } ~ 07 { | ) ~ 34 { | } ) 08 { ) } ~ 35 { ) } ~ 09 { ) } ~ 36 { | ) ~ 10 { | ) ~ 37 { ) } ~ 11 { | } ) 38 ) | } ~ 12 { | } ) 39 { ) } ~ 13 { ) } ~ 40 { | } ) 14 ) | } ~ 41 { | } ) 15 { ) } ~ 42 { | ) ~ 16 { ) } ~ 43 { | ) ~ 17 ) | } ~ 44 ) | } ~ 18 { | } ) 45 ) | } ~ 19 ) | } ~ 46 { | } ) 20 { | ) ~ 47 { ) } ~ 21 { | ) ~ 48 { ) } ~ 22 ) | } ~ 49 ) | } ~ 23 ) | } ~ 50 { ) } ~ 24 { | ) ~ 51 ) | } ~ 25 { | ) ~ 52 { | ) ~ 26 ) | } ~ 53 { | ) ~ 27 { | ) ~ 54 { | } ) 9 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI THPT 2017
CHUYÊN ĐỀ : MŨ – LÔGARIT ĐỀ 010 C©u 1 : 1 3 xx
Giả sử phương trình x 2 x 1 2 2 9 2 2 3    
có nghiệm là a . Khi đó giá trị biểu thức 1 a  log 2 là: 9 2 2 1 1 log 2 1 A. 1 log 2 log 2 9 B. 1 C. 9 D. 2 9 2 2 2 2
C©u 2 : Phương trình log 9  2x  3 x tương đương với phương trình nào dưới đây 2  
A. 9  2x  3  x B. 2 x  3x  0 C. 2 x  3x  0
D. 9  2x  3  2x C©u 3 : Cho phương trình : x 2x 1 81 4.3  
 27  0 .Tổng các nghiệm của phương trình là bao nhiêu ? 1 3 A. B. 1 C. 2 D. 2 2
C©u 4 : Tìm miền xác định của hàm số sau: y  log (x  2)  3 3 A. 29;  B. 2;  C. 29;  D. 2;29
C©u 5 : Đạo hàm của hàm số f (x)  x ln x x bằng 1 A.
f '(x)  ln x B. f '(x)  1
C. f '(x)  ln x 1
D. f '(x)  ln x x x C©u 6 : 1 1 Biểu thức P   log 5 log 5 bằng 49 7 1 A. log 5 B. log 7 7 C. 2 D. 5 2
C©u 7 : Số giá trị nguyên của n thỏa mãn bất đẳng thức log n   1  log n  2 là: n n 1    A. 0 B. Vô số C. 2 D. 1
C©u 8 : Cho phương trình : logx 2 x
1000x .Tích các nghiệm của phương trình là bao nhiêu A. 10 B. 100 C. 1 D. 100
C©u 9 : Cho bất phương trình log x a  2 , khẳng định nào sau đây là sai: x 1
Với a  1 thì phương trình đã cho vô 1 1 1 4a A.
B. Nếu 0  a
thì a x  . nghiệm. 4 2 1 4a
Nếu a  0 thì bất phương trình đã cho tồn
C. Nếu a  0 thì 1  x  . D. 2 tại ngiệm. C©u 10 : 1  a b c c a  3 log log . . 
Cho log b  5;log c  3.Giá trị biểu thức M .c   là: a a 9 1 1 A. 9 B. C. 81 D. 9 81 C©u 11 : 1
Cho hàm số sau: y
. Hãy chọn hệ thức đúng” 1 x  ln x
A. xy '   y ln x   1 y
B. xy   y 'ln x   1 y
C. xy   y ln x   1 y '
D. xy '   y ln x   1 y
C©u 12 : Giá trị của log a (0  a  1) bằng 2 a 1 1 A. 2 B. 2  C. D.  2 2 C©u 13 : 2 log
Nghiệm của bất phương trình 3 x2 5 1 là: A. x  2  B. x  0 C. x  0 D. x  0
C©u 14 : Cho phương trình : 2log x 3  log x  42  0 .Một học sinh giải bài toán như sau : 3 3  x  3  0 x  3
Bước 1: Điều kiện :    x  4    0 x  4
Bước 2: Ta có : 2log (x 3)  2log (x  4)  0 3 3
 log x  3 x  4  0 3   
 x  3x  4 1 Bước 3: 2
x  7x 11  0  7  5 x  2   7 5 x   2 7  5
Vậy phương trình có nghiệm : x  2 2
Học sinh đó giải sai ở bước nào ?
Tất cả các Bước A. đều đúng B. Bước 3 C. Bước 2 D. Bước 1
C©u 15 : Đạo hàm của hàm số sau: f x   2 ( )
ln x  1 x  bằng 1 x 1 2x x A. f '(x)  B. f '(x) 
C. f '(x) 
D. f '(x)  2 1 x 2 1 x 2 1 x 2 1 x C©u 16 :  Phương trình 2a x log
 log x  0;(a  0, a 1) có nghiệm là: 1 a a a
A. x  2a 1.
B. x a 1.
C. x  2a .
D. x a . C©u 17 : log x log x 3 3 2x
Cho bất phương trình :  10   1   10   1 
.Tập nghiệm của bất phương trình là 3 ? A. x  2 B. x  4
C. 2  x  4 D. x  3
C©u 18 : Tìm m để bất phương trình .9x  (2 1).6x  .4x m m m
 0 có nghiệm với mọi x0,  1 A. m  6  B. m  4  C. 6   m  4  D. m  6 
C©u 19 : Nhận xét nào dưới đây là đúng
A. Hàm số 2017x e đồng biến trên . B. log . b log .
c log a 1, , a , b c a b c
Hàm số ln x là hàm số nghịch biến trên
C. log a b  log a  log , b  , a , b c  0 2   2 2 D. 0;.
C©u 20 : Cho a  log 18,b  log 54. Hệ thức nào dưới đây là đúng. 12 24
A. 5ab a b 1
B. ab  5a b  1
C. ab  5a b  1
D. 5ab a b 1 C©u 21 : 2 1
Cho hàm số sau: ( )  5 x f x e
và biểu thức A f ' x  2xf x  f 0  f '0 . 5
Đâu là hệ thức đúng của biểu thức A? A. A 1 B. A  2 C. A  3 D. A  5 C©u 22 : Phương trình 2 log
((ax) 1)  1;( a  1, a  2) có: 2 2 a x A. Vô nghiệm. B. 3 nghiệm. C. 1 nghiệm. D. 2 nghiệm. 3 C©u 23 : Cho log 5  ; a log 7  ;
b log 3  c . Khi đó biểu thức log 35 được biểu diễn là: 27 8 2 6 2(b ac) b ac 3(b ac) b ac A. . B. . C. . D. . 1 c 2(1 c) 1 c 1 c
C©u 24 : Số tiệm cận của đồ thị hàm số x y xe là A. 0 B. 1 C. 2 D. 3
C©u 25 : Đạo hàm của hàm số 2
y  log (2x x 1) là: 2 4x 1 2
A. y '  (4x 1).log (2x x 1) . B. y '  . 2 2
(2x x 1).ln 2 2(4x 1) 2 C. y '  .
D. y '  2(4x 1) log (2x x 1) . 2
(2x x 1).ln 2 2
C©u 26 : Phương trình log ( 1)  2x x
x x 1 có 2 nghiệm x ; x .Tổng 2 2
x x x x có giá trị là: 2 1 2 1 2 1 2 A. 0 B. 1 C. 2 D. 3
C©u 27 : Cho phương trình : 3 log x  log 3x 1  0 .Bình phương một tổng của các nghiệm của 3 3
phương trình là bao nhiêu ? A. 90 B. 6570 C. 144 D. 7056
C©u 28 : Tích các nghiệm của phương trình 2x 2 3 3   x  30 là A. 1 B. 2  C. 1  D. 2 C©u 29 : 2 x
Cho hàm số y f (x)  . x e
. Trong các hệ thức sau đậy, hệ thức nào đúng? 2 2 2 2 2
A. xy '  1 x y
B. xy  1 x y '
C. xy  1 x y '
D. xy '  1 x y ' C©u 30 : Phương trình 2 2 sin x cos 2 5.2 x   7 có nghiệm là: 2  A. x   k2 .
B. x k  3 . C. x   k . D. x   . 3 2 C©u 31 : cos x f '  2 
Cho hàm số f (x)  e .sinx . Tính A. 1 B. 2 C. 1  D. 2 
C©u 32 : Cho a  log 18,b  log 54. Hệ thức nào dưới đây là đúng. 12 24 4
A. 5ab a b 1
B. ab  5a b  1
C. ab  5a b  1
D. 5ab a b 1
C©u 33 : Phương trình log ( 1)  2x x
x x 1 có 2 nghiệm x ; x .Tổng 2 2
x x x x có giá trị là: 2 1 2 1 2 1 2 A. 0 B. 1 C. 2 D. 3
C©u 34 : Phương trình log 9  2x  3 x tương đương với phương trình nào dưới đây 2   A. 2 x  3x  0 B. 2 x  3x  0
C. 9  2x  3  x
D. 9  2x  3  2x C©u 35 : 2 2 Cho hàm số sin x cos 5 5 x y  
.Tổng giá trị lớn nhất và nhỏ nhất của hàm số là bao nhiêu ? A. 7  5 B. 7  3 5 C. 6  4 5 D. 6  2 5
C©u 36 : Giả sử bất đẳng thức log 2x 1  log
x  3  0 đúng với x  1 và x  4 . Khi đó giá trị 2a 1    a   của a là: A. 0  a 1 B. a  1 C. a  1 D. 0  , a a 1 C©u 37 : 3x 1
Tập nghiệm của bất phương trình log 1 là: 1 x  2 3  1    A. S  2;    . B. S    5 2; 2  ;    .  3   8   
C. S   ;  2 .
D. S    5 ; 2  ;    .  8  C©u 38 : 1 3 xx
Giả sử phương trình x 2 x 1 2 2 9 2 2 3    
có nghiệm là a . Khi đó giá trị biểu thức 1 a  log 2 là: 9 2 2 1 1 1 log 2 A. 1 log 2 log 2 9 B. 1 C. D. 9 2 9 2 2 2 2
C©u 39 : Cho phương trình : 2xx x8 2 2
 2  x  8 2x có hai nghiệm x , x .Tính 3 3 x x 1 2 1 2 A. 28 B. 65 C. 9 D. 72 C©u 40 : 3 a
Biết log a  3 b  0,b  1, a  0 . Giá trị của P  log là: ba b b  3 3 1 A.  3 . B. . C.  . D.  . 2 3 3 5
C©u 41 : Cho hàm số f x
x  x 2 ( ) 4 ln 4  x  4x .
Biểu thức f     f    2 4 ' 8  .ln 2 
bằng số nào trong các số sau: A. 2ln 2 B. 6ln 2 C. 8ln 2 D. 4ln 2
C©u 42 : Nhận xét nào dưới đây là đúng A. log . b log .
c log a 1, , a , b c a b c
B. Hàm số 2017x e đồng biến trên .
Hàm số ln x là hàm số nghịch biến trên C.
D. log a b  log a  log , b  , a , b c  0 2   0;  . 2 2
C©u 43 : Giả sử bất đẳng thức log 2x 1  log
x  3  0 đúng với x  1 và x  4 . Khi đó giá trị 2a 1    a   của a là: A. a  1 B. 0  a 1 C. a  1 D. 0  , a a 1 C©u 44 : 1  a b c c a  3 log log . . 
Cho log b  5;log c  3.Giá trị biểu thức M .c   là: a a 9 1 1 A. B. 9 C. 81 D. 9 81 C©u 45 : Cho hàm số : 2 y
x  3  x ln x trên đoạn 1, 2 .Tích của giá trị lớn nhất và giá trị nhỏ nhất là bao nhiêu ? A. 4ln 2  4 7 B. 7  4ln 2 C. 4ln 2  3 7 D. 2 7  4ln 2
C©u 46 : Nghiệm của bất phương trình 2x7x 12 5 1 là: x  3 x  2 x  3 A. B. C.
D. 3  x  4 x  5 x  4 x  4 C©u 47 : Phương trình 4 2
2 log 2x  log (x 1)  có : 8 8 3 Phương trình đã A. cho vô nghiệm. B. 2 nghiệm. C. 1 nghiệm. D. 3 nghiệm. C©u 48 : Cho hàm số sau: cos ( ) x f x e .
Biểu thức f   f '  f "  f '" bằng số nào trong các số sau: 2 1 e A. B. e C. D. e e 2 6
C©u 49 : Phương trình x  42 2 2
log (x 1)  2log (x 1)  (x  4) log 4.log 16 có: 4 4 x 1  x 1  A. Vô nghiệm. B. 1 nghiệm. C. 2 nghiệm. D. 3 nghiệm. C©u 50 : x e  Tính đạ 2
o hàm của hàm số f (x)  sin x x
e (sin x  cosx)  cosx x
e (sin x  cosx)  2 cosx
A. f '(x) 
B. f '(x)  2 sin x 2 sin x x
e (sin x  cosx)  2 cosx x
e (sin x  cosx)  2 cosx
C. f '(x) 
D. f '(x)  2 sin x 2 sin x C©u 51 : 2 2
Nhận xét nào dưới đây là đúng khi nói về biểu thức   log2 log 9  2 x A   2 ln e x 3 
A. Biểu thức A luôn luôn tồn tại và giá trị của A không phụ thuộc vào giá trị của . x
B. Biểu thức A chỉ xác định khi x  0 và giá trị của A không phụ thuộc vào giá trị của . x
C. Biểu thức A chỉ xác định khi x  0 và giá trị của A phụ thuộc vào giá trị của . x
D. Biểu thức A chỉ xác định khi x  0, x  1 và giá trị của A phụ thuộc vào giá trị của . x C©u 52 :  Đạ x 1
o hàm của hàm số f (x)  ln bằng x 1 2 x 1 1 1
A. f '(x)  B. f '(x) 
C. f '(x) 
D. f '(x)  2 x   x 1 x 1 2 x 1 1 C©u 53 : Cho hàm số x
y xe có đạo hàm y’ và y”. Hệ thức nào sau đây đúng?
A. y" 2y ' y  0
B. y" 2y '1  0
C. y" 2y ' 3  0
D. y" 2y ' 3y  0
C©u 54 : Cho 2x  2y  4, giá trị nhỏ nhất của x y là A. 1 B. 3 C. 2 D. 4
C©u 55 : Số giá trị nguyên của n thỏa mãn bất đẳng thức log n   1  log n  2 là: n n 1    A. Vô số B. 0 C. 1 D. 2
C©u 56 : Giá trị a thỏa mãn 15 7 5 2 a a là A. a  1 B. a  0 C. a  1 D. 0  a 1 C©u 57 : Đạ 2 o hàm của hàm số sin ( ) x f x e bằng 7 2 2 A. sin '( ) x f x e .sin 2x B. 2 sin '( )  cos x f x xe 2 2 C. sin '( ) x f x e cos 2x D. sin '( )  2 x f x e cos x
C©u 58 : Số tiệm cận của đồ thị hàm số x y xe là A. 0 B. 1 C. 2 D. 3 C©u 59 : 2 2
Nhận xét nào dưới đây là đúng khi nói về biểu thức   log2 log 9  2 x A   2 ln e x 3 
A. Biểu thức A chỉ xác định khi x  0 và giá trị của A không phụ thuộc vào giá trị của . x
B. Biểu thức A luôn luôn tồn tại và giá trị của A không phụ thuộc vào giá trị của . x
C. Biểu thức A chỉ xác định khi x  0, x  1 và giá trị của A phụ thuộc vào giá trị của . x
D. Biểu thức A chỉ xác định khi x  0 và giá trị của A phụ thuộc vào giá trị của . x
C©u 60 : Cho phương trình : x x 1x   2 2 2 1 4  2 1 2 x
.Tổng bình phương các nghiệm của phương trình là bao nhiêu ? A. 0 B. 1 C. 4 D. 2 8 ĐÁP ÁN 01 { ) } ~ 28 { | ) ~ 55 ) | } ~ 02 { ) } ~ 29 ) | } ~ 56 { | ) ~ 03 { | } ) 30 { | ) ~ 57 ) | } ~ 04 { | ) ~ 31 { | ) ~ 58 { ) } ~ 05 ) | } ~ 32 { ) } ~ 59 ) | } ~ 06 { | ) ~ 33 { ) } ~ 60 { | } ) 07 { ) } ~ 34 { ) } ~ 08 { | } ) 35 { | } ) 09 { | } ) 36 { ) } ~ 10 ) | } ~ 37 { | } ) 11 ) | } ~ 38 { ) } ~ 12 { | ) ~ 39 { | } ) 13 { | ) ~ 40 { | ) ~ 14 { | } ) 41 ) | } ~ 15 ) | } ~ 42 { ) } ~ 16 { | } ) 43 ) | } ~ 17 { | } ) 44 { ) } ~ 18 { | } ) 45 { | } ) 19 ) | } ~ 46 { | ) ~ 20 { ) } ~ 47 { | ) ~ 21 ) | } ~ 48 ) | } ~ 22 { | } ) 49 { | } ) 23 { | ) ~ 50 { | ) ~ 24 { ) } ~ 51 { ) } ~ 25 { | ) ~ 52 ) | } ~ 26 { ) } ~ 53 ) | } ~ 27 { | } ) 54 { | ) ~ 9