Top 57 bài toán VD – VDC hàm số mũ – logarit có lời giải chi tiết

Tài liệu gồm 38 trang tuyển chọn 57 bài toán mức độ vận dụng và vận dụng cao về chủ đề hàm số lũy thừa, hàm số mũ và hàm số logarit trong chương trình Giải tích 12 chương 2

Môn:

Toán 11 3.3 K tài liệu

Thông tin:
38 trang 1 năm trước
Tác giả:
K
Kim Oanh
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Top 57 bài toán VD – VDC hàm số mũ – logarit có lời giải chi tiết

Tài liệu gồm 38 trang tuyển chọn 57 bài toán mức độ vận dụng và vận dụng cao về chủ đề hàm số lũy thừa, hàm số mũ và hàm số logarit trong chương trình Giải tích 12 chương 2

155 78 lượt tải Tải xuống

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT) 188 tài liệu

Môn: Toán 11 3.3 K tài liệu

Thông tin:

38 trang 1 năm trước

Tác giả:

Profile Kim Oanh
QUYEÅN SOÁ 2
Tuyeån taäp 57 caâu hoûi vaän duïng –
vaän duïng cao töø caùc ñeà thi thöû treân
caû nöôùc naêm 2019 –coù ñaùp aùn chi
tieát thöïc hieän giaûi bôûi taäp theå giaùo
vieân Dieãn Ñaøn Giaùo Vieân Toaùn
HAØM SOÁ MUÕ-
LOGARIT
TOÅNG HÔÏP: NGUYEÃN BAÛO VÖÔNG
FACEBOOK: https://www.facebook.com/phong.baovuong
SÑT: 0946798489
Naêm hoïc: 2018 – 2019
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 1
Câu 1.
Giá trị thực của tham số
m
để phương trình
4 2 3 .2 64 0
x x
m
có hai nghiệm thực
1
x
,
2
x
thỏa
mãn
1 2
2 2 24
x x
thuộc khoảng nào sau đây?
A.
3
0;
2
. B.
3
;0
2
. C.
21 29
;
2 2
. D.
11 19
;
2 2
.
Câu 2.
Cho điểm
(0;4),C
đường thẳng
4y
cắt hai đồ thị hàm số
x
y a
và
x
y b
lần lượt tại
A
và
B
sao
cho
AB AC
(hình vẽ). Khẳng định nào sau đây đúng?
A.
2 .a b
B.
2
.b a
C.
2 .b a
D.
2
.a b
Câu 3.
Cho các số thực dương
,a b
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Giá trị nhỏ nhất của biểu thức
2P a b
bằng
A.
2 10 1
2
. B.
2 10 3
2
. C.
3 10 7
2
. D.
2 10 5
2
.
Câu 4.
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
5 10 25 4
x x
m
có
nghiệm duy nhất. Số tập con của
S
là
A.
3
. B.
4
. C.
16
. D.
15
.
Câu 5.
Anh X muốn mua một chiếc xe máy Yamaha Exciter 150 giá 47.500.000 của cửa hàng Phú Tài nhưng
vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước 25 triệu đồng và trả góp
trong 12 tháng, với lã suất 0.6% tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho cửa hàng Phú Tài số tiền
là bao nhiêu(quy tròn đến hàng đơn vị).
A.
1.948.927
đồng. B.
1.948.926
đồng. C.
2.014.545
đồng. D.
2.014.546
đồng.
Câu 6.
Biết rằng bất phương trình
5
2
2
log 5 2 2.log 2 3
x
x
có tập nghiệm là
log ;
a
S b 
, với
a
,
b
là các số nguyên dương nhỏ hơn 6 và 1a
. Tính
2 3P a b
.
A.
7
P
. B.
11.
P
C.
18
P
. D.
16.
P
Câu 7.
Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất
7%
năm. Biết rằng nếu không rút tiền ra
khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo và từ
năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số
tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt thời gian gửi lãi suất không
thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn đến hàng nghìn).
A.
1.686.898.000
VNĐ. B.
743.585.000
VNĐ.
C.
739.163.000
VNĐ. D.
1.335.967.000
VNĐ.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2
Câu 8. Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
. Tìm giá trị nhỏ nhất của biểu
thức
2 2
T a b
A.
. B.
1
. C.
. D.
.
Câu 9.
Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả sử 1 tế bào E.
Coli khối lượng khoảng
15
15.10
g. Hỏi sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là bao
nhiêu? (chọn đáp án chính xác nhất).
A.
29
2,34.10
g
. B.
29
3,36.10
g
. C.
26
2,25.10
kg
. D.
26
3,35.10
kg
.
Câu 10.
Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với mọi
x
dương,
1x
. Tìm giá trị của biểu thức
2 3P n
.
A.
32
P
. B.
23
P
. C.
43
P
. D.
41P
.
Câu 11.
Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
5; 1;1;5
S
. B.
1;1
S
.
C.
5;5
S
. D.
7 5; 1;1;5;7
S
.
Câu 12. Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có
nghiệm.
A.
1
0;
e
. B.
1
0; ln 2
2
. C.
1
; ln 2
2

. D.
1
ln 2;
2

.
Câu 13. Cho
,x y
là hai số thực dương thoả mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của
biểu thức
3 .P x y
A.
min
8
P
. B.
min
17
2
P
. C.
min
25 2
4
P
. D.
min
9
P
.
Câu 14.
Một người vay ngân hàng 90.000.000 đồng theo hình thức trả góp trong 3 năm, mỗi tháng người đó
phải trả số tiền gốc là như nhau và tiền lãi. Giả sử lãi suất không thay đổi trong toàn bộ quá trình trả
nợ là 0.8% trên tháng. Tổng số tiền mà người đó phải trả cho ngân hàng trong toàn bộ quá trình trả nợ
là
A. 103.120.000 đồng. B. 103.420.000 đồng. C. 103.220.000 đồng. D. 103.320.000 đồng.
Câu 15. Cho hai số thực
a
,
b
thỏa mãn
2 2
1
a b
và
2 2
log 1
a b
a b
. Giá trị lớn nhất của biểu thức
2 4 3
P a b
là
A. . B. . C. . D. .
Câu 16.
Một thầy giáo cứ đầu mỗi tháng lại gửi ngân hàng 8 000 000 VNĐ với lãi suất
0,5%
/ tháng. Hỏi sau
bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để mua được một chiếc xe ô tô trị giá
400 000 000 VNĐ?
10
2
10
102
10
1
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 3
A.
60
. B.
50
. C.
55
. D.
45
.
Câu 17. Tích các nghiệm của phương trình
2
25
log 125 .log 1
x
x x
.
A.
630
. B.
1
125
. C.
630
625
. D.
7
125
Câu 18.
Gọi
x
,
y
là các số thực dương thỏa mãn điều kiện
9 6 4
log log log
x y x y
và
2
x a b
y
,
với
a
,
b
là hai số nguyên dương. Tính
2 2
T a b
.
A.
26
T
. B.
29
T
. C.
20
T
. D.
25
T
.
Câu 19.
Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0,7%/ tháng với tổng số tiền
vay là 1 tỉ đồng. Giả sử mỗi tháng ba người đều trả cho ngân hàng một số tiền như nhau để trừ vào tiền
gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần 10 tháng, Bình cần 15 tháng và Cường cần
25 tháng. Hỏi tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân hàng là bao nhiêu (làm tròn đến
hàng nghìn)?
A. 6426800. B. 45672000. C. 46712000. D. 63271000.
Câu 20.
Tìm tất cả các giá trị của tham số
m
để bất phương trình
1
4 2 1 0
x x
m
nghiệm đúng với mọi
x
.
A.
;0
m 
. B.
0;m
.
C.
0;1
m
. D.
;0 1;m
.
Câu 21.
Với mọi số thực
,x y
thỏa điều kiện
2 2
2
2 2
1
log 2
xy
x y xy
x y
. Gọi
M
và
m
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức
4 4
2 1
x y
P
xy
. Tính giá trị biểu thức
2
15 2log
Q m M
.
A.
0
Q
. B.
1
Q
. C.
2
Q
. D.
1
Q
.
Câu 22.
Cho
2019 2019
log 9 log 673 2018
a b
với
,a b
. Khẳng định nào đúng trong các
khẳng định sau đây?
A.
2b a
. B.
2
b a
. C.
2
a b
. D.
2a b
.
Câu 23.
Cho hai số thực
x
,
y
thay đổi thỏa mãn đẳng thức
2
2 1
.2
1 .2 0.
1
x
x y xy
x
y
x
Tìm giá trị lớn nhất
M
của
y
, biết rằng
1x
.
A.
7
2
M
. B.
3
M
. C.
1M
. D.
0
M
.
Câu 24.
Cho
a
,
b
là các số dương thỏa mãn
9 16 12
5
log log log
2
b a
a b
. Giá trị của
a
b
bằng
A.
1 6
a
b
. B.
7 2 6
25
a
b
. C.
1 6
5
a
b
. D.
7 2 6
a
b
.
Câu 25.
Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2 4 3 2 1
x x m x
có hai nghiệm phân
biệt.
A.
3
1 log 4
m
. B.
4
log 3 1
m
. C.
3
1 log 4
m
. D.
4
log 3 1
m
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 4
Câu 26.
Cho phương trình
5
5 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
20;20
m
để phương trình đã cho có nghiệm?
A. 20. B. 21. C. 9. D. 19.
Câu 27.
Nhằm tạo môi trường xanh, sạch, đẹp và thân thiện. Đoàn trường THPT Hậu Lộc 2 đã phát động
phong trào trồng hoa toàn bộ khuôn viên đường vào trường. Sau một ngày thực hiện đã trồng được
một phần diện tích. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 ngày nữa sẽ hoàn thành.
Nhưng thấy công việc có ý nghĩa nên mỗi ngày số lượng đoàn viên tham gia đông hơn vì vậy từ ngày
thứ hai mỗi ngày diện tích trồng tăng lên
4%
so với ngày kế trước. Hỏi công việc sẽ hoàn thành vào
ngày bao nhiêu? Biết rằng ngày
08/ 03
là ngày bắt đầu thực hiện và làm liên tục.
A.
25 / 03
. B.
26 / 03
. C.
23/ 03
. D.
24 / 03
.
Câu 28.
Cho các số thực dương
x
,
y
thỏa mãn
2 2
2 3
log 11 20 40 1
x xy y
x y
. Gọi
M
,
m
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của
y
S
x
. Tính
M m
.
A.
2 14
M m
. B.
10
M m .
C.
7
2
M m
. D.
11
6
M m
.
Câu 29. Tổng tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23
x x
x x
bằng
A.
1
. B.
0
. C.
2
. D.
1
.
Câu 30.
Đồ thị hàm số
y f x
đối xứng với đồ thị của hàm số
0, 1
x
y a a a
qua điểm
1;1
I
. Giá trị
của biểu thức
1
2 log
2018
a
f
bằng:
A.
2016
.
B.
2020
.
C.
2016
.
D.
2020
.
Câu 31.
Cho các số thực
,a b
thỏa mãn
1
, 1
3
a b
. Khi biểu thức
4 2
3
log log 9 81
a b
b a a
đạt giá trị nhỏ
nhất thì tổng
a b
bằng
A.
3
9 2
. B.
2
3 9
. C.
3 3 2
. D.
2 9 2
.
Câu 32.
Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất 0,85% một
tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là 10 triệu
đồng bao gồm cả tiền lãi vay và tiền gốc. Biết phương thức trả lãi và gốc không thay đổi trong suốt
quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng thì anh trả hết nợ ngân hàng? (tháng cuối có thể trả
dưới 10 triệu đồng).
A.
67
. B.
68
. C.
66
. D.
65
.
Câu 33.
Một người vay ngân hàng 100 triệu đồng với lãi suất là 0,7%/tháng theo thỏa thuận cứ cuối mỗi tháng
người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết nợ (tháng
cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng?
A.
21
. B.
24
. C.
22
. D.
23
.
Câu 34.
Cho
2
6
2
log 5
log 45
log 3
b
a
c
, với
, ,a b c
. Tính tổng
a b c
A.
2
. B.
1
. C.
4
. D.
0
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 5
Câu 35. Xét các số nguyên dương
, a b
sao cho phương trình
2
ln ln 5 0
a x b x
có hai nghiệm phân biệt
1 2
, x x
và phương trình
2
5log log 0
x b x a
có hai nghiệm phân biệt
3 4
, x x
thỏa mãn
1 2 3 4
x x x x
.
Tìm giá trị nhỏ nhất của
2 3S a b
A.
min
33
S
. B.
min
30
S
. C.
min
17
S
. D.
min
25
S
.
Câu 36.
Bất phương trình
3
9 ln 5 0
x x x
có bao nhiêu nghiệm nguyên?
A. 4. B. 7. C. 6. D. Vô số.
Câu 37.
Cho hàm số
2 2
x x
f x
. Gọi
0
m
là số lớn nhất trong các số nguyên thõa mãn
12
2 2 0
f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019
m
. B.
0
1009;1513
m
.
C.
0
505;1009
m
. D.
0
1;505
m
.
Câu 38.
Tính tổng tất cả các nghiệm nguyên của bất phương trình
2 2
2 2
log 3 log 4 1 0
x x x x
.
A.
4
. B.
6
. C.
5
. D.
3
.
Câu 39.
Cho hàm số
y f x
liên tục và đồng biến trên
0;
2
, bất phương trình
ln cos
x
f x x e m
(với
m
là tham số) thỏa mãn với mọi
0;
2
x
khi và chỉ khi:
A.
0 1
m f
. B.
0 1
m f
. C.
0 1
m f
. D.
0 1
m f
.
Câu 40.
Ông An có 200 triệu đồng gửi ngân hàng với kì hạn 1 tháng với lãi suất
0,6%
/1 tháng được trả vào
cuối kì. Sau mỗi kì hạn, ông đến tất toán cả lãi và gốc, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại
ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi luất không thay đổi trong
suốt quá trình ông gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông An tất toán và rút toàn
bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng)
A. 169234 (nghìn đồng). B. 165288 (nghìn đồng).
C. 169269 (nghìn đồng). D. 165269 (nghìn đồng).
Câu 41.
Cho
x
,
y
thỏa mãn
3
2 2
log 9 9
2
x y
x x y y xy
x y xy
. Tìm giá trị lớn nhất của
3 2 9
10
x y
P
x y
khi
x
,
y
thay đổi.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 42.
Cho hai số thực
a
,
b
thỏa mãn
0
a
,
0 2
b
. Tìm giá trị nhỏ nhất của biểu thức
2
2
2 2.
2.
2
a
a a
a
a a
b
b
P
b
b
.
A.
min
9
4
P
. B.
min
7
4
P
. C.
min
13
4
P
. D.
min
4
P
.
Câu 43. Cho các số thực
, 1
a b
thỏa mãn điều kiện
2 3
log log 1a b
. Tìm giá trị lớn nhất của biểu thức
3 2
log logP a b
.
A.
2 3
log 3 log 2
. B.
3 2
log 2 log 3
. C.
2 3
1
log 3 log 2
2
. D.
2 3
2
log 3 log 2
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 6
Câu 44.
Với giá trị nào của tham số m để phương trình
1
4 .2 2 3 0
x x
m m
có hai nghiệm
1 2
,x x
thỏa mãn
1 2
4
x x
.
A.
5
.
2
m
B.
2.
m
C.
8.
m
D.
13
.
2
m
Câu 45.
Cho dãy số
n
a
thỏa mãn
1
1
a
và
1
3
5 1
3 2
n n
a a
n
, với mọi
1n
. Tìm số nguyên dương
1
n
nhỏ nhất để
n
a
là một số nguyên.
A.
41
n
. B.
39
n
. C.
49
n
. D.
123
n
.
Câu 46.
Có bao nhiêu giá trị nguyên của tham số
8;m
để phương trình sau có nhiều hơn hai nghiệm
phân biệt
2
2 2
1 2 2 2
x m x x
x x x m x x m
.
A.
6
. B.
7
. C.
5
. D.
8
.
Câu 47. Tổng tất cả các giá trị của tham số
m
để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x m
x x
x m
có đúng
ba nghiệm phân biệt là:
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 48. Cho phương trình
2 2
1 1 1 1
25 2 .5 2 1 0
x x
m m
, với
m
là tham số. Giá trị nguyên dương lớn
nhất của tham số
m
để phương trình trên có nghiệm là:
A.
5
B.
26
. C.
25
. D.
6
.
Câu 49. So sánh ba số
64
1001 2
1000 , 2
a b
và
1 2 3 1000
1 2 3 ... 1000c
?
A.
c a b
. B.
b a c
. C.
c b a
. D.
a c b
.
Câu 50.
Cho các số thực dương
x
,
y
thay đổi và thỏa mãn điều kiện
1x y
. Giá trị nhỏ nhất của biểu thức
2 2
log 3log
x y
y
x
T x
y
là
A.
19
. B.
13
. C.
14
. D.
15
T
.
Câu 51.
Bất phương trình
1
4 1 2 0
x x
m m
nghiệm đúng với mọi
0
x
. Tập tất cả cá giá trị của
m
là
A.
;12

. B.
; 1
. C.
;0

. D.
1;16
.
Câu 52.
Phương trình
4 1 2 . .cos
x x
m x
có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là
A. Vô số. B. 1. C. 2. D. 0.
Câu 53.
Cho a, b, c là ba số thực dương,
1
a
và thỏa mãn
2
2 3 3 2
log log 4 4 0
4
a a
bc
bc b c c
. Số
bộ
; ;a b c
thỏa mãn điều kiện đã cho là
A. 0. B. 1. C. 2. D. Vô số.
Câu 54.
Tính tổng
T
của các giá trị nguyên của tham số
m
để phương trình
x 2
e e 2
x
m m m
có đúng
hai nghiệm phân biệt nhỏ hơn
1
loge
.
A.
28
T
. B.
20
T
. C.
21T
. D.
27
T
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
THI THỬ 2019
CHUYÊN ĐỀ 1
. ỨNG DỤNG ĐẠO HÀM VÀ
KHẢO SÁT HÀM SỐ
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 7
Câu 55.
Cho hai số thực
,x y
lớn hơn 1 và thỏa mãn
.( ) .( ) .
y x
x x e y y e
y e x e
Tìm giá trị nhỏ nhất của biểu thức
log log .
x y
P xy x
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Câu 56.
Tập hợp các giá trị thực của tham số m để phương trình
2
2019 1
2019
log (4 ) log (2 1) 0
x x m
có hai
nghiệm thực phân biệt là
( ; )T a b
. Tính
2
S a b
.
A.
18
. B.
8
. C.
20
. D.
16
.
Câu 57.
Một anh sinh viên nhập học đại học vào tháng 8 năm 2014. Bắt đầu từ tháng 9 năm 2014, cứ vào ngày
mồng một hàng tháng anh vay ngân hàng 3 triệu đồng với lãi suất cố định
0,8%
/tháng. Lãi tháng
trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo( lãi kép). Vào ngày mồng một hàng
tháng kể từ tháng 9/2016 về sau anh không vay ngân hàng nữa và anh còn trả được cho ngân hàng 2
triệu đồng do có việc làm thêm. Hỏi ngay sau khi kết thúc ngày anh ra trường
30/ 06/ 2018
anh còn
nợ ngân hàng bao nhiêu tiền( làm tròn đến hàng nghìn đồng)?
A.
49.024.000
đồng. B.
47.401.000
đồng.
C.
46.641.000
đồng. D.
45.401.000
đồng.
BẢNG ĐÁP ÁN
1.D 2.D 3.B 4.C 5.A 6.D 7.D 8.D 9.D 10.D
11.A 12.C 13.D 14.D 15.A 16.D 17.B 18.A 19.A 20.A
21.C 22.A 23.B 24.D 25.C 26.D 27.A 28.C 29.B 30.A
31.B 32.C 33.C 34.B 35.B 36.C 37.B 38.B 39.A 40.C
41.C 42.C 43.A 44.D 45.A 46.B 47.B 48.C 49.A 50.D
51.B 52.B 53.B 54.D 55.C 56.D 57.C
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 1
Câu 1. Giá trị thực của tham số
m
để phương trình
4 2 3 .2 64 0
x x
m
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
1 2
2 2 24x x
thuộc khoảng nào sau đây?
A.
3
0;
2
. B.
3
;0
2
. C.
21 29
;
2 2
. D.
11 19
;
2 2
.
Lời giải
Chọn D
Đặt
2
x
t
, điều kiện
0t
. Phương trình ban đầu trở thành
2
2 3 . 64 0 *t m t
.
Để phương trình ban đầu có hai nghiệm thực
1
x
và
2
x
thì phương trình
*
phải có hai nghiệm
1
t
,
2
t
dương
0
0
0
S
P
2
4 12 247 0
2 3 0
m m
m
19
2
13
2
3
2
m
m
m
13
2
m
.
Theo định lý Vi-ét, ta có
1 2
. 64t t
1 2
2 .2 64
x x
1 2
2 64
x x
1 2
6x x
.
Ta có
1 2
2 2 24
x x
1 2 1 2
. 2 4 24
x x x x
1 2
. 8x x
.
Từ
1 2
1 2
6
. 8
x x
x x
1
2
1
2
2
4
4
2
x
x
x
x
.
Khi đó, ta có
1 2
1 2
2 2 20 2 3
x x
t t m
17
2
m
.
Câu 2. Cho điểm
(0;4),C
đường thẳng
4y
cắt hai đồ thị hàm số
x
y a
và
x
y b
lần lượt tại
A
và
B
sao cho
AB AC
(hình vẽ). Khẳng định nào sau đây đúng?
A.
2 .a b
B.
2
.b a
C.
2 .b a
D.
2
.a b
Lời giải
Chọn D
Ta có
(0;4), (log 4;4), B(log 4;4).
a b
C A
Khi đó
2
4 4
0 log 4
log 4 log 2log .
2
b
a
AB AC a b a b
Câu 3. Cho các số thực dương
,a b
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Giá trị nhỏ nhất của biểu
thức
2P a b
bằng
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2
A.
2 10 1
2
. B.
2 10 3
2
. C.
3 10 7
2
. D.
2 10 5
2
.
Lời giải
Chọn B
Từ giả thiết ta có điều kiện:
1ab
.
Ta có
2 2
2 2
1 2 2
log 2 3 log 2 3
2
log 2 2 2 2 log 1
ab ab
ab a b ab a b
a b a b
ab ab a b a b
Xét hàm số
2
log , 0f t t t t
,
Có
1
1 0, 0
ln 2
f t t
t
nên
f t
đồng biến trên
0;

.
Do đó:
2
1 2 2 2 2
1 2
a
f ab f a b ab a b b
a
.
Suy ra:
4 2 1 5 3 3 2 10 3
1 2 10
1 2 2 1 2 2 2 2
a
P a a
a a
.
Giá trị nhỏ nhất của
P
là
2 10 3
2
, đạt được khi
2
0, 0, 1
10 1
2
2
1 2
10 2
2 1 10
4
a b ab
a
a
b
a
b
a
Câu 4. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
để phương trình
5 10 25 4
x x
m
có nghiệm duy nhất. Số tập con của
S
là
A.
3
. B.
4
. C.
16
. D.
15
.
Lời giải
Chọn C
5 10
5 10 25 4 1
25 4
x
x x
x
m m
.
TH 1:
0
m
. Phương trình
1
vô nghiệm.
TH 2:
0
m
.
2
2
5 10
(1)
25 4
x
x
m
Đặt
5
x
t
,
0t
. Ta có:
2
2
2
10
(2)
4
t
m
t
Xét hàm số
2
2
10
4
t
f t
t
trên khoảng
0;

2
2
2
10( )
20 192 80
. ( ) 0 .
2
( )
4
5
t l
t t
f t f t
t tm
t
Bảng biến thiên:
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 3
Đề phương trình
1
có đúng một nghiệm
Phương trình
2
có đúng một nghiệm
0t
2
2
26
.
1 25
m
m
Do điều kiện
0
2,3,4,5
m
m
m
.
Vậy
2,3,4,5S
, do đó số tập con của
S
là
4
2 16
.
Câu 5. Anh X muốn mua một chiếc xe máy Yamaha Exciter 150 giá 47.500.000 của cửa hàng Phú Tài
nhưng vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước 25 triệu
đồng và trả góp trong 12 tháng, với lã suất 0.6% tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho
cửa hàng Phú Tài số tiền là bao nhiêu(quy tròn đến hàng đơn vị).
A.
1.948.927
đồng. B.
1.948.926
đồng. C.
2.014.545
đồng. D.
2.014.546
đồng.
Lời giải
Chọn A
Đặt x là số tiền Anh X phải trả 1 tháng,
22.500.000A
,
0,006r
.
Sau 1 tháng, số tiền anh X còn nợ cửa hàng là:
1
1
T A r x
.
Sau 2 tháng, số tiền anh X còn nợ cửa hàng là:
2
2
1 1 1 1T A r x r x A r x r x
.
Tương tự, sau 12 tháng, số tiền anh X còn nợ cửa hàng là:
12 11 10 9
12
1 1 1 1 ... 1 1T A r x r r r r
.
Sau 12 tháng, anh X trả hết nợ, do đó:
12 12
12
12 12
1 1
0 1.948.926,902
1 1 1 1
1.
1 1
A r Ar r
T x
r r
r
.
Làm tròn đến hàng đơn vị ta được:
1.948.927x
đồng.
Câu 6.
Biết rằng bất phương trình
5
2
2
log 5 2 2.log 2 3
x
x
có tập nghiệm là
log ;
a
S b 
,
với
a
,
b
là các số nguyên dương nhỏ hơn 6 và 1a
. Tính
2 3P a b
.
A.
7
P
. B.
11.
P
C.
18
P
. D.
16.
P
Lời giải
Chọn D
Đặt
2
log (5 2)
x
t
. Do
5 2 2
x
với mọi
x
nên
2 2
log (5 2) log 2 1
x
hay
1t
.
Bất phương trình đã cho trở thành:
2
2
3 3 2 0t t t
t
(do
1t
)
1
2
t
t
.
Đối chiếu với
1t
ta lấy
2t
.
Khi đó
2 5
log (5 2) 2 5 2 log 2
x x
x
.
Vậy bất phương trình có nghiệm là
5
S (log 2; ) 
, ta có
5, 2 2 3 16a b a b
.
Câu 7. Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất
7%
năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 4
Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt
thời gian gửi lãi suất không thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn đến
hàng nghìn).
A.
1.686.898.000
VNĐ. B.
743.585.000
VNĐ.
C.
739.163.000
VNĐ. D.
1.335.967.000
VNĐ.
Lời giải
Chọn D
Gọi
200
a
triệu;
20
b
triệu;
7%
.
Số tiền sau 1 năm:
1a
.
Số tiền sau 2 năm:
2
1 1a b
.
Số tiền sau 3 năm:
3 2
1 1 1a b b
.
……………………
Số tiền sau 18 năm:
18 17 16
1 1 1 ... 1a b
17
18
1 1
1 1 .a b
Vậy số tiền ông Chính nhận sau 18 năm là:
1.335.967.000
VNĐ.
Câu 8. Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
. Tìm giá trị nhỏ nhất
của biểu thức
2 2
T a b
A.
1
2
. B.
1
. C.
3
2
. D.
5
2
.
Lời giải
Chọn D
5 5 5
4 2 5
log 3 4 log 4 2 5 log 3 4
a b
a b a b a b a b
a b
5 5
log 4 2 5 4 2 5 log 5 5
a b a b a b a b
(*).
Xét hàm
5
log , 0
f x x x x
.
Đạo hàm
1
1 0, 0
.ln5
f x x
x
. Suy ra hàm số
f x
đồng biến trên
0;

.
Phương trình (*) viết lại:
4 2 5 5 4 2 5 5 3 5
f a b f a b a b a b a b
.
Mặt khác:
2
2 2 2 2 2 2 2
5
5 3 1 3 .
2
a b a b T a b
.
Dấu
" "
xảy ra
1 3
a b
1 3
;
2 2
a b
.
Câu 9.
Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả sử 1 tế
bào E. Coli khối lượng khoảng
15
15.10
g. Hỏi sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh
ra là bao nhiêu? (chọn đáp án chính xác nhất).
A.
29
2,34.10
g
. B.
29
3,36.10
g
. C.
26
2,25.10
kg
. D.
26
3,35.10
kg
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 5
Lời giải
Chọn D.
Một tế bào E. Coli
Sau 20 phút thành:
1
2 2
tế bào.
Sau
40 2.20
phút thành:
2
4 2
tế bào.
Sau
60 3.20
phút thành:
3
8 2
tế bào.
………………………………………………………….
Sau 2 ngày
144.20
phút thành
144
2
tế bào.
Vậy sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là:
144 15 29 26
2 .15.10 3,34511178.10 3,35.10
g kg
.
Câu 10. Gọi
n
là số nguyên dương sao cho
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
n
x x x x x
đúng với
mọi
x
dương,
1x
. Tìm giá trị của biểu thức
2 3P n
.
A.
32
P
. B.
23
P
. C.
43
P
. D.
41P
.
Lời giải
Chọn D
2 3
3 3
3 3 3
1 1 1 1 190
...
log log log log log
log 3 2log 3 3log 3 ... log 3 190log 3
log 3 1 2 3 ... 190log 3
1 2 3 ... 190
1
190
2
n
x x x x x
x x
x x x x x
n
n
n
n n
2
380 0
n n
19
19
20
n
n
n
(do
n
nguyên dương)
2 3 41
P n
Câu 11. Tìm tập
S
tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp số
;x y
thỏa mãn
2 2
2
2
log 4 4 6 1
x y
x y m
và
2 2
2 4 1 0
x y x y
.
A.
5; 1;1;5
S
. B.
1;1
S
.
C.
5;5
S
. D.
7 5; 1;1;5;7
S
.
Lời giải
Chọn A
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 6
Nhận thấy
2 2
2 1
x y
với mọi
,x y
nên:
2 2
2
2
log 4 4 6 1
x y
x y m
2 2 2
4 4 6 2
x y m x y
2 2 2
4 4 8 0
x y x y m
2 2
2
2 2
x y m
(*).
Khi
0
m
thì (*)
2
2
x
y
. Cặp
2;2
không là nghiệm của phương trình
2 2
2 4 1 0
x y x y
.
Khi
0
m
, tập hợp các điểm
;x y
thỏa mãn (*) là hình tròn tâm
2;2
J
, bán kính là
m
.
Trường hợp này, yêu cầu bài toán trở thành tìm
m
để đường tròn tâm
1;2
I
, bán kính
2
và
hình tròn tâm
2;2
J
, bán kính
m
có đúng một điểm chung (hình vẽ)
Điều này xảy ra khi
1
5
m
m
1
5
m
m
(thỏa mãn
0
m
).
Vậy
5; 1;1;5
S
.
Câu 12. Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm.
A.
1
0;
e
. B.
1
0; ln 2
2
. C.
1
; ln 2
2

. D.
1
ln 2;
2

.
Lời giải
Chọn C
Điều kiện:
1;1
x
Đặt
2
1 .x x t
Vì
1;1 1; 2
x t
Ta có:
2
2
2 2 2 2
1
1 1 2 1 1 .
2
t
t x x x x x x
Phương trình đã cho trở thành:
3 3
.
m m
e e t t
Xét hàm số
3 2
, 3 1 0
f u u u f u u u
do đó hàm số
đồng biến trên
.
Phương trình
3 3m m m m
e e t t f e f t e t
.
Phương trình có nghiệm khi và chỉ khi
1 2 0 2
m m
e e
( do
0
m
e
)
1
ln 2 ; ln 2
2
m m

.
m
-3
y
x
2
2
1
-1
O
J
I
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 7
Câu 13. Cho
,x y
là hai số thực dương thoả mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3 .P x y
A.
min
8
P
. B.
min
17
2
P
. C.
min
25 2
4
P
. D.
min
9
P
.
Lời giải
Chọn D
Ta có:
2 2 2 2
1 1 1 1 1
2 2 2 2 2
log log log log log 1 1 .
x y x y xy x y xy x y y x x
Vì
,x y
là hai số thực dương, do đó:
Từ
2 2
1
1 1 3 3 4 1 5 9.
1 1 1
x x
x y P x y x x
x x x
(Áp dụng bất đẳng thức Cô si:
1
4 1 4
1
x
x
).
Dấu “=” xảy ra khi và chỉ khi
3 9
;
2 2
x y
.
Vậy giá trị nhỏ nhất của biểu thức
là
min
9
P
.
Câu 14. Một người vay ngân hàng 90.000.000 đồng theo hình thức trả góp trong 3 năm, mỗi tháng
người đó phải trả số tiền gốc là như nhau và tiền lãi. Giả sử lãi suất không thay đổi trong toàn
bộ quá trình trả nợ là 0.8% trên tháng. Tổng số tiền mà người đó phải trả cho ngân hàng trong
toàn bộ quá trình trả nợ là
A. 103.120.000 đồng. B. 103.420.000 đồng. C. 103.220.000 đồng. D. 103.320.000 đồng.
Lời giải.
Chọn D
Gọi
0
P
là số tiền vay ban đầu,
a
là số tiền gốc trả hàng tháng,
r
là lãi suất
Sau tháng 1
Số tiền nợ là
0
(1 )P r
.
Số tiền trả là
a Pr
.
Số tiền nợ còn lại
0
P a
.
Sau tháng 2
Số tiền nợ là
0
(1 )P a r
.
Số tiền trả là
a P a r
.
Số tiền nợ còn lại
0
2P a
.
…
Sau tháng n
Số tiền nợ là
0
1 (1 )P n a r
.
Số tiền trả là
1
a P n a r
.
Số tiền nợ còn lại
0
P na
.
Theo giả thiết trả hết sau 36 tháng nên
90.000.000 36 0 2.500.000
a a
.
Tổng số tiền đã trả là
0
35.36
... 1 36 36
2
T a Pr a P a r a P n a r a P a r
.
Thay
0
90.000.000, 2.500.000, 0.008
P a r
được
103.320.000
T
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 8
Câu 15. Cho hai số thực
a
,
b
thỏa mãn
2 2
1
a b
và
2 2
log 1
a b
a b
. Giá trị lớn nhất của biểu thức
2 4 3
P a b
là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có
2 2
log 1
a b
a b
2 2
a b a b
2 2
1 1 1
2 2 2
a b
.
Theo bất đẳng thức Cauchy – Schwarz:
2 2
2 2
1 1 1 1 1
2 4 3 2 4 2 4 20. 10
2 2 2 2 2
P a b a b a b
.
Dấu
" "
xảy ra khi
2 2
0
1 1
2 2
2 4
1 1 1
2 2 2
a b
a b
a b
5 10
10
5 2 10
10
a
b
.
Vậy
max
10
P
.
Câu 16. Một thầy giáo cứ đầu mỗi tháng lại gửi ngân hàng 8 000 000 VNĐ với lãi suất
0,5%
/ tháng.
Hỏi sau bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để mua được một chiếc xe ô tô trị giá
400 000 000 VNĐ?
A.
60
. B.
50
. C.
55
. D.
45
.
Lời giải
Chọn D
Đặt
8 000 000
T
Số tiền thầy giáo thu được sau tháng thứ nhất, thứ 2, thứ 3,., thứ
n
lần lượt là
1 2 3
, , ,...,
n
T T T T
Ta có:
1
1
T T r
2
2 1
1 1 1
T T T r T r T r
3 2
3 2
1 1 1 1
T T T r T r T r T r
.
1
1 1
1 1 ... 1 1
n
n n
n
r
T T r T r T r T r
r
Theo bài ra ta có
1 1
400 000 000 1 400 000 000
n
n
r
T T r
r
1.005
251 251
1 log 44,54
201 201
n
r n
Vậy sau 45 tháng thầy giáo sẽ mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ.
Câu 17. Tích các nghiệm của phương trình
2
25
log 125 .log 1
x
x x
.
A.
630
. B.
1
125
. C.
630
625
. D.
7
125
Lời giải
10
2
10
102
10
1
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 9
Chọn B
Điều kiện
0; 1x x
.
Ta có
2
2 2
25 5 5
1
log 125 .log 1 log 125 log log 1 3.log 5 1 log 4
2
x x x x
x x x x x
Đặt
5
log
x t
phương trình tương đương:
5
2 2
5
5
log 1
1
3
1 4 3 4 0
1
log 4
4
625
x
x
t
t t t
x
t
t
x
Vậy tích các nghiệm của phương trình là
1
125
.
Câu 18. Gọi
x
,
y
là các số thực dương thỏa mãn điều kiện
9 6 4
log log log
x y x y
và
2
x a b
y
,
với
a
,
b
là hai số nguyên dương. Tính
2 2
T a b
.
A.
26
T
. B.
29
T
. C.
20
T
. D.
25
T
.
Lời giải
Chọn A
Đặt
9 6 4
log log log
x y x y t
, suy ra
9
t
x
,
6
t
y
,
4
t
x y
.
Khi đó ta có:
9 6 4
t t t
2
3 3
1 0
2 2
t t
3 1 5
2 2
t
(Vì
3
0
2
t
).
Lại có
3
2
t
x
y
1 5
2
x
y
1a
,
5
b
hay
26
T
.
Câu 19. Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0,7%/ tháng với tổng
số tiền vay là 1 tỉ đồng. Giả sử mỗi tháng ba người đều trả cho ngân hàng một số tiền như nhau
để trừ vào tiền gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần 10 tháng, Bình cần 15
tháng và Cường cần 25 tháng. Hỏi tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân
hàng là bao nhiêu (làm tròn đến hàng nghìn)?
A. 6426800. B. 45672000. C. 46712000. D. 63271000.
Lời giải
Chọn A
Gọi A, B, C lần lượt là số tiền mà An, Bình, Cường vay ngân hàng thì ta có:
9
10 1
A B C
Gọi X là số tiền mà mỗi người trả cho ngân hàng vào mỗi tháng. Để trả hết gốc và lãi cho ngân
hàng thì An cần 10 tháng nên áp dụng công thức vay vốn trả góp ta có:
10 10
10
10
1 1 1 1
1 0 2
1
r r
A r X A X
r
r r
,
Bình cần 15 tháng nên:
15 15
15
15
1 1 1 1
1 0 3
1
r r
B r X B X
r
r r
,
Cường cần 25 tháng nên:
25 25
25
25
1 1 1 1
1 0 4
1
r r
C r X C X
r
r r
(Với
0,7
100
r
).
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
10
Từ (1), (2), (3), (4) suy ra tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân hàng là:
3 64268000X
Câu 20. Tìm tất cả các giá trị của tham số
m
để bất phương trình
1
4 2 1 0
x x
m
nghiệm đúng với
mọi
x
.
A.
;0m 
. B.
0;m
.
C.
0;1
m
. D.
;0 1;m

.
Lời giải
Chọn A
Đặt
2
x
t
,
0 1 0t t
.
Bài toán đã cho trở thành:
Tìm tất cả các giá trị của tham số
m
để bất phương trình:
2
, 0 1
4 1
t
m t
t
.
Đặt
2 2
2
2
, 0 0 0 2
4 1
4 1
t t t
f t t f t f t t l t l
t
t
.
Bảng biến thiên:
Nhìn vào bảng biến thiên ta có
;0m 
thỏa yêu cầu bài toán.
Câu 21. Với mọi số thực
,x y
thỏa điều kiện
2 2
2
2 2
1
log 2
xy
x y xy
x y
. Gọi
M
và
m
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
4 4
2 1
x y
P
xy
. Tính giá trị biểu thức
2
15 2logQ m M
.
A.
0
Q
. B.
1
Q
. C.
2
Q
. D.
1
Q
.
Lời giải
Chọn C
Điều kiện:
1 0xy
.
2 2
2
2 2
1
log 2
xy
x y xy
x y
2 2
2
2 2
1
log 2 1
2
xy
x y xy
x y
2 2 2 2
2 2
log 1 1 log 2 2
xy xy x y x y
.
Xét hàm số:
2
logf t t t
0t
1
1 0
ln 2
f t
t
0t
hàm số đồng biến trên
0;
.
Do đó:
2 2 2 2
1 2 1 2f xy f x y xy x y
Ta có:
2 2 2 2
2 2
x y x y
xy
2 2 2 2
2 2
1 2 1
2 2
x y x y
x y
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
11
2 2
2 2
5 3
x y
.
Khi đó:
2
2
2 2
4 4
2
2 1 2 1
x y xy
x y
P
xy xy
.
Thay
2 2
2 1
xy x y
, đặt
2 2
t x y
rút gọn ta được
2
7 8 2
4 1
t t
P t
t
với
2 2
5 3
t
.
2
2
28 14
0
4 1
t t
P t
t
0
1
2
t
t
.
Lập bảng biến thiên dễ thấy:
1 1
max
2 4
P P
,
2 2 2
min
5 3 15
P P P
.
Do đó:
2 1
,
15 4
m M
2
15 2log 2
Q m M
.
Câu 22. Cho
2019 2019
log 9 log 673 2018
a b
với
,a b
. Khẳng định nào đúng trong các
khẳng định sau đây?
A.
2b a
. B.
2
b a
. C.
2
a b
. D.
2a b
.
Lời giải
Chọn A
Ta có:
2019 2019 2019 2019
log 9 log 673 2018 log 9 log 673 2018
a b
a b
2018
2019
log 9 .673 2018 9 .673 2019
a b a b
2 2018 2018
3 .673 673 .3
a b
2018 2 2018
673 3
b a
.
Do
673
và
3
nguyên tố cùng nhau nên
2 2018 1009
2
2018 2018
a a
b a
b b
.
Câu 23. Cho hai số thực
x
,
y
thay đổi thỏa mãn đẳng thức
2
2 1
.2
1 .2 0.
1
x
x y xy
x
y
x
Tìm giá trị lớn
nhất
M
của
y
, biết rằng
1x
.
A.
7
2
M
. B.
3
M
. C.
1M
. D.
0
M
.
Lời giải
Chọn B
Ta có:
2
2
2 1
2 1
.2
1 .2 0 .2 1 .2 *
1
x
x y xy x x y xy
x
y x x y xy
x
Xét hàm số
.2
t
f t t
trên
0;
.
2 .2 ln 2 0 0
t t
f t t t
Vậy hàm số
.2
t
f t t
đồng biến trên
0;
. Suy ra:
2 2
* 1 1
f x f x y xy x y xy x
2
1
1
1
x x
y x
x
Ta có:
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
12
2
2
2 2
0
2 1 1 1
2
; 0
2
1 1
x
x x x x
x x
y y
x
x x
Bảng biến thiên:
Từ bảng biến thiên suy ra:
3M
.
Câu 24. Cho
a
,
b
là các số dương thỏa mãn
9 16 12
5
log log log
2
b a
a b
. Giá trị của
a
b
bằng
A.
1 6
a
b
. B.
7 2 6
25
a
b
. C.
1 6
5
a
b
. D.
7 2 6
a
b
.
Lời giải
Chọn D
Điều kiện:
, 0
, 0
5 0
5
a b
a b
a
b a
b
.
Đặt
9 16 12
5
log log log
2
b a
a b t
, ta có
9
t
a
,
16
t
b
,
5
12
2
t
b a
.
Suy ra
2
2 2
5
14 25 0
2
b a
ab a ab b
2
7 2 6
14 25 0
7 2 6
a
a a
b
a
b b
b
.
So điều kiện ta nhận
7 2 6
a
b
.
Câu 25. Tìm tất cả các giá trị thực của tham số
m
để phương trình
4 2 4 3 2 1
x x m x
có hai
nghiệm phân biệt.
A.
3
1 log 4m
. B.
4
log 3 1m
. C.
3
1 log 4m
. D.
4
log 3 1m
.
Lời giải
Chọn C
Ta có
4 2 4
4 2 4 3 2 1 3
2 1
x x
x x m x m
x
(*).
Đặt
2 , 0
x
t t
.
2
4
* 3
1
m
t t
t
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
13
Đây là phương trình hoành độ giao điểm của đồ thị hàm số
2
4
1
t t
y
t
và đường thẳng
3
m
y
song song với trục hoành.
Xét
2
4
, 0
1
t t
y t
t
.
Ta có
2
2
2 3
1
t t
y
t
.
Cho
2
3
0 2 3 0
1 3
t
y t t
t y
.
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy đường thẳng
3
m
y
cắt đồ thị hàm số
2
4
1
t t
y
t
tại hai
điểm phân biệt
3
3 3 4 1 log 4
m
m
.
Vậy
3
1 log 4m
.
Câu 26. Cho phương trình
5
5 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
20;20m
để phương trình đã cho có nghiệm?
A. 20. B. 21. C. 9. D. 19.
Lời giải
Chọn D
Ta có
5
5 log
x
m x m
(*).
Đặt
5
x
t m
.
5
* log 5 5
t t
t x m x m x m
.
Ta có hệ
5
5 5 5 5
5
x
x t x t
t
t m
t x x t
x m
(1).
Xét hàm số
5
u
f u u
có
1 5 .ln 5 0
u
f u
,
u
nên hàm số đồng biến trên
.
1 x t
.
Khi đó ta được
5 5
x x
x m x m
.
Đây là phương trình hoành độ giao điểm của đồ thị hàm số
5
x
y x
và đường thẳng
y m
song song hoặc trùng trục hoành.
Xét
5
x
y x
có
1 5 ln5
x
y
.
Cho
5
1
0 log
ln5
y x
.
Bảng biến thiên
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
14
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm
5
1
log 1;0
ln5
m f
Vì
20;20
m
m
nên
19; 18;...; 1m
.
Vậy có 19 giá trị nguyên của
m
thỏa bài toán.
Câu 27. Nhằm tạo môi trường xanh, sạch, đẹp và thân thiện. Đoàn trường THPT Hậu Lộc 2 đã phát
động phong trào trồng hoa toàn bộ khuôn viên đường vào trường. Sau một ngày thực hiện đã
trồng được một phần diện tích. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 ngày
nữa sẽ hoàn thành. Nhưng thấy công việc có ý nghĩa nên mỗi ngày số lượng đoàn viên tham gia
đông hơn vì vậy từ ngày thứ hai mỗi ngày diện tích trồng tăng lên
4%
so với ngày kế trước.
Hỏi công việc sẽ hoàn thành vào ngày bao nhiêu? Biết rằng ngày
08/ 03
là ngày bắt đầu thực
hiện và làm liên tục.
A.
25 / 03
. B.
26 / 03
. C.
23/ 03
. D.
24 / 03
.
Lời giải
Chọn A
Gọi số lượng công việc đã hoàn thành trong ngày đầu là
0a a
, khi đó số lượng công việc
phải hoàn thành trong 23 ngày tiếp theo là
23a
Đặt
4%r
Số lượng công việc làm được trong ngày thứ 2, thứ 3,. thứ
n
lần lượt là
1 ,a r
2
1 ,a r
.
1
, 1
n
a r
Công việc được hoàn thành khi và chỉ khi
1a r
2
1 ...a r
1
1 23
n
a r a
1
1
1
1 1
23
1 23 1 1
1
23
1 log 1 17.157
1
n
n
r
r
r
r r
r r
r
n n
r
Do đó, kể từ ngày 08/03 số ngày cần để hoàn thành công việc là 18 ngày
Vậy công việc được hoàn thành vào ngày 25/03
Câu 28. Cho các số thực dương
x
,
y
thỏa mãn
2 2
2 3
log 11 20 40 1
x xy y
x y
. Gọi
M
,
m
lần lượt
là giá trị lớn nhất và giá trị nhỏ nhất của
y
S
x
. Tính
M m
.
A.
2 14M m
. B. 10M m .
C.
7
2
M m
. D.
11
6
M m
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
15
Lời giải
Chọn C
Do
y
S
x
nên
.y Sx
Ta có
2 2
2 2
2 3
2 2 2
2 2
log 11 20 40 1 11 20 40 2 3
11 20 40 2 3
3 2 20 11 40 0 1
x xy y
x y x y x xy y
x Sx x xSx S x
S S x S x
Biệt thức
2
2 2
20 11 4 40 3 2 80 280 199.
S S S S S
Để có các số thực dương
x
,
y
thỏa mãn giả thiết trước hết ta phải có:
2
1 2
35 230 35 230
0 80 280 199 0 .
20 20
S S S S S
Từ đó ta suy ra
1
2
1 1
1
20S 11
x 0
35 230
3S S 2
M maxS khi
20
y S x 0
2
2
2 2
2
20S 11
x 0
35 230
3S S 2
m minS khi
20
y S x 0
Vậy
7
M m .
2
Câu 29. Tổng tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23
x x
x x
bằng
A.
1
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn B
Tập xác định
.
Ta có
1
15 .5 5 27 23 5.5 . 3 1 27 23 0 1
x x x
x x x x
.
Với
1
3
x
không phải là nghiệm của phương trình.
Với
1
3
x
ta có
27 23
1 5.5 0 2
3 1
x
x
x
.
Xét hàm số
27 23
5.5 ,
3 1
x
x
f x
x
2
96 1
5.5 ln 5 0
3
3 1
x
f x x
x
.
Suy ra hàm số đồng biến trên các khoảng
1
; ,
3

1
;
3

nên trên mỗi khoảng hàm số có
nhiều nhất một nghiệm.
Ta thấy
1 1 0
f f
1
x
là nghiệm của phương trình.
Tổng tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23
x x
x x
bằng
0
.
Câu 30.
Đồ thị hàm số
y f x
đối xứng với đồ thị của hàm số
0, 1
x
y a a a
qua điểm
1;1
I
.
Giá trị của biểu thức
1
2 log
2018
a
f
bằng:
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
16
A.
2016
.
B.
2020
.
C.
2016
.
D.
2020
.
Lời giải
Chọn A
Xét
1 1
2 log ; 2 log
2018 2018
a a
M f
thuộc đồ thị hàm số
y f x
.
Điểm
1 1
log ;2 2 log
2018 2018
a a
N f
đối xứng với
M
qua
1;1
I
thuộc đồ thị hàm số
x
y a
nên ta có:
1
log
log 2018
2018
1 1
2 2 log 2 log 2 2 2018 2016
2018 2018
a
a
a a
f a f a
.
Câu 31. Cho các số thực
,a b
thỏa mãn
1
, 1
3
a b
. Khi biểu thức
4 2
3
log log 9 81
a b
b a a
đạt giá
trị nhỏ nhất thì tổng
a b
bằng
A.
3
9 2
. B.
2
3 9
. C.
3 3 2
. D.
2 9 2
.
Lời giải
Chọn B
Ta có
3 1, 1a b
nên
3
log 0,log 3 0
a b
b a
. Theo bất đẳng thức Cauchy ta được:
4 2 2 2
3 3 3
log log 9 81 log log 18 9 log 2log 3 2 2
a b a b a b
b a a b a a b a
Đẳng thức xảy ra khi và chỉ khi:
4
2
3
3 1, 1
3
81
9
log 2log 3
a b
a b
a
a
b
b a
Khi đó ta được
2
3 9
a b .
Câu 32. Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất
0,85% một tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền
cố định là 10 triệu đồng bao gồm cả tiền lãi vay và tiền gốc. Biết phương thức trả lãi và gốc
không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng thì anh trả hết nợ
ngân hàng? (tháng cuối có thể trả dưới 10 triệu đồng).
A.
67
. B.
68
. C.
66
. D.
65
.
Lời giải
Chọn C
Đặt
500; 10; 0,85%
N A r
.
Sau một tháng anh An còn nợ:
. 1
N r A
.
Sau hai tháng anh An còn nợ:
2 2 2
. 1 . 1 . 1 . 1 1 . 1 1 1
A
N r A r A N r A r N r r
r
.
Tương tự sau
n
tháng anh An còn nợ:
. 1 1 1
n n
A
N r r
r
.
Anh An trả hết nợ sau
n
tháng khi
n
là nghiệm nguyên dương nhỏ nhất của bất phương trình:
10
. 1 1 1 0 500. 1 0,85% 1 0,85% 1 0
0,85%
n n n n
A
N r r
r
1 0,85%
40 40
1 0,85% 65,38 66
23 23
n
n log n
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
17
Câu 33. Một người vay ngân hàng 100 triệu đồng với lãi suất là 0,7%/tháng theo thỏa thuận cứ cuối mỗi
tháng người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết
nợ (tháng cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết
nợ ngân hàng?
A.
21
. B.
24
. C.
22
. D.
23
.
Lời giải
Chọn C
Xét bài toán tổng quát:
Gọi
A
là số tiền vay từ ngân hàng với lãi suất là
r
(%) mỗi tháng. Số tiền trả hàng tháng là
a
và sau
n
tháng thì trả được hết nợ.
Cuối tháng thứ 1, số tiền còn nợ là
1
1
N A r a
.
Cuối tháng thứ 2, số tiền còn nợ là
2
2 1 1
. 1 1
N N N r a A r a r a
.
Cuối tháng thứ 3, số tiền còn nợ là
3 2
3
1 1 1
N A r a r a r a
.
…
Cuối tháng thứ
n
, số tiền còn nợ là
1 2
1 1 1 1
n n n
n
N A r a r a r a r a
1 1 1 1
1 . 1 .
1 1
n n
n n
r r
A r a A r a
r r
.
Để hết nợ thì
. . 1
0 *
1 1
n
n
n
A r r
N a
r
.
Từ đề bài ta có
8 6 3
100.000.000 10 , 5.000.000 5.10 , 0,7% 0,007 7.10
A a r
.
Thay vào
*
ta được
8 3
6
1,007
10 .7.10 .1,007 50 50
5.10 1,007 log
1,007 1 43 43
n
n
n
n
.
Suy ra
21,6
n
.
Vậy sau 22 tháng thì người đó trả hết nợ.
Câu 34. Cho
2
6
2
log 5
log 45
log 3
b
a
c
, với
, ,a b c
. Tính tổng
a b c
A.
2
. B.
1
. C.
4
. D.
0
.
Lời giải
Chọn B
Ta có:
2 2 2 2
6
2 2 2
log 45 2log 3 log 5 log 5 2
log 45 2
log 6 log 3 1 log 3 1
Vậy
2, 2, 1 2 2 1 1
a b c a b c
.
Câu 35. Xét các số nguyên dương
, a b
sao cho phương trình
2
ln ln 5 0
a x b x
có hai nghiệm phân
biệt
1 2
, x x
và phương trình
2
5log log 0
x b x a
có hai nghiệm phân biệt
3 4
, x x
thỏa mãn
1 2 3 4
x x x x
. Tìm giá trị nhỏ nhất của
2 3S a b
A.
min
33
S
. B.
min
30
S
. C.
min
17
S
. D.
min
25
S
.
Lời giải
Chọn B.
Điều kiện để hai phương trình
2
ln ln 5 0
a x b x
và
2
5log log 0
x b x a
có hai nghiệm
phân biệt là:
2
20 0
b a
. (*)
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
18
Theo giả thiết ta có
1 2 1 2
1 2
5
3 4 3 4
3 4
ln ln ln
log log log
10
5 5
b
a
b
b b
x x x x
x x e
a a
b b
x x x x
x x
.
Mà
5
1 2 3 4
10
b b
a
x x x x e
ln10
5
b b
a
(Vì
, a b
là các số nguyên dương)
5
3
ln10
a a
. (1)
Theo điều kiện (*) có
2 2
20 0 20 60 8b a b a b
. (2)
Từ (1) và (2) suy ra
min
3
2 3 30 30
8
a
S a b S
b
(thỏa mãn các điều kiện đề bài).
Câu 36. Bất phương trình
3
9 ln 5 0x x x
có bao nhiêu nghiệm nguyên?
A. 4. B. 7. C. 6. D. Vô số.
Lời giải
Chọn C
Điều kiện:
5x
.
Cho
3
3
3
9 0
0
9 ln 5 0
3
ln 5 0
4
x
x x
x
x x x
x
x
x
.
Bảng xét dấu:
Dựa vào bảng xét dấu ta thấy
4 3
0
0 3
x
f x
x
.
Vì
4; 3;0;1;2;3x x
.
Vậy có 6 giá trị nguyên của
x
thỏa bài toán.
Câu 37. Cho hàm số
2 2
x x
f x
. Gọi
0
m là số lớn nhất trong các số nguyên thõa mãn
12
2 2 0f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019
m
. B.
0
1009;1513
m
.
C.
0
505;1009m
. D.
0
1;505m
.
Lời giải
Chọn B
Hàm số ( ) 2 2
x x
f x
xác định
x R
.
Khi đó
x R
, ta có ( ) 2 2 (2 2 ) ( )
x x x x
f x f x
.
Suy ra
( )f x
là hàm số lẻ
(1)
Mặt khác ( ) (2 2 )ln 2 0
x x
f x
,
x R
.
Do đó hàm số
( )f x
đồng biến trên
R
(2)
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
19
Ta có
12
( ) (2 2 ) 0
f m f m
12
(2 2 ) ( )f m f m
.
Theo
(1)
suy ra
12
(2 2 ) ( )f m f m
.
Theo
(2)
ta được
12
12 12
2
2 2 3 2
3
m m m m
.
Vì
m Z
nên
0
1365 1365
m m
.
Vậy
0
1009;1513
m
.
Câu 38. Tính tổng tất cả các nghiệm nguyên của bất phương trình
2 2
2 2
log 3 log 4 1 0
x x x x
.
A.
4
. B.
6
. C.
5
. D.
3
.
Lời giải
Chọn B
Điều kiện:
0
x
.
Ta có
2 2 2 2
2 2 2 2
log 3 log 4 1 0 log 3 3 log 4 4 *
x x x x x x x x
.
Xét hàm số
2
log
f t t t
trên
0;D
. Ta có
1
1 0
ln2
f t t D
t
hàm số
f
đồng biến trên
D
.
Suy ra
2 2
* 3 4 3 4 1 3
f x f x x x x
.
Vậy tập hợp các nghiệm nguyên của bất phương trình là
1; 2; 3
.
Nhận xét: Với cách hỏi và đáp án của câu này ta chỉ cần mở MOD7 của máy tính cầm tay, nhập
vế trái của bất phương trình và cho biến chạy từ 1 đến 6 là tìm được đáp án ngay.
Câu 39. Cho hàm số
y f x
liên tục và đồng biến trên
0;
2
, bất phương trình
ln cos
x
f x x e m
(với
m
là tham số) thỏa mãn với mọi
0;
2
x
khi và chỉ khi:
A.
0 1
m f
. B.
0 1
m f
. C.
0 1
m f
. D.
0 1
m f
.
Lời giải
Chọn A
Ta có:
ln cos , 0; ln cos , 0; 1
2 2
x x
f x x e m x m f x x e x
Do
f x
đồng biến trên
0;
2
nên
0, 0;
2
f x x
.
Xét
ln cos , 0;
2
x
g x f x x e x
0
tan 0 tan 0 , 0;
2
x
g x f x x e e x
Suy ra
g x
đơn điệu tăng trên
0;
2
, do đó:
0
1 0 tan 0 0 1
m f e f
.
Câu 40. Ông An có 200 triệu đồng gửi ngân hàng với kì hạn 1 tháng với lãi suất
0,6%
/1 tháng được trả
vào cuối kì. Sau mỗi kì hạn, ông đến tất toán cả lãi và gốc, rút ra 4 triệu đồng để tiêu dùng, số
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
20
tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi luất
không thay đổi trong suốt quá trình ông gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi,
ông An tất toán và rút toàn bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn
đến nghìn đồng)
A. 169234 (nghìn đồng). B. 165288 (nghìn đồng).
C. 169269 (nghìn đồng). D. 165269 (nghìn đồng).
Lời giải
Chọn C
Nếu cuối mỗi kì hạn, ông An không rút ra 4 triệu thì số tiền ông có được sau 1 năm là
12
200000. 1 0,6%
A
nghìn đồng
Đầu tháng thứ 2 ông An rút về 4 triệu đồng, nếu để nguyên số tiền đó để gửi thì đến hết tháng
thứ 12 ngân hàng phải trả cả gốc và lãi cho ông ứng với 4 triệu đồng đó là
11
11
1
4000. 1 0,6% 4000.B R
(nghìn đồng) nên đến hết tháng thứ 12, số tiền giả định là A
không còn được lấy nguyên vẹn mà bị trừ đi số tiền
1
B
Tương tự, với 4 triệu đồng ông rút ở tháng thứ 3, 4,., 11 sẽ bị trừ đi tương ứng là:
10 9 1
2 3 11
4000. , 4000. ,..., 4000.B R B R B R
Do vậy, số tiền ông An nhận được khi tất toán ở lần cuối cùng là:
12 11 10
2 3 11
... 200000. 4000
A B B B R R R R
11
12
1
200000. 4000 169269
1
R
R R
R
(nghìn đồng).
Câu 41. Cho
x
,
y
thỏa mãn
3
2 2
log 9 9
2
x y
x x y y xy
x y xy
. Tìm giá trị lớn nhất của
3 2 9
10
x y
P
x y
khi
x
,
y
thay đổi.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn C
Điều kiện:
0
x y
(do
2
2
2 2
3
2 2 0
2 4
y y
x y xy x
).
Đẳng thức đã cho tương đương với
3
2 2
9
log 9 9 2 *
2
x y
x x y y xy
x y xy
.
Đặt
2 2
2 0
u x y xy
,
9 9 0
v x y
, ta có.
3 3 3
* log log log
v
u v u u v v
u
.
Mà hàm số
3
logf t t t
đồng biến trên
0;
nên suy ra
2 2
* 9 9 2 0
u v x y xy x y
.
Ta có
2
2
2 2 2
3 9 3 19
9 9 2 0 9 2 3
2 2 4 2 4 4
y y
x y xy x y x x y y y
.
Dẫn đến
2
19 1 19
9 1 2 19
2 2 4 2 2 2
y y y
x x x x y
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
21
Suy ra
3 2 9 10 2 19 2 19
1 1
10 10 10
x y x y x y x y
P
x y x y x y
.
2 19 8
1
3 3
x y x
P
y y
.
Vậy
max 1P
.
Cách 2:
Từ giả thiết, ta có
2 2
9 9 2 0 *x y xy x y
Ta thấy
8, 3x y
thỏa mãn
*
, đặt
8, 3x a y b
khi đó:
2 2 2 2 2 2
9 9 2 0 10a 5 0 10a 5
10a 5 0 2a 0
x y xy x y a b ab b a ab b
b b
Ta có:
3 2 9 3 2 21 2
1 1
10 21 21
x y a b a b
P
x y a b a b
Dấu “=” xảy ra khi và chỉ khi
8, 3x y
. Vậy
P
đạt giá trị lớn nhất bằng 1.
Câu 42. Cho hai số thực
a
,
b
thỏa mãn
0a
,
0 2b
. Tìm giá trị nhỏ nhất của biểu thức
2
2
2 2.
2.
2
a
a a
a
a a
b
b
P
b
b
.
A.
min
9
4
P
. B.
min
7
4
P
. C.
min
13
4
P
. D.
min
4P .
Lời giải
Chọn C
Do
0 2b
và
0a
nên
0 2
a a
b
.
2 2
2
2 . 1 2 1 2
. 2 . 1
2 2
2
2
1
a
a a a a
a
a a
a a
a
a
b
b
P
b b
b
b
. Đặt
2
a
a
t
b
, khi đó ta được
1t
.
Yêu cầu bài toán trở thành tìm giá trị nhỏ nhất của hàm số
2
1
1
2
1
t
f t t
t
với
1;t 
Có
3 2
3
3 3
2 1
t t t
f t
t
3 2
0 3 3 0f t t t t
2
3 1 0 3t t t
(do
2
1 0,t t ).
1
lim
t
f t

;
lim
t
f t


.
Bảng biến thiên
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
22
Từ bảng biến thiên ta được
min
13
4
P
. Dấu bằng diễn ra khi và chỉ khi
2
3 3 3. 2
a
a a
a
t b
b
với
0 2
b
và
0
a
.
Câu 43. Cho các số thực
, 1
a b
thỏa mãn điều kiện
2 3
log log 1a b
. Tìm giá trị lớn nhất của biểu
thức
3 2
log logP a b
.
A.
2 3
log 3 log 2
. B.
3 2
log 2 log 3
. C.
2 3
1
log 3 log 2
2
. D.
2 3
2
log 3 log 2
.
Lời giải
Chọn A.
Đặt
3
2
3 3
2 2
log 1
0 1
log
log log 2
log 1 log 3
b x
x
a x
a x
b x
Đặt
3 2
3 2
1 log 2 log 3
log 2 1 log 3
2 1
x x
P f x x x f x
x x
.
3
3 2
2 3
log 2
0 1 log 2 log 3
log 3 log 2
f x x x x
.
Ta có bảng biến thiên
x
0
3
2 3
log 2
log 3 log 2
1
f x
0
f x
3
log 2
2 3
log 3 log 2
2
log 3
Vậy
max 2 3
log 3 log 2
P
.
Câu 44. Với giá trị nào của tham số m để phương trình
1
4 .2 2 3 0
x x
m m
có hai nghiệm
1 2
,x x
thỏa
mãn
1 2
4
x x
.
A.
5
.
2
m
B.
2.
m
C.
8.
m
D.
13
.
2
m
Lời giải
Chọn D
1
4 .2 2 3 0
x x
m m
(1)
Đặt
2 ( 0)
x
t t
Phương trình (1) trở thành
2
2 2 3 0
t mt m
(2)
2 2
' (2 3) 2 3
m m m m
Phương trình (1) có hai nghiệm
Phương trình (2) có hai nghiệm dương
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
23
2
' 0 2 3 0 1 3
0 2 0 0 3
0 2 3 0 3
2
m m m m
S m m m
P m
m
Theo giả thiết:
1 2
4
x x
1 2 1 2
4
1 2
13
2 2 2 .2 16 . 16 2 3 16
2
x x x x
t t m m
(Thỏa ĐK)
Câu 45. Cho dãy số
n
a
thỏa mãn
1
1
a
và
1
3
5 1
3 2
n n
a a
n
, với mọi
1n
. Tìm số nguyên dương
1
n
nhỏ nhất để
n
a
là một số nguyên.
A.
41
n
. B.
39
n
. C.
49
n
. D.
123
n
.
Lời giải
Chọn A
Ta có:
1 1
3 1 2
3 3 5
5 1 5
3 2 3 2 3 2
n n n n
a a a a
n
n
n n n
1 5 5 5
3 1 2
log log 3 1 2 log 3 2 ; 1
3 2
n n
n
a a n n n
n
Áp dụng cho:
2 1 5 5
3 2 5 5
4 3 5 5
1 5 5
1 log 8 log 5
2 log 11 log 8
3 log 14 log 11
...........
1 log 3 2 log 3 1 2
n n
n a a
n a a
n a a
n n a a n n
Cộng vế với vế
1
n
đẳng thức trên ta được:
1 5 5 5 1 5
log 3 2 log 5 log 3 2 ; 1 log 5
n n
a a n a n Do a
Thử các đáp án từ nhỏ tới lớn ta được:
5 5
5 5
39 log 3 2 log 119
41 log 3 2 log 125 3
n n
n n
Vậy chọn đáp án A.
Câu 46. Có bao nhiêu giá trị nguyên của tham số
8;m
để phương trình sau có nhiều hơn hai
nghiệm phân biệt
2
2 2
1 2 2 2
x m x x
x x x m x x m
.
A.
6
. B.
7
. C.
5
. D.
8
.
Lời giải
Chọn B
Phương trình đã cho tương đương với
2 2
2
2 2 2 2
2 2 1
x m x x
x x
x m x x x m x x
.
Đặt
2 2
;
x m a x x b
ta có phương trình
1
trở thành
.2 .2
a b b
a b a b
.2 .2
b a
a b a b
2 1 2 1 0 2
b a
a b
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
24
Trường hợp 1: Nếu
0ab
thì phương trình
2 1 2 1
2 0 3
a b
a b
.
+ Nếu
2 1
0 2 1 0 0
a
a
a
a
.
+ Nếu
2 1
0 2 1 0 0
a
a
a
a
.
Do đó
2 1
0,
a
a
với
0a
.
Tương tự ta có
2 1
0,
b
b
với
0b
. Do vậy phương trình
3
vô nghiệm.
Trường hợp 2: Nếu
0ab
thì phương trình
2
2
1
0
x m
x x
.
Phương trình
1
có nhiều hơn hai nghiệm phân biệt
2
0
0.
0
m
m
m m
Do
m
nguyên và
8;m
nên có
7
giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 47. Tổng tất cả các giá trị của tham số
m
để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x m
x x
x m
có
đúng ba nghiệm phân biệt là:
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn B
Phương trình tương đương
2
2 3 (2 2)
2
ln 2 2
3
ln 2 3
x x x m
x m
x x
2
2 2
2 3 2
3 .ln 2 3 3 .ln 2 2
x m
x x
x x x m
(*).
Xét hàm đặc trưng
3 .ln , 2
t
f t t t
là hàm số đồng biến nên từ phương trình (*) suy ra
2
2 3 2 2
x x x m
2
2 2 1 0
g x x x x m
.
Có
2
2
4 2 1 2 4
'
2
2 1
x x m khi x m x khi x m
g x g x
x khi x m
x m khi x m
và
2
' 0
0
x khi x m
g x
x khi x m
.
Xét các trường hợp sau:
TH1:
0m
ta có bảng biến thiên của
g x
như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có
m
thoả mãn.
TH2:
2m
tương tự.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
25
TH3:
0 2m
, bảng biến thiên
g x
như sau:
Phương trình có 3 nghiệm khi
2
1
1 0
1
2 1 0 2 3
2
2 1 0 2 3
3
2
m
m
m m m
m m
m
.
Cả 3 giá trị trên đều thoả mãn, nên tổng của chúng bằng 3.
Câu 48. Cho phương trình
2 2
1 1 1 1
25 2 .5 2 1 0
x x
m m
, với
m
là tham số. Giá trị nguyên
dương lớn nhất của tham số
m
để phương trình trên có nghiệm là:
A.
5
B.
26
. C.
25
. D.
6
.
Lời giải
Chọn C
Đặt
2
1 1t x
với
1;1x
ta được
1;2t
.
Phương trình trở thành
2
5 2 .5 2 1 0
t t
m m
với
1; 2t
.
Đặt
5 5;25
t
a a
và
2
2 1
2
a a
m
a
.
Hàm
2
2 1
2
a a
f a
a
đồng biến trên
5;25
nên để phương trình có nghiệm thì
5 25f m f
suy ra
16 576
;
3 23
m
.
Vậy giá trị nguyên dương lớn nhất của
m
bằng
25
.
Câu 49. So sánh ba số
64
1001 2
1000 , 2 a b
và
1 2 3 1000
1 2 3 ... 1000c
?
A.
c a b
. B.
b a c
. C.
c b a
. D.
a c b
.
Lời giải
Chọn A
Ta có:
1 1000 2 1000 999 1000
1 1000 ; 2 1000 ...999 1000
1 2 3 1000 1000
1 2 3 ... 1000 1000.1000c c a
Mặt khác:
10
2 1000
64
4
6
64 10 10 6 2 1001
2
2 .ln2 . 2 .ln 2 1000 .ln1000 1001.ln1000 2 1000
10
a b
Vậy
.c a b
Câu 50. Cho các số thực dương
x
,
y
thay đổi và thỏa mãn điều kiện
1x y
. Giá trị nhỏ nhất của
biểu thức
2 2
log 3log
x y
y
x
T x
y
là
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
26
A.
19
. B.
13
. C.
14
. D.
15T
.
Lời giải
Chọn D
Từ giả thiết
2
2log 3 log 1
x y
y
T x x
2
4 1
3 1
log
1 log
x
x
y
y
.
Đặt log
x
t y vì
1 0;1y x t
.
Yêu cầu bài toán trở thành tìm giá trị nhỏ nhất của hàm
2
4 3
3
1
f t
t
t
với
0;1t
.
Dễ thấy hàm số
f t
liên tục trên khoảng
0;1
và
2
3 2
3 3
2 2
3 1 3
3 9 3
1 1
t t
t t t
f t
t t t t
,
1
0 3 1 0
3
f t t t
.
0
lim
t
f t

;
1
lim
t
f t

.
Bảng biến thiên
Từ bảng biến thiên suy ra
0;1
1
min 15
3
f t f
. Vậy
min 15P
đạt được khi và chỉ khi
3
1
log
3
x
y y x
trong đó
1 y x
.
Câu 51. Bất phương trình
1
4 1 2 0
x x
m m
nghiệm đúng với mọi
0x
. Tập tất cả cá giá trị của
m
là
A.
;12

. B.
; 1
. C.
;0

. D.
1;16
.
Lời giải
Chọn B
Bất phương trình
1
4 1 2 0 1
x x
m m
4 2 1 2 0
x x
m m
.
Đặt
2
x
t
bất phương trình trở thành
2
2 1 0 2t m t m
.
Bất phương trình
1
nghiệm đúng với mọi
0x
khi và chỉ khi bất phương trình
2
nghiệm
đúng với mọi
1t
.
2
2
2
2 2 1 2
2 1
t t
t m t t m
t
(do
1t
).
Đặt
2
2
2 1
t t
f t
t
với
1t
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2
. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
27
2
2
2 2 2
' 0 1
2 1
t t
f t t
t
.
Bảng biến thiên
Từ bảng biến thiên ta có
1;f t m t 
1m
. Vậy chọn B
Câu 52. Phương trình
4 1 2 . .cos
x x
m x
có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là
A. Vô số. B. 1. C. 2. D. 0.
Lời giải
Chọn B
Ta có:
4 1 2 . .cos 2 2 .cos 2 2 .cos 0
x x x x x x
m x m x m x
.
Đặt:
2 2 .cos
x x
f x m x
có tập xác định
D
.
f x
là hàm số chẵn.
0f x
có nghiệm duy nhất
0x
.
Thay
0x
vào phương trình
2m
.
Câu 53. Cho a, b, c là ba số thực dương,
1a
và thỏa mãn
2
2 3 3 2
log log 4 4 0
4
a a
bc
bc b c c
. Số bộ
; ;a b c
thỏa mãn điều kiện đã cho là
A. 0. B. 1. C. 2. D. Vô số.
Lời giải
Chọn B
Đặt:
2
2 3 3 2
log log 4 4
4
a a
bc
P bc b c c
Ta có:
2
3 3 4 4
4
bc
b c b c
.
Do
1a
nên:
2
3 3 4 4
log log 4log
4
a a a
bc
b c b c bc
2
2 log 4 0
a
P bc c
2
2 2
2
4 0
1
0 2 log 0
4
1
2
4
a
a
c
P bc b
c
b c
Câu 54. Tính tổng
T
của các giá trị nguyên của tham số
m
để phương trình
x 2
e e 2
x
m m m
có
đúng hai nghiệm phân biệt nhỏ hơn
1
loge
.
A.
28T
. B.
20T
. C.
21T
. D.
27T
.
Lời giải
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
28
Chọn D
Đặt
e , 0
x
t t
ta được
2
2 1 2 2
2 2 0 *
t m m t m t mt m m t m m
.
Ta có
1
0 10
loge
x t
. Bài toán quy về tìm
m
phương trình
*
có hai nghiệm phân biệt
thỏa mãn
0 10
t
. Tức là:
0
21 41
0 10 1
2
0 10
m
m m m
m m
. Do đó tổng
T
của các giá
trị nguyên của tham số
m
để phương trình
x 2
e e 2
x
m m m
có đúng hai nghiệm phân
biệt nhỏ hơn
1
loge
là
2 3 4 5 6 7 27
T
.
Câu 55. Cho hai số thực
,x y
lớn hơn 1 và thỏa mãn
.( ) .( ) .
y x
x x e y y e
y e x e
Tìm giá trị nhỏ nhất của
biểu thức
log log .
x y
P xy x
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Lời giải
Chọn C
Với
, 1x y
, ta có
.( ) .( )
ln .( ) ln .( )
ln ln
ln ln
(1).
y x
y x
x x e y y e
x x e y y e
y x
y x
y e x e
y e x e
x y xe y x ye
y e x e
y y x x
Xét hàm số
( ) 1 ln
t t
g t te e t
trên
1; ,
có
1
'( ) 0, 1.
t
g t te t
t
Hàm số
( )g t
đồng biến trên
1;

nên
( ) (1) 1 0, 1.
g t g t
Xét hàm số
ln
( )
t
t e
f t
t t
trên
1;

, có
2
( )
'( ) 0, 1,
g t
f t t
t
nên
( )f t
đồng biến trên
(1; ).
Với
, 1x y
thì
(1) ( ) ( ) .f y f x y x
Đặt
log .
x
u y
Do
1y x
nên
1.
u
Ta có
1 1
( ) .
2
u
P h u
u
Nhận thấy
2
2
2
'( )
2
u
h u
u
,
nên
'( ) 0
h u
khi
2,
u
'( ) 0
h u
khi
1 2,
u
'( ) 0
h u
khi
2.
u
Dẫn tới
1 2 2
( ) 2 , 1,
2
P h u h u
đẳng thức xảy ra khi
2.
u
Vậy
1 2 2
min ,
2
P
đạt
được khi
2
y x
và
1.
x
Câu 56. Tập hợp các giá trị thực của tham số m để phương trình
2
2019 1
2019
log (4 ) log (2 1) 0
x x m
có hai nghiệm thực phân biệt là
( ; )T a b
. Tính
2
S a b
.
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
29
A.
18
. B.
8
. C.
20
. D.
16
.
Lời giải
Chọn D
TXĐ:
1
( 2;2) ( ; )
2
m
D

.
Khi đó, phương trình đã cho trở thành
2
2 2
2019
4
log 0 4 2 1 2 5 0 (*)
2 1
x
x x m x x m
x m
Phương trình
(*)
có 2 nghiệm phân biệt
2
1 1.(m 5) 6 m 0 6 (1)
m
Khi đó phương trình
(1)
có 2 nghiệm lần lượt là
1 2
1 6 ; 1 6
x m x m
.
TH1:
1
2 5
2
m
m
(2).
2;2
D
.
Phương trình (1) có 2 nghiệm
1 2
,
x x D
1 6 2 6 3
5
1 6 2 6 1
m m
m
m m
(3).
Từ (1), (2) và (3) suy ra
5 6
m
.
TH2:
1
2 2 3 5
2
m
m
(4).
1
;2
2
m
D
.
Phương trình (1) có 2 nghiệm
1 2
,
x x D
3
1 6 2 6 3
5
3
1 3
1 6 6
5
2 2
m
m m
m
m
m m
m m
m
(5).
Từ (4) và (5) suy ra
m
.
Vậy
5 6
m
.
Suy ra
5, 6
a b
2 16
a b
.
Câu 57. Một anh sinh viên nhập học đại học vào tháng 8 năm 2014. Bắt đầu từ tháng 9 năm 2014, cứ
vào ngày mồng một hàng tháng anh vay ngân hàng 3 triệu đồng với lãi suất cố định
0,8%
/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo( lãi kép).
Vào ngày mồng một hàng tháng kể từ tháng 9/2016 về sau anh không vay ngân hàng nữa và
anh còn trả được cho ngân hàng 2 triệu đồng do có việc làm thêm. Hỏi ngay sau khi kết thúc
ngày anh ra trường
30 / 06/ 2018
anh còn nợ ngân hàng bao nhiêu tiền( làm tròn đến hàng
nghìn đồng)?
A.
49.024.000
đồng. B.
47.401.000
đồng.
C.
46.641.000
đồng. D.
45.401.000
đồng.
Lời giải
Chọn C
Đặt
0,8% 0,008 ; 3.000.000
o
r V
+) Tính tổng số tiền anh sinh viên vay từ 01/09/2014 đến hết 30/08/2016 (24 tháng)
- Số tiền anh vay sau tháng thứ nhất, thứ hai, thứ 3,., tháng thứ 24 lần lượt là:
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
ĐỀ THI THỬ 2019
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA -
LOGARIT
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489
30
1
2
2 1
3 2
3 2
24 23
24
1
1 1 1
1 1 1 1
....
1 1 ... 1
o
o o o
o o o o
o o o
V V r
V V V r V r V r
V V V r V r V r V r
V V r V r V r
24
1 1
1 79.661.701
o
r
V r
r
( đồng) = T
+) Tính số tiền anh sinh viên còn nợ sau mỗi tháng, tính từ 01/09/2016 đến hết 30/06/2018( 22
tháng). Đặt
2.000.000
o
T
- Số tiền anh còn nợ sau tháng thứ nhất, thứ hai, thứ 3,., tháng thứ 22 lần lượt là:
1
2 2
2 1
3 3 2
3 2
22 22 21
22 21
1 1 1
1 1 1 1
1 1 1 1 1
....
1 1 1 1 ... 1
o o
o o o
o o o o
o o o o
T T T r T r T r
T T T r T r T r T r
T T T r T r T r T r T r
T T T r T r T r T r T r
22
22
1 1
1 1 46.641.000
o
r
T r T r
r
( đồng)
| 1/38

Tài liệu khác của Toán 11

Preview text:

QUYEÅN SOÁ 2
Tuyeån taäp 57 caâu hoûi vaän duïng –
vaän duïng cao töø caùc ñeà thi thöû treân
caû nöôùc naêm 2019 –coù ñaùp aùn chi
tieát thöïc hieän giaûi bôûi taäp theå giaùo
vieân Dieãn Ñaøn Giaùo Vieân Toaùn HAØM SOÁ MUÕ- LOGARIT
TOÅNG HÔÏP: NGUYEÃN BAÛO VÖÔNG
FACEBOOK: https://www.facebook.com/phong.baovuong SÑT: 0946798489
Naêm hoïc: 2018 – 2019
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ Câu 1.
Giá trị thực của tham số m để phương trình 4x  2  3.2x m
 64  0 có hai nghiệm thực x , x thỏa 1 2
mãn  x  2 x  2  24 thuộc khoảng nào sau đây? 1  2   3   3   21 29   11 19  A. 0;   . B.  ; 0   . C. ;   . D. ;   .  2   2   2 2   2 2  C y x y a x y b Câu 2.
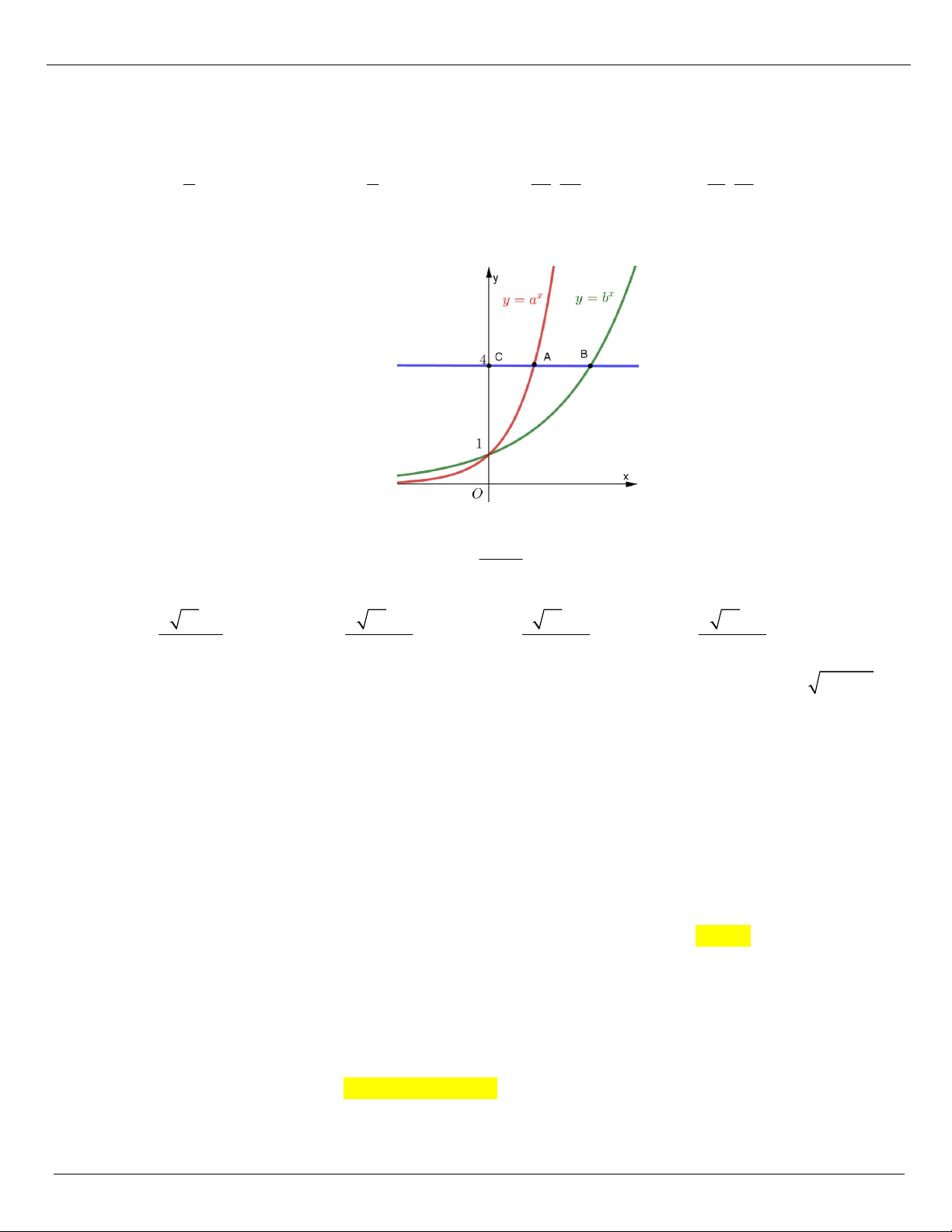
Cho điểm (0; 4), đường thẳng
4 cắt hai đồ thị hàm số và
lần lượt tại A và B sao
cho AB AC (hình vẽ). Khẳng định nào sau đây đúng? A. a  2 . b B. 2
b a . C. b  2 . a D. 2
a b . 1 ab Câu 3.
Cho các số thực dương a, b thỏa mãn log
 2ab a b  3 . Giá trị nhỏ nhất của biểu thức 2 a b
P a  2b bằng 2 10 1 2 10  3 3 10  7 2 10  5 A. . B. . C. . D. . 2 2 2 2 Câu 4.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 5x 10  25x m  4 có
nghiệm duy nhất. Số tập con của S là A. 3 . B. 4 . C. 16 . D. 15 . Câu 5.
Anh X muốn mua một chiếc xe máy Yamaha Exciter 150 giá 47.500.000 của cửa hàng Phú Tài nhưng
vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước 25 triệu đồng và trả góp
trong 12 tháng, với lã suất 0.6% tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho cửa hàng Phú Tài số tiền
là bao nhiêu(quy tròn đến hàng đơn vị).
A. 1.948.927 đồng.
B. 1.948.926 đồng.
C. 2.014.545 đồng.
D. 2.014.546 đồng. x Câu 6.
Biết rằng bất phương trình log 5  2  2.log
 có tập nghiệm là S  log ;
b  , với a , b ax 2 3 2   5 2
là các số nguyên dương nhỏ hơn 6 và a  1. Tính P  2a  3b . A. P  7 . B. P 11. C. P 18. D. P 16. Câu 7.
Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất 7% năm. Biết rằng nếu không rút tiền ra
khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo và từ
năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số
tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt thời gian gửi lãi suất không
thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn đến hàng nghìn).
A. 1.686.898.000 VNĐ. B. 743.585.000 VNĐ.
C. 739.163.000 VNĐ. D. 1.335.967.000 VNĐ.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 1
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ
 4a  2b  5  Câu 8.
Cho a , b là hai số thực dương thỏa mãn log
a  3b  4 . Tìm giá trị nhỏ nhất của biểu 5    a b  thức 2 2
T a b 1 3 5 A. . B. 1. C. . D. . 2 2 2 Câu 9.
Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả sử 1 tế bào E. Coli khối lượng khoảng 15
15.10 g. Hỏi sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là bao
nhiêu? (chọn đáp án chính xác nhất). A. 29 2,34.10  g  . B. 29 3, 36.10  g  . C. 26 2, 25.10 kg  . D. 26 3,35.10 kg  . 1 1 1 1 190 Câu 10.
Gọi n là số nguyên dương sao cho    ...   đúng với mọi x log x log x log x log x x n log 2 3 3 3 3 3 3
dương, x  1. Tìm giá trị của biểu thức P  2n  3 .
A. P  32 .
B. P  23.
C. P  43.
D. P  41. Câu 11.
Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số  x; y  thỏa mãn 2 log
4x  4 y  6  m  1 và 2 2
x y  2x  4 y 1  0 . 2 2 x y 2  
A. S  5; 1;1;  5 .
B. S  1;  1 .
C. S  5;  5 .
D. S  7  5; 1;1;5;  7 . Câu 12.
Tìm tất cả các giá trị thực của tham số m để phương trình 3m m ee   2 x   x  2 2 1
1 x 1 x  có nghiệm.  1   1   1   1  A. 0;   . B. 0; ln 2   . C. ; ln 2   . D. ln 2;    . e   2   2   2  Câu 13.
Cho x, y là hai số thực dương thoả mãn log x  log y  log  2 x y
. Tìm giá trị nhỏ nhất P của 1 1 1  min 2 2 2
biểu thức P  3x  . y 17 25 2 A. P  8 . B. P  . C. P  . D. P  9 . min min 2 min 4 min Câu 14.
Một người vay ngân hàng 90.000.000 đồng theo hình thức trả góp trong 3 năm, mỗi tháng người đó
phải trả số tiền gốc là như nhau và tiền lãi. Giả sử lãi suất không thay đổi trong toàn bộ quá trình trả
nợ là 0.8% trên tháng. Tổng số tiền mà người đó phải trả cho ngân hàng trong toàn bộ quá trình trả nợ là
A. 103.120.000 đồng.
B. 103.420.000 đồng. C. 103.220.000 đồng. D. 103.320.000 đồng. 2 2
Câu 15. Cho hai số thực a , b thỏa mãn a b  1 và log
a b  1. Giá trị lớn nhất của biểu thức 2 2   a b
P  2a  4b  3 là 10 1 A. 10 . B. . C. 2 10 . D. . 2 10 Câu 16.
Một thầy giáo cứ đầu mỗi tháng lại gửi ngân hàng 8 000 000 VNĐ với lãi suất 0, 5% / tháng. Hỏi sau
bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ?
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ A. 60 . B. 50 . C. 55 . D. 45 .
Câu 17. Tích các nghiệm của phương trình log 125x 2 .log x  1 x 25 . 1 630 7 A. 630 . B. . C. . D. 125 625 125 xa b Câu 18.
Gọi x , y là các số thực dương thỏa mãn điều kiện log x  log y  log x y và  , 9 6 4   y 2
với a , b là hai số nguyên dương. Tính 2 2
T a b .
A. T  26 .
B. T  29 .
C. T  20 .
D. T  25 . Câu 19.
Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0,7%/ tháng với tổng số tiền
vay là 1 tỉ đồng. Giả sử mỗi tháng ba người đều trả cho ngân hàng một số tiền như nhau để trừ vào tiền
gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần 10 tháng, Bình cần 15 tháng và Cường cần
25 tháng. Hỏi tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân hàng là bao nhiêu (làm tròn đến hàng nghìn)? A. 6426800. B. 45672000. C. 46712000. D. 63271000. Câu 20.
Tìm tất cả các giá trị của tham số m để bất phương trình x 1 4   2x m  
1  0 nghiệm đúng với mọi x   .
A. m   ;  0 .
B. m  0;   .
C. m  0  ;1 .
D. m   ;
 0  1;   .  xy 1  Câu 21. Với mọi số thực ,
x y thỏa điều kiện log  2    2 2 x y
xy . Gọi M và m lần lượt là giá trị 2 2 2  x y   4 4 x y
lớn nhất và giá trị nhỏ nhất của biểu thức P
. Tính giá trị biểu thức Q  15m  2 log M . 2xy 1 2
A. Q  0 .
B. Q 1. C. Q  2  . D. Q  1  . Câu 22. Cho a log 9  b log
673  2018 với a,b   . Khẳng định nào đúng trong các 2019 2019
khẳng định sau đây?
A. b  2a . B. 2
b a . C. 2
a b .
D. a  2b . 2 2 x 1 x .2  Câu 23.
Cho hai số thực x , y thay đổi thỏa mãn đẳng thức   y  
1 .2xyxy  0. Tìm giá trị lớn nhất x 1
M của y , biết rằng x  1 . 7 A. M   .
B. M  3 .
C. M  1 . D. M  0 . 2 5b a a Câu 24.
Cho a , b là các số dương thỏa mãn log a  log b  log . Giá trị của bằng 9 16 12 2 b a a 7  2 6 a 1 6 a A.  1   6 . B.  . C.  . D.  7  2 6 . b b 25 b 5 b Câu 25.
Tìm tất cả các giá trị thực của tham số m để phương trình 4x 2x 4 3m 2x      1 có hai nghiệm phân biệt.
A. 1  m  log 4 .
B. log 3  m  1.
C. 1  m  log 4 .
D. log 3  m  1. 3 4 3 4
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 3
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ Câu 26.
Cho phương trình 5x m  log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 5  
m  20; 20 để phương trình đã cho có nghiệm? A. 20. B. 21. C. 9. D. 19. Câu 27.
Nhằm tạo môi trường xanh, sạch, đẹp và thân thiện. Đoàn trường THPT Hậu Lộc 2 đã phát động
phong trào trồng hoa toàn bộ khuôn viên đường vào trường. Sau một ngày thực hiện đã trồng được
một phần diện tích. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 ngày nữa sẽ hoàn thành.
Nhưng thấy công việc có ý nghĩa nên mỗi ngày số lượng đoàn viên tham gia đông hơn vì vậy từ ngày
thứ hai mỗi ngày diện tích trồng tăng lên 4% so với ngày kế trước. Hỏi công việc sẽ hoàn thành vào
ngày bao nhiêu? Biết rằng ngày 08 / 03 là ngày bắt đầu thực hiện và làm liên tục. A. 25 / 03 . B. 26 / 03 . C. 23 / 03 . D. 24 / 03 . Câu 28.
Cho các số thực dương x , y thỏa mãn log
11x  20 y  40  1 . Gọi M , m lần lượt là giá trị 2 2  
2 x xy3 y y
lớn nhất và giá trị nhỏ nhất của S
. Tính M m . x
A. M m  2 14 .
B. M m  10 . 7 11
C. M m  .
D. M m  . 2 6 x x 1  Câu 29.
Tổng tất cả các nghiệm thực của phương trình 15 . x 5  5
 27x  23 bằng A. 1 . B. 0 . C. 2 . D. 1 . x Câu 30.
Đồ thị hàm số y f x đối xứng với đồ thị của hàm số y a a  0, a  
1 qua điểm I 1;  1 . Giá trị  1 
của biểu thức f 2  log  bằng: a  2018  A. 2  016 . B. 2  020 . C. 2016 . D. 2020 . 1 Câu 31.
Cho các số thực a, b thỏa mãn a
,b  1. Khi biểu thức log b  log a a  đạt giá trị nhỏ a b  4 2 9 81 3  3
nhất thì tổng a b bằng A. 3 9  2 . B. 2 3  9 . C. 3  3 2 . D. 2  9 2 . Câu 32.
Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất 0,85% một
tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là 10 triệu
đồng bao gồm cả tiền lãi vay và tiền gốc. Biết phương thức trả lãi và gốc không thay đổi trong suốt
quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng thì anh trả hết nợ ngân hàng? (tháng cuối có thể trả
dưới 10 triệu đồng). A. 67 . B. 68 . C. 66 . D. 65 . Câu 33.
Một người vay ngân hàng 100 triệu đồng với lãi suất là 0,7%/tháng theo thỏa thuận cứ cuối mỗi tháng
người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết nợ (tháng
cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng? A. 21. B. 24 . C. 22 . D. 23 . log 5  b 2 log 45  a  6 log 3  c a b c   Câu 34. Cho 2 , với , ,
. Tính tổng a b c A. 2 . B. 1. C. 4  . D. 0 .
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 4
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ
Câu 35. Xét các số nguyên dương a, b sao cho phương trình 2
a ln x b ln x  5  0 có hai nghiệm phân biệt
x , x và phương trình 2
5 log x b log x a  0 có hai nghiệm phân biệt x , x thỏa mãn x x x x . 1 2 3 4 1 2 3 4
Tìm giá trị nhỏ nhất của S  2a  3b A. S  33 . B. S  30 . C. S  17 . D. S  25 . min min min min Câu 36. Bất phương trình  3
x  9x ln  x  5  0 có bao nhiêu nghiệm nguyên? A. 4. B. 7. C. 6. D. Vô số. Câu 37. Cho hàm số   2x 2 x f x   
. Gọi m là số lớn nhất trong các số nguyên thõa mãn 0
f m  f  12
2m  2   0 . Mệnh đề nào sau đây đúng?
A. m  1513; 2019 .
B. m  1009;1513 . 0   0  
C. m  505;1009 .
D. m  1;505 . 0   0   Câu 38.
Tính tổng tất cả các nghiệm nguyên của bất phương trình log  2 x  3 2
 log x x  4x 1  0 . 2 2 A. 4 . B. 6 . C. 5 . D. 3 .    Câu 39.
Cho hàm số y f x liên tục và đồng biến trên 0;  x
, bất phương trình f x  ln cos x  e m 2      
(với m là tham số) thỏa mãn với mọi x  0;   khi và chỉ khi:  2 
A. m f 0 1.
B. m f 0 1.
C. m f 0 1.
D. m f 0 1. Câu 40.
Ông An có 200 triệu đồng gửi ngân hàng với kì hạn 1 tháng với lãi suất 0, 6% /1 tháng được trả vào
cuối kì. Sau mỗi kì hạn, ông đến tất toán cả lãi và gốc, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại
ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi luất không thay đổi trong
suốt quá trình ông gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông An tất toán và rút toàn
bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng)
A. 169234 (nghìn đồng). B. 165288 (nghìn đồng).
C. 169269 (nghìn đồng). D. 165269 (nghìn đồng). x y Câu 41.
Cho x , y thỏa mãn log
x x  9  y y  9  xy . Tìm giá trị lớn nhất của 3 2 2    
x y xy  2 3x  2 y  9 P
khi x , y thay đổi. x y 10 A. 2 . B. 3 . C. 1. D. 0 . Câu 42.
Cho hai số thực a , b thỏa mãn a  0 , 0  b  2 . Tìm giá trị nhỏ nhất của biểu thức  a 2b 2a  2. a b P   . a a  2 2. a 2 b b 9 7 13 A. P  . B. P  . C. P  . D. P  4 . min 4 min 4 min 4 min
Câu 43. Cho các số thực a, b  1 thỏa mãn điều kiện log a  log b  1 . Tìm giá trị lớn nhất của biểu thức 2 3
P  log a  log b . 3 2 1 2 A. log 3  log 2 .
B. log 2  log 3 . C. log 3 log 2 . D. . 2 3  2 3 3 2 2 log 3  log 2 2 3
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 5
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ Câu 44.
Với giá trị nào của tham số m để phương trình x x 1 4 .2 m  
 2m  3  0 có hai nghiệm x , x thỏa mãn 1 2 x x  4 . 1 2 5 13 A. m  . B. m  2. C. m  8. D. m  . 2 2 a a 3 Câu 45.
Cho dãy số a thỏa mãn a  1 và n 1 5   n 1 
, với mọi n  1. Tìm số nguyên dương n  1 n  1 3n  2
nhỏ nhất để a là một số nguyên. n A. n  41 . B. n  39 . C. n  49 . D. n  123 . Câu 46.
Có bao nhiêu giá trị nguyên của tham số m  8
 ;   để phương trình sau có nhiều hơn hai nghiệm phân biệt
    xm       2 2 2 1 2 2 2xx x x x m x x m . A. 6 . B. 7 . C. 5 . D. 8 . 2
Câu 47. Tổng tất cả các giá trị của tham số m để phương trình x 2x 1  2 3 xm  log
2 x m  2 có đúng 2 x 2 x3   ba nghiệm phân biệt là: A. 2 . B. 3 . C. 1. D. 0 . 2 2
Câu 48. Cho phương trình 1 1 x     1 1 25 2 .5 x m
 2m 1  0 , với m là tham số. Giá trị nguyên dương lớn
nhất của tham số m để phương trình trên có nghiệm là: A. 5 B. 26 . C. 25 . D. 6 . 64 1001 2 a  1000 , b  2 1 2 3 1000 Câu 49. So sánh ba số
và c 1  2  3  ... 1000 ?
A. c a b .
B. b a c .
C. c b a .
D. a c b . Câu 50.
Cho các số thực dương x , y thay đổi và thỏa mãn điều kiện x y  1 . Giá trị nhỏ nhất của biểu thức x 2 T   2 log x   3log là x y y y A. 19 . B. 13 . C. 14 . D. T  15 . x xCâu 51. Bất phương trình  m   1 4 1 2
m  0 nghiệm đúng với mọi x  0 . Tập tất cả cá giá trị của m là
A. ;12 . B. ;   1 . C.  ;  0 .
D. 1;16 . Câu 52.
Phương trình 4x 1  2 . x .c
m os  x có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là A. Vô số. B. 1. C. 2. D. 0. 2  bc Câu 53.
Cho a, b, c là ba số thực dương, a  1 và thỏa mãn 2 bc b c     c  . Số a   3 3 2 log log 4 4 0 a    4  bộ  ; a ;
b c thỏa mãn điều kiện đã cho là A. 0. B. 1. C. 2. D. Vô số. Câu 54.
Tính tổng T của các giá trị nguyên của tham số m để phương trình x   2 e  ex m m  2m có đúng 1
hai nghiệm phân biệt nhỏ hơn . log e A. T  28 . B. T  20 . C. T  21. D. T  27 .
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 6
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC ĐỀ
CHUYÊN ĐỀ 1. ỨNG DỤNG ĐẠO HÀM VÀ THI THỬ 2019 KHẢO SÁT HÀM SỐ y x x x e y y e Câu 55.
Cho hai số thực x, y lớn hơn 1 và thỏa mãn y .(e )
x .(e ) . Tìm giá trị nhỏ nhất của biểu thức P  log xy  log . x y x 2 1 2 2 1 2 A. . B. 2 2 . C. . D. . 2 2 2 Câu 56.
Tập hợp các giá trị thực của tham số m để phương trình 2 log (4  x )  log
(2x m 1)  0 có hai 2019 1 2019
nghiệm thực phân biệt là T  ( ;
a b) . Tính S  2a b . A. 18 . B. 8 . C. 20 . D. 16 . Câu 57.
Một anh sinh viên nhập học đại học vào tháng 8 năm 2014. Bắt đầu từ tháng 9 năm 2014, cứ vào ngày
mồng một hàng tháng anh vay ngân hàng 3 triệu đồng với lãi suất cố định 0,8% /tháng. Lãi tháng
trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo( lãi kép). Vào ngày mồng một hàng
tháng kể từ tháng 9/2016 về sau anh không vay ngân hàng nữa và anh còn trả được cho ngân hàng 2
triệu đồng do có việc làm thêm. Hỏi ngay sau khi kết thúc ngày anh ra trường 30 / 06 / 2018 anh còn
nợ ngân hàng bao nhiêu tiền( làm tròn đến hàng nghìn đồng)?
A. 49.024.000 đồng.
B. 47.401.000 đồng.
C. 46.641.000 đồng.
D. 45.401.000 đồng. BẢNG ĐÁP ÁN 1.D 2.D 3.B 4.C 5.A 6.D 7.D 8.D 9.D 10.D 11.A 12.C 13.D 14.D 15.A 16.D 17.B 18.A 19.A 20.A 21.C 22.A 23.B 24.D 25.C 26.D 27.A 28.C 29.B 30.A 31.B 32.C 33.C 34.B 35.B 36.C 37.B 38.B 39.A 40.C 41.C 42.C 43.A 44.D 45.A 46.B 47.B 48.C 49.A 50.D 51.B 52.B 53.B 54.D 55.C 56.D 57.C
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 7
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Câu 1.
Giá trị thực của tham số m để phương trình 4x  2  3.2x m
 64  0 có hai nghiệm thực x , 1
x thỏa mãn  x  2 x  2  24 thuộc khoảng nào sau đây? 1  2  2  3   3   21 29   11 19  A. 0;   . B.  ; 0   . C. ;   . D. ;   .  2   2   2 2   2 2  Lời giải Chọn D Đặt 2x t
, điều kiện t  0 . Phương trình ban đầu trở thành 2
t  2m  3.t  64  0 * .
Để phương trình ban đầu có hai nghiệm thực x và x thì phương trình   * phải có hai nghiệm 1 2  19 m      0 2   2
4m 12m  247  0  13 13
t , t dương  S  0     m   m  . 1 2   2m  3  0  2 2 P  0     3 m     2
Theo định lý Vi-ét, ta có t .t  64 x x x x 1 2  2 .2  64 1 2  2
 64  x x  6 . 1 2 1 2
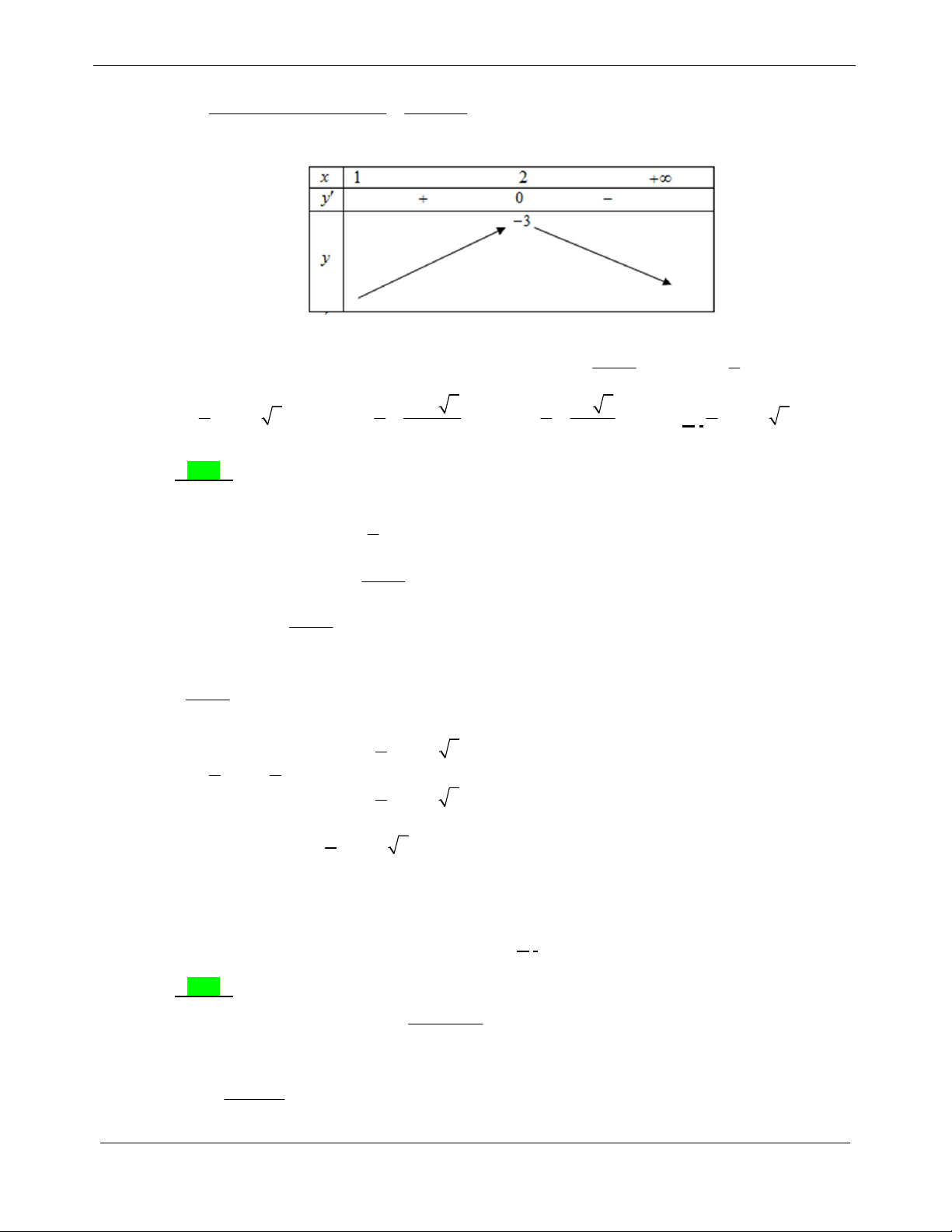
Ta có  x  2 x  2  24  x .x  2 x x  4  24  x .x  8 . 1 2  1 2  1  2  1 2 x  2 1  x x  6 x  4  2 Từ 1 2   . x .x  8   x  4 1 2 1   x  2  2 17 Khi đó, ta có x x 1 2
t t  2  2
 20  2m  3  m  . 1 2 2 x x Câu 2.
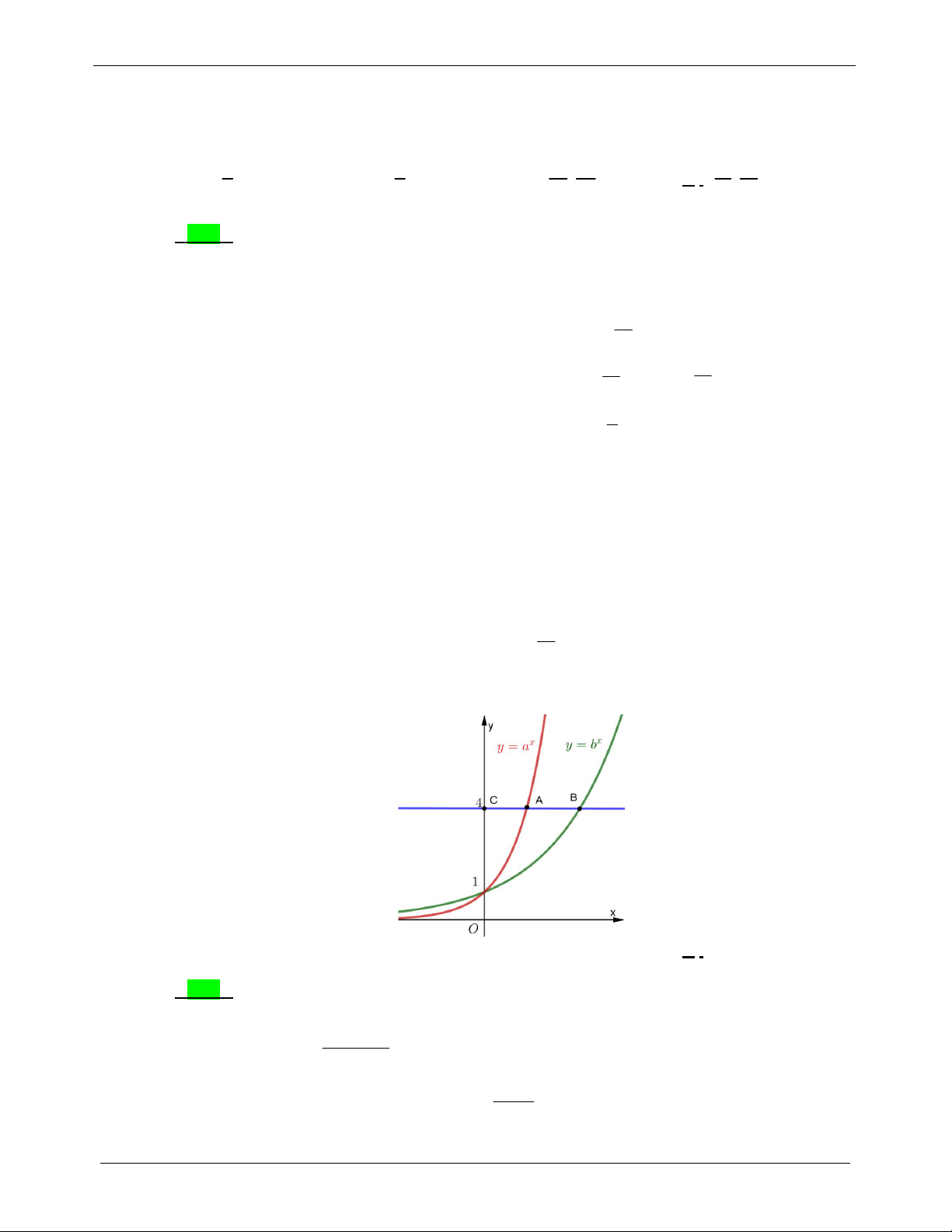
Cho điểm C(0; 4), đường thẳng y  4 cắt hai đồ thị hàm số y a và y b lần lượt tại A và
B sao cho AB AC (hình vẽ). Khẳng định nào sau đây đúng? A. a  2 . b B. 2
b a . C. b  2 . a D. 2
a b . Lời giải Chọn D Ta có C(0; 4), (l
A og 4; 4), B(log 4; 4). a b 0  log 4 Khi đó b 2 AB AC
 log 4  log a  2 log b a b . a 4 4 2 1 ab Câu 3.
Cho các số thực dương a, b thỏa mãn log
 2ab a b  3 . Giá trị nhỏ nhất của biểu 2 a b
thức P a  2b bằng
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 1
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2 10 1 2 10  3 3 10  7 2 10  5 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn B
Từ giả thiết ta có điều kiện: ab  1. Ta có 1 ab 2  2ab log
 2ab a b  3  log
 2ab a b  3 2 2 a b 2a b  log
2  2ab  2  2ab  log
a b a b 1 2     2      
Xét hàm số f t   log t t, t  0 , 2 1
Có f t  
 1  0, t  0 nên f t  đồng biến trên 0;  . t ln 2 2  a Do đó:  
1  f 2  2ab  f a b  2  2ab a b b  . 1  2a Suy ra: 4  2a 1 5 3 3 2 10  3 P a   1 2a    10   . 1 2a 2 1 2a 2 2 2
a  0, b  0, ab  1  10 1  a   2 10  3  2  a  2
Giá trị nhỏ nhất của P là , đạt được khi b     2 1 2a   10  2 b    2a 2 1 10     4  Câu 4.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 5x 10  25x m  4
có nghiệm duy nhất. Số tập con của S là A. 3 . B. 4 . C. 16 . D. 15 . Lời giải Chọn C 5x x x 10
5 10  m 25  4   m   1 . 25x  4
TH 1: m  0 . Phương trình   1 vô nghiệm. 5x 102 TH 2: m  0 . 2 (1)   m 25x  4 t 102 Đặt 5x t  , t  0 . Ta có: 2  m (2) 2 t  4 t 102
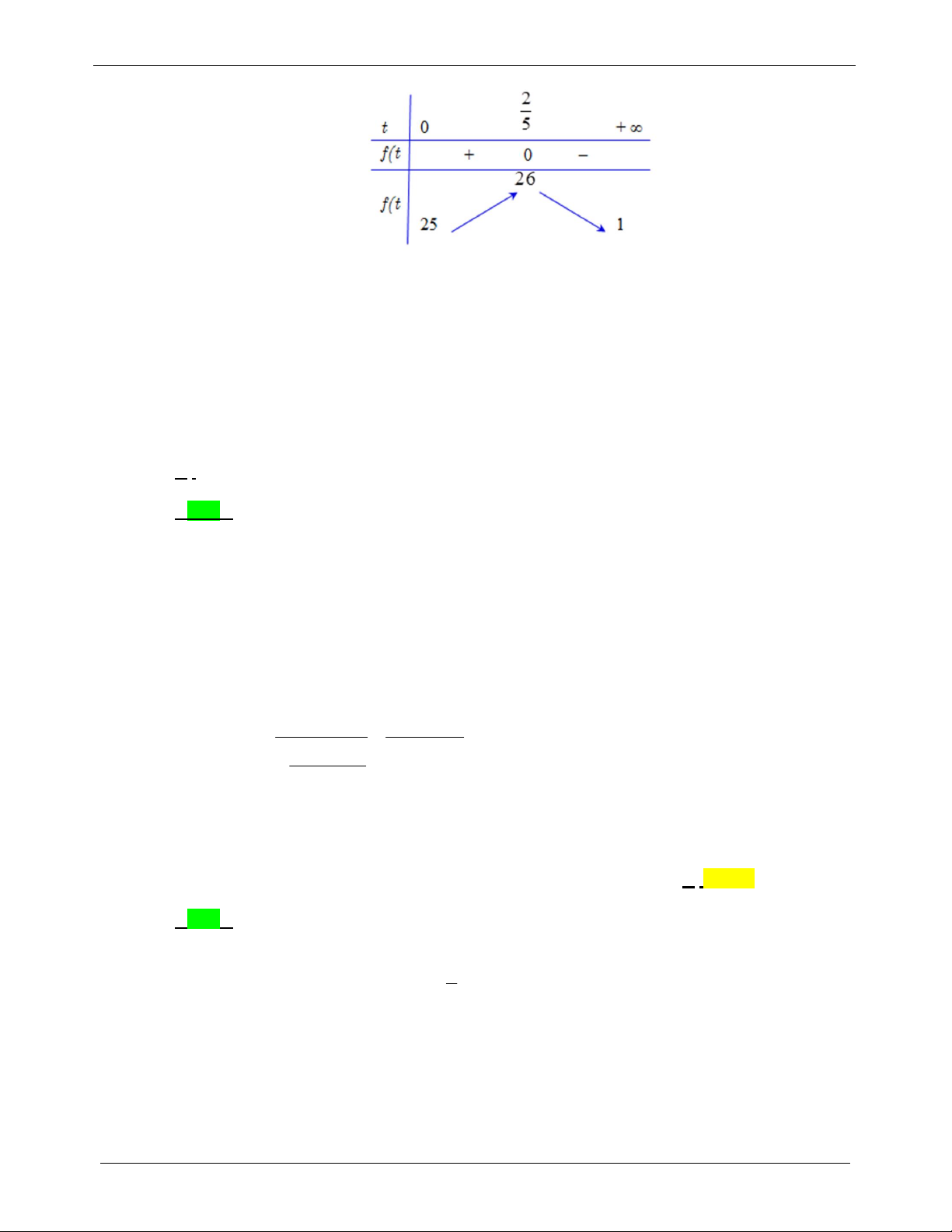
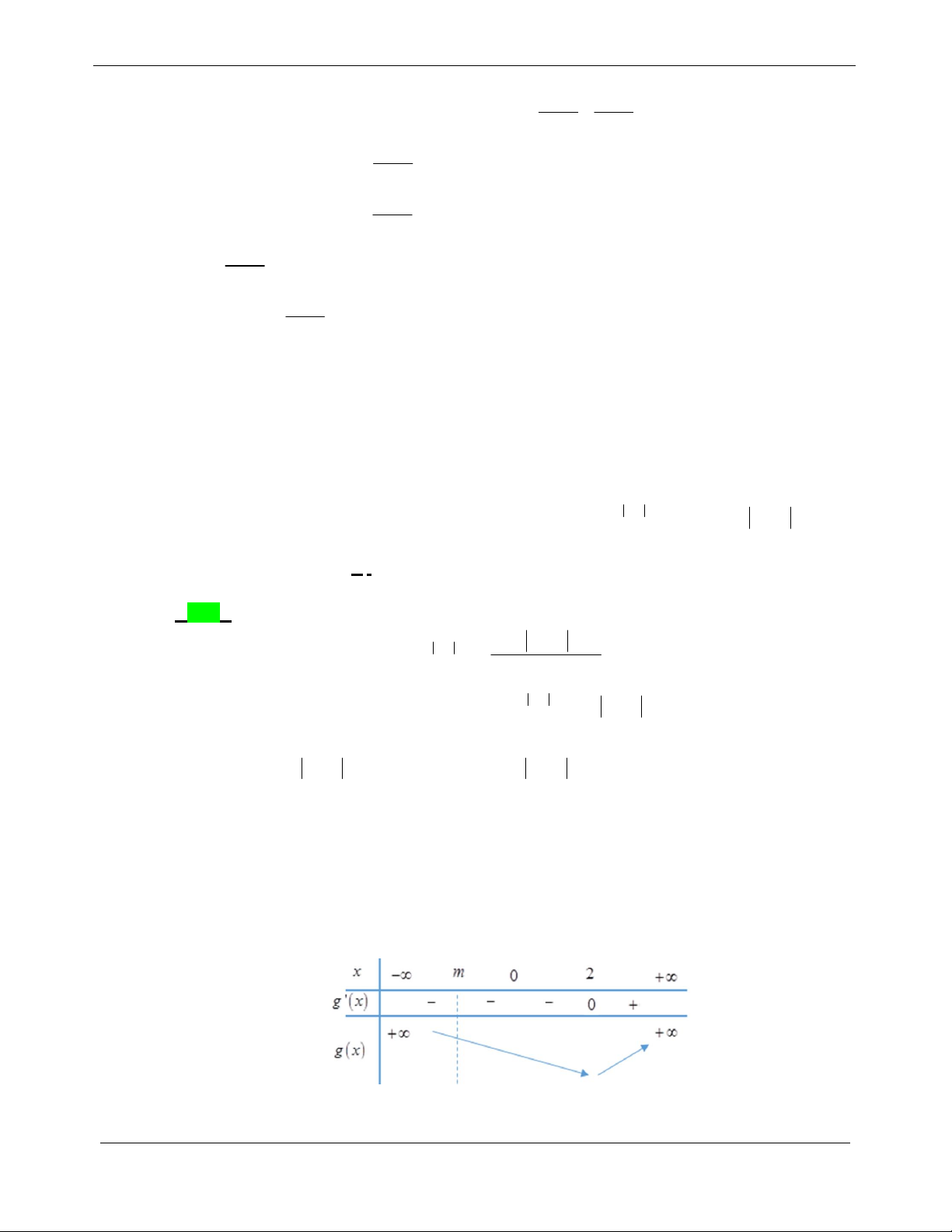
Xét hàm số f t  
trên khoảng 0;  2 t  4
t  10(l) 2 20  t 192t  80 f t   . f (t)  0     2 . t  2 2 t  (tm) 4  5 Bảng biến thiên:
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 2
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Đề phương trình  
1 có đúng một nghiệm  Phương trình 2 có đúng một nghiệm t  0 2 m  26 m  0   . Do điều kiện   m 2,3, 4,  5 . 2 1  m  25  m   
Vậy S  2,3, 4, 
5 , do đó số tập con của S là 4 2  16 . Câu 5.
Anh X muốn mua một chiếc xe máy Yamaha Exciter 150 giá 47.500.000 của cửa hàng Phú Tài
nhưng vì chưa đủ tiền nên anh X đã quyết định mua theo hình thức như sau: trả trước 25 triệu
đồng và trả góp trong 12 tháng, với lã suất 0.6% tháng. Hỏi mỗi tháng, anh X sẽ phải trả cho
cửa hàng Phú Tài số tiền là bao nhiêu(quy tròn đến hàng đơn vị).
A. 1.948.927 đồng.
B. 1.948.926 đồng.
C. 2.014.545 đồng.
D. 2.014.546 đồng. Lời giải Chọn A
Đặt x là số tiền Anh X phải trả 1 tháng, A  22.500.000 , r  0, 006 .
Sau 1 tháng, số tiền anh X còn nợ cửa hàng là: T A 1 r x . 1  
Sau 2 tháng, số tiền anh X còn nợ cửa hàng là:
T   A1 r   x 1 r   x A1 r 2  x 1 r x 2     .
Tương tự, sau 12 tháng, số tiền anh X còn nợ cửa hàng là: T
A1 r 12 x 1 r11 1 r10 1 r9 ... 1 r 1             . 12    
Sau 12 tháng, anh X trả hết nợ, do đó: A1 r 12
Ar 1 r 12
T  0  x    1.948.926, 902 . 12
1 r 12 1 1 r12 1 1. 1 r 1
Làm tròn đến hàng đơn vị ta được: x  1.948.927 đồng. x Câu 6.
Biết rằng bất phương trình log 5  2  2.log
 có tập nghiệm là S  log ; b  , ax 2 3 2   5 2
với a , b là các số nguyên dương nhỏ hơn 6 và a  1. Tính P  2a  3b . A. P  7 . B. P 11. C. P 18. D. P 16. Lời giải Chọn D
Đặt log (5x  2)  t . Do 5x  2  2 với mọi x nên log (5x  2)  log 2  1 hay t  1. 2 2 2 2  t  1
Bất phương trình đã cho trở thành: 2 t
 3  t  3t  2  0 (do t  1)   . t t  2 
Đối chiếu với t  1ta lấy t  2 .
Khi đó log (5x  2)  2  5x  2  x  log 2 . 2 5
Vậy bất phương trình có nghiệm là S  (log 2; ) , ta có a  5, b  2  2a  3b  16 . 5 Câu 7.
Ông Chính gửi 200 triệu đồng vào một ngân hàng với lãi suất 7% năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 3
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả định trong suốt
thời gian gửi lãi suất không thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn đến hàng nghìn).
A. 1.686.898.000 VNĐ. B. 743.585.000 VNĐ.
C. 739.163.000 VNĐ. D. 1.335.967.000 VNĐ. Lời giải Chọn D
Gọi a  200 triệu; b  20 triệu;   7% .
Số tiền sau 1 năm: a 1  . 2
Số tiền sau 2 năm: a 1    b 1   . 3 2
Số tiền sau 3 năm: a 1    b 1    b 1   . …………………… 18 17 16
Số tiền sau 18 năm: a 1   b 1   1   ... 1               18 1 17 1
a 1    b 1  .      
Vậy số tiền ông Chính nhận sau 18 năm là: 1.335.967.000 VNĐ.
 4a  2b  5  Câu 8.
Cho a , b là hai số thực dương thỏa mãn log
a  3b  4 . Tìm giá trị nhỏ nhất 5    a b  của biểu thức 2 2
T a b 1 3 5 A. . B. 1. C. . D. . 2 2 2 Lời giải Chọn D
 4a  2b  5  log
a  3b  4  log 4a  2b  5  log a b a  3b  4 5   5   5    a b   log
4a  2b  5  4a  2b  5  log 5 a b   5 a b 5     5       (*).
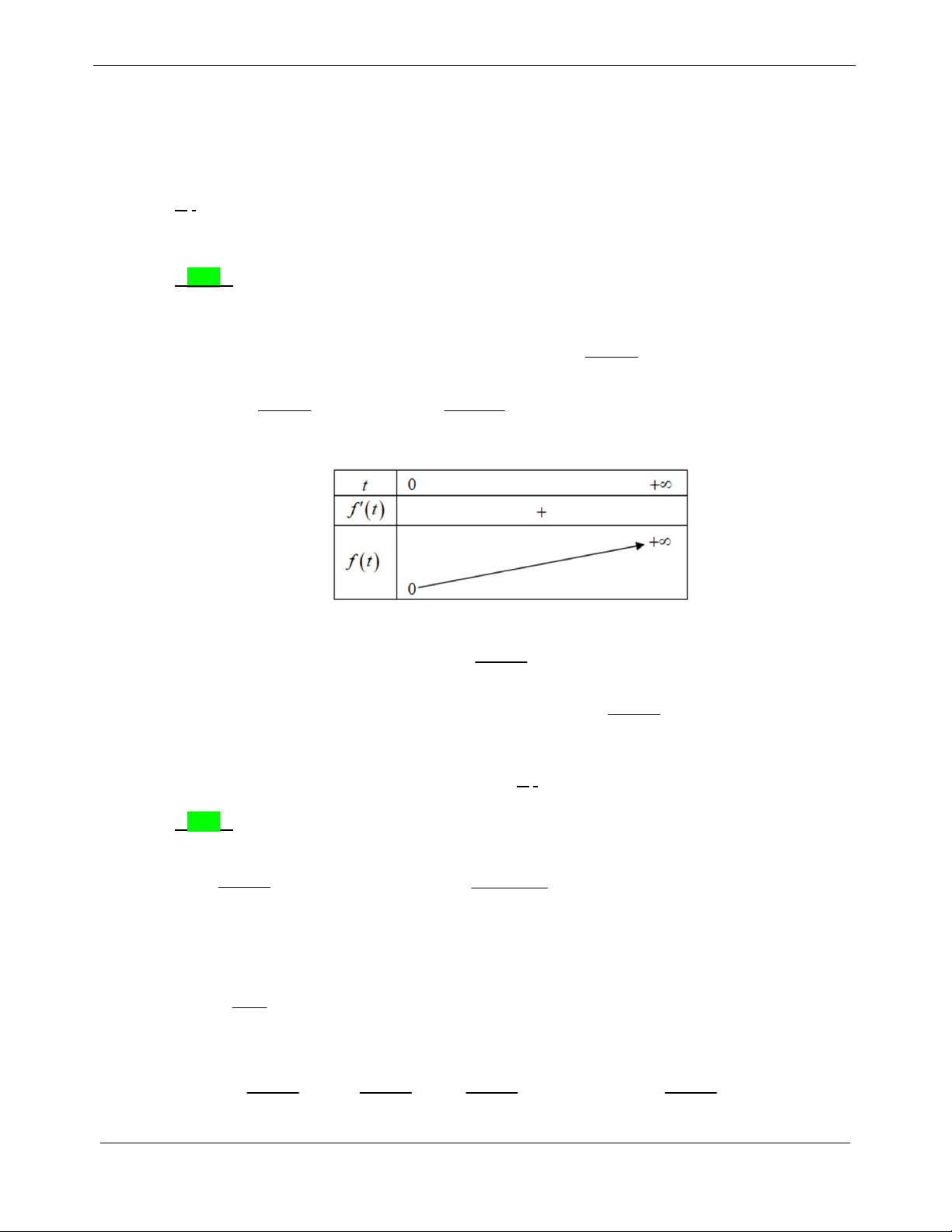
Xét hàm f x  log x x, x  0 . 5 1
Đạo hàm f  x 
 1  0,x  0 . Suy ra hàm số f x đồng biến trên 0; . . x ln 5
Phương trình (*) viết lại:
f 4a  2b  5  f 5a b  4a  2b  5  5a b  a  3b  5 . 2 5 Mặt khác: 2
5  a  3b   2 2 1  3 . 2 2 a b  2 2
T a b  . 2 a b 1 3 Dấu "  " xảy ra    a  ;b  . 1 3 2 2 Câu 9.
Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả sử 1 tế
bào E. Coli khối lượng khoảng 15
15.10 g. Hỏi sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh
ra là bao nhiêu? (chọn đáp án chính xác nhất). A. 29 2,34.10  g  . B. 29 3, 36.10  g  . C. 26 2, 25.10 kg  . D. 26 3, 35.10 kg  .
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 4
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Lời giải Chọn D. Một tế bào E. Coli Sau 20 phút thành: 1 2  2 tế bào. Sau 40  2.20 phút thành: 2 4  2 tế bào. Sau 60  3.20 phút thành: 3 8  2 tế bào.
………………………………………………………….
Sau 2 ngày  144.20 phút thành 144 2 tế bào. Vậy sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là: 144 1  5 29   g  26 2 .15.10 3, 34511178.10
 3, 35.10 kg  . 1 1 1 1 190
Câu 10. Gọi n là số nguyên dương sao cho    ...   đúng với log x log x log x log x x n log 2 3 3 3 3 3 3
mọi x dương, x  1. Tìm giá trị của biểu thức P  2n  3 .
A. P  32 .
B. P  23.
C. P  43.
D. P  41 . Lời giải Chọn D 1 1 1 1 190    ...   log x log x log x log x x n log 2 3 3 3 3 3 3
 log 3  2 log 3  3log 3  ...  n log 3  190 log 3 x x x x x  log 3     n x 1 2 3 ...  190log 3 x
 1 2  3  ...  n  190 n n   1   190 2 2
n n  380  0 n  19   n  19 
(do n nguyên dương)  P  2n  3  41 n  20  
Câu 11. Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số  x; y  thỏa mãn 2 log
4x  4 y  6  m  1 và 2 2
x y  2x  4 y 1  0 . 2 2 x y 2  
A. S  5; 1;1;  5 .
B. S  1;  1 .
C. S  5;  5 .
D. S  7  5; 1;1;5;  7 . Lời giải Chọn A
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 5
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
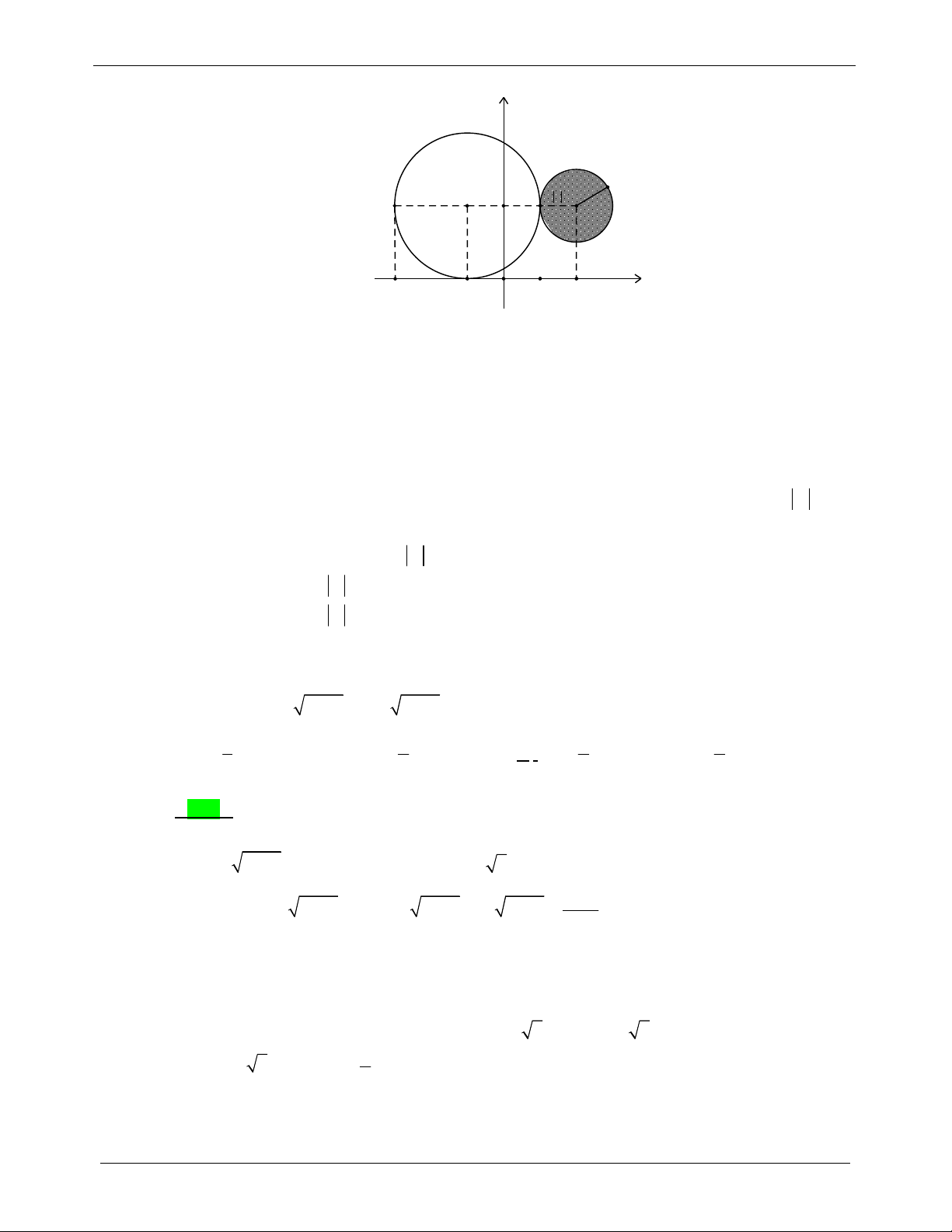
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT y 2 m I J -3 1 2 -1 O x Nhận thấy 2 2
x y  2  1 với mọi , x y   nên: 2 log
4x  4 y  6  m  1 2 2 2
 4x  4 y  6  m x y  2 2 2 x y 2   2 2 2 2 2
x y  4x  4 y  8  m  0   x     y   2 2 2  m (*). x  2
Khi m  0 thì (*)  
. Cặp 2; 2 không là nghiệm của phương trình y  2  2 2
x y  2x  4 y 1  0 .
Khi m  0 , tập hợp các điểm  x; y  thỏa mãn (*) là hình tròn tâm J 2; 2 , bán kính là m .
Trường hợp này, yêu cầu bài toán trở thành tìm m để đường tròn tâm I 1; 2 , bán kính 2 và
hình tròn tâm J 2; 2 , bán kính m có đúng một điểm chung (hình vẽ)  m  1 m  1  Điều này xảy ra khi   
(thỏa mãn m  0 ).  m  5  m  5  
Vậy S  5; 1;1;  5 . Câu 12. Tìm tất cả các giá trị thực của tham số m để phương trình 3m m ee   2 x   x  2 2 1
1 x 1 x  có nghiệm.  1   1   1   1  A. 0;   . B. 0; ln 2   . C. ; ln 2   . D. ln 2;    . e   2   2   2  Lời giải Chọn C
Điều kiện: x 1;  1 Đặt 2
x  1 x t . Vì x  1  ; 
1  t  1; 2    2 2 t 1 Ta có: 2 t   2 x  1 x  2 2
 1 2x 1 x x 1 x  . 2
Phương trình đã cho trở thành: 3m m 3 e
e t t.
Xét hàm số f u  3  u u f  u  2 ,
 3u  1  0 u do đó hàm số f đồng biến trên  . Phương trình 3m m 3      m     m e e t t f e
f t e t .
Phương trình có nghiệm khi và chỉ khi 1 m   2  0 m ee  2 ( do m e  0 )  1 
m  ln 2  m   ;  ln 2  . 2   
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 6
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
Câu 13. Cho x, y là hai số thực dương thoả mãn log x  log y  log  2 x y
. Tìm giá trị nhỏ nhất 1 1 1  2 2 2 P
của biểu thức P  3x  . y min 17 25 2 A. P  8 . B. P  . C. P  . D. P  9 . min min 2 min 4 min Lời giải Chọn D Ta có:
log x  log y  log  2
x y  log  xy  log  2 x y 2
xy x y y x   2 1  x 1 . 1 1 1 1 1   2 2 2 2 2
Vì x, y là hai số thực dương, do đó: 2 2 x x 1 Từ  
1  x  1  y
P  3x y  3x   4  x   1   5  9. x 1 x 1 x 1 1
(Áp dụng bất đẳng thức Cô si: 4  x   1   4 ). x 1 3 9
Dấu “=” xảy ra khi và chỉ khi x  ; y  . 2 2
Vậy giá trị nhỏ nhất của biểu thức P là P  9 . min
Câu 14. Một người vay ngân hàng 90.000.000 đồng theo hình thức trả góp trong 3 năm, mỗi tháng
người đó phải trả số tiền gốc là như nhau và tiền lãi. Giả sử lãi suất không thay đổi trong toàn
bộ quá trình trả nợ là 0.8% trên tháng. Tổng số tiền mà người đó phải trả cho ngân hàng trong
toàn bộ quá trình trả nợ là
A. 103.120.000 đồng.
B. 103.420.000 đồng. C. 103.220.000 đồng. D. 103.320.000 đồng. Lời giải. Chọn D
Gọi P là số tiền vay ban đầu, a là số tiền gốc trả hàng tháng, r là lãi suất 0 Sau tháng 1
Số tiền nợ là P (1 r) . 0
Số tiền trả là a Pr .
Số tiền nợ còn lại P a . 0 Sau tháng 2
Số tiền nợ là  P a (1 r) . 0 
Số tiền trả là a   P ar .
Số tiền nợ còn lại P  2a . 0 … Sau tháng n
Số tiền nợ là P n 1 a (1 r)  0    .
Số tiền trả là a  P  n   1 ar   .
Số tiền nợ còn lại P na . 0
Theo giả thiết trả hết sau 36 tháng nên 90.000.000  36a  0  a  2.500.000 .
Tổng số tiền đã trả là  35.36 
T  a Pr  a   P ar  ... a  P  n  
1 ar  36a  36P a r        . 0   2 
Thay P  90.000.000, a  2.500.000, r  0.008 được T  103.320.000 . 0
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 7
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2 2
Câu 15. Cho hai số thực a , b thỏa mãn a b  1 và log
a b  1. Giá trị lớn nhất của biểu thức 2 2   a b
P  2a  4b  3 là 10 1 A. 10 . B. . C. 2 10 . D. . 2 10 Lời giải Chọn A 2 2  1   1  1 Ta có log
a b  1  2 2
a b a b a   b   . 2 2   a b      2   2  2
Theo bất đẳng thức Cauchy – Schwarz: 2 2 1 1          
P  2a  4b  3  2 a   4 b        1 1 1 2 2 2  4   a   b        20.  10 .  2   2   2   2  2   a b  0   1 1  5  10 a b  a    10 Dấu "  " xảy ra khi 2 2     . 2 4   5  2 10 2 2 b   1   1  1   10  a   b        2    2  2 Vậy P  10 . max
Câu 16. Một thầy giáo cứ đầu mỗi tháng lại gửi ngân hàng 8 000 000 VNĐ với lãi suất 0, 5% / tháng.
Hỏi sau bao nhiêu tháng thầy giáo có thể tiết kiệm tiền để mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ? A. 60 . B. 50 . C. 55 . D. 45 . Lời giải Chọn D
Đặt T  8 000 000
Số tiền thầy giáo thu được sau tháng thứ nhất, thứ 2, thứ 3,., thứ n lần lượt làT , T , T ,..., T 1 2 3 n Ta có:
T T 1 r 1  
T  T T 1 r   T 1 r 2  T 1 r 2 1  
T  T T 1 r   T 1 r 3  T 1 r 2  T 1 r 3 2   . n n n 1  1 r  1 T TrTr   Tr Tr n 1  1  ... 1  1  rn 1  r  1
Theo bài ra ta có T  400 000 000  Tr   n 1  400 000 000 r n 251 251  1 r    n  log  44, 54 1.005 201 201
Vậy sau 45 tháng thầy giáo sẽ mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ.
Câu 17. Tích các nghiệm của phương trình log 125x 2 .log x  1 x 25 . 1 630 7 A. 630 . B. . C. . D. 125 625 125 Lời giải
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 8
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Chọn B
Điều kiện x  0; x  1. 2  1  Ta có log x x    x x    x x 125  2 .log 1 log 125 log x x  log 1   3.log 5 x  2 1 log 4 25 5 5  2 
Đặt log x t phương trình tương đương: 5  x  5  3   t  1  log x  1 2 2 5 1 t 4 t 3t 4 0               1  tt  4  log x  4 x    5  625 1
Vậy tích các nghiệm của phương trình là . 125 xa b
Câu 18. Gọi x , y là các số thực dương thỏa mãn điều kiện log x  log y  log x y và  , 9 6 4   y 2
với a , b là hai số nguyên dương. Tính 2 2
T a b .
A. T  26 .
B. T  29 .
C. T  20 .
D. T  25 . Lời giải Chọn A
Đặt log x  log y  log
x y t , suy ra 9t x  , 6t y  ,   4t x y . 9 6 4   2t t  3   3  Khi đó ta có: 9t 6t 4t     1  0      2   2  t t  3  1 5  3      (Vì  0   ).  2  2  2  t x  3  x 1   5 Lại có     
a  1, b  5 hay T  26 . y  2  y 2
Câu 19. Ba anh em An, Bình, Cường cùng vay tiền ở một ngân hàng với lãi suất 0,7%/ tháng với tổng
số tiền vay là 1 tỉ đồng. Giả sử mỗi tháng ba người đều trả cho ngân hàng một số tiền như nhau
để trừ vào tiền gốc và lãi. Để trả hết gốc và lãi cho ngân hàng thì An cần 10 tháng, Bình cần 15
tháng và Cường cần 25 tháng. Hỏi tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân
hàng là bao nhiêu (làm tròn đến hàng nghìn)? A. 6426800. B. 45672000. C. 46712000. D. 63271000. Lời giải Chọn A
Gọi A, B, C lần lượt là số tiền mà An, Bình, Cường vay ngân hàng thì ta có: 9
A B C  10   1
Gọi X là số tiền mà mỗi người trả cho ngân hàng vào mỗi tháng. Để trả hết gốc và lãi cho ngân
hàng thì An cần 10 tháng nên áp dụng công thức vay vốn trả góp ta có: 10 1 r 10 1 1 r10 1
A1 r   X
 0  A X 2 , 10   r r 1 r  1 r 15 1 1 r 15 15 1
Bình cần 15 tháng nên: B 1 r   X
 0  B X 3 , 15   r r 1 r  1 r25 1 1 r 25 25 1
Cường cần 25 tháng nên: C 1 r   X
 0  C X 4 25   r r 1 r  0, 7 (Với r  ). 100
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 9
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
Từ (1), (2), (3), (4) suy ra tổng số tiền mà ba anh em trả ở tháng thứ nhất cho ngân hàng là:
3X  64268000
Câu 20. Tìm tất cả các giá trị của tham số m để bất phương trình x 1 4   2x m   1  0 nghiệm đúng với mọi x   . A. m  ;  0 .
B. m  0;   .
C. m  0;  1 .
D. m   ;
 0  1;   . Lời giải Chọn A Đặt 2x t
, t  0  t 1  0 .
Bài toán đã cho trở thành: 2 t
Tìm tất cả các giá trị của tham số m để bất phương trình:  m , t   0   1 . 4 t   1 2 2 t t  2t
Đặt f t  
, t  0  f t  
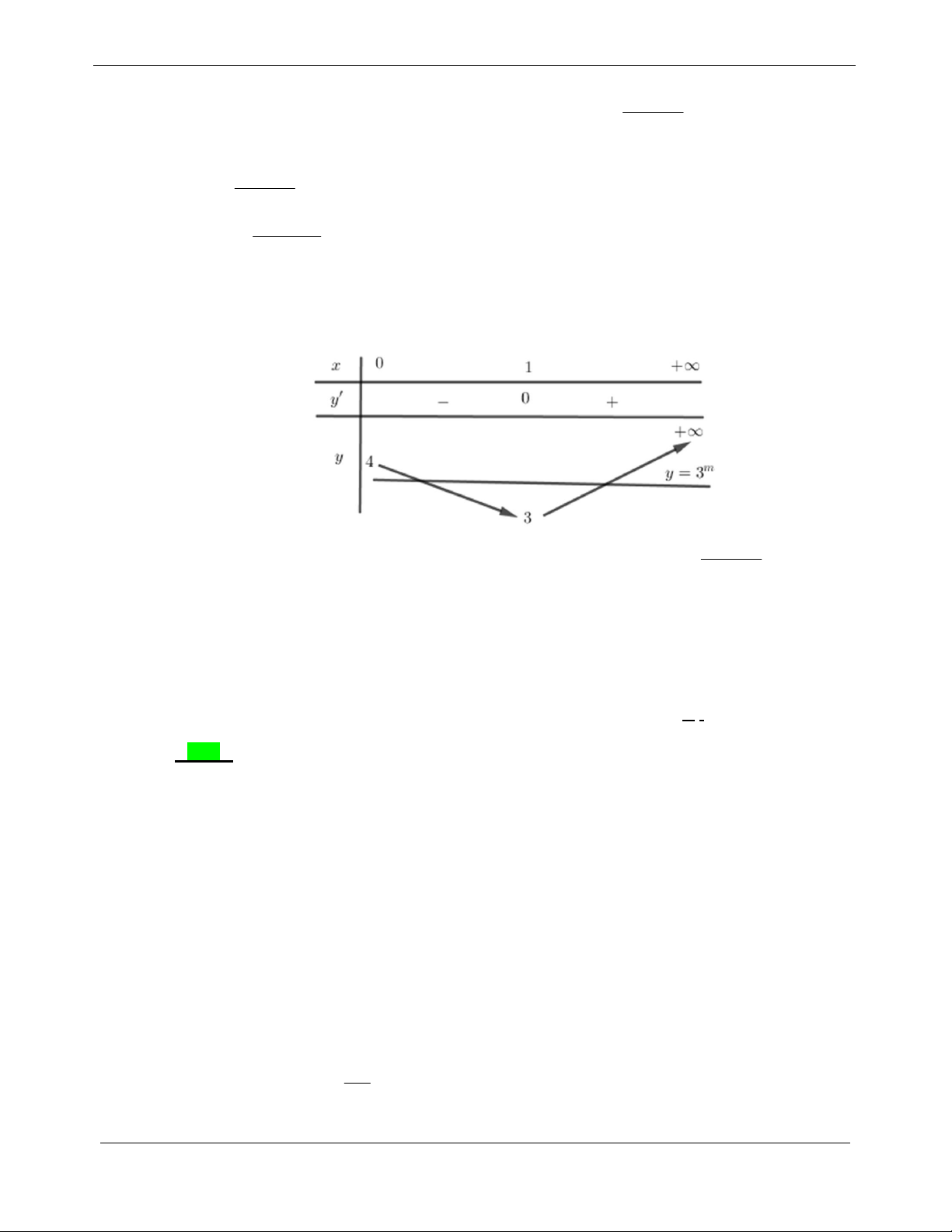
f t  0  t  0 l t  2  l . 2       4 t   1 4 t   1 Bảng biến thiên:
Nhìn vào bảng biến thiên ta có m  ;
 0 thỏa yêu cầu bài toán.  xy 1 
Câu 21. Với mọi số thực ,
x y thỏa điều kiện log  2    2 2 x y
xy . Gọi M và m lần lượt là 2 2 2  x y   4 4 x y
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P
. Tính giá trị biểu thức 2xy 1
Q  15m  2 log M . 2
A. Q  0 .
B. Q  1. C. Q  2  . D. Q  1  . Lời giải Chọn C
Điều kiện: xy 1  0 .  xy 1   xy 1   log  2 2 2    2 2 x yxy  log 
  2 x yxy 1 2 2 2   2 2 2  x y  
 2 x y      log  xy   1   xy   1  log 2 2 2
x y   2 2 2 x y . 2 2   
Xét hàm số: f t   log t t t  0 2 1
f t  
1  0 t  0  hàm số đồng biến trên 0; . t ln 2
Do đó: f xy    f   2 2
x y   xy    2 2 1 2 1 2 x y  2 2 2 2  x y x y 2 2 2 2  x y   x y  Ta có:   xy  2 2     1  2  
x y   1   2 2   2 2    
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 10
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2 2 2 2   x y  . 5 3
x y 2    xy x y 2 2 2 4 4 2 Khi đó: P   . 2xy 1 2xy 1 Thay xy   2 2
2 x y  1, đặt 2 2
t x y rút gọn ta được 2 7
t  8t  2 2 2 P t   với  t  . 4t 1 5 3 t  0 2 2  8t 14t Pt    0   1 . 4t  2 1 t   2  1  1  2   2  2
Lập bảng biến thiên dễ thấy: max P P    , min P PP      .  2  4  5   3  15 2 1 Do đó: m  , M
Q  15m  2 log M  2  . 15 4 2
Câu 22. Cho a log 9  b log 673  2018 với ,
a b   . Khẳng định nào đúng trong các 2019 2019
khẳng định sau đây?
A. b  2a . B. 2
b a . C. 2
a b .
D. a  2b . Lời giải Chọn A Ta có: log 9  log 673  2018  log 9a  log 673b a b  2018 2019 2019 2019 2019  log 9a.673b a b 2018  2018  9 .673  2019 2a b 2018 2018  3 .673  673 .3 2019 2018 b  2a2018  673  3 . 2a  2018 a  1009
Do 673 và 3 nguyên tố cùng nhau nên     b  2a . b  2018 b  2018   2 2 x 1 x .2 
Câu 23. Cho hai số thực x , y thay đổi thỏa mãn đẳng thức   y  
1 .2xyxy  0. Tìm giá trị lớn x 1
nhất M của y , biết rằng x  1 . 7 A. M   .
B. M  3 .
C. M  1 . D. M  0 . 2 Lời giải Chọn B 2 2 x 1  2 x .2 Ta có:  y
xyxy 2 1 .2 0 x .2xx y xy
xyxy 1 1 .2          * x 1 Xét hàm số    .2t f t t trên 0;   .
   2t  .2t f t t ln 2  0 t   0 Vậy hàm số    .2t f t t
đồng biến trên 0;   . Suy ra:    f  2
x   f x y xy   2 *
1  x y xy 1  x 2 x x 1 y   x   1 1 x Ta có:
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 11
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
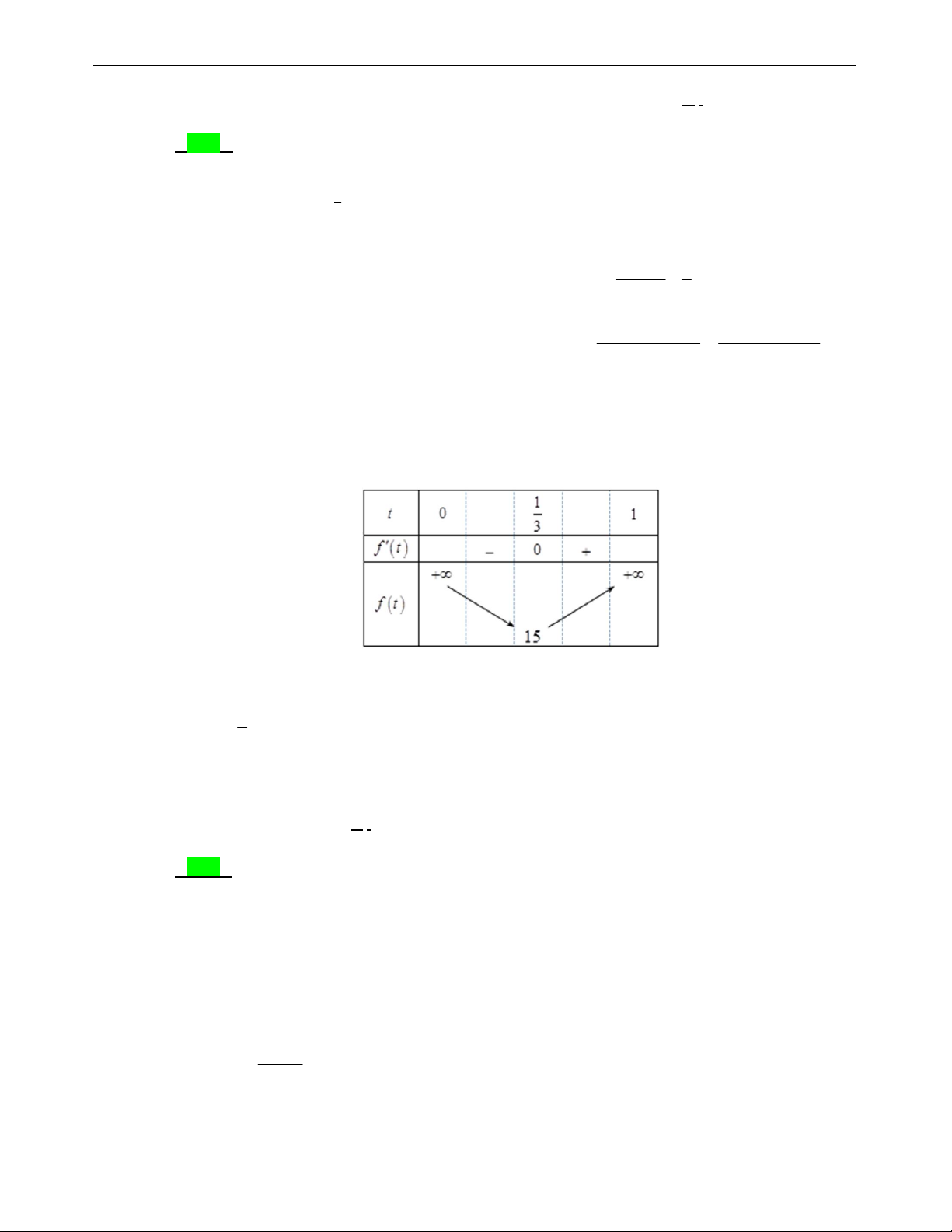
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2x   1 1 x 2 2  x x 1 x  2xx  0 y   ; y  0   1 x2 1 x2 x  2  Bảng biến thiên:
Từ bảng biến thiên suy ra: M  3 . 5b a a
Câu 24. Cho a , b là các số dương thỏa mãn log a  log b  log . Giá trị của bằng 9 16 12 2 b a a 7  2 6 a 1 6 a A.  1   6 . B.  . C.  . D.  7  2 6 . b b 25 b 5 b Lời giải Chọn D  , a b  0  , a b  0  Điều kiện:   a . 5b a  0  5   b 5b a
Đặt log a  log b  log  t , ta có 9 16 12 2 5b a 9t a  , 16t b  ,  12t . 2 Suy ra 2  5b a  2 2
ab a 14ab  25b  0    2   a 2  7  2 6 a a    b  14  25  0     .  b b a   7  2 6 b a So điều kiện ta nhận  7  2 6 . b
Câu 25. Tìm tất cả các giá trị thực của tham số m để phương trình 4x 2x 4 3m 2x      1 có hai nghiệm phân biệt.
A. 1  m  log 4 .
B. log 3  m  1.
C. 1  m  log 4 .
D. log 3  m  1. 3 4 3 4 Lời giải Chọn C x x   Ta có x x m     x   4 2 4 4 2 4 3 2 1   3m (*). 2x 1 Đặt  2x t , t  0 . 2 t t  4 *   3m . t 1
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 12
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2 t t  4
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y  và đường thẳng t 1 3m y
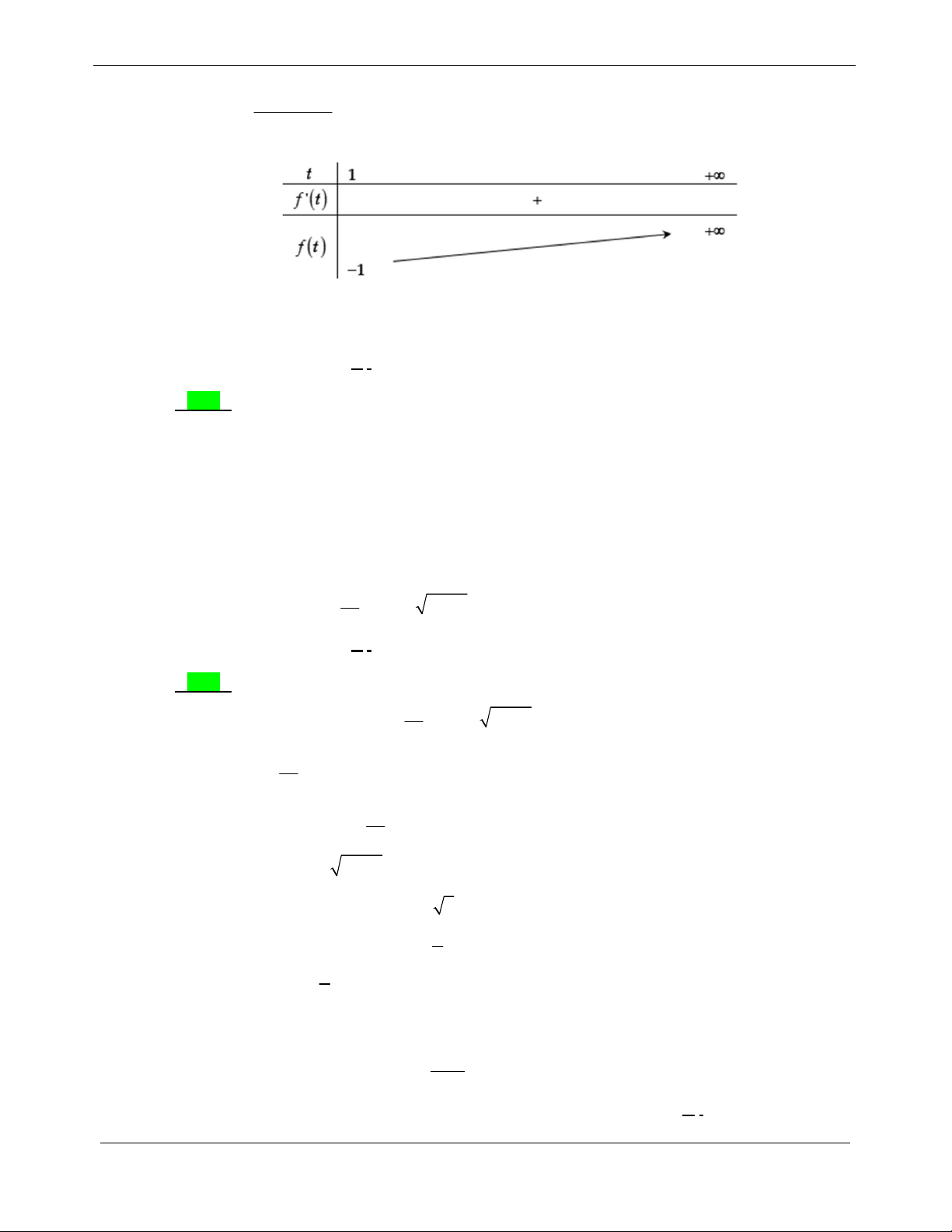
song song với trục hoành. 2 t t  4 Xét y  , t  0 . t 1 2 t  2t  3 Ta có y  . t  2 1 t  3  Cho 2
y  0  t  2t  3  0   .
t  1  y  3  Bảng biến thiên 2 t t  4
Dựa vào bảng biến thiên ta thấy đường thẳng 3m y
cắt đồ thị hàm số y  tại hai t 1
điểm phân biệt  3  3m  4  1  m  log 4 . 3
Vậy 1  m  log 4 . 3
Câu 26. Cho phương trình 5x m  log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 5  
m  20; 20 để phương trình đã cho có nghiệm? A. 20. B. 21. C. 9. D. 19. Lời giải Chọn D
Ta có 5x m  log x m (*). 5   Đặt  5x tm . *   log     5t   5t t x m x m xm . 5   t    5x m Ta có hệ 
t x  5x  5t x  5x t  5t (1).
x  5t m  Xét hàm số     5u f u u
có    1 5u f u .ln 5  0 , u
 nên hàm số đồng biến trên  .   1  x t .
Khi đó ta được  5x    5x x m xm .
Đây là phương trình hoành độ giao điểm của đồ thị hàm số   5x y x
và đường thẳng y m
song song hoặc trùng trục hoành. Xét   5x y x có 1 5x y   ln 5 .  1 
Cho y  0  x  log . 5    ln 5  Bảng biến thiên
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 13
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
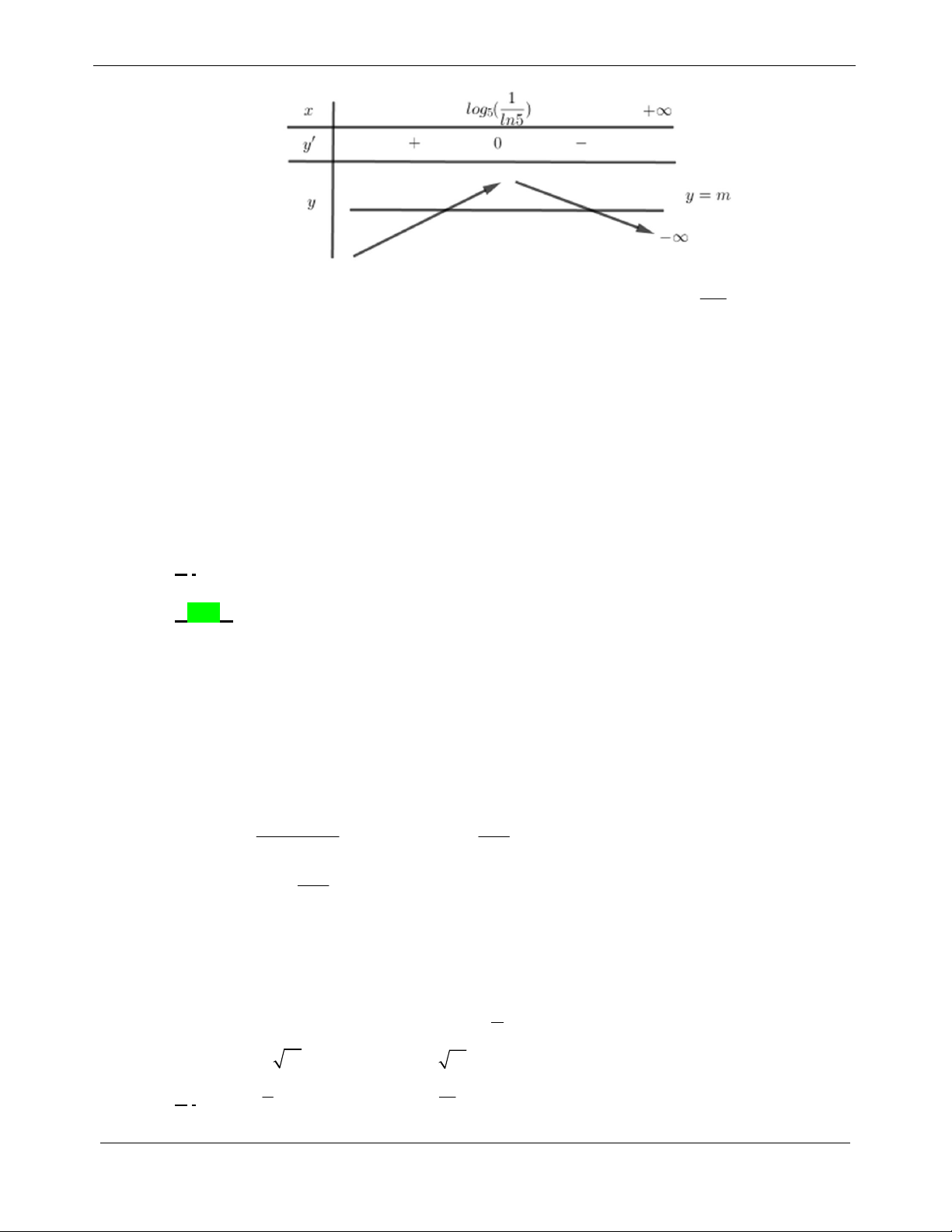
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT   1  
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm  m f log  1; 0  5        ln 5   m    Vì 
nên m 19; 18;...;   1 . m    20  ; 20 
Vậy có 19 giá trị nguyên của m thỏa bài toán.
Câu 27. Nhằm tạo môi trường xanh, sạch, đẹp và thân thiện. Đoàn trường THPT Hậu Lộc 2 đã phát
động phong trào trồng hoa toàn bộ khuôn viên đường vào trường. Sau một ngày thực hiện đã
trồng được một phần diện tích. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 ngày
nữa sẽ hoàn thành. Nhưng thấy công việc có ý nghĩa nên mỗi ngày số lượng đoàn viên tham gia
đông hơn vì vậy từ ngày thứ hai mỗi ngày diện tích trồng tăng lên 4% so với ngày kế trước.
Hỏi công việc sẽ hoàn thành vào ngày bao nhiêu? Biết rằng ngày 08 / 03 là ngày bắt đầu thực hiện và làm liên tục. A. 25 / 03 . B. 26 / 03 . C. 23 / 03 . D. 24 / 03 . Lời giải Chọn A
Gọi số lượng công việc đã hoàn thành trong ngày đầu là a a  0 , khi đó số lượng công việc
phải hoàn thành trong 23 ngày tiếp theo là 23a Đặt r  4%
Số lượng công việc làm được trong ngày thứ 2, thứ 3,. thứ n lần lượt là a 1 r , a   r2 1 , . 
a   rn 1 , 1 n
Công việc được hoàn thành khi và chỉ khi a 1 r  a  r2 1
 ... a   r  1 1  23a n 1 r  1 1 n 23r  1 r 
 23  1 r  1  1 r 1 r  23r   n 1  log 1  n  17.157 1r    1 r
Do đó, kể từ ngày 08/03 số ngày cần để hoàn thành công việc là 18 ngày
Vậy công việc được hoàn thành vào ngày 25/03
Câu 28. Cho các số thực dương x , y thỏa mãn log
11x  20 y  40  1 . Gọi M , m lần lượt 2 2  
2 x xy3 y y
là giá trị lớn nhất và giá trị nhỏ nhất của S
. Tính M m . x
A. M m  2 14 .
B. M m  10 . 7 11
C. M m  .
D. M m  . 2 6
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 14
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Lời giải Chọn C y Do S  nên y  . Sx x Ta có 2 2 log
11x  20 y  40  1  11x  20 y  40  2x xy  3y 2 2  
2 x xy3 y 2 2 2
 11x  20Sx  40  2x xSx  3S x   2
3S S  2 2
x  20S   11 x  40  0   1 2 Biệt thức    S      2 S S   2 20 11 4 40 3 2  8
 0S  280S 199.
Để có các số thực dương x , y thỏa mãn giả thiết trước hết ta phải có: 35  230 35  230 2   0  80 
S  280S 199  0 
S S S  . 1 2 20 20  20S 11 1 x   0 35  230  Từ đó ta suy ra 2 M  max S  khi 3S  S  2  1 1 20 y  S x  0  1  20S 11 2 x   0 35  230  2 m  min S  khi 3S  S  2  2 2 20 y  S x  0  2 7 Vậy M  m  . 2 x x 1 
Câu 29. Tổng tất cả các nghiệm thực của phương trình 15 .5 x  5
 27x  23 bằng A. 1 . B. 0 . C. 2 . D. 1 . Lời giải Chọn B Tập xác định  . Ta có x x 1 15 .5 5    27  23  5.5 . x x x 3x  
1  27x  23  0   1 . 1 Với x
không phải là nghiệm của phương trình. 3 1 x x 27 23 Với x  ta có   1  5.5   0 2 . 3 3x 1 x x 96 1 x 27 23
Xét hàm số f x  5.5 
, f  x  5.5 ln 5   0 x   . 3x 1 3x  2 1 3  1   1 
Suy ra hàm số đồng biến trên các khoảng  ;  ,   ;  
 nên trên mỗi khoảng hàm số có  3   3 
nhiều nhất một nghiệm. Ta thấy f   1  f   1  0  x  1
 là nghiệm của phương trình. x x 1 
Tổng tất cả các nghiệm thực của phương trình 15 .5 x  5
 27x  23 bằng 0 .
Câu 30. Đồ thị hàm số y f x đối xứng với đồ thị của hàm số x
y a a  0, a  
1 qua điểm I 1;  1 .  1 
Giá trị của biểu thức f 2  log  bằng: a  2018 
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 15
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT A. 2  016 . B. 2  020 . C. 2016 . D. 2020 . Lời giải Chọn A  1  1   Xét M 2  log ; f 2  log 
thuộc đồ thị hàm số y f x . a    2018 a   2018    1  1   Điểm N  log ; 2  f 2  log 
đối xứng với M qua I 1; 
1 thuộc đồ thị hàm số a    2018 a   2018  x
y a nên ta có: 1 . log  1  a  1  log 2018 2018 2  f 2  log  af 2  log  2 aa  2  2018  20  16  a     2018 a   2018  1
Câu 31. Cho các số thực a, b thỏa mãn a
,b  1. Khi biểu thức log b  log a a  đạt giá a b  4 2 9 81 3  3
trị nhỏ nhất thì tổng a b bằng A. 3 9  2 . B. 2 3  9 . C. 3  3 2 . D. 2  9 2 . Lời giải Chọn B
Ta có 3a  1,b  1 nên log b  0, log 3a  0 . Theo bất đẳng thức Cauchy ta được: 3a b log b  log a a   b a ab a a b  4 2 9  81 log log a b  2 2 18 9 log 2 log 3 2 2 3 3  3a b
Đẳng thức xảy ra khi và chỉ khi: 3
a  1, b  1 a  3  4  a  81   2 b    9
log b  2 log 3a  3a b  Khi đó ta được 2
a b  3  9 .
Câu 32. Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất
0,85% một tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền
cố định là 10 triệu đồng bao gồm cả tiền lãi vay và tiền gốc. Biết phương thức trả lãi và gốc
không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng thì anh trả hết nợ
ngân hàng? (tháng cuối có thể trả dưới 10 triệu đồng). A. 67 . B. 68 . C. 66 . D. 65 . Lời giải Chọn C
Đặt N  500; A  10; r  0,85% .
Sau một tháng anh An còn nợ: N.1 r   A .
Sau hai tháng anh An còn nợ:  A N r A  r A N r 2 A  r   N r 2  r 2 . 1 . 1 . 1 . 1 1 . 1 1 1                 . r   n A n
Tương tự sau n tháng anh An còn nợ: N.1 r  1 r 1     . r  
Anh An trả hết nợ sau n tháng khi n là nghiệm nguyên dương nhỏ nhất của bất phương trình: n A n n 10 n N.1 r  1 r 1 0 500.1 0,85% 1 0,85% 1            0 r   0,85%   n 40 40  1 0,85%   n log
 65, 38  n  66 10,85% 23 23
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 16
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
Câu 33. Một người vay ngân hàng 100 triệu đồng với lãi suất là 0,7%/tháng theo thỏa thuận cứ cuối mỗi
tháng người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết
nợ (tháng cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng? A. 21. B. 24 . C. 22 . D. 23 . Lời giải Chọn C
Xét bài toán tổng quát:
Gọi A là số tiền vay từ ngân hàng với lãi suất là r (%) mỗi tháng. Số tiền trả hàng tháng là a
và sau n tháng thì trả được hết nợ.
Cuối tháng thứ 1, số tiền còn nợ là N A 1 r a . 1   2
Cuối tháng thứ 2, số tiền còn nợ là N N N .r a A 1 r
a 1 r a . 2 1 1     3 2
Cuối tháng thứ 3, số tiền còn nợ là N A 1 ra 1 r
a 1  r a . 3       … n n 1  n2
Cuối tháng thứ n , số tiền còn nợ là N Arararar a n 1  1  1  1   n n n 1 r  1 n 1 r  1
A1 r   . a
A1 r   . a . 1 r 1 r n .
A r.1 r
Để hết nợ thì N  0  a  . n n * 1 r 1 Từ đề bài ta có 8 6 3
A 100.000.000 10 , a 5.000.000 5.10 , r 0, 7% 0, 007 7.10        . 8 3 10 .7.10 .1, 007n n 50  50  Thay vào * ta được 6 5.10   1, 007   n  log . n 1,007   1, 007 1 43  43  Suy ra n  21, 6 .
Vậy sau 22 tháng thì người đó trả hết nợ. log 5  b 2 log 45  a  6 log 3  c Câu 34. Cho a b c   2 , với , ,
. Tính tổng a b c A. 2 . B. 1. C. 4  . D. 0 . Lời giải Chọn B log 45 2 log 3  log 5 log 5  2 Ta có: 2 2 2 2 log 45    2  6 log 6 log 3 1 log 3 1 2 2 2
Vậy a  2, b  2, c  1  a b c  2  2 1  1.
Câu 35. Xét các số nguyên dương a, b sao cho phương trình 2
a ln x b ln x  5  0 có hai nghiệm phân
biệt x , x và phương trình 2
5 log x b log x a  0 có hai nghiệm phân biệt x , x thỏa mãn 1 2 3 4
x x x x . Tìm giá trị nhỏ nhất của S  2a  3b 1 2 3 4 A. S  33 . B. S  30 . C. S  17 . D. S  25 . min min min min Lời giải Chọn B.
Điều kiện để hai phương trình 2
a ln x b ln x  5  0 và 2
5 log x b log x a  0 có hai nghiệm phân biệt là: 2
b  20a  0 . (*)
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 17
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT bb b
ln x  ln x   ln x x     1 2  1 2  a     x x e a a Theo giả thiết ta có 1 2      . b b b
log x  log x    log  x x   5   3 4 3 4 x x  10  3 4   5   5 b b   Mà a 5
x x x x e  10 1 2 3 4 b b    
ln10 (Vì a, b là các số nguyên dương) a 5 5  a   a  3. (1) ln10 Theo điều kiện (*) có 2 2
b  20a  0  b  20a  60  b  8 . (2) a  3
Từ (1) và (2) suy ra S  2a  3b  30  S  30 
(thỏa mãn các điều kiện đề bài). min b  8 
Câu 36. Bất phương trình  3
x  9x ln  x  5  0 có bao nhiêu nghiệm nguyên? A. 4. B. 7. C. 6. D. Vô số. Lời giải Chọn C
Điều kiện: x  5 .  x  3  3 x 9x 0     x  0 Cho  3 x
9xln  x 5 0        .
ln  x  5  0  x  3   x  4   Bảng xét dấu:  4   x  3 
Dựa vào bảng xét dấu ta thấy f x  0   . 0  x  3 
Vì x    x  4  ;  3;0;1; 2;  3 .
Vậy có 6 giá trị nguyên của x thỏa bài toán. Câu 37. Cho hàm số   2x 2 x f x   
. Gọi m là số lớn nhất trong các số nguyên thõa mãn 0
f m  f  12
2m  2   0 . Mệnh đề nào sau đây đúng?
A. m  1513; 2019 .
B. m  1009;1513 . 0   0  
C. m  505;1009 .
D. m  1;505 . 0   0   Lời giải Chọn B Hàm số ( ) 2x 2 x f x    xác định x   R .
Khi đó x R , ta có ( )  2x  2x  (2x  2x f x
)   f (x) .
Suy ra f (x) là hàm số lẻ (1) Mặt khác ( ) (2x 2 x f x     ) ln 2  0 , x   R .
Do đó hàm số f (x) đồng biến trên R (2)
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 18
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Ta có 12
f (m)  f (2m  2 )  0 12
f (2m  2 )   f (m) . Theo (1) suy ra 12
f (2m  2 )  f (m) . 12 2 Theo (2) ta được 12 12
2m  2  m  3m  2  m  . 3
Vì m Z nên m  1365  m  1365 . 0
Vậy m  1009;1513 . 0  
Câu 38. Tính tổng tất cả các nghiệm nguyên của bất phương trình log  2 x  3 2
 log x x  4x 1  0 . 2 2 A. 4 . B. 6 . C. 5 . D. 3 . Lời giải Chọn B
Điều kiện: x  0 . Ta có log  2 x  3 2
 log x x  4x 1  0  log  2 x  3 2
x  3  log 4x  4x * . 2 2 2 2  
Xét hàm số f t   log t t trên D  0;   . Ta có 2 1
f t   1  0 t
  D  hàm số f đồng biến trên D . t ln 2 Suy ra    f  2
x    f x 2 * 3 4
x  3  4x  1  x  3 .
Vậy tập hợp các nghiệm nguyên của bất phương trình là 1; 2;  3 .
Nhận xét: Với cách hỏi và đáp án của câu này ta chỉ cần mở MOD7 của máy tính cầm tay, nhập
vế trái của bất phương trình và cho biến chạy từ 1 đến 6 là tìm được đáp án ngay.    Câu 39. Cho hàm số
y f x liên tục và đồng biến trên 0;  , bất phương trình 2          ln cos   x f x x e
m (với m là tham số) thỏa mãn với mọi x  0;   khi và chỉ khi:  2 
A. m f 0 1.
B. m f 0 1 .
C. m f 0 1 .
D. m f 0 1 . Lời giải Chọn A Ta có:          ln cos   x   ,   0;        ln cos   x f x x e m x m f x
x e , x   0;     1  2   2       
Do f x đồng biến trên 0;  
nên f x  0, x   0; . 2       2    
Xét       ln cos   x g x f x
x e , x  0;    2    
g x  f  x  x 0
 tan x   e
 0  tan 0   e   , x   0;    2    
Suy ra g x đơn điệu tăng trên 0;   , do đó:  2 
   m f    0 1 0  tan 0  ef 0 1.
Câu 40. Ông An có 200 triệu đồng gửi ngân hàng với kì hạn 1 tháng với lãi suất 0, 6% /1 tháng được trả
vào cuối kì. Sau mỗi kì hạn, ông đến tất toán cả lãi và gốc, rút ra 4 triệu đồng để tiêu dùng, số
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 19
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi luất
không thay đổi trong suốt quá trình ông gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi,
ông An tất toán và rút toàn bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng)
A. 169234 (nghìn đồng). B. 165288 (nghìn đồng).
C. 169269 (nghìn đồng). D. 165269 (nghìn đồng). Lời giải Chọn C
Nếu cuối mỗi kì hạn, ông An không rút ra 4 triệu thì số tiền ông có được sau 1 năm là A    12 200000. 1 0,6% nghìn đồng
Đầu tháng thứ 2 ông An rút về 4 triệu đồng, nếu để nguyên số tiền đó để gửi thì đến hết tháng
thứ 12 ngân hàng phải trả cả gốc và lãi cho ông ứng với 4 triệu đồng đó là
B  4000.1 0,6%11 11
 4000.R (nghìn đồng) nên đến hết tháng thứ 12, số tiền giả định là A 1
không còn được lấy nguyên vẹn mà bị trừ đi số tiền B 1
Tương tự, với 4 triệu đồng ông rút ở tháng thứ 3, 4,., 11 sẽ bị trừ đi tương ứng là: 10 9 1
B  4000.R , B  4000.R ,..., B  4000.R 2 3 11
Do vậy, số tiền ông An nhận được khi tất toán ở lần cuối cùng là:
A  B B  ...  B  12
 200000.R  4000 11 10
R R R 2 3 11  11 1  R 12
 200000.R  4000R  169269 (nghìn đồng). 1  R x y
Câu 41. Cho x , y thỏa mãn log
x x  9  y y  9  xy . Tìm giá trị lớn nhất của 3 2 2    
x y xy  2 3x  2 y  9 P
khi x , y thay đổi. x y 10 A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn C 2 2  y  3y
Điều kiện: x y  0 (do 2 2
x y xy  2  x    2  0   ).  2  4
Đẳng thức đã cho tương đương với 9 x y log
x x  9  y y  9  xy  2 * . 3 2 2      
x y xy  2 Đặt 2 2
u x y xy  2  0 , v  9x  9 y  0 , ta có. v *  log
u v u  log u v  log v . 3 3 3 u
Mà hàm số f t   t  log t đồng biến trên 0;   nên suy ra 3   2 2
*  u v x y xy  9x  9 y  2  0 . Ta có 2  y   y  3 9 3 19
x y xy  9x  9 y  2  0  x   9 x    y
y  2    y  32 2 2 2      .  2   2  4 2 4 4 Dẫn đến 2  y   y  19 1 y 19 x   9 x      x    1
  2x y  19     .  2   2  4 2 2 2
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 20
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Suy ra 3x  2 y  9
x y 10  2x y 19 2x y 19 P    1  1. x y 10 x y 10 x y 10
2x y  19 x  8 P  1     . y  3 y  3   Vậy max P  1. Cách 2: Từ giả thiết, ta có 2 2
x y xy  9x  9 y  2  0  *
Ta thấy x  8, y  3 thỏa mãn  
* , đặt x a  8, y b  3 khi đó: 2 2 2 2
x y xy x y  
a b ab      b    2 2 9 9 2 0 10a 5 0 10a 5
a ab b
 10a  5b  0  2a  b  0 3x  2 y  9 3a  2b  21 2a b P    1  1 Ta có: x y 10 a b  21 a b  21
Dấu “=” xảy ra khi và chỉ khi x  8, y  3 . Vậy P đạt giá trị lớn nhất bằng 1.
Câu 42. Cho hai số thực a , b thỏa mãn a  0 , 0  b  2 . Tìm giá trị nhỏ nhất của biểu thức  a 2b 2a  2. a b P   . a a  2 2. a 2 b b 9 7 13 A. P  . B. P  . C. P  . D. P  4 . min 4 min 4 min 4 min Lời giải Chọn C
Do 0  b  2 và a  0 nên 0 a   2a b . 2a 2a. a b 1 2a 1 2a a 2a   .  2 b P   . 1. Đặt t
, khi đó ta được t  1.  a a a  2 a 2 2 a b 2 a 2  2 b b   b 1  a   b    t 1
Yêu cầu bài toán trở thành tìm giá trị nhỏ nhất của hàm số f t    t 1 với t  2 1 2 t  1;  3 2
t  3t t  3
Có f t   2 t  3 1 f t  3 2
 0  t  3t t  3  0  t   2 3 t  
1  0  t  3 (do 2 t 1  0, t   ).
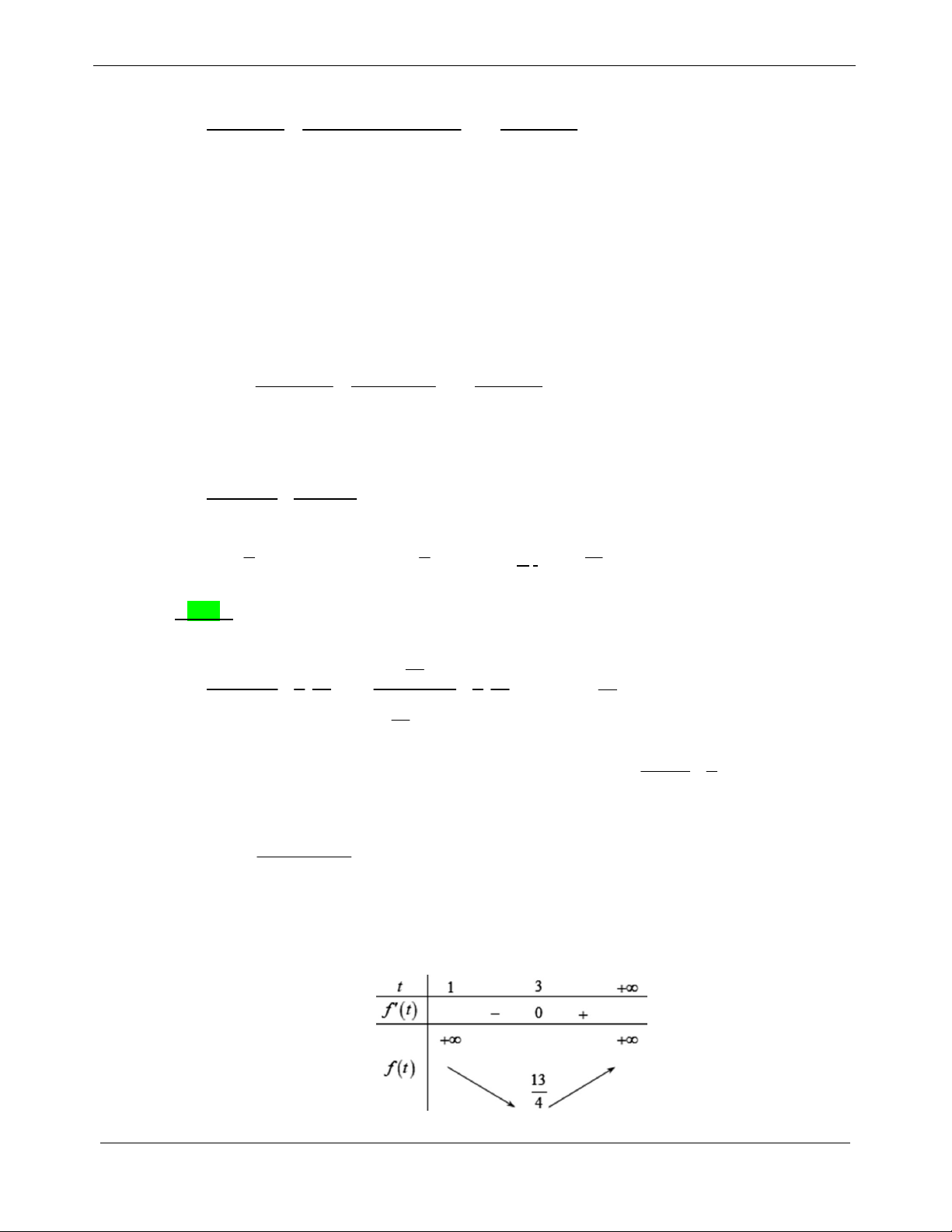
lim f t    ; lim f t    . t 1  t Bảng biến thiên
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 21
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 13
Từ bảng biến thiên ta được P
. Dấu bằng diễn ra khi và chỉ khi min 4 2a t  3   3  3. a
b  2a với 0  b  2 và a  0 . a b
Câu 43. Cho các số thực a, b  1 thỏa mãn điều kiện log a  log b  1. Tìm giá trị lớn nhất của biểu 2 3
thức P  log a  log b . 3 2 1 2 A. log 3  log 2 .
B. log 2  log 3 . C. log 3 log 2 . D. . 2 3  2 3 3 2 2 log 3  log 2 2 3 Lời giải Chọn A.
log b  1 x 3 0  x 1 
Đặt log a x  2
log a x log 2 3 3 
log b  1 x log 3 2   2 
1 xlog 2  x log 3 3 2
Đặt P f x  x log 2 
1 x log 3  f x  . 3   2   2 x 1 x log 2
f  x  0  1 x 3
log 2  x log 3  x  . 3 2 log 3  log 2 2 3 Ta có bảng biến thiên log 2 x 0 3 1 log 3  log 2 2 3 f  x  0  log 3  log 2 f x 2 3 log 2  log 3 3 2 Vậy P  log 3  log 2 . max 2 3
Câu 44. Với giá trị nào của tham số m để phương trình x x 1 4 . m 2  
 2m  3  0 có hai nghiệm x , x thỏa 1 2
mãn x x  4 . 1 2 5 13 A. m  . B. m  2. C. m  8. D. m  . 2 2 Lời giải Chọn D x x 1 4 . m 2    2m  3  0 (1) Đặt  2x t (t  0)
Phương trình (1) trở thành 2
t  2mt  2m  3  0 (2) 2 2
 '  m  (2m  3)  m  2m  3
Phương trình (1) có hai nghiệm  Phương trình (2) có hai nghiệm dương
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 22
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT  2  '  0
m  2m  3  0 m  1   m  3   
 S  0  2m  0  m  0  m  3 P 0 2m 3 0     3   m   2
Theo giả thiết: x x  4 1 2 x x x x 13 1 2 4 1 2  2  2  2 .2
 16  t .t  16  2m  3  16  m  (Thỏa ĐK) 1 2 2 a a 3
Câu 45. Cho dãy số a thỏa mãn a  1 và n 1 5   n 1 
, với mọi n  1. Tìm số nguyên dương n  1 3n  2
n  1 nhỏ nhất để a là một số nguyên. n A. n  41 . B. n  39 . C. n  49 . D. n  123 . Lời giải Chọn A      n n a a 3 a a 3 5 3  1 2 Ta có: n 1  n n 1 5 1   5  n   3n  2 3n  2 3n  2  3n   1  2   aa  log
 log 3 n 1  2  log 3n  2 ; n   1 n 1  n 5   5     5   3n  2  
n  1  a a  log 8  log 5 2 1 5 5
n  2  a a  log 11 log 8 3 2 5 5
Áp dụng cho: n  3  a a  log 14  log 11 4 3 5 5 ...........
n n 1  a a  log 3n  2  log 3 n 1  2 n n 1  5   5    
Cộng vế với vế n  
1 đẳng thức trên ta được: a a  log
3n  2  log 5  a  log 3n  2 ;
Do a  1  log 5 n 1 5   5 n 5    1 5 
Thử các đáp án từ nhỏ tới lớn ta được:
n  39  log 3n  2  log 119   5   5
Vậy chọn đáp án A.
n  41  log 3n  2  log 125  3  5   5
Câu 46. Có bao nhiêu giá trị nguyên của tham số m  8
 ;   để phương trình sau có nhiều hơn hai nghiệm phân biệt
    xm       2 2 2 1 2 2 2xx x x x m x x m . A. 6 . B. 7 . C. 5 . D. 8 . Lời giải Chọn B
Phương trình đã cho tương đương với 2 2
       x mx x         2 2 2 2 2 2  2xx x m x x x m x x   1 .   Đặt 2 2 x m  ;
a x x b ta có phương trình   1 trở thành
 .2ab    .2b a b a b  .2b  .2a a b
a b  2b   1  2a a b   1  0 2 .
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 23
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2a 1 2b 1
Trường hợp 1: Nếu ab  0 thì phương trình 2    0 3 . a b 2a a 1
+ Nếu a  0  2 1  0   0 . a 2a a 1
+ Nếu a  0  2 1  0   0 . a 2a 1 Do đó  0, với a  0 . a 2b 1 Tương tự ta có
 0, với b  0 . Do vậy phương trình 3 vô nghiệm. b 2 x  m
Trường hợp 2: Nếu ab  0 thì phương trình   1   . 2 x x  0  m  0 Phương trình  
1 có nhiều hơn hai nghiệm phân biệt    m  0. 2 m m  0 
Do m nguyên và m   8
 ;   nên có 7 giá trị của m thỏa mãn yêu cầu bài toán. 2
Câu 47. Tổng tất cả các giá trị của tham số m để phương trình x 2x 1  2 3 xm  log
2 x m  2 có 2 x 2 x3  
đúng ba nghiệm phân biệt là: A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn B 2
ln 2 x m  2
x 2 x3(2 xm 2)  
Phương trình tương đương 3  ln  2
x  2x  3 2 x 2 x3   2 3
.ln x  2x  3 2 xm 2  3
.ln 2 x m  2 (*). Xét hàm đặc trưng    3t f t
.ln t, t  2 là hàm số đồng biến nên từ phương trình (*) suy ra 2
x  2x  3  2 x m  2  g x 2
x  2x  2 x m  1  0 . 2 
x  4x  2m 1 khi x m
2x  4 khi x m
Có g x  
g ' x   2 x  2m 1 khi x m 2x khi x m  
x  2 khi x m
và g ' x  0   .
x  0 khi x m
Xét các trường hợp sau:
TH1: m  0 ta có bảng biến thiên của g x như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có m thoả mãn.
TH2: m  2 tương tự.
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 24
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
TH3: 0  m  2 , bảng biến thiên g x như sau:      m  2 m 1 1  0   1
Phương trình có 3 nghiệm khi  2m 1 0 2m 3        m  .  2  2
m 1  0  2m  3   3 m   2
Cả 3 giá trị trên đều thoả mãn, nên tổng của chúng bằng 3. 2 2
Câu 48. Cho phương trình 1 1x     1 1 25 2 .5  x m
 2m 1  0 , với m là tham số. Giá trị nguyên
dương lớn nhất của tham số m để phương trình trên có nghiệm là: A. 5 B. 26 . C. 25 . D. 6 . Lời giải Chọn C Đặt 2
t  1  1 x với x 1 
;1 ta được t  1; 2 . Phương trình trở thành 2
5 t    2.5t m
 2m  1  0 với t  1; 2 . 2 a  2a 1 Đặt  5t a
a 5; 25 và m  . a  2 2 a  2a 1
Hàm f a 
đồng biến trên 5; 25 nên để phương trình có nghiệm thì a  2 16 576 
f 5  m f 25 suy ra m  ;  . 3 23   
Vậy giá trị nguyên dương lớn nhất của m bằng 25 . 64 1001 2 1 2 3 1000
Câu 49. So sánh ba số a  1000 , b  2
và c 1  2  3  ... 1000 ?
A. c a b .
B. b a c .
C. c b a .
D. a c b . Lời giải Chọn A Ta có: 1 1000 2 1000 999 1000 1  1000 ; 2  1000 ...999  1000 1 2 3 1000 1000
c  1  2  3  ... 1000  1000.1000  c a Mặt khác: 10 2  1000 4 64 2  2 .ln 2  . 10 2 6 64 10 6 2 1001 .ln 2
 1000 .ln1000  1001.ln1000  2  1000  a b 10
Vậy c a  . b
Câu 50. Cho các số thực dương x , y thay đổi và thỏa mãn điều kiện x y  1 . Giá trị nhỏ nhất của x biểu thức 2 T   2 log x   3log là x y y y
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 25
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT A. 19 . B. 13 . C. 14 . D. T  15 . Lời giải Chọn D 2   4  1 
Từ giả thiết T   2 log x   3log x   1   3 1 . x y     1 log y log y y    2  x x
Đặt t  log y vì 1  y x t 0;  1 . x 4 3
Yêu cầu bài toán trở thành tìm giá trị nhỏ nhất của hàm f t   
 3 với t  0  ;1 . 1 t 2 t
t t t  3t   1  2 3 2 t  3 3 9 3 
Dễ thấy hàm số f t liên tục trên khoảng 0; 
1 và f t    , t 1 t 3 t 1 t 3 2 2 1
f t   0  3t 1  0  t  . 3
lim f t    ; lim f t    . t 0  t 1  Bảng biến thiên  1 
Từ bảng biến thiên suy ra min f t   f  15  
. Vậy min P  15 đạt được khi và chỉ khi 0;  1  3  1 3 log y
y x trong đó 1  y x . x 3
Câu 51. Bất phương trình xm x 1 4 1 2   
m  0 nghiệm đúng với mọi x  0 . Tập tất cả cá giá trị của m là A.  ;  12 . B. ;   1 .
C. ;0 .
D. 1;16 . Lời giải Chọn B Bất phương trình xm x 1 4 1 2     m  0  
1  4x  2   1 2x mm  0 .
Đặt 2x t bất phương trình trở thành 2
t  2m   1 t m  0 2 . Bất phương trình  
1 nghiệm đúng với mọi x  0 khi và chỉ khi bất phương trình 2 nghiệm
đúng với mọi t  1 . 2 t  2t
2  2t   2
1 m t  2t m  (do t  1 ). 2t 1 2 t  2t
Đặt f t   với t  1 . 2t 1
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 26
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT 2 2t  2t  2
f 't    0 t   1 . 2t  2 1 Bảng biến thiên
Từ bảng biến thiên ta có f t   m t 1;   m  1 . Vậy chọn B
Câu 52. Phương trình 4x 1  2 . x .c
m os  x có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là A. Vô số. B. 1. C. 2. D. 0. Lời giải Chọn B
Ta có: 4x 1  2 . x
.cos    2x  2x  .cos   2x  2x m x m x  .c
m os  x  0 . Đặt:
   2x  2x f x  .c
m os  x có tập xác định D   .
f x là hàm số chẵn.
f x  0 có nghiệm duy nhất  x  0 .
Thay x  0 vào phương trình  m  2 . Câu 53. Cho a, b, c là ba số thực dương, a  1 và thỏa mãn 2  bc 2  bc b c     c  . Số bộ  ; a ;
b c thỏa mãn điều kiện đã cho là a   3 3 2 log log 4 4 0 a    4  A. 0. B. 1. C. 2. D. Vô số. Lời giải Chọn B 2  bc  Đặt: 2 P bc b c     c a   3 3 2 log log 4 4 a    4  2  bc  Ta có: 3 3 4 4 b c   b c   .  4  2  bc  Do a  1 nên: 3 3 4 4 log b c
 log b c  4 log bc a    4 a a   P    bc 2 2 log  4  c  0 a  a  2 2 4  c  0    1
P  0  2  log bc  0  b   a 4  1  2 2 bc  c  2 4  
Câu 54. Tính tổng T của các giá trị nguyên của tham số m để phương trình x   2 e  ex m m  2m có 1
đúng hai nghiệm phân biệt nhỏ hơn . log e A. T  28 . B. T  20 . C. T  21. D. T  27 . Lời giải
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 27
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT Chọn D 2 Đặt  ex t
, t  0 ta được t   2 m m 1  2 2 t
 2m t  2mt m m  0  t m  m * . 1 Ta có x
 0  t  10 . Bài toán quy về tìm m phương trình * có hai nghiệm phân biệt log e m  0  21 41
thỏa mãn 0  t 10 . Tức là: 0  m m  10  1  m
. Do đó tổng T của các giá 2
0  m m 10 
trị nguyên của tham số m để phương trình x   2 e  ex m m
 2m có đúng hai nghiệm phân 1 biệt nhỏ hơn
là T  2  3  4  5  6  7  27 . log e y x
Câu 55. Cho hai số thực x, y lớn hơn 1 và thỏa mãn x.( x )e y  .( y )e y e x e
. Tìm giá trị nhỏ nhất của biểu thức P  log xy  log . x y x 2 1 2 2 1 2 A. . B. 2 2 . C. . D. . 2 2 2 Lời giải Chọn C
Với x, y  1, ta có y x x y .( x e )e yx .( y e )e y x  ln  x y .( x
e )e   ln y x .( y e )e   x ln y
y xe y ln x x ye ln y y e ln x x e     (1). y y x x t 1 Xét hàm số ( ) t t
g t te e 1 ln t trên 1; , có g '(t)  te   0, t   1. t
Hàm số g (t) đồng biến trên 1; nên g(t)  g(1)  1  0,t  1. ln t t e g(t)
Xét hàm số f (t)  
trên 1; , có f '(t)   0, t
  1, nên f (t) đồng biến trên t t 2 t
(1; ). Với x, y  1 thì (1)  f ( y)  f (x)  y  . x 1 u 1 2 u  2 Đặt u  log .
x y Do y x  1 nên u  1. Ta có P h(u)  
. Nhận thấy h '(u)  , 2 u 2 2u
nên h '(u)  0 khi u  2, h '(u)  0 khi 1  u  2, h '(u)  0 khi u  2. Dẫn tới  1 2 2
P h u h   1 2 2 ( ) 2  , u
  1, đẳng thức xảy ra khi u  2. Vậy min P  , đạt 2 2 được khi 2 y x và x  1.
Câu 56. Tập hợp các giá trị thực của tham số m để phương trình 2 log (4  x )  log
(2x m 1)  0 2019 1 2019
có hai nghiệm thực phân biệt là T  ( ;
a b) . Tính S  2a b .
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 28
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT A. 18 . B. 8 . C. 20 . D. 16 . Lời giải Chọn D 1 m TXĐ: D  ( 2  ; 2)  ( ; ) . 2
Khi đó, phương trình đã cho trở thành 2 4  x 2 2 log
 0  4  x  2x m 1  x  2x m  5  0 (*)
2019 2x m 1
Phương trình (*) có 2 nghiệm phân biệt 2
   1 1.(m 5)  6  m  0  m  6 (1)
Khi đó phương trình (1) có 2 nghiệm lần lượt là x  1
  6  m; x  1   6  m . 1 2 1 m TH1:
 2  m  5 (2). 2  D   2  ; 2 . 
 1 6  m  2   6  m  3
Phương trình (1) có 2 nghiệm x , x D      m  5 (3). 1 2  1
  6  m  2   6  m  1 
Từ (1), (2) và (3) suy ra 5  m  6 . 1 m TH2: 2 
 2  3  m  5 (4). 2  1 m   D  ; 2   .  2 
Phương trình (1) có 2 nghiệm x , x D 1 2        m  3 1 6 m 2 6  m  3            m  3   m  5 1 m m 3 (5). 1   6  m  6  m     m  5  2  2 
Từ (4) và (5) suy ra m  . Vậy 5  m  6 .
Suy ra a  5, b  6  2a b  16 .
Câu 57. Một anh sinh viên nhập học đại học vào tháng 8 năm 2014. Bắt đầu từ tháng 9 năm 2014, cứ
vào ngày mồng một hàng tháng anh vay ngân hàng 3 triệu đồng với lãi suất cố định 0,8%
/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo( lãi kép).
Vào ngày mồng một hàng tháng kể từ tháng 9/2016 về sau anh không vay ngân hàng nữa và
anh còn trả được cho ngân hàng 2 triệu đồng do có việc làm thêm. Hỏi ngay sau khi kết thúc
ngày anh ra trường 30 / 06 / 2018 anh còn nợ ngân hàng bao nhiêu tiền( làm tròn đến hàng nghìn đồng)?
A. 49.024.000 đồng.
B. 47.401.000 đồng.
C. 46.641.000 đồng.
D. 45.401.000 đồng. Lời giải Chọn C
Đặt r  0,8%  0, 008 ; V  3.000.000 o
+) Tính tổng số tiền anh sinh viên vay từ 01/09/2014 đến hết 30/08/2016 (24 tháng)
- Số tiền anh vay sau tháng thứ nhất, thứ hai, thứ 3,., tháng thứ 24 lần lượt là:
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 29
TUYỂN CHỌN CÂU HỎI VD-VDC TỪ CÁC
CHUYÊN ĐỀ 2. HÀM SỐ MŨ-LŨY THỪA - ĐỀ THI THỬ 2019 LOGARIT
V V 1 r 1 o  
V  V Vr VrVr o  1  o 1 2 1 2 1 o  
V  V Vr VrVrVr o  1  o 1 3 o 1 2 1 3 2 o   .... V VrVr  Vr o 1 24 o 1 23 ... 1 24 o     r 24 1 1
V 1 r   79.661.701( đồng) = T o r
+) Tính số tiền anh sinh viên còn nợ sau mỗi tháng, tính từ 01/09/2016 đến hết 30/06/2018( 22
tháng). Đặt T  2.000.000 o
- Số tiền anh còn nợ sau tháng thứ nhất, thứ hai, thứ 3,., tháng thứ 22 lần lượt là:
T T T
1 r T 1 r T 1 r 1  o      o  
T  T Tr TrTrTr o  1  1 2 o 1 2 1 2 1 o  
T  T Tr TrTrTrTr o  1  1 3 o 1 3 o 1 2 1 3 2 o   ....
T  T Tr TrTrTr  Tr o  1  1 22 o 1 22 o 1 21 ... 1 22 21 o   22 1 r 22 1
T 1 r  T 1 r 
 46.641.000 ( đồng) o r
TỔNG HỢP: NGUYỄN BẢO VƯƠNG - 0946798489 30