TOP 80 câu trắc nghiệm Hai đường thẳng vuông góc Hình 11 (có đáp án)

TOP 80 câu trắc nghiệm Hai đường thẳng vuông góc Hình 11 có đáp án và lời giải được viết dưới dạng file Word gồm 27 trang. Bài tập trắc nghiệm có các dạng: Lý thuyết; tính góc giữa hai đường thẳng; Chứng minh hai đường thẳng vuông góc và các bài toán liên quan. Các bạn xem và tải về ở dưới.

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

27 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
HAI ĐƯỜNG THẲNG VUÔNG GÓC
A – LÝ THUYẾT TÓM TẮT
1. Vectơ chỉ phương của đường thẳng: là VTCP của d nếu giá của song song hoặc trùng với
d.
2. Góc giữa hai đường thẳng:
• a¢//a, b¢//b Þ
• Giả sử là VTCP của a, là VTCP của b, .
Khi đó:
• Nếu a//b hoặc a º b thì
Chú ý:
3. Hai đường thẳng vuông góc:
• a ^ b Û
• Giả sử là VTCP của a, là VTCP của b. Khi đó .
• Lưu ý: Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
B – BÀI TẬP
Câu 1: Trong không gian cho ba đường thẳng phân biệt , , . Khẳng định nào sau đây đúng?
A. Nếu và cùng vuông góc với thì .
B. Nếu và thì .
C. Nếu góc giữa và bằng góc giữa và thì .
D. Nếu và cùng nằm trong mp thì góc giữa và bằng góc giữa và .
Hướng dẫn giải:
Chọn B.
Nếu và cùng vuông góc với thì và hoặc song song hoặc chéo nhau.
C sai do:
Giả sử hai đường thẳng và chéo nhau, ta dựng đường thẳng là đường vuông góc chung của
và . Khi đó góc giữa và bằng với góc giữa và và cùng bằng , nhưng hiển nhiên hai
đường thẳng và không song song.
D sai do: giả sử vuông góc với , song song với , khi đó góc giữa và bằng , còn góc
giữa và bằng .
Do đó B đúng.
Câu 2: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và khi song song với
(hoặc trùng với ).
B. Góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và thì song song với
C. Góc giữa hai đường thẳng là góc nhọn.
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.
Hướng dẫn giải:
Chọn A.
Câu 3: Cho tứ diện có hai cặp cạnh đối vuông góc. Trong các mệnh đề sau mệnh đề nào đúng?
A. Tứ diện có ít nhất một mặt là tam giác nhọn.
B. Tứ diện có ít nhất hai mặt là tam giác nhọn.
C. Tứ diện có ít nhất ba mặt là tam giác nhọn.
D. Tứ diện có cả bốn mặt là tam giác nhọn.
Hướng dẫn giải:
Chọn A.
0¹
!
!
a
!
a
∂
( )
∑
( )
,','=ab a b
!
u
!
v
(,)=
!!
a
uv
∂
( )
00
000
0 180
,
180 90 180
ne·u
ab
ne·u
ì
ï
££
=
í
-<£
ï
î
aa
aa
∂
( )
0
,0=ab
∂
( )
00
0 , 90££ab
!
u
!
v
.0^Û =
!!
ab uv
a
b
c
a
b
c
//ab
//ab
ca^
cb^
a
c
b
c
//ab
a
b
( )
// c
a
a
c
b
c
a
b
c
a
b
a
b
c
a
b
a
c
b
c
90°
a
b
a
c
b
c
a
c
90°
b
c
0°
a
b
a
c
b
c
b
c
a
b
a
c
b
c
ABCD
Trang 2
Câu 4: Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng
vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song
song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Hướng dẫn giải:
Chọn A.
Theo lý thuyết.
Câu 5: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Nếu đường thẳng vuông góc với đường thẳng và đường thẳng vuông góc với đường
thẳng thì vuông góc với
B. Cho ba đường thẳng vuông góc với nhau từng đôi một. Nếu có một đường thẳng
vuông góc với thì song song với hoặc
C. Nếu đường thẳng vuông góc với đường thẳng và đường thẳng song song với đường thẳng
thì vuông góc với
D. Cho hai đường thẳng và song song với nhau. Một đường thẳng vuông góc với thì
vuông góc với mọi đường thẳng nằm trong mặt phẳng .
Hướng dẫn giải:
Chọn C.
Câu 6: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một
mặt phẳng
B. Ba đường thẳng cắt nhau từng đôi một và không nằm trong một mặt phẳng thì đồng quy
C. Một đường thẳng cắt hai đường thẳng cắt nhau cho trước thì cả ba đường thẳng đó cùng nằm
trong một mặt phẳng
D. Ba đường thẳng cắt nhau từng đôi một thì cùng nằm trong một mặt phẳng
Hướng dẫn giải:
Chọn B.
Gọi , , là 3 đường thẳng cắt nhau từng đôi một. Giả sử , cắt nhau tại , vì không
nằm cùng mặt phẳng với , mà cắt , nên phải đi qua . Thật vậy giả sử không đi
qua thì nó phải cắt , tại hai điểm , điều này là vô lí, một đường thẳng không thể cắt một
mặt phẳng tại hai điểm phân biệt.
Câu 7: Trong các khẳng định sau, khẳng định nào đúng ?
A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
B. Nếu đường thẳng vuông góc với đường thẳng và đường thẳng vuông góc với đường
thẳng thì vuông góc với .
C. Cho hai đường thẳng phân biệt và . Nếu đường thẳng c vuông góc với và thì , ,
không đồng phẳng.
D. Cho hai đường thẳng và song song, nếu vuông góc với thì cũng vuông góc với .
Hướng dẫn giải:
Theo nhận xét phần hai đường thẳng vuông góc trong SGK thì đáp án D đúng.
Câu 8: Mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường
thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường
thẳng kia.
Hướng dẫn giải:
Theo nhận xét phần hai đường thẳng vuông góc trong SGK thì đáp án D đúng.
a
b
b
c
a
c
, , abc
d
a
d
b
c
a
b
b
c
a
c
a
b
c
a
c
( )
, ab
1
d
2
d
3
d
1
d
2
d
A
3
d
1
d
2
d
3
d
1
d
2
d
3
d
A
3
d
A
1
d
2
d
B
C
a
b
b
c
a
c
a
b
a
b
a
b
c
a
b
a
c
b
c
Trang 3
Câu 9: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với
đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường
thẳng kia.
Hướng dẫn giải:
Theo nhận xét phần hai đường thẳng vuông góc trong SGK thì đáp án D đúng.
Câu 10: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Cho hai đường thẳng song song với nhau. Một đường thẳng vuông góc với thì
vuông góc với mọi đường thẳng nằm trong mặt phẳng
B. Cho ba đường thẳng vuông góc với nhau từng đôi một. Nếu có một đường thẳng
vuông góc với thì song song với hoặc .
C. Nếu đường thẳng vuông góc với đường thẳng và đường thẳng vuông góc với đường
thẳng thì đường thẳng vuông góc với đường thẳng .
D. Nếu đường thẳng vuông góc với đường thẳng và đường thẳng song song với đường thẳng
thì đường thẳng vuông góc với đường thẳng .
Hướng dẫn giải:
Chọn D. Theo định lý-sgk
,ab
c
a
c
( )
,.ab
,,abc
d
a
d
b
c
a
b
b
c
a
c
a
b
b
c
a
c
Trang 4
DẠNG 1: TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG.
Phương pháp:
Để tính góc giữa hai đường thẳng trong không gian ta có thể thực hiện theo hai cách
Cách 1. Tìm góc giữa hai đường thẳng bằng cách chọn một điểm thích hợp ( thường nằm
trên một trong hai đường thẳng).
Từ dựng các đường thẳng lần lượt song song ( có thể tròng nếu nằm trên một trong hai
đường thẳng) với và . Góc giữa hai đường thẳng chính là góc giữa hai đường thẳng .
Lưu ý 1: Để tính góc này ta thường sử dụng định lí côsin trong tam giác
.
Cách 2. Tìm hai vec tơ chỉ phương của hai đường thẳng
Khi đó góc giữa hai đường thẳng xác định bởi .
Lưu ý 2: Để tính ta chọn ba vec tơ không đồng phẳng mà có thể tính được độ dài
và góc giữa chúng,sau đó biểu thị các vec tơ qua các vec tơ rồi thực hiện các tính toán
Câu 1: Cho tứ diện có , ( , lần lượt là trung điểm của và
). Số đo góc giữa hai đường thẳng và là
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn C.
Gọi , lần lượt là trung điểm , .
Ta có:
là hình thoi.
Gọi là giao điểm của và .
Ta có: .
Xét vuông tại , ta có: .
Mà: .
12
,dd
12
,dd
O
O
d
1
d
2
d'
2
d'
1
O
O
''
12
,dd
O
1
d
2
d
''
12
,dd
12
,dd
222
cos
2
bca
A
bc
+-
=
12
,uu
!!" !!"
12
,dd
12
,dd
( )
12
12
12
.
cos ,
uu
dd
uu
=
!!" !!"
!!" !!"
12 1 2
,,uu u u
!!" !!" !!" !!"
,,abc
!!!
12
,uu
!!" !!"
,,abc
!!!
ABCD
AB CD a==
3
2
IJ
a
=
I
J
BC
AD
AB
CD
30°
45°
60°
90°
M
N
AC
BC
11
222
// // //
a
MI NI AB CD
MINJ
MI AB CD NI
ì
== = =
ï
Þ
í
ï
î
O
MN
IJ
∑
∑
2MIN MIO=
MIOD
O
∑ ∑
∑
3
3
4
cos 30 60
2
2
a
IO
MIO MIO MIN
a
MI
== =Þ =°Þ =°
( ) ( )
∑
, , 60===°AB CD IM IN MIN
O
J
M
I
N
B
D
C
A
Trang 5
Câu 2: Cho hình hộp . Giả sử tam giác và đều có 3 góc nhọn. Góc giữa
hai đường thẳng và là góc nào sau đây?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Ta có: (tính chất của hình hộp)
(do giả thiết cho nhọn).
Câu 3: Cho tứ diện đều (Tứ diện có tất cả các cạnh bằng nhau).
Số đo góc giữa hai đường thẳng và bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là tâm đường tròn ngoại tiếp .
Gọi là trung điểm (do đều).
Do .
Ta có: .
Câu 17. [1H3-2] Cho tứ diện đều , là trung điểm của cạnh . Khi đó
bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn A.
Không mất tính tổng quát, giả sử tứ diện có cạnh bằng .
Gọi là tâm đường tròn ngoại tiếp .
Gọi là trung điểm
Ta có: .
Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của :
, .
Xét , ta có: .
Từ đó: .
Câu 4: Cho hình chóp có đáy là hình vuông cạnh bằng và các cạnh bên đều bằng
. Gọi và lần lượt là trung điểm của và . Số đo của góc bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là tâm của hình vuông là tâm đường tròn
ngoại tiếp của hình vuông (1).
.ABCD A B C D
¢¢¢¢
AB C
¢
ADC
¢¢
AC
AD
¢
∑
BDB
¢
∑
AB C
¢
∑
DB B
¢
// AC A C
¢¢
( ) ( )
∑
,,AC A D A C A D DA C
¢¢¢¢ ¢¢
Þ= =
DA C
¢¢
D
ABCD
AB
CD
30°
45°
60°
90°
H
( )
BCD AH BCDDÞ^
E
CD
BE CDÞ^
BCDD
( )
AH BCD AH CD^Þ^
( ) ( )
∑
, 90
CD BE
CD ABE CD AB AB CD
CD AH
^
ì
Þ^ Þ^Þ =°
í
^
î
ABCD
M
BC
( )
cos ,AB DM
6
3
2
2
2
3
2
1
ABCD
a
H
( )
BCD AH BCDDÞ^
E
AC
( ) ( )
// , ,ME AB AB DM ME MDÞÞ =
( ) ( )
( )
∑
cos , cos , cos , cosAB DM ME MD ME MD EMD== =
!!! " !!! !"
MEDD
ME a=
3
2
a
ED MD==
MEDD
∑
22
2
222
33
22 2
3
cos
2. 6
3
2. .
22
aa a
ME MD ED
EMD
ME MD
aa
æöæö
æö
+-
ç÷ç÷
ç÷
èø
+-
èøèø
== =
( )
33
cos ,
66
AB DM ==
.S ABCD
ABCD
a
a
M
N
AD
SD
( )
,MN SC
30°
45°
60°
90°
O
ABCD
OÞ
ABCD
D'
B'
C'
B
A
D
C
A'
H
E
B
D
C
A
E
H
M
B
D
C
A
N
M
O
D
A
B
C
S
Trang 6
Ta có: nằm trên trục của đường tròn ngoại
tiếp hình vuông (2).
Từ (1) và (2) .
Từ giả thiết ta có: (do là đường trung bình
của ). .
Xét , ta có: vuông tại .
.
Câu 5: Cho hình chóp có tất cả các cạnh đều bằng . Gọi và lần lượt là trung điểm của
và . Số đo của góc bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn C.
Gọi là tâm của hình vuông là tâm đường tròn
ngoại tiếp của hình vuông (1).
Ta có: nằm trên trục của đường tròn ngoại
tiếp hình vuông (2).
Từ (1) và (2) .
Từ giả thiết ta có: (do là đường trung bình của
). .
Mặt khác, ta lại có đều, do đó .
Câu 6: Cho tứ diện có . Gọi , , , lần lượt là trung điểm của , ,
, . Góc giữa bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Từ giả thiết ta có: (tính chất đường trung bình trong
tam giác)
Từ đó suy ra tứ giác là hình bình hành.
Mặt khác: là hình thoi
(tính chất hai đường chéo của hình thoi)
.
Câu 7: Cho hình lập phương . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Hướng dẫn giải:
Chọn B.
Câu 8: Trong không gian cho hai hình vuông và có chung cạnh và nằm trong
hai mặt phẳng khác nhau, lần lượt có tâm và . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Hướng dẫn giải:
Chọn D.
Vì và là hình vuông nên là hình bình hành
SA SB SC SD S== =Þ
ABCD
( )
SO ABCDÞ^
// MN SA
MN
SADD
( ) ( )
,,MN SC SA SCÞ=
SACD
22222
22
2
22
SA SC a a a
SAC
AC AD a
ì
+=+=
ï
ÞD
í
==
ï
î
S
SA SCÞ^
( ) ( )
, , 90SA SC MN SCÞ= =°
.S ABCD
a
I
J
SC
BC
( )
,IJ CD
30°
45°
60°
90°
O
ABCD
OÞ
ABCD
SA SB SC SD S== =Þ
ABCD
( )
SO ABCDÞ^
// IJ SB
IJ
SABD
( ) ( )
,,IJ CD SB ABÞ=
SABD
∑
( ) ( )
60 , 60 , 60SBA SB AB IJ CD=°Þ =°Þ =°
ABCD
AB CD=
I
J
E
F
AC
BC
BD
AD
( )
,IE JF
30°
45°
60°
90°
// //
// //
IJ EF AB
JE IF CD
ì
í
î
IJEF
11
22
AB CD IJ AB JE CD ABCD=Þ= == Þ
IE JFÞ^
( )
, 90IE JFÞ=°
.ABCD EFGH
AB
!!!"
DH
!!! !"
45°
90°
120°
60°
( )
∑
, 90
//
AB AE
AB DH AB DH
AE DH
^
ü
Þ^ Þ =°
ý
þ
ABCD
''ABC D
AB
O
'O
AB
!!!"
'OO
!!!!"
60°
45°
120°
90°
ABCD
''ABC D
// '; ' 'AD BC AD BC ADBC=Þ
J
I
O
D
A
B
C
S
J
I
F
E
B
D
C
A
Trang 7
Mà là tâm của 2 hình vuông nên là trung điểm của và là đường trung
bình của
Mặt khác, nên
Câu 9: Cho tứ diện có và . Gọi và lần
lượt là trung điểm của và Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Hướng dẫn giải:
Chọn B.
Ta có và là 2 tam giác đều, là trung điểm của nên (2 đường trung tuyến
của 2 tam giác đều chung cạnh ) nên là tam giác cân ở . Do đó
Câu 10: Cho hình chóp có và . Hãy xác định góc giữa cặp
vectơ và ?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Ta có: .
Do đótam giác đều. Gọi là trọng tâm của tam giác .
Vì hình chóp có
nên hình chiếu của trùng với
Hay .
Ta có:
Suy ra .
Vậy góc giữa cặp vectơ và bằng .
Câu 11: Cho tứ diện có và . Gọi và lần
lượt là trung điểm của và . Hãy xác định góc giữa cặp vectơ và ?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Xét tam giác có là trung điểm đoạn .
Ta có:
Vì tam giác có và
Nên tam giác đều. Suy ra:
Tương tự ta có tam giác đều nên .
Xét .
Suy ra . Hay góc giữa cặp vectơ và bằng .
Câu 12: Cho tứ diện có trọng tâm . Chọn khẳng định
đúng?
A. .
B. .
C. .
D. .
Hướng dẫn giải:
;'OO
;'OO
BD
'AC
'OOÞ
'ADBC
' //OO ADÞ
AD AB^
( )
∑
' ', 90
o
OO AB OO AB^ ^Þ =
ABCD
AB AC AD==
∑
∑ ∑
00
60 , 90BAC BAD CAD== =
I
J
AB
.CD
IJ
!!"
CD
!!!"
45°
90°
60°
120°
BAC
BAD
I
AB
CI DI=
AB
CID
I
.IJ CD^
.S ABC
SA SB SC==
∑
∑
∑
ASB BSC CSA==
SB
!! "
AC
!!!"
60°
120°
45°
90°
( )
SAB SBC SCA c g cD=D =D --
AB BC CAÞ==
ABC
G
ABC
.S ABC
SA SB SC==
S
G
( )
SG ABC^
( )
AC BG
AC SBG
AC SG
^
ì
Þ^
í
^
î
AC SB^
SB
!! "
AC
!!!"
0
90
ABCD
AB AC AD==
∑
∑ ∑
00
60 , 90BAC BAD CAD== =
I
J
AB
CD
AB
!!!"
IJ
!!"
120°
90°
60°
45°
ICD
J
CD
( )
1
2
IJ IC ID=+
!!" !!" !!"
ABC
AB AC=
∑
60BAC =°
ABC
CI AB^
ABD
DI AB^
( )
111
....0
222
IJ AB IC ID AB IC AB ID AB=+ = + =
!!" !!!" !!" !!" !!!" !!" !!!" !!" !!!" "
I J AB^
!!" !!!"
AB
!!!"
IJ
!!"
0
90
ABCD
G
( )
222222 2222
3AB AC AD BC BD CD GA GB GC GD+++++= +++
( )
222222 2222
4AB AC AD BC BD CD GA GB GC GD+++++= +++
( )
222222 2222
6AB AC AD BC BD CD GA GB GC GD+++++= +++
( )
222222 2222
2AB AC AD BC BD CD GA GB GC GD+++++= +++
Trang 8
Chọn B.
Lại có:
Từ (1) và (2) ta có điều phải chứng minh.
Câu 13: Cho tứ diện có hai mặt và là các tam giác
đều. Góc giữa và là?
A. . B. .
C. . D. .
Hướng dẫn giải:
Chọn C.
Gọi là trung điểm của
Vì và là các tam giác đều
Nên .
Suy ra .
Câu 14: Cho hình chóp có tất cả các cạnh đều bằng . Gọi và lần lượt là trung điểm của
và . Số đo của góc bằng:
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là tâm của hình thoi .
Ta có: .
Nên góc giữa và bằng góc giữa và .
Xét tam giác có
.
Nên tam giác đều.
Vậy góc giữa và bằng góc giữa và
bằng góc .
Câu 15: Cho hình hộp . Giả sử tam giác và đều có 3 góc nhọn. Góc
giữa hai đường thẳng và là góc nào sau đây?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Ta có: nên góc giữa hai đường thẳng và
là góc giữa hai đường thẳng và
( ) ( ) ( ) ( ) ( ) ( )
222222
222222
222 2
33332. . . . .
AB AC AD BC BD CD
AG GB AG GC AG GD BG GC BG GD CG GD
AG BG CG DG AG GB AG GC AG GD BG GD BG GD
+++++
=+ ++ ++ ++ ++ ++
=++++ + + + +
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
( )
( )
.1CG GD+
!!!" !!!" !!!"
( )
( )
( )
22 2 2
D0
D
2. . . . . . 2
GA GB GC G
GA GB GC G
AG GB AG GC AG GD BG GD BG GD CG GD
+++ =
Û+++
=+++++
!! !" !!!" !!!" !!!" "
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
ABCD
ABC
ABD
AB
CD
120°
60°
90°
30°
I
AB
ABC
ABD
CI AB
DI AB
^
ì
í
^
î
( )
AB CID AB CD^Þ^
.S ABCD
a
I
J
SC
BC
( )
, IJ CD
90°
45°
30°
60°
O
ABCD
//OJ CD
IJ
CD
IJ
OJ
IOJ
11 1
,,
22 2 2 22
aaa
I J SB OJ CD IO SA== = = ==
IOJ
IJ
CD
IJ
OJ
∑
0
O 60IJ =
.ABCD A B C D
¢¢¢¢
AB C
¢
ADC
¢¢
AC
AD
¢
∑
AB C
¢
∑
DA C
¢¢
∑
BB D
¢
//AC A C
¢¢
AC
AD
¢
AC
¢¢
AD
¢
Trang 9
bằng góc nhọn (Vì tam giác đều có 3 góc nhọn
Câu 16: Cho tứ diện đều . Số đo góc giữa hai đường thẳng và bằng:
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn C.
Gọi là trọng tâm tam giác .
Vì tứ diện đều nên .
Ta có: .
Vậy số đo góc giữa hai đường thẳng và bằng
Câu 17: Cho tứ diện có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song
song với một cặp cạnh đối diện của tứ diện. Trong các mệnh đề sau mệnh đề nào đúng?
A. Thiết diện là hình chữ nhật. B. Thiết diện là hình vuông.
C. Thiết diện là hình bình hành. D. Thiết diện là hình thang.
Hướng dẫn giải:
Chọn A.
Gỉa sử thiết diện là tứ giác .
Ta có: và nên là hình bình hành
Lại có
Vậy tứ giác là hình chữ nhật.
Câu 18: Cho tứ diện . Chứng minh rằng nếu thì ,
, . Điều ngược lại đúng không?
Sau đây là lời giải:
Bước 1:
Bước 2: Chứng minh tương tự, từ ta được và
ta được .
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương
đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Sai ở bước 3. B. Đúng C. Sai ở bước 2. D. Sai ở bước 1.
Hướng dẫn giải:
Chọn B.
Bài giải đúng.
∑
DA C
¢¢
ADC
¢¢
ABCD
AB
CD
60°
30°
90°
45°
G
ABC
ABCD
( )
AG BCD^
( )
CD AG
CD ABG CD AB
CD BG
^
ì
Þ^ Þ^
í
^
î
AB
CD
0
90
ABCD
MNPQ
//MN PQ
MN PQ=
MNPQ
AC BD MQ PQ^Þ ^
MNPQ
ABCD
... .AB AC AC AD AD AB==
!!!" !!!" !!!" !!!" !!!" !!!"
AB CD^
AC BD^
AD BC^
...AB AC AC AD=
!!!" !!!" !!!" !!!"
Û
.( ) 0AC AB AD-=
!!!" !!!" !!!"
Û
Û
AC BD^
..AC AD AD AB=
!!!" !!!" !!!" !!!"
AD BC^
..AB AC AD AB=
!!!" !!!" !!!" !!!"
AB CD^
A
B
C
D
M
Q
P
N
Trang 10
Câu 19: Cho hình chóp có và . Hãy xác định góc giữa cặp
vectơ và ?
A. B. C. D.
Hướng dẫn giải:
Chọn D.
Ta có:
Vì và
Do đó:
Câu 20: Cho hình chóp có đáy là hình vuông cạnh bằng và các cạnh bên đều bằng
. Gọi và lần lượt là trung điểm của và . Số đo của góc bằng:
A. B. C. D.
Hướng dẫn giải:
Chọn C.
Ta có:
vuông tại .
Khi đó:
Câu 21: Cho hình lập phương . Chọn khẳng định sai?
A. Góc giữa và bằng . B. Góc giữa và bằng .
C. Góc giữa và bằng . D. Góc giữa và bằng .
Hướng dẫn giải:
Chọn B.
Ta có:
(vì và )
Do đó:
Câu 22: Cho hình lập phương có cạnh . Gọi là trung điểm . Giá trị
là:
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn A.
Ta có:
.S ABC
SA SB SC==
∑
∑
∑
ASB BSC CSA==
SC
!! !"
AB
!!!"
120°
45°
60°
90°
( )
.. ..SC AB SC SB SA SC SB SC SA=-=-
!! !" !!!" !! !" !! " !!" !! !" !! " !! !" !!"
∑
∑
. cos . .cos 0SA SB BSC SC SA ASC=- =
SA SB SC==
∑
∑
BSC ASC=
( )
0
, 90SC AB =
!! !" !!!"
.S ABCD
ABCD
a
a
M
N
AD
SD
( )
,MN SC
45°
30°
90°
60°
2AC a=
22 2 2
2AC a SA SCÞ==+
SACÞD
S
( )
1
. . 0 , 90
2
NM SC SA SC NM SC==Û =°
!!!!" !! !" !!" !! !" !!!!" !! !"
( )
, 90MN SCÞ=°
111 1
.ABCD A B C D
AC
11
BD
90°
11
BD
1
AA
60°
AD
1
BC
45°
BD
11
AC
90°
( )
111 1 1
...AA B D BB BD BB BA BC== +
!!! " !!!!" !!! " !!!" !!! " !!!" !!!"
11
..0BB BA BB BC=+ =
!!! " !! !" !!! " !!!"
( )
0
1
, 90BB BA =
!!! " !!!"
( )
0
1
, 90BB BC =
!!! " !!!"
( )
( )
00
111 111
, 90 , 90AA B D AA B D=Þ =
!!! " !!!!"
111 1
.ABCD A B C D
a
M
AD
11
.B M BD
!!!!" !!! !"
2
1
2
a
2
a
2
3
4
a
2
3
2
a
( )( )
111 1
.B M BD B B BA AM BA AD DD=++ ++
!!!!" !!! !" !!! " !! !" !!!!" !! !" !!!" !!!!"
A
B
S
C
1
A
1
B
A
1
C
1
D
B
C
D
Trang 11
Câu 23: Cho hình hộp có tất cả các cạnh đều bằng
nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?
A. B. C. D.
Hướng dẫn giải:
Chọn B.
Ta có:
Vì và là hai hình thoi bằng nhau nên
+ suy ra không vuông góc với
+ suy ra
Nên đáp án B có thể sai vì chưa có điều kiện của góc và
Chọn B.
Câu 24: Cho hình lập phương . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Hướng dẫn giải:
Chọn C.
Ta có: (do là hình chữ nhật)
Câu 25: Cho tứ diện đều cạnh bằng . Gọi là trung điểm , là góc giữa và .
Chọn khẳng định đúng?
A. B. C. D.
Hướng dẫn giải:
Chọn C.
Gọi là trọng tâm của
Trên đường thẳng qua và song song lấy điểm sao cho
là hình chữ nhật, từ đó suy ra:
Có: và
;
2
11
2
22
2
..
2
2
B B DD BA AM AD
a
aa
a
=++
=- + +
=
!!! " !!!!" !!!" !!!!" !!!"
.ABCD A B C D
¢¢¢¢
A C BD
¢¢
^
BB BD
¢
^
AB DC
¢¢
^
BC A D
¢¢
^
( )
.. ..BB BD BB BA BC BB BA BB BC
¢¢ ¢¢
=+=+
!!! " !!!" !!! " !! !" !!!" !!! " !! !" !!! " !!!"
∑
∑
( )
.BB BA cosB BA cosB BC
¢¢ ¢
=+
AA B B
¢¢
ABCD
∑
∑
B BA B BC
¢¢
=Þ
.0BB BD
¢
¹
!!! " !!!"
BB
¢
BD
∑
∑
∑
∑
0
180B BA B BC cos B BA cosB BC
¢¢ ¢ ¢
+=Þ =- Þ
.0BB BD
¢
=
!!! " !!!"
BB BD
¢
^
∑
B BA
¢
∑
B BC
¢
.ABCD EFGH
AB
!!!"
EG
!!!"
90°
60°
45°
120°
//EG AC
ACGE
( ) ( )
∑
, , 45AB EG AB AC BACÞ===°
!!!" !!!" !!!" !!!"
ABCD
a
M
CD
a
AC
BM
0
60
a
=
O
BCDD
( )
AO BCDÞ^
d
C
BM
N
BMCN
∑
( )
∑
( )
∑
( )
,,AC BM AC CN ACN
a
===
3
2
CN BM a==
2
a
BN CN==
2
2222 2
22
33
AO AB BO AB BM a
æö
=-=- =
ç÷
èø
222 2
7
12
ON BN BO a=+=
22
5
2
AN AO ON a=+=
222
3
cos
2. 6
AC CN AN
AC CN
a
+-
Þ= =
1
A
1
B
A
1
C
1
D
B
C
D
M
E
F
A
G
H
B
C
D
Trang 12
Câu 26: Trong không gian cho hai tam giác đều và có chung cạnh và nằm trong hai
mặt phẳng khác nhau. Gọi lần lượt là trung điểm của các cạnh và .
Hãy xác định góc giữa cặp vectơ và ?
A. 45
0
B. 120
0
C. 60
0
D. 90
0
Hướng dẫn giải:
Chọn C.
Gọi là trung điểm
cân tại
cân tại
Kết luận: góc giữa và là
Câu 27: Cho góc giữa và bằng . Chọn khẳng định sai trong các khẳng đính sau?
A. B. C. D.
Hướng dẫn giải:
Chọn A.
Ta có:
Câu 28: Cho hình lập phương . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Hướng dẫn giải:
Chọn B.
Đặt cạnh của hình lập phương trên là
Gọi là giao trung điểm
Qua kẻ đường thẳng
Qua kẻ đường thẳng
Suy ra cắt tại .
Từ đó suy ra
Câu 29: Cho tứ diện có và . Hãy xác định góc giữa cặp
vectơ và ?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có
ABC
'ABC
AB
,,,MNPQ
,, 'AC CB BC
'CA
AB
!!!"
'CC
!!!!"
I
CC
¢
CAC
¢
D
A
(1)CC AI
¢
Þ^
CBC
¢
D
B
(2)CC BI
¢
Þ^
( )
(1),(2)
CC AIB CC AB CC AB
¢¢¢
¾¾¾® ^ Þ ^ Þ =
!!!!" !!!"
CC
¢
!!!!"
AB
!!!"
90°
3, 5ab==
!!
a
!
b
!
120°
19ab+=
!
!
7ab-=
!
!
2 139ab-=
!
!
29ab+=
!
!
( )
2
22
2 . .cos , 19ab a b ab ab+=++ =
!!!!
!! !!
( )
a b a b a.b.cos a,b+=++ =
2
22
2 19
!! ! ! !! !!
.ABCD EFGH
AF
!!!"
EG
!!!"
0
90
0
60
0
45
0
120
a
I
EG
A
//d FI
I
//d FA
¢
d
d
¢
J
∑
( )
∑
,EG AF EIJ
a
==
!!!!" !!!"
222 2IJ AF EI FI AJ a== = = =
222
3
2
EJ AE AJ=+=
22 2
1
cos 60
2. . 2
EI IJ AJ
EI EJ
aa
++
==Þ=°
ABCD
AB AC AD==
∑
∑
0
60BAC BAD==
AB
!!!"
CD
!!!"
0
60
0
45
0
120
0
90
( )
00
.. ..
. .cos 60 . .cos 60 0
AB CD AB AD AC AB AD AB AC
AB AD AB AC
=-=-
=-=
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
Trang 13
Câu 30: Cho hình lập phương . Góc giữa và là
A. . B. . C. . D. .
Hướng dẫn giải:
Vì nên góc giữa và là .
Vì tam giác đều nên .
Vậy góc giữa và bằng .
Câu 31: Cho hình chóp có và . Hãy xác định góc giữa cặp
vectơ và ?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có
Câu 32: Cho tứ diện đều , là trung điểm của cạnh . Khi đó bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Giả sử cạnh của tứ diện là .
Ta có
Mặt khác
Do có . Suy ra .
Câu 33: Cho tứ diện có vuông góc với , . là điểm thuộc cạnh
sao cho . song song với và lần lượt cắt tại
. Diện tích lớn nhất của tứ giác bằng bao nhiêu ?
A. . B. . C. . D. .
Hướng dẫn giải:
Xét tứ giác có
là hình bình hành.
( )
0
, 90AB CDÞ=
!!!" !!!"
111 1
.ABCD A B C D
AC
1
DA
0
45
0
90
0
60
0
120
' ' //A C AC
AC
1
DA
∑
11
DA C
11
DA C
∑
0
11
60DA C =
AC
1
DA
0
60
.S ABC
SA SB SC==
∑
∑
∑
ASB BSC CSA==
SA
!!"
BC
!!!"
0
120
0
90
0
60
0
45
( )
∑
∑
.. ..
. .cos . .cos 0
SA BC SA SC SB SA SC SA SB
SA SC ASC SA SB ASB
=-=-
=-=
!!" !!!" !!" !! !" !! " !!" !! !" !!" !!"
( )
0
, 90SA BCÞ=
!!" !!!"
ABCD
M
BC
( )
cos ,AB DM
2
2
3
6
1
2
3
2
a
( )
..
cos ,
3
.
.
2
AB DM AB DM
AB DM
a
AB DM
a
==
!!!" !!!!" !!!" !!!!"
!!!" !!!!"
!!!" !!!!"
( )
00
22 2
. . . . .cos 30 . .cos 60
33 13
.. .. .
22 2 4 2 4
AB DM AB AM AD AB AM AB AD AB AM AB AD
aaaa
aaa
=-=-= -
=-=-=
!!!" !!!!" !!!" !!!!" !!!" !!!" !!!!" !!!" !!!"
( )
os ,
3
c
6
AB DM =
!!!" !!!!"
( )
cos ,
3
6
AB DM =
ABCD
AB
CD
6AB CD==
M
BC
( )
. 0 1MC x BC x=<<
( )
mp P
AB
CD
,,,BC DB AD AC
,,,MNPQ
9
11
10
MNPQ
// //
// //
MQ N P AB
MN PQ CD
ì
í
î
MNPQÞ
Trang 14
Mặt khác, .
Do đó, là hình chữ nhật.
Vì nên .
Theo giả thiết .
Vì nên .
Diên tích hình chữ nhật là
.
Ta có khi
Vậy diện tích tứ giác lớn nhất bằng 9 khi là trung điểm của .
Câu 34: Cho tứ diện đều cạnh bằng . Gọi là tâm đường tròn ngoại tiếp tam giác .
Góc giữa và bằng bao nhiêu ?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có
Suy ra .
Câu 35: Cho tứ diện có . Gọi lần lượt là trung điểm của .
Góc bằng
A. . B. . C. . D. .
Hướng dẫn giải:
Tứ giác là hình bình hành.
Mặt khác mà nên .
Do đó là hình thoi.
Suy ra .
Câu 36: Cho tứ diện với . Gọi là góc giữa và
. Chọn khẳng định đúng ?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có
AB CD MQ MN^Þ ^
MNPQ
//MQ AB
.6
MQ CM
x MQ x AB x
AB CB
==Þ= =
( )
.1MC x BC BM x BC=Þ=-
//MN CD
( ) ( )
11.61
MN BM
xMN xCD x
CD BC
==-Þ=- =-
MNPQ
( ) ( )
2
1
. 6 1 .6 36. . 1 36 9
2
MNPQ
xx
SMNMQ xxxx
+-
æö
==-=-£ =
ç÷
èø
9
MNPQ
S =
1
1
2
xxx=- Û =
MNPQ
M
BC
ABCD
a
O
BCD
AO
CD
0
0
0
30
0
90
0
60
( )
.AO CD CO CA CD=-
!!!" !!!" !!!" !! !" !!!"
00
22
. . . .cos 30 . .cos 60
33 1
. . . . 0.
32 222
CO CD CA CD CO CD CA CD
aaa
aaa
=-= -
=-=-=
!!!" !!!" !! !" !!!"
AO CD^
ABCD
AB CD=
,,,IJEF
,,,AC BC BD AD
( )
, IE JF
0
30
0
45
0
60
0
90
IJEF
1
2
1
2
IJ AB
JE CD
ì
=
ï
ï
í
ï
=
ï
î
AB CD=
IJ JE=
IJEF
( )
0
0, 9IE JF =
ABCD
∑
∑
0
3
, 60 ,
2
AC AD CAB DAB CD AD====
j
AB
CD
cos
3
4
j
=
0
60
j
=
0
30
j
=
cos
1
4
j
=
( )
..
cos ,
.
.
AB CD AB CD
AB CD
AB
AB CD
CD
==
!!!" !!!" !!!" !!!"
!!!" !!!"
!!!" !!!"
Trang 15
Mặt khác
Do có . Suy ra .
Câu 37: Trong không gian cho hai hình vuông và có chung cạnh và nằm trong
hai mặt phẳng khác nhau, lần lượt có tâm và . Tứ giác là hình gì?
A. Hình bình hành. B. Hình vuông. C. Hình thang. D. Hình chữ nhật.
Hướng dẫn giải:
Tứ giác là hình bình hành. Lại có:
Vậy tứ giác là hình chữ nhật.
Câu 38: Cho tứ diện có ( lần lượt là trung điểm của và ).
Số đo góc giữa hai đường thẳng AB và CD là :
A. B. C. D.
Hướng dẫn giải:
Gọi M là trung điểm của AC.
Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường
thẳng MI và MJ.
Tính được:
Từ đó suy ra số đo góc giữa hai đường thẳng AB và CD là:
Câu 38: Cho tứ diện với . Gọi lần lượt là trung điểm của và
. Góc giữa và là?
A. B. C. D.
Hướng dẫn giải:
Câu 39: Cho hai vectơ thỏa mãn: . Gọi là góc giữa hai vectơ . Chọn
khẳng định đúng?
A. . B. . C. . D. .
Hướng dẫn giải:
Do đó: .
Câu 40: Cho tứ diện . Tìm giá trị của k thích hợp thỏa mãn:
A. B. C. D.
Hướng dẫn giải:
( )
00
...
. .cos 60 . .cos 60
1311 1
.. . . . ..
2224 4
AB CD AB AD AC AB AD AB AC
AB AD AB AC
AB AD AB AD AB AD AB CD
=-=-
=-
=- =-=-
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
( )
1
.
1
4
cos ,
4.
AB CD
AB CD
AB CD
-
==-
!!!" !!!"
cos
1
4
j
=
ABCD
''ABC D
AB
O
'O
''CDD C
''CDD C
( )
''.DC ADD DC DD^Þ^
''CDD C
ABCD
3
, IJ=
2
a
AB CD a==
,IJ
BC
AD
0
30 .
0
45 .
0
60 .
0
90 .
222
IJ
co
1
2. 2
sIMJ
IM MJ
MI MJ
+-
==-
0
60 .
ABCD
,AB AC AB BD^^
,PQ
AB
CD
PQ
AB
0
90 .
0
60 .
0
30 .
0
45 .
.AB PQ AB PQÞ^
!!!" !!!"
,ab
!!
4; 3 ; 4abab==-=
!!!!
a
,ab
!!
3
cos
8
a
=
0
30
a
=
1
cos
3
a
=
0
60
a
=
22
2
9
() 2. . .
2
ab a b ab ab-=+- Þ=
!! ! ! !! !!
.3
8
cos
.
ab
ab
a
==
!!
!!
ABCD
...AB CD AC DB AD BC k++=
!!!" !!!" !!!" !!!" !!!" !!!"
1.k =
2.k =
0.k =
4.k =
Trang 16
Chọn đáp án C.
Câu 41: Trong không gian cho tam giác có trọng tâm . Chọn hệ thức đúng?
A.
B.
C.
D.
Hướng dẫn giải:
Cách 1
Ta có
Cách 2: Ta có:
Tương tự ta suy ra được
Chọn đáp án D.
Cách 3: Chuẩn hóa giả sử tam giác đều có cạnh là Khi đó
Chọn đáp án D.
Câu 42: Trong không gian cho tam giác . Tìm sao cho giá trị của biểu thức
đạt giá trị nhỏ nhất.
A. là trọng tâm tam giác .
B. là tâm đường tròn ngoại tiếp tam giác .
C. là trực tâm tam giác .
D. là tâm đường tròn nội tiếp tam giác .
Hướng dẫn giải:
Gọi là trọng tâm tam giác cố định và
( )
( ) ( )
... ...
. . 0.
AB CD AC DB AD BC AC CB CD AC DB AD CB
AC CD DB CB CD AD AC CB CB AC
++=+ +-
=++-=+=
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
ABC
G
( )
222 222
2.AB AC BC GA GB GC++= ++
222222
.AB AC BC GA GB GC++=++
( )
222 222
4.AB AC BC GA GB GC++= ++
( )
222 222
3.AB AC BC GA GB GC++= ++
( )
( ) ( ) ( )
( )
2
22 2
22 2 222 2 2 2 2 2 2
222 222
0
2. 2. 2. 0
0
3
GA GB GC
GA GB GC GA GB GA GC GB GC
GA GB GC GA GB AB GA GC AC GB GC BC
AB AC BC GA GB GC
++ =
Û+++ + + =
Û+++ +- + +- + +- =
Û++= ++
!!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!"
222
2
222
2
4
24
.
92 4
2
3
AB AC BC
MA
AB AC BC
GA
GA MA
Ï
Ô
+
Ô
=-
Ô
ʈ
+
Ô
˜
Ô
Á
˜
fi= -
Á
Ì
˜
Á
˜
Á
Ô
˯
Ô
=
Ô
Ô
Ô
Ó
( )
( )
22222 2222
22 2
222
22 2 2 22
4
.
92 4 2 4 2 4
1
.
3
3
AB AC BC BA BC AC CA CB AB
GA GB GC
AB BC CA
GA GB GC AB BC CA
ʈ
+++
˜
Á
˜
++ = - + - + -
Á
˜
Á
˜
Á
˯
=++
€++=++
ABC
1.
( )
222
22 2 2 22
22 2
3
3.
1
AB BC CA
GA GB GC AB BC CA
GA GB GC
Ï
Ô
++=
Ô
fi++=++
Ì
Ô
++ =
Ô
Ó
ABC
M
22 2
PMA MB MC=++
M
ABC
M
ABC
M
ABC
M
ABC
G
ABC Gfi
0.GA GB GC++ =
uur uu ur uuur r
Trang 17
Dấu bằng xảy ra
Vậy với là trọng tâm tam giác
Chọn đáp án A.
Câu 43: Cho hai vectơ thỏa mãn: . Độ dài vectơ bằng?
A. B. . C. D. .
Hướng dẫn giải:
Câu 44: Cho tứ diện có và . Trong các
mặt của tứ diện đó:
A. Tam giác có diện tích lớn nhất. B. Tam giác có diện tích lớn nhất.
C. Tam giác có diện tích lớn nhất. D. Tam giác có diện tích lớn nhất.
Hướng dẫn giải:
Đặt
Tam giác đều cạnh nên diện tích .
Tam giác vuôn tại nên diện tích .
Diện tích tam giác là .
Tam giác có nên tam giác
vuông tại . Diện tích tam giác là .
Vậy diện tích tam giác lớn nhất.
Câu 45: Cho hai vectơ thỏa mãn: . Xét hai vectơ . Gọi
α là góc giữa hai vectơ . Chọn khẳng định đúng.
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có .
.
.
( ) ( ) ( )
( )
22 2
2222
222 2 2 2 2
32.
3.
PMGGA MGGB MGGC
MG MG GA GB GC GA GB GC
MG GA GB GC GA GB GC
=+++++
=+ +++++
=+++≥++
uuur uur uuur uuur uuur uuur
uuur uur uu ur uuur
.MG€∫
22 2
min
PGAGBGC=++
MG∫
.ABC
,ab
!!
26; 28; 48abab==+=
!!!!
ab-
!!
25.
616
9.
618
( )
( )
( )
( )
22
2
22 22
22 2
22 2
2. 2
2 2 26 28 48 616
616.
ab ab a b ab a b ab
ab ab
ab
-=- =+- = + -+
æö
=+-+=+-=
ç÷
èø
Þ-=
!! !! ! ! !! ! ! !!
!! !!
!!
ABCD
DA DB DC==
∑
∑
∑
00 0
60 , 90 , 120BDA ADC BDC===
ABD
BCD
ACD
ABC
DA DB DC a== =
ABD
a
2
3
4
ABD
a
S =
ACD
D
2
1
.
22
ACD
a
SDADC==
BCD
2
0
13
. sin120
24
BCD
a
SDBDC==
ABC
,2,3AB a AC a BC a== =
ABC
A
ABC
2
12
.
22
ABC
a
S AB AC==
ABC
,ab
!!
4; 3; . 10== =
!!!!
abab
=-
!" " "
yab
2,=-
!! !
xa b
,
!"!
xy
2
cos
15
-
=
a
1
cos
15
=
a
3
cos
15
=
a
2
cos
15
=
a
( )( ) ( ) ( )
22
.2 23.4=- -= + - =
!"! ! ! ! ! ! ! !!
xy a b a b a b ab
( ) ( ) ( ) ( )
2222
244.23==-=+-=
!! !! ! !!!
xx ab a bab
( ) ( ) ( ) ( )
2222
2. 5==-=+-=
!" !" " " " " " "
yy ab abab
.42
cos
2 3. 5 15
.
== =
!"!
!"!
xy
xy
a
Trang 18
Câu 46: Cho tam giác có diện tích . Tìm giá trị của thích hợp thỏa mãn:
.
A. . B. k = 0. C. . D. .
Hướng dẫn giải:
.
Chọn C.
Câu 47: Cho tứ diện có hai mặt và là các tam giác đều
a) Khẳng định nào sau đây đúng nhất.
A. AB và CD chéo nhau
B. AB và CD vuông góc với nhau
C. AB và CD đồng phẳng
D. AB và CD cắt nhau
b) Gọi lần lượt là trung điểm các cạnh . Khẳng định nào sau đây là đúng
nhất?
Chứng minh là hình chữ nhật.
A. là hình vuông B. là hình bình hành
C. là hình chữ nhật D. là hình thoi
Hướng dẫn giải:
a) Đặt
Ta có
Vậy .
b) Ta có và nên tứ giác
là hình bình hành.
Lại có , do đó là hình chữ nhật.
Câu 48: Cho hình chóp có và . Tính góc giữa hai đường thẳng
và .
A. B.
C. D.
Hướng dẫn giải:
Gọi lần lượt là trung điểm của , khi đó
nên
.
Đặt , trong tam giác có
.
ABC
S
k
( )
2
22
1
.2.
2
=-
!!!" !!!" !!!" !!!"
S AB AC k AB AC
1
4
=k
1
2
=k
1=k
( )
222 22 2
11 1
. .sin . si n . 1 cos
22 2
== =-S AB AC C AB AC C AB AC C
( )
2
22
1
..
2
=-
!!!" !!!" !!!" !!!"
AB AC AB AC
ABCD
ABC
ABD
,,,MNPQ
,,,AC BC BD DA
MNPQ
MNPQ
MNPQ
MNPQ
MNPQ
===AB AD AC a
( )
. =-
!!!" !!!" !!!" !!!" !!!"
CD AB AD AC AB
00
cos 60 cos 60=-
!!!" !!!" !!!" !!!"
AB AD AB AC
11
.. .. 0
22
=-=aa aa
^AB CD
!!MN PQ AB
22
== =
AB a
MN PQ
MNPQ
ì
ï
Þ^
í
ï
^
î
!
!
MN AB
NP CD MN NP
AB CD
MNPQ
.S ABC
== =SA SB SC a
2=BC a
AB
SC
( )
∑
0
, 60=AB SC
( )
∑
0
, 45=AB SC
( )
∑
0
, 30=AB SC
( )
∑
0
, 90=AB SC
,,MNP
!MN AB
( )
∑
( )
∑
,,=AB SC MN SC
∑
= NMP
j
MNP
( )
222
cos 1
2.
+-
=
MN MP NP
MN MP
j
Q
P
N
M
C
A
D
B
φ
N
P
M
S
A
B
C
Trang 19
Ta có , vuông tại , vì vậy ,
.Trong tam giác theo công thứ tính đường trung tuyến ta có
.
Thay vào ta được .
Vậy .
Câu 49: Cho hình chóp có đáy là hình thoi, và .
a) Tính góc giữa hai đường thẳng và .
A. B. C. D.
b) Gọi lần lượt là các điểm thuộc và sao cho . Chứng minh góc giữa và
không phụ thuộc vào vị trí của và .
A. B. C. D.
Hướng dẫn giải:
a) b) .
Câu 50: Cho hai tam giác cân và có chung cạnh đáy nằm trong hai mặt phẳng khác
nhau.
a) Khẳng định nào sau đây là đúng nhất?
A. B. AD cắt BC
C. AD và BC chéo nhau D. Cả A, B, C đều đúng
b) Gọi là các điểm lần lượt thuộc các đường thẳng và sao cho .
Tính góc giữa hai đường thẳng và .
A. B.
C. D.
Hướng dẫn giải:
a) Gọi là trung điểm của , thì các tam giác
và cân nên .
Ta có
Vậy .
b) Ta có ,
suy ra ( Theo câu a)
Câu 51: Cho hình hộp thoi có tất cả các cạnh đều bằng và
.Tính góc giữa hai đường thẳng AC và B’D’.
2
==
a
MN MP
22 2
+=ÞDAB AC BC ABC
A
2
222
5
4
=+ =
a
PB AP AC
2
2
3
4
=
a
PS
PBS
22
22 2 22
2
53
3
44
24244
+
+
=-=-=
aa
PB PS SB a a
PN
,,MN MP NP
( )
1
0
1
cos 120
2
=- Þ =
jj
( )
∑
( )
∑
0
, , 60==AB SC MN SC
.S ABCD
ABCD
=SA AB
^SA BC
SD
BC
( )
∑
0
, 30=BC SD
( )
∑
0
, 45=BC SD
( )
∑
0
, 60=BC SD
( )
∑
0
, 50=BC SD
,IJ
SB
SD
!IJ BD
AC
IJ
I
J
( )
∑
0
, 90=IJ AC
( )
∑
0
, 60=IJ AC
( )
∑
0
, 30=IJ AC
( )
∑
0
, 45=IJ AC
( )
∑
0
, 45=BC SD
( )
∑
0
, 90=IJ AC
ABC
DBC
BC
^AD BC
,MN
AB
DB
,==
!!!" !!!" !!!" !!!"
MA k MB ND k NB
MN
BC
( )
∑
0
, 90=MN BC
( )
∑
0
, 80=MN BC
( )
∑
0
, 60=MN BC
( )
∑
0
, 45=MN BC
P
BC
ABC
DBC
^
ì
í
^
î
AP BC
DP BC
( )
.0=-=
!!!" !!!" !!!" !!!" !! !"
BC AD BC PD PA
^BC AD
=Þ=
!!!" !!!"
MA
MA k MB k
MB
=Þ=
!!!" !!!"
ND
ND k NB k
NB
Þ=
MA ND
MB NB
( )
∑
( )
∑
0
, , 90Þ==!MN AD MN BC AD BC
.' ' ' 'ABCD A B C D
a
∑
∑
∑
0
' ' 60== =ABC B BA B BC
P
A
B
D
C
M
N
Trang 20
A. B. C. D.
Hướng dẫn giải:
HS tự giải.
Câu 52: Cho tứ diện . Gọi lần lượt là trung điểm các cạnh và . Cho biết
và . Tính góc giữa hai đường thẳng và .
A. B.
C. D.
Hướng dẫn giải:
Gọi là trung điểm của , ta có .
Áp dụng định lí côsin cho tam giác ta có
.
Vậy .
Câu 53: Cho tứ diện có
.
a)Khẳng định nào sau đây là đúng nhất.
A. các đoạn nối trung điểm các cặp cạnh đối thì vuông góc với hai cạnh đó
B. các đoạn nối trung điểm các cặp cạnh đối thì không vuông góc với hai cạnh đó
C. các đoạn nối trung điểm các cặp cạnh đối thì có thể vuông góc có thể không vuông góc với hai
cạnh đó
D. cả A, B, C đều sai
b) Tính góc giữa hai đường thẳng và .
A.
B.
C.
D.
Hướng dẫn giải:
Gọi lần lượt là trung điểm của các cạnh .
( )
∑
0
AC, 'D' 90=B
( )
∑
0
AC, 'D' 60=B
( )
∑
0
AC, 'D' 45=B
( )
∑
0
AC, 'D' 30=B
ABCD
,MN
BC
AD
2==AB CD a
3=MN a
AB
CD
( )
∑
0
, 30=AB CD
( )
∑
0
, 45=AB CD
( )
∑
0
, 60=AB CD
( )
∑
0
, 90=AB CD
O
AC
==OM ON a
( )
∑
( )
∑
,,
ì
Þ=
í
î
!
!
OM AB
AB CD OM ON
ON CD
OMN
∑
22 2
cos
2.
+-
=
OM ON MN
MON
OM ON
( )
2
22
3
1
2. . 2
+-
==-
aa a
aa
( )
∑
0
, 60=AB CD
ABCD
,,== == ==AB CD a AC BD b AD BC c
AC
BD
( )
∑
( )
22
2
, arccos
-
=
ac
AC BD
b
( )
∑
( )
22
2
2
, arccos
+
=
ac
AC BD
b
( )
∑
( )
22
2
2
, arccos
3
-
=
ac
AC BD
b
( )
∑
( )
22
2
2
, arccos
-
=
ac
AC BD
b
,,MNP
,,AB CD AD
N
M
O
A
B
D
C
N
M
A
B
D
C
P
Trang 21
a) Do hai tam giác và có chung và nên chúng bằng nhau, suy ra
Vậy tam giác cân tại và có trung tuyến nên .
Tương tự .
Chứng minh tương tự cho hai cặp cạnh đối còn lại.
b) Ta có
Theo công thức tính đường trung tuyến ta có
Tương tự , nên
Áp dụng định lí cô sin cho tam giác ta có
Vậy .
ACD
BCD
CD
,==AC BD AD BC
=MC MD
MCD
M
MN
^MN CD
^MN AB
( )
∑
( )
∑
,,
ì
Þ=
í
î
!
!
PM BD
BD AC PM PN
PN AC
( )
22 2
22 2
2
2
24 4
+-
+
=-=
bc a
CA CB AB
CM
( )
22 2
2
2
4
+-
=
bc a
DM
( )
22 2
222 2222
2
2
24 442
+-
++-
=-= -=
bc a
MC MD CD a b c a
MN
PMN
∑
( )
22
22 2
22
22 2
2
2
22 2
cos
2. .
2
22
+-
æö æö
+-
ç÷ ç÷
-
+-
èø èø
== =
æöæö
ç÷ç÷
èøèø
bbbca
ac
PM PN MN
MPN
bb
PM PN b
( )
∑
( )
22
2
2
, arccos
-
=
ac
AC BD
b
Trang 22
DẠNG 2: CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC VÀ CÁC BÀI
TOÁN LIÊN QUAN
Phương pháp:
Để chứng minh ta có trong phần này ta có thể thực hiện theo các cách sau:
• Chứng minh ta chứng minh trong đó lần lượt là các vec tơ chỉ phương
của và .
• Sử dụng tính chất .
• Sử dụng định lí Pitago hoặc xác định góc giữa và tính trực tiếp góc đó.
• Tính độ dài đoạn thẳng, diện tích của một đa giác
• Tính tích vô hướng…
Câu 1: Cho hình hộp có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau,
mệnh đề nào có thể sai?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Chú ý: Hình hộp có tất cả các cạnh bằng nhau còn
gọi là hình hộp thoi.
A đúng vì:
.
B sai vì:
C đúng vì: .
D đúng vì: .
Câu 2: Cho tứ diện . Chứng minh rằng nếu thì ,
, . Điều ngược lại đúng không?
Sau đây là lời giải:
Bước 1: .
Bước 2: Chứng minh tương tự, từ ta được và ta được
.
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Đúng. B. Sai từ bước 1. C. Sai từ bước 1. D. Sai ở bước 3.
Hướng dẫn giải:
Chọn A.
Câu 4: Cho tứ diện có vuông góc với . Mặt phẳng song song với và lần
lượt cắt tại . Tứ giác là hình gì?
A. Hình thang. B. Hình bình hành.
C. Hình chữ nhật. D. Tứ giác không phải là hình thang.
Hướng dẫn giải:
Chọn C.
12
dd^
12
dd^
12
0uu =
!!" !!"
12
,uu
!!" !!"
1
d
2
d
bc
ab
ac
ì
Þ^
í
^
î
!
12
,dd
.ABCD A B C D
¢¢¢¢
A C BD
¢¢
^
BB BD
¢
^
AB DC
¢¢
^
BC A D
¢¢
^
//
AC BD
A C BD
B D BD
¢¢ ¢¢
^
ì
¢¢
Þ^
í
¢¢
î
//
A B AB
AB DC
AB DC
¢¢
^
ì
¢¢
Þ^
í
¢¢
î
//
BC B C
BC A D
BC AD
¢¢
^
ì
¢¢
Þ^
í
¢¢
î
ABCD
...AB AC AC AD AD AB==
!!!" !!!" !!!" !!!" !!!" !!!"
AB CD^
AC BD^
AD BC^
..AB AC AC AD=
!!!" !!!" !!!" !!!"
Û
( )
.0AC AB AD-=
!!!" !!!" !!!"
Û
0. =DBAC
Û
AC BD^
ABADADAC .. =
AD BC^
ABADACAB .. =
AB CD^
ABCD
AB
CD
( )
P
AB
CD
, , , BC DB AD AC
, , , MNPQ
MNPQ
D'
B'
C'
B
A
D
C
A'
Trang 23
Ta có:
Tương tự ta có: .
Do đó tứ giác là hình bình hành
lại có .
Vậy tứ giác là hình chữ nhật.
Câu 5: Cho tứ diện đều có cạnh bằng . Gọi lần lượt là trung điểm của
và .
a) Khẳng định nào sau đây là đúng nhất?
A. B. MN cắt RQ
C. MN chéo RP; MN chéo RQ D. Cả A, B, C đều sai
b) Tính góc của hai đường thẳng AB và CD?
A. B.
C. D.
Hướng dẫn giải:
a) Ta có nên tam giác cân tại , do đó .
Lại có .
b) Tương tự ta có
Trong tam giác vuông ta có
Ta có :
Do đó tam giác vuông tại , hay .
Vì vậy .
Câu 6: Trong không gian cho hai tam giác đều và có chung cạnh và nằm trong hai
mặt phẳng khác nhau. Gọi lần lượt là trung điểm của các cạnh và . Tứ
giác là hình gì?
A. Hình bình hành. B. Hình chữ nhật. C. Hình vuông. D. Hình thang.
Hướng dẫn giải:
Chọn B.
Vì nên dễ thấy tứ giác là hình bhình hành.
Gọi là trung điểm của .
Vì hai tam giác và nên
Suy ra . Do đó .
( )
( ) ( )
//
// .
MNPQ AB
MQ AB
MNPQ ABC MQ
ì
ï
Þ
í
Ç=
ï
î
// , // , // DMN CD NP AB QP C
MNPQ
( )
MN MQ do AB CD^^
MNPQ
ABCD
a
,,,,MNPQR
,,,AB CD AD BC
AC
,^^MN RP MN RQ
,^MN RP
( )
∑
0
, 60=AB CD
( )
∑
0
, 30=AB CD
( )
∑
0
, 45=AB CD
( )
∑
0
, 90=AB CD
3
2
==
a
MC MD
MCD
M
^MN CD
Þ^!RP CD MN RQ
^QP AD
PDQ
2
2
2
222
3
222
æö
æö
=-= - =
ç÷
ç÷
ç÷
èø
èø
aaa
QP QD DP
22
22 2 2
22
æö æö
+= + ==
ç÷ ç÷
èø èø
aa
RQ RP a QP
RPQ
R
^RP RQ
ì
ï
Þ^
í
ï
^
î
!
!
AB RQ
CD RP AB CD
RP RQ
ABC
ABC
¢
AB
, , , MNPQ
, , AC CB BC
¢
CA
¢
MNPQ
, , , MNPQ
MNPQ
H
AB
ABC
ABC
¢
CH AB
C H AB
^
ì
í
¢
^
î
( )
AB CHC
¢
^
AB CC
¢
^
N
M
P
Q
R
A
B
D
C
Trang 24
Ta có: .
Vậy tứ giác là hình chữ nhật.
Câu 7: Cho hình chóp có đáy là hình bình hành với .
Tam giác vuông can tại , là một điểm trên cạnh ( khác và ). Mặt phẳng
đi qua và song sog với cắt lần lượt tại .
a) là hình gi?.
A. là hình thang vuông. B. là hình vuông.
C. là hình chữ nhật. D. là hình bình hành.
b)Tính diện tích của theo .
A. B. C. D.
Hướng dẫn giải:
a) Ta có .
Tương tự
Dễ thấy nên là hình bình hành
Lại có .
Vậy là hình thang vuông.
b) Ta có , , .
Vậy .
Câu 8: Cho hình lập phương cạnh . Trên các cạnh và lấy các điểm
và sao cho . Khẳng định nào sau đây là đúng?
a) Khẳng định nào sau đây là đúng?
A. B. AC’ cắt B’D’
C. AC’và B’D’ đồng phẳng D. Cả A, B, C
đều đúng
b) khẳng định nào sau đây là đúng ?.
A.
B. AC’ và MN cắt nhau
C. AC’ và MN đồng phẳng
//
//
PQ AB
PN CC PQ PN
AB CC
ì
ï
¢
Þ^
í
ï
¢
^
î
MNPQ
.S ABCD
,2==AB a AD a
SAB
A
M
AD
M
A
D
( )
a
M
( )
SAB
,,BC SC SD
,,NPQ
MNPQ
MNPQ
MNPQ
MNPQ
MNPQ
MNPQ
a
2
3
8
=
MNPQ
a
S
2
3
4
=
MNPQ
a
S
( ) ( )
( ) ( )
( ) ( )
ì
ï
Ç=
í
ï
Ç=
î
! SAB
SAB ABCD AB
ABCD MN
a
a
Þ !MN AB
( ) ( )
( ) ( )
( ) ( )
ì
ï
Ç=Þ
í
ï
Ç=
î
!
!
SAB
SBC SAB SB NP SB
SBC NP
a
a
( ) ( )
( ) ( )
( ) ( )
ì
ï
Ç=Þ
í
ï
Ç=
î
!
!
SAB
SAD SAB SA MQ SA
SAD MQ
a
a
!!!MN PQ AB CD
MNPQ
ì
ï
Þ^
í
ï
^
î
!
!
MN AB
MQ SA MN MQ
AB SA
MNPQ
==MN AB a
22
==
SA a
MQ
22
==
CD a
PQ
( )
1
.
2
=+
MNPQ
S MN PQ MQ
2
13
2228
æö
=+ =
ç÷
èø
aa a
a
.' ' ' 'ABCD A B C D
a
DC
'BB
M
N
( )
0== ££MD NB x x a
'''^AC B D
Q
P
N
M
A
B
C
D
S
B
C
D
A'
D'
C'
B'
A
M
N
Trang 25
D. Cả A, B, C đều đúng
Hướng dẫn giải:
Đặt .
a) Ta có , nên
.
b)
Từ đó ta có
.
Vậy .
Câu 9: Cho tứ diện có , . Gọi và lần lượt là trung điểm của và
. Biết vuông góc với . Tính .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn A.
Gọi , lần lượt là trung điểm của và .
Ta có: (1).
Mà: (2).
Từ (1), (2) là hình chữ nhật.
Từ đó ta có: .
Chọn D
Câu 10: Trong không gian cho ba điểm bất kỳ, chọn đẳng thức đúng?
A. B.
C. D.
Hướng dẫn giải:
Chọn A.
Câu 11: Cho hình lập phương có cạnh bằng . Tính
A. . B. C. D.
Hướng dẫn giải:.
Chọn B.
Ta có , mặt khác .
Suy ra
', ,===
!!!" " !!!" " !!!" "
AA a AB b AD c
' =++
!!!!" " " "
AC a b c
''=-
!!!!!" " "
BD c b
( )( )
'. ' ' =++ -
!!!!" !!!!!" " " " " "
AC B D a b c c b
( )
22
22
0=-+-=-=
!! ! ! !
ac b c b a a
'''Þ^AC B D
( ) ( )
=- = + - +
!!! !" !!!" !!!!" !!!" !!!" !!!" !!!!"
MN AN AM AB BN AD DM
-1--
æöæö æö
=+ + = +
ç÷ç÷ ç÷
èøèø èø
!!!! ! !!
xxxx
bacb a bc
aaaa
( )
'. [ - 1 - - ]
æöæö æö
=++ + + = +
ç÷ç÷ ç÷
èøèø èø
!!!!" !!! !" " " " " " " " " " "
xxxx
AC MN a b c b a c b a b c
aaaa
222
22
1.10
æö æö
=+- -=+- -=
ç÷ ç÷
èø èø
!!!
xx x
abcxaaa
aa a
ABCD
AC a=
3BD a=
M
N
AD
BC
AC
BD
MN
10
2
a
MN =
6
3
a
MN =
32
2
a
MN =
23
3
a
MN =
E
F
AB
CD
( ) ( )
//
, , 90
//
EN AC
AC BD NE NF NE NF
NF BD
ì
Þ==°Þ^
í
î
1
2
1
2
NE FM AC
NF ME BD
ì
==
ï
ï
í
ï
==
ï
î
MENFÞ
2222
22
3 10
22 222
AC BD a a a
MN NE NF
æöæö æöæö
=+= + = + =
ç÷ç÷ ç÷ç÷
èøèø èøèø
,,ABC
222
2.AB AC AB AC BC=+-
!!!" !!!"
22 2
2. 2AB AC AB AC BC=+-
!!!" !!!"
22 2
.2AB AC AB AC BC=+-
!!!" !!!"
222
.AB AC AB AC BC=+-
!!!" !!!"
( )
222 22
2 . .cos , 2. .BC AB AC AB AC AB AC AB AC AB AC=+- =+-
!!!" !!!"
.ABCD EFGH
a
.AB EG
!!!" !!!"
2
3a
2
a
2
2
2
a
2
2a
..AB EG AB AC=
!!!" !!!" !!!" !!!"
AC AB AD=+
!!!" !!!" !!!"
( )
22
.. .AB EG AB AC AB AB AD AB AB AD a== +=+=
!!!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
M
F
N
E
C
D
B
A
Trang 26
Câu 12: Cho tứ diện có . Gọi lần lượt là trung điểm của và .
Biết vuông góc với . Tính
A.
B. C. D.
Hướng dẫn giải:
Chọn B.
Kẻ , nối .
là đường trung bình .
là đường trung bình .
Lại có suy ra
vuông tại .
Vậy .
Câu 13: Cho tứ diện trong đó , , góc giữa và là và điểm trên
sao cho . Mặt phẳng qua song song với và cắt , , lần
lượt tại , , . Diện tích bằng:
A. B. C. D.
Hướng dẫn giải:
Chọn C.
Thiết diện là hình bình hành.
Ta có .
Suy ra .
Lại có
Do đó .
Câu 14: Cho tứ diện có vuông góc với , . là điểm thuộc cạnh
sao cho . Mặt phẳng đi qua song song với và . Diện tích thiết diện
của với tứ diện là?
A. 5 B. 6 C. D.
Hướng dẫn giải:
Ta có .
Suy ra thiết diện là hình chữ nhật.
Lại có:
ABCD
,3AB a BD a==
,MN
AD
BC
AC
BD
MN
6
3
a
MN =
10
2
a
MN =
23
3
a
MN =
32
2
a
MN =
( )
//ANP C P ABÎ
MP
NP
ABCD
1
22
a
PN ACÞ= =
MP
ABDD
13
22
a
PM BDÞ= =
( ) ( )
, , 90AC BD PN PM NPM===°
!!!!! !"
MNPÞD
P
22
10
2
a
MN PN PM=+=
ABCD
6AB =
3CD =
AB
CD
60°
M
BC
2BM MC=
( )
P
M
AB
CD
BD
AD
AC
M
N
Q
MNPQ
22
2
23
3
2
MNPQ
( ) ( )
∑
, , 60AB CD QM MP QMP===°
. .sin 60
MPNQ
SQNQN=°
1
2
3
CM MO
CMQ CBA MQ
AB AB
DDÞ==Þ=#
2
2
3
AQ QN
AQN ACD QN
AC CD
DDÞ==Þ=#
. .sin 60 2.2.sin 60 2 3
MPNQ
SQMQN=°=°=
ABCD
AB
CD
4, 6AB CD==
M
BC
2MC BM=
( )
P
M
AB
CD
( )
P
17
3
16
3
( ) ( )
∑
, , 90AB CD MN MQ NMQ===°
MNPQ
CM MN
CMN CBA MN
CB AB
AN NP
ANP ACD MP
AC CD
DDÞ==Þ=
DDÞ==Þ=
14
33
2
4
3
!
!
Trang 27
Suy ra .
MNPQ
S MN.NP==
16
3
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

HAI ĐƯỜNG THẲNG VUÔNG GÓC
A – LÝ THUYẾT TÓM TẮT ! ! !
1. Vectơ chỉ phương của đường thẳng: a ¹ 0 là VTCP của d nếu giá của a song song hoặc trùng với d.
2. Góc giữa hai đường thẳng: • a¢//a, b¢//b Þ ( ∂ a,b) = ( ∑ a ',b ') ! ! ! !
• Giả sử u là VTCP của a, v là VTCP của b, (u,v) = a . ìïa £ a £ Khi đó: ∂ (a b) 0 0 ne·u 0 180 , = í 0 0 0 180 ïî -a ne·u 90 < a £ 180
• Nếu a//b hoặc a º b thì ( ∂ a b) 0 , = 0 Chú ý: 0 £ ( ∂ a b) 0 0 , £ 90
3. Hai đường thẳng vuông góc: • a ^ b Û ( ∂ a b) 0 , = 90 ! ! ! !
• Giả sử u là VTCP của a, v là VTCP của b. Khi đó a ^ b Û u.v = 0.
• Lưu ý: Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau. B – BÀI TẬP
Câu 1: Trong không gian cho ba đường thẳng phân biệt a , b , c . Khẳng định nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a // b .
B. Nếu a // b và c ^ a thì c ^ b .
C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b .
D. Nếu a và b cùng nằm trong mp (a ) // c thì góc giữa a và c bằng góc giữa b và c.
Hướng dẫn giải: Chọn B.
Nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau. C sai do:
Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của a
và b . Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng 90° , nhưng hiển nhiên hai
đường thẳng a và b không song song.
D sai do: giả sử a vuông góc với c , b song song với c , khi đó góc giữa a và c bằng 90° , còn góc
giữa b và c bằng 0°. Do đó B đúng.
Câu 2: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với c
(hoặc b trùng với c ).
B. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c
C. Góc giữa hai đường thẳng là góc nhọn.
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.
Hướng dẫn giải: Chọn A.
Câu 3: Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Trong các mệnh đề sau mệnh đề nào đúng?
A. Tứ diện có ít nhất một mặt là tam giác nhọn.
B. Tứ diện có ít nhất hai mặt là tam giác nhọn.
C. Tứ diện có ít nhất ba mặt là tam giác nhọn.
D. Tứ diện có cả bốn mặt là tam giác nhọn.
Hướng dẫn giải: Chọn A. Trang 1
Câu 4: Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng
vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Hướng dẫn giải: Chọn A. Theo lý thuyết.
Câu 5: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường
thẳng c thì a vuông góc với c
B. Cho ba đường thẳng a, ,
b c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d
vuông góc với a thì d song song với b hoặc c
C. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng
c thì a vuông góc với c
D. Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c
vuông góc với mọi đường thẳng nằm trong mặt phẳng (a, b) .
Hướng dẫn giải: Chọn C.
Câu 6: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng
B. Ba đường thẳng cắt nhau từng đôi một và không nằm trong một mặt phẳng thì đồng quy
C. Một đường thẳng cắt hai đường thẳng cắt nhau cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng
D. Ba đường thẳng cắt nhau từng đôi một thì cùng nằm trong một mặt phẳng
Hướng dẫn giải: Chọn B.
Gọi d , d , d là 3 đường thẳng cắt nhau từng đôi một. Giả sử d , d cắt nhau tại A , vì d không 1 2 3 1 2 3
nằm cùng mặt phẳng với d , d mà d cắt d , d nên d phải đi qua A . Thật vậy giả sử d không đi 1 2 3 1 2 3 3
qua A thì nó phải cắt d , d tại hai điểm B , C điều này là vô lí, một đường thẳng không thể cắt một 1 2
mặt phẳng tại hai điểm phân biệt.
Câu 7: Trong các khẳng định sau, khẳng định nào đúng ?
A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
B. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường
thẳng c thì a vuông góc với c .
C. Cho hai đường thẳng phân biệt a và b . Nếu đường thẳng c vuông góc với a và b thì a, b , c không đồng phẳng.
D. Cho hai đường thẳng a và b song song, nếu a vuông góc với c thì b cũng vuông góc với c.
Hướng dẫn giải:
Theo nhận xét phần hai đường thẳng vuông góc trong SGK thì đáp án D đúng.
Câu 8: Mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Hướng dẫn giải:
Theo nhận xét phần hai đường thẳng vuông góc trong SGK thì đáp án D đúng. Trang 2
Câu 9: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Hướng dẫn giải:
Theo nhận xét phần hai đường thẳng vuông góc trong SGK thì đáp án D đúng.
Câu 10: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Cho hai đường thẳng a, b song song với nhau. Một đường thẳng c vuông góc với a thì c
vuông góc với mọi đường thẳng nằm trong mặt phẳng(a,b).
B. Cho ba đường thẳng a, ,
b c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d
vuông góc với a thì d song song với b hoặc c .
C. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường
thẳng c thì đường thẳng a vuông góc với đường thẳng c .
D. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng
c thì đường thẳng a vuông góc với đường thẳng c .
Hướng dẫn giải:
Chọn D. Theo định lý-sgk Trang 3
DẠNG 1: TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG. Phương pháp:
Để tính góc giữa hai đường thẳng d ,d trong không gian ta có thể thực hiện theo hai cách 1 2
Cách 1. Tìm góc giữa hai đường thẳng d ,d bằng cách chọn một điểm O thích hợp ( O thường nằm 1 2
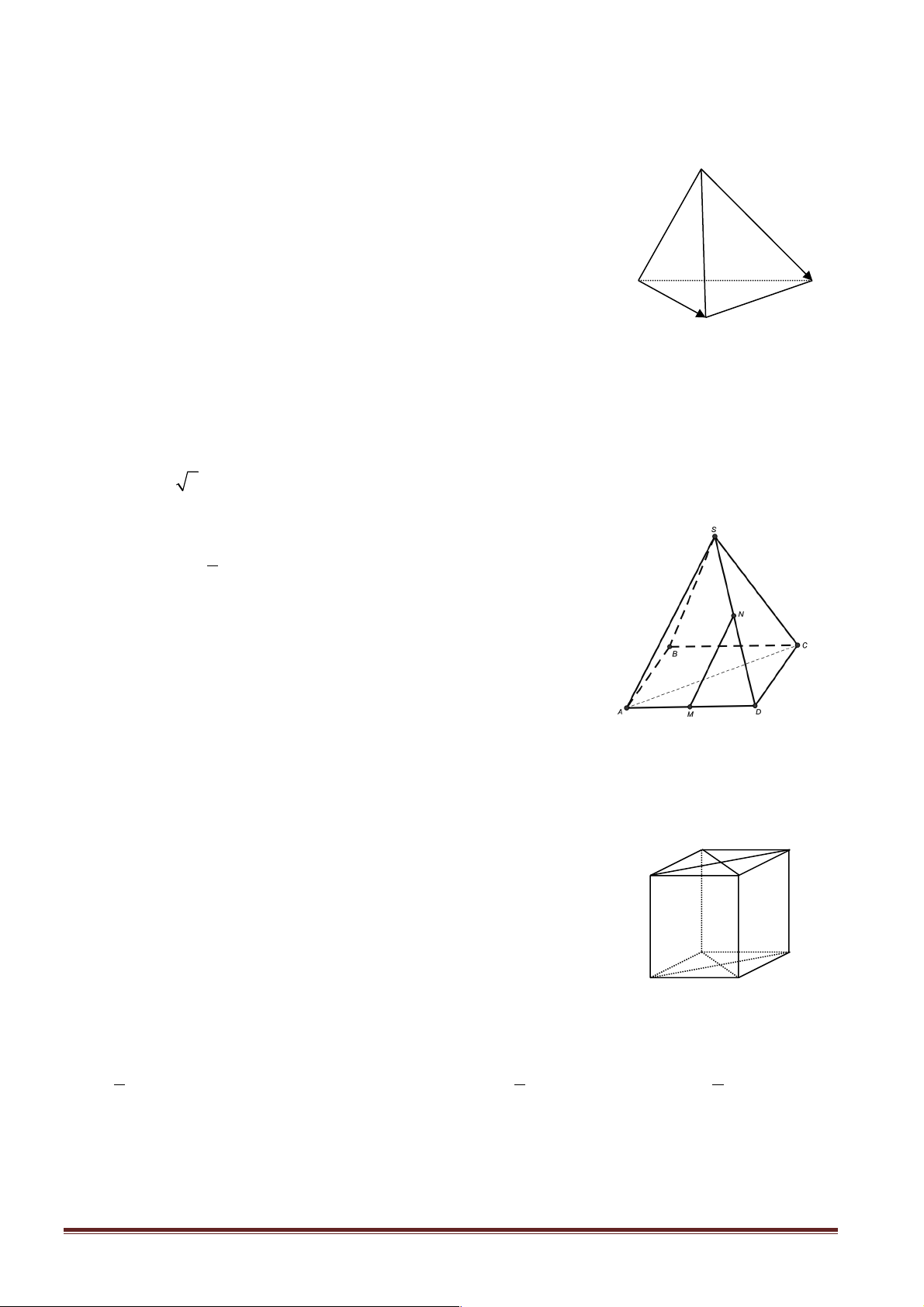
trên một trong hai đường thẳng). d1 d'1 O d'2 d2
Từ O dựng các đường thẳng ' '
d ,d lần lượt song song ( có thể tròng nếu O nằm trên một trong hai 1 2
đường thẳng) với d và d . Góc giữa hai đường thẳng ' '
d ,d chính là góc giữa hai đường thẳng d ,d . 1 2 1 2 1 2
Lưu ý 1: Để tính góc này ta thường sử dụng định lí côsin trong tam giác 2 2 2 cos b + c - a A = . 2bc !!" !!"
Cách 2. Tìm hai vec tơ chỉ phương u ,u của hai đường thẳng d ,d 1 2 1 2!!" !!" u .u
Khi đó góc giữa hai đường thẳng d ,d xác định bởi cos(d ,d = 1 2 ) 1 2 !!" !!" . 1 2 u u 1 2 !!"!!" !!" !!" ! ! !
Lưu ý 2: Để tính u u , u , u ta chọn ba vec tơ a,b,c không đồng phẳng mà có thể tính được độ dài 1 2 1 2 !!" !!" ! ! !
và góc giữa chúng,sau đó biểu thị các vec tơ u ,u qua các vec tơ a,b,c rồi thực hiện các tính toán 1 2 a 3
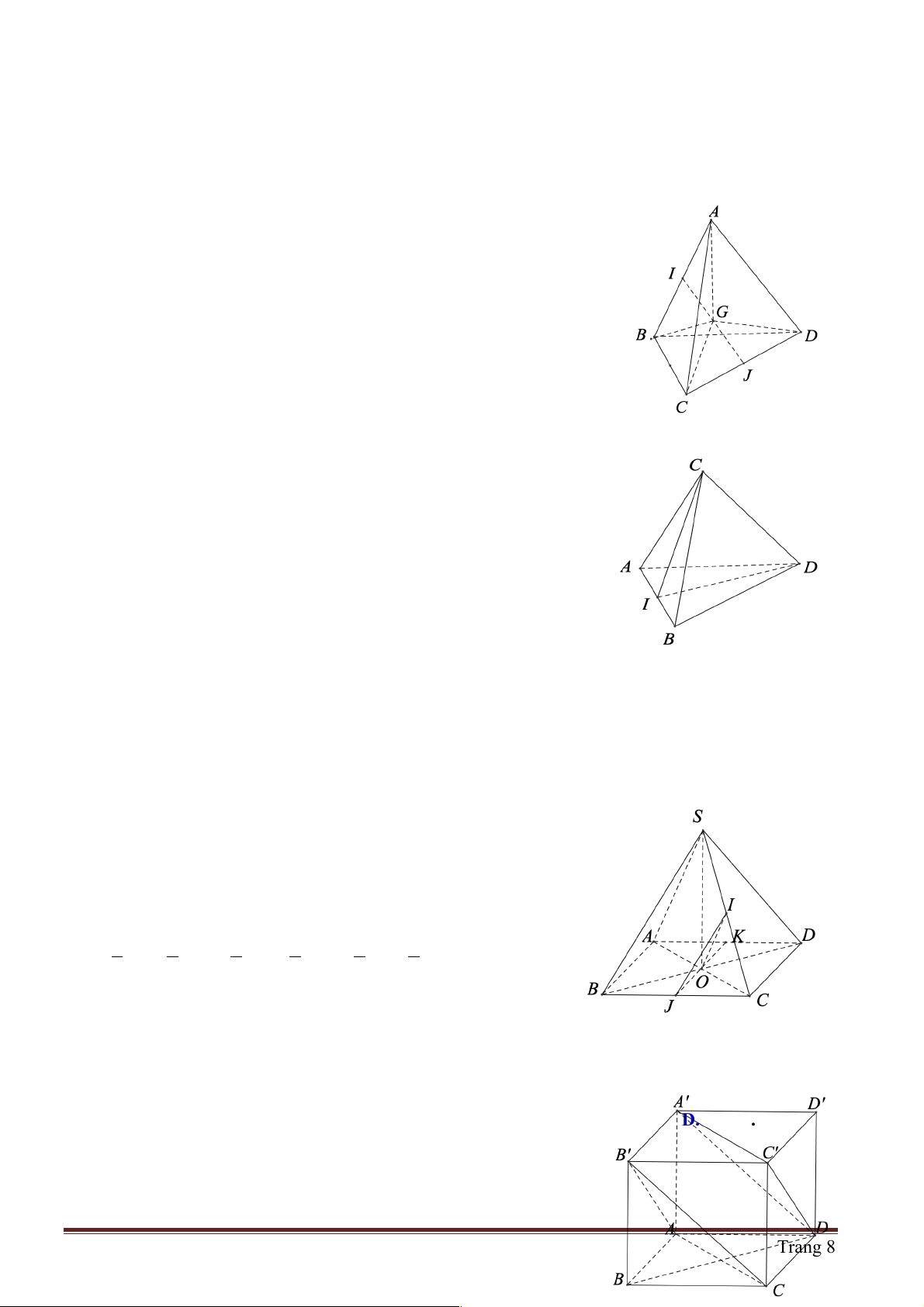
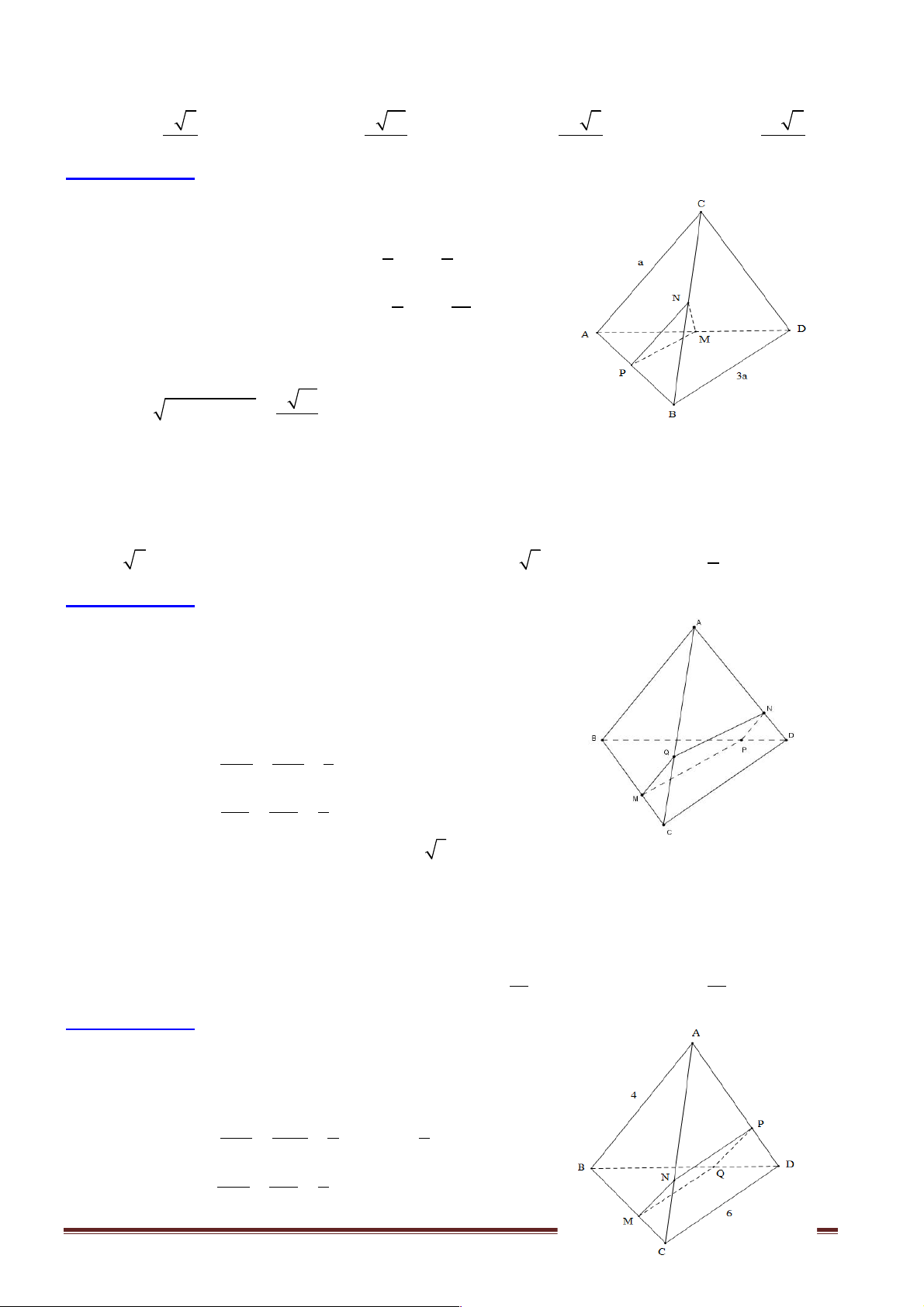
Câu 1: Cho tứ diện ABCD có AB = CD = a , IJ =
( I , J lần lượt là trung điểm của BC và 2
AD ). Số đo góc giữa hai đường thẳng AB và CD là A. 30° . B. 45°. C. 60° . D. 90° .
Hướng dẫn giải: Chọn C. A
Gọi M , N lần lượt là trung điểm AC , BC . Ta có: J ì 1 1 a
ïMI = NI = AB = CD = M í 2 2
2 Þ MINJ là hình thoi. O
ïîMI // AB // CD // NI B D N
Gọi O là giao điểm của MN và IJ . I Ta có: ∑ ∑ MIN = 2MIO . C a 3 IO 3 Xét MI
D O vuông tại O , ta có: ∑ 4 ∑ ∑ cos MIO = = =
Þ MIO = 30° Þ MIN = 60° . MI a 2 2
Mà: ( AB CD) = (IM IN ) ∑ , , = MIN = 60°. Trang 4
Câu 2: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Giả sử tam giác AB C
¢ và A¢DC¢ đều có 3 góc nhọn. Góc giữa
hai đường thẳng AC và A¢D là góc nào sau đây? A. ∑ BDB¢ . B. ∑ AB C ¢ . C. ∑ DB B ¢ . D. .
Hướng dẫn giải: A' D' Chọn D. B'
Ta có: AC // A C
¢ ¢ (tính chất của hình hộp) C'
Þ ( AC A¢D) = ( A¢C¢ A¢D) ∑ , ,
= DA¢C¢ (do giả thiết cho DA D ¢C¢ nhọn). A D
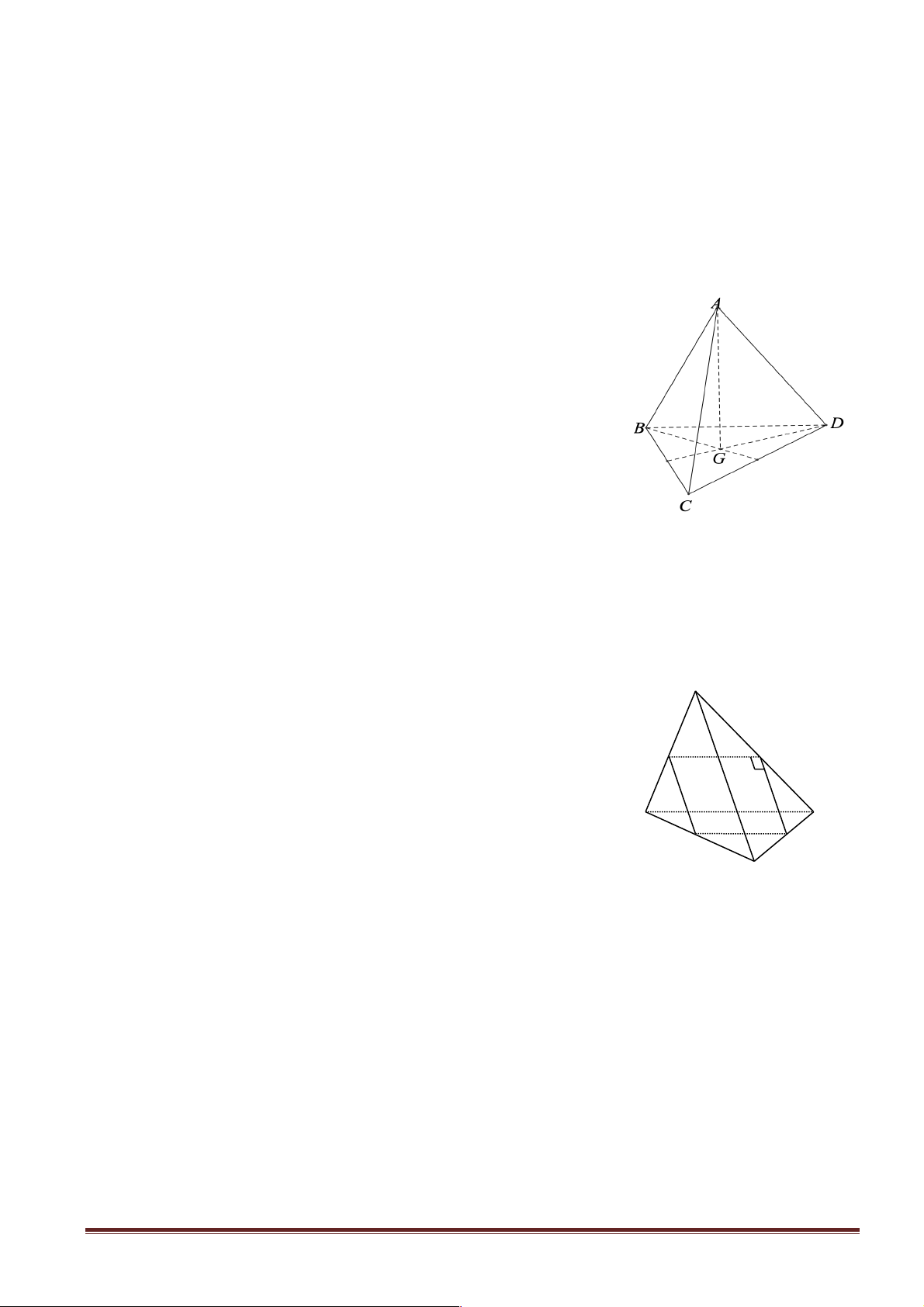
Câu 3: Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). B C
Số đo góc giữa hai đường thẳng AB và CD bằng A. 30° . B. 45°. C. 60° . D. 90° .
Hướng dẫn giải: Chọn D. A
Gọi H là tâm đường tròn ngoại tiếp BCD D Þ AH ^ (BCD) .
Gọi E là trung điểm CD Þ BE ^ CD (do BCD D đều).
Do AH ^ (BCD) Þ AH ^ CD . B D C ì D ^ BE H Ta có: í
Þ CD ^ ( ABE) Þ CD ^ AB Þ (∑ AB,CD) = 90°. E C î D ^ AH C
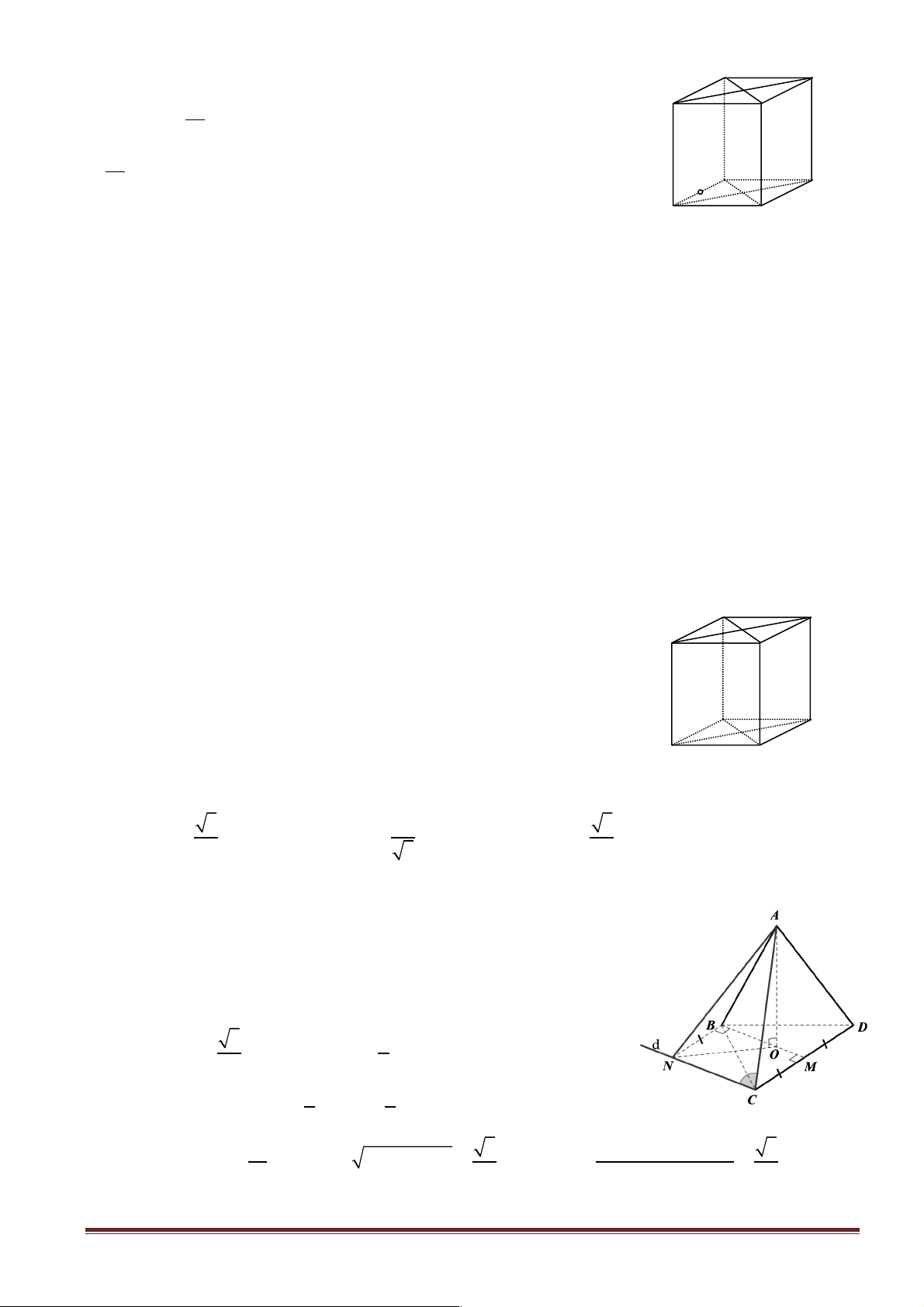
Câu 17. [1H3-2] Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos( AB, DM ) bằng 3 2 3 1 A. . B. . C. . D. . 6 2 2 2
Hướng dẫn giải: A Chọn A.
Không mất tính tổng quát, giả sử tứ diện ABCD có cạnh bằng a .
Gọi H là tâm đường tròn ngoại tiếp BCD D Þ AH ^ (BCD) . E B D
Gọi E là trung điểm AC Þ ME // AB Þ ( AB, DM ) = (ME,MD) H !!!" !!!!" M Ta có: ( AB DM ) = (ME MD) = (ME MD) ∑ cos , cos , cos , = cos EMD . C
Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của M D ED : a ME = 3
a , ED = MD = . 2 2 2 2 æ a ö
æ a 3 ö æ a 3 ö + ç ÷ ç ÷ - ç ÷ 2 2 2
ME + MD - ED è 2 ø 2 2 è ø è ø 3 Xét M D ED , ta có: ∑ cos EMD = = = . 2ME.MD a a 3 6 2. . 2 2 Từ đó: ( AB DM ) 3 3 cos , = = . 6 6
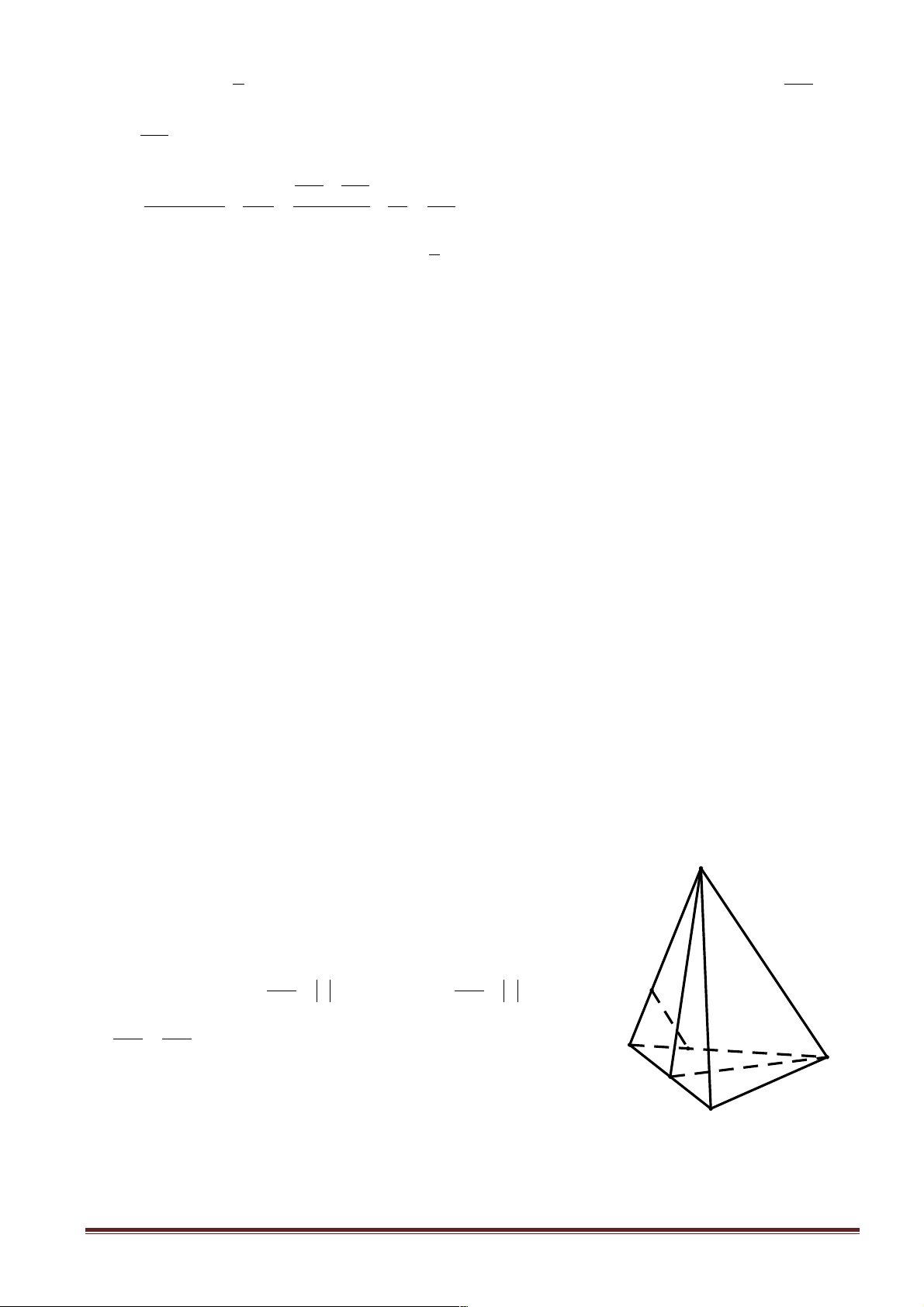
Câu 4: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng
a . Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc (MN,SC) bằng A. 30° . B. 45°. C. 60° . D. 90° .
Hướng dẫn giải: Chọn D.
Gọi O là tâm của hình vuông ABCD Þ O là tâm đường tròn S
ngoại tiếp của hình vuông ABCD (1). N Trang 5 A B M O D C
Ta có: SA = SB = SC = SD Þ S nằm trên trục của đường tròn ngoại
tiếp hình vuông ABCD (2).
Từ (1) và (2) Þ SO ^ ( ABCD) .
Từ giả thiết ta có: MN // SA (do MN là đường trung bình của SA
D D ). Þ (MN,SC) = ( , SA SC ) . 2 2 2 2 2
ìïSA + SC = a + a = 2a Xét SA D C , ta có: í Þ SAC D
vuông tại S Þ SA ^ SC . 2 2
ïîAC = 2AD = 2a Þ ( ,
SA SC ) = (MN,SC) = 90° .
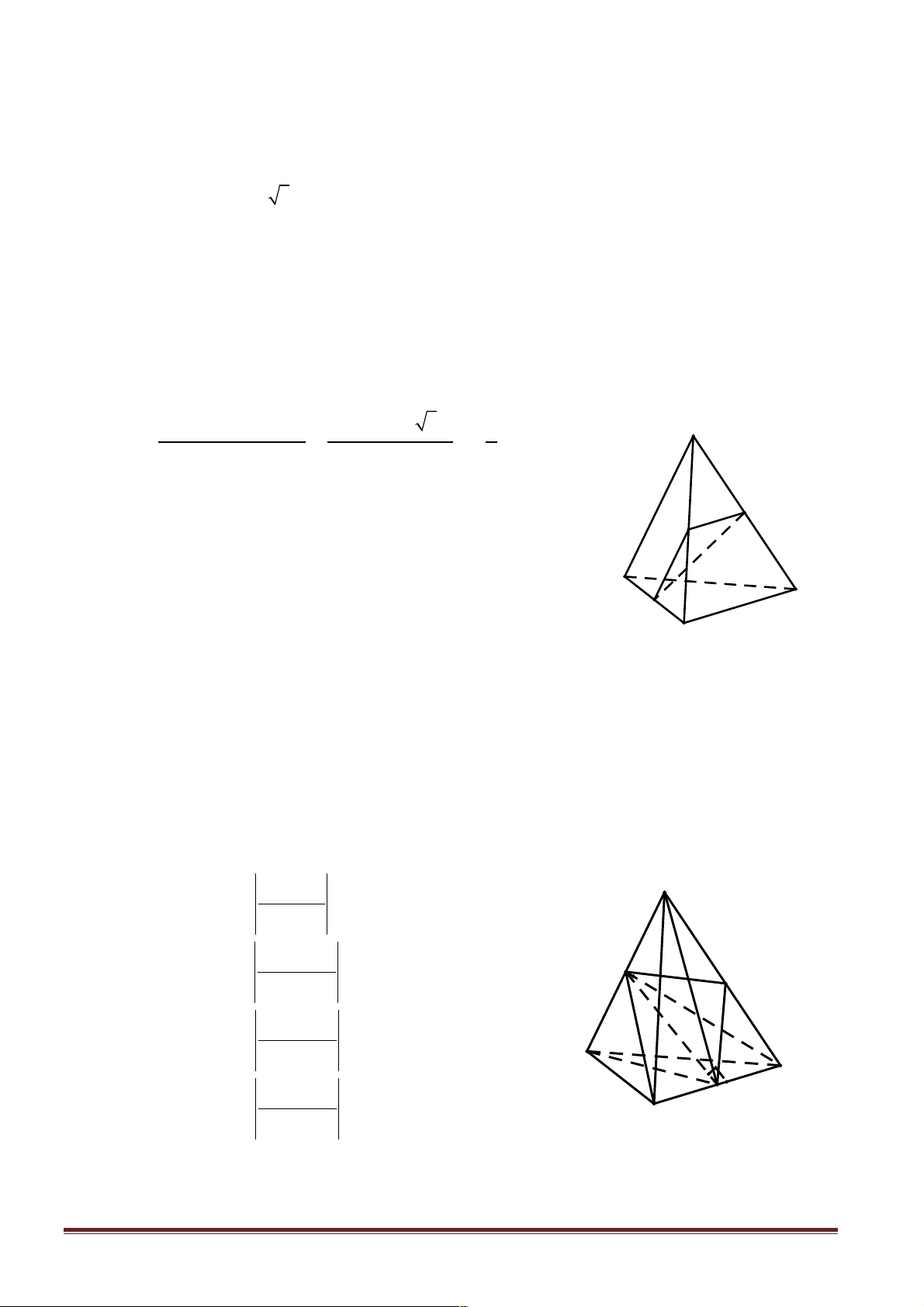
Câu 5: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của
SC và BC . Số đo của góc (IJ,CD) bằng A. 30° . B. 45°. C. 60° . D. 90° .
Hướng dẫn giải: Chọn C. S
Gọi O là tâm của hình vuông ABCD Þ O là tâm đường tròn
ngoại tiếp của hình vuông ABCD (1).
Ta có: SA = SB = SC = SD Þ S nằm trên trục của đường tròn ngoại
tiếp hình vuông ABCD (2). I A
Từ (1) và (2) Þ SO ^ ( ABCD) . B
Từ giả thiết ta có: IJ // SB (do IJ là đường trung bình của O J SA
D B ). Þ (IJ,CD) = (SB, AB) . D C
Mặt khác, ta lại có SA
D B đều, do đó ∑
SBA = 60° Þ (SB, AB) = 60° Þ (IJ,CD) = 60° .
Câu 6: Cho tứ diện ABCD có AB = CD . Gọi I , J , E , F lần lượt là trung điểm của AC , BC ,
BD , AD . Góc giữa (IE, JF ) bằng A. 30° . B. 45°. C. 60° . D. 90° .
Hướng dẫn giải: Chọn D. A
ìIJ // EF // AB Từ giả thiết ta có: í
(tính chất đường trung bình trong
îJE // IF // CD F tam giác) I
Từ đó suy ra tứ giác IJEF là hình bình hành. B 1 1 E D
Mặt khác: AB = CD Þ IJ = AB = JE = CD Þ ABCD là hình thoi 2 2 J
Þ IE ^ JF (tính chất hai đường chéo của hình thoi) Þ ( C
IE, JF ) = 90° . !!!" !!!!"
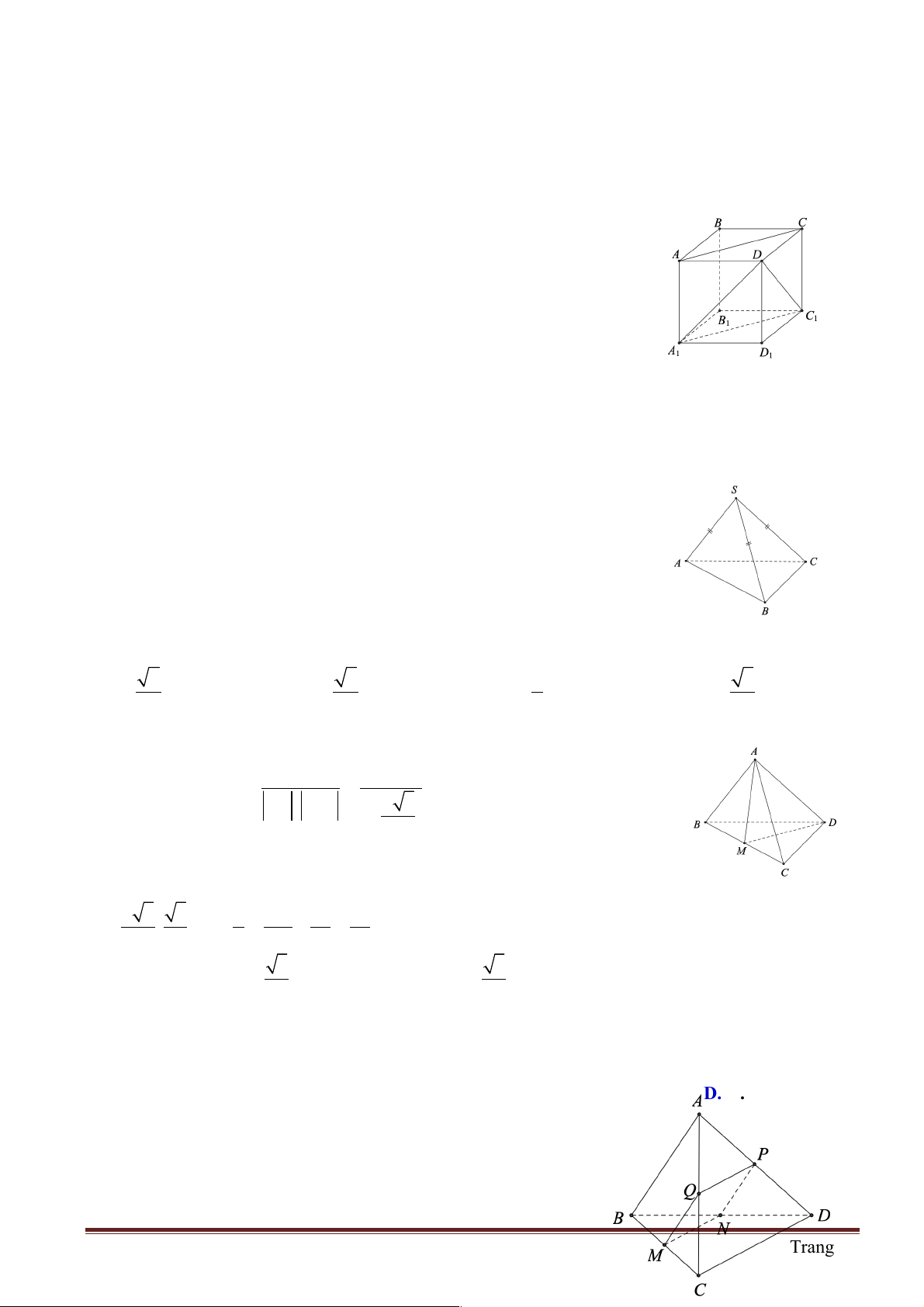
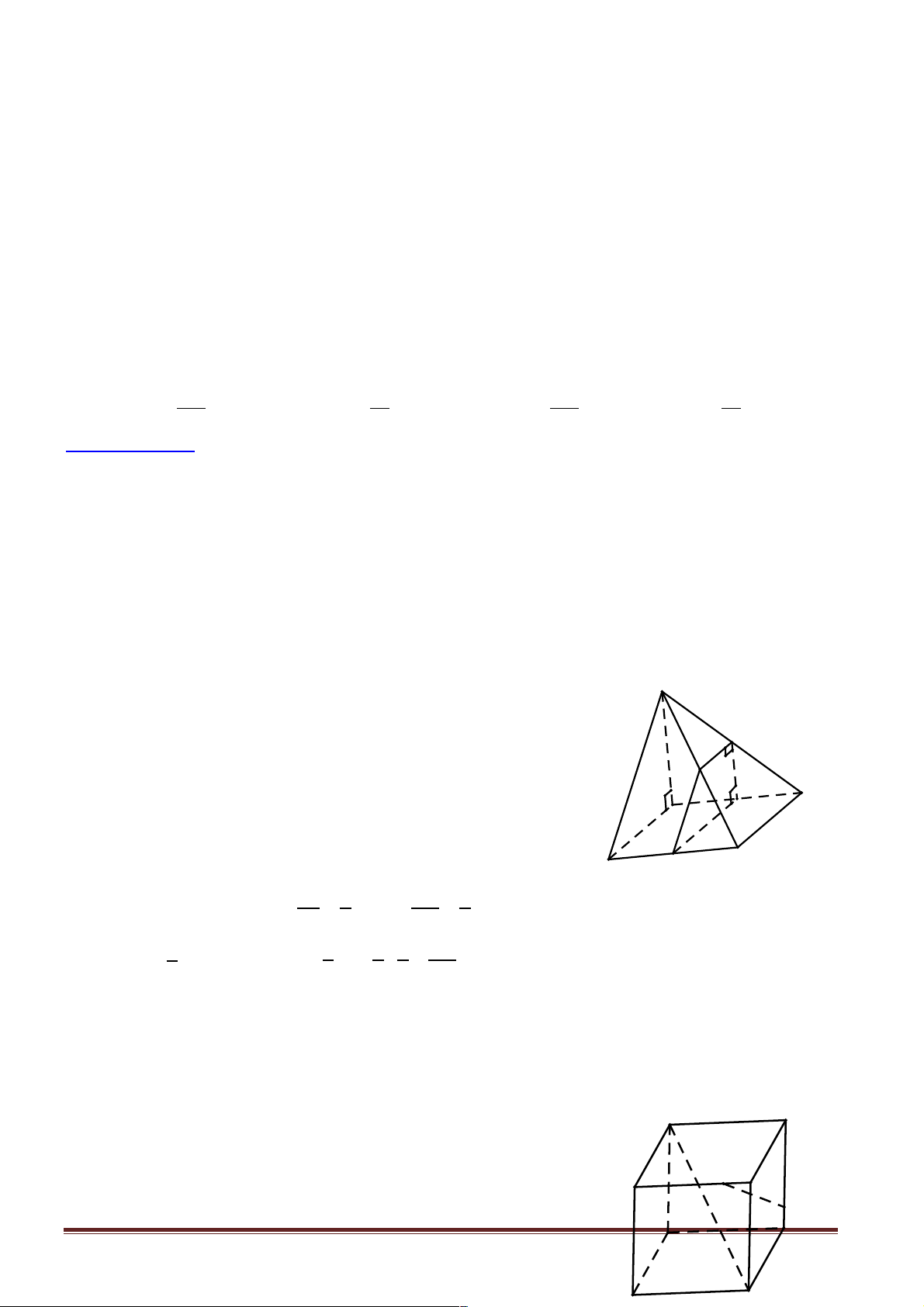
Câu 7: Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và DH ? A. 45° B. 90° C. 120° D. 60°
Hướng dẫn giải: Chọn B.
AB ^ AE üýÞ AB ^ DH Þ(∑ AB, DH ) = 90° AE // DH þ
Câu 8: Trong không gian cho hai hình vuông ABCD và ABC ' D ' có chung cạnh AB và nằm trong !!!" !!!!"
hai mặt phẳng khác nhau, lần lượt có tâm O và O ' . Hãy xác định góc giữa cặp vectơ AB và OO '? A. 60° B. 45° C. 120° D. 90°
Hướng dẫn giải: Chọn D.
Vì ABCD và ABC ' D ' là hình vuông nên AD // BC '; AD = BC ' Þ ADBC ' là hình bình hành Trang 6 Mà ;
O O ' là tâm của 2 hình vuông nên ;
O O ' là trung điểm của BD và AC ' Þ OO ' là đường trung
bình của ADBC ' Þ OO ' // AD
Mặt khác, AD ^ AB nên ^ ^Þ (∑ ' ', ) = 90o OO AB OO AB
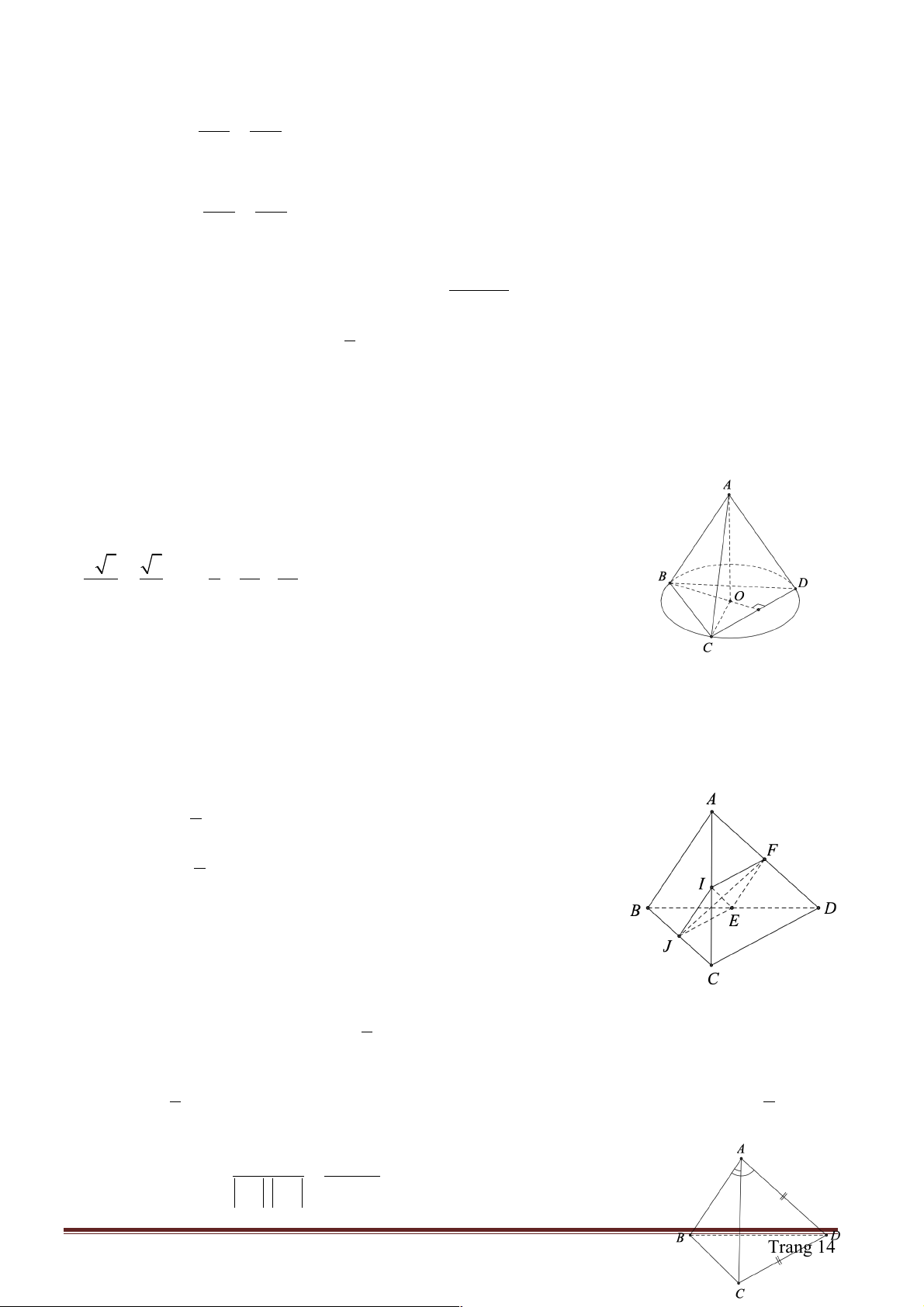
Câu 9: Cho tứ diện ABCD có AB = AC = AD và ∑ ∑ 0 ∑ 0
BAC = BAD = 60 , CAD = 90 . Gọi I và J lần !!" !!!"
lượt là trung điểm của AB và .
CD Hãy xác định góc giữa cặp vectơ IJ và CD? A. 45° B. 90° C. 60° D. 120°
Hướng dẫn giải: Chọn B.
Ta có BAC và BAD là 2 tam giác đều, I là trung điểm của AB nên CI = DI (2 đường trung tuyến
của 2 tam giác đều chung cạnh AB ) nên CID là tam giác cân ở I . Do đó IJ ^ C . D
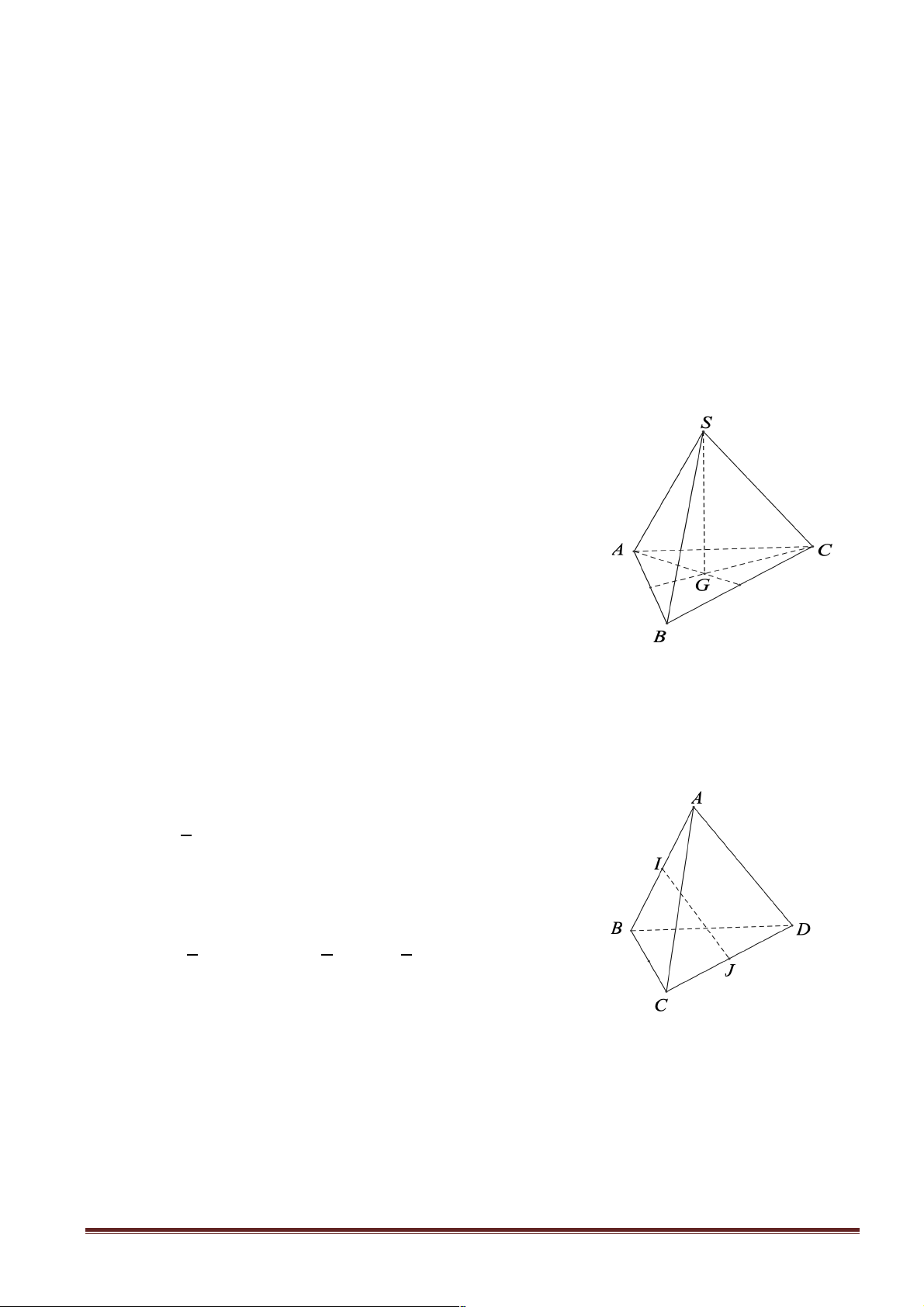
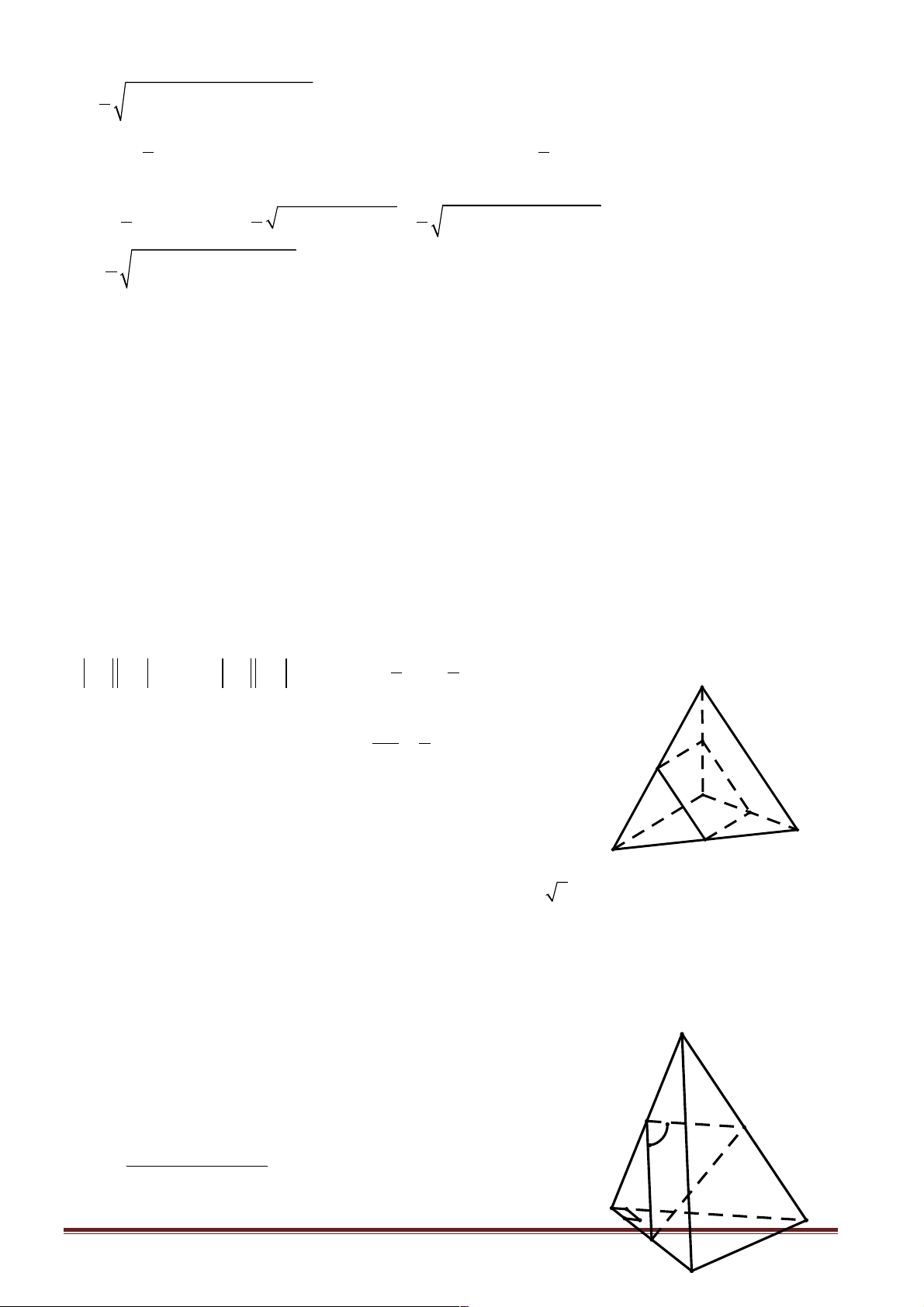
Câu 10: Cho hình chóp S.ABC có SA = SB = SC và ∑ ∑ ∑
ASB = BSC = CSA . Hãy xác định góc giữa cặp !!" !!!"
vectơ SB và AC ? A. 60° . B. 120° . C. 45°. D. 90° .
Hướng dẫn giải: Chọn D. Ta có: SA D B = SB D C = SC
D A (c - g - c) Þ AB = BC = CA.
Do đótam giác ABC đều. Gọi G là trọng tâm của tam giác ABC .
Vì hình chóp S.ABC có SA = SB = SC
nên hình chiếu của S trùng với G
Hay SG ^ ( ABC) . ìAC ^ BG Ta có: í Þ AC ^ (SBG) îAC ^ SG
Suy ra AC ^ SB . !!" !!!"
Vậy góc giữa cặp vectơ SB và AC bằng 0 90 .
Câu 11: Cho tứ diện ABCD có AB = AC = AD và ∑ ∑ 0 ∑ 0
BAC = BAD = 60 ,CAD = 90 . Gọi I và J lần !!!" !!"
lượt là trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơ AB và IJ ? A. 120° . B. 90° . C. 60° . D. 45°.
Hướng dẫn giải: Chọn B.
Xét tam giác ICD có J là trung điểm đoạn CD . !!" 1 !!" !!"
Ta có: IJ = (IC + ID) 2
Vì tam giác ABC có AB = AC và ∑ BAC = 60°
Nên tam giác ABC đều. Suy ra: CI ^ AB
Tương tự ta có tam giác ABD đều nên DI ^ AB .
!!" !!!" 1 !!" !!" !!!" 1 !!" !!!" 1 !!" !!!" "
Xét IJ.AB = (IC + ID).AB = IC.AB + I . D AB = 0 . 2 2 2 !!" !!!" !!!" !!"
Suy ra IJ ^ AB . Hay góc giữa cặp vectơ AB và IJ bằng 0 90 .
Câu 12: Cho tứ diện ABCD có trọng tâm G . Chọn khẳng định đúng? A. 2 2 2 2 2 2
AB + AC + AD + BC + BD + CD = ( 2 2 2 2
3 GA + GB + GC + GD ) . B. 2 2 2 2 2 2
AB + AC + AD + BC + BD + CD = ( 2 2 2 2
4 GA + GB + GC + GD ) . C. 2 2 2 2 2 2
AB + AC + AD + BC + BD + CD = ( 2 2 2 2
6 GA + GB + GC + GD ). D. 2 2 2 2 2 2
AB + AC + AD + BC + BD + CD = ( 2 2 2 2
2 GA + GB + GC + GD ) .
Hướng dẫn giải: Trang 7 Chọn B. 2 2 2 2 2 2
AB + AC + AD + BC + BD + CD !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
= ( AG +GB)2 +( AG +GC)2 + ( AG +GD)2 + (BG +GC)2 + (BG +GD)2 + (CG +GD)2
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" 2 2 2 2
= 3AG + 3BG + 3CG + 3DG + 2( . AG GB + . AG GC + A . G GD + . BG GD + . BG GD + . CG GD)( ) 1 Lại có: (!!!" !!!" !!!" !!!" "
GA + GB + GC + D G ) = 0 2 2 2 2
Û GA + GB + GC + D G
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" = 2( . AG GB + . AG GC + A . G GD + . BG GD + .
BG GD + CG.GD)(2)
Từ (1) và (2) ta có điều phải chứng minh.
Câu 13: Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác
đều. Góc giữa AB và CD là? A. 120° . B. 60° . C. 90° . D. 30° .
Hướng dẫn giải: Chọn C.
Gọi I là trung điểm của AB
Vì ABC và ABD là các tam giác đều C ì I ^ AB Nên í . îDI ^ AB
Suy ra AB ^ (CID) Þ AB ^ CD .
Câu 14: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của
SC và BC . Số đo của góc ( IJ, CD) bằng: A. 90° . B. 45°. C. 30° . D. 60° .
Hướng dẫn giải: Chọn D.
Gọi O là tâm của hình thoi ABCD .
Ta có: OJ //CD .
Nên góc giữa IJ và CD bằng góc giữa IJ và OJ .
Xét tam giác IOJ có 1 a 1 a 1 a
IJ = SB = ,OJ = CD = , IO = SA = . 2 2 2 2 2 2
Nên tam giác IOJ đều.
Vậy góc giữa IJ và CD bằng góc giữa IJ và OJ bằng góc ∑ 0 O IJ = 60 .
Câu 15: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Giả sử tam giác AB C
¢ và A¢DC¢ đều có 3 góc nhọn. Góc
giữa hai đường thẳng AC và A¢D là góc nào sau đây? A. ∑ AB C ¢ . B. ∑
DA¢C¢ . C. ∑ BB D ¢ . D. .
Hướng dẫn giải: Chọn B.
Ta có: AC//A¢C¢ nên góc giữa hai đường thẳng AC và A¢D
là góc giữa hai đường thẳng A¢C¢ và A¢D Trang 8 bằng góc nhọn ∑
DA¢C¢ (Vì tam giác A¢DC¢ đều có 3 góc nhọn
Câu 16: Cho tứ diện đều ABCD . Số đo góc giữa hai đường thẳng AB và CD bằng: A. 60° . B. 30° . C. 90° . D. 45°.
Hướng dẫn giải: Chọn C.
Gọi G là trọng tâm tam giác ABC .
Vì tứ diện ABCD đều nên AG ^ (BCD). C ì D ^ AG Ta có: í
Þ CD ^ ( ABG) Þ CD ^ AB . C î D ^ BG
Vậy số đo góc giữa hai đường thẳng AB và CD bằng 0 90
Câu 17: Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song
song với một cặp cạnh đối diện của tứ diện. Trong các mệnh đề sau mệnh đề nào đúng?
A. Thiết diện là hình chữ nhật.
B. Thiết diện là hình vuông.
C. Thiết diện là hình bình hành.
D. Thiết diện là hình thang.
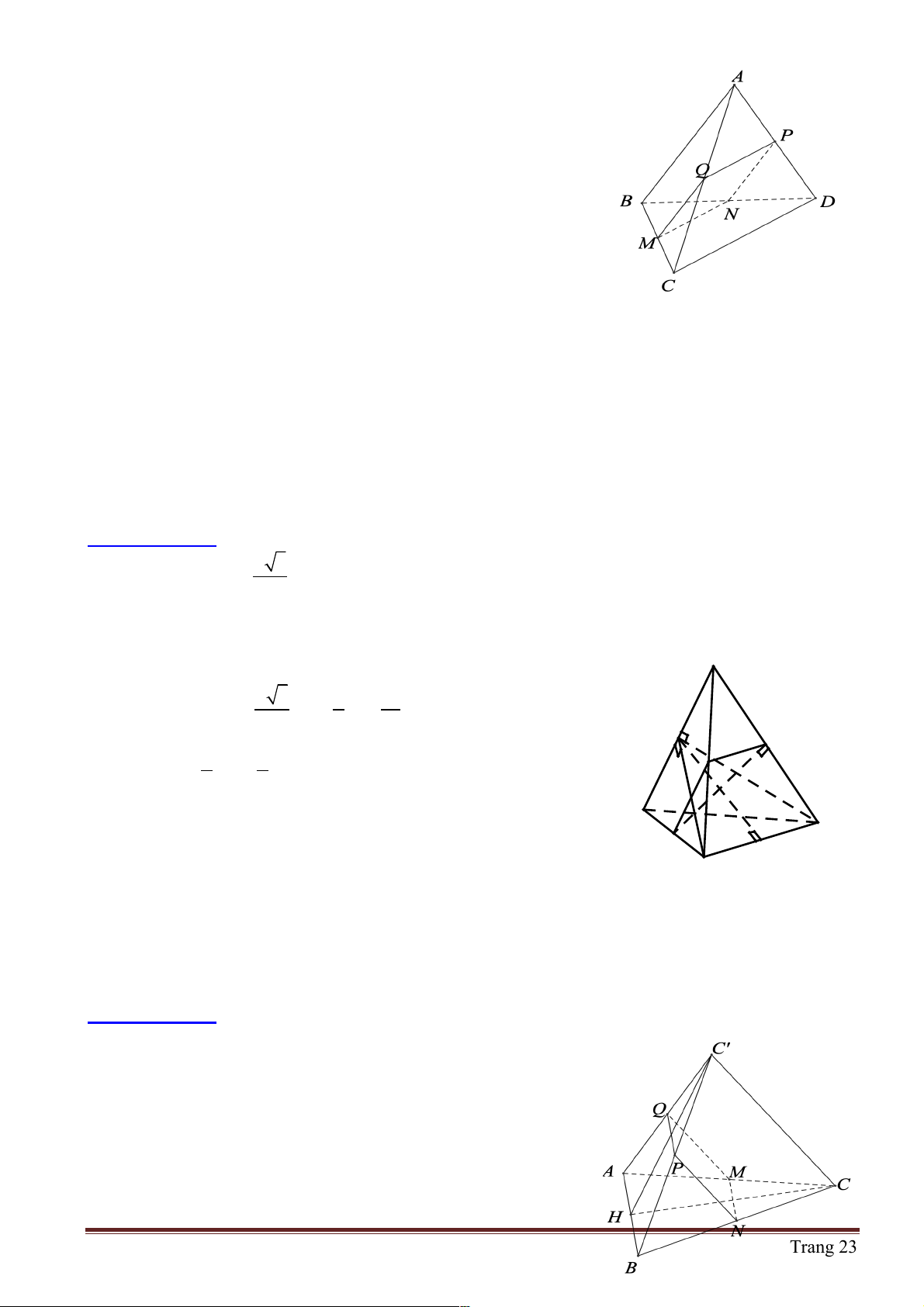
Hướng dẫn giải: Chọn A. A
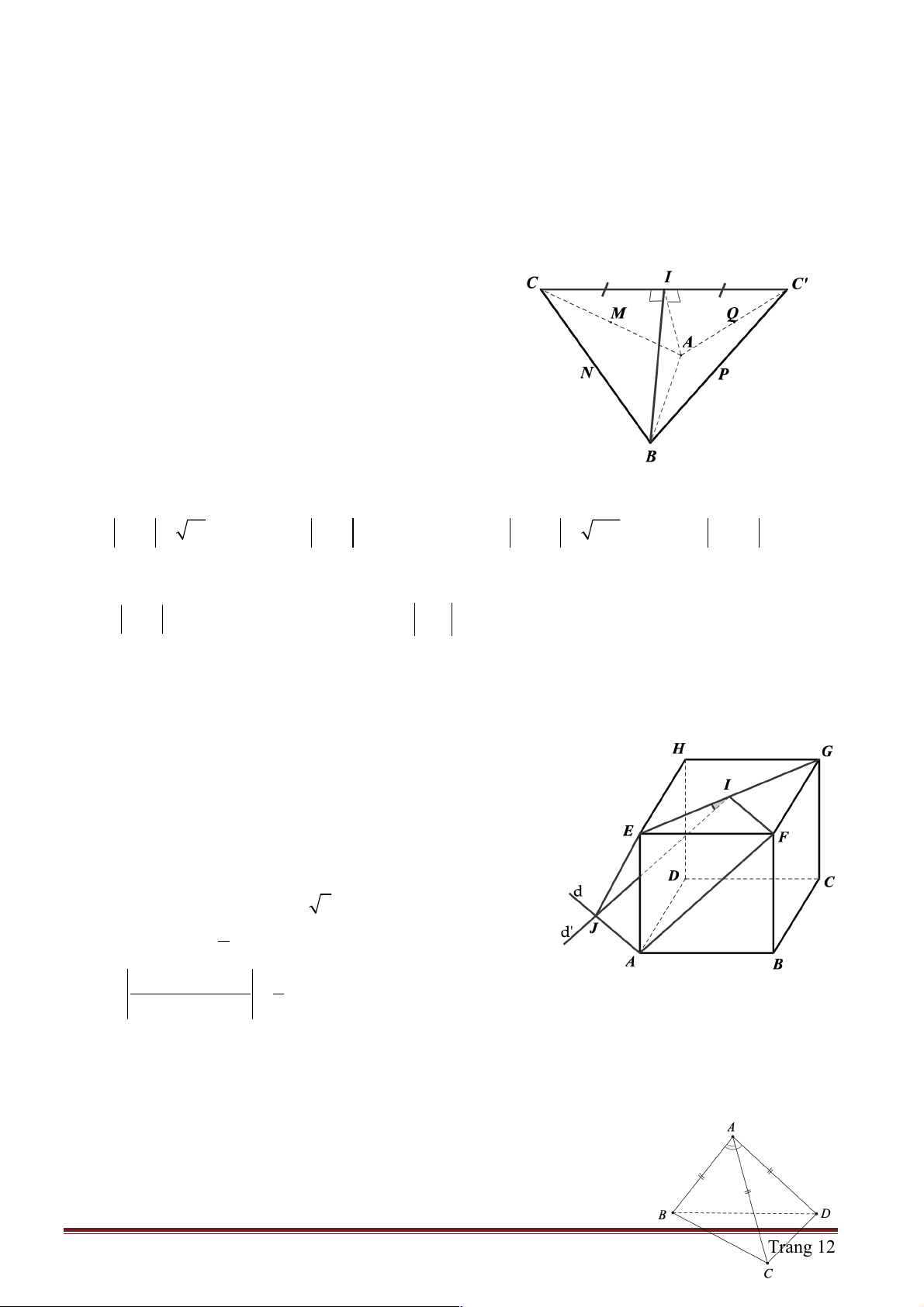
Gỉa sử thiết diện là tứ giác MNPQ .
Ta có: MN //PQ và MN = PQ nên MNPQ là hình bình hành
Lại có AC ^ BD Þ MQ ^ PQ M Q
Vậy tứ giác MNPQ là hình chữ nhật. B D P N C !!!" !!!" !!!" !!!" !!!" !!!"
Câu 18: Cho tứ diện ABCD . Chứng minh rằng nếu .
AB AC = .AC.AD = .
AD AB thì AB ^ CD ,
AC ^ BD , AD ^ BC . Điều ngược lại đúng không?
Sau đây là lời giải: !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" Bước 1: .
AB AC = .AC.AD Û AC.(AB - AD) = 0 Û AC.DB = 0 Û AC ^ BD !!!" !!!" !!!" !!!" Bước 2:
Chứng minh tương tự, từ AC.AD = .
AD AB ta được AD ^ BC và !!!" !!!" !!!" !!!" . AB AC = .
AD AB ta được AB ^ CD . Bước 3:
Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu? A. Sai ở bước 3. B. Đúng C. Sai ở bước 2. D. Sai ở bước 1.
Hướng dẫn giải: Chọn B. Bài giải đúng. Trang 9
Câu 19: Cho hình chóp S.ABC có SA = SB = SC và ∑ ∑ ∑
ASB = BSC = CSA . Hãy xác định góc giữa cặp !!!" !!!"
vectơ SC và AB ? A. 120° B. 45° C. 60° D. 90°
Hướng dẫn giải: Chọn D. S !!!" !!!" !!!" !!" !!" !!!" !!" !!!" !!"
Ta có: SC.AB = SC.(SB - SA) = SC.SB - SC.SA ∑ ∑ = .
SA SB cos BSC - SC. . SA cos ASC = 0
Vì SA = SB = SC và ∑ ∑ BSC = ASC !!!" !!!" A C Do đó: (SC AB) 0 , = 90 B
Câu 20: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng
a . Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc (MN, SC) bằng: A. 45° B. 30° C. 90° D. 60°
Hướng dẫn giải: Chọn C.
Ta có: AC = a 2 2 2 2 2
Þ AC = 2a = SA + SC Þ SA
D C vuông tại S . !!!!" !!!" 1 !!" !!!" !!!!" !!!"
Khi đó: NM .SC = .
SA SC = 0 Û (NM ,SC) = 90° 2
Þ (MN,SC) = 90°
Câu 21: Cho hình lập phương ABC .
D A B C D . Chọn khẳng định sai? 1 1 1 1
A. Góc giữa AC và B D bằng 90° .
B. Góc giữa B D và AA bằng 60°. 1 1 1 1 1
C. Góc giữa AD và B C bằng 45°.
D. Góc giữa BD và A C bằng 90° . 1 1 1
Hướng dẫn giải: Chọn B. A
!!!" !!!!" !!!" !!!" !!!" !!!" !!!" 1 D1
Ta có: AA .B D = BB .BD = BB . BA + BC 1 1 1 1 1 ( ) B !!!" !!!" !!!" !!!" 1 C1
= BB .BA + BB .BC = 0 1 1 !!!" !!!" !!!" !!!"
(vì (BB , BA = 90 (BB ,BC =90 1 ) 0 1 ) 0 và ) A D !!!" !!!!"
Do đó: ( AA , B D = 90 Þ AA , B D = 90 B 1 1 1 ) 0 ( 1 1 1) 0 C
Câu 22: Cho hình lập phương ABC .
D A B C D có cạnh a . Gọi M là trung điểm AD . Giá trị 1 1 1 1 !!!!" !!!!" B M .BD là: 1 1 1 3 3 A. 2 a . B. 2 a . C. 2 a . D. 2 a . 2 4 2
Hướng dẫn giải: Chọn A. !!!!" !!!!"
!!!" !!!" !!!!" !!!" !!!" !!!!"
Ta có: B M .BD = B B + BA + AM BA + AD + DD 1 1 ( 1 )( 1 ) Trang 10 !!!" !!!!" !!!"2 !!!!" !!!" = B .
B DD + BA + AM .AD A1 B 1 1 1 2 a D 2 2 = -a + a + 1 C1 2 2 a = A 2 M B D C
Câu 23: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có tất cả các cạnh đều bằng
nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?
A. A¢C¢ ^ BD
B. BB¢ ^ BD
C. A¢B ^ DC¢
D. BC¢ ^ A¢D
Hướng dẫn giải: Chọn B. !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
Ta có: BB .¢BD = BB .¢(BA+ BC) = BB .¢BA+ BB .¢BC = ¢ ∑¢ ∑
BB .BA(cosB BA+ cosB BC ¢ ) Vì AA¢B B
¢ và ABCD là hai hình thoi bằng nhau nên !!!" !!!" + ∑¢ ∑ B BA = B BC ¢
Þ BB .¢BD ¹ 0 suy ra BB¢ không vuông góc với BD !!!" !!!" + ∑¢ ∑ 0 + ¢ ∑ = Þ ¢ ∑ B BA B BC 180
cosB BA = -cosB BC ¢
Þ BB .¢BD = 0 suy ra BB¢ ^ BD
Nên đáp án B có thể sai vì chưa có điều kiện của góc ∑ B BA ¢ và ∑ B BC ¢ Chọn B. !!!" !!!"
Câu 24: Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 90° B. 60° C. 45° D. 120°
Hướng dẫn giải: Chọn C. E H
Ta có: EG//AC (do ACGE là hình chữ nhật) !!!" !!!" !!!" !!!" F Þ ( G
AB EG) = ( AB AC) ∑ , , = BAC = 45° A D B C
Câu 25: Cho tứ diện ABCD đều cạnh bằng a . Gọi M là trung điểm CD , a là góc giữa AC và BM .
Chọn khẳng định đúng? 3 A. cosa = 1 B. cosa = 3 C. cosa = D. 0 a = 60 4 3 6
Hướng dẫn giải: Chọn C.
Gọi O là trọng tâm của BCD D Þ AO ^ ( BCD)
Trên đường thẳng d qua C và song song BM lấy điểm N sao cho
BMCN là hình chữ nhật, từ đó suy ra: ∑ (AC,BM) ∑ = (AC,CN ) ∑ = (ACN ) =a 3 a Có: CN = BM =
a và BN = CN = 2 2 2 æ 2 ö 2 2 2 2 2 2
AO = AB - BO = AB - BM = a ç ÷ è 3 ø 3 7 5 2 2 2 AC CN AN 3 2 2 2 2
ON = BN + BO = a ; 2 2
AN = AO + ON = a cosa + - Þ = = 12 2 2AC.CN 6 Trang 11
Câu 26: Trong không gian cho hai tam giác đều ABC và ABC ' có chung cạnh AB và nằm trong hai
mặt phẳng khác nhau. Gọi M , N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC ' và C ' A . !!!" !!!!"
Hãy xác định góc giữa cặp vectơ AB và CC '? A. 450 B. 1200 C. 600 D. 900
Hướng dẫn giải: Chọn C.
Gọi I là trung điểm CC¢ C
D AC¢ cân tại A Þ CC¢ ^ AI (1) C
D BC¢ cân tại B Þ CC¢ ^ BI (2) !!!!" !!!" (1),(2)
¾¾¾®CC¢ ^ ( AIB) Þ CC¢ ^ AB Þ CC¢ = AB !!!!" !!!"
Kết luận: góc giữa CC¢ và AB là 90° ! ! ! !
Câu 27: Cho a = 3, b = 5 góc giữa a và b bằng 120°. Chọn khẳng định sai trong các khẳng đính sau? ! ! ! ! ! ! ! !
A. a + b = 19
B. a - b = 7
C. a - 2b = 139
D. a + 2b = 9
Hướng dẫn giải: Chọn A. ! 2 ! ! ! ! ! ! ! ! ! 2 !2 !2 ! ! ! ! Ta có: 2 2
a + b = a + b + 2a.b.cos (a,b ) =19 a + b = a + b + 2a.b.cos(a,b) = 19 !!!" !!!"
Câu 28: Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AF và EG ? A. 0 90 B. 0 60 C. 0 45 D. 0 120
Hướng dẫn giải: Chọn B.
Đặt cạnh của hình lập phương trên là a
Gọi I là giao trung điểm EG
Qua A kẻ đường thẳng d //FI
Qua I kẻ đường thẳng d¢//FA
Suy ra d cắt d¢ tại J . !!!!"!!!" Từ đó suy ra ∑ EG AF = EIJ = a ( ) ∑ ,
IJ = AF = 2EI = 2FI = 2AJ = a 2 3 2 2 2
EJ = AE + AJ = 2 2 2 2
EI + IJ + AJ 1 cosa = = Þ a = 60° 2.EI.EJ 2
Câu 29: Cho tứ diện ABCD có AB = AC = AD và ∑ ∑ 0
BAC = BAD = 60 . Hãy xác định góc giữa cặp !!!" !!!"
vectơ AB và CD ? A. 0 60 . B. 0 45 . C. 0 120 . D. 0 90 .
Hướng dẫn giải: Ta có !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" . AB CD = .
AB ( AD - AC) = . AB AD - . AB AC 0 0 = . AB . AD cos 60 - . AB AC.cos 60 = 0 Trang 12 !!!" !!!" Þ ( AB CD) 0 , = 90
Câu 30: Cho hình lập phương ABC .
D A B C D . Góc giữa AC và DA là 1 1 1 1 1 A. 0 45 . B. 0 90 . C. 0 60 . D. 0 120 .
Hướng dẫn giải:
Vì A'C ' //AC nên góc giữa AC và DA là ∑ DA C . 1 1 1
Vì tam giác DA C đều nên ∑ 0 DA C = 60 . 1 1 1 1
Vậy góc giữa AC và DA bằng 0 60 . 1
Câu 31: Cho hình chóp S.ABC có SA = SB = SC và ∑ ∑ ∑
ASB = BSC = CSA . Hãy xác định góc giữa cặp !!" !!!"
vectơ SA và BC ? A. 0 120 . B. 0 90 . C. 0 60 . D. 0 45 .
Hướng dẫn giải: Ta có !!" !!!" !!" !!!" !!" !!" !!!" !!" !!" . SA BC = .
SA (SC - SB) = . SA SC - . SA SB ∑ ∑ = . SA SC.cos ASC - . SA . SB cos ASB = 0 !!" !!!" Þ (SA BC) 0 , = 90
Câu 32: Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos ( AB, DM ) bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2
Hướng dẫn giải:
Giả sử cạnh của tứ diện là a . !!!" !!!!" !!!" !!!!" !!!" !!!!" AB DM AB DM Ta có (AB DM ) . . cos , = !!!" !!!!" = AB . DM a 3 . a 2 Mặt khác !!!" !!!!" !!!" !!!!" !!!" !!!" !!!!" !!!" !!!" .
AB DM = AB ( AM - AD) 0 0 = . AB AM - . AB AD = . AB AM .cos30 - . AB . AD cos 60 2 2 2 a 3 3 1 3a a a = . a . - . a . a = - = . 2 2 2 4 2 4 !!!" !!!!" 3 3 Do có os c ( AB, DM ) =
. Suy ra cos( AB, DM ) = . 6 6
Câu 33: Cho tứ diện ABCD có AB vuông góc với CD , AB = CD = 6 . M là điểm thuộc cạnh BC sao cho MC = .
x BC (0 < x < )
1 . mp(P) song song với AB và CD lần lượt cắt BC, DB, AD, AC tại
M , N, P,Q . Diện tích lớn nhất của tứ giác bằng bao nhiêu ? A. 9 . B. 11. C. 10 . D. .
Hướng dẫn giải:
ìMQ//NP//AB
Xét tứ giác MNPQ có í
îMN //PQ//CD
Þ MNPQ là hình bình hành. Trang 13
Mặt khác, AB ^ CD Þ MQ ^ MN .
Do đó, MNPQ là hình chữ nhật. MQ CM
Vì MQ//AB nên = = x Þ MQ = . x AB = 6x . AB CB
Theo giả thiết MC = .
x BC Þ BM = (1- x) BC . MN BM
Vì MN //CD nên =
= 1- x Þ MN = (1- x).CD = 6(1- x). CD BC
Diên tích hình chữ nhật MNPQ là 2 æ x + - x ö S = MN MQ = - x x = x - x £ = MNPQ ( ) ( ) 1 . 6 1 .6 36. . 1 36 9 . ç ÷ è 2 ø Ta có S = 1
9 khi x = 1- x Û x = MNPQ 2
Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là trung điểm của BC .
Câu 34: Cho tứ diện ABCD đều cạnh bằng a . Gọi O là tâm đường tròn ngoại tiếp tam giác BCD .
Góc giữa AO và CD bằng bao nhiêu ? A. 0 0 . B. 0 30 . C. 0 90 . D. 0 60 .
Hướng dẫn giải: !!!" !!!" !!!" !!!" !!!" Ta có .
AO CD = (CO -CA)CD !!!" !!!" !!!" !!!" 0 0 = . CO CD - . CA CD = . CO . CD cos30 - . CA . CD cos 60 2 2 a 3 3 1 a a = . . a - . a . a = - = 0. 3 2 2 2 2
Suy ra AO ^ CD .
Câu 35: Cho tứ diện ABCD có AB = CD . Gọi I , J , E, F lần lượt là trung điểm của AC, BC, BD, AD .
Góc (IE, JF ) bằng A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Hướng dẫn giải:
Tứ giác IJEF là hình bình hành. ì 1 IJ = AB ïï Mặt khác 2 í
mà AB = CD nên IJ = JE . 1 ïJE = CD ïî 2
Do đó IJEF là hình thoi. Suy ra (IE, JF ) 0 = 0 9 . 3
Câu 36: Cho tứ diện ABCD với ∑ ∑ 0
AC = AD,CAB = DAB = 60 ,CD = AD . Gọi j là góc giữa AB và 2
CD . Chọn khẳng định đúng ? 3 1 A. cos j = . B. 0 j = 60 . C. 0 j = 30 . D. cos j = . 4 4
Hướng dẫn giải: !!!" !!!" !!!" !!!" !!!" !!!" AB CD AB CD Ta có (AB CD) . . cos , = !!!" !!!" = AB . CD . AB CD Trang 14 Mặt khác !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" .
AB CD = AB ( AD - AC) = . AB AD - . AB AC 0 0 = . AB . AD cos 60 - . AB AC.cos 60 1 3 1 1 1 = . AB . AD - . AB . AD = - . AB AD = - . AB C . D 2 2 2 4 4 1 - . AB CD !!!" !!!" 1 1 Do có (AB CD) 4 cos , = = - . Suy ra cosj = . . AB CD 4 4
Câu 37: Trong không gian cho hai hình vuông ABCD và ABC ' D ' có chung cạnh AB và nằm trong
hai mặt phẳng khác nhau, lần lượt có tâm O và O ' . Tứ giác CDD 'C ' là hình gì? A. Hình bình hành. B. Hình vuông. C. Hình thang. D. Hình chữ nhật.
Hướng dẫn giải:
Tứ giác CDD 'C ' là hình bình hành. Lại có: DC ^ ( ADD ') Þ DC ^ DD '.
Vậy tứ giác CDD 'C ' là hình chữ nhật. a 3
Câu 38: Cho tứ diện ABCD có AB = CD = a, IJ=
( I, J lần lượt là trung điểm của BC và AD ). 2
Số đo góc giữa hai đường thẳng AB và CD là : A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Hướng dẫn giải:
Gọi M là trung điểm của AC.
Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường thẳng MI và MJ. 2 2 2 IM + MJ - IJ 1 Tính được: cos IMJ = = - 2MI.MJ 2
Từ đó suy ra số đo góc giữa hai đường thẳng AB và CD là: 0 60 .
Câu 38: Cho tứ diện ABCD với AB ^ AC, AB ^ BD . Gọi P, Q lần lượt là trung điểm của AB và
CD . Góc giữa PQ và AB là? A. 0 90 . B. 0 60 . C. 0 30 . D. 0 45 .
Hướng dẫn giải: !!!" !!!" .
AB PQ Þ AB ^ PQ ! ! ! ! ! ! ! !
Câu 39: Cho hai vectơ a,b thỏa mãn: a = 4; b = 3; a - b = 4 . Gọi a là góc giữa hai vectơ a,b . Chọn khẳng định đúng? 3 A. cosa = . B. 0 a = 1 30 . C. cosa = . D. 0 a = 60 . 8 3
Hướng dẫn giải: ! ! ! 2 ! 2 ! ! ! ! 9 2
(a - b) = a + b - 2 . a b Þ . a b = . 2 ! ! . a b 3 Do đó: cos a = ! ! = . a . b 8 !!!" !!!" !!!" !!!" !!!" !!!"
Câu 40: Cho tứ diện ABCD . Tìm giá trị của k thích hợp thỏa mãn: .
AB CD + AC.DB + . AD BC = k A. k = 1. B. k = 2. C. k = 0.
D. k = 4.
Hướng dẫn giải: Trang 15 !!!" !!!" !!!" !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" .
AB CD + AC.DB + .
AD BC = ( AC + CB).CD + AC.DB - . AD CB !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
= AC (CD + DB) + CB(CD - AD) = AC.CB + C . B AC = 0. Chọn đáp án C.
Câu 41: Trong không gian cho tam giác ABC có trọng tâm G . Chọn hệ thức đúng? A. 2 2 2
AB + AC + BC = ( 2 2 2
2 GA + GB + GC ). B. 2 2 2 2 2 2
AB + AC + BC = GA + GB + GC . C. 2 2 2
AB + AC + BC = ( 2 2 2
4 GA + GB + GC ). D. 2 2 2
AB + AC + BC = ( 2 2 2
3 GA + GB + GC ).
Hướng dẫn giải: Cách 1 Ta có (!!!" !!!" !!!"
GA + GB + GC )2 = 0 !!!"!!!" !!!"!!!" !!!"!!!" 2 2 2
Û GA + GB + GC + 2 . GA GB + 2 . GA GC + 2 . GB GC = 0 2 2 2
Û GA + GB + GC + ( 2 2 2
GA + GB - AB ) + ( 2 2 2
GA + GC - AC ) + ( 2 2 2
GB + GC - BC ) = 0 2 2 2
Û AB + AC + BC = 3( 2 2 2
GA + GB + GC )
Cách 2: Ta có: 2 2 2 ÏÔ AB + AC BC 2 MA Ô Ô = - 2 2 2 Ô Ô 2 4 4 AB Ê + AC BC ˆ 2 Ì fi GA Á ˜ = Á - ˜. Ô 2 9 Á Ë 2 4 ˜˜¯ GA Ô Ô = MA Ô Ô Ó 3
Tương tự ta suy ra được 2 2 2 2 2 2 2 2 2 4 AB Ê + AC BC BA + BC AC CA + CB AB ˆ 2 2 2
GA + GB + GC Á ˜ = Á - + - + - ˜. 9 Á Ë 2 4 2 4 2 4 ˜˜¯ 1 = ( 2 2 2
AB + BC + CA ). 3 € 3( 2 2 2
GA + GB + GC ) 2 2 2
= AB + BC + CA Chọn đáp án D.
Cách 3: Chuẩn hóa giả sử tam giác ABC đều có cạnh là 1. Khi đó 2 2 2 Ï AB Ô + BC + CA = 3 Ô Ì fi 3( 2 2 2
GA + GB + GC ) 2 2 2
= AB + BC + CA . 2 2 2 GA Ô Ô + GB + GC = 1 Ó Chọn đáp án D.
Câu 42: Trong không gian cho tam giác ABC . Tìm M sao cho giá trị của biểu thức 2 2 2
P = MA + MB + MC đạt giá trị nhỏ nhất.
A. M là trọng tâm tam giác ABC .
B. M là tâm đường tròn ngoại tiếp tam giác ABC .
C. M là trực tâm tam giác ABC .
D. M là tâm đường tròn nội tiếp tam giác ABC .
Hướng dẫn giải: uur uuur uuur r
Gọi G là trọng tâm tam giác ABC fi G cố định và GA+ GB + GC = 0. Trang 16 uuur uur uuur uuur uuur uuur
P = (MG + G )2
A + (MG + GB)2 + (MG + GC)2 uuur uur uuur uuur 2 = 3MG + 2 .
MG (GA+ GB + GC) 2 2 2
+ GA + GB + GC 2 2 2 2 2 2 2
= 3MG + GA + GB + GC ≥ GA + GB + GC .
Dấu bằng xảy ra € M ∫ . G Vậy 2 2 2
P = GA + GB + GC với M ∫ G là trọng tâm tam giác ABC. min Chọn đáp án A. ! ! ! ! ! ! ! !
Câu 43: Cho hai vectơ a,b thỏa mãn: a = 26; b = 28; a + b = 48 . Độ dài vectơ a - b bằng? A. 25. B. 616 . C. 9. D. 618 .
Hướng dẫn giải: ! ! 2 ! ! ! ! ! ! ! ! ! !
a - b = (a -b)2 2 2 = a + b - 2 . a b = 2( 2 2
a + b )-(a +b)2 ! 2 ! 2 ! ! 2 2æç a b ö = +
÷ - a + b = 2( 2 2 26 + 28 ) 2 - 48 = 616 è ø ! ! Þ a - b = 616.
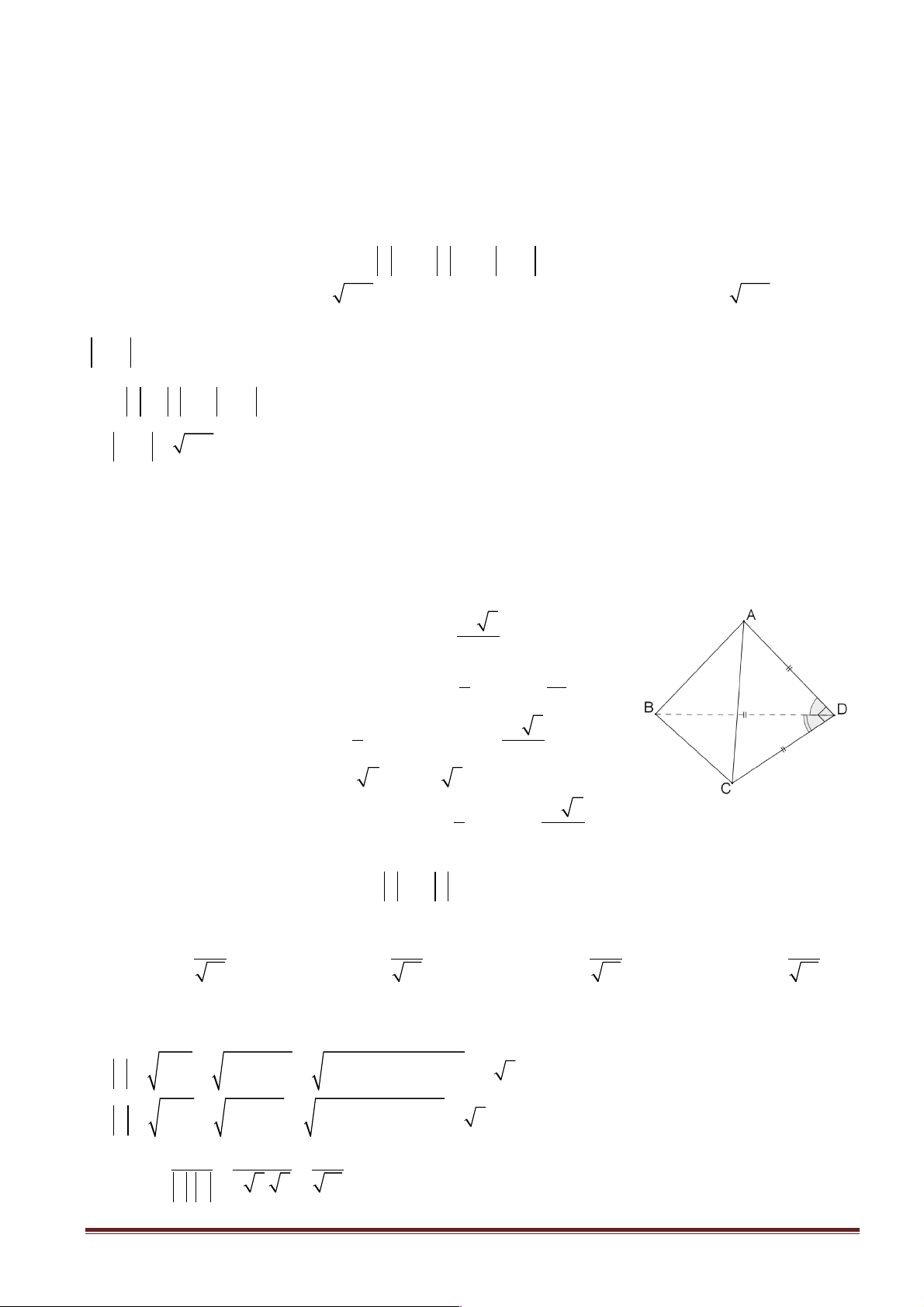
Câu 44: Cho tứ diện ABCD có DA = DB = DC và ∑ 0 ∑ 0 ∑ 0
BDA = 60 , ADC = 90 , BDC = 120 . Trong các
mặt của tứ diện đó:
A. Tam giác ABD có diện tích lớn nhất.
B. Tam giác BCD có diện tích lớn nhất.
C. Tam giác ACD có diện tích lớn nhất.
D. Tam giác ABC có diện tích lớn nhất.
Hướng dẫn giải:
Đặt DA = DB = DC = a 2 a 3
Tam giác ABD đều cạnh a nên diện tích S = . ABD 4 2 1 a
Tam giác ACD vuôn tại D nên diện tích S = D . A DC = . ACD 2 2 2 1 a 3
Diện tích tam giác BCD là 0 S = D . B DC sin120 = . BCD 2 4
Tam giác ABC có AB = a, AC = a 2, BC = a 3 nên tam giác ABC 2 1 a 2
vuông tại A . Diện tích tam giác ABC là S = . AB AC = . ABC 2 2
Vậy diện tích tam giác ABC lớn nhất. ! ! ! ! ! ! !" " " ! ! !
Câu 45: Cho hai vectơ a,b thỏa mãn: a = 4; b = 3; .
a b = 10 . Xét hai vectơ y = a - b x = a - 2b, . Gọi ! "!
α là góc giữa hai vectơ x, y . Chọn khẳng định đúng. 2 - 1 3 2 A. cosa = . B. cosa = . C. cosa = . D. cosa = . 15 15 15 15
Hướng dẫn giải: ! "! ! ! ! ! ! 2 ! 2 ! ! Ta có .
x y = (a - 2b)(a -b) = (a) + 2(b) -3 . a b = 4 . ! ! 2 ! ! 2 ! 2 ! 2 ! !
x = (x) = (a - 2b) = (a) + 4(b) - 4 . a b = 2 3 . !" !" 2 " " 2 " 2 " 2 " "
y = ( y) = (a -b) = (a) + (b) - 2 . a b = 5 . ! "! . x y 4 2 cosa = ! "! = = x . y 2 3. 5 15 Trang 17
Câu 46: Cho tam giác ABC có diện tích S . Tìm giá trị của k thích hợp thỏa mãn: 1 !!!"2 !!!"2 !!!" !!!" S =
AB .AC - 2k ( . AB AC )2 . 2 1 1 A. k = . B. k = 0. C. k = . D. k = 1. 4 2
Hướng dẫn giải: 1 1 1 2 2 2 2 2 S = . AB AC.sin C =
AB .AC sin C = AB .AC ( 2 1- cos C ) 2 2 2 1 !!!"2 !!!"2 !!!" !!!" = AB .AC - ( . AB AC )2 . 2 Chọn C.
Câu 47: Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều
a) Khẳng định nào sau đây đúng nhất.
A. AB và CD chéo nhau
B. AB và CD vuông góc với nhau
C. AB và CD đồng phẳng
D. AB và CD cắt nhau
b) Gọi M , N, P,Q lần lượt là trung điểm các cạnh AC, BC, BD, DA. Khẳng định nào sau đây là đúng nhất?
Chứng minh MNPQ là hình chữ nhật.
A. MNPQ là hình vuông
B. MNPQ là hình bình hành
C. MNPQ là hình chữ nhật
D. MNPQ là hình thoi Hướng dẫn giải:
a) Đặt AB = AD = AC = a !!!" !!!" !!!" !!!" !!!" Ta có C .
D AB = ( AD - AC) AB !!!" !!!" !!!" !!!" 1 1 0 0
= AB AD cos 60 - AB AC cos 60 = . a . a - . a . a = 0 C 2 2 Vậy AB ^ CD . AB a
b) Ta có MN ! PQ ! AB và MN = PQ = = nên tứ giác N 2 2 M
MNPQ là hình bình hành. ìMN ! AB P B ï
Lại có íNP ! CD Þ MN ^ NP , do đó MNPQ là hình chữ nhật. D ïAB ^ î CD A Q
Câu 48: Cho hình chóp S.ABC có SA = SB = SC = a và BC = a 2 . Tính góc giữa hai đường thẳng AB và SC . A. (∑ AB SC ) 0 , = 60 B. (∑ AB SC ) 0 , = 45 C. (∑ AB SC ) 0 , = 30 D. (∑ AB SC ) 0 , = 90
Hướng dẫn giải: S
Gọi M , N, P lần lượt là trung điểm của ,
SA SB, AC , khi đó MN ! AB nên (∑ AB SC ) = (∑ , MN, SC ) . Đặt ∑
j = NMP , trong tam giác MNP có M N φ 2 2 2 + - cosj = MN MP NP ( )1. 2MN.MP A B Trang 18 P C 2 5 Ta có = = a MN MP , 2 2 2
AB + AC = BC Þ DABC vuông tại A , vì vậy 2 2 2 = + = a PB AP AC , 2 4 2 3 2 = a PS
.Trong tam giác PBS theo công thứ tính đường trung tuyến ta có 4 2 2 5a 3a 2 2 2 + 2 2 PB + PS SB a 3a 2 4 4 PN = - = - = . 2 4 2 4 4 1
Thay MN, MP, NP vào ( ) 1 ta được 0 cosj = - Þ j = 120 . 2 Vậy (∑ AB SC ) = (∑ MN SC ) 0 , , = 60 .
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA = AB và SA ^ BC .
a) Tính góc giữa hai đường thẳng SD và BC . A. (∑ BC SD) 0 , = 30 B. (∑ BC SD) 0 , = 45 C. (∑ BC SD) 0 , = 60 D. (∑ BC SD) 0 , = 50
b) Gọi I, J lần lượt là các điểm thuộc SB và SD sao cho IJ ! BD . Chứng minh góc giữa AC và IJ
không phụ thuộc vào vị trí của I và J . A. (∑ IJ AC ) 0 , = 90 B. (∑ IJ AC ) 0 , = 60 C. (∑ IJ AC ) 0 , = 30 D. (∑ IJ AC ) 0 , = 45 Hướng dẫn giải: a) (∑ BC SD) 0 , = 45 b) (∑ IJ AC ) 0 , = 90 .
Câu 50: Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau.
a) Khẳng định nào sau đây là đúng nhất?
A. AD ^ BC B. AD cắt BC
C. AD và BC chéo nhau
D. Cả A, B, C đều đúng !!!" !!!" !!!" !!!"
b) Gọi M , N là các điểm lần lượt thuộc các đường thẳng AB và DB sao cho MA = k MB, ND = k NB .
Tính góc giữa hai đường thẳng MN và BC . A. (∑ MN BC ) 0 , = 90 B. (∑ MN BC ) 0 , = 80 C. (∑ MN BC ) 0 , = 60 D. (∑ MN BC ) 0 , = 45 Hướng dẫn giải:
a) Gọi P là trung điểm của BC , thì các tam giác A ìAP ^ BC
ABC và DBC cân nên í . îDP ^ BC !!!" !!!" !!!" !!!" !!!"
Ta có BC.AD = BC (PD - PA) = 0 Vậy BC ^ AD . !!!" !!!" MA !!!" !!!" ND
b) Ta có MA = k MB Þ
= k , ND = k NB Þ = k M MB NB Þ MA = ND N MB NB B D
suy ra MN ! AD Þ (∑ MN BC ) = (∑ AD BC ) 0 , , = 90 ( Theo câu a) P C
Câu 51: Cho hình hộp thoi ABC .
D A' B 'C ' D ' có tất cả các cạnh đều bằng a và ∑ ∑ ∑ 0
ABC = B ' BA = B ' BC = 60 .Tính góc giữa hai đường thẳng AC và B’D’. Trang 19 A. (∑ B ) 0 AC, 'D' = 90 B. (∑ B ) 0 AC, 'D' = 60 C. (∑ B ) 0
AC, 'D' = 45 D. (∑ B ) 0 AC, 'D' = 30 Hướng dẫn giải:
HS tự giải.
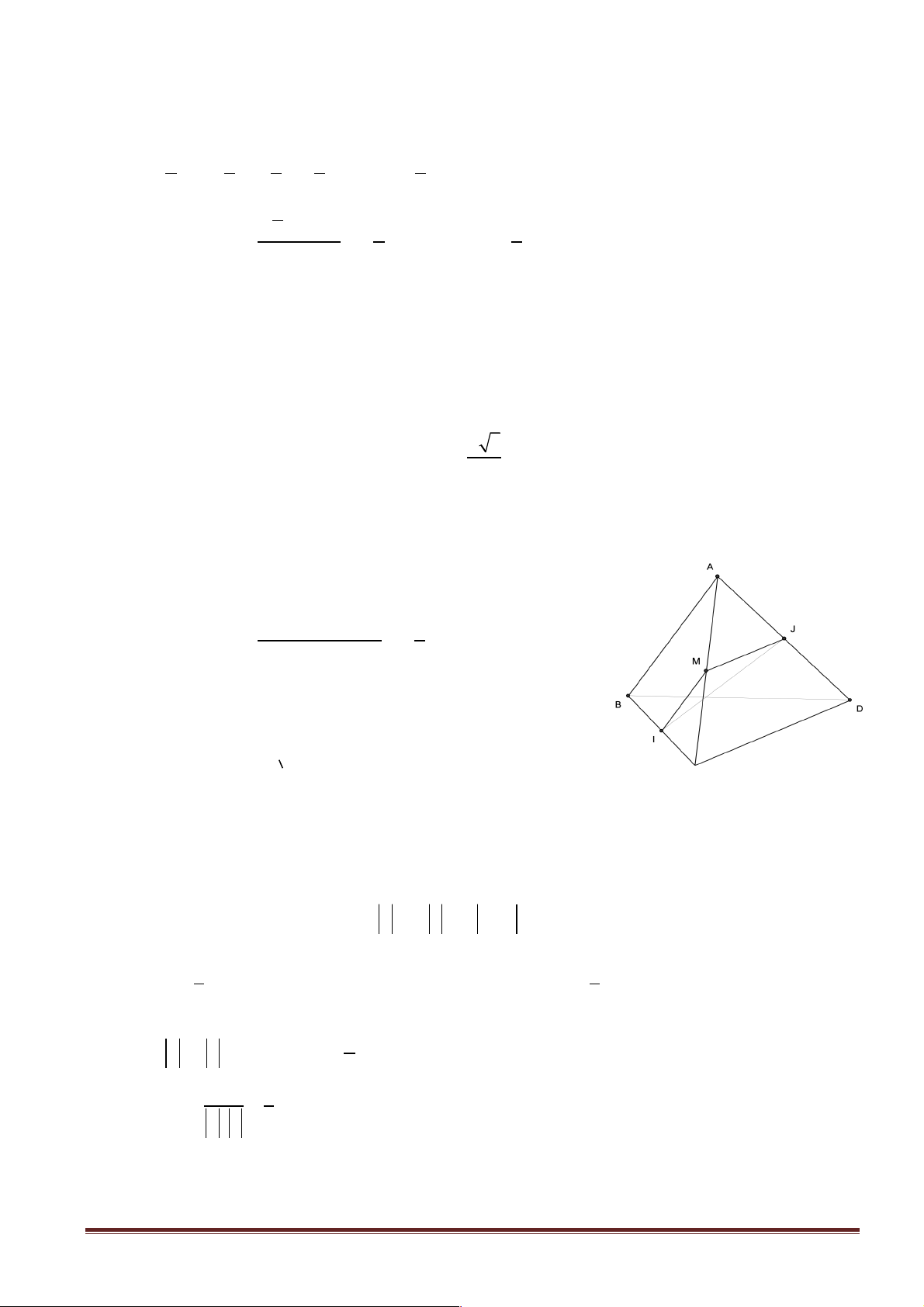
Câu 52: Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm các cạnh BC và AD . Cho biết
AB = CD = 2a và MN = a 3 . Tính góc giữa hai đường thẳng AB và CD . A. (∑ AB CD) 0 , = 30 B. (∑ AB CD) 0 , = 45 C. (∑ AB CD) 0 , = 60 D. (∑ AB CD) 0 , = 90 Hướng dẫn giải:
Gọi O là trung điểm của AC , ta có OM = ON = a . ìOM ! AB í Þ (∑ AB CD) = (∑ , OM ,ON ) îON ! CD
Áp dụng định lí côsin cho tam giác OMN ta có
a + a - (a 3)2 2 2 ∑ 2 2 2 + - 1 A cos = OM ON MN MON = = - . 2OM .ON 2. . a a 2 Vậy (∑ AB CD) 0 , = 60 . N O B D M C
Câu 53: Cho tứ diện ABCD có
AB = CD = a, AC = BD = b, AD = BC = c .
a)Khẳng định nào sau đây là đúng nhất.
A. các đoạn nối trung điểm các cặp cạnh đối thì vuông góc với hai cạnh đó
B. các đoạn nối trung điểm các cặp cạnh đối thì không vuông góc với hai cạnh đó
C. các đoạn nối trung điểm các cặp cạnh đối thì có thể vuông góc có thể không vuông góc với hai cạnh đó
D. cả A, B, C đều sai
b) Tính góc giữa hai đường thẳng AC và BD . 2 2 a - c A A. (∑ ( ) AC, BD) = arccos 2 b 2 2 2 a + c B. (∑ ( ) AC, BD) = arccos M 2 b P 2 2 2 a - c C. (∑ ( ) AC, BD) = arccos 2 3b B D 2 2 2 a - c D. (∑ ( ) AC, BD) = arccos N 2 b C Hướng dẫn giải:
Gọi M , N, P lần lượt là trung điểm của các cạnh AB,CD, AD . Trang 20
a) Do hai tam giác ACD và BCD có CD chung và AC = BD, AD = BC nên chúng bằng nhau, suy ra MC = MD
Vậy tam giác MCD cân tại M và có trung tuyến MN nên MN ^ CD .
Tương tự MN ^ AB .
Chứng minh tương tự cho hai cặp cạnh đối còn lại. ìPM ! BD b) Ta có í Þ (∑ BD AC ) = (∑ , PM , PN ) îPN ! AC
Theo công thức tính đường trung tuyến ta có CA + CB AB 2( 2 2 b + c ) 2 2 2 2 - a 2 CM = - = 2 4 4
2 b + c - a 2 ( 2 2) 2 Tương tự DM = , nên 4 MC + MD CD 2( 2 2 b + c ) 2 2 2 2 2 2 2 2 - a a b + c - a 2 MN = - = - = 2 4 4 4 2
Áp dụng định lí cô sin cho tam giác PMN ta có 2 2 2 2 2 æ b ö æ b ö b + c - + - a ç ÷ ç ÷
PM + PN - MN 2 è 2 ø è 2 ø 2 ( 2 2 2 2 2 a - c ) ∑ cos MPN = = = 2 2.PM .PN æ b öæ b ö 2 b ç ÷ç ÷ è 2 øè 2 ø 2 2 2 a - c Vậy (∑ ( ) AC, BD) = arccos . 2 b Trang 21
DẠNG 2: CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC VÀ CÁC BÀI TOÁN LIÊN QUAN Phương pháp:
Để chứng minh d ^ d ta có trong phần này ta có thể thực hiện theo các cách sau: 1 2 !!"!!" !!" !!" •
Chứng minh d ^ d ta chứng minh u u = 0 trong đó u ,u lần lượt là các vec tơ chỉ phương 1 2 1 2 1 2
của d và d . 1 2 ìb ! c • Sử dụng tính chất í Þ a ^ b . a ^ î c •
Sử dụng định lí Pitago hoặc xác định góc giữa d ,d và tính trực tiếp góc đó. 1 2 •
Tính độ dài đoạn thẳng, diện tích của một đa giác • Tính tích vô hướng…
Câu 1: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau,
mệnh đề nào có thể sai?
A. A¢C¢ ^ BD .
B. BB¢ ^ BD .
C. A¢B ^ DC¢ .
D. BC¢ ^ A¢D .
Hướng dẫn giải: Chọn B. A' D'
Chú ý: Hình hộp có tất cả các cạnh bằng nhau còn gọi là hình hộp thoi. A đúng vì: B' C'
ìA¢C¢ ^ B D ¢ ¢ í
Þ A¢C¢ ^ BD . B D ¢ ¢ î // BD B sai vì: A D
ìA¢B ^ AB¢ C đúng vì: í
Þ A¢B ^ DC¢ . AB¢ // DC¢ î B ìBC¢ ^ B C ¢ C D đúng vì: í
Þ BC¢ ^ A¢D . B C ¢ // A D ¢ î !!!" !!!" !!!" !!!" !!!" !!!"
Câu 2: Cho tứ diện ABCD . Chứng minh rằng nếu .
AB AC = AC.AD = .
AD AB thì AB ^ CD ,
AC ^ BD , AD ^ BC . Điều ngược lại đúng không? Sau đây là lời giải: !!!" !!!" !!!" !!!" !!!" !!!" !!!" Bước 1: .
AB AC = AC.AD Û AC.( AB - AD) = 0 Û AC.DB = 0 Û AC ^ BD.
Bước 2: Chứng minh tương tự, từ AC.AD = AD.AB ta được AD ^ BC và AB.AC = AD.AB ta được AB ^ CD .
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu? A. Đúng. B. Sai từ bước 1. C. Sai từ bước 1. D. Sai ở bước 3.
Hướng dẫn giải: Chọn A.
Câu 4: Cho tứ diện ABCD có AB vuông góc với CD . Mặt phẳng ( P) song song với AB và CD lần
lượt cắt BC, DB, AD, AC tại M , N, P, Q . Tứ giác MNPQ là hình gì? A. Hình thang. B. Hình bình hành. C. Hình chữ nhật.
D. Tứ giác không phải là hình thang.
Hướng dẫn giải: Chọn C. Trang 22 ( ì MNPQ ï )//AB Ta có: í Þ MQ// . AB ( ï MNPQ î )Ç( ABC) = MQ
Tương tự ta có: MN //CD, NP//AB, QP//CD .
Do đó tứ giác MNPQ là hình bình hành
lại có MN ^ MQ (do AB ^ CD ) .
Vậy tứ giác MNPQ là hình chữ nhật.
Câu 5: Cho tứ diện đều ABCD có cạnh bằng a . Gọi M , N, P,Q, R lần lượt là trung điểm của
AB,CD, AD, BC và AC .
a) Khẳng định nào sau đây là đúng nhất?
A. MN ^ RP, MN ^ RQ
B. MN ^ RP, MN cắt RQ
C. MN chéo RP; MN chéo RQ
D. Cả A, B, C đều sai
b) Tính góc của hai đường thẳng AB và CD? A. (∑ AB CD) 0 , = 60 B. (∑ AB CD) 0 , = 30 C. (∑ AB CD) 0 , = 45 D. (∑ AB CD) 0 , = 90
Hướng dẫn giải: 3 a) Ta có = = a MC MD
nên tam giác MCD cân tại M , do đó MN ^ CD . 2
Lại có RP ! CD Þ MN ^ RQ .
b) Tương tự ta có QP ^ AD
Trong tam giác vuông PDQ ta có A 2 2 2 æ a 3 ö a a 2 2 2 æ ö
QP = QD - DP = ç ÷ - = Ta có : ç ÷ ç ÷ 2 è ø è 2 ø 2 M P 2 2 a a R 2 2 æ ö æ ö 2 2 RQ + RP = + = a = QP ç ÷ ç ÷ è 2 ø è 2 ø
Do đó tam giác RPQ vuông tại R , hay RP ^ RQ . B ìAB ! RQ D ï Q N
Vì vậy íCD ! RP Þ AB ^ CD . C ïRP ^ î RQ
Câu 6: Trong không gian cho hai tam giác đều ABC và ABC¢ có chung cạnh AB và nằm trong hai
mặt phẳng khác nhau. Gọi M , N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC¢ và C A ¢ . Tứ
giác MNPQ là hình gì? A. Hình bình hành. B. Hình chữ nhật. C. Hình vuông. D. Hình thang.
Hướng dẫn giải: Chọn B.
Vì M , N, P, Q nên dễ thấy tứ giác MNPQ là hình bhình hành.
Gọi H là trung điểm của AB . C ì H ^ AB
Vì hai tam giác ABC và ABC¢ nên í C î H ¢ ^ AB
Suy ra AB ^ (CHC¢) . Do đó AB ^ CC¢. Trang 23 ìPQ//AB ï
Ta có: íPN //CC¢ Þ PQ ^ PN . ïAB ^ CC¢ î
Vậy tứ giác MNPQ là hình chữ nhật.
Câu 7: Cho hình chóp S.ABCD có đáy là hình bình hành với AB = a, AD = 2a .
Tam giác SAB vuông can tại A , M là một điểm trên cạnh AD ( M khác A và D ). Mặt phẳng (a )
đi qua M và song sog với (SAB)cắt BC, SC, SD lần lượt tại N, P,Q .
a) MNPQ là hình gi?.
A. MNPQ là hình thang vuông.
B. MNPQ là hình vuông.
C. MNPQ là hình chữ nhật.
D. MNPQ là hình bình hành.
b)Tính diện tích của MNPQ theo a . 2 3a 2 a 2 3a 2 a A. S = B. S = C. S = D. S = MNPQ 8 MNPQ 8 MNPQ 4 MNPQ 4
Hướng dẫn giải: ( ì a ) ! (SAB) ï a) Ta có (
í SAB) Ç( ABCD) = AB Þ MN ! AB . ( ï a)Ç(ABCD) = î MN ( ì a ) ! (SAB) ï Tương tự (
í SBC) Ç(SAB) = SB Þ NP ! SB ( ï a)Ç(SBC) = î NP ( ì a ) ! (SAB) ( ï S
í SAD) Ç(SAB) = SA Þ MQ ! SA ( ï a)Ç(SAD) = î MQ Q
Dễ thấy MN ! PQ ! AB ! CD nên MNPQ là hình bình hành P ìMN ! AB ï D
Lại có íMQ ! SA Þ MN ^ MQ . M A ïAB ^ î SA C
Vậy MNPQ là hình thang vuông. B N SA a CD a
b) Ta có MN = AB = a , MQ = = , PQ = = . 2 2 2 2 1 2 1 æ a ö a 3a Vậy S = (MN + PQ MQ = a + = MNPQ ). ç ÷ . 2 2 è 2 ø 2 8
Câu 8: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Trên các cạnh DC và BB ' lấy các điểm M
và N sao cho MD = NB = x (0 £ x £ a) . Khẳng định nào sau đây là đúng?
a) Khẳng định nào sau đây là đúng?
A. AC ' ^ B ' D '
B. AC’ cắt B’D’
C. AC’và B’D’ đồng phẳng D. Cả A, B, C đều đúng A B
b) khẳng định nào sau đây là đúng ?.
A. AC ' ^ MN M
B. AC’ và MN cắt nhau D C
C. AC’ và MN đồng phẳng N B' A' Trang 24 D' C'
D. Cả A, B, C đều đúng
Hướng dẫn giải: !!!" " !!!" " !!!" "
Đặt AA' = a, AB = b, AD = c . !!!!" " " " !!!!!" " "
a) Ta có AC ' = a + b + c , B ' D ' = c - b nên !!!!" !!!!!" " " " " "
AC '.B ' D ' = (a + b + c)(c -b) ! ! ! ! !
= a (c -b) 2 2 2 2
+ c - b = a - a = 0
Þ AC ' ^ B ' D ' . !!!!" !!!" !!!!" !!!" !!!" !!!" !!!!"
æ ! x ! ö æ ! x ! ö x ! æ x ö ! !
b) MN = AN - AM = ( AB + BN ) -( AD + DM ) = b + a - c + b = a + 1- b -c ç ÷ ç ÷ ç ÷ è a ø è a ø a è a ø !!!!" !!!!"
" " " æ " x " ö æ" x " ö x " æ x ö " "
Từ đó ta có AC '.MN = (a + b + c)[ b + a - c + b = a + 1- b -c] ç ÷ ç ÷ ç ÷ è a ø è a ø a è a ø x !2 x !2 !2 æ ö æ x ö 2 2 = a + 1- b - c = . x a + 1- a - a = 0 . ç ÷ ç ÷ a è a ø è a ø
Vậy AC ' ^ MN .
Câu 9: Cho tứ diện ABCD có AC = a , BD = 3a . Gọi M và N lần lượt là trung điểm của AD và
BC . Biết AC vuông góc với BD . Tính MN . a 10 a a a A. MN = 6 . B. MN = 3 2 . C. MN = 2 3 . D. MN = . 2 3 2 3
Hướng dẫn giải: Chọn A.
Gọi E , F lần lượt là trung điểm của AB và CD . A ìEN // AC Ta có: í
Þ ( AC,BD) = (NE, NF ) = 90° Þ NE ^ NF (1). îNF // BD M ì 1 E
NE = FM = AC ïï Mà: 2 í (2). C 1 D ï F
NF = ME = BD ïî 2 N
Từ (1), (2) Þ MENF là hình chữ nhật. B 2 2 2 2 æ AC ö æ BD ö æ a ö æ 3a ö a 10 Từ đó ta có: 2 2
MN = NE + NF = + = + = . ç ÷ ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø è 2 ø 2 Chọn D
Câu 10: Trong không gian cho ba điểm ,
A B, C bất kỳ, chọn đẳng thức đúng? !!!" !!!" !!!" !!!" A. 2 2 2 2 .
AB AC = AB + AC - BC B. 2 2 2 2 .
AB AC = AB + AC - 2BC !!!" !!!" !!!" !!!" C. 2 2 2 .
AB AC = AB + AC - 2BC D. 2 2 2 .
AB AC = AB + AC - BC
Hướng dẫn giải: Chọn A. !!!" !!!" 2 2 2 2 2
BC = AB + AC - 2 .
AB AC.cos ( AB, AC) = AB + AC - 2. . AB AC !!!" !!!"
Câu 11: Cho hình lập phương ABC .
D EFGH có cạnh bằng a . Tính . AB EG 2 a 2 A. 2 a 3 . B. 2 a C. D. 2 a 2 2
Hướng dẫn giải:. Chọn B. !!!" !!!" !!!" !!!" !!!" !!!" !!!" Ta có . AB EG = .
AB AC , mặt khác AC = AB + AD .
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!" !!!" !!!"
Suy ra AB EG = AB AC = AB ( AB + AD) 2 2 . . = AB + . AB AD = a Trang 25
Câu 12: Cho tứ diện ABCD có AB = a, BD = 3a . Gọi M , N lần lượt là trung điểm của AD và BC .
Biết AC vuông góc với BD . Tính MN a 6 a a a A. MN = 10 B. MN = 2 3 C. MN = 3 2 D. MN = 3 2 3 2
Hướng dẫn giải: Chọn B.
Kẻ NP//AC (P Î AB) , nối MP . a
NP là đường trung bình ABC D 1 Þ PN = AC = . 2 2 a
MP là đường trung bình ABD D 1 3 Þ PM = BD = . 2 2 !!!!!!"
Lại có ( AC, BD) = (PN, PM ) = NPM = 90° suy ra Þ MN D P vuông tại P . a 10 Vậy 2 2
MN = PN + PM = . 2
Câu 13: Cho tứ diện ABCD trong đó AB = 6 , CD = 3 , góc giữa AB và CD là 60° và điểm M trên
BC sao cho BM = 2MC . Mặt phẳng (P) qua M song song với AB và CD cắt BD , AD , AC lần
lượt tại M , N , Q . Diện tích MNPQ bằng: 3 A. 2 2 B. 2 C. 2 3 D. 2
Hướng dẫn giải: Chọn C.
Thiết diện MNPQ là hình bình hành.
Ta có ( AB CD) = (QM MP) ∑ , , = QMP = 60° . Suy ra S
= QN.QN.sin 60°. MPNQ Lại có CM MO 1 C D MQ # C D BA Þ = = Þ MQ = 2 AB AB 3 AQ QN 2 AQ D N # ACD D Þ = = Þ QN = 2 AC CD 3 Do đó S
= QM.QN.sin 60° = 2.2.sin 60° = 2 3 . MPNQ
Câu 14: Cho tứ diện ABCD có AB vuông góc với CD , AB = 4, CD = 6 . M là điểm thuộc cạnh
BC sao cho MC = 2BM . Mặt phẳng (P) đi qua M song song với AB và CD . Diện tích thiết diện
của (P) với tứ diện là? 17 16 A. 5 B. 6 C. D. 3 3
Hướng dẫn giải:
Ta có ( AB CD) = (MN MQ) ∑ , , = NMQ = 90° .
Suy ra thiết diện MNPQ là hình chữ nhật. Lại có: CM MN C 1 4 D MN ! C D BA Þ = = Þ MN = CB AB 3 3 AN NP A 2 D NP ! A D CD Þ = = Þ MP = 4 AC CD 3 Trang 26 16 Suy ra S = MN.NP = . MNPQ 3 Trang 27