
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
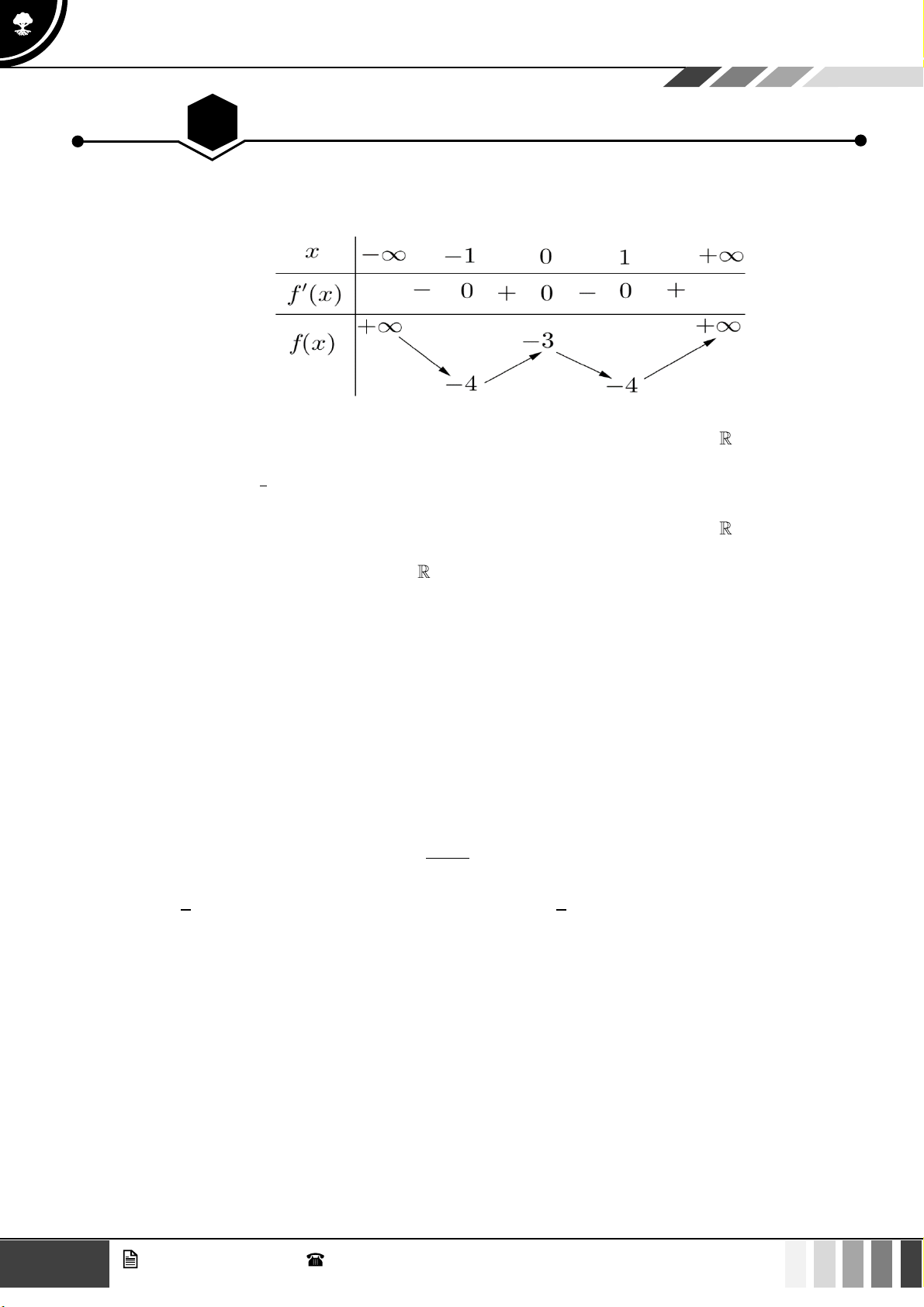
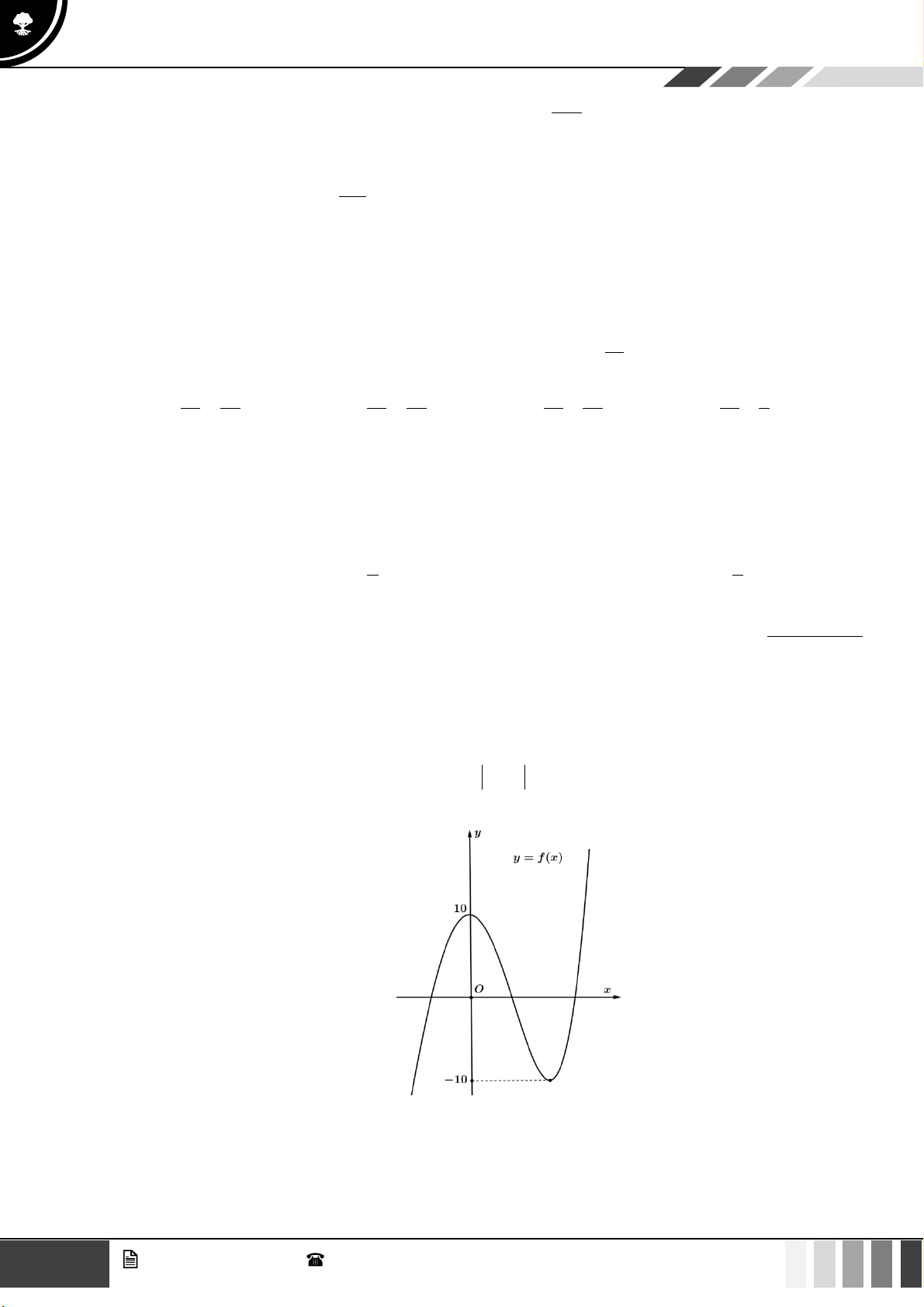
Câu 1: Cho hàm số bậc bốn
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1; +
. B.
( )
1;1−
. C.
( )
;0−
. D. .
Câu 2: Hàm số
1
2
yx=
có tập xác định là:
A.
( )
0;+
. B.
)
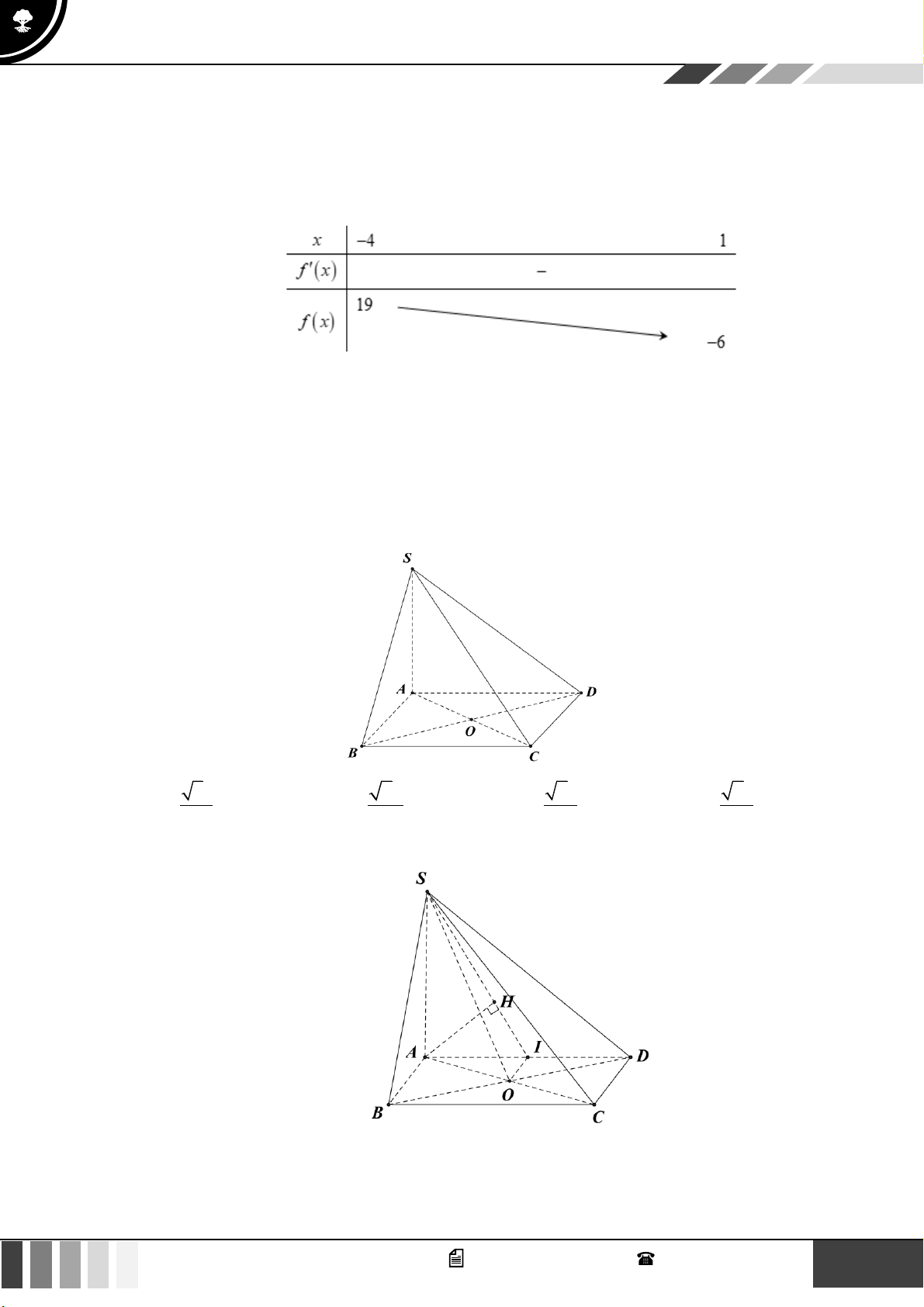
0;+
. C.
( )
1; +
. D. .
Câu 3: Cho hàm số
( )
y f x=
liên tục trên và có đạo hàm
( ) ( )( )
11f x x x
= + −
. Số điểm cực trị của
hàm số
( )
y f x=
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 4: Điểm cực đại của đồ thị hàm số
42
29y x x= − +
có tọa độ là:
A.
( )
1;9
. B.
( )
2;9
. C.
( )
2;9−
. D.
( )
0;9
.
Câu 5: Cho hình nón
( )
N
có đường kính đáy bằng
4a
, đường sinh bằng
5a
. Tính diện tích xung quanh
S
của hình nón
( )
N
.
A.
2
10Sa
=
. B.
2
14Sa
=
. C.
2
36Sa
=
. D.
2
20Sa
=
.
Câu 6: Tìm giá trị lớn nhất của hàm số
31
3
x
y
x
−
=
−
trên
0;2
.
A.
1
3
. B.
5
. C.
1
3
−
. D.
5−
.
Câu 7: Cho hàm số
( )
y f x=
có
( )
lim 2024
x
fx
→+
=
và
( )
lim 2024
x
fx
→−
=−
. Khẳng định nào sau đây
đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
2024y =
và
2024x =−
.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
2024y =
và
2024y =−
.
Câu 8: Cho hình trụ có bán kính đáy bằng
4
và độ dài đường sinh bằng
3l =
. Thể tích của khối trụ đã
cho bằng
A.
12
. B.
24
. C.
19
. D.
48
.
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
01
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
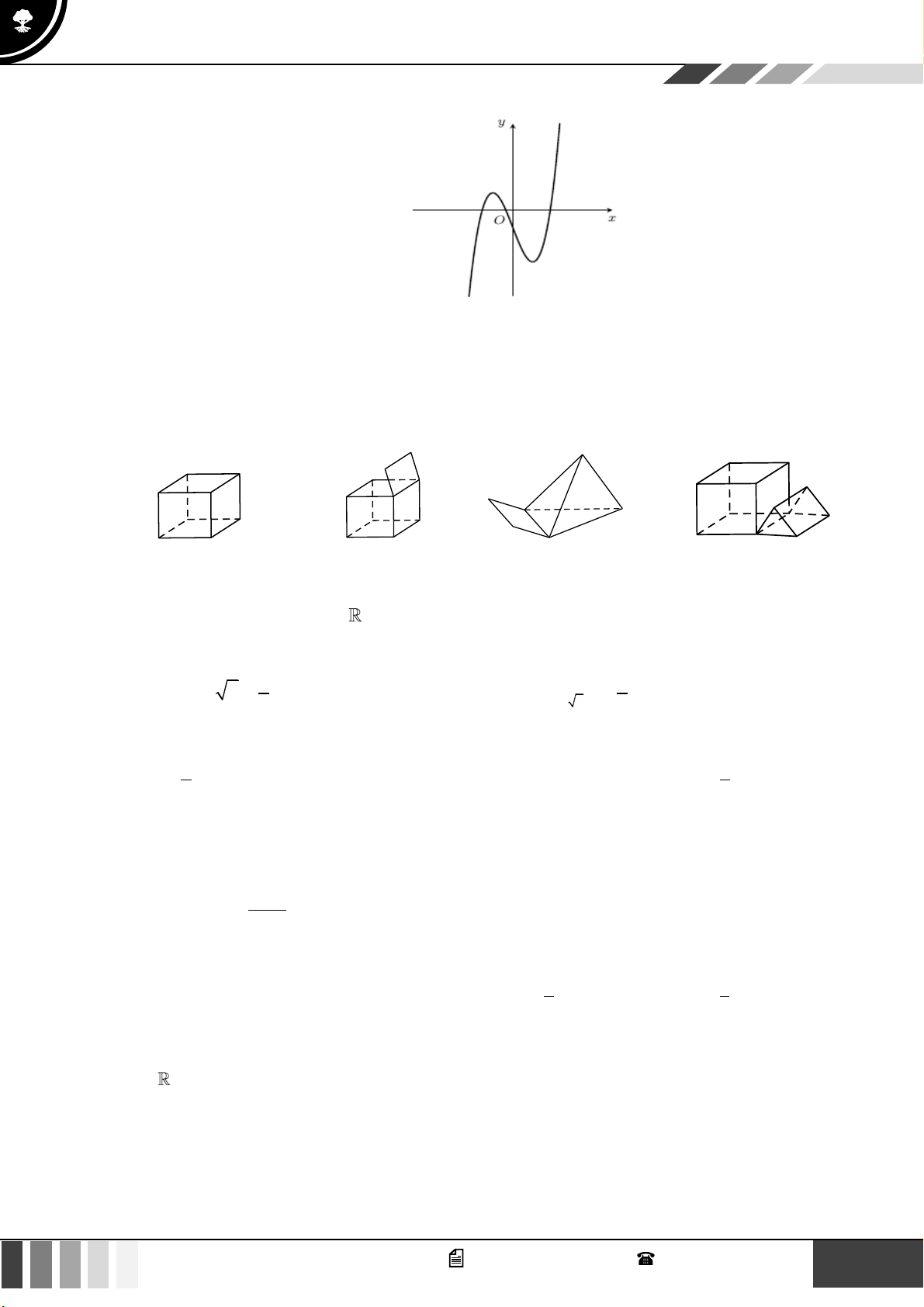
Câu 9: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây.
A.
42
1y x x= − + −
. B.
42
31y x x= − −
. C.
3
31y x x= − − −
. D.
3
31y x x=−−
.
Câu 10: Tìm số giao điểm của
( )
3
:3C y x x= + −
và đường thẳng
2yx=−
?
A.
2
. B.
0
. C.
3
. D.
1
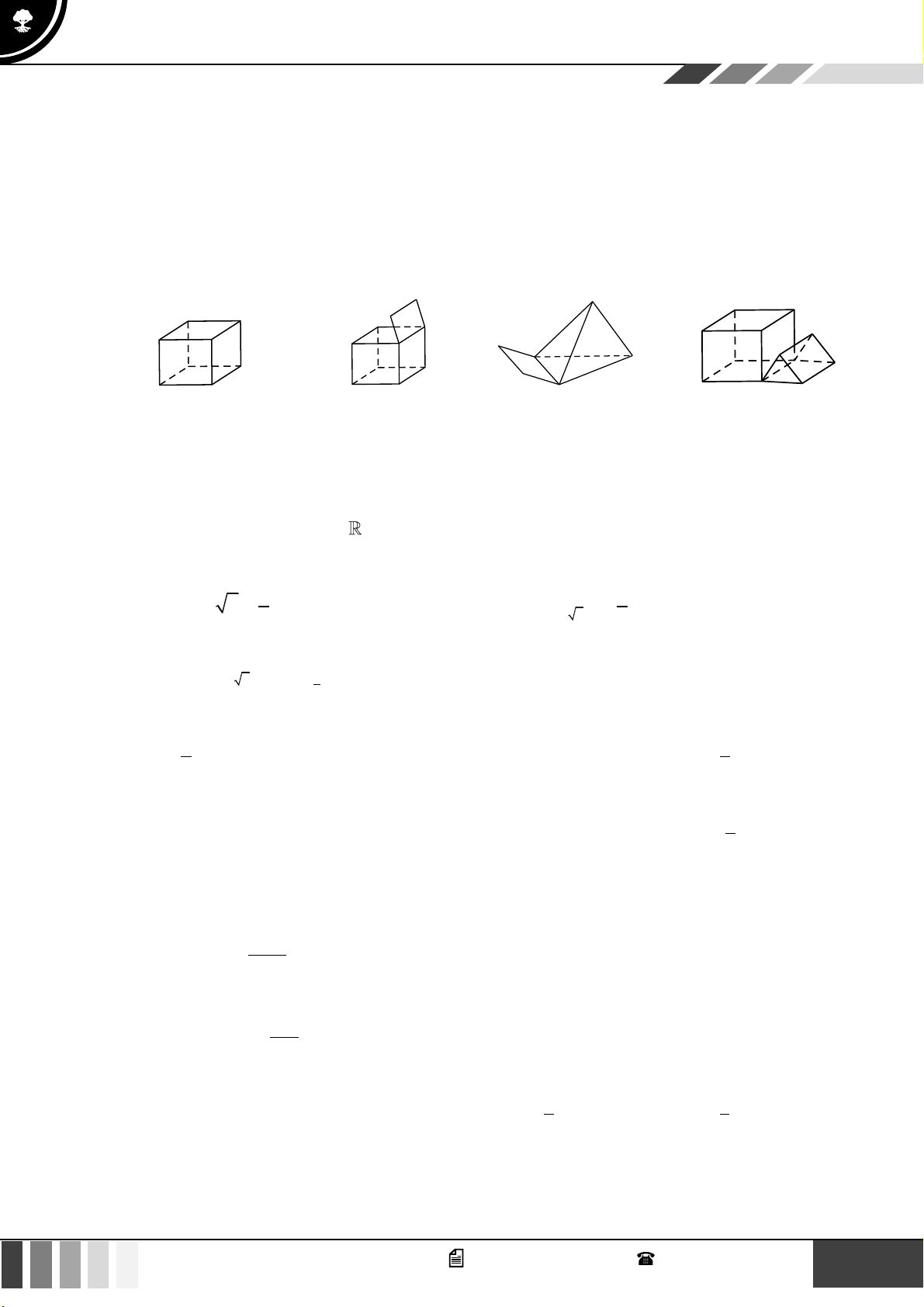
.
Câu 11: Mỗi hình sau gồm một số hữu hạn đa giác phẳng, tìm hình đa diện.
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1.
Câu 12: Cho
, , 0; 1;a x y a
. Khẳng định nào sau đây sai?
A.
( )
log . log log
a a a
x y x y=+
. B.
log log
aa
xx
=
.
C.
1
log log
2
aa
xx=
. D.
1
log log
2
a
a
xx=
.
Câu 13: Thể tích của khối chóp có diện tích đáy bằng
B
và cạnh bên bằng
h
là
A.
1
.
2
Bh
. B.
3.Bh
. C.
.Bh
. D.
1
.
3
Bh
.
Câu 14: Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( )
df x x f x C
=+
. B.
cos d sinx x x C=+
.
C.
1
d , 1
1
x
x x C
+
= + −
+
. D.
d ln
xx
a x a a C=+
( )
01a
.
Câu 15: Thể tích của khối lập phương cạnh
a
bằng:
A.
3
a
. B.
2
a
. C.
3
1
3
a
. D.
2
1
3
a
.
Câu 16: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
3 2 2
1 3 2y x m x x m= − + + − +
đồng biến trên
.
A.
2
4
m
m
−
. B.
42m−
. C.
42m−
. D.
2
4
m
m
−
.
Câu 17: Số nghiệm thực của phương trình
( )
( )
2
2024 2024
log 3 2 log 1x x x− + = −
là
A.
0
. B.
1
. C.
2
. D.
3
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Câu 18: Cho hình nón có thiết diện qua trục là tam giác đều có cạnh bằng
4
. Diện tích toàn phần của
hình nón đã cho bằng
A.
3
. B.
8
. C.
12
. D.
9
.
Câu 19: Tìm giá trị nhỏ nhất của hàm số
( )
cosx
fx
x
=
trên đoạn
;
63
.
A.
33
. B.
32
. C.
33
2
. D.
3
2
.
Câu 20: Tập nghiệm của bất phương trình
( )
1
9
1
log 1
2
x − −
là
A.
( )
1;4
. B.
(
1;4
. C.
)
4;+
. D.
(
;4−
.
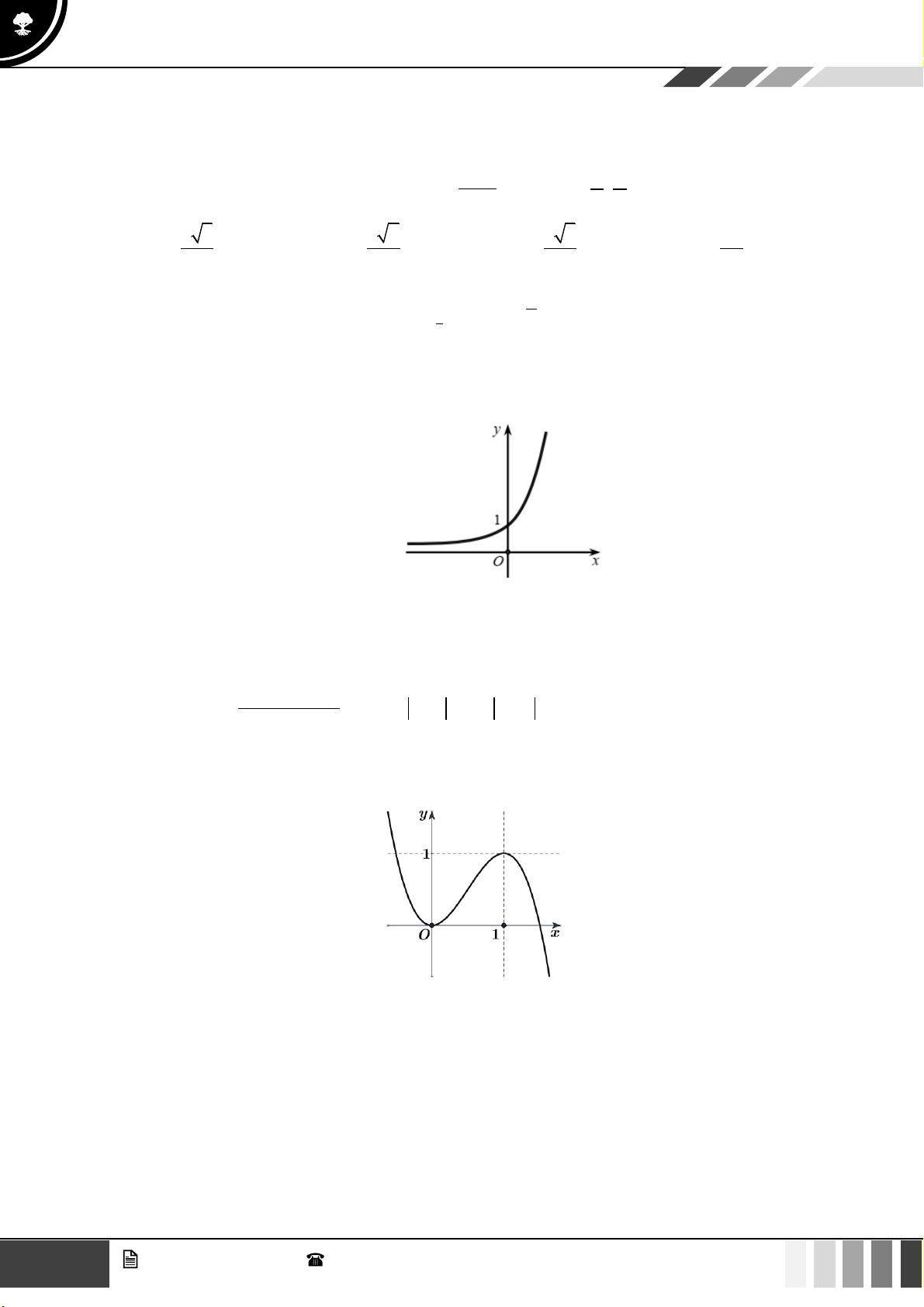
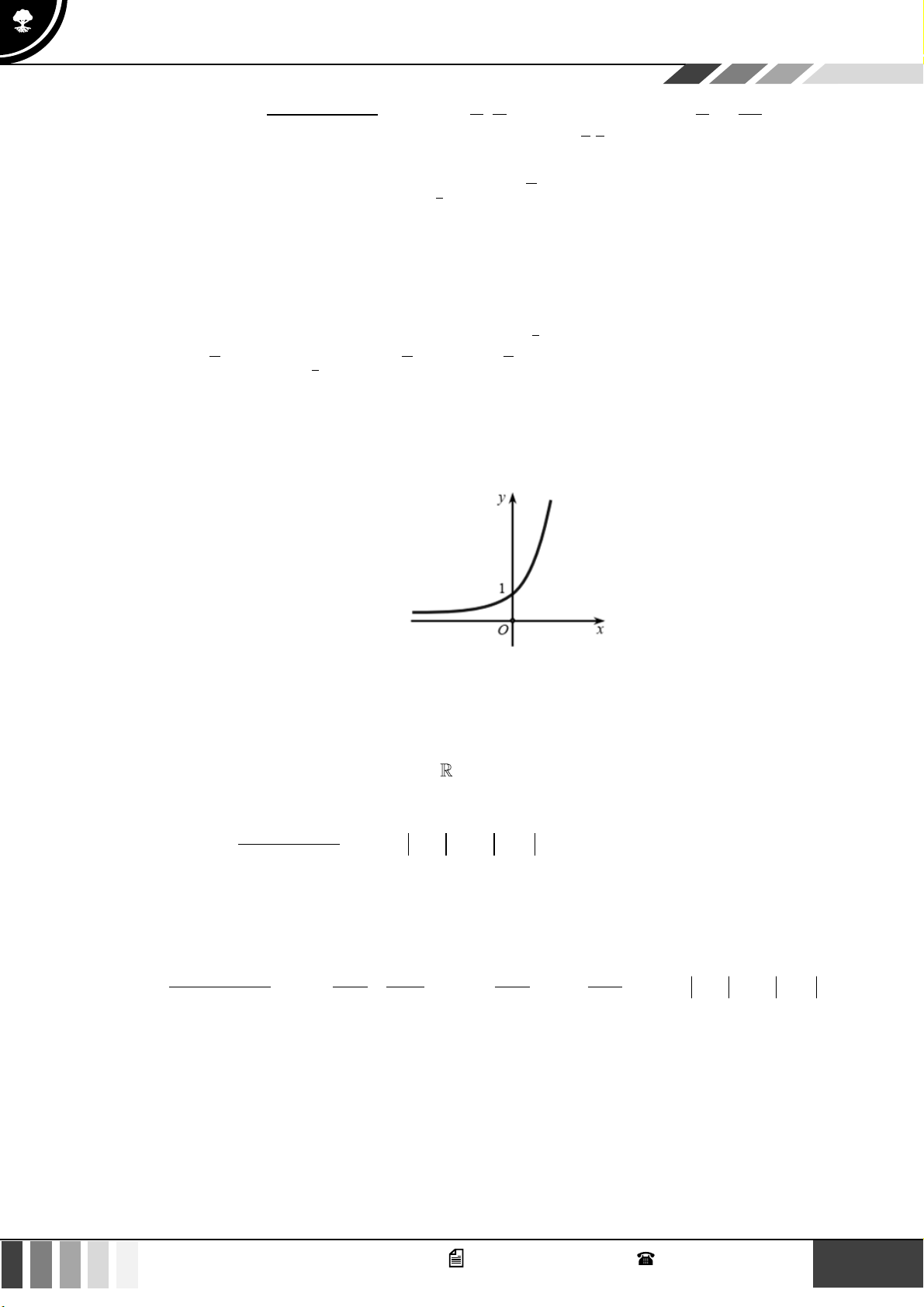
Câu 21: Hàm số nào dưới đây có dạng đồ thị như hình vẽ?
A.
3
31y x x=−+
B.
42
21y x x= − +
.
C.
2024
x
y =
. D.
( )
2024
log 2024yx=+
.
Câu 22: Cho biết
( )( )
2 13
d ln 1 ln 2
12
x
x a x b x C
xx
−
= + + − +
+−
. Mệnh đề nào sau đây đúng?
A.
28ab+=
. B.
8ab+=
. C.
28ab−=
. D.
8ab−=
.
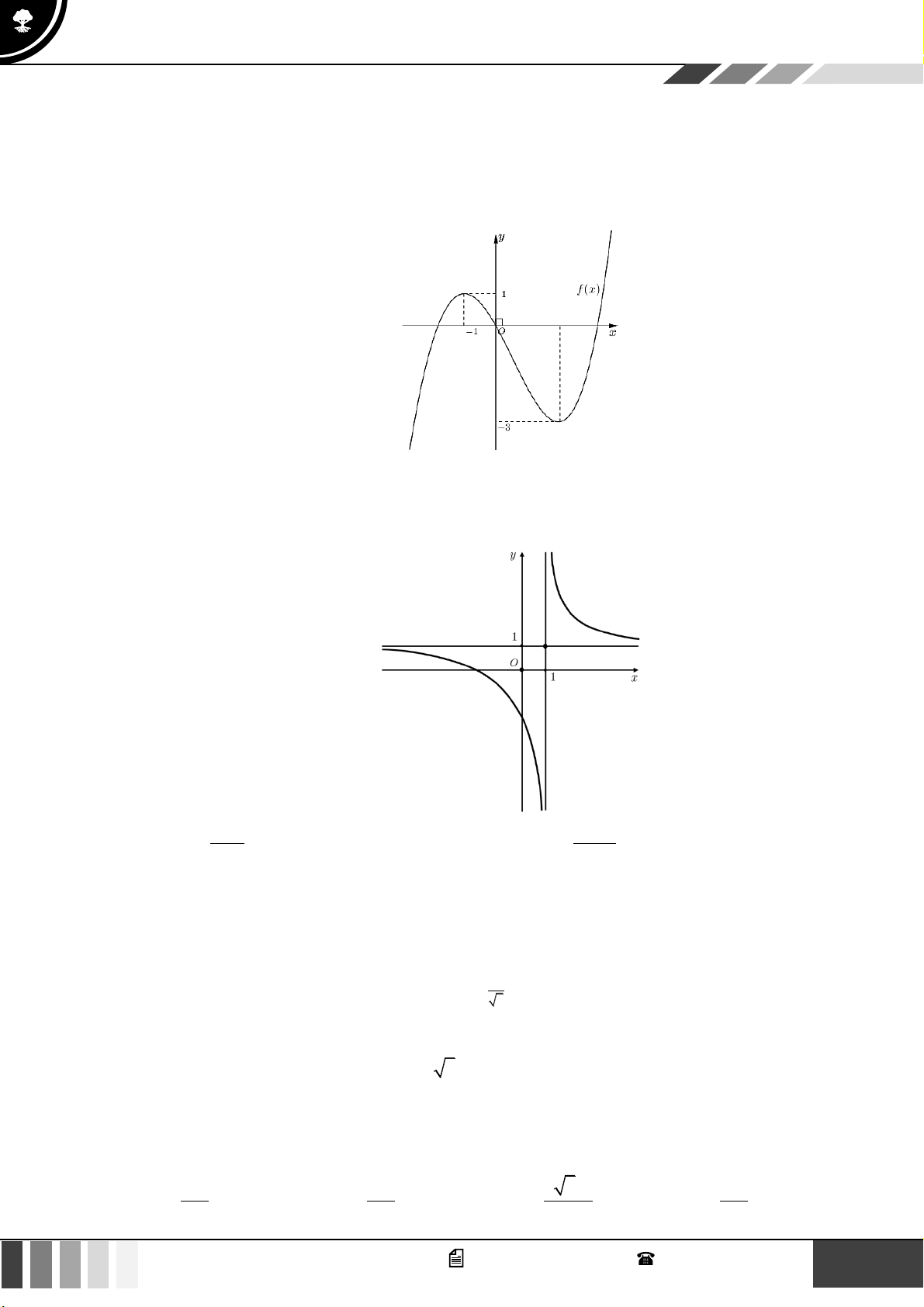
Câu 23: Cho đồ thị hàm số
( )
y f x=
có đồ thị như hình vẽ. Số nghiệm của phương trình
( )
f x x=
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 24: Cho hàm số
( )
2
2 4 3f x x x= − +
. Tìm
m
để phương trình
( )
2
31f x m m= − +
có 2 nghiệm
phân biệt.
A.
3
0
m
m
. B.
03m
. C.
3
0
m
m
. D.
03m
.
Câu 25: Cho hàm số
3
=−y x x
có đồ thị
( )
C
. Gọi
,MN
là hai điểm phân biệt trên
( )
C
và các tiếp
tuyến của
( )
C
tại các điểm
,MN
song song với nhau. Tính
+
MN
xx
.
A.
1
. B.
2
. C.
0
. D.
2−
.
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Câu 26: Cho hàm số
( )
P
với
m
là tham số. Có bao nhiêu giá trị nguyên của
m
để hàm số nghịch biến
trên
( )
;− +
A.
6
. B.
3
. C.
7
. D.
4
.
Câu 27: Cho hàm số bậc ba
32
y ax bx cx d= + + +
có đồ thị như hình vẽ sau.
Có bao nhiêu số dương trong các số
, , ,a b c d
?
A. 0. B. 1. C. 2. D. 3.
Câu 28: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
+
=
−
. B.
3
31y x x= − −
. C.
21
1
x
y
x
−
=
−
. D.
42
1y x x= + +
.
Câu 29: Một người gửi ngân hàng
100
triệu theo hình thức lãi kép với lãi suất
0,5%
một tháng. Sau ít
nhất bao nhiêu tháng người đó có nhiều hơn
125
triệu.
A. 44 tháng. B. 45 tháng. C. 46 tháng. D. 47 tháng.
Câu 30: Tích tất cả các nghiệm của phương trình
( )
1
1
5
log 6 36 2
xx+
− = −
là:
A.
6
log 5
. B.
0
. C.
5
. D.
1
.
Câu 31: Cho lăng trụ
.ABC A B C
có
3AC a=
,
3BC a=
,
30ACB =
. Gọi
H
là điểm nằm trên cạnh
BC
sao cho
2HC HB=
. Hai mặt phẳng
( )
A AH
và
( )
A BC
cùng vuông góc với
( )
ABC
.
Cạnh bên hợp với đáy một góc
60
. Thể tích khối lăng trụ
.ABC A B C
là:
A.
3
9
4
a
. B.
3
3
4
a
. C.
3
33
4
a
. D.
3
9
2
a
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Câu 32: Tìm nguyên hàm của hàm số
53
1dx x x−
.
A.
( )
2
33
3
11
21
3 2 3
xx
x
C
−−
−
−+
. B.
( )
3
2
3
3
2 1 1
1
35
31
x
xC
x
−
− − + +
−
.
C.
( )
3
2
3
3
2 1 1
1
35
31
x
xC
x
−
− − − +
−
. D.
( )
2
33
3
11
21
3 2 3
xx
x
C
−−
−
++
.
Câu 33: Cho hàm số
( )
32
12y x mx m x= − + − +
. Để hàm số đạt cực tiểu tại
1x =
thì tham số
m
thuộc
khoảng nào trong các khoảng sau?
A.
( )
1;1−
. B.
( )
1;3
. C.
( )
4;7
. D.
( )
5; 3−−
.
Câu 34: Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng
48
và chiều dài gấp đôi chiều rộng.
Chất liệu làm đáy và
4
mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp
hộp. Gọi
h
là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết
m
h
n
=
với
m
,
n
là các
số nguyên dương nguyên tố cùng nhau. Tổng
mn+
là
A.
12
. B.
13
. C.
11
. D.
14
.
Câu 35: Một khách hàng gửi ngân hàng
20
triệu đồng, kỳ hạn
3
tháng, với lãi suất
0,65
một tháng
theo phương thức lãi kép. Hỏi sau bao lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc
ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.
A.
8
năm. B.
19
tháng. C.
18
tháng. D.
9
năm.
Câu 36: Cho phương trình
( )
( )
2
0,2 5
log 5 1 log 4 3 0x m x x+ + + − − =
(
m
là tham số). Có bao nhiêu giá
trị nguyên dương của
m
để phương trình có nghiệm thực?
A.
18
B.
17
C.
23
D.
15
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
, cạnh
a
. Cạnh bên
SA
vuông
góc với đáy và
60SBD =
(tham khảo hình bên dưới). Khoảng cách giữa hai đường thẳng
AB
và
SO
bằng
A.
5
5
a
. B.
5
2
a
. C.
2
2
a
. D.
2
5
a
.
Câu 38: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
( )
2
ln 1 1f x x mx= + − +
đồng biến
trên khoảng
( )
;− +
là:
A.
( )
1;− +
. B.
(
;1− −
. C.
1;1−
. D.
( )
;1− −
.

6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Câu 39: Cho hàm số
( )( )
1y f x x=−
xác định và liên tục trên có đồ thị như hình dưới đây.
Có tất cả bao nhiêu giá trị nguyên của tham số
24;24m−
để phương trình
( )
2
1f x x m m− = −
có hai nghiệm có hoành độ nằm ngoài đoạn
1;1−
.
A.
45
. B.
47
. C.
44
. D.
46
.
Câu 40: Khối bát diện đều có độ dài cạnh bằng
a
thì mặt cầu nội tiếp mặt cầu có diện tích bằng:
A.
2
2 a
. B.
2
a
. C.
2
4 a
. D.
2
3 a
.
Câu 41: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích
V
. Gọi
E
là điểm trên
cạnh
SC
sao cho
2EC ES=
,
( )
là mặt phẳng chứa đường thẳng
AE
và song song với đường
thẳng
BD
,
( )
cắt hai cạnh
,SB SD
lần lượt tại hai điểm
,MN
. Tính theo
V
thể tích khối chóp
.S AMEN
.
A.
3
V
. B.
6
V
. C.
12
V
. D.
2
9
V
.
Câu 42: Cho phương trình
2
2
33
log 3 log 2 2 1 0
3
x
m x m m
+ + − − =
. Có bao nhiêu giá trị nguyên của
tham số
m
lớn hơn
2024−
sao cho phương trình đã cho có hai nghiệm phân biệt
12
,xx
thoả
12
10xx+
?
A.
2023
. B.
2019
. C.
2020
. D.
2021
.
Câu 43: Số giá trị thực của tham số
0;24m
để phương trình
4 2 2 2 0
xx
mm− + + =
có hai nghiệm
phân biệt.
A.
22
. B.
21
. C.
24
. D.
20
.
Câu 44: Số các giá trị nguyên của tham số
m
để phương trình
( ) ( )
2
2
log 1 log 8x mx− = −
có hai
nghiệm thực phân biệt?
A. 4. B. 5. C. Vô số. D. 3.
Câu 45: Cho hai số thực dương
a
và
b
thỏa mãn hàm số
( )
3
4
cos 2 1
1
aa
y x x b
b
+
= + +
+
đồng biến trong
khoảng
( )
;− +
. Tìm giá trị lớn nhất của biểu thức
3
27 8S b a=−
.
A.
40
. B.
351
. C.
345
. D.
81
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Câu 46: Năm
2023
, tỉ lệ thể tích khí
2
CO
trong không khí là
6
397
10
. Biết rằng tỉ lệ thể tích khí
2
CO
trong
không khí tăng
0,4%
mỗi năm. Vậy ít nhất đến năm bao nhiêu thì tỉ lệ thể tích khí
2
CO
trong
không khí vượt ngưỡng
5
41
10
.
A.
2029
. B.
2031
. C.
2028
. D.
2033
.
Câu 47: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
( )
ABC
,
0
3 , 60 .SA AC AB BAC= = =
Gọi
,HK
lần lượt là hình chiếu của
A
lên
,SB SC
. Gọi
12
,SS
lần lượt là diện tích của mặt cầu
ngoại tiếp hình chóp
.S AHK
và hình chóp
.A BCKH
. Tính
1
2
S
S
A.
1
2
27
28
S
S
=
. B.
1
2
27
92
S
S
=
. C.
1
2
81
28
S
S
=
. D.
1
2
4
3
S
S
=
.
Câu 48: Cho các số thực
,,x y z
thỏa mãn
2
33
2 1 0.
xy
x y z y yz
− + − − + =
. Tìm giá trị nhỏ nhất của biểu
thức
( ) ( )
22
, , 9 2 3 1P x y z x y x y z= + − − +
.
A.
0
. B.
1
2
. C.
1
. D.
1
2
−
.
Câu 49: Có bao nhiêu giá trị nguyên của tham số
0;2024m
để đồ thị của hàm số
2
1
24
x
y
x mx
−
=
−+
có đúng 3 đường tiệm cận.
A.
2024
. B.
2021
. C.
2022
. D.
2022
.
Câu 50: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới. Hỏi có bao nhiêu giá trị nguyên của tham
số
2024;2024m−
để phương trình
( ) ( ) ( )
3
22
4 2 0f x f x mf x m− + − =
có đúng hai
nghiệm thực (Giả thiết rằng các nghiệm bội chỉ được tính là một nghiệm)?
A.
3976
. B.
3971
. C.
3974
. D.
3975
.
-----------------------HẾT-----------------------
8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
BẢNG ĐÁP ÁN
1.A
2.A
3.C
4.D
5.A
6.A
7.D
8.D
9.D
10.D
11.D
12.D
13.D
14.D
15.A
16.B
17.B
18.C
19.D
20.B
21.C
22.D
23.D
24.A
25.C
26.C
27.B
28.A
29.B
30.B
31.A
32.C
33.B
34.C
35.D
36.A
37.A
38.B
39.B
40.A
41.B
42.A
43.A
44.D
45.B
46.D
47.A
48.A
49.C
50.A
HƯỚNG DẪN GIẢI CHI TIẾT
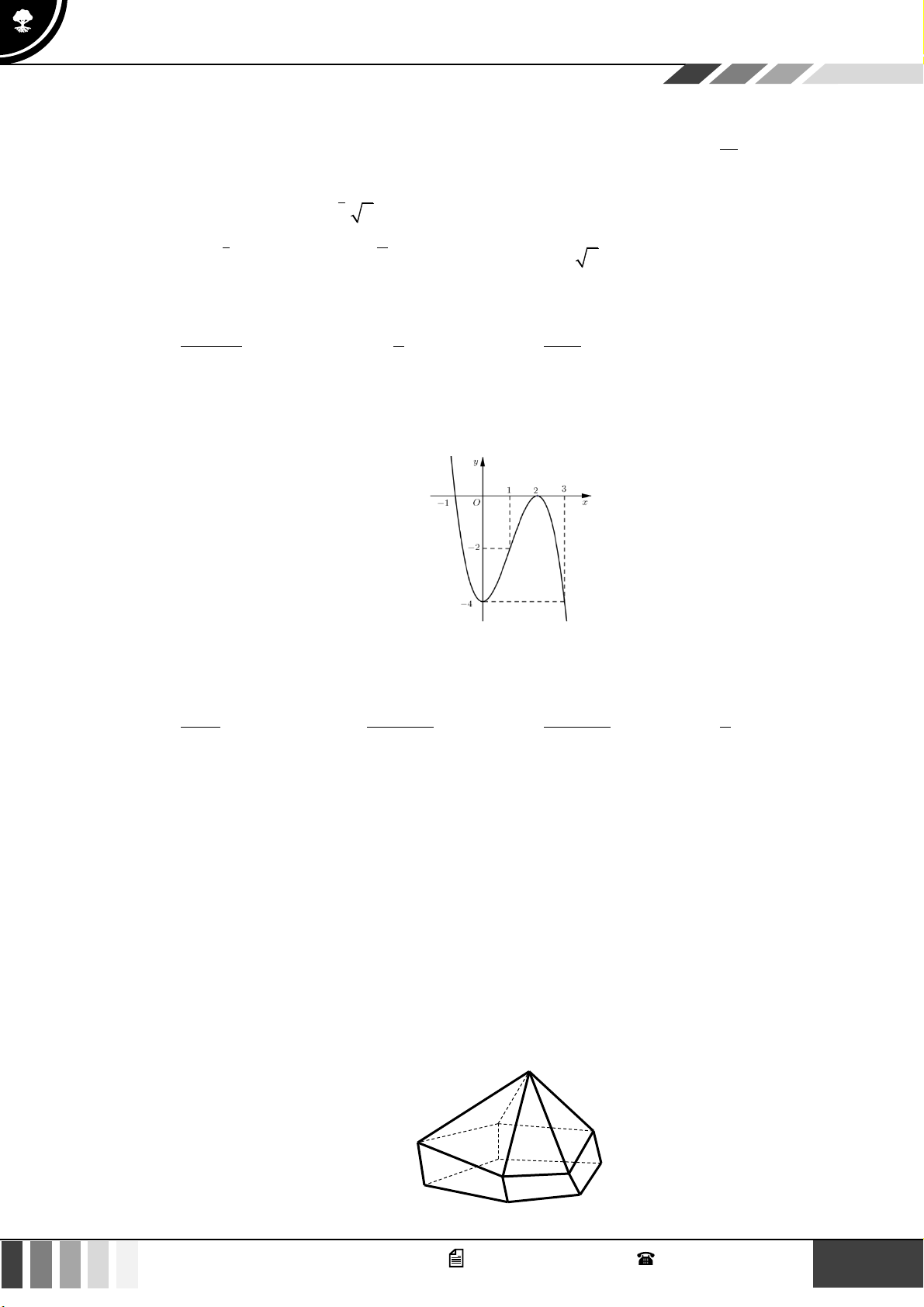
Câu 1: Cho hàm số bậc bốn
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1; +
. B.
( )
1;1−
. C.
( )
;0−
. D. .
Lời giải
Nhìn đồ thị ta thấy đồ thị hàm số đi lên trên khoảng
( )
1; +
.
Câu 2: Hàm số
1
2
yx=
có tập xác định là
A.
( )
0;+
. B.
)
0;+
. C.
( )
1; +
. D. .
Lời giải
Do
1
2
nên tập xác định của hàm số là
( )
0;+
.
Câu 3: Cho hàm số
( )
y f x=
liên tục trên và có đạo hàm
( ) ( )( )
11f x x x
= + −
. Số điểm cực trị của
hàm số
( )
y f x=
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Ta có:
( ) ( )( )
1
1 1 0
1
x
f x x x
x
=
= + − =
=−
Phương trình
( )
0fx
=
có hai nghiệm bội lẻ nên hàm số có hai điểm cực trị.
Câu 4: Điểm cực đại của đồ thị hàm số
42
29y x x= − +
có tọa độ là:
A.
( )
1;9
. B.
( )
2;9
. C.
( )
2;9−
. D.
( )
0;9
.
Lời giải
Ta có:
3
44y x x
=−
. Giải phương trình:
0y
=
3
4 4 0xx−=
1;0;1x =−
Bảng biến thiên:

GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Vậy điểm cực đại của đồ thị hàm số là
( )
0;9
.
Câu 5: Cho hình nón
( )
N
có đường kính đáy bằng
4a
, đường sinh bằng
5a
. Tính diện tích xung quanh
S
của hình nón
( )
N
.
A.
2
10Sa
=
. B.
2
14Sa
=
. C.
2
36Sa
=
. D.
2
20Sa
=
.
Lời giải
Diện tích xung quanh của hình nón
( )
N
là:
S rl
=
.2 .5aa
=
2
10 a
=
.
Câu 6: Tìm giá trị lớn nhất của hàm số
31
3
x
y
x
−
=
−
trên
0;2
.
A.
1
3
. B.
5
. C.
1
3
−
. D.
5−
.
Lời giải
Hàm số đã cho xác định và liên tục trên đoạn
0;2
và có đạo hàm:
( )
2
8
0, 0;2
3
yx
x
−
=
−
Khi đó:
( ) ( )
1
0 ; 2 5
3
yy= = −
nên suy ra
0;2
1
max
3
y =
khi
0.x =
Câu 7: Cho hàm số
( )
y f x=
có
( )
lim 2024
x
fx
→+
=
và
( )
lim 2024
x
fx
→−
=−
. Khẳng định nào sau đây
đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
2024y =
và
2024x =−
.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
2024y =
và
2024y =−
.
Lời giải
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
2024y =
và
2024y =−
.
Câu 8: Cho hình trụ có bán kính đáy bằng
4
và độ dài đường sinh bằng
3l =
. Thể tích của khối trụ đã
cho bằng
A.
12
. B.
24
. C.
19
. D.
48
.
Lời giải
Thể tích của khối trụ đã cho bằng
22
.4 .3 48V r l
= = =
.
Câu 9: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây.
A.
42
1y x x= − + −
. B.
42
31y x x= − −
. C.
3
31y x x= − − −
. D.
3
31y x x=−−
.
Lời giải
Đường cong trong hình vẽ là đồ thị của hàm số
32
y ax bx cx d= + + +
với
0a
.
10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Do đó đây là đồ thị của hàm số
3
31y x x=−−
.
Câu 10: Tìm số giao điểm của
( )
3
:3C y x x= + −
và đường thẳng
2yx=−
?
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Phương trình hoành độ giao điểm:
33
3 2 1 1x x x x x+ − = − = =
.
Vậy có
1
giao điểm giữa
( )
C
và đường thẳng
2yx=−
.
Câu 11: Mỗi hình sau gồm một số hữu hạn đa giác phẳng, tìm hình đa diện.
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 4. B. Hình 2. C. Hình 3. D. Hình 1.
Lời giải
Đoạn thẳng nối hai điểm bất kì từ hai cạnh của đa giác đều phải nằm trong đa giác đó
Hình
2,3,4 không thỏa mãn.
Câu 12: Cho
, , 0; 1;a x y a
. Khẳng định nào sau đây sai?
A.
( )
log . log log
a a a
x y x y=+
. B.
log log
aa
xx
=
.
C.
1
log log
2
aa
xx=
. D.
1
log log
2
a
a
xx=
.
Lời giải
Ta có:
1
2
log log 2log
a
a
a
x x x==
nên đáp án D sai.
Câu 13: Thể tích của khối chóp có diện tích đáy bằng
B
và cạnh bên bằng
h
là
A.
1
.
2
Bh
. B.
3.Bh
. C.
.Bh
. D.
1
.
3
Bh
.
Lời giải
Thể tích của khối chóp có diện tích đáy bằng
B
và cạnh bên bằng
h
là
1
.
3
V B h=
.
Câu 14: Trong các mệnh đề sau, mệnh đề nào sai?
A.
( ) ( )
df x x f x C
=+
. B.
cos d sinx x x C=+
.
C.
1
d , 1
1
x
x x C
+
= + −
+
. D.
d ln
xx
a x a a C=+
( )
01a
.
Lời giải
Ta có
d
ln
x
x
a
a x C
a
=+
( )
01a
nên phương án D sai.
Câu 15: Thể tích của khối lập phương cạnh
a
bằng:
A.
3
a
. B.
2
a
. C.
3
1
3
a
. D.
2
1
3
a
.
Lời giải
Thể tích của khối lập phương có cạnh
a
bằng:
3
Va=
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Câu 16: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
3 2 2
1 3 2y x m x x m= − + + − +
đồng biến trên
.
A.
2
4
m
m
−
. B.
42m−
. C.
42m−
. D.
2
4
m
m
−
.
Lời giải
Hàm số
( )
3 2 2
1 3 2y x m x x m= − + + − +
có
( )
2
3 2 1 3y x m x
= − + +
.
Để hàm số đã cho đồng biến trên
0y
,
x
.
Ta có
( )
2
3 2 1 3y x m x
= − + +
là tam thức bậc hai có hệ số của
2
x
bằng
30
và biệt thức
( )
2
19m
= + −
.
Do đó
0
( )
2
1 9 0m + −
( )
2
19m +
3 1 3m− +
42m −
.
Câu 17: Số nghiệm thực của phương trình
( )
( )
2
2024 2024
log 3 2 log 1x x x− + = −
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Điều kiện:
2
3 2 0
10
xx
x
− +
−
2
1
1
x
x
x
2x
.
Phương trình đã cho tương đương với
2
3 2 1x x x− + = −
2
4 3 0xx − + =
1
3
x
x
=
=
.
Kết hợp với điều kiện
2x
, suy ra phương trình có nghiệm duy nhất
3x =
.
Câu 18: Cho hình nón có thiết diện qua trục là tam giác đều có cạnh bằng
4
. Diện tích toàn phần của
hình nón đã cho bằng
A.
3
. B.
8
. C.
12
. D.
9
.
Lời giải
Theo bài ra, thiết diện qua trục là tam giác đều cạnh bằng
4
nên ta có:
4l =
;
2
2
l
r ==
.
Diện tích toàn phần của hình nón đã cho là:
22
.2.4 .2 12
tp xq day
S S S rl r
= + = + = + =
.
Câu 19: Tìm giá trị nhỏ nhất của hàm số
( )
cosx
fx
x
=
trên đoạn
;
63
.
A.
33
. B.
32
. C.
33
2
. D.
3
2
.
Lời giải
12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Ta có
( )
2
sin cos
0
x x x
fx
x
−−
=
,
;
63
x
suy ra
( )
;
63
3
min
32
f x f
==
.
Câu 20: Tập nghiệm của bất phương trình
( )
1
9
1
log 1
2
x − −
là
A.
( )
1;4
. B.
(
1;4
. C.
)
4;+
. D.
(
;4−
.
Lời giải
Điều kiện xác định:
1 0 1xx−
Vì
1
01
9
nên
( )
1
2
1
9
11
log 1 1 1 3 4
29
x x x x
−
− − − −
.
Kết hợp với điều kiện, ta có
14x
. Vậy tập nghiệm của bất phương trình là
(
1;4S =
.
Câu 21: Hàm số nào dưới đây có dạng đồ thị như hình vẽ?
A.
3
31y x x=−+
B.
42
21y x x= − +
.
C.
2024
x
y =
. D.
( )
2024
log 2024yx=+
.
Lời giải
Do đồ thị hàm số luôn đồng biến trên nên loại các phương án A, B.
Mà đồ thị luôn nằm phía trên trục
Ox
nên loại phương án D.
Câu 22: Cho biết
( )( )
2 13
d ln 1 ln 2
12
x
x a x b x C
xx
−
= + + − +
+−
. Mệnh đề nào sau đây đúng?
A.
28ab+=
. B.
8ab+=
. C.
28ab−=
. D.
8ab−=
.
Lời giải
Ta có
( )( )
2 13
d
12
x
x
xx
−
+−
53
d
12
x
xx
=−
+−
11
5 d 3 d
11
xx
xx
=−
+−
5ln 1 3ln 2x x C= + − − +
.
Vậy
5
3
a
b
=
=−
8ab − =
.
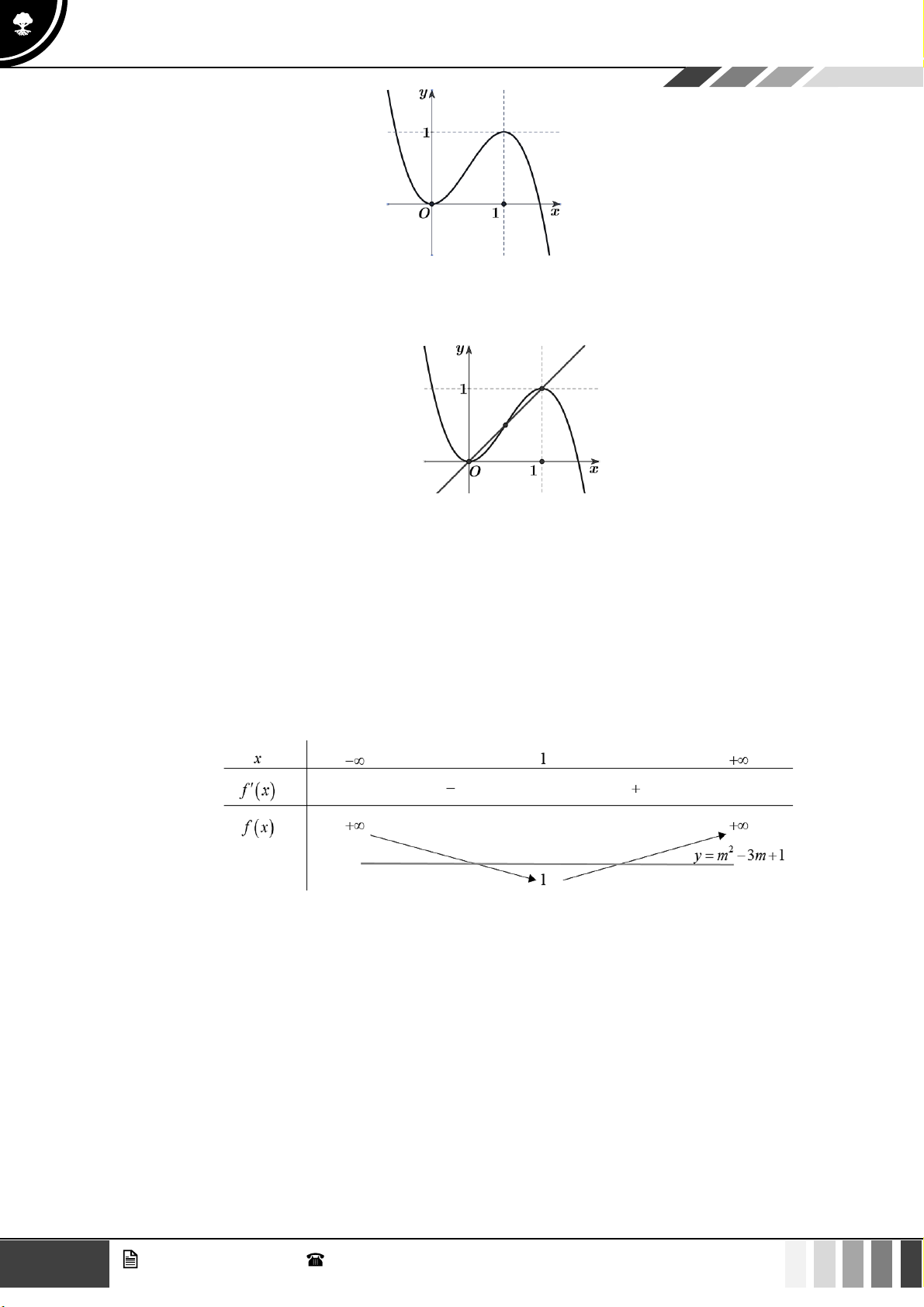
Câu 23: Cho đồ thị hàm số
( )
y f x=
có đồ thị như hình vẽ. Số nghiệm của phương trình
( )
f x x=
là:
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Số nghiệm của phương trình
( )
f x x=
bằng số giao điểm của đồ thị hàm số
( )
y f x=
và
yx=
.
Dựa và hình vẽ suy ra phương trình
( )
f x x=
có
3
nghiệm.
Câu 24: Cho hàm số
( )
2
2 4 3f x x x= − +
. Tìm
m
để phương trình
( )
2
31f x m m= − +
có 2 nghiệm
phân biệt.
A.
3
0
m
m
. B.
03m
. C.
3
0
m
m
. D.
03m
.
Lời giải
Ta có:
( )
4 4 0 1f x x x
= − = =
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy:
Phương trình
( )
2
31f x m m= − +
có 2 nghiệm phân biệt
2
3
3 1 1
0
m
mm
m
− +
Câu 25: Cho hàm số
3
=−y x x
có đồ thị
( )
C
. Gọi
,MN
là hai điểm phân biệt trên
( )
C
và các tiếp
tuyến của
( )
C
tại các điểm
,MN
song song với nhau. Tính
+
MN
xx
.
A.
1
. B.
2
. C.
0
. D.
2−
.
Lời giải
Ta có
2
31
=−yx
.
Vì các tiếp tuyến của
( )
C
tại các điểm
,MN
song song với nhau nên:
( ) ( ) ( )( )
22
3 1 3 1 0
M N M N M N M N
y x y x x x x x x x
= − = − − + =
0
MN
xx + =
do
,MN
là hai điểm phân biệt.
14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Câu 26: Cho hàm số
( )
P
với
m
là tham số. Có bao nhiêu giá trị nguyên của
m
để hàm số nghịch biến
trên
( )
;− +
A.
6
. B.
3
. C.
7
. D.
4
.
Lời giải
Ta có:
2
3 2 4 9y x mx m
= − − + +
Hàm số nghịch biến trên
2
30
93
12 27 0
a
m
mm
= −
− −
= + +
Mà
9; 8;...; 3mm = − − −
. Vậy có tất cả 7 giá trị nguyên của m thỏa mãn yêu cầu bài
toán.
Câu 27: Cho hàm số bậc ba
32
y ax bx cx d= + + +
có đồ thị như hình vẽ sau.
Có bao nhiêu số dương trong các số
, , ,a b c d
?
A. 0. B. 1. C. 2. D. 3.
Lời giải
Ta có:
2
32y ax bx c
= + +
Dựa vào hình dạng đồ thị ta có
0a
.
Đồ thị hàm số qua gốc tọa độ nên
0d =
.
Hàm số có hai điểm cực trị
12
,xx
với
12
xx
nên
12
2
0 0 0
3
b
x x b
a
+ −
Khi đó:
12
0 0 0
3
c
x x c
a
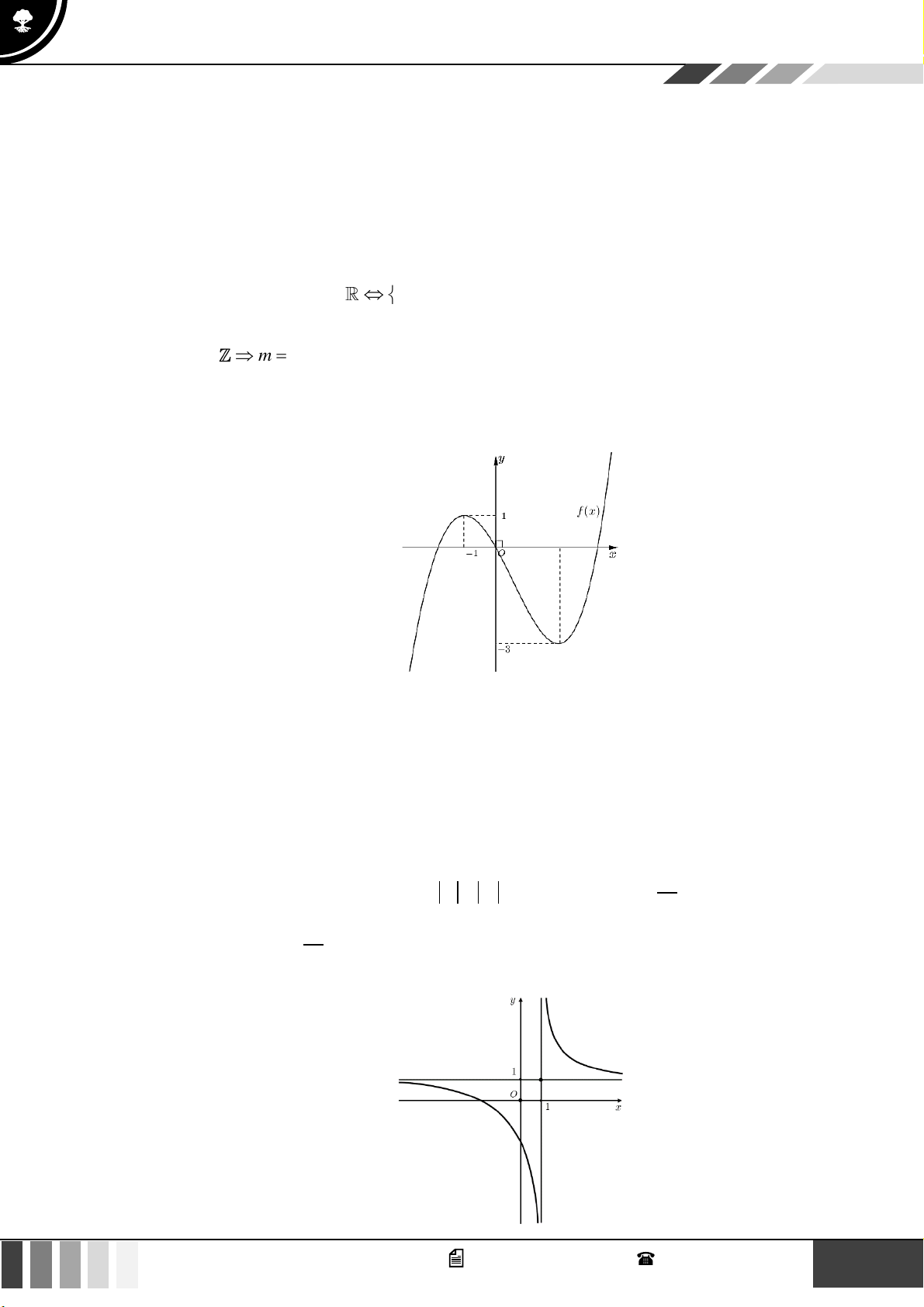
Câu 28: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
A.
1
1
x
y
x
+
=
−
. B.
3
31y x x= − −
. C.
21
1
x
y
x
−
=
−
. D.
42
1y x x= + +
.
Lời giải
Đồ thị hàm số có một tiệm cận ngang
1y =
và một tiệm cận đứng
1x =
.
Vậy hàm số đó là:
1
1
x
y
x
+
=
−
Câu 29: Một người gửi ngân hàng
100
triệu theo hình thức lãi kép với lãi suất
0,5%
một tháng. Sau ít
nhất bao nhiêu tháng người đó có nhiều hơn
125
triệu.
A. 44 tháng. B. 45 tháng. C. 46 tháng. D. 47 tháng.
Lời giải
Số tiền thu được sau n tháng là
( )
100 1 0,5%
n
n
P =+
Ta có
125
n
P
( )
1 0,5%
125
log 44,7
100
n
+
.
Vậy sau ít nhất
45
tháng thì người đó có nhiều hơn 125 tr.
Câu 30: Tích tất cả các nghiệm của phương trình
( )
1
1
5
log 6 36 2
xx+
− = −
là:
A.
6
log 5
. B.
0
. C.
5
. D.
1
.
Lời giải
Phương trình tương đương
1
6
0
61
6 36 5 36 6.6 5 0
log 5
65
x
x x x x
x
x
x
+
=
=
− = − + =
=
=
.
Vậy tích các nghiệm bằng
0
.
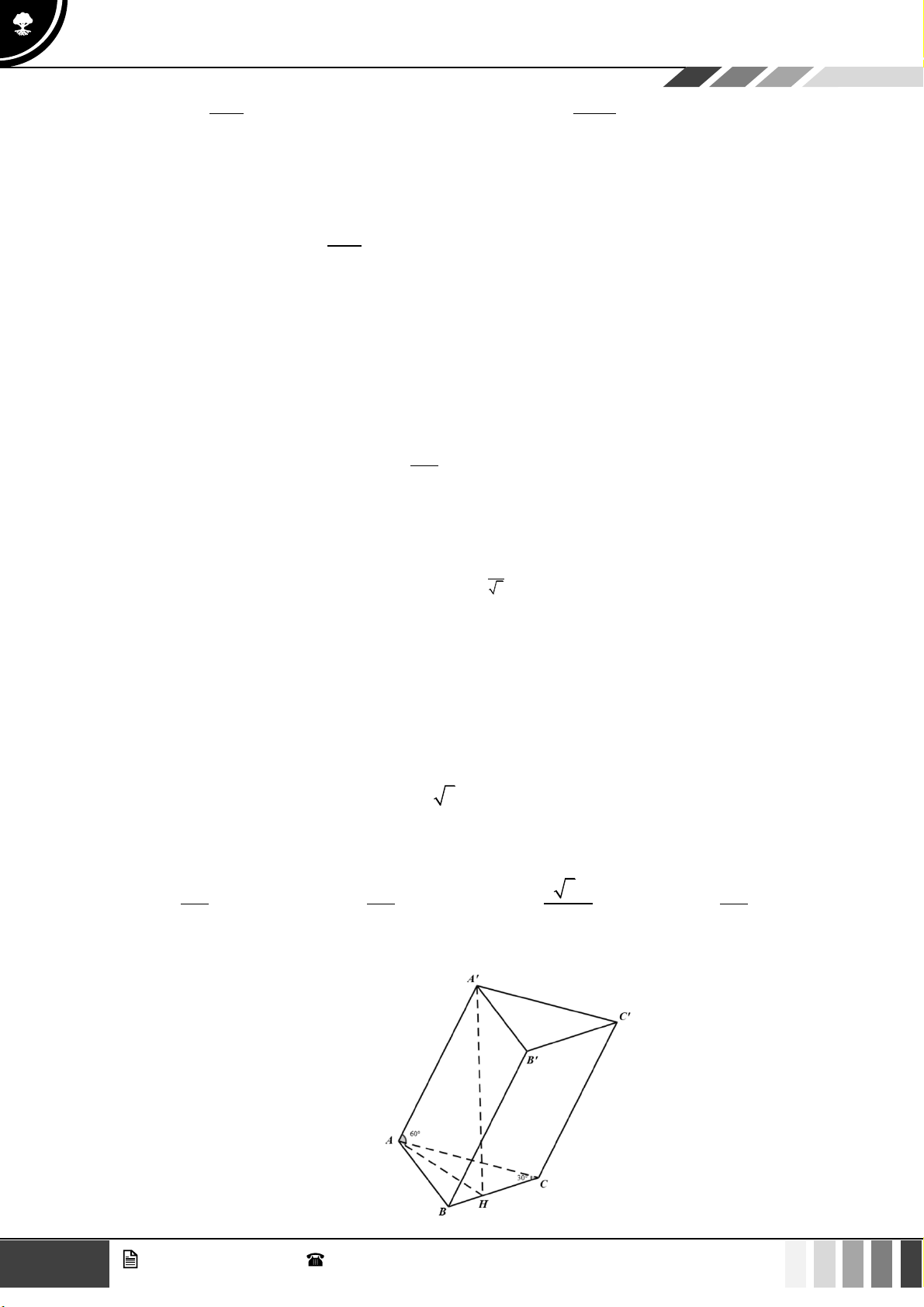
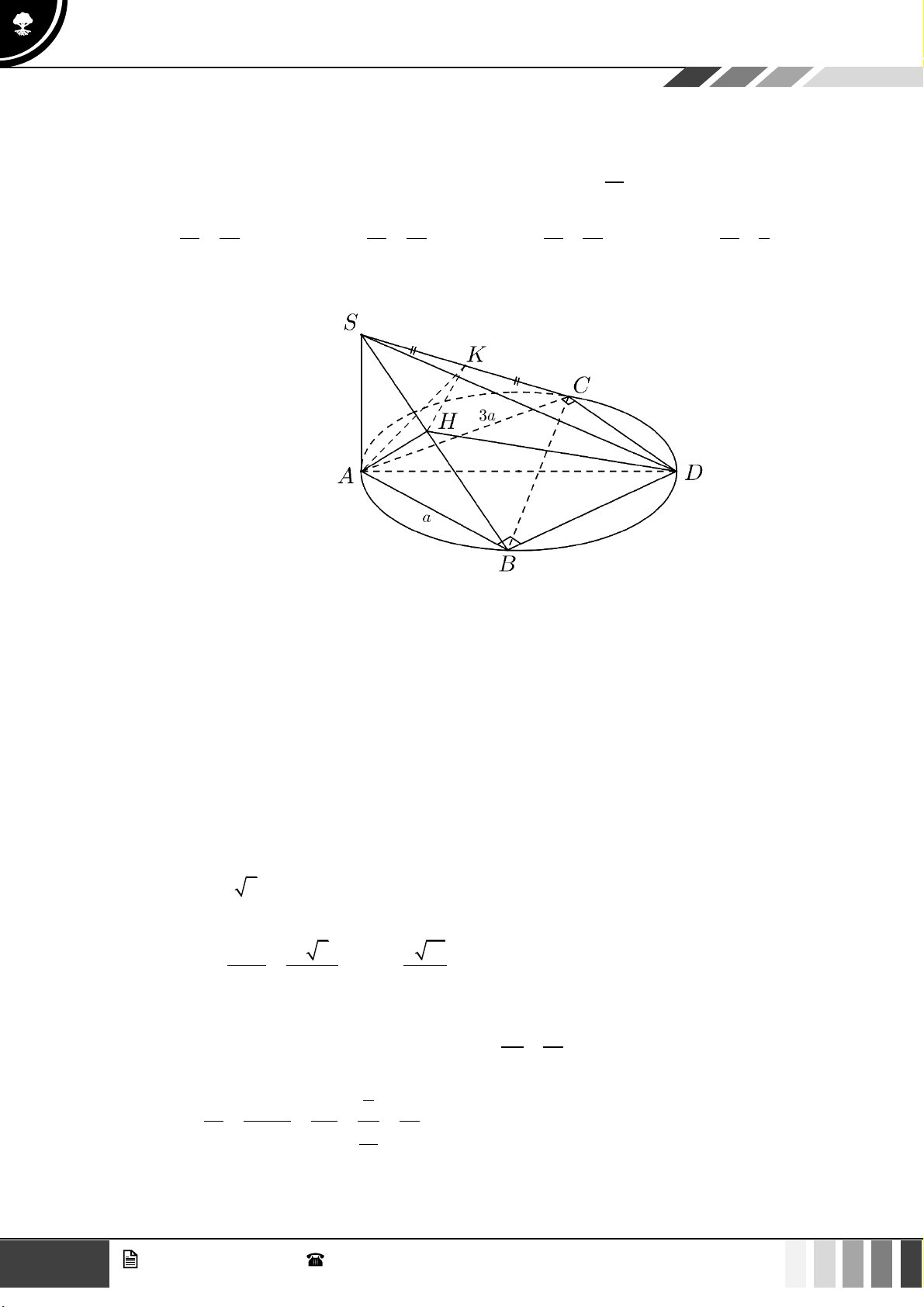
Câu 31: Cho lăng trụ
.ABC A B C
có
3AC a=
,
3BC a=
,
30ACB =
. Gọi
H
là điểm nằm trên cạnh
BC
sao cho
2HC HB=
. Hai mặt phẳng
( )
A AH
và
( )
A BC
cùng vuông góc với
( )
ABC
.
Cạnh bên hợp với đáy một góc
60
. Thể tích khối lăng trụ
.ABC A B C
là:
A.
3
9
4
a
. B.
3
3
4
a
. C.
3
33
4
a
. D.
3
9
2
a
.
Lời giải

16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Ta có
2
1 3 3
. .sin
24
ABC
a
S CB CA C
==
.
Từ giả thiết
( ) ( )
( ) ( )
( ) ( )
( )
A AH ABC
A BC ABC A H ABC
A AH A BC A H
⊥
⊥ ⊥
=
.
Do đó góc hợp bởi cạnh bên
AA
và đáy
( )
ABC
là
60A AH
=
.
Xét tam giác
AA H
ta có:
( )
( )
2
2
2 2 2 2
2 . .cos 3 2 2. 3 .2 cos30AH AC HC AC HC C a a a a a= + − = + − =
nên
AH a=
.
Xét tam giác
ACH
vuông tại
H
ta có
.tan60 3A H AH a
= =
.
Vậy thể tích khối lăng trụ
.ABC A B C
là:
23
3 3 9
. 3.
44
ABC
aa
V A H S a
= = =
.
Câu 32: Tìm nguyên hàm của hàm số
53
1dx x x−
.
A.
( )
2
33
3
11
21
3 2 3
xx
x
C
−−
−
−+
. B.
( )
3
2
3
3
2 1 1
1
35
31
x
xC
x
−
− − + +
−
.
C.
( )
3
2
3
3
2 1 1
1
35
31
x
xC
x
−
− − − +
−
. D.
( )
2
33
3
11
21
3 2 3
xx
x
C
−−
−
++
.
Lời giải
Ta có:
5 3 2 3 3
1 d 1 dI x x x x x x x= − = −
Đặt
3
1ux=−
23
1ux = −
22
2
2 d 3 d d d
3
u u x x x x u u = − = −
Khi đó:
( ) ( )
35
2 2 4
2 2 2
1 d d
3 3 3 3 5
uu
I u u u u u u u C
= − − = − − = − − +
Suy ra:
( )
3
2
3
3
2 1 1
1
35
31
x
I x C
x
−
= − − − +
−
Câu 33: Cho hàm số
( )
32
12y x mx m x= − + − +
. Để hàm số đạt cực tiểu tại
1x =
thì tham số
m
thuộc
khoảng nào trong các khoảng sau?
A.
( )
1;1−
. B.
( )
1;3
. C.
( )
4;7
. D.
( )
5; 3−−
.
Lời giải
Ta có:
2
3 2 1y x mx m
= − + −
62y x m
= −
Hàm số
( )
y f x=
đạt cực tiểu tại
1x =
( )
( )
10
10
f
f
=
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
( )
3 2 1 0 2
2 1;3
6 2 0 3
m m m
m
mm
− + − = =
=
−
Câu 34: Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng
48
và chiều dài gấp đôi chiều rộng.
Chất liệu làm đáy và
4
mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp
hộp. Gọi
h
là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết
m
h
n
=
với
m
,
n
là các
số nguyên dương nguyên tố cùng nhau. Tổng
mn+
là
A.
12
. B.
13
. C.
11
. D.
14
.
Lời giải
Gọi chiều dài, chiều rộng của hộp là
2x
và
x
( 0)x
.
Khi đó, ta có thể tích của cái hộp là:
2 2 2
2 . 2 . 48 . 24V x h x h x h= = =
Do giá thành làm đáy và mặt bên hộp là
3,
giá thành làm nắp hộp là
1
nên giá thành làm hộp là
( )
22
3 2 2 4 2L x xh xh x= + + +
Áp dụng bất đẳng thức Cô-si cho ba số không âm, ta được:
2
8 9 9L x xh xh= + +
3
2
3 8 .9 .9x xh xh
( )
2
2
3
3 648 216xh==
Dấu bằng xảy ra khi và chỉ khi:
2
2
89
24
x xh
xh
=
=
2
3
2
9
8
9
. 24
8
h
x
h
=
=
3
8
3
x
h
=
=
Vậy
8m =
,
3n =
và
11mn+=
.
Câu 35: Một khách hàng gửi ngân hàng
20
triệu đồng, kỳ hạn
3
tháng, với lãi suất
0,65
một tháng
theo phương thức lãi kép. Hỏi sau bao lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc
ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.
A.
8
năm. B.
19
tháng. C.
18
tháng. D.
9
năm.
Lời giải
Lãi suất theo kỳ hạn
3
tháng là
3.0,65 1,95 =
Gọi
n
là số kỳ hạn cần tìm. Theo giả thiết, ta có
n
là số tự nhiên nhỏ nhất thỏa:
20(1 0,0195) 20 20 35.89
n
n+ −
Ta chọn
36n =
, một kỳ hạn là
3
tháng, nên thời gian cần là
108
tháng, tức là
9
năm.
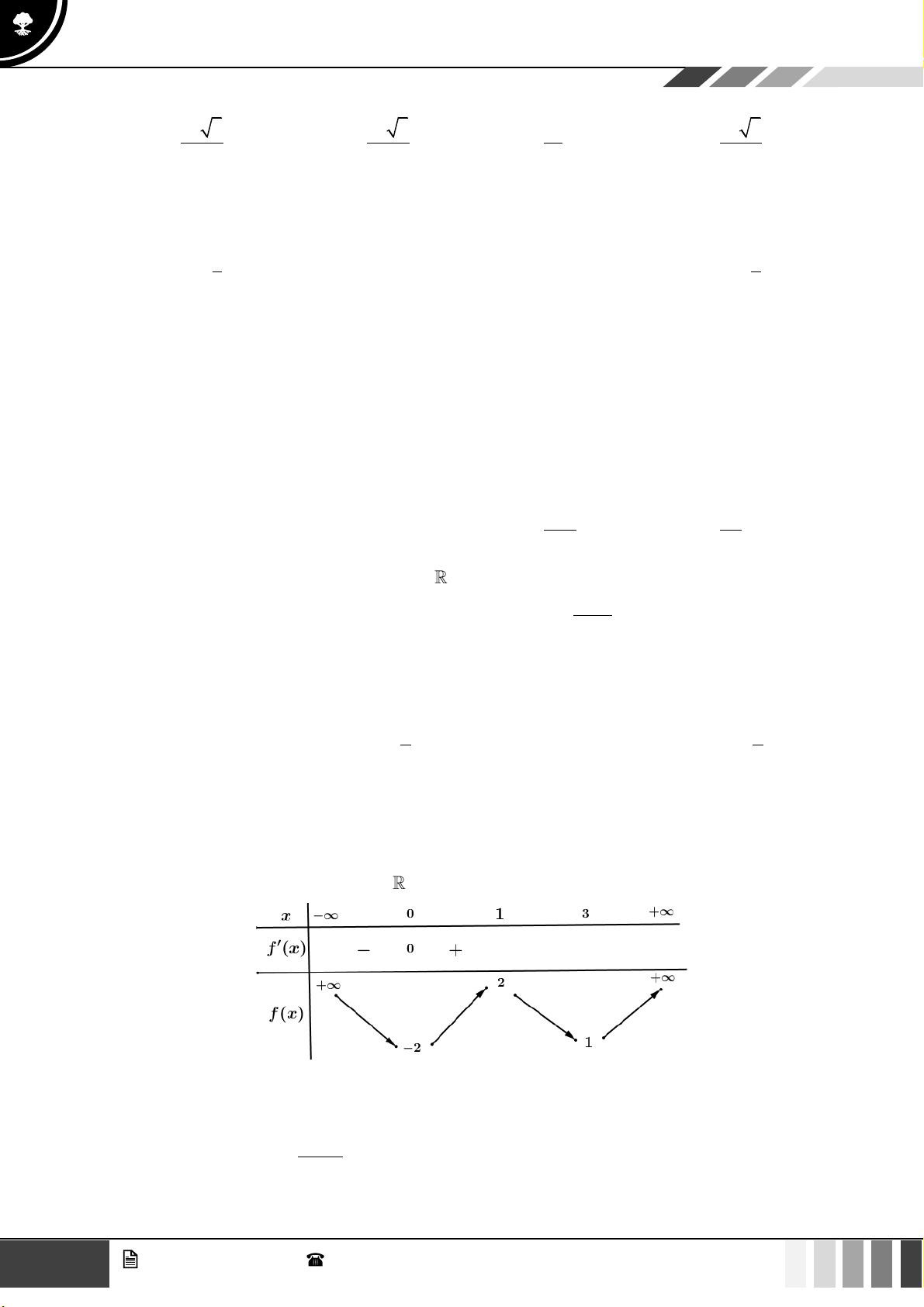
Câu 36: Cho phương trình
( )
( )
2
0,2 5
log 5 1 log 4 3 0x m x x+ + + − − =
(
m
là tham số). Có bao nhiêu giá
trị nguyên dương của
m
để phương trình có nghiệm thực?
A.
18
B.
17
C.
23
D.
15
Lời giải
Điều kiện
2
5 1 0
41
5 1 0
4 3 0
xm
x
xm
xx
+ +
−
+ +
− −
.
18
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Khi đó,
( )
( )
2
0,2 5
log 5 1 log 4 3 0x m x x+ + + − − =
( )
( )
2
55
log 4 3 log 5 1x x x m − − = + +
2
4 3 5 1x x x m − − = + +
2
38x x m − − =
( )
*
.
Xét hàm số
( )
2
83f x x x= − − +
trên
( )
4;1−
, ta có
( )
28f x x
= − −
;
( )
04f x x
= = −
.
Bảng biến thiên
Từ bảng biến thiên suy ra phương trình
( )
*
có nghiệm trên
( )
4;1−
6 19m −
.
Do
m
nguyên dương nên
1;2;...;18m
.
Vậy có
18
giá trị của
m
.
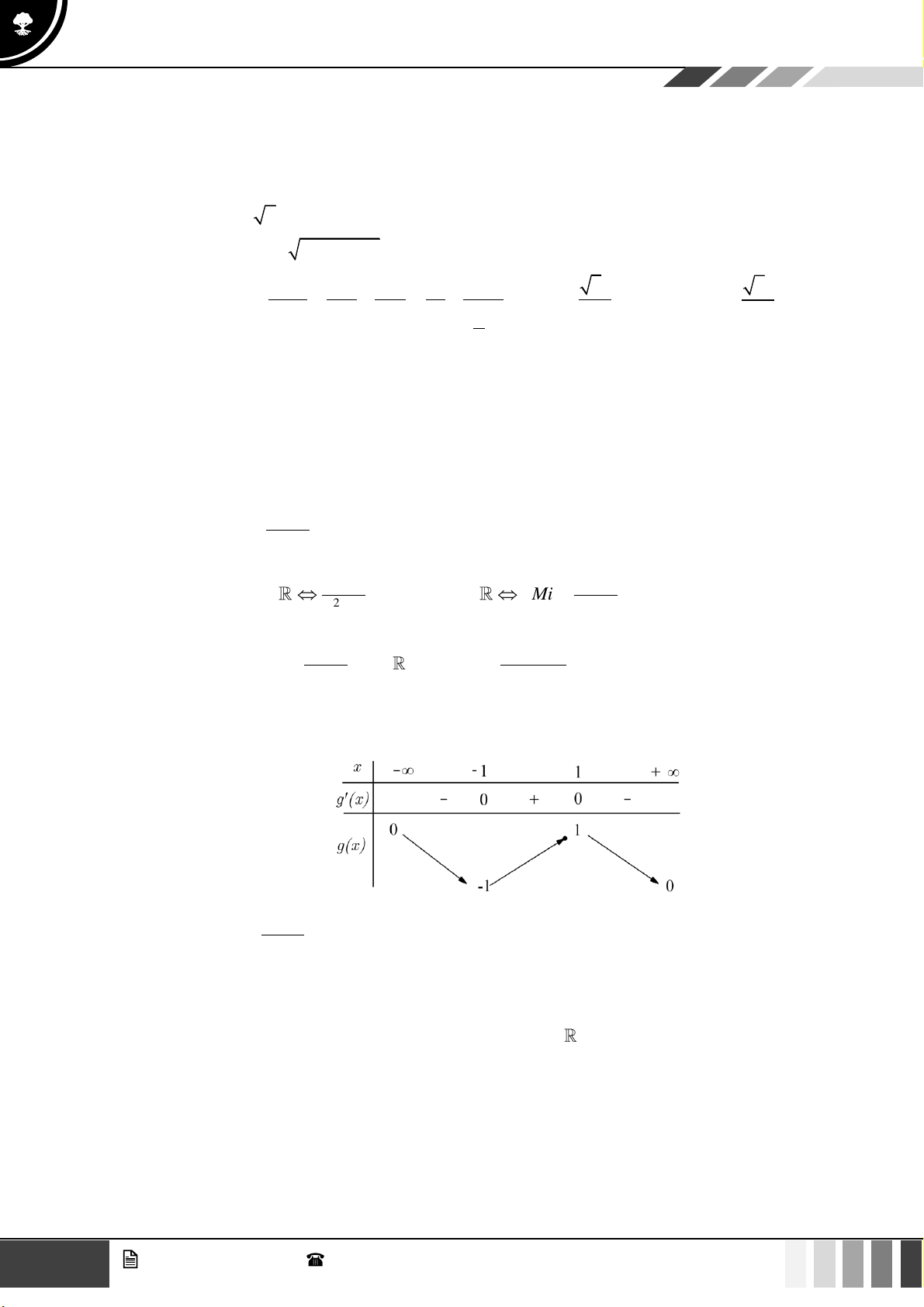
Câu 37: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
, cạnh
a
. Cạnh bên
SA
vuông
góc với đáy và
60SBD =
(tham khảo hình bên dưới). Khoảng cách giữa hai đường thẳng
AB
và
SO
bằng
A.
5
5
a
. B.
5
2
a
. C.
2
2
a
. D.
2
5
a
.
Lời giải
Gọi
I
là trung điểm
AD
suy ra
( )
//OI AB OI SAB⊥
Ta có:
( ) ( ) ( ) ( )
( )
( )
( )
/ / / / ; ; ;AB OI SOI AB SOI d AB SO d AB SOI d A SOI = =
GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Trong
( )
SAI
kẻ
( )
AH SI H SI⊥
OI AH⊥
Do đó:
( )
AH SOI⊥
( )
( )
;d A SOI AH=
Ta có:
( )
SAB SAD c g c SB SD = − − =
mà
60SBD SAD=
là tam giác đều.
2SB BD a==
.
Xét
SAB
:
22
SA SB AB a= − =
.
Xét
SAI
có:
2
2 2 2 2
1 1 1 1 1 5
5
2
a
AH
AH SA AI a
a
= + = + =
( )
5
;
5
a
d AB SO=
.
Câu 38: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
( )
2
ln 1 1f x x mx= + − +
đồng biến
trên khoảng
( )
;− +
là:
A.
( )
1;− +
. B.
(
;1− −
. C.
1;1−
. D.
( )
;1− −
.
Lời giải
Ta có
( )
2
2
1
x
f x m
x
=−
+
. Hàm số đồng biến trên khoảng
( )
;− +
khi và chỉ khi
( )
0fx
,
2
2
0
1
x
xm
x
−
+
,
( )
2
;
2
1
x
x Min m
x
− +
+
Xét hàm số
( )
2
2
1
x
gx
x
=
+
trên có
( )
( )
2
2
2
22
1
x
gx
x
−
=
+
và
( )
1
0
1
x
gx
x
=−
=
=
Bảng biến thiên :
Suy ra
( )
2
;
2
1
1
x
min
x
− +
=−
+
Vậy hàm số đồng biến trên khoảng
( )
;− +
khi và chỉ khi
1m −
.
Câu 39: Cho hàm số
( )( )
1y f x x=−
xác định và liên tục trên có đồ thị như hình dưới đây.
20
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Có tất cả bao nhiêu giá trị nguyên của tham số
24;24m−
để phương trình
( )
2
1f x x m m− = −
có hai nghiệm có hoành độ nằm ngoài đoạn
1;1−
.
A.
45
. B.
47
. C.
44
. D.
46
.
Lời giải
Số nghiệm của phương trình
( )
2
1f x x m m− = −
bằng số giao điểm của đường thẳng
2
y m m=−
và đồ thị hàm số
( )
1y f x x=−
.
Ta có
( )
1y f x x=−
( )( )
( )( )
1 khi 1
1 khi 1
f x x x
f x x x
−
=
− −
nên hàm số
( )
1y f x x=−
có đồ thị:
Giữ nguyên phần đồ thị của hàm số
( )( )
1y f x x=−
ứng với miền
1x
.
Lấy đối xứng qua
Ox
phần đồ thị của hàm số
( )( )
1y f x x=−
ứng với miền
1x
và bỏ phần
đồ thị của hàm số
( )( )
1y f x x=−
ứng với miền
1x
.
Để đường thẳng
2
y m m=−
cắt đồ thị hàm số
( )
1y f x x=−
tại
2
điểm có hoành độ nằm
ngoài đoạn
1;1−
thì đường thẳng
2
y m m=−
nằm hoàn toàn trên trục hoành.
Khi đó
2
0mm−
1m
hoặc
0m
suy ra có
47
giá trị
m
thỏa mãn.
Câu 40: Khối bát diện đều có độ dài cạnh bằng
a
thì mặt cầu nội tiếp mặt cầu có diện tích bằng:
A.
2
2 a
. B.
2
a
. C.
2
4 a
. D.
2
3 a
.
Lời giải
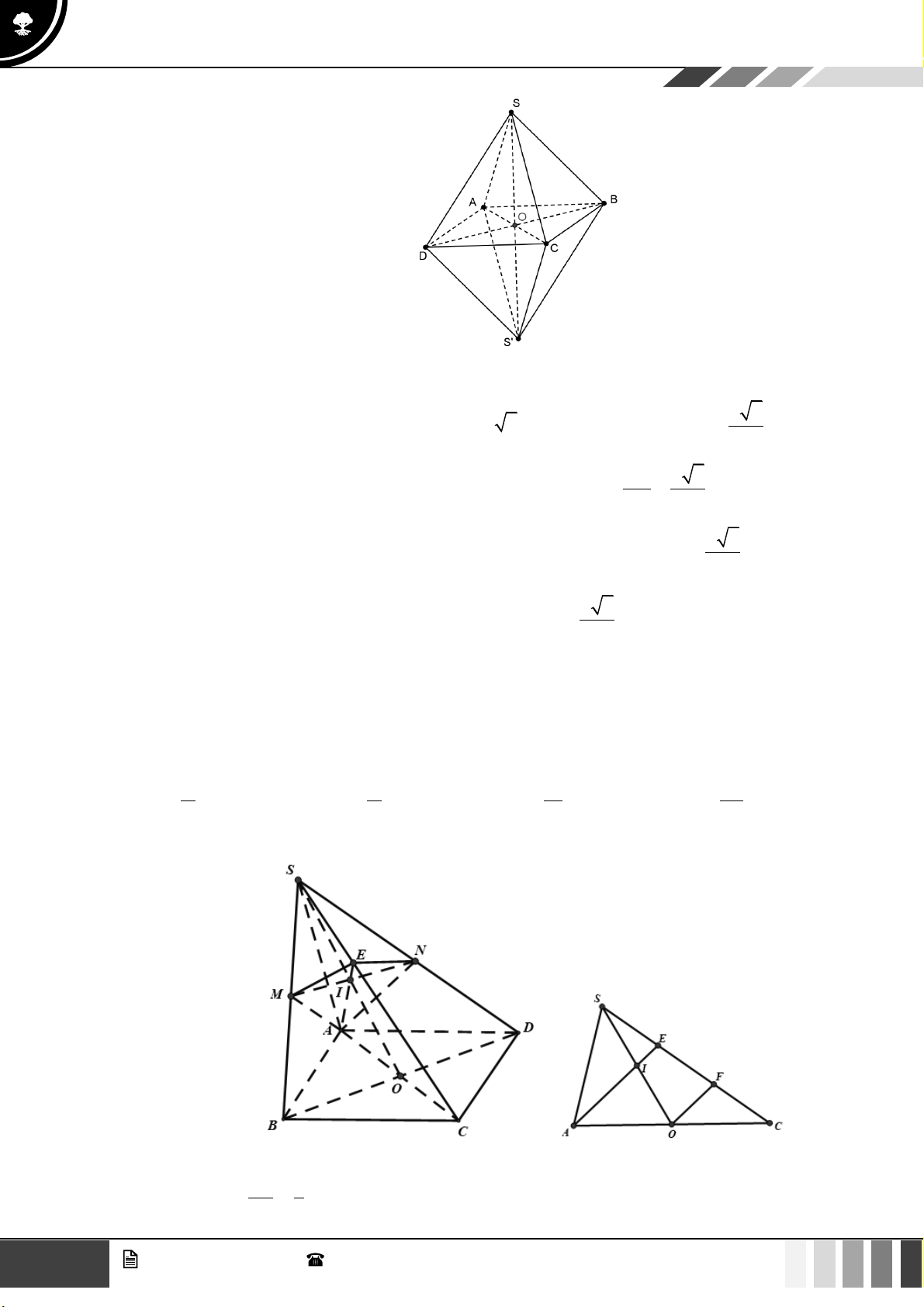
GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Xét bát diện đều
'SABCDS
cạnh
a
.
Vì
ABCD
là hình vuông cạnh
a
nên
2BD a=
2
2
a
DO BO AO OC = = = =
.
Lại có
2 2 2
SD SB BD SBD+ =
vuông cân tại
S
nên
2
'
22
BD a
SO S O= = =
O
là tâm mặt cầu ngoại tiếp bát diện đều, bán kính của mặt cầu là
2
2
a
r =
.
Diện tích mặt cầu ngoại tiếp bát diện đều là:
2
22
2
4 4 . 2
2
a
ra
==
.
Câu 41: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích
V
. Gọi
E
là điểm trên
cạnh
SC
sao cho
2EC ES=
,
( )
là mặt phẳng chứa đường thẳng
AE
và song song với đường
thẳng
BD
,
( )
cắt hai cạnh
,SB SD
lần lượt tại hai điểm
,MN
. Tính theo
V
thể tích khối chóp
.S AMEN
.
A.
3
V
. B.
6
V
. C.
12
V
. D.
2
9
V
.
Lời giải
Gọi
O
là tâm hình bình hành
ABCD
;
I
là giao điểm của
AE
và
SO
.
Theo bài ra:
1
3
SE
SC
=
;
MN
đi qua điểm
I
và
// MN BD
.

22
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Ta có:
.
.
.
S AME
S ABC
V
SM SE
V SB SC
=
;
.
.
.
S ANE
S ADC
V
SN SE
V SD SC
=
,
..
.
2
S ABC S ADC
V
VV==
Kẻ
// ,OF AE F SC
. Vì
O
là trung điểm của
AC
nên
F
là trung điểm của
EC
, theo giả
thiết suy ra
E
là trung điểm của
SF
.
Xét tam giác
SOF
có
E
là trung điểm của
SF
và
//OF IE
, suy ra
I
là trung điểm của
SO
.
1
2
SI
SO
=
1
2
SM SN
SB SD
= =
.
Do đó
..
1
11
6
22
S AME S ANE
VV
VV
= =
1
6
SAMEN
VV=
.
Câu 42: Cho phương trình
2
2
33
log 3 log 2 2 1 0
3
x
m x m m
+ + − − =
. Có bao nhiêu giá trị nguyên của
tham số
m
lớn hơn
2024−
sao cho phương trình đã cho có hai nghiệm phân biệt
12
,xx
thoả
12
10xx+
?
A.
2023
. B.
2019
. C.
2020
. D.
2021
.
Lời giải
Điều kiện:
0x
.
Ta có:
( )
2
2
22
3 3 3 3
log 3 log 2 2 1 0 log 1 3 log 2 2 1 0
3
x
m x m m x m x m m
+ + − − = − + + − − =
Đặt
3
logtx=
thì phương trình trở thành:
( ) ( )
2
2 2 2
1 3 2 2 1 0 3 2 2 2 0
22
tm
t mt m m t m t m m
tm
=−
− + + − − = + − + − =
= − +
22
3
3
m
m
x
x
−
−+
=
=
Do
2 2 2
12
10 3 3 10 9.3 3 10 0 3 1 0 0
m m m m m
x x m m
− − + − − −
+ + + − −
Vì
m
và
2024m −
nên
2023; 2019;...; 1m − − −
.
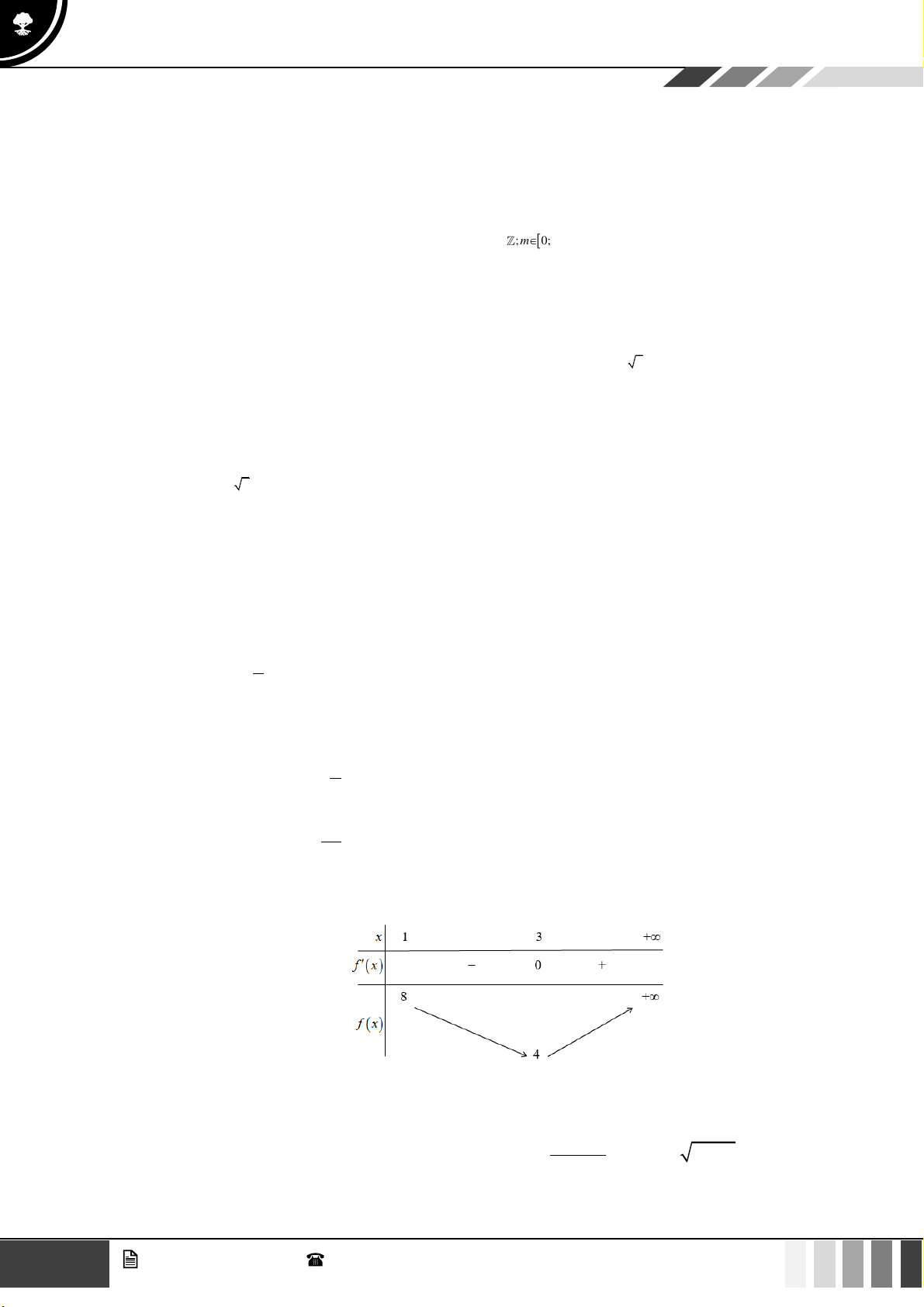
Câu 43: Số giá trị thực của tham số
0;24m
để phương trình
4 2 2 2 0
xx
mm− + + =
có hai nghiệm
phân biệt.
A.
22
. B.
21
. C.
24
. D.
20
.
Lời giải
Đặt
20
x
t =
ta có phương trình
2
2 2 0t mt m− + + =
( )
1
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Phương trình đã cho có hai nghiệm phân biệt khi
( )
1
có hai nghiệm dương phân biệt
0
0
0
S
P
2
20
20
20
mm
m
m
− −
+
1
2
0
2
m
m
m
m
−
−
; 0;24
2 3 24
mm
mm
⎯⎯⎯⎯⎯⎯→
.
Câu 44: Số các giá trị nguyên của tham số
m
để phương trình
( ) ( )
2
2
log 1 log 8x mx− = −
có hai
nghiệm thực phân biệt?
A. 4. B. 5. C. Vô số. D. 3.
Lời giải
Ta có:
( ) ( )
2
2
log 1 log 8x mx− = −
22
10
80
2log ( 1) log ( 8)
x
mx
x mx
−
−
− = −
2
22
10
80
log ( 1) log ( 8)
x
mx
x mx
−
−
− = −
2
10
( 1) 8
x
x mx
−
− = −
( )
1
9
21
x
mx
x
= + −
Phương trình đã cho có hai nghiệm phân biệt
pt có hai nghiệm phân biệt lớn hơn 1.
Xét hàm số
9
( ) 2f x x
x
= + −
trên khoảng
(1; )+
Đạo hàm:
( )
2
9
1 0 3f x x
x
= − = =
Bảng biến thiên:
Từ bảng biến thiên suy ra
48m
. Vậy
5;6;7m
.
Câu 45: Cho hai số thực dương
a
và
b
thỏa mãn hàm số
( )
3
4
cos 2 1
1
aa
y x x b
b
+
= + +
+
đồng biến trong
khoảng
( )
;− +
. Tìm giá trị lớn nhất của biểu thức
3
27 8S b a=−
.
A.
40
. B.
351
. C.
345
. D.
81
.

24
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Lời giải
Theo giả thiết ta có:
( )
3
4
2 1sin 2 1
1
aa
y b b x
b
+
= − + +
+
Hàm số đồng biến trong khoảng
( )
;− +
( )
3
4
2 1sin 2 1 0
1
aa
y b b x
b
+
= − + +
+
,
x
( )
3
4
min 2 1sin 2 1 0
1
aa
b b x
b
+
− + +
+
3
4
2 1 0
1
aa
b
b
+
− +
+
( )
3
4 1 2 1a a b b+ + +
( )
3
8 2a 2 1 1 2 1a b b+ + + +
( )
( )
3
3
2 2 2 1 2 1a a b b+ + + +
2 2 1ab+
.
Khi đó
( )
( )
( )
( )
3
0;
27 2 1S f b b b max f b
+
= − +
.
Xét hàm số
( )
( )
3
27 2 1f b b b= − +
với
0b
;
( )
27 3 2 1 0f b b
= − + =
40b =
Bảng biến thiên hàm
( )
fb
Do đó:
( )
( ) ( )
0;
40 351S max f b f
+
= =
Câu 46: Năm
2023
, tỉ lệ thể tích khí
2
CO
trong không khí là
6
397
10
. Biết rằng tỉ lệ thể tích khí
2
CO
trong
không khí tăng
0,4%
mỗi năm. Vậy ít nhất đến năm bao nhiêu thì tỉ lệ thể tích khí
2
CO
trong
không khí vượt ngưỡng
5
41
10
.
A.
2029
. B.
2031
. C.
2028
. D.
2033
.
Lời giải
Sau
n
năm, tỉ lệ thể tích khí
2
CO
đạt:
( )
6
397
. 1 0,4%
10
n
T =+
.
Do đó: tỉ lệ thể tích khí
2
CO
trong không khí vượt ngưỡng
5
41
10
khi
( ) ( )
1,004
5 6 5
41 397 41 410 410
. 1 0,4% 1 0,4% log 8,1
10 10 10 397 397
nn
Tn + +
Vậy
9n =
nên ít nhất đến năm
2033
thì tỉ lệ thể tích khí
2
CO
trong không khí vượt ngưỡng
5
41
10
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
25
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Câu 47: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
( )
ABC
,
0
3 , 60 .SA AC AB BAC= = =
Gọi
,HK
lần lượt là hình chiếu của
A
lên
,SB SC
. Gọi
12
,SS
lần lượt là diện tích của mặt cầu
ngoại tiếp hình chóp
.S AHK
và hình chóp
.A BCKH
. Tính
1
2
S
S
A.
1
2
27
28
S
S
=
. B.
1
2
27
92
S
S
=
. C.
1
2
81
28
S
S
=
. D.
1
2
4
3
S
S
=
.
Lời giải
3 3 .SA AC AB a= = =
Gọi
AD
là đường kính của đường tròn ngoại tiếp
,ABC AC CD AB BD ⊥ ⊥
.
Ta có
( )
AC CD
CD SAC CD AK
SA CD
⊥
⊥ ⊥
⊥
.
Ta có
( )
AK SC
AK SCD AK KD
AK CD
⊥
⊥ ⊥
⊥
.
Tương tự
AH HD⊥
.
Vậy hình chóp
.A BCKH
có
, , ,H K B C
nhìn
AD
dưới một góc vuông nên hình chóp có mặt
cầu ngoại tiếp đường kính
AD
.
Xét
ABC
có
2 2 2
2. . .cosBC AB AC AB AC A= + −
2 2 0 2
9 2. .3 .cos60 7a a a a a= + − =
7BC a=
.
Gọi
2
R
là bán kính mặt cầu ngoại tiếp hình chóp
.A BCKH
22
0
7 21
2
sin sin60 3
BC a a
RR
A
= = =
.
Hình chóp
.S AHK
có
,AH HS AK KS⊥⊥
nên mặt cầu ngoại tiếp hình chóp là mặt cầu
đường kính
SA
, vậy bán kính mặt cầu là
1
3
22
SA a
R ==
.
Ta có
22
1 1 1
22
2 2 2
9
4
27
4
21
4 28
9
S R R
S R R
= = = =
.

26
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Câu 48: Cho các số thực
,,x y z
thỏa mãn
2
33
2 1 0.
xy
x y z y yz
− + − − + =
. Tìm giá trị nhỏ nhất của biểu
thức
( ) ( )
22
, , 9 2 3 1P x y z x y x y z= + − − +
.
A.
0
. B.
1
2
. C.
1
. D.
1
2
−
.
Lời giải
Ta có
( ) ( ) ( )
2
2 2 2 2
, , 9 2 3 1 6 9 2 3 2P x y z x y x y z x xy y y z x y y z= + − − + = − + + + = − + +
.
Suy ra
2P y z+
.
Theo đề bài:
22
2 1 0 2 1x y z y yz x y z y yz− + − − + = = − + + −
.
Do
3x
nên
22
2 1 3 4 4 8 4 16 0y z y yz y yz y z− + + − + + − −
( ) ( ) ( )
22
2 2 2
4 4 8 16 8 4 0 2 4 2 4y yz z z z y z y z y z z + + − − − + + + + + +
( ) ( ) ( ) ( ) ( )
2 2 2 2
2 4 2 4 4 4 2 2 4 4 4y z y z z y z z + + + + + + + + + +
.
Mặt khác vì
( ) ( ) ( ) ( )
2 2 2 2
2 2 4 4 2 2 4 4 0y z z y z z+ + + + + + − +
Hay
( )( )
2 2 2 2 6 0y y z− + +
.
Vì
3 3 2 2 0yy −
nên
2 2 6 0 3 0 2 3y z y z y z y+ + + + + −
.
Mà
1 3 2 2 2y y y z − − + −
.
Từ ta có
( ) ( )
22
2 2 2 2 2 2P y z P y z+ + + + + +
.
Từ ta suy ra
( )
2
2 2 0
24
2 2 4
PP
P
PP
+
+
+ − −
.
Do
22P y z + −
nên loại
4P −
. Suy ra
0P
.
Vậy giá trị nhỏ nhất của
P
bằng 0, dấu
""=
xảy ra
44
32
2 0 6
zz
x y y
y z x
= − = −
= =
+ = =
.
Câu 49: Có bao nhiêu giá trị nguyên của tham số
0;2024m
để đồ thị của hàm số
2
1
24
x
y
x mx
−
=
−+
có đúng 3 đường tiệm cận.
A.
2024
. B.
2021
. C.
2022
. D.
2022
.
Lời giải
Ta có:
lim 0, lim 0
xx
yy
→− →+
==
nên đồ thị hàm số có đường tiệm cận ngang
0,ym=
.
Do đó đồ thị hàm số đã cho có 3 đường tiệm cận
Phương trình
2
2 x 4 0xm− + =
có hai nghiệm phân biệt khác
1
2
0
40
5
5
2
2
m
m
m
−
; 0;2024
5
2
3 2024
2
2
mm
m
m
m
m
⎯⎯⎯⎯⎯⎯→
−
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
27
Tuyển tập 10 đề ôn HK1
Năm học 2023 - 2024
Câu 50: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới. Hỏi có bao nhiêu giá trị nguyên của tham
số
2024;2024m−
để phương trình
( ) ( ) ( )
3
22
4 2 0f x f x mf x m− + − =
có đúng hai
nghiệm thực (Giả thiết rằng các nghiệm bội chỉ được tính là một nghiệm)?
A.
3976
. B.
3971
. C.
3974
. D.
3975
.
Lời giải
Xét phương trình
( )
f x t=
.
Nếu
10t
thì phương trình có
3
nghiệm,
10t =
thì phương trình có
2
nghiệm và
10t
thì
phương trình có
1
nghiệm duy nhất.
Phương trình đã cho
( ) ( ) ( ) ( )
3
2 2 2
32f x f x f x mf x m − = − +
Đặt
( )
t f x=
thì phương trình trở thành
( )
( )
( )
3
2
2
t t t m g t h t+ = − =
và
( )
10 700g =
.
Từ sơ đồ ta có các nhận xét như sau :
Nếu
0m =
thì có
3
nghiệm
( )
10;10t −
Có tất cả
9
nghiệm thực của
x
nên không thỏa
mãn.
Nếu
1
0 mm
thì có
2
nghiệm
( )
10;10t −
Có tất cả
6
nghiệm thực của
x
nên không
thỏa mãn.

28
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Năm học: 2023 - 2024
Nếu
1
mm=
thì có 1 nghiệm
10t =
và
1
nghiệm
( )
10;10t −
Có tất cả
5
nghiệm thực của
x
nên không thỏa mãn.
Nếu
12
m m m
thì có
1
nghiệm
( )
10;10t −
và 1 nghiệm
10t
và
Có tất cả
4
nghiệm
thực của
x
nên không thỏa mãn.
Nếu
2
mm=
thì có 1 nghiệm
10t =
và
1
nghiệm
10t
Có tất cả
3
nghiệm thực của
x
nên không thỏa mãn.
Nếu
2
mm
thì có
2
nghiệm
10t
Có tất cả
2
nghiệm thực của
x
nên thỏa mãn.
Ta có hàm số
( )
2
2
y t m=−
đi qua
( )
10;700
nên
2
36,5m =
Suy ra yêu cầu bài toán
2024 37
36,5
37 2024
m
m
m
− −
có
3976
giá trị
m
thỏa mãn.
-----------------------HẾT-----------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HK1
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Số điểm cực trị của hàm số
( )
1
1
x
fx
x
+
=
−
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 2: Bảng biến thiên dưới đây là bảng biến thiên của hàm số nào trong các hàm số được liệt kê ở bốn
đáp án A, B, C, D?
A.
32
31y x x= − −
. B.
32
32y x x= − + −
. C.
32
31y x x= − + −
. D.
3
32y x x= − − −
.
Câu 3: Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây?
A.
42
23y x x= − +
. B.
42
23y x x= − −
.
C.
42
23y x x= − + −
. D.
42
33y x x= + −
.
Câu 4: Hàm số
1
2
x
y
=
có đạo hàm là
A.
1
ln2
2
x
y
=−
. B.
1
ln2
2
x
y
=
. C.
1
1
.
2
x
yx
−
=
. D.
1
2
x
y
=
.
Câu 5: Đường cong trong hình vẽ bên dưới là của đồ thị hàm số nào sau đây?
A.
2 2x
.
1
y
x
−
=
+
B.
42
2 2.y x x= + +
C.
21
.
2
x
y
x
−+
=
+
D.
3
2 1.y x x= − +
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
02
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 6: Giá trị lớn nhất của hàm số
42
31y x x= − + +
trên
1;2−
là
A.
29
. B.
1
. C.
3
. D.
13
4
.
Câu 7: Rút gọn biểu thức
9
5
5
.P x x=
với
0x
.
A.
8
5
Px=
. B.
11
5
x
. C.
Px=
. D.
2
Px=
.
Câu 8: Với
a
là số thực dương tùy ý,
( ) ( )
log 7 log 2aa−
bằng
A.
( )
( )
log 7
log 2
a
a
. B.
7
log
2
. C.
log7
log2
. D.
( )
log 5a
.
Câu 9: Cho hàm số bậc bốn
( )
y f x=
có đồ thị hàm số
( )
y f x
=
là đường cong trong hình vẽ, hàm số
( )
y f x=
đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
4;0−
. B.
( )
;1− −
. C.
( )
2;+
. D.
( )
0;2
.
Câu 10: Cho hàm số
( )
2022
logf x x=
. Khi đó
( )
2f
bằng
A.
1
2022
. B.
1
2022ln2
. C.
1
2ln2022
. D.
1
2
.
Câu 11: Tập xác định của hàm số
( )
7
log 1yx=−
là
A.
( )
0;+
. B.
( )
;1−
. C.
( )
;− +
. D.
( )
1; +
.
Câu 12: Tập nghiệm của bất phương trình
2
13 3
33
x −
là
A.
( )
4;+
. B.
( )
;4−
. C.
( )
4;4−
. D.
( )
0;4
.
Câu 13: Nghiệm của phương trình
1
28
x−
=
là
A.
5x =
. B.
3x =−
. C.
3x =
. D.
4x =
.
Câu 14: Nghiệm của phương trình
4
log ( 1) 3x −=
là
A.
65x =
. B.
63x =
. C.
80x =
. D.
82x =
.
Câu 15: Hình đa diện bên dưới có bao nhiêu mặt?
A.
12
. B.
10
. C.
13
. D.
11
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 16: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
.a
A.
3
3
12
a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
3
4
a
.
Câu 17: Gọi
,,l h R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón
( )
N
. Thể tích
V
của khối nón
( )
N
bằng
A.
2
1
3
V R h
=
. B.
2
V R h
=
. C.
2
V R l
=
. D.
2
1
3
V R l
=
.
Câu 18: Cho hình nón có thể tích
3
36Va
=
và bán kính đáy bằng 3a.Tính độ dài đường cao h của hình
nón đã cho.
A.
4a
. B.
12a
. C.
5a
. D.
a
.
Câu 19: Cho hình lăng trụ có bán kính đáy
7r =
và độ dài đường sinh
3l =
. Diện tích xung quanh của
hình trụ đã cho bằng
A.
21
. B.
49
. C.
147
. D.
42
.
Câu 20: Cho khối cầu có bán kính
2r =
. Thể tích khối cầu đã cho là
A.
16
. B.
32
. C.
32
3
. D.
8
3
.
Câu 21: Hàm số nào dưới đây đồng biến trên ?
A.
3
3y x x=+
. B.
42
32y x x= − +
. C.
1
2
x
y
x
+
=
+
. D.
2
2y x x=−
.
Câu 22: Tìm các giá trị của tham số
m
để hàm số
32
38y x x mx= + − +
đạt cực trị tại
12
;xx
thỏa mãn
22
12
5xx+=
.
A.
3m =
. B.
1
2
m =
. C.
2m =
. D.
3
2
m =
.
Câu 23: Giá trị lớn nhất của hàm số
( )
32
3 9 10f x x x x= − − +
trên đoạn
4;4−
là
A.
( )
4;4
max 0fx
−
=
. B.
( )
4;4
max 25fx
−
=
. C.
( )
4;4
max 15fx
−
=
. D.
( )
4;4
max 10fx
−
=−
.
Câu 24: Hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình bên dưới
Số nghiệm thực dương của phương trình
( )
0fx=
là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 25: Đồ thị hàm số
2
3
9
x
y
x
−
=
−
có bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.

4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 26: Trên khoảng
( )
0;+
, đạo hàm của hàm số
3
5
yx=
là
A.
3
2
1
3
yx
=
. B.
3
2
5
3
yx
=
. C.
5
3
yx
=
. D.
3
'5yx=
.
Câu 27: Với mọi
,ab
dương thỏa mãn
3
2
2
log log 5ab+=
. Khẳng định nào dưới đây đúng?
A.
23
32ab =
. B.
32
32ab =
. C.
2
32ab =−
. D.
22
32ab =−
.
Câu 28: Đạo hàm của hàm số
( )
1
2
x
fx
=
là
A.
( )
1
ln2
2
x
fx
=
. B.
( )
1
lg2
2
x
fx
=
.
C.
( )
1
ln2
2
x
fx
=−
. D.
( )
1
lg2
2
x
fx
=−
.
Câu 29: Tập xác định
D
của hàm số
( )
2
5
log 3 2y x x= + +
là
A.
( ) ( )
; 2 1:D= − − − +
. B.
( )
1;D= − +
.
C.
(
)
; 2 1;D= − − − +
. D.
( )
2; 1D= − −
.
Câu 30: Phương trình
9 5.3 6 0
xx
− + =
có tổng các nghiệm là:
A.
3
log 6
. B.
3
2
log
3
. C.
3
2
log
3
. D.
3
log 6−
.
Câu 31: Nghiệm của phương trình
( ) ( )
1
2
2
log 1 log 1 1xx− + + =
nằm trong khoảng nào sau đây?
A.
( )
1;0−
. B.
( )
0;1
. C.
( )
2;3
. D.
( )
4;5
.
Câu 32: Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
A. Khối bát diện đều. B. Khối mười hai mặt đều.
C. Khối tứ diện đều. D. Khối hai mươi mặt đều.
Câu 33: Tính thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
.
A.
3
2
3
a
V =
. B.
3
3
4
a
V =
. C.
3
2
4
a
V =
. D.
3
3
2
a
V =
.
Câu 34: Cho hình nón có góc ở đỉnh bằng và chiều cao bằng
23
. Độ dài đường sinh của hình nón
bằng
A. . B.
4
. C. . D.
43
.
Câu 35: Tìm mệnh đề đúng trong các mệnh đề sau.
A. Tồn tại hình chóp có số cạnh gấp đôi số mặt.
B. Tồn tại hình lăng trụ có số cạnh gấp đôi số mặt.
C. Tồn tại hình lăng trụ có số cạnh bằng số mặt.
D. Tồn tại hình chóp có số cạnh bằng số mặt.
Câu 36: Một mặt cầu có diện tích bằng
2
16 a
. Thể tích của khối cầu tương ứng là
60
3
23
( )
S
( )
S

GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HK1
Toán 12
A.
3
32
3
a
. B. . C. . D. .
Câu 37: Cho ba hàm số lũy thừa
yx
=
,
yx
=
và
yx
=
có đồ thị như hình vẽ bên dưới. Chọn khẳng
định đúng trong các khẳng định sau
A.
. B.
. C.
. D.
.
Câu 38: Giá trị của biểu thức
3 2022
log 2023 log 2023 log 2023 ... log 2023
a
a
aa
S = + + + +
( 0; 1)aa
là:
A.
1011.2022.log 2023
a
. B.
1012.2024.log 2023
a
.
C.
1012.2022.log 2023
a
. D.
1011.2023.log 2023
a
.
Câu 39: Cho các số thực dương
,,abc
( với
,ac
khác 1) thỏa mãn các điều kiện
( ) ( )
23
log log
ac
ac b c=
và
2log log 8
ac
cb+=
. Tính giá trị của biểu thức
(
)
2
log log
ac
P b ab=+
.
A.
31
3
. B.
32
3
. C.
29
3
. D.
28
3
.
Câu 40: Có bao nhiêu số nguyên
m
thuộc đoạn
2022;2022−
để phương trình
2
33
2
0
log 2log
x
m
xx
−
=
−
có nghiệm.
A.
1510
. B.
1513
. C.
1512
. D.
1509
.
Câu 41: Tập nghiệm của bất phương trình
2
3 10
2
1
3
3
xx
x
−−
−
chứa mấy số nguyên.
A.
10
. B.
9
. C.
8
. D.
7
.
Câu 42: Gọi
S
là tập hợp các giá trị của tham số
m
để đồ thị hàm số
( )
3 2 2 2
3 3 1 3 1y x x m x m= − + + − − −
có điểm cực đại và cực tiểu cùng với gốc tọa độ tạo thành
tam giác vuông tại
O
. Tích tất cả các giá trị của tập
S
bằng
A.
1−
. B.
3
2
−
. C.
3
2
. D.
1
.
Câu 43: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật có
23AB a=
;
2.AD a=
Mặt bên
( )
SAB
là
tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp
.S ABD
là
A.
3
4 3 .a
. B.
3
23
.
3
a
. C.
3
4.a
. D.
3
2 3 .a
3
12 a
3
4 a
3
43a
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
,B
1,BA BC==
2.AD =
Cạnh bên
SA
vuông góc với đáy và
2.SA =
Gọi
H
là hình chiếu vuông góc của
A
trên
.SB
Thể tích của khối đa diện
SAHCD
bằng
A.
22
.
9
B.
22
.
3
C.
42
.
9
D.
42
.
3
Câu 45: Số nghiệm thực của phương trình
11
44
2 2 4
x
x
xx
++
+=
là:
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 46: Cho hình lăng trụ
ABCA B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
lên
mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
3
3
a
. Tính thể tích
V
của khối lăng trụ
.ABCA B C
A.
3
5
24
a
V =
. B.
3
5
10
a
V =
. C.
3
5
3
a
V =
. D.
3
5
6
a
V =
.
Câu 47: Cho hình trụ có hai đáy là hình tròn tâm
O
và
O
, chiều cao
3ha=
. Mặt phẳng đi qua tâm
O
và tạo với
OO
một góc
30
, cắt hai đường tròn tâm
O
và
O
tại bốn điểm là bốn đỉnh của một
hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng
2
3a
. Thể tích của khối trụ được giới
hạn bởi hình trụ đã cho bằng
A.
3
3
3
a
. B.
3
3a
. C.
3
3
12
a
. D.
3
3
4
a
.
Câu 48: Cho hàm số . Biết hàm số có bảng biến thiên như hình vẽ sau
Số giá trị nguyên dương của tham số để hàm có giá trị lớn nhất?
A. . B. . C. Vô số. D. .
Câu 49: Một anh sinh viên T nhập học đại học vào tháng
8
năm
2020
. Bắt đầu từ tháng
9
năm
2020
,
cứ vào ngày mồng một hàng tháng anh vay ngân hàng
3
triệu đồng với lãi suất cố định
0,8%
/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo (lãi kép). Vào
ngày mồng một hàng tháng kể từ tháng
9
năm
2022
về sau anh không vay ngân hàng nữa và
anh còn trả được cho ngân hàng
2
triệu đồng do việc làm thêm. Hỏi vào ngày anh ra trường
( )
30 / 6 / 2024
, số tiền anh nợ ngân hàng gần nhất với số nào sau đây?
A.
49.024.000
đồng B.
46.640.000
đồng C.
47.024.000
đồng D.
45.401.000
đồng
Câu 50: Cho hàm đa thức bậc năm
( )
y f x=
và hàm số
( )
y f x
=
có đồ thị như trong hình bên.
( )
y f x=
( )
52y f x=−
m
( )
( )
2
2 4 3g x f x x m= − + −
5
4
3
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HK1
Toán 12
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
( )
32
32g x f x x m m= + + −
có đúng
ba điểm cực đại?
A.
3
. B.
0
. C.
4
. D.
1
.
-----------------------HẾT-----------------------

8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
BẢNG ĐÁP ÁN
1.D
2.B
3.B
4.A
5.A
6.D
7.D
8.B
9.B
10.C
11.D
12.C
13.D
14.A
15.D
16.D
17.A
18.B
19.D
20.C
21.A
22.D
23.C
24.D
25.C
26.B
27.B
28.C
29.A
30.A
31.D
32.B
33.B
34.B
35.B
36.A
37.A
38.D
39.A
40.A
41.B
42.A
43.D
44.C
45.D
46.B
47.B
48.D
49.B
50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Số điểm cực trị của hàm số
( )
1
1
x
fx
x
+
=
−
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Hàm số
( )
1
1
x
fx
x
+
=
−
luôn nghịch biến trên từng khoảng xác định và không có cực trị.
Câu 2: Bảng biến thiên dưới đây là bảng biến thiên của hàm số nào trong các hàm số được liệt kê ở bốn
đáp án A, B, C, D?
A.
32
31y x x= − −
. B.
32
32y x x= − + −
. C.
32
31y x x= − + −
. D.
3
32y x x= − − −
.
Lời giải
Ta nhận thấy đồ thị hàm số đi qua điểm
( )
0; 2−
nên ta loại được các phương án A,C.
Đồ thị hàm số đi qua điểm
( )
2;2
nên ta loại phương án D.
Câu 3: Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây?
A.
42
23y x x= − +
. B.
42
23y x x= − −
.
C.
42
23y x x= − + −
. D.
42
33y x x= + −
.
Lời giải
Dựa vào đồ thị ta thấy đường cong là hàm bậc
4
trùng phương với hệ số
0a
,
3d =−
và hàm
số có ba cực trị suy ra
00ab b
.
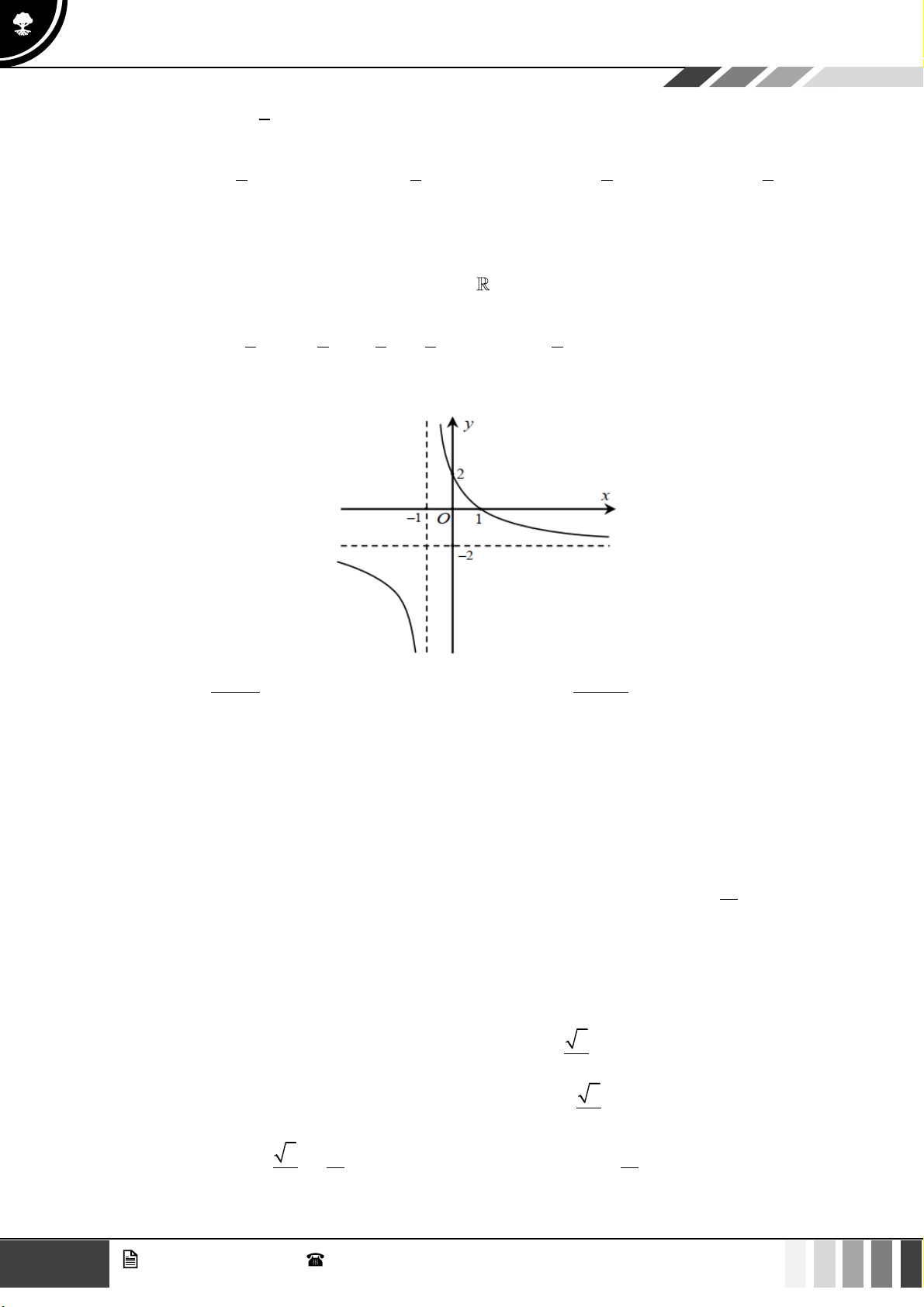
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 4: Hàm số
1
2
x
y
=
có đạo hàm là
A.
1
ln2
2
x
y
=−
. B.
1
ln2
2
x
y
=
. C.
1
1
.
2
x
yx
−
=
. D.
1
2
x
y
=
.
.
Lời giải
Với
0, 1aa
ta có:
( )
ln ,
xx
a a a x
=
.
Vậy
( )
1
1 1 1 1 1
ln ln 2 ln2
2 2 2 2 2
x x x x
y
−
= = = = −
.
Câu 5: Đường cong trong hình vẽ bên dưới là của đồ thị hàm số nào sau đây?
A.
2 2x
.
1
y
x
−
=
+
B.
42
2 2.y x x= + +
C.
21
.
2
x
y
x
−+
=
+
D.
3
2 1.y x x= − +
Lời giải
Đây là độ thị của hàm nhất biến nên loại đáp án B và D.
Từ đồ thị suy ra: Tiệm cận đứng
1x =−
và tiệm cận ngang
2y =−
.
Loại đáp án C.
Câu 6: Giá trị lớn nhất của hàm số
42
31y x x= − + +
trên
1;2−
là
A.
29
. B.
1
. C.
3
. D.
13
4
.
Lời giải
Hàm số xác định và liên tục trên [-1; 2]
Ta có
( )
32
0 1; 2
6
4 6 2 2 3 0 1; 2
2
6
1; 2
2
x
y x x x x y x
x
= −
= − + = − − = = −
= − −
Vì
( ) ( ) ( )
6 13
0 1; ; 2 3; 1 3
24
y y y y
= = = − − =
nên
1; 2
13
max
4
y
−
=
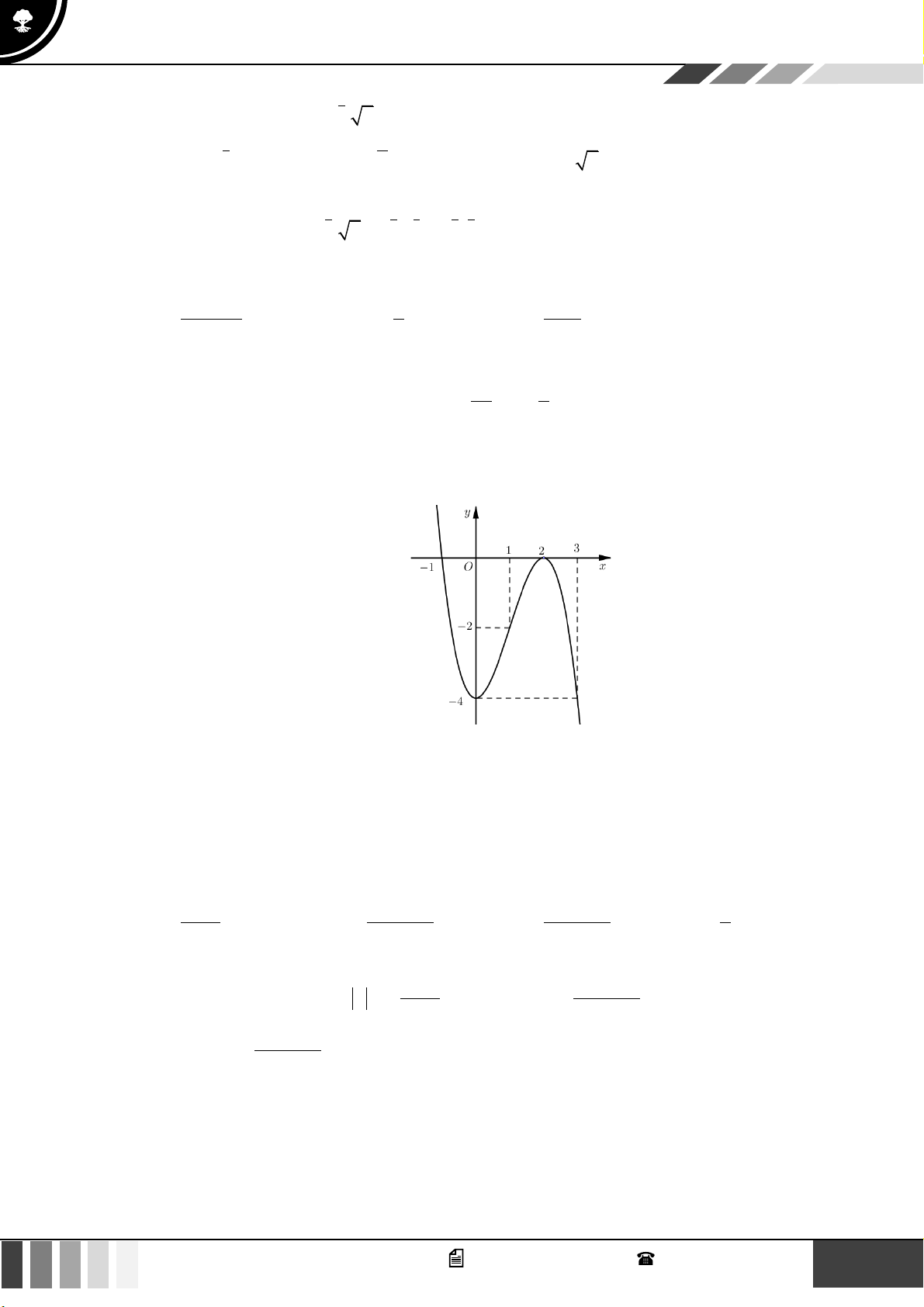
10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 7: Rút gọn biểu thức
9
5
5
.P x x=
với
0x
.
A.
8
5
Px=
. B.
11
5
x
. C.
Px=
. D.
2
Px=
.
Lời giải
Với
0x
, ta có
9 9 1 9 1
2
5
5 5 5 5 5
..P x x x x x x
+
= = = =
Câu 8: Với
a
là số thực dương tùy ý,
( ) ( )
log 7 log 2aa−
bằng
A.
( )
( )
log 7
log 2
a
a
. B.
7
log
2
. C.
log7
log2
. D.
( )
log 5a
.
Lời giải
Với
0a
, ta có:
( ) ( )
77
log 7 log 2 log log
22
a
aa
a
− = =
.
Câu 9: Cho hàm số bậc bốn
( )
y f x=
có đồ thị hàm số
( )
y f x
=
là đường cong trong hình vẽ, hàm số
( )
y f x=
đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
4;0−
. B.
( )
;1− −
. C.
( )
2;+
. D.
( )
0;2
.
Lời giải
Dựa vào đồ thị ta có
( ) ( )
0, ; 1f x x
− −
. Vậy hàm số
( )
y f x=
đồng biến trên khoảng
( )
;1− −
.
Câu 10: Cho hàm số
( )
2022
logf x x=
. Khi đó
( )
2f
bằng
A.
1
2022
. B.
1
2022ln2
. C.
1
2ln2022
. D.
1
2
.
Lời giải
Áp dụng công thức:
( )
1
log
ln
a
x
xa
=
ta được
( )
1
2
2ln2022
f
=
.
Vậy
( )
1
2
2ln2022
f
=
.
Câu 11: Tập xác định của hàm số
( )
7
log 1yx=−
là
A.
( )
0;+
. B.
( )
;1−
. C.
( )
;− +
. D.
( )
1; +
.
Lời giải
Hàm số
( )
7
log 1yx=−
xác định khi
1 0 1xx−
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HK1
Toán 12
Vậy tập xác định của hàm số
( )
7
log 1yx=−
là
( )
1;D = +
.
Câu 12: Tập nghiệm của bất phương trình
2
13 3
33
x −
là
A.
( )
4;+
. B.
( )
;4−
. C.
( )
4;4−
. D.
( )
0;4
.
Lời giải
Ta có:
2
13 3 2 2
3 3 13 3 16 0 4 4
x
x x x
−
− − −
.
Vậy tập nghiệm của bất phương trình đã cho là
( )
4;4S =−
.
Câu 13: Nghiệm của phương trình
1
28
x−
=
là
A.
5x =
. B.
3x =−
. C.
3x =
. D.
4x =
.
Lời giải
Ta có:
1 1 3
2 8 2 2 1 3 4
xx
xx
−−
= = − = =
.
Vậy nghiệm của phương trình đã cho là
4x =
.
Câu 14: Nghiệm của phương trình
4
log ( 1) 3x −=
là
A.
65x =
. B.
63x =
. C.
80x =
. D.
82x =
.
Lời giải
Ta có:
( )
4
log 1 3x −=
3
1 4 65xx − = =
.
Câu 15: Hình đa diện bên dưới có bao nhiêu mặt?
A.
12
. B.
10
. C.
13
. D.
11
.
Lời giải
Hình đa diện đã cho có
11
mặt.
Câu 16: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
.a
A.
3
3
12
a
. B.
3
3
2
a
. C.
3
2
a
. D.
3
3
4
a
.
Lời giải
Ta có
23
33
..
44
aa
V B h a= = =
Câu 17: Gọi
,,l h R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón
( )
N
. Thể tích
V
của khối nón
( )
N
bằng
A.
2
1
3
V R h
=
. B.
2
V R h
=
. C.
2
V R l
=
. D.
2
1
3
V R l
=
.
Lời giải
Ta có:
2
1
3
V R h
=
.

12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 18: Cho hình nón có thể tích
3
36Va
=
và bán kính đáy bằng 3a.Tính độ dài đường cao h của hình
nón đã cho.
A.
4a
. B.
12a
. C.
5a
. D.
a
.
Lời giải
Ta có
( )
2
23
11
36 3 12
33
V R h a a h h a
= = =
.
Câu 19: Cho hình lăng trụ có bán kính đáy
7r =
và độ dài đường sinh
3l =
. Diện tích xung quanh của
hình trụ đã cho bằng
A.
21
. B.
49
. C.
147
. D.
42
.
Lời giải
Diện tích xung quanh của hình trụ là:
2 2 .7.3 42S rl
= = =
.
Câu 20: Cho khối cầu có bán kính
2r =
. Thể tích khối cầu đã cho là
A.
16
. B.
32
. C.
32
3
. D.
8
3
.
Lời giải
Thể tích khối cầu bán kính
2r =
là
3
4
3
Vr
=
3
4 32
. .2
33
==
.
Câu 21: Hàm số nào dưới đây đồng biến trên ?
A.
3
3y x x=+
. B.
42
32y x x= − +
. C.
1
2
x
y
x
+
=
+
. D.
2
2y x x=−
.
Lời giải
Xét hàm số
3
3y x x=+
. Tập xác định:
D =
.
2
3 3 0yx
= +
,
x
nên hàm số
3
3y x x=+
đồng biến trên .
Câu 22: Tìm các giá trị của tham số
m
để hàm số
32
38y x x mx= + − +
đạt cực trị tại
12
;xx
thỏa mãn
22
12
5xx+=
.
A.
3m =
. B.
1
2
m =
. C.
2m =
. D.
3
2
m =
.
Lời giải
Tập xác định
D =
. Ta có:
2
36y x x m
= + −
.
Hàm số có đạt cực trị tại
12
;xx
thỏa mãn
22
12
5xx+=
khi phương trình
2
' 3 6 0y x x m= + − =
có
2 nghiệm phân biệt thỏa mãn
22
12
5xx+=
.
( )
2
22
12
1 2 1 2
3
9 3 0
5
25
m
m
xx
x x x x
−
+
+=
+ − =
3
4 2. 5
3
m
m
−
− − =
3
3
3
2
2
m
m
m
−
=
=
.
Vậy
3
2
m =
thỏa mãn yêu cầu đề bài.
Câu 23: Giá trị lớn nhất của hàm số
( )
32
3 9 10f x x x x= − − +
trên đoạn
4;4−
là
A.
( )
4;4
max 0fx
−
=
. B.
( )
4;4
max 25fx
−
=
. C.
( )
4;4
max 15fx
−
=
. D.
( )
4;4
max 10fx
−
=−
.
Lời giải
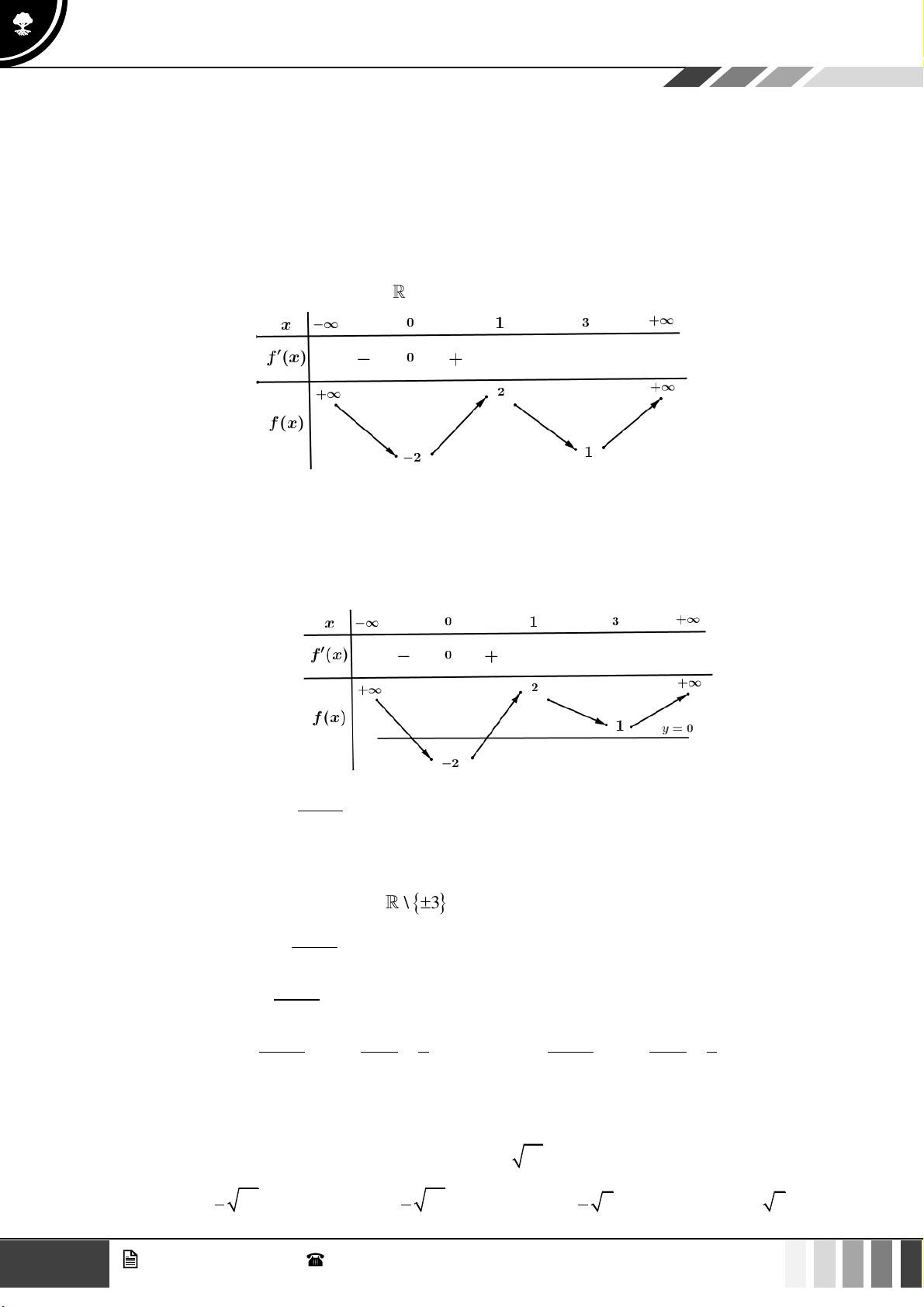
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HK1
Toán 12
Hàm số liên tục trên
4;4−
. Ta có:
( )
2
' 3 6 9f x x x= − −
;
( )
2
1 4;4
' 0 3 6 9 0
3 4;4
x
f x x x
x
= − −
= − − =
= −
.
Ta có:
( )
4 66f − = −
;
( )
1 15f −=
;
( )
3 17f =−
;
( )
4 10f =−
.
Vậy
( ) ( )
4;4
max 1 15f x f
−
= − =
.
Câu 24: Hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình bên dưới
Số nghiệm thực dương của phương trình
( )
0fx=
là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Vẽ đường thẳng
0y =
ta thấy cắt đồ thị tại đúng một điểm có hoành độ dương. Vậy phương
trình đã cho có 1 nghiệm dương.
.
Câu 25: Đồ thị hàm số
2
3
9
x
y
x
−
=
−
có bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Tập xác định của hàm số:
\3D =
. Ta có:
2
3
lim 0 lim 0 0
9
xx
x
yy
x
→ →
−
= = = =
−
là đường tiệm cận ngang.
2
33
3
lim lim 3
9
xx
x
yx
x
++
→− →−
−
= = + = −
−
là đường tiệm cận đứng.
2
3 3 3
3 1 1
lim lim lim
36
9
x x x
x
y
x
x
+ + +
→ → →
−
= = =
+
−
;
2
3 3 3
3 1 1
lim lim lim
36
9
x x x
x
y
x
x
− − −
→ → →
−
= = =
+
−
.
3x=
không là đường tiệm cận đứng.
Vậy đồ thị hàm số có 1 đường tiệm cận ngang và 1 đường tiệm cận đứng.
Câu 26: Trên khoảng
( )
0;+
, đạo hàm của hàm số
3
5
yx=
là
A.
3
2
1
3
yx
=
. B.
3
2
5
3
yx
=
. C.
5
3
yx
=
. D.
3
'5yx=
.

14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Lời giải
Trên khoảng
( )
0;+
ta có
5
3
5
3
y x x==
, khi đó
52
3
2
33
55
33
y x x x
= = =
.
Câu 27: Với mọi
,ab
dương thỏa mãn
3
2
2
log log 5ab+=
. Khẳng định nào dưới đây đúng?
A.
23
32ab =
. B.
32
32ab =
. C.
2
32ab =−
. D.
22
32ab =−
.
Lời giải
Với mọi
,ab
dương ta có
33
2 2 2
2
log log 5 log 2.log 5a b a b+ = + =
( )
3 2 3 2 3 2 5
2 2 2
log log 5 log 5 2a b a b a b + = = =
32
32ab=
.
Câu 28: Đạo hàm của hàm số
( )
1
2
x
fx
=
là
A.
( )
1
ln2
2
x
fx
=
. B.
( )
1
lg2
2
x
fx
=
.
C.
( )
1
ln2
2
x
fx
=−
. D.
( )
1
lg2
2
x
fx
=−
.
Lời giải
Ta có:
( ) ( ) ( ) ( )
1
1 1 1 1 1
' ln ln 2 ln 2
2 2 2 2 2
x x x x
f x f x
−
= = = = −
.
Câu 29: Tập xác định
D
của hàm số
( )
2
5
log 3 2y x x= + +
là
A.
( ) ( )
; 2 1:D= − − − +
. B.
( )
1;D= − +
.
C.
(
)
; 2 1;D= − − − +
. D.
( )
2; 1D= − −
.
Lời giải
Hàm số
( )
2
5
log 3 2y x x= + +
xác định khi:
2
1
3 2 0
2
x
xx
x
−
+ +
−
.
Vậy tập xác định của hàm số đã cho là:
( ) ( )
; 2 1:D= − − − +
.
Câu 30: Phương trình
9 5.3 6 0
xx
− + =
có tổng các nghiệm là:
A.
3
log 6
. B.
3
2
log
3
. C.
3
2
log
3
. D.
3
log 6−
.
Lời giải
Xét phương trình:
9 5.3 6 0
xx
− + =
Đặt
( )
3 , 0
x
tt=
thì phương trình trở thành
2
5. 6 0tt− + =
.
Phương trình
2
5. 6 0tt− + =
có
10=
.
Theo định lý Vi-ét:
12
12
. 3 .3 6
xx
tt ==
12
36
xx+
=
1 2 3
log 6xx + =
.
Câu 31: Nghiệm của phương trình
( ) ( )
1
2
2
log 1 log 1 1xx− + + =
nằm trong khoảng nào sau đây?
A.
( )
1;0−
. B.
( )
0;1
. C.
( )
2;3
. D.
( )
4;5
.
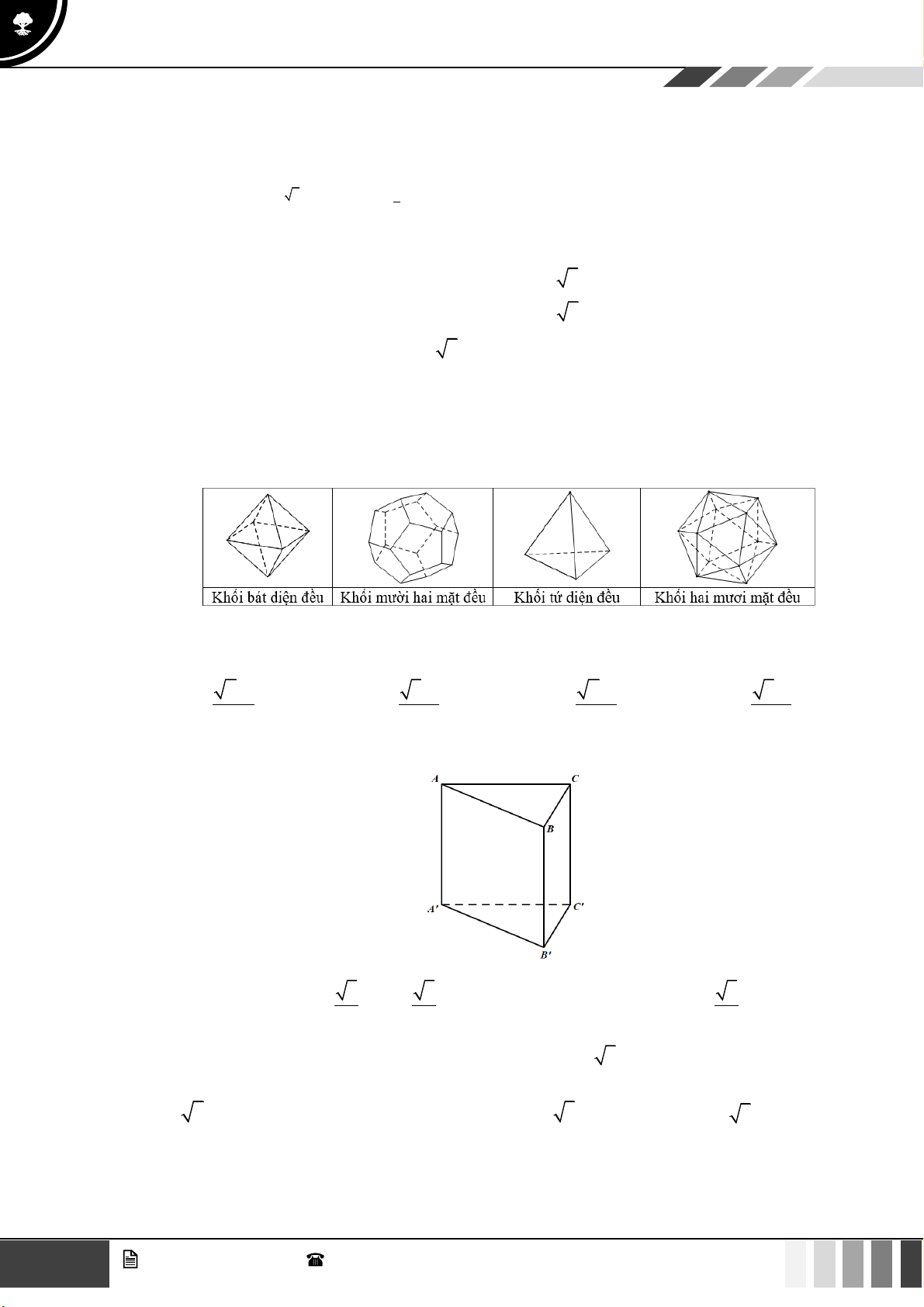
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HK1
Toán 12
Lời giải
Điều kiện
10
1
10
x
x
x
−
+
Phương trình
( ) ( ) ( ) ( )
1 2 2
2
2
log 1 log 1 1 2log 1 log 1 1x x x x− + + = − − + =
( ) ( )
2 2 2
2log 1 log 1 log 2xx − = + +
( ) ( )
2
22
log 1 log 2 1xx − = +
2
2 1 2 2x x x − + = +
( )
2
25
4 1 0
25
xL
xx
x
=−
− − =
=+
.
Tập nghiệm phương trình là
25S =+
.
Câu 32: Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
A. Khối bát diện đều. B. Khối mười hai mặt đều.
C. Khối tứ diện đều. D. Khối hai mươi mặt đều.
Lời giải
Khối mười hai mặt đều có các mặt không phải là tam giác đều
Câu 33: Tính thể tích
V
của khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
.
A.
3
2
3
a
V =
. B.
3
3
4
a
V =
. C.
3
2
4
a
V =
. D.
3
3
2
a
V =
.
Lời giải
Ta có
23
33
.AA .
44
ABC
V S a a a
= = =
. Vậy thể tích khối lăng trụ là
3
3
4
Va=
.
Câu 34: Cho hình nón có góc ở đỉnh bằng và chiều cao bằng
23
. Độ dài đường sinh của hình nón
bằng
A. . B.
4
. C. . D.
43
.
Lời giải
60
3
23

16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Theo đề bài ta có góc ở đỉnh bằng suy ra và chiều cao .
Vậy độ dài đường sinh của hình nón là:
23
4
cos30
3
2
OI
l OM= = = =
.
Câu 35: Tìm mệnh đề đúng trong các mệnh đề sau.
A. Tồn tại hình chóp có số cạnh gấp đôi số mặt.
B. Tồn tại hình lăng trụ có số cạnh gấp đôi số mặt.
C. Tồn tại hình lăng trụ có số cạnh bằng số mặt.
D. Tồn tại hình chóp có số cạnh bằng số mặt.
Lời giải
Với
n
là số nguyên dương lớn hơn hoặc bằng
3
.
Hình chóp
n −
giác có
2n
cạnh và
( )
1n +
mặt.
Xét đáp án A:
( )
2 2 1 0 1nn= + =
(vô lý), vì thế không tồn tại hình chóp có số cạnh gấp đôi
số mặt.
Xét đáp án D:
2 1 1 3n n n= + =
nên không tồn tại hình chóp có số cạnh bằng số mặt.
Hình lăng trụ
n −
giác có
3n
cạnh và
( )
2n +
mặt.
Xét đáp án C:
3 2 1 3n n n= + =
, vì thế không tồn tại hình lăng trụ có số cạnh bằng số mặt.
Xét đáp án B:
( )
3 2 2 4n n n= + =
. Vậy tồn tại hình lăng trụ tứ giác có số cạnh gấp đôi số
mặt.
Câu 36: Một mặt cầu có diện tích bằng
2
16 a
. Thể tích của khối cầu tương ứng là
A.
3
32
3
a
. B. . C. . D. .
Lời giải
Ta có
22
4 16 2S R a R a
= = =
. Vậy thể tích mặt cầu
( )
3
3
4 32
2
33
V a a
==
.
Câu 37: Cho ba hàm số lũy thừa
yx
=
,
yx
=
và
yx
=
có đồ thị như hình vẽ bên dưới. Chọn khẳng
định đúng trong các khẳng định sau
60
30MOI =
2OI =
( )
S
( )
S
3
12 a
3
4 a
3
43a
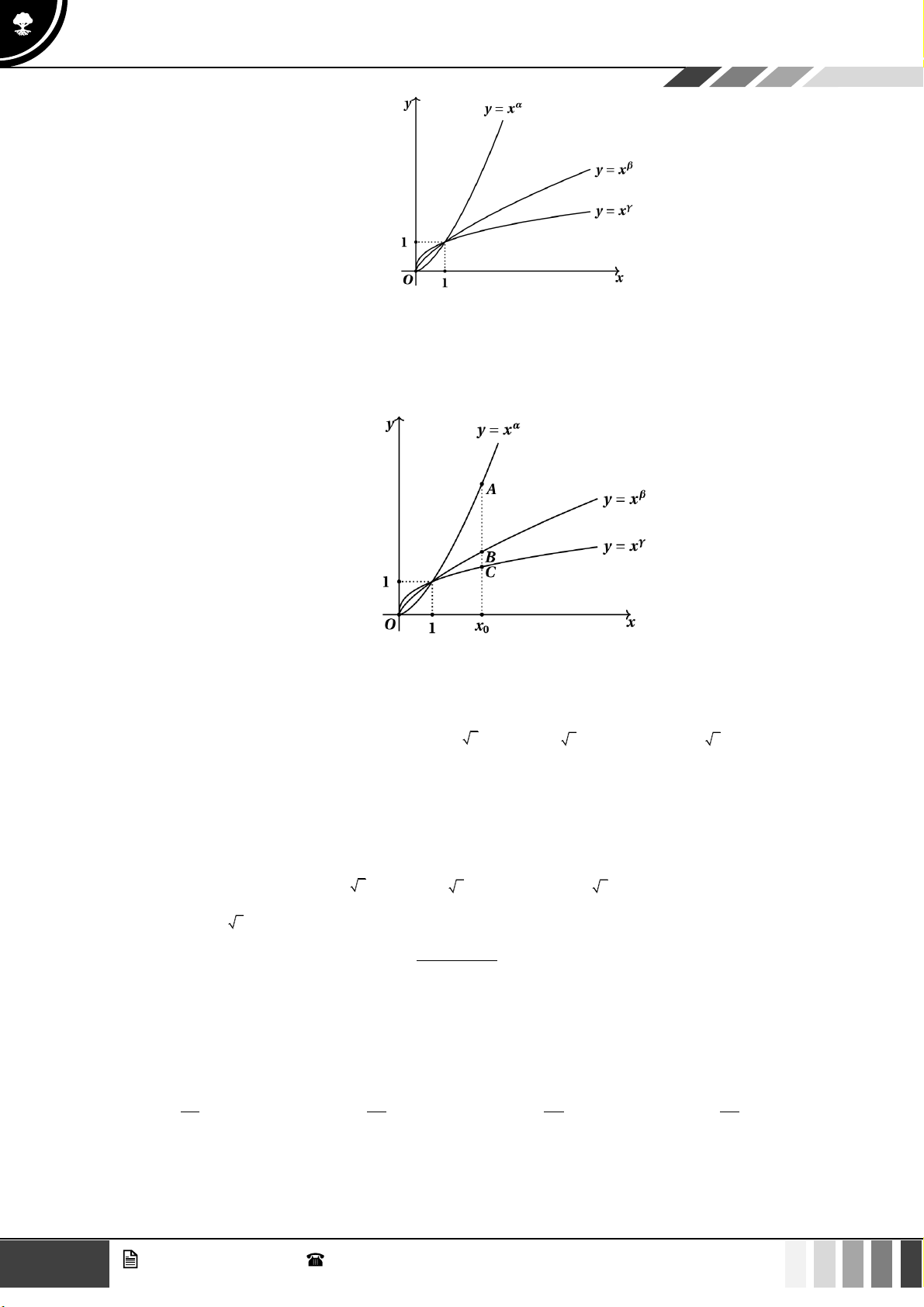
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HK1
Toán 12
A.
. B.
. C.
. D.
.
Lời giải
Chọn một giá trị
0
1x
, đường thẳng
0
xx=
cắt ba đồ thị hàm số lần lượt tại
,,A B C
như hình
vẽ.
Khi đó tung độ của các điểm
,,A B C
lần lượt là
0 0 0
,,x x x
.
Từ vị trí của
,,A B C
ta có
0 0 0
x x x
, suy ra
.
Câu 38: Giá trị của biểu thức
3 2022
log 2023 log 2023 log 2023 ... log 2023
a
a
aa
S = + + + +
( 0; 1)aa
là:
A.
1011.2022.log 2023
a
. B.
1012.2024.log 2023
a
.
C.
1012.2022.log 2023
a
. D.
1011.2023.log 2023
a
.
Lời giải
Ta có:
3 2022
S log 2023 log 2023 log 2023 ... log 2023
a
a
aa
= + + + +
(*)
Ta có
log 2023 .log 2023,
n
a
a
nn=
. Suy ra
( )
2022.2023
1 2 ... 2022 .log 2023 .log 2023 1011.2023.log 2023
2
a a a
S = + + + = =
Câu 39: Cho các số thực dương
,,abc
( với
,ac
khác 1) thỏa mãn các điều kiện
( ) ( )
23
log log
ac
ac b c=
và
2log log 8
ac
cb+=
. Tính giá trị của biểu thức
(
)
2
log log
ac
P b ab=+
.
A.
31
3
. B.
32
3
. C.
29
3
. D.
28
3
.
Lời giải
Từ giả thiết ta có:
( ) ( )
23
log log
2log log 8
ac
ac
ac b c
cb
=
+=

18
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
1 2log 1 3log 2log 3log 0
2log log 8 2log log 8
a c a c
a c a c
c b c b
c b c b
+ = + − =
+ = + =
log 3
log 2
a
c
c
b
=
=
.
Khi đó
(
)
2
1 31
log log log log log 2log 2.3 2.2
33
a c a c c c
P b ab c b a b= + = + + = + + =
.
Câu 40: Có bao nhiêu số nguyên
m
thuộc đoạn
2022;2022−
để phương trình
2
33
2
0
log 2log
x
m
xx
−
=
−
có nghiệm.
A.
1510
. B.
1513
. C.
1512
. D.
1509
.
Lời giải
Điều kiện
3
2
33
3
0
0
0
01
log 2
9
9
log 2log 0
log 0 1
x
x
x
x
x
x
x
xx
xx
−
.
Ta có:
2
33
2
0 2 0 2
log 2log
x
xx
m
mm
xx
−
= − = =
−
.
Do
01
9
0 1 2 2 2 1 2 2
9
2 2 2 512
xx
xx
x
x
nên phương trình đã cho có nghiệm khi và chỉ khi
12
512
m
m
. Mà
m
nguyên thuộc đoạn
2022;2022−
nên
513,514,...2022m
.
Vậy ta có
2022 513 1 1510− + =
giá trị của
m
thoả mãn.
Câu 41: Tập nghiệm của bất phương trình
2
3 10
2
1
3
3
xx
x
−−
−
chứa mấy số nguyên.
A.
10
. B.
9
. C.
8
. D.
7
.
Lời giải
Điều kiện:
( )
2
2
3 10 0 *
5
x
xx
x
−
− −
Ta có:
2
2
3 10
2 3 10 2
1
3 3 3
3
xx
x x x x
−−
− − − − −
( )
2
2
2
20
2
3 10 2
14
3 10 2
x
x
x x x
x
x x x
−
− − −
− − −
Kết hợp với điều kiện
( )
*
5 14x
Vậy tập nghiệm của bất phương trình chứa 9 số nguyên.
Câu 42: Gọi
S
là tập hợp các giá trị của tham số
m
để đồ thị hàm số
( )
3 2 2 2
3 3 1 3 1y x x m x m= − + + − − −
có điểm cực đại và cực tiểu cùng với gốc tọa độ tạo thành
tam giác vuông tại
O
. Tích tất cả các giá trị của tập
S
bằng
A.
1−
. B.
3
2
−
. C.
3
2
. D.
1
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HK1
Toán 12
Ta có
22
3 6 3 3 0y x x m
= − + + − =
22
2 1 0x x m − + + − =
( )
1
Để hàm số có hai điểm cực đại và cực tiểu thì
( )
1
phải có hai nghiệm phân biệt, nên
2
0m
=
suy ra
0m
.
Dễ thấy
( )
1
có hai nghiệm
1
1xm=−
và
2
1xm=+
nên
( )
3
1 ; 2 2A m m− − −
và
( )
3
1 ; 2 2B m m+ − +
là hai điểm cực trị của đồ thị hàm số
Tam giác
OAB
vuông ở
O
.0OAOB=
( )( )
( )( )
33
1 1 2 2 2 2 0m m m m − + + − − − + =
( )
26
1 4 1 0mm − + − =
( )( )
24
1 4 4 5 0m m m − + + =
2
1m=
1m =
.
Do đó tích các giá trị thỏa mãn của
m
bằng
1−
.
Câu 43: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật có
23AB a=
;
2.AD a=
Mặt bên
( )
SAB
là
tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp
.S ABD
là
A.
3
4 3 .a
. B.
3
23
.
3
a
. C.
3
4.a
. D.
3
2 3 .a
Lời giải
Gọi
H
là trung điểm của đoạn thẳng
AB
suy ra
SH
là đường cao của tam giác
SAB
SH AB⊥
.
Mà
( ) ( ) ( )
SAB ABCD SH ABCD⊥ ⊥
Vì tam giác
ABC
đều cạnh
23a
nên
3
. 3 .
2
SH AB a==
Diên tích tam giác
ABD
:
2
11
. .2 3.2 2 3.
22
ABD
S AB AD a a a
= = =
Thể tích khối chóp
.S ABD
:
23
.
11
. .2 3.3 2 3 .
33
S ABD ABD
V S SH a a a
= = =
.
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
,B
1,BA BC==
2.AD =
Cạnh bên
SA
vuông góc với đáy và
2.SA =
Gọi
H
là hình chiếu vuông góc của
A
trên
.SB
Thể tích của khối đa diện
SAHCD
bằng
A.
22
.
9
B.
22
.
3
C.
42
.
9
D.
42
.
3
Lời giải
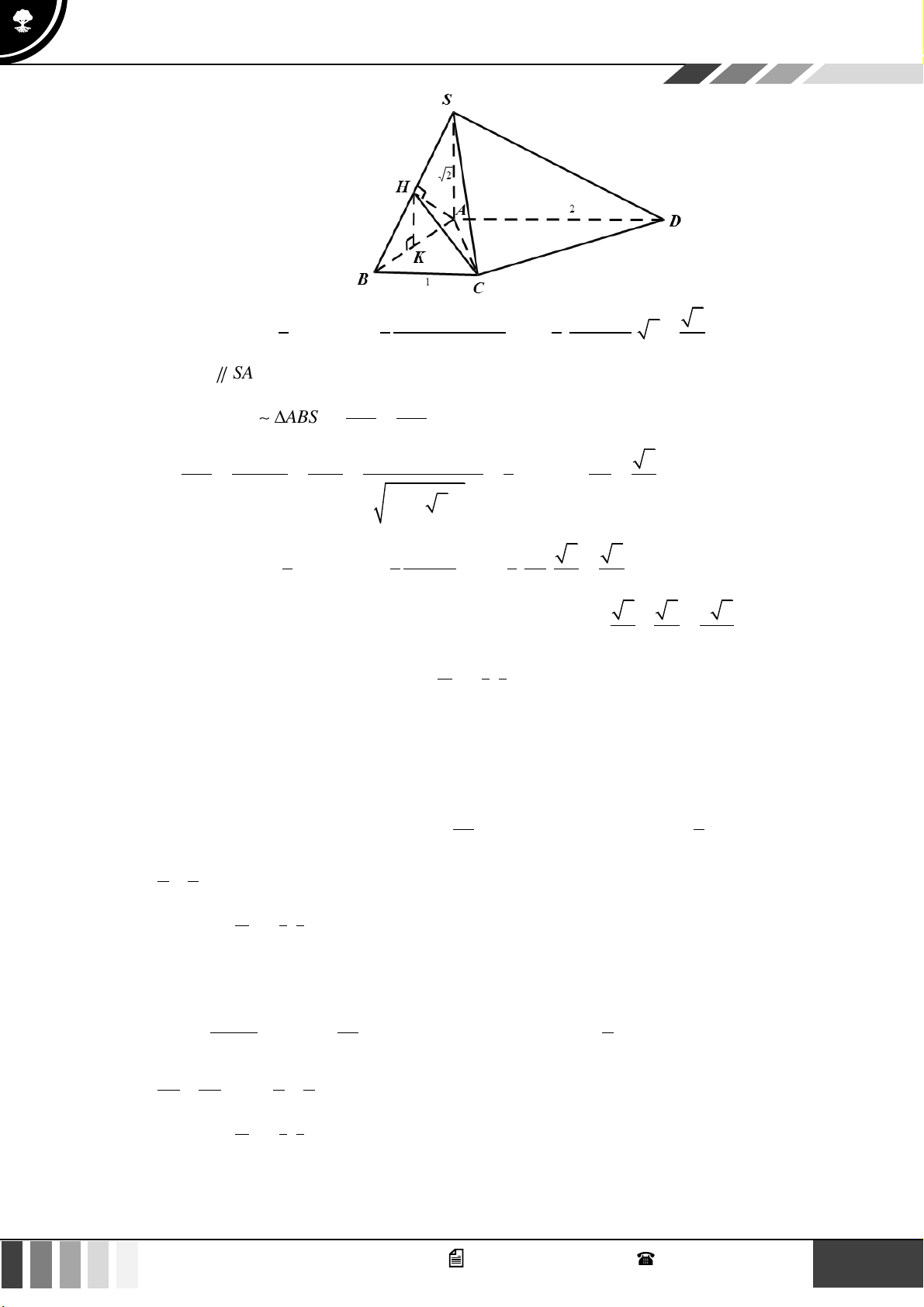
20
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Ta có
( ) ( )
.
1 2 .1
1 1 1 2
. . . . 2 .
3 3 2 3 2 2
S ABCD ABCD
BC AD AB
V S SA SA
++
= = = =
Kẻ
HK SA
( ) ( )
.K AB HK ABC ⊥
Ta có
HK BH
KBH ABS
SA BS
=
( )
22
22
2
2
. 1 1 2
.
. 3 3 3
12
HK BH BS AB SA
HK
SA BS BS
BS
= = = = = =
+
Khi đó
.
1 1 . 1 1.1 2 2
. . . .
3 3 2 3 2 3 18
H ABC ABC
BA BC
V S HK HK
= = = =
Suy ra thể tích đa diện cần tính:
..
2 2 4 2
.
2 18 9
SAHCD S ABCD H ABC
V V V= − = − =
Câu 45: Số nghiệm thực của phương trình
11
44
2 2 4
x
x
xx
++
+=
là:
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Điều kiện
0x
.
Trường hợp 1:
0x
Áp dụng bất đẳng thức Cô sy ta có:
1
1
4
x
x
+
, dấu
""=
xảy ra khi
1
2
x =
.
1
1
4
x
x
+
, dấu
""=
xảy ra khi
2x =
.
Suy ra
( )
11
11
44
2 2 2 2 4 1
x
x
xx
++
+ + =
.
Trường hợp 2:
00xx −
Áp dụng bất đẳng thức Cô sy ta có:
( )
( )
11
11
44
xx
xx
− + + −
−
, dấu
""=
xảy ra khi
1
2
x =−
.
11
11
44
xx
xx
−
+ + −
−
, dấu
""=
xảy ra khi
2x =−
.
Suy ra
( )
11
11
44
2 2 2 2 1 4 2
x
x
xx
++
−−
+ + =
.
Từ
( ) ( )
1 , 2
suy ra phương trình đã cho vô nghiệm.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 46: Cho hình lăng trụ
ABCA B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
lên
mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường thẳng
AA
và
BC
bằng
3
3
a
. Tính thể tích
V
của khối lăng trụ
.ABCA B C
A.
3
5
24
a
V =
. B.
3
5
10
a
V =
. C.
3
5
3
a
V =
. D.
3
5
6
a
V =
.
Lời giải
M
là trung điểm của
BC
thì
( )
BC AA M
⊥
.
Gọi
MH
là đường cao của tam giác
A AM
thì
MH A A
⊥
và
HM BC⊥
nên
HM
là khoảng cách
AA
và
BC
.
Ta có
..HM A A A G AM
=
2
2
33
.
3 2 3
a a a
A A A A
= −
2
22
49
3
a
A A A A
= −
22
53A A a
=
2
2
3
5
a
AA
=
15
5
a
AA
=
.
Đường cao của lăng trụ là
22
3 3 2 15
5 9 15
a a a
AG
= − =
.
Thể tích
23
2 15 3 5
.
15 4 10
a a a
V ==
.
Câu 47: Cho hình trụ có hai đáy là hình tròn tâm
O
và
O
, chiều cao
3ha=
. Mặt phẳng đi qua tâm
O
và tạo với
OO
một góc
30
, cắt hai đường tròn tâm
O
và
O
tại bốn điểm là bốn đỉnh của một
hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng
2
3a
. Thể tích của khối trụ được giới
hạn bởi hình trụ đã cho bằng
A.
3
3
3
a
. B.
3
3a
. C.
3
3
12
a
. D.
3
3
4
a
.
Lời giải
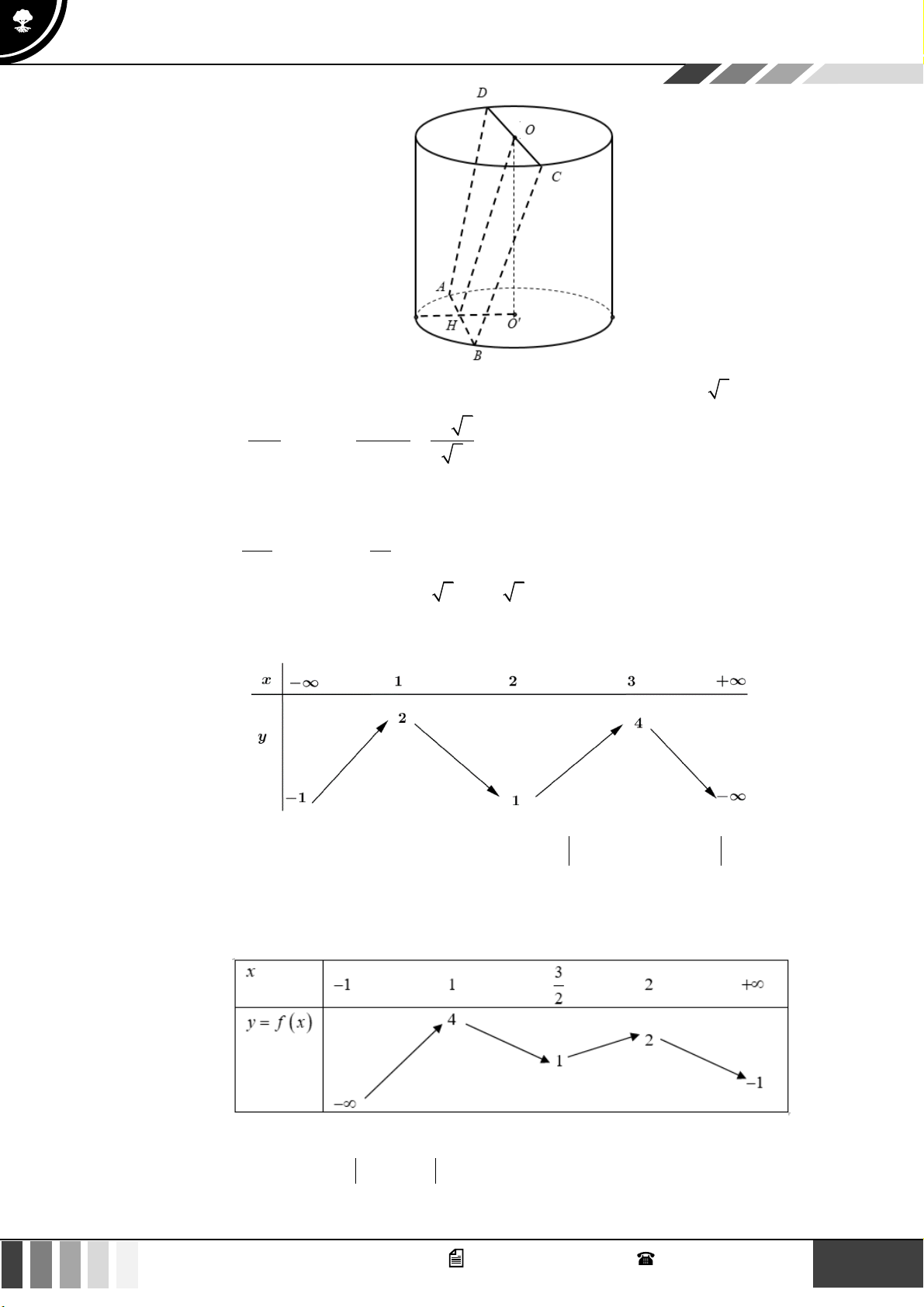
22
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Ta có góc giữa mặt phẳng
( )
ABCD
và
OO
là góc
30HOO
=
,
3OO a
=
.
23
cos 2
cos30
3
OO OO a
HOO OH a
OH
= = = =
Ta có
2CD r AB r= =
Theo giả thiết diện tích hình thang
ABCD
bằng
2
3a
nên ta có:
( )
22
2
3 3 . 3
22
OH a
AB CD a r a r a+ = = =
Vậy thể tích khối trụ bằng
23
. 3 3V a a a
==
.
Câu 48: Cho hàm số . Biết hàm số có bảng biến thiên như hình vẽ sau
Số giá trị nguyên dương của tham số để hàm có giá trị lớn nhất?
A. . B. . C. Vô số. D. .
Lời giải
Vẽ lại bảng biến thiên
( )
:fx
Đặt
( )
2
4 3 1x x t t− + = −
Hàm số trở thành:
( )
2,y f t m=−
với
)
1;t − +
Do
) ( ) (
( ) (
1; 1;4 2 2 ;8t f t f t m m m − + − − − − −
( )
y f x=
( )
52y f x=−
m
( )
( )
2
2 4 3g x f x x m= − + −
5
4
3

GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HK1
Toán 12
Để hàm số
( )
2y f t m=−
có GTLN
80
2
28
m
m
mm
−
− − −
Câu 49: Một anh sinh viên T nhập học đại học vào tháng
8
năm
2020
. Bắt đầu từ tháng
9
năm
2020
,
cứ vào ngày mồng một hàng tháng anh vay ngân hàng
3
triệu đồng với lãi suất cố định
0,8%
/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo (lãi kép). Vào
ngày mồng một hàng tháng kể từ tháng
9
năm
2022
về sau anh không vay ngân hàng nữa và
anh còn trả được cho ngân hàng
2
triệu đồng do việc làm thêm. Hỏi vào ngày anh ra trường
( )
30 / 6 / 2024
, số tiền anh nợ ngân hàng gần nhất với số nào sau đây?
A.
49.024.000
đồng B.
46.640.000
đồng C.
47.024.000
đồng D.
45.401.000
đồng
Lời giải
Anh sinh viên vay hàng tháng
3a =
triệu đồng từ tháng
9
/
2020
đến hết tháng
8 / 2022
, tổng
cộng
24
tháng.
Cuối tháng thứ 1:
( )
1
1T a ar a r= + = +
Cuối tháng thứ 2:
( ) ( ) ( )
2
2 1 1
. . 1 . 1T T a T a r a r a r= + + + = + + +
….
Cuối tháng n:
( ) ( ) ( )
1
. 1 . 1 ... . 1
nn
n
T a r a r a r
−
= + + + + + +
Suy ra
( )
( )
11
. 1 .
n
n
r
T a r
r
+−
=+
Vậy tổng số tiền vay đến cuối tháng
8 / 2022
là
( )
( )
24
24
1 0,8% 1
3. 1 0,8% . 79,662
0,8%
T
+−
= + =
triệu.
Tính từ cuối tháng
8 / 2022
anh sinh viên T thiếu ngân hàng
79,662A =
và bắt đầu trả đầu hàng
tháng
2m =
triệu từ
9 / 2022
đến
6 / 2024
, tổng cộng được
22
tháng
Đầu tháng
9 / 2022
: còn nợ
79,662 2 77,662Am− = − =
triệu
Cuối tháng
9 / 2022
: tiền nợ có lãi đến cuối tháng:
( )
1
77,662 1Tr=+
Đầu tháng
10 / 2022
sau khi trả nợ
m
thì còn nợ
( )
77,662 1rm+−
Cuối tháng
10 / 2022
: còn nợ
( )( ) ( ) ( ) ( )
2
2
77,662 1 1 77,662 1 1T r m r r m r= + − + = + − +
Cuối tháng
11/ 2022
: còn nợ
( ) ( ) ( )
32
3
77,662 1 1 1T r m r m r= + − + − +
….
Cuối tháng
6 / 2024
còn nợ:
( ) ( ) ( ) ( )
( ) ( )
( )
22 21 20
22
21
22
77,662 1 1 1 ... 1
11
77,662 1 . 1
T r m r m r m r
r
r m r
r
= + − + − + − − +
+−
= + − +
( ) ( )
( )
21
22
1 0,8% 1
77,662. 1 0,8% 2. 1 0,8% . 46,64
0,8%
+−
= + − + =
triệu đồng.
Câu 50: Cho hàm đa thức bậc năm
( )
y f x=
và hàm số
( )
y f x
=
có đồ thị như trong hình bên.
24
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
( )
32
32g x f x x m m= + + −
có đúng
ba điểm cực đại?
A.
3
. B.
0
. C.
4
. D.
1
.
Lời giải
Ta có
( )
( )
( )( )
23
32
3
3 3 3
32
3
x x x
g x f x x m m
xx
++
= + + −
+
Ta có
( ) ( )
3 2 3 2
3 2 3 2
3 2 3 2
3 2 3 2
3 2 3 3 2 3
3 2 1 3 2 1
0*
3 2 2 3 2 2
3 2 5 3 2 5
x x m m x x m m
x x m m x x m m
gx
x x m m x x m m
x x m m x x m m
+ + − = − + = − −
+ + − = − + = − −
=
+ + − = + = − +
+ + − = + = − +
và
( )
gx
không
xác định tại
0x =
.
Do
( )
lim
x
gx
→+
= +
nên để hàm số
( )
gx
có ba điểm cực đại khi và chỉ khi hàm số
( )
gx
có bảy
điểm cực trị.
Xét hàm số
( )
3
3h x x x=+
, ta có
( )
2
3 3 0,h x x x
= +
nên
( )
hx
đồng biến trên
( )
;− +
.
Khi đó, ta có được bảng biến của hàm số
( )
3
3y h x x x= = +
như sau:
Để hàm số
( )
gx
có bảy điểm cực trị thì
( )
*
phải có
6
nghiệm phân biệt:
2
2
1
2 1 0
1
2
2 3 0
13
m
mm
m
mm
m
− −
−
− −
−
, mà
m
là số nguyên nên
1;2;3m−
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HK1
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Hàm số nào dưới đây nghịch biến trên khoảng
( )
;− +
?
A.
1
2
x
y
x
−
=
−
. B.
3
y x x=+
. C.
3
3y x x= − −
. D.
1
3
x
y
x
+
=
+
.
Câu 2: Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
A.
32
41y x x= − + +
B.
32
34y x x= − +
C.
42
2 10y x x= − + +
D.
42
91y x x= − +
.
Câu 3: Hàm số
23
1
x
y
x
−
=
+
có bao nhiêu điểm cực trị?
A. 0. B. 1. C. 2. D. 3.
Câu 4: Giá trị nhỏ nhất của hàm số
( )
3
22f x x x=−
trên đoạn
5;22
bằng
A. 15. B. 17. C. 22. D. 37.
Câu 5: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1
x
y
x
+
=
−
. B.
3
1
x
y
x
−
=
−
. C.
2
41y x x= − +
. D.
3
35y x x=−−
.
Câu 6: Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
+
=
−
là
A.
2x =
. B.
2x =−
. C.
1.x =
D.
1x =−
.
Câu 7: Hàm số nào dưới đây không là hàm số lũy thừa?
A.
4
1
y
x
=
.
B.
2
yx
−
=
.
C.
x
ye=
.
D.
yx
=
.
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
03
ĐỀ SỐ

2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 8: Với mọi số thực dương
, , ,a b x y
và
,1ab
, mệnh đề nào sau đây sai?
A.
( )
log log log
a a a
xy x y=+
. B.
11
log
log
a
a
xx
=
.
C.
log .log log
b a b
a x x=
. D.
log log log
a a a
x
xy
y
=−
.
Câu 9: Cho
,ab
là hai số thực dương tùy ý và
1b
. Khẳng định nào dưới đây đúng?
A.
( )
ln ln lna b a b+ = +
. B.
( )
ln ln .lna b a b+=
.
C.
( )
ln ln lna b a b− = −
. D.
ln
log
ln
b
a
a
b
=
.
Câu 10: Tìm tập xác định
D
của hàm số
( )
2
3
log 4 3y x x= − +
.
A.
( )
1;3D =
. B.
( ) ( )
;1 3;D = − +
.
C.
( ) ( )
;2 2 2 2;D = − − + +
. D.
( ) ( )
2 2;1 3;2 2D = − +
.
Câu 11: Hàm số
2
2
xx
y
−
=
có đạo hàm là
A.
2
2 .ln2
xx−
. B.
( )
2
2 1 .2 .ln2
xx
x
−
−
. C.
( )
2
21
.2
xx
xx
−−
−
. D.
( )
2
2 1 .2
xx
x
−
−
.
Câu 12: Tập nghiệm của phương trình
( )
2
3
log 3 1xx+ + =
là
A.
1;0S =−
. B.
0;1S =
. C.
0S =
. D.
1S =−
.
Câu 13: Nghiệm của phương trình
( )
2
log 1 3x −=
là
A.
8x =
. B.
10x =
. C.
7x =
. D.
9x =
.
Câu 14: Tập nghiệm của bất phương trình
52
x
là
A.
( )
5
;log 2−
. B.
( )
5
log 2;+
. C.
( )
2
;log 5−
. D.
( )
2
log 5;+
.
Câu 15: Hình bát diện đều có bao nhiêu cạnh?
A. 8 cạnh. B. 6 cạnh. C. 12 cạnh. D. 20 cạnh.
Câu 16: Cho khối lăng trụ có diện tích đáy
2
6Ba=
và chiều cao
2ha=
. Thể tích khối lăng trụ đã cho
bằng
A.
3
12a
. B.
3
4a
. C.
3
3a
. D.
3
6a
.
Câu 17: Cho hình trụ có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích xung quanh
xq
S
của hình trụ
đã cho được tính theo công thức nào dưới đây?
A.
4
xq
S rl
=
. B.
2
xq
S rl
=
. C.
3
xq
S rl
=
. D.
xq
S rl
=
.
Câu 18: Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích xung quanh
xq
S
của hình
nón đã cho được tính theo công thức nào dưới đây?
A.
4
xq
S rl
=
. B.
xq
S rl
=
. C.
3
xq
S rl
=
. D.
2
xq
S rl
=
.
Câu 19: Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích toàn phần
tp
S
của hình nón
đã cho được tính theo công thức nào dưới đây?

GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HK1
Toán 12
A.
2
tp
S rl l
=+
. B.
2
tp
S rl r
=+
. C.
1
3
tp
S rl
=
. D.
2
22
tp
S rl r
=+
.
Câu 20: Cho khối cầu có bán kính
r
. Thể tích
V
của khối cầu đã cho được tính theo công thức nào dưới
đây?
A.
3
3
4
Vr
=
. B.
3
4
3
Vr
=
. C.
3
3
4
Vr
=
. D.
3
4
3
Vr
=
.
Câu 21: Cho hàm số
( )
y f x=
có đạo hàm
( )
2022f x x
=+
với mọi
x
. Hàm số đã cho đồng biến
trên khoảng nào dưới đây?
A.
( )
2022;− +
. B.
( )
2022;+
. C.
( )
; 2022− −
. D.
( )
;2022−
.
Câu 22: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
12f x x x x
= − +
, . Số điểm cực tiểu của hàm số
đã cho là
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 23: Trên đoạn
4; 1−−
, hàm số
42
8 13y x x= − +
đạt giá trị nhỏ nhất tại điểm nào trong các điểm
sau?
A.
2x =−
. B.
1x =−
. C.
4x =−
. D.
3x =−
.
Câu 24: Cho hàm số
( )
1ax
fx
bx c
+
=
+
( )
,,a b c R
có bảng biến thiên như sau:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A. 1 B. 3. C. 2. D. 0.
Câu 25: Tìm số tiệm cận đứng của đồ thị hàm số
2
2
34
16
xx
y
x
−−
=
−
.
A. 2. B. 3. C. 1. D. 0.
Câu 26: Cho
a
là số thực dương. Rút gọn của biểu thức
4
3
m
n
P a a a==
với
m
n
tối giản,
0n
. Khi đó
mn+
bằng
A.
5
. B.
11
. C.
17
. D.
6
.
Câu 27:
Cho hàm số
3 x
y e x e
−
=+
. Nghiệm của phương trình
0y
=
là
A.
3x =−
. B.
0x =
. C.
ln3x =
. D.
ln2x =
.
Câu 28: Đạo hàm cấp hai
y
của hàm số
( )
ln 3 2yx=+
là
A.
( )
2
3ln 3 2yx
=+
. B.
9
32
y
x
−
=
+
. C.
( )
2
3
32
y
x
=
+
. D.
( )
2
9
32
y
x
−
=
+
.
Câu 29: Hàm số
( )
2
log 2 1y x x m= − + +
có tập xác định là khi
x

4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
A.
0.m
B.
0 3.m
C.
0
.
1
m
m
−
D.
0.m =
Câu 30: Số nghiệm thực của phương trình
( )
2
58
0
ln 1
xx
x
+−
=
−
là?
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 31: Tổng tất cả các nghiệm của phương trình
21
2 5.2 2 0
xx+
− + =
bằng bao nhiêu?
A.
3
.
2
B.
1.
C.
5
.
2
D.
0.
Câu 32: Hình lập phương có bao nhiêu mặt phẳng đối xứng?
A. 6. B. 7. C. 8. D. 9.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông có cạnh bằng
2a
,
( )
SA ABCD⊥
,
2SA a=
. Tính thể tích khối chóp
.S ABCD
.
A.
3
2
3
a
V =
. B.
3
4Va=
. C.
3
2Va=
. D.
3
4
3
a
V =
.
Câu 34: Hình nón có góc ở đỉnh bằng
60
và chiều cao bằng
3
. Độ dài đường sinh của hình nón bằng
A.
2
. B.
22
. C.
23
. D.
3
.
Câu 35: Quay một miếng bìa hình tròn có diện tích
2
16 a
quanh một trong những đường kính, ta được
khối tròn xoay có thể tích là
A.
3
64
3
a
. B.
3
128
3
a
. C.
3
256
3
a
. D.
3
32
3
a
.
Câu 36: Có bao nhiêu giá trị nguyên của
m
thuộc
2023;2023−
để hàm số
( )
2
2
22y x x m= − + +
có
tập xác định là ?
A.
2024
. B.
2023
. C.
4045
. D.
4044
.
Câu 37: Cho hàm số
( )
2
2022 ln
x
fx
x
+
=−
. Tính tổng
( ) ( ) ( )
1 3 ... 2023S f f f
= + + +
.
A.
2024
2025
S =
. B.
2026
2025
S =
. C.
2024
2023
S =
. D.
2022
2023
S =
.
Câu 38: Biết phương trình
4 4 2
log log log 8
9 12.3 3 0
xx
− + =
có hai nghiệm
1
x
,
2
x
. Khi đó
22
12
xx+
bằng
A.
90
. B.
10
. C.
20
. D.
272
.
Câu 39: Với giá trị nào của tham số
m
thì phương trình
1
4 .2 2 0
xx
mm
+
− + =
có hai nghiệm phân biệt
12
,xx
thỏa mãn
12
3xx+=
?
A.
2m =
. B.
1m =
. C.
3m =
. D.
4m =
.
Câu 40: Tập nghiệm của bất phương trình
( ) ( )
2 2 2 2 2
.2 9 2 .2 8 2 .2 9 .2 8 16
x x x x
x x x x x x+ + + + + + +
là
A.
(
; 1 0;2− −
. B.
1;0 2;3−
. C.
)
0;2 3; +
. D.
) (
1;0 2;3−
.
Câu 41: Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh
của tứ diện cũng là đỉnh của hình lập phương?

GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HK1
Toán 12
A.
4
. B.
6
. C.
2
. D.
8
.
Câu 42: Cho hình chóp tứ giác đều
.S ABCD
, gọi
,MN
lần lượt là trung điểm của
SA
và
BC
. Biết góc
giữa đường thẳng
MN
và mặt phẳng
( )
ABCD
bằng
60
, khoảng cách từ
M
đến mặt phẳng
( )
ABCD
bằng
30
4
a
. Thể tích khối chóp
.S ABCD
theo
a
bằng
A.
3
10
3
a
. B.
3
30
6
a
. C.
3
30
2
a
. D.
3
10
6
a
.
Câu 43: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với đáy,
mặt phẳng
( )
SAD
tạo với đáy một góc
60
. Thể tích khối chóp
.S ABCD
là:
A.
3
33
4
a
V =
. B.
3
83
9
a
V =
. C.
3
83
3
a
V =
. D.
3
43
3
a
V =
.
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
( )
ABCD
, góc giữa hai mặt phẳng
( )
SBD
và
ABCD
bằng
0
60
. Gọi
,MN
lần lượt là trung điểm của
,SB SC
. Thể tích khối chóp
.S ADNM
là:
A.
3
6
16
a
V =
. B.
3
6
24
a
V =
. C.
3
36
16
a
V =
. D.
3
6
8
a
V =
.
Câu 45: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và đáy bằng
o
60
.
Diện tích xung quanh của hình nón đỉnh
S
, có đáy là hình tròn ngoại tiếp tam giác
ABC
bằng
A.
2
10
8
a
. B.
2
3
3
a
. C.
2
7
6
a
. D.
2
7
4
a
.
Câu 46: Cho hàm số
( )
y f x=
có đạo hàm trên và bảng xét dấu đạo hàm như sau:
Có bao nhiêu số nguyên
m
để hàm số
( )
3
2y f x x m= + +
nghịch biến trên khoảng
( )
1;1−
?
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 47: Một mảnh đất hình chữ nhật
ABCD
có chiều dài
25mAB =
, chiều rộng
20mAD =
được chia
thành hai phần bằng nhau bởi vạch chắn
MN
(
,MN
lần lượt là trung điểm
BC
và
AD
). Một
đội xây dựng làm một con đường đi từ
A
đến
C
qua vạch chắn
MN
, biết khi làm đường trên
miền
ABMN
mỗi giờ làm được
15m
và khi làm trong miền
CDNM
mỗi giờ làm được
30m
.
Tính thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ
A
đến
C
.
A.
25
3
. B.
10 2 725
30
+
. C.
20 725
30
+
. D.
5
.
Câu 48: Số giá trị nguyên của tham số
m
để hàm số
( )
1
22
2022
21y x mx m m= − − + +
xác định trên khoảng
( )
0;+
là
A.
0
. B.
2
. C.
1
. D.
3
.

6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 49: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình
(
)
2
log 2 2
x
m m x+ + =
có nghiệm thực không âm?
A. 2018. B. 2019. C. 2020. D. 2021.
Câu 50: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ sau.
Gọi
0
m
là giá trị nhỏ nhất của tham số
m
để đồ thị hàm số
( ) ( ) ( )
2
3g x f x f x m= + +
có số
điểm cực trị ít nhất. Tìm mệnh đề đúng trong các mệnh đề sau?
A.
( )
0
;2m − −
. B.
( )
0
2;3m
. C.
( )
0
3;m +
. D.
( )
0
2;2m −
.
-----------------------HẾT-----------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HK1
Toán 12
BẢNG ĐÁP ÁN
1.C
2.B
3.A
4.A
5.B
6.C
7.C
8.B
9.D
10.B
11.B
12.A
13.D
14.B
15.C
16.A
17.B
18.B
19.B
20.B
21.A
22.B
23.A
24.A
25.C
26.C
27.A
28.D
29.A
30.D
31.D
32.D
33.D
34.A
35.C
36.A
37.A
38.D
39.D
40.B
41.B
42.B
43.C
44.A
45.C
46.B
47.A
48.C
49.C
50.B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Hàm số nào dưới đây nghịch biến trên khoảng
( )
;− +
?
A.
1
2
x
y
x
−
=
−
. B.
3
y x x=+
. C.
3
3y x x= − −
. D.
1
3
x
y
x
+
=
+
.
Lời giải
Ta có:
32
3 ' 3 3 0y x x y x= − − = − −
với
.x
Nên ta chọn phương án C.
Câu 2: Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
A.
32
41y x x= − + +
B.
32
34y x x= − +
C.
42
2 10y x x= − + +
D.
42
91y x x= − +
.
Lời giải
Dựa vào đồ thị ta thấy đây là hình ảnh đồ thị của hàm số bậc ba nên loại đáp án
C
và
D
; Mặt
khác dựa vào đồ thị ta có
lim
x
y
→+
= +
nên hệ số của
3
x
dương nên ta chọn đáp án
B
.
Câu 3: Hàm số
23
1
x
y
x
−
=
+
có bao nhiêu điểm cực trị?
A. 0. B. 1. C. 2. D. 3.
Lời giải
Có
( )
2
5
0, 1
1
yx
x
= −
+
nên hàm số không có cực trị.
Câu 4: Giá trị nhỏ nhất của hàm số
( )
3
22f x x x=−
trên đoạn
5;22
bằng
A. 15. B. 17. C. 22. D. 37.
Lời giải
Trên đoạn
5;22
, ta có:
2
22
5;22
3
' 3 22 ' 0 .
22
5;22
3
x
y x y
x
= −
= − =
=

8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Ta có:
( ) ( )
5 15; 22 10164yy==
. Vậy
min
15.y =
Câu 5: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1
x
y
x
+
=
−
. B.
3
1
x
y
x
−
=
−
. C.
2
41y x x= − +
. D.
3
35y x x=−−
.
Lời giải
Đồ thị hàm số dạng
ax b
y
cx d
+
=
+
và hàm số đồng biến trên tập xác định.
Câu 6: Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
+
=
−
là
A.
2x =
. B.
2x =−
. C.
1.x =
D.
1x =−
.
Lời giải
Ta có
11
22
lim lim
1
xx
x
y
x
++
→→
+
= = +
−
và
11
22
lim lim
1
xx
x
y
x
−−
→→
+
= = −
−
Nên đường thẳng
1x =
là tiệm cận đứng của đồ
thị hàm số.
Câu 7: Hàm số nào dưới đây không là hàm số lũy thừa?
A.
4
1
y
x
=
.
B.
2
yx
−
=
.
C.
x
ye=
.
D.
yx
=
.
Lời giải
Dựa vào định nghĩa của hàm số lũy thừa: Hàm số
()yx
=
được gọi là hàm số lũy thừa.
Các hàm số ở mỗi phương án A, B, D đều là hàm số lũy thừa.
Vậy hàm số ở phương án C không là hàm số lũy thừa.
Câu 8: Với mọi số thực dương
, , ,a b x y
và
,1ab
, mệnh đề nào sau đây sai?
A.
( )
log log log
a a a
xy x y=+
. B.
11
log
log
a
a
xx
=
.
C.
log .log log
b a b
a x x=
. D.
log log log
a a a
x
xy
y
=−
.
Lời giải
Theo các tính chất logarit thì các phương án A, C và D đều đúng.
Với mọi số thực dương
, , ,a b x y
và
,1ab
. Ta có:
1
11
log log
log
aa
a
x
xx
−
=
.
Vậy phương án B sai.
Câu 9: Cho
,ab
là hai số thực dương tùy ý và
1b
. Khẳng định nào dưới đây đúng?
A.
( )
ln ln lna b a b+ = +
. B.
( )
ln ln .lna b a b+=
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HK1
Toán 12
C.
( )
ln ln lna b a b− = −
. D.
ln
log
ln
b
a
a
b
=
.
Lời giải
Dựa vào tích chất của logarit chỉ có khẳng định đúng là
ln
log
ln
b
a
a
b
=
nên ta chọn phương án
D
.
Câu 10: Tìm tập xác định
D
của hàm số
( )
2
3
log 4 3y x x= − +
.
A.
( )
1;3D =
. B.
( ) ( )
;1 3;D = − +
.
C.
( ) ( )
;2 2 2 2;D = − − + +
. D.
( ) ( )
2 2;1 3;2 2D = − +
.
Lời giải
Hàm số đã cho xác định khi và chỉ khi
2
1
4 3 0
3
x
xx
x
− +
. Nên tập xác định của hàm số
là:
( ) ( )
;1 3;D = − +
.
Câu 11: Hàm số
2
2
xx
y
−
=
có đạo hàm là
A.
2
2 .ln2
xx−
. B.
( )
2
2 1 .2 .ln2
xx
x
−
−
. C.
( )
2
21
.2
xx
xx
−−
−
. D.
( )
2
2 1 .2
xx
x
−
−
.
Lời giải
Ta có
( )
( )
22
2
2 ln2 2 1 .2 .ln2
x x x x
y x x x
−−
= − = −
.
Câu 12: Tập nghiệm của phương trình
( )
2
3
log 3 1xx+ + =
là
A.
1;0S =−
. B.
0;1S =
. C.
0S =
. D.
1S =−
.
Lời giải
Phương trình đã cho tương đương
2
0
33
1
x
xx
x
=
+ + =
=−
.
Vậy tập nghiệm của phương trình là
1;0S =−
.
Câu 13: Nghiệm của phương trình
( )
2
log 1 3x −=
là
A.
8x =
. B.
10x =
. C.
7x =
. D.
9x =
.
Lời giải
Ta có
( )
3
2
log 1 3 1 2 9x x x− = − = =
. Vậy phương trình đã cho có nghiệm là
9x =
.
Câu 14: Tập nghiệm của bất phương trình
52
x
là
A.
( )
5
;log 2−
. B.
( )
5
log 2;+
. C.
( )
2
;log 5−
. D.
( )
2
log 5;+
.
Lời giải
Ta có
5
5 2 log 2
x
x
. Vậy bất phương trình đã cho có tập nghiệm là
( )
5
log 2;+
.
Câu 15: Hình bát diện đều có bao nhiêu cạnh?
A. 8 cạnh. B. 6 cạnh. C. 12 cạnh. D. 20 cạnh.
Lời giải
Hình bát diện đều có 12 cạnh.

10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 16: Cho khối lăng trụ có diện tích đáy
2
6Ba=
và chiều cao
2ha=
. Thể tích khối lăng trụ đã cho
bằng
A.
3
12a
. B.
3
4a
. C.
3
3a
. D.
3
6a
.
Lời giải
Thể tích khối lăng trụ đã cho là
3
. 12V B h a==
.
Câu 17: Cho hình trụ có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích xung quanh
xq
S
của hình trụ
đã cho được tính theo công thức nào dưới đây?
A.
4
xq
S rl
=
. B.
2
xq
S rl
=
. C.
3
xq
S rl
=
. D.
xq
S rl
=
.
Lời giải
Diện tích xung quanh
xq
S
của hình trụ đã cho là
2
xq
S rl
=
.
Câu 18: Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích xung quanh
xq
S
của hình
nón đã cho được tính theo công thức nào dưới đây?
A.
4
xq
S rl
=
. B.
xq
S rl
=
. C.
3
xq
S rl
=
. D.
2
xq
S rl
=
.
Lời giải
Diện tích xung quanh
xq
S
của hình nón đã cho là
xq
S rl
=
.
Câu 19: Cho hình nón có bán kính đáy
r
và độ dài đường sinh
l
. Diện tích toàn phần
tp
S
của hình nón
đã cho được tính theo công thức nào dưới đây?
A.
2
tp
S rl l
=+
. B.
2
tp
S rl r
=+
. C.
1
3
tp
S rl
=
. D.
2
22
tp
S rl r
=+
.
Lời giải
Diện tích toàn phần
tp
S
của hình nón đã cho là
2
tp
S rl r
=+
.
Câu 20: Cho khối cầu có bán kính
r
. Thể tích
V
của khối cầu đã cho được tính theo công thức nào dưới
đây?
A.
3
3
4
Vr
=
. B.
3
4
3
Vr
=
. C.
3
3
4
Vr
=
. D.
3
4
3
Vr
=
.
Lời giải
Thể tích
V
của khối cầu đã cho là
3
4
3
Vr
=
.
Câu 21: Cho hàm số
( )
y f x=
có đạo hàm
( )
2022f x x
=+
với mọi
x
. Hàm số đã cho đồng biến
trên khoảng nào dưới đây?
A.
( )
2022;− +
. B.
( )
2022;+
. C.
( )
; 2022− −
. D.
( )
;2022−
.
Lời giải
Ta có
( )
0 2022f x x
= = −
.
Bảng xét dấu
Hàm số đã cho đồng biến trên khoảng
( )
2022;− +
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 22: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
12f x x x x
= − +
, . Số điểm cực tiểu của hàm số
đã cho là
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Ta có
( ) ( )( )
3
0
0 1 2 0 1
2
x
f x x x x x
x
=
= − + = =
=−
.
Bảng xét dấu
Hàm số đã cho có
2
điểm cực tiểu.
Câu 23: Trên đoạn
4; 1−−
, hàm số
42
8 13y x x= − +
đạt giá trị nhỏ nhất tại điểm nào trong các điểm
sau?
A.
2x =−
. B.
1x =−
. C.
4x =−
. D.
3x =−
.
Lời giải
Hàm số
42
8 13y x x= − +
xác định và liên tục trên đoạn
4; 1−−
.
3
4 16y x x
=−
;
3
2 4; 1
0 4 16 0 0 4; 1
2 4; 1
x
y x x x
x
= − − −
= − = = − −
= − −
.
Ta có
( )
4 141f −=
;
( )
23f − = −
;
( )
16f −=
.
Vậy hàm số
42
8 13y x x= − +
đạt giá trị nhỏ nhất tại điểm
2x =−
.
Câu 24: Cho hàm số
( )
1ax
fx
bx c
+
=
+
( )
,,a b c R
có bảng biến thiên như sau:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A. 1 B. 3. C. 2. D. 0.
Lời giải
Đồ thị hàm số cắt trục tung tại điểm có tung độ
1
1 0 0yc
c
=
.
Đồ thị hàm số
( )
1ax
fx
bx c
+
=
+
có đường tiệm cận đứng là đường thẳng
2 0 0
c
xb
b
= − =
.
Đồ thị hàm số
( )
1ax
fx
bx c
+
=
+
có đường tiệm cận ngang là đường thẳng
1 0 0
a
ya
b
= =
.
Vậy
0c
và
0, 0ab
.
x

12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 25: Tìm số tiệm cận đứng của đồ thị hàm số
2
2
34
16
xx
y
x
−−
=
−
.
A. 2. B. 3. C. 1. D. 0.
Lời giải
Ta có
2
16 0 4xx− = =
.
2
2
4
8
l
1
im
3 4 5
6
x
xx
x
→
−−
=
−
.
( )
2
2
4
3
lim
4
16
x
xx
x
+
→−
−−
= −
−
.
Vậy đồ thị hàm số có một tiệm cận đứng.
Câu 26: Cho
a
là số thực dương. Rút gọn của biểu thức
4
3
m
n
P a a a==
với
m
n
tối giản,
0n
. Khi đó
mn+
bằng
A.
5
. B.
11
. C.
17
. D.
6
.
Lời giải
Ta có
4 4 4 1 11
1
3 3 3 2 6
2
.P a a a a a a
+
= = = =
.
Khi đó
11, 6mn==
. Suy ra
17mn+=
.
Câu 27:
Cho hàm số
3 x
y e x e
−
=+
. Nghiệm của phương trình
0y
=
là
A.
3x =−
. B.
0x =
. C.
ln3x =
. D.
ln2x =
.
Lời giải
Ta có:
3 x
y e e
−
=−
cho
3
0 0 3
x
y e e x
−
= − = = −
.
Câu 28: Đạo hàm cấp hai
y
của hàm số
( )
ln 3 2yx=+
là
A.
( )
2
3ln 3 2yx
=+
. B.
9
32
y
x
−
=
+
. C.
( )
2
3
32
y
x
=
+
. D.
( )
2
9
32
y
x
−
=
+
.
Lời giải
Ta có
( )
2
39
;
32
32
yy
x
x
= = −
+
+
.
Câu 29: Hàm số
( )
2
log 2 1y x x m= − + +
có tập xác định là khi
A.
0.m
B.
0 3.m
C.
0
.
1
m
m
−
D.
0.m =
Lời giải
Yêu cầu bài toán
2
2 1 0x x m− + +
với mọi
x
thuộc
2
( 2) 4( 1) 0 0mm = − − +
.
Câu 30: Số nghiệm thực của phương trình
( )
2
58
0
ln 1
xx
x
+−
=
−
là?
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
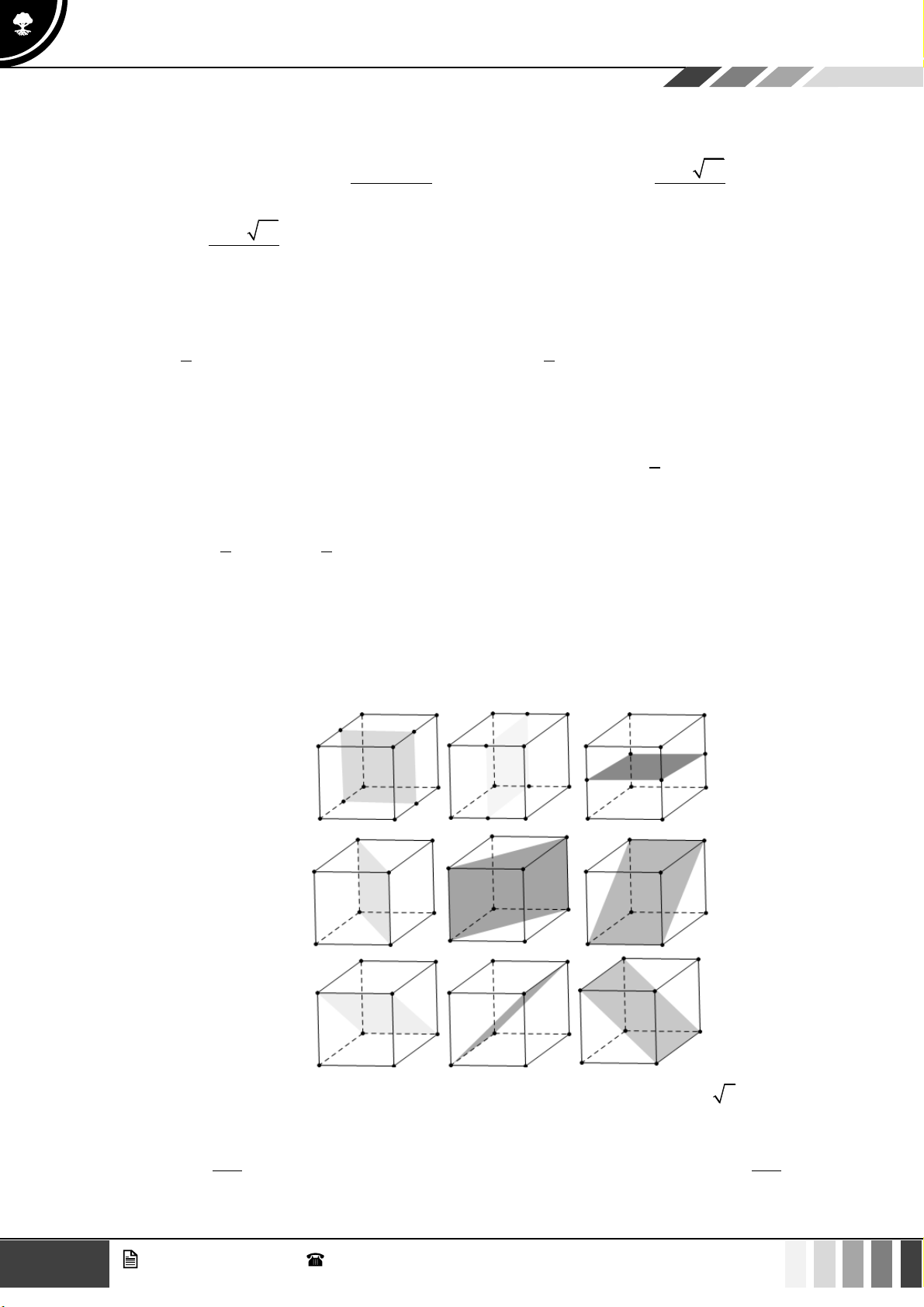
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HK1
Toán 12
Điều kiện
( )
10
1
ln 1 0
2
x
x
x
x
−
−
.
Với điều kiện trên, ta có:
( )
2
2
5 8 5 57
0 5 8 0
ln 1 2
xx
x x x
x
+ − −
= + − = =
−
kết hợp điều kiện
5 57
2
x
−+
=
.
Vậy phương trình có 1 nghiệm.
Câu 31: Tổng tất cả các nghiệm của phương trình
21
2 5.2 2 0
xx+
− + =
bằng bao nhiêu?
A.
3
.
2
B.
1.
C.
5
.
2
D.
0.
Lời giải
Đặt
( )
20
x
tt=
, phương trình trở thành
2
2
2 5 2 0
1
2
t
tt
t
=
− + =
=
(thỏa mãn).
Với,
2t =
ta có
2 2 1
x
x= =
.
Với,
1
2
t =
ta có
1
21
2
x
x= = −
.
Vậy tổng các nghiệm bằng 0.
Câu 32: Hình lập phương có bao nhiêu mặt phẳng đối xứng?
A. 6. B. 7. C. 8. D. 9.
Lời giải
Hình lập phương có 9 mặt phẳng đối xứng.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông có cạnh bằng
2a
,
( )
SA ABCD⊥
,
2SA a=
. Tính thể tích khối chóp
.S ABCD
.
A.
3
2
3
a
V =
. B.
3
4Va=
. C.
3
2Va=
. D.
3
4
3
a
V =
.
Lời giải
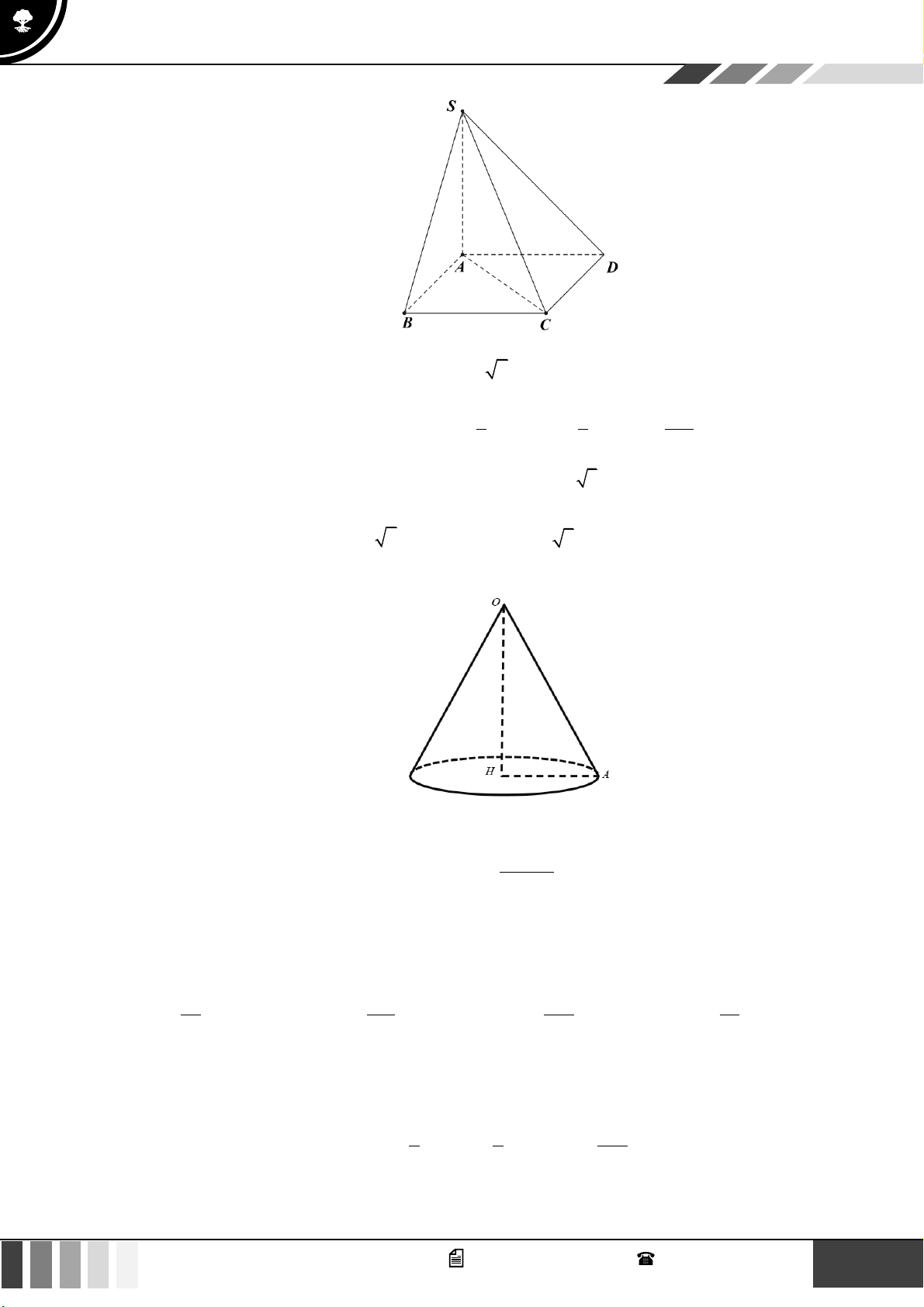
14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Diện tích hình vuông
ABCD
là:
( )
2
2
22
ABCD
S a a==
.
Thể tích khối chóp
.S ABCD
là:
3
2
.
1 1 4
. .2 .2
3 3 3
S ABCD ABCD
a
V SA S a a= = =
.
Câu 34: Hình nón có góc ở đỉnh bằng
60
và chiều cao bằng
3
. Độ dài đường sinh của hình nón
bằng
A.
2
. B.
22
. C.
23
. D.
3
.
Lời giải
Ta có góc ở đỉnh của hình nón bằng
60
nên
30HOA =
.
Trong tam giác
HAO
vuông tại
H
có
2
cos30
OH
OA ==
.
Vậy độ dài đường sinh của hình nón bằng
2
.
Câu 35: Quay một miếng bìa hình tròn có diện tích
2
16 a
quanh một trong những đường kính, ta được
khối tròn xoay có thể tích là
A.
3
64
3
a
. B.
3
128
3
a
. C.
3
256
3
a
. D.
3
32
3
a
.
Lời giải
Gọi
R
là bán kính đường tròn. Theo giả thiết, ta có
22
16 4S R a R a
= = =
.
Khi quay miếng bìa hình tròn quanh một trong những đường kính của nó thì ta được một khối
cầu. Thể tích khối cầu này là
( )
3
33
4 4 256
4
3 3 3
V R a a
= = =
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 36: Có bao nhiêu giá trị nguyên của
m
thuộc
2023;2023−
để hàm số
( )
2
2
22y x x m= − + +
có
tập xác định là ?
A.
2024
. B.
2023
. C.
4045
. D.
4044
.
Lời giải
Vì số mũ
2
nên hàm số xác định với
x
khi và chỉ khi
2
2 2 0,x x m x− + +
0 1 2 0
1
0 1 0
m
m
a
− −
−
.
Mà
2023;2023
0;1;2;...;2023
m
m
m
−
.
Vậy có
2023
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 37: Cho hàm số
( )
2
2022 ln
x
fx
x
+
=−
. Tính tổng
( ) ( ) ( )
1 3 ... 2023S f f f
= + + +
.
A.
2024
2025
S =
. B.
2026
2025
S =
. C.
2024
2023
S =
. D.
2022
2023
S =
.
Lời giải
Ta có:
( )
( )
2
2 1 1
2
22
x
x
fx
x
x x x x
x
+
= − = = −
+
++
.
Suy ra:
( )
11
1
13
f
=−
và
( )
11
3
35
f
=−
( )
11
2023
2023 2025
f
=−
.
( ) ( ) ( )
1 2024
1 3 ... 2023 1
2025 2025
S f f f
= + + + = − =
.
Câu 38: Biết phương trình
4 4 2
log log log 8
9 12.3 3 0
xx
− + =
có hai nghiệm
1
x
,
2
x
. Khi đó
22
12
xx+
bằng
A.
90
. B.
10
. C.
20
. D.
272
.
Lời giải
Điều kiện:
0.x
Ta có
4 4 2
log log log 8
9 12.3 3 0
xx
− + =
44
2log log
3
3 12.3 3 0 (1)
xx
− + =
.
Đặt
4
log
3
x
t =
,
0t
.
( )
2
3
1 12 27 0
9
t
tt
t
=
− + =
=
.
Với
4
log
4
3 3 3 log 1 4
x
t x x= = = =
.
Với
4
log
2
4
9 3 3 log 2 16
x
t x x= = = =
.
Vậy tập nghiệm của phương trình đã cho là
22
12
4;16 272S x x= + =
.
Câu 39: Với giá trị nào của tham số
m
thì phương trình
1
4 .2 2 0
xx
mm
+
− + =
có hai nghiệm phân biệt
12
,xx
thỏa mãn
12
3xx+=
?
A.
2m =
. B.
1m =
. C.
3m =
. D.
4m =
.
Lời giải

16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Ta có:
( )
1
4 .2 2 0 4 2 .2 2 0 1
x x x x
m m m m
+
− + = − + =
.
Đặt:
( )
20
x
tt=
.
Phương trình
( )
1
trở thành:
( )
2
2 2 0 2t mt m− + =
.
Phương trình
( )
1
có hai nghiệm phân biệt
12
,xx
thỏa mãn
12
3xx+=
Phương trình
( )
2
có hai nghiệm dương
12
,tt
phân biệt thỏa mãn
1 2 1 2
3
12
2 2 2 2 8
x x x x
tt
+
= = = =
2
0 2 0
8 2 8
0 2 0
mm
Pm
Sm
−
= =
4m=
.
Câu 40: Tập nghiệm của bất phương trình
( ) ( )
2 2 2 2 2
.2 9 2 .2 8 2 .2 9 .2 8 16
x x x x
x x x x x x+ + + + + + +
là
A.
(
; 1 0;2− −
. B.
1;0 2;3−
. C.
)
0;2 3; +
. D.
) (
1;0 2;3−
.
Lời giải
Ta có
( ) ( )
2 2 2 2 2
.2 9 2 .2 8 2 .2 9 .2 8 16
x x x x
x x x x x x+ + + + + + +
( ) ( ) ( )
2 2 2 2
2 .2 9 2 .2 8 2 0
xx
x x x x x x − − − − − + − −
( ) ( )
2
2
22
2
2
20
2 9.2 8 0
2 . 2 9.2 8 0
20
2 9.2 8 0
xx
xx
xx
xx
xx
xx
− −
− +
− − − +
− −
− +
1
1
2
2
1 2 8
03
23
12
10
12
0
21
3
28
x
x
x
x
x
x
x
x
x
x
x
x
x
x
−
−
−
−
−
.
Vậy bất phương trình có tập nghiệm là:
1;0 2;3S = −
.
Câu 41: Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh
của tứ diện cũng là đỉnh của hình lập phương?
A.
4
. B.
6
. C.
2
. D.
8
.
Lời giải
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HK1
Toán 12
Ta chia khối lập phương
. ' ' ' 'ABCD A B C D
thành hai khối lăng trụ đứng:
. ' ' 'ABD A B D
và
. ' ' 'BCD B C D
Ứng với mỗi khối lăng trụ đứng trên, ta có thể chia thành ba khối tứ diện mà các đỉnh của tứ diện
cũng là đỉnh của hình lập phương.
Khối lăng trụ
.BCD B C D
chia thành ba khối tứ diện:
', ' ' ' , ' 'BCDB B C D D CDB C
.
Ta chứng minh các khối tứ diện này có thể tích bằng nhau như sau:
Hai khối tứ diện
B C D D
và
DCB C
bằng nhau vì đối xứng với nhau qua
( )
''mp DB C
Hai khối tứ diện
DCB C
và
'BCDB
bằng nhau vì đối xứng với nhau qua
( )
'mp B CD
(hoặc có thể chứng minh
. . .
1
3
D B C D B BCD BCC B BCD B C D
V V V V
= = =
)
Tương tự khối lăng trụ
. ' ' 'ABD A B D
chia thành ba khối tứ diện có thể tích bằng nhau là:
', ' ' ' , ' 'ABCB A B D D ADA B
Vậy có tất cả là
6
khối tứ diện có thể tích bằng nhau.
Câu 42: Cho hình chóp tứ giác đều
.S ABCD
, gọi
,MN
lần lượt là trung điểm của
SA
và
BC
. Biết góc
giữa đường thẳng
MN
và mặt phẳng
( )
ABCD
bằng
60
, khoảng cách từ
M
đến mặt phẳng
( )
ABCD
bằng
30
4
a
. Thể tích khối chóp
.S ABCD
theo
a
bằng
A.
3
10
3
a
. B.
3
30
6
a
. C.
3
30
2
a
. D.
3
10
6
a
.
Lời giải
18
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Gọi
( )
O AC BD SO ABCD= ⊥
.
Gọi
H
là trung điểm của
AO
( )
//MH SO MH ABCD ⊥
.
( )
( )
( )
, , 60MN ABCD MN NH MNH = = =
và
( )
( )
30
,
4
a
d M ABCD MH==
.
Ta có:
30
2
2
a
SO MH==
;
10
tan60 4
MH a
NH ==
.
Đặt
3 3 3 2
0 ; . 2
2 4 4 4
xx
AB x CN CH AC x= = = = =
.
22
2
2 2 2
10 3 2 3 2 2
2. . .cos45 2. . .
4 4 2 4 2 2
a x x x x
HN CH CN CH CN
= + − = + −
22
55
88
xa
xa = =
.
Vậy thể tích khối chóp
.S ABCD
là
3
2
1 30 30
.a .
3 2 6
a
Va==
.
Câu 43: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với đáy,
mặt phẳng
( )
SAD
tạo với đáy một góc
60
. Thể tích khối chóp
.S ABCD
là:
A.
3
33
4
a
V =
. B.
3
83
9
a
V =
. C.
3
83
3
a
V =
. D.
3
43
3
a
V =
.
Lời giải
Ta có:
AD AB⊥
(do
ABCD
là hình vuông) (1)
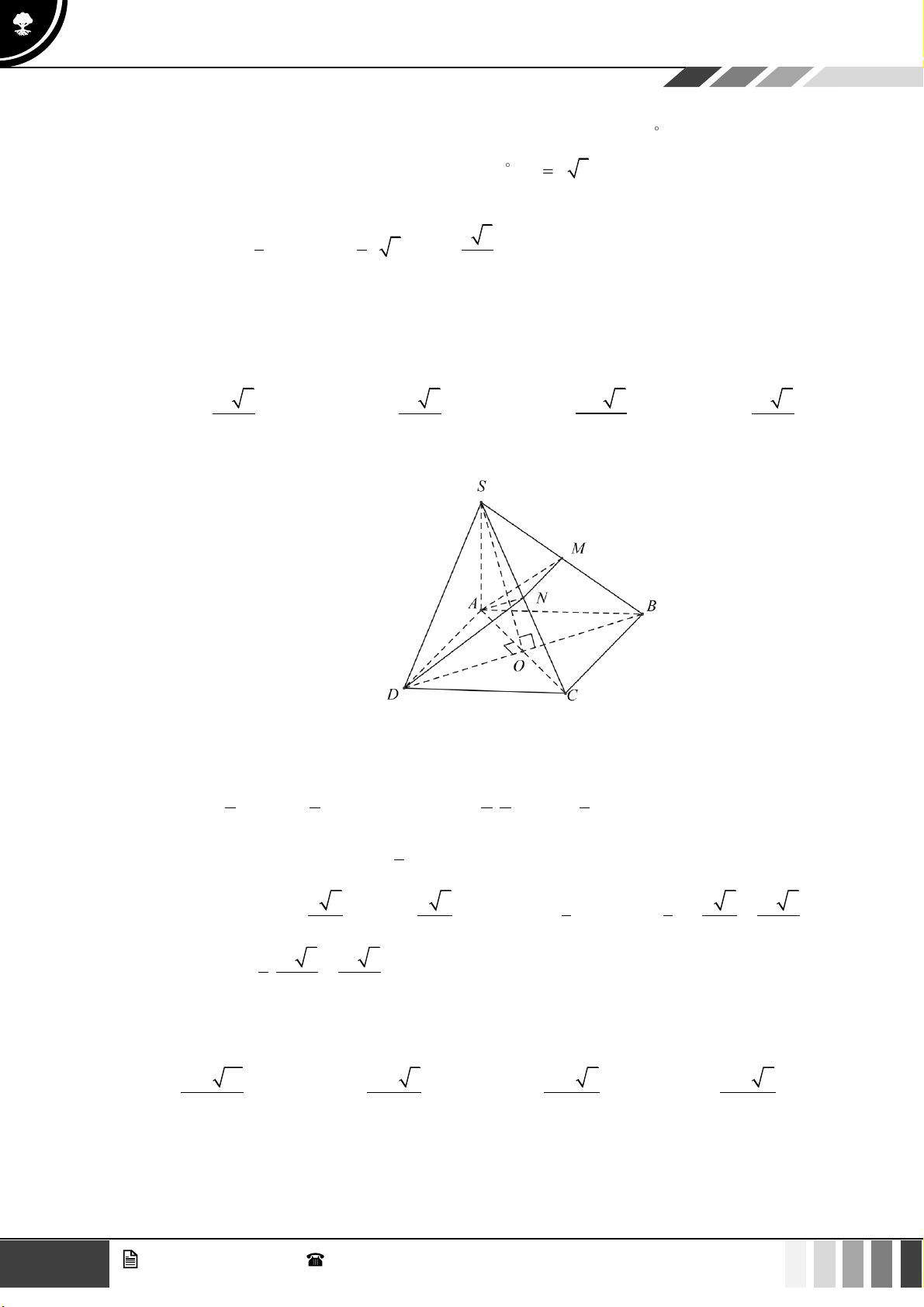
GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HK1
Toán 12
SB AD⊥
(
()SB ABCD⊥
AD SA⊥
(2)
Từ (1) và (2) suy ra góc giữa
( )
SAD
và
( )
ABCD
là góc
60SAB =
Xét tam giác
SAB
vuông tại
B
có
tan60 . 2 3SB AB a==
.
Lại có
22
4
ABCD
S AB a==
23
.
1 1 8 3
. 2 3 .4
3 3 3
S ABCD ABCD
V SB S a a a = = =
(đvdt).
Câu 44: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
( )
ABCD
, góc giữa hai mặt phẳng
( )
SBD
và
ABCD
bằng
0
60
. Gọi
,MN
lần lượt là trung điểm của
,SB SC
. Thể tích khối chóp
.S ADNM
là:
A.
3
6
16
a
V =
. B.
3
6
24
a
V =
. C.
3
36
16
a
V =
. D.
3
6
8
a
V =
.
Lời giải
Gọi
O AC BD=
.
AO BD SO BD⊥ ⊥
. Nên góc của
( )
SBD
và
( )
ABCD
là góc
0
60SOA =
.
. . .
11
..
24
S ADN S ADC S ABCD
V V V==
và
. . .
1 1 1
.
2 2 8
S AMN S ABC S ABCD
V V V==
.
. . . .
3
8
S ADNM S ADN S AMN S ABCD
V V V V = + =
.
0
26
.tan tan60
22
aa
SA AO SOA= = =
3
2
.
1 1 6 6
. . .
3 3 2 6
S ABCD ABCD
aa
V S SA a = = =
.
33
.
3 6 6
.
8 6 16
S ADNM
aa
V = =
.
Câu 45: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và đáy bằng
o
60
.
Diện tích xung quanh của hình nón đỉnh
S
, có đáy là hình tròn ngoại tiếp tam giác
ABC
bằng
A.
2
10
8
a
. B.
2
3
3
a
. C.
2
7
6
a
. D.
2
7
4
a
.
Lời giải
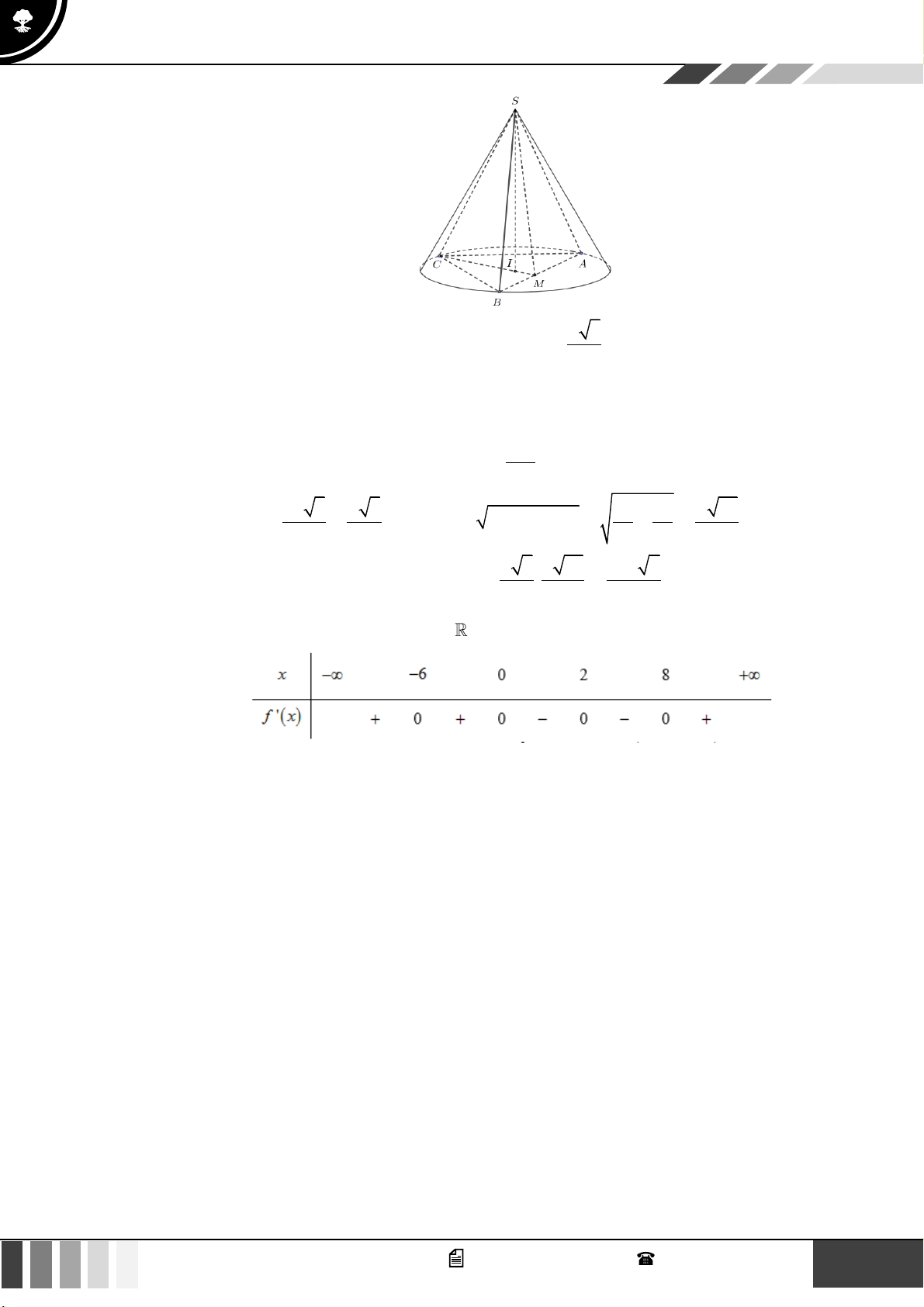
20
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Gọi
I
là tâm đường tròn ngoại tiếp
ABC
3
3
a
IA r = =
.
Gọi
M
là trung điểm của
AB
( )
AB SMC⊥
Góc giữa mặt bên và mặt đáy là góc
o
60SMC =
Trong tam giác
SIM
vuông tại
I
có
cos60
IM
SM
=
23
2
6
a
SM IM = =
3
3
a
=
22
l SA SM MA= = +
22
34
aa
=+
21
6
a
=
.
Diện tích xung quanh hình nón
xq
S rl
=
3 21
..
36
aa
=
2
7
6
a
=
.
Câu 46: Cho hàm số
( )
y f x=
có đạo hàm trên và bảng xét dấu đạo hàm như sau:
Có bao nhiêu số nguyên
m
để hàm số
( )
3
2y f x x m= + +
nghịch biến trên khoảng
( )
1;1−
?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Đặt
32
2 ' 3 2t x x m t x= + + = +
. Do đó, trên khoảng
( )
1;1−
thì
t
đồng biến và
( )
3; 3t m m − +
.
Yêu cầu bài toán trở thành tìm
m
để hàm số
( )
y f t=
nghịch biến trên khoảng
( )
3; 3mm−+
.
Dựa vào bảng xét dấu trên, ta được:
3 0 3
35
3 8 5
mm
m
mm
−
+
.
Vì
m
nguyên nên
3,4,5m
.
Vậy có 3 giá trị của m thỏa mãn yêu cầu.
Câu 47: Một mảnh đất hình chữ nhật
ABCD
có chiều dài
25mAB =
, chiều rộng
20mAD =
được chia
thành hai phần bằng nhau bởi vạch chắn
MN
(
,MN
lần lượt là trung điểm
BC
và
AD
). Một
đội xây dựng làm một con đường đi từ
A
đến
C
qua vạch chắn
MN
, biết khi làm đường trên
miền
ABMN
mỗi giờ làm được
15m
và khi làm trong miền
CDNM
mỗi giờ làm được
30m
.
Tính thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ
A
đến
C
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HK1
Toán 12
A.
25
3
. B.
10 2 725
30
+
. C.
20 725
30
+
. D.
5
.
Lời giải
Do cần thời gian xây là ngắn nhất nên con đường làm trên mỗi miền phải là những đường thẳng.
Gọi
AE
và
EC
lần lượt là đoạn đường cần làm. Đặt
( )
mNE x=
.
( )
25 mEM x = −
. Ta có điều kiện:
0 25x
Ta được
( )
2 2 2
2
22
100
100 25
AE AN EN x
EC MC EM x
= + = +
= + = + −
.
Thời gian để làm đoạn đường từ
A
đến
C
là:
( )
( )
( )
2
2
25 100
100
h
15 30 15 30
x
AE EC x
tx
−+
+
= + = +
( )
( )
22
25
15 100
30. 25 100
xx
tx
x
x
−
= −
+
−+
.
Xét
( )
( )
22
25
00
15 100
30. 25 100
xx
tx
x
x
−
= − =
+
−+
( ) ( ) ( )
( )
( )
( )
2 2 2
2 2 2
2 25 100 25 100 4 25 100 25 100x x x x x x x x − + = − + − + = − +
( ) ( ) ( )
( )
( )
( )
( )
( ) ( ) ( ) ( )
( )
2 2 2
2 2 2
22
2 2 2
2
2
4 25 400 100 25 25 0
4 25 25 20 25 0
5 4 25 5 45 0 5
x x x x x x
x x x x
x x x x x x
− + − − − − =
− − + − − =
− − + + − = =
.
Vì
0 25x
nên
( ) ( ) ( )
( )
2
2
4 25 5 45x x x x− + + −
>0

22
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Ta được
( )
( )
( )
4 29
0
6
25
5
3
1 29
25
3
t
t
t
+
=
=
+
=
.
Vậy thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ
A
đến
C
là
( )
25
h
3
.
Câu 48: Số giá trị nguyên của tham số
m
để hàm số
( )
1
22
2022
21y x mx m m= − − + +
xác định trên khoảng
( )
0;+
là
A.
0
. B.
2
. C.
1
. D.
3
.
.Lời giải
Đặt
( )
22
21f x x mx m m= − − + +
.
Hàm số đã cho xác định trên khoảng
( ) ( ) ( )
0; 0, 0;f x x+ +
.
( )
fx
là một tam thức bậc 2 có
2
21mm
= − −
.
Nếu
( ) ( ) ( )
1
0 1 0 0, 0;
2
m f x x f x x
− +
.
Nếu
1
0
1
2
m
m
=
=
=−
Với
1m=
thì
( )
0, \ 1 1f x x m =
không thỏa mãn.
Với
1
2
m=−
thì
( ) ( ) ( )
11
0 \ 0, 0;
22
f x x f x x m
− + = −
(nhận).
Nếu
1
0
1
2
m
m
−
.
Khi đó
( )
fx
có hai nghiệm phân biệt
12
,xx
và
( ) ( )
12
0, 0; 0f x x x x +
12
2
12
0
20
15
0
1 5 1 5
2
10
22
m
x x m
m
x x m m
m
+ =
−
−+
=− + +
.
Vậy trong trường hợp này
( ) ( )
0, 0;f x x +
khi
1 5 1
22
m
−
−
.
Kết hợp lại ta thấy hàm số đã cho xác định trên khoảng
( )
0;+
khi
15
1
2
m
−
.
Từ đó suy ra chỉ có một giá trị nguyên của tham số m thỏa mãn yêu cầu bài ra.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 49: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình
(
)
2
log 2 2
x
m m x+ + =
có nghiệm thực không âm?
A. 2018. B. 2019. C. 2020. D. 2021.
Lời giải
Phương trình:
(
)
2
log 2 2 , 0
x
m m x x+ + =
(1)
Đặt
2
x
tm=+
. Do
2 0,
x
x
và m nguyên dương nên
0t
.
Khi đó phương trình (1) tương đương:
( )
2
log 2 4 4
xx
m t x m t t m+ = + = = −
4 2 4 2 4 2 2 2 (2).
x x x x x x x x
m m m m m m − = + = + + + = + + +
Xét hàm đặc trưng
( )
2
, 0.f t t t t= +
( )
' 2 1 0, 0.f t t t= +
( )
ft
đồng biến trên
( )
0;+
. Khi đó:
( )
( )
(
)
2 2 2 2 2 4 2
x x x x x x
f f m m m = + = + = −
.
Xét hàm
( )
42
xx
gx=−
có
( ) ( ) ( )
' 4 2ln 2 2 ln 2
xx
gx=−
có
( )
' 0 1g x x= = −
Bảng biến thiên của hàm số g(x)
Phương trình (1) có nghiệm thực không âm
Đồ thị hàm số
( )
y g x=
có giao điểm (hoành
độ không âm) với đường thẳng
ym=
0m
.
Vì m nguyên dương và nhỏ hơn 2021 nên
1;2020m
.
Vậy có 2020 giá trị nguyên
m
thỏa mãn yêu cầu đề bài.
Câu 50: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ sau.
Gọi
0
m
là giá trị nhỏ nhất của tham số
m
để đồ thị hàm số
( ) ( ) ( )
2
3g x f x f x m= + +
có số
điểm cực trị ít nhất. Tìm mệnh đề đúng trong các mệnh đề sau?
A.
( )
0
;2m − −
. B.
( )
0
2;3m
. C.
( )
0
3;m +
. D.
( )
0
2;2m −
.
Lời giải
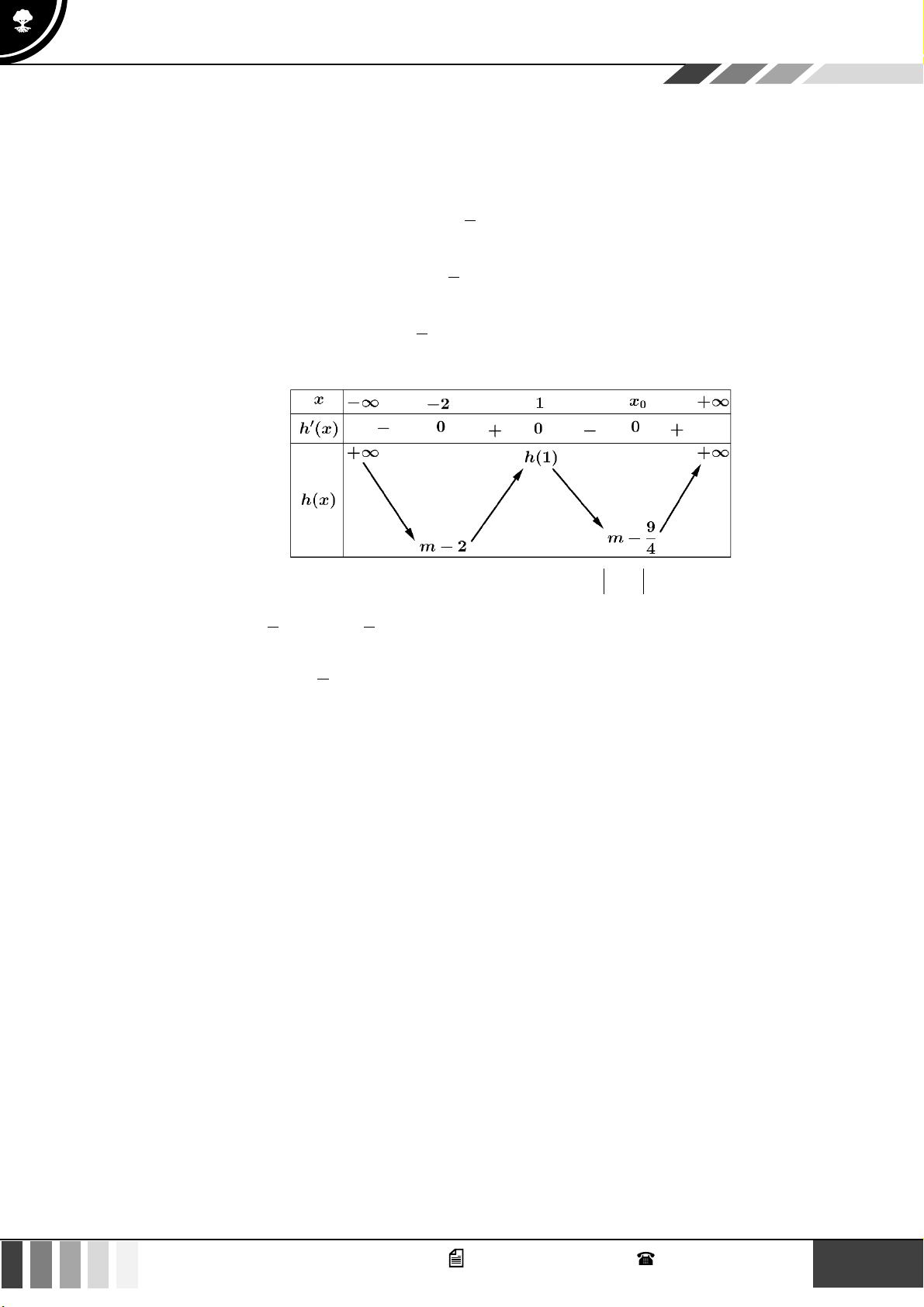
24
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Xét hàm số
( ) ( ) ( )
2
3h x f x f x m= + +
.
Ta có:
( ) ( ) ( ) ( )
2 . 3h x f x f x f x
=+
( ) ( ) ( )
23h x f x f x
= +
.
Xét phương trình:
( )
( )
( )
0
0
3
2
fx
hx
fx
=
=
=−
.
Ta có:
( )
2
0
1
x
fx
x
=−
=
=
;
( )
0
3
1
2
f x x x= − =
.
Ta có
( )
22hm− = −
;
( )
0
9
4
h x m=−
.
Bảng biến thiên:
Từ bảng biến thiên của hàm số
( )
hx
suy ra hàm số
( ) ( )
g x h x=
có số điểm cực trị ít nhất khi
và chỉ khi
99
0
44
mm−
.
Khi đó
0
9
min
4
mm==
nên
( )
0
2;3m
.
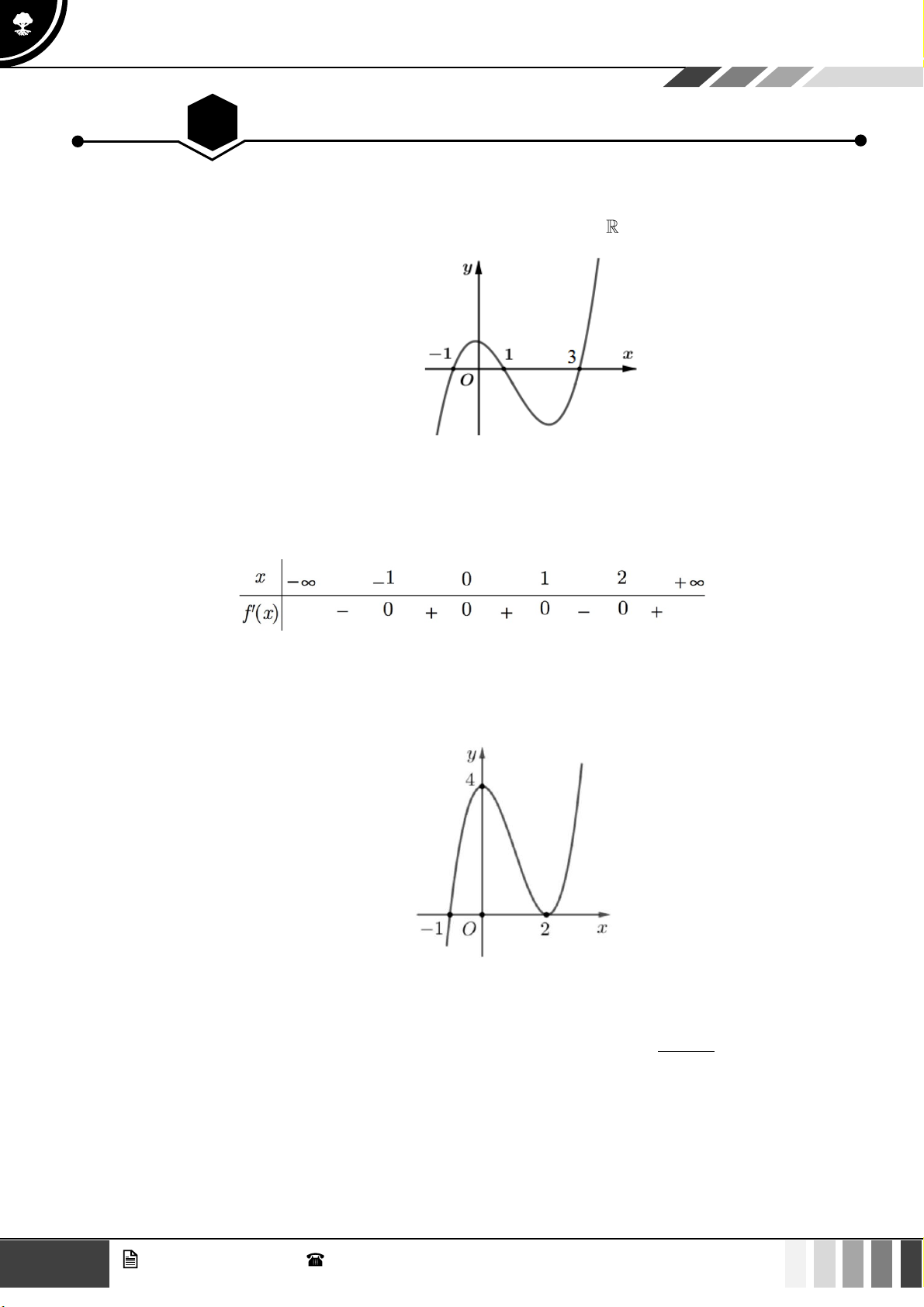
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HK1
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Cho hàm số
( )
fx
có đạo hàm
( )
fx
xác định, liên tục trên và có đồ thị như hình vẽ
Hàm số
( )
y f x=
nghịch biến trên khoảng nào
A.
( )
1;1−
. B.
( )
3;+
. C.
( )
1;3
. D.
( )
;3−
.
Câu 2: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
0x =
. B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực đại tại
1x =
. D. Hàm số đạt cực đại tại
2x =
.
Câu 3: Cho hàm số
( )
fx
có đồ thị như hình vẽ:
Điểm cực tiểu của hàm số đã cho là
A.
1x =−
. B.
0x =
. C.
2x =
. D.
4x =
.
Câu 4: Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số
2
2
2
4
xx
y
x
−
=
−
A.
2x =−
. B.
2x =
. C.
2y =
. D.
1y =
.
Câu 5: Tọa độ giao điểm của đồ thị hàm số
( )
3
:5C y x x= + +
và đường thẳng
( )
: 2 1d y x= − +
là
A.
( )
1; 1−
. B.
( )
0;1
. C.
( )
0;5
. D.
( )
1;3−
.
Câu 6: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
04
ĐỀ SỐ
2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
A.
42
21y x x= − + −
. B.
42
21y x x= − −
. C.
32
31y x x= − −
. D.
32
31y x x= − + −
.
Câu 7: Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ bên dưới?
A.
3
3 2.y x x=−+
B.
2
.
1
x
y
x
+
=
−
C.
2
.
1
x
y
x
−
=
−
D.
42
5 4.y x x= − + −
Câu 8: Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ bên?
A.
32
1y x x= − + −
. B.
42
1y x x= − −
. C.
32
1y x x=−−
. D.
42
1y x x= − + −
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;2− −
. B.
( )
4;0−
. C.
( )
0; ;+
. D.
( )
2;0−
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 10: Biểu thức
3
3
222
333
viết dạng lũy thừa với số mũ hữu tỉ là
A.
5
18
2
3
. B.
1
12
2
3
. C.
7
6
2
3
. D.
1
2
2
3
.
Câu 11: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét dấu của
( )
fx
như sau:
Số điểm cực đại của hàm số
( )
y f x=
là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 12: Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
( )
2
x
y =
. B.
( )
0,5
x
y =
. C.
x
e
y
=
. D.
2
3
x
y
=
.
Câu 13: Cho
0a
,
1a
, giá trị của
3
log
a
a
bằng
A.
1
3
. B.
1
3
−
. C.
3−
. D.
3
.
Câu 14: Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
( )
31
x
y =−
. B.
( )
x
ye
=−
. C.
x
y
=
. D.
( )
2
x
ye=−
.
Câu 15: Tính đạo hàm của hàm số
( )
2
log 2 1 .yx=+
A.
1
21
y
x
=
+
. B.
2
21
y
x
=
+
. C.
( )
1
2 1 ln2
y
x
=
+
. D.
( )
2
2 1 ln2
y
x
=
+
.
Câu 16: Tập nghiệm của phương trình
( ) ( )
2020 2020
log 1 log 2 1xx− = +
là
A.
1
2;
2
−
. B.
2
.
C.
2−
.
D.
.
Câu 17: Nghiệm của bất phương trình
42
22
33
xx−
là
A.
2
5
x
. B.
2
3
x −
. C.
2
5
x
. D.
2
3
x
.
Câu 18: Các giá trị
x
thỏa mãn bất phương trình
( )
2
log 3 1 3x −
là
A.
3x
. B.
1
3
3
x
. C.
3x
. D.
10
3
x
.
Câu 19: Vật thể nào dưới đây không phải là khối đa diện?

4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 3. B. Hình 1. C. Hình 4. D. Hình 2.
Câu 20: Khối đa diện đều loại
{5;3}
có số mặt là bao nhiêu?
A.
14
. B.
12
. C.
10
. D.
8
.
Câu 21: Cho hình chóp
.S ABC
có
( )
,SA ABC⊥
ABC
vuông cân tại A,
2SA AB==
. Thể tích của
khối chóp
.S ABC
là.
A.
2
3
. B.
8
3
. C.
4
3
. D.
4
.
Câu 22: Cho một khối chóp có diện tích đáy là
B
và chiều cao là
h
. Khi đó thể tích
V
của khối chóp
đó là
A.
V Bh=
. B.
3V Bh=
. C.
3
V Bh=
. D.
1
3
V Bh=
.
Câu 23: Tính thể tích khối hộp chữ nhật
.ABCD A B C D
biết
6 AB cm=
,
8 BC cm=
,
10 AA cm
=
.
A.
3
480 cm
. B.
3
48 cm
. C.
3
160 cm
. D.
3
1440 cm
.
Câu 24: Cho khối nón có bán kính đáy
3r =
và chiều cao
4h =
. Tính thể tích
V
của khối nón đã cho.
A.
16 3V
=
. B.
12V
=
. C.
4V
=
. D.
4V =
.
Câu 25: Một khối lăng trụ có chiều cao
3a
, diện tích đáy
2
2a
thì có thể tích bằng
A.
3
2a
. B.
3
a
. C.
3
18a
. D.
3
6a
.
Câu 26: Cho hàm số
21
2
x
y
x
−
=
−
. Mệnh đề nào sau đây là mệnh đề đúng
A. Hàm số đồng biến trên khoảng
( )
;2−
.
B. Hàm số đồng biến trên khoảng
( )
;− +
.
C. Hàm số nghịch biến trên khoảng
( )
2;+
.
D. Hàm số đồng biến trên khoảng
( )
2;+
.
Câu 27: Cho hàm số
( )
fx
có đạo hàm
( )
2 1,f x x x
= −
. Hỏi hàm số
( )
fx
có bao nhiêu điểm cực
trị?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 28: Tìm giá trị nhỏ nhất m của hàm số
42
13y x x= − +
trên đoạn
2;3−
.
A.
13m =
. B.
25m =
. C.
85m =
. D.
51
4
m =
.
Câu 29: Số đường tiệm cận đứng của đồ thị hàm số
22
2
4 1 3 2
22
xx
y
xx
− + +
=
−
là:
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 30: Cho hàm số
( )
y f x=
có đồ thị như vẽ. Số nghiệm của phương trình
( )
2 3 0fx−=
là:
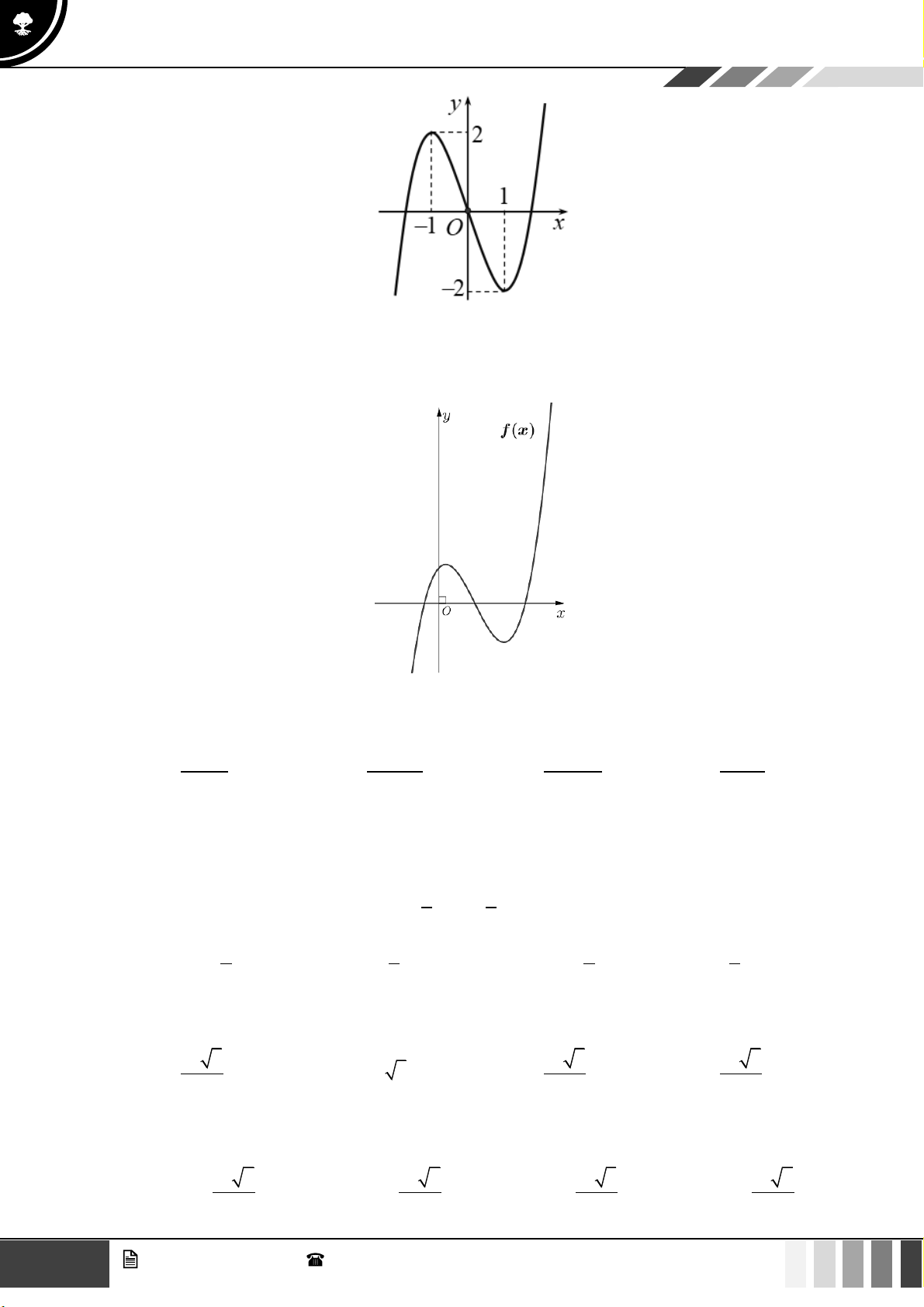
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HK1
Toán 12
A.
5
. B.
3
. C.
4
. D.
6
.
Câu 31: Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị như hình vẽ bên dưới. Mệnh đề nào dưới đây
đúng?
A.
0ad
. B.
0cd
. C.
0bd
. D.
0ac
.
Câu 32: Cho
2
log 3 a=
,
2
log 5 b=
Khi đó
6
log 225
được biểu diễn theo
,ab
là đáp án nào sau đây?
A.
13
ab b
a
+
+
. B.
22
1
ab
a
+
+
. C.
22
1
ab
a
+
+
. D.
12
ab
a
+
+
.
Câu 33: Số nghiệm của phương trình
( )
2 2 2
log log 6 log 7xx+ − =
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 34: Tập nghiệm của bất phương trình
42
45
54
xx−
là:
A.
2
;
3
−
. B.
2
;
3
− +
. C.
2
;
5
−
. D.
2
;
5
+
.
Câu 35: Tính thể tích khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, biết cạnh bên
SA
vuông
góc với mặt phẳng đáy và góc giữa cạnh bên
SD
và mặt phẳng đáy bằng
60
.
A.
3
3
6
a
. B.
3
3a
. C.
3
3
9
a
. D.
3
3
3
a
.
Câu 36: Cho lăng trụ đứng tam giác
.ABC A B C
. Tính thể tích
V
của hình lăng trụ này biết tam giác
ABC
vuông cân tại
A
,
AB a=
, góc giữa
()mp ABC
và
()mp A BC
bằng
60
.
A.
3
6
36
a
V =
. B.
3
6
4
a
V =
. C.
3
3
6
a
V =
. D.
3
6
12
a
V =
.

6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 37: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có cạnh
huyền bằng
6a
. Thể tích
V
của khối nón đó bằng?
A.
3
6
4
a
V
=
. B.
3
6
3
a
V
=
. C.
3
6
6
a
V
=
. D.
3
6
2
a
V
=
.
Câu 38: Thiết diện qua trục của một hình trụ là hình vuông có cạnh
4a
. Thể tích của khối trụ này bằng
A.
3
32 a .
B.
3
8 a .
C.
3
4 a .
D.
3
16 a .
Câu 39: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
.
A.
5
;
2
m
−
−
. B.
5
;
2
m
−
−
. C.
5
;
2
m
+
. D.
5
;
2
m
+
.
Câu 40: Tính tổng bình phương tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
2
23
xm
y
xx
+
=
+−
có đúng một tiệm cận đứng.
A.
10
. B. 9. C. 81. D.
82
.
Câu 41: Cho phương trình
( ) ( )
.25 2 3 .5 5 0 1
xx
m m m− − + − =
. Tập hợp tất cả các giá trị dương của
m
để phương trình
( )
1
có 2 nghiệm phân biệt là một khoảng
( )
;ab
. Khi đó, giá trị của
2Q b a=−
bằng
A.
1Q =−
. B.
13Q =
. C.
16Q =
. D.
1Q =
.
Câu 42: Bất phương trình
( )
( ) ( )
22
1
4 1 log 4 1 0
e
x x x x− − − + +
có tổng tất cả các nghiệm nguyên là?
A.
6
. B.
8
. C.
4
. D.
10
.
Câu 43: Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi điểm của mỗi
tháng trong ba năm đầu tiên là
9
triệu đồng/ tháng. Tính từ ngày đầu làm việc, cứ sau đúng ba
năm liên tiếp thì tăng lương
10%
so với mức lương một tháng người đó đang hưởng. Nếu tính
theo hợp đồng thì tháng đầu tiên của năm thứ
19
người đó nhận được mức lương là bao nhiêu?
A.
6
9.1,1
(triệu đồng). B.
8
9.1,1
(triệu đồng).
C.
5
9.1,1
(triệu đồng). D.
7
9.1,1
(triệu đồng).
Câu 44: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân ở
,B
2,AC a=
( )
,SA ABC⊥
.SA a=
Gọi
G
là trọng tâm của tam giác
SBC
,
( )
mp
đi qua
AG
và song song với
BC
chia
khối chóp thành hai phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
.V
A.
3
4
9
a
B.
3
4
27
a
C.
3
2
9
a
D.
3
5
54
a
Câu 45: Cho hình nón có chiều cao và bán kính hình tròn đáy đều bằng
2.a
Mặt phẳng
( )
đi qua đỉnh
và tạo với đáy của hình nón một góc
60
. Tính diện tích thiết diện của hình nón cắt bởi mặt
phẳng
( )
.
A.
2
82
3
a
. B.
2
42
3
a
. C.
2
82a
. D.
2
42a
.
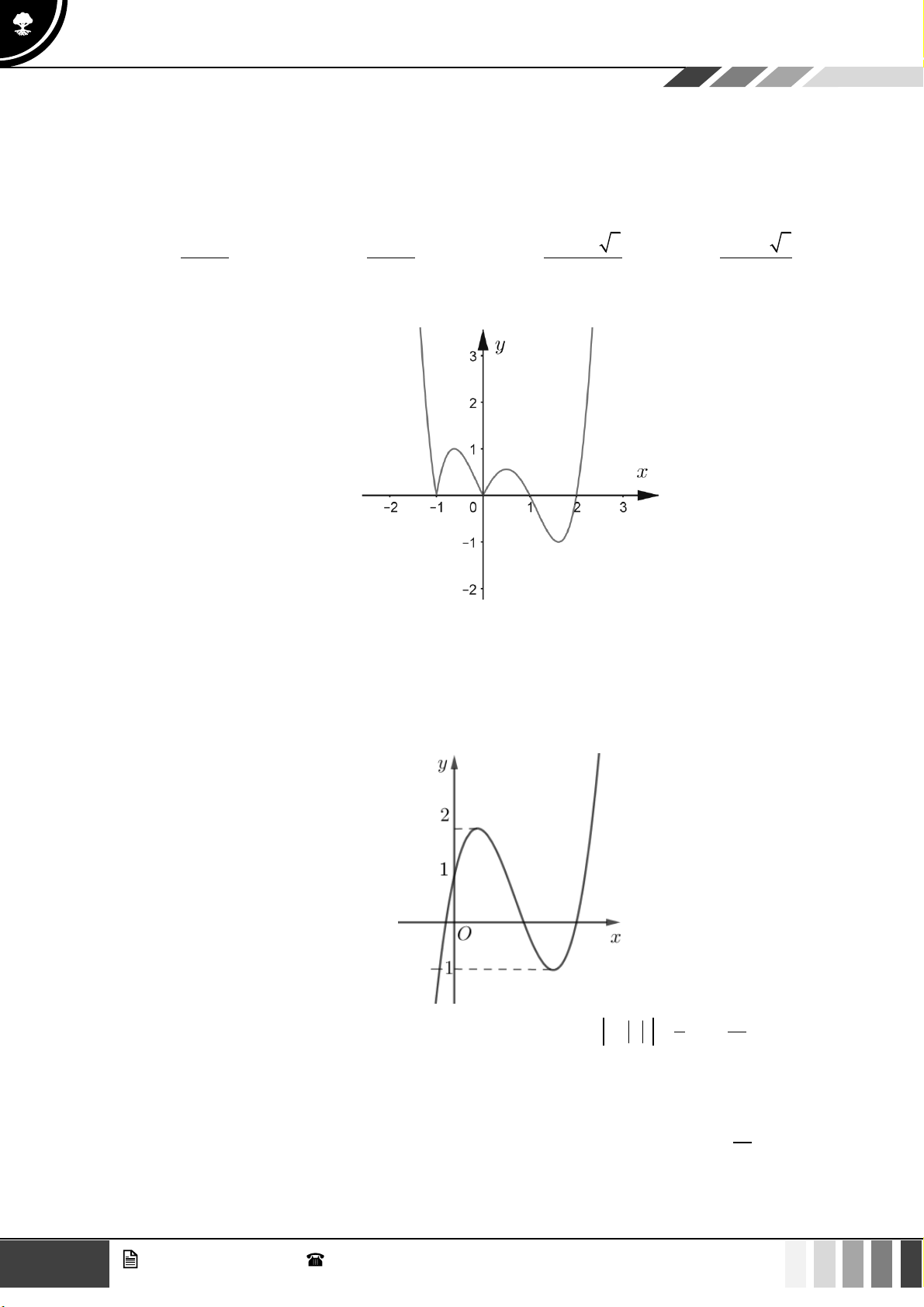
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 46: Bạn Nam muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam
giác đều
ABC
có cạnh bằng
( )
90 cm
. Bạn muốn cắt mảnh tôn hình chữ nhật
MNPQ
từ mảnh
tôn nguyên liệu (với
M
,
N
thuộc cạnh
BC
;
P
và
Q
tương ứng thuộc cạnh
AC
và
AB
) để
tạo thành hình trụ có chiều cao bằng
MQ
. Thể tích lớn nhất của chiếc thùng mà bạn Nam có thể
làm được là:
A.
( )
3
91125
4
cm
. B.
( )
3
91125
2
cm
. C.
( )
3
108000 3
cm
. D.
( )
3
13500. 3
cm
.
Câu 47: Cho hàm số
( )
y f x=
là hàm đa thức bậc 6 có đồ thị hàm số
( )
y f x
=
như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( ) ( )
7
3
1g x f x m
= + +
có 2 điểm cực
trị?
A.
2.
B.
0.
C.
1.
D. Vô số.
Câu 48: Cho hàm số đa thức bậc ba
( )
y f x=
có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
24
21
9 81
f x m m=−
có 8 nghiệm
phân biệt?
A.
9
. B.
8
. C.
6
. D.
3
.
Câu 49: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
15 5 3
10
x x x
m
− − =
có hai nghiệm
thực phân biệt?
A. Vô số. B.
18
. C.
9
. D.
10
.

8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 50: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành thỏa mãn
2,AB a=
2,BC a=
6BD a=
. Hình chiếu vuông góc của đỉnh
S
lên mặt phẳng
( )
ABCD
là trọng tâm của tam
giác
BCD
. Tính theo
a
thể tích khối chóp
.S ABCD
, biết rằng khoảng cách giữa hai đường
thẳng
AC
và
SB
bằng
a
.
A.
3
2
3
a
. B.
3
53
3
a
. C.
3
3
2
a
. D.
3
42
3
a
.
-----------------------HẾT-----------------------
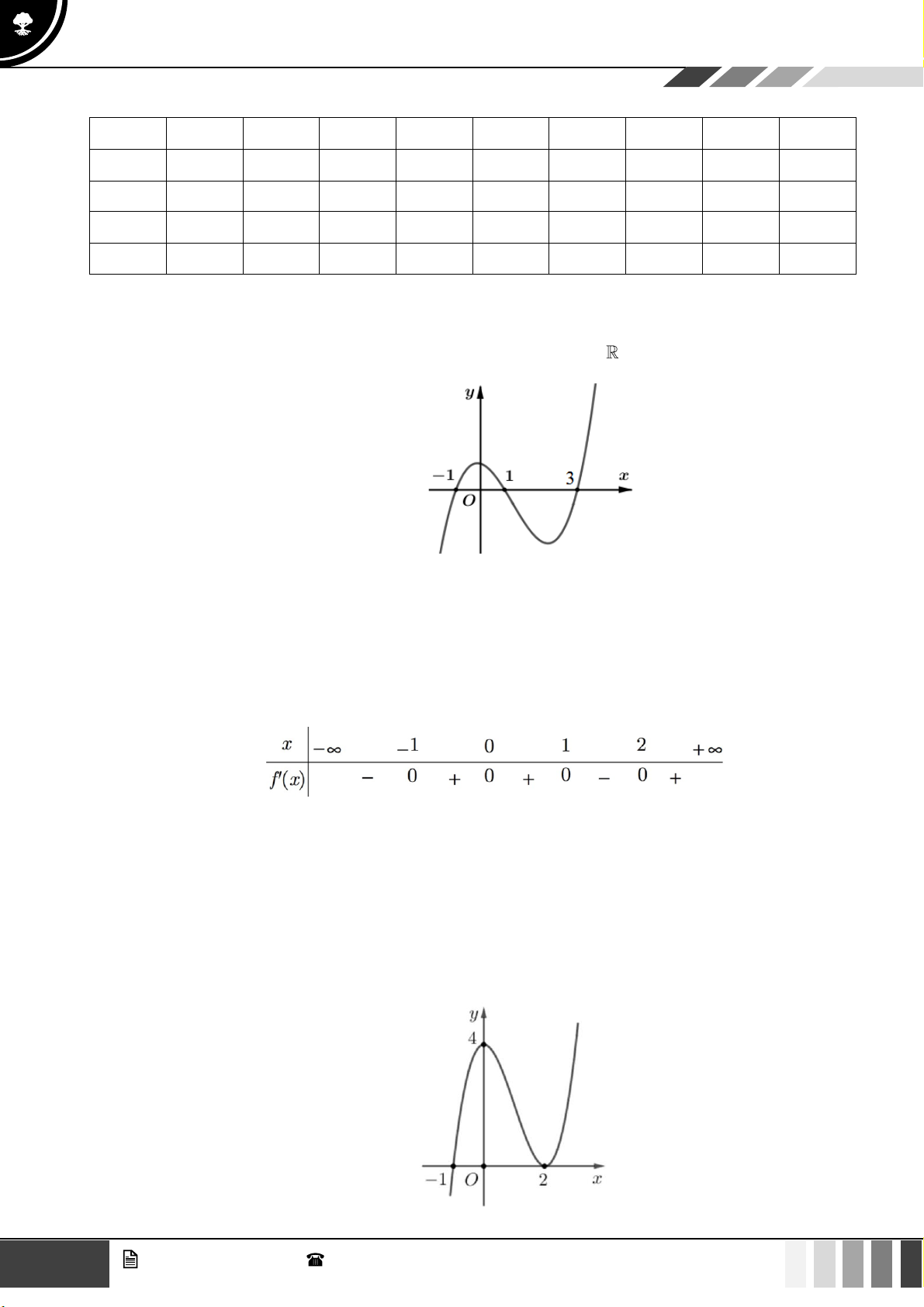
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HK1
Toán 12
BẢNG ĐÁP ÁN
1.C
2.C
3.C
4.A
5.D
6.B
7.C
8.B
9.D
10.D
11.B
12.A
13.A
14.C
15.D
16.D
17.B
18.A
19.A
20.B
21.C
22.D
23.A
24.C
25.D
26.C
27.B
28.D
29.B
30.D
31.D
32.C
33.B
34.B
35.D
36.B
37.A
38.D
39.B
40.D
41.B
42.C
43.A
44.D
45.A
46.D
47.D
48.C
49.C
50.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
có đạo hàm
( )
fx
xác định, liên tục trên và có đồ thị như hình vẽ
Hàm số
( )
y f x=
nghịch biến trên khoảng nào
A.
( )
1;1−
. B.
( )
3;+
. C.
( )
1;3
. D.
( )
;3−
.
Lời giải
Từ đồ thị ta thấy hàm số nghịch biến trên khoảng
( )
1;3
.
Câu 2: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại
0x =
. B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực đại tại
1x =
. D. Hàm số đạt cực đại tại
2x =
.
Lời giải
Hàm số
( )
fx
có
( )
'fx
đổi dấu từ
+
sang
−
khi
( )
'fx
đi qua điểm
1x =
.
Vậy hàm số
( )
fx
cực đại tại
1x =
.
Câu 3: Cho hàm số
( )
fx
có đồ thị như hình vẽ:
Điểm cực tiểu của hàm số đã cho là

10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
A.
1x =−
. B.
0x =
. C.
2x =
. D.
4x =
.
Lời giải
Nhìn đồ thị ta thấy hàm số có điểm cực tiểu
2x =
.
Câu 4: Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số
2
2
2
4
xx
y
x
−
=
−
A.
2x =−
. B.
2x =
. C.
2y =
. D.
1y =
.
Lời giải
Ta có
2
2
2
2
4
x x x
yy
x
x
−
= =
+
−
.
Có
2
lim
x
y
−
→−
= +
và
2
lim
x
y
+
→−
= −
nên đường thẳng
2x =−
là tiệm cận đứng của đồ thị hàm số.
Câu 5: Tọa độ giao điểm của đồ thị hàm số
( )
3
:5C y x x= + +
và đường thẳng
( )
: 2 1d y x= − +
là
A.
( )
1; 1−
. B.
( )
0;1
. C.
( )
0;5
. D.
( )
1;3−
.
Lời giải
Phương trình hoành độ giao điểm
3
5 2 1x x x+ + = − +
3
3 4 0xx + + =
1x = −
3y=
.
Câu 6: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
42
21y x x= − + −
. B.
42
21y x x= − −
. C.
32
31y x x= − −
. D.
32
31y x x= − + −
.
Lời giải
Dựa vào đồ thị có ba điểm cực trị, nhận thấy đây là đồ thị của hàm đa thức bậc bốn nên loại
phương án C và D.
Vì
lim
x
y
→+
= +
nên hệ số
0a
Câu 7: Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ bên dưới?
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HK1
Toán 12
A.
3
3 2.y x x=−+
B.
2
.
1
x
y
x
+
=
−
C.
2
.
1
x
y
x
−
=
−
D.
42
5 4.y x x= − + −
Lời giải
Hàm số trên có dạng
ax b
y
cx d
+
=
+
nên loại
,AD
.
Ta có
( )
02y =
nên loại
B
.
Câu 8: Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ bên?
A.
32
1y x x= − + −
. B.
42
1y x x= − −
. C.
32
1y x x=−−
. D.
42
1y x x= − + −
.
Lời giải
Dựa vào hình dáng đồ thị suy ra đồ thị là đồ thị của hàm số bậc bốn có hệ số
0a
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;2− −
. B.
( )
4;0−
. C.
( )
0; ;+
. D.
( )
2;0−
.
Lời giải
Hàm số đã cho đồng biến trên khoảng
( )
2;0−
.
Câu 10: Biểu thức
3
3
222
333
viết dạng lũy thừa với số mũ hữu tỉ là
A.
5
18
2
3
. B.
1
12
2
3
. C.
7
6
2
3
. D.
1
2
2
3
.
Lời giải
Ta có
1 1 1
1 1 1 1 3 1
3 3 3
1
3 6 3 6 2 2
3
3
2 2 2 2 2 2 2 2 2
..
3 3 3 3 3 3 3 3 3
++
= = = =
Câu 11: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét dấu của
( )
fx
như sau:
Số điểm cực đại của hàm số
( )
y f x=
là

12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Dựa vào bảng biến thiên ta thấy, hàm số
( )
y f x=
đạt cực đại tại
2x =−
nên hàm số đã cho có
1
điểm cực đại.
Câu 12: Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
( )
2
x
y =
. B.
( )
0,5
x
y =
. C.
x
e
y
=
. D.
2
3
x
y
=
.
Lời giải
Hàm số
( )
2
x
y =
đồng biến trên tập xác định vì
21
.
Hàm số
( )
0,5
x
y =
nghịch biến trên tập xác định vì
0 0,5 1
.
Hàm số
x
e
y
=
nghịch biến trên tập xác định vì
01
e
.
Hàm số
2
3
x
y
=
nghịch biến trên tập xác định vì
2
01
3
.
Câu 13: Cho
0a
,
1a
, giá trị của
3
log
a
a
bằng
A.
1
3
. B.
1
3
−
. C.
3−
. D.
3
.
Lời giải
Ta có:
3
11
log log .
33
a
a
aa==
Câu 14: Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
( )
31
x
y =−
. B.
( )
x
ye
=−
. C.
x
y
=
. D.
( )
2
x
ye=−
.
Lời giải
Hàm số
x
ya=
với
0a
,
1a
đồng biến trên khi và chỉ khi
1a
.
Ta có
1
nên hàm số
x
y
=
đồng biến trên .
Câu 15: Tính đạo hàm của hàm số
( )
2
log 2 1 .yx=+
A.
1
21
y
x
=
+
. B.
2
21
y
x
=
+
.
C.
( )
1
2 1 ln2
y
x
=
+
. D.
( )
2
2 1 ln2
y
x
=
+
.
Lời giải
Tập xác định của hàm số
1
;
2
D
= − +
.
Xét hàm số
( )
2
log 2 1 .yx=+
Ta có:
( )
( )
( )
( ) ( )
2
21
2
log 2 1
2 1 ln2 2 1 ln2
x
yx
xx
+
= + = =
++
.
Câu 16: Tập nghiệm của phương trình
( ) ( )
2020 2020
log 1 log 2 1xx− = +
là

GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HK1
Toán 12
A.
1
2;
2
−
. B.
2
.
C.
2−
.
D.
.
Lời giải
Ta có phương trình đã cho
1 2 1
1
xx
x
− = +
2
1
x
x
=−
Hệ phương trình trên vô nghiệm nên ta chọn D.
Câu 17: Nghiệm của bất phương trình
42
22
33
xx−
là
A.
2
5
x
. B.
2
3
x −
. C.
2
5
x
. D.
2
3
x
.
Lời giải
Ta có:
42
2 2 2
4 2 .
3 3 3
xx
x x x
−
− −
.
Câu 18: Các giá trị
x
thỏa mãn bất phương trình
( )
2
log 3 1 3x −
là
A.
3x
. B.
1
3
3
x
. C.
3x
. D.
10
3
x
.
Lời giải
Ta có
( )
2
log 3 1 3 3 1 8 3x x x− −
.
Câu 19: Vật thể nào dưới đây không phải là khối đa diện?
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 3. B. Hình 1. C. Hình 4. D. Hình 2.
Lời giải
Vật thể cho bởi hình
1,2,4
là các khối đa diện.
Vật thể cho bởi hình
3
không phải khối đa diện, vi phạm điều kiện mỗi cạnh của đa giác nào
cũng là cạnh chung của đúng hai đa giác.
Câu 20: Khối đa diện đều loại
{5;3}
có số mặt là bao nhiêu?
A.
14
. B.
12
. C.
10
. D.
8
.
Lời giải
Khối đa diện đều loại
{5;3}
là khối 12 mặt đều.
Câu 21: Cho hình chóp
.S ABC
có
( )
,SA ABC⊥
ABC
vuông cân tại A,
2SA AB==
. Thể tích của
khối chóp
.S ABC
là.
A.
2
3
. B.
8
3
. C.
4
3
. D.
4
.
Lời giải
Ta có:
ABC
vuông cân tại A nên
2AB AC==
.

14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Mặt khác:
1
. . 2
2
ABC
S AB AC
==
(đvdt).
Suy ra:
.
1 1 4
. . .2.2
3 3 3
S ABC ABC
V SA S
= = =
(đvtt).
Câu 22: Cho một khối chóp có diện tích đáy là
B
và chiều cao là
h
. Khi đó thể tích
V
của khối chóp
đó là
A.
V Bh=
. B.
3V Bh=
. C.
3
V Bh=
. D.
1
3
V Bh=
.
Lời giải
Thể tích
V
của khối chóp đó là:
1
3
V Bh=
Câu 23: Tính thể tích khối hộp chữ nhật
.ABCD A B C D
biết
6 AB cm=
,
8 BC cm=
,
10 AA cm
=
.
A.
3
480 cm
. B.
3
48 cm
. C.
3
160 cm
. D.
3
1440 cm
.
Lời giải
Gọi
V
là thể tích khối hộp chữ nhật
.ABCD A B C D
.
Ta có
( )
3
. . 6.8.10 480 V AB BC AA cm
= = =
.
Câu 24: Cho khối nón có bán kính đáy
3r =
và chiều cao
4h =
. Tính thể tích
V
của khối nón đã cho.
A.
16 3V
=
. B.
12V
=
. C.
4V
=
. D.
4V =
.
Lời giải
2
1
. . . 4
3
V r h
==
.
Câu 25: Một khối lăng trụ có chiều cao
3a
, diện tích đáy
2
2a
thì có thể tích bằng
A.
3
2a
. B.
3
a
. C.
3
18a
. D.
3
6a
.
Lời giải
Thể tích của khối lăng trụ là:
22
. 2 .3 6V S h a a a= = =
.
Câu 26: Cho hàm số
21
2
x
y
x
−
=
−
. Mệnh đề nào sau đây là mệnh đề đúng
A. Hàm số đồng biến trên khoảng
( )
;2−
.
B. Hàm số đồng biến trên khoảng
( )
;− +
.
C. Hàm số nghịch biến trên khoảng
( )
2;+
.
D. Hàm số đồng biến trên khoảng
( )
2;+
.
Lời giải
Tập xác định:
\2D =
.
Ta có:
( )
2
3
0, .
2
y x D
x
−
=
−
Vậy hàm số nghịch biến trên khoảng
( )
;2−
và
( )
2;+
.
Câu 27: Cho hàm số
( )
fx
có đạo hàm
( )
2 1,f x x x
= −
. Hỏi hàm số
( )
fx
có bao nhiêu điểm cực
trị?
A.
3
. B.
1
. C.
0
. D.
2
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HK1
Toán 12
Lời giải
Ta có
( )
1
0
2
f x x
= =
, dễ thấy
( )
1
0, ;
2
f x x
+
và
( )
1
0, ;
2
f x x
−
nên
hàm số có 1 điểm cực trị.
Câu 28: Tìm giá trị nhỏ nhất m của hàm số
42
13y x x= − +
trên đoạn
2;3−
.
A.
13m =
. B.
25m =
. C.
85m =
. D.
51
4
m =
.
Lời giải
Ta có:
( )
32
0
1
4 2 ; ' 0 2 2 1 0
2
1
2
x
y x x y x x x
x
=
= − = − = =
−
=
( ) ( ) ( )
1 51 1 51
2 25; ; 0 13; ; 3 85
44
22
f f f f f
− = − = = = =
Giá trị nhỏ nhất của hàm số hàm số
42
13y x x= − +
trên đoạn
2;3−
là:
( ) ( ) ( )
1 1 51
min 2 ; ; 0 ; ; 3
4
22
m f f f f f
= − − =
Câu 29: Số đường tiệm cận đứng của đồ thị hàm số
22
2
4 1 3 2
22
xx
y
xx
− + +
=
−
là:
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Tập xác định:
( )
11
; ;1 1;
22
D
= − − +
Tiệm cận đứng:
( )
22
11
4 1 3 2
lim lim
21
xx
xx
y
xx
++
→→
− + +
= = +
−
( Do
(
)
( )
( )
( )
22
11
lim 4 1 3 2 5 3 0; lim 2 1 0; 2 1 0, 1
xx
x x x x x x x
++
→→
− + + = + − = −
)
( )
22
11
4 1 3 2
lim lim
21
xx
xx
y
xx
−−
→→
− + +
= = −
−
( Do
(
)
( )
( )
( )
22
11
lim 4 1 3 2 5 3 0; lim 2 1 0; 2 1 0, :0 1
xx
x x x x x x x x
−−
→→
− + + = + − = −
)
Suy ra đường thẳng
1x =
là đường tiệm cận đứng.
Câu 30: Cho hàm số
( )
y f x=
có đồ thị như vẽ. Số nghiệm của phương trình
( )
2 3 0fx−=
là:

16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
A.
5
. B.
3
. C.
4
. D.
6
.
Lời giải
Ta có:
( ) ( )
( )
( )
3
3
2
2 3 0
3
2
2
fx
f x f x
fx
=
− = =
=−
Dựa vào đồ thị ta có:
Số nghiệm của phương trình
( )
3
2
fx=
là
3
Số nghiệm của phương trình
( )
3
2
fx=−
là
3
Vậy số nghiệm của phương trình
( )
2 3 0fx−=
là
6
Câu 31: Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị như hình vẽ bên dưới. Mệnh đề nào dưới đây
đúng?
A.
0ad
. B.
0cd
. C.
0bd
. D.
0ac
.
Lời giải
Từ đồ thị ta thấy
Vì
( )
lim
x
fx
→+
= +
nên
0a
.
Vì đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0d
.
Vì
;0
CD CT
xx
nên
2
0
0
3
0
.0
3
CD CT
CD CT
b
xx
b
a
cc
xx
a
+ = −
=
. Vậy
0ac
.
Câu 32: Cho
2
log 3 a=
,
2
log 5 b=
Khi đó
6
log 225
được biểu diễn theo
,ab
là đáp án nào sau đây?
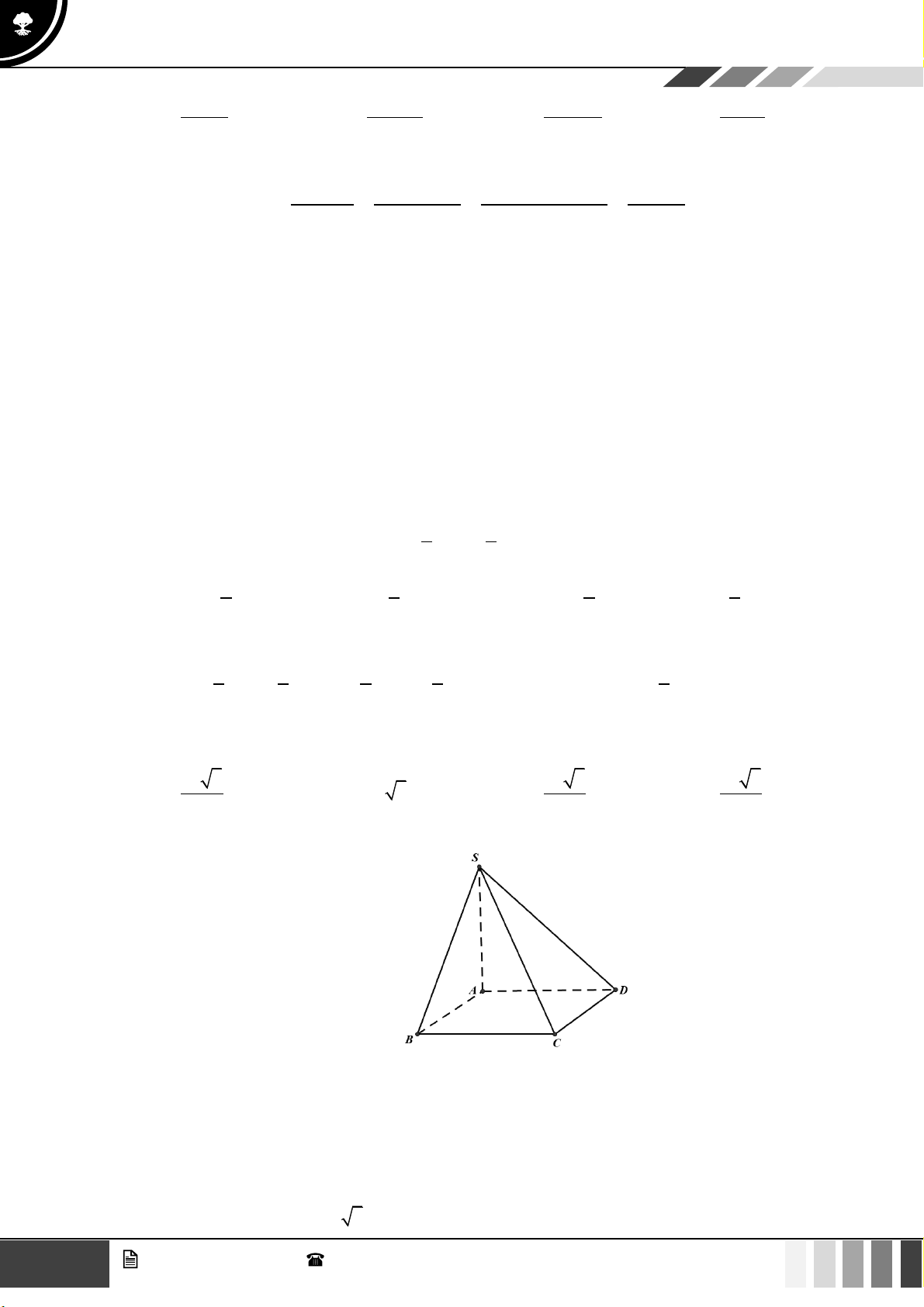
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HK1
Toán 12
A.
13
ab b
a
+
+
. B.
22
1
ab
a
+
+
. C.
22
1
ab
a
+
+
. D.
12
ab
a
+
+
.
Lời giải
Ta có:
( )
( )
22
2
2 2 2
6
2 2 2
log 3 .5
log 225 2log 3 2log 5 2 2
log 225
log 6 log 2.3 1 log 3 1
ab
a
++
= = = =
++
Câu 33: Số nghiệm của phương trình
( )
2 2 2
log log 6 log 7xx+ − =
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Điều kiện:
0
6
60
x
x
x
−
Phương trình đã cho tương đương
( )
2
22
log . 6 log 7 6 7 0x x x x− = − − =
( )
1
7
x loai
x
=−
=
Vậy phương trình đã cho có 1 nghiệm.
Câu 34: Tập nghiệm của bất phương trình
42
45
54
xx−
là:
A.
2
;
3
−
. B.
2
;
3
− +
. C.
2
;
5
−
. D.
2
;
5
+
.
Lời giải
Ta có
4 2 4 2
4 5 5 5 2
42
5 4 4 4 3
x x x x
x x x
− − −
− − −
.
Câu 35: Tính thể tích khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, biết cạnh bên
SA
vuông
góc với mặt phẳng đáy và góc giữa cạnh bên
SD
và mặt phẳng đáy bằng
60
.
A.
3
3
6
a
. B.
3
3a
. C.
3
3
9
a
. D.
3
3
3
a
.
Lời giải
Ta có
( )
SA ABCD⊥
nên hình chiếu của
SD
lên
( )
ABCD
là
AD
.
Vậy
( )
( )
( )
, , 60SD ABCD SD AD SDA= = =
.
Theo giả thiết,
ABCD
là hình vuông cạnh
a
nên diện tích của
ABCD
là
2
ABCD
Sa=
.
Mặt khác, do
( )
SA ABCD⊥
nên
SA AD⊥
hay tam giác
SAD
vuông tại
A
.
.tan 3SA AD SDA a = =
.
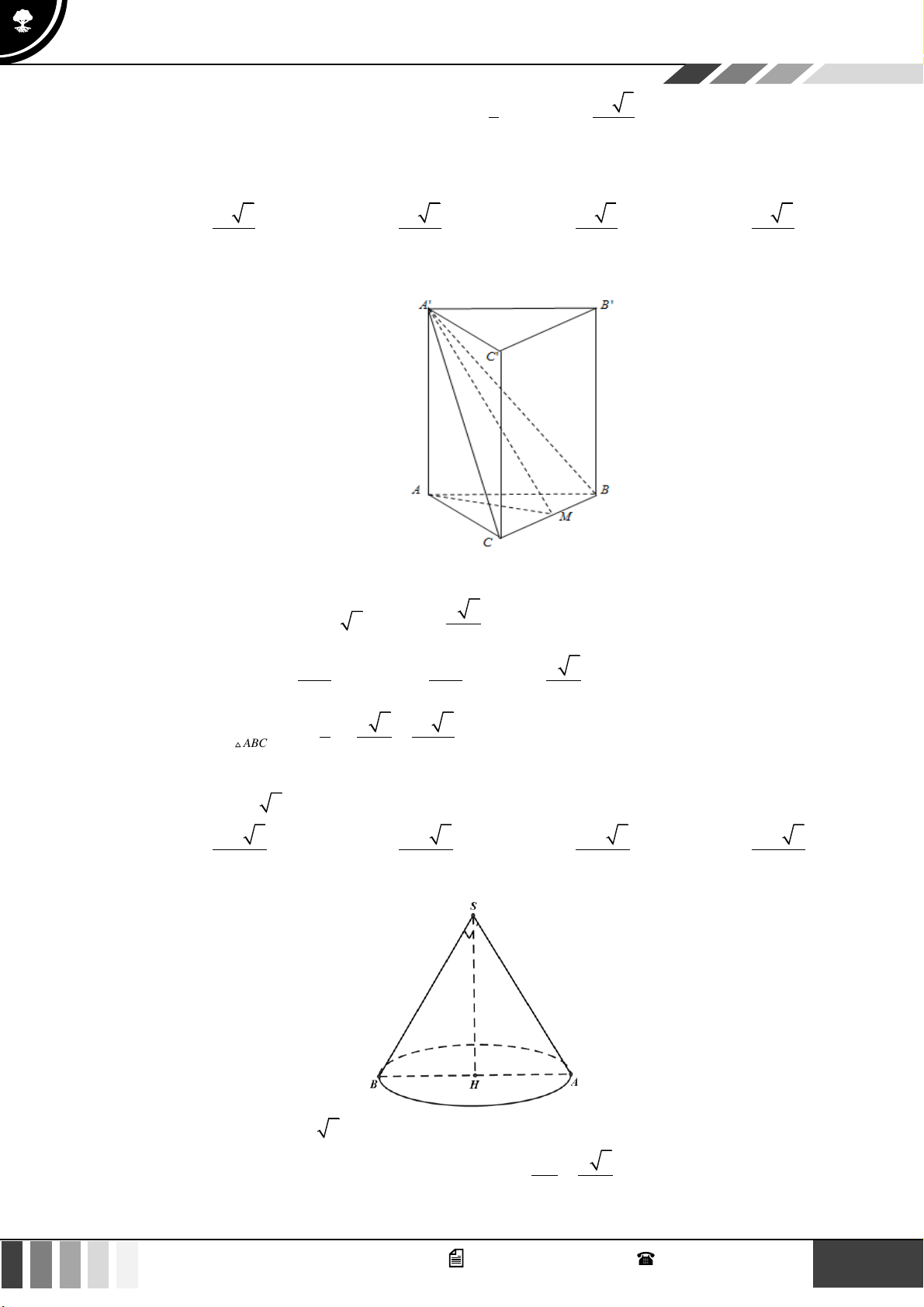
18
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Vậy thể tích của khối chóp
.S ABCD
là
3
13
..
33
ABCD
a
V SAS==
.
Câu 36: Cho lăng trụ đứng tam giác
.ABC A B C
. Tính thể tích
V
của hình lăng trụ này biết tam giác
ABC
vuông cân tại
A
,
AB a=
, góc giữa
()mp ABC
và
()mp A BC
bằng
60
.
A.
3
6
36
a
V =
. B.
3
6
4
a
V =
. C.
3
3
6
a
V =
. D.
3
6
12
a
V =
.
Lời giải
Góc giữa
()mp ABC
và
()mp A BC
là
A MA
(
M
là trung điểm của đoạn thẳng
BC
).
Ta có
AB a=
2BC a=
2
2
a
AM=
.
Lại có
tan tan60
A A A A
A MA
AM AM
= =
6
'
2
a
AA=
.
Vậy
3
2
1 6 6
..
2 2 4
ABC
aa
V S A A a
= = =
.
Câu 37: Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có cạnh
huyền bằng
6a
. Thể tích
V
của khối nón đó bằng?
A.
3
6
4
a
V
=
. B.
3
6
3
a
V
=
. C.
3
6
6
a
V
=
. D.
3
6
2
a
V
=
.
Lời giải
Theo đề ta có
6AB a=
.
Ngoài ra
SAB
vuông cân tại
S
nên
6
22
AB a
SH AH= = =
.
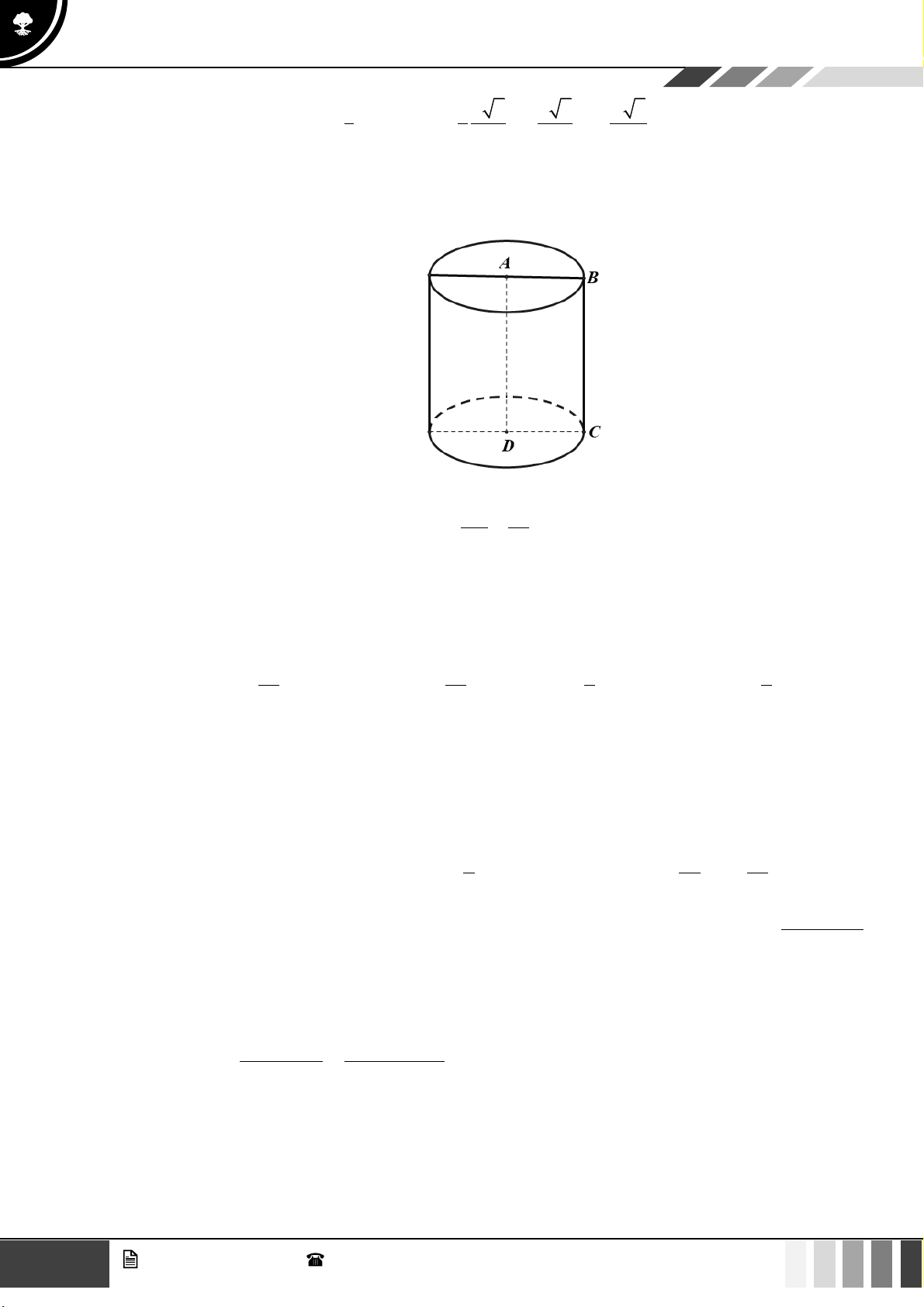
GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HK1
Toán 12
Thể tích khối nón là
2
1
..
3
V SH AH
=
2
1 6 6
..
3 2 2
aa
=
3
6
4
a
=
.
Câu 38: Thiết diện qua trục của một hình trụ là hình vuông có cạnh
4a
. Thể tích của khối trụ này bằng
A.
3
32 a .
B.
3
8 a .
C.
3
4 a .
D.
3
16 a .
Lời giải
Thiết diện qua trục của một hình trụ là hình vuông
''ABB A
có cạnh
4a
nên ta có chiều cao hình
trụ là
'4h OO a==
và bán kính đáy
4
2
22
AB a
ra= = =
.
Thể tích của khối trụ
2 2 3
4 .4a 16 a .
ktru
V h R a
= = =
Câu 39: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
.
A.
5
;
2
m
−
−
. B.
5
;
2
m
−
−
. C.
5
;
2
m
+
. D.
5
;
2
m
+
.
Lời giải
Ta có:
( )
2
3 12 2y x m x
= − + +
.
Hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
khi và chỉ khi:
( ) ( )
2
3 12 2 0, 2 ; 1y x m x x
= − + + − −
( )
2
4 8 0, 2 ; 1x mx x x − + + − −
( )
2
4 8 , 2 ; 1mx x x x − − −
( )
2, 2 ; 1
4
x
mx − − −
25
2
42
m
−−
− =
.
Câu 40: Tính tổng bình phương tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
2
23
xm
y
xx
+
=
+−
có đúng một tiệm cận đứng.
A.
10
. B. 9. C. 81. D.
82
.
Lời giải
Ta có:
2
2
23
xm
y
xx
+
=
+−
( )( )
2
13
xm
xx
+
=
−+
.
Nhận xét: Đồ thì hàm số nếu có tiệm cận đứng chỉ có thể có nhận đường thẳng
1x =
hoặc
3x =−
hoặc cả hai đường thẳng đó.
Vậy đồ thị hàm số có đúng một tiệm cận đứng nếu
2
0xm+=
nhận nghiệm
1x =
hoặc
3x =−
.
Khi đó:
1
9
m
m
=−
=−
.

20
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Với
1m =−
có một tiệm cận đứng
3x =−
.
Với
9m =−
có một tiệm cận đứng
1x =
.
Vậy
{ 1; 9}m − −
. Vậy giá trị cần tìm là
81 1 82+=
Câu 41: Cho phương trình
( ) ( )
.25 2 3 .5 5 0 1
xx
m m m− − + − =
. Tập hợp tất cả các giá trị dương của
m
để phương trình
( )
1
có 2 nghiệm phân biệt là một khoảng
( )
;ab
. Khi đó, giá trị của
2Q b a=−
bằng
A.
1Q =−
. B.
13Q =
. C.
16Q =
. D.
1Q =
.
Lời giải
Đặt
( )
50
x
tt=
, khi đó phương trình
( )
1
trở thành:
( ) ( )
2
. 2 3 5 0 *mt m t m− − + − =
.
Phương trình
( )
1
có hai nghiệm phân biệt
( )
*
có hai nghiệm dương phân biệt
( )
0
00
90
0 9 0
23
0
0 0 3 5 9
0 0 5
5
0
m
am
m
mm
m
S m hay m m
m
P m hay m
m
m
− +
−
−
.
Vậy tập hợp các giá trị dương của
m
để phương trình
( )
1
có 2 nghiệm phân biệt là
( )
5;9
5; 9 2 13a b b a = = − =
.
Câu 42: Bất phương trình
( )
( ) ( )
22
1
4 1 log 4 1 0
e
x x x x− − − + +
có tổng tất cả các nghiệm nguyên là?
A.
6
. B.
8
. C.
4
. D.
10
.
Lời giải
Ta có:
( )
( ) ( )
22
1
4 1 log 4 1 0
e
x x x x− − − + +
( )
( )
2
2
1
2 log 4 1 0
e
x x x − − + +
( )
2
2
1
20
2
log 4 1 0
4 1 1
e
x
x
xx
xx
−
− + +
− + +
2
2
40
x
xx
− +
2
04
x
x
.
Vì
1;3xx
. Vậy tổng tất cả các nghiệm nguyên bằng .
Câu 43: Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi điểm của mỗi
tháng trong ba năm đầu tiên là
9
triệu đồng/ tháng. Tính từ ngày đầu làm việc, cứ sau đúng ba
năm liên tiếp thì tăng lương
10%
so với mức lương một tháng người đó đang hưởng. Nếu tính
theo hợp đồng thì tháng đầu tiên của năm thứ
19
người đó nhận được mức lương là bao nhiêu?
A.
6
9.1,1
(triệu đồng). B.
8
9.1,1
(triệu đồng).
C.
5
9.1,1
(triệu đồng). D.
7
9.1,1
(triệu đồng).
Lời giải
Sau
3
năm, bắt đầu từ tháng đầu tiên của năm thứ
4
số tiền lương người đó nhận được sau mỗi
tháng là
9 9.10% 9.1,1+=
(triệu đồng).
Sau
6
năm (
2.3
năm), bắt đầu từ tháng đầu tiên của năm thứ
7
số tiền lương người đó nhận
được sau mỗi tháng là
( )
2
9.1,1 9.1,1.10% 9.1,1. 1 10% 9.1,1+ = + =
(triệu đồng).
4
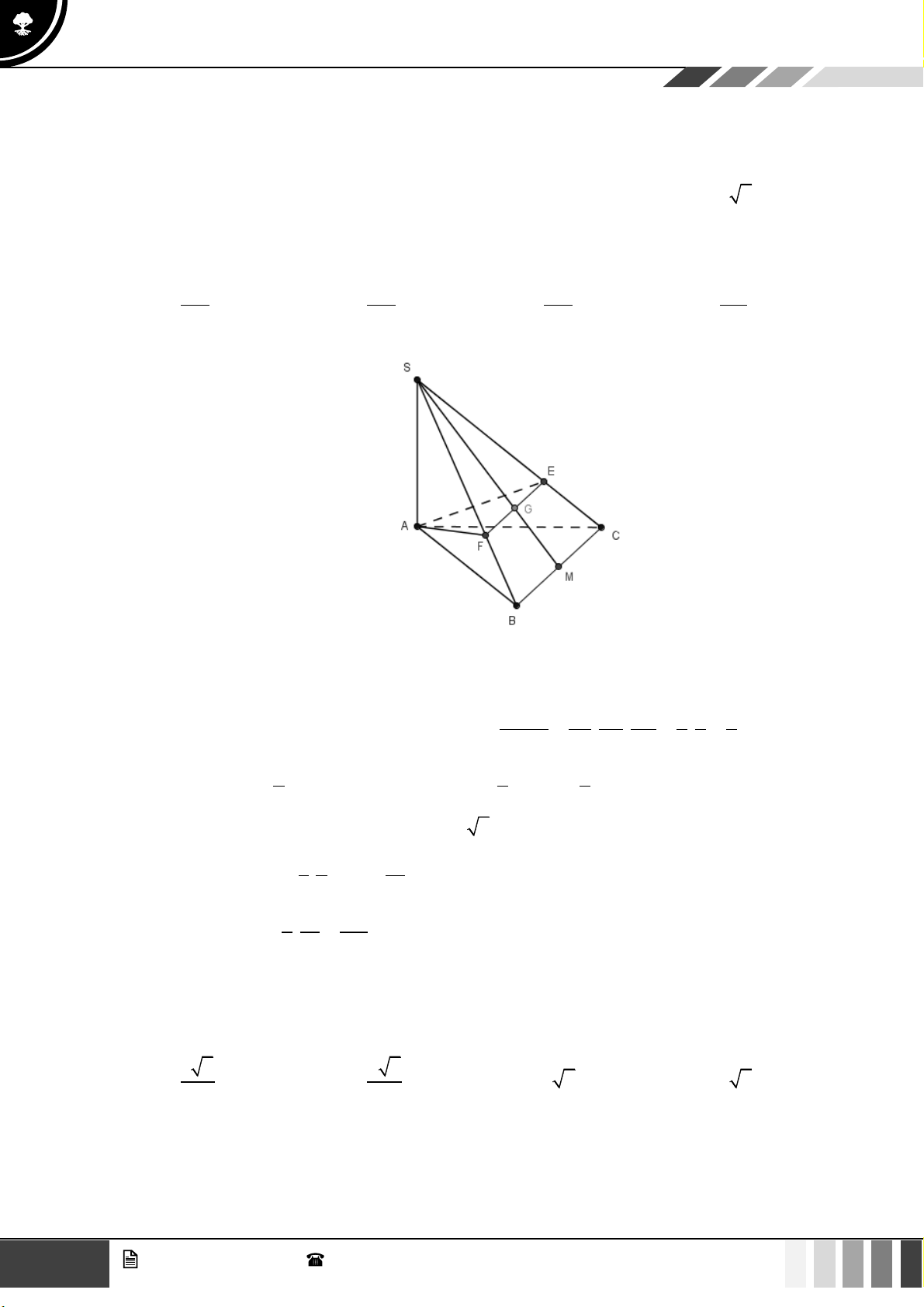
GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HK1
Toán 12
Tương tự như vậy sau
18
năm (
6.3
năm), bắt đầu từ tháng đầu tiên của năm thứ
19
số tiền người
đó nhận được sau mỗi tháng là
6
9.1,1
(triệu đồng).
Vậy tháng đầu tiên của năm thứ
19
, người đó nhận được mức lương là
6
9.1,1
(triệu đồng).
Câu 44: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân ở
,B
2,AC a=
( )
,SA ABC⊥
.SA a=
Gọi
G
là trọng tâm của tam giác
SBC
,
( )
mp
đi qua
AG
và song song với
BC
chia
khối chóp thành hai phần. Gọi
V
là thể tích của khối đa diện không chứa đỉnh
S
. Tính
.V
A.
3
4
9
a
B.
3
4
27
a
C.
3
2
9
a
D.
3
5
54
a
Lời giải
Trong mặt phẳng
( )
SBC
. Qua
G
kẻ đường thẳng song song với
BC
và lần lượt cắt
,SC SB
tại
,EF
. Khi đó ta được khối đa diện không chứa đỉnh
S
là
.ABCEF
Ta có
G
là trọng tâm của tam giác
SBC
nên
.AF
.
2 2 4
. . . .
3 3 9
SE
S ABC
V
SA SF SE
V SA SB SC
= = =
Do đó
.
.AF . . .
4 4 5
. . .
9 9 9
S ABC
S E S ABC ABCEF S ABC S ABC
V V V V V V= = − =
.
Vì tam giác
ABC
vuông cân ở
,B
2AC a=
nên
AB BC a==
.
Mặt khác
3
.
11
. . . .
3 2 6
S ABC
a
V a a a==
Suy ra
33
55
.
9 6 54
ABCEF
aa
V ==
.
Câu 45: Cho hình nón có chiều cao và bán kính hình tròn đáy đều bằng
2.a
Mặt phẳng
( )
đi qua đỉnh
và tạo với đáy của hình nón một góc
60
. Tính diện tích thiết diện của hình nón cắt bởi mặt
phẳng
( )
.
A.
2
82
3
a
. B.
2
42
3
a
. C.
2
82a
. D.
2
42a
.
Lời giải

22
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Gọi
O
là tâm hình tròn đáy, thiết diện qua trục là tam giác
SAB
như hình vẽ.
Gọi
H
là trung điểm
AB
.
Ta có
OH AB⊥
và
SH AB⊥
nên góc giữa
( )
và mặt đáy của hình nón là
60 .SHO =
23
tan .
tan60 3
SO SO
SHO OH a
OH
= = =
43
sin
sin60 3
SO SO
SHO SH a
SH
= = =
.
2
2 2 2
4 4 6
2 2 2 4
33
a
AB HB OB OH a a= = − = − =
.
2
1 1 4 3 4 6 8 2
. . . .
2 2 3 3 3
SAB
S SH AB a a a
= = =
Câu 46: Bạn Nam muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam
giác đều
ABC
có cạnh bằng
( )
90 cm
. Bạn muốn cắt mảnh tôn hình chữ nhật
MNPQ
từ mảnh
tôn nguyên liệu (với
M
,
N
thuộc cạnh
BC
;
P
và
Q
tương ứng thuộc cạnh
AC
và
AB
) để
tạo thành hình trụ có chiều cao bằng
MQ
. Thể tích lớn nhất của chiếc thùng mà bạn Nam có thể
làm được là:
A.
( )
3
91125
4
cm
. B.
( )
3
91125
2
cm
. C.
( )
3
108000 3
cm
. D.
( )
3
13500. 3
cm
.
Lời giải
Gọi
I
là trung điểm
BC
. Suy ra
I
là trung điểm
MN
.
Đặt
MN x=
(
0 90x
);
3
(90 )
2
MQ BM
MQ x
AI BI
= = −
.
Gọi R là bán kính của trụ
2
x
R
=
2 3 2
33
( ) (90 ) ( 90 )
2 2 8
T
x
V x x x
= − = − +
.
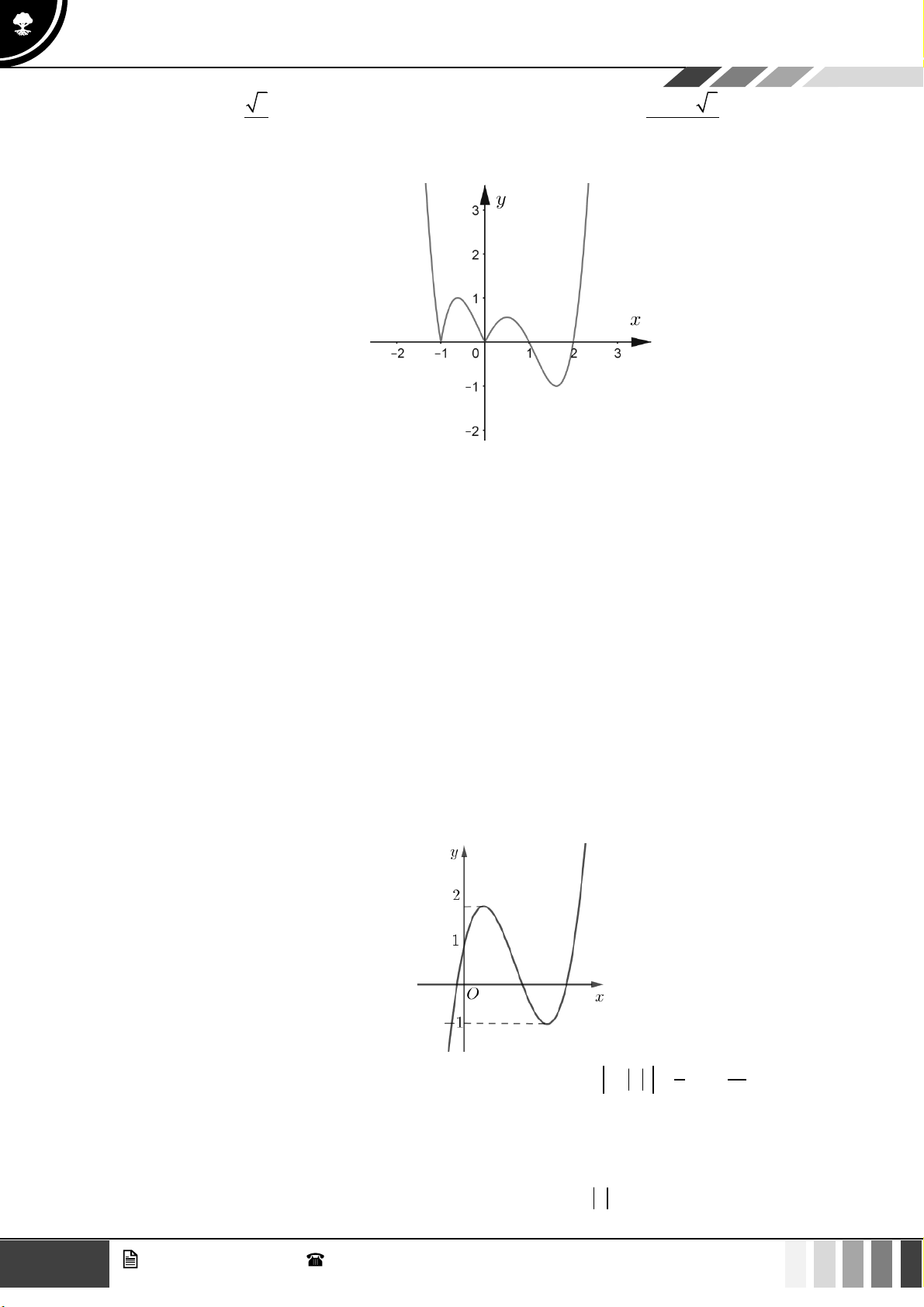
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HK1
Toán 12
Xét
32
3
( ) ( 90 )
8
f x x x
= − +
với
0 90x
. Khi đó:
(0;90)
13500. 3
max ( )
x
fx
=
khi
60x =
.
Câu 47: Cho hàm số
( )
y f x=
là hàm đa thức bậc 6 có đồ thị hàm số
( )
y f x
=
như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( ) ( )
7
3
1g x f x m
= + +
có 2 điểm cực
trị?
A.
2.
B.
0.
C.
1.
D. Vô số.
Lời giải
Ta có
( ) ( )
7
3
1g x f x m
= + +
( ) ( ) ( ) ( )
6
32
21. 1 . 1 . 1g x f x m f x f x
= + + + +
Ta có
( ) ( )
6
32
1 . 1 0f x m f x
+ + +
nên dấu của
( )
gx
phụ thuộc vào dấu
( )
1fx
+
.
Hàm số
( )
fx
cắt trục hoành tại 2 điểm phân biệt là
1, 2xx==
(và đổi dấu khi
x
đi qua hai
điểm đó) nên hàm số
( )
y f x=
có 2 điểm cực trị, số điểm cực trị hàm
( )
1fx+
bằng số điểm
cực trị hàm
( )
fx
nên
( )
gx
có 2 điểm cực trị với mọi
m
.
Vậy với mọi
m
hàm số
( )
gx
đều có 2 điểm cực trị.
Câu 48: Cho hàm số đa thức bậc ba
( )
y f x=
có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
24
21
9 81
f x m m=−
có 8 nghiệm
phân biệt?
A.
9
. B.
8
. C.
6
. D.
3
.
Lời giải
Từ đồ thị hàm số
( )
y f x=
ta suy ra đồ thị hàm số
( )
y f x=
như sau
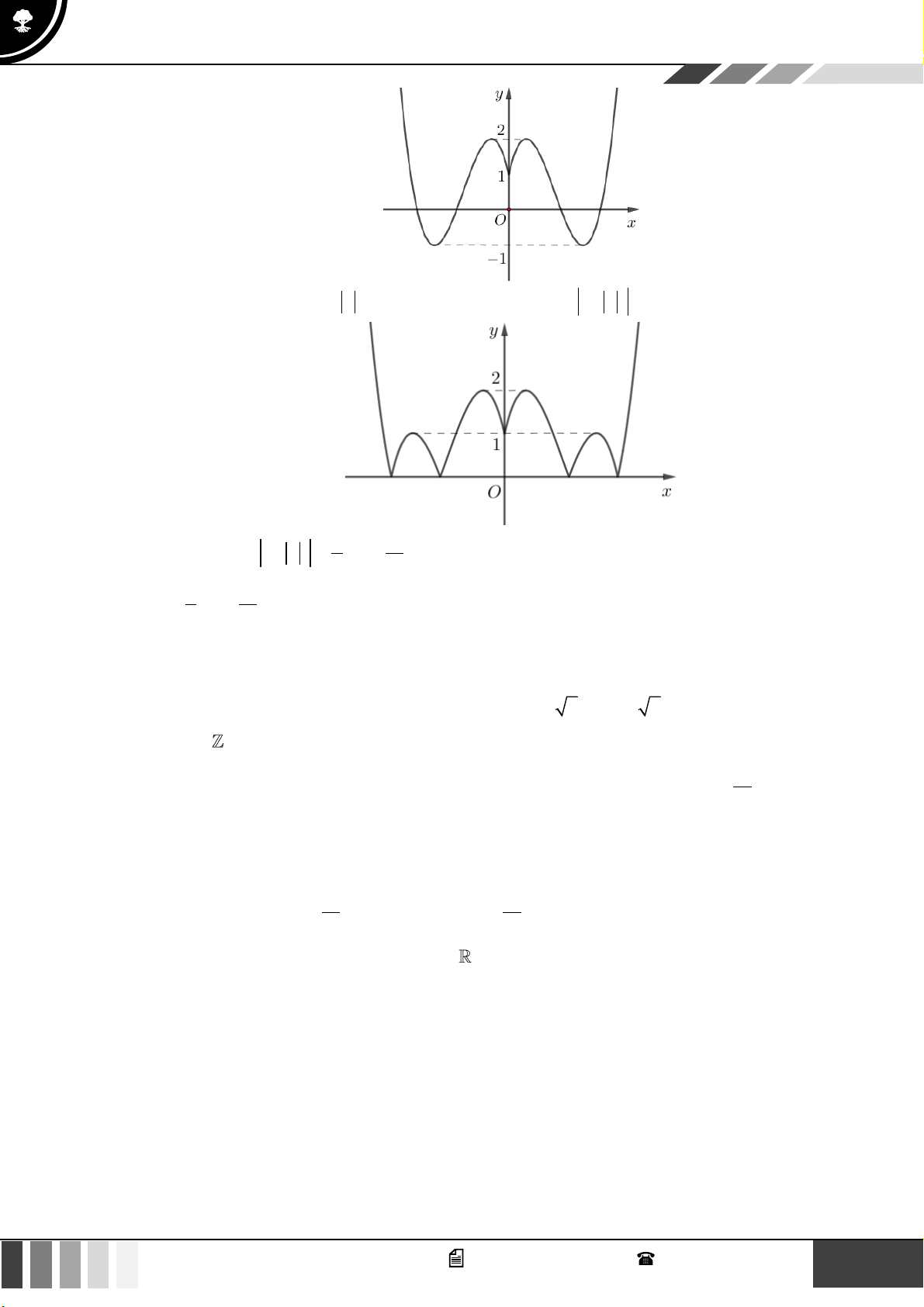
24
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Từ đồ thị hàm số
( )
y f x=
ta suy ra đồ thị hàm số
( )
y f x=
như sau
Phương trình
( )
24
21
9 81
f x m m=−
có 8 nghiệm phân biệt khi chỉ khi
2 4 2 4
21
0 1 0 18 81
9 81
m m m m − −
( )
( )
2
2
42
42
22
90
18 81 0
18 0
18 0
m
mm
mm
mm
−
− +
−
−
3
0
3 2 3 2
m
m
m
−
Vì
m
nên
4; 2; 1;1;2;4m − − −
.
Câu 49: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
15 5 3
10
x x x
m
− − =
có hai nghiệm
thực phân biệt?
A. Vô số. B.
18
. C.
9
. D.
10
.
Lời giải
Ta có:
15 5 3
10
x x x
m
− − =
( )( )
5 1 3 1 1
10
xx
m
− − = +
.
Xét hàm số
( )
( )( )
5 1 3 1
xx
fx= − −
trên có đạo hàm
( )
( ) ( )
3 1 5 ln5 5 1 3 ln3
x x x x
fx
= − + −
.
Nếu
0x
( )
0fx
Nếu
0x
( )
0fx
Nếu
0x =
( )
0fx
=
Bảng biến thiên:
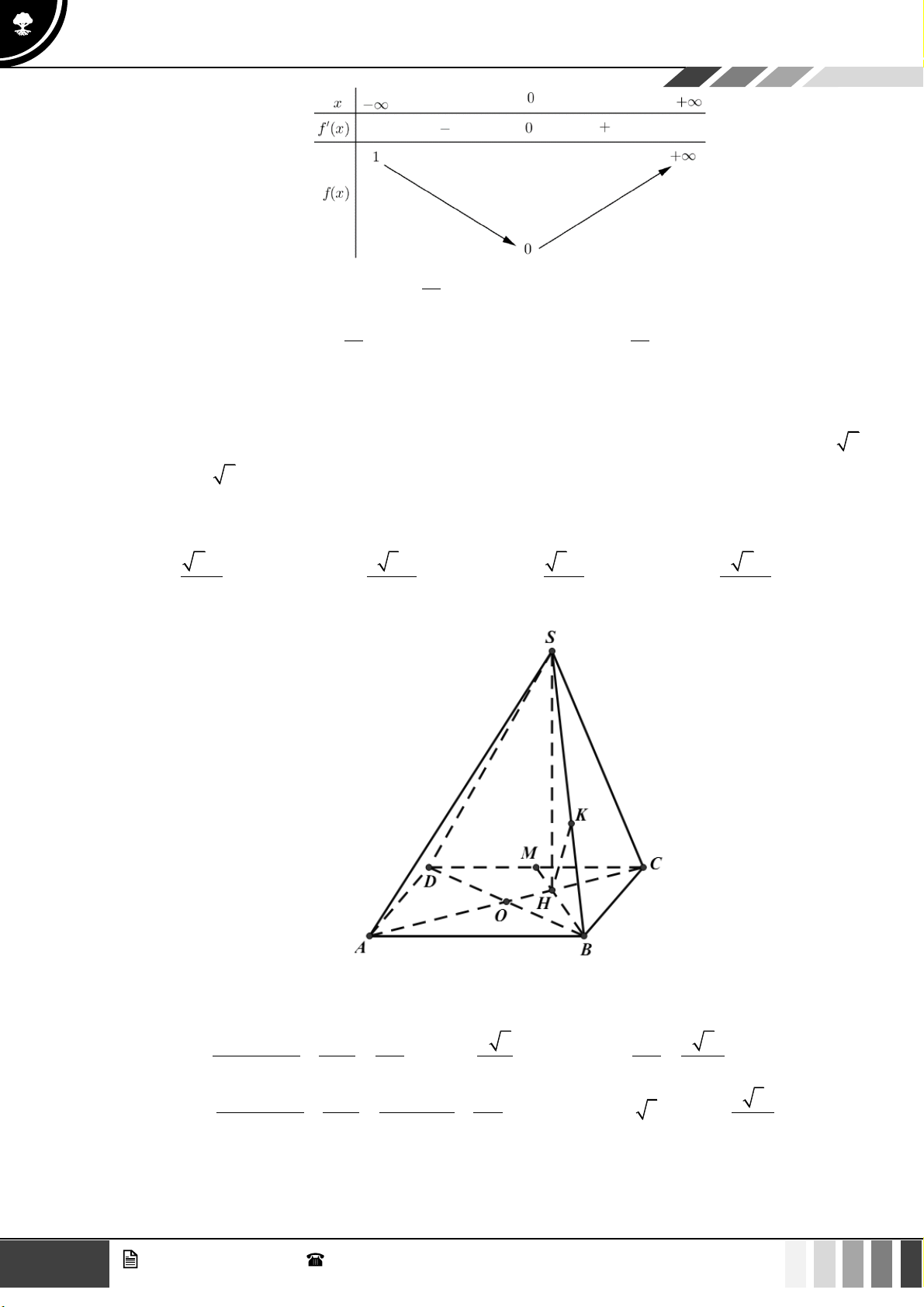
GV. Phan Nhật Linh -
SĐT: 0817 098 716
25
Tuyển tập 10 đề ôn HK1
Toán 12
Do đó phương trình
15 5 3
10
x x x
m
− − =
có hai nghiệm thực phân biệt
Phương trình
( )
1
10
m
fx=+
có hai nghiệm phân biệt
0 1 1
10
m
+
10 0m−
.
Do
m
nguyên nên
9; 8;...; 1m − − −
.
Vậy có
9
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 50: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành thỏa mãn
2,AB a=
2,BC a=
6BD a=
. Hình chiếu vuông góc của đỉnh
S
lên mặt phẳng
( )
ABCD
là trọng tâm của tam
giác
BCD
. Tính theo
a
thể tích khối chóp
.S ABCD
, biết rằng khoảng cách giữa hai đường
thẳng
AC
và
SB
bằng
a
.
A.
3
2
3
a
. B.
3
53
3
a
. C.
3
3
2
a
. D.
3
42
3
a
.
Lời giải
Gọi
H
là hình chiếu vuông góc của đỉnh
S
lên mặt phẳng
( )
ABCD
,
M
là trung điểm của
CD
và
O
là tâm của đáy
ABCD
. Do
AO
là trung tuyến của tam giác
ABD
nên:
2 2 2 2
2
3 6 2 6
2 4 2 2 3 3
AB AD BD a a AO a
AO AO AH AO
+
= − = = = + =
.
2 2 2 2 2 2
22
6 2 4 2 3
33
2 4 2 4 3
BD BC CD a a a a
BM a BM a BH
++
= − = − = = =
.
Ta có
2 2 2 2
4AH BH a AB AH BH+ = = ⊥
kết hợp với
( )
AH SH AH SHB⊥ ⊥
.
Kẻ
( )
HK SB K SB⊥
, theo chứng minh trên ta được
( )
AH SHB AH HK HK⊥ ⊥
là
đoạn vuông góc chung của
AC
và
SB
, suy ra
HK a=
.

26
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Trong tam giác vuông
SHB
ta có:
2 2 2
1 1 1
SH a
HK SH HB
= + =
.
3
.
1 1 4 4 2
. . . .4 . . .
3 3 3 3
S ABCD ABCD OAB
a
V SH S SH S SH OA BH= = = =
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HK1
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Hàm số nào sau đây nghịch biến trên ?
A.
3
2y x x= − −
. B.
42
2y x x= − +
. C.
3
2y x x= − +
. D.
42
2y x x= − −
.
Câu 2: Cho hàm số
()y f x=
có bảng biến thiên như bên dưới.
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
2;0−
. B. Hàm số đồng biến trên khoảng
( )
0;2
.
C. Hàm số nghịch biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
1;0−
.
Câu 3: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Cực đại của hàm số đã cho là
A.
1y =
. B.
2x =
. C.
1x =−
. D.
3y =−
.
Câu 4: Tìm giá trị nhỏ nhất
m
của hàm số
( )
3
2
31
3
x
f x x x= − − + +
trên
0;2
A.
1m =
. B.
1
3
m =
. C.
8
3
m =
. D.
0m =
.
Câu 5: Đường tiệm cận ngang của đồ thị hàm số
32
1
x
y
x
−+
=
+
là
A.
1y =−
. B.
1x =−
. C.
3y =−
. D.
2y =
.
Câu 6: Đường cong trong hình vẽ sau là đồ thị của hàm số nào?
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
05
ĐỀ SỐ

2
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
A.
42
2y x x= − −
. B.
42
2y x x= + −
. C.
42
2y x x= − − −
. D.
42
2y x x= − + −
.
Câu 7: Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
3
31y x x= − + −
là
A.
6
. B.
1−
. C.
6−
. D.
0
.
Câu 8: Tập xác định của hàm số
( )
2
2
3
1yx=−
là
A.
( ) ( )
; 1 1;− − +
. B.
1;1−
. C.
( )
;1−
. D.
( )
1;1−
.
Câu 9: Cho số thực
a
dương và
1a
. Giá trị của biểu thức
3
4
2
log
a
Pa=
là
A.
1
. B.
8
3
. C.
3
2
. D.
3
.
Câu 10: Tìm tập xác định của hàm số
( )
3
2020
log 1yx=−
.
A.
( )
1; +
. B.
( )
1;− +
. C.
)
1; +
. D.
( )
;1− −
.
Câu 11: Nghiệm của phương trình
2
22
log logxx=
là
A.
1x =
. B.
2x =
. C.
0x =
. D.
1
2
x =
.
Câu 12: Bất phương trình
1
25
x−
có tập nghiệm là
A.
( )
2
;1 log 5S = − +
. B.
( )
2
;log 5S = −
.
C.
( )
;1S = −
. D.
( )
5
;1 log 2S = − +
.
Câu 13: Một người gửi ngân hàng
70
triệu đồng theo hình thức lãi kép kì hạn
1
năm với lãi suất
5,6%
/năm. Hỏi sau
3
năm người đó có bao nhiêu tiền cả gốc và lãi? (đơn vị: triệu đồng, kết quả làm
tròn đến hàng phần trăm)
A.
75,6
triệu đồng. B.
80
triệu đồng. C.
82,43
triệu đồng. D.
78,06
triệu đồng.
Câu 14: Khối đa diện đều nào có số cạnh bằng số cạnh khối bát diện đều?
A. Khối nhị thập diện đều (
20
mt đều). B. Khối lập phương.
C. Khối thập nhị diện đều (
12
mt đều). D. Khối tứ diện đều.
Câu 15: Khối đa điện đều loại nào có số đỉnh bằng số mt?
A.
5;3
. B.
3;4
. C.
4;3
. D.
3;3
.
Câu 16: Khối lập phương có cạnh bằng
3a
có thể tích là?
A.
3
6a
. B.
3
9a
. C.
2
27a
. D.
3
27a
.
Câu 17: Cho mt cầu có bán kính bằng
R
. Diện tích của mt cầu đó là:
A.
2
SR
=
. B.
2
2SR
=
. C.
2
4
3
SR
=
. D.
2
4SR
=
.
Câu 18: Cho hình trụ có bán kính đáy bằng
R
và đường sinh bằng đường kính đáy. Diện tích toàn phần
của hình trụ đó là:
A.
2
5 R
. B.
2
2 R
. C.
2
6 R
. D.
2
3 R
.
Câu 19: Diện tích xung quanh của một hình nón có đường sinh bằng
10
và đường kính đáy bằng
5
là:
A.
25
. B.
50
. C.
100
. D.
120
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 20: Cho hàm số
( )
y f x=
liên tục trên và có
( ) ( )( )( )
3
3 5 7 ,f x x x x x
= − − −
. Kết luận
nào sau đây đng?
A. Hàm số
( )
y f x=
đồng biến trên khoảng
( )
1;5
.
B. Hàm số
( )
y f x=
nghịch biến trên khoảng
( )
5;+
.
C. Hàm số
( )
y f x=
đồng biến trên khoảng
( )
5;6
.
D. Hàm số
( )
y f x=
nghịch biến trên khoảng
( )
;3−
.
Câu 21: Các khoảng nghịch biến của hàm số
21
2
x
y
x
+
=
−
là:
A.
\2
B.
( ) ( )
;2 2;− +
C.
( )
;2−
và
( )
2;+
. D.
( )
;− +
.
Câu 22: Cho hàm số
( )
y f x=
xác định và liên tục trên mỗi khoảng
( )
3
;x−
và
( )
3
;x +
, có bảng biến
thiên như sau:
Khẳng định nào sau đây là đng?
A. Hàm số đã cho có một điểm cực đại và không có điểm cực tiểu.
B. Hàm số đã cho có một điểm cực tiểu và không có điểm cực đại.
C. Hàm số đã cho có một điểm cực tiểu và một điểm cực đại.
D. Hàm số đã cho có hai điểm cực tiểu và một điểm cực đại.
Câu 23: Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
x
−
=
+
trên đoạn
1;5
bằng
4−
. Tính tổng các phần tử của
S
.
A.
0
B.
5
C.
5−
D.
10
Câu 24: Có bao nhiêu giá trị nguyên
10;10m−
để đồ thị hàm số
2
2
4
1
x
y
x mx
+
=
++
có đng 3 đường
tiệm cận?
A.
16
B.
18
C.
14
D.
20
Câu 25: Cho hàm số
( )
32
, , ,y x bx cx d b c d= + + +
có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đng?
A.
0, 0, 0b c d
. B.
0, 0, 0b c d
. C.
0, 0, 0b c d
. D.
0, 0, 0b c d
.
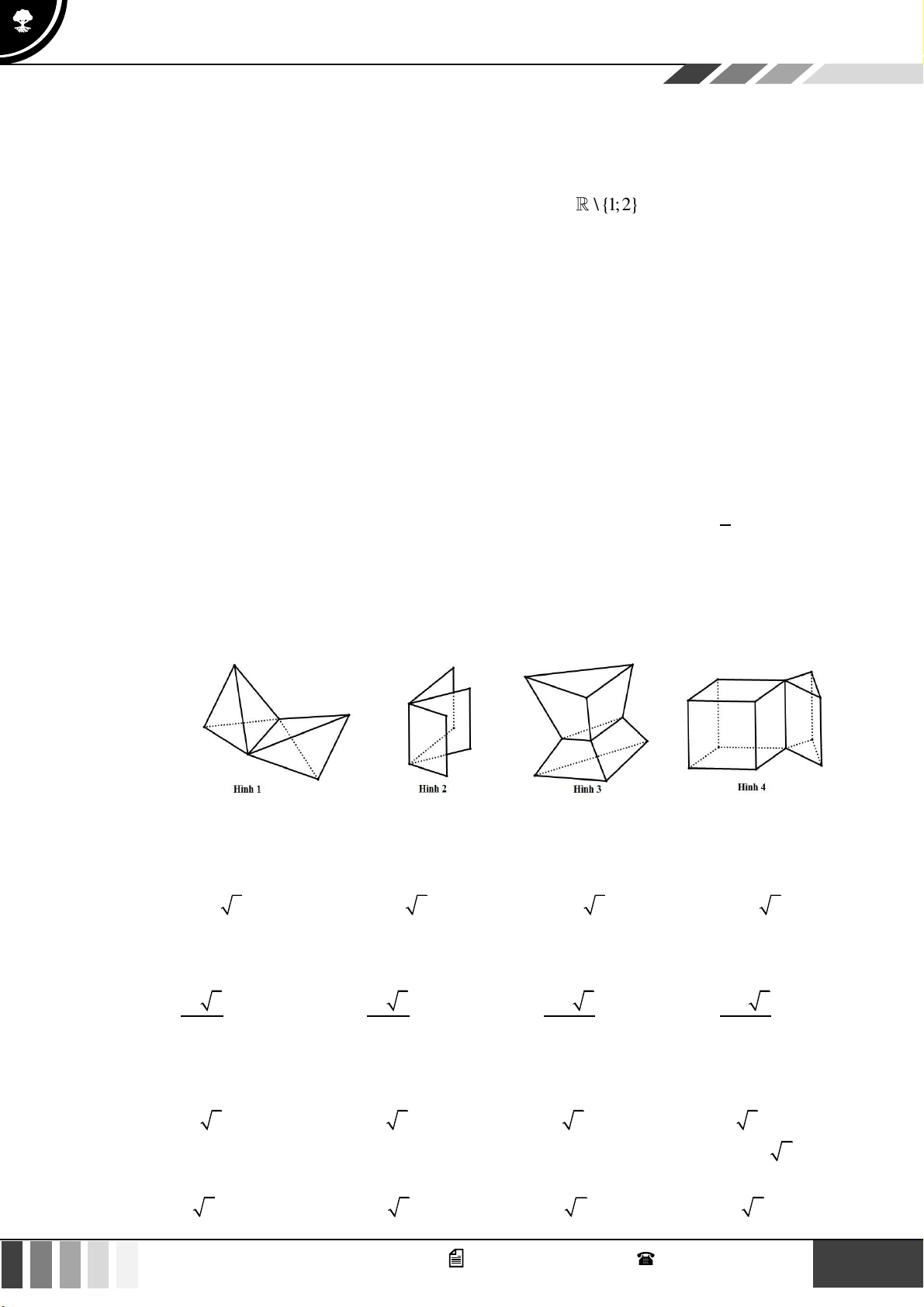
4
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 26: Phương trình tiếp tuyến với đồ thị hàm số
42
22y x x= + −
tại điểm có hoành độ
0
2x =−
là
A.
40 102yx= − −
. B.
40 58yx= − −
. C.
40 102yx= − +
. D.
40 58yx= − +
.
Câu 27: Tập xác định của hàm số
2
( 3 2)
e
y x x
−
= − +
là:
A.
( ;1) (2; )D = − +
B.
\{1;2}D =
C.
(0; )D = +
D.
(1;2)D =
Câu 28: Cho
( )
( )
22
22
log 1 log 0x y xy xy+ = +
. Chọn khẳng định đng trong các khẳng định sau?
A.
xy
. B.
xy=
. C.
xy
.
D.
2
xy=
.
Câu 29: Tập xác định của hàm số
( )
ln 2yx
=−
là
A.
( )
0;+
. B.
( )
2;+
. C.
( )
3;+
. D.
R
Câu 30: Cho phương trình
22
1 1 2
2 2 2 2
x x x x x+ − −
− = −
. Gọi
12
,xx
là nghiệm nhỏ nhất và nghiệm lớn nhất
của phương trình. Tích
12
.xx
bằng
A. -1. B. 0. C. 1. D.
5
2
.
Câu 31: Tập nghiệm của bất phương trình
( ) ( )
22
2log 2 log 12 3xx+ −
là
A.
(
8;4−
. B.
( )
2;4−
. C.
)
8;1−
. D.
(
2;1−
.
Câu 32: Trong các hình dưới đây, hình nào là hình đa diện?
A. Hình 3. B. Hình 1. C. Hình 2. D. Hình 4.
Câu 33: Cho hình bát diện đều cạnh
2a
. Gọi
S
là tổng diện tích tất cả các mt của hình bát diện đó, giá
trị của
S
là
A.
2
23Sa=
. B.
2
83Sa=
. C.
2
43Sa=
. D.
2
63Sa=
.
Câu 34: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, biết góc tạo bởi mt phẳng bên và mt
phẳng đáy bằng
0
60
. Thể tích của khối chóp đã cho là
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
23
3
a
. D.
3
43
3
a
.
Câu 35: Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
2
36 a
. Tính thể
tích
V
của lăng trụ lục giác đều nội tiếp hình trụ.
A.
3
27 3a
. B.
3
24 3a
. C.
3
36 3a
. D.
3
81 3a
.
Câu 36: Thiết diện qua trục một hình nón là một tam giác vuông cân có cạnh huyền bằng
26
. Thể tích
của khối nón này là
A.
6
. B.
33
. C.
32
. D.
26
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 37: Cho hàm số
( )
y f x=
có đạo hàm trên và có đồ thị như hình vẽ dưới đây. Nhận xét nào đng
về hàm số
( ) ( )
2
g x f x=
?
Hàm số
( )
gx
đồng biến trên khoảng nào?
A. . B.
( )
;1−
. C.
( )
2;+
. D.
( )
;2−
.
Câu 38: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
Hàm số
( ) ( )
42
3 2 2023y f x f x= + +
có số điểm cực trị là
A.
3
. B.
5
. C.
6
. D.
7
.
Câu 39: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
4;7
. B.
( )
;1− −
. C.
( )
2;3
. D.
( )
1;2−
.
Câu 40: Một con cá bơi ngược dòng từ A đến B với khoảng cách là
( )
300 km
. Vận tốc dòng nước là
( )
6/km h
. Nếu vận tốc của con cá khi nước đứng yên là
( )
/v km h
thì năng lượng tiêu hao trong
thời gian
t
giờ được cho bởi công thức
( )
3
E v cv t=
, trong đó
c
là một hằng số,
E
được tính
bằng
Jun
. Vận tốc của con cá khi nước đứng yên là bao nhiêu để năng lượng tiêu hao là ít nhất?
A.
7/km h
. B.
10 /km h
. C.
6/km h
. D.
9/km h
.
6
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 41: Có bao nhiêu giá trị nguyên của tham số
m
trong đoạn
2023;2023−
để hàm số
2023
2024y x mx= − +
đồng biến trên .
A.
2020
. B.
2024
. C.
2022
. D.
2023
.
Câu 42: Biết rằng phương trình
2
2
2
2
log 4 9
25
x
xx
x
+
= − + +
+
có hai nghiệm
x a b c=+
và
x a b c=−
với
,,abc
là các số nguyên dương. Tính tích
..abc
.
A.
8
. B.
8−
. C.
12−
. D.
12
.
Câu 43: Tập nghiệm của bất phương trình
2
2
2
1
log
log
2 10 3 0
x
x
x− +
là:
A.
( )
1
0; 2;
2
S
= +
. B.
( )
1
2;0 ;
2
S
= − +
.
C.
( )
1
;0 ;2
2
S
= −
. D.
( )
1
; 2;
2
S
= − +
.
Câu 44: Cho tứ diện
ABCD
có tam giác
BCD
vuông tại
B
,
BC a=
,
3BD a=
,
4AB a=
và
0
90ACB ADB==
. Thể tích khối tứ diện
ABCD
bằng
A.
3
a
. B.
3
3a
. C.
3
5a
. D.
3
2a
.
Câu 45: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
a
, mt bên
SAB
là tam giác
đều và nằm trong mt phẳng vuông góc với mt phẳng đáy. Tính diện tích
S
của khối cầu ngoại
tiếp hình chóp đã cho.
A.
2
5
3
a
S
=
. B.
2
5
12
a
S
=
. C.
2
5
6
a
S
=
. D.
2
3
8
a
S
=
.
Câu 46: Một cốc uống bia có hình nón cụt còn lon bia thì có hình trụ (như hình vẽ dưới đây). Khi rót bia
từ lon ra cốc thì chiều cao của phần bia còn lại trong lon và chiều cao của phần bia có trong
cốc là như nhau. Hỏi khi đó chiều cao của bia trong lon gần nhất là số nào sau đây?
A. B. C. D.
h
h
8,58.
14,2.
7,5.
9,18.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 47: Cho hàm số
3 2 3
34y x mx m= − +
. Có tất cả bao nhiêu giá trị của tham số
m
để các điểm cực đại
và cực tiểu của đồ thị hàm số đối xứng nhau qua đường phân giác
()d
của góc phần tư thứ nhất
và thứ ba.
A.
1
B.
4
C.
2
. D.
3
Câu 48: Gọi
;ab
là tập hợp tất cả các giá trị của tham số
m
để hệ bất phương trình
2
32
3 4 0
3 15 0
xx
x x x m m
− −
− − −
có nghiệm. Tính
ab+
.
A.
17−
. B.
15
. C.
17
. D.
15−
.
Câu 49: Cho tứ diện
SABC
có
AB a=
, tam giác
SBC
đều, hình chiếu vuông góc của
S
lên mt phẳng
( )
ABC
là trực tâm
H
của tam giác
ABC
, mt phẳng
( )
SCH
tạo với mt phẳng
( )
SBC
một
góc
0
60
. Tính thể tích khối tứ diện
GABC
với
G
là trọng tâm của tam giác
SAC
.
A.
3
3
38
a
. B.
3
3
144
a
. C.
3
33
32
a
. D.
3
3
32
a
.
Câu 50: Cho nửa hình cầu bán kính
R
không đổi. Một hình nón có chiều cao
,h
bán kính đáy là
r
tiếp
xc với nửa hình cầu như hình vẽ. Khi diện tích xung quanh của hình nón là nhỏ nhất, khẳng
định nào sau đây đng ?
A.
23hr=
. B.
hr=
. C.
3hr=
. D.
2hr=
.
-----------------------HẾT-----------------------
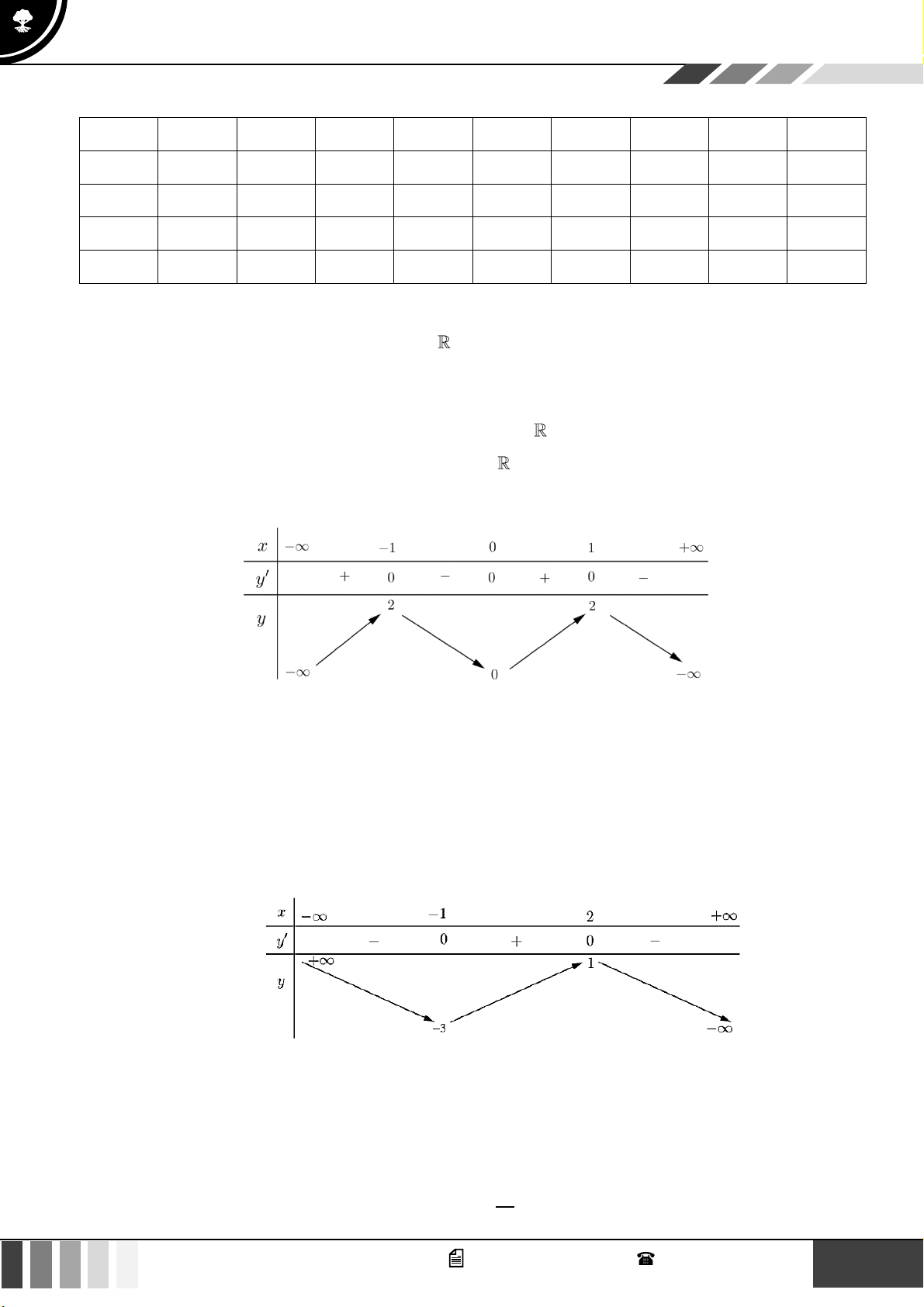
8
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
BẢNG ĐÁP ÁN
1.A
2.C
3.A
4.B
5.D
6.A
7.D
8.A
9.C
10.A
11.A
12.A
13.C
14.B
15.D
16.D
17.D
18.C
19.A
20.C
21.C
22.C
23.A
24.A
25.D
26.B
27.A
28.B
29.C
30.A
31.D
32.A
33.B
34.A
35.D
36.D
37.C
38.D
39.D
40.D
41.B
42.D
43.A
44.A
45
46.A
47.C
48.D
49.D
50.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Hàm số nào sau đây nghịch biến trên ?
A.
3
2y x x= − −
. B.
42
2y x x= − +
. C.
3
2y x x= − +
. D.
42
2y x x= − −
.
Lời giải
Nhận xét
3
2y x x= − −
có
2
3 2 0yx
= − −
,
x
Do đó hàm số
3
2y x x= − −
nghịch biến trên .
Câu 2: Cho hàm số
()y f x=
có bảng biến thiên như bên dưới.
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
2;0−
. B. Hàm số đồng biến trên khoảng
( )
0;2
.
C. Hàm số nghịch biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
1;0−
.
Lời giải
Dựa vào bảng biến thiên: Hàm số nghịch biến trên khoảng
( )
1; +
.
Câu 3: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Cực đại của hàm số đã cho là
A.
1y =
. B.
2x =
. C.
1x =−
. D.
3y =−
.
Lời giải
Dựa vào bảng biến thiên ta có cực đại của hàm số
( )
y f x=
là
1y =
.
Câu 4: Tìm giá trị nhỏ nhất
m
của hàm số
( )
3
2
31
3
x
f x x x= − − + +
trên
0;2
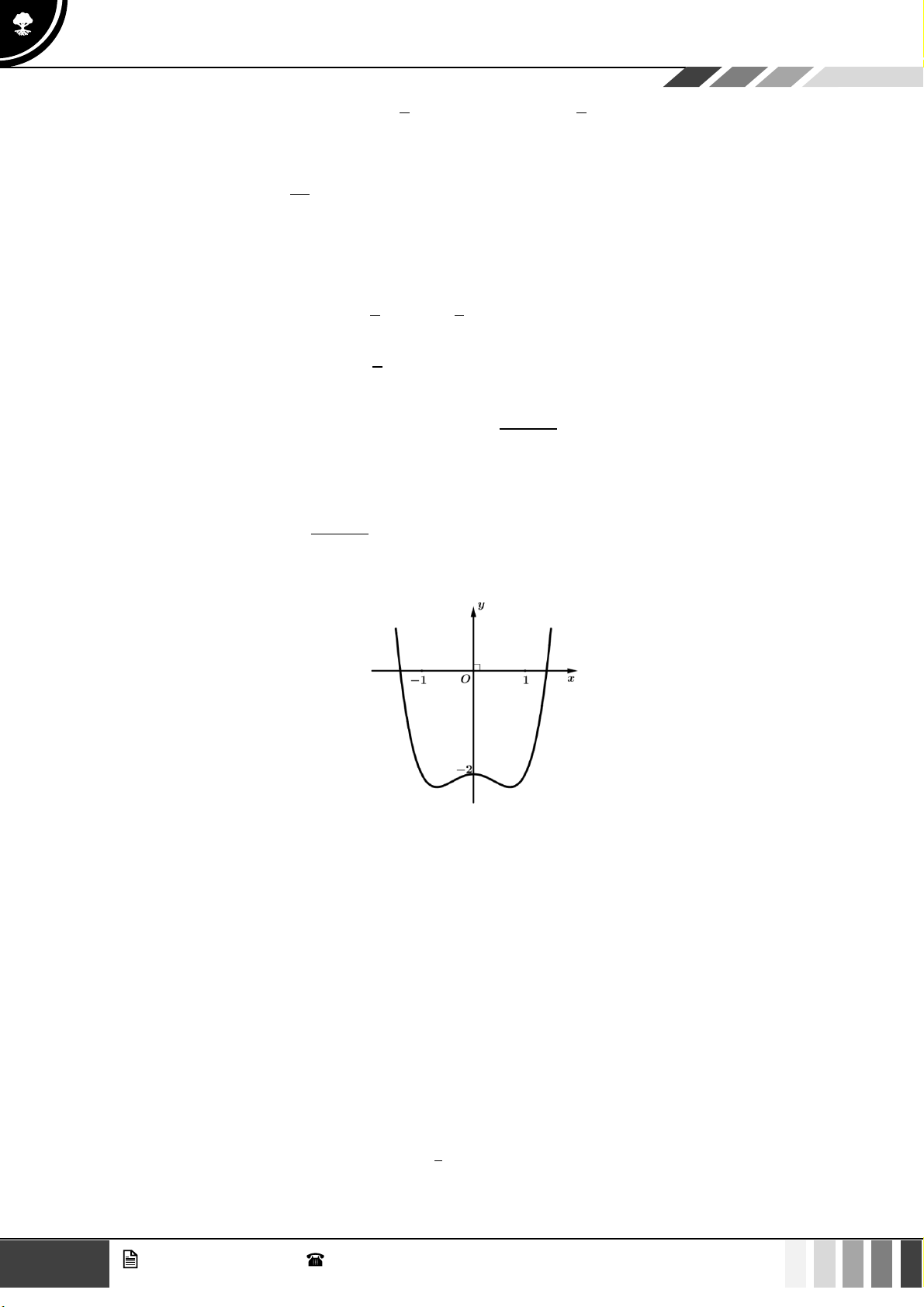
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HK1
Toán 12
A.
1m =
. B.
1
3
m =
. C.
8
3
m =
. D.
0m =
.
Lời giải
Hàm số
( )
3
2
31
3
x
f x x x= − − + +
xác định và liên tục trên đoạn
0;2
.
Ta có
2
1 0;2
2 3 0
3 0;2
x
y x x
x
=
= − − + =
= −
.
Mt khác:
( )
01f =
;
( )
8
1
3
f =
;
( )
1
2
3
f =
.
Vậy
( ) ( )
0;2
1
2
3
m min f x f= = =
.
Câu 5: Đường tiệm cận ngang của đồ thị hàm số
32
1
x
y
x
−+
=
+
là
A.
1y =−
. B.
1x =−
. C.
3y =−
. D.
2y =
.
Lời giải
Ta có
32
lim lim 2
1
xx
x
y
x
→ →
−+
==
+
nên đồ thị hàm số có tiệm cận ngang là
2y =
.
Câu 6: Đường cong trong hình vẽ sau là đồ thị của hàm số nào?
A.
42
2y x x= − −
. B.
42
2y x x= + −
. C.
42
2y x x= − − −
. D.
42
2y x x= − + −
.
Lời giải
Đồ thị hàm số đã cho có hệ số
0a
.
Đồ thị hàm số có 3 cực trị nên
0ab
nên hệ số
0b
.
Suy ra đồ thị hàm số chỉ có thể là đồ thị của hàm số
42
2y x x= − −
.
Câu 7: Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
3
31y x x= − + −
là
A.
6
. B.
1−
. C.
6−
. D.
0
.
Lời giải
Ta có
( )
2
33y x x
= − +
.
Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
đã cho là:
( ) ( )
2
1 3 1 3 0y
= − + =
.
Câu 8: Tập xác định của hàm số
( )
2
2
3
1yx=−
là
A.
( ) ( )
; 1 1;− − +
. B.
1;1−
. C.
( )
;1−
. D.
( )
1;1−
.

10
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Lời giải
Điều kiện xác định của hàm số
( )
2
2
3
1yx=−
là:
2
1
10
1
x
x
x
−
−
.
Vậy tập xác định của hàm số là
( ) ( )
; 1 1;− − +
.
Câu 9: Cho số thực
a
dương và
1a
. Giá trị của biểu thức
3
4
2
log
a
Pa=
là
A.
1
. B.
8
3
. C.
3
2
. D.
3
.
Lời giải
Ta có
4
3
4
3
22
33
log log 2. log
42
a
a
a
P a a a= = = =
.
Câu 10: Tìm tập xác định của hàm số
( )
3
2020
log 1yx=−
.
A.
( )
1; +
. B.
( )
1;− +
. C.
)
1; +
. D.
( )
;1− −
.
Lời giải
Điều kiện xác định của hàm số là
3
1 0 1xx−
.
Câu 11: Nghiệm của phương trình
2
22
log logxx=
là
A.
1x =
. B.
2x =
. C.
0x =
. D.
1
2
x =
.
Lời giải
Điều kiện
0x
.
Ta có:
22
2 2 2 2 2 2 2
log log log log 0 2log log 0 log 0 1x x x x x x x x= − = − = = =
.
Câu 12: Bất phương trình
1
25
x−
có tập nghiệm là
A.
( )
2
;1 log 5S = − +
. B.
( )
2
;log 5S = −
.
C.
( )
;1S = −
. D.
( )
5
;1 log 2S = − +
.
Lời giải
Ta có:
1
22
2 5 1 log 5 1 log 5
x
xx
−
− +
.
Vậy tập nghiệm là
( )
2
;1 log 5S = − +
.
Câu 13: Một người gửi ngân hàng
70
triệu đồng theo hình thức lãi kép kì hạn
1
năm với lãi suất
5,6%
/năm. Hỏi sau
3
năm người đó có bao nhiêu tiền cả gốc và lãi? (đơn vị: triệu đồng, kết quả làm
tròn đến hàng phần trăm)
A.
75,6
triệu đồng. B.
80
triệu đồng. C.
82,43
triệu đồng. D.
78,06
triệu đồng.
Lời giải
Tổng số tiền cả gốc và lãi người gửi nhận được sau
n
năm là
( )
1
n
T A r=+
, với
A
là số tiền
ban đầu đem gửi (tính theo triệu đồng),
r
là lãi suất.
Áp dụng vào bài toán với
70A =
,
0,056r =
và
3n =
ta được số tiền cả gốc và lãi người đó
nhận được sau
3
năm là
( )
3
70. 1 0,056 82,43T = +
(triệu đồng).
Câu 14: Khối đa diện đều nào có số cạnh bằng số cạnh khối bát diện đều?

GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HK1
Toán 12
A. Khối nhị thập diện đều (
20
mt đều). B. Khối lập phương.
C. Khối thập nhị diện đều (
12
mt đều). D. Khối tứ diện đều.
Lời giải
Khối bát diện và khối lập phương đều có số cạnh bằng
12
.
Câu 15: Khối đa điện đều loại nào có số đỉnh bằng số mt?
A.
5;3
. B.
3;4
. C.
4;3
. D.
3;3
.
Lời giải
Dựa vào bảng phân loại sách giáo khoa.
Câu 16: Khối lập phương có cạnh bằng
3a
có thể tích là?
A.
3
6a
. B.
3
9a
. C.
2
27a
. D.
3
27a
.
Lời giải
Ta có thể tích khối lập phương là:
( )
3
3
3 27aa=
Câu 17: Cho mt cầu có bán kính bằng
R
. Diện tích của mt cầu đó là:
A.
2
SR
=
. B.
2
2SR
=
. C.
2
4
3
SR
=
. D.
2
4SR
=
.
Lời giải
Câu 18: Cho hình trụ có bán kính đáy bằng
R
và đường sinh bằng đường kính đáy. Diện tích toàn phần
của hình trụ đó là:
A.
2
5 R
. B.
2
2 R
. C.
2
6 R
. D.
2
3 R
.
Lời giải
Vì
2lR=
nên diện tích toàn phần của hình trụ bằng:
22
2 2 6Rl R R
+=
.
Câu 19: Diện tích xung quanh của một hình nón có đường sinh bằng
10
và đường kính đáy bằng
5
là:
A.
25
. B.
50
. C.
100
. D.
120
.
Lời giải
Diện tích xung quanh của hình nón là:
5
. .10 25
2
xq
S rl
= = =
.
Câu 20: Cho hàm số
( )
y f x=
liên tục trên và có
( ) ( )( )( )
3
3 5 7 ,f x x x x x
= − − −
. Kết luận
nào sau đây đng?
A. Hàm số
( )
y f x=
đồng biến trên khoảng
( )
1;5
.
B. Hàm số
( )
y f x=
nghịch biến trên khoảng
( )
5;+
.
C. Hàm số
( )
y f x=
đồng biến trên khoảng
( )
5;6
.
D. Hàm số
( )
y f x=
nghịch biến trên khoảng
( )
;3−
.
Lời giải
Ta có:
( )
3
05
7
x
f x x
x
=
= =
=
Bảng biến thiên
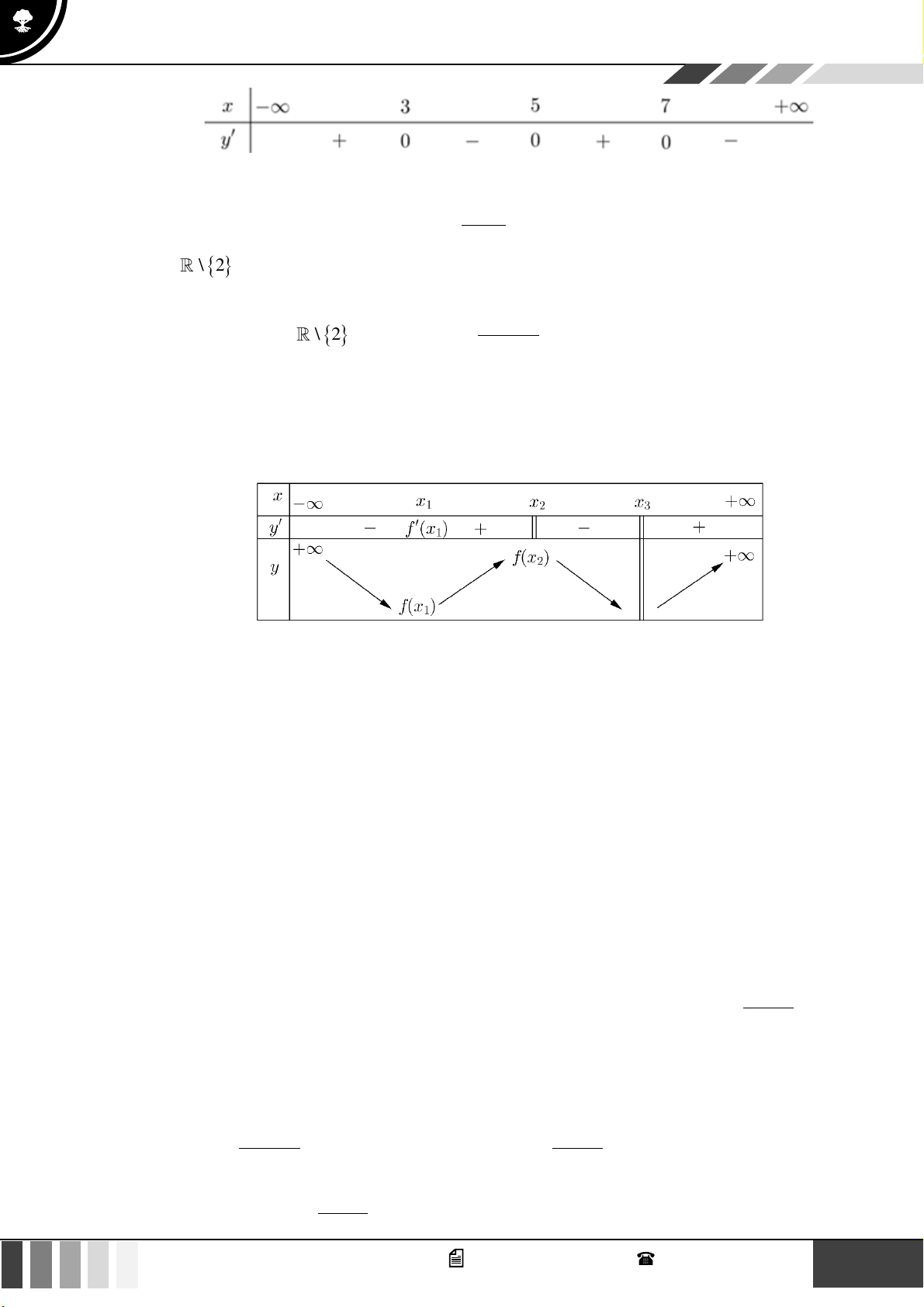
12
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Dựa vào bảng biến thiên ta thấy hàm số
( )
y f x=
đồng biến trên khoảng
( )
5;6
.
Câu 21: Các khoảng nghịch biến của hàm số
21
2
x
y
x
+
=
−
là:
A.
\2
B.
( ) ( )
;2 2;− +
C.
( )
;2−
và
( )
2;+
. D.
( )
;− +
.
Lời giải
Tập xác định:
D \ 2=
. Đạo hàm:
( )
/
2
5
0, 2.
2
yx
x
−
=
−
Vậy hàm số nghịch biến trên các khoảng
( )
;2−
và
( )
2;+
.
Câu 22: Cho hàm số
( )
y f x=
xác định và liên tục trên mỗi khoảng
( )
3
;x−
và
( )
3
;x +
, có bảng biến
thiên như sau:
Khẳng định nào sau đây là đng?
A. Hàm số đã cho có một điểm cực đại và không có điểm cực tiểu.
B. Hàm số đã cho có một điểm cực tiểu và không có điểm cực đại.
C. Hàm số đã cho có một điểm cực tiểu và một điểm cực đại.
D. Hàm số đã cho có hai điểm cực tiểu và một điểm cực đại.
Lời giải
Dựa vào bảng biến thiên, ta thấy
( )
fx
•
đổi dấu từ
""−
sang
""+
khi
x
đi qua điểm
1
x
suy ra
1
x
là điểm cực tiểu của hàm số.
( )
fx
•
đổi dấu từ
""+
sang
""−
khi
x
đi qua điểm
2
x
suy ra
2
x
là điểm cực đại của hàm số.
( )
fx
•
đổi dấu từ
""−
sang
""+
khi
x
đi qua điểm
3
x
nhưng tại
3
x
hàm số
( )
fx
không xác
định nên
3
x
không phải là điểm cực tiểu.
Do đó hàm số đã cho có một điểm cực tiểu và một điểm cực đại.
Câu 23: Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
x
−
=
+
trên đoạn
1;5
bằng
4−
. Tính tổng các phần tử của
S
.
A.
0
B.
5
C.
5−
D.
10
Lời giải
Ta có
( )
2
2
2
' 0, 2.
2
m
yx
x
+
= −
+
Suy ra hàm số
2
2
xm
y
x
−
=
+
đồng biến trên đoạn
1;5
Do đó
2
1;5
5
(5)
7
m
max y y
−
==
.
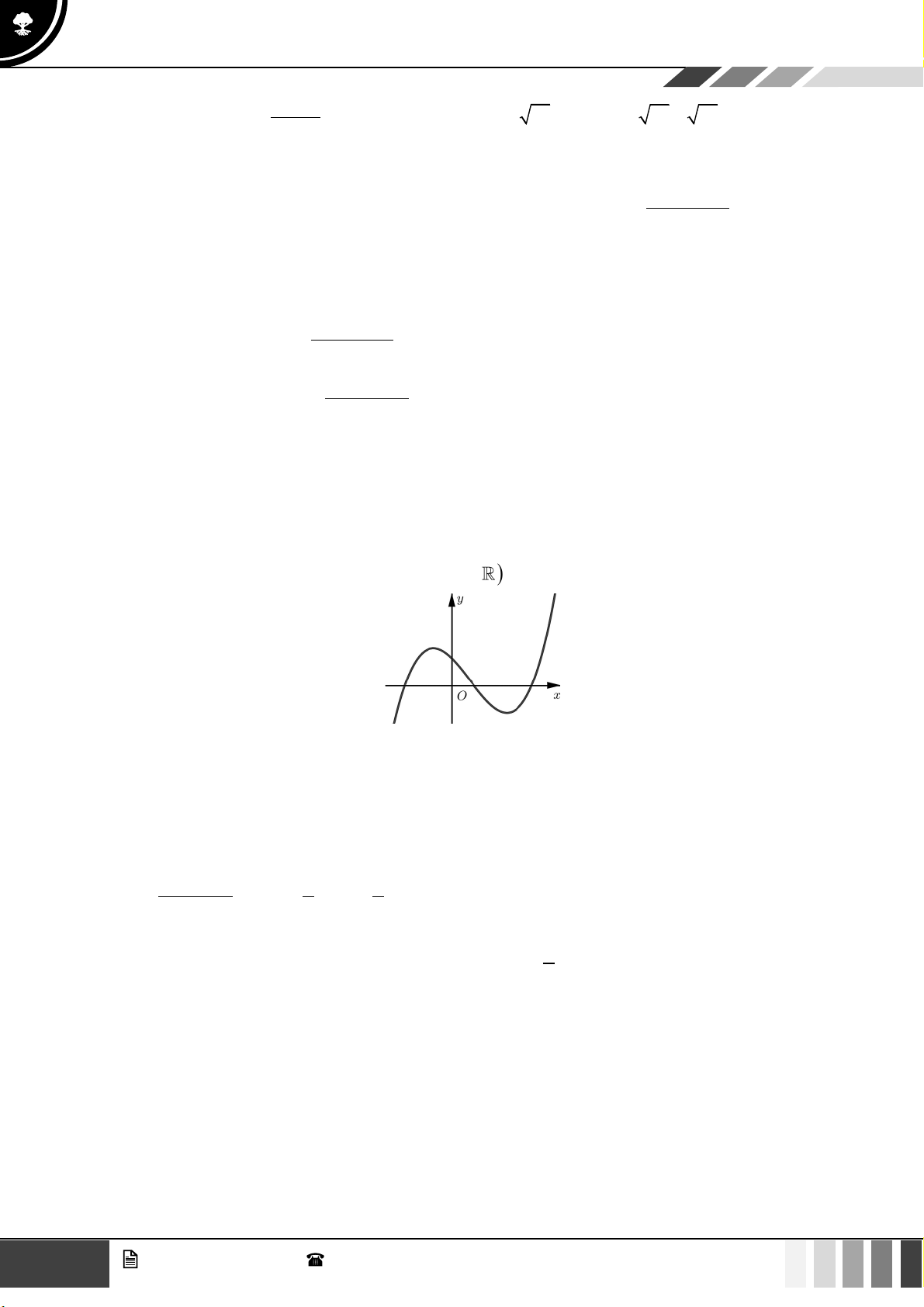
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HK1
Toán 12
Theo giả thiết,
2
2
5
4 33 33
7
m
mm
−
= − = =
. Vậy
33; 33S =−
nên tổng các phần
tử của
S
bằng 0.
Câu 24: Có bao nhiêu giá trị nguyên
10;10m−
để đồ thị hàm số
2
2
4
1
x
y
x mx
+
=
++
có đng 3 đường
tiệm cận?
A.
16
B.
18
C.
14
D.
20
Lời giải
Ta có
2
2
4
lim lim 1
1
xx
x
y
x mx
→ →
+
==
++
nên đồ thị hàm số có 1 đường tiệm cận ngang là
1y =
.
Để đồ thị hàm số
2
2
4
1
x
y
x mx
+
=
++
có đng 3 đường tiệm cận thì đồ thị hàm số cần có đng 2
đường tiệm cận đứng, suy ra phương trình
2
10x mx+ + =
có 2 nghiệm phân biệt
2
40m = −
2
.
2
m
m
−
Kết hợp với giả thiết
m
là số nguyên và
10;10m−
nên có 16 giá trị
m
thỏa mãn.
Câu 25: Cho hàm số
( )
32
, , ,y x bx cx d b c d= + + +
có đồ thị như hình vẽ sau:
Mệnh đề nào dưới đây đng?
A.
0, 0, 0b c d
. B.
0, 0, 0b c d
. C.
0, 0, 0b c d
. D.
0, 0, 0b c d
.
Lời giải
Đồ thị cắt trục tung tại tung độ nằm phía trên trục hoành nên
0d
.
Trung điểm của điểm cực đại và điểm cực tiểu nằm bên phải trục tung nên ta có
D
0 0 0 0
2
C CT
xx
bb
b
aa
+
−
.
Hoành độ hai điểm cực đại và cực tiểu trái dấu nên
00
c
c
a
.
Câu 26: Phương trình tiếp tuyến với đồ thị hàm số
42
22y x x= + −
tại điểm có hoành độ
0
2x =−
là
A.
40 102yx= − −
. B.
40 58yx= − −
. C.
40 102yx= − +
. D.
40 58yx= − +
.
Lời giải
Với
00
2 22xy= − =
.
Ta có
3
44y x x
=+
( )
2 40y
− = −
.
Phương trình tiếp tuyến tại điểm có hoành độ
0
2x =−
là
( )
40 2 22yx= − + +
hay
40 58yx= − −
.

14
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 27: Tập xác định của hàm số
2
( 3 2)
e
y x x
−
= − +
là:
A.
( ;1) (2; )D = − +
B.
\{1;2}D =
C.
(0; )D = +
D.
(1;2)D =
Lời giải
Hàm số
2
( 3 2)
e
y x x
−
= − +
xác định
2
2
3x 2 0
1
x
x
x
− +
Vậy tập xác định của hàm số
2
( 3 2)
e
y x x
−
= − +
là:
( ;1) (2; )D = − +
Câu 28: Cho
( )
( )
22
22
log 1 log 0x y xy xy+ = +
. Chọn khẳng định đng trong các khẳng định sau?
A.
xy
. B.
xy=
. C.
xy
.
D.
2
xy=
.
Lời giải
Ta có:
( )
( )
22
22
log 1 log 0x y xy xy+ = +
( )
22
22
log log 2x y xy + =
( )
2
22
20x y xy x y x y + = − = =
Câu 29: Tập xác định của hàm số
( )
ln 2yx
=−
là
A.
( )
0;+
. B.
( )
2;+
. C.
( )
3;+
. D.
R
Lời giải
Hàm số đã cho xác định
( )
ln 2 0
2 1 3
3
2 0 2
20
x
xx
x
xx
x
−
−
−
−
Câu 30: Cho phương trình
22
1 1 2
2 2 2 2
x x x x x+ − −
− = −
. Gọi
12
,xx
là nghiệm nhỏ nhất và nghiệm lớn nhất
của phương trình. Tích
12
.xx
bằng
A. -1. B. 0. C. 1. D.
5
2
.
Lời giải
Phương trình:
( ) ( ) ( )
(
)
22
11
2 2 1 2 2 1 2 1 2 2 0
x x x x x x x−−
− = − − − =
22
22
11
0
2 1 0 2 1
00
15
1 1 0
2 2 0 2 2
2
xx
x x x x
x
xx
x x x x
x
−−
=
− = =
==
− = − − =
=
− = =
Suy ra nghiệm nhỏ nhất là
1
15
2
x
−
=
, nghiệm lớn nhất là
2
15
2
x
+
=
Vậy
12
.1xx =−
Câu 31: Tập nghiệm của bất phương trình
( ) ( )
22
2log 2 log 12 3xx+ −
là
A.
(
8;4−
. B.
( )
2;4−
. C.
)
8;1−
. D.
(
2;1−
.
Lời giải
Điều kiện:
2 0 2
12 3 0 4
xx
xx
+ −
−
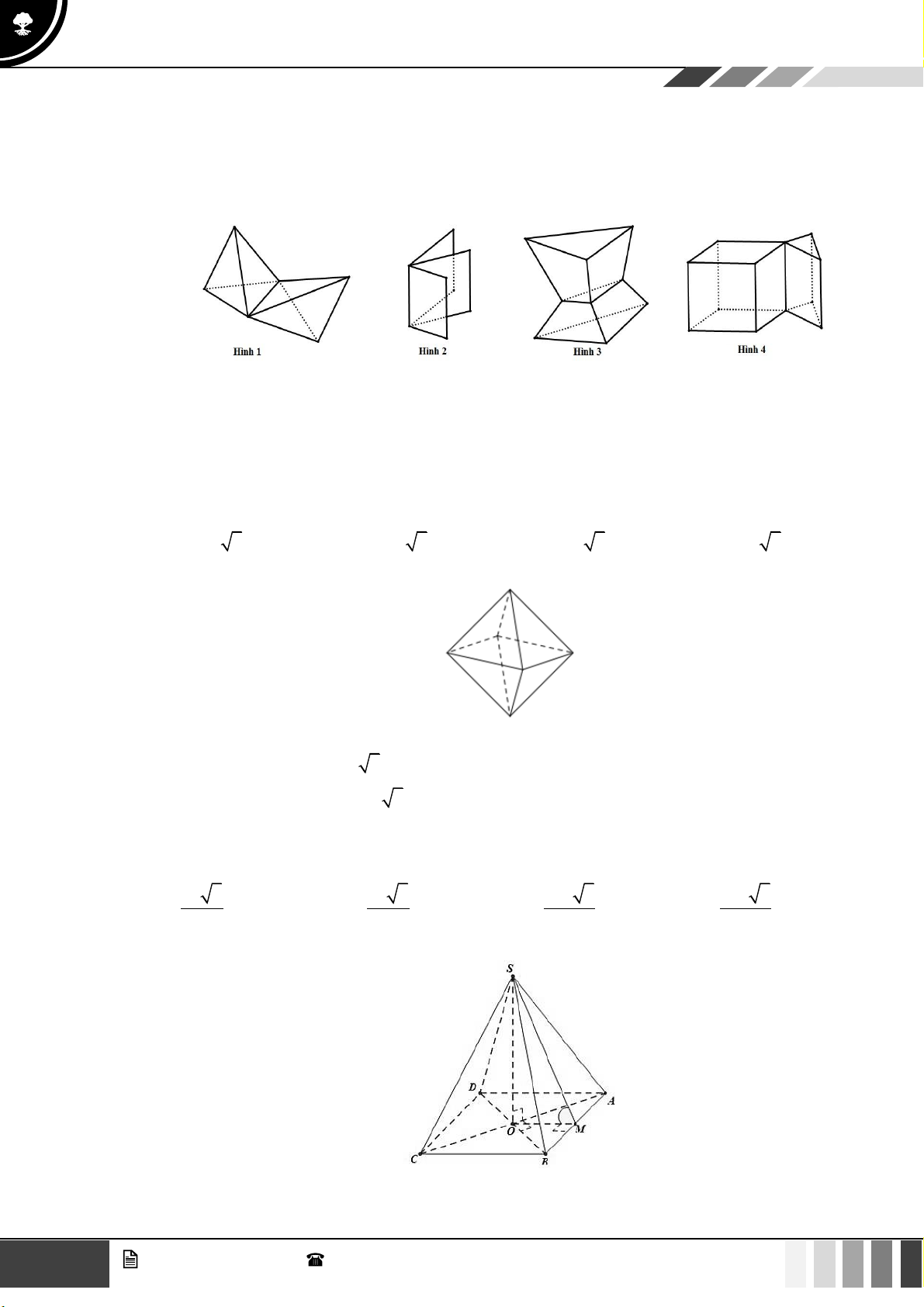
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HK1
Toán 12
Khi đó ta có:
( ) ( ) ( )
2
2 2 2 2
2log 2 log 12 3 log 2 log (12 3 )x x x x+ − + −
( )
2
2 12 3xx + −
2
7 8 0 8 1x x x + − −
Kết hợp điều kiên ta có
21x−
Câu 32: Trong các hình dưới đây, hình nào là hình đa diện?
A. Hình 3. B. Hình 1. C. Hình 2. D. Hình 4.
Lời giải
Trong các hình 1; 2; 4 có một cạnh là cạnh chung của từ 3 mt nên không phải là hình đa diện.
Hình đa diện là hình số 3
Câu 33: Cho hình bát diện đều cạnh
2a
. Gọi
S
là tổng diện tích tất cả các mt của hình bát diện đó, giá
trị của
S
là
A.
2
23Sa=
. B.
2
83Sa=
. C.
2
43Sa=
. D.
2
63Sa=
.
Lời giải
Hình bát diện đều là hình có tám mt bằng nhau, mỗi mt là một tam giác đều.
Diện tích mỗi mt:
2
0
3Sa=
Diện tích tất cả các mt:
2
83Sa=
Câu 34: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, biết góc tạo bởi mt phẳng bên và mt
phẳng đáy bằng
0
60
. Thể tích của khối chóp đã cho là
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
23
3
a
. D.
3
43
3
a
.
Lời giải
16
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Theo tính chất của hình chóp đều ta có:
( ) ( )
SM AB
MO AB
SAB ABCD SO
⊥
⊥
=
Góc giữa hai mt phẳng
( )
SAB
và
( )
ABCD
là góc
0
60SMO =
0
1
.tan60 3
2
SO OM a = =
3
2
1 1 3
.3
3 2 6
a
V a a==
.
Câu 35: Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
2
36 a
. Tính thể
tích
V
của lăng trụ lục giác đều nội tiếp hình trụ.
A.
3
27 3a
. B.
3
24 3a
. C.
3
36 3a
. D.
3
81 3a
.
Lời giải
Thiết diện qua trục là hình vuông nên
2l h r==
.
Ta có diện tích xung quanh của hình nón:
22
2 4 36
xq
S rl r a
= = =
3ra=
.
Diện tích đáy của lăng trụ:
( )
2
2
3 27 3
6. 6. 3 .
42
d OAB
a
S S a
= = =
.
Thể tích lăng trụ:
2
3
27 3
. .6 81 3
2
d
a
V S h a a= = =
.
Câu 36: Thiết diện qua trục một hình nón là một tam giác vuông cân có cạnh huyền bằng
26
. Thể tích
của khối nón này là
A.
6
. B.
33
. C.
32
. D.
26
.
Lời giải
Gọi thiết diện qua trục là
SAB
, tâm đường tròn đáy là
O
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HK1
Toán 12
Xét
SAB
vuông cân tại
S
:
11
.2 6 6
22
SO AO AB= = = =
.
( )
( )
2
2
2
1 1 1
. . . . . 6. 6 2 6
3 3 3
V h r SO OA
= = = =
.
Câu 37: Cho hàm số
( )
y f x=
có đạo hàm trên và có đồ thị như hình vẽ dưới đây. Nhận xét nào đng
về hàm số
( ) ( )
2
g x f x=
?
Hàm số
( )
gx
đồng biến trên khoảng nào?
A. . B.
( )
;1−
. C.
( )
2;+
. D.
( )
;2−
.
Lời giải
Từ đồ thị hàm số
( )
y f x=
ta có:
Phương trình
( )
0fx=
có hai nghiệm
1
2
x
x
=−
=
, trong đó
1x =−
là nghiệm kép.
Phương trình
( )
0fx
=
có hai nghiệm
1
1
x
x
=−
=
và
( )
0fx
khi
11x−
.
Xét hàm số
( ) ( )
2
g x f x=
có
( ) ( ) ( )
2.g x f x f x
=
có
( )
( )
( )
1
0
2
0
1
0
1
x
fx
x
gx
x
fx
x
=−
=
=
=
=−
=
=
.
Ta có bảng xét dấu
Từ bảng xét dấu ta có
( )
0gx
khi
( ) ( )
1;1 2;x − +
nên hàm số
( )
gx
đồng biến trên
khoảng
( )
1;1−
và
( )
2;+
.
Câu 38: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
18
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Hàm số
( ) ( )
42
3 2 2023y f x f x= + +
có số điểm cực trị là
A.
3
. B.
5
. C.
6
. D.
7
.
Lời giải
Ta có
( ) ( ) ( ) ( )
3
12 4y f x f x f x f x
=+
.
( ) ( ) ( ) ( )
( )
( )
3
0
0 12 4 0
0
fx
y f x f x f x f x
fx
=
= + =
=
.
Quan sát đồ thị hàm số ta thầy đồ thị hàm số cắt trục hoành tại bốn điểm phân biệt và hàm số có
ba điểm cực trị. Do đó phương trình
( )
0fx=
có bốn nghiệm phân biệt và
( )
0fx
=
có ba
nghiệm phân biệt, các nghiệm này đôi một khác nhau cho nên hàm
( ) ( )
42
3 2 2023y f x f x= + +
có bảy điểm cực trị.
Câu 39: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
4;7
. B.
( )
;1− −
. C.
( )
2;3
. D.
( )
1;2−
.
Lời giải
Ta có:
( )
3
3
3
x
y f x
x
−
=−
−
. Ta có:
y
không xác định tại điểm
3x =
.
Hàm số đồng biến khi
( )
( )
33
30
1 3 1 2 4
30
3 4 1
34
0
12
3 0 3 3
1 3 4 1 2
30
3 1 4
xx
x
xx
fx
xx
x
y
x
x x x
xx
fx
xx
−
− −
−
−
−
−
− −
−
− −
.
Hàm số
( )
3y f x=−
đồng biến trên khoảng
( )
1;2−
và
( )
3;4
.
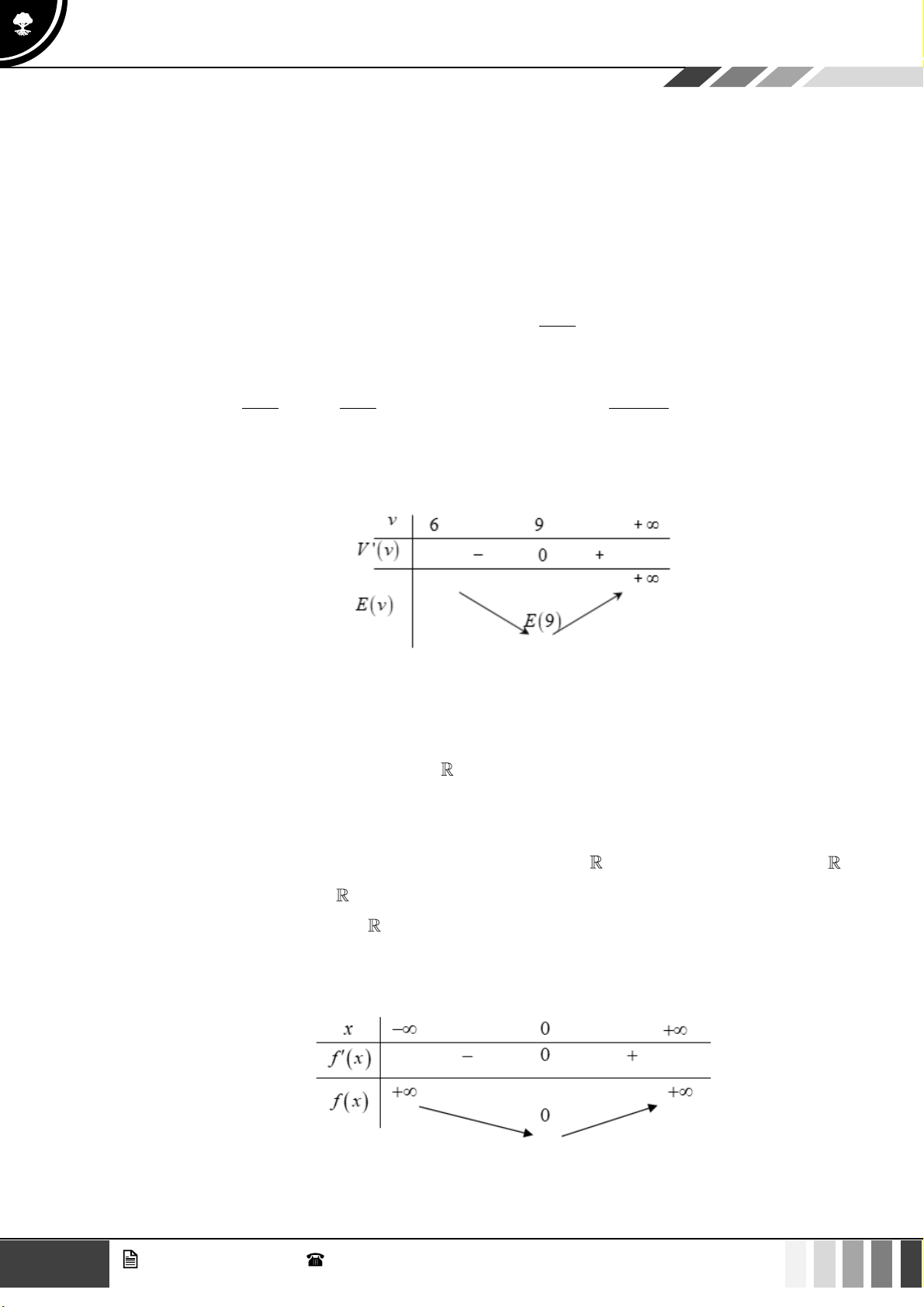
GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 40: Một con cá bơi ngược dòng từ A đến B với khoảng cách là
( )
300 km
. Vận tốc dòng nước là
( )
6/km h
. Nếu vận tốc của con cá khi nước đứng yên là
( )
/v km h
thì năng lượng tiêu hao trong
thời gian
t
giờ được cho bởi công thức
( )
3
E v cv t=
, trong đó
c
là một hằng số,
E
được tính
bằng
Jun
. Vận tốc của con cá khi nước đứng yên là bao nhiêu để năng lượng tiêu hao là ít nhất?
A.
7/km h
. B.
10 /km h
. C.
6/km h
. D.
9/km h
.
Lời giải
Vận tốc của con cá bơi ngược dòng là:
6v −
( )
/km h
Thời gian để con cá bơi khoảng cách 300
km
là
300
6
t
v
=
−
( )
h
Năng lượng tiêu hao của con cá vượt khoảng cách đó là:
( ) ( )
3
3
300
. 300 . 6
66
v
E v cv c jun v
vv
= =
−−
có
( )
( )
2
2
9
600
6
v
E v cv
v
−
=
−
Cho
( )
( )
0
0
9
v loai
Ev
v
=
=
=
Vậy để năng lượng tiêu hao là ít nhất thì vận tốc vận tốc của con cá khi nước đứng yên là
( )
9/v km h=
.
Câu 41: Có bao nhiêu giá trị nguyên của tham số
m
trong đoạn
2023;2023−
để hàm số
2023
2024y x mx= − +
đồng biến trên .
A.
2020
. B.
2024
. C.
2022
. D.
2023
.
Lời giải
Ta có
2022
2023.y x m
=−
. Hàm số đã cho đồng biến trên
2022
2023. 0xm−
x
2022
2023.mx
x
.
Xét
( )
2022
2023.f x x=
x
( )
2021
' 2023.2022.f x x=
( )
2021
' 0 2023.2022. 0 0f x x x= = =
Bảng biến thiên:
Suy ra
0m
,
m
là số nguyên trong đoạn
2023;2023−
nên có
2024
số.

20
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Câu 42: Biết rằng phương trình
2
2
2
2
log 4 9
25
x
xx
x
+
= − + +
+
có hai nghiệm
x a b c=+
và
x a b c=−
với
,,abc
là các số nguyên dương. Tính tích
..abc
.
A.
8
. B.
8−
. C.
12−
. D.
12
.
Lời giải
Điều kiện xác định:
2
25
0
2 5 2
x
x
x
+−
+
2
2
2
2
log 4 9
25
x
xx
x
+
= − + +
+
( )
( )
22
22
log 2 log 2 5 4 9x x x x + − + = − + +
( )
( )
22
2 2 2
log 2 2 log 2 5 log 2 4 10x x x x + + + = + + + +
( )
( )
22
22
log 2 2 log 4 10 4 10x x x x + + + = + + +
Xét hàm số:
( )
2
logf t t t=+
có
( )
1
1 0, 0
ln2
f t t
t
= +
Hàm số
( )
ft
đồng biến trên
( )
0;+
. Đt:
2
20
4 10 0
ux
vx
= +
= +
Khi đó ta được
22
log logu u v v+ = +
( ) ( )
f u f v=
Do đó
( ) ( )
2
2 4 10f u f v u v x x= = + = +
2
2 2 3
4 8 0
2 2 3
x
xx
x
=+
− − =
=−
(thỏa mãn điều kiện).
Vì
,,abc
là các số nguyên dương nên
2, 2, 3abc= = =
. Vậy
. . 12abc=
.
Câu 43: Tập nghiệm của bất phương trình
2
2
2
1
log
log
2 10 3 0
x
x
x− +
là:
A.
( )
1
0; 2;
2
S
= +
. B.
( )
1
2;0 ;
2
S
= − +
.
C.
( )
1
;0 ;2
2
S
= −
. D.
( )
1
; 2;
2
S
= − +
.
Lời giải
Điều kiện:
0 (*)x
. Đt
2
log 2 .
u
u x x= =
Bất phương trình đã cho trở thành
( )
22
2
10
2 10 2 3 0 2 3 0 (1)
2
u
u u u
u
−
− + − +
Đt
( )
2
2
5
2 , 1. 1 3 10 0
2
u
t
t t t t
t
−
= + −
So điều kiện ta suy ra
2
2
1
2 2 2 1
1
u
u
tu
u
−
Với
2
1 log 1 2u x x
Với
2
1
1 log 1 .
2
u x x − −
GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HK1
Toán 12
Kết hợp điều kiện (*), ta được nghiệm của bất phương trình đã cho là
2x
hoc
1
0
2
x
.
Câu 44: Cho tứ diện
ABCD
có tam giác
BCD
vuông tại
B
,
BC a=
,
3BD a=
,
4AB a=
và
0
90ACB ADB==
. Thể tích khối tứ diện
ABCD
bằng
A.
3
a
. B.
3
3a
. C.
3
5a
. D.
3
2a
.
Lời giải
Gọi S là trung điểm của AB, suy ra
SB SC SD==
, Gọi
I
là trung điểm DC suy ra
()SI BCD⊥
2
3
2
BCD
a
S =
;
23DC a BI a SI a= = =
3
3
.
1
.
32
S BCD BCD ABCD
a
V SI S V a = = =
.
Câu 45: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
a
, mt bên
SAB
là tam giác
đều và nằm trong mt phẳng vuông góc với mt phẳng đáy. Tính diện tích
S
của khối cầu ngoại
tiếp hình chóp đã cho.
A.
2
5
3
a
S
=
. B.
2
5
12
a
S
=
. C.
2
5
6
a
S
=
. D.
2
3
8
a
S
=
.
Lời giải
( ) ( )
SAB ABC⊥
theo giao tuyến
AB
Kẻ
( )
;SM AB SM ABC⊥ ⊥
Và có
M
là trung điểm
AB
.
Gọi
,OG
lần lượt là tâm đường tròn ngoại tiếp tam giác
,ABC SAB
.
Dựng đường thẳng qua
O
vuông góc với
( )
ABC
và đường thẳng qua
G
vuông góc
( )
SAB
.
Hai đường thẳng đó cắt nhau tại
I
. Ta có
I OI IA IB IC = =
I GI IA IB IS = =
22
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Nên
IA IB IC IS= = =
hay
I
là tâm mt cầu ngoại tiếp hình chóp
.S ABC
. Mt cầu có bán kính
là
R IA=
.
22
2
2 2 2
5
12
3 2 3
a a a
IA AO IO
= + = + =
Vậy diện tích
S
của khối cầu ngoại tiếp hình chóp là:
22
2
55
4 4 . .
12 3
aa
SR
= = =
Câu 46: Một cốc uống bia có hình nón cụt còn lon bia thì có hình trụ (như hình vẽ dưới đây). Khi rót bia
từ lon ra cốc thì chiều cao của phần bia còn lại trong lon và chiều cao của phần bia có trong
cốc là như nhau. Hỏi khi đó chiều cao của bia trong lon gần nhất là số nào sau đây?
A. B. C. D.
Lời giải
Gọi phần nước trong cốc là nón cụt có bán kính đáy dưới bằng , bán kính đáy trên bằng
Phần bia trong cốc chính là bia từ lon rót ra nên ta có
Theo tỉ số đồng dạng ta có thế vào (1) ta có
.
Câu 47: Cho hàm số
3 2 3
34y x mx m= − +
. Có tất cả bao nhiêu giá trị của tham số
m
để các điểm cực đại
và cực tiểu của đồ thị hàm số đối xứng nhau qua đường phân giác
()d
của góc phần tư thứ nhất
và thứ ba.
A.
1
B.
4
C.
2
. D.
3
Lời giải
Tập xác định:
DR=
Đạo hàm:
2
' 3 6y x mx=−
. Hàm số có 2 cực trị khi
0m
h
h
8,58.
14,2.
7,5.
9,18.
2
r
( )
( )
( )
( )
2 2 2
2
2 2. .9 15 2 4 9 30 2 (1)
33
hh
r r h r r h
+ + = − + + = −
2 15
15rh
=
+
30 2 15 2 15 30h r h r + = = −
( )
( ) ( )
( )
( )
22
15 30
2 4 9 30 15 30 5 10 2 4 9 60 15
3
r
r r r r r r r
−
+ + = − + − + + = −
( )
( )
( )
23
2 2 4 9 12 3 27 116 0 3,14r r r r r r r − + + = − + − =
2 17,1 8,55hh

GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HK1
Toán 12
3
04
'0
20
x y m
y
x m y
= =
=
= =
Khi đó hai điểm cực trị của đồ thị là
3
(0;4 ), (2 ;0)A m B m
. Gọi
I
là trung điểm
AB
Các điểm cực trị này đối xứng nhau qua đường thẳng
( ):d y x=
khi
()
()
AB d
Id
⊥
3
( ;2 ) ( )
d
AB a
I m m d
⊥
3
3
2 4 0
20
mm
mm
−=
−=
2
2
2
2
m
m
=
=−
thỏa mãn điều kiện
Vây có 2 giá trị của
m
Câu 48: Gọi
;ab
là tập hợp tất cả các giá trị của tham số
m
để hệ bất phương trình
2
32
3 4 0
3 15 0
xx
x x x m m
− −
− − −
có nghiệm. Tính
ab+
.
A.
17−
. B.
15
. C.
17
. D.
15−
.
Lời giải
Xét hệ
2
32
3 4 0 (1)
3 15 0 (2)
xx
x x x m m
− −
− − −
.
Bất phương trình (1):
2
3 4 0 1 4x x x− − −
. Bài toán tương đương tìm tất các các giá trị
của tham số
m
sao cho bất phương trình (2) có nghiệm
1;4x −
.
Đt
32
( ) 3 15f x x x x m m= − − −
. Ta có
3 2 2
3 2 2
3 15 , 1 0
()
3 15 , 0 4
x x m m x
fx
x x m m x
+ − − −
=
− − −
.
Suy ra
2
2
3 6 , 1 0
'( )
3 6 , 0 4
x x x
fx
x x x
+ −
=
−
.
Ta thấy khi
12x−
thì
'( ) 0fx
, khi
24x
thì
'( ) 0fx
.
Do đó:
2
1;4
( ) ( 1), (4) (4) 15 16Max f x Max f f f m m
−
= − = = − − +
.
Để bất phương trình
( ) 0fx
có nghiệm thuộc
1;4−
thì
2
1;4
( ) 15 16 0 16 1Max f x m m m
−
= − − + −
.
Vậy
15ab+ = −
.
Câu 49: Cho tứ diện
SABC
có
AB a=
, tam giác
SBC
đều, hình chiếu vuông góc của
S
lên mt phẳng
( )
ABC
là trực tâm
H
của tam giác
ABC
, mt phẳng
( )
SCH
tạo với mt phẳng
( )
SBC
một
góc
0
60
. Tính thể tích khối tứ diện
GABC
với
G
là trọng tâm của tam giác
SAC
.
A.
3
3
38
a
. B.
3
3
144
a
. C.
3
33
32
a
. D.
3
3
32
a
.
Lời giải
24
GV. Phan Nhật Linh -
SĐT: 0817 098 716
Tuyển tập 10 đề ôn HK1
Toán 12
Gọi
O
là trọng tâm của
SBC
;
,MK
lần lượt là chân đường cao kẻ từ
,AC
của
ABC
;
N
là
trung điểm của
SC
. Do
SBC
đều nên
O
là trực tâm của
SBC
. Mà theo giả thiết ta có
SABC
là tứ diện trực tâm nên ta có
( )
AO SBC⊥
. Do đó hình chóp
.A SBC
là hình chóp đều.
Ta có
( )
SC ABN⊥
do
,SC OA BN⊥
( ) ( )
(
)
0
, 60SCH SBC KNB = =
. Suy ra
AOB
vuông
tại
O
có
AB a=
,
0
30ABO =
. Do đó:
.sin30
2
o
a
AO AB==
,
3
. 30
2
o
a
BO AB cos==
.
Suy ra
3
.3
2
a
BC BO==
.
Vậy
2
3
1 1 1 3 3 3
. . . .
3 9 9 2 2 4 32
GABC SABC SBC
a a a
V V AO S
= = = =
.
Câu 50: Cho nửa hình cầu bán kính
R
không đổi. Một hình nón có chiều cao
,h
bán kính đáy là
r
tiếp
xc với nửa hình cầu như hình vẽ. Khi diện tích xung quanh của hình nón là nhỏ nhất, khẳng
định nào sau đây đng ?
A.
23hr=
. B.
hr=
. C.
3hr=
. D.
2hr=
.
Lời giải
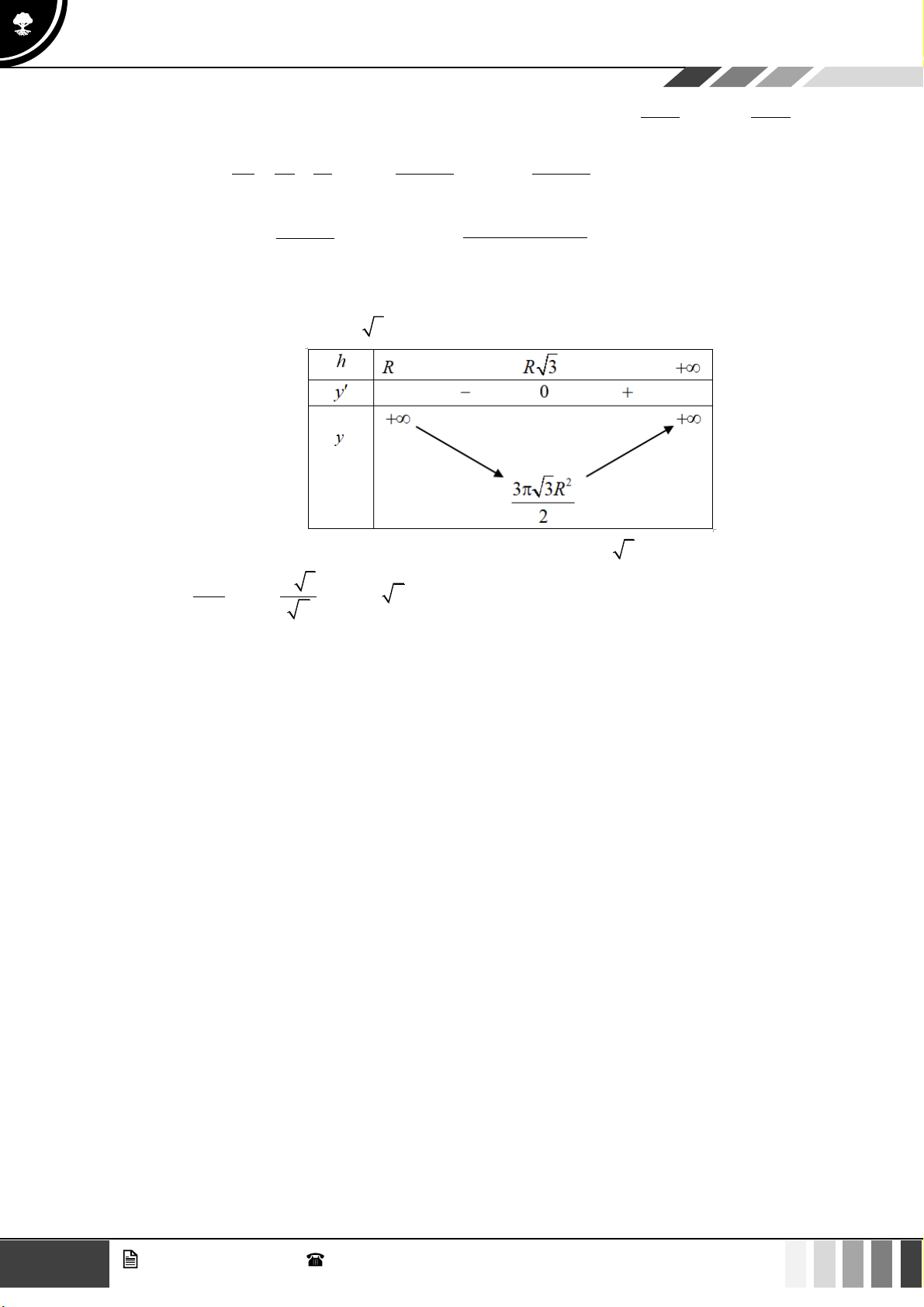
GV. Phan Nhật Linh -
SĐT: 0817 098 716
25
Tuyển tập 10 đề ôn HK1
Toán 12
Gọi
l
là độ dài đường sinh của hình nón. Ta có
22
xq
hr hr
Rl hr rl S
RR
= = =
.
Mt khác
22
2
2 2 2 2 2
1 1 1 Rh
r
R h r h R
= + =
−
3
22
xq
Rh
S
hR
=
−
.
Xét
( )
3
22
Rh
y f h
hR
==
−
( )
( )
( )
2 2 2
2
22
3Rh h R
y f h
hR
−
= =
−
.
Đạo hàm
0
0
3
h
y
hR
=
=
=
. Ta có bảng biến thiên:
Vậy diện tích xung quanh của hình nón là nhỏ nhất khi
3hR=
, thay vào được
2
2
33
2
2
2
RR
r r h r= = =
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HKI
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số trên nghịch biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
;2− −
. C.
( )
0;+
. D.
( )
2;− +
.
Câu 2: Cho hàm số
( )
y f x=
có đồ thị như sau
Hàm số trên đạt cực đại tại điểm nào dưới đây?
A.
0x =
. B.
1x =
. C.
2x =
. D.
3x =
.
Câu 3: Giá trị lớn nhất của hàm số
( )
2
7f x x x= + −
trên đoạn
2;3
là:
A.
5
. B.
1−
. C.
29
4
−
. D.
1
2
−
.
Câu 4: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
35
3
x
y
x
−+
=
−
?
A.
3y =
. B.
3x =−
. C.
3y =−
. D.
1y =
.
Câu 5: Cho hàm số có đồ thị như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
D.
0, 0, 0abc
.
42
y ax bx c= + +
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
06
ĐỀ SỐ
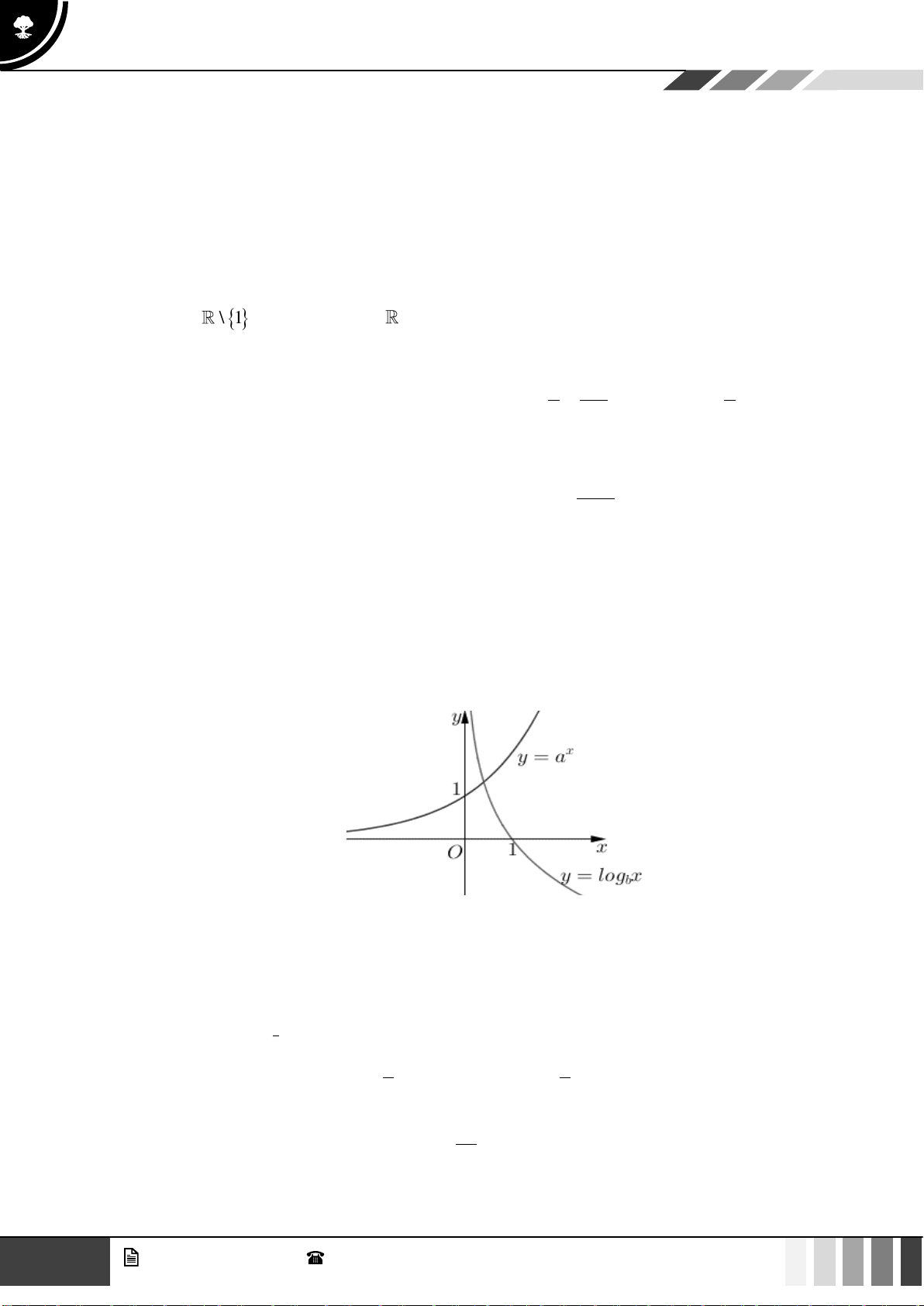
GV. Phan Nhật Linh -
SĐT: 0817 098 716
2
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 6: Cho hàm số
( )
y f x=
có
lim 1
x
y
→+
=
và
lim 1
x
y
→−
=−
. Khẳng định nào sau đây là khẳng định
đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1x =
và
1x =−
.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1y =
và
1y =−
.
C. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng
1x =
và
1x =−
.
Câu 7: Tìm tập xác định
D
của hàm số
( )
1yx
=−
.
A.
\1D =
. B.
D =
. C.
( )
1;D = +
. D.
)
1;D = +
.
Câu 8: Cho các số thực dương
,ab
với
1b
. Khẳng định nào sau đây là khẳng định đúng ?
A.
( )
ln ln ln .ab a b=+
B.
( )
ln ln .ln .ab a b=
C.
ln
ln .
ln
aa
bb
=
D.
ln ln ln .
a
ba
b
=−
.
Câu 9: Đạo hàm của hàm số
12x
ye
−
=
là
A.
12
2
x
ye
−
=
. B.
12
2
x
ye
−
=−
. C.
12
2
x
e
y
−
=−
. D.
12x
ye
−
=
.
Câu 10: Tìm tập xác định D của hàm số
( )
2
2
log 2 3y x x= − −
.
A.
(
)
; 1 3;D = − − +
. B.
1;3D =−
.
C.
( ) ( )
; 1 3;D = − − +
. D.
( )
1;3D =−
.
Câu 11: Cho đồ thị hàm số
x
ya=
và
log
b
yx=
như hình vẽ. Trong các khẳng định sau, đâu là khẳng
định đúng
A.
0 1,0 1ab
. B.
01ab
. C.
1, 1ab
. D.
01ba
.
Câu 12: Nghiệm của phương trình là
A. . B. . C. . D. .
Câu 13: Phương trình có nghiệm là
A. . B. . C. . D. .
Câu 14: Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
3 4 2
39
xx−−
=
0x =
1x =
2x =
3x =
( )
1
2
log 1 2x − = −
2x =
5
2
x =
3
2
x =
5x =
2
1
5
25
x
x
−
+
( )
;2−
( )
;1−
( )
1;+
( )
2;+
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 15: Mỗi đỉnh của bát diện đều là đỉnh chung của bao nhiêu cạnh?
A.
3
. B.
8
. C.
5
. D.
4
.
Câu 16: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và cạnh bên
2SA a=
vuông góc
với đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
2a
. B.
3
4
3
a
. C.
3
2
3
a
. D.
3
a
.
Câu 17: Cho hình trụ có bán kính đáy
r
và chiều cao
h
. Thể tích của khối trụ bằng
A.
rh
. B.
2
rh
. C.
2 rh
. D.
2
1
3
rh
.
Câu 18: Cho hình nón có chu vi đáy
2
và độ dài đường cao là 3. Diện tích xung quanh của hình nón
bằng
A.
rh
. B.
2
rh
. C.
2 rh
. D.
2
1
3
rh
.
Câu 19: Cho mặt cầu có đường kính là 6. Diện tích mặt cầu đã cho bằng
A.
12
. B.
36
. C.
48
. D.
2
36
.
Câu 20: Cho mặt cầu có chu vi đường tròn lớn là
3
. Thể tích khối cầu đã cho bằng
A.
4
. B.
3,6
. C.
9
2
. D.
8
.
Câu 21: Cho hàm số
()y f x=
có đạo hàm
( )
2
'2f x x x=−
. Hàm số
()y f x=
nghịch biến trong khoảng
nào dưới đây?
A.
( )
;1−
. B.
( )
1;2
. C.
( )
1;+
. D.
( )
2;+
.
Câu 22: Cho hàm số
( ) ( )
32
1
2 1 2
3
f x x mx m x= + + − +
. Tất cả các giá trị thực của tham số
m
để hàm số
đã cho có điểm cực trị là
A.
1m
. B.
1m =
. C.
1m
. D.
1m
.
Câu 23: Giá trị lớn nhất của hàm số
2
()
1
x
fx
x
−
=
−
trên đoạn
2;3
bằng
A.
1
2
−
. B.
0
. C.
3−
. D.
2
.
Câu 24: Cho hàm số
()y f x=
có bảng biến thiên như hình vẽ.
Hỏi hàm số đã cho là hàm số nào trong các hàm số sau?
A.
2
1
x
y
x
=
−
. B.
21
1
x
y
x
−
=
+
. C.
23
1
x
y
x
+
=
+
. D.
21
1
x
y
x
−
=
−
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
4
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 25: Tiệm cận đứng của đồ thị hàm số
2
1
32
x
y
xx
+
=
− + −
là đường thẳng
A.
1x =
. B.
1x =−
. C.
2x =
. D.
1x =
và
2x =
.
Câu 26: Tập xác định của hàm số
( )
2
2
2 5 3y x x
−
= − +
là
A.
3
\ 1;
2
D
=
. B.
3
\
2
D
=
. C.
\1D =
. D.
D =
.
Câu 27: Cho
, , a b c
là các số thực khác
0
thỏa mãn
4 25 10
a b c
==
. Tính
.
cc
T
ab
=+
A.
1
10
T =
B.
1
2
T =
C.
2T =
D.
7T =
Câu 28: Tập xác định
D
của hàm số
( )
ln 2yx
=−
là
A.
D =
. B.
( )
3;D = +
. C.
( )
0;D = +
. D.
( )
2;D = +
.
Câu 29: Cho hàm số
1
1 ln
y
xx
=
++
với
0x
. Khi đó
2
'y
y
−
bằng
A.
1
x
x +
. B.
1
1
x
+
. C.
1 ln
x
xx++
. D.
1
1 ln
x
xx
+
++
.
Câu 30: Tập nghiệm của phương trình
2
log( 2 1) log(5 3 )x x x− − = −
A.
3;1−
. B.
3
. C.
3−
. D.
3;2−
.
Câu 31: Tổng tất cả các nghiệm của phương trình:
2
33
28
x x x− − −
=
A.
0
. B.
3
. C.
3−
. D.
23
.
Câu 32: Khối bát diện đều là khối đa diện đều loại nào?
A.
3;3
. B.
3;5
. C.
4;3
. D.
3;4
.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, tam giác
SCD
đều và nằm trong mặt
phẳng vuông góc với đáy,
CD a=
,
3BC a=
. Thể tích khối chóp
.S ABCD
bằng
A.
3
3
2
a
B.
3
6
a
C.
3
2
a
D.
3
a
Câu 34: Cho khối nón có bán kính đáy bằng
3
và khoảng cách từ tâm của đáy đến một đường sinh bất
kỳ bằng
12
5
. Thể tích của khối nón đã cho bằng
A.
36
B.
12
C.
18
D.
24
Câu 35: Một khối trụ có bán kính đáy là
3,a
chiều cao
2 3.a
Thể tích của khối cầu ngoại tiếp khối trụ
là
A.
3
4
6
3
a
B.
3
43a
C.
3
66a
D.
3
86a
Câu 36: Bạn Hoa được gia đình gửi vào sổ tiết kiệm 100 triệu đồng với lãi suất 0,5% một tháng theo hình
thức lãi kép. Nếu mỗi tháng Hoa rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì hàng

GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HKI
Toán 12
tháng Hoa rút ra số tiền gần nhất với số nào sau đây để đúng 4 năm vừa hết số tiền trong sổ tiết
kiệm?
A.
2.351.000
. B.
2.392.000
. C.
2.306.000
. D.
2.349.000
.
Câu 37: Có bao nhiêu giá trị nguyên của
2023;2023m−
để hàm số
2
2
2
mx
xm
y
+
+
=
đồng biến trên
( )
1;2
?
A.
4041
. B.
4044
. C.
4042
. D.
4040
Câu 38: Cho
2023!x =
. Tính
2023 2023 2023 2023
2 3 2022 2023
1 1 1 1
...
log log log log
T
x x x x
= + + + +
.
A.
2022T =
. B.
1
2023
T =
. C.
1
2022
T =
. D.
2023T =
.
Câu 39: Biết nghiệm lớn nhất của phương trình
( )
2
1
log log 10 log4 2
2
xx+ + + =
là
x a b c=+
(
,,abc
là các số nguyên). Giá trị của
abc++
bằng
A. 0. B. -
6
. C.
2−
. D.
2
Câu 40: Gọi
S
là tập chứa tất cả những giá trị nguyên
[ 24;24]m−
để bất phương trình
( )
22
sin 1 cos
3 2 1 3 4
xx
m
+
+ −
đúng với mọi
x
nằm trên . Số phần tử của tập
S
là:
A. 18. B. 19. C. 21. D. 24.
Câu 41: Cho hình lập phương
.ABCD A B C D
. Gọi
, , , , ,I J K L M N
lần lượt là tâm của 6 mặt hình
vuông. Khi đó khối đa diện
IJKLMN
là khối gì?
A. Khối lăng trụ tam giác đều. B. Khối lăng trụ tam giác.
C. Khối đa diện đều loại
4;3
. D. Khối bát diện đều.
Câu 42: Cho hình lăng trụ
.ABC A B C
, đáy
ABC
là tam giác vuông cân tại
C
. Hình chiếu vuông góc
của
A
trên mặt phẳng
( )
ABC
là trọng tâm
G
của tam giác
ABC
. Biết diện tích tam giác
A AB
bằng
2
3
, góc giữa hai mặt phẳng
( )
A AB
và
( )
ABC
bằng
60
. Tính thể tích khối lăng trụ
.ABC A B C
.
A.
1
3
. B. 3. C.
3
. D.
3
3
.
Câu 43: Cho khối lăng trụ
ABC A B C
có thể tích bằng
27
.
,MN
lần lượt là trung điểm các cạnh
,AA BB
. Thể tích khối chóp
MNAC
bằng:
A.
9
2
. B.
27
2
. C.
9
. D.
3
Câu 44: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều,
SAB
vuông góc với đáy
ABC
và tam
giác
SAB
đều, khoảng cách từ điểm
A
tới mặt phẳng
SCB
bằng
2 15
5
a
. Thể tích của khối
chóp
.S ABC
là
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
a
. D.
3
a
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
6
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 45: Một hình trụ có bán kính đáy
5cmr =
và khoảng cách giữa hai đáy
8cmh =
. Cắt khối trụ bởi
một mặt phẳng song song với trục và cách trục
4cm
. Diện tích của thiết diện được tạo thành là
A.
( )
2
48 cm
. B.
( )
2
56 cm
. C.
( )
2
42 cm
. D.
( )
2
44 cm
.
Câu 46: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
42
2 1 3 2 1 , .f x x x x x m x
= + + + −
Số giá trị
nguyên của tham số
2024;2024m−
để hàm số
( ) ( )
2 2024g x f x= − +
đồng biến trên
khoảng
( )
3;+
?
A.
2022.
B.
2020
. C.
2019.
D.
2023
.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm
( )
( )( )
22
42f x x x x
= − −
, với
x
. Tổng các giá trị
nguyên của tham số
m
để hàm số
( )
( )
32
3g x f x x m= − +
có số điểm cực trị nhiều nhất là
A.
1
. B.
3
. C.
6
. D.
5
.
Câu 48: Cho các số thực
,xy
thỏa mãn
( )
2e
ln 2 2 2
2
x
x y x
xy
+ + +
+
. Giá trị nhỏ nhất của
y
là
A.
2
. B.
1
. C.
1−
. D.
3
.
Câu 49: Gọi S là tập hợp các giá trị nguyên của tham số m để tập nghiệm của bất phương trình
(
)
( )
2
22
log 2 2log 2 1
11
0
55
x x m x+ + −
−
chứa đúng 4 số nguyên. Số phần tử của
S
bằng:
A. 15. B.
21.
C. 20. D. 16.
Câu 50: Có bao nhiêu số nguyên
m
để phương trình
( )
( )
ln 2sin ln 3sin sinm x m x x+ + + =
có nghiệm
thực?
A.
5
. B.
6
. C.
3
. D.
4
.
-------------------------HẾT-------------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HKI
Toán 12
BẢNG ĐÁP ÁN
1.B
2.A
3.A
4.C
5.A
6.B
7.C
8.A
9.B
10.C
11.D
12.A
13.D
14.D
15.D
16.C
17.B
18.B
19.B
20.C
21.B
22.A
23.B
24.B
25.D
26.A
27.C
28.B
29.B
30.C
31.A
32.D
33.C
34.B
35.D
36.D
37.A
38.D
39.D
40.D
41.D
42.D
43.A
44.D
45.A
46.D
47.A
48.B
49.B
50.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số trên nghịch biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
;2− −
. C.
( )
0;+
. D.
( )
2;− +
.
Lời giải
Dựa vào bảng biến thiên ta thấy, trên khoảng
( )
;2− −
có
0y
nên hàm số nghịch biến.
Câu 2: Cho hàm số
( )
y f x=
có đồ thị như sau
Hàm số trên đạt cực đại tại điểm nào dưới đây?
A.
0x =
. B.
1x =
. C.
2x =
. D.
3x =
.
Lời giải
Dựa vào đồ thị ta thấy, hàm số đạt cực đại tại
0x =
.
Câu 3: Giá trị lớn nhất của hàm số
( )
2
7f x x x= + −
trên đoạn
2;3
là:
A.
5
. B.
1−
. C.
29
4
−
. D.
1
2
−
.
Lời giải
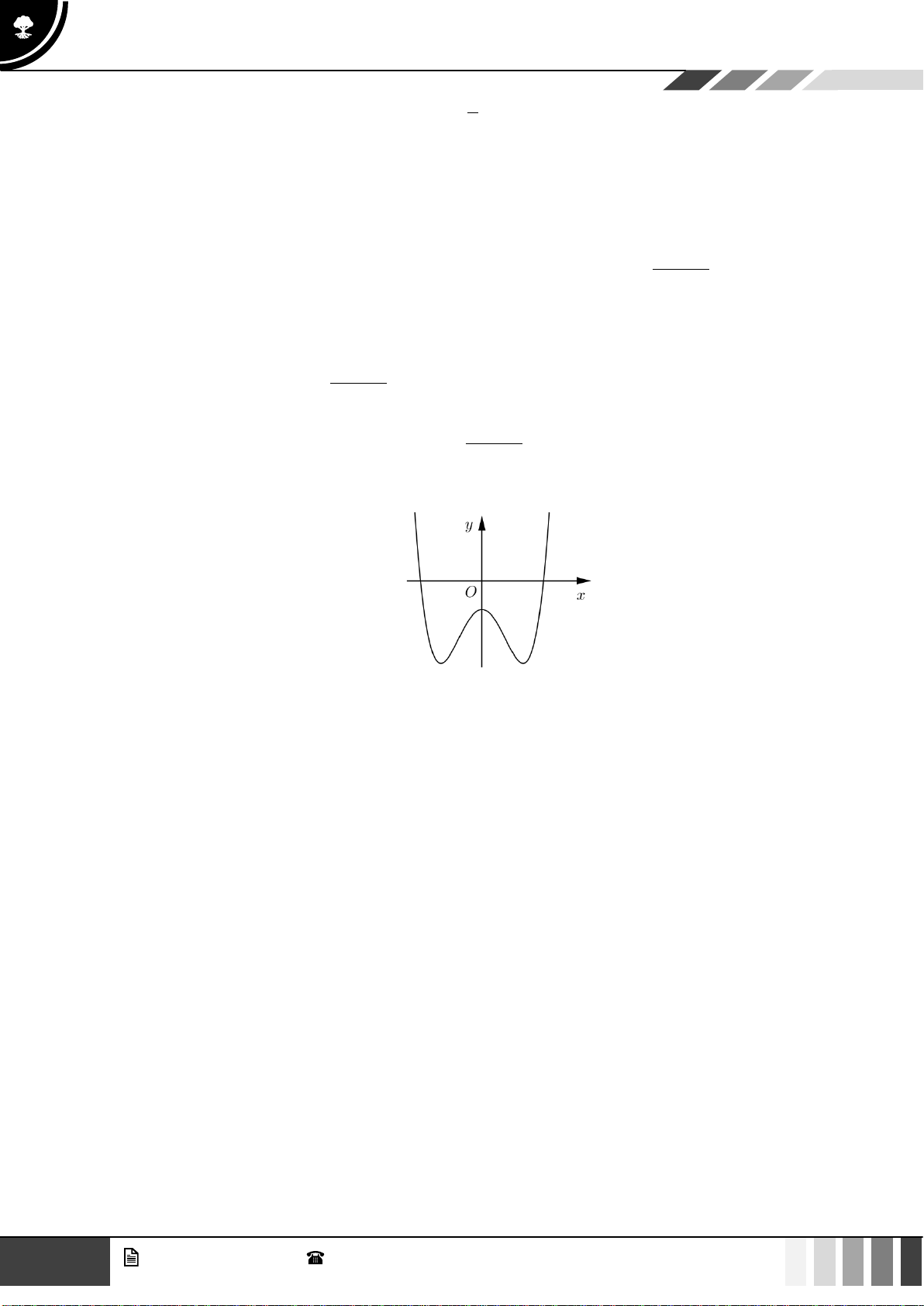
GV. Phan Nhật Linh -
SĐT: 0817 098 716
8
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có đạo hàm:
( )
1
2 1 0
2
f x x x
= + = = −
( loại)
Ta có:
( )
21f =−
và
( )
35f =
Vậy
( ) ( )
[2;3]
max 3 5f x f==
.
Câu 4: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
35
3
x
y
x
−+
=
−
?
A.
3y =
. B.
3x =−
. C.
3y =−
. D.
1y =
.
Lời giải
Ta có:
( )
35
lim lim 3
3
xx
x
fx
x
→ →
−+
= = −
−
Vậy tiệm cận ngang của đồ thị hàm số
35
3
x
y
x
−+
=
−
là
3y =−
.
Câu 5: Cho hàm số có đồ thị như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
D.
0, 0, 0abc
.
Lời giải
Đồ thị hướng lên
0.a
Hàm số có 3 điểm cực trị
. 0 0. a b b
Đồ thị
Oy
tại điểm nằm dưới
0.Ox c
Câu 6: Cho hàm số
( )
y f x=
có
lim 1
x
y
→+
=
và
lim 1
x
y
→−
=−
. Khẳng định nào sau đây là khẳng định
đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1x =
và
1x =−
.
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1y =
và
1y =−
.
C. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng
1x =
và
1x =−
.
Lời giải
Ta có
lim 1
x
y
→+
=
và
lim 1
x
y
→−
=−
nên đồ thị hàm số đã cho có hai tiệm cận ngang là các đường
thẳng
1y =
và
1y =−
.
Câu 7: Tìm tập xác định
D
của hàm số
( )
1yx
=−
.
42
y ax bx c= + +
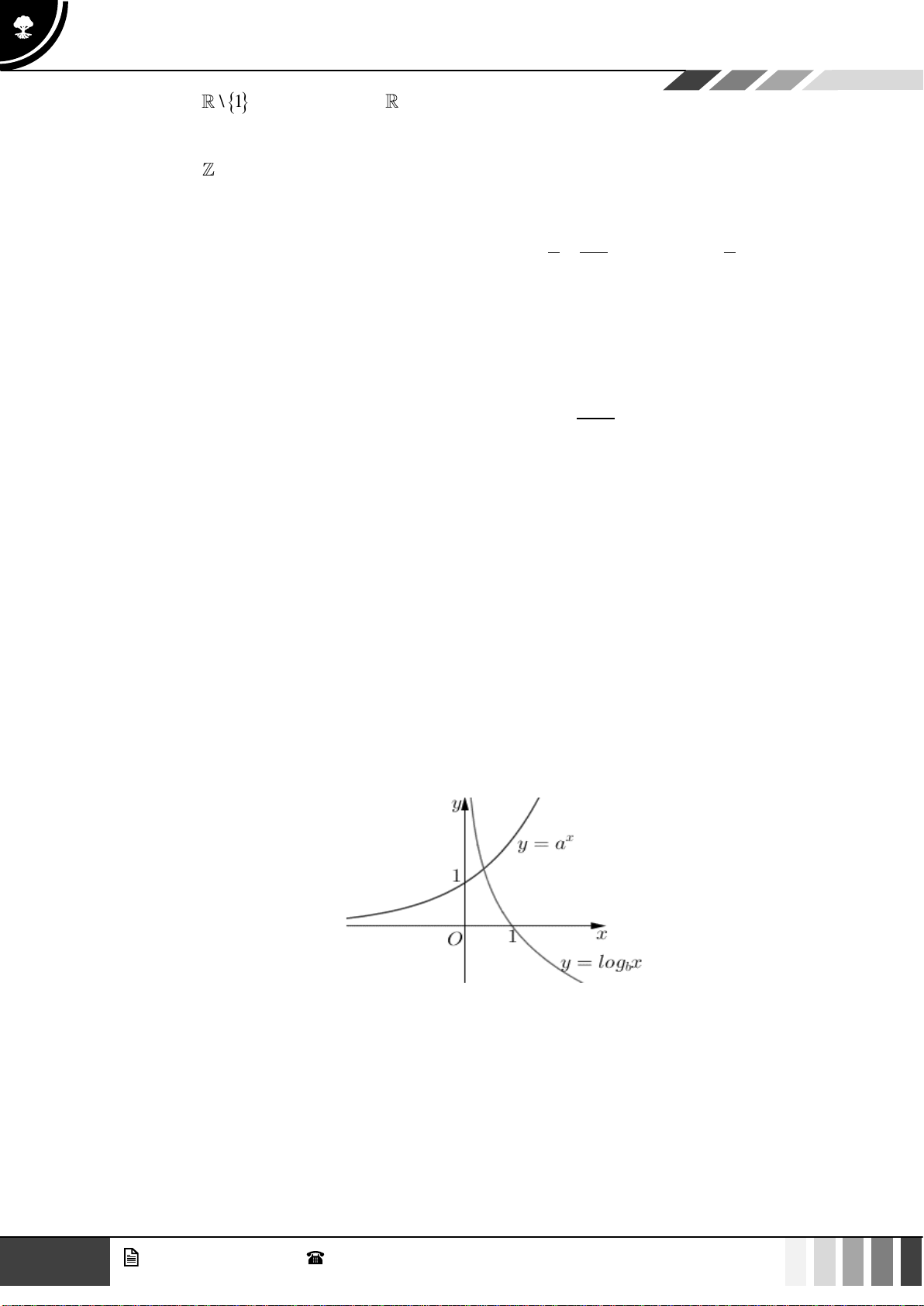
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HKI
Toán 12
A.
\1D =
. B.
D =
. C.
( )
1;D = +
. D.
)
1;D = +
.
Lời giải
Do
nên điều kiện xác định là
1 0 1xx−
( )
1;D = +
.
Câu 8: Cho các số thực dương
,ab
với
1b
. Khẳng định nào sau đây là khẳng định đúng ?
A.
( )
ln ln ln .ab a b=+
B.
( )
ln ln .ln .ab a b=
C.
ln
ln .
ln
aa
bb
=
D.
ln ln ln .
a
ba
b
=−
.
Lời giải
Ta có
( )
ln ln ln .ab a b=+
Câu 9: Đạo hàm của hàm số
12x
ye
−
=
là
A.
12
2
x
ye
−
=
. B.
12
2
x
ye
−
=−
. C.
12
2
x
e
y
−
=−
. D.
12x
ye
−
=
.
Lời giải
Ta có
( )
1 2 1 2
1 2 2
xx
y x e e
−−
= − = −
.
Câu 10: Tìm tập xác định D của hàm số
( )
2
2
log 2 3y x x= − −
.
A.
(
)
; 1 3;D = − − +
. B.
1;3D =−
.
C.
( ) ( )
; 1 3;D = − − +
. D.
( )
1;3D =−
.
Lời giải
Ta có điều kiện xác định
2
1
2 3 0
3
x
xx
x
−
− −
( ) ( )
; 1 3;D = − − +
.
Câu 11: Cho đồ thị hàm số
x
ya=
và
log
b
yx=
như hình vẽ. Trong các khẳng định sau, đâu là khẳng
định đúng
A.
0 1,0 1ab
. B.
01ab
. C.
1, 1ab
. D.
01ba
.
Lời giải
Ta có đồ thị hàm số
x
ya=
đi lên theo chiều từ trái sang phải nên
1a
.
Đồ thị hàm số
log
b
yx=
đi xuống theo chiều từ trái sang phải nên
01b
.
Câu 12: Nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
3 4 2
39
xx−−
=
0x =
1x =
2x =
3x =

GV. Phan Nhật Linh -
SĐT: 0817 098 716
10
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có: .
Câu 13: Phương trình có nghiệm là
A. . B. . C. . D. .
Lời giải
Ta có .
Câu 14: Tập nghiệm của bất phương trình là
A. . B. . C. . D. .
Lời giải
.
Vậy tập nghiệm của bất phương trình là .
Câu 15: Mỗi đỉnh của bát diện đều là đỉnh chung của bao nhiêu cạnh?
A.
3
. B.
8
. C.
5
. D.
4
.
Lời giải
Câu 16: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và cạnh bên
2SA a=
vuông góc
với đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
2a
. B.
3
4
3
a
. C.
3
2
3
a
. D.
3
a
.
Lời giải
Vì
ABCD
là hình vuông cạnh
a
2
ABCD
Sa=
(đvdt).
( )
SA ABCD⊥
3
2
1 1 2
. 2 .
3 3 3
ABCD
a
V SAS a a = = =
(đvtt)
Câu 17: Cho hình trụ có bán kính đáy
r
và chiều cao
h
. Thể tích của khối trụ bằng
A.
rh
. B.
2
rh
. C.
2 rh
. D.
2
1
3
rh
.
Lời giải
Thể tích của hình trụ là
2
.
d
V S h r h
==
Câu 18: Cho hình nón có chu vi đáy
2
và độ dài đường cao là 3. Diện tích xung quanh của hình nón
bằng
A.
rh
. B.
2
rh
. C.
2 rh
. D.
2
1
3
rh
.
Lời giải
( )
22
3 4 2 3 4
3 9 3 3 3 4 2 4 0
x
x x x
xxx
−
− − −
= = − = − =
( )
1
2
log 1 2x − = −
2x =
5
2
x =
3
2
x =
5x =
( )
1
2
log 1 2x − = −
2
1
1
2
x
−
−=
5x =
2
1
5
25
x
x
−
+
( )
;2−
( )
;1−
( )
1;+
( )
2;+
2 2 2
1
5 5 5 2 2 2
25
x
x x x
x x x
−
++
+
( )
2;= +S

GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HKI
Toán 12
Diện tích xung quanh của hình nón là:
2
.3 3
22
xq
p
S rl l
= = = =
(đvdt)
Câu 19: Cho mặt cầu có đường kính là 6. Diện tích mặt cầu đã cho bằng
A.
12
. B.
36
. C.
48
. D.
2
36
.
Lời giải
Diện tích mặt cầu đã cho là:
2
2 2 2
4 4 .6 36
2
d
S R d
= = = = =
(đvdt)
Câu 20: Cho mặt cầu có chu vi đường tròn lớn là
3
. Thể tích khối cầu đã cho bằng
A.
4
. B.
3,6
. C.
9
2
. D.
8
.
Lời giải
Chu vi đường tròn lớn là:
3
23
2
P R R
= = =
.
Thể tích khối cầu đã cho là:
3
3
4 4 3 9
3 3 2 2
VR
= = =
(đvtt)
Câu 21: Cho hàm số
()y f x=
có đạo hàm
( )
2
'2f x x x=−
. Hàm số
()y f x=
nghịch biến trong khoảng
nào dưới đây?
A.
( )
;1−
. B.
( )
1;2
. C.
( )
1;+
. D.
( )
2;+
.
Lời giải
Ta có:
( ) ( )
2
' 2 0 0;2f x x x x= −
.
Suy ra hàm số nghịch biến trên khoảng
( )
0;2
, do đó hàm số nghịch biến trên khoảng
( )
1;2
.
Câu 22: Cho hàm số
( ) ( )
32
1
2 1 2
3
f x x mx m x= + + − +
. Tất cả các giá trị thực của tham số
m
để hàm số
đã cho có điểm cực trị là
A.
1m
. B.
1m =
. C.
1m
. D.
1m
.
Lời giải
Hàm số đã cho có điểm cực trị khi:
( ) ( )
2
2
1
3. . 2 1 0 1 0 1
3
m m m m− − −
Câu 23: Giá trị lớn nhất của hàm số
2
()
1
x
fx
x
−
=
−
trên đoạn
2;3
bằng
A.
1
2
−
. B.
0
. C.
3−
. D.
2
.
Lời giải
Ta có:
( )
( )
2
1
' 0, 1
1
f x x
x
−
=
−
nên hàm số nghịch biến trên đoạn
2;3
.
Do đó
( ) ( )
2;3
Max 2 0.f x f==
GV. Phan Nhật Linh -
SĐT: 0817 098 716
12
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 24: Cho hàm số
()y f x=
có bảng biến thiên như hình vẽ.
Hỏi hàm số đã cho là hàm số nào trong các hàm số sau?
A.
2
1
x
y
x
=
−
. B.
21
1
x
y
x
−
=
+
. C.
23
1
x
y
x
+
=
+
. D.
21
1
x
y
x
−
=
−
.
Lời giải
Từ bảng biến thiên ta có đồ thị hàm số có hai tiệm cận
1x =−
và
2y =
.
Hơn nữa
0y
. Do đó hàm số thỏa mãn là
21
1
x
y
x
−
=
+
.
Câu 25: Tiệm cận đứng của đồ thị hàm số
2
1
32
x
y
xx
+
=
− + −
là đường thẳng
A.
1x =
. B.
1x =−
. C.
2x =
. D.
1x =
và
2x =
.
Lời giải
Vì
( )
1
lim
x
fx
→
= +
nên đồ thị hàm số có một tiệm cận đứng là đường thẳng
1x =
.
( )
2
lim
x
fx
→
= −
nên đồ thị hàm số có một tiệm cận đứng là đường thẳng
2x =
.
Câu 26: Tập xác định của hàm số
( )
2
2
2 5 3y x x
−
= − +
là
A.
3
\ 1;
2
D
=
. B.
3
\
2
D
=
. C.
\1D =
. D.
D =
.
Lời giải
Ta có
( )
( )
2
2
2
2
1
2 5 3
2 5 3
y x x
xx
−
= − + =
−+
Hàm số xác định khi
2
2 5 3 0xx− +
1
3
2
x
x
.
Vậy tập xác định của hàm số đã cho là
3
\ 1;
2
D
=
Câu 27: Cho
, , a b c
là các số thực khác
0
thỏa mãn
4 25 10
a b c
==
. Tính
.
cc
T
ab
=+
A.
1
10
T =
B.
1
2
T =
C.
2T =
D.
7T =
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HKI
Toán 12
Giả sử
4
25
10
log
4 25 10 log .
log
a b c
at
t b t
ct
=
= = = =
=
Do
, , a b c
là các số thực khác
0
nên
0, 1tt
.
Ta có
10 10
10 10
4 25
log log log 4 log 25
log 4 log 25
log log log 10 log 10
tt
tt
tt
cc
T
a b t t
= + = + = + = +
( )
10 10
log 4.25 log 100 2.= = =
Câu 28: Tập xác định
D
của hàm số
( )
ln 2yx
=−
là
A.
D =
. B.
( )
3;D = +
. C.
( )
0;D = +
. D.
( )
2;D = +
.
Lời giải
Điều kiện xác định:
( )
ln 2 0
21
2 1 3
20
20
x
x
xx
x
x
−
−
−
−
−
.
Tập xác định:
( )
3;D = +
.
Câu 29: Cho hàm số
1
1 ln
y
xx
=
++
với
0x
. Khi đó
2
'y
y
−
bằng
A.
1
x
x +
. B.
1
1
x
+
. C.
1 ln
x
xx++
. D.
1
1 ln
x
xx
+
++
.
Lời giải
( )
2
1 1 1 1
1 ln 1 ln 1
1 ln
y
y x x x x
x x y y x
y
= = + + = + + − = +
++
.
Câu 30: Tập nghiệm của phương trình
2
log( 2 1) log(5 3 )x x x− − = −
A.
3;1−
. B.
3
. C.
3−
. D.
3;2−
.
Lời giải
Ta có:
2
2
2
5
5
5 3 0
3
3
log( 2 1) log(5 3 ) 3
2
2 1 5 3
60
3
x
x
x
x x x x
x
x x x
xx
x
−
− − = − = −
=
− − = −
+ − =
=−
Câu 31: Tổng tất cả các nghiệm của phương trình:
2
33
28
x x x− − −
=
A.
0
. B.
3
. C.
3−
. D.
23
.
Lời giải
Ta có
22
3 3 3 3 3 2 2
3
2 8 2 2 3 3 3 3
3
x x x x x x
x
x x x x
x
− − − − − −
=
= = − − = − =
=−
Tổng các nghiệm của phương trình là
3 3 0T =−=
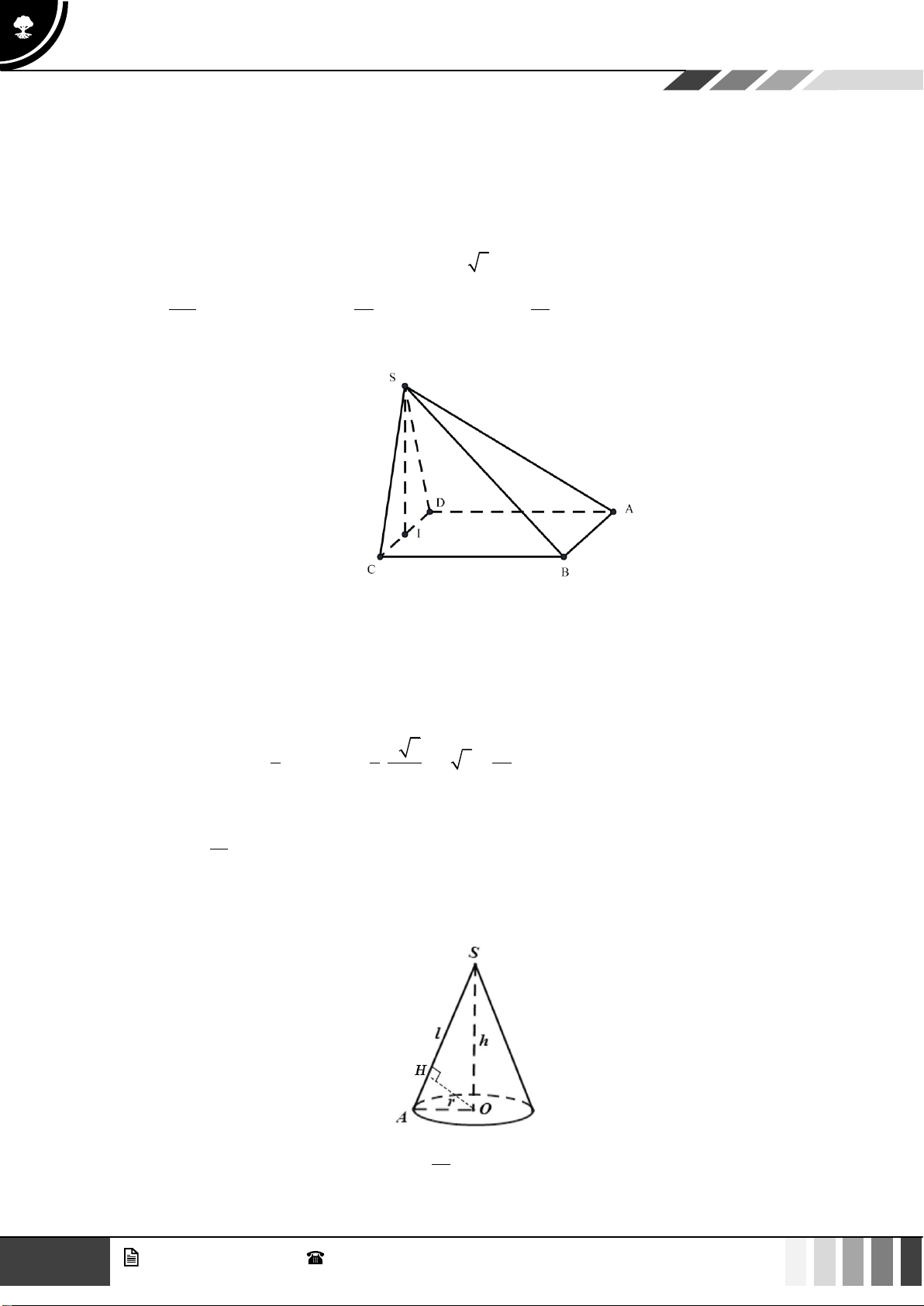
GV. Phan Nhật Linh -
SĐT: 0817 098 716
14
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 32: Khối bát diện đều là khối đa diện đều loại nào?
A.
3;3
. B.
3;5
. C.
4;3
. D.
3;4
.
Lời giải
Ta có khối bát diện đều là khối đa diện đều loại
3;4
.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, tam giác
SCD
đều và nằm trong mặt
phẳng vuông góc với đáy,
CD a=
,
3BC a=
. Thể tích khối chóp
.S ABCD
bằng
A.
3
3
2
a
B.
3
6
a
C.
3
2
a
D.
3
a
Lời giải
Gọi
I
là trung điểm
CD
SI CD⊥
.
Ta có
( ) ( )
( ) ( )
( )
;
SCD ABCD
SCD ABCD CD
SI SCD SI CD
⊥
=
⊥
( )
SI ABCD⊥
.
Do đó
3
.
1 1 3
. . . . 3
3 3 2 2
S ABCD ABCD
aa
V SI S a a= = =
.
Câu 34: Cho khối nón có bán kính đáy bằng
3
và khoảng cách từ tâm của đáy đến một đường sinh bất
kỳ bằng
12
5
. Thể tích của khối nón đã cho bằng
A.
36
B.
12
C.
18
D.
24
Lời giải
Theo giả thiết ta có:
12
3;
5
r OA OH= = =
.
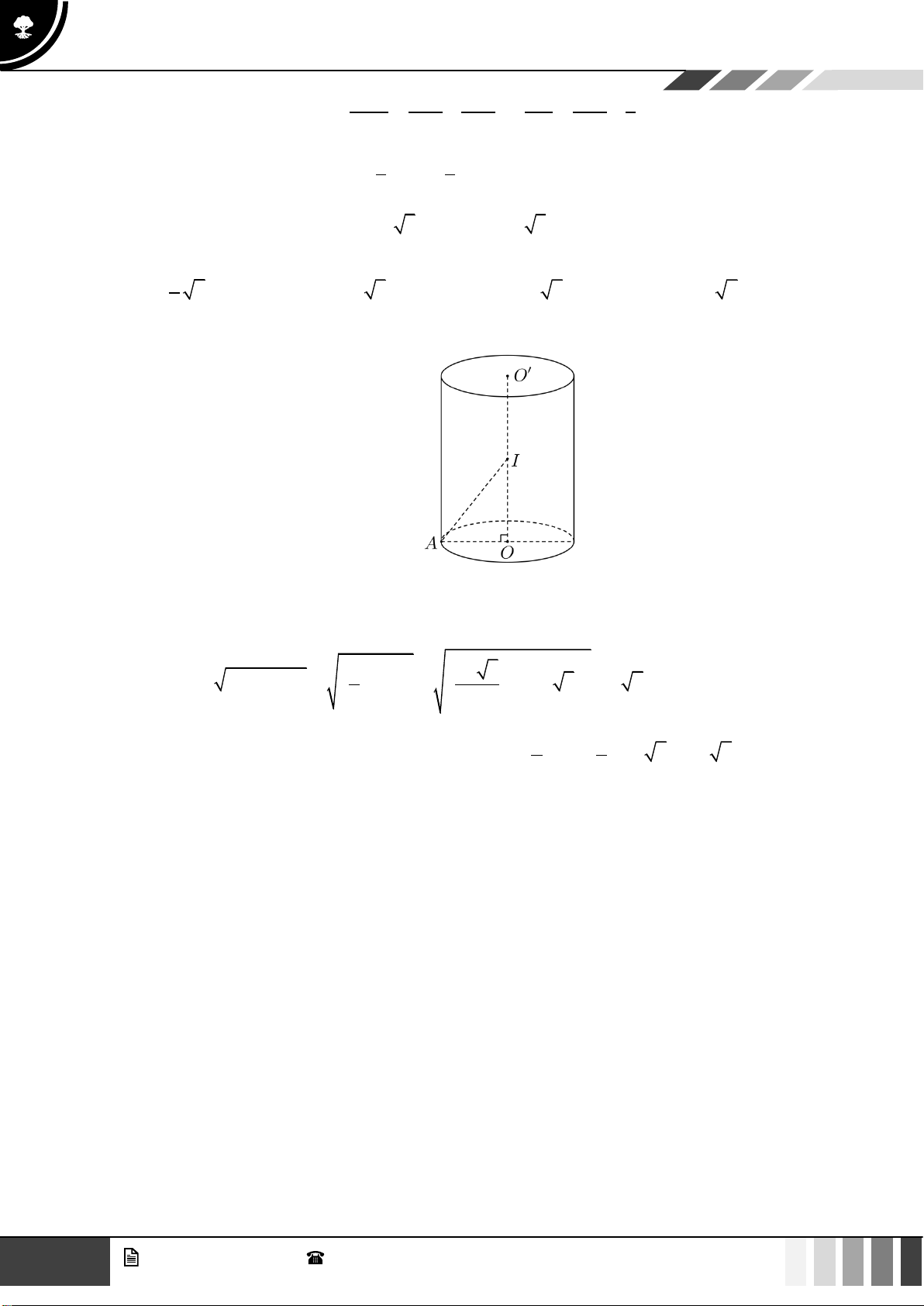
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HKI
Toán 12
Xét
SOA
vuông ở
O
có:
2 2 2 2
1 1 1 25 1 1
4
144 9
SO h
OH SO OA SO
= + = + = =
.
Do đó thể tích khối nón là
22
11
. .3 .4 12
33
V r h
= = =
.
Câu 35: Một khối trụ có bán kính đáy là
3,a
chiều cao
2 3.a
Thể tích của khối cầu ngoại tiếp khối trụ
là
A.
3
4
6
3
a
B.
3
43a
C.
3
66a
D.
3
86a
Lời giải
Gọi
I
là trung điểm của
.OO
Khi đó bán kính mặt cầu ngoại tiếp hình trụ đã cho là
( )
2
2
2
2 2 2
23
3 6.
22
ha
R IA OI OA r a a
= = + = + = + =
Vậy thể tích của khối cầu ngoại tiếp khối trụ là
( )
3
33
44
. 6 8 6
33
V R a a
= = =
.
Câu 36: Bạn Hoa được gia đình gửi vào sổ tiết kiệm 100 triệu đồng với lãi suất 0,5% một tháng theo hình
thức lãi kép. Nếu mỗi tháng Hoa rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì hàng
tháng Hoa rút ra số tiền gần nhất với số nào sau đây để đúng 4 năm vừa hết số tiền trong sổ tiết
kiệm?
A.
2.351.000
. B.
2.392.000
. C.
2.306.000
. D.
2.349.000
.
Lời giải
Gọi số tiền bạn Hoa rút ra hàng tháng là
x
(triệu đồng)
( )
0x
, số tiền ban đầu là
P
(triệu
đồng)
( )
0P
, lãi suất tiền gửi hàng tháng là
r
,
( )
0r
.
Lãi suất nhận được sau tháng thứ nhất là:
.Pr
(triệu đồng).
Số tiền cuối tháng thứ nhất sau khi rút còn lại:
( )
1
1P P r x= + −
(triệu đồng).
Lãi suất nhận được sau tháng thứ hai là:
1
.Pr
(triệu đồng).
Số tiền cuối tháng thứ hai sau khi rút còn lại:
( ) ( ) ( )
2
21
1 1 1P P r x P r x r x= + − = + − + −
(triệu
đồng).

GV. Phan Nhật Linh -
SĐT: 0817 098 716
16
Tuyển tập 10 đề ôn HKI
Toán 12
Cứ như thế, số tiền còn lại sau
n
tháng là:
( ) ( ) ( ) ( )
12
1 1 1 .... 1
n n n
n
P P r x r x r x r x
−−
= + − + − + − − + −
( )
( )
11
1.
n
n
n
r
P P r x
r
+−
= + −
(triệu đồng).
Sau 48 tháng, số vừa hết khi và chỉ khi
0
n
P =
( )
( )
48
48
11
1 . 0
r
P r x
r
+−
+ − =
( )
( )
48
48
1,005 1
100 1,005 . 0
0,005
x
−
− =
2,349x
(triệu đồng).
Câu 37: Có bao nhiêu giá trị nguyên của
2023;2023m−
để hàm số
2
2
2
mx
xm
y
+
+
=
đồng biến trên
( )
1;2
?
A.
4041
. B.
4044
. C.
4042
. D.
4040
Lời giải
Điều kiện xác định của hàm số:
2
m
x −
Đạo hàm
( )
2
2
2
2
4
2 ln2
2
mx
xm
m
y
xm
+
+
−
=
+
.
Hàm số đồng biến trên
( )
1;2
( )
2
40
22
1
0, 1;2 4 2.
2
2
4
2
2
m
mm
m
y x m m
m
m
m
−
−
−
−
−
−
−
.
Kết hợp điều kiện:
(
2023;2023 2023; 4 2;2023 .
mm
mm
− − −
Vậy có
4041
giá trị
m
thỏa yêu cầu bài toán.
Câu 38: Cho
2023!x =
. Tính
2023 2023 2023 2023
2 3 2022 2023
1 1 1 1
...
log log log log
T
x x x x
= + + + +
.
A.
2022T =
. B.
1
2023
T =
. C.
1
2022
T =
. D.
2023T =
.
Lời giải
Ta có:
2023 2023 2023 2023
2 3 2022 2023
1 1 1 1
...
log log log log
T
x x x x
= + + + +
2023 2023 2023 2023
log 2 log 3 ... log 2022 log 2023
x x x x
= + + + +
2023.log 2 2023.log 3 ... 2023.log 2022 2023.log 2023
x x x x
= + + + +
( )
2023. log 2 log 3 ... log 2022 log 2023
x x x x
= + + + +

GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HKI
Toán 12
( )
2023.log 2.3.....2022.2023
x
=
2023!
2023.log 2023!=
2023=
.
Vậy
2023T =
.
Câu 39: Biết nghiệm lớn nhất của phương trình
( )
2
1
log log 10 log4 2
2
xx+ + + =
là
x a b c=+
(
,,abc
là các số nguyên). Giá trị của
abc++
bằng
A. 0. B. -
6
. C.
2−
. D.
2
Lời giải
Điều kiện xác định:
2
0
10 0
x
x
+
0
10
x
x
−
.
Ta có:
( )
2
1
log log 10 2 log4
2
xx+ + = −
( )
log log 10 log25xx+ + =
.
( )
( )
log . 10 log25xx+=
. (*)
Với
0x
thì (*)
2
10 25 0xx + − =
5 5 2( )
5 5 2( )
xn
xl
= − +
= − −
.
Với
10 0x−
thì (*)
2
10 25 0xx − − − =
5x = −
(nhận).
Nghiệm lớn nhất của phương trình là
5 5 2 5, 5,c 2 2x a b a b c= − + = − = = + + =
.
Câu 40: Gọi
S
là tập chứa tất cả những giá trị nguyên
[ 24;24]m−
để bất phương trình
( )
22
sin 1 cos
3 2 1 3 4
xx
m
+
+ −
đúng với mọi
x
nằm trên . Số phần tử của tập
S
là:
A. 18. B. 19. C. 21. D. 24.
Lời giải
Đặt
2 2 2
2
sin 0 1 1 cos 2 sin
sin
99
3 3 ;3 [1;3] 3 3
3
x x x
x
t
t
+−
= = = = =
Bất phương trình trở thành:
( ) ( )
2
9
2 1 4 9 2 1 4t m m t t
t
+ − − −
với
[1;3]t
Ta đặt
( )
2
4f t t t=−
( ) ( )
( )
2
[1;3] [1;3]
9 2 1 max max 4 4
xx
m f t t t
− = − =
Suy ra
( )
13
9 2 1 4 1 24
18
m m m−
Có 24 giá trị nguyên của
m
thỏa mãn.
Câu 41: Cho hình lập phương
.ABCD A B C D
. Gọi
, , , , ,I J K L M N
lần lượt là tâm của 6 mặt hình
vuông. Khi đó khối đa diện
IJKLMN
là khối gì?
A. Khối lăng trụ tam giác đều. B. Khối lăng trụ tam giác.
C. Khối đa diện đều loại
4;3
. D. Khối bát diện đều.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
18
Tuyển tập 10 đề ôn HKI
Toán 12
Nếu gọi cạnh đáy của hình lập phương là
a
. Khi đó tất cả các cạnh của khối
IJKLMN
bằng
2
2
a
,
Lại có
ML
//
CB
và
MJ
//
CB
suy ra
ML MJ⊥
. Do đó tứ giác KJML là hình vuông.
Vậy khối
IJKLMN
là khối bát diện đều.
Câu 42: Cho hình lăng trụ
.ABC A B C
, đáy
ABC
là tam giác vuông cân tại
C
. Hình chiếu vuông góc
của
A
trên mặt phẳng
( )
ABC
là trọng tâm
G
của tam giác
ABC
. Biết diện tích tam giác
A AB
bằng
2
3
, góc giữa hai mặt phẳng
( )
A AB
và
( )
ABC
bằng
60
. Tính thể tích khối lăng trụ
.ABC A B C
.
A.
1
3
. B. 3. C.
3
. D.
3
3
.
Lời giải
Gọi
I
là trung điểm
AB
. Góc giữa hai mặt phẳng
( )
A AB
và
( )
ABC
là góc
60A IC
=
.
Đặt
AB x=
. Ta có:
1 1 1
.
3 3 2 6
x
IG IC AB= = =
.
Khi đó:
1
6
cos
23
x
IG x
A IG A I
A I A I
= = =
.
2 1 2 1 2
. . . . 2
3 2 3 2 3 3
A AB
x
S A I AB x x
= = = =
và
22
3
3
A G A I IG
= − =
.
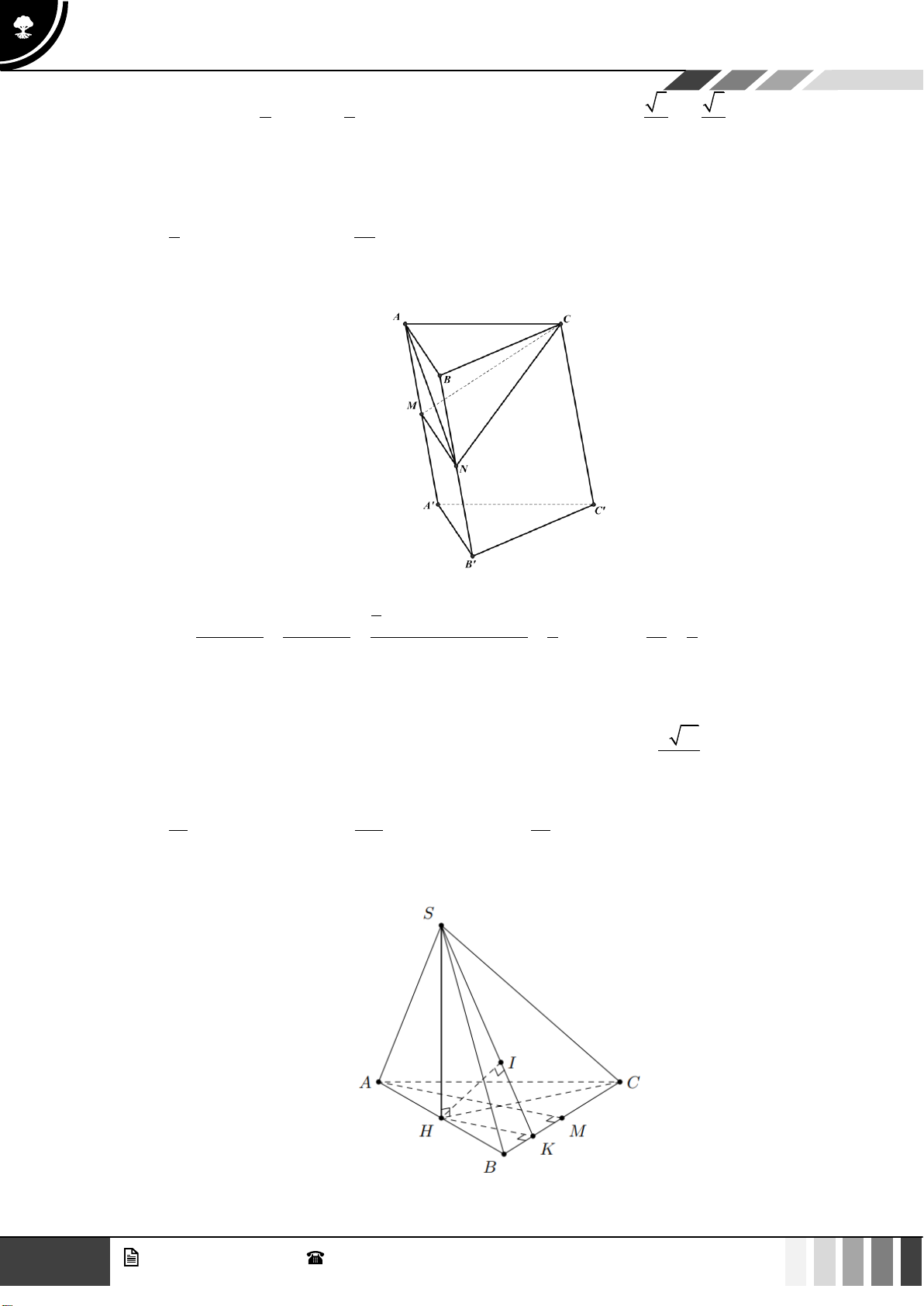
GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HKI
Toán 12
Suy ra:
11
. . .1.2 1
22
ABC
S CI AB= = =
. Vậy
.
33
. .1
33
ABC A B C ABC
V A G S
= = =
.
Câu 43: Cho khối lăng trụ
ABC A B C
có thể tích bằng
27
.
,MN
lần lượt là trung điểm các cạnh
,AA BB
. Thể tích khối chóp
MNAC
bằng:
A.
9
2
. B.
27
2
. C.
9
. D.
3
Lời giải
Ta có:
( )
( )
( )
( )
..
1
. . ,
1 27 9
3
6 6 2
.,
ABC
MNAC CABN
MNAC
ABC A B C ABC A B C
ABC
S d N ABC
VV
V
VV
S d B ABC
= = = = =
.
Câu 44: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều,
SAB
vuông góc với đáy
ABC
và tam
giác
SAB
đều, khoảng cách từ điểm
A
tới mặt phẳng
SCB
bằng
2 15
5
a
. Thể tích của khối
chóp
.S ABC
là
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
a
. D.
3
a
.
Lời giải
Gọi
H
và
M
lần lượt là trung điểm của
AB
và
BC
.
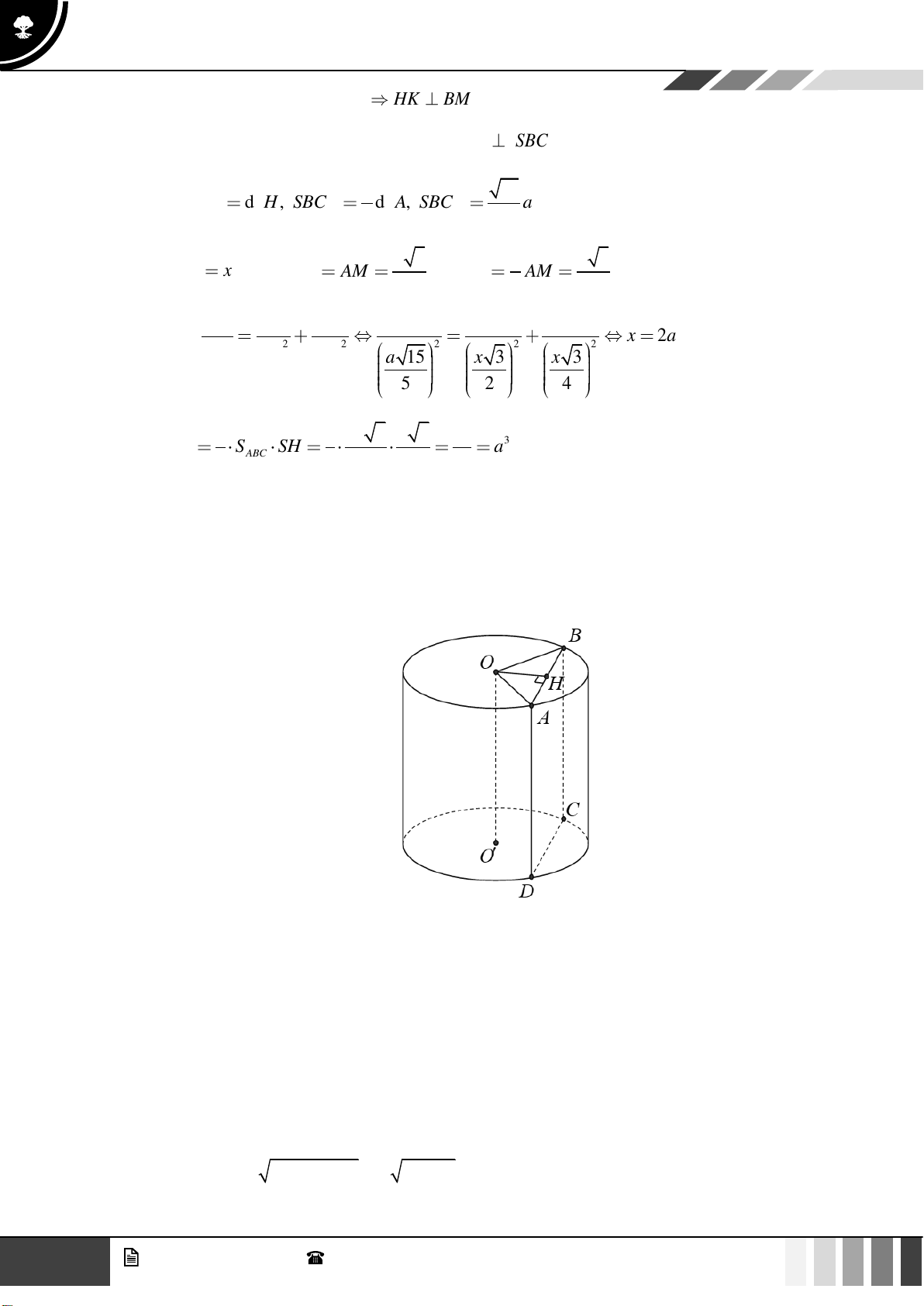
GV. Phan Nhật Linh -
SĐT: 0817 098 716
20
Tuyển tập 10 đề ôn HKI
Toán 12
Gọi
K
là trung điểm của
BM HK BM
.
Gọi
I
là hình chiếu của
H
lên
SK
suy ra
HI SBC
.
Khi đó
1 15
d , d ,
25
HI H SBC A SBC a
.
Đặt
AB x
suy ra
3
2
x
SH AM
và
13
24
x
HK AM
.
Do đó:
2 2 2
2 2 2
1 1 1 1 1 1
2
15 3 3
5 2 4
xa
HI HS HK
a x x
.
Vậy
23
3
1 1 3 3
3 3 4 2 8
ABC
x x x
V S SH a
.
Câu 45: Một hình trụ có bán kính đáy
5cmr =
và khoảng cách giữa hai đáy
8cmh =
. Cắt khối trụ bởi
một mặt phẳng song song với trục và cách trục
4cm
. Diện tích của thiết diện được tạo thành là
A.
( )
2
48 cm
. B.
( )
2
56 cm
. C.
( )
2
42 cm
. D.
( )
2
44 cm
.
Lời giải
Gọi
O
,
O
là tâm của hai đáy của hình trụ và
( )
P
là mặt phẳng song song với trục và cách trục
OO
một khoảng
4cm
.
( )
P
cắt hai hình tròn đáy
( )
O
,
( )
O
theo hai dây cung lần lượt là
AB
,
CD
và cắt mặt xung
quanh theo hai đường sinh là
AD
,
BC
. Khi đó
ABCD
là hình chữ nhật.
Gọi
H
là trung điểm của
AB
. Ta có
( )
OH AD
OH ABCD
OH AB
⊥
⊥
⊥
( )
( )
( )
( )
, , 4d OO P d O ABCD OH cm
= = =
.
2AB AH=
22
2 OA OH=−
22
2 5 4 6= − =
;
'AD OO=
8cmh==
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy diện tích hình chữ nhật
ABCD
là:
( )
2
. 8.6 48
ABCD
S AB AD cm= = =
Câu 46: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
42
2 1 3 2 1 , .f x x x x x m x
= + + + −
Số giá trị
nguyên của tham số
2024;2024m−
để hàm số
( ) ( )
2 2024g x f x= − +
đồng biến trên
khoảng
( )
3;+
?
A.
2022.
B.
2020
. C.
2019.
D.
2023
.
Lời giải
Ta có
( ) ( ) ( ) ( )
( )
4
2
2 2 5 2 7 2 9 .g x f x x x x x m
= − − = − − − − + +
Để hàm số
( )
gx
đồng biến trên
( ) ( ) ( )
3; 0, 3;g x x
+ +
( ) ( )
( )
( )
4
2
2 5 2 7 2 9 0, 3;x x x x m x − − − − + + +
( )
2
7 2 9 0, 3;x x m x − + + +
(do
( ) ( )
4
2 5 2 0, 3x x x− − −
)
)
)
( )
22
3;
2 7 9, 3; 2 7 9 .m x x x m max x x
+
− + − + − + −
Xét
)
2
7 9, 3; .y x x x= − + − +
Ta có
2 7.yx
= − +
Cho
7
0 2 7 0 .
2
y x x
= − + = =
Bảng biến thiên:
Do đó ta có
)
( )
2
3;
13
79
4
Max x x
+
− + − =
13 13
2.
48
mm
Mà
, 2024;2024 2;3;4;...;2024 .m m m −
Vậy có
2023
tham số
m
thỏa mãn yêu cầu bài toán.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm
( )
( )( )
22
42f x x x x
= − −
, với
x
. Tổng các giá trị
nguyên của tham số
m
để hàm số
( )
( )
32
3g x f x x m= − +
có số điểm cực trị nhiều nhất là
A.
1
. B.
3
. C.
6
. D.
5
.
Lời giải
Theo đề bài ta có:
( )
( )( )
( )( )
2
22
4 2 2 2f x x x x x x x
= − − = + −
GV. Phan Nhật Linh -
SĐT: 0817 098 716
22
Tuyển tập 10 đề ôn HKI
Toán 12
Ta lại có:
( )
( ) ( )
2 3 2
3 6 . 3g x x x f x x m
= − − +
( )
( )( )( )( )
2
2 3 2 3 2 3 2
3 6 3 3 2 3 2g x x x x x m x x m x x m
= − − + − + + − + −
( )
( )
( )
( )
32
32
32
0; 2
3 1
0
3 2 2
3 2 3
xx
x x m
gx
x x m
x x m
==
− = −
=
− = − −
− = − +
Ta thấy (1), (2), (3) không có nghiệm chung và
( )
2
32
3 2 0x x m− + −
với
.x
Để hàm số
( )
gx
có số điểm cực trị nhiều nhất thì các phương trình (1), (2) đều có ba nghiệm
phân biệt khác 0 và 2.
Xét hàm số
( )
32
3h x x x=−
với mọi
x
ta có đạo hàm
( )
2
36h x x x
=−
.
Giải phương trình:
( )
2
0
3 6 0
2
x
h x x x
x
=
= − =
=
Bảng biến thiên:
Từ bảng biến thiên ta thấy để phương trình
( ) ( )
1 , 2
đều có ba nghiệm phân biệt khác 0 và 2 thì
4 0 0 4
02
4 2 0 2 2
mm
m
mm
− −
− − − −
Do
m
nên
1m =
Tổng các giá trị nguyên của
m
thỏa mãn yêu cầu đề bài là
1.
Câu 48: Cho các số thực
,xy
thỏa mãn
( )
2e
ln 2 2 2
2
x
x y x
xy
+ + +
+
. Giá trị nhỏ nhất của
y
là
A.
2
. B.
1
. C.
1−
. D.
3
.
Lời giải
Điều kiện:
20xy+
.
Ta có
( )
2e
ln 2 2 2
2
x
x y x
xy
+ + +
+
( )
e1
ln 2 1
2
2
x
x y x
xy
+ + +
+
ln 2
e
ln 2 1
e
x
xy
x y x
+
+ + +
( )
ln 2
e ln 2 1
x x y
x x y
−+
− − +
( )
1
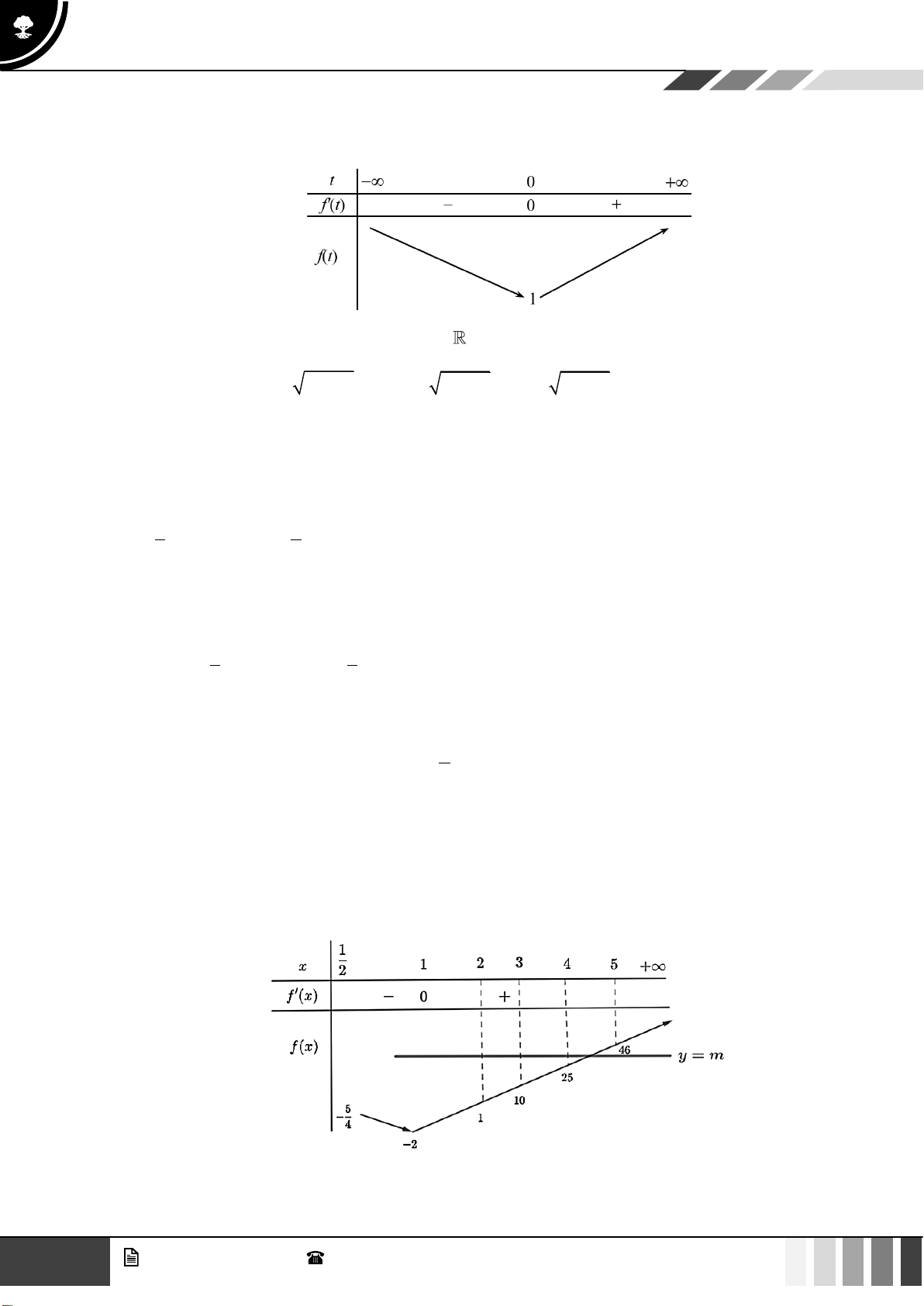
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HKI
Toán 12
Xét hàm số
( )
e
t
f t t=−
. Có
( )
e1
t
ft
=−
;
( )
0 e 1 0
t
f t t
= = =
.
Bảng biến thiên:
Từ bảng biến thiên, ta thấy
( )
1,f t t
. Nên
( ) ( )
1 1 0f t f t t = =
.
Khi đó
( )
1 ln 2 0x x y − + =
ln 2x y x + =
2e
x
xy + =
2
e 2 1
x
yx = −
(từ bảng
biến thiên của hàm số
()ft
).
Vậy
y
đạt giá trị nhỏ nhất bằng
1
khi
0x =
.
Câu 49: Gọi S là tập hợp các giá trị nguyên của tham số m để tập nghiệm của bất phương trình
(
)
( )
2
22
log 2 2log 2 1
11
0
55
x x m x+ + −
−
chứa đúng 4 số nguyên. Số phần tử của
S
bằng:
A. 15. B.
21.
C. 20. D. 16.
Lời giải
Ta có :
(
)
( )
2
22
log 2 2log 2 1
11
55
x x m x+ + −
( )
( ) ( )
2
22
log 2 2log 2 1 *x x m x + + −
Điều kiện xác định :
2
20
1
2 1 0
2
x x m
xx
+ +
−
( ) ( )
2
2
* 2 2 1x x m x + + −
2 2 2
2 4 4 1 3 6 1x x m x x m x x + + − + − +
Đặt
( )
2
3 6 1f x x x= − +
có
( )
6 6 0 1f x x x
= − = =
Bảng biến thiên :
Yêu cầu bài toán
25 46 26;27;28;...;46mm

GV. Phan Nhật Linh -
SĐT: 0817 098 716
24
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy có 21 giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 50: Có bao nhiêu số nguyên
m
để phương trình
( )
( )
ln 2sin ln 3sin sinm x m x x+ + + =
có nghiệm
thực?
A.
5
. B.
6
. C.
3
. D.
4
.
Lời giải
Điều kiện:
( )
3sin 0
2sin ln 3sin 0
mx
m x m x
+
+ + +
.
Phương trình đã cho
( )
sin
2sin ln 3sin e
x
m x m x + + + =
( )
sin
3sin ln 3sin e sin
x
m x m x x + + + = +
( )
( )
ln 3sin
sin
e ln 3sin e sin
mx
x
m x x
+
+ + = +
( )
1
Xét hàm số
( )
e,
t
f t t t= +
có
( )
e 1 0,
t
f t t
= +
nên hàm số
( )
ft
đồng biến trên .
Vậy
( ) ( ) ( )
1 ln 3sin sinf m x f x + =
( )
ln 3sin sinm x x+=
Đặt
sinax=
,
1;1a−
.
Phương trình trở thành:
( )
ln 3m a a+=
e3
a
am = −
.
Xét
( )
e 3 , 1;1
a
g a a a= − −
;
( )
e 3 0, 1;1
a
g a a
= − −
.
Hàm số
( )
ga
luôn nghịch biến trên
1;1−
.
Phương trình có nghiệm thực khi và chỉ khi
( ) ( )
11g m g −
1
e 3 3
e
m − +
.
Mà
mZ
nên
0;1;2;3m
.
Vậy có
4
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HKI
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Tính diện tích xung quanh của khối trụ có chiều cao
2h =
và bán kính đáy
3R =
.
A.
36
xq
S
=
. B.
4
xq
S
=
. C.
6
xq
S
=
. D.
12
xq
S
=
.
Câu 2: Số đường tiệm cận của đồ thị hàm số
19
2
y
x
=
+
là
A. 0. B. 1. C. 3. D. 2.
Câu 3: Công thức tìm thể tích khối lăng trụ nghiêng có độ dài cạnh bên
l
, chiều cao
h
và diện tích đáy
B
là
A.
V Bl=
. B.
1
3
V Bh=
. C.
V Bh=
. D.
V Bl
=
.
Câu 4: Hình tròn xoay tạo ra khi quay một đường thẳng quanh trục là đường thẳng song song với nó gọi
là gì?
A. Hình trụ. B. Mặt trụ. C. Hình lăng trụ. D. Mặt nón.
Câu 5: Tập xác định của hàm số
( )
3
21yx
−
=+
là:
A.
1
;
2
D
= − −
. B.
1
\
2
D
=−
. C.
1
;
2
D
= − +
. D.
1
;
2
D
= − +
.
Câu 6: Cho khối nón
( )
C
có bán kính đáy
R
và độ dài đường sinh
l
và chiều cao
h
. Công thức nào
sau đây đúng?
A.
2
1
3
V R l
=
. B.
2
V R l
=
. C.
2
1
3
V R h
=
. D.
2
V R h
=
.
Câu 7: Cho khối nón
( )
C
, có bán kính đáy
3R =
và độ dài đường sinh
4l =
. Tính chiều cao
h
của khối
nón?
A.
13h =
. B.
1h =
. C.
7h =
. D.
5h =
.
Câu 8: Đồ thị hàm số
( )
2022
2023
x
fx
x
−
=
+
có bao nhiêu điểm cực đại?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 9: Cho khối cầu bán kính
2R
. Gọi
V
là thể tích khối cầu và
S
là diện tích mặt cầu. Công thức nào
sau đây đúng?
A.
( )
3
4
2
3
VR
=
. B.
( )
3
42SR
=
. C.
2
4SR
=
. D.
3
4
3
VR
=
.
Câu 10: Có bao nhiêu loại đa diện đều mà các mặt là các tam giác đều.
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 11: Tìm tập nghiệm của phương trình:
( )
3
log 3 2x−=
.
A.
( )
3;S = − +
. B.
6S =−
. C.
0S =
. D.
3S =−
.
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
07
ĐỀ SỐ
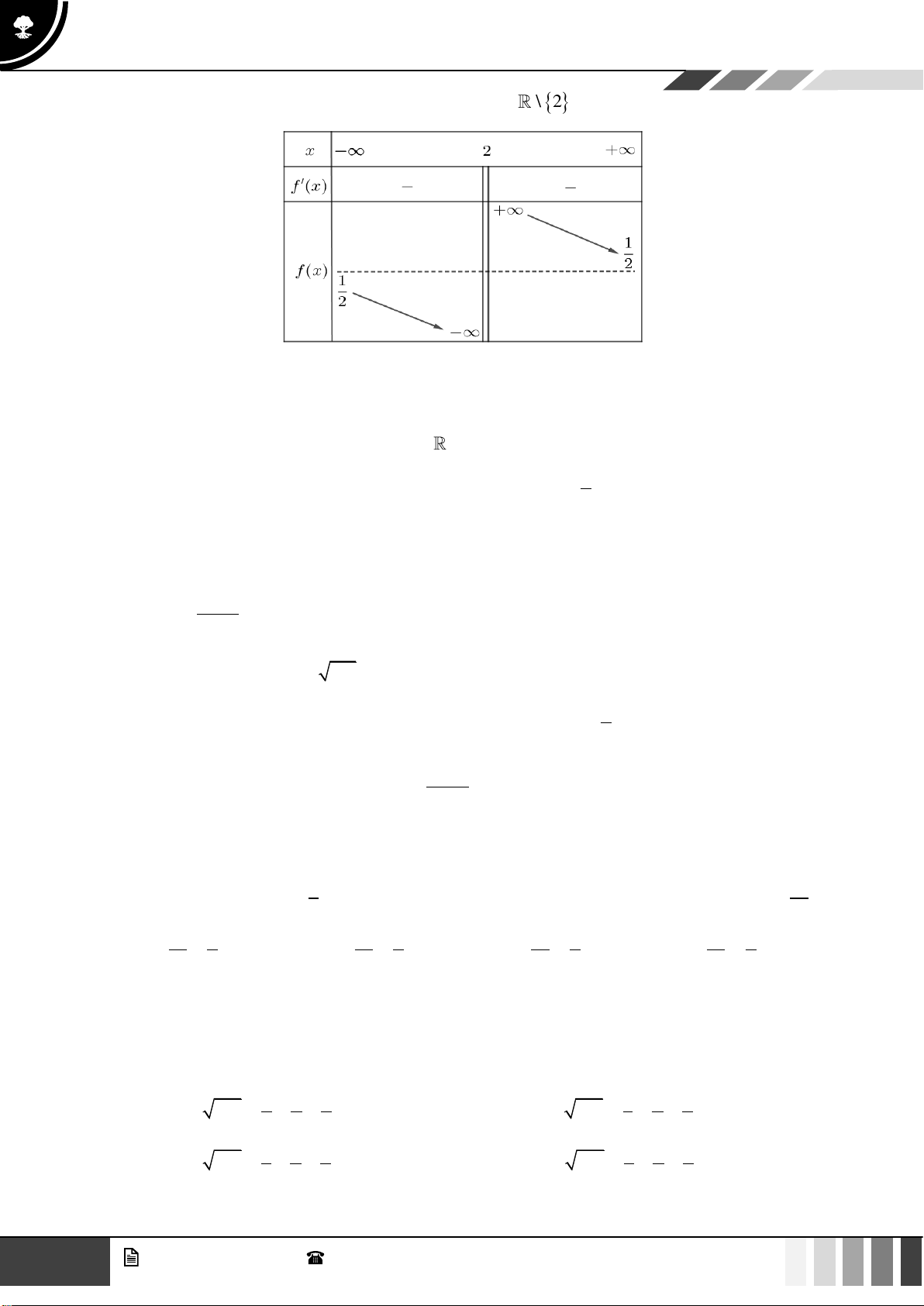
GV. Phan Nhật Linh -
SĐT: 0817 098 716
2
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 12: Cho hàm số
( )
y f x=
xác định, liên tục trên
\2D =
và có bảng biến thiên như sau:
Khẳng định nào sau đây sai?
A. Hàm số
( )
y f x=
không có cực trị.
B. Hàm số
( )
y f x=
nghịch biến trên .
C. Đồ thị hàm số
( )
y f x=
có đường tiệm cận ngang
1
2
y =
.
D. Đồ thị hàm số
( )
y f x=
có đường tiệm cận đứng
2x =
.
Câu 13: Cho các số thực dương
a
,
b
,
x
thỏa
3 3 3
log 10log 7logx a b=+
. Tìm
x
.
A.
10 7
1
x
ab
=
. B.
10 7
x a b=+
. C.
10 7x a b=+
. D.
10 7
x a b=
.
Câu 14: Giải bất phương trình
( )
3
1
101 101
x
x+
.
A.
(
;2S = −
. B.
( )
;0S = −
. C.
1
;
2
S
= −
. D.
( )
;2S = −
.
Câu 15: Với giá trị nào của
m
thì hàm số
2
xm
y
x
−
=
−
đồng biến trên từng khoảng xác định?
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Câu 16: Cho khối nón có thể tích
V
. Nếu tăng bán kính đáy của khối nón lên
2
lần, nhưng giảm chiều
cao của khối nón còn
1
3
chiều cao ban đầu thì khối nón mới có thể tích
V
. Tính tỷ số
V
V
A.
2
3
V
V
=
. B.
1
6
V
V
=
. C.
3
4
V
V
=
. D.
4
3
V
V
=
.
Câu 17: Giá trị lớn nhất của hàm số
( )
42
4 10f x x x=− + +
trên đoạn
0;2
là
A.
12−
. B.
15
. C.
6
. D.
14
.
Câu 18: Nếu
2
log 3a =
;
2
log 5b =
thì
A.
6
2
1
log 180
6 3 6
ab
= + +
. B.
6
2
1
log 180
3 3 6
ab
= + +
.
C.
6
2
1
log 180
3 3 3
ab
= + +
. D.
6
2
1
log 180
3 2 6
ab
= + +
.
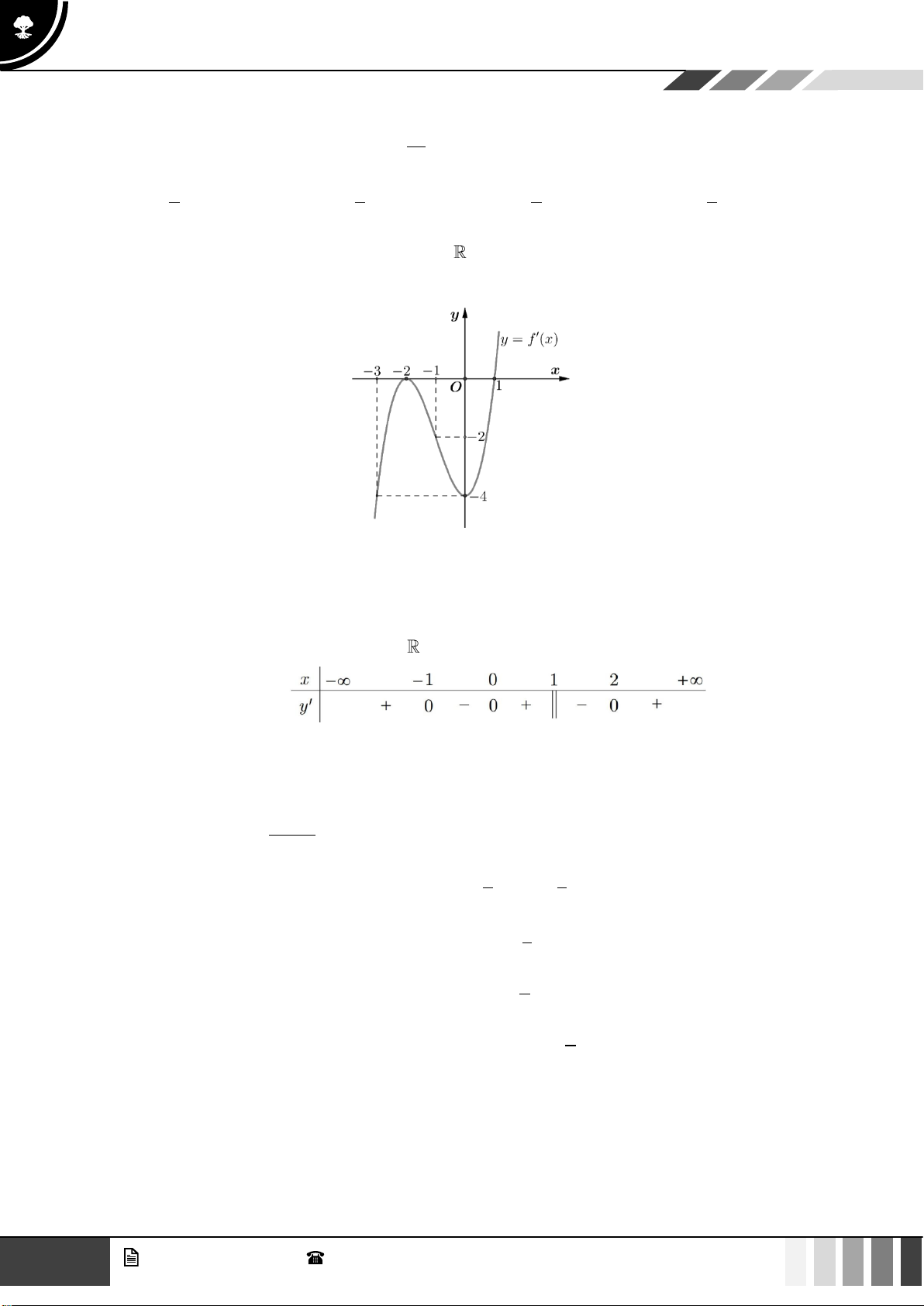
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 19: Cho khối hộp
.ABCD A B C D
. Mặt phẳng
( )
AB D
chia khối hộp thành hai phần có thể tích
tương ứng là
( )
1 2 1 2
;V V V V
. Tỉ số
1
2
V
V
bằng
A.
1
4
. B.
1
5
. C.
1
6
. D.
1
3
.
Câu 20: Cho hàm số
( )
y f x=
có đạo hàm trên và hàm số
( )
y f x
=
là hàm số bậc ba có đồ thị là
đường cong trong hình vẽ.
Hàm số
( )
y f x=
nghịch biến trên
A.
( )
;1−
. B.
( )
2;0−
. C.
( )
1; +
. D.
( )
1;− +
.
Câu 21: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét dấu đạo hàm như hình vẽ:
Hàm số đã cho có bao nhiêu điểm cực đại?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 22: Cho hàm số
23
31
x
y
x
−
=
+
. Phát biểu nào sau đây sai?
A. Hàm số đồng biến trên các khoảng
1
;
3
− −
và
1
;
3
− +
.
B. Đồ thị hàm số có đường tiệm cận đứng là
1
3
x =−
.
C. Đồ thị hàm số có đường tiệm cận ngang là
2
3
y =
.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
3
2
.
Câu 23: Cho hàm số bậc ba
( )
y f x=
có đồ thị đạo hàm
( )
'y f x=
như hình sau:
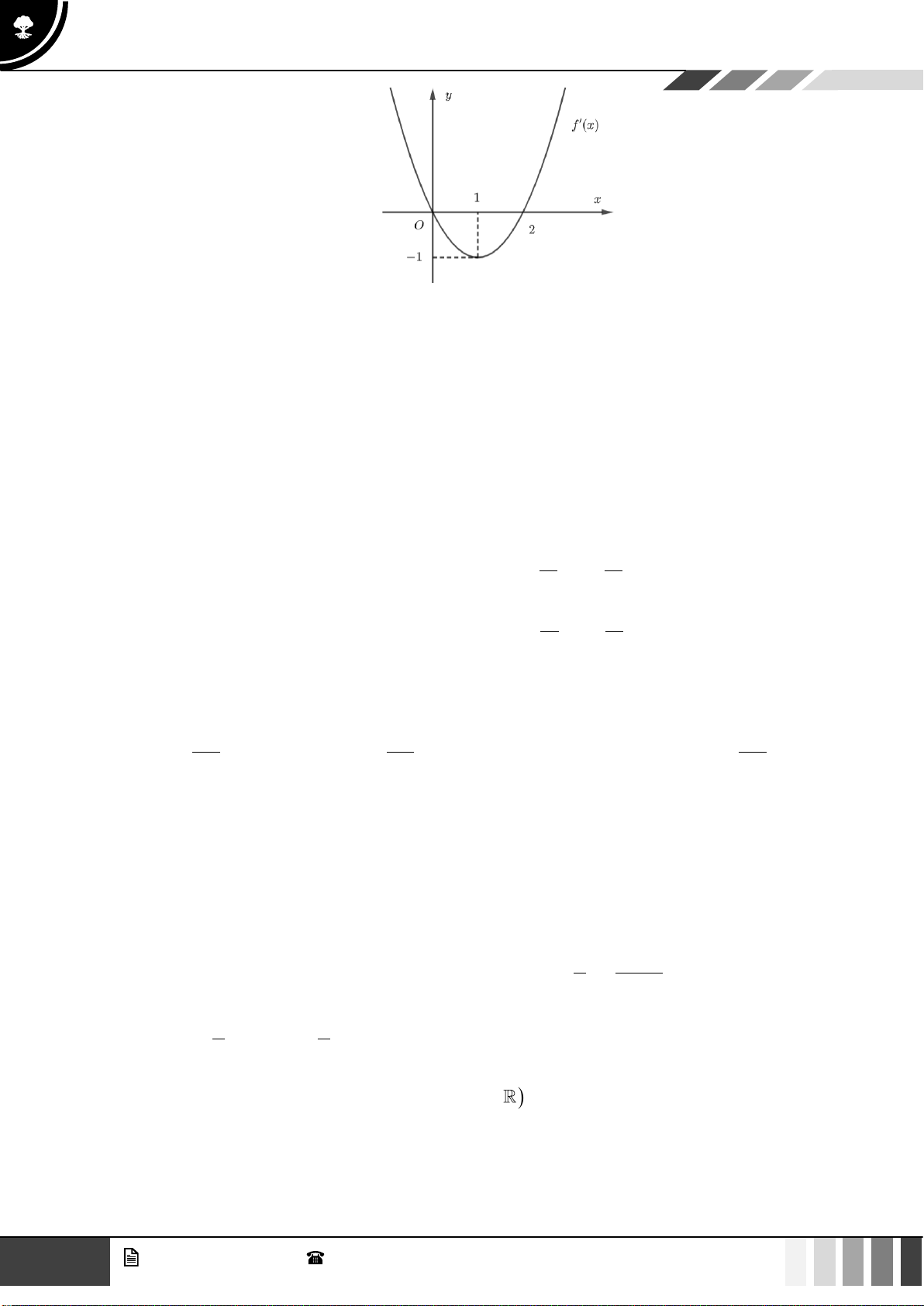
GV. Phan Nhật Linh -
SĐT: 0817 098 716
4
Tuyển tập 10 đề ôn HKI
Toán 12
Hàm số đã cho nghịch biến trên khoảng nào?
A.
( )
1;2 .
B.
( )
3;4 .
C.
( )
2;3 .
D.
( )
1;0 .−
Câu 24: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chóp có đáy là hình thoi luôn có mặt cầu ngoại tiếp.
B. Hình lăng trụ đứng luôn có mặt cầu ngoại tiếp.
C. Hình chóp có đáy là hình thang cân luôn có mặt cầu ngoại tiếp.
D. Hình lăng trụ có đáy là hình chữ nhật luôn có mặt cầu ngoại tiếp.
Câu 25: Cho
,xy
là các số thực. Chọn mệnh đề đúng trong các mệnh đề sau:
A.
10 10
xy
xy
. B.
11
10 10
xy
xy
.
C.
10 10
xy
xy
. D.
11
10 10
xy
xy
.
Câu 26: Giả sử cứ sau mỗi năm diện tích rừng của nước ta giảm
x
phần trăm diện tích hiện có. Hỏi sau
5
năm nữa diện tích rừng của nước ta sẽ là bao nhiêu phần diện tích hiện nay?
A.
5
1
100
x
−
. B.
5
1
100
x
−
. C.
( )
100 5 %x−
. D.
5
1
100
x
−
.
Câu 27: Cắt hình trụ có bán kính
( )
1RR
bởi một mặt phẳng đi qua trục của nó ta được một hình chữ
nhật có diện tích
2
12cm
. Tính diện tích xung quanh
xq
S
của hình trụ đó?
A.
( )
3
12 cm
xq
SR
=
. B.
( )
22
36 cm
xq
SR=
. C.
( )
2
24 cm
xq
S
=
. D.
( )
2
12 cm
xq
S
=
.
Câu 28: Cho các số thực dương
,,x y a
( )
1a
. Mệnh đề nào sau đây là mệnh đề đúng?
A.
( )
log log .log
a a a
xy x y=
. B.
log
log
log
a
a
a
x
x
yy
=
.
C.
log log , 0
n
aa
xx
nn
yy
=
. D.
( )
log log log
a a a
x y x y+ = +
.
Câu 29: Cho hàm số
( )
42
y f x ax bx c= = + +
,
( )
,,abc
có đồ thị là đường cong như hình bên dưới.
Điểm cực đại của hàm số
( )
2y f x=+
là
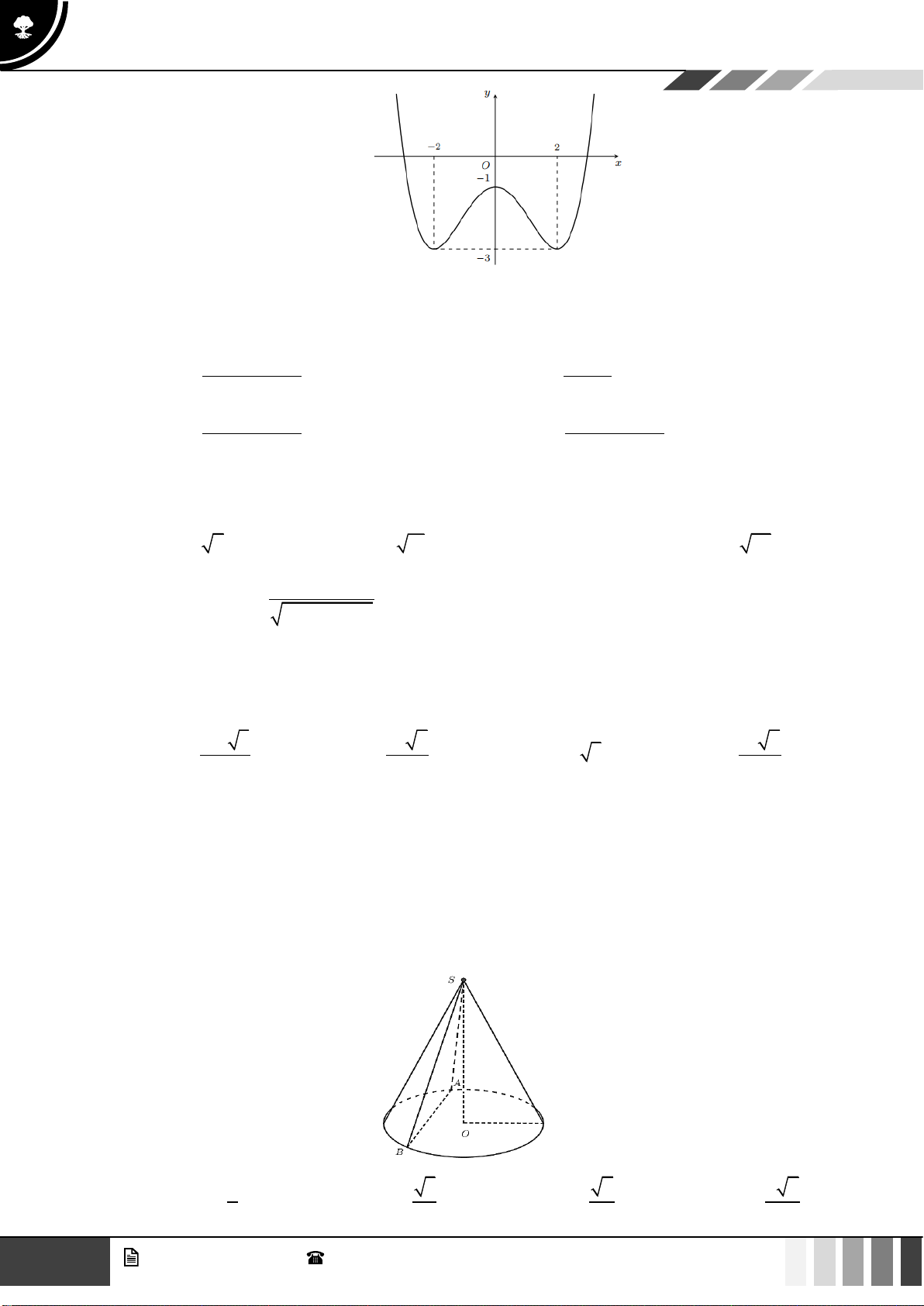
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HKI
Toán 12
A.
4x =−
. B.
0x =
. C.
2x =−
. D.
2x =
.
Câu 30: Tính đạo hàm
y
của hàm số
( )
29
log 2 7yx=+
.
A.
( )
2
2 7 ln29
y
x
=
+
. B.
29
27
y
x
=
+
.
C.
( )
1
2 7 ln29
y
x
=
+
. D.
( )
29
2 7 ln29
y
x
=
+
.
Câu 31: Cho khối chóp tứ giác đều có thể tích
3
48V cm=
, biết độ dài cạnh đáy là
6cm
. Gọi độ dài cạnh
bên của khối chóp là
m
thì ta có:
A.
6m =
. B.
4 11m =
C.
2m =
D.
34m =
Câu 32: Cho hàm số
2
42
59
43
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A.
2.
B.
5.
C.
3.
D.
6.
Câu 33: Cho lăng trụ tam giác
.ABC A B C
có đáy là tam giác đều,
( )
;A B ABC
⊥
AB a=
,
3CC a
=
.
Tính thể tích
V
của khối lăng trụ
A.
3
33
4
a
V =
. B.
3
6
2
a
V =
. C.
3
3Va=
. D.
3
6
6
a
V =
.
Câu 34: Dự kiến mỗi năm giá xăng tăng 5%. Năm 2019 giá xăng là 15.000 đồng/lít. Hỏi giá xăng năm
2026 theo dự kiến gần nhất với số nào sau đây?
A. 21.106,6 đồng. B. 22.106,5 đồng. C. 21.106,5 đồng. D. 22.106,8 đồng.
Câu 35: Cho hình nón
( )
C
đỉnh
S
có bán kính đáy
3R =
, hai đường sinh vuông góc với nhau
,SA SB
cùng dây cung
AB
tạo ra một tam giác có diện tích bằng 8. Gọi
là góc giữa
( )
SAB
và mặt
đáy của hình nón
( )
C
. Tính
cos
?
A.
1
cos
2
=
. B.
3
cos
4
=
. C.
2
cos
4
=
. D.
22
cos
3
=
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
6
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 36: Cho hàm số
( )
fx
, bảng xét dấu của
( )
'fx
như sau:
Hàm số
( )
32y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
3;4 .
. B.
( )
0;2 .
. C.
( )
; 3 .− −
. D.
( )
2;3 .
Câu 37: Hàm số
( )
2
2
log 2y x x=−
nghịch biến trên khoảng nào sau đây?
A.
( )
;1−
. B.
( )
;0−
. C.
( )
1;1−
. D.
( )
0;+
.
Câu 38: Một quán cà-phê có các ly pha cooktail có lòng là hình trụ cao
15cm
dung tích
300ml
. Để thay
đổi phong cách cho mùa giáng sinh và năm mới, người ta đặt hàng loại ly mới cũng hình trụ
nhưng có chiều cao bằng
5
3
chiều cao loại ly cũ. Hỏi khi đó, đường kính đáy phần chứa nước
của loại ly mới bằng bao nhiêu để lượng cooktail chứa trong mỗi ly không thay đổi quá
30ml
so
với loại ly cũ?
A.
4,2cm
. B.
3,6cm
. C.
3,9cm
. D.
3,5cm
.
Câu 39: Phương trình
1
4 3.2 0
xx
m
+
− + =
có hai nghiệm thực
12
,xx
thỏa mãn
12
2xx+=
. Giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
0;1 .
B.
( )
3;5 .
C.
( )
5;0 .−
D.
( )
7; 5 .−−
Câu 40: Tính diện tích xung quanh
S
của khối cầu đi qua 6 đỉnh của một lăng trụ tam giác đều có tất cả
các cạnh đều bằng
a
.
A.
2
4Sa
=
. B.
2
13
4
a
S
=
. C.
2
7
3
a
S
=
D.
2
40
3
a
S
=
Câu 41: Một chiếc đồng hồ cát được thiết kế (như hình vẽ bên dưới), với hai đáy của phần chứa cát là các
hình vuông nội tiếp hình vuông đáy của khối hộp bên ngoài. Tỉ số thể tích của phần chứa cát và
phần còn lại giữa phần chứa cát và khối hộp đứng bên ngoài là?
A.
2
5
. B.
1
6
. C.
3
8
. D.
1
5
.
Câu 42: Tính tổng các nghiệm của phương trình:
( ) ( )
2 2 2
3
log 2 2 log 2 log 2 1
2
x x x− = −
.
A.
4
. B.
82
2
−
. C.
2
2
. D.
82
2
+
.
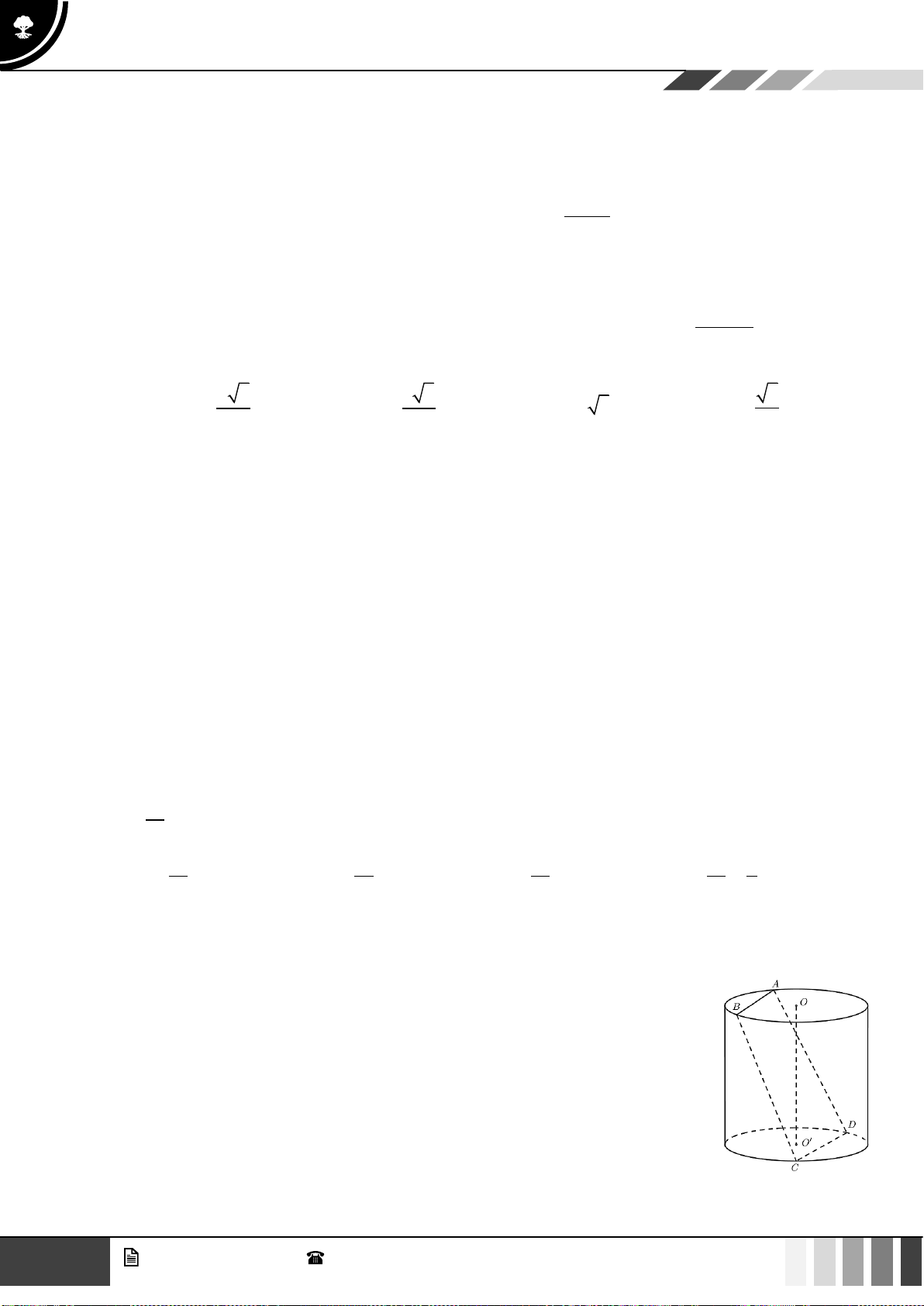
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 43: Cho tam giác nhọn
ABC
có
6BC =
và diện tích
12S =
. Cho tam giác
ABC
quay quanh trục
là đường thẳng chứa cạnh
BC
ta được khối tròn xoay
( )
H
. Tính thể tích của
( )
H
.
A.
( )
24
H
V
=
. B.
( )
36
H
V
=
. C.
( )
32
H
V
=
. D.
( )
12
H
V
=
.
Câu 44: Có bao nhiêu điểm
M
thuộc đồ thị
( )
C
của hàm số
1
10
y
x
=
+
sao cho tổng khoảng cách từ
M
đến
2
đường tiệm cận của đồ thị hàm số là nhỏ nhất.
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 45: Gọi
,KH
là hai giao điểm của đường thẳng
: 2 3d y x=+
và
( )
6
:
22
x
Cy
x
+
=
−+
. Tính độ dài
đoạn
KH
?
A.
25
4
KH =
. B.
35
4
KH =
. C.
35KH =
. D.
5
4
KH =
.
Câu 46: Khi nuôi ong trong vườn nhà, người ta thấy rằng: Nếu trên một đơn vị diện tích vườn có
n
con
ong thì trung bình mỗi con sau vụ thu hoạch được số mật là
( )
240 10P n n=−
(gam). Hỏi phải
thả bao nhiêu con ong trên một đơn vị diện tích vườn để một vụ thu được nhiều mật nhất?
A.
12
. B.
24
. C.
10
. D.
48
.
Câu 47: Ông A muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích
bằng
2
288m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây
bể là
2
500000 /đm
. Nếu ông A biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân
công sẽ thấp nhất. Hỏi ông A trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?
A.
168
triệu đồng B.
90
triệu đồng C.
54
triệu đồng D.
108
triệu đồng
Câu 48: Cho khối chóp tứ giác
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là trung điểm của
SC
, mặt phẳng
( )
P
chứa
AM
và song song
BD
chia khối chóp thành hai khối đa diện. Đặt
1
V
là
thể tích khối đa diện có chứa đỉnh
S
và
2
V
là thể tích khối đa diện có chứa đáy
ABCD
. Tỉ số
2
1
V
V
là
A.
2
1
3
V
V
=
. B.
2
1
2
V
V
=
. C.
2
1
1
V
V
=
. D.
2
1
3
2
V
V
=
.
Câu 49: Cho hàm số
( )
( )
22
2y x m m x x= − − −
có đồ thị là
( )
m
C
với
m
là tham số thực. Khi
m
thay
đổi
( )
m
C
cắt trục
Ox
tại ít nhất bao nhiêu điểm ?
A.
1
. B.
4
.
C.
3
. D.
2
.
Câu 50: Cho hình trụ
( )
H
có hai đáy lá các đường tròn
( )
;6O
và
( )
;6O
, chiều cao
8h =
. Một mặt phẳng cắt trục
OO
của hình trụ và cắt các đường tròn
( )
O
,
( )
O
theo các dây cung
,AB CD
(tham khảo hình vẽ). Biết
9, 3CD AB==
. Diện tích tứ giác
ABCD
gần với số nào nhất trong các số sau:
A.
75
. B.
76
. C.
65
. D.
66

GV. Phan Nhật Linh -
SĐT: 0817 098 716
8
Tuyển tập 10 đề ôn HKI
Toán 12
BẢNG ĐÁP ÁN
1.D
2.D
3.C
4.B
5.B
6.C
7.C
8.A
9.A
10.D
11.B
12.B
13.D
14.A
15.A
16.C
17.D
18.B
19.B
20.A
21.A
22.D
23.A
24.C
25.A
26.B
27.D
28.C
29.C
30.A
31.D
32.B
33.B
34.C
35.C
36.A
37.B
38.C
39.B
40.C
41.D
42.D
43.C
44.B
45.B
46.A
47.D
48.B
49.D
50.B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Tính diện tích xung quanh của khối trụ có chiều cao
2h =
và bán kính đáy
3R =
.
A.
36
xq
S
=
. B.
4
xq
S
=
. C.
6
xq
S
=
. D.
12
xq
S
=
.
Lời giải
Ta có
2 . 2 3.2 12
xq
S R h
= = =
.
Câu 2: Số đường tiệm cận của đồ thị hàm số
19
2
y
x
=
+
là
A. 0. B. 1. C. 3. D. 2.
Lời giải
Tập xác định:
\2D =−
Ta có:
22
19
lim lim
2
xx
y
x
++
→− →−
= = +
+
, suy ra đường thẳng
2x =−
là đường tiệm cận đứng của đồ
thị hàm số đã cho.
Mặt khác:
19
lim lim 0
2
xx
y
x
→ →
==
+
, suy ra đường thẳng
0y =
là đường tiệm cận ngang của đồ
thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Câu 3: Công thức tìm thể tích khối lăng trụ nghiêng có độ dài cạnh bên
l
, chiều cao
h
và diện tích đáy
B
là
A.
V Bl=
. B.
1
3
V Bh=
. C.
V Bh=
. D.
V Bl
=
.
Lời giải
Công thức tìm thể tích khối lăng trụ là:
V Bh=
Câu 4: Hình tròn xoay tạo ra khi quay một đường thẳng quanh trục là đường thẳng song song với nó gọi
là gì?
A. Hình trụ. B. Mặt trụ. C. Hình lăng trụ. D. Mặt nón.
Lời giải
Hình tròn xoay tạo ra khi quay một đường thẳng quanh trục là đường thẳng song song với nó gọi
là mặt trụ.
Câu 5: Tập xác định của hàm số
( )
3
21yx
−
=+
là:

GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HKI
Toán 12
A.
1
;
2
D
= − −
. B.
1
\
2
D
=−
. C.
1
;
2
D
= − +
. D.
1
;
2
D
= − +
.
Lời giải
Vì
3
−
−
nên hàm số xác định khi và chỉ khi
1
2 1 0
2
xx+ −
.
Tập xác định của hàm số đã cho là
1
\
2
D
=−
.
Câu 6: Cho khối nón
( )
C
có bán kính đáy
R
và độ dài đường sinh
l
và chiều cao
h
. Công thức nào
sau đây đúng?
A.
2
1
3
V R l
=
. B.
2
V R l
=
. C.
2
1
3
V R h
=
. D.
2
V R h
=
.
Lời giải
Thể tích khối nón
( )
C
là:
2
1
3
V R h
=
.
Câu 7: Cho khối nón
( )
C
, có bán kính đáy
3R =
và độ dài đường sinh
4l =
. Tính chiều cao
h
của khối
nón?
A.
13h =
. B.
1h =
. C.
7h =
. D.
5h =
.
Lời giải
Ta có:
2 2 2 2 2
16 9 7l R h h l R= + = − = − =
.
Câu 8: Đồ thị hàm số
( )
2022
2023
x
fx
x
−
=
+
có bao nhiêu điểm cực đại?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Ta có hàm số
( )
( )
2
4045
0, 2023
2023
f x x
x
= −
+
hàm số không có cực trị.
Vậy hàm số đã cho không có cực đại.
Câu 9: Cho khối cầu bán kính
2R
. Gọi
V
là thể tích khối cầu và
S
là diện tích mặt cầu. Công thức nào
sau đây đúng?
A.
( )
3
4
2
3
VR
=
. B.
( )
3
42SR
=
. C.
2
4SR
=
. D.
3
4
3
VR
=
.
Lời giải
Ta có công thức tính thể tích khối cầu là:
3
4
3
Vr
=
(
,Vr
lần lượt là thể tích và bán kính khối
cầu).
Theo bài:
( )
3
4
22
3
r R V R
= =
.
Câu 10: Có bao nhiêu loại đa diện đều mà các mặt là các tam giác đều.
A.
5
. B.
2
. C.
1
. D.
3
.
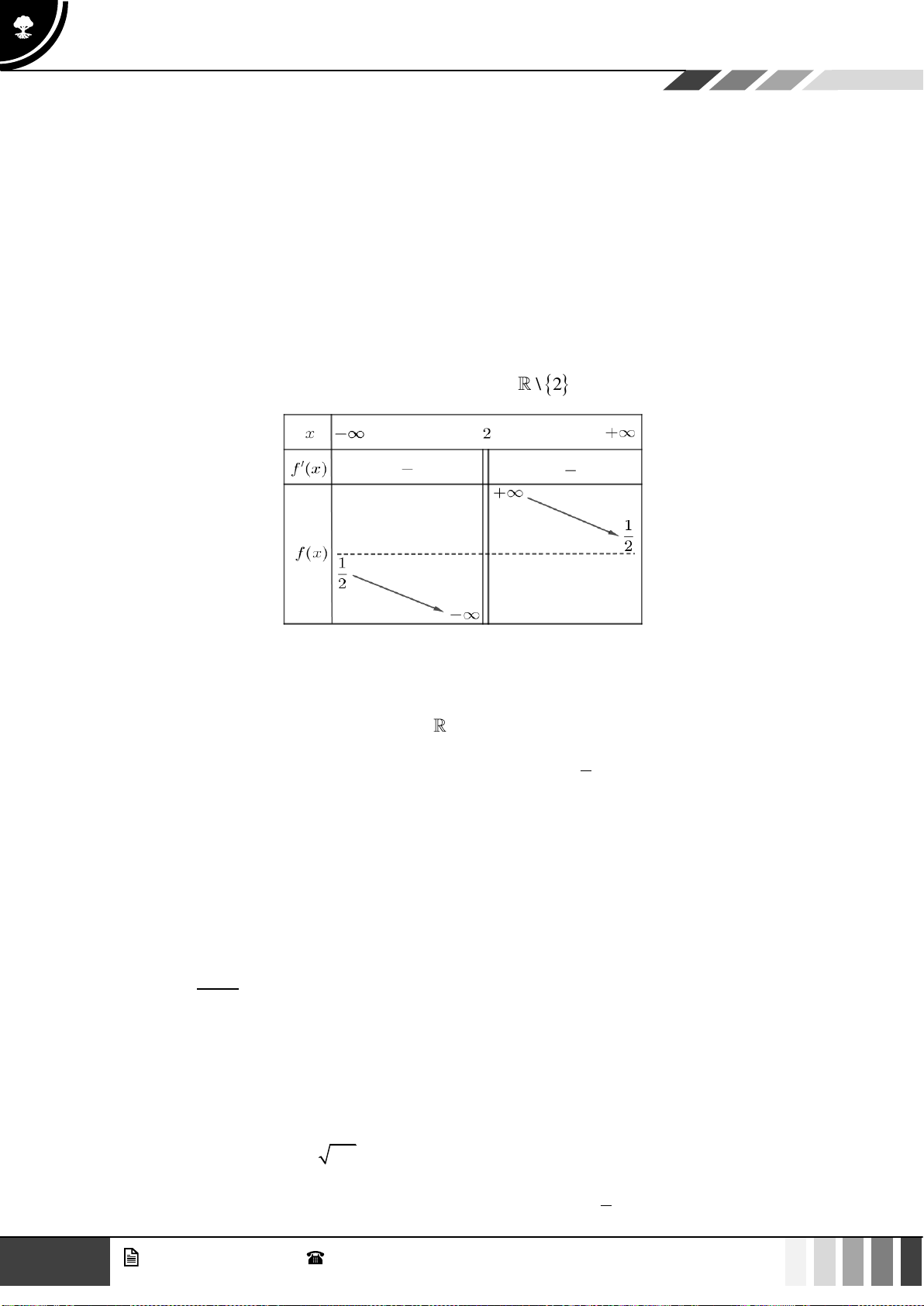
GV. Phan Nhật Linh -
SĐT: 0817 098 716
10
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Có ba loại khối đa diện đều mà các mặt là các tam giác đều: khối tứ diện đều, khối bát diện đều
và khối hai mươi mặt đều.
Câu 11: Tìm tập nghiệm của phương trình:
( )
3
log 3 2x−=
.
A.
( )
3;S = − +
. B.
6S =−
. C.
0S =
. D.
3S =−
.
Lời giải
Ta có:
( )
2
3
log 3 2 3 3 3 9 6x x x x− = − = − = = −
.
Vậy
6S =−
.
Câu 12: Cho hàm số
( )
y f x=
xác định, liên tục trên
\2D =
và có bảng biến thiên như sau:
Khẳng định nào sau đây sai?
A. Hàm số
( )
y f x=
không có cực trị.
B. Hàm số
( )
y f x=
nghịch biến trên .
C. Đồ thị hàm số
( )
y f x=
có đường tiệm cận ngang
1
2
y =
.
D. Đồ thị hàm số
( )
y f x=
có đường tiệm cận đứng
2x =
.
Lời giải
Ta có: Hàm số
( )
y f x=
nghịch biến trên các khoảng
( )
;2−
và
( )
2;+
nên khẳng định B là
khẳng định sai.
Câu 13: Cho các số thực dương
a
,
b
,
x
thỏa
3 3 3
log 10log 7logx a b=+
. Tìm
x
.
A.
10 7
1
x
ab
=
. B.
10 7
x a b=+
. C.
10 7x a b=+
. D.
10 7
x a b=
.
Lời giải
Ta có
( )
10 7 10 7 10 7
3 3 3 3 3 3 3 3
log 10log 7log log log log log logx a b x a b x a b x a b= + = + = =
.
Câu 14: Giải bất phương trình
( )
3
1
101 101
x
x+
.
A.
(
;2S = −
. B.
( )
;0S = −
. C.
1
;
2
S
= −
. D.
( )
;2S = −
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Ta có
( )
3
3
11
2
3
101 101 101 101 1 2
2
x
x
xx
x
xx
++
+
.
Vậy tập nghiệm của bất phương trình là
(
;2S = −
.
Câu 15: Với giá trị nào của
m
thì hàm số
2
xm
y
x
−
=
−
đồng biến trên từng khoảng xác định?
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Lời giải
Tập xác định:
\2D =
. Đạo hàm của hàm số là:
( )
2
2
2
m
y
x
−
=
−
.
Hàm số đồng biến trên từng khoảng xác định
0, 2 2 0 2y x m m
−
.
Câu 16: Cho khối nón có thể tích
V
. Nếu tăng bán kính đáy của khối nón lên
2
lần, nhưng giảm chiều
cao của khối nón còn
1
3
chiều cao ban đầu thì khối nón mới có thể tích
V
. Tính tỷ số
V
V
A.
2
3
V
V
=
. B.
1
6
V
V
=
. C.
3
4
V
V
=
. D.
4
3
V
V
=
.
Lời giải
Ta có thể tích khối nón ban đầu:
2
1
3
V r h
=
.
Thể tích khối nón mới là:
( )
2
2
1 1 4 4
2
3 3 3 3 3
h
V r r h V
= = =
.
Suy ra tỷ số
3
4
V
V
=
.
Câu 17: Giá trị lớn nhất của hàm số
( )
42
4 10f x x x=− + +
trên đoạn
0;2
là
A.
12−
. B.
15
. C.
6
. D.
14
.
Lời giải
Ta có:
3
48y x x
= − +
,
0;2x
. Giải phương trình
( )
3
0
0 4 8 0 2
2
x
y x x x
xl
=
= − + = =
=−
.
Mặt khác:
( )
0 10f =
,
( )
2 14f =
,
( )
2 10f =
Vậy giá trị lớn nhất của hàm số trên đoạn
0;2
là: 14.
Câu 18: Nếu
2
log 3a =
;
2
log 5b =
thì
A.
6
2
1
log 180
6 3 6
ab
= + +
. B.
6
2
1
log 180
3 3 6
ab
= + +
.
C.
6
2
1
log 180
3 3 3
ab
= + +
. D.
6
2
1
log 180
3 2 6
ab
= + +
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
12
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Ta có:
( )
1
6
6
2 2 2
1
log 180 log 180 log 180
6
==
( ) ( )
2 2 2 2
2 2 2 2
11
log 2 .3 .5 log 2 log 3 log 5
66
= = + +
( )
22
11
2 2log 3 log 5
6 3 3 6
ab
= + + = + +
.
Câu 19: Cho khối hộp
.ABCD A B C D
. Mặt phẳng
( )
AB D
chia khối hộp thành hai phần có thể tích
tương ứng là
( )
1 2 1 2
;V V V V
. Tỉ số
1
2
V
V
bằng
A.
1
4
. B.
1
5
. C.
1
6
. D.
1
3
.
Lời giải
Giả sử
V
là thể tích của khối hộp
.ABCD A B C D
,
1
V
là thể tích của khối chóp
.A A B D
.
Ta có
( )
( )
1
1
;.
3
ABD
V d A A B D S
=
( )
( )
11
;.
66
A B C D
d A A B C D S V
==
21
1
6
V V V V V = − = −
5
6
V=
. Vậy
1
2
1
1
6
5
5
6
V
V
V
V
==
.
Câu 20: Cho hàm số
( )
y f x=
có đạo hàm trên và hàm số
( )
y f x
=
là hàm số bậc ba có đồ thị là
đường cong trong hình vẽ.
Hàm số
( )
y f x=
nghịch biến trên
A.
( )
;1−
. B.
( )
2;0−
. C.
( )
1; +
. D.
( )
1;− +
.
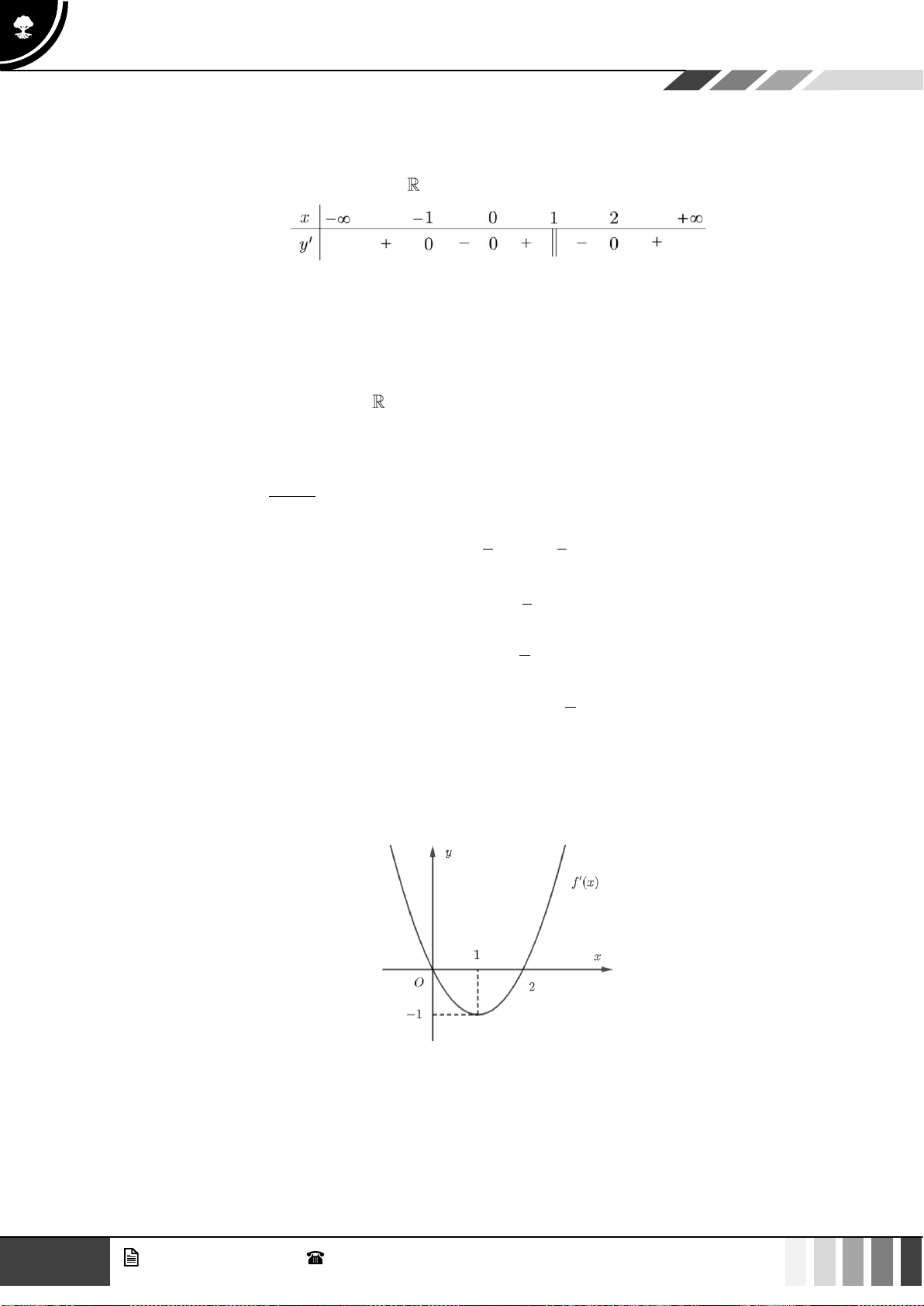
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Dựa vào đồ thị, ta thấy
( )
0, 1f x x
. Do đó hàm số nghịch biến trên khoảng
( )
;1−
.
Câu 21: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét dấu đạo hàm như hình vẽ:
Hàm số đã cho có bao nhiêu điểm cực đại?
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Hàm số
( )
y f x=
liên tục trên và có
y
đổi dấu dương sang âm khi qua hai điểm
1; 1xx= − =
nên hàm số đã cho có hai điểm cực đại.
Câu 22: Cho hàm số
23
31
x
y
x
−
=
+
. Phát biểu nào sau đây sai?
A. Hàm số đồng biến trên các khoảng
1
;
3
− −
và
1
;
3
− +
.
B. Đồ thị hàm số có đường tiệm cận đứng là
1
3
x =−
.
C. Đồ thị hàm số có đường tiệm cận ngang là
2
3
y =
.
D. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
3
2
.
Lời giải
Phát biểu D sai vì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
3−
.
Câu 23: Cho hàm số bậc ba
( )
y f x=
có đồ thị đạo hàm
( )
'y f x=
như hình sau:
Hàm số đã cho nghịch biến trên khoảng nào?
A.
( )
1;2 .
B.
( )
3;4 .
C.
( )
2;3 .
D.
( )
1;0 .−
Lời giải
Hàm số nghịch biến khi và chỉ khi
( )
' 0 0 2.f x x
GV. Phan Nhật Linh -
SĐT: 0817 098 716
14
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy hàm số nghịch biến trên
( )
1;2 .
Câu 24: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chóp có đáy là hình thoi luôn có mặt cầu ngoại tiếp.
B. Hình lăng trụ đứng luôn có mặt cầu ngoại tiếp.
C. Hình chóp có đáy là hình thang cân luôn có mặt cầu ngoại tiếp.
D. Hình lăng trụ có đáy là hình chữ nhật luôn có mặt cầu ngoại tiếp.
Lời giải
Hình chóp có đáy là đa giác có đường tròn ngoại tiếp thì có mặt cầu ngoại tiếp.
Câu 25: Cho
,xy
là các số thực. Chọn mệnh đề đúng trong các mệnh đề sau:
A.
10 10
xy
xy
. B.
11
10 10
xy
xy
.
C.
10 10
xy
xy
. D.
11
10 10
xy
xy
.
Lời giải
Theo tính chất
1,
xy
a a a x y
.
Câu 26: Giả sử cứ sau mỗi năm diện tích rừng của nước ta giảm
x
phần trăm diện tích hiện có. Hỏi sau
5
năm nữa diện tích rừng của nước ta sẽ là bao nhiêu phần diện tích hiện nay?
A.
5
1
100
x
−
. B.
5
1
100
x
−
. C.
( )
100 5 %x−
. D.
5
1
100
x
−
.
Lời giải
Gọi diện tích rừng hiện nay là
S
.
Sau
1
năm thì diện tích rừng là
1
1
100 100
xx
S S S S
= − = −
.
Sau
2
năm thì diện tích rừng là
2
2 1 1 1
11
100 100 100
x x x
S S S S S
= − = − = −
.
…
Sau
5
năm thì diện tích rừng là
5
5
1
100
x
SS
=−
.
Vậy diện tích rừng sau 5 năm bằng
5
1
100
x
−
phần diện tích hiện nay.
Câu 27: Cắt hình trụ có bán kính
( )
1RR
bởi một mặt phẳng đi qua trục của nó ta được một hình chữ
nhật có diện tích
2
12cm
. Tính diện tích xung quanh
xq
S
của hình trụ đó?
A.
( )
3
12 cm
xq
SR
=
. B.
( )
22
36 cm
xq
SR=
. C.
( )
2
24 cm
xq
S
=
. D.
( )
2
12 cm
xq
S
=
.
Lời giải
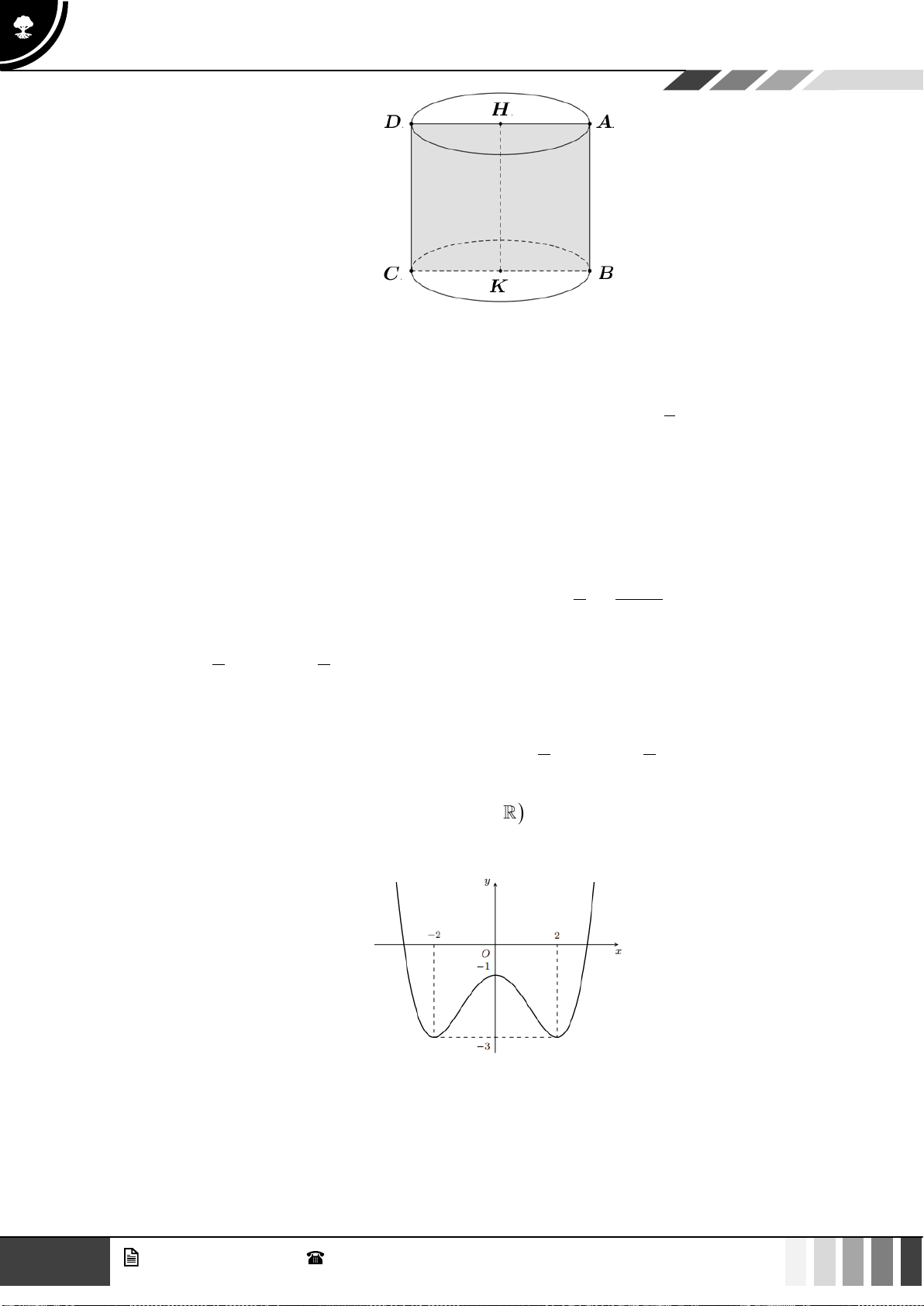
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HKI
Toán 12
Gọi thiết diện qua trục hình trụ là hình chữ nhật
ABCD
.
Gọi
,HK
lần lượt là tâm đường tròn hai đáy hình trụ.
Gọi độ dài đường sinh hình trụ là
l AB=
. Bán kính đáy là
1
2
R AH AD==
.
Theo giả thiết ta có
. 12 .2 12 . 6AB AD l R l R= = =
.
Khi đó, diện tích xung quanh của hình trụ là
( )
2
2 12 cm
xq
S Rl
==
.
Câu 28: Cho các số thực dương
,,x y a
( )
1a
. Mệnh đề nào sau đây là mệnh đề đúng?
A.
( )
log log .log
a a a
xy x y=
. B.
log
log
log
a
a
a
x
x
yy
=
.
C.
log log , 0
n
aa
xx
nn
yy
=
. D.
( )
log log log
a a a
x y x y+ = +
.
Lời giải
Theo tính chất của logarit thì mệnh đề đúng là
log log , 0
n
aa
xx
nn
yy
=
.
Câu 29: Cho hàm số
( )
42
y f x ax bx c= = + +
,
( )
,,abc
có đồ thị là đường cong như hình bên dưới.
Điểm cực đại của hàm số
( )
2y f x=+
là
A.
4x =−
. B.
0x =
. C.
2x =−
. D.
2x =
.
Lời giải
Đồ thị hàm số
( )
2y f x=+
có được bằng cách tịnh tiến đồ thị hàm số
( )
y f x=
sang trái
2
đơn vị.
Do đó ta được đồ thị
GV. Phan Nhật Linh -
SĐT: 0817 098 716
16
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy hàm số đạt cực đại tại điểm
2x =−
.
Câu 30: Tính đạo hàm
y
của hàm số
( )
29
log 2 7yx=+
.
A.
( )
2
2 7 ln29
y
x
=
+
. B.
29
27
y
x
=
+
.
C.
( )
1
2 7 ln29
y
x
=
+
. D.
( )
29
2 7 ln29
y
x
=
+
.
Lời giải
Với
7
2
x −
ta có
( )
( ) ( )
27
2
2 7 ln29 2 7 ln29
x
y
xx
+
==
++
.
Câu 31: Cho khối chóp tứ giác đều có thể tích
3
48V cm=
, biết độ dài cạnh đáy là
6cm
. Gọi độ dài cạnh
bên của khối chóp là
m
thì ta có:
A.
6m =
. B.
4 11m =
C.
2m =
D.
34m =
Lời giải
Xét khối chóp đều
.S ABCD
có
6 , ( 3 2)AB cm SA m m= =
.
2
36, 2 6 2 3 2
ABCD
S AB AC AB AO= = = = =
.
2 2 2
18SO SA AO m= − = −
.
2
.
11
. .36. 18
33
S ABCD ABCD
V SO S m= = −
.
Ta có phương trình:
2 2 2
12 18 48 18 4 18 16 34m m m m− = − = − = =
(vì
32m
).
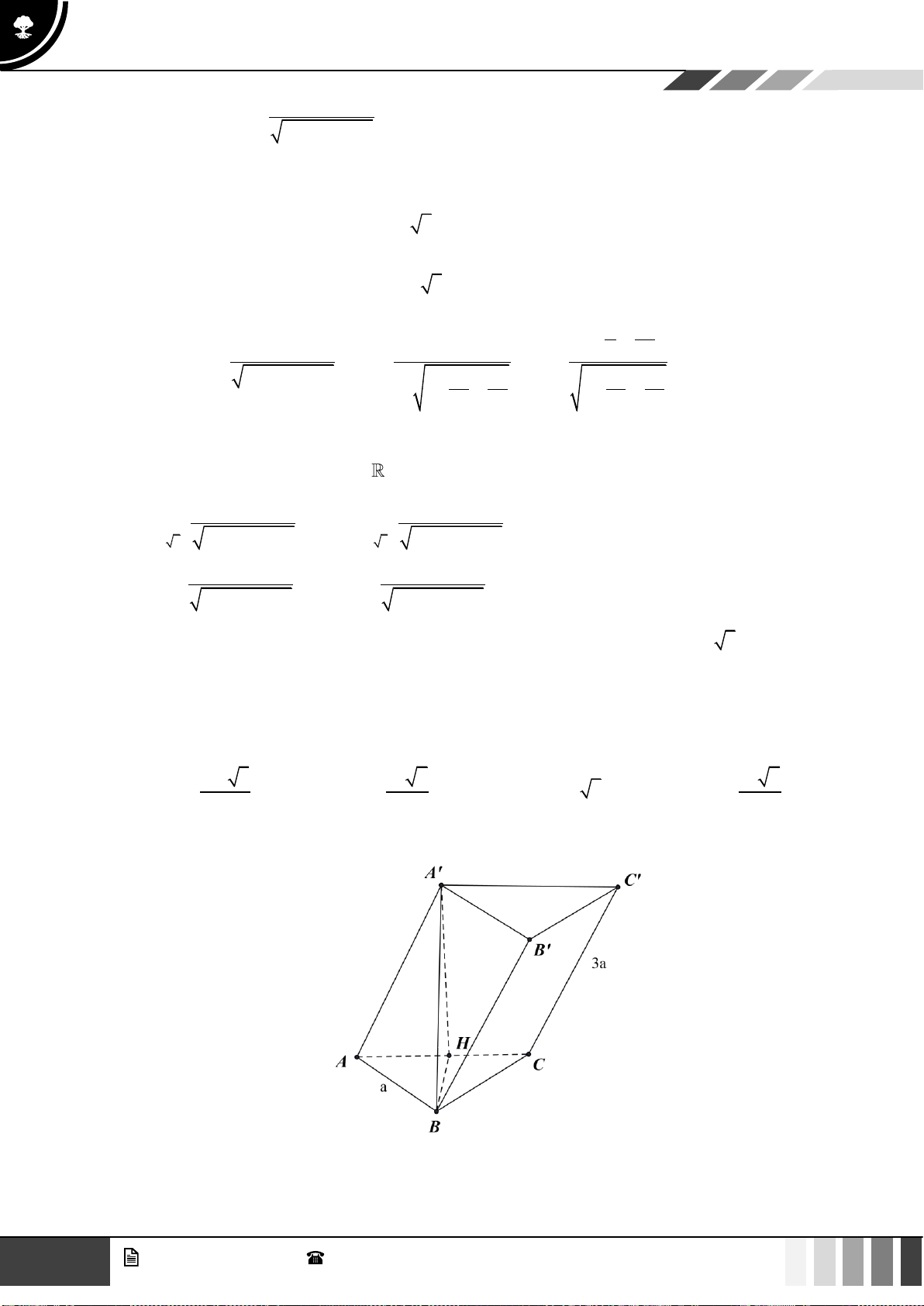
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 32: Cho hàm số
2
42
59
43
xx
y
xx
++
=
−+
. Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A.
2.
B.
5.
C.
3.
D.
6.
Lời giải
Điều kiện:
42
3
4 3 0 1 1
3
x
x x x
x
− + −
−
.
Ta có:
22
2
42
2
2 4 2 4
59
1
5 9 5 9
lim lim lim 1
4 3 4 3
43
11
x x x
x x x x
x
x
xx
x
x x x x
→ → →
++
+ + + +
= = =
−+
− + − +
. Như vậy đồ thị hàm
số có một đường tiệm cận ngang là đường thẳng
1y =
.
Nhận xét:
2
5 9 0x x x+ +
.
22
4 2 4 2
33
5 9 5 9
lim ; lim
4 3 4 3
xx
x x x x
x x x x
+−
→ →−
+ + + +
= + = +
− + − +
22
4 2 4 2
11
5 9 5 9
lim ; lim
4 3 4 3
xx
x x x x
x x x x
+−
→− →
+ + + +
= + = +
− + − +
Suy ra đồ thị hàm số có bốn đường tiệm cận đứng là các đường
1; 3xx= =
.
Vậy đồ thị hàm số đã cho có
5
đường tiệm cận.
Câu 33: Cho lăng trụ tam giác
.ABC A B C
có đáy là tam giác đều,
( )
;A B ABC
⊥
AB a=
,
3CC a
=
.
Tính thể tích
V
của khối lăng trụ
A.
3
33
4
a
V =
. B.
3
6
2
a
V =
. C.
3
3Va=
. D.
3
6
6
a
V =
.
Lời giải
Gọi
H
là trung điểm của
AC
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
18
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có:
BH AC
A B AC
⊥
⊥
( )
AC A BH
⊥
A H AC
⊥
Xét
A HB
có
90AHA
=
có
2
a
AH =
và
3AA a
=
.
( )
2
2
2
2 2 2
39
24
aa
A H AA AH a a
= − = − = −
35
2
a
=
Xét
A HB
có
0
90A BH
=
có
3
2
a
BH =
và
35
2
a
AH
=
Suy ra:
22
A B A H HB
=−
22
35 3
22
44
aa
a= − =
.
Vậy thể tích
V
của khối lăng trụ đã cho bằng:
23
.
36
. 2 2.
42
ABC A B C ABC
aa
V A B S a
= = =
.
Câu 34: Dự kiến mỗi năm giá xăng tăng 5%. Năm 2019 giá xăng là 15.000 đồng/lít. Hỏi giá xăng năm
2026 theo dự kiến gần nhất với số nào sau đây?
A. 21.106,6 đồng. B. 22.106,5 đồng. C. 21.106,5 đồng. D. 22.106,8 đồng.
Lời giải
Do mỗi năm tăng 5% nên từ năm 2019 đến năm 2026 giá xăng sẽ tăng 7 lần.
Vậy giá xăng năm 2026 là:
( )
7
15.000 1 5% 21.106,5+
đồng.
Câu 35: Cho hình nón
( )
C
đỉnh
S
có bán kính đáy
3R =
, hai đường sinh vuông góc với nhau
,SA SB
cùng dây cung
AB
tạo ra một tam giác có diện tích bằng 8. Gọi
là góc giữa
( )
SAB
và mặt
đáy của hình nón
( )
C
. Tính
cos
?
A.
1
cos
2
=
. B.
3
cos
4
=
. C.
2
cos
4
=
. D.
22
cos
3
=
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HKI
Toán 12
Xét
SAB
vuông cân tại
S
, ta có
2
1
8 8 4
2
SAB
S SA SA
= = =
;
2 2 2 2
2 2.4 4 2.AB SA SB SA= + = = =
Gọi
I
là trung điểm của
AB
, ta có
11
2 2; 2 2
22
SI AB AI AB= = = =
.
Xét
AIO
vuông tại
I
, ta có
( )
2
2 2 2
3 2 2 1IO AO AI= − = − =
.
11
. .1.4 2 2 2
22
OAB
S IO AB
= = =
.
Ta có
( )
SO OAB⊥
suy ra
OAB
là hình chiếu của
SAB
lên
( )
OAB
Suy ra
.cos
OAB SAB
SS
=
(Định lý diện tích hình chiếu của đa giác)
2 2 2
cos
84
OAB
SAB
S
S
= = =
.
Câu 36: Cho hàm số
( )
fx
, bảng xét dấu của
( )
'fx
như sau:
Hàm số
( )
32y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
3;4 .
B.
( )
0;2 .
C.
( )
; 3 .− −
D.
( )
2;3 .
Lời giải
Ta có:
( )
' 2 ' 3 2y f x= − −
( ) ( ) ( ) ( )
( ) ( )
' 0 2 ' 3 2 0 ' 3 2 0 3 2 ; 3 1;1
1;2 3;
y f x f x x
x
− − − − − − −
+
Câu 37: Hàm số
( )
2
2
log 2y x x=−
nghịch biến trên khoảng nào sau đây?
A.
( )
;1−
. B.
( )
;0−
. C.
( )
1;1−
. D.
( )
0;+
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
20
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Hàm số xác định khi
2
0
20
2
x
xx
x
−
. Tập xác định của hàm số là
( ) ( )
;0 2;D = − +
.
Khi đó
( )
2
22
0 0 2 2 0 1.
2 ln2
x
y x x
xx
−
−
−
Kết hợp với tập xác định ta được
00yx
.
Vậy hàm số đã cho nghịch biến trên khoảng
( )
;0 .−
Câu 38: Một quán cà-phê có các ly pha cooktail có lòng là hình trụ cao
15cm
dung tích
300ml
. Để thay
đổi phong cách cho mùa giáng sinh và năm mới, người ta đặt hàng loại ly mới cũng hình trụ
nhưng có chiều cao bằng
5
3
chiều cao loại ly cũ. Hỏi khi đó, đường kính đáy phần chứa nước
của loại ly mới bằng bao nhiêu để lượng cooktail chứa trong mỗi ly không thay đổi quá
30ml
so
với loại ly cũ?
A.
4,2cm
. B.
3,6cm
. C.
3,9cm
. D.
3,5cm
.
Lời giải
Chiều cao của loại ly mới là
( )
5
.15 25
3
h cm==
.
Gọi
r
là bán kính và
d
là đường kính đáy phần chứa nước của loại ly mới.
Khi đó, thể tích của loại ly mới là
2
25Vr
=
.
Theo bài ra ta có:
22
54 66
270 330 270 25 330
55
V r r
3 30 330 6 30 2 330
3,7 4,1
5 5 5 5
r d d
.
Câu 39: Phương trình
1
4 3.2 0
xx
m
+
− + =
có hai nghiệm thực
12
,xx
thỏa mãn
12
2xx+=
. Giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
0;1 .
B.
( )
3;5 .
C.
( )
5;0 .−
D.
( )
7; 5 .−−
Lời giải
Ta có:
12
4 3.2 0 2 6.2 0
x x x x
mm
+
− + = − + =
.
Đặt
( ) ( )
2
2 0 6 0 *
x
t t t t m= − + =
Để phương trình
( )
*
có hai nghiệm dương
0 9 0
0 6 0 0 9
00
m
Sm
Pm
−
Ta có:
( )
12
2
12
. 2 2 4
xx
t t m tm
+
= = = =
GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 40: Tính diện tích xung quanh
S
của khối cầu đi qua 6 đỉnh của một lăng trụ tam giác đều có tất cả
các cạnh đều bằng
a
.
A.
2
4Sa
=
. B.
2
13
4
a
S
=
. C.
2
7
3
a
S
=
D.
2
40
3
a
S
=
Lời giải
Ta có
.ABC A B C
là lăng trụ tam giác đều có
,OO
lần lượt là tâm của 2 đáy.
Tâm mặt cầu đi qua 6 đỉnh của lăng trụ này là trung điểm
I
của
,OO
2 2 2
OO AA a
OI
= = =
nên
23
33
a
AO AH==
Bán kính khối cầu là:
2
2
22
3 21
3 2 6
a a a
R AI AO OI
= = + = + =
Diện tích S của mặt cầu là:
2
2
2
21 7
44
63
aa
SR
= = =
.
Câu 41: Một chiếc đồng hồ cát được thiết kế (như hình vẽ bên dưới), với hai đáy của phần chứa cát là các
hình vuông nội tiếp hình vuông đáy của khối hộp bên ngoài. Tỉ số thể tích của phần chứa cát và
phần còn lại giữa phần chứa cát và khối hộp đứng bên ngoài là?
A.
2
5
. B.
1
6
. C.
3
8
. D.
1
5
.
Lời giải
GV. Phan Nhật Linh -
SĐT: 0817 098 716
22
Tuyển tập 10 đề ôn HKI
Toán 12
Gọi hình hộp bên ngoài của đồng hồ cát là
.ABCD A B C D
có diện tích đáy
ABCD
SS=
, có
chiều cao
h
và có thể tích
.V S h=
. (tham khảo hình vẽ).
Gọi thể tích của phần chứa cát là
1
V
, phần còn lại là
2
V
.
Thể tích của phần chứa cát là
1
V
bằng hai lần thể tích khối chóp
.I MNPQ
.
Khối chóp
.I MNPQ
có diện tích đáy
1
22
MNPQ ABCD
S
SS==
, chiều cao
2
h
.
Suy ra
.
1
..
3 2 2 12
I MNPQ
S h V
V ==
1.
2
6
I MNPQ
V
VV = =
.
Thể tích của phần còn lại là
21
5
66
VV
V V V V= − = − =
.
Vậy tỉ số thể tích của phần chứa cát và phần còn lại giữa phần chứa cát và khối hộp đứng bên
ngoài là
1
2
1
5
V
V
=
.
Câu 42: Tính tổng các nghiệm của phương trình:
( ) ( )
2 2 2
3
log 2 2 log 2 log 2 1
2
x x x− = −
.
A.
4
. B.
82
2
−
. C.
2
2
. D.
82
2
+
.
Lời giải
Điều kiện:
0x
.
Ta có:
( ) ( ) ( ) ( )
2
2 2 2 2 2
3 7 3
log 2 2 log 2 log 2 1 log 2 log 2 0
2 2 2
x x x x x− = − − + =
( )
( )
2
2
4
log 2 3
1
2
log 2
2
2
x
x
x
x
=
=
=
=
(thỏa mãn). Tổng các nghiệm là
2 8 2
4
22
+
+=
.
Câu 43: Cho tam giác nhọn
ABC
có
6BC =
và diện tích
12S =
. Cho tam giác
ABC
quay quanh trục
là đường thẳng chứa cạnh
BC
ta được khối tròn xoay
( )
H
. Tính thể tích của
( )
H
.
A.
( )
24
H
V
=
. B.
( )
36
H
V
=
. C.
( )
32
H
V
=
. D.
( )
12
H
V
=
.
Lời giải
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HKI
Toán 12
Gọi
K
là hình chiếu của
A
trên cạnh
BC
, ta có
2 2.12
4
6
S
AK
BC
= = =
.
Khối tròn xoay
( )
H
là hợp của hai khối nón tròn xoay đỉnh
,BC
có chung mặt đáy là hình tròn
tâm
K
bán kính
AK
.
Thể tích của khối tròn xoay
( )
H
là
( )
22
11
..
33
H
V AK BK AK CK
=+
22
11
. .4 .6 32
33
AK BC
= = =
.
Câu 44: Có bao nhiêu điểm
M
thuộc đồ thị
( )
C
của hàm số
1
10
y
x
=
+
sao cho tổng khoảng cách từ
M
đến
2
đường tiệm cận của đồ thị hàm số là nhỏ nhất.
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Đồ thị
( )
C
của hàm số
1
10
y
x
=
+
có tiệm cận đứng là đường thẳng
10x =−
và tiệm cận
ngang là đường thẳng
0y =
.
Gọi
( )
1
; , 10
10
M a C a
a
−
+
.
Tổng khoảng cách từ điểm
M
đến
2
đường tiệm cận của
( )
C
là
1
10 2, 10
10
d a a
a
= + + −
+
.
Ta có
9
1
2 10 10 1
11
10
a
d a a
a
a
=−
= + = + =
=−
+
.
Vậy có
2
điểm
M
thỏa mãn bài toán là
( )
9;1M −
hoặc
( )
11; 1M −−
.
Câu 45: Gọi
,KH
là hai giao điểm của đường thẳng
: 2 3d y x=+
và
( )
6
:
22
x
Cy
x
+
=
−+
. Tính độ dài
đoạn
KH
?
A.
25
4
KH =
. B.
35
4
KH =
. C.
35KH =
. D.
5
4
KH =
.
Lời giải
Điều kiện
1x
.
Phương trình hoành độ giao điểm của đường thẳng
d
và đồ thị
( )
C
là:
6
23
22
x
x
x
+
+=
−+
2
0
4 3 0
3
4
x
xx
x
=
+ =
=−
(thỏa mãn).
Với
( )
0 3 0;3x y H= =
.
Với
3 3 3 3
;
4 2 4 2
x y K
= − = −
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
24
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có
22
3 3 3 3 3 5
;
4 2 4 2 4
HK HK
= − − = − + − =
.
Câu 46: Khi nuôi ong trong vườn nhà, người ta thấy rằng: Nếu trên một đơn vị diện tích vườn có
n
con
ong thì trung bình mỗi con sau vụ thu hoạch được số mật là
( )
240 10P n n=−
(gam). Hỏi phải
thả bao nhiêu con ong trên một đơn vị diện tích vườn để một vụ thu được nhiều mật nhất?
A.
12
. B.
24
. C.
10
. D.
48
.
Lời giải
Điều kiện:
0;24n
.
Ta có trung bình mỗi con sau vụ thu hoạch được số mật là
( )
240 10P n n=−
(gam).
Vậy với
n
con thì khối lượng mật thu được (đơn vị: gam) là
( ) ( )
. 240 10T n P n n n= = −
( )
( ) ( )
22
22
10 24 10 12 12 10 12 1440 1440T n n n n
= − − = − − − = − − +
Vậy
max 1440T =
(gam) khi
12n =
(con).
Nhn xt: Ta có thể xét hàm số
( )
2
10 240f n n n= − +
khi
0;24n
.
Ta có
( )
20 240f n n
= − +
.
Có
( )
0 20 240 0 12f n n n
= − + = =
.
Ta có
( ) ( ) ( )
0 0; 12 1440; 24 0f f f= = =
.
Vậy
( )
0;24
max max 1440T f n==
(gam) khi
12n =
(con).
Câu 47: Ông A muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích
bằng
2
288m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây
bể là
2
500000 /đm
. Nếu ông A biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân
công sẽ thấp nhất. Hỏi ông A trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?
A.
168
triệu đồng B.
90
triệu đồng C.
54
triệu đồng D.
108
triệu đồng
Lời giải
Gọi chiều rộng đáy bể là
x
, chiều dài đáy bể là
2x
, chiều cao của bể là
h
( )
( )
,0mx
Theo bài ra ta có:
2
2
144
2 . 288V x h h
x
= = =
Tổng diện tích bể là:
2 2 2
2
144 864
2 6 2 6 . 2S x xh x x x
x
x
= + = + = +
Ta có:
2 3 2
432 432 432 432
2 3 2 . . 216S x x
x x x x
= + + =
Dấu “= ” xảy ra khi và chỉ khi
2
432
26xx
x
= =
2
min
216Sm=
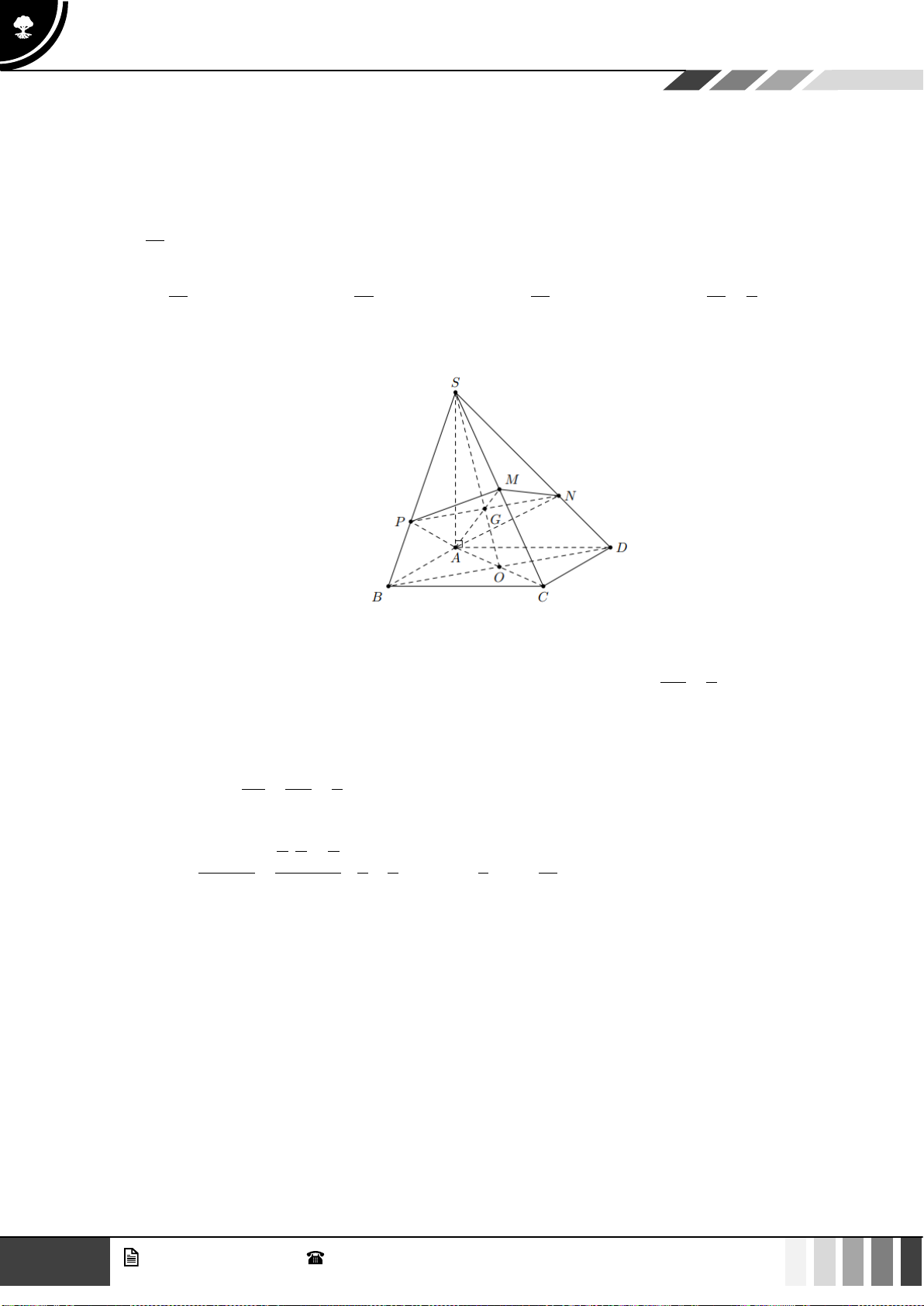
GV. Phan Nhật Linh -
SĐT: 0817 098 716
25
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy ông A trả chi phí thấp nhất là
216.500000 108=
(triệu đồng)
Câu 48: Cho khối chóp tứ giác
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là trung điểm của
SC
, mặt phẳng
( )
P
chứa
AM
và song song
BD
chia khối chóp thành hai khối đa diện. Đặt
1
V
là
thể tích khối đa diện có chứa đỉnh
S
và
2
V
là thể tích khối đa diện có chứa đáy
ABCD
. Tỉ số
2
1
V
V
là
A.
2
1
3
V
V
=
. B.
2
1
2
V
V
=
. C.
2
1
1
V
V
=
. D.
2
1
3
2
V
V
=
.
Lời giải
Gọi
O
là tâm của hình bình hành
ABCD
.
Khi đó
SO
cắt
AM
tại
G
. Suy ra
G
là trọng tâm tam giác
SAC
2
3
SG
SO
=
.
Trong mặt phẳng
( )
SBD
, qua
G
kẻ
d
song song
BD
cắt
SD
,
SB
tại hai điểm
N
,
P
.
Khi đó ta có
2
3
SP SN
SB SD
==
.
Suy ra
1
.
2 2 1
. .1.
3 3 1
3 3 2
. 1 2
4 2 2 3
S ABCD
V
V
= + + + =
. Vậy
2
1
2
V
V
=
.
Câu 49: Cho hàm số
( )
( )
22
2y x m m x x= − − −
có đồ thị là
( )
m
C
với
m
là tham số thực. Khi
m
thay
đổi
( )
m
C
cắt trục
Ox
tại ít nhất bao nhiêu điểm ?
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
( )
m
C
cắt trục
Ox
tại các điểm có hoành độ thỏa mãn phương trình
( )
( )
22
20x m m x x− − − =
.
Trường hợp 1:
0m =
, phương trình thành
( )
20xx− − =
, dễ thấy phương trình có hai nghiệm
phân biệt.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
26
Tuyển tập 10 đề ôn HKI
Toán 12
Trường hợp 2:
0m
,
( )
( )
( )
22
22
22
0
20
2 0 *
20
xm
xm
x m m x x
m x x
m x x
=
−=
− − − =
− − =
− − =
.
Phương trình
( )
*
có hai nghiệm phân biệt trái dấu nên phương trình
( )
( )
22
20x m m x x− − − =
có ít nhất hai nghiệm phân biệt.
Vậy khi
m
thay đổi
( )
m
C
cắt trục
Ox
tại ít nhất 2 điểm phân biệt.
Câu 50: Cho hình trụ
( )
H
có hai đáy lá các đường tròn
( )
;6O
và
( )
;6O
, chiều cao
8h =
. Một mặt
phẳng cắt trục
OO
của hình trụ và cắt các đường tròn
( )
O
,
( )
O
theo các dây cung
,AB CD
(tham khảo hình vẽ). Biết
9, 3CD AB==
. Diện tích tứ giác
ABCD
gần với số nào nhất trong
các số sau:
A.
75
. B.
76
. C.
65
. D.
66
Lời giải
Gọi
,IJ
lần lượt là trung điểm của
AB
và
CD
.
Gọi
,,A B I
lần lượt là hình chiếu của
,,A B I
lên mặt phẳng chứa
( )
;6O
.
Dễ thấy tứ giác
A B CD
là hình thang cân nên
IJ
đi qua
O
và do mặt phẳng
( )
ABCD
cắt
trục
OO
nên
O
nằm trên đoạn thẳng
IJ
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
27
Tuyển tập 10 đề ôn HKI
Toán 12
Tam giác
A I O
vuông tại
I
nên
2
2 2 2
3 3 15
6
22
I O O A I A
= − = − =
.
Tam giác
CJO
vuông tại
J
nên
2
2 2 2
9 3 7
6
22
JO O C JC
= − = − =
.
Từ đó
( )
3
15 7
2
IJ
=+
.
Tam giác
II J
vuông tại
I
nên
( )
2
2 2 2
9 454 18 105
15 7 8
42
IJ I J II
+
= + = + + =
.
Vậy diện tích tứ giác
ABCD
bằng
( )
.
3 454 18 105
2
AB CD IJ+
=+
75,8024
.
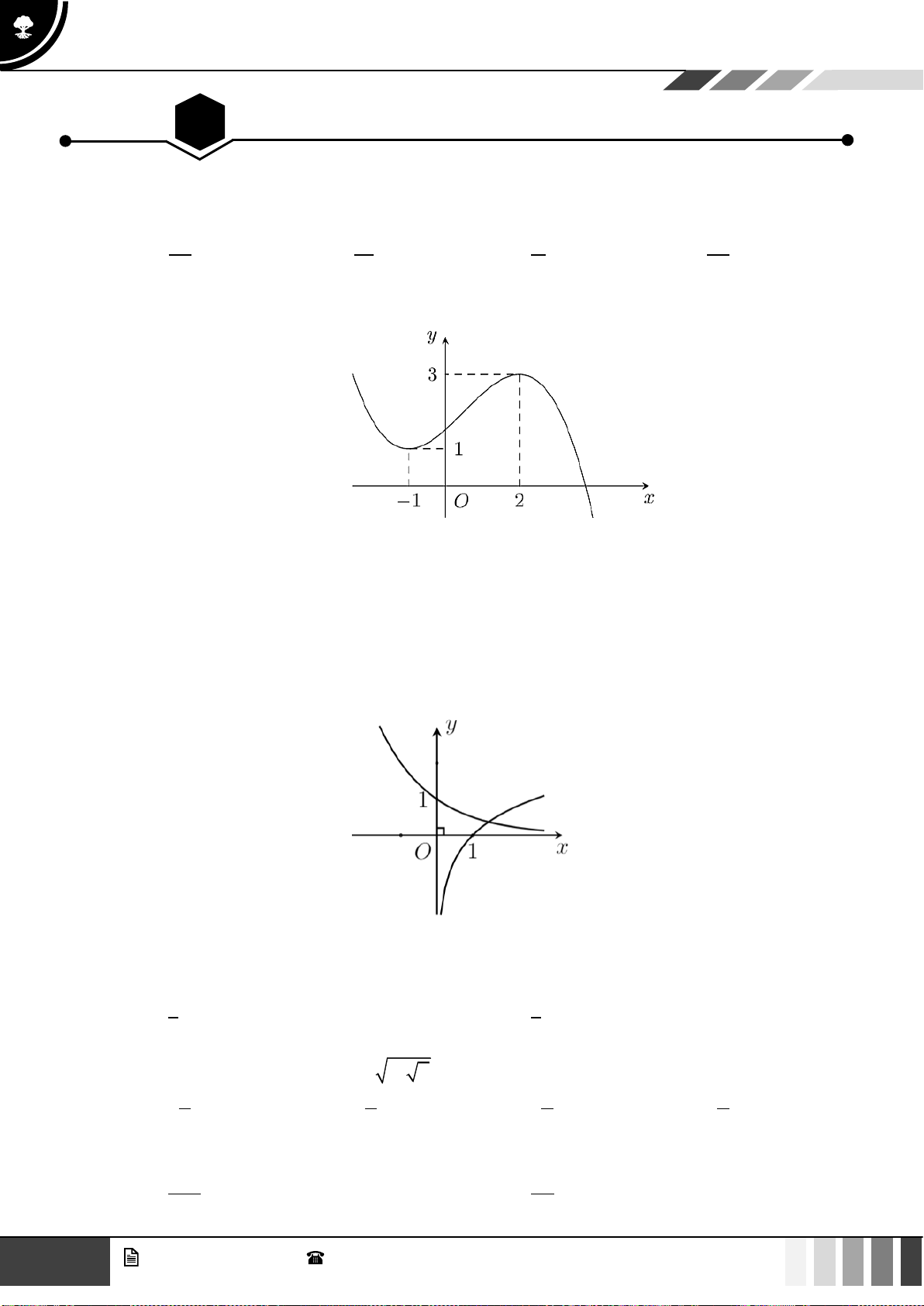
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HKI
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Cho khối chóp có thể tích
V
và chiều cao
h
. Khi đó diện tích đáy của khối chóp bằng
A.
3
h
V
. B.
3
V
h
. C.
V
h
. D.
3V
h
.
Câu 2: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
1;2−
.
B. Hàm số đồng biến trên khoảng
( )
0;2
.
C. Hàm số đồng biến trên khoảng
( )
0;+
.
D. Hàm số nghịch biến trên khoảng
( )
;0−
.
Câu 3: Cho các đồ thị hàm số
x
ya=
và
log
b
yx=
như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
01ba
. B.
1 ba
. C.
01ab
. D.
01ab
.
Câu 4: Thể tích khối trụ tròn xoay có bán kính đáy
R
và chiều cao
h
bằng
A.
2
1
3
Rh
. B.
2
Rh
. C.
2
1
3
Rh
. D.
2
Rh
Câu 5: Với
a
là số thực dương tùy ý,
3
4
aa
bằng
A.
13
6
a
. B.
13
8
a
. C.
17
4
a
. D.
17
6
a
.
Câu 6: Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
2h
là
A.
2
3
Bh
. B.
2Bh
. C.
3
Bh
. D.
Bh
.
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
08
8
ĐỀ SỐ

GV. Phan Nhật Linh -
SĐT: 0817 098 716
2
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 7: Khối lập phương cạnh
3a
có thể tích bằng
A.
3
9a
. B.
3
27a
. C.
2
9a
. D.
3
3a
.
Câu 8: Hàm số nào sau đây nghịch biến trên khoảng
( )
0;+
?
A.
1
2
x
y
=
. B.
21
logyx
+
=
. C.
2
logyx=
. D.
3
x
y =
.
Câu 9: Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2;+
. B.
( )
;2− −
. C.
( )
2;− +
. D.
( )
2;1−
.
Câu 10: Cho hàm số
1
4
yx
−
=
. Khẳng định nào sau đây sai?
A. Hàm số không có điểm cực trị. B. Hàm số nghịch biến trên .
C. Đồ thị hàm số đi qua điểm
( )
1;1A
. D. Đồ thị hàm số có hai đường tiệm cận.
Câu 11: Cho
a
là số thực dương. Biểu thức
2
3
5
3
aa
viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
1
a
−
. B.
10
3
a
. C.
19
5
a
. D.
7
3
a
.
Câu 12: Phương trình tiếp tuyến của đồ thị hàm số
( )
32
31f x x x= − +
tại điểm
( )
4;17M
là
A.
24 113yx=+
. B.
24 113yx=−
. C.
24 79yx=−
. D.
24 79yx=+
.
Câu 13: Giá trị nhỏ nhất của hàm số
42
1
2
4
y x x= − −
trên đoạn
2;4
bằng
A.
37
4
. B.
2−
. C.
3−
. D. 46.
Câu 14: Cho
a
là số thực dương khác 1 thỏa
log 2 3
a
=
. Khẳng định nào sau đây đúng?
A.
2
3a =
. B.
3
2a =
. C.
23
a
=
. D.
32
a
=
.
Câu 15: Cho
,xy
là hai số thực dương và
,mn
là hai số thực tùy ý. Đẳng thức nào sau đây sai?
A.
( ) ( )
mn
nm
xx=
. B.
( )
3
3
mm
xx=
. C.
( )
.
n
nn
xy x y=
. D.
.
m n m n
x x x
+
=
.
Câu 16: Tiệm cận ngang của đồ thị hàm số
21
3
x
y
x
−
=
+
có phương trình là
A.
2y =
. B.
1
3
y =−
. C.
3y =−
. D.
2x =
.
Câu 17: Cho
,,abc
là các số thực dương khác
1
thỏa mãn
log 6, log 3
ac
bb==
. Khi đó
log
a
c
bằng
A.
2
. B.
9
. C.
1
2
. D.
3
.
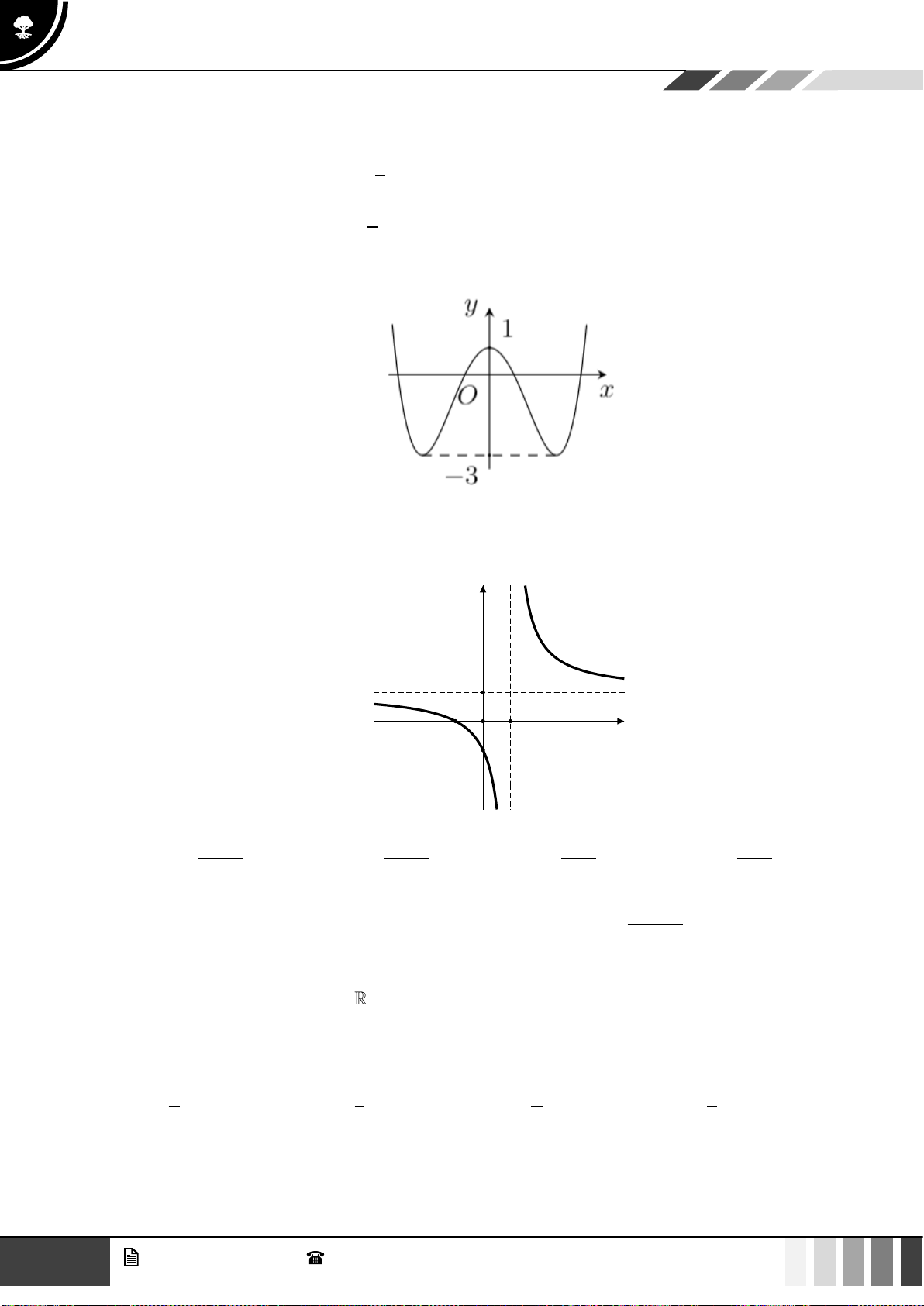
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 18: Cho hình trụ
()T
có bán kính đáy
5R =
, chiều cao
3.h =
Diện tích xung quanh của
()T
là
A.
55
. B.
75
. B.
15
. D.
30
.
Câu 19: Giá trị cực đại của hàm số
32
1
31
3
y x x x= + − +
bằng
A.
3−
. B.
2
3
−
. C.
1
. D.
10
.
Câu 20: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Số nghiệm của phương trình
( )
2 3 0fx−=
là
A.
0
. B.
3
. C.
4
. D.
2
.
Câu 21: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
21
1
x
y
x
−
=
−
. B.
21
1
x
y
x
−
=
−
. C.
1
1
x
y
x
−
=
+
. D.
1
1
x
y
x
+
=
−
.
Câu 22: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
2
1
1
mx
fx
x
−
=
+
có giá trị lớn nhất trên
đoạn
0;1
bằng
4
là
A.
3; 1−−
. B. . C.
3; 2
. D.
3; 3−
.
Câu 23: Cho hình chóp
.S ABC
. Gọi
', 'AB
lần lượt là trung điểm của
,SA SB
. Khi đó tỉ số thể tích của
hai khối chóp
. ' 'S A B C
và
.S ABC
bằng
A.
1
4
. B.
1
8
. C.
1
2
. D.
1
3
.
Câu 24: Cho hàm số
( )
( ) ln 1
x
f x e=+
. Khi đó
''(ln2)f
bằng
A.
9
2
−
. B.
2
9
. C.
2
9
−
. D.
9
2
.
x
y
O
1
1
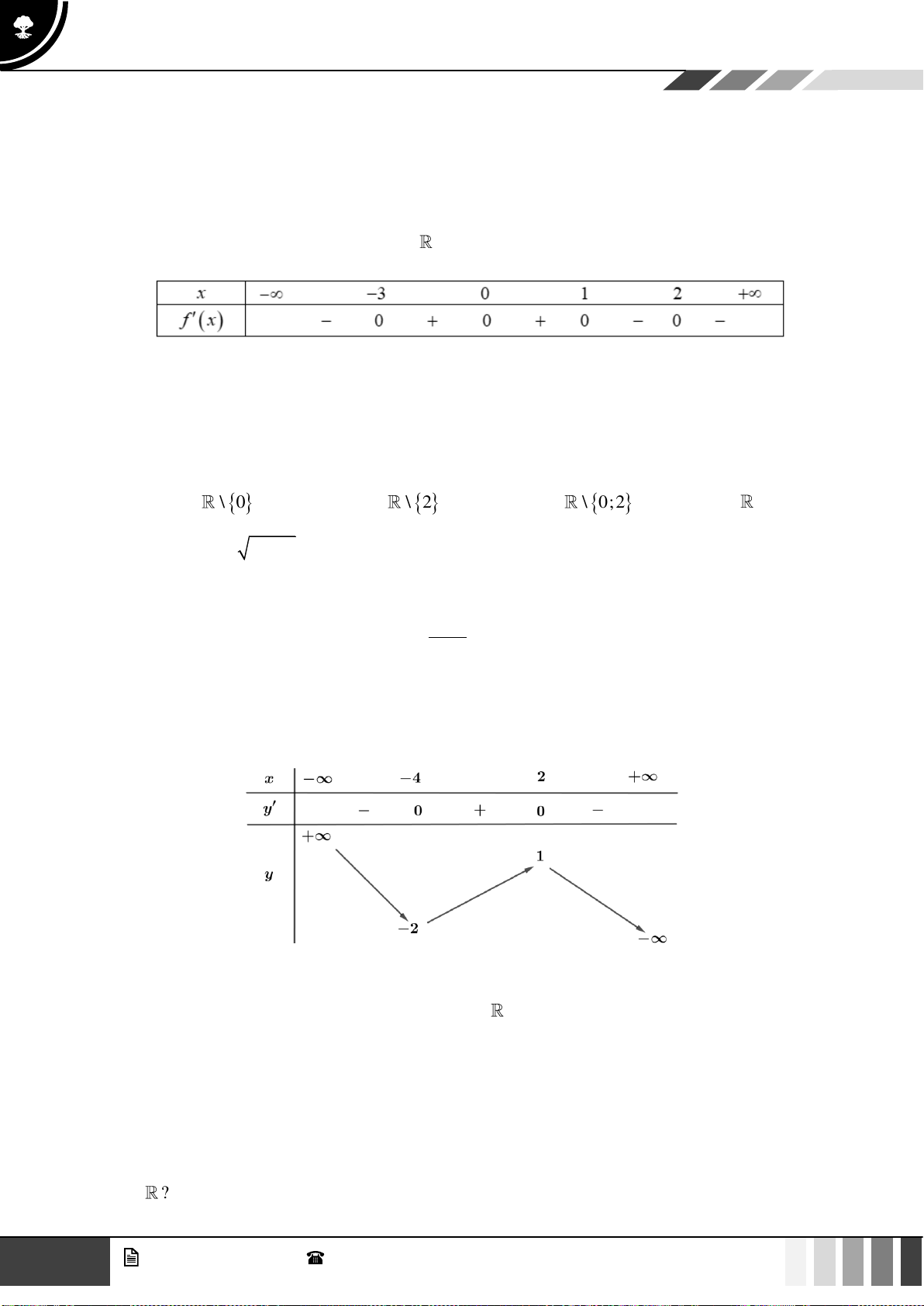
GV. Phan Nhật Linh -
SĐT: 0817 098 716
4
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 25: Cho hình nón
( )
N
có độ dài đường sinh bằng
5
và bán kính đáy bằng
3
.
( )
N
có chiều cao bằng
A.
4
. B.
2
. C.
3
. D.
5
.
Câu 26: Thể tích của khối nón
( )
N
có bán kính
Ra=
và chiều cao
3ha=
là
A.
2
3 a
. B.
3
2 a
. C.
3
a
. D.
3
3 a
.
Câu 27: Cho hàm số
( )
y f x=
xác định trên và có bảng xét dấu
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
4
B.
1
C.
3
D.
2
Câu 28: Tập xác định
D
của hàm số
( )
10
2
2y x x
−
=−
là
A.
\0D =
. B.
\2D =
. C.
\ 0;2D =
. D.
D =
.
Câu 29: Hàm số
2
4yx=−
đồng biến trên khoảng nào sau đây?
A.
( )
0;2
. B.
( )
1;1−
. C.
( )
2;0−
. D.
( )
2;2−
.
Câu 30: Biết tiếp tuyến của đồ thị hàm số
1
2
x
y
x
+
=
−
song song với đường thẳng
31yx= − +
có phương
trình
y ax b=+
. Khi đó giá trị
ab−
bằng
A.
4
. B.
16−
. C.
4−
. D.
16
.
Câu 31: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Khẳng định nào sau đây là khẳng định sai?
A. Giá trị nhỏ nhất của hàm số
( )
y f x=
trên bằng
2−
.
B. Phương trình
( )
0fx=
có 3 nghiệm phân biệt.
C. Đồ thị hàm số
( )
y f x=
không có tiệm cận.
D. Giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2;4
bằng
( )
4f
.
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
2
log 2 9y x mx= − +
có tập xác định là
?
A.
5
. B.
4
. C.
6
. D.
7
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 33: Giá trị nhỏ nhất của tham số
m
đề hàm số
2
1
mx
y
xm
−
=
−+
đồng biến trên khoảng
( )
;1− −
là
A.
1
2
m =
. B.
1m =
. C.
3m =−
. D.
0m =
.
Câu 34: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
và
'AA AB a==
.
Thể tích khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
6
a
. B.
3
2
a
. C.
3
a
. D.
3
3
a
.
Câu 35: Cho hàm số
( )
y f x=
và
( )
fx
có bảng xét dấu như hình dưới. Số điểm cực trị của hàm số
( )
fx
là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 36: Biết rằng
( )
0;2A
và
( )
1;1B −
là hai trong ba điểm cực trị của đồ thị hàm số
( ) ( )
42
, , ,f x ax bx c a b c= + +
. Khi đó giá trị của
( )
2f
bằng
A.
10
. B.
65
. C.
226
. D.
1
.
Câu 37: Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông tại
A
;
AB a=
,
30ACB =
, góc giữa
hai mặt phẳng
( )
BA C
và
( )
ABC
bằng
45
. Gọi
( )
T
là hình trụ ngoại tiếp lăng trụ
.ABC A B C
. Thể tích của khối trụ sinh bởi
( )
T
là
A.
3
a
. B.
3
6
a
. C.
3
3
a
. D.
3
2 a
.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
, 3 , ,D AB a AD CD a SA= = =
vuông góc với mặt phẳng
( )
ABCD
. Nếu góc giữa đường thẳng
SD
và mặt phẳng
( )
ABCD
bằng
60
thì khối chóp
.S ABCD
có thể tích bằng
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
23a
. D.
3
3
2
a
.
Câu 39: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
3
30x x m− − =
có
3 nghiệm phân biệt trong đó có
2
nghiệm dương. Khẳng định nào sau đây đúng
A.
( )
0;2S =
. B.
2;2S =−
. C.
( )
2;2S =−
. D.
( )
2;0S =−
.
Câu 40: Diện tích xung quanh của hình nón ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng
2
là
A.
23
. B.
42
. C.
22
. D.
2
.
Câu 41: Cho hình hộp chữ nhật
.ABCD A B C D
có
AB a=
,
2AD a=
, góc giữa hai mặt phẳng
( )
ABC D
và
( )
ABCD
bằng
45
. Khối hộp
.ABCD A B C D
có thể tích bằng
A.
3
4a
. B.
3
2a
. C.
3
8a
. D.
3
6a
.
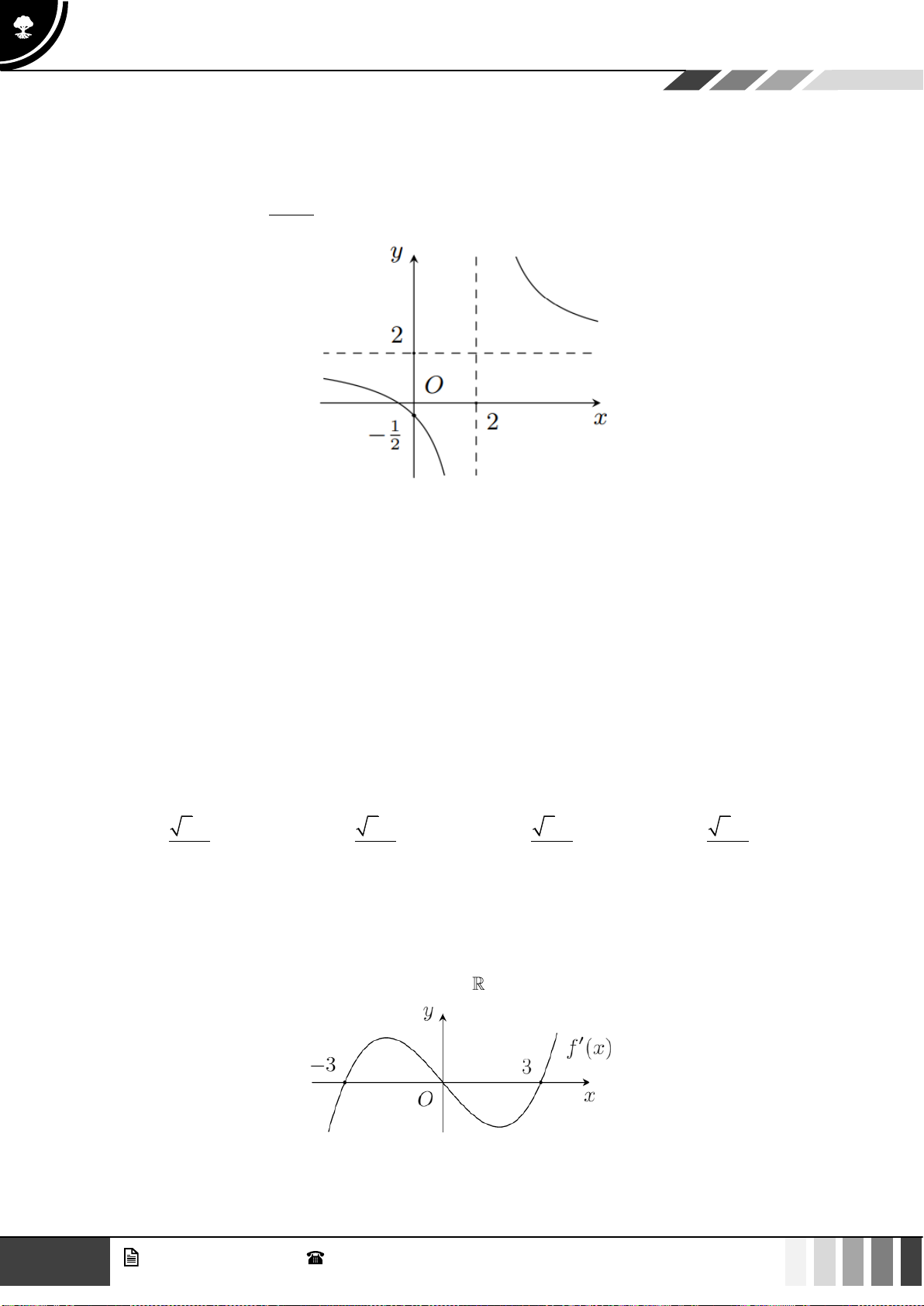
GV. Phan Nhật Linh -
SĐT: 0817 098 716
6
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 42: Cho hình nón
( )
N
có thiết diện qua trục là một tam giác vuông cân có diện tích bằng
9
. Khối
nón sinh bởi
( )
N
có thể tích bằng
A.
6
. B.
3
. C.
9
. D.
Câu 43: Cho hàm số
1ax
y
bx c
+
=
+
có đồ thị như hình bên. Giá trị
abc++
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 44: Cắt một hình trụ
( )
T
bởi một mặt phẳng qua trục của nó được thiết diện là hình vuông cạnh
2a
. Tính diện tích toàn phần của
( )
T
A.
2
2 a
. B.
2
4 a
. C.
2
8 a
. D.
2
6 a
.
Câu 45: Xét các số thực dương
,ab
thỏa
22
20ab+=
. Khẳng định nào sau đây đúng?
A. Giá trị nhỏ nhất của
log( )ab
bằng
0
. B. Giá trị lớn nhất của
log( )ab
bằng
0
.
C. Giá trị nhỏ nhất của
log( )ab
bằng
1
. D. Giá trị lớn nhất của
log( )ab
bằng
1
.
Câu 46: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác đều cạnh
a
. Gọi
,MN
lần lượt là rung điểm
của
''AB
và
'CC
. Nếu
AM
và
'AN
vuông góc với nhau thì khối lăng trụ
. ' ' 'ABC A B C
có thể
tích bằng
A.
3
6
8
a
. B.
3
6
2
a
. C.
3
6
4
a
. D.
3
6
24
a
.
Câu 47: Xét khối trụ
( )
T
có bán kính
R
và chiều cao
h
thỏa mãn
23Rh+=
. Thể tích của
( )
T
có giá
trị lớn nhất bằng
A.
2
. B.
3
. C.
. D.
4
.
Câu 48: Cho hàm số
( )
fx
, biết
( )
fx
liên tục trên và có đồ thị như hình dưới đây.
Hàm số
( )
( )
2
4 2020g x f x= − +
đồng biến trên khoảng nào sau đây?
A.
( )
2;0−
. B.
( )
0;2
. C.
( )
2;+
. D.
( )
1;2
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 49: Cho khối lăng trụ
.ABC A B C
có thể tích bằng
a
. Gọi
M
là trung điểm của
AB
. Nếu tam giác
MB C
có diện tích bằng
b
thì khoảng cách từ
C
đến mặt phẳng
( )
MB C
bằng
A.
2
a
b
. B.
a
b
. C.
2
b
a
. D.
6
a
b
.
Câu 50: Có bao nhiêu số nguyên dương
m
để phương trình
( )
( )
2
e 1 ln 1 2e e 1
x x x
m mx− + + = +
có hai
nghiệm phân biệt không lớn hơn
5
.
A.
29
. B.
27
. C.
28
. D.
26
.
-------------------------HẾT-------------------------
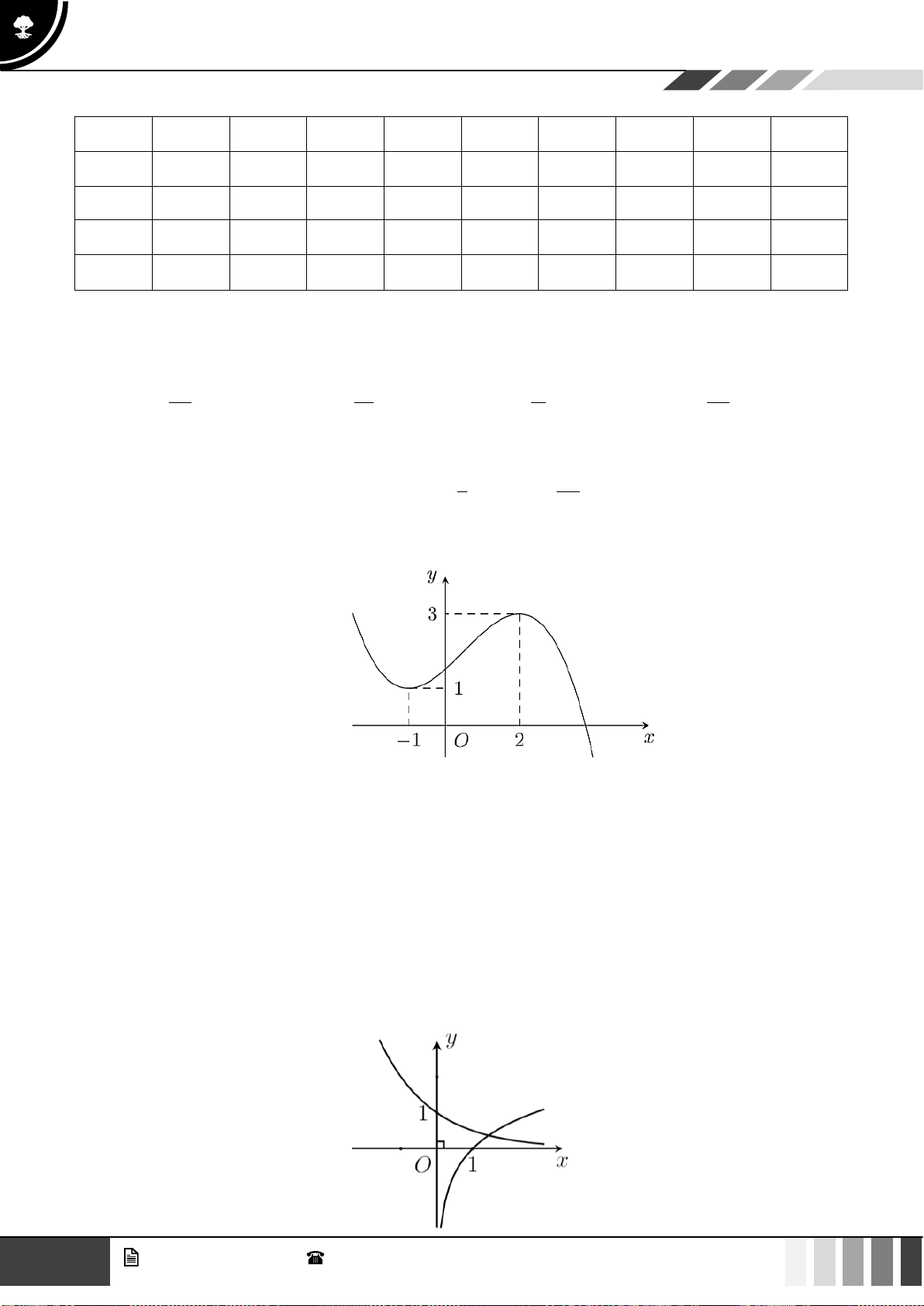
GV. Phan Nhật Linh -
SĐT: 0817 098 716
8
Tuyển tập 10 đề ôn HKI
Toán 12
BẢNG ĐÁP ÁN
1.D
2.B
3.C
4.D
5.B
6.B
7.B
8.A
9.A
10.B
11.D
12.C
13.B
14.B
15.B
16.A
17.A
18.D
19.D
20.D
21.D
22.D
23.A
24.B
25.A
26.C
27.D
28.C
29.C
30.B
31.A
32.A
33.D
34.B
35.A
36.A
37.A
38.A
39.D
40.C
41.A
42.C
43.A
44.D
45.D
46.A
47.C
48.D
49.A
50.C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho khối chóp có thể tích
V
và chiều cao
h
. Khi đó diện tích đáy của khối chóp bằng
A.
3
h
V
. B.
3
V
h
. C.
V
h
. D.
3V
h
.
Lời giải
Ta có công thức thể tích khối chóp là
13
.
3
V
V B h B
h
= =
.
Câu 2: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
1;2−
.
B. Hàm số đồng biến trên khoảng
( )
0;2
.
C. Hàm số đồng biến trên khoảng
( )
0;+
.
D. Hàm số nghịch biến trên khoảng
( )
;0−
.
Lời giải
Dựa vào đồ thị ta thấy hàm số
( )
y f x=
đồng biến trên khoảng
( )
0;2
.
Câu 3: Cho các đồ thị hàm số
x
ya=
và
log
b
yx=
như hình vẽ bên. Mệnh đề nào sau đây đúng?
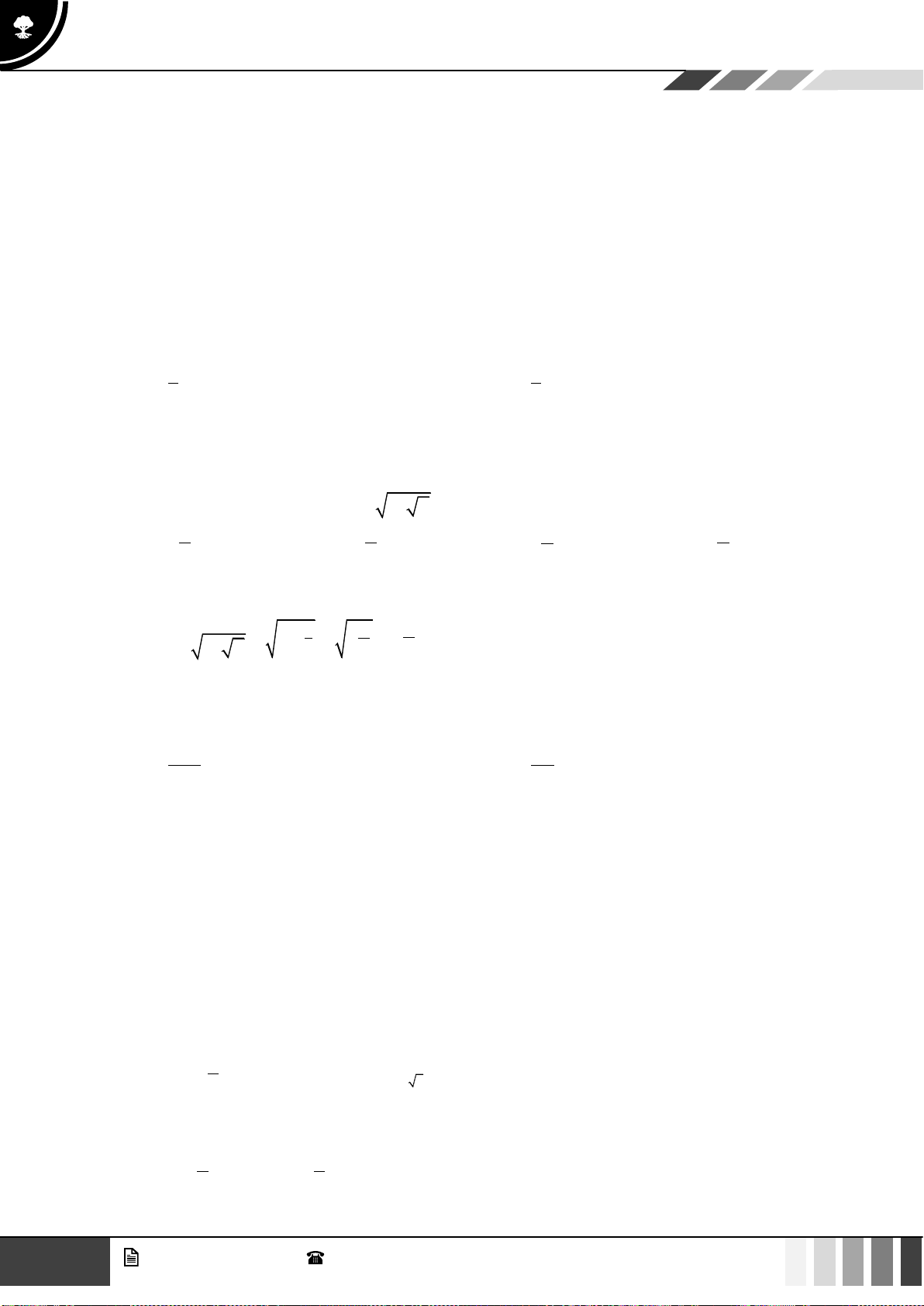
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HKI
Toán 12
A.
01ba
. B.
1 ba
. C.
01ab
. D.
01ab
.
Lời giải
Đồ thị hàm số
x
ya=
là đường cong đi qua điểm có tọa độ
( )
0;1
và là đường cong có chiều “đi
xuống” nên hàm số là hàm nghịch biến
01a
.
Đồ thị hàm số
log
b
yx=
là đường cong đi qua điểm có tọa độ
( )
1;0
và là đường cong có chiều
“đi lên” nên hàm số là hàm đồng biến
1b
.
Vậy
01ab
.
Câu 4: Thể tích khối trụ tròn xoay có bán kính đáy
R
và chiều cao
h
bằng
A.
2
1
3
Rh
. B.
2
Rh
. C.
2
1
3
Rh
. D.
2
Rh
Lời giải
Thể tích khối trụ tròn xoay là
2
.V B h R h
==
.
Câu 5: Với
a
là số thực dương tùy ý,
3
4
aa
bằng
A.
13
6
a
. B.
13
8
a
. C.
17
4
a
. D.
17
6
a
.
Lời giải
Ta có
13
1 13
33
4
8
44
a a a a a a= = =
.
Câu 6: Thể tích khối lăng trụ có diện tích đáy
B
và chiều cao
2h
là
A.
2
3
Bh
. B.
2Bh
. C.
3
Bh
. D.
Bh
.
Lời giải
Thể tích khối lăng trụ là
.2 2V B h Bh==
.
Câu 7: Khối lập phương cạnh
3a
có thể tích bằng
A.
3
9a
. B.
3
27a
. C.
2
9a
. D.
3
3a
.
Lời giải
Thể tích khối lập phương cạnh
3a
là
( )
3
3
3 27V a a==
(đvtt).
Câu 8: Hàm số nào sau đây nghịch biến trên khoảng
( )
0;+
?
A.
1
2
x
y
=
. B.
21
logyx
+
=
. C.
2
logyx=
. D.
3
x
y =
.
Lời giải
Vì
1
01
2
nên
1
2
x
y
=
nghịch biến trên
( )
0;+
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
10
Tuyển tập 10 đề ôn HKI
Toán 12
Vì các cơ số
2 1, 2, 3 1+
nên
21
logyx
+
=
,
2
logyx=
,
3
x
y =
đồng biến trên
( )
0;+
.
Câu 9: Cho hàm số
( )
fx
có bảng xét dấu của đạo hàm như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2;+
. B.
( )
;2− −
. C.
( )
2;− +
. D.
( )
2;1−
.
Lời giải
Từ bảng biến thiên suy ra hàm số nghịch biến trên khoảng
( )
2;+
.
Câu 10: Cho hàm số
1
4
yx
−
=
. Khẳng định nào sau đây sai?
A. Hàm số không có điểm cực trị. B. Hàm số nghịch biến trên .
C. Đồ thị hàm số đi qua điểm
( )
1;1A
. D. Đồ thị hàm số có hai đường tiệm cận.
Lời giải
Vì tập xác định của hàm số là
( )
0;D = +
nên không thể nghịch biến trên được.
Câu 11: Cho
a
là số thực dương. Biểu thức
2
3
5
3
aa
viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
1
a
−
. B.
10
3
a
. C.
19
5
a
. D.
7
3
a
.
Lời giải
Với
0a
ta có
2 2 5 7
3
5
3 3 3 3
a a a a
+
==
.
Câu 12: Phương trình tiếp tuyến của đồ thị hàm số
( )
32
31f x x x= − +
tại điểm
( )
4;17M
là
A.
24 113yx=+
. B.
24 113yx=−
. C.
24 79yx=−
. D.
24 79yx=+
.
Lời giải
( ) ( )
3 2 2
3 1 3 6f x x x f x x x
= − + = −
Ta có
( )
4 24f
=
.
Tiếp tuyến của đồ thị hàm số
( )
32
31f x x x= − +
tại điểm
( )
4;17M
là
( ) ( )
4 . 4 17y f x
= − +
( )
24 4 17yx = − +
24 79yx = −
.
Câu 13: Giá trị nhỏ nhất của hàm số
42
1
2
4
y x x= − −
trên đoạn
2;4
bằng
A.
37
4
. B.
2−
. C.
3−
. D. 46.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Ta có
4 2 3
1
( ) 2 2
4
y f x x x y x x
= = − − = −
.
( )
32
0 2;4
0 2 0 2 0 .
2 2;4
x
y x x x x
x
=
= − = − =
=
( )
22f =−
,
( )
4 46f =
Giá trị nhỏ nhất của hàm số đã cho trên đoạn
2;4
bằng
2−
.
Câu 14: Cho
a
là số thực dương khác 1 thỏa
log 2 3
a
=
. Khẳng định nào sau đây đúng?
A.
2
3a =
. B.
3
2a =
. C.
23
a
=
. D.
32
a
=
.
Lời giải
Theo định nghĩa logarit ta có
3
log 2 3 2
a
a= =
.
Câu 15: Cho
,xy
là hai số thực dương và
,mn
là hai số thực tùy ý. Đẳng thức nào sau đây sai?
A.
( ) ( )
mn
nm
xx=
. B.
( )
3
3
mm
xx=
. C.
( )
.
n
nn
xy x y=
. D.
.
m n m n
x x x
+
=
.
Lời giải
Ta có
( )
3
3
3m m m
x x x=
. Vậy đẳng thức
( )
3
3
mm
xx=
sai.
Câu 16: Tiệm cận ngang của đồ thị hàm số
21
3
x
y
x
−
=
+
có phương trình là
A.
2y =
. B.
1
3
y =−
. C.
3y =−
. D.
2x =
.
Lời giải
Ta có
21
lim lim 2
3
xx
x
y
x
→+ →+
−
==
+
. Nên
2y =
là đường tiệm cận ngang của đồ thị hàm số.
Câu 17: Cho
,,abc
là các số thực dương khác
1
thỏa mãn
log 6, log 3
ac
bb==
. Khi đó
log
a
c
bằng
A.
2
. B.
9
. C.
1
2
. D.
3
.
Lời giải
Ta có:
1
1
log log
3
log 2.
11
log
log 6
bc
a
b
a
cb
c
a
b
= = = =
Câu 18: Cho hình trụ
()T
có bán kính đáy
5R =
, chiều cao
3.h =
Diện tích xung quanh của
()T
là
A.
55
. B.
75
. B.
15
. D.
30
.
Lời giải
Diện tích xung quanh hình trụ:
2 . . 2 .5.3 30
xq
S R h
= = =
.
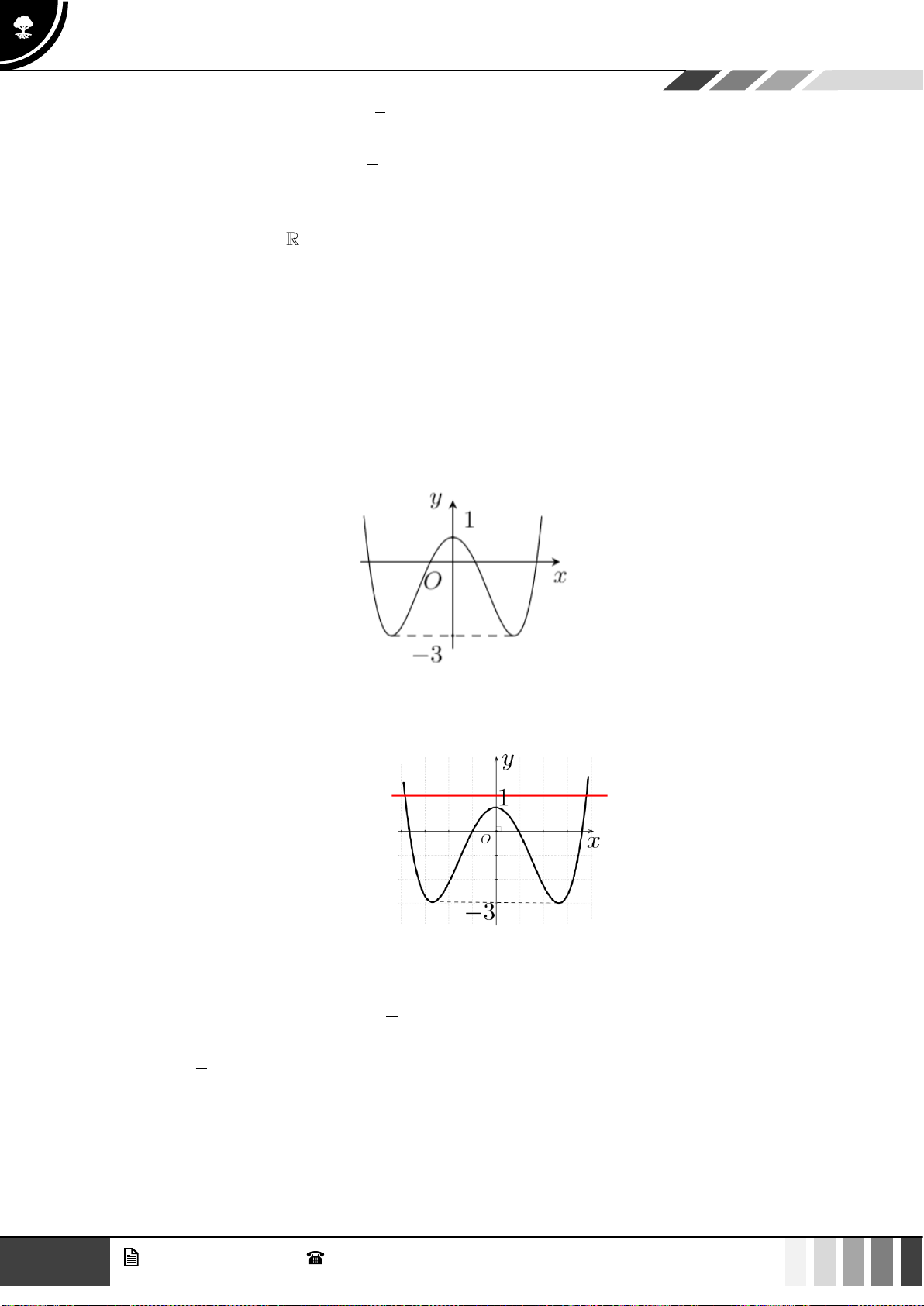
GV. Phan Nhật Linh -
SĐT: 0817 098 716
12
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 19: Giá trị cực đại của hàm số
32
1
31
3
y x x x= + − +
bằng
A.
3−
. B.
2
3
−
. C.
1
. D.
10
.
Lời giải
Tập xác định:
D =
.
Ta có
2
23y x x
= + −
,
22yx
=+
.
Cho
0y
=
2
2 3 0xx + − =
3
1
x
x
=−
=
.
Do
( )
3 4 0y
− = −
,
( )
1 4 0y
=
nên hàm số đạt cực đại tại
3x =−
và giá trị cực đại bằng
10y =
.
Câu 20: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Số nghiệm của phương trình
( )
2 3 0fx−=
là
A.
0
. B.
3
. C.
4
. D.
2
.
Lời giải
Giả sử hàm số
( )
y f x=
có đồ thị
( )
C
.
Ta có:
( )
2 3 0fx−=
( )
3
2
fx=
là phương trình hoành độ giao điểm của
( )
C
và đường thẳng
3
:
2
dy=
. Do đó số nghiệm của phương trình chính là số giao điểm của
( )
C
và
( )
d
.
Dựa vào đồ thị hai hàm số ta có
( )
C
và
( )
d
có
2
điểm chung nên phương trình có
2
nghiệm.
Câu 21: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
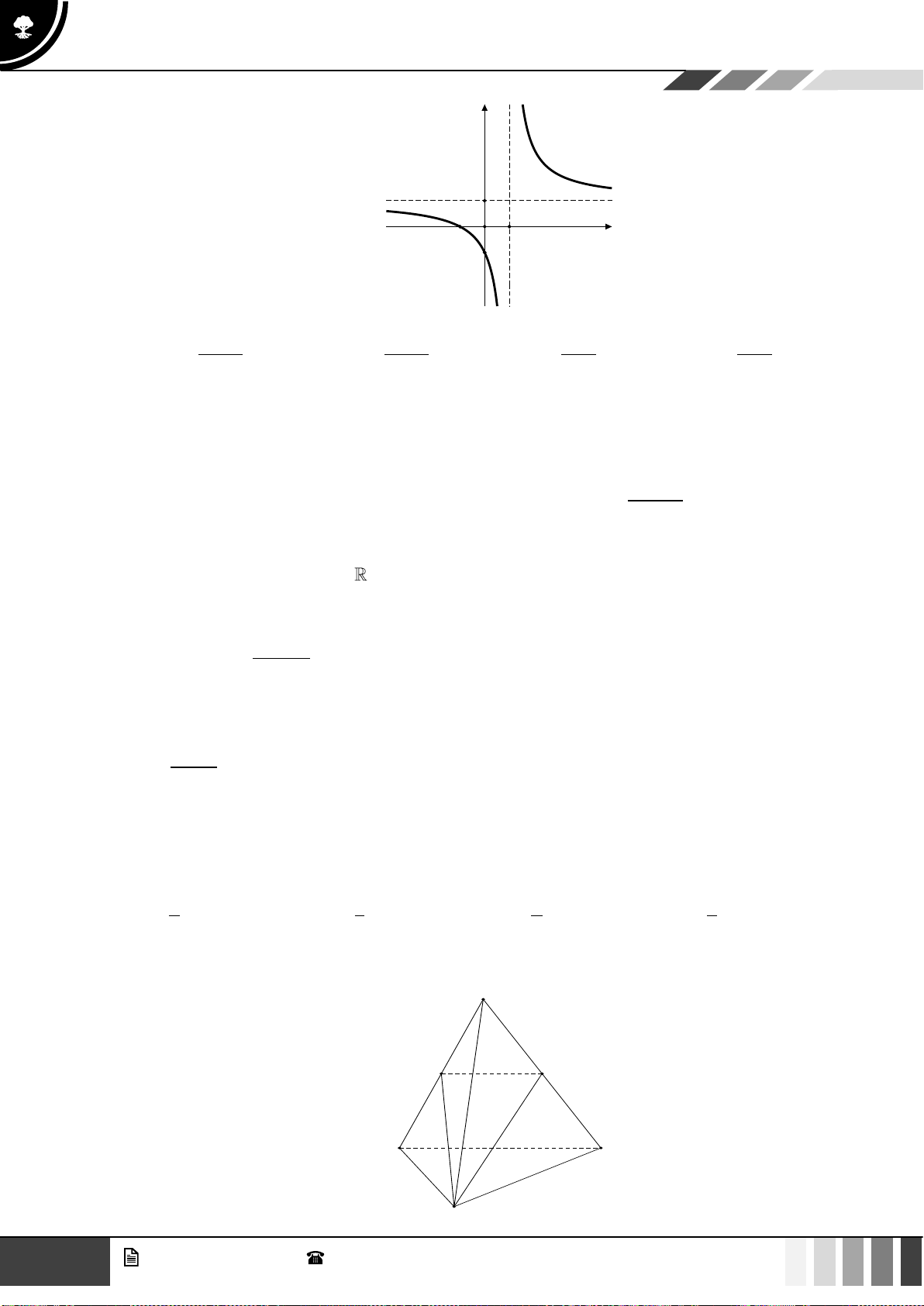
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HKI
Toán 12
A.
21
1
x
y
x
−
=
−
. B.
21
1
x
y
x
−
=
−
. C.
1
1
x
y
x
−
=
+
. D.
1
1
x
y
x
+
=
−
.
Lời giải
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng và ngang
1; 1xy==
.
Câu 22: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
2
1
1
mx
fx
x
−
=
+
có giá trị lớn nhất trên
đoạn
0;1
bằng
4
là
A.
3; 1−−
. B. . C.
3; 2
. D.
3; 3−
.
Lời giải
Ta có
( )
( )
2
2
1
0, 0;1
1
m
f x x
x
+
=
+
.
Do đó giá trị lớn nhất của hàm số trên đoạn
0;1
bằng
4
khi và chỉ khi
( )
14f =
.
2
1
4
2
m −
=
3m =
.
Vậy tập hợp các giá trị của
m
là
3; 3−
.
Câu 23: Cho hình chóp
.S ABC
. Gọi
', 'AB
lần lượt là trung điểm của
,SA SB
. Khi đó tỉ số thể tích của
hai khối chóp
. ' 'S A B C
và
.S ABC
bằng
A.
1
4
. B.
1
8
. C.
1
2
. D.
1
3
.
Lời giải
x
y
O
1
1
B'
A'
A
B
C
S
GV. Phan Nhật Linh -
SĐT: 0817 098 716
14
Tuyển tập 10 đề ôn HKI
Toán 12
Áp dụng công thức tỉ số thể tích của khối chóp ta có:
. ' '
.
' ' 1 1 1
..
2 2 4
S A B C
S ABC
V
SA SB
V SA SB
= = =
Câu 24: Cho hàm số
( )
( ) ln 1
x
f x e=+
. Khi đó
''(ln2)f
bằng
A.
9
2
−
. B.
2
9
. C.
2
9
−
. D.
9
2
.
Lời giải
Ta có:
( )
'
1
x
x
e
fx
e
=
+
( )
( )
2
''
1
x
x
e
fx
e
=
+
( )
( )
ln2
22
ln2
22
'' ln2
9
3
1
e
f
e
= = =
+
.
Câu 25: Cho hình nón
( )
N
có độ dài đường sinh bằng
5
và bán kính đáy bằng
3
.
( )
N
có chiều cao bằng
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Đường cao hình nón:
2 2 2 2
5 3 4h l R= − = − =
Câu 26: Thể tích của khối nón
( )
N
có bán kính
Ra=
và chiều cao
3ha=
là
A.
2
3 a
. B.
3
2 a
. C.
3
a
. D.
3
3 a
.
Lời giải
Thể tích khối nón:
2 2 3
11
.3
33
V R h a a a
= = =
Câu 27: Cho hàm số
( )
y f x=
xác định trên và có bảng xét dấu
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
4
B.
1
C.
3
D.
2
Lời giải
Ta có
y
đổi dấu khi đi qua
3x =−
và qua
1x =
nên số điểm cực trị là
2
.
Câu 28: Tập xác định
D
của hàm số
( )
10
2
2y x x
−
=−
là
A.
\0D =
. B.
\2D =
. C.
\ 0;2D =
. D.
D =
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HKI
Toán 12
Điều kiện xác định:
2
0
20
2
x
xx
x
−
.
Vậy nên tập xác định của hàm số là
\ 0;2D =
Câu 29: Hàm số
2
4yx=−
đồng biến trên khoảng nào sau đây?
A.
( )
0;2
. B.
( )
1;1−
. C.
( )
2;0−
. D.
( )
2;2−
.
Lời giải
Tập xác định
2;2D =−
. Ta có
2
00
4
x
yx
x
−
= = =
−
.
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có hàm số đã cho đồng biến trên khoảng
( )
2;0−
.
Câu 30: Biết tiếp tuyến của đồ thị hàm số
1
2
x
y
x
+
=
−
song song với đường thẳng
31yx= − +
có phương
trình
y ax b=+
. Khi đó giá trị
ab−
bằng
A.
4
. B.
16−
. C.
4−
. D.
16
.
Lời giải
Ta có
( )
2
3
'
2
y
x
−
=
−
. Gọi
( )
00
;xy
là tọa độ tiếp điểm.
Do tiếp tuyến song song với đường thẳng
31yx= − +
nên hệ số góc
( )
( )
0
0
2
0
0
1
3
3
3
2
x
yx
x
x
=
−
= = −
=
−
.
Trường hợp 1:
00
12xy= = −
: Phương trình tiếp tuyến là
( )
3 1 2 3 1y x y x= − − − = − +
(loại).
Trường hợp 2:
00
34xy= =
: Phương trình tiếp tuyến là
( )
3 3 4 3 13y x y x= − − + = − +
(thỏa).
Khi đó,
3, 13ab= − =
nên
16ab− = −
.
Câu 31: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
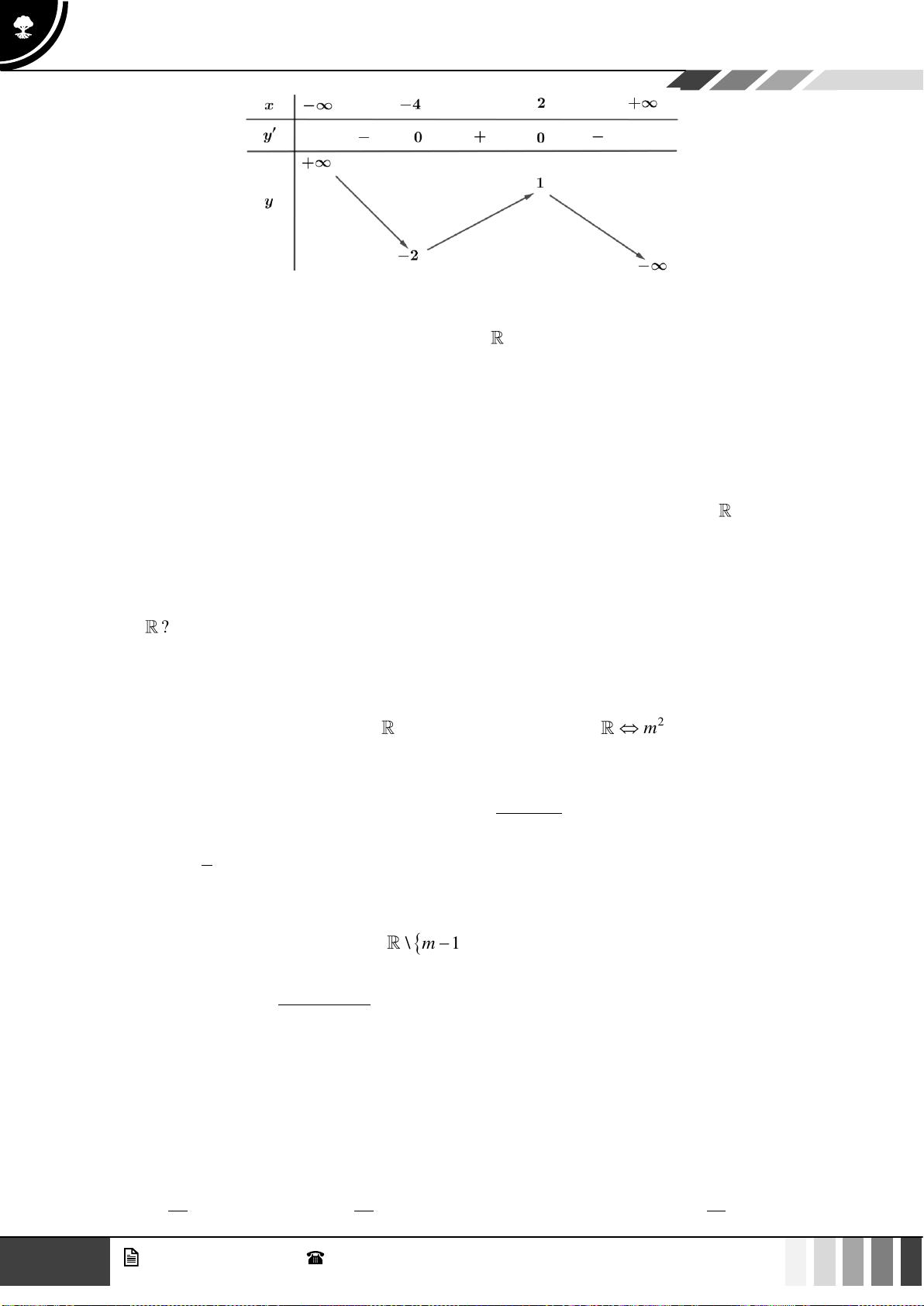
GV. Phan Nhật Linh -
SĐT: 0817 098 716
16
Tuyển tập 10 đề ôn HKI
Toán 12
Khẳng định nào sau đây là khẳng định sai?
A. Giá trị nhỏ nhất của hàm số
( )
y f x=
trên bằng
2−
.
B. Phương trình
( )
0fx=
có 3 nghiệm phân biệt.
C. Đồ thị hàm số
( )
y f x=
không có tiệm cận.
D. Giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2;4
bằng
( )
4f
.
Lời giải
Ta có
( )
lim
x
fx
→+
= −
nên hàm số
( )
y f x=
không có giá trị nhỏ nhất trên . Do đó khẳng
định A là sai.
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
2
log 2 9y x mx= − +
có tập xác định là
?
A.
5
. B.
4
. C.
6
. D.
7
.
Lời giải
Để hàm số có tập xác định
D =
thì:
22
2 9 0 9 0 3 3x mx x m m− + − −
Vậy có
5
giá trị nguyên
m
thỏa mãn.
Câu 33: Giá trị nhỏ nhất của tham số
m
đề hàm số
2
1
mx
y
xm
−
=
−+
đồng biến trên khoảng
( )
;1− −
là
A.
1
2
m =
. B.
1m =
. C.
3m =−
. D.
0m =
.
Lời giải
Tập xác định của hàm số là
\1Dm=−
.
Ta tính được
( )
2
2
2
1
mm
y
xm
− + +
=
−+
. Do đó điều kiện của
m
đề hàm số đồng biến trên
( )
;1− −
là
2
11
0
02
12
20
m
m
m
m
mm
− −
−
− + +
. Vậy giá trị nhỏ nhất của
m
là
0m =
.
Câu 34: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
và
'AA AB a==
.
Thể tích khối lăng trụ
. ' ' 'ABC A B C
bằng
A.
3
6
a
. B.
3
2
a
. C.
3
a
. D.
3
3
a
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Ta có thể tích khối lăng trụ là
3
1
'. . .
22
ABC
a
V AA S a a a
= = =
.
Câu 35: Cho hàm số
( )
y f x=
và
( )
fx
có bảng xét dấu như hình dưới. Số điểm cực trị của hàm số
( )
fx
là
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Ta có
( )
fx
đổi dấu
3
lần nên hàm số
( )
y f x=
có
3
điểm cực trị.
Câu 36: Biết rằng
( )
0;2A
và
( )
1;1B −
là hai trong ba điểm cực trị của đồ thị hàm số
( ) ( )
42
, , ,f x ax bx c a b c= + +
. Khi đó giá trị của
( )
2f
bằng
A.
10
. B.
65
. C.
226
. D.
1
.
Lời giải
Ta có:
( ) ( )
4 2 3
42f x ax bx c f x ax bx
= + + = +
.
Vì
( )
0;2A
và
( )
1;1B −
là hai điểm cực trị của đồ thị hàm số nên
( )
( )
( )
02
21
1 1 2 1 2
4 2 0 2
10
f
ca
f a b b
a b c
f
=
==
− = + + = = −
− − = =
−=
. Vậy
( ) ( )
42
2 2 2 10f x x x f= − + =
.
Câu 37: Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác vuông tại
A
;
AB a=
,
30ACB =
, góc giữa
hai mặt phẳng
( )
BA C
và
( )
ABC
bằng
45
. Gọi
( )
T
là hình trụ ngoại tiếp lăng trụ
.ABC A B C
. Thể tích của khối trụ sinh bởi
( )
T
là
A.
3
a
. B.
3
6
a
. C.
3
3
a
. D.
3
2 a
.
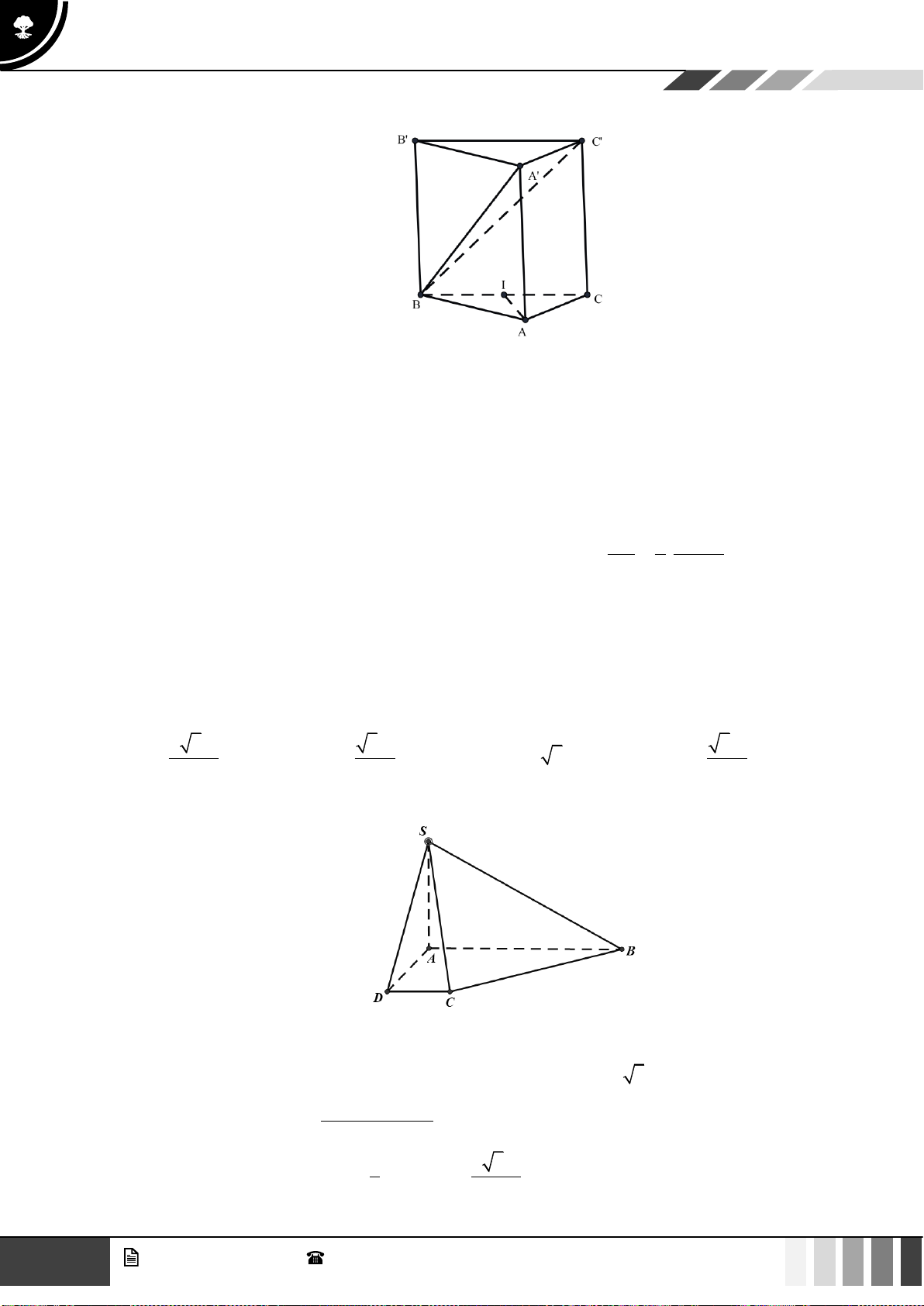
GV. Phan Nhật Linh -
SĐT: 0817 098 716
18
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Ta có
( ) ( )
BA C A B C A C
=
,
( )
AA B B A C
⊥
Do đó góc giữa hai mặt phẳng
( )
BA C
và
( )
ABC
là
45BA B
=
.
Tam giác
BB A
vuông cân tại
B
nên
BB B A a
==
.
Hình trụ
( )
T
ngoại tiếp lăng trụ
.ABC A B C
có chiều cao
h BB a==
, đường tròn đáy là
đường tròn ngoại tiếp tam giác vuông
ABC
nên bán kính
1
.
2 2 sin30
BC BA
ra= = =
Thể tích khối trụ
( )
T
là:
2 2 3
. . .V r h a a a
= = =
.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
, 3 , ,D AB a AD CD a SA= = =
vuông góc với mặt phẳng
( )
ABCD
. Nếu góc giữa đường thẳng
SD
và mặt phẳng
( )
ABCD
bằng
60
thì khối chóp
.S ABCD
có thể tích bằng
A.
3
23
3
a
. B.
3
3
3
a
. C.
3
23a
. D.
3
3
2
a
.
Lời giải
Do
( ) ( )
(
)
( )
, , 60SA ABCD SD ABCD SD AD SDA SDA⊥ = = =
.
Tam giác
SAD
vuông tại
, 60 tan60 3A SDA SA AD a= = =
.
Diện tích đáy:
( )
2
2
2
ABCD
AD AB CD
Sa
+
==
.
Thể tích khối chóp:
3
.
1 2 3
.
33
S ABCD ABCD
a
V SAS==
.
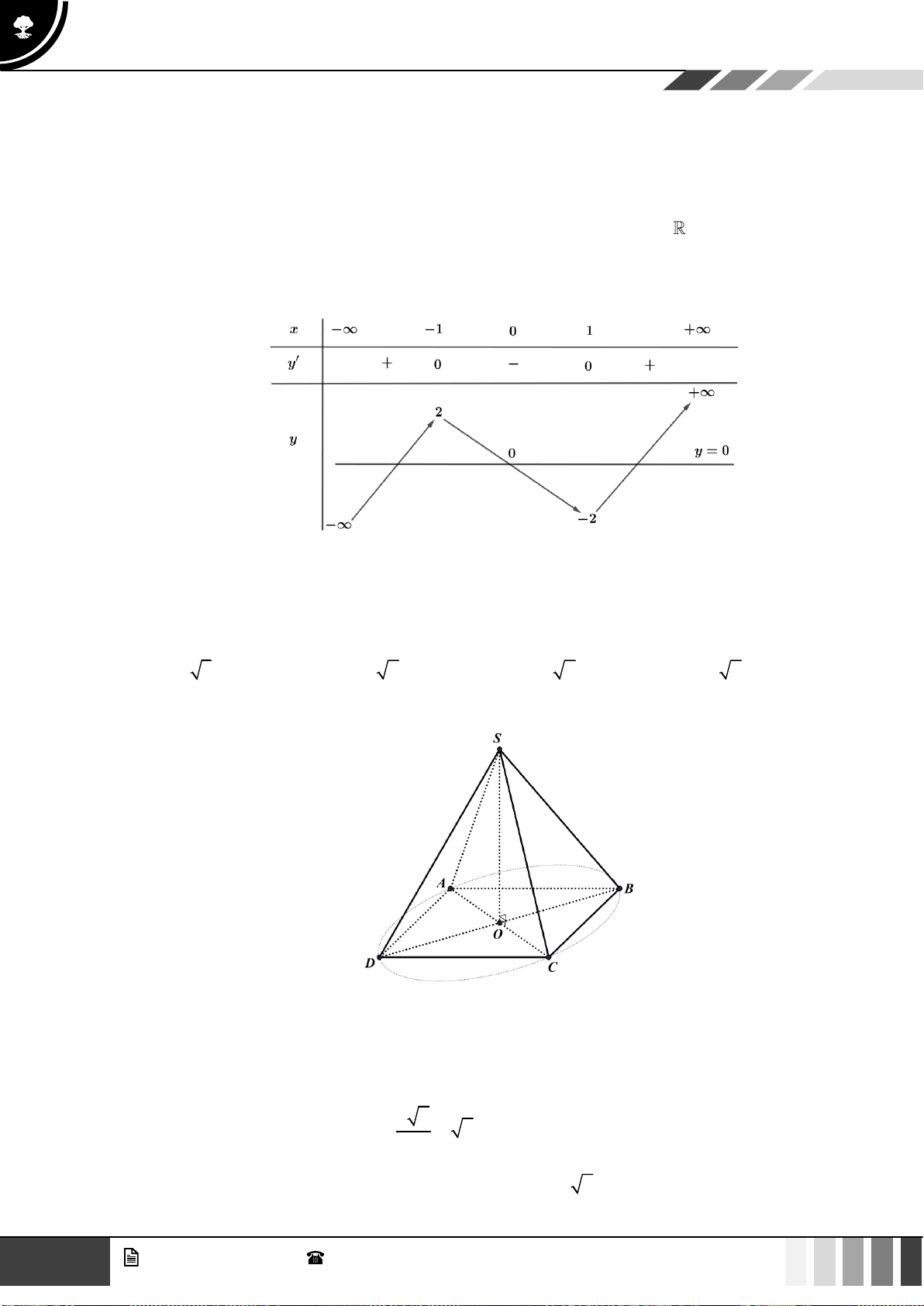
GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 39: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
3
30x x m− − =
có
3 nghiệm phân biệt trong đó có
2
nghiệm dương. Khẳng định nào sau đây đúng
A.
( )
0;2S =
. B.
2;2S =−
. C.
( )
2;2S =−
. D.
( )
2;0S =−
.
Lời giải
Ta có
33
3 0 3x x m x x m− − = − =
. Xét hàm số
( )
3
3g x x x=−
trên .
( )
( )
22
3 3 3 1g x x x
= − = −
( )
10g x x
==
.
Bảng biến thiên
Dựa vào bảng biến thiên, yêu cầu bài toán
20m −
Vậy
( )
2;0m−
.
Câu 40: Diện tích xung quanh của hình nón ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng
2
là
A.
23
. B.
42
. C.
22
. D.
2
.
Lời giải
Hình nón ngoại tiếp hình chóp tứ giác đều (có đáy là hình vuông) là hình nón có đỉnh là đỉnh
của hình chóp và đáy là đường tròn ngoại tiếp đáy của hình chóp.
Do đó chiều dài đường sinh của hình nón là
2l =
.
Bán kính của đáy hình nón là
22
2
2
r ==
.
Vậy diện tích xung quanh của hình nón là
22
xq
S rl
==
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
20
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 41: Cho hình hộp chữ nhật
.ABCD A B C D
có
AB a=
,
2AD a=
, góc giữa hai mặt phẳng
( )
ABC D
và
( )
ABCD
bằng
45
. Khối hộp
.ABCD A B C D
có thể tích bằng
A.
3
4a
. B.
3
2a
. C.
3
8a
. D.
3
6a
.
Lời giải
Ta có:
( ) ( )
( ) ( )
( )
, 45
ABC D ABCD AB
AD AB ABC D ABCD D AD
AD AB
=
⊥ = =
⊥
.
.tan45 2DD AD a
= =
.
23
.
2 .2 4
ABCD A B C D
V a a a
==
.
Câu 42: Cho hình nón
( )
N
có thiết diện qua trục là một tam giác vuông cân có diện tích bằng
9
. Khối
nón sinh bởi
( )
N
có thể tích bằng
A.
6
. B.
3
. C.
9
. D.
Lời giải
Giả sử thiết diện qua trục của hình nón
( )
N
là tam giác vuông cân
SAB
.
Giả sử cạnh
SA SB a==
. Khi đó diện tích của tam giác
SAB
là
2
1
9 3 2
2
SAB
S a a= = =
.
Ta có bán kính đáy của
( )
N
là
1
3
2
2
SA
R AH AB= = = =
.
Đường cao của
( )
N
là
1
3
2
h SH AB= = =
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy thể tích khối nón sinh bởi
( )
N
là
22
11
. .3 .3 9
33
V R h
= = =
.
Câu 43: Cho hàm số
1ax
y
bx c
+
=
+
có đồ thị như hình bên. Giá trị
abc++
bằng
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Vì đồ thị hàm số qua điểm
1
(0; )
2
M
−
nên ta có:
11
2
2
c
c
−
= = −
.
Tiệm cận đứng của đồ thị:
21
c
xb
b
−
= = =
.
Tiệm cận ngang của đồ thị:
22
a
ya
b
= = =
.
Vậy
1abc+ + =
.
Câu 44: Cắt một hình trụ
( )
T
bởi một mặt phẳng qua trục của nó được thiết diện là hình vuông cạnh
2a
. Tính diện tích toàn phần của
( )
T
A.
2
2 a
. B.
2
4 a
. C.
2
8 a
. D.
2
6 a
.
Lời giải
Chiều cao của khối trụ là
2ha=
.
Bán kính đáy:
ra=
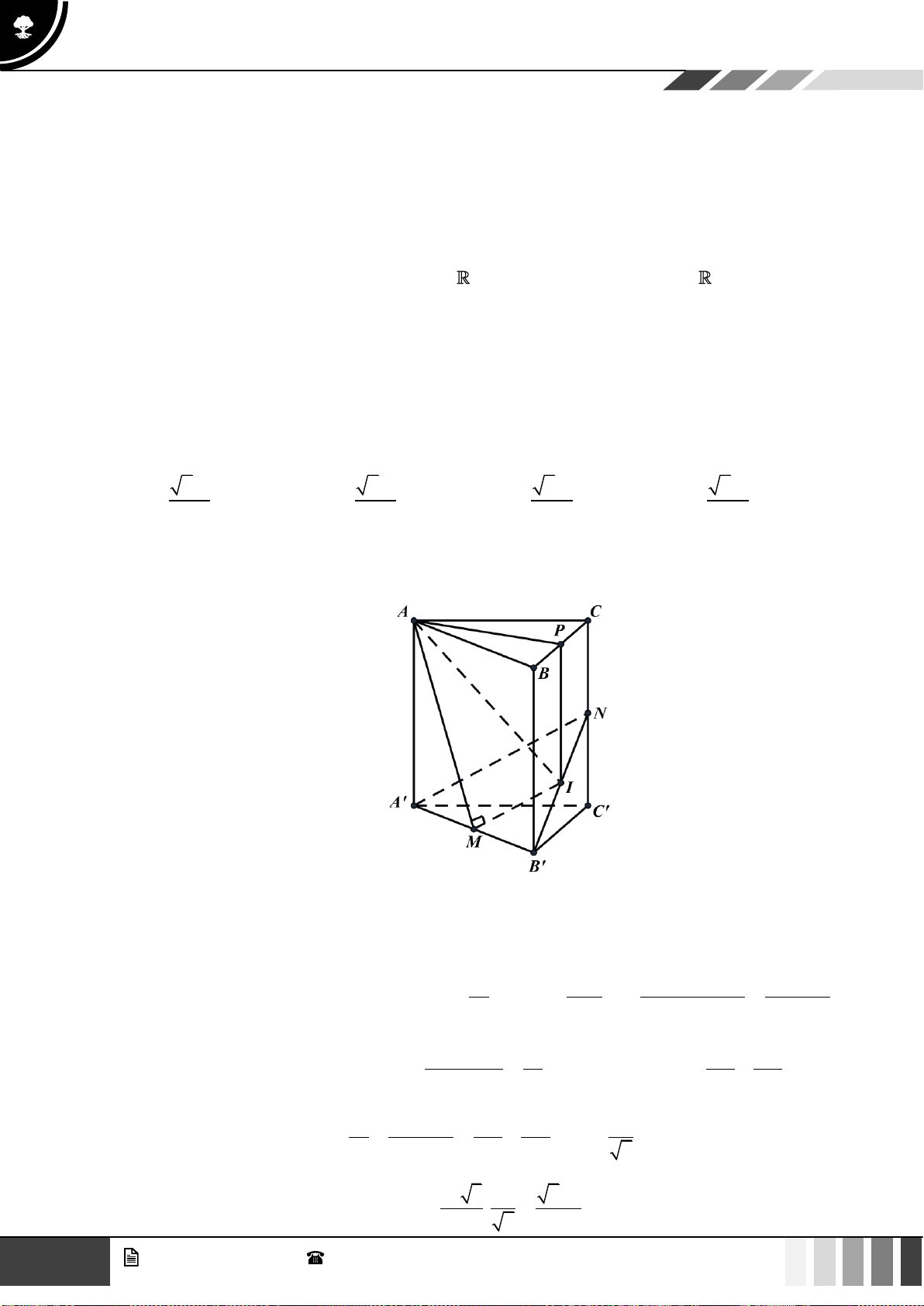
GV. Phan Nhật Linh -
SĐT: 0817 098 716
22
Tuyển tập 10 đề ôn HKI
Toán 12
Diện tích toàn phần là:
2 2 2 2
2 2 2 4 6
tp
S r rh a a a
= + = + =
.
Câu 45: Xét các số thực dương
,ab
thỏa
22
20ab+=
. Khẳng định nào sau đây đúng?
A. Giá trị nhỏ nhất của
log( )ab
bằng
0
. B. Giá trị lớn nhất của
log( )ab
bằng
0
.
C. Giá trị nhỏ nhất của
log( )ab
bằng
1
. D. Giá trị lớn nhất của
log( )ab
bằng
1
.
Lời giải
Ta có
2 2 2
2 ( ) 0, ,a ab b a b a b− + = −
do đó
22
2ab a b+
,,ab
.
Do đó mọi số thực dương
,ab
thỏa
22
20ab+=
ta có
10ab
suy ra
log( ) 1ab
.
Vậy giá trị lớn nhất của
log( )ab
bằng
1
.
Câu 46: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác đều cạnh
a
. Gọi
,MN
lần lượt là rung điểm
của
''AB
và
'CC
. Nếu
AM
và
'AN
vuông góc với nhau thì khối lăng trụ
. ' ' 'ABC A B C
có thể
tích bằng
A.
3
6
8
a
. B.
3
6
2
a
. C.
3
6
4
a
. D.
3
6
24
a
.
Lời giải
Cách 1:
Gọi
I
là trung điểm
'NB
. Khi đó
MI
là đường trung bình trong tam giác
''A B N
.
'AM A N AM MI⊥ ⊥
. Hay tam giác
AMI
vuông tại
M
.
Đặt
'A A x=
.
2
2 2 2 2
''
4
a
AM A A A M x= + = +
,
2
2 2 2 2
2
' ' ' ' 4
2 4 16
A N A C C N a x
MI
++
= = =
Gọi
P
là trung điểm
BC
. Ta có
'3
24
B B CN x
PI
+
==
,
22
2 2 2
39
4 16
ax
AI AP PI= + = +
.
2 2 2 2 2
2 2 2 2
4 3 9
4 16 4 16
2
a a x a x a
AM MI AI x x
+
+ = + + = + =
.
Thể tích khối lăng trụ
23
3 6.
. ' .
48
2
ABC
a a a
V S A A
= = =
.
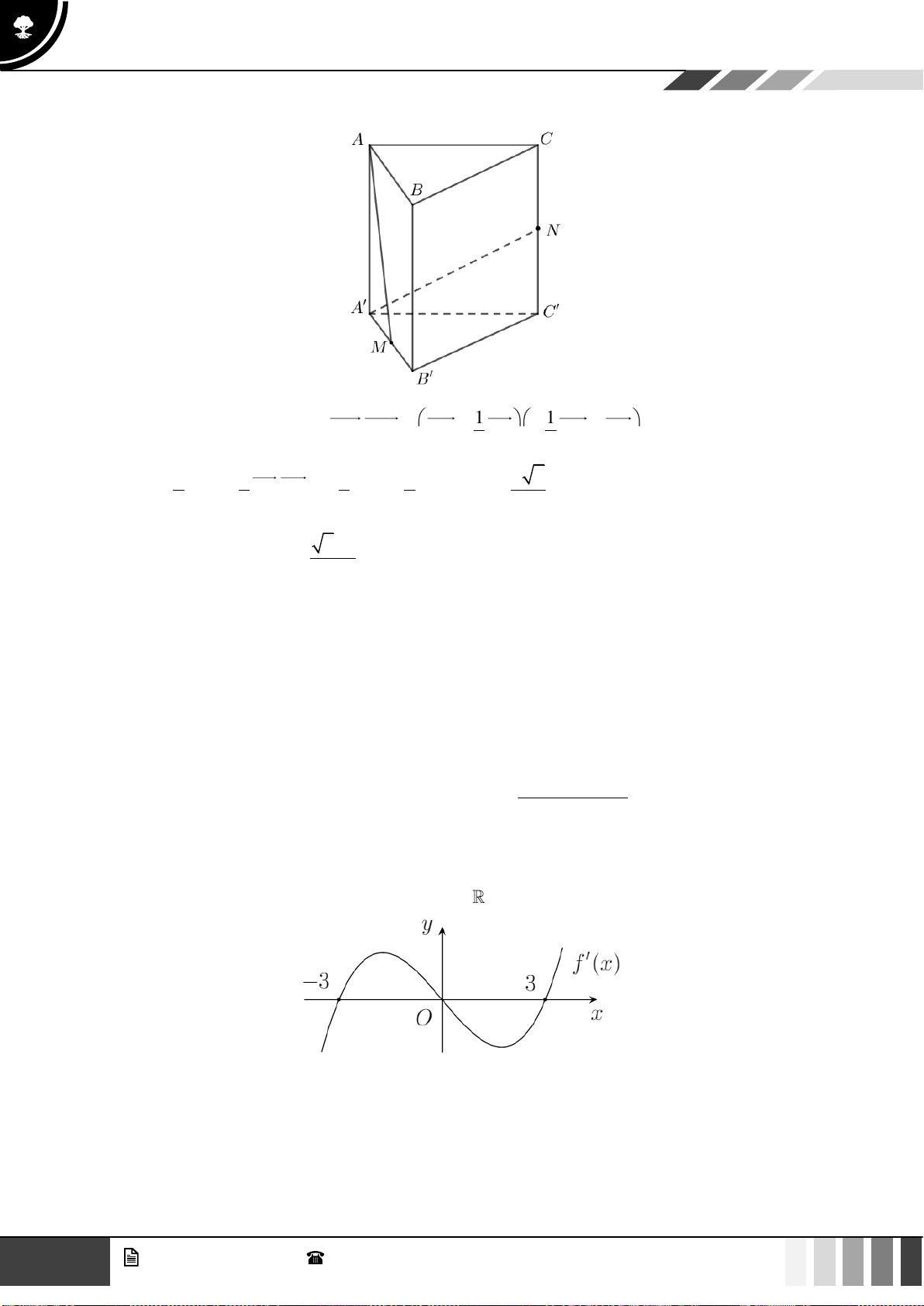
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HKI
Toán 12
Cách 2:
Do
'AM A N⊥
nên
11
0 . ' ' '
22
AM A N AA AB AA AC
= = + − +
2 2 2
1 1 1 1
' . '
2 2 2 4
AA AB AC AA a= − + = − +
2
'
2
a
AA=
.
Vậy
3
6.
.'
8
ABC
a
V S A A
==
.
Câu 47: Xét khối trụ
( )
T
có bán kính
R
và chiều cao
h
thỏa mãn
23Rh+=
. Thể tích của
( )
T
có giá
trị lớn nhất bằng
A.
2
. B.
3
. C.
. D.
4
.
Lời giải
Ta có thể tích khối
( )
T
là
( )
22
32V h R R R
= = −
.
Theo bất đẳng thức Cauchy ta có
( )
3
32
. 3 2 1
3
R R R
R R R
+ + −
− =
.
Vậy
max
1V R h
= = =
.
Câu 48: Cho hàm số
( )
fx
, biết
( )
fx
liên tục trên và có đồ thị như hình dưới đây.
Hàm số
( )
( )
2
4 2020g x f x= − +
đồng biến trên khoảng nào sau đây?
A.
( )
2;0−
. B.
( )
0;2
. C.
( )
2;+
. D.
( )
1;2
.
Lời giải
Xét hàm số
( )
( )
2
4 2020g x f x= − +
có
( )
( )
2
24g x xf x
=−
GV. Phan Nhật Linh -
SĐT: 0817 098 716
24
Tuyển tập 10 đề ôn HKI
Toán 12
( )
2
0
( ) 0
' 4 0
x
gx
fx
=
=
−=
2
2
0
40
43
x
x
x
=
− =
− =
0
2
1
7
x
x
x
x
=
=
=
=
.
Ta có bảng xét dấu
Vậy hàm số
( )
gx
đồng biến trên
( )
1;2
.
Câu 49: Cho khối lăng trụ
.ABC A B C
có thể tích bằng
a
. Gọi
M
là trung điểm của
AB
. Nếu tam giác
MB C
có diện tích bằng
b
thì khoảng cách từ
C
đến mặt phẳng
( )
MB C
bằng
A.
2
a
b
. B.
a
b
. C.
2
b
a
. D.
6
a
b
.
Lời giải
Ta có
( ) ( )
( )
( )
( )
// // d , d ,BC B C BC MB C C MB C B MB C
=
.
Ta có
. . . .
1 1 1
.
2 2 3 6
B MB C C MBB C ABB ABC A B C
a
V V V V
= = = =
.
Ta có
( )
( )
( )
( )
.
.
3.
3
1
6
.d , . d ,
32
B MB C
B MB C MB C
MB C
a
V
a
V B MB C S B MB C
S b b
= = = =
.
Câu 50: Có bao nhiêu số nguyên dương
m
để phương trình
( )
( )
2
e 1 ln 1 2e e 1
x x x
m mx− + + = +
có hai
nghiệm phân biệt không lớn hơn
5
.
A.
29
. B.
27
. C.
28
. D.
26
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
25
Tuyển tập 10 đề ôn HKI
Toán 12
Lời giải
Ta có:
( )
( )
2
e 1 ln 1 2e e 1
x x x
m mx− + + = +
( )
1
( )
( )
( )
2
e 1 ln x 1 e 1 0
xx
mm − + − − =
( )
( )
( )
e 1 ln 1 e 1 0
xx
m mx
− + − − =
( )
( )
e 1 0
ln 1 e 1 0
x
x
m mx
−=
+ − − =
( )
e 1
ln 1 e 1
x
x
m mx
=
+ = −
( )
( )
0 /
ln 1 e 1
x
x t m
m mx
=
+ = −
Phương trình
( )
1
có hai nghiệm phân biệt không lớn hơn
5
Phương trình
( )
ln 1 e 1
x
m mx + = −
có một nghiệm duy nhất khác
0
và nhỏ hơn hoặc bằng
5
.
Vì
0x
nên
( )
ln 1 e 1
x
m mx + = −
( )
ln 1 1 e
x
m mx + + =
( )
2
.
Đặt
( )
ln 1t mx=+
1e
x
mx +=
.
Ta có
1e
ee
1e
t
xt
x
mx
mx mt
mt
+=
+ = +
+=
( )
**
.
Xét hàm số đặc trưng:
( )
e
u
f u mu=+
trên .
Ta có
( )
e0
u
f u m
= +
,
u
và
m
+
.
Suy ra
( )
** e 1 0
x
x t mx = − − =
.
Xét hàm số
( )
e1
x
g x mx= − −
, có
( )
e
x
g x m
=−
, suy ra
( )
0 lng x x m
= =
.
Nếu
1m =
loại.
Nếu
1m
, ta có
Để thỏa mãn bài toán thì
( )
5
e1
50
5
gm
−
.
Kết hợp điều kiện, suy ra
2;3; ;29m
.
Vậy có
28
giá trị nguyên dương
m
thỏa mãn.
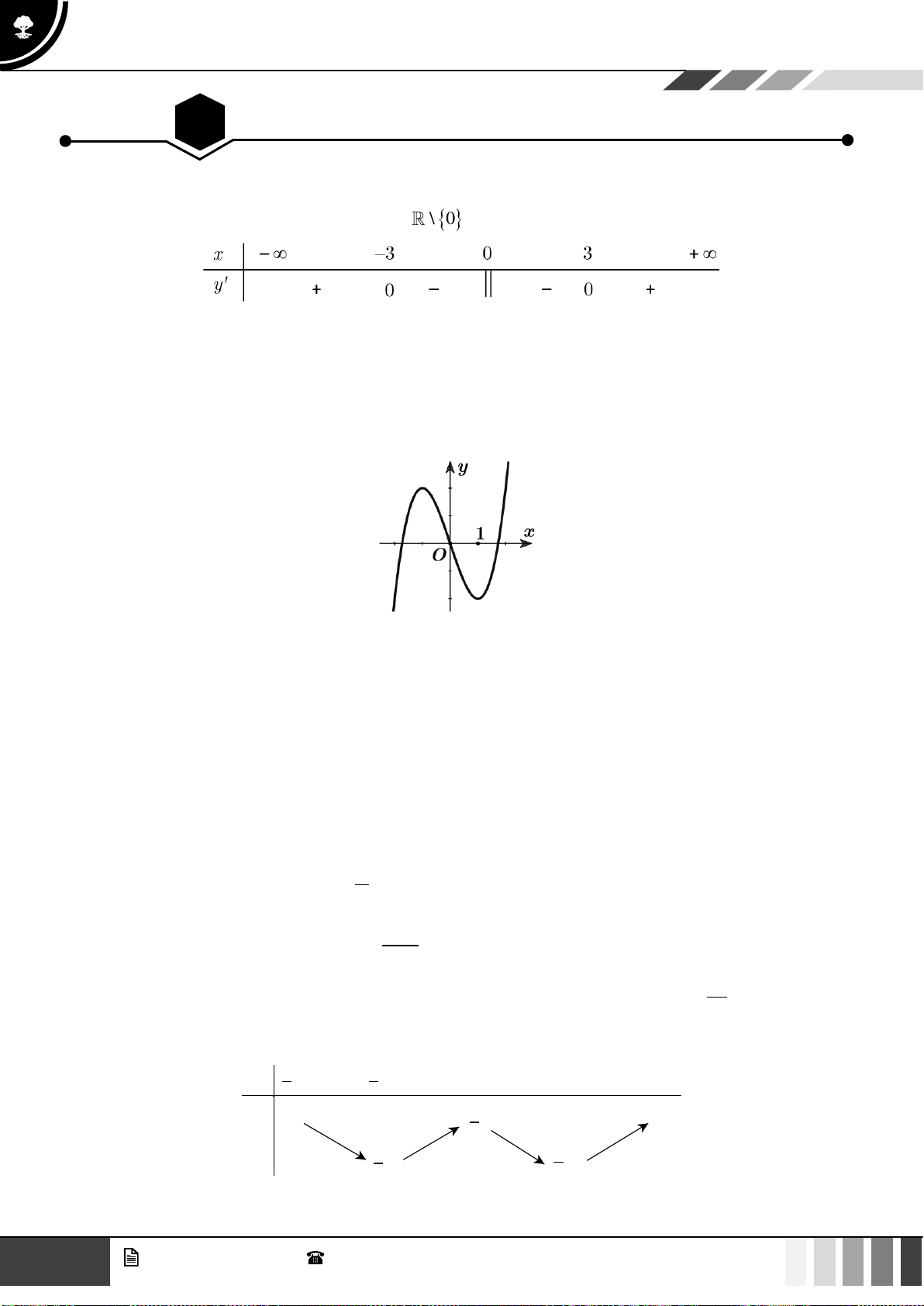
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HKI
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Cho hàm số
( )
y f x=
liên tục trên
\0
và có bảng xét dấu đạo hàm như sau
Hàm số đã cho:
A. Nghịch biến trên khoảng
( )
3;3−
. B. Đồng biến trên khoảng
( )
;3− −
.
C. Đồng biến trên khoảng
( )
3;0−
. D. Nghịch biến trên khoảng
( )
0;+
.
Câu 2: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
A.
3
3y x x=+
. B.
3
3y x x=−
. C.
3
3y x x= − −
. D.
3
3y x x= − +
.
Câu 3: Thể tích của khối chóp có diện tích đáy
2
6mS =
và chiều cao
3mh =
bằng
A.
3
12m .
B.
3
4m .
C.
3
18m .
D.
3
6m .
Câu 4: Với
a
và
b
là các số thực dương tùy ý,
a
khác 1 thì
( )
7
log
a
ab
bằng
A.
7 log
a
b+
. B.
1 7log
a
b+
. C.
7log
a
b
. D.
7 log
a
b−
.
Câu 5: Với
a
và
b
là các số thực dương, khác
1
và
là số thực bất kỳ thì
log
a
b
bằng
A.
log
a
b
−
. B.
1
log
a
b
. C.
log
b
a
−
. D.
log
a
b
.
Câu 6: Giá trị lớn nhất của hàm số
3
1
x
y
x
−
=
+
trên đoạn
0;50
là
A.
1−
. B.
3−
. C.
0
. D.
47
51
.
Câu 7: Tìm hàm số
42
y ax bx c= + +
có bảng biến thiên như hình vẽ bên
A.
42
23y x x= − −
. B.
42
23y x x= − + −
. C.
42
23y x x= + −
. D.
42
23y x x= − + +
.
4
4
+
∞
0
+
∞
x
∞
+
∞
1
1
y
3
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
09
8
ĐỀ SỐ
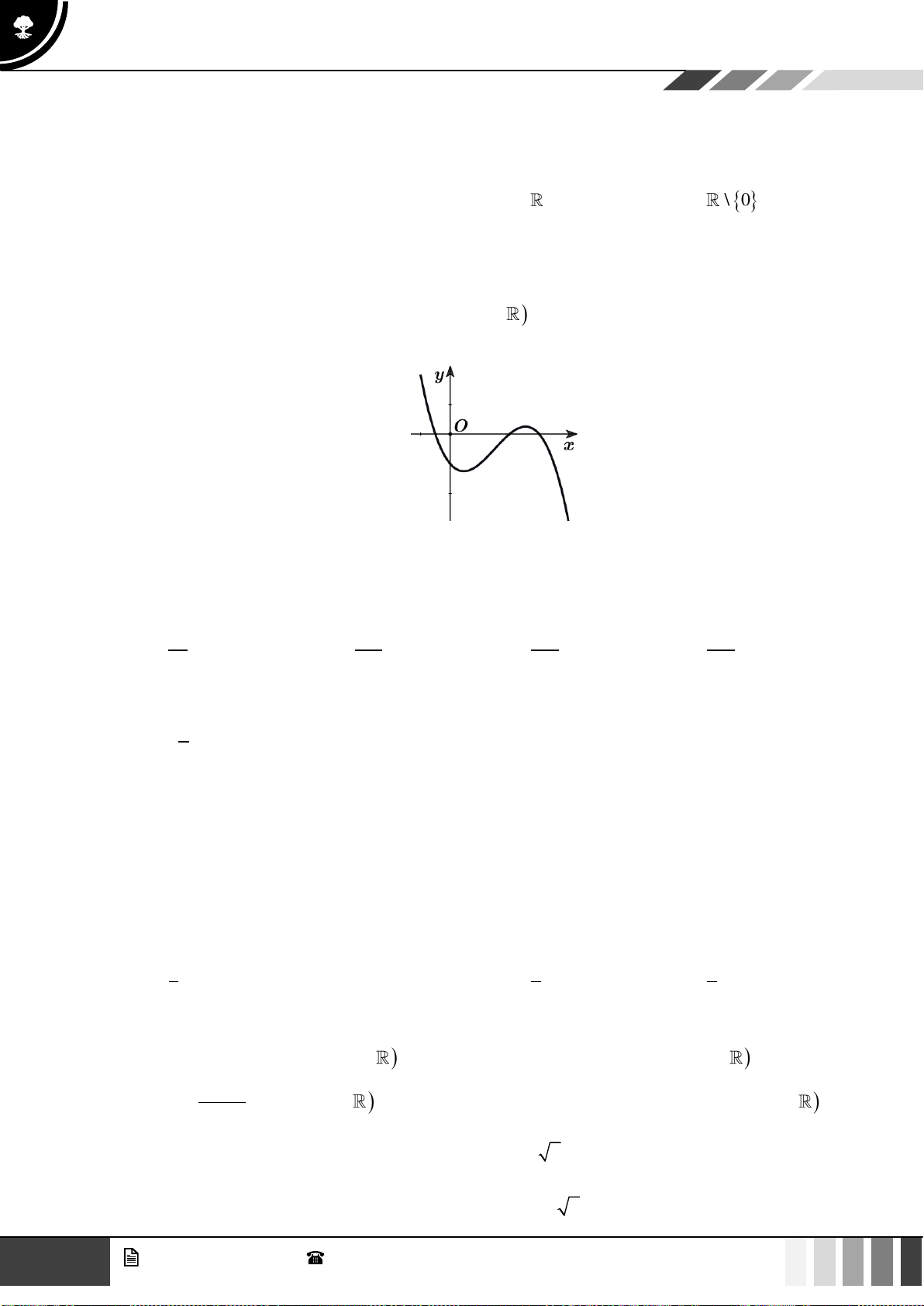
GV. Phan Nhật Linh -
SĐT: 0817 098 716
2
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 8: Nghiệm của phương trình
2
log 3x =
là
A.
8x =
. B.
5x =
. C.
6x =
. D.
9x =
.
Câu 9: Tập xác định của hàm số
3
x
y =
là
A.
( )
0;+
. B.
)
0;+
. C. . D.
\0
.
Câu 10: Phương trình
( )
3
log 1 2x +=
có nghiệm là
A.
10x =
. B.
7x =
. C.
5x =
. D.
8x =
.
Câu 11: Cho hàm số
32
y ax bx cx d= + + +
( )
, , ,a b c d
có đồ thị như hình vẽ bên. Có bao nhiêu số
dương trong các số
, , ,a b c d
?
A. 3. B. 2. C. 4. D. 1.
Câu 12: Cho hình lăng trụ đứng
.ABC A B C
. Có đáy là tam giác đều cạnh
a
và
AC
tạo với mặt phẳng
đáy một góc
60
.Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
4
a
. B.
3
3
4
a
. C.
3
3
8
a
. D.
3
3
2
a
.
Câu 13: Tập nghiệm của phương trình
32
x
=
là
A.
2
3
. B.
2
log 3
. C.
. D.
3
log 2
.
Câu 14: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
,B
SA
vuông góc với mặt phẳng đáy
và
4SA a=
,
6AC a=
. Thể tích khối chóp
.S ABC
bằng
A.
3
16a
. B.
3
48a
. C.
3
12a
. D.
3
24a
.
Câu 15: Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình
A. lăng trụ đều. B. chóp đều. C. bát diện đều. D. lục giác đều.
Câu 16: Khối nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
thì có thể tích bằng
A.
2
1
3
rl
. B.
2
rh
. C.
1
3
rh
. D.
2
1
3
rh
.
Câu 17: Hàm số nào sau đây có tối đa 3 điểm cực trị?
A.
( )
42
, ,y ax bx c a b c= + +
. B.
( )
2
, ,y ax bx c a b c= + +
.
C.
( )
, , ,
ax b
y a b c d
cx d
+
=
+
. D.
( )
32
, , ,y ax bx cx d a b c d= + + +
.
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
,
SA
vuông góc với mặt phẳng đáy và
3SA a=
. Khi đó, thể tích của khối chóp
.S ABCD
bằng
A.
3
6a
. B.
3
3a
. C.
3
32a
. D.
3
2a
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
41x x m− + + =
có 3 nghiệm phân
biệt?
A. 17. B. 5. C. 7. D. 15.
Câu 20: Diện tích xung quanh của hình nón có độ dài đường sinh
3l =
và bán kính đáy bằng
2r =
là
A.
18
. B.
24
. C.
6
. D.
12
.
Câu 21: Một khu rừng có trữ lượng gỗ là
53
5.10 m
. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4%
mỗi năm. Hỏi sau 6 năm, khu rừng đó sẽ có số mét khối gỗ gần với giá trị nào sau đây?
A.
( )
3
729990 m
. B.
( )
3
608326 m
. C.
( )
3
657966 m
. D.
( )
3
632660 m
.
Câu 22: Tiệm cận ngang của đồ thị hàm số
2
x
y
x
−
=
−
là đường thẳng
A.
2.y =
B.
0.y =
C.
1
2
y =
D.
1.y =−
Câu 23: Tìm đạo hàm của hàm số
e
( 1)yx=−
trên khoảng
(1; ).+
A.
e1
e( 1) .yx
+
=−
B.
e
( 1) .yx
=−
C.
e1
e( 1) .yx
−
=−
D.
e
(e 1)( 1) .yx
= − −
Câu 24: Có tất cả bao nhiêu loại khối đa diện đều?
A.
5
. B.
4
. C.
7
. D.
6
.
Câu 25: Hàm số
4
9yx=−
A. Nghịch biến trên khoảng
( )
3;+
. B. Đồng biến trên khoảng
( )
0;+
.
C. Đồng biến trên khoảng
( )
;0−
. D. Nghịch biến trên khoảng
( )
;3−
.
Câu 26: Tính đạo hàm của hàm số
3
logyx=
trên khoảng
( )
0;+
.
A.
1
y
x
=
. B.
1
ln3
y
x
=
. C.
ln3
y
x
=
. D.
.ln3yx
=
.
Câu 27: Hàm số
32
37y x x= − + −
đạt cực tiểu tại điểm
A.
0x =
. B.
3x =−
. C.
7x =−
. D.
2x =
.
Câu 28: Cho khối tứ diện
ABCD
và gọi
M
là trung điểm của đoạn thẳng
.AB
Khi đó, mặt phẳng
()P
chứa đường cạnh
CM
, song song với
BD
chia khối tứ diện
ABCD
thành
A. Một khối tứ diện và một khối chóp tứ giác. B. Một khối tứ diện và một khối lăng trụ.
C. Hai khối chóp tứ giác. D. Hai khối tứ diện.
Câu 29: Tiếp tuyến của đồ thị hàm số
32
32y x x= + −
tại điểm có hoành độ bằng 2 là đường thẳng đi
qua điểm:
A.
( )
1;72H
. B.
( )
4;38L
. C.
( )
0;2G
. D.
( )
3;42K
.
Câu 30: Thể tích của khối hộp chữ nhật
.ABCD A B C D
có
,AA a
=
2AB a=
và
5AC a=
bằng
A.
3
15a
. B.
3
6a
. C.
3
25a
. D.
3
2a
.
Câu 31: Khối lăng trụ tam giác đều có cạnh đáy bằng
1m
và cạnh bên bằng
12m
thì có thể tích là

GV. Phan Nhật Linh -
SĐT: 0817 098 716
4
Tuyển tập 10 đề ôn HKI
Toán 12
A.
3
12m
. B.
3
3m
. C.
3
3 3 m
. D.
3
6m
.
Câu 32: Điểm cực đại của đồ thị hàm số
42
64y x x= − −
là:
A.
( )
0; 4N −
. B.
( )
3;23Q
. C.
( )
0;0M
. D.
( )
3; 13P −
.
Câu 33: Số cạnh của khối mười hai mặt đều là:
A.
20
. B.
30
. C.
12
. D.
16
.
Câu 34: Giá trị lớn nhất của hàm số
3
31y x x=−+
trên đoạn
2;2−
là:
A.
1−
. B.
2
. C.
3
. D.
2−
.
Câu 35: Số giao điểm của đồ thị hàm số
42
2y x x= − +
và đường thẳng
1y =−
là
A.
4
. B.
0
. C.
2
. D.
3
.
Câu 36: Giao điểm hai đường tiệm cận của đồ thị hàm số
2
3
x
y
x
+
=
−
là điểm
A.
(1;3)F
. B.
(3;1)E
. C.
( 2;3)H −
. D.
(3; 2)G −
.
Câu 37: Nếu đặt
5
x
t =
thì phương trình
2 1 1
5 5 250
xx−+
+=
trở thành
A.
2
25 1250 0.tt+ − =
B.
2
5 250 0.tt+ − =
C.
2
5 1250 0.tt+ + =
D.
2
25 250 0.tt+ − =
Câu 38: Với số thực
a
dương, khác 1 và các số thực
,
bất kì thì ta có
A.
a a a
+
=+
. B.
a a a
+
=−
. C.
( )
aa
+
=
. D.
.a a a
+
=
.
Câu 39: Tìm tọa độ giao điểm của đồ thị hàm số
42
23y x x= − −
với trục hoành.
A.
( )
1;0−
và
( )
1;0
. B.
( )
3;0−
và
( )
3;0
.
C.
( )
0; 3−
. D.
( )
3;60
và
( )
3;60−
.
Câu 40: Giá trị
5 1 5 1
:
+−
bằng
A.
4
. B.
2
. C.
25
. D.
.
Câu 41: Đặt
3
log 2a =
, khi đó
72
log 768
được biểu diễn dưới dạng
2
ma n
pa
+
+
, với
,,m n p
là các số nguyên.
Giá trị
23
m n p++
bằng:
A.
17
. B.
36
. C.
10
. D.
73
.
Câu 42: Nếu khối lăng trụ đều
.ABC A B C
có cạnh đáy bằng
a
và thể tích bằng
3
3
4
a
thì khoảng cách
giữa hai đường thẳng
AB
và
AC
là
A.
15
3
a
B.
15
5
a
C.
5
3
a
D.
3
5
a
Câu 43: Có bao nhiêu giá trị nguyên thuộc khoảng
( 30;30)−
của tham số
m
để mọi tiếp tuyến của đồ thị
hàm số
32
(2 3) 1y x mx m x= − + − −
đều có hệ số góc dương?
A.
59
. B.
1
. C.
58
. D.
0
.
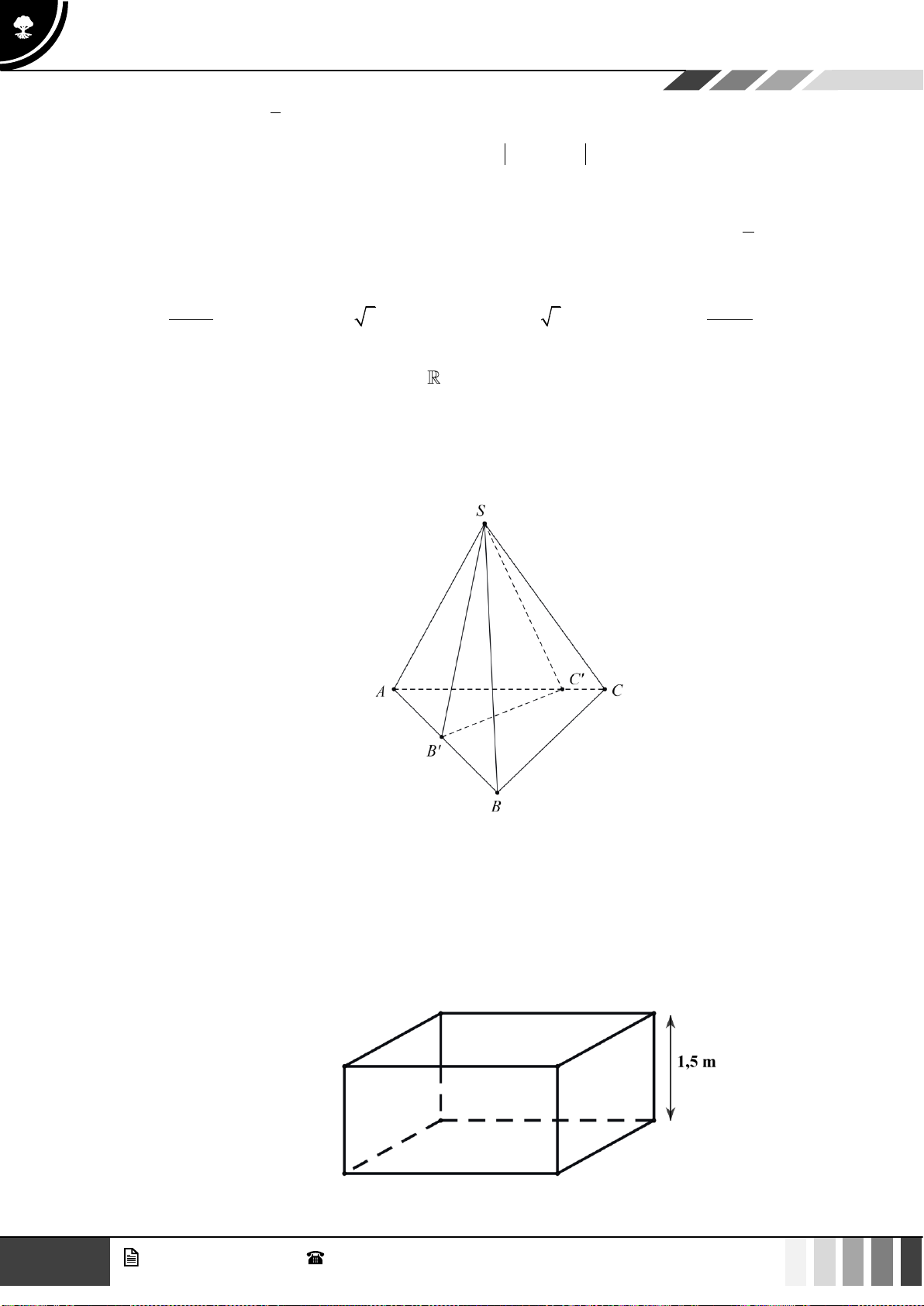
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 44: Cho hàm số
( )
32
1
2 9 1
3
y x m x x= − − − +
, với
m
là tham số. Gọi
12
,xx
là các điểm cực trị của
hàm số đã cho thì giá trị nhỏ nhất của biểu thức
12
9 25xx−
bằng
A.
15
. B.
450
. C.
90
. D.
45
.
Câu 45: Biết tập nghiệm của bất phương trình
( ) ( )
2 2 2
2 3 2 3
2
log 1 log 1 log log 2 0
3
xx− − − +
là
;;S a b c d=
với
a b c d
. Giá trị của biểu thức
2a b c d+ + +
bằng
A.
2
1
log 3
. B.
3
. C.
3−
. D.
2
1
1
log 3
+
.
Câu 46: Cho hàm số
( )
fx
có
( )
0,f x x
. Có bao nhiêu giá trị nguyên
x
để
( )
( )
2
24f x f x
A.
21
. B.
20
. C.
23
. D.
22
.
Câu 47: Cho khối chóp
.S ABC
có thể tích
3
24 cm
. Gọi
B
là trung điểm của
AB
và
C
là điểm trên cạnh
AC
sao cho
3AC CC
=
(minh họa như hình vẽ)
Thể tích của khối chóp
.S AB C
bằng
A.
3
8 cm
. B.
3
6 cm
. C.
3
2 cm
. D.
3
9 cm
.
Câu 48: Người ta cần xây một hồ chứa nước dạng hình hộp chữ nhật không nắp, cao
1,5m
và chiều dài
gấp đôi chiều rộng (minh họa như hình vẽ dưới). Nếu tổng diện tích bốn mặt xung quanh của hồ
là
2
18m
thì dung tích của hồ là
A.
3
12m
. B.
3
18m
. C.
3
5m
. D.
3
48m
.
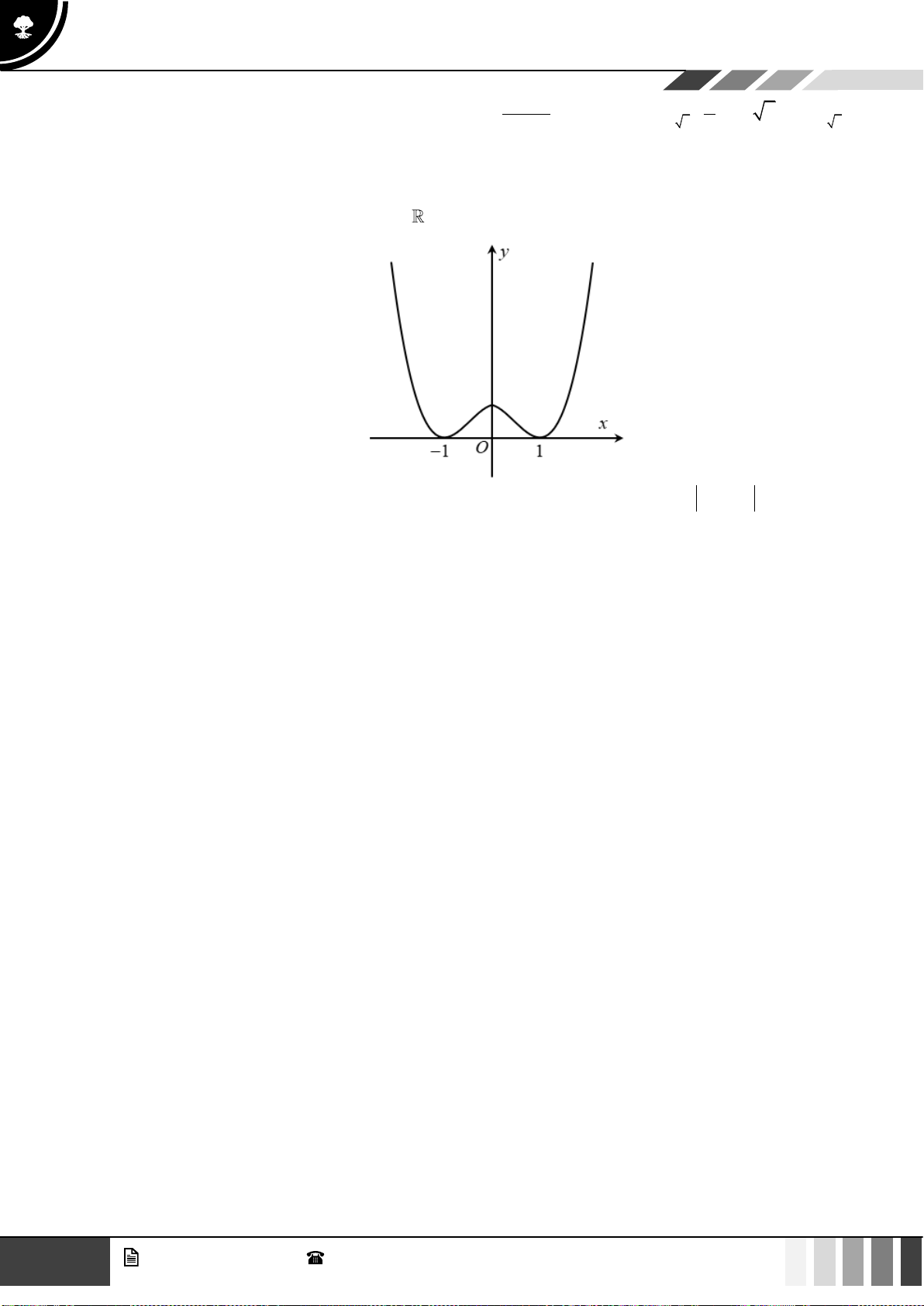
GV. Phan Nhật Linh -
SĐT: 0817 098 716
6
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 49: Cho
0, 0ab
thỏa mãn
4 25
4
log log log
4
ba
ab
−
= =
Giá trị của
66
log 4 2 log
2
a
bb
+−
bằng
A.
1
. B.
2
. C.
6
. D.
4
.
Câu 50: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số
0;23m
để hàm số
( )
( )
2
2 2023g x f x x m= − + +
đồng biến trên khoảng
( )
2; ?+
A.
23
. B.
20
. C.
21
. D.
22
.
-------------------------HẾT-------------------------
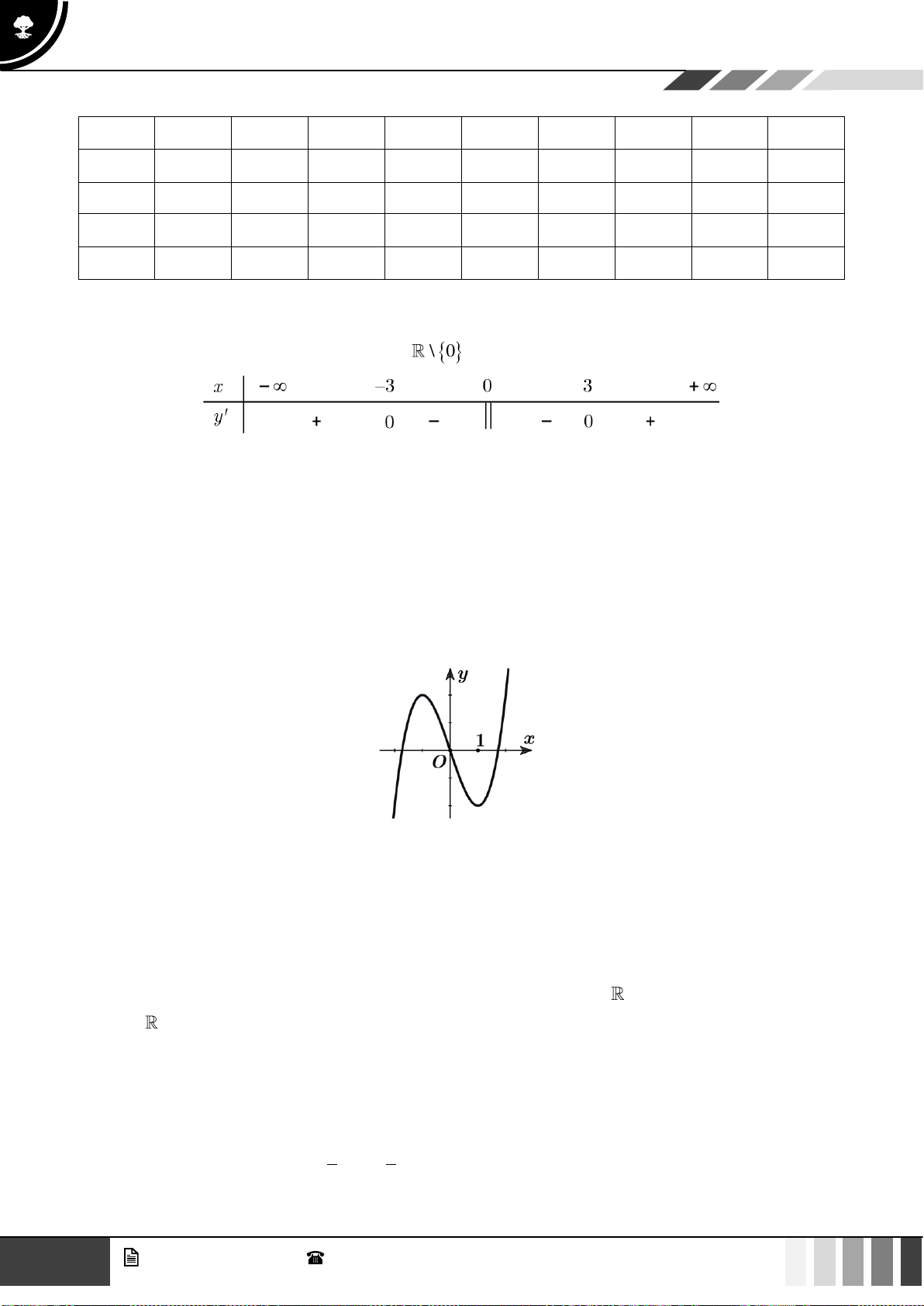
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HKI
Toán 12
BẢNG ĐÁP ÁN
1.B
2.B
3.D
4.A
5.D
6.D
7.A
8.A
9.C
10.D
11.D
12.B
13.D
14.C
15.C
16.D
17.A
18.D
19.C
20.C
21.D
22.D
23.C
24.A
25.B
26.B
27.A
28.A
29.D
30.C
31.C
32.A
33.B
34.C
35.C
36.B
37.A
38.D
39.B
40.B
41.B
42.B
43.D
44.C
45.B
46.C
47.D
48.A
49.B
50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
y f x=
liên tục trên
\0
và có bảng xét dấu đạo hàm như sau
Hàm số đã cho:
A. Nghịch biến trên khoảng
( )
3;3−
. B. Đồng biến trên khoảng
( )
;3− −
.
C. Đồng biến trên khoảng
( )
3;0−
. D. Nghịch biến trên khoảng
( )
0;+
.
Lời giải
Dựa vào bảng xét dấu đạo hàm
y
, ta thấy hàm số đã cho
đồng biến trên khoảng
( )
;3− −
.
Câu 2: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
A.
3
3y x x=+
. B.
3
3y x x=−
. C.
3
3y x x= − −
. D.
3
3y x x= − +
.
Lời giải
Dựa vào đồ thị hàm số ta thấy đây là đồ thị của hàm số bậc 3 và có hệ số
0a
.
Đồ thị hàm số đã cho có 2 điểm cực trị.
Ta xét đạo hàm của hàm số ở đáp án A là
2
' 3 3 0y x x= +
hàm số luôn đồng biến trên
hàm số không có cực trị.
Câu 3: Thể tích của khối chóp có diện tích đáy
2
6mS =
và chiều cao
3mh =
bằng
A.
3
12m .
B.
3
4m .
C.
3
18m .
D.
3
6m .
Lời giải
Thể tích khối chóp:
( )
3
11
. . .6.3 6 m
33
V S h= = =
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
8
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 4: Với
a
và
b
là các số thực dương tùy ý,
a
khác 1 thì
( )
7
log
a
ab
bằng
A.
7 log
a
b+
. B.
1 7log
a
b+
. C.
7log
a
b
. D.
7 log
a
b−
.
Lời giải
Ta có:
( )
77
log log log 7 log
a a a a
a b a b b= + = +
Câu 5: Với
a
và
b
là các số thực dương, khác
1
và
là số thực bất kỳ thì
log
a
b
bằng
A.
log
a
b
−
. B.
1
log
a
b
. C.
log
b
a
−
. D.
log
a
b
.
Lời giải
Ta có:
log log
aa
bb
=
Câu 6: Giá trị lớn nhất của hàm số
3
1
x
y
x
−
=
+
trên đoạn
0;50
là
A.
1−
. B.
3−
. C.
0
. D.
47
51
.
Lời giải
Tập xác định:
\1D =−
có
( )
2
4
0
1
y
x
=
+
,
xD
.
Hàm số đồng biến
( )
0;50
, liên tục trên
0;50
.
Do đó
( )
0;50
47
max 50
51
yy==
.
Câu 7: Tìm hàm số
42
y ax bx c= + +
có bảng biến thiên như hình vẽ bên
A.
42
23y x x= − −
. B.
42
23y x x= − + −
. C.
42
23y x x= + −
. D.
42
23y x x= − + +
.
Lời giải
Do
lim
x
y
→+
= +
nên hàm số
42
y ax bx c= + +
có
0a
Do hàm số
42
y ax bx c= + +
có
3
cực trị nên
0ab
Câu 8: Nghiệm của phương trình
2
log 3x =
là
A.
8x =
. B.
5x =
. C.
6x =
. D.
9x =
.
Lời giải
Ta có:
3
2
log 3 2 8xx= = =
.
4
4
+
∞
0
+
∞
x
∞
+
∞
1
1
y
3

GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 9: Tập xác định của hàm số
3
x
y =
là
A.
( )
0;+
. B.
)
0;+
. C. . D.
\0
.
Lời giải
Tập xác định của hàm số mũ
3
x
y =
là .
Câu 10: Phương trình
( )
3
log 1 2x +=
có nghiệm là
A.
10x =
. B.
7x =
. C.
5x =
. D.
8x =
.
Lời giải
Điều kiện:
1x −
.
( )
2
3
log 1 2 1 3 8x x x+ = + = =
thỏa mãn điều kiện bài toán.
Vậy
8S =
.
Câu 11: Cho hàm số
32
y ax bx cx d= + + +
( )
, , ,a b c d
có đồ thị như hình vẽ bên. Có bao nhiêu số
dương trong các số
, , ,a b c d
?
A. 3. B. 2. C. 4. D. 1.
Lời giải
Khi
0x =
yd=
. Dựa vào đồ thị thì
0d
.
Dựa vào hình dáng đồ thị thì
0a
.
2
3 2 0y ax bx c
= + + =
có hai nghiệm dương phân biệt
0
0
0
00
0
3
0
0
2
0
3
c
c
P
a
b
S
b
a
−
.
Câu 12: Cho hình lăng trụ đứng
.ABC A B C
. Có đáy là tam giác đều cạnh
a
và
AC
tạo với mặt phẳng
đáy một góc
60
.Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
4
a
. B.
3
3
4
a
. C.
3
3
8
a
. D.
3
3
2
a
.
Lời giải
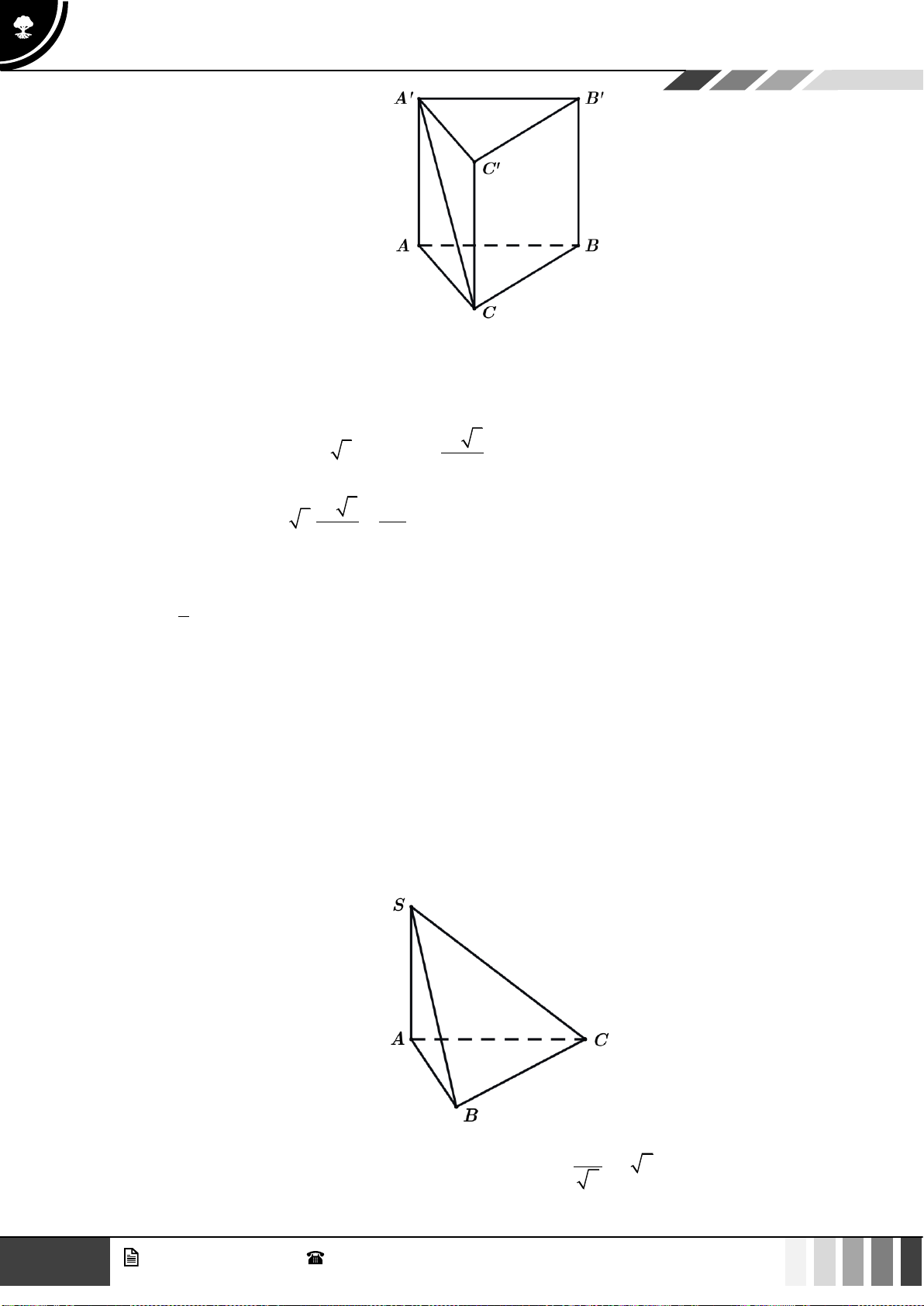
GV. Phan Nhật Linh -
SĐT: 0817 098 716
10
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có góc giữa đường thẳng
AC
và mặt phẳng
( )
ABC
là
60A CA
=
.
Xét tam giác
A AC
vuông tại
A
.
Có
.tan60 3AA AC a
= =
và
2
3
4
ABC
a
S =
.
Vậy:
23
.
33
3.
44
ABC A B C
aa
Va
==
.
Câu 13: Tập nghiệm của phương trình
32
x
=
là
A.
2
3
. B.
2
log 3
. C.
. D.
3
log 2
.
Lời giải
Ta có
3
3 2 log 2
x
x= =
.
Vậy tập nghiệm
3
log 2S =
.
Câu 14: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
,B
SA
vuông góc với mặt phẳng đáy
và
4SA a=
,
6AC a=
. Thể tích khối chóp
.S ABC
bằng
A.
3
16a
. B.
3
48a
. C.
3
12a
. D.
3
24a
.
Lời giải
Vì tam giác
ABC
vuông cân tại
B
nên ta có
32
2
AC
AB BC a= = =
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HKI
Toán 12
( )
2
2
11
. 3 2 9
22
ABC
S AB BC a a
= = =
.
Thể tích khối chóp:
23
.
11
. .4 .9 12
33
S ABC ABC
V SAS a a a
= = =
.
Câu 15: Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình
A. lăng trụ đều. B. chóp đều. C. bát diện đều. D. lục giác đều.
Lời giải
Trung điểm các cạnh của một tứ diện đều là các đỉnh của một hình bát diện đều.
Câu 16: Khối nón có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
thì có thể tích bằng
A.
2
1
3
rl
. B.
2
rh
. C.
1
3
rh
. D.
2
1
3
rh
.
Lời giải
Khối nón có chiều cao
,h
độ dài đường sinh
,l
bán kính đáy
r
thì có thể tích bằng
2
1
3
rh
.
Câu 17: Hàm số nào sau đây có tối đa 3 điểm cực trị?
A.
( )
42
, ,y ax bx c a b c= + +
. B.
( )
2
, ,y ax bx c a b c= + +
.
C.
( )
, , ,
ax b
y a b c d
cx d
+
=
+
. D.
( )
32
, , ,y ax bx cx d a b c d= + + +
.
Lời giải
Xét hàm số
( )
42
0y ax bx c a= + +
. Với
0ab
thì hàm số
42
y ax bx c= + +
có 3 điểm cực
trị.
Câu 18: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
,
SA
vuông góc với mặt phẳng đáy và
3SA a=
. Khi đó, thể tích của khối chóp
.S ABCD
bằng
A.
3
6a
. B.
3
3a
. C.
3
32a
. D.
3
2a
.
Lời giải
Thể tích của khối chóp
.S ABCD
là:
( )
2
3
11
. . .3 . 2 2
33
ABCD
V SAS a a a= = =
.
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
41x x m− + + =
có 3 nghiệm phân
biệt?
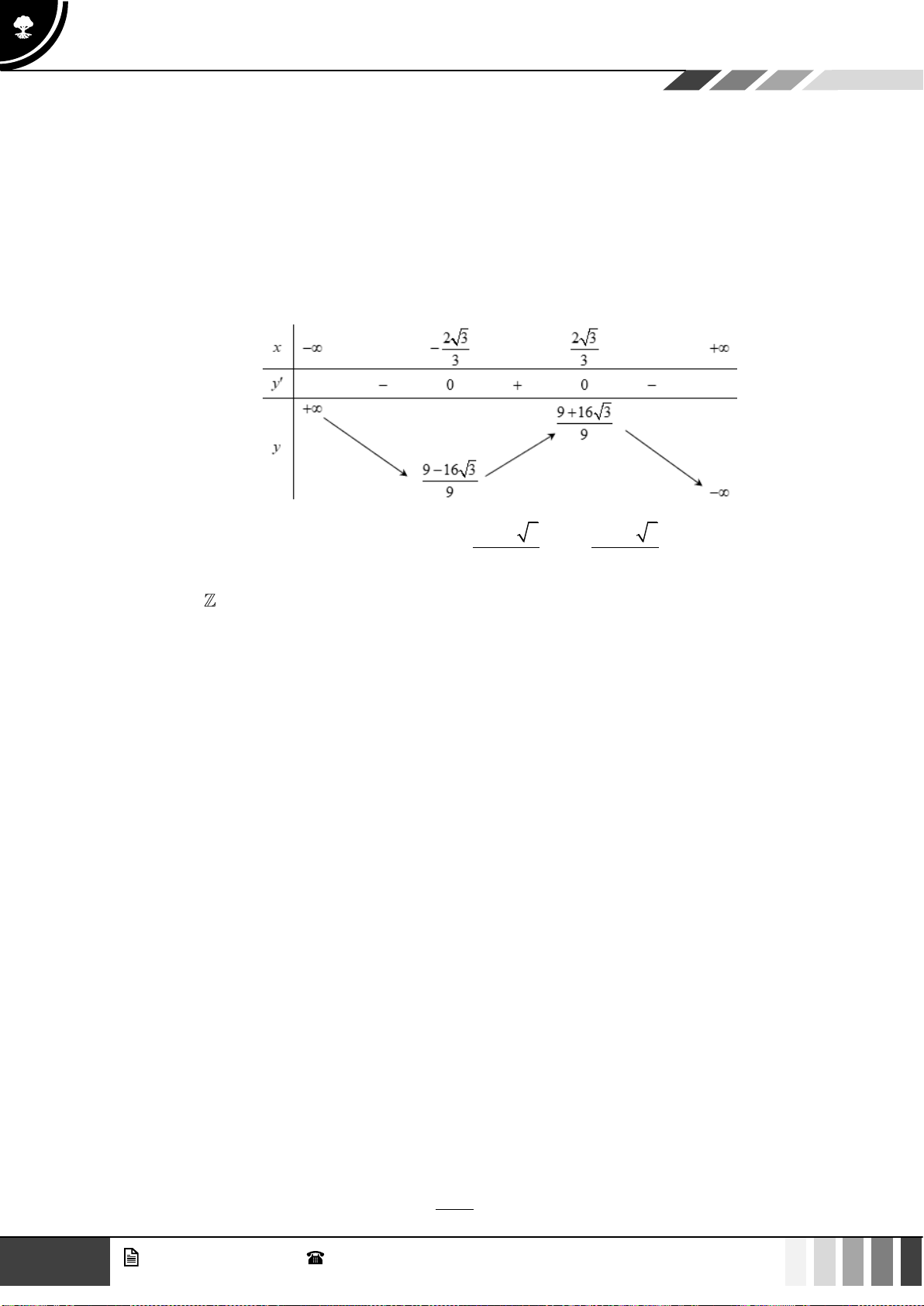
GV. Phan Nhật Linh -
SĐT: 0817 098 716
12
Tuyển tập 10 đề ôn HKI
Toán 12
A. 17. B. 5. C. 7. D. 15.
Lời giải
Phương trình
3
41x x m− + + =
.
Đặt
3
41y x x= − + +
.
ym=
(đường thẳng song song hoặc trùng với trục
Ox
).
Hàm số
3
41y x x= − + +
có bảng biến thiên:
Để phương trình có
3
nghiệm phân biệt thì
9 16 3 9 16 3
99
m
−+
.
Do
m
nên
2; 1;0;1;2;3;4m − −
.
Câu 20: Diện tích xung quanh của hình nón có độ dài đường sinh
3l =
và bán kính đáy bằng
2r =
là
A.
18
. B.
24
. C.
6
. D.
12
.
Lời giải
Ta có
2.3 6
xq
S rl
= = =
.
Câu 21: Một khu rừng có trữ lượng gỗ là
53
5.10 m
. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là
4%
mỗi năm. Hỏi sau 6 năm, khu rừng đó sẽ có số mét khối gỗ gần với giá trị nào sau đây?
A.
( )
3
729990 m
. B.
( )
3
608326 m
. C.
( )
3
657966 m
. D.
( )
3
632660 m
.
Lời giải
Gọi trữ lượng gỗ ban đầu là
0
V
, tốc độ sinh trưởng hàng năm của rừng là
%r
. Ta có:
Sau 1 năm, trữ lượng gỗ là:
( )
1 0 0 0
.1V V rV V r= + = +
.
Sau 2 năm, trữ lượng gỗ là:
( ) ( )
2
2 1 1 1 0
. 1 1V V rV V r V r= + = + = +
.
Tổng quát, sau
n
năm trữ lượng gỗ là:
( )
0
1
n
n
V V r=+
.
Áp dụng công thức ta có trữ lượng gỗ sau 6 năm trong bài toán là:
( )
( )
6
53
5
5.10 1 4% 632660Vm= +
.
Câu 22: Tiệm cận ngang của đồ thị hàm số
2
x
y
x
−
=
−
là đường thẳng

GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HKI
Toán 12
A.
2.y =
B.
0.y =
C.
1
2
y =
D.
1.y =−
Lời giải
Ta có
1
lim lim lim 1
2
2
1
x x x
x
y
x
x
→+ →+ →+
−−
= = = −
−
−
và
1
lim lim lim 1
2
2
1
x x x
x
y
x
x
→− →− →−
−−
= = = −
−
−
.
Vậy đồ thị của hàm số
2
x
y
x
−
=
−
có tiệm cận ngang là đường thẳng
1y =−
Câu 23: Tìm đạo hàm của hàm số
e
( 1)yx=−
trên khoảng
(1; ).+
A.
e1
e( 1) .yx
+
=−
B.
e
( 1) .yx
=−
C.
e1
e( 1) .yx
−
=−
D.
e
(e 1)( 1) .yx
= − −
Lời giải
( )
e1
e
( 1) e 1y x y x
−
= − = −
.
Câu 24: Có tất cả bao nhiêu loại khối đa diện đều?
A.
5
. B.
4
. C.
7
. D.
6
.
Lời giải
Có 5 loại khối đa diện đều. Cụ thể
Khối đa diện đều loại
3;3
:Khối tứ diện đều.
Khối đa diện đều loại
4;3
:Khối lập phương.
Khối đa diện đều loại
3;4
:Khối bát diện đều.
Khối đa diện đều loại
3;5
:Khối hai mươi mặt đều.
Khối đa diện đều loại
5;3
:Khối mười hai mặt đều.
Câu 25: Hàm số
4
9yx=−
A. Nghịch biến trên khoảng
( )
3;+
. B. Đồng biến trên khoảng
( )
0;+
.
C. Đồng biến trên khoảng
( )
;0−
. D. Nghịch biến trên khoảng
( )
;3−
.
Lời giải
Ta có
3
4 ; 0 0y x y x
= = =
.
Bảng biến thiên:
GV. Phan Nhật Linh -
SĐT: 0817 098 716
14
Tuyển tập 10 đề ôn HKI
Toán 12
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng
( )
0;+
.
Câu 26: Tính đạo hàm của hàm số
3
logyx=
trên khoảng
( )
0;+
.
A.
1
y
x
=
. B.
1
ln3
y
x
=
. C.
ln3
y
x
=
. D.
.ln3yx
=
.
Lời giải
Ta có
( )
3
1
log
.ln3
yx
x
==
.
Câu 27: Hàm số
32
37y x x= − + −
đạt cực tiểu tại điểm
A.
0x =
. B.
3x =−
. C.
7x =−
. D.
2x =
.
Lời giải
Ta có
2
0
3 6 0
2
x
y x x y
x
=
= − + =
=
;
66yx
= − +
Có
(0) 6 0y
=
suy ra hàm số đạt cực tiểu tại
0x =
Có
(2) 6 0y
= −
suy ra hàm số đạt cực đại tại
2x =
.
Câu 28: Cho khối tứ diện
ABCD
và gọi
M
là trung điểm của đoạn thẳng
.AB
Khi đó, mặt phẳng
()P
chứa đường cạnh
CM
, song song với
BD
chia khối tứ diện
ABCD
thành
A. Một khối tứ diện và một khối chóp tứ giác. B. Một khối tứ diện và một khối lăng trụ.
C. Hai khối chóp tứ giác. D. Hai khối tứ diện.
Lời giải
Gọi
N
là giao điểm của mặt phẳng
()P
với cạnh
AD
. Vì
()P
song song với
BD
nên ta có
MN
song song với
BD
(
N
là trung điểm của đoạn thẳng
AD
). Khi đó mặt phẳng
()P
chia
khối tứ diện
ABCD
thành một khối chóp (tứ diện)
CMNA
và một khối chóp tứ giác
.C MNDB
0
x
+
∞
+
0
0
+
∞∞
y
y'
+
∞

GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 29: Tiếp tuyến của đồ thị hàm số
32
32y x x= + −
tại điểm có hoành độ bằng 2 là đường thẳng đi
qua điểm:
A.
( )
1;72H
. B.
( )
4;38L
. C.
( )
0;2G
. D.
( )
3;42K
.
Lời giải
Gọi thuộc đồ thị thì ta có phương trình tiếp tuyến có dạng:
Đạo hàm:
Theo giả thiết hoành độ: nên .
Thay vào ta được phương trình tiếp tuyến:
Thay điểm thì ta được đáp án D .
Câu 30: Thể tích của khối hộp chữ nhật
.ABCD A B C D
có
,AA a
=
2AB a=
và
5AC a=
bằng
A.
3
15a
. B.
3
6a
. C.
3
25a
. D.
3
2a
.
Lời giải
3
.
. . 2 . 5 . 2 5
ABCD A B C D
V AB AC AA a a a a
= = =
(đvtt).
Câu 31: Khối lăng trụ tam giác đều có cạnh đáy bằng
1m
và cạnh bên bằng
12m
thì có thể tích là
A.
3
12m
. B.
3
3m
. C.
3
3 3 m
. D.
3
6m
.
Lời giải
3
. .12 3 3
4
LT
V S h= = =
(
3
m
).
Câu 32: Điểm cực đại của đồ thị hàm số
42
64y x x= − −
là:
A.
( )
0; 4N −
. B.
( )
3;23Q
. C.
( )
0;0M
. D.
( )
3; 13P −
.
Lời giải
Tập xác định:
D =
. Ta có:
3
4 12y x x
=−
;
2
12 12yx
=−
;
0
03
3
x
yx
x
=
= =
=−
( )
0 12 0y
= −
0x =
là điểm cực đại của hàm số; giá trị cực đại của hàm số là
( )
04f =−
.
( ) ( )
3 3 24 0yy
= − =
3x =
và
3x =−
là hai điểm cực tiểu của hàm số.
Vậy điểm cực đại của đồ thị hàm số là
( )
0; 4N −
.
Câu 33: Số cạnh của khối mười hai mặt đều là:
A.
20
. B.
30
. C.
12
. D.
16
.
Lời giải
( )
00
;N x y
( ) ( )
00
. *y k x x y= − +
2
36y x x
=+
0
2x =
( )
( )
32
0
2 2 3.2 2 18
2 24
yf
ky
= = + − =
==
( )
*
( )
24. 2 18 24 30y x y x= − + = −
( )
42 24.3 30=−

GV. Phan Nhật Linh -
SĐT: 0817 098 716
16
Tuyển tập 10 đề ôn HKI
Toán 12
Số cạnh của khối mười hai mặt đều là 30.
Câu 34: Giá trị lớn nhất của hàm số
3
31y x x=−+
trên đoạn
2;2−
là:
A.
1−
. B.
2
. C.
3
. D.
2−
.
Lời giải
Ta có:
2
33yx
=−
;
1 2;2
0
1 2;2
x
y
x
= −
=
= − −
.
( )
21y − = −
;
( )
13y −=
;
( )
11y =−
;
( )
23y =
.
Vậy giá trị lớn nhất của hàm số trên đoạn
2;2−
là:
3
.
Câu 35: Số giao điểm của đồ thị hàm số
42
2y x x= − +
và đường thẳng
1y =−
là
A.
4
. B.
0
. C.
2
. D.
3
.
Lời giải
Phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng là:
42
21xx− + = −
.
42
2 1 0xx − + + =
2
2
12
12
x
x
=+
=−
12
12
x
x
=+
= − +
.
Vậy đồ thị hàm số
42
2y x x= − +
và đường thẳng
1y =−
có hai giao điểm.
Câu 36: Giao điểm hai đường tiệm cận của đồ thị hàm số
2
3
x
y
x
+
=
−
là điểm
A.
(1;3)F
. B.
(3;1)E
. C.
( 2;3)H −
. D.
(3; 2)G −
.
Lời giải
Đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số có phương trình lần lượt là
1y =
và
3x =
.
Giao điểm của hai đường tiệm cận của đồ thị hàm số là điểm
(3;1)E
.
Câu 37: Nếu đặt
5
x
t =
thì phương trình
2 1 1
5 5 250
xx−+
+=
trở thành
A.
2
25 1250 0.tt+ − =
B.
2
5 250 0.tt+ − =
C.
2
5 1250 0.tt+ + =
D.
2
25 250 0.tt+ − =
Lời giải
Ta có:
2 1 1 2
1
5 5 250 .5 5.5 250 0
5
x x x x−+
+ = + − =
( )
2
5 25.5 1250 0
xx
+ − =
.
Đặt
5
x
t =
thì phương trình trở thành
2
25 1250 0.tt+ − =
Câu 38: Với số thực
a
dương, khác 1 và các số thực
,
bất kì thì ta có
A.
a a a
+
=+
. B.
a a a
+
=−
. C.
( )
aa
+
=
. D.
.a a a
+
=
.
Lời giải
Với số thực
a
dương, khác 1 và các số thực
,
bất kì thì ta có
.a a a
+
=
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 39: Tìm tọa độ giao điểm của đồ thị hàm số
42
23y x x= − −
với trục hoành.
A.
( )
1;0−
và
( )
1;0
. B.
( )
3;0−
và
( )
3;0
.
C.
( )
0; 3−
. D.
( )
3;60
và
( )
3;60−
.
Lời giải
Phương trình hoành độ giao điểm của đồ thị hàm số
42
23y x x= − −
với trục hoành là:
42
3
2 3 0
3
x
xx
x
=
− − =
=−
.
Vậy tọa độ giao điểm của đồ thị hàm số
42
23y x x= − −
với trục hoành là
( )
3;0−
và
( )
3;0
Câu 40: Giá trị
5 1 5 1
:
+−
bằng
A.
4
. B.
2
. C.
25
. D.
.
Lời giải
Ta có:
5 1 5 1 5 1 5 1 2
:
+ − + − +
==
.
Câu 41: Đặt
3
log 2a =
, khi đó
72
log 768
được biểu diễn dưới dạng
2
ma n
pa
+
+
, với
,,m n p
là các số nguyên.
Giá trị
23
m n p++
bằng:
A.
17
. B.
36
. C.
10
. D.
73
.
Lời giải
( )
( )
8
3
3
72
32
3
3
log 2 .3
log 768
81
log 768
log 72 3 2
log 2 .3
a
a
+
= = =
+
Vậy
23
8, 1, 3 36.m n p m n p= = = + + =
Câu 42: Nếu khối lăng trụ đều
.ABC A B C
có cạnh đáy bằng
a
và thể tích bằng
3
3
4
a
thì khoảng cách
giữa hai đường thẳng
AB
và
AC
là
A.
15
3
a
B.
15
5
a
C.
5
3
a
D.
3
5
a
Lời giải
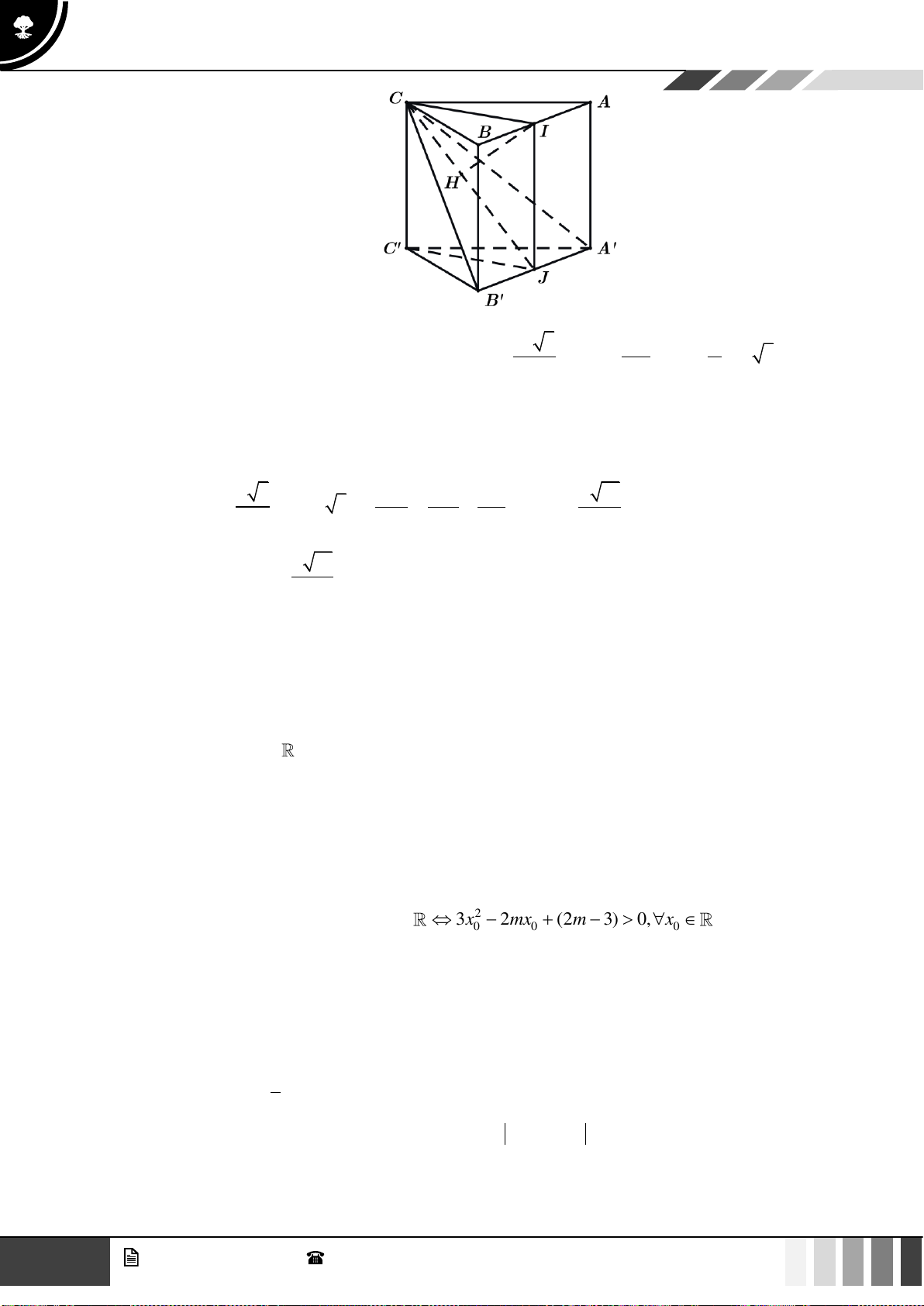
GV. Phan Nhật Linh -
SĐT: 0817 098 716
18
Tuyển tập 10 đề ôn HKI
Toán 12
Tam giác
ABC
có cạnh đáy bằng
a
, suy ra:
2
3
4
a
B =
có
2
3
4
a
V =
3
V
ha
B
= =
.
Gọi
;IJ
là trung điểm của
;AB AB
. Dựng
IH CJ⊥
.
Mặt khác:
( ; ) ( ;( ))d AB CAAd AB C B
=
( ;( )) ( ; )d I C d I CJ IHAB =
=
=
Ta có:
3
;3
2
a
CI IJ a==
2 2 2
1 1 1
IH CI IJ
= +
15
5
a
IH=
Vậy:
15
( ; )
5
a
d AAB C =
.
Câu 43: Có bao nhiêu giá trị nguyên thuộc khoảng
( 30;30)−
của tham số
m
để mọi tiếp tuyến của đồ thị
hàm số
32
(2 3) 1y x mx m x= − + − −
đều có hệ số góc dương?
A.
59
. B.
1
. C.
58
. D.
0
.
Lời giải
Tập xác định
D =
.
2
3 2 (2 3)y x mx m
= − + −
Lấy
( )
00
;M x y
tùy ý trên đồ thị hàm số đã cho, khi đó hệ số góc của tiếp tuyến của đồ thị hàm
số tại điểm
( )
00
;M x y
được tính bởi
( )
2
0 0 0
3 2 (2 3)y x x mx m
= − + −
.
Yêu cầu bài toán:
( )
2
0 0 0 0 0
0, 3 2 (2 3) 0,y x x x mx m x
− + −
( )
2
30
3 2 3 0mm
− −
2
6 9 0mm − +
(vô nghiệm).
Vậy không có
m
thỏa đề.
Câu 44: Cho hàm số
( )
32
1
2 9 1
3
y x m x x= − − − +
, với
m
là tham số. Gọi
12
,xx
là các điểm cực trị của
hàm số đã cho thì giá trị nhỏ nhất của biểu thức
12
9 25xx−
bằng
A.
15
. B.
450
. C.
90
. D.
45
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có
( )
2
2 2 9y x m x
= − − −
,
( )
2
2 9 0m
= − +
hàm số luôn có hai điểm cực trị với
m
Theo định lí Viete ta có:
( )
12
1 2 2
1
22
9
.9
x x m
x x x
x
+ = −
= − = −
.
Ta có
1 2 1 1
11
9 25
9 25 9 25. 9x x x x
xx
− = + = +
9.2. 25 90=
.
Vậy giá trị nhỏ nhất của biểu thức bằng
90
.
Câu 45: Biết tập nghiệm của bất phương trình
( ) ( )
2 2 2
2 3 2 3
2
log 1 log 1 log log 2 0
3
xx− − − +
là
;;S a b c d=
với
a b c d
. Giá trị của biểu thức
2a b c d+ + +
bằng
A.
2
1
log 3
. B.
3
. C.
3−
. D.
2
1
1
log 3
+
.
Lời giải
Điều kiện:
1
1
x
x
−
. Đặt
( )
2
2
log 1tx=−
.
Khi đó bất phương trình đã cho trở thành
2
3 3 3
log 2 log 2 1 0 log 2 1;1t t t− + − −
.
Suy ra
( )
( )
3
3
log 2 1
log 2 1
2 1 3
3 2 1
x
x
−
−
+
− − +
, kết hợp với điều kiện ta được tập nghiệm của bpt là
( ) ( )
33
log 2 1 log 2 1
3; 2 1 2 1; 3S
−−
= − − + +
.
Vậy
23a b c d+ + + =
.
Câu 46: Cho hàm số
( )
fx
có
( )
0,f x x
. Có bao nhiêu giá trị nguyên
x
để
( )
( )
2
24f x f x
A.
21
. B.
20
. C.
23
. D.
22
.
Lời giải
Vì
( )
fx
có
( )
0,f x x
nên
( )
fx
đồng biến trên
Do đó
( )
( )
2 2 2
24 24 24 0 0 24f x f x x x x x x −
Vì
x
nên có 23
giá trị nguyên
x
thỏa mãn bài toán.
Câu 47: Cho khối chóp
.S ABC
có thể tích
3
24 cm
. Gọi
B
là trung điểm của
AB
và
C
là điểm trên cạnh
AC
sao cho
3AC CC
=
(minh họa như hình vẽ)
GV. Phan Nhật Linh -
SĐT: 0817 098 716
20
Tuyển tập 10 đề ôn HKI
Toán 12
Thể tích của khối chóp
.S AB C
bằng
A.
3
8 cm
. B.
3
6 cm
. C.
3
2 cm
. D.
3
9 cm
.
Ta có:
.
.
' ' 1 3 3
..
2 4 8
S AB C
S ABC
V
S AB C AB AC
V S ABC AB AC
= = = =
3
..
33
.24 9 cm
88
S AB C S ABC
VV
= = =
Câu 48: Người ta cần xây một hồ chứa nước dạng hình hộp chữ nhật không nắp, cao
1,5m
và chiều dài
gấp đôi chiều rộng (minh họa như hình vẽ dưới). Nếu tổng diện tích bốn mặt xung quanh của hồ
là
2
18m
thì dung tích của hồ là
A.
3
12m
. B.
3
18m
. C.
3
5m
. D.
3
48m
.
Lời giải
Gọi
x
là chiều rộng của hồ cần xây (
0x
). Suy ra chiều dài của hồ là:
2x
.
Tổng diện tích bốn mặt xung quanh của hồ là:
( ) ( )
.1,5 .2 2 .1,5 .2 18xx+=
39x=
3x=
.
Thể tích của hồ là:
3
3.6.1,5 12Vm==
.
Câu 49: Cho
0, 0ab
thỏa mãn
4 25
4
log log log
4
ba
ab
−
= =
Giá trị của
66
log 4 2 log
2
a
bb
+−
bằng
A.
1
. B.
2
. C.
6
. D.
4
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có
( )
( )
( )
4 25
41
4
4
log log log 25 25 2
4
4
4.25 4
10
10 3
4
4
t
t
tt
tt
t
t
a
a
ba
a b t b b
ba
=
=
−
= = = = =
−
−
=
=
Có
( )
( ) ( )
22
3 4.25 4 4.10 2 4.2 .5 4. 5 0
t t t t t t t
− = + − =
( )
( )
2
2
2
2
2 2 2
5
2 2 2
4 4 0 2 2 2 12 8 2
5 5 5
5
2 2 2
2
t
t t t
t
a
b
VN
= − +
+ − = = = − = −
= − −
6 6 6 6
42
2
log 4 2 log log log 4 2
22
a
b
aa
bb
bb
+
+ − = = +
( )
66
log 6 4 2 4 2 log 6 2= − + = =
.
Câu 50: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số
0;23m
để hàm số
( )
( )
2
2 2023g x f x x m= − + +
đồng biến trên khoảng
( )
2; ?+
A.
23
. B.
20
. C.
21
. D.
22
.
Lời giải:
Để hàm số
( )
( )
2
2 2023g x f x x m= − + +
đồng biến trên khoảng
( )
2;+
thì
( )
( )
( )
( )
( )
2
2
2
2 2 2
2 0, 2;
2
x x x
g x f x x m x
xx
−−
= − + +
−
Mà
( )
( )
( )
2
2
2 2 2
0, 2;
2
x x x
x
xx
−−
+
−
( )
( )
2
2 0, 2;f x x m x
− + +
Từ đồ thị, hàm số
( )
y f x=
đồng biến trên
1;0−
và
)
1; +
.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
22
Tuyển tập 10 đề ôn HKI
Toán 12
Suy ra
( )
22
22
2 1 2 1
, 2;
1 2 0 1 2
x x m x x m
x
x x m m x x m
− + − −
+
− − + − − − −
.
Nhận xét: Ta thấy
( )
; 0;23
2
2 0, 2; 0 1 1 1 23
mm
x x x m m m
− + − ⎯⎯⎯⎯⎯→
.
Vậy có tất cả
23
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
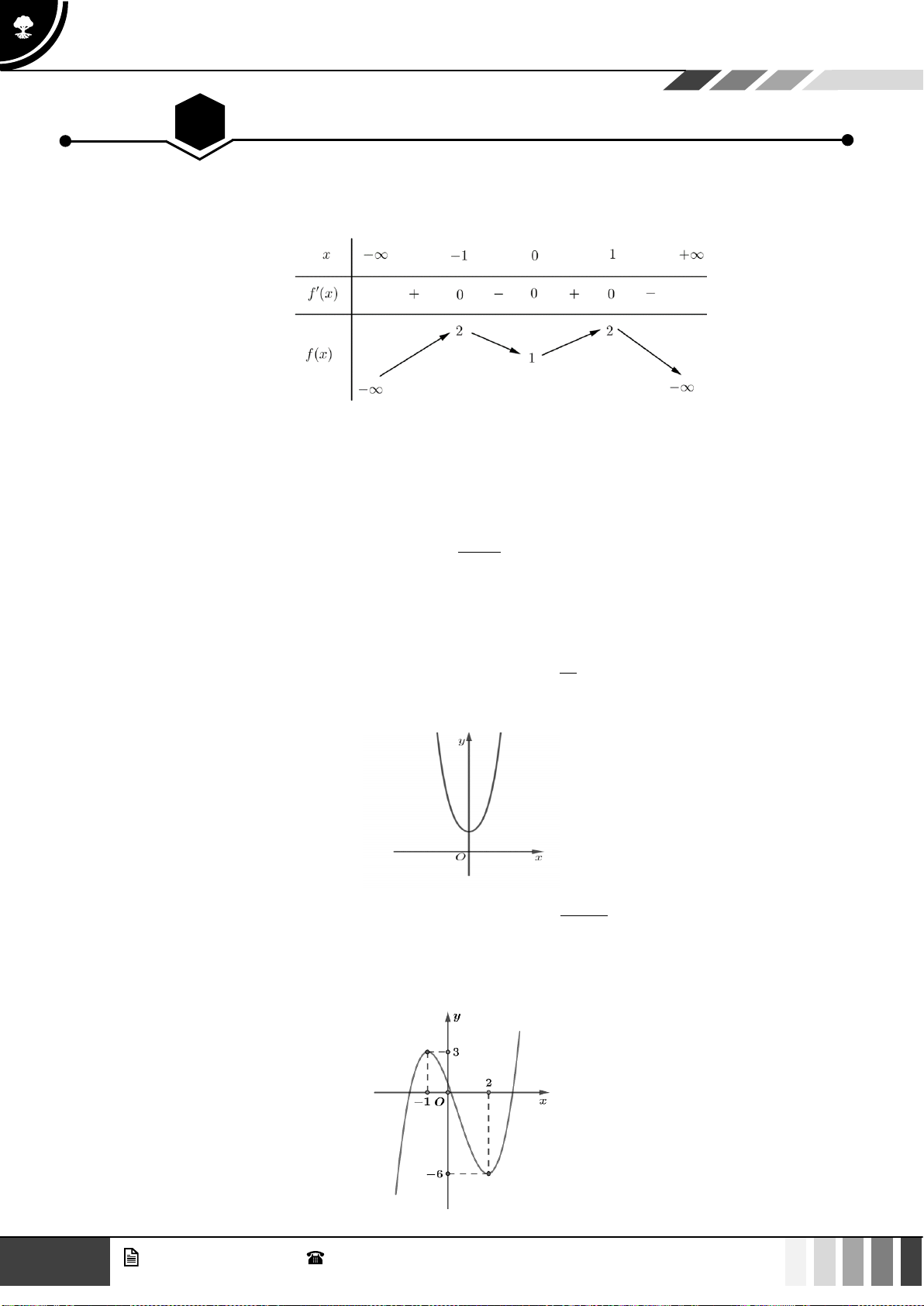
GV. Phan Nhật Linh -
SĐT: 0817 098 716
1
Tuyển tập 10 đề ôn HKI
Toán 12
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
1−
. B.
0
. C.
1
. D.
2
.
Câu 2: Nghiệm của phương trình
1
24
x+
=
là
A.
1x =−
. B.
0x =
. C.
2x =
. D.
1x =
.
Câu 3: Tìm tiệm cận đứng của đồ thị hàm số
31
2
x
y
x
−
=
+
.
A.
2x =−
. B.
2x =
. C.
2y =−
. D.
3x =
.
Câu 4: Nghiệm của phương trình
3
log (2 1) 2x −=
là
A.
10x =
. B.
4x =
. C.
11
2
x =
. D.
5x =
.
Câu 5: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1yx=+
. B.
42
21y x x= + +
. C.
32
2
x
y
x
+
=
+
. D.
42
21y x x= − +
.
Câu 6: Cho hàm số bậc ba
32
y ax bx cx d= + + +
có đồ thị là đường cong trong hình bên. Hàm số đã
cho đạt cực đại tại điểm nào dưới đây?
A.
2x =
. B.
3x =
. C.
6x =−
. D.
1x =−
.
ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 12
10
8
ĐỀ SỐ

GV. Phan Nhật Linh -
SĐT: 0817 098 716
2
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 7: Cho
a
là số thực dương và
,mn
là các số thực tùy ý. Khẳng định nào dưới đây là đúng?
A.
m n m n
a a a
−
+=
. B.
.
.
m n m n
a a a=
. C.
.m n m n
a a a+=
. D.
.
m n m n
a a a
+
=
.
Câu 8: Tập xác định của hàm số
2
logyx=
là
A.
)
0;+
. B.
\0
. C. . D.
( )
0;+
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số đường tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 10: Cho khối nón có bán kính đáy
1r =
và chiều cao
3h =
. Thể tích của khối nón đã cho bằng
A.
3
. B.
22
3
. C.
22
. D.
.
Câu 11: Tập xác định của hàm số
2
yx
−
=
là
A.
( )
0;+
. B.
)
0;+
. C.
\0
. D. .
Câu 12: Cho hàm số
()fx
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( ;2)−
. B.
( 1;2)−
. C.
( 1; )− +
. D.
(2; )+
.
Câu 13: Cho khối chóp có diện tích đáy
12B =
và chiều cao
6.h =
Thể tích của khối chóp đã cho bằng
A.
72
. B.
24
. C.
6
. D.
36
.
Câu 14: Cho hình nón có bán kính đáy
2r =
và độ dài đường sinh
4l =
. Diện tích xung quanh của hình
nón đã cho bằng
A.
9
. B.
16
. C.
3
. D.
8
.
Câu 15: Cho khối lập phương có cạnh bằng
5
. Thể tích của khối lập phương bằng
A.
125
. B.
25
. C.
15
. D.
50
.
Câu 16: Cho hình trụ có bán kính đáy
3r =
và độ dài đường sinh
1l =
. Diện tích xung quanh của hình
trụ đã cho bằng
A.
24
. B.
3
. C.
6
. D.
9
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
3
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 17: Cho khối lăng trụ
.ABCD A B C D
có chiều cao
9h =
. Đáy
ABCD
là hình vuông có cạnh bằng
2
. Thể tích của khối lăng trụ đã cho bằng
A.
36
. B.
12
. C.
18
. D.
6
.
Câu 18: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
,
,3AB a SA a==
và
SA
vuông góc với
mặt phẳng đáy (tham khảo hình vẽ bên). Góc giữa
SB
và mặt phẳng đáy bằng
A.
90
. B.
60
. C.
30
. D.
45
.
Câu 19: Tập nghiệm của bất phương trình
1
5
25
x
là
A.
( )
1;− +
. B.
( )
2;− +
. C.
( )
5;+
. D.
( )
2;+
.
Câu 20: Cho khối trụ có bán kính đáy
6r =
và chiều cao
2h =
. Thể tích của khối trụ đã cho bằng
A.
36
. B.
24
. C.
72
. D.
18
.
Câu 21: Cắt hình nón
S
bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có
cạnh huyền bằng 2. Tính thể tích của khối nón tạo nên bởi hình nón đã cho bằng
A.
. B.
2
3
. C.
3
. D.
4
3
.
Câu 22: Giá trị nhỏ nhất của hàm số
( )
3
31f x x x=−+
trên đoạn
0;2
bằng
A.
2−
. B.
3
. C.
1
. D.
1−
.
Câu 23: Cho khối lăng trụ tam giác đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
và cạnh bên bằng
4a
( tham
khảo hình vẽ bên). Thể tích khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
3
3
a
. C.
3
a
. D.
3
3a
.
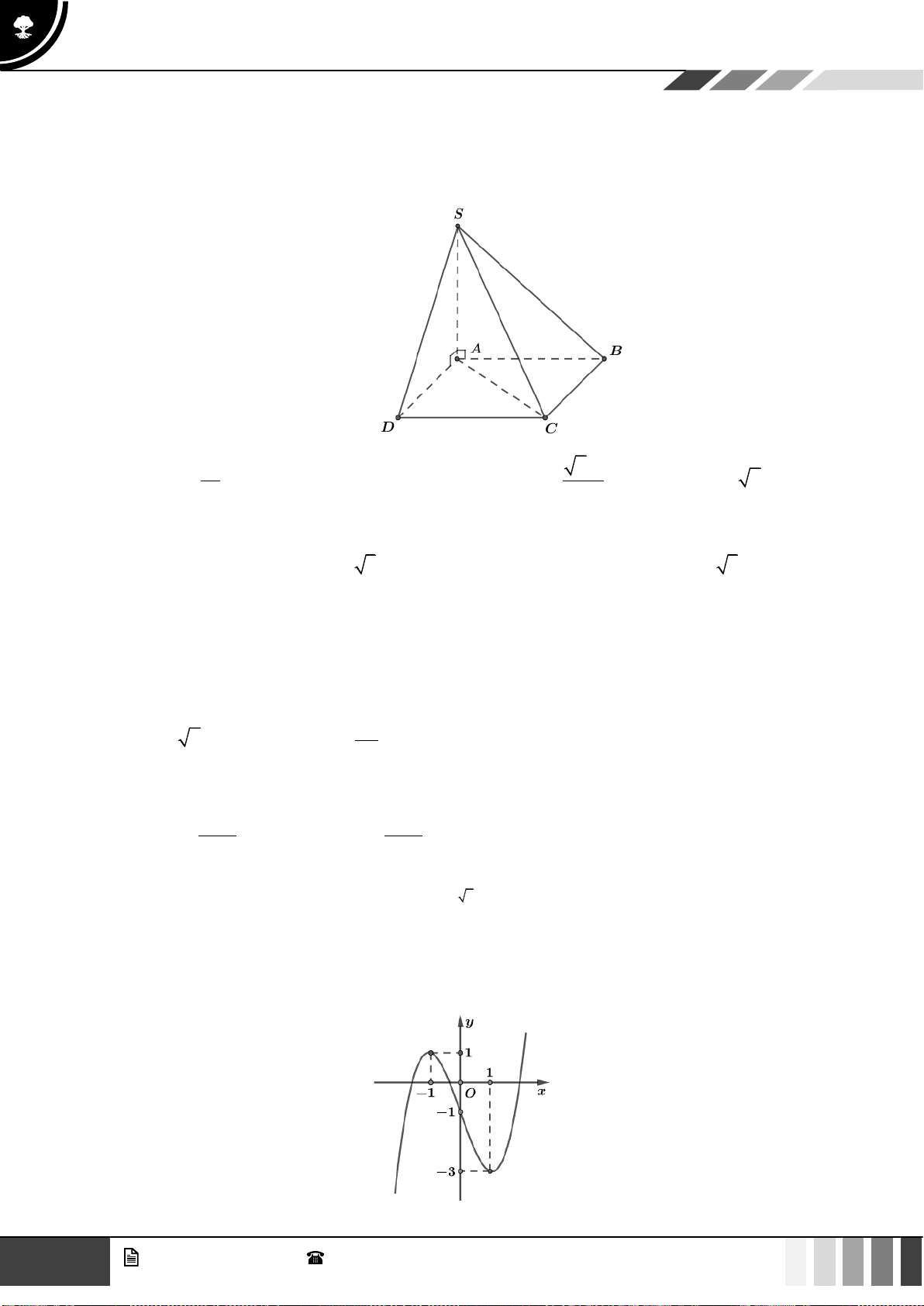
GV. Phan Nhật Linh -
SĐT: 0817 098 716
4
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 24: Số giao điểm của đồ thị hàm số
3
y x x=−
và trục hoành là
A.
0.
B.
2.
C.
1.
D.
3.
Câu 25: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và tam
giác
SAC
là tam giác cân (tham khảo hình vẽ bên). Tính thể tích
V
của khối chóp đã cho.
A.
3
3
a
V =
. B.
3
Va=
. C.
3
2
3
a
V =
. D.
3
2Va=
.
Câu 26: Tổng tất cả các nghiệm của phương trình
2
33
28
x x x− − −
=
bằng
A.
0
. B.
3
. C.
3−
. D.
23
.
Câu 27: Tính đạo hàm của hàm số
1
3.
x
y
−
=
A.
1
3
x
y
−
=−
. B.
1
3 .ln3
x
y
−
=−
. C.
1
3 .ln3
x
y
−
=
. D.
1
3
x
y
−
=
.
Câu 28: Cắt hình trụ bởi một mặt phẳng đi qua trục ta được thiết diện là một hình vuông có diện tích bằng
4. Thể tích của khối trụ tạo nên bởi hình trụ đã cho bằng
A.
22
. B.
2
3
. C.
2
. D.
8
.
Câu 29: Hàm số nào dưới đây đồng biến trên khoảng
( )
;− +
?
A.
2
3
x
y
x
−
=
+
. B.
5
2
x
y
x
+
=
−
. C.
3
y x x= − −
. D.
3
3y x x=+
.
Câu 30: Cho
a
là số thực dương,
1a
và
4
log
a
Pa=
. Mệnh đề nào dưới đây đúng?
A.
8P =
. B.
6P =
. C.
2P =
. D.
4P =
.
Câu 31: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong trong hình dưới. Số nghiệm thực của
phương trình
( )
2fx=−
là
A. 0. B. 3. C. 2. D. 1.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
5
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 32: Tập nghiệm của bất phương trình
( )
1
5
log 1 1x − −
là
A.
( )
0;6
. B.
( )
1;6
. C.
( )
6;+
. D.
( )
;6−
.
Câu 33: Cho hàm số liên tục trên và có bảng xét dấu của
( )
fx
như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 34: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
5AC a=
,
2BC a=
,
3AA a
=
(tham khảo hình vẽ). Khoảng cách từ
C
đến
( )
A BC
bằng
A.
3
2
a
. B.
3
4
a
. C.
3a
. D.
3
2
a
.
Câu 35: Cho
,ab
là các số thực dương và
a
khác 1. Khẳng định nào dưới đây đúng?
A.
6
11
log ( ) log
66
a
a
ab b=+
. B.
6
1
log ( ) log
6
a
a
ab b=
.
C.
6
11
log ( ) log
56
a
a
ab b=+
. D.
6
log ( ) 6 6log
a
a
ab b=+
.
Câu 36: Cho
,,abc
là ba số thực dương và khác 1. Đồ thị các hàm số
, log , log
x
bc
y a y x y x= = =
được
cho trong hình bên. Mệnh đề nào dưới đây đúng?
A.
abc
. B.
c b a
. C.
b c a
. D.
bac
.
( )
fx
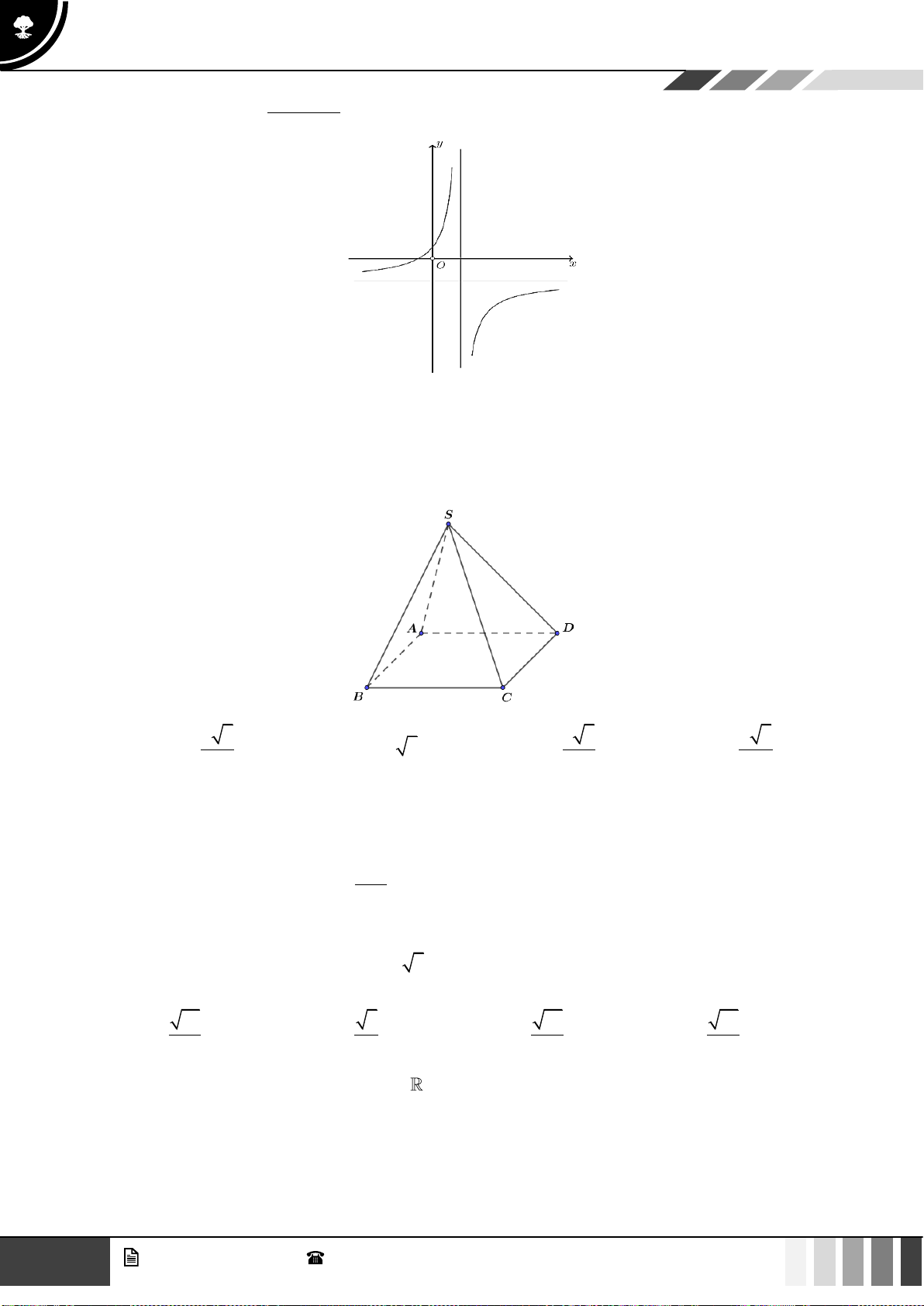
GV. Phan Nhật Linh -
SĐT: 0817 098 716
6
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 37: Cho hàm số
4ax b
y
cx b
+−
=
+
có đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
A.
0, 4, 0abc
. B.
0,0 4, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0 4, 0a b c
.
Câu 38: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Tam giác
SAB
là tam giác đều, tam
giác
SCD
vuông tại
S
(tham khảo hình vẽ bên). Tính thể tích
V
của khối chóp đã cho.
A.
43
3
V =
. B.
23V =
. C.
83
3
V =
. D.
23
3
V =
.
Câu 39: Cho hình nón có chiều cao bằng
4
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo
thiết diện là tam giác vuông có diện tích bằng
32
. Thể tích của khối nón giới hạn bởi hình nón
đã cho bằng
A.
32
. B.
64
3
. C.
64
. D.
192
.
Câu 40: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Các điểm
,MN
lần lượt là trung
điểm các cạnh
BC
và
CD
.
5SA =
và
SA
vuông góc với đáy. Khoảng cách giữa hai đường
thẳng
SN
và
DM
bằng
A.
10
10
. B.
5
10
. C.
10
5
. D.
10
2
.
Câu 41: Cho hàm số
( )
fx
có đạo hàm trên . Đồ thị của hàm số
( )
y f x
=
trên đoạn
2;2−
là đường
cong hình bên. Mệnh đề nào dưới đây đúng?
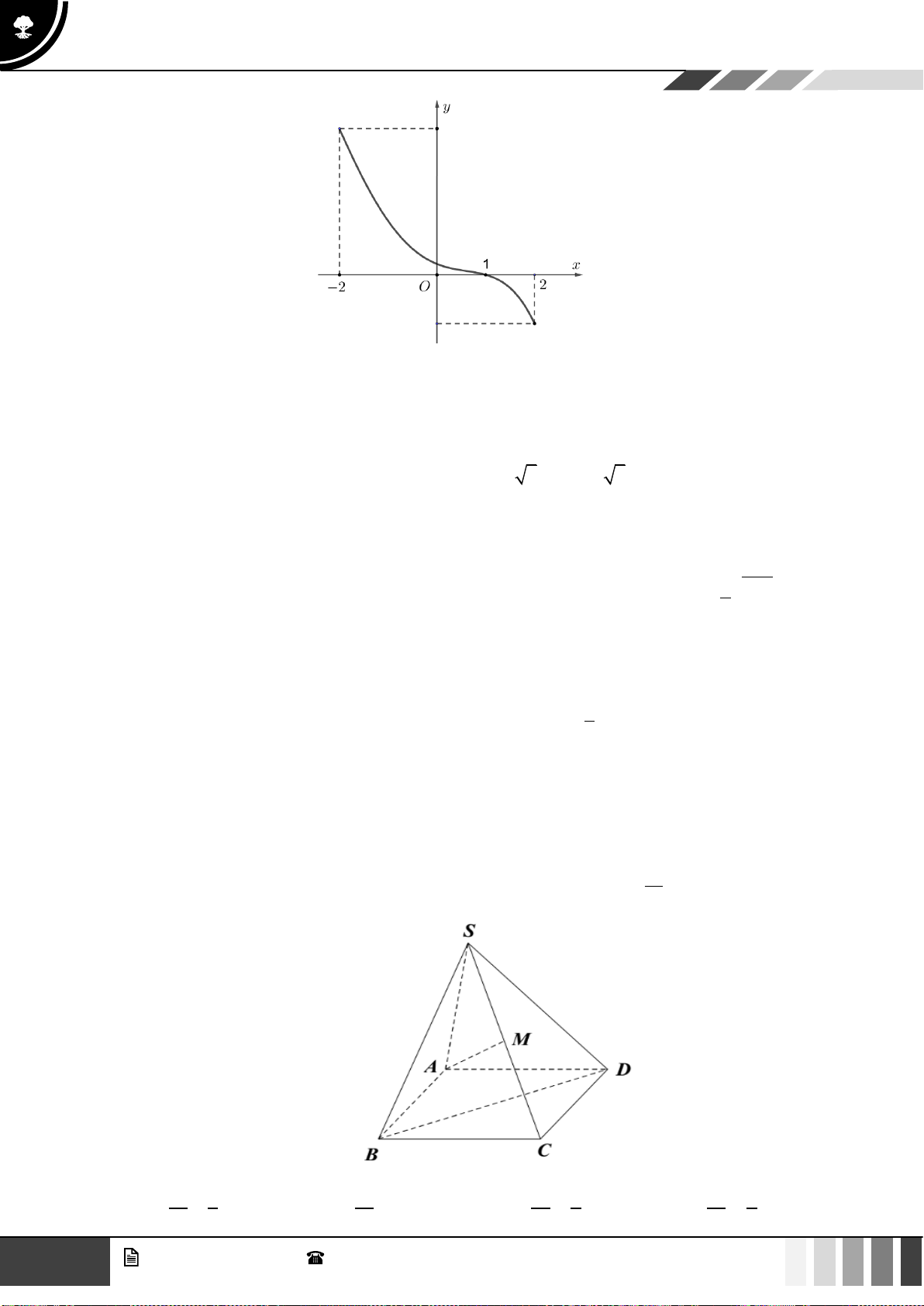
GV. Phan Nhật Linh -
SĐT: 0817 098 716
7
Tuyển tập 10 đề ôn HKI
Toán 12
A.
( ) ( )
2;2
max 2f x f
−
=
. B.
( ) ( )
2;2
min 1f x f
−
=
.
C.
( ) ( )
2;2
max 1f x f
−
=
. D.
( ) ( )
2;2
max 2f x f
−
=−
.
Câu 42: Biết rằng tập nghiệm của bất phương trình
( ) ( )
3 5 3 5 3.2
xx
x
+ + −
là khoảng
( )
;ab
, hãy
tính
S b a=−
A.
2S =
B.
3S =
C.
1S =
D.
4S =
Câu 43: Có bao nhiêu giá trị nguyên của tham số
2024;2024m−
để hàm số
21
3
7
9
x
xm
y
+
+
=
đồng biến
trên khoảng
( )
3;+
?
A.
2014
. B.
9
. C.
8
. D.
2015
.
Câu 44: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
32
1
16 10
3
y x mx x= − + +
đồng biến trên
khoảng
( ; )− +
?
A.
7
. B.
9
. C.
8
. D.
10
.
Câu 45: Cho khối chóp
.S ABCD
có đáy là hình bình hành.
M
là trung điểm của
.SC
Mặt phẳng qua
AM
và song song với
BD
chia khối chóp thành hai phần, trong đó phần chứa đỉnh
S
có thể tích
1
V
, phần còn lại có thể tích
2
V
(tham khảo hình vẽ bên). Tính tỉ số
1
2
V
V
A.
1
2
1
3
V
V
=
. B.
1
2
1
V
V
=
. C.
1
2
1
2
V
V
=
. D.
1
2
2
7
V
V
=
.
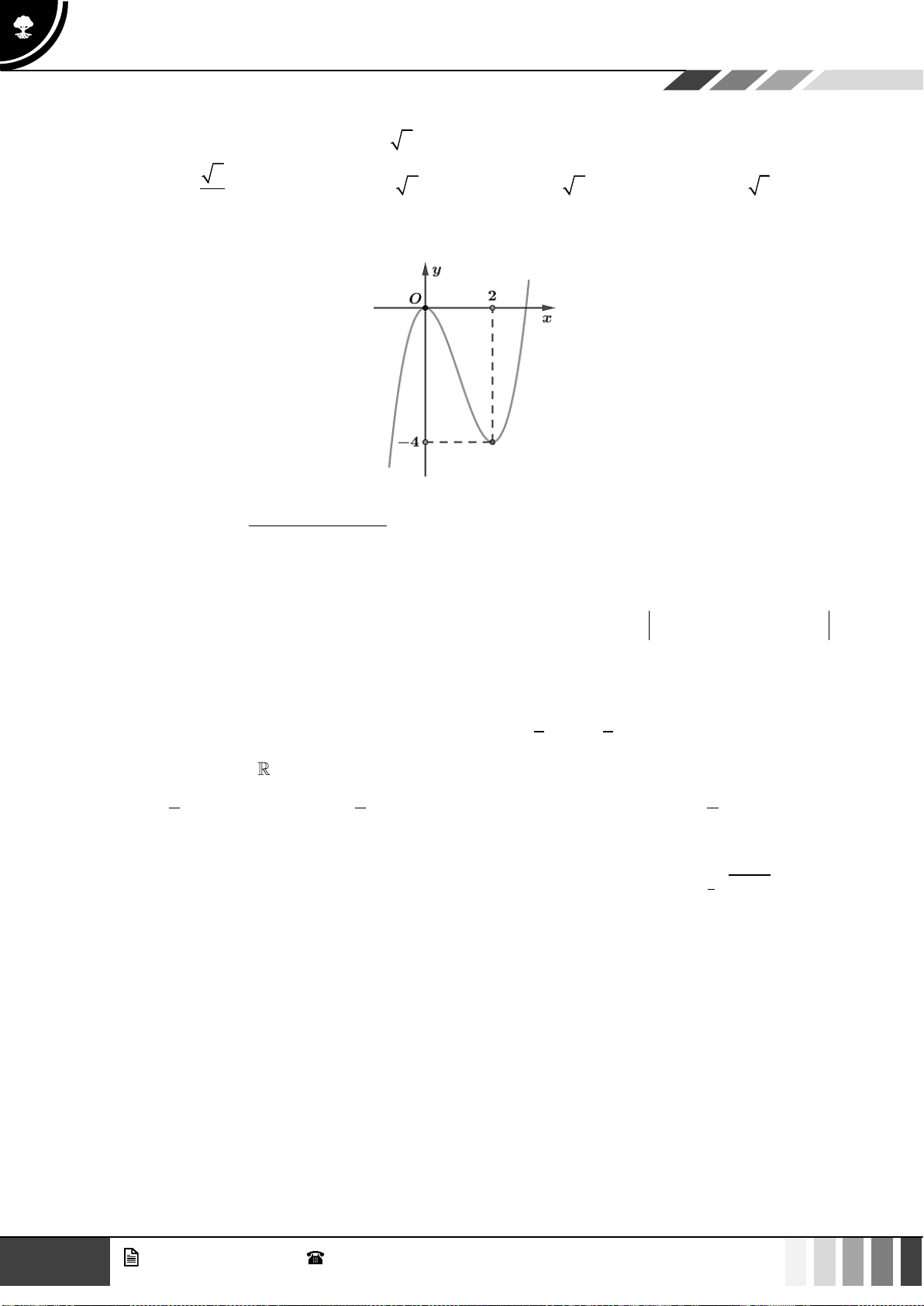
GV. Phan Nhật Linh -
SĐT: 0817 098 716
8
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 46: Cho khối hộp
.ABCD A B C D
có
2 2 , 90 ,AA AB AD BAD
= = =
60BAA
=
,
120 , 6DAA AC
==
. Tính thể tích
V
của khối hộp đã cho.
A.
2
2
V =
. B.
22V =
. C.
2V =
. D.
23V =
.
Câu 47: Cho hàm số
( )
32
3y f x x x= = −
có đồ thị là đường cong trong hình dưới đây.
Phương trình
( )
( )
( ) ( )
2
4
4
21
f f x
f x f x
−
=−
++
có bao nhiêu nghiệm?
A.
7
. B.
6
. C.
9
. D.
3
.
Câu 48: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
32
98y x x m x m= − + + −
có
năm điểm cực trị?
A.
14
. B. Vô số. C.
15
. D.
13
.
Câu 49: Tổng tất cả các giá trị của tham số
m
để hàm số
( )
2 5 3 2 2
11
10 1
3
20
5
ymxmm mx x x=− −+ − +−
đồng biến trên bằng
A.
1
2
. B.
5
2
. C.
2−
. D.
3
2
.
Câu 50: Số nghiệm nguyên thuộc
100;100−
của bất phương trình
( )
51
5
31
log 3 1 .log 143
25
x
x
−
− −
là
A.
81.
B.
79.
C.
83.
D.
84.
-------------------------HẾT-------------------------
GV. Phan Nhật Linh -
SĐT: 0817 098 716
9
Tuyển tập 10 đề ôn HKI
Toán 12
BẢNG ĐÁP ÁN
1.C
2.D
3.A
4.D
5.B
6.D
7.D
8.D
9.D
10.D
11.C
12.D
13.B
14.D
15.A
16.C
17.A
18.B
19.B
20.C
21.C
22.D
23.D
24.D
25.C
26.A
27.B
28.C
29.D
30.A
31.B
32.B
33.B
34.A
35.A
36.D
37.B
38.D
39.C
40.A
41.C
42.A
43.C
44.B
45.C
46.C
47.A
48.A
49.A
50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
1−
. B.
0
. C.
1
. D.
2
.
Lời giải
Từ bảng biến thiên ta suy ra giá trị cực tiểu của hàm số đã cho bằng 1.
Câu 2: Nghiệm của phương trình
1
24
x+
=
là
A.
1x =−
. B.
0x =
. C.
2x =
. D.
1x =
.
Lời giải
Ta có:
1
24
x+
=
12
22
x+
=
12x + =
1x=
.
Câu 3: Tìm tiệm cận đứng của đồ thị hàm số
31
2
x
y
x
−
=
+
.
A.
2x =−
. B.
2x =
. C.
2y =−
. D.
3x =
.
Lời giải
Gọi
( )
C
là đồ thị của hàm số
31
2
x
y
x
−
=
+
.
Vì
2
31
lim
2
x
x
x
+
→−
−
= −
+
(hoặc
2
31
lim
2
x
x
x
−
→−
−
= +
+
) nên đường thẳng
2x =−
là tiệm cận đứng của
đồ thị
( )
C
.
Câu 4: Nghiệm của phương trình
3
log (2 1) 2x −=
là
A.
10x =
. B.
4x =
. C.
11
2
x =
. D.
5x =
.
Lời giải
3
log (2 1) 2 (1)x −=
.
Điều kiện:
1
2 1 0
2
xx−
.
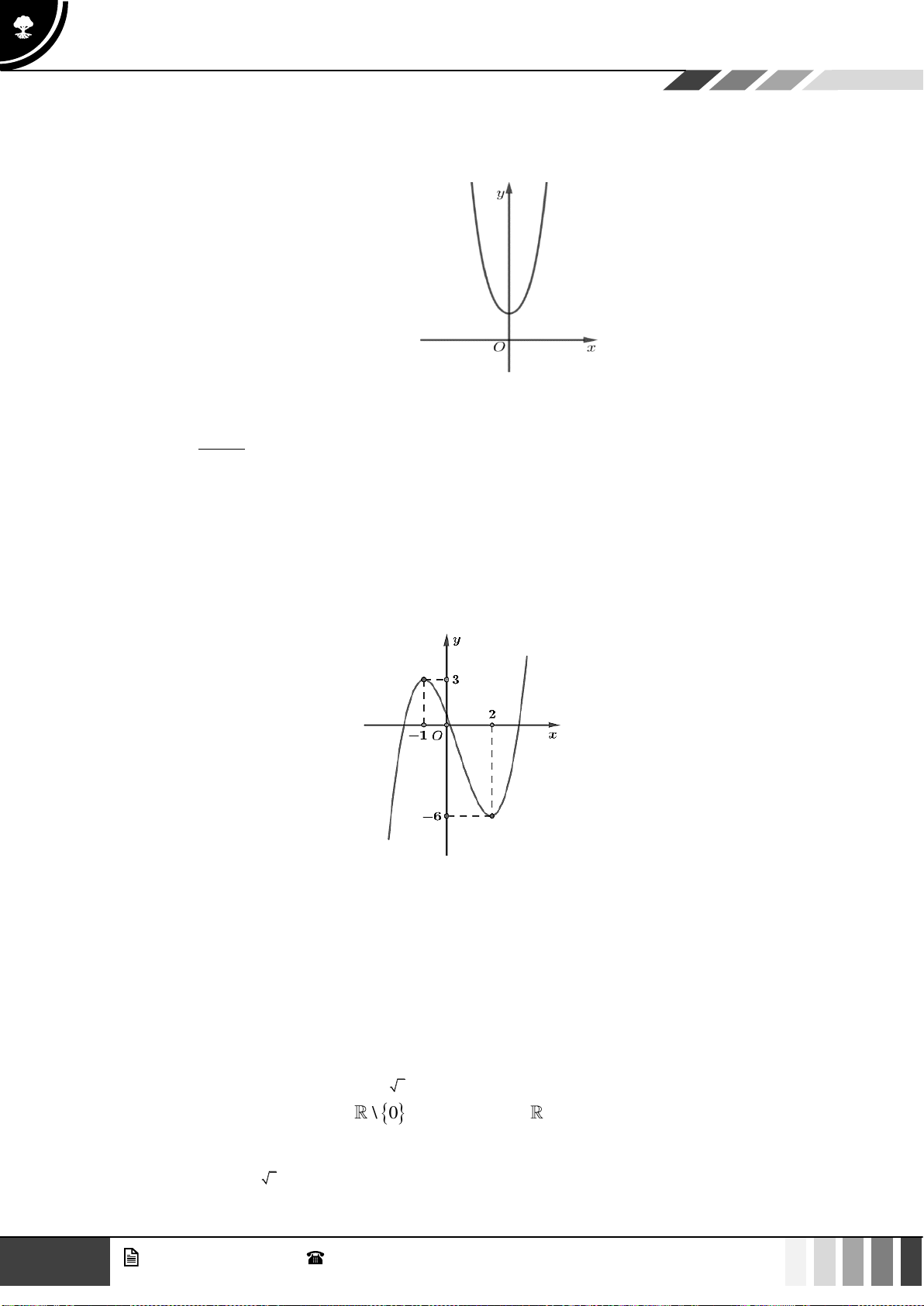
GV. Phan Nhật Linh -
SĐT: 0817 098 716
10
Tuyển tập 10 đề ôn HKI
Toán 12
Với điều kiện trên:
2
(1) 2 1 3 2 1 9 2 10 5x x x x − = − = = =
.
Giá trị
5x =
thỏa mãn điều kiện.
Câu 5: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1yx=+
. B.
42
21y x x= + +
.
C.
32
2
x
y
x
+
=
+
. D.
42
21y x x= − +
.
Lời giải
Đồ thị trên là của hàm số bậc 4 trùng phương, có 1 cực trị nên
,ab
cùng dấu, bề lõm quay lên
nên hệ số
0a
. Vậy đó là đồ thị hàm số
42
21y x x= + +
.
Câu 6: Cho hàm số bậc ba
32
y ax bx cx d= + + +
có đồ thị là đường cong trong hình bên. Hàm số đã
cho đạt cực đại tại điểm nào dưới đây?
A.
2x =
. B.
3x =
. C.
6x =−
. D.
1x =−
.
Lời giải
Từ đồ thị ta thấy
1x =−
là điểm cực đại của hàm số đã cho.
Câu 7: Cho
a
là số thực dương và
,mn
là các số thực tùy ý. Khẳng định nào dưới đây là đúng?
A.
m n m n
a a a
−
+=
. B.
.
.
m n m n
a a a=
.C.
.m n m n
a a a+=
. D.
.
m n m n
a a a
+
=
.
Lời giải
Ta thấy đáp án D là hoàn toàn chính xác.
Câu 8: Tập xác định của hàm số
2
logyx=
là
A.
)
0;+
. B.
\0
. C. . D.
( )
0;+
.
Lời giải
Hàm số
2
logyx=
xác định khi và chỉ khi
0x
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:

GV. Phan Nhật Linh -
SĐT: 0817 098 716
11
Tuyển tập 10 đề ôn HKI
Toán 12
Số đường tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Do
lim 5
lim 3
x
x
y
y
→+
→−
=
=−
nên đồ thị hàm số
( )
y f x=
có 2 đường tiệm cận ngang là
3, 5yy= − =
.
Câu 10: Cho khối nón có bán kính đáy
1r =
và chiều cao
3h =
. Thể tích của khối nón đã cho bằng
A.
3
. B.
22
3
. C.
22
. D.
.
Lời giải
Thể tích của khối nón là
22
11
.1 .3
33
V r h
= = =
.
Câu 11: Tập xác định của hàm số
2
yx
−
=
là
A.
( )
0;+
. B.
)
0;+
. C.
\0
. D. .
Lời giải
Điều kiện xác định của hàm số là
0x
(do
2
−
−
). Vậy tập xác định của hàm số đã cho là
\0D =
.
Câu 12: Cho hàm số
()fx
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( ;2)−
. B.
( 1;2)−
. C.
( 1; )− +
. D.
(2; )+
.
Lời giải
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng
(2; )+
.
Câu 13: Cho khối chóp có diện tích đáy
12B =
và chiều cao
6.h =
Thể tích của khối chóp đã cho bằng
A.
72
. B.
24
. C.
6
. D.
36
.
Lời giải
Thể tích của khối chóp là
11
. .12.6 24.
33
V B h= = =

GV. Phan Nhật Linh -
SĐT: 0817 098 716
12
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 14: Cho hình nón có bán kính đáy
2r =
và độ dài đường sinh
4l =
. Diện tích xung quanh của hình
nón đã cho bằng
A.
9
. B.
16
. C.
3
. D.
8
.
Lời giải
Diện tích xung quanh của hình nón là:
8
xq
S rl
==
.
Câu 15: Cho khối lập phương có cạnh bằng
5
. Thể tích của khối lập phương bằng
A.
125
. B.
25
. C.
15
. D.
50
.
Lời giải
Thể tích của khối lập phương là:
3
5 125V ==
.
Câu 16: Cho hình trụ có bán kính đáy
3r =
và độ dài đường sinh
1l =
. Diện tích xung quanh của hình
trụ đã cho bằng
A.
24
. B.
3
. C.
6
. D.
9
.
Lời giải
Diện tích xung quanh của hình trụ
2 2 .3.1 6
xq
S rl
= = =
.
Câu 17: Cho khối lăng trụ
.ABCD A B C D
có chiều cao
9h =
. Đáy
ABCD
là hình vuông có cạnh bằng
2
. Thể tích của khối lăng trụ đã cho bằng
A.
36
. B.
12
. C.
18
. D.
6
.
Lời giải
Đáy là hình vuông có cạnh bằng
2
nên diện tích đáy
4
d
S =
.
Thể tích của khối lăng trụ
. 4.9 36
d
V S h= = =
.
Câu 18: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
,
,3AB a SA a==
và
SA
vuông góc với
mặt phẳng đáy (tham khảo hình vẽ bên). Góc giữa
SB
và mặt phẳng đáy bằng
A.
90
. B.
60
. C.
30
. D.
45
.
Lời giải
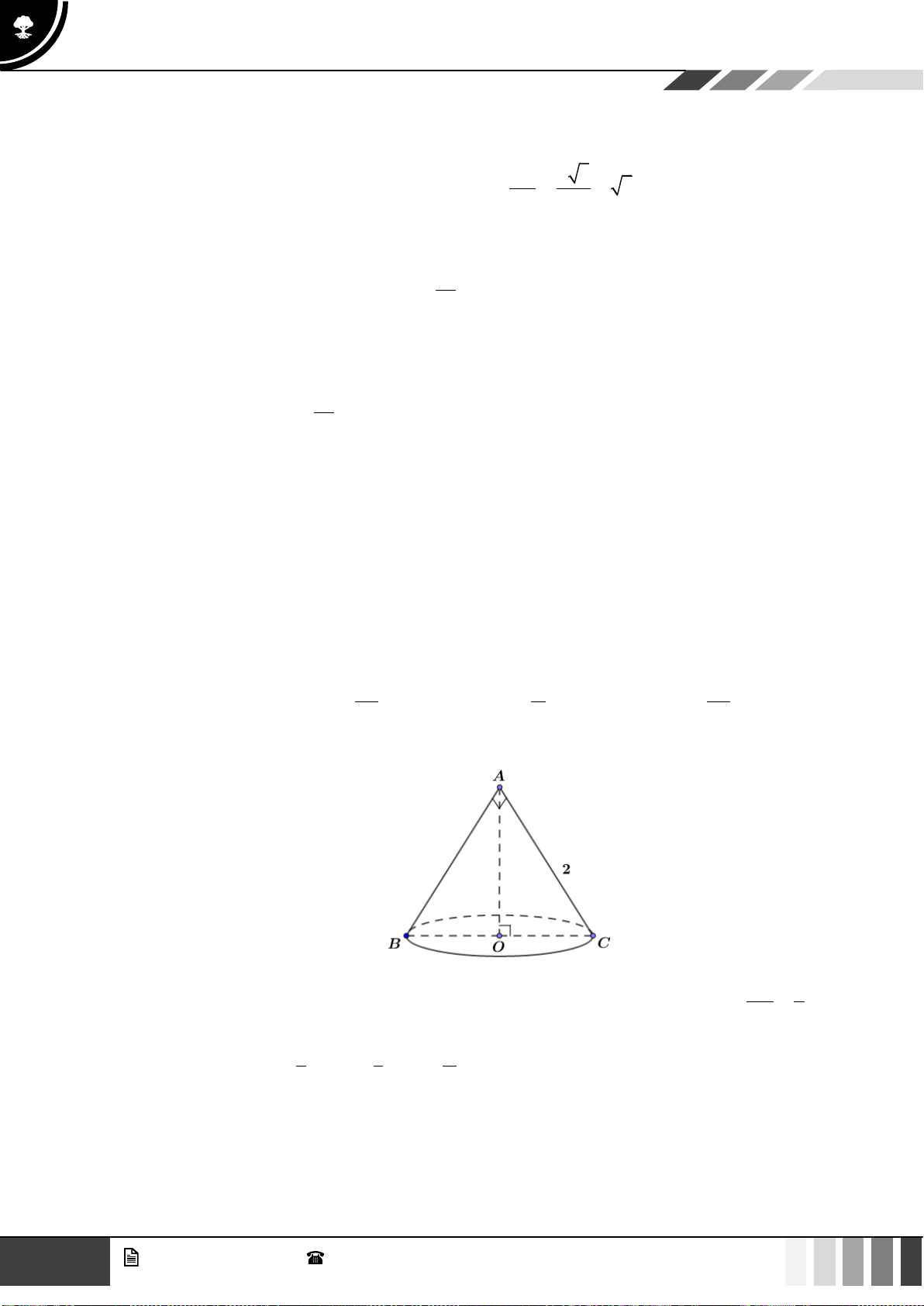
GV. Phan Nhật Linh -
SĐT: 0817 098 716
13
Tuyển tập 10 đề ôn HKI
Toán 12
Vì
( )
SA ABC⊥
nên
AB
là hình chiếu vuông góc của
SB
lên
( )
ABC
.
Suy ra
( )
( )
( )
,,SB ABC SB AB SBA==
.
Xét tam giác
SAB
vuông tại
A
ta có:
3
tan 3
SA a
SBA
AB a
= = =
60SBA =
.
Vậy
( )
( )
, 60SB ABC SBA= =
.
Câu 19: Tập nghiệm của bất phương trình
1
5
25
x
là
A.
( )
1;− +
. B.
( )
2;− +
. C.
( )
5;+
. D.
( )
2;+
.
Lời giải
Bất phương trình
2
1
5 5 5 2
25
xx
x
−
−
.
Vậy tập nghiệm của bpt là
( )
2;− +
.
Câu 20: Cho khối trụ có bán kính đáy
6r =
và chiều cao
2h =
. Thể tích của khối trụ đã cho bằng
A.
36
. B.
24
. C.
72
. D.
18
.
Lời giải
Thể tích của khối trụ là
22
.6 .2 72V r h
= = =
.
Câu 21: Cắt hình nón
S
bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có
cạnh huyền bằng 2. Tính thể tích của khối nón tạo nên bởi hình nón đã cho bằng
A.
. B.
2
3
. C.
3
. D.
4
3
.
Lời giải
Vì thiết diện là một tam giác vuông cân có cạnh huyền bằng 2 nên
2
1
22
BC
R h OA= = = = =
.
Vậy thể tích là:
2
11
. .1.1
3 3 3
V R h
= = =
.
Câu 22: Giá trị nhỏ nhất của hàm số
( )
3
31f x x x=−+
trên đoạn
0;2
bằng
A.
2−
. B.
3
. C.
1
. D.
1−
.
Lời giải
Ta có:
( )
2
' 3 3f x x=−
.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
14
Tuyển tập 10 đề ôn HKI
Toán 12
( )
2
' 0 3 3 0 1f x x x= − = =
.
Ta có bảng biến thiên:
Vậy giá trị nhỏ nhất của hàm số trên đoạn
0;2
là
( )
0;2
min 1
x
fx
=−
.
Câu 23: Cho khối lăng trụ tam giác đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
và cạnh bên bằng
4a
( tham
khảo hình vẽ bên). Thể tích khối lăng trụ đã cho bằng
A.
3
23a
. B.
3
3
3
a
. C.
3
a
. D.
3
3a
.
Lời giải
Ta có lăng trụ
. ' ' 'ABC A B C
đều nên
. ' ' '
.'
ABC A B C ABC
V S BB=
.
Mà
2
3
4
ABC
a
S =
,
'4BB a=
. Suy ra
2
3
. ' ' '
3
.4 3
4
ABC A B C
a
V a a==
.
Câu 24: Số giao điểm của đồ thị hàm số
3
y x x=−
và trục hoành là
A.
0.
B.
2.
C.
1.
D.
3.
Lời giải
Phương trình hoành độ giao điểm của đồ thị hàm số
3
y x x=−
và trục hoành là
3
0
01
1
x
x x x
x
=
− = =
=−
Vậy đồ thị hàm số cắt trục hoành tại
3
điểm.
Câu 25: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và tam
giác
SAC
là tam giác cân (tham khảo hình vẽ bên). Tính thể tích
V
của khối chóp đã cho.
GV. Phan Nhật Linh -
SĐT: 0817 098 716
15
Tuyển tập 10 đề ôn HKI
Toán 12
A.
3
3
a
V =
. B.
3
Va=
. C.
3
2
3
a
V =
. D.
3
2Va=
.
Lời giải
( )
SA ABCD SA AC SAC⊥ ⊥
vuông cân tại
2A SA AC a = =
3
2
1 1 2
. 2.
3 3 3
ABCD
a
V SA S a a = = =
.
Câu 26: Tổng tất cả các nghiệm của phương trình
2
33
28
x x x− − −
=
bằng
A.
0
. B.
3
. C.
3−
. D.
23
.
Lời giải
22
3 3 3 3 3 2 2
2 8 2 2 3 3 3 3 0
x x x x x x
x x x x
− − − − − −
= = − − = − − =
Phương trình có tổng
2
nghiệm bằng
0
.
Câu 27: Tính đạo hàm của hàm số
1
3.
x
y
−
=
A.
1
3
x
y
−
=−
. B.
1
3 .ln3
x
y
−
=−
. C.
1
3 .ln3
x
y
−
=
. D.
1
3
x
y
−
=
.
Lời giải
Hàm số
1
3
x
y
−
=
có đạo hàm:
( )
11
1 .3 .ln3 3 .ln3
xx
yx
−−
= − = −
.
Câu 28: Cắt hình trụ bởi một mặt phẳng đi qua trục ta được thiết diện là một hình vuông có diện tích bằng
4. Thể tích của khối trụ tạo nên bởi hình trụ đã cho bằng
A.
22
. B.
2
3
. C.
2
. D.
8
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
16
Tuyển tập 10 đề ôn HKI
Toán 12
Thiết diện qua trục của hình trụ là hình vuông có diện tích
4S =
.
Ta có:
2
2 . 4 2; 1.S r h h h r= = = = =
Vậy thể tích khối trụ
22
.1 .2 2 .V r h
= = =
Câu 29: Hàm số nào dưới đây đồng biến trên khoảng
( )
;− +
?
A.
2
3
x
y
x
−
=
+
. B.
5
2
x
y
x
+
=
−
. C.
3
y x x= − −
. D.
3
3y x x=+
.
Lời giải
Ta có: Hàm số xác
3
3y x x=+
định với
( )
;x − +
.
( )
2
' 3 3 0 ;y x x= + − +
.
Do đó hàm số luôn đồng biến trên khoảng
( )
;− +
.
Câu 30: Cho
a
là số thực dương,
1a
và
4
log
a
Pa=
. Mệnh đề nào dưới đây đúng?
A.
8P =
. B.
6P =
. C.
2P =
. D.
4P =
.
Lời giải
Ta có:
1
2
4 4 4 4
1
log log log 2.log 2.4 8
1
2
aa
a
a
P a a a a= = = = = =
.
Câu 31: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong trong hình dưới. Số nghiệm thực của
phương trình
( )
2fx=−
là
A. 0. B. 3. C. 2. D. 1.
Lời giải
Dựa vào đồ thị ta thấy đường thẳng
2y =−
cắt đồ thị hàm số
( )
y f x=
tại ba điểm phân biệt
nên phương trình
( )
2fx=−
có ba nghiệm thực.
Câu 32: Tập nghiệm của bất phương trình
( )
1
5
log 1 1x − −
là
A.
( )
0;6
. B.
( )
1;6
. C.
( )
6;+
. D.
( )
;6−
.
Lời giải
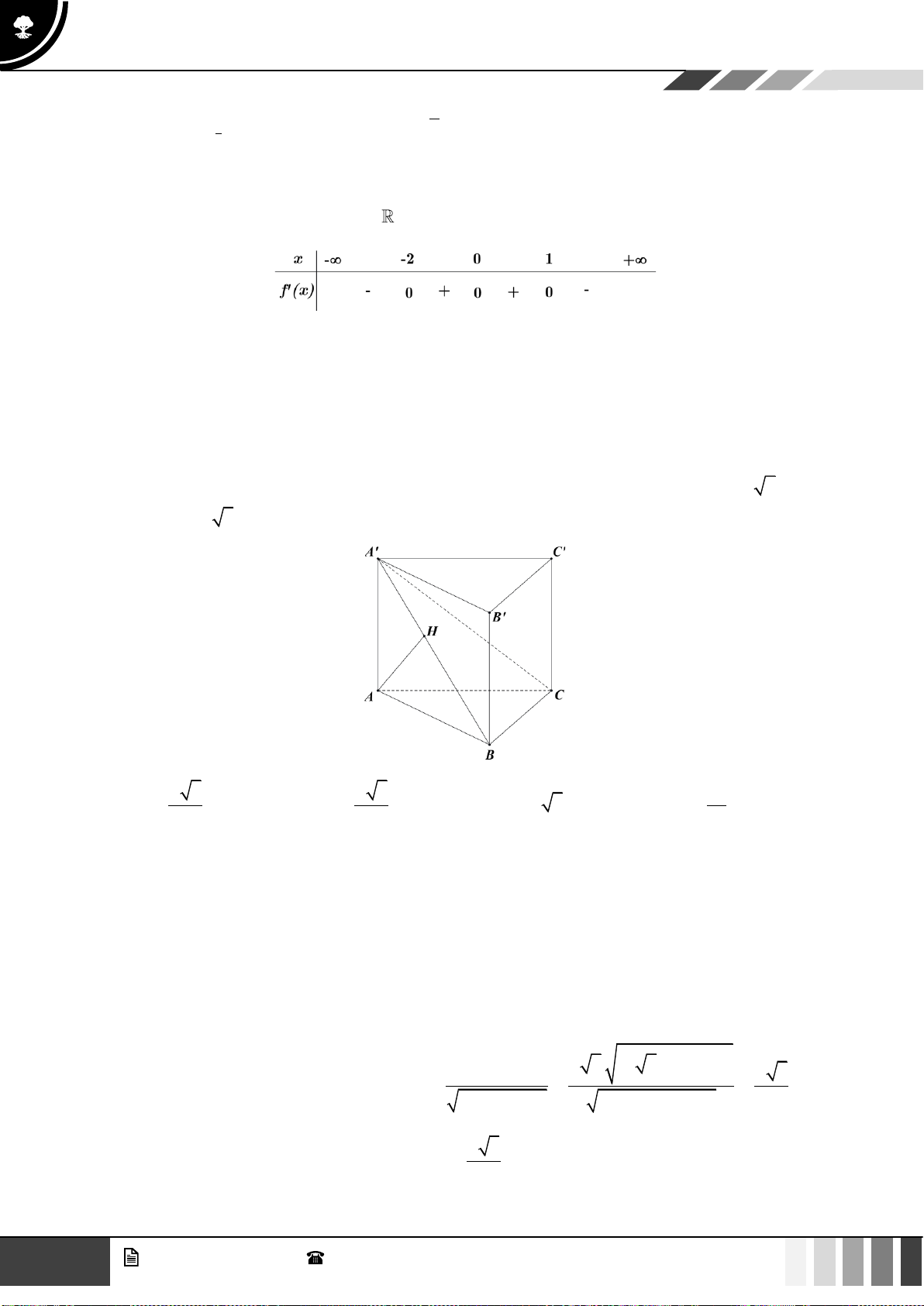
GV. Phan Nhật Linh -
SĐT: 0817 098 716
17
Tuyển tập 10 đề ôn HKI
Toán 12
Ta có
( )
1
5
log 1 1x − −
1
1
01
5
x
−
−
0 1 5x −
16x
.
Vậy tập nhiệm của bất phương trình đã cho là (1; 6).
Câu 33: Cho hàm số liên tục trên và có bảng xét dấu của
( )
fx
như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Từ bảng xét dấu ta thấy
( )
fx
đổi dấu
2
lần nên hàm số đã cho có
2
cực trị.
Câu 34: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
5AC a=
,
2BC a=
,
3AA a
=
(tham khảo hình vẽ). Khoảng cách từ
C
đến
( )
A BC
bằng
A.
3
2
a
. B.
3
4
a
. C.
3a
. D.
3
2
a
.
Lời giải
Dựng
( )
AH A B H A B
⊥
Khi đó:
( ) ( )
( )
( )
,
AH A B
AH A BC
AH BC BC A BC AH A BC
⊥
⊥
⊥ ⊥
.
Ta có:
( )
( )
( )
( )
, , d C A BC d A A BC AH
==
.
Xét tam giác
A AB
vuông tại
A
:
( )
( )
2
2
2 2 2 2 2
3. 5 2
.3
2
3 5 4
a a a
AA AB a
AH
AA AB a a a
−
= = =
+ + −
.
Vậy khoảng cách từ
C
đến
( )
A BC
bằng
3
2
a
.
Câu 35: Cho
,ab
là các số thực dương và
a
khác 1. Khẳng định nào dưới đây đúng?
( )
fx
GV. Phan Nhật Linh -
SĐT: 0817 098 716
18
Tuyển tập 10 đề ôn HKI
Toán 12
A.
6
11
log ( ) log
66
a
a
ab b=+
. B.
6
1
log ( ) log
6
a
a
ab b=
.
C.
6
11
log ( ) log
56
a
a
ab b=+
. D.
6
log ( ) 6 6log
a
a
ab b=+
.
Lời giải
( )
6
1 1 1 1
log ( ) log ( ) 1 log log
6 6 6 6
a a a
a
ab ab b b= = + = +
Câu 36: Cho
,,abc
là ba số thực dương và khác 1. Đồ thị các hàm số
, log , log
x
bc
y a y x y x= = =
được
cho trong hình bên. Mệnh đề nào dưới đây đúng?
A.
abc
. B.
c b a
. C.
b c a
. D.
bac
.
Lời giải
Đường thẳng
1x =
cắt đồ thị hàm số
x
ya=
tại điểm
(1; )Ma
. Khi đó, gọi
(0; )Aa
là hình
chiếu của điểm
M
trên trục
Oy
.
Đường thẳng
1y =
cắt các đồ thj hàm số
log
b
yx=
và
log
c
yx=
lần lượt tại
( ;1)Nb
và
( ;1)Pc
. Khi đó, gọi
( ;0)Bb
và
( ;0)Cc
lần lượt là hình chiếu của
N
và
P
trên trục
Ox
.
Nhận thấy
OB OA OC
nên
bac
.
Câu 37: Cho hàm số
4ax b
y
cx b
+−
=
+
có đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?

GV. Phan Nhật Linh -
SĐT: 0817 098 716
19
Tuyển tập 10 đề ôn HKI
Toán 12
A.
0, 4, 0abc
. B.
0,0 4, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0 4, 0a b c
.
Lời giải
Dựa vào đồ thị, ta thấy tiệm cận ngang, tiệm cận đứng, giao của đồ thị với trục tung và trục
hoành, suy ra
0
04
0
0
4
0
0
4
0
a
c
b
b
c
a
b
c
b
b
a
−
−
−
.
Câu 38: Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Tam giác
SAB
là tam giác đều, tam
giác
SCD
vuông tại
S
(tham khảo hình vẽ bên). Tính thể tích
V
của khối chóp đã cho.
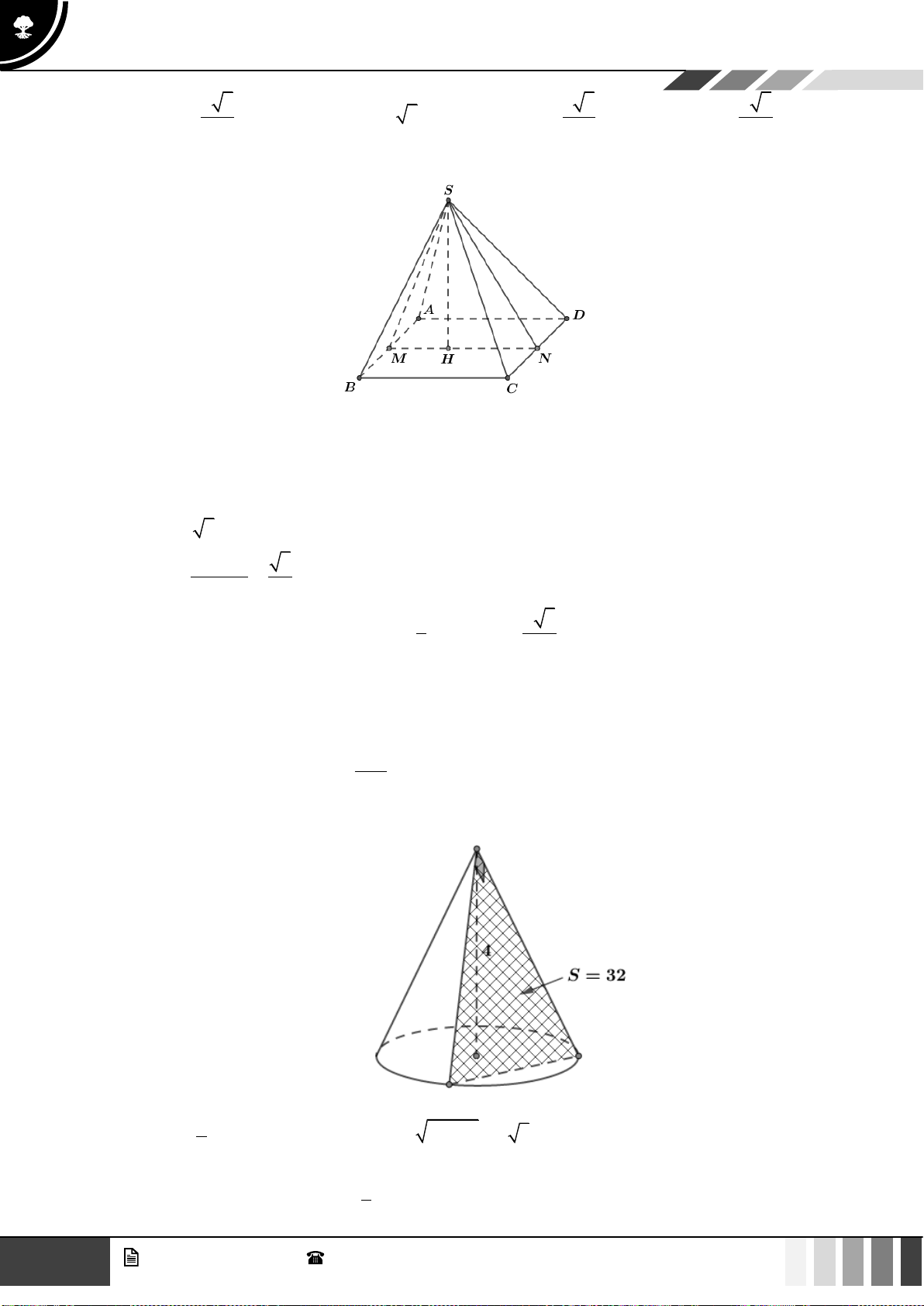
GV. Phan Nhật Linh -
SĐT: 0817 098 716
20
Tuyển tập 10 đề ôn HKI
Toán 12
A.
43
3
V =
. B.
23V =
. C.
83
3
V =
. D.
23
3
V =
.
Lời giải
Gọi
,MN
lần lượt là trung điểm
,AB CD
( )
1MN AB⊥
Do
SAB
đều nên
( )
2SM AB⊥
, từ
( ) ( )
1 , 2
suy ra
( ) ( ) ( )
AB SMN SMN ABCD⊥ ⊥
Kẻ
SH MN⊥
( )
SH ABCD⊥
.
2 2 2
3, 2, 1SM MN SN SM SN MN= = = + =
SMN
vuông tại
S
nên
.3
2
SM SN
SH
MN
==
.
Thể tích khối chóp
.S ABCD
là
1 2 3
.
33
ABCD
V SH S==
.
Câu 39: Cho hình nón có chiều cao bằng
4
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo
thiết diện là tam giác vuông có diện tích bằng
32
. Thể tích của khối nón giới hạn bởi hình nón
đã cho bằng
A.
32
. B.
64
3
. C.
64
. D.
192
.
Lời giải
Ta có:
2
1
32 8
2
ll= =
. Suy ra
22
43r l h= − =
.
Vậy thể tích khối nón là
2
1
64
3
V r h
==

GV. Phan Nhật Linh -
SĐT: 0817 098 716
21
Tuyển tập 10 đề ôn HKI
Toán 12
Câu 40: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh bằng
2
. Các điểm
,MN
lần lượt là trung
điểm các cạnh
BC
và
CD
.
5SA =
và
SA
vuông góc với đáy. Khoảng cách giữa hai đường
thẳng
SN
và
DM
bằng
A.
10
10
. B.
5
10
. C.
10
5
. D.
10
2
.
Lời giải
Ta chứng minh
AN DM⊥
, thật vậy ta có:
ADN DCM =
suy ra
NAD MDC=
Mà
0
90ADM MDC+=
nên
0
90ADM NAD+=
. Từ đó ta có
()MD SAN⊥
Gọi
I AN DM=
, kẻ
IK SN⊥
(
K SN
)
( , )d SN DM IK=
Trong
ADN
ta có
5AN =
,
2
1
5
DN
IN
AN
==
. Suy ra
1
5
IN
AN
=
; từ đó
1
5
IK
AH
=
với
H
là
hình chiếu của
A
lên
SN
. Trong tam giác
SAN
ta có
2 2 2
1 1 1
AH SA AN
=+
, suy ra
10
2
AH =
.
Vậy
10
( , )
10
d SN DM =
.
Câu 41: Cho hàm số
( )
fx
có đạo hàm trên . Đồ thị của hàm số
( )
y f x
=
trên đoạn
2;2−
là đường
cong hình bên. Mệnh đề nào dưới đây đúng?
GV. Phan Nhật Linh -
SĐT: 0817 098 716
22
Tuyển tập 10 đề ôn HKI
Toán 12
A.
( ) ( )
2;2
max 2f x f
−
=
. B.
( ) ( )
2;2
min 1f x f
−
=
.
C.
( ) ( )
2;2
max 1f x f
−
=
. D.
( ) ( )
2;2
max 2f x f
−
=−
.
Lời giải.
Dựa vào thị của hàm số
( )
y f x
=
trên đoạn
2;2−
ta thấy
( )
0fx
=
1x=
.
Bảng biến thiên:
Do đó
( ) ( )
2;2
max 1f x f
−
=
.
Câu 42: Biết rằng tập nghiệm của bất phương trình
( ) ( )
3 5 3 5 3.2
xx
x
+ + −
là khoảng
( )
;ab
, hãy
tính
S b a=−
A.
2S =
B.
3S =
C.
1S =
D.
4S =
Lời giải.
Ta có
( ) ( )
3 5 3 5 3.2
xx
x
+ + −
.
3 5 2
3
2
35
x
x
+
+
+
.
Đặt
35
2
x
t
+
=
với
0t
1
3t
t
+
2
3 1 0tt − +
3 5 3 5
22
t
−+
3 5 3 5 3 5
2 2 2
x
− + +
3 5 3 5
22
3 5 3 5
log log
22
x
++
−+
11x −
.
Suy ra:
( ) ( )
; 1;1ab =−
2S=
.
Câu 43: Có bao nhiêu giá trị nguyên của tham số
2024;2024m−
để hàm số
21
3
7
9
x
xm
y
+
+
=
đồng biến
trên khoảng
( )
3;+
?
A.
2014
. B.
9
. C.
8
. D.
2015
.
Lời giải
Xét hàm số
( )
7
9
fx
y
=
với
( )
21
3
x
fx
xm
+
=
+
. Ta có
( )
( )
77
. .ln
99
fx
y f x
=
.
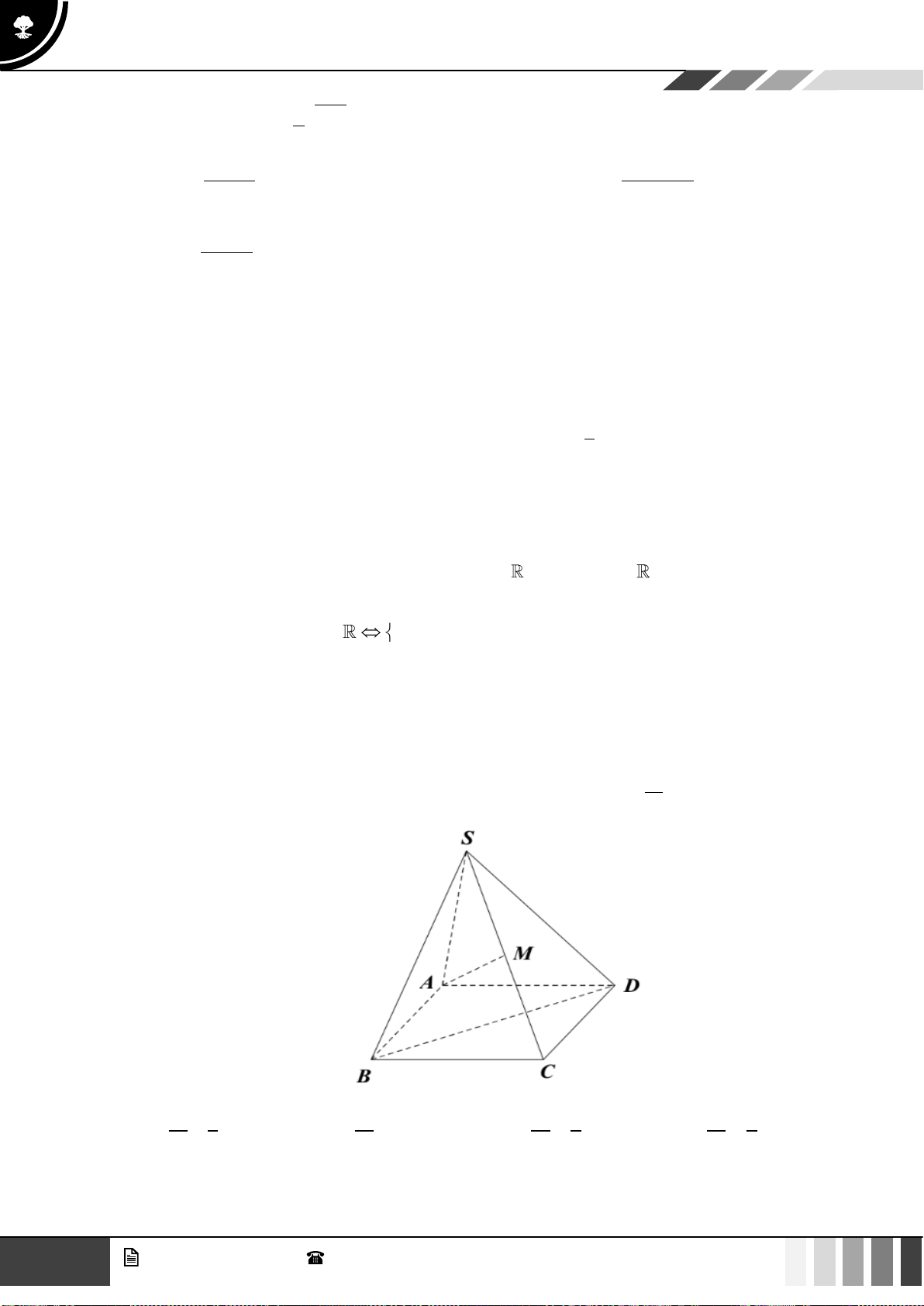
GV. Phan Nhật Linh -
SĐT: 0817 098 716
23
Tuyển tập 10 đề ôn HKI
Toán 12
Do đó hàm số
21
3
7
9
x
xm
y
+
+
=
đồng biến trên khoảng
( )
3;+
khi và chỉ khi hàm số
( )
21
3
x
fx
xm
+
=
+
nghịch biến trên khoảng
(3; )+
. Ta có
2
3 21
()
( 3 )
m
fx
xm
−
=
+
.
21
()
3
x
fx
xm
+
=
+
nghịch biến trên khoảng
(3; )+
( ) 0 (3; )f x x
+
3 21 0
3 (3; )
m
m
−
− +
77
17
3 3 1
mm
m
mm
−
− −
.
Do
m
nguyên và
2024;2024m−
nên có
8
giá trị của
m
thỏa mãn.
Câu 44: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
32
1
16 10
3
y x mx x= − + +
đồng biến trên
khoảng
( ; )− +
?
A.
7
. B.
9
. C.
8
. D.
10
.
Lời giải
Ta có
2
2 16y x mx
= − +
. Hàm số đồng biến trên
0yx
2
2
0
16 0
2 16 0 4 4
0
10
m
x mx x m
a
−
− + −
.
Do
m
nguyên nên có
9
giá trị của
m
thỏa mãn.
Câu 45: Cho khối chóp
.S ABCD
có đáy là hình bình hành.
M
là trung điểm của
.SC
Mặt phẳng qua
AM
và song song với
BD
chia khối chóp thành hai phần, trong đó phần chứa đỉnh
S
có thể tích
1
V
, phần còn lại có thể tích
2
V
(tham khảo hình vẽ bên). Tính tỉ số
1
2
V
V
A.
1
2
1
3
V
V
=
. B.
1
2
1
V
V
=
. C.
1
2
1
2
V
V
=
. D.
1
2
2
7
V
V
=
.
Lời giải
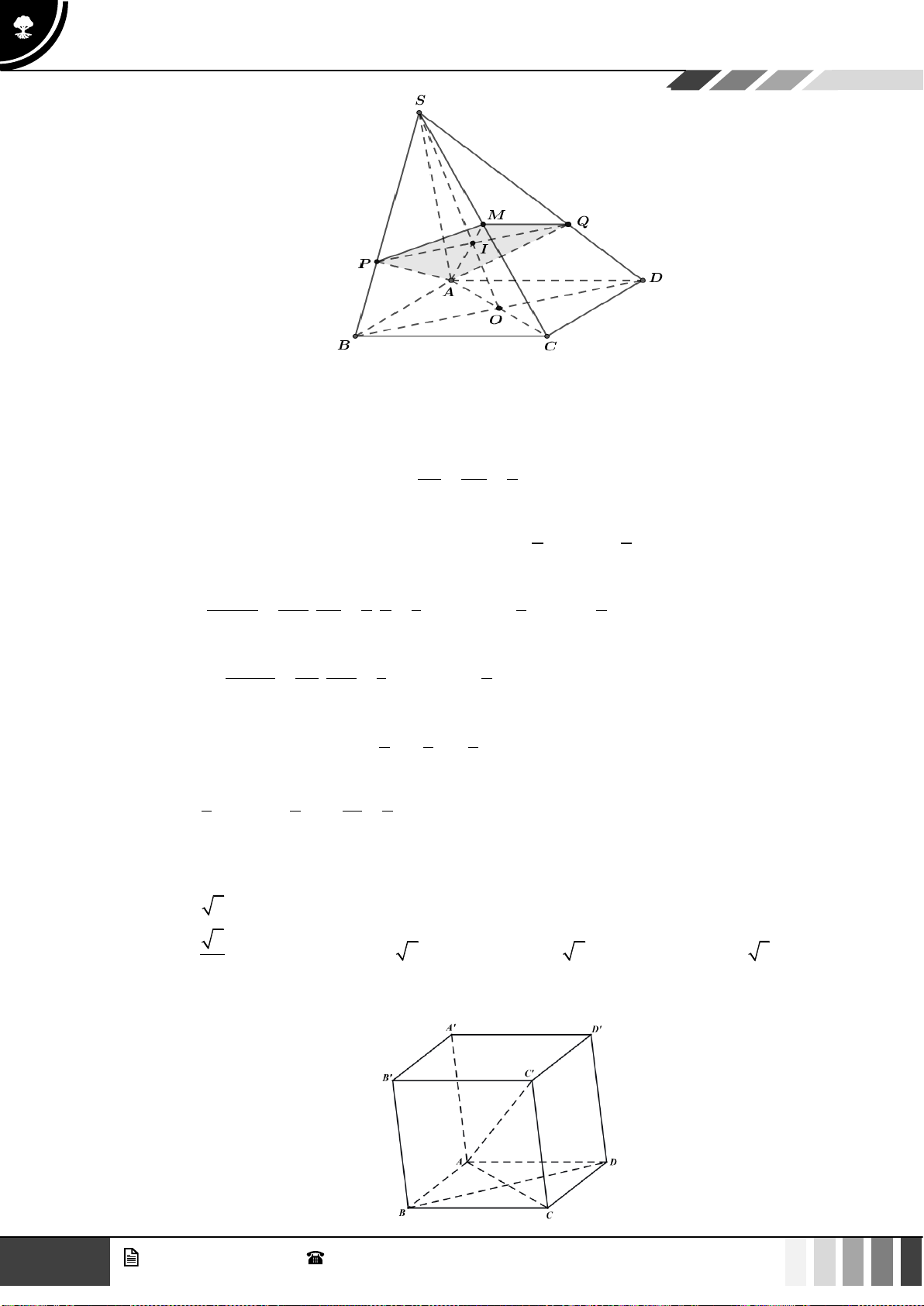
GV. Phan Nhật Linh -
SĐT: 0817 098 716
24
Tuyển tập 10 đề ôn HKI
Toán 12
Gọi
()P
là mặt phẳng qua
AM
và song song với
.BD
Ta gọi
,PQ
là giao điểm của
()P
với
,,SB SD
khi đó tứ giác
APMQ
là thiết diện.
Gọi
I
là trọng tâm tam giác
2
3
SP SQ
SAC
SB SD
= =
Do
ABCD
là hình bình hành nên
. . .
11
22
S ABC S ACD S ABCD
V V V V= = =
Khi đó:
.
..
1 2 1 1 1
..
2 3 3 3 6
S AMQ
S MAQ S ACD
SACD
V
SM SQ
V V V
V SC SD
= = = = =
Tương tự:
.
.
.
11
.
36
S AMP
S AMP
S ABC
V
SP SM
VV
V SB SC
= = =
. . .
1 1 1
6 6 3
S APMQ S AMQ S AMP
V V V V V V = + = + =
1
12
2
1 2 1
3 3 2
V
V V V V
V
= = =
.
Câu 46: Cho khối hộp
.ABCD A B C D
có
2 2 , 90 ,AA AB AD BAD
= = =
60BAA
=
,
120DAA
=
và
,6AC
=
. Tính thể tích
V
của khối hộp đã cho.
A.
2
2
V =
. B.
22V =
. C.
2V =
. D.
23V =
.
Lời giải
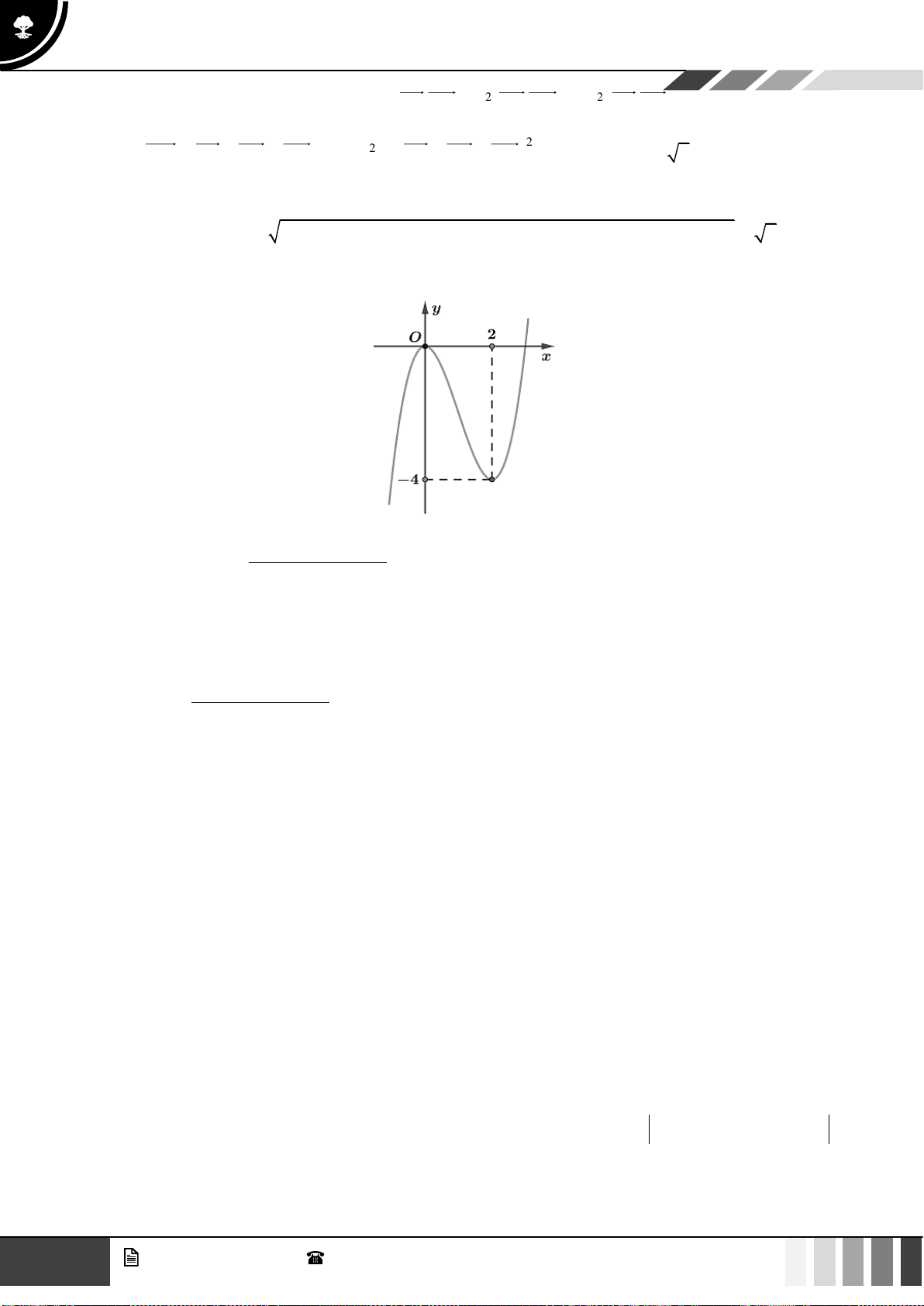
GV. Phan Nhật Linh -
SĐT: 0817 098 716
25
Tuyển tập 10 đề ôn HKI
Toán 12
Gọi
'2AB AD x AA x= = =
22
. ' , . ' , . 0AB AA x AD AA x AB AD = = − =
( )
2
22
' ' ' ' 6AC AB AD AA AC AB AD AA x= + + = + + =
mà
' 6 1AC x= =
Áp dụng công thức
0 0 0 2 0 2 0 2 0
. . '. 1 2cos60 .cos90 .cos120 cos 90 cos 60 cos 120 2V AB AD AA= + − − − =
Câu 47: Cho hàm số
( )
32
3y f x x x= = −
có đồ thị là đường cong trong hình dưới đây.
Phương trình
( )
( )
( ) ( )
2
4
4
21
f f x
f x f x
−
=−
++
có bao nhiêu nghiệm?
A.
7
. B.
6
. C.
9
. D.
3
.
Lời giải
Ta có
( )
( )
( ) ( )
2
4
4
21
f f x
f x f x
−
=−
++
( )
( )
( ) ( )
( )
2
4 4 2 1f f x f x f x − = − + +
( ) ( ) ( ) ( )
( )
3 2 2
3 4 4 2 1f x f x f x f x − − = − + +
( ) ( ) ( )
32
5 4 0f x f x f x + + =
( )
( ) ( )
( )
0
1 4;0
4
fx
fx
fx
=
= − −
=−
.
Từ đồ thị hàm số
( )
y f x=
ta thấy:
Phương trình
( )
0fx=
có 2 nghiệm.
Phương trình
( )
1fx=−
có 3 nghiệm.
Phương trình
( )
4fx=−
có 2 nghiệm.
Vậy phương trình đã cho có 7 nghiệm.
Câu 48: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
32
98y x x m x m= − + + −
có
năm điểm cực trị?
A.
14
. B. Vô số. C.
15
. D.
13
.
Lời giải

GV. Phan Nhật Linh -
SĐT: 0817 098 716
26
Tuyển tập 10 đề ôn HKI
Toán 12
Hàm số đã cho có 5 điểm cực trị
Đồ thị hàm số
( ) ( )
32
98f x x x m x m= − + + −
cắt trục
Ox
tại 3 điểm phân biệt
Phương trình
( )
32
9 8 0x x m x m− + + − =
(1) có 3 nghiệm phân biệt
Ta có
( ) ( )
( )
2
1 1 8 0x x x m − − + =
( )
2
1
8 0 2
x
x x m
=
− + =
.
Do đó, điều kiện bài toán
( )
2
có hai nghiệm phân biệt khác
1
16 0 16
1 8 0 7
mm
mm
= −
− +
.
Mà
m
nguyên dương nên có 14 giá trị
m
thỏa mãn.
Câu 49: Tổng tất cả các giá trị của tham số
m
để hàm số
( )
2 5 3 2 2
11
10 1
3
20
5
ymxmm mx x x=− −+ − +−
đồng biến trên bằng
A.
1
2
. B.
5
2
. C.
2−
. D.
3
2
.
Lời giải
Ta có:
( )
2 4 2 2
20 20xy xmmmxm− + − − −
=
.
Hàm số đồng biến trên khi và chỉ khi:
0,yx
( )
2 4 2 2
20 20 0mx mx x mmx −+ − − −
.
TH1:
0m =
khi đó
120 20 0yx x= + −
. Suy ra
0m =
không thỏa mãn.
TH2:
0m
khi đó:
( ) ( )
( ) ( )
( )
( ) ( )
2 4 2 2 2
01120 1 1 1 11 2y m x m x x x m x x m x
= − + + = +
− − + − − − +
.
Để
0yx
thì phương trình
( )
( ) ( )
22
1 1 21 00m x x m x−−+ − + =
cũng phải có
nghiệm
1x =−
. Nghĩa là:
2
2
2 20 04
5
2
m
m
m
m
=−
+ + =
=
−
.
Với
2m =−
khi đó
( )
( )
2
4 2 2
4 +2x 0120 14 4 8 14y x x xx xx
= + + = + − +
.
Suy ra
2m =−
thỏa mãn.
Với
5
2
m =
khi đó
( )
2
2
1
25 50 5106
4
y x x x x
+= − +
.
Suy ra
5
2
m =
thỏa mãn.

GV. Phan Nhật Linh -
SĐT: 0817 098 716
27
Tuyển tập 10 đề ôn HKI
Toán 12
Vậy
5
2;
2
m
−
thỏa mãn yêu cầu đề bài. Suy ra tổng các giá trị của
m
bằng
1
2
.
Câu 50: Số nghiệm nguyên thuộc
100;100−
của bất phương trình
( )
51
5
31
log 3 1 .log 143
25
x
x
−
− −
là
A.
81.
B.
79.
C.
83.
D.
84.
Lời giải
Điều kiện xác định của bất phương trình là
3 1 0 0
x
x−
(*).
Ta có,
( ) ( )
5 1 5 5
5
3 1 25
log 3 1 .log 143 log 3 1 log 143
25
31
x
xx
x
−
− − − −
−
( ) ( )
55
log 3 1 2 log 3 1 143 0
xx
− − − +
(1)
Đặt
( )
5
log 3 1
x
t =−
, bất phương trình (1) trở thành
( )
2
11
2 143 0 2 143 0
13
t
t t t t
t
−
− + − + +
.
Với
( )
11
5
11 log 3 1 11 3 1 5 1
xx
tx
−
− − − −
. Do
x
nguyên thoả điều kiện
0x
nên trường hợp này không tồn tại giá trị
x
.
Với
( )
13 13
5
13 log 3 1 13 3 1 5 3 1 5
x x x
t − − +
. Do
x
nguyên thoả điều kiện
0x
và
100;100x −
nên chọn
20,21,...,100x
. Vậy có
81
số nguyên
x
thoả mãn điều kiện.
Bấm Tải xuống để xem toàn bộ.




