TOP18 đề thi HK2 lớp 10 trường THPT Ernst Thalmann – TP. HCM

Giới thiệu đến quý thầy, cô và các em học sinh 18 đề thi HK2 lớp 10 trường THPT Ernst Thalmann – TP. HCM. Đề được biên soạn dưới hình thức tự luận, mời bạn đọc đón xem 

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

32 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
THPT ERNST THÄLMANN
TỔ TOÁN- NHÓM TOÁN 10
TÀI LIỆU ÔN THI
HỌC KÌ 2
MÔN TOÁN
LỚP 10
Năm học 2013- 2014
-Lưu hành nội bộ-
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 2
MỤC LỤC
BỘ ĐỀ ÔN KI ỂM TRA GI ỮA HK2 ............................. 3
Đề số 1 ..................................................................... 3
Đề số 2..................................................................... 4
Đề số 3..................................................................... 5
Đề số 4..................................................................... 7
Đề số 5..................................................................... 8
ĐỀ THI GI ỮA HK2 các năm trước . ........................... 11
Năm học 2008- 2009 .................................................. 11
Năm học 2009- 2010 .................................................. 11
Năm học 2010- 2011 .................................................. 12
Năm học 2012- 2013 .................................................. 13
BỘ ĐỀ ÔN THI HK2 . ............................................... 15
Đề số 1 ................................................................... 15
Đề số 2 ................................................................... 16
Đề số 3 ................................................................... 17
Đề số 4 ................................................................... 19
Đề số 5 ................................................................... 20
ĐỀ THI HK2 các năm trước . ..................................... 23
Năm 2008- 2009 ........................................................ 23
Năm 2010- 2011 ........................................................ 25
Năm 2011- 2012 ........................................................ 27
Năm 2012- 2013 ........................................................ 29
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 3
BỘ ĐỀ ÔN KIỂM TRA GIỮA HK2
Đề số 1
Bài 1. Giải các bất phương trình sau:
a.
2
3 (2 3)( 1)x x x
; b
2
22
(3 ) ( 9)
0
( 2 )( 2 1)( 5)
xx
x x x x
.
Bài 2. Giải các bất phương trình sau:
a.
3
2 2 2 2 5
2
x x x
; b.
22
7 12 1 5 7 x x x x
;
c.
2
2
35
2 2 1
2 4 4
x
x x x
; d.
2
7 10 1x x x
;
e.
22
2 3 2x x x x
.
Bài 3. Tìm m để
2
( 4) ( 12) 7 0 m x m x m
(1)
a. có 2 nghiệm trái dấu; b. có 2 nghiệm phân biệt.
c. có 2 nghiệm cùng dấu; d. có hai nghiệm nhỏ hơn 0.
Bài 4. a. Cho tam giác ABC có
0
30C
. Tính
cạnh c, góc A, R, r, S,
a
m
;
b. Cho tam giác ABC có
7, 5, 8a b c
. Tính
, , , , , , , , , , ,
a b c a b c
S R r h h h m m m A B C
.
c. Cho
ABC
thỏa
2
bc a
. Chứng m inh rằng
2
.
b c a
h h h
;
d. Cho
ABC
, chứng minh
(sin sin sin )S Rr A B C
.
Bài 5. Cho
ABC
với
(1; 2), ( 7;0), ( 5;6) A B C
a. Viết PTTS của cạnh AB; b. Viết PTTQ của trung
tuy ến kẻ từ C; c. Viết PTCT đường trung bình qua
trung điểm 2 cạnh BC và AC; d. Viết PTTS của
đường thẳng qua A và song song với BC; e. Viết
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 4
PTTQ của đường thẳng qua B và vuông góc với
:3 2 9 0xy
; f. Viết PTCT trung trực của cạnh
AC; g. Tính độ dài đường cao BH; h. Viết PTTS của
đường cao kẻ từ C.
Bài 6. a. Tìm điểm A thuộc
22
:
3
xt
d
yt

, sao cho A
cách B(0;3) một khoảng bằng 5;
b. Tính góc giữa 2 đường thẳng
:3 4 5 0d x y
và
/
:6 8 1 0d x y
.
Đề số 2
Bài 1. Giải các bất phương trình sau:
a.
12
21
3
x
x

; b.
22
2
( 5)( 3)
0
2( 1) ( 1)
x x x
xx
.
Bài 2. Giải các bất phương trình sau:
a.
2 3 5 7 4 x x x
; b.
1
25
23x
;
c.
2
3 4 4x x x
; d.
2
4 36 2 1xx
;
e.
2
2 3 5 3 0x x x
.
Bài 3. Tìm m để
2
( 2) 2( 1) 3 0 m x m x m
(1)
a. có hai nghiệm có tích nhỏ hơn 0; b. có hai nghiệm ;
c. có 2 nghiệm cùng dấu; d.có 2 nghiệm dương phân biệt.
Bài 4. a.Cho
ABC
có
1
5, 7,cos
2
b c A
. Tính
, , ,
ab
h R r m
;
b. Cho
ABC
có
0
120 , 8, 7B a c
. Tính
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 5
, , , , , , , , , , ,
a b c a b c
b S R r h h h m m m A C
;
c.Cho
ABC
có
2b c a
. Chứng m inh
2 1 1
a b c
h h h

;
d. Cho
ABC
, chứng minh
2
2 sin sin sinS R A B C
.
Bài 5. Cho
ABC
với
(0;3), ( 2;5), (4;1)A B C
a. Viết PTTQ của cạnh AC; b. Viết PTCT của trung
tuy ến kẻ từ B; c. Viết PTTQ đường trung bình qua
trung điểm 2 cạnh AB và BC; d. Viết PTCT của
đường thẳng qua D(5;3) và vuông góc với AB; e. Viết
PTTQ của đường thẳng qua C và song song với
23
:
5
xt
y

; f. Viết PTTS trung trực của cạnh BC; g.
Tính độ dài đường cao CK; h. Viết PTTQ của đường
cao kẻ từ B.
Bài 6. a.Cho
:2 3 5 0d x y
và
3
':
12
xt
d
yt


.
Chứng m inh d//d’ rồi tính khoảng cách giữa d và d’.
b. Tính góc giữa 2 đường thẳng
:5 12 1 0xy
và
/
14
:
3
xt
yt

.
Đề số 3
Bài 1. Giải các bất phương trình sau:
a.
2
( 1)
21
3

x
x
x
; b.
2
2
22
2
4

xx
x
.
Bài 2. Giải các bất phương trình sau:
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 6
a.
4 2 3 x x x
; b.
22
5 6 7 9 7 x x x x
;
c.
22
2 2 3 2 0x x x x
; d.
2 3 4 2xx
;
e.
22
6 3 5 6 0x x x x
.
Bài 3. Tìm m để
2
2( 1) 3 0 x m x m
(1)
a. có 2 nghiệm trái dấu; b. có 2 nghiệm phân biệt;
c. có 2 nghiệm cùng dấu; d. có 2 nghiệm âm phân biệt.
Bài 4. a.Cho
ABC
có
00
45 , 75 , 2 3B C a
. Tính
,,A b R
;
b. Cho
ABC
. Chứng m inh rằng
1 1 1 1
a b c
h h h r
;
c. Cho
ABC
. Chứng minh
2 sin sin
a
h R B C
.
Bài 5. Cho
ABC
với
(0;7), ( 4;1), (6; 1)A B C
a. Viết PTCT của cạnh BC; b. Viết PTTS của trung
tuy ến kẻ từ C; c. Viết PTTQ đường trung bình qua
trung điểm 2 cạnh BC và AC; d. Viết PTTQ của
đường thẳng qua A và song song với BC; e. Viết PTTS
của đường thẳng qua C và vuông góc với
32
:
51
xy

; f. Viết PTTQ trung trực của cạnh AC;
g. Tính độ dài đường cao AH; h. Viết PTTQ của đường
cao kẻ từ C.
Bài 6. a. Cho
(2; 5)N
. Tìm điểm M thuộc đường thẳng
:2 11 0d x y
, sao cho độ dài đoạn MN=10.
b. Tính góc giữa 2 đường thẳng
3
:
1
xt
d
y
và
/
3
:
25
x
d
yt


.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 7
Đề số 4
Bài 1. Giải các bất phương trình sau:
a.
2
(4 10)(2 6) 9x x x
; b.
22
12
4 2 8 13 5
x x x x
.
Bài 2. Giải các bất phương trình sau:
a.
3 7 2 2 3 x x x
; b.
2
2
43
3 12 2
2

xx
xx
;
c.
2
2
3
2 5 2 3 0
4 2 4
xx
xx
; d.
2
1 9 3 6 3x x x
;
e.
22
4 5 4 5 2x x x
.
Bài 3. Tìm m để
2
( 2) 2(2 3) 5 6 0 m x m x m
(1)
a. có 2 nghiệm trái dấu; b. có 2 nghiệm phân biệt;
c. có 2 nghiệm phân biệt cùng dấu; d. có 2 nghiệm lớn hơn
0.
Bài 4. a. Cho
ABC
có
5, 8AB AC
, diện tích
10 3S
và
bán kính đường tròn ngoại tiếp bằng
73
3
. Tính cạnh BC, độ
dài đường cao kẻ từ A, bán kính đường tròn nội tiếp
ABC
,
độ lớn góc A;
b. Cho
ABC
. Chứng m inh
( )sin (sin sin )b c A a B C
;
c. Cho
ABC
. Chứng m inh rằng: Nếu
23b a c
thì ta có
1 2 3
b a c
h h h

.
Bài 5. Cho
ABC
với
( 3;2), (1;8), (5;0)A B C
a. Viết PTTQ của cạnh AB; b. Viết PTTS của trung
tuy ến BN; c. Viết PTTQ đường trung bình qua trung
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 8
điểm 2 cạnh AB và AC; d. Viết PTTQ của đường
thẳng qua D(1;5) và vuông góc với BC; e. Viết PTTS
của đường thẳng qua E(4;-1) và song song với
:2 5 1 0xy
; f. Viết PTTQ trung trực của cạnh AB;
g. Tính độ dài đường cao kẻ từ B; h. Viết PTTQ của
đường cao AH.
Bài 6. a. Tính khoảng cách từ
(1;2)A
đến
2
:
6
xt
yt
;
b. Tính góc giữa 2 đường thẳng
:4 3 7 0d x y
và
/
:5 12 11 0d x y
.
Đề số 5
Bài 1. Giải các bất phương trình sau:
a.
2
( 5)(3 6) 4x x x
; b.
3 2 2
25
x
x

e.
6 2 12
(2 )(3 15) 2


xx
x x x
; d.
2
22
2( 5) 3( 25)
0
( 4)( 9)
xx
x x x
.
Bài 2. Giải các bất phương trình sau:
a.
2
2
53
3 3 7
3

xx
xx
; b.
22
5 4 2 6 7x x x x
;
c.
3
2
2
x
x
; d.
2
2
9 18
2 2 18 0
4
xx
x
;
e.
2
1 2 3 4 1x x x
; f.
2
3 4 2 2x x x
.
Bài 3. Tìm m để
2
2 (3 1) 1 0 x m x m
(1)
a. có 2 nghiệm m ột âm , một dương; b. có 2 nghiệm ;
c. có 2 nghiệm phân biệt cùng dấu; d. có 2 nghiệm > 0.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 9
Bài 4. a. Cho
ABC
có
3, 5AC AB
,
15 3
4
S
. Tính
góc A (biết góc A tù);
b. Cho
ABC
có
21, 17, 10a b c
. Tính
, , , , , , , , ,cos ,sin ,cos
a b c a b c
S R r h h h m m m A B C
;
c. Cho
ABC
có
0
60 , 8, 5A b c
. Tính
, , , , , , , , , ,cos ,cos
a b c a b c
a S R r h h h m m m B C
;
d. Cho
ABC
có
00
30 , 45 , 3 2A B b
. Tính
, , .C a R
e. Cho
ABC
. Chứng m inh
2 2 2
cos cos cos
2
A B C a b c
a b c abc

;
f. Cho
ABC
. Chứng m inh rằng:
2
a
bc
R
h
.
Bài 5. Cho
ABC
với
( 8;1), (2; 3), ( 2; 4) A B C
a. Viết PTTS của cạnh AC; b. Viết PTTQ của trung
tuy ến BN; c. Viết PTTS đường trung bình qua trung
điểm 2 cạnh AC và BC; d. Viết PTCT của đường
thẳng qua A và song song với BC; e. Viết PTTQ của
đường thẳng qua B và vuông góc với
23
:
10
xt
yt


; f.
Viết PTCT trung trực của cạnh AB; g. Tính độ dài
đường cao kẻ từ C; h. Viết PTTS của đường cao AH.
Bài 6. a. Tính khoảng cách từ
( 4;6)A
đến
37
:
5
xt
yt

;
b. Tính góc giữa 2 đường thẳng
:4 3 7 0d x y
và
/
:5 12 11 0d x y
;
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 10
c. (ok) Tìm điểm M thuộc
45
:
8
xt
d
yt


, sao cho M
cách
(4; 3)N
m ột khoảng bằng 13.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 11
ĐỀ THI GIỮA HK2 các năm trước
Năm học 2008-2009
Bài 1. Tìm m để phương trình:
2
1 2 1 2 3 0m x m x m
(1)
a) Có hai nghiệm trái dấu b) Có hai nghiệm dương phân biệt
Bài 2.Giải các bất phương trình sau:
a)
2
2
1
23
x
xx

b)
2
2 5 3 0xx
Bài 3. Cho tam giác ABC với
(2;6), ( 3; 4), (4;0)A B C
a) Viết phương trình tham số của trung tuy ến AM
b) Viết phương trình tổng quát đường cao BH
c) Viết phương trình chính tắc đường trung trực của cạnh
AC
Năm học 2009-2010
Bài 1.Giải các bất phương trình sau:
a)
2
2
6
1
3 4 11


xx
xx
b)
2
20 x x x
Bài 2. Tìm m để phương trình:
2
2 2 1 3 0m x m x m
(1)
có hai nghiệm dương .
Bài 3. Cho tam giác ABC có
17 , 21, 10 a b c
Hãy tính
, , , , ,cos .
bb
S h R r m A
Bài 4. Cho tam giác ABC có
,,BC a AB c CA b
và
đường trung tuy ến
AM b AC
.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 12
Chứng m inh:
2 2 2
2( )a c b
Năm học 2010-2011
ĐỀ A
Bài 1( 5 đ ) : Giải các bất phương trình :
a/
2
4 10 2 6 9x x x
; b/
2
20x x x
;
c/
2
7 6 2x x x
Bài 2 ( 1 đ) : Tìm m để phương trình
2
2 2 2 3 5 6 0m x m x m
có 2 nghiệm cùng
dấu
Bài 3 ( 3 đ) : Cho tam giác ABC với a =16 , c = 14 và
B = 120
0
. Hãy tính b , S, R,r , h
b
,m
a
Bài 4 ( 1 đ) : Cho tam giác ABC . Chứng minh :
sin sin sinS Rr A B C
ĐỀ B
Bài 1( 5 đ ) : Giải các bất phương trình :
a/
2
4 10 2 6 9x x x
b/
2
30x x x
c/
2
7 6 2x x x
Bài 2 ( 1 đ) : Tìm m để phương trình
2
2 2 2 3 5 6 0m x m x m
có 2 nghiệm cùng
dấu
Bài 3 ( 3 đ) : Cho tam giác ABC với b =8 , c = 7 và A
= 120
0
. Hãy tính a , S, R,r , h
a
,m
b
Bài 4 ( 1 đ) : Cho tam giác ABC . Chứng minh
2
2 sin sin sinS R A B C
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 13
Năm học 2012-2013
ĐỀ A
Câu 1 ( 3 đ) : Giải bất phương trình
a/
2
4 5 7x x x
b/
2
3 5 11xx
Câu 2 ( 2 đ) : Tìm m để phương trình sau có hai
nghiệm cùng dấu
2
1 2 1 2 5 0m x m x m
Câu 3 ( 3 đ) : Trong mặt phẳng tọa độ Oxy cho
2, 1 , 3, 1AB
a/ Viết phương trình tham số của đường thẳng AB
b/ Viết phương trình tổng quát của đường thẳng OB
c/ Viết phương trình tổng quát của trung tuy ến OM
của tam giác OAB
Câu 4 ( 2 đ) : Cho tam giác ABC với
0
13, 7, 120b c B
. Tính :
, , ,
b
a S R h
ĐỀ B
Câu 1 ( 3 đ) : Giải bất phương trình
a/
2
4 5 7x x x
b/
2
3 4 8xx
Câu 2 ( 2 đ) : Tìm m để phương trình sau có hai
nghiệm cùng dấu
2
1 2 1 2 5 0m x m x m
Câu 3 ( 3 đ) : Trong mặt phẳng tọa độ Oxy cho
1, 3 , 1,2AB
a/ Viết phương trình tham số của đường thẳng AB
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 14
b/ Viết phương trình tổng quát của đường thẳng OA
c/ Viết phương trình tổng quát của trung tuy ến OM của
tam giác OAB
Câu 4 ( 2 đ) : Cho tam giác ABC với
0
13, 7, 120a c A
. Tính :
, , ,
a
b S R h
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 15
BỘ ĐỀ ÔN THI HK2
Đề số 1
Câu 1. a. Cho
5
sin , 0 .
13 2
aa
Tính
sin ,a
cos ,sin2 ,cos2 ,tan2 ,cot2 ,a a a a a
sin ,
6
a



cos( ),tan( 2 )
43
aa


,
sin ,cos ,tan
2 2 2
a a a
.
b. Tính
sin 3cos
2sin cos
xx
A
xx
biết
tan 8x
.
c. Tính
22
22
tan cot
4tan 3cot
dd
B
dd
biết
1
sin
5
d
.
Câu 2. a. Chứng m inh rằng:
cos 1
tan
1 sin cos

x
x
xx
b. CMR:
sin2 sin2 sin2 4sin sin sinA B C A B C
.
Câu 3. Cho tam giác
( 4;6); (5;1); (1;3)A B C
a. PTTQ của cạnh BC. b.Viết PTTS của trung tuy ến
BN
c. Viết PTTS của đường cao CK; d. Viết phương
trình đường thẳng qua A và song song với
( ):2 100 0a x y
;
e. Viết phương trình đường thẳng qua B và vuông góc
với
( ):5 4 6 0b x y
; f. Viết phương trình đường
tròn ngoại tiếp tam giác ABC. g. Viết phương trình
đường tròn có tâm A, đi qua B;
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 16
Câu 4. Lập phương trình tiếp tuy ến với đường tròn
22
( ): 16 –8 64 0C x y x y
:
a. tại
( 4;4) ( )AC
; b. biết tiếp tuy ến song song với
đường thẳng
1
( ):3 4 2008 0d x y
;
Câu 5. a. Xác định các y ếu tố của elip
22
( ):16 25 400E x y
;
b. Viết phương trình chính tắc của elip (E) biết (E) có
độ dài trục lớn bằng 8 và (E) đi qua điểm
27
(2; )
2
A
.
Đề số 2
Câu 1. a. Cho
00
3
cos (90 180 )
5
bb
. Tính sin2b,
cos2b, tan2b,
0 0 0
cos( 60 ),sin(2 135 ),tan(30 )b b b
,
sin ,cos ,tan
2 2 2
b b b
.
b. Tính giá trị
22
22
7sin 3cos
2sin 3cos
dd
A
dd
biết
cot 4d
;
c. Tính giá trị
7tan 3cot
2tan cot
cc
B
cc
biết
1
cos
4
c
.
Câu 2. a. Chứng m inh rằng:
sin cos 1 2cos
1 cos sin cos 1

x x x
x x x
b. Cho A, B và C là ba góc của tam giác. Chứng minh
rằng:
cos cos cos 4cos cos sin 1
2 2 2
A B C
A B C
.
Câu 3. Cho
ABC
có
(1;3), (3; 1); ( 5;5)A B C
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 17
a. Viết PTTS của đường cao AH. b.Viết PTTQ trung
trực cạnh AC; c. Viết phương trình đường thẳng
qua C và vuông góc với
( ):11 3 26 0b x y
;
d. Viết phương trình đường tròn nhận AC làm đường
kính; e. Viết phương trình đường tròn có tâm B và
tiếp xúc với
( ):8 6 11 0xy
;
Câu 4. Cho đường tròn
22
( ):( 3) ( 7) 25C x y
.
a. Viết phương trình tiếp tuy ến với (C) tại
(6; 3) ( )BC
;
b.Lập phương trình tiếp tuy ến với đường tròn biết tiếp
tuy ến vuông góc với
( ): 3 4 2009 0a x y
;
Câu 5. a. Xác định các y ếu tố của elip
22
( ): 9 16 1E x y
;
b. Viết phương trình chính tắc của elip (E) biết (E) có
độ dài trục nhỏ bằng 8 và tỉ số
3
5
c
a
;
Đề số 3
Câu 1. a.Tính
sin ,cos ,sin2 ,cos2 ,x x x x
và
sin( 2 ),cos ,tan
4 6 3
x x x
,
sin ,cos ,
22
xx
tan
2
x
biết
tan 2 2,
2
xx
.
b.Cho
22
22
5 os sin
3sin os
c a a
A
a c a
biết
4
cot
3
a
.
c. Tính giá trị
22
2
7tan 3cot
1 2cot
cc
B
c
biết
2
cos
5
c
;
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 18
Câu 2. a. Chứng m inh rằng:
2
2
(cos sin ) 1
2tan
cot sin .cos

xx
x
x x x
b. Cho A, B và C là ba góc của tam giác. CMR:
sin sin sin 4cos os os
2 2 2
A B C
A B C c c
.
Câu 3. Cho
ABC
với
(3;8), (5;2), ( 1;10)A B C
a.Viết PTTQ của cạnh BC. b.Viết PTTS của trung
tuy ến BN; c. Viết PTTQ của đường cao CK;
d. Viết PTTS của đường trung bình qua trung điểm 2
cạnh AC, BC; e.Viết PTTQ trung trực cạnh AB ;
f. Viết phương trình đường thẳng qua A và song song
với
( ):5 2 11 0a x y
; g. Viết phương trình đường
thẳng qua B và vuông góc với
( ):3 7 16 0b x y
;
h. Viết phương trình đường tròn ngoại tiếp tam giác
ABC. i. Viết phương trình đường tròn có tâm A, đi
qua B;
j. Viết phương trình đường tròn nhận BC làm đường
kính; k. Viết phương trình đường tròn có tâm B và
tiếp xúc với
( ):6 8 7 0xy
;
Câu 4. a. Lập phương trình tiếp tuy ến với đường tròn
(C):
22
( 2) ( 1) 25xy
biết tiếp tuy ến song song với
đường thẳng
( ): 0d x y
.
b. Lập phương trình tiếp tuy ến với đường tròn
22
( ): 8 8 16 0C x y x y
biết tiếp tuy ến vuông góc
với đường thẳng
( ): 5 12 3 0d x y
.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 19
Câu 5. a. Xác định các y ếu tố của elip
2
2
( ): 1
16
x
Ey
;
b. Viết phương trình chính tắc của elip (E) biết (E) có
tiêu cự bằng
6
và (E) đi qua điểm
16
( 3; )
5
A 
;
c. Viết phương trình chính tắc của elip (E) biết (E)có
m ột tiêu điểm là
1
( 3;0)F
và qua
3
(1; )
2
M
;
Đề số 4
Câu 1.
a. Cho
31
os 0 ,sin 0
5 2 3 2
c a a b b

.
Tính
sin( ),tan ,cos
63

a b a b
.
b. Cho
1
tan
3
a
, tính
2
2
2sin cos 4cos
3sin cos 5sin
a a a
A
a a a
;
c. Tính
7tan 3cot
tan 2cot
bb
B
bb
biết
4
sin
5
b
Câu 2. a. Chứng m inh rằng:
2
2
1 (cos sin )
cot sin .cos
2tan

xx
x x x
x
b. Cho A, B và C là các góc của tam giác. CMR:
cos2 cos2 cos2 1 4cos cos cosA B C A B C
Câu 3. Cho
ABC
với
(3;8), (5;2), ( 1;10)A B C
a.Viết PTTS cạnh AB. b. PTTQ của trung tuy ến AM;
c. PTTQ của đường cao CK; d. PTTS của đường
trung bình qua trung điểm 2 cạnh AC, BC. e. PTTS
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 20
trung trực cạnh BC; f. Viết phương trình đường
thẳng qua A và song song với
( ):5 2 11 0a x y
;
g. Viết phương trình đường thẳng qua B và vuông góc
với
( ):3 7 16 0b x y
; h. Viết phương trình
đường tròn ngoại tiếp tam giác ABC. i. Viết
phương trình đường tròn có tâm A, đi qua B;
j. Viết phương trình đường tròn nhận BC làm đường
kính; k. Viết phương trình đường tròn có tâm C và
tiếp xúc với
:5 12 17 0xy
;
Câu 4. Lập phương trình tiếp tuy ến với đường tròn
(C):
22
16 12 75 0x y x y
:
a.tại điểm
(11; 2) ( )NC
. b. biết tiếp tuy ến vuông
góc với đường thẳng
( ): 3 4 2 0a x y
; c. biết tiếp
tuy ến song song với đường thẳng
( ):5 12 21 0b x y
;
Câu 5. a. Xác định các y ếu tố của elip
2
2
25
( ): 1
4
y
Ex
;
b. Viết phương trình chính tắc của elip (E) biết (E) đi
qua hai điểm
8 6 16
(1; ); ( 3; )
55
AB
.
Đề số 5
Câu 1. a. Cho
00
1
cos2 (45 90 )
3
bb
. Tính sin2b ,
sinb, cosb, tanb,
0 0 0
cos( 60 ),sin(2 135 ),tan(45 )b b b
.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 21
b. Cho
4
sin2 ( 0)
54
yy
. Tính cos2y , siny,
cosy, tany,
cos( ),sin(2 ),tan( )
6 3 4
y y y
.
c. Tính giá trị
2
2
7sin cos 3cos
2sin 3sin cos
d d d
A
d d d
biết
cot 7d
;
d. Tính giá trị
2
2
7 3cot
2tan 1
c
B
c
biết
1
sin
5
c
;
Câu 2. a. Chứng m inh rằng:
sin cos 1 2cos
1 cos sin cos 1

x x x
x x x
b. Cho A, B và C là ba góc của tam giác. Chứng m inh
rằng:
cos cos cos 4cos cos sin 1
2 2 2
A B C
A B C
.
Câu 3. Cho
ABC
có
(2;15), (6; 1); ( 10;7)A B C
a.Viết PTTQ của cạnh BA.
b.Viết PTTS của trung tuyến ; c. Viết PTTS của
đường cao AH d. Viết PTTQ của đường trung bình
qua trung điểm 2 cạnh AB, AC ; e.Viết PTTQ trung
trực cạnh AC ; f. Viết phương trình đường thẳng qua
B và song song với
( ):3 11 29 0a x y
; g. Viết
phương trình đường thẳng qua C và vuông góc với
( ):11 6 21 0b x y
;
h. Viết phương trình đường tròn ngoại tiếp tam giác
ABC. i. Viết phương trình đường tròn có tâm B, đi
qua A;
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 22
j. Viết phương trình đường tròn nhận AC làm đường
kính; k. Viết phương trình đường tròn có tâm B và
tiếp xúc với
( ):3 4 114 0xy
;
Câu 4. Cho đường tròn
22
( ):( 5) ( 10) 100C x y
.
a. Viết phương trình tiếp tuy ến với (C) tại
(1;2) ( )BC
;
b.Lập phương trình tiếp tuy ến với đường tròn biết tiếp
tuy ến vuông góc với
( ): 3 4 2011 0a x y
;
c. Lập phương trình tiếp tuy ến với đường tròn biết tiếp
tuy ến song song với
( ): 5 12 20 0b x y
;
Câu 5. Xác định các y ếu tố của elip:
a.
22
( ): 1
169 144

xy
E
; b.
22
( ):16 81 1E x y
;
e.
22
( ):4 9 36E x y
; f.
2
2
81
( ): 1
16

y
Ex
;
Câu 6. Hãy lập phương trình chính tắc của elip (E)
biết (E) có:
a. độ dài trục nhỏ bằng 24 và tiêu cự bằng 8;
b. Độ dài trục lớn bằng 30 và tỉ số
7
15
c
a
;
c. Tiêu cự bằng 10 và tỉ số
13
12
a
b
d. Tiêu điểm
1
( 8;0)F
và tỉ số
2
5
c
a
;
e. Một đỉnh trên trục lớn là A(5 ;0) và một tiêu điểm là
2
( 3;0)F
;
f. (E) đi qua hai điểm
2 2 2
(2; ); (1; )
55
AB
.
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 23
ĐỀ THI HK2 các năm trước
Năm 2008-2009
Đề A ( Thời gian 90 phút )
Bài 1 ( 3đ) : Tính :
a)
3sin 4cos
sin cos
xx
A
xx
biết
tan 2x
b)
3
cos , cos
4




biết
12
sin
13 2



c)
sin2 , tan2aa
biết
8
cos2
17 2
aa



Bài 2 ( 2đ) : Chứng minh :
a)
1 cos10 sin10
tan5
1 cos10 sin10
xx
x
xx


b)
sin2 sin2 sin2 4cos sin cosA B C A B C
với
A,B,C là ba góc của một tam giác
Bài 3 ( 3đ) : Cho đường tròn ( C) có phương trình
22
2 4 20 0x y x y
a.Xác định tọa độ tâm I và bán kính R của đường tròn (
C)
b.Viết phương trình tiếp tuy ến của đường tròn ( C) tại
điểm A
4,2
c.Viết phương trình tiếp tuy ến của đường tròn ( C) biết
tiếp tuy ến song song với (d) :
3 4 2009 0xy
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 24
Bài 4 ( 2đ): Lập phương trình chính tắc của elip ( E)
biết ( E) qua hai điểm
3
1,
2
A




,
2
2,
2
B




Bài 5: Cho elip ( E) :
22
16 25 9xy
. Xác định ,tiêu
cự, đỉnh , tiêu điểm , độ dài các trục của elip (E)
Đề B ( Thời gian 90 phút )
Bài 1 ( 3đ) : Tính :
a)
sin cos
3sin 4cos
xx
B
xx
biết
cot 2x
b)
3
sin , cos
4




biết
5
cos
13 2



c)
sin2 , tan2aa
biết
15
cos2
17 2
aa



Bài 2 ( 2đ) : Chứng minh :
a)
1 cos10 sin10
cot5
1 cos10 sin10
xx
x
xx


b)
sin2 sin2 sin2 4cos cos sinA B C A B C
với
A,B,C là ba góc của một tam giác
Bài 3 ( 3đ) : Cho đường tròn ( C) có phương trình
22
4 2 20 0x y x y
a/ Xác định tọa độ tâm I và bán kính R của đường tròn
( C)
b/ Viết phương trình tiếp tuy ến của đường tròn ( C) tại
điểm B
2,4
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 25
c/ Viết phương trình tiếp tuy ến của đường tròn ( C)
biết tiếp tuy ến song song với (d) :
4 3 2009 0xy
Bài 4 ( 2đ) : a.Lập phương trình chính tắc của elip ( E)
biết ( E) qua hai điểm
3
1,
2
A




,
2
2,
2
B




a/ Cho elip ( E) :
22
9 25 16xy
. Xác định tiêu cự,
đỉnh, tiêu điểm , độ dài các trục của elip (E)
Năm 2010-2011
Đề A ( Thời gian 90 phút )
Câu 1(2đ) : a/ Chứng minh

22
1 sin2 tan 1
tan 1
sin cos
xx
x
xx
b/ Cho tam giác ABC. Chứng minh
cos sin cos sin cos
2 2 2 2 2
A B C C B
Câu 2(1đ): Cho
5
cot
3
x
. Tính

22
1
2cos sin sin cos
A
x x x x
Câu 3 (2đ ): Cho
3
cos 0
52
aa



và
5
sin
13 2
bb



Tính




sin , cos2a , sin2b , cos 2
4
a b a
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 26
Câu 4 (4đ): Cho tam giác ABC với
5, 2 , B 1,4 , C 3,6A 
a/ Viết phương trình tổng quát của đường thẳng AC
b/ Viết phương trình tham số của trung tuy ến AM
c/ Viết phương trình đường tròn ( C) đường kính AC
d/ Viết phương trình tiếp tuy ến của đường tròn ( C)
tại điểm A
Câu 5 (1đ): Cho elip

22
: 9 144E x y
.
Tính tọa độ đỉnh, tiêu điểm, tiêu cự và độ dài các trục
của elip ( E).
Đề B ( Thời gian 90 phút )
Câu 1 (2đ): a/ Chứng m inh

22
1 sin2 cot 1
cot 1
cos sin
xx
x
xx
b/ Cho tam giác ABC. Chứng m inh
sin cos cos sin sin
2 2 2 2 2
A B C C B
Câu 2 (1đ): Cho
5
tan
3
x
. Tính

22
1
2cos sin sin cos
B
x x x x
Câu 3 (2đ): Cho
53
cos 2
13 2
aa



và
3
sin
52
bb



THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 27
Tính
cos , cos2 , sin2 , sin 2
4
a b b a b




Câu 4 ( 4 đ ) : Cho tam giác ABC với
4,1 , B 2,5 , C 6, 3A 
a/ Viết phương trình tổng quát của đường thẳng BC
b/ Viết phương trình tham số của trung tuy ến BM
c/ Viết phương trình đường tròn ( C) đường kính BC
d/ Viết phương trình tiếp tuy ến của đường tròn ( C) tại
điểm B
Câu 5 (1đ) : Cho elip

22
: 16 144E x y
Tính tọa độ đỉnh, tiêu điểm, tiêu cự và độ dài các trục
của elip ( E)
Năm 2011-2012
Đề A ( Thời gian 90 phút )
Câu 1 (2 đ) : Chứng minh
a/
22
1
cos sin cos sin sin4
4
a a a a a
b/ Cho tam giác ABC . Chứng minh
sin sin sin 4sin cos sin
2 2 2
A B C
A B C
Câu 2 (2 đ) : Cho
12
cos
13
a 
với
2
a

. Tinh
sin2 , cos2aa
,
tan
4
a



THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 28
Câu 3 (1 đ) : Cho
3
cot
2
x
. Tinh
2
22
9sin 3sin cos
3sin 2cos
x x x
A
xx
Câu 4 (3 đ) : Cho đường tròn
C
có phương trình
22
4 4 17 0x y x y
a/ Xác định tọa độ tâm I và bán kính R của đường tròn
( C)
b/ Viết phương trình tiếp tuy ến của đường tròn ( C) tại
điểm
2,5A
c/ Viết phương trình tiếp tuy ến của ( C) biết tiếp tuy ến
song song với
:3 4 11 0d x y
Câu 5 (2 đ) : a/ Cho elip
22
: 4 1E x y
. Tìm tọa độ
các tiêu điểm và độ dài các trục của
E
b/ Lập phương trình chính tắc của elip
'
biết
'
qua hai điểm
2 2 6
1, , 3,
33
AB

Đề B ( Thời gian 90 phút )
Câu 1 (2 đ) : Chứng minh a/
22
1
sin cos sin cos sin4
4
b b b b b
b/ Cho tam giác ABC . Chứng m inh
sin sin sin 4sin sin cos
2 2 2
A B C
A B C
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 29
Câu 2 (2 đ) : Cho
12
sin
13
b 
với
3
2
b

. Tinh
sin2 , cos2bb
,
tan
4
b



Câu 3 (1 đ): Cho
3
tan
2
x
. Tinh
2
22
9cos 3sin cos
3cos 2sin
x x x
B
xx
Câu 4 (3 đ): Cho đường tròn
C
có phương trình
22
4 4 17 0x y x y
a/ Xác định tọa độ tâm I và bán kính R của đường tròn
( C)
b/ Viết phương trình tiếp tuy ến của đường tròn ( C) tại
điểm
5,2B
c/ Viết phương trình tiếp tuy ến của ( C) biết tiếp tuy ến
song song với
:4 3 11 0d x y
Câu 5 (2 đ): a/ Cho elip
22
: 9 1E x y
. Tìm tọa độ
các tiêu điểm và độ dài các trục của
E
b/ Lập phương trình chính tắc của elip
'
biết
'
qua hai điểm
32
1, , 2,
22
AB

Năm 2012-2013
ĐỀ A
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 30
Câu 1 (2 đ) : a/ Chứng minh
2
2
1 cos
1 2cot
1 cos 1 cos
x
x
xx


b/ Cho tam giác ABC . Chứng m inh
tan tan tan tan .tan .tanA B C A B C
Câu 2 (2 đ) : Cho
0
24
sin2 0 45
25
xx
. Tính
00
sin , cos , sin 30 , cot 45x x x x
Câu 3 (1 đ) : Cho
1
cos
4
x 
. Tinh
3tan 2cot
tan cot
xx
A
xx
Câu 4 (3 đ) : Cho đường tròn
C
:
22
2 8 8 0x y x y
và đường thẳng
:5 12 12 0d x y
a/ Chứng tỏ đường thẳng d tiếp xúc đường tròn ( C)
b/ Viết phương trình tiếp tuy ến của đường tròn ( C)
biết tiếp tuy ến vuông góc với đường thẳng d
c/ Chứng tỏ điểm
1, 9A
nằm trên đường tròn ( C).
Viết phương trình tiếp tuy ến của ( C) tại
A
Câu 5 (2 đ) : a/ Cho elip
22
: 4 9E x y
. Xác định
các y ếu tố của
E
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 31
b/ Lập phương trình chính tắc của elip
'
biết
'
có tiêu cự là 12 và tỉ số
5
4
a
b
ĐỀ B
Câu 1 (2 đ) : a/ Chứng minh
2
2
1 sin
1 2tan
1 sin 1 sin
x
x
xx


b/ Cho tam giác ABC . Chứng m inh
tan .tan .tan tan tan tanA B C A B C
Câu 2 (2 đ) : Cho
0
7
sin2 0 45
25
xx
. Tính
00
sin , cos , cos 60 , cot 45x x x x
Câu 3 (1 đ) : Cho
1
sin
3
x 
. Tinh
2tan 3cot
cot tan
xx
B
xx
Câu 4 (3 đ) : Cho đường tròn
C
:
22
8 2 8 0x y x y
và đường thẳng
:12 5 12 0d x y
a/ Chứng tỏ đường thẳng d tiếp xúc đường tròn ( C)
b/ Viết phương trình tiếp tuy ến của đường tròn ( C)
biết tiếp tuy ến vuông góc với đường thẳng d
c/ Chứng tỏ điểm
9,1B
nằm trên đường tròn ( C).
Viết phương trình tiếp tuy ến của ( C) tại
B
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Trang 32
Câu 5 (2 đ) : a/ Cho elip
22
: 9 4E x y
. Xác định
các y ếu tố của
E
b/ Lập phương trình chính tắc của elip
'
biết
'
có tiêu cự là 18 và tỉ số
4
5
b
a
.
-CHÚC CÁC EM THI TỐT!
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

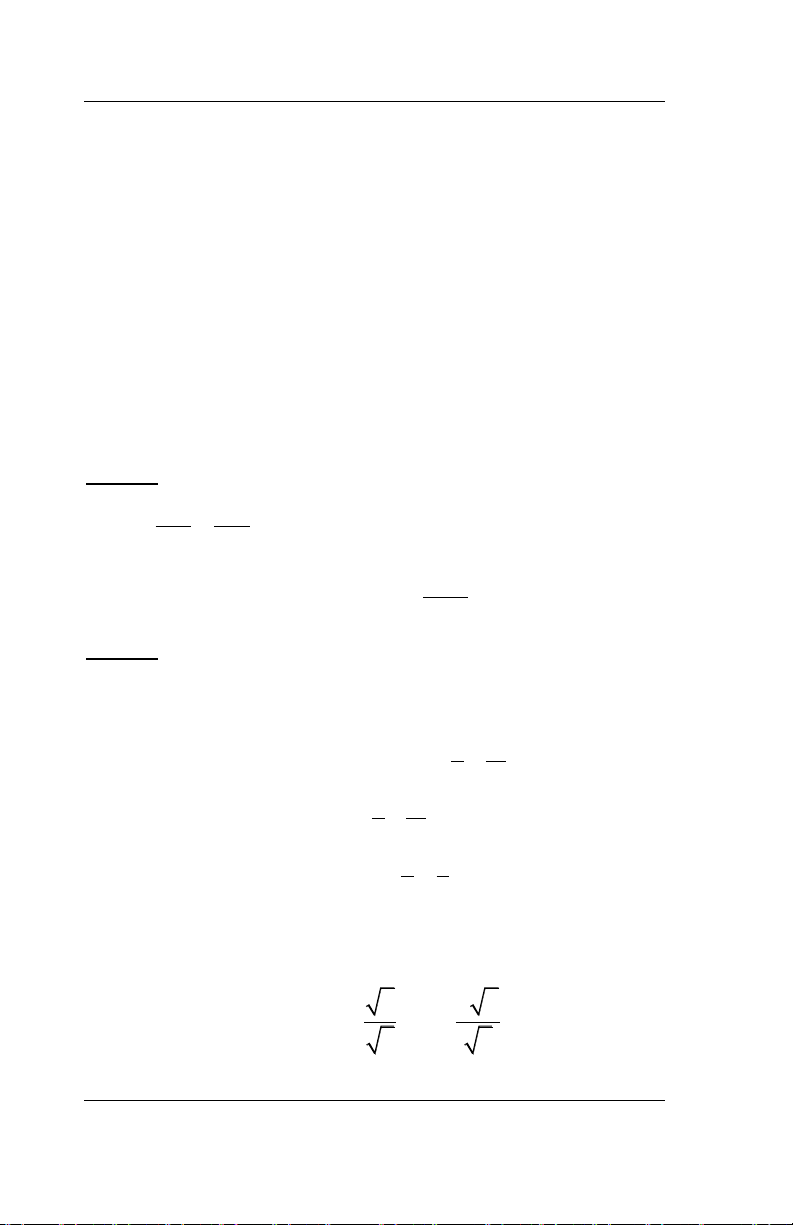
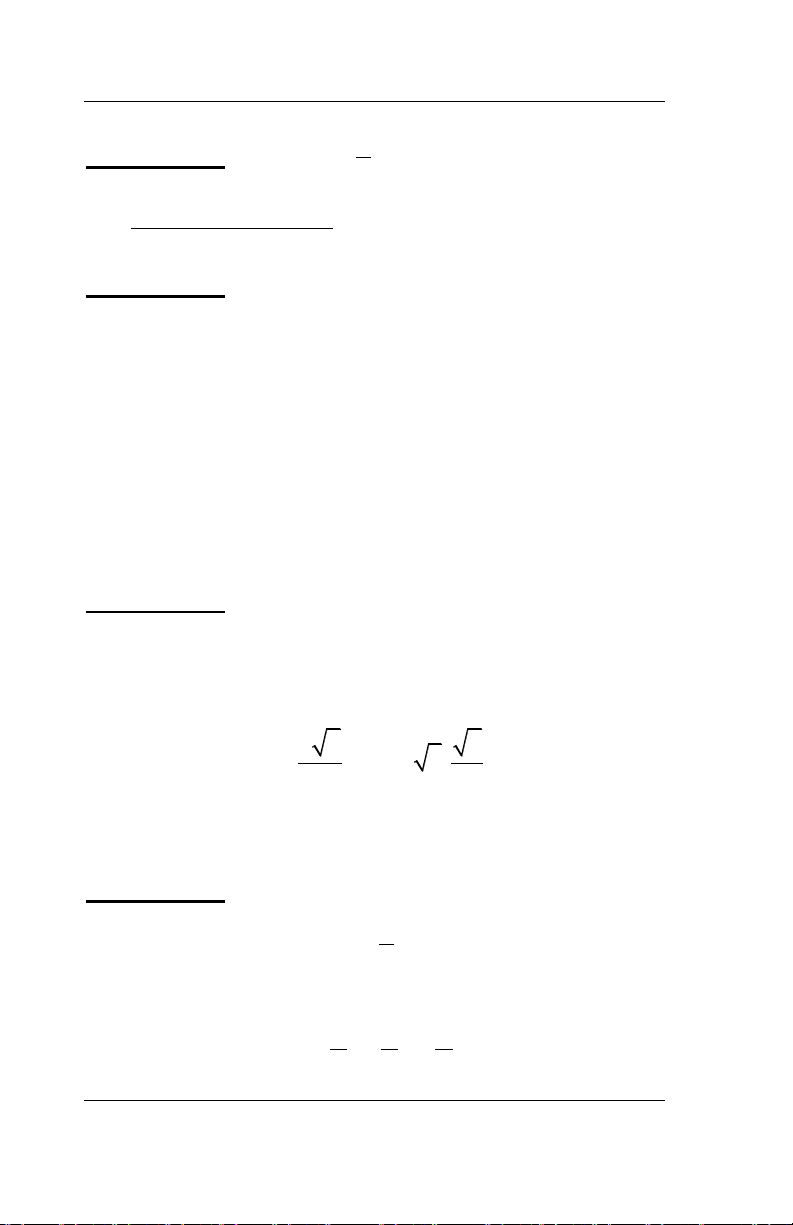
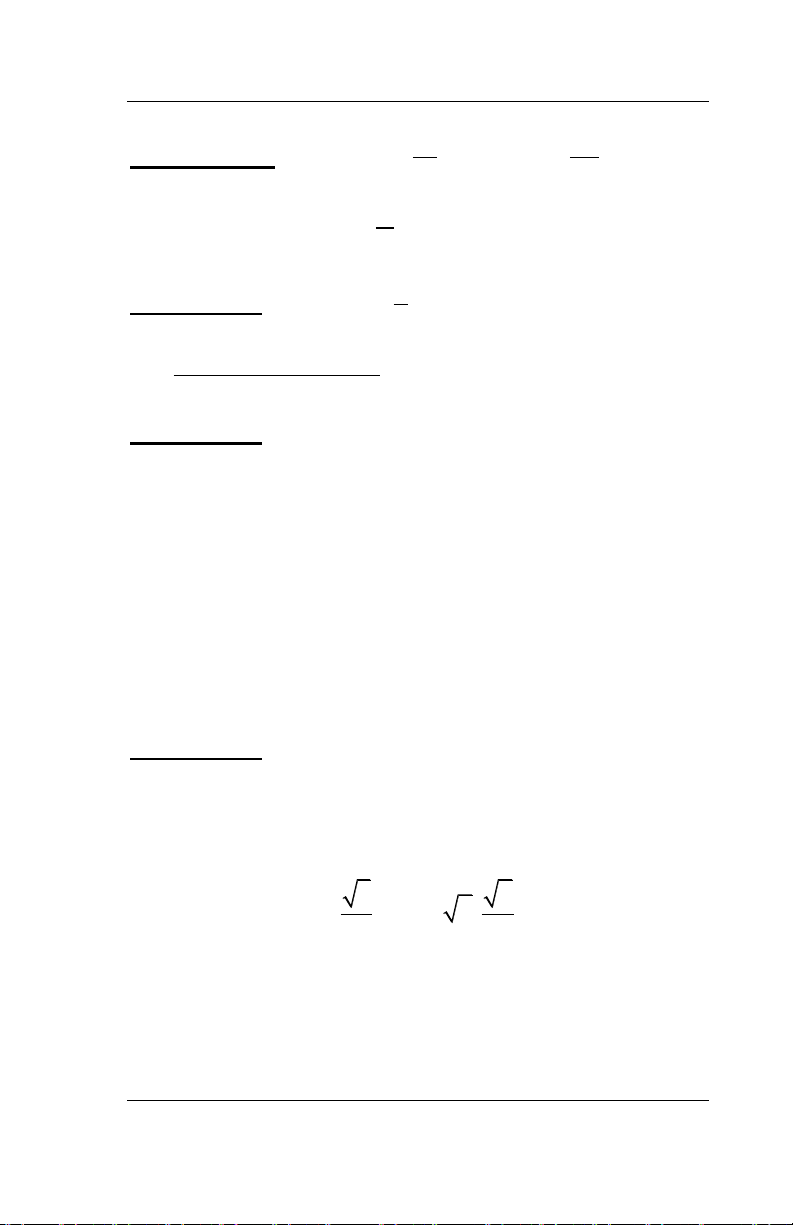
Preview text:

THPT ERNST THÄLMANN
TỔ TOÁN- NHÓM TOÁN 10 TÀI LIỆU ÔN THI HỌC KÌ 2 MÔN TOÁN LỚP 10 Năm học 2013- 2014
-Lưu hành nội bộ-
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 MỤC LỤC
BỘ ĐỀ ÔN KIỂM TRA GIỮA HK2 ............................. 3
Đề số 1 ..................................................................... 3
 Đề số 2..................................................................... 4
 Đề số 3..................................................................... 5
 Đề số 4..................................................................... 7
 Đề số 5..................................................................... 8
ĐỀ THI GIỮA HK2 các năm trước . ........................... 11
Năm học 2008-2009 .................................................. 11
Năm học 2009-2010 .................................................. 11
Năm học 2010-2011 .................................................. 12
Năm học 2012-2013 .................................................. 13
BỘ ĐỀ ÔN THI HK2 . ............................................... 15
Đề số 1 ................................................................... 15
Đề số 2 ................................................................... 16
Đề số 3 ................................................................... 17
Đề số 4 ................................................................... 19
Đề số 5 ................................................................... 20
ĐỀ THI HK2 các năm trước . ..................................... 23
Năm 2008-2009 ........................................................ 23
Năm 2010-2011 ........................................................ 25
Năm 2011-2012 ........................................................ 27
Năm 2012-2013 ........................................................ 29 Trang 2
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
BỘ ĐỀ ÔN KIỂM TRA GIỮA HK2 Đề số 1
Bài 1. Giải các bất phương trình sau: 2
(3  x)  (x  9) a. 2
x  3  (2x 3)(x 1) ; b  0. 2 2 ( 2
  x )(x  2x 1)(x 5)
Bài 2. Giải các bất phương trình sau: 3 a. 2
 2x  2x  2  5x ; b. 2 2
 x  7x 12  x 1 5  x  7 ; 2 2 x 3 5 c. 2 2 
x    x  2x 1
x x x   2 4 4 ; d. 2 7 10 1; e. 2 2
x 2x 3   x x  2 .
Bài 3. Tìm m để 2
(m  4)x  (m 12)x m  7  0 (1)
a. có 2 nghiệm trái dấu; b. có 2 nghiệm phân biệt.
c. có 2 nghiệm cùng dấu; d. có hai nghiệm nhỏ hơn 0.
Bài 4. a. Cho tam giác ABC có a  2 3,b  2, 0 C  30 . Tính
cạnh c, góc A, R, r, S, ma ;
b. Cho tam giác ABC có a  7,b  5,c  8 . Tính S, ,
R r,h ,h ,h ,m ,m ,m , , A , B C a b c a b c . c. Cho ABC thỏa 2
bc a . Chứng minh rằng 2
h .h h b c a ; d. Cho A
BC , chứng minh S Rr(sin A  sin B  sinC) . Bài 5. Cho ABC với ( A 1; 2  ), B( 7  ;0),C( 5  ;6)
a. Viết PTTS của cạnh AB; b. Viết PTTQ của trung
tuyến kẻ từ C; c. Viết PTCT đường trung bình qua
trung điểm 2 cạnh BC và AC; d. Viết PTTS của
đường thẳng qua A và song song với BC; e. Viết Trang 3
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
PTTQ của đường thẳng qua B và vuông góc với
 : 3x  2y  9  0 ; f. Viết PTCT trung trực của cạnh
AC; g. Tính độ dài đường cao BH; h. Viết PTTS của đường cao kẻ từ C. x  2   2t
Bài 6. a. Tìm điểm A thuộc d :  , sao cho A y  3 t
cách B(0;3) một khoảng bằng 5;
b. Tính góc giữa 2 đường thẳng d : 3x  4y  5  0 và /
d : 6x  8y 1  0.  Đề số 2
Bài 1. Giải các bất phương trình sau: 12 2 2
(x x  5)(x  3) a. 2x 1   x ; b. 0 .  3 2
2(x 1)  (x 1)
Bài 2. Giải các bất phương trình sau: 1 a.  2
x 3 5x 7  4x ; b. 2  5 2x ;  3 c. 2
x 3x 4  4 x ; d. 2  4x 36  2  x 1; e. 2
2x x 3  5  x 3  0.
Bài 3. Tìm m để 2
(m  2)x  2(m 1)x  3  m  0 (1)
a. có hai nghiệm có tích nhỏ hơn 0; b. có hai nghiệm;
c. có 2 nghiệm cùng dấu; d.có 2 nghiệm dương phân biệt. 1 Bài 4. a.Cho A
BC có b  5,c  7,cos A h R r m 2 . Tính , , , a b ; b. Cho ABC có 0
B 120 ,a  8,c  7 . Tính Trang 4
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 , b S, ,
R r,h ,h ,h ,m ,m ,m , , A C a b c a b c ; 2 1 1 c.Cho A
BC có b c  2a. Chứng minh   h h h ; a b c d. Cho ABC , chứng minh 2
S  2R sin AsinBsinC . Bài 5. Cho ABC với ( A 0;3), B( 2  ;5),C(4;1)
a. Viết PTTQ của cạnh AC; b. Viết PTCT của trung
tuyến kẻ từ B; c. Viết PTTQ đường trung bình qua
trung điểm 2 cạnh AB và BC; d. Viết PTCT của
đường thẳng qua D(5;3) và vuông góc với AB; e. Viết
PTTQ của đường thẳng qua C và song song với
x  2  3t  : 
; f. Viết PTTS trung trực của cạnh BC; g. y  5
Tính độ dài đường cao CK; h. Viết PTTQ của đường cao kẻ từ B. x  3  t
Bài 6. a.Cho d : 2x  3y  5  0 và d ' :  . y  1 2t
Chứng minh d//d’ rồi tính khoảng cách giữa d và d’.
b. Tính góc giữa 2 đường thẳng  : 5x 12y 1  0 và x  1 4t /  :  . y  3t Đề số 3
Bài 1. Giải các bất phương trình sau: 2 (x 1) 2 2x  2x a. 2x 1  ; b.  2  . x  3 2 4  x
Bài 2. Giải các bất phương trình sau: Trang 5
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
a. 4  x x  2  3x ; b. 2 2
x  5x  6  x  7  9  x  7; c. 2 2 2
x 2x x 3x 2  0; d. 2x  3  x  4  2; e. 2 2
 x  6x 3  x  5x 6  0 .
Bài 3. Tìm m để 2
x  2(m 1)x  3  m  0 (1)
a. có 2 nghiệm trái dấu; b. có 2 nghiệm phân biệt;
c. có 2 nghiệm cùng dấu; d. có 2 nghiệm âm phân biệt. Bài 4. a.Cho ABC có 0 0
B  45 ,C  75 ,a  2 3 . Tính , A ,bR ; 1 1 1 1 b. Cho A
BC . Chứng minh rằng    h h h r ; a b c c. Cho A
BC . Chứng minh h  2Rsin BsinC a . Bài 5. Cho ABC với ( A 0;7), ( B 4  ;1),C(6; 1  )
a. Viết PTCT của cạnh BC; b. Viết PTTS của trung
tuyến kẻ từ C; c. Viết PTTQ đường trung bình qua
trung điểm 2 cạnh BC và AC; d. Viết PTTQ của
đường thẳng qua A và song song với BC; e. Viết PTTS
của đường thẳng qua C và vuông góc với x 3 y  2  :  5
1 ; f. Viết PTTQ trung trực của cạnh AC; 
g. Tính độ dài đường cao AH; h. Viết PTTQ của đường cao kẻ từ C.
Bài 6. a. Cho N(2; 5
 ) . Tìm điểm M thuộc đường thẳng
d : 2x y 11 0 , sao cho độ dài đoạn MN=10. x  3tx  3 
b. Tính góc giữa 2 đường thẳng d :  và / d :  . y 1
y  2  5t Trang 6
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10  Đề số 4
Bài 1. Giải các bất phương trình sau: 1 2 a. 2
(4x 10)(2x 6)  x 9; b.  . 2 2 x  4x  2 8
x 13x 5
Bài 2. Giải các bất phương trình sau: 2  4  3
a. 3 7x  2x  2  3x ; b. 2  3 12  x x x x 2 ; 2 2 x x 3 c. 2 2      5
x 2x 3  0 ; d. 2 1
  9x 3x 6  3  x ; 4 2 4 e. 2 2
 4x 5   4x  5x  2 .
Bài 3. Tìm m để 2
(m  2)x  2(2m  3)x  5m  6  0 (1)
a. có 2 nghiệm trái dấu; b. có 2 nghiệm phân biệt;
c. có 2 nghiệm phân biệt cùng dấu; d. có 2 nghiệm lớn hơn 0. Bài 4. a. Cho A
BC có AB  5, AC  8, diện tích S 10 3 và 7 3
bán kính đường tròn ngoại tiếp bằng 3 . Tính cạnh BC, độ
dài đường cao kẻ từ A, bán kính đường tròn nội tiếp ABC , độ lớn góc A; b. Cho A
BC . Chứng minh (b  ) c sin A  (
a sinB sinC); c. Cho A
BC . Chứng minh rằng: Nếu b 2a  3c thì ta có 1 2 3   h h h . b a c Bài 5. Cho ABC với ( A 3  ;2), ( B 1;8),C(5;0)
a. Viết PTTQ của cạnh AB; b. Viết PTTS của trung
tuyến BN; c. Viết PTTQ đường trung bình qua trung Trang 7
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
điểm 2 cạnh AB và AC; d. Viết PTTQ của đường
thẳng qua D(1;5) và vuông góc với BC; e. Viết PTTS
của đường thẳng qua E(4;-1) và song song với
 : 2x  5y 1  0 ; f. Viết PTTQ trung trực của cạnh AB;
g. Tính độ dài đường cao kẻ từ B; h. Viết PTTQ của đường cao AH. x  2t
Bài 6. a. Tính khoảng cách từ ( A 1;2) đến  :  ; y  6   t
b. Tính góc giữa 2 đường thẳng d : 4x  3y  7  0 và /
d : 5x 12y 11  0 . Đề số 5
Bài 1. Giải các bất phương trình sau: 3  x  2 2 a. 2
(x 5)(3x  6)  x  4 ; b.  2 x  5 6  x 2x 12 2
2(x  5)  3(x  25) e.   ; d.  0.
(2  x)(3x 15) 2  x 2 2
(x  4)(x x  9)
Bài 2. Giải các bất phương trình sau: 2 x  5x  3 a. 2 3 
 3x  x  7 ; b. 2 2
x  5x  4  x  2  6x  7 ; 3 3 x 2 x 9x 18 c.  2 2 2  2x 18  0 x ; d. ;  2 4 e. 2
12x   3x 4x 1; f. 2  3
x x 4  2x 2.
Bài 3. Tìm m để 2 2
x  (3m 1)x 1 m  0 (1)
a. có 2 nghiệm một âm, một dương; b. có 2 nghiệm;
c. có 2 nghiệm phân biệt cùng dấu; d. có 2 nghiệm > 0. Trang 8
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 15 3 Bài 4. a. Cho A
BC có AC  3, AB  5, S  4 . Tính góc A (biết góc A tù); b. Cho A
BC có a  21,b 17,c  10 . Tính S, ,
R r,h ,h ,h ,m ,m ,m ,cos , A sin , B cosC a b c a b c ; c. Cho ABC có 0
A  60 ,b  8,c  5 . Tính , a S, ,
R r,h ,h ,h ,m ,m ,m ,cos , B cosC a b c a b c ; d. Cho ABC có 0 0
A  30 ,B  45 ,b  3 2 . Tính , C , a . R 2 2 2
cos A cosB cosC a b c e. Cho ABC . Chứng minh    a b c 2abc ; bc f. Cho A
BC . Chứng minh rằng: R  2h . a Bài 5. Cho ABC với ( A 8  ;1), ( B 2; 3  ),C( 2  ; 4  )
a. Viết PTTS của cạnh AC; b. Viết PTTQ của trung
tuyến BN; c. Viết PTTS đường trung bình qua trung
điểm 2 cạnh AC và BC; d. Viết PTCT của đường
thẳng qua A và song song với BC; e. Viết PTTQ của
x  2  3t
đường thẳng qua B và vuông góc với  :  ; f.
y  10  t
Viết PTCT trung trực của cạnh AB; g. Tính độ dài
đường cao kẻ từ C; h. Viết PTTS của đường cao AH. x  3 7t
Bài 6. a. Tính khoảng cách từ ( A 4  ;6) đến  :  ; y  5t
b. Tính góc giữa 2 đường thẳng d : 4x  3y  7  0 và /
d : 5x 12y 11  0 ; Trang 9
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
x  4  5t
c. (ok) Tìm điểm M thuộc d :  , sao cho M y  8  t cách N(4; 3
 ) một khoảng bằng 13. Trang 10
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
ĐỀ THI GIỮA HK2 các năm trước Năm học 2008-2009
Bài 1. Tìm m để phương trình: m  2
1 x  2m  
1 x  2m  3  0(1)
a) Có hai nghiệm trái dấu b) Có hai nghiệm dương phân biệt
Bài 2.Giải các bất phương trình sau: 2 x a) 1 b) 2
2x  5x  3  0 2 x  2x  3
Bài 3. Cho tam giác ABC với ( A 2;6), ( B 3  ; 4  ),C(4;0)
a) Viết phương trình tham số của trung tuyến AM
b) Viết phương trình tổng quát đường cao BH
c) Viết phương trình chính tắc đường trung trực của cạnh AC Năm học 2009-2010
Bài 1.Giải các bất phương trình sau: 2 x x  6 a) 1 b) 2
x  2x x  0 2 3x  4x 11
Bài 2. Tìm m để phương trình: m  2
2 x  2m 
1 x 3 m  0 (1) có hai nghiệm dương .
Bài 3. Cho tam giác ABC có a  17 ,b  21, c 10
Hãy tính S, h , R, r, m , cos . A b b
Bài 4. Cho tam giác ABC có BC  , a AB  , c CA b và
đường trung tuyến AM b AC . Trang 11
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 Chứng minh: 2 2 2
a  2(c b ) Năm học 2010-2011 ĐỀ A
Bài 1( 5 đ ) : Giải các bất phương trình :
a/  x   x   2 4 10 2 6  x  9 ; b/ 2
x  2x x  0 ; c/ 2
x  7x  6  x  2
Bài 2 ( 1 đ) : Tìm m để phương trình m  2
2 x  22m  
3 x  5m  6  0 có 2 nghiệm cùng dấu
Bài 3 ( 3 đ) : Cho tam giác ABC với a =16 , c = 14 và
B = 120 0 . Hãy tính b , S, R,r , h ,m b a
Bài 4 ( 1 đ) : Cho tam giác ABC . Chứng minh :
S Rr sin A  sin B  sin CĐỀ B
Bài 1( 5 đ ) : Giải các bất phương trình : a/  x   x  2 4 10 2 6  x  9 b/ 2
x  3x x  0 c/ 2
x  7x  6  x  2
Bài 2 ( 1 đ) : Tìm m để phương trình m  2
2 x  22m  
3 x  5m  6  0 có 2 nghiệm cùng dấu
Bài 3 ( 3 đ) : Cho tam giác ABC với b =8 , c = 7 và A
= 120 0 . Hãy tính a , S, R,r , h ,m a b
Bài 4 ( 1 đ) : Cho tam giác ABC . Chứng minh 2
S  2R sin Asin B sin C Trang 12
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Năm học 2012-2013 ĐỀ A
Câu 1 ( 3 đ) : Giải bất phương trình a/ 2
x  4x  5  x 7 b/ 2
x  3 x  5  1  1
Câu 2 ( 2 đ) : Tìm m để phương trình sau có hai nghiệm cùng dấu m  2
1 x  2m  
1 x  2m  5  0
Câu 3 ( 3 đ) : Trong mặt phẳng tọa độ Oxy cho A2,  1 ,B 3  ,  1
a/ Viết phương trình tham số của đường thẳng AB
b/ Viết phương trình tổng quát của đường thẳng OB
c/ Viết phương trình tổng quát của trung tuyến OM của tam giác OAB
Câu 4 ( 2 đ) : Cho tam giác ABC với 0
b  13,c  7,B  120 . Tính : a,S,R,hb ĐỀ B
Câu 1 ( 3 đ) : Giải bất phương trình a/ 2
x  4x  5  x 7 b/ 2
x  3 x  4  8 
Câu 2 ( 2 đ) : Tìm m để phương trình sau có hai nghiệm cùng dấu m  2
1 x  2m  
1 x  2m  5  0
Câu 3 ( 3 đ) : Trong mặt phẳng tọa độ Oxy cho A 1  , 3  ,B 1  ,2
a/ Viết phương trình tham số của đường thẳng AB Trang 13
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
b/ Viết phương trình tổng quát của đường thẳng OA
c/ Viết phương trình tổng quát của trung tuyến OM của tam giác OAB
Câu 4 ( 2 đ) : Cho tam giác ABC với 0
a  13,c  7,A  120 . Tính : ,
b S, R, ha Trang 14
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
BỘ ĐỀ ÔN THI HK2 Đề số 1 5 
Câu 1. a. Cho sin a  , 0  a  . Tính sin , a 13 2 cos , a sin2 , a cos2 , a tan2 , a cot 2 ,
a sina    ,  6    cos( ) a ,tan( a a a   2 ) a 4 3 , sin ,cos ,tan 2 2 2 . sin x  3cos x b. Tính A  biết tan x  8 . 2sin x  cos x 2 2 tan d  cot d 1 c. Tính B  biết sin d  . 2 2
4 tan d  3cot d 5 cos x 1
Câu 2. a. Chứng minh rằng:  tan x  1 sin x cos x
b. CMR: sin 2A sin 2B  sin 2C  4sin A sinB sinC . Câu 3. Cho tam giác ( A 4  ;6); ( B 5;1);C(1;3)
a. PTTQ của cạnh BC. b.Viết PTTS của trung tuyến BN
c. Viết PTTS của đường cao CK; d. Viết phương
trình đường thẳng qua A và song song với ( )
a :2x y 100  0 ;
e. Viết phương trình đường thẳng qua B và vuông góc với ( )
b : 5x  4y  6  0; f. Viết phương trình đường
tròn ngoại tiếp tam giác ABC. g. Viết phương trình
đường tròn có tâm A, đi qua B; Trang 15
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Câu 4. Lập phương trình tiếp tuyến với đường tròn 2 2
(C): x y 16x –8y  64  0 : a. tại ( A 4
 ;4)(C); b. biết tiếp tuyến song song với
đường thẳng (d ) : 3x  4y  2008  0 1 ;
Câu 5. a. Xác định các yếu tố của elip 2 2
(E):16x  25y  400 ;
b. Viết phương trình chính tắc của elip (E) biết (E) có 27
độ dài trục lớn bằng 8 và (E) đi qua điểm ( A 2; ) 2 . Đề số 2 3 Câu 1. a. Cho 0 0
cosb   (90  b 180 ) 5 . Tính sin2b, cos2b, tan2b, 0 0 0
cos(b 60 ),sin(2b 135 ),tan(30  ) b ,
sin b ,cos b ,tan b 2 2 2 . 2 2
7sin d  3cos d
b. Tính giá trị A  biết cot d  4 ; 2 2
2sin d  3cos d
7 tan c  3cot c 1
c. Tính giá trị B  biết cos c  .
2 tan c  cot c 4
Câu 2. a. Chứng minh rằng:
sin x  cos x 1 2 cos  x 1 cos x
sin x  cos x 1
b. Cho A, B và C là ba góc của tam giác. Chứng minh A B C
rằng: cos A  cos B  cosC  4 cos cos sin 1 2 2 2 .
Câu 3. Cho ABC có ( A 1;3), (
B 3;1); C(5;5) Trang 16
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
a. Viết PTTS của đường cao AH. b.Viết PTTQ trung
trực cạnh AC; c. Viết phương trình đường thẳng
qua C và vuông góc với ( )
b :11x 3y  26  0 ;
d. Viết phương trình đường tròn nhận AC làm đường
kính; e. Viết phương trình đường tròn có tâm B và tiếp xúc với ( )
 : 8x  6y 11  0 ;
Câu 4. Cho đường tròn 2 2
(C):(x 3) (y  7)  25.
a. Viết phương trình tiếp tuyến với (C) tại ( B 6; 3  )(C);
b.Lập phương trình tiếp tuyến với đường tròn biết tiếp tuyến vuông góc với ( )
a : 3x  4y  2009  0 ;
Câu 5. a. Xác định các yếu tố của elip 2 2
(E): 9x 16y 1;
b. Viết phương trình chính tắc của elip (E) biết (E) có c 3
độ dài trục nhỏ bằng 8 và tỉ số  a 5 ; Đề số 3 Câu 1. a.Tính sin , x cos , x sin 2 , x cos 2 , x và        x x x sin(  2 ) x , cos  x , tan     x  , sin ,cos , tan 4  6   3  2 2 2 
biết tan x  2 2,    x   . 2 2 2 5 o
c s a  sin a 4 b.Cho A  biết cot a   . 2 2 3sin a  o c s a 3 2 2
7 tan c  3cot c 2
c. Tính giá trị B  biết cos c   ; 2 1 2cot c 5 Trang 17
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Câu 2. a. Chứng minh rằng: 2
(cos x  sin x) 1 2  2tan x cot x  sin . x cos x
b. Cho A, B và C là ba góc của tam giác. CMR: A B C
sin A  sin B  sin C  4 cos o c s o c s . 2 2 2
Câu 3. Cho ABC với ( A 3;8), ( B 5;2), C( 1  ;10)
a.Viết PTTQ của cạnh BC. b.Viết PTTS của trung
tuyến BN; c. Viết PTTQ của đường cao CK;
d. Viết PTTS của đường trung bình qua trung điểm 2
cạnh AC, BC; e.Viết PTTQ trung trực cạnh AB ;
f. Viết phương trình đường thẳng qua A và song song với ( )
a :5x 2y 11 0 ; g. Viết phương trình đường
thẳng qua B và vuông góc với ( )
b :3x  7y 16  0;
h. Viết phương trình đường tròn ngoại tiếp tam giác
ABC. i. Viết phương trình đường tròn có tâm A, đi qua B;
j. Viết phương trình đường tròn nhận BC làm đường
kính; k. Viết phương trình đường tròn có tâm B và tiếp xúc với ( )
 : 6x 8y  7  0 ;
Câu 4. a. Lập phương trình tiếp tuyến với đường tròn (C): 2 2
(x  2)  ( y 1)  25 biết tiếp tuyến song song với
đường thẳng (d) : x y  0 .
b. Lập phương trình tiếp tuyến với đường tròn 2 2
(C) : x y 8x  8y 16  0 biết tiếp tuyến vuông góc
với đường thẳng (d) : 5
x 12y  3  0. Trang 18
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 2 x
Câu 5. a. Xác định các yếu tố của elip 2 (E):  y 1 16 ;
b. Viết phương trình chính tắc của elip (E) biết (E) có 16
tiêu cự bằng 6 và (E) đi qua điểm ( A 3  ; ) 5 ;
c. Viết phương trình chính tắc của elip (E) biết (E)có
một tiêu điểm là F ( 3; 0) 1 và qua 3 M (1; ) ; 2 Đề số 4 Câu 1. 3    1    a. Cho o c sa  0  a  ,sin b     b  0     . 5  2  3  2        Tính sin(a  ) b , tan a  , cos b      .  6   3  1 2
2sin a cos a  4 cos a
b. Cho tan a   , tính A  ; 3 2
3sin a cos a  5sin a
7 tan b  3cot b 4 c. Tính B  biết sin b  
tan b  2 cot b 5
Câu 2. a. Chứng minh rằng: 2 1
  (cos x  sin x)  cot xsin .xcosx 2 2 tan x
b. Cho A, B và C là các góc của tam giác. CMR:
cos2A cos2Bcos2C  1
 4cos AcosBcosC
Câu 3. Cho ABC với ( A 3;8), ( B 5;2), C( 1  ;10)
a.Viết PTTS cạnh AB. b. PTTQ của trung tuyến AM;
c. PTTQ của đường cao CK; d. PTTS của đường
trung bình qua trung điểm 2 cạnh AC, BC. e. PTTS Trang 19
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
trung trực cạnh BC; f. Viết phương trình đường
thẳng qua A và song song với ( )
a : 5x  2y 11 0 ;
g. Viết phương trình đường thẳng qua B và vuông góc với ( )
b :3x  7y 16  0; h. Viết phương trình
đường tròn ngoại tiếp tam giác ABC. i. Viết
phương trình đường tròn có tâm A, đi qua B;
j. Viết phương trình đường tròn nhận BC làm đường
kính; k. Viết phương trình đường tròn có tâm C và
tiếp xúc với  : 5x 12y 17  0 ;
Câu 4. Lập phương trình tiếp tuyến với đường tròn (C): 2 2
x y 16x 12y  75  0 : a.tại điểm N(11; 2  ) ( )
C . b. biết tiếp tuyến vuông
góc với đường thẳng ( ) a : 3
x  4y  2  0; c. biết tiếp
tuyến song song với đường thẳng ( )
b : 5x 12y  21 0 ;
Câu 5. a. Xác định các yếu tố của elip 2 2 25 ( ): y E x  1 4 ;
b. Viết phương trình chính tắc của elip (E) biết (E) đi 8 6 16 qua hai điểm ( A 1; ); ( B 3  ; ) 5 5 . Đề số 5 1 Câu 1. a. Cho 0 0
cos2b   (45  b  90 ) 3 . Tính sin2b ,
sinb, cosb, tanb, 0 0 0
cos(b 60 ),sin(2b 135 ),tan(45  ) b . Trang 20
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 4 
b. Cho sin 2y   (  y  0) 5 4
. Tính cos2y , siny,   
cosy, tany, cos(y  ),sin(2y  ),tan(  y) 6 3 4 . 2
7sin d cos d  3cos d
c. Tính giá trị A  biết cot d  7  ; 2
2sin d  3sin d cos d 2 7  3cot c 1
d. Tính giá trị B  biết sin c  ; 2 2 tan c 1 5
Câu 2. a. Chứng minh rằng:
sin x  cos x 1 2 cos  x 1 cos x
sin x  cos x 1
b. Cho A, B và C là ba góc của tam giác. Chứng minh A B C
rằng: cos A  cos B  cosC  4 cos cos sin 1 2 2 2 .
Câu 3. Cho ABC có ( A 2;15), ( B 6; 1  ); C( 1  0;7)
a.Viết PTTQ của cạnh BA.
b.Viết PTTS của trung tuyến ; c. Viết PTTS của
đường cao AH d. Viết PTTQ của đường trung bình
qua trung điểm 2 cạnh AB, AC ; e.Viết PTTQ trung
trực cạnh AC ; f. Viết phương trình đường thẳng qua B và song song với ( )
a :3x 11y 29  0 ; g. Viết
phương trình đường thẳng qua C và vuông góc với ( )
b :11x 6y  21 0 ;
h. Viết phương trình đường tròn ngoại tiếp tam giác
ABC. i. Viết phương trình đường tròn có tâm B, đi qua A; Trang 21
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
j. Viết phương trình đường tròn nhận AC làm đường
kính; k. Viết phương trình đường tròn có tâm B và tiếp xúc với ( )
 :3x  4y 114  0 ;
Câu 4. Cho đường tròn 2 2
(C):(x 5) (y 10) 100 .
a. Viết phương trình tiếp tuyến với (C) tại ( B 1;2)(C);
b.Lập phương trình tiếp tuyến với đường tròn biết tiếp tuyến vuông góc với ( )
a : 3x  4y  2011 0 ;
c. Lập phương trình tiếp tuyến với đường tròn biết tiếp tuyến song song với ( )
b : 5x 12y 20  0 ;
Câu 5. Xác định các yếu tố của elip: 2 2 x y a. (E) :  1; b. 2 2
(E) :16x  81y  1 ; 169 144 2 81y e. 2 2
(E) : 4x  9 y  36 ; f. 2 (E) : x  1; 16
Câu 6. Hãy lập phương trình chính tắc của elip (E) biết (E) có:
a. độ dài trục nhỏ bằng 24 và tiêu cự bằng 8;
b. Độ dài trục lớn bằng 30 và tỉ số c 7  ; a 15
c. Tiêu cự bằng 10 và tỉ số a 13  b 12 d. Tiêu điểm c F ( 8  ;0) và tỉ số 2  ; 1 a 5
e. Một đỉnh trên trục lớn là A(5 ;0) và một tiêu điểm là F ( 3  ;0) ; 2 2 2 2 f. (E) đi qua hai điểm ( A 2; ); ( B 1; ) . 5 5 Trang 22
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
ĐỀ THI HK2 các năm trước Năm 2008-2009
Đề A ( Thời gian 90 phút )
Bài 1 ( 3đ) : Tính :
3sin x  4 cos x a) A  biết tan x  2 sin x  cos x  3  b) cos, cos     biết  4  12    sin        13  2  8     c) sin 2 ,
a tan 2a biết cos 2a   a     17  2 
Bài 2 ( 2đ) : Chứng minh :
1 cos10x  sin10x a)  tan 5x
1 cos10x  sin10x
b) sin 2Asin 2B  sin 2C  4cos Asin BcosC với
A,B,C là ba góc của một tam giác
Bài 3 ( 3đ) : Cho đường tròn ( C) có phương trình 2 2
x y  2x  4 y  20  0
a.Xác định tọa độ tâm I và bán kính R của đường tròn ( C)
b.Viết phương trình tiếp tuyến của đường tròn ( C) tại điểm A 4,2
c.Viết phương trình tiếp tuyến của đường tròn ( C) biết
tiếp tuyến song song với (d) : 3x  4y  2009  0 Trang 23
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Bài 4 ( 2đ): Lập phương trình chính tắc của elip ( E)  3    2 
biết ( E) qua hai điểm A 1  ,   , B  2,  2      2   Bài 5: Cho elip ( E) : 2 2
16x  25y  9 . Xác định ,tiêu
cự, đỉnh , tiêu điểm , độ dài các trục của elip (E)
Đề B ( Thời gian 90 phút )
Bài 1 ( 3đ) : Tính : sin x  cos x a) B x  3sin x  biết cot 2 4 cos x  3  b) sin, cos     biết  4  5     cos        13  2  15    c) sin 2 ,
a tan 2a biết cos 2a   a     17  2 
Bài 2 ( 2đ) : Chứng minh :
1 cos10x  sin10x a)  cot 5x
1 cos10x  sin10x
b) sin 2A sin 2B sin 2C  4cos Acos Bsin C với
A,B,C là ba góc của một tam giác
Bài 3 ( 3đ) : Cho đường tròn ( C) có phương trình 2 2
x y  4x  2 y  20  0
a/ Xác định tọa độ tâm I và bán kính R của đường tròn ( C)
b/ Viết phương trình tiếp tuyến của đường tròn ( C) tại điểm B 2,4 Trang 24
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
c/ Viết phương trình tiếp tuyến của đường tròn ( C)
biết tiếp tuyến song song với (d) : 4x  3y  2009  0
Bài 4 ( 2đ) : a.Lập phương trình chính tắc của elip ( E)   3   2 
biết ( E) qua hai điểm A1,   , B   2,  2      2   a/ Cho elip ( E) : 2 2
9x  25y  16 . Xác định tiêu cự,
đỉnh, tiêu điểm, độ dài các trục của elip (E) Năm 2010-2011
Đề A ( Thời gian 90 phút ) 1 sin2x tan x 1
Câu 1(2đ) : a/ Chứng minh  2 sin x  2 cos x tan x 1
b/ Cho tam giác ABC. Chứng minh cos A B C C B  sin cos sin cos 2 2 2 2 2 5
Câu 2(1đ): Cho cot x  3 . Tính 1 A  2 2cos x  2
sin x sin x cos x 3  
Câu 3 (2đ ): Cho cos a  0  a   5 2  và   5 sinb   b       13 2     
Tính sina b 
, cos2a , sin2b , cos 2a     4  Trang 25
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Câu 4 (4đ): Cho tam giác ABC với A5, 2  , B1,4, C 3  ,6
a/ Viết phương trình tổng quát của đường thẳng AC
b/ Viết phương trình tham số của trung tuyến AM
c/ Viết phương trình đường tròn ( C) đường kính AC
d/ Viết phương trình tiếp tuyến của đường tròn ( C) tại điểm A
Câu 5 (1đ): Cho elip E 2 x  2 : 9y 144 .
Tính tọa độ đỉnh, tiêu điểm, tiêu cự và độ dài các trục của elip ( E).
Đề B ( Thời gian 90 phút ) 1 sin2x cot x 1
Câu 1 (2đ): a/ Chứng minh  2 cos x  2 sin x cot x 1
b/ Cho tam giác ABC. Chứng minh sin A B C C B  cos cos sin sin 2 2 2 2 2 5
Câu 2 (1đ): Cho tan x  3 . Tính 1 B  2 2cos x  2
sin x sin x cos x 5  3 
Câu 3 (2đ): Cho cos a   a  2   13 2  và   3 sinb   b       5 2    Trang 26
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10  
Tính cosa b, cos2 , b sin2 , a sin 2b    4   
Câu 4 ( 4 đ ) : Cho tam giác ABC với A4  ,1 , B 2  ,5, C6, 3  
a/ Viết phương trình tổng quát của đường thẳng BC
b/ Viết phương trình tham số của trung tuyến BM
c/ Viết phương trình đường tròn ( C) đường kính BC
d/ Viết phương trình tiếp tuyến của đường tròn ( C) tại điểm B
Câu 5 (1đ) : Cho elip E 2 x  2 : 16y 144
Tính tọa độ đỉnh, tiêu điểm, tiêu cự và độ dài các trục của elip ( E) Năm 2011-2012
Đề A ( Thời gian 90 phút )
Câu 1 (2 đ) : Chứng minh 1 a/ cos asin a 2 2
cos a sin a  sin4a 4
b/ Cho tam giác ABC . Chứng minh
sin sin  sin  4sin A cos B sin C A B C 2 2 2 12 
Câu 2 (2 đ) : Cho cosa    a   13 với 2 . Tinh sin2a , cos2a   , tan a    4    Trang 27
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 3
Câu 3 (1 đ) : Cho cot x  2 . Tinh 2
9sin x 3sin x cos x A  2 2
3sin x  2cos x
Câu 4 (3 đ) : Cho đường tròn C có phương trình 2 2
x y  4x  4y 17  0
a/ Xác định tọa độ tâm I và bán kính R của đường tròn ( C)
b/ Viết phương trình tiếp tuyến của đường tròn ( C) tại điểm A2,5
c/ Viết phương trình tiếp tuyến của ( C) biết tiếp tuyến
song song với d : 3x  4y 11  0
Câu 5 (2 đ) : a/ Cho elip E 2 2
: x  4y 1 . Tìm tọa độ
các tiêu điểm và độ dài các trục của E
b/ Lập phương trình chính tắc của elip ' biết '  2 2   6 
qua hai điểm A 1, ,B   3,   3   3     
Đề B ( Thời gian 90 phút )
Câu 1 (2 đ) : Chứng minh a/ b b 2 2 b b 1 sin cos sin cos   sin 4b 4
b/ Cho tam giác ABC . Chứng minh
sin sin sin  4sin A sin B cosC A B C 2 2 2 Trang 28
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10 12 3
Câu 2 (2 đ) : Cho sin b   b     13 với 2 . Tinh sin2b , cos2b   , tan b    4    3
Câu 3 (1 đ): Cho tan x  2 . Tinh 2
9cos x 3sin x cos x B  2 2
3cos x  2sin x
Câu 4 (3 đ): Cho đường tròn C có phương trình 2 2
x y  4x  4y 17  0
a/ Xác định tọa độ tâm I và bán kính R của đường tròn ( C)
b/ Viết phương trình tiếp tuyến của đường tròn ( C) tại điểm B5,2
c/ Viết phương trình tiếp tuyến của ( C) biết tiếp tuyến
song song với d : 4x  3y 11  0
Câu 5 (2 đ): a/ Cho elip E 2 2
: x  9y 1 . Tìm tọa độ
các tiêu điểm và độ dài các trục của E
b/ Lập phương trình chính tắc của elip ' biết '  3   2 
qua hai điểm A 1, ,B   2,   2   2      Năm 2012-2013 ĐỀ A Trang 29
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Câu 1 (2 đ) : a/ Chứng minh 2 1 cos x 2     x  x 1 2cot x 1 cos 1 cos
b/ Cho tam giác ABC . Chứng minh
tan A  tanB  tanC  tan . A tan . B tanC 24
Câu 2 (2 đ) : Cho sin 2x   0 0  x  45  25 . Tính x x  0 x    0 sin , cos , sin 30 , cot x  45  1
Câu 3 (1 đ) : Cho cos x   4 . Tinh
3tan x  2cot x
A  tanxcot x
Câu 4 (3 đ) : Cho đường tròn C: 2 2
x y  2x  8y 8  0 và đường thẳng
d : 5x 12y 12  0
a/ Chứng tỏ đường thẳng d tiếp xúc đường tròn ( C)
b/ Viết phương trình tiếp tuyến của đường tròn ( C)
biết tiếp tuyến vuông góc với đường thẳng d
c/ Chứng tỏ điểm A1, 9
  nằm trên đường tròn ( C).
Viết phương trình tiếp tuyến của ( C) tại A
Câu 5 (2 đ) : a/ Cho elip E 2 2
: x  4y  9 . Xác định
các yếu tố của E Trang 30
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
b/ Lập phương trình chính tắc của elip ' biết ' a 5
có tiêu cự là 12 và tỉ số  b 4 ĐỀ B
Câu 1 (2 đ) : a/ Chứng minh 2 1 sin x 2    
x  x 1 2tan x 1 sin 1 sin
b/ Cho tam giác ABC . Chứng minh tan . A tan .
B tanC  tan A  tanB  tanC 7
Câu 2 (2 đ) : Cho sin 2x   0 0  x  45  25 . Tính x x  0 x    0 sin , cos , cos 60 , cot x  45  1
2tan x  3cot x
Câu 3 (1 đ) : Cho sin x   B  3 . Tinh cot x  tan x
Câu 4 (3 đ) : Cho đường tròn C: 2 2
x y  8x  2y 8  0 và đường thẳng
d :12x  5y 12  0
a/ Chứng tỏ đường thẳng d tiếp xúc đường tròn ( C)
b/ Viết phương trình tiếp tuyến của đường tròn ( C)
biết tiếp tuyến vuông góc với đường thẳng d
c/ Chứng tỏ điểm B 9  , 
1 nằm trên đường tròn ( C).
Viết phương trình tiếp tuyến của ( C) tại B Trang 31
THPT ERNST THÄLMANN TỔ TOÁN- NHÓM TOÁN 10
Câu 5 (2 đ) : a/ Cho elip E 2 2
: x  9y  4 . Xác định
các yếu tố của E
b/ Lập phương trình chính tắc của elip ' biết ' b 4
có tiêu cự là 18 và tỉ số  a 5 .
-CHÚC CÁC EM THI TỐT! Trang 32