
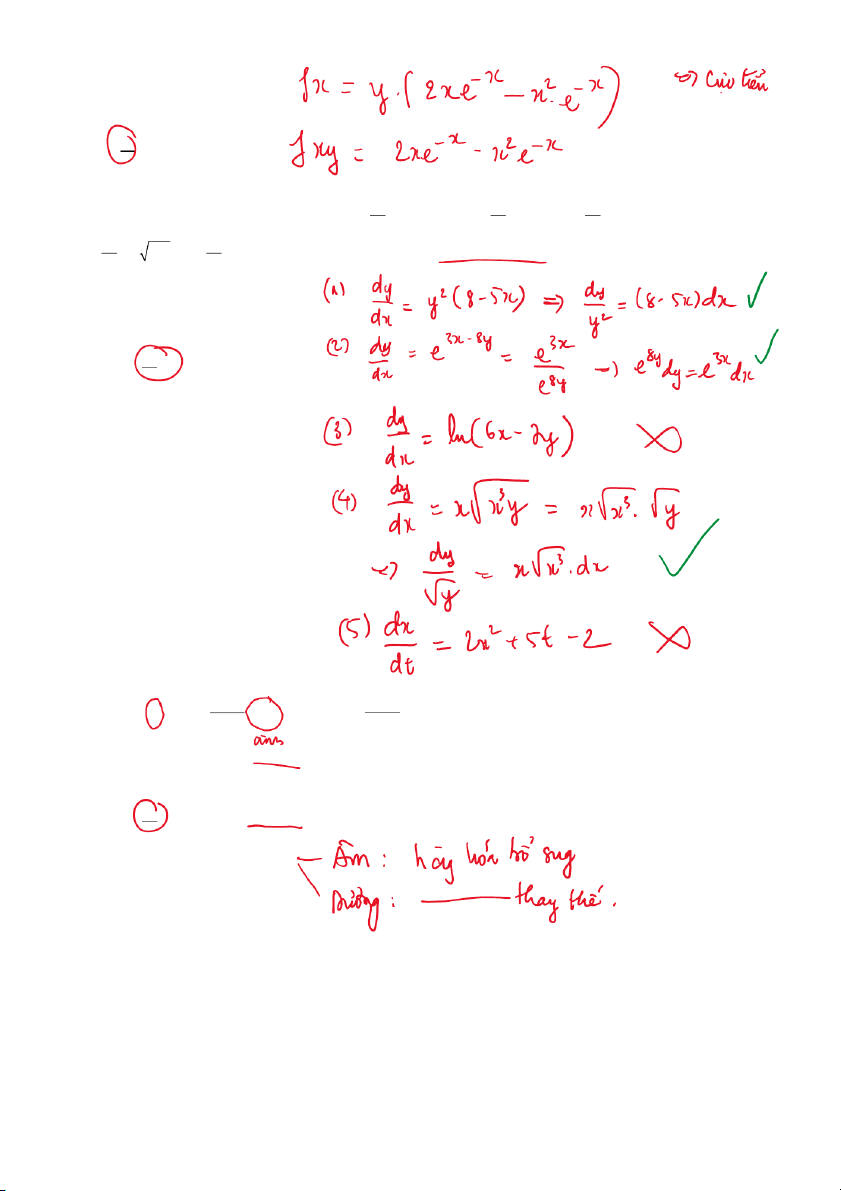
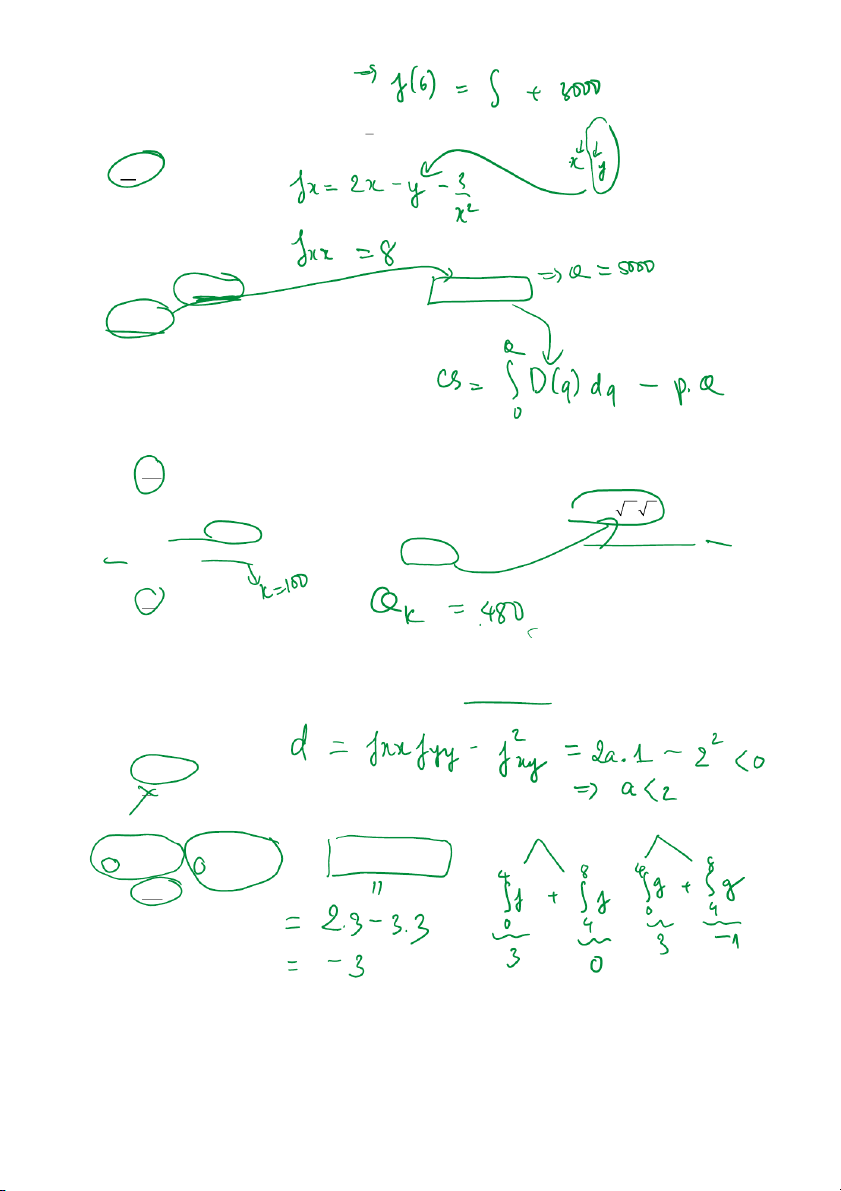


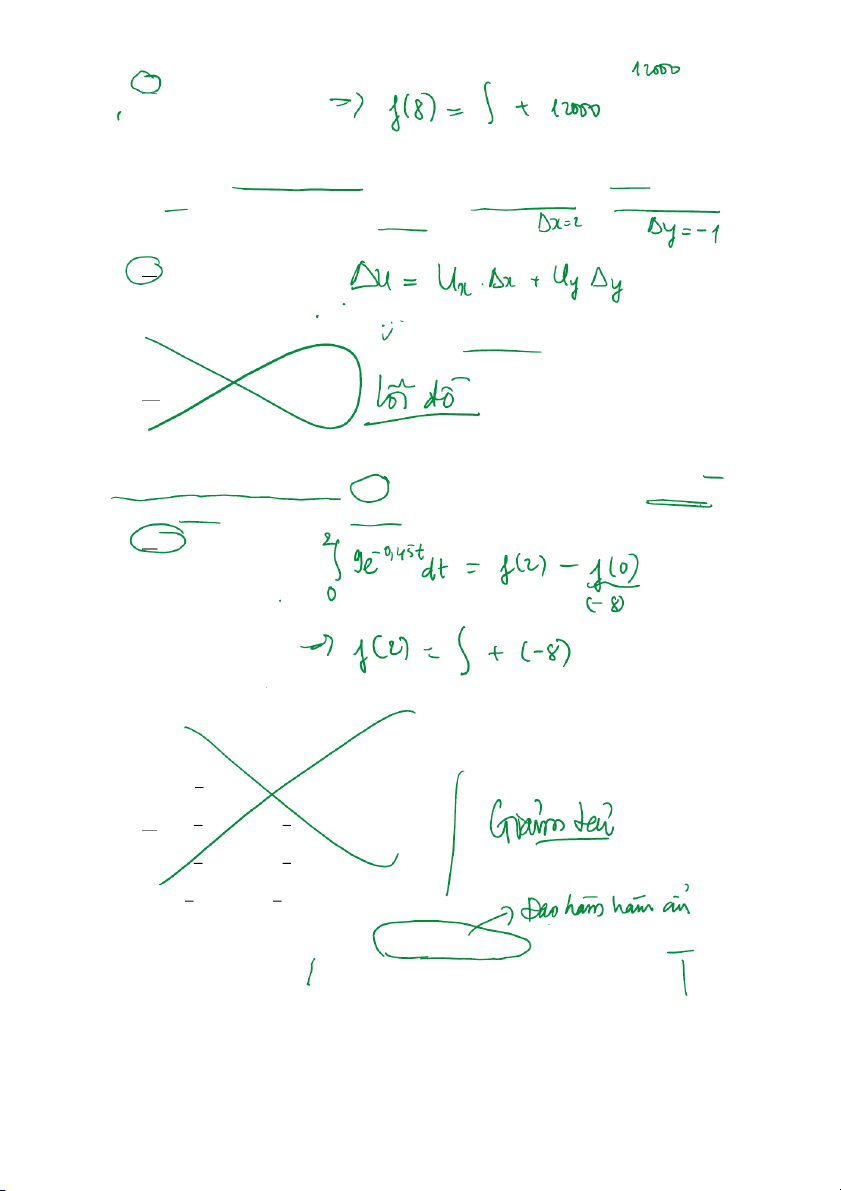
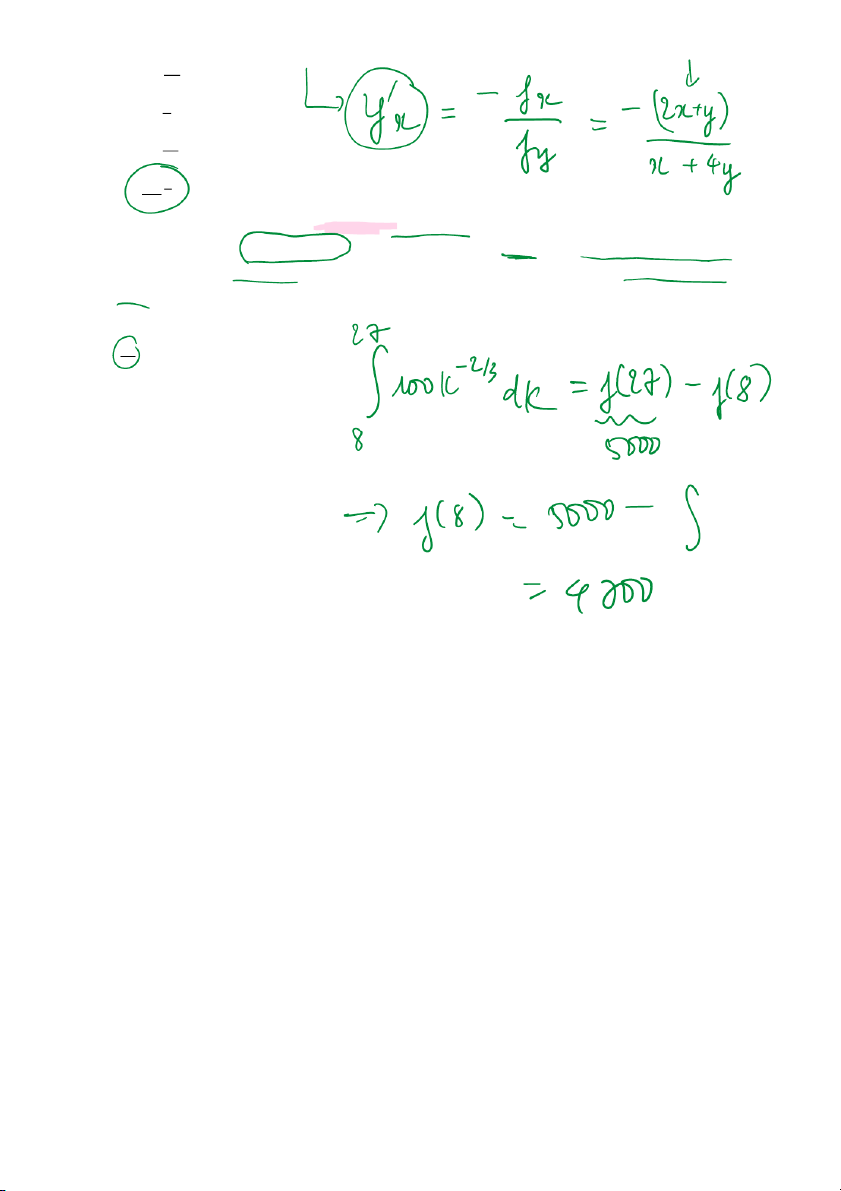
Preview text:
Câu 1. Một loại sản phẩm, với mức giá ban đầu là $5 mỗi đơn vị, có tốc độ thay đổi giá p(t) sau t
tháng bằng 5% của mức thiếu hụt D – S, trong đó lượng cung S( p) và lượng cầu D( p) sản
phẩm (tính theo nghìn đơn vị) được cho bởi D = 50 − p và S = 30 + pvới 0 p 10 . Hàm giá
p(t) tìm được là A. 0.1 ( ) = 5−10 t p t e 0.1 B. ( ) = 10−10 t p t e C. 0.1 ( ) 10 5 t p t e− = − D. ( ) =10 −5 t p t e
Câu 2. Chi phí cận biên của một nhà máy là 2
6(q − 5) đô la mỗi đơn vị khi mức ả
s n lượng là q đơn
vị. Biết rằng chi phí cố định (chi phí tại mức sản lượng bằng 0) là $250. Chi phí để nhà máy sản xuất 15 đơn vị l à A. $1250 B. $250 C. $2500 D. $3100 Câu 3. Giả sử hàm số 1 2 2 f ( , x )
y = ax + xy +
y + 2x có điểm tới hạn là (x , y ) . Khi đó điểm (x , y ) là 2 0 0 0 0
A. Điểm cực tiểu nếu a 1
B. Điểm cực tiểu nếu a 0
C. Điểm cực đại nếu a 0 D. Điểm cực ạ đ i nếu a 1 Câu 4. Cho hàm số 2 ( , ) x f x y x ye− =
khi đó đạo hàm riêng cấp 2 f là xy 2 A. ( ) x x x y e− − B.(2 ) x y x e− − 2 C. (2 ) x x x e− − 2 D. (2 ) x x x y e− −
Câu 5. Cho các phương trình vi phân: (1) dy 2 2 = 8 dy − dy y − 5xy (2) 3x 8 y = e (3) = ln(6 x −7 ) y (4) dx dx dx dy 3 = dx x x y (5) 2
= 2 x +5t −2 . Số phương trình vi phân phân ly biến số trong các phương trình đã dx dt cho là A. 1 B. 2 C. 3 D. 4
Câu 6. Có hai loại hàng hóa được bán trong một của hàng, biết hàm cầu đối với mỗi mặt hàng lần lượt là 100 50 D = 200 + − 5 và D = 300 + −8
. Hai loại hàng hóa trên là 1 p2 2 p2 p + 2 p + 3 1 2 A. Hai hàng hóa thay thế
B. Chưa thể kết luận được trên đây là hai hàng hóa thay thế hay bổ sung
C. Hai hàng hóa vừa thay thế vừa bổ sung D. Hai hàng hóa bổ sung Câu 7. Cho hàm số 2
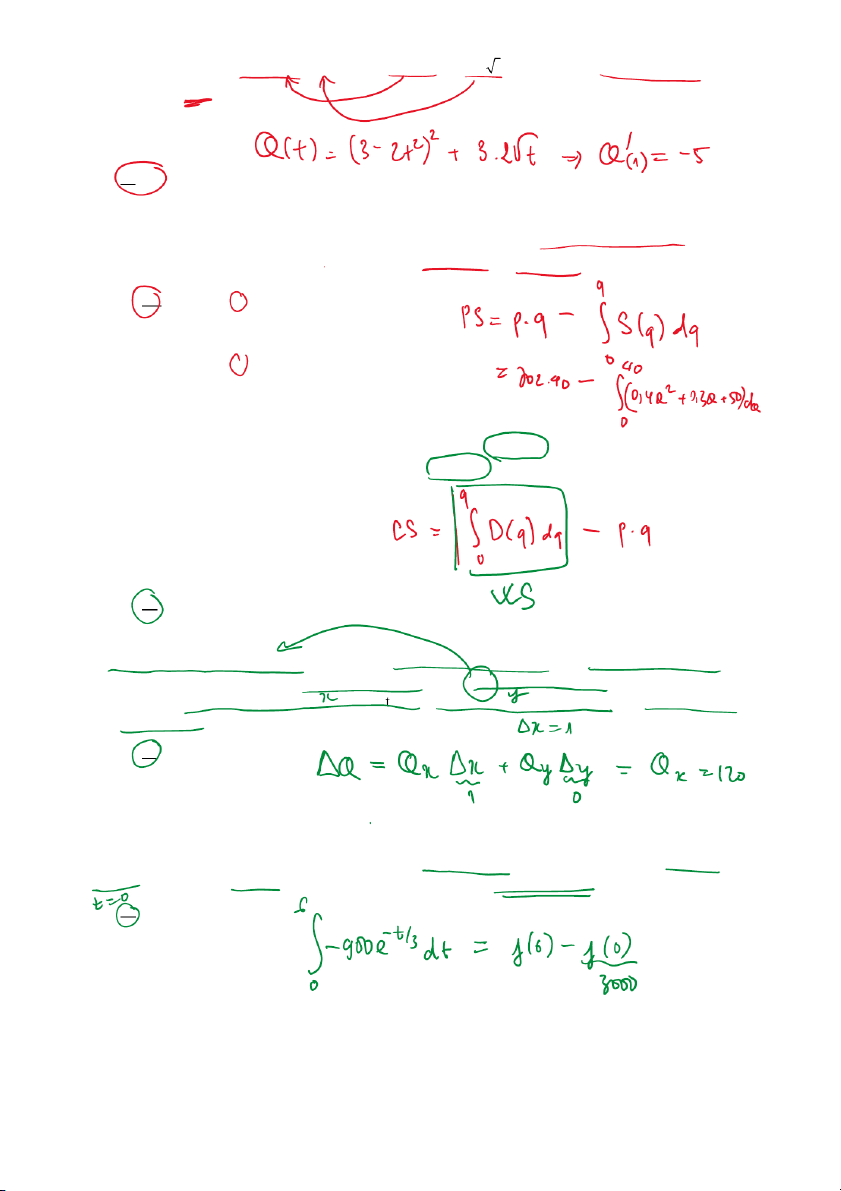
Q(x, y) = x + 3 y trong đó 2
x = 3 − 2t , y = 2 t đạo hàm của Q( ,
x y) theo biến t tại t = 1 l à A. -12 B. 10 C. -5 D. 12
Câu 8. Cho biết hàm cung ngược đối với một loại sản phẩm là −1 2
p = S (Q) = 0.4Q + 0.3Q+ 50và điểm
cân bằng thị trường là ( p Q ) = (702,40). Khi đó, thặng dư của nhà sản xuất tại mức giá cân bằng là 0, 0 A. 40 2 PS = 28080 −
(0.4Q + 0.3Q + 50)dQ 0 B. 40 2 PS = 28080 +
(0.4Q + 0.3Q + 50)dQ 0 C. 702 2 PS = 28080 −
(0.4Q + 0.3Q + 50)dQ 0 702 2 PS = 28080+
(0.4Q + 0.3Q + 50) D. dQ 0
Câu 9. Cho biết hàm cầu đối cới một loại hàng hóa là 2
D(q) = 3(81− q ) đô la mỗi đơn vị. ổ T ng lượng
tiền mà người tiêu dùng sẵn lòng chi tiêu để sở hữu 5 đơn vị hàng hóa đó là A. 5 2
WS = 15(81− q )dq 0 B. 5 2
WS = 3(81− q )dq + 5 0 C. 5 2
WS = 3(81− q )dq −15.56 0 D. 5 2 WS = 3(81− q )dq 0
Câu 10. Người ta ước tính rằng, sản lượng hàng tuần của một nhà máy là 2 2
Q(x, y) = 120x + 200 y + xy − x − 2 y . Trong đó, x là số lao động có kỹ thuật, y là số lao động giản đơn,
hiện tại nhà máy đang sử dụng 10 lao động có kỹ thuật và 20 lao động giản đơn. Sử dụng phân tích
cận biên ước lượng sản lượng hàng tuần khi ăng thêm một lao động có kỹ thuật và giữ nguyên số
lao động giản đơn thì sản lượng thay đổi xấp xỉ A. 120 sản phẩn B. 130 sản phẩm C. 150 sản phẩm D. 100 sản phẩm
Câu 11. Giá trị bán lại của một loại máy công nghiệp giảm với tốc độ p ụ
h thuộc vào tuổi của nó.
Khi máy t năm tuổi thì giá trị của nó thay đổi với tốc độ /3 900 t e− −
đô la mỗi năm. Nếu giá trị ban
đầu của chiếc máy là $3000 thì giá trị của chiếc máy khi nó được 6 năm tuổi xấp xỉ bằng A. $665 B. $1650 C. $1665 D. $1000 Câu 12. Cho hàm số 3 2 u = f ( ,
x y) = x − xy +
khi đó đạo hàm riêng cấp 2 f (1;−1)có giá trị l à x xx A. 8 B. -1 C. 3 D. -4
Câu 13. Cho hàm cầu đối với một loại sản phẩm là p = 350 −0.04Q và mức giá cân bằng thị trường
là p = 150 . Khi đó, thặng dư của người tiêu dùng tại mức giá cân bằng là 0 A. 5000 CS = −
(350− 0,04Q)dQ+ 750,000 0 B. 150 CS = −
(350− 0,04Q)dQ+ 750,000 0 150 CS =
(350 − 0,04Q)dQ − 750,000 C. 0 D. 5000 CS =
(350 −0,04Q)dQ −750,000 0
Câu 14. Một nhà máy ước tính rằng sản lượng hằng năm của nhà máy là 3 Q = 240 K L , trong đó K
là vốn tính bằng 1000$ và L là lượng lao động tính bằng số giờ lao động. sản lượng cận biên của
vốn khi vốn là 100,000$ và quy mô lao động là 64,000 giờ l à A.240 sản phẩm B.480 sản phẩm C.300 sản phẩm D.840 sản phẩm
Câu 15. Cho hàm số u = u( ,
x y) thỏa mãn f = 2ax + 2y − 2 , f = 2x + y − 3 và M (x , y ) là điểm tới hạn x y 0 0
của hàm số đã cho. Tìm điều kiện của a để M (x , y ) là điểm yên ngựa 0 0 A.a 1 B.a 2 C.a 2 D.a 1 Câu 16. Cho các hàm số 8
f (x), g(x) liên tục trên 0,8 và thỏa mãn
f (x)dx = 3
, 8g(x)dx = 2 , 0 0 8 4
f (x)dx = 0
, 8g(x)dx = 1 −
. Khi đó 2 f (x)−3g(x)dx bằn g 4 4 0 A.-3 B.-7 C.-12 D.5
Câu 17. Một công ty sản xuất hai loại máy nghe nhạc, chi phí để sản xuất máy loại 1 là $40 mỗi
chiếc, chi phí để sản xuất máy loại 2 là $20 mỗi chiếc. Nếu công ty sản xuất x chiếc máy loại 1 và y
chiếc máy loại 2 thì hàm chi phí của công ty là A. C( ,
x y) = 40x − 20 y
B. C(x, y) = 20x + 40y C. C( ,
x y) = 40x + 20 y
D. C(x, y) = 20x − 40y
Câu 18. Chi phí cận biên của một loại sản phẩm của một nhà sản xuất là 2
6q − 8q + 200 đô la mỗi đơn
bị khi q đơn vị được sản xuất. Chi phí để sản xuất 3 đơn vị đầu tiên là 718 đô la. Chi phí để sản
xuất 5 đơn vị đầu tiên là A. $1250 B. $1520 C. $2510 D. $2150
Câu 19. Một cửa hàng sơn bán hai thương thiệu sơn A và B, người ta nhận thấy rằng nếu giá bán
hai loại sơn lần lượt là x, y đô la một thùng thì lượng cầu đối với hai loại sơn trên lần lượt là
D (x, y) = 300 − y + 2 , D (x, y) = 100 + x − 2 thùng một tháng. Khi đó hàm doanh thu hằng tháng của 1 y 2 y cửa hàng là A. R( ,
x y) = (100 + x − 2 y)y B. R( ,
x y) = (300 − y + 2y) + (100 + x − 2 y)y C. R( ,
x y) = (300 − y + 2y)x D. R( ,
x y) = (300 − y + 2y)x + (100 + x − 2y) y
Câu 20. Một nghiên cứu cho thấy, nếu người lao động làm việc 100x giờ trên y mẫu đất thì sẽ sản xuất được 0.5 0.5 f ( , x y) = Ax y
giạ lúa mỳ, trong đó A là một hằng số dương. Giả sử các yếu tố sản xuất
x và y được tăng gấp ba. Khi đó mức ả
s n lượng sản xuất lúa mỳ sẽ A. Không thay đổi B. Tăng gấp đôi C. Giảm đi 3 lần D. Tăng gấp ba Câu 21. Gọi dy y = y( )
x là nghiệm của phương trình phân ly biến số 2
=2 xy với điều kiện ban đầu dx y(0) = 1
− . Giá trị y(2) là A. 0.2 B. -0.2 C. -0.3 D. 0.3
Câu 22. Sản lượng hàng ngày tại một nhà máy là Q =120 K L trong đó K là lượng vốn đầu tư tính
theo đơn vị 1000$ và L là số lao động tính bằng số giờ lao động. Hiện tại nhà máy đang đầu tư
9000$ và 100 giờ lao động. Nếu nhà máy tăng thêm vốn đầu tư là 1000$ và giảm 3 giờ lao động thì sản lượng sẽ
A. Tăng thêm 364 sản phẩm
B. Giảm đi 146 sản phẩm
C. Giảm đi 364 sản phẩm
D. Tăng thêm 146 sản phẩm
Câu 23. Cho hàm số f (x) liên tục trên 2,8. Khi đó, tích phân 6 8 f (x)dx + f (x)dx = 0 3 A. 8 6
f (x)dx + 2 f (x)dx 2 3 B. 8 6 f (x)dx + f (x)dx 2 3
C. 8 f (x)dx 2 D. 8 8 f (x)dx + f (x)dx 2 3
Câu 24. Người ta ước tính rằng, t tháng kể từ bây giờ, dân số của một thị trấn sẽ tăng với tốc độ 2/3 6 +10t
người mỗi tháng. Giả sử dân số hiện tại của thị trấn là 12,000 người, thì sau 8 tháng dân số của thị trấn là A. 12.440 người B. 12.240 người C. 24.240 người D. 24.120 người
Câu 25. Một nhà đầu tư sẽ n ậ
h n được U(x, y)đơn vị lợi ích khi sở hữu ĩi đơn vị cổ phiếu và y đơn vị
trái phiếu, trong đó U(x, y) = (x + 3)(2y +5) . Hiện tại nhà đầu tư đó đang sở hữu x = 20đơn vị cổ
phiếu và y = 10 đơn vị trái phiếu. nếu nhà đầu tư đó thêm 2 đơn vị cổ phiếu và bớt 1 đơn vị trái
phiếu trong danh mục đầu tư của mình thì lợi ích của nhà đầu tư sẽ:
A. Tăng khoảng 40 đơn vị
B. Tăng khoảng 4 đơn vị
C. Giảm khoảng 4 đơn vị D. Không thay đổi Câu 26. Cho hàm số 2
u = f (x, y) = x − 3x + 5 y . Hàm số có điểm tới hạn là A. M (1,1) B. M (1, 1 − ) C. M ( 1 − ,1) D. M ( 1 − , 1 − )
Câu 27. Một miếng thịt được lấy k ỏ
h i ngăn đá của tủ lạnh và được đặt trên quầy để rã đông. Nhiệt
độ miếng thịt khi lấy ra khỏi ngăn đá là -8oC và tốc độ tăng nhiệt của nó sauu t giờ là 0.45 '(t) 9 t T e− =
độ C/giờ. Nhiệt độ của miếng thịt sau 2 giờ là bao nhiêu A.3.9 B.6.5 C.5.5 D.5.8
Câu 28. Cho hàm số f (x) thỏa mãn f '(x)là hàm liên tục. Áp dụng công thức tính tích phân từng
phần đối với tích phân I = f (x)sin 2xdx , ta được A. 1 I = −
f (x) cos 2x +
f '(x) cos 2xdx 2 B. 1 1 I = −
f (x) cos 2x +
f '(x) cos 2xdx 2 2 C. 1 1 I = −
f (x)cos 2x +
f '(x)sin 2xdx 2 2 D. 1 1 I =
f (x ) cos 2x −
f '(x) cos 2xdx 2 2 Câu 29. Cho hàm số 2 2
f (x, y) = x + xy + 2 y . Độ dốc của đường mức của hàm số tại điểm (-1,1) là A. 2 − 3 B. 2 3 1 − C. 3 D. 1 3
Câu 30. Tại một nhà máy, khi K nghìn đô la được đầu tư vào máy và thiết bị thì tốc độ thay đổi sản lượng Q được cho bởi 2/3 Q '(K ) 100K − =
đơn vị trên nghìn đô la đầu tư. Khi 27000 đô la được đầu tư
thì mức sản lượng là 5000 đơn vị. Hãy xác định mức sản lượng của nhà máy khi 8000 đô la được đầu tư A. 4100 đơn vị B. 4700 đơn vị C. 41000 đơn vị D. 47000 đơn vị




