Trắc nghiệm dãy số, cấp số cộng và cấp số nhân trong các đề thi thử Toán 2018

Tài liệu gồm 86 trang tổng hợp, phân loại và giải chi tiết các câu hỏi và bài tập trắc nghiệm dãy số, cấp số cộng và cấp số nhân trong các đề thi thử Toán 2018.

 

66 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT)

Môn: Toán 11

Thông tin:

86 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Câu 1:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Cho cấp số cộng
n
u
có
1
2
u
và công sai
3
d
. Tìm số hạng
10
u
.
A.
9
10
2.3
u
. B.
10
25
u
. C.
10
28
u
. D.
10
29
u
.
Lời giải
Chọn B
Ta có
10 1
9u u d
.
Câu 2:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Cho một cấp số cộng
n
u
có
1
1
3
u
,
8
26.
u
Tìm công sai
d
A.
11
3
d
. B.
10
3
d
. C.
3
10
d
. D.
3
11
d
.
Lời giải
Chọn A
8 1
7u u d
1
26 7
3
d
11
3
d
.
Câu 3:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Cho một cấp số cộng
n
u
có
1
1
3
u
,
8
26.
u
Tìm công sai
d
A.
11
3
d
. B.
10
3
d
. C.
3
10
d
. D.
3
11
d
.
Lời giải
Chọn A
8 1
7u u d
1
26 7
3
d
11
3
d
.
Câu 4:
(THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018)
Cho dãy số
n
u
với
3 .
n
n
u
Tính
1
?
n
u
A.
1
3 3.
n
n
u
B.
1
3.3 .
n
n
u
C.
1
3 1.
n
n
u
D.
1
3 1 .
n
u n
Lời giải
Chọn B
Ta có
1
1
3 3.3 .
n n
n
u
Câu 5:
(THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018)
Cho
cấp
số cộng
: 2, , 6, .
n
u a b
Tích
ab
bằng?
A.
32
. B.
40
. C.
12
. D.
22
.
Lời giải
Chọn A
Ta có
2 6 2 4
32.
2.6 8
a a
ab
a b b
Câu 6:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Trong các dãy số sau đây dãy số nào
là cấp số nhân?
A. Dãy số
2
,
2
,
2
,
2
, …,
2
,
2
,
2
,
2
, …
B. Dãy số
n
u
, xác định bởi công thức
3 1
n
n
u
với
*
n
.
C. Dãy số
n
u
, xác định bởi hệ:
1
*
1
1
2 : 2
n n
u
u u n n
.
D. Dãy số các số tự nhiên
1
,
2
,
3
, ….
Lời giải
Chọn A
Dãy số
2
,
2
,
2
,
2
, …,
2
,
2
,
2
,
2
, …. là cấp số nhân với số hạng đầu
1
2
u
, công bội
1
q
.
Dãy số
n
u
xác định bởi công thức
3 1
n
n
u
có
1
1
3 1 4
u
,
2
2
u
,
3
3
u
. Nhận xét:
3
2
2 1
u
u
u u
nên
n
u
không là cấp số nhân.
Dãy số
n
u
, xác định bởi hệ:
1
*
1
1
2 : 2
n n
u
u u n n
có
1
1
u
,
1
3
u
,
3
5
u
. Nhận
xét:
3
2
2 1
u
u
u u
nên
n
u
không là cấp số nhân.
Dãy số các số tự nhiên
1
,
2
,
3
, …. có
1
1
u
,
1
2
u
,
3
3
u
. Nhận xét:
3
2
2 1
u
u
u u
nên không là
cấp số nhân.
Câu 7:
(THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018)
Tính giới hạn
2 1
lim
1
n
I
n
A.
1
2
I
. B.
I 
. C.
2I
. D.
1I
.
Lời giải
Chọn C
Ta có
2 1
lim
1
n
I
n
1
2
lim 2
1
1
n
n
.
Câu 8:
(THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018)
Cho một cấp số cộng có
4
2
u
,
2
4
u
. Hỏi
1
u
bằng bao nhiêu?
A.
1
6
u
. B.
1
1
u
. C.
1
5
u
. D.
1
1
u
.
Lời giải
Chọn C
Theo giả thiết ta có
4
2
2
4
u
u
1
1
3 2
4
u d
u d
1
5
1
u
d
.
Câu 1:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
có số hạng tổng
quát là
3 2
n
u n
. Tìm công sai
d
của cấp số cộng.
A.
3
d
. B.
2
d
. C.
2
d
. D.
3
d
.
Lời giải
Chọn A
Ta có
1
3 1 2 3 2 3
n n
u u n n
Suy ra
3
d
là công sai của cấp số cộng.
Câu 2:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Tổng
2
1 1 1
3 3 3
n
S
có giá trị là:
A.
1
9
. B.
1
4
. C.
1
3
. D.
1
2
.
Lời giải
Chọn D
Ta có
2
1 1 1
3 3 3
n
S
là tổng của cấp số nhân lùi vô hạn
n
u
với
1
3
n
n
u
có số hạng
đầu
1
1
3
u
, công sai
1
3
q
.
Do đó
1
1
1
3
1
1 2
1
3
u
S
q
.
Câu 3:
(THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018)
Trong các phát biểu sau, phát biểu
nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Một cấp số cộng có công sai dương là một dãy số dương.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
Lời giải
Chọn B
Một phản ví dụ: dãy số
n
u
, với
2
n
u n
là cấp số cộng có công sai
1 0
d
.
Nhưng dạng khai triển của nó là
1
;
0
;
1
… không phải là một dãy số dương.
Câu 4:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
có
1
11
u
và công
sai
4
d
. Hãy tính
99
u
.
A.
401
. B.
403
. C.
402
. D.
404
.
Lời giải
Chọn B
Ta có :
99 1
98u u d
11 98.4
403
.
Câu 5:
(THPT Ninh Giang-Hải Dương năm 2017-2018)
Dãy số nào sau đây là một cấp số cộng ?
A.
1
1
1
:
2, 1
n
n n
u
u
u u n
. B.
1
1
3
:
2 1, 1
n
n n
u
u
u u n
.
C.
:
n
u
1
;
3
;
6
;
10
;
15
;
. D.
:
n
u
1
;
1
;
1
;
1
;
1
;
.
Lời giải
Chọn A
Dãy số ở đáp án A thỏa
1
2
n n
u u
với mọi
1n
nên là cấp số cộng.
Câu 6:
(THPT Quãng Xương 1-Thanh Hóa năm 2017-2018)
Cho tứ diện
ABCD
, các điểm
M
,
N
lần
lượt là trung điểm của
AB
,
CD
. Không thể kết luận
G
là trọng tâm tứ diện
ABCD
trong
trường hợp
A.
0
GM GN
.
B.
GM GN
.
C.
0
GA GB GC GD
.
D.
4
PG PA PB PC PD
với
P
là điểm bất kỳ.
Lời giải
Chọn B
Theo giả thiết ta có
GM GN
thì chưa thể kết luận ngay được
G
là trung điểm
MN
.
GV GIẢI đã đề xuất sửa đáp án D của đề gốc, từ
4
PG PA PB PC PC
 
thành
4
PG PA PB PC PD
với
P
là điểm bất kỳ.
Các phương án còn lại ta kết luận được ngay
G
là trọng tâm của tứ diện
ABCD
.
Câu 7:
(THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018)
Một cấp số nhân có số hạng đầu
1
3
u
,
công bội
2
q
. Biết
765
n
S
. Tìm
n
?
A.
7
n
. B.
6
n
. C.
8
n
. D.
9
n
.
Hướng dẫn giải
Chọn C
Áp dụng công thức của cấp số nhân ta có:
1
1 3. 1 2
765
1 1 2
n n
n
u q
S
q
8
n
.
Câu 1:
(THPT Lê Quý Đôn-Hà Nội năm 2017-2018)
Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình
vuông tâm
O
,
SA ABCD
. Gọi
I
là trung điểm của
SC
. Khoảng cách từ
I
đến mặt phẳng
ABCD
bằng độ dài đoạn thẳng nào?
A.
IO
. B.
IA
. C.
IC
. D.
IB
.
Lời giải
Chọn A
Do
I
là trung điểm của
SC
và
O
là trung điểm
AC
nên
//IO SA
. Do
SA ABCD
nên
IO ABCD
, hay khoảng cách từ
I
đến mặt phẳng
ABCD
bằng độ dài đoạn thẳng
IO
.
O
I
C
A
B
D
S
Câu 2:
(THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018)
Cho
2
2
4 5
lim
4 1
n n
I
n n
. Khi đó giá trị
của
I
là
A.
1I
. B.
5
3
I
. C.
1I
. D.
3
4
I
.
Lời giải
Chọn A
Ta có
2
2
4 5
lim
4 1
n n
I
n n
2
2
5
4 1
lim
1
4 1
n
n
1
Câu 3:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Cho cấp số cộng có
1
3
u
,
4
d
. Chọn
khẳng định đúng trong các khẳng định sau?
A.
5
15
u
. B.
4
8
u
. C.
3
5
u
. D.
2
2
u
.
Lời giải
Chọn C
Ta có
3 1
2u u d
3 2.4
5
.
Câu 4:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Từ các chữ số
0
,
1
,
2
,
3
,
4
,
5
,
8
lập được
bao nhiêu số có ba chữ số đôi một khác nhau, chia hết cho
2
và
3
.
A.
35
số. B.
52
số. C.
32
số. D.
48
số.
Lời giải
Chọn A
Số chia hết cho
2
và
3
là số chẵn và có tổng các chữ số của nó chia hết cho
3
.
Gọi
1 2 3
a a a
là số tự nhiên có ba chữ số đôi một khác nhau, chia hết cho
2
và
3
được lập từ các
chữ số
0
,
1
,
2
,
3
,
4
,
5
,
8
.
 Trường hợp 1:
3
0
a
Khi đó các chữ số
1 2
,a a
được lập từ các tập
1;2
,
1;5
,
1;8
,
2;4
,
4;5
,
4;8
.
Trường hợp này có
6.2! 12
số.
 Trường hợp 2:
3
2
a
Khi đó các chữ số
1 2
,a a
được lập từ các tập
1;0
,
4;0
,
1;3
,
3;4
,
5;8
.
Trường hợp này có
2 3.2! 8
số.
 Trường hợp 3:
3
4
a
Khi đó các chữ số
1 2
,a a
được lập từ các tập
2;0
,
2;3
,
3;5
,
3;8
.
Trường hợp này có
1 3.2! 7
số.
 Trường hợp 4:
3
8
a
Khi đó các chữ số
1 2
,a a
được lập từ các tập
0;1
,
0;4
,
1;3
,
2;5
,
3;4
.
Trường hợp này có
2 3.2! 8
số.
Vậy có tất cả
12 8 7 8 35
số cần tìm.
Câu 5:
(THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018)
Cho cấp số nhân
n
u
có
1
2
u
và công
bội
3
q
. Số hạng
2
u
là
A.
2
6
u
. B.
2
6
u
. C.
2
1
u
. D.
2
18
u
.
Lời giải
Chọn A
Số hạng
2
u
là
2 1
.u u q
6
Câu 6:
(THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018)
Cho dãy số
n
u
thỏa mãn
1
2 1
n
n
u
n
.
Tìm số hạng thứ
10
của dãy số đã cho.
A.
51,2
. B.
51,3
. C.
51,1
. D.
102,3
.
Lời giải
Chọn B
Ta có:
10 1
10
2 1
10
u
51,3
.
Câu 7:
(THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018)
Cho dãy số
1
1
4
n n
u
u u n
. Tìm số
hạng thứ
5
của dãy số.
A.
16
. B.
12
. C.
15
. D.
14
.
Lời giải
Chọn D
Ta có
2 1
1 5
u u
;
3 2
2 7
u u
;
4 3
3 10
u u
. Do đó số hạng thứ
5
của dãy số là
5 4
4 14
u u
.
Câu 8: (THPT Chuyên Thái Bình-lần 4 năm 2017-2018) Tính
2018
1
lim
1
x
x
x

.
A.
1
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn D
2
2018 2017
2017
1 1
1 1
lim lim . 0
1
1
1
x x
x
x x
x x
x
 
.
Câu 9:
(THPT Lê Xoay-Vĩnh phúc-lần 1 năm 2017-2018)
4
4
2 2 2
lim
4 2 5
n n
n n
bằng
A.
2
11
. B.
1
2
. C.

. D.
0
.
Lời giải
Chọn B
Ta có
4
3 4
4
3 4
2 2
2
2 2 2 1
lim lim
2 5
4 2 5 2
4
n n
n n
n n
n n
.
Câu 10: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Trong các dãy số sau, dãy
số nào là dãy số giảm?
A.
2
n
u n
. B.
2
n
u n
. C.
3
1
n
u n
. D.
2 1
1
n
n
u
n
.
Lời giải
Chọn D
*
n
ta có:
2
2
1
n n
nên A sai;
2 2 1
n n
nên B sai;
3
3
1 1 1
n n
nên C sai.
Với
2 1
1
n
n
u
n
thì
1
3
0
1 .
n n
u u
n n
nên dãy
2 1
1
n
n
u
n
giảm.
Câu 11: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Cấp số cộng
n
u
có số hạng đầu
1
3
u
, công sai
2
d
thì số hạng thứ 5 là
A.
5
8
u
. B.
5
1
u
. C.
5
5
u
. D.
5
7
u
.
Lời giải
Chọn C
Ta có:
5 1
4 3 4. 2 5
u u d
.
Câu 12: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Cho dãy số
n
u
là một cấp số cộng có
1
3
u
và công sai
4
d
. Biết tổng
n
số hạng đầu của dãy số
n
u
là
253
n
S
. Tìm
n
.
A.
9
. B.
11
. C.
12
. D.
10
.
Lời giải
Chọn B
Ta có
1
2 1 2.3 1 .4
253
2 2
n
n u n d n n
S
2
11
4 2 506 0
23
2
n
n n
n L
.
Câu 1:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Có bao nhiêu tập con gồm
3
phần tử
của tập hợp
1;2;3;4;7;8;9
X
?
A.
3
7
A
. B.
3
9
C
. C.
3
7
C
. D.
3
9
A
.
Lời giải
Chọn C
Số tập con gồm
3
phần tử của tập hợp
1;2;3;4;7;8;9
X
là số tổ hợp chập
3
của
7
phần tử.
Vậy có
3
7
C
tập hợp.
Câu 2:
3 2
lim
2 4
x
x
x

bằng
A.
1
2
. B.
3
4
. C.
1
. D.
3
2
.
Câu 3:
3 2
lim
2 4
x
x
x

bằng
A.
1
2
. B.
3
4
. C.
1
. D.
3
2
.
Lời giải
Chọn D
Ta có:
3 2
lim
2 4
x
x
x

2
3
lim
4
2
x
x
x

3
2
.
Câu 4: Cho cấp số cộng
n
u
thỏa mãn
4
4 6
10
26
u
u u
có công sai là
A.
3
d
. B.
3
d
. C.
5
d
. D.
6
d
.
Câu 5: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 2; 3; 4; 5
.
B.
1; 2; 4; 8; 16
. C.
1; 1; 1; 1; 1
. D.
1; 2; 4; 8; 16
.
Câu 6: Cho cấp số cộng
n
u
thỏa mãn
4
4 6
10
26
u
u u
có công sai là
A.
3
d
. B.
3
d
. C.
5
d
. D.
6
d
.
Lời giải
Chọn B
Gọi
d
là công sai.
Ta có:
4
1
1
4 6 1
10 3 10
1
26
2 8 26
3
u u d
u
u u
u d
d
.
Vậy công sai
3
d
.
Câu 7: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 2; 3; 4; 5
.
B.
1; 2; 4; 8; 16
. C.
1; 1; 1; 1; 1
. D.
1; 2; 4; 8; 16
.
Lời giải
Chọn A
Dãy
1; 2; 4; 8; 16
là cấp số nhân với công bội
2
q
.
Dãy
1; 1; 1; 1; 1
là cấp số nhân với công bội
1
q
.
Dãy
1; 2; 4; 8; 16
là cấp số nhân với công bội
2
q
.
Dãy
1; 2; 3; 4; 5
là cấp số cộng với công sai
1
d
.
Câu 8: Cho dãy số
n
u
với
2 1
n
u n
. Dãy số
n
u
là dãy số
A.Bị chặn trên bởi 1. B. Giảm.
C. Bị chặn dưới bởi 2. D. Tăng.
Câu 9: Cho dãy số
n
u
với
2 1
n
u n
. Dãy số
n
u
là dãy số
A.Bị chặn trên bởi 1. B. Giảm.
C. Bị chặn dưới bởi 2. D. Tăng.
Lời giải
Chọn D
*
n
ta có:
1
2 1 1 2 1 2 0
n n
u u n n
nên
1
n n
u u
vậy dãy số
n
u
tăng.
Câu 10: Cho cấp số nhân
n
u
có số hạng đầu
1
5
u
và công bội
2
q
. Số hạng thứ sáu của
n
u
là:
A.
6
160
u
. B.
6
320
u
. C.
6
160
u
. D.
6
320
u
.
Câu 11: Biết bốn số
5
;
x
;
15
;
y
theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức
3 2x y
bằng.
A.
50
. B.
70
. C.
30
. D.
80
.
Câu 12: Cho cấp số nhân
n
u
có số hạng đầu
1
5
u
và công bội
2
q
. Số hạng thứ sáu của
n
u
là:
A.
6
160
u
. B.
6
320
u
. C.
6
160
u
. D.
6
320
u
.
Hướng dẫn giải
Chọn C
Ta có
5
5
6 1
5. 2 160
u u q
.
Câu 13: Biết bốn số
5
;
x
;
15
;
y
theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức
3 2x y
bằng.
A.
50
. B.
70
. C.
30
. D.
80
.
Hướng dẫn giải
Chọn B
Ta có:
5 15
10
2
x
20
y
. Vậy
3 2 70
x y
.
Câu 14: Số cách sắp xếp
6
học sinh vào một bàn dài có
10
chỗ ngồi là:
A.
6
10
6.A
. B.
6
10
C
. C.
6
10
A
. D.
6
10P
.
Câu 15: Số cách sắp xếp
6
học sinh vào một bàn dài có
10
chỗ ngồi là:
A.
6
10
6.A
. B.
6
10
C
. C.
6
10
A
. D.
6
10P
.
Lời giải
Chọn C
Số cách sắp xếp
6
học sinh vào một bàn dài có
10
chỗ ngồi là số chỉnh hợp chập
6
của
10
phần tử. Vậy số cách sắp xếp là:
6
10
A
.
Câu 16: Cho cấp số cộng
n
u
có
1 2
4; 1
u u
. Giá trị của
10
u
bằng
A.
10
31
u
. B.
10
23
u
. C.
10
20
u
. D.
10
15.
u
Câu 17: Cho cấp số cộng
n
u
có
1 2
4; 1
u u
. Giá trị của
10
u
bằng
A.
10
31
u
. B.
10
23
u
. C.
10
20
u
. D.
10
15.
u
Hướng dẫn giải
Chọn B
1 2
4; 1
u u
3
d
. Vậy
10 1
9 4 9. 3 23
u u d
Câu 18: Cấp số cộng
n
u
có số hạng đầu
1
3
u
, công sai
5
d
, số hạng thứ tư là
A.
4
23
u
. B.
4
18
u
. C.
4
8
u
. D.
4
14
u
.
Câu 19: Cấp số cộng
n
u
có số hạng đầu
1
3
u
, công sai
5
d
, số hạng thứ tư là
A.
4
23
u
. B.
4
18
u
. C.
4
8
u
. D.
4
14
u
.
Lời giải
Chọn B
4 1
3u u d
3 5.3
18
.
Câu 20: Khẳng định nào dưới đây sai?
A. Số hạng tổng quát của cấp số nhân
n
u
là
1
1
.
n
n
u u q
, với công bội
q
và số hạng đầu
1
u
.
B. Số hạng tổng quát của cấp số cộng
n
u
là
1
1
n
u u n d
, với công sai
d
và số hạng
đầu
1
u
.
C. Số hạng tổng quát của cấp số cộng
n
u
là
1n
u u nd
, với công sai
d
và số hạng đầu
1
u
.
D. Nếu dãy số
n
u
là một cấp số cộng thì
2
1
2
n n
n
u u
u
*
n
.
Câu 21: Khẳng định nào dưới đây sai?
A. Số hạng tổng quát của cấp số nhân
n
u
là
1
1
.
n
n
u u q
, với công bội
q
và số hạng đầu
1
u
.
B. Số hạng tổng quát của cấp số cộng
n
u
là
1
1
n
u u n d
, với công sai
d
và số hạng
đầu
1
u
.
C. Số hạng tổng quát của cấp số cộng
n
u
là
1n
u u nd
, với công sai
d
và số hạng đầu
1
u
.
D. Nếu dãy số
n
u
là một cấp số cộng thì
2
1
2
n n
n
u u
u
*
n
.
Lời giải
Chọn C
Câu 22: Cho cấp số cộng
n
u
có số hạng đầu
1
3
u
và công sai
2
d
. Tính
5
u
.
A.
11
. B.
15
. C.
12
. D.
14
.
Câu 23: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông.
SA
vuông góc với
ABCD
và
H
là
hình chiếu vuông góc của
A
lên
SB
. Khẳng định nào sau đây là sai?
A.
AH BC
. B.
AH SC
. C.
BD SC
. D.
AC SB
.
Câu 24: Cho cấp số cộng
n
u
có số hạng đầu
1
3
u
và công sai
2
d
. Tính
5
u
.
A.
11
. B.
15
. C.
12
. D.
14
.
Lời giải
Chọn A
Ta có
5 1
4u u d
3 4.2 11
.
Câu 25: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông.
SA
vuông góc với
ABCD
và
H
là
hình chiếu vuông góc của
A
lên
SB
. Khẳng định nào sau đây là sai?
A.
AH BC
. B.
AH SC
. C.
BD SC
. D.
AC SB
.
Lời giải
Chọn D
Đáp án A đúng do
BC SAB
nên
AH BC
.
Đáp án B đúng do
AH SBC
nên
AH SC
.
Đáp án C đúng do
BD SAC
nên
BD SC
.
Câu 26: Dãy số nào sau đây có giới hạn bằng
0
?
A.
1 4 n
. B.
3
3
1
n n
n
. C.
2
1n
n
. D.
3
3
1 2
5
n
n n
.
Câu 27: Dãy số nào sau đây có giới hạn bằng
0
?
A.
1 4 n
. B.
3
3
1
n n
n
. C.
2
1n
n
. D.
3
3
1 2
5
n
n n
.
Lời giải
Chọn C
Ta có
2 2
1 1 1
lim lim 0
n
n n n
.
Câu 28: Cho dãy số
n
u
là một cấp số nhân có số hạng đầu
1
u
và công bội
q
. Đẳng thức nào sau đây
sai?
A.
1
n n
u u q
,
1
n
. B.
1
1
n
n
u u q
,
2
n
.
C.
1
n
n
u u q
,
2
n
. D.
2
1 1k k k
u u u
,
2
k
.
Câu 29: Cho dãy số
n
u
là một cấp số nhân có số hạng đầu
1
u
và công bội
q
. Đẳng thức nào sau đây
sai?
A.
1
n n
u u q
,
1
n
. B.
1
1
n
n
u u q
,
2
n
.
C.
1
n
n
u u q
,
2
n
. D.
2
1 1k k k
u u u
,
2
k
.
Lời giải
Chọn C .
Cho dãy số
n
u
là một cấp số nhân có số hạng đầu
1
u
và công bội
q
.
Từ định nghĩa của cấp số nhân ta có các kết quả sau:
1
n n
u u q
,
1
n
,
1
1
n
n
u u q
,
2
n
,
2
1 1k k k
u u u
,
2
k
.
Kết quả của đáp án C là sai.
Câu 1:
(THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018)
Trong các phát biểu sau, phát
biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương.
Lời giải.
Chọn D
A. Đúng vì dãy số đã cho là cấp số nhân với công bội
1
q
.
B. Đúng vì dãy số đã cho là cấp số cộng với công sai
0
d
.
C. Đúng vì dãy số đã cho là cấp số cộng có công sai dương nên:
1
0
n n
u u d
1
n n
u u
.
D. Sai. Ví dụ dãy
5
;
2
;
1
;
3
; … là dãy số có
3 0
d
nhưng không phải là dãy số dương.
Câu 2:
(THTT Số 1-484 tháng 10 năm 2017-2018)
Cho cấp số cộng
n
u
và gọi
n
S
là tổng
n
số hạng
đầu tiên của nó. Biết
7
77
S
và
12
192
S
. Tìm số hạng tổng quát
n
u
của cấp số cộng đó
A.
5 4
n
u n
. B.
3 2
n
u n
. C.
2 3
n
u n
. D.
4 5
n
u n
.
Lời giải
Chọn B
Giả sử cấp số cộng có số hạng đầu là
1
u
và công sai
d
.
Ta có:
1
7 1
1
1
12
1
7.6.
7 77
77 7 21 77
5
2
12.11. 12 66 192192
2
12 192
2
d
u
S u d
u
d u dS
d
u
.
Khi đó:
1
1 5 2 1 3 2
n
u u n d n n
.
Câu 3:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Cho cấp số nhân
1
; 1, 2
n
u u q
. Hỏi số
1024
là số hạng thứ mấy?
A.
11
. B.
9
. C.
8
. D.
10
.
Lời giải
Chọn A
Ta có
1 1 1 10
1
. 1.2 1024 2 2 1 10 11
n n n
n
u u q n n
.
Câu 4:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Trong các dãy số sau, dãy nào là cấp số nhân?
A.
1
n
n
u n
. B.
2
n
u n
. C.
2
n
n
u
. D.
3
n
n
n
u
.
Lời giải
Chọn C
Lập tỉ số
1
n
n
u
u
A:
1
1
1 . 1
1
1 .
n
n
n
n
n
u
n
u n
n
n
u
không phải cấp số nhân.
B:
2
1
2
1
n
n
n
u
u n
n
u
không phải là cấp số nhân.
C:
1
1
1
2
2 2
2
n
n
n n
n
n
u
u u
u
n
u
là cấp số nhân có công bội bằng
2
.
D:
1
1
3
n
n
u
n
u n
n
u
không phải là cấp số nhân.
Câu 5:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Xác định số hạng đầu và công bội của cấp số
nhân
n
u
có
4 2
54
u u
và
5 3
108
u u
.
A.
1
3
u
và
2
q
. B.
1
9
u
và
2
q
. C.
1
9
u
và
–2
q
. D.
1
3
u
và
–2
q
.
Lời giải
Chọn B
Gọi số hạng đầu của cấp số nhân là
1
u
và công bội là
q
.
Theo giả thiết, ta có
4 2
5 3
54
108
u u
u u
3
1 1
4 2
1 1
. . 54
. . 108
u q u q
u q u q
2
2 2
1
54 1
108 2
1
q q
q q
2
q
.
Với
2
q
, ta có
1 1
8 2 54
u u
1
6 54
u
1
9
u
.
Câu 6:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Xác định số hàng đầu
1
u
và công sai
d
của cấp
số cộng
n
u
có
9 2
5u u
và
13 6
2 5
u u
.
A.
1
3
u
và
4
d
. B.
1
3
u
và
5
d
. C.
1
4
u
và
5
d
. D.
1
4
u
và
3
d
.
Lời giải
Chọn A
Ta có:
1
1
n
u u n d
. Theo đầu bài ta có hpt:
1 1
1 1
8 5
12 2 5 5
u d u d
u d u d
1
1
1
4 3 0
3
2 5
4
u d
u
u d
d
.
Câu 7:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Với mọi
*
n
, dãy số
n
u
nào sau đây không phải
là cấp số cộng hay cấp số nhân?
A.
2017 2018
n
u n
. B.
2017
1
2018
n
n
n
u
.
C.
1
1
1
, 1,2,3,...
2018
n
n
u
u
u n
. D.
1
1
1
2017 2018
n n
u
u u
.
Lời giải
Chọn D
 Xét dãy số
n
u
trong phương án A, ta có
1
2017 1 2018 2017 2018 2017
n n
u u n n
với mọi
*
n
. Vậy dãy số này là
một cấp số cộng.
 Xét dãy số
n
u
trong phương án B, ta có
1
1
1
2017
1
2017
2018
2018
2017
1
2018
n
n
n
n
n
n
u
u
với mọi
*
n
. Vậy dãy số này là một cấp số nhân.
 Xét dãy số
n
u
trong phương án C, ta có
1
1
2018
2018
n
n
n n
u
u
u u
với mọi
*
n
. Vậy dãy số này là một cấp số nhân.
 Xét dãy số
n
u
trong phương án D, ta có
1 1 1
2
1 2
3
2 3
1 1
2 1
2017 2018 2017 2018 2017
2017
2017
...
2017 2017 2017 2018 1 2.2017
n n n n n n
n n
n n
n n n
u u u u u u
u u
u u
u u
Vậy dãy số này không phải là cấp số cộng.
Mặt khác, ta có
1
2017 2018
2018
2017
n n
n n n
u u
u u u
.
Tỷ số này thay đổi khi
n
u
thay đổi nên dãy
n
u
không là cấp số nhân.
Câu 8:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Cho ba số
,a
,b
c
theo thứ tự đó vừa lập
thành cấp số cộng, vừa lập thành cấp số nhân khi và chỉ khi
A.
1;
a
2;
b
3
c
. B.
;a d
2 ;b d
3c d
với
0
d
cho trước.
C.
;a q
2
;b q
3
c q
với
0
q
cho trước. D.
a b c
.
Lời giải
Chọn D
Gọi
d
và
q
lần lượt là công sai của cấp số cộng và công bội của cấp số nhân.
Ta có:
2
2
b a d aq
c a d aq
2
d aq aq
2
a aq aq aq
2
2 1 0
q q
1 0
q d
a b c
.
Câu 9:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Cho chuyển động xác định bởi
phương trình
3 2
3 9S t t t
, trong đó
t
được tính bằng giây và
S
được tính bằng mét. Tính
vận tốc tại thời điểm gia tốc triệt tiêu.
A.
2
12
m/s
. B.
s
21
m/
. C.
2
12
m/s
. D.
s
12
m/
.
Lời giải
Chọn D
Ta có
2
' 3 6 9v t S t t t
và
' 6 6.
a t v t t
Tại thời điểm gia tốc triệt tiêu thì
6 6 0 1t t
.
Vận tốc tại thời điểm gia tốc triệt tiêu là
2
1 12
m/s
v
.
Câu 10:
(THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018)
Cho cấp số cộng
n
u
có
1
123
u
,
3 15
84
u u
. Số hạng
17
u
bằng
A.
235
. B.
11
. C.
3
96000cm
. D.
3
81000cm
.
Lời giải
Chọn B
Giả sử cấp số cộng
n
u
có công sai
d
.
Theo giả thiết ta có:
3 15
84
u u
1 1
2 14 84
u d u d
12 84
d
7
d
.
Vậy
17 1
16u u d
123 16. 7
11
.
Câu 11:
(THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018)
Cho cấp số nhân
n
u
có
2 3
4; 13
S S
.
Biết
2
0
u
, giá trị
5
S
bằng
A.
35
16
. B.
181
16
. C.
2
. D.
121
.
Lời giải
Chọn B
Ta có:
2
1
2
2
1
2
3
1
1
1
3
1
1 4
4 1
1 4
1 1 13
4
1 13
1
2
13
1
1
u q
q
S
u q
q q q
u q q
u q
u
S
q
q
Xét
1
2
2
1
3 1
1 4
1 : 4 9 9 0
3
1 13
16
4
q u
q
q q
q q
q u
Với
1 2 1
3; 1 . 3 0
q u u u q
(loại)
Với
1 2 1
3
; 16 . 12 0
4
q u u u q
(Thỏa mãn).
Vậy
5
5
1
5
3
16 1
1 4
181
3
1 16
1
4
u q
S
q
.
Câu
12:
(THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018)
Một cấp số cộng có số
hạng đầu
1
2018
u
công sai
5
d
. Hỏi bắt đầu từ số hạng nào của cấp số cộng đó thì nó
nhận giá trị âm.
A.
406
u
.
B.
403
u
.
C.
405
u
.
D.
404
u
.
Lời
giải
Chọn
C
Ta có
1
1
n
u n d u
.
n
Theo đề ra
2018 5 1 0
n
u n
2018 5 1
n
2023
2023 5 405
5
n n n
PP
trắc
nghiệm
:
Vì
1
1 2018 5 1
n
u n d u n
Thay từng giá trị vào ta có:
403
404
2018 5.402 8
2018 5.403 3
u
u
405
2018 5.404 2
u
.
Câu
13:
(THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018)
Một cấp số cộng có tổng
của
n
số hạng đầu
n
S
tính theo công thức
2
5 3
n
S n n
,
*
n
. Tìm số hạng đầu
1
u
và
công sai
d
của cấp số cộng đó.
A.
1
u d
.
B.
1
8; 10
u d
.
C.
.
1
8; 10
u d
..
D.
1
8; 10
u d
.
Lời giải
Chọn C
Ta có
2
1 1
5.1 3.1 8
S u
Lại có
2 1 2 1
2 26 10.
S u u u d d
Câu
14:
(THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018)
Chọn phát biểu
sai
trong
các phát biểu sau
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
B. Một cấp số nhân có công bội
1
q
là một dãy tăng.
C. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
D. Một cấp số cộng có công sai dương là một dãy tăng.
Lời giải
Chọn B
Xét cấp số nhân
n
u
với
1
2
u
và công bội
3 1
q
. Ta có:
2 1
2 .3 6
u u
;
3 2
2 . 6 12
u u
;
4 3
2 .12 24
u u
; … là dãy số không
tăng, không giảm.
Câu 15:
(THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018)
Cho
n
u
là cấp số cộng có công sai
là
d
,
n
v
là cấp số nhân có công bội là
q
và các khẳng định.
I)
1
2,
n n
u d u n n . II)
1
2,
n
n
v q v n n
.
III)
1 1
2,
2
n n
n
u u
u n n
. IV)
2
1 1
. 2,
n n n
v v v n n
.
V)
1
1 2
... 2,
2
n
n
n v v
v v v n n
.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn B
I) ĐÚNG : theo định nghĩa cấp số cộng.
II) SAI: do
1
1
, 2,
n
n
v q v n n
theo công thức tổng quát của cấp số nhân.
III) ĐÚNG: theo tính chất cấp số cộng.
IV) SAI: do
2
1 1
. , 2,
n n n
v v v n n
theo tính chất cấp số nhân.
V) SAI: do đây là công thức tính tổng
n
số hạng đầu của một cấp số cộng.
Số câu đúng là:
2
.
Câu 16:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Cho cấp số nhân
n
u
có
1
3
u
, công bội
2
q
.
Hỏi
192
là số hạng thứ mấy của
?
n
u
A. Số hạng thứ
6
. B. Số hạng thứ
7
. C. Số hạng thứ
5
. D. Số hạng thứ
8
.
Lời giải
Chọn B
Giả sử
192
là số hạng thứ
n
của
n
u
với
*
n
.
Ta có
1
1
192 .
n
u q
1
192 3 . 2
n
1
64 2
n
6 1
2 2
n
6 1n
7
n
. Do đó
192
là số hạng thứ
7
của
n
u
.
Câu 17:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
có
5
15
u
,
20
60
u
. Tổng
của
10
số hạng đầu tiên của cấp số cộng này là:
A.
10
125
S
. B.
10
250
S
. C.
10
200
S
. D.
10
200
S
.
Lời giải
Chọn A
Gọi
1
u
,
d
lần lượt là số hạng đầu và công sai của cấp số cộng.
Ta có:
5
20
15
60
u
u
1
1
u d
u d
1
35
5
u
d
.
Vậy
10 1
10
. 2 9
2
S u d
5. 2. 35 9.5
125
.
Câu 1:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Xác định
x
dương để
2 3x
;
x
;
2 3x
lập thành cấp số nhân.
A.
3
x
. B.
3
x .
C.
3
x
. D. không có giá trị nào của
x
.
Lời giải
Chọn B
2 3x
;
x
;
2 3x
lập thành cấp số nhân
2
2 3 2 3
x x x
2 2
4 9
x x
2
3
x
3
x
.
Vì
x
dương nên
3
x .
Câu 2:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Cho dãy số
n
u
xác định bởi
1
1
1
2 1, 1
n n
u
u u n n
. Giá trị của
n
để
2017 2018 0
n
u n
là
A. Không có
n
. B.
1009
. C.
2018
. D.
2017
.
Lời giải
Chọn C
Cách 1 :
Với
1
n
ta có:
2
2 1
3 4 2
u u
.
Với
2
n
ta có:
2
3 2
2.2 1 9 3
u u
.
Với
3
n
ta có:
2
4 3
2.3 1 16 4
u u
.
Từ đó ta có:
2
n
u n
.
Suy ra
2017 2018 0
n
u n
2
2017 2018 0
n n
1
2018
n L
n N
.
Cách 2 :
Ta có :
2 1
2.1 1
u u
3 2
2.2 1
u u
4 3
2.3 1
u u
……………….
1
2. 1 1
n n
u u n
Cộng các vế tương ứng ta được :
1
2. 1 2 3 ..... 1 1
n
u u n n
1
1 2. 1 1 1
2
n
n
u n n
2
n
u n
. Suy ra
2017 2018 0
n
u n
2
2017 2018 0
n n
1
2018
n L
n N
.
Câu 3:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Cấp số nhân
n
u
có công bội âm,
biết
3
12
u
,
7
192
u
. Tìm
10
u
.
A.
10
1536
u
. B.
10
1536
u
. C.
10
3072
u
. D.
10
3072
u
.
Lời giải
Chọn B
Gọi
q
là công bội của cấp số nhân đề bài cho
0
q
.
Ta có
2
3 1
6
7 1
12
192
u u q
u u q
6
1
2
1
192
12
u q
u q
4
16
q
.
Mà
0
q
2
q
1
2
12
3
u
q
.
Do đó
9
9
10 1
3. 2 1536
u u q
.
Câu 4:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Cho dãy số
n
u
xác định bởi
1
1
cos 0
1
, 1
2
n
n
u
u
u n
. Số hạng thứ 2017 của dãy số đã cho là
A.
2017
2017
sin
2
u
. B.
2017
2017
cos
2
u
. C.
2017
2016
cos
2
u
. D.
2017
2016
sin
2
u
.
Lời giải
Chọn C
Do
0
nên
Ta có
2
2
1 cos
cos cos
2 2 2
u
.
2
3
1 cos
2
cos cos
2 4 4
u
Vậy
1
cos
2
n
n
u
với mọi
*
n
. Ta sẽ chứng mình bằng quy nạp.
Với
1
n
đúng.
Giả sử với
*
n k
ta có
1
cos
2
k
k
u
. Ta chứng minh
1
1
cos
2
k
k
u
.
Thật vậy
1
2
1
1 cos
1
2
cos cos
2 2 2 2
k
k
k
k k
u
u
.
Từ đó ta có
2017
2016
cos
2
u
.
Câu 5:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Cấp số nhân
n
u
có
20 17
1 5
8
.
272
u u
u u
Tìm
1
u
, biết rằng
1
100
u
.
A.
1
16.
u
B.
1
2.
u
C.
1
16.
u
D.
1
2.
u
Lời giải
Chọn A
Ta có:
16 3
19 16
1
20 17
1 1
4
4
1 5
1 1
1
8 0 1
8 . 8
272
. 272
1 272 2
u q q
u u u q u q
u u
u u q
u q
.
Từ
2
suy ra
1
0
u
do đó:
0
1
2
q
q
.
Nếu
0
q
thì
1
2 272
u
không thõa điều kiện
1
100
u
.
Nếu
2
q
thì
1
2 16
u
thõa điều kiện
1
100
u
.
Câu 6:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
có
1
1
u
và công sai
2
d
. Tổng
10 1 2 3 10
.....
S u u u u
bằng:
A.
10
110
S
. B.
10
100
S
. C.
10
21
S
. D.
10
19
S
.
Lời giải
Chọn B
* Áp dụng công thức
1
1
2 1
2 2
n
n
n u n d
n u u
S
ta được:
10
10 2 10 1 2
100
2
S
.
Câu 7:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Tổng của
n
số hạng đầu tiên của một
dãy số
n
a
,
1n
là
2
2 3
n
S n n
. Khi đó
A.
n
a
là một cấp số cộng với công sai bằng
4
.
B.
n
a
là một cấp số nhân với công bội bằng
4
.
C.
n
a
là một cấp số cộng với công sai bằng
1
.
D.
n
a
là một cấp số nhân với công bội bằng
1
.
Lời giải
Chọn A
Ta có
2
2 3
n
S n n
1 1
5
u S
,
1 2 2
14
u u S
2
9
u
,
1 2 3 3
27
u u u S
3
13
u
Dựa vào nội dung các đáp án ta chọn được đáp án A.
Câu 8:
(THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018)
Cho cấp số cộng
n
u
có
1
3
u
,
6
27
u
.
Tính công sai
d
.
A.
7
d
. B.
5
d
. C.
8
d
. D.
6
d
.
Lời giải
Chọn D
Ta có
6 1
5 27 6
u u d d
.
Câu 9:
(SGD Ninh Bình năm 2017-2018)
Cho cấp số nhân
n
u
, biết
1
1
u
;
4
64
u
. Tính công bội
q
của cấp số nhân.
A.
21
q
. B.
4
q
. C.
4
q
. D.
2 2
q
.
Lời giải
Chọn C
Theo công thức tổng quát của cấp số nhân
3
4 1
u u q
3
64 1.q
4
q
.
Câu 10:
(THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018)
Cho cấp số cộng
n
u
, biết
2
3
u
và
4
7
u
. Giá trị của
15
u
bằng
A.
27
. B.
31
. C.
35
. D.
29
.
Lời giải
Chọn D
Từ giả thiết
2
3
u
và
4
7
u
suy ra ta có hệ phương trình:
1
1
3
3 7
u d
u d
1
1
2
u
d
.
Vậy
15 1
14 29
u u d
.
Câu 11:
(THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018)
Dãy số nào sau đây là dãy số
giảm?
A.
5 3
, *
2 3
n
n
u n
n
. B.
5
, *
4 1
n
n
u n
n
.
C.
3
2 3, *
n
u n n
. D.
cos 2 1 , *
n
u n n
.
Hướng dẫn giải
Chọn A
Xét
5 3
, *
2 3
n
n
u n
n
, ta có
1
5 3 1
5 3
2 1 3 2 3
n n
n
n
u u
n n
2 3 5 3
2 5 2 3
n n
n n
2 3 2 3 2 5 5 3
2 5 2 3
n n n n
n n
2 2
4 6 6 9 10 6 25 15
2 5 2 3
n n n n n n
n n
19
0, *
2 5 2 3
n
n n
.
Vậy
5 3
, *
2 3
n
n
u n
n
là dãy giảm.
Câu 12:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Cho cấp số nhân
n
u
có
1
1,
u
công bội
1
.
10
q
Hỏi
2017
1
10
là số hạng thứ mấy của
n
u
?
A. Số hạng thứ
2018.
B. Số hạng thứ
2017.
C. Số hạng thứ
2019.
D. Số hạng thứ
2016.
Lời giải
Chọn A
Ta có
1
1
1
1
10
n
n
n
u u q
.
Khi đó
1
2017 2017
1 1 1
2018
10 10 10
n
n
u n
.
Do đó
2017
1
10
là số hạng thứ
2018
của
n
u
.
Câu 13:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Cho cấp số cộng
n
u
có
4
12
u
,
14
18
u
. Tính tổng
16
số hạng đầu tiên của cấp số cộng này.
A.
16
24
S
. B.
16
26
S
. C.
16
25
S
. D.
16
24
S
.
Lời giải
Chọn D
Gọi
d
là công sai của cấp số cộng. Theo giả thiết, ta có
1
1
3 12
13 18
u d
u d
1
21
3
u
d
.
Khi đó,
1
16
2 15 .16
2
u d
S
8 42 45 24
.
Câu 14:
(THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018)
Viết ba số xen giữa
2
và
22
để ta được một cấp số cộng có
5
số hạng?
A.
6
,
12
,
18
. B.
8
,
13
,
18
. C.
7
,
12
,
17
. D.
6
,
10
,
14
.
Hướng dẫn giải
Chọn C
Xem cấp số cộng cần tìm là
n
u
có:
1
5
2
22
u
u
. Suy ra:
1
2
5
u
d
.
Vậy cấp số cộng cần tìm là
n
u
:
2
,
7
,
12
,
17
,
22
.
Câu 15:
(THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018)
Cho cấp số nhân
n
u
có
2
1
4
u
,
5
16
u
. Tìm công bội
q
và số hạng đầu
1
u
.
A.
1
2
q
,
1
1
2
u
. B.
1
2
q
,
1
1
2
u
. C.
4
q
,
1
1
16
u
. D.
4
q
,
1
1
16
u
.
Hướng dẫn giải
Chọn D
Ta có
2
5
1
4
16
u
u
1
4
1
1
. 1
4
. 16 2
u q
u q
.
Chia hai vế của
2
cho
1
ta được
3
64
q
4
q
1
1
16
u
.
Câu 16:
(THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018)
Xác định
x
để bộ ba số
2 1x
,
x
,
2 1x
theo thứ tự lập thành một cấp số nhân.
A.
1
3
x
. B.
1
3
x
.
C.
3
x
. D. Không có giá trị nào của
x
.
Hướng dẫn giải
Chọn B
Bộ ba số
2 1x
,
x
,
2 1x
theo thứ tự lập thành một cấp số nhân nên ta có
2
2 1 2 1
x x x
2 2
4 1
x x
1
3
x
.
Câu 17:
(THPT Hoài Ân-Hải Phòng năm 2017-2018)
Tính giới hạn
2
0
4 2 1 1 2
lim
x
x x x
x
.
A.
2
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn D
Ta có:
2
0
4 2 1 1 2
lim
x
x x x
x
2
0
2
4
lim
4 2 1 1 2
x
x
x x x x
0
2
4
lim 0
4 2 1 1 2
x
x
x x x
.
Câu 18:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Trong các dãy số
n
u
cho bởi số hạng
tổng quát
n
u
sau, dãy số nào là dãy số giảm ?
A.
1
2
n
n
u
. B.
3 1
1
n
n
u
n
. C.
2
n
u n
. D.
2
n
u n
.
Lời giải
Chọn A
Ta có
1
2
n
n
u
1
1
1
2
n
n
u
*
n
.
Câu 19:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Tính tổng tất cả các số hạng của một cấp
số nhân có số hạng đầu là
1
2
, số hạng thứ tư là
32
và số hạng cuối là
2048
?
A.
1365
2
. B.
5416
2
. C.
5461
2
. D.
21845
2
.
Lời giải
Chọn C
Theo bài ra ta có
1
1
2
u
,
4
32
u
và
2048
n
u
.
3
4 1
.u u q
3
1
32 .
2
q
4
q
2048
n
u
1
1
. 2048
n
u q
1 6
4 4
n
7
n
Khi đó tổng của cấp số nhân này là
7
7
1
7
1
1 4
1
5461
2
1 1 4 2
u q
S
q
.
Câu 20:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
, biết:
1
3
u
,
2
1
u
. Chọn đáp án đúng.
A.
3
4
u
. B.
3
7
u
. C.
3
2
u
. D.
3
5
u
.
Lời giải
Chọn D
Ta có
n
u
là cấp số cộng nên
2 1 3
2
u u u
suy ra
3 2 1
2 5
u u u
.
Câu 21:
(THPT Ninh Giang-Hải Dương năm 2017-2018)
Cho cấp số nhân
n
u
thỏa mãn:
1 2 3
4 1
13
26
u u u
u u
. Tổng
8
số hạng đầu của cấp số nhân
n
u
là
A.
8
3280
S
. B.
8
9841
S
. C.
8
3820
S
. D.
8
1093
S
.
Lời giải
Chọn A
Ta có :
1 2 3
4 1
13
26
u u u
u u
2
1
3
1
1 13
1 26
u q q
u q
3
2
1
26
13
1
q
q q
1 2
q
3
q
1
1
u
.
8
8
1 1 3
3280
1 3
S
.
Câu 22:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Xen giữa số
3
và số
768
là
7
số để được
một cấp số nhân có
1
3
u
. Khi đó
5
u
là:
A.
72
. B.
48
. C.
48
. D.
48
.
Lời giải
Chọn D
Ta có
1
3
u
và
9
768
u
nên
8
768 3.q
8
256
q
2
q
.
Do đó
4 4
5 1
. 3.2 48
u u q
.
Câu 23:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
, biết
1
5
u
,
2
d
. Số
81
là số hạng thứ bao nhiêu?
A.
100
. B.
50
. C.
75
. D.
44
.
Lời giải
Chọn D
Ta có
1
1
n
u u n d
81 5 1 2
n
44
n
.
Vậy
81
là số hạng thứ
44
.
Câu 24:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Cho hình chóp
.
S ABC
có
SA ABC
,
góc giữa
SB
và
ABC
là
60
,
ABC
đều cạnh
a
. Thể tích khối chóp bằng
A.
3a
. B.
3
4
a
. C.
3
2
a
. D.
3
a
.
Lời giải
Chọn B
A C
B
S
Diện tích
ABC
là
2
3
4
ABC
a
S
.
SA ABC
nên
AB
là hình chiếu của
SB
lên
ABC
.
, , 60
SB ABC SB AB SBA
.
SAB
vuông tại
A
có
60
SBA
, ta có
.tan 3SA AB SBA a
.
Thể tích khối chóp là
2 3
1 1 3
. . . . 3
3 3 4 4
ABC
a a
V S SA a
.
Câu 25:
(THPT Quãng Xương 1-Thanh Hóa năm 2017-2018)
Trong các dãy số sau, có bao nhiêu dãy
số là cấp số cộng ?
a) Dãy số
n
u
với
4
n
u n
. b) Dãy số
n
v
với
2
2 1
n
v n
.
b) Dãy số
n
w
với
7
3
n
n
w
. d) Dãy số
n
t
với
5 5
n
t n
.
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Dãy số
n
u
với
4
n
u n
có
1
4 1 4 4
n
u n n
1
4
n n
u u
,
*
n
dãy số
n
u
là cấp số cộng với công sai
4d
.
Dãy số
n
v
với
2
2 1
n
v n
có
1
3
v
,
2
9
v
,
3
19
v
nên dãy số
n
v
không là cấp số cộng.
Dãy số
n
w
với
7
3
n
n
w
có
1
1
7
3
n
n
w
1
7
3 3
n
1
1
3
n n
u u
,
*
n
dãy
số
n
w
là cấp số cộng với công sai
1
3
d
.
Dãy số
n
t
với
5 5
n
t n
có
1
5 5 5
n
t n
1
5
n n
u u
,
*
n
dãy số
n
w
là cấp số cộng với công sai
5d
.
Vậy có
3
dãy số là cấp số cộng.
Câu 26:
(THPT Tứ Kỳ-Hải Dương năm 2017-2018)
Cho dãy số vô hạn
n
u
là cấp số cộng có công sai
d
, số hạng đầu
1
u
. Hãy chọn khẳng định sai?
A.
1 9
5
2
u u
u
. B.
1n n
u u d
,
2
n
.
C.
12 1
2 11
2
n
S u d
. D.
1
( 1).
n
u u n d
,
*
n
.
Hướng dẫn giải
Chọn C
Ta có công thức tổng
n
số hạng đầu tiên của cấp số cộng là:
1
1
2
n
n n d
S nu
Suy ra
12 1
12.11.
12
2
d
S u
1
6 2 11u d
1
2 11
2
n
u d
.
Câu 27:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Tìm tất cả các giá trị thực của
m
để
hàm số
2
1 1
0
( )
1 0
x
khi x
f x
x
x m khi x

liên tục trên
.
A.
2
3
m
. B.
2
1
m
. C.
2
m
. D.
2
1
m
.
Lời giải
Chọn B
Khi
0
x
ta có:
1 1
( )
x
f x
x
liên tục trên khoảng
0;

.
Khi
0
x
ta có:
2
( ) 1
f x x m
liên tục trên khoảng
;0

.
Hàm số liên tục trên
khi và chỉ khi hàm số liên tục tại
0
x
.
Ta có:
0 0 0
1 1 1 1
lim ( ) lim lim
2
1 1
x x x
x
f x
x
x
.
2
0 0
lim ( ) lim 1 1 0
x x
f x x m m f
.
Do đó hàm số liên tục tại
0
x
khi và chỉ khi
1 1
1
2 2
m m
.
Câu 28:
(THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018)
Một loại vi khuẩn sau mỗi phút
số lượng tăng gấp đôi biết rằng sau
5
phút người ta đếm được có
64000
con hỏi sau bao nhiêu
phút thì có được
2048000
con.
A.
10
. B.
11
. C.
26
. D.
50
.
Hướng dẫn giải
Chọn A
Số lượng vi khuẩn tăng lên là cấp số nhân
n
u
với công bội
2
q
.
Ta có:
6
64000
u
5
1
. 64000
u q
1
2000
u
.
Sau
n
phút thì số lượng vi khuẩn là
1n
u
.
1
2048000
n
u
1
. 2048000
n
u q
2000.2 2048000
n
10
n
.
Vậy sau
10
phút thì có được
2048000
con.
Câu 29:
(THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018)
Tính
( ) sin 2
F x x xdx
. Chọn kết quả
đúng?
A.
1
( ) (2 cos 2 sin 2 )
4
F x x x x C
. B.
1
( ) (2 cos 2 sin 2 )
4
F x x x x C
.
C.
1
( ) (2 cos 2 sin 2 )
4
F x x x x C
. D.
1
( ) (2 cos 2 sin 2 )
4
F x x x x C
.
Hướng dẫn giải
Chọn C
Đặt
1
sin 2
co
d
d
s
2
d
2
du x
u x
v x x
v x
, ta được
1 1
( ) cos 2 cos2
2 2
dF x x x x x
1 1
cos2 sin 2
2 4
x x x C
1
(2 cos 2 sin 2 )
4
x x x C
.
Câu 30:
(THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018)
Cho một cấp số cộng
( )
n
u
có
1
1
u
và
tổng
100
số hạng đầu bằng
24850
. Tính
1 2 2 3 49 50
1 1 1
...S
u u u u u u
A.
123
S
. B.
4
23
S
. C.
9
246
S
. D.
49
246
S
.
Hướng dẫn giải
Chọn D
Ta có
100
24850
S
1
24850
2
n
n
u u
100
496
u
.
Vậy
100 1
99u u d
100 1
99
u u
d
5
d
.
1 2 2 3 49 50
1 1 1
...S
u u u u u u
1 1 1 1
...
1.6 6.11 11.16 241.246
.
5 5 5 5
5 ...
1.6 6.11 11.16 241.246
S
1 1 1 1 1 1
...
1 6 6 11 241 246
1 1
1 246
245
246
49
246
S
.
Câu 1:
(SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018)
Cho ba số
x
;
5
;
2y
theo thứ tự lập thành cấp số
cộng và ba số
x
;
4
;
2y
theo thứ tự lập thành cấp số nhân thì
2x y
bằng
A.
2 8
x y
. B.
2 9
x y
. C.
2 6
x y
. D.
2 10
x y
.
Lời giải
Chọn C
Ta có:
2
2 2.5
. 2 4
x y
x y
2 10
. 2 16
x y
x y
8
2 2
x
y
hoặc
2
2 8
x
y
.
Từ đó, ta có
2 8 2 6
x y
.
Câu 2:
(SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018)
Cho cấp số cộng có tổng
n
số hạng đầu là
2
3 4
n
S n n
,
*
n
. Giá trị của số hạng thứ
10
của cấp số cộng là
A.
10
55
u
. B.
10
67
u
. C.
10
61
u
. D.
10
59.
u
Lời giải
Chọn C
Từ giả thiết ta có
2
1 1
3.1 4.1 7
S u
.
Ta có
2
8 6
3 4
2
n
n n
S n n
7 6 1
2
n n
6 1
n
u n
10
61
u
.
Câu 3:
(SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018)
Cho ba số
x
,
5
,
3y
theo thứ tự lập thành cấp số cộng
và ba số
x
,
3
,
3y
theo thứ tự lập thành cấp số nhân thì
3
y x
bằng?
A.
8
. B.
6
. C.
9
. D.
10
.
Lời giải
Chọn A
Ta có
x
,
5
,
3y
theo thứ tự lập thành cấp số cộng
3 5.2
x y
10 3x y
.
Lại có
x
,
3
,
3y
theo thứ tự lập thành cấp số nhân
2
.3 3
x y
3
xy
.
Do đó
10 3 3
y y
2
3 10 3 0
y y
3 1 3 8
1
9 3 8
3
y x y x
y x y x
Vậy
3 8
y x
.
Câu 4:
(SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018)
Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
60
. Gọi
M
,
N
lần lượt là trung điểm của các cạnh
AB
,
BC
. Khoảng cách từ điểm
C
đến mặt phẳng
SMN
bằng
A.
7
a
. B.
7
3
a
. C.
3
7
a
. D.
3
a
.
Lời giải
Chọn C
Gọi
G
là trọng tâm tam giác
ABC
, khi đó
SG ABC
.
Ta có
; ;
SA ABC SM AG SAG
60
SAG
.
Ta có
2 2 3 3
.
3 3 2 3
a a
AG AM
nên suy ra
3
.tan .tan 60
3
a
SG AG SAG a
.
Gọi
K
là giao điểm của
BG
với
MN
, khi đó
BG MN
, nên suy ra
MN SGK
.
Kẻ
GH SK
, với
H SK
. Từ
MN SGK
MN GH
.
Từ
GH SK
và
MN GH
suy ra
GH SMN
, do đó
;
GH d G SMN
.
Vì
3
CN
GN
nên
; 3 ;
d C SMN d G SMN
3
GH
.
Ta có
1 1 3 3
.
3 3 2 6
a a
GN CN
,
2
2
2 2
3
6 4
4 3
a a a
GK GN NG
.
2 2 2
1 1 1
GH GK SG
2
2 2
1 1 49
7
4 3
a
GH
a a
a
.
Vậy
3
; 3
7
a
d C SMN GH
.
K
G
N
M
A
C
B
S
H
Câu 5:
(THPT Lê Quý Đôn-Hà Nội năm 2017-2018)
Cho cấp số cộng
n
u
có
1
4
u
. Tìm giá trị nhỏ
nhất của
1 2 2 3 3 1
u u u u u u
?
A.
20
. B.
6
. C.
8
. D.
24
.
Lời giải
Chọn D
Ta gọi
d
là công sai của cấp số cộng.
1 2 2 3 3 1
4 4 4 4 2 4 4 2u u u u u u d d d d
2
2
2 24 48 2 6 24 24
d d d
Dấu
" "
xảy ra khi
6
d
Vậy giá trị nhỏ nhất của
1 2 2 3 3 1
u u u u u u
là
24
.
Câu 6:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018)
Một tam giác vuông có chu vi bằng
3
và độ
dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:
A.
1 5
;1;
3 3
. B.
1 7
;1;
4 4
. C.
3 5
;1;
4 4
. D.
1 3
;1;
2 2
.
Lời giải
Chọn C
Gọi
d
là công sai của cấp số cộng và các cạnh có độ dài lần lượt là
a d
,
a
,
a d
0
d a
.
Vì tam giác có chu vi bằng
3
nên
3 3
a
1a
.
Vì tam giác vuông nên theo định lý Pytago ta có
2 2
2
1 1 1
d d
4 1
d
1
4
d
.
Suy ra ba cạnh của tam giác có độ dài là
3 5
;1;
4 4
.
Câu 7:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018)
Cho cấp số nhân
1
1
u
,
6
0,00001
u
.
Khi đó
q
và số hạng tổng quát là
A.
1
10
q
,
1
1
10
n
n
u
. B.
1
10
q
,
1
10
n
n
u
.
C.
1
10
q
,
1
1
10
n
n
n
u
. D.
1
10
q
,
1
1
10
n
n
u
.
Lời giải
Chọn C
Ta có:
5
6 1
. 0,00001
u u q
5
5
1
10
q
1
10
q
1
1
.
n
n
u u q
1
1
1.
10
n
1
1
10
n
n
.
Câu 8:
(THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018)
Cho một cấp số nhân có các số hạng đều
không âm thỏa mãn
2
6
u
,
4
24
u
. Tính tổng của
12
số hạng đầu tiên của cấp số nhân đó.
A.
12
3.2 3
. B.
12
2 1
. C.
12
3.2 1
. D.
12
3.2
.
Lời giải
Chọn A
Gọi công bội của CSN bằng
q
. Suy ra
2
4 2
.u u q
2
q
. Do CSN có các số hạng không âm nên
2
q
.
Ta có
12
12 1
1
.
1
q
S u
q
12
1 2
3.
1 2
12
3 2 1
.
Câu 9: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Tính diện tích hình phẳng giới hạn bởi
các đồ thị
2
2 y x x
và
2
y x x
?
A.
9
8
. B.
6
. C.
12
. D.
10
3
.
Lời giải
Chọn A
Ta có
2 2
0
2
3
2
x
x x x x
x
Nên
3
2
2
0
2 3 dS x x x
3
2
2
0
2 3 dx x x
3
3 2
2
0
9
2 3
3 2 8
x x
.
Câu 10:
(THPT Chuyên Tiền Giang-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
có
5
15
u
,
20
60
u
. Tổng
20
S
của
20
số hạng đầu tiên của cấp số cộng là
A.
20
600
S
. B.
20
60
S
. C.
20
250
S
. D.
20
500
S
.
Lời giải
Chọn C
Ta có:
5
20
15
60
u
u
1
1
4 15
19 60
u d
u d
1
35
5
u
d
.
20 1
20.19
20 .
2
S u d
20.19
20. 35 .5
2
250
.
Câu 11:
(THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018)
Tam giác
ABC
có ba cạnh
a
,
b
,
c
thỏa mãn
2
a
,
2
b
,
2
c
theo thứ tự đó lập thành một cấp số cộng. Chọn khẳng định đúng trong
các khẳng định sau
A.
2
tan A
,
2
tan B
,
2
tan C
theo thứ tự đó lập thành một cấp số cộng.
B.
2
cot A
,
2
cot B
,
2
cot C
theo thứ tự đó lập thành một cấp số cộng.
C.
cos A
,
cos B
,
cosC
theo thứ tự đó lập thành một cấp số cộng.
D.
2
sin A
,
2
sin B
,
2
sin C
theo thứ tự đó lập thành một cấp số cộng.
Lời giải
Chọn D
Áp dụng định lý sin trong tam giác
ABC
ta có
2 sina R A
,
2 sinb R B
,
2 sinc R C
Theo giả thiết
2
a
,
2
b
,
2
c
theo thứ tự đó lập thành một cấp số cộng nên
2 2 2
2a c b
2 2 2 2 2 2
4 .sin 4 .sin 2.4 .sinR A R C R B
2 2 2
sin sin 2.sinA C B
.
Vậy
2
sin A
,
2
sin B
,
2
sin C
theo thứ tự đó lập thành một cấp số cộng.
Câu 12:
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018)
Cho hình chóp
.
S ABCD
có đáy
ABCD
là
hình vuông cạnh
a
,
SA
vuông góc với mặt đáy, góc giữa cạnh
SD
và mặt đáy bằng
30
. Độ
dài cạnh
SD
bằng
A.
2a
. B.
2 3
3
a
. C.
2
a
. D.
3a
.
Lời giải
Chọn B
Vì
SA
vuông góc với mặt đáy nên hình chiếu vuông góc của
SD
lên
ABCD
là
AD
. Do đó
góc giữa
SD
và
ABCD
là
30
SDA
. Suy ra
2 3
cos30 3
AD a
SD
.
Câu 13:
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018)
Cho dãy số
n
u
xác định bởi
1
1
u
và
2
1
2
n n
u u
,
*
n
. Tổng
2 2 2 2
1 2 3 1001
...
S u u u u
bằng
A.
1002001
. B.
1001001
. C.
1001002
. D.
1002002
.
Lời giải
Chọn A
Từ giả thiết
2
1
2
n n
u u
ta có
2 2
1
2
n n
u u
.
Xét dãy số
2
n n
v u
với
*
n
ta có
1
2
1
n
n
v u
2
2
n
u
hay
1
2
n n
v v
dãy số
n
v
là
một cấp số cộng với số hạng đầu
2
1 1
1
v u
và công sai
2
d
.
Do đó
2 2 2 2
1 2 3 1001
...
S u u u u
1 2 3 1001
...
v v v v
1001 2.1 1001 1 2
2
10002001
.
Câu 14:
(SGD Hà Nội-lần 11 năm 2017-2018)
Cho
n
u
là cấp số cộng biết
3 13
80
u u
. Tổng 15 số
hạng đầu của cấp số cộng đó bằng
A.
800
. B.
600
. C.
570
. D.
630
Lời giải
Chọn B
Cách 1:
15 1 2 3 15 1 15 2 14 3 13 7 9 8
... ...
S u u u u u u u u u u u u u
Vì
1 15 2 14 3 13 7 9 8
... 2u u u u u u u u u
và
3 13
80
u u
7.80 40 600
S
.
Cách 2: Gọi
d
là công sai của cấp số cộng.
Ta có
3 13 1 1 1
80 2 12 80 7 40.
u u u d u d u d
Khi đó
15 1 15 1 1 1
15 15
14 15 7 15.40 600.
2 2
S u u u u d u d
Câu 15:
(SGD Hà Nội-lần 11 năm 2017-2018)
2018
2 2018
2018
2
4
lim
2
x
x
x
bằng
A.

. B.
2018
2
. C.
2
. D.
2019
2
.
Lời giải
Chọn D
Ta có
2018
2 2018
2018
2
4
lim
2
x
x
x
2018
2018 2018
2018
2
2 2
lim
2
x
x x
x
2018
2018
2
lim 2
x
x
2018 2018 2019
2 2 2
.
Câu 16:
(THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018)
Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi
một vuông góc với nhau và
OA OB OC a
. Khoảng cách giữa hai đường thẳng
OA
và
BC
bằng
A.
3
2
a
. B.
1
2
a
. C.
2
2
a
. D.
3
2
a
.
Lời giải
Chọn C
Cách 1.
M
O
C
B
A
Gọi
M
là trung điểm của
BC
.
Khi đó:
OM BC
và
OM OA
(do
OA OBC
).
Do đó
2
,
2 2
BC a
d OA BC OM
.
Cách 2. Gắn hệ trục tọa
Oxyz
với gốc tọa độ trùng với điểm
O
,
OA Oz
,
OB Ox
,
OC Oy
.
Khi đó, ta có:
0;0;0
O
,
0;0;A a
,
;0;0
B a
,
0; ;0C a
.
Ta có:
0;0;OA a
,
; ;0BC a a
2 2
, ; ;0
OA BC a a
.
2 2
3
2
4 4 2
, .
. .0 0.0
2
,
2
2
0
,
OA BC OB
a a a
a a
d OA BC
a
a a
OA BC
.
Câu 17:
(THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018)
Cho
4
số thực
a
,
b
,
c
,
d
là
4
số hạng liên
tiếp của một cấp số cộng. Biết tổng của chúng bằng
4
và tổng các bình phương của chúng bằng
24
. Tính
3 3 3 3
P a b c d
.
A.
64
P
. B.
80
P
. C.
16
P
. D.
79
P
.
Lời giải
Chọn A
Theo giả thiết ta có:
2
4
a d b c
a d b c
a b c d
.
2 2
2 2 2 2
2
a b c d a d b c ad bc
2 2
2 2 2 2
8
ad bc a b c d a d b c
.
3 3 3 3
P a b c d
2 2 2 2
a d a ad d b c b bc c
2 2 2 2
2 64
a b c d ad bc
Câu 18: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Một công ti trách nhiệm hữu hạn
thực hiện việc trả lương cho các kĩ sư theo phương thức sau: Mức lương của quý làm việc đầu
tiên cho công ti là
4,5
triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng
thêm
0,3
triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư nhận được sau
3
năm làm
việc cho công ti.
A.
83,7
(triệu đồng). B.
78,3
(triệu đồng). C.
73,8
(triệu đồng). D.
87,3
(triệu đồng).
Lời giải
Chọn C
Ta có
3
năm bằng
12
quý.
Gọi
1
u
,
2
u
, …,
12
u
là tiền lương kĩ sư đó trong các quý (từ quý
1
đến quý
12
).
Suy ra
n
u
là cấp số cộng với công sai
4,5
.
Vậy số tiền lương kĩ sư nhận được là
1
12
2 1
2
u n d
S n
2 4,5 11 0,3
12 73,8
2
(triệu đồng).
Câu 19:
(THPT Chuyên Trần Phú-Hải Phòng-lần 2 năm 2017-2018)
Cho cấp số cộng
n
u
có
2013 6
1000
u u
. Tổng
2018
số hạng đầu tiên của cấp số cộng đó là
A.
1009000
. B.
100800
. C.
1008000
. D.
100900
.
Lời giải
Chọn A
Gọi
d
là công sai của cấp số cộng.
Khi đó:
2013 6
1000
u u
1 1
2012 5 1000
u d u d
1
2 2017 1000
u d
.
Ta có:
2018 1
2017.2018
2018
2
S u d
1
1009. 2 2017u d
1009000
.
Câu 20:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Người ta viết thêm
999
số thực vào giữa số
1
và số
2018
để được cấp số cộng có
1001
số hạng. Tìm số hạng thứ
501
.
A.
1009
. B.
2019
2
. C.
1010
. D.
2021
2
.
Lời giải
Chọn B
Áp dụng công thức cấp số cộng ta có:
1 1001 1
2017
1 1001 1 2018 1 1001 1
1000
n
u u n d u u d d d
.
Vậy số hạng thứ
501
là
501 1
2019
501 1
2
u u d
.
Câu 21: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Trong các dãy số sau, dãy
số nào là dãy số bị chặn?
A.
2 1
1
n
n
u
n
. B.
2 sin
n
u n n
. C.
2
n
u n
. D.
3
1
n
u n
.
Lời giải
Chọn A
Xét đáp án A, ta có
2 1
0
1
n
n
u
n
2, n
.
Câu 22: (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho
3
số
a
,
b
,
c
theo thứ tự đó tạo
thành cấp số nhân với công bội khác
1
. Biết cũng theo thứ tự đó chúng lần lượt là số hạng thứ
nhất, thứ tư và thứ tám của một cấp số cộng với công sai là
0
s
. Tính
a
s
.
A.
4
9
. B.
3
. C.
4
3
. D.
9
.
Lời giải
Chọn D
Theo đề bài ta có hệ phương trình
2
3
7
b ac
b a s
c a s
2
3 7a s a a s
2
9 0
s as
.
Do
0
s
nên
9a s
9
a
s
.
Câu 23: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho hình lăng trụ tứ giác đều
.
ABCD A B C D
có đáy là hình vuông cạnh
a
. Mặt phẳng
cắt các cạnh bên
AA
,
BB
,
CC
,
DD
lần lượt tại
4
điểm
M
,
N
,
P
,
Q
. Góc giữa mặt phẳng
và mặt phẳng
ABCD
là
60
. Diện tích của hình tứ giác
MNPQ
là
A.
2
2a
. B.
2
2
3
a
. C.
2
1
2
a
. D.
2
3
2
a
.
Lời giải
Chọn A
N
P
M
Q
A'
D'
C'
B'
A
B
C
D
Ta có
2
2
2
1
cos60
2
ABCD
MNPQ
S
a
S a
.
Câu 24: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho dãy số
n
u
gồm
89
số
hạng thỏa mãn
tan
n
u n
,
n
,
1 89
n
. Gọi
P
là tích của tất cả
89
số hạng của dãy
số. Giá trị của biểu thức
log P
là
A.
1
. B.
0
. C.
10
. D.
89
.
Lời giải
Chọn B
Ta có:
tan1 .tan 2 ...tan 88 .tan89
P
tan1 .tan89 . tan 2 .tan88 .... tan 44 .tan 46 .tan
45 1
.
log log1 0
P
.
Câu 25: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018) Giải phương trình
1 8 15 22 7944
x
A.
330
x
. B.
220
x
. C.
351
x
. D.
407
x
.
Lời giải
Chọn A
Ta có cấp số cộng với
1
1
u
,
7
d
,
n
u x
,
7944
n
S
.
Áp dụng công thức
1
2
2 1 2.1 1 7
7944 7 5 15888 0
2 2
n
u n d n n n
S n n
48
331
7
n N
n L
.
Vậy
48
1 47.7 330
x u
.
Câu 26:
(ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018)
Viết thêm bốn số vào giữa hai số
160
và
5
để
được một cấp số nhân. Tổng các số hạng của cấp số nhân đó là
A.
215
. B.
315
. C.
415
. D.
515
.
Lời giải
Chọn B
Từ giả thiết ta có
1
6
5
6
1
160
1
5
2
u
u
q
u
u
.
Suy ra tổng các số hạng của cấp số nhân đó là:
6
6
1
1
160 1
1 2
315
1
1
2
u q
S
q
.
Câu 27:
(ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018)
Người ta trồng
465
cây trong một khu vườn
hình tam giác như sau: Hàng thứ nhất có
1
cây, hàng thứ hai có
2
cây, hàng thứ ba có
3
cây….Số hàng cây trong khu vườn là
A.
31
. B.
30
. C.
29
. D.
28
.
Lời giải
Chọn B
Cách trồng
465
cây trong một khu vườn hình tam giác như trên lập thành một cấp số cộng
n
u
với số
n
u
là số cây ở hàng thứ
n
và
1
1
u
và công sai
1
d
.
Tổng số cây trồng được là:
465
n
S
1
465
2
n n
2
930 0
n n
30
31
n
n l
.
Như vậy số hàng cây trong khu vườn là
30
.
Câu 28:
(THPT Trần Phú – Đà Nẵng - Lần 2 – năm 2017 – 2018)
Cho cấp số cộng
n
u
có
1
3
u
và
công sai
7
d
. Hỏi kể từ số hạng thứ mấy trở đi thì các số hạng của
n
u
đều lớn hơn
2018
?
A.
287
. B.
289
. C.
288
. D.
286
.
Lời giải
Chọn B
Ta có:
1
1
n
u u n d
3 7 1
n
7 4
n
;
2018
n
u
7 4 2018
n
2022
7
n
Vậy
289
n
.
Câu 1:
(Tạp chí THTT – Tháng 4 năm 2017 – 2018)
Cho dãy số
n
x
thỏa mãn
1 2
3 3
...
2
n
n n
x x x
với mọi
*
n
. Khẳng định nào dưới đây là đúng và đầy đủ nhất.
A.
n
x
là cấp số cộng với công sai âm.
B.
n
x
là cấp số nhân với công bội âm.
C.
n
x
là cấp số cộng với công sai dương.
D.
n
x
là cấp số nhân với công bội dương.
Lời giải
Chọn C
Ta có:
3 3 3 1 1 3
3 3
2 2
n
n n n n
x n
Ta lại có:
1
3 1 3 3 3 3
n n
x x n n
.
Vậy
n
x
là cấp số cộng với công sai dương.
Câu 2:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Cho cấp số nhân
n
u
, biết
1
12
u
,
3
8
243
u
u
. Tìm
9
u
.
A.
9
2
2187
u
. B.
9
4
6563
u
. C.
9
78732
u
. D.
9
4
2187
u
.
Lời giải
Chọn D
Gọi
q
là công bội của cấp số nhân
n
u
.
Ta có
2
3 1
u u q
,
7
8 1
u u q
3
5
8
1
243
u
u q
1
3
q
.
Do đó
8
9 1
u u q
8
1
12.
3
4
2187
.
Câu 3: [1D3- 2(THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018)] Cho một cấp số
cộng
có
và tổng của
số hạng đầu bằng
. Tìm công thức của số hạng tổng quát
.
A.
. B.
. C.
. D.
.
Lời giải
Chọn A
Ta có:
.
Số hạng tổng quát của cấp số cộng bằng
.
Câu 4: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho cấp số nhân
n
u
có
tổng
n
số hạng đầu tiên là
5 1
n
n
S
với
1,2,...
n
. Tìm số hạng đầu
1
u
và công bội
q
của
cấp số nhân đó?
A.
1
5
u
,
4
q
. B.
1
5
u
,
6
q
. C.
1
4
u
,
5
q
. D.
1
6
u
,
5
q
.
Lời giải
Chọn C
Ta có:
1 1
1
2
2 1
1 2 2
5 1 4
4
24 20
5 1 24
u S
u
u u
u u S
1
4
u
,
2
1
5
u
q
u
.
Câu 5:
(THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018)
Cho hình chóp
.
S ABC
có
tam giác
ABC
vuông cân tại
B
có
AB BC a
, tam giác
SAC
đều và nằm trong mặt phẳng
vuông góc với mặt phẳng
ABC
( tham khảo hình vẽ). Khoảng cách từ
A
đến mặt phẳng
SBC
bằng.
A.
42
14
a
. B.
2a
. C.
42
7
a
. D.
21
14
a
.
Lời giải
Chọn C
M
H
B
A
C
S
K
Gọi
H
và
M
lần lượt là trung điểm của
AC
và
BC
. Ta có
, 2 ,
d A SBC d H SBC
.
Theo giả thiết tam giác
SAC
đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABC
nên
SH ABC
SH BC
1
Do tam giác tam giác
ABC
vuông cân tại
B
nên
HM BC
2
Từ
1
và
2
ta có
BC SHM
SHM SBC
.
Trong mặt phẳng
SHM
kẻ
HK SM
thì
,
d H SBC HK
.
Theo đề bài ta có có tam giác
ABC
vuông cân tại
B
có
AB BC a
2 2
2AC BA BC a
,
1
2 2
a
HM AB
.
Mặt khác tam giác
SAC
đều nên
6
2
a
SH
. Xét tam giác vuông
SHM
ta có
2 2 2
1 1 1
HK HM SH
2 2
2
1 1 1
6
4 4
a a
HK
2 2
1 28
6HK a
42
14
a
HK
.
Vậy
42
, 2
7
a
d A SBC HK
Câu 6: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho cấp số nhân
n
u
thỏa mãn
1 2 3
4 1
13
26
u u u
u u
.
Tổng
8
số hạng đầu của cấp số nhân
n
u
là
A.
8
1093
S
. B.
8
3820
S
. C.
8
9841
S
. D.
8
3280
S
.
Hướng dẫn giải
Chọn D
Ta có
1 2 3
4 1
13
26
u u u
u u
2
1 1 1
3
1 1
. . 13
. 26
u u q u q
u q u
2
1
2
1
1 13
. 1 1 26
u q q
u q q q
2
1
1 13
3
u q q
q
1
1
3
u
q
.
Vậy tổng
1
8
1
1
S
8
1 1 3
3280
1 3
.
Câu 7:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Cho cấp số cộng
n
u
,
*
n
có số hạng tổng
quát
1 3
n
u n
. Tổng của
10
số hạng đầu tiên của cấp số cộng bằng
A.
59048
. B.
59049
. C.
155
. D.
310
.
Lời giải
Chọn C
Ta có:
1 3
n
u n
1
10
1 3.1 2
1 3.10 29
u
u
.
Áp dụng công thức:
1 1 10
10
155
2 2
n
n u u u u
S
.
Câu 8: Cho cấp số nhân
n
u
biết
6
2
u
và
9
6
u
. Tìm giá trị của
21
u
.
A.
18
. B.
54
. C.
162
. D.
486
.
Câu 9: Cho cấp số nhân
n
u
biết
6
2
u
và
9
6
u
. Tìm giá trị của
21
u
.
A.
18
. B.
54
. C.
162
. D.
486
.
Lời giải
Chọn D
Gọi
n
u
có số hạng đầu
1
u
và công bội
q
.
Ta có
5
6
1
8
9
1
2
2
6
6
u
u q
u
u q
3
1
2
3
3
2
3 3
q
u
Suy ra
20
21 1
.u u q
20
3
2
3
2
. 3
3 3
486
.
Câu 10: Bốn số tạo thành một cấp số cộng có tổng bằng
28
và tổng các bình phương của chúng bằng
276
. Tích của bốn số đó là :
A.
585
. B.
161
. C.
404
. D.
276
.
Câu 11: Bốn số tạo thành một cấp số cộng có tổng bằng
28
và tổng các bình phương của chúng bằng
276
. Tích của bốn số đó là :
A.
585
. B.
161
. C.
404
. D.
276
.
Lời giải
Chọn A
Gọi
4
số cần tìm là
3a r
,
a r
,
a r
,
3a r
.
Ta có:
2 2 2 2
3 3 28
3 3 276
a r a r a r a r
a r a r a r a r
2
7
4
a
r
7
2
a
r
.
Bốn số cần tìm là
1
,
5
,
9
,
13
có tích bằng
585
.
Câu 12: Sinh nhật lần thứ
17
của An vào ngày
01
tháng
5
năm
2018
. Bạn An muốn mua một chiếc
máy ảnh giá
3850000
đồng để làm quà sinh nhật cho chính mình nên An quyết định bỏ ống
heo
1000
đồng vào ngày
01
tháng
02
năm
2018
. Trong các ngày tiếp theo, ngày sau bỏ ống
nhiều hơn ngày trước
1000
đồng. Hỏi đến ngày sinh nhật của mình, An có bao nhiêu tiền (tính
đến ngày
30
tháng
4
năm
2018
)?
A.
4095000
đồng. B.
89000
đồng. C.
4005000
đồng. D.
3960000
đồng.
Câu 13: Sinh nhật lần thứ
17
của An vào ngày
01
tháng
5
năm
2018
. Bạn An muốn mua một chiếc
máy ảnh giá
3850000
đồng để làm quà sinh nhật cho chính mình nên An quyết định bỏ ống
heo
1000
đồng vào ngày
01
tháng
02
năm
2018
. Trong các ngày tiếp theo, ngày sau bỏ ống
nhiều hơn ngày trước
1000
đồng. Hỏi đến ngày sinh nhật của mình, An có bao nhiêu tiền (tính
đến ngày
30
tháng
4
năm
2018
)?
A.
4095000
đồng. B.
89000
đồng. C.
4005000
đồng. D.
3960000
đồng.
Lời giải
Chọn C
* Số tiền bỏ heo của An mỗi ngày tạo thành một cấp số cộng có số hạng đầu
1
1000
u
công sai
1000
d
.
* Tổng số tiền bỏ heo tính đến ngày thứ n là:
1
1
1 2
2 1
...
2 2
n
n n
n u n d
n u u
S u u u
* Tính đến ngày
30
tháng
4
năm
2018
(tính đến ngày thứ
89
) tổng số tiền bỏ heo là:
89
89 2.1000 89 1 .1000
45.89.1000 4005000
2
S
đồng.
Câu 14: Cho cấp số nhân
n
u
có số hạng đầu
1
3
u
và công bội
2
3
q
. Số hạng thứ năm của
n
u
là
A.
27
16
. B.
16
27
. C.
27
16
. D.
16
27
.
Câu 15: Cho cấp số nhân
n
u
có số hạng đầu
1
3
u
và công bội
2
3
q
. Số hạng thứ năm của
n
u
là
A.
27
16
. B.
16
27
. C.
27
16
. D.
16
27
.
Lời giải
Chọn D
Ta có
1
1
.
n
n
u u q
4
5
2
3.
3
u
16
27
.
Câu 16: Cho khối chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
ABC
và
SA a
.
Đáy
ABC
thỏa mãn
3AB a
(tham khảo hình vẽ). Tìm số đo góc giữa
đường thẳng
SB
và mặt phẳng
ABC
.
A.
30
. B.
45
.
C.
90
. D.
60
.
Câu 17: Cho khối chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
ABC
và
SA a
. Đáy
ABC
thỏa mãn
3AB a
(tham khảo hình vẽ).
Tìm số đo góc giữa đường thẳng
SB
và mặt phẳng
ABC
.
A.
30
. B.
45
. C.
90
. D.
60
.
Lời giải
Chọn A
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
là
SBA
.
Ta có:
1
tan
3
SBA
30
SBA
.
Câu 18: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là
80.000
đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
S
a
A
B
3a
C
S
a
A
B
3a
C
thêm
5.000
đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống
50m
mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
A.
4.000.000
đồng. B.
10.125.000
đồng. C.
52.500.000
đồng. D.
52.500.000
đồng.
Câu 19: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là
80.000
đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm
5.000
đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống
50m
mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
A.
4.000.000
đồng. B.
10.125.000
đồng. C.
52.500.000
đồng. D.
52.500.000
đồng.
Lời giải
Chọn B
* Áp dụng công thức tính tổng của
n
số hạng đầu của cấp số nhân có số hạng đầu
1
80.000
u
,
công sai
5.000
d
ta được số tiền phải trả khi khoan đến mét thứ
n
là
1
1
2 1
2 2
n
n
n u n d
n u u
S
* Khi khoan đến mét thứ
50
, số tiền phải trả là
50
50 2.80000 50 1 .5000
10.125.000
2
S
đồng.
Câu 20: Cho cấp số cộng có
1
1
u
và công sai
2
d
. Tổng
n
số hạng đầu tiên của cấp số cộng này là
9800
n
S
. Giá trị
n
là
A.
100
. B.
99
. C.
101
. D.
98
.
Câu 21: Cho cấp số cộng có
1
1
u
và công sai
2
d
. Tổng
n
số hạng đầu tiên của cấp số cộng này là
9800
n
S
. Giá trị
n
là
A.
100
. B.
99
. C.
101
. D.
98
.
Lời giải
Chọn A
1
2 1 9800 2 2 1 19600 0
2
n
n
S u n d n n
100
n
.
Câu 22: Cho dãy số
n
u
là cấp số cộng với
1
3
u
;
5
19
u
. Tính
12
u
.
A.
12
51
u
. B.
12
57
u
. C.
12
47
u
. D.
12
207
5
u
.
Câu 23: Cho dãy số
n
u
là cấp số cộng với
1
3
u
;
5
19
u
. Tính
12
u
.
A.
12
51
u
. B.
12
57
u
. C.
12
47
u
. D.
12
207
5
u
.
Lời giải
Chọn C
Ta có:
5
19
u
1
4 19
u d
3 4 19
d
4
d
Do đó:
12 1
11 3 11.4 47
u u d
.
Câu 24: Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy và cạnh bên đều bằng
a
. Tính cosin của góc
giữa hai mặt phẳng
SAB
và
SAD
.
S
D
C
B
A
A.
1
3
. B.
1
3
. C.
2 2
3
. D.
2 2
3
.
Câu 25: Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy và cạnh bên đều bằng
a
. Tính cosin của góc
giữa hai mặt phẳng
SAB
và
SAD
.
S
D
C
B
A
A.
1
3
. B.
1
3
. C.
2 2
3
. D.
2 2
3
.
Lời giải
Chọn A
I
A
C
D
B
S
Gọi
I
là trung điểm
SA
.
Vì các tam giác
SAB
và
SAD
là tam giác đều nên ta có
BI
và
DI
cùng vuông góc với
SA
góc giữa hai mặt phẳng
SAB
và
SAD
là
,
BI DI
.
Trong tam giác
BID
ta có:
2 2 2
1
cos , cos
2 . 3
DI BI BD
BI DI BID
BI DI
.
Vậy cosin của góc giữa mặt phẳng
SAB
và
SAD
bằng
1
3
.
Câu 26: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích
của đế tháp (có diện tích là
2
12288 m
). Tính diện tích mặt trên cùng.
A.
2
8m
. B.
2
6m
. C.
2
12m
. D.
2
10m
.
Câu 27: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích
của đế tháp (có diện tích là
2
12288 m
). Tính diện tích mặt trên cùng.
A.
2
8m
. B.
2
6m
. C.
2
12m
. D.
2
10m
.
Hướng dẫn giải
Chọn B
Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội
1
2
q
Số hạng đầu
1
12288
u
. Khi đó mặt trên cùng tầng 11 ứng với
12
u
.
Do đó
11
12 1
.u u q
11
1
12288.
2
6
.
Câu 28: Xác định
x
để
3
số
2 1x
;
x
;
2 1x
theo thứ tự lập thành cấp số nhân?
A.
1
3
x
. B.
1
3
x
. C.
1
3
x
. D.
3
x
.
Câu 29: Xác định
x
để
3
số
2 1x
;
x
;
2 1x
theo thứ tự lập thành cấp số nhân?
A.
1
3
x
. B.
1
3
x
. C.
1
3
x
. D.
3
x
.
Lời giải
Chọn B
Vì
2 1x
;
x
;
2 1x
theo thứ tự lập thành cấp số nhân
nên
2
2 1 2 1
x x x
2 2
x x
2
1
3
x
1
3
x
.
Câu 30: Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có
1
cây, ở hàng thứ hai có
2
cây, ở hàng thứ ba có
3
cây,… ở hàng thứ
n
có
n
cây. Biết rằng người ta trồng hết
4950
cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
A.
99
. B.
100
. C.
101
. D.
98
.
Câu 31: Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có
1
cây, ở hàng thứ hai có
2
cây, ở hàng thứ ba có
3
cây,… ở hàng thứ
n
có
n
cây. Biết rằng người ta trồng hết
4950
cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
A.
99
. B.
100
. C.
101
. D.
98
.
Lời giải
Chọn A
Ta thấy số cây ở mỗi hàng tạo nên một cấp số cộng có số hạng đầu
1
1
u
và công sai
1
d
.
Ta có
2
1
2 1
4950
2 2
n
u n d n
n n
S
2
9900 0 99
n n n
.
Câu 32: Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn?
A.
2
3
,
4
9
,
8
27
,…,
2
3
n
,…. B.
1
3
,
1
9
,
1
27
,…,
1
3
n
,….
C.
3
2
,
9
4
,
27
8
,…,
3
2
n
,…. D.
1
,
1
2
,
1
4
,
1
8
,
1
16
,…,
1
1
2
n
,….
Câu 33: Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn?
A.
2
3
,
4
9
,
8
27
,…,
2
3
n
,…. B.
1
3
,
1
9
,
1
27
,…,
1
3
n
,….
C.
3
2
,
9
4
,
27
8
,…,
3
2
n
,…. D.
1
,
1
2
,
1
4
,
1
8
,
1
16
,…,
1
1
2
n
,….
Lời giải
Chọn C
Chọn đáp án C vì dãy ở đây là một CSN có công bội
3
1
2
q
, nên dãy
3
2
,
9
4
,
27
8
,…,
3
2
n
,…
không phải là dãy lùi vô hạn
Câu 34: Một du khách vào chuồng đua ngựa đặt cược, lần đầu tiên đặt
20000
đồng, mỗi lần sau tiền đặt
gấp đôi tiền đặt lần trước. Người đó thua
9
lần liên tiếp và thắng ở lần thứ
10
. Hỏi du khách đó
thắng hay thua bao nhiêu?
A. Thắng
20000
đồng. B. Hòa vốn.
C. Thua
20000
đồng. D. Thua
40000
đồng.
Câu 35: Một du khách vào chuồng đua ngựa đặt cược, lần đầu tiên đặt
20000
đồng, mỗi lần sau tiền đặt
gấp đôi tiền đặt lần trước. Người đó thua
9
lần liên tiếp và thắng ở lần thứ
10
. Hỏi du khách đó
thắng hay thua bao nhiêu?
A. Thắng
20000
đồng. B. Hòa vốn.
C. Thua
20000
đồng. D. Thua
40000
đồng.
Hướng dẫn giải
Chọn A
Số tiền du khách đó đặt cược là một cấp số nhân với
1
20000
2
u
q
.
9
lần đầu người đó thua
số tiền thua là tổng
9
số hạng đầu của cấp số nhân ở trên. Vậy
số tiền người đó thua là
9
9
1 2
20000 10220000
1 2
S
(đồng)
 Số tiền người đó thắng được ở lần thứ
10
là
9 9
10 1
. 20000.2 10240000
u u q
(đồng)
Ta có
10 9
10240000 10220000 20000
u S
(đồng)
Vậy người đó thắng
20000
đồng.
Câu 1:
(THTT Số 1-484 tháng 10 năm 2017-2018)
Một hình vuông
ABCD
có cạnh
AB a
, diện tích
1
S
. Nối 4 trung điểm
1
A
,
1
B
,
1
C
,
1
D
theo thứ tự của 4 cạnh
AB
,
BC
,
CD
,
DA
ta được hình
vuông thứ hai là
1 1 1 1
A B C D
có diện tích
2
S
. Tiếp tục như thế ta được hình vuông thứ ba
2 2 2 2
A B C D
có diện tích
3
S
và cứ tiếp tục như thế, ta được diện tích
4 5
, ,...
S S Tính
1 2 3 100
...
S S S S S
.
A.
100
99 2
2 1
.
2
S
a
B.
100
99
2 1
.
2
a
S
C.
2 100
99
2 1
.
2
a
S
D.
2 99
99
2 1
.
2
a
S
Lời giải
Chọn C
Dễ thấy:
2 2 2
2
1 2 3 100
99
; ; ;...; .
2 4 2
a a a
S a S S S
Như vậy
1 2 3 100
, , ,...,S S S S
là cấp số nhân với công bội
1
2
q
.
2 100
2
1 2 100
2 99 99
2 1
1 1 1
... 1 ... .
2 2 2 2
a
S S S S a
Câu 2:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Trong các dãy số sau, dãy số nào là dãy số
giảm
A.
3
1
n
n
u
n
. B.
2
n
n
u
. C.
2
2
n
u
n
. D.
1
3
n
n
n
u
.
Lời giải
Chọn C
Xét A:
Ta có
3
;
1
n
n
u
n
1
2
2
n
n
u
n
. Khi đó :
1
2 3 4
0
2 1 1 2
n n
n n
u u
n n n n
n
Vậy
n
u
là dãy số tăng.
Xét B:
Ta có
;
2
n
n
u
1
1
2
n
n
u
. Khi đó :
1
1 1
0
2 2 2
n n
n n
u u
n
Vậy
n
u
là dãy số tăng.
Xét C:
Ta có
2
2
n
u
n
,
1
2
2
1
n
u
n
2 2
1
2
2
1,
1
n
n
u
n n
n
u n
n
. Vậy
n
u
là dãy giảm.
Xét D:
Ta có
1
1
;
3
u
2
1
;
9
u
3
1
27
u
. Vậy
n
u
là dãy số không tăng không giảm .
Câu 3: [1D3 - 2] (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Trong các mệnh đề sau, mệnh đề
nào đúng?
A.
. B.
. C.
. D.
.
Lời giải
Chọn A
Vì
. Vậy A đúng.
Câu 4:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Cho hàm số
2
khi 1, 0
0 khi 0
khi 1
x
x x
x
f x x
x x
.
Khẳng định nào đúng
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn
0;1
.
B. Hàm số liên tục tại mọi điểm trừ điểm
0
x
.
C. Hàm số liên tục tại mọi điểm thuộc
.
D. Hàm số liên tục tại mọi điểm trừ điểm
1x
.
Lời giải
Chọn C
Tập xác định
D
.
 Nếu
0
x
,
1x
thì hàm số
y f x
liên tục trên mỗi khoảng
;0 , 0;1
và
1;

.
 Nếu
0
x
thì
0 0
f
và
2 2
0 0 0 0 0 0
lim lim lim 0; lim lim lim 0
x x x x x x
x x
f x x f x x
x x
.
Suy ra:
0
lim 0 0
x
f x f
.
Do đó, hàm số
y f x
liên tục tại
0
x
.
 Nếu
1x
thì
1 1
f
và
2
1 1 1
1
1 1
lim lim lim 1
lim 1 1
lim lim 1
x x x
x
x x
x
f x x
x
f x f
f x x
.
Do đó, hàm số
y f x
liên tục tại
1x
.
Vậy hàm số
y f x
liên tục trên
.
Câu 5:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Cho dãy số
n
u
được xác định bởi
1
1
3
.
2 1 2
n n
u
n u nu n
Tính
lim .
n
u
A.
lim 1.
n
u
B.
lim 4.
n
u
C.
lim 3.
n
u
D.
lim 0.
n
u
Lời giải
Chọn A
Ta có
1
2
(*)
2 2 2 2
n n
n n
u u
n n
Đặt
a lim ,
n
u
trong biểu thức
(*)
cho
n 
ta được
1 1
1 lim .
2 2
n
a a a u
Chú ý: Để chặt chẽ hơn ta có thể lập luận như sau:
Sử dụng quy nạp toán học, ta chứng minh được
1
n
u
với mọi
*
n
, nên dãy
n
u
bị
chặn dưới.
Khi đó ta cũng có
1
. .
2 2
.
2 2 2 2 2 2 2 2
n
n
n n
n
n u n u
n n
u u u
n n n n
nên dãy
n
u
là dãy giảm.
Vậy, dãy
n
u
có giới hạn (Học sinh cần chú ý tính chất: một dãy giảm và bị chặn dưới,
hoặc tăng và bị chặn trên, thì có giới hạn).
Đặt
lim ,
n
a u
trong biểu thức
(*)
cho
n 
ta được
1 1
1 lim .
2 2
n
a a a u
Câu 6:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Cho dãy số
n
u
với
1
n
n
u n
.
Mệnh đề nào sau đây đúng?
A. Dãy số
n
u
là dãy số bị chặn. B. Dãy số
n
u
là dãy số giảm.
C. Dãy số
n
u
là dãy số tăng. D. Dãy số
n
u
là dãy số không bị chặn.
Lời giải
Chọn D
Dãy số
1
n
n
u n
là dãy số không bị chặn vì
lim lim
n
u n

.
Câu 7:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Cho dãy số
sin
n
u
n
. Chọn khẳng định sai
trong các khẳng định sau đây:
A. Dãy số tăng. B.
1
sin
1
n
u
n
.
C. Dãy số bị chặn. D. Dãy số không tăng, không giảm.
Lời giải
Chọn A
1
sin
1
n
u
n
nên B đúng.
Do
1 sin 1
n
nên dãy số bị chặn, do đó C đúng.
1
sin 0
u
,
2
sin 1
2
u
,
3
3
sin
3 2
u
. Do
1 2
2 3
u u
u u
nên dãy số không tăng, không
giảm. Vậy D đúng. Do đó A sai.
Câu
8:
(THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018)
Cho tam giác
ABC
cân tại
A
. Biết rằng độ dài cạnh
BC
, trung tuyến
AM
và độ dài cạnh
AB
theo thứ tự đó lập thành
một cấp số nhân có công bội
q
. Tìm công bội
q
của cấp số nhân đó.
A.
1 2
2
q
. B.
2 2 2
2
q
. C.
1 2
2
q
. D.
2 2 2
2
q
.
Lời giải
Chọn B
Ta có:
2 2 2
2
2
4
AB AC BC
AM
1
.
Do ba cạnh
BC
,
AM
,
AB
lập thành cấp số nhân nên ta có:
.
2
Thay
2
vào
1
ta được
2 2 2
2
.
4
AB AC BC
BC AB
2 2
4 4 . 0
AB AB BC BC
2
4 4 1 0
AB AB
BC BC
1 2
2
1 2
2
AB
BC
AB
loai
BC
1 2
2
AB
BC
1 2 2 2 2
2 2
q
.
Câu 9:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Tìm tất cả các giá trị của tham số m để
phương trình
3 2
3 2 0
x x mx m
có 3 nghiệm lập thành cấp số cộng.
A.
3
m
. B.
3
m
. C.
0
m
. D.
m
tùy ý.
Lời giải
Chọn A
3 2
3 2 0
x x mx m
(1)
2
1 2 2 0
x x x m
2
1
2 2 0 (2)
x
x x m
Phương trình (1) có
3
nghiệm lập thành cấp số cộng khi phương trình (2) có
2
nghiệm
1 2
;x x
thoả mãn
1 2
1 2
1
2
x x
x x
(Vì pt (2) nếu có nghiệm thì tổng các nghiệm là
2
)
phương trình (2) có
2
nghiệm
0
3 0
m
3.
m
Câu 10:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Cho dãy số
n
x
thoả mãn
1
40
x
và
1
1,1.
n n
x x
với mọi
2,3,4,...
n
Tính giá trị của
1 2 12
...
S x x x
(làm tròn đến chữ số thập phân thứ
nhất).
A.
855,4
. B.
855,3
. C.
741,2
. D.
741,3
.
Lời giải
Chọn A
Ta có
1
1,1.
n n
x x
và
1
40
x
nên dãy số
n
x
là một cấp số nhân có số hạng đầu
1
40
x
và
công bội
1
1,1
n
n
x
q
x
.
12
1 2 12
1 1,1
... 40. 855,4
1 1,1
S x x x
.
Câu 11:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Cho dãy số
n
u
với
1
2
1
1
,
n n
u
u u n n
.
Tính
21
.u
A.
21
3080.
u
B.
21
3312.
u
C.
21
2871.
u
D.
21
3011.
u
Lời giải
Chọn C
Từ
2
1
,
n n
u u n
với mọi
n
, ta có:
2
2 1
1
u u
.
2
3 2
2
u u
.
...
2
1
1
n n
u u n
.
2
1n n
u u n
.
Cộng
n
đẳng thức trên theo vế ta được:
2 2 2
1
1 1 2 ...
n
u n
, với mọi
n
.
Mặt khác, ta luôn có:
2 2 2
1 2 1
1 2 ...
6
n n n
n
nên suy ra:
1
1 2 1
1
6
n
n n n
u
, với mọi
n
.
Cho
20
n
, ta được:
21
20.21. 2.20 1
1 2871.
6
u
Câu 12:
(THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018)
Có bao nhiêu cấp số nhân có
5
số hạng? Biết
rằng tổng
5
số hạng đó là
31
và tích của chúng là
1024
.
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn C
Gọi cấp số nhân thỏa yêu cầu bài toán có số hạng đầu
1
u
và công bội
q
.
Theo giả thiết ta có
2 3 4 5 10 2
1 1 1 1 1 1 1
. . . . 1024 . 1024 4
u u q u q u q u q u q u q
1
.
Lại có
2 3 4 2 3 4
1 1 1 1 1 1
31 1 31
u u q u q u q u q u q q q q
2
.
Giải hệ hai phương trình
1
và
2
ta được các nghiệm:
1
2
q
,
2
1
2
q
,
3
7 33
4
q
,
4
7 33
4
q
.
Vậy có
4
cấp số nhân thỏa yêu cầu bài toán.
Câu 1:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Trong sân vận động có tất cả
30
dãy ghế, dãy đầu tiên có
15
ghế, các dãy liền sau nhiều hơn dãy trước
4
ghế, hỏi sân vận động
đó có tất cả bao nhiêu ghế?
A.
2250
. B.
1740
. C.
4380
. D.
2190
.
Lời giải
Chọn C
Gọi
1 2 30
, ,...u u u
lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba mươi. Ta
có công thức truy hồi ta có
1
4
n n
u u
,
2,3,...,30
n
.
Ký hiệu:
30 1 2 30
...
S u u u
, theo công thức tổng các số hạng của một cấp số cộng với
1
15
u
,
4
d
ta được:
30 1
30
2 30 1 4 15 2.15 29.4 2190
2
S u
.
Câu 2:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Cho hình vuông
1 1 1 1
A B C D
có cạnh
bằng 1. Gọi
1k
A
,
1k
B
,
1k
C
,
1k
D
thứ tự là trung điểm các cạnh
k k
A B
,
k k
B C
,
k k
C D
,
k k
D A
(với
1, 2, ...).
k
Chu vi của hình vuông
2018 2018 2018 2018
A B C D
bằng
A.
2018
2
.
2
B.
1007
2
.
2
C.
2017
2
.
2
D.
1006
2
.
2
Lời giải :
Chọn B
Hình vuông có cạnh bằng
a
thì có chu vi là
4a
. Hình vuông có các đỉnh là trung điểm của hình
vuông ban đầu có cạnh bằng
2
2
a
có chu vi là
2 2
a
.
Đường chéo của hình vuông
1 1 1 1
A B C D
có độ dài bằng
2
nên cạnh của hình vuông
2 2 2 2
A B C D
có độ dài bằng
2
.
2
Đường chéo của hình vuông
2 2 2 2
A B C D
có độ dài bằng
1
nên cạnh của hình vuông
3 3 3 3
A B C D
có độ dài bằng
1
.
2
Đường chéo của hình vuông
3 3 3 3
A B C D
có độ dài bằng
2
2
nên cạnh của hình vuông
4 4 4 4
A B C D
có độ dài bằng
1
.
2 2
Cứ như thế độ dài các cạnh hình vuông tạo thành một cấp số nhân có
1
1
u
, công bội
1
2
q
nên độ dài cạnh của hình vuông
2018 2018 2018 2018
A B C D là:
2008
2017
1
2
u
nên chu vi hình vuông
đó là:
2018
2017
1007
4 2
4 .
2
2
u
Câu 3:
(THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018)
Cho dãy số
n
u
với
1 1 1
...
1.3 3.5 2 1 2 1
n
u
n n
. Tính
lim
n
u
.
A.
0
. B.
1
2
. C.
1
4
. D.
1
.
Lời giải
Chọn B
* Cách 1:
Ta có
1 1 1 1
2 1 2 1 2 2 1 2 1
n n n n
suy ra
1 1 1 1
1.3 2 1 3
1 1 1 1
3.5 2 3 5
…
…
1 1 1 1 1 1
...
1.3 3.5 2 1 2 1 2 1 2 1
n
u
n n n
nên
1 1 1 1
lim lim
2 1 2 1 2
n
u
n
.
* Cách 2:
Ta có
1 2 3
1 2 3
; ;
3 5 7
u u u
. Ta chứng minh
*
2 1
n
n
u
n
bằng qui nạp
+ Với
1
n
, công thức
*
đúng.
+ Giả sử công thức
*
đúng với
1
2 1
k
k
n k u
k
. Ta cần chứng minh
1
1
2 1 1
k
k
u
k
. Thật vậy, ta có
1
1
2 1 1 2 1 1
k k
u u
k k
2
1 2 3 1
2 1 2 1 2 3 2 1 2 3
k k k
k k k k k
1 2 1
1
2 1 2 3 2 1 1
k k
k
k k k
. Vậy công thức
*
2 1
n
n
u
n
đúng với mọi
*
n
.
Khi đó
1
lim lim
2 1 2
n
n
u
n
.
Câu 4:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Cho tứ diện
.
S ABC
có
SA SB SC AB AC a
và
2BC a
. Tính góc giữa hai đường thẳng
AB
và
SC
.
A.
45
. B.
120
. C.
60
.
D.
90
.
Lời giải
Chọn C
Cách 1: Gọi
M
là trung điểm của
BC
.
Ta có:
2 2 2
BC AB AC
nên tam giác
ABC
vuông cân tại
A
.
Và
2 2 2
BC SB SC
nên tam giác
SBC
vuông cân tại
S
.
Vẽ hình chữ nhật (cũng là hình vuông)
ABDC
,
AB SC SCD
và
SC CD a
.
2
2
2 2
2 2
a a
AM SM MD a
.
SAM
vuông tại
M
.
SM BC ABCD
SM ABCD
SM AM ABCD
SM MD
.
2 2 2
SD SM MD
2 2
2 2
2 2
a a
2 2
2 2
a a
SD a
.
Suy ra tam giác
SCD
đều
, 60
AB SC SCD
.
Cách 2:
.
.
cos ,
. .
SC SB SA
SC AB
SC AB
SC AB SC AB

. .cos . .cos
.
SC SB BSC SC SA ASC
SC AB
. .cos90 . .cos60 1
. 2
a a a a
a a
; 120
SC AB
.
Vậy góc giữa hai đường thẳng
AB
và
SC
là
60
.
Câu 5:
(THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018)
Cho dãy số
n
a
xác định bởi
1
2
a
,
1
2
n n
a a
,
1n
,
n
. Tính tổng của
10
số hạng đầu tiên của dãy số.
A.
2050
3
. B.
2046
. C.
682
. D.
2046
.
Lời giải
Chọn C
Vì
1
2
n
n
a
a
suy ra
n
a
là một cấp số nhân với
1
2
2
a
q
.
Suy ra
10
1
10
1
682
1
a q
S
q
.
Câu 6:
(THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018)
Cho dãy số
n
u
xác định bởi
1
41
20
u
và
1
21 1
n n
u u
với mọi
1.
n
Tìm số hạng thứ
2018
của dãy số đã cho.
A.
2018
2018
1
2.21 .
20
u
B.
2017
2018
1
2.21 .
20
u
C.
2017
2018
1
2.21 .
20
u
D.
2018
2018
1
2.21 .
20
u
Lời giải
Chọn C
Ta có
1
21 1
n n
u u
1
1
2
1
21
20
0
n n
u u
.
Đặt
1
20
n n
v u
, ta có
1
21
n n
v v
.
Do đó
n
v
là một CSN với
1
41 1
2
20 20
v
và công bội
21
q
.
Do đó số hạng tổng quát của dãy
n
v
là
1 1
1
. 2.21
n n
n
v v q
1
1
2.21
20
n
n
u
.
Khi đó
2017
2018
1
2.21
20
u
.
Câu 7:
(SGD Bắc Ninh năm 2017-2018)
Cho hình vuông
1
C
có cạnh bằng
a
. Người ta chia mỗi cạnh
của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình
vuông
2
C
(Hình vẽ).
Từ hình vuông
2
C
lại tiếp tục làm như trên ta nhận được dãy các hình vuông
1
C
,
2
C
,
3
C
,.,
n
C
... Gọi
i
S
là diện tích của hình vuông
1, 2,3,.....
i
C i
. Đặt
1 2 3
... ...
n
T S S S S
.
Biết
32
3
T
, tính
a
?
A.
2
. B.
5
2
. C.
2
. D.
2 2
.
Lời giải
Chọn A
Cạnh của hình vuông
2
C
là:
2 2
2
3 1 10
4 4 4
a
a a a
. Do đó diện tích
2
2
5
8
S a
1
5
8
S
.
Cạnh của hình vuông
3
C
là:
2
2 2
2
3 2 2
10
3 1 10
4 4 4 4
a
a a a a
. Do đó diện tích
2
2
3 2
5 5
8 8
S a S
. Lý luận tương tự ta có các
1
S
,
2
S
,
3
,... ...
n
S S
. tạo thành một dãy cấp số
nhân lùi vô hạn có
1 1
u S
và công bội
5
8
q
.
1
1
S
T
q
2
8
3
a
. Với
32
3
T
ta có
2
4 2
a a
.
Câu 8:
(THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018)
Cho hai cấp số cộng
n
a
:
1
4
a
;
2
7
a
;...;
100
a
và
n
b
:
1
1
b
;
2
6
b
;...;
100
b
. Hỏi có bao nhiêu số có mặt đồng thời
trong cả hai dãy số trên.
A.
32
. B.
20
. C.
33
. D.
53
.
Lời giải
Chọn B
Cấp số cộng
n
a
:
1
4
a
;
2
7
a
;...;
100
a
có số hạng tổng quát:
4 1 3 3 1
n
a n n
.
Cấp số cộng
n
b
:
1
1
b
;
2
6
b
;...;
100
b
có số hạng tổng quát:
1 1 5 5 4
m
b m m
.
Các số có mặt đồng thời trong cả hai dãy số trên thỏa mãn hệ:
3 5 1
3 1 5 4
1 100 1 100
1 100 1 100
n m
n m
n n
m m
.
Vì
3 5 1
n m
nên
5n
và
1 3
m
với
1 0
m
Ta lại có
100 3 300 5 1 300 61
n n m m
.
Có
1 3 3 1m m t
,
*
t
. Vì
1 61 1 3 1 61 0 20
m t t
.
Vì
* 1;2;3;...;20
t t
.
Vậy có
20
số hạng có mặt đồng thời ở hai dãy số trên.
Câu 9:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Cho cấp số cộng
n
u
biết
5
18
u
và
2
4
n n
S S
. Tìm số hạng đầu tiên
1
u
và công sai
d
của cấp số cộng.
A.
1
2
u ;
4
d
. B.
1
2
u ;
3
d
. C.
1
2
u ;
2
d
. D.
1
3
u ;
2
d
.
Lời giải
Chọn A
Ta có:
5 1
18 4 18
u u d
1
.
2
4
n n
S S
1 1
1 2 2 1
4 2
2 2
n n d n n d
nu nu
1 1
4 2 2 2 2
u nd d u nd d
1
2 0
u d
2
.
Từ
1
và
2
suy ra
1
2
u
;
4
d
.
Câu 10:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
biết
5
18
u
và
2
4
n n
S S
. Giá trị
1
u
và
d
là
A.
1
2
u
,
3
d
. B.
1
3
u
,
2
d
. C.
1
2
u
,
2
d
. D.
1
2
u
,
4
d
.
Lời giải
Chọn D
Ta có
5
18
u
1
4 18
u d
.
Lại có
5 10
4
S S
1 1
5.4 10.9
4 5 10
2 2
u d u d
1
2 0
u d
.
Khi đó ta có hệ phương trình
1
1
4 18
2 0
u d
u d
1
2
4
u
d
.
Câu 11:
(THPT Tứ Kỳ-Hải Dương năm 2017-2018)
Giả sử
sin
6
,
cos
,
tan
theo thứ tự đó là một
cấp số nhân. Tính
cos 2
.
A.
3
2
. B.
3
2
. C.
1
2
. D.
1
2
.
Hướng dẫn giải
Chọn D
Điều kiện:
cos 0
2
k
k
.
Theo tính chất của cấp số nhân, ta có:
2
sin
cos .tan
6
2
2
sin
6cos
cos
.
3 2
6cos sin 0
3 2
6cos cos 1 0
1
cos
2
.
Ta có:
2
2
1 1
cos2 2cos 1 2. 1
2 2
.
Câu 12:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Cho bốn số
, a b
,
, c d
theo thứ tự đó tạo
thành cấp số nhân với công bội khác
1
. Biết tổng ba số hạng đầu bằng
148
9
, đồng thời
theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số
cộng. Tính giá trị biểu thức
T a b c d
.
A.
101
27
T
. B.
100
27
T
. C.
100
27
T
. D.
101
27
T
.
Lời giải
Chọn C
Ta có
2
2
1
2
148
3
9
ac b
bd c
a b c
.
Và cấp số cộng có
1
u a
,
4
u b
,
8
u c
. Gọi
x
là công sai của cấp số cộng. Vì cấp số nhân
có công bội khác
1
nên
0
x
.
Ta có :
3
7
b a x
c a x
4
.
Từ
1
và
4
ta được :
2
7 3a a x a x
2
9 0
ax x
.
Do
0
x
nên
9a x
.
Từ
3
và
4
, suy ra
3 10
a x
.
Do đó :
4
4
9
a
x
16
3
64
9
256
27
b
c
d
.
Vậy
100
27
T a b c d
.
Câu 13:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Tính tổng
201732
2.2018........2.42.32.21 S
A.
2018
2017.2 1
S
. B.
2018
2017.2
S
. C.
2018
2018.2 1
S
. D.
2018
2019.2 1
S
.
Lời giải
Chọn A
Ta có
2 3
1 2 2 2 ... 2
n
A
1
2 1
n
Xét
20182017432
2.20182.2017...2.42.32.22.12 S
Và
2017201632
2.20182.2017...2.42.32.21 S
Suy ra
2018 2 3 2017
2018.2 1 2 2 2 ... 2S
2018 2018 2018
2018.2 2 1 2017.2 1
.
Câu 14:
(THTT số 5-488 tháng 2 năm 2018)
Ba số phân biệt có tổng là
217
có thể coi là các số hạng
liên tiếp của một cấp số nhân, cũng có thể coi là số hạng thứ
2
, thứ
9
, thứ
44
của một cấp số
cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng này để tổng của chúng bằng
820
?
A.
20
. B.
42
. C.
21
. D.
17
.
Lời giải
A
C
B
S
M
Chọn A
Gọi ba số đó là
x
,
y
,
z
. Do ba số là các số hạng thứ
2
, thứ
9
và thứ
44
của một cấp số cộng
nên ta có:
x
;
7y x d
;
42z x d
(với
d
là công sai của cấp số cộng).
Theo giả thiết, ta có:
x y z
7 42x x d x d
3 49x d
217
.
Mặt khác, do
x
,
y
,
z
là các số hạng liên tiếp của một cấp số nhân nên:
2
y xz
2
7 42x d x x d
4 7 0
d x d
0
4 7 0
d
x d
Với
0
d
, ta có:
217
3
x y z
. Suy ra
217 2460
820 :
3 217
n
.
Với
4 7 0
x d
, ta có:
4 7 0
3 49 217
x d
x d
7
4
x
d
. Suy ra
1
7 4 3
u
.
Do đó,
820
n
S
1
2 1
820
2
u n d n
2.3 4 1
820
2
n n
20
41
2
n
n
Vậy
20
n
.
Câu 15:
(THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018)
Cho hình chóp
.
S ABC
có đáy
ABC
là
tam giác đều cạnh bằng
1
, cạnh bên
SA
vuông góc với đáy. Gọi
M
là trung điểm của
SA
(hình vẽ bên cạnh). Biết hai đường
thẳng
CM
và
SB
hợp nhau một góc
45
, khoảng cách giữa hai
đường thẳng
CM
và
SB
bằng bao nhiêu?
A.
1
5
. B.
1
6
.
C.
1
3
. D.
1
2
.
Lời giải
Chọn B
A
C
B
S
M
N
H
Gọi
N
là trung điểm cạnh
AB
nên
//MN SB
.
, ,
CM SB CM MN
CMN
Ta có
CN AB
,
CN SA
suy ra
CN SAB
hay
CN NM
3
2
CN
,
tan
CN
CMN
MN
3
2
a
MN
,
2 2
AM MN AN
3 1
4 4
2
2
, d CM SB
,
d SB CMN
,
d B CMN
,
d A CMN
Kẻ
AH MN
suy ra
,
d A CMN AH
2 2 2
1 1 1
AH AN AM
2
1
4 2
AH
6
6
AH
.
THI THỬ – THPT MỘ ĐỨC 2 – QUẢNG NGÃI
GV giải: Đặng Thanh Quang – CÂU 38 – 39
Câu 16:
(THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018)
Cho dãy số
n
u
xác định bởi
2017sin 2018cos
2 3
n
n n
u
. Mệnh đề nào dưới đây đúng?
A.
9
n n
u u
,
n
. B.
15
n n
u u
,
n
. C.
12
n n
u u
,
n
. D.
6
n n
u u
,
n
.
Lời giải
Chọn C
Ta có
12
2017sin 12 2018cos 12
2 3
n
u n n
2017sin 6 2018cos 4
2 3
n n
2017sin 2018cos
2 3
n
n n
u
.
Câu 17:
(THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018)
Cho hai cấp số cộng
: 4
n
x
,
7
,
10
,… và
n
y
:
1
,
6
,
11
,…. Hỏi trong
2018
số hạng đầu tiên của mỗi cấp số có bao
nhiêu số hạng chung?
A.
404
. B.
673
. C.
403
. D.
672
.
Lời giải
Chọn C
Số hạng tổng quát của cấp số cộng
n
x
là:
4 1 .3
n
x n
3 1n
.
Số hạng tổng quát của cấp số cộng
n
y
là:
1 1 .5
m
y m
5 4
m
.
Giả sử
k
là
1
số hạng chung của hai cấp số cộng trong
2018
số hạng đầu tiên của mỗi cấp số.
Vì
k
là
1
số hạng của cấp số cộng
n
x
nên
3 1k i
với
1 2018
i
và
*
i
.
Vì
k
là
1
số hạng của cấp số cộng
n
y
nên
5 4k j
với
1 2018
j
và
*
j
.
Do đó
3 1 5 4i j
3 5 5i j
5i
5;10;15;...;2015
i
có
403
số hạng chung.
Câu 1:
(SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018)
Ông Trung vay ngân hàng
800
triệu đồng theo
hình thức trả góp hàng tháng trong
60
tháng. Lãi suất ngân hàng cố định
0,5
/tháng. Mỗi
tháng ông Trung phải trả (lần đầu tiên phải trả là
1
tháng sau khi vay) số tiền gốc là số tiền vay
ban đầu chia cho
60
và số tiền lãi sinh ra từ số tiền gốc còn nợ ngân hàng. Tổng số tiền lãi mà
ông Trung phải trả trong toàn bộ quá trình trả nợ là bao nhiêu?
A.
118.000.000
đồng. B.
126.066.666
đồng.
C.
122.000.000
đồng. D. 135.500.000 đồng.
Lời giải
Chọn C
Gọi số tiền gốc ban đầu là
N
và phần trăm lãi là
r
.
Tháng thứ nhất ông Trung phải trả số tiền lãi là
.N r
.
Tháng thứ hai ông Trung phải trả số tiền lãi là
59
.
60
N r
.
Tháng thứ ba ông Trung phải trả số tiền lãi là
58
.
60
N r
.
..
Tháng thứ sáu mươi ông Trung phải trả số tiền lãi là
1
.
60
N r
.
Tổng số tiền lãi mà ông Trung phải trả trong suốt quá trình lãi là
59 58 1
. . . . . ... . .
60 60 60
N r N r N r N r
59 58 1
1 ... .
60 60 60
N r
60. 60 1
1 .
2.60
N r
61
.800.0,5% 122.000.000
2
.
Vậy tổng số tiền lãi mà ông Trung phải trả trong toàn bộ quá trình trả nợ là
122.000.000
đồng.
Câu 2:
(THPT Lê Quý Đôn-Hà Nội năm 2017-2018)
Tính diện tích
D
S
của hình phẳng
D
được giới
hạn bởi các đường
ln x
y
x
, trục hoành
Ox
và các đường
1
e
x
;
2
x
?
A.
1
1 ln 2
2
D
S
. B.
2
1
1 ln 2
2
D
S
.
C.
2
1 1
ln 2
2 2
D
S
. D.
2
1
1 ln 2
2
D
S
.
Lời giải
Chọn B
Diện tích hình phẳng cần tìm là
2
1
e
ln
d
D
x
S x
x
1 2
1
1
e
ln ln
d d
x x
x x
x x
1 2
1
1
e
ln ln
d d
x x
x x
x x
1 2
2 2 2
1
1
e
ln ln ln 2
1
2 2 2 2
x x
2
1
1 ln 2
2
.
Câu 3:
(THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018)
Trong hội chợ tết Mậu Tuất
2018
, một
công ty sữa muốn xếp
900
hộp sữa theo số lượng
1
,
3
,
5
,
...
từ trên xuống dưới (số hộp sữa
trên mỗi hàng xếp từ trên xuống là các số lẻ liên tiếp - mô hình như hình bên). Hàng dưới cùng
có bao nhiêu hộp sữa?
A.
59.
B.
30.
C.
61.
D.
57.
Lời giải
Chọn A
Cách 1: p dụng công thức tính tổng n số hạng liên tiếp của CSC:
1
2 1
2
n
n
S u n d
900 2.1 1 .2
2
n
n
2
900
n
30.
n
Vậy
30
1 29*2 59.
u
Cách 2: Áp dụng công thức
2
1 3 5 ..... 2 1
n n
, suy ra
30.
n
Vậy
2 1 59.
n
Câu 4:
(THPT Chuyên Lam Sơn-Thanh Hóa-lần 2 năm 2017-2018)
Cho dãy số
n
u
xác định bởi:
1
1
3
u
và
1
1
.
3
n n
n
u u
n
. Tổng
3 10
2
1
...
2 3 10
u u
u
S u
bằng
A.
3280
6561
. B.
29524
59049
. C.
25942
59049
. D.
1
243
.
Lời giải
Chọn B
Theo đề ta có:
1
1
.
3
n n
n
u u
n
1
1
1 3
n n
u u
n n
mà
1
1
3
u
hay
1
1
1 3
u
Nên ta có
2
2
1 1 1
.
2 3 3 3
u
;
2 3
3
1 1 1
.
3 3 3 3
u
; … ;
10
10
1
10 3
u
.
Hay dãy
n
u
n
là một cấp số nhân có số hạng đầu
1
1
3
u
, công bội
1
3
q
.
Khi đó
3 10
2
1
...
2 3 10
u u
u
S u
10
10
3 1
2.3
10
59048
2.3
29524
59049
.
Câu 5: (THPT Chuyên Thái Bình-lần 4 năm 2017-2018) Có bao nhiêu giá trị thực của tham số
m
để
hàm số
2 2
khi 2
1 khi 2
m x x
f x
m x x
liên tục trên
?
A.
0
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có hàm số luôn liên tục
2
x
.
Tại
2
x
, ta có
2 2
lim lim 1 1 2
x x
f x m x m
;
2 2 2
2 2
lim lim 4
x x
f x m x m
;
2
2 4f m
.
Hàm số liên tục tại
2
x
khi và chỉ khi
2 2
2 2
lim lim 2 4 1 2 4 2 2 0 1
x x
f x f x f m m m m
Phương trình (1) luôn có hai nghiệm thực phân biệt. Vậy có hai giá trị của
m
.
Câu 6:
(SGD Hà Nội-lần 11 năm 2017-2018)
Giá trị của tổng
4 44 444 ... 44...4
(tổng đó có
2018
số hạng) bằng
A.
2018
40
10 1 2018
9
. B.
2019
4 10 10
2018
9 9
.
C.
2019
4 10 10
2018
9 9
. D.
2018
4
10 1
9
.
Lời giải
Chọn B
Cách 1: Đặt
4 44 444 ... 44...4
S
(tổng đó có
2018
số hạng). Ta có:
9
9 99 999 ... 99...9
4
S
2 3 2018
10 1 10 1 10 1 ... 10 1
Suy ra:
9
4
S
2 3 2018
10 10 10 ... 10 2018
2018
A
.
Với
2 3 2018
10 10 10 ... 10
A
là tổng
2018
số hạng của một cấp số nhân có số hạng đầu
1
10
u
, công bội
10
q
nên ta có
2018
1
1
1
q
A u
q
2018
1 10
10
9
2019
10 10
9
.
Do đó
2019
9 10 10
2018
4 9
S
2019
4 10 10
2018
9 9
S
.
Cách 2: Xét dãy số có
1
1
1 1
4
4
4 4
10 4 10
9 9
n n n n
u
u
u u u u
Đặt
1
1
40
4
9
9
10
n n
n n
v
v u v n
v v
là cấp số nhân.
Ta có:
1 2 2018 1 2 2018 1 2 2018
4 4 2018.4
....... ... ...
9 9 9 9
n
v
S u u u v v v v v v
Trong đó
2018
2018
1
2018
40. 10 1
1 1 10 40
. .
1 1 10 9 81
n
v
q
S v
q
Vậy tổng là
2019
2018
40 4 4 10 10
10 1 .2018 2018 .
81 9 9 9
S
Câu 7:
(THPT Nguyễn Trãi-Đà Nẵng-lần 1 năm 2017-2018)
Cho cấp số cộng
n
u
thỏa
2 3 5
4 6
10
26
u u u
u u
.
Tính
1 4 7 2011
...
S u u u u
A.
2023736
S
. B.
2023563
S
. C.
6730444
S
. D.
6734134
S
.
Lời giải
Chọn A
2 3 5
4 6
10
26
u u u
u u
1 1 1
1 1
2 4 10
3 5 26
u d u d u d
u d u d
1
1
3 10
2 8 26
u d
u d
1
1
3
u
d
.
4
10
u
,
7
19
u
,
10
28
u
…
Ta có
1
u
,
4
u
,
7
u
,
10
u
, …,
2011
u
là cấp số cộng có
1
1
9
671
u
d
n
671
2.1 670.9 2023736
2
S
.
Câu 8: Cho dãy số
n
u
thỏa mãn
1
6
n n
u u
,
2
n
và
2 5 9
2
log log 8 11
u u
. Đặt
1 2
...
n n
S u u u
. Tìm số tự nhiên
n
nhỏ nhất thỏa mãn
20172018
n
S
.
A.
2587
. B.
2590
. C.
2593
. D.
2584
.
Câu 9:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Cho dãy số
n
u
thỏa mãn
1
6
n n
u u
,
2
n
và
2 5 9
2
log log 8 11
u u
. Đặt
1 2
...
n n
S u u u
. Tìm số tự nhiên
n
nhỏ nhất
thỏa mãn
20172018
n
S
.
A.
2587
. B.
2590
. C.
2593
. D.
2584
.
Lời giải
Chọn C
Ta có dãy số
n
u
là cấp số cộng có công sai
6
d
.
2 5 9 2 5 9
2
log log 8 11 log 8 11
u u u u
*
với
5
0
u
.
Mặt khác
5 1 1
4 24
u u d u
và
9 1 1
8 48
u u d u
.
Thay vào
*
ta được
1 5
1 5
8 32
88 64
u u
u u
. Suy ra
1
8
u
.
2
1
20172018 2 1 20172018 3 5 20172018 0
2
n
n
S u n d n n
.
Vậy số tự nhiên
n
nhỏ nhất thỏa mãn
20172018
n
S
là
2593
n
.
Câu 10: (SGD Quảng Nam – năm 2017 – 2018) Cho hình vuông
ABCD
có cạnh bằng
a
và có diện
tích
1
S
. Nối
4
trung điểm
1
A
,
1
B
,
1
C
,
1
D
theo thứ tự của
4
cạnh
AB
,
BC
,
CD
,
DA
ta được
hình vuông thứ hai có diện tích
2
S
. Tiếp tục làm như thế, ta được hình vuông thứ ba
là
2 2 2 2
A B C D
có diện tích
3
S
, …và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt
có diện tích
4
S
,
5
S
,…,
100
S
(tham khảo hình bên). Tính tổng
1 2 3 100
... S
S S S S
.
A.
2 100
100
2 1
2
a
S
. B.
2 100
99
2 1
2
a
S
. C.
2
100
2
a
S
. D.
2 99
98
2 1
2
a
S
.
Lời giải
Chọn B
Ta có
2
1
S a
;
2
2
1
2
S a
;
2
3
1
4
S a
,…
Do đó
1
S
,
2
S
,
3
S
,…,
100
S
là cấp số nhân với số hạng đầu
2
1 1
u S a
và công bội
1
2
q
.
Suy ra
1 2 3 100
... S
S S S S
1
1
.
1
n
q
S
q
2 100
99
2 1
2
a
.
Câu 11:
(SGD Nam Định – năm 2017 – 2018)
Cho dãy số
n
u
xác định bởi
1
3 *
1
1
,
n n
u
u u n n
.
Tìm số nguyên dương
n
nhỏ nhất sao cho
1 2039190
n
u
.
A.
2017
n
. B.
2019
n
. C.
2020
n
. D.
2018
n
.
Lời giải
Chọn C
Ta có
1
3
2 1
3
3 3 3
3 2
3
1
1
1
2 1 1 2 ... 1
.................
n
n n
u
u u
u u u n
u u n
Ta lại có
2
3 2
3 3
1
1 2 ... 1 1 2 3 ... 1
2
n n
n n
Suy ra
2
1
1
2
n
n n
u
Theo giả thiết ta có
1
1 2039190 2039190
2
n
n n
u
2020
1 4078380
2019
n
n n
n
mà
n
là số
nguyên dương nhỏ nhất nên
2020
n
.
Câu 1:
(SGD Thanh Hóa – năm 2017 – 2018)
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc
1
2 m/s
v t t
. Đi được
12
giây, người lái xe gặp chướng ngại vật và phanh gấp, ô tô tiếp tục
chuyển động chậm dần đều với gia tốc
a
. Tính quãng đường
m
s
đi được của
ôtô từ lúc bắt đầu chuyển động đến khi dừng hẳn?
A.
168 m
s
. B.
166 m
s
. C.
144 m
s
. D.
152 m
s
.
Lời giải
Chọn A
Giai đoạn 1: Xe bắt đầu chuyển động đến khi gặp chướng ngại vật.
Quãng đường xe đi được là:
12
1 1
0
dS v t t
12
0
2 dt t
12
2
0
t
144 m
.
Giai đoạn 2: Xe gặp chướng ngại vật đến khi dừng hẳn.
Ôtô chuyển động chậm dần đều với vận tốc
2
d 12
v t a t t c
.
Vận tốc của xe khi gặp chướng ngại vật là:
2 1
0 12 2.12 24 m/s
v v
.
12.0 24
c
24
c
2
12 24
v t t
.
Thời gian khi xe gặp chướng ngại vật đến khi xe dừng hẳn là nghiệm phương trình:
12 24 0
t
2t
.
Khi đó, quãng đường xe đi được là:
2
2 2
0
dS v t t
2
0
12 24 dt t
2
2
0
6 24 24 m
t t
.
Vậy tổng quãng đường xe đi được là:
1 2
168 m
S S S
.
Câu 2: (Tạp chí THTT – Tháng 4 năm 2017 – 2018) Có hai cơ sở khoan giếng A và B. Cơ sở A giá
mét khoan đầu tiên là
8000
(đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm
500
(đồng) so với giá của mét khoan ngay trước đó. Cơ sở B: Giá của mét khoan đầu tiên là
6000
(đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm
7%
giá của mét
khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần
lượt là
20
m
và
25
m
để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng
của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất?
A. luôn chọn A.
B. luôn chọn B.
C. giếng
20
m
chọn A còn giếng
25
m
chọn B.
D. giếng
20
m
chọn B còn giếng
25
m
chọn B.
Lời giải
Chọn D
Cơ sở
A
giá mét khoan đầu tiên là
8000
(đồng) và kể từ mét khoan thứ hai, giá của mỗi mét
sau tăng thêm
500
(đồng) so với giá của mét khoan ngay trước đó. Do đó theo tổng của một
cấp số cộng ta có:
+ Nếu đào giếng
20
m
hết số tiền là:
20
20
2.8000 20 1 500 255000
2
S
(đồng).
+ Nếu đào giếng
25
m
hết số tiền là:
25
25
2.8000 25 1 500 350000
2
S
(đồng).
Cơ sở
B
giá của mét khoan đầu tiên là
6000
(đồng) và kể từ mét khoan thứ hai, giá của mỗi
mét khoan sau tăng thêm
7%
giá của mét khoan ngay trước đó. Do đó theo tổng của một cấp
số nhân ta có:
+ Nếu đào giếng
20
m
hết số tiền là:
20
20
1 1,07
6000 245973
1 1,07
S
(đồng).
+ Nếu đào giếng
25
m
hết số tiền là:
25
25
1 1,07
6000 379494
1 1,07
S
(đồng).
Ta thấy
20 20
S S
,
25 25
S S
nên giếng
20
m
chọn B còn giếng
25
m
chọn A.
Câu 3: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Cho
1
10
lim 5
1
x
f x
x
. Giới hạn
1
10
lim
1 4 9 3
x
f x
x f x
bằng
A.
1
. B.
2
. C.
10
. D.
5
3
.
Lời giải
Chọn A
1
10
lim 5
1
x
f x
x
nên
1
10 5 1
x
f x x

hay
1
5 5
x
f x x

Do đó
1
10
lim
1 4 9 3
x
f x
x f x
1
5 5 10
lim
1 4 5 5 9 3
x
x
x x
1
5 1 1
lim
1 20 29 3
x
x x
x x
1
5 1
lim
20 29 3
x
x
x
1
.
Cách 2:
Giả sử:
10 1
f x x g x
.
Ta có:
1
10
lim
1
x
f x
x
1
1
lim
1
x
x g x
x
1
lim
x
g x
5
.
Vậy
1
10
lim
1 4 9 3
x
f x
x f x
1
1 1
lim
1 4 1 10 9 3
x
x g x x
x x g x
1
1
lim
4 1 10 9 3
x
g x x
x g x
5 1 1
1
4 0.5 10 9 3
.
Câu 4: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho dãy số
n
u
bởi công thức truy hồi sau
1
1
0
; 1
n n
u
u u n n
;
218
u
nhận giá trị nào sau đây?
A.
23653
. B.
46872
. C.
23871
. D.
23436
.
Lời giải
Chọn A
Đặt
1n n n
v u u n
, suy ra
n
v
là một câp số cộng với số hạng đầu
1 2 1
1
v u u
và công
sai
1
d
.
Xét tổng
217 1 2 217
...
S v v v
.
Ta có
217 1 2 217
...
S v v v
1 217
217.
2
v v
217. 1 217
23653
2
.
Mà
1
n n n
v u u
suy ra
217 1 2 217 2 1 3 2 218 217
... ...S v v v u u u u u u
218 1
u u
218 217 1
23653
u S u
.
Câu 5:
(THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018)
Cho dãy số
n
a
thỏa mãn
1
1
a
và
1
10 1
n n
a a
,
2
n
. Tìm giá trị nhỏ nhất của
n
để
log 100
n
a
.
A.
100
. B.
101
. C.
102
. D.
103
.
Hướng dẫn giải
Chọn C
1 1
1 1
10 1 10 (1)
9 9
n n n n
a a a a
.
Đặt
1 1
1 1 8
9 9 9
n n
b a b a
. Từ
1
(1) 10 , 2
n n
b b n
Dãy
n
b
là cấp số nhân với công bội là
10
q
. Nên
1 1
1
8
. .10
9
n n
n
b b q
.
Do đó
1
1 8 1
10 , 1,2,...
9 9 9
n
n n
a b n
.
Ta có
100 1 100
8 1
log 100 10 10 10
9 9
n n
n
a a
.
Vậy giá trị nhỏ nhất của
n
để
log 100
n
a
là
102
n
.
Câu 6:
(Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018)
Cho cấp số cộng
n
u
có các số hạng
đều dương, số hạng đầu
1
1
u
và tổng của
100
số hạng đầu tiên bằng
14950
. Tính giá trị của
tổng
2 1 1 2 3 2 2 3 2018 2017 2017 2018
1 1 1
...S
u u u u u u u u u u u u
.
A.
1 1
1
3
6052
. B.
1
1
6052
. C.
2018
. D.
1
.
Hướng dẫn giải
Chọn A
Gọi
d
là công sai của cấp số cộng. Khi đó:
100 1
100.99
100 100 4950 14950 3
2
S u d d d
.
Do đó
2018 1
2017 6052
u u d
.
Ta có:
1
1 1 1 1
1 1
1 1 1 1 1 1
. .
.
. .
k k
k k k k k k k k
k k k k
u u
d d
u u u u u u u u
u u u u
.
Do đó:
1 2 2 3 2017 2018 1 2018
1 1 1 1 1 1 1 1 1 1 1 1
. . ... . .S
d d d d
u u u u u u u u
1 1
1
3
6052
.
Câu 7:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Cho cấp số cộng
n
u
có tất cả các số hạng
đều dương thoả mãn
1 2 2018 1 2 1009
... 4 ...u u u u u u
. Giá trị nhỏ nhất của biểu thức
2 2 2
3 2 3 5 3 14
log log log
P u u u
bằng
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Ta có
2018 1
2018
2 2017
2
S u d
,
1009 1
1009
2 1008
2
S u d
1 2 2018 1 2 1009
... 4 ...u u u u u u
1
2018
2 2017
2
u d
1
1009
4. 2 1008
2
u d
1 1
2 2017 2 2 1008u d u d
1
2
d
u
.
Dãy số
n
u
:
2
d
,
3
2
d
,
5
2
d
, ...
Ta có
2 2 2
3 2 3 5 3 14
log log log
P u u u
2 2 2
3 3 3
3 9 27
log log log
2 2 2
d d d
2 2 2
3 3 3
1 log 2 log 3 log
2 2 2
d d d
. Đặt
3
log
2
d
x
thì
2 2 2
1 2 3
P x x x
2
3 12 14
x x
2
3 2 2 2
x
.
Dấu bằng xảy ra khi
2
2
9
x d
. Vậy giá trị nhỏ nhất của
P
bằng 2.
Câu 8: Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
. Khoảng cách từ
A
đến mặt phẳng
CB D
bằng
A.
3
3
a
. B.
3
2
a
. C.
2
2
a
. D.
2 3
3
a
.
Câu 9: Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
. Khoảng cách từ
A
đến mặt phẳng
CB D
bằng
A.
3
3
a
. B.
3
2
a
. C.
2
2
a
. D.
2 3
3
a
.
Hướng dẫn giải
Chọn D
I
O'
A'
B'
B
C'
D
A
C
D'
H
Gọi
I AC CO
ta có
I AC CB D
. Gọi
H
là hình chiếu của
C
lên
CO
. Khi đó
;
d C CB D C H
2 2
.CC C O
CC C O
3
3
a
.
Mặt khác, ta có
2AI C I
nên
;
d A CB D
2 ;
d C CB D
2 3
3
a
.
Câu 10: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng
1
cây, hàng
thứ hai trồng
2
cây, hàng thứ ba trồng
3
cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Câu 11: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng
1
cây, hàng
thứ hai trồng
2
cây, hàng thứ ba trồng
3
cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Lời giải
Chọn A
Gọi số cây ở hàng thứ
n
là
n
u
.
Ta có:
1
1
u
,
2
2
u
,
3
3
u
, … và
1 2 3
... 3003
n
S u u u u
.
Nhận xét dãy số
n
u
là cấp số cộng có
1
1
u
, công sai
1
d
.
Khi đó
1
2 1
2
n u n d
S
3003
.
Suy ra
2.1 1 1
3003
2
n n
1 6006
n n
2
6006 0
n n
77
78
n
n
77
n
(vì
n
).
Vậy số hàng cây được trồng là
77
.
Câu 12: Trong tủ đồ chơi của bạn An có
5
con thú bông gồm: vịt, chó, mèo, gấu, voi. Bạn An muốn lấy ra một số
thú bông. Xác suất để trong những con thú bông An lấy ra không có con vịt.
A.
16
31
. B.
1
2
. C.
15
32
. D.
15
31
.
Câu 13: Trong tủ đồ chơi của bạn An có
5
con thú bông gồm: vịt, chó, mèo, gấu, voi. Bạn An muốn lấy ra một số
thú bông. Xác suất để trong những con thú bông An lấy ra không có con vịt.
A.
16
31
. B.
1
2
. C.
15
32
. D.
15
31
.
Lời giải
Chọn D
Trường hợp 1: Bạn An chỉ lấy 1 con thú bông
có 5 cách.
Trường hợp 2: Bạn An lấy 2 con thú bông
có
2
5
C
cách.
Trường hợp 3: Bạn An lấy 3 con thú bông
có
3
5
C
cách.
Trường hợp 4: Bạn An lấy 4 con thú bông
có
4
5
C
cách.
Trường hợp 5: Bạn An lấy cả 5 con thú bông
có
5
5
C
cách.
Do đó, số phần tử của không gian mẫu là
2 3 4 5
5 5 5 5
5 31
n C C C C
.
Gọi A là biến cố: “trong những con thú bông An lấy ra không có con vịt”
Do đó, số kết quả thuận lợi cho biến cố A là
2 3 4
4 4 4
4 15
n A C C C
Vậy xác suất cần tìm là
15
31
n A
P A
n
.
Câu 14: Một quả bóng cao su được thả từ độ cao
81m
. Mỗi lần chạm đất quả bóng lại nảy lên hai phần
ba độ cao của lần rơi trước. Tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho
đến lúc bóng không nảy nữa bằng
A.
234
. B.
567
. C.
162
. D.
405
.
Câu 15: Một quả bóng cao su được thả từ độ cao
81m
. Mỗi lần chạm đất quả bóng lại nảy lên hai phần
ba độ cao của lần rơi trước. Tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho
đến lúc bóng không nảy nữa bằng
A.
234
. B.
567
. C.
162
. D.
405
.
Lời giải
Chọn D
Gọi
i
r
là khoảng cách lần rơi thứ
i
Ta có
1
81
r
,
2
2
.81
3
r
,…,
1
2
.81
3
n
n
r
,…
Suy ra tổng các khoảng cách rơi của quả bóng từ lúc thả bóng cho đến lần rơi thứ
n
bằng
2
1
3
81.
2
1
3
n
.
Gọi
i
t
là khoảng cách lần nảy thứ
i
Ta có
1
2
.81
3
t
,
2
2 2
. 81
3 3
t
,…,
1
2 2
.81
3 3
n
n
t
,…
Suy ra tổng các khoảng cách nảy của quả bóng từ lúc thả bóng cho đến đến lần nảy thứ
n
bằng
1
2
1
2
3
.81.
2
3
1
3
n
.
Vậy tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy
nữa bằng
1
2 2
1 1
2
3 3
S lim 81. .81. 405
2 2
3
1 1
3 3
n n
.
Câu 16: Cho dãy
n
u
:
3
1
e
u
,
2
1
n n
u u
,
*
k
thỏa mãn
765
1 2
. ... e
k
u u u
. Giá trị của
k
là:
A.
6
. B.
7
. C.
8
. D.
9
.
Câu 17: Cho dãy
n
u
:
3
1
e
u
,
2
1
n n
u u
,
*
k
thỏa mãn
765
1 2
. ... e
k
u u u
. Giá trị của
k
là:
A.
6
. B.
7
. C.
8
. D.
9
.
Hướng dẫn giải
Chọn C
Ta có
e
n
v
n
u
, với
1
3.2
n
n
v
,
*
n
.
1 2
2 1
... 3. 3 2 1
2 1
k
k
k
v v v
.
1 2
...
1 2
. ... e
k
v v v
k
u u u
.
Suy ra
3 2 1 765 2 1 255
k k
2 256
k
8
k
.
Câu 18: Cho dãy số
n
u
có
1
1
5
u
và
1
1
5
n n
n
u u
n
,
1
n
. Tìm tất cả giá trị
n
để
2018
2018
1
5 1
4.5
n
k
k
u
S
k
.
A.
2019
n
. B.
2018
n
. C.
2020
n
. D.
2017
n
.
Câu 19: Cho dãy số
n
u
có
1
1
5
u
và
1
1
5
n n
n
u u
n
,
1
n
. Tìm tất cả giá trị
n
để
2018
2018
1
5 1
4.5
n
k
k
u
S
k
.
A.
2019
n
. B.
2018
n
. C.
2020
n
. D.
2017
n
.
Lời giải
Chọn B
Ta có
1
1
1 1
5 1 5
n n
n n
u u
n
u u
n n n
.
Đặt
n
n
u
v
n
,
1
n
. Suy ra
n
v
là cấp số nhận có công bội
1
5
q
và
1
1
5
v
.
Ta có
1
1 1
1
1
1 1 1 5 1
5
1
1 5 4 5
1
5
n
n n
n n
k
k n
n
k k
u
q
S v v T
k q
.
Do
0
n
v
,
1
n
nên
n
T
là dãy tăng. Suy ra
2018
2018
2018
5 1
2018
4.5
n
T T n
.
Câu 20: Xét các số thực dương
a
,
b
sao cho
25
,
2a
,
3b
là cấp số cộng và
2
,
2
a
,
3b
là cấp số
nhân. Khi đó
2 2
3a b ab
bằng :
A.
59
. B.
89
. C.
31
. D.
76
.
Câu 21: Xét các số thực dương
a
,
b
sao cho
25
,
2a
,
3b
là cấp số cộng và
2
,
2
a
,
3b
là cấp số
nhân. Khi đó
2 2
3a b ab
bằng :
A.
59
. B.
89
. C.
31
. D.
76
.
Lời giải
Chọn A
Vì
25
,
2a
,
3b
là cấp số cộng nên
25 3 4b a
3 9 4 16
b a
.
Vì
2
,
2
a
,
3b
là cấp số nhân nên
2
2 3 2
b a
.
Suy ra
2
4 16
2 2
3
a
a
2
2 4 16 3 2
a a
2
3 4 20 0
a a
Vì
0
a
nên
2
a
suy ra
11
b
.
Vậy
2 2
3a b ab
4 121 66 59
Câu 22: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác
ABC
được gọi là tam giác
trung bình của tam giác
ABC
. Ta xây dựng dãy các tam giác
1 1 1
A B C
,
2 2 2
A B C
,
3 3 3
A B C
,… sao
cho
1 1 1
A B C
là một tam giác đều cạnh bằng
3
và với mỗi số nguyên dương
2
n
, tam giác
n n n
A B C
là tam giác trung bình của tam giác
1 1 1n n n
A B C
. Với mỗi số nguyên dương
n
, kí hiệu
n
S
tương ứng là diện tích hình tròn ngoại tiếp tam giác
n n n
A B C
. Tính tổng
1 2
... ...
n
S S S S
?
A.
15
.
4
S
B.
4 .
S
C.
9
.
2
S
D.
5 .
S
Câu 23: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác
ABC
được gọi là tam giác
trung bình của tam giác
ABC
. Ta xây dựng dãy các tam giác
1 1 1
A B C
,
2 2 2
A B C
,
3 3 3
A B C
,… sao
cho
1 1 1
A B C
là một tam giác đều cạnh bằng
3
và với mỗi số nguyên dương
2
n
, tam giác
n n n
A B C
là tam giác trung bình của tam giác
1 1 1n n n
A B C
. Với mỗi số nguyên dương
n
, kí hiệu
n
S
tương ứng là diện tích hình tròn ngoại tiếp tam giác
n n n
A B C
. Tính tổng
1 2
... ...
n
S S S S
?
A.
15
.
4
S
B.
4 .
S
C.
9
.
2
S
D.
5 .
S
Lời giải
Chọn B
Ta có
2
1
3
. 3. 3
3
S
;
2
2 1
3 3 3 1
. . .
2 3 4 4
S S
;
2
3 2
3 3 3 1
. . .
4 3 16 4
S S
Ta có
1
S
,
2
S
,
3
S
, …,
n
S
tạo thành cấp số nhân lùi vô hạn với số hạng đầu là
1
3
S
và công
bội
1
4
q
Suy ra
1
1 2
3
... ... 4
1
1
1
4
n
S
S S S S
q
.
Câu 24: Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp
được tháp có
10
tầng thì bạn An cần đúng bao nhiêu que diêm?
A.
210
. B.
39
. C.
100
. D.
270
.
Câu 25: Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp
được tháp có
10
tầng thì bạn An cần đúng bao nhiêu que diêm?
A.
210
. B.
39
. C.
100
. D.
270
.
Lời giải
Chọn A
Số que ở
1
tầng là
1
3
u
.
Tổng số que ở
2
tầng là
1 2
3 7
u u
.
Tổng số que ở
3
tầng là
1 2 3
3 7 11
u u u
.
.
Ta có cấp số cộng
1
3
u
,
4
d
, tính
10
S
?
Để cần có
10
tầng cần tổng
10
10
2.3 9.4 210
2
S
que.
Câu 26: Cho
a b c
là ba số nguyên. Biết
a
,
b
,
c
theo thứ tự tạo thành một cấp số cộng và
a
,
c
,
b
theo thứ tự tạo thành một cấp số nhân. Tìm giá trị nhỏ nhất của
c
.
A.
2
. B.
2
. C.
1
. D.
4
.
Câu 27: Cho
a b c
là ba số nguyên. Biết
a
,
b
,
c
theo thứ tự tạo thành một cấp số cộng và
a
,
c
,
b
theo thứ tự tạo thành một cấp số nhân. Tìm giá trị nhỏ nhất của
c
.
A.
2
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn B
Ta có
2
2
0
b a c
c ab
. Suy ra:
2 2 2
2 2 0
2 4 2
c a L
c a a c c ac a
a a c
c b
.
Suy ra
a
,
b
trái dấu với
c
0
0
a
c
.
Do
a
,
b
,
c
nguyên nên
c
chia hết cho
2
.
Do đó
c
nhỏ nhất bằng
2
khi đó
4
a
,
1
b
(thỏa mãn).
Câu 28: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân tại
A
,
120
BAC
,
AB BB a
. Gọi
I
là trung điểm của
CC
. Tính
cosin của góc giữa hai mặt phẳng
ABC
và
AB I
.
A.
70
10
. B.
5
5
.
A
B
C
B
A
C
I
C.
30
10
. D.
15
5
.
Câu 29: Cho dãy số
n
u
thỏa mãn
1
2
u
và
1
2
n n
u u
với mọi
1n
. Tìm
2018
u
.
A.
2018
2017
2 cos
2
u
. B.
2018
2019
2cos
2
u
. C.
2018
2018
2 cos
2
u
. D.
2018
2
u
.
Câu 30: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân tại
A
,
120
BAC
,
AB BB a
. Gọi
I
là trung điểm của
CC
. Tính cosin của góc giữa hai mặt phẳng
ABC
và
AB I
.
A.
70
10
. B.
5
5
. C.
30
10
. D.
15
5
.
Lời giải
Chọn C
Chọn hệ trục
Oxyz
như hình vẽ và độ dài đơn vị trên các trục là
a
ta có:
3BC a
,
2
a
OA
nên
1
0; ;0
2
A
,
3
;0;1
2
B
,
3
;0;0
2
C
,
3
;0;1
2
C
,
3 1
;0;
2 2
I
3 1
; ;1 // 3; 1;2
2 2
AB
;
3 1 1 1
; ; = 3; 1;1
2 2 2 2
AI
.
Mặt phẳng
ABC
có véc tơ pháp tuyến là
1
0;0;1
n k
.
Mặt phẳng
AB I
có véc tơ pháp tuyến là
2
; 1; 3 3; 2 3
n AB AI

.
I
B
A
C
B'
A'
C'
O
x
y
z
A
B
C
B
A
C
I
1 2
1 2
.
30
cos ;
10
.
n n
ABC AB I
n n
.
Cách 2: Dùng công thức hình chiếu:
cos ;
ABC
AB I
S
ABC AB I
S
.
Câu 31: Cho dãy số
n
u
thỏa mãn
1
2
u
và
1
2
n n
u u
với mọi
1n
. Tìm
2018
u
.
A.
2018
2017
2 cos
2
u
. B.
2018
2019
2cos
2
u
. C.
2018
2018
2 cos
2
u
. D.
2018
2
u
.
Lời giải
Chọn B
Ta có:
1
2
2 2cos 2cos
4 2
u
.
2
3
2 2 2cos 2cos
8 2
u
.
Dự đoán:
1
2cos
2
n
n
u
.
Chứng minh theo quy nạp ta có.
1
co
2 2
4
su
, công thức
1
đúng với
1
n
. Giả sử công thức
1
đúng với
n k
,
1
k
ta có
1
cos2
2
k
k
u
.
Ta có:
1
2
1
2 2
1
2 2 2 2 1 4cos 2cos
2 2
cos cos
2 2
k
k
k
kk k
u u
(vì
2
0
2 2
k
với mọi
1
k
).
Công thức
1
đúng với
1n k
.
Vậy
1
2cos
2
n
n
u
,
n N
. Suy ra
2018
2019
2cos
2
u
.
Câu 32: Cho dãy
n
x
thỏa lim
n
x

. Tính giới hạn
1
lim cos 1
n
n
x
x
A. Không tồn tại. B.
1
. C.
0
. D.
1
.
Câu 33: Cho dãy
n
x
thỏa
lim
n
x

. Tính giới hạn
1
lim cos 1
n
n
x
x
A. Không tồn tại. B.
1
. C.
0
. D.
1
.
Lời giải
Chọn C
1
lim cos 1
n
n
x
x
2
1 1
lim 2sin
1
2
n
n
x
x
2
2
1
sin
2 2
lim .
1
2
n
n
n
x
x
x
0.1 0
.
Câu 1:
(THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018)
Cho hình lập phương
.
ABCD A B C D
có
cạnh bằng
1
. Cắt hình lập phương bằng một mặt phẳng đi qua đường chéo
BD
. Tìm giá trị
nhỏ nhất của diện tích thiết diện thu được.
A.
6
2
. B.
6
4
. C.
2
. D.
6
3
.
Lời giải
Chọn A
Gọi
O
là tâm của hình lập phương. Vì các mặt bên của hình lập phương là các mặt phẳng song
song nên mặt phẳng qua đường chéo
BD
cắt các mặt bên theo các giao tuyến song song. Thiết
diện là hình bình hành
BMD N
.
Ta có
2 .
BMD N BMD
S S BD MH
.
Có
3
BD
nên diện tích đạt GTNN khi và chỉ khi
MH
nhỏ nhất. Do
AA
và
BD
chéo
nhau nên
MH
là đoạn vuông góc chung của
AA
và
BD
hay
2
2
MH OI
.
Vậy
' '
2 6
2 . 3.
2 2
BMD N BMD
S S BD MH
.
Câu 2:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Trong dịp hội trại hè 2017, bạn Anh thả một
quả bóng cao su từ độ cao
6 m
so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên một độ
cao bằng ba phần tư độ cao lần rơi trước. Biết rằng quả bóng luôn chuyển động vuông góc với
mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa)
khoảng:
A.
44 m
. B.
45 m
. C.
42 m
. D.
43 m
.
Lời giải
Chọn C
Ta có quãng đường bóng bay bằng tổng quảng đường bóng nảy lên và quãng đường bóng rơi
xuống.
Vì mỗi lần bóng nảy lên bằng
3
4
lần nảy trước nên ta có tổng quãng đường bóng nảy lên là
2 3
1
3 3 3 3
6. 6. 6. ... 6. ...
4 4 4 4
n
S
B
A
C
D
B
C
D
A
I
O
H
M
N
K
Đây là tổng của cấp số nhân lùi vô hạn có số hạng đầu
1
3 9
6.
4 2
u
và công bội
3
4
q
. Suy ra
1
9
2
18
3
1
4
S
.
Tổng quãng đường bóng rơi xuống bằng khoảng cách độ cao ban đầu và tổng quãng đường
bóng nảy lên nên là
2
2
3 3 3
6 6. 6. ... 6. ...
4 4 4
n
S
Đây là tổng của cấp số nhân lùi vô hạn với số hạng đầu
1
6
u
và công bội
3
4
q
. Suy ra
2
6
24
3
1
4
S
.
Vậy tổng quãng đường bóng bay là
1 2
18 24 42
S S S
.
Câu 3:
(THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018)
Cho dãy số
n
u
thỏa mãn
1
1
2
2 1
1 2 1
n
n
n
u
u
u
u
,
*
n
. Tính
2018
u
.
A.
2018
u
. B.
2018
2
u
. C.
2018
u
. D.
2018
7 2
u
.
Lời giải
Chọn A
Đặt
tan 2
. Ta có
tan 2 1
8
. Suy ra
1
tan
8
1 tan .
8
n
n
n
u
u
u
Có
2
u
tan tan
8
tan
8
1 tan .tan
8
n
u
.
Bằng quy nạp, ta chứng minh được
tan 1
8
n
u n
.
Vậy
2018
tan tan
2017
8
tan tan 7 5 2
8 8
1 tan .tan
8
u
.
Câu 1:
(THPT Triệu Sơn 1-lần 1 năm 2017-2018)
Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình
vuông cạnh
2a
. Gọi
M
,
N
lần lượt là trung điểm của các cạnh
AB
,
AD
;
H
là giao điểm
của
CN
và
DM
. Biết
3SH a
và vuông góc với mặt đáy
ABCD
. Khoảng cách giữa hai
đường thẳng
MD
và
SC
là
A.
12 15
.
61
a
B.
61
.
61
a
C.
12 61
.
61
a
D.
6 61
.
61
a
Lời giải
Chọn C
2a
E
H
M
N
D
C
A
B
Cách 1: Dựng đường thẳng
d
qua
C
và song song với
.DM
d AB E
.
Dựng
HK SC
,
K SC
.
Ta có
( . . )DMA CDN c c c
Suy ra
NCD ADM
Lại có
90 90
NCD CND ADM CND
90
CHD MD CN
tại
H
.
Suy ra
. (1)
CE CH
CE CSH CE HK
CE SH
Suy ta
(1)HK CE
HK CSE
HK CS
, , , .d DM SC d DM CSE d H CSE HK
Ta có
2 2 2 2
4 5.
NC DC DN a a a
E
H
K
M
D
A
B
C
S
K
Xét tam giác vuông
NCD
ta có
2 2
4 4 5
.
5
5
DC a a
HC
NC
a
Suy ta
2 2
. 12 61
61
HS HC
HK a
HS HC
.
Cách 2: Dễ thấy
CN DM CH DM
Tam giác
ADM
vuông tại
A
có:
2 2
5
2
a
DM AD AM
Ta có :
CH DM
DM SHC
SH DM
2
1 4
. 2
2
5
DCM
a
S CH DM a CH
Trong
SHC
hạ
HK SC
,
d DM SC HK
Tam giác
SHC
vuông tại
H
có:
2 2 2
1 1 1 12 61
61
a
HK
HK SH HC
.
Câu 2:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Tam giác mà ba đỉnh của nó là ba trung điểm ba
cạnh của tam giác
ABC
được gọi là tam giác trung bình của tam giác
ABC
.
Ta xây dựng dãy các tam giác
1 1 1 2 2 2 3 3 3
, , ,...
A B C A B C A B C
sao cho
1 1 1
A B C
là một tam giác đều
cạnh bằng
3
và với mỗi số nguyên dương
2
n
, tam giác
n n n
A B C
là tam giác trung bình của
tam giác
1 1 1n n n
A B C
. Với mỗi số nguyên dương
n
, kí hiệu
n
S
tương ứng là diện tích hình tròn
ngoại tiếp tam giác
n n n
A B C
. Tính tổng
1 2
... ...
n
S S S S
?
A.
15
.
4
S
B.
4 .
S
C.
9
.
2
S
D.
5 .
S
Lời giải
Chọn B
Vì dãy các tam giác
1 1 1 2 2 2 3 3 3
, , ,...
A B C A B C A B C
là các tam giác đều nên bán kính đường tròn
ngoại tiếp các tam giác bằng cạnh
3
3
.
Với
1
n
thì tam giác đều
1 1 1
A B C
có cạnh bằng
3
nên đường tròn ngoại tiếp tam giác
1 1 1
A B C
có bán kính
1
3
3.
3
R
2
1
3
3.
3
S
.
Với
2
n
thì tam giác đều
2 2 2
A B C
có cạnh bằng
3
2
nên đường tròn ngoại tiếp tam giác
2 2 2
A B C
có bán kính
2
1 3
3. .
2 3
R
2
2
1 3
3. .
2 3
S
.
Với
3
n
thì tam giác đều
3 3 3
A B C
có cạnh bằng
3
4
nên đường tròn ngoại tiếp tam giác
2 2 2
A B C
có bán kính
3
1 3
3. .
4 3
R
2
3
1 3
3. .
4 3
S
.
...................
Như vậy tam giác đều
n n n
A B C
có cạnh bằng
1
1
3.
2
n
nên đường tròn ngoại tiếp tam giác
n n n
A B C
có bán kính
1
1 3
3. .
2 3
n
n
R
2
1
1 3
3. .
2 3
n
n
S
.
Khi đó ta được dãy
1
S
,
2
S
,
... ...
n
S
là một cấp số nhân lùi vô hạn với số hạng đầu
1 1
3
u S
và công bội
1
4
q
.
Do đó tổng
1 2
... ...
n
S S S S
1
4
1
u
q
.
Câu 1:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Cho dãy số xác định bởi
1
1
u
,
*
1
2
1 1
2 ;
3 3 2
n n
n
u u n
n n
. Khi đó
2018
u
bằng
A.
2016
2018
2017
2 1
3 2019
u
. B.
2018
2018
2017
2 1
3 2019
u
.
C.
2017
2018
2018
2 1
3 2019
u
.
D.
2017
2018
2018
2 1
3 2019
u
.
Lời giải
Chọn A
Ta có:
1
2
1 1
u 2u
3 3 2
n n
n
n n
1 3 2
2
3 2 1
n
u
n n
2 1 2 1
.
3 2 3 1
n
u
n n
.
1
1 2 1
2 3 1
n n
u u
n n
1
Đặt
1
1
n n
v u
n
, từ
1
ta suy ra:
1
2
3
n n
v v
.
Do đó
n
v
là cấp số nhân với
1 1
1 1
2 2
v u
, công bội
2
3
q
.
Suy ra:
1
1
1
1 2
. .
2 3
n
n
n
v v q
1
1 1 2
.
1 2 3
n
n
u
n
1
1 2 1
.
2 3 1
n
n
u
n
.
Vậy
2017
2018
1 2 1
.
2 3 2019
u
2016
2017
2 1
3 2019
.
Câu 2: ----------HẾT----------
(THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018)
Cho dãy số
n
u
được xác định bởi
1
2
u
;
1
2 3 1
n n
u u n
. Công thức số hạng tổng quát của dãy số đã cho là
biểu thức có dạng
.2
n
a bn c
, với
a
,
b
,
c
là các số nguyên,
2
n
;
n
. Khi đó tổng
a b c
có giá trị bằng
A.
4
. B.
4
. C.
3
. D.
3
.
Lời giải
Chọn C
Ta có
1
2 3 1
n n
u u n
1
3 5 2 3 1 5
n n
u n u n
, với
2
n
;
n
.
Đặt
3 5
n n
v u n
, ta có
1
2
n n
v v
với
2
n
;
n
.
Như vậy,
n
v
là cấp số nhân với công bội
2
q
và
1
10
v
, do đó
1
10.2 5.2
n n
n
v
.
Do đó
3 5 5.2
n
n
u n
, hay
5.2 3 5
n
n
u n
với
2
n
;
n
.
Suy ra
5
a
,
3
b
,
5
c
. Nên
5 3 5 3
a b c
.
Câu 3:
(THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018)
Cho dãy số
n
u
như sau:
2 4
1
n
n
u
n n
,
1
n
,
2
,
...
Tính giới hạn
1 2
lim ...
n
x
u u u

.
A.
1
4
. B.
1
. C.
1
2
. D.
1
3
.
Lời giải
Chọn C
Ta có
2
2 2
2 2
2 2
1 1 1
2 1 1
1 1
1
n
n n
u
n n n n
n n n n
n n
Ta có
1 2
2 2
1 1 1 1 1 1 1 1 1 1
... 1 ...
2 3 3 7 7 13 13 21 1 1
n
u u u
n n n n
2
2 2
1 1 1
1
2 1 2 1
n n
n n n n
Suy ra
1 2
2
1
1
1 1
lim ... lim
1 1
2 2
1
n
n
u u u
n n
.
Câu 4:
(THPT Chuyên Trần Phú-Hải Phòng-lần 2 năm 2017-2018)
Trong năm đầu tiên đi làm, anh A
được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi
tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương anh A đều cất đi phần
lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh
A mua được ô tô giá 500 triệu biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe?
A.
11
. B.
12.
C.
13
. D.
10
.
Lời giải
Chọn C
Số tiền anh A cần tiết kiệm là
500 500.0,12 340
(triệu).
Gọi số tiền mà anh A nhận được ở mỗi tháng trong năm đầu tiên là
1
10
u
(triệu).
Thì số tiền mà anh A nhận được ở mỗi tháng trong năm thứ hai là
2 1 1
. 1 0,12 .1,12
u u u
(triệu).
Số tiền mà anh
A
nhận được ở mỗi tháng trong năm thứ ba là
2 2
3 1 1
. 1 0,12 . 1,12
u u u
(triệu).
…
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ
n
là
1
1
. 1 0,12
n
n
u u
1
1
. 1,12
n
u
(triệu).
Vậy số tiền mà anh A tiết kiệm được sau
n
năm là
2 1 3 2 1 2 1
12.
n n n n
u u u u u u u u
1
12.
n
u u
1
1 1
12. . 1,12
n
u u
.
Cho
1
1 1
12. . 1,12 340
n
u u
1
23
1,12
6
n
1,12
23
log 1
6
n
13
n
.
Vậy sau ít nhất
13
năm thì anh A sẽ tiết kiệm đủ tiền để mua ô tô.
Câu 5: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Cho lăng trụ tam giác đều
.
ABC A B C
có
AB a
.
M
là một điểm di động trên đoạn
AB
. Gọi
H
là hình chiếu của
A
trên đường
thẳng
CM
. Tính độ dài đoạn thẳng
BH
khi tam giác
AHC
có diện tích lớn nhất.
A.
3
3
a
. B.
2
a
. C.
3 1
2
a
. D.
3
1
2
a
.
Lời giải
Chọn C
C'
B'
A
B
C
A'
M
H
Ta có
AA ABC
nên
AA CM
. Mặt khác
A H CM
. Do đó
. Suy ra
CM AH
. Vậy
H
còn là hình chiếu của
A
trên
CM
.
Ta có
2 2
2 2
1 1 1
. .
2 2 2 4 4
AHC
AC a
S AH HC AH HC
. Dấu bằng xảy ra khi
AH HC
, tức
là khi
45
ACM
. Vậy tam giác
AHC
có diện tích lớn nhất khi
M
ở vị trí sao cho
45
ACM
. Khi đó
2
2
a
HC
và
15
HCB
.
Trong tam giác
HBC
:
2 2 2
2 . .cos
BH HC BC HC BC HCB
2
2
2
4 2 3
2 2 6
2. . .
2 2 4 4
a
a a
a a
3 1
2
a
BH
.
Câu 6: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Cho dãy số
n
u
thỏa mãn
2 2
1 2 1 2
ln 10 ln 2 6u u u u
và
2 1
2 1
n n n
u u u
với mọi
1.
n
Giá trị nhỏ nhất của
n
để
5050
n
u
bằng.
A.
100
. B.
99
. C.
101
. D.
102
.
Lời giải
Chọn D
Ta có:
2 2
1 2 1 2
ln 10 ln 2 6u u u u
2 2
1 2 1 2
10 2 6u u u u
2 2
1 2
1 3 0
u u
1
2
1
3
u
u
.
Đặt
1
n n n
v u u
với
1n
1 2 1
2
v u u
.
Theo giả thiết:
2 1
2 1
n n n
u u u
2 1 1 1
1 1
n n n n n n
u u u u v v
,
1
n
.
Suy ra
n
v
là cấp số cộng có công sai
1
d
1
1 3
n
v v n d n
.
Ta có:
1
1 2
1 1 1 3 2 2 1 1 1
...
n n
n n n n n n
v
v v v
u u u u u u u u u u S u
.
Với
1 2 1
1
...
2 2
n n n
n n
n
S v v v v v
.
Suy ra:
1
1 1 2
1 1
2 2
n n
n n n n
u u
.
Ta có:
2
1 2
5050 1 5050 3 10096 0 101,99
2
n
n n
u n n n
.
Vậy số
n
nhỏ nhất thỏa yêu cầu là
102
.
| 1/86
| | Tải xuống

Có thể bạn quan tâm:

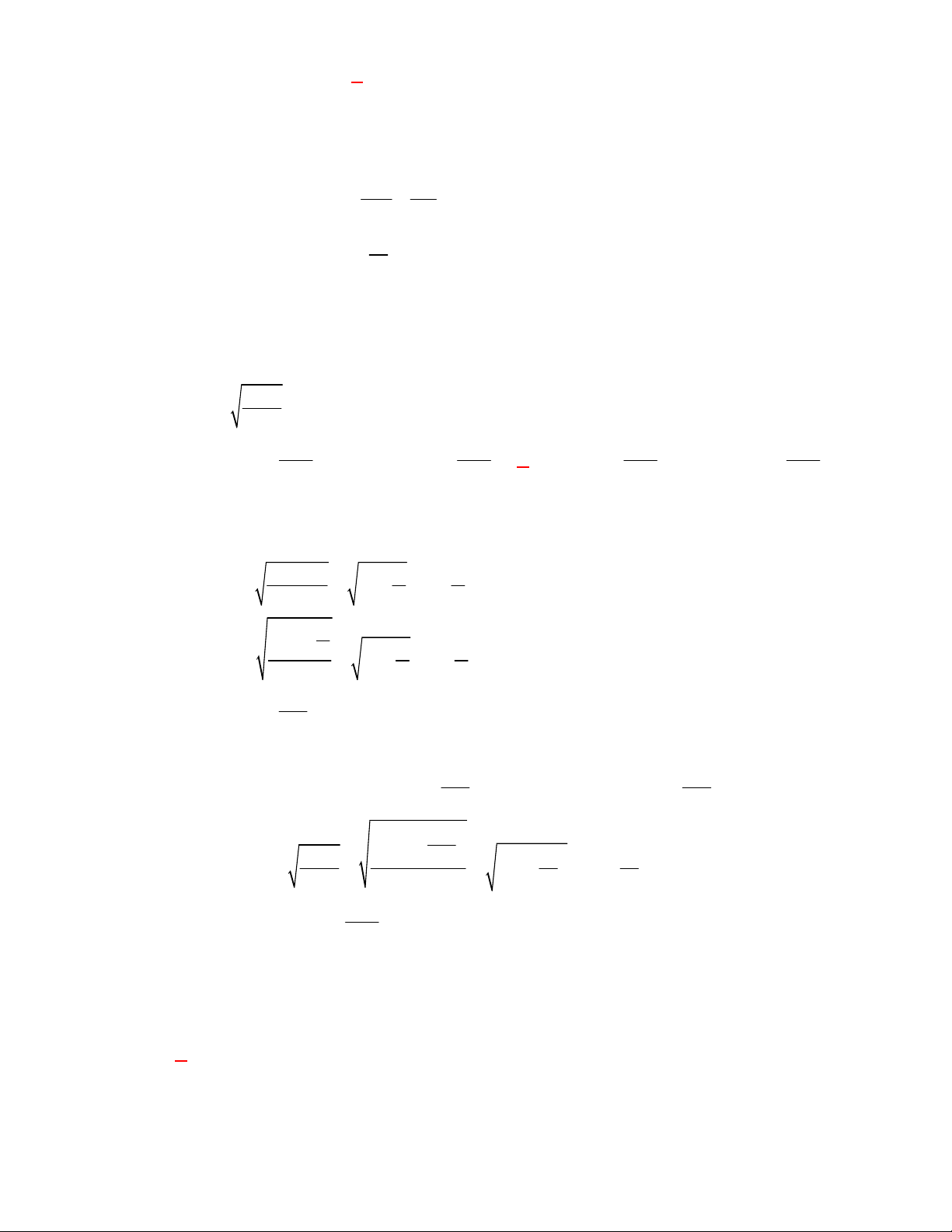
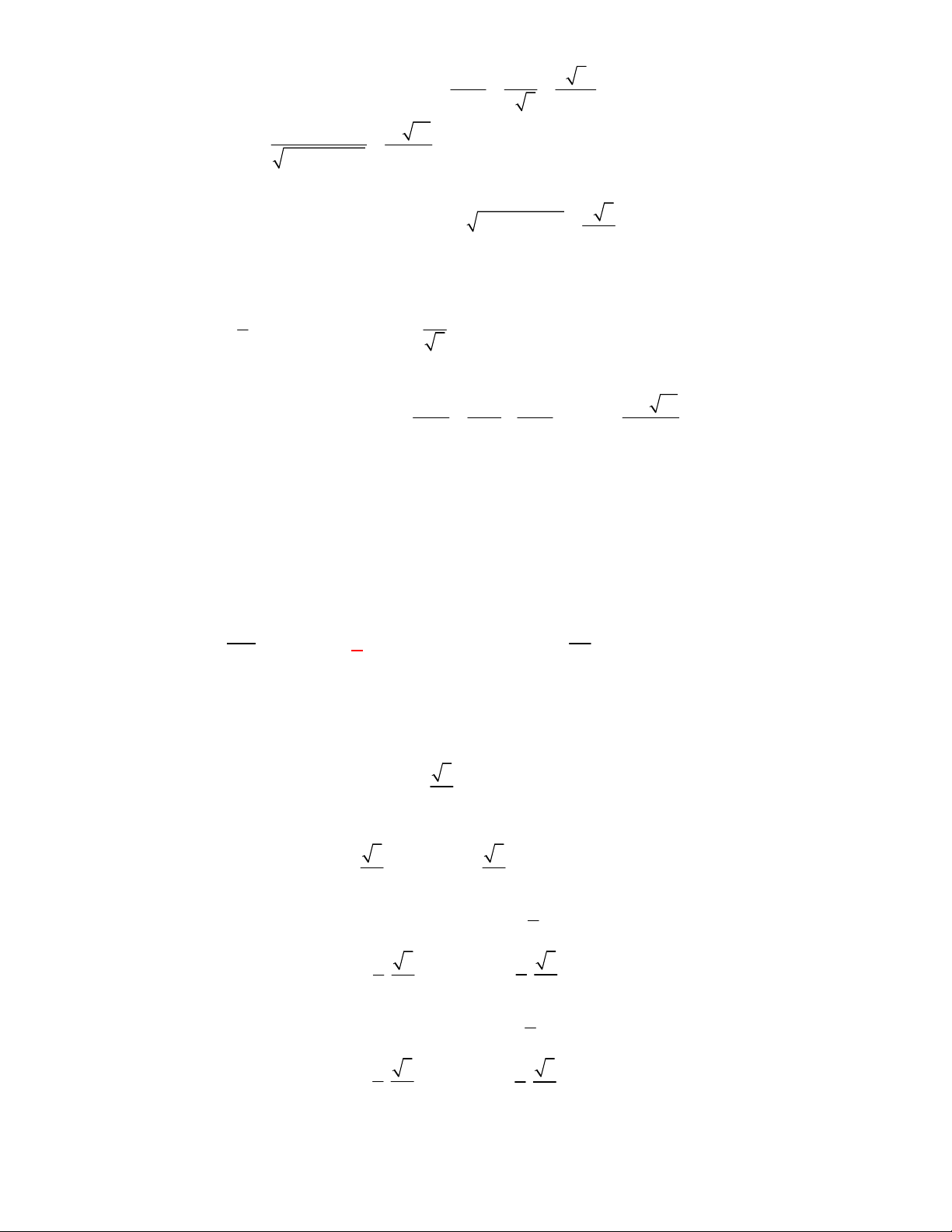
Preview text:

Câu 1: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Cho cấp số cộng u có u  2 và công sai n  1
d  3 . Tìm số hạng u . 10 A. 9 u  2.  3 . B. u  25 . C. u  28 . D. u  29  . 10 10 10 10 Lời giải Chọn B
Ta có u u  9d  2   9.3  25 . 10 1 1
Câu 2: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Cho một cấp số cộng u có u  , n  1 3
u  26. Tìm công sai d 8 11 10 3 3 A. d  . B. d  . C. d  . D. d  . 3 3 10 11 Lời giải Chọn A 1 11
u u  7d  26   7d d  . 8 1 3 3 1
Câu 3: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Cho một cấp số cộng u có u  , n  1 3
u  26. Tìm công sai d 8 11 10 3 3 A. d  . B. d  . C. d  . D. d  . 3 3 10 11 Lời giải Chọn A 1 11
u u  7d  26   7d d  . 8 1 3 3
Câu 4: (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Cho dãy số u với u  3n. Tính u ? n n n 1  A. u  3n  3. B. u  3.3n. C. u  3n 1. D. u  3 n 1 . n 1    n 1  n 1  n 1  Lời giải Chọn B Ta có n 1 u  3   3.3 . n n 1 
Câu 5: (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Cho cấp số cộng u  : 2, a, 6, . b Tích ab n bằng? A. 32 . B. 40 . C. 12 . D. 22 . Lời giải Chọn A 2  6  2aa  4 Ta có     ab  32. a b  2.6 b  8  
Câu 6: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Trong các dãy số sau đây dãy số nào là cấp số nhân? A. Dãy số 2  , 2 , 2  , 2 , …, 2  , 2 , 2  , 2 , …
B. Dãy số u , xác định bởi công thức u  3n 1 với * n   . n n u   1 1 
C. Dãy số u , xác định bởi hệ: . n
u u  2      * n : n 2 n n 1  
D. Dãy số các số tự nhiên 1, 2 , 3 , …. Lời giải Chọn A Dãy số 2  , 2 , 2  , 2 , …, 2  , 2 , 2
 , 2 , …. là cấp số nhân với số hạng đầu u  2 , công bội 1 q  1  .
Dãy số u xác định bởi công thức u  3n 1 có 1 u  3 1  4 , 2 u  3 1  10 , n n 1 2 u u 3
u  3 1  28 . Nhận xét: 3 2 
nên u không là cấp số nhân. n  3 u u 2 1 u   1 1 
Dãy số u , xác định bởi hệ:
có u  1, u  3 , u  5 . Nhận n
u u  2   1 1 3    * n : n 2 n n 1   u u xét: 3 2 
nên u không là cấp số nhân. n u u 2 1 u u
Dãy số các số tự nhiên 1, 2 , 3 , …. có u  1, u  2 , u  3 . Nhận xét: 3 2  nên không là 1 1 3 u u 2 1 cấp số nhân. 2n 1
Câu 7: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Tính giới hạn I  lim n 1 1 A. I  .
B. I   . C. I  2 . D. I  1. 2 Lời giải Chọn C 1 2  2n 1 Ta có I  lim  lim n  2 . n 1 1 1 n
Câu 8: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Cho một cấp số cộng có u  2 , u  4 . Hỏi 4 2 u bằng bao nhiêu? 1 A. u  6 . B. u  1. C. u  5 . D. u  1  . 1 1 1 1 Lời giải Chọn C Theo giả thiết ta có u   2 u   3d  2 u   5 4 1 1      . u  4  u d  4 d  1  2  1 
Câu 1: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Cho cấp số cộng u có số hạng tổng n
quát là u  3n  2 . Tìm công sai d của cấp số cộng. n A. d  3 . B. d  2 . C. d  2  . D. d  3 . Lời giải Chọn A Ta có u
u  3 n 1  2  3n  2  3 n 1  n  
Suy ra d  3 là công sai của cấp số cộng. 1 1 1
Câu 2: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Tổng S     
  có giá trị là: 2 3 3 3n 1 1 1 1 A. . B. . C. . D. . 9 4 3 2 Lời giải Chọn D 1 1 1 1 Ta có S     
  là tổng của cấp số nhân lùi vô hạn u với u  có số hạng n  2 3 3 3n n 3n 1 1 đầu u  , công sai q  . 1 3 3 1 u 1 Do đó 1 3 S    . 1 q 1 2 1 3
Câu 3: (THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018) Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Một cấp số cộng có công sai dương là một dãy số dương.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng. Lời giải Chọn B
Một phản ví dụ: dãy số u , với u n  2 là cấp số cộng có công sai d  1  0 . n n
Nhưng dạng khai triển của nó là 1
 ; 0 ; 1… không phải là một dãy số dương.
Câu 4: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Cho cấp số cộng u có u  11 và công n  1
sai d  4 . Hãy tính u . 99 A. 401. B. 403. C. 402 . D. 404 . Lời giải Chọn B
Ta có : u u  98d  11 98.4  403 . 99 1
Câu 5: (THPT Ninh Giang-Hải Dương năm 2017-2018) Dãy số nào sau đây là một cấp số cộng ?  u  1  u  3 A.u . B.u . n  1 : n  1 :   uu  2, n   1  u  2u 1, n   1 n 1  nn 1  n
C.u  : 1; 3 ; 6 ; 10 ; 15 ; . D.u 1; 1; 1; 1; 1  ;  . n  : n Lời giải Chọn A
Dãy số ở đáp án A thỏa u
u  2 với mọi n  1 nên là cấp số cộng. n 1  n
Câu 6: (THPT Quãng Xương 1-Thanh Hóa năm 2017-2018) Cho tứ diện ABCD , các điểm M , N lần
lượt là trung điểm của AB , CD . Không thể kết luận G là trọng tâm tứ diện ABCD trong trường hợp
  
A. GM GN  0 .
B. GM GN .
    
C. GA GB GC GD  0 .
    
D. 4PG PA PB PC PD với P là điểm bất kỳ. Lời giải Chọn B
Theo giả thiết ta có GM GN thì chưa thể kết luận ngay được G là trung điểm MN .
    
GV GIẢI đã đề xuất sửa đáp án D của đề gốc, từ 4PG PA PB PC PC thành
    
4PG PA PB PC PD với P là điểm bất kỳ.
Các phương án còn lại ta kết luận được ngay G là trọng tâm của tứ diện ABCD .
Câu 7: (THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018) Một cấp số nhân có số hạng đầu u  3, 1
công bội q  2 . Biết S  765 . Tìm n ? n A. n  7 . B. n  6 . C. n  8 . D. n  9 .
Hướng dẫn giải Chọn C u 1 nq 3. 1 2n 1    
Áp dụng công thức của cấp số nhân ta có: S  
 765  n  8 . n 1 q 1 2
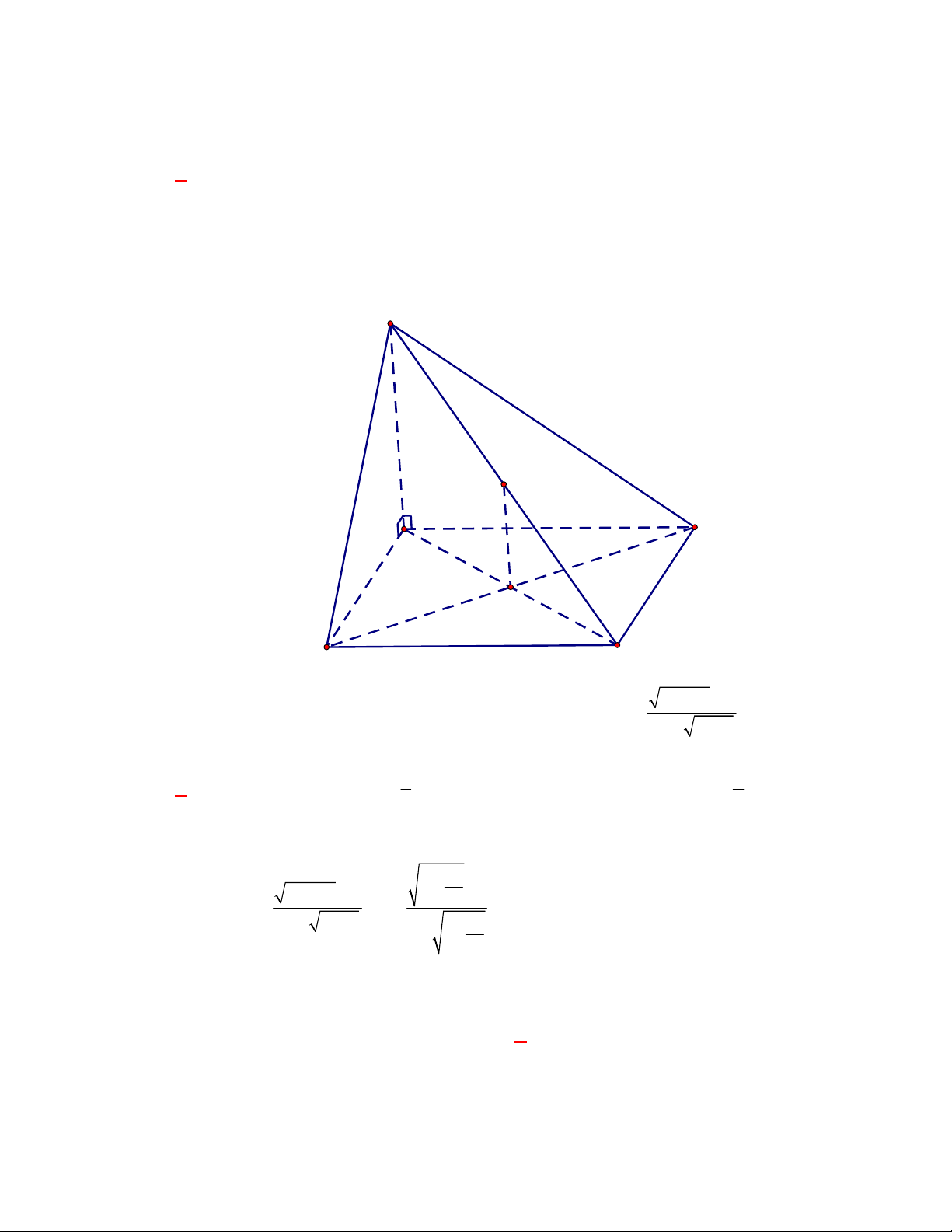
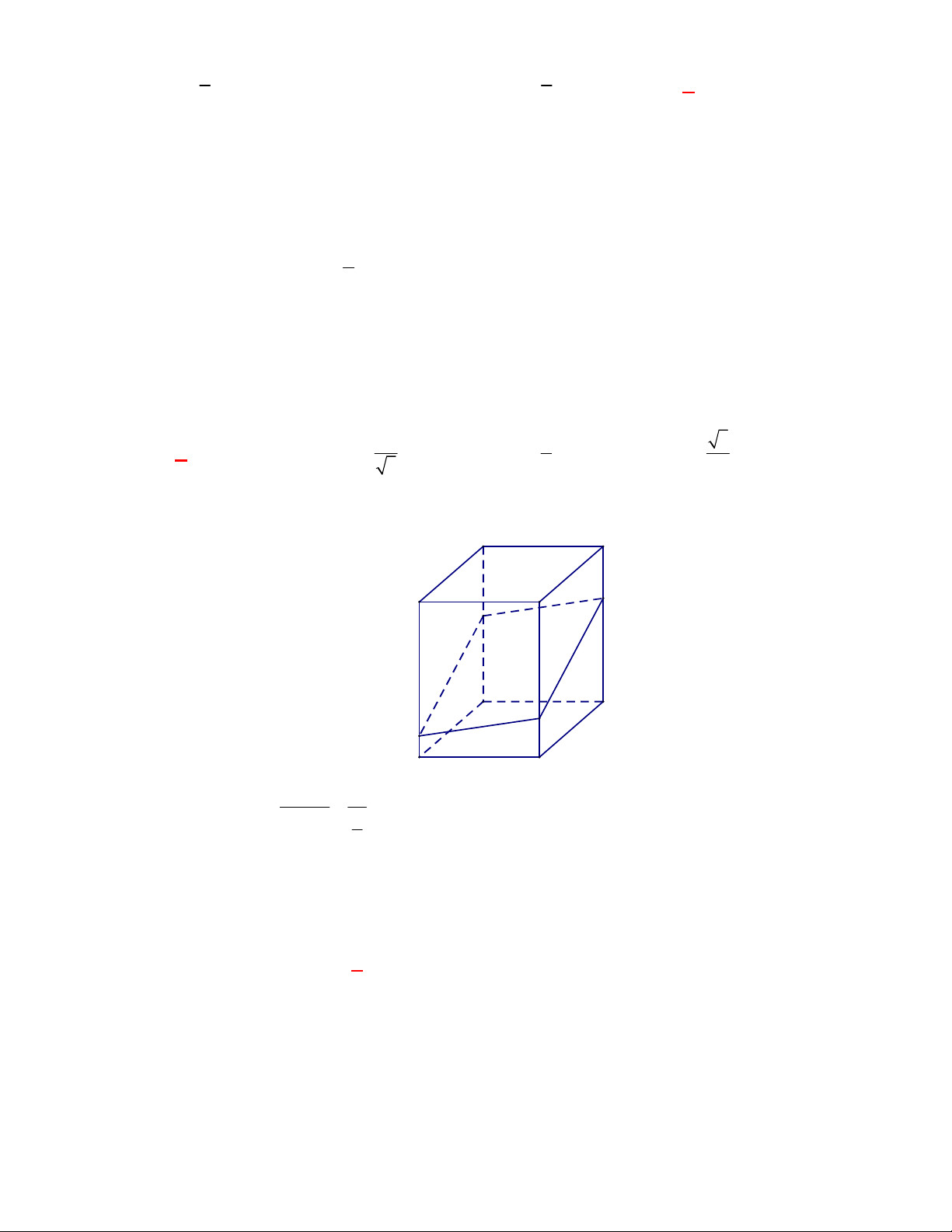
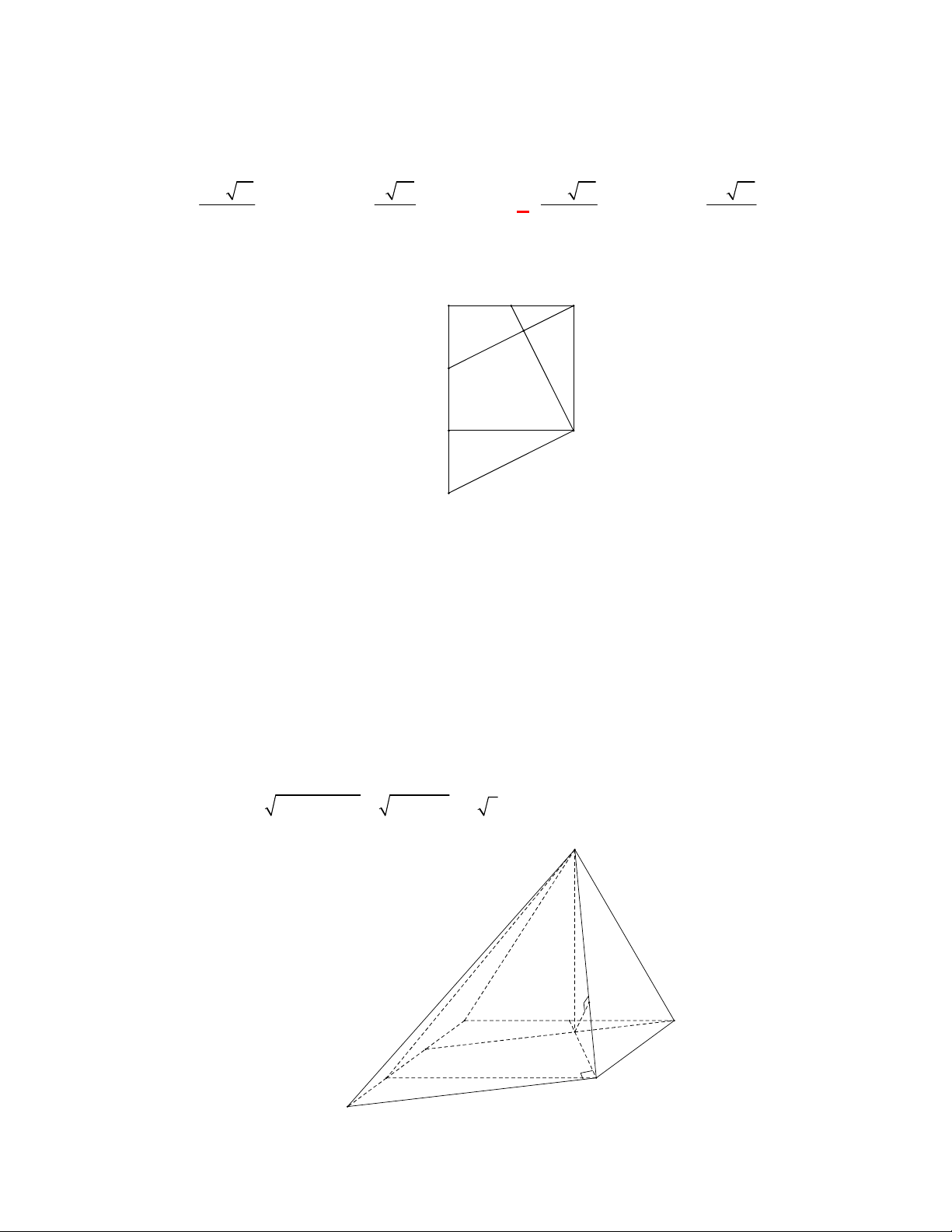
Câu 1: (THPT Lê Quý Đôn-Hà Nội năm 2017-2018) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông tâm O , SA   ABCD . Gọi I là trung điểm của SC . Khoảng cách từ I đến mặt phẳng
ABCD bằng độ dài đoạn thẳng nào? A. IO . B. IA . C. IC . D. IB . Lời giải
Chọn A
Do I là trung điểm của SC và O là trung điểm AC nên IO//SA . Do SA   ABCD nên
IO   ABCD , hay khoảng cách từ I đến mặt phẳng  ABCD bằng độ dài đoạn thẳng IO . S I B A O D C 2 4n  5  n
Câu 2: (THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018) Cho I  lim . Khi đó giá trị 2 4n n 1 của I là 5 3 A. I  1. B. I  . C. I  1. D. I  . 3 4 Lời giải Chọn A 5 2 4  1 4n  5  n 2 n Ta có I  lim  lim  1 2 4n n 1 1 4  1 2 n
Câu 3: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Cho cấp số cộng có u  3  , d  4 . Chọn 1
khẳng định đúng trong các khẳng định sau? A. u  15 . B. u  8 . C. u  5 . D. u  2 . 5 4 3 2 Lời giải Chọn C
Ta có u u  2d  3   2.4  5 . 3 1
Câu 4: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Từ các chữ số 0 , 1, 2 , 3 , 4 , 5 , 8 lập được
bao nhiêu số có ba chữ số đôi một khác nhau, chia hết cho 2 và 3 . A. 35 số. B. 52 số. C. 32 số. D. 48 số. Lời giải Chọn A
Số chia hết cho 2 và 3 là số chẵn và có tổng các chữ số của nó chia hết cho 3 .
Gọi a a a là số tự nhiên có ba chữ số đôi một khác nhau, chia hết cho 2 và 3 được lập từ các 1 2 3
chữ số 0 , 1, 2 , 3 , 4 , 5 , 8 .
 Trường hợp 1: a  0 3
Khi đó các chữ số a , a được lập từ các tập 1;  2 , 1;  5 , 1;  8 , 2;  4 , 4;  5 , 4;  8 . 1 2
Trường hợp này có 6.2!  12 số.
 Trường hợp 2: a  2 3
Khi đó các chữ số a , a được lập từ các tập 1;  0 , 4;  0 , 1;  3 , 3;  4 , 5;  8 . 1 2
Trường hợp này có 2  3.2!  8 số.
 Trường hợp 3: a  4 3
Khi đó các chữ số a , a được lập từ các tập 2;  0 , 2;  3 , 3;  5 , 3;  8 . 1 2
Trường hợp này có 1 3.2!  7 số.
 Trường hợp 4: a  8 3
Khi đó các chữ số a , a được lập từ các tập 0;  1 , 0;  4 , 1;  3 , 2;  5 , 3;  4 . 1 2
Trường hợp này có 2  3.2!  8 số.
Vậy có tất cả 12  8  7  8  35 số cần tìm.
Câu 5: (THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018) Cho cấp số nhân u có u  2 và công n  1
bội q  3. Số hạng u là 2 A. u  6  . B. u  6 . C. u  1. D. u  18  . 2 2 2 2 Lời giải Chọn A
Số hạng u là u u .q  6  2 2 1 n 1 2  1
Câu 6: (THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018) Cho dãy số u thỏa mãn u  . n n n
Tìm số hạng thứ 10 của dãy số đã cho. A. 51, 2 . B. 51, 3 . C. 51,1. D. 102, 3 . Lời giải Chọn B 10 1 2  1 Ta có: u   51, 3 . 10 10 u   4
Câu 7: (THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018) Cho dãy số 1  . Tìm số uu nn 1  n
hạng thứ 5 của dãy số. A. 16 . B. 12 . C. 15 . D. 14 . Lời giải Chọn D
Ta có u u 1  5 ; u u  2  7 ; u u  3  10 . Do đó số hạng thứ 5 của dãy số là 2 1 3 2 4 3
u u  4  14 . 5 4 x 1
Câu 8: (THPT Chuyên Thái Bình-lần 4 năm 2017-2018) Tính lim . 2018 x x 1 A. 1. B. 1. C. 2 . D. 0 . Lời giải Chọn D 1 1  2 x 1 1 x x lim  lim .  0 . 2018 2017 x x 1 x x 1 1 2017 x 4 2n  2n  2
Câu 9: (THPT Lê Xoay-Vĩnh phúc-lần 1 năm 2017-2018) lim bằng 4 4n  2n  5 2 1 A. . B. . C.  . D. 0 . 11 2 Lời giải Chọn B 2 2 4 2   3 4 2n  2n  2 1 Ta có lim  lim n n  . 4 4n  2n  5 2 5 2 4   3 4 n n
Câu 10: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Trong các dãy số sau, dãy
số nào là dãy số giảm? 2n 1 A. 2 u n .
B. u  2n . C. 3 u n 1 . D. u  . n n n n n 1 Lời giải Chọn D * n
   ta có: n  n  2 2
1 nên A sai; 2n  2n  
1 nên B sai; n   n  3 3 1 1 1 nên C sai. 2n 1 3 2n 1 Với u  thì uu   0 nên dãy u  giảm. n n 1 n 1  nn   1 .n n n 1
Câu 11: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Cấp số cộng u có số hạng đầu n
u  3 , công sai d  2
 thì số hạng thứ 5 là 1 A. u  8 . B. u  1 . C. u  5  . D. u  7 . 5 5 5 5 Lời giải Chọn C
Ta có: u u  4d  3  4. 2   5 . 5 1  
Câu 12: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Cho dãy số u là một cấp số cộng có n
u  3 và công sai d  4 . Biết tổng n số hạng đầu của dãy số u là S  253 . Tìm n . n  1 n A. 9 . B. 11. C. 12 . D. 10 . Lời giải
Chọn B
n 2u n 1 d
n 2.3  n 1 .4 1        Ta có S    253 n 2 2 n  11 2 4n 2n 506 0       23 . n   L  2
Câu 1: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Có bao nhiêu tập con gồm 3 phần tử
của tập hợp X  1;2;3; 4;7;8;  9 ? A. 3 A . B. 3 C . C. 3 C . D. 3 A . 7 9 7 9 Lời giải Chọn C
Số tập con gồm 3 phần tử của tập hợp X  1;2;3; 4;7;8; 
9 là số tổ hợp chập 3 của 7 phần tử. Vậy có 3 C tập hợp. 7 3x  2 Câu 2: lim bằng
x  2x  4 1 3 3 A.  . B.  . C.1. D. . 2 4 2 3x  2 Câu 3: lim bằng
x  2x  4 1 3 3 A.  . B.  . C.1. D. . 2 4 2 Lời giải Chọn D 2 3  3x  2 3 Ta có: lim  lim x  .
x 2x  4 x 4 2 2  x u   10
Câu 4: Cho cấp số cộng un  thỏa mãn 4  có công sai là u  4  6 u  26 A. d  3. B. d  3 . C. d  5 . D. d  6 .
Câu 5: Dãy số nào sau đây không phải là cấp số nhân? A. 1; 2; 3; 4; 5 . B. 1; 2; 4; 8; 16 .
C. 1; 1; 1; 1; 1.
D. 1;  2; 4;  8; 16 . u   10
Câu 6: Cho cấp số cộng un  thỏa mãn 4  có công sai là u  4  6 u  26 A. d  3. B. d  3 . C. d  5 . D. d  6 . Lời giải Chọn B
Gọi d là công sai. u   10 u   3d  10 u   1 Ta có: 4 1 1      . u  4  6 u  26 2  1 u  8d  26 d  3 
Vậy công sai d  3 .
Câu 7: Dãy số nào sau đây không phải là cấp số nhân? A. 1; 2; 3; 4; 5 . B. 1; 2; 4; 8; 16 .
C. 1; 1; 1; 1; 1.
D. 1;  2; 4;  8; 16 . Lời giải Chọn A
Dãy 1; 2; 4; 8; 16 là cấp số nhân với công bội q  2 .
Dãy 1; 1; 1; 1; 1 là cấp số nhân với công bội q  1  .
Dãy 1;  2; 4;  8; 16 là cấp số nhân với công bội q  2  .
Dãy 1; 2; 3; 4; 5 là cấp số cộng với công sai d  1.
Câu 8: Cho dãy số u với u  2n 1. Dãy số u là dãy số n n n
A.Bị chặn trên bởi 1. B. Giảm.
C. Bị chặn dưới bởi 2. D. Tăng.
Câu 9: Cho dãy số u với u  2n 1. Dãy số u là dãy số n n n
A.Bị chặn trên bởi 1. B. Giảm.
C. Bị chặn dưới bởi 2. D. Tăng. Lời giải Chọn D * n    ta có: u
u  2 n 1 1 2n 1  2  0 nên u
u vậy dãy số u tăng. n n 1  n     n 1  n
Câu 10: Cho cấp số nhân u có số hạng đầu u  5 và công bội q  2
 . Số hạng thứ sáu của u là: n n  1 A. u  160 . B. u  320  . C. u  160  . D. u  320 . 6 6 6 6
Câu 11: Biết bốn số 5 ; x ; 15 ; y theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức 3x  2 y bằng. A. 50 . B. 70 . C. 30 . D. 80 .
Câu 12: Cho cấp số nhân u có số hạng đầu u  5 và công bội q  2
 . Số hạng thứ sáu của u là: n n  1 A. u  160 . B. u  320  . C. u  160  . D. u  320 . 6 6 6 6
Hướng dẫn giải Chọn C
Ta có u u q  5. 2  5 5  160  . 6 1
Câu 13: Biết bốn số 5 ; x ; 15 ; y theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức 3x  2 y bằng. A. 50 . B. 70 . C. 30 . D. 80 .
Hướng dẫn giải Chọn B 5 15 Ta có: x
 10  y  20 . Vậy 3x  2 y  70 . 2
Câu 14: Số cách sắp xếp 6 học sinh vào một bàn dài có 10 chỗ ngồi là: A. 6 6.A . B. 6 C . C. 6 A . D. 10P . 10 10 10 6
Câu 15: Số cách sắp xếp 6 học sinh vào một bàn dài có 10 chỗ ngồi là: A. 6 6.A . B. 6 C . C. 6 A . D. 10P . 10 10 10 6 Lời giải Chọn C
Số cách sắp xếp 6 học sinh vào một bàn dài có 10 chỗ ngồi là số chỉnh hợp chập 6 của 10
phần tử. Vậy số cách sắp xếp là: 6 A . 10
Câu 16: Cho cấp số cộng u có u  4;u  1. Giá trị của u bằng n  1 2 10 A. u  31 .
B. u  23 . C. u  20  . D. u  15. 10 10 10 10
Câu 17: Cho cấp số cộng u có u  4;u  1. Giá trị của u bằng n  1 2 10 A. u  31 .
B. u  23 . C. u  20  . D. u  15. 10 10 10 10
Hướng dẫn giải Chọn B
u  4;u  1  d  3 . Vậy u u  9d  4  9. 3   23 10 1   1 2
Câu 18: Cấp số cộng u có số hạng đầu u  3 , công sai d  5 , số hạng thứ tư là n  1 A. u  23 . B. u  18 . C. u  8 . D. u  14 . 4 4 4 4
Câu 19: Cấp số cộng u có số hạng đầu u  3 , công sai d  5 , số hạng thứ tư là n  1 A. u  23 . B. u  18 . C. u  8 . D. u  14 . 4 4 4 4 Lời giải Chọn B
u u  3d  3  5.3  18 . 4 1
Câu 20: Khẳng định nào dưới đây sai?
A. Số hạng tổng quát của cấp số nhân u là 1 u u . n q  
, với công bội q và số hạng đầu u . n n 1 1
B. Số hạng tổng quát của cấp số cộng u là u u n 1 d , với công sai d và số hạng n 1   n  đầu u . 1
C. Số hạng tổng quát của cấp số cộng u là u u nd , với công sai d và số hạng đầu u . n n 1 1 u u
D. Nếu dãy số u là một cấp số cộng thì n n 2 u   * n    . n n 1  2
Câu 21: Khẳng định nào dưới đây sai?
A. Số hạng tổng quát của cấp số nhân u là 1 u u . n q  
, với công bội q và số hạng đầu u . n n 1 1
B. Số hạng tổng quát của cấp số cộng u là u u n 1 d , với công sai d và số hạng n 1   n  đầu u . 1
C. Số hạng tổng quát của cấp số cộng u là u u nd , với công sai d và số hạng đầu u . n n 1 1 u u
D. Nếu dãy số u là một cấp số cộng thì n n 2 u   * n    . n n 1  2 Lời giải Chọn C
Câu 22: Cho cấp số cộng u có số hạng đầu u  3 và công sai d  2 . Tính u . n  1 5 A. 11. B. 15 . C. 12 . D. 14 .
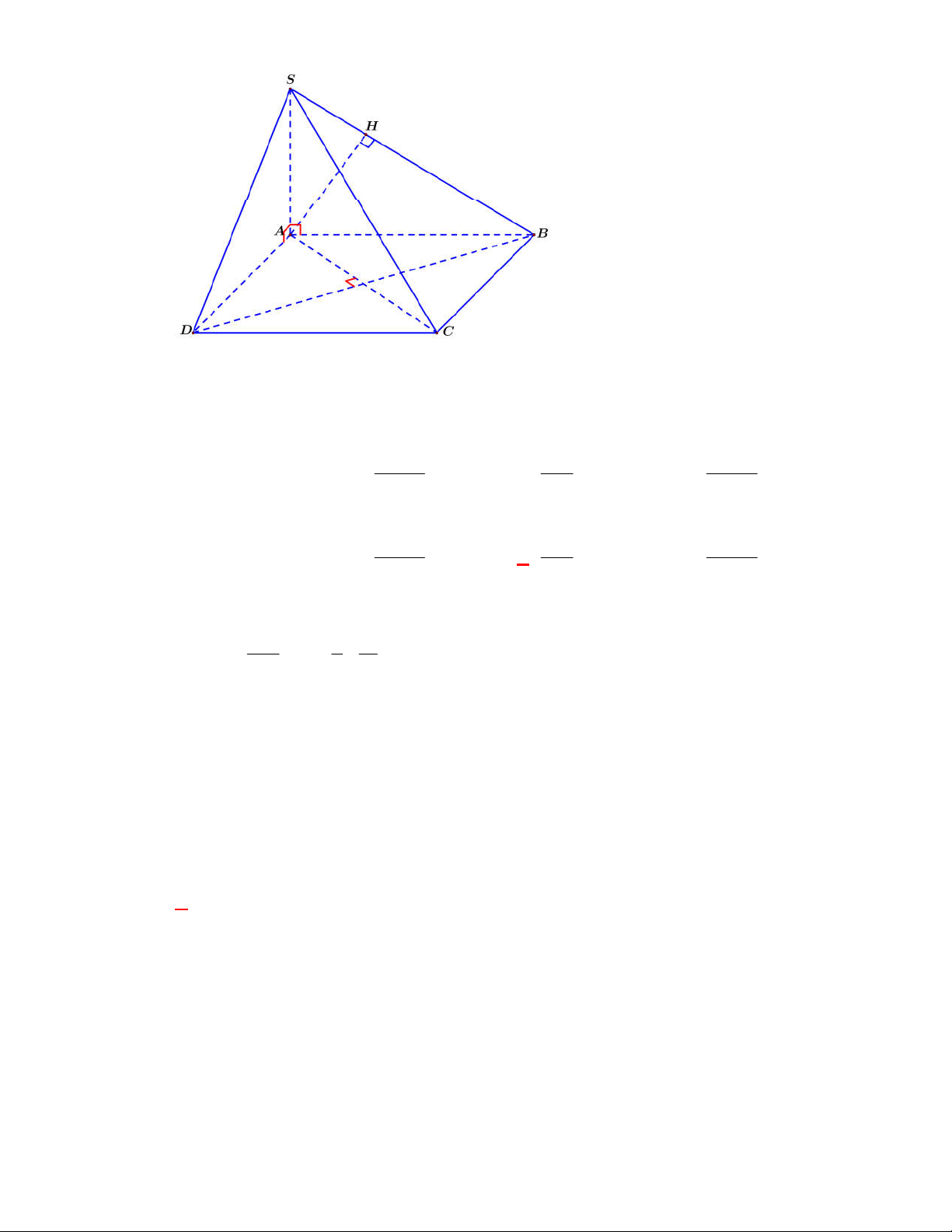
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA vuông góc với  ABCD và H là
hình chiếu vuông góc của A lên SB . Khẳng định nào sau đây là sai?
A. AH BC .
B. AH SC .
C. BD SC .
D. AC SB .
Câu 24: Cho cấp số cộng u có số hạng đầu u  3 và công sai d  2 . Tính u . n  1 5 A. 11. B. 15 . C. 12 . D. 14 . Lời giải
Chọn A
Ta có u u  4d  3  4.2  11 . 5 1
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA vuông góc với  ABCD và H là
hình chiếu vuông góc của A lên SB . Khẳng định nào sau đây là sai?
A. AH BC .
B. AH SC .
C. BD SC .
D. AC SB . Lời giải
Chọn D
Đáp án A đúng do BC   SAB nên AH BC .
Đáp án B đúng do AH   SBC  nên AH SC .
Đáp án C đúng do BD   SAC  nên BD SC .
Câu 26: Dãy số nào sau đây có giới hạn bằng 0 ? 3 n  3n n 1 3 1 2n A. 1 4n . B. . C. . D. . n 1 2 n 3 n  5n
Câu 27: Dãy số nào sau đây có giới hạn bằng 0 ? 3 n  3n n 1 3 1 2n A. 1 4n . B. . C. . D. . n 1 2 n 3 n  5n Lời giải Chọn C n 1  1 1  Ta có lim  lim   0 . 2  2  nn n
Câu 28: Cho dãy số u là một cấp số nhân có số hạng đầu u và công bội q . Đẳng thức nào sau đây n  1 sai? A. u
u q , n   1 . B. n 1 u u q   , n  2 . n 1  n n 1 C. n
u u q , n  2 . D. 2 u u u , k  2 . n 1 k k 1  k 1 
Câu 29: Cho dãy số u là một cấp số nhân có số hạng đầu u và công bội q . Đẳng thức nào sau đây n  1 sai? A. u
u q , n   1 . B. n 1 u u q  
, n  2 . n 1  n n 1 C. n
u u q , n  2 . D. 2 u u u , k  2 . n 1 k k 1  k 1  Lời giải
Chọn C .
Cho dãy số u là một cấp số nhân có số hạng đầu u và công bội q . n  1
Từ định nghĩa của cấp số nhân ta có các kết quả sau: u
u q , n   1 , n 1  n n 1 u u q   , n  2 , n 1 2 u u u , k  2 . k k 1  k 1 
Kết quả của đáp án C là sai.
Câu 1: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Trong các phát biểu sau, phát biểu nào là sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương. Lời giải. Chọn D
A. Đúng vì dãy số đã cho là cấp số nhân với công bội q  1.
B. Đúng vì dãy số đã cho là cấp số cộng với công sai d  0 .
C. Đúng vì dãy số đã cho là cấp số cộng có công sai dương nên: u
u d  0  uu . n 1  n n 1  n D. Sai. Ví dụ dãy 5  ; 2
 ; 1; 3 ; … là dãy số có d  3  0 nhưng không phải là dãy số dương.
Câu 2: (THTT Số 1-484 tháng 10 năm 2017-2018) Cho cấp số cộng u và gọi S là tổng n số hạng n n
đầu tiên của nó. Biết S  77 và S  192 . Tìm số hạng tổng quát u của cấp số cộng đó 7 12 n
A. u  5  4n .
B. u  3  2n .
C. u  2  3n .
D. u  4  5n . n n n n Lời giải
Chọn B
Giả sử cấp số cộng có số hạng đầu là u và công sai d . 1  7.6.d 7u   77 1 S  77  
7u  21d  77 u   5 2 Ta có: 7 1 1        . S  192 12.11.d
12u  66d  192 d  2  12   1 12u   192  1   2
Khi đó: u u n 1 d  5  2 n 1  3  2n . n 1    
Câu 3: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Cho cấp số nhân u ;u  1, q  2 . Hỏi số n 1
1024 là số hạng thứ mấy? A. 11. B. 9 . C. 8 . D. 10 . Lời giải Chọn A Ta có n 1  n 1  n 1  10
u u .q  1.2  1024  2
 2  n 1  10  n  11. n 1
Câu 4: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Trong các dãy số sau, dãy nào là cấp số nhân? n n A. u   n . B. 2 u n .
C. u  2n . D. u  . n   1 n n n 3n Lời giải Chọn C u Lập tỉ số n 1  unun n n  n 1 1 . 1 1 1   A:   
 u không phải cấp số nhân. n u  n n n n 1 . u n 1 n 1   2 B: 
 u không phải là cấp số nhân. n  2 u n n n 1 u 2  C: n 1    2  u
 2u  u là cấp số nhân có công bội bằng 2 . n n n 1 u 2  n n u n 1 D: n 1  
 u không phải là cấp số nhân. n u 3n n
Câu 5: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Xác định số hạng đầu và công bội của cấp số
nhân u có u u  54 và u u  108 . n  4 2 5 3
A. u  3 và q  2 .
B. u  9 và q  2 .
C. u  9 và q  –2 . D. u  3 và q  –2 . 1 1 1 1 Lời giải Chọn B
Gọi số hạng đầu của cấp số nhân là u và công bội là q . 1 Theo giả thiết, ta có u 2   u  54 3 u
 .q u .q  54 q q   1 4 2 1 1 54 1        q  2 . u u  108 4 2 2 2  q q   1 108 2 5 3 u
 .q u .q  108  1 1
Với q  2 , ta có 8u  2u  54  6u  54  u  9 . 1 1 1 1
Câu 6: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Xác định số hàng đầu u và công sai d của cấp 1
số cộng u có u  5u và u  2u  5 . n  9 2 13 6
A. u  3 và d  4 .
B. u  3 và d  5 .
C. u  4 và d  5 .
D. u  4 và d  3 . 1 1 1 1 Lời giải Chọn A u
 8d  5 u d  1  1 
Ta có: u u n 1 d . Theo đầu bài ta có hpt: n 1  
u 12d  2 u 5d 5   1  1 
4u  3d  0 u  3 1 1     . u  2d  5  d  4  1 
Câu 7: (THTT Số 2-485 tháng 11-năm học 2017-2018) Với mọi *
n   , dãy số u nào sau đây không phải n
là cấp số cộng hay cấp số nhân? n n  2017 
A. u  2017n  2018 . B. u   . n   1 n    2018  u   1 1  u   1 C.u . D. 1  . n u  , n  1, 2,3,...  u  2017u  2018 n 1   n 1  n  2018 Lời giải
Chọn D
 Xét dãy số u trong phương án A, ta có n u
u  2017 n 1  2018  2017n  2018  2017 n 1  n       với mọi *
n   . Vậy dãy số này là một cấp số cộng.
 Xét dãy số u trong phương án B, ta có n n 1  n  2017   1  1 u   n  2018  2017 1    với mọi *
n   . Vậy dãy số này là một cấp số nhân. n u n n  2017 2018    1    2018 
 Xét dãy số u trong phương án C, ta có n un u 1 n 1  2018   với mọi *
n   . Vậy dãy số này là một cấp số nhân. u u 2018 n n
 Xét dãy số u trong phương án D, ta có n u
u  2017u  2018  2017u
 2018  2017 u u n 1  nn   n 1    n n 1   2  2017 uu n 1  n2  3  2017 uu n2 n3  ... n 1
 2017  u u n 1
 2017   2017  2018 1  2.2017n 2 1    
Vậy dãy số này không phải là cấp số cộng. Mặt khác, ta có u 2017u  2018 2018 n 1  n   2017  . u u u n n n
Tỷ số này thay đổi khi u thay đổi nên dãy u không là cấp số nhân. n n
Câu 8: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Cho ba số a, b, c theo thứ tự đó vừa lập
thành cấp số cộng, vừa lập thành cấp số nhân khi và chỉ khi
A. a  1; b  2; c  3.
B. a d; b  2d; c  3d với d  0 cho trước. C. a  ; q 2 b q ; 3
c q với q  0 cho trước.
D. a b c . Lời giải Chọn D
Gọi d và q lần lượt là công sai của cấp số cộng và công bội của cấp số nhân. b
  a d aq Ta có:  2
d aq aq 2
a aq aq aq 2
q  2q 1  0 2
c a  2d aq
q  1  d  0  a b c .
Câu 9: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Cho chuyển động xác định bởi phương trình 3 2
S t  3t  9t , trong đó t được tính bằng giây và S được tính bằng mét. Tính
vận tốc tại thời điểm gia tốc triệt tiêu. A. 2 12 m/s . B. 21 m s / . C. 2 12 m/s . D. 12  m/s . Lời giải Chọn D
Ta có v t   S t  2 '
 3t  6t  9 và a t   v 't   6t  6.
Tại thời điểm gia tốc triệt tiêu thì 6t  6  0  t  1.
Vận tốc tại thời điểm gia tốc triệt tiêu là v   2 1  12  m/s .
Câu 10: (THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018) Cho cấp số cộng u có u  123, n  1
u u  84 . Số hạng u bằng 3 15 17 A. 235 . B. 11. C. 3 96000cm . D. 3 81000cm . Lời giải Chọn B
Giả sử cấp số cộng u có công sai d . n
Theo giả thiết ta có: u u  84  u  2d u 14d  84  12 
d  84  d  7  . 3 15 1 1
Vậy u u 16d  123 16.7  11. 17 1
Câu 11: (THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018) Cho cấp số nhân u có S  4; S  13 . n  2 3
Biết u  0 , giá trị S bằng 2 5 35 181 A. . B. . C. 2 . D. 121. 16 16 Lời giải Chọn Bu  2 1 q 1   1 q 4  S   4  1 2 u  1 q  4  1 q   1   2   1   q q 13 Ta có:       u 1 q u   2 3 1 q q  13 4 1 1    u  2 1   S   13  3  1 1  q q   
q  3  u  1 1 1 q 4  Xét   2 1 : 
 4q  9q  9  0  2  3 1 q q 13 q    u  16  1  4
Với q  3;u  1  u u .q  3  0 (loại) 1 2 1 3
Với q   ;u  16  u u .q  12   0 (Thỏa mãn). 1 2 1 4 5  3    16 1     u  5 1 q   4   1     181 Vậy S    . 5 1 q 3 16 1 4
Câu 12: (THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018) Một cấp số cộng có số
hạng đầu u  2018 công sai d  5. Hỏi bắt đầu từ số hạng nào của cấp số cộng đó thì nó 1 nhận giá trị âm. A. u . B. u . C. u . D. u . 406 403 405 404 Lời giải
Chọn C
Ta có u  n  
1 d u n  . n 1
Theo đề ra u  2018  5 n n    1  0
 2018  5n   1 2023
 2023  5n n   n  405 5
PP trắc nghiệm: Vì u n d u n n    1   2018  5 1 1  
Thay từng giá trị vào ta có: u  2018  5.402  8 403 u  2018  5.403  3 404 u  2018  5.404  2  . 405
Câu 13: (THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018) Một cấp số cộng có tổng
của n số hạng đầu S tính theo công thức 2
S  5n  3n ,  *
n    . Tìm số hạng đầu u và n n 1
công sai d của cấp số cộng đó.
A. u  8; d  10 . B. u  8  ; d  10  .
C. . u  8; d  10 ..
D. u  8; d  10  . 1 1 1 1 Lời giải
Chọn C Ta có 2
S  5.1  3.1  8  u 1 1
Lại có S u u  2u d  26  d  10. 2 1 2 1
Câu 14: (THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018) Chọn phát biểu sai trong các phát biểu sau
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
B. Một cấp số nhân có công bội q  1 là một dãy tăng.
C. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
D. Một cấp số cộng có công sai dương là một dãy tăng. Lời giải
Chọn B
Xét cấp số nhân u với u  2 và công bội q  3  1. Ta có: n  1 u  2 .3  6
  u ; u  2  . 6 
 12  u ; u  2 .12  24 
u ; … là dãy số không 4   3     2   1 2 3 tăng, không giảm.
Câu 15: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Cho u là cấp số cộng có công sai n
là d , v là cấp số nhân có công bội là q và các khẳng định. n
I) u d u
n  2, n   . II) v n q v
n  2, n   . n n 1  n 1 uu III) n 1  n 1  u
n  2, n   . IV) 2
v .v v
n  2, n   . n 2 n 1  n n 1 
n v v 1 n
V) v v  ...  v
n  2, n   . 1 2 n 2
Có bao nhiêu khẳng định đúng trong các khẳng định trên? A. 4 . B. 2 . C. 3 . D. 5 . Lời giải Chọn B
I) ĐÚNG : theo định nghĩa cấp số cộng. II) SAI: do n 1  v q
v , n  2, n   theo công thức tổng quát của cấp số nhân. n 1
III) ĐÚNG: theo tính chất cấp số cộng. IV) SAI: do 2 v .v
v , n  2, n   theo tính chất cấp số nhân. n 1  n 1  n
V) SAI: do đây là công thức tính tổng n số hạng đầu của một cấp số cộng. Số câu đúng là: 2 .
Câu 16: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Cho cấp số nhân u có u  3, công bội q  2  . n  1
Hỏi 192 là số hạng thứ mấy của u ? n
A. Số hạng thứ 6 .
B. Số hạng thứ 7 .
C. Số hạng thứ 5 .
D. Số hạng thứ 8 . Lời giải Chọn B
Giả sử 192 là số hạng thứ n của u với * n   . n nn 6 n 1  Ta có 1 192 . n u q           1 192 3 . 2     1 64 2  2   2    6  n 1 1
 7  n . Do đó 192 là số hạng thứ 7 của u . n
Câu 17: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Cho cấp số cộng u có u  15  , u  60 . Tổng n  5 20
của 10 số hạng đầu tiên của cấp số cộng này là: A. S  125  . B. S  250  . C. S  200 . D. S  200  . 10 10 10 10 Lời giải Chọn A
Gọi u , d lần lượt là số hạng đầu và công sai của cấp số cộng. 1 u   15 u   4d  15  u   35  Ta có: 5   1   1  . u  60  u 19d  60 d  5 20  1  10 Vậy S
. 2u  9d  5.2. 35    9.5   . 10  1  2   125
Câu 1: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Xác định x dương để 2x  3 ; x ;
2x  3 lập thành cấp số nhân. A. x  3 . B. x  3 .
C. x   3 .
D. không có giá trị nào của x . Lời giải Chọn B
2x  3 ; x ; 2x  3 lập thành cấp số nhân 2
x  2x  32x  3 2 2
x  4x  9 2  x  3  x   3 .
Vì x dương nên x  3 .
Câu 2: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Cho dãy số u xác định bởi n  u  1 1 
. Giá trị của n để u  2017n  2018  0 là u
u  2n 1, n  1 nn 1  n
A. Không có n . B. 1009 . C. 2018 . D. 2017 . Lời giải Chọn C Cách 1 : Với n  1 ta có: 2
u u  3  4  2 . 2 1 Với n  2 ta có: 2
u u  2.2 1  9  3 . 3 2 Với n  3 ta có: 2
u u  2.3 1  16  4 . 4 3 Từ đó ta có: 2 u n . nn  1   L
Suy ra u  2017n  2018  0 2
 n  2017n  2018  0  . n
n  2018 N   Cách 2 : Ta có :
u u  2.11 2 1
u u  2.2 1 3 2
u u  2.3 1 4 3 ………………. u u  2. n 1 1 n n 1   
Cộng các vế tương ứng ta được :
u u  2. 1 2  3  .....n 1  n 1 n 1   n 1 u  1 2.  n   n n 1  1 1 2
n  1 L 2
u n . Suy ra u  2017n  2018  0 2
 n  2017n  2018  0  . n n
n  2018 N  
Câu 3: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Cấp số nhân u có công bội âm, n
biết u  12 , u  192 . Tìm u . 3 7 10 A. u  1536 . B. u  1536  . C. u  3072 . D. u  3072  . 10 10 10 10 Lời giải Chọn B
Gọi q là công bội của cấp số nhân đề bài cho q  0 . 2 u   12  u q  6 u q 192 Ta có 3 1 1    4  q  16 . 6 2 u   192  u qu q 12 7 1 1 12
Mà q  0  q  2  u   3 . 1 2 q
Do đó u u q  3. 2  9 9  1  536 . 10 1
Câu 4: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Cho dãy số u xác định bởi n u   cos 0     1     1 u
. Số hạng thứ 2017 của dãy số đã cho là n u   , n  1 n 1   2             A. u  sin . B. u  cos . C. u  cos . D. u  sin . 2017  2017         2  2017 2017  2  2017 2016  2  2017 2016  2  Lời giải Chọn C Do 0     nên 1 cos   Ta có 2 u   cos  cos . 2 2 2 2  1 cos   2 2 u   cos  cos 3 2 4 4    Vậy u  cos với mọi *
n  . Ta sẽ chứng mình bằng quy nạp. nn 1   2   Với n  1 đúng.       Giả sử với *
n k  ta có u  cos . Ta chứng minh u  cos . kk 1     2   k 1  k 1  2      1 cos  k 1 1 u           k 2 Thật vậy 2 u    cos  cos . k 1      2 2  2k   2k     Từ đó ta có u  cos . 2017  2016   2  u   8u
Câu 5: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Cấp số nhân u có 20 17  . Tìm n u u  272  1 5
u , biết rằng u  100 . 1 1 A. u  16. B. u  2. C. u  16.  D. u  2.  1 1 1 1 Lời giải Chọn A Ta có: 16    uq u u uq u q   3 19 16 q  8  0 1 8 . 8 1    20 17 1 1      . 4 u u  272  u   u .q  272  u   4 1 5 1 q  272 2 1 1 1     q  0
Từ 2 suy ra u  0 do đó:   1  . 1 q  2 
Nếu q  0 thì 2  u  272 không thõa điều kiện u  100 . 1 1
Nếu q  2 thì 2  u  16 thõa điều kiện u  100 . 1 1
Câu 6: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Cho cấp số cộng u có u  1 và công sai n  1
d  2 . Tổng S u u u .....  u bằng: 10 1 2 3 10 A. S  110 . B. S  100 . C. S  21. D. S  19 . 10 10 10 10 Lời giải Chọn B
n u u
n 2u n 1 d n 1   1   * Áp dụng công thức  S   n ta được: 2 2 10 2  10   1 2 S     100 10 . 2
Câu 7: (THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Tổng của n số hạng đầu tiên của một
dãy số a , n  1 là 2
S  2n  3n . Khi đó n n
A.a là một cấp số cộng với công sai bằng 4 . n
B.a là một cấp số nhân với công bội bằng 4 . n
C.a là một cấp số cộng với công sai bằng 1. n
D.a là một cấp số nhân với công bội bằng 1. n Lời giải Chọn A Ta có 2
S  2n  3n u S  5 ,
u u S  14  u  9 ,
u u u S  27 n 1 1 1 2 2 2 1 2 3 3  u  13  3
Dựa vào nội dung các đáp án ta chọn được đáp án A.
Câu 8: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Cho cấp số cộng u có u  3  , u  27 . n  1 6 Tính công sai d . A. d  7 . B. d  5 . C. d  8 . D. d  6 . Lời giải Chọn D
Ta có u u  5d  27  d  6 . 6 1
Câu 9: (SGD Ninh Bình năm 2017-2018) Cho cấp số nhân u , biết u  1; u  64 . Tính công bội q n  1 4 của cấp số nhân. A. q  21. B. q  4  . C. q  4 . D. q  2 2 . Lời giải Chọn C
Theo công thức tổng quát của cấp số nhân 3 u u q  3
64  1.q q  4 . 4 1
Câu 10: (THPT Chuyên ĐH KHTN-Hà Nội năm 2017-2018) Cho cấp số cộng u , biết u  3 và n  2
u  7 . Giá trị của u bằng 4 15 A. 27 . B. 31. C. 35 . D. 29 . Lời giải Chọn D u   d  3 u   1
Từ giả thiết u  3 và u  7 suy ra ta có hệ phương trình: 1 1  . 2 4   u  3d  7  d  2 1 
Vậy u u 14d  29 . 15 1
Câu 11: (THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018) Dãy số nào sau đây là dãy số giảm? 5  3n n  5 A. u  , n   . B. u  , n   . n   * n   * 2n  3 4n 1 C. 3
u  2n  3,n   * . D. u  cos n n   . n 2  1 ,  * n
Hướng dẫn giải Chọn A 5  3n 5  3n   1 5  3n 2  3n 5  3n Xét u  , n   , ta có uu     n   * 2n  3 n 1  n 2 n   1  3 2n  3 2n  5 2n  3
2  3n2n  3  2n  55  3n 
2n  52n  3 2 2
4n  6n  6  9n 10n  6n  25 15n 19     0, n    * .
2n  52n  3
2n  52n  3 5  3n Vậy u  , n   là dãy giảm. n   * 2n  3
Câu 12: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho cấp số nhân u có u  1  , công bội n  1 1 1 q   . Hỏi
là số hạng thứ mấy của u ? n  10 2017 10
A. Số hạng thứ 2018.
B. Số hạng thứ 2017. C. Số hạng thứ 2019. D. Số hạng thứ 2016. Lời giải
Chọn A n 1  n  1  Ta có 1 u u q    . n 1    10  n 1  1  1  1 Khi đó u       n  2018 . n 2017   2017 10  10  10 1 Do đó
là số hạng thứ 2018 của u . n  2017 10
Câu 13: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho cấp số cộng u có u  12  , n  4
u  18 . Tính tổng 16 số hạng đầu tiên của cấp số cộng này. 14 A. S  24  . B. S  26 . C. S  25  . D. S  24 . 16 16 16 16 Lời giải
Chọn D u   3d  12  u   21 
Gọi d là công sai của cấp số cộng. Theo giả thiết, ta có 1  1   . u 13d  18  d  3 1  2u 15d .16 1  Khi đó, S
 842  45  24 . 16 2
Câu 14: (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Viết ba số xen giữa 2 và 22
để ta được một cấp số cộng có 5 số hạng? A. 6 , 12 , 18 . B. 8 , 13 , 18 . C. 7 , 12 , 17 .
D. 6 , 10 , 14 .
Hướng dẫn giải Chọn C u   2 u   2
Xem cấp số cộng cần tìm là u có: 1 . Suy ra: 1 . n    u  22  d  5 5 
Vậy cấp số cộng cần tìm là u : 2 , 7 , 12 , 17 , 22 . n
Câu 15: (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Cho cấp số nhân u có n 1 u
, u  16 . Tìm công bội q và số hạng đầu u . 2 4 5 1 1 1 1 1 1 1 A. q  , u  . B. q   , u   . C. q  4  , u  
. D. q  4 , u  . 2 1 2 2 1 2 1 16 1 16
Hướng dẫn giải Chọn D  1  1 u   u .q  1  1   Ta có 2  4  4  . u   16 4   u .q  16 2  1   5 1
Chia hai vế của 2 cho   1 ta được 3
q  64  q  4  u  . 1 16
Câu 16: (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Xác định x để bộ ba số
2x 1, x , 2x 1 theo thứ tự lập thành một cấp số nhân. 1 1 A. x   . B. x   . 3 3
C. x   3 .
D. Không có giá trị nào của x .
Hướng dẫn giải Chọn B
Bộ ba số 2x 1, x , 2x 1 theo thứ tự lập thành một cấp số nhân nên ta có 1
x   x   2 2 1 2 1  x 2 2
 4x 1  x x   . 3 2
4x  2x 1  1 2x
Câu 17: (THPT Hoài Ân-Hải Phòng năm 2017-2018) Tính giới hạn lim . x0 x A. 2 . B. 1. C. 2  . D. 0 . Lời giải Chọn D Ta có: 2
4x  2x 1  1 2x 2 4x lim  lim x0 x x0 x  2
4x  2x 1  1 2x  4x  lim  0 . x0  2
4x  2x 1  1 2x
Câu 18: (THPT Hồng Quang-Hải Dương năm 2017-2018) Trong các dãy số u cho bởi số hạng n
tổng quát u sau, dãy số nào là dãy số giảm ? n 1 3n 1 A. u  . B. u  . C. 2 u n . D. u n  2 . n 2n n n 1 n n Lời giải Chọn A 1 1 Ta có u    u * n    . n 2n n 1  1 2 n
Câu 19: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Tính tổng tất cả các số hạng của một cấp 1
số nhân có số hạng đầu là
, số hạng thứ tư là 32 và số hạng cuối là 2048 ? 2 1365 5416 5461 21845 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn C 1
Theo bài ra ta có u
, u  32 và u  2048 . 1 2 4 n 1 3
u u .q 3  32  .q q  4 4 1 2 u  2048 n 1 u .q    2048 n 1  6  4  4  n  7 n 1 1 1 4 u 1 q 1    7 7  5461
Khi đó tổng của cấp số nhân này là 2 S    . 7 1 q 1 4 2
Câu 20: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Cho cấp số cộng u , biết: u  3 n  1 ,
u  1. Chọn đáp án đúng. 2 A. u  4 . B. u  7 . C. u  2 . D. u  5  . 3 3 3 3 Lời giải Chọn D
Ta có u là cấp số cộng nên 2u u u suy ra u  2u u  5  . n  2 1 3 3 2 1
Câu 21: (THPT Ninh Giang-Hải Dương năm 2017-2018) Cho cấp số nhân u thỏa mãn: n u
u u  13 1 2 3 
. Tổng 8 số hạng đầu của cấp số nhân u là n u u  26  4 1 A. S  3280 . B. S  9841. C. S  3820 . D. S  1093 . 8 8 8 8 Lời giải Chọn A Ta có : 2 u 3 
u u  13 u  1 q q  13 1    q   1 1 2 3 26     
q 1  2  q  3  u  1. u u  26 2 1  3
1 q q  13 4 1 uq 1  26 1    1 8 1 3  S   3280 . 8 1 3
Câu 22: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Xen giữa số 3 và số 768 là 7 số để được
một cấp số nhân có u  3 . Khi đó u là: 1 5 A. 72 . B. 48 . C. 48 . D. 48 . Lời giải Chọn D
Ta có u  3 và u  768 nên 8 768  3.q 8
q  256  q  2 . 1 9 Do đó 4 4
u u .q  3.2  48 . 5 1
Câu 23: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Cho cấp số cộng u , biết u  5, n  1
d  2 . Số 81 là số hạng thứ bao nhiêu? A. 100 . B. 50 . C. 75 . D. 44 . Lời giải Chọn D
Ta có u u n 1 d  81  5  n   1 2  n  44 . n 1  
Vậy 81 là số hạng thứ 44 .
Câu 24: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Cho hình chóp S.ABC có SA   ABC  ,
góc giữa SB và  ABC là 60 , A
BC đều cạnh a . Thể tích khối chóp bằng 3 a 3 a A. a 3 . B. . C. . D. 3 a . 4 2 Lời giải Chọn B S A C B 2 a 3 Diện tích ABC là S  . ABC 4
SA   ABC  nên AB là hình chiếu của SB lên  ABC .
 SB ABC    SB AB   , ,  SBA  60 . SAB
vuông tại A có  SBA  60 , ta có  SA A .
B tan SBA a 3 . 2 3 1 1 a 3 a
Thể tích khối chóp là V  .S .SA  . .a 3  . 3 ABC 3 4 4
Câu 25: (THPT Quãng Xương 1-Thanh Hóa năm 2017-2018) Trong các dãy số sau, có bao nhiêu dãy số là cấp số cộng ?
a) Dãy số u với u  4n .
b) Dãy số v với 2 v  2n  1. n n n n n
b) Dãy số w với w
 7 . d) Dãy số t với t  5  5n . n n n 3 n A. 4 . B. 2 . C. 1. D. 3 . Lời giải Chọn D
Dãy số u với u  4n có u
 4 n  1  4n  4  uu  4 , * n
    dãy số u n n 1    n n n 1  n
là cấp số cộng với công sai d  4 . Dãy số v với 2
v  2n  1 có v  3, v  9 , v  19 nên dãy số v không là cấp số cộng. n n n 1 2 3 n n  1 n 1 1
Dãy số w với w   7 có w   7   7   uu  , * n     dãy n n 3 n 1  3 3 3 n 1  n 3 1
số w là cấp số cộng với công sai d  . n  3
Dãy số t với t  5  5n có t
 5  5n  5  uu  5 , * n
    dãy số w n n n n 1  n 1  n
là cấp số cộng với công sai d  5  .
Vậy có 3 dãy số là cấp số cộng.
Câu 26: (THPT Tứ Kỳ-Hải Dương năm 2017-2018) Cho dãy số vô hạn u là cấp số cộng có công sai n
d , số hạng đầu u . Hãy chọn khẳng định sai? 1 u u A. 1 9 u  .
B. u u
d , n  2 . 5 2 n n 1  n C. S
2u 11d . D. u u  (n 1).d , * n    . 12  1  2 n 1 Hướng dẫn giải Chọn C n n   1 d
Ta có công thức tổng n số hạng đầu tiên của cấp số cộng là: S nu n 1 2 12.11.d n
Suy ra S  12u
 6 2u 11d  2u 11d . 1  1  12 1 2 2
Câu 27: (THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Tìm tất cả các giá trị thực của m để  x 1 1 
khi x  0
hàm số f (x)   x liên tục trên  .  2
x 1  m khi x  0  3 1 1 A. m  . B. m  . C. m  2  . D. m   . 2 2 2 Lời giải
Chọn B x 1 1
Khi x  0 ta có: f (x) 
liên tục trên khoảng 0;  . x Khi x  0 ta có: 2 f (x) 
x 1  m liên tục trên khoảng  ;  0 .
Hàm số liên tục trên  khi và chỉ khi hàm số liên tục tại x  0 . x 1 1 1 1
Ta có: lim f (x)  lim  lim  . x 0 x 0 x 0 x     x 1 1 2
lim f (x)  lim
x   m   m f .  x     2 1 1 0 x 0 0    1 1
Do đó hàm số liên tục tại x  0 khi và chỉ khi
 1 m m  . 2 2
Câu 28: (THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018) Một loại vi khuẩn sau mỗi phút
số lượng tăng gấp đôi biết rằng sau 5 phút người ta đếm được có 64000 con hỏi sau bao nhiêu
phút thì có được 2048000 con. A. 10 . B. 11. C. 26 . D. 50 .
Hướng dẫn giải Chọn A
Số lượng vi khuẩn tăng lên là cấp số nhân u với công bội q  2 . n  Ta có: u  64000 5
u .q  64000  u  2000 . 6 1 1
Sau n phút thì số lượng vi khuẩn là u . n 1  u  2048000  . n u q  2048000 2000.2n
 2048000  n  10 . n 1  1
Vậy sau 10 phút thì có được 2048000 con.
Câu 29: (THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018) Tính F (x)  x sin 2xdx  . Chọn kết quả đúng? 1 1
A. F (x) 
(2x cos 2x  sin 2x)  C .
B. F (x)  
(2x cos 2x  sin 2x)  C . 4 4 1 1
C. F (x)  
(2x cos 2x  sin 2x)  C .
D. F (x) 
(2x cos 2x  sin 2x)  C . 4 4
Hướng dẫn giải Chọn C du  dx u   x  Đặt    1 , ta được dv  sin 2 d x x v   cos 2x    2 1 1 1 1 1 F (x)   x cos 2x  cos 2 d x x    x cos 2x
sin 2x C   (2x cos 2x  sin 2x)  C . 2 2 2 4 4
Câu 30: (THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018) Cho một cấp số cộng (u ) có u  1 và n 1 1 1 1
tổng 100 số hạng đầu bằng 24850 . Tính S    ...  u u u u u u 1 2 2 3 49 50 4 9 49 A. S  123. B. S  . C. S  . D. S  . 23 246 246
Hướng dẫn giải Chọn D n Ta có S  24850 
u u  24850  u  496 . 1  100 2 n 100 uu Vậy uu  99d 100 1  d   d  5 . 100 1 99 1 1 1 1 1 1 1 S    ...      ...  . u u u u u u 1.6 6.11 11.16 241.246 1 2 2 3 49 50 5 5 5 5 1 1 1 1 1 1  5S     ...       ...   1.6 6.11 11.16 241.246 1 6 6 11 241 246 1 1 245 49     S  . 1 246 246 246
Câu 1: (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) Cho ba số x ; 5 ; 2 y theo thứ tự lập thành cấp số
cộng và ba số x ; 4 ; 2 y theo thứ tự lập thành cấp số nhân thì x  2 y bằng
A. x  2 y  8 .
B. x  2 y  9 .
C. x  2 y  6 .
D. x  2 y  10 . Lời giải Chọn C Ta có: x   2y  2.5
x  2 y  10  x  8 x  2      hoặc  . . x  2 y 2  4 . x  2 y   16   2 y  2  2 y  8 
Từ đó, ta có x  2 y  8  2  6 .
Câu 2: (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) Cho cấp số cộng có tổng n số hạng đầu là 2
S  3n  4n , n   * . Giá trị của số hạng thứ 10 của cấp số cộng là n A. u  55 . B. u  67 . C. u  61. D. u  59. 10 10 10 10 Lời giải Chọn C Từ giả thiết ta có 2
S u  3.1  4.1  7 . 1 1 n 8  6n
n 7  6n   1 2  
Ta có S  3n  4n  
u  6n 1  u  61. n 2 2 n 10
Câu 3: (SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018) Cho ba số x , 5 , 3y theo thứ tự lập thành cấp số cộng
và ba số x , 3 , 3y theo thứ tự lập thành cấp số nhân thì 3y x bằng? A. 8 . B. 6 . C. 9 . D. 10 . Lời giải Chọn A
Ta có x , 5 , 3y theo thứ tự lập thành cấp số cộng  x  3y  5.2  x  10  3y .
Lại có x , 3 , 3y theo thứ tự lập thành cấp số nhân 2  .
x 3y  3  xy  3 .
y  3  x  1  3y x  8
Do đó y 10  3y  3 2
 3y 10 y  3  0   1
y   x  9  3y x  8  3
Vậy 3y x  8 .
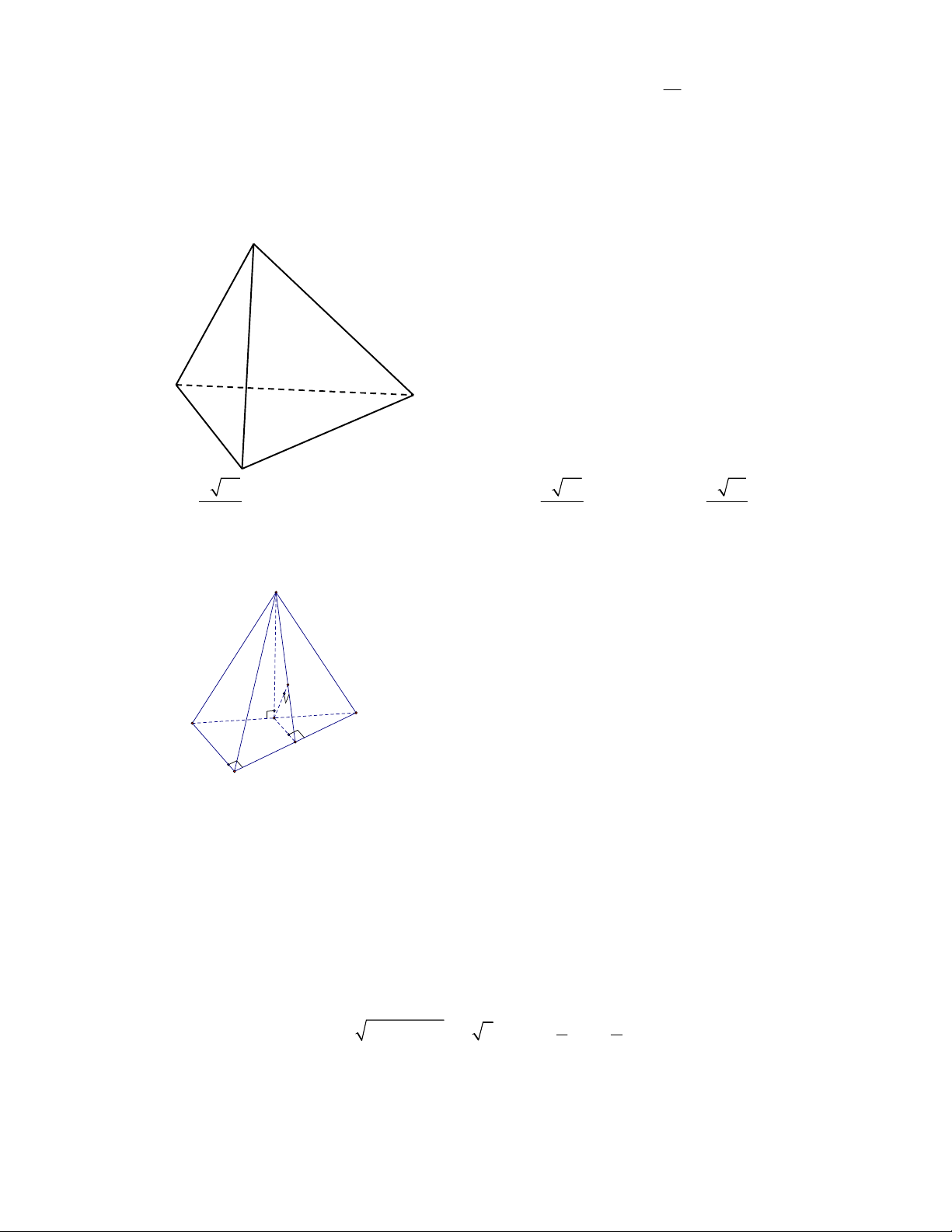
Câu 4: (SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018) Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng
a , góc giữa cạnh bên và mặt đáy bằng 60 . Gọi M , N lần lượt là trung điểm của các cạnh AB ,
BC . Khoảng cách từ điểm C đến mặt phẳng  SMN  bằng a 7a 3a a A. . B. . C. . D. . 7 3 7 3 Lời giải Chọn C
Gọi G là trọng tâm tam giác ABC , khi đó SG   ABC  .
Ta có SA ABC    SM AG   ; ;  SAG   SAG  60 . 2 2 a 3 a 3 Ta có AG AM  .  nên suy ra 3 3 2 3  a 3
SG AG.tan SAG  .tan 60  a . 3
Gọi K là giao điểm của BG với MN , khi đó BG MN , nên suy ra MN   SGK  .
Kẻ GH SK , với H SK . Từ MN   SGK   MN GH .
Từ GH SK và MN GH suy ra GH  SMN  , do đó GH d G;SMN  . CN Vì
 3 nên d C;SMN   3d G;SMN   3GH . GN 2 2 1 1 a 3 a 3  a 3   a a
Ta có GN CN  .  , 2 2
GK GN NG        . 3 3 2 6  6   4  4 3   1 1 1 1 1 49 a       GH  . 2 2 2 GH GK SG 2 2 2 a a 7  a     4 3  a
Vậy d C SMN  3 ;  3GH  . 7 S H N A B K G M C
Câu 5: (THPT Lê Quý Đôn-Hà Nội năm 2017-2018) Cho cấp số cộng u có u  4 . Tìm giá trị nhỏ n  1
nhất của u u u u u u ? 1 2 2 3 3 1 A. 20 . B. 6 . C. 8 . D. 2  4. Lời giải Chọn D
Ta gọi d là công sai của cấp số cộng.
u u u u u u  4 4  d  4  d
4  2d  4 4  2d 1 2 2 3 3 1         d d   d  2 2 2 24 48 2 6  24  2  4
Dấu "  " xảy ra khi d  6 
Vậy giá trị nhỏ nhất của u u u u u u là 24 . 1 2 2 3 3 1
Câu 6: (THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018) Một tam giác vuông có chu vi bằng 3 và độ
dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là: 1 5 1 7 3 5 1 3 A. ;1; . B. ;1; . C. ;1; . D. ;1; . 3 3 4 4 4 4 2 2 Lời giải Chọn C
Gọi d là công sai của cấp số cộng và các cạnh có độ dài lần lượt là a d , a , a d
0  d a .
Vì tam giác có chu vi bằng 3 nên 3a  3  a  1. 2 2 1
Vì tam giác vuông nên theo định lý Pytago ta có   d     d  2 1 1
1  4d  1  d  . 4 3 5
Suy ra ba cạnh của tam giác có độ dài là ;1; . 4 4
Câu 7: (THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018) Cho cấp số nhân u  1, u  0, 00001. 1 6
Khi đó q và số hạng tổng quát là 1 1  1  A. q  , u  . B. q  , 1 u 10n   . 10 n n 1 10  10 n n 1    1 1 1 C. q  , u  . D. q  , u  . 10 n n 1 10  10 n n 1 10  Lời giải Chọn C n 1  n 1  1   1    1 Ta có: 5
u u .q  0, 00001 5  q   q  1 u u . n q     1.   . 6 1 5   10 10 n 1 n 1   10  10
Câu 8: (THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018) Cho một cấp số nhân có các số hạng đều
không âm thỏa mãn u  6 , u  24 . Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó. 2 4 A. 12 3.2  3 . B. 12 2 1 . C. 12 3.2 1. D. 12 3.2 . Lời giải Chọn A
Gọi công bội của CSN bằng q . Suy ra 2
u u .q q  2
 . Do CSN có các số hạng không âm nên 4 2 q  2 . 12 1 q 12 1 2 Ta có S u .  3.   12 3 2   1 . 12 1 1 q 1 2
Câu 9: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Tính diện tích hình phẳng giới hạn bởi các đồ thị 2
y x  2x và 2
y  x x ? 9 10 A. . B. 6 . C. 12 . D. . 8 3 Lời giải Chọn A x   0  Ta có 2 2
x  2x   x x   3 x    2 3 3 3 2 2 3 2 2  x x  9 Nên 2 S 2 
2x  3x dx   2x  3   x dx  2  3   .  3 2  8 0 0   0
Câu 10: (THPT Chuyên Tiền Giang-lần 1 năm 2017-2018) Cho cấp số cộng u có u  15  , n  5 u
 60 . Tổng S của 20 số hạng đầu tiên của cấp số cộng là 20 20 A. S  600 . B. S  60 . C. S  250 . D. S  500 . 20 20 20 20 Lời giải Chọn C u   15 u   4d  15 u   35  Ta có: 5 1 1      . u  60  u 19d  60 d  5 20  1  20.19 20.19  S  20u
.d  20.35  .5  250 . 20 1 2 2
Câu 11: (THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018) Tam giác ABC có ba cạnh a , b , c thỏa mãn 2 a , 2 b , 2
c theo thứ tự đó lập thành một cấp số cộng. Chọn khẳng định đúng trong các khẳng định sau A. 2 tan A , 2 tan B , 2
tan C theo thứ tự đó lập thành một cấp số cộng. B. 2 cot A , 2 cot B , 2
cot C theo thứ tự đó lập thành một cấp số cộng.
C. cos A , cos B , cos C theo thứ tự đó lập thành một cấp số cộng. D. 2 sin A , 2 sin B , 2
sin C theo thứ tự đó lập thành một cấp số cộng. Lời giải Chọn D
Áp dụng định lý sin trong tam giác ABC ta có
a  2R sin A , b  2R sin B , c  2R sin C Theo giả thiết 2 a , 2 b , 2
c theo thứ tự đó lập thành một cấp số cộng nên 2 2 2
a c  2b 2 2 2 2 2 2
 4R .sin A  4R .sin C  2.4R .sin B 2 2 2
 sin A  sin C  2.sin B . Vậy 2 sin A , 2 sin B , 2
sin C theo thứ tự đó lập thành một cấp số cộng.
Câu 12: (THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Cho hình chóp S.ABCD có đáy ABCD là
hình vuông cạnh a , SA vuông góc với mặt đáy, góc giữa cạnh SD và mặt đáy bằng 30 . Độ
dài cạnh SD bằng 2a 3 a A. 2a . B. . C. . D. a 3 . 3 2 Lời giải
Chọn B
Vì SA vuông góc với mặt đáy nên hình chiếu vuông góc của SD lên  ABCD là AD . Do đó AD 2a 3
góc giữa SD và  ABCD là 
SDA  30 . Suy ra SD   . cos 30 3
Câu 13: (THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Cho dãy số u xác định bởi u  1 và n  1 2 uu  2 , * n    . Tổng 2 2 2 2
S u u u  ...  u bằng n 1  n 1 2 3 1001 A. 1002001. B. 1001001. C. 1001002 . D. 1002002 . Lời giải
Chọn A Từ giả thiết 2 uu  2 ta có 2 2 uu  2 . n 1  n n 1  n Xét dãy số 2 v u với * n    ta có 2 vu 2
u  2 hay v
v  2  dãy số v là n n n n 1  n 1  n n 1  n
một cấp số cộng với số hạng đầu 2
v u  1 và công sai d  2 . 1 1 Do đó 10012.1 1001  1 2 2 2 2 2  
S u u u  ...  u
v v v  ...  v   10002001. 1 2 3 1001 1 2 3 1001 2
Câu 14: (SGD Hà Nội-lần 11 năm 2017-2018) Cho u là cấp số cộng biết u u  80 . Tổng 15 số n  3 13
hạng đầu của cấp số cộng đó bằng A. 800 . B. 600 . C. 570 . D. 630 Lời giải Chọn B
Cách 1: S u u u  ...  u u uu uu u
 ...  u uu 15 1 2 3 15  1 15   2 14   3 13   7 9  8
Vì u u u u u u  ...  u u  2u và u u  80  S  7.80  40  600 . 1 15 2 14 3 13 7 9 8 3 13
Cách 2: Gọi d là công sai của cấp số cộng.
Ta có u u  80  u  2d u 12d  80  u  7d  40. 3 13  1   1  1 15 15 Khi đó S u u
u u 14d  15 u  7d  15.40  600. 15  1 15   1 1   1  2 2 2 2018 x  4
Câu 15: (SGD Hà Nội-lần 11 năm 2017-2018) lim bằng 2018 2018 x2 x  2 A.  . B. 2018 2 . C. 2 . D. 2019 2 . Lời giải Chọn D 2 2018 2018 2018 x  4
x  2 x  2  Ta có lim  lim 2018  lim x  2 2018 2018 2019  2  2  2 . 2018   2018 2018 2018 x2 x  2 2018 x2 x  2 x2
Câu 16: (THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018) Cho tứ diện OABC có OA , OB , OC đôi
một vuông góc với nhau và OA OB OC a . Khoảng cách giữa hai đường thẳng OA và BC bằng 3 1 2 3 A. a . B. a . C. a . D. a . 2 2 2 2 Lời giải Chọn C Cách 1. A O C M B
Gọi M là trung điểm của BC .
Khi đó: OM BC và OM OA (do OA  OBC  ). BC a 2 Do đó d O ,
A BC   OM   . 2 2
Cách 2. Gắn hệ trục tọa Oxyz với gốc tọa độ trùng với điểm O , OA Oz , OB Ox , OC Oy .
Khi đó, ta có: O 0;0;0 , A0;0;a , B  ;
a 0;0 , C 0; ; a 0 .    
Ta có: OA0;0;a , BC  ; a ;
a 0  OA BC    2 2 ,
a ; a ;0 .  
   2 2   3 , OA BC .OB
a .a a .0  0.0   a a 2 d O , A BC        . 2 4 4 2  , OA BC a a  0 a 2 2  
Câu 17: (THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018) Cho 4 số thực a , b , c , d là 4 số hạng liên
tiếp của một cấp số cộng. Biết tổng của chúng bằng 4 và tổng các bình phương của chúng bằng 24 . Tính 3 3 3 3
P a b c d . A. P  64 . B. P  80 . C. P  16 . D. P  79 . Lời giải Chọn A
a d b c Theo giả thiết ta có: 
a d b c  2 .
a b c d  4 
a b c d  a d 2  b c2 2 2 2 2
 2 ad bc
ad bc a b c d  a d 2  b c2 2 2 2 2  8  . 3 3 3 3
P a b c d     2 2        2 2 a d a ad d
b c b bc c    2 2 2 2
2 a b c d ad bc  64
Câu 18: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Một công ti trách nhiệm hữu hạn
thực hiện việc trả lương cho các kĩ sư theo phương thức sau: Mức lương của quý làm việc đầu
tiên cho công ti là 4,5 triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng
thêm 0, 3 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư nhận được sau 3 năm làm việc cho công ti.
A. 83, 7 (triệu đồng).
B. 78, 3 (triệu đồng). C. 73,8 (triệu đồng). D. 87, 3 (triệu đồng). Lời giải Chọn C Ta có 3 năm bằng 12 quý.
Gọi u , u , …, u là tiền lương kĩ sư đó trong các quý (từ quý 1 đến quý 12 ). 1 2 12
Suy ra u là cấp số cộng với công sai 4,5. n
Vậy số tiền lương kĩ sư nhận được là
2u n 1 d 2  4, 5 11 0,3 1   S n  12  73,8 (triệu đồng). 12 2 2
Câu 19: (THPT Chuyên Trần Phú-Hải Phòng-lần 2 năm 2017-2018) Cho cấp số cộng u có n u
u  1000 . Tổng 2018 số hạng đầu tiên của cấp số cộng đó là 2013 6 A. 1009000 . B. 100800 . C. 1008000 . D. 100900 . Lời giải Chọn A
Gọi d là công sai của cấp số cộng. Khi đó: u
u  1000  u  2012d u  5d  1000  2u  2017d  1000 . 2013 6 1 1 1 2017.2018 Ta có: S  2018u
d  1009.2u  2017d  1009000 . 1  2018 1 2
Câu 20: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Người ta viết thêm 999 số thực vào giữa số 1
và số 2018 để được cấp số cộng có 1001 số hạng. Tìm số hạng thứ 501. 2019 2021 A. 1009 . B. . C. 1010 . D. . 2 2 Lời giải Chọn B
Áp dụng công thức cấp số cộng ta có: 2017
u u n 1 d u
u  10011 d  2018  1 10011 d d  . n 1   1001 1     1000 2019
Vậy số hạng thứ 501 là u
u  5011 d  . 501 1   2
Câu 21: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Trong các dãy số sau, dãy
số nào là dãy số bị chặn? 2n 1 A. u  .
B. u  2n  sin n . C. 2 u n . D. 3 u n 1 . n n 1 n n n Lời giải Chọn A 2n 1
Xét đáp án A, ta có 0  u   2, n    . n n 1
Câu 22: (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Cho 3 số a , b , c theo thứ tự đó tạo
thành cấp số nhân với công bội khác 1. Biết cũng theo thứ tự đó chúng lần lượt là số hạng thứ a
nhất, thứ tư và thứ tám của một cấp số cộng với công sai là s  0 . Tính . s 4 4 A. . B. 3 . C. . D. 9 . 9 3 Lời giải Chọn D 2 b   ac  2
Theo đề bài ta có hệ phương trình b 2
  a  3s  a  3s  a a  7s  9s as  0 .
c a  7sa
Do s  0 nên a  9s   9 . s
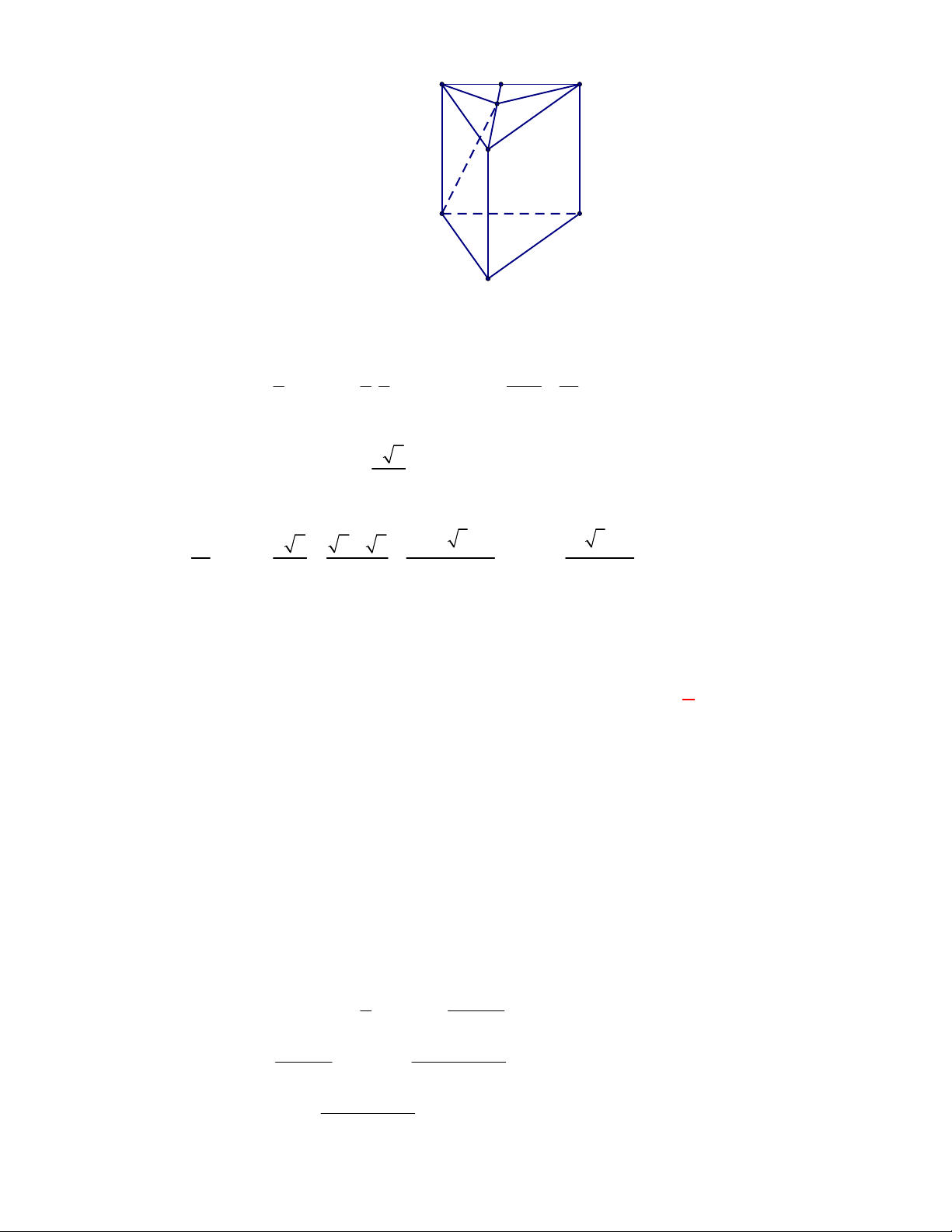
Câu 23: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho hình lăng trụ tứ giác đều . ABCD AB CD
  có đáy là hình vuông cạnh a . Mặt phẳng   cắt các cạnh bên AA , BB ,
CC , DD lần lượt tại 4 điểm M , N , P , Q . Góc giữa mặt phẳng   và mặt phẳng
ABCD là 60 . Diện tích của hình tứ giác MNPQ là 2 1 3 A. 2 2a . B. 2 a . C. 2 a . D. 2 a . 3 2 2 Lời giải Chọn A A' B' N D' C' M A B P Q D C 2 S a Ta có ABCD 2 S    2a . MNPQ cos60 1 2
Câu 24: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho dãy số u gồm 89 số n
hạng thỏa mãn u  tan n , n
   , 1  n  89 . Gọi P là tích của tất cả 89 số hạng của dãy n
số. Giá trị của biểu thức log P là A. 1. B. 0 . C. 10 . D. 89 . Lời giải Chọn B Ta có: P  tan1 .  tan 2 ...  tan 88 .  tan 89  tan1 .  tan 89.tan 2 .
 tan 88.... tan 44 .
 tan 46.tan 45  1.
 log P  log1  0 .
Câu 25: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018) Giải phương trình
1 8 15  22  x  7944 A. x  330 . B. x  220 . C. x  351 . D. x  407 . Lời giải Chọn A
Ta có cấp số cộng với u  1 , d  7 , u x , S  7944 . 1 n n Áp dụng công thức
n  48 N
2u n 1 d n
2.1 n 1 7 n  1        2 S   7944 
 7n  5n 15888  0   . n 331 2 2 n    L  7 Vậy x u  1 47.7  330 . 48
Câu 26: (ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Viết thêm bốn số vào giữa hai số 160 và 5 để
được một cấp số nhân. Tổng các số hạng của cấp số nhân đó là A. 215 . B. 315 . C. 415 . D. 515 . Lời giải Chọn B u   160 u 1 Từ giả thiết ta có 1 6   q  5  . u  5 u 2  6 1 6  1    160 1    u  6 1 q   2   1  
Suy ra tổng các số hạng của cấp số nhân đó là:   S    315 . 1 q 1 2
Câu 27: (ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Người ta trồng 465 cây trong một khu vườn
hình tam giác như sau: Hàng thứ nhất có 1 cây, hàng thứ hai có 2 cây, hàng thứ ba có 3
cây….Số hàng cây trong khu vườn là A. 31. B. 30 . C. 29 . D. 28 . Lời giải Chọn B
Cách trồng 465 cây trong một khu vườn hình tam giác như trên lập thành một cấp số cộng
u với số u là số cây ở hàng thứ n và u  1 và công sai d  1. n n 1 n n   1 n  30
Tổng số cây trồng được là: S  465   465 2
n n  930  0  . n  2
n  31l  
Như vậy số hàng cây trong khu vườn là 30 .
Câu 28: (THPT Trần Phú – Đà Nẵng - Lần 2 – năm 2017 – 2018) Cho cấp số cộng u có u  3 và n  1
công sai d  7 . Hỏi kể từ số hạng thứ mấy trở đi thì các số hạng của u đều lớn hơn 2018 ? n A. 287 . B. 289 . C. 288 . D. 286 . Lời giải Chọn B 2022
Ta có: u u n 1 d  3  7 n  
1  7n  4 ; u  2018  7n  4  2018  n n 1   n 7 Vậy n  289 .
Câu 1: (Tạp chí THTT – Tháng 4 năm 2017 – 2018) Cho dãy số  x thỏa mãn n  3n n  3
x x  ...  x
với mọi n   * . Khẳng định nào dưới đây là đúng và đầy đủ nhất. 1 2 n 2
A.x là cấp số cộng với công sai âm. n
B.x là cấp số nhân với công bội âm. n
C.x là cấp số cộng với công sai dương. n
D.x là cấp số nhân với công bội dương. n Lời giải Chọn C
3n n  3 3n   1 n 1 3 Ta có: x    3n  3 n 2 2 Ta lại có: x
x  3 n 1  3  3n  3  3 . n 1  n  
Vậy  x là cấp số cộng với công sai dương. n
Câu 2: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Cho cấp số nhân u
u , biết u 12 , 3  243 . Tìm u . n  1 u 9 8 2 4 4 A. u  . B. u  .
C. u  78732 . D. u  . 9 2187 9 6563 9 9 2187 Lời giải Chọn D
Gọi q là công bội của cấp số nhân u . n u 1 1 Ta có 2 u u q , 7 u u q 3    243  q  . 3 1 8 1 5 u q 3 8 8  1  4 Do đó 8
u u q  12.  . 9 1    3  2187
Câu 3: [1D3- 2(THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018)] Cho một cấp số
cộng có và tổng của số hạng đầu bằng . Tìm công thức của số hạng tổng quát . A. . B. .
C. . D. . Lời giải
Chọn A Ta có: .
Số hạng tổng quát của cấp số cộng bằng .
Câu 4: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Cho cấp số nhân u có n
tổng n số hạng đầu tiên là S  5n 1 với n  1, 2,... . Tìm số hạng đầu u và công bội q của n 1 cấp số nhân đó?
A. u  5 , q  4 .
B. u  5 , q  6 .
C. u  4 , q  5 .
D. u  6 , q  5 . 1 1 1 1 Lời giải Chọn C u   S  5 1  4 u   4 1 1 u Ta có: 1     u  4 , 2 q   5 . 2 1
u u S  5 1  24
u  24  u  20  u 1 2 2  2 1 1
Câu 5: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Cho hình chóp S.ABC có
tam giác ABC vuông cân tại B có AB BC a , tam giác SAC đều và nằm trong mặt phẳng
vuông góc với mặt phẳng  ABC  ( tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng
SBC  bằng. a 42 a 42 a 21 A. . B. 2a . C. . D. . 14 7 14 Lời giải
Chọn C S K C A H M B
Gọi H và M lần lượt là trung điểm của AC và BC . Ta có d  ,
A SBC   2d H ,SBC  .
Theo giả thiết tam giác SAC đều và nằm trong mặt phẳng vuông góc với mặt phẳng  ABC
nên SH   ABC   SH BC   1
Do tam giác tam giác ABC vuông cân tại B nên HM BC 2 Từ  
1 và 2 ta có BC  SHM   SHM   SBC  .
Trong mặt phẳng  SHM  kẻ HK SM thì d H ,SBC   HK . Theo đề bài ta có có tam giác ABC vuông cân tại B 1 a
có AB BC a 2 2  AC
BA BC a 2 , HM AB  . 2 2 a 6
Mặt khác tam giác SAC đều nên SH
. Xét tam giác vuông SHM ta có 2 1 1 1 1 1 1 1 28 a 42         HK  . 2 2 2 HK HM SH 2 2 2 HK 6a a 2 2 HK 6a 14 4 4 a
Vậy d A SBC  42 ,  2HK  7 u
u u  13
Câu 6: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho cấp số nhân u thỏa mãn 1 2 3 . n  u u  26  4 1
Tổng 8 số hạng đầu của cấp số nhân u là n A. S  1093 . B. S  3820 . C. S  9841. D. S  3280 . 8 8 8 8
Hướng dẫn giải Chọn D 2 u
u u  13 2 u   
u .q u .q  13
u 1 q q  13 1    Ta có 1 2 3 1 1 1      u u  26 3  2 4 1 u
 .q u  26  u
 . q 1 1 q q  26 1    1 1  u    2 1 q q  13 u   1 1   1    . q  3  q  3  u  8 1 q  8 1 1 3  1  Vậy tổng S    3280 . 8 1 q 1 3
Câu 7: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Cho cấp số cộng u , *
n   có số hạng tổng n
quát u  1 3n . Tổng của 10 số hạng đầu tiên của cấp số cộng bằng n A. 5  9048 . B. 59049  . C. 155 . D. 3  10 . Lời giải
Chọn C u   1 3.1  2 
Ta có: u  1 3n  1 . nu 13.10  29   10
n u u 10 u u 1 n   1 10 
Áp dụng công thức: S    155  . 2 2
Câu 8: Cho cấp số nhân u biết u  2 và u  6 . Tìm giá trị của u . n  6 9 21 A. 18 . B. 54 . C. 162 . D. 486 .
Câu 9: Cho cấp số nhân u biết u  2 và u  6 . Tìm giá trị của u . n  6 9 21 A. 18 . B. 54 . C. 162 . D. 486 . Lời giải Chọn D
Gọi u có số hạng đầu u và công bội q . n  1 3 q  3 5 u   2 u   q  2   Ta có 6 1     2  8 u  6 u   1 9 uq  6  2 1  3   3 3  2 Suy ra 20
u u .q  . 3  486 . 2  20 3 21 1 3 3 3
Câu 10: Bốn số tạo thành một cấp số cộng có tổng bằng 28 và tổng các bình phương của chúng bằng
276 . Tích của bốn số đó là : A. 585 . B. 161. C. 404 . D. 276 .
Câu 11: Bốn số tạo thành một cấp số cộng có tổng bằng 28 và tổng các bình phương của chúng bằng
276 . Tích của bốn số đó là : A. 585 . B. 161. C. 404 . D. 276 . Lời giải Chọn A
Gọi 4 số cần tìm là a  3r , a r , a r , a  3r .
a  3r a r a r a  3r  28  a  7 a  7 Ta có:      . a  3r 2 
2  a r 2  a r2  a  3r 2  276  r  4  r  2  
Bốn số cần tìm là 1, 5 , 9 , 13 có tích bằng 585 .
Câu 12: Sinh nhật lần thứ 17 của An vào ngày 01 tháng 5 năm 2018 . Bạn An muốn mua một chiếc
máy ảnh giá 3850000 đồng để làm quà sinh nhật cho chính mình nên An quyết định bỏ ống
heo 1000 đồng vào ngày 01 tháng 02 năm 2018 . Trong các ngày tiếp theo, ngày sau bỏ ống
nhiều hơn ngày trước 1000 đồng. Hỏi đến ngày sinh nhật của mình, An có bao nhiêu tiền (tính
đến ngày 30 tháng 4 năm 2018 )? A. 4095000 đồng. B. 89000 đồng. C. 4005000 đồng. D. 3960000 đồng.
Câu 13: Sinh nhật lần thứ 17 của An vào ngày 01 tháng 5 năm 2018 . Bạn An muốn mua một chiếc
máy ảnh giá 3850000 đồng để làm quà sinh nhật cho chính mình nên An quyết định bỏ ống
heo 1000 đồng vào ngày 01 tháng 02 năm 2018 . Trong các ngày tiếp theo, ngày sau bỏ ống
nhiều hơn ngày trước 1000 đồng. Hỏi đến ngày sinh nhật của mình, An có bao nhiêu tiền (tính
đến ngày 30 tháng 4 năm 2018 )? A. 4095000 đồng. B. 89000 đồng. C. 4005000 đồng. D. 3960000 đồng. Lời giải Chọn C
* Số tiền bỏ heo của An mỗi ngày tạo thành một cấp số cộng có số hạng đầu u  1000 công sai 1 d  1000 .
* Tổng số tiền bỏ heo tính đến ngày thứ n là:
n u u
n 2u n 1 d  1 n   1   S u u ... u        n 1 2 n 2 2
* Tính đến ngày 30 tháng 4 năm 2018 (tính đến ngày thứ 89 ) tổng số tiền bỏ heo là: 89 2.1000  89   1 .1000   S
 45.89.1000  4005000 đồng. 89 2 2
Câu 14: Cho cấp số nhân u có số hạng đầu u  3
 và công bội q
. Số hạng thứ năm của u là n n  1 3 27 16 27 16 A. . B. . C.  . D.  . 16 27 16 27 2
Câu 15: Cho cấp số nhân u có số hạng đầu u  3
 và công bội q
. Số hạng thứ năm của u là n n  1 3 27 16 27 16 A. . B. . C.  . D.  . 16 27 16 27 Lời giải Chọn D 4  2  16 Ta có 1 u u . n q    u  3.    . n 1 5    3  27
Câu 16: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng  ABC  và SA a . S
Đáy ABC thỏa mãn AB a 3 (tham khảo hình vẽ). Tìm số đo góc giữa a
đường thẳng SB và mặt phẳng  ABC  . A C A. 30 . B. 45 . a 3 B C. 90 . D. 60 .
Câu 17: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng  ABC và SA a . Đáy ABC thỏa mãn
AB a 3 (tham khảo hình vẽ). S a A C a 3 B
Tìm số đo góc giữa đường thẳng SB và mặt phẳng  ABC  . A. 30 . B. 45 . C. 90 . D. 60 . Lời giải Chọn A
Góc giữa đường thẳng SB và mặt phẳng  ABC là  SBA . Ta có:  1  tan SBA   SBA  30 . 3
Câu 18: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm 5.000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? A. 4.000.000 đồng.
B. 10.125.000 đồng. C. 52.500.000 đồng. D. 52.500.000 đồng.
Câu 19: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước. Biết giá
của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ hai giá của mỗi mét khoan tăng
thêm 5.000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50m mới
có nước. Hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? A. 4.000.000 đồng.
B. 10.125.000 đồng. C. 52.500.000 đồng. D. 52.500.000 đồng. Lời giải Chọn B
* Áp dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu u  80.000 , 1
công sai d  5.000 ta được số tiền phải trả khi khoan đến mét thứ n là
n u u
n 2u n 1 d  1 n   1   S    n 2 2
* Khi khoan đến mét thứ 50 , số tiền phải trả là
50 2.80000  50   1 .5000   S   10.125.000 đồng. 50 2
Câu 20: Cho cấp số cộng có u  1 và công sai d  2
 . Tổng n số hạng đầu tiên của cấp số cộng này là 1 S  9800  . Giá trị n là n A. 100 . B. 99 . C. 101. D. 98 .
Câu 21: Cho cấp số cộng có u  1 và công sai d  2
 . Tổng n số hạng đầu tiên của cấp số cộng này là 1 S  9800  . Giá trị n là n A. 100 . B. 99 . C. 101. D. 98 . Lời giải
Chọn A n S u n d    n   n      n  . n 2 1 9800 2 2 1 19600 0 1      2   100
Câu 22: Cho dãy số u là cấp số cộng với u  3; u  19 . Tính u . n  1 5 12 207 A. u  51 . B. u  57 . C. u  47 . D. u  . 12 12 12 12 5
Câu 23: Cho dãy số u là cấp số cộng với u  3; u  19 . Tính u . n  1 5 12 207 A. u  51 . B. u  57 . C. u  47 . D. u  . 12 12 12 12 5 Lời giải Chọn C
Ta có: u  19  u  4d  19  3  4d  19  d  4 5 1
Do đó: u u 11d  3 11.4  47 . 12 1
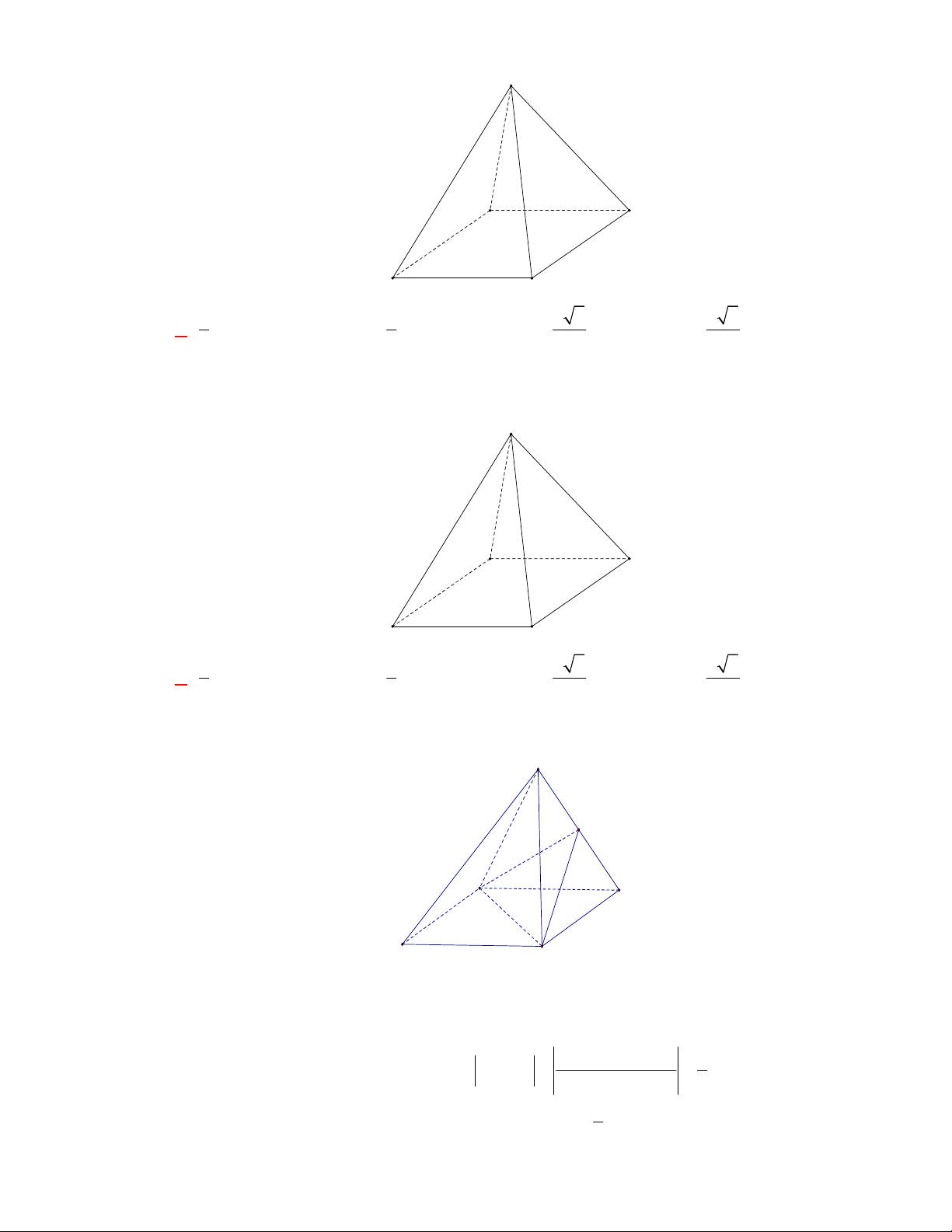
Câu 24: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên đều bằng a . Tính cosin của góc
giữa hai mặt phẳng  SAB và  SAD . S D A C B 1 1 2 2 2 2 A. . B.  . C.  . D. . 3 3 3 3
Câu 25: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên đều bằng a . Tính cosin của góc
giữa hai mặt phẳng  SAB và  SAD . S D A C B 1 1 2 2 2 2 A. . B.  . C.  . D. . 3 3 3 3 Lời giải Chọn A S I A D C B
Gọi I là trung điểm SA .
Vì các tam giác SAB và SAD là tam giác đều nên ta có BI và DI cùng vuông góc với SA
 góc giữa hai mặt phẳng SAB và SAD là  BI, DI  .
DI BI BD
Trong tam giác BID ta có: BI DI   2 2 2 1 cos ,  cos BID   . 2BI.DI 3 1
Vậy cosin của góc giữa mặt phẳng SAB và SAD bằng . 3
Câu 26: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích
của đế tháp (có diện tích là 2
12288 m ). Tính diện tích mặt trên cùng. A. 2 8m . B. 2 6m . C. 2 12m . D. 2 10m .
Câu 27: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích
của đế tháp (có diện tích là 2
12288 m ). Tính diện tích mặt trên cùng. A. 2 8m . B. 2 6m . C. 2 12m . D. 2 10m .
Hướng dẫn giải Chọn B 1
Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội q  2
Số hạng đầu u  12288 . Khi đó mặt trên cùng tầng 11 ứng với u . 1 12 11  1  Do đó 11
u u .q  12288.  6 . 12 1    2 
Câu 28: Xác định x để 3 số 2x 1; x ; 2x 1 theo thứ tự lập thành cấp số nhân? 1 1 1 A. x  . B. x   . C. x   .
D. x   3 . 3 3 3
Câu 29: Xác định x để 3 số 2x 1; x ; 2x 1 theo thứ tự lập thành cấp số nhân? 1 1 1 A. x  . B. x   . C. x   .
D. x   3 . 3 3 3 Lời giải Chọn B
Vì 2x 1; x ; 2x 1 theo thứ tự lập thành cấp số nhân 1 1 nên 2
x  2x   1 2x   1 2 2
x  4x 1 2  x   x   . 3 3
Câu 30: Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có
2 cây, ở hàng thứ ba có 3 cây,… ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4950
cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu? A. 99 . B. 100 . C. 101. D. 98 .
Câu 31: Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có
2 cây, ở hàng thứ ba có 3 cây,… ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4950
cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu? A. 99 . B. 100 . C. 101. D. 98 . Lời giải Chọn A
Ta thấy số cây ở mỗi hàng tạo nên một cấp số cộng có số hạng đầu u  1 và công sai d  1. 1
2u n 1 d n 1    2 n n Ta có S    4950 2
n n  9900  0  n  99 . n 2 2
Câu 32: Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn? n 2 4 8  2  1 1 1 1 A. , , ,…,   ,…. B. , , ,…, ,…. 3 9 27  3  3 9 27 3n n n 1  3 9 27  3  1 1 1 1  1  C. , , ,…,   ,…. D. 1,  , ,  , ,…,    ,…. 2 4 8  2  2 4 8 16  2 
Câu 33: Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn? n 2 4 8  2  1 1 1 1 A. , , ,…,   ,…. B. , , ,…, ,…. 3 9 27  3  3 9 27 3n n n 1  3 9 27  3  1 1 1 1  1  C. , , ,…,   ,…. D. 1,  , ,  , ,…,    ,…. 2 4 8  2  2 4 8 16  2  Lời giải Chọn C n 3 3 9 27  3 
Chọn đáp án C vì dãy ở đây là một CSN có công bội q   1, nên dãy , , ,…,   ,… 2 2 4 8  2 
không phải là dãy lùi vô hạn
Câu 34: Một du khách vào chuồng đua ngựa đặt cược, lần đầu tiên đặt 20000 đồng, mỗi lần sau tiền đặt
gấp đôi tiền đặt lần trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10 . Hỏi du khách đó thắng hay thua bao nhiêu?
A. Thắng 20000 đồng. B. Hòa vốn. C. Thua 20000 đồng. D. Thua 40000 đồng.
Câu 35: Một du khách vào chuồng đua ngựa đặt cược, lần đầu tiên đặt 20000 đồng, mỗi lần sau tiền đặt
gấp đôi tiền đặt lần trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10 . Hỏi du khách đó thắng hay thua bao nhiêu?
A. Thắng 20000 đồng. B. Hòa vốn. C. Thua 20000 đồng. D. Thua 40000 đồng.
Hướng dẫn giải Chọn A u   20000
Số tiền du khách đó đặt cược là một cấp số nhân với 1  . q  2 
9 lần đầu người đó thua  số tiền thua là tổng 9 số hạng đầu của cấp số nhân ở trên. Vậy 9 1 2
số tiền người đó thua là S  20000  10220000 (đồng) 9 1 2
Số tiền người đó thắng được ở lần thứ 10 là 9 9
u u .q  20000.2  10240000 (đồng) 10 1
Ta có u S  10240000 10220000  20000 (đồng) 10 9
Vậy người đó thắng 20000 đồng.
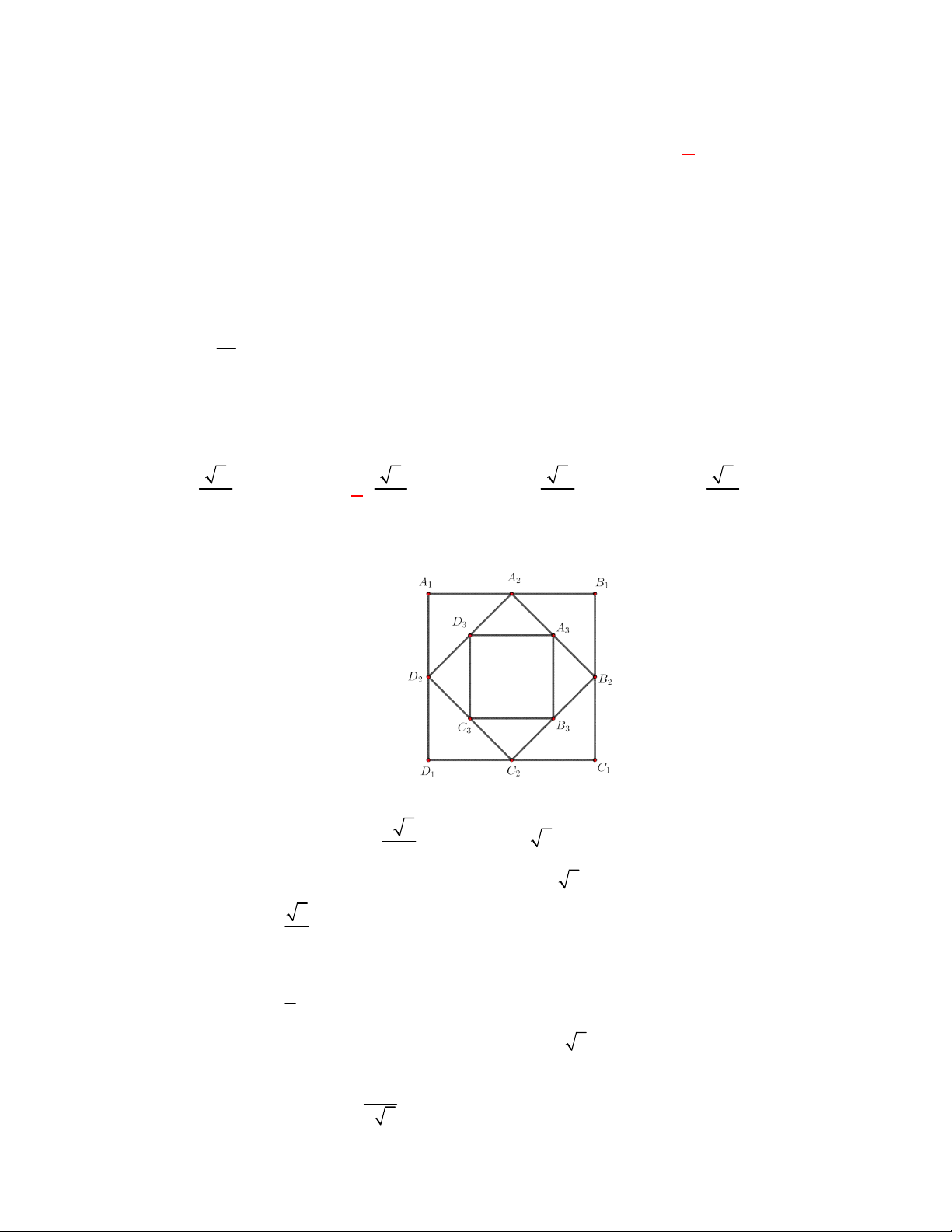
Câu 1: (THTT Số 1-484 tháng 10 năm 2017-2018) Một hình vuông ABCD có cạnh AB a , diện tích
S . Nối 4 trung điểm A , B , C , D theo thứ tự của 4 cạnh AB , BC , CD , DA ta được hình 1 1 1 1 1
vuông thứ hai là A B C D có diện tích S . Tiếp tục như thế ta được hình vuông thứ ba 1 1 1 1 2
A B C D có diện tích S và cứ tiếp tục như thế, ta được diện tích S , S ,... Tính 2 2 2 2 3 4 5
S S S S  ...  S . 1 2 3 100 100 100 2 100 2 99 2 1 a 2   1 a 2   1 a 2   1 A. S  . B. S  . C. S  . D. S  . 99 2 2 a 99 2 99 2 99 2 Lời giải Chọn C 2 2 2 a a a Dễ thấy: 2
S a ; S  ; S  ;...; S  . 1 2 3 100 99 2 4 2 1
Như vậy S , S , S ,..., S
là cấp số nhân với công bội q  . 1 2 3 100 2 2 a    100 2 1 1 1 1 2 
S S S  ...  Sa 1   ...   . 1 2 100  2 99  99  2 2 2  2
Câu 2: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Trong các dãy số sau, dãy số nào là dãy số giảm n n  3 n 2   1 A. u  . B. u  . C. u  . D. u  . n n 1 n 2 n 2 n n 3n Lời giải Chọn C Xét A: n  3 n  2 n  2 n  3 4 Ta có u  ; u  . Khi đó : uu     0 n    n n 1 n 1  n  2 n 1  n n  2 n  1 n   1 n  2
Vậy u là dãy số tăng. n Xét B: n n 1 n 1 n 1 Ta có u  ; u  . Khi đó : uu     0 n    n 2 n 1  2 n 1  n 2 2 2
Vậy u là dãy số tăng. n Xét C: 2 2 Ta có u  , un 2 n n 1  n  2 1 2 2 u n n n 1     1, n
  . Vậy u là dãy giảm. n u n n n  2 2 1
Xét D: 1  1 1  Ta có u  ; u  ; u
. Vậy u là dãy số không tăng không giảm . n  1 3 2 9 3 27
Câu 3: [1D3 - 2] (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Trong các mệnh đề sau, mệnh đề nào đúng? A. . B. .
C. . D. . Lời giải
Chọn A
Vì . Vậy A đúng. 2  x
khi x  1, x  0  x  
Câu 4: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Cho hàm số f x  0 khi x  0 .  x khi x 1    Khẳng định nào đúng
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn 0  ;1 .
B. Hàm số liên tục tại mọi điểm trừ điểm x  0 .
C. Hàm số liên tục tại mọi điểm thuộc  .
D. Hàm số liên tục tại mọi điểm trừ điểm x  1 . Lời giải Chọn C
Tập xác định D   . 
Nếu x  0 , x  1 thì hàm số y f x liên tục trên mỗi khoảng  ;  0,0;  1 và 1; .  Nếu x  0 thì f 0  0 và 2 2 x x
lim f x  lim
 lim x  0; lim f x  lim  lim x  0 . x 0 x 0 x 0 x 0 x 0 x 0       x x
Suy ra: lim f x  0  f 0 . x0
Do đó, hàm số y f x liên tục tại x  0 . 2  x lim f   x  lim  lim x  1 
Nếu x  1 thì f   1  1 và x 1  x 1  x 1 x   
 lim f x  1  f   1 . x 1 
 lim f x  lim x 1  x 1  x 1 
Do đó, hàm số y f x liên tục tại x  1.
Vậy hàm số y f x liên tục trên  .
Câu 5: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Cho dãy số u được xác định bởi n u   3  1  . Tính lim u . 2 n  n   1 u
nu n  2  n 1  n A. lim u  1. B. lim u  4. C. lim u  3. D. lim u  0. n n n n Lời giải Chọn A n n  2 Ta có uu  (*) n 1  2n  2 n 2n  2 1 1
Đặt a  lim u , trong biểu thức (*) cho n   ta được a a
a  1  lim u . n 2 2 n 
Chú ý: Để chặt chẽ hơn ta có thể lập luận như sau:
Sử dụng quy nạp toán học, ta chứng minh được u  1 với mọi n   * , nên dãy u bị n n chặn dưới. . n u n  2 . n u n  2 Khi đó ta cũng có n n u    
.u u nên dãy u là dãy giảm. n n 1  2n  2 2n  2 2n  2 2n  2 n n
Vậy, dãy u có giới hạn (Học sinh cần chú ý tính chất: một dãy giảm và bị chặn dưới, n
hoặc tăng và bị chặn trên, thì có giới hạn). 1 1
Đặt a  lim u , trong biểu thức (*) cho n   ta được a a
a  1  lim u . n 2 2 n n
Câu 6: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Cho dãy số u với u   n . n   1 n
Mệnh đề nào sau đây đúng?
A. Dãy số u là dãy số bị chặn.
B. Dãy số u là dãy số giảm. n n
C. Dãy số u là dãy số tăng.
D. Dãy số u là dãy số không bị chặn. n n Lời giải Chọn D n Dãy số u  
n là dãy số không bị chặn vì lim u  lim n   . n   1 n
Câu 7: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Cho dãy số u  sin . Chọn khẳng định sai n n
trong các khẳng định sau đây:  A. Dãy số tăng. B. u  sin . n 1  n 1
C. Dãy số bị chặn.
D. Dãy số không tăng, không giảm. Lời giải Chọn A   u  sin nên B đúng. n 1  n 1   Do 1  sin
 1 nên dãy số bị chặn, do đó C đúng. n   3 u   u
u  sin   0 , u  sin  1, u  sin  . Do 1
2 nên dãy số không tăng, không 1 2  2 3 3 2 u u  2 3
giảm. Vậy D đúng. Do đó A sai.
Câu 8: (THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018) Cho tam giác ABC cân tại
A . Biết rằng độ dài cạnh BC , trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành
một cấp số nhân có công bội q . Tìm công bội q của cấp số nhân đó. 1 2 2  2 2 1   2 2  2 2 A. q  . B. q  . C. q  . D. q  . 2 2 2 2 Lời giải
Chọn B 2 AB ACBC 2  2 2  2 Ta có: AM    1 . 4
Do ba cạnh BC , AM , AB lập thành cấp số nhân nên ta có: 2
BC.AB AM 2  2 2 AB AC  2 2  BC Thay 2 vào   1 ta được  BC.AB 2 2
 4 AB  4 A .
B BC BC  0 4  AB 1 2 2    AB AB BC 2  4  4 1  0      BC BCAB 1 2   loai  BC 2 AB 1 2 1 2 2  2 2    q   . BC 2 2 2
Câu 9: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Tìm tất cả các giá trị của tham số m để phương trình 3 2
x  3x mx  2  m  0 có 3 nghiệm lập thành cấp số cộng. A. m  3 . B. m  3 . C. m  0 . D. m tùy ý. Lời giải Chọn A 3 2
x  3x mx  2  m  0 (1) x  1   x   2
1 x  2x  2  m  0   2
x  2x  2  m  0 (2) 
Phương trình (1) có 3 nghiệm lập thành cấp số cộng khi phương trình (2) có 2 nghiệm x ; x 1 2 x  1  x thoả mãn 1 2 
(Vì pt (2) nếu có nghiệm thì tổng các nghiệm là 2 ) x x  2  1 2
 phương trình (2) có 2 nghiệm    0  3  m  0  m  3.
Câu 10: (THTT Số 3-486 tháng 12 năm 2017-2018) Cho dãy số  x thoả mãn x  40 và x  1,1.x n  1 n n 1 
với mọi n  2, 3, 4,... Tính giá trị của S x x  ...  x (làm tròn đến chữ số thập phân thứ 1 2 12 nhất). A. 855, 4 . B. 855, 3 . C. 741, 2 . D. 741, 3 . Lời giải Chọn A
Ta có x  1,1.x
và x  40 nên dãy số  x là một cấp số nhân có số hạng đầu x  40 và n n n 1  1 1 x công bội q n  1,1. xn 1  12 11,1
S x x  ...  x  40.  855, 4 . 1 2 12 11,1 u   1 1
Câu 11: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Cho dãy số u với . n   2 u
u n , n     n 1  n Tính u . 21 A. u  3080. B. u  3312. C. u  2871. D. u  3011. 21 21 21 21 Lời giải Chọn C Từ 2 u
u n , với mọi n    , ta có: n 1  n 2 u u 1 . 2 1 2 u u  2 . 3 2 ... u u  n  .  2 1 n n 1 2 uu n . n 1  n
Cộng n đẳng thức trên theo vế ta được: u  1    , với mọi n    .   2 2 2 1 2 ... n n 1  n n 1 2n 1 2 2 2   
Mặt khác, ta luôn có: 1  2  ...  n  nên suy ra: 6 n n   1 2n   1 u  1 , với mọi n    . n 1  6 20.21.2.20   1
Cho n  20 , ta được: u  1  2871. 21 6
Câu 12: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Có bao nhiêu cấp số nhân có 5 số hạng? Biết
rằng tổng 5 số hạng đó là 31 và tích của chúng là 1024 . A. 1. B. 2 . C. 4 . D. 3 . Lời giải Chọn C
Gọi cấp số nhân thỏa yêu cầu bài toán có số hạng đầu u và công bội q . 1 Theo giả thiết ta có 2 3 4 5 10 2 u .u .
q u q .u q .u q  1024  u .q  1024  u q  4   1 . 1 1 1 1 1 1 1 Lại có 2 3 4
u u q u q u q u q  31  u  2 3 4
1 q q q q  31 2 . 1 1 1 1 1 1 
Giải hệ hai phương trình  
1 và 2 ta được các nghiệm: 1 7   33 7   33 q  2 , q  , q  , q  . 1 2 2 3 4 4 4
Vậy có 4 cấp số nhân thỏa yêu cầu bài toán.
Câu 1: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Trong sân vận động có tất cả 30
dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền sau nhiều hơn dãy trước 4 ghế, hỏi sân vận động
đó có tất cả bao nhiêu ghế? A. 2250 . B. 1740 . C. 4380 . D. 2190 . Lời giải Chọn C
Gọi u , u ,...u lần lượt là số ghế của dãy ghế thứ nhất, dãy ghế thứ hai,… và dãy ghế số ba mươi. Ta 1 2 30
có công thức truy hồi ta có u u
 4 , n  2,3,...,30 . n n 1  Ký hiệu: S
u u  ...  u , theo công thức tổng các số hạng của một cấp số cộng với 30 1 2 30
u  15 , d  4 ta được: 1 30 S
2u  30 1 4  15 2.15  29.4  2190 . 30  1      2
Câu 2: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Cho hình vuông A B C D có cạnh 1 1 1 1 bằng 1. Gọi A , B , C , D
thứ tự là trung điểm các cạnh A B , B C , C D , D A k 1  k 1  k 1  k 1  k k k k k k k k
(với k  1, 2, ...). Chu vi của hình vuông A B C D bằng 2018 2018 2018 2018 2 2 2 2 A. . B. . C. . D. . 2018 2 1007 2 2017 2 1006 2
Lời giải : Chọn B
Hình vuông có cạnh bằng a thì có chu vi là 4a . Hình vuông có các đỉnh là trung điểm của hình a 2
vuông ban đầu có cạnh bằng có chu vi là 2a 2 . 2
Đường chéo của hình vuông A B C D có độ dài bằng 2 nên cạnh của hình vuông A B C D 1 1 1 1 2 2 2 2 2 có độ dài bằng . 2
Đường chéo của hình vuông A B C D có độ dài bằng 1 nên cạnh của hình vuông A B C D 2 2 2 2 3 3 3 3 1 có độ dài bằng . 2 2
Đường chéo của hình vuông A B C D có độ dài bằng
nên cạnh của hình vuông 3 3 3 3 2 1
A B C D có độ dài bằng . 4 4 4 4 2 2 1
Cứ như thế độ dài các cạnh hình vuông tạo thành một cấp số nhân có u  1, công bội q  1 2 1
nên độ dài cạnh của hình vuông A B C D là: u  nên chu vi hình vuông 2018 2018 2018 2018 2008  22017 4 2 đó là: 4u   . 2018  2017 1007 2 2
Câu 3: (THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018) Cho dãy số u với n  1 1 1 u    ...  . Tính lim u . n 1.3 3.5 2n   1 2n   1 n 1 1 A. 0 . B. . C. . D. 1. 2 4 Lời giải Chọn B * Cách 1: 1 1  1 1  Ta có   suy ra    2n   1 2n   1
2  2n 1 2n 1 1 1  1 1      1.3 2  1 3  1 1  1 1      … 3.5 2  3 5  … 1 1 1 1  1 1  1  1 1  1 u    ...    nên lim u  lim   . n     1.3 3.5 2n   1 2n   1 2 n  1 2n 1  2  1 2n 1  2 * Cách 2: 1 2 3 n
Ta có u  ; u  ; u  . Ta chứng minh u  bằng qui nạp n   * 1 2 3 3 5 7 2n 1
+ Với n  1 , công thức * đúng. k
+ Giả sử công thức * đúng với n k  1  u  . Ta cần chứng minh k 2k 1 k 1 u  . Thật vậy, ta có k 1  2 k   1 1 1 2 k 1 2k  3k 1 uu     k 1  k 2 k  
1 1 2 k   1 1     2k 1 2k   1 2k  3 2k   1 2k  3 k   1 2k   1 k 1 n  
. Vậy công thức u  đúng với mọi * n   . n   * 2k   1 2k  3 2 k   1 1 2n 1 n 1 Khi đó lim u  lim  . n 2n 1 2
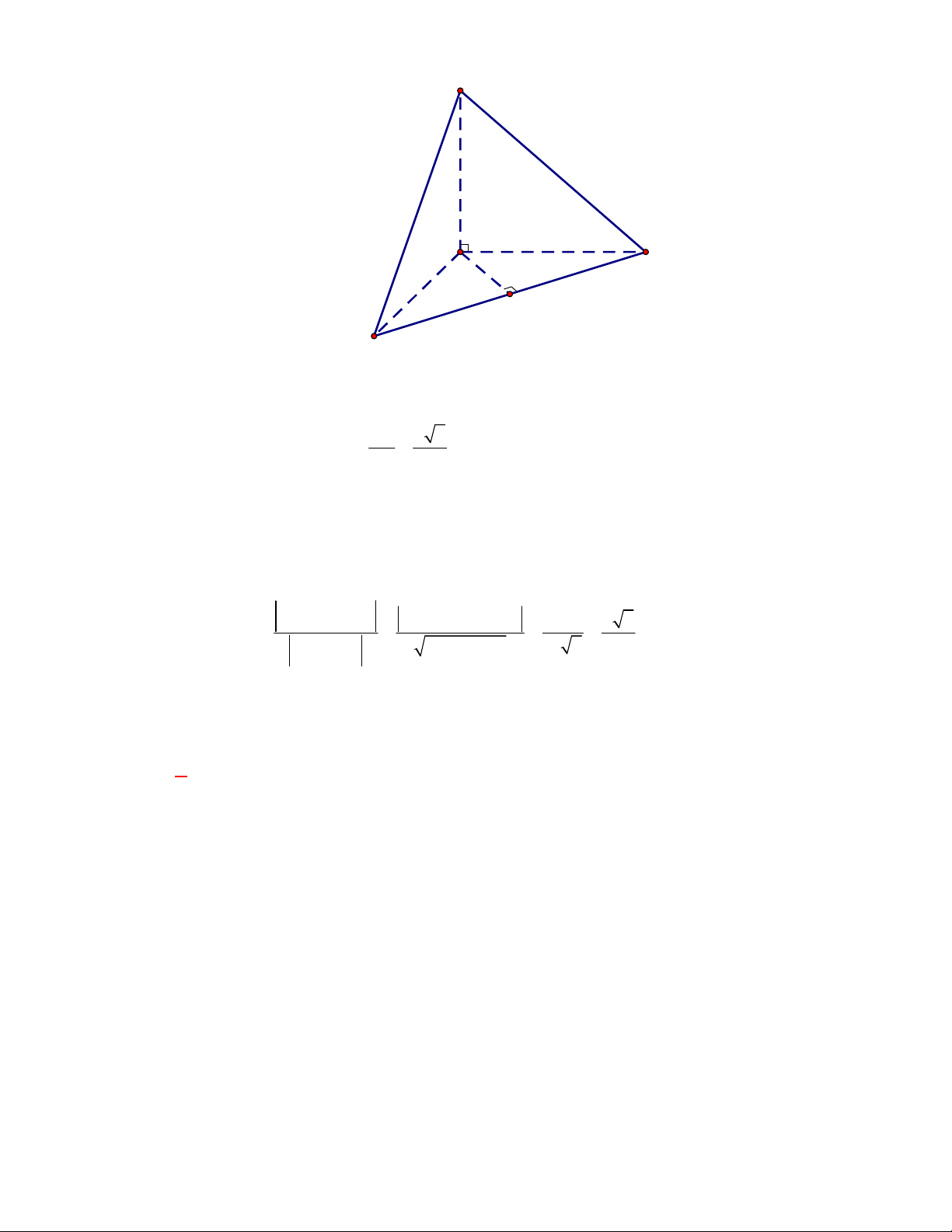
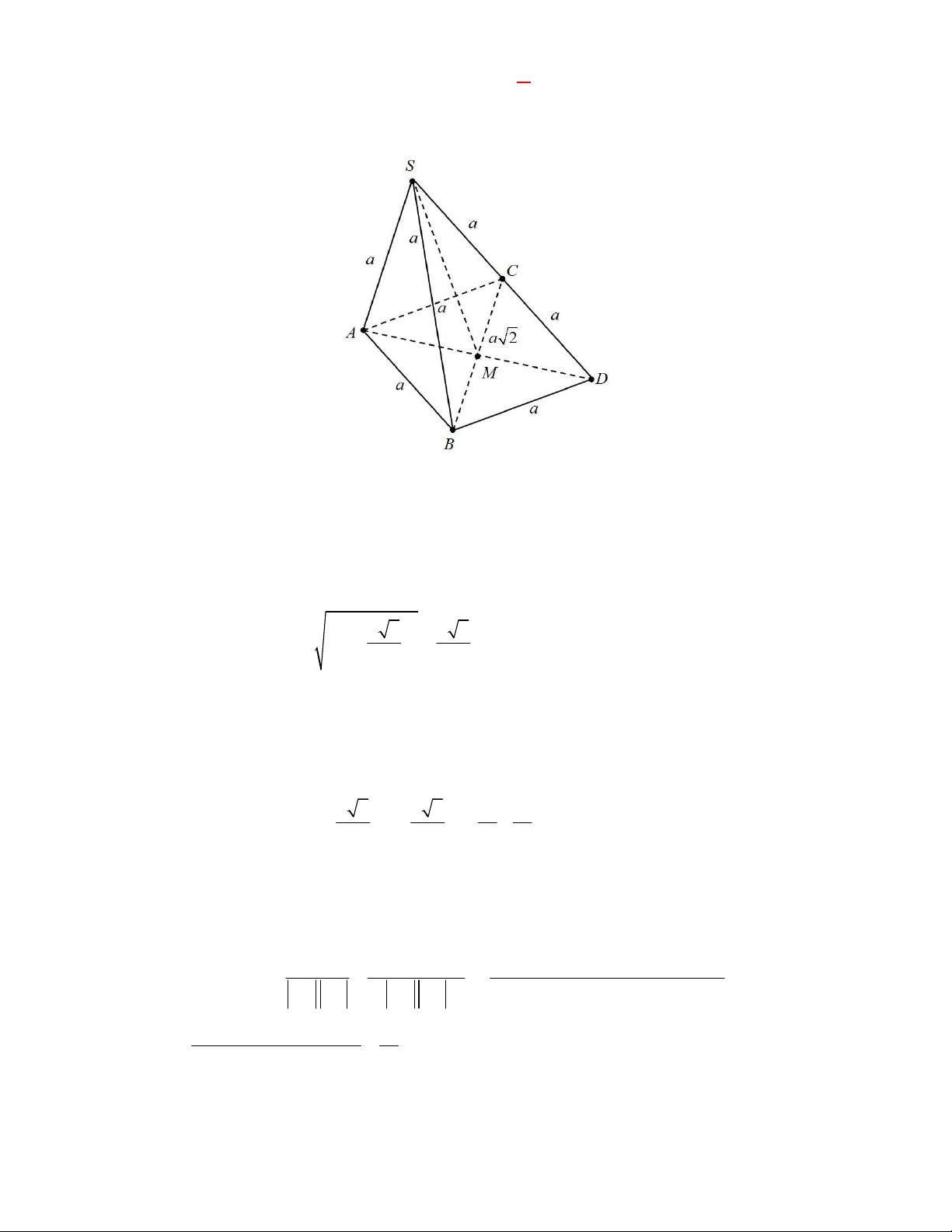
Câu 4: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Cho tứ diện S.ABC có
SA SB SC AB AC a và BC a 2 . Tính góc giữa hai đường thẳng AB và SC . A. 45 . B. 120 . C. 60 . D. 90 . Lời giải Chọn C
Cách 1: Gọi M là trung điểm của BC . Ta có: 2 2 2
BC AB AC nên tam giác ABC vuông cân tại A . Và 2 2 2
BC SB SC nên tam giác SBC vuông cân tại S .
Vẽ hình chữ nhật (cũng là hình vuông) 
ABDC   AB SC  ,
SCD và SC CD a . 2  a 2  a 2 2
AM SM MD a     .  2  2    SA
M vuông tại M .
SM BC   ABCD  SM  ABCD  SM MD .
SM AM   ABCD 2 2  a 2   a 2  2 2 a a 2 2 2
SD SM MD          SD a .  2   2      2 2
Suy ra tam giác SCD đều    AB SC  ,  SCD  60 . Cách 2:
      SC. . SB SA SC AB    SC. .
SB cos BSC SC. . SA cos ASC
cos SC, AB        SC. AB SC. AB SC.AB . a . a cos 90  . a . a cos 60 1     
 SC; AB 120 . . a a 2
Vậy góc giữa hai đường thẳng AB và SC là 60 .
Câu 5: (THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018) Cho dãy số a xác định bởi n a  2 , a
 2a , n  1, n   . Tính tổng của 10 số hạng đầu tiên của dãy số. 1 n 1  n 2050 A. . B. 2046 . C. 682 . D. 2046 . 3 Lời giải Chọn C aa  2 Vì n 1   2  suy ra a
là một cấp số nhân với 1 . n   a q  2  na  10 1 q 1  Suy ra S   682 . 10 1 q 41
Câu 6: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Cho dãy số u xác định bởi u   và n  1 20 u
 21u 1 với mọi n  1. Tìm số hạng thứ 2018 của dãy số đã cho. n 1  n 1 1 A. 2018 u  2.21  . B. 2017 u  2.21  . 2018 20 2018 20 1 1 C. 2017 u  2.21   . D. 2018 u  2.21   . 2018 20 2018 20 Lời giải Chọn C 1  1  Ta có u
 21u 1  u   21 u  . n 1  n n 1    20 n  20  1
Đặt v u  , ta có v  21v . n n 20 n 1  n 41 1
Do đó v là một CSN với v     2
 và công bội q  21. n  1 20 20 n 1
Do đó số hạng tổng quát của dãy v là n 1 n 1 v v .q  2.21     1  u  2.21   . n n 1 n 20 1 Khi đó 2017 u  2.2  1  . 2018 20
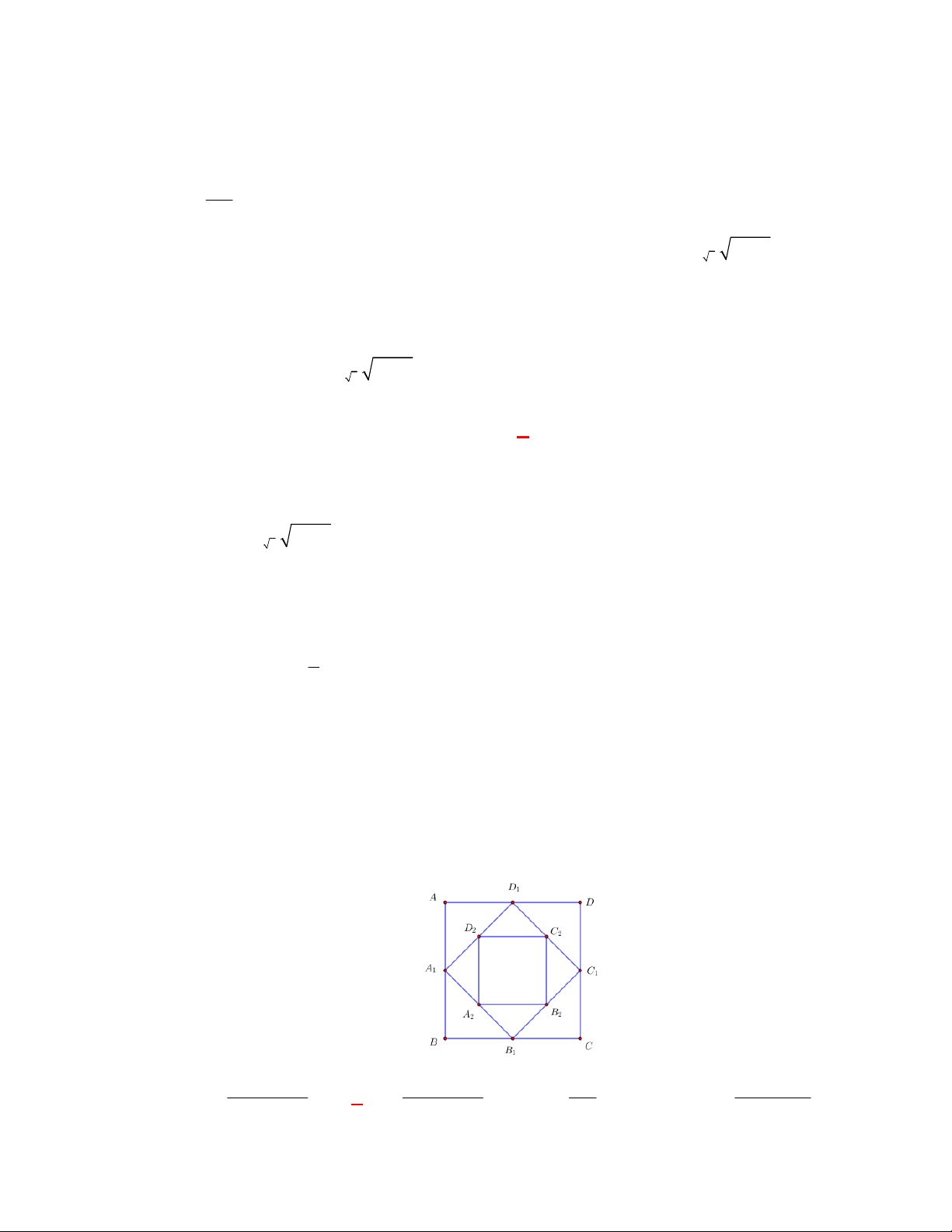
Câu 7: (SGD Bắc Ninh năm 2017-2018) Cho hình vuông C có cạnh bằng a . Người ta chia mỗi cạnh 1 
của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình
vuông C (Hình vẽ). 2 
Từ hình vuông C lại tiếp tục làm như trên ta nhận được dãy các hình vuông C , C , C ,., 2  1 2 3
C ... Gọi S là diện tích của hình vuông C i 1, 2,3,. 
.... . Đặt T S S S  ...S  .... in i 1 2 3 n 32 Biết T  , tính a ? 3 5 A. 2 . B. . C. 2 . D. 2 2 . 2 Lời giải Chọn A 2 2  3   1  a 10
Cạnh của hình vuông C là: a aa  . Do đó diện tích 2  2      4   4  4 5 5 2 S a S . 2 8 1 8 2 2 2 3 1 a 10  10     
Cạnh của hình vuông C là: 2 a aa   a . Do đó diện tích 3  3  2   2    4 4 4  4        2  5  5 2 S a
S . Lý luận tương tự ta có các S , S , S ,...S .... tạo thành một dãy cấp số 3   2 1 2 3 n  8  8 5
nhân lùi vô hạn có u S và công bội q  . 1 1 8 S 2 8a 32 1 T   . Với T  ta có 2
a  4  a  2 . 1 q 3 3
Câu 8: (THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018) Cho hai cấp số cộng a : n
a  4 ; a  7 ;...; a
và b : b 1; b  6 ;...; b . Hỏi có bao nhiêu số có mặt đồng thời n  1 2 100 1 2 100
trong cả hai dãy số trên. A. 32. B. 20 . C. 33. D. 53. Lời giải Chọn B
Cấp số cộng a : a  4 ; a  7 ;...; a có số hạng tổng quát: a  4  n   n  . n   1 3 3 1 n  1 2 100
Cấp số cộng b : b 1; b  6 ;...; b có số hạng tổng quát: b  1 m   m  . m   1 5 5 4 n  1 2 100
Các số có mặt đồng thời trong cả hai dãy số trên thỏa mãn hệ: 3
n 1  5m  4 3
n  5m   1   1   n  100  1   n  100 . 1  m 100 1     m  100  
Vì 3n  5m  
1 nên n5 và m 13 với m 1  0
Ta lại có n  100  3n  300  5m  
1  300  m  61 .
Có m 13  m  3t 1, t *. Vì 1  m  61  1 3t 1  61  0  t  20 . Vì t  *
  t  1;2;3;...;  20 .
Vậy có 20 số hạng có mặt đồng thời ở hai dãy số trên.
Câu 9: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho cấp số cộng u biết u  18 và n  5
4S S . Tìm số hạng đầu tiên u và công sai d của cấp số cộng. n 2n 1
A. u  2 ; d  4 .
B. u  2 ; d  3 .
C. u  2 ; d  2 .
D. u  3 ; d  2 . 1 1 1 1 Lời giải
Chọn A
Ta có: u  18  u  4d  18   1 . 5 1  n n   1 d   2n 2n   1 d  4S S  4 nu   2nu
 4u  2nd  2d  2u  2nd d n 2n  1   1  2 2 1 1    
 2u d  0 2 . 1 Từ  
1 và 2 suy ra u  2 ; d  4 . 1
Câu 10: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Cho cấp số cộng u biết u  18 và n  5
4S S . Giá trị u và d là n 2n 1
A. u  2 , d  3 .
B. u  3 , d  2 .
C. u  2 , d  2 .
D. u  2 , d  4 . 1 1 1 1 Lời giải Chọn D
Ta có u  18  u  4d  18 . 5 1  5.4  10.9
Lại có 4S S  4 5u d  10u
d  2u d  0 . 5 10  1  1 1  2  2 u   4d  18 u   2
Khi đó ta có hệ phương trình 1   1  . 2u d  0  d  4 1  sin 
Câu 11: (THPT Tứ Kỳ-Hải Dương năm 2017-2018) Giả sử
, cos , tan  theo thứ tự đó là một 6
cấp số nhân. Tính cos 2 . 3 3 1 1 A. . B.  . C. . D.  . 2 2 2 2 Hướng dẫn giải Chọn D
Điều kiện: cos  0   
k k   . 2 sin  2 sin 
Theo tính chất của cấp số nhân, ta có: 2 cos   .tan  2  6 cos   . 6 cos 1 3 2
 6 cos   sin   0 3 2
 6 cos   cos  1  0  cos  . 2 2  1  1 Ta có: 2
cos 2  2 cos  1  2. 1     .  2  2
Câu 12: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Cho bốn số , a b , ,
c d theo thứ tự đó tạo 148
thành cấp số nhân với công bội khác 1. Biết tổng ba số hạng đầu bằng , đồng thời 9
theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số
cộng. Tính giá trị biểu thức T a b c d . 101 100 100 101 A. T  . B. T  . C. T   . D. T   . 27 27 27 27 Lời giải
Chọn C  2
ac b   1  Ta có 2 bd   c 2 .  148
a b c  3  9
Và cấp số cộng có u a , u b , u c . Gọi x là công sai của cấp số cộng. Vì cấp số nhân 1 4 8
có công bội khác 1 nên x  0 . b   a  3x Ta có :  4 .
c a  7x  Từ  
1 và 4 ta được : a a x  a x2 7 3 2
ax  9x  0 .
Do x  0 nên a  9x . 148
Từ 3 và 4 , suy ra 3a 10x  . 9  16 b   3 a  4    64 Do đó :  4  c  . x   9   9  256 d    27 1  00
Vậy T a b c d  . 27 Câu 13:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Tính tổng 2 3 2017 S  1  2 2 .  3 2 .  4 2 .  ........  2018 2 . A. 2018 S  2017.2 1. B. 2018 S  2017.2 . C. 2018 S  2018.2 1. D. 2018 S  2019.2 1. Lời giải Chọn A Ta có 2 3 1 2 2 2 ... 2n A       n 1 2   1 Xét 2 3 4 2017 2018 2S  1 2 .  2 2 .  3 2 .  4 2 .  ...  2017.2  2018.2 Và 2 3 2016 2017 S  1  2.2  3 2 .  4.2  ...  2017.2  2018 2 . Suy ra 2018 S    2 3 2017 2018.2
1 2  2  2  ...  2  2018    2018   2018 2018.2 2 1  2017.2 1 .
Câu 14: (THTT số 5-488 tháng 2 năm 2018) Ba số phân biệt có tổng là 217 có thể coi là các số hạng
liên tiếp của một cấp số nhân, cũng có thể coi là số hạng thứ 2 , thứ 9 , thứ 44 của một cấp số
cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng này để tổng của chúng bằng 820 ? A. 20 . B. 42 . C. 21 . D. 17 . Lời giải Chọn A
Gọi ba số đó là x , y , z . Do ba số là các số hạng thứ 2 , thứ 9 và thứ 44 của một cấp số cộng
nên ta có: x ; y x  7d ; z x  42d (với d là công sai của cấp số cộng).
Theo giả thiết, ta có: x y z x x  7d x  42d  3x  49d  217 .
Mặt khác, do x , y , z là các số hạng liên tiếp của một cấp số nhân nên: d  0 2 2
y xz   x  7d   x x  42d   d  4
x  7d   0   4
x  7d  0  217 217 2460
Với d  0 , ta có: x y z  . Suy ra n  820 :    . 3 3 217
4x  7d  0 x  7
Với 4x  7d  0 , ta có:   
. Suy ra u  7  4  3 .
3x  49d  217 1  d  4  n  20
2u  n   1 d n
2.3  4n   1  n Do đó, S  820  1    820   820   n 41 2 2 n    2 Vậy n  20 .
Câu 15: (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Cho hình chóp S.ABC có đáy ABC là
tam giác đều cạnh bằng 1, cạnh bên SA vuông góc với đáy. Gọi S
M là trung điểm của SA (hình vẽ bên cạnh). Biết hai đường
thẳng CM và SB hợp nhau một góc 45 , khoảng cách giữa hai
đường thẳng CM và SB bằng bao nhiêu? M 1 1 A. . B. . 5 6 A C 1 1 C. . D. . 3 2 B Lời giải Chọn B S M H A C N B
Gọi N là trung điểm cạnh AB nên MN //SB . CM SB   CM MN  , ,   CMN
Ta có CN AB , CN SA suy ra CN  SAB hay CN NM 3 CN a 3 3 1 2 CN  ,  tan CMN   MN  , 2 2 AM MN AN    2 MN 2 4 4 2
d CM , SB  d SB,  CMN   d B,  CMN   d  , A CMN 
Kẻ AH MN suy ra d  , A
CMN   AH 1 1 1 1 6     4  2  AH  . 2 2 2 AH AN AM 2 AH 6
THI THỬ – THPT MỘ ĐỨC 2 – QUẢNG NGÃI
GV giải: Đặng Thanh Quang – CÂU 38 – 39
Câu 16: (THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018) Cho dãy số u xác định bởi n nnu  2017 sin  2018cos
. Mệnh đề nào dưới đây đúng? n 2 3 A. uu , n    . B. uu , n
   . C. uu , n
   . D. uu , n    . n9 n n 1  5 n n 1  2 n n6 n Lời giải Chọn C   Ta có u  2017 sin n 12  2018 cos n 12 n 12      2 3  n   n  nn  2017 sin  6  2018 cos  4      2017 sin  2018 cos  u .  2   3  2 3 n
Câu 17: (THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018) Cho hai cấp số cộng  x  : 4 , n
7 , 10 ,… và  y : 1, 6 , 11,…. Hỏi trong 2018 số hạng đầu tiên của mỗi cấp số có bao n  nhiêu số hạng chung? A. 404 . B. 673. C. 403. D. 672 . Lời giải Chọn C
Số hạng tổng quát của cấp số cộng  x là: x  4  n   3n 1. n   1 .3 n
Số hạng tổng quát của cấp số cộng  y là: y  1 m   5m  4 . m   1 .5 n
Giả sử k là 1 số hạng chung của hai cấp số cộng trong 2018 số hạng đầu tiên của mỗi cấp số.
Vì k là 1 số hạng của cấp số cộng  x nên k  3i 1 với 1  i  2018 và * i   . n
Vì k là 1 số hạng của cấp số cộng  y nên k  5 j  4 với 1  j  2018 và * j   . n
Do đó 3i 1  5 j  4  3i  5 j  5  i5  i 5;10;15;...; 2 
015  có 403 số hạng chung.
Câu 1: (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) Ông Trung vay ngân hàng 800 triệu đồng theo
hình thức trả góp hàng tháng trong 60 tháng. Lãi suất ngân hàng cố định 0, 5 /tháng. Mỗi
tháng ông Trung phải trả (lần đầu tiên phải trả là 1 tháng sau khi vay) số tiền gốc là số tiền vay
ban đầu chia cho 60 và số tiền lãi sinh ra từ số tiền gốc còn nợ ngân hàng. Tổng số tiền lãi mà
ông Trung phải trả trong toàn bộ quá trình trả nợ là bao nhiêu?
A. 118.000.000 đồng.
B. 126.066.666 đồng.
C. 122.000.000 đồng.
D. 135.500.000 đồng. Lời giải Chọn C
Gọi số tiền gốc ban đầu là N và phần trăm lãi là r .
Tháng thứ nhất ông Trung phải trả số tiền lãi là N.r . 59
Tháng thứ hai ông Trung phải trả số tiền lãi là N.r . 60 58
Tháng thứ ba ông Trung phải trả số tiền lãi là N.r . 60 .. 1
Tháng thứ sáu mươi ông Trung phải trả số tiền lãi là N.r . 60
Tổng số tiền lãi mà ông Trung phải trả trong suốt quá trình lãi là 59 58 1  59 58 1   60.60   1  N.r  .N.r  .N.r  ...  .N.r  1   ...  N.r    1 N.r   60 60 60  60 60 60  2.60   61  .800.0,5%  122.000.000 . 2
Vậy tổng số tiền lãi mà ông Trung phải trả trong toàn bộ quá trình trả nợ là 122.000.000 đồng.
Câu 2: (THPT Lê Quý Đôn-Hà Nội năm 2017-2018) Tính diện tích S của hình phẳng D được giới D ln x 1
hạn bởi các đường y
, trục hoành Ox và các đường x  ; x  2 ? x e 1 1 A. S   . B. S   . D  2 1 ln 2 D 1 ln 2 2 2 1 1 1 C. 2 S  ln 2  . D. S   . D  2 1 ln 2 D 2 2 2 Lời giải Chọn B
Diện tích hình phẳng cần tìm là 2 ln x 1 2 ln x ln x S  dx  dx  dx D    x x x 1 1 1 e e 1 2 1 2 2 2 2 ln x ln x ln x ln x 1 ln 2 1   dx  dx          2 1 ln 2 . x x 2 2 2 2 2 1 1 1 1 e e
Câu 3: (THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018) Trong hội chợ tết Mậu Tuất 2018 , một
công ty sữa muốn xếp 900 hộp sữa theo số lượng 1, 3 , 5 , ... từ trên xuống dưới (số hộp sữa
trên mỗi hàng xếp từ trên xuống là các số lẻ liên tiếp - mô hình như hình bên). Hàng dưới cùng có bao nhiêu hộp sữa? A. 59. B. 30. C. 61. D. 57. Lời giải Chọn A
Cách 1: p dụng công thức tính tổng n số hạng liên tiếp của CSC: n n S
2u n 1 d   900  2.1 n 1 .2 2
n  900  n  30. n  1   2    2  
Vậy u  1 29 * 2  59. 30
Cách 2: Áp dụng công thức      n   2 1 3 5 ..... 2
1  n , suy ra n  30. Vậy 2n 1  59. 1
Câu 4: (THPT Chuyên Lam Sơn-Thanh Hóa-lần 2 năm 2017-2018) Cho dãy số u xác định bởi: u n  1 3 n 1 u u u và u  .u . Tổng 2 3 10 S u    ...  bằng n 1  3 n n 1 2 3 10 3280 29524 25942 1 A. . B. . C. . D. . 6561 59049 59049 243 Lời giải Chọn B n 1 u 1 u 1 u 1 Theo đề ta có: u  .u n 1  n   mà u  hay 1  n 1  3 n n n 1 3 n 1 3 1 3 2 2 3 10 u 1 1  1  u 1  1   1  u  1  Nên ta có 2  .  3 10   ;  .      ; … ;    . 2 3 3  3  3 3  3   3  10  3   u  1 1 Hay dãy n
 là một cấp số nhân có số hạng đầu u  , công bội q  . 1  n  3 3 u u u 10 3 1 59048 29524 Khi đó 2 3 10 S u    ...     1 . 2 3 10 10 2.3 10 2.3 59049
Câu 5: (THPT Chuyên Thái Bình-lần 4 năm 2017-2018) Có bao nhiêu giá trị thực của tham số m để 2 2  m x khi x  2
hàm số f x   liên tục trên  ? 1 m
x khi x  2  A. 0 . B. 2 . C. 3 . D. 4 . Lời giải Chọn B
Ta có hàm số luôn liên tục x   2 .
Tại x  2 , ta có lim f x  lim 1 mx  1 m 2 ; x 2 x 2  
lim f x  lim  ; f   2 2  4m .    2 2 m x  2 4m x2 x2
Hàm số liên tục tại x  2 khi và chỉ khi
lim f x  lim f x  f 2 2
 4m  1 m 2
2  4m  2m  2  0  1 x 2 x 2  
Phương trình (1) luôn có hai nghiệm thực phân biệt. Vậy có hai giá trị của m .
Câu 6: (SGD Hà Nội-lần 11 năm 2017-2018) Giá trị của tổng 4  44  444  ...  44...4 (tổng đó có 2018 số hạng) bằng 40 2019 4  10 10  A.  2018 10   1  2018 . B.  2018   . 9 9 9   2019 4  10 10  4 C.  2018 2018   . D. 10   1 . 9 9   9 Lời giải Chọn B
Cách 1: Đặt S  4  44  444  ...  44...4 (tổng đó có 2018 số hạng). Ta có:
9 S  9 99 999...99...9     2   3    2018 10 1 10 1 10 1 ... 10   1 4 9 Suy ra: S   2 3 2018 10 10 10  ... 10
  2018  A 2018. 4 Với 2 3 2018
A  10 10 10  ... 10
là tổng 2018 số hạng của một cấp số nhân có số hạng đầu 2018 1 q 2018 110 2019 10 10
u  10 , công bội q  10 nên ta có A u  10  . 1 1 1 q 9  9 2019 9 10 10 2019 4  10 10  Do đó S   2018  S   2018   . 4 9 9 9   u   4 1 u   4 
Cách 2: Xét dãy số có 1    4  4  u  10u  4 u   10 u   n 1  n n 1     9 n   9   40 4 v  Đặt 1 v u   
v n là cấp số nhân. n n 9   9 v  10vn 1  n 4 v 4 2018.4
Ta có: S u u  .......  uv
v  ...  v
v v  ...  vn 1 2 2018 1 2 2018 1 2 2018 9 9 9 9 n 40. q  2018 2018 10     1 1 1 10 40 Trong đó S  .v  .  v2018 1 1 q 110 9 81 2019 40 4 4  10 10  Vậy tổng là S   2018 10   1  .2018   2018 .   81 9 9 9  
Câu 7: (THPT Nguyễn Trãi-Đà Nẵng-lần 1 năm 2017-2018) Cho cấp số cộng u thỏa n u
u u  10 2 3 5 
. Tính S u u u  ...  u u u  26 1 4 7 2011  4 6
A. S  2023736 .
B. S  2023563 .
C. S  6730444 .
D. S  6734134 . Lời giải Chọn A u
u u  10 u
d u  2d u  4d  10 u   3d  10 u   1 2 3 5 1 1 1 1 1        . u u  26 
u  3d u  5d  26 2u  8d  26 d  3 4 6  1 1  1 
u  10 , u  19 , u  28 … 4 7 10 u   1 1 
Ta có u , u , u , u , …, u
là cấp số cộng có d  9 1 4 7 10 2011 n  671  671 S
2.1 670.9  2023736 . 2
Câu 8: Cho dãy số u thỏa mãn u u  6 , n
  2 và log u  log u  8  11. Đặt n n n 1  2 5 9 2
S u u  ...  u . Tìm số tự nhiên n nhỏ nhất thỏa mãn S  20172018 . n 1 2 n n A. 2587 . B. 2590 . C. 2593. D. 2584 .
Câu 9: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Cho dãy số u thỏa mãn u u  6 , n n n 1 
n  2 và log u  log
u  8  11. Đặt S u u  ...  u . Tìm số tự nhiên n nhỏ nhất 2 5 9 2 n 1 2 n
thỏa mãn S  20172018 . n A. 2587 . B. 2590 . C. 2593. D. 2584 . Lời giải Chọn C
Ta có dãy số u là cấp số cộng có công sai d  6 . n  log u  log
u  8  11  log u u  8  11 * với u  0 . 2 5 9 2 5  9  2 5
Mặt khác u u  4d u  24 và u u  8d u  48 . 5 1 1 9 1 1
u  8  u  32
Thay vào * ta được 1 5  . Suy ra u  8 . u  88   u  64 1  1 5 n S  20172018  2u n d    n n   n   2 1 20172018 3 5 20172018 0  1 2  .
Vậy số tự nhiên n nhỏ nhất thỏa mãn S  20172018 là n  2593 . n
Câu 10: (SGD Quảng Nam – năm 2017 – 2018) Cho hình vuông ABCD có cạnh bằng a và có diện
tích S . Nối 4 trung điểm A , B , C , D theo thứ tự của 4 cạnh AB , BC , CD , DA ta được 1 1 1 1 1
hình vuông thứ hai có diện tích S . Tiếp tục làm như thế, ta được hình vuông thứ ba 2
là A B C D có diện tích S , …và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt 2 2 2 2 3
có diện tích S , S ,…, S
(tham khảo hình bên). Tính tổng S S S S  ...  S . 4 5 100 1 2 3 100 2 a  100 2   1 2 a  100 2   1 2 2 99 a a 2   1 A. S  . B. S  . C. S  . D. S  . 100 2 99 2 100 2 98 2 Lời giải Chọn B 1 1 Ta có 2 S a ; 2 S a ; 2 S a ,… 1 2 2 3 4 1
Do đó S , S , S ,…, S
là cấp số nhân với số hạng đầu 2
u S a và công bội q  . 1 2 3 100 1 1 2 2 100 1 nq a 2   1
Suy ra S S S S  ...  S  S .  . 1 2 3 100 1 1 q 99 2 u   1 1
Câu 11: (SGD Nam Định – năm 2017 – 2018) Cho dãy số u xác định bởi . n   3 * uu n , n     n 1  n
Tìm số nguyên dương n nhỏ nhất sao cho u 1  2039190 . n
A. n  2017 . B. n  2019 . C. n  2020 . D. n  2018 . Lời giải
Chọn C u   1 1  3 u u 1 2 1   3 Ta có 3 3 3 u   u  2
u  11  2  ...  n 1 3 2 n   ........  .........  3 u   u n n 1  n   n n 1  3 3   2 3 2
Ta lại có 1  2  ...  n   1
 1 2  3  ...  n   1    2  
n n   2 1  Suy ra u  1 n   2   Theo giả thiết ta có n n   1 n  2020 u 1  2039190 
 2039190  n n   1  4078380  mà n là số n  2 n  2019 
nguyên dương nhỏ nhất nên n  2020 .
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc
v t  2t m/s . Đi được 12 giây, người lái xe gặp chướng ngại vật và phanh gấp, ô tô tiếp tục 1    
chuyển động chậm dần đều với gia tốc a    2
12 m/s  . Tính quãng đường s m đi được của
ôtô từ lúc bắt đầu chuyển động đến khi dừng hẳn?
A. s  168m .
B. s  166 m .
C. s  144 m .
D. s  152 m . Lời giải
Chọn A
Giai đoạn 1: Xe bắt đầu chuyển động đến khi gặp chướng ngại vật.
Quãng đường xe đi được là: 12 12 12
S v t dt  2 d t t 2  t  144m . 1 1     0 0 0
Giai đoạn 2: Xe gặp chướng ngại vật đến khi dừng hẳn.
Ôtô chuyển động chậm dần đều với vận tốc v t  d a t  12  t c 2    .
Vận tốc của xe khi gặp chướng ngại vật là: v 0  v 12  2.12  24 m/s . 2   1      12. 
0  c  24  c  24  v t  12t  24 . 2  
Thời gian khi xe gặp chướng ngại vật đến khi xe dừng hẳn là nghiệm phương trình:
12t  24  0  t  2 .
Khi đó, quãng đường xe đi được là: 2 2 2
S v t dt  12  t  24 dt 2
 6t  24t  24 m . 2 2           0 0 0
Vậy tổng quãng đường xe đi được là: S S S  168 m . 1 2  
Câu 2: (Tạp chí THTT – Tháng 4 năm 2017 – 2018) Có hai cơ sở khoan giếng A và B. Cơ sở A giá
mét khoan đầu tiên là 8000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm
500 (đồng) so với giá của mét khoan ngay trước đó. Cơ sở B: Giá của mét khoan đầu tiên là
6000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 7% giá của mét
khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần
lượt là 20 m và 25 m để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng
của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất? A. luôn chọn A. B. luôn chọn B.
C. giếng 20 m chọn A còn giếng 25 m chọn B.
D. giếng 20 m chọn B còn giếng 25 m chọn B. Lời giải Chọn D
Cơ sở A giá mét khoan đầu tiên là 8000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét
sau tăng thêm 500 (đồng) so với giá của mét khoan ngay trước đó. Do đó theo tổng của một cấp số cộng ta có: 20
+ Nếu đào giếng 20 m hết số tiền là: S
2.8000  20 1 500  255000 20   2   (đồng). 25
+ Nếu đào giếng 25 m hết số tiền là: S
2.8000  25 1 500  350000 25   2   (đồng).
Cơ sở B giá của mét khoan đầu tiên là 6000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi
mét khoan sau tăng thêm 7% giá của mét khoan ngay trước đó. Do đó theo tổng của một cấp số nhân ta có: 1 1,0720
+ Nếu đào giếng 20 m hết số tiền là: S  6000  245973 (đồng). 20 11, 07 1 1, 0725
+ Nếu đào giếng 25 m hết số tiền là: S  6000  379494 (đồng). 25 11, 07
Ta thấy S  S , S  S nên giếng 20 m chọn B còn giếng 25 m chọn A. 20 20 25 25
Câu 3: (THPT Chuyên Lương Thế Vinh - Hà Nội – Lần 2 năm 2017 – 2018) Cho f x 10 f x 10 lim  5 . Giới hạn lim bằng x 1  x 1 x 1   x  
1  4 f x  9  3 5 A. 1. B. 2 . C. 10 . D. . 3 Lời giải
Chọn A f x 10 lim
 5 nên f xx 1 10    5 x   1 hay f xx 1   5x  5 x 1  x 1 Do đó f x 10 5x  5 10 5 x   1  x   1 lim  lim  lim x 1   x  
1  4 f x  9  3 x 1   x  
1  45x  5  9  3 x 1   x  
1  20x  29  3 5 x   1  lim  1. x 1
  20x  29  3 Cách 2:
Giả sử: f x 10   x   1 g x . f x 10  x   1 g x Ta có: lim  lim
 lim g x  5 . x 1  x 1 x 1  x 1 x 1  Vậy f x 10  x  
1 g x x   1 lim  lim x 1   x  
1  4 f x  9  3 x 1   x   1  4x  
1 g x 10  9  3   
g x x   1 51  1  lim   1 . x 1  4  x  
1 g x 10  9  3   4 0.5 10  9  3
Câu 4: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Cho dãy số u bởi công thức truy hồi sau n  u  0 1  ; u
nhận giá trị nào sau đây? uu  ; n n  1 218  n 1  n A. 23653 . B. 46872 . C. 23871 . D. 23436 . Lời giải Chọn A Đặt v u
u n , suy ra v là một câp số cộng với số hạng đầu v u u  1 và công n n n 1  n 1 2 1 sai d  1 . Xét tổng S
v v  ...  v . 217 1 2 217 217.v v 217.1 217 1 217  Ta có S
v v  ...  v    23653. 217 1 2 217 2 2 Mà v uu suy ra n n 1  n S
v v  ...  v
u u u u  ...  uuuu 217 1 2 217  2 1   3 2   218 217  218 1  uSu  23653. 218 217 1
Câu 5: (THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018) Cho dãy số a thỏa mãn n
a  1 và a  10a 1, n
  2 . Tìm giá trị nhỏ nhất của n để log a  100 . 1 n n 1  n A. 100 . B. 101. C. 102 . D. 103 .
Hướng dẫn giải Chọn C 1  1  a  10a 1  a   10 a  (1) . n n 1  nn 1  9   9  1 1 8 Đặt b a   b a  
. Từ (1)  b  10b , n   2 n n 1 1 9 9 9 n n 1  n 8
Dãy b là cấp số nhân với công bội là q  10 . Nên 1 n 1 b b .q  .10    . n n 1 9 1 8 n 1 Do đó 1 a b   10  , n   1, 2,... . n n 9 9 9 n 8 n 1 Ta có 100 1 100
log a  100  a  10  10   10 . n 9 9
Vậy giá trị nhỏ nhất của n để log a  100 là n  102 . n
Câu 6: (Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018) Cho cấp số cộng u có các số hạng n
đều dương, số hạng đầu u  1 và tổng của 100 số hạng đầu tiên bằng 14950 . Tính giá trị của 1 tổng 1 1 1 S    ...  . u u u u u u u u u uu u 2 1 1 2 3 2 2 3 2018 2017 2017 2018 1  1  1 A. 1   . B. 1 . C. 2018 . D. 1. 3  6052  6052
Hướng dẫn giải Chọn A
Gọi d là công sai của cấp số cộng. Khi đó: 100.99 S  100u
d  100  4950d  14950  d  3 . 100 1 2 Do đó u
u  2017d  6052 . 2018 1 1 1 1 uu   k k 1 1 1 Ta có: 1   .  .   . u u u u      u u u u d u u d u u k k k k . . . 1 1 k k 1   k k 1   k k 1  k k 1    Do đó: 1  1 1  1  1 1  1  1 1  1  1 1  S  .    .    ...  .    .   d u u d u u d u ud u u   1 2   2 3   2017 2018   1 2018  1  1   1   . 3  6052 
Câu 7: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Cho cấp số cộng u
có tất cả các số hạng n
đều dương thoả mãn u u  ...  u
 4 u u  ...  u
. Giá trị nhỏ nhất của biểu thức 1 2 2018  1 2 1009  2 2 2
P  log u  log u  log u bằng 3 2 3 5 3 14 A. 3 . B. 1. C. 2 . D. 4 . Lời giải Chọn C 2018 1009 Ta có S
2u  2017d , S  2u 1008d 1009  1  2018  1  2 2 2018 1009
u u  ...  u
 4 u u  ...  u
2u  2017d  4. 2u 1008d 1  1  1 2 2018  1 2 1009  2 2 d
 2u  2017d  2 2u 1008d u  . 1  1  1 2 d 3d 5d Dãy số u : , , , ... n  2 2 2 3d 9d 27d Ta có 2 2 2
P  log u  log u  log u 2 2 2  log  log  log 3 2 3 5 3 14 3 3 3 2 2 2 2 2 2  d   d   d d  1 log  2  log  3  log  . Đặt log  x thì 3   3   3  3  2   2   2  2
P    x2    x2    x2 1 2 3 2
 3x 12x 14   x  2 3 2  2  2 . 2
Dấu bằng xảy ra khi x  2   d
. Vậy giá trị nhỏ nhất của P bằng 2. 9
Câu 8: Cho hình lập phương . ABCD AB CD
  có cạnh bằng a . Khoảng cách từ A đến mặt phẳng CB D   bằng a 3 a 3 a 2 2a 3 A. . B. . C. . D. . 3 2 2 3
Câu 9: Cho hình lập phương . ABCD AB CD
  có cạnh bằng a . Khoảng cách từ A đến mặt phẳng CB D   bằng a 3 a 3 a 2 2a 3 A. . B. . C. . D. . 3 2 2 3
Hướng dẫn giải Chọn D C B D A I H C' B' O' A' D'
Gọi I AC  CO ta có I AC  CB D
  . Gọi H là hình chiếu của C lên CO . Khi đó CC .C O   a 3
d C ;CB D    C H    . 2 2 CC  C O   3 2a 3
Mặt khác, ta có AI  2C I  nên d  ; A CB D
   2d C ;CB D    . 3
Câu 10: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 .
Câu 11: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 . Lời giải Chọn A
Gọi số cây ở hàng thứ n là u . n
Ta có: u  1 , u  2 , u  3 , … và S u u u  ...  u  3003 . 1 2 3 1 2 3 n
Nhận xét dãy số u là cấp số cộng có u  1 , công sai d  1. n  1
n 2u n 1 d   1   Khi đó S    3003 . 2
n 2.1 n   1 1 n  77 Suy ra 
  3003  nn   1  6006 2
n n  6006  0    n  77 2 n  78  (vì n   ).
Vậy số hàng cây được trồng là 77 .
Câu 12: Trong tủ đồ chơi của bạn An có 5 con thú bông gồm: vịt, chó, mèo, gấu, voi. Bạn An muốn lấy ra một số
thú bông. Xác suất để trong những con thú bông An lấy ra không có con vịt. 16 1 15 15 A. . B. . C. . D. . 31 2 32 31
Câu 13: Trong tủ đồ chơi của bạn An có 5 con thú bông gồm: vịt, chó, mèo, gấu, voi. Bạn An muốn lấy ra một số
thú bông. Xác suất để trong những con thú bông An lấy ra không có con vịt. 16 1 15 15 A. . B. . C. . D. . 31 2 32 31 Lời giải Chọn D
Trường hợp 1: Bạn An chỉ lấy 1 con thú bông  có 5 cách.
Trường hợp 2: Bạn An lấy 2 con thú bông  có 2 C cách. 5
Trường hợp 3: Bạn An lấy 3 con thú bông  có 3 C cách. 5
Trường hợp 4: Bạn An lấy 4 con thú bông  có 4 C cách. 5
Trường hợp 5: Bạn An lấy cả 5 con thú bông  có 5 C cách. 5
Do đó, số phần tử của không gian mẫu là n  2 3 4 5
 5  C C C C  31. 5 5 5 5
Gọi A là biến cố: “trong những con thú bông An lấy ra không có con vịt”
Do đó, số kết quả thuận lợi cho biến cố A là n A 2 3 4
 4  C C C  15 4 4 4 n A 15
Vậy xác suất cần tìm là P A   . n  31
Câu 14: Một quả bóng cao su được thả từ độ cao 81m . Mỗi lần chạm đất quả bóng lại nảy lên hai phần
ba độ cao của lần rơi trước. Tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho
đến lúc bóng không nảy nữa bằng A. 234 . B. 567 . C. 162 . D. 405 .
Câu 15: Một quả bóng cao su được thả từ độ cao 81m . Mỗi lần chạm đất quả bóng lại nảy lên hai phần
ba độ cao của lần rơi trước. Tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho
đến lúc bóng không nảy nữa bằng A. 234 . B. 567 . C. 162 . D. 405 . Lời giải Chọn D
Gọi r là khoảng cách lần rơi thứ i i n 1  2  2 
Ta có r  81, r  .81 ,…, r  .81 ,… 1 2   3 n  3 
Suy ra tổng các khoảng cách rơi của quả bóng từ lúc thả bóng cho đến lần rơi thứ n bằng n  2  1    3  81. . 2 1 3
Gọi t là khoảng cách lần nảy thứ i i n 1  2  2  2  2  2 Ta có t  .81, t  . 81,…, t  .81 ,… 1     3 2 n  3  3  3  3
Suy ra tổng các khoảng cách nảy của quả bóng từ lúc thả bóng cho đến đến lần nảy thứ n bằng n 1   2  1 2    3  .81. . 3 2 1 3
Vậy tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy n n 1   2 2       1 1        3  2  3 nữa bằng  S lim 81. .81.     405 .  2 3 2  1 1  3 3   
Câu 16: Cho dãy u : 3 u  e , 2 uu , * k   thỏa mãn 765
u .u ...u  e
. Giá trị của k là: n  1 n 1  n 1 2 k A. 6 . B. 7 . C. 8 . D. 9 .
Câu 17: Cho dãy u : 3 u  e , 2 uu , * k   thỏa mãn 765
u .u ...u  e
. Giá trị của k là: n  1 n 1  n 1 2 k A. 6 . B. 7 . C. 8 . D. 9 .
Hướng dẫn giải Chọn C Ta có u  e n v , với 1 v 3.2n  , * n   . n n 2k 1
v v  ...  v  3.  3 2k 1 . 1 2 k   2 1 1 v  2 v ...
u .u ...u  e vk . 1 2 k Suy ra 32k  1 765 2k    1  255 2k   256  k  8 . 1 n 1
Câu 18: Cho dãy số u có u  và uu , n
  1 . Tìm tất cả giá trị n để n  1 5 n 1  5 n n n 2018 u 5 1 k S    . 2018 k 1  k 4.5 A. n  2019 . B. n  2018 . C. n  2020 . D. n  2017 . 1 n 1
Câu 19: Cho dãy số u có u  và uu , n
  1 . Tìm tất cả giá trị n để n  1 5 n 1  5 n n n 2018 u 5 1 k S    . 2018 k 1  k 4.5 A. n  2019 . B. n  2018 . C. n  2020 . D. n  2017 . Lời giải
Chọn B n 1 u 1 u Ta có n 1  n uu    . n 1  5 n n n 1 5 n u 1 1 Đặt n v  , n
  1 . Suy ra v là cấp số nhận có công bội q  và v  . n n n 5 1 5 n  1  1 n n u 1 n q 1       k 5 1 5n 1 Ta có S   v v      T   . k 1   kq k k 1 5 1 4 5n n 1 1 1 5 2018 5 1 Do v  0 , n
  1 nên T là dãy tăng. Suy ra T   Tn  2018 . n n n 2018 2018 4.5
Câu 20: Xét các số thực dương a , b sao cho 2
 5 , 2a , 3b là cấp số cộng và 2 , a  2 , b  3 là cấp số nhân. Khi đó 2 2
a b  3ab bằng : A. 59 . B. 89 . C. 31 . D. 76 .
Câu 21: Xét các số thực dương a , b sao cho 25 , 2a , 3b là cấp số cộng và 2 , a  2 , b  3 là cấp số nhân. Khi đó 2 2
a b  3ab bằng : A. 59 . B. 89 . C. 31 . D. 76 . Lời giải Chọn A
Vì 25 , 2a , 3b là cấp số cộng nên 25  3b  4a  3b  9  4a 16 .
Vì 2 , a  2 , b  3 là cấp số nhân nên b    a  2 2 3 2 . 4a 16 Suy ra 2
 a  22   a    a  2 2 4 16 3 2 2
 3a  4a  20  0 3
Vì a  0 nên a  2 suy ra b  11 . Vậy 2 2
a b  3ab  4 121 66  59
Câu 22: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC . Ta xây dựng dãy các tam giác A B C , A B C , A B C ,… sao 1 1 1 2 2 2 3 3 3
cho A B C là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác 1 1 1
A B C là tam giác trung bình của tam giác A B C
. Với mỗi số nguyên dương n , kí hiệu n n n n 1  n 1  n 1 
S tương ứng là diện tích hình tròn ngoại tiếp tam giác A B C . Tính tổng n n n n
S S S  ...  S  ... ? 1 2 n 15 9 A. S  . B. S  4 . C. S  . D. S  5 . 4 2
Câu 23: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC . Ta xây dựng dãy các tam giác A B C , A B C , A B C ,… sao 1 1 1 2 2 2 3 3 3
cho A B C là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác 1 1 1
A B C là tam giác trung bình của tam giác A B C
. Với mỗi số nguyên dương n , kí hiệu n n n n 1  n 1  n 1 
S tương ứng là diện tích hình tròn ngoại tiếp tam giác A B C . Tính tổng n n n n
S S S  ...  S  ... ? 1 2 n 15 9 A. S  . B. S  4 . C. S  . D. S  5 . 4 2 Lời giải Chọn B 2 2 2  3   3 3  3 1  3 3  3 1 Ta có S   .3.
  3 ; S   . .   
.S ; S   . .    .S 1  3  2 1   3 2     2 3 4 4   4 3 16 4  
Ta có S , S , S , …, S tạo thành cấp số nhân lùi vô hạn với số hạng đầu là S  3 và công 1 2 3 n 1 1 bội q  4 S 3 Suy ra 1
S S S  ...  S  ...    4 . 1 2 n 1 q 1 1 4
Câu 24: Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp
được tháp có 10 tầng thì bạn An cần đúng bao nhiêu que diêm? A. 210 . B. 39. C. 100. D. 270 .
Câu 25: Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp
được tháp có 10 tầng thì bạn An cần đúng bao nhiêu que diêm? A. 210 . B. 39. C. 100. D. 270 . Lời giải Chọn A
Số que ở 1 tầng là u  3 . 1
Tổng số que ở 2 tầng là u u  3  7 . 1 2
Tổng số que ở 3 tầng là u u u  3  7 11 . 1 2 3 .
Ta có cấp số cộng u  3 , d  4 , tính S ? 1 10 10
Để cần có 10 tầng cần tổng S  2.3  9.4  210 que. 10   2
Câu 26: Cho a b c là ba số nguyên. Biết a , b , c theo thứ tự tạo thành một cấp số cộng và a , c , b
theo thứ tự tạo thành một cấp số nhân. Tìm giá trị nhỏ nhất của c . A. 2  . B. 2 . C. 1. D. 4 .
Câu 27: Cho a b c là ba số nguyên. Biết a , b , c theo thứ tự tạo thành một cấp số cộng và a , c , b
theo thứ tự tạo thành một cấp số nhân. Tìm giá trị nhỏ nhất của c . A. 2  . B. 2 . C. 1. D. 4 . Lời giải Chọn B
c a L
 2b a c Ta có 2 2 2  
. Suy ra: 2c a a c  2c ac a  0  . 2 a a c c ab  0 
c    b     2 4 2 a  0
Suy ra a , b trái dấu với c   . c  0 
Do a , b , c nguyên nên c chia hết cho 2 .
Do đó c nhỏ nhất bằng 2 khi đó a  4
 , b  1 (thỏa mãn).
Câu 28: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân tại A , 
BAC  120 , AB BB  a . Gọi I là trung điểm của CC . Tính BC
cosin của góc giữa hai mặt phẳng  ABC và  AB I   . 70 5 AI A. . B. . 10 5 B C A 30 15 C. . D. . 10 5
Câu 29: Cho dãy số u thỏa mãn u  2 và u
 2  u với mọi n  1. Tìm u . n  1 n 1  n 2018    A. u  2 cos . B. u  2 cos . C. u  2 cos . D. u  2 . 2018 2017 2 2018 2019 2 2018 2018 2 2018
Câu 30: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân tại A ,  BAC  120 ,
AB BB  a . Gọi I là trung điểm của CC . Tính cosin của góc giữa hai mặt phẳng  ABC và  AB I   . BC AI B C A 70 5 30 15 A. . B. . C. . D. . 10 5 10 5 Lời giải Chọn C a
Chọn hệ trục Oxyz như hình vẽ và độ dài đơn vị trên các trục là a ta có: BC a 3 , OA  2  1   3   3   3   3 1  nên A 0; ; 0   , B ; 0;1 , C  
; 0; 0  , C  ; 0;1 , I   ; 0;   2   2          2   2   2 2   z B' C' A' x I B O C A y   3 1    3 1 1  1  AB   ;  ;1 // ; AI    ;  ;  = .    3; 1   ;1    3; 1  ; 2 2 2   2 2 2 2    
Mặt phẳng  ABC  có véc tơ pháp tuyến là n k  0;0;1 . 1      Mặt phẳng  AB I
  có véc tơ pháp tuyến là n   AB ; AI   1; 3  3; 2  3 . 2       n .n   30
cos  ABC ; AB I   1 2     . n . n 10 1 2 S
Cách 2: Dùng công thức hình chiếu: cos  ABC ; AB I  ABC  . SAB I
Câu 31: Cho dãy số u thỏa mãn u  2 và u
 2  u với mọi n  1. Tìm u . n  1 n 1  n 2018    A. u  2 cos . B. u  2 cos . C. u  2 cos . D. u  2 . 2018 2017 2 2018 2019 2 2018 2018 2 2018 Lời giải Chọn B Ta có:   u  2  2 cos  2 cos . 1 2 4 2   u  2  2  2 cos  2 cos . 2 3 8 2 
Dự đoán: u  2 cos . n n 1 2 
Chứng minh theo quy nạp ta có.  u  2 cos  2 , công thức  
1 đúng với n  1 . Giả sử công thức  
1 đúng với n k , k  1 1 4  ta có u  2 cos . k k 1 2          Ta có: 2 u
 2  u  2  2 cos  2 1 cos  4 cos  2 cos k 1  k k 1   k 1    k2  k 2 2  2   2  2   (vì 0  
với mọi k  1 ). k 2 2 2 Công thức  
1 đúng với n k 1 .   Vậy u  2 cos , n
  N . Suy ra u  2 cos . n n 1 2  2018 2019 2   1 
Câu 32: Cho dãy  x thỏa lim x   . Tính giới hạn lim x cos 1 n n n   x   n  A. Không tồn tại. B. 1. C. 0 . D. 1  .   1 
Câu 33: Cho dãy  x thỏa lim x   . Tính giới hạn lim x cos 1 n n n   x   n  A. Không tồn tại. B. 1. C. 0 . D. 1  . Lời giải Chọn C     1 2 sin    1   1 1    2  2x  lim 2  x cos 1  lim  2sin   lim . n  0.1  0 . n     x 1 2      2x x n   n  n  1     x     n   2x    n  
Câu 1: (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Cho hình lập phương . ABCD
A BCD có
cạnh bằng 1. Cắt hình lập phương bằng một mặt phẳng đi qua đường chéo BD . Tìm giá trị
nhỏ nhất của diện tích thiết diện thu được. 6 6 6 A. . B. . C. 2 . D. . 2 4 3 Lời giải Chọn A ADI BCM O N D A H K B C
Gọi O là tâm của hình lập phương. Vì các mặt bên của hình lập phương là các mặt phẳng song
song nên mặt phẳng qua đường chéo BD cắt các mặt bên theo các giao tuyến song song. Thiết
diện là hình bình hành BMDN . Ta có S  2SBD .MH . BMDN BMD
Có BD  3 nên diện tích đạt GTNN khi và chỉ khi MH nhỏ nhất. Do 
AA và BD chéo 2
nhau nên MH là đoạn vuông góc chung của 
AA và BD hay MH OI  . 2 2 6 Vậy S  2S
BD .MH  3.  . BMD ' N BMD ' 2 2
Câu 2: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Trong dịp hội trại hè 2017, bạn Anh thả một
quả bóng cao su từ độ cao 6 m so với mặt đất, mỗi lần chạm đất quả bóng lại nảy lên một độ
cao bằng ba phần tư độ cao lần rơi trước. Biết rằng quả bóng luôn chuyển động vuông góc với
mặt đất. Tổng quãng đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng: A. 44 m . B. 45m . C. 42 m . D. 43m . Lời giải Chọn C
Ta có quãng đường bóng bay bằng tổng quảng đường bóng nảy lên và quãng đường bóng rơi xuống. 3
Vì mỗi lần bóng nảy lên bằng
lần nảy trước nên ta có tổng quãng đường bóng nảy lên là 4 2 3 n 3  3   3   3  S  6.  6.  6.  ...  6.  ... 1       4  4   4   4  3 9 3
Đây là tổng của cấp số nhân lùi vô hạn có số hạng đầu u  6.  và công bội q  . Suy ra 1 4 2 4 9 2 S   18 . 1 3 1 4
Tổng quãng đường bóng rơi xuống bằng khoảng cách độ cao ban đầu và tổng quãng đường 2 n  3   3   3 
bóng nảy lên nên là S  6  6.  6.  ...  6.  ... 2        4   4   4  3
Đây là tổng của cấp số nhân lùi vô hạn với số hạng đầu u  6 và công bội q  . Suy ra 1 4 6 S   24 . 2 3 1 4
Vậy tổng quãng đường bóng bay là S S S  18  24  42 . 1 2
Câu 3: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Cho dãy số u thỏa mãn n u   2 1  u  2 1  , * n    . Tính u . n u  2018 n 1   1  2   1 unA. u  7  5 2 . B. u  2 . C. u  7  5 2 . D. u  7  2 . 2018 2018 2018 2018 Lời giải Chọn Au  tan  n
Đặt tan   2 . Ta có tan  2 1. Suy ra 8 u  8 n 1   1 tan .u 8 n  tan   tan    Có u 8   tan   . 2     8 1 tan . tan u   8 n   
Bằng quy nạp, ta chứng minh được u  tan   n  . n   1  8     tan  tan  2017     Vậy 8 u  tan    tan     7  5 2 . 2018      8   8   1 tan .tan 8
Câu 1: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh 2a . Gọi M , N lần lượt là trung điểm của các cạnh AB , AD ; H là giao điểm
của CN và DM . Biết SH  3a và vuông góc với mặt đáy  ABCD . Khoảng cách giữa hai
đường thẳng MD và SC là 12a 15 a 61 12a 61 6a 61 A. . B. . C. . D. . 61 61 61 61 Lời giải Chọn C A D N H 2a M B C E
Cách 1: Dựng đường thẳng d qua C và song song với DM . d AB E .
Dựng HK SC , K SC .
Ta có DMA CDN ( . c . c c) Suy ra   NCD ADM Lại có    
NCD CND  90  ADM CND  90 
CHD  90  MD CN tại H . CE   CH Suy ra 
CE  CSH   CE HK. (1) CE SH  HK CE (1) Suy ta 
HK  CSE HK CS
d DM , SC   d DM ,CSE  d H,CSE  HK. Ta có 2 2 2 2 NC
DC DN  4a a a 5. S K K D A H M B C E 2 2 DC 4a 4 5a
Xét tam giác vuông NCD ta có HC    . NC a 5 5 HS.HC 12 61 Suy ta HK   a . 2 2 61 HS HC
Cách 2: Dễ thấy CN DM CH DM a 5
Tam giác ADM vuông tại A có: 2 2 DM AD AM  2 CH DM Ta có : 
DM  SHC SH DM  1 4a 2 S
CH .DM  2a CH DCM 2 5 Trong S
HC hạ HK SC d DM , SC   HK 1 1 1 12a 61
Tam giác SHC vuông tại H có:    HK  . 2 2 2 HK SH HC 61
Câu 2: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Tam giác mà ba đỉnh của nó là ba trung điểm ba
cạnh của tam giác ABC được gọi là tam giác trung bình của tam giác ABC .
Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho A B C là một tam giác đều 1 1 1 2 2 2 3 3 3 1 1 1
cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác A B C là tam giác trung bình của n n n tam giác A B C
. Với mỗi số nguyên dương n , kí hiệu S tương ứng là diện tích hình tròn n 1  n 1  n 1  n
ngoại tiếp tam giác A B C . Tính tổng S S S  ...  S  ... ? n n n 1 2 n 15 9 A. S  . B. S  4. C. S  . D. S  5 . 4 2 Lời giải
Chọn B
Vì dãy các tam giác A B C , A B C , A B C ,... là các tam giác đều nên bán kính đường tròn 1 1 1 2 2 2 3 3 3 3
ngoại tiếp các tam giác bằng cạnh . 3
Với n  1 thì tam giác đều A B C có cạnh bằng 3 nên đường tròn ngoại tiếp tam giác 1 1 1 2 3  3 
A B C có bán kính R  3.  S   3. . 1 1 1 1  3 1  3    3
Với n  2 thì tam giác đều A B C có cạnh bằng
nên đường tròn ngoại tiếp tam giác 2 2 2 2 2 1 3  1 3 
A B C có bán kính R  3. .  S   3. . . 2 2 2 2  2 3 2  2 3    3
Với n  3 thì tam giác đều A B C có cạnh bằng
nên đường tròn ngoại tiếp tam giác 3 3 3 4 2 1 3  1 3 
A B C có bán kính R  3. .  S   3. . . 2 2 2 3  4 3 3  4 3    ................... n 1   1 
Như vậy tam giác đều A B C có cạnh bằng 3.
nên đường tròn ngoại tiếp tam giác n n n    2  2 n 1  n 1   1  3  1 3   
A B C có bán kính R  3. .  S    3. .    . n n n n   n  2  3  2 3     
Khi đó ta được dãy S , S , ...S ... là một cấp số nhân lùi vô hạn với số hạng đầu u S  3 1 2 n 1 1 1 và công bội q  . 4 u
Do đó tổng S S S  ...  S  ... 1   4 . 1 2 n 1 q
Câu 1: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Cho dãy số xác định bởi u  1, 1 1  n 1  * u  2u
; n   . Khi đó u bằng n 1   n 2  3 2018 
n  3n  2  2016 2 1 2018 2 1 A. u   . B. u   . 2018 2017 3 2019 2018 2017 3 2019 2017 2 1 2017 2 1 C. u   . u   . 2018 2018 D. 3 2019 2018 2018 3 2019 Lời giải Chọn A 1  n 1  1  3 2  2 1 2 1 Ta có: u  2u   2u    u   . . n 1   n 2    3 n n
n  3n  2  3  n  2 n 1  3 n  2 3 n 1 1 2  1   u   u    1 n 1    n  2 3 nn 1  1 2
Đặt v u  , từ   1 ta suy ra: vv . n n n 1 n 1  3 n 1 1 2
Do đó v là cấp số nhân với v u   , công bội q  . n  1 1 2 2 3 n 1  n 1  n 1  1 1  2 1  2  1 n 1  2   Suy ra: 1
v v .q  .  u   .  u  .  . n 1       2 n n  3  n 1 2  3  2  3  n 1 2017 1  2  1 2016 2 1 Vậy u  .    . 2018   2 2017  3  2019 3 2019
Câu 2: ----------HẾT----------(THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018) Cho dãy số u n
được xác định bởi u  2 ; u  2u
 3n 1. Công thức số hạng tổng quát của dãy số đã cho là 1 n n 1 
biểu thức có dạng .2n a
bn c , với a , b , c là các số nguyên, n  2 ; n   . Khi đó tổng
a b c có giá trị bằng A. 4  . B. 4 . C. 3  . D. 3 . Lời giải Chọn C Ta có u  2u
 3n 1  u  3n  5  2 u  3 n 1  5
n  ; n   . nn 1    n n 1   , với 2
Đặt v u  3n  5 , ta có v  2v
với n  2 ; n   . n n n n 1 
Như vậy, v là cấp số nhân với công bội q  2 và v  10 , do đó n 1 v 10.2    5.2n . n  1 n
Do đó u  3n  5  5.2n , hay u  5.2n  3n  5 với n  2 ; n   . n n
Suy ra a  5 , b  3  , c  5
 . Nên a b c  5   3     5    3  .
Câu 3: (THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018) Cho dãy số u như sau: n n u  , n
  1 , 2 ,... Tính giới hạn lim u u  ...  u . 1 2 n n 2 4 1 n n x 1 1 1 A. . B. 1. C. . D. . 4 2 3 Lời giải Chọn C n n 1  1 1  Ta có u     n   1 2   2 n n   1  2 2 2 n n n n   2 2 1
2  n n 1 n n 1  1  1 1 1 1 1 1 1 1 1 
Ta có u u  ...  u  1        ...   1 2 n  2 2  2  3 3 7 7 13 13 21 n n 1 n n 1  2 1  1  1 n n  1   2  2 2  n n 1  2 n n 1 1 1 1 1 Suy ra lim    ...   lim n u u u  . 1 2 n  2 1 1 2 1  2 n n
Câu 4: (THPT Chuyên Trần Phú-Hải Phòng-lần 2 năm 2017-2018) Trong năm đầu tiên đi làm, anh A
được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi
tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương anh A đều cất đi phần
lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh
A mua được ô tô giá 500 triệu biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe? A. 11. B. 12. C. 13 . D. 10 . Lời giải Chọn C
Số tiền anh A cần tiết kiệm là 500  500.0,12  340 (triệu).
Gọi số tiền mà anh A nhận được ở mỗi tháng trong năm đầu tiên là u  10 (triệu). 1
Thì số tiền mà anh A nhận được ở mỗi tháng trong năm thứ hai là
u u . 1 0,12  u .1,12 (triệu). 2 1   1
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ ba là
u u .1 0,122  u .1,122 (triệu). 3 1 1 …
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ n là nnu u .   u . 1,12 (triệu). 1   1 n 1 0,12 1 1
Vậy số tiền mà anh A tiết kiệm được sau n năm là n
12.u u u u    uuu u
 12.u u 12. u . 1,12 u    . 1   1 n 1  2 1 3 2 n 1  n2 n n 1   1   nn 23
Cho 12.u .1,12 1 u    340    1 23 1,12   n  log 1  n  13. 1 1   6 1,12 6
Vậy sau ít nhất 13 năm thì anh A sẽ tiết kiệm đủ tiền để mua ô tô.
Câu 5: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Cho lăng trụ tam giác đều ABC.AB C  
có AB a . M là một điểm di động trên đoạn AB . Gọi H là hình chiếu của A trên đường
thẳng CM . Tính độ dài đoạn thẳng BH khi tam giác AHC có diện tích lớn nhất. a 3 a a  3   1  3  A. . B. . C. . D. a  1 . 3 2 2  2    Lời giải
Chọn C A M B H C A' B' C'
Ta có AA   ABC  nên AA  CM . Mặt khác A H
CM . Do đó CM   AA H  . Suy ra
CM AH . Vậy H còn là hình chiếu của A trên CM . 2 2 1 1 1 AC a Ta có SAH.HC  . AH HC  
. Dấu bằng xảy ra khi AH HC , tức AHC  2 2  2 2 2 4 4 là khi 
ACM  45 . Vậy tam giác AHC có diện tích lớn nhất khi M ở vị trí sao cho  a 2
ACM  45 . Khi đó HC  và  HCB  15 . 2 Trong tam giác HBC : 2 2 2 
BH HC BC  2HC.BC.cos HCB  4 2 3 2 2 6  2 2 a a a a  3   1 2   a  2. . . a   BH  . 2 2 4 4 2
Câu 6: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Cho dãy số u thỏa mãn n  ln  2 2
u u 10  ln 2u  6u và uu  2u
1 với mọi n  1. Giá trị nhỏ nhất của n 1 2   1 2  n2 n n 1 
để u  5050 bằng. n A. 100 . B. 99 . C. 101. D. 102 . Lời giải Chọn D Ta có: ln  2 2
u u 10  ln 2u  6u 2 2
u u 10  2u  6u 1 2   1 2  1 2 1 2 u   1  u  2
1  u  32  0 1  . 1 2 u  3  2 Đặt v u
u với n  1  v u u  2 . n n 1  n 1 2 1 Theo giả thiết: uu  2u 1  uuuu 1  vv 1 , n   1 . n2 n n 1  n2 n 1  n 1  n n 1  n
Suy ra v là cấp số cộng có công sai d  1  v v n 1 d n  3 . n 1   n  Ta có: uu
u u u
 ...  u u u u u S u . n 1  n 1  n n n 1  3 2 2 1 1 n 1         v v v v n n 1  2 1 n n n   1
Với S v v  ...  v v v  . n 1 2 n  1 n  2 2 n n   1 n   1 n  2 Suy ra: u  1  u  1. n 1  2 n 2 n   1 n  2 Ta có: 2 u  5050 
1  5050  n  3n 10096  0  n  101,99 . n 2
Vậy số n nhỏ nhất thỏa yêu cầu là 102 .
Document Outline

  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 1 Phần 1
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 1 Phần 2
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 1 Phần 3
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 1 Phần 4
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 2 Phần 1
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 2 Phần 2
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 2 Phần 3
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 2 Phần 4
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 3 Phần 1
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 3 Phần 2
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 3 Phần 3
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 3 Phần 4
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 4 Phần 1
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 4 Phần 2
  • Chương 3 - DÃY SỐ - CẤP SỐ NHÂN - CẤP SỐ CỘNG - Mức độ 4 Phần 3