Trắc nghiệm hàm số mũ, hàm số logarit và một số bài toán liên quan

Nhằm giúp các em học sinh khối 12 tự học chương trình Giải tích 12 chương 2: hàm số lũy thừa, hàm số mũ và hàm số logarit và ôn tập chuẩn bị cho kỳ thi THPT Quốc gia môn Toán năm học 2019 – 2020,

73 37 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

65 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 11
HÀM SỐ MŨ, HÀM SỐ LOGARIT
VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN
MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 1
Dạng 1. Tìm tập xác định ............................................................................................................................................... 1
Dạng 1.1 Không chứa tham số .................................................................................................................................. 1
Dạng 1.2 Chứa tham số .............................................................................................................................................. 2
Dạng 2. Tìm đạo hàm ..................................................................................................................................................... 4
Dạng 3. Khảo sát hàm số mũ, logarit ............................................................................................................................ 7
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…) .................................................................................................... 16
Dạng 5. Bài toán cực trị ............................................................................................................................................... 21
Dạng 6. Một số bài toán khác ...................................................................................................................................... 24
PHẦN B. ĐÁP ÁN THAM KHẢO ............................................................................................................................. 25
Dạng 1. Tìm tập xác định ............................................................................................................................................. 25
Dạng 1.1 Không chứa tham số ................................................................................................................................ 25
Dạng 2. Chứa tham số .............................................................................................................................................. 26
Dạng 2. Tìm đạo hàm ................................................................................................................................................... 29
Dạng 3. Khảo sát hàm số mũ, logarit .......................................................................................................................... 32
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…) .................................................................................................... 41
Dạng 5. Bài toán cực trị ............................................................................................................................................... 53
Dạng 6. Một số bài toán khác ...................................................................................................................................... 63
PHẦN A. CÂU HỎI
Dạng 1. Tìm tập xác định
Dạng 1.1 Không chứa tham số
Câu 1. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm tập xác định
D
của hàm số
5
3
log .
2
x
y
x
A.
( ; 2) (3; )D
B.
( 2; 3)D
C.
( ; 2) [3; )D
D.
\{ 2}D
Câu 2. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tập xác định D của hàm số
2
2
log 2 3
y x x
A.
; 1 3;D
 
B.
1;3
D
C.
; 1 3;D

D.
D
Câu 3. (MĐ 104 BGD&DT NĂM 2017) Tìm tập xác định
D
của hàm số
2
3
log 4 3
y x x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
A.
1;3
D
B.
;1 3;D
 
C.
;2 2 2 2;D
 
. D.
2 2;1 3;2 2
D
Câu 4. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm tập xác định của hàm số
2
2018
log 3
y x x
.
A.
D
B.
0;D
C.
; 0 3;D

D.
0; 3
D
Câu 5. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tập xác định của
2
ln 5 6
y x x
là
A.
2; 3
B.
2; 3
C.
; 2 3;
D.
; 2 3;

Câu 6. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Tìm tập xác định của hàm số
5
1
log
6
y
x
.
A.
;6
B.
C.
0;
D.
6;
Câu 7. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Tập xác định của hàm số
2
2
log 3 2
y x x
là
A.
( 1;1)D
. B.
( 1; 3)D
. C.
( 3;1)D
. D.
(0;1)D
.
Câu 8. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tập xác định của hàm số
2
2
log 2 3
y x x
là
A.
1;3
. B.
1;3
.
C.
; 1 3;

. D.
; 1 3;

.
Câu 9. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Tìm tập xác định
của hàm số:
x
y x
2 log 3
A.
0;

. B.
0;3
. C.
;3

. D.
0;3
.
Câu 10. (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Tập xác định của hàm số
ln 2
y x
là
A.
. B.
3;

. C.
0;

. D.
2;

.
Câu 11. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm tập xác định D của hàm số
2019
2
2019
y log 4 x 2x 3 .
A.
3 3
D 2; ;2
2 2
. B.
3 3
D 2; ;2
2 2
.
C.
3
D ;2
2
. D.
D 2;2
.
Câu 12. Tìm tập xác định của hàm số
0
2
2
2 log 9
y x x
là
A.
2;3 .
D
B.
3;3 \ 2 .
D
C.
3; .
D
. D.
3;3 .
D
.
Dạng 1.2 Chứa tham số
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
Câu 13. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
log 2 1
y x x m có tập xác định là
.
A.
2m
B.
2m
C.
0m
D.
0m
Câu 14. (MĐ 104 BGD&DT NĂM 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
ln 2 1
y x x m
có tập xác định là
.
A.
0 3
m
B.
1
m
hoặc
0
m
C.
0
m
D.
0
m
Câu 15. Hàm số
2
ln 1
y x mx
xác định với mọi giá trị của
x
khi.
A.
2
2
m
m
. B.
2
m
. C.
m
. D.
2
m
.
Câu 16. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Tìm tất cả các giá trị của tham số
m
để hàm số
2
3 3
1
log 4log 3
y
m x x m
xác định trên khoảng
0;

A.
; 4 1;m

. B.
1;m
.
C.
4;1
m
. D.
1;m
.
Câu 17. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Tìm tất cả các giá trị của
m
để hàm số
2
ln 2 1
y x mx m
xác định với mọi
1;2
x
.
A.
1
3
m
. B.
3
4
m
. C.
3
4
m
. D.
1
3
m
.
Câu 18. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Tìm tất cả các giá trị thực của
tham số
m
để hàm số
2
log( 4 1)
y x x m
có tập xác định là
.
A.
4
m
. B.
0
m
. C.
4
m
. D.
3
m
.
Câu 19. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Có bao nhiêu giá trị nguyên của tham
số
m
trên
2018; 2018
để hàm số
2
ln 2 1
y x x m
có tập xác định là
?
A.
2019
B.
2017
C.
2018
D.
1009
Câu 20. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Tìm tất cả các giá trị thực của tham số
m
để
hàm số
2
log 2 4
y x mx
có tập xác định là
.
A.
2 2
m
. B.
2
m
. C.
2
2
m
m
. D.
2 2
m
.
Câu 21. Số các giá trị nguyên của tham số
m
để hàm số
log 2
y mx m
xác định trên
1
;
2
là
A.
4
B.
5
C. Vô số D.
3
Câu 22. (KTNL GIA BÌNH NĂM 2018-2019) Tìm tất cả các giá trị của
m
để hàm số
2
2018
log 2018
2
x
x
y x m
xác định với mọi giá trị
x
thuộc
0;

A.
9
m
B.
1
m
C.
0 1
m
D.
2
m
Câu 23. Hàm số
2
log 4 2
x x
y m
có tập xác định là
thì
A.
1
4
m
. B.
0
m
. C.
1
4
m
. D.
1
4
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 24. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Tập hợp tất cả các giá trị của tham số
m
để
hàm số
2 2
2018
3 5
log 2 4 5
x
y
x x m m
xác định với mọi
x
là
A.
;1 3;
 
. B.
(1;3) \ 2
. C.
;1
. D.
1;3 \ 2
.
Câu 25. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2018
log 2017 1
2
x
x
y x m
xác định với mọi
x
thuộc
0;
?
A.
1
. B.
2
. C.
2018
. D. Vô số.
Câu 26. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Có tất cả bao nhiêu giá
trị nguyên dương của tham số
m
để hàm số
3
1
log
2 1
y x m
m x
xác định trên khoảng
2;3
?
A.
1
. B.
2
. C.
4
. D.
3
.
Dạng 2. Tìm đạo hàm
Câu 27. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm đạo hàm của hàm số
logy x
.
A.
ln10
y
x
B.
1
ln10
y
x
C.
1
10ln
y
x
D.
1
y
x
Câu 28. (Mã 103 - BGD - 2019) Hàm số
2
2
x x
y
có đạo hàm là
A.
2
2 .ln 2
x x
. B.
2
(2 1).2 .ln 2
x x
x
. C.
2
2 1
( ).2
x x
x x
. D.
2
(2 1).2
x x
x
.
Câu 29. (Mã đề 104 - BGD - 2019) Hàm số
2
3
x x
y
có đạo hàm là
A.
2
2 1 .3
x x
x
. B.
2
2 1
.3
x x
x x
. C.
2
2 1 .3 .ln 3
x x
x
. D.
2
3 .ln3
x x
.
Câu 30. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính đạo hàm của hàm số
13
x
y
A.
13
ln13
x
y
B.
1
.13
x
y x
C.
13 ln13
x
y
D.
13
x
y
Câu 31. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1 ln 2
y
x
B.
1
2 1 ln 2
y
x
C.
2
2 1
y
x
D.
1
2 1
y
x
Câu 32. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính đạo hàm của hàm số
1
4
x
x
y
A.
2
1 2 1 ln 2
'
2
x
x
y
B.
2
1 2 1 ln 2
'
2
x
x
y
C.
2
1 2 1 ln 2
'
2
x
x
y
D.
2
1 2 1 ln 2
'
2
x
x
y
Câu 33. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Hàm số
2
2
log 2x
f x x
có đạo hàm
A.
2
ln2
'
2x
f x
x
B.
2
1
'
2x ln2
f x
x
C.
2
2x 2 ln 2
'
2x
f x
x
D.
2
2x 2
'
2x ln2
f x
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
Câu 34. (Mã đề 101 - BGD - 2019) Hàm số
2
3
2
x x
y
có đạo hàm là
A.
2
3
2 3 2 ln 2
x x
x
. B.
2
3
2 ln 2
x x
. C.
2
3
2 3 2
x x
x
. D.
2
2 3 1
3 2
x x
x x
.
Câu 35. (Mã 102 - BGD - 2019) Hàm số
2
3
3
x x
y
có đạo hàm là
A.
2
3
2 3 .3
x x
x
. B.
2
3
3 .ln3
x x
. C.
2
2 3 1
3 .3
x x
x x
. D.
2
3
2 3 .3 .ln 3
x x
x
.
Câu 36. Tính đạo hàm của hàm số
y = ln 1+ x +1
.
A.
1
1 1 1
y
x x
B.
2
1 1 1
y
x x
C.
1
2 1 1 1
y
x x
D.
1
1 1
y
x
Câu 37. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số
ln x
y
x
, mệnh đề nào dưới đây đúng?
A.
2
1
2y xy
x
. B.
2
1
y xy
x
. C.
2
1
y xy
x
. D.
2
1
2y xy
x
.
Câu 38. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Đạo hàm của hàm số
1 2x
y e
là
A.
1 2
2
x
y e
B.
1 2
2
x
y e
C.
1 2
2
x
e
y
D.
1 2x
y e
Câu 39. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Đạo hàm của hàm số
2
3
log 1
y x x
là:
A.
2
2 1 ln 3
'
1
x
y
x x
B.
2
2 1
'
1 ln 3
x
y
x x
C.
2
2 1
'
1
x
y
x x
D.
2
1
'
1 ln 3
y
x x
Câu 40. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Tính đạo hàm của hàm số
2
x x
y e
.
A.
2 1
x
x e
B.
2
2 1
x x
x e
C.
2 1
2 1
x
x e
D.
2 2 1x
x x e
Câu 41. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
2
2
log 1
f x x
, tính
1
f
A
1 1
f
. B.
1
1
2ln 2
f
. C.
1
1
2
f
. D.
1
1
ln 2
f
.
Câu 42. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Tìm đạo hàm của hàm số
2
ln 1
x
y e
.
A.
2
2
2
2
1
x
x
e
y
e
. B.
2
2
1
x
x
e
y
e
. C.
2
1
1
x
y
e
. D.
2
2
2
1
x
x
e
y
e
.
Câu 43. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Tính đạo hàm của hàm số
1
2
x
x
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
A.
2
2
x
x
y
. B.
2
ln 2. 1 1
2
x
x
y
C.
2
2
x
x
y
. D.
ln 2. 1 1
2
x
x
y
.
Câu 44. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Tính đạo hàm của hàm số
2
9
log 1
y x
.
A.
2
1
1 ln 9
y
x
. B.
2
1 ln 3
x
y
x
. C.
2
2 ln9
1
x
y
x
. D.
2
2ln 3
1
y
x
.
Câu 45. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Tính đạo hàm hàm số
.sin 2
x
y e x
A.
sin 2 cos 2
x
e x x
. B.
.cos2
x
e x
.
C.
sin 2 cos2
x
e x x
. D.
sin 2 2cos 2
x
e x x
.
Câu 46. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Đạo hàm của hàm số
1
4
x
x
y
là
A.
2
1 2 1 ln 2
2
x
x
B.
2
1 2 1 ln 2
2
x
x
C.
2
1 2 1 ln 2
2
x
x
D.
2
1 2 1 ln 2
2
x
x
Câu 47. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số
2
x x
f x e
. Biết phương
trình
0
f x
có hai nghiệm
1
x
,
2
x
. Tính
1 2
.x x
.
A.
1 2
1
.
4
x x
B.
1 2
. 1
x x
C.
1 2
3
.
4
x x
D.
1 2
. 0
x x
Câu 48. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Cho hàm
cos ln s ln
y x x in x
.
Khẳng định nào sau đây đúng?
A.
2
2 4 0
x y xy y
. B.
2
2 0
x y xy xy
.
C.
2
2 2 5 0
x y xy y
. D.
2
2 0
x y xy y
.
Câu 49. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Tính đạo hàm của hàm số
2019
log , 0
xy x
.
A.
1
ln 2019
y
x
. B.
1
y
x
. C.
1
ln 2019
y
x
. D.
ln 2019
y x
.
Câu 50. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Cho hàm số
1
1 ln
y
x x
với
0
x
. Khi đó
2
'y
y
bằng
A.
1
x
x
. B.
1
1
x
. C.
1 ln
x
x x
. D.
1
1 ln
x
x x
.
Câu 51. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Tính đạo hàm của hàm số
x
1
2 ln
e
x
y x
.
A.
1 1
2 ln2 ln
e
x
x
y x
x
. B.
1
2 ln 2 e
x x
y
x
.
C.
x
1 1
2 ln 2
e
x
y
x
. D.
x
1
2 ln 2 e
x
y
x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 52. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Tập xác định của hàm
số
2020 2019 2018 2017
log log log log
y x
là
; .
D a
Giá trị của
a
bằng
A.
2019
2018
. B.
2020
2019
. C.
2018
2017
. D.
0
.
Câu 53. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Đạo hàm của hàm số
2
2
( ) log 2f x x x
là
A.
2
2 2
2 ln 2
x
x x
B.
2
2 l 2
1
n
x x
C.
2
(2 2)ln
2
2
x
x
x
D.
2
2 2
2 ln 2
x
x x
Câu 54. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Đạo hàm của hàm số
(x) ln(lnx)
f
là:
A.
1
( )
x ln ln ln
f x
x x
. B.
1
( )
2 ln ln
f x
x
C.
1
( )
2x lnx ln ln
f x
x
. D.
1
( )
lnx ln ln
f x
x
.
Câu 55. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hàm số
ln 2018 ln
1
x
f x
x
. Tính
' 1 ' 2 ' 3 ' 2017 .
S f f f f
A.
4035
2018
S
B.
2017
2018
S
C.
2016
2017
S
D.
2017
S
Câu 56. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hàm số
2018
ln
1
x
f x
x
. Tính tổng
1 2 ... 2018
S f f f
.
A.
ln 2018
. B.
1
. C.
2018
. D.
2018
2019
.
Câu 57. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số
lnf x x x
. Một trong bốn đồ thị cho
trong bốn phương án A, B, C, D dưới đây là đồ thị của hàm số
y f x
. Tìm đồ thị đó?
A. Hình 2 B. Hình 3 C. Hình 4 D. Hình 1
Dạng 3. Khảo sát hàm số mũ, logarit
Câu 58. Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
y ln 1 1x mx
đồng biến trên
khoảng
;
A.
1;

B.
; 1
C.
1;1
D.
; 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Câu 59. Cho ba số thực dương
, ,a b c
khác
1
. Đồ thị các hàm số , ,
x x x
y a y b y c được cho trong hình
vẽ bên
Mệnh đề nào dưới đây đúng?
A.
b c a
B.
c a b
C.
a b c
D.
a c b
Câu 60. (MĐ 105 BGD&ĐT NĂM 2017)
Cho hàm số
,
x x
y a y b
với , a b là hai số thực dương khác
1, lần lượt có đồ thị là
1
C
và
2
C
như hình bên. Mệnh đề nào dưới đây đúng
?
A.
0 1b a
B.
0 1a b
C.
0 1b a
D.
0 1a b
Câu 61. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Trong các hàm số sau hàm số nào
nghịch biến trên
?
A.
2
3
log x
B.
3
logy x
C.
e
4
x
y
D.
2
5
x
y
Câu 62. Mệnh đề nào trong các mệnh đề dưới đây sai?
A. Hàm số
2
1
2018
x
y
đồng biến trên
.
B. Hàm số
logy x
đồng biến trên
0;
.
C. Hàm số
lny x
nghịch biến trên khoảng
;0
.
D. Hàm số 2
x
y đồng biến trên
.
Câu 63. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Hàm số nào dưới đây đồng biến trên
tập xác định của nó?
A.
1
π
x
y
B.
2
3
x
y
C.
3
x
y
D.
0,5
x
y
Câu 64. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số
2
logy x . Mệnh đề nào
dưới đây sai?
O
1
C
2
C
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
A. Đạo hàm của hàm số là
1
ln 2
y
x
B. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng
C. Tập xác định của hàm số là
;

D. Hàm số đồng biến trên khoảng
0;

Câu 65. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Trong các hàm số sau, hàm số
nào luôn đồng biến trên
?
A.
2015
y
2016
x
B.
3
y
2016 2
x
C.
2x
y (0,1)
D.
2
(2016)
x
y
Câu 66. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
e
x
y
. B.
lny x
. C.
lny x
. D.
e
x
y
.
Câu 67. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Tìm hàm số đồng biến trên
.
A.
3
x
f x
. B.
f x
. C.
1
3
x
f x
. D.
3
3
x
f x
.
Câu 68. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho hàm số
5
log
y x
. Mệnh đề nào dưới
đây là mệnh đề sai?
A. Hàm số đã cho đồng biến trên tập xác định.
B. Hàm số đã cho có tập xác định
0\
D
.
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục tung.
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
Câu 69. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ.
Khẳng định nào sau đây đúng?
A.
1
0
2
a b
. B.
0 1
a b
. C.
0 1
b a
. D.
0 1a
,
1
0
2
b
.
Câu 70. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Trong các hàm số sau, hàm
số nào nghịch biến?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
A.
ln .y x
B.
2018
1
2019
log
y x
C.
D.
4 3
log .y x
Câu 71. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Đồ thị hàm số
lny x
đi qua điểm
A.
1; 0
. B.
2
2; e
. C.
2 ; 2e
. D.
0;1
.
Câu 72. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Trong các hàm số
sau,hàm số nào luôn nghịch biến trên tập xác định của nó?
A.
2
1
2
y
. B.
logy x
. C.
2
x
y
. D.
2
3
x
y
.
Câu 73. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Chọn khẳng định sai
trong các khẳng định sau:
A. Hàm số
2
logy x
đồng biến trên
.
B. Hàm số
1
2
logy x
nghịch biến trên tập xác định của nó.
C. Hàm số
2
x
y
đồng biến trên
.
D. Hàm số
2
y x
có tập xác định là
0;

.
Câu 74. (KTNL GV BẮC GIANG NĂM 2018-2019) Hàm số nào dưới đây đồng biến trên khoảng
(0; )
?
A.
3
log
y x
. B.
6
logy x
. C.
3
log
e
y x
. D.
1
4
logy x
.
Câu 75. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Trong các mệnh
đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số
2
x
y
và
2
logy x
đối xứng với nhau qua đường thẳng
y x
.
B. Đồ thị của hai hàm số
x
y e
và
lny x
đối xứng với nhau qua đường thẳng
y x
.
C. Đồ thị của hai hàm số
2
x
y
và hàm số
1
2
x
y
đối xứng với nhau qua trục hoành.
D. Đồ thị của hai hàm số
2
logy x
và
2
1
log
y
x
đối xứng với nhau qua trục tung.
Câu 76. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong hình dưới đây, điểm
B
là trung
điểm của đoạn thẳng
AC
. Khẳng định nào sau đây là đúng?
A.
2a c b
. B.
2
ac b
. C.
2
2ac b
. D.
ac b
.
Câu 77. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Hàm số nào sau đây có
đồ thị như hình bên?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
A.
3
logy x
. B.
2
log 1y x
. C.
2
log 1
y x
. D.
3
log 1
y x
Câu 78. (CHUYÊN QUỐC HỌC HUẾ NĂM 2018-2019 LẦN 1) Trong các hàm số dưới đây, hàm số nào
nghịch biến trên tập số thực
R
.
A.
3
x
y
B.
2
4
log 2 1
y x
C.
2
x
y
e
D.
2
3
logy x
Câu 79. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Hàm số nào dưới đây nghịch biến trên
tập xác định của nó?
A.
3
log
y x
B.
2
log 1
y x
C.
4
logy x
D.
3
x
y
Câu 80. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hàm số
3
9 17
ln3
x
y x
. Mệnh
đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng
;0

B. Hàm số đồng biến trên khoảng
0;

C. Hàm số đạt cực trị tại
2
x
D. Hàm số có giá trị cực tiểu là
9
y
Câu 81. Cho các số thực
,a b
sao cho
0 , 1
a b
, biết răng đô thi cac ham sô
x
y a
và
log
b
y x
căt nhau
tai điêm
5 1
2018; 2019
M
. Mệnh đề nào dưới đây đúng?
A.
1, 1
a b
B.
1,0 1a b
C.
0 1, 1a b
D.
0 1,0 1
a b
Câu 82. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Đồ thị
L
của hàm số
lnf x x
cắt trục hoành tại điểm
A
, tiếp tuyến của
L
tại
A
có phương trình là:
A.
2 1y x
B.
1y x
C.
3y x
D.
4 3y x
Câu 83. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số
3x
y xe
đạt cực đại
tại
A.
1
3
x
e
. B.
1
3
x
. C.
1
x
e
. D.
0
x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Câu 84. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Hàm số
2
3
log 2y x x
nghịch
biến trên khoảng nào?
A.
2;
. B.
;0

. C.
1;
. D.
0;1
.
Câu 85. (HỌC MÃI NĂM 2018-2019-LẦN 02) Cho đồ thị hàm số
x
y a
và
log
b
y x
như hình vẽ. Trong
các khẳng định sau, đâu là khẳng định đúng
A.
0 1,0 1
a b
. B.
1, 1
a b
. C.
0 1
b a
. D.
0 1
a b
.
Câu 86. (TT HOÀNG HOA THÁM - 2018-2019) Hình vẽ bên thể hiện đồ thị của ba trong bốn hàm số
6
x
y
,
8
x
y
,
1
5
x
y
và
1
.
7
x
y
Hỏi (C
2
) là đồ thị hàm số nào?
A.
6
x
y
. B.
1
7
x
y
. C.
1
5
x
y
. D.
8
x
y
Câu 87. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Tập tất cả các giá trị của tham số
m
để hàm số
2
ln 1 1y x mx
đồng biến trên
là
A.
1;1
. B.
; 1
. C.
1;1
. D.
; 1
.
Câu 88. (THPT ĐÔNG SƠN THANH HÓA NĂM 2018-2019 LẦN 02) Trong hình vẽ bên có đồ thị các
hàm số
, , log
x x
c
y a y b y x
. Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
A.
a c b
. B.
c a b
. C.
a b c
. D.
b c a
.
Câu 89. (GKI CS2 LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 01) Cho đô thi cua ba ham sô
, ,
x x x
y a y b y c như hinh ve bên. Khăng đinh nao sau đây đung?
A.
b a c
. B.
a c b
. C.
c a b
. D.
c b a
.
Câu 90. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Cho
, ,a b c
là các số thực dương khác 1. Hình
vẽ bên là đồ thị của ba hàm số
log , log , log
a b c
y x y x y x
.
Khẳng định nào sau đây là đúng?
A.
a c b
. B.
a b c
. C.
c b a
. D.
c a b
.
Câu 91. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Giá trị nhỏ nhất
của hàm số
ln x
y
x
trên đoạn
2;3
bằng
A.
ln 2
2
. B.
ln 3
3
. C.
2
3
e
. D.
1
e
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Câu 92. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Cho , ,a b c là các số thực dương khác 1. Hình
vẽ bên là đồ thị hàm số log , log , log
a b c
y x y y x y x . Khẳng định nào sau đây là đúng?
A.
a b c
. B.
a c b
. C.
b a c
. D.
b a c
.
Câu 93. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hàm số
ln 6
ln 2
x
y
x m
với
m
là tham số. Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số đồng biến trên khoảng
1; e
.
Tìm số phần tử của
S
.
A.
3
B.
1
C.
2
D.
4
Câu 94. Tìm tất cả các giá trị thực của tham số m để hàm số
2
2
log 2
log 1
m x
y
x m
nghịch biến trên
4;
A.
2m
hoặc
1m
. B.
2m
hoặc
1m
.
C.
2m
hoặc
1m
. D.
2m
.
Câu 95. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hàm số
lnf x x x
. Khẳng định
nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;1
.
B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số đồng biến trên các khoảng
;0
và
1;
.
D. Hàm số đồng biến trên khoảng
1;
.
Câu 96. (HSG BẮC NINH NĂM 2018-2019) Cho hàm số
2018
1
logy
x
có đồ thị
1
C
và hàm số
y f x
có đồ thị
2
C
. Biết
1
C
và
2
C
đối xứng nhanh qua gốc tọa độ. Hỏi hàm số
y f x
nghịch
biến trên khoảng nào dưới đây?
A.
0;1
B.
1;0
C.
; 1
D.
1;
Câu 97. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Có bao nhiêu giá trị nguyên của tham
số
2019;2019m
để hàm số
ln 6
ln 3
x
y
x m
đồng biến trên khoảng
6
1;e
?
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Câu 98. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2018;2018
để hàm số
1 ln 2 y f x x x m x
đồng biến trên khoảng
2
0;e
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
A.
2016
. B.
2022
. C.
2014
. D.
2023
.
Câu 99. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho
2
ln 1 sin 6f x a x x b x
với
,a b
.
Biết rằng
log log 2f e
. Tính giá trị của
log ln10f
.
A.
10
. B.
2
. C.
4
. D.
8
.
Câu 100. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Cho
, ,a b c
dương và khác 1. Các hàm số
log
a
y x , log
b
y x , log
c
y x có đồ thị như hình vẽ
Khẳng định nào dưới đây đúng?
A.
a c b
. B.
a b c
. C.
c b a
. D.
b c a
.
Câu 101. Đồ thị hàm số
y f x
đối xứng với đồ thị hàm số
0, 1
x
y a a a
qua điểm
1;1I
. Giá trị
của biểu thức
1
2 log
2018
a
f
bằng
A.
2016
. B.
2016
. C.
2020
. D.
2020
.
Câu 113. (TRƯƠNG THPT HOANG HOA THAM HƯNG YÊN NĂM 2018-2019) Hình vẽ bên thể hiện
đồ thị của ba trong bốn hàm số
6
x
y
,
8
x
y
,
1
5
x
y
và
1
.
7
x
y
Hỏi
2
C
là đồ thị hàm số nào?
A.
6 .
x
y
B.
1
.
7
x
y
C.
1
.
5
x
y
D.
8 .
x
y
Câu 114. (HSG BẮC NINH NĂM 2018-2019) Giá trị nhỏ nhất của hàm số
2 2
2
x
f x x e
trên đoạn
1;2
bằng:
A.
4
2e
B.
2
e
C.
2
2e
D.
2
2e
3C
2C
1C
O
x
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Câu 115. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Giá trị nhỏ nhất của hàm số
1
4
2 8
3
x x
y
trên
1;0
bằng
A.
4
9
. B.
5
6
. C.
2 2
3
. D.
2
3
.
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…)
Câu 102. (ĐỀ THAM KHẢO BGD & ĐT 2018) Một người gửi
100
triệu đồng vào ngân hàng với lãi suất
0,4%/
tháng. Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào
vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau
6
tháng, người đó được lĩnh số tiền ( cả vốn ban đầu và
lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất
không thay đổi?
A.
102.16.000
đồng B.
102.017.000
đồng C.
102.424.000
đồng D.
102.423.000
đồng
Câu 103. (Mã đề 104 BGD&ĐT NĂM 2018) Một người gửi tiết kiệm vào một ngân hàng với lãi suất
6,1% /
năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào
vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và
lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không
rút tiền ra?
A.
11
năm B.
12
năm C.
13
năm D.
10
năm
Câu 104. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với lãi
suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu
hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết
tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền
m
mà ông A sẽ phải trả cho ngân hàng
trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng, lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn
nợ.
A.
3
3
120.(1,12)
(1,12) 1
m
(triệu đồng) B.
3
100.(1,01)
3
m (triệu đồng)
C.
3
3
(1,01)
(1,01) 1
m
(triệu đồng) D.
100.1,03
3
m
(triệu đồng)
Câu 105. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Ông A vay ngân hàng 100 triệu đồng với lãi
suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt
đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau và
ông A trả hết nợ sau đúng năm năm kể từ ngày vay. Biết rằng mỗi tháng ngâng hàng chỉ tính lãi trên số dư nợ
thực tế của tháng đó. Hỏi số tiền mỗi tháng ông ta cần trả cho ngâng hàng gần nhất với số tiền nào dưới đây?
A.
2,20
triệu đồng B.
2,22
triệu đồng C.
3,03
triệu đồng D.
2,25
triệu đồng
Câu 106. Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9
tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không
thay đổi trong thời gian gửi.
A.
0,8 %
B.
0,6 %
C.
0,7 %
D.
0,5 %
Câu 107. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Một người gửi
100
triệu đồng vào
một ngân hàng với lãi suất
0,6%
/tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng,
số tiền lãi sẽ được nhập làm vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng, người
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
đó được lĩnh số tiền không ít hơn
110
triệu đồng (cả vốn ban đầu và lãi), biết rằng trong suốt thời gian gửi
tiền người đó không rút tiền và lãi suất không thay đổi?
A.
18
tháng B.
16
tháng C.
17
tháng D.
15
tháng
Câu 108. Một người lần đầu gửi vào ngân hàng
100
triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ
trước được cộng vào vốn của kỳ kế tiếp) với kì hạn
3
tháng, lãi suất
2%
một quý. Sau đúng
6
tháng, người
đó gửi thêm
100
triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau
1
năm
gửi tiền vào ngân hàng gần bằng với kết quả nào sau đây? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân
hàng không thay đổi và người đó không rút tiền ra.
A.
212
triệu đồng B.
216
triệu đồng C.
210
triệu đồng D.
220
triệu đồng
Câu 109. (KTNL GIA BÌNH NĂM 2018-2019) Ông An gửi tiết kiệm
50
triệu đồng vào ngân hàng với kỳ
hạn
3
tháng, lãi suất
8,4%
một năm theo hình thức lãi kép. Ông gửi được đúng
3
kỳ hạn thì ngân hàng thay
đổi lãi suất, ông gửi tiếp
12
tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là
12%
một năm thì
ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi là: (làm tròn đến chữ số hàng đơn vị)
A.
62255910
đồng. B.
59895767
đồng. C.
59993756
đồng. C.
63545193
đồng.
Câu 110. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Ngày 01 tháng 01năm 2017, ông An
đem 800 triệu đồng gửi vào một ngân hàng với lãi suất 0,5% một tháng. Từ đó, cứ tròn mỗi tháng, ông đến
ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01tháng 01 năm 2018, sau khi rút tiền, số tiền tiết
kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi suất trong suốt thời gian ông An gửi không thay đổi
A.
11
800.(1,005) 72
(triệu đồng) B.
12
1200 400.(1,005)
(triệu đồng)
C.
12
800.(1,005) 72
(triệu đồng) D.
11
1200 400.(1,005)
(triệu đồng)
Câu 111. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Để đủ tiền mua nhà,
anh An vay ngân hàng
500
triệu theo phương thức trả góp với lãi suất
0,85%
/tháng. Nếu sau mỗi tháng, kể
từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là
10
triệu đồng bao gồm cả tiền lãi vay và tiền
gốc. Biết rằng phương thức trả lãi và gốc không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu
tháng thì anh trả hết nợ ngân hàng? (Tháng cuối có thể trả dưới
10
triệu đồng).
A.
68
B.
66
C.
65
D.
67
Câu 112. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Ông An gửi
100
triệu vào tiết
kiệm ngân hàng theo thể thức lãi kép trong một thời gian khá lâu mà không rút ra với lãi suất ổn định trong
mấy chục năm qua là
10% /1
năm. Tết năm nay do ông kẹt tiền nên rút hết ra để gia đình đón Tết. Sau khi rút
cả vốn lẫn lãi, ông trích ra gần
10
triệu để sắm sửa đồ Tết trong nhà thì ông còn
250
triệu. Hỏi ông đã gửi
tiết kiệm bao nhiêu lâu?
A.
10
năm B.
17
năm C.
15
năm D.
20
năm
Câu 116. (TT HOÀNG HOA THÁM - 2018-2019) Một học sinh
A
khi
15
tuổi được hưởng tài sản thừa
kế
200 000 000
VNĐ. Số tiền này được bảo quản trong ngân hàng
B
với kì hạn thanh toán
1
năm và học
sinh
A
chỉ nhận được số tiền này khi
18
tuổi. Biết rằng khi
18
tuổi, số tiền mà học sinh
A
được nhận sẽ là
231 525 000
VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng
B
là bao nhiêu?
A.
8% /
năm. B.
7%/
năm. C.
6%/
năm. D.
5% /
năm.
Câu 117. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Ông Anh gửi vào ngân hàng
60
triệu đồng
theo hình thức lãi kép. Lãi suất ngân hàng là
8%
trên năm. Sau
5
năm ông An tiếp tục gửi thêm
60
triệu
đồng nữa. Hỏi sau
10
năm kể từ lần gửi đầu tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao nhiêu?
(Biết lãi suất không thay dổi qua các năm ông gửi tiền).
A.
231,815
(triệu đồng). B.
197,201
(triệu đồng).
C.
217,695
(triệu đồng). D.
190,271
(triệu đồng).
Câu 118. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Ông Chính gửi 200 triệu đồng vào một
ngân hàng với lãi suất
7%
năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi
sẽ được nhập vào gốc để tính lãi cho năm tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả
định trong suốt thời gian gửi lãi suất không thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn
đến hàng nghìn).
A.
1.686.898.000
VNĐ. B.
743.585.000
VNĐ.
C.
739.163.000
VNĐ. D.
1.335.967.000
VNĐ.
Câu 119. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Một người mỗi tháng đều đặn gửi
vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng người
đó có số tiền là
10
triệu đồng. Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng B.
645.000
đồng C.
635.000
đồng D.
535.000
đồng
Câu 120. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Anh Nam gửi 100 triệu đồng
vào ngân hàng theo thể thức lãi kép kì hạn là một quý với lãi suất 3% một quý. Sau đúng 6 tháng anh Nam
gửi thêm 100 triệu đồng với kì hạn và lãi suất như trước đó.Hỏi sau 1 năm số tiền (cả vốn lẫn lãi) anh Nam
nhận được là bao nhiêu? ( Giả sử lãi suất không thay đổi).
A.
218,64
triệu đồng. B.
208,25
triệu đồng.
C.
210,45
triệu đồng. D.
209,25
triệu đồng.
Câu 121. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Ông A gửi vào ngân hàng
50
triệu đồng
với lãi suất
0,5% /
tháng. Hỏi sau ít nhất bao nhiêu tháng thì ông A có được số tiền cả gốc lẫn lãi nhiều hơn
60 triệu đồng? Biết rằng trong suốt thời gian gửi, lãi suất ngân hàng không đổi và ông A không rút tiền ra.
A.
36
tháng. B.
38
tháng. C.
37
tháng. D.
40
tháng.
Câu 122. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho biết sự tăng dân số được
ước tính theo công thức
.
Nr
S Ae
(trong đó
A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số hằng năm). Đầu năm 2010 dân số tỉnh Bắc Ninh là
1.038.229
người tính đến đầu năm
2015 dân số của tỉnh là
1.153.600
người. Hỏi nếu tỉ lệ tăng dân số hằng năm giữ nguyên thì đầu năm 2020
dân số của tỉnh nằm trong khoảng nào?
A.
1.281.600;1.281.700
. B.
1.281.700;1.281.800
.
C.
1.281.800;1.281.900
. D.
1.281.900;1.282.000
.
Câu 123. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Một người gửi
300
triệu
đồng vào một ngân hàng với lãi suất
7%/
năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi
năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó
nhận được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất
không đổi và người đó không rút tiền ra.
A.
9
năm. B.
10
năm. C.
11
năm. D.
12
năm.
Câu 124. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Một người gửi tiết kiệm số tiền
80000000
đồng với lãi suất
6,9%
/ năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5
năm người đó rút được cả tiền gốc lẫn tiền lãi gần với con số nào sau đây?
A.
105370000
đồng B.
111680000
đồng C.
107667000
đồng D.
116570000
đồng
Câu 125. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Một người mỗi tháng đều đặn gửi
vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng,
người đó có số tiền là
10
triệu đồng. Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng B.
645.000
đồng C.
635.000
đồng D.
535.000
đồng
Câu 126. Một người muốn có
1
tỉ tiền tiết kiệm sau
6
năm gửi ngân hàng bằng cách bắt đầu từ ngày
01/01/2019 đến 31/12/2024, vào ngày 01/01 hàng năm người đó gửi vào ngân hàng một số tiền bằng nhau với
lãi suất ngân hàng là
7% /1
năm (tính từ ngày 01/01 đến ngày 31/12) và lãi suất hàng năm được nhập vào
vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng hàng năm là bao nhiêu (với giả thiết lãi suất không thay
đổi và số tiền được làm tròn đến đơn vị đồng)?
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
A.
130 650 280
(đồng). B.
130 650 000
(đồng).
C.
139 795 799
(đồng). D.
139 795 800
(đồng).
Câu 127. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Một người vay ngân hàng
100
triệu đồng với lãi
suất là
0,7%
/tháng theo thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng
5
triệu đồng và cứ trả hàng
tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới
5
triệu). Hỏi sau bao nhiêu tháng thì người
đó trả được hết nợ ngân hàng.
A.
22
. B.
23
. C.
24
. D.
21
.
Câu 128. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Anh Bảo gửi 27 triệu đồng vào ngân
hàng theo thể thức lãi kép, kỳ hạn là một quý, với lãi suất
1,85%
một quý. Hỏi thời gian tối thiểu bao nhiêu
để anh Bảo có được ít nhất 36 triệu đồng tính cả vỗn lẫn lãi?
A. 16 quý. B. 20 quý. C. 19 quý. D. 15 quý.
Câu 129. (HSG BẮC NINH NĂM 2018-2019) Vào ngày
15
hàng tháng ông An đều đến gửi tiết kiệm tại
ngân hàng
SHB
số tiền
5
triệu đồng theo hình thức lãi kép với kì hạn một tháng, lãi suất tiết kiệm không đổi
trong suốt quá trình gửi là
7,2%/
năm. Hỏi sau đúng
3
năm kể từ ngày bắt đầu gửi ông An thu được số tiền
cả gốc và lãi là bao nhiêu (làm tròn đến nghìn đồng)?.
A.
195251000
(đồng) B.
201453000
(đồng) C.
195252000
(đồng) D.
201452000
(đồng)
Câu 130. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Anh Bình gửi
200
triệu vào ngân
hàng VB với kì hạn cố định
12
tháng và hưởng lãi suất
0,65% /
tháng. Tuy nhiên sau khi gửi được tròn 8
tháng anh phải dùng đến
200
triệu trên. Anh đến ngân hàng định rút tiền thì được nhân viên ngân hàng tư
vấn: “Nếu rút tiền trước kì hạn, toàn bộ số tiền anh gửi chỉ có lãi suất không kỳ hạn là
0,02% /
thángAnh nên
thế chấp sổ tiết kiệm đó tại ngân hàng để vay ngân hàng
200
triệu với lãi suất
0,7% /
tháng. Khi sổ của anh
đến kì hạn, anh có thể rút tiền để trả nợ ngân hàng”. Nếu làm theo tư vấn của nhân viên ngân hàng anh Bình
sẽ đỡ thiệt một số tiền gần nhất với con số nào dưới đây (biết ngân hàng tính lãi theo thể thức lãi kép).
A.
10,85
triệu đồng. B.
10,51
triệu đồng. C.
10,03
triệu đồng. D.
10,19
triệu đồng.
Câu 131. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Một thầy giáo cứ đầu mỗi
tháng lại gửi ngân hàng 8 000 000 VNĐ với lãi suất
0,5%
/ tháng. Hỏi sau bao nhiêu tháng thầy giáo có thể
tiết kiệm tiền để mua được một chiếc xe ô tô trị giá
400 000 000 VNĐ?
A.
60
. B.
50
. C.
55
. D.
45
.
Câu 132. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Ông An gửi 100 triệu đồng vào một ngân
hàng với lãi suất 0,8%/ tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi
sẽ được nhập vào gốc để tính lãi cho tháng tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi them vào
tài khoản với số tiền 2 triệu đồng. Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu?
Biết rằng trong suốt thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra (kết quả được làm tròn
đến hàng nghìn).
A.
169.871.000
đồng. B.
171.761.000
đồng. C.
173.807.000
đồng. D.
169.675.000
đồng.
Câu 133. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Một người vay ngân
hàng số tiền
400
triệu đồng, mỗi tháng trả góp
10
triệu đồng và lãi suất cho số tiền chưa trả là
1%
mỗi tháng.
Kỳ trả đầu tiên là cuối tháng thứ nhất. Biết lãi suất không đổi trong suốt quá trình gửi, hỏi số tiền còn phải trả
ở kỳ cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn).
A.
2.921.000
. B.
3.387.000
. C.
2.944.000
. D.
7.084.000
.
Câu 134. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Một người gửi
100
triệu
đồng vào ngân hàng với lãi suất
0,5% /
tháng và ông ta rút đều đặn mỗi tháng một triệu đồng kể từ sau ngày
gửi một tháng cho đến khi hết tiền ( tháng cuối cùng có thể không còn đủ một triệu đồng). Hỏi ông ta rút hết
tiền sau bao nhiêu tháng?
A.
139
. B.
140
. C.
100
. D.
138
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Câu 135. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Một bà mẹ Việt Nam anh hùng được
hưởng số tiền là
4
triệu đồng trên
1
tháng (chuyển vào tài khoản ngân hàng của mẹ ở ngân hàng vào đầu
tháng). Từ tháng
1
năm
2019
mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi
1%
trên
1
tháng.
Đến đầu tháng
12
năm
2019
mẹ đi rút toàn số tiền ( gồm số tiền của tháng
12
và số tiền gửi từ tháng
1
). Hỏi
khi đó mẹ lĩnh về bao nhiêu tiền? (kết quả làm tròn theo đơn vị nghìn đồng).
A.
50970000
đồng. B.
50560000
đồng. C.
50670000
đồng. D.
50730000
đồng.
Câu 136. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Bạn H trúng tuyển vào trường Đại học Ngoại
Thương nhưng vì do không đủ tiền nộp học phí nên H quyết định vay ngân hàng trong bốn năm mỗi năm 4
triệu đồng để nộp học phí với lãi suất ưu đãi 3%/năm (theo thể thức lãi suất kép) biết rằng tiền vay mỗi năm
H nhận được từ ngày đầu tiên của năm học và trong suốt bốn năm học H không trả tiền cho ngân hàng. Ngay
sau khi tốt nghiệp Đại học (tròn 4 năm kể từ khi bạn H bắt đầu vay ngân hàng) bạn H thực hiện trả góp hàng
tháng cho ngân hàng số tiền (không đổi và tiền trả vào ngày cuối của tháng) với lãi suất theo cách tính mới là
0,25%/tháng và lãi suất được tính theo dư nợ thực tế, bạn H trả đúng 5 năm thì hết nợ. Tính số tiền hàng tháng
mà bạn H phải trả cho ngân hàng (kết quả làm tròn đến hàng đơn vị).
A. 323.582 (đồng). B. 398.402 (đồng). C. 309.718 (đồng. D. 312.518 (đồng).
Câu 137. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Ông A muốn mua một chiếc ôtô trị giá 1 tỉ
đồng nhưng vì chưa đủ tiền nên chọn mua bằng hình thức trả góp hàng tháng (số tiền trả góp mỗi tháng như
nhau) với lãi suất
12%
/năm và trả trước
500
triệu đồng. Hỏi mỗi tháng ông phải trả số tiền gần nhất với số
tiền nào dưới đây để sau đúng 2 năm, kể từ ngày mua xe, ông trả hết nợ, biết kì trả nợ đầu tiên sau ngày mua
ôtô đúng một tháng và chỉ tính lãi hàng tháng trên số dư nợ thực tế của tháng đó?
A.
23 537 000
đồng B.
24 443 000
đồng C.
22 703 000
đồng D.
23 573 000
đồng
Câu 138. (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Một người vay ngân hàng
50
triệu đồng, mỗi tháng trả ngân hàng
4
triệu đồng và phải trả lãi suất cho số tiền còn nợ là
1,1%
một tháng
theo hình thức lãi kép. Giả sử sau
n
tháng người đó trả hết nợ. Khi đó
n
gần nhất với số nào sau?
A.
14
. B.
13
. C.
16
. D.
15
.
Câu 139. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Ông
A
vay ngân hàng
100
triệu đồng với
lãi suất
1%
/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông
bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau
và sau đúng một năm kể từ ngày vay ông
A
còn nợ ngân hàng tổng số tiền
50
triệu đồng. Biết rằng mỗi tháng
ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tiền mỗi tháng ông ta cần trả cho ngân hàng
gần nhất với số tiền nào dưới đây?
A.
4,95
triệu đồng B.
4, 42
triệu đồng C.
4,5
triệu đồng D.
4,94
triệu đồng
Câu 140. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Một người nhận hợp đồng dài hạn làm
việc cho một công ty với mức lương khởi điểm của mỗi tháng trong ba năm đầu tiên là
6
triệu đồng/ tháng.
Tính từ ngày đầu làm việc, cứ sau đúng ba năm liên tiếp thì tăng lương
10%
so với mức lương một tháng
người đó đang hưởng. Nếu tính theo hợp đồng thì tháng đầu tiên của năm thứ
16
người đó nhận được mức
lương là bao nhiêu?
A.
4
6.1,1
(triệu đồng). B.
6
6.1,1
(triệu đồng). C.
5
6.1,1
(triệu đồng). D.
16
6.1,1
(triệu đồng).
Câu 141. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Một người gửi
50
triệu đồng vào
một ngân hàng với lãi suất
6% /
năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số
tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được
số tiền nhiều hơn 100 triệu đồng bao gồm gốc và lãi?
A.
11
năm. B.
12
năm. C.
13
năm. D.
14
năm.
Câu 142. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Anh
C
đi làm với mức lương khởi điểm là
x
(triệu đồng)/ tháng, và số tiền lương này được nhận vào ngày đầu tháng. Vì làm việc chăm chỉ và có trách
nhiệm nên sau
36
tháng kể từ ngày đi làm, anh
C
được tăng lương thêm
10%
. Mỗi tháng, anh ta giữ lại
20%
số tiền lương để gửi tiết kiệm ngân hàng với kì hạn
1
tháng và lãi suất là
0,5%
/tháng, theo hình thức lãi kép
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
(tức tiền lãi của tháng này được nhập vào vốn để tính lãi cho tháng tiếp theo). Sau
48
tháng kể từ ngày đi
làm, anh
C
nhận được số tiền cả gốc và lãi là
100
triệu đồng. Hỏi mức lương khởi điểm của người đó là bao
nhiêu?
A.
8.991.504
đồng. B.
9.991.504
đồng. C.
8.981.504
đồng. D.
9.881.505
đồng.
Câu 143. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Bạn Nam vừa trúng tuyển đại
học, vì hoàn cảnh gia đình khó khăn nên được ngân hàng cho vay vốn trong 4 năm học đại học, mỗi năm
10
triệu đồng vào đầu năm học để nạp học phí với lãi suất
7,8%
/năm (mỗi lần vay cách nhau đúng 1 năm). Sau
khi tốt nghiệp đại học đúng 1 tháng, hàng tháng Nam phải trả góp cho ngân hàng số tiền là
m
đồng/tháng với
lãi suất
0,7%
/tháng trong vòng
4
năm. Số tiền
m
mỗi tháng Nam cần trả cho ngân hàng gần nhất với số nào
sau đây (ngân hàng tính lãi trên số dư nợ thực tế).
A.
1.468.000
(đồng). B.
1.398.000
(đồng). C.
1.191.000
(đồng). D.
1.027.000
(đồng).
Câu 144. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Một anh sinh viên nhập học đại học vào tháng
8
năm
2014
. Bắt đầu từ tháng
9
năm
2014
, cứ vào ngày mồng một hàng tháng anh vay ngân hàng
3
triệu
đồng với lãi suất cố định
0,8%
/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp
theo (lãi kép). Vào ngày mồng một hàng tháng kể từ tháng
9 / 2016
về sau anh không vay ngân hàng nữa và
anh còn trả được cho ngân hàng
2
triệu đồng do việc làm thêm. Hỏi ngay sau khi kết thức ngày anh ra trường
30 / 6 / 2018
anh còn nợ ngân hàng bao nhiêu tiền (làm tròn đến hàng nghìn đồng)?
A.
49.024.000
đồng B.
47.401.000
đồng C.
47.024.000
đồng D.
45.401.000
đồng
Câu 145. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cường độ ánh sáng đi qua môi trường nước biển giảm
dần theo công thức
0
e
x
I I
, với
0
I
là cường độ ánh sáng lúc ánh sáng bắt đầu đi vào môi trường nước biển
và
x
là độ dày của môi trường đó (
x
tính theo đơn vị mét). Biết rằng môi trường nước biển có hằng số hấp
thụ là
1,4
. Hỏi ở độ sâu 30 mét thì cường độ ánh sáng giảm đi bao nhiêu lần so với cường độ ánh sáng
lúc ánh sáng bắt đầu đi vào nước biển?
A.
21
e
lần. B.
42
e
lần. C.
21
e
lần. D.
42
e
lần
Câu 146. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Một người thả một lá bèo vào
một chậu nước. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong chậu. Biết rằng sau mỗi giờ lượng bèo tăng
gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì bèo phủ kín
1
5
mặt nước trong
chậu (kết quả làm tròn đến 1 chữ số phần thập phân).
A.
9,1
giờ. B.
9,7
giờ. C.
10,9
giờ. D.
11,3
giờ.
Dạng 5. Bài toán cực trị
Câu 147. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho
0, 0
a b
thỏa mãn
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
. Giá trị của
a 2b
bằng
A.
6
B.
27
4
C.
20
3
D.
9
Câu 148. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 2 4
2
xy
xy x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
P x y
A.
min
2 11 3
3
P
B.
min
9 11 19
9
P
C.
min
18 11 29
21
P
D.
min
9 11 19
9
P
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
Câu 149. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Xét các số thực dương
, a b
thỏa mãn
2
1
log 2 3
ab
ab a b
a b
. Tìm giá trị nhỏ nhất
min
P
của
2P a b
.
A.
min
3 10 7
2
P
B.
min
2 10 1
2
P
C.
min
2 10 3
2
P
D.
min
2 10 5
2
P
Câu 150. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hai số thực dương
, x y
thỏa
mãn
ln
ln
ln5
2
2 .5 2
x y
x y
. Tìm giá trị lớn nhất của biểu thức
( 1)ln ( 1) lnP x x y y
.
A.
max
10
P
. B.
max
0
P
. C.
max
1
P
. D.
max
ln 2
P
.
Câu 151. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Cho các số thực
,x y
thỏa mãn
0 , 1
x y
và
3
log 1 1 2 0
1
x y
x y
xy
. Tìm giá trị nhỏ nhất của
2
P x y
.
A.
2
. B.
1
. C.
1
2
. D.
0
.
Câu 152. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho các số thực
,a b
thỏa mãn
1.
a b
Biết
rằng biểu thức
1
log
log
a
ab
a
P
a b
đạt giá trị lớn nhất khi
.
k
b a
Khẳng định nào sau đây là sai
A.
2;3
k . B.
0;1
k
. C.
0;1
k . D.
3
0;
2
k
.
Câu 153. Cho hai số thực
, a b
thỏa mãn
2 2
4 1
log 2 8 1
a b
a b
. Tính
a
P
b
khi biểu thức
4 6 5 S a b
đạt giá trị lớn nhất.
A.
8
5
B.
13
2
C.
13
4
D.
17
44
Câu 154.
Cho các số thực
,x y
thỏa mãn bất đẳng thức
2 2
4 9
log 2 3 1
x y
x y
. Giá trị lớn nhất của biểu thức
3P x y
là
A.
3
2
. B.
2 10
4
. C.
5 10
4
. D.
3 10
4
.
Câu 155. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Cho
a
,
b
là các số dương thỏa mãn
1b
và
. Tìm giá trị nhỏ nhất của biểu thức
log 2log
a
b
b
a
P a
b
.
A.
6
. B.
7
. C.
5
. D.
4
.
Câu 156. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho các số thực
,a b
thay đổi, thỏa mãn
1
, 1.
3
a b
Khi biểu thức
4 2
3
log log 9 81
a b
P b a a
đạt giá trị nhỏ nhất thì tổng
a b
bằng
A.
2
3 9
B.
3
9 2
C.
2 9 2
D.
3 3 2
Câu 157. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho
a
,
b
là hai số thực dương thỏa
mãn
5
4 2 5
log 3 4
a b
a b
a b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
T a b
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
A.
1
2
. B.
1
. C.
3
2
. D.
5
2
.
Câu 158. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho các số thực
, ,ca b
thỏa
mãn
1 3
0 1; 1; 1
8 8
a b c
. Gọi
M
là giá trị nhỏ nhất của biểu thức
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
. Khẳng định nào sau đây đúng?
A.
3 2
M
. B.
2M
. C.
2 3
M . D.
2
M
.
Câu 159. Cho các số thực
, , ,a b m n
sao cho
2 0
m n
và thoả mãn điều kiện:
2 2
2 2
4
2
2
log 9 1 log 3 2
9 .3 .3 ln 2 2 1 81
m n
m n
a b a b
m n
Tìm giá trị nhỏ nhất của biểu thức
2 2
P a m b n
A.
2 5 2
. B.
2
. C.
5 2
. D.
2 5
Câu 160. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Với hai số thực
,a b
bất kì, ta kí hiệu
,
2 3
a b
f x x a x b x x
.Biết rằng luôn tồn tại duy nhất số thực
0
x
để
0
, ,
min
a b a b
x R
f x f x
với mọi số thực
,a b
thỏa mãn
b a
a b
và
0
a b
. Số
0
x
bằng
A.
2 1e
B.
2,5
C.
e
D.
2e
Câu 161. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Cho hai số thực
1, 1
a b
. Biết phương trình
2
1
1
x x
a b
có hai nghiệm phân biệt
1 2
,x x
. Tìm giá trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4
x x
S x x
x x
.
A.
3
3 4
. B.
4
C.
3
3 2
. D.
3
4
.
Câu 162. Cho các số thực
, ,ca b
thỏa mãn
1 3
0 1; 1; 1
8 8
a b c
. Gọi
M
là giá trị nhỏ nhất của biểu
thức
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
. Khẳng định nào sau đây đúng?
A.
3 2
M
. B.
2M
. C.
2 3
M . D.
2
M
.
Câu 163. (CHUYÊN QUỐC HỌC HUẾ NĂM 2018-2019 LẦN 1) Cho
,x y
là các số thực lớn hơn
1
sao
cho
y x
e e
x x y y
y e x e
. Tìm giá trị nhỏ nhất của biểu thức:
log log
x y
P xy x
.
A.
2
2
B.
2 2
C.
1 2 2
2
D.
1 2
2
Câu 164. Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Câu 165. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Xét các số thực dương
x
,
y
thỏa
mãn
2
1 1 1
2 2 2
log log log
x y x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
3P x y
.
A.
min
9
P
B.
min
8
P
C.
min
25 2
4
P
D.
min
17
2
P
Câu 166. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho
,x y
là các số thực dương thỏa
mãn
2019 201 2
2
9 019
log log logx y
x y
. Gọi
min
T
là giá trị nhỏ nhất của biểu thức
2
T x y
. Mệnh đề nào
dưới đây đúng?
A.
min
7;8
T
B.
min
6;7
T
C.
min
5;6
T
D.
min
8;9
T
Dạng 6. Một số bài toán khác
Câu 167. (MĐ 105 BGD&ĐT NĂM 2017) Xét hàm số
2
9
9
t
t
f t
m
với
m
là tham số thực. Gọi
S
là
tập hợp tất cả các giá trị của
m
sao cho
1
f x f y
với mọi số thực
,x y
thỏa mãn
x y
e e x y
.Tìm
số phần tử của
S
.
A.
0
B. Vô số C.
1
D.
2
Câu 168. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số
y f x
liên tục
trên
, có bảng biến thiên như hình vẽ và có đạo hàm cấp hai
0, xf x
.
Gọi
, , ,a b c n
là các số thực và biểu thức:
2
3
e e e 1
2 3
f a f b f c
a b c
P f
. Khẳng định đúng
với mọi
, , ,a b c n
là
A.
0 3
P
. B.
7 3e P 0
. C.
3
P
. D.
7 3e
P
.
Câu 169. (HỌC MÃI NĂM 2018-2019-LẦN 02) Có bao nhiêu giá trị nguyên của
m
để giá trị nhỏ nhất
của hàm số
2
ln 2
y x x m
trên đoạn
2
1;e
đạt giá trị nhỏ nhất
A.
11
. B.
12
. C.
107
. D.
106
.
Câu 170. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Cho hàm số
( ) 2 2
x x
f x
.
Gọi
0
m
là số lớn nhất trong các số nguyên
m
thỏa mãn
12
( ) (2 2 ) 0
f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019
m
B.
0
1009;1513
m
C.
0
505;1009
m
D.
0
1;505
m
Câu 171. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Tìm tất cả các giá trị của tham số
m
đề đồ thị
hàm số
2
2 2
log 2log 2 1
y m x x m
cắt trục hoành tại một điểm duy nhất có hoành độ thuộc khoảng
1;

.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
A.
1 1
;
2 2
m
. B.
1 1
;0
2 2
m
.
C.
1 1
;
2 2
m
. D.
1 1
;0
2 2
m
.
PHẦN B. ĐÁP ÁN THAM KHẢO
Dạng 1. Tìm tập xác định
Dạng 1.1 Không chứa tham số
Câu 1. Chọn A
Tập xác định của là tập các số
x
để
3
3
0 3 2 0
2
2
x
x
x x
x
x
Suy ra
 
; 2 3;D
.
Câu 2. Chọn C
2
2
log 2 3
y x x
. Hàm số xác định khi
2
2 3 0
x x
1
x
hoặc
3
x
Vậy tập xác định:
; 1 3;D
 
Câu 3. Chọn B
Điều kiện
2
1
4 3 0
3
x
x x
x
.
Câu 4. Chọn D
Hàm số xác định khi:
2
3 0 0; 3
x x x
Vậy
0; 3
D
Câu 5. Chọn B
Hàm số xác định khi và chỉ khi
2
5 6 0 2 3.
x x x
Vậy tập xác định của hàm số là
2;3 .
D
Câu 6. Chọn A
Điều kiện:
1
0 6 0 6
6
x x
x
. Do đó tập xác định của hàm số là
;6
.
Câu 7. Hàm số
2
2
log 3 2
y x x
xác định khi:
2
3 2 0 3 1x x x
.
Vậy tập xác định của hàm số đã cho là:
3;1
D
.
Câu 8. Hàm số xác định khi
2
1
2 3 0
3
x
x x
x
.
Vậy
; 1 3;D

.
Câu 9. Chọn D
Điều kiện xác định:
x x
D
x x
0 0
0;3
3 0 3
Câu 10. ĐKXĐ:
ln 2 0
2 1
2 1 3
2 0
2 0
x
x
x x
x
x
.
TXĐ:
3;D

.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
Câu 11. Điều kiện có nghĩa của hàm số là
2
2 x 2
4 x 0
3
x
2x 3 0
2
Vậy tập xác định của hàm số là
3 3
D 2; ;2
2 2
Câu 12. + Điều kiện xác định:
2
2 0
2
3 3
9 0
x
x
x
x
+ Vậy tập xác định của hàm số là:
3;3 \ 2 .
D
Dạng 2. Chứa tham số
Câu 13. Chọn D
Để hàm số có tâp xác định
khi và chỉ khi
2
2 1 0,x x m x
.
0
2
1 1. 1 0
m
0m
.
Câu 14. Chọn C
Hàm số có tâp xác định
khi và chỉ khi
2
1 0( )
2 1 0,
1 1 0 0
a ld
x x m x
m m
.
Câu 15. Chọn C
Yêu cầu bài toán
2
1 0
x mx
,
x
2
4 0
m
2 2
m
.
Câu 16. Cách 1
Điêu kiện:
0
x
.
Hàm số xác định khi:
2
3 3
log 4log 3 0
m x x m
2
3 3
log 1 4log 3m x x
3
2
3
4log 3
log 1
x
m
x
,
0;x

.
Để hàm số xác định trên
0;
thì phương trình
3
2
3
4log 3
log 1
x
m
x
vô nghiệm
0;x

Xét hàm số
3
2
3
4log 3
log 1
x
y
x
.
Đặt
3
log
x t
khi đó ta có
2
4 3
1
t
y
t
,
2
2
2
4 6 4
1
t t
y
t
0
y
1
2
2
t
t
.
Ta có BBT:
t

1
2
2
y
0
0
y
1
0
0
4
Để hàm số xác định trên
0;
thì
; 4 1;m

.
Cách 2:
Đê ham sô xac đinh trên khoang
0;

thi phương trinh
2
3 3
.log 4log 3 0
m x x m
vô nghiệm.
TH1:
0
m
thì PT trở thành
3
4log 3 0
x
3
3
log
4
x
3
4
3
x
.
Vậy
0
m
không thỏa mãn.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
TH2:
0
m
thì để PT vô nghiệm
2
4 4 3 0
m m
2
4 12 16 0
m m
4
1
m
m
.
Để hàm số xác định trên
0;

thì
; 4 1;m
 
.
Câu 17. Hàm số xác định với mọi
1; 2
x
khi
2
2 1 0, 1;2
x mx m x
.
2
2 1 0, 1; 2
f x x mx m x
.
0
f x
có
2
nghiệm thỏa mãn
1 2
1 2
x x
.
1 0
3 0
3
4 3 0
4
2 0
f
m
m
m
f
.
Câu 18. Hàm số
2
log( 4 1)
y x x m
có tập xác định là
khi và chỉ khi
2
4 1 0
x x m
x
Câu 19. Hàm số
2
ln 2 1
y x x m
có tập xác định là
khi và chỉ khi:
2
2 1 0 x x m x
' 0 1 1 0 0
m m
.
Kết hợp với điều kiện
m
nguyên thuộc
2018; 2018
ta có 2018 giá trị của
m
.
Câu 20.
2
log 2 4
y x mx
Điều kiện xác định của hàm số trên:
2
2 4 0
x mx
.
Để tập xác định của hàm số là
thì
2
1 0,
0
2 2
0
4 0
m
a
m
m
.
Vậy đáp án đúng là đáp án D.
Câu 21. Chọn A
Điều kiện xác định
2 0 2 (1)
mx m mx m
Trường hợp 1.
0
m
.
1 2 0
(luôn đúng với
1
;
2
x

).
Trường hợp 2.
0
m
.
2
1
m
x
m
Để hàm số
log 2
y mx m
xác định trên
1
;
2
thì
2 1
0 4.
2
m
m
m
Vì
m
nên
1;2;3 .
m
Trường hợp 3.
0
m
.
2
1
m
x
m
.
Suy ra tập xác định của hàm số
log 2
y mx m
là
2
; .
m
D
m

Do đó
1
;
2
D

suy ra không có giá trị
0
m
nào thỏa yêu cầu bài toán.
Từ
3
trường hợp trên ta được
0;1;2;3 .
m
Câu 22. Chọn B
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
Hàm số đã cho xác định
0;x

2
2018 0, 0;
2
x
x
x m x
2
2018 , 0;
2
x
x
x m x

.
YCBT
0;
min
x
m f x

.
Đặt
2
2018 , 0;
2
x
x
f x x x

2018 ln 2018 1
x
f x x
2
2018 ln 2018 1 0, 0;
x
f x x

Khi đó
f x
đồng biến trên
0;x

và
0 ln 2018 1 0
f
Suy ra
f x
đồng biến trên
0;x

và
0 1
f
Vậy
1
m
thì thỏa YCBT.
Câu 23. Chọn D
Điều kiện xác định:
4 2 0
x x
m
Hàm số đã cho có tập xác định là 4 2 0, 4 2 ,
x x x x
m x m x
(*)
Đặt
2 , 0
x
t t
Khi đó (*) trở thành
2
, 0
m t t t
0;
max ( )m f t

với
2
( ) , 0f t t t t
Ta có:
' 2 1f t t
,
1
' 0
2
f t t
Bảng biến thiên của hàm số
2
( ) , 0f t t t t
:
t
0
1
2

'f t
+ 0 -
f t
0
1
4

Từ BBT ta thấy
0;
1
max ( )
4
f t

đạt được khi
1
2
t
Vậy
0;
1
max
4
m f t m

Câu 24. Xét hàm số
2 2
2018
3 5
log 2 4 5
x
y
x x m m
ĐKXĐ:
2 2
2 2
2 2
2 2
2018
2 4 5 0
2 4 5 0
log 2 4 5 0
2 4 5 1
x x m m
x x m m
x x m m
x x m m
.
Nên điều kiện để hàm số xác định với mọi
x
là
2 2
2 2
2 4 5 0
2 4 4 0
x x m m
x x m m
với
x
.
Điều này xảy ra khi và chỉ khi :
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
2
1
2
2
1 4 5 0
1 4 4 0
m m
m m
2
2
4 4 0
4 3 0
m m
m m
2
1
4 3 0
3
m
m m
m
.
Vậy
;1 3;m
 
.
Câu 25. Chọn D
Điều kiện
2
2017 1 0, 0;
2
x
x
x m x
2
2017 1, 0;
2
x
x
x m x
.
Xét hàm số
2
2017 , 0;
2
x
x
f x x x

liên tục có
2017 ln 2017 1 , 0;
x
f x x x

2
2017 ln 2017 1 0, 0;
x
f x x

Vậy hàm số
f x
đồng biến trên
0;

suy ra
0 ln 2017 1 0, 0;f x f x

Vậy hàm số
y f x
đồng biến trên
0;

suy ra
0;
min 0 1
f x f

.
Mặt khác
0;
1 min 0 1 2
m f x f m

.
Vậy có vô số giá trị nguyên
m
thỏa mãn.
Câu 26. Hàm số xác định
2 1 0 2 1
0
m x x m
x m x m
;2 1
D m m
.
Hàm số đã cho xác định trên khoảng
2;3
nên
2;3 ;2 1
D m m
2 3 2 1
m m
2
1 2
2 1 3
m
m
m
.
Vì
m
nguyên dương nên
1;2
m
.
Dạng 2. Tìm đạo hàm
Câu 27. Chọn B
Áp dụng công thức
1
log
ln
a
x
x a
, ta được
1
ln10
y
x
.
Câu 28. Chọn B
Ta có
2 2
2
' ( )'.2 .ln 2 (2 1).2 .ln 2
x x x x
y x x x
.
Câu 29. Chọn C
Ta có:
. .ln
u u
a u a a
nên
2 2
3 ' 2 1 .3 .ln3
x x x x
x
.
Câu 30. Chọn C
Ta có:
13 ln13
x
y
.
Câu 31. Chọn A
Ta có
2
2 1
2
log 2 1
2 1 ln 2 2 1 ln 2
x
y x
x x
.
Câu 32. Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
Ta có:
2 2
1 .4 1 . 4
4 1 .4 .ln 4
'
4 4
x x
x x
x x
x x
x
y
2
2
4 . 1 .ln 4 ln 4 1 2 1 ln 2
1 .2ln 2 2ln 2
4 2
4
x
x x
x
x x
x
.
Câu 33. Chọn D
2
2 2
2x '
2x 2
'
2x ln 2 2x ln 2
x
f x
x x
Câu 34. Chọn A
2 2
3 3
' 2 ' 2 3 2 ln 2
x x x x
y x
.
Câu 35. Chọn D
Ta có:
2 2
3 3
3 2 3 .3 .ln 3
x x x x
y x
.
Câu 36. Chọn C
Ta có:
1 1
1
ln 1 1
1 1
2 1 1 1
x
y x
x
x x
.
Câu 37.
Lơi giai
Chọn A
Cách 1.
2 2 2
1
. ln
ln . .ln
1 ln
x x
x x x x
x
x
y
x x x
2 2
4
1 ln . 1 lnx x x x
y
x
2
4
1
. 2 1 lnx x x
x
x
4 3 3
2 1 ln 1 2 1 ln
3 2ln
x x x x
x
x x x
Suy ra:
2 3
1 ln 3 2ln
2 2.
x x
y xy x
x x
2 2
2 2ln 3 2ln 1
x x
x x
.
Cách 2. Ta có
lnxy x
, lấy đạo hàm hai vế, ta được
1
y xy
x
.
Tiếp tục lấy đạo hàm hai vế của biểu thức trên, ta được
2
1
y y xy
x
, hay
2
1
2y xy
x
.
Câu 38. Chọn B
1 2 1 2
' . 1 2 ' 2.
x x
y e x e
Câu 39. Chọn B
2
2 2
1 '
2 1
'
1 ln 3 1 ln 3
x x
x
y
x x x x
Câu 40. Chọn B
2 2 2
'
'
2
. 2 1
x x x x x x
e e x x x e
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Câu 41. Ta có:
2
2
2
2 2
1
2
ln 1
1 1
x
x
x
x x
e
e
y e
e e
.
Câu 43. Ta có
2
1 .2 2 . 1
2
x x
x
x x
y
2
1.2 2 .ln 2. 1
2
x x
x
x
ln 2. 1 1
2
x
x
Câu 44. Ta có
2
2 2 2 2 2
1
2 2
1 ln9 1 ln3 1 2ln3 1 ln3
x
x x x
y
x x x x
.
Câu 45. Chọn D
' .sin 2 .sin 2 . sin 2 .sin 2 2 .cos 2 sin 2 2cos 2
x x x x x x
y e x e x e x e x e x e x x
Câu 46. Chọn A
2
2
1 4 1 4
4
1 2 1 ln 2
2
x x
x
x
x
y
x
x
Câu 47. Chọn A
Ta có:
2
1 2
x x
f x x e
.
2 2 2
2
2 1 2 1 2 1 4 4
x x x x x x
f x e x x e x x e
2
2 2
0 1 4 4 0 1 4 4 0
x x
f x x x e x x
khi đó
1 2
1
4
c
x x
a
.
Câu 48. Chọn D
Ta có
cos ln s ln
y x x in x
cos ln s ln s ln cos ln 2cos lny x in x in x x x
2
sin lny x
x
Từ đó kiểm tra thấy đáp án
D
đúng vì :
2
2 2 sin ln 2 cos ln 2 cos ln sin ln 0
x y xy y y x x x x x x x
.
Câu 49.
2019
2019
2019
log , 0
log
log , 0
x khi x
x
x hi x
y
k
1
, 0
ln 2019
1
, 0
ln 2019
khi x
x
khi x
x
y
1
ln 2019
y
x
.
Câu 50.
2
1 1 1 1
1 ln 1 ln 1
1 ln
y
y x x x x
x x y y y x
.
Câu 51.
Ta có
x
2 1 1 1
2 ln 2 ln ln 2 ln
e e
x
x
x
y x x
x x
.
Câu 52. Điều kiện xác định của hàm số đã cho là:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
2017
2017
2017
2018 2017
2018 2017
2018 2017
2019 2018 2017 2018 2017
0
0
0
log 0
log 0
log 0
log log 0
log log 0
log log 1
log log log 0 log log 1
x
x
x
x
x
x
x
x
x
x x
2018
2017
2018
2017
2017
0
0
0
log 0 2017
log 2018
2017
log 2018
x
x
x
x x
x
x
x
.
Câu 53. Ta có
2
2 2
2
2 2
( )
2 ln 2 2 ln2
x x
x
f x
x x x x
Câu 54. Áp dụng các công thức
ln
ln
u
u
u
và
2
u
u
u
ta có
1
( )
2 ln ln(ln )
f x
x x x
.
Câu 55. Chọn B
Ta có
ln 2018 ln
1
x
f x
x
1 1 1
1 1
f x
x x x x
Do đó
1 1 1 1 1 1
...
1 2 2 3 2017 2018
S
1 2017
1
2018 2018
.
Câu 56. Ta có:
2018 1 2018
ln . .
2018
1 1
1
x x
f x
x
x x
x
2
1 2018 1
.
2018 . 1
1
x
x x x
x
Vậy
1 2 ... 2018
S f f f
1 1 1
...
1.2 2.3 2018.2019
1 1 1 1 1 1
...
1 2 2 3 2018 2019
1 2018
1
2019 2019
.
Dạng 3. Khảo sát hàm số mũ, logarit
Câu 57. Chọn B
Tập xác định
0;D
Ta có
ln ln 1f x x x f x g x x
.
Ta có
1 1
g
nên đồ thị hàm số đi qua điểm
1;1
. Loại hai đáp án B và D
Và
0 0
lim lim ln 1
x x
g x x
. Đặt
1
t
x
. Khi
0x
thì
t
.
Do đó
0
1
lim lim ln 1 lim ln 1
t t
x
g x t
t
 

nên loại đáp án A
Câu 58. Chọn D
Ta có:
2
2
1
x
y m
x
.
Hàm số
2
ln 1 1y x mx
đồng biến trên khoảng
;
0, ;y x
 
.
2
2
( ) , ;
1
x
g x m x
x
 
. Ta có
2
2
2
2 2
( ) 0 1
1
x
g x x
x
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
Bảng biến thiên:
Dựa vào bảng biến thiên ta có:
2
2
( ) , ;
1
x
g x m x
x

1m
Câu 59. Chọn D
Đường thẳng
1x
đồ thị các hàm số , ,
x x x
y a y b y c tại các điểm có tung độ lần lượt là
, ,y a y b y c
như hình vẽ:
Từ đồ thị kết luận
a c b
Câu 60.
Chọn A
Theo hình ta thấy hàm
x
y a
là hàm đồng biến nên
1a
, còn hàm
x
y b
là hàm nghịch biến nên
0 1b
. Suy ra
0 1 .b a
Câu 61. Chọn C
Hàm số mũ
x
y a với
0 1a
nghịch biến trên
.
Ta có
e
0 1
4
nên hàm số
e
4
x
y
nghịch biến trên
.
Câu 62. Chọn C
Hàm số
ln( )y x
TXĐ
;0D 
Cơ số
1a e
do đó hàm số đồng biết trên
;0

Câu 63. Chọn C
Hàm số
x
y a đồng biến trên
khi và chỉ khi
1a
.
Thấy các số
1 2
; ; 0,5
π 3
nhỏ hơn
1
, còn 3 lớn hơn 1 nên chọn
.C
Câu 64. Chọn C
Hàm số
2
logy x có tập xác định là
0;D =
.
Câu 65. Chọn D
2
y 0,01(0,1)
x
x
,
2
40642(2016 56)
x x
y
Ta có các cơ số
2015
2016
;
3
2016 2
;
0,01
đều nhỏ hơn
1
nên các hàm số ở A, B, C nghịch biến trên
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
Cơ số
4064256 1
nên hàm số
2
(2016)
x
y đồng biến trên
.
Câu 66. Đồ thị hàm số đi qua điểm
; 1
e
và nằm cả trên và dưới trục hoành nên chỉ có hàm số
lny x
thoả mãn.
Câu 67. Hàm số
x
f x a
đồng biến trên
nếu
1
a
và nghịch biến trên
nếu
0 1a
.
Vậy hàm số
3
x
f x
là hàm số đồng biến trên
.
Câu 68. Ta có tập xác định của hàm số
5
log
y x
là
0D ;

. Do đó đáp án B sai.
Câu 69. Chọn B
Xét hàm số
x
y a
đi qua
0;1
suy ra đồ thị hàm số
1
là đồ thị của hàm nghịch biến nên
0 1a
.
Xét đồ thị hàm số
log
b
y x
đi qua
1;0
suy ra đồ thị của hàm số
2
là đồ thị của hàm đồng biến suy ra
1b
.
Vậy
0 1
a b
.
Câu 70.
+)
lny x
; TXĐ:
0;D

1e
suy ra hàm số
lny x
đồng biến trên
D
.
+)
2018
1
2019
log
y x
; TXĐ:
0;D

2018 2018
0 1 0 1 1
2019 2019
suy ra hàm số
2018
1
2019
log
y x
là hàm nghịch biến
D
.
+)
logy x
; TXĐ:
0;D

1
suy ra hàm số
logy x
đồng biến trên
D
.
+)
4 3
log
y x
; TXĐ:
0;D

4 3 1
suy ra hàm số
4 3
log
y x
đồng biến trên
D
.
Câu 71. Với
1x
lny x
ln1
0
.
Với
2
x
lny x
ln 2
.
Với
2x e
lny x
ln2e
ln 2 1
.
Với
0
x
, hàm số không xác định.
Câu 72. Ta thấy hàm số
2
3
x
y
là hàm số mũ có có tập xác định là
cơ số
2
1
3
a
nên nghịch biến
trên tập xác định của nó.
Ngoài ra ta có thể loại các đáp án khác bằng cách giải thích cụ thể đặc điểm các hàm đó như sau:
Đáp án A loại vì: Hàm số
2
1
2
y
là hàm hằng nên không nghịch biến củng không đồng biến.
Đáp án B loại vì: Hàm số
logy x
là hàm số logarit có tập xác định là
(0; )
D
có cơ số
10 1
a
nên
luôn đồng biến trên tập xác định của nó.
Đáp án C loại vì: hàm số
2
x
y
là hàm số mũ có tập xác định là
có cơ số
2 1
a
Câu 73. Hàm số
2
logy x
đồng biến trên khoảng
0;

.
Câu 74. Chọn A.
Hàm số
log
a
y x
đồng biến trên khoảng
(0; )
⇔
1
a
⇒ Chọn A
Câu 75. Chọn B
Đồ thị hàm số
x
y a
và đồ thị hàm số
log
a
y x
đối xứng với nhau qua đường phân giác góc
phần tư thứ nhất (
y x
), suy ra chọn B.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Câu 76. Ta có
0;lnA a
,
0;lnB b
,
0;lnC c
và
B
là trung điểm của
AC
nên
2 2
ln ln 2ln ln ln
a c b ac b ac b
.
Vậy
2
ac b
.
Câu 77. Đồ thị hàm số đi qua điểm
0;0
nên loại đáp án A và B.
Đồ thị hàm số đi qua điểm
1;1
nên loại D.
Vậy đáp án C thỏa mãn.
Câu 78. Vì
2
1
e
nên
2
x
y
e
nghịch biến trên
R
.
Câu 79. Xét hàm số
4
logy x
có tập xác định:
0;D

.
Nhận thấy cơ số
1
4
nên
4
logy x
nghịch biến trên tập xác định.
Câu 80. Chọn B
Ta có:
3 ln 3
' 9 3 9
ln3
x
x
y
' 0 3 9 2
x
y x
Câu 81. Chọn C
5 1
2018; 2019
M
thuộc đồ thị hàm số
x
y a
nên ta có:
2018 5 1 0
5
1
2019 1 0 1
2019
a a a
5 1
2018; 2019
M
thuộc đồ thị hàm số
log
b
y x
nên ta có:
5
1
5 1 0
2019
log 2018 2019 2018 1 1
b
b b b
Vậy
0 1, 1.
a b
Câu 82. Chọn B
TXĐ
0;D

.
1
f x
x
Xét phương trình hoành độ giao điểm:
ln 0 1 1;0
x x A
Vậy phương trình tiếp tuyến của đồ thị hàm số
L
tại điểm
A
là:
(1) 1 0 1y f x x
, chọn B.
Câu 83. Tập xác định là
.
3
1 3
x
y e x
.
Vì
3
0,
x
e x
nên dấu của
y
là dấu của nhị thức
1 3x
, suy ra
y
đổi dấu từ dương sang âm khi
x
đi
qua
1
3
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
Do đó,
1
3
x
là điểm cực đại của hàm số.
Câu 84. Hàm số
2
3
log 2y x x
có tập xác định
;0 2;D

.
Ta có
2
2 2
2 ln3
x
y
x x
. Khi đó
0
y
1x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số
y
nghịch biến trên
;0

.
Câu 85. Dựa vào đồ thị ta thấy khi
0
x y

do đó đồ thị hàm số
x
y a
có
1
a
. Nên ta loại đáp
án A và. D.
Ở đồ thị hàm số
log
y
b
y x x b
ta thấy khi
x y  
do đó ta có
0 1b
.
Câu 86.
Hàm số có đồ thị (C
2
) là hàm số nghịch biến, do đó loại đáp án A,D. Cho
1x
suy ra
1 1
5
7
Do đó đồ thị hàm số (C
2
) là
1
.
5
x
y
Câu 87. Tập xác định:
D
.
Ta có:
2
2 2
2 2
1 1
x mx x m
y m
x x
Để hàm số đồng biến trên
điều kiện là
2
2
0
0; 2 0; ; 1
1 0
m
y x mx x m x m
m

.
Câu 88. Dựa vào đồ thị các hàm số
, , log
x x
c
y a y b y x
,ta có:
Hàm số
x
y a
nghịch biến trên
nên ta có:
0 1a
. (1)
Các hàm số
, log
x
c
y b y x
đồng biến trên tập xác định của nó nên ta có:
1
1
b
c
.(2)
Từ (1),(2)
a b
a c
. Do đó loại hai phương án B, D.
Nếu
b c
thì ta có đồ thị hai hàm số
, log
x
b
y b y x
đối xứng nhau qua đường thẳng
y x
.
Tuy nhiên nhìn hình dáng hai đồ thị hàm số
, log
x
b
y b y x
không có tính chất đối xứng nhau qua đường
thẳng
y x
. Do đó phương án đúng là A.
Cách khác:
Hàm số
x
y a
nghịch biến trên
nên ta có:
0 1a
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
Các hàm số
, log
x
c
y b y x
đồng biến biến trên tập xác định của nó nên ta có:
1
1
b
c
.
Xét đồ thị hàm số log
c
y x , ta có: log 2 1 2
c
c .
Xét đồ thị hàm số
x
y b , ta có:
1
2 2b b
.
Do đó:
0 a c b
.
Câu 89. Chọn C
Xét hàm số
x
y b : Dựa vào hình dáng đồ thị ta thấy
lim 0
x
x
b

, do đó
0 1b
.
Xét hàm số
x
y a : Dựa vào hình dáng đồ thị ta thấy
lim


x
x
a
, do đó
1a
.
Tư đo suy ra:
a b
. Loai đap an A, D.
Xét tại
1x
đồ thị hàm số
x
y c có tung độ lớn hơn tung độ của đồ thị hàm số
x
y a nên
c a
. Vậy
1c a b
.
Câu 90. Chọn D
Theo hình dạng của đồ thị ta có
, 1
0 1
a b
c
.
Vẽ đường thẳng
1y
cắt đồ thị hai hàm số
log , log
a b
y x y x
lần lượt tại 2 điểm
( ;1), ( ;1)M a N b
. Ta
thấy điểm
N
bên phải điểm
M
nên
b a
.
Vậy
c a b
.
Câu 91. Chọn A
Xét
ln x
y f x
x
. Hàm số
y f x
liên tục trên đoạn
2;3
/
2
1 ln x
y
x
;
/
0y
2
1 ln
0
x
x
2;3x e
Có
ln2
2 0,3466
2
f ;
1
0,3679f e
e
;
ln3
3 0,366
3
f ,
Suy ra
2;3
ln2
2
x
Min f x
.
Vậy giá trị nhỏ nhất của hàm số
ln x
y
x
trên đoạn
2;3
bằng
ln 2
2
.
Câu 92. Do log
b
y x và log
c
y x là hai hàm đồng biến nên , 1b c .
Do log
a
y x nghịch biến nên
0 1a
. Vậy
a
bé nhất.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
Mặt khác: Lấy
y m
, khi đó tồn tại
1 2
, 0
x x
để
1
1
2
2
log
log
m
b
m
c
x m
b x
x m
c x
.
Dễ thấy
1 2
m m
x x b c b c
. Vậy
a b c
.
Câu 93. Chọn C
Điều kiện:
2
ln 2 e
m
x m x
. Có
2
6 2
ln 2
m
y
x x m
Hàm số đồng biến trên
1; e
0 1; e
y x
2
6 2
0 1; e
ln 2
m
x
x x m
2
2
2
6 2 0
6 2 0
e 1
e 1; e
e e
m
m
m
m
m
3
0
0
1
3
1
2
2
m
m
m
m
m
.
Do
m
nguyên dương nên
1; 2
m
. Vậy tập
S
có
2
phần tử.
Câu 94. Chọn D
Đặt
2
logt x
.
Ta có
4; 2;x t
.
Hàm số được viết lại
2
1
mt
y
t m
(1).
Vì
2
logt x
đồng biến trên
0;

nên yêu cầu bài toán
(1) nghịch biến trên
2;

2
1 2 0
2
1
1 2
1
m
m m
m
m
m
m
.
Câu 95. Tập xác định của hàm số
f x
:
0;D

Ta có
1 1
1
x
f x
x x
0 1f x x
Bảng xét dấu
f x
:
Câu 96. Ta có
2018
1
logy
x
thì
2
1 1
0
ln 2018
y
x x
hàm số nghịch biến ta vẽ được đồ thị hàm số
1
C
như hình
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
Do
2
C
đối xứng với
1
C
qua
O
nên có dạng như hình dưới
Từ đó đồ thị hàm số
y f x
là
Dựa vào đồ thị trên ta có hàm số
y f x
nghịch biến trên khoảng
; 1
Câu 97. Đặt
lnt x
.
Khi đó hàm số
ln 6
ln 3
x
y
x m
đồng biến trên khoảng
6
1;e
thì hàm số
6
3
t
y t
t m
đồng biến trên khoảng
0;6
.
Ta có
2
3 6
3
m
y t
t m
Để hàm số
y t
đồng biến trên khoảng
0;6
thì
2019;2019
2
3 6 0
0 2019; 2018;... 1;0
0
3 0;6
2
m
m
m
m
m m
m
m
m

.
Vậy có tất cả:
2020
số nguyên
m
thoả mãn yêu cầu bài toán.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
Câu 98. Ta có:
1
' ' ln 2
x
y f x x m
x
Yêu cầu bài toán
1 1
ln 3 0 ln 3
f x x m x m
x x
;
2
0; x e
.
Xét hàm số:
1
ln 3 g x x
x
với
2
0;x e
.
Ta có:
2
1 1
' 0 1 g x x
x x
.
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra
4g x
với mọi
2
0;x e
.
Từ đó suy ra
2018 4 m
.
Vậy có
2023
giá trị của
m
thỏa mãn.
Câu 99. Ta có
log loge log ln10 log1 0
.
Mặt khác
2 2
ln 1 sin 6 ln 1 sin 6f x f x a x x b x a x x b x
2 2
ln 1 1 sin sin 12a x x x x b x b x
ln1 12 12a
x
.
Khi đó suy ra
log loge log ln10 12f f
log ln10 10f
.
Câu 100.
Kẻ đường thẳng
( ) : 1d y
. Hoành độ giao điểm của
( )d
với các đồ thị hàm số log
a
y x , log
b
y x ,
log
c
y x lần lượt là
, ,a b c
. Dựa vào đồ thị hàm số ta thấy
a c b
.
Câu 101.
Lờigiải
Chọn B
Gọi
C
là đồ thị hàm số
x
y a
;
1
C
là đồ thị hàm số
y f x
.
1
1
2 log ;
2018
a M
M y C
1
2 log
2018
M a
y f
.
Gọi
N
đối xứng với
M
qua
1;1I
1
log ;2
2018
a M
N y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
Do đồ thị
1
C
đối xứng
C
qua
1;1
I
nên
1
log ;2
2018
a M
N y C
.
N C
1
log
2018
2
a
M
y a
log 2018
2
a
M
y a
2 2018
M
y
2016
M
y
.
Vậy
1
2 log 2016
2018
a
f
.
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…)
Câu 102.
Lơi giai
Chọn C
Ta có
6
0
0,4
1 100.000.000 1 102.424.128
100
n
n
A A r
Câu 103. Chọn B
Gọi
x
số tiền gửi ban đầu.
Theo giả thiết
6,1 6,1
2 1 2 1
100 100
N N
x x
1,061
6,1
2 1 log 2 11,7
100
N
N
Vậy sau ít nhất 12 năm người đó thu được số tiền thỏa yêu cầu.
Câu 104. Chọn C
Cách 1: Công thức: Vay số tiền
A
lãi suất
%r
/ tháng. Hỏi trả số tiền
a
là bao nhiêu để
n
tháng hết nợ
3
3
. . 1 100.0, 01. 1 0,01
1 1 1 0, 01 1
n
n
Ar r
a
r
.
Cách 2: Theo đề ta có: ông A trả hết tiền sau 3 tháng vậy ông A hoàn nợ 3 lần
Với lãi suất 12%/năm suy ra lãi suất một tháng là 1%
Hoàn nợ lần 1:
-Tổng tiền cần trả (gốc và lãi) là :
100.0, 01 100 100.1, 01
(triệu đồng)
- Số tiền dư :
100.1, 01 m
(triệu đồng)
Hoàn nợ lần 2:
- Tổng tiền cần trả (gốc và lãi) là :
2
100.1,01 .0,01 100.1,01 100.1,01 .1,01 100. 1,
01 1,01.m m m m
(triệu đồng)
- Số tiền dư:
2
100. 1,01 1,01.
m m
(triệu đồng)
Hoàn nợ lần 3:
- Tổng tiền cần trả (gốc và lãi) là :
2 3 2
100. 1,01 1,01. .1,01 100. 1,01 1,01 1,01m m m m
(triệu đồng)
- Số tiền dư:
3 2
100. 1,01 1,01 1,01
m m m
(triệu đồng)
3
3 2
2
100. 1,01
100. 1,01 1,01 1,01 0
1,01 1,01 1
m m m m
3 3
3
2
100. 1,01 . 1,01 1 1,01
1,01 1
1,01 1,01 1 . 1,01 1
m
(triệu đồng).
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
Câu 105. Chọn B
Ta xây dựng bài toán tổng quát như sau
Gọi số tiền người đó vay ngâng hàng là
0
V
triệu đồng
Số tiền hàng tháng người đó phải trả là
a
triệu đồng
Lãi suất là
r
%/ tháng
Vậy số tiền nợ ngân hàng sau tháng thứ nhất là
0
1 0,0V r
Số tiền người đó còn nợ ngân hàng sau khi trả tiền tháng 1 là
1 0
1 0,0
T V r a
Số tiền người đó còn nợ ngân hàng sau khi trả tiền tháng 2 là
2 1
2
1 0,0
1 0,0 1 0,0
1 0,0 1 0,0
o
o
T T r a
V r a r a
V r a r a
Số tiền người đó còn nợ ngâng hàng sau tháng thứ n là
1
1 0,0 1 0, 0 ... 1 0,0
n n
n o
T V r a r a r a
Vì sau n tháng thì trả hết tiền nên ta có
1
1
0 1 0,0 1 0,0 ... 1 0,0 0
1 0,0 1 0,0 ... 1 0,0 1
1 0,0 1
1 0,0
1 0,0 1
.0,0 . 1 0,0
1 0,0 1
n n
n o
n n
o
n
n
o
n
o
n
T V r a r a r a
V r a r r
r
V r a
r
V r r
a
r
Áp dụng
60
60
100.0,01 1,01
2,224444768
1,01 1
a
Câu 106. Chọn C
Áp dụng công thức
0
1
n
n
A A r
với
n
là số kỳ hạn,
0
A
là số tiền ban đầu,
n
A
là số tiền có được sau
n
kỳ hạn,
r
là lãi suất.
Suy ra
9
9
9
9 0
0
1 1 0,7%
A
A A r r
A
.
Câu 107. Chọn B
Sau
n
tháng, người đó lĩnh được số tiền là:
100. 1 0,6%
n
(triệu đồng).
Sau
n
tháng, người đó được lĩnh số tiền không ít hơn
110
triệu đồng (cả vốn ban đầu và lãi)
1 0,6%
11
100. 1 0,6% 110 log 15,9
10
n
n
.
Câu 108. Chọn A
Ta có:
2% 0,02
r
Số tiền
100
triệu đồng gửi lần đầu thì sau 1 năm (4 quý) nhận được cả vốn lẫn lãi là:
4
1
100 1 0,02 108,24
T
triệu đồng
Số tiền
100
triệu đồng gửi lần thứ hai thì sau 6 tháng (2 quý) nhận được cả vốn lẫn lãi là:
2
2
100 1 0,02 104,04
T
triệu đồng
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
Vậy tổng số tiền nhận được là:
1 2
212,28
T T T
triệu đồng.
Câu 109. Chọn B
Gửi ngân hàng số tiền là A đồng với lãi suất
%r
./tháng. Mỗi tháng vào ngày ngân hàng tính lãi, rút ra số
tiền là X đồng. Sô tiền còn lại sau n tháng đươc tính theo công thức:
12
1
12
2
1 1 1,005 1
1 800 1,005 6. 775.3288753
0
1200 400.(1,0
%
5
,5
0 )
n
n
n
r
S A r X
r
Câu 111. Chọn B
Giả sử anh An vay số tiền là
A
với lãi suất
r
trên tháng và trả nợ cho ngân hàng số tiền cố định là x. Anh An
sau các tháng còn nợ ngân hàng với số tiền là:
Tháng thứ
1
:
1
A r x
Tháng thứ 2:
2
2 2
1 1
1 1 1 1 1 1 .
r
A r x r x A r r x A r x
r
Tháng thứ
3
:
3
3
1 1
1 .
r
A r x
r
…
Tháng thứ
n
:
1 1
1 .
n
n
r
A r x
r
Áp dụng công thức ta có:
500; 0,0085; 10
A r x
và sau
n
tháng trả hết nợ ta có:
1 0,0085 1
500. 1 0,0085 10. 0
0,0085
n
n
1,0085
1,0085 1
40 40
50. 1,0085 1,0085 log 65,4
0,0085 23 23
n
n n
n
Câu 112. Chọn A
Số tiền ông An tích lũy được gồm cả vốn và lãi là
260
triệu
Công thức tính lãi kép
1
n
n
A A r
6 6
260.10 100.10 1 10%
n
10
n
Câu 113.
Lờigiải
Tácgiả: Mai Tiến Linh; Fb:Mai Tiến Linh
Vì hàm số
x
y a
đồng biến trên
khi
1
a
và nghịch biến trên
khi
0 1a
nên dựa vào đồ thị ta có:
1
B
A
3C
2C
1C
O
x
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
+
3
C
là đồ thị của hàm số đồng biến trên
. Do đó
3
C
có thể là đồ thị của hàm số
6
x
y
hoặc
8
x
y
.
+
1
C
,
2
C
là đồ thị của các hàm nghịch biến trên
nên
2
C
có thể là đồ thị của hàm số
1
5
x
y
hoặc
1
7
x
y
.
+ Kẻ đường thẳng
1x
lần lượt cắt
2
C
và
1
C
tại
A
và
B
. Vì
A B
y y
và
1 1
5
7
nên đồ
Câu 114. Ta có:
2 2 2 2 2
2 2 2 2 2
x x x
f x x e xe x x e
1 1;2
0
2 1;2
x
f x
x
.
Và
2
1
f e
;
4
2 2f e
;
2
1
f e
Giá trị nhỏ nhất của hàm số
2 2
2
x
f x x e
trên đoạn
1;2
bằng
2
e
tại
1x
.
Câu 115. Chọn D
3
1
2 0
1
4
2 ln 2 8 ln8 0 2 2 2 0
1
1/ 2
3
2
2
x
x x x x
x
x
y
x
Xét
y(-1)=5/6 ; y(-1/2)=0,9428 ; y(0)=2/3
. Ta có:
min
2
3
y
.
Câu 116. Ta có: số tiền nhận được của gốc và lãi là:
3
200 000 000 1 231 525 000
r
5%
r
/năm
Câu 117. Số tiền ông An nhận được sau
5
năm đầu là:
5
60 1 8% 88,160
(triệu đồng)
Số tiền ông An nhận được (toàn bộ tiền gốc và tiền lãi) sau
10
năm là:
5
88,16 60 1 8% 217,695
(triệu đồng).
Câu 118.
Lời giai
Gọi
200
a
triệu;
20
b
triệu;
7%
.
Số tiền sau 1 năm:
1a
.
Số tiền sau 2 năm:
2
1 1a b
.
Số tiền sau 3 năm:
3 2
1 1 1a b b
.
……………………
Số tiền sau 18 năm:
18 17 16
1 1 1 ... 1a b
17
18
1 1
1 1 .a b
Vậy số tiền ông Chính nhận sau 18 năm là:
1.335.967.000
VNĐ.
Câu 119. Ta có: Số tiền cả lãi lẫn gốc sau
15
tháng gửi:
15
15
1 1 1
T
S r r
r
Vậy:
15
10.000.000 1 0,006 1 0,00
635.301
6 1
0,006
T
T
Câu 120. • Số tiền anh Nam nhận được sau 6 tháng (tức 2 quý) là:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
2
0
1 0
100 1 3 / 106,09
T
triệu đồng.
• Số tiền anh Nam nhận được sau một năm (tức 2 quý còn lại của năm) là:
2
0
2 0
106,09 100 1 3 / 218,64
T
triệu đồng.
Câu 121. Gọi
A
là số tiền gửi vào ngân hàng,
r
là lãi suất,
T
là số tiền cả gốc lẫn lãi thu được sau
n
tháng. Ta có
1
n
T A r
.
Theo đề
1,005
6
50. 1,005 60 log 36,6
5
n
T n
.
Vậy sau ít nhất
37
tháng thì ông A thu được số tiền cả gốc lẫn lãi hơn 60 triệu.
Câu 122. Chọn B
Áp dụng công thức
.
Nr
S Ae
từ đầu năm 2010 đến đầu năm 2015 ta có:
5
1
1038229. ln
5 10
1153600
11536
9
00
3822
r
e r
.
Đầu năm 2020 dân số của tỉnh Bắc Ninh là
115361 0
ln
5 1038
0
2
.
2 9
10
10382
. 1281792
29S e
người.
Vậy Chọn B.
Câu 123. Kí hiệu số tiền gửi ban đầu là
A
, lãi suất một kì hạn là
m
thì số tiền cả gốc và lãi có được sau
n
kì hạn là
. 1
n
A m
.
Do đó, số tiền cả gốc và lãi người đó nhận được sau
n
năm là
300.1,07
n
triệu đồng.
Số tiền cả gốc và lãi nhận được nhiều hơn
600
triệu đồng
300.1,07 600
n
1,07
log 2 10,245
n
.
Vậy sau ít nhất
11
năm thì người đó nhận được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc và lãi.
Câu 124. Gọi
0
P
là số tiền gửi ban đầu,
r
là lãi suất / năm.
Số tiền gốc và lãi sau năm thứ nhất:
1 0 0 0
. 1
P P P r P r
.
Số tiền gốc và lãi sau năm thứ hai:
2
2 1 1 0
. 1
P P P r P r
.
….
Số tiền gốc và lãi người đó rút ra được sau 5 năm là
5 5
5 0
. 1 80000000. 1 6,9% 111680799
P P r
(đồng).
Câu 125. Chọn C
Số tiền nhận được khi gửi khoản tiền
T
ở tháng đầu tiên là
15 15
(1 0,006) .1,006
T T .
Số tiền nhận được khi gửi khoản tiền
T
ở tháng thứ 2 là
14 14
(1 0,006) .1,006
T T .
Cứ như vậy, số tiền nhận được khi gửi khoản tiền
T
ở tháng thứ 14 là
(1 0,006) .1,006
T T
.
Vậy tổng số tiền nhận được sau
15
tháng là:
15
15 14 2
1,006 1
(1,006 1,006 ... 1,006 1,006) .1,006.
0,006
T T
.
Theo giả thiết có:
15
1,006 1
10000000 .1,006. 635301,46
0,006
T T
.
Câu 126. Chọn A
Gọi
0
T
là số tiền người đó gửi vào ngân hàng vào ngày 01/01 hàng năm,
n
T
là tổng số tiền cả vốn lẫn lãi người
đó có được ở cuối năm thứ
n
, với
*
n
,
r
là lãi suất ngân hàng mỗi năm.
Ta có:
1 0 0 0
1
T T rT T r
.
Đầu năm thứ
2
, người đó có tổng số tiền là:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
2 2
0 0
0 0 0
1 1 1 1 1 1 1
1 1
T T
T r T T r r r
r
r
.
Do đó:
2 2
2
0 0 0
2
. 1 1 . 1 1 . . 1 1 1
T T T
T r r r r r
r r r
.
……
Ta có:
0
. 1 1 1
n
n
T
T r r
r
.
Áp dụng vào bài toán, ta có:
6
0
0
10 . 1 0,07 1 1 0,07 130 650 280
0,07
T
T
đồng.
Câu 127. Gọi số tiền vay ban đầu là
M
, số tiền hoàn nợ mỗi tháng là
m
, lãi suất một tháng là
r
.
Hết tháng thứ nhất, số tiền cả vốn lẫn nợ ngân hàng là
1
M Mr M r
(triệu đồng).
Sau khi hoàn nợ lần thứ nhất, số tiền còn nợ là
1
M r m
(triệu đồng).
Sau khi hoàn nợ lần thứ hai, số tiền còn nợ là
2
1 1 1 1
M r m M r m r m M r m r m
(triệu đồng).
Sau khi hoàn nợ lần thứ ba, số tiền còn nợ là
2 2
1 1 1 1
M r m r m M r m r m r m
3 2
1 1 1
M r m r m r m
(triệu đồng).
Lập luận tương tự, sau khi hoàn nợ lần thứ
n
, số tiền còn nợ là
1 2
1 1 1 ... 1
n n n
M r m r m r m r m
1
1 1
1
n
n
m r
M r
r
.
Sau tháng thứ
n
trả hết nợ thì ta có
1
1 1
1 0
n
n
m r
M r
r
1
1 1
n
n
Mr r
m
r
1
n
m m Mr r
1
n
m
r
m Mr
1
log
r
m
n
m Mr
Thay số với
100.000.000
M
,
0,7%
r
,
5.000.000
m
ta tính được
21,62
n
(tháng).
Vậy sau
22
tháng người đó trả hết nợ ngân hàng.
Câu 128. Bài toán lãi kép:
Kí hiệu số tiền gửi ban đầu là
A
, lãi suất một kì hạn là
%r
thì số tiền cả gốc và lãi có được sau
n
kì hạn là
. 1 %
n
n
S A r
.
Anh Bảo nhận được số tiền ít nhất 36 triệu đồng tính cả vốn và lãi nên ta có:
27 1 1,85% 36 15.693
n
n
.
Vậy thời gian tối thiểu để anh Bảo nhận được ít nhất 36 triệu đồng tính cả vốn lẫn lãi là 16 quý.
Câu 129. Gọi
n
T
là số tiền cả gốc lẫn lãi sau
n
tháng,
a
là số tiền gốc,
r
là lãi xuất, ta có:
Cuối tháng thứ
1
ông An có số tiền là:
1
1
T a r
Đầu tháng thứ
2
ông An có số tiền là:
2
1
T a r a
Cuối tháng thứ
2
ông An có số tiền là:
2
2
1 1 1 1
T a r a a r a r a r a r
……………………………………………………………
Cuối tháng thứ
n
ông An có số tiền là::
2
1 1 ... 1
n
n
T a r a r a r
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
2
1 1 1 1 1 1
1 1 ... 1 . 1
1 1
n n
n
r r a r r
a r r r a
r r
.
Với kì hạn một tháng, suy ra 3 năm có 36 kỳ. Lãi xuất của một năm là
7,2%
, suy ra lãi xuất của 1 tháng là:
7,2
% 0.6%
12
. Áp dụng
1
ta có:
5000000; 0.6% 0.072; 36
a r n
36
36
5000000 1 0.6% 1 0.6% 1
201453000
0.6%
 T
Câu 130. Số tiền trả cho ngân hàng nếu vay 200 triệu trong 4 tháng
4
200. 1 0,7% 200 5,65907
N
Tổng số tiền lãi nếu anh Bình gửi đúng kì hạn là
12
1
200. 1 0,65% 200 16,16996
L
Số tiền lãi nếu anh Bình làm theo tư vấn của nhân viên ngân hàng
16,16996 5,65907 10,51089.
L
Số tiền lãi nếu gửi 8 tháng theo hình thức lãi suất không kì hạn
8
2
200. 1 0,02% 200 0,32022.
L
Số tiền anh Bình đỡ thiệt nếu làm theo tư vấn của nhân viên ngân hàng
16,16996 5,65907 0,32022 10,19067.
Câu 131. Đặt
8 000 000
T
Số tiền thầy giáo thu được sau tháng thứ nhất, thứ 2, thứ 3,., thứ
n
lần lượt là
1 2 3
, , ,...,
n
T T T T
Ta có:
1
1
T T r
2
2 1
1 1 1
T T T r T r T r
3 2
3 2
1 1 1 1
T T T r T r T r T r
.
1
1 1
1 1 ... 1 1
n
n n
n
r
T T r T r T r T r
r
Theo bài ra ta có
1 1
400 000 000 1 400 000 000
n
n
r
T T r
r
1.005
251 251
1 log 44,54
201 201
n
r n
Vậy sau 45 tháng thầy giáo sẽ mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ.
Câu 132. Với 100 triệu ban đầu số tiền cả lãi và gốc thu được sau hai năm là
24
6
1
100. 1 0,8% .10 121074524
T
Mỗi tháng tiếp theo gửi 2 triệu thì tổng số tiền cả lãi và gốc là
23
6
2
2
. 1 0,008 1 . 1 0,008 10 50686310
0,008
T
Vậy tổng số tiền là
1 2
171.761.000
T T T
Câu 133. Cuối tháng thứ nhất, tiền gốc và lãi là
400 1,01
triệu đồng. Sau khi trả
10
triệu thì số tiền người
đó còn nợ ngân hàng là
400 1,01 10
triệu đồng.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
Cuối tháng thứ hai, tiền gốc và lãi là:
2
400 1,01 10 1,01
triệu đồng. Sau khi trả
10
triệu thì số tiền người
đó còn nợ ngân hàng là
2
400 1,01 10 1,01 10
triệu đồng.
Như vậy ở cuối tháng thứ
1
n n
người đó nếu còn nợ thì số tiền nợ là:
1 2
400 1,01 10 1,01 10 1,01 10
n n n
triệu đồng.
Xét
1 2
400 1,01 10 1,01 10 1,01 10 0
n n n
1,01 1
400 1,01 10 0
0,01
n
n
600 1,01 1000
n
1,01
5
log 51,33
3
n
Do vậy kỳ cuối cùng người đó phải trả tiền là tháng thứ
52
. Cuối tháng thứ
51
, số tiền còn nợ lại là
51
51
1,01 1
400 1,01 10 3,3531596
0,01
triệu đồng.
Vậy kỳ cuối người đó phải trả số tiền là
3,3531596 1,01 3,386647
triệu đồng
3387000
đồng.
Câu 134. Gọi số tiền lúc đầu người đó gửi là
A
(triệu đồng), lãi suất gửi ngân hàng một tháng là
r
,
n
S
là
số tiền còn lại sau
n
tháng.
Sau 1 tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
1
1 1
S A r
.
Sau 2 tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
2
2
1 1 1 1 1 1 1
S A r r A r r
.
…
Sau
n
tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
1 2
1 1 1 1 1
n n n
n
S A r r r r
1 1
1
n
n
r
A r
r
.
Giả sử sau
n
tháng người đó rút hết tiền. Khi đó ta có
1 1
0 1 0
n
n
n
r
S A r
r
1 1 1 0
n
r Ar
1 1
1
log log 1
1
r r
n n Ar
Ar
.
Câu 135. Gọi sô tiền mẹ gửi vào ngân hàng vào đầu tháng hàng tháng là
A
đồng.
Số tiền mẹ lĩnh vào đầu tháng
12
là T đồng.
Lãi suất hàng tháng mẹ gửi tại ngân hàng là r %.
Vì mẹ rút tiền vào đầu tháng
12
năm
2019
nên thời gian được tính lãi suất là
11
tháng.
Ta có:
+) Đầu tháng
1
mẹ gửi vào
A
đồng.
cuối tháng
1
số tiền của mẹ là:
1
A Ar A r
đồng.
+) Đầu tháng
2
số tiền của mẹ gửi vào là:
1
A A r
đồng.
cuối tháng
2
số tiền của mẹ là:
2
+ 1 1 1 1
A A r r A r A r
đồng.
+) Đầu tháng
3
số tiền mẹ gửi vào là:
2
1 1
A A r A r
.
cuối tháng
3
số tiền của mẹ là:
2 2 3
1 1 1 1 1 1
A A r A r r A r A r A r
.
Cứ như vậy đến cuối tháng thứ
11
số tiền của mẹ là:
2 11 2 11
1
1 1 ... 1 1 1 ... 1
A r A r A r A r r r T
.
Ta thấy
2 11
1 1 ... 1r r r
là tổng của 1 cấp số nhân với
1
1 ,n 11,q 1u r r
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
11
1
1
1
1
u q
T A
q
. Ta có:
4000000
1% 0.01
A
r
1
46730000
T đồng.
Vì mẹ rút tiền vào đầu tháng
12
năm
2019
1
4000000 50730000
T T đồng.
Câu 136. Xét bài toán 1: Vay nhận vốn định kì lãi suất kép.
Gọi
A
là số tiền mỗi năm bạn H vay ngân hàng,
1
r
là lãi suất theo năm.
Cuối năm thứ nhất, H nợ ngân hàng với số tiền là
1
. 1
A r
.
Đầu năm thứ hai, H nợ ngân hàng với số tiền là
1
. 1
A A r
.
Cuối năm thứ hai, H nợ ngân hàng với số tiền là
2
1 1 1 1 1
. 1 1 1 1
A A r A A r r A r A r
.
Tiếp tục như vậy, cuối năm thứ n số tiền mà H nợ ngân hàng là:
1 1
2
1 1 1
1
1 1 1
1 1 ... 1
n
n
A r r
B A r A r A r
r
.
Xét bài toán 2: Vay trả góp, lãi suất dư nợ thực tế.
Gọi
a
là số tiền mà bạn H phải trả hàng tháng sau khi ra trường,
2
r
là lãi suất mỗi tháng, số tiền H nợ ngân
hàng là B.
Cuối tháng thứ nhất bạn H còn nợ ngân hàng số tiền là:
2 2
. . 1
B B r a B r a
.
Cuối tháng thứ hai bạn H còn nợ ngân hàng số tiền là:
2 2 2
. 1 . 1
B r a B r a r a
=
2
2 2
. 1 1
B r a a r
.
Cứ tiếp tục như vậy ta có công thức tổng quát.
Cuối tháng thứ m bạn H còn nợ ngân hàng số tiền là
2 1
2 2 2 2
. 1 1 1 ... 1
m m
B r a r a r a r a
=
2
2
2
1 1
. 1
m
m
r
B r a
r
.
Áp dụng 2 bài toán trên vào câu 42, ta có phương trình.
4
60
60
4.1,03 1,03 1
1,0025 1
1,0025 . 0 0,309718
0,03 0,0025
a a
(triệu đồng).
Vậy số tiền mà H cần phải trả hàng tháng là 309.718 triệu đồng.
Câu 137. Chọn A
Gọi
a
là số tiền trả hàng tháng.
Sau tháng thứ 1, số tiền còn lại:
1
500 1
P r a
.
Sau tháng thứ 2, số tiền còn lại:
2 1
1
P P r a
2
500 1 1
r a r a
.
.
Sau tháng thứ
n
, số tiền còn lại:
1
500 1 1 ... 1
n n
n
P r a r a r a
.
Vậy sau 24 tháng:
24
24
1 1
500 1 0
r
r a
r
24
24
500 1 .
1 1
r r
a
r
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
24
24
500 1 1% .1%
1 1% 1
a
23,537
triệu đồng.
Câu 138. Phương pháp:Sử dụng công thức trả góp
(1 ) (1 ) 1
n n
M
P r r
r
, trong đó:
P
: là số tiền phải trả sau
n
tháng
r
: Lãi suất/ tháng
M
: số tiền phải trả mỗi tháng
Áp dụng công thức ta có:
(1 ) (1 ) 1
n n
M
P r r
r
4
50(1 1,1%) (1 1,1%) 1
1,1%
n n
4 4
50(1 1,1%) (1 1,1%)
1,1% 1,1%
n n
4 3450
(1 1,1%)
1,1% 11
n
1 1,8
80 80
(1 1,1%) log 13,52
69 69
n
n
Câu 139. Gọi
X
là số tiền mỗi tháng ông
A
trả cho ngân hàng.
Số tiền còn nợ sau
n
kì hạn là
1 1
. 1 .
n
n
n
r
T T r X
r
(triệu đồng), trong đó
100
T
(triệu đồng) là
số tiền mà ông
A
vay.
Sau đúng một năm, số tiền ông còn nợ là
50
triệu đồng nên ta có
12
12
1 0,01 1
50 100. 1 0,01 .
0,01
X
12
12
100.1,01 50 .0,01
4,94
1,01 1
X
(triệu đồng).
Vậy mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền
4,94
triệu đồng.
Câu 140. Sau
3
năm, bắt đầu từ tháng đầu tiên của năm thứ
4
số tiền lương người đó nhận được sau mỗi
tháng là
6 6.10% 6.1,1
(triệu đồng).
Sau
6
năm (
2.3
năm), bắt đầu từ tháng đầu tiên của năm thứ
7
số tiền lương người đó nhận được sau mỗi
tháng là
2
6.1,1 6.1,1.10% 6.1,1. 1 10% 6.1,1
(triệu đồng).
Tương tự như vậy sau
15
năm (
5.3
năm), bắt đầu từ tháng đầu tiên của năm thứ
16
số tiền người đó nhận
được sau mỗi tháng là
5
6.1,1
(triệu đồng).
Vậy tháng đầu tiên của năm thứ
16
, người đó nhận được mức lương là
5
6.1,1
(triệu đồng).
Câu 141. Dạng toán lãi kép:
Bài toán tổng quát: gửi
a
đồng vào ngân hàng với lãi suất
%r
(sau mỗi kì hạn không rút tiền lãi ra).
Gọi
n
A
là số tiền có được sau
n
năm.
Sau
1
năm:
1
%. 1 %A a r a a r
.
Sau
2
năm:
2
2
1 % 1 % . % 1 %
A a r a r r a r
.
Sau
3
năm:
2 2 3
3
1 % 1 % . % 1 %
A a r a r r a r
.
Sau
n
năm:
1 %
n
n
A a r
.
Người đó nhận được số tiền hơn
100
triệu. Suy ra:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
1,06
50 1 6% 100
50.1,06 100
1,06 2
log 2 11,9
n
n
n
n
Vậy
12
n
.
Câu 142. Gọi số tiền mỗi tháng anh gửi tiết kiệm ngân hàng trong
36
tháng đầu là
A
; số tiền mỗi tháng
anh gửi tiết kiệm sau tháng thứ
36
là
B
.
Đặt
1 0,5% 1, 005
q
Gọi
n
S
là số tiền sau tháng thứ
n
ta có
1
.0,5% .
S A A A q
2
2 1 1 1
.0,5% .
S S A S A S A q Aq Aq
.
….
36
36 35
36 35 35 35
1
.0,5% . .
1
q
S S A S A S A q Aq Aq Aq Aq
q
.
37 36 36 36 36
.0,5% . . .
S S B S B S B q S q B q
.
2 2
38 37 37 37 36
.0,5% .
S S B S B S B q S q Bq Bq
.
….
36 12
12 12 11 13
48 36
1 1
. ... . .
1 1
q q
S S q Bq Bq Bq Aq Bq
q q
.
Theo giả thiết ta có
20% 0,2 A x x
;
20% 10% 0,22
B x x x
;
8
48
10
S
.
Vậy
36 12
13 8
1 1
0,2 . 0,22 . . 10
1 1
q q
xq x q
q q
36 12
8 13
1 1
10 : 0,2 . 0,22. .
1 1
q q
x q q
q q
8991504
x
đồng.
Câu 143. Bài toán được chia làm hai giai đoạn
* Giai đoạn 1: vay vốn để học đại học trong 4 năm. Đặt
7,8
0,078
100
r
Ở năm thứ nhất:
4
1
10(1 )M r
(triệu đồng)
Ở năm thứ hai:
3
2
10(1 )M r
(triệu đồng)
Ở năm thứ ba:
2
3
10(1 )M r
(triệu đồng)
Ở năm thứ tư:
1
4
10(1 )M r
(triệu đồng)
Như vậy tổng số tiền mà Nam đã vay trong 4 năm là
4
0
1
48,4324
i
i
M M
(triệu đồng)
* Giai đoạn 2: trả góp cho ngân hàng số tiền đã vay hàng tháng
Sau tháng thứ nhất, người đó còn số nợ là:
1
0,7
1
100
o
P M m
. Đặt
0,7
1
100
y
Sau tháng thứ hai người đó còn nợ:
2
2 2
2 1
1
( 1)
1
o o a
y
P P y m M y m y m M y m y M y m
y
Sau tháng thứ ba người đó còn nợ:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
3
3 2 3
3 2
1
1
1
o o
y
P P y m M y m y y M y m
y
Bằng phương pháp quy nạp, sau
n
tháng số tiền trả hết sẽ là
( 1)
1
0
1
1
n
n
o
o
n
M y y
y
M y m m
y
y

Đồng thời ta có:
48n
tháng và
0,7
1 1,007
100
y
suy ra
1,914m
(triệu đồng).
Câu 144. Chọn
Anh sinh viên vay hàng tháng
3
a
triệu đồng từ
9
/
2014
đến
8 / 2016
, tổng cộng
24
tháng.
Cuối tháng thứ 1:
1
ar 1
T a a r
Cuối tháng thứ 2:
2
2 1 1
. . 1 . 1
T T a T a r a r a r
….
Cuối tháng n:
1
. 1 . 1 ... . 1
n n
n
T a r a r a r
Suy ra
1 1
. 1 .
n
n
r
T a r
r
Vậy tổng số tiền vay đến cuối tháng 8/2016 là
24
24
1 0,8% 1
3. 1 0,8% . 79,662
0,8%
T
triệu
Tính từ cuối tháng 8/2016 Anh sinh viên thiếu ngân hàng
79,662
A
và bắt đầu trả đầu hàng tháng
2
m
triệu từ
9 / 2016
đến
6 / 2018
, tổng cộng được
22
tháng
Đầu tháng
9 / 2016
: còn nợ
79,662 2 77,662
A m
triệu
Cuối tháng
9 / 2016
: tiền nợ có lãi đến cuối tháng:
1
77,662 1
T r
Đầu tháng
10/ 2016
sau khi trả nợ
m
thì còn nợ
77,662 1
r m
Cuối tháng
10/ 2016
: còn nợ
2
2
77,662 1 1 77,662 1 1
T r m r r m r
Cuối tháng
11/ 2016
: còn nợ
3 2
3
77,662 1 1 1
T r m r m r
….
Cuối tháng
6 / 2018
còn nợ
22 21 20
22
21
22
77,662 1 1 1 ... 1
1 1
77,662 1 . 1
T r m r m r m r
r
r m r
r
21
22
1 0,8% 1
77,662. 1 0,8% 2. 1 0,8% . 46,64
0,8%
triệu đồng.
Câu 145. Khi mới bắt đầu đi vào môi trường nước biển thì
0
x
1
.e
o
o
I I
Ở độ sâu 30 mét thì
.30
2
e.
o
I I
Vậy ta có:
.30
42
2
2 1
1
e
e
e
.
.
.
o
o
o
I
I
I I
I I
 , vậy
2
I
tăng
42
e
lần so với
1
I
, nói cách khác,
2
I
giảm
42
e
lần so với
1
I
Câu 146. Gọi
S
là diện tích lá bèo thả ban đầu.
Vì sau mỗi giờ, lượng bèo tăng gấp 10 lần lượng bèo trước đó nên sau 12 giờ, tổng diện tích các lá bèo trong
chậu là
12
10 S
.
Theo đề bài: Sau 12 giờ, bèo phủ kín mặt nước trong chậu nên diện tích mặt nước trong chậu là
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
12
10 S
. Giả sử sau
x
giờ thì bèo phủ kín
1
5
mặt nước trong chậu.
Ta có:
12
1
10 .10
5
x
S S
12
10 5
x
12 log5 11,3
x
.
Vậy sau
11,3
giờ thì bèo phủ kín
1
5
mặt nước trong chậu.
Dạng 5. Bài toán cực trị
Câu 147. Chọn B
Từ giả thiết suy ra
2 2
4 5 1
log 16 1 0
a b
a b
và
8a 1
log 4 5 1 0
b
a b
.
Áp dụng BĐT Côsi ta có
2 2
4 5 1 8a 1
log 16 1 log 4 5 1
a b b
a b a b
2 2
4 5 1 8a 1
2log 16 1 .log 4 5 1
a b b
a b a b
8a 1
2 2
2log 16 1
b
a b
.
Mặt khác
2
2 2
16 1 4 8a 1 8a 1 , 0
a b a b b b a b
,
suy ra
8a 1
2 2
2log 16 1 2
b
a b
.
Khi đó
2 2
4 5 1 8a 1
log 16 1 log 4 5 1 2
a b b
a b a b
4 5 1 8a 1
log 8 1 log 4 5 1
4
a b b
ab a b
b a
2
24 1
log 32 1 1
4
a
a
b a
2
3
32 24
4
4
3
a
a a
b a
b
.
Vậy
3 27
2 6
4 4
a b
.
Câu 148. Chọn A
Với
,x y
dương và kết hợp với điều kiện của biểu thức
3
1
log 3 2 4
2
xy
xy x y
x y
ta được
1 0xy
Biến đổi
3
1
log 3 2 4
2
xy
xy x y
x y
3 3 3
log 1 log 2 3 1 2 log 3
xy x y xy x y
3 3 3
log 1 log 3 3 1 log 2 2xy xy x y x y
3 3
log 3 1 3 1 log 2 2 1
xy xy x y x y
Xét hàm số
3
log
f t t t
trên

0;D
1
' 1 0
.ln 3
f t
t
với mọi
x D
nên hàm số
3
log
f t t t
đồng biến trên

0;D
Từ đó suy ra
3 2
1 3 1 2 3 2 1 3
1 3
y
xy x y y x y x
y
(do
0y
)
Theo giả thiết ta có
0, 0x y
nên từ
3 2
1 3
y
x
y
ta được
3
0
2
y
.
2
3 2 3 3
1 3 3 1
y y y
P x y y
y y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
Xét hàm số
2
3 3
3 1
y y
g y
y
với
3
0
2
y
2
2
9 6 10
' 0
3 1
y y
g y
y
ta được
1 11
3
y
.
Từ đó suy ra
1 11
mi
2 11
.
3
n
3
3
P g
Câu 149. Chọn C
Điều kiện:
1ab
.
Ta có
2 2 2
1
log 2 3 log 2 1 2 1 log *
ab
ab a b ab ab a b a b
a b
.
Xét hàm số
2
log
y f t t t
trên khoảng
0;
.
Ta có
1
1 0, 0
.ln 2
f t t
t
. Suy ra hàm số
f t
đồng biến trên khoảng
0;
.
Do đó
2
* 2 1 2 1 2 1 2
2 1
b
f ab f a b ab a b a b b a
b
.
Do
0, 0
a b
nên
2
0 0 2
2 1
b
b
b
.
Khi đó:
2
2 2
2 1
b
P a b b
b
. Xét hàm số
2
( ) 2
2 1
b
g b b
b
trên khoảng
0;2
.
2
2
2 10
0;2
5 5
4
2 0 2 1
2
2 1
2 10
0;2
4
b
g b b
b
b
Lập bảng biến thiên
Vậy
min
10 2 2 10 3
4 2
P g
.
Câu 150.
ln
ln( ) ln5 ln( ) ln 2 ln( ) ln5 ln( ) ln( ) ln5 ln2
2
2 .5 2 2 .5 2 2 .5 2 .2
x y
x y x y x y x y x y
ln( ) ln10
10 2
x y
ln10 ln( ) ln10.log 2
ln( ) log 2 ln( ) ln10.log 2
x y
x y x y e e
log2
10 2
x y x y
.
Do đó
1 ln 3 ln 2
P x x x x
.
Xét hàm số
( ) ( 1)ln (3 ) ln(2 )f x x x x x
1 3 2 2
( ) ln ln(2 ) ln
2 2 (2 )
x x x x
f x x x
x x x x x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
2
2 2
2
1 2 2 4 4
. 0, 0;2
2
2
x x x
f x x
x
x
x x
Do đó
0
f x
có nhiều nhất một nghiệm trên
0;2
Mà
1x
là một nghiệm của pt
0
f x
nên phương trình
0
f x
có nghiệm duy nhất là
1
x
.
Lập bảng biến thiên ta được
max 1 0
f x f
.
Câu 151. Với điều kiện biểu thức đề bài có nghĩa, ta có
3 3 3
log 1 1 2 0 log log 1 1 0
1
x y
x y x y xy xy x y
xy
3 3
log log 1 1 *
x y x y xy xy
Xét hàm số
3
log
f x t t
trên
0;2
1
ln3 1 0, 0;2
f t t
t
nên hàm số
f t
đồng biến trên
0;2
.
Do đó từ
*
ta có
1
1 1 1
1
x
x y xy y x x y
x
1
2 2
1
x
P x y x
x
2
2
2 0, 0;1
1
P x x
x
Suy ra
min 0 1
P P
đạt được khi
0, 1
x y
.
Câu 152. Ta có
1 log 0
a
a b b
.
1
log log log log 1 log 1 log .
log
a a a a a a
ab
a
P ab a b b b
a b
Đặt
2
1 log 0 log 1
a a
t b t b t
. Ta có:
2
2P t t
trên
0;

Bảng biến thiên
t
1
2
P
9
2
Hàm số đạt giá trị lớn nhất tại
1
.
2
t
Với
3
4
1 1 3 3
1 log log .
2 2 4 4
a a
t b b b a k
Câu 153. Chọn B
2 2
2 2
4 1
log 2 8 1 2 8 4 1
a b
a b a b a b
Ta có:
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
2 2
2 2
2
2
2 2 2
2 2
2 8 4 1
2 8 4 1
6 5
4 6 5
4
6 5 6 5
2 8 4 1
4 4
6 5
4
8 48 40 128 36 25 12 10 60 64 16
6 5
4
100 2(58 6 ) 2 1 0
a b a b
a b a b
S b
S a b
a
S b S b
b b
S b
a
S b b S b Sb S b b
S b
a
b S b S S
S
a
2 2 2
6 5
4
(58 6 ) 100.(1 ) 0 64 896 3264 0
17 3
b
S S S S
S
Giá trị lớn nhất của S là:
13
5
3
2
5
a
b
Suy ra
13
2
a
b
Câu 154.
Điều kiện
2 2
4 9 1
x y
.
Trường hợp 1:
2 2
4 9 1
x y
.
Ta có
2 2
2 1
2 3 1
3 1
x
x y
y
1 3
3 1
2 2
x y P
.
1
Trường hợp 2:
2 2
4 9 1
x y
.
Khi đó
2 2
2 2
4 9
log 2 3 1 2 3 4 9
x y
x y x y x y
2 2
1 1 1
2 3
2 2 2
x y
.
1 1 1 3
3 2 3
2 2 2 4
P x y x y
.
Áp dụng BĐT Bunhiacopski ta được:
2
2 2
1 1 1 1 1 1 5
2 3 1 2 3
2 2 2 4 2 2 8
x y x y
.
Suy ra
1 1 1 3 3 10
2 3
2 2 2 4 4
P x y
.
2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
Dấu bằng xẩy ra khi và chỉ khi
1 1
5 10
2 2 3
8 6 1
2 2
20
4 12 3 10
5 2 10
3 10
3
30
4
x y
x
x y
x y
y
x y
. Từ
1
và
2
suy ra giá trị lớn nhất của
P
là
3 10
4
.
Câu 155. Chọn D
Ta có:
1 1
4. log 1 4. log 1
1
1 log
1
log
b b
a
b
P a a
b
a
Đặt
log
b
t a
. Vì
log 1 log 1 1 2
2
b b
t
a b a a a t t
.
1
4 1 4 1
1
1
1
t
P t t
t
t
với
1;2
t
.
Xét hàm số
( ) 4 1
1
t
f t t
t
với
1;2
t
.
2
2
3
1 1
2
( ) 4, ( ) 0 1
1
4
1
2
t tm
f t f t t
t
t l
.
Bảng biến thiên
Từ bảng biến thiên suy ra:
1;2
3
minf 5.
2
t f
Vậy giá trị nhỏ nhất của biểu thức
P
bằng
5
.
Câu 156. Chọn A
Do
2
4 2 2 2
9 81 9 9 0
a a a a
đúng
1
;
3
a
Dấu bằng xảy ra khi
3
a
Suy ra
2
3 3
log log 3 log 2log 3 2 2
a b a b
P b a b a
5
6
+∞
+
-
0
3
2
3
2
2
1
+∞
-∞
f (t)
f '(t)
t
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
Dấu bằng xảy ra khi và chỉ khi
2
3
3
3
log 2log 3
9
a b
a
a
b a
b
Vậy, khi
P
đạt giá trị nhỏ nhất thì
2
3 9 .
a b
Câu 157.
5 5 5
4 2 5
log 3 4 log 4 2 5 log 3 4
a b
a b a b a b a b
a b
5 5
log 4 2 5 4 2 5 log 5 5
a b a b a b a b
(*).
Xét hàm
5
log , 0
f x x x x
.
Đạo hàm
1
1 0, 0
.ln5
f x x
x
. Suy ra hàm số
f x
đồng biến trên
0;

.
Phương trình (*) viết lại:
4 2 5 5 4 2 5 5 3 5
f a b f a b a b a b a b
.
Mặt khác:
2
2 2 2 2 2 2 2
5
5 3 1 3 .
2
a b a b T a b
.
Dấu
" "
xảy ra
1 3
a b
1 3
;
2 2
a b
.
Câu 158. Ta có:
1 8 1 1 8 1
.
2 16 16 4 4
b b b
2
2
2
2
b
b
.
3 8 3 1 1 1 8 3
. . .
2 16 16 2 2 2 2
c c c
4
4
4
4
c
c
.
Suy ra
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
2 4
3 1 1
log log log
16 4 3
a b a
b c c
3
2 3
3.
16 2
.
Vậy
min
3
2
P
1
4
8 1 1
1
8 3 1
2
3 1
log log log
2
8 3
4
a b c
b
b
c c
b c a
a
.
Câu 159.
2 2 2 2 2 2
2 2
log 9 1 log 3 2 9 6 4 6 4 9 0
a b a b a b a b a b a b
1
Gọi
;A a b
. Từ
1
ta suy ra điểm
A
thuộc điểm đường tròn
C
có tâm
3;2
I
, bán kính
2R
.
4 4
2
2 2
2 2
9 .3 .3 ln 2 2 1 81 ln 2 2 1 81 3
m n
m n
m n m n
m n m n
Theo bất đẳng thức Cô-si:
4 4
2 2 2 . 4
2 2
m n m n
m n m n
4
2
2
3 81
m n
m n
.
(Đẳng thức xảy ra khi:
4
2 2 2
2
m n m n
m n
)
Từ
2 2 2
ln 2 2 1 0 2 2 1 1 2 2 0
m n m n m n
2 2 0 2
m n
.
Gọi
;B m n
. Từ
2
ta suy ra điểm
B
thuộc đường thẳng
:
2 2 0
x y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
Ta có:
2 2
P a m b n AB
2 2
3.2 2 2
min min ; 2 2 5 2.
2 1
P AB d I R
Câu 160. Ta có
b a
a b
ln lnb a a b
ln ln
*
a b
a b
.
Xét hàm số
lnx
y
x
, trên tập xác định
0;D
2
1 ln x
y
x
,
0y x e
Bảng biến thiên
Có
0 a b
f a f b
Kết hợp với bảng biến thiên suy ra
1a e b
.
Ta lại có
,
2 3
a b
f x x a b x x x
2 3 1x a b x x x b a
.
Suy ra
,
min 1
x
a b
f x b a
2
2 3
a x b
x
Từ
1
và
2
suy ra số thực duy nhất thỏa mãn yêu cầu bài toán là
x e
Thử lại: khi
x e
thì
1f e b a
.
Vậy
0
, , ,
min
a b a b a b
x R
f x f x f e
Câu 161. Chọn A
Ta có
2
1 2 2
1 1 log 0 log log 0
x x
a a a
a b x x b b x x b
1
e
ba
+
0
x
y
/
y
+∞
0
_
0
e
-∞
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
Do phương trình có hai nghiệm
1 2
,x x
nên theo định lý Viet ta có:
1 2
1 2
1
log
log
1
b
a
x x a
b
x x
Khi đó
2
1
4log
log
b
b
S a
a
Đặt
log
b
t a
, do
1, 1 0a b t
. Khi đó
3
2 2
1 1
4 2 2 3 4
S t t t
t t
.
Đẳng thức xảy ra khi
2
3
1 1
2
2
t t
t
. Vậy
3
min 3 4
S
Câu 162. Chọn C
Ta có:
1 8 1 1 8 1
.
2 16 16 4 4
b b b
2
2
2
2
b
b
.
3 8 3 1 1 1 8 3
. . .
2 16 16 2 2 2 2
c c c
4
4
4
4
c
c
.
Suy ra
3 1 1 3 1
log log log
16 2 16 4 2 16 3
a b c
b c
P a
2 4
3 1 1
log log log
16 4 3
a b a
b c c
3
2 3
3.
16 2
.
Vậy
min
3
2
P
1
4
8 1 1
1
8 3 1
2
3 1
log log log
2
8 3
4
a b c
b
b
c c
b c a
a
.
Câu 163. Cách 1.
Ta có:
ln ln
y x y x
e e e e
x x y y x x y y
y e x e y e x e
ln ln
ln ln
y x
x y
x y
x y xe y x ye
x e y e
(*) (vì
ln
x
y e x
có
1
' 0; 1
x
y e x
x
nên
1 0
y y e
)
Xét hàm số:
ln
t
t
f t
t e
trên
1;
ta có
2
ln 1
'
ln
t t
t
t e te
f t
t e
. Với hàm số
ln 1
t t
g t t e te
có
1
' ln 1 ' 0, 1
t t t
g t t e te te t
t
Nên
1 1 ' 0; 1g t g f t t
y f t
là hàm nghịch biến trên
1;

nên với (*)
1f x f y y x
Khi đó
1 1 1 1 1 1 1 2 2
log log log 2 log .
2 2 log 2 2 log 2
x y x x
x x
P xy x y y
y y
Dấu “=” xảy ra khi:
2
2
1 1
log log 2
2 log
x x
x
y y y x
y
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
Vậy:
min
1 2 2
2
P
.
Cách 2:
Với
, 1x y
thì
log ;log
x y
y x
là các số dương, ta có:
log log
x y
P xy x
1 1 1 1 1 1 1 2 2
log 2 log .
2 2 log 2 2 log 2
x x
x x
y y
y y
Dấu “=” xảy ra khi:
2
2
1 1
log log 2
2 log
x x
x
y y y x
y
,
Thay
2
1
y x
x
vào điều kiện thấy thỏa mãn điều kiện ban đầu.
Vậy
min
1 2 2
2
P
.
Câu 164. Để
1
0
3
y
x xy
mà từ giả thiết
, 0
x y
suy ra
1 0 1y y
. Vậy ĐKXĐ:
0;0 1x y
.
Ta có:
3
1
log 3 3 4
3
y
xy x y
x xy
3 3 4
1
3
3
xy x y
y
x xy
3 3 3
3 1
3
3
xy x y
y
x xy
3
3 3
3 1
3
3 3
xy x
y
y
x xy
3 3 3
3 3 .3 3 .3 (*)
y xy x
y xy x
Xét
.3
t
f t t
với
0t
. Ta có
3 .3 .ln3 0
t t
f t t
với
0
t
, suy ra
f t
đồng biến trên khoảng
0;

. Từ
(*)
ta có
3 3 3
f y f xy x
với
3 3 0,3 0
y xy x
nên
3
3 3 3
3( 1)
x
y xy x y
x
.
Ta có
3 3 1 4
1
3 1 3 1 3 3
x x
P x y x x
x x
4 4 4 4 4 3 4
1 2 1 .
3 1 3 3 1 3 3
P x x
x x
.
Vậy
min
4
1
3 1
2 3 3
4 3 4 3
3
3 3 1
2 3 1
0;0 1
3
x
x
x
x
P y
x
y
x y
.
Câu 165. Ta có:
2
1 1 1
2 2 2
log log log
x y x y
2 2
1 1
2 2
log log
xy x y xy x y
2
2
1
1
1
y
x
x y y
y
y
( Vì
; 0
x y
).
Ta có:
2
1
3 3 4 1
1 1
y
P x y y y
y y
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
Xét hàm số:
1
4 1 ; 1
1
f y y y
y
.
Đạo hàm:
/
2
1
4
1
f y
y
.
/
3
2
0
1
2
y n
f y
y l
.
Bảng biến thiên.
Câu 166. Ta có:
2019 201 2
2
9 019
log log logx y
x y
2019 2019
2
log logxy
x y
2
xy x y
2
1
y x x
2
1
1
x
y
x
x
Ta có:
2
1
2 2 3 1
1 1
x
T x y x x
x x
.
Xét hàm số:
1
3 1 ; 1
1
f x x x
x
.
Đạo hàm:
/
2
1
3
1
f x
x
.
/
3
0 1 ( 1)
3
f x x do x
.
Bảng biến thiên.
Do đó:
min
4 2 3
T
.
A.
0,014
B.
0,0495
C.
0,079
D.
0,055
Chọn số tự nhiên có 4 chữ số bất kỳ có:
9.10.10.10 9000
n
(cách).
Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có:
1m n m n
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
Do đó nếu đặt:
1
2
3
x a
y b
z c
t d
Từ giả thuyết
1 9
a b c d
ta suy ra:
1 12
x y z t
(**).
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ
1,2,...,12
ta đều có được duy nhất một
bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số
, , ,a b c d
thoả mãn (*). Số cách chọn tập
con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó:
4
12
495
n A C
.
Vậy:
495
0,055
9000
n A
P A
n
.
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có:
9.10.10.10 9000
n
(cách).
Mỗi tập con có 4 phần tử được lấy từ tập
1, 2,...,9
(trong đó mỗi phần tử có thể được chọn lặp lại nhiều
lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được một số tự nhiên có dạng
abcd
(trong đó
1 9
a b c d
). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử.
Do đó theo công thức tổ hợp lặp ta có:
4
9 4 1
495
n A C
.
Vậy:
495
0,055
9000
n A
P A
n
.
Dạng 6. Một số bài toán khác
Câu 167. Chọn D
Ta có
4 4 2
9 3
1 9 log log
x y
f x f y m x y m m
Đặt
, 0x y t t
. Vì
1 ln 1 ln 0, 0
x y
t
e e x y e et t t t t t
(1)
Xét hàm
ln 1f t t t
với
0t
.
1 1
1 0 0
t
f t t
t t
Bảng biến thiên
Dựa vào bảng biến thiên, ta có
1 , 0
f t f t
1 ln 0, 0t t t
(2)
Từ
1
và
2
ta có
2 2
3
1 log 1 3 3
t m m m
Câu 168. Ta có
3
e e e 3
f a f b f c f a f b f c
e
.
Mặt khác do
0, xf x
nên
f x
là hàm lồi, áp dụng bất đẳng thức lồi ta có
3
3
a b c
f a f b f c f
Do đó
3
3
3 3
e e e 3 3
a b c a b c
f f
f a f b f c
e e
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
Suy ra
2
3
3
3 1
2 3
a b c
f
a b c
P e f
. Đặt
2
, 0
3
a b c
t f t n
Ta có
P g t
với
2
3
3 1
2
t
g t e t
3e 3 1 ; " 3e 3 3 e 1 0, 0.
t t t
g t t g t t
Nên
g t
là hàm nghịch biến trên
0;
.
'( ) (0) 0, 0; ( ) (0)g t g t g t g

Do đó
3
0 7 3e.
2
P g
Câu 169. Ta có
2
ln 2 0
y x x m
, suy ra
2
1;
min
e
y
nhỏ nhất bằng
0
2
ln 2 0
x x m
có nghiệm
2
1;x e
1
.
Đặt
2
ln 2f x x x
. Khi đó
1
f x m
,
2
1;x e
.
Ta có
2
2
1 1 4
4 0, 1;
x
f x x x e
x x
.
BBT
Dựa vào bảng biến thiên suy ra
4
2;2 2
m e
.
Suy ra
2;3;4;5;...;106;107
m
.
Vậy có tất cả
106
số nguyên
m
thỏa mãn yêu cầu bài toán.
Câu 170. Chọn B
Hàm số
( ) 2 2
x x
f x
xác định
x
.
Khi đó
x
, ta có
( ) 2 2 (2 2 ) ( )
x x x x
f x f x
.
Suy ra
( )f x
là hàm số lẻ.
1
Mặt khác
( ) (2 2 )ln2 0
x x
f x
,
x
.
Do đó hàm số
( )f x
đồng biến trên
.
2
Ta có
12
( ) (2 2 ) 0
f m f m
12
(2 2 ) ( )f m f m
.
Theo
1
suy ra
12
(2 2 ) ( )f m f m
.
Theo
2
ta được
12
12 12
2
2 2 3 2
3
m m m m .
Vì
m
nên
0
1365 1365
m m
. Vậy
0
1009;1513
m
.
Câu 171. Xét phương trình hoành độ giao điểm
2
2 2
log 2log 2 1 0
m x x m
.
Ycbt
Phương trình có duy nhất một nghiệm thuộc khoảng
1;

.
Đặt
2
log 0
t x
1;

x
.
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
Phương trình
2
2 2 1 0
mt t m
2
2 1
2
t
m
t
.
Ycbt
Phương trình có duy nhất một nghiệm
0;

t
.
Xét hàm số
2
2 1
2
t
f t
t
trên
0;

.
Ta có
2
2
2 2
2 2
2 2 2 2 1
2 2 4
1 1
t t t
t t
f t
t t
0
f t
2
2 2 4 0
t t
1 0;
2 0;


t
t
.
Bảng biến thiên
Từ bảng biến thiên ta suy ra: ycbt
1 1
;0
2 2
m
.
------------- HẾT -------------
| 1/65
| | Tải xuống

Có thể bạn quan tâm:

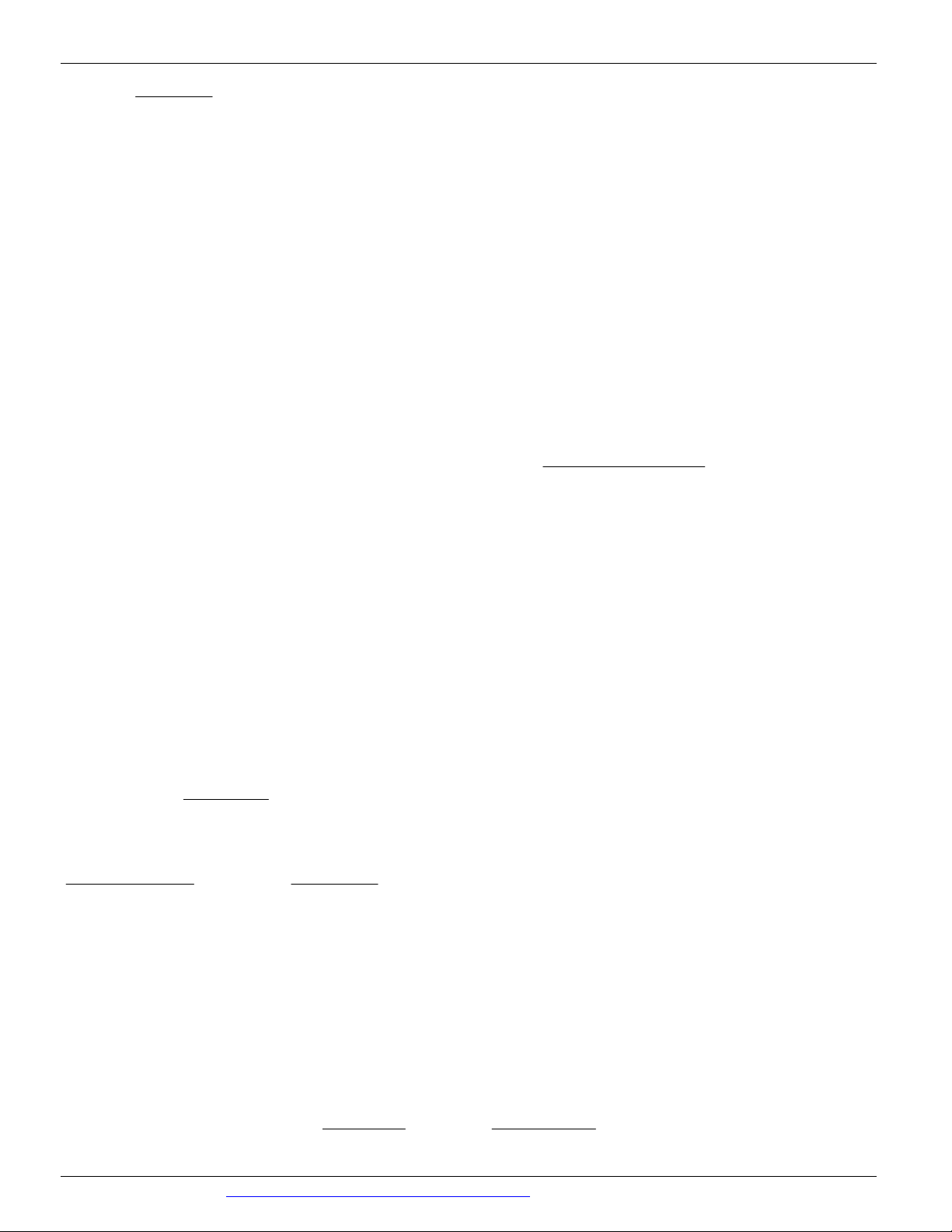
Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 CHUYÊN
HÀM SỐ MŨ, HÀM SỐ LOGARIT ĐỀ 11
VÀ MỘT SỐ BÀI TOÁN LIÊN QUAN MỤC LỤC
PHẦN A. CÂU HỎI ....................................................................................................................................................... 1
Dạng 1. Tìm tập xác định ............................................................................................................................................... 1
Dạng 1.1 Không chứa tham số .................................................................................................................................. 1
Dạng 1.2 Chứa tham số .............................................................................................................................................. 2
Dạng 2. Tìm đạo hàm ..................................................................................................................................................... 4
Dạng 3. Khảo sát hàm số mũ, logarit ............................................................................................................................ 7
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…) .................................................................................................... 16
Dạng 5. Bài toán cực trị ............................................................................................................................................... 21
Dạng 6. Một số bài toán khác ...................................................................................................................................... 24
PHẦN B. ĐÁP ÁN THAM KHẢO ............................................................................................................................. 25
Dạng 1. Tìm tập xác định ............................................................................................................................................. 25
Dạng 1.1 Không chứa tham số ................................................................................................................................ 25
Dạng 2. Chứa tham số .............................................................................................................................................. 26
Dạng 2. Tìm đạo hàm ................................................................................................................................................... 29
Dạng 3. Khảo sát hàm số mũ, logarit .......................................................................................................................... 32
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…) .................................................................................................... 41
Dạng 5. Bài toán cực trị ............................................................................................................................................... 53
Dạng 6. Một số bài toán khác ...................................................................................................................................... 63 PHẦN A. CÂU HỎI
Dạng 1. Tìm tập xác định
Dạng 1.1 Không chứa tham số x  3
Câu 1. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm tập xác định D của hàm số y  log . 5 x  2
A. D  (; 2)  (3; )
B. D  (2; 3)
C. D  (; 2)  [3; ) D. D   \{2}
Câu 2. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm tập xác định D của hàm số y  log  2
x  2x  3 2  A. D   ;    1 3;  B. D   1  ;  3 C. D   ;    1 3; D. D   1  ;  3
Câu 3. (MĐ 104 BGD&DT NĂM 2017) Tìm tập xác định D của hàm số y  log  2
x  4x  3 . 3 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. D  1;3 B. D   
;1  3;  C. D   ;
 2  2  2  2; . D. D  2  2  ;1  3;2  2
Câu 4. (GKI THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019) Tìm tập xác định của hàm số y  log  2 3x x . 2018  A. D  
B. D  0;   C. D   ;  0  3;   D. D  0; 3
Câu 5. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Tập xác định của y   2
ln x  5x  6 là A. 2;  3 B. 2; 3 C.  ;
 23;   D.  ;
 2 3;  
Câu 6. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Tìm tập xác định của hàm số 1 y  log . 5 6  x A.  ;  6 B.  C. 0; D. 6;
Câu 7. (THPT LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 1) Tập xác định của hàm số y  log  2
3  2x x là 2  A. D  (1;1) . B. D  (1; 3) . C. D  (3;1) .
D. D  (0;1) .
Câu 8. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Tập xác định của hàm số y  log  2
x  2x  3 là 2  A. 1;3 . B. 1;  3 . C. ; 
1  3;   . D. ;   1  3;   .
Câu 9. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Tìm tập xác định của hàm số: x y  2  log3 x A. 0;   . B. 0;  3 . C.  ;   3 . D. 0;   3 .
Câu 10. (CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Tập xác định của hàm số 
y  ln  x  2   là A.  . B. 3;  . C. 0;  . D. 2;  .
Câu 11. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Tìm tập xác định D của hàm số  y  log
4  x  2x 3 2019 2 . 2019  3   3   3   3  A. D  2;  ; 2    . B. D  2;  ; 2     . 2 2       2   2   3  C. D  ; 2   . D. D   2  ; 2 .  2  0
Câu 12. Tìm tập xác định của hàm số y   x  2  log  2 9  x là 2  A. D  2;  3 . B. D   3  ;  3 \   2 .
C. D  3;.. D. D   3  ;  3 ..
Dạng 1.2 Chứa tham số
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 13. (MĐ 105 BGD&ĐT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để hàm số y   2
log x  2x m  1 có tập xác định là  . A. m  2 B. m  2 C. m  0 D. m  0
Câu 14. (MĐ 104 BGD&DT NĂM 2017) Tìm tất cả các giá trị thực của tham số m để hàm số y   2
ln x  2x m  
1 có tập xác định là .
A. 0  m  3 B. m  1
 hoặc m  0 C. m  0 D. m  0
Câu 15. Hàm số y   2
ln x mx  
1 xác định với mọi giá trị của x khi. m  2 A.  . B. m  2 . C. 2   m  2 . D. m  2 . m  2 
Câu 16. (THPT CẨM GIÀNG 2 NĂM 2018-2019) Tìm tất cả các giá trị của tham số m để hàm số 1 y
xác định trên khoảng 0;  2
m log x  4 log x m  3 3 3
A. m  ; 4  1;  .
B. m  1;   . C. m  4;  1 .
D. m  1;   .
Câu 17. (ĐỀ 15 LOVE BOOK NĂM 2018-2019) Tìm tất cả các giá trị của m để hàm số y   2
ln x mx  2m  
1 xác định với mọi x  1; 2 . 1 3 3 1 A. m   . B. m  . C. m  . D. m   . 3 4 4 3
Câu 18. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Tìm tất cả các giá trị thực của
tham số m để hàm số 2
y  log(x  4x m 1) có tập xác định là  . A. m  4  . B. m  0 . C. m  4  . D. m  3  .
Câu 19. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Có bao nhiêu giá trị nguyên của tham số m trên  2018 
; 2018 để hàm số y   2
ln x  2x m  
1 có tập xác định là  ? A. 2019 B. 2017 C. 2018 D. 1009
Câu 20. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Tìm tất cả các giá trị thực của tham số m để hàm số y   2
log x  2mx  4 có tập xác định là  . m  2 A. 2   m  2 . B. m  2 . C.  . D. 2   m  2 . m  2    1 
Câu 21. Số các giá trị nguyên của tham số m để hàm số y  log mx m  2 xác định trên ;  là    2  A. 4 B. 5 C. Vô số D. 3
Câu 22. (KTNL GIA BÌNH NĂM 2018-2019) Tìm tất cả các giá trị của m để hàm số 2  xy  log
 2018x x
m xác định với mọi giá trị x thuộc 0;  2018   2  A. m  9 B. m  1 C. 0  m  1 D. m  2 Câu 23. Hàm số  log 4x  2x y
m có tập xác định là  thì 2   1 1 1 A. m  . B. m  0 . C. m  . D. m  . 4 4 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 24. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Tập hợp tất cả các giá trị của tham số m để 3x  5 hàm số y
xác định với mọi x   là log  2 2
x  2x m  4m  5 2018  A.   ;1  3;  . B. (1;3) \   2 . C.  ;   1 . D. 1;  3 \   2 .
Câu 25. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Có bao nhiêu giá trị nguyên của tham số 2   m để hàm số  log  2017x x yx
m 1 xác định với mọi x thuộc 0;   ? 2018  2   A. 1. B. 2 . C. 2018 . D. Vô số.
Câu 26. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Có tất cả bao nhiêu giá 1
trị nguyên dương của tham số m để hàm số y   log
x m xác định trên khoảng 2;3 ? 3 2m 1 x A. 1. B. 2 . C. 4 . D. 3 .
Dạng 2. Tìm đạo hàm
Câu 27. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm đạo hàm của hàm số y  log x . ln10 1 1 1 A. y  B. y  C. y  D. y  x x ln10 10 ln x x 2
Câu 28. (Mã 103 - BGD - 2019) Hàm số 2x x y   có đạo hàm là 2 2 2 2
A. 2x x.ln 2 . B. (2 1).2x . x x   ln 2 . C. 2 1 ( ).2x x x x    . D. (2 1).2x x x   . 2
Câu 29. (Mã đề 104 - BGD - 2019) Hàm số 3x x y   có đạo hàm là 2 A.   2 2 1 .3x x x   . B.   2 2 1 .3x x x x    . C.   2 2 1 .3x . x x  
ln 3 . D. 3x  . x ln 3.
Câu 30. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính đạo hàm của hàm số 13x y 13x A. y  B. 1 .13x y x    C. 13x y  ln13 D. 13x y  ln13
Câu 31. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tính đạo hàm của hàm số y  log 2x 1 . 2   2 1 2 1 A. y  B. y  C. y  D. y  2x   1 ln 2 2x   1 ln 2 2x 1 2x 1 x 1
Câu 32. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tính đạo hàm của hàm số y 4x 1 2 x   1 ln 2 1 2  x   1 ln 2 1  2  x   1 ln 2 1  2  x   1 ln 2 A. y '  B. y '  C. y '  D. y '  2 2 x 2 2 x 2 2 2x 2x
Câu 33. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Hàm số f x  log  2
x  2x có đạo hàm 2  ln 2 1
A. f ' x 
B. f ' x  2 x  2x  2 x  2xln 2 2x  2ln 2 2x  2
C. f ' x 
D. f ' x  2 x  2x  2 x  2xln 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2
Câu 34. (Mã đề 101 - BGD - 2019) Hàm số 3 2x x y   có đạo hàm là 2 A.   2x 3 2 3 2 x x   ln 2 . B. x 3 2 x ln 2 . C.   2 3 2 3 2x x x   . D.   2 2 3 1 3 2x x x x    . 2
Câu 35. (Mã 102 - BGD - 2019) Hàm số 3 3x x y   có đạo hàm là 2 A.   2 3 2 3 .3x x x   . B. x 3 3 . x ln 3 . C.   2 2 3 1 3 .3x x x x    . D.   2x 3 2 3 .3 x x   .ln 3 .
Câu 36. Tính đạo hàm của hàm số y = ln 1+ x +1 . 1 2 A. y  B. y 
x 1 1 x 1
x 1 1 x 1 1 1 C. y  D. y 
2 x 1 1 x 1 1 x 1 ln x
Câu 37. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số y
, mệnh đề nào dưới đây đúng? x 1 1 1 1
A. 2 y  xy   .
B. y  xy  .
C. y  xy   .
D. 2 y  xy  . 2 x 2 x 2 x 2 x
Câu 38. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Đạo hàm của hàm số 1 2 x y e   là 12 x e A. 1 2 2 x y e    B. 1 2 2 x y e     C. y   D. 1 2 x y e    2
Câu 39. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Đạo hàm của hàm số y  log  2
x x 1 là: 3  2x   1 ln 3 2x 1 2x  1 1 A. y '  B. y '  C. y '  D. y '  2 x x  1  2 x x   1 ln 3 2 x x  1  2 x x   1 ln 3
Câu 40. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Tính đạo hàm của hàm số 2 x x y e   . A. 2   1 x x e B.   2 2 1 x x x e   C.   2 1 2 1 x x e   D.  2 x x  2x 1 e  
Câu 41. (THPT HÙNG VƯƠNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 01) Cho hàm số
f x  log  2
x 1 , tính f    1 2  1 1 1 A f   1  1. B. f   1  . C. f   1  . D. f   1  . 2 ln 2 2 ln 2
Câu 42. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Tìm đạo hàm của hàm số   2 ln 1 x ye  . 2 2 xe 2 x e 1 2 2 x e A. y  . B. y  . C. y  . D. y  .  x 2 x 2 x 2 x e  2 2 1 e 1 e 1 e 1
Câu 43. (CHUYEN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 02) Tính đạo hàm của hàm số 1 x y 2x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2  x ln 2. x   1 1 x  2 ln 2. x   1 1 A. y  . B. y  C. y  . D. y  . 2x 2x 2 2x 2x
Câu 44. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Tính đạo hàm của hàm số y  log  2 x 1 . 9  1 x 2x ln 9 2 ln 3 A. y  . B. y  . C. y  . D. y  .  2 x   1 ln 9  2 x   1 ln 3 2 x 1 2 x 1
Câu 45. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Tính đạo hàm hàm số x
y e .sin 2x A. x
e sin 2x  cos 2x . B. x e .cos 2x . C. x
e sin 2x  cos 2x . D. x
e sin 2x  2 cos 2x . x 1
Câu 46. (ĐỀ THI THỬ VTED 03 NĂM HỌC 2018 - 2019) Đạo hàm của hàm số y  là 4x 1 2 x   1 ln 2 1 2 x   1 ln 2 1 2  x   1 ln 2 1 2  x   1 ln 2 A. B. C. D. 2 2 x 2 2 x 2 2 2x 2x
Câu 47. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số   2 x x f x e   . Biết phương
trình f  x  0 có hai nghiệm x , x . Tính x .x . 1 2 1 2 1 3 A. x .x   B. x .x  1 C. x .x  D. x .x  0 1 2 4 1 2 1 2 4 1 2
Câu 48. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Cho hàm y x cos ln x  s in ln x   .
Khẳng định nào sau đây đúng? A. 2
x y  xy  2 y  4  0 . B. 2
x y  xy  2xy  0 . C. 2
2x y  xy  2 y  5  0 . D. 2
x y  xy  2 y  0 .
Câu 49. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Tính đạo hàm của hàm số y  log x , x   0 . 2019 1 1 1 A. y  . B. y  . C. y  .
D. y  x ln 2019 . x ln 2019 x x ln 2019 1
Câu 50. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Cho hàm số y x 1 ln x y '
với x  0 . Khi đó  bằng 2 y x 1 x x 1 A. . B. 1 . C. . D. . x 1 x 1 x  ln x 1 x  ln x
Câu 51. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Tính đạo hàm của hàm số x 1 y  2 ln x  . x e x  1  1 x 1 A. y  2
 ln 2ln x   x   . B. y  2 ln 2   e .  x  ex x x 1 x 1 1 C. y  2 ln 2  . D. x y  2 ln 2   e . x x e x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 52. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Tập xác định của hàm số y  log log log log x
là D  a;  . Giá trị của a bằng 2020  2019  2018  2017  A. 2019 2018 . B. 2020 2019 . C. 2018 2017 . D. 0 .
Câu 53. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Đạo hàm của hàm số 2
f (x)  log x  2x là 2 2x  2 1 (2x  2) ln 2 2x  2 A. B. C. D.  2 x  2xln 2  2 x  2xln 2 2 x  2x 2 x  2x ln 2
Câu 54. (CHUYÊN KHTN LẦN 2 NĂM 2018-2019) Đạo hàm của hàm số f (x)  ln(lnx) là: 1 1 A. f (  x)  . B. f (  x) 
x ln x ln ln x 2 ln ln x 1 1 C. f (  x)  . D. f (  x)  . 2 x lnx ln ln x lnx ln ln xCâu 55. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hàm số  x
f x  ln 2018  ln 
 . Tính S f ' 
1  f '2  f '3  f '2017.  x 1  4035 2017 2016 A. S  B. S  C. S  D. S  2017 2018 2018 2017
Câu 56. (SỞ GIÁO DỤC ĐÀO TẠO VĨNH PHÚC NĂM 2018 - 2019 LẦN 01) Cho hàm số 2018x
f x  ln
. Tính tổng S f  
1  f 2  ... f 2018 . x 1 2018 A. ln 2018 . B. 1. C. 2018 . D. . 2019
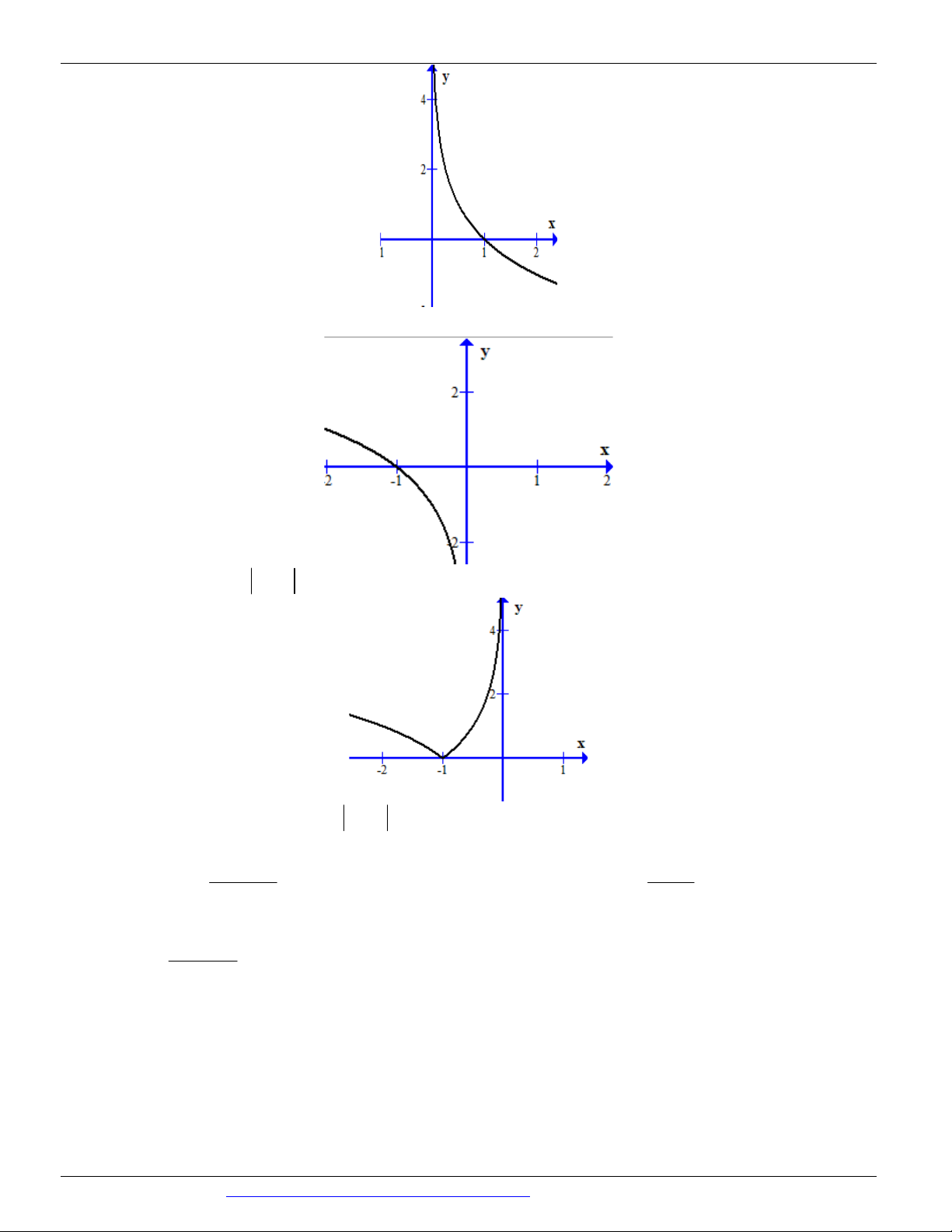
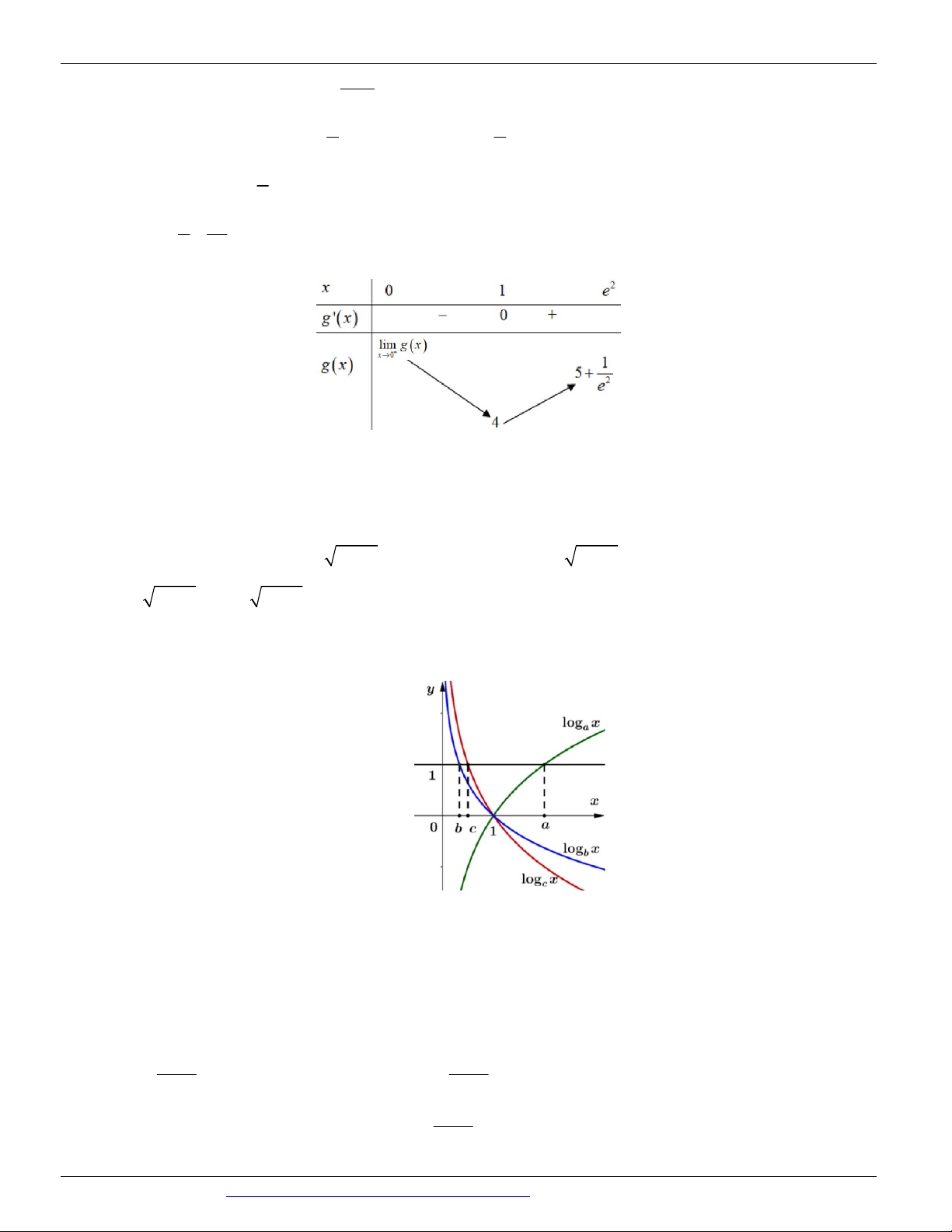
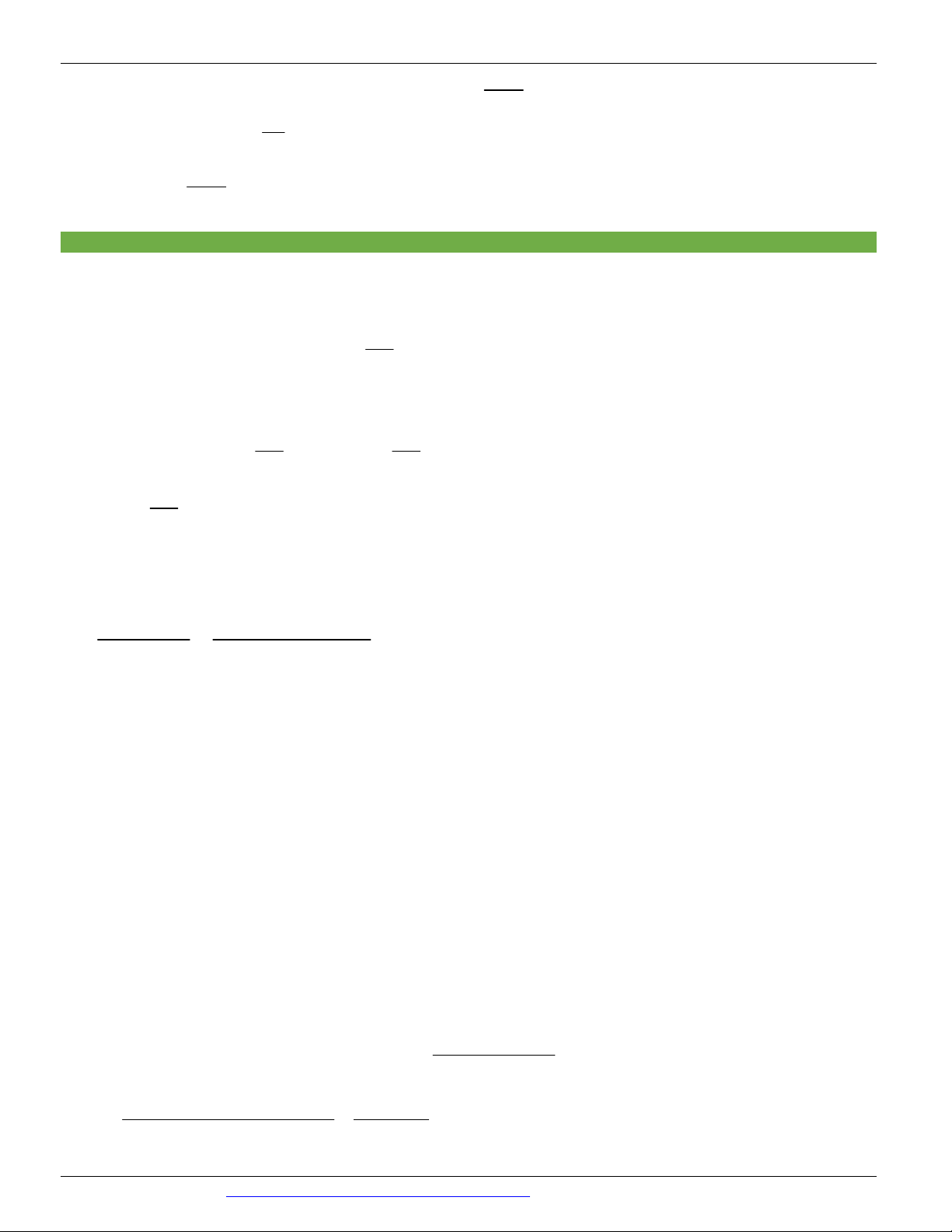
Câu 57. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số f x  x ln x . Một trong bốn đồ thị cho
trong bốn phương án A, B, C, D dưới đây là đồ thị của hàm số y f  x . Tìm đồ thị đó? A. Hình 2 B. Hình 3 C. Hình 4 D. Hình 1
Dạng 3. Khảo sát hàm số mũ, logarit
Câu 58. Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số   2 y ln x  
1  mx  1 đồng biến trên khoảng  ;   A. 1; B.  ;    1 C. 1;  1 D.  ;    1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
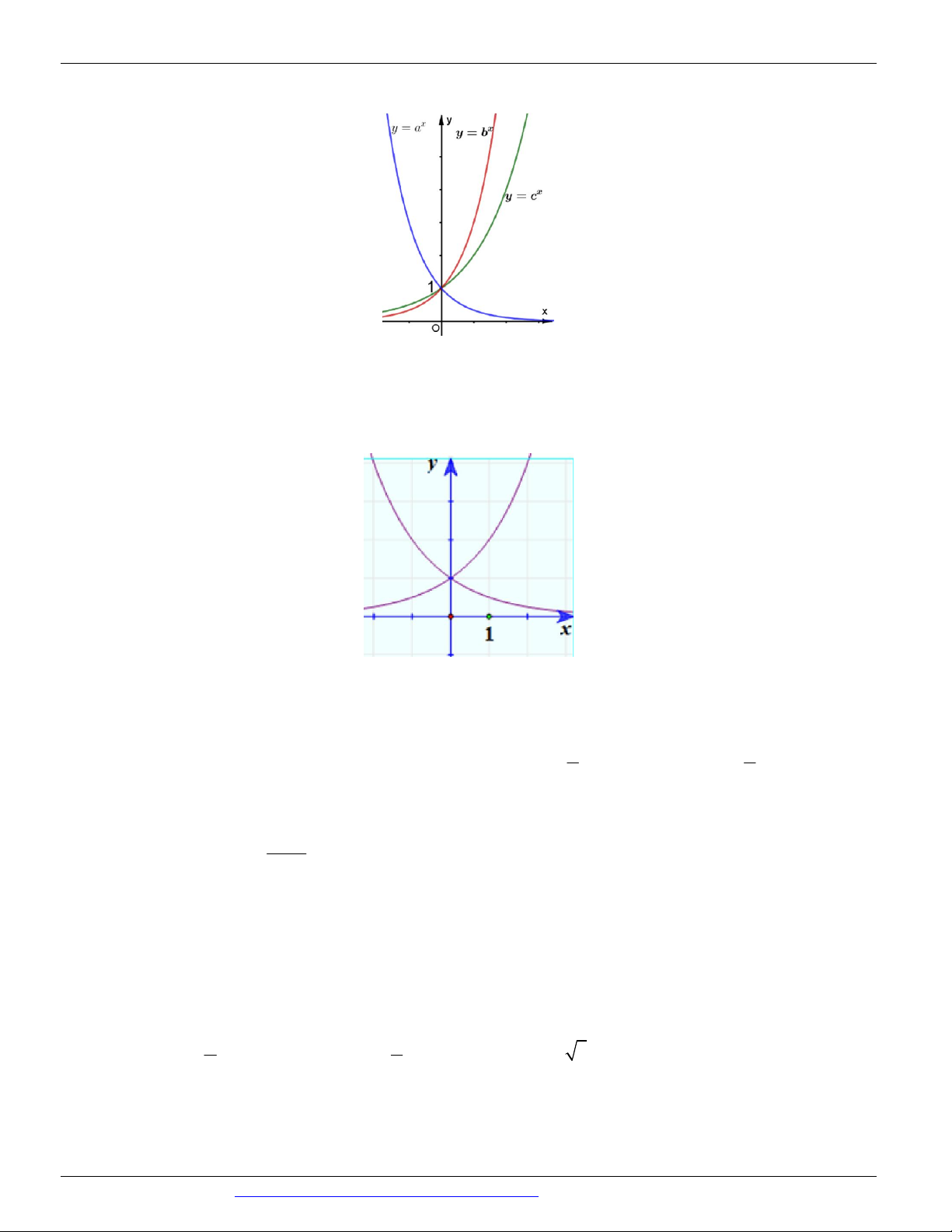
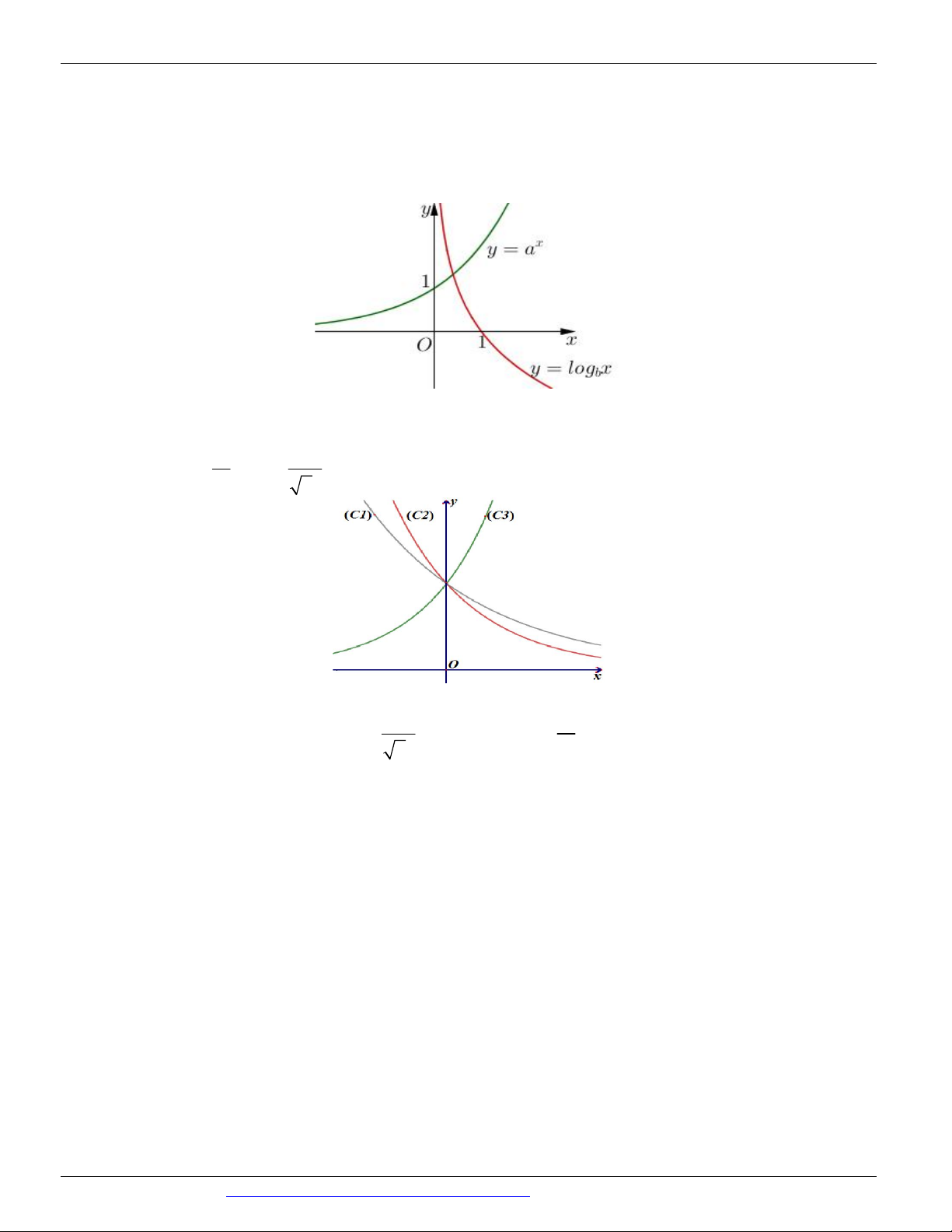
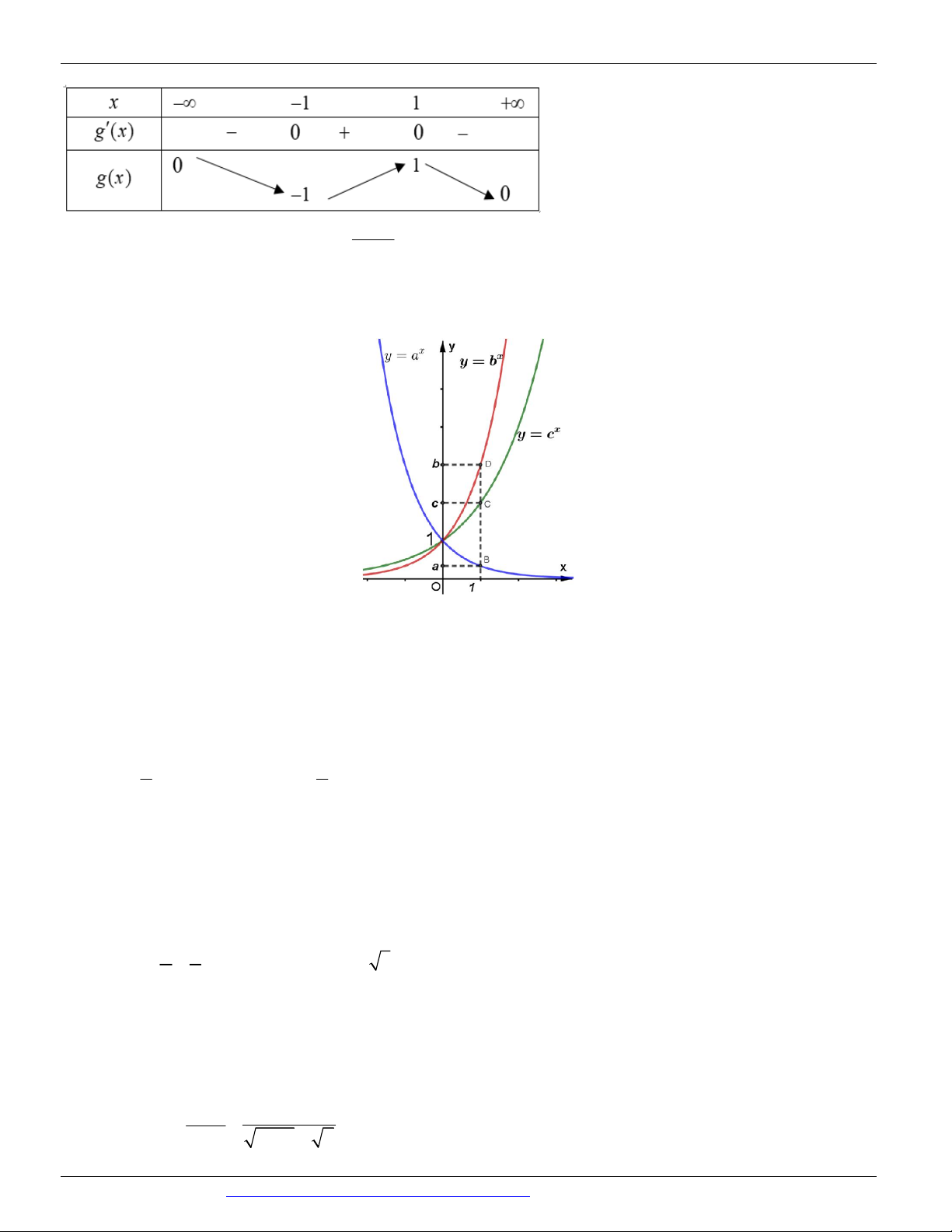
Câu 59. Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số x  , x  , x y a y
b y c được cho trong hình vẽ bên
Mệnh đề nào dưới đây đúng?
A. b c a
B. c a b
C. a b c
D. a c b x x
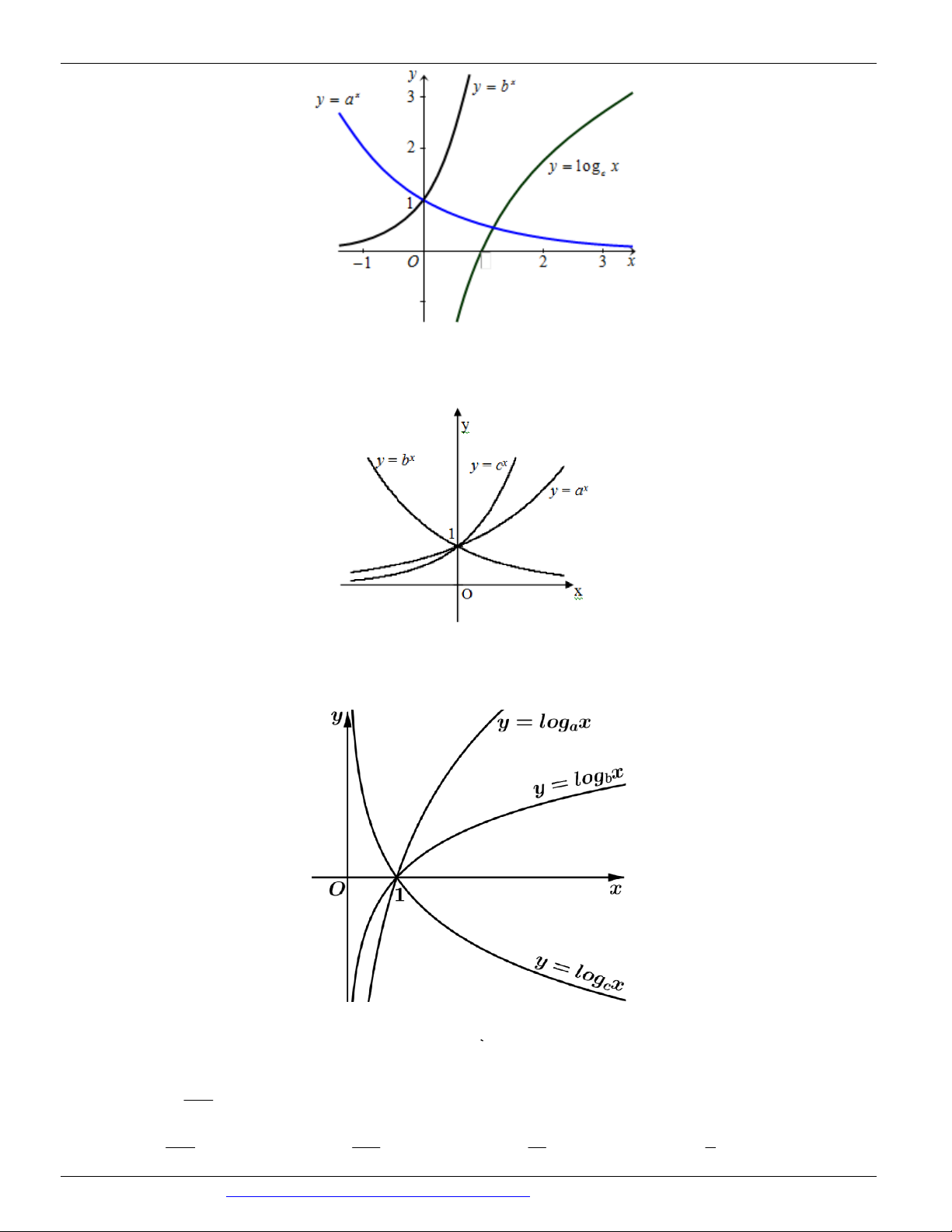
Câu 60. (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y a , y b với a, b là hai số thực dương khác
1, lần lượt có đồ thị là C và C
như hình bên. Mệnh đề nào dưới đây đúng ? 2  1  C2  C1 O
A. 0  b  1  a
B. 0  a b  1
C. 0  b a  1
D. 0  a  1  b
Câu 61. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Trong các hàm số sau hàm số nào
nghịch biến trên  ? xx  e   2  A. 2 log x B. y   3 log x  C. y  D. y  3      4   5 
Câu 62. Mệnh đề nào trong các mệnh đề dưới đây sai? 2 x 1   2018  A. Hàm số y    đồng biến trên  .   
B. Hàm số y  log x đồng biến trên 0;  .
C. Hàm số y  ln x nghịch biến trên khoảng  ;  0 . D. Hàm số 2x y  đồng biến trên  .
Câu 63. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Hàm số nào dưới đây đồng biến trên tập xác định của nó? x x  1   2  x x A. y    B. y    C. y   3 D. y  0,5  π   3 
Câu 64. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho hàm số y  log x . Mệnh đề nào 2 dưới đây sai?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1
A. Đạo hàm của hàm số là y  x ln 2
B. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
C. Tập xác định của hàm số là ; 
D. Hàm số đồng biến trên khoảng 0; 
Câu 65. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Trong các hàm số sau, hàm số
nào luôn đồng biến trên  ? x x  2015   3  A. y    B. y    C. 2 x y  (0,1) D. 2 (2016) x y   2016   2016  2 
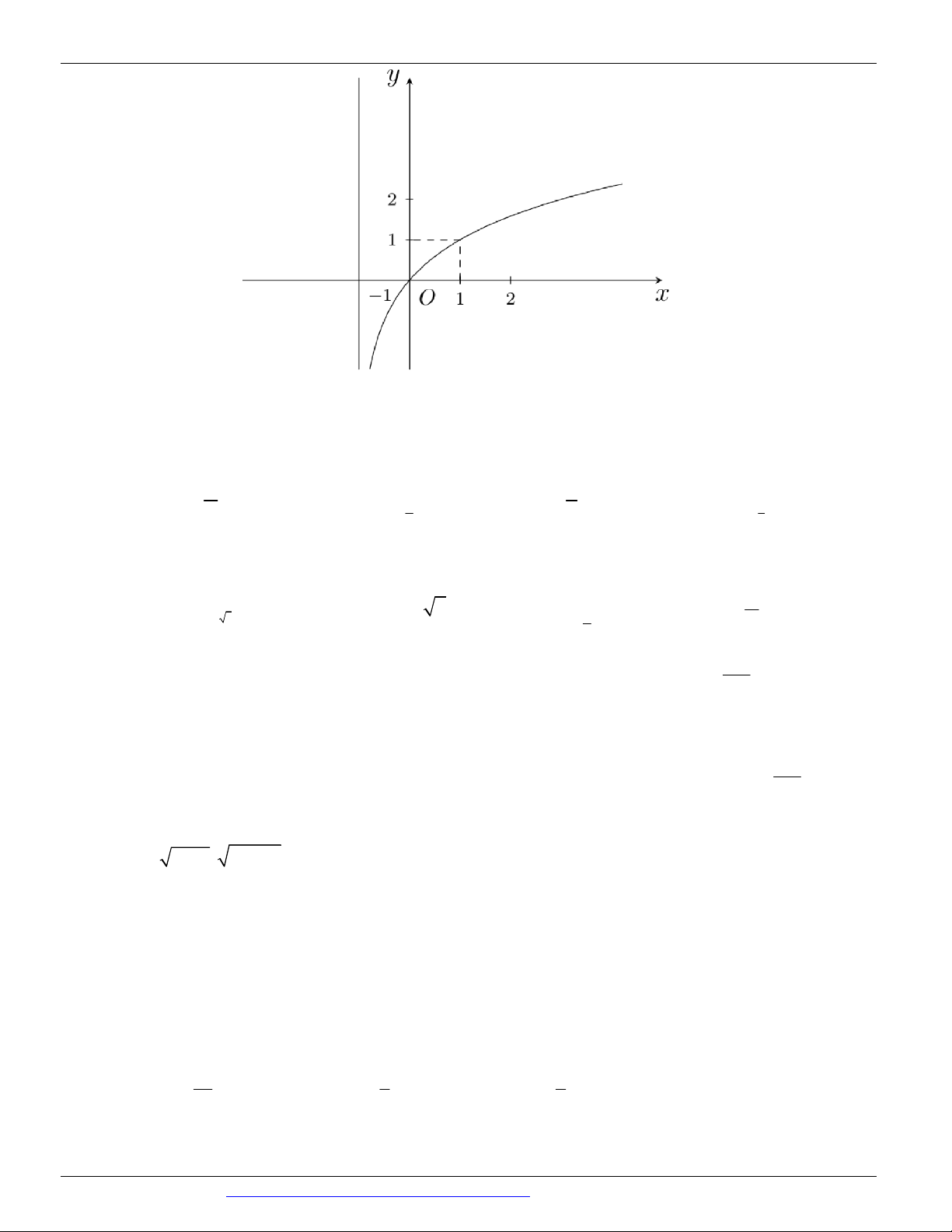
Câu 66. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. ex y   . B. y  ln x . C. y  ln x . D. ex y  .
Câu 67. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Tìm hàm số đồng biến trên  . x  1  3 A.   3x f x  . B.   3 x f x   .
C. f x    .
D. f x  .  3  3x
Câu 68. (CHUYÊN BẮC NINH NĂM 2018-2019 LẦN 03) Cho hàm số y  log
x . Mệnh đề nào dưới 5
đây là mệnh đề sai?
A. Hàm số đã cho đồng biến trên tập xác định.
B. Hàm số đã cho có tập xác định D  \  0 .
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục tung.
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
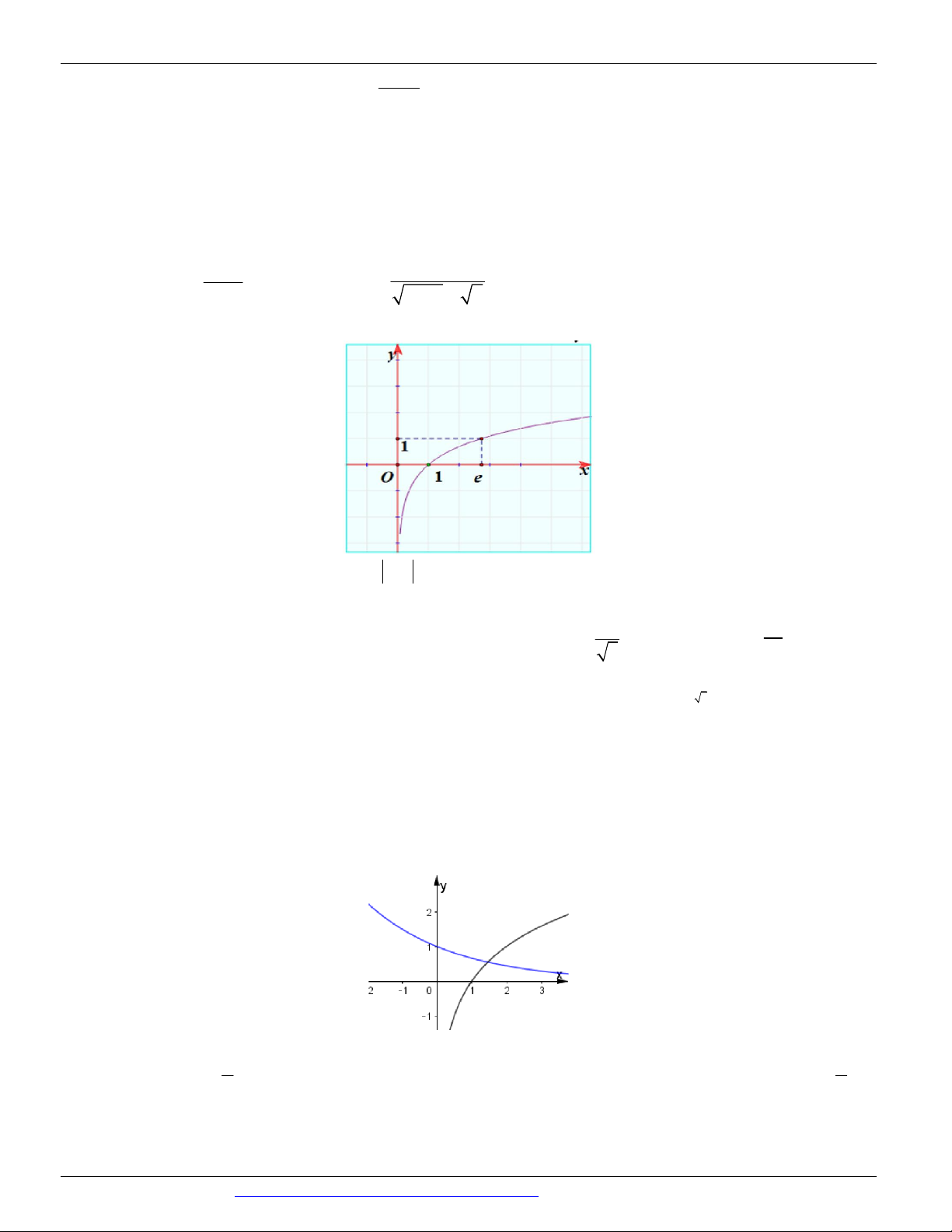
Câu 69. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Cho đồ thị hàm số x
y a và y  log x b như hình vẽ.
Khẳng định nào sau đây đúng? 1 1 A. 0  a   b .
B. 0  a  1  b .
C. 0  b  1  a .
D. 0  a  1, 0  b  . 2 2
Câu 70. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Trong các hàm số sau, hàm
số nào nghịch biến?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. y  ln . x B. y  log x C. y  log x. D. y  log x.  4  3 2018 1 2019
Câu 71. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Đồ thị hàm số y  ln x đi qua điểm A. 1; 0 . B.  2 2; e  . C. 2e; 2 . D. 0;1 .
Câu 72. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Trong các hàm số
sau,hàm số nào luôn nghịch biến trên tập xác định của nó? 2 x  1   2  A. y    .
B. y  log x . C. 2x y  . D. y    .  2   3 
Câu 73. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Chọn khẳng định sai
trong các khẳng định sau:
A. Hàm số y  log x đồng biến trên  . 2
B. Hàm số y  log x nghịch biến trên tập xác định của nó. 1 2 C. Hàm số 2x y  đồng biến trên  . D. Hàm số 2 y x
có tập xác định là 0;  .
Câu 74. (KTNL GV BẮC GIANG NĂM 2018-2019) Hàm số nào dưới đây đồng biến trên khoảng (0;  ) ? A. y  log x .
B. y  log x .
C. y  log x .
D. y  log x . 3  e 1 6 3 4
Câu 75. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Trong các mệnh
đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số 2x y
và y  log x đối xứng với nhau qua đường thẳng y  x . 2
B. Đồ thị của hai hàm số x
y e và y  ln x đối xứng với nhau qua đường thẳng y x . 1
C. Đồ thị của hai hàm số 2x y  và hàm số y
đối xứng với nhau qua trục hoành. 2x 1
D. Đồ thị của hai hàm số y  log x và y  log
đối xứng với nhau qua trục tung. 2 2 x
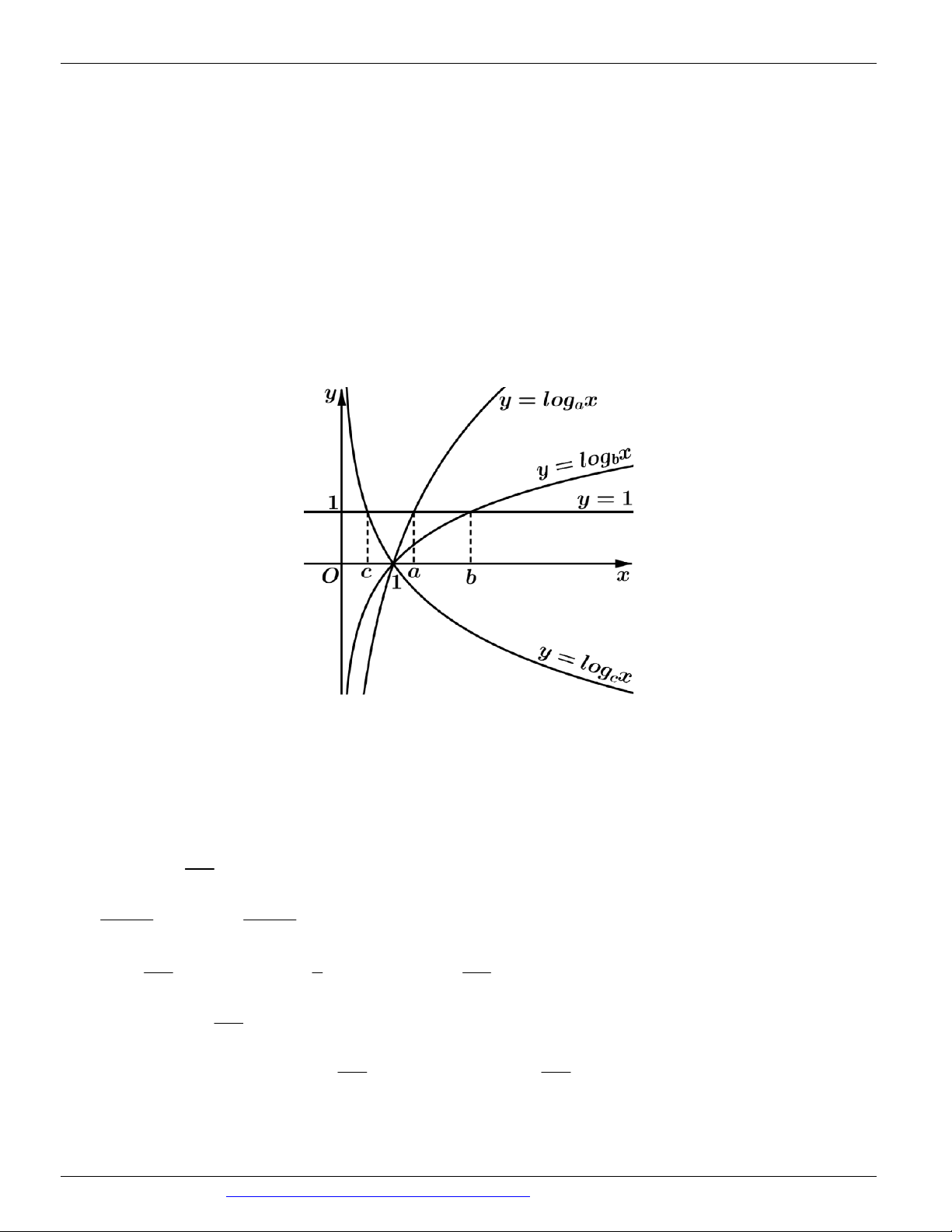
Câu 76. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Trong hình dưới đây, điểm B là trung
điểm của đoạn thẳng AC . Khẳng định nào sau đây là đúng?
A. a c  2b . B. 2 ac b . C. 2 ac  2b . D. ac b .
Câu 77. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Hàm số nào sau đây có đồ thị như hình bên?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. y  log x .
B. y  log x 1. C. y  log x 1 . D. y  log x 1 3   2   3 2
Câu 78. (CHUYÊN QUỐC HỌC HUẾ NĂM 2018-2019 LẦN 1) Trong các hàm số dưới đây, hàm số nào
nghịch biến trên tập số thực R . x x     2  A. y  2  
B. y  log 2x   1 C. D. y  log x y    2  3  e 4   3
Câu 79. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x    A. y  log x B. y  log x 1 C. y  log x D. y  2   3     3  4 3x
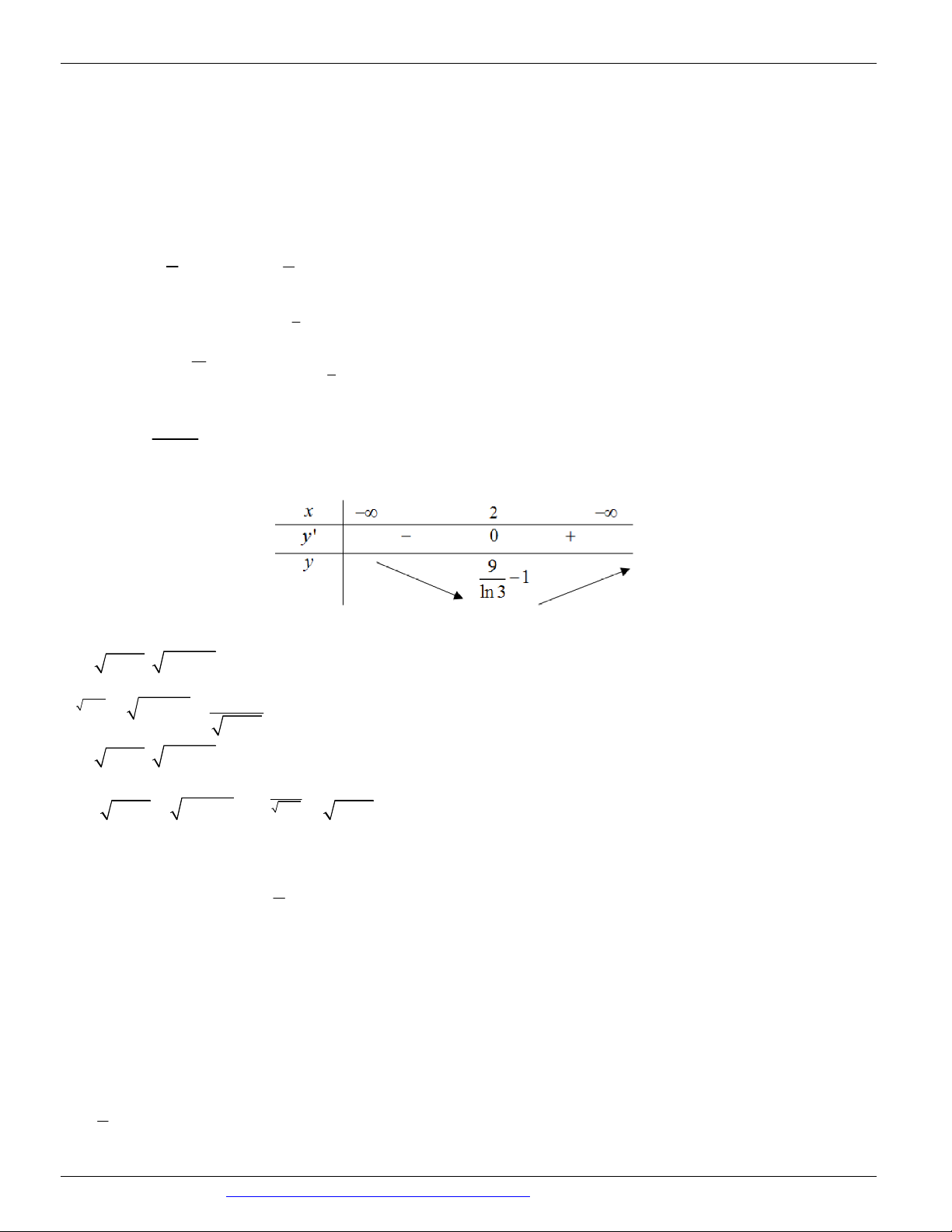
Câu 80. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Cho hàm số y   9x 17 . Mệnh ln 3
đề nào sau đây sai?
A. Hàm số nghịch biến trên khoảng  ;  0
B. Hàm số đồng biến trên khoảng 0;  9
C. Hàm số đạt cực trị tại x  2
D. Hàm số có giá trị cực tiểu là y  1 ln 3
Câu 81. Cho các số thực a, b sao cho 0  a, b  1 , biết rằng đồ thị các hàm số x
y a và y  log x cắt nhau b tại điểm M  5 1
2018; 2019 . Mệnh đề nào dưới đây đúng?
A. a  1, b  1
B. a  1, 0  b  1
C. 0  a  1, b  1
D. 0  a  1, 0  b  1
Câu 82. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Đồ thị  L của hàm số
f x  ln x cắt trục hoành tại điểm A , tiếp tuyến của  L tại A có phương trình là:
A. y  2x 1 B. y x 1 C. y  3x
D. y  4x  3
Câu 83. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Hàm số 3x y xe  đạt cực đại tại 1 1 1 A. x  . B. x  . C. x  . D. x  0 . 3e 3 e
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
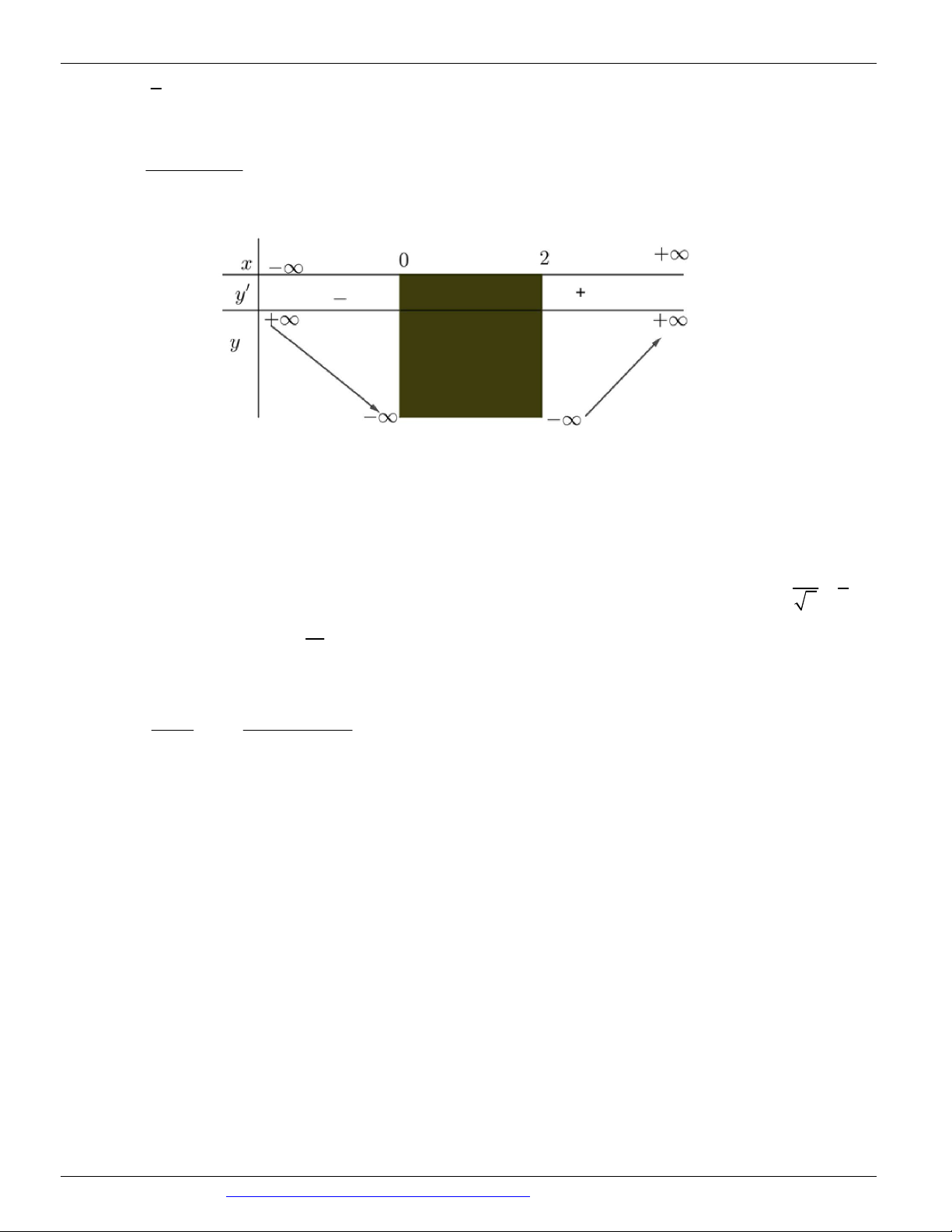
Câu 84. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Hàm số y  log  2
x  2x nghịch 3  biến trên khoảng nào? A. 2;   . B. ;0 . C. 1;   . D. 0  ;1 .
Câu 85. (HỌC MÃI NĂM 2018-2019-LẦN 02) Cho đồ thị hàm số x
y a và y  log x như hình vẽ. Trong b
các khẳng định sau, đâu là khẳng định đúng
A. 0  a  1, 0  b  1 .
B. a  1,b  1 .
C. 0  b  1  a .
D. 0  a  1  b .
Câu 86. (TT HOÀNG HOA THÁM - 2018-2019) Hình vẽ bên thể hiện đồ thị của ba trong bốn hàm số 1 1 6x y  , 8x y  , y  và y  . 5x x 7
Hỏi (C2) là đồ thị hàm số nào? 1 1 A. 6x y  . B. y  . C. y  . D. 8x y x 7 5x
Câu 87. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Tập tất cả các giá trị của tham số m để hàm số y   2 ln x  
1  mx  1 đồng biến trên  là A.  1   ;1 . B.  ;    1 . C.  1   ;1 . D.  ;    1 .
Câu 88. (THPT ĐÔNG SƠN THANH HÓA NĂM 2018-2019 LẦN 02) Trong hình vẽ bên có đồ thị các hàm số x y a , x
y b , y  log x . Hãy chọn mệnh đề đúng trong các mệnh đề sau đây? c
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. a c b .
B. c a b .
C. a b c .
D. b c a .
Câu 89. (GKI CS2 LƯƠNG THẾ VINH HÀ NỘI NĂM 2018-2019 LẦN 01) Cho đồ thị của ba hàm số x  , x  , x y a y b
y c như hình vẽ bên. Khẳng định nào sau đây đúng?
A. b a c .
B. a c b .
C. c a b .
D. c b a .
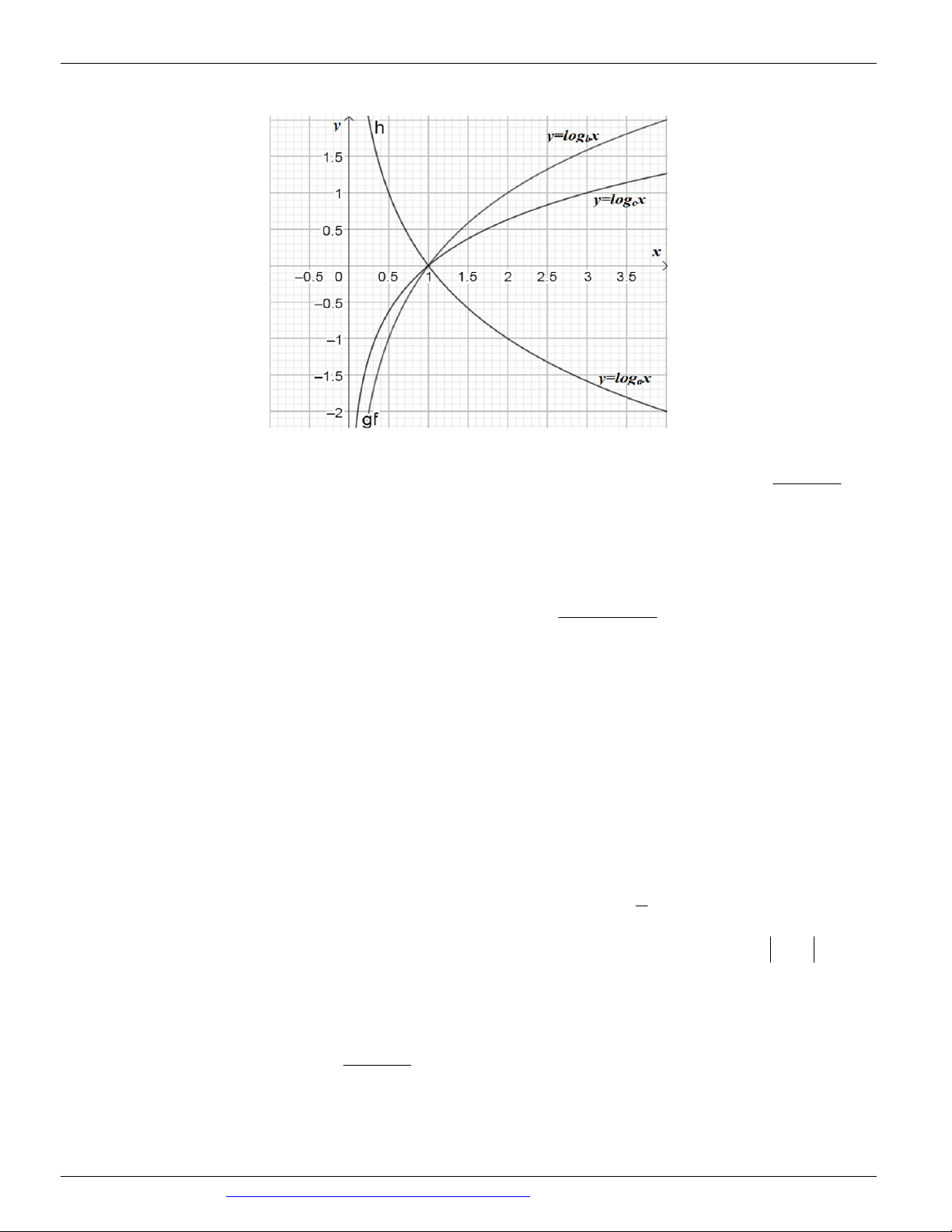
Câu 90. (KTNL GV THPT LÝ THÁI TỔ NĂM 2018-2019) Cho a, b, c là các số thực dương khác 1. Hình
vẽ bên là đồ thị của ba hàm số y  log , x y  log ,
x y  log x . a b c
Khẳng định nào sau đây là đúng?
A. a c b .
B. a b c .
C. c b a .
D. c a b .
Câu 91. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Giá trị nhỏ nhất ln x của hàm số y  trên đoạn 2;  3 bằng x ln 2 ln 3 3 1 A. . B. . C. . D. . 2 3 2 e e
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
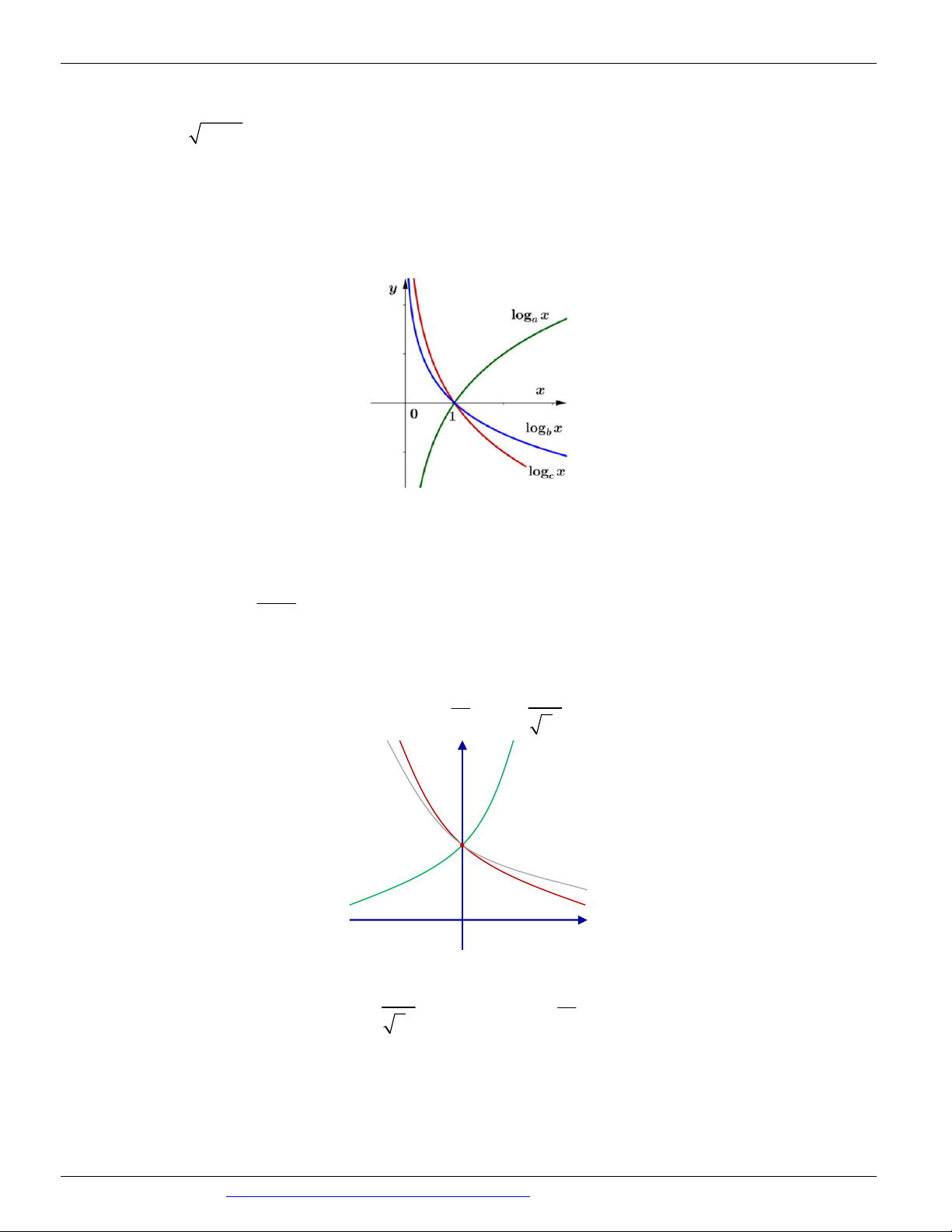
Câu 92. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Cho a, ,
b c là các số thực dương khác 1. Hình
vẽ bên là đồ thị hàm số y  log x, y y  log x, y  log x . Khẳng định nào sau đây là đúng? a b c
A. a b c .
B. a c b .
C. b a c .
D. b a c . ln x  6
Câu 93. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Cho hàm số y  với ln x  2m
m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng 1; e .
Tìm số phần tử của S . A. 3 B. 1 C. 2 D. 4 m log x  2
Câu 94. Tìm tất cả các giá trị thực của tham số m để hàm số 2 y
nghịch biến trên 4;  log x m 1 2 A. m  2  hoặc m  1. B. m  2  hoặc m  1. C. m  2  hoặc m  1. D. m  2  .
Câu 95. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Cho hàm số f x  ln x x . Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0  ;1 .
B. Hàm số đồng biến trên khoảng 0; .
C. Hàm số đồng biến trên các khoảng  ;  0 và 1; .
D. Hàm số đồng biến trên khoảng 1;  .  1 
Câu 96. (HSG BẮC NINH NĂM 2018-2019) Cho hàm số y  log
có đồ thị C và hàm số 1  2018    x
y f x có đồ thị C . Biết C và C đối xứng nhanh qua gốc tọa độ. Hỏi hàm số y f x nghịch 2  1  2 
biến trên khoảng nào dưới đây? A. 0  ;1 B. 1;0 C.  ;    1 D. 1; 
Câu 97. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Có bao nhiêu giá trị nguyên của tham ln x  6
số m 2019; 2019 để hàm số y
đồng biến trên khoảng  6 1;e  ? ln x  3m A. 2020 . B. 2021. C. 2018 . D. 2019 .
Câu 98. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Có bao nhiêu giá trị nguyên của tham số thực
m thuộc đoạn  2  018;201 
8 để hàm số y f x   x  
1 ln x  2  mx đồng biến trên khoảng  2 0;e  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 A. 2016 . B. 2022 . C. 2014 . D. 2023. Câu 99. (THPT QUANG TRUNG ĐỐNG ĐA HÀ NỘI NĂM 2018-2019) Cho
f x   a  2 ln x
x  1   b sin x  6 với a,b   .
Biết rằng f loglog e  2 . Tính giá trị của f log ln10 . A. 10 . B. 2. C. 4. D. 8 .
Câu 100. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Cho a, b, c dương và khác 1. Các hàm số
y  log x , y  log x , y  log x có đồ thị như hình vẽ a b c
Khẳng định nào dưới đây đúng?
A. a c b .
B. a b c .
C. c b a .
D. b c a . x
Câu 101. Đồ thị hàm số y f x đối xứng với đồ thị hàm số y a a  0, a  
1 qua điểm I 1;  1 . Giá trị  1 
của biểu thức f 2  log  a  bằng  2018  A. 2016 . B. 2  016 . C. 2020 . D. 2  020 .
Câu 113. (TRƯỜNG THPT HOÀNG HOA THÁM HƯNG YÊN NĂM 2018-2019) Hình vẽ bên thể hiện 1 1
đồ thị của ba trong bốn hàm số 6x y  , 8x y  , y  và y  . 5x x 7   1 C   2 C y   3 C O x
Hỏi C là đồ thị hàm số nào? 2  1 1 A. 6 . x y  B. y  . C. y  . D. 8 . x y x 7 5x
Câu 114. (HSG BẮC NINH NĂM 2018-2019) Giá trị nhỏ nhất của hàm số     2   2 2 x f x x e trên đoạn 1;2 bằng: A. 4 2e B. 2 e C. 2 2e D. 2 2e
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x 4
Câu 115. (PEN I - THẦY LÊ ANH TUẤN - ĐỀ 3 - NĂM 2019) Giá trị nhỏ nhất của hàm số 1 2 8x y     3 trên 1;0 bằng 4 5 2 2 2 A. . B. . C. . D. . 9 6 3 3
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…)
Câu 102. (ĐỀ THAM KHẢO BGD & ĐT 2018) Một người gửi 100 triệu đồng vào ngân hàng với lãi suất
0, 4% / tháng. Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào
vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền ( cả vốn ban đầu và
lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất không thay đổi? A. 102.16.000 đồng
B. 102.017.000 đồng C. 102.424.000 đồng D. 102.423.000 đồng
Câu 103. (Mã đề 104 BGD&ĐT NĂM 2018) Một người gửi tiết kiệm vào một ngân hàng với lãi suất
6,1% / năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào
vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và
lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra? A. 11 năm B. 12 năm C. 13 năm D. 10 năm
Câu 104. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với lãi
suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu
hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết
tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m mà ông A sẽ phải trả cho ngân hàng
trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng, lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ. 3 120.(1,12) 3 100.(1, 01) A. m  (triệu đồng) B. m  (triệu đồng) 3 (1,12) 1 3 3 (1, 01) 100.1, 03 C. m  (triệu đồng) D. m  (triệu đồng) 3 (1, 01) 1 3
Câu 105. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Ông A vay ngân hàng 100 triệu đồng với lãi
suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt
đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau và
ông A trả hết nợ sau đúng năm năm kể từ ngày vay. Biết rằng mỗi tháng ngâng hàng chỉ tính lãi trên số dư nợ
thực tế của tháng đó. Hỏi số tiền mỗi tháng ông ta cần trả cho ngâng hàng gần nhất với số tiền nào dưới đây?
A. 2, 20 triệu đồng
B. 2, 22 triệu đồng
C. 3, 03 triệu đồng D. 2, 25 triệu đồng
Câu 106. Anh An gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9
tháng thì lĩnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không
thay đổi trong thời gian gửi. A. 0,8 % B. 0,6 % C. 0,7 % D. 0,5 %
Câu 107. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Một người gửi 100 triệu đồng vào
một ngân hàng với lãi suất 0, 6% /tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng,
số tiền lãi sẽ được nhập làm vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng, người
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
đó được lĩnh số tiền không ít hơn 110 triệu đồng (cả vốn ban đầu và lãi), biết rằng trong suốt thời gian gửi
tiền người đó không rút tiền và lãi suất không thay đổi? A. 18 tháng B. 16 tháng C. 17 tháng D. 15 tháng
Câu 108. Một người lần đầu gửi vào ngân hàng 100 triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ
trước được cộng vào vốn của kỳ kế tiếp) với kì hạn 3 tháng, lãi suất 2% một quý. Sau đúng 6 tháng, người
đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm
gửi tiền vào ngân hàng gần bằng với kết quả nào sau đây? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân
hàng không thay đổi và người đó không rút tiền ra. A. 212 triệu đồng B. 216 triệu đồng C. 210 triệu đồng D. 220 triệu đồng
Câu 109. (KTNL GIA BÌNH NĂM 2018-2019) Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với kỳ
hạn 3 tháng, lãi suất 8, 4% một năm theo hình thức lãi kép. Ông gửi được đúng 3 kỳ hạn thì ngân hàng thay
đổi lãi suất, ông gửi tiếp 12 tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là 12% một năm thì
ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi là: (làm tròn đến chữ số hàng đơn vị) A. 62255910 đồng. B. 59895767 đồng. C. 59993756 đồng. C. 63545193 đồng.
Câu 110. (THPT AN LÃO HẢI PHÒNG NĂM 2018-2019 LẦN 02) Ngày 01 tháng 01năm 2017, ông An
đem 800 triệu đồng gửi vào một ngân hàng với lãi suất 0,5% một tháng. Từ đó, cứ tròn mỗi tháng, ông đến
ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01tháng 01 năm 2018, sau khi rút tiền, số tiền tiết
kiệm của ông An còn lại là bao nhiêu? Biết rằng lãi suất trong suốt thời gian ông An gửi không thay đổi A. 11
800.(1, 005)  72 (triệu đồng) B. 12
1200  400.(1, 005) (triệu đồng) C. 12
800.(1, 005)  72 (triệu đồng) D. 11
1200  400.(1, 005) (triệu đồng)
Câu 111. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Để đủ tiền mua nhà,
anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất 0,85% /tháng. Nếu sau mỗi tháng, kể
từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là 10 triệu đồng bao gồm cả tiền lãi vay và tiền
gốc. Biết rằng phương thức trả lãi và gốc không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu
tháng thì anh trả hết nợ ngân hàng? (Tháng cuối có thể trả dưới 10 triệu đồng). A. 68 B. 66 C. 65 D. 67
Câu 112. (THPT LÊ QUY ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 01) Ông An gửi 100 triệu vào tiết
kiệm ngân hàng theo thể thức lãi kép trong một thời gian khá lâu mà không rút ra với lãi suất ổn định trong
mấy chục năm qua là 10% /1 năm. Tết năm nay do ông kẹt tiền nên rút hết ra để gia đình đón Tết. Sau khi rút
cả vốn lẫn lãi, ông trích ra gần 10 triệu để sắm sửa đồ Tết trong nhà thì ông còn 250 triệu. Hỏi ông đã gửi
tiết kiệm bao nhiêu lâu? A. 10 năm B. 17 năm C. 15 năm D. 20 năm
Câu 116. (TT HOÀNG HOA THÁM - 2018-2019) Một học sinh A khi 15 tuổi được hưởng tài sản thừa
kế 200 000 000 VNĐ. Số tiền này được bảo quản trong ngân hàng B với kì hạn thanh toán 1 năm và học
sinh A chỉ nhận được số tiền này khi 18 tuổi. Biết rằng khi 18 tuổi, số tiền mà học sinh A được nhận sẽ là
231 525 000 VNĐ. Vậy lãi suất kì hạn một năm của ngân hàng B là bao nhiêu? A. 8% / năm. B. 7% / năm. C. 6% / năm. D. 5% / năm.
Câu 117. (THPT MINH KHAI HÀ TĨNH NĂM 2018-2019) Ông Anh gửi vào ngân hàng 60 triệu đồng
theo hình thức lãi kép. Lãi suất ngân hàng là 8% trên năm. Sau 5 năm ông An tiếp tục gửi thêm 60 triệu
đồng nữa. Hỏi sau 10 năm kể từ lần gửi đầu tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao nhiêu?
(Biết lãi suất không thay dổi qua các năm ông gửi tiền).
A. 231,815(triệu đồng). B. 197, 201(triệu đồng).
C. 217, 695 (triệu đồng). D. 190, 271(triệu đồng).
Câu 118. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Ông Chính gửi 200 triệu đồng vào một
ngân hàng với lãi suất 7% năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi
sẽ được nhập vào gốc để tính lãi cho năm tiếp theo và từ năm thứ 2 trở đi, mỗi năm ông gửi thêm vào tài
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
khoản với số tiền 20 triệu đồng. Hỏi sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là bao nhiêu? Giả
định trong suốt thời gian gửi lãi suất không thay đổi và ông Chính không rút tiền ra (kết quả được làm tròn đến hàng nghìn).
A. 1.686.898.000 VNĐ. B. 743.585.000 VNĐ.
C. 739.163.000 VNĐ. D. 1.335.967.000 VNĐ.
Câu 119. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Một người mỗi tháng đều đặn gửi
vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0, 6% mỗi tháng. Biết sau 15 tháng người
đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau. A. 613.000 đồng B. 645.000 đồng C. 635.000 đồng D. 535.000 đồng
Câu 120. (CHUYÊN HÙNG VƯƠNG GIA LAI NĂM 2018-2019 LẦN 01) Anh Nam gửi 100 triệu đồng
vào ngân hàng theo thể thức lãi kép kì hạn là một quý với lãi suất 3% một quý. Sau đúng 6 tháng anh Nam
gửi thêm 100 triệu đồng với kì hạn và lãi suất như trước đó.Hỏi sau 1 năm số tiền (cả vốn lẫn lãi) anh Nam
nhận được là bao nhiêu? ( Giả sử lãi suất không thay đổi).
A. 218, 64 triệu đồng. B. 208, 25 triệu đồng.
C. 210, 45 triệu đồng. D. 209, 25 triệu đồng.
Câu 121. (THPT CHUYÊN SƠN LA NĂM 2018-2019 LẦN 01) Ông A gửi vào ngân hàng 50 triệu đồng
với lãi suất 0, 5% / tháng. Hỏi sau ít nhất bao nhiêu tháng thì ông A có được số tiền cả gốc lẫn lãi nhiều hơn
60 triệu đồng? Biết rằng trong suốt thời gian gửi, lãi suất ngân hàng không đổi và ông A không rút tiền ra. A. 36 tháng. B. 38 tháng. C. 37 tháng. D. 40 tháng.
Câu 122. (KTNL GV THUẬN THÀNH 2 BẮC NINH NĂM 2018-2019) Cho biết sự tăng dân số được
ước tính theo công thức  . Nr S A e
(trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau N năm,
r là tỉ lệ tăng dân số hằng năm). Đầu năm 2010 dân số tỉnh Bắc Ninh là 1.038.229 người tính đến đầu năm
2015 dân số của tỉnh là 1.153.600 người. Hỏi nếu tỉ lệ tăng dân số hằng năm giữ nguyên thì đầu năm 2020
dân số của tỉnh nằm trong khoảng nào?
A. 1.281.600;1.281.700 .
B. 1.281.700;1.281.800 .
C. 1.281.800;1.281.900 .
D. 1.281.900;1.282.000 .
Câu 123. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH LẦN 1 NĂM 2018-2019) Một người gửi 300 triệu
đồng vào một ngân hàng với lãi suất 7% / năm. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi
năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó
nhận được số tiền nhiều hơn 600 triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất
không đổi và người đó không rút tiền ra. A. 9 năm. B. 10 năm. C. 11 năm. D. 12 năm.
Câu 124. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Một người gửi tiết kiệm số tiền
80 000 000 đồng với lãi suất 6,9% / năm. Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5
năm người đó rút được cả tiền gốc lẫn tiền lãi gần với con số nào sau đây? A. 105370000 đồng B. 111680000 đồng C. 107 667 000 đồng D. 116570000 đồng
Câu 125. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Một người mỗi tháng đều đặn gửi
vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0, 6% mỗi tháng. Biết sau 15 tháng,
người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau. A. 613.000 đồng B. 645.000 đồng C. 635.000 đồng D. 535.000 đồng
Câu 126. Một người muốn có 1 tỉ tiền tiết kiệm sau 6 năm gửi ngân hàng bằng cách bắt đầu từ ngày
01/01/2019 đến 31/12/2024, vào ngày 01/01 hàng năm người đó gửi vào ngân hàng một số tiền bằng nhau với
lãi suất ngân hàng là 7% / 1 năm (tính từ ngày 01/01 đến ngày 31/12) và lãi suất hàng năm được nhập vào
vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng hàng năm là bao nhiêu (với giả thiết lãi suất không thay
đổi và số tiền được làm tròn đến đơn vị đồng)?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
A. 130 650 280 (đồng). B. 130 650 000 (đồng).
C. 139 795 799 (đồng). D. 139 795 800 (đồng).
Câu 127. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Một người vay ngân hàng 100 triệu đồng với lãi
suất là 0, 7% /tháng theo thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng
tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người
đó trả được hết nợ ngân hàng. A. 22 . B. 23 . C. 24 . D. 21 .
Câu 128. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 01) Anh Bảo gửi 27 triệu đồng vào ngân
hàng theo thể thức lãi kép, kỳ hạn là một quý, với lãi suất 1,85% một quý. Hỏi thời gian tối thiểu bao nhiêu
để anh Bảo có được ít nhất 36 triệu đồng tính cả vỗn lẫn lãi? A. 16 quý. B. 20 quý. C. 19 quý. D. 15 quý.
Câu 129. (HSG BẮC NINH NĂM 2018-2019) Vào ngày 15 hàng tháng ông An đều đến gửi tiết kiệm tại
ngân hàng SHB số tiền 5 triệu đồng theo hình thức lãi kép với kì hạn một tháng, lãi suất tiết kiệm không đổi
trong suốt quá trình gửi là 7,2% / năm. Hỏi sau đúng 3 năm kể từ ngày bắt đầu gửi ông An thu được số tiền
cả gốc và lãi là bao nhiêu (làm tròn đến nghìn đồng)?. A. 195251000 (đồng)
B. 201453000 (đồng) C. 195252000 (đồng) D. 201452000 (đồng)
Câu 130. (THPT-THANG-LONG-HA-NOI-NAM-2018-2019 LẦN 01) Anh Bình gửi 200 triệu vào ngân
hàng VB với kì hạn cố định 12 tháng và hưởng lãi suất 0, 65% / tháng. Tuy nhiên sau khi gửi được tròn 8
tháng anh phải dùng đến 200 triệu trên. Anh đến ngân hàng định rút tiền thì được nhân viên ngân hàng tư
vấn: “Nếu rút tiền trước kì hạn, toàn bộ số tiền anh gửi chỉ có lãi suất không kỳ hạn là 0, 02% / thángAnh nên
thế chấp sổ tiết kiệm đó tại ngân hàng để vay ngân hàng 200 triệu với lãi suất 0, 7% / tháng. Khi sổ của anh
đến kì hạn, anh có thể rút tiền để trả nợ ngân hàng”. Nếu làm theo tư vấn của nhân viên ngân hàng anh Bình
sẽ đỡ thiệt một số tiền gần nhất với con số nào dưới đây (biết ngân hàng tính lãi theo thể thức lãi kép). A. 10,85 triệu đồng. B. 10,51 triệu đồng. C. 10, 03 triệu đồng. D. 10,19 triệu đồng.
Câu 131. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN NĂM 2018-2019 LẦN 02) Một thầy giáo cứ đầu mỗi
tháng lại gửi ngân hàng 8 000 000 VNĐ với lãi suất 0, 5% / tháng. Hỏi sau bao nhiêu tháng thầy giáo có thể
tiết kiệm tiền để mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ? A. 60 . B. 50 . C. 55 . D. 45 .
Câu 132. (SỞ GD&ĐT BẮC GIANG NĂM 2018-2019 LẦN 01) Ông An gửi 100 triệu đồng vào một ngân
hàng với lãi suất 0,8%/ tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi
sẽ được nhập vào gốc để tính lãi cho tháng tiếp theo và từ tháng thứ hai trở đi, mỗi tháng ông gửi them vào
tài khoản với số tiền 2 triệu đồng. Hỏi sau đúng 2 năm số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu?
Biết rằng trong suốt thời gian gửi lãi suất không thay đổi và ông An không rút tiền ra (kết quả được làm tròn đến hàng nghìn).
A. 169.871.000 đồng.
B. 171.761.000 đồng. C. 173.807.000 đồng. D. 169.675.000 đồng.
Câu 133. (CHUYÊN LƯƠNG THẾ VINH ĐỒNG NAI NĂM 2018-2019 LẦN 01) Một người vay ngân
hàng số tiền 400 triệu đồng, mỗi tháng trả góp 10 triệu đồng và lãi suất cho số tiền chưa trả là 1% mỗi tháng.
Kỳ trả đầu tiên là cuối tháng thứ nhất. Biết lãi suất không đổi trong suốt quá trình gửi, hỏi số tiền còn phải trả
ở kỳ cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn). A. 2.921.000 . B. 3.387.000 . C. 2.944.000 . D. 7.084.000 .
Câu 134. (CHUYÊN LÊ QUÝ ĐÔN QUẢNG TRỊ NĂM 2018-2019 LẦN 01) Một người gửi 100 triệu
đồng vào ngân hàng với lãi suất 0, 5% / tháng và ông ta rút đều đặn mỗi tháng một triệu đồng kể từ sau ngày
gửi một tháng cho đến khi hết tiền ( tháng cuối cùng có thể không còn đủ một triệu đồng). Hỏi ông ta rút hết tiền sau bao nhiêu tháng? A. 139 . B. 140 . C. 100 . D. 138 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 135. (THPT QUỲNH LƯU 3 NGHỆ AN NĂM 2018-2019) Một bà mẹ Việt Nam anh hùng được
hưởng số tiền là 4 triệu đồng trên 1 tháng (chuyển vào tài khoản ngân hàng của mẹ ở ngân hàng vào đầu
tháng). Từ tháng 1 năm 2019 mẹ không đi rút tiền mà để lại ngân hàng và được tính lãi 1% trên 1 tháng.
Đến đầu tháng 12 năm 2019 mẹ đi rút toàn số tiền ( gồm số tiền của tháng 12 và số tiền gửi từ tháng1). Hỏi
khi đó mẹ lĩnh về bao nhiêu tiền? (kết quả làm tròn theo đơn vị nghìn đồng). A. 50970000 đồng. B. 50560000 đồng. C. 50670000 đồng. D. 50730000 đồng.
Câu 136. (SỞ GD&ĐT THANH HÓA NĂM 2018 - 2019) Bạn H trúng tuyển vào trường Đại học Ngoại
Thương nhưng vì do không đủ tiền nộp học phí nên H quyết định vay ngân hàng trong bốn năm mỗi năm 4
triệu đồng để nộp học phí với lãi suất ưu đãi 3%/năm (theo thể thức lãi suất kép) biết rằng tiền vay mỗi năm
H nhận được từ ngày đầu tiên của năm học và trong suốt bốn năm học H không trả tiền cho ngân hàng. Ngay
sau khi tốt nghiệp Đại học (tròn 4 năm kể từ khi bạn H bắt đầu vay ngân hàng) bạn H thực hiện trả góp hàng
tháng cho ngân hàng số tiền (không đổi và tiền trả vào ngày cuối của tháng) với lãi suất theo cách tính mới là
0,25%/tháng và lãi suất được tính theo dư nợ thực tế, bạn H trả đúng 5 năm thì hết nợ. Tính số tiền hàng tháng
mà bạn H phải trả cho ngân hàng (kết quả làm tròn đến hàng đơn vị). A. 323.582 (đồng). B. 398.402 (đồng). C. 309.718 (đồng. D. 312.518 (đồng).
Câu 137. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Ông A muốn mua một chiếc ôtô trị giá 1 tỉ
đồng nhưng vì chưa đủ tiền nên chọn mua bằng hình thức trả góp hàng tháng (số tiền trả góp mỗi tháng như
nhau) với lãi suất 12% /năm và trả trước 500 triệu đồng. Hỏi mỗi tháng ông phải trả số tiền gần nhất với số
tiền nào dưới đây để sau đúng 2 năm, kể từ ngày mua xe, ông trả hết nợ, biết kì trả nợ đầu tiên sau ngày mua
ôtô đúng một tháng và chỉ tính lãi hàng tháng trên số dư nợ thực tế của tháng đó? A. 23 537 000 đồng B. 24 443 000 đồng
C. 22 703 000 đồng D. 23 573 000 đồng
Câu 138. (THPT CHUYÊN THÁI NGUYÊN LẦN 01 NĂM 2018-2019) Một người vay ngân hàng 50
triệu đồng, mỗi tháng trả ngân hàng 4 triệu đồng và phải trả lãi suất cho số tiền còn nợ là 1,1% một tháng
theo hình thức lãi kép. Giả sử sau n tháng người đó trả hết nợ. Khi đó n gần nhất với số nào sau? A. 14 . B. 13 . C. 16 . D. 15 .
Câu 139. (ĐỀ THI THỬ VTED 02 NĂM HỌC 2018 - 2019) Ông A vay ngân hàng 100 triệu đồng với
lãi suất 1% /tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông
bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau
và sau đúng một năm kể từ ngày vay ông A còn nợ ngân hàng tổng số tiền 50 triệu đồng. Biết rằng mỗi tháng
ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tiền mỗi tháng ông ta cần trả cho ngân hàng
gần nhất với số tiền nào dưới đây? A. 4,95 triệu đồng B. 4, 42 triệu đồng C. 4, 5 triệu đồng D. 4, 94 triệu đồng
Câu 140. (CHUYÊN ĐHSP HÀ NỘI NĂM 2018-2019 LẦN 01) Một người nhận hợp đồng dài hạn làm
việc cho một công ty với mức lương khởi điểm của mỗi tháng trong ba năm đầu tiên là 6 triệu đồng/ tháng.
Tính từ ngày đầu làm việc, cứ sau đúng ba năm liên tiếp thì tăng lương 10% so với mức lương một tháng
người đó đang hưởng. Nếu tính theo hợp đồng thì tháng đầu tiên của năm thứ 16 người đó nhận được mức lương là bao nhiêu? A. 4 6.1,1 (triệu đồng). B. 6 6.1,1 (triệu đồng). C. 5 6.1,1 (triệu đồng). D. 16 6.1,1 (triệu đồng).
Câu 141. (ĐỀ THI CÔNG BẰNG KHTN LẦN 02 NĂM 2018-2019) Một người gửi 50 triệu đồng vào
một ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số
tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được
số tiền nhiều hơn 100 triệu đồng bao gồm gốc và lãi? A. 11 năm. B. 12 năm. C. 13 năm. D. 14 năm.
Câu 142. (THPT NGHĨA HƯNG NĐ- GK2 - 2018 - 2019) Anh C đi làm với mức lương khởi điểm là x
(triệu đồng)/ tháng, và số tiền lương này được nhận vào ngày đầu tháng. Vì làm việc chăm chỉ và có trách
nhiệm nên sau 36 tháng kể từ ngày đi làm, anh C được tăng lương thêm 10% . Mỗi tháng, anh ta giữ lại 20%
số tiền lương để gửi tiết kiệm ngân hàng với kì hạn 1 tháng và lãi suất là 0, 5% /tháng, theo hình thức lãi kép
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
(tức tiền lãi của tháng này được nhập vào vốn để tính lãi cho tháng tiếp theo). Sau 48 tháng kể từ ngày đi
làm, anh C nhận được số tiền cả gốc và lãi là 100 triệu đồng. Hỏi mức lương khởi điểm của người đó là bao nhiêu? A. 8.991.504 đồng. B. 9.991.504 đồng. C. 8.981.504 đồng. D. 9.881.505 đồng.
Câu 143. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Bạn Nam vừa trúng tuyển đại
học, vì hoàn cảnh gia đình khó khăn nên được ngân hàng cho vay vốn trong 4 năm học đại học, mỗi năm 10
triệu đồng vào đầu năm học để nạp học phí với lãi suất 7,8% /năm (mỗi lần vay cách nhau đúng 1 năm). Sau
khi tốt nghiệp đại học đúng 1 tháng, hàng tháng Nam phải trả góp cho ngân hàng số tiền là m đồng/tháng với
lãi suất 0, 7% /tháng trong vòng 4 năm. Số tiền m mỗi tháng Nam cần trả cho ngân hàng gần nhất với số nào
sau đây (ngân hàng tính lãi trên số dư nợ thực tế). A. 1.468.000 (đồng).
B. 1.398.000 (đồng). C. 1.191.000 (đồng). D. 1.027.000 (đồng).
Câu 144. (CHUYÊN PHAN BỘI CHÂU NĂM 2018-2019) Một anh sinh viên nhập học đại học vào tháng
8 năm 2014 . Bắt đầu từ tháng 9 năm 2014 , cứ vào ngày mồng một hàng tháng anh vay ngân hàng 3 triệu
đồng với lãi suất cố định 0,8% /tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp
theo (lãi kép). Vào ngày mồng một hàng tháng kể từ tháng 9 / 2016 về sau anh không vay ngân hàng nữa và
anh còn trả được cho ngân hàng 2 triệu đồng do việc làm thêm. Hỏi ngay sau khi kết thức ngày anh ra trường
30 / 6 / 2018 anh còn nợ ngân hàng bao nhiêu tiền (làm tròn đến hàng nghìn đồng)? A. 49.024.000 đồng B. 47.401.000 đồng C. 47.024.000 đồng D. 45.401.000 đồng
Câu 145. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cường độ ánh sáng đi qua môi trường nước biển giảm dần theo công thức  e x I I
 , với I là cường độ ánh sáng lúc ánh sáng bắt đầu đi vào môi trường nước biển 0 0
và x là độ dày của môi trường đó ( x tính theo đơn vị mét). Biết rằng môi trường nước biển có hằng số hấp
thụ là   1,4 . Hỏi ở độ sâu 30 mét thì cường độ ánh sáng giảm đi bao nhiêu lần so với cường độ ánh sáng
lúc ánh sáng bắt đầu đi vào nước biển? A. 21 e lần. B. 42 e lần. C. 21 e lần. D. 42 e lần
Câu 146. (CHUYÊN LÊ QUÝ ĐÔN ĐIỆN BIÊN LẦN 3 NĂM 2018-2019) Một người thả một lá bèo vào
một chậu nước. Sau 12 giờ, bèo sinh sôi phủ kín mặt nước trong chậu. Biết rằng sau mỗi giờ lượng bèo tăng 1
gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì bèo phủ kín mặt nước trong 5
chậu (kết quả làm tròn đến 1 chữ số phần thập phân). A. 9,1 giờ. B. 9, 7 giờ. C. 10,9 giờ. D. 11,3 giờ.
Dạng 5. Bài toán cực trị Câu 147. (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho
a  0, b  0 thỏa mãn log a b   a b
 . Giá trị của a  2b bằng a b  2 2 16 1 log 4 5 1 2 4 5 1  8ab 1    27 20 A. 6 B. C. D. 9 4 3
Câu 148. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Xét các số thực dương x, y thỏa mãn 1  xy log
 3xy x  2y  4 . Tìm giá trị nhỏ nhất P
của P x y 3 x  2y min 2 11  3 9 11  19 18 11  29 9 11  19 A. P B. P C. P D. P min 3 min 9 min 21 min 9
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 149. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Xét các số thực dương ,
a b thỏa mãn 1 ab log
 2ab a b  3 . Tìm giá trị nhỏ nhất P
của P a  2b . 2 a b min 3 10  7 2 10 1 2 10  3 2 10  5 A. P B. P C. P D. P min 2 min 2 min 2 min 2
Câu 150. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 01) Cho hai số thực dương , x y thỏa  xy  ln  mãn  2 ln   xy ln 5 2 .5  2
. Tìm giá trị lớn nhất của biểu thức P  (x 1) ln x  ( y 1) ln y . A. P  10 . B. P  0 . C. P  1 . D. P  ln 2 . max max max max
Câu 151. (THPT BẠCH ĐẰNG QUẢNG NINH NĂM 2018-2019) Cho các số thực x, y thỏa mãn x y
0  x, y  1 và log  x  1
y  1  2  0 . Tìm giá trị nhỏ nhất của P  2x y . 3     1  xy 1 A. 2 . B. 1 . C. . D. 0 . 2
Câu 152. (CHUYÊN HẠ LONG NĂM 2018-2019 LẦN 02) Cho các số thực a, b thỏa mãn a b  1. Biết 1 a
rằng biểu thức P   log
đạt giá trị lớn nhất khi k
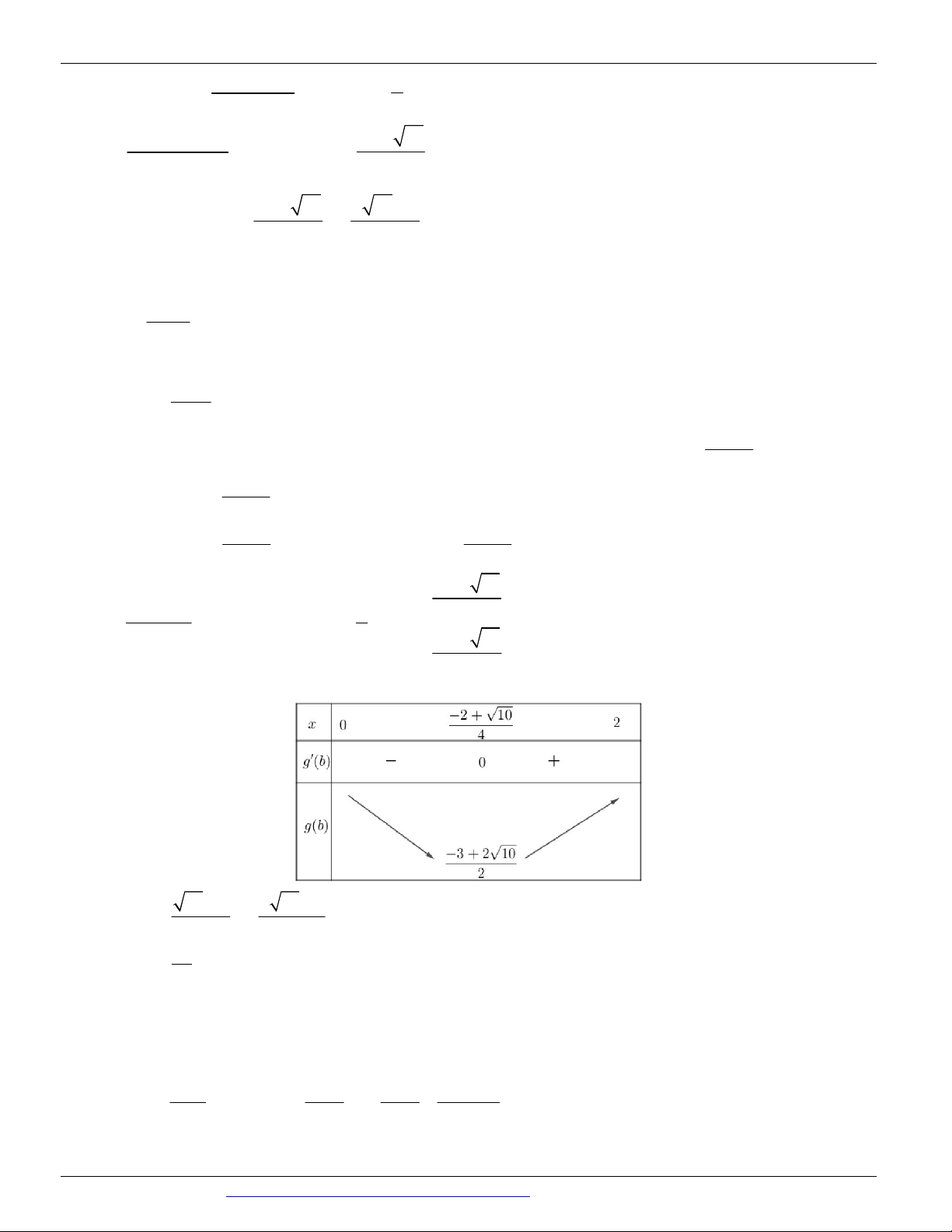
b a . Khẳng định nào sau đây là sai log a a b ab  3  A. k 2;  3 . B. k  0  ;1 . C. k  0;  1 . D. k  0;   .  2  a
Câu 153. Cho hai số thực ,
a b thỏa mãn log
2a  8b  1 . Tính P
khi biểu thức S  4a  6b  5 2 2   a 4b 1  b
đạt giá trị lớn nhất. 8 1  3 1  3 17 A. B. C. D. 5 2 4 44
Cho các số thực x , y thỏa mãn bất đẳng thức log
2x  3y  1. Giá trị lớn nhất của biểu thức 2 2   Câu 154. 4 x 9 y
P x  3 y là 3 2  10 5  10 3  10 A. . B. . C. . D. . 2 4 4 4
Câu 155. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Cho a , b là các số dương thỏa mãn  a
b  1 và a b a . Tìm giá trị nhỏ nhất của biểu thức P  log a  2 log . a b    b b A. 6 . B. 7 . C. 5 . D. 4 .
Câu 156. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho các số thực a, b 1
thay đổi, thỏa mãn a
, b  1. Khi biểu thức P  log b  log a a
đạt giá trị nhỏ nhất thì tổng a b  4 2 9 81 3  3 a b bằng A. 2 3  9 B. 3 9  2 C. 2  9 2 D. 3  3 2
Câu 157. (THPT ĐOÀN THƯỢNG - HẢI DƯƠNG - 2018 2019) Cho a , b là hai số thực dương thỏa
 4a  2b  5  mãn log
a  3b  4 . Tìm giá trị nhỏ nhất của biểu thức 2 2
T a b 5    a b
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 3 5 A. . B. 1. C. . D. . 2 2 2
Câu 158. (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Cho các số thực a, b, c thỏa 1 3 mãn 0  a  1;  b  1;  c  1 . Gọi M là giá trị nhỏ nhất của biểu thức 8 8 3  b 1  1  c 3  1 P  log   log   log a    
. Khẳng định nào sau đây đúng? 16 a  2 16  4 b  2 16  3 c A. 3  M  2 . B. M  2 . C. 2  M  3 . D. M  2 .
Câu 159. Cho các số thực a, b, m, n sao cho 2m n  0 và thoả mãn điều kiện: log  2 2
a b  9  1 log 3a  2b 2  2    4   9  .3 m  .3 n
mn  ln 2m n  22 2 1  81    2 2
Tìm giá trị nhỏ nhất của biểu thức P  a m  b n A. 2 5  2 . B. 2 . C. 5  2 . D. 2 5
Câu 160. (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Với hai số thực ,
a b bất kì, ta kí hiệu f
x x a x b x  2  x  3 .Biết rằng luôn tồn tại duy nhất số thực x để min f x f x a,b   a ,b  0  a,b     0     x R  với mọi số thực ,
a b thỏa mãn b a
a b và 0  a b . Số x bằng 0 A. 2e 1 B. 2, 5 C. e D. 2e
Câu 161. (THPT CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019 LẦN 01) Cho hai số thực 2
a  1, b  1 . Biết phương trình x x 1
a b   1 có hai nghiệm phân biệt x , x . Tìm giá trị nhỏ nhất của biểu thức 1 2 2  x x  1 2 S   4    x x . 1 2  x x  1 2  A. 3 3 4 . B. 4 C. 3 3 2 . D. 3 4 . 1 3
Câu 162. Cho các số thực a, b, c thỏa mãn 0  a  1;  b  1;
c  1 . Gọi M là giá trị nhỏ nhất của biểu 8 8 3  b 1  1  c 3  1 thức P  log   log   log a    
. Khẳng định nào sau đây đúng? 16 a  2 16  4 b  2 16  3 c A. 3  M  2 . B. M  2 . C. 2  M  3 . D. M  2 .
Câu 163. (CHUYÊN QUỐC HỌC HUẾ NĂM 2018-2019 LẦN 1) Cho x, y là các số thực lớn hơn 1 sao y x e e cho x x y   y y e x
e  . Tìm giá trị nhỏ nhất của biểu thức: P  log xy  log x . x y 2 1 2 2 1  2 A. B. 2 2 C. D. 2 2 2 1 y
Câu 164. Xét các số thực dương x, y thỏa mãn log
 3xy x  3y  4 . Tìm giá trị nhỏ nhất P 3 x  3xy min
của P x y . 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 165. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Xét các số thực dương x , y thỏa
mãn log x  log y  log  2 x y
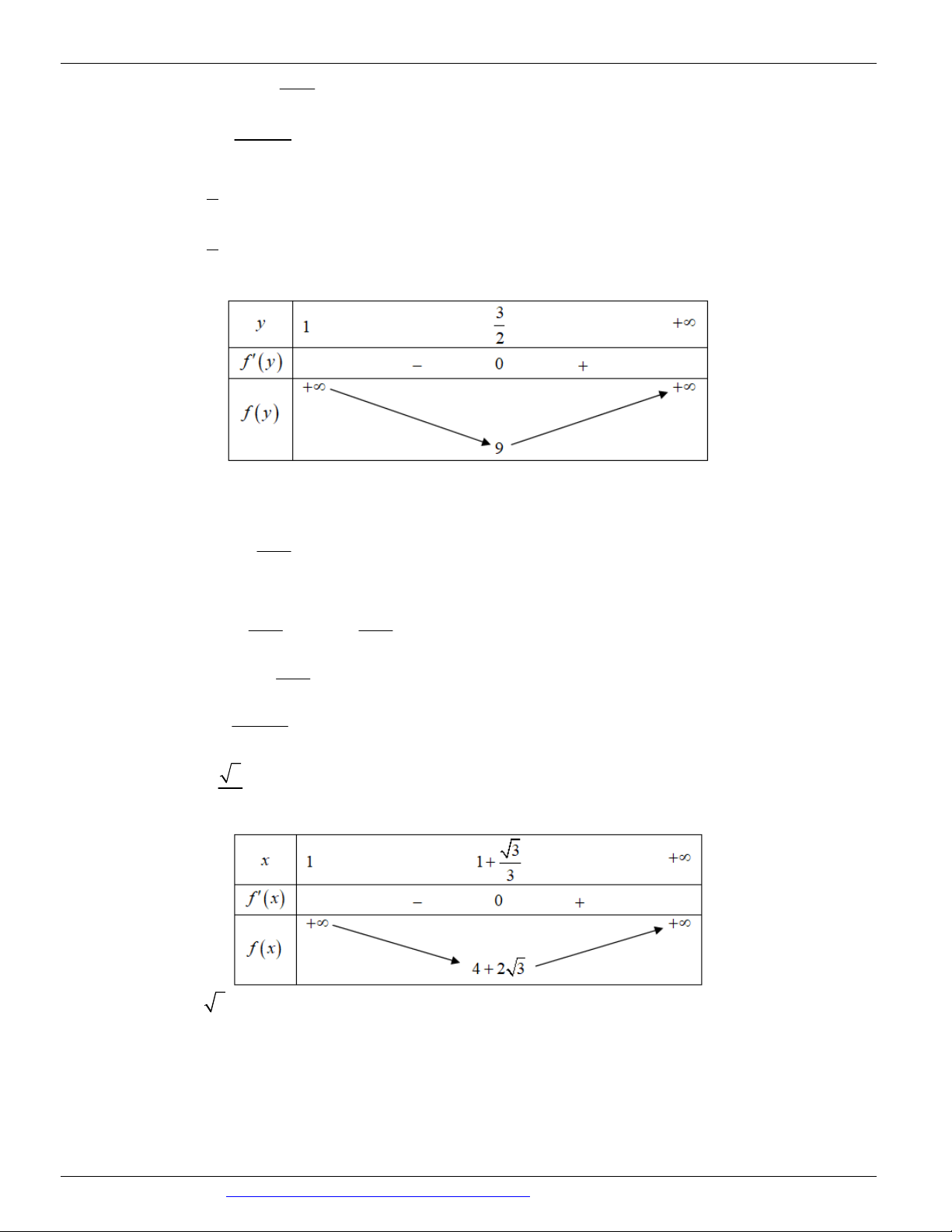
. Tìm giá trị nhỏ nhất P của biểu thức P x  3 y . 1 1 1  min 2 2 2 25 2 17 A. P  9 B. P  8 C. P  D. P  min min min 4 min 2
Câu 166. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Cho ,
x y là các số thực dương thỏa mãn 2 log x  log y  log
x y . Gọi T
là giá trị nhỏ nhất của biểu thức T  2x y . Mệnh đề nào 2019 2019 2019   min dưới đây đúng? A. T  7;8 B. T  6;7 C. T  5; 6 D. T  8;9 min   min   min   min  
Dạng 6. Một số bài toán khác 9t
Câu 167. (MĐ 105 BGD&ĐT NĂM 2017) Xét hàm số f t 
với m là tham số thực. Gọi S là 9t  2 m
tập hợp tất cả các giá trị của m sao cho f x  f y  1 với mọi số thực x, y thỏa mãn xy e
e x y .Tìm
số phần tử của S . A. 0 B. Vô số C. 1 D. 2
Câu 168. (THCS - THPT NGUYỄN KHUYẾN NĂM 2018-2019 LẦN 01) Cho hàm số y f x liên tục
trên  , có bảng biến thiên như hình vẽ và có đạo hàm cấp hai f   x  0, x   . 2 f a f b f c
3   a b c   Gọi a, ,
b c, n là các số thực và biểu thức:       P   e  e  e  f 1     . Khẳng định đúng 2   3   với mọi a, ,
b c, n   là
A. 0  P  3 .
B. 7  3e  P  0 . C. P  3 .
D. P  7  3e .
Câu 169. (HỌC MÃI NĂM 2018-2019-LẦN 02) Có bao nhiêu giá trị nguyên của m để giá trị nhỏ nhất của hàm số 2
y  ln x  2x m trên đoạn 2 1  ;e  
 đạt giá trị nhỏ nhất A. 11. B. 12 . C. 107 . D. 106 .
Câu 170. (THPT CHUYÊN ĐẠI HỌC VINH NĂM 2018-2019 LẦN 01) Cho hàm số ( ) 2x 2 x f x    .
Gọi m là số lớn nhất trong các số nguyên m thỏa mãn 12 f ( )
m f (2m  2 )  0 . Mệnh đề nào sau đây đúng? 0 A. m  1513; 2019
B. m  1009;1513 C. m  505;1009 D. m  1;505 0   0   0   0  
Câu 171. (ĐỀ GK2 VIỆT ĐỨC HÀ NỘI NĂM 2018-2019) Tìm tất cả các giá trị của tham số m đề đồ thị hàm số 2
y mlog x  2 log x  2m 1 cắt trục hoành tại một điểm duy nhất có hoành độ thuộc khoảng 1;  2 2 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1  1   1  1  A. m   ;        . B. m   ; 0      .  2  2   2   2   1  1   1  1  C. m   ;       .
D. m   ;0   . 2       2   2  2 
PHẦN B. ĐÁP ÁN THAM KHẢO
Dạng 1. Tìm tập xác định
Dạng 1.1 Không chứa tham số Câu 1. Chọn A x  3 x  3
Tập xác định của là tập các số x để
 0  x  3 x  2  0   x  2 x    2
Suy ra D  ; 2  3;  . Câu 2. Chọn C y  log  2
x  2x  3 . Hàm số xác định khi 2
x  2x  3  0  x  1  hoặc x  3 2 
Vậy tập xác định: D   ;    1  3;  Câu 3. Chọn B x  1 Điều kiện 2
x  4x  3  0   . x  3  Câu 4. Chọn D Hàm số xác định khi: 2
3x x  0  x  0; 3 Vậy D  0; 3 Câu 5. Chọn B
Hàm số xác định khi và chỉ khi 2
x  5x  6  0  2  x  3. Vậy tập xác định của hàm số là D  2;3. Câu 6. Chọn A 1 Điều kiện:
 0  6  x  0  x  6 . Do đó tập xác định của hàm số là  ;  6 . 6  x Câu 7.
Hàm số y  log  2
3  2x x xác định khi: 2
3  2x x  0  3  x  1 . 2 
Vậy tập xác định của hàm số đã cho là: D   3  ;  1 . x  1 Câu 8. Hàm số xác định khi 2
x  2x  3  0   . x  3 
Vậy D  ;   1  3;   . Câu 9. Chọn D Điều kiện xác định: x  0 x  0     D  0;   3 3 x  0 x  3   
ln  x  2  0 x  2  1 Câu 10. ĐKXĐ:   
x  2  1  x  3 . x  2  0 x  2  0  
TXĐ: D  3;  .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  2   x  2 2 4  x  0 
Câu 11. Điều kiện có nghĩa của hàm số là    3 2x  3  0 x     2  3   3 
Vậy tập xác định của hàm số là D  2;  ; 2      2   2  x  2  0 x  2
Câu 12. + Điều kiện xác định:    2 9  x  0 3   x  3  
+ Vậy tập xác định của hàm số là: D   3  ;  3 \   2 .
Dạng 2. Chứa tham số
Câu 13. Chọn D
Để hàm số có tâp xác định  khi và chỉ khi 2
x  2x m  1  0, x   . 2
   0  1  1.m  1  0  m  0 .
Câu 14. Chọn C
a  1  0(ld ) 
Hàm số có tâp xác định  khi và chỉ khi 2
x  2x m 1  0, x      .   1 
1 m  0  m  0 
Câu 15. Chọn C Yêu cầu bài toán  2
x mx  1  0 , x   2  m  4  0  2   m  2 .
Câu 16. Cách 1
Điều kiện: x  0 .
Hàm số xác định khi: 4 log x  3 2
m log x  4 log x m  3  0  m 2
log x 1  4 log x  3 3  m  , x  0; . 3  3 3 3 2 log x  1 3 4 log x  3
Để hàm số xác định trên 0;   thì phương trình 3 m
vô nghiệm x  0;  2 log x  1 3 4 log x  3 Xét hàm số 3 y  . 2 log x 1 3  1 4t  3 2 4
t  6t  4 t
Đặt log x t khi đó ta có y  , y   y  0   . 3 2 2 t 1 t  2 2 1 t  2  Ta có BBT: 1 t   2  2 y 0  0 1 y 0 0 4 
Để hàm số xác định trên 0;   thì m  ; 4  1;  . Cách 2:
Đề hàm số xác định trên khoảng 0;  thi phương trình 2 .
m log x  4 log x m  3  0 vô nghiệm. 3 3 3 3
TH1: m  0 thì PT trở thành 4
 log x  3  0  log x  4  x  3 . 3 3 4
Vậy m  0 không thỏa mãn.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2
TH2: m  0 thì để PT vô nghiệm    4
   4mm  3  0 m  4 2
 4m 12m 16  0   . m  1 
Để hàm số xác định trên 0;  thì m  ;  4   1; .
Câu 17. Hàm số xác định với mọi x  1; 2 khi 2
x mx  2m  1  0, x  1; 2 .  f x 2
x mx  2m 1  0, x  1; 2 .
f x  0 có 2 nghiệm thỏa mãn x  1  2  x . 1 2  f    1  0 3m  0 3      m  . f  2  0 4m  3  0 4   Câu 18. Hàm số 2
y  log(x  4x m 1) có tập xác định là  khi và chỉ khi 2
x  4x m 1  0 x  
Câu 19. Hàm số y   2
ln x  2x m  
1 có tập xác định là  khi và chỉ khi: 2
x  2x m 1  0 x
     '  0  1 m 1  0  m  0 .
Kết hợp với điều kiện m nguyên thuộc  2018 
; 2018 ta có 2018 giá trị của m . Câu 20. y   2
log x  2mx  4
Điều kiện xác định của hàm số trên: 2
x  2mx  4  0 . a  0 1   0, m
Để tập xác định của hàm số là  thì     2   m  2 . 2   0  m  4  0 
Vậy đáp án đúng là đáp án D.
Câu 21. Chọn A
Điều kiện xác định
mx m  2  0  mx m  2 (1)
Trường hợp 1. m  0 .    1 
1  2  0 (luôn đúng với x   ;    ).  2 
Trường hợp 2. m  0 . m  2   1  x m  1 
Để hàm số y  log mx m  2 xác định trên ;    thì  2  m  2 1   0  m  4. m 2
Vì m   nên m 1;2;  3 .
Trường hợp 3. m  0 . m  2   1  x  . mm  2 
Suy ra tập xác định của hàm số y  log mx m  2 là D  ; .    m   1  Do đó ;   D  
suy ra không có giá trị m  0 nào thỏa yêu cầu bài toán.  2 
Từ 3 trường hợp trên ta được m 0;1;2;  3 .
Câu 22. Chọn B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Hàm số đã cho xác định x  0; 2 x
 2018x x   m  0, x  0;  2 2 x
 2018x x   m, x  0;  . 2
YCBT  m  min f x  . x   0; 2 x
Đặt f x   2018x x  , x 0;  2      2018x f x
ln  2018  1  x     x f x   2 2018 ln 2018  1  0, x  0; 
Khi đó f   x  đồng biến trên x 0; và f 0  ln 2018 1  0
Suy ra f x  đồng biến trên x 0; và f 0  1
Vậy m  1 thì thỏa YCBT.
Câu 23. Chọn D
Điều kiện xác định: 4x  2x m  0
Hàm số đã cho có tập xác định là   4x  2x   0,      4x   2x m x m , x    (*) Đặt  2x t ,t  0 Khi đó (*) trở thành 2
m  t t, t
  0  m  max f (t) với 2
f (t)  t t, t  0 0; 1
Ta có: f 't   2
t 1 , f 't   0  t  2
Bảng biến thiên của hàm số 2
f (t)  t t, t  0 : 1 t 0  2 f 't  + 0 - 1 f t  4 0  1 1
Từ BBT ta thấy max f (t) 
đạt được khi t  0; 4 2 1
Vậy m  max f t   m  0; 4 3x  5
Câu 24. Xét hàm số y  log  2 2
x  2x m  4m  5 2018  2 2 2 2
x  2x m  4m  5  0  
x  2x m  4m  5  0 ĐKXĐ:    . log   2 2
x  2x m  4m  5 2 2  0
x  2x m  4m  5  1 2018   2 2 
x  2x m  4m  5  0
Nên điều kiện để hàm số xác định với mọi x   là  với x    . 2 2
x  2x m  4m  4  0 
Điều này xảy ra khi và chỉ khi :
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   1 2   2
m  4m  5  0 1  
m  4m  4  0 m  1 2   
 m  4m  3  0  . 2    1  2
m  4m  4  0
m  4m  3  0 m  3  2   
Vậy m    ;1  3;  .
Câu 25. Chọn D 2 2 Điều kiện 2017x xx
m 1  0, x
 0;  2017x xx   m 1, x  0; . 2 2 2 Xét hàm số    2017x x f xx  , x
 0; liên tục có 2    2017x f x
ln 2017 1 x, x  0;  f  xx 2
 2017 ln 2017 1  0, x  0; 
Vậy hàm số f  x đồng biến trên 0;  suy ra f  x  f 0  ln 2017 1  0, x
 0;  Vậy hàm số
y f x đồng biến trên 0;  suy ra min f x  f 0  1. 0;
Mặt khác m 1  min f x  f 0  1  m  2 . 0;
Vậy có vô số giá trị nguyên m thỏa mãn.
2m 1 x  0 x  2m 1
Câu 26. Hàm số xác định      D   ; m 2m   1 . x m  0 x m  
Hàm số đã cho xác định trên khoảng 2;3 nên 2;3  D   ; m 2m  
1  m  2  3  2m 1 m  2    1  m  2 . 2m 1  3 
Vì m nguyên dương nên m 1;  2 . Dạng 2. Tìm đạo hàm
Câu 27. Chọn B 1 1
Áp dụng công thức log x   , ta được y  . ax ln a l x n10
Câu 28. Chọn B 2 2 Ta có 2 '  (
 ) '.2x x.ln 2  (2 1).2x x y x x x .ln 2 .
Câu 29. Chọn C  2 2
Ta có:  u   . u a
ua .ln a nên 3x x ' 2  1 .3x    . x x ln 3 .
Câu 30. Chọn C Ta có: 13x y  ln13 .
Câu 31. Chọn A  2x  1   2
Ta có y  log 2x 1   . 2   2x   1 ln 2 2x   1 ln 2
Câu 32. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
x   x x  1 .4   x   1 .4 
4x   x   1 .4x.ln 4 Ta có: y '   4x 2 4x 2 4 . x 1 .
x ln 4  ln 4 1 .2 x ln 2  2 ln 2 1 2 x   1 ln 2    . x 2 x 2 4 2 x 4
Câu 33. Chọn D  2 x  2x ' 2x  2 f ' x    2 x  2x ln 2  2 x  2x ln 2
Câu 34. Chọn A
  2xx      2 3 x 3 ' 2 ' 2 3 2 x y x ln 2 .
Câu 35. Chọn D 2 2 
Ta có:    x 3x      x 3 3 2 3 .3 x y x .ln 3 .
Câu 36. Chọn C Ta có:    1 x 1
y     x   1 ln 1 1   . 1 x 1
2 x 11 x 1 Câu 37. Lời giải Chọn A 1   .x  ln ln .  .ln x x x x x 1 ln x Cách 1. x y    2 2 2 x x x 1 2    1 ln x  2 .x   2
x  1 ln x
 .x  2x 1 ln x
x  2x 1 ln x 1 21 ln x 3  2 ln x y  x       4 x 4 x 4 3 3 x x x 1 ln x 3  2 ln x
2  2 ln x  3  2 ln x 1
Suy ra: 2 y  xy  2.  x    . 2 3 x x 2 2 x x 1
Cách 2. Ta có xy  ln x , lấy đạo hàm hai vế, ta được y xy  . x 1 1
Tiếp tục lấy đạo hàm hai vế của biểu thức trên, ta được y  y  xy  
, hay 2 y  xy   . 2 x 2 x
Câu 38. Chọn B 12x     12 ' . 1 2 '  2  . x y e x e
Câu 39. Chọn B  2 x x   1 ' 2x  1 y '    2 x x   1 ln 3  2 x x   1 ln 3
Câu 40. Chọn B  ' 2 x x  2 x x    ' 2 .  2   2 1 x x e e x x x e
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1 xee x 2 x 2  2  2
Câu 41. Ta có: y  ln 1 e    . 2 x 2   1 e 1 xe   
1 x .2x  2x  .1 x 1.  2x  2 .
x ln 2.1 x ln 2. x   1 1
Câu 43. Ta có y    2x 2 2x 2 2x  2  x   1 2x 2x x
Câu 44. Ta có y     .  2 x   1 ln 9  2 x   2 1 ln 3  2 x   1 2 ln 3  2 x   1 ln 3
Câu 45. Chọn D   '
x.sin 2   x  .sin 2 x .sin 2  x      .sin 2  2 x .cos 2 x y e x e x e x e x e
x e sin 2x  2 cos 2x
Câu 46. Chọn A    x  
1 4x   x   1 4x  1 2 x   1 ln 2 y    x 4x 2 2 2
Câu 47. Chọn A Ta có:     2 1 2 x x f x x e     .   2 xx         2 xx      2 2 2 1 2 1 2 1 4 4 xx f x e x x e x x e c 1
f  x     x x  2 2 xx 2 0 1 4 4 e  0  1
  4x  4x  0 khi đó x x    . 1 2 a 4
Câu 48. Chọn D
Ta có y x cos ln x  s in ln x  
y  cos ln x  s in ln x  s in ln x  cos ln x  2 cos ln x 2
y   sin ln xx
Từ đó kiểm tra thấy đáp án D đúng vì : 2
x y  xy  2 y y  2
x sin ln x  2x cosln x  2x cosln x  sin ln x  0   . l  og x , khi x  0 2019 
Câu 49. y  log x   2019 l  og x , h k i x  0  2019     1  , khi x  0 xln 2019  1 y        y . 1   x ln 2019 x , khi x 0 ln 2019   1 1  1  y 1 Câu 50. y x 1 ln x
x 1 ln x             1   . 2 x 1 ln x y y y x   2x x 1  1  1
Câu 51. Ta có y  2 ln 2ln x     ln 2 ln x  x     . x e  x  ex
Câu 52. Điều kiện xác định của hàm số đã cho là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x  0 x  0    x  0 log x  0 log x  0 2017 2017        log x  0 log log x  0 log log x 2017  0 2018 2017 2018 2017   log log x  1    2018  2017  log log log x  0 log log x  1 2019  2018  2017    2018  2017  x  0  x  0 x  0 2018  log x  0      x  2017 . 2017 2018 log x  2018 x  2017   2017  log x  2018  2017      2 x 2x 2x 2
Câu 53. Ta có f (x)    2
x  2xln 2  2 x  2xln 2 u  u 1
Câu 54. Áp dụng các công thức ln u   và  u   ta có f (  x)  . ln u 2 u
2x ln x ln(ln x)
Câu 55. Chọn B x  1 1 1
Ta có f x  ln 2018  ln 
  f  x     x 1  x x   1 x x  1 1 1 1 1 1 1 1 2017 Do đó S      ...    1  . 1 2 2 3 2017 2018 2018 2018 2018x  1 2018x      x 1 2018 1
Câu 56. Ta có: f  x  ln  . .      .  2  x 1 2018x   x 1 
2018x x   1 . x x   1 x 1
Vậy S f  
1  f 2  ... f 2018 1 1 1 1 1 1 1 1 1    ...       ...   1.2 2.3 2018.2019 1 2 2 3 2018 2019 1 2018  1  . 2019 2019
Dạng 3. Khảo sát hàm số mũ, logarit
Câu 57. Chọn B
Tập xác định D  0; 
Ta có f x  x ln x f  x  g x  ln x 1. Ta có g  
1  1 nên đồ thị hàm số đi qua điểm 1 
;1 . Loại hai đáp án B và D 1 Và lim     t  . Khi x 0  thì t   .
  g x   lim ln  x 1   . Đặt x 0 x 0   x   1   Do đó lim            
nên loại đáp án A
  g x   lim ln 1 lim ln t  1    x0 t  t   t   
Câu 58. Chọn D 2x Ta có: y   m . 2 x 1 Hàm số y   2 ln x  
1  mx  1 đồng biến trên khoảng  ;
   y  0, x   ;   . 2x 2 2x  2  g(x)   , m x    ;   . Ta có g (  x)   0  x  1 2   x 1 x  2 2 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 Bảng biến thiên: 2x
Dựa vào bảng biến thiên ta có: g(x)   , m x    ;    m  1  2   x 1
Câu 59. Chọn D
Đường thẳng x  1đồ thị các hàm số x  , x  , x y a y
b y c tại các điểm có tung độ lần lượt là
y a, y b, y c như hình vẽ:
Từ đồ thị kết luận a c b
Câu 60. Chọn A Theo hình ta thấy hàm  x y
a là hàm đồng biến nên a  1, còn hàm  x
y b là hàm nghịch biến nên
0  b  1 . Suy ra 0  b  1  . a
Câu 61. Chọn C Hàm số mũ x
y a với 0  a  1 nghịch biến trên  . x e  e  Ta có 0 
 1 nên hàm số y    nghịch biến trên  . 4  4 
Câu 62. Chọn C
Hàm số y  ln( x) TXĐ D   ;  0
Cơ số a e  1 do đó hàm số đồng biết trên  ;  0
Câu 63. Chọn C Hàm số x
y a đồng biến trên  khi và chỉ khi a  1. 1 2 Thấy các số ;
; 0, 5 nhỏ hơn 1, còn 3 lớn hơn 1 nên chọn . C π 3
Câu 64. Chọn C
Hàm số y  log x có tập xác định là D = 0;  . 2
Câu 65. Chọn D 2 x
y  (0,1) x  0, 0  1 , 2  (2016) x 4064256x y  2015 3 Ta có các cơ số ;
; 0, 01 đều nhỏ hơn 1 nên các hàm số ở A, B, C nghịch biến trên  . 2016 2016  2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Cơ số 4064256  1 nên hàm số 2 (2016) x y  đồng biến trên  .
Câu 66. Đồ thị hàm số đi qua điểm e ; 
1 và nằm cả trên và dưới trục hoành nên chỉ có hàm số y  ln x thoả mãn. Câu 67. Hàm số   x
f x a đồng biến trên  nếu a  1 và nghịch biến trên  nếu 0  a  1. Vậy hàm số   3x f x
là hàm số đồng biến trên  .
Câu 68. Ta có tập xác định của hàm số y  log
x là D  0; . Do đó đáp án B sai. 5
Câu 69. Chọn B Xét hàm số x
y a đi qua 0 
;1 suy ra đồ thị hàm số  
1 là đồ thị của hàm nghịch biến nên 0  a  1.
Xét đồ thị hàm số y  log x đi qua 1;0 suy ra đồ thị của hàm số 2 là đồ thị của hàm đồng biến suy ra b b  1.
Vậy 0  a  1  b .
Câu 70. +) y  ln x ; TXĐ: D  0;
e  1 suy ra hàm số y  ln x đồng biến trên D . +) y  log
x ; TXĐ: D  0;  2018 1 2019 2018 2018 0   1  0  1
 1 suy ra hàm số y  log
x là hàm nghịch biến 2019 2019 2018 1 2019 D .
+) y  log x ; TXĐ: D  0;  
  1 suy ra hàm số y  log x
đồng biến trên D . +) y  log
x ; TXĐ: D  0;  4 3
4  3  1 suy ra hàm số y  log x 4 3
đồng biến trên D .
Câu 71. Với x  1  y  ln x  ln1  0 .
Với x  2  y  ln x  ln 2 .
Với x  2e y  ln x  ln 2 e  ln 2  1 .
Với x  0 , hàm số không xác định. x  2  2
Câu 72. Ta thấy hàm số y    là hàm số mũ có có tập xác định là  cơ số a   1 nên nghịch biến  3  3
trên tập xác định của nó.
Ngoài ra ta có thể loại các đáp án khác bằng cách giải thích cụ thể đặc điểm các hàm đó như sau: 2  1 
Đáp án A loại vì: Hàm số y    là hàm hằng nên không nghịch biến củng không đồng biến.  2 
Đáp án B loại vì: Hàm số y  log x là hàm số logarit có tập xác định là D  (0; ) có cơ số a  10  1 nên
luôn đồng biến trên tập xác định của nó.
Đáp án C loại vì: hàm số 2x y
là hàm số mũ có tập xác định là  có cơ số a  2  1
Câu 73. Hàm số y  log x đồng biến trên khoảng 0;  . 2
Câu 74. Chọn A.
Hàm số y  log x đồng biến trên khoảng (0;  ) ⇔ a  1 ⇒ Chọn A a
Câu 75. Chọn B Đồ thị hàm số x
y a và đồ thị hàm số y  log x đối xứng với nhau qua đường phân giác góc a
phần tư thứ nhất ( y x ), suy ra chọn B.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 76. Ta có A0;ln a , B 0;ln b , C 0;ln c và B là trung điểm của AC nên a c b  ac 2 2 ln ln 2ln ln
 ln b ac b . Vậy 2 ac b .
Câu 77. Đồ thị hàm số đi qua điểm 0;0 nên loại đáp án A và B.
Đồ thị hàm số đi qua điểm 1  ;1 nên loại D.
Vậy đáp án C thỏa mãn. 2 x  2  Câu 78. Vì
 1 nên y    nghịch biến trên R . ee
Câu 79. Xét hàm số y  log x có tập xác định: D  0;  .  4  Nhận thấy cơ số
 1 nên y  log x nghịch biến trên tập xác định. 4  4
Câu 80. Chọn B 3x ln 3 Ta có: ' 9 3x y     9 ln 3 '  0  3x y  9  x  2
Câu 81. Chọn C M  5 1
2018; 2019  thuộc đồ thị hàm số x
y a nên ta có:  1 2018 5 1 0 a  2019 
 1  a  0  a  1 5 2019 M  5 1
2018; 2019  thuộc đồ thị hàm số y  log x nên ta có: b 1 5 5 1 2019 0 log 2018  2019  b
2018  1  b b  1 b
Vậy 0  a  1, b  1.
Câu 82. Chọn B 1
TXĐ D  0;  . f  x  x
Xét phương trình hoành độ giao điểm: ln x  0  x  1  A1;0
Vậy phương trình tiếp tuyến của đồ thị hàm số  L tại điểm A là: y f (  1)  x  
1  0  x 1, chọn B.
Câu 83. Tập xác định là  . 3  x y  e 1 3x . Vì 3  x e  0, x
   nên dấu của y là dấu của nhị thức 1 3x , suy ra y đổi dấu từ dương sang âm khi x đi 1 qua . 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 Do đó, x
là điểm cực đại của hàm số. 3
Câu 84. Hàm số y  log  2
x  2x có tập xác định D  ;0  2;   . 3  2x  2 Ta có y 
. Khi đó y  0  x  1 .  2 x  2xln 3 Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số y nghịch biến trên ;0 .
Câu 85. Dựa vào đồ thị ta thấy khi x    y  0 do đó đồ thị hàm số x
y a có a  1 . Nên ta loại đáp án A và. D.
Ở đồ thị hàm số y  log y
x x b ta thấy khi x    y   do đó ta có 0  b  1 . b 1 1
Câu 86. Hàm số có đồ thị (C2) là hàm số nghịch biến, do đó loại đáp án A,D. Cho x 1 suy ra  7 5 1
Do đó đồ thị hàm số (C2) là y  . 5x
Câu 87. Tập xác định: D   . 2 2x
mx  2x m Ta có: y   m  2 2 x 1 x 1
Để hàm số đồng biến trên  điều kiện là m  0 2 y  0; x
    mx  2x m  0; x       m   ;    1 . 2   1 m  0 
Câu 88. Dựa vào đồ thị các hàm số x y a , x
y b , y  log x ,ta có: c Hàm số x
y a nghịch biến trên  nên ta có: 0  a  1 . (1) b   1 Các hàm số x
y b , y  log x đồng biến trên tập xác định của nó nên ta có: .(2) cc 1  a b Từ (1),(2)  
. Do đó loại hai phương án B, D. a c
Nếu b c thì ta có đồ thị hai hàm số x
y b , y  log x đối xứng nhau qua đường thẳng y x . b
Tuy nhiên nhìn hình dáng hai đồ thị hàm số x
y b , y  log x không có tính chất đối xứng nhau qua đường b
thẳng y x . Do đó phương án đúng là A. Cách khác: Hàm số x
y a nghịch biến trên  nên ta có: 0  a  1 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 b   1 Các hàm số x
y b , y  log x đồng biến biến trên tập xác định của nó nên ta có: . cc 1 
Xét đồ thị hàm số y  log x , ta có: log 2  1  c  2 . c c Xét đồ thị hàm số x
y b , ta có: 1
b  2  b  2 .
Do đó: 0  a c b .
Câu 89. Chọn C Xét hàm số x
y b : Dựa vào hình dáng đồ thị ta thấy lim x
b  0 , do đó 0  b  1. x Xét hàm số  x y
a : Dựa vào hình dáng đồ thị ta thấy lim x
a   , do đó a  1 . x
Từ đó suy ra: a b . Loại đáp án A, D.
Xét tại x  1 đồ thị hàm số x
y c có tung độ lớn hơn tung độ của đồ thị hàm số x
y a nên c a . Vậy
c a  1  b .
Câu 90. Chọn D a,b  1
Theo hình dạng của đồ thị ta có  . 0  c  1 
Vẽ đường thẳng y  1 cắt đồ thị hai hàm số y  log ,
x y  log x lần lượt tại 2 điểm M ( ;1 a ), N ( ;1 b ) . Ta a b
thấy điểm N bên phải điểm M nên b a .
Vậy c a b .
Câu 91. Chọn A ln x
Xét y f x 
. Hàm số y f x liên tục trên đoạn 2;  3 x 1 ln x 1 ln x /  y  ; / y  0 
 0  x e 2;  3 2 x 2 x   ln2 1 ln3 Có f 2   0,3466 ; f   e   0,3679 ; f   3   0,366 , 2 e 3 ln2
Suy ra Min f x  . x   2    ;3 2 ln x ln 2
Vậy giá trị nhỏ nhất của hàm số y  trên đoạn 2;  3 bằng . x 2
Câu 92. Do y  log x và y  log x là hai hàm đồng biến nên , b c  1 . b c
Do y  log x nghịch biến nên 0  a  1 . Vậy a a bé nhất.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 log m x mb x
Mặt khác: Lấy y m , khi đó tồn tại x , x  0 để b 1 1   . 1 2  log m x mc 2 c x  2 Dễ thấy m m
x x b c b c . Vậy a b c . 1 2
Câu 93. Chọn C 6  2m Điều kiện: 2 ln  2   e m x m x . Có y 
x ln x  2m2 6  2m
Hàm số đồng biến trên 1; e  y  0 x  1; e   0 x   1; e 2  
x ln x  2m m  3 6  2m  0  m  0 6  2m  0   2 m  0      e m  1     . 2 1 e m    1; e    1   m  3 2  e m  e   m   2   2
Do m nguyên dương nên m 1; 
2 . Vậy tập S có 2 phần tử.
Câu 94. Chọn D
Đặt t  log x . 2
Ta có x 4;   t 2;  . mt  2
Hàm số được viết lại y  (1). t m 1
Vì t  log x đồng biến trên 0;  nên yêu cầu bài toán  (1) nghịch biến trên 2;  2 m  2  
m m   1  2  0   
  m  1  m  2   . m 1  2  m 1 
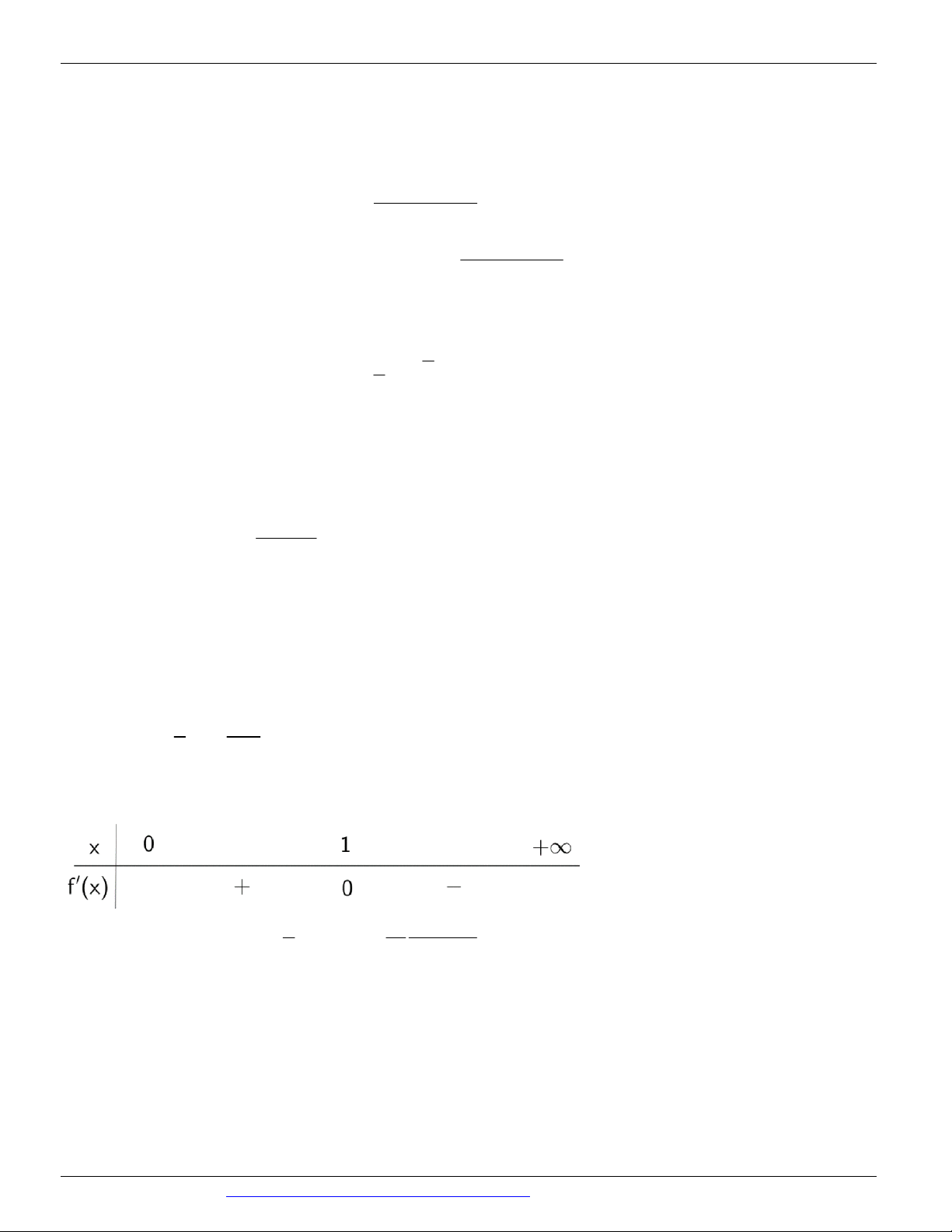
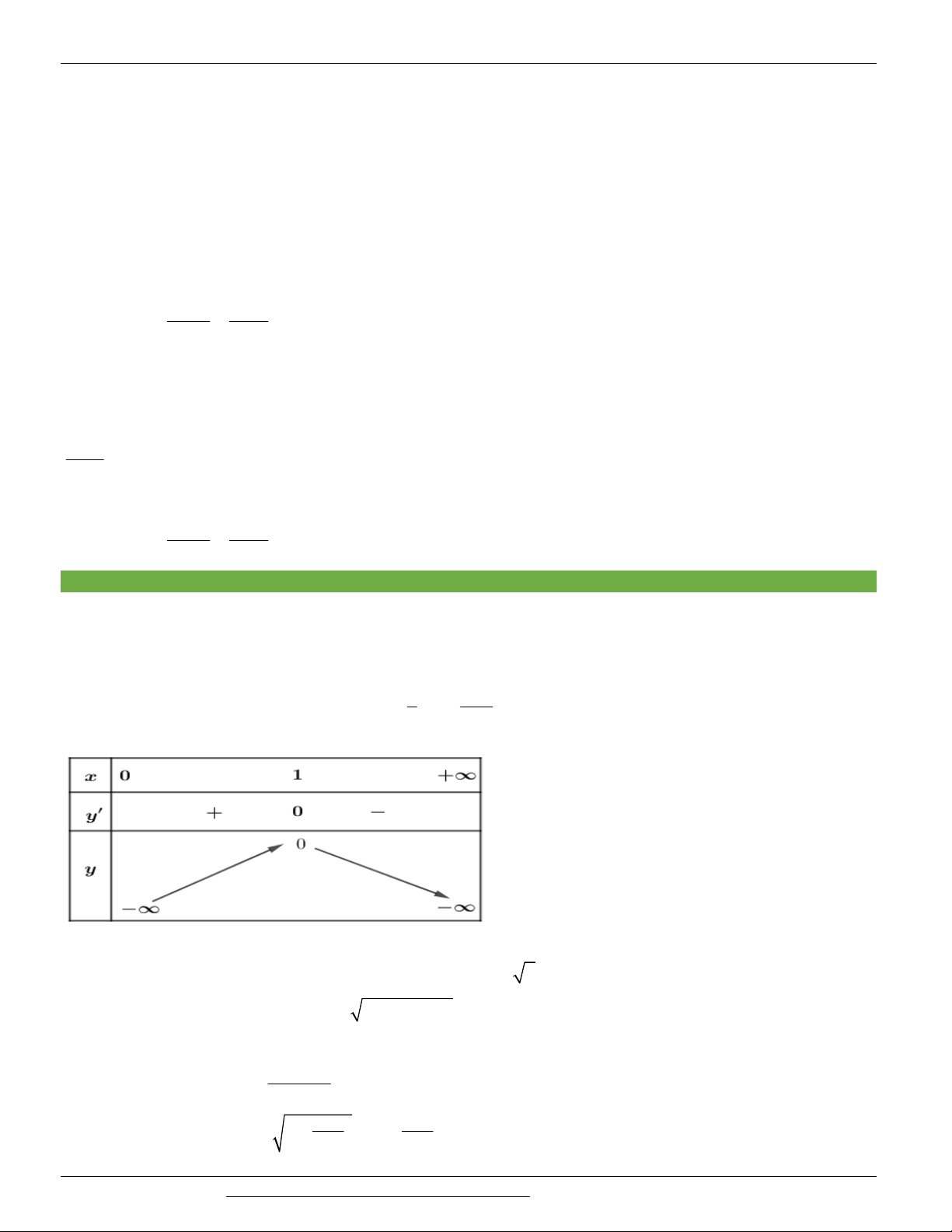
Câu 95. Tập xác định của hàm số f x : D  0; 1 1 x
Ta có f  x  1  x x
f  x  0  x 1
Bảng xét dấu f  x :  1  1 1
Câu 96. Ta có y  log thì y  
 0 hàm số nghịch biến ta vẽ được đồ thị hàm số 2018   2  x x x ln 2018 C như hình 1 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Do C đối xứng với C qua O nên có dạng như hình dưới 1  2 
Từ đó đồ thị hàm số y f x là
Dựa vào đồ thị trên ta có hàm số y f x nghịch biến trên khoảng  ;    1
Câu 97. Đặt t  ln x . ln x  6 t  6
Khi đó hàm số y
đồng biến trên khoảng  6
1;e  thì hàm số y t  
đồng biến trên khoảng ln x  3m t  3m 0;6 . 3  m  6
Ta có yt   t  3m2
Để hàm số y t  đồng biến trên khoảng 0;6 thì m  2  3  m  6  0    
 m  0  m  0 m
 m  2019  ; 20  18;... 1;0 . m 2019  ;2019   3m   0;6    m  2 
Vậy có tất cả: 2020 số nguyên m thoả mãn yêu cầu bài toán.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x 1
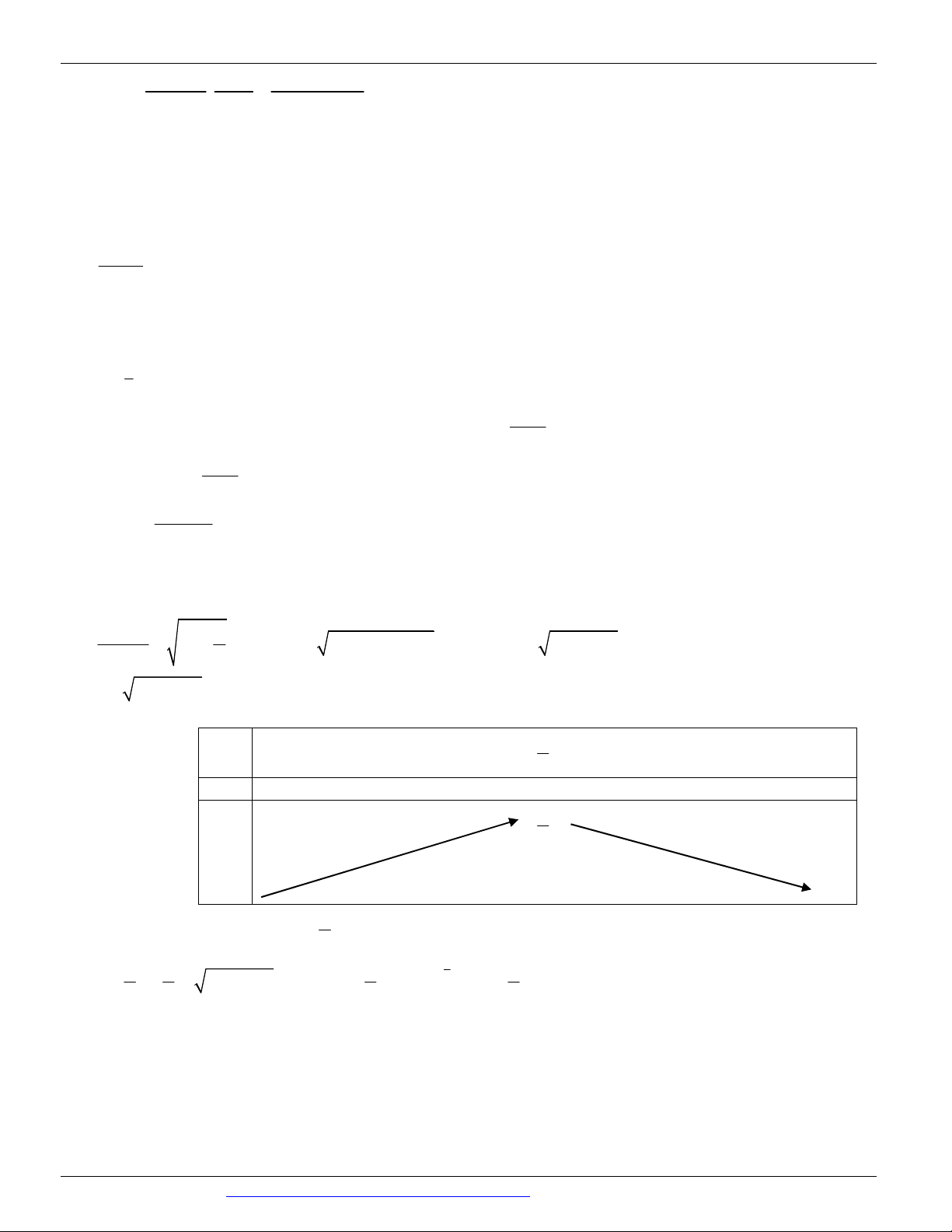
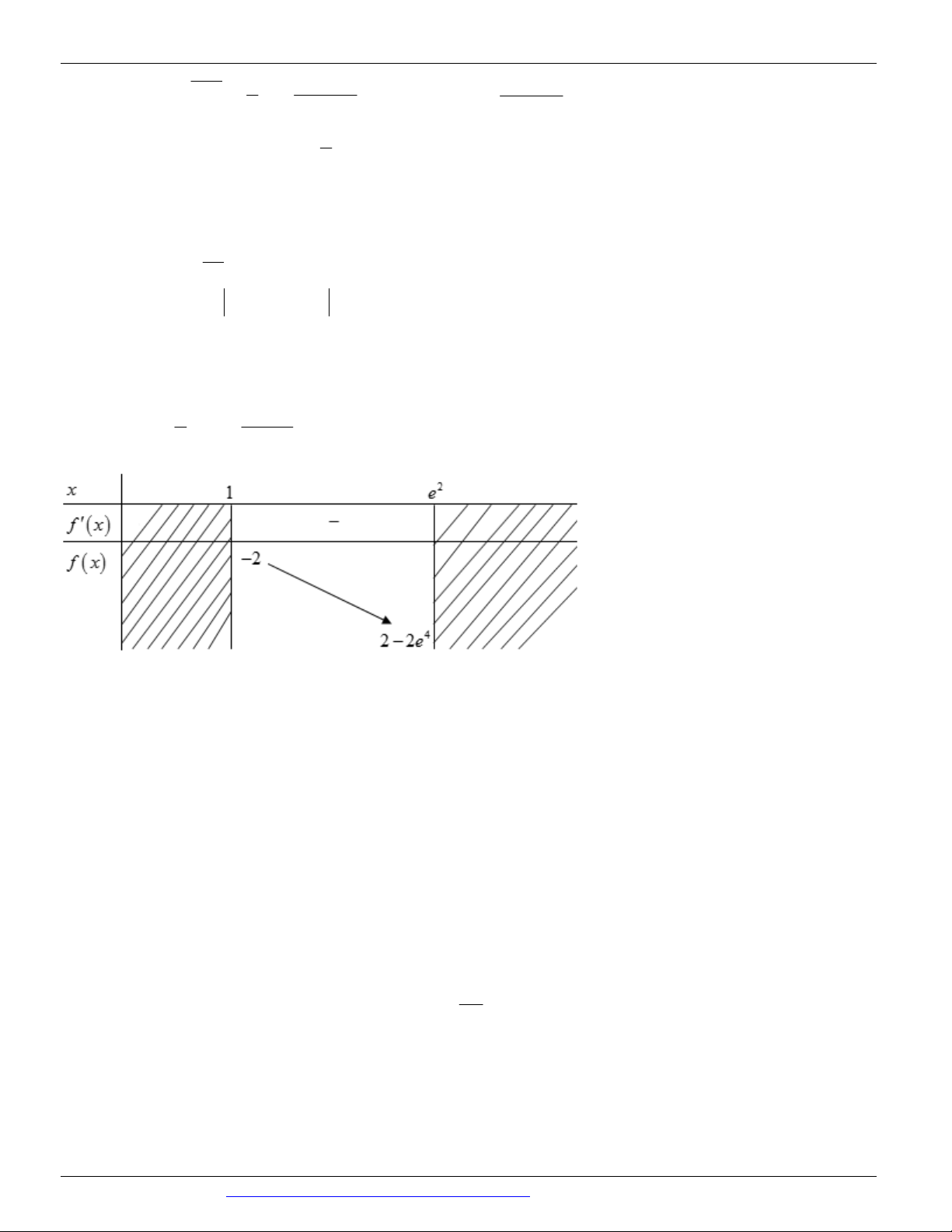
Câu 98. Ta có: y '  f ' x  ln x   2  m x 1 1
Yêu cầu bài toán  f  x  ln x   3  m  0  ln x   3  m ; x   2 0; e  . x x 1
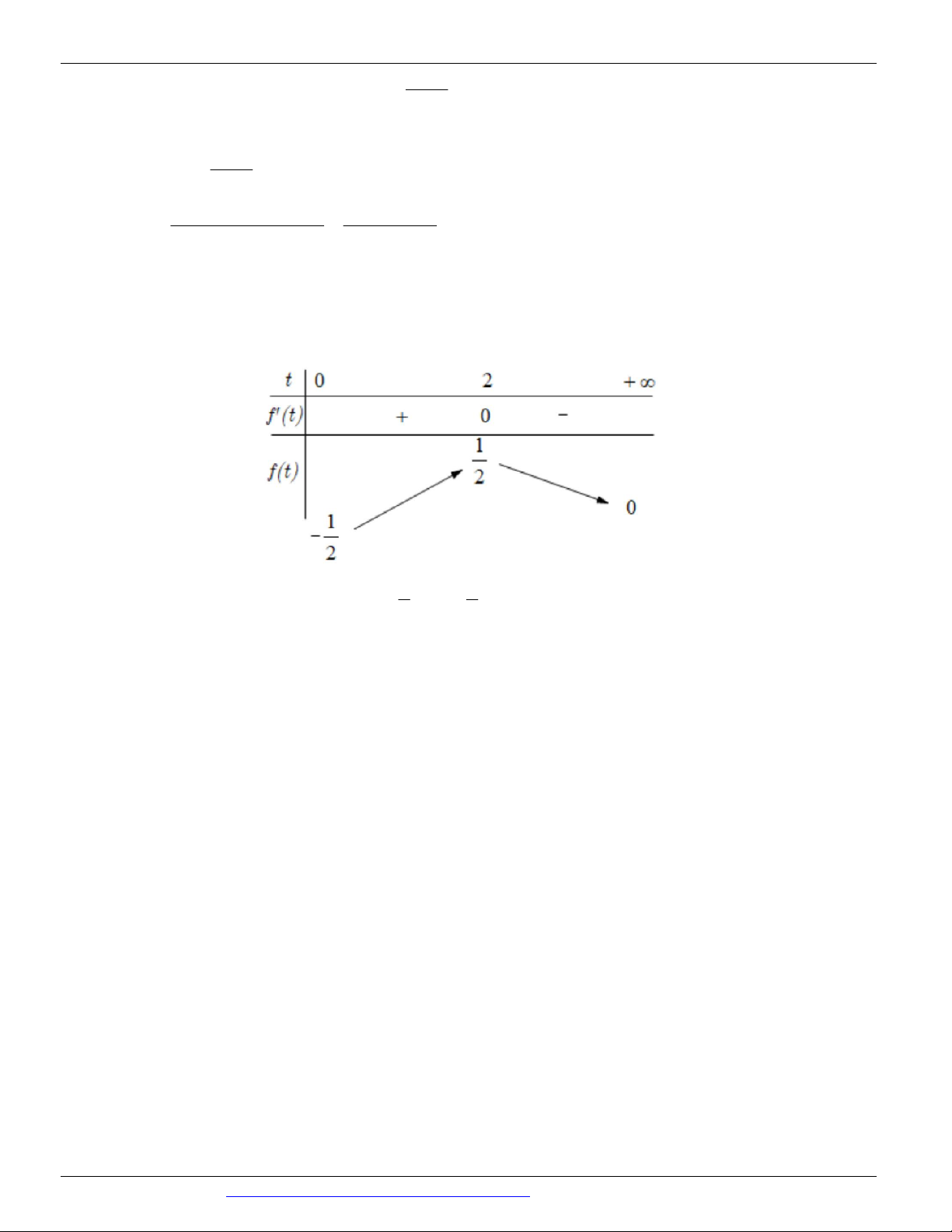
Xét hàm số: g x  ln x   3 với x  2 0;e  . x 1 1
Ta có: g ' x    0  x  1 . 2 x x Bảng biến thiên:
Dựa vào bảng biến thiên suy ra g x  4 với mọi x  2 0;e  . Từ đó suy ra 2  018  m  4 .
Vậy có 2023 giá trị của m thỏa mãn.
Câu 99. Ta có log log e  log ln10  log1  0 .
Mặt khác f x  f  x   a  2 x x    b x   a  2 ln 1 sin 6 ln  x
x  1   b sin x  6  a  2 x x   2 ln 1  x
x  1  b sin x bsin x 12
a ln112 12  x   .
Khi đó suy ra f loglog e  f log ln10 12  f logln10 10 . Câu 100.
Kẻ đường thẳng (d ) : y  1. Hoành độ giao điểm của (d ) với các đồ thị hàm số y  log x , y  log x , a b
y  log x lần lượt là a, b, c . Dựa vào đồ thị hàm số ta thấy a c b . c Câu 101. Lờigiải Chọn B
Gọi C  là đồ thị hàm số x
y a ; C là đồ thị hàm số y f x . 1   1   1  M 2  log ; yC   yf 2  log . a M   1  Ma   2018   2018   1 
Gọi N đối xứng với M qua I 1;  1  N  log ; 2  y  . a   2018 M
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1 
Do đồ thị C đối xứng C  qua I 1;  1 nên N  log ; 2  yC  . a M    1   2018  1  loga N  C  2018
 2  y a log 2018  2 aya
 2  y  2018  y  2  016 . M M M M  1  Vậy f 2  log  2016  . a   2018 
Dạng 4. Bài toán thực tế (lãi suất, tăng trưởng…) Câu 102. Lời giải Chọn C 6 n  0, 4 
Ta có A A 1 r 100.000.000 1 102.424.128 n 0      100 
Câu 103. Chọn B
Gọi x số tiền gửi ban đầu. N N  6,1   6,1 
Theo giả thiết 2x x 1  2  1      100   100  N  6,1   2  1  N  log 2  11, 7   1,06  1  100 
Vậy sau ít nhất 12 năm người đó thu được số tiền thỏa yêu cầu.
Câu 104. Chọn C
Cách 1: Công thức: Vay số tiền A lãi suất r% / tháng. Hỏi trả số tiền a là bao nhiêu để n tháng hết nợ n .
A r.1  r  100.0, 01.1  0,013 a   .  n 1  r   1 1  0,013  1
Cách 2: Theo đề ta có: ông A trả hết tiền sau 3 tháng vậy ông A hoàn nợ 3 lần
Với lãi suất 12%/năm suy ra lãi suất một tháng là 1% Hoàn nợ lần 1:
-Tổng tiền cần trả (gốc và lãi) là : 100.0, 01  100  100.1, 01 (triệu đồng)
- Số tiền dư : 100.1, 01  m (triệu đồng) Hoàn nợ lần 2:
- Tổng tiền cần trả (gốc và lãi) là :   m    m    m   2 100.1, 01 .0, 01 100.1, 01 100.1, 01
.1, 01 100. 1, 01 1, 01.m (triệu đồng) - Số tiền dư:  2 100. 1, 01
1, 01.m m (triệu đồng) Hoàn nợ lần 3:
- Tổng tiền cần trả (gốc và lãi) là :   2 m m     3   2 100. 1, 01 1, 01. .1, 01 100. 1, 01
1, 01 m 1, 01m (triệu đồng)   3 2
- Số tiền dư:100.1, 0  1  1, 
01 m 1, 01m m (triệu đồng) 3 2 100.1, 3 01  100.1,  01  1, 
01 m 1, 01m m  0  m  1,0 2 1 1, 011 100.1, 3 01 .1, 01  1 1, 3 01  m   (triệu đồng). 1, 2
01 1, 011 .1, 01  1 1, 3 01 1  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Câu 105. Chọn B
Ta xây dựng bài toán tổng quát như sau
Gọi số tiền người đó vay ngâng hàng là V triệu đồng 0
Số tiền hàng tháng người đó phải trả là a triệu đồng
Lãi suất là r %/ tháng
Vậy số tiền nợ ngân hàng sau tháng thứ nhất là V 1 0, 0r 0  
Số tiền người đó còn nợ ngân hàng sau khi trả tiền tháng 1 là
T V 1 0, 0r a 1 0  
Số tiền người đó còn nợ ngân hàng sau khi trả tiền tháng 2 là
T T 1 0, 0r a 2 1    V   r a  r ao 1 0, 0  1 0,0    Vrar a o 1 0, 0 2 1 0,0 
Số tiền người đó còn nợ ngâng hàng sau tháng thứ n là  T Vrar   ar a n o  n  n 1 1 0, 0 1 0, 0 ... 1 0, 0  n nT  0  Vrar   ar a n o 1 0, 0  1 0,0  1 ... 1 0,0  0  V r a r r          o n n 1 0, 0 
1 0,0  1 ... 1 0,0  1   n
Vì sau n tháng thì trả hết tiền nên ta có n 1 0,0r 1  Vra o 1 0, 0  1 0,0r 1 n V .0, 0r.  r o 1 0,0   a   n 1 0, 0r  1 Áp dụng 100.0, 01 60 1, 01  a   2, 224444768 60 1, 01 1
Câu 106. Chọn C n
Áp dụng công thức A A 1 r
với n là số kỳ hạn, A là số tiền ban đầu, A là số tiền có được sau n n 0   0 n
kỳ hạn, r là lãi suất. A
Suy ra A A 1 r 9 9  r  9 1  0, 7% . 9 0 A0
Câu 107. Chọn B n
Sau n tháng, người đó lĩnh được số tiền là: 100.1 0,6% (triệu đồng).
Sau n tháng, người đó được lĩnh số tiền không ít hơn 110 triệu đồng (cả vốn ban đầu và lãi) n 11
 100.1 0, 6%  110  n  log  15, 9 . 10,6% 10 Câu 108. Chọn A
Ta có: r  2%  0, 02
 Số tiền 100 triệu đồng gửi lần đầu thì sau 1 năm (4 quý) nhận được cả vốn lẫn lãi là:
T  100 1 0, 024  108, 24 triệu đồng 1
 Số tiền 100 triệu đồng gửi lần thứ hai thì sau 6 tháng (2 quý) nhận được cả vốn lẫn lãi là:
T  1001 0, 022  104, 04 triệu đồng 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
T T T  212, 28
Vậy tổng số tiền nhận được là: 1 2 triệu đồng. Câu 109. Chọn B
Gửi ngân hàng số tiền là A đồng với lãi suất r% ./tháng. Mỗi tháng vào ngày ngân hàng tính lãi, rút ra số
tiền là X đồng. Sô tiền còn lại sau n tháng đươc tính theo công thức:  n n 1 r  1 12 1,00512 1 S ArX      n 1  800 1, 005 12 6. 775.3288753 1200 400.(1, 005) r 0, 5%
Câu 111. Chọn B
Giả sử anh An vay số tiền là A với lãi suất r trên tháng và trả nợ cho ngân hàng số tiền cố định là x. Anh An
sau các tháng còn nợ ngân hàng với số tiền là:
Tháng thứ 1: A1 r  x   r 2 2 2 1 1
Tháng thứ 2:  A1 r   x 1 r   x A1 r   1
  1 r  x A1 r   . x     r   r3 3 1 1
Tháng thứ 3 : A1 r   . x r …  n n 1 r  1
Tháng thứ n : A1 r   . x r
Áp dụng công thức ta có: A  500; r  0, 0085; x  10 và sau n tháng trả hết nợ ta có:  n n 1 0, 0085 1 500.1 0, 0085 10.  0 0, 0085  n n 1, 0085 1 n 40 40  50.1, 0085   1, 0085   n  log  65, 4 1,0085 0, 0085 23 23
Câu 112. Chọn A
Số tiền ông An tích lũy được gồm cả vốn và lãi là 260 triệu n
Công thức tính lãi kép A Ar n 1  6 6 n
 260.10  100.10 110%  n  10 Câu 113. Lờigiải
Tácgiả: Mai Tiến Linh; Fb:Mai Tiến Linh  1 C   2 C y   3 C B A O 1 x Vì hàm số x
y a đồng biến trên  khi a  1 và nghịch biến trên  khi 0  a  1 nên dựa vào đồ thị ta có:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
+ C là đồ thị của hàm số đồng biến trên  . Do đó C có thể là đồ thị của hàm số 6x y  hoặc 8x y  . 3  3  1
+ C , C là đồ thị của các hàm nghịch biến trên  nên C có thể là đồ thị của hàm số y  hoặc 2  2  1  5x 1 y  . x 7 1 1
+ Kẻ đường thẳng x  1 lần lượt cắt C và C tại A và B . Vì y y và  nên đồ 1  2  A B 5 7
Câu 114. Ta có:     2   2x 2 x    2    2 2 2 2 2 2 x f x x e xe x x e
x  11; 2
f  x  0   . x  2   1;2  Và f   2 1 e    ; f   4
2  2e ; f   2 1  e
Giá trị nhỏ nhất của hàm số     2   2 2 x f x x
e trên đoạn 1; 2 bằng 2
e tại x  1 .
Câu 115. Chọn D  2x  0  x   x 4 1 y 2 ln 2 8x ln 8 0 2x 2 2x 3 1 0            x 1  3 2  x  1  / 2   2 2
Xét y(-1)=5/6 ; y(-1/2)=0,9428 ; y(0)=2/3 . Ta có: y  . min 3
Câu 116. Ta có: số tiền nhận được của gốc và lãi là:   r3 200 000 000 1  231 525 000  r  5% /năm
Câu 117. Số tiền ông An nhận được sau 5 năm đầu là:   5 60 1 8%  88,160 (triệu đồng)
Số tiền ông An nhận được (toàn bộ tiền gốc và tiền lãi) sau 10 năm là:     5 88,16 60 1 8%
 217, 695 (triệu đồng). Câu 118. Lời giải
Gọi a  200 triệu; b  20 triệu;   7% .
Số tiền sau 1 năm: a 1  . 2
Số tiền sau 2 năm: a 1    b 1   . 3 2
Số tiền sau 3 năm: a 1    b 1    b 1   . …………………… 18 17 16
Số tiền sau 18 năm: a 1   b 1   1   ... 1               18 1 17 1
a 1    b 1 .      
Vậy số tiền ông Chính nhận sau 18 năm là: 1.335.967.000 VNĐ. T  
Câu 119. Ta có: Số tiền cả lãi lẫn gốc sau 15 tháng gửi: S
1 r 1 r15 1 15   r   T   Vậy:       615 10.000.000 1 0, 006 1 0, 00 1  T  635.301   0, 006  
Câu 120. • Số tiền anh Nam nhận được sau 6 tháng (tức 2 quý) là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
T  100 1 3 / 2 0  106, 09 triệu đồng. 1 0
• Số tiền anh Nam nhận được sau một năm (tức 2 quý còn lại của năm) là:
T  106, 09 1001 3 / 2 0  218, 64 triệu đồng. 2 0
Câu 121. Gọi A là số tiền gửi vào ngân hàng, r là lãi suất, T là số tiền cả gốc lẫn lãi thu được sau n tháng. Ta có   n T A 1  r  . n 6
Theo đề T  50.1, 005  60  n  log  36, 6 . 1,005 5
Vậy sau ít nhất 37 tháng thì ông A thu được số tiền cả gốc lẫn lãi hơn 60 triệu.
Câu 122. Chọn B Áp dụng công thức  . Nr S A e
từ đầu năm 2010 đến đầu năm 2015 ta có: 5r 1 1153600 1153600  1038229.er  ln . 5 1038229 1 1153600 10. ln
Đầu năm 2020 dân số của tỉnh Bắc Ninh là 5 1038229 S  10382 . 29 e  1281792 người. Vậy Chọn B.
Câu 123. Kí hiệu số tiền gửi ban đầu là A , lãi suất một kì hạn là m thì số tiền cả gốc và lãi có được sau n n kì hạn là .
A 1 m .
Do đó, số tiền cả gốc và lãi người đó nhận được sau n năm là 300.1, 07n triệu đồng.
Số tiền cả gốc và lãi nhận được nhiều hơn 600 triệu đồng 300.1, 07n   600  n  log 2  10, 245 . 1,07
Vậy sau ít nhất 11 năm thì người đó nhận được số tiền nhiều hơn 600 triệu đồng bao gồm cả gốc và lãi.
Câu 124. Gọi P là số tiền gửi ban đầu, r là lãi suất / năm. 0
Số tiền gốc và lãi sau năm thứ nhất: P P P .r P 1 r . 1 0 0 0  
Số tiền gốc và lãi sau năm thứ hai: P P P.r P 1 r 2 . 2 1 1 0 …. 5 5
Số tiền gốc và lãi người đó rút ra được sau 5 năm là P P . 1 r  80 000 000. 1 6, 9%  111680 799 5 0     (đồng).
Câu 125. Chọn C
Số tiền nhận được khi gửi khoản tiền T ở tháng đầu tiên là 15 15
T (1 0,006)  T.1, 006 .
Số tiền nhận được khi gửi khoản tiền T ở tháng thứ 2 là 14 14
T (1 0,006)  T.1, 006 .
Cứ như vậy, số tiền nhận được khi gửi khoản tiền T ở tháng thứ 14 là T (1 0, 006)  T .1, 006 .
Vậy tổng số tiền nhận được sau 15 tháng là: 15 1,006 1 15 14 2
T (1, 006 1,006  ... 1,006 1,006)  T.1, 006. . 0,006 15 1,006 1
Theo giả thiết có: 10000000  T.1,006.  T  635301, 46 . 0,006
Câu 126. Chọn A
Gọi T là số tiền người đó gửi vào ngân hàng vào ngày 01/01 hàng năm, T là tổng số tiền cả vốn lẫn lãi người 0 n
đó có được ở cuối năm thứ n , với *
n   , r là lãi suất ngân hàng mỗi năm.
Ta có: T T rT T 1 r . 1 0 0 0  
Đầu năm thứ 2 , người đó có tổng số tiền là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 T T
T 1 r T
T 1 r  1   1 r2 1 1 r2 0 0 1            . 0 0 0   1 r  1    r       T 2 T 2 T Do đó: 0 T  . 1 r  0 1  . 1 r  0 1 .r  . 1 r 1 1 r . 2  2    r   r   r   …… T n Ta có: 0 T . r      r . n 1  1 1  r   T 6
Áp dụng vào bài toán, ta có:  0 10 .1 0, 07 1   
1 0,07  T  130 650 280 đồng. 0 0, 07  
Câu 127. Gọi số tiền vay ban đầu là M , số tiền hoàn nợ mỗi tháng là m , lãi suất một tháng là r .
Hết tháng thứ nhất, số tiền cả vốn lẫn nợ ngân hàng là M Mr M 1 r  (triệu đồng).
Sau khi hoàn nợ lần thứ nhất, số tiền còn nợ là M 1 r   m (triệu đồng).
Sau khi hoàn nợ lần thứ hai, số tiền còn nợ là
M   r  m  M   r  mr m M   r2 1 1 1
m 1 r  m   (triệu đồng).
Sau khi hoàn nợ lần thứ ba, số tiền còn nợ là M r 2 m
r m M r 2 1 1 1
m 1 rm          r m  
M   r 3  m   r 2 1 1
m 1 r   m (triệu đồng).
Lập luận tương tự, sau khi hoàn nợ lần thứ n , số tiền còn nợ là  m  r n 1 1 1     n  
M   r n m   r n 1  m   r n 2 1 1 1
 ...  m 1 r   m M 1 r   . r
Sau tháng thứ n trả hết nợ thì ta có  m  r n 1 1 1   n   Mr 1 r M n 1 r    0  m rn 1 r  1 n mm       n m m
Mr 1 r   1 r    n  log   m Mr
1r   m Mr
Thay số với M  100.000.000 , r  0, 7% , m  5.000.000 ta tính được n  21, 62 (tháng).
Vậy sau 22 tháng người đó trả hết nợ ngân hàng.
Câu 128. Bài toán lãi kép:
Kí hiệu số tiền gửi ban đầu là A , lãi suất một kì hạn là r% thì số tiền cả gốc và lãi có được sau n kì hạn là n S  . Ar . n 1 %
Anh Bảo nhận được số tiền ít nhất 36 triệu đồng tính cả vốn và lãi nên ta có: n
27 11,85%  36  n  15.693 .
Vậy thời gian tối thiểu để anh Bảo nhận được ít nhất 36 triệu đồng tính cả vốn lẫn lãi là 16 quý.
Câu 129. Gọi T là số tiền cả gốc lẫn lãi sau n tháng, a là số tiền gốc, r là lãi xuất, ta có: n
Cuối tháng thứ 1 ông An có số tiền là: T a 1 r 1  
Đầu tháng thứ 2 ông An có số tiền là: T a 1 r a 2  
Cuối tháng thứ 2 ông An có số tiền là: T a 1 r   a  a 1 r   ar a 1 r  a 1 r2 2
…………………………………………………………… 2 n
Cuối tháng thứ n ông An có số tiền là:: T a r a r a r n
1   1  ... 1 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 n n
1 r  1 r 1 a 1 r 1 r 1 2 n       
a 1 r  1 r ... 1 r   . a    1 . 1 r 1 r
Với kì hạn một tháng, suy ra 3 năm có 36 kỳ. Lãi xuất của một năm là 7,2%, suy ra lãi xuất của 1 tháng là:
7,2 % 0.6%. Áp dụng  1 ta có: a  5000000;r  0.6%  0.072;n  36 12
5000000 1 0.6%1 0.6%36   1  T   201453000 36 0.6%
Câu 130. Số tiền trả cho ngân hàng nếu vay 200 triệu trong 4 tháng N    4 200. 1 0, 7%  200  5, 65907
Tổng số tiền lãi nếu anh Bình gửi đúng kì hạn là
L  200.1 0,65%12  200  16,16996 1
Số tiền lãi nếu anh Bình làm theo tư vấn của nhân viên ngân hàng
L  16,16996  5, 65907  10,51089.
Số tiền lãi nếu gửi 8 tháng theo hình thức lãi suất không kì hạn
L  200.1 0, 02%8  200  0,32022. 2
Số tiền anh Bình đỡ thiệt nếu làm theo tư vấn của nhân viên ngân hàng
16,16996  5, 65907  0, 32022  10,19067.
Câu 131. Đặt T  8 000 000
Số tiền thầy giáo thu được sau tháng thứ nhất, thứ 2, thứ 3,., thứ n lần lượt làT , T , T ,..., T 1 2 3 n Ta có:
T T 1 r 1  
T  T T 1 r   T 1 r 2  T 1 r 2 1  
T  T T 1 r   T 1 r 3  T 1 r 2  T 1 r 3 2   . n n n 1  1 r  1 T TrTr   Tr Tr n 1  1  ... 1  1  rn 1 r  1
Theo bài ra ta có T  400 000 000  Tr   n 1  400 000 000 r n 251 251  1 r    n  log  44, 54 1.005 201 201
Vậy sau 45 tháng thầy giáo sẽ mua được một chiếc xe ô tô trị giá 400 000 000 VNĐ.
Câu 132. Với 100 triệu ban đầu số tiền cả lãi và gốc thu được sau hai năm là
T  100.1 0,8%24 6 .10  121074524 1
Mỗi tháng tiếp theo gửi 2 triệu thì tổng số tiền cả lãi và gốc là 2 T .   1 0,00823 1    .1 0,008 6 10  50686310 2 0, 008  
Vậy tổng số tiền là T T T  171.761.000 1 2
Câu 133. Cuối tháng thứ nhất, tiền gốc và lãi là 400 1, 01 triệu đồng. Sau khi trả 10 triệu thì số tiền người
đó còn nợ ngân hàng là 4001, 0110 triệu đồng.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Cuối tháng thứ hai, tiền gốc và lãi là:  2 400 1, 01 10 1, 
01 triệu đồng. Sau khi trả 10 triệu thì số tiền người
đó còn nợ ngân hàng là  2
400 1, 01 101, 0110 triệu đồng.
Như vậy ở cuối tháng thứ n n  
1 người đó nếu còn nợ thì số tiền nợ là:  n n 1  n2 400 1, 01 10 1, 01 10 1, 01
 10 triệu đồng. Xét n n 1  n2 400 1, 01 101, 01 101, 01 10  0 1, 01n  5 n 1  400 1, 01 10   0 600 1, 01n    1000  n  log  51,33 1,01 0, 01 3
Do vậy kỳ cuối cùng người đó phải trả tiền là tháng thứ 52 . Cuối tháng thứ 51, số tiền còn nợ lại là 51 1, 01 1 51 400 1, 01 10 
 3,3531596 triệu đồng. 0, 01
Vậy kỳ cuối người đó phải trả số tiền là 3, 3531596 1, 01  3,386647 triệu đồng  3387000 đồng.
Câu 134. Gọi số tiền lúc đầu người đó gửi là A (triệu đồng), lãi suất gửi ngân hàng một tháng là r , S là n
số tiền còn lại sau n tháng.
Sau 1 tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
S A 1 r 1. 1  
Sau 2 tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là:
S   A1 r 1 1 r 1  A1 r 2  1 r 1 2     . …
Sau n tháng kể từ ngày gửi tiền, số tiền còn lại của người đó là: n   n 1 r 1 S Ar   r   r     r
A1 r   . n  n  n 1  n 2 1 1 1 1  1 rn n 1 r  1
Giả sử sau n tháng người đó rút hết tiền. Khi đó ta có S  0  Ar   n 1  0 r 1   n
1 r   Ar  
1 1  0  n  log  n   log 1 Ar . 1r 1r       1 Ar
Câu 135. Gọi sô tiền mẹ gửi vào ngân hàng vào đầu tháng hàng tháng là A đồng.
Số tiền mẹ lĩnh vào đầu tháng 12 là T đồng.
Lãi suất hàng tháng mẹ gửi tại ngân hàng là r %.
Vì mẹ rút tiền vào đầu tháng 12 năm 2019 nên thời gian được tính lãi suất là 11 tháng. Ta có:
+) Đầu tháng 1 mẹ gửi vào A đồng.
 cuối tháng 1 số tiền của mẹ là: A Ar A1 r đồng.
+) Đầu tháng 2 số tiền của mẹ gửi vào là: A A1 r đồng.
 cuối tháng 2 số tiền của mẹ là:  A
A  r   r   A  r  A  r2 + 1 1 1 1   đồng.
+) Đầu tháng 3 số tiền mẹ gửi vào là: A A  r   A  r 2 1 1 . 2 2 3
 cuối tháng 3 số tiền của mẹ là:  A
A1 rA1 r     
1 r  A1 r  A1 r  A1 r .  
Cứ như vậy đến cuối tháng thứ 11 số tiền của mẹ là:
A1 r A1 r 2 ... A1 r11
A 1 r 1 r2 ... 1 r11               T . 1   2 11 Ta thấy 
 1 r  1 r ... 1 r       
là tổng của 1 cấp số nhân với u  1 r, n  11, q  1 r .   1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 u  11 1 q 1   T A . Ta có: 1 1 q A  4000000 r  1%  0.01
T  46730000 đồng. 1
Vì mẹ rút tiền vào đầu tháng 12 năm 2019  T T  4000000  50730000 đồng. 1
Câu 136. Xét bài toán 1: Vay nhận vốn định kì lãi suất kép.
Gọi A là số tiền mỗi năm bạn H vay ngân hàng, r là lãi suất theo năm. 1
Cuối năm thứ nhất, H nợ ngân hàng với số tiền là . A 1 r . 1 
Đầu năm thứ hai, H nợ ngân hàng với số tiền là A  . A 1 r . 1 
Cuối năm thứ hai, H nợ ngân hàng với số tiền là A  .
A 1 r   A A1 r  r A1 r   A1 r 2 1  1  . 1 1 1
Tiếp tục như vậy, cuối năm thứ n số tiền mà H nợ ngân hàng là: An 1 r  1 r 1    1   1  B An
1 r A1 r 2 ... A 1 r           . 1 1  1  r1
Xét bài toán 2: Vay trả góp, lãi suất dư nợ thực tế.
Gọi a là số tiền mà bạn H phải trả hàng tháng sau khi ra trường, r là lãi suất mỗi tháng, số tiền H nợ ngân 2 hàng là B.
Cuối tháng thứ nhất bạn H còn nợ ngân hàng số tiền là: B  . B r a  .
B 1 r a . 2  2 
Cuối tháng thứ hai bạn H còn nợ ngân hàng số tiền là: 2 .
B 1 r a   .
B 1 r ar a . B 1 r
 a a 1 r  2    2   =  2    2  2  .
Cứ tiếp tục như vậy ta có công thức tổng quát.
Cuối tháng thứ m bạn H còn nợ ngân hàng số tiền là m m . B 1 r
a 1 r a 1 r 2 a ... 1 r  1 a          2 2 2 2    m m 1 r 1 2  = . B 1 ra . 2  r2
Áp dụng 2 bài toán trên vào câu 42, ta có phương trình. 4 60 4.1, 03 1  , 03 1   1, 0025 1 60 1, 0025  . a
 0  a  0, 309718 (triệu đồng). 0, 03 0, 0025
Vậy số tiền mà H cần phải trả hàng tháng là 309.718 triệu đồng.
Câu 137. Chọn A
Gọi a là số tiền trả hàng tháng.
Sau tháng thứ 1, số tiền còn lại: P  500 1 r a . 1   2
Sau tháng thứ 2, số tiền còn lại: P P 1 r a  500 1 r   a 1 r   a . 2 1   . n n 1 
Sau tháng thứ n , số tiền còn lại: P  500 r a r a r a . n
1   1   ... 1    24  r 24 24 1 1
5001 r  .r
Vậy sau 24 tháng: 5001 r   a  0  a r 1 r 24 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 50011%24 .1%  a   23, 537 triệu đồng. 11%24 1 M
Câu 138. Phương pháp:Sử dụng công thức trả góp P(1 r)n (1 r)n 1       r  , trong đó:
P : là số tiền phải trả sau n tháng
r : Lãi suất/ tháng
M : số tiền phải trả mỗi tháng
Áp dụng công thức ta có: M P(1 r)n (1 r)n 1       rn 4 50(1 1,1%) (1  1,1%)n 1        1,1%  n 4 n 4  50(11,1%)  (1 1,1%)  1,1% 1,1% 4 3450 (1 1,1%)n    1,1% 11 n 80 80  (11,1%)   n  log  13,52 11,8 69 69
Câu 139. Gọi X là số tiền mỗi tháng ông A trả cho ngân hàng.  n n 1 r  1
Số tiền còn nợ sau n kì hạn là T T .  rX
(triệu đồng), trong đó T  100 (triệu đồng) là n 1  . r số tiền mà ông A vay.
Sau đúng một năm, số tiền ông còn nợ là 50 triệu đồng nên ta có  12 100.1, 01  50.0,01 12 1 0,0 12 1 1 50  100.1 0, 0  1  X .  X   4,94 (triệu đồng). 0, 01 12 1, 01 1
Vậy mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền 4, 94 triệu đồng.
Câu 140. Sau 3 năm, bắt đầu từ tháng đầu tiên của năm thứ 4 số tiền lương người đó nhận được sau mỗi
tháng là 6  6.10%  6.1,1 (triệu đồng).
Sau 6 năm ( 2.3 năm), bắt đầu từ tháng đầu tiên của năm thứ 7 số tiền lương người đó nhận được sau mỗi tháng là      2 6.1,1 6.1,1.10%
6.1,1. 1 10%  6.1,1 (triệu đồng).
Tương tự như vậy sau 15 năm ( 5.3 năm), bắt đầu từ tháng đầu tiên của năm thứ 16 số tiền người đó nhận được sau mỗi tháng là 5 6.1,1 (triệu đồng).
Vậy tháng đầu tiên của năm thứ 16 , người đó nhận được mức lương là 5 6.1,1 (triệu đồng).
Câu 141. Dạng toán lãi kép:
Bài toán tổng quát: gửi a đồng vào ngân hàng với lãi suất r% (sau mỗi kì hạn không rút tiền lãi ra).
Gọi A là số tiền có được sau n năm. n
Sau 1 năm: A a r%.a a 1 r% . 1  
Sau 2 năm: A a 1 r%  a 1 r%.r%  a 1 r%2 . 2 2 2 3
Sau 3 năm: A a 1 r%
a 1 r% .r%  a 1 r% . 3       n
Sau n năm: A ar . n 1 %
Người đó nhận được số tiền hơn 100 triệu. Suy ra:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 n 50 1 6%  100  50.1, 06n  100  1, 06n  2  n  log 2  11, 9 1,06 Vậy n  12 .
Câu 142. Gọi số tiền mỗi tháng anh gửi tiết kiệm ngân hàng trong 36 tháng đầu là A ; số tiền mỗi tháng
anh gửi tiết kiệm sau tháng thứ 36 là B .
Đặt q  1 0, 5%  1, 005
Gọi S là số tiền sau tháng thứ n ta có n S A  .0 A , 5%  . A q 1
S  S A  S A.0,5%  S A 2
.q Aq Aq . 2 1 1 1 …. 36 1        .0,5%     36 35 .    q S S A S A S A q Aq AqAq A . q . 36 35 35 35 q 1
S S B S B .0,5%  S B .q S .q  . B q . 37  36   36   36  36
S  S B  S B.0,5%  S B 2 2
.q S q Bq Bq . 38 37 37 37 36 …. 36 12 q 1 q 1 12 12 11 13 S
S .q Bq Bq  ...  Bq Aq .  B . q . 48 36 q 1 q 1
Theo giả thiết ta có A  20% x  0, 2x ; B  20% x 10%x  0, 22x ; 8 S  10 . 48 36 12 q 1 q 1 36 12  q 1 q 1  Vậy 13 8 0, 2xq .  0, 22 . x . q  10 8 13
x  10 : 0, 2q .  0, 22. .  q   x  8991504 q 1 q 1 q 1 q 1   đồng.
Câu 143. Bài toán được chia làm hai giai đoạn 7, 8
* Giai đoạn 1: vay vốn để học đại học trong 4 năm. Đặt r   0,078 100 Ở năm thứ nhất: 4
M  10(1 r) (triệu đồng) 1 Ở năm thứ hai: 3
M  10(1 r) (triệu đồng) 2 Ở năm thứ ba: 2
M  10(1 r) (triệu đồng) 3 Ở năm thứ tư: 1
M  10(1 r) (triệu đồng) 4 4
Như vậy tổng số tiền mà Nam đã vay trong 4 năm là M   M  48,4324 (triệu đồng) 0 i i 1 
* Giai đoạn 2: trả góp cho ngân hàng số tiền đã vay hàng tháng  0,7    0,7
Sau tháng thứ nhất, người đó còn số nợ là: P M 1  
 m . Đặt y  1 1 o   100   100
Sau tháng thứ hai người đó còn nợ: 2 
P P y m  M y my 1 2 2
y m M y  (
m y  1)  M y m 2 1 o o a y 1
Sau tháng thứ ba người đó còn nợ:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 y
P P y m M y m y y   M y m o   3 1 3 2 3 1 3 2 o y 1
Bằng phương pháp quy nạp, sau n tháng số tiền trả hết sẽ là n    y 1 n M y (y 1) M y m  0 om o y 1 n y 1 0,7
Đồng thời ta có: n  48 tháng và y  1
 1,007 suy ra m  1,914 (triệu đồng). 100 Câu 144. Chọn
Anh sinh viên vay hàng tháng a  3 triệu đồng từ 9 / 2014 đến 8 / 2016 , tổng cộng 24 tháng.
Cuối tháng thứ 1: T a  ar  a 1 r 1   2
Cuối tháng thứ 2: T T a T a .r  . a 1 r  . a 1 r 2 1  1      …. n n 1 
Cuối tháng n: T  . arar   ar n 1  .1  ... .1   n 1 r  1 Suy ra T  . ar n 1 . r 1 0,8%24 1
Vậy tổng số tiền vay đến cuối tháng 8/2016 là T  3. 1 0,8% .  79, 662 triệu 24   0,8%
Tính từ cuối tháng 8/2016 Anh sinh viên thiếu ngân hàng A  79, 662 và bắt đầu trả đầu hàng tháng m  2
triệu từ 9 / 2016 đến 6 / 2018 , tổng cộng được 22 tháng
Đầu tháng 9 / 2016 : còn nợ A m  79, 662  2  77, 662 triệu
Cuối tháng 9 / 2016 : tiền nợ có lãi đến cuối tháng: T  77, 662 r 1 1  
Đầu tháng 10 / 2016 sau khi trả nợ m thì còn nợ 7 7, 662r   1  m 2
Cuối tháng 10 / 2016 : còn nợ T   77, 662 r 1  m 1 r  77, 662 1 rm 1 r 2            3 2
Cuối tháng 11/ 2016 : còn nợ T  77, 662 1 rm 1  rm 1  r 3       ….
Cuối tháng 6 / 2018 còn nợ
T  77, 662 1 r 22  m 1 r 21  m 1 r 20  ...  m 1 r 22   22 1 r 21 1
 77, 662 1 r   . m 1 r r 22 1 0,8%21 1
 77, 662.1 0,8%  2.1 0,8%.  46, 64 triệu đồng. 0,8%
Câu 145. Khi mới bắt đầu đi vào môi trường nước biển thì x  0  I I .eo 1 o Ở độ sâu 30 mét thì .30 I I e . 2 o   .30 I I e . Vậy ta có: 2 o 42 I e   
.I , vậy I tăng 42
e lần so với I , nói cách khác, I giảm 42 e lần so với o 2 1 I I e . 2 1 2 1 o I 1
Câu 146. Gọi S là diện tích lá bèo thả ban đầu.
Vì sau mỗi giờ, lượng bèo tăng gấp 10 lần lượng bèo trước đó nên sau 12 giờ, tổng diện tích các lá bèo trong chậu là 12 10 S .
Theo đề bài: Sau 12 giờ, bèo phủ kín mặt nước trong chậu nên diện tích mặt nước trong chậu là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 12 1
10 S . Giả sử sau x giờ thì bèo phủ kín mặt nước trong chậu. 5 x 1 Ta có: 12 10 S  .10 S 12
10 x  5  x 12  log 5  11,3. 5 1
Vậy sau 11,3 giờ thì bèo phủ kín mặt nước trong chậu. 5
Dạng 5. Bài toán cực trị
Câu 147. Chọn B
Từ giả thiết suy ra log a b   và log
4a  5b 1  0 . 8ab 1    a b  2 2 16 1 0 4 5 1  Áp dụng BĐT Côsi ta có log a b   a b   2 log a b a b ab  2 2 16 1 .log 4 5 1 4 5 1  8ab 1    a b  2 2 16 1 log 4 5 1 4 5 1  8ab 1    2 2  2 log
16a b  1 . 8 ab 1    2 Mặt khác 2 2
16a b 1  4a b  8ab 1  8ab 1 a  , b  0 , suy ra 2 2 2 log
16a b  1  2 . 8ab 1    Khi đó log a b   a b   a b  2 2 16 1 log 4 5 1 2 4 5 1  8ab 1     log 8ab 1  log 4a  5b 1 4 a5b 1    8ab 1      b  4a   3  2 log a   32  a  24aa a  2 32 1 1 24 1        4 . b   4ab  4ab   3  3 27
Vậy a  2b   6  . 4 4
Câu 148. Chọn A 1  xy
Với x, y dương và kết hợp với điều kiện của biểu thức log
 3xy x  2y  4 ta được 1 xy  0 3 x  2y 1  xy Biến đổi log
 3xy x  2y  4 3 x  2y
 log 1  xy  log x  2y  31  xy  x  2y  log 3 3 3 3  log 1 xy log 3 3 1 xy log x 2y x 2y 3       3     3           log 3 1 xy 3 1 xy log x 2y x 2y 1 3
        3          
Xét hàm số f t  log t t trên D  0;  3 f t 1 ' 
 1  0 với mọi x D nên hàm số f t  log t t đồng biến trên D  0;  t.ln 3 3 3 2y Từ đó suy ra   1
31 xyx 2y 3 2y x 1 3y           x  (do y  0 ) 1  3y 3  2y 3
Theo giả thiết ta có x  0, y  0 nên từ x
ta được 0  y  . 1  3y 2  2 3 2y 3y y  3
P x y   y  1  3y 3y  1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 3y y 3 3
Xét hàm số g y    với 0  y  3y  1 2 2 1  11
g y 9y  6y  10 '   0 ta được y  .  2 3y  1 3   1  11 2 11  3
Từ đó suy ra min P g    .    3  3 Câu 149. Chọn C
Điều kiện: ab  1. 1 ab Ta có log
 2ab a b  3  log 2 1 ab   2 1 ab  log
a b a b * . 2 2       2       a b
Xét hàm số y f t   log t t trên khoảng 0; . 2 1
Ta có f t   1  0, t
  0 . Suy ra hàm số f t  đồng biến trên khoảng 0; . t.ln 2 b   2
Do đó *  f 21 ab  f a b  2 1 ab  a b a 2b  
1  2  b a    . 2b 1 b  2
Do a  0, b  0 nên
 0  0  b  2 . 2b 1 b  2 b   2
Khi đó: P a  2b
 2b . Xét hàm số g(b) 
 2b trên khoảng 0; 2 . 2b 1 2b 1  2   10 b    0;2 5  5 gb 4   2  0  2b 1    2  2 2b   1 2  2   10 b  0; 2  4 Lập bảng biến thiên  10  2  2 10  3 Vậy Pg    . min  4  2    xy  ln  Câu 150.  2  ln( xy ) ln 5
ln( xy )ln 2 ln( xy ) ln 5 ln( xy ) ln( xy ) ln 5 ln 2 2 .5  2  2 .5  2  2 .5  2 .2 ln( xy) ln10  10  2     ln10  ln(  ) ln10.log 2 ln( ) log 2  ln(  )  ln10.log 2 x y x y x yee log 2
x y  10
x y  2 .
Do đó P   x  
1 ln x  3  x ln 2  x .
Xét hàm số f (x)  (x 1) ln x  (3  x) ln(2  x) x  1 3  x x 2  2x f (
x)  ln x   ln(2  x)   ln  . x 2  x 2  x x(2  x)
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 1 2  x 2x  4x  4
f  x   .   0,x  0; 2 2 2   2  xx  2 2x x
Do đó f  x  0 có nhiều nhất một nghiệm trên 0;2
Mà x  1 là một nghiệm của pt f  x  0 nên phương trình f  x  0 có nghiệm duy nhất là x  1 .
Lập bảng biến thiên ta được max f x  f   1  0 .
Câu 151. Với điều kiện biểu thức đề bài có nghĩa, ta có x y log  x  1
y  1  2  0  log
x y  log 1  xy xy x y  1  0 3     3   3   1  xy  log
x y x y  log 1  xy  1  xy * 3     3     
Xét hàm số f x  log t t trên 0;2 3 1
f t  ln 3  1  0, t
  0;2 nên hàm số f t đồng biến trên 0;2 . t 1  x
Do đó từ * ta có x y  1  xy y 1  x  1  x y  1  x 1  x
P  2x y  2x  1  x 2
P x  2   0, x   0;1 2   1 x
Suy ra min P P 0  1 đạt được khi x  0, y  1.
Câu 152. Ta có a b  1  log b  0 . a 1 a P   log
 log ab  log a  log b  1  log b  1  log b. log a a a a a a a b ab Đặt t   b t   2 1 log
0  log b  1  t . Ta có: 2 P t
  t  2 trên 0;  a a Bảng biến thiên t  1  2 P 9 2 1
Hàm số đạt giá trị lớn nhất tại t  . 2 3 1 1 3 3 Với 4 t  
 1  log b  log b
b a k  . 2 2 a a 4 4
Câu 153. Chọn B 2 2 log
2a  8b  1  2a  8b a  4b 1 2 2   a  4b 1  Ta có:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2  2 2
2a  8b a  4b 1
2a  8b a  4b 1     S  6b  5
S  4a  6b  5 a     4 2
  S  6b  5 
S  6b  5  2 2  8b   4b 1       4   4     S  6b  5 a    4 2 2 2 8
S  48b  40 128b S  36b  25 12Sb 10S  60b  64b 16    S  6b  5 a    4 2 2 10 
0b  2(58  6S )b  2S 1 S  0    S  6b  5 a    4 2 2 2
  (58  6S) 100.(1 S )  0  64S  896S  3264  0  17  S  3  13 a    5
Giá trị lớn nhất của S là: 3   2  b    5 a 13 Suy ra  b 2 Điều kiện 2 2
4x  9 y  1. Câu 154. Trường hợp 1: 2 2
4x  9 y  1. 2 2 2x  1 1 3
Ta có 2x  3y  1    x  3y  1  P  .   1 3y  1  2 2 Trường hợp 2: 2 2
4x  9 y  1. 2 2  1   1  1 Khi đó 2 2 log
2x  3y  1  2x  3y  4x  9 y  2x   3y   . 2 2   4 x 9 y      2   2  2 1  1   1  3
P x  3y  2x   3y       . 2  2   2  4
Áp dụng BĐT Bunhiacopski ta được: 2 2 2 1  1   1   1    1   1     5 2x   3y   1         2x   3y        . 2   2   2   4   2   2  8   1  1   1  3 3  10 Suy ra P  2x   3y        . 2 2  2   2  4 4
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489   1  1  5  10 2 2x   3y     x    2  2 8  x 6 y 1      20
Dấu bằng xẩy ra khi và chỉ khi      . Từ   1 và  3  10
4x 12 y  3  10   5  2 10 x  3y y    4   30  3  10
2 suy ra giá trị lớn nhất của P là . 4
Câu 155. Chọn D 1 1 Ta có: P   4.log a    a b  1 4.logb  1 1 log b 1 a 1 log a b t
Đặt t  log a . Vì a b a  log a   a
  t   t  . b   1 log 1 1 2 b b 2 1 tP   4t   1   4t  
1 với t  1;2 . 1 t 1 1 t t
Xét hàm số f (t)   4t  
1 với t  1;2 . t 1  3 t  tm 1 1   2 f (  t)   4, f (
t)  0  t 1    . 2  2 t   1 4 1 t  l  2 Bảng biến thiên 3 3 t -∞ 1 2 +∞ 2 2 f '(t) - 0 + +∞ f (t) 6 5  3 
Từ bảng biến thiên suy ra: minf t   f  5.   1;2  2 
Vậy giá trị nhỏ nhất của biểu thức P bằng 5 .
Câu 156. Chọn A 1 Do a a
a  a  2 4 2 2 2 9 81 9 9  0 đúng a  
; Dấu bằng xảy ra khi a  3 3
Suy ra P  log b  log ab a a b 3 2 log 2 log 3 2 2 3 3a b
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 a  3 a  3 
Dấu bằng xảy ra khi và chỉ khi    2
log b  2 log 3a  3a bb  9 
Vậy, khi P đạt giá trị nhỏ nhất thì 2
a b  3  9 .
 4a  2b  5  Câu 157. log
a  3b  4  log 4a  2b  5  log a b a  3b  4 5   5   5    a b   log
4a  2b  5  4a  2b  5  log 5 a b   5 a b 5     5       (*).
Xét hàm f x  log x x, x  0 . 5 1
Đạo hàm f  x 
 1  0, x  0 . Suy ra hàm số f x đồng biến trên 0; . x.ln 5
Phương trình (*) viết lại:
f 4a  2b  5  f 5a b  4a  2b  5  5a b  a  3b  5 . 2 5 Mặt khác: 2
5  a  3b   2 2 1  3 . 2 2 a b  2 2
T a b  . 2 a b 1 3 Dấu "  " xảy ra    a  ;b  . 1 3 2 2 2 b 1 8b 1 1 8b 1  2b Câu 158. Ta có:    . 2   b   . 2 16 16 4 4  2  4 c 3 8c  3 1 1 1 8c  3  4c     . . . 4   c   . 2 16 16 2 2 2 2  4  3  b 1  1  c 3  1 Suy ra P  log   log   log a     16 a  2 16  4 b  2 16  3 c 3 1 1 2 4 2 3  log b
log c  log c 3  3.  . 16 a 4 b 3 a 16 2  1  b   4 8  b 1  1  3   1 Vậy P   8  c  3  1  c  . min 2 2 3 1 
 log b  log c  log aa b c 2 8 3 a   4 Câu 159.  log  2 2
a b  9 1 log 3a  2b 2 2 2 2
a b  9  6a  4b a b  6a  4b  9  0   1 2 2
Gọi Aa;b . Từ  
1 ta suy ra điểm A thuộc điểm đường tròn C có tâm I 3; 2 , bán kính R  2 . 4 4  2 2 2 mn
 m n 2mn      2 9 .3 .3 ln 2 2 1 81 ln 2 2 1           81 3 mn m n m n      4 4 4 
2mn
Theo bất đẳng thức Cô-si:  2m n 
 2  2m n.  4 2  3 mn  81. 2m n 2m n 4 
(Đẳng thức xảy ra khi:  2m n 
 2m n  2  ) 2m n 2 2 2 Từ   ln 2m n 2 1     
 0  2m n  2 1  1  2m n  2  0  
 2m n  2  0 2 . Gọi B  ;
m n . Từ 2 ta suy ra điểm B thuộc đường thẳng  : 2x y  2  0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2 2
Ta có: P  a m  b n  AB 3.2  2  2
 min P  min AB d I;   R   2  2 5  2. 2 2 2 1 lna lnb
Câu 160. Ta có b a
a b blna alnb   * . a b lnx Xét hàm số y
, trên tập xác định D  0;  x 1 ln x y 
, y  0  x e 2 x Bảng biến thiên x 0 a e b +∞ y / + 0 _ 1 y e 0 -∞ 0  a b  Có  f
 a  f b 
Kết hợp với bảng biến thiên suy ra a e b   1 . Ta lại có f
x x a b x x  2  3 x x a b x x  2  3 x b a  1. , a b    
a x b Suy ra min f
x b a  1   2 , a b   x   2  x  3  Từ  
1 và 2 suy ra số thực duy nhất thỏa mãn yêu cầu bài toán là x e
Thử lại: khi x e thì f  
e b a  1. Vậy min f x f xf e a,b   a,b  0  a,b          x R
Câu 161. Chọn A 2 Ta có x x 1
a b    x   2 x   b   b x x b aa  2 1 1 log 0 log log 0 a
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489  1 x x    log a  1 2 b
Do phương trình có hai nghiệm x , x nên theo định lý Viet ta có: log b 1 2  ax x  1  1 2 1 Khi đó S   4 log a 2 log b a b 1 1
Đặt t  log a , do a  1, b  1  t  0 . Khi đó 3 S   4t
 2t  2t  3 4 . b 2 2 t t 1 1 Đẳng thức xảy ra khi  2t t  . Vậy 3 min S  3 4 2 3 t 2
Câu 162. Chọn C 2 b 1 8b 1 1 8b 1  2b  Ta có:    . 2   b   . 2 16 16 4 4  2  4 c 3 8c  3 1 1 1 8c  3  4c     . . . 4   c   . 2 16 16 2 2 2 2  4  3  b 1  1  c 3  1 Suy ra P  log   log   log a     16 a  2 16  4 b  2 16  3 c 3 1 1 2 4 2 3  log b
log c  log c 3  3.  . 16 a 4 b 3 a 16 2  1  b   4 8  b 1  1  3   1 Vậy P   8  c  3  1  c  . min 2 2 3 1 
 log b  log c  log aa b c 2 8 3 a   4
Câu 163. Cách 1. y x y x e e e e    
Ta có: x x y
y   ln x
x    ln y   y y e x e y e x e       x y x 1  x ln y
y xe y ln x x ye   (*) (vì x
y e  ln x có y '  e   0; x   1 nên ln x x e ln y y e x y y   1  e  0 ) t ln t t e 1 tte
Xét hàm số: f t  
trên 1; ta có f 't  
. Với hàm số    ln t  1 t g t t ete ln t t e ln t t e 2 có     t t     1 ' ln 1 ' t g t t e te   te  0, t   1 t
Nên g t   g   1  1
  f 't   0; t   1
y f t là hàm nghịch biến trên 1; nên với (*) f x  f y  y x  1 1 1 1 1 1 1 1 2 2 Khi đó P  log xy  log x   log y    2 log . yx y 2 2 x log y 2 2 x log y 2 x x 1 1 Dấu “=” xảy ra khi: log y   y   y x x logx 2 2 2 2 log y x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1 2 2 Vậy: P  . min 2 Cách 2:
Với x, y  1 thì log ;
y log x là các số dương, ta có: x y 1 1 1 1 1 1 1  2 2 P  log xy  log x   log y    2 log . yx y 2 2 x log y 2 2 x log y 2 x x 1 1 Dấu “=” xảy ra khi: log y   y   y x , x logx 2 2 2 2 log y x 2   y x Thay 
vào điều kiện thấy thỏa mãn điều kiện ban đầu. x  1  1 2 2 Vậy P  . min 2 1 y Câu 164. Để  0 mà từ giả thiết ,
x y  0 suy ra 1 y  0  y  1. Vậy ĐKXĐ: x  0; 0  y  1. x  3xy 1 y 1 y 31 y Ta có: log
 3xy x  3y  4
3xyx3 y 4   3
3xyx3 y3   3 3 x  3xy x  3xy x  3xy 31 y 3 3 xyx       33y     3 3 3 .3 3 .3 xyx y xy x (*) 3 3 x  3xy 3  y Xét    .3t f t t với t  0 . Ta có
   3t  .3t f t t .ln 3  0 với t
  0 , suy ra f t  đồng biến trên khoảng 3  x
0; . Từ (*) ta có f 3 3y  f 3xy x với 3 3y  0,3xy x  0 nên 3 3y  3xy x y  3(x1) . 3  x  3  x 1  4
Ta có P x y x    x   1      3 x  1  3 x  1 3    3   4 4 4 4 4 3  4
P   x   1    2  x   1 .   . 3 x   1 3 3 x   1 3 3  4 x 1   3 x   1  2 3  3  x  4 3  4  3  x  3 Vậy P    y   . min  3 3 x   1   2 3 1 y   x 0;0 y 1      3   Câu 165. Ta có:
log x  log y  log  2 x y  log xy  log x y
xy x y 1   1  2  2 1 1 1  2 2 2 2 2 2  y x  
x y   2 1  y   y 1 ( Vì ; x y  0 ).  y 1  2 y 1
Ta có: P x  3y
 3y  4 y 1 . y 1 y 1
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 1
Xét hàm số: f y  4 y 1 ; y  1. y 1 1 Đạo hàm: /
f y  4  .  y  2 1  3 y  n  / f y 2  0   . 1
y  l  2 Bảng biến thiên. Câu 166. Ta có: 2 log x  log y  log x y 2  log xy  log x y 2
xy x y 2019 2019   2019 2019 2019   2  xy
y x   2 1  x   x 1 x  1  2 x 1
Ta có: T  2x y  2x   3x  1 . x 1 x 1 1
Xét hàm số: f x  3x 1 ; x  1 . x 1 1 Đạo hàm: /
f x  3  .  x  2 1 3 /
f x  0  x  1 (do x  1) . 3 Bảng biến thiên. Do đó: T  4  2 3 . min
A. 0, 014 B. 0, 0495 C. 0, 079
D. 0, 055 Chọn số tự nhiên có 4 chữ số bất kỳ có:
n   9.10.10.10  9000 (cách).
Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có: m n m n 1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 x a   y b 1 Do đó nếu đặt:  z c  2  t   d  3 
Từ giả thuyết 1  a b c d  9 ta suy ra: 1  x y z t  12 (**).
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ 1, 2,...,1 
2 ta đều có được duy nhất một
bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số a,b, c, d  thoả mãn (*). Số cách chọn tập
con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó: n A 4  C  495 . 12 n A 495
Vậy: P A    0, 055 . n  9000
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có: n   9.10.10.10  9000 (cách).
Mỗi tập con có 4 phần tử được lấy từ tập 1, 2,..., 
9 (trong đó mỗi phần tử có thể được chọn lặp lại nhiều
lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được một số tự nhiên có dạng
abcd (trong đó 1  a b c d  9 ). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử.
Do đó theo công thức tổ hợp lặp ta có: n A 4  C  495 . 94 1  n A 495
Vậy: P A    0, 055 . n  9000
Dạng 6. Một số bài toán khác
Câu 167. Chọn D Ta có     x   1  9 y f x f y  4
m x y  4 log m  2 log m 9 3
Đặt x y t,t  0 . Vì xy      t e e x y
e et t  1  ln t  1  ln t t  0,t  0 (1) 1 1 t
Xét hàm f t  ln t  1 t với t  0 . f t     1   0  t  0 t t Bảng biến thiên
Dựa vào bảng biến thiên, ta có f t  f 1 ,t  0  1 ln t t  0,t  0 (2)
Từ 1 và 2 ta có t  1  2 log m  1  2
m  3  m   3 3
Câu 168. Ta có f af bf c 3
f a f bf c e e e 3 e      .
Mặt khác do f   x  0, x   nên f x là hàm lồi, áp dụng bất đẳng thức lồi ta có
a b c
f a  f b  f c  3 f    3 
abc
abc  3 3 f f    
Do đó f af bf c  3   3 e e e 3 e 3e     
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
abc 2  f  
3   a b c  
a b c  Suy ra  3 P  3  e   f 1     . Đặt 2 t f , t n  0   2   3    3  t 3
Ta có P g t  với g t   3e  t  2 1 2    3  et  3   1 ; "   3  et  3  3  et g t t g t   1  0, t
  0. Nên gt là hàm nghịch biến trên0; .
g '(t)  g(0)  0, t
 0;  g(t)  g(0) 3
Do đó P g 0   7  3e. 2 Câu 169. Ta có 2
y  ln x  2x m  0 , suy ra min y nhỏ nhất bằng 0 2 1  ;e     2
ln x  2x m  0 có nghiệm 2 x  1  ; e      1 .
Đặt f x 2
 ln x  2x . Khi đó  
1  f x  m , 2 x   1  ; e    . 2 1 1 4x
Ta có f  x 2   4x   0, x   1  ; e x x   . BBT
Dựa vào bảng biến thiên suy ra 4
m  2; 2e  2   .
Suy ra m 2;3; 4;5;...;106;10  7 .
Vậy có tất cả 106 số nguyên m thỏa mãn yêu cầu bài toán.
Câu 170. Chọn B Hàm số ( ) 2x 2 x f x    xác định x    .
Khi đó x   , ta có ( )  2x  2x  (2x   2x f x )   f ( ) x .
Suy ra f (x) là hàm số lẻ.   1 Mặt khác ( ) (2x 2 x f x     ) ln 2  0, x    .
Do đó hàm số f (x) đồng biến trên  . 2 Ta có 12 f ( )
m f (2m  2 )  0 12
f (2m  2 )   f ( ) m . Theo   1 suy ra 12
f (2m  2 )  f ( ) m . 12 2 Theo 2 ta được 12 12
2m  2  m  3m  2  m  . 3
Vì m   nên m 1365  m  1365. Vậy m  1009;1513 . 0   0
Câu 171. Xét phương trình hoành độ giao điểm 2
mlog x  2log x  2m 1  0 . 2 2
Ycbt  Phương trình có duy nhất một nghiệm thuộc khoảng 1;  .
Đặt t  log x  0 x 1;  . 2
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489 2t 1 Phương trình 2
mt  2t  2m 1  0  m  . 2 t  2
Ycbt  Phương trình có duy nhất một nghiệm t 0; . 2t 1
Xét hàm số f t   trên 0; . 2 t  2 2 2
t  2  2t 2t   2 1 2
t  2t  4
Ta có f t    t  2 1 t  2 2 2 1
t  10; 
f t   0 2  2
t  2t  4  0   .
t  2 0;   Bảng biến thiên  1  1 
Từ bảng biến thiên ta suy ra: ycbt  m   ; 0     . 2     2 
------------- HẾT -------------
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65