Trắc nghiệm nâng cao dãy số, cấp số cộng và cấp số nhân – Đặng Việt Đông

Tài liệu trắc nghiệm nâng cao dãy số, cấp số cộng và cấp số nhân được biên soạn bởi thầy Đặng Việt Đông gồm 52 trang tuyển tập các câu hỏi và bài tập trắc nghiệm chủ đề dãy số, cấp số cộng và cấp số nhân có đáp án 

Môn:

Toán 11 3.3 K tài liệu

Thông tin:
52 trang 1 năm trước
Tác giả:
K
Kim Oanh
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Trắc nghiệm nâng cao dãy số, cấp số cộng và cấp số nhân – Đặng Việt Đông

Tài liệu trắc nghiệm nâng cao dãy số, cấp số cộng và cấp số nhân được biên soạn bởi thầy Đặng Việt Đông gồm 52 trang tuyển tập các câu hỏi và bài tập trắc nghiệm chủ đề dãy số, cấp số cộng và cấp số nhân có đáp án 

77 39 lượt tải Tải xuống

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT) 63 tài liệu

Môn: Toán 11 3.3 K tài liệu

Thông tin:

52 trang 1 năm trước

Tác giả:

Profile Kim Oanh
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
A – LÝ THUYẾT CHUNG
I – DÃY SỐ
Một hàm số
*
:u N
được gọi là một dãy số vô hạn, kí hiệu là
n
u
.
Khi
n u n
, khi đó
n
u u n
gọi là số hạng tổng quát của dãy
n
u
Một hàm số
u
xác định trên tập hợp
m
số nguyên dương đầu tiên được gọi là dãy số hữu hạn.
Dãy số
n
u
là dãy số tăng nếu
*
1
0,
n n
u u n
Dãy số
n
u
là dãy số giảm nếu
*
1
0,
n n
u u n
Dãy số
n
u
được gọi là bị chặn trên nếu tồn tại số
M
sao cho
*
,
n
u M n
Dãy số
n
u
được gọi là bị chặn dưới nếu tồn tại số
M
sao cho
*
,
n
u M n
Dãy số được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới.
II - CẤP SỐ CỘNG
1. Định nghĩa:
n
u
là cấp số cộng nếu
1n n
u u d
, với
*
n
,
d
là hằng số
2. Các khái niệm:
Cho cấp số cộng
n
u
, Khi đó:
1
1
n
u u n d
: số hạng tổng quát của cấp số cộng
d
: công sai của cấp số cộng
1 2
...
n n
S u u u
: tổng
n
số hạng đầu tiên của cấp số cộng
3. Tính chất:
1 1
n n
n
u u
u
1
2
n n
n
S u u
1
2 1
2
n
n
s u n d
III - CẤP SỐ NHÂN
1. Định nghĩa:
n
u
là cấp số nhân
1
.
n n
u u q
,
*
n
2. Các khái niệm:
1
1
. , 1
n
n
u u q n
: số hạng tổng quát của cấp số nhân
:
q
công bội của cấp số nhân
3. Tính chất:
2
1 1
.
n n n
u u u
2
n
1
1
. 1
...
1
n
n n
u q
S u u
q
;
1
q
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
B - BÀI TẬP
DÃY SỐ
Câu 1. Cho dãy số có các số hạng đầu là:
0,1;0,01;0,001;0,0001;...
. Số hạng tổng quát của dãy số này
có dạng?
A.
0
01...00,0
soá
chöõ
n
u
n
. B.
0
1
01...00,0
soá
chöõ
n
u
n
. C.
1
10
1
n
n
u . D.
1
10
1
n
n
u .
Câu 2. Cho dãy số
n
u với
nuu
u
nn 1
1
5
.Số hạng tổng quát
n
u của dãy số là số hạng nào dưới đây?
A.
2
)1( nn
u
n
. B.
2
)1(
5
nn
u
n
.
C.
2
)1(
5
nn
u
n
. D.
2
)2)(1(
5
nn
u
n
.
Câu 3. Cho dãy số
n
u
với
1
2
1
1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1 2 1
1
6
n
n n n
u
. B.
1 2 2
1
6
n
n n n
u
.
C.
1 2 1
1
6
n
n n n
u
. D.
1 2 2
1
6
n
n n n
u
.
Câu 4. Cho dãy số
n
u
với
1
1
2
2 1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
2
2 1
n
u n
. B.
2
2
n
u n
. C.
2
2 1
n
u n
. D.
2
2 1
n
u n
.
Câu 5. Cho dãy số
n
u
với
1
1
2
1
2
n
n
u
u
u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
. B.
1
n
n
u
n
. C.
1
n
n
u
n
. D.
1
n
n
u
n
.
Câu 6. Cho dãy số
n
u
với
1
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
2 1
2
n
u n
. B.
1
2 1
2
n
u n
. C.
1
2
2
n
u n
. D.
1
2
2
n
u n
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
Câu 7. Cho dãy số
n
u
với
1
2
1
1
1
n
n n
u
u u
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1
n
u n
. B.
1
n
u n
. C.
2
1 1
n
n
u . D.
n
u n
.
Câu 8. Cho dãy số
n
u
với
1
2 1
1
1
1
n
n n
u
u u
. Số hạng tổng quát
n
u
của dãy số là số hạng nào
dưới đây?
A. 2
n
u n
. B.
n
u
không xác định.
C.
1
n
u n
. D.
n
u n
với mọi
n
.
Câu 9. Cho dãy số
n
u
với
1
2
1
1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1 2 1
1
6
n
n n n
u
. B.
1 2 2
1
6
n
n n n
u
.
C.
1 2 1
1
6
n
n n n
u
. D.
1 2 2
1
6
n
n n n
u
.
Câu 10. Cho dãy số
n
u
với
1
1
2
2 1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
2
2 1
n
u n
. B.
2
2
n
u n
. C.
2
2 1
n
u n
. D.
2
2 1
n
u n
.
Câu 11. Cho dãy số
n
u
với
1
1
2
1
2
n
n
u
u
u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
. B.
1
n
n
u
n
. C.
1
n
n
u
n
. D.
1
n
n
u
n
.
Câu 12. Cho dãy số
n
u
với
1
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
2 1
2
n
u n
. B.
1
2 1
2
n
u n
. C.
1
2
2
n
u n
. D.
1
2
2
n
u n
.
Câu 13. Cho dãy số
n
u
với
1
1
1
2
n
n
u
u
u
. Công thức số hạng tổng quát của dãy số này là:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
A.
1
1 .
2
n
n
u
. B.
1
1
1 .
2
n
n
u
. C.
1
1
2
n
n
u
. D.
1
1
1 .
2
n
n
u
.
Câu 14. Cho dãy số
n
u
với
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này:
A.
1
n
n
u n
. B.
2
n
n
u
. C.
1
2
n
n
u
. D.
2
n
u
.
Câu 15. Cho dãy số
n
u
với
1
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này:
A.
1
2
n
n
u
. B.
1
1
2
n
n
u
. C.
1
2
n
n
u
. D.
2
2
n
n
u
.
Câu 16. Cho dãy số
n
u
với
1
2
1
1
1
n
n n
u
u u
. Số hạng tổng quát
n
u
của dãy số là số hạng nào
dưới đây?
A.
1
n
u n
. B.
1
n
u n
. C.
2
1 1
n
n
u . D.
n
u n
.
Câu 17. Đặt
2 2 2 ... 2
n
T (có
n
dấu căn). Mệnh đề nào dưới đây là mệnh đề đúng?
A.
3
n
T . B.
1
2cos
2
n
n
T
. C.
1
cos
2
n
n
T
. D.
5
n
T .
Câu 18. Cho dãy số
1
2
1
1
3 2
n n
u
u u
và
2 2 2
1 2 2018
... 2018
S u u u . Khi đó S có bao nhiêu chữ
số?
A. 963 B. 962 C. 607 D. 608
Câu 19. Cho dãy số
n
u
được xác định bởi công thức
1
2
1
2
2018 2017
n n n
u
u u u
. Tìm giới hạn của dãy
số
1 2
2 3 1
...
1 1 1
n
n
n
u
u u
S
u u u
?
A.
1
lim
2018
n
S B.
lim 2018
n
S C.
2017
lim
2018
n
S D.
lim 1
n
S
Câu 20. Cho dãy số
n
a
xác định bởi
2 *
1 1
3 5
1; 1,
2 2
n n n
a a a a n
. Số hạng thứ 201 của dãy
số
n
a
có giá trị bằng bao nhiêu?
A.
2018
2
a
. B.
2018
1
a
. C.
2018
0
a
. D.
2018
5
a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
Câu 21. Cho dãy số
n
u
xác định bởi
1
1
cos 0
1
, 1
2
n
n
u
u
u n
. Số hạng thứ 2017 của dãy số đã cho là:
A.
2017
2016
cos
2
u
B.
2017
2017
cos
2
u
C.
2017
2016
sin
2
u
D.
2017
2017
sin
2
u
Câu 22. Cho dãy số
n
a
xác định bởi
1 2
5, 0
a a và
2 1
6 , 1
n n n
a a a n
. Số hạng thứ
14
của
dãy là số hạng nào?
A.
3164070
. B.
9516786
. C.
1050594
. D.
9615090
.
Câu 23. Cho dãy số
n
a
xác định bởi
1
3
a và
2
1
3 4, *
n n
a a n n n
. Số
1391
là số hạng
thứ mấy của dãy số đã cho?
A.
18
. B.
17
. C.
20
. D.
19
Câu 24. Biết rằng
2
2
1 1 1
...
1.2.3 2.3.4 1 2 16
an bn
n n n cn dn
, trong đó
, , ,
a b c d
và
n
là các số
nguyên dương. Tính giá trị của biểu thức
T a c b d
.
là :
A.
75
T
. B.
364
T
. C.
300
T
. D.
256
T
.
Câu 25. Cho dãy số
n
a
xác định bởi 2017sin 2018cos
2 3
n
n n
a
. Mệnh đề nào dưới đây là mệnh
đề đúng?
A.
*
6
,
n n
a a n
. B.
*
9
,
n n
a a n
.
C.
*
12
,
n n
a a n
. D.
*
15
,
n n
a a n
.
Câu 26. Cho dãy số
n
a
có
2
, *
100
n
n
a n
n
. Tìm số hạng lớn nhất của dãy số
n
a
.
A.
1
20
. B.
1
30
. C.
1
25
. D.
1
21
.
Câu 27. Cho dãy số
( )
n
u
thỏa mãn
*
2018 2017, .
n
u n n n
Khẳng định nào sau đây
sai?
A. Dãy số
( )
n
u
là dãy tăng. B.
lim 0.
n
n
u

C.
*
1
0 , .
2 2018
n
u n
D.
1
lim 1.
n
n
n
u
u

Câu 28. Cho dãy số
n
x
với
4
2
n
an
x
n
. Dãy số
n
x
là dãy số tăng khi:
A.
2
a
. B.
2
a
. C.
2
a
. D.
1
a
.
Câu 29. Trong các dãy số sau dãy số nào là dãy bị chặn ?
A. Dãy
n
a
, với
2
16, *
n
a n n .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
B. Dãy
n
b
, với
1
, *
2
n
b n n
n
.
C. Dãy
n
c
, với
2 3, *
n
n
c n
.
D. Dãy
n
d
, với
2
, *
4
n
n
d n
n
.
Câu 30. Cho dãy số
n
u
với
2
,
n
an
u a
n
là tham số. Tìm tất cả các giá trị của a để dãy số
n
u
là
một dãy số tăng
A.
1
a
B.
1
a
C.
2
a
D.
2
a
Câu 31. Cho dãy số
( )
n
z
xác định bởi
sin 2cos .
2 3
n
n n
z
Gọi M, m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất trong các số hạng của dãy số
( )
n
z
. Tính giá trị biểu thức
2 2
.
T M m
A.
13.
T
B.
5.
T
C.
18.
T
D.
7.
T
Câu 32. Cho dãy số
( )
n
u
thỏa mãn
1 1 1 2
1 2017
; , 1. ...
2 2( 1) 1 2018
n
n n n
n
u
u u n S u u u
n u
khi
n
có giá trị nguyên dương lớn nhất.
A.
2017.
B.
2015.
C.
2016.
D.
2014.
Câu 33. Cho hàm số
cos 2017
2
3 2
x
f x x x
và dãy số
n
u
được xác định bởi công thức tổng
quát
log 1 log 2 ... log
n
u f f f n
. Tìm tổng tất cả các giá trị của
n
thỏa mãn điều kiện
2018
1
n
u
?
A.
21
B.
18
C.
3
D.
2018
Câu 34. Cho
2
2 *
1 1f n n n n
và đặt
1 3 ... 2 1
2 4 ... 2
n
f f f n
u
f f f n
. Tìm số nguyên
dương n nhỏ nhất sao cho
2
10239
log
1024
n n
u u ?
A.
23
n
B.
29
n
C.
33
n
D.
21
n
Câu 35. Cho dãy số
n
a
thỏa mãn điều kiện
1
1
3
1; 5 1
3 2
n n
a a
a
n
với mọi n
. Tìm số
nguyên dương
1
n
nhỏ nhất để
n
a
?
A.
39
n
B.
41
n
C.
49
n
D.
123
n
Câu 36. Cho dãy số
n
u
xác định bởi
1
1 1
5; 2 2.3
n n n n
n n
u u u
với mọi
1
n
. Tìm số nguyên nhỏ
nhất thỏa mãn
100
2 5
n n
n
u
.
A.
146
B.
233
C.
232
D.
147
Câu 37. Biết rằng
2 2018
2 2018
2019
4
4 4
2
2 2
...
lim
...
n n
n n
n n
n n
u u u u
a b
L
c
u u u u
trong đó
n
u
xác định bởi
1 1
0; 4 3
n n
u u u n
và
, ,
a b c
là các số nguyên dương và
2019
b
. Tính
S a b c
?
A.
1
B.
0
C.
2017
D.
2018
CẤP SỐ CỘNG
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
Câu 38. Cho dãy số
n
u
(u
n
) có
3
12
2
n
u
n
. Khẳng định nào sau đây sai?
A. Là cấp số cộng có ;
3
1
1
u
2
3
d
. B. Số hạng thứ n+1:
2
1
2( 1) 1
3
n
n
u
.
C. Hiệu
3
)12(2
1
n
uu
nn
. D. Không phải là một cấp số cộng.
Câu 39. Cho hai cấp số cộng
:4,7,10,...
n
x
và
:1,6,11,...
n
y
. Hỏi trong 2018 số hạng đầu tiên của
mỗi cấp số có bao nhiêu số hạng chung?
A. 404. B. 673. C. 403. D. 672.
Câu 40. Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
thể coi là số hạng thứ 2,thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp
số cộng này để tổng của chúng bằng 820?
A. 20. B.
42.
C.
21.
D.
17.
Câu 41. Cho cấp số cộng
n
u
biết
5
18
u
và
2
4 .
n n
S S
Tìm số hạng đầu tiên
1
u
và công sai
d
của
cấp số cộng.
A.
1
2, 4
u d
. B.
1
2, 3
u d
. C.
1
2, 2
u d
. D.
1
3, 2
u d
.
Câu 42. Một cấp số cộng có tổng
n
số hạng đầu
n
S
được tính theo công thức
2 *
5 3 , .
n
S n n n
Tìm số hạng đầu
1
u
và công sai
d
của cấp số cộng đó
A.
1
8, 10
u d
B.
1
8, 10
u d
C.
1
8, 10
u d
D.
1
8, 10
u d
Câu 43. Cho cấp số cộng
n
u
và gọi
n
S
là tổng
n
số đầu tiên của nó. Biết
7
77
S
và
12
192.
S
Tìm
số hạng tổng quát
n
u
của cấp số cộng đó.
A.
5 4
n
u n
. B.
3 2
n
u n
. C.
2 3
n
u n
. D.
4 5
n
u n
Câu 44. Cho ba số dương
a
,
b
,
c
theo thứ tự lập thành cấp số cộng. Giá trị lớn nhất của biểu thức
2
2
8 3
2 1
a bc
P
a c
có dạng
, .
x y x y
Hỏi
x y
bằng bao nhiêu:
A.
9
B.
11
C.
13
D.
7
Câu 45. Chu vi của một đa giác là
158
cm
, số đo các cạnh của nó lập thành một cấp số cộng với công
sai
3
d cm
. Biết cạnh lớn nhất là 44cm. Số cạnh của đa giác đó là:
A. 3. B. 4. C. 5. D. 6
Câu 46. Chu vi của một đa giác n cạnh là 158, số đo các cạnh đa giác lập thành một cấp số cộng với
công sai
3.
d
Biết cạnh lớn nhất có độ dài là 44. Tính số cạnh của đa giác.
A. 6. B. 4. C. 9. D. 5
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
Câu 47. Cho tam giác ABC có độ dài các cạnh là a, b, c theo thứ tự lập thành một cấp số cộng. Biết
tan tan ,
2 2
A C x
x y
y
, giá trị
x y
là:
A.
4
B.
1
C.
2
D.
3
Câu 48. Cho các số hạng dương a, b, c là số hạng thứ m, n, p của một cấp số cộng và một cấp số nhân.
Tính giá trị của biểu thức
( ) (c a) ( )
2
log . .
b c a b
a b c
A. 0 B. 2 C. 1 D. 4
Câu 49. Cho
2
a b c
và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng
A. 1 B. 2 C. 3 D. 4
Câu 50. Cho a, b, c theo thứ tự tạo thành cấp số cộng. Giá trị
x y
là bao nhiêu biết
2 2 2 2 2
2 2
log 2 log ,P a ab b bc c x a ac c y x y
.
A. 0 B. 1 C.
1
D. 2
Câu 51. Cho ba (bố số chứ) số
, , ,
a b c d
theo thứ tự đó tạo thành cấp số nhân với công bội khác
1
. Biết
tổng ba số hạng đầu bằng
148
9
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và
thứ tám của một cấp số cộng. Tính giá trị biểu thức
T a b c d
?
A.
101
.
27
T B.
100
.
27
T C.
100
.
27
T D.
101
.
27
T
Câu 52. Cho cấp số cộng
n
u
. Mệnh đề nào dưới đây là mệnh đề đúng?
A.
0
m n p
n p u p m u m n u
. B.
0
m n p
m n u n p u p m u
.
C.
0
m n p
m p u n m u p n u
. D.
0
m n p
p n u m p u m n u
.
Câu 53. Cho ba số dương
, ,
a b c
thỏa mãn điều kiện
1 1 1
, ,
b c c a a b
lập thành một cấp
số cộng. Mệnh đề nào dưới đây là đúng?
A. Ba số
, ,
a b c
lập thành một cấp số cộng.
B. Ba số
1 1 1
, ,
a b c
lập thành một cấp số cộng.
C. Ba số
2 2 2
, ,
a b c
lập thành một cấp số cộng.
D. Ba số
, ,
a b c
lập thành một cấp số cộng
Câu 54. Biết rằng tồn tại các giá trị của
0;2
x
để ba số
2
1 sin ,sin ,1 sin3
x x x
lập thành một
cấp số cộng, tính tổng
S
các giá trị đó của
x
.
A.
5
S
. B.
3
S
. C.
7
2
S
. D.
23
6
S
.
Câu 55. Tìm tất cả các giá trị của tham số
m
để phương trình
3 2 2
3 1 0
x x x m có ba nghiệm
phân biệt lập thành một cấp số cộng.
A.
16
m
. B.
2
m
. C.
2
m
. D.
2
m
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay
Câu 56. Biết rằng tồn tại đúng ba giá trị
1 2 3
, ,
m m m
của tham số
m
để phương trình
3 2 3 2
9 23 4 9 0
x x x m m m có ba nghiệm phân biệt lập thành một cấp số cộng, tính giá trị
của biểu thức
3 3 3
1 2 3
P m m m
.
A.
34
P
. B.
36
P
. C.
64
P
. D.
34
P
.
Câu 57. Biết rằng tồn tại hai giá trị của tham số
m
để phương trình sau có bốn nghiệm phân biệt lập
thành một cấp số cộng:
4 2 2
10 2 7 0
x x m m
, tính tổng lập phương của hai giá trị đó.
A.
343
8
. B.
721
8
. C.
721
8
. D.
343
8
.
Câu 58. Cho một cấp số cộng
n
u
có
1
1
u
và tổng của 100 số hạng đầu tiên
24850
. Tính giá trị của
biểu thức
1 2 2 3 48 49 49 50
1 1 1 1
...S
u u u u u u u u
?
A.
123
S
B.
4
23
S C.
9
246
S D.
49
246
S
Câu 59. Cho cấp số cộng
n
a
; cấp số nhân
n
b
thỏa mãn
2 1 2 1
0; 1
a a b b
và hàm số
3
3
f x x x
sao cho
2 1
2
f a f a
và
2 2 2
log 2 log
f b f b
. Số nguyên dương
1
n
nhỏ
nhất thỏa mãn điều kiện
2018
n n
b a
là?
A.
16
B.
15
C.
17
D.
18
Câu 60. Cho cấp số cộng
u
có số hạng đầu
1
2
u và công sai
3
d
. Trên mặt phẳng tọa độ
Oxy
, lấy các điểm
1 2
, ,...
A A sao cho với mỗi số nguyên dương
n
, điểm
n
A
có tọa độ
;
n
n u
. Biết rằng khi
đó tất cả các điểm
1 2
, ,..., ,...
n
A A A cùng nằm trên một đường thẳng. Hãy viết phương trình của đường
thẳng đó.
A.
3 5
y x
. B.
3 2
y x
. C.
2 3
y x
. D.
2 5
y x
Câu 61. Trong mặt phẳng tọa độ
Oxy
, cho đồ thị
C
của hàm số
3 2
y x
. Với mỗi số nguyên
dương
n
, gọi
n
A
là giao điểm của đồ thị
C
với đường thẳng
: 0
d x n
. Xét dãy số
n
u
với
n
u
là
tung độ của điểm
n
A
. Mệnh đề nào dưới đây là mệnh đề đúng?
A. Dãy số
n
u
là một cấp số cộng có công sai
2
d
.
B. Dãy số
n
u
là một cấp số cộng có công sai
3
d
.
C. Dãy số
n
u
là một cấp số cộng có công sai
1
d
.
D. Dãy số
n
u
không phải là một cấp số cộng.
Câu 62. Trên tia
Ox
lấy các điểm
1 2
, ,..., ,...
n
A A A sao cho với mỗi số nguyên dương
n
,
n
OA n
.
Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia
Ox
, vẽ các nửa đường tròn đường kính
n
OA
,
1,2,...
n
Kí hiệu
1
u
là diện tích nửa đường tròn đường kính
1
OA
và với mỗi
2
n
, kí hiệu
n
u
là
diện tích của hình giới hạn bởi nửa đường tròn đường kính
1
n
OA
, nửa đường tròn đường kính
n
OA
và
tia
Ox
. Mệnh đề nào dưới đây là đúng?
A. Dãy số
n
u
không phải là một cấp số cộng.
B. Dãy số
n
u
là một cấp số cộng có công sai
4
d
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay
C. Dãy số
n
u
là một cấp số cộng có công sai
8
d
.
D. Dãy số
n
u
không phải là một cấp số cộng có công sai
2
d
.
Câu 63. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000
đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm
30000
đồng so với giá của mét khoan
ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu
20
mét lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó
phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
A.
7700000
đồng. B.
15400000
đồng. C.
8000000
đồng. D.
7400000
đồng.
Câu 64. Trên một bàn cờ có nhiều ô vuông. Người ta đặt 7 hạt dẻ vào ô vuông đầu tiên, sau đó đặt tiếp
vào ô thứ hai số hạt dẻ nhiều hơn ô đầu tiên là 5, tiếp tục đặt vào ô thứ ba số hạt dẻ nhiều hơn ô thứ hai
là 5, … và cứ thế tiếp tục đến ô cuối cùng. Biết rằng đặt hết số ô trên bàn cờ người ta đã phải sử dụng
hết
25450
hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô?
A.
98
ô. B.
100
ô. C.
102
ô. D.
104
ô.
Câu 65. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức
sau: Mức lương của quý làm việc đầu tiên cho công ty là
13,5
triệu đồng/quý, và kể từ quý làm việc
thứ hai, múc lương sẽ được tăng thêm
500.000
đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận
được sau ba năm làm việc cho công ty.
A.
198
triệu đồng. B.
195
triệu đồng. C.
228
triệu đồng. D. 114 triệu đồng.
Câu 66. Mặt sàn tầng của một ngôi nhà cao hơn mặt sân
0,5m
. Cầu thang đi từ tầng một lên tầng hai
gồm 21 bậc, một bậc cao
18cm
. Kí hiệu
n
h là độ cao của bậc thứ
n
so với mặt sân. Viết công thức để
tìm độ cao
n
h .
A.
0,18 0,32
n
h n m
. B.
0,18 0,5
n
h n m
.
C.
0,5 0,18
n
h n m
. D.
0,5 0,32
n
h n m
.
Câu 67. Trên tia Ox lấy các điểm
1 2
,..., ., ..,
n
A A A sao cho với mỗi số nguyên dương n, .
n
OA n Trong
cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính
, 1, 2...
n
OA n Kí hiệu
1
u là diện tích của nửa hình tròn đường kính
1
OA và với mỗi 2,n kí hiệu
n
u
là diện tích của hình giới hạn bởi nửa đường tròn đường kính
1
,
n
OA
nửa đường tròn đường kính
n
OA
và tia Ox. Chứng minh rằng dãy số ( )
n
u là một cấp số cộng. Hãy xác định công sai của cấp số cộng
đó.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay
A.
4
d
B.
2
d
C.
3
d
D.
2
3
d
CẤP SỐ NHÂN
Câu 68. Cho tam giác
ABC
biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng
25
. Tìm 2 góc còn lại?
A.
65 ,90
B.
75 ,80
. C.
60 ,95
. D.
60 ,90
.
Câu 69. Cho dãy số
n
a
xác định bởi
1 1
5, . 3
n n
a a q a
với mọi
1,
n
trong đó q là hằng số,
0, 1.
a q
Biết công thức số hạng tổng quát của dãy số viết được dưới dạng
1
1
1
. .
1
n
n
n
q
a q
q
Tính
2 ?
A. 13. B. 9. C. 11. D. 16.
Câu 70. Trong dịp hội trại hè 2017 bạn A thả một quả bóng cao su từ độ cao 3m so với mặt đất, mỗi
lần chạm đất quả bóng lại nảy lên một độ cao bằng hai phần ba độ cao lần rơi trước. Tổng quãng
đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng:
A. 13m. B. 14m. C. 15m. D. 16m.
Câu 71. Có hai cấp số nhân thỏa mãn
1 2 3 4
2 2 2 2
1 2 3 4
15
85
u u u u
u u u u
với công bội lần lượt là
1 2
, .
q q
Hỏi giá
trị của
1 2
q q
là:
A.
1
2
B.
3
2
C.
5
2
D.
7
2
Câu 72. Cho tứ giác
ABCD
biết
4
góc của tứ giác lập thành một cấp số cộng và góc
A
bằng 30
o
. Tìm
các góc còn lại?
A.
75 ,120 ,65
. B.
72 ,114 ,156
. C. 70
o
; 110
o
; 150
o
. D. 80
o
; 110
o
; 135
o
.
Câu 73. Cho một cấp số cộng
( )
n
u
có
1
1
u và tổng 100 số hạng đầu bằng
24850
. Tính
1 2 2 3 49 50
1 1 1
... S
u u u u u u
.
A.
9
246
S . B.
4
23
S . C.
123
S
. D.
49
246
S .
Câu 74. Cho
, ,
a b c
theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A.
2 2
2 2 2
a c ab bc ac
. B.
2 2
2 2 2
a c ab bc ac
.
C.
2 2
2 2 2
a c ab bc ac
. D.
2 2
2 2 2
a c ab bc ac
.
Câu 75. Cho dãy số
n
u
được xác định như sau:
1
1
2
.
4 4 5 1
n n
u
u u n n
Tính tổng
2018 2017
2 .
S u u
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay
A.
2017
2015 3.4
S B.
2018
2016 3.4
S C.
2018
2016 3.4
S D.
2017
2015 3.4
S
Câu 76. Cho số hạng thứ
m
và thứ
n
của một cấp số nhân biết số hạng thứ
( )
m n
bằng
A
, sổ hạng
thứ
( )
m n
bằng
B
và các số hạng đểu dương. Số hạng thứ m là:
A.
2
m
n
B
A
A
B.
AB
C.
m
n
A
B
D.
2
n
AB
Câu 77.
Cho dãy số
n
U
xác định bởi:
1
1
3
U
và
1
1
.
3
n n
n
U U
n
. Tổng
3 10
2
1
..
2 3 10
U U
U
S U
bằng:
A.
3280
6561
.
B.
29524
59049
.
C.
25942
59049
.
D.
1
243
.
Câu 78. Phương trình
2 2 4
1 ... 1 1 1
x
a a a a a a
với
0 1
a
có bao nhiêu nghiệm?
A.
0
B.
1
C.
2
D.
3
Câu 79. Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập thành
một cấp số nhân:
3 2
3 1 5 4 8 0.
x x x m x
A.
2.
m
B.
2.
m
C.
4.
m
D.
4.
m
Câu 80. Biết rằng tồn tại hai giá trị
1
m
và
2
m
để phương trình sau có ba nghiệm phân biệt lập thành
một cấp số nhân:
3 2 2 2
2 2 2 1 7 2 2 54 0.
x m m x m m x
Tính giá trị của biểu thức
3 3
1 2
.
P m m
A.
56
P
B.
8.
P
C.
56
P
D.
8.
P
Câu 81. Ba số
, ,
x y z
lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số
2;3;9
vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính
2 2 2
.
F x y z
A.
389.
F
hoặc
395.
F
B.
395.
F
hoặc
179.
F
C.
389.
F
hoặc
179.
F
D.
441
F
hoặc
357.
F
Câu 82. Cho cấp số nhân
n
a
có
1
7,
a
6
224
a
và
3577.
k
S
Tính giá trị của biểu thức
1 .
k
T k a
A.
17920.
T
B.
8064.
T
C.
39424.
T
D.
86016.
T
Câu 83. Cho cấp số nhân
n
a
có
1
2
a
và biểu thức
1 2 3
20 10
a a a
đạt giá trị nhỏ nhất. Tìm số
hạng thứ bảy của cấp số nhân đó.
A.
7
156250.
a B.
7
31250.
a C.
7
2000000.
a D.
7
39062.
a
Câu 84. Trong các mệnh đề dưới đây, mệnh đề nào là sai?
A. Dãy số
n
a
, với
1
3
a
và
1
6,
n n
a a
1,
n
vừa là cấp số cộng vừa là cấp số
nhân.
B. Dãy số
n
b
, với
1
1
b
và
2
1
2 1 3,
n n
b b
1,
n
vừa là cấp số cộng vừa là cấp số
nhân.
C. Dãy số
n
c
, với
1
2
c
và
2
1
3 10
n n
c c
1,
n
vừa là cấp số cộng vừa là cấp số nhân.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay
D. Dãy số
n
d
, với
1
3
d
và
2
1
2 15,
n n
d d
1,
n
vừa là cấp số cộng vừa là cấp số
nhân.
Câu 85. Xét bảng ô vuông gồm
4 4
ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số
1
hoặc
1
sao cho tổng các số trong mỗi hang và tổng các số trong mỗi cột đều bằng
0
. Hỏi có bao
nhiêu cách?
A.
72
B.
90
C.
80
D.
144
Câu 86. Số đo ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân. Biết thể tích của khối
hộp là
3
125
cm
và diện tích toàn phần là
2
175 .
cm
Tính tổng số đo ba kích thước của hình hộp chữ nhật
đó.
A.
30 .
cm
B.
28 .
cm
C.
31 .
cm
D.
17,5 .
cm
Câu 87. Một của hàng kinh doanh, ban đầu bán mặt hàng A với giá 100 (đơn vị nghìn đồng). Sau đó,
cửa hàng tăng giá mặt hàng A lên
10%.
Nhưng sau một thời gian, cửa hàng lại tiếp tục tăng giá mặt
hàng đó lên
10%.
Hỏi giá của mặt hàng A của cửa hàng sau hai làn tăng giá là bao nhiêu?
A.
120.
B.
121.
C.
122.
D.
200.
Câu 88. Một người đem 100 triệu đồng đi gửi tiết kiệm với kỳ han 6 tháng, mỗi tháng lãi suất là
0,7%
số tiền mà người đó có. Hỏi sau khi hết kỳ hạn, người đó được lĩnh về bao nhiêu tiền?
A.
5
8
10 . 0,007
(đồng) B.
5
8
10 . 1,007
(đồng)
C.
6
8
10 . 0,007
(đồng) D.
6
8
10 . 1,007
(đồng)
Câu 89. Tỷ lệ tăng dân số của tỉnh M là
1,2%.
Biết rằng số dân của tỉnh M hiện nay là 2 triệu người.
Nếu lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
A.
10320
nghìn người. B.
3000
nghìn người.
C.
2227
nghìn người. D.
2300
nghìn người.
Câu 90. Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc
đầu có
12
10
tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào?
A.
12
1024.10
tế bào. B.
12
256.10
tế bào. C.
12
512.10
tế bào. D.
13
512.10
tế bào.
Câu 91. Người ta thiết kế một cái tháp gồm 11 tầng theo cách: Diện tích bề mặt trên của mỗi tầng
bằng nửa diện tích mặt trên của tầng ngay bên dưới và diện tích bề mặt trên của tầng 1 bằng nửa diện
tích đế tháp. Biết diện tích đế tháp là
2
12288 ,
m
tính diện tích mặt trên cùng.
A.
2
6 .
m
B.
2
12 .
m
C.
2
24 .
m
D.
2
3 .
m
Câu 92. Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất
bằng
1
9
số đo của góc nhỏ thứ ba. Hãy tính số đo của các góc trong tứ giác đó.
A.
0 0 0 0
5 ,15 ,45 ,225 .
B.
0 0 0 0
9 ,27 ,81 ,243 .
C.
0 0 0 0
7 ,21 ,63 ,269 .
D.
0 0 0 0
8 ,32 ,72 ,248 .
Câu 93. Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác
ABC
được gọi là tam giác
trung bình của tam giác
ABC
. Ta xây dựng dãy các tam giác
1 1 1
A BC
,
2 2 2
A B C
,
3 3 3
,...
A B C sao cho
1 1 1
A BC
là một tam giác đều cạnh bằng
3
và với mỗi số nguyên dương
2
n
, tam giác
n n n
A B C
là tam
giác trung bình của tam giác
1 1 1
n n n
A B C
. Với mỗi số nguyên dương
n
, kí hiệu
n
S
tương ứng là diện
tích hình tròn ngoại tiếp tam giác
n n n
A B C
. Tính tổng
1 2
... ...
n
S S S S
?
A.
15
4
S
. B.
4
S
. C.
9
2
S
. D.
5
S
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay
Câu 94. Cho tam giác ABC cân tại đỉnh
.
A
Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB
theo thứ tự lập thành cấp số nhân công bội q. Gía trị của
2
q
bằng
A.
2 2
2
. B.
2 2
2
. C.
2 1
2
. D.
2 1
2
.
Câu 95. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức như
sau: mức lương của quý làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ
hai mức lương sẽ được tăng thêm 1,5 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư được
nhận sau 3 năm làm việc cho công ty.
A.
495
triệu đồng. B.
279
triệu đồng. C.
384
triệu đồng. D.
558
triệu đồng.
Câu 96. Một hình vuông
ABCD
có cạnh
,
AB a
diện tích
1
.
S
Nối 4 trung điểm
1 1 1 1
, , ,
A B C D
theo
thứ tự của 4 cạnh
, , ,
AB BC CD DA
ta được hình vuông thứ hai là
1 1 1 1
A B C D
có diện tích
2
.
S
Tiếp tục
như thế, ta được hình vuông thứ ba là
2 2 2 2
A B C D
có diện tích
3
S
và cứ tiếp tục như thế, ta được diện
tích
4 5
, ,...
S S Tính
1 2 100
... .
S S S S
A.
100
99 2
2 1
2
S
a
. B.
100
99
2 1
2
a
S
. C.
2 100
99
2 1
2
a
S
. D.
2 99
99
2 1
2
a
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay
C – HƯỚNG DẪN GIẢI
DÃY SỐ
Câu 1. Cho dãy số có các số hạng đầu là:
0,1;0,01;0,001;0,0001;...
. Số hạng tổng quát của dãy số này
có dạng?
A.
0
01...00,0
soá
chöõ
n
u
n
. B.
0
1
01...00,0
soá
chöõ
n
u
n
. C.
1
10
1
n
n
u . D.
1
10
1
n
n
u .
Hướng dẫn giải
Chọn A.
Ta có:
Số hạng thứ
1
có
1
chữ số
0
Số hạng thứ
2
có
2
chữ số
0
Số hạng thứ
3
có
3
chữ số
0
…………………………….
Suy ra
n
u
có
n
chữ số
0
.
Câu 2. Cho dãy số
n
u với
nuu
u
nn 1
1
5
.Số hạng tổng quát
n
u của dãy số là số hạng nào dưới đây?
A.
2
)1( nn
u
n
. B.
2
)1(
5
nn
u
n
.
C.
2
)1(
5
nn
u
n
. D.
2
)2)(1(
5
nn
u
n
.
Hướng dẫn giải
Chọn B.
Ta có
1
5 1 2 3 ... 1 5
2
n
n n
u n
.
Câu 3. Cho dãy số
n
u
với
1
2
1
1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1 2 1
1
6
n
n n n
u
. B.
1 2 2
1
6
n
n n n
u
.
C.
1 2 1
1
6
n
n n n
u
. D.
1 2 2
1
6
n
n n n
u
.
Hướng dẫn giải
Chọn C.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay
Ta có:
1
2
2 1
2
3 2
2
1
1
1
2
...
1
n n
u
u u
u u
u u n
. Cộng hai vế ta được
2
2 2
1 2 1
1 1 2 ... 1 1
6
n
n n n
u n
.
Câu 4. Cho dãy số
n
u
với
1
1
2
2 1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
2
2 1
n
u n
. B.
2
2
n
u n
. C.
2
2 1
n
u n
. D.
2
2 1
n
u n
.
Hướng dẫn giải
Chọn A.
Ta có:
1
2 1
3 2
1
2
1
3
...
2 3
n n
u
u u
u u
u u n
. Cộng hai vế ta được
2
2 1 3 5 ... 2 3 2 1
n
u n n
.
Câu 5. Cho dãy số
n
u
với
1
1
2
1
2
n
n
u
u
u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
. B.
1
n
n
u
n
. C.
1
n
n
u
n
. D.
1
n
n
u
n
.
Hướng dẫn giải
Chọn C.
Ta có:
1 2 3
3 4 5
; ; ;...
2 3 4
u u u Dễ dàng dự đoán được
1
n
n
u
n
.
Câu 6. Cho dãy số
n
u
với
1
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
2 1
2
n
u n
. B.
1
2 1
2
n
u n
. C.
1
2
2
n
u n
. D.
1
2
2
n
u n
.
Hướng dẫn giải
Chọn B.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay
Ta có:
1
2 1
3 2
1
1
2
2
2
...
2
n n
u
u u
u u
u u
. Cộng hai vế ta được
1 1
2 2... 2 2 1
2 2
n
u n
.
Câu 7. Cho dãy số
n
u
với
1
2
1
1
1
n
n n
u
u u
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
1
n
u n
. B.
1
n
u n
. C.
2
1 1
n
n
u . D.
n
u n
.
Hướng dẫn giải
Chọn D
Ta có
2
1 2 3 4
1 1 2; 3; 4;...
n
n n n
u u u u u u
Dễ dàng dự đoán được
n
u n
.
Thật vậy, ta chứng minh được
n
u n
*
bằng phương pháp quy nạp như sau:
+ Với
1
1 1
n u
. Vậy
*
đúng với
1
n
+ Giả sử
*
đúng với mọi
*
n k k
, ta có:
k
u k
. Ta đi chứng minh
*
cũng đúng
với
1
n k
, tức là:
1
1
k
u k
+ Thật vậy, từ hệ thức xác định dãy số
n
u
ta có:
2
1
1 1
k
k k
u u k
. Vậy
*
đúng
với mọi
*
n
.
Câu 8. Cho dãy số
n
u
với
1
2 1
1
1
1
n
n n
u
u u
. Số hạng tổng quát
n
u
của dãy số là số hạng nào
dưới đây?
A. 2
n
u n
. B.
n
u
không xác định.
C.
1
n
u n
. D.
n
u n
với mọi
n
.
Hướng dẫn giải
Chọn A
Ta có:
2 3 4
0; 1; 2
u u u
,. Dễ dàng dự đoán được 2
n
u n
.
Câu 9. Cho dãy số
n
u
với
1
2
1
1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay
A.
1 2 1
1
6
n
n n n
u
. B.
1 2 2
1
6
n
n n n
u
.
C.
1 2 1
1
6
n
n n n
u
. D.
1 2 2
1
6
n
n n n
u
.
Hướng dẫn giải
Chọn C
Ta có:
1
2
2 1
2
3 2
2
1
1
1
2
...
1
n n
u
u u
u u
u u n
.
Cộng hai vế ta được
2
2 2
1 2 1
1 1 2 ... 1 1
6
n
n n n
u n
.
Câu 10. Cho dãy số
n
u
với
1
1
2
2 1
n n
u
u u n
. Số hạng tổng quát
n
u
của dãy số là số hạng nào dưới
đây?
A.
2
2 1
n
u n
. B.
2
2
n
u n
. C.
2
2 1
n
u n
. D.
2
2 1
n
u n
.
Hướng dẫn giải
Chọn A
Ta có:
1
2 1
3 2
1
2
1
3
...
2 3
n n
u
u u
u u
u u n
.
Cộng hai vế ta được
2
2 1 3 5 ... 2 3 2 1
n
u n n
.
Câu 11. Cho dãy số
n
u
với
1
1
2
1
2
n
n
u
u
u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
n
n
u
n
. B.
1
n
n
u
n
. C.
1
n
n
u
n
. D.
1
n
n
u
n
.
Hướng dẫn giải
Chọn C
Ta có:
1 2 3
3 4 5
; ; ;...
2 3 4
u u u Dễ dàng dự đoán được
1
n
n
u
n
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay
Câu 12. Cho dãy số
n
u
với
1
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
2 1
2
n
u n
. B.
1
2 1
2
n
u n
. C.
1
2
2
n
u n
. D.
1
2
2
n
u n
.
Hướng dẫn giải
Chọn B
Ta có:
1
2 1
3 2
1
1
2
2
2
...
2
n n
u
u u
u u
u u
.
Cộng hai vế ta được
1 1
2 2... 2 2 1
2 2
n
u n
.
Câu 13. Cho dãy số
n
u
với
1
1
1
2
n
n
u
u
u
. Công thức số hạng tổng quát của dãy số này là:
A.
1
1 .
2
n
n
u
. B.
1
1
1 .
2
n
n
u
. C.
1
1
2
n
n
u
. D.
1
1
1 .
2
n
n
u
.
Hướng dẫn giải
Chọn D
Ta có:
1
1
2
2
3
1
1
2
2
...
2
n
n
u
u
u
u
u
u
u
.
Nhân hai vế ta được
1
1 2 3 1
1 2 3
1
1 lan
. . ...
1 1
. . ... 1 . 1 . 1 .
2.2.2...2 2 2
n
n
n n
n
n
u u u u
u u u u u
Câu 14. Cho dãy số
n
u
với
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay
A.
1
n
n
u n
. B.
2
n
n
u
. C.
1
2
n
n
u
. D.
2
n
u
.
Hướng dẫn giải
Chọn B
Ta có:
1
2 1
3 2
1
2
2
2
...
2
n n
u
u u
u u
u u
.
Nhân hai vế ta được
1
1 2 3 1 2 1
. . ... 2.2 . . ... 2
n n
n n n
u u u u u u u u
.
Câu 15. Cho dãy số
n
u
với
1
1
1
2
2
n n
u
u u
. Công thức số hạng tổng quát của dãy số này:
A.
1
2
n
n
u
. B.
1
1
2
n
n
u
. C.
1
2
n
n
u
. D.
2
2
n
n
u
.
Hướng dẫn giải
Chọn D
Ta có:
1
2 1
3 2
1
1
2
2
2
...
2
n n
u
u u
u u
u u
.
Nhân hai vế ta được
1 2
1 2 3 1 2 1
1
. . ... .2 . . ... 2
2
n n
n n n
u u u u u u u u
.
Câu 16. Cho dãy số
n
u
với
1
2
1
1
1
n
n n
u
u u
. Số hạng tổng quát
n
u
của dãy số là số hạng nào
dưới đây?
A.
1
n
u n
. B.
1
n
u n
. C.
2
1 1
n
n
u . D.
n
u n
.
Hướng dẫn giải
Chọn D.
Ta có:
2
1 2 3 4
1 1 2; 3; 4;...
n
n n n
u u u u u u
Dễ dàng dự đoán được
n
u n
Thật vậy, ta chứng minh được
n
u n
*
bằng phương pháp quy nạp như sau:
+ Với
1
1 1
n u
. Vậy
*
đúng với
1
n
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay
+ Giả sử
*
đúng với mọi
*
n k k
, ta có:
k
u k
. Ta đi chứng minh
*
cũng đúng
với
1
n k
, tức là:
1
1
k
u k
+ Thật vậy, từ hệ thức xác định dãy số
n
u
ta có:
2
1
1 1
k
k k
u u k
. Vậy
*
đúng
với mọi
*
n
.
Câu 17. Đặt
2 2 2 ... 2
n
T (có
n
dấu căn). Mệnh đề nào dưới đây là mệnh đề đúng?
A.
3
n
T . B.
1
2cos
2
n
n
T
. C.
1
cos
2
n
n
T
. D.
5
n
T .
Hướng dẫn giải
Chọn B.
Ta chứng minh
1
2cos
2
n
n
T
bằng phương pháp quy nạp toán học. Thật vậy:
Bước 1: Với
1
n
thì vế trái bằng
2
, còn vế phải bằng
1 1
2cos 2cos 2
2 4
.
Vậy đẳng thức đúng với
1
n
.
Bước 2: Giả sử đẳng thức đúng với
1
n k
, nghĩa là
1
2cos
2
k
k
T
.
Ta phải chứng minh đẳng thức cũng đúng với
1
n k
, tức là chứng minh
1
2
2cos
2
k
k
T
.
Thật vậy, vì
1
2
k k
T T
nên theo giả thiết quy nạp ta có
1
1
2 2 2cos
2
k k
k
T T
.
Mặt khác,
2
1 2 2
1 cos 1 cos 2. 2cos
2 2 2
k k k
nên
2
1
2 2
2.2cos 2cos
2 2
k
k k
T
.
Câu 18. Cho dãy số
1
2
1
1
3 2
n n
u
u u
và
2 2 2
1 2 2018
... 2018
S u u u . Khi đó S có bao nhiêu chữ
số?
A. 963 B. 962 C. 607 D. 608
Hướng dẫn giải
Ta có
2 2 2
1
3. 2 .3
n
n n n
u u u a b
.
Vì
2
5
u
ta có hệ phương trình
2
5 9
3
1 3
1
a b
a
a b
b
. Vậy
2 1
2
.3 1 2.3 1
3
n n
n
u
Khi đó
1 2 2017 2018
2 1 3 3 ... 3 3 1
S
. Số chữ số của
2018log3 1 963
S
.
Chọn A.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay
Câu 19. Cho dãy số
n
u
được xác định bởi công thức
1
2
1
2
2018 2017
n n n
u
u u u
. Tìm giới hạn của dãy
số
1 2
2 3 1
...
1 1 1
n
n
n
u
u u
S
u u u
?
A.
1
lim
2018
n
S B.
lim 2018
n
S C.
2017
lim
2018
n
S D.
lim 1
n
S
Hướng dẫn giải
Ta có:
1 1
1
1 1
2018 1
2018 1 2018 1 1 1
n n n n n n
n n n n
n n n n
u u u u u u
u u u u
u u u u
1
1 1 1 1
1 1
2018
2018 1 1 1 1 1 1
n n n n
n n n n n n
u u u u
u u u u u u
.
Như vậy:
1 1
1 1 1 1
2018 lim 2018 lim 2018
1 1 2 1 lim 1
n n n
n n
S S S
u u u
.
Câu 20. Cho dãy số
n
a
xác định bởi
2 *
1 1
3 5
1; 1,
2 2
n n n
a a a a n
. Số hạng thứ 201 của dãy
số
n
a
có giá trị bằng bao nhiêu?
A.
2018
2
a
. B.
2018
1
a
. C.
2018
0
a
. D.
2018
5
a
.
Hướng dẫn giải
Chọn A.
Nhận thấy dãy số trên là dãy số cho bởi công thức truy hồi.
Ta có
1 2 3 4 2 6
1; 2; 0; 1; 2; 0; 1
a a a a a a
.
Từ đây chúng ta có thể dự đoán
*
3
,
n n
a a n
. Chúng ta khẳng định dự đoán đó bằng
phương pháp quy nạp toán học. Thật vậy:
Với
1
n
thì
1
1
a
và
4
1
a
. Vậy đẳng thức đúng với
1
n
.
Giả sử đẳng thức đúng với
1
n k
, nghĩa là
3
k k
a a
.
Ta phải chứng minh đẳng thức đúng với
1
n k
, nghĩa là chứng minh
4 1
k k
a a
.
Thật vậy, ta có
2
4 3 3
3 5
1
2 2
k k k
a a a
(theo hệ thức truy hồi).
Theo giả thiết quy nạp thì
3
k k
a a
nên
2
4 1
3 5
1
2 2
k k k k
a a a a
.
Vậy đẳng thức đúng với
1
n k
. Suy ra
*
3
,
n n
a a n
.
Từ kết quả phần trên, ta có: nếu
mod3
m p
thì
m p
a a
.
Ta có
2018 2 mod3
nên
2018
2
a
.
Câu 21. Cho dãy số
n
u
xác định bởi
1
1
cos 0
1
, 1
2
n
n
u
u
u n
. Số hạng thứ 2017 của dãy số đã cho là:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay
A.
2017
2016
cos
2
u
B.
2017
2017
cos
2
u
C.
2017
2016
sin
2
u
D.
2017
2017
sin
2
u
Hướng dẫn giải
Đáp án A
Ta có
2
2 3 4
2 3
1 cos
1 cos
2
cos cos cos
2 2 1 2 2
u u u
Suy ra
2017
2016
cos
2
u
Câu 22. Cho dãy số
n
a
xác định bởi
1 2
5, 0
a a và
2 1
6 , 1
n n n
a a a n
. Số hạng thứ
14
của
dãy là số hạng nào?
A.
3164070
. B.
9516786
. C.
1050594
. D.
9615090
.
Hướng dẫn giải
Chọn A.
+ Ta có
2 1 2 1 1
6 , 1 2 3 2 , 1
n n n n n n n
a a a n a a a a n
.
Do đó ta có
1 2 1
2 10
b a a và
1
3 , 1
n n
b b n
.
Từ hệ thức truy hồi của dãy số
n
b
, ta có
2 3
2 1 3 2 1 4 3 1
3 ; 3 3 ; 3 3
b b b b b b b b
.
Bằng phương pháp quy nạp toán học, chúng ta chứng minh được rằng:
1 1
1
3 10.3 , 1
n n
n
b b n
.
+ Ta có
2 1 2 1 1
6 , 1 3 2 3 , 1
n n n n n n n
a a a n a a a a n
.
Do đó ta có:
1 2 1
3 15
c a a và
1
2 , 1
n n
c c n
.
Từ hệ thức truy hồi của dãy số
n
c
, ta có
2 3
2 1 3 1 4 1
2 ; 2 ; 2
c c c c c c
.
Bằng phương pháp quy nạp toán học, chúng ta chứng minh được rằng:
1 1
1
2 15. 2 , 1
n n
n
c c n
.
+ Từ các kết quả trên, ta có hệ phương trình:
1
1
1
1
1
1
2 10.3
2.3 3. 2
3 15. 2
n
n n
n
n
n
n
n n
a a
a
a a
.
Do đó số hạng tổng quát của dãy số
n
a
là
1
1
2.3 3. 2 , 1
n
n
n
a n
.
Vậy suy ra
14
3164070
a .
Câu 23. Cho dãy số
n
a
xác định bởi
1
3
a và
2
1
3 4, *
n n
a a n n n
. Số
1391
là số hạng
thứ mấy của dãy số đã cho?
A.
18
. B.
17
. C.
20
. D.
19
Hướng dẫn giải
Chọn A.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay
Từ hệ thức truy hồi của dãy số
n
a
ta có:
3 2
2
2 2
1
6 17 21
1 2 ... 1 3 1 2 ... 1 4 1
3
n n
n n n
a a n n n a
.
Suy ra số hạng tổng quát của dãy số
n
a
là
3 2
6 17 21
3
n
n n n
a
.
Giải phương trình
1391
n
a ta được
18
n
Câu 24. Biết rằng
2
2
1 1 1
...
1.2.3 2.3.4 1 2 16
an bn
n n n cn dn
, trong đó
, , ,
a b c d
và
n
là các số
nguyên dương. Tính giá trị của biểu thức
T a c b d
.
là :
A.
75
T
. B.
364
T
. C.
300
T
. D.
256
T
.
Hướng dẫn giải
Chọn C .
Phân tích phần tử đại diện, ta có:
1 1 1 1
1 2 2 1 1 2
k k k k k k k
.
Suy ra:
1 1 1
...
1.2.3 2.3.4 1 2
n n n
1 1 1 1 1 1 1
. ...
2 1.2 2.3 2.3 3.4 1 1 2
n n n n
1 1 1
2 2 1 2
n n
=
2 2
2 2
3 2 6
4 12 8 8 24 16
n n n n
n n n n
.
Đối chiếu với hệ số, ta được:
2; 6; 8; 24
a b c d
.
Suy ra:
300
T a c b d .
Câu 25. Cho dãy số
n
a
xác định bởi 2017sin 2018cos
2 3
n
n n
a
. Mệnh đề nào dưới đây là mệnh
đề đúng?
A.
*
6
,
n n
a a n
. B.
*
9
,
n n
a a n
.
C.
*
12
,
n n
a a n
. D.
*
15
,
n n
a a n
.
Hướng dẫn giải
Chọn C
Kiểm tra từng phương án đến khi tìm được đáp án đúng.
+ Ta có
6
6 6
2017sin 2018cos 2017sin 2018cos
2 3 2 3
n n
n n
n n
a a
+ Ta có
6
9 9
2017sin 2018cos 2017sin 2018cos
2 3 2 3
n n
n n
n n
a a
.
+ Ta có
12
12 12
2017sin 2018cos 2017sin 2018cos
2 3 2 3
n n
n n
n n
a a
.
+ Ta có
15
15 15
2017sin 2018cos 2017sin 2018cos
2 3 2 3
n n
n n
n n
a a
.
Câu 26. Cho dãy số
n
a
có
2
, *
100
n
n
a n
n
. Tìm số hạng lớn nhất của dãy số
n
a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay
A.
1
20
. B.
1
30
. C.
1
25
. D.
1
21
.
Hướng dẫn giải
Chọn A.
Ta có
2
2
1
.
100 20
2 .100
n
n n
a
n
n
Dấu bằng xảy ra khi
2
100 10.
n n
Vậy số hạng lớn nhất của dãy là số hạng bằng
1
20
.
Câu 27. Cho dãy số
( )
n
u
thỏa mãn
*
2018 2017, .
n
u n n n
Khẳng định nào sau đây
sai?
A. Dãy số
( )
n
u
là dãy tăng. B.
lim 0.
n
n
u

C.
*
1
0 , .
2 2018
n
u n
D.
1
lim 1.
n
n
n
u
u

Hướng dẫn giải
Chọn A
Câu 28. Cho dãy số
n
x
với
4
2
n
an
x
n
. Dãy số
n
x
là dãy số tăng khi:
A.
2
a
. B.
2
a
. C.
2
a
. D.
1
a
.
Hướng dẫn giải
Chọn B.
Ta có
1
( 1) 4
.
3
n
a n
x
n
Xét hiệu
1
( 1) 4 4 2 4
.
3 2 ( 2)( 3)
n n
a n an a
x x
n n n n
( )
n
x
là dãy tăng khi và chỉ khi
1
0, 1 2 4 0 2.
n n
x x n a a
Câu 29. Trong các dãy số sau dãy số nào là dãy bị chặn ?
A. Dãy
n
a
, với
2
16, *
n
a n n .
B. Dãy
n
b
, với
1
, *
2
n
b n n
n
.
C. Dãy
n
c
, với
2 3, *
n
n
c n
.
D. Dãy
n
d
, với
2
, *
4
n
n
d n
n
.
Hướng dẫn giải
Chọn D.
Dãy số
( )
n
a
là dãy số tăng và chỉ bị chặn dưới vì
2
16 17, 1.
n
a n n
Dãy số
( )
n
b
là dãy số tăng và chỉ bị chặn dưới vì
1 1
2 . 2, 1.
2 2
n
b n n n
n n
Dãy số
( )
n
c
là dãy số tăng và chỉ bị chặn dưới vì
2 3 5, 1.
n
n
c n
Dãy số
( )
n
d
là dãy số bị chặn vì
1
0 , 1.
4
n
d n
2
1
0 .
4 4 4
n n
do
n n
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay
Câu 30. Cho dãy số
n
u
với
2
,
n
an
u a
n
là tham số. Tìm tất cả các giá trị của a để dãy số
n
u
là
một dãy số tăng
A.
1
a
B.
1
a
C.
2
a
D.
2
a
Hướng dẫn giải
Chọn C
Câu 31. Cho dãy số
( )
n
z
xác định bởi
sin 2cos .
2 3
n
n n
z
Gọi M, m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất trong các số hạng của dãy số
( )
n
z
. Tính giá trị biểu thức
2 2
.
T M m
A.
13.
T
B.
5.
T
C.
18.
T
D.
7.
T
Hướng dẫn giải
Chọn A.
Dựa vào chu kì của hàm số
sin ; cos ,
y x y x
ta có
12
, 1.
n n
z z n
Do đó tập hợp các phần tử của dãy số là
1 2 12
; ;...; 3; 2; 1;0;2 .
S z z z
Suy ra
2; 3.
M m
Do đó
13.
T
Câu 32. Cho dãy số
( )
n
u
thỏa mãn
1 1 1 2
1 2017
; , 1. ...
2 2( 1) 1 2018
n
n n n
n
u
u u n S u u u
n u
khi
n
có giá trị nguyên dương lớn nhất.
A.
2017.
B.
2015.
C.
2016.
D.
2014.
Hướng dẫn giải
Chọn C .
Dễ chỉ ra được
0, 1.
n
u n
Từ hệ thức truy hồi của dãy số, ta có
1
1 1
2 2, 1.
n n
n n
u u
Suy ra
2
1
1 1 1 1
2(1 2 .. 1) 2( 1) 2 ( 1) 2( 1) .
( 1)
n
n n
n n n n n n n u
u u u n n
Do đó
1 1
, 1.
1
n
u n
n n
Vậy
1 2
1
... 1 .
1 1
n n
n
S u u u
n n
Vì
2017
2018
n
S nên
2017
2017.
1 2018
n
n
n
Suy ra số nguyên dương lớn nhất để
2017
2018
n
S là
2016
n
.
Câu 33. Cho hàm số
cos 2017
2
3 2
x
f x x x
và dãy số
n
u
được xác định bởi công thức tổng
quát
log 1 log 2 ... log
n
u f f f n
. Tìm tổng tất cả các giá trị của
n
thỏa mãn điều kiện
2018
1
n
u
?
A.
21
B.
18
C.
3
D.
2018
Hướng dẫn giải
Ta có:
1 1
log cos 2017 log 1 log 2
n n
n
k k
u f k k k k
(
k
chẵn)
(
k
lẻ).
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay
Trường hợp 1:
2
n p
(Chẵn), khi đó ta có khai triển sau:
log3 log4 ... log 2 1 log 2 2 log2 log3 ... log 2 log 2
1
n
u p p p p
.
Như vậy
log 1
n
u p
cho nên
2018
1 9 18
n
u p n .
Trường hợp 1:
2 1
n p
(Lẻ), khi đó ta có khai triển sau:
log3 log4 ... log 2 1 log 2 2 log2 log3 ... log 2 2 log
2 3
n
u p p p p
.
Như vậy
log 4 6
n
u p
cho nên
2018
1 1 3
n
u p n
.
Kết luận: Tổng các giá trị của
n
thỏa mãn điều kiện
2018
1
n
u
là 21.
Chọn A.
Câu 34. Cho
2
2 *
1 1f n n n n
và đặt
1 3 ... 2 1
2 4 ... 2
n
f f f n
u
f f f n
. Tìm số nguyên
dương n nhỏ nhất sao cho
2
10239
log
1024
n n
u u ?
A.
23
n
B.
29
n
C.
33
n
D.
21
n
Hướng dẫn giải
Ta có:
2
2
2 2 *
1 1 1 1 1f n n n n n n
.
Đến đây ta dễ dàng có:
2 2
2 2 2 2
2
2 2
2 2 2 2
1 1 2 1 3 1 4 1 ... 2 1 1 2 1
1
2 2 1
2 1 3 1 4 1 5 1 ... 2 1 2 1 1
n
n n
u
n n
n n
.
Ta có:
2 2
10239 1 1 1
log log 23
1024 1024 1024 1024
n n n
u u u n .
Chọn A.
Câu 35. Cho dãy số
n
a
thỏa mãn điều kiện
1
1
3
1; 5 1
3 2
n n
a a
a
n
với mọi n
. Tìm số
nguyên dương
1
n
nhỏ nhất để
n
a
?
A.
39
n
B.
41
n
C.
49
n
D.
123
n
Hướng dẫn giải
Ta có:
1 1 2 2 1
3 3 3
5 1 ; 5 1 ; ...5 1
3 1 3 4 5
n n n n
a a a a a a
n n
.
Nhân vế với vế ta được:
1
8.11.14... 3 1 3 2
3 3 3 3 2
5 1 1 .... 1
3 1 3 4 5 5.8.11.... 3 4 3 1 5
n
a a
n n
n
n n n n
.
Khi đó ta có công thức tổng quát
5
log 3 2
n
a n
.
Chọn B.
Chú ý: Tới đoạn này sử dụng lệnh CALC là nhanh nhất. Nhưng nếu bài toán không cho
trước đáp số có thể sử dụng Bảng TABLE để truy tìm giá trị nguyên dương
1
n
nhỏ nhất
để
n
a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay
Câu 36. Cho dãy số
n
u
xác định bởi
1
1 1
5; 2 2.3
n n n n
n n
u u u
với mọi
1
n
. Tìm số nguyên nhỏ
nhất thỏa mãn
100
2 5
n n
n
u
.
A.
146
B.
233
C.
232
D.
147
Hướng dẫn giải
Ta có:
1 1 1
1
1 2 2 2
2 1 2 1
1 2
2 1
2 1
2 2.3
2 2.3
2 1 2 2 ... 2 2 1 3 3 ... 3
...
2 2.3
n n n n
n n
n n n n
n n n
n n
n
u u
u u
u
u u
.
Do vậy:
2 3
n n n
n
u
nên
100 100
3
2 5 3 5 100log 5 147
n n n
n
u n n .
Chọn D.
Câu 37. Biết rằng
2 2018
2 2018
2019
4
4 4
2
2 2
...
lim
...
n n
n n
n n
n n
u u u u
a b
L
c
u u u u
trong đó
n
u
xác định bởi
1 1
0; 4 3
n n
u u u n
và
, ,
a b c
là các số nguyên dương và
2019
b
. Tính
S a b c
?
A.
1
B.
0
C.
2017
D.
2018
Hướng dẫn giải
2
1
4 1 2 3
n n n
u u n u n n
.
Xét
2 2018
1
,4 ,4 ,...4
S n n n n
và
2 2018
2
,2 ,2 ,...2
S n n n n
.
Ta có:
2
2 3 2. 2.
k
u k k k k
2
3
2.
2 3 2.
k
k
k k k
.
Vậy
1
2
2019
2019
2
2019
2
3 4 1
2 .
3
2 1
2 3 2.
lim
3
3
2 . 2 1
2 3 2.
k S
k S
k
n
k k k
L
k
n
k k k
.
Chọn B.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay
CẤP SỐ CỘNG
Câu 38. Cho dãy số
n
u
(u
n
) có
3
12
2
n
u
n
. Khẳng định nào sau đây sai?
A. Là cấp số cộng có ;
3
1
1
u
2
3
d
. B. Số hạng thứ n+1:
2
1
2( 1) 1
3
n
n
u
.
C. Hiệu
3
)12(2
1
n
uu
nn
. D. Không phải là một cấp số cộng.
Hướng dẫn giải
Chọn A
Ta có
2 2
1
2(n 1) 1 2 1 2(2 n 1)
.
3 3 3
n n
n
u u
Vậy dãy số trên không phải cấp số cộng.
Câu 39. Cho hai cấp số cộng
:4,7,10,...
n
x
và
:1,6,11,...
n
y
. Hỏi trong 2018 số hạng đầu tiên của
mỗi cấp số có bao nhiêu số hạng chung?
A. 404. B. 673. C. 403. D. 672.
Hướng dẫn giải
Chọn C
Cấp số cộng
:4,7,10,...
n
x
có
1
4
x
, công sai
3
d
.
Số hạng tổng quát
4 ( 1).3 3 1
n
x n n
Cấp số cộng
:1,6,11,16,21...
n
y
có
1
1
y
,công sai
5
d
.
Số hạng tổng quát
'
1 ( 1).5
n
y n
5 4
n
Xét phương trình
'n n
x y
3 1 5 4
n n
3
1,
5
n
n
0 , 2018
n n
. Do
n
là số
nguyên dương nên n chia hết cho 5 và
0 2018
n
. Suy ra số các giá trị n cần tìm là
2018
403
5
.
Vậy có 403 số hạng chung.
Câu 40. Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
thể coi là số hạng thứ 2,thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp
số cộng này để tổng của chúng bằng 820?
A. 20. B.
42.
C.
21.
D.
17.
Hướng dẫn giải
Chọn A
Câu 41. Cho cấp số cộng
n
u
biết
5
18
u
và
2
4 .
n n
S S
Tìm số hạng đầu tiên
1
u
và công sai
d
của
cấp số cộng.
A.
1
2, 4
u d
. B.
1
2, 3
u d
. C.
1
2, 2
u d
. D.
1
3, 2
u d
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải
Chọn A
Giả sử
1 5 1
1 4 18 1 .
n
u u n d u u d
Ta có:
1 1
2
2 1 2 2 2 1
;
2 2
n n
n u n d n u n d
S S
Do
2 1
1 1 1
4 2 2 2 1
4 2 1 2 2 1 4 2 2
n n
S S n u n d
n u n d u n d u n d
1
2 2 .
u d
Từ (1) và (2) suy ra
1
2, 4.
u d
Câu 42. Một cấp số cộng có tổng
n
số hạng đầu
n
S
được tính theo công thức
2 *
5 3 , .
n
S n n n
Tìm số hạng đầu
1
u
và công sai
d
của cấp số cộng đó
A.
1
8, 10
u d
B.
1
8, 10
u d
C.
1
8, 10
u d
D.
1
8, 10
u d
Hướng dẫn giải
Chọn C
Tổng n số hạng đầu
2 *
1 2
... 5 3 ;
n n
S u u u n n n
Tổng số hạng đầu tiên là
2
1 1
5.1 3.1 8
S u
Tổng 2 số hạng đầu là
2
2 1 2 2 2 1
5.2 3.2 26 8 18 8 10 10
S u u u u u d d
Câu 43. Cho cấp số cộng
n
u
và gọi
n
S
là tổng
n
số đầu tiên của nó. Biết
7
77
S
và
12
192.
S
Tìm
số hạng tổng quát
n
u
của cấp số cộng đó.
A.
5 4
n
u n
. B.
3 2
n
u n
. C.
2 3
n
u n
. D.
4 5
n
u n
Hướng dẫn giải
Chọn B
Ta có
1
7 1
1
112
1
7.6.
7 77
77 7 21 77
5
2
12.11. 12 66 192192
2
12 192
2
d
u
S u d
u
d u dS
d
u
Khi đó
1
1 5 2 1 3 2
n
u u n d n n
Câu 44. Cho ba số dương
a
,
b
,
c
theo thứ tự lập thành cấp số cộng. Giá trị lớn nhất của biểu thức
2
2
8 3
2 1
a bc
P
a c
có dạng
, .
x y x y
Hỏi
x y
bằng bao nhiêu:
A.
9
B.
11
C.
13
D.
7
Hướng dẫn giải
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay
Chọn B
Ta có:
2 2
2 2 2 2 2
2 2 2 8 4 4 8 2
a c b a b c a b c a bc b bc c a bc b c
Do đó
2 2
2 3 3
10
1
2 1
b c t
P
t
b c
với
2
t b c
, dấu bằng xảy ra khi
1
2 .
3
b c
Vậy
11.
x y
Câu 45. Chu vi của một đa giác là
158
cm
, số đo các cạnh của nó lập thành một cấp số cộng với công
sai
3
d cm
. Biết cạnh lớn nhất là 44cm. Số cạnh của đa giác đó là:
A. 3. B. 4. C. 5. D. 6
Hướng dẫn giải
Chọn B
Câu 46. Chu vi của một đa giác n cạnh là 158, số đo các cạnh đa giác lập thành một cấp số cộng với
công sai
3.
d
Biết cạnh lớn nhất có độ dài là 44. Tính số cạnh của đa giác.
A. 6. B. 4. C. 9. D. 5
Hướng dẫn giải
Chọn B
Câu 47. Cho tam giác ABC có độ dài các cạnh là a, b, c theo thứ tự lập thành một cấp số cộng. Biết
tan tan ,
2 2
A C x
x y
y
, giá trị
x y
là:
A.
4
B.
1
C.
2
D.
3
Hướng dẫn giải
Đáp án D
Ta có:
2 sin sin 2sin
2sin os 4sin . os 4sin . os
2 2 2 2 2 2
os 2 os os os sin sin 2 os os 2sin sin
2 2 2 2 2 2 2 2 2 2
1
3sin sin os os 3tan tan 1 tan tan
2 2 2 2 2 2 2 2 3
a c b A C B
A C A C B B A C A C
c c c
A C A C A C A C A C A C
c c c c c c
A C A C A C A C
c c
Câu 48. Cho các số hạng dương a, b, c là số hạng thứ m, n, p của một cấp số cộng và một cấp số nhân.
Tính giá trị của biểu thức
( ) (c a) ( )
2
log . .
b c a b
a b c
A. 0 B. 2 C. 1 D. 4
Hướng dẫn giải
Đáp án C
Ta có a, b, c là số hạng thứu m, n, p của một cấp số cộng và một cấp số nhân nên:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay
1
1 1
1
1 1
1
1 1
1
1
1
m
n
p
a u m d a q
a b m n d
b u n d a q b c n p d
c a p m d
c u p d a q
Do đó
1 1 0 0
2 2 1 1 2 1
log . . log log 0
n p d m n d
b c c a a b
m p
P a b c a q a q a q
Câu 49. Cho
2
a b c
và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng
A. 1 B. 2 C. 3 D. 4
Hướng dẫn giải
Đáp án C
Ta có
cota.cot 1 1
cot cot tan
2 2 2 cot a cot cot
cota.cot 1 1
cot cot tan
2 2 2 cot a cot cot
cota.cot .cot cota cot cot
b
a b c a b a b c c
b c
b
a b c a b a b c c
b c
b c b c
Mà
cota cot 2cot
c b
Do đó ta được
cota.cot .cot 3cot cot a.cot 3
b c b c
2 sin sin 2sin
2sin os 4sin . os 4sin . os
2 2 2 2 2 2
os 2 os os os sin sin 2 os os 2sin sin
2 2 2 2 2 2 2 2 2 2
1
3sin sin os os 3tan tan 1 tan tan
2 2 2 2 2 2 2 2 3
a c b A C B
A C A C B B A C A C
c c c
A C A C A C A C A C A C
c c c c c c
A C A C A C A C
c c
Câu 50. Cho a, b, c theo thứ tự tạo thành cấp số cộng. Giá trị
x y
là bao nhiêu biết
2 2 2 2 2
2 2
log 2 log ,P a ab b bc c x a ac c y x y
.
A. 0 B. 1 C.
1
D. 2
Hướng dẫn giải
Đáp án D
Theo đề a, b, c theo thứ tự tạo thành cấp số cộng nên
2
2
2 4
a c b a c b
2
2
2 2 2 2 2
2
2a 2 2
b a c b a c
ab b bc c a ac c
Do đó
2 2 2 2 2
2 2
log a 2 log 1
ab b bc c a ac c
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay
Câu 51. Cho ba (bố số chứ) số
, , ,
a b c d
theo thứ tự đó tạo thành cấp số nhân với công bội khác
1
. Biết
tổng ba số hạng đầu bằng
148
9
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và
thứ tám của một cấp số cộng. Tính giá trị biểu thức
T a b c d
?
A.
101
.
27
T B.
100
.
27
T C.
100
.
27
T D.
101
.
27
T
Hướng dẫn giải
Chọn C
Gọi e là công sai. Ta có:
148
3 10 1
9
a b c a e
(Đề xuất
3
b a e
,
7
c a e
)
Gọi q là công bội khác 1 ta lại có:
2 2 2
b a q ac
2
3 7 3
a e a e
9 0 2
a e
.
Từ (1) và (2)
4
16 64 256 100
; ;
4
3 9 27 27
9
a
b c d T
e
.
Câu 52. Cho cấp số cộng
n
u
. Mệnh đề nào dưới đây là mệnh đề đúng?
A.
0
m n p
n p u p m u m n u
. B.
0
m n p
m n u n p u p m u
.
C.
0
m n p
m p u n m u p n u
. D.
0
m n p
p n u m p u m n u
.
Hướng dẫn giải
Chọn A.
Kiểm tra từng phương án cho đến khi tìm được phương án đúng.
Ta có:
1 1 1
1 ; 1 ; 1
m n p
u u m d u u n d u u p d
.
- Phương án A: Ta có:
m n p
n p u p m u m n u
1 1 1
1 1 1 0
n p u m d p m u n d m n u p d .
Câu 53. Cho ba số dương
, ,
a b c
thỏa mãn điều kiện
1 1 1
, ,
b c c a a b
lập thành một cấp
số cộng. Mệnh đề nào dưới đây là đúng?
A. Ba số
, ,
a b c
lập thành một cấp số cộng.
B. Ba số
1 1 1
, ,
a b c
lập thành một cấp số cộng.
C. Ba số
2 2 2
, ,
a b c
lập thành một cấp số cộng.
D. Ba số
, ,
a b c
lập thành một cấp số cộng
Hướng dẫn giải
Chọn A.
Theo giả thiết ta có:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay
1 1 2
2 2 2
b c a b c a
c a a c b b c a b a c b
Suy ra ba số
, ,
a b c
hoặc
, ,
c b a
lập thành một cấp số cộng.
Câu 54. Biết rằng tồn tại các giá trị của
0;2
x
để ba số
2
1 sin ,sin ,1 sin3
x x x
lập thành một
cấp số cộng, tính tổng
S
các giá trị đó của
x
.
A.
5
S
. B.
3
S
. C.
7
2
S
. D.
23
6
S
.
Hướng dẫn giải
Chọn A.
Theo tính chất của cấp số cộng ta có:
2
3 2 3 2
2
1 sin 1 sin3 2sin
2 4sin 4sin 2sin 2sin sin 2sin 1 0
1
sin
2sin 1 sin 1 0
2
cos 0
x x x
x x x x x x
x
x x
x
+)
2
1
6
sin
7
2
2
6
x k
x
x k
.
+)
cos 0
2
x x k
Với nghiệm
2
x k
và
0;2
x
, ta tìm được
11
6
x
. Với nghiệm
7
2
6
x k
và
0;2
x
, ta tìm được
7
6
x
. Với nghiệm
2
x k
và
0;2
x
ta tìm được
nghiệm
3
;
2 2
x x
Do đó
11 7 3
5
6 6 2 2
S
.
Câu 55. Tìm tất cả các giá trị của tham số
m
để phương trình
3 2 2
3 1 0
x x x m có ba nghiệm
phân biệt lập thành một cấp số cộng.
A.
16
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Hướng dẫn giải
Chọn D.
Áp dụng kết quả phần lý thuyết, ta có phương trình đã cho có 3 nghiệm phân biệt thì điều
kiện cần là
3
1
3a 3
b
là nghiệm của phương trình.
Suy ra
3 2 2
1 3.1 1 1 0 2
m m .
Với
2
m
, ta có phương trình
3 2
3 3 0
x x x .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay
2
3 1 0 1, 1, 3
x x x x x
Ba số
1,1,3
lập thành cấp số cộng.
Vậy các giá trị cần tìm là
2
m
. Do đó D là phương án đúng.
Câu 56. Biết rằng tồn tại đúng ba giá trị
1 2 3
, ,
m m m
của tham số
m
để phương trình
3 2 3 2
9 23 4 9 0
x x x m m m có ba nghiệm phân biệt lập thành một cấp số cộng, tính giá trị
của biểu thức
3 3 3
1 2 3
P m m m
.
A.
34
P
. B.
36
P
. C.
64
P
. D.
34
P
.
Hướng dẫn giải
Chọn A.
Áp dụng kết quả ở phần lý thuyết, ta có phương trình đã cho có 3 nghiệm phân biệt thì điều
kiện cần là:
9
3
3 3
b
a
là nghiệm của phương trình.
Suy ra
3 2 3 2
3 9.3 23.3 4 9 0
m m m
3 2
4 6 0
m m m
1, 2, 3
m m m
Với
1, 2, 3
m m m
thì
3 2
4 6 0
m m m
nên
3 2
4 9 15
m m m
.
Do vậy, với
1, 2, 3
m m m
ta có phương trình
3 2 2
9 23 15 0 3 6 5 0
x x x x x x
1, 3, 5
x x x
.
Ba số 1,3,5 lập thành cấp số cộng.
Vậy
1, 2, 3
m m m
là các giá trị cần tìm.
Do đó
3
3 3
1 2 3 34
Câu 57. Biết rằng tồn tại hai giá trị của tham số
m
để phương trình sau có bốn nghiệm phân biệt lập
thành một cấp số cộng:
4 2 2
10 2 7 0
x x m m
, tính tổng lập phương của hai giá trị đó.
A.
343
8
. B.
721
8
. C.
721
8
. D.
343
8
.
Hướng dẫn giải
Chọn C .
Đặt
2
0
t x t
. Khi đó ta có phương trình:
2 2
10 2 7 0 (*)
t t m m .
Phương trình đã cho có
4
nghiệm phân biệt khi và chỉ khi phương trình
(*)
có
2
nghiệm
dương phân biệt
2 2
2
2
5 (2 7 ) 0
0 2 7 25.
2 7 0
m m
m m
m m
(do tổng hai nghiệm bằng
10 0
nên không cần điều kiện này).
+ Với điều kiện trên thì
(*)
có hai nghiệm dương phân biệt là
1 2 1 2
, ( )
t t t t
.
Khi đó phương trình đã cho có bốn nghiệm phân biệt là
2 1 1 2
; ; ;
t t t t
.
Bốn nghiệm này lập thành một cấp số cộng khi
1 2 1 1 2 1 2 1
9 .
t t t t t t t t
Theo định lý Vi-ét ta có:
2
1 2 1 2
10; . 2 7
t t t t m m
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay
Suy ra ta có hệ phương trình
2 1 1
1 2 2
2 2
1 2
9 1
1
10 9
9
2
. 2 7 2 7 9
t t t
m
t t t
m
t t m m m m
.
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được.
Do đó
3
3
9 721
1
2 8
.
Câu 58. Cho một cấp số cộng
n
u
có
1
1u và tổng của 100 số hạng đầu tiên
24850
. Tính giá trị của
biểu thức
1 2 2 3 48 49 49 50
1 1 1 1
...S
u u u u u u u u
?
A.
123S
B.
4
23
S C.
9
246
S D.
49
246
S
Hướng dẫn giải
Ta có:
100 1 100 50
497 496 1 99 5 246u u u d d u .
Lại có:
3 2 49 48 50 492 1
1 2 2 3 48 49 49 50 1 50
1 1 1 49
5 ... 1
246 246
u u u u u uu u
S S
u u u u u u u u u u
.
Câu 59. Cho cấp số cộng
n
a
; cấp số nhân
n
b
thỏa mãn
2 1 2 1
0; 1a a b b và hàm số
3
3f x x x
sao cho
2 1
2f a f a
và
2 2 2
log 2 logf b f b
. Số nguyên dương
1n
nhỏ
nhất thỏa mãn điều kiện 2018
n n
b a là?
A.
16
B.
15
C.
17
D.
18
Hướng dẫn giải
Tính bảng biến thiên:
Vì
2 1 1 2
, 0;1f a f a a a
và
2 1
1; 0a a .
Tương tự
2 2
log 1b và
2 1
log 0b .
Khi đó 1
n
a n và
1
2
n
n
b
.
Vậy
1
2018 2 2018 1
n
n n
b a n
.
Chọn A.
Câu 60. Cho cấp số cộng
u
có số hạng đầu
1
2u và công sai
3 d
. Trên mặt phẳng tọa độ
Oxy
, lấy các điểm
1 2
, ,...A A sao cho với mỗi số nguyên dương
n
, điểm
n
A có tọa độ
;
n
n u
. Biết rằng khi
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay
đó tất cả các điểm
1 2
, ,..., ,...
n
A A A cùng nằm trên một đường thẳng. Hãy viết phương trình của đường
thẳng đó.
A.
3 5
y x
. B.
3 2
y x
. C.
2 3
y x
. D.
2 5
y x
Hướng dẫn giải
Chọn A.
Số hạng tổng quát của cấp số cộng
n
u
là
1
1 3 5
n
u u n d n
.
Nhận thấy toạ độ của các điểm
n
A
đều thoả mãn phương trình
3 5
y x
nên phương trình
đường thẳng đi qua các điểm
1 2
, ,..., ,...
n
A A A là
3 5
y x
.
Suy ra A là phương án đúng.
Câu 61. Trong mặt phẳng tọa độ
Oxy
, cho đồ thị
C
của hàm số
3 2
y x
. Với mỗi số nguyên
dương
n
, gọi
n
A
là giao điểm của đồ thị
C
với đường thẳng
: 0
d x n
. Xét dãy số
n
u
với
n
u
là
tung độ của điểm
n
A
. Mệnh đề nào dưới đây là mệnh đề đúng?
A. Dãy số
n
u
là một cấp số cộng có công sai
2
d
.
B. Dãy số
n
u
là một cấp số cộng có công sai
3
d
.
C. Dãy số
n
u
là một cấp số cộng có công sai
1
d
.
D. Dãy số
n
u
không phải là một cấp số cộng.
Hướng dẫn giải
Chọn B.
Ta có
;
n n
A n u
trong đó
3 2
n
u n
.
Do
1
3, n 1
n n
u u
nên
n
u
là một cấp số cộng với công sai
3
d
.
Suy ra B là phương án đúng.
Câu 62. Trên tia
Ox
lấy các điểm
1 2
, ,..., ,...
n
A A A sao cho với mỗi số nguyên dương
n
,
n
OA n
.
Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia
Ox
, vẽ các nửa đường tròn đường kính
n
OA
,
1,2,...
n
Kí hiệu
1
u
là diện tích nửa đường tròn đường kính
1
OA
và với mỗi
2
n
, kí hiệu
n
u
là
diện tích của hình giới hạn bởi nửa đường tròn đường kính
1
n
OA
, nửa đường tròn đường kính
n
OA
và
tia
Ox
. Mệnh đề nào dưới đây là đúng?
A. Dãy số
n
u
không phải là một cấp số cộng.
B. Dãy số
n
u
là một cấp số cộng có công sai
4
d
.
C. Dãy số
n
u
là một cấp số cộng có công sai
8
d
.
D. Dãy số
n
u
không phải là một cấp số cộng có công sai
2
d
.
Hướng dẫn giải
Chọn B.
Bán kính đường tròn có đường kính
n
OA
là
2
n
n
r
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay
Diên tích nửa đường tròn đường kính
n
OA
là
2
2
1
2 2 8
n
n n
S
.
Suy ra
2
2
1
2 1
1 , 2
8 8
n n n
n
u s s n n n
.
Ta có
2
1
1 1
2 2 8
u
.
Do
1
, n 1
4
n n
u u
nên
n
u
là cấp số cộng với công sai
4
d
.
Suy ra B là phương án đúng.
Câu 63. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000
đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm
30000
đồng so với giá của mét khoan
ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu
20
mét lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó
phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
A.
7700000
đồng. B.
15400000
đồng. C.
8000000
đồng. D.
7400000
đồng.
Hướng dẫn giải
Chọn A.
Gọi
n
u
là giá của mét khoan thứ
n
, trong đó
1 20.
n
Theo giả thiết, ta có
1
100000
u
và
1
30000
n n
u u
với
1 19
n
.
Ta có
( )
n
u
là cấp số cộng có số hạng đầu
1
100000
u
và công sai
30000
d
.
Tổng số tiền gia đình thanh toán cho cơ sở khoan giếng chính là tổng các số hạng của cấp số
cộng
( )
n
u
. Suy ra số tiền mà gia đình phải thanh toán cho cơ sở khoan giếng là
1
20 1 2 20
20[2 (20 1) ]
.... 7700000
2
u d
S u u u
(đồng).
Câu 64. Trên một bàn cờ có nhiều ô vuông. Người ta đặt 7 hạt dẻ vào ô vuông đầu tiên, sau đó đặt tiếp
vào ô thứ hai số hạt dẻ nhiều hơn ô đầu tiên là 5, tiếp tục đặt vào ô thứ ba số hạt dẻ nhiều hơn ô thứ hai
là 5, … và cứ thế tiếp tục đến ô cuối cùng. Biết rằng đặt hết số ô trên bàn cờ người ta đã phải sử dụng
hết
25450
hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô?
A.
98
ô. B.
100
ô. C.
102
ô. D.
104
ô.
Hướng dẫn giải
Chọn B.
Kí hiệu
n
u
là số hạt dẻ ở ô thứ
n
.
Khi đó, ta có
1
7
u
và
1
5, 1
n n
u u n
.
Dãy số
n
u
là cấp số cộng với
1
7
u
và công sai
5
d
nên có
2
1
2 1
5 9
2 2
n
n u n d
n n
S
.
Theo giả thiết, ta có
2
5 9
25450
2
n n
100
n
.
Suy ra bàn cờ có 100 ô.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay
Câu 65. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức
sau: Mức lương của quý làm việc đầu tiên cho công ty là
13,5
triệu đồng/quý, và kể từ quý làm việc
thứ hai, múc lương sẽ được tăng thêm
500.000
đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận
được sau ba năm làm việc cho công ty.
A.
198
triệu đồng. B.
195
triệu đồng. C.
228
triệu đồng. D.
114
triệu đồng.
Hướng dẫn giải
Chọn B.
Kí hiệu
n
u
là mức lương của quý thứ
n
làm việc cho công ty. Khi đó
1
13,5
u và
1
0,5, 1
n n
u u n
.
Dãy số
n
u
lập thành cấp số cộng có số hạng đầu
1
13,5
u và công sai
0,5
d
.
Một năm có 4 quý nbên 3 năm có tổng 12 quý.
Số tiền lương sau 3 năm bằng tổng số tiền lương của 12 quý và bằng tổng 12 số hạng đầu
tiên của cấp số cộng
n
u
. Vậy, tổng số tiền lương nhận được sau 3 năm làm việc cho công
ty của kỹ sư là
12
12. 2.13,5 11.0,5
195
2
S
(triệu đồng).
Câu 66. Mặt sàn tầng của một ngôi nhà cao hơn mặt sân
0,5
m
. Cầu thang đi từ tầng một lên tầng hai
gồm
21
bậc, một bậc cao
18
cm
. Kí hiệu
n
h
là độ cao của bậc thứ
n
so với mặt sân. Viết công thức để
tìm độ cao
n
h
.
A.
0,18 0,32
n
h n m
. B.
0,18 0,5
n
h n m
.
C.
0,5 0,18
n
h n m
. D.
0,5 0,32
n
h n m
.
Hướng dẫn giải
Chọn A.
Ký hiệu
n
h
là độ cao của bậc thứ
n
so với mặt sân.
Khi đó, ta có
1
0,18
n n
h h
(mét), trong đó
1
0,5
h (mét). Dãy số
n
h
lập thành một cấp
số cộng có
1
0,5
h và công sai
0,18
d
. Suy ra số hạng tổng quát của cấp số cộng này là
0,5 1 .0,18 0,18. 0,32
n
h n n
(mét).
Câu 67. Trên tia Ox lấy các điểm
1 2
,..., .
,
..
,
n
A A A sao cho với mỗi số nguyên dương n,
.
n
OA n
Trong
cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính
, 1, 2...
n
OA n Kí hiệu
1
u
là diện tích của nửa hình tròn đường kính
1
OA
và với mỗi
2,
n
kí hiệu
n
u
là diện tích của hình giới hạn bởi nửa đường tròn đường kính
1
,
n
OA
nửa đường tròn đường kính
n
OA
và tia Ox. Chứng minh rằng dãy số
( )
n
u
là một cấp số cộng. Hãy xác định công sai của cấp số cộng
đó.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay
A.
4
d
B.
2
d
C.
3
d
D.
2
3
d
Hướng dẫn giải
Đáp án A
Đặt
0
0,OA ta có
2 2
2
2
1
2 1
1
1 , 1
2 4 4 8 8
n n
n
n
OA OA
u n n n
Suy ra
1
2 1 2 1
, 1
8 8 4
n n
n n
u u n
Do đó
n
u
là một cấp số cộng công sai
4
d
CẤP SỐ NHÂN
Câu 68. Cho tam giác
ABC
biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng
25
. Tìm 2 góc còn lại?
A. 65 ,90 B. 75 ,80 . C. 60 ,95 . D. 60 ,90 .
Hướng dẫn giải
Chọn D
Ta có:
1 2 3
180 25 25 25 2 180 35u u u d d d .
Vâỵ
2 3
60; 90.u u
Câu 69. Cho dãy số
n
a
xác định bởi
1 1
5, . 3
n n
a a q a
với mọi 1,n trong đó q là hằng số,
0, 1.a q Biết công thức số hạng tổng quát của dãy số viết được dưới dạng
1
1
1
. .
1
n
n
n
q
a q
q
Tính 2 ?
A. 13. B. 9. C. 11. D. 16.
Hướng dẫn giải
Chọn C
Cách 1.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay
Ta có:
1
3
3
1
n n
a k q a k k kq k
q
Đặt
2
1 1 1
. . ...
n
n n n n n
v a k v q v q v q v
Khi đó
1 1 1
1 1
3
. . . 5
1
n n n
n
v q v q a k q
q
Vậy
1
1 1 1
3 3 3 1
. 5 . 5 5 3
1 1 1 1
n
n n n
n n
q
a v k q k q q
q q q q
Do dó:
5; 3 2 5 2.3 11
Cách 2.
Theo giả thiết ta có
1 2
5, 5 3.
a a q
Áp dụng công thức tổng quát, ta được
1 1
1 1
1
2 1
2 1
2
1
.
1
,
1
. .
1
q
a q
q
q
a q q
q
suy ra
5
,
5 3 .q q
hay
5
3
2 5 2.3 11
Câu 70. Trong dịp hội trại hè 2017 bạn A thả một quả bóng cao su từ độ cao 3m so với mặt đất, mỗi
lần chạm đất quả bóng lại nảy lên một độ cao bằng hai phần ba độ cao lần rơi trước. Tổng quãng
đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng:
A. 13m. B. 14m. C. 15m. D. 16m.
Hướng dẫn giải
Chọn C
Gọi S là tổng quãng đường bóng đã bay, khi đó ta có:
2 3 4 5
2 2 2 2 2 2
3 3. .3 3. 3. 3. ... 3. ...
3 3 3 3 3 3
n
S
S là tổng của cấp số nhân lùi vô hạn có số hạng đầu tiên là
1
3
u
, công bội là
2
3
q
nên
1
3
9
2
1
1
3
u
S
q
Vậy tổng quãng đường đã bay của bóng là khoảng 9m.
Do đó
x 2
y
Câu 71. Có hai cấp số nhân thỏa mãn
1 2 3 4
2 2 2 2
1 2 3 4
15
85
u u u u
u u u u
với công bội lần lượt là
1 2
, .
q q
Hỏi giá
trị của
1 2
q q
là:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay
A.
1
2
B.
3
2
C.
5
2
D.
7
2
Hướng dẫn giải
Đáp án C
Biến đổi giả thiết thành
2
2 4
4
1
1
2
2
4 2
2
2
8
2 8
2 8
1
1
2
2
1
1
225
15
1 1
1
225
1
85
1 1
1
1
85
85
1
1
u q
u q
q q
q
q
q q
u q
u q
q
q
4 3 2
1
14 17 17 17 14 0 .
2
2
q
q q q q
q
Do đó
1 2
5
.
2
q q
Câu 72. Cho tứ giác
ABCD
biết
4
góc của tứ giác lập thành một cấp số cộng và góc
A
bằng 30
o
. Tìm
các góc còn lại?
A.
75 ,120 ,65
. B.
72 ,114 ,156
. C. 70
o
; 110
o
; 150
o
. D. 80
o
; 110
o
; 135
o
.
Hướng dẫn giải
Chọn C
Ta có:
1 2 3 4
360 30 30 30 2 30 3 360 40
u u u u d d d d
.
Vâỵ
2 3 4
70; 110; u 150
u u .
Câu 73. Cho một cấp số cộng
( )
n
u
có
1
1
u và tổng 100 số hạng đầu bằng
24850
. Tính
1 2 2 3 49 50
1 1 1
... S
u u u u u u
.
A.
9
246
S . B.
4
23
S . C.
123
S
. D.
49
246
S .
Hướng dẫn giải
Chọn D
Gọi
d
là công sai của cấp số đã cho
Ta có:
1
100 1
497 2
50 2 99 24850 5
99
u
S u d d
1 2 2 3 49 50
5 5 5
5 ... S
u u u u u u
3 2 50 49
2 1
1 2 2 3 49 50
...
u u u u
u u
u u u u u u
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay
1 2 2 3 48 49 49 50
1 1 1 1 1 1 1 1
...
u u u u u u u u
1 50 1 1
1 1 1 1 245
49 246
u u u u d
49
246
S .
Câu 74. Cho
, ,
a b c
theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A.
2 2
2 2 2
a c ab bc ac
. B.
2 2
2 2 2
a c ab bc ac
.
C.
2 2
2 2 2
a c ab bc ac
. D.
2 2
2 2 2
a c ab bc ac
.
Hướng dẫn giải
Chọn C
, ,
a b c
theo thứ tự lập thành cấp số cộng khi và chỉ khi
2 2
2 2
2 2
b a c b b a c b a c ab bc
2 2 2
2 2 2 2 2
2 2 2 2 2
a c c ab bc ab c c b
ab c b a ab bc ac
Câu 75. Cho dãy số
n
u
được xác định như sau:
1
1
2
.
4 4 5 1
n n
u
u u n n
Tính tổng
2018 2017
2 .
S u u
A.
2017
2015 3.4
S B.
2018
2016 3.4
S C.
2018
2016 3.4
S D.
2017
2015 3.4
S
Hướng dẫn giải
Chọn C
Câu 76. Cho số hạng thứ
m
và thứ
n
của một cấp số nhân biết số hạng thứ
( )
m n
bằng
A
, sổ hạng
thứ
( )
m n
bằng
B
và các số hạng đểu dương. Số hạng thứ m là:
A.
2
m
n
B
A
A
B.
AB
C.
m
n
A
B
D.
2
n
AB
Hướng dẫn giải
Chọn B
Ta có
1
1
2
2
1
1
.
.
m n
m n
n
n
m n
m n
u A u q
A
A Bq q
B
u B u q
Mặt khác
1
1
2
1
1
.
.
n
m
m
n
m
n
m
m n
m n
u u q
u
A
q u A AB
A B
u u q
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay
Tương tự ta có thể tính được
2
m
n
n
B
u A
A
Câu 77.
Cho dãy số
n
U
xác định bởi:
1
1
3
U
và
1
1
.
3
n n
n
U U
n
. Tổng
3 10
2
1
..
2 3 10
U U
U
S U
bằng:
A.
3280
6561
.
B.
29524
59049
.
C.
25942
59049
.
D.
1
243
.
Hướng dẫn giải
Chọn B
Ta có
1
1
3
n n
n
u u
n
1
1
.
1 3
n n
u u
n n
1
1
3
n
u
.
2
1
1
2 3
u
u
;
2
3
1
2
1 1
3 3 2 3
u
u
u
;…;
10
1
9
1
10 3
u
u
.
Khi đó:
3 10
2
1
2 10
1 1 1
... ...
2 3 10 3 3 3
u u
u
S u
10
1 1
1
3 3
1
1
3
29524
59049
.
Câu 78. Phương trình
2 2 4
1 ... 1 1 1
x
a a a a a a
với
0 1
a
có bao nhiêu nghiệm?
A.
0
B.
1
C.
2
D.
3
Hướng dẫn giải
Chọn B
Phương trình biến đổi thành
1
2 4 1 8
1
1 1 1 1 1 7.
1
x
x
a
a a a a a x
a
Câu 79. Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập thành
một cấp số nhân:
3 2
3 1 5 4 8 0.
x x x m x
A.
2.
m
B.
2.
m
C.
4.
m
D.
4.
m
Hướng dẫn giải
Chọn B.
Phương pháp 1: Ta có
8
8.
1
d
a
Điều kiện cần để phương trình đã choc ó ba nghiệm lập thành một cấp số nhân là
3
8 2
x
là nghiệm của phương trình.
Thay
2
x
vào phương trình đã cho, ta được
4 2 0
m
2.
m
Với
2,
m
ta có phương trình
3 2
7 14 8 0
x x x
1; 2; 4
x x x
Ba nghiệm này lập thành một cấp số nhân nên
2
m
là giá trị cần tìm. Vậy,
B
là phương
án đúng.
Phương pháp 2: Kiểm tra từng phương án đến khi tìm được phương án đúng.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay
Câu 80. Biết rằng tồn tại hai giá trị
1
m
và
2
m
để phương trình sau có ba nghiệm phân biệt lập thành
một cấp số nhân:
3 2 2 2
2 2 2 1 7 2 2 54 0.
x m m x m m x
Tính giá trị của biểu thức
3 3
1 2
.
P m m
A.
56
P
B.
8.
P
C.
56
P
D.
8.
P
Hướng dẫn giải
Chọn A.
Ta có
54
27.
2
d
a
Điều kiện cần để phương trình đã cho có ba nghiệm phân biệt lập thành một cấp số nhân là
3
27 3
x
phải là nghiệm của phương trình đã cho.
2
2 8 0
m m
2; 4.
m m
Vì giả thiết cho biết tồn tại đúng hai giá trị của tham số
m
nên
2
m
và
4
m
là các giá
trị thỏa mãn
Suy ra
3
3
2 4 56.
P
Câu 81. Ba số
, ,
x y z
lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số
2;3;9
vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính
2 2 2
.
F x y z
A.
389.
F
hoặc
395.
F
B.
395.
F
hoặc
179.
F
C.
389.
F
hoặc
179.
F
D.
441
F
hoặc
357.
F
Hướng dẫn giải
Chọn C .
Theo tính chất của cấp số cộng, ta có
2
x z y
.
Kết hợp với giả thiết
21
x y z
, ta suy ra
3 21 7
y y
.
Gọi
d
là công sai của cấp số cộng thì 7
x y d d
và 7
z y d d
.
Sau khi thêm các số
2;3;9
vào ba số
, ,
x y z
ta được ba số là
2, 3, 9
x y z
hay
9 ,10,16
d d
.
Theo tính chất của cấp số nhân, ta có
2 2
9 16 10 7 44 0
d d d d
.
Giải phương trình ta được
11
d
hoặc
4
d
.
Với
11
d
, cấp số cộng
18,7, 4
. Lúc này
389
F
.
Với
4
d
, cấp số cộng
3,7,11
. Lúc này
179
F
.
Câu 82. Cho cấp số nhân
n
a
có
1
7,
a
6
224
a
và
3577.
k
S
Tính giá trị của biểu thức
1 .
k
T k a
A.
17920.
T
B.
8064.
T
C.
39424.
T
D.
86016.
T
Hướng dẫn giải
Chọn A.
Ta có
6
224
a
5
1
224
a q
2
q
(do
1
7
a
).
Do
1
1
7 2 1
1
k
k
k
a q
S
q
nên
3577
k
S
7 2 1 3577
k
9
2 2
k
9.
k
Suy ra
8
9 1
10 10 17920.
T a a q
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay
Câu 83. Cho cấp số nhân
n
a
có
1
2
a
và biểu thức
1 2 3
20 10
a a a
đạt giá trị nhỏ nhất. Tìm số
hạng thứ bảy của cấp số nhân đó.
A.
7
156250.
a B.
7
31250.
a C.
7
2000000.
a D.
7
39062.
a
Hướng dẫn giải
Chọn B.
Gọi
q
là công bội của cấp số nhân
n
a
.
Ta có
2
1 2 3
20 10 2 10 20
a a a q q
2
2 5 10 10, .
q q
Dấu bằng xảy ra khi
5.
q
Suy ra
6 6
7 1
. 2.5 31250.
a a q
Câu 84. Trong các mệnh đề dưới đây, mệnh đề nào là sai?
A. Dãy số
n
a
, với
1
3
a
và
1
6,
n n
a a
1,
n
vừa là cấp số cộng vừa là cấp số
nhân.
B. Dãy số
n
b
, với
1
1
b
và
2
1
2 1 3,
n n
b b
1,
n
vừa là cấp số cộng vừa là cấp số
nhân.
C. Dãy số
n
c
, với
1
2
c
và
2
1
3 10
n n
c c
1,
n
vừa là cấp số cộng vừa là cấp số nhân.
D. Dãy số
n
d
, với
1
3
d
và
2
1
2 15,
n n
d d
1,
n
vừa là cấp số cộng vừa là cấp số
nhân.
Hướng dẫn giải
Chọn D.
Kiểm tra từng phương án đến khi tìm được phương án sai.
+ Phương án A:Ta có
2 2
3; 3;...
a a Bằng phương pháp quy nạp toán học chúng ra chứng
minh được rằng
3, 1
n
a n
. Do đó
n
a
là dãy số không đổi. Suy ra nó vừa là cấp số
cộng (công sai bằng
0
) vừa là cấp số nhân (công bội bằng
1
).
+ Phương án B: Tương tự như phương án A, chúng ta chỉ ra được
1, 1
n
b n
. Do đó
n
b
là dãy số không đổi. Suy ra nó vừa là cấp số cộng (công sai bằng
0
) vừa là cấp số nhân
(công bội bằng
1
).
+ Phương án C: Tương tự như phương án A, chúng ta chỉ ra được
2, 1
n
c n
. Do đó
n
c
là dãy số không đổi. Suy ra nó vừa là cấp số cộng (công sai bằng
0
) vừa là cấp số
nhân (công bội bằng
1
).
+ Phương án D: Ta có:
1 2 3
3, 3, 3
d d d
. Ba số hạng này không lập thành cấp số cộng
cũng không lập thành cấp số nhân nên dãy số
n
d
không phải là cấp số cộng và cũng
không là cấp số nhân.
Câu 85. Xét bảng ô vuông gồm
4 4
ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số
1
hoặc
1
sao cho tổng các số trong mỗi hang và tổng các số trong mỗi cột đều bằng
0
. Hỏi có bao
nhiêu cách?
A.
72
B.
90
C.
80
D.
144
Hướng dẫn giải
Xét 1 hàng (hay 1 cột bất kì). Giả sử trên hàng đó có
x
số 1 và
y
số -1. Ta có tổng các chữ
số trên hàng đó là
x y
. Theo đề bài có 0
x y x y
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay
Lần lượt xếp các số vào các hàng ta có số cách sắp xếp là 3!.3!.2.1 =72 (Cách)
Câu 86. Số đo ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân. Biết thể tích của khối
hộp là
3
125
cm
và diện tích toàn phần là
2
175 .
cm
Tính tổng số đo ba kích thước của hình hộp chữ nhật
đó.
A.
30 .
cm
B.
28 .
cm
C.
31 .
cm
D.
17,5 .
cm
Hướng dẫn giải
Chọn D.
Vì ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân nên ta có thể gọi ba kích
thước đó là
, , .
a
q aq
q
Thể tích của khối hình hộp chữ nhật là
3
. . 125 5.
a
V a qa a a
q
Diện tích toàn phần của hình hộp chữ nhật là
2
1 1
2 . . . 2 1 50 1 .
tp
a a
S a a aq aq a q q
q q q q
Theo giả thiết, ta có
2
2
1
50 1 175 2 5 2 0 .
1
2
q
q q q
q
q
Với
2
q
hoặc
1
2
q
thì kích thước của hình hộp chữ nhật là
2,5 ;5 ;10 .
cm cm cm
Suy ra tổng của ba kích thước này là
2,5 5 10 17,5
cm.
Câu 87. Một của hàng kinh doanh, ban đầu bán mặt hàng A với giá 100 (đơn vị nghìn đồng). Sau đó,
cửa hàng tăng giá mặt hàng A lên
10%.
Nhưng sau một thời gian, cửa hàng lại tiếp tục tăng giá mặt
hàng đó lên
10%.
Hỏi giá của mặt hàng A của cửa hàng sau hai làn tăng giá là bao nhiêu?
A.
120.
B.
121.
C.
122.
D.
200.
Hướng dẫn giải
Chọn B.
Sau lần tăng giá thứ nhất thì giá của mặt hàng
A
là:
1
100 100.10% 110.
M
Sau lần tăng giá thứ hai thì giá của mặt hàng
A
là:
2
110 110.10% 121.
M
Câu 88. Một người đem 100 triệu đồng đi gửi tiết kiệm với kỳ han 6 tháng, mỗi tháng lãi suất là
0,7%
số tiền mà người đó có. Hỏi sau khi hết kỳ hạn, người đó được lĩnh về bao nhiêu tiền?
A.
5
8
10 . 0,007
(đồng) B.
5
8
10 . 1,007
(đồng)
C.
6
8
10 . 0,007
(đồng) D.
6
8
10 . 1,007
(đồng)
Hướng dẫn giải
Chọn D.
Số tiền ban đầu là
8
0
10
M
(đồng).
Đặt
0,7% 0,007
r
.
Số tiền sau tháng thứ nhất là
1 0 0 0
1
M M M r M r
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay
Số tiền sau tháng thứ hai là
2
2 1 1 0
1
M M M r M r
.
Lập luận tương tự, ta có số tiền sau tháng thứ sáu là
6
6 0
1
M M r
.
Do đó
6
8
6
10 1,007
M .
Câu 89. Tỷ lệ tăng dân số của tỉnh M là
1,2%.
Biết rằng số dân của tỉnh M hiện nay là 2 triệu người.
Nếu lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
A.
10320
nghìn người. B.
3000
nghìn người.
C.
2227
nghìn người. D.
2300
nghìn người.
Hướng dẫn giải
Chọn C .
Đặt
6
0
2000000 2.10
P
và
1,2% 0,012
r
.
Gọi
n
P
là số dân của tỉnh
M
sau
n
năm nữa.
Ta có:
1
1
n n n n
P P P r P r
.
Suy ra
n
P
là một cấp số nhân với số hạng đầu
0
P
và công bội
1
q r
.
Do đó số dân của tỉnh
M
sau
10
năm nữa là:
9 10
6
9 0
1 2.10 1,012 2227000
P M r .
Câu 90. Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc
đầu có
12
10
tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào?
A.
12
1024.10
tế bào. B.
12
256.10
tế bào. C.
12
512.10
tế bào. D.
13
512.10
tế bào.
Hướng dẫn giải
Chọn C .
Lúc đầu có
22
10
tế bào và mỗi lần phân chia thì một tế bào tách thành hai tế bào nên ta có
cấp số nhân với
22
1
10
u
và công bội
2
q
.
Do cứ
20
phút phân đôi một lần nên sau
3
giờ sẽ có
9
lần phân chia tế bào. Ta có
10
u
là số
tế bào nhận được sau
3
giờ. Vậy, số tế bào nhận được sau
3
giờ là
9 12
10 1
512.10
u u q
.
Câu 91. Người ta thiết kế một cái tháp gồm 11 tầng theo cách: Diện tích bề mặt trên của mỗi tầng
bằng nửa diện tích mặt trên của tầng ngay bên dưới và diện tích bề mặt trên của tầng 1 bằng nửa diện
tích đế tháp. Biết diện tích đế tháp là
2
12288 ,
m
tính diện tích mặt trên cùng.
A.
2
6 .
m
B.
2
12 .
m
C.
2
24 .
m
D.
2
3 .
m
Hướng dẫn giải
Chọn A.
Gọi
0
u
là diện tích đế tháp và
n
u
là diện tích bề mặt trên của tầng thứ
n
, với
1 11
n
.
Theo giả thiết, ta có
1
1
0 10
2
n n
u u n
.
Dãy số
n
u
lập thành cấp số nhân với số hạng đầu
0
12288
u và công bội
1
2
q
.
Diện tích mặt trên cùng của tháp là
11
11 2
11 0
1
. 12288. 6m
2
u u q
.
Câu 92. Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất
bằng
1
9
số đo của góc nhỏ thứ ba. Hãy tính số đo của các góc trong tứ giác đó.
A.
0 0 0 0
5 ,15 ,45 ,225 .
B.
0 0 0 0
9 ,27 ,81 ,243 .
C.
0 0 0 0
7 ,21 ,63 ,269 .
D.
0 0 0 0
8 ,32 ,72 ,248 .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải
Chọn B.
Phương pháp 1: Kiểm tra các dãy số trong mỗi phương án có thỏa mãn yêu cầu của bài
toán không.
+ Phương án
:A
Các góc
0 0 0 0
5 ,15 ,45 ,225 không lập thành cấp số nhân vì
0 0
15 3.5 ;
0 0
45 3.15 ;
0 0
225 3.45 .
+ Phương án
:B
Các góc
0 0 0 0
9 ,27 ,81 ,243 lập thành cấp số nhân và
0 0 0 0 0
9 27 81 243 360 . Hơn nữa,
0 0
1
9 81
9
nên B là phương án đúng.
+ Phương án
C
và
:D
Kiểm tra như phương án
.A
Phương pháp 2: Gọi các góc của tứ giác là
2 3
, , , ,a aq aq aq trong đó 1.q
Theo giả thiết, ta có
2
1
9
a aq nên 3.q
Suy ra các góc của tứ giác là ,3 ,9 ,27 .a a a a
Vì tổng các góc trong tứ giác bằng
0
360 nên ta có:
0
3 9 27 360a a a a
0
9 .a
Do đó, phương án đúng là B (vì trong ba phương án còn lại không có phương án nào có góc
0
9 ).
Câu 93. Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác
ABC
được gọi là tam giác
trung bình của tam giác
ABC
. Ta xây dựng dãy các tam giác
1 1 1
A BC ,
2 2 2
A B C ,
3 3 3
,...A B C sao cho
1 1 1
A BC là một tam giác đều cạnh bằng
3
và với mỗi số nguyên dương
2n
, tam giác
n n n
A B C là tam
giác trung bình của tam giác
1 1 1n n n
A B C
. Với mỗi số nguyên dương
n
, kí hiệu
n
S tương ứng là diện
tích hình tròn ngoại tiếp tam giác
n n n
A B C . Tính tổng
1 2
... ...
n
S S S S ?
A.
15
4
S
. B.
4S
. C.
9
2
S
. D.
5S
.
Hướng dẫn giải
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay
*Gọi
i
R
là bán kính đường tròn ngoại tiếp
i i i
ABC
1;
i n
.
Ta có
1 1 1 2 1
2
3 3
3
R OA A A S
.
*Dễ thấy
1 1 1 2 2 2 2 1 2 1
1
;
2
1 1
: .
2 4
o
V A B C A B C R R S S
2 2 2 3 3 3 3 2 1 3 1
1
2
;
2
1 1 1
: .
2 4 4
o
V A B C A B C R R R S S
Tương tự, ta có:
1
1
1
4
n
n
S S
.
Suy ra:
1 2 1
2 1
1 1 1
... ... 1 ... ...
4 4 4
n
n
S S S S S
1 1
1 4
. 4
1
3
1
4
S S
. (Áp dụng công thức tính tổng của một cấp số nhân lùi vô hạn).
Câu 94. Cho tam giác ABC cân tại đỉnh
.
A
Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB
theo thứ tự lập thành cấp số nhân công bội q. Gía trị của
2
q
bằng
A.
2 2
2
. B.
2 2
2
. C.
2 1
2
. D.
2 1
2
.
Hướng dẫn giải
Chọn C
, ,
BC AH AB
theo thứ tự lập thành CSN
2
2
.
AH BC AB
AB
q
BC
Ta có:
2 2
2 2
2
. 4 4 1 0
4
2 1
2
BC AB AB
AH AB AB BC
BC BC
AB
q
BC
Câu 95. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức như
sau: mức lương của quý làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ
hai mức lương sẽ được tăng thêm 1,5 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư được
nhận sau 3 năm làm việc cho công ty.
A.
495
triệu đồng. B.
279
triệu đồng. C.
384
triệu đồng. D.
558
triệu đồng.
Hướng dẫn giải
Chọn B
A
C
H
B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay
Câu 96. Một hình vuông
ABCD
có cạnh
,
AB a
diện tích
1
.
S
Nối 4 trung điểm
1 1 1 1
, , ,
A B C D
theo
thứ tự của 4 cạnh
, , ,
AB BC CD DA
ta được hình vuông thứ hai là
1 1 1 1
A B C D
có diện tích
2
.
S
Tiếp tục
như thế, ta được hình vuông thứ ba là
2 2 2 2
A B C D
có diện tích
3
S
và cứ tiếp tục như thế, ta được diện
tích
4 5
, ,...
S S Tính
1 2 100
... .
S S S S
A.
100
99 2
2 1
2
S
a
. B.
100
99
2 1
2
a
S
. C.
2 100
99
2 1
2
a
S
. D.
2 99
99
2 1
2
a
S
Hướng dẫn giải
Đáp án C
Dễ thấy
2 2 2
2
1 2 3 100
99
; ; ;...;
2 4 2
a a a
S a S S S
Như vậy
1 2 3 100
, , ,...,
S S S S
là cấp số nhân với công bội
1
2
q
2 100
2
1 2 100
2 99 99
2 1
1 1 1
... 1 ...
2 2 2 2
a
S S S S a
| 1/52

Tài liệu khác của Toán 11

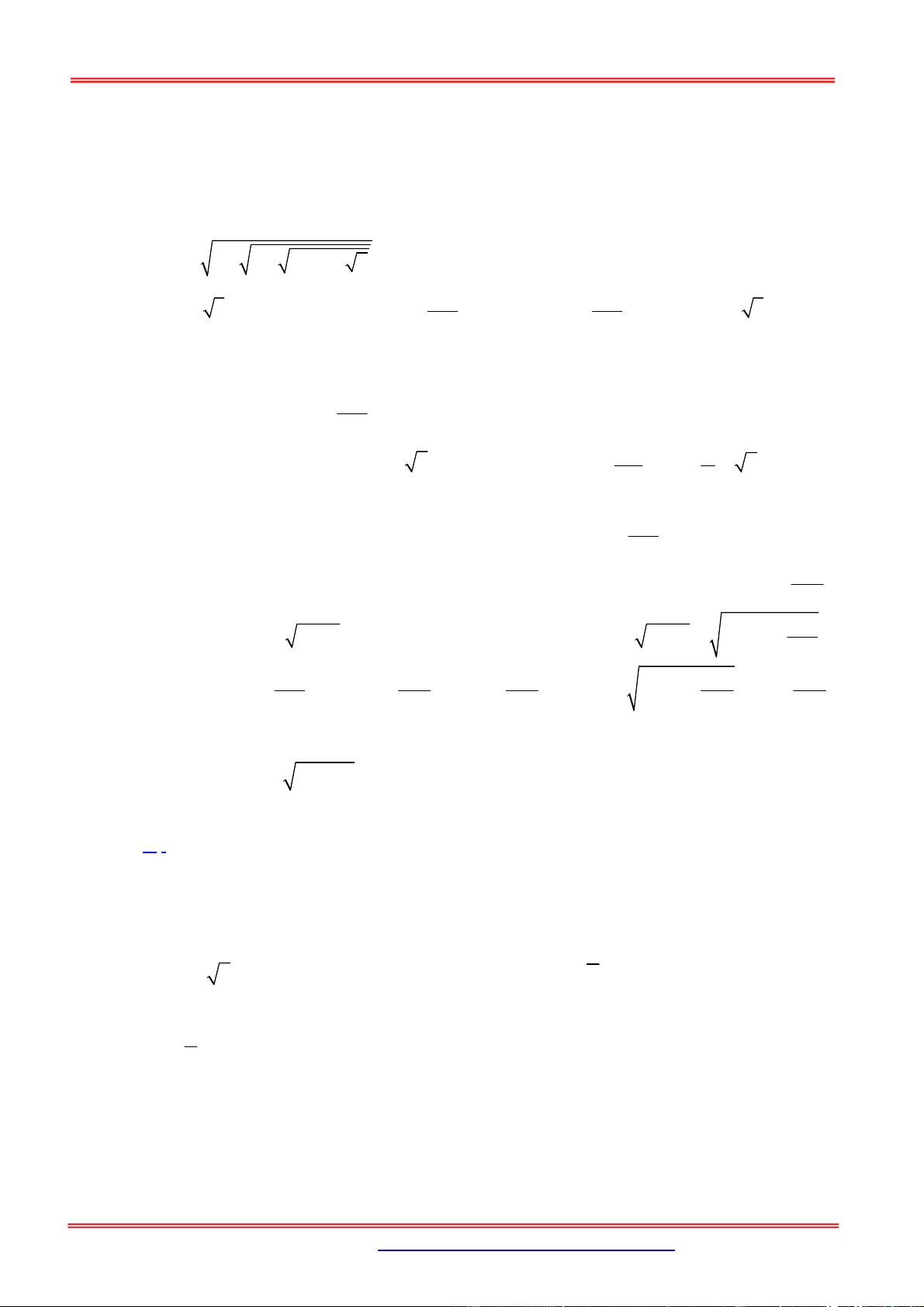
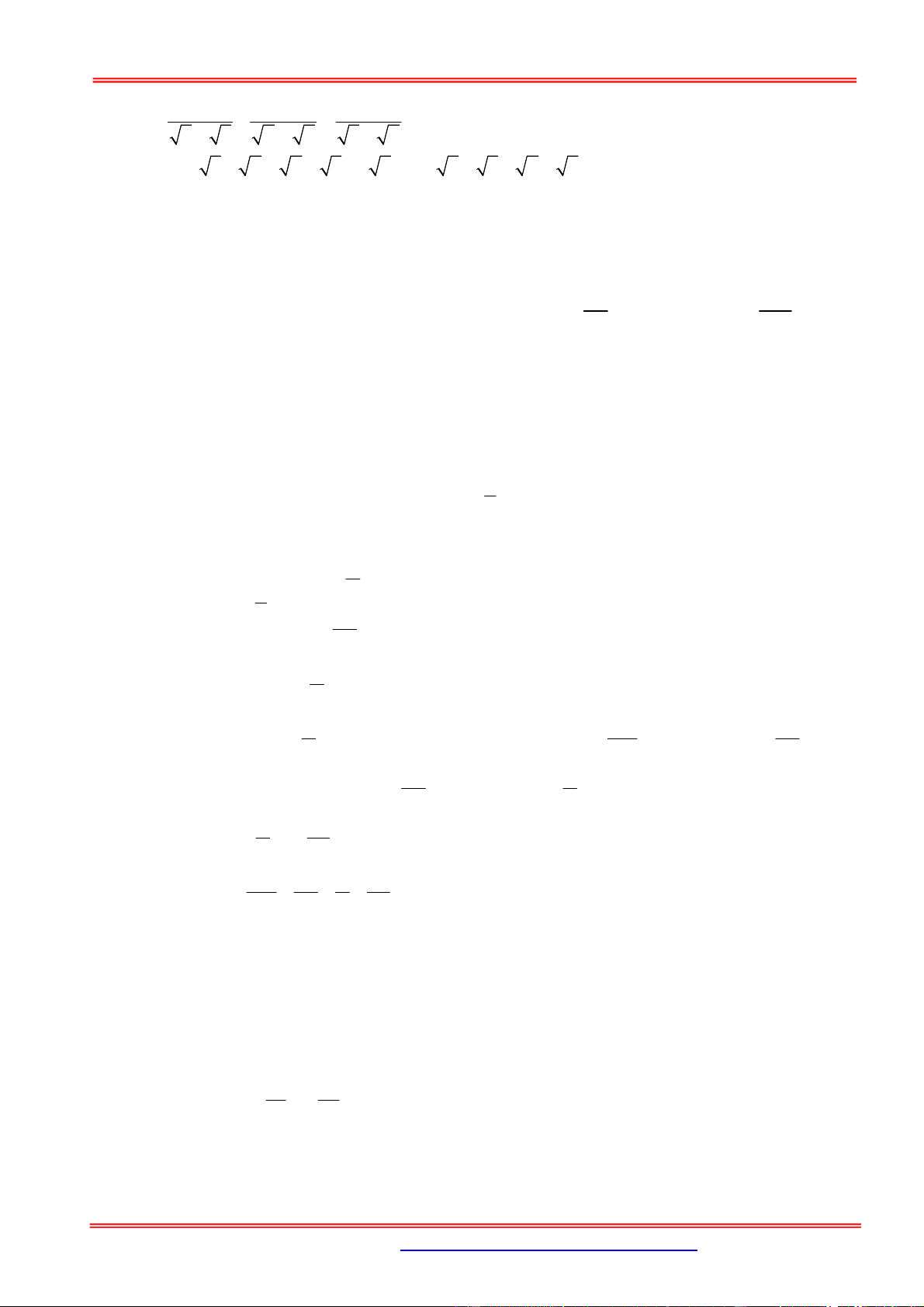
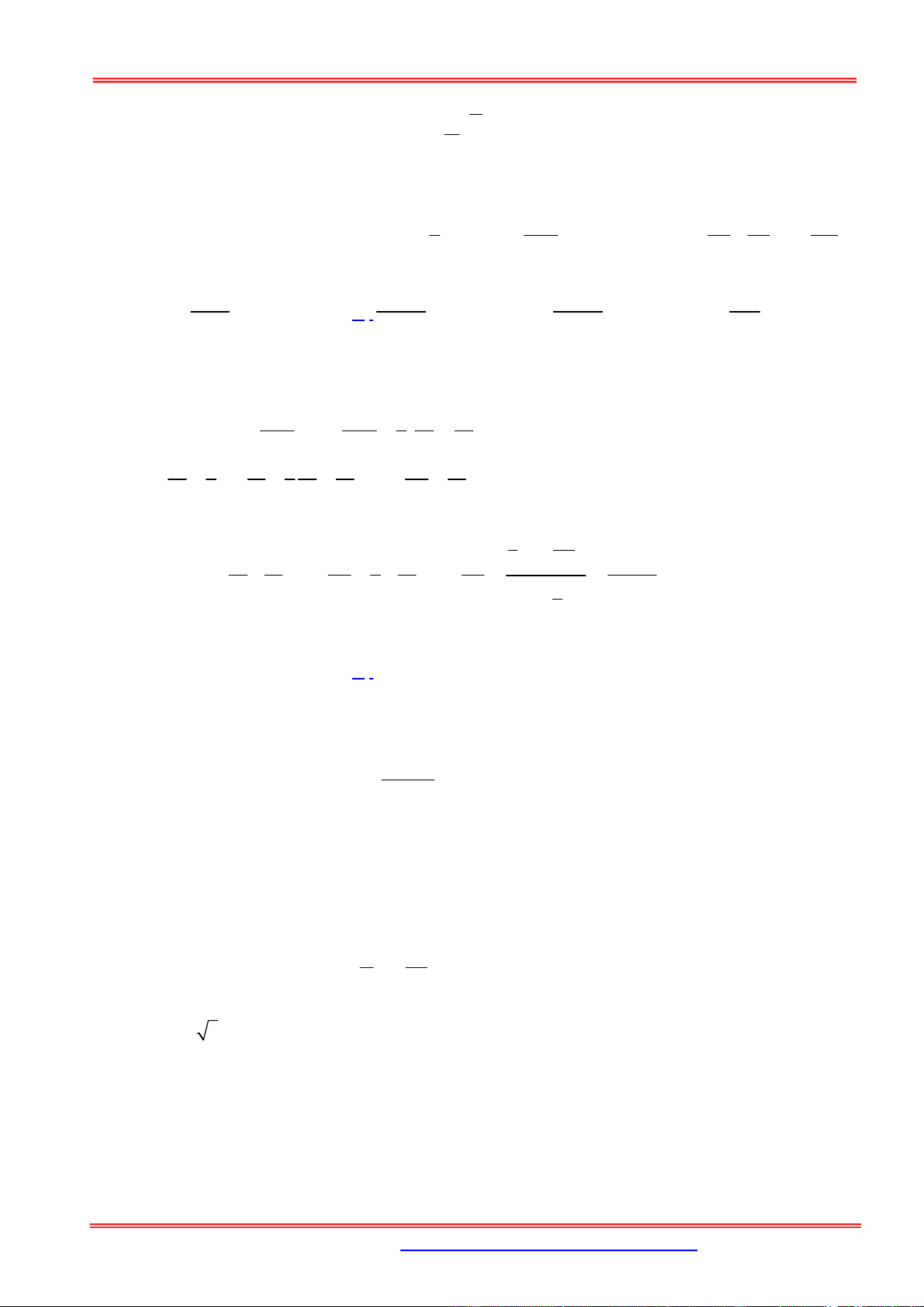
Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
DÃY SỐ, CẤP SỐ CỘNG, CẤP SỐ NHÂN
A – LÝ THUYẾT CHUNG I – DÃY SỐ  Một hàm số *
u : N   được gọi là một dãy số vô hạn, kí hiệu là u . n
Khi n u n , khi đó u u n gọi là số hạng tổng quát của dãy un n   
Một hàm số u xác định trên tập hợp m số nguyên dương đầu tiên được gọi là dãy số hữu hạn.  Dãy số u là dãy số tăng nếu * u
u  0, n   n n 1  n Dãy số u là dãy số giảm nếu * u
u  0, n   n n 1  n
Dãy số u được gọi là bị chặn trên nếu tồn tại số M sao cho *
u M , n   n n
Dãy số u được gọi là bị chặn dưới nếu tồn tại số M sao cho *
u M , n   n n
Dãy số được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới. II - CẤP SỐ CỘNG
1. Định nghĩa: u là cấp số cộng nếu u
u d , với * n
   , d là hằng số n n 1  n 2. Các khái niệm:
Cho cấp số cộng u , Khi đó: n
u u n 1 d : số hạng tổng quát của cấp số cộng n 1  
d : công sai của cấp số cộng
S u u  ...  u : tổng n số hạng đầu tiên của cấp số cộng n 1 2 n 3. Tính chất: uun 1 n 1 u    n 2 nS u u n  1 n  2 ns u n d n 2 1 1    2 III - CẤP SỐ NHÂN
1. Định nghĩa: u
là cấp số nhân  uu .q , * n    n n 1  n 2. Các khái niệm: n 1 u u .q  
, n  1 : số hạng tổng quát của cấp số nhân n 1
q :công bội của cấp số nhân 3. Tính chất:  2 uu .un  2 n n 1  n 1  u . n q 1 1   
S u  ...  u
; q  1 n 1 n q 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao B - BÀI TẬP DÃY SỐ
Câu 1. Cho dãy số có các số hạng đầu là: 0,1;0, 01;0,001;0, 0001;... . Số hạng tổng quát của dãy số này có dạng? 1 1 A. un   0 , 0 . 0  . 0 . 1 . B. u n   , 0 0 . 0  . 0 . 1 . C. u  . D. u  . n n 1 n 10  n 1 10  n c höõso á 0 n 1  c höõso á 0 u  5
Câu 2. Cho dãy số u với 1
.Số hạng tổng quát u của dãy số là số hạng nào dưới đây? n   nuu n n1 n (n  ) 1 n (n  ) 1 n A. u  . B. u  5  . n 2 n 2 (n  ) 1 n (n  ) 1 (n  ) 2 C. u  5  . D. u  5  . n 2 n 2 u   1
Câu 3. Cho dãy số u với 1
. Số hạng tổng quát u của dãy số là số hạng nào dưới n   2 n uu nn 1  n đây? n n   1 2n   1 n n   1 2n  2 A. u  1 . B. u  1 . n 6 n 6 n n   1 2n   1 n n   1 2n  2 C. u  1 . D. u  1 . n 6 n 6 u   2 1
Câu 4. Cho dãy số u với 
u của dãy số là số hạng nào dưới n u
u  2n 1  . Số hạng tổng quát n 1  n n đây? A. u   n  2 2 1 . B. 2 u  2  n . C. u   n  . D. u   n  . n  2 2 1 n  2 2 1 n n u   2  1 
Câu 5. Cho dãy số u với 
1 . Công thức số hạng tổng quát của dãy số này là: n u  2   n 1   un n 1 n 1 n 1 n A. u   . B. u  . C. u   . D. u   . n n n n n n n n 1  1 u  
Câu 6. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này là: n   2 u   u  2  n 1  n 1 1 1 1 A. u   2 n  . B. u   2 n  . C. u   2n . D. u   2n . n   1 n   1 2 2 n 2 n 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao u   1 1 
Câu 7. Cho dãy số u với
. Số hạng tổng quát u của dãy số là số hạng nào dưới n   n uu     nn  2n 1 1 đây? n
A. u  1 n .
B. u  1 n . C. u    .
D. u n . n  2 1 1 n n n u   1 1 
Câu 8. Cho dãy số u với
. Số hạng tổng quát u của dãy số là số hạng nào n    n uu     nn  2n 1 1 1 dưới đây?
A. u  2  n .
B. u không xác định. n n
C. u  1 n .
D. u  n với mọi n . n n u   1
Câu 9. Cho dãy số u với 1
. Số hạng tổng quát u của dãy số là số hạng nào dưới n   2 n uu nn 1  n đây? n n   1 2n   1 n n   1 2n  2 A. u  1 . B. u  1 . n 6 n 6 n n   1 2n   1 n n   1 2n  2 C. u  1 . D. u  1 . n 6 n 6 u   2
Câu 10. Cho dãy số u với 1
. Số hạng tổng quát u của dãy số là số hạng nào dưới n
u u  2n 1 nn 1  n đây? A. u   n  2 2 1 . B. 2 u  2  n . C. u   n  . D. u   n  . n  2 2 1 n  2 2 1 n n u   2  1 
Câu 11. Cho dãy số u với 
1 . Công thức số hạng tổng quát của dãy số này là: n u  2   n 1   un n 1 n 1 n 1 n A. u   . B. u  . C. u   . D. u   . n n n n n n n n 1  1 u  
Câu 12. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này là: n   2 u   u  2  n 1  n 1 1 1 1 A. u   2 n  . B. u   2 n  . C. u   2n . D. u   2n . n   1 n   1 2 2 n 2 n 2 u   1 1 
Câu 13. Cho dãy số u với
. Công thức số hạng tổng quát của dãy số này là: n   un u   n 1   2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao n n 1  n 1  n 1   1   1   1   1  A. u   . B. u   . C. u  . D. u   n   1 . n   1 . n   1 .    n      2   2   2   2  . u   2
Câu 14. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này: n  u  2un 1  n A. n 1 u n   .
B. u  2n . C. 1 u 2n  . D. u  2 . n n n n  1 u  
Câu 15. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này: n   2 u   2un 1  n 1  1  A. 1 u 2n   . B. u  . C. u  . D.  2 u  2n . n n n 1 2  n 2n n u   1 1 
Câu 16. Cho dãy số u với
. Số hạng tổng quát u của dãy số là số hạng nào n   n uu     nn  2n 1 1 dưới đây? n
A. u  1 n .
B. u  1 n . C. u    .
D. u n . n  2 1 1 n n n
Câu 17. Đặt T
2  2  2  ...  2 (có n dấu căn). Mệnh đề nào dưới đây là mệnh đề đúng? n A. T  3 . B. T  2 cos . C. T  cos . D. T  5 . n n n 1 2  n n 1 2  n u   1 1 
Câu 18. Cho dãy số  và 2 2 2
S u u  ...  u
 2018 . Khi đó S có bao nhiêu chữ 2 1 2 2018 u  3u  2  n 1  n  số? A. 963 B. 962 C. 607 D. 608 u   2 1
Câu 19. Cho dãy số u
được xác định bởi công thức
. Tìm giới hạn của dãy n   2 2018uu  2017un 1  n n u u u số 1 2 S    ... n  ? n u 1 u 1 u 1 2 3 n 1  1 2017 A. lim S
B. lim S  2018 C. lim S
D. lim S  1 n 2018 n n 2018 n 3 5
Câu 20. Cho dãy số a xác định bởi 2 * a  1; a   a a 1, n
   . Số hạng thứ 201 của dãy n  1 n 1  2 n 2 n
số a có giá trị bằng bao nhiêu? n A. a  2 . B. a  1 . C. a  0 . D. a  5 . 2018 2018 2018 2018
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
u  cos0  1   
Câu 21. Cho dãy số u xác định bởi
. Số hạng thứ 2017 của dãy số đã cho là: n   1 uun ,n  1 n 1   2    A. u  cos B. u  cos 2017  2016  2017  2017   2   2     C. u  sin D. u  sin 2017  2016  2017  2017   2   2 
Câu 22. Cho dãy số a xác định bởi a  5, a  0 và aa
 6a ,n  1. Số hạng thứ 14 của n  1 2 n2 n 1  n dãy là số hạng nào? A. 3164070 . B. 9516786 . C. 1050594 . D. 9615090 .
Câu 23. Cho dãy số a xác định bởi a  3  và 2 a
a n  3n  4, n   * . Số 1391 là số hạng n  1 n 1  n
thứ mấy của dãy số đã cho? A. 18 . B. 17 . C. 20 . D. 19 2 1 1 1 an bn Câu 24. Biết rằng   ...   , trong đó , a , b ,
c d và n là các số 1.2.3 2.3.4 n n   1 n  2 2 cn dn 16
nguyên dương. Tính giá trị của biểu thức T  a cb d  . là : A. T  75 . B. T  364 . C. T  300 .
D. T  256 . n n
Câu 25. Cho dãy số a xác định bởi a  2017sin  2018 cos
. Mệnh đề nào dưới đây là mệnh n n 2 3 đề đúng? A. * a
a , n   . B. * a
a , n   . n  6 n n 9 n C. * a
a , n   . D. * a
a , n   . n 1  2 n n 1  5 na nan n Câu 26. Cho dãy số có a  , n
   * . Tìm số hạng lớn nhất của dãy số . n 2 n 100 1 1 1 1 A. . B. . C. . D. . 20 30 25 21 (u ) * u
n  2018  n  2017, n    . Câu 27. Cho dãy số n thỏa mãn n
Khẳng định nào sau đây sai?
A. Dãy số (u ) là dãy tăng.
B. lim u  0. n n n 1 u C. * 0  u  ,n   . D. n 1 lim   1. n 2 2018 n unx an  4  xn n Câu 28. Cho dãy số với x  . Dãy số là dãy số tăng khi: n n  2
A. a  2 .
B. a  2 .
C. a  2 .
D. a  1.
Câu 29. Trong các dãy số sau dãy số nào là dãy bị chặn ?
A. Dãy a , với 2 a
n 16, n   * . n n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 1
B. Dãy b , với b n  ,n   * . n n 2n
C. Dãy c , với c  2n  3, n   *. n n n
D. Dãy d , với d  ,n   * . n n 2 n  4 an  2
Câu 30. Cho dãy số u với u
, a là tham số. Tìm tất cả các giá trị của a để dãy số u là n n n n 1 một dãy số tăng A. a  1 B. a  1 C. a  2 D. a  2 n n
Câu 31. Cho dãy số (z ) xác định bởi z  sin  2 cos
. Gọi M, m lần lượt là giá trị lớn nhất và n n 2 3
giá trị nhỏ nhất trong các số hạng của dãy số (z ) . Tính giá trị biểu thức 2 2
T M m . n A. T  13. B. T  5. C. T  18. D. T  7. 1 u 2017
Câu 32. Cho dãy số (u ) thỏa mãn u  ; n u
, n  1.S u u  ...  u  khi n n 1 n 1  n 1 2 2
2(n  1)u  1 n 2018 n
có giá trị nguyên dương lớn nhất. A. 2017. B. 2015. C. 2016. D. 2014. cos 2017 x
Câu 33. Cho hàm số f x   2
x  3x  2 
 và dãy số u được xác định bởi công thức tổng n
quát u  log f  
1  log f 2  ... log f n . Tìm tổng tất cả các giá trị của n thỏa mãn điều kiện n   2018 u  1? n A. 21 B. 18 C. 3 D. 2018 f  
1 f 3... f 2n   1
Câu 34. Cho f n  n n  2 2 * 1 1 n
  và đặt u  . Tìm số nguyên n
f 2 f 4... f 2n 10239
dương n nhỏ nhất sao cho log u u   ? 2 n n 1024 A. n  23 B. n  29 C. n  33 D. n  21 a a 3
Câu 35. Cho dãy số a thỏa mãn điều kiện n 1
a  1; 5   n 1  với mọi n   . Tìm số n  1 3n  2
nguyên dương n  1 nhỏ nhất để a ? n A. n  39 B. n  41 C. n  49 D. n  123
Câu 36. Cho dãy số u xác định bởi n 1 u  5;  n u
u  2n  2.3n với mọi n  1. Tìm số nguyên nhỏ n  1 n 1  n nhất thỏa mãn n n 100 u  2  5 . n A. 146 B. 233 C. 232 D. 147 2019 u uu  ...  u 2 2018 n 4n ab Câu 37. Biết rằng 4 n 4 L  lim n  trong đó u xác định bởi n u uu  ...  u c 2 2018 n 2n 2 n 2 n u  0;u
u  4n  3 và , a ,
b c là các số nguyên dương và b  2019 . Tính S a b c ? 1 n 1  n A. 1  B. 0 C. 2017 D. 2018
CẤP SỐ CỘNG
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 2 2 n  1
Câu 38. Cho dãy số u (u u n  n) có n
. Khẳng định nào sau đây sai? 3 1 2 2 2(n  1) 1
A. Là cấp số cộng có u ; 1  d  .
B. Số hạng thứ n+1: u  . 3 3 n 1  3 ( 2 2n  ) 1
C. Hiệu un 1  u   n .
D. Không phải là một cấp số cộng. 3
Câu 39. Cho hai cấp số cộng  x  : 4, 7,10,... và  y
. Hỏi trong 2018 số hạng đầu tiên của n  :1, 6,11, ... n
mỗi cấp số có bao nhiêu số hạng chung? A. 404. B. 673. C. 403. D. 672.
Câu 40. Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
thể coi là số hạng thứ 2,thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp
số cộng này để tổng của chúng bằng 820? A. 20. B. 42. C. 21. D. 17.
Câu 41. Cho cấp số cộng u
biết u  18 và 4S S . Tìm số hạng đầu tiên u và công sai d của n  5 n 2n 1 cấp số cộng.
A. u  2, d  4 .
B. u  2, d  3 .
C. u  2, d  2 .
D. u  3, d  2 . 1 1 1 1
Câu 42. Một cấp số cộng có tổng n số hạng đầu S được tính theo công thức 2
S n n n   n  * 5 3 , . n
Tìm số hạng đầu u và công sai d của cấp số cộng đó 1
A. u  8, d  10
B. u  8, d  10
C. u  8, d  10
D. u  8, d  1  0 1 1 1 1 S S  77 S  192.
Câu 43. Cho cấp số cộng u và gọi n là tổng n số đầu tiên của nó. Biết 7 và 12 Tìm n u
số hạng tổng quát n của cấp số cộng đó.
A. u  5  4n .
B. u  3  2n .
C. u  2  3n .
D. u  4  5n n n n n
Câu 44. Cho ba số dương a , b , c theo thứ tự lập thành cấp số cộng. Giá trị lớn nhất của biểu thức 2 a  8bc  3 P
có dạng x y x, y  . Hỏi x y bằng bao nhiêu:
2a c2 1 A. 9 B. 11 C. 13 D. 7
Câu 45. Chu vi của một đa giác là158cm , số đo các cạnh của nó lập thành một cấp số cộng với công
sai d  3cm . Biết cạnh lớn nhất là 44cm. Số cạnh của đa giác đó là: A. 3. B. 4. C. 5. D. 6
Câu 46. Chu vi của một đa giác n cạnh là 158, số đo các cạnh đa giác lập thành một cấp số cộng với
công sai d  3. Biết cạnh lớn nhất có độ dài là 44. Tính số cạnh của đa giác. A. 6. B. 4. C. 9. D. 5
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 47. Cho tam giác ABC có độ dài các cạnh là a, b, c theo thứ tự lập thành một cấp số cộng. Biết A C x tan tan   ,
x y   , giá trị x y là: 2 2 y A. 4 B. 1 C. 2 D. 3
Câu 48. Cho các số hạng dương a, b, c là số hạng thứ m, n, p của một cấp số cộng và một cấp số nhân.
Tính giá trị của biểu thức (bc ) (c a) ( ab ) log a .b .c 2 A. 0 B. 2 C. 1 D. 4
Câu 49. Cho a b c
và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng 2 A. 1 B. 2 C. 3 D. 4
Câu 50. Cho a, b, c theo thứ tự tạo thành cấp số cộng. Giá trị x y là bao nhiêu biết P  log  2 2 2
a ab  2b bc c   x log  2 2
a ac cy x, y   . 2 2    A. 0 B. 1 C. 1  D. 2
Câu 51. Cho ba (bố số chứ) số a, b, c, d theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết 148
tổng ba số hạng đầu bằng
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và 9
thứ tám của một cấp số cộng. Tính giá trị biểu thức T a b c d ? 101 100 100 101 A. T  . B. T  . C. T   . D. T   . 27 27 27 27
Câu 52. Cho cấp số cộng u . Mệnh đề nào dưới đây là mệnh đề đúng? n
A. n pu   p mu  m nu  0 .
B. m nu n p u p m u  . m   n   0 m n p p
C. m pu  n mu   p nu  0 .
D. p nu m p u m n u  . m   n   0 m n p p 1 1 1
Câu 53. Cho ba số dương , a ,
b c thỏa mãn điều kiện , , lập thành một cấp b c c a a b
số cộng. Mệnh đề nào dưới đây là đúng? A. Ba số , a ,
b c lập thành một cấp số cộng. 1 1 1 B. Ba số , ,
lập thành một cấp số cộng. a b c C. Ba số 2 2 2
a ,b , c lập thành một cấp số cộng.
D. Ba số a , b , c lập thành một cấp số cộng
Câu 54. Biết rằng tồn tại các giá trị của x 0;2 để ba số 2
1  sin x,sin x,1 sin 3x lập thành một
cấp số cộng, tính tổng S các giá trị đó của x . 7 23
A. S  5.
B. S  3. C. S  . D. S  . 2 6
Câu 55. Tìm tất cả các giá trị của tham số m để phương trình 3 2 2
x  3x x m 1  0 có ba nghiệm
phân biệt lập thành một cấp số cộng. A. m  16 . B. m  2  . C. m  2 . D. m  2  .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 56. Biết rằng tồn tại đúng ba giá trị m , m , m của tham số m để phương trình 1 2 3 3 2 3 2
x  9x  23x m  4m m  9  0 có ba nghiệm phân biệt lập thành một cấp số cộng, tính giá trị của biểu thức 3 3 3
P m m m . 1 2 3 A. P  34 . B. P  36 . C. P  64 . D. P  34 .
Câu 57. Biết rằng tồn tại hai giá trị của tham số m để phương trình sau có bốn nghiệm phân biệt lập
thành một cấp số cộng: 4 2 2
x 10x  2m  7m  0 , tính tổng lập phương của hai giá trị đó. 343 721 721 343 A.  . B. . C.  . D. . 8 8 8 8
Câu 58. Cho một cấp số cộng u
có u  1 và tổng của 100 số hạng đầu tiên 24850 . Tính giá trị của n  1 1 1 1 1 biểu thức S    ...   ? u u u u u u u u 1 2 2 3 48 49 49 50 4 9 49 A. S  123 B. S C. S D. S  23 246 246 abn n
Câu 59. Cho cấp số cộng ; cấp số nhân
thỏa mãn a a  0;b b  1 và hàm số 2 1 2 1 f x 3  x  3x
f a  2  f a
f log b  2  f log b 2 2   2  2   1 sao cho và
. Số nguyên dương n  1 nhỏ
nhất thỏa mãn điều kiện b  2018a là? n n A. 16 B. 15 C. 17 D. 18
Câu 60. Cho cấp số cộng u  có số hạng đầu u  2 và công sai d  3 . Trên mặt phẳng tọa độ Oxy 1
, lấy các điểm A , A ,... sao cho với mỗi số nguyên dương n , điểm A có tọa độ  ; n u . Biết rằng khi n  1 2 n
đó tất cả các điểm A , A ,..., A ,... cùng nằm trên một đường thẳng. Hãy viết phương trình của đường 1 2 n thẳng đó. A. y  3  x  5. B. y  3  x  2 .
C. y  2x 3 .
D. y  2x 5
Câu 61. Trong mặt phẳng tọa độ Oxy , cho đồ thị C  của hàm số y  3x  2 . Với mỗi số nguyên
dương n , gọi A là giao điểm của đồ thị C  với đường thẳng d : x n  0 . Xét dãy số u với u là n n n
tung độ của điểm A . Mệnh đề nào dưới đây là mệnh đề đúng? n
A. Dãy số u
là một cấp số cộng có công sai d  2 . n
B. Dãy số u
là một cấp số cộng có công sai d  3 . n
C. Dãy số u
là một cấp số cộng có công sai d  1 . n
D. Dãy số u
không phải là một cấp số cộng. n
Câu 62. Trên tia Ox lấy các điểm A , A ,..., A ,... sao cho với mỗi số nguyên dương n , OA n . 1 2 n n
Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox , vẽ các nửa đường tròn đường kính
OA , n 1,2,... Kí hiệu u là diện tích nửa đường tròn đường kính OA và với mỗi n  2 , kí hiệu u là n 1 1 n
diện tích của hình giới hạn bởi nửa đường tròn đường kính OA
, nửa đường tròn đường kính OA và n 1  n
tia Ox . Mệnh đề nào dưới đây là đúng?
A. Dãy số u
không phải là một cấp số cộng. n
B. Dãy số u
là một cấp số cộng có công sai d  . n  4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
C. Dãy số u
là một cấp số cộng có công sai d  . n  8
D. Dãy số u
không phải là một cấp số cộng có công sai d  . n  2
Câu 63. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là 100000
đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30000 đồng so với giá của mét khoan
ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu 20
mét lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó
phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu? A. 7700000 đồng. B. 15400000 đồng. C. 8000000 đồng. D. 7400000 đồng.
Câu 64. Trên một bàn cờ có nhiều ô vuông. Người ta đặt 7 hạt dẻ vào ô vuông đầu tiên, sau đó đặt tiếp
vào ô thứ hai số hạt dẻ nhiều hơn ô đầu tiên là 5, tiếp tục đặt vào ô thứ ba số hạt dẻ nhiều hơn ô thứ hai
là 5, … và cứ thế tiếp tục đến ô cuối cùng. Biết rằng đặt hết số ô trên bàn cờ người ta đã phải sử dụng
hết 25450 hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô? A. 98 ô. B. 100 ô. C. 102 ô. D. 104 ô.
Câu 65. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức
sau: Mức lương của quý làm việc đầu tiên cho công ty là 13,5 triệu đồng/quý, và kể từ quý làm việc
thứ hai, múc lương sẽ được tăng thêm 500.000 đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận
được sau ba năm làm việc cho công ty. A. 198 triệu đồng. B. 195 triệu đồng. C. 228 triệu đồng. D. 114 triệu đồng.
Câu 66. Mặt sàn tầng của một ngôi nhà cao hơn mặt sân 0,5m . Cầu thang đi từ tầng một lên tầng hai
gồm 21 bậc, một bậc cao 18cm . Kí hiệu h là độ cao của bậc thứ n so với mặt sân. Viết công thức để n tìm độ cao h . n
A. h  0,18n  0, 32 m .
B. h  0,18n  0, 5 m . n   n  
C. h  0, 5n  0,18 m .
D. h  0, 5n  0, 32 m . n   n  
Câu 67. Trên tia Ox lấy các điểm A , A ,..., A ,... sao cho với mỗi số nguyên dương n, OA  . n Trong 1 2 n n
cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính
OA , n  1, 2... Kí hiệu u là diện tích của nửa hình tròn đường kính OA và với mỗi n  2, kí hiệu u n 1 1 n
là diện tích của hình giới hạn bởi nửa đường tròn đường kính OA , nửa đường tròn đường kính OA n 1  n
và tia Ox. Chứng minh rằng dãy số (u ) là một cấp số cộng. Hãy xác định công sai của cấp số cộng n đó.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 2 A. d B. d C. d D. d  4 2 3 3
CẤP SỐ NHÂN
Câu 68. Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng
25 . Tìm 2 góc còn lại? A. 65 ,  90 B. 75 ,  80 . C. 60 ,  95 . D. 60 ,  90 .
Câu 69. Cho dãy số a xác định bởi a  5, a  .
q a  3 với mọi n  1, trong đó q là hằng số, n  1 n 1  n n 1   q n 1
a  0, q  1. Biết công thức số hạng tổng quát của dãy số viết được dưới dạng 1
a .q . n 1 q
Tính  2? A. 13. B. 9. C. 11. D. 16.
Câu 70. Trong dịp hội trại hè 2017 bạn A thả một quả bóng cao su từ độ cao 3m so với mặt đất, mỗi
lần chạm đất quả bóng lại nảy lên một độ cao bằng hai phần ba độ cao lần rơi trước. Tổng quãng
đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng: A. 13m. B. 14m. C. 15m. D. 16m. u
u u u  15  1 2 3 4
Câu 71. Có hai cấp số nhân thỏa mãn 
với công bội lần lượt là q , q . Hỏi giá 2 2 2 2 1 2 u
u u u  85  1 2 3 4
trị của q q là: 1 2 1 3 5 7 A. B. C. D. 2 2 2 2
Câu 72. Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và góc A bằng 30o. Tìm các góc còn lại? A. 75 ,  120 ,  65 . B. 72 ,  114 ,  156 . C. 70o; 110o; 150o. D. 80o; 110o; 135o.
Câu 73. Cho một cấp số cộng (u ) có u  1 và tổng 100 số hạng đầu bằng 24850 . Tính n 1 1 1 1 S    ...  . u u u u u u 1 2 2 3 49 50 9 4 49 A. S  . B. S  . C. S  123 . D. S  . 246 23 246 Câu 74. Cho , a ,
b c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng? A. 2 2
a c  2ab  2bc  2ac . B. 2 2
a c  2ab  2bc  2ac . C. 2 2
a c  2ab  2bc  2ac . D. 2 2
a c  2ab  2bc  2ac . u   2  1
Câu 75. Cho dãy số u được xác định như sau:  . Tính tổng n u
 4u  4  5n n  1   n 1  n   S u  2u . 2018 2017
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao A. 2017 S  2015  3.4 B. 2018 S  2016  3.4 C. 2018 S  2016  3.4 D. 2017 S  2015  3.4
Câu 76. Cho số hạng thứ m và thứ n của một cấp số nhân biết số hạng thứ (m n) bằng A , sổ hạng thứ (m  )
n bằng B và các số hạng đểu dương. Số hạng thứ m là: m m 2nB nA  2 A. A  B. AB C.   D.  n ABA   B  1 n 1 U U U
Câu 77. Cho dãy số U U U  .U 2 S U    .. 
n  xác định bởi: và . Tổng 3 10 1 3 n 1  3 n n 1 2 3 10 bằng: 3280 29524 25942 1 A. . B. . C. . D. . 6561 59049 59049 243
Câu 78. Phương trình 2 xa a
a    a  2  a  4 1 ... 1 1
1 a  với 0  a  1 có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. 3
Câu 79. Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3
x   x   2 3
1 x  5m  4 x  8  0. A. m  2  . B. m  2. C. m  4. D. m  4  .
Câu 80. Biết rằng tồn tại hai giá trị m và m để phương trình sau có ba nghiệm phân biệt lập thành 1 2 một cấp số nhân: 3 x   2
m m   2 x   2 2 2 2 1
7 m  2m  2 x  54  0. Tính giá trị của biểu thức 3 3
P m m . 1 2 A. P  56 B. P  8. C. P  56 D. P  8.
Câu 81. Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2;3;9
vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính 2 2 2
F x y z .
A. F  389. hoặc F  395.
B. F  395. hoặc F  179.
C. F  389. hoặc F  179.
D. F  441 hoặc F  357.
a  7, a  224 S  3577.
Câu 82. Cho cấp số nhân a có 1 6 và k
Tính giá trị của biểu thức n
T  k   1 a . k A. T  17920. B. T  8064. C. T  39424. D. T  86016.
Câu 83. Cho cấp số nhân a có a  2 và biểu thức 20a 10a a đạt giá trị nhỏ nhất. Tìm số n  1 1 2 3
hạng thứ bảy của cấp số nhân đó.
A. a  156250. B. a  31250.
C. a  2000000. D. a  39062. 7 7 7 7
Câu 84. Trong các mệnh đề dưới đây, mệnh đề nào là sai?
A. Dãy số a , với a  3 và a
a  6, n  1, vừa là cấp số cộng vừa là cấp số n  1 n 1  n nhân.
B. Dãy số b , với b  1 và b  
n  1, vừa là cấp số cộng vừa là cấp số   2 2b 1 3, n 1 nn  1 nhân.
C. Dãy số c , với c  2 và 2 c
 3c  10 n  1, vừa là cấp số cộng vừa là cấp số nhân. n  1 n 1  n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
D. Dãy số d , với d  3 và 2 d
 2d  15, n  1, vừa là cấp số cộng vừa là cấp số n  1 n 1  n nhân.
Câu 85. Xét bảng ô vuông gồm 4 4 ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số 1 hoặc 1
 sao cho tổng các số trong mỗi hang và tổng các số trong mỗi cột đều bằng 0 . Hỏi có bao nhiêu cách? A. 72 B. 90 C. 80 D. 144
Câu 86. Số đo ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân. Biết thể tích của khối hộp là 3
125 cm và diện tích toàn phần là 2
175 cm . Tính tổng số đo ba kích thước của hình hộp chữ nhật đó. A. 30c . m B. 28c . m C. 31c . m D. 17,5c . m
Câu 87. Một của hàng kinh doanh, ban đầu bán mặt hàng A với giá 100 (đơn vị nghìn đồng). Sau đó,
cửa hàng tăng giá mặt hàng A lên 10%. Nhưng sau một thời gian, cửa hàng lại tiếp tục tăng giá mặt
hàng đó lên 10%. Hỏi giá của mặt hàng A của cửa hàng sau hai làn tăng giá là bao nhiêu? A. 120. B. 121. C. 122. D. 200.
Câu 88. Một người đem 100 triệu đồng đi gửi tiết kiệm với kỳ han 6 tháng, mỗi tháng lãi suất là 0, 7%
số tiền mà người đó có. Hỏi sau khi hết kỳ hạn, người đó được lĩnh về bao nhiêu tiền? A.  5 8 10 . 0, 007 (đồng) B.  5 8 10 . 1, 007 (đồng) C.  6 8 10 . 0, 007 (đồng) D.  6 8 10 . 1, 007 (đồng)
Câu 89. Tỷ lệ tăng dân số của tỉnh M là 1, 2%. Biết rằng số dân của tỉnh M hiện nay là 2 triệu người.
Nếu lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
A. 10320 nghìn người.
B. 3000 nghìn người.
C. 2227 nghìn người.
D. 2300 nghìn người.
Câu 90. Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc đầu có 12
10 tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào? A. 12 1024.10 tế bào. B. 12 256.10 tế bào. C. 12 512.10 tế bào. D. 13 512.10 tế bào.
Câu 91. Người ta thiết kế một cái tháp gồm 11 tầng theo cách: Diện tích bề mặt trên của mỗi tầng
bằng nửa diện tích mặt trên của tầng ngay bên dưới và diện tích bề mặt trên của tầng 1 bằng nửa diện
tích đế tháp. Biết diện tích đế tháp là 2
12288m , tính diện tích mặt trên cùng. A. 2 6m . B. 2 12m . C. 2 24m . D. 2 3m .
Câu 92. Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất 1 bằng
số đo của góc nhỏ thứ ba. Hãy tính số đo của các góc trong tứ giác đó. 9 A. 0 0 0 0 5 ,15 , 45 , 225 . B. 0 0 0 0 9 , 27 ,81 , 243 . C. 0 0 0 0 7 , 21 , 63 , 269 . D. 0 0 0 0 8 , 32 , 72 , 248 .
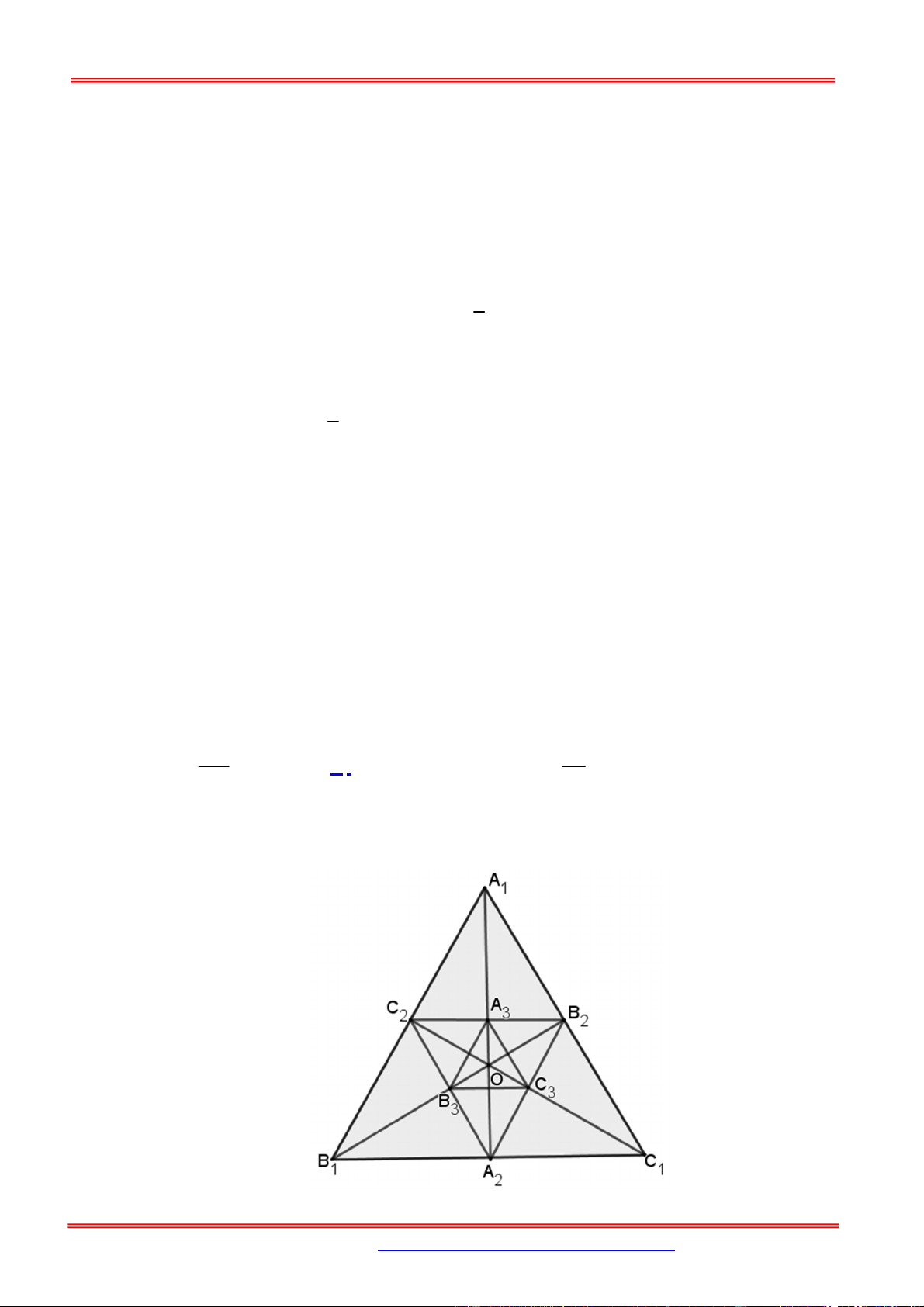
Câu 93. Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC . Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho 1 1 1 2 2 2 3 3 3
A B C là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác A B C là tam 1 1 1 n n n
giác trung bình của tam giác A B C
. Với mỗi số nguyên dương n , kí hiệu S tương ứng là diện n 1  n 1  n 1  n
tích hình tròn ngoại tiếp tam giác A B C . Tính tổng S S S  ...  S  ... ? n n n 1 2 n 15 9 A. S  .
B. S  4. C. S  .
D. S  5. 4 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
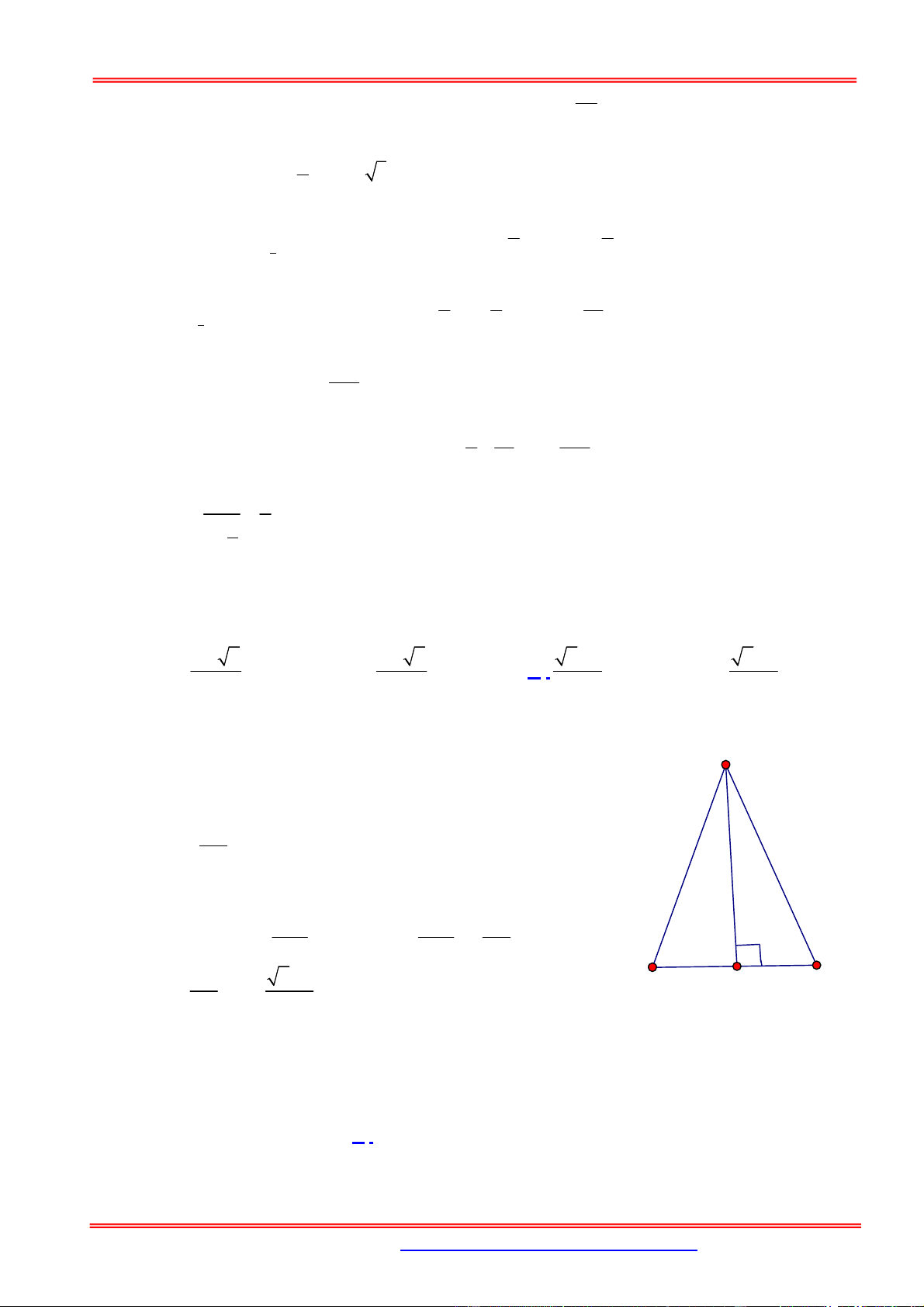
Câu 94. Cho tam giác ABC cân tại đỉnh .
A Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB
theo thứ tự lập thành cấp số nhân công bội q. Gía trị của 2 q bằng 2  2 2  2 2  1 2 1 A. . B. . C. . D. . 2 2 2 2
Câu 95. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức như
sau: mức lương của quý làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ
hai mức lương sẽ được tăng thêm 1,5 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư được
nhận sau 3 năm làm việc cho công ty. A. 495 triệu đồng. B. 279 triệu đồng. C. 384 triệu đồng. D. 558 triệu đồng.
Câu 96. Một hình vuông ABCD có cạnh AB a, diện tích S . Nối 4 trung điểm A , B ,C , D theo 1 1 1 1 1
thứ tự của 4 cạnh AB, BC,C ,
D DA ta được hình vuông thứ hai là A B C D có diện tích S . Tiếp tục 1 1 1 1 2
như thế, ta được hình vuông thứ ba là A B C D có diện tích S và cứ tiếp tục như thế, ta được diện 2 2 2 2 3
tích S , S ,... Tính S S S  ...  S . 4 5 1 2 100 100 100 2 100 2 99 2 1 a 2   1 a 2   1 a 2   1 A. S  . B. S  . C. S  . D. S  99 2 2 a 99 2 99 2 99 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
C – HƯỚNG DẪN GIẢI DÃY SỐ
Câu 1. Cho dãy số có các số hạng đầu là: 0,1;0, 01;0,001;0, 0001;... . Số hạng tổng quát của dãy số này có dạng? 1 1 A. un   0 , 0 . 0  . 0 . 1 . B. u n   , 0 0 . 0  . 0 . 1 . C. u  . D. u  . n n 1 n 10  n 1 10  n c höõso á 0 n 1  c höõso á 0 Hướng dẫn giải Chọn A. Ta có:
Số hạng thứ 1 có 1 chữ số 0
Số hạng thứ 2 có 2 chữ số 0
Số hạng thứ 3 có 3 chữ số 0
…………………………….
Suy ra u có n chữ số 0 . nu  5
Câu 2. Cho dãy số u với 1
.Số hạng tổng quát u của dãy số là số hạng nào dưới đây? n   nuu n n1 n (n  ) 1 n (n  ) 1 n A. u  . B. u  5  . n 2 n 2 (n  ) 1 n (n  ) 1 (n  ) 2 C. u  5  . D. u  5  . n 2 n 2 Hướng dẫn giải Chọn B. n n   1
Ta có u  5 1 2  3  ...  n 1  5  . n 2 u   1
Câu 3. Cho dãy số u với 1
. Số hạng tổng quát u của dãy số là số hạng nào dưới n   2 n uu nn 1  n đây? n n   1 2n   1 n n   1 2n  2 A. u  1 . B. u  1 . n 6 n 6 n n   1 2n   1 n n   1 2n  2 C. u  1 . D. u  1 . n 6 n 6 Hướng dẫn giải Chọn C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao u   1 1  2 u u 1  2 1  Ta có: 2 u   u  2 . Cộng hai vế ta được 3 2 .  ..  u   u  n    2 1 n n 1 2 n n 1 2n 1 2 2   
u  1 1  2  ...  n    . n   1 1 6 u   2 1
Câu 4. Cho dãy số u với 
u của dãy số là số hạng nào dưới n u
u  2n 1  . Số hạng tổng quát n 1  n n đây? A. u   n  2 2 1 . B. 2 u  2  n . C. u   n  . D. u   n  . n  2 2 1 n  2 2 1 n n Hướng dẫn giải Chọn A. u   2 1 u u 1 2 1   Ta có: u   u  3
. Cộng hai vế ta được u       n    n  . n    2 2 1 3 5 ... 2 3 2 1 3 2 .  ..  u   u  2n  3  n n 1  u   2  1 
Câu 5. Cho dãy số u với 
1 . Công thức số hạng tổng quát của dãy số này là: n u  2   n 1   un n 1 n 1 n 1 n A. u   . B. u  . C. u   . D. u   . n n n n n n n n 1 Hướng dẫn giải Chọn C. 3 4 5 n 1
Ta có: u   ;u   ;u   ;... Dễ dàng dự đoán được u   . 1 2 3 2 3 4 n n  1 u  
Câu 6. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này là: n   2 u   u  2  n 1  n 1 1 1 1 A. u   2 n  . B. u   2 n  . C. u   2n . D. u   2n . n   1 n   1 2 2 n 2 n 2 Hướng dẫn giải Chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao  1 u  1  2 u u 2  2 1  1 1 Ta có: u
u  2 . Cộng hai vế ta được u   2  2...  2   2 n  . n   1 3 2 2 2 .  ..  u   u  2 n n 1    u   1 1 
Câu 7. Cho dãy số u với
. Số hạng tổng quát u của dãy số là số hạng nào dưới n   n uu     nn  2n 1 1 đây? n
A. u  1 n .
B. u  1 n . C. u    .
D. u n . n  2 1 1 n n n Hướng dẫn giải Chọn D n Ta có uu  
u   u u u nn  2 1 1 2; 3; 4;... 1 n 2 3 4
Dễ dàng dự đoán được u n . n
Thật vậy, ta chứng minh được u n * bằng phương pháp quy nạp như sau: n
+ Với n  1  u  1 . Vậy * đúng với n  1 1
+ Giả sử * đúng với mọi   * n
k k    , ta có: u k . Ta đi chứng minh * cũng đúng k
với n k 1 , tức là: uk 1 k 1  k
+ Thật vậy, từ hệ thức xác định dãy số u ta có: uu  1
k 1 . Vậy * đúng k 1  k  2 n  với mọi * n   . u   1 1 
Câu 8. Cho dãy số u với
. Số hạng tổng quát u của dãy số là số hạng nào n    n uu     nn  2n 1 1 1 dưới đây?
A. u  2  n .
B. u không xác định. n n
C. u  1 n .
D. u  n với mọi n . n n Hướng dẫn giải Chọn A
Ta có: u  0;u  1
 ;u  2 ,. Dễ dàng dự đoán được u  2  n . 2 3 4 n u   1
Câu 9. Cho dãy số u với 1
. Số hạng tổng quát u của dãy số là số hạng nào dưới n   2 n uu nn 1  n đây?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao n n   1 2n   1 n n   1 2n  2 A. u  1 . B. u  1 . n 6 n 6 n n   1 2n   1 n n   1 2n  2 C. u  1 . D. u  1 . n 6 n 6 Hướng dẫn giải Chọn C u   1 1  2 u u 1  2 1  Ta có: 2 u   u  2 . 3 2 .  ..  u   u  n    2 1 n n 1 2 n n 1 2n 1 2 2   
Cộng hai vế ta được u  1 1  2  ...  n    . n   1 1 6 u   2
Câu 10. Cho dãy số u với 1
. Số hạng tổng quát u của dãy số là số hạng nào dưới n
u u  2n 1 nn 1  n đây? A. u   n  2 2 1 . B. 2 u  2  n . C. u   n  . D. u   n  . n  2 2 1 n  2 2 1 n n Hướng dẫn giải Chọn A u   2 1 u u 1 2 1   Ta có: u   u  3 . 3 2 .  ..  u   u  2n  3  n n 1 
Cộng hai vế ta được u     
  n     n  2 2 1 3 5 ... 2 3 2 1 . n u   2  1 
Câu 11. Cho dãy số u với 
1 . Công thức số hạng tổng quát của dãy số này là: n u  2   n 1   un n 1 n 1 n 1 n A. u   . B. u  . C. u   . D. u   . n n n n n n n n 1 Hướng dẫn giải Chọn C 3 4 5 n 1
Ta có: u   ;u   ;u   ;... Dễ dàng dự đoán được u   . 1 2 3 2 3 4 n n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao  1 u  
Câu 12. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này là: n   2 u   u  2  n 1  n 1 1 1 1 A. u   2 n  . B. u   2 n  . C. u   2n . D. u   2n . n   1 n   1 2 2 n 2 n 2 Hướng dẫn giải Chọn B  1 u  1  2 u u 2  2 1  Ta có: u   u  2 . 3 2 .  ..  u   u  2 n n 1    1 1
Cộng hai vế ta được u   2  2...  2   2 n  . n   1 2 2 u   1 1 
Câu 13. Cho dãy số u với
. Công thức số hạng tổng quát của dãy số này là: n   un u   n 1   2 n n 1  n 1  n 1   1   1   1   1  A. u   . B. u   . C. u  . D. u   n   1 . n   1 . n   1 .    n      2   2   2   2  . Hướng dẫn giải Chọn D u   1 1  u1 u   2  2   u Ta có: 2 u   . 3 2  .  ..  un 1 u    n   2 n 1 
u .u .u ...u 1  1 
Nhân hai vế ta được u .u .u ...u     u     n   1 2 3 n 1 1 . 1 . 1 . 1 2 3 n
  n 1     2.2.2...2 2     2  n 1  lan u   2
Câu 14. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này: n  u  2un 1  n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao A. n 1 u n   .
B. u  2n . C. 1 u 2n  . D. u  2 . n n n n Hướng dẫn giải Chọn B u   2 1 u  2u 2 1   Ta có: u   2u . 3 2 .  ..  u   2un n 1  Nhân hai vế ta được n 1
u .u .u ...u  2.2  .u .u ...uu  2n . 1 2 3 n 1 2 n 1  n  1 u  
Câu 15. Cho dãy số u với 1
. Công thức số hạng tổng quát của dãy số này: n   2 u   2un 1  n 1  1  A. 1 u 2n   . B. u  . C. u  . D.  2 u  2n . n n n 1 2  n 2n n Hướng dẫn giải Chọn D  1 u  1  2 u  2u  2 1  Ta có: u   2u . 3 2 .  ..  u   2u n n 1    1 Nhân hai vế ta được n 1  n2
u .u .u ...u
.2 .u .u ...uu  2 . 1 2 3 n 1 2 n 1 2  n u   1 1 
Câu 16. Cho dãy số u với
. Số hạng tổng quát u của dãy số là số hạng nào n   n uu     nn  2n 1 1 dưới đây? n
A. u  1 n .
B. u  1 n . C. u    .
D. u n . n  2 1 1 n n n Hướng dẫn giải Chọn D. n Ta có: uu  
u   u u u
Dễ dàng dự đoán được u n nn  2 1 1 2; 3; 4;... 1 n 2 3 4 n
Thật vậy, ta chứng minh được u n * bằng phương pháp quy nạp như sau: n
+ Với n  1  u  1 . Vậy * đúng với n  1 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
+ Giả sử * đúng với mọi   * n
k k    , ta có: u k . Ta đi chứng minh * cũng đúng k
với n k 1 , tức là: uk 1 k 1  k
+ Thật vậy, từ hệ thức xác định dãy số u ta có: uu  1
k 1 . Vậy * đúng k 1  k  2 n  với mọi * n   .
Câu 17. Đặt T
2  2  2  ...  2 (có n dấu căn). Mệnh đề nào dưới đây là mệnh đề đúng? n A. T  3 . B. T  2 cos . C. T  cos . D. T  5 . n n n 1 2  n n 1 2  n Hướng dẫn giải Chọn B.
Ta chứng minh T  2 cos
bằng phương pháp quy nạp toán học. Thật vậy: n n 1 2 
Bước 1: Với n  1 thì vế trái bằng 2 , còn vế phải bằng 2 cos  2 cos  2 . 1 1 2  4
Vậy đẳng thức đúng với n  1 .
Bước 2: Giả sử đẳng thức đúng với n k  1 , nghĩa là T  2 cos . k k 1 2 
Ta phải chứng minh đẳng thức cũng đúng với n k  1 , tức là chứng minh T  2 cos . k 1  k 2 2 Thật vậy, vì T
2  T nên theo giả thiết quy nạp ta có T  2  T  2  2 cos . k 1  k k 1  k k 1 2  Mặt khác, 2 1  cos  1  cos 2.  2 cos nên 2 T  2.2 cos  2 cos . k 1   k 2  k 2 2 k 1  k 2 k  2  2  2 2 2 u   1 1 
Câu 18. Cho dãy số  và 2 2 2
S u u  ...  u
 2018 . Khi đó S có bao nhiêu chữ 2 1 2 2018 u  3u  2  n 1  n  số? A. 963 B. 962 C. 607 D. 608 Hướng dẫn giải Ta có 2 2 2 u
 3.u  2  u  .
a 3n b . n 1  n n  2 5   9a ba  Vì u
5  ta có hệ phương trình    3 . Vậy 2 1  3a b  b  1  2 2 n n 1 u  .3 1  2.3 1 n 3 Khi đó S   1 2 2017      2018 2 1 3 3 ... 3  3
1. Số chữ số của S  2018log  3 1  963. Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao u   2 1
Câu 19. Cho dãy số u
được xác định bởi công thức
. Tìm giới hạn của dãy n   2 2018uu  2017un 1  n n u u u số 1 2 S    ... n  ? n u 1 u 1 u 1 2 3 n 1  1 2017 A. lim S
B. lim S  2018 C. lim S
D. lim S  1 n 2018 n n 2018 n Hướng dẫn giải u uu u uu Ta có: 2018uuu u         n n nn n 1 n n n 1 1 n n 1 2018 u 1 2018 uu un  1 1 1 n 1    n  n 1  u uu u  1 1  n n 1  n n     2018    . 2018u 1 u 1 u 1 u 1 u 1 u 1 n 1    n  n 1  n 1   n n 1   Như vậy:  1 1   1 1  S  2018   lim S  2018   lim S  2018 . n     u 1 u 1 n 2 1 lim u 1 n  1 n 1    n  3 5
Câu 20. Cho dãy số a xác định bởi 2 * a  1; a   a a 1, n
   . Số hạng thứ 201 của dãy n  1 n 1  2 n 2 n
số a có giá trị bằng bao nhiêu? n A. a  2 . B. a  1 . C. a  0 . D. a  5 . 2018 2018 2018 2018 Hướng dẫn giải Chọn A.
Nhận thấy dãy số trên là dãy số cho bởi công thức truy hồi.
Ta có a  1; a  2; a  0; a  1; a  2; a  0; 1  . 1 2 3 4 2 6
Từ đây chúng ta có thể dự đoán * a
a , n   . Chúng ta khẳng định dự đoán đó bằng n 3 n
phương pháp quy nạp toán học. Thật vậy:
Với n  1 thì a  1 và a  1. Vậy đẳng thức đúng với n  1 . 1 4
Giả sử đẳng thức đúng với n k  1 , nghĩa là aa . k 3 k
Ta phải chứng minh đẳng thức đúng với n k 1 , nghĩa là chứng minh aa . k 4 k 1  3 5 Thật vậy, ta có 2 a   aa
1 (theo hệ thức truy hồi). k 4 k 3 k 3 2 2 3 5
Theo giả thiết quy nạp thì aa nên 2 a   a a 1  a . k 3 k k 4 k k k 1 2 2 
Vậy đẳng thức đúng với n k 1 . Suy ra * a
a , n   . n 3 n
Từ kết quả phần trên, ta có: nếu m p mod3 thì a a . m p
Ta có 2018  2mod 3 nên a  2 . 2018
u  cos0  1   
Câu 21. Cho dãy số u xác định bởi
. Số hạng thứ 2017 của dãy số đã cho là: n   1 uun ,n  1 n 1   2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 23
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao     A. u  cos B. u  cos C. u  sin D. 2017  2016  2017  2017  2017  2016   2   2   2   u  sin 2017  2017   2  Hướng dẫn giải Đáp án A 1 cos 1 cos Ta có 2 2 u   cos  u   cos  u  cos 2 3 2 4 3 2 2 1 2 2   Suy ra u  cos 2017  2016   2 
Câu 22. Cho dãy số a xác định bởi a  5, a  0 và aa
 6a ,n  1. Số hạng thứ 14 của n  1 2 n2 n 1  n dãy là số hạng nào? A. 3164070 . B. 9516786 . C. 1050594 . D. 9615090 . Hướng dẫn giải Chọn A. + Ta có aa
 6a ,n  1  a  2a  3 a
 2a ,n  1 . n2 n 1  n n2 n 1   n 1 n
Do đó ta có b a  2a  10 và b
 3b ,n  1. 1 2 1 n 1  n
Từ hệ thức truy hồi của dãy số b , ta có 2 3
b  3b ; b  3b  3 b ; b  3b  3 b . n  2 1 3 2 1 4 3 1
Bằng phương pháp quy nạp toán học, chúng ta chứng minh được rằng: n 1  n 1 b 3 b 10.3    , n  1 . n 1 + Ta có aa
 6a , n  1  a  3a  2 a
 3a ,n  1. n2 n 1  n n2 n 1   n 1 n
Do đó ta có: c a  3a  1  5 và c  2
c ,n  1. 1 2 1 n 1  n 2 3
Từ hệ thức truy hồi của dãy số c , ta có c  2c ;c  2 c ; c  2 c . 2 1 3   1 4   n  1
Bằng phương pháp quy nạp toán học, chúng ta chứng minh được rằng: c c n . nnn  2 1
 15.2 1 ,   1 1
+ Từ các kết quả trên, ta có hệ phương trình: n 1 a  2a  10.3   n 1  n nn
a  2.3   3. 2 . n 1  n   1 1 a  3a  15. 2    n 1  n   n
Do đó số hạng tổng quát của dãy số a là na   n . n   1 1 2.3 3. 2 ,   1 n
Vậy suy ra a  3164070 . 14
Câu 23. Cho dãy số a xác định bởi a  3  và 2 a
a n  3n  4, n   * . Số 1391 là số hạng n  1 n 1  n
thứ mấy của dãy số đã cho? A. 18 . B. 17 . C. 20 . D. 19 Hướng dẫn giải Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Từ hệ thức truy hồi của dãy số a ta có: n  3 2
n  6n 17n  21 a a 1  2 ... n n n a . n  2 2 2 1         3 1   2  ...  1   4 1   1         n 3 3 2
n  6n 17n  21
Suy ra số hạng tổng quát của dãy số a là a  . n n 3
Giải phương trình a  1391 ta được n  18 n 2 1 1 1 an bn Câu 24. Biết rằng   ...   , trong đó , a , b ,
c d và n là các số 1.2.3 2.3.4 n n   1 n  2 2 cn dn 16
nguyên dương. Tính giá trị của biểu thức T  a cb d  . là : A. T  75 . B. T  364 . C. T  300 .
D. T  256 . Hướng dẫn giải Chọn C . 1 1  1 1 
Phân tích phần tử đại diện, ta có:   . k k  1  k 2 2  k k  1 k  1 k 2        1 1 1 Suy ra:   ...  1.2.3 2.3.4 n n   1  n  2 1  1 1 1 1 1 1      .  ...   2 1.2 2.3 2.3 3.4 n n  1 n  1 n 2      1  1 1  2 2 n  3n 2n  6n   =  . 2  2 n  1  n 2     2 2 4n 12n  8
8n  24n  16
Đối chiếu với hệ số, ta được: a  2;b  6;c  8; d  24 .
Suy ra: T   a c b d   300 . n n
Câu 25. Cho dãy số a xác định bởi a  2017sin  2018 cos
. Mệnh đề nào dưới đây là mệnh n n 2 3 đề đúng? A. * a
a , n   . B. * a
a , n   . n  6 n n 9 n C. * a
a , n   . D. * a
a , n   . n 1  2 n n 1  5 n Hướng dẫn giải Chọn C
Kiểm tra từng phương án đến khi tìm được đáp án đúng. n  6n  6 n n + Ta có a  2017 sin  2018 cos  2017 sin  2018 cos  a n 6 2 3 2 3 nn  9n  9 n n + Ta có a  2017 sin  2018 cos  2017 sin  2018 cos  a . n 6 2 3 2 3 nn 12n 12 n n + Ta có a  2017 sin  2018 cos  2017 sin  2018 cos  a . n 1  2 2 3 2 3 nn 15n 15 n n + Ta có a  2017 sin  2018 cos  2017 sin  2018 cos  a . n 1  5 2 3 2 3 na nan n Câu 26. Cho dãy số có a  , n
   * . Tìm số hạng lớn nhất của dãy số . n 2 n 100
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 1 1 1 1 A. . B. . C. . D. . 20 30 25 21 Hướng dẫn giải Chọn A. n n 1 Ta có a    . Dấu bằng xảy ra khi 2
n  100  n  10. n 2 2 n 100 20 2 n .100 1
Vậy số hạng lớn nhất của dãy là số hạng bằng . 20 (u ) * u
n  2018  n  2017, n    . Câu 27. Cho dãy số n thỏa mãn n
Khẳng định nào sau đây sai?
A. Dãy số (u ) là dãy tăng.
B. lim u  0. n n n 1 u C. * 0  u  ,n   . D. n 1 lim   1. n 2 2018 n un Hướng dẫn giải Chọn A x an  4  xn n Câu 28. Cho dãy số với x  . Dãy số là dãy số tăng khi: n n  2
A. a  2 .
B. a  2 .
C. a  2 .
D. a  1. Hướng dẫn giải Chọn B. a(n 1)  4 a(n 1)  4 an  4 2a  4 Ta có x  . Xét hiệu xx    . n 1  n  3 n 1  n n  3 n  2
(n  2)(n  3)
(x ) là dãy tăng khi và chỉ khi xx  0, n
  1  2a  4  0  a  2. n n 1  n
Câu 29. Trong các dãy số sau dãy số nào là dãy bị chặn ?
A. Dãy a , với 2 a
n 16, n   * . n n 1
B. Dãy b , với b n  ,n   * . n n 2n
C. Dãy c , với c  2n  3, n   *. n n n
D. Dãy d , với d  ,n   * . n n 2 n  4 Hướng dẫn giải Chọn D. (a ) 2 a
n 16  17, n   1. Dãy số n
là dãy số tăng và chỉ bị chặn dưới vì n 1 1
Dãy số (b ) là dãy số tăng và chỉ bị chặn dưới vì b n   2 . n  2, n   1. n n 2n 2n (c )
c  2n  3  5, n  1.
Dãy số n là dãy số tăng và chỉ bị chặn dưới vì n 1  n n 1 
Dãy số (d ) là dãy số bị chặn vì 0  d  , n   1. do0    . n n   4 2  n  4 4n 4 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao an  2
Câu 30. Cho dãy số u với u
, a là tham số. Tìm tất cả các giá trị của a để dãy số u là n n n n 1 một dãy số tăng A. a  1 B. a  1 C. a  2 D. a  2 Hướng dẫn giải Chọn C n n
Câu 31. Cho dãy số (z ) xác định bởi z  sin  2 cos
. Gọi M, m lần lượt là giá trị lớn nhất và n n 2 3
giá trị nhỏ nhất trong các số hạng của dãy số (z ) . Tính giá trị biểu thức 2 2
T M m . n A. T  13. B. T  5. C. T  18. D. T  7. Hướng dẫn giải Chọn A.
Dựa vào chu kì của hàm số y  sin ;
x y  cos x, ta có zz , n   1. n 1  2 n
Do đó tập hợp các phần tử của dãy số là S  z ; z ;...; z  3  ; 2  ; 1  ;0; 2 . 1 2 12  
Suy ra M  2; m  3
 . Do đó T  13. 1 u 2017
Câu 32. Cho dãy số (u ) thỏa mãn u  ; n u
, n  1.S u u  ...  u  khi n n 1 n 1  n 1 2 2
2(n  1)u  1 n 2018 n
có giá trị nguyên dương lớn nhất. A. 2017. B. 2015. C. 2016. D. 2014. Hướng dẫn giải Chọn C .
Dễ chỉ ra được u  0, n
  1. Từ hệ thức truy hồi của dãy số, ta có n 1 1 
 2n  2, n  1. u u n 1  n Suy ra 1 1 1 1 2 
 2(1 2  ..  n 1)  2(n 1) 
 2  n(n 1)  2(n 1)  n n u  . n u u u n(n  1) n 1 n 1 1 Do đó u   , n   1. n n n 1 1 n 2017 n 2017
Vậy S u u  ...  u  1  . Vì S  nên   n  2017. n 1 2 n n 1 n 1 n 2018 n 1 2018 2017
Suy ra số nguyên dương lớn nhất để S  là n  2016 . n 2018 cos 2017 x
Câu 33. Cho hàm số f x   2
x  3x  2 
 và dãy số u được xác định bởi công thức tổng n
quát u  log f  
1  log f 2  ... log f n . Tìm tổng tất cả các giá trị của n thỏa mãn điều kiện n   2018 u  1? n A. 21 B. 18 C. 3 D. 2018 Hướng dẫn giải n n Ta có: u  log f k  k k   k
  ( k chẵn) ( k lẻ). n    cos  2017  log   1 log  2   k 1  k 1 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Trường hợp 1: n  2 p (Chẵn), khi đó ta có khai triển sau:
u  log3 log 4  ... log2 p  
1  log 2 p  2  log 2  log3 ... log 2 p  log 2 p   1 n  .
Như vậy u  log  p   1 cho nên 2018 u
 1  p  9  n  18 . n n
Trường hợp 1: n  2 p 1 (Lẻ), khi đó ta có khai triển sau:
u  log3  log 4 ... log2 p  
1  log 2 p  2  log 2  log3 ... log 2 p  2  log 2 p  3 n  .
Như vậy u   log 4 p  6 cho nên 2018 u
 1  p  1  n  3 . nn
Kết luận: Tổng các giá trị của n thỏa mãn điều kiện 2018 u  1 là 21. n Chọn A. f  
1 f 3... f 2n   1
Câu 34. Cho f n  n n  2 2 * 1 1 n
  và đặt u  . Tìm số nguyên n
f 2 f 4... f 2n 10239
dương n nhỏ nhất sao cho log u u   ? 2 n n 1024 A. n  23 B. n  29 C. n  33 D. n  21 Hướng dẫn giải 2 2
Ta có: f n   2
n n      2
n  n     * 1 1 1 1 1 n .
Đến đây ta dễ dàng có: 1   1 2   1 3   1 4   1 ...2n  2 1   1 2n2 2 2 2 2   1 1 u   . n
          n2   n  2 2 2 2 2   2 2n  2n 1 2 1 3 1 4 1 5 1 ... 2 1 2 1 1 10239 1 1 1
Ta có: log u u    log   u   n  23 . 2 n n 2 1024 1024 1024 n 1024 Chọn A. a a 3
Câu 35. Cho dãy số a thỏa mãn điều kiện n 1
a  1; 5   n 1  với mọi n   . Tìm số n  1 3n  2
nguyên dương n  1 nhỏ nhất để a ? n A. n  39 B. n  41 C. n  49 D. n  123 Hướng dẫn giải a a 3 aa 3 a a 3 Ta có: n n 1  n 1  n2 2 1 5  1 ; 5  1 ; ...5  1 . 3n 1 3n  4 5
Nhân vế với vế ta được:       n n    n a a 3 3 3 8.11.14...3  1 3 2 3 2 n 1 5  1 1 .... 1         .  3n 1   3n  4   5 
5.8.11....3n  43n   1 5
Khi đó ta có công thức tổng quát a  log 3n  2 . n 5   Chọn B.
Chú ý: Tới đoạn này sử dụng lệnh CALC là nhanh nhất. Nhưng nếu bài toán không cho
trước đáp số có thể sử dụng Bảng TABLE để truy tìm giá trị nguyên dương n  1 nhỏ nhất
để a . n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 36. Cho dãy số u xác định bởi n 1 u  5;  n u
u  2n  2.3n với mọi n  1. Tìm số nguyên nhỏ n  1 n 1  n nhất thỏa mãn n n 100 u  2  5 . n A. 146 B. 233 C. 232 D. 147 Hướng dẫn giải n n 1  n 1  n 1 u   u  2  2.3  n n 1   n 1  n2 n2 n2 u   u  2  2.3 Ta có: n 1  n2 n   u  2             . n  2 n 1 1 2 2 ... 2  2 2 n 1 1 3 3 ... 3  ...   2 1
u u  2  2.3  2 1 Do vậy: n
u  2n  3n nên n n 100 n 100 u  2  5  3  5
n  100log 5  n  147 . n n 3 Chọn D. 2019 u uu  ...  u 2 2018 n 4n ab Câu 37. Biết rằng 4 n 4 L  lim n  trong đó u xác định bởi n u uu  ...  u c 2 2018 n 2n 2 n 2 n u  0;u
u  4n  3 và , a ,
b c là các số nguyên dương và b  2019 . Tính S a b c ? 1 n 1  n A. 1  B. 0 C. 2017 D. 2018 Hướng dẫn giải 2 u u
 4n  1  u  2n n  3 . n n 1  n Xét S   2 2018
n, 4n, 4 n,...4 n và S   2 2018
n, 2n, 2 n,...2 n . 2  1  k  3 Ta có: 2
u  2k k  3  2.k  2.k   2.k . k 2
2k k  3  2.k 2019 k  3  4 1   2 . n    2019 2 k S  3
2k k  3  2.k   2 1 Vậy 1 L  lim  . k  3  n   2019   3 2 . 2 1 2 k S
2k k  3  2.k 2 Chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
CẤP SỐ CỘNG 2 2 n  1
Câu 38. Cho dãy số u (u u n  n) có n
. Khẳng định nào sau đây sai? 3 1 2 2 2(n  1) 1
A. Là cấp số cộng có u ; 1  d  .
B. Số hạng thứ n+1: u  . 3 3 n 1  3 ( 2 2n  ) 1
C. Hiệu un 1  u   n .
D. Không phải là một cấp số cộng. 3 Hướng dẫn giải Chọn A 2 2 2(n1) 1 2n 1 2(2 n1) Ta có uu   
. Vậy dãy số trên không phải cấp số cộng. n 1  n 3 3 3
Câu 39. Cho hai cấp số cộng  x  : 4, 7,10,... và  y
. Hỏi trong 2018 số hạng đầu tiên của n  :1, 6,11, ... n
mỗi cấp số có bao nhiêu số hạng chung? A. 404. B. 673. C. 403. D. 672. Hướng dẫn giải Chọn C
Cấp số cộng  x  : 4, 7,10,... có x  4 , công sai d  3. n 1
Số hạng tổng quát x  4  (n 1).3  3n 1 n
Cấp số cộng  y  :1, 6,11,16, 21... có y  1 ,công sai d  5 . n 1
Số hạng tổng quát y  1 (n 1).5  5n  4 n' 3n
Xét phương trình x y  3n 1  5n  4  n  1, 0  ,
n n  2018 . Do n là số n n' 5
nguyên dương nên n chia hết cho 5 và 0  n  2018 . Suy ra số các giá trị n cần tìm là  2018   403  . 5   
Vậy có 403 số hạng chung.
Câu 40. Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có
thể coi là số hạng thứ 2,thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp
số cộng này để tổng của chúng bằng 820? A. 20. B. 42. C. 21. D. 17. Hướng dẫn giải Chọn A
Câu 41. Cho cấp số cộng u
biết u  18 và 4S S . Tìm số hạng đầu tiên u và công sai d của n  5 n 2n 1 cấp số cộng.
A. u  2, d  4 .
B. u  2, d  3 .
C. u  2, d  2 .
D. u  3, d  2 . 1 1 1 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao Hướng dẫn giải Chọn A
Giả sử u u n 1 d u u  4d  18 1 . n 1   5 1  
n 2u n 1 d
2n 2u  2n 1 d   1     1    Ta có: S  ; Sn 2 2 n 2 S
 4S  2n 2u  2n 1 d  2n n 1     Do
 4n 2u n 1 d   2u  2n 1 d  4u  2n  2 d  1    1   1  
 2u d 2 . Từ (1) và (2) suy ra u  2, d  4. 1   1
Câu 42. Một cấp số cộng có tổng n số hạng đầu S được tính theo công thức 2
S n n n   n  * 5 3 , . n
Tìm số hạng đầu u và công sai d của cấp số cộng đó 1
A. u  8, d  10
B. u  8, d  10
C. u  8, d  10
D. u  8, d  1  0 1 1 1 1 Hướng dẫn giải Chọn C Tổng n số hạng đầu 2
S u u  ...  u  5n  3 ; n n   n n  * 1 2 
Tổng số hạng đầu tiên là 2
S u  5.1  3.1  8 1 1
Tổng 2 số hạng đầu là 2
S u u  5.2  3.2  26  8  u u  18  8  10  u d d  10 2 1 2 2 2 1 S S  77 S  192.
Câu 43. Cho cấp số cộng u
và gọi n là tổng n số đầu tiên của nó. Biết 7 và 12 Tìm n u
số hạng tổng quát n của cấp số cộng đó.
A. u  5  4n .
B. u  3  2n .
C. u  2  3n .
D. u  4  5n n n n n Hướng dẫn giải Chọn B  7.6.d 7u   77 1 S  77  
7u  21d  77 u   5 2 Ta có 7 1 1        S  192 12.11.d
12u  66d  192 d  2  12   1 12u   192  1   2
Khi đó u u n 1 d  5  2 n 1  3  2n n 1    
Câu 44. Cho ba số dương a , b , c theo thứ tự lập thành cấp số cộng. Giá trị lớn nhất của biểu thức 2 a  8bc  3 P
có dạng x y x, y  . Hỏi x y bằng bao nhiêu:
2a c2 1 A. 9 B. 11 C. 13 D. 7 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao Chọn B Ta có:
a c b a b c a   b c2  a bc b bc c a bc   b c2 2 2 2 2 2 2 2 2 8 4 4 8 2 2b c  3 t  3 1 Do đó P  
 10 với t  2b c , dấu bằng xảy ra khi 2b c  . 2b c2 2 1 t 1 3
Vậy x y  11.
Câu 45. Chu vi của một đa giác là158cm , số đo các cạnh của nó lập thành một cấp số cộng với công
sai d  3cm . Biết cạnh lớn nhất là 44cm. Số cạnh của đa giác đó là: A. 3. B. 4. C. 5. D. 6 Hướng dẫn giải Chọn B
Câu 46. Chu vi của một đa giác n cạnh là 158, số đo các cạnh đa giác lập thành một cấp số cộng với
công sai d  3. Biết cạnh lớn nhất có độ dài là 44. Tính số cạnh của đa giác. A. 6. B. 4. C. 9. D. 5 Hướng dẫn giải Chọn B
Câu 47. Cho tam giác ABC có độ dài các cạnh là a, b, c theo thứ tự lập thành một cấp số cộng. Biết A C x tan tan   ,
x y   , giá trị x y là: 2 2 y A. 4 B. 1 C. 2 D. 3 Hướng dẫn giải Đáp án D Ta có:
a c  2b  sin A  sin C  2sin B A C A C B B A C A C  2 sin os c  4sin . os c  4 sin . os c 2 2 2 2 2 2 A C A C A C A C A C A C  os c  2 os c  os c os c  sin sin  2 os c os c  2 sin sin 2 2 2 2 2 2 2 2 2 2 A C A C A C A C 1  3sin sin  os c os c  3 tan tan  1  tan tan  2 2 2 2 2 2 2 2 3
Câu 48. Cho các số hạng dương a, b, c là số hạng thứ m, n, p của một cấp số cộng và một cấp số nhân.
Tính giá trị của biểu thức (bc ) (c a) ( ab ) log a .b .c 2 A. 0 B. 2 C. 1 D. 4 Hướng dẫn giải Đáp án C
Ta có a, b, c là số hạng thứu m, n, p của một cấp số cộng và một cấp số nhân nên:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 32
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
a u  m   m 1 1 d a q
a b m n d 1 1     
b u  n   n 1 1 d a q
b c n    p d 1 1     c u    p   p 1 1 d a q
c a p m d 1 1     np d mn d Do đó bc ca ab log . . log  m    p P a b c a q a q      1 1 0 0  log a q  0 2 2 1 1 2 1
Câu 49. Cho a b c
và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng 2 A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải Đáp án C Ta có  cot a.cot b 1 1
a b c   a b
 cot a b  cot
c  tan c     2 2  2  cot a  cot b cot c  cot a.cot b 1 1
a b c   a b
 cot a b  cot
c  tan c     2 2  2  cot a  cot b cot c  cot a.cot .
b cot c  cot a  cot b  cot c
Mà cot a  cot c  2 cot b
Do đó ta được cot a.cot .
b cot c  3cot b  cot a.cot c  3
a c  2b  sin A  sin C  2sin B A C A C B B A C A C  2 sin os c  4sin . os c  4 sin . os c 2 2 2 2 2 2 A C A C A C A C A C A C  os c  2 os c  os c os c  sin sin  2 os c os c  2 sin sin 2 2 2 2 2 2 2 2 2 2 A C A C A C A C 1  3sin sin  os c os c  3 tan tan  1  tan tan  2 2 2 2 2 2 2 2 3
Câu 50. Cho a, b, c theo thứ tự tạo thành cấp số cộng. Giá trị x y là bao nhiêu biết P  log  2 2 2
a ab  2b bc c   x log  2 2
a ac cy x, y   . 2 2    A. 0 B. 1 C. 1  D. 2 Hướng dẫn giải Đáp án D
Theo đề a, b, c theo thứ tự tạo thành cấp số cộng nên a c b  a c2 2 2  4b
b a c  2b  a c2 2 2 2 2
 2a  ab  2b bc c  2  2 2
a ac c  Do đó log  2 2 2
a  ab  2b bc c   log  2 2
a ac c 1 2 2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 51. Cho ba (bố số chứ) số a, b, c, d theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết 148
tổng ba số hạng đầu bằng
, đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và 9
thứ tám của một cấp số cộng. Tính giá trị biểu thức T a b c d ? 101 100 100 101 A. T  . B. T  . C. T   . D. T   . 27 27 27 27 Hướng dẫn giải Chọn C 148
Gọi e là công sai. Ta có: a b c  3a 10e    1 9
(Đề xuất b a  3e , c a  7e ) 2
Gọi q là công bội khác 1 ta lại có: 2 2 2
b a q ac  a  3e  a 7  3e  a  9e  02 . a  4  16 64 256 100 Từ (1) và (2)   4  b  ;c  ;d   T   . e  3 9 27 27   9
Câu 52. Cho cấp số cộng u . Mệnh đề nào dưới đây là mệnh đề đúng? n
A. n pu   p mu  m nu  0 .
B. m nu n p u p m u  . m   n   0 m n p p
C. m pu  n mu   p nu  0 .
D. p nu m p u m n u  . m   n   0 m n p p Hướng dẫn giải Chọn A.
Kiểm tra từng phương án cho đến khi tìm được phương án đúng.
Ta có: u u m 1 d;u u n 1 d;u u p 1 d . m 1   n 1   p 1  
- Phương án A: Ta có: n pu   p mu  m n u m np
 n p  u m 1 d   p m u n 1 d   m n u p 1 d   0 . 1     1     1         1 1 1
Câu 53. Cho ba số dương , a ,
b c thỏa mãn điều kiện , , lập thành một cấp b c c a a b
số cộng. Mệnh đề nào dưới đây là đúng? A. Ba số , a ,
b c lập thành một cấp số cộng. 1 1 1 B. Ba số , ,
lập thành một cấp số cộng. a b c C. Ba số 2 2 2
a ,b , c lập thành một cấp số cộng. D. Ba số
a , b , c lập thành một cấp số cộng Hướng dẫn giải Chọn A.
Theo giả thiết ta có:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 34
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 1 1 2   b c a b c a
  c a  a c  2 b   2 b c  a b   a c  2b Suy ra ba số , a , b c hoặc , c ,
b a lập thành một cấp số cộng.
Câu 54. Biết rằng tồn tại các giá trị của x 0;2 để ba số 2
1  sin x,sin x,1 sin 3x lập thành một
cấp số cộng, tính tổng S các giá trị đó của x . 7 23
A. S  5.
B. S  3. C. S  . D. S  . 2 6 Hướng dẫn giải Chọn A.
Theo tính chất của cấp số cộng ta có: 2
1 sin x 1 sin 3x  2 sin x 3 2 3 2
 2  4 sin x  4 sin x  2 sin x  2 sin x  sin x  2 sin x 1  0  1 sin x   2sin x  1  2 sin x  1 0       2 cos x  0   x    k2 1  6 +) sin x     . 2 7x   k 2  6
+) cos x  0  x   k 2 11 7
Với nghiệm x  
k2 và x 0; 2 , ta tìm được x  . Với nghiệm x   k2 6 6 6 7
và x 0; 2 , ta tìm được x  . Với nghiệm x
k và x 0; 2 ta tìm được 6 2 3 nghiệm x  ; x  2 2 11 7 3 Do đó S      5. 6 6 2 2
Câu 55. Tìm tất cả các giá trị của tham số m để phương trình 3 2 2
x  3x x m 1  0 có ba nghiệm
phân biệt lập thành một cấp số cộng. A. m  16 . B. m  2  . C. m  2 . D. m  2  . Hướng dẫn giải Chọn D.
Áp dụng kết quả phần lý thuyết, ta có phương trình đã cho có 3 nghiệm phân biệt thì điều b 3  kiện cần là   
 1 là nghiệm của phương trình. 3a 3 Suy ra 3 2 2
1  3.1 1 m 1  0  m  2  .
Với m  2 , ta có phương trình 3 2
x 3x x  3  0 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 35
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao   x   2 3 x  
1  0  x  1, x  1, x  3 Ba số 1
 ,1,3 lập thành cấp số cộng.
Vậy các giá trị cần tìm là m  2 . Do đó D là phương án đúng.
Câu 56. Biết rằng tồn tại đúng ba giá trị m , m , m của tham số m để phương trình 1 2 3 3 2 3 2
x  9x  23x m  4m m  9  0 có ba nghiệm phân biệt lập thành một cấp số cộng, tính giá trị của biểu thức 3 3 3
P m m m . 1 2 3 A. P  34 . B. P  36 . C. P  64 . D. P  34 . Hướng dẫn giải Chọn A.
Áp dụng kết quả ở phần lý thuyết, ta có phương trình đã cho có 3 nghiệm phân biệt thì điều b 9  kiện cần là:   
 3 là nghiệm của phương trình. 3a 3 Suy ra 3 2 3 2
3  9.3  23.3 m  4m m  9  0  3 2
m  4m m  6  0  m  1
 , m  2, m  3 Với m  1
 , m  2, m  3 thì 3 2
m  4m m  6  0 nên 3 2
m  4m m 9  1  5 . Do vậy, với m  1
 , m  2, m  3 ta có phương trình 3 2 x x x     x   2 9 23 15 0 3
x  6x  5  0  x 1, x  3, x  5.
Ba số 1,3,5 lập thành cấp số cộng. Vậy m  1
 , m  2, m  3 là các giá trị cần tìm. Do đó  3 3 3 1  2  3  34
Câu 57. Biết rằng tồn tại hai giá trị của tham số m để phương trình sau có bốn nghiệm phân biệt lập
thành một cấp số cộng: 4 2 2
x 10x  2m  7m  0 , tính tổng lập phương của hai giá trị đó. 343 721 721 343 A.  . B. . C.  . D. . 8 8 8 8 Hướng dẫn giải Chọn C . Đặt 2
t x t  0 . Khi đó ta có phương trình: 2 2
t 10t  2m  7m  0 (*) .
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm 2 2  5  (2m  7 ) m  0 dương phân biệt 2  
 0  2m  7m  25. 2
2m  7m  0 
(do tổng hai nghiệm bằng 10  0 nên không cần điều kiện này).
+ Với điều kiện trên thì (*) có hai nghiệm dương phân biệt là t , t (t t ) . 1 2 1 2
Khi đó phương trình đã cho có bốn nghiệm phân biệt là  t ;  t ; t ; t . 2 1 1 2
Bốn nghiệm này lập thành một cấp số cộng khi  t   tt   t
t t t  9t . 1  2  1  1  2 1 2 1
Theo định lý Vi-ét ta có: 2
t t  10; t .t  2m  7m . 1 2 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao t   9t t   1 2 1 1 m  1  
Suy ra ta có hệ phương trình t t 10 t 9        . 1 2  2 9 m    2  2
t .t  2m  7m 2m  7m  9  2  1 2 
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được. 3  9   721 Do đó 3 1      .  2  8
Câu 58. Cho một cấp số cộng u
có u  1 và tổng của 100 số hạng đầu tiên 24850 . Tính giá trị của n  1 1 1 1 1 biểu thức S    ...   ? u u u u u u u u 1 2 2 3 48 49 49 50 4 9 49 A. S  123 B. S C. S D. S  23 246 246 Hướng dẫn giải Ta có: u
u  497  u
 496  1 99d d  5  u  246 . 100 1 100 50 u u u u u u u u 1 1 1 49 Lại có: 2 1 3 2 49 48 50 49 5S    ...      1  S  . u u u u u u u u u u 246 246 1 2 2 3 48 49 49 50 1 50 abn n
Câu 59. Cho cấp số cộng ; cấp số nhân
thỏa mãn a a  0;b b  1 và hàm số 2 1 2 1 f x 3  x  3x
f a  2  f a
f log b  2  f log b 2 2   2  2   1 sao cho và
. Số nguyên dương n  1 nhỏ
nhất thỏa mãn điều kiện b  2018a là? n n A. 16 B. 15 C. 17 D. 18 Hướng dẫn giải Tính bảng biến thiên:
Vì f a f a a , a  0;1 và a  1; a  0 . 2   1 1 2   2 1
Tương tự log b  1 và log b  0 . 2 2 2 1
Khi đó a n 1 và 1 b 2n  . n n Vậy n 1 b 2018a 2     2018 n  . n n   1 Chọn A.
Câu 60. Cho cấp số cộng u  có số hạng đầu u  2 và công sai d  3 . Trên mặt phẳng tọa độ Oxy 1
, lấy các điểm A , A ,... sao cho với mỗi số nguyên dương n , điểm A có tọa độ  ; n u . Biết rằng khi n  1 2 n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
đó tất cả các điểm A , A ,..., A ,... cùng nằm trên một đường thẳng. Hãy viết phương trình của đường 1 2 n thẳng đó. A. y  3  x  5. B. y  3  x  2 .
C. y  2x 3 .
D. y  2x 5 Hướng dẫn giải Chọn A.
Số hạng tổng quát của cấp số cộng u là u u n 1 d  3  n  5 . n 1   n
Nhận thấy toạ độ của các điểm A đều thoả mãn phương trình y  3
x  5 nên phương trình n
đường thẳng đi qua các điểm A , A ,..., A ,...là y  3  x  5. 1 2 n
Suy ra A là phương án đúng.
Câu 61. Trong mặt phẳng tọa độ Oxy , cho đồ thị C  của hàm số y  3x  2 . Với mỗi số nguyên
dương n , gọi A là giao điểm của đồ thị C  với đường thẳng d : x n  0 . Xét dãy số u với u là n n n
tung độ của điểm A . Mệnh đề nào dưới đây là mệnh đề đúng? n
A. Dãy số u
là một cấp số cộng có công sai d  2 . n
B. Dãy số u
là một cấp số cộng có công sai d  3 . n
C. Dãy số u
là một cấp số cộng có công sai d  1 . n
D. Dãy số u
không phải là một cấp số cộng. n Hướng dẫn giải Chọn B. Ta có A  ; n u
trong đó u  3n  2 . n n n Do u
u  3,  n  1 nên u
là một cấp số cộng với công sai d  3 . n n 1  n
Suy ra B là phương án đúng.
Câu 62. Trên tia Ox lấy các điểm A , A ,..., A ,... sao cho với mỗi số nguyên dương n , OA n . 1 2 n n
Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox , vẽ các nửa đường tròn đường kính
OA , n 1,2,... Kí hiệu u là diện tích nửa đường tròn đường kính OA và với mỗi n  2 , kí hiệu u là n 1 1 n
diện tích của hình giới hạn bởi nửa đường tròn đường kính OA
, nửa đường tròn đường kính OA và n 1  n
tia Ox . Mệnh đề nào dưới đây là đúng?
A. Dãy số u
không phải là một cấp số cộng. n
B. Dãy số u
là một cấp số cộng có công sai d  . n  4
C. Dãy số u
là một cấp số cộng có công sai d  . n  8
D. Dãy số u
không phải là một cấp số cộng có công sai d  . n  2 Hướng dẫn giải Chọn B. n
Bán kính đường tròn có đường kính OA là r  . n n 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 2 2 1  n n 
Diên tích nửa đường tròn đường kính OA là S  . n n   2  2  8 2 2n 1 2   Suy ra u s sn n 1        , n  2 . n n n 1    8   8 2 1  1  Ta có u  . 1   2  2  8 Do uu  , n  1 nên u
là cấp số cộng với công sai d  . n n 1  n 4 4
Suy ra B là phương án đúng.
Câu 63. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là 100000
đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30000 đồng so với giá của mét khoan
ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu 20
mét lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó
phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu? A. 7700000 đồng. B. 15400000 đồng. C. 8000000 đồng. D. 7400000 đồng. Hướng dẫn giải Chọn A.
Gọi u là giá của mét khoan thứ n , trong đó 1  n  20. n
Theo giả thiết, ta có u  100000 và u
u  30000 với 1  n  19 . 1 n 1  n
Ta có (u ) là cấp số cộng có số hạng đầu u  100000 và công sai d  30000 . n 1
Tổng số tiền gia đình thanh toán cho cơ sở khoan giếng chính là tổng các số hạng của cấp số
cộng (u ) . Suy ra số tiền mà gia đình phải thanh toán cho cơ sở khoan giếng là n
20[2u  (20 1)d ] 1 S
u u  ....  u   7700000 (đồng). 20 1 2 20 2
Câu 64. Trên một bàn cờ có nhiều ô vuông. Người ta đặt 7 hạt dẻ vào ô vuông đầu tiên, sau đó đặt tiếp
vào ô thứ hai số hạt dẻ nhiều hơn ô đầu tiên là 5, tiếp tục đặt vào ô thứ ba số hạt dẻ nhiều hơn ô thứ hai
là 5, … và cứ thế tiếp tục đến ô cuối cùng. Biết rằng đặt hết số ô trên bàn cờ người ta đã phải sử dụng
hết 25450 hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô? A. 98 ô. B. 100 ô. C. 102 ô. D. 104 ô. Hướng dẫn giải Chọn B.
Kí hiệu u là số hạt dẻ ở ô thứ n . n
Khi đó, ta có u  7 và u
u  5, n  1. 1 n 1  n
Dãy số u là cấp số cộng với u  7 và công sai d  5 nên có n  1
n 2u  n   2 1 d   1  5n  9n S   . n 2 2 2 5n  9n Theo giả thiết, ta có
 25450  n  100 . 2 Suy ra bàn cờ có 100 ô.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 65. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức
sau: Mức lương của quý làm việc đầu tiên cho công ty là 13,5 triệu đồng/quý, và kể từ quý làm việc
thứ hai, múc lương sẽ được tăng thêm 500.000 đồng mỗi quý. Tính tổng số tiền lương một kỹ sư nhận
được sau ba năm làm việc cho công ty. A. 198 triệu đồng. B. 195 triệu đồng. C. 228 triệu đồng. D. 114 triệu đồng. Hướng dẫn giải Chọn B.
Kí hiệu u là mức lương của quý thứ n làm việc cho công ty. Khi đó u  13,5 và n 1 u
u  0,5, n  1. n 1  n Dãy số u
lập thành cấp số cộng có số hạng đầu u  13,5 và công sai d  0,5 . n  1
Một năm có 4 quý nbên 3 năm có tổng 12 quý.
Số tiền lương sau 3 năm bằng tổng số tiền lương của 12 quý và bằng tổng 12 số hạng đầu
tiên của cấp số cộng u . Vậy, tổng số tiền lương nhận được sau 3 năm làm việc cho công n  12.2.13,5 11.0, 5
ty của kỹ sư là S   195 (triệu đồng). 12 2
Câu 66. Mặt sàn tầng của một ngôi nhà cao hơn mặt sân 0,5m . Cầu thang đi từ tầng một lên tầng hai
gồm 21 bậc, một bậc cao 18cm . Kí hiệu h là độ cao của bậc thứ n so với mặt sân. Viết công thức để n tìm độ cao h . n
A. h  0,18n  0, 32 m .
B. h  0,18n  0, 5 m . n   n  
C. h  0, 5n  0,18 m .
D. h  0, 5n  0, 32 m . n   n   Hướng dẫn giải Chọn A.
Ký hiệu h là độ cao của bậc thứ n so với mặt sân. n Khi đó, ta có h
h  0,18 (mét), trong đó h  0,5 (mét). Dãy số h lập thành một cấp n n 1  n 1
số cộng có h  0,5 và công sai d  0,18 . Suy ra số hạng tổng quát của cấp số cộng này là 1
h  0,5  n  
1 .0,18  0,18.n  0, 32 (mét). n
Câu 67. Trên tia Ox lấy các điểm A , A ,..., A ,... sao cho với mỗi số nguyên dương n, OA  . n Trong 1 2 n n
cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính
OA , n  1, 2... Kí hiệu u là diện tích của nửa hình tròn đường kính OA và với mỗi n  2, kí hiệu u n 1 1 n
là diện tích của hình giới hạn bởi nửa đường tròn đường kính OA , nửa đường tròn đường kính OA n 1  n
và tia Ox. Chứng minh rằng dãy số (u ) là một cấp số cộng. Hãy xác định công sai của cấp số cộng n đó.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 2 A. d B. d C. d D. d  4 2 3 3 Hướng dẫn giải Đáp án A
Đặt OA  0, ta có 0 2 2 1  OA OA 2 2n 1 n n 1 2   u  n n        n   n     1 , 1 2 4 4 8   8   2n   1 2n   1 Suy ra uu    , n   1 n 1  n 8 8 4 Do đó u
là một cấp số cộng công sai d n  4
CẤP SỐ NHÂN
Câu 68. Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có một góc bằng
25 . Tìm 2 góc còn lại? A. 65 ,  90 B. 75 ,  80 . C. 60 ,  95 . D. 60 ,  90 . Hướng dẫn giải Chọn D
Ta có: u u u  180  25  25  d  25  2d  180  d  35 . 1 2 3
Vâỵ u  60; u  90. 2 3
Câu 69. Cho dãy số a xác định bởi a  5, a  .
q a  3 với mọi n  1, trong đó q là hằng số, n  1 n 1  n n 1   q n 1
a  0, q  1. Biết công thức số hạng tổng quát của dãy số viết được dưới dạng 1
a .q . n 1 q
Tính  2? A. 13. B. 9. C. 11. D. 16. Hướng dẫn giải Chọn C Cách 1.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 3 Ta có: a
k q a k k kq  3  k n 1   n  1 q Đặt 2
v a k v
q.v q .v  ... nq v n n n 1  n n 1  1   nnn 3 Khi đó 1 1 v q .v q
. a k qn   1. 5 1 1   1 q   n 1         q n 3 n 3 3 n 1 Vậy 1 1 1
a v k q . 5   k q . 5    5q  3 n n     1 q 1 q 1 q 1 q    
Do dó:  5;  3   2 5  2.3  11 Cách 2.
Theo giả thiết ta có a  5, a  5q  3. Áp dụng công thức tổng quát, ta được 1 2 1 1    1 q  1 1
a .q  1  1 q 5     5  , suy ra  , hay  2 1  
5q  3  .q  3  1 q  2 1  
a .q
.q 2  1 q
 2 5  2.3  11
Câu 70. Trong dịp hội trại hè 2017 bạn A thả một quả bóng cao su từ độ cao 3m so với mặt đất, mỗi
lần chạm đất quả bóng lại nảy lên một độ cao bằng hai phần ba độ cao lần rơi trước. Tổng quãng
đường quả bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng: A. 13m. B. 14m. C. 15m. D. 16m. Hướng dẫn giải Chọn C
Gọi S là tổng quãng đường bóng đã bay, khi đó ta có: 2 3 4 5 n 2  2   2   2   2   2  S  3  3. .3  3.  3.  3.  ...  3.  ...           3  3   3   3   3   3  2
S là tổng của cấp số nhân lùi vô hạn có số hạng đầu tiên là u  3 , công bội là q  nên 1 3 u 3 1 S    9 1 q 2 1 3
Vậy tổng quãng đường đã bay của bóng là khoảng 9m. Do đó x  y  2 u
u u u  15  1 2 3 4
Câu 71. Có hai cấp số nhân thỏa mãn 
với công bội lần lượt là q , q . Hỏi giá 2 2 2 2 1 2 u
u u u  85  1 2 3 4
trị của q q là: 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 1 3 5 7 A. B. C. D. 2 2 2 2 Hướng dẫn giải Đáp án C 2 
u q   2 1 u  4 4 q 1 1 1    15   225 2  q 1   q  2 1  4 q   1  2 2 q   1 225
Biến đổi giả thiết thành      2 u  8 q   2 8 2 1 u  8 q 1 q 1 85 1 q 1 1       85  2   85 2 q 1   q 1   1 q  4 3 2 14q 17q 17q 17q 14 0        2 . q  2  5
Do đó q q  . 1 2 2
Câu 72. Cho tứ giác ABCD biết 4 góc của tứ giác lập thành một cấp số cộng và góc A bằng 30o. Tìm các góc còn lại? A. 75 ,  120 ,  65 . B. 72 ,  114 ,  156 . C. 70o; 110o; 150o. D. 80o; 110o; 135o. Hướng dẫn giải Chọn C
Ta có: u u u u  360  30  30  d  30  2d  30  3d  360  d  40 . 1 2 3 4
Vâỵ u  70; u  110; u  150 . 2 3 4
Câu 73. Cho một cấp số cộng (u ) có u  1 và tổng 100 số hạng đầu bằng 24850 . Tính n 1 1 1 1 S    ...  . u u u u u u 1 2 2 3 49 50 9 4 49 A. S  . B. S  . C. S  123 . D. S  . 246 23 246 Hướng dẫn giải Chọn D
Gọi d là công sai của cấp số đã cho 497  2u Ta có: S
 50 2u  99d  1  24850  d   5 100 1 99 5 5 5  5S    ...  u u u u u u 1 2 2 3 49 50 u u u u u u 2 1 3 2 50 49    ...  u u u u u u 1 2 2 3 49 50
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao 1 1 1 1 1 1 1 1      ...     u u u u u u u u 1 2 2 3 48 49 49 50 1 1 1 1 245      u u u u  49d 246 1 50 1 1 49  S  . 246 Câu 74. Cho , a ,
b c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng? A. 2 2
a c  2ab  2bc  2ac . B. 2 2
a c  2ab  2bc  2ac . C. 2 2
a c  2ab  2bc  2ac . D. 2 2
a c  2ab  2bc  2ac . Hướng dẫn giải Chọn C , a ,
b c theo thứ tự lập thành cấp số cộng khi và chỉ khi
b a c b  b a2  c b2 2 2
a c  2ab  2bc 2 2 2
a c  2c  2ab  2bc  2ab  2c c b
 2ab  2c b a  2ab  2bc  2ac u   2  1
Câu 75. Cho dãy số u được xác định như sau:  . Tính tổng n u
 4u  4  5n n  1   n 1  n   S u  2u . 2018 2017 A. 2017 S  2015  3.4 B. 2018 S  2016  3.4 C. 2018 S  2016  3.4 D. 2017 S  2015  3.4 Hướng dẫn giải Chọn C
Câu 76. Cho số hạng thứ m và thứ n của một cấp số nhân biết số hạng thứ (m n) bằng A , sổ hạng thứ (m  )
n bằng B và các số hạng đểu dương. Số hạng thứ m là: m m 2nB nA  2 A. A  B. AB C.   D.  n ABA   B Hướng dẫn giải Chọn B mn 1 u
A u .q    A Ta có m n 1 2n 2 n   A Bqq mn 1 u
B u .qBmn 1 m 1 u    u .  n q u   A  Mặt khác m 1 m n 2n    qu AAB   mn 1 m u   u .qAB   mn 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao m 2nB
Tương tự ta có thể tính được u A n    A  1 n 1 U U U
Câu 77. Cho dãy số U U U  .U 2 S U    .. 
n  xác định bởi: và . Tổng 3 10 1 3 n 1  3 n n 1 2 3 10 bằng: 3280 29524 25942 1 A. . B. . C. . D. . 6561 59049 59049 243 Hướng dẫn giải Chọn B n 1 u 1 u 1 Ta có uu n 1    . n u . n 1  3 n n n 1 3 n 1 3n u 1 u 1 u 1 u 1 2  u ; 3 2   u ;…; 10  u . 1 2 3 2 1 3 3 2 3 9 1 10 3 Khi đó: 1  1  1 u u u 1 1 1  10  3  3 29524 2 3 10  S u    ...     ...    . 1 2 10 2 3 10 3 3 3 1 59049 1 3
Câu 78. Phương trình 2 xa a
a    a  2  a  4 1 ... 1 1
1 a  với 0  a  1 có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. 3 Hướng dẫn giải Chọn B x 1 1 a
Phương trình biến đổi thành  1 a 2 1 a  4 1 a x 1  8  1 a
 1 a x  7. 1 a
Câu 79. Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: 3
x   x   2 3
1 x  5m  4 x  8  0. A. m  2  . B. m  2. C. m  4. D. m  4  . Hướng dẫn giải Chọn B. d 8
Phương pháp 1: Ta có     8. a 1
Điều kiện cần để phương trình đã choc ó ba nghiệm lập thành một cấp số nhân là 3
x  8  2 là nghiệm của phương trình.
Thay x  2 vào phương trình đã cho, ta được
4  2m  0  m  2.
Với m  2, ta có phương trình 3 2
x  7x 14x  8  0  x  1; x  2; x  4
Ba nghiệm này lập thành một cấp số nhân nên m  2 là giá trị cần tìm. Vậy, B là phương án đúng.
Phương pháp 2: Kiểm tra từng phương án đến khi tìm được phương án đúng.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 80. Biết rằng tồn tại hai giá trị m và m để phương trình sau có ba nghiệm phân biệt lập thành 1 2 một cấp số nhân: 3 x   2
m m   2 x   2 2 2 2 1
7 m  2m  2 x  54  0. Tính giá trị của biểu thức 3 3
P m m . 1 2 A. P  56 B. P  8. C. P  56 D. P  8. Hướng dẫn giải Chọn A. d 5  4 Ta có     27. a 2
Điều kiện cần để phương trình đã cho có ba nghiệm phân biệt lập thành một cấp số nhân là 3 x
27  3 phải là nghiệm của phương trình đã cho. 2
m  2m  8  0  m  2; m  4  .
Vì giả thiết cho biết tồn tại đúng hai giá trị của tham số m nên m  2 và m  4  là các giá trị thỏa mãn Suy ra P    3 3 2 4  56.
Câu 81. Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2;3;9
vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính 2 2 2
F x y z .
A. F  389. hoặc F  395.
B. F  395. hoặc F  179.
C. F  389. hoặc F  179.
D. F  441 hoặc F  357. Hướng dẫn giải Chọn C .
Theo tính chất của cấp số cộng, ta có x z  2 y .
Kết hợp với giả thiết x y z  21, ta suy ra 3y  21  y  7 .
Gọi d là công sai của cấp số cộng thì x y d  7  d và z y d  7  d .
Sau khi thêm các số 2;3;9 vào ba số x, y, z ta được ba số là x  2, y  3, z  9 hay
9  d ,10,16  d .
Theo tính chất của cấp số nhân, ta có   d   d  2 2 9 16
 10  d  7d  44  0 .
Giải phương trình ta được d  1  1 hoặc d  4 . Với d  1
 1 , cấp số cộng 18, 7, 4
 . Lúc này F  389 .
Với d  4 , cấp số cộng 3,7,11. Lúc này F  179 .
a  7, a  224 S  3577.
Câu 82. Cho cấp số nhân a có 1 6 và k
Tính giá trị của biểu thức n
T  k   1 a . k A. T  17920. B. T  8064. C. T  39424. D. T  86016. Hướng dẫn giải Chọn A. Ta có a  224 5
a q  224  q  2 (do a  7 ). 6 1 1 a 1 kq 1   Do S
 7 2k  nên S  3577 7 2k    1  3577 k 9
 2  2  k  9. k  1 1 q k Suy ra 8
T  10a  10a q  17920. 9 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 83. Cho cấp số nhân a có a  2 và biểu thức 20a 10a a đạt giá trị nhỏ nhất. Tìm số n  1 1 2 3
hạng thứ bảy của cấp số nhân đó.
A. a  156250. B. a  31250.
C. a  2000000. D. a  39062. 7 7 7 7 Hướng dẫn giải Chọn B.
Gọi q là công bội của cấp số nhân a . n
Ta có 20a 10a a  2  2
q 10q  20  q  2 2 5 10  10, q. 1 2 3 
Dấu bằng xảy ra khi q  5. Suy ra 6 6
a a .q  2.5  31250. 7 1
Câu 84. Trong các mệnh đề dưới đây, mệnh đề nào là sai?
A. Dãy số a , với a  3 và a
a  6, n  1, vừa là cấp số cộng vừa là cấp số n  1 n 1  n nhân.
B. Dãy số b , với b  1 và b  
n  1, vừa là cấp số cộng vừa là cấp số   2 2b 1 3, n 1 nn  1 nhân.
C. Dãy số c , với c  2 và 2 c
 3c  10 n  1, vừa là cấp số cộng vừa là cấp số nhân. n  1 n 1  n
D. Dãy số d , với d  3 và 2 d
 2d  15, n  1, vừa là cấp số cộng vừa là cấp số n  1 n 1  n nhân. Hướng dẫn giải Chọn D.
Kiểm tra từng phương án đến khi tìm được phương án sai.
+ Phương án A:Ta có a  3; a  3;... Bằng phương pháp quy nạp toán học chúng ra chứng 2 2
minh được rằng a  3, n
  1. Do đó a là dãy số không đổi. Suy ra nó vừa là cấp số n n
cộng (công sai bằng 0 ) vừa là cấp số nhân (công bội bằng 1).
+ Phương án B: Tương tự như phương án A, chúng ta chỉ ra được b  1, n
  1 . Do đó bn n
là dãy số không đổi. Suy ra nó vừa là cấp số cộng (công sai bằng 0 ) vừa là cấp số nhân (công bội bằng 1).
+ Phương án C: Tương tự như phương án A, chúng ta chỉ ra được c  2, n   1 . Do đó n
c là dãy số không đổi. Suy ra nó vừa là cấp số cộng (công sai bằng 0 ) vừa là cấp số n  nhân (công bội bằng 1).
+ Phương án D: Ta có: d  3
 , d  3, d  3 . Ba số hạng này không lập thành cấp số cộng 1 2 3
cũng không lập thành cấp số nhân nên dãy số d không phải là cấp số cộng và cũng n  không là cấp số nhân.
Câu 85. Xét bảng ô vuông gồm 4 4 ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số 1 hoặc 1
 sao cho tổng các số trong mỗi hang và tổng các số trong mỗi cột đều bằng 0 . Hỏi có bao nhiêu cách? A. 72 B. 90 C. 80 D. 144 Hướng dẫn giải
Xét 1 hàng (hay 1 cột bất kì). Giả sử trên hàng đó có x số 1 và y số -1. Ta có tổng các chữ
số trên hàng đó là x y . Theo đề bài có x y  0  x y .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Lần lượt xếp các số vào các hàng ta có số cách sắp xếp là 3!.3!.2.1 =72 (Cách)
Câu 86. Số đo ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân. Biết thể tích của khối hộp là 3
125 cm và diện tích toàn phần là 2
175 cm . Tính tổng số đo ba kích thước của hình hộp chữ nhật đó. A. 30c . m B. 28c . m C. 31c . m D. 17,5c . m Hướng dẫn giải Chọn D.
Vì ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân nên ta có thể gọi ba kích a thước đó là , q, a . q q a
Thể tích của khối hình hộp chữ nhật là 3 V  . .
a qa a  125  a  5. q
Diện tích toàn phần của hình hộp chữ nhật là  a a   1   1  2 S  2 .a  . a aq a . q  2a 1 q   50 1 q  . tp       q q q q        q  2  1  Theo giả thiết, ta có 2 50 1 q 175 2q 5q 2 0          .   1 qq     2 1
Với q  2 hoặc q
thì kích thước của hình hộp chữ nhật là 2,5c ; m 5c ;1 m 0c . m 2
Suy ra tổng của ba kích thước này là 2,5  5 10  17,5 cm.
Câu 87. Một của hàng kinh doanh, ban đầu bán mặt hàng A với giá 100 (đơn vị nghìn đồng). Sau đó,
cửa hàng tăng giá mặt hàng A lên 10%. Nhưng sau một thời gian, cửa hàng lại tiếp tục tăng giá mặt
hàng đó lên 10%. Hỏi giá của mặt hàng A của cửa hàng sau hai làn tăng giá là bao nhiêu? A. 120. B. 121. C. 122. D. 200. Hướng dẫn giải Chọn B.
Sau lần tăng giá thứ nhất thì giá của mặt hàng A là:
M  100 100.10%  110. 1
Sau lần tăng giá thứ hai thì giá của mặt hàng A là:
M  110 110.10%  121. 2
Câu 88. Một người đem 100 triệu đồng đi gửi tiết kiệm với kỳ han 6 tháng, mỗi tháng lãi suất là 0, 7%
số tiền mà người đó có. Hỏi sau khi hết kỳ hạn, người đó được lĩnh về bao nhiêu tiền? A.  5 8 10 . 0, 007 (đồng) B.  5 8 10 . 1, 007 (đồng) C.  6 8 10 . 0, 007 (đồng) D.  6 8 10 . 1, 007 (đồng) Hướng dẫn giải Chọn D.
Số tiền ban đầu là 8 M  10 (đồng). 0
Đặt r  0, 7%  0, 007 .
Số tiền sau tháng thứ nhất là M M M r M 1 r . 1 0 0 0  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Số tiền sau tháng thứ hai là M M M r M 1 r 2 . 2 1 1 0 M M 1 r 6 0  6
Lập luận tương tự, ta có số tiền sau tháng thứ sáu là .
Do đó M  10 1, 0076 8 . 6
Câu 89. Tỷ lệ tăng dân số của tỉnh M là 1, 2%. Biết rằng số dân của tỉnh M hiện nay là 2 triệu người.
Nếu lấy kết quả chính xác đến hàng nghìn thì sau 9 năm nữa số dân của tỉnh M sẽ là bao nhiêu?
A. 10320 nghìn người.
B. 3000 nghìn người.
C. 2227 nghìn người.
D. 2300 nghìn người. Hướng dẫn giải Chọn C . Đặt 6
P  2000000  2.10 và r  1, 2%  0, 012 . 0
Gọi P là số dân của tỉnh M sau n năm nữa. n Ta có: P
P P r P 1 r . n 1  n n n  
Suy ra  P là một cấp số nhân với số hạng đầu P và công bội q  1 r . n  0 9 10
Do đó số dân của tỉnh M sau 10 năm nữa là: P M 1 r  6  2.10 1, 012  2227000 . 9 0  
Câu 90. Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc đầu có 12
10 tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào? A. 12 1024.10 tế bào. B. 12 256.10 tế bào. C. 12 512.10 tế bào. D. 13 512.10 tế bào. Hướng dẫn giải Chọn C . Lúc đầu có 22
10 tế bào và mỗi lần phân chia thì một tế bào tách thành hai tế bào nên ta có cấp số nhân với 22
u  10 và công bội q  2 . 1
Do cứ 20 phút phân đôi một lần nên sau 3 giờ sẽ có 9 lần phân chia tế bào. Ta có u là số 10
tế bào nhận được sau 3 giờ. Vậy, số tế bào nhận được sau 3 giờ là 9 12 uu q  512.10 . 10 1
Câu 91. Người ta thiết kế một cái tháp gồm 11 tầng theo cách: Diện tích bề mặt trên của mỗi tầng
bằng nửa diện tích mặt trên của tầng ngay bên dưới và diện tích bề mặt trên của tầng 1 bằng nửa diện
tích đế tháp. Biết diện tích đế tháp là 2
12288m , tính diện tích mặt trên cùng. A. 2 6m . B. 2 12m . C. 2 24m . D. 2 3m . Hướng dẫn giải Chọn A.
Gọi u là diện tích đế tháp và u là diện tích bề mặt trên của tầng thứ n , với 1  n  11. 0 n 1
Theo giả thiết, ta có u
u 0  n  10 . n 1  2 n 1 Dãy số u
lập thành cấp số nhân với số hạng đầu u  12288 và công bội q  . n  0 2 11  1 
Diện tích mặt trên cùng của tháp là 11 2
u u .q  12288.  6 m . 11 0    2 
Câu 92. Một tứ giác lồi có số đo các góc lập thành một cấp số nhân. Biết rằng số đo của góc nhỏ nhất 1 bằng
số đo của góc nhỏ thứ ba. Hãy tính số đo của các góc trong tứ giác đó. 9 A. 0 0 0 0 5 ,15 , 45 , 225 . B. 0 0 0 0 9 , 27 ,81 , 243 . C. 0 0 0 0 7 , 21 , 63 , 269 . D. 0 0 0 0 8 , 32 , 72 , 248 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao Hướng dẫn giải Chọn B.
Phương pháp 1: Kiểm tra các dãy số trong mỗi phương án có thỏa mãn yêu cầu của bài toán không.
+ Phương án A : Các góc 0 0 0 0
5 ,15 , 45 , 225 không lập thành cấp số nhân vì 0 0 15  3.5 ; 0 0 45  3.15 ; 0 0 225  3.45 .
+ Phương án B : Các góc 0 0 0 0
9 , 27 ,81 , 243 lập thành cấp số nhân và 1 0 0 0 0 0
9  27  81  243  360 . Hơn nữa, 0 0 9 
81 nên B là phương án đúng. 9
+ Phương án C và D : Kiểm tra như phương án . A
Phương pháp 2: Gọi các góc của tứ giác là 2 3 ,
a aq, aq , aq , trong đó q  1. 1 Theo giả thiết, ta có 2 a
aq nên q  3. 9
Suy ra các góc của tứ giác là ,
a 3a,9a, 27 . a
Vì tổng các góc trong tứ giác bằng 0 360 nên ta có: 0
a  3a  9a  27a  360 0  a  9 .
Do đó, phương án đúng là B (vì trong ba phương án còn lại không có phương án nào có góc 0 9 ).
Câu 93. Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác
trung bình của tam giác ABC . Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho 1 1 1 2 2 2 3 3 3
A B C là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương n  2 , tam giác A B C là tam 1 1 1 n n n
giác trung bình của tam giác A B C
. Với mỗi số nguyên dương n , kí hiệu S tương ứng là diện n 1  n 1  n 1  n
tích hình tròn ngoại tiếp tam giác A B C . Tính tổng S S S  ...  S  ... ? n n n 1 2 n 15 9 A. S  .
B. S  4. C. S  .
D. S  5. 4 2 Hướng dẫn giải Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
*Gọi R là bán kính đường tròn ngoại tiếp A
B C i 1;n. i i i i 2
Ta có R OA
A A  3  S  3. 1 1 1 2 1 3 1 1 *Dễ thấy V : AB C A
B C R R S S .  1  1 1 1 2 2 2 2 1 2 1 o;   2 4  2  1 1 1 V : AB C A
B C R R R S S .  1  2 2 2 3 3 3 3 2 1 3 2 1 o;   2 4 4  2  1
Tương tự, ta có: S S . n n 1  1 4  1 1 1 
Suy ra: S S S  ...  S  ...  S 1   ...   ... 1 2 n 1  2 n 1   4 4 4   1 4  S . 
S  4. (Áp dụng công thức tính tổng của một cấp số nhân lùi vô hạn). 1 1 1 3 1 4
Câu 94. Cho tam giác ABC cân tại đỉnh .
A Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB
theo thứ tự lập thành cấp số nhân công bội q. Gía trị của 2 q bằng 2  2 2  2 2  1 2 1 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải Chọn C A
BC, AH , AB theo thứ tự lập thành CSN 2
AH BC.AB    AB 2  q   BC Ta có: 2 2 BC AB AB 2 2 AH AB   A . B BC  4  4 1  0 2 4 BC BC AB 2  1   q  B H C BC 2
Câu 95. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức như
sau: mức lương của quý làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ
hai mức lương sẽ được tăng thêm 1,5 triệu đồng mỗi quý. Hãy tính tổng số tiền lương một kĩ sư được
nhận sau 3 năm làm việc cho công ty. A. 495 triệu đồng. B. 279 triệu đồng. C. 384 triệu đồng. D. 558 triệu đồng. Hướng dẫn giải Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
DS-CSC-CSN Nâng Cao
Câu 96. Một hình vuông ABCD có cạnh AB a, diện tích S . Nối 4 trung điểm A , B ,C , D theo 1 1 1 1 1
thứ tự của 4 cạnh AB, BC,C ,
D DA ta được hình vuông thứ hai là A B C D có diện tích S . Tiếp tục 1 1 1 1 2
như thế, ta được hình vuông thứ ba là A B C D có diện tích S và cứ tiếp tục như thế, ta được diện 2 2 2 2 3
tích S , S ,... Tính S S S  ...  S . 4 5 1 2 100 100 100 2 100 2 99 2 1 a 2   1 a 2   1 a 2   1 A. S  . B. S  . C. S  . D. S  99 2 2 a 99 2 99 2 99 2 Hướng dẫn giải Đáp án C 2 2 2 a a a Dễ thấy 2
S a ; S  ; S  ;...; S  1 2 3 100 99 2 4 2 1
Như vậy S , S , S ,..., S
là cấp số nhân với công bội q  1 2 3 100 2 2 a    100 2 1 1 1 1 2 
S S S  ...  Sa 1   ...   1 2 100  2 99  99  2 2 2  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay