Trắc nghiệm phép dời hình và phép đồng dạng trong các đề thi thử Toán 2018

Tài liệu gồm 39 trang tổng hợp câu hỏi và bài tập trắc nghiệm phép dời hình và phép đồng dạng trong mặt phẳng có lời giải chi tiết với đầy đủ các mức độ nhận thức khác nhau

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

39 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Câu 1:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai
đường thẳng
1
: 2 3 1 0
d x y
và
2
: 2 0
d x y
. Có bao nhiêu phép tịnh tiến biến
1
d
thành
2
d
.
A. Vô số. B.
4
. C.
1
. D.
0
.
Lời giải
Chọn D
Nhắc lại kiến thức:
"
Phép tịnh tiến theo vectơ
v
biến đường thẳng thành đường thẳng song
song hoặc trùng với nó
"
.
Ta có:
và
2
d
không song song hoặc trùng nhau, suy ra không có phép tịnh tiến nào biến
đường thẳng
thành
.
Câu 2:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Cho
1;5
v
và điểm
4;2
M
. Biết
M
là
ảnh của
M
qua phép tịnh tiến
v
T
. Tìm
M
.
A.
4;10
M
. B.
3;5
M
. C.
3;7
M
. D.
5; 3
M
.
Lời giải
Chọn D
x x a
y y b
4 1
2 5
x
y
5; 3
M
Câu 3:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Cho điểm
1;4
A
và
2;3
u
, biết
A
là ảnh của
A
qua phép tịnh tiến
u
. Tìm tọa độ điểm
A
.
A.
1;4
A
. B.
3; 1
A
. C.
1; 4
A
. D.
3;1
A
.
Lời giải
Chọn D
Gọi
;A x y
. Ta có
AA u
1 2
4 3
x
y
1 2 3
4 3 1
x
y
3;1
A
.
Câu 4:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Cho hai đường thẳng song song
d
và
d
. Trong các khẳng định sau khẳng định nào đúng?
A. Có đúng một phép tịnh tiến biến
d
thành
.d
B. Có vô số phép tịnh tiến biến
d
thành
.d
C. Phép tịnh tiến theo véc tơ
v
có giá vuông góc với đường thẳng
d
biến
d
thành
.d
D. Cả ba khẳng định trên đều đúng.
Lời giải
Chọn B
Có vô số phép tịnh tiến véc tơ
v
với điểm gốc nằm trên
d
và điểm ngọn nằm trên
d
biến
d
thành
.d
Câu 5:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Điểm
2;4
M
là ảnh của điểm nào sau đây
qua phép tịnh tiến theo véctơ
1;7
v
.
A.
1; 3
F
. B.
3;11
P
. C.
3;1
E
. D.
1;3
Q
.
Lời giải
Chọn B
Gọi
;M x y
là ảnh của điểm
M
qua phép tịnh tiến theo véctơ
1;7
v
.
Ta có
2; 4
MM x y
và
v
T M M MM v
2 1 3
4 7 11
x x
y y
.
Câu 6:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Hình nào sau đây có vô số trục đối xứng?
A. Hình vuông. B. Hình tròn. C. Đoạn thẳng. D. Tam giác đều.
Lời giải
Chọn B
R
I
 Hình tròn có vô số trục đối xứng – là các đường thẳng đi qua tâm của đường tròn đó.
 Tam giác đều có 3 tục đối xứng như hình vẽ
 Hình vuông có bốn trục đối xứng như hình vẽ
 Đoạn thẳng có hai trục đối xứng là đường thẳng đi qua 2 đầu đoạn thẳng và đường trung
trực của đoạn thẳng đó.
Câu 7:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Trong mặt phẳng tọa độ
,Oxy
cho
2;3
v
. Tìm
ảnh của điểm
1; 1
A
qua phép tịnh tiến theo vectơ
v
.
A.
2;1
A
. B.
1;2
A
. C.
2; 1
A
. D.
1; 2
A
.
Lời giải
Chọn B
Giả sử
;A x y
. Theo công thức tọa độ của phép tịnh tiến ta có:
1 2
1 3
x
y
1
2
x
y
. Suy
ra
1;2
A
.
Câu 1:
(THPT Triệu Sơn 1-lần 1 năm 2017-2018)
Phép biến hình nào sau đây không là phép dời hình?
A. Phép tịnh tiến. B. Phép đối xứng tâm. C. Phép đối xứng trục. D. Phép vị tự.
Lời giải
Chọn D
Phép vị tự tâm
I
tỷ số
k
biến đoạn thẳng
AB
thành đoạn thẳng
.A B k AB
nên nó không
phải là phép dời hình với
1
k
.
Câu 2:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Cho hình bình hành
ABCD
. Ảnh
của điểm
D
qua phép tịnh tiến theo véctơ
AB
là:
A.
B
. B.
C
. C.
D
. D.
A
.
Lời giải
Chọn B
Ta có :
:
AB
AB DC T D C
Thấy ngay phép tịnh tiến theo véctơ
AB
biến điểm
D
thành điểm
C
vì
AB DC
.
Câu 3:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Cho hình thoi
ABCD
tâm
O
. Trong các mệnh
đề sau, mệnh đề nào là mệnh đề đúng?
A. Phép vị tự tâm
O
, tỉ số
1
k
biến tam giác
ABD
thành tam giác
CDB
.
B. Phép quay tâm
O
, góc
2
biến tam giác
OBC
thành tam giác
OCD
.
C. Phép vị tự tâm
O
, tỉ số
1
k
biến tam giác
OBC
thành tam giác
ODA
.
D. Phép tịnh tiến theo véc tơ
AD
biến tam giác
ABD
thành tam giác
DCB
.
Lời giải
Chọn A
B
C
D
O
A
Ta có:
, 1O
V A C
;
, 1O
V B D
;
, 1O
V D B
. Nên chọn phương án A.
Câu 4:
(THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018)
Trong các khẳng định dưới đây, khẳng định
nào sai?
A. Tam giác đều có ba trục đối xứng.
B. Phép quay biến một đường thẳng thành một đường thẳng song song với nó.
C. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
D. Phép vị tự tâm
I
tỉ số
1
k
là phép đối xứng tâm.
A
B
C
D
Lời giải
Chọn B
Phép quay biến một đường thẳng thành một đường thẳng.
Câu 5:
(SGD Bắc Ninh năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
2;5
M
. Phép
tịnh tiến theo vectơ
1;2
v
biến điểm
M
thành điểm
M
. Tọa độ điểm
M
là:
A.
3;7
M
. B.
1;3
M
. C.
3;1
M
. D.
4;7
M
.
Lời giải
Chọn A
Gọi
;
v
T M M x y
2 1 3
5 2 7
x
y
. Vậy
3;7
M
.
Câu 6:
(THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018)
Hình nào dưới nào dưới đây
không có trục đối xứng?
A. Tam giác cân.
B. Hình thang cân.
C. Hình elip.
D. Hình bình hành.
Hướng dẫn giải
Chọn D
Câu 7:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
, cho véctơ
3; 5
v
. Tìm ảnh của điểm
1; 2
A
qua phép tịnh tiến theo véctơ
v
.
A.
4; 3
A
. B.
2; 3
A
. C.
4; 3
A
. D.
2; 7
A
.
Lời giải
Chọn D
Ta có
3 1 3 2
5 2 5 7
A A
A A
x x
y y
2; 7
A
.
Câu 8:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Cho hình chóp tam giác
.
S ABC
với
SA
,
SB
,
SC
đôi một vuông góc và
SA SB SC a
. Tính thế tích của khối chóp
.
S ABC
.
A.
3
1
3
a
. B.
3
1
2
a
. C.
3
1
6
a
. D.
3
2
3
a
.
Lời giải
Chọn C
Ta có
1
. .
3
SBC
V S SA
1 1
. . . .
3 2
SB SC SA
3
1
.
6
a
.
Câu 9:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Cho lăng trụ tam giác đều
.
ABC A B C
có
tất cả các cạnh bằng
2a
. Tính thể tích khối lăng trụ
.
ABC A B C
.
A.
3
3
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
2 3
a
.
Lời giải
Chọn C
Ta có
2
3
2 3
. .2 2 3
4
ABC
a
V S AA a a
.
Câu 10:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Cho
4 5IA IB
. Tỉ số vị tự
k
của phép vị
tự tâm
I
, biến
A
thành
B
là
A.
4
5
k
. B.
3
5
k
. C.
5
4
k
. D.
1
5
k
.
Lời giải
Chọn A
Ta có
4 5IA IB
4
5
IA IB
. Vậy tỉ số
4
5
k
.
Câu 11:
(THPT Kinh Môn 2-Hải Dương năm 2017-2018)
Trong mặt phẳng
cho đường tròn
C
có phương trình
2 2
1 1 4
x y
. Phép vị tự tâm
O
(với
O
là gốc tọa độ) tỉ số
2
k
biến
C
thành đường tròn nào trong các đường tròn có phương trình sau ?
A.
2 2
1 1 8
x y
. B.
2 2
2 2 8
x y
.
C.
2 2
2 2 16
x y
. D.
2 2
2 2 16
x y
.
Lời giải
Chọn D
Đường tròn
C
có tâm
1;1
I
, bán kính
2R
.
Gọi đường tròn
C
có tâm
I
, bán kính
R
là đường tròn ảnh của đường tròn
C
qua phép
vị tự
;2
O
V
.
Khi đó
;2O
V I I
2OI OI
2
2
x
y
2;2
I
.
Và
2 4R R
.
Vậy phương trình đường tròn
C
:
2 2
2 2 16
x y
.
Câu 12:
(THPT Quãng Xương 1-Thanh Hóa năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
Oxy
,
cho vectơ
2; 1
v
và điểm
3; 2 .
M
Tìm tọa độ ảnh
M
của điểm
M
qua phép tịnh tiến
theo vectơ
.v
A.
5;3
M
. B.
1; 1
M
. C.
1;1
M
. D.
1;1
M
.
Lời giải
Chọn C
2 3 2 1
.
1 2 1 1
v
x x
T M M MM v
y y
Vậy
1;1 .
M
Câu 13:
(THPT Tứ Kỳ-Hải Dương năm 2017-2018)
Cho hình chữ nhật có
O
là tâm đối xứng. Hỏi có
bao nhiêu phép quay tâm
O
góc
,
0 2
biến hình chữ nhật trên thành chính nó?
A. Không có. B. Bốn. C. Hai. D. Ba.
Hướng dẫn giải
Chọn C
Ta có
, 0
O
Q
,
,
O
Q
biến hình chữ nhật có
O
là tâm đối xứng thành chính nó.
Vậy có hai phép quay tâm
O
góc
,
0 2
biến hình chữ nhật trên thành chính nó.
Câu 14:
(THPT Lương Văn ChasnhPhus Yên năm 2017-2018)
Phép tịnh tiến biến gốc tọa độ
O
thành
điểm
1;2
A
sẽ biến điểm
A
thành điểm
A
có tọa độ là:
A.
2;4
A
. B.
1; 2
A
. C.
4;2
A
. D.
3;3
A
.
Lời giải
Chọn A
Phép tịnh tiến biến gốc tọa độ
O
thành điểm
1;2
A
nên vectơ tịnh tiến
1;2 .
u OA
Khi đó,
1 1 2
2 2 4
x
y
2;4
A
.
Câu 15:
(THPT Đô Lương 4-Nghệ An năm 2017-2018)
Số hình đa diện lồi trong các hình dưới đây là
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn C
Quan sát bốn hình trên ta thấy chỉ có một hình thứ tư từ trái qua là hình đa diện lồi vì lấy bất kỳ
hai điểm nào thì đoạn thẳng nối hai điểm đó nằm trong khối đa diện.
Vậy chỉ có một đa diện lồi.
Câu 16:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Chọn khẳng định sai trong các khẳng định sau:
A. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
B. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
C. Phép tịnh tiến biến một đường tròn thành một đường tròn có cùng bán kính.
D. Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với nó.
Lời giải
Chọn D
Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó.
Câu 1:
(THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018)
Trong mặt phẳng với hệ trục tọa độ
Oxy
cho
2; 3
A
,
1;0
B
. Phép tịnh tiến theo
4; 3
u
biến điểm
A
,
B
tương ứng thành
A
,
B
khi đó, độ dài đoạn thẳng
A B
bằng
A.
10
A B
. B.
10
A B
. C.
13
A B
. D.
5
A B
.
Lời giải
Chọn A
Phép tịnh tiến bảo toàn độ dài nên
10
AB A B
.
Câu 2:
(THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018)
Trong mặt phẳng tọa độ
cho
vectơ
3; 1
u
. Phép tịnh tiến theo vectơ
u
biến điểm
1; 4
M
thành
A. Điểm
4; 5
M
. B. Điểm
2; 3
M
. C. Điểm
3; 4
M
. D. Điểm
4;5
M
.
Lời giải
Chọn A
Ta có
M M
M M
x a x
y b y
3 1
1 4
M
M
x
y
4; 5
M
.
Câu 3: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Cho hình chữ nhật
MNPQ
. Phép
tịnh tiến theo véc tơ
MN

biến điểm
Q
thành điểm nào?
A. Điểm
Q
. B. Điểm
N
. C. Điểm
M
. D. Điểm
P
.
Lời giải
Chọn D
Do
MNPQ
là hình chữ nhật nên
MN QP

MN
T Q P
.
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình
hành . Tìm giao tuyến của hai mặt phẳng
SAD
và
SBC
.
C
A
D
B
S
A. Là đường thẳng đi qua đỉnh
S
và tâm
O
đáy.
B. Là đường thẳng đi qua đỉnh
S
và song song với đường thẳng
BC
.
C. Là đường thẳng đi qua đỉnh
S
và song song với đường thẳng
.AB
D. Là đường thẳng đi qua đỉnh
S
và song song với đường thẳng
.BD
Lời giải
Chọn B
Xét hai mặt phẳng
SAD
và
SBC
Có :
S
chung và
//AD BC
Gọi
d
là giao tuyến của hai mặt phẳng
SAD
và
SBC
d
đi qua
S
và song song với
AD
và
BC
.
Câu 2:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
, cho điểm
3; 1
A
.
Tìm tọa độ điểm
B
sao cho điểm
A
là ảnh của điểm
B
qua phép tịnh tiến theo véctơ
2; 1
u
.
A.
1;0
B
. B.
5; 2
B
. C.
1; 2
B
. D.
1;0
B
.
Lời giải
Chọn D
Ta có
u
T B A
BA u
3 2
1 1
x
y
1
0
x
y
1;0
B
.
Câu 3: Cho hình hộp
.
ABCD A B C D
(như hình vẽ).
A'
B'
C'
B
D
C
A
D'
Chọn mệnh đề đúng?
A. Phép tịnh tiến theo
DC
biến điểm
A
thành điểm
B
.
B. Phép tịnh tiến theo
AB
biến điểm
A
thành điểm
C
.
C. Phép tịnh tiến theo
AC
biến điểm
A
thành điểm
D
.
D. Phép tịnh tiến theo
AA
biến điểm
A
thành điểm
B
.
Lời giải
Chọn A
Ta có:
DC A B
.
Nên phép tịnh tiến theo
DC
biến điểm
A
thành điểm
B
.
Câu 4: Trong mặt phẳng tọa độ
, phép tịnh tiến theo vectơ
1;2
v
biến điểm
4;5
M
thành điểm
nào sau đây?
A.
1;6
P
. B.
3;1
Q
. C.
5;7
N
. D.
4;7
R
.
Câu 5: Trong mặt phẳng tọa độ
, phép tịnh tiến theo vectơ
1;2
v
biến điểm
4;5
M
thành điểm
nào sau đây?
A.
1;6
P
. B.
3;1
Q
. C.
5;7
N
. D.
4;7
R
.
Lời giải
Chọn C
Phép tịnh tiến theo vectơ
1;2
v
biến điểm
4;5
M
thành điểm
5;7
N
.
Câu 6: Trong mặt phẳng tọa độ
, cho hai điểm
1;1
A
và
2;3
I
. Phép vị tự tâm
I
tỉ số
2
k
biến điểm
A
thành điểm
'A
. Tọa độ điểm
'A
là
A.
0;7
A
. B.
7;0
A
. C.
7;4
A
. D.
4;7
A
.
Câu 7: Trong mặt phẳng tọa độ
, cho hai điểm
1;1
A
và
2;3
I
. Phép vị tự tâm
I
tỉ số
2
k
biến điểm
A
thành điểm
A
. Tọa độ điểm
A
là
A.
0;7
A
. B.
7;0
A
. C.
7;4
A
. D.
4;7
A
.
Lời giải
Chọn D
Ta có:
'
IA k IA
x a k x a
y b k y b
1
1
x kx k a
y ky k b
2.1 3.2 4
2.1 3.3 7
x
y
Câu 8: Trong mặt phẳng tọa độ
, phép tính tiến theo vectơ
v
biến điểm
;M x y
thành điểm
;M x y
sao cho
2x x
và
4
y y
. Tọa độ của
v
là
A.
2;4
v
. B.
4; 2
v
. C.
2; 4
v
. D.
2;4
v
.
Câu 9: Trong mặt phẳng tọa độ
, phép tính tiến theo vectơ
v
biến điểm
;M x y
thành điểm
;M x y
sao cho
2x x
và
4
y y
. Tọa độ của
v
là
A.
2;4
v
. B.
4; 2
v
. C.
2; 4
v
. D.
2;4
v
.
Hướng dẫn giải
Chọn A
Gọi
;v a b
. Biểu thức tọa độ của phép tịnh tiến theo vectơ
v
là
x x a
y y b
Theo đề bài ta có
2; 4
a b
13
6
.
Câu 10: Trong mặt phẳng
cho điểm
2;1
A
và vectơ
1;3
a
. Phép tịnh tiến theo vectơ
a
biến điểm
A
thành điểm
A
. Tọa độ điểm
A
là
A.
1; 2
A
. B.
1;2
A
. C.
4;3
A
. D.
3;4
A
.
Câu 11: Trong mặt phẳng
cho điểm
2;1
A
và vectơ
1;3
a
. Phép tịnh tiến theo vectơ
a
biến điểm
A
thành điểm
A
. Tọa độ điểm
A
là
A.
1; 2
A
. B.
1;2
A
. C.
4;3
A
. D.
3;4
A
.
Hướng dẫn giải
Chọn D
Ta có:
a
A T A
3;4
A
.
Câu 12: Cho hình thoi
ABCD
tâm
I
. Phép tịnh tiến theo véc tơ
IA
biến điểm
C
thành điểm nào?
A. Điểm
B
. B. Điểm
C
. C. Điểm
D
. D. Điểm
I
.
Câu 13: Cho hình thoi
ABCD
tâm
I
. Phép tịnh tiến theo véc tơ
IA
biến điểm
C
thành điểm nào?
A. Điểm
B
. B. Điểm
C
. C. Điểm
D
. D. Điểm
I
.
Lời giải
Chọn D
Phép tịnh tiến theo véc tơ
IA
biến điểm
C
thành điểm
I
.
Câu 14: Trong mặt phẳng tọa độ
, phép tịnh tiến theo véc tơ
1;3
v
biến điểm
1;2
A
thành điểm
nào trong các điểm sau?
A.
2;5
M
. B.
1;3
P
. C.
3;4
N
. D.
3; 4
Q
.
Câu 15: Trong mặt phẳng tọa độ
, phép tịnh tiến theo véc tơ
1;3
v
biến điểm
1;2
A
thành điểm
nào trong các điểm sau?
A.
2;5
M
. B.
1;3
P
. C.
3;4
N
. D.
3; 4
Q
.
Lời giải
Chọn A
Ta có
;
v
M x y T A
AM v
1 1
2 3
x
y
2
5
x
y
.
Câu 16: Trong các mệnh đề sau, mệnh đề nào là sai?
A. Mọi phép đối xứng trục đều là phép dời hình. B. Mọi phép vị tự đều là phép dời hình.
C. Mọi phép tịnh tiến đều là phép dời hình. D. Mọi phép quay đều là phép dời hình.
Câu 17: Trong các mệnh đề sau, mệnh đề nào là sai?
A. Mọi phép đối xứng trục đều là phép dời hình. B. Mọi phép vị tự đều là phép dời hình.
C. Mọi phép tịnh tiến đều là phép dời hình. D. Mọi phép quay đều là phép dời hình.
Lời giải
I
A
C
D
B
Chọn B
Phép vị tự
,I k
V
chỉ là phép dời hình khi
1
k
.
Câu 18: Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
3;2
M
. Tọa độ của điểm
M
là ảnh của điểm
M
qua phép tịnh tiến theo vectơ
2; 1
v
là
A.
1;1
. B.
3; 2
. C.
5; 3
. D.
5;3
.
Câu 19: Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
3;2
M
. Tọa độ của điểm
M
là ảnh của điểm
M
qua phép tịnh tiến theo vectơ
2; 1
v
là
A.
1;1
. B.
3; 2
. C.
5; 3
. D.
5;3
.
Lời giải
Chọn A
Gọi
;M x y
. Khi đó:
MM v
3 2
2 1
x
y
1
1
x
y
. Vậy
1;1
M
.
Câu 20: Trong các mệnh đề sau, mệnh đề nào sai?
A. Phép quay biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
B. Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng nó.
C. Phép quay biến đường tròn thành đường tròn có cùng bán kính.
D. Phép tịnh tiến biến tam giác thành tam giác bằng nó.
Câu 21: Trong các mệnh đề sau, mệnh đề nào sai?
A. Phép quay biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
B. Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng nó.
C. Phép quay biến đường tròn thành đường tròn có cùng bán kính.
D. Phép tịnh tiến biến tam giác thành tam giác bằng nó.
Lời giải
Chọn A
Phép quay không biến đường thẳng thành đường thẳng song song với nó trong trường hợp góc
quay bất kì.
Câu 22: Trong các phép biến hình sau, phép nào không phải là phép dời hình?
A. Phép vị tự tỉ số
1
. B. Phép đối xứng tâm.
C. Phép quay. D. Phép chiếu vuông góc lên một đường thẳng.
Câu 23: Trong các phép biến hình sau, phép nào không phải là phép dời hình?
A. Phép vị tự tỉ số
1
. B. Phép đối xứng tâm.
C. Phép quay. D. Phép chiếu vuông góc lên một đường thẳng.
Lời giải
Chọn D
Phép dời hình là phép bào toàn khoảng cách giữa hai điểm bất kì nên phép chiếu vuông góc lên
một đường thẳng.
Câu 1:
(THPT Hoa Lư A-Ninh Bình-lần 1-năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
0xy
, phép
quay tâm
4; 3
I
góc quay
180
biến đường thẳng
: 5 0
d x y
thành đường thẳng
d
có
phương trình
A.
3 0
x y
. B.
3 0
x y
. C.
5 0
x y
. D.
3 0
x y
.
Lời giải
Chọn B
Ta có phép quay
o
;180
I
Q
là phép đối xứng tâm
I
( ký hiệu là
I
Đ
)
Vì
I d
nên nếu
I
Đ d d
thì
/ /d d
, suy ra phương trình
: 0 5
d x y m m
.
Xét
0;5
8; 11
4; 3
I
M d
Đ M M M
I
Cho
8; 11
M d
3
m
. Vậy
: 3 0
d x y
.
Câu 2:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Cho hình thoi
ABCD
tâm
O
(như hình vẽ).
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Phép tịnh tiến theo véc tơ
DA
biến tam giác
DCB
thành tam giác
ABD
.
B. Phép vị tự tâm
O
, tỉ số
1
k
biến tam giác
CDB
thành tam giác
ABD
.
C. Phép quay tâm
O
, góc
2
biến tam giác
OCD
thành tam giác
OBC
.
D. Phép vị tự tâm
O
, tỉ số
1
k
biến tam giác
ODA
thành tam giác
OBC
.
Lời giải
Chọn B
Ta có
O
là trung điểm của
AC
và
BD
nên ta có
; ;
OA OC OB OD OD OB

, 1 , 1 , 1
; ;
O O O
V C A V D B V B D
, 1O
V CDB ABD
.
Câu 3:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Cho hình chóp
.
S ABC
đáy
ABC
là tam giác
đều, cạnh bên
SA
vuông góc với đáy. Gọi
,M N
lần lượt là trung điểm của
AB
và
SB
. Trong
các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A.
CM SB
. B.
CM AN
. C.
MN MC
. D.
AN BC
.
Lời giải
Chọn D
M
M
d
d
180
A
B
C
D
O
Ta có
,
CM AB
CM SA CM SAB CM SB
SA AB SAB
Mà
AN SAB CM AN
Mặt khác
MN SA
MN ABC
SA ABC
Vì
MN
MN CM
CM ABC
SAB
.
Vậy
D
sai.
Câu 4:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Cho đường thẳng
d
có phương trình
2 0
x y
. Phép hợp thành của phép đối xứng tâm
O
và phép tịnh tiến theo
3;2
v
biến
d
thành đường thẳng nào sau đây?
A.
4 0.
x y
B.
3 3 2 0.
x y
C.
2 2 0.
x y
D.
3 0.
x y
Lời giải.
Chọn D
Giả sử
d
là ảnh của
d
qua phép hợp thành trên (do
d
song song hoặc trùng với
d
)
: 0
d x y c
.
Lấy
1;1
M d
.
Giả sử
M
là ảnh của
M
qua phép đối xứng tâm
1; 1
O M
.
Giả sử
v
T M N
2;1
N
.
Ta có
N d
1 1 0
c
3
c
.
Vậy phương trình
: 3 0
d x y
.
Câu 5:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong mặt phẳng
, tìm phương trình
đường tròn
C
là ảnh của đường tròn
2 2
: 1
C x y
qua phép đối xứng tâm
1;0
I
.
A.
2
2
2 1
x y
. B.
2
2
2 1
x y
. C.
2
2
2 1
x y
. D.
2
2
2 1
x y
.
Lời giải
Chọn C
C
có tâm
0;0
O
và bán kính
1R
.
Qua phép đối xứng tâm
1;0
I
, ảnh của
0;0
O
là
2;0
O
(vì
I
là trung điểm của
OO
),
R R
với
R
là bán kính của
C
.
Vậy phương trình đường tròn
C
là:
2
2
2 1
x y
.
S
A
B
M
C
N
Câu 6:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Trong mặt phẳng
Oxy
, tìm phương
trình đường tròn
C
là ảnh của đường tròn
2 2
: 1
C x y
qua phép đối xứng tâm
1;0
I
.
A.
2
2
2 1
x y
. B.
2
2
2 1
x y
. C.
2
2
2 1
x y
. D.
2
2
2 1
x y
.
Lời giải
Chọn C
C
có tâm
0;0
O
và bán kính
1R
.
Qua phép đối xứng tâm
1;0
I
, ảnh của
0;0
O
là
2;0
O
(vì
I
là trung điểm của
OO
),
R R
với
R
là bán kính của
C
.
Vậy phương trình đường tròn
C
là:
2
2
2 1
x y
.
Câu 7:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong mặt phẳng
Oxy
, qua phép quay
, 90
Q O
,
3; 2
M
là ảnh của điểm:
A.
3; 2
M
. B.
3;2
M
. C.
2;3
M
. D.
2; 3
M
.
Lời giải
Chọn C
Áp dụng công thức tọa độ của phép quay :
;
: ; ;
O
Q M x y M x y
thì biểu thức tọa độ là :
cos sin
sin cos
x x y
y x y
Áp dụng vào bài ta có
3 cos90 sin 90
2 sin 90 cos90
x y
x y
2
3
x
y
2;3
M
.
Câu 8:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
cho đường tròn
2 2
: 2 4 4 0
C x y x y
và đường tròn
2 2
: 6 4 4 0.
C x y x y
Tìm tâm vị tự của hai đường tròn?
A.
0;1 ; 3;4 .
I J
B.
1; 2 ; 3;2 .
I J
C.
1;2 ; 3; 2 .
I J
D.
1;0 ; 4;3 .
I J
Lời giải
Chọn A
Gọi
1 2
;I I
lần lượt là tâm đường tròn
;
C C
. Ta có
1 2
1; 2 ; 3; 2
I I
và bán kính
1 2
1; 3.
R R
Do đó hai đường tròn này khác tâm và khác bán kính, suy ra sẽ có
một tâm vị tự trong và một tâm vị tự ngoài.
Gọi
;I J
là hai tâm vị tự cần tìm, ta có tỉ số vị tự
1
2
1
.
3
R
k
R
Với đáp A: Ta có
1 2 1 2
1
1; 1 ; 3; 3 .
3
II II II II
1 2 1 2
1
2; 2 ; 6; 6 .
3
JI JI JI JI
Vậy đáp A thỏa mãn nên ta Chọn A
Nhận xét: Câu
12
là câu không đáp ứng được yêu cầu của đề thi THPT vì theo khung chương
trình của Bộ Giáo Dục thì giảm tải nội dung tâm vị tự của hai đường tròn.
Câu 9:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
cho đường thẳng
: 2 6 0.
x y
Viết phương trình đường thẳng
là ảnh của đường thẳng
qua phép quay tâm
O
góc
90 .
A.
2 6 0.
x y
B.
2 6 0.
x y
C.
2 6 0.
x y
D.
2 6 0.
x y
Lời giải
Chọn A
Véc tơ pháp của tuyến của đường thẳng
là
1
1;2
n
. Vì
o
;90
:
O
Q
nên
véctơ pháp của tuyến của đường thẳng
là
2
2; 1
n
.
Lấy
o
;90
6;0
:
O
M
Q M M
0;6M
.
Phương trình đường thẳng
là:
2 6 0
x y
Câu 10:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Cho tứ diện
ABCD
,
M
,
N
lần lượt
là trung điểm của
AB
và
BC
.
P
là điểm trên cạnh
AC
sao cho
2
CP PD
. Mặt phẳng
MNP
cắt
AD
tại
Q
. Tính tỉ số
AQ
QD
?
A.
1
2
. B.
3
. C.
2
3
. D.
2
.
Lời giải
Chọn D
Ta có
//
//
MN AC
MN ACD
AC ACD
Lại có
//
// //
MN ACD
PQ MN AC
MNP ACD PQ
.
Vì
//
PQ AC
nên
1
3
DQ DP
DA DC
Khi đó
2
AQ
QD
.
Câu 11:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Trong mặt phẳng
Oxy
, cho đường
tròn
2 2
: 1 3 4
C x y
. Phép tịnh tiến theo vectơ
3;2
v
biến đường tròn
C
thành
đường tròn có phương trình nào sau đây?
A.
2 2
2 5 4
x y
. B.
2 2
4 1 4
x y
.
A
B
C
D
M
N
P
Q
C.
2 2
1 3 4
x y
. D.
2 2
2 5 4
x y
.
Lời giải
Chọn A
2 2
: 1 3 4
C x y
có tâm
1;3
I
và bán kính
2R
.
C
là ảnh của
C
qua phép tịnh tiến theo vectơ
3;2
v
sẽ có tâm
I
và bán kính
2R R
với
1 3 2
3 2 5
I I
v
I I
x x
T I I
y y
.
Vậy
2 2
: 2 5 4
C x y
.
Câu 12:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Trong mặt phẳng
Oxy
, cho điểm
3;6
B
. Tìm tọa độ điểm
E
sao cho
B
là ảnh của
E
qua phép quay tâm
O
góc quay
90
.
A.
6; 3
E
. B.
3; 6
E
. C.
6;3
E
. D.
3;6
E
.
Lời giải
Chọn A
Ta có:
; 90 ;90O O
Q E B Q B E
.
Theo biểu thức tọa độ của phép quay tâm
O
góc quay
90
, ta có:
6
3
E B
E B
x y
y x
.
Vậy
6; 3
E
.
Câu 13:
(THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
Oxy
,
tìm tọa độ điểm
M
là ảnh của điểm
2;1
M
qua phép đối xứng tâm
3; 2
I
A.
1; 3
M
. B.
5;4
M
. C.
4; 5
M
. D.
1;5
M
.
Lời giải
Chọn C
;
M x y
là ảnh của
M
qua phép đối xứng tâm
3; 2
I
khi và chỉ khi
MM
nhận
I
là trung
điểm
2.3 2 4
2. 2 1 5
x
y
.
Vậy
4; 5
M
.
Câu 14:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có
2; 4
A
,
5;1
B
,
1; 2
C
. Phép tịnh tiến
BC
T
biến tam giác
ABC
tành tam giác
A B C
. Tìm tọa độ trọng tâm của tam giác
A B C
.
A.
4; 2
. B.
4; 2
. C.
4; 2
. D.
4; 2
.
Lời giải
Chọn D
Gọi
G
là trọng tâm tam giác
ABC
và
BC
G T G
.
Ta có
2 5 1 4 1 2
;
3 3
G
hay
2;1
G
.
Lại có
6; 3
BC
mà
6; 3
BC
G T G GG BC
. Từ đó ta có
; 6; 3
G G G G
x x y y
' '
2; 1 6; 3
G G
x y
' '
; 4; 2
G G
x y
.
Câu 15:
(THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018)
Trong mặt phẳng với hệ toạ độ
Oxy
,
cho véctơ
1; 2
v
, điểm
3; 5
A
. Tìm tọa độ của các điểm
A
là ảnh của
A
qua phép tịnh
tiến theo
v
.
A.
2; 7
A
. B.
2; 7
A
. C.
7; 2
A
. D.
2; 7
A
.
Lời giải
Chọn A
Biểu thức tọa độ của phép tịnh tiến theo
v
là:
1 2
2; 7
2 7
x x
A
y y
.
Câu 16:
(THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018)
Trong mặt phẳng
, ảnh của điểm
2; 3
M
qua phép đối xứng trục
: 0
x y
là
A.
3;2
M
. B.
3; 2
M
. C.
3; 2
M
. D.
3;2
M
.
Lời
giải
Chọn D
Gọi
;M x y
. Khi đó
;
MM x x y y
.
Ta có
1;1
n
1;1
u
.
Ta biết
Đ M M
khi và chỉ khi
là trung trực của đoạn
MM
. 0
;
2 2
MM u
x x y y
I
0
0
x x y y
x x y y
y
x y
x
.
Khi
2;3
M
Đ M M
nên
3
:
2
x
M
y
.
Vậy
3;2
M
.
Câu 1:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Trong mặt phẳng
Oxy
, cho
1;2
v
, điểm
2;5
M
. Tìm tọa độ ảnh của điểm
M
qua phép tịnh tiến
v
.
A.
1;6
. B.
3;7
. C.
4;7
. D.
3;1
.
Lời giải
Chọn B
Gọi
;M x y
là ảnh của điểm
M
qua phép tịnh tiến
v
.
Ta có
MM v
2; 5 1;2
x y
2 1
5 2
x
y
3
7
x
y
3;7
M
.
Câu 2:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
cho
các điểm
3;1
I
,
1; 1
J
. Ảnh của
J
qua phép quay
0
90
I
Q
là
A.
1;5
J
. B.
5; 3
J
. C.
3;3
J
. D.
1; 5
J
.
Lời giải
Chọn A
Gọi
;
J x y
là ảnh của điểm
;J x y
qua phép quay tâm
;I a b
góc quay
90
.
Trong đó:
1; 1
J
,
3;1
I
.
Ta có:
cos sin
sin cos
x x a y b a
y x a y b b
3 cos 90 1 sin 90 3
3 sin 90 1 cos 90 1
x x y
y x y
1
5
x
y
Câu 3:
(THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018)
Trong mặt phẳng tọa độ
, cho đường
tròn
2 2
: 1 2 4
C x y
. Tìm ảnh của đường tròn
C
qua phép vị tự tâm
O
tỉ số
2
.
A.
2 2
2 4 16
x y
. B.
2 2
2 4 16
x y
.
C.
2 2
2 4 16
x y
. D.
2 2
2 4 16
x y
.
Lời giải
Chọn B
Gọi
;
M x y C
và
; 2
;
O
M x y V M
, ta có:
2
2
x
OM OM x
;
2
y
y
.
Mà
M C
nên:
2 2
1 2 4
2 2
x y
2 2
2 4 16
x y
.
Vậy, phương trình ảnh của
C
cần tìm là:
2 2
2 4 16
x y
.
Câu 4:
(SGD Ninh Bình năm 2017-2018)
Cho lục giác đều
ABCDEF
tâm
O
như hình bên. Tam giác
EOD
là ảnh
của tam giác
AOF
qua phép quay tâm
O
góc quay
. Tìm
.
A.
o
60
. B.
o
60
.
C.
o
120
. D.
o
120
.
O
F
E
D
C
B
A
Lời giải
Chọn B
; 120O
Q O O
,
; 120O
Q A F
.
; 120O
Q F D
.
Câu 5:
(THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018)
Trong mặt phẳng tọa độ
Oxy
,
cho vectơ
1;2
v
. Tìm ảnh của điểm
2;3
A
qua phép tịnh tiến theo vectơ
v
.
A.
5; 1
A
. B.
1;5
A
. C.
3; 1
A
. D.
3;1
A
.
Hướng dẫn giải
Chọn B
Giả sử
;A x y
.
Ta có
v
T A A AA v
2 1
3 2
x
y
1
5
x
y
1;5
A
.
Câu 6:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 1 0
x y
. Để phép tịnh tiến theo
v
biến đường thẳng
d
thành chính nó
thì
v
phải là vectơ nào trong các vectơ sau đây ?
A.
2;4
v
. B.
2;1
v
. C.
1;2
v
. D.
2; 4
v
.
Lời giải
Chọn A
Phép tịnh tiến theo
v
biến đường thẳng
d
thành chính nó khi vectơ
v
cùng phương với vectơ
chỉ phương của
d
. Mà
d
có VTCP
1;2
u
.
Câu 7:
(THPT Kinh Môn 2-Hải Dương năm 2017-2018)
Trong mặt phẳng tọa độ
cho điểm
1;2
M
. Phép tịnh tiến theo vectơ
3;4
u
biến điểm
M
thành điểm
M
có tọa độ là
A.
2;6
M
. B.
2;5
M
. C.
2; 6
M
. D.
4; 2
M
.
Lời giải
Chọn A
Theo biểu thức tọa độ của phép tịnh tiến
x x a
y y b
1 3
2 4
x
y
2
6
x
y
.
Vậy
2;6
M
.
Câu 8:
(THPT Ninh Giang-Hải Dương năm 2017-2018)
Trong mặt phẳng
Oxy
, cho vectơ
3;2
v
và đường thẳng
: 3 6 0
x y
. Viết phương trình đường thẳng
là ảnh của đường thẳng
qua phép tịnh tiến theo vec-tơ
v
.
A.
:3 15 0
x y
. B.
:3 5 0
x y
. C.
: 3 15 0
x y
. D.
: 3 15 0
x y
.
Lời giải
Chọn D
Ta có
//
: 3 0
x y m
6
m
.
Lấy
0;2M
, giả sử
v
M T M
0 3;2 2
M
3;4
M
.
Do
M
3 12 0
m
15
m
thỏa mãn
6
m
: 3 15 0
x y
.
Câu 9:
(THPT Ninh Giang-Hải Dương năm 2017-2018)
Trong mặt phẳng
, cho đường tròn
2 2
: 4 10 4 0
C x y x y
. Viết phương trình đường tròn
C
biết
C
là ảnh của
C
qua phép quay với tâm quay là gốc tọa độ
O
và góc quay bằng
270
.
A.
2 2
: 10 4 4 0
C x y x y
. B.
2 2
: 10 4 4 0
C x y x y
.
C.
2 2
: 10 4 4 0
C x y x y
. D.
2 2
: 10 4 4 0
C x y x y
.
Lời giải
Chọn B
Đường tròn
C
có tâm
2; 5
I
, bán kính
4 25 4 5
R
.
Ta có
,270O
C Q C
, 90O
C Q C
,90O
C Q C
.
Do đó
,90O
I Q I
. Vì đây là phép quay
90
nên
5
2
I I
I I
x y
y x
, suy ra
5;2
I
.
Bán kính đường tròn
C
là
5
R R
.
Vậy
2 2
: 5 2 25
C x y
2 2
: 10 4 4 0
C x y x y
.
Câu 10:
(THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018)
Trong mặt phẳng
Oxy
, cho đường
thẳng
: 2 0
x y
. Hãy viết phương trình đường thẳng
d
là ảnh của đường thẳng
qua
phép quay tâm
O
, góc quay
90
.
A.
: 2 0
d x y
. B.
: 2 0
d x y
. C.
: 2 0
d x y
. D.
: 4 0
d x y
.
Lời giải
Chọn A
Đường thẳng
d
là ảnh của đường thẳng
qua phép quay tâm
O
, góc quay
90
nên
d
vuông
góc với
.
Phương trình
d
có dạng
0
x y c
1
Chọn
0;2M
,
M
là ảnh của
M
qua phép quay nên
2;0
M d
Thay vào
1
:
2
c
.
Vậy phương trình
: 2 0
d x y
.
Câu 11:
(THPT Tứ Kỳ-Hải Dương năm 2017-2018)
Trong mặt phẳng
Oxy
, cho điểm
(2;5)
A
. Phép
tịnh tiến theo vectơ
1;2
v
biến
A
thành điểm
A.
3;7
P
. B.
1;6
N
. C.
3;1
M
. D.
4;7
Q
.
Hướng dẫn giải
Chọn A
Ta có
2 1 3
: 2;5 ,
5 2 7
v
x x
T A A x y AA v
y y
.
3;7
A
A P
.
Vậy phép tịnh tiến theo vectơ
1;2
v
biến
A
thành điểm
3;7
P
.
Câu 12:
(THPT Xuân Trường-Nam Định năm 2017-2018)
Trong mặt phẳng tọa độ
, tìm phương
trình đường thẳng
là ảnh của đường thẳng
: 2 1 0
x y
qua phép tịnh tiến theo véctơ
1; 1
v
.
A.
: 2 3 0
x y
. B.
: 2 0
x y
. C.
: 2 1 0
x y
. D.
: 2 2 0
x y
.
Lời giải
Chọn B
Gọi
;M x y
là điểm thuộc
.
1 1
;
1 1
v
x x x x
M x y T M
y y y y
.
Thay vào phương trình đường thẳng
ta được:
1 2 1 1 0 2 0
x y x y
.
Vậy phương trình đường thẳng
là ảnh của đường thẳng
có dạng:
2 0
x y
.
Câu 13:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
, cho
đường tròn
C
:
2 2
2 1 9
x y
. Gọi
C
là ảnh của đường tròn
C
qua việc thực hiện
liên tiếp phép vị tự tâm
O
, tỉ số
1
3
k
và phép tịnh tiến theo vectơ
1; 3
v
. Tính bán kính
R
của đường tròn
C
.
A.
9
R
. B.
3
R
. C.
27
R
. D.
1R
.
Lời giải
Chọn D
Đường tròn
C
có bán kính
3
R
.
Qua phép vị tự tâm
O
, tỉ số
1
3
k
, đường tròn
C
biến thành đường tròn
1
C
có bán kính
là
1
.R k R
1
.3 1
3
.
Qua phép tính tiến theo vectơ
1; 3
v
, đường tròn
1
C
biến thành đường tròn
C
có bán
kính
1
1
R R
.
Vậy
R
của đường tròn
C
là
1R
.
Câu 14:
(THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018)
Cho tam giác
ABC
với trọng tâm
G
.
Gọi
A
,
B
,
C
lần lượt là trung điểm của các cạnh
BC
,
AC
,
AB
của tam giác
ABC
. Khi đó
phép vị tự nào biến tam giác
A B C
thành tam giác
ABC
?
A. Phép vị tự tâm
G
, tỉ số
1
2
. B. Phép vị tự tâm
G
, tỉ số
1
2
.
C. Phép vị tự tâm
G
, tỉ số 2. D. Phép vị tự tâm
G
, tỉ số
2
.
Hướng dẫn giải
Chọn D
Vì
G
là trọng tâm tam giác
ABC
nên
2
GB GB
, 2G
V B B
Tương tự
, 2G
V A A
và
, 2G
V C C
Vậy phép vị tự tâm
G
, tỉ số
2
biến tam giác
A B C
thành tam giác
ABC
.
Câu 15:
(THTT số 5-488 tháng 2 năm 2018)
Trong mặt phẳng
Oxy
, cho điểm
2; 1
I
. Gọi
C
là đồ
thị hàm số
sin 3y x
. Phép vị tự tâm
2; 1
I
, tỉ số
1
2
k
biến
C
thành
C
. Viết
phương trình đường cong
C
.
A.
3 1
sin 6 18
2 2
y x
. B.
3 1
sin 6 18
2 2
y x
.
C.
3 1
sin 6 18
2 2
y x
. D.
3 1
sin 6 18
2 2
y x
.
Lời giải
Chọn D
Ta có:
,
:
I k
M C V M N C
N I M I
N I M I
x x k x x
IN k IM
y y k y y
1
2 2
2
1
1 1
2
N M
N M
x x
y y
2 6
2 3
M N
M N
x x
y y
2 6; 2 3
N N
M x y C
Thay tọa độ
M
vào hàm số
sin 3y x
ta có:
2 3 sin 3 2 6
N N
y x
3 1
sin 6 18
2 2
N N
y x
3 1
sin 6 18
2 2
N N
y x
.
Vậy đường cong
C
có phương trình là
3 1
sin 6 18
2 2
y x
.
Câu 16:
(THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018)
Cho tam giác
ABC
có diện tích
bằng
6
2
cm
. Phép vị tự tỷ số
2
k
biến tam giác
ABC
thành tam giác
A B C
. Tính diện
tích tam giác
A B C
?
A.
12
2
cm
. B.
24
2
cm
. C.
6
2
cm
. D.
3
2
cm
.
Lời giải
Chọn B
Phép vị tự tỉ số
k
biến tam giác thành tam giác đồng dạng với tỉ số
k
.
Theo đề bài ta có phép vị tự tỉ số
2
k
biến biến tam giác
ABC
thành tam giác
A B C
nên
2
ABC
A B C
S
k
S
2
.
A B C
ABC
S k S
2
2 .
A B C
ABC
S S
4.6
A B C
S
24
A B C
S
2
cm
.
Câu 1:
(THPT Chuyên Lam Sơn-Thanh Hóa-lần 2 năm 2017-2018)
Trong mặt phẳng tọa độ
Oxy
cho
điểm
3;4
A
. Gọi
A
là ảnh của điểm
A
qua phép quay tâm
0;0
O
, góc quay
90
. Điểm
A
có tọa độ là
A.
3;4
A
. B.
4; 3
A
. C.
3; 4
A
. D.
4;3
A
.
Lời giải
Chọn D
Ta có
.cos90 .sin 90 4
.sin 90 .cos90 3
A A A A
A A A A
x x y y
y x y x
4;3
A
.
Câu 2:
(THPT Chuyên Tiền Giang-lần 1 năm 2017-2018)
Trong mặt phẳng
, cho vectơ
3;3
v
và đường tròn
2 2
: 2 4 4 0
C x y x y
. Ảnh của
C
qua phép tịnh tiến vectơ
v
là đường
tròn nào?
A.
2 2
: 4 1 4
C x y
. B.
2 2
: 4 1 9
C x y
.
C.
2 2
: 4 1 9
C x y
. D.
2 2
: 8 2 4 0
C x y x y
.
Lời giải
Chọn B
Ta có
2 2
: 2 4 4 0
C x y x y
2 2
1 2 9
x y
.
Vậy đường tròn
C
có tâm
1; 2
I
và bán kính
3
R
.
Gọi
;
v
I x y T I
khi đó ta có
1 3
2 3
x
y
4
1
x
y
.
Do phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính nên phương trình đường
tròn
C
là
2 2
: 4 1 9
C x y
.
Câu 3: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:
d y x
. Tìm ảnh của
d
qua phép quay tâm
O
, góc quay
90
.
A.
: 2d y x
. B.
:
d y x
. C.
: 2d y x
. D.
:
d y x
.
Lời giải
Chọn B
Phép quay tâm
O
, góc quay
90
biến điểm
;M x y
thành điểm
;M x y
với
x y
y x
.
Mà
0
TQ
y x x y x y y x
.
Câu 1:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Trong mặt phẳng
Oxy
, tìm phương trình đường tròn
C
là ảnh của đường tròn
C
:
2 2
1
x y
qua phép đối
xứng tâm
1; 0
I
.
A.
2
2
2 1
x y
. B.
2
2
2 1
x y
.
C.
2
2
2 1
x y
. D.
2
2
2 1
x y
.
Lời giải
Chọn C
Đường tròn
C
có tâm
0; 0
O
, bán kính
1R
.
Gọi
O
là ảnh của
O
qua phép đối xứng tâm
1; 0
I
.
Ta có:
2
2
O O
I
O O
I
x x
x
y y
y
2
2
O I O
O I O
x x x
y y y
2.1 0
2.0 0
O
O
x
y
2; 0
O
.
Đường tròn
C
là ảnh của đường tròn
C
qua phép đối xứng tâm
1; 0
I
.
C
có tâm
2; 0
O
, bán kính
1R R
.
Phương trình đường tròn
C
là:
2
2
2 1
x y
.
Câu 2: Trong mặt phẳng tọa độ
Oxy
, phép quay tâm
O
góc quay
90
biến điểm
1; 2
M
thành điểm
M
. Tọa độ điểm
M
là
A.
2;1
M
. B.
2; 1
M
. C.
2; 1
M
. D.
2;1
M
.
Câu 3: Trong mặt phẳng tọa độ
Oxy
, phép quay tâm
O
góc quay
90
biến điểm
1; 2
M
thành điểm
M
. Tọa độ điểm
M
là
A.
2;1
M
. B.
2; 1
M
. C.
2; 1
M
. D.
2;1
M
.
Lời giải
Chọn C
x
y
1
2
M
O
M'
1-1
2
-2
-1
Có
;90
; 90
O
OM OM
M Q M
OM OM
.
Phương trình đường thẳng
OM
qua
O
, vuông góc với
OM
có dạng
2 0
x y
.
Gọi
2 ;M a a
. Do
OM OM
2
2 2 2
4 1 2
a a
1
1
a
a
2;1
2; 1
M
M
.
Có
2;1
M
là ảnh của
M
qua phép quay góc
90
,
2; 1
M
là ảnh của
M
qua phép
quay góc
90
. Vậy chọn
2; 1
M
.
Trắc nghiệm:
Điểm
;M b a
là ảnh của
;M a b
qua phép quay tâm
O
, góc quay
90
. Vậy chọn
2; 1
M
.
Câu 35: [1H1-3]
(THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018)
Cho tứ diện
ABCD
có
2BD
. Hai tam giác
ABD
và
BCD
có diện tích lần lượt là
6
và
10
. Biết thể tích khối tứ
diện
ABCD
bằng
16
. Tính số đo góc giữa hai mặt phẳng
,ABD
BCD
.
A.
4
arccos
15
. B.
4
arcsin
5
. C.
4
arccos
5
. D.
4
arcsin
15
.
Lời giải
Chọn B.
Gọi
H
là hình chiếu của
A
xuống
BCD
. Ta có
1 3 24
.
3 5
ABCD BCD
BCD
V
V AH S AH
S
.
Gọi
K
là hình chiếu của
A
xuống
BD
, dễ thấy
HK BD
. Vậy
,
ABD BCD AKH
Mặt khác
2
1
. 6
2
ABD
ABD
S
S AK BD AK
BD
.
Do đó
4
, arcsin arcsin
5
AH
ABD BCD AKH
AK
.
Câu 32. [1H1-3]
(THTT Số 1-484 tháng 10 năm 2017-2018)
Trong mặt phẳng tọa độ
, cho hai
đường tròn
2 2
: 2 5
C x m y
và
2 2 2
: 2 2 6 12 0
C x y m y x m
. Vectơ
v
nào dưới đây là vectơ của phép tịnh tiến biến
C
thành
C
?
A.
2;1
v
. B.
2;1
v
. C.
1;2
v
. D.
2; 1
v
.
Lời giải
Chọn A.
Điều kiện để
C
là đường tròn
2
2
1
2 9 12 0 4 1 0
4
m m m m
.
Khi đó:
Đường tròn
C
có tâm là
2 ; 3
I m
, bán kính
4 1
R m
.
Đường tròn
C
có tâm là
;2
I m
, bán kính
5
R
.
Phép tịnh tiến theo vectơ
v
biến
C
thành
C
khi và chỉ khi
R R
II v
H
K
B
D
C
A
1
4 1 5
2;1
3 ;
m
m
v
v II m m
.Vậy chọn A
Câu 35: [1H1-3]
(THPT Nguyễn Khuyến-Nam Định-lần 1-năm 2017-2018)
Cho hình chóp
.
S ABC
có
đáy
ABC
là tam giác vuông tại
B
,
AB a
, cạnh bên
SA
vuông góc với mặt đáy và
2SA a
. Gọi
M
là trung điểm của
AB
. Tính khoảng cách
d
giữa hai đường thẳng
SM
và
BC
.
A.
3
2
a
d
. B.
2
3
a
d
. C.
3
3
a
d
. D.
2
a
d
.
Lời giải
Chọn B.
Gọi
N
là trung điểm
AC
Ta có
//
//
MN BC
BC SMN
MN SMN
, , , ,
d SM BC d BC SMN d B SMN d A SMN
(vì
M
là trung điểm
AB
).
Mặt khác
MN AB
MN SAB
MN SA
;
SMN SAB
MN SMN
SMN SAB SM
Trong mặt phẳng
SAB
, kẻ
,
AH SM AH SMN AH d A SMN
Tam giác
SAM
vuông tại
A
có
2 2 2
1 1 1 2
3
a
AH
AH SA AM
.
Vậy
2
,
3
a
d SM BC
.
Câu 50: [1H1-3]
(THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018)
Cho
tứ diện
ABCD
có các tam giác
ABC
và
DBC
vuông cân và nằm trong hai mặt phẳng vuông góc với nhau,
2 .AB AC DB DC a
Tính khoảng cách từ
B
đến mp
.ACD
A.
6.
a
B.
6
.
3
a
C.
6
.
2
a
D.
2 6
.
3
a
Lời giải
Chọn D.
S
A
B
C
M
N
H
Ta có
ABC DBC
và
.ABC DBC BC
Kẻ
.AH BC H BC AH BCD
Tam giác
ABC
vuông cân tại
2
2.
2 2
BC AB
A AH HB HC a
Từ
DBC
vuông cân tại
D
và
2HB HC HD HB HC a
và
.HD BC
Ta có
;
2 ; 2 ; 2 .
;
d B ACD
BC
d B ACD d H ACD h
HC
d H ACD
Để ý
, , HA HC HD
vuông góc với nhau từng đôi một
2 2 2 2 2 2 2
1 1 1 1 1 1 1 2 2 6
; 2 .
2 2 2 3 3
a
h a d B ACD h
h HA HC HD a a a
----------------------------------- HẾT -----------------------------------
Câu 43. [1H1-3]
(THPT Thạch Thành-
Thanh Hóa-năm 2017-2018)
Trong mặt phẳng
cho đường tròn
C
có phương trình
2 2
1 2 4.
x y
Hỏi phép vị tự tâm
O
tỉ số
2
k
biến
C
thành đường tròn nào sau
đây:
A.
2 2
4 2 4
x y
. B.
2 2
4 2 16
x y
.
C.
2 2
2 4 16
x y
. D.
2 2
2 4 16
x y
.
Lời giải
Chọn C.
Gọi
C
là ảnh của đường tròn
C
qua phép vị tự tâm
O
tỉ số
2
k
.
Đường tròn
C
có tâm
1;2
I
và bán kính
2R
.
Gọi
I
và
R
tâm và bán kính của đường tròn
C
.
Ta có:
2 .2 4
R k R
.
Mặt khác:
2 2.1 2
2 2; 4
2 2.2 4
I I
I I
x x
OI OI I
y y

.
Vậy, phương trình đường tròn
C
là
2 2
2 4 16.
x y
Câu 36. [1H1-3]
(TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018)
Cho lăng trụ
.
ABCD A B C D
có đáy
ACBD
là hình thoi cạnh
a
, biết
.
A ABC
là hình chóp đều và
A D
hợp với mặt đáy
một góc
45
. Thể tích khối lăng trụ
.
ABCD A B C D
là :
A.
3
a
. B.
3
6
12
a
. C.
3
3
a
. D.
3
6
3
a
.
Lời giải
Chọn A.
A
B
C
D
H
G
O
A
B
D
A'
C'
B'
D'
C
Ta có
, 45
A D ABCD A DG
.
Ta giác
ABC
đều cạnh
a
nên
3
3
a
BG
,
3DB a
,
2 3
2
3
a
DG BG
.
Tam giác
A DG
vuông cân tại
G
nên
2 3
3
a
A G DG
.
3
.
1 2 3
. . 3.
2 3
ABCD A B C D ABCD
a
V S AG a a a
.
Câu 4: [1H1-3]
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Cho tam giác
ABC
có
1;2
A
,
5;4
B
,
3; 2 .
C
Gọi
A
,
B
,
C
lần lượt là ảnh của
A
,
B
,
C
qua phép vị tự tâm
1;5
I
tỉ số
3
k
. Bán kính đường tròn ngoại tiếp tam giác
A B C
bằng:
A.
3 10
. B.
6 10
. C.
2 5
. D.
3 5
.
Lời giải
Chọn A.
Ta có:
2; 6
BC
,
4;2
AB
,
2; 4
AC
nên
. 0
AB AC
AB AC
.
Vậy tam giác
ABC
vuông tại
A
nên tâm đường tròn ngoại tiếp tam giác
ABC
là trung điểm
cạnh huyền
BC
và bán kính
10
2
BC
R
.
Gọi
R
là bán kính đường tròn ngoại tiếp tam giác
A B C
.
Tam giác
A B C
là ảnh của tam giác
ABC
qua phép vị tự tâm
I
tỉ số
3
k
.
Nên
3 3 10
R R
.
Câu 45. [1H1-3]
(THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018)
Cho hình chóp
SABC
. Bên trong tam giác
ABC
lấy một điểm
O
bất kỳ. Từ
O
dựng các đường thẳng lần lượt
song song với
SA
,
SB
,
SC
và cắt các mặt phẳng
SBC
,
SCA
,
SAB
theo thứ tự lần lượt
tại
A
,
B
,
C
. Khi đó tổng tỉ số
OA OB OC
T
SA SB SC
bằng bao nhiêu ?
A.
3
T
. B.
3
4
T
. C.
1T
. D.
1
3
T
.
Lời giải
Chọn C.
Gọi
M
,
N
,
P
lần lượt là giao điểm của
AO
,
BO
,
CO
với
BC
,
CA
,
AB
.
Từ
O
dựng các đường thẳng lần lượt song song với
SA
,
SB
,
SC
và cắt các đường thẳng
SM
,
SN
,
SP
lần lượt tại
A
,
B
,
C
.
Áp dụng định lý Talet trong các tam giác
SAM
,
SBN
,
SCP
ta có:
OA MO
SA MA
;
OB NO
SB NB
;
OC PO
SC PC
.
Khi đó
OA OB OC MO NO PO
T
SA SB SC MA NB PC
Gọi
1
S
,
2
S
,
3
S
S
lần lượt là diện tích các tam giác
OBC
,
OCA
,
OAB
,
ABC
. Dựng
OH BC
,
AK BC
nên
//
OH AK
.
Khi đó áp dụng định lý Talet trong tam giác
AKM
và tỉ số diện tích ta có
1
S
MO OH
MA AK S
.
Tương tự:
2
S
NO
NB S
và
3
S
PO
PC S
.
Vậy
3
1 2
1
S
S SOA OB OC S
T
SA SB SC S S S S
.
Cách giải nhanh: Đặc biệt hóa bài toán với
O
là trọng tâm tam giác
ABC
sẽ nhanh chóng tìm
ra đáp án.
Câu 49. [1H1-3]
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Cho ba điểm
A
,
B
,
C
thẳng hàng theo
thứ tự đó và
2
AB BC
. Dựng các hình vuông
ABEF
,
BCGH
(đỉnh của hình vuông tính theo chiều
kim đồng hồ). Xét phép quay tâm
B
góc quay
90
biến điểm
E
thành điểm
.A
Gọi
I
là giao điểm
của
EC
và
.GH
Giả sử
I
biến thành điểm
J
qua phép quay trên. Nếu
3
AC
thì
IJ
bằng
A.
10
. B.
5
. C.
2 5
. D.
10
2
.
Lời giải
Chọn D.
S
A
B
C
M
A
B
C
P
N
O
A
B
O
N
P
K
H
M
C
Do
; 90 :
Q B I J
nên
BIJ
vuông cân tại
B
2IJ BI
.
Mà
3
AC
1
BC
. Vì
2
AB BC
2
BE BH
HI
là đường trung bình
EBC
1 1
2 2
HI BC
. Ta có
2 2
1 5
1
4 2
BI BH IH
Vậy
10
2
2
IJ BH
.
Câu 39. [1H1-3]
(THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018)
Ảnh của điểm
2; 3
M
qua phép
quay tâm
1;2
I
góc quay
120
là
A.
5 3 5 3 3 9
;
2 2
M
. B.
5 3 5 3 3 9
;
2 2
M
.
C.
5 3 1 3 3 1
;
2 2
M
. D.
5 3 1 3 3 9
;
2 2
M
.
Lời giải
Chọn B.
Gọi
;M x y
là ảnh của
2; 3
M
qua phép quay tâm
1;2
I
góc quay
120
Ta có:
cos sin a
sin cos
x x a y b
x x a y b b
2 1 cos120 3 2 sin120 1
2 1 sin120 3 2 cos120 2
x
x
.
3 3
5 1
2 2
3 5
3. 2
2 2
x
y
5 3 5
2
3 3 9
2
x
y
. Vậy
5 3 5 3 3 9
;
2 2
M
.
Câu 1:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Trong mặt phẳng
Oxy
, cho đường
tròn
2 2
: 6 4 12
C x y
. Viết phương trình đường tròn là ảnh của đường tròn
C
qua phép
đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
O
tỉ số
1
2
và phép quay tâm
O
góc
90
.
A.
2 2
2 3 3
x y
. B.
2 2
2 3 3
x y
.
C.
2 2
2 3 6
x y
. D.
2 2
2 3 6
x y
.
Lời giải
Chọn A
Đường tròn
C
có tâm
6;4
I
và bán kính
2 3
R
.
Qua phép vị tự tâm
O
tỉ số
1
2
điểm
6;4
I
biến thành điểm
1
3;2
I
; qua phép quay tâm
O
góc
90
điểm
1
3;2
I
biến thành điểm
2;3
I
.
Vậy ảnh của đường tròn
C
qua phép đồng dạng trên là đường tròn có tâm
2;3
I
và bán kính
1
3
2
R R
có phương trình:
2 2
2 3 3
x y
.
Câu 2:
(SGD Ninh Bình năm 2017-2018)
Cho tứ diện
ABCD
có cạnh
AD
vuông góc với mặt phẳng
ABC
,
4
AC AD
,
3
AB
,
5
BC
. Tính khoảng cách
d
từ điểm
A
đến mặt phẳng
BCD
.
A.
12
34
d
. B.
60
769
d
. C.
769
60
d
. D.
34
12
d
.
Lời giải
Chọn A
Ta có
2 2 2
BC AB AC
nên
ABC
vuông tại
A
, gọi
H
là hình chiếu của
A
trên
BCD
.
Tứ diện
ABCD
là tứ diện vuông nên ta có
2 2 2 2 2 2 2
1 1 1 1 1 1 1 17
3 4 4 72AH AB AC AD
Vậy
12
;
34
d A BCD AH
. .
A
D
B
C
H
Câu 3:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Thành phố Hải Đông dự định xây dựng một
trạm nước sạch để cung cấp cho hai khu dân cư
A
và
B
. Trạm nước sạch đặt tại vị trí
C
trên
bờ sông. Biết
3 17 km
AB
, khoảng cách từ
A
và
B
đến bờ sông lần lượt là
3km
AM
,
6km
BN
(hình vẽ). Gọi
T
là tổng độ dài đường ống từ trạm nước đến
A
và
B
. Tìm giá trị
nhỏ nhất của
T
.
A.
15km
. B.
14,32 km
. C.
15,56 km
. D.
16km
.
Lời giải
Chọn C
Gọi
A
đối xứng với
A
qua
MN
,
D
là trung điểm của
NB
.
Do
A
cố định nên
A
cũng cố định.
Ta có:
T CA CB CA CB A B
(không đổi).
Đẳng thức xảy ra khi
C MN A B
.
Khi đó:
1
2
MC MA MA
NC NB NB
(1)
Mặt khác,
2 2
153 9 9 2 km
MN AD AD DB
(2)
Từ (1) và (2) suy ra
3 2
MC km
,
6 2 km
NC
.
Vậy
2 2 2 2
9 18 36 72 9 3 15,56 km
T CA CB AM MC BN NC
.
Câu 4:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Trong mặt phẳng tọa độ
, cho
đường thẳng
:d
023
yx
. Viết phương trình đường thẳng
d
là ảnh của
d
qua phép quay
tâm
O
góc quay
o
90
.
A.
: 3 2 0
d x y
. B.
: 3 2 0
d x y
. C.
:3 6 0
d x y
. D.
: 3 2 0
d x y
.
Lời giải
Chọn B
Qua phép quay tâm
O
góc quay
o
90
đường thẳng
d
biến thành đường thẳng
d
vuông góc
với
d
.
Phương trình đường thẳng
d
có dạng:
3 0
x y m
.
Lấy
0;2
A d
. Qua phép quay tâm
O
góc quay
o
90
, điểm
0;2
A
biến thành điểm
2;0
B d
. Khi đó
2
m
.
Vậy phương trình đường
d
là
3 2 0
x y
.
Câu 1:
(THPT Chuyên Lam Sơn-Thanh Hóa-lần 2 năm 2017-2018)
Cho đường thẳng
d
có phương
trình
4 3 5 0
x y
và đường thẳng
có phương trình
2 5 0
x y
. Phương trình đường
thẳng
d
là ảnh của đường thẳng
d
qua phép đối xứng trục
là
A.
3 0
x
. B.
3 1 0
x y
. C.
3 2 5 0
x y
. D.
3 0
y
.
Lời giải
Chọn D
Gọi
M d
1; 3
M
.
Lấy
2; 1
N d
.
Gọi
1
d
là đường thẳng qua
N
và vuông góc với
, ta có
1
: 2 5 0
d x y
Gọi
1
I d
3;1
I
.
Gọi
N
là ảnh của
N
qua phép đối xứng trục
I
là trung điểm của
NN
nên
4; 3
N
.
d
là ảnh của đường thẳng
d
qua phép đối xứng trục
d
là đường thẳng qua
1; 3
M
và
4; 3
N
.
Vậy
: 3 0
d y
.
Câu 2:
(SGD Hà Nội-lần 11 năm 2017-2018)
Cho tứ diện đều
ABCD
có
M
,
N
lần lượt là trung điểm
của các cạnh
AB
và
CD
. Mệnh đề nào sau đây sai?
A.
MN AB
. B.
MN BD
. C.
MN CD
. D.
AB CD
.
Lời giải
Chọn B
N
M
B
C
D
A
•
NAB
cân tại
N
nên
MN AB
.
•
MCD
cân tại
M
nên
MN CD
.
•
CD ABN
CD AB
.
• Giả sử
MN BD
mà
MN AB
. Suy ra
MN ABD
(Vô lí vì
ABCD
là tứ diện đều)
Vậy phương án B sai.
Câu 1: Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
A
,
SA
vuông góc với mặt phẳng
ABC
và
4 2 cm
BC
. Khoảng cách giữa hai đường thẳng
SA
và
BC
là
A.
4 2 cm
. B.
2 2 cm
. C.
4cm
. D.
2cm
.
Câu 2: Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
A
,
SA
vuông góc với mặt phẳng
ABC
và
4 2 cm
BC
. Khoảng cách giữa hai đường thẳng
SA
và
BC
là
A.
4 2 cm
. B.
2 2 cm
. C.
4cm
. D.
2cm
.
Lời giải
Chọn B .
Gọi
M
là trung điểm
BC
, ta có
AM SA
và
AM BC
.
, 2 2 cm
2
BC
d SA BC AM
.
Câu 3: Cho khối hộp
.
ABCD A B C D
. Gọi
M
là trung điểm của
AB
. Mặt phẳng
MB D
chia khối
hộp thành hai phần. Tính tỉ số thể tích
2
phần đó.
A.
7
24
. B.
5
12
. C.
7
17
. D.
5
17
.
Câu 4: Cho khối hộp
.
ABCD A B C D
. Gọi
M
là trung điểm của
AB
. Mặt phẳng
MB D
chia khối
hộp thành hai phần. Tính tỉ số thể tích
2
phần đó.
A.
7
24
. B.
5
12
. C.
7
17
. D.
5
17
.
Lời giải
Chọn C
M
A
D
B
C
B'
C'
A'
D'
S
Đặc biệt hóa:
.
ABCD A B C D
là hình lập phương cạnh
a
.
Gọi
N
là trung điểm của
AD
suy ra
// // ' 'MN BD B D
suy ra thiết diện là
MND B
.
1
V
là thể tích phần chứa đỉnh
A
;
2
V
là phần còn lại.
Gọi
S AA MB
nên
S
,
N
,
D
thẳng hàng;
1
2
MN B D
1
2
SA SA
1
SA B D SAMN
V V V
1
. .
3
A B D AMN
SA S SA S
2
2
1 1 1 1
2 .
3 2 2 2
a a a
3
3
1
3 8
a
a
3
7
24
a
.
2 1
lp
V V V
3
17
24
a
. Vậy
1
2
7
17
V
V
.
Câu 1:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Trong mặt phẳng tọa độ
, cho tam giác
ABC
có trực tâm
O
. Gọi
M
là trung điểm của
BC
;
N
,
P
lần lượt là chân đường cao kẻ từ
B
và
C
. Đường tròn đi qua ba điểm
M
,
N
,
P
có phương trình là
2
2
1 25
: 1
2 4
T x y
. Phương trình đường tròn ngoại tiếp tam giác
ABC
là:
A.
2 2
1 2 25
x y
. B.
2
2
1 25
x y
.
C.
2
2
1 50
x y
. D.
2 2
2 1 25
x y
.
Lời giải
Chọn D
Ta có
M
là trung điểm của
BC
;
N
,
P
lần lượt là chân đường cao kẻ từ
B
và
C
. Đường tròn
đi qua ba điểm
M
,
N
,
P
là đường tròn Euler. Do đó đường tròn ngoại tiếp tam giác
ABC
chính là ảnh của đường tròn Euler qua phép vị tự tâm là
O
, tỷ số
2
k
.
Gọi
I
và
I
lần lượt là tâm đường tròn ngoại tiếp tam giác
MNP
và tam giác
ABC
.
Gọi
R
và
R
lần lượt là bán kính đường tròn ngoại tiếp tam giác
MNP
và tam giác
ABC
.
Ta có
1
1;
2
I
và do đó
2 2; 1
OI OI I
.
Mặt khác
5
5
2
R R
.
Vậy phương trình đường tròn ngoại tiếp tam giác
ABC
là:
2 2
2 1 25
x y
.
Nhận xét: Đề bài này rất khó đối với học sinh nếu không biết đến đường tròn Euler.
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Câu 1: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy , cho hai
đường thẳng d : 2x  3y 1  0 và d : x y  2  0 . Có bao nhiêu phép tịnh tiến biến d 2  1  1 thành d . 2 A. Vô số. B. 4 . C. 1. D. 0 . Lời giải Chọn D
Nhắc lại kiến thức: "Phép tịnh tiến theo vectơ v biến đường thẳng thành đường thẳng song
song hoặc trùng với nó".
Ta có: d và d không song song hoặc trùng nhau, suy ra không có phép tịnh tiến nào biến 2  1 
đường thẳng d thành d . 2  1  
Câu 2: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Cho v  1;5 và điểm M 4; 2 . Biết M  là
ảnh của M qua phép tịnh tiến T . Tìm M . v
A. M 4;10 . B. M  3  ;5 .
C. M 3;7 .
D. M 5; 3 . Lời giải Chọn D
x  x a 4  x 1     M 5; 3  
y  y b  2  y  5  
Câu 3: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Cho điểm A1;4 và u   2
 ;3 , biết A 
là ảnh của A qua phép tịnh tiến u . Tìm tọa độ điểm A .
A. A1; 4 .
B. A3;   1 .
C. A1; 4 . D. A3;  1 . Lời giải Chọn D   1   x  2  x  1 2  3 Gọi A ;
x y . Ta có AA  u      A3;  1 . 4  y  3  y  4  3  1 
Câu 4: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Cho hai đường thẳng song song d và
d  . Trong các khẳng định sau khẳng định nào đúng?
A. Có đúng một phép tịnh tiến biến d thành d .
B. Có vô số phép tịnh tiến biến d thành d . 
C. Phép tịnh tiến theo véc tơ v có giá vuông góc với đường thẳng d biến d thành d .
D. Cả ba khẳng định trên đều đúng. Lời giải Chọn B
Có vô số phép tịnh tiến véc tơ v với điểm gốc nằm trên d và điểm ngọn nằm trên d  biến d thành d .
Câu 5: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Điểm M  2
 ; 4 là ảnh của điểm nào sau đây 
qua phép tịnh tiến theo véctơ v  1;7 . A. F 1; 3   . B. P 3  ;11 . C. E 3;  1 .
D. Q 1;3 . Lời giải Chọn B 
Gọi M  x ; y là ảnh của điểm M qua phép tịnh tiến theo véctơ v   1  ; 7 .    x  2  1  x  3
Ta có MM    x  2; y  4 và T  M   M   MM   v     . v y  4  7 y  11  
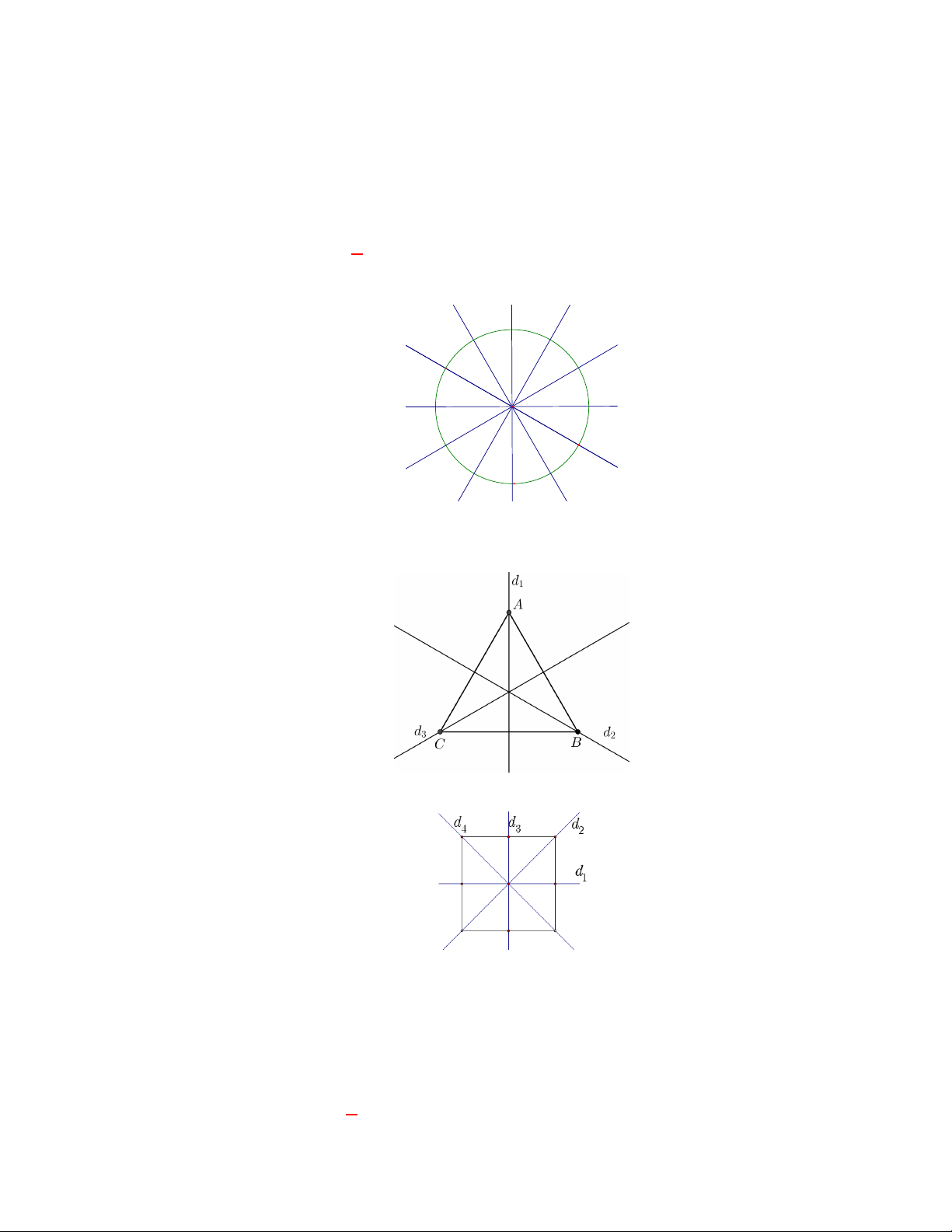
Câu 6: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Hình nào sau đây có vô số trục đối xứng? A. Hình vuông. B. Hình tròn. C. Đoạn thẳng. D. Tam giác đều. Lời giải Chọn B R I
 Hình tròn có vô số trục đối xứng – là các đường thẳng đi qua tâm của đường tròn đó.
 Tam giác đều có 3 tục đối xứng như hình vẽ
 Hình vuông có bốn trục đối xứng như hình vẽ
 Đoạn thẳng có hai trục đối xứng là đường thẳng đi qua 2 đầu đoạn thẳng và đường trung
trực của đoạn thẳng đó. 
Câu 7: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Trong mặt phẳng tọa độ Oxy, cho v  2;3 . Tìm 
ảnh của điểm A1;  
1 qua phép tịnh tiến theo vectơ v . A. A 2   ;1 .
B. A1; 2 .
C. A2;   1 . D. A 1  ; 2   . Lời giải Chọn Bx  1 2 x  1  Giả sử A ;
x y . Theo công thức tọa độ của phép tịnh tiến ta có:    . Suy y  1   3  y  2  ra A1; 2 .
Câu 1: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Phép biến hình nào sau đây không là phép dời hình?
A. Phép tịnh tiến.
B. Phép đối xứng tâm. C. Phép đối xứng trục. D. Phép vị tự. Lời giải Chọn D
Phép vị tự tâm I tỷ số k biến đoạn thẳng AB thành đoạn thẳng AB  k .AB nên nó không
phải là phép dời hình với k  1  .
Câu 2: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Cho hình bình hành ABCD . Ảnh 
của điểm D qua phép tịnh tiến theo véctơ AB là: A. B . B. C . C. D . D. A . Lời giải
Chọn B  
Ta có : AB DC T : D C AB A B D C   
Thấy ngay phép tịnh tiến theo véctơ AB biến điểm D thành điểm C vì AB DC .
Câu 3: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Cho hình thoi ABCD tâm O . Trong các mệnh
đề sau, mệnh đề nào là mệnh đề đúng?
A. Phép vị tự tâm O , tỉ số k  1
 biến tam giác ABD thành tam giác CDB . 
B. Phép quay tâm O , góc
biến tam giác OBC thành tam giác OCD . 2
C. Phép vị tự tâm O , tỉ số k  1 biến tam giác OBC thành tam giác ODA . 
D. Phép tịnh tiến theo véc tơ AD biến tam giác ABD thành tam giác DCB . Lời giải Chọn A D A O C B Ta có: V
A C ; V
B D ; V
D B . Nên chọn phương án A. O, 1    O, 1    O, 1         
Câu 4: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Trong các khẳng định dưới đây, khẳng định nào sai?
A. Tam giác đều có ba trục đối xứng.
B. Phép quay biến một đường thẳng thành một đường thẳng song song với nó.
C. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
D. Phép vị tự tâm I tỉ số k  1
 là phép đối xứng tâm. Lời giải Chọn B
Phép quay biến một đường thẳng thành một đường thẳng.
Câu 5: (SGD Bắc Ninh năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M 2;5 . Phép 
tịnh tiến theo vectơ v  1; 2 biến điểm M thành điểm M  . Tọa độ điểm M  là:
A. M 3;7 .
B. M 1;3 .
C. M 3;  1 .
D. M 4;7 . Lời giải Chọn A
x  2 1  3
Gọi T M   M  x; y 
. Vậy M 3;7 . v
y  5 2  7 
Câu 6: (THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018) Hình nào dưới nào dưới đây
không có trục đối xứng? A. Tam giác cân. B. Hình thang cân. C. Hình elip. D. Hình bình hành.
Hướng dẫn giải Chọn D
Câu 7: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho véctơ  
v  3; 5 . Tìm ảnh của điểm A1; 2 qua phép tịnh tiến theo véctơ v .
A. A4;  3 . B. A 2  ; 3 . C. A 4  ; 3 . D. A 2  ; 7 . Lời giải
Chọn D
x x       AA  3 1 3 2 Ta có   A 2  ; 7 .
y y  5  2  5  7  AA
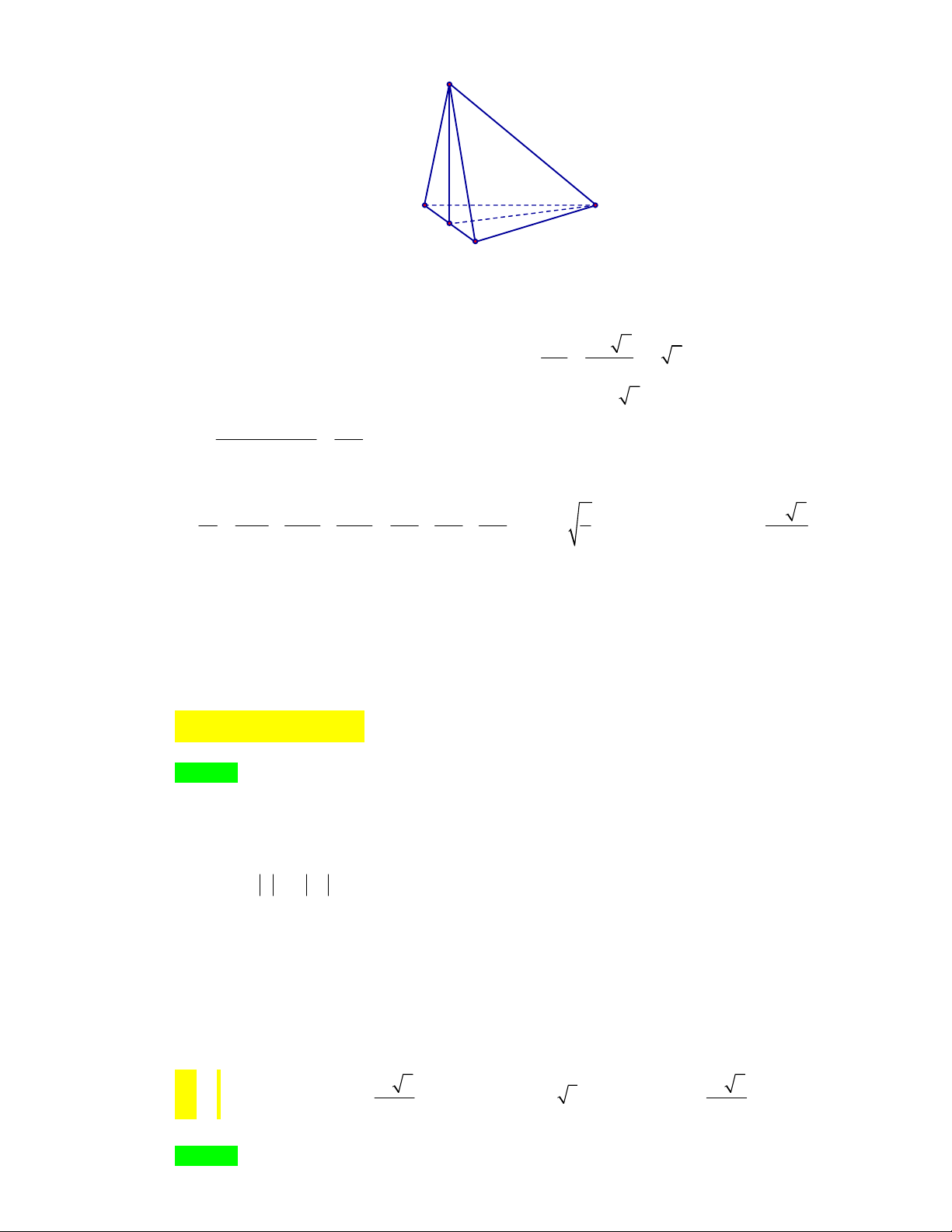
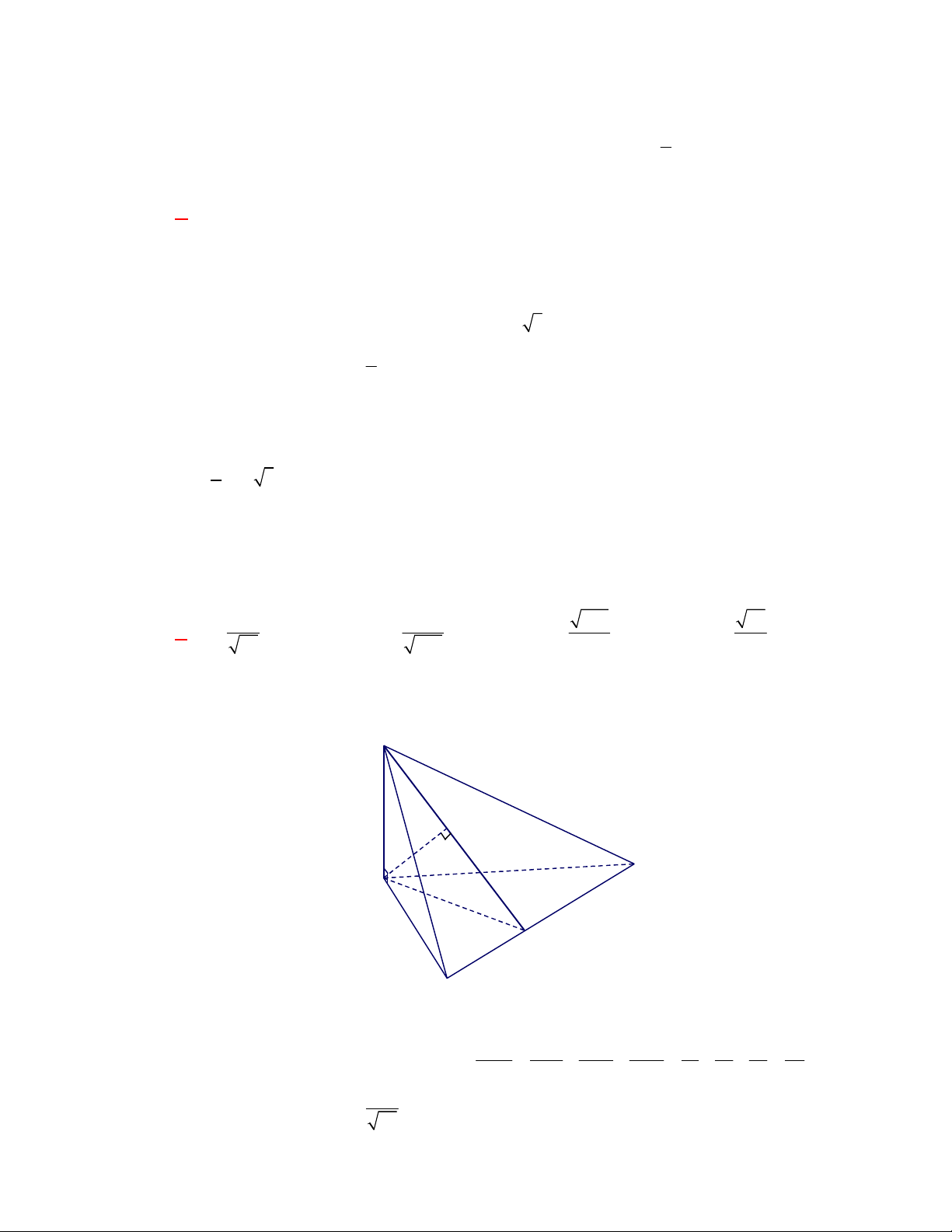
Câu 8: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho hình chóp tam giác S.ABC với SA ,
SB , SC đôi một vuông góc và SA SB SC a . Tính thế tích của khối chóp S.ABC . 1 1 1 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 2 6 3 Lời giải
Chọn C 1 1 1 1 Ta có V  .S .SA  . . . SB SC.SA 3  .a . 3 SBC 3 2 6
Câu 9: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho lăng trụ tam giác đều ABC.AB C   có
tất cả các cạnh bằng 2a . Tính thể tích khối lăng trụ ABC.AB C   . 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. 3 2a 3 . 4 2 Lời giải
Chọn C 2a2 3 Ta có 3 V S .AA  .2a  2a 3 . ABC 4  
Câu 10: (THPT Hồng Quang-Hải Dương năm 2017-2018) Cho 4IA  5IB . Tỉ số vị tự k của phép vị
tự tâm I , biến A thành B là 4 3 5 1 A. k  . B. k  . C. k  . D. k  . 5 5 4 5 Lời giải Chọn A   4   4
Ta có 4IA  5IB
IA IB . Vậy tỉ số k  . 5 5
Câu 11: (THPT Kinh Môn 2-Hải Dương năm 2017-2018) Trong mặt phẳng Oxy cho đường tròn C  2 2
có phương trình  x   1   y   1
 4 . Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k  2 biến
C  thành đường tròn nào trong các đường tròn có phương trình sau ? 2 2 2 2 A.x   1   y   1  8 .
B.x  2   y  2  8 . 2 2 2 2
C.x  2   y  2  16 .
D.x  2   y  2  16 . Lời giải Chọn D
Đường tròn C  có tâm I 1; 
1 , bán kính R  2 .
Gọi đường tròn C có tâm I , bán kính R là đường tròn ảnh của đường tròn C  qua phép vị tự V . O;2   x  2 Khi đó V
I I   OI   2OI   I 2;2 . O;2      y  2 
Và R  2R  4 . 2 2
Vậy phương trình đường tròn C :  x  2   y  2  16 .
Câu 12: (THPT Quãng Xương 1-Thanh Hóa năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy , 
cho vectơ v  2;  1 và điểm M  3
 ; 2. Tìm tọa độ ảnh M  của điểm M qua phép tịnh tiến  theo vectơ . v
A. M 5;3 .
B. M 1;   1 . C. M  1   ;1 .
D. M 1;  1 . Lời giải Chọn C  
x  x  2  3   2  1   T M M MM v Vậy M  1   ;1 . v          .
y  y 1  2 1  1 
Câu 13: (THPT Tứ Kỳ-Hải Dương năm 2017-2018) Cho hình chữ nhật có O là tâm đối xứng. Hỏi có
bao nhiêu phép quay tâm O góc  , 0    2 biến hình chữ nhật trên thành chính nó? A. Không có. B. Bốn. C. Hai. D. Ba. Hướng dẫn giải Chọn C Ta có Q , Q
biến hình chữ nhật có O là tâm đối xứng thành chính nó. O, 0 O,  
Vậy có hai phép quay tâm O góc  , 0    2 biến hình chữ nhật trên thành chính nó.
Câu 14: (THPT Lương Văn ChasnhPhus Yên năm 2017-2018) Phép tịnh tiến biến gốc tọa độ O thành
điểm A1;2 sẽ biến điểm A thành điểm A có tọa độ là:
A. A2; 4 . B. A 1  ; 2   .
C. A4; 2 .
D. A3;3 . Lời giải Chọn A  
Phép tịnh tiến biến gốc tọa độ O thành điểm A1;2 nên vectơ tịnh tiến u OA  1;2. x  11  2 Khi đó,   A2; 4 . y  2  2  4 
Câu 15: (THPT Đô Lương 4-Nghệ An năm 2017-2018) Số hình đa diện lồi trong các hình dưới đây là A. 3 . B. 0 . C. 1. D. 2 . Lời giải Chọn C
Quan sát bốn hình trên ta thấy chỉ có một hình thứ tư từ trái qua là hình đa diện lồi vì lấy bất kỳ
hai điểm nào thì đoạn thẳng nối hai điểm đó nằm trong khối đa diện.
Vậy chỉ có một đa diện lồi.
Câu 16: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Chọn khẳng định sai trong các khẳng định sau:
A. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
B. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
C. Phép tịnh tiến biến một đường tròn thành một đường tròn có cùng bán kính.
D. Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với nó. Lời giải
Chọn D
Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó.
Câu 1: (THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018) Trong mặt phẳng với hệ trục tọa độ Oxy  cho A2; 3
  , B 1;0 . Phép tịnh tiến theo u  4;3 biến điểm A , B tương ứng thành A,
B khi đó, độ dài đoạn thẳng AB bằng
A. AB  10 . B. A B    10 .
C. AB  13 . D. A B    5 . Lời giải Chọn A
Phép tịnh tiến bảo toàn độ dài nên AB A B    10 .
Câu 2: (THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018) Trong mặt phẳng tọa độ Oxy cho  
vectơ u  3;  
1 . Phép tịnh tiến theo vectơ u biến điểm M 1; 4 thành
A. Điểm M 4; 5   .
B. Điểm M  2  ; 3
  . C. Điểm M 3; 4
  . D. Điểm M 4;5 . Lời giải Chọn Axa xx  3 1 Ta có M M M    
M 4;5 . yb yy  1 4 M MM
Câu 3: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Cho hình chữ nhật MNPQ . Phép 
tịnh tiến theo véc tơ MN biến điểm Q thành điểm nào? A. Điểm Q . B. Điểm N . C. Điểm M . D. Điểm P . Lời giải Chọn D  
Do MNPQ là hình chữ nhật nên MN QP T Q  P . MN
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Cho hình chóp S.ABCD có đáy ABCD là hình bình
hành . Tìm giao tuyến của hai mặt phẳng SAD và SBC  . S A D B C
A. Là đường thẳng đi qua đỉnh S và tâm O đáy.
B. Là đường thẳng đi qua đỉnh S và song song với đường thẳng BC .
C. Là đường thẳng đi qua đỉnh S và song song với đường thẳng A . B
D. Là đường thẳng đi qua đỉnh S và song song với đường thẳng BD. Lời giải
Chọn B
Xét hai mặt phẳng SAD và SBC
Có : S chung và AD//BC
Gọi d  là giao tuyến của hai mặt phẳng SAD và SBC
 d  đi qua S và song song với AD và BC .
Câu 2: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho điểm A3;   1 .
Tìm tọa độ điểm B sao cho điểm A là ảnh của điểm B qua phép tịnh tiến theo véctơ u2; 1.
A. B 1;0 . B. B 5; 2   .
C. B 1;2 .
D. B 1;0 . Lời giải Chọn D   3   x  2 x  1
Ta có TB A BA u    B 1;0 . u     1 y  1   y  0 
Câu 3: Cho hình hộp . ABCD AB CD   (như hình vẽ). D' C' A' B' D C A B
Chọn mệnh đề đúng? 
A. Phép tịnh tiến theo DC biến điểm A thành điểm B . 
B. Phép tịnh tiến theo AB biến điểm A thành điểm C . 
C. Phép tịnh tiến theo AC biến điểm A thành điểm D . 
D. Phép tịnh tiến theo AA biến điểm A thành điểm B . Lời giải
Chọn A  
Ta có: DC A B   . 
Nên phép tịnh tiến theo DC biến điểm A thành điểm B . 
Câu 4: Trong mặt phẳng tọa độ Oxy , phép tịnh tiến theo vectơ v  1;2 biến điểm M 4;5 thành điểm nào sau đây? A. P 1;6 . B. Q 3;  1 .
C. N 5;7 .
D. R 4;7 . 
Câu 5: Trong mặt phẳng tọa độ Oxy , phép tịnh tiến theo vectơ v  1;2 biến điểm M 4;5 thành điểm nào sau đây? A. P 1;6 . B. Q 3;  1 .
C. N 5;7 .
D. R 4;7 . Lời giải Chọn C
Phép tịnh tiến theo vectơ v  1;2 biến điểm M 4;5 thành điểm N 5;7 .
Câu 6: Trong mặt phẳng tọa độ Oxy , cho hai điểm A1; 
1 và I 2;3 . Phép vị tự tâm I tỉ số k  2 
biến điểm A thành điểm A' . Tọa độ điểm A' là
A. A0;7 .
B. A7; 0 .
C. A7; 4 .
D. A4;7 .
Câu 7: Trong mặt phẳng tọa độ Oxy , cho hai điểm A1; 
1 và I 2;3 . Phép vị tự tâm I tỉ số k  2 
biến điểm A thành điểm A . Tọa độ điểm A là
A. A0;7 .
B. A7; 0 .
C. A7; 4 .
D. A4;7 . Lời giải Chọn D  
x  a k   x a
x  kx   1 k a
x  2.1 3.2  4
Ta có: IA'  k IA      
y  b k   y b   y  ky   1 k b
y  2.1 3.3  7  
Câu 8: Trong mặt phẳng tọa độ Oxy , phép tính tiến theo vectơ v biến điểm M  ; x y thành điểm 
M  x ; y sao cho x  x  2 và y  y  4 . Tọa độ của v là     A. v   2  ; 4 . B. v  4; 2   . C. v   2  ; 4 .
D. v  2; 4 . 
Câu 9: Trong mặt phẳng tọa độ Oxy , phép tính tiến theo vectơ v biến điểm M  ; x y thành điểm 
M  x ; y sao cho x  x  2 và y  y  4 . Tọa độ của v là     A. v   2  ; 4 . B. v  4; 2   . C. v   2  ; 4 .
D. v  2; 4 .
Hướng dẫn giải Chọn A  
x  x a Gọi v   ;
a b . Biểu thức tọa độ của phép tịnh tiến theo vectơ v là 
y  y b  13
Theo đề bài ta có a  2  ;b  4 . 6  
Câu 10: Trong mặt phẳng Oxy cho điểm A2; 
1 và vectơ a 1;3 . Phép tịnh tiến theo vectơ a biến điểm
A thành điểm A . Tọa độ điểm A là A. A 1  ; 2   .
B. A1; 2 .
C. A4;3 .
D. A3; 4 .  
Câu 11: Trong mặt phẳng Oxy cho điểm A2 
;1 và vectơ a 1;3 . Phép tịnh tiến theo vectơ a biến điểm
A thành điểm A . Tọa độ điểm A là A. A 1  ; 2   .
B. A1; 2 .
C. A4;3 .
D. A3; 4 .
Hướng dẫn giải Chọn D
Ta có: A  T  A  A3;4 . a 
Câu 12: Cho hình thoi ABCD tâm I . Phép tịnh tiến theo véc tơ IA biến điểm C thành điểm nào? A. Điểm B . B. Điểm C . C. Điểm D . D. Điểm I . 
Câu 13: Cho hình thoi ABCD tâm I . Phép tịnh tiến theo véc tơ IA biến điểm C thành điểm nào? A. Điểm B . B. Điểm C . C. Điểm D . D. Điểm I . Lời giải Chọn D D A C I B 
Phép tịnh tiến theo véc tơ IA biến điểm C thành điểm I . 
Câu 14: Trong mặt phẳng tọa độ Oxy , phép tịnh tiến theo véc tơ v  1;3 biến điểm A1; 2 thành điểm
nào trong các điểm sau? A. M 2;  5 . B. P1;  3 .
C. N 3; 4 . D. Q 3  ; 4  . 
Câu 15: Trong mặt phẳng tọa độ Oxy , phép tịnh tiến theo véc tơ v  1;3 biến điểm A1; 2 thành điểm
nào trong các điểm sau? A. M 2;  5 . B. P1;  3 .
C. N 3; 4 . D. Q 3  ; 4  . Lời giải
Chọn A   x 1  1 x  2 Ta có M  ;
x y   T  A  AM v     . v y  2  3  y  5 
Câu 16: Trong các mệnh đề sau, mệnh đề nào là sai?
A. Mọi phép đối xứng trục đều là phép dời hình. B. Mọi phép vị tự đều là phép dời hình.
C. Mọi phép tịnh tiến đều là phép dời hình.
D. Mọi phép quay đều là phép dời hình.
Câu 17: Trong các mệnh đề sau, mệnh đề nào là sai?
A. Mọi phép đối xứng trục đều là phép dời hình. B. Mọi phép vị tự đều là phép dời hình.
C. Mọi phép tịnh tiến đều là phép dời hình.
D. Mọi phép quay đều là phép dời hình. Lời giải Chọn B Phép vị tự V
chỉ là phép dời hình khi k  1 . I ,k
Câu 18: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M  3
 ; 2 . Tọa độ của điểm M  là ảnh của điểm 
M qua phép tịnh tiến theo vectơ v  2;   1 là A.  1   ;1 . B. 3;  2 . C. 5;  3 . D.  5  ;3 .
Câu 19: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M  3
 ; 2 . Tọa độ của điểm M  là ảnh của điểm 
M qua phép tịnh tiến theo vectơ v  2;   1 là A.  1   ;1 . B. 3;  2 . C. 5;  3 . D.  5  ;3 . Lời giải Chọn A   x  3  2 x  1 
Gọi M  x; y . Khi đó: MM   v     . Vậy M  1   ;1 . y  2  1   y  1 
Câu 20: Trong các mệnh đề sau, mệnh đề nào sai?
A. Phép quay biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
B. Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng nó.
C. Phép quay biến đường tròn thành đường tròn có cùng bán kính.
D. Phép tịnh tiến biến tam giác thành tam giác bằng nó.
Câu 21: Trong các mệnh đề sau, mệnh đề nào sai?
A. Phép quay biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
B. Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng nó.
C. Phép quay biến đường tròn thành đường tròn có cùng bán kính.
D. Phép tịnh tiến biến tam giác thành tam giác bằng nó. Lời giải Chọn A
Phép quay không biến đường thẳng thành đường thẳng song song với nó trong trường hợp góc quay bất kì.
Câu 22: Trong các phép biến hình sau, phép nào không phải là phép dời hình?
A. Phép vị tự tỉ số 1.
B. Phép đối xứng tâm. C. Phép quay.
D. Phép chiếu vuông góc lên một đường thẳng.
Câu 23: Trong các phép biến hình sau, phép nào không phải là phép dời hình?
A. Phép vị tự tỉ số 1.
B. Phép đối xứng tâm. C. Phép quay.
D. Phép chiếu vuông góc lên một đường thẳng. Lời giải Chọn D
Phép dời hình là phép bào toàn khoảng cách giữa hai điểm bất kì nên phép chiếu vuông góc lên một đường thẳng.
Câu 1: (THPT Hoa Lư A-Ninh Bình-lần 1-năm 2017-2018) Trong mặt phẳng với hệ tọa độ 0xy , phép quay tâm I 4; 3
  góc quay 180 biến đường thẳng d : x y  5  0 thành đường thẳng d có phương trình
A. x y  3  0 .
B. x y  3  0 .
C. x y  5  0 .
D. x y  3  0 . Lời giải Chọn B Md 180 d M Ta có phép quay Q
là phép đối xứng tâm I ( ký hiệu là Đ )  o I ;180  I
Vì I d nên nếu Đ d d thì d / /d , suy ra phương trình d : x y m  0m  5   . I  
M 0;5  d
Xét Đ M M   M   I   8;  11 I 4;3  Cho M 8; 1  
1  d  m  3 . Vậy d  : x y  3  0 .
Câu 2: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Cho hình thoi ABCD tâm O (như hình vẽ).
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng? B A C O D 
A. Phép tịnh tiến theo véc tơ DA biến tam giác DCB thành tam giác ABD .
B. Phép vị tự tâm O , tỉ số k  1
 biến tam giác CDB thành tam giác ABD . 
C. Phép quay tâm O , góc 
biến tam giác OCD thành tam giác OBC . 2
D. Phép vị tự tâm O , tỉ số k  1 biến tam giác ODA thành tam giác OBC . Lời giải Chọn B      
Ta có O là trung điểm của AC và BD nên ta có OA OC  ;OB  O ; D OD OB   V C  ; A V D  ; B V
B D V CDB ABD . O,1   O, 1    O, 1    O, 1           
Câu 3: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Cho hình chóp S.ABC đáy ABC là tam giác
đều, cạnh bên SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AB và SB . Trong
các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. CM SB .
B. CM AN .
C. MN MC .
D. AN BC . Lời giải Chọn D S N A C M B CM   AB  Ta có CM   SA
CM   SAB  CM SB  ,
SA AB  SAB 
Mà AN  SAB  CM AN MN SA  Mặt khác 
MN   ABC SA    ABC   MN   SAB Vì   MN CM . CM    ABC  Vậy D sai.
Câu 4: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Cho đường thẳng d có phương trình 
x y  2  0 . Phép hợp thành của phép đối xứng tâm O và phép tịnh tiến theo v  3; 2 biến
d thành đường thẳng nào sau đây?
A. x y  4  0.
B. 3x  3y  2  0.
C. 2x y  2  0.
D. x y  3  0. Lời giải. Chọn D
Giả sử d  là ảnh của d qua phép hợp thành trên (do d  song song hoặc trùng với d )
d  : x y c  0 . Lấy M 1  ;1  d .
Giả sử M  là ảnh của M qua phép đối xứng tâm O M 1;  1 .
Giả sử T M   N N 2;  1 . v
Ta có N d  11 c  0  c  3 .
Vậy phương trình d  : x y  3  0 .
Câu 5: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Trong mặt phẳng Oxy , tìm phương trình
đường tròn C là ảnh của đường tròn C  2 2
: x y  1 qua phép đối xứng tâm I 1;0 .
A.x  2 2 2  y  1.
B. x   y  2 2 2  1.
C.x  2 2 2  y  1.
D. x   y  2 2 2  1. Lời giải
Chọn C
C có tâm O 0;0 và bán kính R  1 .
Qua phép đối xứng tâm I 1;0 , ảnh của O 0;0 là O2;0 (vì I là trung điểm của OO ),
R  R với R là bán kính của C .
Vậy phương trình đường tròn C là:  x  2 2 2  y  1.
Câu 6: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Trong mặt phẳng Oxy , tìm phương
trình đường tròn C là ảnh của đường tròn C  2 2
: x y  1 qua phép đối xứng tâm I 1;0 .
A.x  2 2 2  y  1.
B. x   y  2 2 2  1.
C.x  2 2 2  y  1.
D. x   y  2 2 2  1. Lời giải
Chọn C
C có tâm O 0;0 và bán kính R  1 .
Qua phép đối xứng tâm I 1;0 , ảnh của O 0;0 là O2;0 (vì I là trung điểm của OO ),
R  R với R là bán kính của C .
Vậy phương trình đường tròn C là:  x  2 2 2  y  1.
Câu 7: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Trong mặt phẳng Oxy , qua phép quay
Q O, 90 , M 3; 2 là ảnh của điểm: A. M  3  ; 2   . B. M  3  ; 2 .
C. M 2;3 . D. M  2  ; 3   . Lời giải Chọn C
Áp dụng công thức tọa độ của phép quay :
x  x cos  y sin  Q :M ;
x y M x ;
y thì biểu thức tọa độ là : O;      
y  xsin  ycos  3
  x cos 90  y sin 90 x  2
Áp dụng vào bài ta có     M 2;3 .
2  x sin 90  y cos 90  y  3 
Câu 8: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy
cho đường tròn C  2 2
: x y  2x  4 y  4  0
và đường tròn C 2 2
: x y  6x  4 y  4  0. Tìm tâm vị tự của hai đường tròn? A. I 0;  1 ; J 3;4. B. I  1  ; 2  ; J 3;2.
C. I 1;2; J  3  ;  2.
D. I 1;0; J 4;3. Lời giải Chọn A
Gọi I ; I lần lượt là tâm đường tròn C;C . Ta có I 1; 2 ; I 3  ;  2 1   2   1 2
và bán kính R  1; R  3. Do đó hai đường tròn này khác tâm và khác bán kính, suy ra sẽ có 1 2
một tâm vị tự trong và một tâm vị tự ngoài. R 1
Gọi I; J là hai tâm vị tự cần tìm, ta có tỉ số vị tự 1 k     . R 3 2    1 
Với đáp A: Ta có II  1; 1 ; II  3  ;  3  II II . 1   2   1 2 3    1 
JI  2;  2 ; JI  6  ;  6  JI JI . 1   2   1 2 3
Vậy đáp A thỏa mãn nên ta Chọn A
Nhận xét: Câu 12 là câu không đáp ứng được yêu cầu của đề thi THPT vì theo khung chương
trình của Bộ Giáo Dục thì giảm tải nội dung tâm vị tự của hai đường tròn.
Câu 9: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy
cho đường thẳng  : x  2 y  6  0. Viết phương trình đường thẳng 
 là ảnh của đường thẳng
 qua phép quay tâm O góc 90 . 
A. 2x y  6  0.
B. 2x y  6  0.
C. 2x y  6  0.
D. 2x y  6  0. Lời giải Chọn A 
Véc tơ pháp của tuyến của đường thẳng  là n  1; 2 . Vì Q
:    nên     1    o O;90  
véctơ pháp của tuyến của đường thẳng  là n  2; 1 . 2   M 6;0    Lấy
M 0;6   . Q  : M M    o O;90  
Phương trình đường thẳng  là: 2x y  6  0
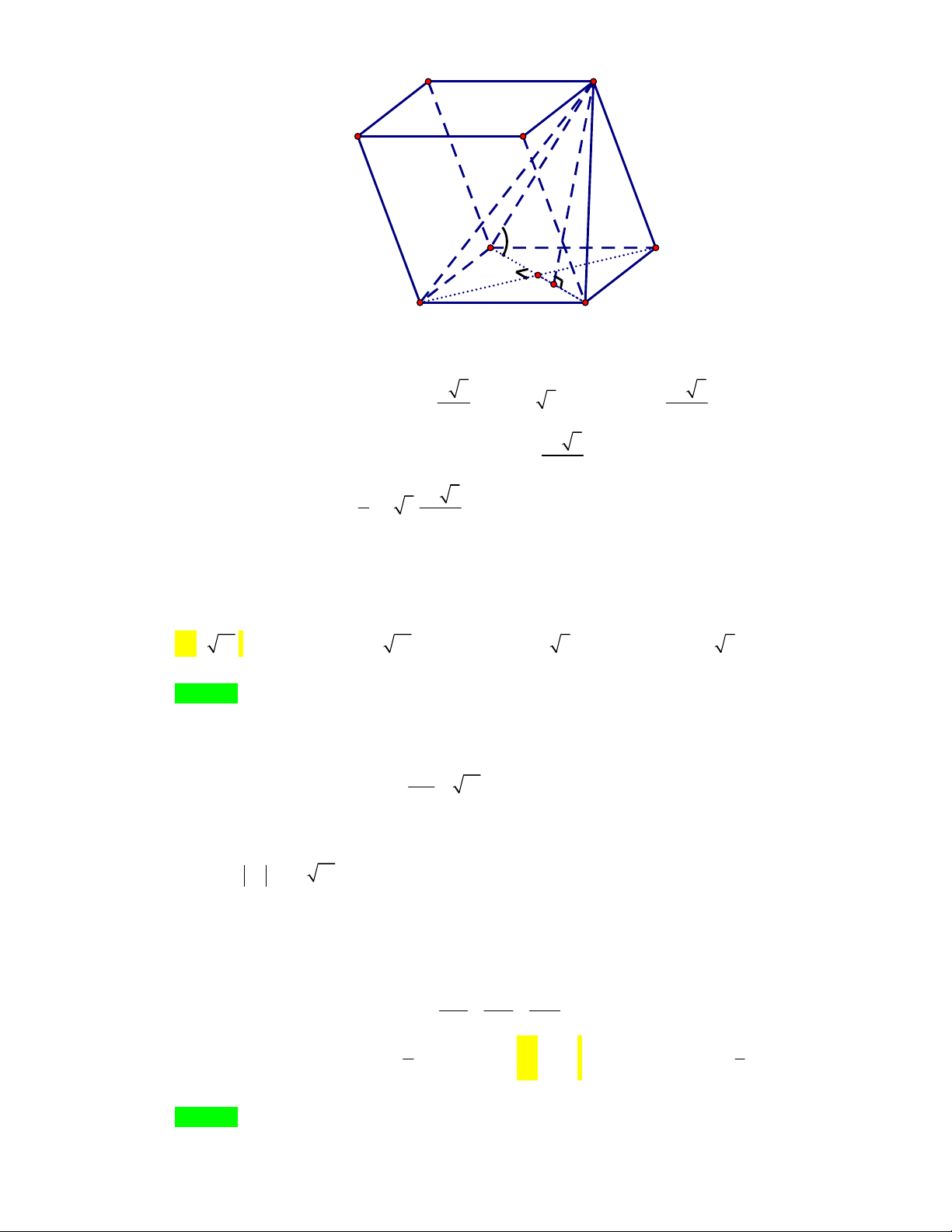
Câu 10: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Cho tứ diện ABCD , M , N lần lượt
là trung điểm của AB và BC . P là điểm trên cạnh AC sao cho CP  2PD . Mặt phẳng AQ
MNP cắt AD tại Q . Tính tỉ số ? QD 1 2 A. . B. 3 . C. . D. 2 . 2 3 Lời giải Chọn D A M Q B D P N CMN // AC  Ta có 
MN //  ACDAC    ACD  MN //   ACD Lại có
PQ // MN // AC  . MNP
   ACD  PQDQ DP 1
Vì PQ // AC nên   DA DC 3 AQ Khi đó  2 . QD
Câu 11: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Trong mặt phẳng Oxy , cho đường 2 2 
tròn C  :  x  
1   y  3  4 . Phép tịnh tiến theo vectơ v  3; 2 biến đường tròn C  thành
đường tròn có phương trình nào sau đây? 2 2 2 2
A.x  2   y  5  4 .
B.x  4   y   1  4 . 2 2 2 2 C.x  
1   y  3  4 .
D.x  2   y  5  4 . Lời giải Chọn A
C   x  2   y  2 : 1 3
 4 có tâm I 1;3 và bán kính R  2 . 
C là ảnh của C  qua phép tịnh tiến theo vectơ v  3;2 sẽ có tâm I và bán kính x  1 3 x  2
R  R  2 với T  I I II      . vy  3  2 y  5  I  I 2 2
Vậy C :  x  2   y  5  4 .
Câu 12: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Trong mặt phẳng Oxy , cho điểm
B 3;6 . Tìm tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay 90   .
A. E 6;  3 .
B. E 3;  6 .
C. E 6;3 .
D. E 3; 6 . Lời giải Chọn A Ta có: Q
E B Q B E . O;90   O;90      
x   y  6
Theo biểu thức tọa độ của phép quay tâm O góc quay 90 , ta có: E B  . y x  3   E B
Vậy E 6;  3 .
Câu 13: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy ,
tìm tọa độ điểm M  là ảnh của điểm M 2; 
1 qua phép đối xứng tâm I 3;2
A. M 1; 3 . B. M  5  ; 4 . C. M 4; 5   .
D. M 1;5 . Lời giải Chọn C M  ;
x y là ảnh của M qua phép đối xứng tâm I 3;2 khi và chỉ khi MM  nhận I là trung
x  2.3  2  4  điểm   . y  2.  2 1  5  Vậy M 4; 5   .
Câu 14: (THTT Số 3-486 tháng 12 năm 2017-2018) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác
ABC có A2; 4 , B 5; 
1 , C 1;  2 . Phép tịnh tiến  T
biến tam giác ABC tành tam giác BC
A BC . Tìm tọa độ trọng tâm của tam giác  A BC . A. 4; 2 . B. 4; 2 . C. 4;  2 . D. 4;  2 . Lời giải Chọn D
Gọi G là trọng tâm tam giác ABC và G   TG . BC
 2  5 1 4 1 2  Ta có G ;   hay G 2  ;1 .  3 3     Lại có BC  6
 ;  3 mà G   T
G  GG  BC   6  ; 3   . Từ đó ta có BC
x x ; y y      x  2; y 1  6
 ; 3   x ; y  4  ;  2 . G ' G '    G ' G '        6; 3 G G G G
Câu 15: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Trong mặt phẳng với hệ toạ độ Oxy ,  cho véctơ v   1
 ; 2 , điểm A3; 5 . Tìm tọa độ của các điểm A là ảnh của A qua phép tịnh  tiến theo v .
A. A2; 7 . B. A 2  ; 7 .
C. A7; 2 . D. A 2  ;  7 . Lời giải Chọn A
x  x 1  2
Biểu thức tọa độ của phép tịnh tiến theo v là:   A2; 7 .
y  y  2  7 
Câu 16: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Trong mặt phẳng Oxy , ảnh của điểm M  2
 ; 3 qua phép đối xứng trục  : x y  0 là
A. M 3; 2 .
B. M 3;  2 .
C. M 3; 2 . D. M  3  ; 2 . Lời giải Chọn D 
Gọi M  x; y . Khi đó MM    x  x; y  y .   Ta có n  1;  1  u    1;1 .   Ta biết Đ
 khi và chỉ khi  là trung trực của đoạn MM    M M  
  MM .u  0   
  x  x   y  y   0
x   y
   x xy y      . I ;          x    x x    y y   0  y    2 2  x  3  Khi M  2  ;3  Đ   nên M  : .   M M    y  2  Vậy M  3  ; 2 .
Câu 1: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Trong mặt phẳng Oxy , cho  
v  1; 2 , điểm M 2;5 . Tìm tọa độ ảnh của điểm M qua phép tịnh tiến v . A. 1;6 . B. 3;7 . C. 4;7 . D. 3  ;1 . Lời giải Chọn B
Gọi M  x ; y là ảnh của điểm M qua phép tịnh tiến v .   x  2  1 x  3
Ta có MM   v   x  2; y  5  1; 2      M 3;7 . y  5  2  y  7 
Câu 2: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Trong mặt phẳng tọa độ Oxy cho 0 các điểm I 3  ;1 , J  1  ;  
1 . Ảnh của J qua phép quay 90 Q là I
A. J 1;5 .
B. J 5; 3 . C. J  3  ;3 .
D. J 1; 5 . Lời giải Chọn A Gọi 
J  x; y là ảnh của điểm J x ; y qua phép quay tâm I a ;b góc quay 9  0 . Trong đó: J  1  ;   1 , I 3;  1 . Ta có:   x  x 
x acos   y bsin   a   x  3 cos 
90   y   1 sin 90   3 x  1     
y   x asin   y b cos     y  b y 
  x  3sin  90     y   1 cos  90   1  5  
Câu 3: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho đường 2 2
tròn C  : x  
1   y  2  4 . Tìm ảnh của đường tròn C  qua phép vị tự tâm O tỉ số 2  . 2 2 2 2
A.x  2   y  4  16 .
B.x  2   y  4  16 . 2 2 2 2
C.x  2   y  4  16 .
D.x  2   y  4  16 . Lời giải Chọn B Gọi M  ;
x y C  và M  x ; y  V M , ta có: O; 2        xyOM   2
OM x   ; y   . 2 2 2 2  x   y  2 2
Mà M  C  nên:  1    2  4    
  x  2   y  4  16 .  2   2  2 2
Vậy, phương trình ảnh của C  cần tìm là:  x  2   y  4  16 .
Câu 4: (SGD Ninh Bình năm 2017-2018) Cho lục giác đều A B
ABCDEF tâm O như hình bên. Tam giác EOD là ảnh
của tam giác AOF qua phép quay tâm O góc quay O
. Tìm . F C A. o  60 . B. o  60 . C. o  120 . D. o
 120 . E D Lời giải Chọn B Q
O O , Q
A F . Q F D . O; 1  20   O; 1  20   O; 1  20        
Câu 5: (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Trong mặt phẳng tọa độ Oxy ,  
cho vectơ v 1;2 . Tìm ảnh của điểm A 2
 ;3 qua phép tịnh tiến theo vectơ v .
A. A5;   1 . B. A 1  ;5 .
C. A3;   1 .
D. A3  ;1 .
Hướng dẫn giải Chọn B
Giả sử A ; x y .   x  2  1 x  1
Ta có T  A  A  AA  v      A 1  ;5 . v y  3  2  y  5 
Câu 6: (THPT Hồng Quang-Hải Dương năm 2017-2018) Trong mặt phẳng Oxy cho đường thẳng d
có phương trình 2x y 1  0 . Để phép tịnh tiến theo v biến đường thẳng d thành chính nó 
thì v phải là vectơ nào trong các vectơ sau đây ?    
A. v  2; 4 .
B. v  2;  1 .
C. v  1; 2 . D. v  2; 4   . Lời giải Chọn A  
Phép tịnh tiến theo v biến đường thẳng d thành chính nó khi vectơ v cùng phương với vectơ 
chỉ phương của d . Mà d có VTCP u  1; 2 .
Câu 7: (THPT Kinh Môn 2-Hải Dương năm 2017-2018) Trong mặt phẳng tọa độ Oxy cho điểm 
M 1; 2 . Phép tịnh tiến theo vectơ u   3
 ; 4 biến điểm M thành điểm M  có tọa độ là A. M  2  ; 6 .
B. M 2;5 . C. M 2; 6   . D. M 4; 2   . Lời giải Chọn A
x  x ax  1 3 x  2 
Theo biểu thức tọa độ của phép tịnh tiến      .
y  y by  2  4  y  6  Vậy M  2  ; 6 . 
Câu 8: (THPT Ninh Giang-Hải Dương năm 2017-2018) Trong mặt phẳng Oxy , cho vectơ v   3  ; 2
và đường thẳng  : x  3y  6  0 . Viết phương trình đường thẳng  là ảnh của đường thẳng 
 qua phép tịnh tiến theo vec-tơ v .
A.  : 3x y 15  0 . B.  : 3x y  5  0 . C.  : x  3y 15  0 . D.  : x  3y 15  0 . Lời giải Chọn D
Ta có //   : x  3y m  0 m  6 .
Lấy M 0; 2   , giả sử M   T M   M 0  3; 2  2  M  3  ; 4 . v
Do M     3
 12  m  0  m  15 thỏa mãn m  6   : x  3y 15  0 .
Câu 9: (THPT Ninh Giang-Hải Dương năm 2017-2018) Trong mặt phẳng Oxy , cho đường tròn C 2 2
: x y  4x 10 y  4  0 . Viết phương trình đường tròn C  biết C là ảnh của C
qua phép quay với tâm quay là gốc tọa độ O và góc quay bằng 270 . A.C  2 2
: x y 10x  4 y  4  0 . B.C  2 2
: x y 10x  4 y  4  0 . C.C  2 2
: x y 10x  4 y  4  0 . D.C  2 2
: x y 10x  4 y  4  0 . Lời giải Chọn B
Đường tròn C có tâm I2; 5 , bán kính R  4  25  4  5 .
Ta có C  Q C
 C  Q C
 C   Q C . O,90    O, 90    O, 270         
x   y  5 Do đó  I Q
I  . Vì đây là phép quay 90 nên I I
, suy ra I 5; 2 . O,90    
y x  2  I I
Bán kính đường tròn C  là R R  5 . 2 2
Vậy C  :  x  5   y  2  25  C  2 2
: x y 10x  4 y  4  0 .
Câu 10: (THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018) Trong mặt phẳng Oxy , cho đường
thẳng  : x y  2  0 . Hãy viết phương trình đường thẳng d là ảnh của đường thẳng  qua
phép quay tâm O , góc quay 90 .
A. d : x y  2  0 .
B. d : x y  2  0 .
C. d : x y  2  0 .
D. d : x y  4  0 . Lời giải
Chọn A
Đường thẳng d là ảnh của đường thẳng  qua phép quay tâm O , góc quay 90 nên d vuông góc với  .
Phương trình d có dạng x y c  0   1
Chọn M 0; 2   , M  là ảnh của M qua phép quay nên M 2;0  d Thay vào   1 : c  2 .
Vậy phương trình d : x y  2  0 .
Câu 11: (THPT Tứ Kỳ-Hải Dương năm 2017-2018) Trong mặt phẳng Oxy , cho điểm ( A 2;5) . Phép 
tịnh tiến theo vectơ v  1;2 biến A thành điểm
A. P 3; 7 .
B. N 1;6 . C. M 3;  1 .
D. Q 4;7 . Hướng dẫn giải Chọn A   x  2  1 x  3 Ta có T : A
Ax y AA  v    . v 2;5  ,   y  5  2 y  7  
A3;7  A  P . 
Vậy phép tịnh tiến theo vectơ v  1; 2 biến A thành điểm P 3;7 .
Câu 12: (THPT Xuân Trường-Nam Định năm 2017-2018) Trong mặt phẳng tọa độ Oxy , tìm phương
trình đường thẳng  là ảnh của đường thẳng  : x  2 y 1  0 qua phép tịnh tiến theo véctơ
v  1; 1.
A.  : x  2 y  3  0 .
B.  : x  2 y  0 .
C.  : x  2 y 1  0 . D.  : x  2 y  2  0 . Lời giải Chọn B Gọi M  ;
x y là điểm thuộc  .
x  x 1
x x 1
M  x ; y  T M      . v y  y 1 y y 1  
Thay vào phương trình đường thẳng  ta được: x 1 2 y  
1 1  0  x  2 y  0 .
Vậy phương trình đường thẳng  là ảnh của đường thẳng  có dạng: x  2 y  0 .
Câu 13: (THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho 2 2
đường tròn C  :  x  2   y   1
 9 . Gọi C là ảnh của đường tròn C  qua việc thực hiện 1 
liên tiếp phép vị tự tâm O , tỉ số k   và phép tịnh tiến theo vectơ v  1;  3 . Tính bán kính 3
R của đường tròn C . A. R  9 . B. R  3 .
C. R  27 .
D. R  1. Lời giải Chọn D
Đường tròn C  có bán kính R  3 . 1
Qua phép vị tự tâm O , tỉ số k   , đường tròn C  biến thành đường tròn C có bán kính 1  3 1
là R k .R  .3  1. 1 3 
Qua phép tính tiến theo vectơ v  1;  3 , đường tròn C biến thành đường tròn C có bán 1 
kính R  R  1. 1
Vậy R của đường tròn C là R 1.
Câu 14: (THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018) Cho tam giác ABC với trọng tâm G .
Gọi A , B , C lần lượt là trung điểm của các cạnh BC , AC , AB của tam giác ABC . Khi đó
phép vị tự nào biến tam giác A BC
  thành tam giác ABC ? 1 1
A. Phép vị tự tâm G , tỉ số  .
B. Phép vị tự tâm G , tỉ số . 2 2
C. Phép vị tự tâm G , tỉ số 2.
D. Phép vị tự tâm G , tỉ số 2  .
Hướng dẫn giải Chọn D  
Vì G là trọng tâm tam giác ABC nên GB  2  GB  V B  B G,2     Tương tự V
A  A và V C  C G,2   G, 2       
Vậy phép vị tự tâm G , tỉ số 2
 biến tam giác A BC
  thành tam giác ABC .
Câu 15: (THTT số 5-488 tháng 2 năm 2018) Trong mặt phẳng Oxy , cho điểm I 2;  
1 . Gọi C  là đồ 1
thị hàm số y  sin 3x . Phép vị tự tâm I 2;  1 , tỉ số k  
biến C  thành C . Viết 2
phương trình đường cong C . 3 1 3 1 A. y   sin 6x 18 . B. y   sin 6x 18 . 2 2 2 2 3 1 3 1 C. y    sin 6x 18 . D. y    sin 6x 18 . 2 2 2 2 Lời giải Chọn D  
x x k x xN IM I  Ta có: M   C  :V
M N C  IN k IM I ,k      
y y k y y   N IM I   1 x  2   x N  2 M    2 x  2  x  6  M N   
M 2x  6; 2
y  3  C N N    1  y  2  y  3 y 1   y   M N NM  1   2
Thay tọa độ M vào hàm số y  sin 3x ta có: 3 1 3 1
2 y  3  sin 32x  6   y    sin 6
x 18  y    sin x  . N 6 18 NNN  NN  2 2 2 2 3 1
Vậy đường cong C có phương trình là  y    sin 6x 18 . 2 2
Câu 16: (THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018) Cho tam giác ABC có diện tích bằng 6 2
cm . Phép vị tự tỷ số k  2
 biến tam giác ABC thành tam giác A BC   . Tính diện tích tam giác A BC   ? A. 12 2 cm . B. 24 2 cm . C. 6 2 cm . D. 3 2 cm . Lời giải Chọn B
Phép vị tự tỉ số k biến tam giác thành tam giác đồng dạng với tỉ số k .
Theo đề bài ta có phép vị tự tỉ số k  2
 biến biến tam giác ABC thành tam giác A BC   nên S ABC   2  k 2  Sk .S 2  S  2 .SS  4.6  S  24 2 cm .               SA B CABCA B CABC A B C A B C ABC
Câu 1: (THPT Chuyên Lam Sơn-Thanh Hóa-lần 2 năm 2017-2018) Trong mặt phẳng tọa độ Oxy cho
điểm A3; 4 . Gọi A là ảnh của điểm A qua phép quay tâm O 0;0 , góc quay 90 . Điểm A có tọa độ là A. A 3  ; 4 . B. A 4  ; 3   . C. A3; 4   . D. A 4  ;3 . Lời giải Chọn D
x x .cos 90  y .sin 90   y  4 Ta có AA A A   A 4  ;3 .
y x .sin 90  y .cos 90  x  3  AA A A
Câu 2: (THPT Chuyên Tiền Giang-lần 1 năm 2017-2018) Trong mặt phẳng Oxy , cho vectơ v  3;3 
và đường tròn C  2 2
: x y  2x  4 y  4  0 . Ảnh của C  qua phép tịnh tiến vectơ v là đường tròn nào? 2 2 2 2
A.C :  x  4   y   1  4 .
B.C :  x  4   y   1  9 . 2 2
C.C :  x  4   y   1  9 . D.C 2 2
: x y  8x  2 y  4  0 . Lời giải Chọn B 2 2 Ta có C  2 2
: x y  2x  4 y  4  0   x  
1   y  2  9 .
Vậy đường tròn C  có tâm I 1; 2 và bán kính R  3 . x  1 3 x  4
Gọi I  x ; y  T  I  khi đó ta có    . v y  2  3  y  1 
Do phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính nên phương trình đường 2 2
tròn C là C :  x  4   y   1  9 .
Câu 3: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Trong mặt phẳng tọa độ
Oxy , cho đường thẳng d : y x . Tìm ảnh của d qua phép quay tâm O , góc quay 90 .
A. d  : y  2x .
B. d  : y  x .
C. d  : y  2  x .
D. d  : y x . Lời giải Chọn B
x   y
Phép quay tâm O , góc quay 90 biến điểm M  ;
x y thành điểm M  x ; y với  . y  xTQ
Mà y x  x  y  x  y  0  y  x .
Câu 1: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Trong mặt phẳng
Oxy , tìm phương trình đường tròn C là ảnh của đường tròn C  : 2 2
x y  1 qua phép đối
xứng tâm I 1; 0 .
A. x   y  2 2 2  1.
B.x  2 2 2  y  1.
C.x  2 2 2  y  1.
D. x   y  2 2 2  1. Lời giải
Chọn C
Đường tròn C  có tâm O 0; 0 , bán kính R  1 .
Gọi O là ảnh của O qua phép đối xứng tâm I 1; 0 .  x x O O  x   2 I
x  2x xx  2.1 0 Ta có: OI O O       O2; 0 . y y
y  2 y y y  2.0  0 O O   yOI OO   2 I
Đường tròn C là ảnh của đường tròn C  qua phép đối xứng tâm I 1; 0 .
C có tâm O2; 0 , bán kính R  R  1.
Phương trình đường tròn C là:  x  2 2 2  y  1.
Câu 2: Trong mặt phẳng tọa độ Oxy , phép quay tâm O góc quay 90 biến điểm M  1  ; 2 thành điểm
M  . Tọa độ điểm M  là
A. M  2;  1 .
B. M 2;   1 .
C. M 2;   1 .
D. M 2;  1 .
Câu 3: Trong mặt phẳng tọa độ Oxy , phép quay tâm O góc quay 90 biến điểm M  1  ; 2 thành điểm
M  . Tọa độ điểm M  là
A. M  2;  1 .
B. M 2;   1 .
C. M 2;   1 .
D. M 2;  1 . Lời giải Chọn C y M 2 1 -2 x -1 O 1 2 -1 M'  
OM ; OM   90 Có M   Q M  . O;90     OM    OM
Phương trình đường thẳng OM  qua O , vuông góc với OM có dạng x  2 y  0 . a  1 M 2;  1 Gọi M 2 ;
a a . Do OM   OM a a   2 2 2 2 4 1  2     . a  1   M  2  ;   1  Có M 2; 
1 là ảnh của M qua phép quay góc 90 , M  2  ;  
1 là ảnh của M qua phép
quay góc 90 . Vậy chọn M 2;   1 .
Trắc nghiệm: Điểm M  ;
b a là ảnh của M  ;
a b qua phép quay tâm O , góc quay 90 . Vậy chọn M  2;   1 .
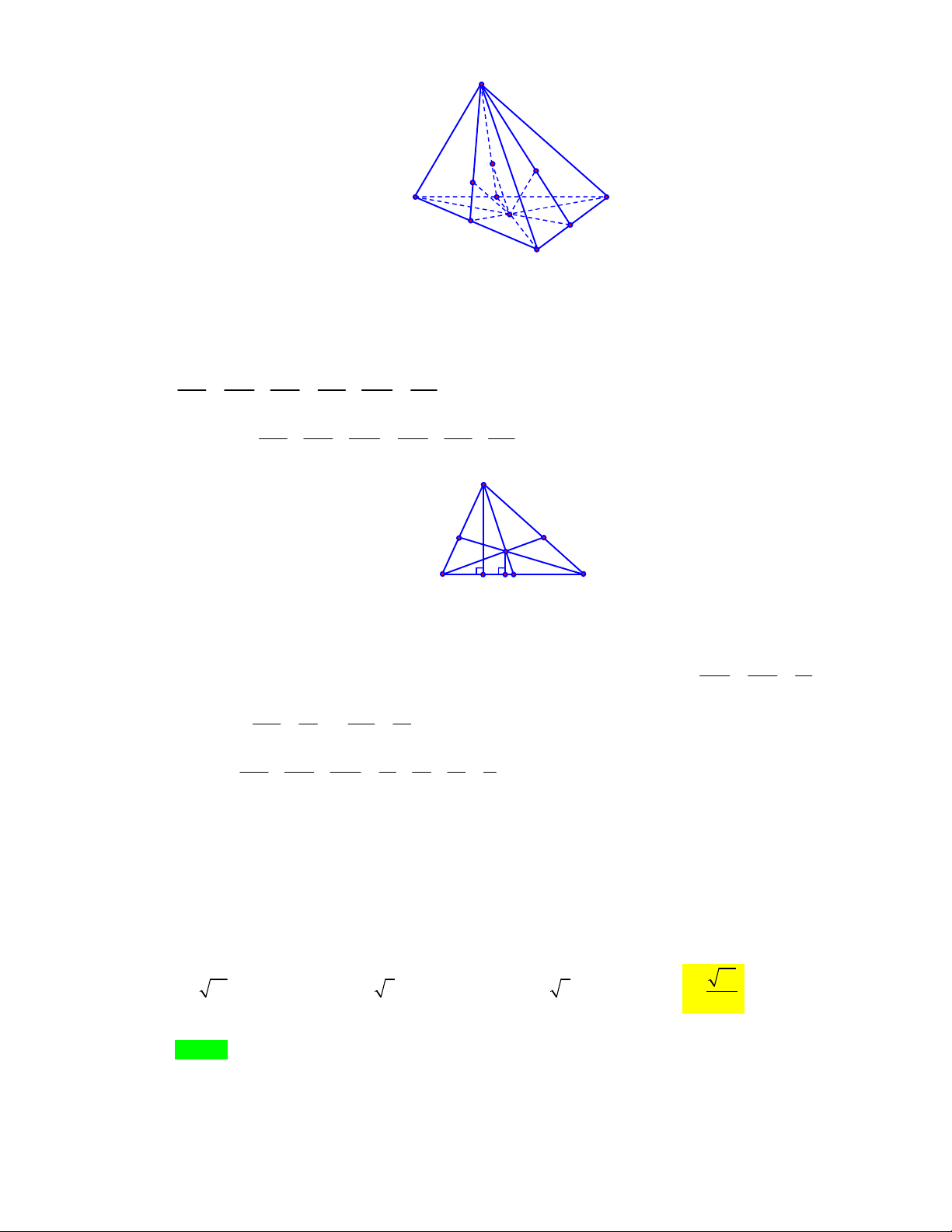
Câu 35: [1H1-3] (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Cho tứ diện ABCD
có BD  2 . Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10 . Biết thể tích khối tứ
diện ABCD bằng 16 . Tính số đo góc giữa hai mặt phẳng  ABD,  BCD .  4   4   4   4  A. arccos   .
B. arcsin   . C. arccos   . D. arcsin   .  15   5   5   15  Lời giải Chọn B. A B C H K D 1 3V 24
Gọi H là hình chiếu của A xuống  BCD . Ta có VAH .SAH   . ABCD 3 BCD S 5 BCD
Gọi K là hình chiếu của A xuống BD , dễ thấy HK BD . Vậy  ABD  BCD     ,  AKH 1 2S Mặt khác SAK. ABD BD AK   6 . ABD 2 BD AH  
Do đó  ABD  BCD     4 ,  AKH  arcsin  arcsin   . AK  5 
Câu 32. [1H1-3] (THTT Số 1-484 tháng 10 năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho hai 2 2
đường tròn C  :  x m   y  2  5 và C 2 2
x y  m   2 : 2
2 y  6x 12  m  0 . Vectơ 
v nào dưới đây là vectơ của phép tịnh tiến biến C  thành C ?    
A. v  2  ;1 . B. v   2  ;  1 .
C. v  1; 2 .
D. v  2;   1 . Lời giải Chọn A. 1
Điều kiện để C là đường tròn m  22 2
 9 12  m  0  4
m 1  0  m  . 4 Khi đó:
Đường tròn C có tâm là I 2  ;
m 3 , bán kính R  4  m 1 .
Đường tròn C  có tâm là I  ;
m 2 , bán kính R  5 .  R  R
Phép tịnh tiến theo vectơ v biến C  thành C khi và chỉ khi   II   v   4  m 1  5 m  1        .Vậy chọn A v II    3  ; m mv   2;  1  
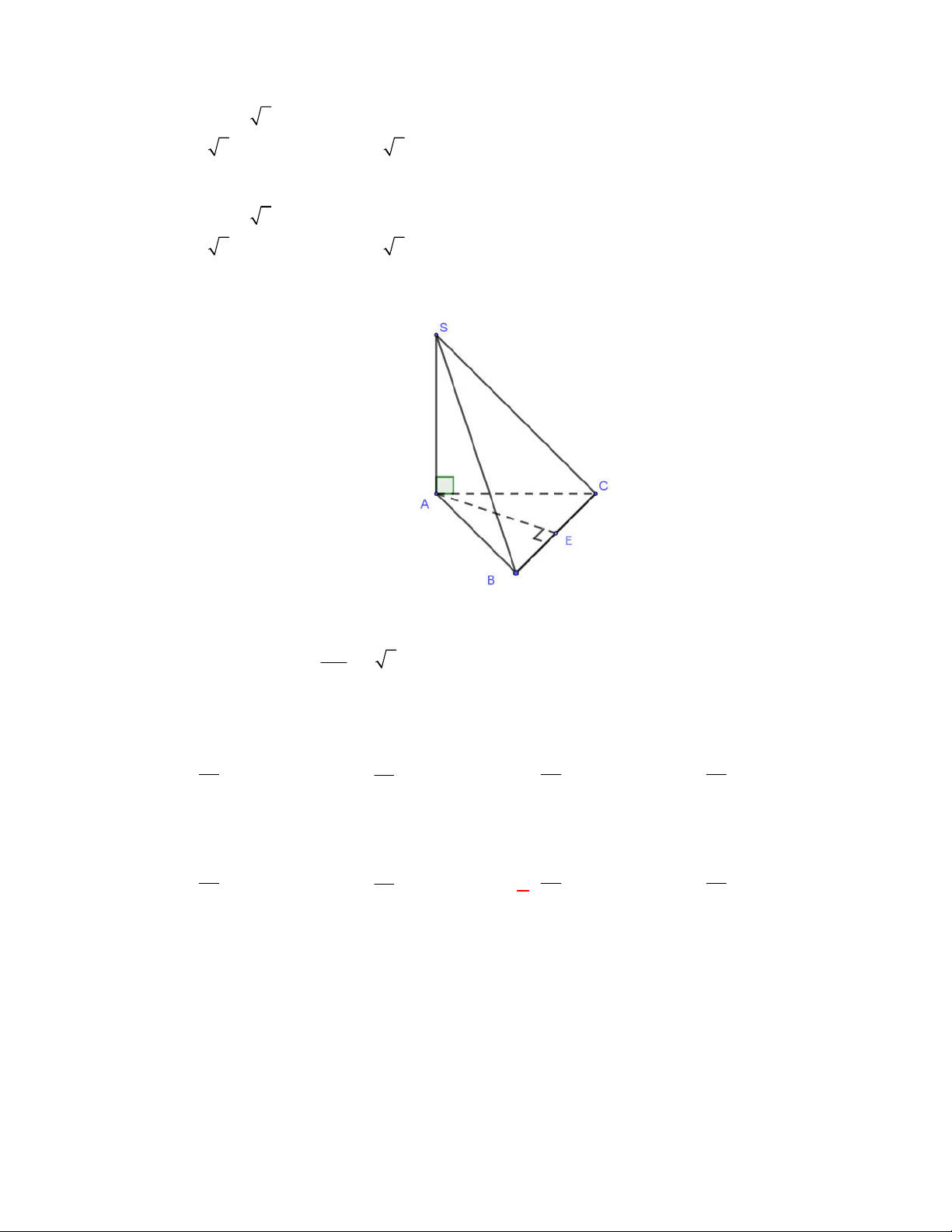
Câu 35: [1H1-3] (THPT Nguyễn Khuyến-Nam Định-lần 1-năm 2017-2018) Cho hình chóp S.ABC có
đáy ABC là tam giác vuông tại B , AB a , cạnh bên SA vuông góc với mặt đáy và
SA a 2 . Gọi M là trung điểm của AB . Tính khoảng cách d giữa hai đường thẳng SM và BC . a 3 a 2 a 3 a A. d  . B. d  . C. d  . D. d  . 2 3 3 2 Lời giải Chọn B. S H A N C M B
Gọi N là trung điểm AC MN // BC  Ta có 
BC //  SMN MN   SMN  
d SM , BC   d BC,SMN   d B,SMN   d  ,
A SMN  (vì M là trung điểm AB ). MN AB Mặt khác 
MN   SAB ; MN SA    SMN    SAB
MN  SMN    SMN
  SAB  SM
Trong mặt phẳng  SAB , kẻ AH SM AH   SMN   AH d  , A SMN  1 1 1 a 2
Tam giác SAM vuông tại A có    AH  . 2 2 2 AH SA AM 3 a 2
Vậy d SM , BC   . 3 Câu 50:
[1H1-3] (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Cho tứ diện ABCD có các tam giác
ABC và DBC vuông cân và nằm trong hai mặt phẳng vuông góc với nhau,
AB AC DB DC  2 .
a Tính khoảng cách từ B đến mp  ACD. a 6 a 6 2a 6 A. a 6. B. . C. . D. . 3 2 3 Lời giải Chọn D. A B D H C
Ta có  ABC    DBC  và  ABC    DBC   BC.
Kẻ AH BC H BC   AH   BCD. BC AB 2
Tam giác ABC vuông cân tại A AH HB HC    a 2. 2 2
Từ DBC vuông cân tại D và HB HC HD HB HC a 2 và HD BC. d  ; B ACD BC Ta có   2  d  ;
B ACD  2d H; ACD  2 . h
d H; ACD HC Để ý ,
HA HC, HD vuông góc với nhau từng đôi một 1 1 1 1 1 1 1 2 2a 6         h ad ; B ACD  2h  . 2 2 2 2 2 2 2    h HA HC HD 2a 2a 2a 3 3
----------------------------------- HẾT -----------------------------------Câu 43.
[1H1-3] (THPT Thạch Thành-
Thanh Hóa-năm 2017-2018) Trong mặt phẳng Oxy cho đường tròn C  có phương trình
x  2   y  2 1 2
 4. Hỏi phép vị tự tâm O tỉ số k  2
 biến C  thành đường tròn nào sau đây: 2 2 2 2
A. x  4   y  2  4 .
B. x  4   y  2  16 . 2 2 2 2
C. x  2   y  4  16 .
D. x  2   y  4  16 . Lời giải Chọn C.
Gọi C là ảnh của đường tròn C  qua phép vị tự tâm O tỉ số k  2  .
Đường tròn C  có tâm I 1;2 và bán kính R  2 .
Gọi I  và R tâm và bán kính của đường tròn C .
Ta có: R  k R  2 .2  4 .   x  2  x  2.1   2
Mặt khác: OI   2 I IOI    I  2  ; 4   . y  2  y  2.2   4  II 2 2
Vậy, phương trình đường tròn C là  x  2   y  4  16.
Câu 36. [1H1-3] (TT Diệu Hiền-Cần Thơ-tháng 11-năm 2017-2018) Cho lăng trụ . ABCD AB CD  
có đáy ACBD là hình thoi cạnh a , biết A .ABC là hình chóp đều và A D  hợp với mặt đáy
một góc 45 . Thể tích khối lăng trụ . ABCD AB CD   là : 3 a 6 3 a 6 A. 3 a . B. . C. 3 a 3 . D. . 12 3 Lời giải Chọn A. D' A' C' B' D A O G C B Ta có  A D   ABCD   ,
ADG  45 . a 3 2a 3
Ta giác ABC đều cạnh a nên BG
, DB a 3 , DG  2BG  . 3 3 2a 3 Tam giác A DG
vuông cân tại G nên AG DG  . 3 1 2a 3 3 VS .AG  . a a 3.  a . ABCD. A BCD   ABCD 2 3 Câu 4:
[1H1-3] (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Cho tam giác ABC có A1; 2 ,
B 5; 4 , C 3; 2
 . Gọi A, B, C lần lượt là ảnh của A , B , C qua phép vị tự tâm I 1;5 tỉ số k  3
 . Bán kính đường tròn ngoại tiếp tam giác A BC   bằng: A. 3 10 . B. 6 10 . C. 2 5 . D. 3 5 . Lời giải Chọn A.      
Ta có: BC  2; 6
  , AB  4; 2 , AC  2; 4   nên A .
B AC  0  AB AC .
Vậy tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm BC
cạnh huyền BC và bán kính R   10 . 2
Gọi R là bán kính đường tròn ngoại tiếp tam giác A BC   . Tam giác A BC
  là ảnh của tam giác ABC qua phép vị tự tâm I tỉ số k  3  .
Nên R  3 R  3 10 .
Câu 45. [1H1-3] (THPT Chuyên Hùng Vương-Bình Phước-lần 2-năm 2017-2018) Cho hình chóp
SABC . Bên trong tam giác ABC lấy một điểm O bất kỳ. Từ O dựng các đường thẳng lần lượt
song song với SA , SB , SC và cắt các mặt phẳng SBC  , SCA , SAB theo thứ tự lần lượt  OA OBOC tại 
A , B , C . Khi đó tổng tỉ số T    bằng bao nhiêu ? SA SB SC 3 1 A. T  3. B. T  . C. T  1. D. T  . 4 3 Lời giải Chọn C. S BACN A C O P M B
Gọi M , N , P lần lượt là giao điểm của AO , BO , CO với BC , CA , AB .
Từ O dựng các đường thẳng lần lượt song song với SA , SB , SC và cắt các đường thẳng SM ,
SN , SP lần lượt tại 
A , B , C .
Áp dụng định lý Talet trong các tam giác SAM , SBN , SCP ta có: O A MO OBNO OCPO  ;  ;  . SA MA SB NB SC PCOA OBOCMO NO PO Khi đó T       SA SB SC MA NB PC A P O N B K H M C
Gọi S , S , S S lần lượt là diện tích các tam giác OBC , OCA , OAB , ABC . Dựng 1 2 3
OH BC , AK BC nên OH // AK . MO OH S
Khi đó áp dụng định lý Talet trong tam giác AKM và tỉ số diện tích ta có 1   . MA AK S NO S PO S Tương tự: 2  và 3  . NB S PC SOA OBOCS S S S Vậy 1 2 3 T         1. SA SB SC S S S S
Cách giải nhanh: Đặc biệt hóa bài toán với O là trọng tâm tam giác ABC sẽ nhanh chóng tìm ra đáp án. Câu 49.
[1H1-3] (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Cho ba điểm A , B , C thẳng hàng theo
thứ tự đó và AB  2BC . Dựng các hình vuông ABEF , BCGH (đỉnh của hình vuông tính theo chiều
kim đồng hồ). Xét phép quay tâm B góc quay 90 biến điểm E thành điểm .
A Gọi I là giao điểm
của EC và GH . Giả sử I biến thành điểm J qua phép quay trên. Nếu AC  3 thì IJ bằng 10 A. 10 . B. 5 . C. 2 5 . D. . 2 Lời giải Chọn D.
Do Q B;90 : I J nên BIJ vuông cân tại B IJ BI 2 .
Mà AC  3  BC  1. Vì AB  2BC BE  2BH HI là đường trung bình EBC 1 1 1 5  HI BC  . Ta có 2 2 BI
BH IH  1  2 2 4 2 10
Vậy IJ BH 2  . 2
Câu 39. [1H1-3] (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Ảnh của điểm M 2; 3   qua phép
quay tâm I 1;2 góc quay 120 là  5 3  5 3 3  9   5 3  5 3 3  9  A. M  ;  . B. M  ; .   2 2      2 2    5 3 1 3  3 1   5  3 1 3 3  9  C. M  ;  . D. M  ; .   2 2      2 2   Lời giải Chọn B.
Gọi M  x ; y là ảnh của M 2; 3
  qua phép quay tâm I 1;2 góc quay 120 
x   x a cos   y b sin   a 
x  2   1 cos120   3   2sin120 1 Ta có:    . x  
x asin   y bcos  bx   2   1 sin120   3   2 cos120  2   3 3  5 3  5 x    5 1  x    2 2  2  5 3  5 3 3  9      . Vậy M  ;  .    3 5  3 3  9 2 2   y  3.   2 y    2 2   2
Câu 1: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Trong mặt phẳng Oxy , cho đường
tròn C  x  2   y  2 : 6 4
12 . Viết phương trình đường tròn là ảnh của đường tròn C  qua phép 1
đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số
và phép quay tâm O góc 2 90 .
A.x  2   y  2 2 3  3 .
B.x  2   y  2 2 3  3 . C.  2 2
x  2   y  2 2 3  6 .
D.x  2   y  3  6. Lời giải Chọn A
Đường tròn C  có tâm I 6; 4 và bán kính R  2 3 . 1
Qua phép vị tự tâm O tỉ số
điểm I 6; 4 biến thành điểm I 3; 2 ; qua phép quay tâm O góc 1   2
90 điểm I 3; 2 biến thành điểm I  2  ;3 . 1  
Vậy ảnh của đường tròn C  qua phép đồng dạng trên là đường tròn có tâm I 2  ;3 và bán kính 1 R 
R  3 có phương trình:  x  2   y  2 2 3  3 . 2
Câu 2: (SGD Ninh Bình năm 2017-2018) Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng
ABC , AC AD  4 , AB  3 , BC  5. Tính khoảng cách d từ điểm A đến mặt phẳng BCD . 12 60 769 34 A. d  . B. d  . C. d  . D. d  . 34 769 60 12 Lời giải Chọn A D H C A B Ta có 2 2 2
BC AB AC nên A
BC vuông tại A , gọi H là hình chiếu của A trên  BCD . 1 1 1 1 1 1 1 17
Tứ diện ABCD là tứ diện vuông nên ta có        2 2 2 2 2 2 2 AH AB AC AD 3 4 4 72
Vậy d A BCD 12 ;  AH  . . 34
Câu 3: (THPT Hồng Quang-Hải Dương năm 2017-2018) Thành phố Hải Đông dự định xây dựng một
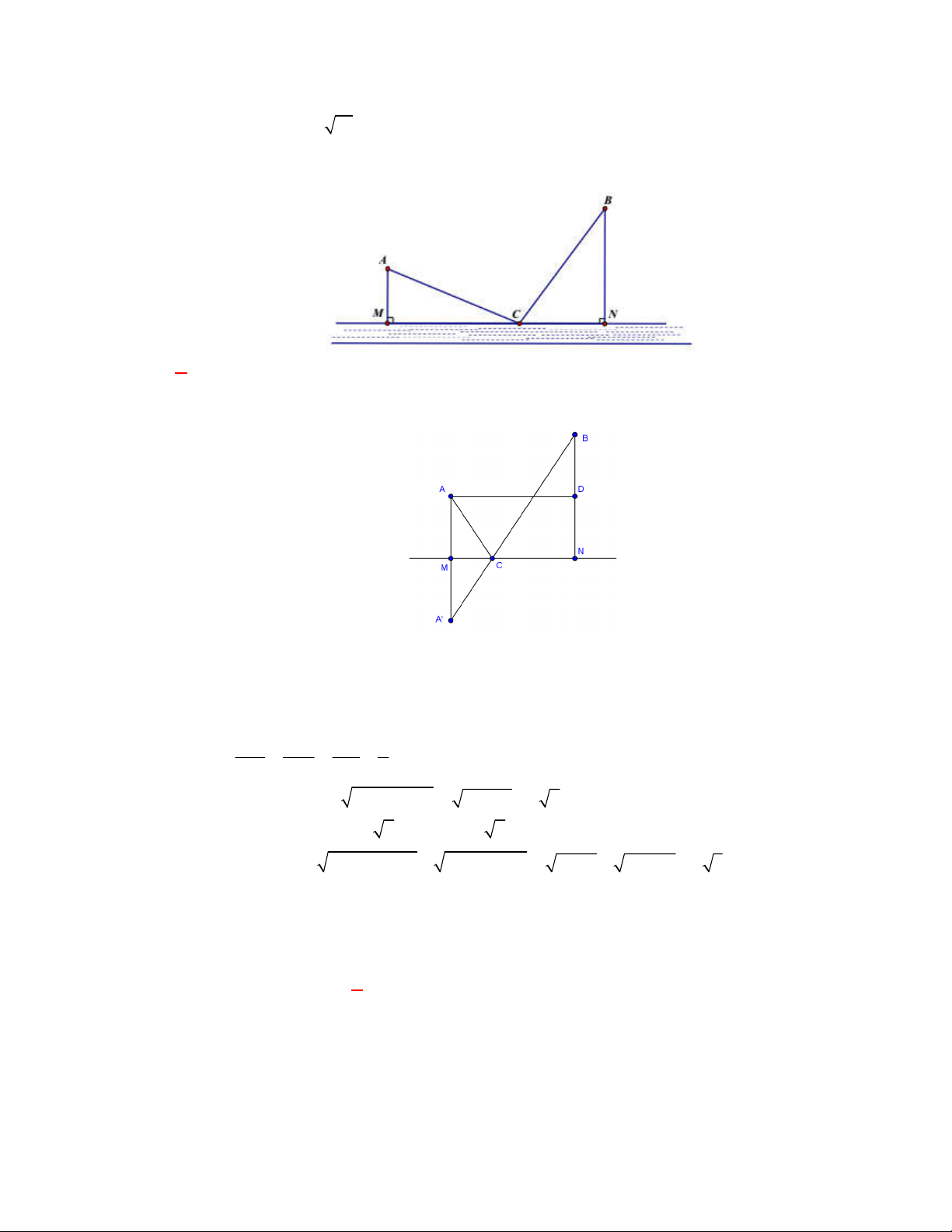
trạm nước sạch để cung cấp cho hai khu dân cư A và B . Trạm nước sạch đặt tại vị trí C trên
bờ sông. Biết AB  3 17 km , khoảng cách từ A và B đến bờ sông lần lượt là AM  3km ,
BN  6 km (hình vẽ). Gọi T là tổng độ dài đường ống từ trạm nước đến A và B . Tìm giá trị nhỏ nhất của T . A. 15 km . B. 14, 32 km . C. 15, 56 km . D. 16 km . Lời giải Chọn C
Gọi A đối xứng với A qua MN , D là trung điểm của NB .
Do A cố định nên A cũng cố định.
Ta có: T CA CB CA  CB AB (không đổi).
Đẳng thức xảy ra khi C  MN A B  . MC MAMA 1 Khi đó:    (1) NC NB NB 2 Mặt khác, 2 2 MN AD
AD DB  153  9  9 2 km (2)
Từ (1) và (2) suy ra MC  3 2 km , NC  6 2 km . Vậy 2 2 2 2
T CA CB
AM MC BN NC  9 18  36  72  9 3  15, 56 km .
Câu 4: (THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho
đường thẳng d : 3x y  2  0 . Viết phương trình đường thẳng d là ảnh của d qua phép quay tâm O góc quay o 90 .
A. d : x  3y  2  0 .
B. d : x  3y  2  0 . C. d : 3x y  6  0 . D. d : x  3y  2  0 . Lời giải Chọn B
Qua phép quay tâm O góc quay o
90 đường thẳng d biến thành đường thẳng d vuông góc với d .
Phương trình đường thẳng d có dạng: x  3y m  0 .
Lấy A0; 2  d . Qua phép quay tâm O góc quay o
90 , điểm A0; 2 biến thành điểm
B 2;0  d . Khi đó m  2  .
Vậy phương trình đường d là x  3y  2  0 .
Câu 1: (THPT Chuyên Lam Sơn-Thanh Hóa-lần 2 năm 2017-2018) Cho đường thẳng d có phương
trình 4x  3y  5  0 và đường thẳng  có phương trình x  2 y  5  0 . Phương trình đường
thẳng d  là ảnh của đường thẳng d qua phép đối xứng trục  là
A. x  3  0 .
B. 3x y 1  0 .
C. 3x  2 y  5  0 .
D. y  3  0 . Lời giải Chọn D
Gọi M d    M 1; 3 . Lấy N 2;   1  d .
Gọi d là đường thẳng qua N và vuông góc với  , ta có d : 2x y  5  0 1 1
Gọi I d    I 3;  1 . 1
Gọi N là ảnh của N qua phép đối xứng trục   I là trung điểm của NN  nên N 4; 3 .
d  là ảnh của đường thẳng d qua phép đối xứng trục 
d  là đường thẳng qua M  1
 ; 3 và N4; 3 .
Vậy d  : y  3  0 .
Câu 2: (SGD Hà Nội-lần 11 năm 2017-2018) Cho tứ diện đều ABCD có M , N lần lượt là trung điểm
của các cạnh AB và CD . Mệnh đề nào sau đây sai?
A. MN AB .
B. MN BD .
C. MN CD .
D. AB CD . Lời giải Chọn B A M B C N D • N
AB cân tại N nên MN AB . • MC
D cân tại M nên MN CD .
• CD   ABN   CD AB .
• Giả sử MN BD
mà MN AB . Suy ra MN   ABD (Vô lí vì ABCD là tứ diện đều) Vậy phương án B sai.
Câu 1: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , SA vuông góc với mặt phẳng  ABC
và BC  4 2 cm . Khoảng cách giữa hai đường thẳng SA và BC là A. 4 2 cm . B. 2 2 cm . C. 4 cm . D. 2 cm .
Câu 2: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , SA vuông góc với mặt phẳng  ABC
và BC  4 2 cm . Khoảng cách giữa hai đường thẳng SA và BC là A. 4 2 cm . B. 2 2 cm . C. 4 cm . D. 2 cm . Lời giải
Chọn B .
Gọi M là trung điểm BC , ta có AM SA và AM BC . BC d  ,
SA BC   AM   2 2 cm . 2
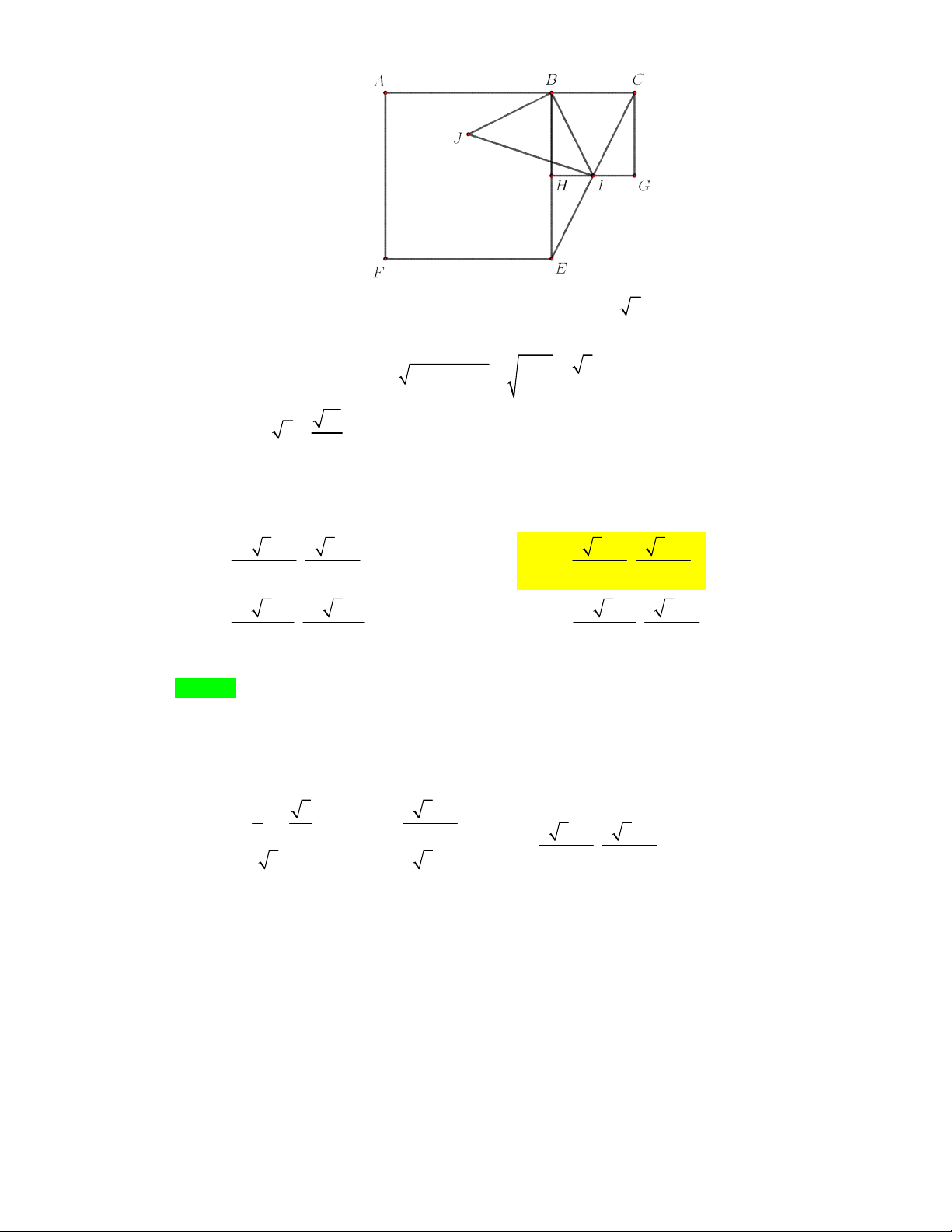
Câu 3: Cho khối hộp ABCD.AB CD
  . Gọi M là trung điểm của AB . Mặt phẳng MB D   chia khối
hộp thành hai phần. Tính tỉ số thể tích 2 phần đó. 7 5 7 5 A. . B. . C. . D. . 24 12 17 17
Câu 4: Cho khối hộp ABCD.AB CD
  . Gọi M là trung điểm của AB . Mặt phẳng MB D   chia khối
hộp thành hai phần. Tính tỉ số thể tích 2 phần đó. 7 5 7 5 A. . B. . C. . D. . 24 12 17 17 Lời giải Chọn C S A D M C B A' D' B' C'
Đặc biệt hóa: ABCD.AB CD
  là hình lập phương cạnh a .
Gọi N là trung điểm của AD suy ra MN //BD //B' D' suy ra thiết diện là MND B   .
V là thể tích phần chứa đỉnh A ; V là phần còn lại. 1 2 1 1
Gọi S AA  MB nên S , N , D thẳng hàng; MN B D    SA SA 2 2 2 1 1  1 1 1    3 1  a  7 V VV  SA .S  . SA S 2  3 3 2a. a aa   a .     1 SA BD   SAMN      3 A B D AMN 3 2 2   2    3 8   24 3 17a V 7
V V V  . Vậy 1  . 2 lp 1 24 V 17 2
Câu 1: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Trong mặt phẳng tọa độ Oxy , cho tam giác
ABC có trực tâm O . Gọi M là trung điểm của BC ; N , P lần lượt là chân đường cao kẻ từ
B và C . Đường tròn đi qua ba điểm M , N ,
P có phương trình là 2   
T   x  2 1 25 : 1  y    
. Phương trình đường tròn ngoại tiếp tam giác ABC là:  2  4 2 2 A.x  
1   y  2  25 .
B. x   y  2 2 1  25 . 2 2
C. x   y  2 2 1  50 .
D.x  2   y   1  25 . Lời giải Chọn D
Ta có M là trung điểm của BC ; N , P lần lượt là chân đường cao kẻ từ B và C . Đường tròn
đi qua ba điểm M , N , P là đường tròn Euler. Do đó đường tròn ngoại tiếp tam giác ABC
chính là ảnh của đường tròn Euler qua phép vị tự tâm là O , tỷ số k  2 .
Gọi I và I  lần lượt là tâm đường tròn ngoại tiếp tam giác MNP và tam giác ABC .
Gọi R và R lần lượt là bán kính đường tròn ngoại tiếp tam giác MNP và tam giác ABC .    1  Ta có I 1;  
 và do đó OI   2OI I 2;   1 .  2  5 Mặt khác R   R  5 . 2 2 2
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là:  x  2   y   1  25 .
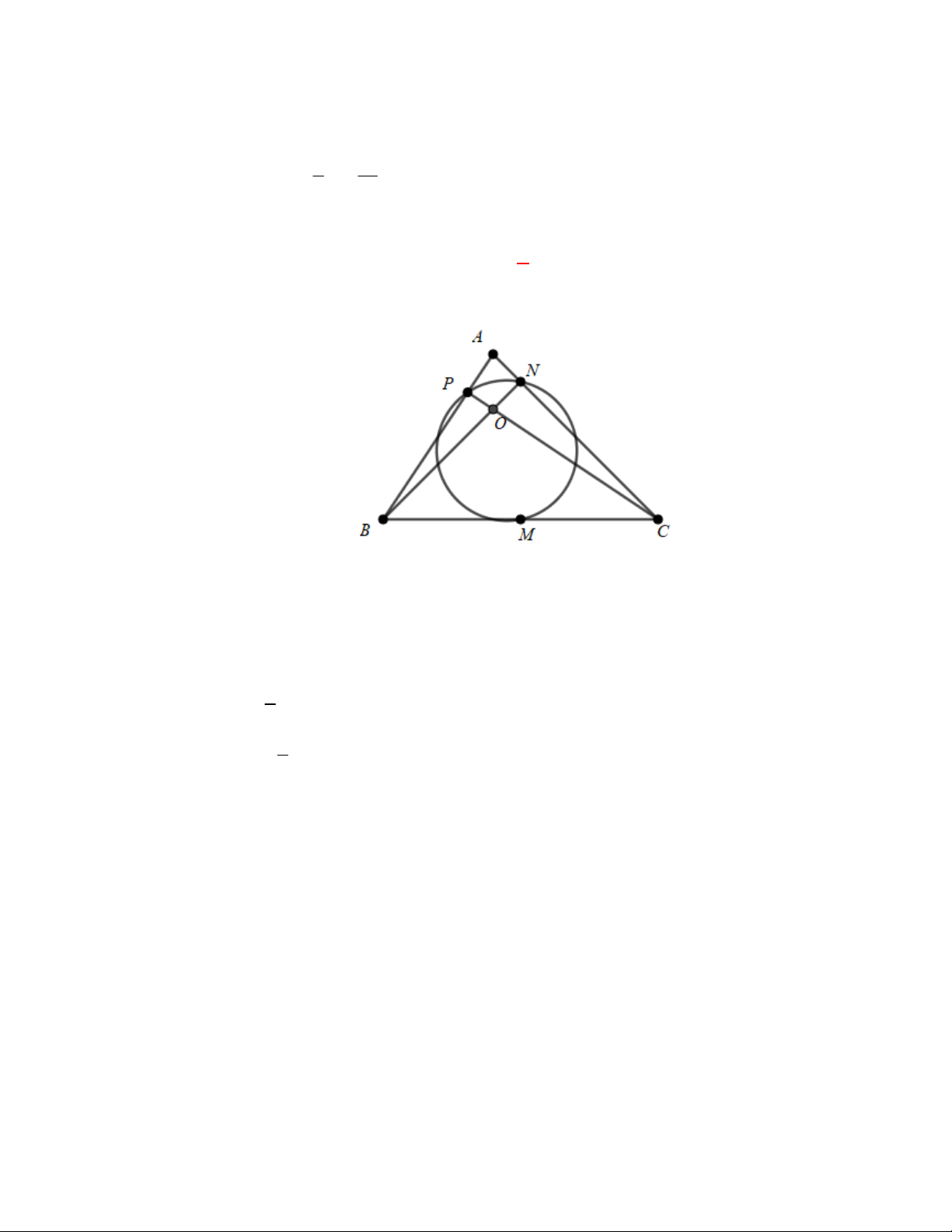
Nhận xét: Đề bài này rất khó đối với học sinh nếu không biết đến đường tròn Euler.
Document Outline

  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 1 Phần 1
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 1 Phần 2
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 1 Phần 3
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 1 Phần 4
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 2 Phần 1
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 2 Phần 2
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 2 Phần 3
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 2 Phần 4
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 3 Phần 1
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 3 Phần 2
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 3 Phần 3
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 3 Phần 4
  • Chương 1 - PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG - Mức độ 4 Phần 2