Thông tin
Quiz

Tuyển chọn một số bài toán PT – BPT – HPT hay – Lương Anh Nhật

Thường thường câu 9 điểm trong đề thi PTTH Quốc gia là câu giải phương trình, bất phương trình hay hệ phương trình. Theo ý kiến cá nhân của tôi thì phương trình là nền tảng cho các dạng còn lại, bất phương trình kế thừa phương trình nhưng mang màu sắc của xét dấu là chủ yếu còn lại là các phép biến đổi. Hệ phương trình là dung hòa của hai (nhiều) phương trình. Nói chung cái khó của các bài toán này nằm ở kinh nghiệm giải của các bạn và do ý đồ kết hợp các phương pháp của tác giả! Các ví dụ trên đây là các dạng thường gặp của “bài toán 9 điểm” trong bài thi PTTH Quốc gia. Cùng xem một số câu tham khảo nhé!

Chủ đề:

Tài liệu chung Toán 10 394 tài liệu

Môn:

Toán 10 2.8 K tài liệu

Thông tin:

21 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tuyển chọn một số bài toán PT – BPT – HPT hay – Lương Anh Nhật

246 123 lượt tải Tải xuống

PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH

Kiến thức cần nhớ:





























































 

00ab

















Ví dụ 1: Giải phương trình:

1 2 1x x x    

HD: biến đổi sao cho hai vế không âm rồi bình phương đưa về dạng cơ bản.

Ví dũ 2: Giải phương trình:

2 2 2

4 4 3 4 2x x x x x x x      

HD: biến đổi hai vế, đặt

4t x x  

đưa về dạng đẳng cấp.

Ví dụ 3: Giải phương trình:





HD: Đặt

sinx





, lượng giác hóa phương trình.

Ví dụ 4: Giải phương trình:

2 2 1 27 27 13 2x x x x    

HD: Dùng đơn điệu.

Ví dụ 5: Giải phương trình:

 

3 2 1 3x x x x    

HD: Dùng lượng liên hiệp.

Ví dụ 6: Giải phương trình:

4 20 4 29 97x x x x     

HD: Dạng này hiếm gặp, xét hai vecto có tọa độ thích hợp rồi đưa về độ dài.

Ví dụ 7: Giải phương trình:

3 1 3 2 0x x x x     

HD: Biến đổi về dạng đẳng cấp, chú ý dấu. (Làm nhiễu thôi!)

Ví dụ 8: Giải bất phương trình:

 

3 2 3 2 0x x x x   

HD: Dạng cơ bản.

Ví dụ 9: Giải bất phương trình:







HD: Chia khoảng theo điều kiện và giải bình thường.

Ví dụ 10: (A-2004) Giải bất phương trình:

 

2 16



  



Ví dụ 11: Giải bất phương trình:

2 2 2

8 15 2 15 4 18 18x x x x x x       

HD: Chia trường hợp theo điều kiện xác định.

Lưu ý: Thường thường câu 9 điểm trong đề thi PTTH Quốc gia là câu giải phương trình, bất phương trình hay hệ phương

trình. Theo ý kiến cá nhân của tôi thì phương trình là nền tảng cho các dạng còn lại, bất phương trình kế thừa phương trình

nhưng mang màu sắc của xét dấu là chủ yếu còn lại là các phép biến đổi. Hệ phương trình là dung hòa của hai (nhiều)

phương trình. Nói chung cái khó của các bài toán này nằm ở kinh nghiệm giải của các bạn và do ý đồ kết hợp các phương

pháp của tác giả! Các ví dụ trên đây là các dạng thường gặp của “bài toán 9 điểm” trong bài thi PTTH Quốc gia. Cùng xem

một số câu tham khảo nhé!

Bài 1. Giải phương trình:





 

7 1 13 2 2 1x x x x x x x      

Hướng dẫn

Điều kiện:

13 3 17





Phương trình đã cho tương trương với:

 

1 2 1

7 1 13 2 1x x x



      





Đặt

2t x t x

     

, từ (1) suy ra t > 0 .

Phương trình (1) trở thành:

   









 

2 2 2

7 2 1 13 2 2

5 9 2 1 2 5

8 2 5

5 20

9 2 1 2 5

t t t

t t t t

t t t

     

      







   



   



   



Vì

9 2 1 2 5t t t



   

và t > 0 nên t = 2.

Suy ra:

2 2 1 0 1 2 3 2 2x x x x x

           

So sánh với điều kiện đề bài, kết luận:

3 2 2x 

Nhận xét: Bài toán này rất hay ở chỗ chia hai vế cho x mới có thể đưa về dạng quen thuộc là kết hợp giữa ẩn phụ và liên

hiệp, có dính dáng đến một chút của phương pháp đánh giá biểu thức nhưng không quá khó. Tiếp tục với một bài nữa về

phương trình cũng rất hay liên quan đến tính đơn điệu.

Bài 2. (PTTH Quốc gia 2015) Giải phương trình:

 

1 2 2



   



Hướng dẫn

Điều kiện:

2x 

Phương trình tương đương với:

  

 

1 .

0 *















   

































Nhìn kỹ phương trình (*) ta thấy một nét đẹp như phép biến đổi sau:

 

   

     

2 2 2 2 1 2 1 2 **

x x x x













         









Xét hàm số:

 

       

2 2 , 0 ' 2 . 2 2 0, 0f t t t t f t t t t f t t            

 

3 13

** 2 1 2 1

2 2 1 3 1 0

f x f x x x x

x x x x x







           



      



Kết luận:

3 13





Nhận xét: Bài toán này hay ở chỗ sau khi liên hiệp xong phần đông học trò sẽ lấn cấn ở chỗ dung đơn điệu, nhưng nếu làm

quen các bạn sẽ dễ dàng thấy rõ được chỗ bí ẩn này. Phần lớn học trò năm 2015 – là các anh chị trước cũng gặp tình trạng

tương tự nên nếu không rõ thì cũng không sao. Tiếp theo đây là một bài cũng nên lưu ý.

Bài 3. Giải phương trình:





2 2 2

2 15 15 3 15 4x x x x x      

Hướng dẫn

Điều kiện:

0 15x

Phương trình tương đương với:





 

2 2 2

15 3 . 15 4 2 15 0 1x x x x x x       

Đặt

 

2 2 2 2 2

15 , : 1 3 4 2 0 3 2 2 4 0u x v x u uv v u v u v u v v              

 

3 2 4 2 4 2

v v v v





       







   

2 15 2 2 19 nhan 2 19 loaiu v x x x x           

2 2 2

2 15 2 15 2 4 15 19 0u v x x x x x x              

Có

0 15 19 0 4 15 19 0 4 15 19 0x x x x x x              

vô nghiệm.

Kết luận:

2 19x   

Nhận xét: Bài toán hay ở chỗ đặt ẩn phụ và dò mối tương quan của các ẩn phụ bằng denta của một phương trình bậc hai

theo một ẩn nào đó thích hợp. Các bạn nên lưu ý dạng toán này.

Bài 4. Giải phương trình:

 

2 4 3 2

4 2 4 4 1 1x x x x x x       

Hướng dẫn

Điều kiện:

22x  

Phương trình tương đương với:

 

2 2 2

4 2 2 2 2x x x x x x      

(1)

Có:





   

2 2 2

4 4 2 4 4, 2;2 4 2, 2;2x x x x x x x x               

Có dấu “=” khi và chỉ khi

02xx   

(2). Đặt

   

2 1;2 , 2,2t x x t x       

Khi đó vế phải của phương trình (1) là:

 

 

   

3 2 2

2 2, 1,2 ' 3 4 ' 0

f t t t t f t t t f t







          







Hàm số f(t) liên tục trên tập xác định của nó nên:

       

 

4 22

1 1, 0 0, , 2 2 2, 1,2

3 27

f f f f f t t



         





Ta có:

 

 

2 2 2 2 2, 2,2x x x x x       

Dấu “=” xảy ra khi và chỉ khi

02xx   

(3).

Từ (2) và (3) cho ta: phương trình có ba nghiệm là

02xx   

Nhận xét: Dạng đánh giá này các bạn ít gặp và nó cũng hơi rắc rối, nên lưu tâm. Dạng này không có kinh nghiệm gì để học

mà kinh nghiệm là do các bạn giải nhiều thôi!

Bài 5. Giải phương trình:

3 2 2 3

2 10 17 8 2 . 5x x x x x x     

Hướng dẫn

Ta nhận thấy x = 0 không là nghiệm của phương trình.

Ta chia 2 vế của phương trình cho x

, ta được:

2 3 2

10 17 8 5

2 2 1

x x x x

     

Đặt

,0tt



phương trình trở thành:

   





 

3 3 3

2 3 2 2 2

2 10 17 8 2 5 1 2 1 2 2 1 5 1 2 5 1 1t t t t t t t t             

Xét hàm số:

     

2 ' 3 2 ' 0,f t t t f t t f t t        

   





 

2 2 2 3 2

1 2 1 5 1 2 1 5 1 2 1 5 1 8 17 6 0

17 97

f t f t t t t t t t t







                











0t 

loại trường hợp này. _

17 97 17 97

16 12



  

. _

17 97 17 97

16 12



  

Kết luận: Phương trình đã cho có nghiệm

17 97





Bài 6. Giải phương trình:

7 14 6

3 7 5 1

x x x

  

    



Hướng dẫn Phương trình tương đương với:

 

      

 

3 2 2

7 14 6 1 2 3 7 5

2 4 3 1 2 1 2 2 4 3

x x x x x x

x x x x x x x x

       

           

Đặt

  

 

2, 1 2 2 4 3a x b x x x x       

. Ta có hệ sau:

 

  

1 2 4 3

1 2 0

1 2 4 3

b x a x x

b a x b a

a b x

a x a x x







    





      







    

    













3 7 5 2b a x x x     

lập phương hai vế ta được ba nghiệm

3 3 2 2xx     

1 2 0

a b x



    





rõ rang là vô nghiệm nhé!

Kết luận: Phương trình có nghiệm là

3 3 2 2xx     

Bài 7. Giải phương trình:





 

3 2 2

5 1 1 4 25 18x x x x    

Hướng dẫn Điều kiện:

1x 

. Phương trình tương đương với:





 

3 4 3 2

3 3 4 2

3 3 2 2 2

3 3 2 2

5 5 1 4 25 18

25 25 5 1 4 18 20

25 25 5 1 4 16 16 2 4

5 1 5 1 2 3 2 3 1

x x x x

x x x x x

x x x x

    

      

        

       

Xét hàm số:

     

, 0 ' 2 1 ' 0, 0f t t t t f t t f t t         

 





   

 

   

 

3 2 3 2 2 2

1 5 1 2 4 5 1 2 2 5 1 1 2 1 1f x f x x x x x x x x x



                



Đặt

1, 0; 1, 0u x u v x x v      

, ta được:

 

2 2 2 2

5 2 2 5 2 0 2 hay 2uv u v u uv v u v v u        

2 1 2 1 4 5 3 0u v x x x x x         

(vô nghiệm)

5 37

2 1 2 1 5 3 0

v u x x x x x x



           

So sánh điều kiện đề bài, kết luận: Phương trình có nghiệm là

5 37





Nhận xét: Bài toán thoạt nhìn có vẻ ngắn ngắn nhưng cũng khó khăn trong khâu xử lý tình huống mà tác giả đặt ra. Bài này

hay ở chỗ phối hợp đơn điệu và ẩn phụ đưa về đẳng cấp, sẽ có nhiều bạn giải đến phân nửa ra được hai hàm bằng nhau rồi

giải lung tung nên sẽ khó lòng mà chu toàn cả bài!

Bài 8. Giải phương trình:

 

4 2 1

log 2 2.8 3.2 1

2.16 2.4 1

x x x



  



Hướng dẫn Phương trình tương đương với:

   

 

log 4 2 1 log 2.16 2.4 1 2.16 3.4 2

log 4 2 1 4 2 1 log 2.16 2.4 1 2.16 2.4 1 1

x x x x x x x

x x x x x x x x

       

           

Xét hàm số:

     

log , 0 ' 1 ' 0, 0

.ln 2

f t t t t f t f t t

         

 

   

 

1 4 2 1 2.16 2.4 1 4 2 1 2.16 2.4 1 2.2 3.2 2 0

1 3 1 3

2 2 1 2 2 0

x x x x x x x x x x x

x x x x

ff               

  

  

    

  

  

log





































Kết luận: Phương trình có nghiệm là

0, log











Nhận xét: Bài toán này không quá khó nhưng tôi mạn phép đưa vào để làm một đường dẫn cho bài luyện tập dười đây!

Mạnh dạng làm bài này nhé, đề bài chỉ là làm nhiễu các bạn thôi!

Bài tập: Giải phương trình:

16 96 208

9 log 2 3 4 3 5 9 6

12 16 45 81

x x x x



      

  

Bài 9. Giải bất phương trình:

2 5 11

  



Hướng dẫn Điều kiện:

02x

Bất phương trình tương đương:

 

7 2 7

2 2 5 2 5

x x x



     



(x = 0 không thỏa mãn bất phương trình)

Đặt





, ta có:

  

7 2 5 7

2 5 0 2 7 1 0

t t t t









        



  



  

1 1 0 2 4

t x x





        

  

7 7 2 1

0 0 2

4 2 1 0

2 2 4









          



  





Kết luận: Bất phương trình có nghiệm

4, 2

xx  

Bài 10. Giải bất phương trình:

2 3 1 3 2 2 5 3 16x x x x x       

Hướng dẫn Điều kiện:

1x 

Bất phương trình tương đương với:

 

2 3 1 2 3 1 20x x x x       

Đặt

2 3 1, 0t x x t    

. Ta có:

 

20 0

t nhan

t loai





    









3 1 0

2 5 3 0

5 2 3 1 5 2 2 5 3 3 1

3 1 0

13 6 5

26 11 0

t x x x x x



  









  







             



  















   





Kết luận: Bất phương trình có nghiệm là

x 

Bài 11. Giải bất phương trình:

2 6 8 2 4 6 3 4 3 3 1 0x x x x x x          

Hướng dẫn Điều kiện:

1x 

. Bất phương trình tương đương với:

   

 

   

 

2 1 . 4 2 1 . 3 3 4 3 3 1 0

2 1 4 3 3 4 3 1

4 3 2 1 3 1

2 1 3

2 1 3 4 3

2 1 3 0

2 1 3 4 3

11 30 0

3 2 1 7 12

x x x x x x

x x x x x

x x x

          

         

      

   

  

      







  



  

   

   





     

  

  

   

















Kết luận: Bất phương trình có nghiệm x > 6.

Bài 12. Giải bất phương trình:





. (Rất đơn giản nhưng không ai chỉ bảo thì cũng khó khăn)

Hường dẫn Điều kiện:

11x  

Bất phương trình tương đương với:

2 2 2

1 3 3

1 2 0

x x x x x



     



Đặt





. Ta có:

3 2 0





   







1 1 1 1

t x x x

















          





















2 2 2 1

t x x x





        









So sánh điều kiện đề bài, kết luận: Bất phương trình có nghiệm:

2 2 5

xx     

Bài 13. Giải bất phương trình:

4 3 6 1 4 15x x x    

Hướng dẫn Bất phương trình tương đương với:

 

   

4 3 2 6 3 4 4 15 0

4 1 1 4

3 2 1 0

4 3 2 4 4 15

2 1 2 1

2 1 2 0 1

4 3 2 4 4 15

x x x

       



    

   





    



   



Ta có:

2 2 2 2

4 3 6 1 4 15 6 1 4 15 4 3 0 2 1 0

x x x x x x x x                

Vì

4 3 2 4 4 15xx    

nên

2 1 2 1

4 3 2 4 4 15





   

Do đó

 

2 1 2 1 1

2 0 : 1 2 1 0

4 3 2 4 4 15



       

   

Kết luận: Bất phương trình có nghiệm

x 

Bài 14. Giải bất phương trình:

 

5 4 1 2 4x x x x x



    





Hướng dẫn Điều kiện:

1 5 0



   



  





. Bất phương trình tương đương với:

   

2 2 2 2

4 2 4 5 4 2 4 4 . 2 4 3 0x x x x x x x x x x x            

Tới đây là dạng đẳng cấp, các bạn giải bình thường nhé!

Đáp án:

1 17 7 65

1 5,0 ,



  



   









Bài 15. Giải bất phương trình:

3 2 9

3 1 3





  

Hướng dẫn Điều kiện:

1 9, 0xx   

. Bất phương trình tương đương với:

 

   

 

    

 

   

3 2 9 3 3 1

3 3 1

3 9 1 2 9 3 3 1

3 3 1

3 3 1 3 3 1 2 9 3 3 1

3 3 1

3 3 1 2 9

1 3 1 2 2 9

1 1 3 2 1 9

8 1 2

0 0 0 8

1 3 1 9

x x x x x

x x x

x x x x x

x x x

x x x x x x x

x x x

     



  

       



  

          



  

    



     



     





       



   



So sánh điều kiện đề bài, kết luận: Bất phương trình có nghiệm

08x

Nhận xét: Tuy bài toán không rầm rầm rộ rộ như những bài khác nhưng để trục được mẫu thì không phải dễ đâu nhé!

Bài 16. Giải bất phương trình:

2 2 1

2 1 3

x x x

  





Hướng dẫn Điều kiện:

1, 13xx  

. Bất phương trình tương đương với:

 

3 3 3

2 1 2

6 6 2 2 1 6

1 1 2 1 *

2 1 3 2 1 3 2 1 3

x x x x x

x x x

  

      

       

     

Vừa có căn bậc ba và căn bậc hai thường thì ta nên nghĩ đến dung đơn điệu, lưu ý nhỏ ta sẽ giải bài toán trên khi trục mẫu

bằng chia trường hợp ; dễ dàng thôi, ta có ngay phép biến đổi sau:

Trường hợp 1:

2 1 3 0 13xx    

       

* 2 1 2 1 1 1 1 **x x x x x        

Xét hàm số:

     

' 3 1 ' 0,f t t t f t t f t t        

 

   

1 5 1 5

** 2 1 1 2 1 1 2 1 1 0

f x f x x x x x x x

   

                

So sánh điều kiện của TH1, vô nghiệm.

Trường hợp 2:

2 1 3 0 13xx    

. Giải tương tự, ta được:

   

2 1 1 1 0

2 1 1

x x x x



   







         



  











  







So sánh điều kiện của TH2, ta được:

1 0 13



     

Kết luận: Bất phương trình có nghiệm là

1 0 13



     

Nhận xét: Bài toán này còn khó khăn hơn cả Bài 15 các bạn nên lưu ý nhé! Tiếp theo đây là một số bài tập tự luyện.

BÀI TẬP TỰ LUYỆN

Bài 1: Giải phương trình:

3 2 3 2 2

3 2 2 3 2 1 2 2 2x x x x x x x         

HD: Đánh giá hai căn thức bằng BĐT Cauchy. ĐS:

1x 

Bài 2: (PTTH Quốc gia 2016)

Giải phương trình:

   

 

3 1 3 1

3log 2 2 2log 2 2 .log 9 1 log 0x x x x x



         





HD: Dạng đẳng cấp. ĐS:

2 17

x 

Bài 3: Giải bất phương trình:

 

3 4 8 9

2 2 1 1

3 2 2 1





   







HD: Tương tự như bài 15. ĐS:

1x 

Bài 4: Giải bất phương trình:

7 7 7 6 2 49 7 42 181 14x x x x x       

HD: Đặt 2 ẩn phụ. ĐS:

x

Bài 5: Giải bất phương trình:

 

  

4 3 2 3 2 3

4 1 2

2 3 3 4 1

x x x x x

    

   

   

HD: Tương tự bài 16. ĐS:

1 5 1 5

; 1 ,12

   

   

  



  



   

Phần tiếp các bạn sẽ làm quen với một số dạng thường gặp của bài toán hệ phương trình là xong chuyên đề về câu 9 điểm

trong đề thi PTTH Quốc gia. Theo quan điểm riêng của tôi, câu hệ phương trình có vẻ dễ thở hơn so với hai dạng trên là

phương trình và bất phương trình. Tuy nhiên tùy theo ý đồ của các giả mà các bạn bí hay không bí. Bình tĩnh khi gải các

bài toán này là điều tất yếu!

Ví dụ 1: Giải hệ phương trình:

x y xy

  









. HD: Thế bình thường.

Ví dụ 2: Giải hệ phương trình:

 

3 3 9 10 3 0

x y x y x y



     





  







. HD: PT trên có dạng đẳng cấp.

Ví dụ 3: Giải hệ phương trình:

2 2 1 3 1

2 1 2 1

y x x x y

y x xy x



    





   





. HD: Dùng đơn điệu ở PT trên.

Ví dụ 4: Giải hệ phương trình:

 



  







  





. HD: Cộng trừ hai vế.

Ví dụ 5: Giải hệ phương trình:

 

6 2 6

1 2 3

1 4 5

y x y x

x y x















. HD: Chia hai vế của mỗi PT cho x

Ví dụ 6: Giải hệ phương trình:

 

2 1 2 4 1

4 2 7

x y x y

x y xy



    





  





. HD: Dùng ẩn phụ.

Ví dụ 7: Giải hệ phương trình:

2 2 2 2

x y x y



   





    





. HD: Dùng 2 ẩn phụ

, u x y v x y   

Ví dụ 8: Giải hệ phương trình:

3 2 2 3

2 7 2 6 0

7 12 6 2 2 0

x y x y

x x y xy y x y



    





      





HD: Biến đổi hợp lý PT dưới để thu được thừa số chung

yx

Ví dụ 9: Giải hệ phương trình:

 

7 1 1 1 1

1 1 13 12

x y x

x y y x x



    







    



. HD: Rút

1x 

ở PT trên rồi thế vào PT dưới.

Ví dụ 10: Giải hệ phương trình:

 

2 2 2 2 2 2

4 3 7 4 5 6 3 2

3 10 34 47

x xy y x xy y x xy y

x xy y



       





  





HD: Chuyển vế rồi liên hiệp ở PT trên.

Các ví dụ nêu trên là các dạng thường gặp trong khi giải hệ phương trình. Bản chất của các bài toán theo quan điểm cá

nhân là một dạng bài tập tích hợp các kỹ năng từ việc giải phương trình. Nhìn chung các dạng này khi cho đi thi sẽ dễ thở

hơn vì sẽ luôn luôn có một phương trình làm cầu nối cho lời giải của bài toán. Dưới đây là một số dạng bài toán hay mà

các bạn nên tham khảo. Một lưu ý, ở phần này tôi chỉ giải chi tiết một số câu cần thiết nếu nó làm khó người giải ở cả hai

phương trình, còn các câu còn lại chỉ là đường dẫn để các bạn tự làm việc.

Bài 1. Giải hệ phương trình:

           

 

6 4 3 3 4 8 2 4 1 2 1

3 22 1 2 3 2

x x y y y x y x y xy

x xy y x y



           







      



Hướng dẫn

Đề bài chỉ có tác dụng gây rối người giải thôi, các biểu thức dong dài chỉ là các bộ phận của một hằng đẳng thức và nếu để

ý kỹ bạn dễ dàng có được phép biến đổi sau:

         

1 3 2 4 3 2 4x y x y y x y x           

Xét hàm số:

     

4 , 0 ' 1 ' 0, 0

f t t t t f t f t t

          



Do đó, ta có:

   

3 2 3 2 1f x y f y x x y y x y x           

Thay vào phương trình (2), ta được:

  

   

2 22 2 1

2 22 5 1 2 3

2 3 1

2 22 5

1 3 1 0

2 22 5

x x x x x

x x x

     

        

  

    



  





    



  









     







  







Vì

0x 

nên A > 0 và B > 0. Do đó

10xy  

Kết luận: Hệ phương trình có nghiệm

 

,xy

là

 

1,0

Bài 2. Giải hệ phương trình:





 

2 2 2 2

4 1 1 3 2 1

2014 2015 4030 2

x x x y y

x y y x y



     







    



Bài toán chỉ là xu thế của năm 2015, chế bài phù hợp với năm ôn thi vậy thôi. Cá nhân tôi có thể chế tác lại các hệ số cho

phù hợp với năm nay nhưng đứng trên tâm thế người viết chuyên đề thì cần tôn trọng tác giả, đó là điều tất yếu. Bài toán

này hay ở phần đánh giá, các phần còn lại nếu bạn làm tốt các bài toán ở trên thì không có gì khó khăn cả!

Hướng dẫn

 

   

 

2 2 2 2 2 2

2 2015 1 0 0 1 1, 1x y x y y x y x y              

+ Xét

1 1 0 0xx    

, thay vào hệ có:

   

3 2 0

1 2 0

2014 2015 4030

y y y



   

   



  



  



  





+ Xét

1 1 0 0xx    

, nhân hai vế của

 

cho

11x 

có:

 





 













    

2 2 2 2 3

2 2 3

1 4 1 1 3 2

4 1 1 3 2

1 4 1 3 3 2

1 1 1 3 2 1 3

x x x x y y

x x y y

      

       

       

Vì

1, 1xy

nên









2 2 2 2

1 1 0, 1 3 0 1 3 1 1 0x x x x           

và

  

2 1 0yy  

Do đó phương trình (3) vô nghiệm.

Kết luận: Hệ phương trình có nghiệm

 

,xy

là

 

0,1

Bài 3. Giải hệ phương trình:

      

 

2 1 1 1

3 8 3 4 1 1 2

x y x y

x x x y



    









    



Hướng dẫn Điều kiện

1, 1xy   

      

 

1 2 1 1

2 1

1 1

x x x

y x y

x x x



    





   



   

     

   



   

Xét hàm số:

     

' 3 1 ' 0,f t t t f t t f t t        

Do đó, ta có:

 

1 1 0

f f y y x



      







. Thay vào phương trình (2), ta có:

 

2 1 1

3 8 3 4 1 2 1 2 1

2 1 1 3

x x x x x x x



  

         



  





2 1 1 3 2 3

6 3 0

3 2 3

x x x







       



  







5 2 13

2 1 1 3

5 2 13

9 10 3 0

x x x















      







  









Vì x > 0 nên ta nhận

4 3 3

3 2 3



   

Kết luận: Hệ phương trình có nghiệm

 

,xy

là

4 3 3

3 2 3,









Bài 4. Giải hệ phương trình:

 

2 2 4 1 2 3 1

4 6 5 2 2 2 2 2 2

x x x y y

x x y xy y x y x



      





          





Hướng dẫn Điều kiện:

2y 

và

  

2 1 0xy  

Bài toán này dễ dàng thấy đơn điệu ở PT (1) nên ta có:

     

1 1 2 1 3 2 3x x y y       

Xét hàm số:

     

2 3 ' 1 ' 0 1

f t t t f t f t t

         



Xét

   

' 0 3 2 1 ' 0 1f t t t t f t t         

Dựa trên điều kiện, ta có:

+ Nếu

2 0 1 1

1 0 1

   







  



thì

   

11f x f y y x    

+ Nếu

2 0 1 1

1 0 1

   







  



thì

   

11f x f y y x    

Thay vào PT (2) ta có:

   

 

1 0 1

4 6 1 2 5 1 3 5 1

4 6 1 2 1 4

4 6 1 2

x x x x x

x x x x

x x x

    





         



     

   





Từ

   

3 , 4

cho ta:

2 1 2 1

4 8 3 0

x x x









     





  



Kết luận: Hệ phương trình có nghiệm

 

,xy

là

 

2 7 7

1; 2 , ;











Bài 5. Giải hệ phương trình:

 

   

1 ln 1

6 2 1 1 2 7 2

y y y x y





  









     



Hướng dẫn

Chắc các bạn còn nhớ Bài 8 ở phần phương trình. Áp dụng bà đó vào PT (1), ta dễ dàng có:

1xy

Thay vào PT (2) ta được:

 

6 1 2 2 2 8 3x x x x x     

Xét

1x 

có:

6 1 2 2 2 3 7 2 8x x x x x       

nên PT (3) vô nghiệm trên khoảng





,1

Xét

1x 

có:

 

10 4

6 1 2 2 2 1 1 1

x x x x x



        





Xét

 

10 4 3

2 8 3 12 12 0 2 0

x x x x x



         

Có đẳng thức khi và chỉ khi x = 2

1y

Kết luận: Hệ phương trình có nghiệm

 

,xy

là

 

2,1

Bài 6. Giải hệ phương trình:

   

 

2 4 2 3

4 1 1

1 3 2 5 2 3 3 2

xy y x

x xy x y x x y x y







   













         





Hướng dẫn Điều kiện:

0, 3 0xy   

     

      





2 2 2 2

1 2 4 4 2 3

4 4 2 3 4 2 3 4 4

4 4 2 3 0

x xy y x y x x y y

xy y x y x y xy y

xy y x y

     

      

    

   

 

   

 

2 3 2 3 3 2 3

3 2 3 2 3 3 0

x x y x y x y x y

x y x x y x y x y

           

            

Kết hợp hai điều kiện trên ta suy ra được hệ có nghiệm duy nhất.

Mà

4, 1xy

thỏa hệ phương trình.

Kết luận: Hệ phương trình có nghiệm

 

,xy

là

 

4,1

Nhận xét: Các bài toán dung phương pháp đánh giá ở dạng như trên cho phép người giải nhẩm nghiệm nếu lý luận chặt chẽ

về mối tương quan giữa các phương trình. Tuy nhiên phải giải rất nhiều thì các bạn mới có thể truy ra được dạng này.

Bài 7. Giải hệ phương trình:

 

16 8 2 2

4 4 1 3 4 8 17 3 1

3 35 88 2

5 3 4 2

x y y

x y y y x

y y x

x x y





        



  











   









Hướng dẫn Điều kiện

xy

 

4 16

16 2

1 4 1 3 4 4 1 3 4

x x y y





         

Xét hàm số

     

4 2 4

4 1 3 , 0 ' 2 .4 ln 4 ' 0, 0

f t t t t f t t f t t



            



Ta có:

   

44f x f y y x    

, thay vào PT (2) ta có:

 

  

 

2 2 2

3 1 4

3 11 4 4 4 1

2 1. 2 2 1 2 1

5 3 2

x x x x

x x x









   



    





   





  











 

2 2 2

3 2 2 1 3 1 2 1 1 0

x x x x x        

(Mò thôi nhé các bạn, phần này chịu khó xíu!)

Đặt

21tx

, có phương trình:

 

2 3 1 1 0 .......

2 2 15

t x t x x













        















Kết luận: Hệ phương trình có 3 nghiệm

 

,xy

là

 

1 6 7 6 2 2 15 30 2 15

4,8 ; , ; ,

2 2 7 7

   

    

   

   

Nhận xét: Một số bài toán bất khả xâm phạm ta chỉ có thể mò cho tới khi ra thôi!

Bài 8. Giải hệ phương trình:

 

      

 

2 5 1

2 3 3

2 3 1 3 1 2 3 2 6 3 1 2

x x y y x y x y















            





Hướng dẫn Điều kiện:

0, 3xy

. Đặt

 

, 3 1a x b y   

     

 

2 2 2 6a a b b a b a b     

Có:

    

 

VT 2 2 3 6 VPa b a b a b a b a b         

Có đẳng thức khi và chỉ khi

3 1 3 1a b x y x y        

. Thay vào phương trình (1), ta được:

 

  

 

2 5

2 3 3

2 5 *

3 2 3 3

x y y





  

   

Theo BĐT Cauchy, ta có:

 

  

2 3 3 2 3 3

2 3 8

3 2 3 3

5 VT VP

3 2 3 3

x y y

   

     

   

    

   

Đẵng thức xảy ra khi và chỉ khi:

 

  

2 3 3

2 3 .....

2 3 2 3 3

x y y











     





   







Kết luận: Hệ phương trình có nghiệm

 

,xy

là

9 13







Bài 9. Giải hệ phương trình:

   

 

3 3 2 2

3 2 3 2 2

2 4 2 5 2 2

x y x y

x y xy

x x x x y x y y







   







       





Hướng dẫn

Biến đổi phương trình (1) về dạng:

   

 

3 3 2 2

5 8 0

x y x y

x y xy



    

rồi chia hai vế cho

được:

2 3 5 8 0

y y y

x x x y x

y y x x y x

   



      

   



   



   

Đặt

3 3 2 2

, : pt 2 3 5 8 0

u v u v u v

u x v y

v u v u v u

   



         

   





   

Đặt

, 2 : pt 2t 3 2 0

t t t t

       

 

2 2 1 0 2t t t t a b x y x y            

Thay x = y vào phương trình (2) ta có:

3 2 3 2 2

2 4 2 5 2 2x x x x x x x x       

 

3 2 3 2 2

3 2 3 2

2 5 2 5 2 1 1

2 5 2 5 1 1

x x x x x x x x x

x x x x x x x x

          

         

Xét hàm đặc trưng:

     





 

2 3 2

, 0 ' 2 1 ' 0, 0 2 5 1f a a a a f a a f a a f x x x f x              

2 5 1 .... 1 1x x x x x y         

So điều kiện nhận x = 1 và y = 1

Kết luận: Hệ phương trình có nghiệm

 

,xy

là

 

1,1

Nhớ: Muốn giải tốt một bài toán Phương trình, Bất phương trình hay Hệ phương trình thì điều nhất thiết là mỗi người

nên đọc và giải thật nhiều các dạng toán thường gặp. Đừng xem thường những ví dụ đơn giản vì bài toán khó là sự dung

hòa các dạng cơ bản một cách có ẩn ý của tác giả. Chung quy lại, những bài mà tôi đưa vào phần tham khảo vừa là bài

toán đại số vừa là bài toán tinh thần đòi hỏi các bạn phải thật bình tĩnh là vô tư giải dù giải đúng hay sai. Kiến thức mà

người khác cung cấp dù nhiều hay ít thì nó cũng chỉ là kiến thức của người ta, muốn biến nó thành của mình thì phải học.

Một câu nữa gửi đến các bạn: CÁCH CHUẨN BỊ TỐT NHẤT CHO MỘT KỲ THI LÀ LÀM THẬT TỐT BÀI TẬP

ÔN THI! Chúc các bạn sinh năm 1999 học vui!

LUYỆN TẬP NHÉ!

Bài 1: Giải bất phương trình:

 

   

2 2 2

2 2 2 2 3 6 3x x x x x x x       

ĐS:





1 5 1 7

, 2,





  









Bài 2: Giải bất phương trình:

x x x

   

   



. ĐS:





3;S  

Bài 3: Giải bất phương trình:

 

2 2 1

6 2 4 2 2

x x x





   

. ĐS:

2 2 3x 

Bài 4: Giải bất phương trình:





2 2 2

1 1 1 1 2x x x x x x       

HD: Chuyển vế rồi liên hiệp hoặc dung ẩn phụ

1u x x  

. ĐS:

 

1;S  

Bài 5: Giải bất phương trình:

 

6 1 2 1 3 9 2x x x x x x x        

HD: Nhẩm được

2, 3xx

rồi dùng liên hiệp. ĐS:

  



1;2 3;S   

Bài 6: Giải bất phương trình:

 

2 2 5 2 2 3x x x x x x x        

HD: Thừa số chung

 

2xx

, liện hiệp rồi đặt 2 ẩn phụ. ĐS:

3 13





Bài 7: Giải bất phương trình:

2 2 2

1 1 2

1 3 5 2 1x x x



   

HD: Dùng ẩn phụ

2tx

. ĐS:

 

; 2 2;S



    



Bài 8: Giải bất phương trình:

5 13 57 10 3

2 3 2 9

3 19 3

x x x

   

    

  

HD: Xem lại các bài tập trang 9, 10. ĐS:

 

2;1S 

Bài 9: Giải hệ phương trình:

 

1 4 1

9 2 7 2 5 2 2

y x y y



  











     





HD: Ẩn phụ

2u x y  

, sau đó dung đơn điệu. ĐS:

   

2;2 , 3;3

Bài 10: Giải hệ phương trình:

  

3 2 2 2 2

3 6 5 2 6 3 1

2 4 2 3 2 1 2 2

x y y x

x y y x x y x y x



     









          



HD: Dùng ẩn phụ

2t y x

rồi đánh giá bằng BĐT Cauchy. ĐS:

 

0; , 1;0









Bài 11: Giải hệ phương trình:

 

3 3 2 2

2 3 2

8 8 3 3

5 5 10 7 2 6 2 13 6 32

x y x y x y

x y y y x x y x



    





         





HD: Đơn điệu ở PT trên, chú ý đoạn sau phải chứng minh phương trình vô nghiệm. ĐS:

 

2,2

Bài 12: Giải hệ phương trình:

 

   

3 2 3 4 2 2

3 3 12 9 3 8 6 1 4

4 9 6 8

y y x x x x x x x x x x

x y x y



         







   



HD: PT trên dung hàm số, chú ý biến cần đặt lại sao cho dễ nhìn. ĐS:

 

3 89 89 5

3 89

1;1 , ; 1

16 2















Bấm Tải xuống để xem toàn bộ.

| 1/21

| | Tải xuống

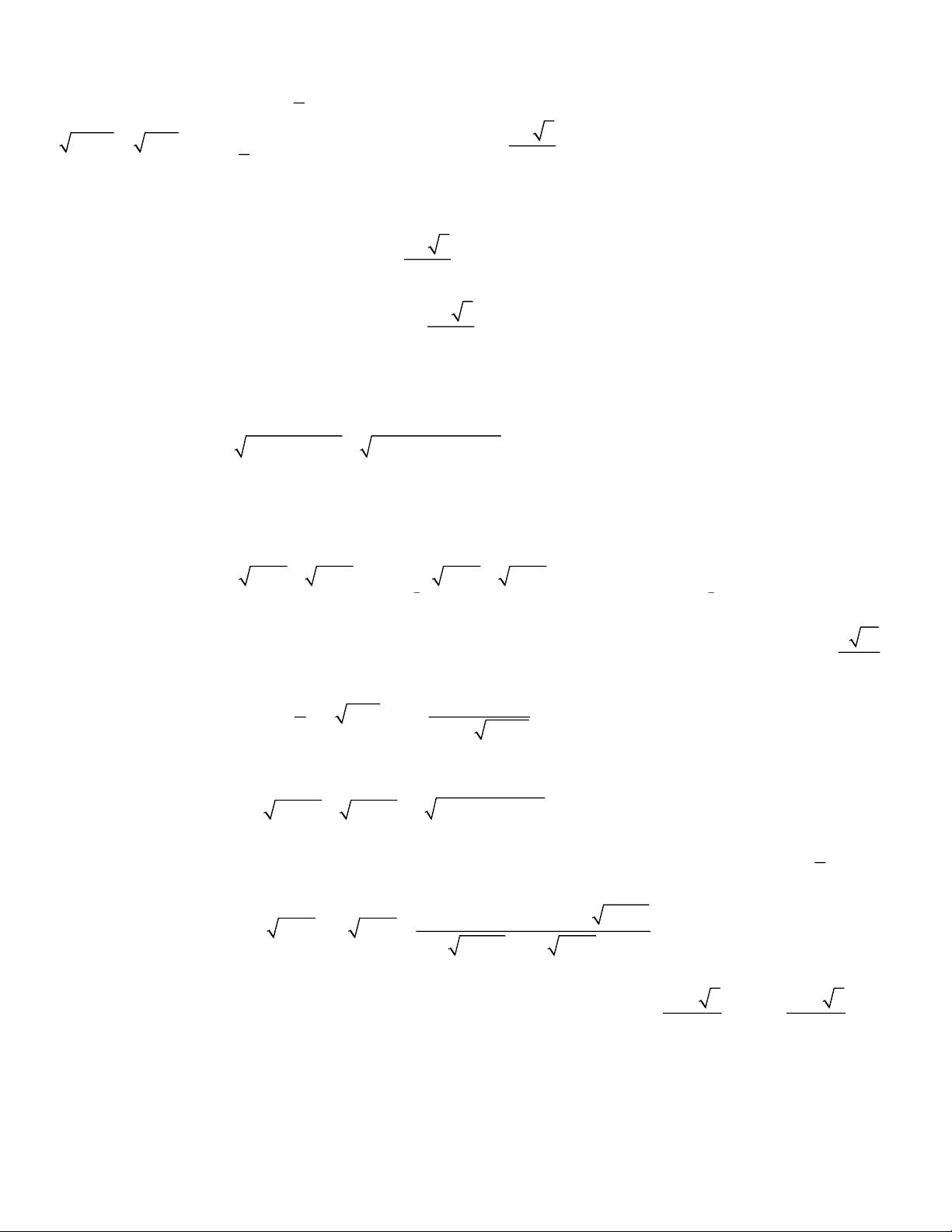
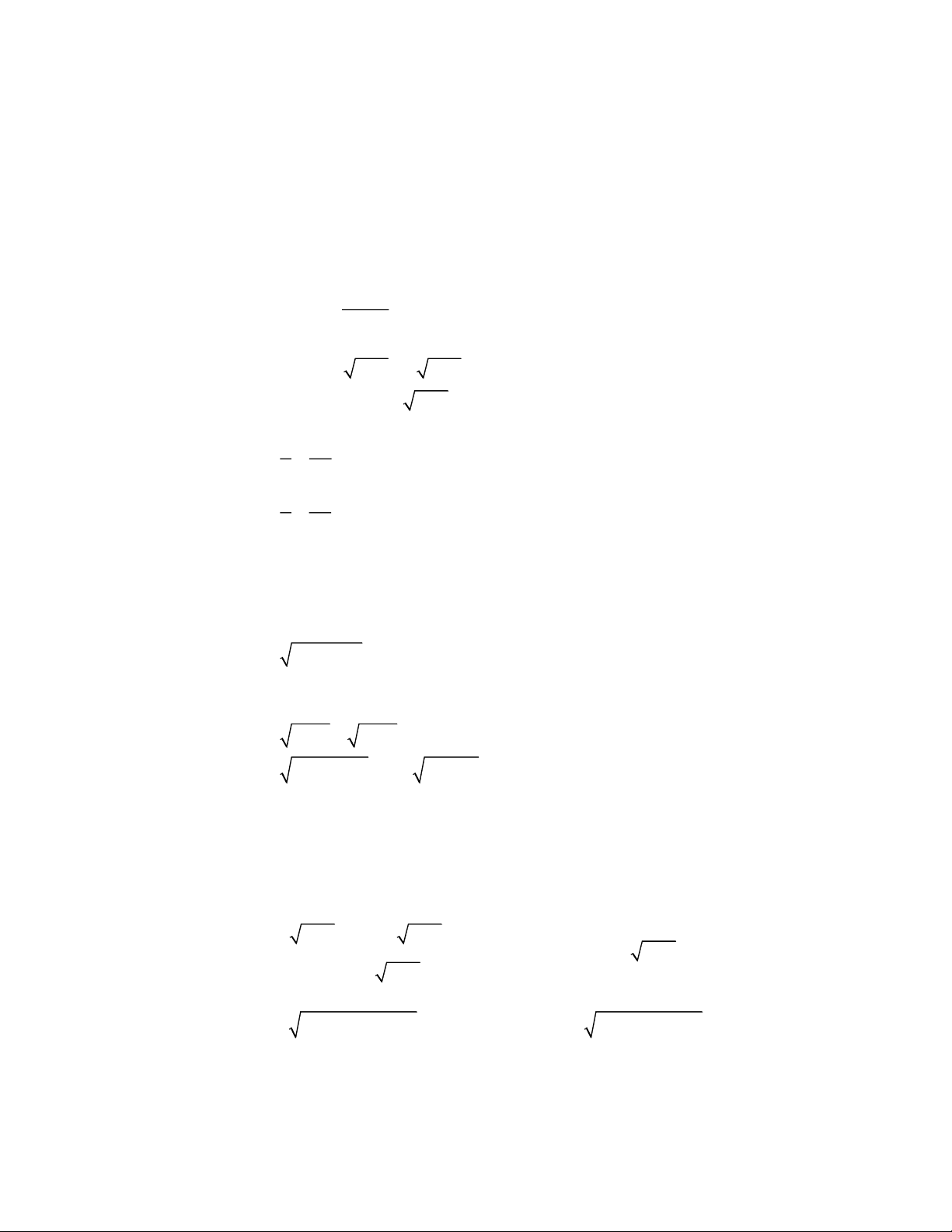
Preview text:

PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH
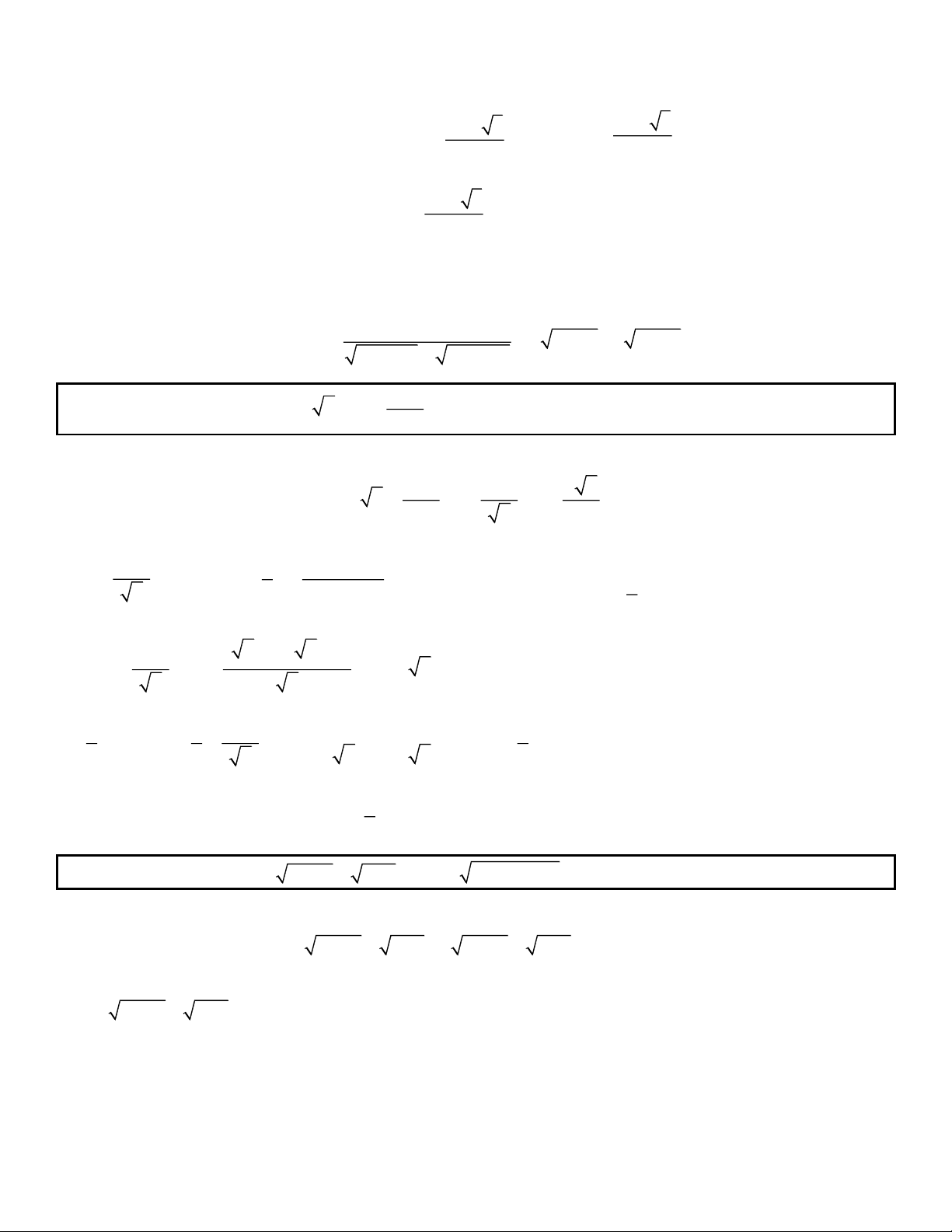
Kiến thức cần nhớ: b  0 a  b 
1. a  b  
4. a  b  b   0  a  b    2 a  b b   0 b   0 2. a  b  
5. a  b   2 a  b 2 a  b
a  0b  0 3.
a  b  a b
Ví dụ 1: Giải phương trình: x 1  x  2  x 1.
HD: biến đổi sao cho hai vế không âm rồi bình phương đưa về dạng cơ bản.
Ví dũ 2: Giải phương trình: 2 2 2
4x  x  4  3x x  x  4  x  2x .
HD: biến đổi hai vế, đặt 2
t  x  x  4 đưa về dạng đẳng cấp. 1 1
Ví dụ 3: Giải phương trình:   2 2 . 2 x 1 x
HD: Đặt x  sin , lượng giác hóa phương trình.
Ví dụ 4: Giải phương trình: 3 3 2
2 2x 1  27x  27x 13x  2 .
HD: Dùng đơn điệu.
Ví dụ 5: Giải phương trình:  x   2 2
3 2x 1  x  x  3 .
HD: Dùng lượng liên hiệp.
Ví dụ 6: Giải phương trình: 2 2
x  4x  20  x  4x  29  97 .
HD: Dạng này hiếm gặp, xét hai vecto có tọa độ thích hợp rồi đưa về độ dài.
Ví dụ 7: Giải phương trình: 2 3
x  3x 1 x  3x  2  0 .
HD: Biến đổi về dạng đẳng cấp, chú ý dấu. (Làm nhiễu thôi!)
Ví dụ 8: Giải bất phương trình: 2 x  x 2 3
2x  3x  2  0 . HD: Dạng cơ bản. x  2  x
Ví dụ 9: Giải bất phương trình:  0 . 3 4  x
HD: Chia khoảng theo điều kiện và giải bình thường.  2 2 x 16 7  x
Ví dụ 10: (A-2004) Giải bất phương trình:  x 3  . x 3 x 3
Ví dụ 11: Giải bất phương trình: 2 2 2
x 8x 15  x  2x 15  4x 18x 18 .
HD: Chia trường hợp theo điều kiện xác định.
Lưu ý: Thường thường câu 9 điểm trong đề thi PTTH Quốc gia là câu giải phương trình, bất phương trình hay hệ phương
trình. Theo ý kiến cá nhân của tôi thì phương trình là nền tảng cho các dạng còn lại, bất phương trình kế thừa phương trình
nhưng mang màu sắc của xét dấu là chủ yếu còn lại là các phép biến đổi. Hệ phương trình là dung hòa của hai (nhiều)
phương trình. Nói chung cái khó của các bài toán này nằm ở kinh nghiệm giải của các bạn và do ý đồ kết hợp các phương
pháp của tác giả! Các ví dụ trên đây là các dạng thường gặp của “bài toán 9 điểm” trong bài thi PTTH Quốc gia. Cùng xem
một số câu tham khảo nhé!
Bài 1. Giải phương trình: 2 x  x   2 7
1 x  13x  2x  2  x x  1. Hướng dẫn 13 3 17
Điều kiện:1 x  . 4 1  2  1
Phương trình đã cho tương trương với: 7  x  1 13 2x    x    1 x  x    x 1 1 Đặt 2 t  x 
 t  x   2 , từ (1) suy ra t > 0 . x x
Phương trình (1) trở thành:
7   2t  2 1 132 2t  2  t 2  5  t  2 9  2t   2
1  t  2 5  t  2 8  2t  2 2 5  t 5t  20   2 2 9  2t 1 t  2 5  t     2 t   2 5 4     0 2 2
 9  2t 1 t  2 5  t  2 5 Vì 
 0 và t > 0 nên t = 2. 2 2
9  2t 1 t  2 5 t 1 Suy ra: x 
 2  x  2 x 1 0  x 1 2  x  3 2 2 . x
So sánh với điều kiện đề bài, kết luận: x  3 2 2 .
Nhận xét: Bài toán này rất hay ở chỗ chia hai vế cho x mới có thể đưa về dạng quen thuộc là kết hợp giữa ẩn phụ và liên
hiệp, có dính dáng đến một chút của phương pháp đánh giá biểu thức nhưng không quá khó. Tiếp tục với một bài nữa về
phương trình cũng rất hay liên quan đến tính đơn điệu. 2 x  2x 8
Bài 2. (PTTH Quốc gia 2015) Giải phương trình:  x   1 x  2  2 . 2   x  2x  3 Hướng dẫn Điều kiện: x  2  .
Phương trình tương đương với:
x  2x  4 x  x2 1 . 2 x  2x  3 x  2  2       x   x 4 x 1 2     0  x  2 1  2 x  2  2   x  2   x  4 x 1    0 * 2  
x  1  2 x  2  2
Nhìn kỹ phương trình (*) ta thấy một nét đẹp như phép biến đổi sau: x  2 2 x 1  x  2 1  2 x  2  2 
  x  22  2 
  x  2  2   x  2 1  2      x   1  2  **
Xét hàm số: f t   2t  t   t   f t  t t   2 2 2 , 0 ' 2 .
2  t  2  f t  0, t   0      
 f  x    f x   x 1 x 1 3 13 ** 2
1  x  2  x 1     x  2 2
x  2  x  2x 1
x  3x 1  0 2 3 13
Kết luận: x  2, x  . 2
Nhận xét: Bài toán này hay ở chỗ sau khi liên hiệp xong phần đông học trò sẽ lấn cấn ở chỗ dung đơn điệu, nhưng nếu làm
quen các bạn sẽ dễ dàng thấy rõ được chỗ bí ẩn này. Phần lớn học trò năm 2015 – là các anh chị trước cũng gặp tình trạng
tương tự nên nếu không rõ thì cũng không sao. Tiếp theo đây là một bài cũng nên lưu ý.
Bài 3. Giải phương trình: 2 x   2  x  x 2 2 15
15 3 15  x  4 x . Hướng dẫn
Điều kiện: 0  x  15 .
Phương trình tương đương với: 2 2  x  x  x  x   2 15 3 . 15 4
2 15  x  x  0  1 Đặt 2 u 
 x v  x   2
 u  uv  v   2 u  v  2
  u   v   2 15 , : 1 3 4 2 0
3 2 u  2v  4v  0 .    u  v 3v  22  4 2 2
2v  4v  v  22   . u  v  2 _ 2
u  2v  15  x  2 x  x  2
  19 nhan  x  2   19 loai . _ 2 2 2
u  v  2  15  x  x  2  15  x  2  x  4 15  x 19  x  0 . Có 2 2
0  x  15 19  x  0  4 15  x 19  x  0  4 15  x 19  x  0 vô nghiệm. Kết luận: x  2   19 .
Nhận xét: Bài toán hay ở chỗ đặt ẩn phụ và dò mối tương quan của các ẩn phụ bằng denta của một phương trình bậc hai
theo một ẩn nào đó thích hợp. Các bạn nên lưu ý dạng toán này.
Bài 4. Giải phương trình: 2 3 4 3 2
4  x  2 x  4x  4x  x  2 1 1 x . Hướng dẫn Điều kiện: 2   x  2.
Phương trình tương đương với: x 
 x  x  x  x  x2 2 2 2 3 4 2 2 2  2(1) 2 Có:  2 x   x  2   x  x  x    2 4 4 2 4 4,
2;2  x  4  x  2, x   2  ;2
Có dấu “=” khi và chỉ khi x  0 x  2  (2). Đặt 3 2
t  x  2x  t  1  ;2, x   2  ,2 . t  0
Khi đó vế phải của phương trình (1) là: f t 3 2 t 2t 2,t  1,2 f 't 2 3t 4t f 't 0             4  . t   3  4  22
Hàm số f(t) liên tục trên tập xác định của nó nên: f   1  1
 , f 0  0, f 
, f 2  2  f t  2,t  1    ,2 .  3  27 2 Ta có: 2
x  x   2 3 2
2 x  2x  2  2, x   2  ,2.
Dấu “=” xảy ra khi và chỉ khi x  0 x  2  (3).
Từ (2) và (3) cho ta: phương trình có ba nghiệm là x  0 x  2  .
Nhận xét: Dạng đánh giá này các bạn ít gặp và nó cũng hơi rắc rối, nên lưu tâm. Dạng này không có kinh nghiệm gì để học
mà kinh nghiệm là do các bạn giải nhiều thôi!
Bài 5. Giải phương trình: 3 2 2 3 3 2
 x 10x 17x  8  2x . 5x  x . Hướng dẫn
Ta nhận thấy x = 0 không là nghiệm của phương trình. 10 17 8 5
Ta chia 2 vế của phương trình cho x3, ta được:      3 2 2 1 . 2 3 2 x x x x 1
Đặtt  ,t  0 phương trình trở thành: x 2 3 3 2
  t  t  t 
t    t     t    3 2t  3 3 3 2 2 10 17 8 2 5 1 2 1 2 2 1 5 1  2 5t 1   1 .
Xét hàm số: f t 3
 t  t  f t 2 2 '
 3t  2  f 't  0, t   t  0   1 f 2t  1 f 3 2 5t 1 3 2 2t 1 5t 1 2t 3 2 3 2 1 5t 1 8t 17t 6t 0                   17   97 . t   16 17  97 17  97 17  97 17  97
_ t  0 loại trường hợp này. _ t   x  . _t   x  . 16 12 16 12 17  97
Kết luận: Phương trình đã cho có nghiệm x  . 12 3 2
x  7x 14x  6
Bài 6. Giải phương trình: 3 2  3
 x  7x  5 1. 1 2x
Hướng dẫn Phương trình tương đương với: 3 2
x  7x 14x  6  1 2x 3 2 3
 x  7x  5  x  23 2
 x  4x 3  1 2x 1 2xx  2   2 3 x  4x 3
Đặt a  x  b    xx     2 3 2, 1 2 2
x  4x  3 . Ta có hệ sau: 3 b
    xa  2x  x    b  a  0 1 2 4 3 3 3  2 
 b  a   1 2x b  a   b  3 3
a  1 2xa  
 2x 4x3    2  a   
b 1 2x  0  2  4 _ 3 2 b  a  3
 x 7x  5  x  2 lập phương hai vế ta được ba nghiệm x  3   x  3   2 2 . 2  b  3 _ 2 a 
 b 1 2x   
0 rõ rang là vô nghiệm nhé!  2  4
Kết luận: Phương trình có nghiệm là x  3   x  3   2 2 .
Bài 7. Giải phương trình:  3   x  2  x  2 5 1 1
4x  25x 18 .
Hướng dẫn Điều kiện: x  1
 . Phương trình tương đương với: 3 4 3 2
5  5 1 x  4x  25x 18x 3 3 4 2
 25x  25  5 1 x  4x 18x  20 3 3 2 2 2
 25x  25  5 1 x  4x 16x 16  2x  4
 5 1 x 2 5 1 x  2x 32 3 3 2 2  2x  3   1
Xét hàm số: f t 2
 t  t,t  0  f 't  2t 1 f 't  0, t   0    f  3
 x   f  2x   3   x   2
x    x   2
x  x     2 1 5 1 2 4 5 1 2 2 5 1 1
2 x  x   1  x   1  Đặt 2
u  x 1,u  0; v  x  x 1,v  0 , ta được: uv   2 2 u  v  2 2 5 2
 2u  5uv  2v  0  u  2v hay v  2u . _ 2 2
u  2v  x 1  2 x  x 1  4x  5x  3  0 (vô nghiệm)  _ 2 2 5 37
v  2u  x  x 1  2 x 1  x 5x 3  0  x  . 2 5  37
So sánh điều kiện đề bài, kết luận: Phương trình có nghiệm là x  . 2
Nhận xét: Bài toán thoạt nhìn có vẻ ngắn ngắn nhưng cũng khó khăn trong khâu xử lý tình huống mà tác giả đặt ra. Bài này
hay ở chỗ phối hợp đơn điệu và ẩn phụ đưa về đẳng cấp, sẽ có nhiều bạn giải đến phân nửa ra được hai hàm bằng nhau rồi
giải lung tung nên sẽ khó lòng mà chu toàn cả bài! 4x  2x 1
Bài 8. Giải phương trình: log
 2x 2.8x 3.2x 1 2 . x x   2.16  2.4 1
Hướng dẫn Phương trình tương đương với:
log 4x  2x 1  log 2.16x  2.4x 1  2.16x 3.4x  2x 2   2  
 log 4x  2x 1  4x  2x 1  log 2.16x  2.4x 1  2.16x  2.4x 1 1 2   2     1
Xét hàm số: f t  log t  t,t  0  f ' t 
1 f ' t  0, t   0 2     . t.ln 2
   f  x x     f  x x    x x x x 4x 2 1 4 2 1
2.16 2.4 1  4  2 1  2.16  2.4 1  2.2  3.2 x  2x  0       x 
 x   x 1 3 x 1 3 2 2 1 2   2    0  2  2     x   x  0 2 1             x 1 3 1 3 2  x  log2    2     2    1   3 
Kết luận: Phương trình có nghiệm là x  0, x  log2    . 2   
Nhận xét: Bài toán này không quá khó nhưng tôi mạn phép đưa vào để làm một đường dẫn cho bài luyện tập dười đây!
Mạnh dạng làm bài này nhé, đề bài chỉ là làm nhiễu các bạn thôi! 2
16x  96x  208
Bài tập: Giải phương trình: 2 x  9  log
 2 3x  4  3 5x  9  6x . 2
12x 16  45x 81 14
Bài 9. Giải bất phương trình: 2x  5 x 11 . x  2
Hướng dẫn Điều kiện: 0  x  2 . x x  x
Bất phương trình tương đương: x   7 2 7 2 2  5 x   2  5 
(x = 0 không thỏa mãn bất phương trình) x  2 x x  2   x t 1  2 2 7 2t  5t  7 Đặt t  , ta có: 2t 5 0
t 2t 7t  1 0           . x 7 t t   t  0  2 x
 x  1 x   2 2  + t 1  1
 0  x  2  x  4 . x x 0  x  2 7 7 x  2  1
+   t  0     0     x  . 2 2 x  x    x   2 4 2 1  0 4 1
Kết luận: Bất phương trình có nghiệm x  4,  x  2 . 4
Bài 10. Giải bất phương trình: 2
2x  3  x 1  3x  2 2x  5x  3 16 .
Hướng dẫn Điều kiện: x  1  .
Bất phương trình tương đương với:
x   x    x   x  2 2 3 1 2 3 1  20 .
t  5 nhan
Đặtt  2x  3  x 1,t  0 . Ta có: 2 t
  t  20  0   t  4   loai  3  x 1 0  2  1
2x  5x  3  0 x  2 t 5 2x 3 x 1 5 2 2x 5x 3 3x 1                3  .  3x 1 0        x 13 6 5 2
x  26x 11 0 1
Kết luận: Bất phương trình có nghiệm là x  . 3
Bài 11. Giải bất phương trình: 2 2
2x  6x 8  2x  4x  6  3 x  4  3 x  3 1  0 .
Hướng dẫn Điều kiện: x 1. Bất phương trình tương đương với: 2x  
1 . x  4  2x  
1 . x  3 3 x  4 3 x  3 1  0  2x  
1  x  4  x 33 x  4  x 3 1
  x  4  x 3 2x  1 3 1  x   1 2
1  3  x4  x3  2x  
1  3  x  4  x  3  11  2    11 1  3  0  11 x x x     x   2    2    2    x  6       2     2 x x x x  3  2x   5 2 1 3 4 3 2  2
1  x  7x 12  
x 11x  30  0  x  6
Kết luận: Bất phương trình có nghiệm x > 6. 3x 1
Bài 12. Giải bất phương trình: 1
. (Rất đơn giản nhưng không ai chỉ bảo thì cũng khó khăn) 2 2 1 x 1 x
Hường dẫn Điều kiện: 1   x 1. 2 2 2 1 x  x 3x x 3x
Bất phương trình tương đương với:  1   2  0 . 2 2 2 2 1 x 1 x 1 x 1 x x t 1 Đặtt  . Ta có: 2
t  3t  2  0   . 2 1 x t  2 x  0  2 x  1   x  0 2 _ 2 t 1 
1  1 x  x   1   x  . 2 1 x x  0 2  2 2x 1 x x  0 2 5 _ 2 t  2 
 2  x  2 1 x    x  2 2 1 x 5  x  4 5 2 2 5
So sánh điều kiện đề bài, kết luận: Bất phương trình có nghiệm: 1   x    x 1. 2 5
Bài 13. Giải bất phương trình: 2 2
4x  3  6x 1 4x 15 .
Hướng dẫn Bất phương trình tương đương với: 2 2
4x  3  2  6x  3 4  4x 15  0 2 2 4x 1      1 4 3 2 1 x x   0 2 2 4x  3  2 4  4x 15       x   2x 1 2x 1 2 1   2    0   1 2 2  4x  3  2 4  4x 15  Ta có: 2 2 2 2 1
4x  3  6x 1 4x 15  6x 1 4x 15  4x  3  0  x   2x 1  0 . 6 2x 1 2x 1 Vì 2 2
4x  3  2  4  4x 15 nên   0 2 2
4x  3  2 4  4x 15 2x 1 2x 1 1 Do đó  2   0 : 
1  2x 1 0  x  . 2 2 4x  3  2 4  4x 15 2 1
Kết luận: Bất phương trình có nghiệm x  . 2
Bài 14. Giải bất phương trình: 2 x x  x 2 5 4 1 x 2x 4        .  1   5  x  0
Hướng dẫn Điều kiện: 
. Bất phương trình tương đương với: x  1   5 x 2 x  x   2
 x  x    2 x  x   2 4 2 4 5 4 2
4  4 x. x  2x  4  3x  0
Tới đây là dạng đẳng cấp, các bạn giải bình thường nhé!  1   17 7  65 
Đáp án: S   1   5,0  ,     . 2 2    x 3 2 9  x
Bài 15. Giải bất phương trình:  .
3 x 1  x  3 x
Hướng dẫn Điều kiện: 1
  x  9, x  0. Bất phương trình tương đương với: 2
x  3x  2 9  x x 33 x 1 
xx   x   0 3 3 1
x 32 9x  
1  2 9  x x 33 x 1  
xx   x   0 3 3 1
x33 x1x33 x12 9xx33 x1  
xx   x   0 3 3 1
x  3 3 x 1  2 9  x   0 x
x 1 3 x 1  2  2 9  x   0 x
x 1 x 13 21 9 x x 8  x 1 2    0   
  0  0  x  8 x x  x 1 3 1 9 x       
So sánh điều kiện đề bài, kết luận: Bất phương trình có nghiệm0  x  8 .
Nhận xét: Tuy bài toán không rầm rầm rộ rộ như những bài khác nhưng để trục được mẫu thì không phải dễ đâu nhé! 2 3
x  x  2 2x 1
Bài 16. Giải bất phương trình: x 1  . 3 2x 1 3
Hướng dẫn Điều kiện: x  1
 , x 13. Bất phương trình tương đương với: 2 3 2 x  2 x x x x x  x1        2 6 6 2 2 1 6  x 1   x 1  2   1 * 3 3 3 2x 1 3 2x 1 3 2x 1 3
Vừa có căn bậc ba và căn bậc hai thường thì ta nên nghĩ đến dung đơn điệu, lưu ý nhỏ ta sẽ giải bài toán trên khi trục mẫu
bằng chia trường hợp ; dễ dàng thôi, ta có ngay phép biến đổi sau:
Trường hợp 1: 3 2x 1 3  0  x 13
    x   3 * 2
1  2x 1  x  
1 x 1  x 1**
Xét hàm số: f t 3
 t  t  f t 2 '
 3t 1 f 't  0, t   .      
 f  x    f  x    x   x    x  2  x  3 3 3 1 5 1 5 ** 2 1 1 2 1 1 2 1 1  x   0  x  2 2
So sánh điều kiện của TH1, vô nghiệm.
Trường hợp 2: 3 2x 1 3  0  x 13. Giải tương tự, ta được:  1 1   x    2   3 1 5
2x 1  x 1   1  1   x  0    .  13  x x  2  2     2x   2 1  x  3 1 1 5
So sánh điều kiện của TH2, ta được: 1   x  0   x 13. 2 1 5
Kết luận: Bất phương trình có nghiệm là 1   x  0   x 13. 2
Nhận xét: Bài toán này còn khó khăn hơn cả Bài 15 các bạn nên lưu ý nhé! Tiếp theo đây là một số bài tập tự luyện.
BÀI TẬP TỰ LUYỆN
Bài 1: Giải phương trình: 3 2 3 2 2
3x  2x  2  3
 x  x  2x 1  2x  2x  2 .
HD: Đánh giá hai căn thức bằng BĐT Cauchy. ĐS: x  1  .
Bài 2: (PTTH Quốc gia 2016) 2   Giải phương trình: 2
3log  2 x  2 x 2log  2 x  2 x.log  2
9x  1log   0 . 3 1 3  1 3  3  2 17
HD: Dạng đẳng cấp. ĐS: x  . 9    x  x
Bài 3: Giải bất phương trình:
  x    2 3 4 8 9 2 2 1 1   .  x  3x  2 2x 1
HD: Tương tự như bài 15. ĐS: x 1.
Bài 4: Giải bất phương trình: 2
7x  7  7x  6  2 49x  7x  42 18114x . 6
HD: Đặt 2 ẩn phụ.
ĐS:  x  6 . 7 3 2 3
x  4x  3x  2 x  3 2x  3
Bài 5: Giải bất phương trình: x  4     1 x  2   .
3 2x  3 3 x  4   1  1   5   1   5 
HD: Tương tự bài 16. ĐS: S   ; 1     ,12 . 2 2     
Phần tiếp các bạn sẽ làm quen với một số dạng thường gặp của bài toán hệ phương trình là xong chuyên đề về câu 9 điểm
trong đề thi PTTH Quốc gia. Theo quan điểm riêng của tôi, câu hệ phương trình có vẻ dễ thở hơn so với hai dạng trên là
phương trình và bất phương trình. Tuy nhiên tùy theo ý đồ của các giả mà các bạn bí hay không bí. Bình tĩnh khi gải các
bài toán này là điều tất yếu!
x  y  xy  3
Ví dụ 1: Giải hệ phương trình:  .
HD: Thế bình thường. 2 2
x y  xy  2 
 x  y2   x  y   x  y2 2 2 3 3 9 10 3  0 
Ví dụ 2: Giải hệ phương trình:  1 .
HD: PT trên có dạng đẳng cấp. 3  x  y   6  3x  y 3
2y  2x 1 x  3 1 x  y
Ví dụ 3: Giải hệ phương trình:  .
HD: Dùng đơn điệu ở PT trên. 2
y  2x 1 2xy 1 x 1 1   2   2 2 x  y   x 2y
Ví dụ 4: Giải hệ phương trình:  .
HD: Cộng trừ hai vế. 1 1  2 2   y  x x 2y y 3 1 2x y 6  3x
Ví dụ 5: Giải hệ phương trình:  .
HD: Chia hai vế của mỗi PT cho x6. 6 2 6 1
  4x y  5x
 x  2y 1 2x  4 y   1
Ví dụ 6: Giải hệ phương trình:  . HD: Dùng ẩn phụ. 2 2
x  4y  2xy  7
 x  y  x  y   2
Ví dụ 7: Giải hệ phương trình:  .
HD: Dùng 2 ẩn phụu  x  ,
y v  x  y . 2 2 2 2
 x  y 1  3 x  y 2 2
2x  y  7x  2y  6  0
Ví dụ 8: Giải hệ phương trình:  . 3 2 2 3  7
 x 12x y  6xy  y  2x  2y  0
HD: Biến đổi hợp lý PT dưới để thu được thừa số chung y  x .
7 x 11 y x1  1
Ví dụ 9: Giải hệ phương trình:  .
HD: Rút x 1 ở PT trên rồi thế vào PT dưới.   x    2
1 y  y x 1 13x 12  2 2
 4x  3xy  7y  4 2 2
x  5xy  6y  2 2
 3x  2xy  y
Ví dụ 10: Giải hệ phương trình:  . 2 2 3
 x 10xy 34y  47
HD: Chuyển vế rồi liên hiệp ở PT trên.
Các ví dụ nêu trên là các dạng thường gặp trong khi giải hệ phương trình. Bản chất của các bài toán theo quan điểm cá
nhân là một dạng bài tập tích hợp các kỹ năng từ việc giải phương trình. Nhìn chung các dạng này khi cho đi thi sẽ dễ thở
hơn vì sẽ luôn luôn có một phương trình làm cầu nối cho lời giải của bài toán. Dưới đây là một số dạng bài toán hay mà
các bạn nên tham khảo. Một lưu ý, ở phần này tôi chỉ giải chi tiết một số câu cần thiết nếu nó làm khó người giải ở cả hai
phương trình, còn các câu còn lại chỉ là đường dẫn để các bạn tự làm việc.
 xx6y 43y3y 48 2x y  x y2 41 xy 2  1
Bài 1. Giải hệ phương trình:  . 2
 3x  xy  22  1 y  x  2y  3  2 Hướng dẫn
Đề bài chỉ có tác dụng gây rối người giải thôi, các biểu thức dong dài chỉ là các bộ phận của một hằng đẳng thức và nếu để
ý kỹ bạn dễ dàng có được phép biến đổi sau:
   x  y  2  x  y     y  x 2 1 3 2 4 3 2 4
   y  x . t
Xét hàm số: f t 2
 t  4  t,t  0  f 't 
1 f 't  0, t   0 . 2 t  4
Do đó, ta có: f  x  3y  2  f  y  x  x  3y  2  y  x  y 1 x .
Thay vào phương trình (2), ta được: 2 2
x  2x  22  x  x  2x 1 2 2
 x  2x  22  5 1 x  x  2x  3 2 x  2x  3 1 x 2  
 x  2x  3 2
x  2x  22  5 1 x
x 3x   1 1 x  
 x  3x   1 2
x  2x  22  5 1 x         x   1   x   1 1 3 1   0 2 1 x 
x  2x  22  5    A    B 
Vì x  0 nên A > 0 và B > 0. Do đó x 1 y  0.
Kết luận: Hệ phương trình có nghiệm  x, y là1,0 .  2 4x    2 1 x  1 2 2
x  y  3y  2   1
Bài 2. Giải hệ phương trình:  . x  y  2 2 2 2 2
 2014y  2015  x  4030y 2
Bài toán chỉ là xu thế của năm 2015, chế bài phù hợp với năm ôn thi vậy thôi. Cá nhân tôi có thể chế tác lại các hệ số cho
phù hợp với năm nay nhưng đứng trên tâm thế người viết chuyên đề thì cần tôn trọng tác giả, đó là điều tất yếu. Bài toán
này hay ở phần đánh giá, các phần còn lại nếu bạn làm tốt các bài toán ở trên thì không có gì khó khăn cả! Hướng dẫn     2 2
x  y 2  2 2
x  y     y  2 2 2 2 2015
1  0  0  x  y 1 x 1, y 1. + Xét 2
x 1 1  0  x  0 , thay vào hệ có: 3
y  3y  2  0  y  2 1  y  2  0     y 1. 4 2 4 2
y  2014y  2015  4030y
y  2014y  2015  4030y + Xét 2
x 1 1  0  x  0 , nhân hai vế của   1 cho 2 x 1 1 có:   2
1  4x  2x 1  2 1  x  2 3
x  y  3y  2
 4 2x 1  2 3
1  x  y  3y  2 2 2 3
 1 x  4 1 x  3  y 3y  2   2 1 x  1 2
1 x 3   y  2 y  2 1 3
Vì x  1, y  1nên 2 2  x    x     2  x   2 1 1 0, 1 3 0 1 3
1 x  1  0 và y   y  2 2 1  0 .
Do đó phương trình (3) vô nghiệm.
Kết luận: Hệ phương trình có nghiệm x, y là0,  1 .  2 x x 
  y  2 x   1  y    1   1
Bài 3. Giải hệ phương trình: 2 x   1 .  2
3x 8x 3  4  x   1 y 1 2
Hướng dẫn Điều kiện x  1  , y  1  . 3 2     1 x x x 
  y  2 x   1  y   1 1 x 2
x  xx   1    y  2   x   y 1 1 x 1 3  x   x   
  y 13  y      1  x 1   x 1 
Xét hàm số: f t 3
 t  t  f t 2 '
 3t 1 f 't  0, t   .  x  x Do đó, ta có: f
 f  y 1 
 y 1  x   
0 . Thay vào phương trình (2), ta có:  x 1  x 1
2 x 1  x 1 2
3x 8x 3  4x x 1  2x  
1  x  2 x 12 2   .
2 x 1 13x x 1 x 1
+ 2 x 1  x 1      x  3 2 3 . 2
x  6x  3  0 x  3 2 3  1  1 x  x   3 5  2 13
+ 2 x 1 1 3x   3    x  . 2 5    2 13 9 9
 x 10x  3  0 x   9 4  3 3
Vì x > 0 nên ta nhận x  3 2 3  y  . 2  4  3 3 
Kết luận: Hệ phương trình có nghiệm x, y là3 2 3,   . 2     2 2
x  2 x  2x  4  y 1 2 y   3   1
Bài 4. Giải hệ phương trình:  . 2
 4x  x  6  5 y  2  xy  2y  x  2  2y  x  2  2
Hướng dẫn Điều kiện: y  2
 vàx  2 y   1  0 .
Bài toán này dễ dàng thấy đơn điệu ở PT (1) nên ta có:
   x   x  2 2 1 1 2
1  3  y  2 y  3 . 2t
Xét hàm số: f t 2
 t  2 t  3  f 't 1
 f 't  0  t 1. 2 t  3 Xét f t 2 '
 0  t  3  2t  t 1 f 't  0  t 1.
Dựa trên điều kiện, ta có: x  2  0 x 11 + Nếu  
thì f  x  
1  f  y  y  x 1. y 1 0    y 1 x  2  0 x 11 + Nếu  
thì f  x  
1  f  y  y  x 1. y 1 0    y 1 Thay vào PT (2) ta có:  
x 1 0  x  1  2
x  x    x  x    x 1 4 6 1 2 5 1 3   5 x 1   . 2
4x  x  6  1 2x 2
 4x  x  6 1 2x  x 1  4  1 x  2  7
Từ 3,4 cho ta: 2 x 1  2x 1   2  x  .  2 2
4x 8x  3  0   
Kết luận: Hệ phương trình có nghiệm  x, y là   2 7 7 1; 2 , ;   . 2 2    2  y  4y  5
x  y 1  ln   1
Bài 5. Giải hệ phương trình: 2  x  2x  2 . 6 y  2   y   2 3
1 y 1  2x  y  7 2 Hướng dẫn
Chắc các bạn còn nhớ Bài 8 ở phần phương trình. Áp dụng bà đó vào PT (1), ta dễ dàng có: x  y 1.
Thay vào PT (2) ta được: 3 2
6 x 1  2x x  2  2x  x  8 3 . Xét x 1 có: 3 2
6 x 1 2x x  2  2 3  7  2x  x 8 nên PT (3) vô nghiệm trên khoảng  ,1 . 4  x  2 x 10x  4
Xét x 1 có: 6 x 1  2x x  2  2 x     2 3 1 11  x   . 2 2 2 x 10x  4 3 Xét 2 2
 2x  x 8  3x 12x 12  0  x  22  0 . 2 2
Có đẳng thức khi và chỉ khi x = 2 y 1.
Kết luận: Hệ phương trình có nghiệm  x, y là 2,  1 .  2 2 2x  4y  2 3    4   
 x  y 1 1
Bài 6. Giải hệ phương trình: xy   y x  .    x  2
1  xy  3x  2y  5  2x x y  3  x  y  3 2 
Hướng dẫn Điều kiện: x  0, 3   y  0 .   2 2
1  2x  xy  4y  4 2x 3y xx  y y   2
4xy  4y    2
2x 3y  4  2 2x 3y 2 4xy  4y 
  4xy  4y  2x 3y2 2 2  0
2  x xy 32 2x y 3  x  y 3  2 x y 3
 x  y  3 2 xx  y  3  2x  y  3   x  y 32  0
Kết hợp hai điều kiện trên ta suy ra được hệ có nghiệm duy nhất.
Mà x  4, y 1 thỏa hệ phương trình.
Kết luận: Hệ phương trình có nghiệm x, y là4,  1 .
Nhận xét: Các bài toán dung phương pháp đánh giá ở dạng như trên cho phép người giải nhẩm nghiệm nếu lý luận chặt chẽ
về mối tương quan giữa các phương trình. Tuy nhiên phải giải rất nhiều thì các bạn mới có thể truy ra được dạng này. 2 2 x 1  6 y   8 y 2 2 4  4
 x 1  3 y  4  y 8y 17  3 x   1  
Bài 7. Giải hệ phương trình: 2
3y  35y  88 x  2   2 .  3 x  x     y     2 2 2x 1 5 3 4 2  2  1
Hướng dẫn Điều kiện x  , y  4. 2   x 1  6 2  y42 2 1  6 1  4
 x 1  3 x  4
  y  42 1  3 y  4 . t  t  3 t
Xét hàm số f t 2  4
 t 1  3 t,t  0  f 't 2 4 2 4  2t.4 ln 4  
 f 't  0, t   0 . 2 2 t t 1
Ta có: f  x  f  y  4  y  x  4 , thay vào PT (2) ta có: x  4 2 3x 11x  4 x  4 3x   1 x  4 x  4  3x 1 1       3  3  3 2
5x  x  3 x  2 2
2x 1. x  2 2 2 2   2x 1  2 3 2x 1 5x x 3 5x  x  3  2  2  2
    2x   x   2 2 3 3 2 2 1
3 1 2x 1  x  x 1  0 (Mò thôi nhé các bạn, phần này chịu khó xíu!) 2  1  1   6 t  x   x  3 Đặt 2
t  2x 1 , có phương trình: 2
2t  3x   2 2 2
1 t  x  x 1  0    .......   . 2  x  2  2 15 t  1  2 x   7         
Kết luận: Hệ phương trình có 3 nghiệm x, y là  1 6 7 6 2 2 15 30 2 15 4,8 ; , ; ,   . 2 2   7 7     
Nhận xét: Một số bài toán bất khả xâm phạm ta chỉ có thể mò cho tới khi ra thôi!
Bài 8. Giải hệ phương trình:  32 2 x      2 y  3  3 5 1 2    .  
x 2 x  y 3  
1   y 3  
1  x  2 y 3  2  6x y 3  2 1  2 
Hướng dẫn Điều kiện: x  0, y  3. Đặt a  x,b   y 3   1 .
   a a b  ba  b   2 2 2 2 2 6 a  b  . Có:
 a  b a  b  a  b 
a b   2 2 VT 2 2 3
6 a  b   VP .
Có đẳng thức khi và chỉ khi a  b  x  y  3 1  x  y  3  1. Thay vào phương trình (1), ta được: 32 2 x    2 y  3  3 5 2 . 32  2 x   
x  y 32 y 3 3 5 * 2   Theo BĐT Cauchy, ta có:     
x  y   2 y 3 3 2 y 3 3 32 2 3     2 2
 x  y32 y33 8 2 . 32  x     
x  y  32 y 3 3 5 VT VP 2  9 2  3  3 x y  32 
Đẵng thức xảy ra khi và chỉ khi:  x  y   4 2 3     . 2 
2 x  y 32 y 3 3 ..... 2 13 y   4  9 13 
Kết luận: Hệ phương trình có nghiệm x, y là , . 4 4    2 3 3
x  y  3 2 2 x  y   
 5x  y   8 xy
Bài 9. Giải hệ phương trình:  xy xy .  3 2 3 2 2
x  2x  4x  x  2y  5x  y  2y  2 Hướng dẫn  3 3 x  y   2 2 2 3 x  y 
Biến đổi phương trình (1) về dạng: 
 5x  y 8 xy  0 rồi chia hai vế cho xy ta xy xy
 x x y y   x y   x y  được: 2    3     5   8  0   y y x x  y x    y x     3 3 2 2     Đặt , : pt 2 u v   3 u v   5 u v u x v y             8  0 3 3 2 2  v u   v
u   v u  u v Đặt 3 2
t   ,t  2: pt  2t 3t  t  2  0 v u  t   2
2 2t  t  
1  0  t  2  a  b  x  y  x  y
Thay x = y vào phương trình (2) ta có: 3 2 3 2 2
x  2x  4x  x  2x  5x  x  2x  2 3 2 3 2 2
 x  2x  5x  x  2x  5x  x  2x 1 x 1 3 2 3 2
 x  2x  5x  x  2x  5x  x  2 1  x 1 Xét hàm đặc trưng: f a 2
 a  a a   f a  a   f a  a    f  3 2 , 0 ' 2 1 ' 0, 0
x  2x  5x   f x  1 3 2
 x  2x  5x  x 1  ....  x 1 y 1
So điều kiện nhận x = 1 và y = 1
Kết luận: Hệ phương trình có nghiệm  x, y là 1,  1 .
Nhớ: Muốn giải tốt một bài toán Phương trình, Bất phương trình hay Hệ phương trình thì điều nhất thiết là mỗi người
nên đọc và giải thật nhiều các dạng toán thường gặp. Đừng xem thường những ví dụ đơn giản vì bài toán khó là sự dung
hòa các dạng cơ bản một cách có ẩn ý của tác giả. Chung quy lại, những bài mà tôi đưa vào phần tham khảo vừa là bài
toán đại số vừa là bài toán tinh thần đòi hỏi các bạn phải thật bình tĩnh là vô tư giải dù giải đúng hay sai. Kiến thức mà
người khác cung cấp dù nhiều hay ít thì nó cũng chỉ là kiến thức của người ta, muốn biến nó thành của mình thì phải học.
Một câu nữa gửi đến các bạn: CÁCH CHUẨN BỊ TỐT NHẤT CHO MỘT KỲ THI LÀ LÀM THẬT TỐT BÀI TẬP
ÔN THI! Chúc các bạn sinh năm 1999 học vui! LUYỆN TẬP NHÉ!
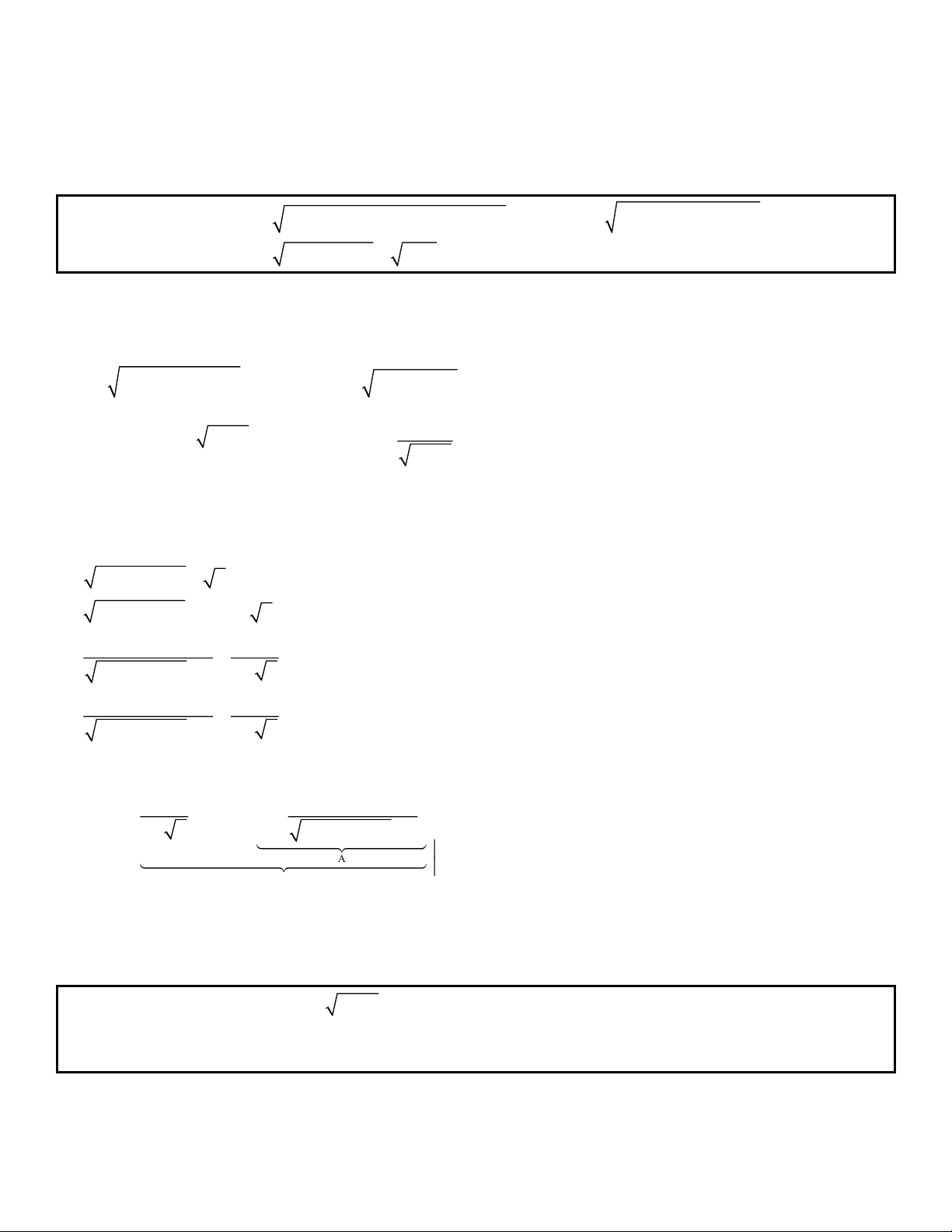
Bài 1: Giải bất phương trình:
x   x  x     x  x  x2 2 2 2 2 2 2 2 3 6  3x . 1 5 1 7  ĐS: S   ,  2,  .  2 2  2
x  x  4  x 1
Bài 2: Giải bất phương trình: x 1 x 1  .
ĐS: S  3; . 2 x  2x  6 x  2  2 1
Bài 3: Giải bất phương trình:   .
ĐS: x  2  2 3 . 2
x  x    x   2 6 2 4 2 2
Bài 4: Giải bất phương trình: 2 2
 x x   x  x   2 1 1
1 1 x  x  2 .
HD: Chuyển vế rồi liên hiệp hoặc dung ẩn phụ 2
u  x  x 1.
ĐS: S  1; .
Bài 5: Giải bất phương trình: 2
x  x   x   x   2 6 1
2 x 1  3x  9x  2 .
HD: Nhẩm được x  2, x  3 rồi dùng liên hiệp.
ĐS: S  1;23; .
Bài 6: Giải bất phương trình: 2
x  x   
 x  x 2 2 2 5 2 2
x  x  3  x . 3 13
HD: Thừa số chung  x  2  x , liện hiệp rồi đặt 2 ẩn phụ. ĐS: x  . 2 1 1 2
Bài 7: Giải bất phương trình:   . 2 2 2 x 1 3x  5 x  2 1 HD: Dùng ẩn phụ 2 t  x  2.
ĐS: S   ;   2   2;   . 2
5x 13 57 10x  3x
Bài 8: Giải bất phương trình: 2
 2 x  3  x  2x  9 .
x  3  19 3x
HD: Xem lại các bài tập trang 9, 10. ĐS: S   2  ;  1 . 1
  4x  y  2 1 3  1 
Bài 9: Giải hệ phương trình:  2x  y  2
2x  y   1 .  3 2
 9y  2  7x  2y 5  2y  2
HD: Ẩn phụ u  x  y  2 , sau đó dung đơn điệu.
ĐS: 2;2,3;3 .  6
3x  6y  5  2 6y  3x 1  
Bài 10: Giải hệ phương trình: x  2y  3  .  3 2 2
x  2y  4y  x  x  2y  3    2x 2 2
1 2y  x   2  1 HD: 
Dùng ẩn phụ t  2y  x rồi đánh giá bằng BĐT Cauchy. ĐS: 0; , 1    ;0 .  2  3 3 2 2
x  y 8x 8y  3x   3y
Bài 11: Giải hệ phương trình:  . 2 5x 5y 10 
 y7 2y6 3 2
x  2  x 13y  6x   32
HD: Đơn điệu ở PT trên, chú ý đoạn sau phải chứng minh phương trình vô nghiệm. ĐS: 2,2 . 3 2
y 3y  x  3
3x 12x x  9  x  4 2
x  3x 8x 6x 2 x   1  4
Bài 12: Giải hệ phương trình:  . 2 2
x  4y 9  6x 8y  3 89   89   5  3 89 
HD: PT trên dung hàm số, chú ý biến cần đặt lại sao cho dễ nhìn. ĐS: 1  ;1 , ; 1   . 8 16 2     