Tuyển tập 100 bài toán Hệ phương trình

Tài liệu gồm 52 trang tuyển chọn và giải chi tiết 100 bài toán hệ phương trình, các bài toán hệ phương trình được tuyển chọn gồm nhiều dạng bài khác nhau, trong mỗi bài toán lại được giải bằng nhiều phương pháp, cách giải khác nhau nhằm giúp học sinh tiếp cận được nhiều dạng toán về hệ phương trình và có nhiều hướng tiếp cận khi giải bài toán này.

105 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

52 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
TUYỂN TẬP 100 HỆ PHƯƠNG TRÌNH LTĐH NĂM HỌC 2014-2015

NHÓM GIÁO VIÊN THỰC HIỆN
1) PHẠM VĂN QUÝ
2) NGUYỄN VIẾT THANH
3) DOÃN TIẾN DŨNG
ĐƠN VỊ CÔNG TÁC:
TRƯỜNG THPT HÙNG VƯƠNG, TX ĐỒNG XOÀI, TỈNH BÌNH PHƯỚC
Bài 1 Giải hệ phương trình:
2
3
12 (12 ) 12 (1)
8 1 2 2 (2)
x y y x
x x y
(x, y R) (ĐH khối A – 2014)
Giải
Điều kiện :
2
2 12
12 0
y
x
2 12
y
x
Cách 1:
Đặt
2
12 , 0 12
y a y a
a
PT (1)
2 2
(12 )(12 ) 12
xa a x
2 2 2 2 2
12 12 12 12
x a x a xa
2 2 2 2 2 2 2 2
12
12 12 12 12 2.12.
xa
x a x a xa x a
2 2
12
12 2.12 12 0
xa
x xa a
2
12
( ) 0
xa
x a
Ta có (x – a)
2
= 0 x =
12
y
(*)
Thế (*) vào (2) được :
(12 ) 12 8 12 1 2 2
y y y y
(4 ) 12 2 2 1
y y y
(3 ) 12 12 3 2 2 2 0
y y y y
3 2(3 )
(3 ) 12 0
12 3 1 2
y y
y y
y y
3
12 3 1 2
y
y
y y
1 2
12 0(vo nghiem)
Vậy
3
3
x
y
Cách 2:
Ta có
2 2 2
12 (12 ) 12 12 12
x y x y x x y y
Dấu “=” xảy ra
2
12
12
y
x
y
y
2
(12 )(12 )
x y y x
(3)
Khi đó (1) tương đương với (3)
(3)
2 2 2 2 2
0 0 0
144 12 12 12 144 12 12 (4)
x x x
x y x y x y y x y x
Thế (4) vào (2) ta có
3 2 3 2
(2) 8 1 2 10 8 1 2 10 0
x x x x x x
3 2
8 3 2 1 10 0
x x x
2
2
2
1 (10 )
3 3 1 2. 0
1 10
x
x x x
x
2
2
2
9
3 3 1 2. 0
1 10
x
x x x
x
2
2
2( 3)
3 3 1 0
1 10
x
x x x
x
2
2
3
2( 3)
x
x
x x
x
3 3
x y
Vậy
3
3
x
y
Cách 3:
Đặt
2
; 12 ; 12 ;
a x x b y y
12
a b
(1)
2 2
2 .
a b a b
a b
12
x y
(2)
3 2
8 3 2 10 2
x x x
3 1 0 (vo nghiem vì x 0)
1 10
2
2
3 3
3 3 1 2
10 1
x x
x x x
x
3
x y
2 2
3 1 10 1 2 3 0
x x x x
Đặt
2 2
3 1 10 1 2 3
f x x x x x
' 0 0
f x x
phương trình vô nghiệm.
Vậy nghiệm của hpt trên: (3;3)
Bài 2 Giải hệ phương trình:
2
(1 ) 2 ( 1)
2 3 6 1 2 2 4 5 3
y x y x x y y
y x y x y x y
(ĐH khối B – 2014)
Giải
Điều kiện:
0
2
4 5 3
y
x y
x y
Phương trình thứ nhất viết lại thành
(1 ) (1 ) ( 1) ( 1)
1
(1 )(x y 1) 1
( 1)
1
1 1
y x y y x y x y y
y
y y
x y
x y
x y y
TH1 :
1
y
thay xuống (2) ta có
9 3 2 2 4 8 3( )
x x x x TM
TH2 :
1
x y
thay xuống (2) ta có
2
2
2
2
2 3 2 2 1 1
2 3 2 1 0
2( 1) ( 1 ) 0
1
( 1) 2 0
1
5 1 5 1
( )
2 2
y y y y
y y y
y y y y
y y
y y
y x TM
Vậy hệ đã cho có nghiệm :
5 1 5 1
( ; ) (3;1),( ; )
2 2
x y
.
Bài 3 Giải hệ phương trình:
2 2
2 2
( 2 2) ( 6)
( 1)( 2 7) ( 1)( 1)
y x x x y
y x x x y
Giải
ĐK:
,
x y R
Đặt
1
a x
b y
, ta có hệ trở thành:
2 2 2 2
2 2 2 2
( 1) ( 1)( 6) ( 1)( 6) ( 1) (*)
( 1)( 6) ( 1) ( 1)( 6) ( 1)(**)
b a a b a b b a
b a a b b a a b
Trừ vế theo vế hai phương trình rồi thu gọn ta có:
( )( 2 7) 0
2 7 0
a b
a b a b ab
a b ab
Trường hợp 1:
a b
thay vào phương trình (*) ta có:
2 2 2
2
( 1)( 6) ( 1) 5 6 0
3
a
a a a a a a
a
1
2
x
x
hệ có 2 nghiệm (x; y) là:
Trường hợp 2:
2 7 0
a b ab
Trừ vế theo vế hai phương trình (*) và (**) rồi rút gọn ta có:
2 2
5 5 1
2 2 2
a b
Vậy ta có hệ phương trình:
2 2
2 7 0
5 5 1
2 2 2
a b ab
a b
Đây là hệ đối xứng loại I, giải hệ ta có các nghiệm:
2 3 2 3
; ; ;
2 3 3 2
a a a a
b b b b
Từ đó ta có các nghiệm (x; y) là:
(1;2),(2; 3),(1;3),(2;2).
Kết luận: Hệ phương trình có 4 nghiệm là:
(1;2),(2; 3),(1;3),(2;2).
Bài 4
Giải hệ phương trình:
3 3 2
2 2 2
12 6 16 0
4 2 4 5 4 6 0
x x y y
x x y y
Giải
ĐK:
2;2 , 0;4
x y
Ta có
3 3 2
(1) ( 2) 6( 2) 6
PT x x y y
Xét hàm số
3
( ) 6 , 0; 4
f t t t t
ta có
2
'( ) 3 12 3 ( 4) 0, 0;4 ( )
f t t t t t t f t
nghịch
biến trên
0;4
. Mà phương trình (1) có dạng:
( 2) ( ) 2
f x f y y x
thay vào phương trình (2) ta
có:
2 2
4 6 3 4 0
x x x
từ đó ta có y = 2.
Kết luận: Hệ phương trình có nghiệm (0; 2).
Bài 5 Giải hệ phương trình:
3 2
2 1 3
4 1 9 8 52 4
x y
x x y x y xy
.
Giải
§K:
1
y
.
3 2
3 2 1
4 1 4 4 13 8 52 0
x y
HPT
x x y xy x x y
2
3 2 1
( 2 1) 13 8 52 0
3 2 1
2 13 0
3 2 1
1 5
x y
x x y x y
x y
x y
x y
y y
2
3 2 1
5
11 24 0
3 2 1
7
5
3
3
8
x y
y
y y
x y
x
y
y
y
y
Kết luận: Hệ phương trình có nghiệm:
7
3
x
y
.
Bài 6 Giải hệ phương trình:
2 2
2
1 0
1 0
y x y x
xy
xy x y
ĐK:
0; 0; 1
x y xy
1 2 0 2 1 0
y x y x xy y x y x
y x y x
thay vào
2
, ta được:
2
1 0 1 1
x x y
KL: hệ pt có tập nghiệm:
1;1
S
Bài 7 Giải hệ phương trình:
3 3 2 2
2 3
5 8
5
5 1 2
2
x y x y
x y xy
xy
xy
x y
x y
ĐK:
1
;0 2
5
x y
Đặt
, 0; , 0
u x y u v xy v
khi đó
2
3 2 2 3
1 2 3 2 0 2 2 1 0 2 2
u u u u
u u v uv v u v
v v v v
2
2 0
x y xy x y x y
thay vào
2
, ta được:
5 5 1 5 1
5 1 2 3 3 3 1 3 0
5 1 2 2 1 5 1 2 2 1
x x
x x x x x
x x x x
1 1
5 1 1
3 0 ì 2
5
5 1 2 2 1
x y
VN v x
x x
KL: tập nghiệm của hệ pt là:
1;1
S
Bài 8
Giải hệ phương trình:
2
3 2
2 2
3 2
2
1 1
2 1 1 3 1
1 4
1 0
x y
x x x
x y
y x y
y y
x x
y
y
ĐK:
0
y
Hệ
2
3 2
3 2 2
3 2 2
1 1 0
1 0
1 4 0
1 4 0
x y x y
x y x y x y
x x y y
x x y y
1 1
1 2
y x x
x y
KL:
1;2
S
Bài 9
Giải hệ phương trình:
2 2 2 2 2 2
2 2
4 3 7 4 5 6 3 2
3 10 34 47
x xy y x xy y x xy y
x xy y
ĐK:
2 2
2 2
3 2 0
4 3 7 0
x xy y
x xy y
Chuyển vế nhân liên hợp ở phương trình
1
, ta được:
2 2
2 2 2 2
1
5 6 4 0
6
4 3 7 3 2
x y n
x xy y
x y n
x xy y x xy y
Với
x y
thay vào
2
, ta được:
2
1 1
1
1 1
x y
x
x y
Với
6
x y
thay vào
2
, ta được:
2
47 47
6
82 82
82 47
47 47
6
82 82
y x
y
y x
KL:
47 47 47 47
1;1 , 1; 1 , ; 6 ; ;6
82 82 82 82
S
Bài 10 Giải hệ phương trình:
2
4 2 2
3 3 0
9 5 0
x xy x y
x y x y x
Hệ
2
2
2 2 2
3 3 3
3 3 5 0
x y x xy
x y x y x
Thay
1
vào
2
, ta được:
2 2
2
0 0
1
9 15 4 0 1
3
4
4 0
3
x y
x y y y x
y x x VN
KL:
1
0;0 ; 1;
3
S
Bài 11
Giải hệ phương trình:
2 2
2 2
2 2
2 4 1 4 13
2 2
x y xy
x xy y
x y
x y
x y
ĐK:
0
0
2 0
x y
x y
x y
Hệ
2 2
4 4 4 8 5 0
2 2
x xy y x y
x y x y x y x y
Ta có PT
2
2 1
1 2 4 2 5 0
2 5
x y
x y x y
x y l
Với
2 1
x y
thay vào
2
, ta được:
3 2
3 1 1 1 3 9 6 13 0 0 1
y y y y y y y x
thỏa mãn
KL:
1;0
S
Bài 12 Giải hệ phương trình:
2 2 2 2
2
5 2 3 2 2 1
3 6
x x y x y x y
x y
ĐK:
2
x y
Ta có
2
2 6 3
x y
thay vào
1
ta được:
1 5 6 5 5 9 1 3
y y y y x
thỏa
mãn
KL:
3;1 ; 3;1
S
Bài 13 Giải hệ phương trình:
2
2
2 2 2 2
1 2
1 1
4 1 6 5 1 1 1 1
x y
y
x y
x y x x x y
ĐK:
2
1 1
1
1 1 0
x x
y
x y
Đặt:
2
1, 0
1, 0
a x a
b y b
, ta được:
2
3 2 2
2
4 5 6
b a b
a ab a b
Nhân chéo hai phương trình giải hệ đẳng cấp ta đươc tập nghiệm:
10;2 ; 10;2
S
Bài 14
Giải hệ phương trình:
3 2
2 2
20 3 3 0
3 1
y y xy x y
x y y
Hệ
3
2 2
20 3 1 3 1 0
3 1
y y y x y
x y y
.
Thế
2
vào
1
, ta được phương trình thuần nhất bậc 3
KL:
3 1 3 1
; ; ;
2 2 5 5
S
Bài 15
Giải hệ phương trình:
2 2
2 2
3 3 0
2 1 2 3 1 0
x y x y
y x y x
ĐK:
1
2
y
Ta có PT
2 2
2
3
3
0
1 3 3
6 6 0
y x
y x
y l
x y y x
y xy
x y
Với
x y
thay vào
2
, ta được:
2 4 3 2
1 1
2 1 3 1 6 11 8 2 0 2 2
2 2 2 2
y x
y y y y y y y y l
y x
KL:
1;1 ; 2 2;2 2
S
Bài 16 Giải hệ phương trình:
4 4 2 2
2 2
2 2 2
2 2
2 2
3 2
3 4 8
x y x y
x y
y x
x y
xy y x
ĐK:
. 0
x y
Ta có PT
4 2 2 4
2
2 2 2 2
2
2 2 2 2
1 0
x y
x x y y
x y x y
x y
x y x y
Với
x y
thay vào
2
, ta được:
1 1
x y
Với
x y
thay vào
2
, ta được:
1 1
y x
KL:
1;1 ; 1; 1
S
Bài 17 Giải hệ phương trình:
2 2
3 3 2
10 5 2 38 6 41 0
6 1 2
x y xy x y
x xy y y x
ĐK:
3
3 2
6 0
1 0
x xy y
y x
Ta có PT
2 2
1 10 2 19 5 6 41 0
x x y y y
.
Tính
Δ
2
' 49 1 0 1
x
y y
thay vào
1
được
2
x
thỏa hệ phương trình
KL:
2;1
S
Bài 18
Giải hệ phương trình:
3 3 2 2
3 2
2 0
2 2
x y x y xy xy x y
x y x x y
ĐK:
x y
Ta có PT
2 2
2 2
1
1 1 0
0
y x
x y x y x y
x y x y
1
y x
thay vào
2
, ta được:
3 2
0 1
2 0
1 0
x y
x x x
x y
2 2
0 0
x y x y x y
ì 0
v x y
thay vào hệ không thỏa
KL:
1;0 ; 0; 1
S
Bài 19 Giải hệ phương trình:
2 2 2 2
3 3
2
2 2 2 2 2
3
3
8 3 1 3 1 1
4 3 1 2 1 12 1 4
y x y y
y y x y x
ĐK:
1 1
2 2
x
Đặt:
2
3
2
1
1 4 , 0
a y
b x b
, ta có:
3 2 2
2
3 2 2
3 2 3 0
3 2 0
a a a b b
a b b
a a a b
thay vào
1
, ta được:
3 2
2 2 2 2
3 2 3 0 0 0
b b b b b b b b b a
.
Khi đó ta có:
2
2
3
1
1 4 0
2
1 0
1
x
x
y
y
KL:
1 1 1 1
;1 ; ; 1 ; ;1 ; ; 1
2 2 2 2
S
Bài 20 Giải hệ phương trình:
6 3 2 2
3
3
3 24 2 9 18 11 0
1 2 2 1 6 1
x y y x x y
y x x y
ĐK:
0
y
Ta có PT
2 4 2 2 2
1 2 3 6 9 12 18 1 0
x y x x y x y y
Với
2
2
x y
thay vào
2
, ta được:
3
3
3
2 2
3
3
3
1 2
1 2 1 4 1 1 0
1
(4 1) 4 1 2 1 (2 1)
x x x x
x
x x x x
1
1
2
x y
KL:
1
1;
2
S
Bài 21 Giải hệ phương trình:
2
2
1 1
4
x y
x y
xy
xy
x y xy
x y
y x
ĐK:
0; 0
x y
Ta có PT
2
2 2
1 0 2
y x xy x y xy x y x y xy
thay vào
2
ta được:
1 4 0 1
xy xy xy xy xy xy
Khi đó ta có:
3 5
3
2
1
3 5
2
x
x y
xy
y
KL: thay vào hệ ta có tập nghiệm:
3 5 3 5
;
2 2
S
Bài 22 Giải hệ phương trình:

1 4 4
2 1 0
1 1
1
1
1 1 1 2 1 2
2
x
x x
y y
y
y
y x x y
ĐK:
1; 1
x y
Đặt:
1, 0
1, 0
a x a
b y b
. Ta có
2
2 2 2
1 2 2 0
b a b ab ab
2
0
b
a
1 0 1
5
1 2
x x
y
y
thỏa hệ phương trình
KL:
1;5
S
Bài 23
Giải hệ phương trình:
3
3
1
4 2
1 1 1
2
3 4 8 1
x y
y x y
x y y
ĐK:
1
2 0
3 4 8
y
x y
x y
Ta có
2
1 4 1 0 4
3 2
x y x y
y x y
thay vào
2
, ta được:
2 2 2
3 6
1 1 1 1 1 1
1 2 1 0 1
2 2 2
2 1 1 1
a a a a a a a
y y y
6
1
1 2 8
1
y x
y
KL:
8;2
S
Bài 24 Giải hệ phương trình sau:
1 1 2 2 0
( , ).
1 4 0
x y y
x y
y y x x
Giải
Điều kiện:
1.
x
Đặt
1, 0.
t x t
Khi đó
2
1
x t
và hệ trở thành
2 2 2 2
(1 2 ) 2 0 2 2 0 ( ) 2 2 0
( ) 3 0 3 0 ( ) 3 3 0
t y y t y ty t y ty
y y t t y ty t t y ty
Suy ra
2
0
2( ) 3( ) 0
3 3
.
2 2
t y y t
t y t y
t y y t
Với
,
y t
ta có
2
2 2 0 1.
t t
Suy ra
2, 1.
x y
Với
3
,
2
y t
ta có
2
3 3 3 13
2 2 0 4 6 1 0 .
2 2 4
t t t t t
Suy ra
19 3 13 3 13
, .
8 4
x y
Vậy nghiệm (x; y) của hệ là
Bài 25 Giải hệ phương trình sau:
2 2
2
( 2) 4 7 3 2 0
1 1
x x x y y x y
x y x y
Giải
Điều kiện:
2
1 0
x y
Phương trình (1)
2 2
( 2) ( 2) 3 2 ( ) 3
x x x y y y
Xét hàm số
2
( ) 3
f t t t t
Có
2
2
2
'( ) 3 1 0
3
t
f t t t
t
Hàm số f(t) đồng biến trên R
Phương trình (1)
2
x y
Thay vào (2) ta có
:
2
2 2 2 2
2
3 3
1 2 3
2 2
1 4 12 9 1 4 12 9
3
3
2
1
1 1 (tmdk)
2
3 13 10 0
10
3
x x
x x x
x x x x x x x x
x
x
x
x y
x x
x
Vậy hệ có nghiệm (x;y) = (-1;-1).
Bài 26 Giải hệ phương trình sau:
2
53 5 10 5 48 9 0
,
2 6 2 11 2 66
x x y y
x y
x y x x y x
1
2
Giải
ĐK:
10 0 10
9 0 9
2 6 0 2 6 0
2 11 0 2 11 0
x x
y y
x y x y
x y x y
Từ PT(1) ta có
5 10 3 10 5 9 3 9 , 3
x x y y
Xét hàm số
2
5 3
f t t t
trên khoảng
0;t

có
/ 2
15 3 0, 0
f t t t
hàm số đồng
biến .Từ (3) ta có
10 9 10 9 1, 4
f x f y x y y x
Thay (4) vào (2) ta
được
2
7 10 2 66 0
x x x x
(5) ĐK:
7;10
x
Giải (5) ta được
2
9 9
7 4 1 10 2 63 0 9 7 0
7 4 1 10
1 1
9 [ 7 ] 0 9, 8
7 4 1 10
x x
x x x x x x
x x
x x x y
x x
Vậy Hệ phương trình có nghiệm duy nhất
; 9;8
x y
Bài 27 Giải hệ phương trình sau:
1
1
1 1 1
1 4 2 2
yx
x y
x y
x y
Giải
ĐK:
0 ; 1
x y
PT(1)
1
1
1 1 1 1 (1 )
yx
x y
x y
(*)
xét h/s
( )
1 1
t
f t t
t
; có
'
2
1 1
(1 1 ) .
2 2 1
( ) 1 0 , (1; )
(1 1 )
t t
t t
f t t
t

vì (*)
( ) (1 ) 1
f x f y x y
, thế vào pt(2) ta được :
2
1 5 2 2 6 2 2 5 6 8
x x x x x
2 2 2
1 1
5 6 1 5 6 ( 1)
2 2
x x x x x x x y
(tmđk)
vậy hệ pt có nghiệm là
1
2
1
2
x
y
Bài 28
Giải hệ phương trình sau:
3 3 3
2 2
27 7 8
9 6
x y y
x y y x
Giải
Nhận xét
0,
y
nhân hai vế phương trình thứ hai với 7y, trừ đi phương trình thứ nhất, được
3 2
(3 ) 7(3 ) 14(3 ) 8 0
xy xy xy
Từ đó tìm được hoặc 3
1
xy
hoặc 3
2
xy
hoặc 3
4
xy
Với 3
1,
xy
thay vào phương trình thứ nhất, được y=1 do đó
1
3
x
Với 3
2,
xy
thay vào phương trình thứ nhất, được y=0 (loại)
Với 3
4,
xy
thay vào phương trình thứ nhất, được y=-2 do đó
2
3
x
Bài 29 Giải hệ phương trình sau:
3 3
2 2
4 2
3 4
x y x y
x y
Giải
Phương trình
3 3
(1) 2(x y ) 4(2 x y)
Từ phương trình (2) thay
2 2
4 3
x y
vào phương trình trên và rút gọn ta được:
2 2 3
0
6 5 0
5
y
x y xy y x y
x y
TH1 :
0
y
thay vào hệ ta được
3
2
4
2
4
x x
x
x
nghiệm
(x;y) ( 2; 0)
TH2 :
x y y x
thay vào hệ ta được :
3
2
2 2
1
4 4
x x
x
x
Hệ có nghiệm
(x; y) (1; 1); ( 1;1)
TH3 :
5
x y
thay vào hệ ta có nghiệm
5 1 5 1
(x; y) ( ; ); ( ; )
7 7 7 7
Bài 30
Giải hệ phương trình sau:
2
2 . 2 . 0
(x; y R).
1. 1 3 . 1 3
y x x y
x y y x y x
Giải
ĐK:
2
1; 0
3 0
x y
x y x
PT (1)
2. . 2 2 0
x y x y x
có
2
2
8 2 4
y
x x x
2 4
2 2
2
0
4 2
x
y
x
y loai
x
với
2 4
2 2
2 2
x
y y x y x
x
, thế vào (1) ta được
2
1 2 1 1 1 2 2
x x x x x
2
1.( 2 1) 1 . 1 1
x x x x
(*)
Vậy hệ đã cho có 6 nghiệm.
Xét hàm số
2 2
( ) 1 1 1
f t t t t t t
, có
2
' 2
2
( ) 1 1 0 ( )
1
t
f t t f t
t
đồng
biến.
Vì PT (*)
2
1
( 1) ( 1) 1 1
1 1
x
f x f x x x
x x
3
x
Với x = 3
5
y
(thỏa mãn). Vậy hệ có nghiệm (x; y) = (3; 5).
Bài 31 Giải hệ phương trình sau:
2 2
1 2 2
2 1 2
x y x y
x y y y
Giải
Lấy (1) + (2) vế theo vế ta được:
2
2
2 1 1 2 4 2 2 2 2 2 0
2 0
x
x xy x y x x y x y x x y
x y
Trường hợp x=2 thay vào (2) ta có y = 1
Trường hợp x+2y = 0 thay vào (2) ta được phương trình vô nghiệm.
Vậy hệ có nghiệm x = 2; y = 1.
Bài 32 Giải hệ phương trình sau:
2
2 2
2
1 1 4
1
2 5
xy y y y
xy x y
y
Giải
Điều kiện
0
y
2
2 2 2
2 2
1 1
1 4 1 4
( )
1 1
2 1 5 1 5
x y y y x x
y y
I
y x x y x
y y
Đặt
1
1 ; 1
u y x v x
y
ta có hệ
2 2
5 5
5 3
10 2
2 5 2 15 0
1 1
1 5 1 3
1 10 1 2
u v v u
u u
v v
u v u u
y x y x
hay
y y
x x
2 2
1 1
10 5 1 0 2 3 1 0
1
9 1
1
2
x y
y y y y
x x
x y
Vậy hệ có các nghiệm (1;1) và (1; 1/2 ).
Bài 33 Giải hệ phương trình sau:
2 2
2 2
3 2
1
1
4
22
y
x
x y
x
x y
y
Giải
Điều kiện: x
0, y
0. và x
2
+ y
2
- 1
0.
Đặt u = x
2
+ y
2
- 1 và v =
x
y
Hệ phương trình (I) trở thành
3 2
1
21 4
u v
u v
2
2 13 21 0
21 4
v v
u v
9
3
u
v
hoặc
7
7
2
u
v
+ Với
9
3
u
v
3
1
x
y
hoặc
3
1
x
y
Với
7
7
2
u
v
2
14
53
2
4
53
x
y
hoặc
2
14
53
2
4
53
x
y
Vậy hệ có nghiệm (3;1), (-3;-1),
2 2
14 ;4
53 53
và
2 2
14 ; 4
53 53
.
Bài 34 Giải hệ phương trình :
3
4
1 1
1
x y x
x y
(I) .
Điều kiện:
1 0 1
0 0
x x
y y
Ta có (I)
2
3
4
1 1 1
1
x x x
x y
Từ phương trình :
2
3
1 1 1
x x x
3 2
1 2 2
x x x x
(1)
Ta thấy hàm số
( ) 1
f x x
là hàm đồng biến trên
1;

Xét hàm số
3 2
( ) 2 2
g x x x x
. Miền xác định:
1;D

Đạo hàm
/ 2
( ) 3 2 2 0
g x x x x D
. Suy ra hàm số nghich biến trên D.
Từ (1) ta thấy
1
x
là nghiệm của phương trình và đó là nghiệm duy nhất.
Vậy hệ có nghiệm
1;0
.
Bài 35 Giải hệ phương trình :
2
2
3 2 3
3 2 3
x x y
y y x
(II). Điều kiện:
0
0
x
y
Ta có (II)
2
2
3 2 3
3 3 2
x x y
x y y
Cộng vế theo vế ta có:
2 2
3 3 3 3 3 3
x x y y
(2)
Xét hàm số
2
( ) 3 3 3
f t t t
. Miền xác định:
1;D

Đạo hàm:
/
2
3
( ) 1 0
2
3
t
f t x D
t
t
. Suy ra hàm số đồng biến trên D.
Từ (*) ta có
( ) ( )
f x f y x y
Lúc đó:
2
3 3
x x
(3)
+ VT (3) là hàm số hàm đồng biến trên D.
+ VP (3) là hàm hằng trên D.
Ta thấy
1
x
là nghiệm của phương trình (3) (thỏa điều kiện)
Suy ra phương trình có nghiệm
1
x
là nghiệm duy nhất.
Vậy hệ có nghiệm
1;1
Bài 36 Giải hệ phương trình :
3
2
2 2. 1 3 1 (1)
1 2 2 1 (2)
y x x x y
y x xy x
ĐK :
1 1
x
Từ (1) ta có :
3
2. 2( 1) 1 2 1 3 1
y x x x x y
(thêm vào vế trái
2 1
x
)
3 3
2 2( 1 ) 1
y y x x
Xét hàm số f(t) = 2.t
3
+t có f’(t ) = 6t
2
+ 1 >0 suy ra hàm số đồng biến
Suy ra y =
1
x
thế vào (2), ta có
2 2
1 1 2 2 1
x x x x
(3)
Vì
1 1
x
nên đặt x = cos(t) với t
[0; ]
sau đó thế vào phương trình (3) là ra kết quả.
Bài 37 Giải hệ phương trình:
2 2
2
1
(1)
5
57
4 3 (3 1) (2)
25
x y
x x y x
Giải
ĐK:
,
x y R
Nhân 2 vế phương trình (1) với 25 và nhân 2 vế phương trình (2) với 50 ta có:
Hệ phương trình
2 2
2
25 25 5
200 150 114 50 (3 1)
x y
x x y x
Cộng vế theo vế hai phương trình của hệ ta có:
2 2
225 25 25 150 150 50 144
x y xy x y
2
15 5 5 12 15 5 7
15 5 5 144
15 5 5 12 15 5 17
x y x y
x y
x y x y
Với
15 5 7
x y
kết hợp với (1) ta có hệ phương trình:
2 2
15 5 7
1
5
x y
x y
2
2 2
2
11
25
5 7 15
2
5 7 15
11
5 7 15
25
25
25 25 5
2
25 7 15 5
2
5
5
1
5
x
y x
y
y x
y x
x
x y
x x
x
x
y
Với
15 5 17
x y
kết hợp với (1) ta có hệ phương trình:
2 2
15 5 17
1
5
x y
x y
2
2 2
2
5 17 15
5 17 15
5 7 15
25 25 5
25 17 15 5
y x
y x
y x
x
x y
x x
hệ vô nghiệm.
Kết luận: Hệ phương trình có hai nghiệm là:
2 11
5 25
;
1 2
5 25
x x
y y
.
Bài 38 Giải hệ phương trình:
3 2 1 (1)
0 (2)
x y x y
x y x y
Giải
Điều kiện :
0
3 2 0
x y
x y
Hệ Phương trình tương đương
1 3 2 2 1 3 2
x y x y x y x y x y
x y y x x y y x
2 2
2 2
y x x y
x y x y
x y y x
x y y x
4 1 4 1
5 1 3 1
y x y x
x y y x x x
2
4 1
1
3
5 1 9 6 1
y x
x
x x x
2
4 1
1
3
9 11 2 0
y x
x
x x
4 1
1
3
1
2
9
y x
x
x
x
1
3
x
y
Kết luận : Hệ phương trình có nghiệm
1
3
x
y
Bài 39 Giải hệ phương trình:
2 2 2 2
3 3
2 2 2 3 (1)
2 2 (2)
x y y x
x y y x
Giải
ĐK:
2 2
2 0
x y
Đặt :
2 2
2 ( 0)
t x y t
2
2 2
2 2
1
1 2 3 0
3
1 2 1
2 1
t
t t
t
t x y
x y
Khi đó hệ phương trình tương đương
2 2
3 3
2 1
2 2
x y
x y y x
2 2
3 3 2 2
2 1
2 2 2
x y
x y y x x y
2 2
3 2 2 3
2 1
5 2 2 0 (3)
x y
x x y xy y
Th 1:
0
y
Hệ phương trình tương đương
2
3
2 1
x
x
( vô lí )
Vậy cặp ( x , 0) không là nghiệm của hệ
TH2 : Chia hai vế ( 3 ) cho
3
y
ta có hệ phương trình tương đương
2 2
3 2
2 1
5 2 2 1 0
x y
x x x
y y y
2 2
2 1
1
x y
x
y
1
1
x y
x y
Kết luận : Hệ phương trình có nghiệm
1;1 , 1; 1
S
Bài 40 Giải hệ phương trình:
2 2
2
1 9
6 0
8
1 5
2 0
4
x y xy
x y
y
x y
Giải
Điều kiện:
0
x y
Hệ phương trình biến đổi tương đương
2 2
2
1 9
2 0
8
1 5
0
4
x y x y
x y
x y x y
x y
Đặt
1
a x y
b x y
x y
Ta có hệ tương đương
2 2
9
2 2 0
8
5
0
4
a b
a b
2 2
25
2
8
5
4
a b
a b
2
2
5 25
2
4 8
5
4
b b
a b
5
4
5
2
a
b
Vậy hệ có nghiệm
7 3 13 3
; ; , ;
8 8 8 8
x y
Bài 41 Giải hệ phương trình:
2 2
2 2
1 25 1
2 8 9
x y x y y
x xy y x y
Giải
Hệ phương trình tương đương
2 2
2
2 2
1 25 1
1 1 10 1 0
x y x y y
x y x y y y
Nhận xét
1 0
y
không là nghiệm hệ phương trình
Chia hai vế phương trình một và hai cho
1
y
ta có
2 2
2 2
1
25
1
1 10
1
x y x y
y
x y
x y
y
Đặt
2 2
1
1
x y
a
y
b x y
Khi đó ta có
. 25
10
a b
a b
2 2
5
5 1
5
1 10
a
x y y
b
x y
Vậy hệ có nghiệm
3 11
; 3;1 , ;
2 2
x y
Bài 42 Giải hệ phương trình:
2 2 2
3 3 2 2 3
4 1 0
4 1 0
x x y y y
x y x y y xy
Giải
Nhận xét
0
y
không là nghiệm hệ phương trình
Chia hai vế phương trình một cho
2
y
và hai
3
y
2
2
2
3
2 3
1 1
4 0
1
4 0
x x
y
y
x x
x
y
y y
Đặt
1
a x
y
x
b
y
Hệ phương trình biến đổi tương đương ta có :
2
3
2 4
a a b
a ab
2
2 4
2
1
4 4
a b a a
b
a a
1
1
x
y
Hệ có nghiệm
; 1;1
x y
Bài 43
Giải hệ phương trình:
2 2
2 2
5
4
5
5 5
x y
x y x y
x y
x y
xy
Giải
Hệ phương trinh tương đương:
2 2
5
4
5 5 5
x y
x y x y
x y
x y
y x
2 2
2 2
5
4
5 5
x y
x y x y
x y y x
x y
2 2
2 2
5
4
1
5
x y
x y x y
x y y x
x y
Đặt
2
2
5
x
a
x y
y
b
x y
khi đó ta có
4
1 1
1
a b
a b
4 2
4 2
a b a
ab b
Hệ có nghiệm
3 3
; ;
2 2
x y
Bài 44 Giải hệ phương trình:
3 2 3 1
5
3 2 2 2
2
x y x y
x
y xy y
Giải
Điều kiện ta có
2
; 3;3
3
y x y x
Phương trình (1) tương đương
2
3 4 3 1
x y x y
2 2
2 5 2 12 12 9 0
x y x y y
6 9
2 1
x y
x y
Với
6 9
x y
3
x
6 9 3 1
y y

Suy ra phương trình vô nghiệm
Với
2 1
x y
thay vào phương trình ( 2 ) ta có
2
3 2 2 2 3 2
y y y y
2 2
2 1 2
3 2 2
y
y y
y y
2
2
2 1( )
3 2 2
y
y vn
y y
Vì
2 2 7
;2 1
3
3 2 2 2
y
y y
Vậy hệ có nghiệm ( 3 ;2 )
Bài 45 Giải hệ phương trình:
2
2 7 10 3 1 1
3
1 2
1
y y x y y x
y x y
x
Giải
Điều kiện
2
2 7 10 3 0; 1 0; 1 0
y y x y y x
Ta có
2
2 7 10 3 1 1
1 1 3 2 1
y y x y x y
x y x y x
2
2
2 7 10 3 1 2 1 1 1
1 1 2 1 3
y y x y x x y y
x y x y x
2
2
2 7 10 3 1 2 1 2 7
1 1 1 2 3
y y x y x x x y
x y x x y
Phương trình ( *) tương đương
2 2
2 4 2 3 3 0
y y xy x x
1 0
2 2 0
x y
x y
Với y = 1 – x thay vào phương trình ( 2 ) ta được
2
1 2 1
x x x x
( VN )
Với x = 2 – 2y thay vào phương trình (2) ta được phương trình đơn giản ẩn y.
Từ đó có nghiệm của hệ.
Bài 46
Giải hệ phương trình:
2 2
2 2
2 2 2 2 1 ( 1 )
2 2 2 0 ( 2 )
x x x y y y
x y x y
Giải
Lấy ( 1 ) – ( 2 )
Ta có
2 2
3 2 2 4 2 2 1
x x x y y y
2 2
( 1) ( 1) 2 4 2 2 1
x x x y y y
Xét hàm số :
2
( ) 1
f t t t t
1
'( ) 2 1
2 1
f t t
t
Áp dụng bất đẳng thức Cauchy
1 1 3 1
2 1 1 1
2 2
4 1 4 1
t
t t
Suy ra
' 0
f t
Vậy
f t
là hàm đồng biến
Suy ra
1 2
x y
Thay
2 1
x y
vào phương trình ( 2 ) ta có
2
2
2 1 2 2 2 1 2 0
y y y y
2
1 1
6 7 1 0
1 2
6 3
y x
y y
y x
Vậy hệ có nghiệm
2 1
1;2 , ;
3 6
S
Bài 47 Giải hệ phương trình:
3
3 2 2 2 1 0
2 2 2 5
x x y y
x y
Giải
Điều kiện
1
2;
2
x y
Phương trình ( 1) tương đương :
2 2 2 2 1 2 1 2 1
x x x y y y
2 2 1 .
f x f y
Xét hàm số
3
f t t t
ta có
2
' 3 1 0
f t t
sauy ra hàm số
f t
đơn điệu tăng .
Từ đó suy ra
2 2 1 2 2 1
f x f y x y
3 2
x y
thay vào phương trình (2)
Ta có
3
5 2 2 2 5
y y
( * )
Đặt
3
5 2
2 0
u y
v y v
(*)
3 2
2 5
2 9
u v
u v
1; 2
3 65 23 65
;
4 8
65 3 23 65
;
4 4
u v
u v
u v
2
233 23 65
32
233 23 65
32
y
y
y
Vậy hệ có nghiệm
23 65 185 233 23 65 23 65 185 233 23 65
1;2 , ; , ;
16 32 16 32
S
Bài 48 Giải hệ phương trình:
2 3 4 6
2
2 2
2 1 1
x y y x x
x y x
Giải
Với
0
x
thay vào hệ phương trình ta có
0
3
4
y
y
( mâu thuẫn )
Chia hai vế phương trình ( 1) cho
3
x
ta có
3
3
2 2
y y
x x
x x
y
f f x
x
Xét hàm số
3
2
f t t t
có
2
' 3 2 0
f t t
sauy ra hàm số
f t
đơn điệu tăng .
Từ đó suy ra
2
0
y
x x y y
x
Thay vào phương trình ( 2) ta có
2
2
2 1 1
x x x
.(*)
Đặt
2
1 0
u x
v x v
(*)
2
2 2
u v v u
2
2 2 0 2 0
v uv v u v u v
2 3
v x
Vậy hệ có nghiệm
3; 3 , 3; 3
S .
Bài 49 Giải hệ phương trình:
2
2 2
4 1 3 5 2 0
4 2 3 4 7
x x y y
x y x
Giải
Điều kiện :
3
4
5
2
x
y
Phương trình ( 1 ) biến đổi ta có
3
3
3
8 2 6 2 5 2 2 2 5 2 5 2
x x y y x x y y
Xét hàm số
3
f t t t
ta có
2
' 3 1 0
f t t
suy ra hàm số
f t
đơn điệu tăng .
Từ đó suy ra
2 5 2
f x f y
2 5 2
x y
2
5 4
0
2
x
y x
Thay vào Phuong trinh ( 2) ta có
2
2
2
5 4
4 2 3 4 7 0
2
x
x x
. Với
3
0;
4
x
. Nhận xét
3
0;
4
x x
đều không là nghiệm
2
2
2
5 4
4 2 3 4 7
2
x
g x x x
Khi đó
2
4
' 4 4 3 0
3 4
g x x x
x
với
3
0;
4
x
Ta có
1 1
0 ; 2
2 2
g x y
là nghiệm duy nhất của hệ.
Bài 50
Giải hệ phương trình:
2
2
2
3
1 1
2
2 5 1 2 2 4 2
y y y x
x x x x y
Giải
Điều kiện
2 4 2 0
x y
Phương trình ( 1 ) tương đương
2 2 2
2 4 2 1 2 1
x y y y y y
2
2
2 4 2 1
x y y y
(*)
Thay vào phương trình (2) ta có
2
2
2
1 1 1 2 1
x x y y
2
2
1 1
1 1
2 2
x x
y y
Xét hàm số
2
( ) 1.
f t t t
Khi dó
2
'( ) 1 0
1
t
f t
t
suy ra hàm số
f t
đơn điệu tăng .
Từ đó suy ra
1
2
x
f f y
1 1
2 1
2 2
x x
f f y y x y
thay vào phương trinh
(*)ta được
2
2
2
2
1 2
3
1 4
4
1 2
y y
y y y
y y
5
2
x
Vậy hệ có nghiệm
5 3
;
2 2
Bài 51 Giải hệ phương trình:
2 2
2 2
2 5 3 4
3 3 1 0
x x x y y
x y x y
Giải
Cộng hai phương trình ta có
2 2 2 2
2 2
2 2
2 1 2 5 4
1 1 4 4
x x x x y y
x x y y
Xét hàm số
4 0
f t t t t
Khi đó
1
' 1 0
2 4
f t
t
suy ra hàm số
f t
đơn điệu
tăng .
Từ đó suy ra
2 2
2 2
1 1
f x f y x y
1
1
y x
y x
Với
1
y x
thay vào phuong trình hai ta có
2 2
2 1 3 3 1 1 0
x x x x x
1 1
2 2
x y
Với
1
y x
thay vào phương trình hai ta có
2 2
2 1 3 3 1 1 0
x x x x x
3 1
4 4
x y
Bài 52 Giải hệ phương trình:
2 2
2 2
2 4 1 2 2 1 32
1
2
x x y y y
x y x y
Giải
Xét phương trình thứ hai của hệ :
2 2
1
0
2
x x y y
Phương trình có nghiệm khi
2 2
1 4 4 2 3 4 4 0
y y y y
3 1
2 2
y
Phương trình thứ hai của hệ biến đổi theo biến y
2 2
1
0
2
y y x x
Phương trình có nghiệm khi
2 2
1 4 4 2 3 4 4 0
x x x x
1 3
2 2
x
Phương trình thứ nhất ta có
3 2 3 2
8 2 4 2 32
x x y y y
Xét hàm số
3 2
8 2
f x x x
Khi đó
2
' 24 4
f x x x
với
0
' 0
1
6
x
f x
x
Ta có
1 1 1 1 3 63
0 0; ; ;
2 2 6 54 2 2
f f f f
Xét hàm số
3 2
4 2 32
g y y y y
khi đó
2
' 12 4 1
g y y y
với
1
6
' 0
1
2
y
g y
y
Ta có
1 63 1 1733 1 63 3 79
; ; ;
2 2 6 54 2 2 2 2
g g g g
Vậy hệ phương trình có hai căp nghiệm
3 1 3 1
; ; ;
2 2 2 2
Bài 53
Giải hệ phương trình:
3 2
2 1 3
4 1 9 8 52 4
x y
x x y x y xy
,x y
Giải
§K:
1
y
.
3 2
2
3 2 1
4 1 4 4 13 8 52 0
3 2 1
( 2 1) 13 8 52 0
3 2 1
3 2 1
2 13 0
1 5
x y
HPT
x x y xy x x y
x y
x x y x y
x y
x y
x y
y y
2
3 2 1
5
11 24 0
3 2 1
7
5
3
3
8
x y
y
y y
x y
x
y
y
y
y
Bài 54
Giải hệ phương trình:
2 2 3
2
2 2
5 4 3 2 0
2
x y xy y x y
xy x y x y
,x y
Giải
Biến đổi phương trình thứ hai của hệ ta có
2 2 2 2 2
2 2
( ) 2 2 ( ) ( ) ( 1) 2( 1)( 1) 0
( 1)( 2) 0
xy x y x y x y x y xy xy xy
xy x y
+)
1
xy
, thay vào phương trình thứ nhất và rút gọn ta được:
Vậy hệ có nghiệm là (7,3).
2 2 3 2
3 6 3 0 ( ) 0.
x y xy y y x y
Vì xy = 1 nên
0
y
, do đó x = y. Do đó x = y =1 hoặc x = y = -1.
+)
2 2
0.
x y
thay vào phương trình thứ nhất và rút gọn ta được:
3 2 2 3 2
4 5 2 0 ( 2 )( ) 0
2
x x y xy y x y x y
x y
x y
Từ đó giải được các nghiệm
2 2 2 2
(1;1),( 1, 1),(2 ; ),( 2 ; )
5 5 5 5
Bài 55
Giải hệ phương trình:
2 2
2 2
2 5 3 4 (1)
3 3 1 0 (2)
x x x y y
x y x y
,x y
Giải
Từ (1):
2 2
2 2
2 1
3
2 5 4
x y x
y x
x x y
, thay (2) vào ta được
2 2
1
( 3 )( 1) 0
2 5 4
x y
x x y
3
x y
Với x = 3y thay vào (2) giải được:
3 1 3 1
( , ) ( ; );( ; )
2 2 4 4
x y
Bài 56 Giải hệ phương trình:
4 4 2 2
2 2 2
1 25 2 (1)
1 (18 ) (2)
x y y x
x y y x
Giải
Dễ thấy với
0
y
hệ pt vô nghiệm
Xét
0
y
.Chia (1) cho
2
y
, chia (2) cho
y
ta được hệ
4 2
2
2 2 2
2
2
1
2 25
1
18
x x
y
y y y
x
y x
y y
2
2 2
2
2
1
( ) 2( 1) 25
1
18
x
y x
y
x
y x
y
Đặt
2
2
1x
a y
y
b x
ta được hệ
2
7
11
2 27
18
9
27
a
b
a b
a b
a
b
+ Với
7
11
a
b
ta giải ra được
2
11
3
x
y
hoặc
2
11
4
x
y
+ Với
9
27
a
b
vô nghiệm
Vậy phương trình đã cho có 4 nghiệm
2
11
3
x
y
hoặc
2
11
4
x
y
Bài 57 Giải hệ phương trình:
3 3
2 2
8 65
2(2 3 ) (1 3 ) 4 5.
x y
y x x y xy
Giải
Hệ
2 2
2
2 2 2 2
(2 )(4 2 ) 65
(2 )[(2 ) 6 ] 65
(2 )[3 (2 )] 5.
4 4 6 3 5.
x y x xy y
x y x y xy
x y xy x y
x xy y x y xy
3
3 2
2
2
2 5
(2 ) 6 (2 ) 65
(2 ) 2(2 ) 75 0
(2 ) 3(2 ) 15 0( )
2.(2 ) +6 (2 ) 10
x y
x y xy x y
x y x y
x y x y VN
x y xy x y
Thay y = 2x – 5 vào (1) ta có
3 3 2
2; 1
8 (2 5) 65 6 15 6 0
1
; 4
2
x y
x x x x
x y
Vậy hệ có 2 nghiệm
1
(2; 1);( ; 4)
2
.
Bài 58 Giải hệ phương trình:
2
2 2( 1) 2
1
2( ) 1
1
y x x
y x
x
Giải
ĐK:
1
x
Hệ phương trình đã cho trở thành
2
2 2( 1) 2
1
2 ( 1)
1
y x x
y x x
x
Đặt
2
1
a y x
b x
. Khi đó hệ đã cho trở thành
2 2 2
1( )
2 2 1 2 2
2
1
1 1
1
1
b L
a b b b b
a
b
b
a b a b
a b
b b
b
Với
2
2
1
a
x y
b
Vậy hệ phương trình đã cho có duy nhất nghiệm
2
x y
.
Bài 59
Giải hệ phương trình:
3
3
1 2 (9 5 )
(5 1) 1 3
xy y xy
xy y y
Giải
Nhận thấy
0
y
không là nghiệm của hệ
Xét
0
y
hệ đã cho được biến đổi thành
3
3
1
1
( ) 2(9 5 )
2(9 5 )
1
1 3
3 5 0
(5 1)
xy
x xy
xy
y
y
y
x xy
x y
y
y
Đặt
1
, 9 5
a x b xy
y
ta được hệ
3
2
2
4
6 0
a
a b
b
a b
Với
2
4
a
b
ta có hệ
1
1
2
1
9 5 4
x
x
y
y
xy
Vậy hệ đã cho có nghiệm
1
x y
Bài 60 Giải hệ phương trình:
2
1 1 4 3
3
2
2
x y x y x y
x y
Giải
§K:
0
x y
.
2
(1) 1 3( ) 4( ) 1
2 2 1
(2 2 1)(2 2 1) 0
1 3( )
1
(2 2 1)( 2( ) 1) 0
1 3( )
2 2 1 0
pt x y x y x y
x y
x y x y
x y x y
x y x y
x y x y
x y
Từ đó ta có hệ
2
2 2 1 0
3
3
1
2
2
6
x y
x
x y
x
Bài 61 Giải hệ phương trình:
3 2
2
3 9 3 1
9 2 3.
x y x xy
x x y
Giải
2
2
2
3 3 1
3 1
3 1
3 2 3 3
x x x y
x x
hpt
x y
x x x y
hoặc
2
3 2
1
3
2
x x
x y
Nếu
2
3 13
3 1
2
3 1
11 3 13
2
x
x x
x y
y
hoặc
3 13
2
11 3 13
2
x
y
Nếu
2
3 17
3 2
2
1
3
10 3 17
2
2
x x
x
x y
y
hoặc
3 17
2
10 3 17
2
x
y
Bài 62 Giải hệ phương trình
2 2 2 2
2
( )( 3) 3( ) 2 (1)
4 2 16 3 8 (2)
x y x xy y x y
x y x
,x y
Giải
ĐK:
16
2,
3
x y
3 3
(1) ( 1) ( 1) 2
x y y x
Thay y = x - 2 vao (2) được
2
4( 2) 3( 2)
4 2 22 3 8 ( 2)( 2)
2 2 22 3 4
x x
x x x x x
x x
2
4 3
( 2) 0(*)
2 2 22 3 4
x
x
x x
Xét f(x) = VT(*) trên
21
2;
3
, có f’(x) > 0 nên hàm số đồng biến. suy ra
1
x
là nghiệm duy
nhất của (*)
Vậy hệ phương trình có 2 nghiệm
2;0 , 1; 3 .
Bài 63
Giải hệ phương trình
2 2
2 2
12
12
x y x y
y x y
,x y
Giải
Điều kiện:
| | | |
x y
Đặt
2 2
; 0
u x y u
v x y
;
x y
không thỏa hệ nên xét
x y
ta có
2
1
2
u
y v
v
.
Hệ phương trình đã cho có dạng:
2
12
12
2
u v
u u
v
v
Đến đây sử dụng phương pháp rút thế ta dễ dàng tìm ra kết quả bài toán.
Bài 64
Giải hệ phương trình
2
2
4 2 2 2
4 3
x y x y y
x x y x y
,x y
Giải
Hệ tương đương
2
2 2 2
(1 2 ) 0 (1)
( ) 3 (1 2 ) 0 (2)
x y x y
x y x y
Thay (1) vào (2) được
2
2 2
0
1
(1 2 ) 3 (1 2 ) 0 2 (1 2 )(2 ) 0
2
2
x
x y x y x y y y
y
Với x = 0 suy ra y = 0
Với
1 2 0
y
thay vào (1) suy ra
2
1
2
x y
(Vô lí)
Với y = 2 suy ra x = 1 hoặc x = 2
Hệ có 3 nghiệm (0; 0), (1; 2), (2; 2).
Bài 65
Giải hệ phương trình
2 2
5 3 6 7 4 0
( 2) 3 3
x y y x
y y x x
( , )
x y R
.
,x y
Giải
Phương trình thứ (2)
2
(2 ) 3 3 0
y x y x
được xem là phương trình bậc hai theo ẩn y có
2
( 4)
x
Phương trình có hai nghiệm:
2 4
3
2
2 4
1
2
x x
y
x x
y x
Thay
y
= -3 vào pt thứ nhất ta được pt vô
nghiệm
Thay
1
y x
vào pt thứ nhất ta được:
2 2
x 5 2 6 5 5 0
x x x
(3)
Giải (3): đặt
2
5 5
x x
=
t
, điều kiện t
0
2
1
3 6 7 0
7 ( )
t tm
t t
t ktm
Với t=1
2
5 5
x x
=1
1 2
4 5
x y
x y
( thỏa mãn)
Vậy, hệ phương trình có 2 nghiệm là:
(1;2)
và (4;5)
Bài 66 Giải hệ phương trình
2 2 2
2 2 2 2
2 2 5 2 0
1 2 2 1
x y x y y
y x y xy x x xy y y
( , )
x y R
.
Giải
Từ phương trình (2) ta có đ/k :
, 0
x y y
2 2
2 2
1 1
y y y x y x y x y
.
Xét hàm số
2 2
1
f t t t t
liên tuc
0;

có
/
2
1
2
.2
1
t
f t t
t
t
2
1 1
2 0 0
2
1
t t
t
t
Suy ra hàm số nghịch biến
0;

nên
2
f y f x y x y
Thay vào (1) ta có
2
2 1 0 2
y x x y
4
x
.Vậy hệ có nghiệm (x ;y) = (4 ; 2).
Bài 67
Giải hệ phương trình
3 1 4 2 1 1 3
2 4 6 3
x x y y
x y x y x y
Giải
Điều kiện:
1
; 1
3
x y
2
2 2
(2) 3 2 6 4 0; 3 5
y x y x x x
Vậy ta có:
1 0
2 4 0
y x
x y
1 0
y x
vô nghiệm vì
1
; 1
3
x y
2 4 0 2 4
x y y x
, thay vào (1) ta có:
3 1 4 2 1 2 3 3 2 4
2 3 1 3 1 2 2 3 2 3 *
x x x x
x x x x
* 3 1 2 3 4 12
x x x y
.Kết luận:
, 4;12
x y
.
Bài 68
Giải hệ phương trình
2 2
5 5
3 3
3
31
7
x xy y
x y
x y
Giải
Điều kiện của phương trình
x y
2 2
2 2
5 5
5 5 3 3
3 3
3
3 1
31
7 31 2
7
x xy y
x xy y
x y
x y x y
x y
Lấy (2) nhân 3 kết hợp với (1) ta được phương trình đồng bậc
5 5 2 2 3 3 5 4 3 2 4 4
21 31 10 31 31 31 10 0 3
x y x xy y x y x x y x y xy y
.
Rõ ràng
0
x y
không phải là nghiệm hệ phương trình. Đặt
x ty
thay vào (3) ta được:
5 5 4 3 5 4 3
4 3 2
4 3 2
10 31 31 31 10 0 10 31 31 31 10 0
1 0
1 10 21 10 21 10 0
10 21 10 21 10 0
y t t t t t t t t
t
t t t t t
t t t t
Với
1 0 1
t t
hay
0
x y x y
(loại).
Với
4 3 2
10 21 10 21 10 0 3
t t t t
. Vì
0
t
không phải là nghiệm của phương trình (3) chia
hai vế phương trình cho
2
t
ta được:
2
2
1 1
10 21 10 0
t t
t
t
,
Đặt
2 2 2 2
2 2
1 1 1
2; u 2 2
u t u t t u
t
t t
. Khi đó (3) trở thành
2
2
5
10 21 10 0
5
2
u loai
u u
u
Với
5
2
u
ta có
2
2
1 5
2 5 2 0
1
2
2
t
t t t
t
t
Với
2
t
ta có
2
x y
thế vào (1) ta có
2 2
3 3 1 1
y y y
tương ứng
2
x
.
Với
1
2
t
ta có
2
y x
thế vào (1) ta có
2 2
3 3 1 1
x x x
tương ứng
2
y
.
Vậy hệ đã cho có bốn nghiệm là
1; 2 , 1;2 , 2; 1 , 2;1 .
Bài 69 Giải hệ phương trình
3 4
2 2 3
7
2 9
x y y
x y xy y
Giải
Hệ phương trình
3 3
2
7 1
9 2
y x y
y x y
Từ hệ suy ra
.y 0; y, y 0
x x
.
Lấy phương trình (1) lũy thừa ba, phương trình (2) lũy thừa bốn. Lấy hai phương trình thu được
chia cho nhau ta thu được phương trình đồng bậc:
3
3 3 3
3
8 4
4
7
9
y x y
y x y
.
Đặt
x ty
ta được phương trình:
3
3
3
8 4
1
7
3
9
1
t
t
. Từ phương trình này suy ra
1
t
.
Xét
3
3
8
1
; t 1.
1
t
f t
t
2 3 2
8 7 7
2 3 3 3 3 2 3
8 8
2
7
3 3 2
8
9 1 1 8 1 1 1 1 9 9 8 8
f'
1 1
1 1 9 8
0 1
1
t t t t t t t t t t
t
t t
t t t t
t
t
Vậy f(t) đồng biến với mọi
1
t
. Nhận thấy
2
t
là nghiệm của (3). Vậy
2
t
là nghiệm duy nhất.
Với
2
t
ta có
2
x y
thế vào (1) ta được
4
1 1
y y
(vì
0
y
) suy ra
2
x
.
Vậy hệ có nghiệm là
2;1
.
Bài 70 Giải hệ phương trình
1 1
2 2 (1)
1 1
2 2 (2)
y
x
x
y
ĐK:
1 1
,
2 2
x y
.
Trừ vế hai pt ta được
1 1 1 1
2 2 0
y x
x y
1 1
2 2
0 0
1 1
1 1
2 2
2 2
y x
y x y x y x
xy
xy x y
xy
y x
y x
TH 1.
0
y x y x
thế vào (1) ta được
1 1
2 2
x
x
Đặt
1
, 0
t t
x
ta được
2
2 2 2
2 0 2
2 2 1 1
2 4 4 2 1 0
t t
t t t x
t t t t t
và
1
y
TH 2.
1 1
0
1 1
2 2
xy x y
xy
y x
. TH này vô nghiệm do ĐK.
Vậy hệ có nghiệm duy nhất (1; 1).
Bài 71
Giải hệ phương trình:
2 2
2 2
8
2 2
2 1
3 3 5 8
x y
y
x y
y x
Điều kiện:
. 0
x y
Quy đồng rồi thế
1
vào
2
, ta được:
3 3 2 2 2 2
3 3 5 2 2 2 2 2
x y xy xy x x y y y y x y y y
2 2
2 1 0 2
x y x xy y x y
thay vào
1
, ta được:
3 2
4 2 2 8 0 1 2
y y y y x
KL:
2;1
S
.
Bài 72 Giải hệ phương trình:
6 3 2 2 2
3 3 2 2
2
8 2 1 4 2 1 (2 )
y y x xy x y
xy y x x y
Giải
2
6 3 2
6 3 2
1 1 1 1
(1) (1) 2
4 2 2 2
2 2 4 1 (3)
VP xy VT y y x
y y x
Từ (2) và (3) suy ra:
3 3 6 3 2 2 2
3 6 2 2
3 6 2 2
2 6 3 2 3 2
8 2 2 2 2 4 4 2 1 (2 )
8 2 2 8 2 1 (2 )
4 1 4 1 (2 )
1 1 (2 ) 4 4 ( 2 ) (4)
xy y y y x x x y
xy y x x y
xy y x x y
x y y xy x y x
(4) 0, (4) 0
VT VP
. Do đó:
3 3
0
0
1
2 2
(4)
2
2
1
1
2
1
x
y
y x y x
x
y x y y
y
x
y
Thử lại chỉ có:
1
( ; ) ( ; 1)
2
x y
thỏa mãn.
Vậy hệ đã cho có nghiệm duy nhất
1
( ; ) ( ; 1)
2
x y
.
Bài 73 Giải hệ phương trình
2
2
2
2 2
2
0 1
1
2 1 3 2
y
x y
x x
x
x y
y
Giải
Từ PT
(1)
ta có:
2 2
( 1 ) 0
x y x x y
do
0
y
2
1 0 (3)
x
y x x
y
Từ
(2) & 3
ta có:
2
1
2 3 0
3
x
y
x x
y
y y
x
y y
y
y
Thay vào
3
giải ra ta có nghiệm
0; 1
Bài 74 Giải hệ phương trình:
3
3
2 2 2 2 1 1
3 1 8 2 1
0
x y x y xy
y x y
x
Giải
Ta có (1)
2 1 2 1 2 1 1 0
x y x y
ĐK: (2x + 1)(y + 1)
0
Mà x > 0
2 1 0
1 0
x
y
Ta có PT (1)
2 1 1 2 1 2 1 0
x y x y
2 1 1 0
x y
2
y x
Thay vào (2):
3
3
6 1 8 4 1
x x x
3
3
6 1 6 1 2 2
x x x x
(3)
Hàm số f(t) = t
3
+ t đồng biến trên R
(3)
3
6 1 2
x x
3
1
4 3
2
x x
Nhận xét: x >1 không là nghiệm của phương trình
Xét 0
x
1: Đặt x = cos
với
0
2
1
cos 3
2
2
9 3
2
9 3
k
k
(k
Z
)
Do
0
2
9
Vậy hệ có nghiệm:
cos ;2 cos
9 9
Bài 75 Giải hệ phương trình:
4
2 2
4 4
3 4
9
7
3
3 ln 0
64 32 8 3
x y x y
x y
x y
x y x
y
Giải
Theo BĐT Cauchy ta có
4 4
4
1 1 1 4 .1.1.1 4 4
x y x y x y x y
Dấu bằng xảy ra
1 (*)
x y
.
Từ đó kết hợp với điều kiện:
3
0 2 , 3
3
x
x y
y
.
PT thứ hai của hệ
4 2 4 2
9 7 9 7
3ln 3 3ln 3
64 32 8 64 32 8
x x x y y y
x y
.
Xét hàm số f(x) =
4 2
9 7
3 ln 3
64 32 8
x x x
x
( với x < 3 )
3
3
'
9 14 3 48
9 7 3
16 16 8 3 16( 3)
x x x
x x
f x
x x
2
2
4 3 2
1 6
3 9 13 6
0
16( 3) 16( 3)
x x x
x x x x
x x
( vì x < 3).
Suy hàm số nghịch biến trên (-2; 3), vậy f(x) = f(y)
x y
( **).
Từ (*), (**) có x = y =
1
2
.
Bài 76 Giải hệ phương trình:
2
2 2
2
5
9
2 6 ln
9
3 1 0
y y
x y x xy y
x x
x y xy
Giải
Từ
2
2 2
2
9
2 6 ln
9
y y
x y x xy y
x x
3 2 3 2
2 6 ln 9 2 6 ln 9 1
x x x x y y y y
Xét
3 2
2 6 ln 9f t t t t t t
2 2
2 2
6 2 2
' 3 2 3
3
9 9
f t t t
t t
Ta có
2
2 2 2
2 2 2 2
2 2 2 29 9 1 1 26 29
9 9
3 3 27 27 3
9 9 9 9
t
t t t
t t t t
2
26 29 26 29 29
1 9 1 0
27 3 3 3 3
t
Suy ra
' 0
f t t
hàm số đồng biến và liên tục trên R
Mà (1)
f x f y x y
Thay vào phương trình còn lại của hệ ta có
6 2
3 1 0 2
x x
Đặt
2
0
x u u
suy ra
3
3 1
u u
(3)
Xét
3
3 1
g u u u
với
0
u
2
' 3 3
g u u
có
' 0 1
g u u
Ta có bảng biến thiên của hàm số:
u -1 0 1 2
g’(u) + 0 - - 0 +
g(u)
Căn cứ vào BBT phương trình (3) có nghiệm duy nhất thuộc (0; 2)
Đặt
2 cos
u
với
0;
2
Khi đó (3) trở thành:
1
os3 = = 2 cos
2 9 9
c x
Vậy hệ có nghiệm
2 cos ; 2 cos ; 2 cos ; 2 cos
9 9 9 9
Bài 77
Giải hệ phương trình:
2 2
2 2 8
2
x y x y
x y
Giải
Ta có:
2
2 2
2
2 2
1
2
2
4
1
2
2
x y x y
x y x y
x y x y
Theo BĐT Cauchy ta có:
2 2 2 2
4
2 2 2 2 2. 2 8
x y y x x y x y
PT
dấu “ = ” xảy ra. Từ đó ta có x = y = 1.
Vậy hệ có nghiệm duy nhất (1; 1).
Bài 78 Giải hệ phương trình:
2 3
2
3
8 2 (1 2 )
2 1
4 1
3
x y xy y
y
x x
Giải
§K: tõ PT (2) ,suy ra x> 0
Ta có PT (1)
2 2
( 2 ) 4 (2 ) ( 2 )( 4 ) 0 2
x x y y y x x y x y x y
( v× x+4y
2
> 0 )
Thay vµo ph¬ng tr×nh (2) cã
3 2
3 4 2 4 (*)
x x x x
Ap dông bÊt d¼ng thøc Cauchy tacã
2 2
2 2 2
2
3 3
4 4 3 3
2 4 ( 4) 2 ( 4 ) 2
4 4 4 4
3 4 3
( 2 ) .2 4 3 4
2 2 2
x x
x x x x x x x x x
x
x x x x x
DÊu ®¼ng thøc x¶y ra khi x = 2. HÖ ph¬ng tr×nh cã nghiÖm (2,1)
-1
-
33
1
+
(Chó ý :C¸ch kh¸c : B×nh ph¬ng 2 vÕ cña pt (*)
2 2
( 2) ( 4) 0
x x x
)
Bài 79
Giải hệ phương trình:
2 2
4 8 ( 2)
( , )
3 3 2 1
xy y x x
x y R
x y y
Giải
2
2
4
(1) 4 2 0
2
x
x y x
x y
Với
4
x
thay vào pt (2) ta được
10 3 10
y
Với
2
2
x y
thế vào pt (2) ta được
2
5 3 2 1
y y y
(*)
Ta có
2 2
5 2 1 ( 1) 5 2 1 5 2 5(2 1) 3 2 1
y y y y y y y y
Do đó pt (*) vô nghiệm.
KL: Nghiệm của hệ
4
x
,
10 3 10
y
.
Bài 80 Giải hệ phương trình:
3 3
2 2
8 2
3 3( 1)
x x y y
x y
Giải
Ta có PT (1)
3 3
2 2
2(4 )(1)
3 6(2)
x y x y
x y
3 2 2
x x y 12xy 0
0
3
4
x
x y
x y
Thay cả 3 trường hợp
x
vào
2
Hệ có các nghiệm là:
6 6 6 6
3;1 , 3; 1 , ( 4 ; ),(4 ; )
13 13 13 13
Bài 81 Giải hệ phương trình:
2 2
2 2
8 3 2
4 2 3 2 5
x y xy y x
x y x y
Giải
Điều kiện:
2
3
x
y
, phương trình
0
(1) 2 8 0
2 8
x y
x y x y
x y
.
Với
2 8
x y
Ta có :
2 2
2 8
3 2 6
x x
x y
y y
Khi đó:
2
2 8
3
x
x y
y
không thỏa hệ.
Với
0
x y y x
thay vào phương trình (2)
Ta có PT
2
(2) 4 2 3 5
x x x
Điều kiện:
3 2
x
Ta có
2
1 1
(2) 4 2 1 3 2 1 4 1 1
2 1 3 2
x x
x x x x x
x x
1 1
4 1
1 0 (*)
2 1 3 2
x y
x
x x
Xét phương trình (*), đặt
4 1
( ) 1
2 1 3 2
f x x
x x
Ta có:
'
2 2
2 1
( ) 1 0; 3;2
2 2 1 2 3 3 2
f x x
x x x x
Mặt khác
( )
f x
liên tục trên
3;2
, suy ra
( )
f x
đồng biến trên
3;2
.
Ta có:
( 2) 0
f
, suy ra (*) có nghiệm duy nhất
2 2
x y
.
Kết hợp điều kiện, hệ có hai nghiệm
1; 1 , 2;2
.
Bài 82 Giải hệ phương trình:
2
2
3( )(1 2) 2 2 1
2 2 2 2
y y x x x
y y x
Giải
ĐK:
2.
x
Ta có
2
2
3( )(1 2) 2 2 1
2 2 2 2
y y x x x
y y x
2
2
3( )(1 2) ( 2 2 2 1) 2
2( ) 1 2 3
y y x x x
y y x
Đặt
2
1 2
a y y
b x
ta được
2
2
1
3 2
3 2
11 4
2 3 10 21 11 0
,
10 5
a b
b a
ab b
a b a a
a b
Với a=b=1 suy ra hệ có hai nghiệm là :
1 5
2,
2
1 5
2,
2
x y
x y
Vì
4
1 2 1
5
b x b
không
Bài 83 Giải hệ phương trình:
3
3
2 2 2 1 1 1
3 2 8 2 2
x y x y
y x y
, với
0
x
và
,
x y R
.
Giải
Điều kiện:
(2 1)( 1) 0
x y
,
Phương trình
(1) 2 1 2 1 2 1 1 0
x y x y
. Từ giả thiết
0
x
ta có
2 1 0 1 0
x y
. Đặt
2 1, 1
a x b y
ta có (1) trở thành:
2 2
2 0
a b ab
2 2 2
0 2 0
2 0( )
a b
a b ab b a b a b
a b l
Với
a b
ta có:
2 1 1 2
x y y x
thay vào phương trình (2) ta có:
3
3
3 3
6 2 8 4 2 6 2 6 2 2 2
x x x x x x x
, (*).
Xét hàm số
3
( )
f t t t
ta có
2
'( ) 3 1 0,
f t t t R
hàm số
( )
f t
đồng biến trên R
Do đó
3
3
(*) 6 2 2 8 6 2 0
PT x x x x
2
1 ( )
2( 1)(4 4 1) 0
1
( )
2
x n
x x x
x l
. Với
1 2
x y
Bài 84 Giải hệ phương trình:
5 2 3
2
2 2
5 4 3 2 0 1
2 2
x y xy y x y
xy y x y
.
Giải
Từ (2) ta có :
2 2 2 2
1 2 0 1 2
xy x y xy x y
Với xy = 1; từ (1) suy ra :
4 2
2 1 0 1
y y y
. Vậy hệ có nghiệm (x;y)=(1;1),(-1;-1).
Với :
2 2 2 2 2 2
2 1 3 4 2 2 0
x y y x y xy x y x y
2 2
6 4 2 2 0
y xy x y x y
1 2 0 1 2
xy y x xy x y
Xét : xy = 1 . Đã giải ở trên
Với : x = 2y , thay vào
2 2
2 10 10 2 10 10
2 ; ; , ;
5 5 5 5
x y x y
Vậy hệ có nghiệm : (x;y)=(1;1),(-1;-1),
2 10 10 2 10 10
; , ;
5 5 5 5
Bài 85 Giải hệ phương trình:
2
4 2 2 2 2 2
1 6 2 1
2 1 12 1 2
x y y
x y x y y x y
.
Giải
Điều kiện :
0; 1
y y
Khi đó :
2 2 2 2
4 4 9 1
1 1 6 2 2 ; 3
1 1
y y
x y y y y x x
y y
.
Thay vào (2) , ta có :
4 2 2 2 2 2 2 2 2
6 2 12 1 2 3 1 0
x y x y y y y y x x y y
2
2
2
2
1 2
1
4 1 9 1
1
1
4 9 1 1
0
1
3
y x
y
y y y
y
y y y
y x
y
Bài 86 Giải hệ phương trình:
2
2
2 4
1 1
3
x y y x xy
x
xy y
x
.
Giải
Điều kiện :
0, 0
x y
. Chia hai vế phương trình (1) cho xy , thêm 1 vào hai vế của phương trình
(2) và nhóm chuyển về dạng tích
1 1 1
4
1 1 1
4
x
x x y
x
x x y
Đặt :
4
1 1 1
; 4
4
u v
u x v u v
uv
x x y
.
Đến đậy bài toán trở thành đơn giản.
Bài 87
Giải hệ phương trình:
2
23
2
2
3
2
2 9
2
2 9
xy
x x y
x x
xy
y y x
y y
.
Giải
Cộng hai vế phương trình của hệ vế với vế ta có :
2 2
2 23
3
2 2
2 9 2 9
xy xy
x y
x x y y
. Ta có : x = y = 0 là một nghiệm của hệ .
Ta có :
2
23
3
2 9 1 8 2 2
x x x VT xy xy xy
. Khi đó :
2 2
2
VP x y xy
.
Cho nên dấu bằng chỉ xảy ra khi : x = y = 1. Vậy hệ có hai nghiệm : (x; y)=(0;0); (1;1).
Bài 88 Giải hệ phương trình:
2 4 7
2 4 7
1 1 1 1
1 1 1 1
x x x y
y y y x
.
Giải
Dễ thấy : x = y = 0 hoặc x = y = -1 là nghiệm của hệ
Xét : x > 0
Ta có:
7 2 4 2 3 4 5 6 7 7
1 1 1 1 1 1
y x x x x x x x x x x x y x
Ta có:
7 2 4 2 3 4 5 6 7 7
1 1 1 1 1 1
x y y y y y y y y y y y x y
Vậy hệ vô nghiệm . Tương tự khi y>0 hệ cũng vô nghiệm
Xét : x < -1
7
1 0 1
x y
Ta có : 1+
2 3 4 5 6 7 7
1
x x x x x x x x y x
. Tương tự khi
1
y
ta có
x y
Hệ cũng vô nghiệm
Xét trường hợp
1 0
x
. Hệ cũng vô nghiệm .
Kết luận : Hệ có nghiệm :
; 0;0 ; 1;
.
1
x y
Bài 89 Giải hệ phương trình:
1
3 (1 ) 2 (1)
1
7 (1 ) 4 2 (2)
x
x y
y
x y
.
Giải
ĐK
0, 0.
x y
Dễ thấy x = 0 hoặc y = 0 không thõa mãn hệ. Với x > 0, y > 0 ta có :
1 2
1 2 2
1
1
1 1 8
3
3 7
1 4 2
3 7
1 1 2 2
1
7
3 7
x y
x
x y
x y x y
x y
x y
y
x y
( nhân vế với vế)
2 2
21 (7 24 )( ) 24 38 7 0 6
xy y x x y x xy y y x
(vì x, y dương).
Thay vào phương trình (1) ta được
1 2 1 1 1 2
. 1 0 7 .
7
3 3 21
x
x x
Từ đó dễ dàng suy ra x và y.
Bài 90
Giải hệ phương trình:
3 2
2 2
3 49 (1)
8 8 17 (2)
x xy
x xy y y x
.
Giải
Với hệ này, cả hai ẩn và ở hai phương trình đều khó có thể rút ẩn này theo ẩn kia. Tuy nhiên, nếu rút
2
y
từ (2) và thế vào (1) thì ta được một phương trình mà ẩn y chỉ có bậc 1:
3 2 3 2 2
3 ( 8 8 17 ) 49 24 ( 1) 2 2 49 49 (3)
x x x xy y x xy x x x x
Nếu x=0 thì (1) vô lí.
Nếu x=-1 thì hệ trở thành
2
16 4
y y
.
Nếu
1 & 0
x x
thì từ (3) suy ra
2
2 49 49
24
x x
y
x
. Thế trở lại phương trình (2) ta được
2
2 2 2
2
2 49 49 2 49 49 2 49 49
8 . 17
24 24 3
x x x x x x
x x x
x x x
2
2 2
4 2 2
4 3 2 3
3 2
2 49 49 49
192 (2 49 49) 49.192
3 24 3
196 196 2205 4606 2401 0 196 2205 2401 0
196 196 2205 2205 0 196 196 2401 0
x x x
x x x x
x x
x x x x x x
x x x x
Phương trình cuối cùng vô nghiệm, chứng tỏ hệ chỉ có hai nghiệm (-1;4) và (-1;-4).
Bài 91
Giải hệ phương trình:
5 4 10 6
2
(1)
4 5 8 6 (2)
x xy y y
x y
.
Giải
ĐK:
5
.
4
x
Nếu y = 0 thì từ phương trình (1) ta suy ra x = 0, thế vào phương trình (2) ta thấy
không thỏa mãn, vậy y khác 0.
Đặt x = ky ta được (1) trở thành :
5 5 5 10 6 5 5
k y ky y y k k y y
(3). Xét hàm số
5
( )
f t t t
trên
, ta có
4
'( ) 5 1 0 .
f t t t
Do đó f(t) là hàm số đồng biến trên
, vậy
2
(3) ( ) ( ) .
f k f y k y x y
Thế vào (2) ta được
2 2
4 5 8 6 5 13 2 4 37 40 36 2 4 37 40 23 5
x x x x x x x x
2 2 2
23 5 0 5 23
1
41
16 148 160 25 230 529 9 378 369 0
x x
x
x
x x x x x x
Suy ra x = 1 và do đó
1
y
.
Bài 92 Giải hệ phương trình:
2 2
4
4
2 2 2 2 2
3 3
x x y y
x y
.
Giải
Điều kiện:
2
2
2 2 0
0
2 2 0
3
0
3 0
x x
x
y y
y
x
y
Mà:
2 2 2
2 2
2
4
2 2 ( 1) 1 1 2 2 1
2 2 ( 1) 1 1
2 2 1
x x x x x
y y y
y y
2 2
4
2 2 2 2 2
x x y y
Vậy (1) có nghiệm x = y = 1 thỏa (2).
Bài 93
Giải hệ phương trình:
2 2 2
2 2 2 2
2 2 5 2 0
1 2 2 1
x y x y y
y x y xy x x xy y y
.
Giải
ĐK:
0; 0 0
x y y x y
Từ (2) :
2
2 2 2 2
1 2 1y x y y y xy x x y y
2 2
2 2
1 1
y y y x y x y x y
Xét hàm số :
2 2
2 2
1 1 1
( ) 1 0 '( ) 2 2 0
2 2
1 1
t
f t t t t t f t t t
t t
t t
(Vì :
2
2 2
1 1
1 1 0 1 2 0
1 1
t
t t
với mọi t>0 )
Như vậy hệ có nghiệm chỉ xảy ra khi :
y x y
hay x = 2y .
Thay vào (1) :
2 2
2 3 2
2 2 2 2 5 2 0 4 10 5 2 0
y y y y y y y y
2
2 4 2 1 0 2
y y y y
vì :
2
4 2 1 0
y y
vô nghiệm .
Vậy hệ có nghiệm : (x; y) = (4; 2).
Bài 94 Giải hệ phương trình:
2
2
2
1
8
1
2
2 4 3 2 1
3 7
2 2
2 2
y
x
x y
y x
x y
.
Giải
Điều kiện :
, 0
x y
Ta có PT (1)
4 4
2
2.2 3 2.2 3 2
x y
x y
Xét hàm số :
4 3
( ) 2. 3 0 '( ) 8 3 0
f t t t t f t t
. Chứng tỏ f(t) luôn đồng biến .
Do vậy để phương trình (1) có nghiệm chỉ khi :
2 4 *
x y x y
Thay vào (2) :
4
5
3 7
2 5
2 2
y
y
. Xét hàm số : f(t)=
4 4
3
3 3
2 '( ) 4 .2 0
2 2
t
t f t t
.
Nhận xét : f(1) = 2 +
3 7
2 2
. Suy ra t = 1 là nghiệm duy nhất .
1
4
4 1
5
; ;
4
5 5
5 1
5
y
x y
x y
y
x
Bài 95 Giải hệ phương trình:
2 2
6 3
4 1 2 1
27x 8 2 (2)
x x y y
x y
Giải
Ta có PT (1)
2
2
4 2 4 2
x x y y
Hàm số
2
4
f t t t
đồng biến trên R nên
1 2
x y
Thế vào PT (2) ta có:
6 3
2 33
3
3 33
27x 4x 3
3x 4x 3
1 1 4x 3 4x 3 3
x
x
x x x x
Lại xét :
3
g t t t
, đồng biến trên R nên:
33
2
3 1 4x 2
3x 1 0
1 13
6
x x
x
x
Bài 96 Giải hệ phương trình:
3
2
2 2 1 3 1
( , )
2 1 4 4
y y x x x
x y
y y x
Giải
Điều kiện:
4 1;
x y
.
Ta có PT
3 3
(1) 2 2 1 2 1 1 2 2(1 ) 1 1
y y x x x x y y x x x
Xét hàm số
3
( ) 2 ,
f t t t
ta có
2
'( ) 6 1 0, ( )
f t t t f t
đồng biến trên
. Vậy
2
0
(1) ( ) ( 1 ) 1
1
y
f y f x y x
y x
Thế vào (2) ta được
3 2 1 4 4
x x x
(3). Xét hàm số
( ) 3 2 1 4,
g x x x x
liên tục trên [-4;1], ta có
1 1 1
'( ) 0
3 2 2 1 2 4
g x
x x x
( 4;1) ( )
x g x
nghịch biến trên [-4;1]. Lại có
( 3) 4
g
nên
3
x
là nghiệm duy nhất của phương trình (3).
Với
3
x
suy ra
2.
y
Vậy hệ có nghiệm duy nhất
3
2.
x
y
Bài 97 Giải hệ phương trình:
2 2
2
( 1)( 1) 3 4 1(1)
1 (2)
x y x y x x
xy x x
Giải
Nhận xét x = 0 không thỏa mãn phương trình (2) nên ta có thể suy ra
2
1
1
x
y
x
(3)
Thay (3) vào (1) ta được
2 2
2 2 2
1 1
( ) 3 4 1 ( 1)( 1)(2 1) ( 1)(3 1)
x x
x x x x x x x x x
x x
3 2 2
0
( 1)(2 2 4 ) 0 2 ( 1) ( 2) 0 1
2
x
x x x x x x x x
x
Loại nghiệm x = 0, vậy phương trình có hai nghiệm:
5
1; 1 , 2;
2
.
Bài 98 Giải hệ phương trình:
2 3 4 6
2
2 2
2 1 1
x y y x x
x y x
Giải
Ta có hệ
3
2 2 2 2 4
2 2 3 2
2
2
2 0
2 0
2 1 1
2 1 1
y x x y yx x
x y x y x
x y x
x y x
Trường hợp 1: y =
2
x
, thay vào (2) :
2 2 2
2 1 1 2 2 2 0 2;
x x x x t x t x t t x
2 2
2
1 2 3 3
.
1
x x x
x x x
Trường hợp 2:
2 2 2 4 2 2 2 4
2 0 yx 2 0
x y yx x y x x
4 2 4 4 2
4 2 3 8 0 0
y y
x x x x x x R
2 2 2 4
(, ) 2 0 ,
f y x y yx x x y
. Phương trình vô nghiệm .
Do đó hệ có hai nghiệm : (x;y)=
3;3 , 3;3
Chú ý:
Ta còn có cách giải khác
Phương trình (1) khi x = 0 và y = 0 không là nghiệm do không thỏa mãn (2).
Chia 2 vế phương trình (1) cho
3
3 3
0 1 2 2
y y
x x x
x x
Xét hàm số :
3 2
2 ' 2 3 0
f t t t f t t t R
. Chứng tỏ hàm số f(t) đồng biến . Để
phương trình có nghiệm thì chỉ xảy ra khi :
2
y
x y x
x
. Đến đây ta giải như ở phần trên.
Bài 99 Giải hệ phương trình:
2 2
1 1 1
6 2 1 4 6 1
x x y y
x x xy xy x
Giải
Ta có hệ
2
2
1 1
6 2 1 4 6 1
x x y y
x x xy xy x
. (nhân liên hợp)
Xét hàm số :
2
2
2 2 2
1
( ) 1 '( ) 1 0
1 1 1
t t
t t t
f t t t f t t R
t t t
Chứng tỏ hàm số đồng biến . Để
f x f y
chỉ xảy ra
x y
(*)
Thay vào phương trình (2) :
2
2 2 2 2
6 2 1 4 6 1 2 6 1
2 4
x
x x x x x x x x
2
2
2 6 1 3
2 6 1 2
x x x
x x x
Trường hợp :
2
2 2 2
0 0
2 6 1 3 1; 1
2 6 1 9 7 6 1 0
x x
x x x x y
x x x x x
Trường hợp :
2
2 2 2
0 0
2 6 1 2
2 6 1 4 2 6 1 0
x x
x x x
x x x x x
3 11 3 11
;
2 2
x y
. Vậy hệ có hai nghiệm : (x; y) = (1;-1),(
3 11 3 11
;
2 2
)
Bài 100 Giải hệ phương trình:
3
2 3 2
8 3 2 1 4 0 1
4 8 2 2 3 0 2
x x y y
x x y y y
Giải
Điều kiện :
1
2
x
.
Ta có PT (1)
3
8 3 2 1 4 *
x x y y
Đặt
2 2 2 3
2 1 2 1 8 3 2 1 4 1 3 4 1 4
t x x t x x t t t t t t
Do đó (*) :
3 3
4 4
t t y y
Xét hàm số : f(u) =
3 2
4 ' 12 1 0
u u f u u u R
. Chứng tỏ hàm số đồng biến . Do đó
phương trình có nghiệm khi : f(t) = f(y)
2
2 1 2 1(**)
x y x y
Thay vào (2) :
2
2 2 3 2 4 3 2
1 4 1 2 2 3 0 2 2 0
y y y y y y y y y
3 2 2
2 2 0 1 3 2 0 1 2 1 0
y y y y y y y y y y y y
Vậy :
2 2
0
0 0
1
1
; ;0 , ; 1;1
1
1
2 1 2 1
2
2
y
y y
y
x y x y
x
x y x y
x
2 2
2
1 2
0
5
; 1;0 , ; ; 2
5
1
2 1 2 1
2
2
y
y y
y
x y x y
x
x y x y
x
.
Hết
Đồng Xoài, ngày 05 tháng 8 năm 2014
Chúc quý thầy cô và các em học sinh có một tài liệu bổ ích.

| 1/52
| | Tải xuống

Có thể bạn quan tâm:

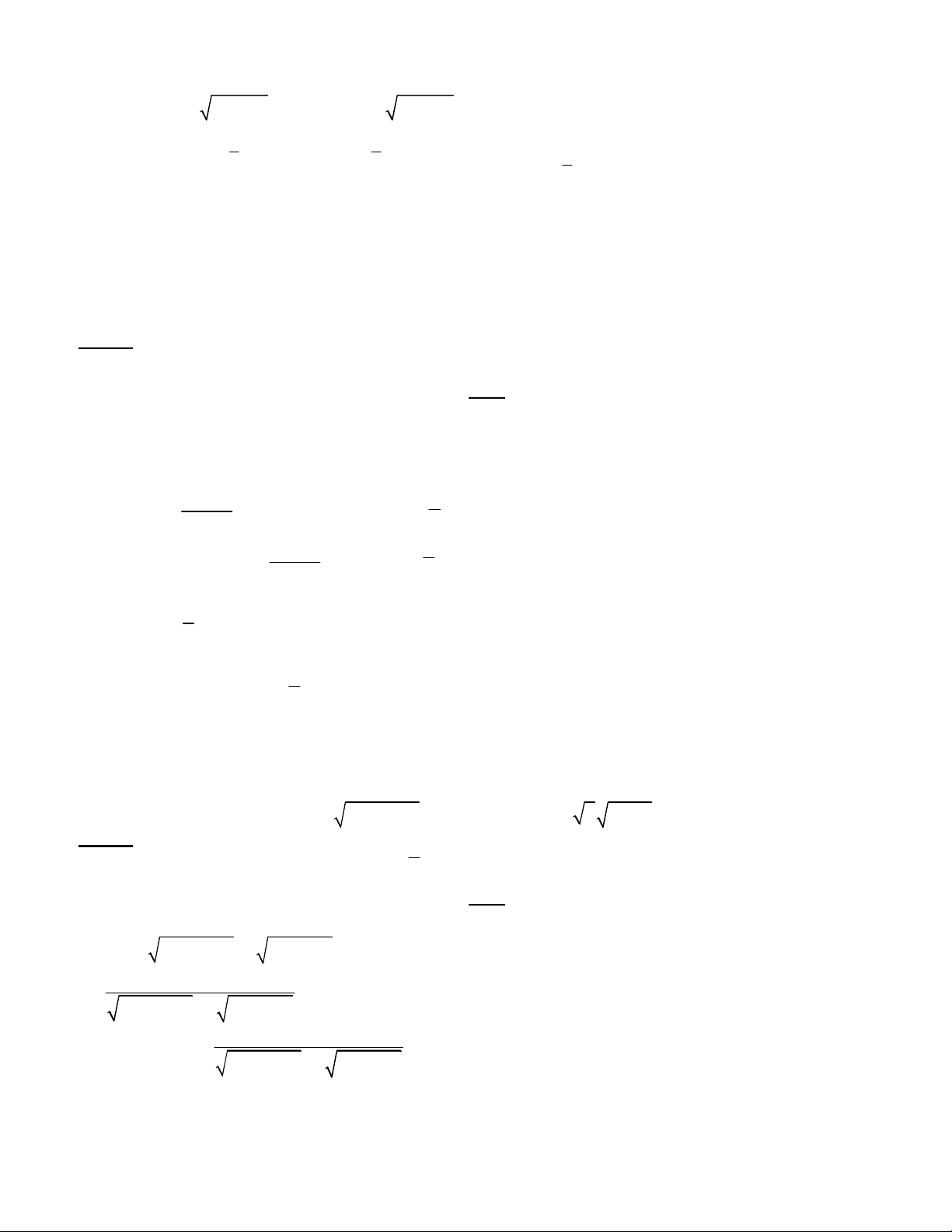
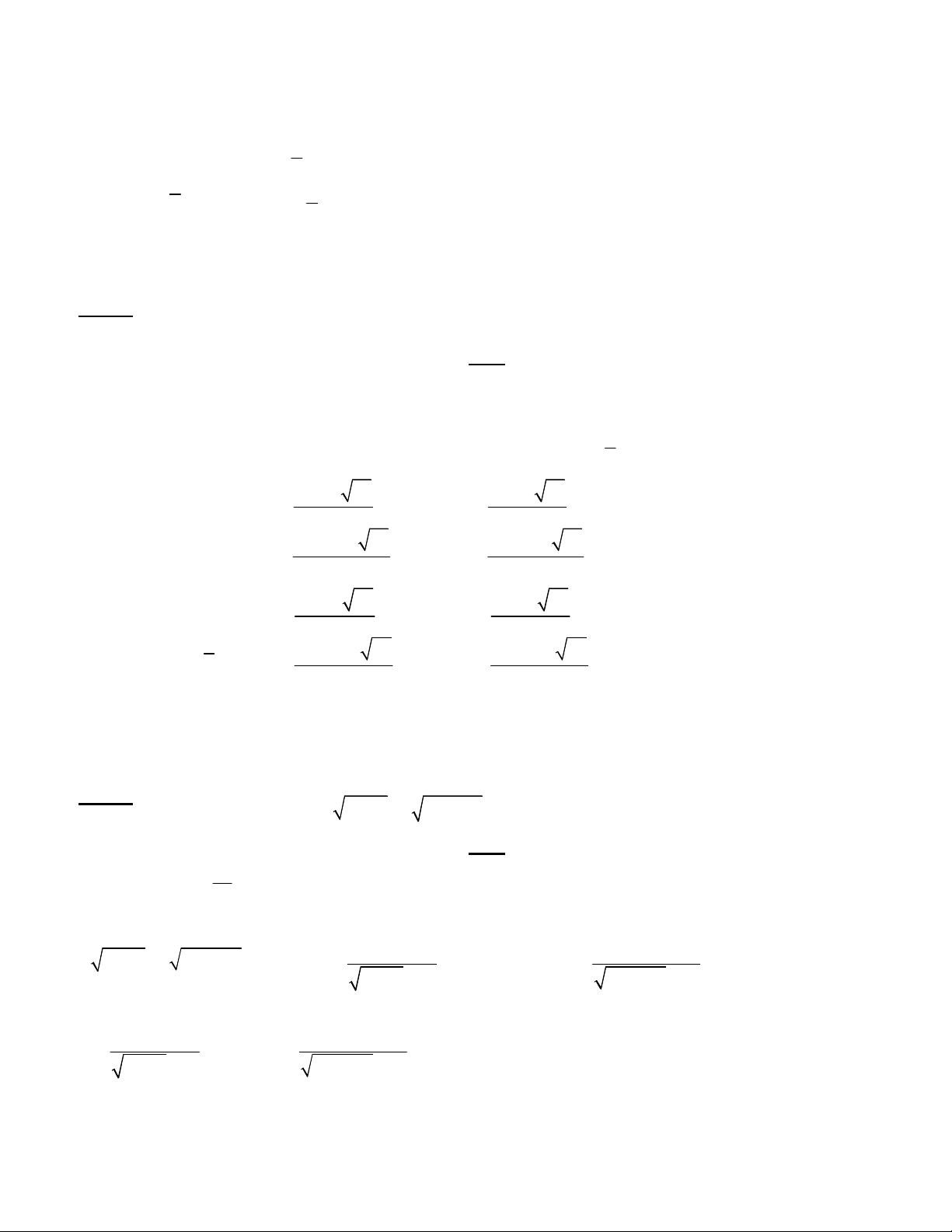
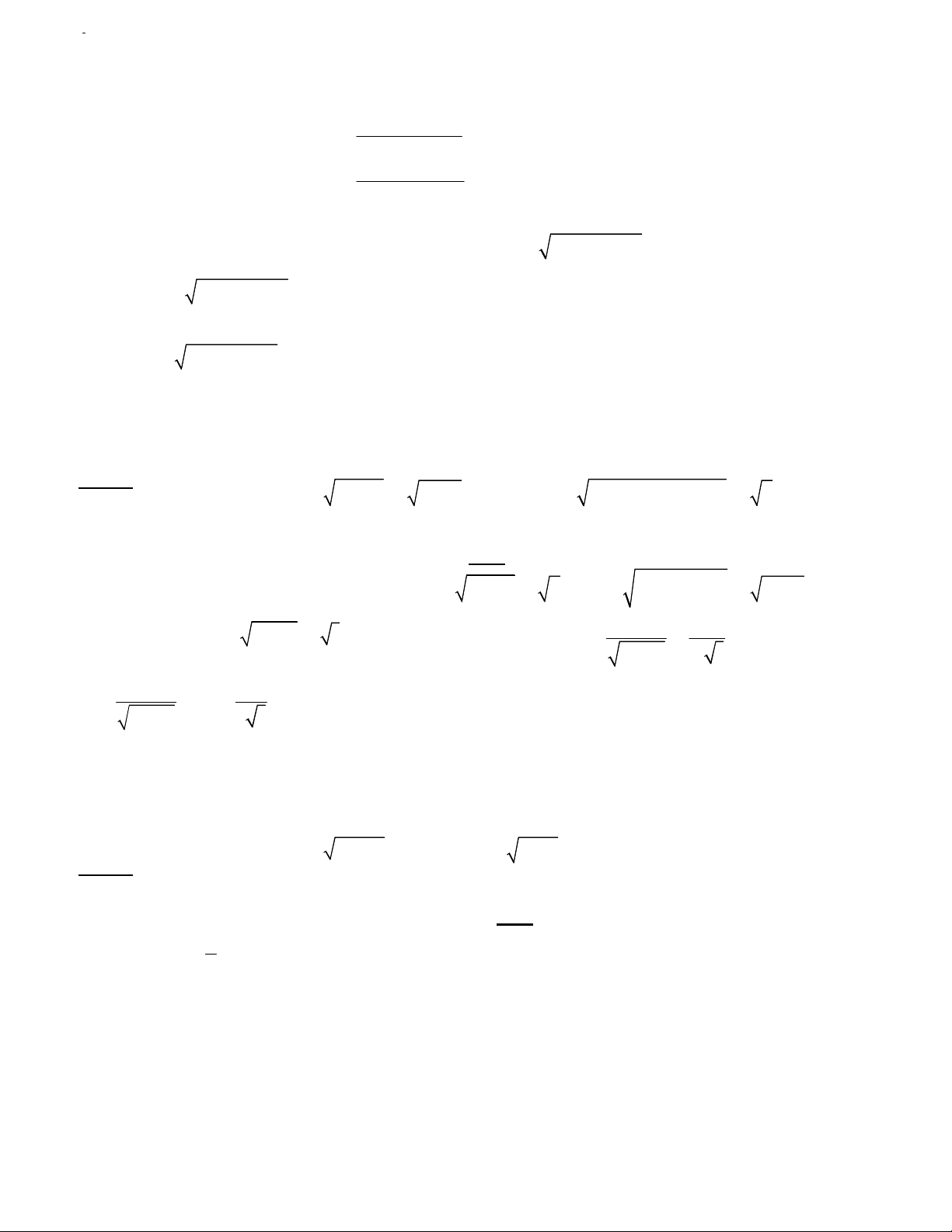
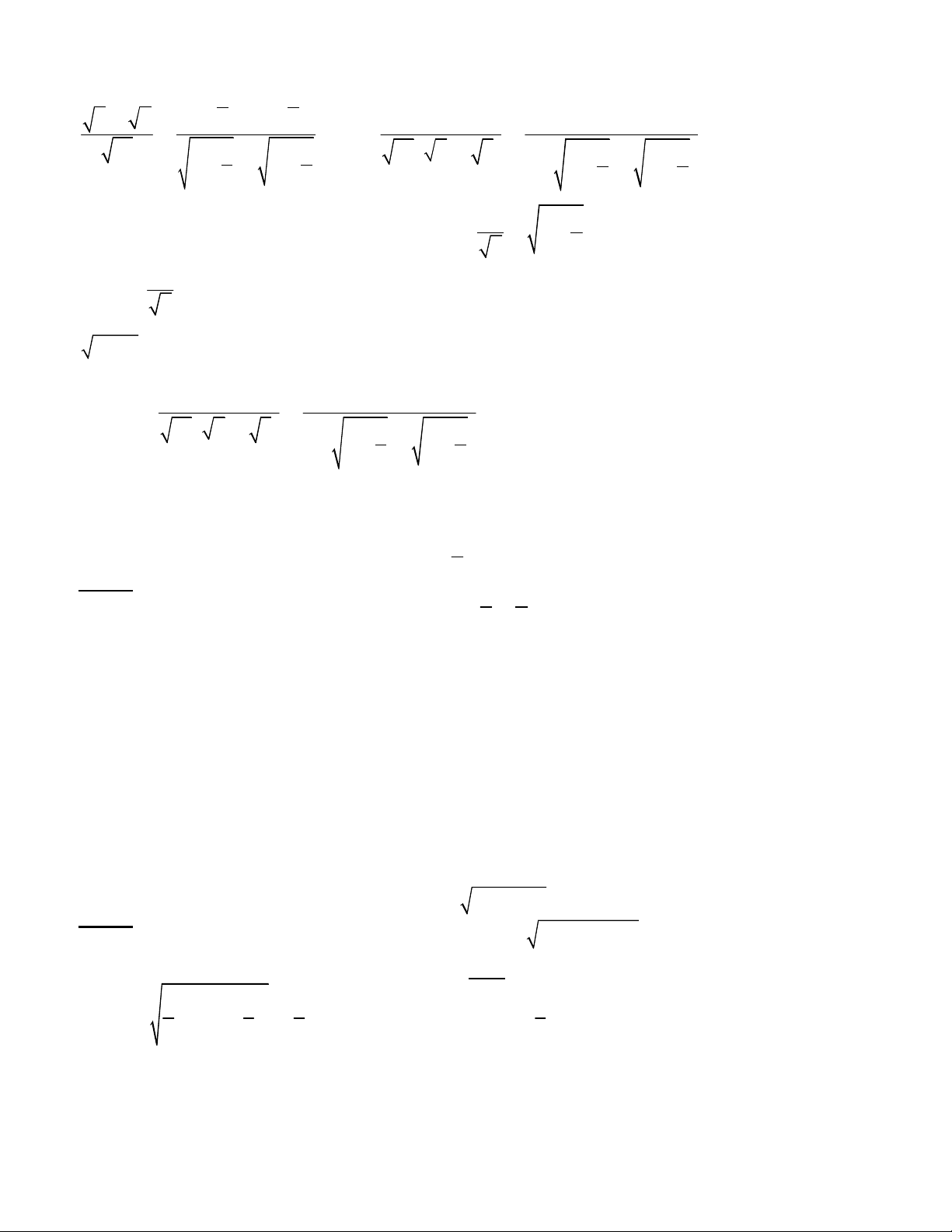
Preview text:

TUYỂN TẬP 100 HỆ PHƯƠNG TRÌNH LTĐH NĂM HỌC 2014-2015 
NHÓM GIÁO VIÊN THỰC HIỆN 1) PHẠM VĂN QUÝ 2) NGUYỄN VIẾT THANH 3) DOÃN TIẾN DŨNG
ĐƠN VỊ CÔNG TÁC: TRƯỜNG THPT HÙNG VƯƠNG, TX ĐỒNG XOÀI, TỈNH BÌNH PHƯỚC  2 x
12  y y(12  x )  12 (1) 
Bài 1 Giải hệ phương trình: 
(x, y  R) (ĐH khối A – 2014) 3 x
  8x 1  2 y  2 (2)  Giải 2   y  12     2  y  12  Điều kiện :    2 12   x  0    2 3  x  2 3  Cách 1: Đặt 2
a  12  y,a  0  y  12  a PT (1) 2 2
xa  (12 a )(12  x )  12  2 2 2 2 2
12  12x  12a x a  12  xa x  a  12    2 2 2 2 2 2 2 2 12 
 12x  12a x a  12  2.12.xa x a  x  a  12    2 2 12
x  2.12xa  12a  0  x  a  12    2 (
x a)  0 
Ta có (x – a)2 = 0  x = 12  y (*)
Thế (*) vào (2) được : (12  y) 12  y  8 12  y  1  2 y  2
 (4  y) 12  y  2 y  2  1
 (3  y) 12  y  12  y  3  2  2 y  2  0 3  y 2(3  y)
 (3  y) 12  y    0 12  y  3 1  y  2 y   3     1 2 12 y     0(vo nghiem)  12  y  3 1  y  2  x   3  Vậy  y   3  Cách 2: Ta có 2 xy   x y   2 2 12 (12 )
x  12  x 12  y y  12 x 12  y Dấu “=” xảy ra   2
x y  (12  y)(12  x ) (3) 2 12  y y
Khi đó (1) tương đương với (3) x   0 x   0 x   0    (3)       2 2 2 2 2 x
y  144  12x 12y x y 12
y  144 12x y   12  x (4)    Thế (4) vào (2) ta có 3 2 3 2
(2)  x  8x  1  2 10  x x  8x  1  2 10  x  0 3
x x    2 8 3
2 1  10  x   0     x
x  3x  3x   2 1 (10 ) 2 1  2.  0 2 1  10  x    x
x  3x  3x   2 9 2 1  2.  0 2 1  10  x    x x 3 2( 3) 2 x  3x 1        0   2  1  10  x  x  3    2(x  3) 2  x x 3  1   0 (vo nghiem vì x   0) 2  1  10  x
x  3  y  3 x   3  Vậy  y   3  Cách 3:   Đặt a   2
x; 12  x ;b   12 y; y   a b  12 2 2  
(1)  a b  2a.b  
a b x  12  y (2) 3 2
x  8x  3  2 10  x  2 3  x 3  x  x   3  2 x  3x      1  2 2 10  x  1
x y  3
 2x x   2 3 1 10  x  
1  23  x  0
Đặt f x   2
x x   2 3 1 10  x   1  23  x
f 'x  0 x  0  phương trình vô nghiệm.
Vậy nghiệm của hpt trên: (3;3) (
 1y) x y x  2 (x y 1) y
Bài 2 Giải hệ phương trình:  (ĐH khối B – 2014) 2 2
 y  3x  6y  1  2 x  2y  4x  5y  3  Giải y   0  Điều kiện: x   2y
4x  5y  3 
Phương trình thứ nhất viết lại thành
(1  y) x y  (1  y)  (x y  1)  (x y  1) y (1  y)(x y 1) y  1 y   1 (x y 1)     
 x y 1 x y  1 y  1 
TH1 : y  1 thay xuống (2) ta có
9  3x  2 x  2  4x  8  x   3 (TM )
TH2 : x y  1 thay xuống (2) ta có 2
2y  3y  2  2 1  y  1  y 2
 2y  3y  2  1  y  0 2
 2(y y  1)  (y  1  y )  0  1  2
 (y y  1) 2       0   
y  1  y  5  1 5  1  y   x  (TM) 2 2 5  1 5  1
Vậy hệ đã cho có nghiệm : (x;y)  (3;1),( ; ) . 2 2  2 2 y
 (x  2x  2)  x(y  6) 
Bài 3 Giải hệ phương trình:  2 2 (
y 1)(x  2x  7)  (x  1)(y  1)  Giải
ĐK: x,y R a   x  1  2 2   2 2 
b(a  1)  (a  1)(b  6) (
a 1)(b  6)  b(a  1) (*)   Đặt 
, ta có hệ trở thành:    b   y 2 2 2 2         (b 1)(a 6) a(b 1)
(b  1)(a  6)  a(b  1)(**)    
Trừ vế theo vế hai phương trình rồi thu gọn ta có: a   b (a b)(a b 2ab 7) 0        a
 b  2ab  7  0 
 Trường hợp 1: a b thay vào phương trình (*) ta có: a   2 2 2 2 (a 1)(a 6) a(a 1) a 5a 6 0           a   3  x  1    
hệ có 2 nghiệm (x; y) là: x  2 
 Trường hợp 2: a b  2ab  7  0 2 2  5  5     1
Trừ vế theo vế hai phương trình (*) và (**) rồi rút gọn ta có: a     b       2    2 2 a
 b  2ab  7  0 
Vậy ta có hệ phương trình: 2 2   5     5   1  a     b       2     2 2  a   2 a   3 a   2 a   3    
Đây là hệ đối xứng loại I, giải hệ ta có các nghiệm:  ; ; ; b   2 b   3 b   3 b   2    
Từ đó ta có các nghiệm (x; y) là: (1;2),(2; 3),(1; 3),(2;2).
Kết luận: Hệ phương trình có 4 nghiệm là: (1;2),(2; 3),(1; 3),(2;2).  3 3 2 x
 12x y  6y  16  0 
Bài 4 Giải hệ phương trình:  2 2 2 4
 x  2 4 x  5 4y y  6  0  Giải ĐK: x  2;2,y 0;4        Ta có 3 3 2
PT(1)  (x  2)  6(x  2)  y  6y Xét hàm số 3 f (t) t 6t,t 0;4        ta có 2
f '(t)  3t  12t  3t(t  4)  0, t  0; 4  f (t)   nghịch biến trên 0; 4 
 . Mà phương trình (1) có dạng: f (x  2)  f (y)  y x  2 thay vào phương trình (2) ta có: 2 2
4x  6  3 4  x x  0 từ đó ta có y = 2.
Kết luận: Hệ phương trình có nghiệm (0; 2). x
 2 y 1  3 
Bài 5 Giải hệ phương trình:  . 3 2 x
  4x y  1  9x  8y  52  4xy  Giải §K: y  1  . x
  3  2 y 1 HPT    3 2 x
  4x y 1  4xy  4x 13x  8y  52  0  x
  3  2 y 1    2 x
 (x  2 y  1) 13x  8y  52  0  x
  3  2 y 1    x   2y  13  0  x
  3  2 y 1 
  y 1  5y  x
  3  2 y 1 y    5  2 y
  11y  24  0   x   3  2 y  1  x   7 y     5     y   3  y  3   y  8   x   7 
Kết luận: Hệ phương trình có nghiệm:  . y   3 
y 2x y x   1  0 
Bài 6 Giải hệ phương trình:  xy   2 2
 1  xy x y  0 
ĐK: x  0;y  0;xy  1
 1  y 2x y x xy  0   y x  y 2 x  1  0  y x y x thay vào   2 , ta được: 2
1  x  0  x  1  y  1
KL: hệ pt có tập nghiệm: S    1; 1   3 3 x y   2 2 2 3 x y   
 5x y  8 xy
Bài 7 Giải hệ phương trình: xyxy   5x y
 5x 1  2 y   2 1
ĐK: x  ; 0  y  2 5
Đặt u x  ,
y u  0;v xy,v  0 khi đó  2    u     u     u  u 3 2 2 3
1  2u  3u v uv  2v  0    2 2       1  0 
 2  u  2v  v    v  v  v    x y
xy   x y 2 2
 0  x y thay vào   2 , ta được: 5x 5 1 x     x   x x  
x   x   5 1 5 1 2 3 3 3 1    3  0   5x 1  2 2 x 1  5x 1 2 2 x 1 
x  1  y  1    5 1 1    3  0 VN vì  x  2       5 5x 1 2 2 x 1
KL: tập nghiệm của hệ pt là: S    1; 1  2    1  1 x y x x   x 2 3   2x  1 1     3y  1   2      2    
Bài 8 Giải hệ phương trình: yy y x y  3 2 x x  1 4    1  0  2  y y  ĐK: y  0        x y   
 x y x y1  0 x y  
1 x y  2 3 2  1  0  y x  1 x   1   Hệ           3 2 2   3 2 2 x
  x  1  4y y  0 x
  x  1  4y y  0 x   1 y   2       KL: S    1;2  2 2
 4x  3xy  7y  4   2 2
x  5xy  6y  2 2
 3x  2xy y
Bài 9 Giải hệ phương trình:  2 2 3
 x  10xy  34y  47   2 2
3x  2xy y  0  ĐK:  2 2
4x  3xy  7y  0 
Chuyển vế nhân liên hợp ở phương trình   1 , ta được:      1  x y n 2 2
x  5xy  6y        4  0     2 2 2 2          x  6 4 3 7 3 2 yn x xy y x xy y  
x  1  y  1
Với x y thay vào   2 , ta được: 2 x 1    
x  1  y  1   47 47 y    x  6  Với x  6  y thay vào   2 , ta được: 2 82 82 82y  47   47 47 y     x  6  82 82                  KL: S     47 47 47 47 1;1 , 1; 1 , ;6  ; ;6         82 82     82 82        2 x   3xy  3 
x y  0 
Bài 10 Giải hệ phương trình:  4 x   9y   2x y 2  5x  0   2 x
 3y  3x  3xy  Hệ     x  3y2 2 2 2
 3x y  5x  0  
x  0  y  0   1 Thay   1 vào   2 , ta được: 2 x  2
9y  15y  4  0  y   x  1  3   4 2 y
x x  4  0 VN   3        KL: S     1 0;0 ; 1  ;      3    x  2  2  4y  2 1  4xy  13 
Bài 11 Giải hệ phương trình: 2 2
x xy  2y 2    x y   2 2  x y x y  x   y  0  ĐK: x   y  0  x  2y  0   2 2 x
  4xy  4y  4x  8y  5  0  Hệ   x y
x 2y x yx y  2   2 x  2y  1  Ta có PT  
1  x  2y  4x  2y  5  0  
x  2y  5  l 
Với x  2y  1 thay vào   2 , ta được:  y   3 2 3
1 y  1  1  3y  9y  6y  13y  0  y  0  x  1 thỏa mãn KL: S    1;0  2  x   2 2 5
x  2y x  3  2y  2 x  2y   1
Bài 12 Giải hệ phương trình:  2 x   3y  6  ĐK: x  2y Ta có   2
2  x  6  3y thay vào  
1 ta được: 1  5y 6  5y  5y  9  y  1  x   3 thỏa mãn KL: S    3; 1; 3; 1    2 x y y 1  2  2 
Bài 13 Giải hệ phương trình:
x  1  y  1   2    x  4y   2 2
x  1  6  5 x  1 1   
 2x  1y  1    x
  1  x  1  ĐK: y   1   2
 x 1  y 1  0   2 a
  x  1,a  0  2 b
 a b  2 Đặt:   , ta được:  b  3 2 2
  y  1,b  0 a
  4ab  5a b  6  
Nhân chéo hai phương trình giải hệ đẳng cấp ta đươc tập nghiệm: S  
 10;2; 10; 2  3 2
20y  3y  3xy x y  0 
Bài 14 Giải hệ phương trình:  2 2 x
y  3y  1   3 20y y
3y  1 x 3y  1  0 Hệ   . 2 2 x
y  3y  1  Thế   2 vào  
1 , ta được phương trình thuần nhất bậc 3   3 1    3 1     KL: S   ; ; ;      2 2     5 5      2 2 x
  3y x  3y  0 
Bài 15 Giải hệ phương trình:  2 2
 2y 1  2x y  3x  1  0  1 ĐK: y  2 3  y x 3y x      Ta có PT   2 2
1  x  3y  3y x     y   0 l 2    6
y  6xy  0      x y  
Với x y thay vào   2 , ta được: y   1  x  1   2 4 3 2 2y  1  y
  3y  1  y  6y  11y  8y  2  0  y   2  2 l
y  2 2  x  2 2  KL: S  
 1; 1;2 2;2 2  3 4 4 x y  2 2 2 2  2x y x y    
Bài 16 Giải hệ phương trình: 2 2 y x  x y 2 2 2  2 2 x
y  3y  4x  8  ĐK: x.y  0    4 2 2 4  
2 x x y y x y   Ta có PT   1   2 2 x y  2 2 
  0  x y       2   2 2 2 2  x y x y x y       
 Với x y thay vào  
2 , ta được: x  1  y  1
 Với x y  thay vào  
2 , ta được: y  1   x  1 KL: S    1; 1;1; 1  2 2 10
x  5y  2xy  38x  6y  41  0 
Bài 17 Giải hệ phương trình:  3 3 2
 x xy  6y y x 1  2   3 x
xy  6y  0  ĐK:  3 2 y   x  1  0  Ta có PT   2 
x x y   2 1 10 2
19  5y  6y  41  0 . 2
Tính Δ '  49y  
1  0  y  1 thay vào  
1 được x  2 thỏa hệ phương trình x KL: S    2; 1  3 3 2 2 x
y x y xy  2xy x y  0 
Bài 18 Giải hệ phương trình:  3 2
x y x  2x y  2  ĐK: x y y   x 1 Ta có PT   1 x y 1 2 2 x y x y 0           2 2
x y x y  0 
x  0  y  1
y x  1 thay vào   2 , ta được: 3 2 x 2x x 0      
x  1  y  0   2 2
x y x y  0  x y  0 vì x y  0 thay vào hệ không thỏa KL: S   1;0;0; 1  2 2 y   8x  3    3 2 1  3 y  1 3 2 y  1 
Bài 19 Giải hệ phương trình:   3 4  3  y  2 2 3 2 2 2 2
1  2 y  1  12x y  1  4x  1 1 ĐK:  x  2 2  3 2 a   y  1  3 2 2 a
 3a  2a  3b b  0  Đặt:   2 
a b b  , ta có: thay vào   1 , ta được: 2 b 3 2 2
  1  4x ,b  0 a
 3a a  2b  0  
b b3  b b2 2 2   2 b b 2 3 2
 3b b  0  b  0  a  0 .    2  1  1  4x  0 x       Khi đó ta có:    2  3 2  y 1 0 y      1     1  1   1   1           KL: S    ;1; ; 1  ;   ;1;   ; 1                 2 2   2     2      6 3
3x  24y   2
2y x  2
9x  18y   11  0 
Bài 20 Giải hệ phương trình:  3 3 1
  2 2y  1  x x  6y  1  ĐK: y  0 Ta có PT     2 x y 4 2 2 2 1 2
3x  6x y  9x  12y  18y   1  0 Với 2
x  2y thay vào   2 , ta được:    1 2  3 3
1  2x  1  x  4x  1  x   1       0   2 3 3 3 3 2  x  1
(4x  1)  4x  1 2x  1  (2x  1)    1
x  1  y  2   1     KL: S  1   ;     2      2   x y x y  2   xy    xy
Bài 21 Giải hệ phương trình: x y xy  1 1  
x y  4  y x 
ĐK: x  0;y  0
Ta có PT     y x xy2 2 2 1
 0  x y xy x y x y  2 xy thay vào   2 ta được:
xy  1xy xy xy xy 4 0  xy 1  3  5    3 x x y      Khi đó ta có: 2    xy  1    3  5 y    2    3 5 3 5      
KL: thay vào hệ ta có tập nghiệm: S    ;      2 2         x  1 4 4 x   2    x  1  0  y  1 y  1
Bài 22 Giải hệ phương trình: y  1     y   x   y 1 1
1 x  1  2 y  1   2  2
ĐK: x  1;y  1 a
  x 1,a  0 b   2  Đặt:  
. Ta có    b  2 2 2 2 1
2  a b  2ab ab  0   b
  y 1,b  0 a   0    x 1  0 x   1        thỏa hệ phương trình  y  1  2 y   5    KL: S    1;5
 x  3 y   1
4y  2x y
Bài 23 Giải hệ phương trình:  1 1 1     3     2 3x 4y 8 y 1  y   1  ĐK: 2
x y  0 
3x  4y  8     
Ta có    x y 2 1 4 1    
  0  x  4y   thay vào   2 , ta được: 
3 y  2x y  1 1 1 1 1  1  2 2 
   a a    a   1  2 2a a   1  0  a  1 a        3 6 2 y  1 y  1 2 2 2  y  1 1 
 1  y  2  x  8 6 y  1 KL: S    8;2
 x 112yy  2  0 
Bài 24 Giải hệ phương trình sau:   y
 y x   (x,y ). 1  x  4  0  Giải
Điều kiện: x  1.
Đặt t x  1, t  0. Khi đó 2
x t  1 và hệ trở thành t
 (1 2y) y  2  0 t
  y  2ty  2  0 (
 t y) 2ty  2  0         2 2 2 2 y
 (y t)  t  3  0 y
  ty t  3  0 (
t y)  3ty  3  0    ty 0 y     t   Suy ra 2
2(t y)  3(t y)  0   3   3 ty y      t  .  2    2
 Với y t, ta có 2
2t  2  0  t  1. Suy ra x  2, y  1. 3 3  3   3  13
 Với y t  , ta có 2   2t t
    2  0  4t  6t  1  0  t  . 2 2  2 4 19  3 13 3  13 Suy ra x  , y  . 8 4
Vậy nghiệm (x; y) của hệ là  2 2 
(x  2) x  4x  7  y y  3  x y  2  0 
Bài 25 Giải hệ phương trình sau:  2
x y  1  x y  1  Giải Điều kiện: 2
x y  1  0 Phương trình (1) 2 2
 (x  2) (x  2)  3  x  2  y  ( y  )  3  y 2 t Xét hàm số 2
f (t)  t t  3  t Có 2
f '(t)  t  3   1  0 t 2 t  3
 Hàm số f(t) đồng biến trên R Phương trình (1)  x  2  y  Thay vào (2) ta có  3  3  x      x   2 x x 1 2x 3  2         2  2 2  2 2 x
  x  1  4x  12x  9 x
  x  1  4x  12x  9      3 :    x    3    2  x       2 
  x  1  x  1  y  1 (tmdk)   2 
3x  13x  10  0    10  x     3
Vậy hệ có nghiệm (x;y) = (-1;-1). 53  5x
 10 x 5y  48 9 y  0  1
Bài 26 Giải hệ phương trình sau: 
x,y   2
 2x y  6  x  2x y  11  2x  66 2  Giải 10   x  0 x   10     9  y 0 y      9   ĐK:    2
x y  6  0 2
x y  6  0      2x y 11 0      
 2x y  11  0   Từ PT(1) ta có 5  10 x  3 10 x 5    9 y 3       9  y,   3  x
Xét hàm số f t   2 5t  
3 t trên khoảng t   0;   / 2 
có f t  15t  3  0, t  0 hàm số đồng
biến .Từ (3) ta có f  10  x   f  9  y   10  x  9  y y x 1,4 Thay (4) vào (2) ta được 2
x  7  10  x x  2x  66  0 (5) ĐK: x  7;10     Giải (5) ta được  x x
x  7  4 1 10  x  9 9 2
x  2x  63  0  
 x  9x  7  0 x  7  4 1  10  xx   1 1 9 [ 
 x  7]  0  x  9,y  8 x  7  4 1  10  x
Vậy Hệ phương trình có nghiệm duy nhất x;y  9;8  x 1  y  
x y  1 
Bài 27 Giải hệ phương trình sau: 1  1  x 1  y
 1x  4  y  2 2  Giải
ĐK: 0  x;y  1 x 1  y PT(1)   x   1  y (*) 1  1  x 1  1  (1  y) 1 1 (1  1  t )  . t t 2 t 2 1  t
xét h/s f (t)   t ; có ' f (t) 
 1  0 ,t  (1; )  1  1  t 2 (1  1  t )
vì (*)  f (x)  f (1  y)  x  1  y , thế vào pt(2) ta được : 2
1  x  5  x  2 2  6  2x  2 5  6x x  8 1 1 2 2 2
 5  6x x x  1  5  6x x  (x  1)  x   y  (tmđk) 2 2  1 x   
vậy hệ pt có nghiệm là 2  1 y    2  3 3 3 27
x y  7y  8 
Bài 28 Giải hệ phương trình sau:  2 2 9  x y y  6x  Giải
Nhận xét y  0, nhân hai vế phương trình thứ hai với 7y, trừ đi phương trình thứ nhất, được 3 2
(3xy)  7(3xy)  14(3xy)  8  0
Từ đó tìm được hoặc 3 xy  1 hoặc 3xy  2 hoặc 3 xy  4 1
Với 3xy  1, thay vào phương trình thứ nhất, được y=1 do đó 3
Với 3xy  2, thay vào phương trình thứ nhất, được y=0 (loại) 2
Với 3xy  4, thay vào phương trình thứ nhất, được y=-2 do đó x   3  3 3 x
y  4x  2y
Bài 29 Giải hệ phương trình sau:  2 2 x   3y  4  Giải Phương trình 3 3
(1)  2(x  y )  4(2 x y) Từ phương trình (2) thay 2 2
4  x  3y vào phương trình trên và rút gọn ta được: y   0  2 2 3 x y 6xy 5y 0 x       y   x    5y   3 x   4x
TH1 : y  0 thay vào hệ ta được 
x  2  nghiệm (x; y)  ( 2  ; 0) 2 x   4   3 2  x  2x  TH2 : x y   y x
 thay vào hệ ta được :   x  1 2 4x  4 
Hệ có nghiệm (x; y)  (1;1); (1;1) 5 1 5 1 TH3 : x  5
y thay vào hệ ta có nghiệm (x; y)  ( ; ); ( ; ) 7 7 7 7
Vậy hệ đã cho có 6 nghiệm. y  
2 . x  2  x. y  0 
Bài 30 Giải hệ phương trình sau:    x  1. 
y  1 y 3.   (x; y R). 2
1  x y  3x   Giải x   1;y  0  ĐK: 2 x
y  3x  0 
PT (1)  x  2.y x. y  2 x  2  0  2x  4  y   2 x  2
có   x  x    x  2 2 8 2 4   y  2  y   0  loai   4 x  2 2x  4 với y
y x  2  y x  2 , thế vào (1) ta được 2 x  2  
x   x     x   2 1 2 1
1 1  x  2x  2 x xx          x  2 1.( 2 1) 1 . 1  1    (*)   2 t
Xét hàm số f t t  2 t    2 ( ) 1
1  t t  1  t , có ' 2
f (t)  t  1 
 1  0  f (t) đồng 2 t  1 biến. x   1 
Vì PT (*)  f ( x  1)  f (x  1)  x  1  x  1    x  3 x
  1  x  2 1 
Với x = 3  y  5 (thỏa mãn). Vậy hệ có nghiệm (x; y) = (3; 5).  2 2 x
y  1  2x  2y
Bài 31 Giải hệ phương trình sau:  2x y  y  1 2y  Giải
Lấy (1) + (2) vế theo vế ta được: x  2 2 x 2xy 1 1 2x 4y
x x 2y 2x 2y
x 2x 2y 0                 x  2y  0 
Trường hợp x=2 thay vào (2) ta có y = 1
Trường hợp x+2y = 0 thay vào (2) ta được phương trình vô nghiệm.
Vậy hệ có nghiệm x = 2; y = 1.  xy  y   2
1  y  1  4y 
Bài 32 Giải hệ phương trình sau:  1 2 xy  x  2 2   y  5 2  y  Giải Điều kiện y  0    x y  1 y y       x   1 1 4 1   x  4   ( )  yy I       y
 x  2x   1 1   5
 y x  2 1 2 2 2 1   5 2 2  yy  
Đặt u y x   1
1  ;v x  1 ta có hệ y u   v  5 v   5  u u   5 u   3            2 2 u   2v  5 u   2u  15  0 v   10 v   2          y  x  1 y       x   1 1 5 1   3 hay y   y   x   1  10 x   1  2       2   2
x  1  y  1
10y  5y  1  0 2
y  3y  1  0          1 x   9 x   1   
x  1  y    2
Vậy hệ có các nghiệm (1;1) và (1; 1/2 ).  3 2y    1 2 2
x y 1 x
Bài 33 Giải hệ phương trình sau:  4x 2 2 x   y   22  y  Giải
Điều kiện: x  0, y  0. và x2 + y2 - 1  0. 3 2 x   2    1  2
v 13v  21  0 
Đặt u = x2 + y2 - 1 và v =
Hệ phương trình (I) trở thành u v   y u   21 4v u   21  4v         2 u   9 u   7  u   9 x   3 x   3 u   7  x   14            hoặc  + Với    hoặc  Với    53  v   3 7 7             v   v 3 y 1 y 1 v    2      2     2 y   4  53  2 x   14  hoặc 53   2 y   4  53  2 2   2 2 
Vậy hệ có nghiệm (3;1), (-3;-1), 14  ;4    14 ;4     và .  53 53       53 53     3
 x 1  y  1 x
Bài 34 Giải hệ phương trình :  (I) .  x  4 1  y  x  1  0 x   1   Điều kiện:    y   0 y   0      x 1   x  2 3 1  1  x Ta có (I)   x  4 1  y 
Từ phương trình : x   x  2 3 1 1  1  x 3 2
x  1  x
  x  2x  2 (1)
Ta thấy hàm số f (x)  x  1 là hàm đồng biến trên 1  ;    Xét hàm số 3 2
g(x)  x
  x  2x  2 . Miền xác định: D 1   ;    Đạo hàm / 2
g (x)  3x  2x  2  0 x D . Suy ra hàm số nghich biến trên D.
Từ (1) ta thấy x  1 là nghiệm của phương trình và đó là nghiệm duy nhất.
Vậy hệ có nghiệm 1;  0 .  2
 3  x  2 x  3  y   x   0 
Bài 35 Giải hệ phương trình : (II). Điều kiện:  2
 3  y  2 y  3  x y   0    2
 3  x  2 x  3  y Ta có (II)    2 3
  x  3  y  2 y  Cộng vế theo vế ta có: 2 2
3  x  3 x  3  3  y  3 y  3 (2) Xét hàm số 2
f (t)  3  t  3 t  3 . Miền xác định: D 1   ;    t 3 Đạo hàm: / f (t)  
 1  0 x D . Suy ra hàm số đồng biến trên D. 2 3  t 2 t
Từ (*) ta có f (x)  f (y)  x y Lúc đó: 2
3  x x  3 (3)
+ VT (3) là hàm số hàm đồng biến trên D.
+ VP (3) là hàm hằng trên D.
Ta thấy x  1 là nghiệm của phương trình (3) (thỏa điều kiện)
Suy ra phương trình có nghiệm x  1 là nghiệm duy nhất.
Vậy hệ có nghiệm 1;  1  3 2
y  2.x 1  x  3 1  x y (1) 
Bài 36 Giải hệ phương trình :  2 y
  1  2x  2xy 1  x (2)  ĐK : 1  x  1 Từ (1) ta có : 3
2.y  2(x  1) 1  x  2 1  x  3 1  x y (thêm vào vế trái 2 1  x ) 3 3
 2y y  2( 1  x )  1  x
Xét hàm số f(t) = 2.t 3 +t có f’(t ) = 6t2 + 1 >0 suy ra hàm số đồng biến
Suy ra y = 1  x thế vào (2), ta có 2 2
1  x  1  2x  2x 1  x (3)
Vì 1  x  1 nên đặt x = cos(t) với t  [0; ] sau đó thế vào phương trình (3) là ra kết quả.  1 2 2 x   y  (1) 
Bài 37 Giải hệ phương trình: 5  57 2 4
 x  3x   y  (3x  1) (2)  25 Giải
ĐK: x,y R
Nhân 2 vế phương trình (1) với 25 và nhân 2 vế phương trình (2) với 50 ta có:  2 2 25
x  25y  5  Hệ phương trình   2 200 
x  150x  114  50y(3x  1) 
Cộng vế theo vế hai phương trình của hệ ta có: 2 2
225x  25y  25  150xy  150x  50y  144         x y 2 15x 5y 5 12 15x 5y 7 15 5 5 144         15  x 5y 5 12 15     
x  5y  17   15
 x  5y  7 
 Với 15x  5y  7 kết hợp với (1) ta có hệ phương trình:  1 2 2 x   y   5  11 x          25 5y 7 15x      2            5y 7 15x 5y 7 15x  11  y       x   25         x y   25  
x  7  15x 2 2 2 2   25 25 25 5 5    2   2 x     x    5  5  1  y      5 15
 x  5y  17 
 Với 15x  5y  17 
kết hợp với (1) ta có hệ phương trình:  1 2 2 x   y   5 5
 y  17 15x 5
 y  17  15x   5
 y  7 15x           hệ vô nghiệm. 25
x  25y  5  25    x    17   15x2 2 2 2  5 x       2  11 x  x      
Kết luận: Hệ phương trình có hai nghiệm là: 5 25  ;   . 1  2 y  y      5  25
 x y  3x  2y  1 (1) 
Bài 38 Giải hệ phương trình:  x y x y  0 (2)  Giải x   y  0  Điều kiện :  3
x  2y  0 
Hệ Phương trình tương đương  x y 1 3x 2y x     
  y  2 x y  1  3x  2y       x y y x    
x y y x   2
 x y  2x y 2  
 y x   2x y      
x y y x
x y y x    y   4x  1 y   4x 1       
x y y x
 5x  1  3x  1     y   4x 1   y   4x  1      1  1 x     x     3   3   2 5
x  1  9x  6x  1  2  9
x  11x  2  0  
y4x1  1 x   1 x         3  y   3    x  1   2   x    9 x   1 
Kết luận : Hệ phương trình có nghiệm  y   3   2 2 2 2 2
 2x y y  2x  3 (1) 
Bài 39 Giải hệ phương trình:  3 3
 x  2y y  2x (2)  Giải ĐK: 2 2 2x y  0 Đặt : 2 2
t  2x y (t  0)    t  1 2 1 t 2t 3 0 
     t  3  2 2
t  1  2x y  1 2 2
 2x y  1  2 2 2
x y  1 
Khi đó hệ phương trình tương đương  3 3 x
 2y y  2x   2 2 2
x y  1   2 2  2
x y  1      3 3 x   2y  3 2 2 3 
y 2x 2 2 2x y  5
x  2x y  2xy y  0 ( 3)   Th 1: y  0 8 8  8 8 
x;y   ; , ;        2 2  x  1 
Hệ phương trình tương đương  ( vô lí ) 3  x  
Vậy cặp ( x , 0) không là nghiệm của hệ
TH2 : Chia hai vế ( 3 ) cho 3
y ta có hệ phương trình tương đương  2 2 2
x y  1   2 2   2x y  1    3 2   x       x     x  x 5
    2   2     1  0   1     y    y    y    y  x y  1    x y  1 
Kết luận : Hệ phương trình có nghiệm S  
 1; 1,1; 1  1 9 2 2 x
  y  6xy    0  x y2 8
Bài 40 Giải hệ phương trình:   1 5 2  y    0  x y 4  Giải
Điều kiện: x y  0
Hệ phương trình biến đổi tương đương
 x y2 x y2 1 9 2    0  x y2 8  x y
x y 1 5    0  x y 4  a
  x y  Đặt  1 b
  x y   x y   9 2 2 2
 a b  2   0  Ta có hệ tương đương 8  5 a  b   0  4  2  25           5 2 2 5 25 2
 a b   2        2 bb a  8          4 8 4     5   5 a  b   5 b      4 a b     4  2 Vậy hệ có nghiệm   7 3 13 3  2 2  x y
x y  1  25y  1
Bài 41 Giải hệ phương trình:  2 2 x
xy  2y x  8y  9  Giải
Hệ phương trình tương đương  2 2
 x y x y   1  25y   1  x
  y x y   1  y  2 2 2 1  10y   1  0 
Nhận xét y  1  0 không là nghiệm hệ phương trình  2 2
x y x y   1   25 
Chia hai vế phương trình một và hai cho y  1 ta có y  1  2 2 x y   
x y  1  10  y  1   2 2  x y a    Đặt  y  1  b
  x y  1  a  .b  25   2 2  a  5 x   y  5   y   1 Khi đó ta có      a   b  10      b 5
x y  1  10      
Vậy hệ có nghiệm x y    3 11 ; 3;1 ,   ;    2 2   2  x x   2 2
y  4y y  1  0
Bài 42 Giải hệ phương trình:  3 3 2 2 3 x
y x y  4y xy  1  0  Giải
Nhận xét y  0 không là nghiệm hệ phương trình
Chia hai vế phương trình một cho 2 y và hai 3 y  1 1 2
 x x 4    0 2  y y  2  x x 1 3 x      4  0 2 3  yy y   1 a   x   y Đặt  x b    y 
Hệ phương trình biến đổi tương đương ta có :
3y  2  y  2
3y  2  y  2  2y  3y  2   2y   1 y   2 2 2y  2
Với x  2y  1thay vào phương trình ( 2 ) ta có x  3
  6y  9  3  y  1 Suy ra phương trình vô nghiệm Với x  6  y  9 x 2y 1      x 6y 9    
x  25  2yx  12y  12y  9  0 2 2
Phương trình (1) tương đương x  3  4 3y x y   1 2 3  2 y  ;x  3  ; 3y x a
  a  2b  4  2     
a  2b  4 a a   2   x   1         3 a   ab   a
 4 a  4 b   1 y   1     
Hệ có nghiệm x;y  1;  1  x 5y    4 2 2
x y x y
Bài 43 Giải hệ phương trình:  2 2  x  5y 5
 x y   5  xy  Giải
Hệ phương trinh tương đương:  x 5y     x 5yx 5y    4    4    4 2 2
x y x y 2 2    2 2     x y x yx y x y     x y 2 2  x y y x 2 2 x y y x 5
 x y   5  5    5    5    1 y x   x y   x 5y   x a   a  b  4 2     x y  a b  4 a   2   Đặt      khi đó ta có   5y 1 1  ab  4 b   2 b     1      2  a  bx y     
Hệ có nghiệm x y 3 3 ;   ;   2 2 x
  3  2 3y xy  1 
Bài 44 Giải hệ phương trình:  x  5  3y  2 
xy  2y  2  2 Giải 2 Điều kiện ta có
Áp dụng bất đẳng thức Cauchy 2 t  1
f '(t)  2t  1  y   2   2 2 7  2   ;2y  1 
 2y  1(vn) Vì 
3y  2  y  2 2 3
 3y  2  y  2 
Vậy hệ có nghiệm ( 3 ;2 )  2
 2y  7y  10  x y  
3  y  1  x  1 
Bài 45 Giải hệ phương trình:  3   y  1   x  2y  x  1 Giải Điều kiện 2
2y  7y  10  x y  
3  0;y  1  0;x  1  0  2
 2y  7y  10  x
y  3  x 1 y 1 Ta có   x  
1 y  1  3  x  2yx   1 
 y y  x
y    x  2 2 2 7 10 3 1  2x  
1 y  1  y  1    x  
1 y  1  x  2yx   1  3 
 y y  x
y    x  2 2 2 7 10 3 1  2x  
1 x  2y  7    x  
1 y  1  x  
1 x  2y  3 
x y 1  0
Phương trình ( *) tương đương 2 2
2y  4y  2  3xy x  3x  0   
x  2y  2  0 
Với y = 1 – x thay vào phương trình ( 2 ) ta được x   2
1 2  x  1  x x ( VN )
Với x = 2 – 2y thay vào phương trình (2) ta được phương trình đơn giản ẩn y.
Từ đó có nghiệm của hệ.  2 2 2
 x x x  2  2y y  2y  1 ( 1 ) 
Bài 46 Giải hệ phương trình:  2 2 x
 2y  2x y  2  0 ( 2 )  Giải Lấy ( 1 ) – ( 2 ) Ta có 2 2
x  3x  2  x  2  4y  2y  2y  1 2 2
(x  1)  (x  1)  x  2  4y  2y  2y  1 Xét hàm số : 2
f (t ) t t t  1 1     16 32   16 32   S   1;2 ,    ; , ;                   t   1 1 3 1 2 1    1   1    2 2 4 t 1 4 t 1
Suy ra f ' t 0
Vậy f t là hàm đồng biến
Suy ra x  1  2y 2
Thay x  2y  1 vào phương trình ( 2 ) ta có  y   2 2
1  2y  22y   1  y  2  0 y   1 x  1  2
 6y  7y  1  0   1 2 y   x   6 3         
Vậy hệ có nghiệm S     2 1 1;2 , ;      3 6    3 x
 2 x 2y 2y 1  0
Bài 47 Giải hệ phương trình:  3
 x  2  2 y  2  5  Giải 1
Điều kiện x  2;y  2
Phương trình ( 1) tương đương : 2  x 2  x  2  x  2y  
1 2y  1  2y  1
f  2  x   f  2y 1. Xét hàm số   3
f t t t ta có f t 2 '
 3t  1  0 sauy ra hàm số f t đơn điệu tăng .
Từ đó suy ra f  2  x   f  2y 1  2  x  2y 1 x  3  2y thay vào phương trình (2)
Ta có 3 5  2y  2 y  2  5 ( * )  3 u   5  2y Đặt   v
  y  2 v  0    u   1;v  2   y  2   u   2v  5    3  65 23  65   233  23 65 (*)    u   ;v   y  3 2 u   2v  9     4 8   32  65  3 23  65  233  23 65 u   ;v     y  4 4  32 Vậy hệ có nghiệm   23 65 185 233 23 65 23 65 185 233 23 65   x      . Nhận xét   3  2 3 4 6 2
x y y  2x x 
Bài 48 Giải hệ phương trình: 
x  2 y  1  x  2 1  Giải y   0 
Với x  0 thay vào hệ phương trình ta có  3 ( mâu thuẫn ) y    4 x  0 ;x  đều không là nghiệm 4 3 yy    y   
Chia hai vế phương trình ( 1) cho 3 x ta có 3
2     2x x f    f   xx x  x 
Xét hàm số f t 3
t  2t có f t 2 '
 3t  2  0 sauy ra hàm số f t đơn điệu tăng . y Từ đó suy ra 2
x x y y  0Thay vào phương trình ( 2) ta có x
x   x   x  2 2 2 1 1 .(*) u   x  Đặt  2 v
  x  1 v    0  (*)  u   2
2 v v  2u 2
v uv  2v  2u  0  v uv  
2  0  v  2  x   3
Vậy hệ có nghiệm S  
  3; 3, 3;3.  2  4x  
1x y 3 52y  0
Bài 49 Giải hệ phương trình:  2 2 4
 x y  2 3  4x  7  Giải  3 x    Điều kiện : 4  5 y    2
Phương trình ( 1 ) biến đổi ta có x x    y
y   x  x    y3 3 3 8 2 6 2 5 2 2 2 5 2  5  2y Xét hàm số   3
f t t t ta có f t 2 '
 3t  1  0 suy ra hàm số f t đơn điệu tăng . 2 5  4x
Từ đó suy ra  f 2x   f  5  2y   2x  5  2y y  x  0 2
Thay vào Phuong trinh ( 2) ta có 2 2 5 4x   3 2 4x    
  2 3  4x  7  0   . Với 0;  2  4 2 4
Xét hàm số f t  t t  4 t  0 Khi đó '   1 0 1 x   1  x  
1  4  y y  4 2 2 2 2
x  2x  1  x  2x  5  y y  4 2 2 2 2
Cộng hai phương trình ta có Giải x  y 3x 3y 1 0
Bài 51 Giải hệ phương trình: 2 2 x       x 2x 5 3y y 4        2 2 2        4  3 g x 2 5 4x 2  4x    
  2 3  4x  7 2    
Khi đó g 'x   4x 4x  3 
 0 với x  0;      2  3  4x  4 1   1
Ta có g    0  x  ;y  2 
là nghiệm duy nhất của hệ. 2 2 y   2 3 2
1  y y  1  x
Bài 50 Giải hệ phương trình:  2 f t  
 suy ra hàm số f t đơn điệu t  tăng .  2 x
  x 2x  5  1  2 2x  4y  2  Giải
Điều kiện 2x  4y  2  0
Phương trình ( 1 ) tương đương
x y    2 y   2 2 2 4 2
1  2y y  1  y x y    y   y2 2 2 4 2 1 (*)
Thay vào phương trình (2) ta có 2 x 1 x 1  
x   x    
y  y2 2 2 1 1 1 2 1   2   
  1  y y  1 2  2  t Xét hàm số 2
f (t)  t t  1. Khi dó f '(t)  1 
 0 suy ra hàm số f t đơn điệu tăng . 2 t  1 x 1    x 1    x  1 Từ đó suy ra f    f   yf    f   y 
y x  2y  1  thay vào phương trinh  2   2  2 (*)ta được  
y    y 5 y  1  y 2 2 1 2 3 2  4    y   x  2
y  1  2  y 4 2  5 3 Vậy hệ có nghiệm ; 2 2 Ta có 1 63 1 1733 1 63 3 79  2 y    1
g ' y  0     y     2 2   y x  1 Từ đó suy ra f   x       f   
 2y  x   2 1 1  yy   1 x 
Với y x  1 thay vào phuong trình hai ta có 1 1  2 x   2 x  2x  
1  3x  3x   1  1  0  x   y  2 2
Với y  1  x thay vào phương trình hai ta có 3 1 2 x                  g    ;g    ;g    ;g                       
 2x 2x  13x  31x1  0 x   y  2 2 6 54 2 2  2  2 4 4  2 2  x  4x   2
1  2y 2y   1  y  32 
Bài 52 Giải hệ phương trình:  1 2 2 x
  y x y   2 Giải 1
Xét phương trình thứ hai của hệ : 2 2
x x y y   0 2
Phương trình có nghiệm khi 2 2
  1  4y  4y  2  3  4y  4y  0 3 1   y  2 2
Phương trình thứ hai của hệ biến đổi theo biến y 1 2 2
y y x x   0 2
Phương trình có nghiệm khi 1  3 2 2
  1  4x  4x  2  3  4x  4x  0   x  2 2
Phương trình thứ nhất ta có 3 2 3 2
8x  2x  4y  2y y  32 Xét hàm số x  0  f x 3 2
 8x  2x Khi đó f x 2 '
 24x  4x với f 'x  0   1  x   6               Ta có f   1 1 1 1 3 63 0  0; f    ; f    ; f      2  2
 6  54 2 2 Xét hàm số 1 g y 3 2  4
y  2y y  32 khi đó g y 2 '  12
y  4y  1 với   6 3 1    3 1   
Vậy hệ phương trình có hai căp nghiệm  ; ; ;   2 2   2 2  x
 2 y 1  3 
Bài 53 Giải hệ phương trình: 
x,y   3 2 x
  4x y  1  9x  8y  52  4xy  Giải §K: y  1  . x
  3  2 y 1 HPT    3 2 x
  4x y 1  4xy  4x 13x  8y  52  0  x
  3  2 y 1    2 x
 (x  2 y  1) 13x  8y  52  0    x
  3  2 y  1 x
  3  2 y  1        x   2y  13  0  
y  1  5  y   x
  3  2 y 1 y    5  2 y
  11y  24  0 
x 32 y1  x   7 y     5     y   3  y  3   y  8  
Vậy hệ có nghiệm là (7,3).  2 2 3 5
x y  4xy  3y  2 
x y  0 
Bài 54 Giải hệ phương trình: 
x,y   x
 yx y   2  x y2 2 2  Giải
Biến đổi phương trình thứ hai của hệ ta có 2 2 2 2 2
xy(x y)  2x y  2  (x y)  (x y) (xy  1)  2(xy  1)(xy  1)  0 2 2
 (xy  1)(x y  2)  0
+) xy  1, thay vào phương trình thứ nhất và rút gọn ta được: 2 2 3 2
3x y  6xy 3y  0  y(x y)  0.
Vì xy = 1 nên y  0 , do đó x = y. Do đó x = y =1 hoặc x = y = -1. +) 2 2
x y  0. thay vào phương trình thứ nhất và rút gọn ta được: 3 2 2 3 2
x  4x y  5xy  2y  0  (x  2y)(x y)  0 x  2y   x y 
Từ đó giải được các nghiệm 2 2 2 2 (1;1),(1,1),(2 ; ),( 2 ; ) 5 5 5 5  2 2 x
  x  2x  5  3y y  4 (1) 
Bài 55 Giải hệ phương trình: 
x,y   2 2 x
 y  3x  3y  1  0 (2)  Giải 2 2
x y  2x  1 Từ (1):
 3y x , thay (2) vào ta được 2 2
x  2x  5  y  4 1 (x  3y)(
 1)  0  x  3y 2 2
x  2x  5  y  4 3 1 3 1
Với x = 3y thay vào (2) giải được: (x,y)  ( ; );( ; ) 2 2 4 4  4 4 2 2 x
y  1  25y  2x (1) 
Bài 56 Giải hệ phương trình:  2 2 2 x
y  1  y(18  x ) (2)  Giải
Dễ thấy với y  0 hệ pt vô nghiệm
Xét y  0 .Chia (1) cho 2
y , chia (2) cho y ta được hệ  4 2 x 1 x  2   y   2  25  2 2 2 y y y  2 x 1  2 
y   x  18  y y  2  x  1  2 2 ( 
y)  2(x  1)  25  y   2 x  1  2 
y x  18  y   a   7   2  x  1    a    y 2  a   2b  27 b   11   Đặt  y     ta được hệ      2 a b 18 b   a  9   x    b   27  a   7  2  2  x   11  x   11  + Với  ta giải ra được  hoặc  b   11     y  3    y 4  a   9  + Với  vô nghiệm b   27   2 x   11   2  x   11 
Vậy phương trình đã cho có 4 nghiệm  hoặc  y   3      y 4   3 3
8x y  65 
Bài 57 Giải hệ phương trình:  2 2 2
 (2  3y)x  (1  3x)y  4xy  5.  Giải  2 2   2
(2x y)(4x  2xy y )  65 (
 2x y)[(2x y)  6xy]  65   Hệ     2 2 2 2
4x  4xy y  6x y  3xy  5. (
 2x y)[3xy  (2x y)]  5.      3 (
 2x y)  6xy(2x y)  65
2x y  5  3 2  (2x y) 2(2x y) 75 0          2  2 2.(
 2x y) +6xy(2x y)  10
(2x y)  3(2x y)  15  0(VN )     x   2;y  1 
Thay y = 2x – 5 vào (1) ta có 3 3 2
8x  (2x  5)  65  6x  15x  6  0   1 x   ;y  4  2 1
Vậy hệ có 2 nghiệm (2; 1  );( ; 4)  . 2  2 2
y x  2(x  1)  2 
Bài 58 Giải hệ phương trình:  1 2
 (y x)  1   x  1 Giải ĐK: x  1
Hệ phương trình đã cho trở thành  2 2
y x  2(x  1)  2   1 2
 y x (x 1)   x  1 Đặt a
  2y x  
. Khi đó hệ đã cho trở thành b   x  1 
 b  1(L)    2  2 2 a   2b  2 b
  1  b 2b  2      a   2    b  1   1   1         b   1 a  b a  b   1   b  b a b        b a   2  Với 
x y  2 b   1 
Vậy hệ phương trình đã cho có duy nhất nghiệm x y  2 . xy   3 3
1  2y (9  5xy)
Bài 59 Giải hệ phương trình:  x
 y(5y 1)  1  3y  Giải
Nhận thấy y  0 không là nghiệm của hệ
Xét y  0 hệ đã cho được biến đổi thành  3   xy  1  1    3     2(9  5xy) (
 x  )  2(9  5xy)   y     y      1  1  3yx   
   3  5xy  0 x(5y 1)   yy     1  3 a   2b a   2  
Đặt a x  , b  9  5xy ta được hệ    y a  b  6  0 b   4    a   2 1    x    2 x   1   Với  ta có hệ  y   b   4      y 1 9   5xy  4    
Vậy hệ đã cho có nghiệm x y  1
 x y     x y2 1 1 4  3 x y
Bài 60 Giải hệ phương trình:  3 2
 x y   2 Giải
§K: x y  0 . 2
pt(1)  x y  1  3(x y)  4(x y)  1 2x  2y  1 
 (2x  2y  1)(2x  2y  1)  0
x y  1  3(x y) 1
 (2x  2y  1)(
 2(x y)  1)  0
x y  1  3(x y)
 2x  2y  1  0 Từ đó ta có hệ   2 2
x  2y  1  0  x     3  3   2
 x y   1   2 x      6  3 3x   9 y 2 x  3xy  1
Bài 61 Giải hệ phương trình:  2 x
 9x  2y  3.  Giải   2 2  x   3x  2  x  3x  3x y  2  1 x   3x  1  hpt       hoặc  2 x   3x  2 1 
3x y  3 3
x y  1     3  x y   2    3  13  3  13  2   3  1 x x x       x    Nếu 2    hoặc 2  3
x y  1      11  3 13   11  3 13 y    y    2  2     2   3  17 x  3x  2  3  17  x       x    Nếu 2  2 1   hoặc  3  x y     10  3 17     10 3 17  2 y    y    2  2  2 2 2 2 (
x y)(x xy y  3)  3(x y )  2 (1) 
Bài 62 Giải hệ phương trình 
x,y   2 4 
x  2  16  3y x  8 (2)  Giải 16 ĐK: x  2  ,y  3 3 3
(1)  (x  1)  (y  1)  y x  2 Thay y = x - 2 vao (2) được 4(x  2) 3(x  2) 2
4 x  2  22  3x x  8 
 (x  2)(x  2)  x  2  2 22  3x  4 x  2    4 3   (x  2)   0(*)   x  2  2 22  3x  4  21 Xét f(x) = VT(*) trên 2  ; 
, có f’(x) > 0 nên hàm số đồng biến. suy ra x  1 là nghiệm duy 3    nhất của (*)
Vậy hệ phương trình có 2 nghiệm 2;0, 1  ; 3  .  2 2 x
  y x y  12 
Bài 63 Giải hệ phương trình  x,y      2 2 yx y  12  Giải
Điều kiện: | x |  | y |  2 2 u
  x y ; u  0   2 1 u    Đặt  ; x y
 không thỏa hệ nên xét x y  ta có y v     . v   x y     2  v  
Hệ phương trình đã cho có dạng: u   v  12    2 u u   v      12    2  v  
Đến đây sử dụng phương pháp rút thế ta dễ dàng tìm ra kết quả bài toán.
x y  2 2
x y y
Bài 64 Giải hệ phương trình  x,y      4 2 2 2 x
 4x y  3x  y  Giải  2 x
y x(1  2y)  0 (1)  Hệ tương đương  2 2 2 (
x y)  3x (1  2y)  0 (2)  x  0   1
Thay (1) vào (2) được x(1 2y 2 2 2 ) 3x (1 2y) 0 2x (1 2y)(2 y) 0 y             2 y  2  Với x = 0 suy ra y = 0 1 
Với 1 2y  0 thay vào (1) suy ra 2 x y   (Vô lí) 2
Với y = 2 suy ra x = 1 hoặc x = 2
Hệ có 3 nghiệm (0; 0), (1; 2), (2; 2).  2 2 x
  5y  3  6 y  7x  4  0 
Bài 65 Giải hệ phương trình 
(x,y R) . x,y   y
 (y x  2)  3x  3  Giải
Phương trình thứ (2)  2
y  (2  x)y  3x  3  0 được xem là phương trình bậc hai theo ẩn y có 3
y x  1  0 vô nghiệm vì ; 1 1 2x y 4 0 (2)  y   x  
3 y  2x  6x  4  0;   3x   5     Vậy ta có: 2 2  2 y x 1 0     x y  2   (x  4) 
x  2  x  4 y    3 
Phương trình có hai nghiệm: 2 
Thay y = -3 vào pt thứ nhất ta được pt vô 
x  2  x  4 y   x  1   2 nghiệm
Thay y x  1 vào pt thứ nhất ta được: 2 2
x  5x  2  6 x  5x  5  0 (3) x y t  1 tm  Giải (3): đặt 2
x  5x  5 = t , điều kiện t 0 3 2  
t  6t  7  0 
t  7 (ktm) 
x  1  y  2 Với t=1  2
x  5x  5 =1   ( thỏa mãn)
x  4  y  5 
Vậy, hệ phương trình có 2 nghiệm là: (1;2)và (4;5)  2 2 2 x
y  2x  2y  5y  2  0 
Bài 66 Giải hệ phương trình  2 2 2 2
 y  1  x y  2xy x x  2xy y  1  y 
(x,y R) . Giải 2 2
Từ phương trình (2) ta có đ/k : x y ,y  0 2 2
y  1  y y  x y  1  x y x y . t 1
Xét hàm số f t 2 2
t  1  t t liên tuc 0; /   
có f t    2t 2 t  1 .2 t  1  1  t   2   
 0 t  0 Suy ra hàm số nghịch biến 0;   nên  2   t  1  2 t
f y  f x yx  2y
Thay vào (1) ta có y   2
2 x x  
1  0  y  2  x  4 .Vậy hệ có nghiệm (x ;y) = (4 ; 2).  3x 1  4 
2x  1  y 1  3y
Bài 67 Giải hệ phương trình  x y
2x y 4  6x  3y  Giải 1 Điều kiện: ; 1 3
Vậy hệ đã cho có bốn nghiệm là 1;  2 ,  1  ;2, 2;  1 ,  2  ;  1 .
t   ta có y  2
x thế vào (1) ta có 3x  3  x  1  x  1 tương ứng y  2 . 2 2
3x  1  42x  
1  2x  3  32x  4
2x y  4  0  y  2x  4 , thay vào (1) ta có:  23x  
1  3x  1  22x   3  2x  3   *  
*  3x  1  2x  3  x  4  y  12 .Kết luận: x,y  4;  12 .  2 2 x
xy y  3 
Bài 68 Giải hệ phương trình 5 5 x y 31    3 3 x y 7  Giải
Điều kiện của phương trình x y   2 2 x
xy y  3   2 2  x
xy y  3    1 5 5  x y 31     7     5 5
x y   31 3 3 x y 2 3 3    x y 7  
Lấy (2) nhân 3 kết hợp với (1) ta được phương trình đồng bậc  5 5
x y    2 2
x xy y  3 3 x y  5 4 3 2 4 4 21 31
 10x  31x y  31x y  31xy  10y  0 3.
Rõ ràng x y  0 không phải là nghiệm hệ phương trình. Đặt x ty thay vào (3) ta được: 5 y  5 4 3
10t  31t  31t  31t  10 5 4 3
 0  10t  31t  31t  31t  10  0    t   t 1  1 0 4 3 2 10t 21t 10t 21t 10 0           4 3 2
10t  21t  10t  21t  10  0 
Với t  1  0  t  1 hay x y
  x y  0 (loại). Với 4 3 2
10t  21t  10t  21t  10  0  
3 . Vì t  0 không phải là nghiệm của phương trình (3) chia  1   1     hai vế phương trình cho 2 t ta được: 2 10 t     21 t     10  0  , 2       t   t  1 1 1 Đặt 2 2 2 2
u t   u  2; u  t   2  t
u  2 . Khi đó (3) trở thành 2 2 t t t  2 u   loai 2  5
10u  21u  10  0    5 u     2 t  2 5 1 5  Với u   ta có 2
t     2t  5t  2  0   1 2 t 2 t    2
Với t  2 ta có x  2
y thế vào (1) ta có 2 2
3y  3  y  1  y  1 tương ứng x  2 . 1 Với 2  3 4 x
y y  7 
Bài 69 Giải hệ phương trình  2 2 3 x
y  2xy y  9  Giải y   3 3
x y   7   1 Hệ phương trình    y
 x y2  9 2 
Từ hệ suy ra x.y  0; x  y, y   0 .
Lấy phương trình (1) lũy thừa ba, phương trình (2) lũy thừa bốn. Lấy hai phương trình thu được
y x y 3 3 3 3 3 7
chia cho nhau ta thu được phương trình đồng bậc:  .
y x y8 4 4 9 t  3 3 3 1 7
Đặt x ty ta được phương trình: 
3 . Từ phương trình này suy ra t  1 . 8 4   t   9 1 t  3 3 1
Xét f t  ; t  1. t  8 1 9t t  2 1 t  8 1  8t  7 1 t  3 1 t  2 1 t  7 2 3 3 3 1  3 2 3
9t  9t  8t   t 8 f'   t  8 1 t  8 1 t  2 1 t  7 3 1  3 2 t  9t   8   0 t  1 t  8 1
Vậy f(t) đồng biến với mọi t  1 . Nhận thấy t  2 là nghiệm của (3). Vậy t  2 là nghiệm duy nhất.
Với t  2 ta có x  2y thế vào (1) ta được 4
y  1  y  1 (vì y  0 ) suy ra x  2 .
Vậy hệ có nghiệm là 2;  1 .  1 1   2   2 (1)  yx
Bài 70 Giải hệ phương trình  1 1   2   2 (2)  x y  1 1
ĐK: x  ,y  . 2 2 1 1 1 1 Trừ vế hai pt ta được   2   2   0  y x x y 1  1 2   2      y x y  x  y x y x   0    xy xy     x y 0 1 1  1 1    2 2 xy  2   2     y xy x    1 1
 TH 1. y x  0  y x thế vào (1) ta được  2   2 x x 1 Đặt t  , t  0 ta được x 2  t  0 t   2 2 2 t 2 t         
t  1  x  1 và y  1 2 2 2 2
 t  4  4t t t   2t  1  0   1 1  TH 2. 
 . TH này vô nghiệm do ĐK. xy x y  0  1 1    xy  2   2      y x   
Vậy hệ có nghiệm duy nhất (1; 1).  8 2 2 x   2y  2   y
Bài 71 Giải hệ phương trình:   2 1  2 2 3
x  3y  5  8         y x  
Điều kiện: x.y  0
Quy đồng rồi thế   1 vào   2 , ta được: 3 3
x y xy xy x  2 2
x y y y  y  2 2 3 3 5 2 2 2
x y  2y  2y
 x y 2 2 2
x xy y  
1  0  x  2y thay vào   1 , ta được: 3 2
4y  2y  2y  8  0  y  1  x  2 KL: S    2; 1.  6 3 2 2 2 y
  y  2x xy x y
Bài 72 Giải hệ phương trình:  3 3 2 2 8
xy  2y  1  4x  2 1  (2x y)  Giải 2 1  1   1 1 6 3 2 VP(1)   xy
   VT(1)  y y  2x  4  2 2 2 6 3 2
 2y  2y  4x  1 (3) Từ (2) và (3) suy ra: 3 3 6 3 2 2 2
8xy  2y  2  2y  2y  4x  4x  2 1  (2x y) 3 6 2 2
 8xy  2  2y  8x  2 1  (2x y) 3 6 2 2
 4xy  1  y  4x  1  (2x y) 2 6 3 2 3 2
 1  1  (2x y)  y  4xy  4x  (y  2x) (4)
VT(4)  0,VP(4)  0 . Do đó:    x   0    y   0    1 y  2x y   2x    x     (4)        3 3 2 y   2x y   y    y   1  1  x     2 y    1    1
Thử lại chỉ có: (x;y)  ( ; 1  ) thỏa mãn. 2 1
Vậy hệ đã cho có nghiệm duy nhất (x;y)  ( ; 1  ). 2  y 2 x    y  0   1  2   
Bài 73 Giải hệ phương trình 1 x x  2  x  2 2 
 2 x  1  y  3 2  2    y  Giải Từ PT (1) ta có: 2 2
x y( x  1  x)  y  0 do y  0 x 2 
y x  1  x  0 (3) yx 2   y  1 x  x       y Từ (2) &  
3 ta có:   y  2  y  3  0    y    y   x   y  3  y
Thay vào 3 giải ra ta có nghiệm 0; 1  2
 x 2y  2x y  2xy 1  1 
Bài 74 Giải hệ phương trình: 3 3
 3y  1  8x  2y  1  x   0  Giải 3
Từ đó kết hợp với điều kiện: 0 2 , 3 x 3
Dấu bằng xảy ra  x y  1 (*) .
x y  1  1  1  4 x y .1.1.1  4 x y  4 x y 4 4 4
Ta có (1)  2x   1  2y   1  2x   1 y   1  0 ĐK: (2x + 1)(y + 1)  0 2  x  1  0  Mà x > 0   y   1  0 
Ta có PT (1)   2x  1  y  1 2x  1  2 y  1  0
 2x  1  y  1  0
     x y  . y  4 2 4 2 x 9x 7x y 9y 7y PT thứ hai của hệ   
 3 ln3  x     3 ln3  y. 64 32 8 64 32 8  y  2x Thay vào (2): 3 3
6x  1  8x  4x  1
  x    x    x3 3 6 1 6 1 2  2x (3)
Hàm số f(t) = t3 + t đồng biến trên R 1 (3) 3
 6x  1  2x 3
 4x  3x  2
Nhận xét: x >1 không là nghiệm của phương trình
Xét 0 x  1: Đặt x = cos với 0   2 1  cos 3 2  2  k  9 3   (k Z )  2
   k   9 3 Do 0     2 9     Vậy hệ có nghiệm: cos  ;2 cos    9 9 
x y
4  3  4x y 
Bài 75 Giải hệ phương trình:  9    2 2 4 4
x y  7x y x y  x  3     3 ln     0  64 32 8 y  3  Giải Theo BĐT Cauchy ta có      
Ta có bảng biến thiên của hàm số:
g 'u  3u  3 có g 'u  0  u  1  2
Xét g u  u  3u  1 với u  0 3
Đặt x u u  
0 suy ra u  3u  1 (3) 2 3
Thay vào phương trình còn lại của hệ ta có x  3x  1  0 2 6 2
Mà (1)  f x   f y  x y 4 2
Suy ra f ' t   0 t  hàm số đồng biến và liên tục trên R 27 3 3 3 3 x 9x 7x  Xét 1  t  9   1     0 2 26 hàm 29 26 29 số 29 f(x) =  
 3 ln3  x ( với x < 3 ) 64 32 8  3 3 x  9x   14 x x x   3  48 9 7 3 ' f x      16 16 8 x  3 16(x  3) x  2  2 4 3 2 1 x x x x x x      6 3 9 13 6    0 ( vì x < 3). 16(x  3) 16(x  3)
Suy hàm số nghịch biến trên (-2; 3), vậy f(x) = f(y)  x y ( **). 1 Từ (*), (**) có x = y = . 2       
y y   x
y x xy y  2 2 9 2 2  6 ln     
Bài 76 Giải hệ phương trình: 2 
x x  9    5 x
y  3xy 1  0  Giải y y   9 
Từ x yx xy y  2 2 2 2  6 ln      2
x x  9  3  x x   2 x x   3  y y   2 2 6 ln 9 2
6 ln y y  9  1 Xét f t 3  t t   2 2
6 ln t t  9 t       f 't 6 2 2 2 2  3t  2   3 t       2  2  3 t  9  t  9  2 2 2 2 29 t  9 1 1 26 29 Ta có 2 2 t    t  9        2t  9 2 2 2 2 3 3 27 27 3 t  9 t  9 t  9 t  9   u -1 0 1 2 g’(u) + 0 - - 0 + g(u) -1 + - 1 33
Căn cứ vào BBT phương trình (3) có nghiệm duy nhất thuộc (0; 2)    
Đặt u  2 cos với  0;    2  1
Khi đó (3) trở thành: cos3=  =  x   2 cos 2 9 9      
Vậy hệ có nghiệm  2 cos ; 2 cos  
 ;  2 cos ; 2 cos       9 9     9 9    2 2 2  x y    2x y   8 
Bài 77 Giải hệ phương trình: 
x y  2  Giải  1 x   y  
x y2  2  Ta có: 2 2 2 
x y x y  4  1 x
  y  x y2 2 2  2  2 2 2 2 2
Theo BĐT Cauchy ta có: x yy xx yxy  4 2  2  2 2  2. 2  8
PT  dấu “ = ” xảy ra. Từ đó ta có x = y = 1.
Vậy hệ có nghiệm duy nhất (1; 1).  2 3 x
  8y  2xy(1  2y) 
Bài 78 Giải hệ phương trình:  2y   2 1 3
x  4x  1   3 Giải
§K: tõ PT (2) ,suy ra x> 0 Ta có PT (1) 2 2
x(x  2y)  4y (2y x)  (x  2y)(x  4y )  0  x  2y ( v× x+4y2> 0 )
Thay vµo ph­¬ng tr×nh (2) cã 3 2
3 x  4x x  2x  4 (*)
Ap dông bÊt d¼ng thøc Cauchy tacã 2 2 x  4 x  4 3 3 2 2 2
x x  2x  4 
 (x  4)  2x x  (x  4x)  2x  4 4 4 4 2 3 x  4 3 3 3  (
 2x)  .2 x  4x  3 x  4x 2 2 2
DÊu ®¼ng thøc x¶y ra khi x = 2. HÖ ph­¬ng tr×nh cã nghiÖm (2,1)
(Chó ý :C¸ch kh¸c : B×nh ph­¬ng 2 vÕ cña pt (*) 2 2
 (x  2) (x x  4)  0 )  2 2 x
y  4y  8  x(x  2) 
Bài 79 Giải hệ phương trình:  (x,y  ) R x
  y  3  3 2y 1  Giải x   (1) x 4 4 2 y x 2 0         2 x y  2 
Với x  4 thay vào pt (2) ta được y  10  3 10 Với 2
x y  2 thế vào pt (2) ta được 2
y y  5  3 2y  1 (*) Ta có 2 2
y y  5  2y  1  (y y  1)  5  2y  1  5  2 5(2y  1)  3 2y  1 Do đó pt (*) vô nghiệm.
KL: Nghiệm của hệ x  4 , y  10  3 10 .  3 3 x
 8x y  2y
Bài 80 Giải hệ phương trình:  2 2 x
  3  3(y  1)  Giải  3 3 x
  y  2(4x y)(1)  Ta có PT (1)   2 2 x   3y  6(2)  x  0  3 2 2  x  x y  12xy  0   x  3y   x  4y
Thay cả 3 trường hợp x vào  
2  Hệ có các nghiệm là:      6 6 6 6 3;1 , 3; 1 , (4 ; ),(4 ; ) 13 13 13 13 8
 x y 2 2
 3xy  2y x
Bài 81 Giải hệ phương trình:  2 2 4 
2  x  3  y  2x y  5  Giải x   2   x y  Điều kiện:  , phương trình x yx y  0 (1) 2 8 0        . y   3      x 2y 8 
Với x  2y  8 x   2 x   2   Ta có :   
x  2y  8 y   3 2  y  6   x   2 
Khi đó: x  2y  8   không thỏa hệ. y   3 
Với x y  0  y x
 thay vào phương trình (2) Ta có PT 2
(2)  4 2  x  3  x x  5 Điều kiện: 3   x  2 1  x x  1
Ta có (2)  4  2  x  
1   3  x  2 2  x  1  4   x   1 x   1 2  x  1 3  x  2
x  1  y  1    4 1    x  1  0 (*)   2  x  1 3  x  2 4 1
Xét phương trình (*), đặt f (x)    x  1 2  x  1 3  x  2 2 1 Ta có: ' f (x)  
 1  0; x  3;2 2 2  
2  x  2  x   1
2 3  x  3  x  2
Mặt khác f (x) liên tục trên  3;2    
 , suy ra f (x) đồng biến trên 3;2   .
Ta có: f (2)  0 , suy ra (*) có nghiệm duy nhất x  2   y  2 .
Kết hợp điều kiện, hệ có hai nghiệm 1;  1 ,2;  2 .  2 3
 (y y)(1  x  2)  x  2 x  2  1 
Bài 82 Giải hệ phương trình:  2 2
 y  2y x  2  2  Giải ĐK: x  2. Ta có  2 3  
 (y y)(1  x  2)  x  2 x  2  1 2   3
 (y y)(1  x  2)  (x  2  2 x  2  1)  2     2 2
 y  2y x  2  2 2        2(y y) 1 x 2 3    2 a   y y   a b  1  2  3ab b  2 b   3  2a    Đặt  ta được      11 4 b   1  x  2 2  2  a b  3 10
a  21a  11  0     a  ,b    10 5  1  5 x  2,y   4
Với a=b=1 suy ra hệ có hai nghiệm là : 2 
b  1  x  2  1  b   Vì không 1  5  5 x  2,y   2 2
 x  2y  
2x  1y  1  1
Bài 83 Giải hệ phương trình:  x x y R  , với 0 và , . 3 3
 3y  2  8x  2y  2  Giải
x y x y y  6y  2y  12y  1  x  2x   Thay vào (2) , ta có :
3 y y  1  0 4 2 2 2 2 2 2 2 2 y  1 y  1 Khi đó :  
1  x y y  
1  6y  2y x  2  ;x  3  . 2 2 2 2 4y  4 9y  1
Điều kiện : y  0;y  1  Giải x  y 2x y y x 1 12y 12
Bài 85 Giải hệ phương trình: 4 . x       2y 2 2 2 y   2 1 6 2 1     2 Điều  5 5   5 5     ; ,        kiện: ; 
(2x  1)(y  1)  0 ,
Phương trình (1)  2x   1  2y   1  2x   1 y  
1  0 . Từ giả thiết x  0 ta có
2x  1  0  y  1  0 . Đặt a  2x  1,b y  1 ta có (1) trở thành: 2 2
a  2b ab  0   a b 2 2 a b   2 ab b  0
a ba 2b 0            a
  2b  0(l) 
Với a b ta có: 2x  1  y  1  y  2x thay vào phương trình (2) ta có: 3
x   x x    x   3 6 2 8 4 2 6
2  6x  2  2x3 3  2x , (*). Xét hàm số 3
f (t)  t t ta có 2
f '(t)  3t  1  0, t R  hàm số f (t) đồng biến trên R Do đó 3 3
PT(*)  6x  2  2x  8x  6x  2  0 x  1 (n)  2
 2(x  1)(4x  4x  1)  0   1 x   y   . Với 1 2 x   (l)  2  5 2 3 5
x y  4xy  3y  2 
x y  0 1 
Bài 84 Giải hệ phương trình:  . x  yy
   2  x y2 2 2   2  Giải
Từ (2) ta có : xy   2 2 x y   2 2 1
2  0  xy  1  x y  2
 Với xy = 1; từ (1) suy ra : 4 2
y  2y  1  0  y  1 . Vậy hệ có nghiệm (x;y)=(1;1),(-1;-1).  Với : 2 2
x y      y  2 2 x y  2 2 2 1 3
 4xy  2x y  2x y  0 2 2
 6y  4xy  2x y  2x y  0
 1  xy2y x  0  xy  1  x  2y
Xét : xy = 1 . Đã giải ở trên 2 10 10  2 10 10    Với : x = 2y , thay vào 2 2
x y  2  x;y   ;   , ;        5 5     5 5    2 10 10 2 10 10
Vậy hệ có nghiệm : (x;y)=(1;1),(-1;-1),  4y   1 9y   2 1 y y   1
y  1  x   2    y   1       y   1
  y  y  y  2 2 2 1 4 9 1 1 y   x  0    3  2 x
y  2y x  4xy 
Bài 86 Giải hệ phương trình:  1 1 x  .    3  2 x xy y Giải
Điều kiện : x  0,y  0 . Chia hai vế phương trình (1) cho xy , thêm 1 vào hai vế của phương trình  1 1 1 x      4  x x y
(2) và nhóm chuyển về dạng tích   1    1 1  x           4   x   x y   1 1 1 u   v  4 
Đặt : u x  ;v    
u v  4 . x x y uv  4 
Đến đậy bài toán trở thành đơn giản.  2xy 2 x    x y  3 2  x  2x  9
Bài 87 Giải hệ phương trình:  . 2xy 2 y    y x  3 2  y  2y  9  Giải
Cộng hai vế phương trình của hệ vế với vế ta có : 2xy 2xy 2 2 
x y . Ta có : x = y = 0 là một nghiệm của hệ . 3 2 3 2 x  2x  9 y  2y  9 Ta có : 3 3
x  2x  9  x  2 2
1  8  2 VT xy xy  2xy . Khi đó : 2 2
VP x y  2xy .
Cho nên dấu bằng chỉ xảy ra khi : x = y = 1. Vậy hệ có hai nghiệm : (x; y)=(0;0); (1;1). 1  x   2 1  x  4 1  x  7  1  y
Bài 88 Giải hệ phương trình:  . 1  y   2 1  y  4 1  y  7  1  x  Giải
Dễ thấy : x = y = 0 hoặc x = y = -1 là nghiệm của hệ Xét : x > 0 Ta có: 7
y    x 2  x  4  x  2 3 4 5 6 7 7 1 1 1 1
 1  x x x x x x x  1  x y x Ta có: 7
x    y 2  y  4  y  2 3 4 5 6 7 7 1 1 1 1
 1  y y y y y y y  1  y x y
Vậy hệ vô nghiệm . Tương tự khi y>0 hệ cũng vô nghiệm Xét : x < -1 7
 1  x  0  y  1 Ta có : 1+ 2
x x    3 4
x x    5 6 x x  7 7
x  1  x y x . Tương tự khi y  1
 ta có x y Hệ cũng vô nghiệm Xét trường hợp 1
  x  0 . Hệ cũng vô nghiệm .
Kết luận : Hệ có nghiệm :  x; y  0;0; 1  ;  1 .  1  3x(1  )  2 (1)  x y
Bài 89 Giải hệ phương trình:  . 1  7y(1 )  4 2 (2)  x y  Giải
ĐK x  0,y  0. Dễ thấy x = 0 hoặc y = 0 không thõa mãn hệ. Với x > 0, y > 0 ta có :  1 2    1 2 2 1    1     x y   3x  3x 7y 1 1 8        ( nhân vế với vế) 1 4 2    1 1 2 2 x y 3x 7 1 y        x y  7y x y  3x 7y  2 2
 21xy  (7y  24x)(x y)  24x  38xy  7y  0  y  6x (vì x, y dương). 1 2 1 1  1 2   
Thay vào phương trình (1) ta được  .  1  0   7  .   7x 3 x x  3 21
Từ đó dễ dàng suy ra x và y.  3 2 x   3xy  49 (1) 
Bài 90 Giải hệ phương trình:  . 2 2 x
  8xy y  8y 17x (2)  Giải
Với hệ này, cả hai ẩn và ở hai phương trình đều khó có thể rút ẩn này theo ẩn kia. Tuy nhiên, nếu rút 2
y từ (2) và thế vào (1) thì ta được một phương trình mà ẩn y chỉ có bậc 1: 3 2 3 2 2
x  3x( x
  8xy  8y  17x)  49  24xy(x  1)  2x  2x  49x  49 (3)
Nếu x=0 thì (1) vô lí.
Nếu x=-1 thì hệ trở thành 2
y  16  y  4 . 2
2x  49x  49
Nếu x  1 & x  0 thì từ (3) suy ra y
. Thế trở lại phương trình (2) ta được 24x 2 2  2  2
2x  49x  49
2x  49x  49  
2x  49x  49 2 x  8x.      17x   24x  24x  3x 2 2  2 x 2x 49x 49     49 4 2 2     
 192x  (2x  49x  49)  49.192x   3  24x  3x 4 3 2 3
 196x  196x  2205x  4606x  2401  0  196x  2205x  2401  0 3 2
 196x  196  2205x  2205  0  196x  196x  2401  0
Phương trình cuối cùng vô nghiệm, chứng tỏ hệ chỉ có hai nghiệm (-1;4) và (-1;-4).  5 4 10 6 x
xy y y (1) 
Bài 91 Giải hệ phương trình:  . 2
 4x  5  y  8  6 (2)  Giải 5
ĐK: x   . Nếu y = 0 thì từ phương trình (1) ta suy ra x = 0, thế vào phương trình (2) ta thấy 4
không thỏa mãn, vậy y khác 0.
Đặt x = ky ta được (1) trở thành : 5 5 5 10 6 5 5
k y ky y y k k y y (3). Xét hàm số 5
f (t)  t t trên  , ta có 4
f '(t)  5t  1  0t  .
 Do đó f(t) là hàm số đồng biến trên  , vậy 2
(3)  f (k)  f (y)  k y x y . Thế vào (2) ta được 2 2
4x  5  x  8  6  5x  13  2 4x  37x  40  36  2 4x  37x  40  23  5x 23   5x  0 5  x  23 x  1         2 2 2
16x  148x  160  25x  230x  529
9x  378x  369  0    x  41     
Suy ra x = 1 và do đó y  1.  2 4 2
x  2x  2  y  2y  2  2 
Bài 92 Giải hệ phương trình:  . 4
 x y  3  3  Giải  2 x   2x  2  0  2y   2y  2  0 x   0   Điều kiện:    x   0 y   3     y   3  0   2 2    2
x  2x  2  (x  1)  1  1 
x  2x  2  1 Mà:      2 2        4 2 y 2y 2 (y 1) 1 1 
y  2y  2  1   2 4 2
x  2x  2  y  2y  2  2
Vậy (1) có nghiệm x = y = 1 thỏa (2).  2 2 2 x
y  2x  2y  5y  2  0 
Bài 93 Giải hệ phương trình:  . 2 2 2 2
 y  1  x y  2xy x x  2xy y  1  y  Giải
ĐK: x y  0;y  0  x y  0
Từ (2) : y   x y y y
  xy x  x y2 2 2 2 2 1 2  1  y
y   y y   x y2   x y  x y2 2 2 1 1 Xét hàm số : t 1  1  1 2 2
f (t)  t  1  t tt   0  f '(t)    2t t   2     0 2  2  t  1 2 t  t  1  2 t 1 1 (Vì : 2 t  1  1  0   1 
 2  0 với mọi t>0 ) 2 2 t  1 t  1
Như vậy hệ có nghiệm chỉ xảy ra khi : y x y hay x = 2y . 2 2
Thay vào (1) :  yy   y 2 3 2 2 2 2
 2y  5y  2  0  4y  10y  5y  2  0  y   2
2 4y  2y  
1  0  y  2 vì : 2
4y  2y  1  0 vô nghiệm .
Vậy hệ có nghiệm : (x; y) = (4; 2).  2 1  2 8y   x 1  2 2   4  3 
2 y x 1
Bài 94 Giải hệ phương trình:  . x y  2 3 7 2   x y    2  2 2 Giải
Điều kiện : x,y  0  x4  y4 2 Ta có PT (1)  2.2  3 x  2.2  32 y Xét hàm số : 4
f t t t t   3 ( ) 2. 3
0  f '(t)  8t  3  0 . Chứng tỏ f(t) luôn đồng biến .
Do vậy để phương trình (1) có nghiệm chỉ khi : x  2 y x  4y   *  y4 5 3 7 4 t 3 4 3 Thay vào (2) : 2
  5y  . Xét hàm số : f(t)= 3
2  t f '(t)  4t .2   0 . 2 2 2 2 3 7 Nhận xét : f(1) = 2 +
 . Suy ra t = 1 là nghiệm duy nhất . 2 2  1 x   4y y               x y 4 1 5 ;    ;   5y  1  4    5 5  x     5  2
x x  4   2
y y  1  2  1
Bài 95 Giải hệ phương trình:  6 3 27
 x  x  8y  2 (2)  Giải 2 Ta có PT (1) 2
x x  4  2y  4  2y
Hàm số f t 2
t  4  t đồng biến trên R nên   1  x  2  y Thế vào PT (2) ta có: 6 3 27x  x  4x  3 2 3 3
 3x  x  4x  3  x  3 1  x   3 3 3
1  x  4x  3  x  4x  3 3 Lại xét :   3
g t t t , đồng biến trên R nên: 3 3 3
x  1  x  4x  2 2
 3x  x  1  0 1  13  x  6  3 2
 y y  2x 1 x  3 1 x
Bài 96 Giải hệ phương trình:  (x,y  ) 2
 2y  1  y  4  x  4  Giải
Điều kiện: 4  x  1;y   . Ta có PT 3 3
(1)  2y y  2 1  x  2x 1  x  1  x  2y y  2(1  x) 1  x  1  x Xét hàm số 3
f (t)  2t t, ta có 2
f '(t)  6t  1  0, t    f (t) đồng biến trên  . Vậy y   0 (1) f (y) f ( 1 x ) y 1 x          2 y   1  x 
Thế vào (2) ta được 3  2x  1  x  4  x  4 (3). Xét hàm số
g(x)  3  2x  1  x x  4, liên tục trên [-4;1], ta có 1 1 1 g '(x)      0 x  ( 4
 ;1)  g(x) nghịch biến trên [-4;1]. Lại có 3  2x 2 1  x 2 x  4 g( 3
 )  4 nên x  3 là nghiệm duy nhất của phương trình (3). x   3 
Với x  3 suy ra y  2. Vậy hệ có nghiệm duy nhất  y   2.   2 2 x
 (y  1)(x y  1)  3x  4x  1(1) 
Bài 97 Giải hệ phương trình:  2 x
y x  1  x (2)  Giải 2 x  1
Nhận xét x = 0 không thỏa mãn phương trình (2) nên ta có thể suy ra y  1  (3) x Thay (3) vào (1) ta được 2 2 x  1 x  1 2 2 2 x  (x
)  3x  4x  1  (x  1)(x  1)(2x  1)  (x  1)(3x  1) x xx  0  3 2 2 (x 1)(2x 2x 4x) 0 2x(x 1) (x 2) 0            x  1   x  2   
Loại nghiệm x = 0, vậy phương trình có hai nghiệm:    5 1; 1 , 2  ;    .  2   2 3 4 6 2
x y y  2x x 
Bài 98 Giải hệ phương trình: 
x  2 y  1  x  2 1  Giải   2  x
y x y x 3  0  2
 y x  2 2 2 4 2 2 3 2
2x y yx x   0  Ta có hệ     x   2
y  1  x   1 x   2
y  1  x  2 2 1   Trường hợp 1: y = 2 x , thay vào (2) : x   2 x    2 x   x 2 2 1 1 2
t  x  2t  2x  0  t  2;t x  2 2
x  1  2  x  3  x   3   . 2
x  1  x x    Trường hợp 2: 2 2 2 4 2 2
x y yx x   y    2 4 2 0 yx
2x x   0 4    x   2 4 x x  4 2 4 2
 3x  8x  0  x R    0 y y 2 2 2 4
f (,y)  2x y yx x  0  x,y . Phương trình vô nghiệm .
Do đó hệ có hai nghiệm : (x;y)= 3;3, 3;3
Chú ý: Ta còn có cách giải khác
Phương trình (1) khi x = 0 và y = 0 không là nghiệm do không thỏa mãn (2). 3
y  y     
Chia 2 vế phương trình (1) cho 3 x     3 0
1  2      2x x  x    x 
Xét hàm số : f t 3
t t f t 2 2 '
 2  3t  0t R . Chứng tỏ hàm số f(t) đồng biến . Để y
phương trình có nghiệm thì chỉ xảy ra khi : 2
x y x . Đến đây ta giải như ở phần trên. x  2  x   x   2 1
y  1  y   1
Bài 99 Giải hệ phương trình:  x
 6x  2xy  1  4xy  6x  1  Giải     x x        y     y  2 2 1 1    Ta có hệ       . (nhân liên hợp) x
 6x  2xy  1  4xy  6x  1  2 1 t t tt t Xét hàm số : 2
f (t)  t  1  t f '(t)  1   
 0t R 2 2 2 1  t t  1 1  t
Chứng tỏ hàm số đồng biến . Để f x   f y chỉ xảy ra x  y (*)
Thay vào phương trình (2) : 2   x  2  
 2x  6x  1  3x 2 2 2 2
x 6x  2x  1  4x  6x  1   2x  6x  1    x      2 4 2
 2x  6x  1  2x  x   0 x   0    Trường hợp : 2
2x  6x  1  3x    
x  1;y  1 2 2 2 2
x  6x  1  9x 7
x  6x 1  0   x   0 x   0    Trường hợp : 2
2x  6x  1  2x     2 2 2 2
x  6x  1  4x 2
x  6x  1  0   3  11 3  11 3  11 3  11  x  ;y
. Vậy hệ có hai nghiệm : (x; y) = (1;-1),( ; ) 2 2 2 2 8x  3   3
2x  1  y  4y  0  1
Bài 100 Giải hệ phương trình:  2 3 2 4
x  8x  2y y  2y  3  0    2  Giải 1 Điều kiện : x  . 2
Ta có PT (1)   x   3 8 3
2x  1  y  4y   *   Đặt 2 t
x   x t    x   x     2t   t    2t   3 2 1 2 1 8 3 2 1 4 1 3 4
1 t  4t t   Do đó (*) : 3 3
4t t  4y y Xét hàm số : f(u) = 3
u u f u 2 4 '
 12u  1  0u R . Chứng tỏ hàm số đồng biến . Do đó
phương trình có nghiệm khi : f(t) = f(y) 2
 2x  1  y  2x y  1(**) 2 Thay vào (2) :  2 y     2 y   3 2 4 3 2 1 4
1  2y y  2y  3  0  y  2y y  2y  0  y  3 2
y y y     y y   2 2 2 0
1 y  3y  
2  0  y y   1 y   2 y   1  0  y   0 y   0     1  y   0 y   1      Vậy :   
x;y   ;0,           x;y  1;1 2 1   2     2x y 1  x    2  2
x y  1 x   1      2       y   2 y 1 y  0 y   2        5    
x;y  1;0 ,      x;y    ;2. 2     2 5   2
x y  1 x   1 2
x y  1       x    2   2 Hết
Đồng Xoài, ngày 05 tháng 8 năm 2014
Chúc quý thầy cô và các em học sinh có một tài liệu bổ ích. 
Document Outline

  • www.VNMATH.com