Tuyển tập 260 bài toán phương trình – Hệ phương trình – Bất phương trình trong các đề thi Quốc gia

Tài liệu gồm 95 trang tuyển chọn 260 bài toán phương trình – hệ phương trình – bất phương trình trong các đề thi Quốc gia.

Các bài toán gồm nhiều dạng bài khác nhau và được phân tích, giải chi tiết, qua đó bạn đọc sẽ năm được các dạng toán thường xuất hiện để có phương pháp, định hướng học tập phù hợp nhằm chinh phục điểm 9, 10 trong đề thi Đại học.

67 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

95 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
260 HỆ PHƯƠNG TRÌNH TRONG CÁC ĐỀ THI
1/ Giải phương trình:
x x x x x
2
2 3 1 3 2 2 5 3 16
.
Giải: Đặt
t x x
2 3 1
> 0. (2)
x
3
2/ Giải bất phương trình:
xx
x
1
2 2 1
0
21

Giải:
x
01
3/ Giải phương trình:
x x x
8
48
2
11
log ( 3) log ( 1) 3log (4 )
24
.
Giải: (1)
x x x
( 3) 1 4
x = 3; x =
3 2 3
4/ Tìm m để phương trình sau có nghiệm x
0; 1 3



:
(2)
Giải: Đặt
2
t x 2x 2
. (2)
2
t2
m (1 t 2),dox [0;1 3]
t1
Khảo sát
2
t2
g(t)
t1
với 1 t 2. g'(t)
2
2
t 2t 2
0
(t 1)


. Vậy g tăng trên [1,2]
Do đó, ycbt
bpt
2
t2
m
t1
có nghiệm t [1,2]
t
m g t g
1;2
2
max ( ) (2)
3
5/ Giải hệ phương trình :
x x y y
x y x y
4 2 2
22
4 6 9 0
2 22 0
(2)
Giải: (2)
2 2 2
22
( 2) ( 3) 4
( 2 4)( 3 3) 2 20 0
xy
xyx
. Đặt
2
2
3


xu
yv
Khi đó (2)
22
4
. 4( ) 8

uv
u v u v
2
0
u
v
hoặc
0
2
u
v
2
3
x
y
;
2
3

x
y
;
2
5
x
y
;
2
5

x
y
6/ 1) Giải phương trình:
2 1 1 1
5.3 7.3 1 6.3 9 0
x x x x
(1)
2) Tìm tất cả các giá trị của tham số m để hệ phương trình sau có 2 nghiệm phân biệt:
xx
x x a
x x m b
2
3
33
2
2
( 2 5)
log ( 1) log ( 1) log 4 ( )
log ( 2 5) log 2 5 ( )

Giải: 1) Đặt
30
x
t 
. (1)
2
5 7 3 3 1 0 t t t
33
3
log ; log 5
5
xx
2)
2
3
33
2
2
( 2 5)
log ( 1) log ( 1) log 4 ( )
log ( 2 5) log 2 5 ( )

xx
x x a
x x m b
Giải (a) 1 < x < 3.
Xét (b): Đặt
2
2
log ( 2 5) t x x
. Từ x (1; 3) t (2; 3).
(b)
2
5t t m
. Xét hàm
2
( ) 5f t t t
, từ BBT
25
;6
4



m
7/ Giải hệ phương trình:
3 3 3
22
8 27 18
46


x y y
x y x y
Giải: (2)
x
y
xx
yy
3
3
3
(2 ) 18
33
2 . 2 3








. Đặt a = 2x; b =
y
3
. (2)
ab
ab
3
1

Hệ đã cho có nghiệm:
3 5 6 3 5 6
; , ;
44
3 5 3 5


8/ Giải bất phương trình sau trên tập số thực:
11
2 3 5 2
x x x
(1)
Giải: Với
1
2
2
x
:
2 3 0, 5 2 0 x x x
, nên (1) luôn đúng
Với
15
22
x
: (1)
2 3 5 2 x x x
5
2
2
x
Tập nghiệm của (1) là
15
2; 2;
22


S
9/ Giải hệ phương trình:
2
2
1 ( ) 4
( 1)( 2)
x y y x y
x y x y
(x, y
)
Giải: (2)
2
2
2
1
22
1
1
1
( 2) 1
21



x
yx
x
y
y
x
yx
yx
y
1
2
x
y
hoặc
2
5

x
y
10/ Giải bất phương trình:
)3(log53loglog
2
4
2
2
2
2
xxx
Giải: BPT
22
2 2 2
log log 3 5(log 3) (1) x x x
Đặt t = log
2
x. (1)
2
2 3 5( 3) ( 3)( 1) 5( 3) t t t t t t
2
2
2
1
log 1
1
3
3 4 3 log 4
( 1)( 3) 5( 3)



t
x
t
t
tx
t t t
1
0
2
8 16


x
x
11/Giải phương trình:
2 2 2 2 2
log ( 1) ( 5)log( 1) 5 0 x x x x
Giải: Đặt
2
log( 1)xy
. PT
2 2 2 2
( 5) 5 0 5 y x y x y y x
; Nghiệm:
99999x
; x = 0
12/ Giải phương trình:
3
1
8 1 2 2 1
xx
Giải: Đặt
3
1
2 0; 2 1
xx
uv
.
PT
33
3
3 2 2
0
1 2 1 2
2 1 0
1 2 ( )( 2) 0






uv
u v u v
uu
v u u v u uv v
2
0
15
log
2

x
x
13/ Tìm m để hệ phương trình:
22
22
2
4
x y x y
m x y x y
có ba nghiệm phân biệt
Giải: Hệ PT
42
2
2
( 1) 2( 3) 2 4 0 (1)
2
1
m x m x m
x
y
x
.
Khi m = 1: Hệ PT
2
2
2
2 1 0
()
2
1

x
VN
x
y
x
Khi m ≠ 1. Đặt t = x
2
,
0t
. Xét
2
( ) ( 1) 2( 3) 2 4 0 (2) f t m t m t m
Hệ PT có 3 nghiệm phân biệt (1) có ba nghiệm x phân biệt
(2) có một nghiệm t = 0 và 1 nghiệm t > 0
(0) 0
... 2
23
0
1

f
m
m
S
m
.
14/ Tìm m để hệ phương trình có nghiệm:
1
13

xy
x x y y m
.
Giải: Đặt
, ( 0, 0) u x v y u v
. Hệ PT
33
1
1
13



uv
uv
uv m
u v m
. ĐS:
1
0
4
m
.
15/ Tìm m để phương trình sau có nghiệm:
( 1) 4( 1)
1
x
x x x m
x
Giải: Đặt
( 1)
1
x
tx
x

. PT có nghiệm khi
2
40t t m
có nghiệm, suy ra
4m 
.
16/ Giải phương trình: 3
x
.2x = 3
x
+ 2x + 1
Giải: Nhận xét; x =
1 là các nghiệm của PT. PT
21
3
21

x
x
x
.
Dựa vào tính đơn điệu PT chỉ có các nghiệm x = 1.
17/ Giải hệ phương trình:
22
22
3 ( )
1 1 4 ( )
x y xy a
x y b
Giải (b)
2 2 2 2 2
2 ( 1).( 1) 14 2 ( ) 4 11 x y x y xy xy xy
(c)
Đặt xy = p.
2
2
3
11
( ) 2 4 11
35
3 26 105 0
3
p
p
c p p p
p
pp
(a)
2
33 x y xy
p = xy =
35
3
(loại) p = xy = 3
23 xy
1/ Với
3
3
23

xy
xy
xy
2/ Với
3
3
23
xy
xy
xy
Vậy hệ có hai nghiệm là:
3; 3 , 3; 3
18/ Giải bất phương trình:
2
21
2
1
log (4 4 1) 2 2 ( 2)log
2



x x x x x
Giải: BPT
01)x21(logx
2
1
2



x
2
1
x
4
1
hoặc x < 0
19/ Giải hệ phương trình:
2
2
1 ( ) 4
( 1)( 2)
x y x y y
x x y y
(x, y
R
)
Giải: y = 0 không phải là nghiệm. Hệ PT
2
2
1
22
1
( 2) 1
x
xy
y
x
xy
y
Đặt
2
1
,2
x
u v x y
y
. Ta có hệ
2
1
1

uv
uv
uv
2
1
1
21
x
y
xy
Nghiệm của hpt đã cho là (1; 2), (–2; 5).
20/ Tìm m sao cho phương trình sau có nghiệm duy nhất:
ln( ) 2ln( 1)mx x
Giải: 1) ĐKXĐ:
1, 0 x mx
. Như vậy trước hết phải có
0m
.
Khi đó, PT
22
( 1) (2 ) 1 0 mx x x m x
(1)
Phương trình này có:
2
4
mm
.
Với
(0;4)m
< 0 (1) vô nghiệm.
Với
0m
, (1) có nghiệm duy nhất
1x
< 0 loại.
Với
4m
, (1) có nghiệm duy nhất x = 1 thoả ĐKXĐ nên PT đã cho có nghiệm duy nhất.
Với
0m
, ĐKXĐ trở thành
10 x
. Khi đó
0
nên (1) có hai nghiệm phân biệt
1 2 1 2
, x x x x
.
Mặt khác,
( 1) 0, (0) 1 0 f m f
nên
12
10 xx
, tức là chỉ có
2
x
là nghiệm của phương trình
đã cho. Như vậy, các giá trị
0m
thoả điều kiện bài toán.
Với
4m
. Khi đó, điều kiện xác định trở thành x > 0 và (1) cũng có hai nghiệm phân biệt
1 2 1 2
, x x x x
. Áp dụng định lý Viet, ta thấy cả hai nghiệm này đều dương nên các giá trị
4m
cũng
bị loại.
Tóm lại, phương trình đã cho có nghiệm duy nhất khi và chỉ khi:
( ;0) 4  m
.
21/ Giải hệ phương trình:
22
22
91 2 (1)
91 2 (2)
x y y
y x x
Giải: Điều kiện: x ≥ 2 và y ≥ 2 : Lấy (1) trừ (2) vế theo vế ta được:
2 2 2 2
91 91 2 2 x y y x y x
22
22
( )( )
22
91 91

x y y x
y x y x
yx
xy
22
1
( ) 0
22
91 91




xy
x y x y
xy
xy
x = y (trong ngoặc luôn dương và x và y đều lớn hơn 2)
Vậy từ hệ trên ta có:
22
91 2 x x x
22
91 10 2 1 9 x x x
2
2
93
( 3)( 3)
21
91 10



xx
xx
x
x
2
11
( 3) ( 3) 1 0
21
91 10









xx
x
x
x = 3
Vậy nghiệm của hệ x = y = 3
22/ Giải bất phương trình:
22
log ( 3 1 6) 1 log (7 10 ) xx
Giải: Điều kiện:
1
10
3
x
BPT
22
3 1 6
log log (7 10 )
2

x
x
3 1 6
7 10
2

x
x
3 1 6 2(7 10 ) xx
3 1 2 10 8 xx
49x
2
– 418x + 369 ≤ 0
1 ≤ x ≤
369
49
(thoả)
23/ Giải phương trình:
22
2 1 2 ( 1) 2 3 0 x x x x x x
Giải:
Đặt:
22
2 2 2
22
22
2
2
21
2, 0 2
1
23
2 3, 0
2



v u x
u x u u x
vu
v x x
x
v x x v
PT
0 ( )
1
( ) ( ) 1 0
1
( ) 1 0 ( )
22
22










v u b
vu
v u v u
vu
v u c
Vì u > 0, v > 0, nên (c) vô nghiệm.
Do đó: PT
22
1
0 2 3 2
2
v u v u x x x x
24/ Giải bất phương trình:
22
3 2 2 3 1 1 x x x x x
Giải: Tập xác định: D =
1
; 1 2;
2

 

x = 1 là nghiệm
x
2: BPT
2 1 2 1 x x x
vô nghiệm
x
1
2
: BPT
2 1 1 2 x x x
có nghiệm x
1
2
BPT có tập nghiệm S=
1
;1
2



25/ Giải phương trình:
22
2( 1) 3 1 2 2 5 2 8 5 x x x x x x
.
Giải:
Điều kiện:
1
3
x
.
PT
2 2 2
22
( 1) 2( 1) 3 1 3 1 2 2 2 5 2 2 1 0


x x x x x x x x
26/
Giải hệ phương trình:
x x y xy y
x y x y
3 2 2 3
6 9 4 0
2
Giải:
x x y xy y
x y x y
3 2 2 3
6 9 4 0 (1)
2 (2)
. Ta có: (1)
x y x y
2
( ) ( 4 ) 0
xy
xy
4
Với x = y: (2) x = y = 2
Với x = 4y: (2)
xy
32 8 15; 8 2 15
27/ Giải phương trình:
x x x x
2 2 2
3 1 tan 1
6
Giải:
PT
x x x x
2 4 2
3
3 1 1
3
(1)
Chú ý:
x x x x x x
4 2 2 2
1 ( 1)( 1)
,
x x x x x x
2 2 2
3 1 2( 1) ( 1)
Do đó: (1)
x x x x x x x x
2 2 2 2
3
2( 1) ( 1) ( 1)( 1)
3
.
Chia 2 vế cho
x x x x
2
22
11
và đặt
xx
tt
xx
2
2
1
,0
1



Ta được: (1)
tt
2
3
2 1 0
3
t
t
3
0
23
1
3

xx
xx
2
2
11
3
1


x
1
.
28/ Giải hệ phương trình:
x x y
x x y xy x
2
3 2 2
59
3 2 6 18
Giải: Hệ PT
y x x
x x x x+
2
4 3 2
95
4 5 18 18 0
xy
xy
xy
xy
1; 3
3; 15
1 7; 6 3 7
1 7; 6 3 7

29/ Giải bất phương trình:
x x x
3 12 2 1
Giải: BPT
x
34
.
30/ Giải hệ phương trình:
x y xy
xy
20
1 4 1 2
.
Giải : Hệ PT
x y x y
xy
20
1 4 1 2
xy
xy
20
1 4 1 2

xy
y
4
4 1 1

y x x
x
x
x
2
95
1
3
17

x
y
2
1
2
31/ Giải hệ phương trình:
x y y
x y x y
3 3 3
22
8 27 7 (1)
4 6 (2)


Giải:
Từ (1) y 0. Khi đó Hệ PT
x y y
x y xy y
3 3 3
2 2 3
8 27 7
46


t xy
t t t
32
8 27 4 6
t xy
t t t
3 1 9
;;
222
Với
t
3
2

: Từ (1) y = 0 (loại). Với
t
1
2
: Từ (1)
xy
3
3
1
;4
24




Với
t
9
2
: Từ (1)
xy
3
3
3
; 3 4
24




32/ Giải phương trình:
xx
xx
3 .2 3 2 1
Giải
PT
x
xx
3 (2 1) 2 1
(1). Ta thấy
x
1
2
không phải là nghiệm của (1).
Với
x
1
2
, ta có: (1)
x
x
x
21
3
21
x
x
x
21
30
21

Đặt
xx
x
fx
xx
2 1 3
( ) 3 3 2
2 1 2 1

. Ta có:
x
f x x
x
2
61
( ) 3 ln3 0,
2
(2 1)
Do đó f(x) đồng biến trên các khoảng
1
;
2




và
1
;
2




Phương trình f(x) = 0 có nhiều nhất 1
nghiệm trên từng khoảng
11
; , ;
22
 
.
Ta thấy
xx
1, 1
là các nghiệm của f(x) = 0. Vậy PT có 2 nghiệm
xx
1, 1
.
33/ Giải phương trình:
x x x x
4
22
1 1 2
Giải:
Điều kiện:
x
xx
2
2
10
1


x 1.
Khi đó:
x x x x x x
4
2 2 2
1 1 1
(do x 1)
VT >
Coâ Si
x x x x x x x x
44
8
2 2 2 2
1 1 2 1 1
= 2 PT vô nghiệm.
34/ Giải hệ phương trình:
xy
xy
xy
x y x y
22
2
2
1
Giải:
xy
xy
xy
x y x y
22
2
2
1 (1)
(2)
. Điều kiện:
xy
0
.
(1)
x y xy
xy
2
1
( ) 1 2 1 0



x y x y x y
22
( 1)( ) 0
xy
10
(vì
xy
0
nên
x y x y
22
0
)
Thay
xy
1
vào (2) ta được:
xx
2
1 (1 )
xx
2
20
xy
xy
1 ( 0)
2 ( 3)

Vậy hệ có 2 nghiệm: (1; 0), (–2; 3).
35/ Giải hệ phương trình:
xx
3
2 3 2 3 6 5 8 0
Giải: Điều kiện:
x
6
5
. Đặt
ux
vx
3
32
65


ux
vx
3
2
32
65


.
Ta có hệ PT:
uv
uv
32
2 3 8
5 3 8


. Giải hệ này ta được
u
v
2
4

x
x
3 2 2
6 5 16

x
2
.
Thử lại, ta thấy
x
2
là nghiệm của PT. Vậy PT có nghiệm
x
2
.
36/ Giải hệ phương trình:
22
33
21
22
yx
x y y x

Giải: Ta có:
3 3 2 2 3 2 2 3
2 2 2 2 2 5 0x y y x y x x x y xy y
Khi
0y
thì hệ VN.
Khi
0y
, chia 2 vế cho
3
0y
ta được:
32
2 2 5 0
x x x
y y y
Đặt
x
t
y
, ta có :
32
2 2 5 0 1t t t t
2
1, 1
1
yx
x y x y
y
37/ Tìm các giá trị của tham số m sao cho hệ phương trình


y x m
y xy
2
1
có nghiệm duy nhất.
Giải:


y x m
y xy
2 (1)
1 (2)
.
Từ (1)

x y m
2
, nên (2)
y my y
2
21
y
my
y
1
1
2
(vì y 0)
Xét
f y y f y
y
y
2
11
2 ' 1 0
Dựa vào BTT ta kết luận được hệ có nghiệm duy nhất

m
2
.
38/ Giải hệ phương trình:
x y xy
xy
33
22
34
9

Giải: Ta có :
22
93x y xy
.
Khi:
3xy
, ta có:
33
4xy
và
33
. 27 xy
Suy ra:
33
; xy
là các nghiệm của phương trình:
2
4 27 0 2 31X X X
Vậy nghiệm của Hệ PT là:
33
2 31, 2 31xy
hoặc
33
2 31, 2 31xy
.
Khi:
3xy 
, ta có:
33
4xy
và
33
. 27xy
Suy ra:
33
;xy
là nghiệm của phương trình:
2
4 27 0 ( ) X X PTVN
39/ Giải hệ phương trình:
y
x
xy
x
xy
y
22
22
3
21
1
4 22


Giải: Điều kiện:
x y x y
22
0, 0, 1 0
Đặt
x
u x y v
y
22
1;
. Hệ PT trở thành:
u v u v
u v u v
3 2 3 2
1 1 (1)
1 4 22 21 4 (2)





Thay (2) vào (1) ta được:
v
vv
v
vv
2
3
32
1 2 13 21 0
7
21 4
2
Nếu v = 3 thì u = 9, ta có Hệ PT:
xy
xx
xy
x
yy
xy
y
22
22
19
33
10
11
3
3



Nếu
v
7
2
thì u = 7, ta có Hệ PT:
yy
xy
xy
x
xy
y
xx
22
22
22
44
17
8
53 53
7
7
22
2
14 14
2
53 53





So sánh điều kiện ta được 4 nghiệm của Hệ PT.
40/ Giải hệ phương trình:
2
32
28
x y xy
xy


Giải:
2
3 2 (1)
2 8 (2)


x y xy
xy
. Điều kiện :
. 0 ;x y x y
Ta có: (1)
2
3( ) 4 (3 )( 3 ) 0 x y xy x y x y
3
3
y
x y hay x
Với
3xy
, thế vào (2) ta được :
2
6 8 0 2 ; 4y y y y
Hệ có nghiệm
6 12
;
24
xx
yy





Với
3
y
x
, thế vào (2) ta được :
2
3 2 24 0yy
Vô nghiệm.
Kết luận: hệ phương trình có 2 nghiệm là:
6 12
;
24
xx
yy





41/ Giải hệ phương trình:
22
22
14
( ) 2 7 2
x y xy y
y x y x y
Giải: Từ hệ PT
0y
. Khi đó ta có:
2
22
22
2
2
1
4
14
.
( ) 2 7 2
1
( ) 2 7
x
xy
y
x y xy y
y x y x y
x
xy
y

Đặt
2
1
,
x
u v x y
y
ta có hệ:
22
4 4 3, 1
2 7 2 15 0 5, 9
u v u v v u
v u v v v u


Với
3, 1vu
ta có hệ:
222
1, 2
1 1 2 0
2, 5
3 3 3
xy
x y x y x x
xy
x y y x y x




.
Với
5, 9vu
ta có hệ:
222
1 9 1 9 9 46 0
5 5 5
x y x y x x
x y y x y x




, hệ này vô nghiệm.
Kết luận: Hệ đã cho có hai nghiệm:
(1; 2), ( 2;5)
.
42/ Giải phương trình:
x x x
2
11 4 3
Giải: Điều kiện
x
0
.
PT
x x x
2
4 1 3 1 0
x
xx
xx
21
(2 1)(2 1) 0
31

xx
xx
1
(2 1) 2 1 0
31




x
2 1 0
x
1
2
.
43 / Giải hệ phương trình:
2
12
12
2log ( 2 2) log ( 2 1) 6
log ( 5) log ( 4) = 1
xy
xy
xy x y x x
yx


Giải: Điều kiện:
2
2 2 0, 2 1 0, 5 0, 4 0
(*)
0 1 1, 0 2 1
xy x y x x y x
xy
Hệ PT
1 2 1 2
1 2 1 2
2log [(1 )( 2)] 2log (1 ) 6 log ( 2) log (1 ) 2 0 (1)
log ( 5) log ( 4) = 1 log ( 5) log ( 4) = 1 (2)





x y x y
x y x y
x y x y x
y x y x
Đặt
2
log (1 )
y
xt

thì (1) trở thành:
2
1
2 0 ( 1) 0 1.t t t
t
Với
1t
ta có:
1 2 1 (3) x y y x
. Thế vào (2) ta có:
2
1 1 1
44
log ( 4) log ( 4) = 1 log 1 1 2 0
44
x x x
xx
x x x x x
xx

0
2
x
x

Với
x
0
y
1
(không thoả (*)).
Với
x
2
y
1
(thoả (*)).
Vậy hệ có nghiệm duy nhất
2, 1xy
.
44/ Giải bất phương trình:
x
xx x
x
1
2
2
4 – 2.2 – 3 .log – 3 4 4

Giải:BPT
x x x x
x
1
2
(4 2.2 3).log 3 2 4
xx
x
2
(4 2.2 3).(log 1) 0
xx
xx
x
x
2
2
2
2
2
2
2.2 3 0
log 1 0
2.2 3 0
log 1 0


x
x
x
x
2
2
23
log 1
23
log 1


x
x
x
x
2
2
log 3
1
2
log 3
1
0
2

x
x
2
log 3
1
0
2

45/ Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất:
x
ax
55
log (25 – log )
Giải: PT
xx
a
5
25 log 5
xx
a
2
5
5 5 log 0
x
tt
t t a
2
5
5 , 0
log 0 (*)

PT đã cho có nghiệm duy nhất (*) có đúng 1 nghiệm dương
t t a
2
5
log
có đúng 1 nghiệm
dương.
Xét hàm số
f t t t
2
()
với t [0; +∞). Ta có:
f t t
( ) 2 1

f t t
1
( ) 0
2
.
f
11
24




,
f
(0) 0
.
Dựa vào BBT ta suy ra phương trình
f t a
5
( ) log
có đúng 1 nghiệm dương
a
a
5
5
log 0
1
log
4

a
a
4
1
1
5
.
46/ Giải hệ phương trình:
x x x
2 2 2
3 3 3
2log – 4 3 log ( 2) log ( – 2) 4
Giải: Điều kiện:
x
x
2
2
3
40
log ( 2) 0


x
x
2
2
40
( 2) 1


x
x
2
3

(**)
PT
x x x
2
2 2 2
3 3 3
log – 4 3 log ( 2) log ( – 2) 4
xx
22
33
log ( 2) 3 log ( 2) 4 0
xx
22
33
log ( 2) 4 log ( 2) 1 0
x
2
3
log ( 2) 1
x
2
( 2) 3
x
23
Kiểm tra điều kiện (**) chỉ có
x
23
thỏa mãn.
Vậy phương trình có nghiệm duy nhất là:
x
23
47 / Giải hệ phương trình:
x y y x
yx
33
22
4 16
1 5(1 )
.
Giải:
x y y x
yx
33
22
4 16 (1)
1 5(1 ) (2)
Từ (2) suy ra
yx
22
– 5 4
(3).
Thế vào (1) được:
yx x y y x
2233
–5 . 16
x x y x
32
– 5 –16 0
x
0
hoặc
x xy
2
– 5 –16 0
Với
x
0
y
2
4
y
2
.
Với
x xy
2
– 5 –16 0
x
y
x
2
16
5
(4). Thế vào (3) được:
x
x
x
2
2
2
16
54
5




x x x x
4 2 4 2
– 32 256 –125 100
x x
42
124 132 – 256 0
x
2
1
xy
xy
1 ( 3)
1 ( 3)
.
Vậy hệ có 4 nghiệm: (x; y) = (0; 2) ; (0; –2); (1; –3); (–1; 3)
48/ Giải hệ phương trình:
x y x y
x y x y
28
2 2 2 2
log 3log ( 2)
13
Giải: Điều kiện:
x y x y
0, 0
Hệ PT
x y x y
x y x y
2 2 2 2
2
13
.
Đặt:
u x y
v x y


ta có hệ:
u v u v u v uv
u v u v
uv uv
2 2 2 2
2 ( ) 2 4
22
33
22





u v uv
u v uv
uv
2
2 4 (1)
( ) 2 2
3 (2)
2

.
Thế (1) vào (2) ta có:
uv uv uv uv uv uv uv
2
8 9 3 8 9 (3 ) 0
.
Kết hợp (1) ta có:
uv
uv
uv
0
4, 0
4

(với u > v). Từ đó ta có: x = 2; y = 2.(thoả đk)
Kết luận: Vậy nghiệm của hệ là: (x; y) = (2; 2).
49/ Giải phương trình: 25
x
– 6.5
x
+ 5 = 0
Giải: Câu 2: 1) 25
x
– 6.5
x
+ 5 = 0
2
(5 ) 6.5 5 0
xx
5
x
= 1 hay 5
x
= 5
x = 0 hay x = 1.
50/ Giải hệ phương trình:
20
1 4 1 2
x y xy
xy
Giải:
2 0 (1)
1 4 1 2 (2)
x y xy
xy
Điều kiện:
1
1
4
x
y
Từ (1)
20
xx
yy
x = 4y
Nghiệm của hệ (2;
1
2
)
51/ Tìm m để bất phương trình: 5
2x
– 5
x+1
– 2m5
x
+ m
2
+ 5m > 0 thỏa với mọi số thực x.
Giải: Đặt X = 5
x
X > 0
Bất phương trình đã cho trở thành: X
2
+ (5 + 2m)X + m
2
+ 5m > 0 (*)
Bpt đã cho có nghiệm với mọi x khi và chỉ khi (*) có nghiệm với mọi X > 0
< 0 hoặc (*) có hai nghiệm X
1
≤ X
2
≤ 0
Từ đó suy ra m
52/ Giải bất phương trình:
2
3 1 1
33
1
log 5 6 log 2 log 3
2
x x x x
Giải: Điều kiện:
3x
; Phương trình đã cho tương đương:
11
2
3
33
1 1 1
log 5 6 log 2 log 3
2 2 2
x x x x

2
3 3 3
1 1 1
log 5 6 log 2 log 3
2 2 2
x x x x
3 3 3
log 2 3 log 2 log 3x x x x


33
2
log 2 3 log
3
x
xx
x





2
23
3
x
xx
x
2
10
91
10
x
x
x

Giao với điều kiện, ta được nghiệm của phương trình đã cho là
10x
53/ Cho phương trình
3
4
1 2 1 2 1x x m x x x x m
Tìm m để phương trình có một nghiệm duy nhất.
Giải: Phương trình
3
4
1 2 1 2 1x x m x x x x m
(1)
Điều kiện :
01x
Nếu
0;1x
thỏa mãn (1) thì 1 – x cũng thỏa mãn (1) nên để (1) có nghiệm duy nhất thì cần có điều kiện
1
1
2
x x x
. Thay
1
2
x
vào (1) ta được:
3
0
11
2. 2.
1
22
m
mm
m

*Với m = 0; (1) trở thành:
2
44
1
10
2
x x x
Phương trình có nghiệm duy nhất.
* Với m = -1; (1) trở thành
4
4
22
44
1 2 1 2 1 1
1 2 1 1 2 1 0
1 1 0
x x x x x x
x x x x x x x x
x x x x
+ Với
44
1
10
2
x x x
+ Với
1
10
2
x x x
Trường hợp này, (1) cũng có nghiệm duy nhất.
* Với m = 1 thì (1) trở thành:
22
44
4
1 2 1 1 2 1 1 1x x x x x x x x x x
Ta thấy phương trình (1) có 2 nghiệm
1
0,
2
xx
nên trong trường hợp này (1) không có nghiệm duy nhất.
Vậy phương trình có nghiệm duy nhất khi m = 0 và m = -1.
54/ Giải phương trình :
23
48
2
log 1 2 log 4 log 4x x x
Giải:
23
48
2
log 1 2 log 4 log 4x x x
(2)
Điều kiện:
10
44
40
1
40
x
x
x
x
x




2
2 2 2 2 2
22
22
(2) log 1 2 log 4 log 4 log 1 2 log 16
log 4 1 log 16 4 1 16
x x x x x
x x x x
+ Với
14x
ta có phương trình
2
4 12 0 (3)xx
;
2
(3)
6
x
x

lo¹i
+ Với
41x
ta có phương trình
2
4 20 0xx
(4);
2 24
4
2 24
x
x


lo¹i
; Vậy phương trình đã cho có hai nghiệm là
2x
hoặc
2 1 6x 
55/ 1). Giải phương trình: 2x +1 +x
22
2 1 2x 3 0
x x x
2) Giải phương trình:
1
4 2 2 2 1 sin 2 1 2 0
x x x x
y
.
3) Giải bất phương trình:
22
12
9 1 10.3
x x x x

.
Giải
1) Giải phương trình : 2x +1 +x
22
2 1 2x 3 0
x x x
. (a)
* Đặt:



22
2 2 2
22
22
2
2
v u 2x 1
u x 2, u 0 u x 2
v u 1
v x 2x 3
x
v x 2x 3, v 0
2
Ta có:










2 2 2 2 2 2 2 2
2 2 2 2
v u 1 v u 1 v u u v u v
(a) v u .u 1 .v 0 v u .u .v 0
2 2 2 2 2 2
v u 0 (b)
v u 1
(v u) (v u) 1 0
v u 1
(v u) 1 0 (c)
22
22
Vì u > 0, v > 0, nên (c) vô nghiệm.
Do đó:
2 2 2 2
1
(a) v u 0 v u x 2x 3 x 2 x 2x 3 x 2 x
2
Kết luận, phương trình có nghiệm duy nhất: x =
1
2
.
2) Giải phương trình
1
4 2 2 2 1 sin 2 1 2 0
x x x x
y
(*)
Ta có: (*)
2
2
2 1 sin 2 1 0(1)
2 1 sin 2 1 os 2 1 0
os 2 1 0(2)
xx
x x x
x
y
y c y
cy
Từ (2)
sin 2 1 1
x
y
.
Khi
sin 2 1 1
x
y
, thay vào (1), ta được: 2
x
= 0 (VN)
Khi
sin 2 1 1
x
y
, thay vào (1), ta được: 2
x
= 2 x = 1.
Thay x = 1 vào (1) sin(y +1) = -1
1,
2
y k k Z
.
Kết luận: Phương trình có nghiệm:
1; 1 ,
2
k k Z



.
3) Giải bất phương trình:
22
12
9 1 10.3
x x x x

. Đặt
2
3
xx
t
, t > 0.
Bất phương trình trở thành: t
2
– 10t + 9 0 ( t 1 hoặc t 9)
Khi t 1
2
2
3 1 0 1 0
xx
t x x x
.(i)
Khi t 9
2
2
2
3 9 2 0
1
xx
x
t x x
x

(2i)
Kết hợp (i) và (2i) ta có tập nghiệm của bpt là: S = (- ; -2][-1;0][1; + ).
56/ Giải phương trình, hệ phương trình:
1.
3
log
1
22
2
x
x x x



; 2.
22
22
12
12
x y x y
y x y

Giải: 1) Phương trình đã cho tương đương:
3
3
log
log
3
20
2
20
1
1
1
log ln 0
ln 0
1
2
2
2
2
2
20
x
x
x
x
x
xx
x
x
x
x
x

















3
2
22
log 0
11
2
1
13
ln 0
1
2
22
22
2
x
xx
x
xx
x
x
xx
xx
x






















Điều kiện:
| | | |xy
Đặt
22
;0u x y u
v x y

;
xy
không thỏa hệ nên xét
xy
ta có
2
1
2
u
yv
v




.
2) Hệ phương trình đã cho có dạng:
2
12
12
2
uv
uu
v
v





4
8
u
v
hoặc
3
9
u
v
+
22
4
4
8
8
u
xy
v
xy



(I)
+
22
3
3
9
9
u
xy
v
xy



(II) Giải hệ (I), (II). Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ
phương trình ban đầu là
5;3 , 5;4S
Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ phương
trình ban đầu là
5;3 , 5;4S
57/ Giải hệ phương trình:
yyxx
yyxyx
)2)(1(
4)(1
2
2
(x, y
R
)
Giải:
2) Hệ phương trình tương đương với
2
2
1
( 2) 2
1
( 2) 1
x
xy
y
x
xy
y
Đặt
2yxv,
y
1x
u
2
Ta có hệ
1vu
1uv
2vu
Suy ra
12yx
1
y
1x
2
.
Giải hệ trên ta được nghiệm của hệ phưng trình đã cho là (1; 2), (-2; 5)
58 / Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
22
1 1 1 1
9 ( 2)3 2 1 0
xx
mm
(1)
Giải: * Đk
[-1;1]
x
, đặt t =
2
11
3
x

;
[-1;1]
x

[3;9]
t
Ta có: (1) viết lại
2
22
21
( 2) 2 1 0 ( 2) 2 1
2
tt
t m t m t m t t m
t

Xét hàm số f(t) =
2
21
2
tt
t

, với
[3;9]
t
. Ta có:
2
//
1
43
( ) , ( ) 0
3
( 2)
t
tt
f t f t
t
t

Lập bảng biến thiên
t
3 9
f
/
(t)
+
f(t)
48
7
4
Căn cứ bảng biến thiêng, (1) có nghiệm
[-1;1]
x
(2) có nghiệm
[3;9]
t
48
4
7
m

59/ Giải phương trình:
( ) ( ) ( )
2 3 3
1 1 1
4 4 4
3
log x 2 3 log 4 x log x 6
2
+ - = - + +
Giải: bất phương trình:
)
7
1
(log)54(log
2
1
2
1
2
2
x
xx
(1)
Đk:

7
);1()5;(
07
054
2
x
x
x
xx
)1()5;7( x
Từ (1)
7
1
log2)54(log
2
2
2
x
xx
2 2 2 2
22
log ( 4 5) log ( 7) 4 5 14 49
27
10 54
5
x x x x x x x
xx
Kết hợp điều kiện: Vậy BPT có nghiệm:
)
5
27
;7(
x
60/ Giải hệ phương trình :
22
1
322
33
yxyyx
yx
Giải:
)2(022
)1(1
22
1
2233
33
322
33
xyyxyx
yx
yxyyx
yx
y
0
. Ta có:
)4(0122
)3(1
23
33
y
x
y
x
y
x
yx
Đặt :
t
y
x
(4) có dạng : 2t
3
– t
2
– 2t + 1 = 0
t =
,1
t =
2
1
.
a) Nếu t = 1 ta có hệ
3
33
2
1
1
yx
yx
yx
b) Nếu t = -1 ta có hệ
yx
yx 1
33
hệ vô nghiệm.
c) Nếu t =
2
1
ta có hệ
3
32
,
3
3
2
1
33
33
yx
xy
yx
61/ Tìm m để phương trình sau có nghiệm thực:
mxx
4
2
1
Giải: D = [0 ; +
)
*Đặt f(x) =
x
x
x
x
xx
xx
xxx
x
x
x
xfxx
.)
1
1(2
)
1
1(
.)1(2
)1(
2
1
)1(2
)('1
4
3
2
2
3
4
3
2
2
3
2
3
4
32
4
32
4
32
4
2
Suy ra: f’(x) =
);0(0
.)
1
1(2
)
1
1(1
4
3
2
4
3
2
x
x
x
x
*
0
)1)(1(
1
lim
1
1
lim)1(lim
2
4
2
22
4
2
2
4
2

xxxx
xx
xx
xx
xx
xxx
* BBT x 0 +
f’(x)
f(x) 1
0
Vậy: 0 < m
1
62/ Giải bất phương trình:
3log3log
3
xx
Giải: ĐK :
3
1
0
x
x
x
Bất phương trình trở thành :
0
1log
1
log
1
1log
1
log
1
3
log
1
log
1
3333
3
3
xxxx
x
x
1log0log0)1(loglog0
)1(loglog
1
3333
33
xxxx
xx
*
10log
3
xx
kết hợp ĐK : 0 < x < 1
*
30log
3
xx
Vậy tập nghiệm của BPT: x
);3()1;0(
63/ .Giải bất phương trình
)3(log53loglog
2
4
2
2
2
2
xxx
Giải: ĐK:
03loglog
0
2
2
2
2
xx
x
Bất phương trình đã cho tương đương với
)1()3(log53loglog
2
2
2
2
2
xxx
Đặt t = log
2
x,
2.BPT (1)
)3(5)1)(3()3(532
2
tttttt
4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t
168
2
1
0
x
x
Vậy bất phương trình đã cho có nghiệm là
)16;8(]
2
1
;0(
64/ Giải hệ phương trình
22
22
91 2 (1)
91 2 (2)
x y y
y x x
Giải: Điều kiện: x ≥ 2 và y ≥ 2 : Lấy (1) trừ (2) vế theo vế ta được:
2 2 2 2
91 91 2 2x y y x y x
22
22
( )( )
22
91 91
x y y x
y x y x
yx
xy

22
1
( ) 0
22
91 91
xy
x y x y
xy
xy




x = y (trong ngoặc luôn dương và x vay đều lớn hơn 2)
Vậy từ hệ trên ta có:
22
91 2x x x
22
91 10 2 1 9x x x
2
2
93
( 3)( 3)
21
91 10
xx
xx
x
x



2
11
( 3) ( 3) 1 0
21
91 10
xx
x
x









x = 3
Vậy nghiệm của hệ x = y = 3
65/ Giải phương trình:
33
x 34 x 3 1
Đặt
33
u x 34, v x 3
. Ta có:
22
33
u v 1
u v 1
u v u v uv 37
u v 37




2
u v 1
u v 1
uv 12
u v 3uv 37




u3
v4
u4
v3

Với = -3 , v = - 4 ta có : x = - 61
Với = 4, v = 3 ta có : x = 30 vậy phương trình đã cho có 2 nghiệm: x = -61 vµ x = 30
66/ Giải bấ phương trình
)3(log53loglog
2
4
2
2
2
2
xxx
Giải: §K:
03loglog
0
2
2
2
2
xx
x
Bất phương trình đã cho tương đương với
)1()3(log53loglog
2
2
2
2
2
xxx
Đặt t = log
2
x,
BPT (1)
)3(5)1)(3()3(532
2
tttttt
4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t
168
2
1
0
x
x
Vậy bất phương trình đã cho có nghiệm là
)16;8(]
2
1
;0(
67/ .
1. Giải phương trình:
3510325.3
22
xx
xx
2.Giải phương trình:
02coscoslogsincoslog
1
xxxx
x
x
.
3) Giải bất phương trình:
01311
23
xxxx
Giải:
1.
015.3315.315.35
3510325.3
2222
22
xxxx
xx
x
xx
2035
1015.3
03515.3
2
2
22
x
x
x
x
xx
Giải:
3log2
3
1
log2
3
1
51
55
2
x
x
352
2
x
x
Vế trái là hàm đồng biến vế phải là hàm nghịch biến mà (2) có nghiệm x = 2 nên là nghiệm duy nhất.
Vậy Pt có nghiệm là: x =
3log2
5
và x = 2
2/
02coscoslogsincoslog
1
xxxx
x
x
Điều kiện:
02coscos
0sincos
10
xx
xx
x
. Khi đó Pt
2
cos2cossin2cos
xxxx
3
2
6
2
2
2
2
2
2
2
2
k
x
kx
kxx
kxx
.
Kết hợp với điều kiện ta được:
3
2
6
k
x
(Với k ∊ N* k 3/ 3/
3/.
02301311
232323
xxxxxxxx
023
2
tt
Đặt
3
2
1 xxt
2
3
22
11
1
33
2
t
t x x x
t
t



68/ Giải phương trình: 3
x
.2x = 3
x
+ 2x + 1
Giải: Ta thấy phương trình: 3
x
.2x = 3
x
+ 2x + 1 (2) có hai nghiệm x =
1.
Ta có x =
1
2
không là nghiệm của phương trình nên
(2)
21
3
21
x
x
x

Ta có hàm số y = 3
x
tăng trên R
hàm số y =
21
21
x
x
luôn giảm trên mỗi khoảng
11
; , ;
22

Vậy Phương trình (2) chỉ có hai nghiệm x =
1
69/ Giải phương trình:
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
Giải:
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
Điều kiện:
.
3
1 0 1
0
x
xx
x

Biến đổi theo logarit cơ số 2 thành phương trình
log log .
x
x x x x x x
x



2
22
1 loaïi
3 1 4 2 3 0 3
3
70/ Tìm các giá trị của tham số
m
để phương trình sau có nghiệm duy nhất thuộc đoạn :
mxxx 12213
232
(
Rm
).
Giải:Đặt
2 3 2
3 1 2 2 1f x x x x
, suy ra
fx
xác định và liên tục trên đoạn
;
1
1
2



.
'
2
2 3 2 2 3 2
3 3 4 3 3 4
1 2 1 1 2 1
x x x x
f x x
x x x x x x




.
;
1
1
2
x



ta có
2 3 2
4 3 3 4
3 4 0 0
3
1 2 1
x
xx
x x x
.
Vậy:
' 00f x x
.Bảng biến thiên:
' || ||
1
01
2
0
1
CÑ
3 3 22
2
4
x
fx
fx

Dựa vào bảng biến thiên, ta có:
Phương trình đã cho có 1 nghiệm duy nhất thuộc
;
1
1
2



3 3 22
4
2
m
hoặc
1m
.
71/ 1.Giaûi baát phöông trình:
2 2 2
3 2 4 3 2. 5 4x x x x x x
2.Cho phöông trình:
2 2 2 2
4 1 2
2log (2 2 4 ) log ( 2 ) 0x x m m x mx m
Xaùc ñònh tham soá m ñeå phöông trình (1) coù 2 nghieäm
1
x
,
2
x
thoûa :
22
12
1xx
Giải: 1) Giaûi baát phöông trình:
2 2 2
3 2 4 3 2. 5 4x x x x x x
Ñieàu kieän:
2
3 2 0
2
4 3 0 1 4
2
5 4 0
xx
x x x x
xx
Ta coù:
Baát phöông trình
( 1)( 2) ( 1)( 3) 2 ( 1)( 4)x x x x x x
(*)
Neáu x = 1 thì hieån nhieân (*) ñuùng . Suy ra x=1 laø nghieäm cuûa phöông trình
Neáu x < 1 thì (*) trôû thaønh :
2 3 2 4x x x
Nhaän xeùt:
24
2 3 2 4
34
xx
x x x
xx
Suy ra Baát phöông trình voâ nghieäm.
Neáu
4x
thì (*) trôû thaønh :
2 3 2 4x x x
Nhaän xeùt:
24
2 3 2 4
34
xx
x x x
xx
Suy ra Baát phöông trình ñuùng
4x
.
Toùm laïi: Baát phöông trình coù nghieäm laø:
14xx
.
2)
2 2 2 2
2log (2 2 4 ) log ( 2 ) 0
41
2
x x m m x mx m
22
20
2 2 2 2
log (2 2 4 ) log ( 2 ) 0
22
22
(1 ) 2 2 0
22
20
2 , 1
12
x mx m
x x m m x mx m
x m x m m
x mx m
x m x m
Yeâu caàu baøi toaùn
22
1
12
22
20
11
22
20
22
xx
x mx m
x mx m

vôùi
1
2xm
,
1
2
xm
2
5 2 0
21
2
4 0 1 0
52
2
2 1 0
mm
m m m
mm

72/ Giải hệ phương trình
2
22
1
22
22
xx
y
y y x y
Giải: ĐK :
0y
hệ
2
2
1
2 2 0
21
20
xx
y
x
yy
đưa hệ về dạng
2
2
2 2 0
2 2 0
u u v
v v u
2
1
1
1
2 2 0
uv
uv
uv
uv
v v u



hoặc
3 7 3 7
22
,
1 7 1 7
22
uu
vv










Từ đó ta có nghiệm của hệ(-1 ;-1),(1 ;1), (
3 7 2
;
2
71
), (
3 7 2
;
2
71
)
73/ Giải bất phương trình
23
34
2
log ( 1) log ( 1)
0
56
xx
xx

Giải: Đk: x > - 1 ; bất phương trình
3
3
3
3log ( 1)
2log ( 1)
log 4
0
( 1)( 6)
x
x
xx



3
log ( 1)
0
6
x
x

06x
74/ Giải phương trình:
x x x x x
2
2 3 1 3 2 2 5 3 16
.
Giải : Đặt
t x x
2 3 1
> 0. (2)
x
3
75/ Giải hệ phương trình:
x y x x y
x
xy y y x
y
22
4 4 4
2
4 4 4
log ( ) log (2 ) 1 log ( 3 )
log ( 1) log (4 2 2 4) log 1



Giải :
x x=2
vôùi >0 tuyø yù vaø
y y= 1



76/ Giải bất phương trình:
2 10 5 10 2x x x
(1)
Giải: Điều kiện:
2x
2
1 2 10 2 5 10 2 6 20 1(2)x x x x x x
Khi
2x
=> x+1>0 bình phương 2 vế phương trình (2)
2 2 2
(2) 2 6 20 2 1 4 11 0 x ; 7 3;x x x x x x 
Kết hợp điều kiện vậy nghiệm của bất phương trình là:
3x
77/ Giải phương trình:
2
2 4 1
2
log (x 2) log (x 5) log 8 0
Giải: . Điều kiện: x > – 2 và x 5 (*)
Với điều kiện đó, ta có phương trình đã cho tương đương với phương trình:
22
22
log (x 2) x 5 log 8 (x 2) x 5 8 (x 3x 18)(x 3x 2) 0


2
2
x 3x 18 0
3 17
x 3; x 6; x
2
x 3x 2 0
Đối chiếu với điều kiện (*), ta được tất cả các nghiệm của phương trình đã cho là:
x6
và
3 17
x
2
78/ Giải phương trình:
23
16 4
2
14 40 0
x x x
log x log x log x .
Giải: Giải phương trình
2
3 4 2 2 2 1 2sin x cos x sinx
Biến đổi phương trình về dạng
2 3 2 1 2 1 0sin x sin x sinx
Do đó nghiệm của phương trình là
7 2 5 2
22
6 6 18 3 18 3
kk
x k ;x k ;x ;x

Giải phương trình
23
16 4
2
14 40 0
x x x
log x log x log x .
Điều kiện:
11
02
4 16
x ;x ;x ;x .
Dễ thấy x = 1 là một nghiệm của pt đã cho Với
1x
. Đặt
2
x
t log
và biến đổi phương trình về dạng
2 42 20
0
1 4 1 2 1t t t
, Giải ra ta được
11
24
2
2
t ;t x ;x .
Vậy pt có 3 nghiệm x =1;
1
4
2
x ;x .
79 / Giải phương trình
12
9.
4
1
4.69.
3
1
4.3
xxxx
.
Giải: Giải phương trình
12
9.
4
1
4.69.
3
1
4.3
xxxx
Biến đổi phương trình đã cho về dạng
2 2 2 2
9
3 2 27 3 6 2 3
4
x x x x
. . . .
Từ đó ta thu được
3
2
3 2 2
2
39 39
x
x log



80/ Cho hàm số
3
2
sin)(
2
x
xexf
x
. Tìm giá trị nhỏ nhất của
)(xf
và chứng minh rằng
0)( xf
có đúng hai nghiệm.
Giải: Ta có
x
f ( x ) e x cos x.
Do đó
0
x
f ' x e x cos x.
Hàm số
x
ye
là hàm đồng biến;
hàm số
y x cosx
là hàm nghịch biến vì
10y' sinx , x
. Mặt khác
0x
là nghiệm của phương
trình
x
e x cos x
nên nó là nghiệm duy nhất. Lập bảng biến thiên của hàm số
y f x
(học sinh tự
làm) ta đi đến kết luận phương trình
0)( xf
có đúng hai nghiệm.
Từ bảng biến thiên ta có
20min f x x .
81/ 1) Giải hệ phương trình:
22
2
2
1
xy
xy
xy
x y x y
2) Giải bất phương trình:
22
1 5 3 1
35
log log 1 log log 1x x x x
Giải:
1)
22
2
2
11
0
2
xy
xy
xy
dk x y
x y x y

23
2
1 2 1 0 2 2 0
xy
x y xy x y xy x y xy x y
xy
2
1 2 1 0
1 1 2 0
x y x y xy x y
x y x y x y xy


22
13
04
xy
x y x y

Dễ thấy (4) vô nghiệm
vì x+y>0
Thế (3) vào (2) ta được
2
1xy
Giải hệ
2
1
1; 0
2; 3
1
xy
xy
xy
xy



……
2)
22
1 5 3 1
35
log log 1 log log 1 (1)x x x x
Đk:
0x
;
22
3 1 3 5
5
2 2 2 2
3 1 5 5
5
1 log log 1 log log 1 0
log log 1 .log 1 0 log 1 1
x x x x
x x x x x x



2
5
0 log 1 1xx
*)
2
5
0 log 1 0x x x
*)
2 2 2
5
12
log 1 1 1 5 1 5 ...
5
x x x x x x x
Vậy BPT có nghiệm
12
0;
5
x



Đề 87.
1. Giải bất phương trình
22
2 3 5 4 6x x x x x
( x
R).
Giải:Điều kiện
2
2
20
02
5 4 6 0
xx
xx
xx
;Bình phương hai vế ta được
2
6 ( 1)( 2) 4 12 4x x x x x
3 ( 1)( 2) 2 ( 2) 2( 1)x x x x x x
( 2) ( 2)
3 2 2
11
x x x x
xx


Đặt
( 2)
0
1
xx
t
x

ta được bpt
2
2 3 2 0tt
1
2
2
2
t
t
t
( do
0t
)
Với
2
( 2)
2 2 6 4 0
1
xx
t x x
x
3 13
3 13
3 13
x
x
x


( do
2x
) Vậy bpt có nghiệm
3 13x 
82/ Giải hệ phương trình
Giải: Điều kiện:
0
0
yx
y

14
4
22
1
log log 1
( , )
25
yx
y
xy
xy

Hệ phương trình
4 4 4
2 2 2 2 2 2
11
log log 1 log 1
4
25 25 25
y x y x
yx
y y y
x y x y x y

2
2 2 2 2
3
33
25
25 9 25
10
xy
x y x y
y
x y y y



15 5
;;
10 10
15 5
;;
10 10
xy
xy






( loại)
Vậy hệ phương trình đã cho vô nghiệm.
83/ Giải hpt :
2
2
3
4 4(( ) 2 )) 7
()
1
( ) 3
xy x y xy
xy
x y x y
xy
Giải:
22
22
2 2 2 2 2
22
33
4 4(( ) 2 )) 7 4( ) 4 7
( ) ( )
11
( ) 3 ( ) 3
33
3( ) (( ) 4 ) 7 3( ) ( 2 ) 7
( ) ( )
11
( ) 3 ( ) 3
xy x y xy x y xy
x y x y
x y x y x y x y
x y x y
x y x y xy x y x y xy
x y x y
x y x y x y x y
x y x y
















22
22
2
2
3
1
3( ) ( ) 7
3 ( ) ( ) 7
()
()
1
1
( ) 3
( ) 3
x y x y
x y x y
xy
xy
x y x y
x y x y
xy
xy








84/ 1. Giải bất phương trình :
32
2log( 8) 2log( 58) log( 4 4)x x x x
.
2. Giải pt :
3 5 10 3 15.3 50 9 1
x x x x
Giải:1. Đk :
32
22
8 ( 2)( 2 4) 0
58 0 2
4 4 ( 2) 0
x x x x
xx
x x x
Bpt đã cho
32
log( 8) log(( 58)( 2)) ( 2) 3 54 0x x x x x x


6; 2 9 (0.25). , : 2 9(0.25)x x So dk ta co x
2.Giải pt :
3 5 10 3 15.3 50 9 1
x x x x
Đặt :
2
3 5 10 3 ( 0) 5 2 15.3 50 9
x x x x
t t t
Ta có pt :
2
3( )
2 3 0 (0.25)
1( )
t nhan
tt
t loai

22
2
3
3 3 5 10 3 3. : 3 ( 0).
:9 5 2 15. 50 15. 50 2
2
9 3 9
15 54 0
log 6
6
36
x x x
x
x
t Dat y y
Ta co pt y y y y
x
y
yy
x
y

85/ Giải hệ phương trình:
1)4(log)5(log
6)12(log)22(log2
21
2
21
xy
xxyxxy
yx
yx
Giải: Hệ phương trình
1)4(log)5(log
6)12(log)22(log2
21
2
21
xy
xxyxxy
yx
yx
ĐK
1;2
0,14
yy
xx
Đưa phương trình thứ nhất của hệ về dạng
21log)2(log
21
xy
yx
Đặt
)2(log
1
yt
x
, Tìm được T=1, kết hợp với phương trình thứ hai của hệ, đối chiếu với điều kiện trên,
tìm được nghiệm
1;2; yx
.
86/ Giai3 phuong trình:
xxx 4log1log
4
1
)3(log
2
1
2
8
4
2
.
87/ 1/.Giải hệ phương trình:
3 3 3
22
8 27 18 (1)
4 6 (2)
x y y
x y x y


Giải: hệ phương trình:
3 3 3
22
8 27 18 (1)
4 6 (2)
x y y
x y x y


(1) y 0
Hệ
3
3
3
3
2
2
27
3
8 18
(2 ) 18
46
33
1
2 . 2 3
x
x
y
y
xx
xx
yy
yy












Đặt a = 2x; b =
3
y
. Ta có hệ:
33
3
18
1
( ) 3
ab
ab
ab
ab a b




Hệ đã cho có 2 nghiệm
3 5 6 3 5 6
; , ;
44
3 5 3 5


88/ Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
(m - 3)
x
+ ( 2- m)x + 3 - m = 0. (1)
Giải: Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
(m - 3)
x
+ ( 2- m)x + 3 - m = 0. (1)
Đk x 0. đặt t =
x
; t 0
(1) trở thành (m–3)t+(2-m)t
2
+3-m = 0
2
2
2 3 3
1
tt
m
tt


(2)
Xét hàm số f(t) =
2
2
2 3 3
1
tt
tt


(t 0)
Lập bảng biến thiên
(1) có nghiệm (2) có nghiệm t 0
5
3
3
m

89/ Giải phương trình:
)12(log1)13(log2
3
5
5
xx
.
Giải: Giải phương trình:
)12(log1)13(log2
3
5
5
xx
.
ĐK :
.
3
1
x
(*)
Với điều kiện trên phương trình đã cho
)12(log31)13(log
5
2
5
xx
32
3
5
2
5
)12()13(5
)12(log)13(5log
xx
xx
8
1
2
0)18()2(
0436338
2
23
x
x
xx
xxx
Đối chiếu với điều kiện trên ta được nghiệm của phương trình đã cho là
.2x
90/ : Giải hệ phương trình:
0222
0964
22
224
yxyx
yyxx
.
Giải:
Hệ phuong trình đã cho tương đương với
022)2(
4)3()2(
22
222
xyx
yx
2 2 2
22
( 2) ( 3) 4
( 2 4)( 3 3) 2 20 0
xy
x y x
2
2
3
xu
yv


* Thay vào hệ phương trình ta có
22
4
. 4( ) 8
uv
u v u v

2
0
u
v
hoặc
0
2
u
v
Thế vào cách đặt ta được các nghiệm của hệ là:
2
3
x
y
;
2
3
x
y

;
2
5
x
y
;
2
5
x
y

;
91/ Giải bất phương trình:
22
35 5 4 24x x x
Giải: Giải bất phương trình:
22
35 5 4 24x x x
BPT tương đương
22
22
22
11
35 24 5 4 5 4
35 24
11 (5 4)( 35 24)
x x x x
xx
x x x
Xét:
a)Nếu x
4
5
không thỏa mãn BPT
b)Nếu x>4/5: Hàm số
22
(5 4)( 35 24)y x x x
với x>4/5
y
'
=
22
22
11
5( 35 24) (5 4)( )
35 24
x x x
xx

>0 mọi x>4/5
Vậy HSĐB. +Nếu 4/5<x
1 thì y(x)
11
+Nếu x>1 thì y(x)>11 Vậy nghiệm BPT x>1
92/ Tìm m để hệ phương trình:
3 3 2
2 2 2
3 3 2 0
1 3 2 0
x y y x
x x y y m
có nghiệm thực
Giải: Điều kiện:
2
2
1 0 1 1
02
20
xx
y
yy



Đặt t = x + 1 t[0; 2]; ta có (1) t
3
3t
2
= y
3
3y
2
.
Hàm số f(u) = u
3
3u
2
nghịch biến trên đoạn [0; 2] nên:
(1) t = y y = x + 1 (2)
22
2 1 0x x m
Đặt
2
1vx
v[0; 1] (2) v
2
+ 2v 1 = m.
Hàm số g(v) = v
2
+ 2v 1 đạt
0;1 0;1
min ( ) 1; m ( ) 2
[ ] [ ]
axg v g v
Vậy hệ phương trình có nghiệm khi và chỉ khi 1 m 2
93/ Giải hệ phương trình:
2
2
3
23
11
(1 ) 4
1
4
xx
yy
xx
x
y y y
.
Giải:
hệ phương trình:
2
2
3
23
11
(1 ) 4
1
4
xx
yy
xx
x
y y y
.
ĐK
0y
2
2
2
2
3
3
3
23
11
11
(1 ) 4
4
11
1
( ) 4
4
xx
xx
yy
yy
x
xx
xx
x
y y y
y y y




Đặt
1
ax
y
x
b
y

Ta có
2 2 2
3 3 2 2
2 4 4 2 4 2 2
1
2 4 ( 4) 4 4 4 0
a a b a a b a a b a
b
a ab a a a a a a
Khi đó
1
1
1
2
xy
y
x
x
x


KL
94/ Giải phương trình
22
3 3 3
log (x 5x 6) log (x 9x 20) 1 log 8
Giải:
22
3 3 3
log (x 5x 6) log (x 9x 20) 1 log 8
(*)
+ Điều kiện :
2
2
x5
x 5x 6 0 x 3 x 2
4 x 3
x 5 x 4
x 9x 20 0
x2



, và có :
33
1 log 8 log 24
+ PT (*)
22
22
33
log (x 5x 6)(x 9x 20) log 24
(x 5x 6)(x 9x 20) 24
(x 5) ( 4 x 3) (x 2)
(x 5) ( 4 x 3) (x 2)




(x 2)(x 3)(x 4)(x 5) 24 (*)
(x 5) ( 4 x 3) (x 2) (**)
+ Đặt
2
t (x 3)(x 4) x 7x 12 (x 2)(x 5) t 2
, PT (*) trở thành :
t(t-2) = 24
2
(t 1) 25 t 6 t 4
t = 6 :
22
x1
x 7x 12 6 x 7x 6 0
x6


( thỏa đkiện (**))
t = - 4 :
22
x 7x 12 4 x 7x 16 0
: vô nghiệm
+ Kết luận : PT có hai nghiệm là x = -1 và x = - 6
95/ Cho khai triển
x1
3
x1
2
2
8
1
log 3 1
log 9 7
5
22




. Hãy tìm các giá trị của x biết rằng số hạng thứ 6 trong khai
triển này là 224
Giải: Ta có :
k8
8
k 8 k k
8
k0
a b C a b

với
x1
3
x1
2
2
1
11
log 3 1
log 9 7
x 1 x 1
5
35
a 2 9 7 b 2 3 1 = ;


+ Theo thứ tự trong khai triển trên , số hạng thứ sáu tính theo chiều từ trái sang phải của khai triển là
35
11
1
5 x 1 x 1 x 1 x 1
35
68
T C 9 7 . 3 1 56 9 7 . 3 1

+ Theo giả thiết ta có :
x1
1
x 1 x 1 x 1 x 1
x1
97
56 9 7 . 3 1 4 9 7 4(3 1)
31
= 224
x1
2
x 1 x 1
x1
3 1 x 1
3 4(3 ) 3 0
x2
33


96/ Giải phương trình
2 2 2
log 9 log log 3
2
.3
x
x x x

Giải: 1.ĐK: x>0.
Ta có phương trình
2 2 2 2
log 9 log log 3 log
22
.3 3 1
xx
x x x x
. Đặt
2
log 2
t
xx

.
Phương trình trở thành
31
3 4 1 1 1 2
44
tt
tt
tx
97/ .1.Cho hệ phương trình
22
2
1
x xy y m
x y xy m
1) Giải phương trình với m=3
2.Giải hệ phương trình sau:
3
1
2
7
)(
3
)(44
2
22
yx
x
yx
yxxy
Giải: 1. Nhận thấy rằng đây là hệ phương trình đối xứng loại 1, khi đó
đặt
,
x y S
xy P

ĐK
2
40SP
ViẾT lại hệ phương trình dưới dạng
2
2
1
1
x y xy m
S P m
SP m
x y xy m


I
Khi đó S,P là nghiệm của phương trình bậc 2
2
1
2 1 0
1
t
t m t m
tm

1
1
1
1
xy
xy m
x y m
xy

2
2
11
1 1 2
f u u u m
g u u m u
Với m=-3. ta có
2
1 1; 2
1 2 0
2 2; 1
u x y
uu
u x y



2
2 1 0 1 1u u u x y
Vậy với m=3, hệ phương trình đã cho có nghiệm là
1;2 , 2; 1 , 1; 1
.
2. Giải hệ phương trình sau:
3
1
2
7
)(
3
)(44
2
22
yx
x
yx
yxxy
ĐK: x + y
0
Ta có hệ
22
2
3
3( ) ( ) 7
()
1
3
x y x y
xy
x y x y
xy
Đặt u = x + y +
1
xy
(
2u
) ; v = x – y ta được hệ :
22
3 13
3
uv
uv


Giải hệ ta được u = 2, v = 1 do (
2u
)
Từ đó giải hệ
1
2
11
10
1
xy
x y x
xy
x y y
xy




98/ 1. Tìm a để hệ phương trình sau có nghiệm:
2
11
33
log 1 log ( )x ax a
2.Gải phương trình:
2
22
log log
3 1 . 3 1 1
xx
xx
Giải:1 ĐK: ax + a > 0 ; Bpt tương đương
2
1 ( 1)x a x
Nếu a>0 thì X+1>0, ta có
2
1
1
x
a
x
Nếu a<0 thì X+1<0, ta có
2
1
1
x
a
x
Xét hàm số y=
2
1
1
x
x
với x
- 1
y’ =
22
1
( 1) 1
x
xx

=0 khi x=1 => a>
2
2
hoặc a < - 1
2 Điều kiện : x>0
Đặt
2
log
31
x
=u,
2
log
31
x
v
ta có phương trình u +uv
2
= 1 + u
2
v
2
(uv
2
-1)(u – 1) = 0
2
1
1
u
uv
. . . x =1
99/ Giải hệ phương trình:
22
22
x y x y 13
x,y .
x y x y 25
Giải: hệ phương trình:
22
22
x y x y 13
x,y .
x y x y 25
3 2 2 3
3 2 2 3
x xy x y y 13 1'
y xy x y x 25 2'
LÊy (2’) - (1’) ta ®îc : x
2
y– xy
2
= 6
x y xy 6
(3)
KÕt hîp víi (1) ta cã :
22
x y x y 13
I
x y xy 6

. §Æt y = - z ta cã :
2
22
x z x z 13 x z x z 2xz 13
I
x z xz 6
x z xz 6







Đặt S = x +z Và P = x.z ta có :
2
3
S S 2P 13
S1
S 2SP 13
P6
SP 6
SP 6






Ta có:
x z 1
x.z 6


. hệ này có nghiệm
x3
z2

hoặc
x2
z3

Vậy hệ phương trình đã cho có 2 nghiệm là: ( 3 ; 2) và ( -2 ; -3 )
Đề 106. a) Giải bất phương trình:
4
log (log (2 4)) 1
x
x

Giải:a) Giải bất phương trình:
4
log (log (2 4)) 1
x
x

4
log (log (2 4)) 1
x
x

. Đk:
42
01
log (2 4) 0 log 5
2 4 0
x
x
x
x


Do
1x 
PT
4
log (2 4) 2 4 4 4 2 4 0
x x x x x
x
đúng với mọi x. Do vậy BPT có
nghiệm:
2
log 5x
Đề 107. Tìm m để phương trình sau có một nghiệm thực:
2
2 2( 4) 5 10 3 0x m x m x
Giải:
2
2 2( 4) 5 10 3 0x m x m x
2
2 2( 4) 5 10 3x m x m x
22
30
2 2( 4) 5 10 ( 3)
x
x m x m x

2
3
21
25
x
xx
m
x

Xét hàm số, lập BBT với
2
21
()
25
xx
fx
x

2
2
2( 5 )
'( )
(2 5)
xx
fx
x

Khi đó ta có:
Bảng biến thiên:
x
-
0
5/2
3 5
+
y’
+
0
-
-
0
+
y
8
24/5
+
Phương trình có 1 nghiệm
24
(8; )
5
m




100/ Tìm m để phương trình:
2
m x 2x 2 1 x(2 x) 0 (2)
có nghiệm x
0; 1 3



Giải: Tìm m để phương trình:
2
m x 2x 2 1 x(2 x) 0 (2)
có nghiệm x
0; 1 3



Đặt
2
t x 2x 2
t
2
2 = x
2
2x Bpt (2)
2
t2
m (1 t 2),dox [0;1 3]
t1
Khảo sát
2
t2
g(t)
t1
với 1 t 2 ; g'(t)
2
2
t 2t 2
0
(t 1)


. Vậy g tăng trên [1,2]
Do đó, ycbt
bpt
2
t2
m
t1
có nghiệm t [1,2]
t 1;2
2
m max g(t) g(2)
3
Vậy m
2
3
101/ . 1) Giải phương trình:
22
33
log 1 log 2x x x x x
2) Giải bất phương trình:
2
x 4 2
(log 8 log x )log 2x 0
Giải:
1. (1)
2
2
3
11
log 2 3 1
xx
xx
x x x
xx

Đặt:f(x)=
2
3
xx
; g(x)=
1
1x
x

(x
0)
Dùng pp kshs =>max f(x)=3; min g(x)=3=>PT f(x)= g(x) max f(x)= min g(x)=3 tại x=1
=>PT có nghiệm x= 1
2. Điều kiện x > 0 , x 1
(1)



42
8
11
2 log x log 2x 0
log x 2





22
2
1
log x log x 1 0
1
log x
3




2
22
2
22
22
log x 1 log x 1
(log x 3) 0 0
log x log x
1
log x 1hayl og x 0 0 x hay x 1
2
102/ Giải phương trình:
2
21
3 2 6
x
x
x
Giải: Giải phương trình:
2
21
3 2 6
x
x
x
Lấy logarit theo cơ số 3 cho hai vế ta được:
2
33
log 2 1 log 2
21
x
x
x
Đưa phương trình về dạng: (x – 1)(2x
2
+ x – 1 - log
2
3
) = 0.
Từ đó suy ra nghiệm x = 1;
3
1 9 8log 2
4
x
103/ .Giải bất phương trình
)3(log53loglog
2
4
2
2
2
2
xxx
Giải: Giải bất phương trình
)3(log53loglog
2
4
2
2
2
2
xxx
ĐK:
03loglog
0
2
2
2
2
xx
x
Bất phương trình đã cho tương đương với
)1()3(log53loglog
2
2
2
2
2
xxx
đặt t = log
2
x,
BPT (1)
)3(5)1)(3()3(532
2
tttttt
4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t
168
2
1
0
x
x
Vậy BPT đã cho có tập nghiệm là:
)16;8(]
2
1
;0(
104/ Giải hệ phương trình:
0322
6)2)(1)(1(
22
yxyx
yxyx
Giải: hệ phương trình:
0322
6)2)(1)(1(
22
yxyx
yxyx
Hệ
052)(
6)(
05
6)(
05)1()1(
6)11)(1)(1(
22222
uvvu
vuuv
vu
vuuv
yx
yxyx
với
1
1
yv
xu
Đặt:
vuP
vuS
.
được
2
3
052
6.
2
P
S
PS
SP
u, v là nghiệm của phương trình: X
2
– 3X + 2 = 0
21
11
11
21
2
1
y
x
y
x
X
X
Vậy nghiệm của hệ: (3 ; 2), (2 ; 3)
105/ 1. Tìm m để phương trình sau có nghiệm: 4
x
– 4m(2
x
– 1) = 0
2.Tìm m để phương trình:
0loglog4
2
1
2
2
mxx
có nghiệm trong khỏang (0 ; 1).
Giải:
1. Đặt t = 2
x
(t > 0) ta có phương trình: t
2
– 4mt + 4m = 0 (*)
(*)
)10(4
1
2
ttm
t
t
Xét
1
2
t
t
y
có
2
2
1
2
'
t
tt
y
y’ = 0
20 tt
Từ bảng biến thiên ta có : m < 0
1 m
2. Pt đã cho
0loglog)1;0(0loglog
2
1
4
2
2
22
2
2
mxxxmxx
(*)
Đặt
)0;()1;0(,log
2
 txxt
(*)
)0;(0
22
 tttmmtt
Xét hàm số y = -t
2
– t có y’ = -2t – 1
y’ = 0
4
1
,
2
1
yt
t -
-
2
1
0
+
-
+
-
4
0
0
0
2
0
1
y
y'
x
+
-
y’ + 0 -
y
4
1
-
0 ĐS : m
4
1
106/ Giải bất phương trình
2
4x 3 x 3x 4 8x 6
Giải:
bất phương trình:
2
4x 3 x 3x 4 8x 6
(1)
(1)
2
4 3 3 4 2 0x x x
Ta có: 4x-3=0<=>x=3/4
2
3 4 2xx
=0<=>x=0;x=3
Bảng xét dấu:
x - 0 ¾ 2 +
4x-3 - - 0 + +
2
3 4 2xx
+ 0 - - 0 +
Vế trái - 0 + 0 - 0 +
Vậy bất phương trình có nghiệm:
3
0; 3;
4
x




107 / Giải phương trình:
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
Giải: phương trình:
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
Điều kiện:
.
3
1 0 1
0
x
xx
x

Biến đổi theo logarit cơ số 2 thành phương trình
log log .
x
x x x x x x
x



2
22
1 loaïi
3 1 4 2 3 0 3
3
108/ Tìm các giá trị của tham số
m
để phương trình sau có nghiệm duy nhất thuộc đoạn
1;
2
1
:
mxxx 12213
232
(
Rm
).
Giải:Đặt
2 3 2
3 1 2 2 1f x x x x
, suy ra
fx
xác định và liên tục trênđoạn
;
1
1
2



.
'
2
2 3 2 2 3 2
3 3 4 3 3 4
1 2 1 1 2 1
x x x x
f x x
x x x x x x




.
;
1
1
2
x



ta có
2 3 2
4 3 3 4
3 4 0 0
3
1 2 1
x
xx
x x x
.
Vậy:
' 00f x x
.
Bảng biến thiên:
' || ||
1
01
2
0
1
CÑ
3 3 22
2
4
x
fx
fx

Dựa vào bảng biến thiên, ta có: Phương trình đã cho có 1 nghiệm duy nhất thuộc
;
1
1
2



3 3 22
4
2
m
hoặc
1m
.
109/ 1. Giải hệ phương trình sau:
2
2
2
2
y2
3y
x
x2
3x
y
2. Giải phương trình:
0322212
333
xxx
Giải:1. Giải hệ phương trình sau:
2
2
2
2
y2
3y
x
x2
3x
y
điều kiện x>0, y>0. Khi đó hệ tương đương
22
22
32
32
x y y
xy x


Trừ vế theo vế hai phương trình ta được: (x-y)(3xy+x+y) = 0
xy
thay lại phương trình Giải tìm
được nghiệm của hệ là: (1;1).
2. Giải phương trình:
0322212
333
xxx
Tập xác định: D = R. Đặt f(x) =
333
322212 xxx
Ta có:
2
3
,1,
2
1
;0
)32(
2
)22(
2
)12(
2
)('
3
2
3
2
3
2
x
xxx
xf
Suy ra hàm số f(x) đồng biến trên tập M=

,
2
3
2
3
,11,
2
1
2
1
,
Ta thấy f(-1)=0 x=-1 là một nghiệm của (1). Ta có:
3)
2
3
(;3)
2
1
( ff
Ta có bảng biến thiên của hàm số f(x):
x
-∞
2
3
-1
2
1
+∞
f’(x)
  
F(x)
+∞
0 3
-∞ -3
Từ bảng biến thiên ta thấy f(x) = 0 x = -1. Vậy phương trình đã cho có duy nhất một nghiệm x = -1.
Cách 2: Hs có thể đặt
3
3
21
23
ux
vx


khi đó ta được hệ
33
33
0
2
2
uv
uv
vu

giải hệ này và tìm được
nghiệm.
110/ Giaûi phöông trình :
3
2 3x 2 3 6 5x 8 0
(x R)
Giải:
3
2 3x 2 3 6 5x 8 0
, ñieàu kieän :
6
6 5 0
5
xx
Ñaët t =
3
3x 2
t
3
= 3x – 2 x =
3
t2
3
vaø 6 – 5x =
3
8 5t
3
Phöông trình trôû thaønh :
3
8 5t
2t 3 8 0
3
3
8 5t
3 8 2t
3

32
t4
15t 4t 32t 40 0
t = -2. Vaäy x = -2
111/ Gæai heä phöông trình :
22
22
22
x xy y
log (x y ) 1 log (xy)
3 81

(x, y R)
Giải: Ñieàu kieän x, y > 0
22
2 2 2 2
22
log (x y ) log 2 log (xy) log (2xy)
x xy y 4
22
22
x y 2xy
x xy y 4

2
(x y) 0
xy 4

xy
xy 4
x2
y2
hay
x2
y2


112/ Tìm các giá trị của tham số m sao cho hệ phương trình
2
1
y x m
y xy


có nghiệm duy nhất
Giải Ta có :
2x y m
, nên :
2
21y my y
. PT
1
1
2
y
my
y
( vì y = 0 PTVN). Xét
2
11
2 ' 1 0f y y f y
y
y
. Lập BTT. KL: Hệ có nghiệm duy nhất
2m
.
113/ 1. Giải phương trình
log log
42
28
xx
x
.
2. Giải bất phương trình
2 4 8
2 1 log log log 0x x x
.
Giải 1. ĐK :
0x
. Ta có:
2 4 2
1 log log 3logx x x
. Đặt
2
logtx
.Ta có:
2
3 2 0 1, 2t t t t
. Khi:
1t
thì
2
log 1 2( )x x th
. Khi:
2t
thì
2
log 2 4( )x x th
. KL:
Nghiệm PT
2, 4xx
.
2. ĐK :
0x
. Đặt
2
logtx
, ta có :
10
3
t
tt
, BPT
2
4
3 4 0 0
3
t t t
. KL:
2
3
41
log 0 1
3
22
xx
.
114/ Giải bất phương trình:
( 1)(4 )
2
2
22
xx
x
x
xx


Giải
ĐK:? bpt
2
3 4 2x x x
2
0;7
7
1;
2
2
1;4
x
x
x
x
x



115/ Giải phương trình:
3
1
8 1 2 2 1
xx
Giải :
3
1
8 1 2 2 1
xx
Đặt
3
1
2 0; 2 1
xx
uv
33
3
3 2 2
0
1 2 1 2
2 1 0
1 2 ( )( 2) 0
uv
u v u v
uu
v u u v u uv v





2
15
0; log
2
xx

116/ Giải hệ phương trình:
2
2
3
23
11
(1 ) 4
1
4
xx
yy
xx
x
y y y
.
Giải : ĐK
0y
2
2
2
2
3
3
3
23
11
11
(1 ) 4
4
11
1
( ) 4
4
xx
xx
yy
yy
x
xx
xx
x
y y y
y y y




Đặt
1
ax
y
x
b
y

Ta có
2 2 2
3 3 2 2
2 4 4 2 4 2 2
1
2 4 ( 4) 4 4 4 0
a a b a a b a a b a
b
a ab a a a a a a
Khi đó
1
1
1
2
xy
y
x
x
x


117/ Giải hệ phương trình:
3
3
1
9 5.3 14.log 0
2
xx
x
x



Giải:
KL:2. +) Đ/K: x>2 or x<-1
3
3
33
3
11
9 5.3 14.log 0 3 7 3 2 log 0
22
1
3 7 log 0
2
x x x x
x
xx
xx
x
x





Xét x>2 ta có
3
1 1 3
log 0 1 0 2
2 2 2
xx
x
x x x

Xét x<-1 ta có
3
1 1 3
log 0 1 0 2
2 2 2
xx
x
x x x




. KL:?
118 / Giải phương trình :
1
4 2 2 2 1 sin 2 1 2 0
x x x x
y
Giải: Đặt
2
x
t
, đ ưa về pt bậc 2 ẩn t ,giải tiếp. Hoặc đưa pt về dạng tổng các bình phương
119/ Tìm m để phương trình sau có nghiệm thực :
mmxxxx 2223
22
Giải Tìm m để phương trình sau có nghiệm thực :
mmxxxx 2223
22
(*)
(*)
2
22
3 2 0
3 2 2 2
xx
x x x mx m
m
x
x
xf
x
xxm
x
2
1
23
)(
21
23)1(2
21
f(x) liên tục trên
1;2
và có
2
5
( ) 0, 1;2
1
f x x
x
)(xf
đồng biến trên
2;1
Bài toán yêu cầu
12
(1) 2 (2)
43
f m f m
120/ Giải hệ phương trình :
22
33
22
22
log log
4
y x y x x xy y
xy

Giải: Điều kiện : x > 0 ; y > 0 . Ta có :
0
4
3
2
2
2
22
y
y
xyxyx
yx,
>0 ; Xét x > y
33
22
VT(*) 0
log log
VP(*) 0
xy
(*) vô nghiệm nên hệ vô nghiệm.
Xét x < y
33
22
VT(*) 0
log log
VP(*) 0
xy
(*) vô nghiệm nên hệ vô nghiệm.
Khi x = y hệ cho ta
22
00
2 2 4xy

x = y =
2
( do x, y > 0). Vậy hệ có ngd nh
; 2; 2xy
Vậy hệ có ngd
121/ Giải phương trình:
1
1
3
2
(x 24) (12 x) 6
.
Giải; Nhận xét: Theo định nghĩa của lũy thừa số mũ hữu tỉ, cơ số phải dương nên điều kiện có nghĩa
của biểu thức là:
x 24 0
24 x 12
12 x 0


.
Đặt:
1
1
3
2
u (x 24) ; v (12 x)
với
u, v 0.
Ta có:
3 2 3 2 3 2 2
u v 6 u v 6 u v 6 u v 6
u v 36 u (6 u) 36 u u 12u 0 u(u u 12) 0
u3
(do u, v 0)
v3

1
3
1
2
(x 24) 3
x 24 27
(12 x) 3 12 x 9 x 3
24 x 12 24 x 12





(thỏa)
122/ Giải phương trình
22
3 3 3
log (x 5x 6) log (x 9x 20) 1 log 8
Giải: Điều kiện :
2
2
x5
x 5x 6 0 x 3 x 2
4 x 3
x 5 x 4
x 9x 20 0
x2



, và có :
33
1 log 8 log 24
+ PT (*)
22
22
33
log (x 5x 6)(x 9x 20) log 24
(x 5x 6)(x 9x 20) 24
(x 5) ( 4 x 3) (x 2)
(x 5) ( 4 x 3) (x 2)




(x 2)(x 3)(x 4)(x 5) 24 (*)
(x 5) ( 4 x 3) (x 2) (**)
+ Đặt
2
t (x 3)(x 4) x 7x 12 (x 2)(x 5) t 2
, PT (*) trở thành :
t(t-2) = 24
2
(t 1) 25 t 6 t 4
t = 6 :
22
x1
x 7x 12 6 x 7x 6 0
x6


( thỏa đkiện (**))
t = - 4 :
22
x 7x 12 4 x 7x 16 0
: vô nghiệm
+ Kết luận : PT có hai nghiệm là x = -1 và x = - 6
123/ Giải hệ phương trình.
Giải: Đặt : t = x + y ; ĐK: t =>
; Hệ đã cho trở thành
Vậy hệ dã cho có một nghiệm
Đề 132 : Giải phương trình:
Giải: ĐK: x > 1; Với ĐK trên phương trình đã cho tương đương
Vậy phương trình đã cho có một nghiệm :
124/ Giải bất phương trình:
2
44
16 6
2
xx
xx
Giải : * Đk:
40
40
x
x


x
4. Đặt t =
44xx
(t > 0)
BPT trở thành: t
2
- t - 6
0
2( )
3
tL
t

* Với t
3
2
2
16x
9 - 2x
22
( )
0 ( )
4( 16) (9 2 )
a
b
xx

x4
9 - 2x 0
x4
9 - 2x
* (a)
x
9
2
. * (b)
145 9
36 2
x<
. *Tập nghệm của BPT là: T=
145
;
36



125/ 1. Giải hệ phương trình:
2
2
3
1
9
1218
yxy
xxy
2. Giải phương trình: 9
x
+ (
x
- 12).3
x
+ 11 -
x
= 0
Giải 1) Giải hệ:
3232
3
1
9
320121218
2
22
xyyxyxy
xxxxy
1832 xyx
32;32 x
, tương ứng y
33;33
Thử lại, thoả mãn hệ đã cho
Vậy,
33;32,33;32; yx
2) Giải phương trình:
0113123
2
xx
xx
x
x
x
113
13
(*)0113)(
0
xxf
x
x
(a + b + c = 0)
(*)
0)2(
,013ln3)('
f
xxf
x
có nghiệm duy nhất
x
= 2
Vậy, tập nghiệm của phương trình: S = {0 ; 2
126/ Giải phương trình:
2
22
1 5 2 4; x x x x R
Giải:
2
22
1 5 2 4; x x x x R
Đặt
2 2 4 2
2 4 2( 2 )t x x t x x
ta được phương trình
2
2
1 5 2 8 0
2
t
t t t
4
2
t
t

+ Với t =
4 Ta có
2
4 2 4 2
00
2 4 4
2( 2 ) 16 2 8 0
xx
xx
x x x x




2
0
2
2
x
x
x
+ Với t = 2 ta có
2
4 2 4 2
00
2 4 2
2( 2 ) 4 2 2 0
xx
xx
x x x x




2
0
31
31
x
x
x

ĐS: phương trình có 2 nghiệm
2, 3 1xx
127/ Giải bất phương trình:
2
12
2
2
1
2
3
log 1 log 1 6
2
log 1
2 log ( 1)
xx
x
x





Giải; Đ ặt
2
log 1xt
rồi giải tiếp
128/ Giải phương trình:
22
7 5 3 2 ( )x x x x x x
Giải
2
22
3 2 0
7 5 3 2
xx
PT
x x x x x
2
3 2 0
5 2( 2)
xx
x x x
31
0
2
5 2.
x
x
x
x
x

2
20
1 16 0
x
xx
1x
; Vậy phương trình đã cho có một nghiệm x = - 1.
129/ Giải hệ phương trình
14
4
22
1
log log 1
( , )
25
yx
y
xy
xy

Giải: Điều kiện:
0
0
yx
y

; Hệ phương trình
4 4 4
2 2 2 2 2 2
11
log log 1 log 1
4
25 25 25
y x y x
yx
y y y
x y x y x y

2
2 2 2 2
3
33
25
25 9 25
10
xy
x y x y
y
x y y y



15 5
;;
10 10
15 5
;;
10 10
xy
xy






(không thỏa mãn đk)
Vậy hệ phương trình đã cho vô nghiệm.
130/ Tìm các giá trị của tham số m để phương trình:
2
4
2
1
x
x
m e e
có nghiệm thực .
Giải: Đặt
2
x
te
ĐK: t > 0 . PT trở thành:
4
4
1m t t
.Xét
4
4
( ) 1f t t t
với t > 0 .
3
4
4
4
'( ) 1 0
1
t
ft
t



hàm số NB trên
0;
.
4 4 2
4
1
lim ( ) lim 0
11
tt
ft
t t t t
 

;
f(0) = 1. KL: 0< m <1.
131/ Giải phương trình:
3
log 4.16 12 2 1
xx
x
.
Giải: PT
2 1 2 2
4.16 12 3 4.4 4 .3 3.3
x x x x x x x
. Chia 2 vế cho
2
30
x
, ta
có:
2
44
4 3 0
33
xx
; Đặt
4
3
x
t



. ĐK:
2
3
0 ; 4 3 0 1( ); ( )
4
t t t t kth t th
.
Khi
3
4
t
, ta có:
1
4 3 4
1
3 4 3
x
x
.
132/ Giải hệ phương trình:
22
22
12
12
x y x y
y x y

Giải: Điều kiện:
| | | |xy
Đặt
22
;0u x y u
v x y

;
xy
không thỏa hệ nên xét
xy
ta có
2
1
2
u
yv
v




.
Hệ phương trình đã cho có dạng:
2
12
12
2
uv
uu
v
v





4
8
u
v
hoặc
3
9
u
v
+
22
4
4
8
8
u
xy
v
xy



(I) ; +
22
3
3
9
9
u
xy
v
xy



(II)
Giải hệ (I), (II).Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ phương trình ban đầu là
5;3 , 5;4S
133/ Giải phương trình:
23
16 4
2
14 40 0
x x x
log x log x log x .
Giải : phương trình
23
16 4
2
14 40 0
x x x
log x log x log x .
Điều kiện:
11
02
4 16
x ;x ;x ;x .
Dễ thấy x = 1 là một nghiệm của pt đã cho;Với
1x
. Đặt
2
x
t log
và biến đổi phương trình về dạng
2 42 20
0
1 4 1 2 1t t t
;Giải ra ta được
11
24
2
2
t ;t x ;x .
Vậy pt có 3 nghiệm x =1;
1
4
2
x ;x .
134/ Giải phương trình
12
9.
4
1
4.69.
3
1
4.3
xxxx
.
Giải: Biến đổi phương trình đã cho về dạng
2 2 2 2
9
3 2 27 3 6 2 3
4
x x x x
. . . .
Từ đó ta thu được
3
2
3 2 2
2
39 39
x
x log



135/ Giải hệ phương trình:
2
2
3
1
9
1218
yxy
xxy
Giải:
Hệ:
3232
3
1
9
320121218
2
22
xyyxyxy
xxxxy
;
1832 xyx
;
32;32 x
,
tương ứng y
33;33
;Thử lại, thoả mãn hệ đã cho
Vậy,
33;32,33;32; yx
136/ Giải phương trình:
3
log 4.16 12 2 1
xx
x
.
Giải; PT
2 1 2 2
4.16 12 3 4.4 4 .3 3.3
x x x x x x x
.Chia 2 vế cho
2
30
x
, ta có
2
44
4 3 0
33
xx
Đặt
4
3
x
t



. ĐK:
2
3
0 ; 4 3 0 1( ); ( )
4
t t t t ktm t tm
. Khi
3
4
t
, ta có:
1
4 3 4
1
3 4 3
x
x
. .
137/ :1.Tìm m để phương trình sau có 2 nghiệm phân biệt :
x10
1).12(48
22
xxmx
.
2..Giải phương trình:
33
log 1 log 2
22
xx
x


.
Giải: Nhận xét: 10x
48
2
x
= 2(2x+1)
2
+2(x
2
+1)
Phương trình tương đương với :
2
(
02)
1
12
()
1
12
2
2
2
x
x
m
x
x
. Đặt
t
x
x
1
12
2
ĐK: -2< t
5
.
Rút m ta có: m=
t
t 22
2
Lập bảng biến thiên của hàm số trên
5,2
ta có kết quả của m để phương trình
có hai nghiệm phân biệt là
5
12
4 m
hoặc -5 <
4m
.
2.ĐK: x > 0 . Đặt
3
log 3
t
t x x
. Ta có:
2
1 9 2 4 2
2.2 2 3 .2 3
4 4 3 9 3
t
t t t t t
.
Khi t = 2 thì
3
log 2 9xx
(th) KL: nghiệm PT là
9x
.
138/ Giải bất phương trình :
2
1 2 1xx
(2) .
Giải:
(2)
2
2
2
2 1 0
10
2 1 1
x
x
xx

2
11
1
2 3 0
xx
x
xx
1
1
13
x
x
x
1
13
x
x


Vậy nghiệm của bất phương trình :
1 1 3xx
.
139 / Giải hệ phương trình , khi a > 1 :
2
2
1
3
1
3
a
x a y a z a
a
a
a x a y a z
a
Giải: Xét các véc tơ :
; ; , 1 ; 1; 1 u x a y a z a v
2
22
2
..
3 3 1

u v u v
x a y a z a a x y z
Tương tự
2
33 a x a y a z a x y z
(2)
22
18x a y a z a a x a y a z a
Mà cộng hai phương trình của hệ ta có :
22
18x a y a z a a x a y a z a
Tức là dấu đẳng thức phải xảy ra trong các bất đẳng thức (1) và (2) , hay :
2
2
1
1
1
a
x a y a z a
a
x y z
a
a
a x a y a z
a
Vậy hệ phương trình có nghiệm là :
1
x y z
a
.
140/ Giaûi heä phöông trình :
22
4
( 1) ( 1) 2
x y x y
x x y y y
Giải: (I)
22
22
x y x y 4
x y x y xy 2

22
x y x y 4
xy 2

2
(x y) x y 0
xy 2

x y 0 hay x y 1
xy 2

x y 0 hay x y 1
xy 2

2
xy
x2
hay
2
x y 1
x x 2 0
x2
y2

V
x2
y2

V
x1
y2

V

x2
y1
141/ Giaûi heä pt :
2x y 1 x y 1
I
3x 2y 4

Giải:
2x y 1 x y 1
I
2x y 1 x y 5
Ñaët
u 2x y 1 0,v x y 0
;(I) thaønh


11
22
22
u v 1
u 2 v 1
u 1 v 2 loaïi
u v 5
Vaäy
2x y 1 2
I
x y 1

2x y 1 4 x 2
x y 1 y 1




142/ Giaûi pt
3x 3 5 x 2x 4 1
Giải:
1/ Giaûi pt
3x 3 5 x 2x 4 1
Ñieàu kieän
3x 3 0
5 x 0 2 x 5
2x 4 0


(1)
3x 3 5 x 2x 4
vaø
2 x 5
3x 3 5 x 2x 4 2 5 x 2x 4
vaø
2 x 5
x 2 5 x 2x 4
vaø
2 x 5
x 2 0
hay[ x 2 5 x 2
vaø
2 x 5
]
x 2 hay [x 2 2 5 x vaø 2 x 5]
x 2 hayx 4
143/ Giaûi baát phöông trình
2
8x 6x 1 4x 1 0
(1)
Giải: (1)
2
8x 6x 1 4x 1





2
22
2
11
x Vx
11
42
8x 6x 1 0
x Vx
1
42
4x 1 0 x
1
4
x 0 hayx
8x 6x 1 (4x 1)
4
8x 2x 0

11
x hay x
42
144/ Giaûi bpt
2x 7 5 x 3x 2
(1)
Giải: bpt
2x 7 5 x 3x 2
(1)
Ñieàu kieän


2x 7 0
2
5 x 0 x 5
3
3x 2 0
(1)
2
2x 7 3x 2 5 x vaø x 5
3
2x 7 3x 2 5 x 2 3x 2 5 x

2
vaø x 5
3
2 3x 2 5 x

2
vaø x 5
3
2
3x 17x 14 0

2
vaø x 5
3
14
(x 1 hay x)
3

2
vaø x 5
3
2 14
x 1 hay x 5
33
145/ Tìm m ñeå heä phöông trình sau coù nghieäm:
2x x 1 2 x 1
2
7 7 2005x 2005 (1)
x m 2 x 2m 3 0 (2)
Giải: Ñieàu kieän laø
x1
.Ta coù
2x x 1 2 x 1
7 7 0, x 1;1
Ta coù: (1)
x 1 2x 2
7 7 7 2005 1 x : ñuùng x 1;1
vaø sai khi x > 1Do ñoù (1)
1x1
. Vaäy, heä bpt coù nghieäm
2
f x x m 2 x 2m 3 0
coù nghieäm
1,1

x 1;1
0 max f( 1),f(1) 0
Maxf(x)
max 3m 6,m 2 0 3m 6 0 hay m 2 0
m2
146/ Giaûi baát phöông trình
2
2
2x x
x 2x
1
9 2 3 1
3




Giải: Ta coù (1)
22
x 2x x 2x
9 2.3 3

. Ñaët

2
x 2x
t 3 0
, (1) thaønh
2
t 2t 3 0 1 t 3
. Do ñoù, (1)

22
x 2x x 2x 1
1 3 3 0 3 3
22
x 2x 1 x 2x 1 0 1 2 x 1 2
147 /Tìm m để hệ phương trình sau có nghiệm:
4
(2 1)[ln(x + 1) - lnx] = (2y + 1)[ln(y + 1) - lny] (1)
y-1 2 ( 1)( 1) 1 0 (2)
x
y x m x
Giải: Đặt f(x) = (2x + 1)[ln(x + 1) – lnx] =
1
(2 1)ln
x
x
x
TXĐ: D = [0;+)
Gọi x
1
; x
2
[0;+) với x
1
> x
2
Ta có :
12
12
12
12
2 1 2 1 0
( ) ( )
11
ln ln 0
xx
f x f x
xx
xx



: f(x) là hàm số tăng
Từ phương trình (1) x = y
(2)
4
1 2 ( 1)( 1) 1 0x x x m x
4
11
20
11
xx
m
xx


Đặt X =
4
1
1
x
x
0 ≤ X < 1
Vậy hệ có nghiêm khi phương trình: X
2
– 2X + m = 0 có nghiệm 0 ≤ X < 1
Đặt f(X) = X
2
– 2X f’(X) = 2X – 2 hệ có nghiệm -1 < m ≤ 0
149/ 1) Giải hệ phương trình:
22
1
2
2
( 1)( 2) 6
xy
xy
xy x y x y


(
,x y R
)
2) Tìm m thực để phương trình sau có nghiệm thực trong đoạn
5
;4
2



:
22
1/2 1/2
1
( 1).log ( 2) 4( 5)log 4 4 0
2
m x m m
x
Giải: 1. Hệ
22
( 1) ( 1) 5
( 1)( 1)[( 1) ( 1)] 6
xy
x y x y
. Đặt
1
1
ux
vy


, thu được hệ
22
5
( ) 6
uv
uv u v


Giải ra được:
3
.2
uv
uv

; * Giải ra được:
11
12
ux
vy
hoặc
12
11
ux
vy
3
2
x
y
hoặc
2
3
x
y
2 / PT
2
1/2 1/2
( 1).log ( 2) ( 5)log ( 2) 1 0m x m x m
*Đặt
1/2
5
log ( 2), ;4 1;1
2
t x x t



;
Thu được pt:
2
2
51
()
1
tt
m f t
tt



;
2
22
44
'( ) ; '( ) 0 1
( 1)
t
f t f t t
tt

Lập BBT của f(t) trên đoạn
1;1
, thấy f(t) liên tục và NB trên đoạn
1;1
, nên
7
3;
3
m




thỏa mãn đề bài.
150/ Tìm m để hệ phương trình sau có 2 nghiệm phân biệt:
x10
1).12(48
22
xxmx
.
Giải: 10x
48
2
x
= 2(2x+1)
2
+2(x
2
+1)
Phương trình tương đương với :
2
(
02)
1
12
()
1
12
2
2
2
x
x
m
x
x
.
Đặt
t
x
x
1
12
2
ĐK: -2< t
5
. Rút m ta có : m=
t
t 22
2
Lập bảng biếm thiên của hàm số trên
5,2
, ta có kết quả của m để hệ phương có 2 nghiệm phân biệt là
5
12
4 m
hoặc -5 <
4m
151/ Giải hệ phương trình:
2
4 2 2
1
log log 16 4
log 2
4 8 16 4
xy
y
x
x x xy x x y
Giải: ÑK:
0, 0, 1, 1
x y xy y
+) Töø PT (1) ta coù: xy = 4 ; +) Theá vaøo (2) ta coù: x
2
–4x + 1 = 0
23
x
+) KL : Heä coù caùc nghieäm laø :
44
2 3; ; 2 3;
2 3 2 3


152/ Tìm m để phương trình sau có nghiệm:
1 6 8 1 6 8
6
xm
x x x x
Giải:+) ÑK:
8
x
+) PT
8 3 8 3
6
xm
xx
; +) Neáu
17
x
, ta coù PT trôû thaønh :
12 8
x x m
. PT coù nghieäm
17
x
77 100
m

+) Neáu
8 17
x

, ta coù PT trôû thaønh : 36 – x = m. PT coù nghieäm
19 28
m

KL:
77 100
m

hoaëc
19 28
m

153/ Giải hệ phương trình:
22
22
14
( ) 2 7 2
x y xy y
y x y x y
,
( , )xyR
.
Giải:
0y
, ta có:
2
22
22
2
2
1
4
14
.
( ) 2 7 2
1
( ) 2 7
x
xy
y
x y xy y
y x y x y
x
xy
y

Đặt
2
1
,
x
u v x y
y
ta có hệ:
22
4 4 3, 1
2 7 2 15 0 5, 9
u v u v v u
v u v v v u


Với
3, 1vu
ta có hệ:
222
1, 2
1 1 2 0
2, 5
3 3 3
xy
x y x y x x
xy
x y y x y x




.
Với
5, 9vu
ta có hệ:
222
1 9 1 9 9 46 0
5 5 5
x y x y x x
x y y x y x




, hệ này vô nghiệm.
KL: Vậy hệ đã cho có hai nghiệm:
( ; ) {(1; 2), ( 2;5)}.xy
154/ Giải hệ phương trình :
2
12
12
2log ( 2 2) log ( 2 1) 6
log ( 5) log ( 4) = 1
xy
xy
xy x y x x
yx


,
( , )xyR
.
Giải:+ Điều kiện:
2
2 2 0, 2 1 0, 5 0, 4 0
()
0 1 1, 0 2 1
xy x y x x y x
I
xy
.
1 2 1 2
1 2 1 2
2log [(1 )( 2)] 2log (1 ) 6 log ( 2) log (1 ) 2 0 (1)
()
log ( 5) log ( 4) = 1 log ( 5) log ( 4) = 1(2).
x y x y
x y x y
x y x y x
I
y x y x






Đặt
2
log (1 )
y
xt

thì (1) trở thành:
2
1
2 0 ( 1) 0 1.t t t
t
Với
1t
ta có:
1 2 1(3).x y y x
Thế vào (2) ta có:
2
1 1 1
44
log ( 4) log ( 4) = 1 log 1 1 2 0
44
x x x
xx
x x x x x
xx

0
2
x
x

. Suy ra:
1
1
y
y

.Kiểm tra thấy chỉ có
2, 1xy
thoả mãn điều kiện trên.
Vậy hệ có nghiệm duy nhất
2, 1xy
.
155/ .Giải phương trình: 8 – x.2
x
+ 2
3-x
- x = 0
Giải:Giải phương trình: 8 – x.2
x
+ 2
3-x
- x = 0 , 8 – x.2
x
-
8
2
x
- x = 0 8(1+
1
)
2
x
- x(2
x
+1) =0
8
(2 1) (2 1) 0
2
xx
x
x
(2
x
+1)(
88
)0
22
xx
xx
Vế trái nghịch biến, vế phải đồng biến
phương trình có nghiệm duy nhất x=2
156/ 1) Giải phương trình
5x
+
x
+
7x
+
16x
= 14.
2)Tìm m để ptrình sau đây có đúng 2 nghiệm:
2 3 2 2
( 2 2) 4 2 2 2 4x x x x x x m
.
Giải: 1.TXĐ: x
5; x= 5 không là nghiệm
Đặt y =
5 7 16 14x x x x
=> y’ =
1 1 1 1
0
2 5 2 2 7 2 16x x x x
Hàm số đồng biến
phương trình y=0 có 1 nghiệm duy nhất. Ta có y(9) = 14
x= 9
2. Đặt t=
22
2 2 ( 1) 1 1x x x
32
( ) 2 4 4
1
f t t t t m
t
f
’
(t)= 3t
2
– 4t- 4=0
t
1
=-2/3; t
2
= 2
BBT
t
-2/3 1 2 +
f
’(t)
0
- 0 +
f(t)
-1/2 +
-4
Từ bảng biến thiên
1
2
4
m
m

157/ Giải bất phương trình:
22
log ( 3 1 6) 1 log (7 10 ) xx
Giải: Điều kiện:
1
10
3
x
BPT
22
3 1 6
log log (7 10 )
2

x
x
3 1 6
7 10
2

x
x
3 1 6 2(7 10 ) xx
3 1 2 10 8 xx
49x
2
– 418x + 369 ≤ 0
1 ≤ x ≤
369
49
(thoả)
158/ Giải hệ phương trình:
log log
2 2 3

yx
xy
xy y
Giải:Điều kiện: x > 0 và x ≠ 1 và y > 0 và y ≠ 1
Ta có
2
log log log log 2 0
y x y y
xy y x x
log 1
log 2

y
y
x
x
2
1
xy
x
y
Với x = y x = y =
2
log 3 1
Với x =
2
1
y
ta có:
2
1
2 2 3
y
y
theo bất đẳng thức Cô-si suy ra PT vô nghiệm
159/ .Giải bất phương trình:
2 10 5 10 2x x x
Giải: *Điều kiện:
2x
;
2
1 2 10 2 5 10 2 6 20 1(2)x x x x x x
Khi
2x
=> x+1>0 bình phương 2 vế phương trình (2)
2 2 2
(2) 2 6 20 2 1 4 11 0 x ; 7 3;x x x x x x 
Kết hợp điều kiện vậy nghiệm của bất phương trình là:
3x
160/ 1) Tìm các giá trị của tham số m để phương trình:
2
2 2 2m x x x
có 2 nghiệm phân biệt.
2) Giải phương trình:
3
18
2
2
log 1 log (3 ) log ( 1) 0 x x x
.
Giải: Ta có:
2
2 2 1xx
nên
2
2 2 2m x x x
2
2
22
x
m
xx


Xét
2
2
()
22
x
fx
xx

, ta có:
22
43
'( )
2 2 2 2
x
fx
x x x x
44
' 0 ; 10; lim ( ) 1; lim ( ) 1
33
xx
f x x f f x f x
 



Bảng biến thiên:
x
-
4
3
+
y’
- 0 +
y
10
-1 1
Dựa vào bảng biến thiên ta có:
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi
1 10m
161/
3
18
2
2
log 1 log (3 ) log ( 1) 0 x x x
Giải:
3
18
2
2
log 1 log (3 ) log ( 1) 0 x x x
2 2 2
log 1 log (3 ) log ( 1) 0
13

x x x
x
1 3 1
13
x x x
x

2
x x 4 0
1 x 3


1 17
x
2

162/ Giải hệ phương trình
22
4 2 2
2 3 15 0
2 4 5 0
x y x y
x y x y
Giải: Hệ pt
22
2 2 2
( 1)( 2) 4( 1) 4( 2) 5
( 1) ( 2) 10
x y x y
xy
. Đặt
2
1
2
ux
vy


Ta có hpt
2 2 2
10 ( ) 2 10
4( ) 5 4( ) 5
u v u v uv
uv u v uv u v



10
45
uv
uv
(vô nghiệm) hoặc
2
3
uv
uv


3
1
u
v

hoặc
1
3
u
v

+)
3
1
u
v

Tìm được 2 nghiệm
( ; ) (2;1)xy
và
( ; ) ( 2;1)xy
+)
1
3
u
v

Tìm được nghiệm
( ; ) (0;5)xy
Kết luận: Hệ phương trình có 3 nghiệm: (2;1), (-2;1), (0;5)
163/ : 1. Giải phương trình:
.25log)20.155.10log( x
xx
2. Giải bất phương trình
22
2
1 log log ( 2) log (6 )x x x
Giải: 1. PT
xxx
10.25log20.155.10log
xxx
10.2520.155.10
0102.254.15
xx
(chia hai vế của phương trình cho
x
5
) Đặt
)0(2 tt
x
, Ta có pt :
15t
2
- 25t +10 = 0
)(
3
2
)(1
tmt
tmt
Với
1t
012 x
x
Với
3
2
log
3
2
2
3
2
2
xt
x
Vậy phương trình đã cho có hai nghiệm là
0x
và
3
2
log
2
x
.
2. Đk: 0< x< 6. BPT
22
22
log (2 4 ) log (6 )x x x
BPT
2 2 2
2 4 (6 ) 16 36 0x x x x x
x < -18 hoặc x > 2 .Kết hợp đk ta có tập
nghiệm BPT là S =(2; 6)
164/ Giải bất phương trình :
x
x
xx
x
92
313
3
Giải:
x
x
xx
x
92
313
3
.
ĐK: -1 ≤ x ≤ 9 và x ≠ 0
Bpt
)11)(11(
92
)11)(21(
)21)(21(
xx
x
xx
xx
11
92
21
x
x
x
TH1:
0011 xx
;
Bpt
xxx 92133
0)922()139()8( xxx
8
0)
922
8
139
9
1)(8(
x
xx
x
Kết hợp đk : 8 < x ≤ 9
TH2:
0011 xx
;
Bpt
892133 xxxx
;
Kết hợp đk: -1 ≤ x < 0
Vậy tập nghiệm của bpt S = [-1; 0) (8; 9]
165/ Giải phương trình
23
9 27
33
log ( 1) log 2 log 4 log ( 4)
x x x
Giải: log
9
(x + 1)
2
+
3
27
33
log 2 log 4 log ( 4) (1)
xx
§ K:
44
1
x
x

(1)
log
3
(x + 1) + log
3
4 = log
3
(4 – x) + log
3
(x + 4)
log
3
4
1
x
= log
3
(16 – x
2
)
4
1
x
= 16 – x
2
;
Giải phương trình tìm được X=2 , hoặc X= -2
166/ 1) Giải phương trình:
3
3
2
2ln x ln 2lnx 0
3
x x x
2) Giải hệ phương trình:
22
3x 3 14
14x 36
y x y xy
x y x y y
Giải: 1. Đặt
3
2lnx 0yx
Đưa về hệ PT đối xứng. PT có nghiệm duy nhất
1x
.
2. Đưa về PT đẳng cấp (bậc 3) bằng cách đặt ẩn phụ
;0u x y v xy
.
167/ Giải hệ phương trình:
22
2
2
1
xy
xy
xy
x y x y
Giải: Điều kiện x+ y >0
2
22
22
( ) 1 2 0 ( 1)( 1 ) 0
xy xy
x y xy x y x y
x y x y
x y x y x y x y






2
( 1)( 1) 0x y x y
x y x y
2
1
12
03
1
xy
xx
h
yy
xy





168/ Giải hệ phương trình:
22
2
2xy
x y 1
xy
x 2y 2 x y 4x 3y 4x 5y.
Giải:
22
2
2xy
x y 1(1)
xy
x 2y 2 x y 4x 3y 4x 5y(2).
Điều kiện: x +y>0, 4x +3y
0, 4x +5y 0.
2
2xy
(1) x+y 1 2xy 0
xy
2xy
x y 1 x y 1 0
xy



22
x y x y
x y 1 0
xy



22
x y x y
x y 1 0 (do 0)
xy
.
Với
y x 1
y =1 -x thay vào (2) ta được
2
4 (x 1) 3 x 5 x
(*)
Ta thấy vế trái (*)
2
4 (x 1) 4
dấu “=” khi x =1.
Ta thấy vế phải (*)
3 x 5 x (1 1)[(3 x) (5 x)] 4
(Bunhiacopski) dấu “=” khi x =1. (*)
x =1 y =0. Ta thấy (x;y) = (1;0) thỏa mãn đk.
Vậy hệ phương trình có một nghiệm duy nhất (x;y) = (1;0)
169/ 1. Giải phương trình:
2
2x 2 x 2x 2 x
x 2 2
22
3 .log (x x 2) 3 3 .log x 2
.
2. Giải phương trình:
x x 1 x x
3 3 3
log 3 2 log 3 1 log 2.9 3 9 1
.
Giải:1. Điều kiện x 2
Phương trình tương đương với
2
2x 2 2x 2
x x 2 2
3 .log(x x 2) 3 3 .log x 2


2
2x 2
x x 2 2
22
3 .log (x x 2) 3 .log (2 x 2)

(*)
Vì
2
x x 2 1
nên vế trái dương vậy vế phải dương
x 2 1
Xét hàm số
t
2
f(t) 3.log t
với t >1,
t
't
2
3
f (t) 3.ln3.log t 0 t 1
t.ln2
. Vậy f(t) đồng biến trên (1; +)
Từ (*) ta có
22
f(x x 2) f(2 x 2) x x 2 2 x 2
22
22
x x 2 2x 4 x 3x 6 0(1)
x x 2 2x 4(2) x x 2 0(2)

pt(1) vô nghiệm, pt(2) có nghiệm x =1 và x = -2 tm điều kiện
Vậy nghiệm của phương trình là:
x1
x2

2. Phương trình tương đương với
x x x x
33
log 3 2 3 3 log 2.9 3 9


x x x x x x
3 2 3 3 2.9 3 9 9 4.3 3 0
(*). Đặt
x
t 3 ,t 0.
(*)
2
t1
t 4t 3 0
t2
(thỏa mãn đk t>0) ; Với t =1
x
3 1 x 0.
Với t =3
x
3 3 x 1.
Vậy phương trình có 2 nghiệm x =0 hoặc x =1.
170/ Giaûi heä phöông trình :
22
4
( 1) ( 1) 2
x y x y
x x y y y
Giải: Giaûi heä phöông trình : (I)
22
4
( 1) ( 1) 2
x y x y
x x y y y
(I)
22
22
x y x y 4
x y x y xy 2 xy 2
Đặt
2 2 2 2 2 2 2
S x y;P xy(S 4P) S x y 2xy x y S 2P
Vaäy





2
2
P2
S 2P S 4
I
S0
S P S 2
S1


1
x y 0
TH :
xy 2
vaäy x, y laø nghieäm cuûa phöông trình
2
X 0X 2 0
Vaäy heä coù 2 nghieäm
x2
x2

hay
x2
y2


2
x y 1
TH :
xy 2
vaäy x,y laø nghieäm cuûa phöông trình
2
X X 2 0
X 1hay X 2
. Vaäy heä coù 2 nghieäm
x1
y2

V
x2
y1

Toùm laïi heä Pt (I) coù 4 nghieäm
x2
y2

V
x2
y2

V
x1
y2

V

x2
y1
171/ 1. Giải phương trình
2( 2x 3 x 1) x 4
2. Giải hệ phương trình
22
22
2 x 5 2 y 1 y
2 y 5 2 x 1 x
Giải: 1.
2( 2x 3 x 1) x 4
(1) - Điều kiện:
3
x.
2
- Nhận thấy x = 4 không là nghiệm của PT. Với
x 4 2x 3 x 1 0.
PT
2( 2x 3 x 1)( 2x 3 x 1) (x 4)( 2x 3 x 1)
2(x 4) ( 2x 3 x 1)(x 4)
2x 3 x 1 2.
(2)
Từ (1) và (2) suy ra
2
x
2x 3
x8
x8
4
x 16 208 (t / m)
x 8 x 32x 48 0
x 16 208
x1
4




Vậy PT có 1 nghiệm
x 16 208.
2.Giải hệ
22
22
2 x 5 2 y 1 y
2 y 5 2 x 1 x
(1)
(2)
- Điều kiện:
x,y 1.
Nhận thấy x = y = 1 không là nghiệm của hệ
x 1 y 1 0.
Hệ
2 2 2 2
2( x 5 y 5) 2( y 1 x 1) (y x )
22
22
22
2(x y ) 2(y x)
(y x )
x 1 y 1
x 5 y 5

22
22
(x y) x y 0
x 1 y 1
x 5 y 5




xy
- Thế vào (1) được:
22
2 x 5 2 x 1 x
22
2( x 5 3) 2( x 1 1) (x 4) 0
2
2
2
2(x 4) 2(x 2)
(x 4) 0
x 1 1
x 5 3



2
2(x 2) 2
(x 2) (x 2) 0 (3)
x 1 1
x 5 3





- Vì
2
22
2 2(x 2)
x 1 x 5 3 2 1 (x 2)
x 5 3 x 5 3
2
2(x 2) 2
(x 2) 0 (*) x 2.
x 1 1
x 5 3


Vậy hệ có 1 nghiệm (2; 2).
172/ Giải phương trình: log
2
2
8x
3
– 9log
2
4x
2
– 36log
4
2x = 0
Giải: Giải phương trình: log
2
2
8x
3
– 9log
2
4x
2
– 36log
4
2x = 0(1) Điều kiện x > 0
(1 )
0log118log229log33
22
2
2
xxx
027log18log9
2
2
2
xx
log
2
x = -1 hoặc log
2
x =3
x = 1/2 hoặc x=8
173 / Giải hệ phương trình:
33
22
x y 9
x 2y x 4y

Giải: Giải hệ
yxyx
yx
42
9
22
33
yyxx
yx
12633
9
22
33
x
3
–3x
2
+3x = y
3
+6y
2
+12y +9
(x-1)
3
= (y +2)
3
x =y +3
Vậy hệ đã cho
33
x1
x y 9
y2
x y 3




hoặc
x2
y1

174/ 1) Giải phương trình :
3
1
8 1 2 2 1
xx
2) Giải bất phương trình:
2
3 1 1 2 3 4 x x x x
Giải: 1/ Giải phương trình:
3
1
8 1 2 2 1
xx
. Đặt
3
1
2 0; 2 1
xx
uv
.
PT
33
3
3 2 2
0
1 2 1 2
2 1 0
1 2 ( )( 2) 0






uv
u v u v
uu
v u u v u uv v
3
1
3
1
21
1
1
2 1 1
0
15
15
2
2
2
15
15
21
2
2
x
x
x
x
u
v
x
u
Vn
v









Phương trình có nghiệm là:
0x
2. Giải bất pt:
2
3 1 1 2 3 4 x x x x
Điều kiện
2
3 0 3
/ 1 0 1 1
3
x 2x 3 0
1
xx
D k x x x
x
x




Nhân hai vế của bpt với
31 xx
, ta được
BPT
22
4. 1 2 3 4. 3 1 1 2 3 3 1 x x x x x x x x
2 2 2 2
2
2 2 2 2 3 2 2 2 2 3 4 0
2

x
x x x x x x x x
x
Kết hợp với điều kiện ta được
2x
là nghiệm của bất pt
175/ Giải hệ phương trình:
x x y y
x y x y
4 2 2
22
4 6 9 0
2 22 0
Giải: Giải hệ pt:
2 2 2
22
( 2) ( 3) 4
( 2 4)( 3 3) 2 20 0
xy
xyx
.
Đặt
2
2
3


xu
yv
Khi đó (2)
22
4
. 4( ) 8

uv
u v u v
2
0
u
v
hoặc
0
2
u
v
2
x 2 2
30y


Hoặc
2
x 2 0
32y


Kết luận:Hệ pt có 4 nghiệm là:
2
3
x
y
;
2
3

x
y
;
2
5
x
y
;
2
5

x
y
176 /Tìm giá trị lớn nhất và nhỏ nhất của hàm số:
y =
444
2323 xxx
Giải:
177/ Giải phương trình
25
4
2
1
4log 2 log 1 ( )
2
x x x
Giải: Giải phương trình
25
4
2
1
4log 2 log 1 ( )
2
x x x
(1)
ĐK:x>0
2
22
1 log 2 5log 1xx
22
2 2 2 2
(log 1) 5log 1 log 3log 2 0(1)x x x x
Đặt t=log
2
x (1)
trở thành
2
1
3 2 0
2
t
tt
t
t=1 ta có log
2
x=1
x=2 ;t=2 ta có log
2
x=2
x=4
kết hợp với ĐKXĐ
phương trình đã cho có 2 nghiệm là x=2 và x=4
179/ 1. Giải phương trình:
10 1 3 5 9 4 2 2x x x x
2
.Giải phương trình
21
2
2log (2 2) log 9 1 1xx
Giải:
Điều kiện: x
5
.;
3
Phương trình đã cho tương đương với 10x 1 2 x 2 9 x 4 3x 5 (1).
Vì x
5
nên cả hai vế của (1) đều dương. Do đó:
3
(1) 12 x 1 2 (10 x 1)(2 x 2) 12 x 1 2 (9 x 4)(3x 5)
7 x
2
15x 18 0 x 3 hay x
6
.
7
Kết hợp với điều kiện ta được nghiệm của phương trình là x = 3.
2/ Điều kiện: x
1
.
9
Phương trình đã cho tương đương với phương trình
log (2x 2)
2
log (9x 1) 1
2 2
log (2x 2)
2
log (9 x 1) log 2 log (2x 2)
2
log (18x 2)
(2x 2)
2
(18x 2) 2 x
2
5x 3 0 = 1 hoặc x
3
.
2
Đối chiếu điều kiện suy ra nghiệm của phương trình là x = 1 hay x
3
.
2
186/ : Giải phương trình
x2
1 1 1
log x 1
2
log log 4 2
2x 1
4
Giải: Giải phương trình
x2
1 1 1
log x 1
2
log log 4 2
2x 1
4
Điều kiện
2, 3xx
; (1)
4 4 4 4
log (x 2) log (2x 1) log 2 log (x 1)
2 2 1 2 1x x x
0
2
2 7 0
7
2
x
xx
x
; Đối chiếu điều kiện ta có
7
2
x
187/ : 1. Giải hệ phương trình
22
4 2 2
2 3 15 0
2 4 5 0
x y x y
x y x y
2. Giải phương trình:
.25log)20.155.10log( x
xx
3. Giải bất phương trình
22
2
1 log log ( 2) log (6 )x x x
Giải:
1/ Hệ pt
22
2 2 2
( 1)( 2) 4( 1) 4( 2) 5
( 1) ( 2) 10
x y x y
xy
. Đặt
2
1
2
ux
vy


Ta có hpt
2 2 2
10 ( ) 2 10
4( ) 5 4( ) 5
u v u v uv
uv u v uv u v



10
45
uv
uv
(vô nghiệm) hoặc
2
3
uv
uv


3
1
u
v

hoặc
1
3
u
v

+)
3
1
u
v

Tìm được 2 nghiệm
( ; ) (2;1)xy
và
( ; ) ( 2;1)xy
+)
1
3
u
v

Tìm được nghiệm
( ; ) (0;5)xy
Kết luận: Hệ phương trình có 3 nghiệm: (2;1), (-2;1), (0;5)
2/. PT
xxx
10.25log20.155.10log
xxx
10.2520.155.10
0102.254.15
xx
(chia hai vế của phương trình cho
x
5
)
Đặt
)0(2 tt
x
, Ta có pt : 15t
2
- 25t +10 = 0
)(
3
2
)(1
tmt
tmt
Với
1t
012 x
x
Với
3
2
log
3
2
2
3
2
2
xt
x
Vậy phương trình đã cho có hai nghiệm là
0x
và
3
2
log
2
x
.
3/ Đk: 0< x< 6. BPT
22
22
log (2 4 ) log (6 )x x x
BPT
2 2 2
2 4 (6 ) 16 36 0x x x x x
x < -18 hoặc x > 2
Kết hợp đk ta có tập nghiệm BPT là S =(2; 6)
188/ : Giải bất phương trình:
23
3 2 3 2
log log 8 .log log 0x x x x
(1)
Giải:
Điều kiện x>0;Biến đổi phương trình tương đương về dạng:
2
3 2 3 2
log 3 log log 3log 0x x x x
Đặt
3
logtx
khi đó bất phương trình có dạng:
2
22
3 log . 3log 0f t t x t x
(2)
Ta có:
22
2 2 2
3 log 12log 3 logx x x
.
Do đó f(t)=0 có nghiệm:
2
3
log
t
tx
Do đó (2) tương đương với:
2 3 3 2
3 log 0 log 3 log log 0t t x x x x
33
3 2 3 2
33
3 2 3 2
log 3 0 log 3
27
log log 0 log log
1
27
01
log 3 0 log 3 27
01
log log 0 log log
xx
x
x x x x
x
x
x
x x x
x
x x x x













Vậy bất phương trình có nghiệm là tập
0;1 27; 
189/ : 1. Giaûi heä phöông trình :
0222
0964
22
224
yxyx
yyxx
2. Giải phương trình:
23
8
2
4
log 1 2 log 4 log 4x x x
3. Giải hệ phương trình:
2
log ( 2 8) 6
8 2 .3 2.3
x x y x y
yx

Giải:
1/
022)2(
4)3()2(
22
222
xyx
yx
0202)33)(42(
4)3()2(
22
222
xyx
yx
0202)33)(42(
4)3()2(
22
222
xyx
yx
Đặt
vy
ux
3
2
2
* Thay vào ta có hệ phương trình
8)(4.
4
22
vuvu
vu
Giải hệ ta được
0
2
v
u
hoặc
2
0
v
u
Thay vào phương trình ta có
3
2
y
x
;
3
2
y
x
;
5
2
y
x
;
5
2
y
x
2 .
23
48
2
log 1 2 log 4 log 4x x x
(2) Điều kiện:
10
44
40
1
40
x
x
x
x
x




2
2 2 2 2 2
22
22
(2) log 1 2 log 4 log 4 log 1 2 log 16
log 4 1 log 16 4 1 16
x x x x x
x x x x
+ Với
14x
ta có phương trình
2
4 12 0 (3)xx
;
2
(3)
6
x
x

lo¹i
Với
41x
ta có phương trình
2
4 20 0xx
(4);
2 24
4
2 24
x
x


lo¹i
Vậy phương trình đã cho có hai nghiệm là
2x
hoặc
2 1 6x 
3. Pt đầu
y – 2x + 8 =
6
2
2yx
thế vào pt thứ hai ta được:
23
8 2 .3 2.3
x x x x

8 18 2.27
x x x
8 18
2
27 27
xx

3
22
2
33
xx
Đặt: t =
2
3
x



, (đk t > 0 ) , ta có pt:
32
2 0 1 2 0t t t t t
0
1
0
x
t
y
190/ : 1. Giải hệ phương trình
22
4 2 2
2 3 15 0
2 4 5 0
x y x y
x y x y
2. Giải phương trình:
.25log)20.155.10log( x
xx
3.Giải bất phương trình
22
2
1 log log ( 2) log (6 )x x x
Giải:
1/ Hệ pt
22
2 2 2
( 1)( 2) 4( 1) 4( 2) 5
( 1) ( 2) 10
x y x y
xy
. Đặt
2
1
2
ux
vy


Ta có hpt
2 2 2
10 ( ) 2 10
4( ) 5 4( ) 5
u v u v uv
uv u v uv u v



10
45
uv
uv
(vô nghiệm) hoặc
2
3
uv
uv


3
1
u
v

hoặc
1
3
u
v

+)
3
1
u
v

Tìm được 2 nghiệm
( ; ) (2;1)xy
và
( ; ) ( 2;1)xy
+)
1
3
u
v

Tìm được nghiệm
( ; ) (0;5)xy
Kết luận: Hệ phương trình có 3 nghiệm: (2;1), (-2;1), (0;5)
2/ PT
xxx
10.25log20.155.10log
xxx
10.2520.155.10
0102.254.15
xx
(chia hai vế của phương trình cho
x
5
)
Đặt
)0(2 tt
x
, Ta có pt : 15t
2
- 25t +10 = 0
)(
3
2
)(1
tmt
tmt
Với
1t
012 x
x
Với
3
2
log
3
2
2
3
2
2
xt
x
Vậy phương trình đã cho có hai nghiệm là
0x
và
3
2
log
2
x
.
3 / Đk: 0< x< 6. BPT
22
22
log (2 4 ) log (6 )x x x
BPT
2 2 2
2 4 (6 ) 16 36 0x x x x x
x < -18 hoặc x > 2
Kết hợp đk ta có tập nghiệm BPT là S =(2; 6)
191/ 1. Giải hệ phương trình :
2
2 2 2
2 2 (1 )
1
( 2 )(1 ) 9
x y xy xy x
xy
xy
2.Giải phương trình:
23
1
2
2
(6 1)log ( 1) ( 1)log ( 1) 7 0x x x x
3. Giải phương trình:
3
2 1 1 3 2
73
2 4 4 6
22
xx
x x x
Giải:
1/ Điều kiện Hệ
22
2 2 2
2 2 2
(2 )(1 ) 2
2 2 2
1
1
( 2 )( ) 12
( 2 )(1 ) 12
x y xy xy
x y xy x y xy
xy
xy
xy
xy
xy





,0xy
.
Do
10xy
,nên hệ
2 2 2
2 2 2
2
2
(1 )
12(2 ) 4( 2 )
( 2 ) 12( )
1
xy
xy
xy
x y x y
xy
xy
xy


22
11 12 0
11
yx
x xy y
yx
Vây hệ có nghiệm (1;1)
2/ Giải phương trình:
23
1
2
2
(6 1)log ( 1) ( 1)log ( 1) 7 0x x x x
HD: Điều kiện:x>-1:Phương trình
2
22
(6 1)log ( 1) (6 6)log ( 1) 7 0x x x x
Đặt
)1(log
2
xt
,Phương trình trở thành:
07)66()16(
2
txtx
(*)
+Nếu
6
1
016 xx
:Pt (*) có a-b+c=0 nên(*)
)1(
16
7
)1(log
2
1
16
7
1
2
x
x
x
x
t
t
Ta có
0
16
7
)1(log)1(
2
x
x
;Đặt
);
6
1
()
6
1
;1(,
16
7
)1(log)(
2

x
x
xxf
);
6
1
()
6
1
;1(,0
)16(
42
2ln)1(
1
)('
2

x
x
x
xf
Do đó hàm số đồng biến trên các khoảng
)
6
1
;1(
và
);
6
1
( 
.
+Với
yx
thay vào hê ta được :x=y=1
+Với y=11x thay vào ta được hệ vô nghiệm
+Nếu
6
1
016 xx
;Pt :
07
6
5
log.7
2
:Vô lý
+Hàm số đồng biến trên
)
6
1
;1(
nên phương trình có nhiều nhất một nghiệm trên
)
6
1
;1(
Thử với
4
3
x
:
02)
4
1
(log)1(
2
Đúng.
+Hàm số đồng biến trên
);
6
1
( 
nên phương trình có nhiều nhất một nghiệm trên
);
6
1
( 
Thử với x=1 ta được:
012log)1(
2
Đúng.
Tóm lại phương trình có 3 nghiệm:
4
3
x
;
2
1
x
; x=1
3/ Giải phương trình:
3
2 1 1 3 2
73
2 4 4 6
22
xx
x x x
16128222
23122
3
xxxx
xx
3122
)12(222
3
xx
xx
Xét hàm số:
3
2)( ttf
t
có
2
'( ) 2 ln2 3 0
t
f t t t R
.Do đó f(t) đồng biến trên R
Phương trình:
122)12()2(
33
xxxfxf
Vậy phương trình có nghiệm x=1.
192/ :
1.Giải phương trình:
22
36 63 27 15 27 2 9 9 3x x x x x
.
2.Cho hai số thực x, y thỏa mãn
1 15
2
xy
xy
Tìm giá trị lớn nhất và nhỏ nhất của
P x y
.
3. Tìm m để phương trình
2
12 4 3 3 24 3 1 2 4 3x x x m x x
có nghiệm .
4.Giải hệ phương trình:
22
22
22
2
log log 9
10
1 log 1 log
9
1 log 2.log 2 log
2
xy
xy
xy
xy



Giải:
1) Từ dấu hiệu
2 2 2
36 63 27; 2 9 9 3 36x 36x 12x x x x
Nhân liên hợp và biện luận ta được nghiệm duy nhất
15
27
x
2.HD.(nhiều cách) Đặt
1 0; 15 0x u y v
ta đưa được về hệ PT đối xứng. Từ đk PT
có nghiệm không âm ta tìm được
2 1 17 16P
3.HD. ĐK. Đặt
3 1 2 4 3x 21; 7t x t


ta chỉ việc tìm GTLN,NN trên đoạn này của hàm
số
1
f t t
t

Hd: Phương trình
3
2 1 1 3 2
73
2 4 4 6
22
xx
x x x
3712822
23122
3
xxx
xx
10)348)(1(037128
223
xxxxxxx
4. ĐK, đặt
22
log ; logx u y v
và
11
; ( , 2)u m v n m n
uv
Ta được 4 nghiệm
4,2 , 2; 2
và giao hoán của bộ số.
193. Giải phương trình:
33
x 34 x 3 1
Giải:
Đặt
33
u x 34, v x 3
. Ta cã :
22
33
u v 1
u v 1
u v u v uv 37
u v 37




2
u v 1
u v 1
uv 12
u v 3uv 37




u3
v4
u4
v3

Với u = -3 , v = - 4 ta có: x = - 61 ;
Với u = 4, v = 3 ta có: x = 30
Vậy phương trình đã cho có 2 nghiệm : x = -61 và x = 30
194/
22
(3x y)(x 3y) xy 14
(x y)(x y 14xy) 36
Giải:
22
(3x y)(x 3y) xy 14
(x y)(x y 14xy) 36
Đk:
0xy
Hệ ban đầu tương đương
2
2
[3(x y) 4xy] xy 14
(x y)[(x y) 12xy] 36
Đặt
0
a x y
b xy


thay vào hệ trên được
2 2 2 3
2 2 3 2
(3 4 ) 14 3 4 14
( 12 ) 36 12 36
a b b a b b
a a b a ab





Nhận thấy a=0 không là nghiệm của hệ trên. Đặt b=ka thay vào hệ trên được
33
32
(3 4 ) 14
(1 12 ) 36(1)
a k k
ak


. Ta suy
ra phương trình 72k
3
-84k
2
+54k-7=0
11
6
66
k b a a b
thay vào (1) được a=3, từ đó b=1/2
3 2 2 3 2 2
33
22
11
3 2 2 3 2 2
24
22
x y x y
xx
hoac
xy xy
yy











195/ . Giải phương trình:
22
x 3 x 1 x x 2 0
(
x
)
Giải: Giải phương trình:
22
x 3 x 1 x x 2 0
(
x
)
ĐK:
2
x 3 0
x3
x 1 0



; Đặt
2
u x 3 ,u 0
,
v x 1 ,v 0
Suy ra:
2 2 2
u v x x 2
Ta được phương trình:
22
u v u v 0
u v u v u v 0
u v 1 u v 0
uv
u v 1
Vì
u 0;v 0
nên loại u + v = – 1
Khi u = v
22
x 3 x 1 x x 2 0
x1
x2

Vì
x3
, nên x = – 1 loại. Vậy phương trình có 1 nghiệm x = 2.
196/. Giải hệ phương trình:
28
2 2 2 2
log 3log ( 2)
13
x y x y
x y x y
.
Giải:
Điều kiện: x+y>0, x-y>0
28
2 2 2 2 2 2 2 2
log 3log (2 ) 2
1 3 1 3
x y x y x y x y
x y x y x y x y





Đặt:
u x y
v x y


ta có hệ:
2 2 2 2
2 ( ) 2 4
22
33
22
u v u v u v uv
u v u v
uv uv





2
2 4 (1)
( ) 2 2
3(2)
2
u v uv
u v uv
uv

. Thế (1) vào (2) ta có:
2
8 9 3 8 9 (3 ) 0uv uv uv uv uv uv uv
. Kết hợp (1) ta có:
0
4, 0
4
uv
uv
uv

(vỡ u>v). Từ đó ta có: x =2; y =2.(T/m)
KL: Vậy nghiệm của hệ là: (x; y)=(2; 2).
197/ . 1.Giải hệ phương trình
3 2 3 2
2
3 5.6 4.2 0
( 2 )( 2 )
x y x x y
x y y y x y x

2. Giải bất phương trình
23
34
2
log ( 1) log ( 1)
0
56
xx
xx

Giải:
1/ ĐK:
,0xy
xy
Hệ phương trình
3 2 3 2 3 2 3 2
3 5.6 4.2 0 3 5.6 4.2 0
(2 )( 2 ) 2 (2 )( 2 )( )
x y x x y x y x x y
x y y y x y x x y y x y x x y y






3 2 3 2
3 2 3 2
3 5.6 4.2 0
3 5.6 4.2 0
20
(2 )[( 2 )( ) 1] 0
x y x x y
x y x x y
yx
y x y x x y y





(do
2 )( ) 1 0y x x y y
)
3 2 3 2 2 2
3 5.6 4.2 0 3 5.6 4.2 0 (1)
2 2 (2)
x y x x y x x x
y x y x






Giải (1):
2 2 2
3
( ) 1
33
2
3 5.6 4.2 0 ( ) 5.( ) 4 0
3
22
( ) 4
2
x
x x x x x
x
3
2
0
log 4
x
x
Với x = 0 thay vao (2) ta được y = 0
Với
3
2
log 4x
thay vao (2) ta được y =
3
2
1
log 4
2
Kết hợp với điều kiện ta được nghiệm của phương trình là
3
2
log 4x
,y =
3
2
1
log 4
2
198/ 1. Giải hệ phương trình:
22
2
25
( 2 )( 3) 3
x y xy x y
x x x y y
(
;
x y R
)
2. Giải hệ phương trình :
2
2
log ( ) log 1
2 3 2 1 2
y x x
yx
Giải:
1/ Nếu y = 0
2
0
20
2
x
xx
x

hệ có nghiệm (0;0);(-2;0)
Nếu
0
y
, hpt
2
2
2
5
2
.( 3) 3
xx
xy
y
xx
xy
y
;đặt
2
2
3
xx
u
y
v x y
ta có hệ:
23
31
u v u
uv v



hoặc
1
3
u
v

Với
2
2
3
31
11
31
xx
ux
y
vy
xy




hoặc
6
8
x
y

Với
1
3
u
v

2
2
1
33
xx
y
xy

(vô nghiệm)
Vậy hệ phương trình đã cho có 4 nghiệm (x; y) là: (0; 0) ; (-2; 0); (1; 1) và (-6; 8)
2/ Đk:
1
2
x
yx
; Pt hai
2 3 2 2 1 2 2 1
y x y x x
Thế vào pt còn lại ta được :
22
2 log 2 2 1 log 1
xx
2
4(2 1) 2 2 2
log 1 4(2 1) 2
33
3
x
x x x y
x
,(tmđk)
KL: hệ có nghiệm (x;y) là (
2
3
;
22
3
3
)
199/ 1) Giải phương trình sau:
2
11
2
2
x
x

.
2/ Giải hệ phương trình :
22
2
2
32
2010
2009
2010
3log ( 2 6) 2log ( 2) 1
yx
x
y
x y x y
Giải: 1/+) ĐK:
( 2; 2) \{0}x
+) Đặt
2
2 , 0y x y
Ta có hệ:
22
2
2
x y xy
xy


+) Giải hệ đx ta được x = y = 1 và
1 3 1 3
22
;
1 3 1 3
22
xx
yy









+) Kết hợp điều kiện ta được: x = 1 và
13
2
x

2/
22
2
2
32
2010
2009 (1)
2010
3log ( 2 6) 2log ( 2) 1(2)
yx
x
y
x y x y
+) ĐK: x + 2y = 6 > 0 và x + y + 2 > 0
+) Lấy loga cơ số 2009 và đưa về pt:
2 2 2 2
2009 2009
log ( 2010) log ( 2010)x x y y
+) Xét và CM HS
2009
( ) log ( 2010), 0f t t t t
đồng biến,
từ đó suy ra x
2
= y
2
x= y, x = - y
+) Với x = y thế vào (2) và đưa về pt: 3log
3
(x +2) = 2log
2
(x + 1) = 6t
Đưa pt về dạng
18
1
99
tt

, cm pt này có nghiệm duy nhất t = 1
x = y =7
+) Với x = - y thế vào (2) được pt: log
3
(y + 6) = 1 y = - 3 x = 3
200. Giải hệ phương trình:
33
2 2 3
x y 1
x y 2xy y 2

Giải:
1 3 4 x y
1 1 3 3
2x
2 x y
2 x y
yx
y x x y
xy
.
13
13
13
2y
2x
2x
xy
yx
yx
xy
13
x y 1
xy
2x
xx
x y 1
xy 2
2
x 2,y 2
y
13
2x
x
yx
x 2,y 2
x3
2x
2x











201. Giải phương trình :
3
2
3
512)13(
22
xxxx
Giải:
PT
631012)13(2
22
xxxx
232)12(412)13(2
222
xxxxx
. Đặt
)0(12
2
txt
Pt trở thành
0232)13(24
22
xxtxt
Ta có:
222
)3()232(4)13(' xxxx
Từ đó ta có phương trình có nghiệm :
2
2
;
2
12
x
t
x
t
Thay vào cách đăt giải ra ta được phương trình có các nghiệm:
7
602
;
2
61
x
202. Giải bất phương trình :
22
11
55
xx
> 24. (2)
Giải: Giải bất phương trình :
22
11
55
xx
> 24. (2)
(2)
22
2
5 5 24 5 5 0
xx

2
55
x
x
2
> 1
1
1
x
x
203. 1)
22
22
14
( ) 2 7 2
x y xy y
y x y x y
; 2)
12
12
2log [(1 )( 2)] 2log (1 ) 6
log ( 5) log ( 4) = 1
xy
xy
x y x
yx


Giải: 1)
0y
, ta có:
2
22
22
2
2
1
4
14
.
( ) 2 7 2
1
( ) 2 7
x
xy
y
x y xy y
y x y x y
x
xy
y

Đặt
2
1
,
x
u v x y
y
ta có hệ:
22
4 4 3, 1
2 7 2 15 0 5, 9
u v u v v u
v u v v v u


+) Với
3, 1vu
ta có hệ:
222
1, 2
1 1 2 0
2, 5
3 3 3
xy
x y x y x x
xy
x y y x y x




.
+) Với
5, 9vu
ta có hệ:
222
1 9 1 9 9 46 0
5 5 5
x y x y x x
x y y x y x




, hệ này vô nghiệm.
KL: Vậy hệ đã cho có hai nghiệm:
( ; ) {(1; 2), ( 2;5)}.xy
2) + Điều kiện:
2
2 2 0, 2 1 0, 5 0, 4 0
()
0 1 1, 0 2 1
xy x y x x y x
I
xy
.
1 2 1 2
1 2 1 2
2log [(1 )( 2)] 2log (1 ) 6 log ( 2) log (1 ) 2 0 (1)
()
log ( 5) log ( 4) = 1 log ( 5) log ( 4) = 1(2).
x y x y
x y x y
x y x y x
I
y x y x






Đặt
2
log (1 )
y
xt

thì (1) trở thành:
2
1
2 0 ( 1) 0 1.t t t
t
Với
1t
ta có:
1 2 1(3).x y y x
Thế vào (2) ta có:
2
1 1 1
44
log ( 4) log ( 4) = 1 log 1 1 2 0
44
x x x
xx
x x x x x
xx

0
2
x
x

. Suy ra:
1
1
y
y

.
+ Kiểm tra thấy chỉ có
2, 1xy
thoả mãn điều kiện trên.
Vậy hệ có nghiệm duy nhất
2, 1xy
.
204. Giải phương trình
8
42
2
11
log 3 log 1 log 4 2
24
x x x
Giải:
Điều kiện:
01x
;
2 3 1 4x x x
Trường hợp 1:
1x
2
2 2 0 2x x x
Trường hợp 2:
01x
2
2 6 3 0 2 3 3x x x
Vậy tập nghiệm của (2) là
2;2 3 3T 
205. Giải hệ phương trình
33
33
xy
yx
Giải: Điều kiện:
0 3,0 3xy
Ta có
33
33
xy
yx
2 (3 ) 0
2 (3 ) 0
x y x y
y x y x
(3 ) (3 ) 0
(3 ) 0
(3 ) 0
x y y x
xy
yx


0
0
3
3
x
y
x
y
Kiểm tra ta thấy
03
,
03
xx
yy





thỏa mãn.
Kết luận : Hệ có hệ có hai nghiệm
03
,
03
xx
yy





206. Giải bất phương trình :
22
11
55
xx
> 24. (2)
Giải:
Giải bất phương trình :
22
11
55
xx
> 24. (2)
(2)
22
2
5 5 24 5 5 0
xx

2
55
x
x
2
> 1
1
1
x
x
207. 1/ Giải phương trình:
22
7 5 3 2 ( )x x x x x x
2/ Giải hệ phương trình
14
4
22
1
log log 1
( , )
25
yx
y
xy
xy

Giải :
1/ Giải phương trình:
22
7 5 3 2 ( )x x x x x x
2
22
3 2 0
7 5 3 2
xx
PT
x x x x x
2
3 2 0
5 2( 2)
xx
x x x
31
0
2
5 2.
x
x
x
x
x

2
20
1 16 0
x
xx
1x
. Vậy phương trình đã cho có một nghiệm x = - 1.
2/ Giải hệ phương trình
14
4
22
1
log log 1
( , )
25
yx
y
xy
xy

Điều kiện:
0
0
yx
y

Hệ phương trình
4 4 4
2 2 2 2 2 2
11
log log 1 log 1
4
25 25 25
y x y x
yx
y y y
x y x y x y

2
2 2 2 2
3
33
25
25 9 25
10
xy
x y x y
y
x y y y



15 5
;;
10 10
15 5
;;
10 10
xy
xy






(không thỏa mãn đk)
Vậy hệ phương trình đã cho vô nghiệm.
208 1/ Giải phương trình: x
2
– 4x - 3 =
x5
2/ Giải phương trình :
5
log x 3
2x
Giải:
2
2
x 2 y 5
x y 0
5 29
x
2
x 2 y 5
x1
x y 3 0
y2




Vậy nghiệm của PT đã cho là : x = 2
208. Giải bất phương trình:
2
4x 3 x 3x 4 8x 6
(1)
Giải: Giải bất phương trình:
2
4x 3 x 3x 4 8x 6
(1)
(1)
2
4 3 3 4 2 0x x x
Ta có: 4x-3=0<=>x=3/4
2
3 4 2xx
=0<=>x=0;x=3
Bảng xét dấu:
x - 0 ¾ 2 +
4x-3 - - 0 + +
2
3 4 2xx
+ 0 - - 0 +
Vế trái - 0 + 0 - 0 +
Vậy bất phương trình có nghiệm:
3
0; 3;
4
x




209. 1/ Giải hệ phương trình :
22
8
7
1
x y x y
xy
y x xy
1/ x
2
- 4x + 3 =
x5
(1)
TX§ : D =
5; ) 
2
1 x 2 7 x 5
®Æt y - 2 =
x5
,
2
y 2 y 2 x 5
Ta cã hÖ :
2
2
2
x 2 y 5
x 2 y 5
y 2 x 5 x y x y 3 0
y 2 y 2




2/ ĐK : x > 0 PT đã cho tương đương với : log
5
( x + 3) = log
2
x (1)
Đặt t = log
2
x, suy ra x = 2
t
t t t
5
2 log 2 3 t 2 3 5
tt
21
31
35
(2)
Xét hàm số : f(t) =
tt
21
3
35
; f'(t) =
tt
21
ln0,4 3 ln0,2 0, t
35
R
Suy ra f(t) nghịch biến trên R
Lại có : f(1) = 1 nên PT (2) có nghiệm duy nhất t = 1 hay log
2
x = 1 hay x =2
2/ Giải bất phương trình :
22
1 5 2 1
25
log log 1 log log 1x x x x
3/ Giải bất phương trình :
1 1 1
3 3 4 0
xx
Giải:
1/ Hệ
2
2
3
( ) 2 8
2
7
1
xy
x y x y xy
xy
x y xy
x y xy



:
Vậy nghiệm của hệ là : (x;y) = (1 ;2) ,( 2 ; 1) ,( 1;-3 ) (-3; 1)
2/
22
3 1 3 5
5
22
3 1 5
5
2 2 2 2
55
2
2
2
k x 0: Bpt log log 1 log log 1 0
log log 1 log 1 0
log 1 1 0 log 1 1 1 5
50
12
15
5
15
Đ x x x x
x x x x
x x x x x x
x
x x x
xx




Kết hợp đk ta có 0 < x <
12
5
3/ Đk :
1x 
Pt
1
2 1 1
1
3 3 1 1 0
3 4.3 3 0
1
10
31
x
xx
x
xx
x
x



Nghiệm bất pt là : T =
1 0;
210. 1.Giải hệ phương trình :
4 3 2 2
32
1
1
x x y x y
x y x xy
2)Giải phương trình:
22
2
(24 1)
(24 1) (24 1)
log log
x
x x x x
Log x x x


3)Giải bất phương trình: log
x
( log
3
( 9
x
– 72 ))
1
Giải:
1/*Biến đổi hệ tương đương với
2 2 3
32
( ) 1
( ) 1
x xy x y
x y x xy
*Đặt ẩn phụ
2
3
x xy u
x y v

, ta được hệ
2
1
1
uv
vu

*Giải hệ trên được nghiệm (u;v) là (1;0) và (-2;-3)
*Từ đó giải được nghiệm (x;y) là (1;0) và (-1;0)
2/ *Điều kiện :x>0
*TH1 : xét x=1 là nghiệm
*TH2 : xét
1x
, biến đổi phương trình tương đương với
1 2 1
1 2log (24 1) 2 log (24 1) log (24 1)
x x x
x x x

Đặt
log ( 1)
x
xt
, ta được phương trình
1 2 1
1 2 2t t t


giải được t=1 và t=-2/3
*Với t=1
log ( 1) 1
x
x
phương trình này vô nghiệm
*Với t=-2/3
2
log ( 1)
3
x
x
23
.(24 1) 1xx
(*)
Nhận thấy
1
8
x
là nghiệm của (*)
Nếu
1
8
x
thì VT(*)>1
Nếu
1
8
x
thì VT(*)<1 , vậy (*) có nghiệm duy nhất
1
8
x
*Kết luận : Các nghiệm của phương trình đã cho là x=1 và
1
8
x
3/ *Điều kiện :
3
0
log (9 72) 0
9 72 0
x
x
x


giải được
9
log 73x
Vì
9
log 73x
>1 nên bpt đã cho tương đương với
3
log (9 72)
x
x
9 72 3
xx
38
39
x
x

2x
*Kết luận tập nghiệm :
9
(log 72;2]T
211. 1. Giải bất phương trình
xxxxx
2
1
log)2(22)144(log
2
1
2
2
2/ Giải hệ phương trình
113
2.322
2
3213
xxyx
xyyx
Giải:
1/ ĐK:
*
2
1
x
2
1
x
2
1
x
0)1x2(
2
1
x
01x4x4
0x
2
1
22
Với điều kiện (*) bất phương trình tương đương với:
1)x21(log)2x(2x2)x21(log2
22
01)x21(logx
2
0x
4
1
x
1)x21(2
0x
1)x21(2
0x
0)x21(2log
0x
0)x21(2log
0x
01)x21(log
0x
01)x21(log
0x
2
2
2
2
Kết hợp với điều kiện (*) ta có:
2
1
x
4
1
hoặc x < 0.
2/
)2(1xxy1x3
)1( 2.322
2
x3y2y1x3
Phương trình (2)
0)13(
1
113
01
2
yxx
x
xxyx
x
xy
x
x
yx
x
x
31
1
0
013
0
1
* Với x = 0 thay vào (1)
11
8
log
11
8
22.12282.322
2
2
y
yyyyy
* Với
xy
x
31
1
thay y = 1 – 3x vào (1) ta được:
2.322
1313
xx
Đặt
13
2
x
t
Vì
1x
nên
4
1
t
)83(log2y
183log
3
1
x
83t
i¹lo83t
01t6t6
t
1
t)3(
2
2
2
212 1. Giải phương trình:
2
2
1 3 2
13
xx
xx
2.Giải hệ phương trình:
2 2 2
3 3 3
log 3 log log
log 12 log log
x y y x
x x y y
. .
Giải: 1/ TXĐ: x
1;3
Đặt t=
1 3 , t > 0xx
=>
2
2
4
32
2
t
xx
đc pt: t
3
- 2t - 4 = 0 t=2 Với t = 2
1
1 3 =2 ( / )
3
x
x x t m
x

2/ TXĐ:
0
0
x
y
2 2 2
3 3 3
log 3 log log
3 . 2 .
log 12 log log
12 . 3 .
xy
xy
x y y x
yx
x x y y
xy

2
3 . 2 .
xy
yx
yx
4
3
4
3
log 2
2log 2
x
y
(t/m TXĐ)
213. Giải bất phương trình:
2
51 2x x
1
1x

.
Giải:
2
2
2
22
10
51 2 0
51 2
1
10
1
51 2 0
51 2 (1 )
x
xx
xx
x
x
xx
x x x




1
1 52; 1 52
1
( ; 5) (5; )
1 52; 1 52
x
x
x
x
x


 


1 52; 5 1; 1 52x


214. a)Giải bất phương trình: 9
2 2 2
2 1 2 2 1
34.15 25 0
x x x x x x
b)Tìm
a
để hệ phương trình sau có nghiệm :
x+1 1
21
ya
x y a
Giải: a)
2 2 2 2 2
2 1 2 2 1 2(2 ) 2
9 34.15 25 0 9.3 34.3
x x x x x x x x x x
.
22
2 2(2 )
5 25.5 0
x x x x

2
2
2
2
2
2(2 ) 2
2
3
1
5
33
9. 34. 25 0
55
3 25
59
xx
x x x x
xx







2
20
( ;1 3) (0;2) (1 3; )
22
xx
x
xx


KL: Bpt có tập nghiệm là T=
( ;1 3) (0;2) (1 3; )
b) đ/k
1; 1xy
.Bất pt
22
11
( 1) ( 1) 2 1
x y a
x y a
2
11
1
1. 1 (2 1)
2
x y a
x y a a


; Vậy
1x
và
1y
là nghiệm của p/t: T
2
2
1
( 2 1) 0*
2
aT a a
.Rõ ràng hệ trên có nghiệm khi p/t*
có 2 nghiệm không âm
22
2
0 2( 2 1) 0
0 0 1 2 2 6
01
( 2 1) 0
2
a a a
S a a
P
aa


215. 1/ Giải hệ phương trình:
2
53
x y x y y
xy

(x, y R)
2/ Giải bất phương trình
2
2
log
2log
2 20 0
x
x
x
2
Giải:
1/ ĐK: x + y 0 , x - y 0, y 0
PT(1)
2 2 2 2
2 2 4 2x x y y x y y x
2
2 0 (3)
5 4 (4)
yx
y xy

Từ PT(4) y = 0 v 5y = 4x
Với y = 0 thế vào PT(2) ta có x = 9 (Không thỏa mãn đk (3))
Với 5y = 4x thế vào PT(2) ta có
2 3 1x x x
KL: HPT có 1 nghiệm
4
( ; ) 1;
5
xy



2/ Điều kiện: x> 0 ; BPT
2
22
4log 2log
2 20 0
xx
x
Đặt
2
logtx
. Khi đó
2
t
x
.
BPT trở thành
22
22
4 2 20 0
tt
. Đặt y =
2
2
2
t
; y 1.
BPT trở thành y
2
+ y - 20 0 - 5 y 4.
Đối chiếu điều kiện ta có :
2
2 2 2
2 4 2 2 1
t
tt
- 1 t 1.
Do đó - 1
2
log x
1
1
2
2
x
216. 1/Giải hệ phương trình:
22
2
2
1
xy
xy
xy
x y x y
2/ Giải bất phương trình:
22
1 5 3 1
35
log log 1 log log 1x x x x
Giải:
1/
22
2
2
11
0
2
xy
xy
xy
dk x y
x y x y

23
2
1 2 1 0 2 2 0
xy
x y xy x y xy x y xy x y
xy
2
22
1 2 1 0 1 1 2 0
13
04
x y x y xy x y x y x y x y xy
xy
x y x y



Dễ thấy (4) vô nghiệm vì x+y>0 ; Thế (3) vào (2) ta được
2
1xy
Giải hệ
2
1
1; 0
2; 3
1
xy
xy
xy
xy



……
2/
22
1 5 3 1
35
log log 1 log log 1 (1)x x x x
Đk:
0x
22
3 1 3 5
5
22
3 1 5
5
22
5
1 log log 1 log log 1 0
log log 1 .log 1 0
log 1 1
x x x x
x x x x
xx



2
5
0 log 1 1xx
*)
2
5
0 log 1 0x x x
*)
2 2 2
5
12
log 1 1 1 5 1 5 ...
5
x x x x x x x
Vậy BPT có nghiệm
12
0;
5
x



217.
1. Giải phương trình:
1
xlog1
4
3logxlog2
3
x93
2. Gii bÊt ph-¬ng tr×nh:
1 2 3x x x
3. Giải phương trình :
21x2log1xlog
3
2
3
Giải:
1. Phương trình:
1
xlog1
4
3logxlog2
3
x93
(1)
(1)
1
xlog1
4
x9log
1
xlog2
33
3
1
xlog1
4
xlog2
xlog2
33
3
đặt: t = log
3
x thành
2
2 t 4
1 t 3t 4 0
2 t 1 t

(vì t = -2, t = 1 không là nghiệm)
t 1 hay t 4
; Do đó, (1)
3
1
log x 1 hay x 4 x hayx 81
3
2. §k:
3x
Bpt
2
1 2 3 2 5 6 4x x x x x x
2
34
40
6 2 3
3
6 2 3 6 2 3
3
3 12 8 0
33
x
x
x
xx
x





3. Giải phương trình:
21x2log1xlog
3
2
3
§k:
1
1
2
x
; pt
33
2log x 1 2 log 2x 1 2
33
log x 1 log 2x 1 1
33
log x 1 2x 1 log 3
x 1 2x 1 3

2
2
1
x1
x1
hoac
2
2x 3x 2 0
2x 3x 4 0(vn)
x2
219 . 1. Giải hệ phương trình
2
22
1
22
22
xx
y
y y x y
2.Giải bất phương trình
23
34
2
log ( 1) log ( 1)
0
56
xx
xx

Giải
1. ĐK :
0y
hệ
2
2
1
2 2 0
21
20
xx
y
x
yy
đưa hệ về dạng
2
2
2 2 0
2 2 0
u u v
v v u
2
3 7 3 7
1
22
1
1
1 7 1 7
2 2 0
22
uv
uu
uv
uv
hoac hoac
uv
vv
v v u











Từ đó ta có nghiệm của hệ : (-1 ;-1),(1 ;1), (
3 7 2
;
2
71
), (
3 7 2
;
2
71
)
2. Đk: x > - 1
bất phương trình
3
3
3
3log ( 1)
2log ( 1)
log 4
0
( 1)( 6)
x
x
xx



3
log ( 1)
0
6
x
x

06x
220. Giải phương trình :
22
1 2 2 1 2 2
2
2
log (5 2 ) log (5 2 ).log (5 2 ) log (2 5) log (2 1).log (5 2 )
x
x x x x x x
Giải: ĐK :
15
22
0
x
x

. Với ĐK trên PT đã cho tương đương với
2
2
2
2 2 2 2
2
log (5 2 )
log (5 2 ) 2log (5 2 ) 2log (5 2 )log (2 1)
log (2 1)
x
x x x x
x
2
22
2
1
4
log (2 1) 1
1
log (5 2 ) 2log (2 1) 2
2
log (5 2 ) 0
2
x
x
x x x x
x
x

Kết hợp với ĐK trên PT đã cho có 3 nghiệm x=-1/4 , x=1/2 và x=2
222. Giải hệ phương trình:
28
2 2 2 2
log 3log ( 2)
13
x y x y
x y x y
.
Giải
Điều kiện: x+y>0, x-y>0
28
2 2 2 2 2 2 2 2
log 3log (2 ) 2
1 3 1 3
x y x y x y x y
x y x y x y x y





Đặt:
u x y
v x y


ta có hệ:
2 2 2 2
2 ( ) 2 4
22
33
22
u v u v u v uv
u v u v
uv uv





2
2 4 (1)
( ) 2 2
3(2)
2
u v uv
u v uv
uv

. Thế (1) vào (2) ta có:
2
8 9 3 8 9 (3 ) 0uv uv uv uv uv uv uv
.Kết hợp (1) ta có:
0
4, 0
4
uv
uv
uv

(vỡ u>v). Từ đó ta có: x =2; y =2.(T/m)
KL: Vậy nghiệm của hệ là: (x; y)=(2; 2).
Đề số 223 Giải phương trình:
2007 2006
2006 x 2007 x 1
Giải Nhận xét :
1 x 2006 1
1 x 2007 1
2006 x 2007
Ta có : 2006 - x
2007
+ 2007 - x
2006
2006 - x+ 2007 - x = x - 2006 + 2007 - x = 1
Vậy phương trình 2006 - x
2007
= 2006 - x và 2007 - x
2006
= 2007 - x
2006 x 0
2006 x 1
2007 x 0
2007 x 1



x 2006
x 2005
x 2007
x 2007
x 2006

x = 2006 hay x = 2007
224 2. Giải hệ phương trình
3 2 3 2
2
3 5.6 4.2 0
( 2 )( 2 )
x y x x y
x y y y x y x

4. Giải bất phương trình
23
34
2
log ( 1) log ( 1)
0
56
xx
xx

Giải:
2. ĐK:
,0xy
xy
Hệ phương trình
3 2 3 2 3 2 3 2
3 5.6 4.2 0 3 5.6 4.2 0
(2 )( 2 ) 2 (2 )( 2 )( )
x y x x y x y x x y
x y y y x y x x y y x y x x y y






3 2 3 2
3 2 3 2
3 5.6 4.2 0
3 5.6 4.2 0
20
(2 )[( 2 )( ) 1] 0
x y x x y
x y x x y
yx
y x y x x y y





(do
2 )( ) 1 0y x x y y
)
3 2 3 2 2 2
3 5.6 4.2 0 3 5.6 4.2 0 (1)
2 2 (2)
x y x x y x x x
y x y x






Giải (1):
2 2 2
3
( ) 1
33
2
3 5.6 4.2 0 ( ) 5.( ) 4 0
3
22
( ) 4
2
x
x x x x x
x
3
2
0
log 4
x
x
Với x 0 thay vao (2) ta được y = 0
Với
3
2
log 4x
thay vao (2) ta được y =
3
2
1
log 4
2
Kết hợp với điều kiện ta được nghiệm của phương trình là
3
2
log 4x
,y =
3
2
1
log 4
2
4. Đk: x > - 1 ; bất phương trình
3
3
3
3log ( 1)
2log ( 1)
log 4
0
( 1)( 6)
x
x
xx



3
log ( 1)
0
6
x
x

06x
225 Giải phương trình: x
2
– 4x - 3 =
x5
x
2
- 4x + 3 =
x5
(1)
TXĐ : D =
5; ) 
;
2
1 x 2 7 x 5
Đặt y - 2 =
x5
,
2
y 2 y 2 x 5
Ta có hệ
2
2
2
x 2 y 5
x 2 y 5
y 2 x 5 x y x y 3 0
y 2 y 2




2
2
x 2 y 5
x y 0
5 29
x
2
x 2 y 5
x1
x y 3 0
y2




Đề số 226.
1. Giải hệ phương trình
22
2
( , )
4 5(2 )
xy
xy
x y x y xy

4.Giải phương trình:
0)2(2)2(log74)2(log2
2
2
2
xxxx
.
5. Giải hệ phương trình:
422)23(log
log)7(log1)(log
2
22
2
yxyx
yyxyx
Giải:
2. ĐK
0xy
xyyxyx )2(54
22
xyyxxyyx )2(54)2(
2
0)42)(2( xyyxxyyx
042
02
xyyx
xyyx
Với
02 xyyx
ta có
1
223
2
2
yx
xxx
yx
(thoả mãn)
Với
02 xyyx
ta có
2
2423
2
xxx
yx
25
6822
25
6822
y
x
(thoả mãn)
Vậy hệ phương trình có hai nghiệm.
4/Điều kiện:
2x
, phương trình đã cho tương đương với:
Giải
042)2(log.1)2(log2
22
xxx
042)2(log
01)2(log2
2
2
xx
x
Với
01)2(log2
2
x
ta có
2
1
2 x
, thoả mãn.
Với
042)2(log
2
xx
, ta có
42)2(log
2
xxy
là hàm số đồng biến trên
;2
nên
2
5
x
là
nghiệm duy nhất. Vậy phương trình có hai nghiệm
2
1
2 x
và
2
5
x
5. Điều kiện
0
07
0
y
yx
yx
; Biến đổi phương trình đầu ta được
yyxyx )7(log)(2log
2
2
2
xy
xy
yxyx
2
032
22
Với
xy
thế vào phương trình thứ hai ta được
94)22(log
2
xx
suy ra
9 yx
, thoả mãn điều kiện.
Với
xy 2
thế vào phương trình thứ hai ta được
xx 24)2(log
2
042)2(log
2
xx
42)2(log
2
xxy
là hàm số đồng biến trên
;2
nên
2
5
x
là nghiệm duy nhất.
Suy ra
5
2
5
y
x
, thoả mãn điều kiện. Vậy hệ đã cho có hai nghiệm
9
9
y
x
và
5
2
5
y
x
Đề số 234. Giải hệ phương trình:
33
2 2 3
x y 1
x y 2xy y 2

Giải:
xy
1 3 4 x y
1 1 3 3
2x
2 x y
2 x y
yx
xy 2
y x x y
xy
2.
13
13
13
13
2y
2x
2x
2x
xy
yx
yx
yx
xy
13
x y 1
2x
xx
x y 1
2
x 2,y 2
y
x
x 2,y 2
x3
2x
2x











Đề số 235 Giải phương trình:
)12(log1)13(log2
3
5
5
xx
.
Giải:
§iÒu kiÖn
.
3
1
x
(*)
Víi ®k trªn, pt ®· cho
)12(log31)13(log
5
2
5
xx
2 3 2 3
55
log 5(3 1) log (2 1) 5(3 1) (2 1)x x x x
3 2 2
2
8 33 36 4 0 2) (8 1) 0
1
8
x
x x x x x
x
§èi chiÕu ®iÒu kiÖn (*), ta cã nghiÖm cña pt lµ
.2x
236. 1. Giải hệ phương trình:
2
53
x y x y y
xy

(x, y R)
4. Giải bất phương trình
2
2
log
2log
2 20 0
x
x
x
2
Giải:
2. ĐK: x + y 0 , x - y 0, y 0
PT(1)
2 2 2 2
2 2 4 2x x y y x y y x
2
2 0 (3)
5 4 (4)
yx
y xy

Từ PT(4) y = 0 v 5y = 4x
Với y = 0 thế vào PT(2) ta có x = 9 (Không thỏa mãn đk (3))
Với 5y = 4x thế vào PT(2) ta có
2 3 1x x x
KL: HPT có 1 nghiệm
4
( ; ) 1;
5
xy



1. Điều kiện: x> 0 ; BPT
2
22
4log 2log
2 20 0
xx
x
Đặt
2
logtx
. Khi đó
2
t
x
.
BPT trở thành
22
22
4 2 20 0
tt
. Đặt y =
2
2
2
t
; y 1. BPT trở thành y
2
+ y - 20 0 - 5 y 4.
Đối chiếu điều kiện ta có :
2
2 2 2
2 4 2 2 1
t
tt
- 1 t 1.
Do đó - 1
2
log x
1
1
2
2
x
Đề số 237.
2. Giải hệ phương trình:
12
4)3()1(3
22
yxyx
xyyyxx
R),( yx
4. Giải phương trình:
2
1
3
9.
3
2
4
3
1
log)23(
x
x
x
Giải:
2/ x
2
-3x(y-1) + y
2
+ y(x-3) = 0
(x-y)
2
+ 3(x-y) - 4 + 0
1
4
xy
xy

* Với x- y = 1, ta có
12
1
yxyx
yx
x = 1; y = 0 và x= -1; y = -2
* Với x - y = -4 ta có
12
4
yxyx
yx
(Hệ PT vô nghiệm)
Vậy hệ phương trình có 2 nghiệm (x; y) = (1; 0) và (x; y) = (-1; -2)
4.Điều kiện: x > 1 Thì Pt
1
2
3
12
(3 2)log 4 .9
33
x
x
x
1
33
3
3
2
43log)1(log)23(
xx
x
xx
x 3.241)1(log)23(
3
023)1(log)23(
3
xx
x
01)1(log)23(
3
x
x
1)1(log
023
3
x
x
3
4
2log
3
x
x
; Vậy PT có nghiệm x =
3
4
Đề số 238 .
1. Giải phương trình
2 2 2
2 3 2 3 9x x x x x
.
4. Giải hệ phương trình:
22
23
42
log (2 ) log (2 ) 1
xy
x y x y

Giải:
1/ Đặt
2
30ux
ta có
22
3ux
. Kết hợp với pt đã cho ta có hệ
(2 1) (2 1) 9 (2 1)( ) 9
( )( ) 3 ( )( ) 3
x x u x x u x
u x u x u x u x



( ) 1 ( ) ( ) 9
( )( ) 3
u x u x u x
u x u x
.
Đặt
u x a
u x b


, ta có hệ
( 1) 9
3
a b a
ab
3
1
a
b
hoặc
4
3
4
a
b

.
Nếu
22
22
3 3 3 3 3
1
3 1 3 1
a x x x x
b
x x x x





1x
Nếu
4
3
4
a
b

2
2
3 4 (*)
3
3
4
xx
xx
(I)
Ta có
22
3 3 0x x x x x x
(*) vô nghiệm
hệ (I) vô nghiệm.
Vậy, pt đã cho có nghiệm duy nhất
1x
.
(Các cách khác:
+ Đặt
2
3t x x
+ Biến đổi pt thành
22
(2 1) 3 9 2x x x x
, đặt đk rồi bình phương hai vế.
+ Biến đổi pt thành
2
(2 1) 3 9x x x
, nhân 2 vế với
2
3 0,x x x
)
4/
22
23
4 2 (1)
log (2 ) log (2 ) 1 (2)
xy
x y x y

(I). Đk:
20
20
xy
xy


22
2 2 2 2
(1) log (4 ) log 2 log (2 ) log (2 ) 1x y x y x y
(3)
23
(2) và (3) log (2 ) log (2 ) 0x y x y
2 2 3
log (2 ) log 3.log (2 ) 0x y x y
22
log (2 ) 1 log 3 0xy


2
log (2 ) 0 2 1x y x y
Vậy, Hệ (I)
22
21
42
xy
xy


3
4
1
2
21
()
22
x
xy
tm
xy
y




.
Vậy nghiệm hệ pt là
3
1
42
( ; ) ;xy
.
Đề số 239. 1. Giải bất phương trình
2
2 5 3 2 3 6 .5
2
3 .5 1
x
x
x x x x
x
2. Giải phương trình
8
42
2
11
log 3 log 1 log 4 2
24
x x x
Giải:
2. Giải phương trình
8
42
2
11
log 3 log 1 log 4 2
24
x x x
Điều kiện:
01x
;
2 3 1 4x x x
Trường hợp 1:
1x
2
2 2 0 2x x x
Trường hợp 1:
01x
2
2 6 3 0 2 3 3x x x
Vậy tập nghiệm của (2) là
2;2 3 3T 
Đề số 240.
1/ Giải phương trình :
011243923
22
xxxxx
2/ Giải hệ phương trình:
6854
24
2
3642
yx
xyyxy
Giải:
1/ Phương trình
22
4442123923 xxxxx
3)12(2123)3(23
22
xxxx
Xét hàm số
3)(2)(
2
tttf
có
0
3
3)(2)(
2
2
2'
t
t
ttf
với
t
Vậy hàm số đồng biến nên:
5
1
123)12()3( xxxxfxf
Vậy phương trình có nghiệm
5
1
x
2 Hệ phương trình
)2(6854
)1(22
2
)(2
3642
yx
xyyxy
Từ (1)
))(()(2
424222
xxyyxyyxy
224242
0)2)(( yxyxxyyxy
thay vào (2) ta có :
6854 xx
11 yx
Vậy hệ có nghiệm ( 1;1) và (1;-1)
Đề số 241.
2. Giải hệ phương trình:
12
4)3()1(3
22
yxyx
xyyyxx
R),( yx
4/ Giải phương trình:
2
1
3
9.
3
2
4
3
1
log)23(
x
x
x
Giải:
2/ x
2
-3x(y-1) + y
2
+ y(x-3) = 0
(x-y)
2
+ 3(x-y) - 4 + 0
4
1
yx
yx
* Với x- y = 1, ta có
12
1
yxyx
yx
x = 1; y = 0 và x= -1; y = -2
* Với x - y = -4 ta có
12
4
yxyx
yx
(Hệ PT vô nghiệm)
Vậy hệ phương trình có 2 nghiệm (x; y) = (1; 0) và (x; y) = (-1; -2)
4/ Điều kiện: x > 1
2
1
3
9.
3
2
4
3
1
log)23(
x
x
x
1
33
3
3
2
43log)1(log)23(
xx
x
xx
x 3.241)1(log)23(
3
023)1(log)23(
3
xx
x
01)1(log)23(
3
x
x
1)1(log
023
3
x
x
3
log 2 ( )
4
3
x loai
x
Vậy PT có nghiệm x =
3
4
Đề số 242. Giải bất phương trình:
22
2 92 2 1 1x x x x x
Giải: Điều kiện:
1x
Bất phương trình
22
2 92 10 ( 2 8) ( 1 1)x x x x x
2
2
2
2 8 2
( 2)( 4)
11
2 92 10
41
( 2) ( 4) 0
11
2 92 10
x x x
xx
x
xx
x
xx
x
xx





2
11
( 2) ( 4)( 1) 0
11
2 92 10
xx
x
xx




Ta có:
2
11
( 4)( 1) 0, 1
11
2 92 10
xx
x
xx

Do đó bất phương trình
2 0 2xx
Kết hợp với điều kiện ta có nghiệm bất phương trình là:
12x
Đề số 243. Giải bất phương trình sau:
2
2 5 3 2 3 6 .5
2
3 .5 1
x
x
x x x x
x
4. Giải phương trình
2
22
2
log log 4
4 6 2.3
xx
x 
5. Giải hệ phương trình
22
22
22
2
log log
9
1 log 1 log 10
9
1 log 2.log 2 .log ( )
2
xy
x
x
xy
y
y


Giải:
2/ Điều kiện:
1
3
2
x
. Bất phương trình tương đương với
2
2 5 3 3 2)5 6
2
3 . 5
5(
xx
x
x x x x
x
3 .5
0
35
5 3 2 1
xx
x
x
x
xx
(1)
Xét hàm số
( ) 3 5
x
g x x
,
5
ln5
'( ) 3 5 .ln5, ( ) 0 log
3
x
g x g x x



.
Lâp bảng biến thiên, ta thấy
5
ln5
( ) log 0
3
g x g







(1)
303 2 1 xxx
( vì
50
x
)
5 157
22
x

Vậy nghiệm của bất phương trình là:
5 157
;3
22
T


4/ Điều kiện
0x
2
22
2
log log 4
4 6 2.3
xx
x 
2
22
2 2 2 2 2
1 log
log 4 log log 4 2log 2 2log 2
6
2 6 2.3 2 2.3 0
6
x
x x x x x
2 2 2
2log 2 1 log 2log 2
6.2 6 12.3 0
x x x
22
2log 2 log 2
22
6. 12 0
33
xx
2
log 2
2 3 1
3 2 4
x
x



5/ Điều kiện:
0 , 1xy
. Đặt
22
log ; loga x b y
.
Khi đó, hệ phương trình trở thành:
22
9
1 1 10
19
1
2
ab
ab
ab
ab





(*)
(**)
22
10 1 9 1 1
2 1 9
a b ab a b
a b ab ab
(1)
(2)
Lấy phương trình (1) chia vế theo vế (2) ta được:
2
22
2
51
5 1 1
1
ab
ab a b
ab
(3)
Từ (*), ta suy ra
22
9
1 10 1
ab
ab


.
Thay vào (3), ta có:
22
22
9 1 1 9
5 5 0
10 1 1 2
b b b b
b b b b





(4)
Đặt
2
1 b
t
b
. Phương trình (4) trở thành:
2
5 9 5
0 2 9 10 0 2;
22
t t t t t
t
.
Với
2t
2
2 1 0 1b b b
2y
2
4
x
x
Với
2
2 4, 2
5
2 5 2 0
1
2
2, 2
2
b y x
t b b
b y x
Vậy hệ có nghiệm
( ; ) (2;4);(2; 2)xy
2;4 , 4;2
.
Đề số244. Giải hệ phương trình:
3 3 3
22
8 27 18 (1)
4 6 (2)
x y y
x y x y


Giải: Giải hệ phương trình:
3 3 3
22
8 27 18 (1)
4 6 (2)
x y y
x y x y


(1) y 0
Hệ
3
3
3
3
2
2
27
3
8 18
(2 ) 18
46
33
1
2 . 2 3
x
x
y
y
xx
xx
yy
yy












Đặt a = 2x; b =
3
y
. Ta có hệ:
33
3
18
1
( ) 3
ab
ab
ab
ab a b




Hệ đã cho có 2 nghiệm
3 5 6 3 5 6
; , ;
44
3 5 3 5


Đề số 245 . Giải phương trình:
)12(log1)13(log2
3
5
5
xx
.
Giải Giải phương trình:
)12(log1)13(log2
3
5
5
xx
.
§iÒu kiÖn
.
3
1
x
(*)
Víi ®k trªn, pt ®· cho
)12(log31)13(log
5
2
5
xx
32
3
5
2
5
)12()13(5
)12(log)13(5log
xx
xx
8
1
2
0)18()2(
0436338
2
23
x
x
xx
xxx
§èi chiÕu ®iÒu kiÖn (*), ta cã nghiÖm cña pt lµ
.2x
Đề số 246 Giải hệ phương trình:
0322
6)2)(1)(1(
22
yxyx
yxyx
Giải Giải hệ phương trình:
0322
6)2)(1)(1(
22
yxyx
yxyx
Hệ
052)(
6)(
05
6)(
05)1()1(
6)11)(1)(1(
22222
uvvu
vuuv
vu
vuuv
yx
yxyx
với
1
1
yv
xu
Đặt:
vuP
vuS
.
được
2
3
052
6.
2
P
S
PS
SP
u, v là nghiệm của phương trình: X
2
– 3X + 2 = 0
21
11
11
21
2
1
y
x
y
x
X
X
Vậy nghiệm của hệ: (3 ; 2), (2 ; 3)
Đề số247.
3. Giải phương trình:
22
33
log 1 log 2x x x x x
4. Giải bất phương trình:
2
x 4 2
(log 8 log x )log 2x 0
Giải
3. Giải phương trình:
22
33
log 1 log 2x x x x x
2
2
3
11
log 2 3 1
xx
xx
x x x
xx

Đặt:f(x)=
2
3
xx
g(x)=
1
1x
x

(x
0)
Dùng pp kshs =>max f(x)=3; min g(x)=3=>PT f(x)= g(x) max f(x)= min g(x)=3 tại x=1
=>PT có nghiệm x= 1
4/ Giải bất phương trình:
2
x 4 2
(log 8 log x )log 2x 0
Điều kiện x > 0 , x 1
(1)



42
8
11
2 log x log 2x 0
log x 2





22
2
1
log x log x 1 0
1
log x
3




2
22
2
22
22
log x 1 log x 1
(log x 3) 0 0
log x log x
1
log x 1hayl og x 0 0 x hay x 1
2
Đề số248 .
1/ Giải các phương trình
2.
22
3 3 3
log (x 5x 6) log (x 9x 20) 1 log 8
Giải:
+ Điều kiện :
2
2
x5
x 5x 6 0 x 3 x 2
4 x 3
x 5 x 4
x 9x 20 0
x2



, và có :
33
1 log 8 log 24
+ PT (*)
22
22
33
log (x 5x 6)(x 9x 20) log 24
(x 5x 6)(x 9x 20) 24
(x 5) ( 4 x 3) (x 2)
(x 5) ( 4 x 3) (x 2)




(x 2)(x 3)(x 4)(x 5) 24 (*)
(x 5) ( 4 x 3) (x 2) (**)
+ Đặt
2
t (x 3)(x 4) x 7x 12 (x 2)(x 5) t 2
, PT (*) trở thành :
t(t-2) = 24
2
(t 1) 25 t 6 t 4
t = 6 :
22
x1
x 7x 12 6 x 7x 6 0
x6


( thỏa đkiện (**))
t = - 4 :
22
x 7x 12 4 x 7x 16 0
: vô nghiệm
+ Kết luận : PT có hai nghiệm là x = -1 và x = - 6
Đề số 249. 1.Giải phương trình
2 2 2
log 9 log log 3
2
.3
x
x x x

2. . Giải hệ phương trình sau:
3
1
2
7
)(
3
)(44
2
22
yx
x
yx
yxxy
Giải:
1. Giải phương trình
2 2 2
log 9 log log 3
2
.3
x
x x x

ĐK: x>0.
Ta có phương trình
2 2 2 2
log 9 log log 3 log
22
.3 3 1
xx
x x x x
. Đặt
2
log 2
t
xx

.
Phương trình trở thành
31
3 4 1 1 1 2
44
tt
tt
tx
2. Giải hệ phương trình sau:
3
1
2
7
)(
3
)(44
2
22
yx
x
yx
yxxy
ĐK: x + y
0
Ta có hệ
22
2
3
3( ) ( ) 7
()
1
3
x y x y
xy
x y x y
xy
Đặt u = x + y +
1
xy
(
2u
) ; v = x – y ta được hệ :
22
3 13
3
uv
uv


Giải hệ ta được u = 2, v = 1 do (
2u
)
Từ đó giải hệ
1
2
11
10
1
xy
x y x
xy
x y y
xy




Đề số250.
Giải hệ phương trình:
3 1 2 3
2
2 2 3.2
3 1 1
x y y x
x xy x

PT
2
1
x+1 0
1
2
3 1 0
0 1 3
3 1 1
x
x
x x y
x y x
x xy x


Với x = 0 thay vào (1) :
2
2
88
2 2 3.2 8 2 12.2 2 log
11 11
y y y y y
y
Với
1
13
x
yx


thay y = 1 – 3x vào (1) ta được :
3 1 3 1
2 2 3.2 3
xx

Đặt
31
2
x
t
, vì
1x 
nên
1
4
t 
PT (3) :
2
3 2 2
1
6 6 1 0
3 2 2
t
t t t
t
t


Đối chiếu điều kiện
1
4
t 
ta chọn
3 2 2t 
.
Khi đó
31
2
1
2 3 2 2 log 3 2 2 1
3
x
x


2
1 3 2 log 3 2 2yx
Vậy HPT đã cho có 2 nghiệm
2
0
8
log
11
x
y
và
2
2
1
log 3 2 2 1
3
2 log 3 2 2
x
y


Đề số 251. Giải hệ phương trình:
22
22
x y x y 13
x,y .
x y x y 25
Giải:
Giải hệ phương trình:
22
22
x y x y 13
x,y .
x y x y 25
3 2 2 3
3 2 2 3
x xy x y y 13 1'
y xy x y x 25 2'
Lấy (2’) - (1’) ta có: x
2
y– xy
2
= 6
x y xy 6
(3)
Kết hợp với 1 ta có
22
x y x y 13
I
x y xy 6

. Đặt y = - z ta có :
2
22
x z x z 13 x z x z 2xz 13
I
x z xz 6
x z xz 6







Đặt S = x +z và P = xz ta có :
2
3
S S 2P 13
S1
S 2SP 13
P6
SP 6
SP 6






Ta cã :
x z 1
x.z 6


. Hệ này có nghiệm
x3
z2

hoặc
x2
z3

Vậy hệ đã cho có hai nghiệm là: ( 3 ; 2) vµ ( -2 ; -3 )
Đề số252 . Giải bất phương trình:
4
log (log (2 4)) 1
x
x

Giải:
Giải bất phương trình:
4
log (log (2 4)) 1
x
x

4
log (log (2 4)) 1
x
x

. Đk:
42
01
log (2 4) 0 log 5
2 4 0
x
x
x
x


Do
1x 
PT
4
log (2 4) 2 4 4 4 2 4 0
x x x x x
x
đúng với mọi x. Do vậy BPT có
nghiệm:
2
log 5x
Đề số 253.
2: Giải bất phương trình:
22
35 5 4 24x x x
5. Giải hệ phương trình
2010
22
2( 1)
log
23
x
yx
y
y x x y

Giải:
2: Giải bất phương trình:
22
35 5 4 24x x x
BPT tương đương
22
22
22
11
35 24 5 4 5 4
35 24
11 (5 4)( 35 24)
x x x x
xx
x x x
Xét:
a)Nếu x
4
5
không thỏa mãn BPT
b)Nếu x>4/5: Hàm số
22
(5 4)( 35 24)y x x x
với x>4/5
y
'
=
22
22
11
5( 35 24) (5 4)( )
35 24
x x x
xx

>0 mọi x>4/5
Vậy HSĐB. +Nếu 4/5<x
1 thì y(x)
11
+Nếu x>1 thì y(x)>11 Vậy nghiệm BPT x>1
Đề số254. Giải phương trình:
2
21
3 2 6
x
x
x
Giải: Giải phương trình:
2
21
3 2 6
x
x
x
Lấy logarit theo cơ số 3 cho hai vế ta được:
2
33
log 2 1 log 2
21
x
x
x
Đưa phương trình về dạng: (x – 1)(2x
2
+ x – 1 - log
2
3
) = 0.
Từ đó suy ra nghiệm x = 1;
3
1 9 8log 2
4
x
Đề số255. .Giải bất phương trình
)3(log53loglog
2
4
2
2
2
2
xxx
Giải: Giải bất phương trình
)3(log53loglog
2
4
2
2
2
2
xxx
ĐK:
03loglog
0
2
2
2
2
xx
x
Bất phương trình đã cho tương đương với
)1()3(log53loglog
2
2
2
2
2
xxx
đặt t = log
2
x, BPT (1)
)3(5)1)(3()3(532
2
tttttt
4log3
1log
43
1
)3(5)3)(1(
3
1
2
2
2
x
x
t
t
ttt
t
t
168
2
1
0
x
x
Vậy BPT đã cho có tập nghiệm là:
)16;8(]
2
1
;0(
Đề số 256
2,Giải hệ phương trình:
1)4(log)5(log
6)12(log)22(log2
21
2
21
xy
xxyxxy
yx
yx
4,Giải phương trình:
xxx 4log1log
4
1
)3(log
2
1
2
8
4
2
.
Giải 2,Giải hệ phương trình:
1)4(log)5(log
6)12(log)22(log2
21
2
21
xy
xxyxxy
yx
yx
§K
1;2
0,14
yy
xx
Đưa phương trình thứ nhất của hệ về dạng :
21log)2(log
21
xy
yx
Đặt
)2(log
1
yt
x
, tìm được T=1 kết hợp với phương trình thứ 2 của hệ, đối chiếu với điều kiện trên, tìm
được nghiệm :
1;2; yx
4Giải phương trình:
xxx 4log1log
4
1
)3(log
2
1
2
8
4
2
.
ĐK x > 0 và
1x
. Đưa phương trình về dạng :
xxx 4log1log)3(log
222
.
Xét hai khả năng 0<X<1 và X>1, đối chiếu với điều kiện ta tìm được nghiệm của phương trình là
323x
và x = 3.
Đề số 257. Giải phương trình:
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
Giải Giải phương trình:
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
)4(log3)1(log
4
1
)3(log
2
1
8
8
4
2
xxx
.
Điều kiện:
.
3
1 0 1
0
x
xx
x

Biến đổi theo logarit cơ số 2 thành phương trình
log log .
x
x x x x x x
x



2
22
1 loaïi
3 1 4 2 3 0 3
3
Đề số 258.
1. Giải hệ phương trình sau:
2
2
2
2
y2
3y
x
x2
3x
y
2. Giải phương trình:
0322212
333
xxx
Giải:
1. Giải hệ phương trình sau:
2
2
2
2
y2
3y
x
x2
3x
y
điều kiện x>0, y>0. Khi đó hệ tương đương
22
22
32
32
x y y
xy x


Trừ vế theo vế hai phương trình ta được: (x-y)(3xy+x+y) = 0
xy
thay lại phương trình Giải tìm
được nghiệm của hệ là: (1;1).
2. Giải phương trình:
0322212
333
xxx
Tập xác định: D = R. Đặt f(x) =
333
322212 xxx
Ta có:
2
3
,1,
2
1
;0
)32(
2
)22(
2
)12(
2
)('
3
2
3
2
3
2
x
xxx
xf
Suy ra hàm số f(x) đồng biến trên tập M=

,
2
3
2
3
,11,
2
1
2
1
,
Ta thấy f(-1)=0 x=-1 là một nghiệm của (1). Ta có:
3)
2
3
(;3)
2
1
( ff
Ta có bảng biến thiên của hàm số f(x):
x
-∞
2
3
-1
2
1
+∞
f’(x)
  
F(x)
+∞
0 3
-∞ -3
Từ bảng biến thiên ta thấy f(x) = 0 x = -1. Vậy phương trình đã cho có duy nhất một nghiệm x = -1.
Cách 2: Học sinh có thể đặt
3
3
21
23
ux
vx


khi đó ta được hệ
33
33
0
2
2
uv
uv
vu

giải hệ này và tìm được nghiệm.
Đề số 259. Giải hệ phương trình:
2
2
3
23
11
(1 ) 4
1
4
xx
yy
xx
x
y y y
.
Giải
Giải hệ phương trình:
2
2
3
23
11
(1 ) 4
1
4
xx
yy
xx
x
y y y
.
§k
0y
2
2
2
2
3
3
3
23
11
11
(1 ) 4
4
11
1
( ) 4
4
xx
xx
yy
yy
x
xx
xx
x
y y y
y y y




®Æt
1
ax
y
x
b
y

Ta ®-îc
2 2 2
3 3 2 2
2 4 4 2 4 2 2
1
2 4 ( 4) 4 4 4 0
a a b a a b a a b a
b
a ab a a a a a a
Đề số 260.
2. Giải phương trình :
3
2 3x 2 3 6 5x 8 0
(x R)
4. Giải hệ phương trình :
22
22
22
x xy y
log (x y ) 1 log (xy)
3 81

(x, y R)
Giải
2.Giải phương trình :
3
2 3x 2 3 6 5x 8 0
(x R)
3
2 3x 2 3 6 5x 8 0
, ñieàu kieän :
6
6 5 0
5
xx
Ñaët t =
3
3x 2
t
3
= 3x – 2 x =
3
t2
3
vaø 6 – 5x =
3
8 5t
3
Phöông trình trôû thaønh :
3
8 5t
2t 3 8 0
3
3
8 5t
3 8 2t
3

32
t4
15t 4t 32t 40 0
t = -2. Vaäy x = -2
4. Gæai heä phöông trình :
22
22
22
x xy y
log (x y ) 1 log (xy)
3 81

(x, y R)
Ñieàu kieän x, y > 0
22
2 2 2 2
22
log (x y ) log 2 log (xy) log (2xy)
x xy y 4
22
22
x y 2xy
x xy y 4

2
(x y) 0
xy 4

xy
xy 4
x2
y2
hay
x2
y2


………………………………………………………………………………………………………………….
| 1/95
| | Tải xuống

Có thể bạn quan tâm:

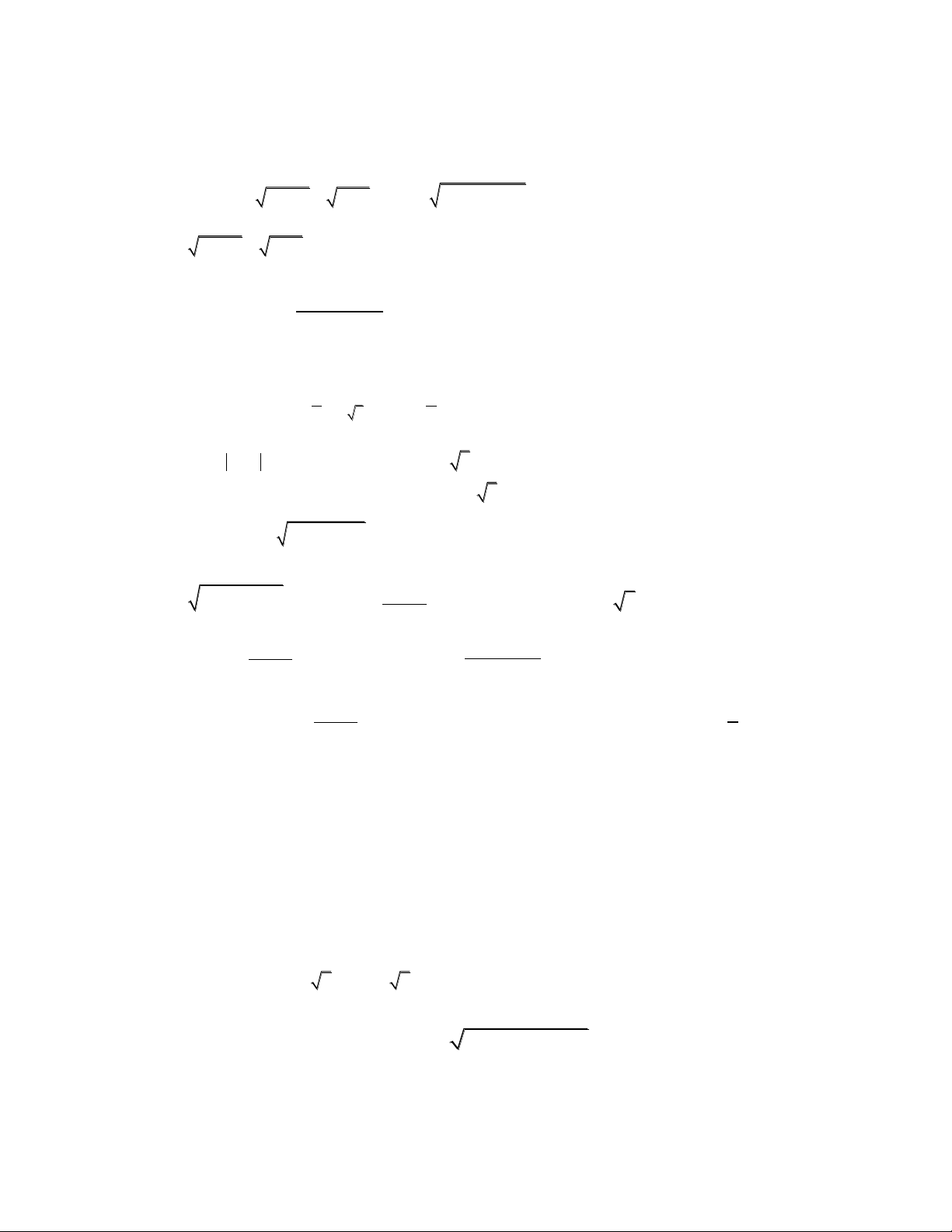
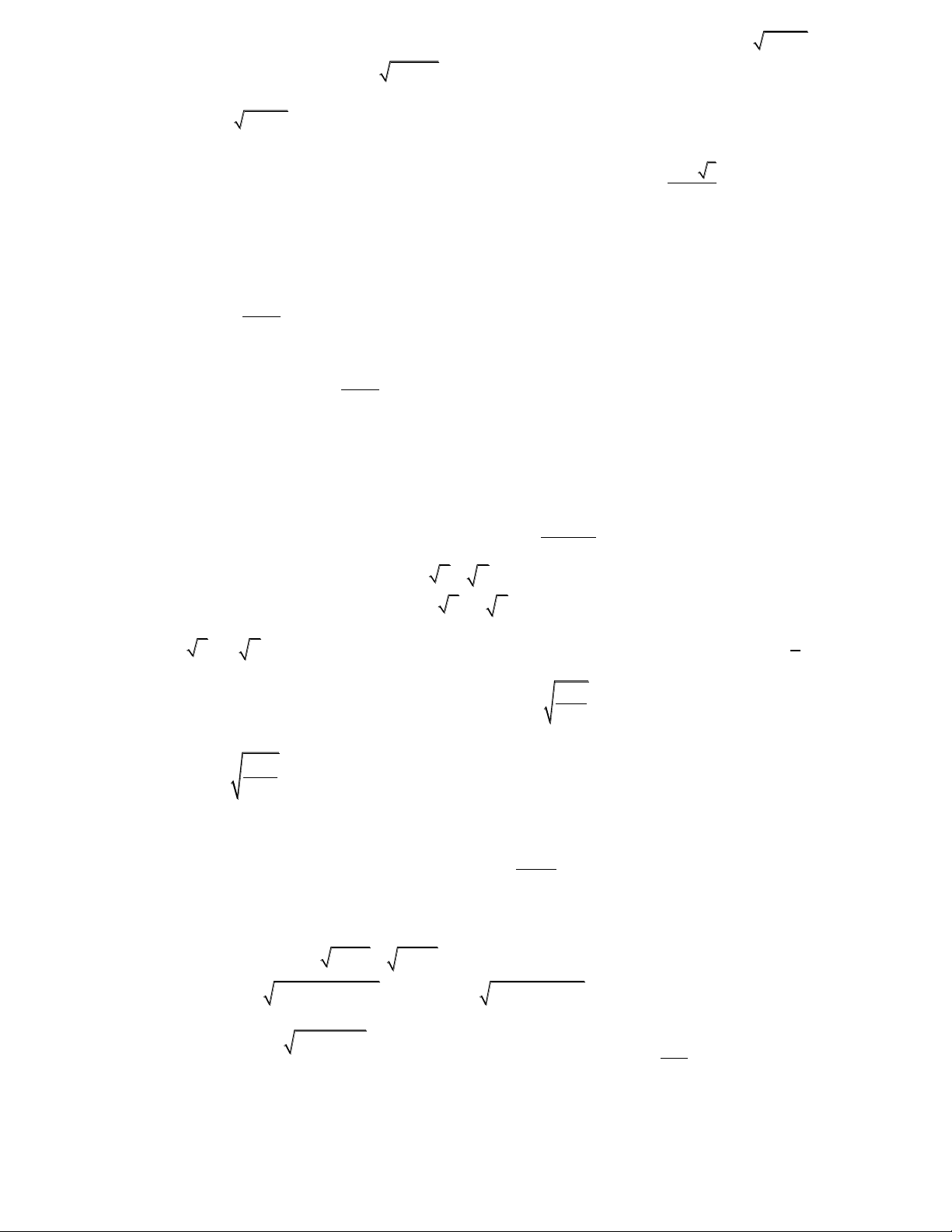
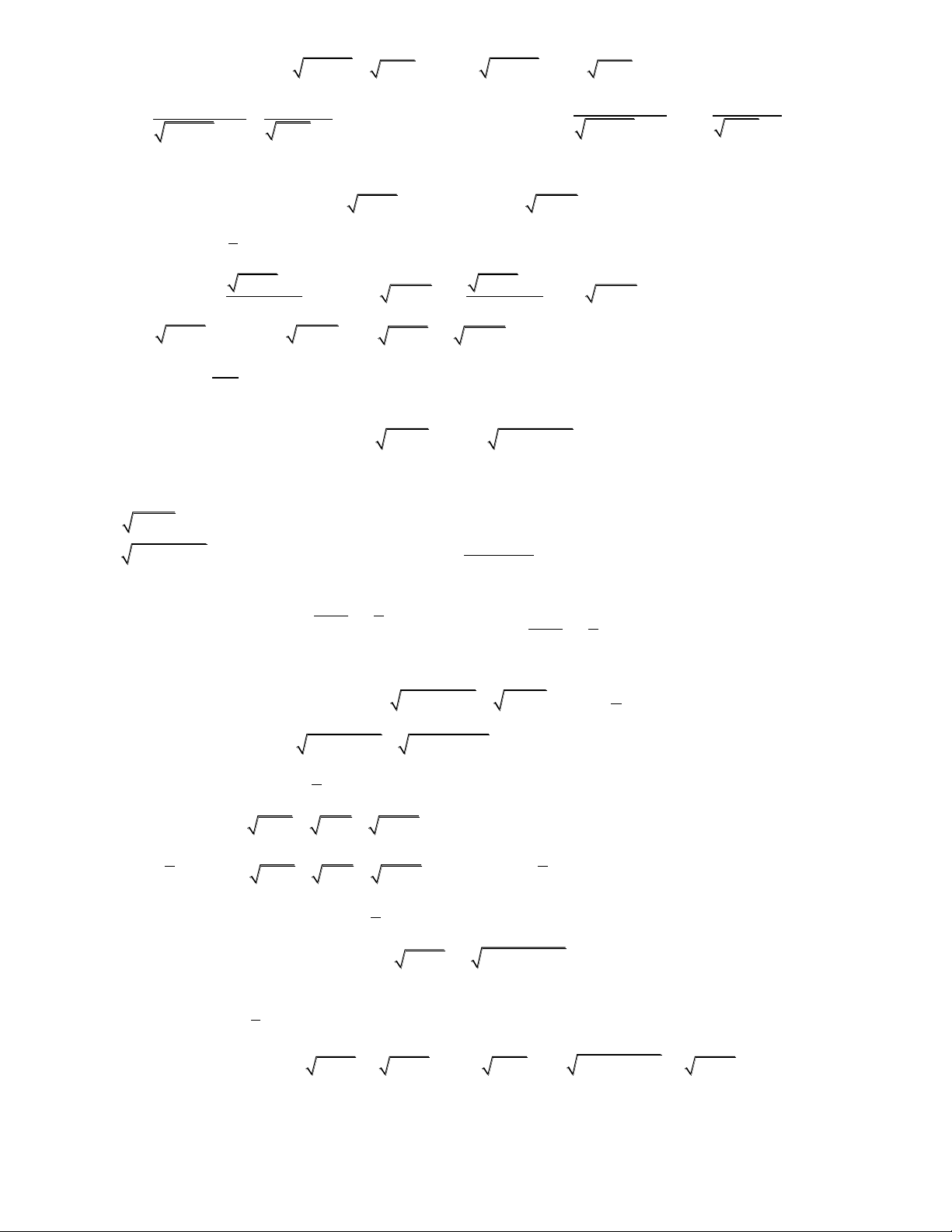
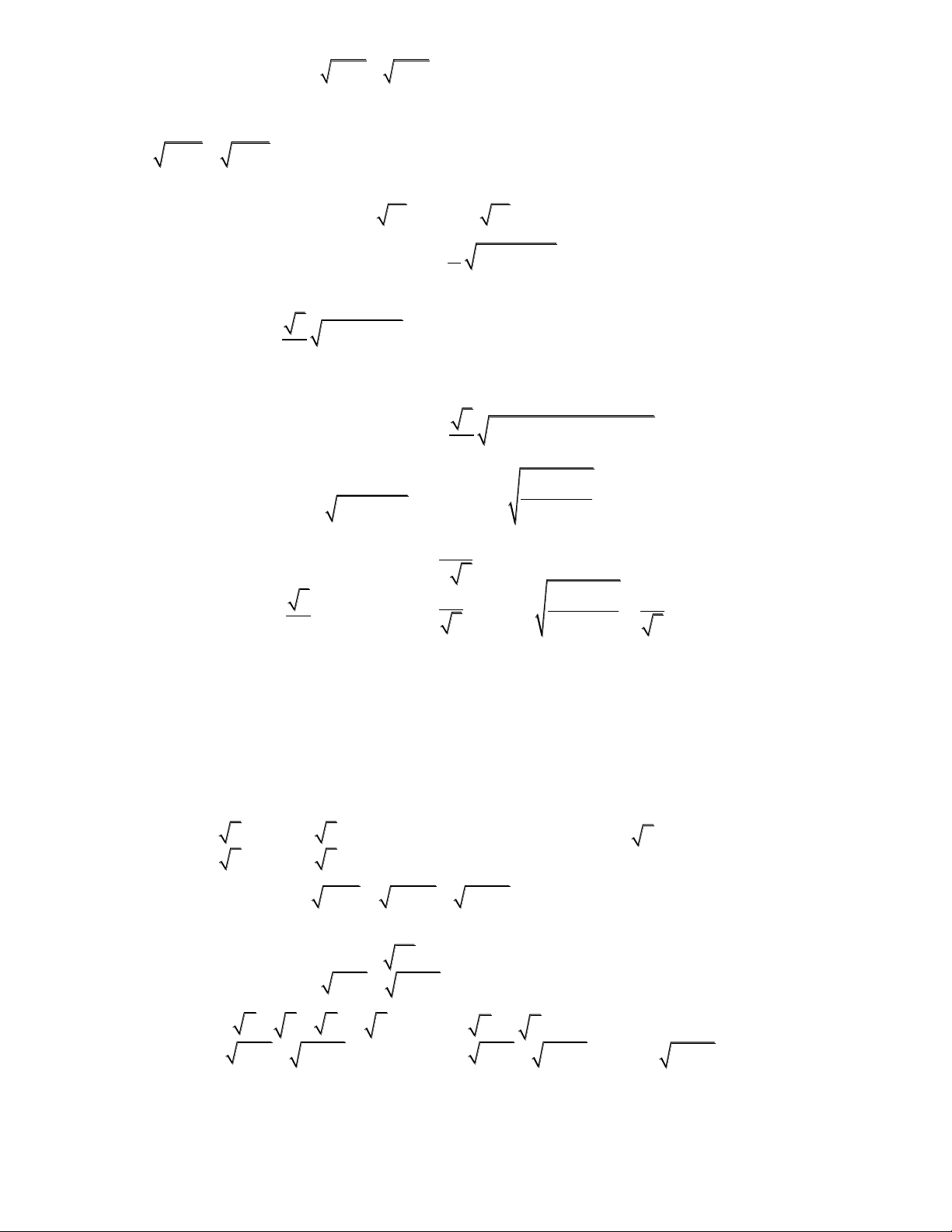
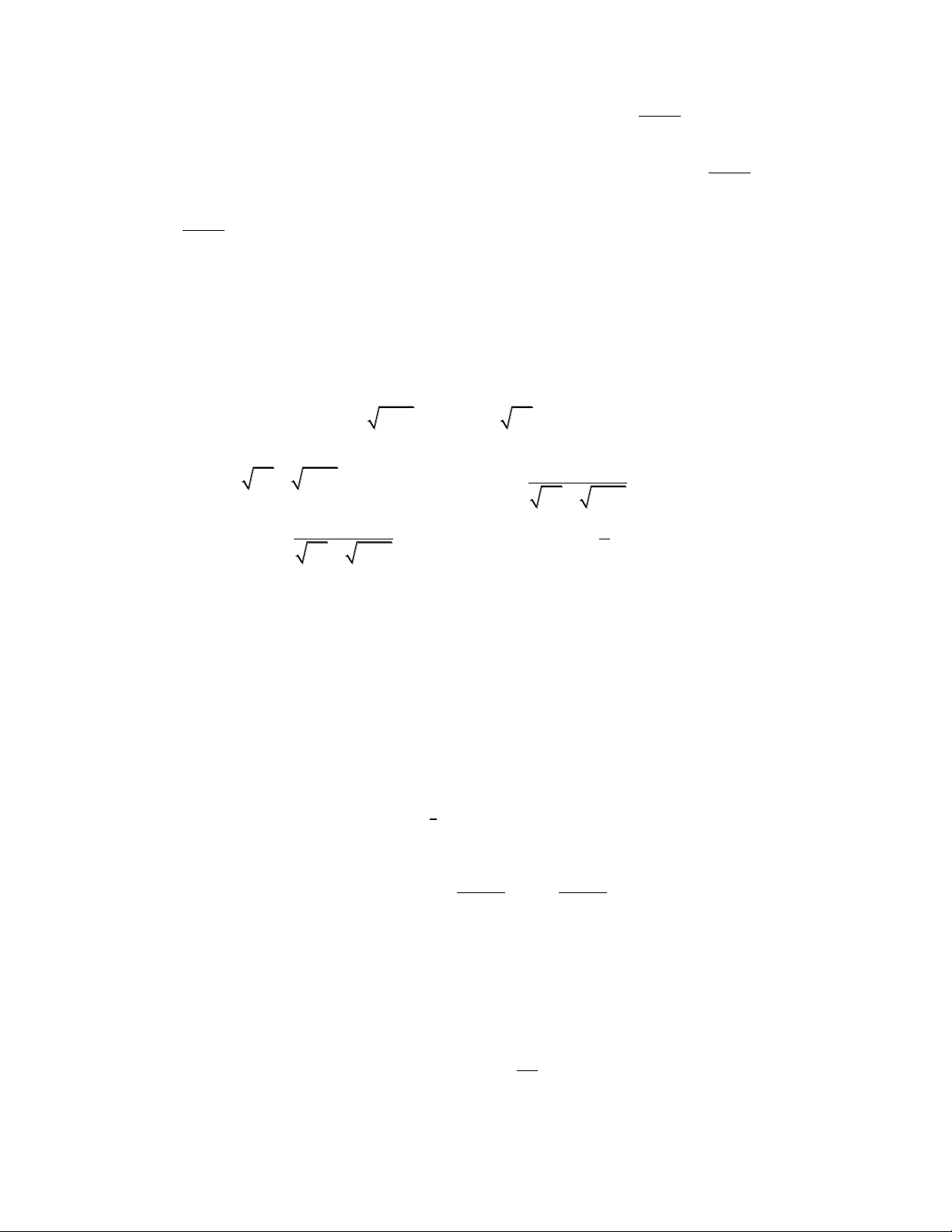
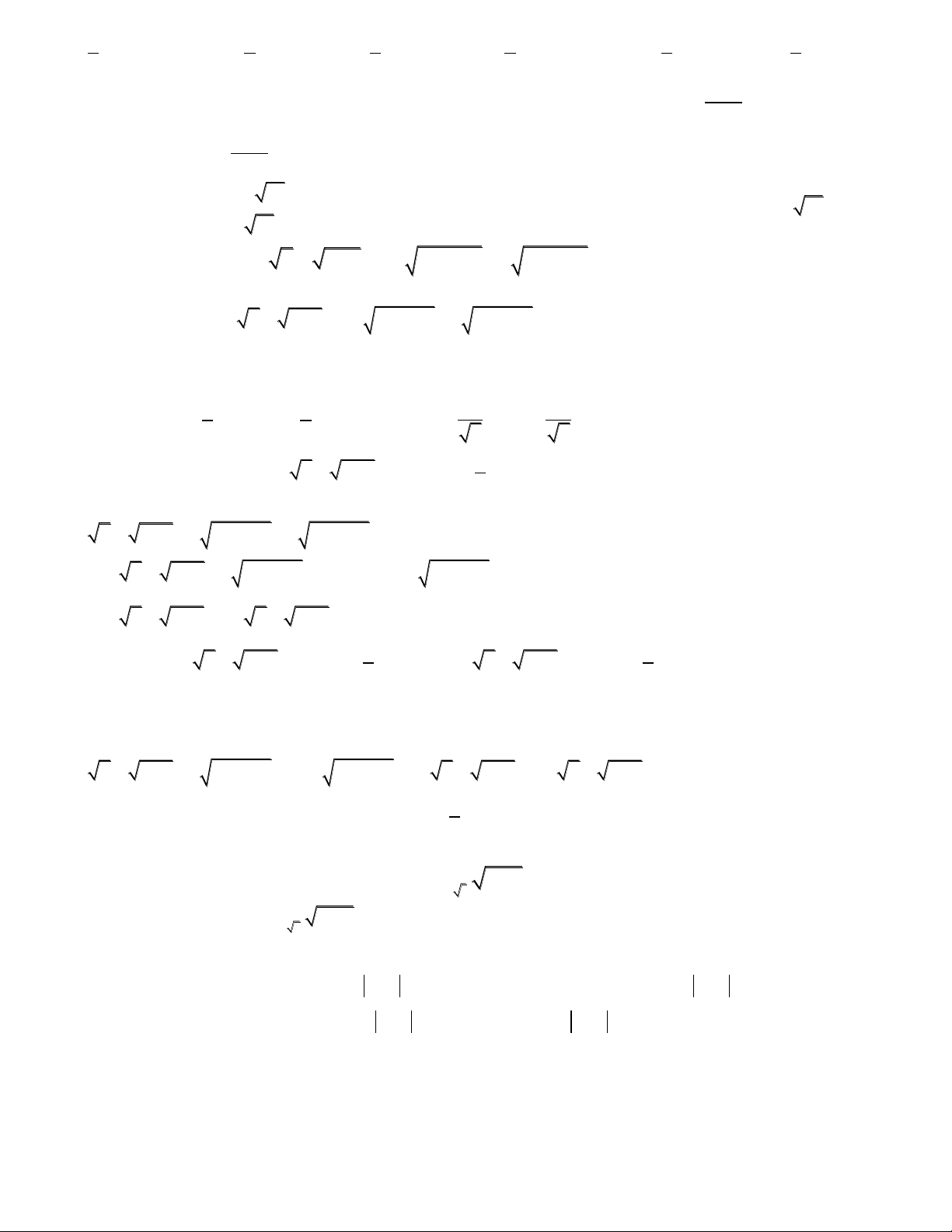
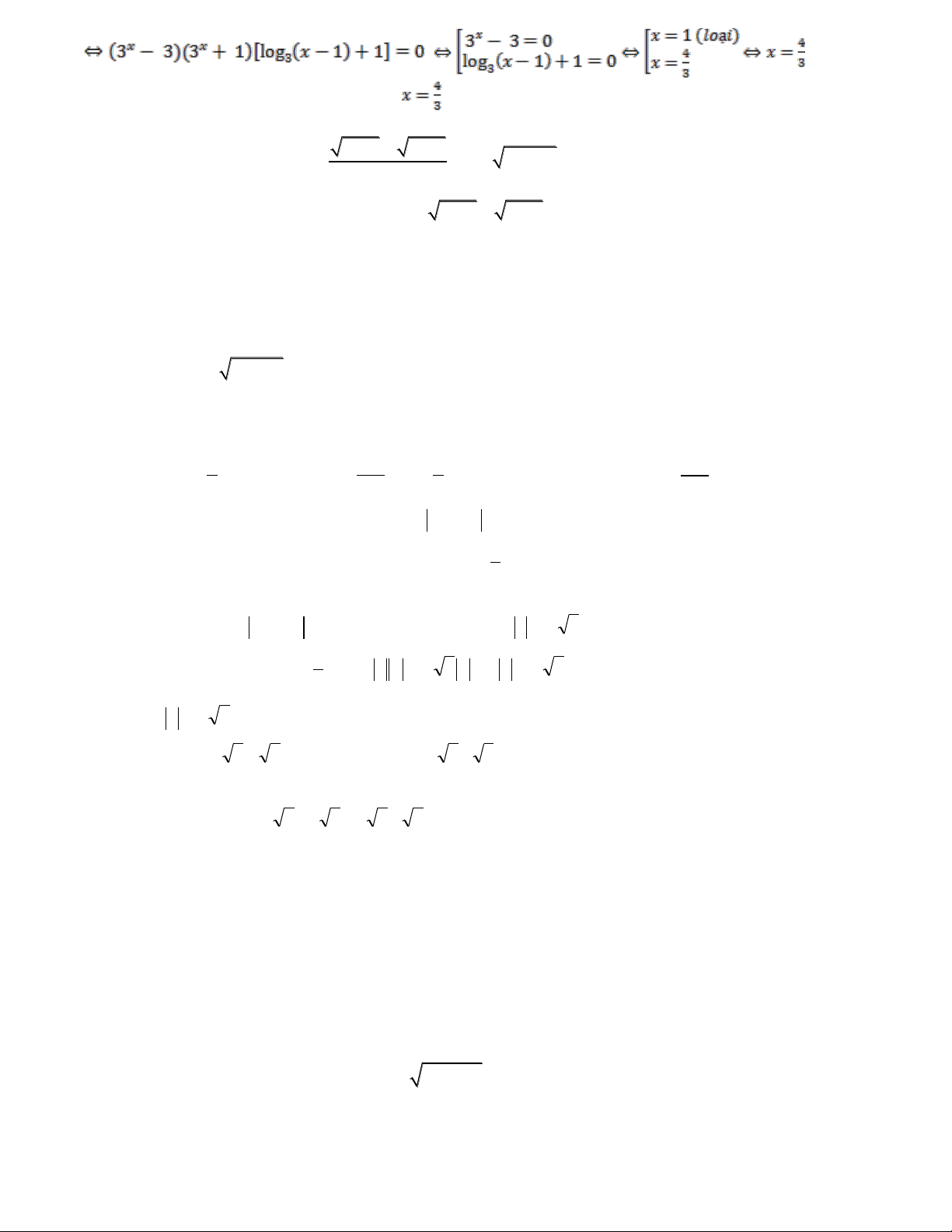
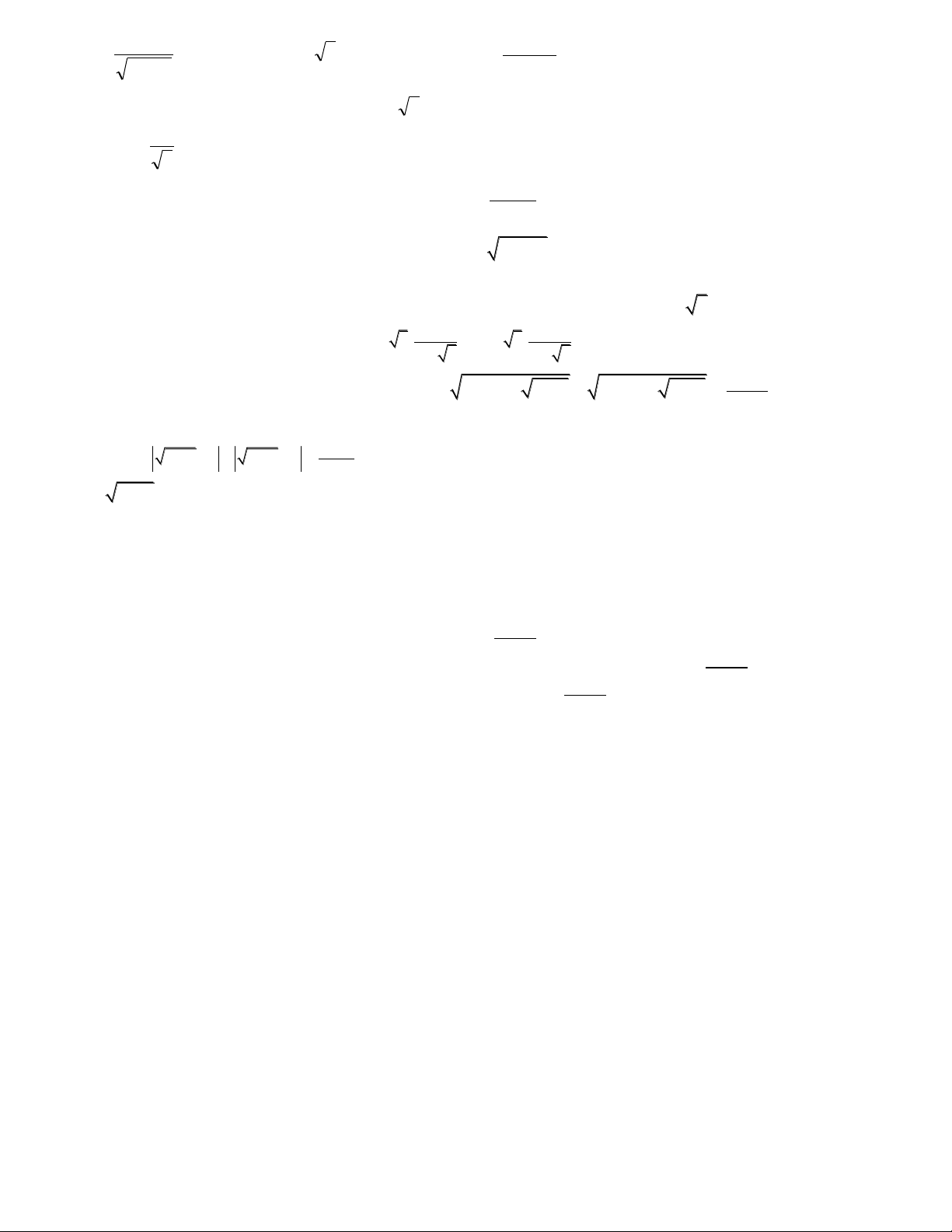
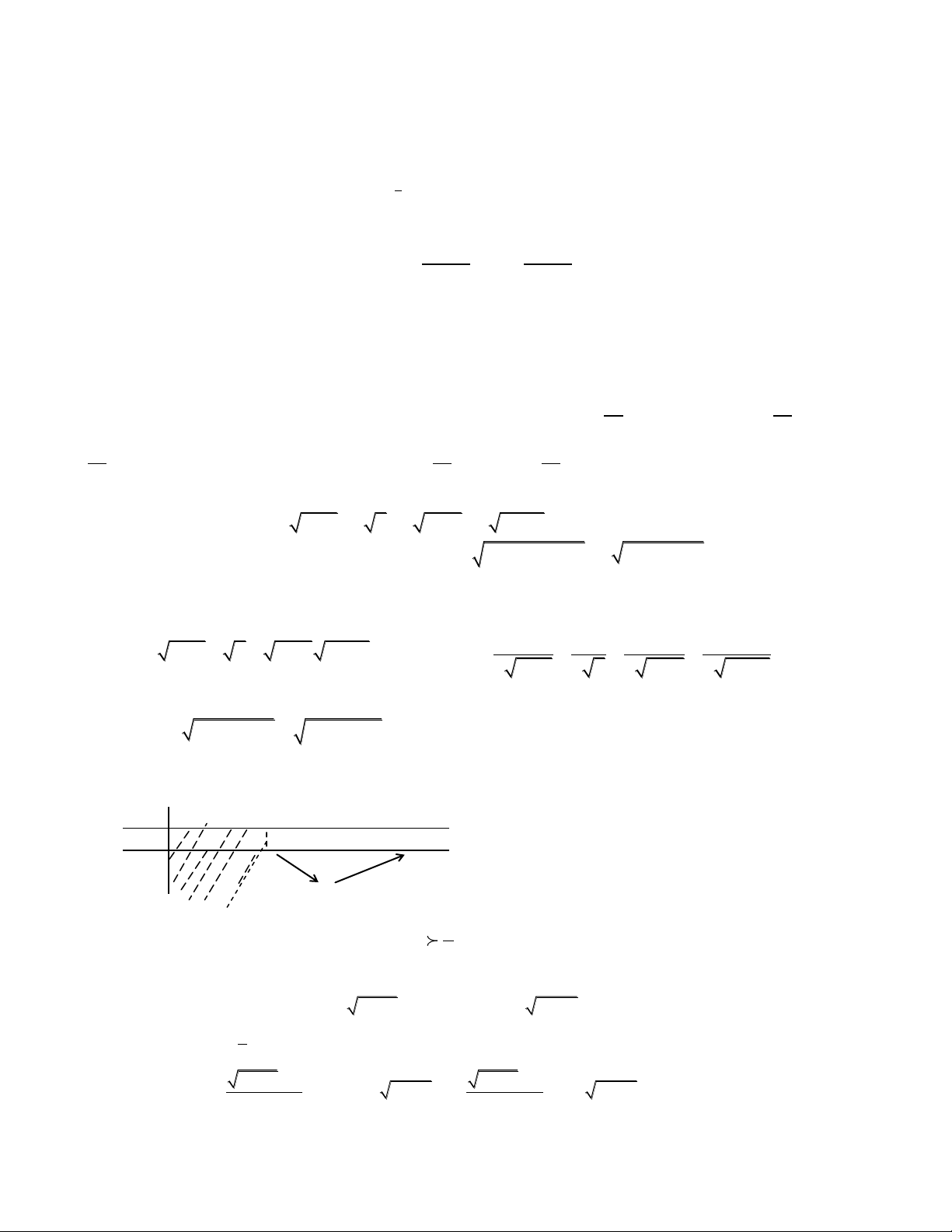
Preview text:


260 HỆ PHƯƠNG TRÌNH TRONG CÁC ĐỀ THI 2
1/ Giải phương trình: 2x  3  x 1  3x  2 2x  5x  3 16 .
Giải: Đặt t  2x  3  x 1 > 0. (2)  x  3 1x x 2  2 1
2/ Giải bất phương trình: 0 x 2 1 Giải: 0  x  1 1 1
3/ Giải phương trình: log (x  3)  log (x 8 1)  3log (4x) . 2 4 8 2 4
Giải: (1)  (x  3) x 1  4x  x = 3; x = 3   2 3
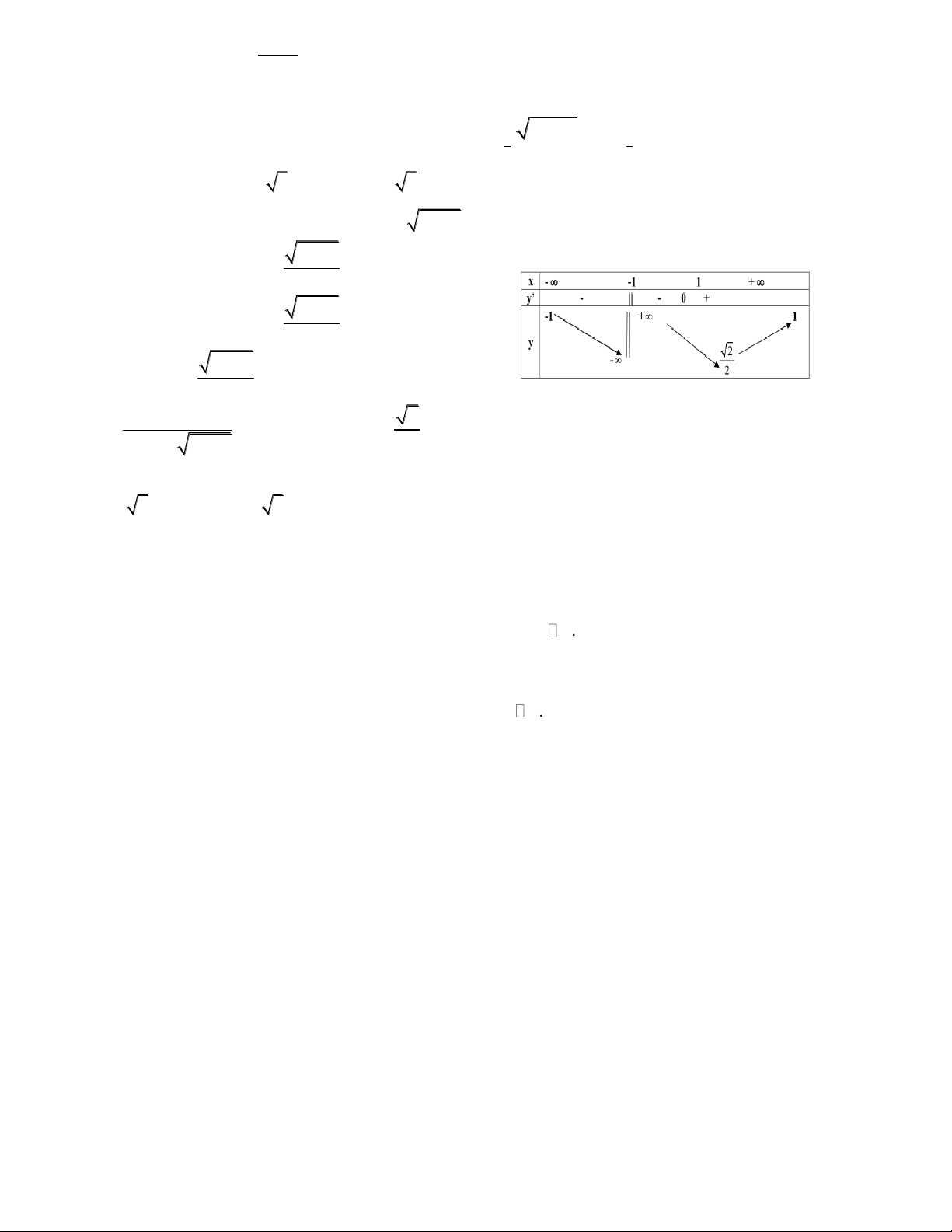
4/ Tìm m để phương trình sau có nghiệm x 0; 1 3     : m x2  2x  2   1  x(2  x)  0 (2) 2 t  2 Giải: Đặt 2
t  x  2x  2 . (2)  m 
(1 t  2),dox[0;1 3] t 1 2 t  2 2 t  2t  2 Khảo sát g(t)  
 0 . Vậy g tăng trên [1,2]
t 1 với 1  t  2. g'(t) 2 (t 1) 2 t  2 2 Do đó, ycbt  bpt m  m  max g(t)  g(2) 
t 1 có nghiệm t  [1,2]  t   1;2 3
x4  4x2  y2  6y 9  0
5/ Giải hệ phương trình :  (2)
x2y  x2  2y  22  0 2 2 2
(x  2)  (y  3)  4 2 x   Giải: 2 u (2)   . Đặt  2 2
(x  2  4)(y  3 3)  x  2  20  0 y  3  v 2 2 u v  4 u  2 u  Khi đó (2)     hoặc 0   .
u v  4(u v)  8 v  0 v  2
x  2 x  2 
x  2 x   2 ; ; ;
y  3 y  3 y  5 y  5
6/ 1) Giải phương trình: 2 x 1  x 1  x x 1 5.3 7.3 1 6.3 9       0 (1)
2) Tìm tất cả các giá trị của tham số m để hệ phương trình sau có 2 nghiệm phân biệt:
log (x 1)  log (x 1)  log 4 (a)  3 3 3  log (x2  2x  5)  mlog 2  5 ( ) 2 b  2  (x 2x5) Giải: 1) Đặt 3 3x t   0 . (1)  2
5t  7t  3 3t 1  0  x  log ; x   log 5 3 3 5
log (x 1)  log (x 1)  log 4 (a) 3  2) 3 3  2
log (x  2x  5)  m log 2  5 ( ) b 2  2  ( x 2 x5)
 Giải (a)  1 < x < 3.  Xét (b): Đặt 2
t  log (x  2x  5) . Từ x  (1; 3)  t  (2; 3). 2   (b)  2
t  5t m . Xét hàm 2
f (t)  t  5t , từ BBT  25 m    ; 6    4  3 3 3 8
 x y  27 18y
7/ Giải hệ phương trình:  2 2 
4x y  6x y  3  x 3  3  (2 )    18  3 a  b Giải:  y  3 (2)    . Đặt a = 2x; b = . (2)    y ab  1 x 3  x 3  2 . 2    3  y   y   3 5 6   3 5 6   
Hệ đã cho có nghiệm:  ; , ;   4 3 5   4 3 5       
8/ Giải bất phương trình sau trên tập số thực: 1 1  (1)
x  2  3  x 5  2x Giải:  Với 1 2
  x  : x  2  3 x 0, 5 2 
x 0 , nên (1) luôn đúng 2 5  Với 1 5
x  : (1)  x  2  3 x  5  2x  2  x  2 2 2     Tập nghiệm của (1) là 1 5 S  2  ;  2;      2   2  2
x 1 y(y x) 4y
9/ Giải hệ phương trình:  (x, y  ) 2
(x 1)(y x  2)  y 2  x 1 2
y x  2  2   x 1  y    x  x   Giải: 1 1 (2)     y   hoặc 2  2  x 1   y  2  y  5
( y x  2)  1
y x  2  1  y
10/ Giải bất phương trình: log 2 x  log 2 x  3  5(log 2 x  ) 3 2 2 4 Giải: BPT  2 2
log x  log x  3  5(log x  3) (1) 2 2 2 Đặt t = log t t   t   t t   t  2x. (1)  2 2 3 5( 3) ( 3)( 1) 5( 3) t  1     1 t  1  log x  1  0  x  2  t  3         2  3  t  4 3  log x  4   2 2
(t 1)(t 3)  5(t 3) 8   x 16
11/Giải phương trình: 2 2 2 2 2
log (x 1)  (x  5)log(x 1)  5x  0 Giải: Đặt 2
log(x 1)  y . PT  2 2 2 2
y  (x  5) y  5x  0  y  5  y  x ;
Nghiệm: x   99999 ; x = 0
12/ Giải phương trình: x 3 x 1 8 1 2 2    1
Giải: Đặt x 3 x 1 2 u 0; 2    1  v . x  0 3 3
u 1  2v
u 1  2vu v  0 PT           3 2 2 3  1 5   v 1  2u (
 u v)(u uv v  2)  0
u  2u 1  0 x  log2  2 2 2
x y x y  2 
13/ Tìm m để hệ phương trình:  có ba nghiệm phân biệt m 2 x y 2  x y  4 4 2
(m 1)x  2(m  3)x  2m  4  0 (1) Giải:  Hệ PT  2  x  2 . y  2  x 1 2 2x 1  0   Khi m = 1: Hệ PT  2  (VN ) x  2 y  2  x 1
 Khi m ≠ 1. Đặt t = x2 , t  0 . Xét 2
f (t)  (m 1)t  2(m  3)t  2m  4  0 (2)
Hệ PT có 3 nghiệm phân biệt  (1) có ba nghiệm x phân biệt  f (0)  0 
 (2) có một nghiệm t = 0 và 1 nghiệm t > 0   2m  3  ...  m  2 . S   0  1 m
 x y 1
14/ Tìm m để hệ phương trình có nghiệm:  .
x x y y 1 3  mu v 1 u v  Giải: Đặt 1 u x,v
y (u  0, v  0) . Hệ PT     . ĐS: 1 0  m  . 3 3
u v 1 3muv m 4 x
15/ Tìm m để phương trình sau có nghiệm: x(x 1)  4(x 1)  m x 1 x
Giải: Đặt t  (x 1) . PT có nghiệm khi 2
t  4t m  0 có nghiệm, suy ra m  4  . x 1
16/ Giải phương trình: 3x.2x = 3x + 2x + 1 x x
Giải: Nhận xét; x =  1 là các nghiệm của PT. PT 2 1  3  . 2x 1
Dựa vào tính đơn điệu  PT chỉ có các nghiệm x =  1. 2 2
x y xy  3 (a) 
17/ Giải hệ phương trình:  2 2
x 1  y 1  4 (b)  Giải (b)  2 2 2 2 2
x y  2 (x 1).( y 1) 14  xy  2 (xy)  xy  4  11 (c)  p  3  p 11 Đặt xy = p. 2 
(c)  2 p p  4  11  p    35  2 3
p  26 p 105  0  p   3 35
(a)   x y2  3xy  3  p = xy =  (loại)
 p = xy = 3  x y  2  3 3 xy  3  xy  3  1/ Với 
x y  3 2/ Với 
x y   3
x y  2 3
x y  2  3
Vậy hệ có hai nghiệm là:  3; 3,  3; 3  1 
18/ Giải bất phương trình: 2
log (4x  4x 1)  2x  2  (x  2) log  x 2 1    2  2 Giải:  1  1 1 BPT   x log 1 (  x 2 ) 
  x     x  hoặc x < 0 2 1 0  2 4 2 2
x 1 y(x y)  4y
19/ Giải hệ phương trình: 
(x, yR ) 2
(x 1)(x y  2)  y 2
x 1  x y 2  2   y
Giải: y = 0 không phải là nghiệm. Hệ PT   2
x 1(x y  2) 1  y 2  x 1 2 x 1 u v   1 Đặt u
,v x y  2 . Ta có hệ 2 
u v 1   y yuv 1 
x y  2 1
Nghiệm của hpt đã cho là (1; 2), (–2; 5).
20/ Tìm m sao cho phương trình sau có nghiệm duy nhất: ln(mx)  2ln(x 1)
Giải: 1) ĐKXĐ: x  1
 ,mx  0 . Như vậy trước hết phải có m  0 . Khi đó, PT  2 2
mx  (x 1)  x  (2  ) m x 1  0 (1) Phương trình này có: 2
  m  4m.
 Với m(0;4)   < 0  (1) vô nghiệm.
 Với m  0, (1) có nghiệm duy nhất x  1  < 0  loại.
 Với m  4, (1) có nghiệm duy nhất x = 1 thoả ĐKXĐ nên PT đã cho có nghiệm duy nhất.
 Với m  0 , ĐKXĐ trở thành 1
  x  0 . Khi đó   0 nên (1) có hai nghiệm phân biệt x , x x x . 1 2  1 2  Mặt khác, f ( 1
 )  m  0, f (0) 1 0 nên x  1
  x  0 , tức là chỉ có x là nghiệm của phương trình 1 2 2
đã cho. Như vậy, các giá trị m  0 thoả điều kiện bài toán.
 Với m  4. Khi đó, điều kiện xác định trở thành x > 0 và (1) cũng có hai nghiệm phân biệt x , x
x x . Áp dụng định lý Viet, ta thấy cả hai nghiệm này đều dương nên các giá trị m  4 cũng 1 2  1 2  bị loại.
Tóm lại, phương trình đã cho có nghiệm duy nhất khi và chỉ khi: m( ;  0)   4 . 2 2
 x 91  y  2  y (1)
21/ Giải hệ phương trình:  2 2
y  91  x  2  x (2) 
Giải: Điều kiện: x ≥ 2 và y ≥ 2 : Lấy (1) trừ (2) vế theo vế ta được: 2 2 2 2 x   y
y   x   y  91 91 2 2 x 2 2 x y y    x
 (y x)(y x) 2 2 x  91  y  91 y  2  x  2   x y 1  (x y) 
x y   0  2 2 x   y x   y   91 91 2 2  
 x = y (trong ngoặc luôn dương và x và y đều lớn hơn 2) 2 2 Vậy từ hệ trên ta có: 2 2 x  91 
x  2  x x  91 10  x  2 1 x  9 2     x  9 x  3 1 1  
 (x  3)(x  3)  (x  3)(x  3) 1    0   2   x    x   2 x  91 10 x  2 1 91 10 2 1  x = 3
Vậy nghiệm của hệ x = y = 3
22/ Giải bất phương trình: log ( 3x 1  6) 1 log (7  10  x) 2 2 1   x 10
Giải: Điều kiện: 3 3x 1  6 3x 1  6 log
 log (7  10  x)  7  10  x BPT  2 2 2  2
 3x 1  6  2(7  10  x)  3x 1  2 10  x  8  49x2 – 418x + 369 ≤ 0 369  1 ≤ x ≤ 49 (thoả)
23/ Giải phương trình: 2 2
2x 1 x x  2  (x 1) x  2x  3  0 Giải: Đặt: 2 2
v u x  2 2 2 2 1
u x  2, u  0
u x  2      2 2  v u  2 2 1 2 2
v x x v
v x  2x  3 2 3, 0  x   2 v u  0 (b)   v u  1  
(v u) (v u) 1    0       v u  1   2  2   (v u) 1    0 (c)    PT    2  2
Vì u > 0, v > 0, nên (c) vô nghiệm. 1 2 2
v u  0  v u
x  2x  3 
x  2  x   Do đó: PT  2
24/ Giải bất phương trình: 2 2
x  3x  2  2x  3x 1  x 1  1    ;    1  2; Giải: 
Tập xác định: D =  2   x = 1 là nghiệm
 x 2: BPT  x  2  x 1  2x 1 vô nghiệm 1  1 
 x 2 : BPT  2  x  1 x  1 2x có nghiệm x 2  1    ;    1 
 BPT có tập nghiệm S=  2 
25/ Giải phương trình: 2 2
x  2(x 1) 3x 1  2 2x  5x  2  8x  5 . Giải: 1 x   Điều kiện: 3 .    
(x 1)  2(x 1) 3x 1   3x 12   
x  22  2 2x  5x  2   2x 12 2 2   PT  0
x3  6x2y 9xy2  4y3 Giải hệ phương trình:  0 26/   x  y  x  y  2  Giải: x3  x2y xy2  y3 6 9 4  0 (1)  x  y  x  y  x  y  2 (2) x  y 2 ( ) (x  4y)  0 x  4y  . Ta có: (1)    Với x = y: (2)  x = y = 2
x  32 8 15; y  82 15  Với x = 4y: (2)  2  2 2
27/ Giải phương trình: x 3x 1  tan x  x 1 6 Giải: x2  x 3 3 1   x4  x2 1 PT  3 (1)
x4 x2   x2  x x2 1 ( 1)(  x 1)
x2  x   x2  x  x2 3 1 2( 1) (  x 1) Chú ý: , x2  x   x2  x 3 2( 1) ( 1)   (x2  x 1)(x2  x 1) Do đó: (1)  3 . 2 2 x  x t 1  , t  0 x2  x    x2 1  x 1 2 Chia 2 vế cho và đặt x  x 1 t 3    0  2 3   1 x2  x 1 1 t2 3 2  t 1  0 t    2 Ta được: (1)  3   3  x  x 1 3  x 1. x2  5x y  9
28/ Giải hệ phương trình: 
3x3  x2y 2xy 6x2 18 y  9 x2 5x  4 3 2 Giải:
x  4x  5x 18x+18  0 Hệ PT   y   x2 9  5x x  1; y  3 x 1 x  3  ; y  15   x  3   x  1   7; y  6  3 7 x  1   7 x  1   7; y  6  3 7 
29/ Giải bất phương trình: x 3  x12  2x1
Giải: BPT  3  x  4 . x 2y xy  0
30/ Giải hệ phương trình:  .  x 1  4y1  2 
 x  y x 2 y  0  x 2 y  0 x  4y     x 1  4y1  2  x 1  4y1  2 4y1  1 Giải : Hệ PT       x  2  y 1     2 8  x3y3  27  7y3 (1)
31/ Giải hệ phương trình:  4x2y 6x  y2 (2) Giải: 8  x3y3  27  7y3 t  xy
Từ (1)  y  0. Khi đó Hệ PT      3 2 4x2y2  6xy  y3  t 8  27  4t  6t t  xy   t 3   t 1  t 9 ; ;   2 2 2  1   Với t 3   : Từ (1)   : Từ (1)   ;  4 2 y = 0 (loại).  Với t 12  x y 3 3   2 4   3   Với t 9  : Từ (1)   ;  3 4 2  x y 3 3   2 4  x x
32/ Giải phương trình: 3 .2x  3  2x 1 Giải x
PT  3 (2x 1)  2x 1 (1). Ta thấy x 1
 2 không phải là nghiệm của (1). x 2x 1 x 2x 1 Với x 1  3  3   0 2 , ta có: (1)  2x  1 2x 1 2x 1 3 x 6 1 Đặt x x f(x)  3   3  2  f(x)  3 ln3   0, x   2x . Ta có: 1 2x 1 (2x 2 1) 2  1   1 
Do đó f(x) đồng biến trên các khoảng  ;   ; 2     và  2
  Phương trình f(x) = 0 có nhiều nhất 1  1   1 
nghiệm trên từng khoảng   ;  ,  ; 2 2      . Ta thấy x  1, x  1
 là các nghiệm của f(x) = 0. Vậy PT có 2 nghiệm x 1, x  1  . 4 2 2
33/ Giải phương trình:
x  x 1  x  x 1  2 Giải: x2 1 0 Điều kiện:   x  1. x  x2 1 2 2 4 2
Khi đó: x  x 1  x  x 1  x  x 1 (do x  1) CoâSi 4 x x2 4   x  x2 8   x x2  x x2 1 1 2 1 1  VT > = 2  PT vô nghiệm.  2 2 2xy x  y   1
34/ Giải hệ phương trình:  x  y  x  y  x2  y   2 2 2xy x  y   1 (1) Giải:  x  y .
Điều kiện: x  y  0 .  x  y  x2  y (2)   1  (1)  (x  y 2 ) 1 2xy 2 2 1
  0  (x  y 1)(x  y  x  y)  0  x  y 1  0  x  y 
(vì x  y  0 nên x2  y2  x  y  0 ) x 1 (y  0)
Thay x  1 y vào (2) ta được:  x2 1
 (1 x)  x2  x  2  0   x  2  (y  3)
Vậy hệ có 2 nghiệm: (1; 0), (–2; 3). 3
35/ Giải hệ phương trình:
2 3x 2 3 6 5x 8  0  3  3 Giải:   3  2 u  3x  2 Điều kiện: x 6  . Đặt u x  . 5   v  6  5x v2  6  5x 2u  v 3  8 u  2  3  x  2  2  Ta có hệ PT: 
. Giải hệ này ta được     x  2  .  u3 5  v2 3  8 v  4 6  5x 16 Thử lại, ta thấy x  2
 là nghiệm của PT. Vậy PT có nghiệm x  2  . 2 2
2y x 1
36/ Giải hệ phương trình:  3 3
2x y  2y x Giải: Ta có: 3 3 x y   2 2
y x  y x 3 2 2 3 2 2 2
x  2x y  2xy 5y  0
Khi y  0 thì hệ VN. 3 2  x   x   x
Khi y  0 , chia 2 vế cho 3 y  0 ta được:  2  2  5  0        y   y   y  y x  Đặt x t  , ta có : 3 2
t  2t  2t  5  0  t  1  
x y 1, x y  1  y 2 y 1 2y x  m
37/ Tìm các giá trị của tham số m sao cho hệ phương trình y có nghiệm duy nhất.  xy   1 2y x  m (1) Giải: y xy   1 (2) . y  1 2 
Từ (1)  x  2y m, nên (2)  2y  my  1 y  m 1  y    2 (vì y  0)  y 1 1
Xét f y  y   2  f 'y  1  0 y y2
Dựa vào BTT ta kết luận được hệ có nghiệm duy nhất  m  2 . 3  x3  y3  4xy
38/ Giải hệ phương trình:  x2y2  9 Giải: Ta có : 2 2
x y  9  xy  3  .
 Khi: xy  3 , ta có: 3 3
x y  4 và 3 x  3 .  y   2  7 Suy ra: 3 x  3
;  y  là các nghiệm của phương trình: 2
X  4X  27  0  X  2  31
Vậy nghiệm của Hệ PT là: 3 3 x
2  31, y   2  31 hoặc 3 3 x
2  31, y   2  31 .  Khi: xy  3  , ta có: 3 3 x y  4  và 3 x  3 .  y   27 Suy ra: 3 x  3
;  y  là nghiệm của phương trình: 2
X  4X  27  0 (PTVN)  3 y  2  1 x2  y2 1 x
39/ Giải hệ phương trình:   2 2 x x  y  4  22  y Giải: 2 2
Điều kiện: x  0, y  0, x  y 1  0 3 2 3 2 2 2 x    1   1 (1)
Đặt u  x  y 1; v  . Hệ PT trở thành:   y u v u v
u1 4v  22 u  21 4v (2) v  3 3 2 2
Thay (2) vào (1) ta được:   1  2v 1 v 3  21  0   7 21  4v v v   2 x2  y2 1 9  x2  y2 10 x  3 x  3 
 Nếu v = 3 thì u = 9, ta có Hệ PT:  x       3  x  3y y 1   y  1   y  Nếu v 7
 2 thì u = 7, ta có Hệ PT:   x2  y2 2 2 1  7 x2  y2  8 y  4 y  4     53  53  x 7      x 7  y   y  2 x 2   x 2 2 14  1  4  53    53
So sánh điều kiện ta được 4 nghiệm của Hệ PT.
 3x y  2 xy
40/ Giải hệ phương trình:  2
2x y  8
 3x y  2 xy (1) Giải:  . Điều kiện : .
x y  0 ; x y 2
2x y  8 (2) y Ta có: (1)  2
3(x y)  4xy  (3x y)(x  3y)  0  x  3y hay x  3
 Với x  3y , thế vào (2) ta được : 2
y  6y  8 0  y 2 ; y 4
x  6 x 12  Hệ có nghiệm  ; 
y  2 y  4 y
 Với x  , thế vào (2) ta được : 2
3y  2y  24  0 Vô nghiệm. 3
x  6 x 12
Kết luận: hệ phương trình có 2 nghiệm là:  ; 
y  2 y  4 2 2
x y xy 1 4y
41/ Giải hệ phương trình:  2 2
y(x y)  2x  7y  2 2
x 1  xy  4  2 2
x y xy 1  4yy
Giải: Từ hệ PT  y  0 . Khi đó ta có:    . 2 2 2
y(x y)  2x  7y  2  x 1 2 (x y)  2  7  y 2 x 1
u v  4  u  4  v
v  3, u 1 Đặt u
, v x y ta có hệ:      y 2 2
v  2u  7
v  2v 15  0 v  5  , u  9 2 2 2 x 1  yx 1 y
x x  2  0
x 1, y  2
 Với v  3, u 1ta có hệ:        .
x y  3  y  3 xy  3 xx  2  , y  5 2 2 2 x 1  9yx 1  9y
x  9x  46  0  Với v  5
 , u  9 ta có hệ:      , hệ này vô nghiệm.
x y  5   y  5   xy  5   x
Kết luận: Hệ đã cho có hai nghiệm: (1; 2), ( 2  ; 5) . 2
42/ Giải phương trình: x 1 1   4x  3x
Giải: Điều kiện x  0. 2 2x 1
PT  4x 1 3x  x 1  0  (2x 1)(2x 1)   0 3x  x 1  1   (2x 1) 2  x 1  0   2x 1  0  x 1  .  3x  x 1  2
43 / Giải hệ phương trình: 2
2log (xy  2x y  2)  log (x  2x 1)  6 1 x 2 y
log (y  5)  log (x  4) = 1  1 x 2 y 2
xy  2x y  2  0, x  2x 1 0, y  5  0, x  4  0
Giải: Điều kiện:  (*) 0
 1 x  1, 0  2  y  1 Hệ PT 
2log [(1 x)(y  2)]  2log (1 x)  6 l  y x x y
 og (  2)  log (1 )  2  0 (1) 1 2  1 x 2 y   
log (y  5)  log (x  4) = 1 l  y x x y
 og (  5)  log (  4) = 1 (2) 1 2  1 x 2 y 1 Đặt log
(1 x)  t thì (1) trở thành: 2
t   2  0  (t 1)  0  t  1. 2 y t
Với t 1 ta có: 1 x y  2  y  x 1 (3) . Thế vào (2) ta có: x  4 x  4 2 log (x  4)  log (x  4) = 1  log 1 
1 x x  2x  0 1x 1x 1x x  4 x  4  x  0   x  2   Với x  0  y  1  (không thoả (*)).  Với x  2   y  1 (thoả (*)).
Vậy hệ có nghiệm duy nhất x  2  , y 1. x  1  x x 4 – 2.2 – 3 2 x
44/ Giải bất phương trình: .log x – 3  4  2 4 Giải:BPT  x x x x x x (4  2.2  3).log x 1 2  3  2
 4  (4  2.2 3).(log x 2 1)  0 x  log 3  2x x 2 2  2.2  3  0  x 2   3   1 log x 1 0 log x   1  x   x  log 3  2 2   2  2      1  2x x 2  2.2  3  0  x x  log 3 0  x   2  3   2   2  log x   1 2 1  0 log x  2  1    0  x    2
45/ Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất: x log (25 – log a)  x 5 5  x t  5 , t  0 Giải: x x 2x x PT  25  log a 5  5  5  5  log a 5  0   t2  t  log a  5  0 (*) 2
PT đã cho có nghiệm duy nhất  (*) có đúng 1 nghiệm dương  t  t  log a 5 có đúng 1 nghiệm dương.   Xét hàm số f t t2
( )   t với t  [0; +∞). Ta có: f t()  2t 1  f t   t 1 ( ) 0  . f 1 1
    , f (0)  0 . 2  2  4
Dựa vào BBT ta suy ra phương trình f t ( )  log a
5 có đúng 1 nghiệm dương log a a  1 5  0    1  a 1 log  a  . 5    4 4  5 2log x2 – 4 2 2
46/ Giải hệ phương trình:  3 log (x  2)  log (x 3 3 3 – 2)  4 x2  4  0  2    2 Giải: x  4  0 Điều kiện:     x  (**) log (x 2 2  x  3  3  2)  0 (  x  2) 1 log  2 x2 – 4 2 2 PT   3 log (x  2)  log (x 3 3 3 – 2)  4 2 2  log (x 2  2)  4 log (x 2 3 3  2)    log (x  2)  3 log (x 3 3  2)  4  0  1  0  log (x 2 3  2) 1  x 2 (  2)  3  x  2   3
Kiểm tra điều kiện (**) chỉ có x  2   3 thỏa mãn.
Vậy phương trình có nghiệm duy nhất là: x  2   3 x3  4y  y3 16x
47 / Giải hệ phương trình:  . 1   y2  5(1 x2) x3  4y  y3 16x Giải: (1)  1   y2  5(1 x2) (2) 2 2
Từ (2) suy ra y – 5x  4 (3). 3 2 2 3 3 2
Thế vào (1) được: x  y – 5x  y
.  y 16x  x – 5x y–16 x  0 2
 x  0 hoặc x – 5xy –16  0
 Với x  0  y2  4  y  2  . 2 2  2 2 x 16 x 16   2
 Với x – 5xy –16  0  y     5x  4
5x (4). Thế vào (3) được:  5x  4 2 4 2 4 2 x 1 (y  3  )
 x – 32x  256 –125x 100x  124 x 132x – 256  0  x2 1   . x  1  (y  3)
Vậy hệ có 4 nghiệm: (x; y) = (0; 2) ; (0; –2); (1; –3); (–1; 3)
log x  y  3log ( x  y  2 8  2)
48/ Giải hệ phương trình:  
x2  y2 1  x2  y2  3 
Giải: Điều kiện: x  y  0, x  y  0  x  y  2  x  y Hệ PT   .
 x2  y2 1  x2  y2  3   u v 2 (u v)     u  v  2 uv  4 u  x  y   Đặt:  ta có hệ:  2 2   2 2 v  x  y u  v  2 u  v   uv  2  3   uv  3  2  2 u  v  2 uv  4 (1)    (u v 2) 2uv2 .   uv  3 (2)  2 2
Thế (1) vào (2) ta có: uv 8 uv  9  uv  3  uv 8 uv  9  (3  uv)  uv  0 .  uv  0 Kết hợp (1) ta có: 
 u  4, v  0 (với u > v). Từ đó ta có: x = 2; y = 2.(thoả đk) u  v  4
Kết luận: Vậy nghiệm của hệ là: (x; y) = (2; 2).
49/ Giải phương trình: 25x – 6.5x + 5 = 0
Giải: Câu 2: 1) 25x – 6.5x + 5 = 0  x 2 (5 ) 6.5x
 5  0  5x = 1 hay 5x = 5  x = 0 hay x = 1.
x  2y xy  0
50/ Giải hệ phương trình: 
x 1  4y 1  2      x 1
x  2 y xy  0 (1)  Giải:  Điều kiện:  1
x 1  4y 1  2 (2)  y   4 x x Từ (1)    2  0  x = 4y y y Nghiệm của hệ (2; 1 ) 2
51/ Tìm m để bất phương trình: 52x – 5x+1 – 2m5x + m2 + 5m > 0 thỏa với mọi số thực x.
Giải: Đặt X = 5x  X > 0
Bất phương trình đã cho trở thành: X2 + (5 + 2m)X + m2 + 5m > 0 (*)
Bpt đã cho có nghiệm với mọi x khi và chỉ khi (*) có nghiệm với mọi X > 0
 < 0 hoặc (*) có hai nghiệm X1 ≤ X2 ≤ 0 Từ đó suy ra m 1
52/ Giải bất phương trình: 2 log
x  5x  6  log x  2  log x  3 3 1 1   2 3 3
Giải: Điều kiện: x  3; Phương trình đã cho tương đương: 1 1 1 1 log  1 1 2
x  5x  6  log     log  2
x  5x  6  log x  2   log x  3 3  3   3    x 2 log  x 3 3  1   1   3 3 2 2 2 2 2 2    x 2  log  x  2 x  3   log x  2  log
x  3  log  x  2 x  3   log 3    3    3   3    3    x  3   
x  x   x 2 2 3  x  3 x   10 2
x  9 1  
Giao với điều kiện, ta được nghiệm của phương trình đã cho là x  10 x  10
53/ Cho phương trình x
x m x  x  x   x 3 4 1 2 1 2 1  m
Tìm m để phương trình có một nghiệm duy nhất.
Giải: Phương trình x
x m x  x  x   x 3 4 1 2 1 2 1  m (1)
Điều kiện : 0  x 1 Nếu x 0; 
1 thỏa mãn (1) thì 1 – x cũng thỏa mãn (1) nên để (1) có nghiệm duy nhất thì cần có điều kiện 1 1 1 1 m  0
x  1 x x  . Thay x  vào (1) ta được: 3 2.  m  2.  m   2 2 2 2 m  1 
*Với m = 0; (1) trở thành:  x  1 x2 1 4 4
 0  x  Phương trình có nghiệm duy nhất. 2
* Với m = -1; (1) trở thành
x  1 x  2 x 1 x 4
 2 x1 x  1    4
x  1 x  2 x 1 x   x 1 x  2 x1 x  0
  x  1 x2  x  1 x 2 4 4  0 1 + Với 4 4
x  1 x  0  x  + Với 1
x  1 x  0  x  2 2
Trường hợp này, (1) cũng có nghiệm duy nhất.
* Với m = 1 thì (1) trở thành: x   x
x   x  
x   x   x
x 2   x   x2 4 4 4 1 2 1 1 2 1 1 1
Ta thấy phương trình (1) có 2 nghiệm 1 x  0, x
nên trong trường hợp này (1) không có nghiệm duy nhất. 2
Vậy phương trình có nghiệm duy nhất khi m = 0 và m = -1. 2 3
54/ Giải phương trình : log  x   1  2  log
4  x  log 4  x 4 8 2 Giải: 2 3 log x 1  2  log
4  x  log 4  x (2) 4   8   2 Điều kiện: x 1  0   2 4
  x  4 (2)  log x 1  2  log 4  x  log 4  x  log x 1  2  log 16  x 2 2   2   2 2  
4  x  0    x  1 
 log 4 x 1  log 16  x  4 x 1 16  x 2 2  2  2 4  x  0  x  2 + Với 1
  x  4 ta có phương trình 2
x  4x 12  0 (3) ; (3)   x  6   lo¹i + Với 4   x  1  ta có phương trình 2
x  4x  20  0 (4);    x  2  24 4  
; Vậy phương trình đã cho có hai nghiệm là x  2 hoặc x  21 6 x  2  24  lo¹i 2 2
55/ 1). Giải phương trình: 2x +1 +x x  2  x  1 x  2x  3  0 x x 1  x x
2) Giải phương trình: 4  2  22   1 sin2  y  1  2  0. 2 2 x x 1  x x2
3) Giải bất phương trình: 9 110.3 . Giải
1) Giải phương trình : 2x +1 +x 2 x   x  2 2 1 x  2x  3  0 . (a)   2 v  2 2 2 2 u  2x 1 u  x  2, u  0 u  x  2  * Đặt:      2 v  2 2 2 2 u 1 v  2 x  2x  3, v  0 v  x  2x  3  x   2  Ta có:  2 2 2 v  2 u 1  2 v  2 u 1   2 2 2 v  2 u  u  2 v  2 u  v (a) v  u   .u  
1.v  0 v  u   .u    .v           0  2   2   2  2  2  2 v  u  0 (b)   v  u  1   (v  u)(v  u) 1      0   v  u   1 2 2 (v  u) 1         0 (c)   2  2
 Vì u > 0, v > 0, nên (c) vô nghiệm.  Do đó: 2 2 2 2 1
(a)  v  u  0  v  u  x  2x  3  x  2  x  2x  3  x  2  x   2 1
Kết luận, phương trình có nghiệm duy nhất: x =  . 2 x x 1  x x
2) Giải phương trình 4  2  22   1 sin2  y  1  2  0(*) x x       2 2 1 sin 2 y 1 0(1) 
Ta có: (*)  2x 1 sin 2x y   1 2  o
c s 2x y     1  0    o c s 
2x y  1  0(2)
Từ (2)  sin 2x y   1  1  .
Khi sin 2x y  
1  1, thay vào (1), ta được: 2x = 0 (VN)
Khi sin 2x y   1  1
 , thay vào (1), ta được: 2x = 2  x = 1. 
Thay x = 1 vào (1)  sin(y +1) = -1  y  1
   k ,k Z . 2   
Kết luận: Phương trình có nghiệm: 1; 1
   k ,k Z  .  2  
3) Giải bất phương trình: 2 2 x x 1  x x2 9 110.3 . Đặt 2  3x x t , t > 0.
Bất phương trình trở thành: t2 – 10t + 9  0  ( t  1 hoặc t  9) 2  Khi t  1  x x 2 t  3
1  x x  0  1   x  0 .(i)    2 x 2  Khi t  9  x x 2 t  3
 9  x x  2  0   (2i) x 1
Kết hợp (i) và (2i) ta có tập nghiệm của bpt là: S = (- ; -2][-1;0][1; + ).
56/ Giải phương trình, hệ phương trình:  log x 2 2
x y x y 12    x   3 1 2 x   x  2      2 2
y x y 12 1. 2 ; 2. 
Giải: 1) Phương trình đã cho tương đương:  x  2  0 x  2  0 x  2    log log x 3 x 3    1    1    1    x  1  ln x   0      
log x ln x   0 3     2    2    2        x  2  0 x  2 x  2 x  2 x  2 x  2    log x  0      3 x 1 x 1          1    1   3  x  2 
Điều kiện: | x |  | y |  ln x   0     x  1   x     2   2  2    x  2  x  2  x  2 2 2     2 1  u  Đặt u x y ; u 0 
; x   y không thỏa hệ nên xét x   y ta có y  v   .
v x y 2  v
2) Hệ phương trình đã cho có dạng: u   v  12  u   4 u   3 2 u u    hoặc   v   12 v  8 v  9 2   v  2 2 u   4
 x y  4 +    (I) v  8
x y  8 2 2 u   3
 x y  3 +   
(II) Giải hệ (I), (II). Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ v  9
x y  9
phương trình ban đầu là S  
 5;3,5;4 Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ phương
trình ban đầu là S    5;3,5;4
x2  1  y(x  y)  4y (x2  )( 1 x  y  2) 
57/ Giải hệ phương trình: 
y (x, yR ) Giải: 2
x 1 (xy 2)  2   y x2  1
2) Hệ phương trình tương đương với  Đặt u  , v  x  y  2 2  x 1 y
(x y  2)  1  y x2 1 u   v  2   1 Ta có hệ   u  v  1 Suy ra  y . uv   1  x  y  2  1
Giải hệ trên ta được nghiệm của hệ phưng trình đã cho là (1; 2), (-2; 5)
58 / Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực: 2 2 1 1x 1 1x 9  (m 2)3  2m1  0 (1)
Giải: * Đk x[-1;1], đặt t = 2 1 1
3 x ; x[-1;1]  t [3;9] 2 t  2t 1 Ta có: (1) viết lại 2 2
t (m 2)t  2m1  0  (t  2)m  t  2t 1  m  t 2 2 t  2t 1 2 t  4t  3 t  1 Xét hàm số f(t) = t  / / f (t)  , f (t)  0  t  2 , với [3;9]. Ta có: (t  2)  t  3 Lập bảng biến thiên t 3 9 f/(t) + 48 7 f(t) 4
Căn cứ bảng biến thiêng, (1) có nghiệm x[-1;1] 48
 (2) có nghiệm t [3;9]  4  m  7 3 log (x + )2 2
- 3 = log (4 - x)3 + log (x + 6)3 1 1 1
59/ Giải phương trình: 2 4 4 4
Giải: bất phương trình: 1 2 1
log (x  4x  ) 5  log ( ) (1) 2 2 1 x  7 2  2
x  4x  5  0 x(  ; ) 5   ; 1 ( ) Đk:     x ( ; 7  ) 5  1 (  )  x  7  0 x  7 Từ (1) 2 1
 log (x  4x  ) 5  2  log 2 2 x  7 2 2 2 2
 log (x  4x  5)  log (x  7)  x  4x  5  x 14x  49 2 2 27   1
 0x  54  x  5 
Kết hợp điều kiện: Vậy BPT có nghiệm: 27 x  ( ; 7 ) 5  3 x  3 y  1   2 x y  2 2 xy  3 y  2
60/ Giải hệ phương trình :  Giải:  3 x  3 y  1  3 x  3 y  1 ) 1 (     2 x y  2 2 xy  3 y  2   2 3 x  3 y  2 x y  2 2 xy  0 ( ) 2  3 x  3 y  1 ) 3 ( 
y  0. Ta có:   x 3  x 2  x  2   2 1        0 ( ) 4   y   y   y  Đặt : x  1
t (4) có dạng : 2t3 – t2 – 2t + 1 = 0  t =  1 , t = . y 2 3 3 x y  1 1 a) Nếu t = 1 ta có hệ   x y  3 x y 2
x3  y3  1
b) Nếu t = -1 ta có hệ   hệ vô nghiệm. x  y 1 3 3 x y  1 3 3 23 3 c) Nếu t = ta có hệ   x  , y  2 y  2x 3 3 4 2 1  
61/ Tìm m để phương trình sau có nghiệm thực: x x m Giải: D = [0 ; + ) 3 3 1   2 3 x 2 x 3 2 4 1 ( )   4 2 x 1 x x 4 (x ) 1 2 *Đặt f(x) = x x  1 
x f '(x)     3 24 (x2  ) 1 3 2 x 24 (x 2  ) 1 3 . x 1 2x 3 2 4 1 (  ) . x x 2 1 1 3  4 1 (  ) 2 Suy ra: f’(x) = x
 0 x  (0 ;  ) 1 2 3 4 1 (  ) . x 2 x 2     x   x x   x 4 2 1 2 1 2 * lim ( x  1  x )  lim    lim    0 x x   4 2 
x 1  x x(4 2 x  1  x )( 2
x  1  x)  * BBT x 0 +  f’(x) f(x) 1 0 Vậy: 0 < m  1 log 3  log 3
62/ Giải bất phương trình: x x 3 x  0 
Giải: ĐK : x  1 Bất phương trình trở thành :  x  3 1 1 1 1 1 1       0 log x x log x log x 1 log x log x 1 3 log 3 3 3 3 3 3 1 
 0  log x(log x  )
1  0  log x  0  log x  1
log x(log x  ) 1 3 3 3 3 3 3
* log x  0  x  1 kết hợp ĐK : 0 < x < 1 3
* log x  0  x  3 3
Vậy tập nghiệm của BPT: x 0 ( ; ) 1  3 ( ;  )  log 2 x  log 2 x  3  5(log 2 x  ) 3
63/ .Giải bất phương trình 2 2 4 x  0 Giải: ĐK:  log 2 x  log 2 x  3  0 2 2
Bất phương trình đã cho tương đương với log2 x  log 2
x  3  5(log x  ) 3 ) 1 ( 2 2 2 Đặt t = log2x, 2.BPT (1)  2
t  2t  3  5(t  ) 3  (t  )( 3 t  ) 1  5(t  ) 3 t  1    1 t  1 log x   0  x   t  3   1     2  2  t x  2 3   4 3  log   4 2 (t  )( 1 t  ) 3  ( 5 t  ) 3 8  x  16
Vậy bất phương trình đã cho có nghiệm là 1 ( ; 0 ]  ) 16 ; 8 ( 2 2 2
 x 91  y 2  y (1)  2 2     
64/ Giải hệ phương trình y 91 x 2 x (2) 
Giải: Điều kiện: x ≥ 2 và y ≥ 2 : Lấy (1) trừ (2) vế theo vế ta được: 2 2 2 2 x  91  y  91 
y  2  x  2  y x 2 2 x y y x  
 (y x)(y x) 2 2 x  91  y  91 y  2  x  2   x y 1
 (x y)  
x y   0  2 2        x 91 y 91 x 2 y 2  
 x = y (trong ngoặc luôn dương và x vay đều lớn hơn 2) Vậy từ hệ trên ta có: 2 2 x  91  x  2  x 2 2
x  91 10  x  2 1 x 9 2 x  9 x  3        1 1
(x  3)(x  3)  (x  3)  (x  3) 1    0 2   x  91 10 x  2 1 2   x  91 10  x  2 1   x = 3
Vậy nghiệm của hệ x = y = 3 3 3    
65/ Giải phương trình: x 34 x 3 1 Giải: Đặt 3 3 u  x  34, v  x  3 . Ta có: u  v 1 u  v 1     3 3 u  v  37 u  v     2 2 u  v  uv  37 u  3   u  v  1  u  v 1 v  4       u  v  2 3uv  37 uv 12 u  4  v  3
Với = -3 , v = - 4 ta có : x = - 61
Với = 4, v = 3 ta có : x = 30 vậy phương trình đã cho có 2 nghiệm: x = -61 vµ x = 30 log 2 x  log 2 x  3  5(log 2 x
66/ Giải bấ phương trình ) 3 2 2 4 x  0 Giải: §K:  log2 x  log 2 x  3  0 2 2
Bất phương trình đã cho tương đương với log2 x  log 2
x  3  5(log x  ) 3 ) 1 ( 2 2 2 Đặt t = log2x, BPT (1)  2
t  2t  3  5(t  ) 3  (t  )( 3 t  ) 1  5(t  ) 3 t  1    1 t  1 log x   0  x   t  3   1     2  2  t x  2 3   4 3  log   4 2 (t  )( 1 t  ) 3  ( 5 t  ) 3 8  x  16
Vậy bất phương trình đã cho có nghiệm là 1 ( ; 0 ]  ) 16 ; 8 ( 2 67/ . xx 25 . 3
2  3x 10 2  x  1. Giải phương trình: 5 3
log x cosx  sin x  log x x  1 cos cos2  0 2.Giải phương trình: x .
 3x  1  2x   x x  
3) Giải bất phương trình: 1 3 1 0 Giải: xx 25 . 3
2  3x 105 2  x  3 1.  xxxx 5 2  5 . 3 2   1  x 5 . 3 2   1   3 5 . 3 2   1  0   x 5 . 3 2   1  x 5 2  x   3  0 x  5 . 3 2 1  0    1   x 5 2  x  3  0 2   x 2 1 1 1   5   x  2  log
 2  log 3 2  x 5 2  x  3 3 5 3 5
Vế trái là hàm đồng biến vế phải là hàm nghịch biến mà (2) có nghiệm x = 2 nên là nghiệm duy nhất.
Vậy Pt có nghiệm là: x = 2  log 3 và x = 2 5 2/ log
x cos x  sin x  log x x  1 cos cos2  0 x 0  x  1 
Điều kiện: cosx  sin x  0 . Khi đó Pt 
cosx  cos2x  0   
 cos2x  sin x  cos2x  co  s x    2      2x x   k2 x   k   2  2     2 .     k 2
2x  x   k2 x     2  6 3  k2
Kết hợp với điều kiện ta được: x    (Với k ∊ N* k 3/ 3/ 6 3
 3x  1  2x  13x x 10 3 2 x x  3/.  3 3 2
x x  2  0  2 t    2  2  3 2 2
t  3t  2  0 Đặt t x x  1    
t    x x 1    x  1 3 t  1  3 3  t  2 
68/ Giải phương trình: 3x.2x = 3x + 2x + 1
Giải: Ta thấy phương trình: 3x.2x = 3x + 2x + 1 (2) có hai nghiệm x =  1. 1 Ta có x =
không là nghiệm của phương trình nên 2 x x 2 1 (2)  3  2x 1
Ta có hàm số y = 3x tăng trên R x      hàm số y = 2
1 luôn giảm trên mỗi khoảng 1 1  ;  , ;      2x 1  2   2 
Vậy Phương trình (2) chỉ có hai nghiệm x =  1 1 1 log (x  ) 3  log (x  ) 1 8  3log (4x) 4 8
69/ Giải phương trình: 2 2 4 . Giải: 1 1
log (x  ) 3  log (x  )
1 8  3log (4x) . 2 2 4 4 8 Điều kiện: x  3  
x  1  0  x  .
1 Biến đổi theo logarit cơ số 2 thành phương trình x  0  1 loaïi  2 3 1 4 2 3 0 3 2    
x   x     2  xx   log log
x x      x  . x  3
70/ Tìm các giá trị của tham số m để phương trình sau có nghiệm duy nhất thuộc đoạn :
3 1 x2  2 x3  2x2 1  m ( m R ). f x 2 3 2
 3 1 x  2 x  2x 1 f x  1  Giải:Đặt , suy ra
xác định và liên tục trên đoạn  ;1  . 2    2 3x 3x  4x  3 3x  4 
f ' x     x   . 2 3 2 2 3 2 1 x x  2x 1  1 x
x  2x 1   1  4 3 3x  4 x    ;1  ta có x    3x  4  0    0 . 2    2 3 2 3 1 x x  2x 1 Vậy:
f ' x  0  x  0 .Bảng biến thiên: 1 x  0 1 2 f '  x  ||  0  || 1 CÑ  f x  3 3 22 2  4
Dựa vào bảng biến thiên, ta có:  1  3 3  22
Phương trình đã cho có 1 nghiệm duy nhất thuộc  ;1   4    m  2  m hoặc 1.   2 71/
1.Giaûi baát phöông trình: 2 2 2
x  3x  2  x  4x  3  2. x  5x  4 2 2 2 2
2log (2x x  2m  4m )  log (x mx  2m )  0 2.Cho phöông trình: 4 1 2 2 2  
Xaùc ñònh tham soá m ñeå phöông trình (1) coù 2 nghieäm x x x x 1 1 , 2 thoûa : 1 2
Giải: 1) Giaûi baát phöông trình: 2 2 2
x  3x  2  x  4x  3  2. x  5x  4  2
x  3x  2  0   Ñieàu kieän: 2
x  4x  3  0  x  1 x  4  2
x  5x  4  0  Ta coù:
Baát phöông trình  (x 1)(x  2)  (x 1)(x  3)  2 (x 1)(x  4) (*)
Neáu x = 1 thì hieån nhieân (*) ñuùng .
Suy ra x=1 laø nghieäm cuûa phöông trình
Neáu x < 1 thì (*) trôû thaønh :
2  x  3  x  2 4  x
 2 x  4 x Nhaän xeùt: 
 2  x  3 x  2 4  x
Suy ra Baát phöông trình voâ nghieäm.
 3 x  4  x
Neáu x  4 thì (*) trôû thaønh :
x  2  x  3  2 x  4
 x  2  x  4 Nhaän xeùt: 
x  2  x  3  2 x  4 Suy ra Baát phöông trình ñuùng x   4 .
 x 3  x  4
Toùm laïi: Baát phöông trình coù nghieäm laø: x 1 x  4 . 2 2 2 2
2) 2 log (2x x  2m  4m )  log
(x mx  2m )  0 4 12  2 2
x mx  2m  0 2 2 2 2
 log (2x x  2m  4m )  log (x mx  2m )  0   2 2 2 2
x  (1 m)x  2m  2m  0  2 2
x mx  2m  0  x  2 , m x  1 m  1 2  2 2 xx  1  1 2 Yeâu caàu baøi toaùn  2 2     vôùi x 2m , x 1 m x
mx  2m  0 1 2 1 1   2 2 x
mx  2m  0  2 2  2 5m  2m  0   2 1 2  4m  0  1   m  0   m  5 2  2  2
m m 1  0   1 2 2x x   2  y   2 2     
72/ Giải hệ phương trình y y x 2 y 2 Giải: ĐK : y  0  1 2 2x x   2  0  y 2
2u u v  2  0   hệ   u v đưa hệ về dạng  
u v  1 2 1  2
 u  1 v   
2v v u  2  0  x  2  0  u v  1  2  2       y y 2v v u 2 0  3  7  3  7 u   u    2  2 hoặc  ,   1   7  1   7 v v     2  2  
Từ đó ta có nghiệm của hệ( 3 7 2 3 7 2 -1 ;-1),(1 ;1), ( ; ), ( ; ) 2 7 1 2 7 1 2 3
log (x 1)  log (x 1) 3 4  0 2
73/ Giải bất phương trình x  5x  6 3log (x 1) 3 2 log (x 1)  3 log 4 log (x 1)
Giải: Đk: x > - 1 ; bất phương trình 3   0 3 
 0  0  x  6
(x 1)(x  6) x  6 2
74/ Giải phương trình: 2x  3  x 1  3x  2 2x  5x  3 16 .
Giải : Đặt t  2x  3  x 1 > 0. (2)  x  3
75/ Giải hệ phương trình:
log (x2  y2)  log (2x) 1 log (x  3y 4 4 4 )   2  x 
log (xy 1)  log (4y  2y  2x  4 4  4)  log4   1   y  x   x=2 Giải : 
vôùi >0 tuyø yù vaø y    y=1
76/ Giải bất phương trình:
2x 10  5x 10  x  2 (1)
Giải: Điều kiện: x  2   2
1  2x 10  x  2  5x 10  2x  6x  20  x 1(2)
Khi x  2 => x+1>0 bình phương 2 vế phương trình (2) 2 2 2
(2)  2x  6x  20  x  2x 1  x  4x 11  0  x  ;  7  3;
Kết hợp điều kiện vậy nghiệm của bất phương trình là: x  3
77/ Giải phương trình: 2
log (x  2)  log (x  5)  log 8  0 2 4 1 2
Giải: . Điều kiện: x > – 2 và x  5 (*)
Với điều kiện đó, ta có phương trình đã cho tương đương với phương trình: 2 2
log (x  2) x  5   log 8  (x  2) x  5  8  (x  3x 18)(x  3x  2)  0 2   2 2 x  3x 18  0 3  17    x  3  ; x  6; x  2 x  3x  2  0 2 
Đối chiếu với điều kiện (*), ta được tất cả các nghiệm của phương trình đã cho là: 3 17 x  6 và x  2
78/ Giải phương trình: 2 3 log x 14log x  40log x  0. x 16 x 4 x 2
Giải: Giải phương trình 2
3  4 sin 2x  2cos 2x 1 2 sin x
Biến đổi phương trình về dạng 2 sin3x2sin x  
1  2 sin x   1  0
 Do đó nghiệm của phương trình là  7  k2 5 k2 x  
k2 ; x
k2 ; x   ; x   6 6 18 3 18 3 Giải phương trình 2 3 log x 14log x  40log x  0. x 16 x 4 x 2  Điều kiện: 1 1
x  0; x  2; x ; x . 4 16
 Dễ thấy x = 1 là một nghiệm của pt đã cho Với x 1. Đặt t log 2 và biến đổi phương trình về dạng x 2 42 20    0 , Giải ra ta được 1 1 t ;t  2
  x  4; x
. Vậy pt có 3 nghiệm x =1; 1 t 4t 1 2t 1 2 2 1 x  4; x . 2 79 / Giải phương trình x 1 xx 1 2 x 1 4 . 3  9 .  4 . 6  9 .  3 4 .
Giải: Giải phương trình x 1 xx 1 2 x 1 4 . 3  9 .  4 . 6  9
.  Biến đổi phương trình đã cho về dạng 3 4 x  3  2 2 x x x 9 2 2 2 2 3 2  27 3  6 2  3 x . . . . Từ đó ta thu được   x log   4 3  2  39 39 2 2 x x
f (x)  e  sin x   3 80/ Cho hàm số 2
. Tìm giá trị nhỏ nhất của f (x) và chứng minh rằng f (x)  0 có đúng hai nghiệm. Giải: Ta có x f (
x ) e x cos x. Do đó    0 x f ' x
e  x cos x. Hàm số x
y e là hàm đồng biến;
hàm số y  x cosx là hàm nghịch biến vì y'  1
  sin x  0, x
 . Mặt khác x  0 là nghiệm của phương trình x
e  x cos x nên nó là nghiệm duy nhất. Lập bảng biến thiên c ủa hàm số y f x (học sinh tự
làm) ta đi đến kết luận phương trình f (x)  0 có đúng hai nghiệm.
Từ bảng biến thiên ta có min f x  2
  x  0.
81/ 1) Giải hệ phương trình:  2xy 2 2 x y  1  x y   2
x y x y  log log  2
x 1  x  log log  2 x 1  x 1 5 3 1 
2) Giải bất phương trình: 3 5 Giải: 1)  2xy 2 2 x y  1   1  x y
dk x y  0  2
x y x y  2
   x y2 2xy 1  2xy
1 0  x y3  2xyx y  2xy  x y  0 x y
 x y x y2  
1  2xy x y   1  0
x y 1 3   Dễ thấy (4) vô nghiệm   2 2 x y   1 
x y x y  0  4
 x y x y   1  2xy  0  vì x+y>0 x y 1
x 1; y  0
Thế (3) vào (2) ta được 2
x y  1 Giải hệ   ……  2 x y 1 x  2  ; y  3
2) log log  2x 1  x  log log  2x 1  x (1) 1 5 3 1  3 5 Đk: x  0;   1  log log  2
x  1  x  log log  2
x  1  x  0 3 1 3 5  5    log log 
 2x 1x.log  2x 1 x 2  0  log 
 2x 1 x 1 3 1 5 5    5
 0  log  2x 1  x 1 5  *) 0  log  2
x 1  x x  0 5  12 *) log  2 x 1  x 2 2
1 x 1  x  5  x 1  5  x  ...  x  5 5  12 
Vậy BPT có nghiệm x  0;    5  Đề 87.
1. Giải bất phương trình 2 2
x x  2  3 x  5x  4x  6 ( x  R). 2
x x  2  0 
Giải:Điều kiện x  0
x  2 ;Bình phương hai vế ta được 2
6 x(x 1)(x  2)  4x 12x  4  2
5x  4x  6  0     x(x 2) x(x 2)
3 x(x 1)(x  2)  2 (
x x  2)  2(x 1)  3  2  2 x 1 x  1  1  x(x  2) t  Đặt t   0 t t    
2  t  2 ( do t  0 ) x  ta được bpt 2 2 3 2 0 1  t  2 x(x  2) x  3 13 Với 2 t  2 
 2  x  6x  4  0    x  3 13 x 1 x  3 13
( do x  2 ) Vậy bpt có nghiệm x  3  13
82/ Giải hệ phương trình  1 log y x  log 1  1   4 y   4 (x, y )  2 2     y x  0 x y 25 Giải: Điều kiện:  y  0  1  y xy x 1 log y x  log  1  log  1    4   Hệ phương trình 4  4   y   y   y 4   2 2  2 2  2 2
x y  25
x y  25
x y  25     ; x y  15 5   ; x  3y   x  3yx  3y   10 10    ( loại)       25 2 2 2 2 2
x y  25 9
y y  25 y       15 5 10  ; x y    ;      10 10 
Vậy hệ phương trình đã cho vô nghiệm. 83/ Giải hpt :  3 2
4xy  4((x y)  2xy))   7  2  (x y)  1 x y
 (x y)  3  x y Giải:  3  3 2 2
4xy  4((x y)  2xy))   7
4(x y)  4xy   7  2  2  (x y)  (x y)    1 1 x y (x y) 3       x y
 (x y)  3  x y  x y  3  3 2 2 2 2 2             3(x y) ((x y) 4xy) 7 3(x y) (x y 2xy) 7  2  2  (x y)  (x y)     1 1 x y
 (x y)  3 x y
 (x y)  3  x y  x y  3    2 2 1 2 2 3(x y) 
 (x y)  7 3 
 (x y) 
 (x y)  7 2   2  (x y)   (x y)      1   1 x y
 (x y)  3 x y
 (x y)  3  x y  x y      
84/ 1. Giải bất phương trình : 3 2 2log(x 8) 2log(x 58) log(x 4x 4) . x x x x
2. Giải pt : 3  5  10  3  15.3  50  9  1 3 2
x  8  (x  2)(x  2x  4)  0 
Giải:1. Đk : x  58  0  x  2   2 2
x  4x  4  (x  2)  0  Bpt đã cho  3 2
log(x  8)  log((x  58)(x  2))  (x  2) x  3x  54  0    x  6
 ;  2  x  9 (0.25) .So dk, ta co : 2   x  9 (0.25) 2.Giải pt : 3x 5 10 3x 15.3x 50 9x       1 Đặt : x x 2
 3 5  10 3 (  0)   5 2 15.3x 50 9x t t tt  3(nhan) Ta có pt : 2
t  2t  3  0 (0.25)   t  1  (loai)
t  3  3x  5  10  3x  3.
Dat : y  3x ( y  0). 2 2
Ta co pt : 9  5  2 15.y  50  y  15.y  50  y  2  y  9 3x  9 x  2 2
y 15y  54  0        y  6 3x  6 x  log 6  3
2log (xy  2x y  ) 2  log ( 2 x  2x  ) 1   1 x 2 6
85/ Giải hệ phương trình:  y log (y  ) 5  log (x  ) 4   1 x 2 1 y
2log (xy  2x y  ) 2  log ( 2 x  2x  ) 1  6 Giải  1 x 2 : Hệ phương trình  y log (y  ) 5  log (x  ) 4   1 x 2 1 y  4  x  , 1 x  0 ĐK  y   ; 2 y  1
Đưa phương trình thứ nhất của hệ về dạng log (2  y)  log   1 x x 2 y 1  2
Đặt t  log (2  y) 1
, Tìm được T=1, kết hợp với phương trình thứ hai của hệ, đối chiếu với điều kiện trên, x tìm được nghiệm  ; x y   1 ; 2 . 1 1
86/ Giai3 phuong trình: log (x  ) 3  log   . 4 x 18 log 4x 2 2 4 2 3 3 3 8  x y  27  18y (1)
87/ 1/.Giải hệ phương trình:  2 2 4x y  6x  y (2) 3 3 3 8  x y  27  18y (1)
Giải: hệ phương trình:  2 2 4x y  6x  y (2) (1)  y  0 3 3  27  3 8x   18  3  x  3 (2 )   18 y  y     Hệ    2  4x 6x    1  3  3  2 2 . x 2x   3  y y  y y  3 3 a  b  18 a  b  3
Đặt a = 2x; b = 3 . Ta có hệ:   y a  ( b a  b)  3 ab  1      
 Hệ đã cho có 2 nghiệm 3 5 6 3 5 6  ; , ; 4   3  5   4 3  5 
88/ Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực: (m - 3) x + ( 2- m)x + 3 - m = 0. (1)
Giải: Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực: (m - 3) x + ( 2- m)x + 3 - m = 0. (1) Đk x  0. đặt t = x ; t  0 2 2t 3t 3
(1) trở thành (m–3)t+(2- m)t2 +3-m = 0  m  2 t t 1 (2) 2 2t 3t  3 Xét hàm số f(t) = 2 t t 1 (t  0) Lập bảng biến thiên (1) có nghiệm  5 (2) có nghiệm t  0   m  3 3
89/ Giải phương trình: 2log 3 ( x  ) 1 1  log x  . 3 (2 ) 1 5 5
Giải: Giải phương trình: 2log 3 ( x  ) 1 1  log x  . 3 (2 ) 1 5 5 ĐK 1 : x  . (*) 3
Với điều kiện trên phương trình đã cho  log 3 ( x  )
1 2 1  3log (2x  ) 1 5 5 2 3  log 3 ( 5 x  ) 1  log (2x  ) 1 5 5 2 3  3 ( 5 x  ) 1  (2x  ) 1  8 3 x  33 2
x  36x  4  0  (x  ) 2 2 8 ( x  ) 1  0 x  2   x  1  8
Đối chiếu với điều kiện trên ta được nghiệm của phương trình đã cho là x  . 2  4 x  4 2 x  2
y  6 y  9  0
90/ : Giải hệ phương trình:   .  2 x y  2
x  2 y  22  0 Giải: ( 2 x  ) 2 2  ( y  ) 3 2  4 2 2 2
(x  2)  (y 3)  4
Hệ phuong trình đã cho tương đương với   ( 2 x  ) 2 y  2 x  22  0 2 2
(x  2  4)(y 3 3)  x  2  20  0 2 x  2  u 2 2 u   v  4 
* Thay vào hệ phương trình ta có  y  3  v  .
u v  4(u v)  8 u   2  v  0 u   0 hoặc  v  2
x  2 x  2
 x  2 x   2
Thế vào cách đặt ta được các nghiệm của hệ là :  ;  ;  ;  ;
y  3 y  3 y  5 y  5
91/ Giải bất phương trình: 2 2
x  35  5x  4  x  24
Giải: Giải bất phương trình: 2 2
x  35  5x  4  x  24 BPT tương đương 11 2 2
x  35  x  24  5x  4   5x  4 2 2
x  35  x  24 2 2
 11 (5x  4)( x  35  x  24) Xét: a)Nếu x 4  không thỏa mãn BPT 5 b)Nếu x>4/5: Hàm số 2 2
y  (5x  4)( x  35  x  24) với x>4/5 1 1 y'= 2 2 5( x  35 
x  24)  (5x  4)(  ) >0 mọi x>4/5 2 2 x  35 x  24
Vậy HSĐB. +Nếu 4/5 +Nếu x>1 thì y(x)>11 Vậy nghiệm BPT x>1 3 3 2
x y  3y  3x  2  0 
92/ Tìm m để hệ phương trình:  có nghiệm thực 2 2 2
x  1 x  3 2y y m  0  2 1   x  0  1   x 1 Giải: Điều kiện:    2
2y y  0 0  y  2
Đặt t = x + 1  t[0; 2]; ta có (1)  t3  3t2 = y3  3y2.
Hàm số f(u) = u3  3u2 nghịch biến trên đoạn [0; 2] nên: 2 2
(1)  t = yy = x + 1  (2)  x  2 1  x m  0 Đặt 2
v  1 x v[0; 1]  (2)  v2 + 2v  1 = m.
Hàm số g(v) = v2 + 2v  1 đạt min g(v)  1
 ; max g(v)  2 [0;1] [0;1]
Vậy hệ phương trình có nghiệm khi và chỉ khi 1  m 2  1 1 2 x x  (1 )  4  y y
93/ Giải hệ phương trình: 2 x x 1  . 3    4  x 2 3  y y y Giải:  1 1 2 x x  (1 )  4  y y  hệ phương trình: 2 x x 1  . 3    4  x 2 3  y y y  1 1  2 1 1 2  x x  (1 )  4 x   x   4 1     2  a x y yy y  y ĐK y  0    Đặt  2 x x 1 1 x 1  3 3     x 4  x x   (  x)  4 b   2 3 3  y y y  y y y  y 2 2 2
a a  2b  4
a a  4  2b
a a  4  2ba  2 Ta có        3 3 2 2
a  2ab  4
a a(a a  4)  4
a  4a  4  0 b  1 x y  y 1 Khi đó  1   KL x   2  x 1  x
94/ Giải phương trình 2 2
log (x  5x  6)  log (x  9x  20)  1 log 8 3 3 3 Giải: 2 2
log (x  5x  6)  log (x  9x  20)  1 log 8 (*) 3 3 3 x  5  + Điều kiện : 2 x  5x  6  0 x  3   x  2         4   x  3
 , và có : 1 log 8 log 24 3 3 2  x  9x  20  0 x  5   x  4  x  2   2 2 2 2         + PT (*) log (x 5x 6)(x 9x 20) log 24
(x  5x  6)(x  9x  20)  24 3   3     (x  5  )  ( 4   x  3  )  (x  2  ) (x  5  )  ( 4   x  3  )  (x  2  )
(x  2)(x  3)(x  4)(x  5)  24 (*)   (x  5  )  ( 4   x  3  )  (x  2  ) (**) + Đặt 2
t  (x  3)(x  4)  x  7x 12  (x  2)(x  5)  t  2 , PT (*) trở thành : t(t-2) = 24 2
 (t 1)  25  t  6 t  4      t = 6 : x 1 2 2
x  7x 12  6  x  7x  6  0   ( thỏa đkiện (**)) x  6   t = - 4 : 2 2 x  7x 12  4
  x  7x 16  0 : vô nghiệm
+ Kết luận : PT có hai nghiệm là x = -1 và x = - 6     log   log 9 7  8 1 x 1 3 x 1 2 3 1
95/ Cho khai triển 2 5  2  2
 . Hãy tìm các giá trị của x biết rằng số hạng thứ 6 trong khai   triển này là 224  1 1 x 1  1   Giải: Ta có :  3 x 1   log2 3 1    a  b k 8 8 k 8k k  C a b với log2 9 7  = x 1     3 ;    x 1 5   5 a 2 9 7 b 2 3 1 8 k0
+ Theo thứ tự trong khai triển trên , số hạng thứ sáu tính theo chiều từ trái sang phải của khai triển là 3 5 1 1      1  5 T  C  x 1 9   7  . x 1 3    1   56 x 1 9   7. x 1  3 5 3 1 6 8       + Theo giả thiết ta có :  
569   7.3    x 1 1 9 7 x 1 x 1 x 1  x 1 1 = 224 
 4  9  7  4(3  1) x 1 3  1 3  1 x 1  3   x 1 2 x 1 x 1
 4(3  )  3  0     x 1 3   3 x  2 log 9 2 log log 3
96/ Giải phương trình 2 2 2  .3 x x x  x Giải: 1.ĐK: x>0. Ta có phương trình lo x x 2 g 9 2 log2 log2 3 lo 2 g 2 x  x .3  x  3  x 1. Đặt log   2t x x 2 . t t  3 t  1 t
Phương trình trở thành 3  4 1    1     t 1 x  2  4   4 
97/ .1.Cho hệ phương trình
x xy y m  2  2 2
x y xy m 1
1) Giải phương trình với m=3
4xy  (4 2x  2y  3 )  7  (x y)2
2.Giải hệ phương trình sau:   x  1 2   3  x y
Giải: 1. Nhận thấy rằng đây là hệ phương trình đối xứng loại 1, khi đó
x y S đặt  , ĐK 2 S  4P  0 xy P   x y
 xy m 2 S P m 2
ViẾT lại hệ phương trình dưới dạng     I   x y   xy m1 SP m 1
Khi đó S,P là nghiệm của phương trình bậc 2 t 1 2
t  m  2t m 1  0   t m 1
x y 1  2
xy m 1
f u  u u m 1  1    
x y m 1 g  u 2
u  m   1 u 12  xy 1 Với m=-3. ta có u  1  x  1  ; y  2   2
1  u u  2  0     u  2
x  2; y  1    2
2  u u 1  0  u  1
  x y  1 
Vậy với m=3, hệ phương trình đã cho có nghiệm là  1  ;2,2;  1 , 1  ;  1 .
4xy  (4 2x  2y  3 )  7  (x y)2
2. Giải hệ phương trình sau:   x  1 2   3  x y ĐK: x + y  0  3 2 2
3(x y)  (x y)   7  2  (x y) Ta có hệ   1 x y
x y  3  x y 2 2 3
u v  13
Đặt u = x + y + 1 ( u  2) ; v = x – y ta được hệ :  x y u   v  3
Giải hệ ta được u = 2, v = 1 do ( u  2)  1 x y   2 x y  1 x  1 Từ đó giải hệ  x y      x y  1 y  0 x y  1
98/ 1. Tìm a để hệ phương trình sau có nghiệm: 2 log
x 1  log (ax a) 1 1 3 3 log x log x
2.Gải phương trình:  3   2 1  . x  3   2 2 1 1 x
Giải:1 ĐK: ax + a > 0 ; Bpt tương đương 2
x 1  a(x 1) 2 
Nếu a>0 thì X+1>0, ta có x 1  a x 1 2 x 1
Nếu a<0 thì X+1<0, ta có  a x 1 2  Xét hàm số y x 1 = với x  - 1 x 1  y’ = x 1 2 =0 khi x=1 => a> hoặc a < - 1 2 2 (x 1) x 1 2 2 Điều kiện : x>0 log x log x Đặt  3   2 1 =u,  3   2 1
v ta có phương trình u +uv2 = 1 + u2 v2  (uv2-1)(u – 1) = 0 u 1   2  . . . x =1 uv 1    x  y   2 2 x  y  13
99/ Giải hệ phương trình:  x, y  .   x  y   2 2 x  y     25   x  y   2 2 x  y  13
Giải: hệ phương trình:  x, y  .   x  y   2 2 x  y     25   x  y   2 2 x  y  13   1 3 2 2 3
x  xy  x y  y 13 1'      3 2 2 3
y  xy  x y  x  25  2' x  y   2 2 x  y   25 2
LÊy (2’) - (1’) ta ®­îc : x2 y– xy2 = 6  x  yxy  6 (3) KÕt hîp víi (1) ta cã :      2 2 x y x  y  13 
I. §Æt y = - z ta cã :   x  y  xy  6 2 2 2      
x zx z  13
x z x z 2xz 13       I      x  zxz  6 x  z  xz  6 
Đặt S = x +z Và P = x.z ta có :   2   3 S S 2P  13 S  2SP  13 S  1         SP  6  P  6 SP 6  x  z  1      Ta có:  . hệ này có nghiệm x 3  hoặc x 2  x.z  6  z  2  z  3
Vậy hệ phương trình đã cho có 2 nghiệm là: ( 3 ; 2) và ( -2 ; -3 )
Đề 106. a) Giải bất phương trình: log (log x   x 4 (2 4)) 1
Giải:a) Giải bất phương trình: log (log x   x 4 (2 4)) 1 0  x  1  log (log x
 . Đk: log (2x  4)  0  x  log 5 x 4 (2 4)) 1 4 2  2x  4  0
Do x  1 PT  log x x x x x          4 (2 4) x 2 4 4 4 2 4
0 đúng với mọi x. Do vậy BPT có nghiệm: x  log2 5
Đề 107. Tìm m để phương trình sau có một nghiệm thực: 2
2x  2(m  4)x  5m 10  x  3  0 Giải: 2
2x  2(m  4)x  5m 10  x  3  0 2
 2x  2(m  4)x  5m 10  x 3    x 3 x  3  0      2    2 2  x 2x 1
2x  2(m  4)x  5m 10  (x  3) m   2x  5 2   2 2(x  5x)
Xét hàm số, lập BBT với x 2x 1 f (x)   f '(x)  2x  5 2 (2x  5) Khi đó ta có: Bảng biến thiên: x -  0 5/2 3 5 +  y’ + 0 - - 0 + y 8 +  24/5  
Phương trình có 1 nghiệm 24 m    (8;)  5 
100/ Tìm m để phương trình:  2 m x  2x  2  
1  x(2  x)  0 (2) có nghiệm x  0; 1 3  
Giải: Tìm m để phương trình:  2 m x  2x  2  
1  x(2  x)  0 (2) có nghiệm x  0; 1 3   2 t  2 Đặt 2
t  x  2x  2  t2  2 = x2  2x Bpt (2)  m 
(1 t  2),dox[0;1 3] t 1 2 t  2 2 t  2t  2 Khảo sát g(t)  
 0 . Vậy g tăng trên [1,2]
t 1 với 1  t  2 ; g'(t) 2 (t 1) 2 t  2 2 Do đó, ycbt  bpt m  m  max g(t)  g(2)  t có nghiệm t  [1,2]  1 t   1;2 3 Vậy m 23
101/ . 1) Giải phương trình: log  2 x x   2
1  log x  2x x 3 3
2) Giải bất phương trình: 2 (log   x 8 log4 x )log2 2x 0 Giải: 2 x x 1 xx 1 1. (1)  log
x 2  x  3  x 1 3   2  x x Đặt:f(x)= 2  1 3x
x ; g(x)= x 1 (x  0) x
Dùng pp kshs =>max f(x)=3; min g(x)=3=>PT f(x)= g(x)  max f(x)= min g(x)=3 tại x=1 =>PT có nghiệm x= 1
2. Điều kiện x > 0 , x  1    1  1  1  (1)    2 log4 x log 2x  2 0    log2 x log x 1  2 0  log 1 8 x  2    log x   2 3   2 log x 1 log x 1  (log x  2 3) 2   0  2  0 log x log x  2  2 1
 log x  1hayl og x  0  0  x  hay x  2 2 1 2 x 2
102/ Giải phương trình: x 2 x 1 3 2   6 x
Giải: Giải phương trình: 2x 2x 1 3 2   6 x
Lấy logarit theo cơ số 3 cho hai vế ta được: 2 x  log 2  1 log 2 3 3 2x 1
Đưa phương trình về dạng: (x – 1)(2x2 + x – 1 - log 2 ) = 0. 3 1   9  8log 2
Từ đó suy ra nghiệm x = 1; 3 x  4
103/ .Giải bất phương trình log 2 x  log 2 x  3  5(log 2 x  ) 3 2 2 4
Giải: Giải bất phương trình log2 x  log 2 x  3  5(log 2 x  ) 3 2 2 4 x  0 ĐK:  log2 x  log 2 x  3  0 2 2
Bất phương trình đã cho tương đương với log2 x  log 2
x  3  5(log x  ) 3 ) 1 ( 2 2 2 đặt t = log2x, BPT (1)  2
t  2t  3  5(t  ) 3  (t  )( 3 t  ) 1  5(t  ) 3 t  1  t  1 log x    t  3   1    2  t x 2 3   4 3  log   4 2 (t  )( 1 t  ) 3  ( 5 t  ) 3  1 0  x   1  
2 Vậy BPT đã cho có tập nghiệm là: ( ; 0 ] ) 16 ; 8 ( 2 8  x  16 (x  )( 1 y  )( 1 x y  ) 2  6
104/ Giải hệ phương trình:   2 x  2
y  2x  2 y  3  0 (x  )( 1 y  )( 1 x y  ) 2  6
Giải: hệ phương trình:   2 x  2
y  2x  2 y  3  0 (x  )( 1 y  )(
1 x 1  y  ) 1  6
uv(u v)  6
uv(u v)  6 u x 1 Hệ       với  (x  ) 1 2  ( y  ) 1 2  5  0  2 u  2 v  5  0
(u v)2  2uv  5  0 v y 1
S u v  . P S  6 S  3 Đặt:  được    P u v .  2
S  2P  5  0 P  2 X  1
x 1  2 x 1  1
u, v là nghiệm của phương trình: X2 – 3X + 2 = 0       X  2
y 1  1 y 1  2
Vậy nghiệm của hệ: (3 ; 2), (2 ; 3)
105/ 1. Tìm m để phương trình sau có nghiệm: 4x – 4m(2x – 1) = 0 2
2.Tìm m để phương trình:  4 log x
x m  có nghiệm trong khỏang (0 ; 1). 2  log 0 1 2 Giải:
1. Đặt t = 2x (t > 0) ta có phương trình: t2 – 4mt + 4m = 0 (*) 2 t (*) 
 4m (t  0  t  ) 1 - + t 1 x 0 1 2 2 t 2 t  2t y' 0 0 Xét y  có y'  + + 0  t 1 t  2 1 y
y’ = 0  t  0  t  2 - - 4
Từ bảng biến thiên ta có : m < 0  m  1 2   2. Pt đã cho 1
 4 log x  log x m  0 x (0 ; )
1  log 2 x  log x m  0 (*)  2 2 2 2 2 
Đặt t  log x , x  0 ( ; ) 1  t  ( ; ) 0 2 (*) 2
t t m  0 2
m  t t t ( ; ) 0
Xét hàm số y = -t2 – t có y’ = -2t – 1 1 1 y’ = 0  t   , y  2 4 1 t -  - 0 2 y’ + 0 - 1 y 4 1 -  0 ĐS : m  4
106/ Giải bất phương trình    2 4x 3 x  3x  4  8x  6 Giải: bất phương trình:    2 4x 3
x  3x  4  8x  6 (1)
(1)   x   2 4 3
x  3x  4  2  0 Ta có: 4x-3=0<=>x=3/4 2
x  3x  4  2=0<=>x=0;x=3 Bảng xét dấu: x - 0 ¾ 2 +  4x-3 - - 0 + + 2
x  3x  4  2 + 0 - - 0 + Vế trái - 0 + 0 - 0 +  
Vậy bất phương trình có nghiệm: 3 x  0; 3;    4 1 1
107 / Giải phương trình: log (x  ) 3  log (x  ) 1 8  3log (4x) . 2 2 4 4 8 Giải: 1 1 phương trình: log (x  ) 3  log (x  ) 1 8  3log (4x) . 2 2 4 4 8 1 1 log (x  ) 3  log (x  ) 1 8  3log (4x) . 2 2 4 4 8 x  3  
Điều kiện: x  1  0  x  .
1 Biến đổi theo logarit cơ số 2 thành phương trình x  0  1 loaïi  2 3 1 4 2 3 0 3 2    
x   x     2  xx   log log
x x      x  . x  3  1 
108/ Tìm các giá trị của tham số m để phương trình sau có nghiệm duy nhất thuộc đoạn   1 ; :  2 
3 1 x2  2 x3  2x2 1  m ( m R ).  1 
Giải:Đặt f x 2 3 2
 3 1 x  2 x  2x 1, suy ra f x xác định và liên tục trênđoạn  ;1  2  .   2 3x 3x  4x  3 3x  4 
f ' x     x   . 2 3 2 2 3 2 1 x x  2x 1  1 x
x  2x 1   1  4 3 3x  4 x    ;1  x    3x  4  0    0 2  ta có .   2 3 2 3 1 x x  2x 1
Vậy: f ' x  0  x  0 . Bảng biến thiên: 1 x  0 1 2 f '  x  ||  0  || 1 CÑ  f x  3 3 22 2  4
Dựa vào bảng biến thiên, ta có: Phương trình đã cho có 1 nghiệm duy nhất thuộc  1  3 3  22  ;1   4    hoặc m  1 . 2  m   2 2  y  2
109/ 1. Giải hệ phương trình sau: 3y  2  x  2  x  2 3x   2  y 2. Giải phương trình: 3 2x 1 3  2x  2 3  2x  3  0
Giải:1. Giải hệ phương trình sau: 2  y  2 3y  2  x  2  x  2 3x   2  y 2 2 3
 x y y  2
điều kiện x>0, y>0. Khi đó hệ tương đương  2 2 3
 xy x  2
Trừ vế theo vế hai phương trình ta được: (x-y)(3xy+x+y) = 0  x y thay lại phương trình Giải tìm
được nghiệm của hệ là: (1;1). 2. Giải phương trình: 3 2x 1 3  2x  2 3  2x  3  0
Tập xác định: D = R. Đặt f(x) = 3 3 3
2x 1  2x  2  2x  3 Ta có: 2 2 2 1 3 f ' (x)     ; 0 x   , , 1  (2x  ) 1 (2x  ) 2 3 (2x  ) 3 2 3 2 3 2 2 2
Suy ra hàm số f(x) đồng biến trên tập M=  1   1   3   3 
 ,    ,  1    ,
1      ,  2   2   2   2  1 3
Ta thấy f(-1)=0  x=-1 là một nghiệm của (1). Ta có: f ( )  ; 3 f ( )  3  2 2
Ta có bảng biến thiên của hàm số f(x): x 3 -∞  -1 1  +∞ 2 2 f’(x)    F(x) +∞ 0 3 -∞ -3
Từ bảng biến thiên ta thấy f(x) = 0  x = -1. Vậy phương trình đã cho có duy nhất một nghiệm x = -1. 3 3  u v 3 u   2x 1 u   v   0
Cách 2: Hs có thể đặt  khi đó ta được hệ  2
giải hệ này và tìm được 3
v  2x  3  3 3 v u  2 nghiệm.
110/ Giaûi phöông trình : 3
2 3x  2  3 6  5x  8  0 (x  R) Giải: 6 3
2 3x  2  3 6  5x  8  0 , ñieàu kieän : 6  5x  0  x  5 3 t  2 3 8  5t
Ñaët t = 3 3x  2  t3 = 3x – 2  x = vaø 6 – 5x = 3 3 3 8  5t
Phöông trình trôû thaønh : 2t  3  8  0 3 3 8  5t t  4  3  8  2t   3 2 3
15t  4t  32t  40   t = -2. Vaäy x = -2 0 2 2
log (x  y ) 1 log (xy)
111/ Gæai heä phöông trình : 2 2  (x, y  R) 2 2 x xyy 3  81 2 2
log (x  y )  log 2  log (xy)  log (2xy)
Giải: Ñieàu kieän x, y > 0 2 2 2 2  2 2 x  xy  y  4 2 2 x  y  2xy 2 (x  y)  0 x  y x  2 x  2         hay  2 2 x  xy  y  4 xy  4 xy  4 y  2 y  2 
2y x m
112/ Tìm các giá trị của tham số m sao cho hệ phương trình  có nghiệm duy nhất y xy 1  y 1 
Giải Ta có : x  2y m  , nên : 2
2 y my  1 y . PT   1 ( vì y = 0 PTVN). Xét m y   2  y f y 1
y    f y 1 2 ' 1
 0. Lập BTT. KL: Hệ có nghiệm duy nhất  m  2 . 2 y y
113/ 1. Giải phương trình log x log 4 2 2 8 x x  .
2. Giải bất phương trình 21 log x log x  log x  0 2  4 8 .
Giải 1. ĐK : x  0 . Ta có: 1 log x log x  3log
x . Đặt t  log x .Ta có: 2 4 2 2 2
t  3t  2  0  t  1,t  2 . Khi: t  1 thì log x  1  x  2(t )
h . Khi: t  2 thì log x  2  x  4(t ) h . KL: 2 2
Nghiệm PT x  2, x  4. t
2. ĐK : x  0 . Đặt t  log x , ta có : 1 t t   0 , BPT 2 4
 3t  4t  0    t  0 . KL: 2 3 3 4 1   log x  0   x 1. 2 3 3 2 2
(x 1)(4  x) 2x
114/ Giải bất phương trình:  x  2  x  2 x  2 Giải x  2   x   0;7  7  ĐK:? bpt 2
 x  3x  4  x  2   x  1  ;    x  2   2    x    1  ;4 
115/ Giải phương trình: x 3 x 1 8 1  2 2 1  Giải : x 3 x 1 8 1  2 2 1 Đặt x 3 x 1 2 u 0; 2    1  v 3 3 u  1 2v u  1 2v u   v  0    1 5     
x  0; x  log 3 2 2 3  2 v 1  2u
(u v)(u uv v  2)  0 u   2u 1  0 2  1 1 2 x x  (1 )  4  y y
116/ Giải hệ phương trình: 2 x x 1  . 3    4  x 2 3  y y y  1 1  2 1 1 2  x x  (1 )  4 x   x   4 1     2  a x y yy y  y
Giải : ĐK y  0    Đặt  2 x x 1 1 x 1  3 3     x 4  x x   (  x)  4 b   2 3 3  y y y  y y y  y 2 2 2
a a  2b  4
a a  4  2b
a a  4  2ba  2 Ta có        3 3 2 2
a  2ab  4
a a(a a  4)  4
a  4a  4  0 b  1 x y  y 1 Khi đó  1   x   2  x 1  x    3 x x x 1
117/ Giải hệ phương trình: 9  5.3 1  4.log 0    3  x  2  Giải:
KL:2. +) Đ/K: x>2 or x<-1       3 x x x 1 x x x 1 3 9  5.3 14.log  0  3  7 3  2 log  0     3    3  x  2   x  2       x   x 1 3 7 log  0   3  x  2   x 1   x 1  3 Xét x>2 ta có log  0  1  0  x  2     3  x  2   x  2  x  2  x 1  x 1 3 Xét x<-1 ta có log  0  1  0  x  2   . KL:? 3  x  2  x  2 x  2 x x 1  x x
118 / Giải phương trình : 4  2  22  
1 sin 2  y   1  2  0
Giải: Đặt 2x t , đ ưa về pt bậc 2 ẩn t ,giải tiếp. Hoặc đưa pt về dạng tổng các bình phương
119/ Tìm m để phương trình sau có nghiệm thực :  x2  3x  2   x2  mx 2  m 2
Giải Tìm m để phương trình sau có nghiệm thực :  x2  3x  2   x2  mx 2  m 2 (*) 2    1  x
x  3x  2  0  1  x  2  2 (*)       3x  2 2 2
x  3x  2  x  2mx  2mf (x)   2m(x  ) 1  3x  2m  2  x 1 5
f(x) liên tục trên 1; 2 và có f (  x)   0, x
  1;2  f (x) đồng biến trên  ; 1 2 2   x   1 Bài toán yêu cầu 1 2
f (1)  2m f (2)   m  4 3
log y  log x   y x 2 2
x xy y 3 3  
120/ Giải hệ phương trình :  2 2  2 2 x y  4 2  y  2 2 3
Giải: Điều kiện : x > 0 ; y > 0 . Ta có : 2
x xy y   x
  y  0 x
 , y >0 ; Xét x > y  2  4 VT(*)  0
 log x  log y  
 (*) vô nghiệm nên hệ vô nghiệm. 3 3 VP(*)  0 2 2 VT(*)  0
Xét x < y  log x  log y  
 (*) vô nghiệm nên hệ vô nghiệm. 3 3 VP(*)  0 2 2 0  0
Khi x = y hệ cho ta 
x = y = 2 ( do x, y > 0). Vậy hệ có ngd nh  ; x y   2; 2 2 2
2x  2y  4 Vậy hệ có ngd 1 1
121/ Giải phương trình: 3 2
(x  24)  (12  x)  6 .
Giải; Nhận xét: Theo định nghĩa của lũy thừa số mũ hữu tỉ, cơ số phải dương nên điều kiện có nghĩa x  24  0 của biểu thức là:   2  4  x  12. 1  2  x  0 1 1 Đặt: 3 2
u  (x  24) ; v  (12  x) với u , v  0. u  v  6 u  v  6 u  v  6 u  v  6 Ta có:        3 2 3 2 3 2 2 u  v  36 u  (6  u)  36 u  u 12u  0 u(u  u 12)  0 1  3 (x  24)  3  x  24  27 u  3  1     (do u, v  0) 2  (12  x)  3  1  2  x  9  x  3 (thỏa) v  3   2  4  x  12 2  4  x  12   
122/ Giải phương trình 2 2
log (x  5x  6)  log (x  9x  20)  1 log 8 3 3 3 x  5  Giải: Điều kiện : 2 x  5x  6  0 x  3   x  2       , và có :   4   x  3  1 log 8 log 24 3 3 2  x  9x  20  0 x  5   x  4  x  2   2 2 2 2          + PT (*) log (x 5x 6)(x 9x 20) log 24
(x  5x  6)(x  9x  20)  24 3   3     (x  5  )  ( 4   x  3  )  (x  2  ) (x  5  )  ( 4   x  3  )  (x  2  )
(x  2)(x  3)(x  4)(x  5)  24 (*)   (x  5  )  ( 4   x  3  )  (x  2  ) (**) + Đặt 2
t  (x  3)(x  4)  x  7x 12  (x  2)(x  5)  t  2 , PT (*) trở thành : t(t-2) = 24 2
 (t 1)  25  t  6 t  4   t = 6 : x  1  2 2
x  7x 12  6  x  7x  6  0   ( thỏa đkiện (**)) x  6   t = - 4 : 2 2 x  7x 12  4
  x  7x 16  0 : vô nghiệm
+ Kết luận : PT có hai nghiệm là x = -1 và x = - 6
123/ Giải hệ phương trình.
Giải: Đặt : t = x + y ; ĐK: t => ; Hệ đã cho trở thành
Vậy hệ dã cho có một nghiệm
Đề 132 : Giải phương trình:
Giải: ĐK: x > 1; Với ĐK trên phương trình đã cho tương đương
Vậy phương trình đã cho có một nghiệm : x  4  x  4
124/ Giải bất phương trình: 2
x x 16  6 2 x  4  0 Giải : * Đk:   x  4. Đặt t =
x  4  x  4 (t > 0) x  4  0 t   L
BPT trở thành: t2 - t - 6  0  2( )  t  3 x  4  (a) 9 - 2x  0 * Với t   3  2 2
x 16  9 - 2x x   4  9 - 2x  0 (b)  2 2
4(x 16)  (9  2x) 9 145 9   * (a)  x  . * (b) 
 x < . *Tập nghệm của BPT là: T= 145 ;   2 36 2  36 
xy 18  12  2  x
125/ 1. Giải hệ phương trình:  1 xy  9  2 y  3
2. Giải phương trình: 9x + ( x - 12).3x + 11 - x = 0
xy 18  12  2 x  12  2
x  0  x   2 3
Giải 1) Giải hệ:  1 xy  9  2
y x y  2 3 y x  2 3  3
x  2 3  xy 18  x  2 2 ; 3
3, tương ứng y  3 3 3 ; 3
Thử lại, thoả mãn hệ đã cho Vậy,  ; x y  2 ;3 3 3,2 3; 3 3 2
2) Giải phương trình: 3x   x 123x 11 x  0  x 3  x  0  1    (a + b + c = 0)  x x 3  11  x
f (x)  3  x 11  ( 0 *)
f '(x)  3x ln 3 1  , 0 x
  (*) có nghiệm duy nhất x = 2 f ( ) 2  0 
Vậy, tập nghiệm của phương trình: S = {0 ; 2
126/ Giải phương trình:  x  2 2 2 1
 5  x 2x  4; x R Giải:  x  2 2 2 1
 5  x 2x  4; x R 2 t Đặt 2 2 4 2
t x 2x  4  t  2(x  2x ) ta được phương trình 2
1  5  t t  2t 8  0 2 t  4    t  2 x  0 x  0 x  0 + Với t = 4 Ta có 2 x 2x  4  4         x   2 4 2 4 2
2(x  2x ) 16
x  2x 8  0 2 x  2 + Với t = 2 ta có x  0 x  0 x  0  2
x 2x  4  2        x  3 1 4 2 4 2
2(x  2x )  4
x  2x  2  0 2 x  3 1
ĐS: phương trình có 2 nghiệm x   2, x  3 1 2   3 log
x 1   log x 1  6 1 2   2  
127/ Giải bất phương trình: 2  log x 1 2   2  log (x 1) 1 2 Giải; Đ ặt log
x 1  t rồi giải tiếp 2  
128/ Giải phương trình: 2 2
7  x x x  5  3  2x x (x  ) Giải   3   x 1 2 3
  2x x  0 2 3
  2x x  0  PT      x  0 2 2
7  x x x  5  3 2x x x x  5  2  (x  2)  x  2  x  5  2.   x  2   x  0     x  1
 ; Vậy phương trình đã cho có một nghiệm x = - 1. x    1   2x 16  0  1 log y x  log 1  1   4
129/ Giải hệ phương trình y   4 (x, y )  2 2
x y  25 y x  0 Giải: Điều kiện: 
; Hệ phương trình y  0  1  y xy x 1 log y x  log  1  log  1    4   4  4  y   y   y 4   2 2  2 2  2 2
x y  25
x y  25
x y  25   15 5    ; x y x  3y  ;    x  3yx  3y   10 10         25  (không thỏa mãn đk) 2 2 2 2 2
x y  25 9
y y  25 y       15 5 10  ; x y    ;      10 10 
Vậy hệ phương trình đã cho vô nghiệm. x
130/ Tìm các giá trị của tham số m để phương trình: 2 4 2 x m e e  1 có nghiệm thực . x Giải: Đặt 2
t e ĐK: t > 0 . PT trở thành: 4 4
m t 1  t .Xét 4 4
f (t)  t 1  t với t > 0 . 3 4  t   1 4 f '(t) 
 1 0 hàm số NB trên 0;  . lim f (t)  lim  0 ; 4  t 1 t 
t  4 4t 1t 4 2 t 1  t  f(0) = 1. KL: 0< m <1.
131/ Giải phương trình: log
4.16x  12x  2x  1. 3   Giải: PT x x 2x 1  2x x x 2 4.16 12  3
 4.4  4 .3  3.3 x . Chia 2 vế cho 2 3 x  0 , ta 2 x xx 4   4    3 có: 4   3  0     ; Đặt 4 t    . ĐK: 2
t  0 ; 4t t  3  0  t  1
 (kth);t  (th) .  3   3   3  4 x 1  3  4  3  4  Khi t  , ta có:    x  1      . 4  3  4  3  2 2
x y x y 12
132/ Giải hệ phương trình:  2 2
y x y 12 
Giải: Điều kiện: | x |  | y | 2 2 u
  x y ; u  0 2 1  u  Đặt 
; x   y không thỏa hệ nên xét x   y ta có y  v   .
v x y 2  v u   v  12  u   4 u   3
Hệ phương trình đã cho có dạng: 2 u u    hoặc   v   12 v  8 v  9 2   v  2 2 u   4
 x y  4 2 2 u   3
 x y  3 +    (I) ; +    (II) v  8
x y  8 v  9
x y  9
Giải hệ (I), (II).Sau đó hợp các kết quả lại, ta được tập nghiệm của hệ phương trình ban đầu là S    5;3,5;4
133/ Giải phương trình: 2 3 log x 14log x  40log x  0. x 16 x 4 x 2 Giải : phương trình 2 3 log x 14log x  40log x  0. x 16 x 4 x 2  Điều kiện: 1 1
x  0; x  2; x ; x
. Dễ thấy x = 1 là một nghiệm của pt đã cho;Với x  1 . Đặt 4 16
t log 2 và biến đổi phương trình về dạng 2 42 20    0 ;Giải ra ta được x 1 t 4t 1 2t 1 1 1 t ;t  2
  x  4; x
. Vậy pt có 3 nghiệm x =1; 1 x  4; x . 2 2 2 x 1 xx 1
134/ Giải phương trình 2 x 1 4 . 3  9 .  4 . 6  9 .  . 3 4 x x x 9
Giải: Biến đổi phương trình đã cho về dạng 2 2 2 2 3 2  27 3  6 2  3 x . . . . Từ đó ta thu được 4 x  3  2 2   x log   3  2  39 39 2
xy 18  12  2  x
135/ Giải hệ phương trình:  1 xy  9  2 y  3 Giải:
xy 18  12  2 x  12  2
x  0  x   2 3 Hệ:   x   xy  1 ; 2 3 18 ;  x  2 2 ; 3 3, xy  9  2
y x y  2 3 y x  2 3  3
tương ứng y  3 3 3 ;
3;Thử lại, thoả mãn hệ đã cho Vậy,  ; x y  2 ;3 3 3,2 3; 3 3
136/ Giải phương trình: log
4.16x  12x  2x  1. 3   2 x x  4   4  Giải; PT x x 2x 1  2x x x 2 4.16 12  3
 4.4  4 .3  3.3 x .Chia 2 vế cho 2 3 x  0 , ta có 4   3  0      3   3  x   3 3 Đặt 4 t    . ĐK: 2
t  0 ; 4t t  3  0  t  1  (kt ) m ;t  (t ) m . Khi t  , ta có:  3  4 4 x 1   4  3  4     x  1      . .  3  4  3 
137/ :1.Tìm m để phương trình sau có 2 nghiệm phân biệt : 10x 2 8  x  4  ( m 2x  ). 1 2 x 1 . log x 1  log x2
2..Giải phương trình: 3 3 2  2  x . Giải: Nhận xét: 10x 2 8
x  4= 2(2x+1)2 +2(x2 +1) x x  2 
Phương trình tương đương với 2 1 x 1 2 2 1 : 2 ( )  ( m )  2  0 . Đặt
t ĐK: -2< t  5 . 2 x  1 2 x  1 x 2  1 t 2 2  2 Rút m ta có: m=
Lập bảng biến thiên của hàm số trên  , 2
5 ta có kết quả của m để phương trình t
có hai nghiệm phân biệt là 12 4  m
hoặc -5 < m  4  . 5 t 2     t 1 t t 9 t t 2 4 2
2.ĐK: x > 0 . Đặt  log   3 t t x x . Ta có: 2.2  2  3  .2  3    . 3     4 4  3  9  3 
Khi t = 2 thì log x  2  x  9 (th) KL: nghiệm PT là x  9 . 3
138/ Giải bất phương trình : x    2 1 2 x   1 (2) . Giải:
2 2x  1  0  x  1   x  1 x  1     x  1 
(2)  x 1  0  x  1   x  1      1   x  3 2 2      x   1   x   2 2 1
x  2x  3  0 1 x 3
Vậy nghiệm của bất phương trình : x  1  1 x  3 .
139 / Giải hệ phương trình , khi a > 1 : 2  a  1
x a y a z a  3  a  2  a 1
a x a y a z  3  a
Giải: Xét các véc tơ : u   x a ; y a ; z a  , v  1 ; 1 ;  1
  u .v 2 2 2  u . v
  x a y a z a 2  33a x y z   1 2
Tương tự  a x a y a z   33a x y z (2) 2 2
  x a y a z a    a x a y a z   18a
Mà cộng hai phương trình của hệ ta có : 2 2
x a y a z a    a x a y a z   18a
Tức là dấu đẳng thức phải xảy ra trong các bất đẳng thức (1) và (2) , hay : 2  a  1
x a y a z a   a 1 
x y z  2  a 1 a a x a y a z   a
Vậy hệ phương trình có nghiệm là : 1
x y z  . a 2 2
x y x y  4
140/ Giaûi heä phöông trình : 
x(x y 1)  y(y 1)  2  2 x  2 y  x  y  4  2  2 x y  x  y  4   2 (x y)  x  y 0 Giải: (I)        2 x  2 y  x  y  xy  2 xy  2 xy  2
x  y  0 hay x  y 1
x  y  0 hay x  y 1     xy  2 xy  2 x  y  x  y  1 x  2 x   2 x  1 x  2    hay    V  V  V   2 x  2  2 x  x  2  0 y   2 y  2 y  2  y  1
 2x  y 1  x  y 1
141/ Giaûi heä pt :  I 3  x  2y  4 Giải: 
   2x  y 1  x  y 1 I    2x  y    1  x  y  5 u  v   1 u  2  v  1 1 1 Ñaët u 
2x  y 1  0,v  x  y  0 ;(I) thaønh   2 2  u  v  5 u  1 v    2 2 2loaïi     2x  y 1  4 x  2 Vaäy   2x y 1 2 I        x  y  1  x  y  1 y  1  142/ Giaûi pt
3x  3  5  x  2x  4   1 Giải: 1/ Giaûi pt
3x  3  5  x  2x  4   1 3x   3  0 
Ñieàu kieän 5  x  0  2  x  5 2x  4  0  (1) 
3x  3  5  x  2x  4 vaø 2  x  5
 3x  3  5  x  2x  4  2 5  x2x  4 vaø 2  x  5
 x  2  5  x2x  4 vaø 2  x  5
 x  2  0 hay[ x  2  5 x2 vaø 2  x  5]
 x  2 hay [x  2  25  xvaø 2 x5]  x  2 hayx  4 2
143/ Giaûi baát phöông trình
8x  6x 1  4x 1  0 (1) 2 Giải: (1)  8x  6x 1  4x 1  1 1 x  Vx    2 4 2  8x  6x 1  1 1 0  x  Vx   1    4 2 1 1  4x 1  0  x     x  hay x   4 1 4 2 2 2  x  0hayx  8x  6x 1 (4x   1)  2 8x  2x 0  4  144/ Giaûi bpt
2x  7  5  x  3x  2 (1) Giải: bpt
2x  7  5  x  3x  2 (1) 2x  7  0  2
Ñieàu kieän 5  x  0   x  5  3 3x  2   0 2 (1) 
2x  7  3x  2  5  x vaø x5 3 2
 2x  7  3x  2  5  x  2 3x  25  x vaø x5 3 2 2
 2  3x  25  x 2 vaø
x5  3x 17x 14  0 vaø x 5 3   3 14 2 2 14  (x  1 hay  x) vaø x 5 x 1 hay x 5 3   3     3 3
145/ Tìm m ñeå heä phöông trình sau coù nghieäm:  2x x1 2 x 7  1 7  2005x  2005 (1)   2 x  
m  2x  2m 3  0 (2) 2x x1 2 x1
Giải: Ñieàu kieän laø x  1.Ta coù 7  7  0,x 1;  1 x1 2x 2 Ta coù: (1)  7
7 7 20051x:ñuùngx1; 1vaø sai khi x > 1Do ñoù (1)  1   x 1 2
. Vaäy, heä bpt coù nghieäm  f x  x  m  2x  2m  3  0 coù nghieäm  1  ,  1
 Maxf(x)0  maxf(1),f(1  )  0 x   1;1   max3m 6,m  
2  0  3m  6  0hay m  2  0 m 2 2 2xx 2 x 2x  1 
146/ Giaûi baát phöông trình 9  2  3     1  3  2 2 x 2  x x 2  x 2 x 2x Giải: Ta coù (1)  9  2.3  3. Ñaët t  3  0 , (1) thaønh 2 2 2 x 2x x 2x 1
t  2t  3  0  1  t  3 . Do ñoù, (1)  1  3  3  0  3  3 2 2
 x  2x  1  x  2x 1  0  1 2  x  1 2
147 /Tìm m để hệ phương trình sau có nghiệm:
(2x 1)[ln(x + 1) - lnx] = (2y + 1)[ln(y + 1) - lny] (1)   4
 y-1  2 (y 1)(x 1)  m x 1  0 (2)  x 1
Giải: Đặt f(x) = (2x + 1)[ln(x + 1) – lnx] = (2x 1) ln TXĐ: D = [0;+) x
Gọi x1; x2  [0;+) với x1 > x2
2x 1  2x 1  0  1 2  Ta có : x 1 x 1
  f (x )  f (x ) : f(x) là hàm số tăng 1 2 1 2 ln  ln  0 x x  1 2
Từ phương trình (1)  x = y x 1 x 1 (2) 4
x 1  2 (x 1)(x 1)  m x 1  0 4   2  m  0 x 1 x  1 x 1
Đặt X = 4 x   0 ≤ X < 1 1
Vậy hệ có nghiêm khi phương trình: X2 – 2X + m = 0 có nghiệm 0 ≤ X < 1
Đặt f(X) = X2 – 2X  f’(X) = 2X – 2  hệ có nghiệm  -1 < m ≤ 0 2 2  x y 1   2
149/ 1) Giải hệ phương trình:  x y  2 ( , x y R ) 
(xy x y 1)(x y  2)  6 5 
2) Tìm m thực để phương trình sau có nghiệm thực trong đoạn ;4   :  2  1 2 2        (m 1).log (x 2) 4(m 5) log 4m 4 0 1/ 2 1/ 2 x  2 2 2 2 2  
(x 1)  ( y 1)  5 u   x 1 u v  5 Giải: 1. Hệ   . Đặt  , thu được hệ 
(x 1)(y 1)[(x 1)  (y 1)]  6 v y 1 u
v(u v)  6 u   v  3 u   x 1  1 u   x 1  2 x  3 x  2 Giải ra được:  ; * Giải ra được    hoặc  :   . u v  2  hoặc
v y 1  2
v y 1  1 y  2  y  3 2 2 / PT  (m 1).log
(x  2)  (m  5) log
(x  2)  m 1  0 1/ 2 1/ 2   *Đặt 5 t  log (x  2), x  ; 4  t  1  ;1 ; 1/ 2     2  2   2  Thu được pt t 5t 1 4t 4 :
m f (t)  f '(t) 
; f '(t)  0  t  1
 Lập BBT của f(t) trên đoạn 2 t t  ; 1 2 2 (t t 1)   7  1  
;1 , thấy f(t) liên tục và NB trên đoạn  1   ;1 , nên m  3;    thỏa mãn đề bài.  3 
150/ Tìm m để hệ phương trình sau có 2 nghiệm phân biệt: 10x 2 8  x  4  ( m 2x  ). 1 2 x 1 . Giải: 10x 2 8
x  4= 2(2x+1)2 +2(x2 +1) 2x  1 x  2 2 1
Phương trình tương đương với : 2 ( )  ( m )  2  0 . 2 x  1 2 x  1 2  Đặt x 1  t 2 2  2
t ĐK : -2< t  5 . Rút m ta có : m= x 2  1 t
Lập bảng biếm thiên của hàm số trên  , 2
5 , ta có kết quả của m để hệ phương có 2 nghiệm phân biệt là 12 4  m hoặc -5 < m  4  5  1
log x  log 16  4   xy
151/ Giải hệ phương trình: 2 log 2 y   4 2 2
4x  8x xy  16x 4x y
Giải: ÑK: x  0, y  0, xy  1, y  1
+) Töø PT (1) ta coù: xy = 4 ; +) Theá vaøo (2) ta coù: x2–4x + 1 = 0  x  2  3    
+) KL : Heä coù caùc nghieäm laø : 4 4 2  3; ; 2  3;      2  3   2  3  x m
152/ Tìm m để phương trình sau có nghiệm:
x 1 6 x  8 
x 1 6 x  8  6 Giải:+) ÑK: x  8 x  m
+) PT  x  8  3  x  8  3 
; +) Neáu x  17 , ta coù PT trôû thaønh : 6
12 x  8  x  m. PT coù nghieäm x  17  77  m  100
+) Neáu 8  x  17, ta coù PT trôû thaønh : 36 – x = m. PT coù nghieäm  19  m  28
KL: 77  m  100 hoaëc 19  m  28 2 2
x y xy 1 4y
153/ Giải hệ phương trình:  , ( , x y  ) R . 2 2
y(x y)  2x  7y  2 2
x 1  xy  4  2 2
x y xy 1  4yy 2 x 1
Giải: y  0 , ta có:    . Đặt u
, v x y ta có hệ: 2 2 2
y(x y)  2x  7y  2  x 1 y 2 (x y)  2  7  y
u v  4  u  4  v
v  3, u 1      2 2
v  2u  7
v  2v 15  0 v  5  , u  9 2 2 2 x 1  yx 1 y
x x  2  0
x 1, y  2
Với v  3, u 1ta có hệ:        .
x y  3  y  3 xy  3 xx  2  , y  5 2 2 2 x 1  9yx 1  9y
x  9x  46  0 Với v  5
 , u  9 ta có hệ:      , hệ này vô nghiệm.
x y  5   y  5   xy  5   x
KL: Vậy hệ đã cho có hai nghiệm: ( ; x y)  {(1; 2), ( 2  ; 5)}. 2
2log (xy  2x y  2)  log (x  2x 1)  6 1 x 2 y
154/ Giải hệ phương trình :  , ( , x y  ) R .
log (y  5)  log (x  4) = 1  1 x 2 y Giải:+ Điều kiện: 2
xy  2x y  2  0, x  2x 1 0, y  5  0, x  4  0  (I ) . 0
 1 x  1, 0  2  y  1
2log [(1 x)(y  2)]  2log (1 x)  6 l 
 og (y  2)  log (1 x)  2  0 (1) 1 x 2 y  1 x 2 y (I )    
log (y  5)  log (x  4) = 1 l 
 og (y  5)  log (x  4) = 1(2). 1 x 2 y  1 x 2 y Đặt 1 log
(1 x)  t thì (1) trở thành: 2
t   2  0  (t 1)  0  t  1. 2 y t
Với t 1 ta có: 1 x y  2  y  x 1(3). Thế vào (2) ta có: x  4 x  4 2 log (x  4)  log (x  4) = 1  log 1 
1 x x  2x  0 1x 1x 1x x  4 x  4  x  0     y 1  . Suy ra: 
.Kiểm tra thấy chỉ có x  2
 , y 1thoả mãn điều kiện trên. x  2   y 1
Vậy hệ có nghiệm duy nhất x  2  , y 1.
155/ .Giải phương trình: 8 – x.2x + 23-x- x = 0 8 1
Giải:Giải phương trình: 8 – x.2x + 23-x- x = 0 ,  8 – x.2x - - x = 0  8(1+ ) - x(2x+1) =0 2x 2x 8 8 8
(2x 1)  x(2x 1)  0  (2x+1)(  x)  0   x 2x 2x 2x
Vế trái nghịch biến, vế phải đồng biến  phương trình có nghiệm duy nhất x=2
156/ 1) Giải phương trình
x  5 + x + x  7 + x 16 = 14.
2)Tìm m để ptrình sau đây có đúng 2 nghiệm: 2 3 2 2
(x  2x  2)  4 x  2x  2  2x  4x m .
Giải: 1.TXĐ: x  5; x= 5 không là nghiệm Đặt y =
x  5  x x  7 x 16 14 => y’ = 1 1 1 1     0 2 x  5 2 x 2 x  7 2 x 16
Hàm số đồng biến  phương trình y=0 có 1 nghiệm duy nhất. Ta có y(9) = 14  x= 9 3 2
f (t)  t  2t  4t  4  m 2. Đặt t= 2 2
x  2x  2  (x 1) 1  1   t  1
f’(t)= 3t2 – 4t- 4=0  t1=-2/3; t2= 2 BBT t -2/3 1 2 +  f’(t) 0 - 0 + -1/2 +  f(t) -4  1 m  Từ bảng biến thiên 2  m  4
157/ Giải bất phương trình: log ( 3x 1  6) 1 log (7  10  x) 2 2 Giải: Điều kiện: 1   x 10 3 3x 1  6 x   BPT  log
 log (7  10  x)  3 1 6  7  10  x 2 2 2 2
 3x 1  6  2(7  10  x)  3x 1  2 10  x  8  49x2 – 418x + 369 ≤ 0  1 ≤ x ≤ 369 (thoả) 49
log xy  log y y x
158/ Giải hệ phương trình: 
2x  2y  3
Giải:Điều kiện: x > 0 và x ≠ 1 và y > 0 và y ≠ 1 x   y log x  1 y  Ta có 2 log
xy  log y  log x  log x  2  0    1 y x y y log x  2    x y 2  y
 Với x = y  x = y = log 31 2 1 1 2  Với x =
ta có: 2 y  2y  3 theo bất đẳng thức Cô-si suy ra PT vô nghiệm 2 y
159/ .Giải bất phương trình:
2x 10  5x 10  x  2
Giải: *Điều kiện: x  2 ;   2
1  2x 10  x  2  5x 10  2x  6x  20  x 1(2)
Khi x  2 => x+1>0 bình phương 2 vế phương trình (2) 2 2 2
(2)  2x  6x  20  x  2x 1  x  4x 11  0  x  ;  7  3;
Kết hợp điều kiện vậy nghiệm của bất phương trình là: x  3
160/ 1) Tìm các giá trị của tham số m để phương trình: 2
m x  2x  2  x  2 có 2 nghiệm phân biệt. 2) Giải phương trình: 3 log
x 1  log (3  x)  log (x 1)  0 . 1 8 2 2 x  2 Giải: Ta có: 2
x  2x  2  1nên 2
m x  2x  2  x  2  m  2 x  2x  2 x  2 Xét f (x)  , ta có: 2 x  2x  2 4  3x   f '(x)   f x 4 4 '
 0  x  ; f
 10; lim f (x)  1
 ; lim f (x) 1   2
x  2x  2 2 x  2x  2 3  3 x x  Bảng biến thiên: x -  4 +  3 y’ - 0 + y 10 -1 1
Dựa vào bảng biến thiên ta có:
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi 1 m  10 161/ 3 log
x 1  log (3  x)  log (x 1)  0 1 8 2 2 Giải:
log x 1  log (3 x)  log (x 1)  0 2   3 log
x 1  log (3  x)  log (x 1)  0  2 2  1 8 2 1   x  3 2   x   1 3  x   2   x 1 x  x  4  0 1 17     x  1   x  3 1   x  3 2 2 2
x y  2x  3y 15  0
162/ Giải hệ phương trình 4 2 2
x y  2x  4y  5  0 2 2
(x 1)(y  2)  4(x 1)  4(y  2)  5 2 u   x 1 Giải: Hệ pt   . Đặt  2 2 2
(x 1)  (y  2) 10 v y  2 2 2 2 u   v 10 (
u v)  2uv 10 u   v   Ta có hpt     10  (vô nghiệm) hoặc u
v  4(u v)  5 u
v  4(u v)  5 uv   45 u   v  2 u   3 u   1  u   3    hoặc  +)  Tìm được 2 nghiệm ( ; x y)  (2;1) và uv   3  v  1  v  3 v  1  u   1  ( ; x y)  ( 2  ;1) +)  Tìm được nghiệm ( ; x y)  (0;5) v  3
Kết luận: Hệ phương trình có 3 nghiệm: (2;1), (-2;1), (0;5)
163/ : 1. Giải phương trình: log( 5 . 10 x  20 . 15
x )  x  log . 25
2. Giải bất phương trình
1 log x  log (x  2)  log (6  x) 2 2 2 Giải: 1. P T  log x x 5 . 10  20 . 15  log x 10 . 25  x x x  5 . 10  20 . 15  10 . 25  4 . 15 x  2 .
25 x 10  0 (chia hai vế của phương trình cho x
5 ) Đặt t  2x (t  ) 0 , Ta có pt : t  ( 1 tm) 15t 2 - 25t +10 = 0   t   x   x   Với 1 2 1 0 t  2 (tm)  3 Với 2 x 2  2  t   2   x  log 2   3 3  3 
Vậy phương trình đã cho có hai nghiệm là  2 
x  0 và x  log . 2    3 
2. Đk: 0< x< 6. BPT  2 2
log (2x  4x)  log (6  x) BPT 2 2  2 2 2
2x  4x  (6  x)  x 16x  36  0  x < -18 hoặc x > 2 .Kết hợp đk ta có tập nghiệm BPT là S =(2; 6) x  3 2 9  x
164/ Giải bất phương trình : 
3 x 1  x  3 x x  3 2 9  x Giải:  .
3 x 1  x  3 x
ĐK: -1 ≤ x ≤ 9 và x ≠ 0 ( x 1  )( 2 x 1  ) 2 2 9  x 2 9  x Bpt    x 1  2  ( x 1  )( 2 x 1  ) 1 ( x 1  )( 1 x 1  ) 1 x 1 1 TH1: x 1 1  0  x  0   3 3 1  2 9  ;Bpt x x x 9 8  (x  1 )( 8   )  0  (x  ) 8  9 (  3 x  )
1  (2  2 9  x)  0 9  3 x 1 2  2 9  xx  8
Kết hợp đk : 8 < x ≤ 9 TH2: x 1 1  0  x  0  x   x    x x  ;Bpt 3 3 1 2 9
8; Kết hợp đk: -1 ≤ x < 0
Vậy tập nghiệm của bpt S = [-1; 0) (8; 9]
165/ Giải phương trình 2 3 log (x 1)  log 2  log 4  x  log (x  4) 9 27 3 3 Giải: log     9(x + 1)2 + 3 log 2 log 4 x log (x 4) (1) 27 3 3  4   x  4 § K:  x  1 
(1)  log3(x + 1) + log34 = log3(4 – x) + log3(x + 4)
 log34 x 1 = log3(16 – x2)  4 x 1 = 16 – x2 ;
Giải phương trình tìm được X=2 , hoặc X= -2 2
166/ 1) Giải phương trình: 3 3
x x  2 ln x 
ln  x  2ln x  0 3
 3x  yx 3yxy 14
2) Giải hệ phương trình:  x y     2 2
x 14xy y   36 Giải: 1. Đặt 3 y
x  2ln x  0 Đưa về hệ PT đối xứng. PT có nghiệm duy nhất x  1 .
2. Đưa về PT đẳng cấp (bậc 3) bằng cách đặt ẩn phụ u x  ; y v xy  0 .  2xy 2 2 x y  1 
167/ Giải hệ phương trình: x y   2
x y x y
Giải: Điều kiện x+ y >0  2xy  2xy 2
(x y) 1 2xy   0
(x y 1)(x y 1 )  0   x y   x y   2  2
x y x y
x y x y  
(x y 1)(x y 1)  0  x y 1
x 1 x  2       h  2
x y x y  2 x y 1
y  0 y  3  2xy 2 2 x  y  1 
168/ Giải hệ phương trình: x  y   2
x  2y  2  x  y  4x  3y  4x  5y.   2xy 2 2 x  y  1(1)  Giải: x  y   2
x  2y  2  x  y  4x  3y  4x  5y(2). 
Điều kiện: x +y>0, 4x +3y  0, 4x +5y 0.   2 2xy   (1) x+y 1
 2xy  0      2xy x y 1 x  y  1   0   x  y  x  y  2 2         2 2  x  y  x  y  x y x y x y 1  0    x  y 1 0 (do  0).  x  y  x  y
Với y  x 1  y =1 -x thay vào (2) ta được 2
4  (x 1)  3  x  5  x (*) Ta thấy vế trái (*) 2
4  (x 1)  4 dấu “=” khi x =1.
Ta thấy vế phải (*) 3  x  5  x  (11)[(3  x)  (5  x)]  4 (Bunhiacopski) dấu “=” khi x =1. (*)
 x =1  y =0. Ta thấy (x;y) = (1;0) thỏa mãn đk.
Vậy hệ phương trình có một nghiệm duy nhất (x;y) = (1;0) 2 x 2 2 2 x2 x 2 x2 x
169/ 1. Giải phương trình: 3 .log (x  x  2)  3  3 .log x  2 2 2 . x x 1  x x
2. Giải phương trình: log 3  2  log 3
1  log 2.9  3  9 1. 3   3   3  
Giải:1. Điều kiện x 2
Phương trình tương đương với 2 x x2 2 2 x2 2 x2 3 .log(x  x  2)  3  3 .log x  2 2 x x2 2 2 x2  3 .log (x  x  2)  3 .log (2 x  2 ) (*) 2 2 Vì 2
x  x  2 1 nên vế trái dương vậy vế phải dương  x  2 1 t Xét hàm số t 3
f (t)  3 .log t với t >1, ' t  
   . Vậy f(t) đồng biến trên (1; +) 2 f (t) 3 .ln 3.log t 0 t 1 2 t.ln 2 Từ (*) ta có 2 2
f (x  x  2)  f (2 x  2 )  x  x  2  2 x  2 2 2          x x 2 2x 4 x 3x 6 0(1)     2 2 x  x  2  2  x  4(2)   x  x  2  0(2)
pt(1) vô nghiệm, pt(2) có nghiệm x =1 và x = -2 tm điều kiện  
Vậy nghiệm của phương trình là: x 1  x  2 
2. Phương trình tương đương với log  x  3  2   x3 3 log   x x 2.9  3  9 3 3 
  x   x     x x    x x 3 2 3 3 2.9 3
9  9  4.3  3  0 (*). Đặt x t  3 , t  0. (*)  t 1 2
 t  4t  3  0  
(thỏa mãn đk t>0) ; Với t =1 x  3 1 x  0. t  2 Với t =3 x
 3  3  x 1. Vậy phương trình có 2 nghiệm x =0 hoặc x =1. 2 2
x y x y  4
170/ Giaûi heä phöông trình : 
x(x y 1)  y(y 1)  2 2 2
x y x y  4
Giải: Giaûi heä phöông trình : (I) 
x(x y 1)  y(y 1)  2  2 x  2 y  x  y  4 (I)    2 x  2
y  x  y xy  2 xy  2 Đặt    2   2  2  2   2  2  2 S x y;P xy(S 4P) S x y 2xy x y S  2P P  2  2 S  2P  S  4  Vaäy I    S  0  2 S  P  S  2  S  1 x  y  0 TH : 2 1  X 0X 2 0
xy  2 vaäy x, y laø nghieäm cuûa phöông trình    x  2 x   2 Vaäy heä coù 2 nghieäm  hay  x   2 y  2 x  y  1 TH : 2 2  X  X  2  0
xy  2 vaäy x,y laø nghieäm cuûa phöông trình x  1 x  2 
 X 1hay X  2. Vaäy heä coù 2 nghieäm  V  y  2  y  1 x  2 x   2 x  1 x  2
Toùm laïi heä Pt (I) coù 4 nghieäm  V  V  V  y   2 y  2 y  2  y  1
171/ 1. Giải phương trình 2( 2x  3  x  1)  x  4 2 2
2 x  5  2 y 1  y
2. Giải hệ phương trình  2 2
2 y  5  2 x 1  x 3 Giải: 1. 2( 2x  3 
x  1)  x  4 (1) - Điều kiện: x  . 2
- Nhận thấy x = 4 không là nghiệm của PT. Với x  4  2x  3  x 1  0. PT  2( 2x  3 
x 1)( 2x  3  x 1)  (x  4)( 2x  3  x 1)
 2(x  4)  ( 2x  3  x 1)(x  4) 
2x  3  x 1  2. (2) Từ (1) và (2) suy ra  x 2x  3    x  8  x  8 4        x  16  208 (t / m) 2 x  8  x  32x  48  0 x 16  208 x 1   4
Vậy PT có 1 nghiệm x  16  208. 2 2
2 x  5  2 y 1  y (1)  2.Giải hệ 2 2  2 y  5  2 x  1  x (2)
- Điều kiện: x, y  1. Nhận thấy x = y = 1 không là nghiệm của hệ  x 1  y 1  0. Hệ 2 2 2 2
 2( x  5  y  5)  2( y 1  x 1)  (y  x ) 2 2 2(x  y ) 2(y  x) 2 2    (y  x ) 2 2 x  5  y  5 x 1  y 1   2 2  (x  y)    x  y  0    x y 2 2        x 5 y 5 x 1 y 1   - Thế vào (1) được: 2 2 2 x  5  2 x 1  x 2 2
 2( x  5  3)  2( x 1 1)  (x  4)  0 2 2(x  4) 2(x  2) 2    (x  4)  0 2 x  5  3 x 1 1  2(x  2) 2   (x  2)  (x  2)    0 (3) 2  x  5  3 x 1 1 2 2(x  2) - Vì 2 x  1  x  5  3  2  1  (x  2) 2 2 x  5  3 x  5  3 2(x  2) 2   (x  2)   0  (*)  x  2. 2 x  5  3 x 1 1
Vậy hệ có 1 nghiệm (2; 2).
172/ Giải phương trình: log228x3 – 9log24x2 – 36log42x = 0
Giải: Giải phương trình: log228x3 – 9log24x2 – 36log4 2x = 0(1) Điều kiện x > 0 2
(1 )  3  3log x   x   x  2   9 2 2log 2  181 log2  0 2  9 log
x 18log x  27  0  log 2 2
2x = -1 hoặc log2 x =3  x = 1/2 ho ặc x=8 3 3 x  y  9
173 / Giải hệ phương trình:  2 2 x  2y  x  4y
x3  y3 9
x3  y3  9 Giải: Giải hệ   
x2  2y2  x  4y
3x2  3x   6y2 12y
x3 –3x2 +3x = y3 +6y2 +12y +9  (x-1)3 = (y +2)3  x =y +3 3 3  x  y  9 x 1 x  2 Vậy hệ đã cho    hoặc  x  y 3 y  2  y  1 
174/ 1) Giải phương trình : x 3 x 1 8 1 2 2    1
2) Giải bất phương trình:  x   x   2 3 1 1
x  2x  3  4
Giải: 1/ Giải phương trình: x 3 x 1 8 1 2 2    1 . Đặt x 3 x 1 2 u 0; 2    1  v . PT  xu   1 2 1   3 x 1 v  1  2  1 1 3 3
u 1 2v u 1 2vu v  0            x 0 1   5       3 2 2 3  x 1 5  v 1  2u (
 u v)(u uvv 2)  0 u 2u 1 0 u    2   2 Vn   2     1   5     x 1 5 3 1 v   2 1   2   2
Phương trình có nghiệm là: x  0
2. Giải bất pt:  x   x   2 3 1 1
x  2x  3  4   x  3  0 x  3    
Điều kiện D / k x 1  0
 x 1  x 1   2 x  2x  3  0 x  3   x 1
Nhân hai vế của bpt với x  3  x 1 , ta được BPT   2
x x     x   x   2 4. 1 2 3 4. 3 1 1
x  2x  3  x  3  x 1 x  2  2 2 2 2
x  2x  2  2 x  2x  3  2x  2  2 x  2x  3  x  4  0   x  2
Kết hợp với điều kiện ta được x  2 là nghiệm của bất pt
x4  4x2  y2  6y 9  0
175/ Giải hệ phương trình:
x2y  x2  2y  22  0 2 2 2
(x  2)  (y  3)  4 Giải: Giải hệ pt:  . 2 2
(x  2  4)(y  3 3)  x  2  20  0 2 x   2 2 u v  u  u  Đặt 2 u 4 2  Khi đó (2)     hoặc 0  y  3  v  .
u v  4(u v)  8 v  0 v  2 2 x  2  2 2 x  2  0  Hoặc  y  3  0 y  3  2 x
x   x  x  
Kết luận:Hệ pt có 4 nghiệm là: 2 2 2 2  ;  ;  ; 
y  3 y  3 y  5 y  5
176 /Tìm giá trị lớn nhất và nhỏ nhất của hàm số: y = 4 4 4
3 x  2  x  3  2x Giải: 1
177/ Giải phương trình 2 5 4 log 2x  log x 1 (x  ) 4 2 2 1
Giải: Giải phương trình 2 5 4 log 2x  log
x 1 (x  ) (1) 4 2 2 ĐK:x>0   2
1  log 2x 5log x 1 2 2
 (log x 1)  5log x 1 log x 3log x  2  0(1) Đặt t=log 2 2 2 2 2 2 2x (1 ) t 1 trở thành 2
t  3t  2  0   t  2
t=1 ta có log2x=1  x=2 ;t=2 ta có log2x=2  x=4
kết hợp với ĐKXĐ  phương trình đã cho có 2 nghiệm là x=2 và x=4
179/ 1. Giải phương trình: 10x 1  3x  5  9x  4  2x  2
2 .Giải phương trình 2log (2x  2)  log
9x 1  1 2 1   2 Giải: 5
Điều kiện: x .;3
Phương trình đã cho tương đương với 10x 1 2 x 2 9 x 4 3x 5 (1). 5 Vì x
nên cả hai vế của (1) đều dương. Do đó: 3
(1) 12 x 1 2 (10 x 1)(2 x 2) 12 x 1 2 (9 x 4)(3x 5) 6
7 x 2 15x 18 0 x 3 hay x . 7
Kết hợp với điều kiện ta được nghiệm của phương trình là x = 3. 2/ Đ 1 iều kiện: x . 9
Phương trình đã cho tương đương với phương trình
log (2x 2)2 log (9x 1) 1 2 2
log (2x 2)2 log (9 x 1) log 2 log (2x 2)2 log (18x 2) 3
(2x 2)2 (18x 2) 2 x2 5x 3 0 = 1 hoặc x . 2 Đố 3
i chiếu điều kiện suy ra nghiệm của phương trình là x = 1 hay x . 2 1 1 1    log x 1 2 log 4 log 4 2
186/ : Giải phương trình x2 2x 1  1 1 1
Giải: Giải phương trình    log x 1 2 log 4 log 4 2 x2 2x 1 
Điều kiện x  2, x  3; (1)  log (x  2)  log (2x 1)  log 2  log (x 1) 4 4 4 4  x  0
x 22x   1  2 x   1 2
 2x  7x  0   7 
; Đối chiếu điều kiện ta có 7 x x   2 2 2 2
x y  2x  3y 15  0
187/ : 1. Giải hệ phương trình  4 2 2
x y  2x  4y  5  0
2. Giải phương trình: log( 5 . 10 x  20 . 15
x )  x  log . 25
3. Giải bất phương trình
1 log x  log (x  2)  log (6  x) 2 2 2 Giải: 2 2
(x 1)(y  2)  4(x 1)  4(y  2)  5 2 u   x 1 1/ Hệ pt   . Đặt  2 2 2
(x 1)  (y  2) 10 v y  2 2 2 2 u   v 10 (
u v)  2uv 10 Ta có hpt    u
v  4(u v)  5 u
v  4(u v)  5              u v 10 u v 2 u 3 u 1  (vô nghiệm) hoặc    hoặc  uv   45 uv   3  v  1  v  3 u   3 +)  Tìm được 2 nghiệm ( ; x y)  (2;1) và ( ; x y)  ( 2  ;1) v  1  u   1  +)  Tìm được nghiệm ( ; x y)  (0;5) v  3
Kết luận: Hệ phương trình có 3 nghiệm: (2;1), (-2;1), (0;5) 2/. PT  log x x 5 . 10  20 . 15  log x 10 . 25  x x x  5 . 10  20 . 15  10 . 25  4 . 15 x  2 .
25 x 10  0 (chia hai vế của phương trình cho x 5 ) t  ( 1 tm) Đặt 
t  2x (t  )
0 , Ta có pt : 15t 2 - 25t +10 = 0   t  2 (tm)  3
Với t  1  2x  1  x  0 2 x 2  2  Với t   2   x  log 2   3 3  3   2 
Vậy phương trình đã cho có hai nghiệm là x  0 và x  log . 2    3 
3/ Đk: 0< x< 6. BPT  2 2
log (2x  4x)  log (6  x) 2 2 BPT  2 2 2
2x  4x  (6  x)  x 16x  36  0  x < -18 hoặc x > 2
Kết hợp đk ta có tập nghiệm BPT là S =(2; 6) 2
log x  log 8x .log x  log x  0 3 2   3
188/ : Giải bất phương trình: 3 2 (1) Giải:
Điều kiện x>0;Biến đổi phương trình tương đương về dạng: 2
log x  3  log x log x  3log x  0 3  2  3 2
Đặt t  log x 3
khi đó bất phương trình có dạng: f t 2
t 3log x .t 3log x  0 2  2 (2)
  3 log x 12log x  3log x 2 2 2  2 2 Ta có: . t  3 t  log x
Do đó f(t)=0 có nghiệm:  2
t  3t log x  0  log x3 log xlog x  0 2   3  3 2 
Do đó (2) tương đương với: log x  3  0 log x  3 x  27 3 3   
log x  log x  0 log x  log x   x 1   3 2 3 2 x 27         log x  3  0 log x  3 x  27 0  x 1 3 3      
 log x  log x  0
 log x  log x   0  x 1 3 2 3 2 0;  1  27;
Vậy bất phương trình có nghiệm là tập  4 x  4 2 x  2
y  6 y  9  0
189/ : 1. Giaûi heä phöông trình :    2 x y  2
x  2 y  22  0 log  x  2 1  2  log
4  x  log 4  x3 2. Giải phương trình: 4 8 2
log (y  2x  8)  6 
3. Giải hệ phương trình: 2  8x
  2x.3y  2.3xy Giải: ( 2 x  ) 2 2  ( y  ) 3 2  4 1/   ( 2 x  ) 2 y  2 x  22  0 ( 2 x  ) 2 2  ( y  ) 3 2  4 ( 2 x  ) 2 2  ( y  ) 3 2  4    ( 2 x  2  )( 4 y  3  ) 3  2
x  2  20  0  ( 2 x  2  )( 4 y  3  ) 3  2 x  2  20  0
x2  2  u  2 u  2 v  4 Đặt 
* Thay vào ta có hệ phương trình  y  3  v  . u v  ( 4 u v)  8 u  2 u  0 Giải hệ ta được  hoặc  v  0 v  2
x  2 x  2 x  2 x   2
Thay vào phương trình ta có  ;  ;  ; 
y  3 y  3 y  5 y  5 x 1  0   4   x  4 2 3 2 . log x 1  2  log
4  x  log 4  x (2) Điều kiện: 4  x  0   4   8   2  x  1  4  x  0 
(2)  log x 1  2  log 4  x  log 4  x  log x 1  2  log  2 16  x 2 2 2 2 2 
 log 4 x 1  log  2 16  x  2
 4 x 1 16  x 2 2 + Với 1
  x  4 ta có phương trình 2
x  4x 12  0 (3) ; x  2 (3)   x  6   lo¹i x  2  24 Với 4   x  1  ta có phương trình 2
x  4x  20  0 (4); 4   x  2  24  lo¹i
Vậy phương trình đã cho có hai nghiệm là x  2 hoặc x  21 6
3. Pt đầu  y – 2x + 8 =  6 2  y  2x
thế vào pt thứ hai ta được: x x     3x x     x x 2x 3 2 2 8 2 .3 2.3 x   8x 18x 2.27x    8 18    2        2      27   27   3   3  x Đặt: t =  2 
  , (đk t > 0 ) , ta có pt: 3 t t    t   2 2 0
1 t t  2  0  3  x  0  t 1  y  0 2 2
x y  2x  3y 15  0
190/ : 1. Giải hệ phương trình 4 2 2
x y  2x  4y  5  0
2. Giải phương trình: log( 5 . 10 x  20 . 15
x )  x  log . 25
3.Giải bất phương trình 1 log x  log (x  2)  log (6  x) 2 2 2 Giải: 2 2
(x 1)(y  2)  4(x 1)  4(y  2)  5 2 u   x 1 1/ Hệ pt   . Đặt  2 2 2
(x 1)  (y  2) 10 v y  2 2 2 2 u   v 10 (
u v)  2uv 10 Ta có hpt    u
v  4(u v)  5 u
v  4(u v)  5              u v 10 u v 2 u 3 u 1  (vô nghiệm) hoặc    hoặc  uv   45 uv   3  v  1  v  3 u   3 +)  Tìm được 2 nghiệm ( ; x y)  (2;1) và ( ; x y)  ( 2  ;1) v  1  u   1  +)  Tìm được nghiệm ( ; x y)  (0;5) v  3
Kết luận: Hệ phương trình có 3 nghiệm: (2;1), (-2;1), (0;5) 2/ P T  log x x 5 . 10  20 . 15  log x 10 . 25  x x x  5 . 10  20 . 15  10 . 25  4 . 15 x  2 .
25 x 10  0 (chia hai vế của phương trình cho x 5 ) t  ( 1 tm) Đặt 
t  2x (t  )
0 , Ta có pt : 15t 2 - 25t +10 = 0   t  2 (tm)  3
Với t  1  2x  1  x  0 Với 2 x 2  2  t   2   x  log 2   3 3  3 
Vậy phương trình đã cho có hai nghiệm là  2 
x  0 và x  log . 2    3 
3 / Đk: 0< x< 6. BP T  2 2
log (2x  4x)  log (6  x) 2 2 BP T  2 2 2
2x  4x  (6  x)  x 16x  36  0  x < -18 hoặc x > 2
Kết hợp đk ta có tập nghiệm BPT là S =(2; 6) 2
2x y xy  2xy(1 x) 
191/ 1. Giải hệ phương trình :  1 2 2 2
(x  2 y )(1 )  9   xy 2.Giải phương trình: 2 3
(6x 1) log (x 1)  (x 1) log (x 1)  7  0 1 2 2 3 x x 7 3 2 1 1 3 2 3. Giải phương trình: 2
 4  4x  6x x  2 2 Giải: 2 2
2x y xy  2x y  2xy
(2x y)(1 xy)  2xy   1/ Điều kiện Hệ   1   1 xy , x y  0 . 2 2 2 2 2 2
(x  2 y )(1 )  12 (x  2 y )( )  12    xyxy
Do 1 xy  0 ,nên hệ  2xy 2x y   (1 xy) 2 2 2  
12(2x y)  4(x  2y )  y x xy 2 2
 11x 12xy y  0  2 2 2  
(x  2 y )  12( )   y 11x  1 xy
+Với y x thay vào hê ta được :x=y=1
+Với y=11x thay vào ta được hệ vô nghiệm Vây hệ có nghiệm (1;1) 2/ Giải phương trình: 2 3
(6x 1) log (x 1)  (x 1) log (x 1)  7  0 1 2 2
HD: Điều kiện:x>-1:Phương trình 2
 (6x 1)log (x 1)  (6x  6)log (x 1) 7  0 2 2
Đặt t  log (x  )
1 ,Phương trình trở thành: 6 ( x  ) 1 2 t  6 ( x  ) 6 t  7  0 (*) 2 +Nếu 1 5
6x  1  0  x   ;Pt :  . 7 log  7  0 :Vô lý 6 2 6   t   1 1 x  +Nếu 1  2
6x  1  0  x  
:Pt (*) có a-b+c=0 nên(*)  7   6 t   7  6x  1 log (x  ) 1  ) 1 (  2 6x  1 7 7 1 1 Ta có ) 1 (  log (x  ) 1 
 0;Đặt f (x)  log (x  ) 1  ,x  ( ; 1 )  ( ; )  2 6x  1 2 6x  1 6 6 1 42 1 1 f '(x)    0 ,x  ( ; 1 )  ( ; )  (x  ) 1 ln 2 (6x  ) 1 2 6 6  
Do đó hàm số đồng biến 1 1 trên các khoảng ( ; 1 ) và ( ; )  . 6 6  
+Hàm số đồng biến trên 1 1 ( ; 1
) nên phương trình có nhiều nhất một nghiệm trên ( ; 1 ) 6 6  Thử với 3 1 x  : ) 1 (
 log ( )  2  0 Đúng. 4 2 4  
+Hàm số đồng biến trên 1 1 ( ; )
 nên phương trình có nhiều nhất một nghiệm trên ( ; )  6 6 Thử với x=1 ta được: ) 1 (  log 2 1  0Đúng. 2  
Tóm lại phương trình có 3 nghiệm: 3 1 x  ; x  ; x=1 4 2 3 x x 7 3 2 1 1 3 2 3/ Giải phương trình: 2
 4  4x  6x x  2 2 x x 7 3 Hd: Phương trình 3 2 1 1 3 2  3 2
 4  4x  6x x   2 2x  22x 1  8 3 x 12 2 x  7x  3 2 2 3 3
2 2x  2  x  22x 1   8 3 x 12 2 x  6x 1 2x 2 x 1  3  2  2  x  2  (2x  ) 1 Xét hàm số: t 3
f (t)  2  t có t 2
f '(t)  2 ln 2  3t  0 t
  R .Do đó f(t) đồng biến trên R
Phương trình:  f (3 2  x)  f (2x  ) 1 3
 2  x  2x 1 Vậy phương trình 3 2 2
x x x    x x x    x  có nghiệm x=1. 8 12 7 3 0 ( 8 )( 1 4 ) 3 0 1 192/ : 1.Giải phương trình: 2 2
36x  63x  27  15  27x  2 9x  9x  3 . x y
2.Cho hai số thực x, y thỏa mãn x 1  y 15 
Tìm giá trị lớn nhất và nhỏ nhất của P x y . 2
3. Tìm m để phương trình 2
12 4  x  3x  3x  24  m3 x 1  2 4  3x  có nghiệm .
4.Giải hệ phương trình:  log x log y 9 2 2   1   log x 1  log y 10 2 2  2 2     xy x y  9 1 log 2.log 2 log2  2 Giải: 1) Từ dấu hiệu 2 2 2
36x  63x  27; 2 9x  9x  3  36x  36x 12 15
Nhân liên hợp và biện luận ta được nghiệm duy nhất x  27      
2.HD.(nhiều cách) Đặt x 1 u 0; y 15 v
0 ta đưa được về hệ PT đối xứng. Từ đk PT
có nghiệm không âm ta tìm được 21 17   P 16
3.HD. ĐK. Đặt t  3 x 1  2 4  3x  t   21; 7 
 ta chỉ việc tìm GTLN,NN trên đoạn này của hàm số   1 f t t t   1 1 4. ĐK, đặt log x ; u log y v      2 2 và u ; m v n ( , m n 2) u v
Ta được 4 nghiệm 4, 2,2; 2  và giao hoán của bộ số.
193. Giải phương trình: 3 3 x  34  x  3  1 Giải: Đặt 3 3 u  x  34, v  x  3 . Ta cã : u  3  u  v 1 u  v 1  u  v 1  u  v 1 v  4         3 3 u  v  37 u  v      2 2 u  v  uv  37   u  v  2 3uv 37 uv 12 u  4  v  3
Với u = -3 , v = - 4 ta có: x = - 61 ;
Với u = 4, v = 3 ta có: x = 30
Vậy phương trình đã cho có 2 nghiệm : x = -61 và x = 30
(3x  y)(x  3y) xy 14 194/  2 2
(x  y)(x  y 14xy)  36 Giải:
(3x  y)(x  3y) xy 14  2 2
(x  y)(x  y 14xy)  36 2 [
 3(x  y)  4xy] xy 14
Đk: xy  0 Hệ ban đầu tương đương  2
(x  y)[(x  y) 12xy]  36
a x y  2 2 2 3
(3a  4b )b 14 3
 a b  4b 14 Đặt 
thay vào hệ trên được    b   xy  0  2 2 3 2
a(a 12b )  36
a 12ab  36 3 3
a (3k  4k ) 14
Nhận thấy a=0 không là nghiệm của hệ trên. Đặt b=ka thay vào hệ trên được  . Ta suy 3 2
a (112k )  36(1) ra phương trình 72k3 1 1 -84k2+54k-7=0  k
b a a  6b thay vào (1) được a=3, từ đó b=1/2 6 6  3  2 2  3  2 2 x y  3 x y  3 x  x     2  2   1   1   hoac xy xy     3  2 2  3  2 2  2  4 y y     2  2
195/ . Giải phương trình: 2 2
x  3  x 1  x  x  2  0 ( x  )
Giải: Giải phương trình: 2 2
x  3  x 1  x  x  2  0 ( x  ) 2 x 3  0 ĐK:   x  3 ; Đặt 2 u  x  3 , u  0 , v  x 1 , v  0 x 1 0 Suy ra: 2 2 2 u  v  x  x  2 Ta được phương trình: 2 2 u  v  u  v  0    u v
u  v  u  vu  v  0  u  v1 u  v  0   u  v  1 
Vì u  0; v  0 nên loại u + v = – 1 x  1  Khi u = v 2 2
 x 3  x 1  x  x  2  0   x  2
Vì x  3 , nên x = – 1 loại. Vậy phương trình có 1 nghiệm x = 2.
log x y  3log ( x y  2) 
196/. Giải hệ phương trình: 2 8  . 2 2 2 2 
x y 1  x y  3  Giải:
Điều kiện: x+y>0, x-y>0
log x y  3log (2  x y) 
x y  2  x y   2 8    2 2 2 2 2 2 2 2 
x y 1  x y  3 
x y 1  x y  3  
u v  2 (u v) 
u v  2 uv  4 u   x y   Đặt:  ta có hệ: 2 2   2 2      
v x y u v 2 u v 2   uv  3   uv  3  2  2
u v  2 uv  4 (1)   2  . Thế (1) vào (2) ta có:
(u v)  2uv  2   uv  3 (2)  2 2
uv  8 uv  9  uv  3  uv  8 uv  9  (3  uv)  uv  0 . Kết hợp (1) ta có:  uv  0 
u  4, v  0 (vỡ u>v). Từ đó ta có: x =2; y =2.(T/m) u   v  4
KL: Vậy nghiệm của hệ là: (x; y)=(2; 2). 3x2 y x 3x2 3   5.6  4.2 y  0
197/ . 1.Giải hệ phương trình  2
x y y  ( 2y x)( 2y x)  2 3
log (x 1)  log (x 1)
2. Giải bất phương trình 3 4  0 2 x  5x  6 Giải:x, y  0 1/ ĐK:  x y 3x2 y x 3x2 y 3x2 y x 3x2 3   5.6  4.2  0 3   5.6  4.2 y  0 Hệ phương trình    
x y y  (2y x)( 2y x) 
x  2y  (2y x)( 2y x)( x y y)  3x2 y x 3x2 y 3x2 y x 3x2 3   5.6  4.2  0 3   5.6  4.2 y  0    
(2y x)[( 2y x)( x y y) 1]  0 
2y x  0
(do 2y x)( x y y ) 1  0 ) 3x2 y x 3x2 y 2 x x 2 3   5.6  4.2  0 3 
 5.6  4.2 x  0 (1)     2y x 2y x (2)  3 ( )x  1  x  0 Giải (1): x x x 3 x 3 2 2 2 x 2 3  5.6  4.2
 0  ( )  5.( )  4  0      2 2 3  x log 4 3  ( )x  4    2 2
Với x = 0 thay vao (2) ta được y = 0 Với 1
x  log 4 thay vao (2) ta được y = log 4 3 3 2 2 2
Kết hợp với điều kiện ta được nghiệm của phương trình là 1 x  log 4 ,y = log 4 3 3 2 2 2 2 2
x  y  xy 2x  5y
198/ 1. Giải hệ phương trình:  ( ; x y R) 2 (  x  2 ) x (x  y  3)  3  y log (y  ) x  log x  1 
2. Giải hệ phương trình : 2 2   2y  3  2x 1  2  Giải: x  0 1/ Nếu y = 0 2  x  2x  0  
 hệ có nghiệm (0;0);(-2;0) x  2  2  x  2x  x y  5  2  x  2x  y u  Nếu y  0, hpt   ;đặt  y ta có hệ: 2  x  2x  .(x  y  3)  3   v  x  y  3  y u  v  2 u  3 u  1     hoặc  uv  3  v  1  v  3 2  x  2x u  3   3 x  1 x  6  Với    y   hoặc  v  1   y  1 y  8 x  y  3  1  2    x 2x u  1    1  Với    y (vô nghiệm) v  3  x  y  3  3
Vậy hệ phương trình đã cho có 4 nghiệm (x; y) là: (0; 0) ; (-2; 0); (1; 1) và (-6; 8)  1 x  2/ Đk: 
2 ; Pt hai  2y  3  2  2x 1  y  x  2 2x 1 y  x
Thế vào pt còn lại ta được : 4(2x 1) 2 2 2
2 log 2 2x 1  log x  1  log
 1  4(2x 1)  2x  x   y   ,(tmđk) 2 2 2 x 3 3 3
KL: hệ có nghiệm (x;y) là ( 2 2 2 ;  ) 3 3 3 1 1  
199/ 1) Giải phương trình sau: 2 x . 2 2  x
2/ Giải hệ phương trình :  2 2 2 y x x  2010 2009  2  y  2010 3log        3( x 2 y 6) 2 log2(x y 2) 1
Giải: 1/+) ĐK: x( 2; 2) \{0}
x y  2xy +) Đặ 2 t y
2  x , y  0 Ta có hệ:  2 2 x y  2  1   3  1   3 x  x   2  2
+) Giải hệ đx ta được x = y = 1 và  ;   1   3  1   3 y y     2  2 1   3
+) Kết hợp điều kiện ta được: x = 1 và x  2  2 2 2 y x x  2010 2009  (1) 2 2/  y  2010 3log        3(x 2 y 6) 2 log2(x y 2) 1(2)
+) ĐK: x + 2y = 6 > 0 và x + y + 2 > 0
+) Lấy loga cơ số 2009 và đưa về pt: 2 2 2 2 x  log
(x  2010)  y  log ( y  2010) 2009 2009
+) Xét và CM HS f (t)  t  log
(t  2010),t  0 2009 đồng biến,
từ đó suy ra x2 = y2  x= y, x = - y
+) Với x = y thế vào (2) và đưa về pt: 3log3(x +2) = 2log2(x + 1) = 6t t t  1   8  Đưa pt về dạng   1      9   9 
, cm pt này có nghiệm duy nhất t = 1  x = y =7
+) Với x = - y thế vào (2) được pt: log3(y + 6) = 1  y = - 3  x = 3 3 3 x  y 1
200. Giải hệ phương trình:  2 2 3 x y  2xy  y  2 Giải:  1 3    
     1 1   3 3    2x 2 x y         2  x  y 4x y    y x   y x   x y   xy .     1 3   1 3 1 3 2y    2x   2x    x y  y x    y x x  y  1 3    x  y  1 x y 2x      x x x  y  1 xy 2         2    1 3  y   x  2, y   2 2x     x   y x   x   2, y  2 x 3   2x    2 x 2 2 3
201. Giải phương trình : 3 ( x  ) 1
2x 1  5x x  3 2 Giải: PT  3 ( 2 x  ) 1 2 2 x 1  10 2 x  3x  6 3 ( 2 x  ) 1 2 2 x 1  ( 4 2 2 x  ) 1  2 2
x  3x  2 . Đặt t  2 2 x  ( 1 t  ) 0 Pt trở thành 4 2 t  3 ( 2 x  ) 1 t  2 2
x  3x  2  0 2x 1  2 Ta có: 2 2 2 '   3 ( x  ) 1  (
4 2x  3x  ) 2  (x  )
3 Từ đó ta có phương trình có nghiệm : t x ;t  2 2 1 6 2  60 
Thay vào cách đăt giải ra ta được phương trình có các nghiệm: x   ;   2 7  2 2 1 x 1x
202. Giải bất phương trình : 5 5 > 24. (2) 2 2   Giải: 1 x 1 x
Giải bất phương trình : 5 5 > 24. (2) 2  2 2 x (2)  55x  245x
5 0  25x 5 x2 > 1 1  x 1  2 2
x y xy 1 4y
2log [(1 x)(y  2)]  2log (1 x)  6  1 x 2 y 203. 1)  ; 2)  2 2
y(x y)  2x  7y  2
log (y  5)  log (x  4) = 1  1 x 2 y 2
x 1  xy  4  2 2
x y xy 1  4yy
Giải: 1) y  0 , ta có:    . 2 2 2
y(x y)  2x  7y  2  x 1 2 (x y)  2  7  y 2 
u v  4  u  4  v
v  3, u 1 Đặt x 1 u
, v x y ta có hệ:      y 2 2
v  2u  7
v  2v 15  0 v  5  , u  9 2 2 2 x 1  yx 1 y
x x  2  0
x 1, y  2
+) Với v  3, u 1ta có hệ:        .
x y  3  y  3 xy  3 xx  2  , y  5 2 2 2 x 1  9yx 1  9y
x  9x  46  0 +) Với v  5
 , u  9 ta có hệ:      , hệ này vô nghiệm.
x y  5   y  5   xy  5   x
KL: Vậy hệ đã cho có hai nghiệm: ( ; x y)  {(1; 2), ( 2  ; 5)}. 2
xy  2x y  2  0, x  2x 1 0, y  5  0, x  4  0 2) + Điều kiện:  (I ) . 0
 1 x  1, 0  2  y  1
2log [(1 x)(y  2)]  2log (1 x)  6 l 
 og (y  2)  log (1 x)  2  0 (1) 1 x 2 y  1 x 2 y (I )    
log (y  5)  log (x  4) = 1 l 
 og (y  5)  log (x  4) = 1(2). 1 x 2 y  1 x 2 y Đặt 1 log
(1 x)  t thì (1) trở thành: 2
t   2  0  (t 1)  0  t  1. 2 y t
Với t 1 ta có: 1 x y  2  y  x 1(3). Thế vào (2) ta có: x  4 x  4 2 log (x  4)  log (x  4) = 1  log 1 
1 x x  2x  0 1x 1x 1x x  4 x  4  x  0     y 1  . Suy ra:  . x  2   y 1
+ Kiểm tra thấy chỉ có x  2
 , y 1thoả mãn điều kiện trên.
Vậy hệ có nghiệm duy nhất x  2
 , y 1. 1 1 8
204. Giải phương trình log x 3 log   4  x  1
log2 4x 2 2 2 4 Giải:
Điều kiện: 0  x  1 ; 2   x  3 x 1  4x
Trường hợp 1: x  1   2
2  x  2x  0  x  2
Trường hợp 2: 0  x  1   2
2  x  6x  3  0  x  2 3  3
Vậy tập nghiệm của (2) là T  2;2 3   3
 x  3 y  3
205. Giải hệ phương trình 
y  3 x  3 
Giải: Điều kiện: 0  x  3,0  y  3
 x  3 y  3
x y  2 x(3 y)  0 Ta có   
y  3 x  3 
y x  2 y(3 x)  0  x  0
x(3 y)  y(3 x)  0   y  0
x  0 x  3
x(3 y)  0  Kiểm tra ta thấy  ,  thỏa mãn.   x  3
y  0 y  3
y(3 x)  0  y  3
x  0 x  3
Kết luận : Hệ có hệ có hai nghiệm  , 
y  0 y  3 2 2 1 x 1x
206. Giải bất phương trình : 5 5 > 24. (2) Giải: 2 2   Giải bất phươ 1 x 1 x ng trình : 5 5 > 24. (2) 2  2 2 x
(2)  55x  245x
5 0  25x 5 x2 > 1 1  x 1 
207. 1/ Giải phương trình: 2 2
7  x x x  5  3  2x x (x  )  1 log y x  log 1  1   4
2/ Giải hệ phương trình y   4 (x, y )  2 2
x y  25 Giải : 1/ Giải phương trình: 2 2
7  x x x  5  3  2x x (x  )   3   x 1 2 3
  2x x  0 2 3
  2x x  0  PT      x  0 2 2
7  x x x  5  3 2x x x x  5  2  (x  2)  x  2  x  5  2.   x  2   x  0     x  1
 . Vậy phương trình đã cho có một nghiệm x = - 1. x    1   2x 16  0  1 log y x  log 1  1   4
2/ Giải hệ phương trình y   4 (x, y )  2 2
x y  25 y x  0 Điều kiện:  Hệ phương trình y  0  1  y xy x 1 log y x  log  1  log  1    4     4 4  y   y   y 4   2 2  2 2  2 2
x y  25
x y  25
x y  25 x  3yx  3yx  3y        25 2 2 2 2 2
x y  25 9
y y  25 y   10     x y  15 5 ;  ;    10 10     (không thỏa mãn đk)    x y  15 5 ;   ;      10 10 
Vậy hệ phương trình đã cho vô nghiệm.
208 1/ Giải phương trình: x2 – 4x - 3 = x  5 log  5  x  2/ Giải phương trình : 3 2  x Giải: 1/ x2 - 4x + 3 = x  5 (1) TX§ : D =  5
 ;)      2 1 x 2  7  x  5 ®Æt y - 2 = x  5 ,     2 y 2 y 2  x  5   x  22  y 5   x  22  y 5     Ta cã hÖ : 
 y  22  x  5  
 x  yx  y  3  0   y  2 y  2    
 x 22  y5  x  y  0  5  29         x  2 x 2  y  5 2   x  1 
x  y  3  0  y  2
2/ ĐK : x > 0 PT đã cho tương đương với : log5( x + 3) = log2x (1)
Đặt t = log2x, suy ra x = 2t t t   2   1  2  log  t 2  3 t t  t  2  3  5   3 1 (2) 5      3   5  t t     t t     Xét hàm số 2 1 2 1 : f(t) =  3     ; f'(t) = ln 0, 4  3 ln 0, 2  0, t       R  3   5   3   5 
Suy ra f(t) nghịch biến trên R
Lại có : f(1) = 1 nên PT (2) có nghiệm duy nhất t = 1 hay log2x = 1 hay x =2
Vậy nghiệm của PT đã cho là : x = 2
208. Giải bất phương trình:    2 4x 3
x  3x  4  8x  6 (1)
Giải: Giải bất phương trình:    2 4x 3
x  3x  4  8x  6 (1)
(1)   x   2 4 3
x  3x  4  2  0 Ta có: 4x-3=0<=>x=3/4 2
x  3x  4  2=0<=>x=0;x=3 Bảng xét dấu: x - 0 ¾ 2 +  4x-3 - - 0 + + 2
x  3x  4  2 + 0 - - 0 + Vế trái - 0 + 0 - 0 +
Vậy bất phương trình có nghiệm:  3 x  0; 3;    4  2 2
x y x y  8 
209. 1/ Giải hệ phương trình : x y 7   1  y x xy
2/ Giải bất phương trình : log log  2
x 1  x  log log  2
x 1  x 1 5 2 1  2 5 x 1  1 x 1 
3/ Giải bất phương trình : 3 3 4  0 Giải:
x y  3 2
(x y)  x y  2xy  8   1/ Hệ         :  x y   x y 2 2  xy  7 
x y xy 1
Vậy nghiệm của hệ là : (x;y) = (1 ;2) ,( 2 ; 1) ,( 1;-3 ) (-3; 1) 2/ k x Đ
 0 : Bpt  log log  2x 1 xlog log  2x 1 x  0 3 1 3 5  5  
 log log  2x 1 xlog  2x 1 x   0 3 1 5    5 2
 log  2x 1 x 1 0  log  2x 1 x 2
 1  x 1  x  5 5 5 5   x  0  12 2
x 1  5  x    x  x 1  5 x2 2 5
Kết hợp đk ta có 0 < x < 12 5 3/ Đk : x  1  x 1 3   3  x 1 1 x  0 Pt 2 x 1  x 1  3
 4.3   3  0       x 1       x  1 3 1 x 1 0 
Nghiệm bất pt là : T =  
1 0; 4 3 2 2 x
 x y x y 1
210. 1.Giải hệ phương trình :  3 2 x
 y x xy  1  2)Giải phương trình: 2 Log   2 x log 2 x log x
x (24x 1  )
x (24x 1  ) (24x 1  )
3)Giải bất phương trình: logx( log3( 9x – 72 ))  1 Giải: 2 2 3
(x xy ) 1x y
1/*Biến đổi hệ tương đương với  3 2 x
 y  (x xy )  1  2 x
 xy u 2 u  1v *Đặt ẩn phụ  , ta được hệ  3 x
 y v v  u  1 
*Giải hệ trên được nghiệm (u;v) là (1;0) và (-2;-3)
*Từ đó giải được nghiệm (x;y) là (1;0) và (-1;0) 2/ *Điều kiện :x>0 *TH1 : xét x=1 là nghiệm
*TH2 : xét x  1 , biến đổi phương trình tương đương với 1 2 1  
1 2 log (24x 1)
2  log (24x 1) log (24x  1) x x x
Đặt log (x 1)  t , ta được phương trình x 1 2 1 
 giải được t=1 và t=-2/3 1 2t 2  t t
*Với t=1  log (x 1) 1 phương trình này vô nghiệm x *Với t= 2
-2/3  log (x 1)   x 3 2 3
x .(24x 1) 1 (*) Nhận thấy 1 x  là nghiệm của (*) 8 Nếu 1 x  thì VT(*)>1 8 Nếu 1 x
thì VT(*)<1 , vậy (*) có nghiệm duy nhất 1 x  8 8
*Kết luận : Các nghiệm của phương trình đã cho là x=1 và 1 x  8 x   0 
3/ *Điều kiện : log (9x  72)  0 giải được x  log 73 3 9 9x   72  0
Vì x  log 73>1 nên bpt đã cho tương đương với 9 3x   8 
log (9x  72)  x 9x 72 3x       x  2 3 3x   9
*Kết luận tập nghiệm : T  (log 72;2] 9 2  1 
211. 1. Giải bất phương trình log (4x  4x  )
1  2x  2  (x  2)log 2 1   x 2  2   3x 2 1  y 2 2  y 2 . 3 3 x
2/ Giải hệ phương trình   3 2 x  1  xy  x  1 Giải:  1 1  1 x    x  0 x    2 1 1/ ĐK: 2   2    x  * 1 2    4x2  4x 1  0 (  2x  ) 1 2  0 x    2
Với điều kiện (*) bất phương trình tương đương với: 2log 1 (  ) x 2  x 2  2  x (    2 ) 2 log 1 ( ) x 2 2 1   x log 1 (  x 2 )   2 1 0 x  0 x  0 x  0     1 log 1 (  2x)  1  0 2 log 1 ( 2  2x)  0 2  1 ( 2  2x)  1 x         4 x  0 x  0 x      0    x  0 log 1 (  2x)  1  0 2   log 1 ( 2  2x)  0 2  1 ( 2  2x)  1
Kết hợp với điều kiện (*) ta có: 1 1  x  hoặc x < 0. 4 2  3x 2 1  y 2 2  y  2 . 3 3x ) 1 ( 2/   x 3 2  1  xy  x  1 (2) x 1  0 x  1 Phương trình (2)     3 2
x  1  xy x  1 x 3 ( x y  ) 1  0 x  1 x  0    x  0  x  1
3x y 1  0  
y  1 3x * Với x = 0 thay vào (1) y2 y y y y 8 8 2  2  2 . 3  8  2  2 . 12  2   y  log 11 2 11 x  1 * Với 
thay y = 1 – 3x vào (1) ta được: 23x 1   2 3  x 1   2 . 3 y  1 3x Đặt 1 3 1 2   x t Vì x  1  nên t  4  1 t  3  8lo¹i  1 x  log2 2 3 8 1 ) 3 (
 t   6  t  6t 1  0     3 t t  3  8 y  2  log 3( 8) 2
212 1. Giải phương trình: 2 2
1 3 2x x
x 1  3  x
x log 3  log y y  log x
2.Giải hệ phương trình: 2 2 2  . .
x log 12  log x y  log y  3 3 3 2  Giải: 1/ t 4 TXĐ: x 1  ;  3 Đặt t=
x 1  3  x , t > 0 => 2
3  2x x  2 x  1 
đc pt: t3 - 2t - 4 = 0  t=2 Với t = 2  x 1  3  x =2  (t / m)  x  3 x  0 2/ TXĐ:   y  0 x  log 2
x log 3 log y y  log x 3
 .xy  2y.xy  2x 4 2 2 2       3   (t/m TXĐ)
x log 12  log x y  log x y y    3
 .xy  2y.x y  2 log 2 3 3 3 12 .x 3 .y  4  3 2 51 2x  x
213. Giải bất phương trình: 1 1 . x Giải:    x 1 1   x  0            2 x 1 52; 1 52 5
 1 2x x  0     2 51 2x x  1  1   x  0    1 x  x 1  2   5
 1 2x x  0   x ( ;  5  )  (5;)   2 2
 51 2x x  (1 x)    x   1   52; 1   52      x   1   52; 5  
1; 1 52 2 2 2
214. a)Giải bất phương trình: 9 2xx 1  2xx 2xx 1 34.15 25     0   y   a
b)Tìm a để hệ phương trình sau có nghiệm : x+1 1 
x y  2a 1 Giải: 2 2 2 2 2 2 2
a) 2xx 1  2xx 2xx 1  2(2xx ) 2 9 34.15  25  0  9.3
34.3 xx . 2xx 2(2 xx ) 5  25.5  0 2  2 xx  3   2  2 1 2(2 xx ) 2 xx    3   3   5   9.  34.  25  0       2  5   5  2 xx  3  25      5  9 2
2x x  0    x( ;1
  3) (0;2) (1 3;)
2x x  2 
KL: Bpt có tập nghiệm là T= ( ;
 1 3) (0;2) (1 3; ) 
x 1  y 1  a   x 1  y 1  a   b) đ/k x  1
 ; y 1 .Bất pt   1 2  ; Vậy
x 1. y 1 
a  (2a 1) 2 2
( x 1)  ( y 1)  2a 1     2 1 x 1 và
y 1 là nghiệm của p/t: T 2 2
aT  (a  2a 1)  0*.Rõ ràng hệ trên có nghiệm khi p/t* 2  2 2   0
a  2(a  2a 1)  0  
có 2 nghiệm không âm  S  0  a  0
 1 2  a  2  6   P  0 1  2
 (a  2a 1)  0 2
 x y x y  2 y
215. 1/ Giải hệ phương trình:  (x, y R)
x  5y  3  2 log x 2log x
2/ Giải bất phương trình 2 2 2  x  20  0 Giải:
1/ ĐK: x + y  0 , x - y  0, y  0
2y x  0 (3) PT(1)  2 2 2 2
2x  2 x y  4 y
x y  2 y x   2 5
y  4xy (4)
Từ PT(4)  y = 0 v 5y = 4x
Với y = 0 thế vào PT(2) ta có x = 9 (Không thỏa mãn đk (3))
Với 5y = 4x thế vào PT(2) ta có x  2 x  3  x  1  4 
KL: HPT có 1 nghiệm (x; y)  1;    5  2
2/ Điều kiện: x> 0 ; BPT  4log2 x 2log2 2 xx
 20  0 Đặt t  log x . Khi đó 2t x  . 2 BPT trở thành 2 2 2t 2 4 2 t   20  0 . Đặt y = 2 2 2 t ; y  1.
BPT trở thành y2 + y - 20  0  - 5  y  4.
Đối chiếu điều kiện ta có 2 : 2t 2 2 2
 4  2t  2  t  1  - 1  t  1. Do đó 1
- 1  log x  1 
x  2 2 2
216. 1/Giải hệ phương trình:  2xy 2 2 x y  1  x y   2
x y x y
2/ Giải bất phương trình: log log  2
x 1  x  log log  2 x 1  x 1 5 3 1  3 5 Giải:  2xy 2 2 x y  1   1  x y
dk x y  0  2
x y x y  2 1/
   x y2 2xy 1  2xy
1 0  x y3  2xyx y  2xy  x y  0 x y
 x y x y2  
1  2xy x y  
1  0   x y  
1 x yx y   1  2xy  0 
x y 1 3   2 2
x y x y  0  4
Dễ thấy (4) vô nghiệm vì x+y>0 ; Thế (3) vào (2) ta được 2 x y  1 x y 1
x 1; y  0 Giải hệ    …… 2 x y 1 x  2  ; y  3 2/ log log  2
x 1  x  log log  2 x 1  x (1) 1 5 3 1  3 5 Đk: x  0   1  log log  2
x  1  x  log log  2
x 1  x  0 3 1 3 5  5    log log 
 2x 1 x.log  2x 1 x 0  3 1 5    5 2
 log  2x 1  x 1 5 
 0  log  2x 1  x 1*) 0  log  2x 1  x x  0 5  5  12 *) log  2 x 1  x 2 2
1 x 1  x  5  x 1  5  x  ...  x  5 5  12 
Vậy BPT có nghiệm x  0;    5  217. 2  log x 3  4 log 3   1 1. Giải phương trình: 9x 1 log x 3
2. Gi¶i bÊt ph-¬ng tr×nh:
x 1  x  2  x  3 log     3 x  1 2 log 2x  1 2 3. Giải phương trình : 3 Giải: 4
1. Phương trình: 2  log x 3 log 3   1 9x 1 (1)  log x 3 1 4 2  log x 4 (1)  2  log x 3 3    1   1 log 9x 1  log x 3 3 2  log x 1 log x 3 3 2  t 4 đặt: t = log   1  t  3t  4  0 3x thành 2 2
(vì t = -2, t = 1 không là nghiệm)  t 1 t 1  t  1
 hay t  4 ; Do đó, (1)  log x  1
 hay x 4  x  hay x 81 3 3 2. §k: x  3 2            Bpt x 1 x 2 x 3 2 x 5x 6 4 x 3   x  4 4  x  0  6  2 3      3  x    2 6 2 3 6 2 3 3
x 12x  8  0   x  3  3 3 2 3. Giải phương trình: log     3 x  1 log 2x  1 2 3 1 §k:
x  1 ; pt  2log x 1  2log 2x 1  2  log x 1  log 2x 1 1 3 3   3 3   2
 log x 1 2x 1  log 3  x 1 2x 1  3 3   3   1    x  1 x 1  hoac 2  2  x  2 2 2x  3x  2   0 2x  3x  4  0(vn)  1 2 2x x   2 
219 . 1. Giải hệ phương trình y   2 2
y y x  2y  2  2 3
log (x 1)  log (x 1)
2.Giải bất phương trình 3 4  0 2 x  5x 6 Giải
1. ĐK : y  0  1 2 2x x   2  0  y 2
2u u v  2  0 hệ   đưa hệ về dạng  2 1  2  
2v v u  2  0 x  2  0 2  y y  3  7  3  7 u v u   u    u v 1  2  2
 u 1 vhoac   hoac   u v  1   1   7  1   7 2
2v v u  2  0 v v     2  2 3  7 2 3  7 2
Từ đó ta có nghiệm của hệ : (-1 ;-1),(1 ;1), ( ; ), ( ; ) 2 7 1 2 7 1
2. Đk: x > - 1 3log (x 1) 3 2 log (x 1)  3 log 4 log (x 1)
bất phương trình 3   0 3 
 0  0  x  6
(x 1)(x  6) x  6
220. Giải phương trình : 2 2
log (5  2x)  log (5  2x).log
(5  2x)  log (2x  5)  log (2x 1).log (5  2x) 1 2 2 x 1  2 2 2 2  1  5   x
Giải: ĐK :  2
2 . Với ĐK trên PT đã cho tương đương với x  0 2 log (5  2x) 2 2 log (5  2x) 
 2log (5  2x)  2log (5  2 ) x log (2x 1) 2 2 2 2 log (2x 1) 2  1  x   4 log (2x 1)  1   2  1 
 log (5  2x)  2log (2x 1)  x   x  2  2 2   2 log (5  2x)  0   2 x  2  
Kết hợp với ĐK trên PT đã cho có 3 nghiệm x=-1/4 , x=1/2 và x=2
log x y  3log ( x y  2) 
222. Giải hệ phương trình: 2 8  . 2 2 2 2 
x y 1  x y  3  Giải
Điều kiện: x+y>0, x-y>0
log x y  3log (2  x y) 
x y  2  x y   2 8    2 2 2 2 2 2 2 2 
x y 1  x y  3 
x y 1  x y  3  
u v  2 (u v) 
u v  2 uv  4 u   x y   Đặt:  ta có hệ: 2 2   2 2      
v x y u v 2 u v 2   uv  3   uv  3  2  2
u v  2 uv  4 (1)   2  . Thế (1) vào (2) ta có:
(u v)  2uv  2   uv  3 (2)  2 2
uv  8 uv  9  uv  3  uv  8 uv  9  (3  uv)  uv  0 .Kết hợp (1) ta có:  uv  0 
u  4, v  0 (vỡ u>v). Từ đó ta có: x =2; y =2.(T/m) u   v  4
KL: Vậy nghiệm của hệ là: (x; y)=(2; 2). 2007 2006 Đề số    
223 Giải phương trình: 2006 x 2007 x 1
Giải Nhận xét :  1   x  2006 1   1
  x  2007 1  2006  x  2007
Ta có : 2006 - x2007 + 2007 - x2006  2006 - x+ 2007 - x = x - 2006 + 2007 - x = 1
Vậy phương trình  2006 - x2007 = 2006 - x và 2007 - x2006 = 2007 - x x  2006     2006  x  0 x  2005      2006  x  1  x  2007    2007  x  0 x  2007        
 2007 x 1  x 2006 x = 2006 hay x = 2007 3x2 y x 3x2 3   5.6  4.2 y  0
224 2. Giải hệ phương trình  2
x y y  ( 2y x)( 2y x)  2 3
log (x 1)  log (x 1)
4. Giải bất phương trình 3 4  0 2 x  5x  6 Giải: x, y  0 2. ĐK:  x y 3x2 y x 3x2 y 3x2 y x 3x2 3   5.6  4.2  0 3   5.6  4.2 y  0 Hệ phương trình    
x y y  (2y x)( 2y x) 
x  2y  (2y x)( 2y x)( x y y)  3x2 y x 3x2 y 3x2 y x 3x2 3   5.6  4.2  0 3   5.6  4.2 y  0    
(2y x)[( 2y x)( x y y) 1]  0 
2y x  0
(do 2y x)( x y y ) 1  0 ) 3x2 y x 3x2 y 2 x x 2 3   5.6  4.2  0 3 
 5.6  4.2 x  0 (1)     2y x 2y x (2)  3 ( )x  1  x  0 Giải (1): x x x 3 x 3 2 2 2 x 2 3  5.6  4.2
 0  ( )  5.( )  4  0      2 2 3  x log 4 3  ( )x  4    2 2
Với x 0 thay vao (2) ta được y = 0 Với 1
x  log 4 thay vao (2) ta được y = log 4 3 3 2 2 2
Kết hợp với điều kiện ta được nghiệm của phương trình là 1 x  log 4 ,y = log 4 3 3 2 2 2 3log (x 1) 3 2 log (x 1)  3 log 4
4. Đk: x > - 1 ; bất phương trình 3   0
(x 1)(x  6) log (x 1) 3 
 0  0  x  6 x  6
225 Giải phương trình: x2 – 4x - 3 = x  5
Giải x2 - 4x + 3 = x 5 (1) TXĐ : D =  5
 ;) ;      2 1 x 2  7  x  5
Đặt y - 2 = x  5 ,     2 y 2 y 2  x  5
 x 22  y5    x  22  y  5   x  22  y 5      x y 0     5 29    Ta có hệ   x
y  22  x  5  
 x  yx  y  3  0       x  22  y  5 2     y  2 y  2      x 1  
x  y  3  0  y  2 Đề số 226. x y  2 
1. Giải hệ phương trình  (x, y  ) 2 2
4x y  5(2x y) xy
4.Giải phương trình: 2 log 2 (x  ) 2  x x   x   . 2 4 7log ( ) 2 ( 2 ) 2 0 2
log (x y) 1  log (7x y)  log y 2 2
5. Giải hệ phương trình:  2 log 3 ( x y  )
2  2x  2 y  4 2 Giải: 2. ĐK xy  0 4x2  y2  (
5 2x y) xy
2x y xy  0
 (2x y)2  4xy  (
5 2x y) xy  (2x y xy )(2x y  4 xy )  0   Với
2x y  4 xy  0 x y  2 
2x y xy  0 ta có 
x y  1(thoả mãn) 3  x  2  2 2 x x  22  x  8 6
x y  2  Với 25
2x y xy  0 ta có    (thoả mãn)
3x  2  4 x  2 2 x  22  8 6 y   25
Vậy hệ phương trình có hai nghiệm.
4/Điều kiện: x  2 , phương trình đã cho tương đương với: 2log (x  ) 2  1  0 2 2log (x  ) 2  x   x     2 1.log ( ) 2 2 4 2
 0 log (x )22x40 2 1
Với 2 log (x  )
2  1  0 ta có x  2  , thoả mãn. 2 2 5
Với log (x  )
2  2x  4  0 , ta có y  log (x  )
2  2x  4 là hàm số đồng biến trên    ; 2 nên x  là 2 2 2
nghiệm duy nhất. Vậy phương trình có hai nghiệm 1 5 x  2  và x  2 2 x y  0 
5. Điều kiện 7x y  0 ; Biến đổi phương trình đầu ta được log (
2 x y) 2  log 7
( x y) y  2 2 y  0 y x
2x 2  3xy y 2  0   y  2x
Với y x thế vào phương trình thứ hai ta được log (2x  ) 2  4  x  9 2
suy ra x y  9, thoả mãn điều kiện.
Với y  2x thế vào phương trình thứ hai ta được log (x  )
2  4  2x  log (x  ) 2  2x  4  0 2 2 5
y  log (x  )
2  2x  4 là hàm số đồng biến trên    ; 2 nên x  là nghiệm duy nhất. 2 2    5 x  5 x  9 x  Suy ra 
2 , thoả mãn điều kiện. Vậy hệ đã cho có hai nghiệm  và  2 y  9   y  5 y  5 3 3 x  y 1
Đề số 234. Giải hệ phương trình:  2 2 3 x y  2xy  y  2 Giải:  1 3    
     1 1   3 3      2x 2 x y         2  x  y 4x y x y     y x   y x   x y   xy xy  2  2.       1 3   1 3 1 3   1 3 2y   2x   2x   2x    x y  y x  y x     y x x  y  1 3  x  y  1 2x     x x x  y  1     2     y   x  2, y   2   x    x   2,y  2 x 3   2x    2 x
Đề số 235 Giải phương trình: 2log 3 ( x  ) 1 1  log x  . 3 (2 ) 1 5 5 Giải: 1
§iÒu kiÖn x  . (*) 3
Víi ®k trª n, pt ®· cho  log 3 ( x  )
1 2 1  3log (2x  ) 1 5 5 2 3 2 3
 log 5(3x 1)  log (2x 1)  5(3x 1)  (2x 1) 5 5 x  2 3 2 2 
 8x  33x  36x  4  0  x  2) (8x 1)  0  1  x   8
§èi chiÕu ®iÒu kiÖn (*), ta cã nghiÖm cña pt lµ x  . 2
 x y x y  2 y
236. 1. Giải hệ phương trình:  (x, y R)
x  5y  3  2 log x 2log x
4. Giải bất phương trình 2 2 2  x  20  0 Giải:
2. ĐK: x + y  0 , x - y  0, y  0
2y x  0 (3) PT(1)  2 2 2 2
2x  2 x y  4 y
x y  2 y x   2 5
y  4xy (4)
Từ PT(4)  y = 0 v 5y = 4x
Với y = 0 thế vào PT(2) ta có x = 9 (Không thỏa mãn đk (3))
Với 5y = 4x thế vào PT(2) ta có x  2 x  3  x  1 KL: HPT có 1 nghiệm  4  ( x; y)  1;    5  2
1. Điều kiện: x> 0 ; BPT  4log2 x 2log2 2 xx  20  0
Đặt t  log x . Khi đó 2t x  . 2 BPT trở thành 2 2 2t 2 4 2 t   20  0 . Đặt y = 2 2
2 t ; y  1. BPT trở thành y2 + y - 20  0  - 5  y  4.
Đối chiếu điều kiện ta có 2 : 2t 2 2 2
 4  2t  2  t 1  - 1  t  1. Do đó 1
- 1  log x  1 
x  2 2 2 Đề số 237.  2
x  3x( y  ) 1  2
y y(x  ) 3  4
2. Giải hệ phương trình:  ( , x y  R)
x xy  2y  1 x 1  x x 1 2 4. Giải phương trình: 2 3 (  ) 2 log  4  9 . 3 3 3 Giải: x y 1
2/ x2 -3x(y-1) + y2 + y(x-3) = 0  (x-y)2 + 3(x- y) - 4 + 0   x y  4  x y  1 * Với x- y = 1, ta có 
 x = 1; y = 0 và x= -1; y = -2
x xy  2y  1
x y  4 * Với x - y = -4 ta có  (Hệ PT vô nghiệm)
x xy  2y  1
Vậy hệ phương trình có 2 nghiệm (x; y) = (1; 0) và (x; y) = (-1; -2)
4.Điều kiện: x > 1 Thì Pt x 1  x x 2 x 1 2 2  (3  2)log  4  .9  3 (   ) 2 log (x  ) 1  log 3  4 3x  3 3  1 3 3 3 3  x 3 (   ) 2 log (x  ) 1     3 ( x  ) 2 log (x  ) 1  3x  2  0 3  x 1 4 3 . 2 3  x  log 2 3x  2  3  0  4 3 ( x  ) 2 log (x  ) 1     
; Vậy PT có nghiệm x = 3 1 0 4 log (x  ) 1  1 x  3 3  3 Đề số 238 .
1. Giải phương trình 2 2 2 2x x
x  3  2x x  3  9 . 2 2
4x y  2
4. Giải hệ phương trình: 
log (2x y)  log (2x y)  1  2 3 Giải: 1/ Đặt 2 u x  3  0 ta có 2 2
u x  3 . Kết hợp với pt đã cho ta có hệ
x(2x 1)  u(2x 1)  9 (
 2x 1)(u x)  9
(u x) 1(u x)(u x)  9      .
(u x)(u x)  3 (
u x)(u x)  3
(u x)(u x)  3 a  4 u   x a
(a b 1)a  9 a  3  Đặt  , ta có hệ    hoặc  3  . u   x bab  3 b   1 b   4 2 2 a 3
 x 3 x 3     
x  3  3  x Nếu       x 1   2 2 b 1
 x  3  x 1
 x  3 1 xa  4 2  
x  3  x  4 (*)  Nếu  3    3  (I) b   2 
x  3  x  4  4 Ta có 2 2
x  3  x
x  3  x x x  0  (*) vô nghiệm  hệ (I) vô nghiệm.
Vậy, pt đã cho có nghiệm duy nhất x  1.
(Các cách khác: + Đặt 2
t x x  3
+ Biến đổi pt thành 2 2
(2x 1) x  3  9  x  2x , đặt đk rồi bình phương hai vế.
+ Biến đ ổi pt thành x   2 (2 1)
x  3  x  9, nhân 2 vế với 2
x  3  x  0, x ) 2 2
4x y  2 (1)
2x y  0 4/  (I). Đk: 
log (2x y)  log (2x y) 1 (2) 
2x y  0 2 3 2 2
(1)  log (4x y )  log 2  log (2x y)  log (2x y)  1 (3) 2 2 2 2
(2) và (3)  log (2x y)  log (2x y)  0 2 3
 log (2x y)  log 3.log (2x y)  0  log (2x y) 1   log 3  0 2 2 3 2  2 
 log (2x y)  0  2x y 1 2 2x y 1 3 2x y 1 x  Vậy, Hệ (I)   4   (tm)   . 2 2
4x y  2 1
2x y  2 y   2 Vậy nghiệm hệ pt là ( ; x y)   3 1 ; . 4 2  2 2
x  5x  3  2  3x  6 . x 5x
Đề số 239. 1. Giải bất phương trình  2 3 . x 5x  1 1 1
2. Giải phương trình log
x 3 log x  8  4 1
log2 4x 2 2 2 4 Giải: 1 1 8 2. Giải phương trình log x 3 log   4  x  1 log2 4x 2 2 2 4
Điều kiện: 0  x 1 ; 2  x  3 x 1  4x
Trường hợp 1: x 1   2
2  x  2x  0  x  2
Trường hợp 1: 0  x 1   2
2  x  6x  3  0  x  2 3  3
Vậy tập nghiệm của (2) là T  2;2 3   3 Đề số 240.
1/ Giải phương trình : 3x2  9 2
x  3 4x  21 1 2
x x  0  2 xy  4 6 3 4 yy  2 x
2/ Giải hệ phương trình:  4x  5  2 y  8  6 Giải:
1/ Phương trình  3x 2 2  9x  3   2x   1  2 2 
4  4x  4x   3x2  3 ( x) 2  3    2x   1 2  (2x  ) 1 2  3 2 Xét hàm số t '
f (t)  2  (t)2  3
f (t)  t2  (t)2  3 có   0 với t  2 t  3
Vậy hàm số đồng biến nên 1 : f 3 ( x)  f ( 2  x  ) 1  3x  2
x 1  x   5
Vậy phương trình có nghiệm 1 x   5   2( 2 xy  4 6 3 2 y )  y  2 x ) 1 (
2 Hệ phương trình     4x  5  2 y  8  ( 6 ) 2 2 2 2 4 2 4
Từ (1)  2 y (x y )  ( y x)( y xy x ) 2 4 2 4 2 2
 (y x)(y xy x  2y )  0  x y thay vào (2) ta có : 4x  5 
x  8  6  x  1  y  1 
Vậy hệ có nghiệm ( 1;1) và (1;-1) Đề số 241.  2
x  3x( y  ) 1  2
y y(x  ) 3  4
2. Giải hệ phương trình:  ( , x y  R)
x xy  2y  1 x 1  x x 1 2 4/ Giải phương trình: 2 3 (  ) 2 log  4  9 . 3 3 3 Giải:
2/ x2 -3x(y-1) + y2 + y(x-3) = 0  (x-y)2 + 3(x- y) - 4 + 0 x y  1 
x y  4 x y  1 * Với x- y = 1, ta có 
x xy  2y  1
 x = 1; y = 0 và x= -1; y = -2
x y  4 * Với x - y = -4 ta có  (Hệ PT vô nghiệm)
x xy  2y  1
Vậy hệ phương trình có 2 nghiệm (x; y) = (1; 0) và (x; y) = (-1; -2)
4/ Điều kiện: x > 1 x 1  x x 2 x 1 2 2 3 (  ) 2 log  4  9 .  3 (   ) 2 log (x  ) 1  log 3  4 3x  3 3  1 3 3 3 3  x 3 (   ) 2 log (x  ) 1     3 ( x  ) 2 log (x  ) 1  3x  2  0 3  x 1 4 3 . 2 3 
x  log 2 ( loai ) 3x  2  3  0  3 ( x  ) 2 log (x  ) 1      3 1 0 4 log (x  ) 1  1 x  3  3 4
Vậy PT có nghiệm x = 3
Đề số 242. Giải bất phương trình: 2 2
x  2x  92  x  2x x 1 1
Giải: Điều kiện: x 1 Bất phương trình 2 2
x  2x  92 10  (x  2x 8)  ( x 1 1) 2 x  2x  8 x  2 
 (x  2)(x  4)  2
x  2x  92 10 x 1 1  x  4 1   (x  2)   (x  4)    0 2
x  2x  92 10 x 1 1  1 1 
 (x  2) (x  4)( 1)    0 2 
x  2x  92 10 x 1 1 1 1 Ta có: (x  4)( 1)   0, x  1 2
x  2x  92 10 x 1 1
Do đó bất phương trình  x  2  0  x  2
Kết hợp với điều kiện ta có nghiệm bất phương trình là: 1 x  2 2 x       Đề số 243 2x 5x 3 2 3x 6 . x 5
. Giải bất phương trình sau:  2  3 . x 5 x 1 2 4. Giải phương trình x x 2 log log 4 2 2 4x  6  2.3  log x log y 9 2 2    2 2
1 log x 1 log y 10
5. Giải hệ phương trình 2 2    xy x y   9 1 log 2.log 2 .log ( ) 2  2 Giải: 2/ Điều kiện: 1
  x  3. Bất phương trình tương đương với 2 x 2 x x 5 2
x  5x  3  3
( x  2)5x  6x 5
3 x2x   1  3 . x 5  2   0 (1) 3 . x  5x 3x  5x   Xét hàm số x ln 5 ( )  3  5x g x x
, g '(x)  3  5 .ln 5, g(x)  0  x  log . 5    3    
Lâp bảng biến thiên, ta thấy ln 5
g(x)  g log  0  5     3  5  157 (1) 
3 x2x  1 3x  0( vì 5x  0) x  22   
Vậy nghiệm của bất phương trình là: 5 157 T   ;3  22  
4/ Điều kiện x  0 1log x 2 2 x x x x 6 2 log x log 4x 2 2 2 2 4x  6  2.3 log 4 log log 4 2log 2 2log 2 x 2 2 2 2 2  2  6  2.3  2   2.3  0 6 2log 2 x log 2 x log 2 x 2 2     2   2log 2 x 1log x 2log 2 x 2 2 2 3 1 2 2 2  6.2  6 12.3  0  6.  12  0       x     3   3   3  2 4 5/ Điều kiện: 0  ,
x y  1. Đặt a  log ; x b  log y . 2 2
Khi đó, hệ phương trình trở thành:  a b 9    2 2 2 2 1   a 1 b 10 (*) 1  0
 a b1 ab  91 a 1 b  (1)     1     (**) 2
 a b1 ab  (2) a b 9 1    9ab   ab  2 
Lấy phương trình (1) chia vế theo vế (2) ta được: a b
5ab  1 a 1 b  2 5 1 2 2   2 1 (3) a b Từ (*), ta suy ra a 9 b   . 2 2 1 a 10 1 b 2 2  9 b  1 b 1 b b 9 Thay vào (3), ta có: 5     5   0   (4) 2 2 10 1 b b b 1 b 2 2  Đặt 1 b 5 9 5 t
. Phương trình (4) trở thành: 2 t
  0  2t  9t 10  0  t  2;t  . b t 2 2   Với x t  2   2 b  2b  
1  0  b  1  y  2 2   x  4
b  2  y  4, x  2 Với 5 2  t
 2b  5b  2  0  1 2
b   y  2, x  2  2 Vậy hệ có nghiệm ( ;
x y)  (2; 4);(2; 2)  2;4,4;2. 3 3 3 8  x y  27  18y (1)
Đề số244. Giải hệ phương trình:  2 2 4x y  6x  y (2) 3 3 3 8  x y  27  18y (1)
Giải: Giải hệ phương trình:  2 2 4x y  6x  y (2) (1)  y  0 3 3  27  3 8x   18  3  x  3 (2 )   18 y  y     Hệ    2  4x 6x    1  3  3  2 2 . x 2x   3  y y  y y  3 3 a  b  18 a  b  3
Đặt a = 2x; b = 3 . Ta có hệ:   y a  ( b a  b)  3 ab  1      
 Hệ đã cho có 2 nghiệm 3 5 6 3 5 6  ; , ; 4   3  5   4 3  5 
Đề số 245 . Giải phương trình: 2log 3 ( x  ) 1 1  log x  . 3 (2 ) 1 5 5
Giải Giải phương trình: 2log 3 ( x  ) 1 1  log x  . 3 (2 ) 1 5 5 1 §iÒu kiÖn x  . (*) 3
Víi ®k trª n, pt ®· cho  log 3 ( x  )
1 2 1  3log (2x  ) 1 5 5 2 3  log 3 ( 5 x  ) 1  log (2x  ) 1 5 5 2 3  3 ( 5 x  ) 1  (2x  ) 1  8 3 x  33 2
x  36x  4  0  (x  ) 2 2 8 ( x  ) 1  0
§èi chiÕu ®iÒu kiÖn (*), ta cã nghiÖm cña pt lµ x  . 2 x  2   x  1  8 (x  )( 1 y  )( 1 x y  ) 2  6
Đề số 246 Giải hệ phương trình:   2 x  2
y  2x  2 y  3  0 (x  )( 1 y  )( 1 x y  ) 2  6
Giải Giải hệ phương trình:   2 x  2
y  2x  2 y  3  0 (x  )( 1 y  )(
1 x 1  y  ) 1  6
uv(u v)  6
uv(u v)  6 u x 1 Hệ       với  (x  ) 1 2  ( y  ) 1 2  5  0  2 u  2 v  5  0
(u v)2  2uv  5  0 v y 1
S u v  . P S  6 S  3 Đặt:  được    P u v .  2
S  2P  5  0 P  2 X  1
x 1  2 x 1  1
u, v là nghiệm của phương trình: X2 – 3X + 2 = 0       X  2
y 1  1 y 1  2
Vậy nghiệm của hệ: (3 ; 2), (2 ; 3) Đề số247.
3. Giải phương trình: log  2 x x   2
1  log x  2x x 3 3
4. Giải bất phương trình: 2 (log   x 8 log4 x )log2 2x 0 Giải
3. Giải phương trình: log  2 x x   2
1  log x  2x x 3 3 2 x x 1 xx 1  log
x 2  x  3  x 1 3   2  x x Đặt:f(x)= 2  1 3x
x g(x)= x 1 (x  0) x
Dùng pp kshs =>max f(x)=3; min g(x)=3=>PT f(x)= g(x)  max f(x)= min g(x)=3 tại x=1 =>PT có nghiệm x= 1
4/ Giải bất phương trình: 2 (log   x 8 log4 x )log2 2x 0
Điều kiện x > 0 , x  1    1  1  1  (1)    2 log4 x log 2x  2 0    log2 x log x 1  2 0  log 1 8 x  2    log x   2 3   2 log x 1 log x 1  (log x  2 3) 2   0  2  0 log x log x  2  2 1
 log x  1hayl og x  0  0  x  hay x  2 2 1 2 Đề số248 .
1/ Giải các phương trình 2. 2 2
log (x  5x  6)  log (x  9x  20)  1 log 8 3 3 3 Giải: x  5  + Điều kiện : 2 x  5x  6  0 x  3   x  2         4   x  3
 , và có : 1 log 8 log 24 3 3 2  x  9x  20  0 x  5   x  4  x  2   2 2 2 2          + PT (*) log (x 5x 6)(x 9x 20) log 24
(x  5x  6)(x  9x  20)  24 3   3     (x  5  )  ( 4   x  3  )  (x  2  ) (x  5  )  ( 4   x  3  )  (x  2  )
(x  2)(x  3)(x  4)(x  5)  24 (*)   (x  5  )  ( 4   x  3  )  (x  2  ) (**) + Đặt 2
t  (x  3)(x  4)  x  7x 12  (x  2)(x  5)  t  2 , PT (*) trở thành : t(t-2) = 24 2
 (t 1)  25  t  6 t  4      t = 6 : x 1 2 2
x  7x 12  6  x  7x  6  0   ( thỏa đkiện (**)) x  6   t = - 4 : 2 2 x  7x 12  4
  x  7x 16  0 : vô nghiệm
+ Kết luận : PT có hai nghiệm là x = -1 và x = - 6 Đề số log 9 2 log log 3
249. 1.Giải phương trình 2 2 2  .3 x x x  x
4xy  (4 2x  2y  3 )  7  (x y)2
2. . Giải hệ phương trình sau:   x  1 2   3  x y Giải: log 9 2 log log 3 1. Giải phương trình 2 2 2  .3 x x x  x ĐK: x>0. Ta có phương trình lo x x 2 g 9 2 log2 log2 3 lo 2 g 2 x  x .3  x  3  x 1. Đặt log   2t x x 2 . t t  3 t  1 t
Phương trình trở thành 3  4 1    1     t 1 x  2  4   4 
4xy  (4 2x  2y  3 )  7  (x y)2
2. Giải hệ phương trình sau:   x  1 2   3  x y ĐK: x + y  0  3 2 2
3(x y)  (x y)   7  2  (x y) Ta có hệ   1 x y
x y  3  x y 2 2 3
u v  13
Đặt u = x + y + 1 ( u  2) ; v = x – y ta được hệ :  x y u   v  3
Giải hệ ta được u = 2, v = 1 do ( u  2)  1 x y   2 x y  1 x  1 Từ đó giải hệ  x y      x y  1 y  0 x y  1 Đề số250. 3x 1  y2 y3 2  2  3.2 x
Giải hệ phương trình:  2
 3x 1 xy x 1  x+1 0 x  1   x  1  PT 2       2 3
x 1 xy x 1 x
 3x y   1  0
x  0  y 1 3x Với x = 0 thay vào (1) : yy y y y 8 8 2 2  2
 3.2  8  2 12.2  2   y  log 2 11 11 x  1  Với    
thay y = 1 – 3x vào (1) ta được : 3x 1 3x 1 2  2  3.23 y 1 3x Đặt 1 3 1 2 x t   , vì x  1  nên t   4 1 t  3 2 2 PT (3) : 2
t   6  t  6t 1  0   t t  3 2 2 Đối chiếu điều kiện 1 t  
ta chọn t  3  2 2 . 4 Khi đó x 1 3 1 2
 3 2 2  x  log 3 2 2 1 2    3 
y  1 3x  2  log 3  2 2 2   x  0   1 x  log 3 2 2 1  2   
Vậy HPT đã cho có 2 nghiệm   8 và 3  y  log  2   11 y  2  log 3  2 2 2      x  y   2 2 x  y  13
Đề số 251. Giải hệ phương trình:  x, y  .   x  y   2 2 x  y     25 Giải:   x  y   2 2 x  y  13
Giải hệ phương trình:  x, y  .   x  y   2 2 x  y     25   x  y   2 2 x  y  13   1 3 2 2 3
x  xy  x y  y 13 1'      3 2 2 3
y  xy  x y  x  25  2' x  y   2 2 x  y   25 2
Lấy (2’) - (1’) ta có: x2 y– xy2 = 6  x  y xy  6 (3)      2 2 x y x  y  13 Kết hợp với 1 ta có 
I. Đặt y = - z ta có :   x  y  xy  6 2 2 2      
x zx z  13
x z x z 2xz 13       I      x  zxz  6 x  z  xz  6 
Đặt S = x +z và P = xz ta có :   2   3 S S 2P  13 S  2SP  13 S  1         SP  6  P  6 SP 6  x  z  1 x  3 x  2  Ta cã :  . Hệ này có nghiệm  hoặc  x.z  6  z  2  z  3
Vậy hệ đã cho có hai nghiệm là: ( 3 ; 2) vµ ( -2 ; -3 )
Đề số252 . Giải bất phương trình: log (log x   x 4 (2 4)) 1 Giải:
Giải bất phương trình: log (log x   x 4 (2 4)) 1 0  x  1  log (log x
 . Đk: log (2x  4)  0  x  log 5 x 4 (2 4)) 1 4 2  2x  4  0
Do x  1 PT  log x x x x x       
  đúng với mọi x. Do vậy BPT có 4 (2 4) x 2 4 4 4 2 4 0 nghiệm: x  log 2 5 Đề số 253.
2: Giải bất phương trình: 2 2
x  35  5x  4  x  24  2(x 1) log  y x
5. Giải hệ phương trình 2010 y   2 2
y x  2  x  3yGiải:
2: Giải bất phương trình: 2 2
x  35  5x  4  x  24 BPT tương đương 11 2 2
x  35  x  24  5x  4   5x  4 2 2
x  35  x  24 2 2
 11 (5x  4)( x  35  x  24) Xét: a)Nếu x 4  không thỏa mãn BPT 5 b)Nếu x>4/5: Hàm số 2 2
y  (5x  4)( x  35  x  24) với x>4/5 1 1 y'= 2 2 5( x  35 
x  24)  (5x  4)(  ) >0 mọi x>4/5 2 2 x  35 x  24
Vậy HSĐB. +Nếu 4/5 +Nếu x>1 thì y(x)>11 Vậy nghiệm BPT x>1 x Đề số254.
Giải phương trình: 2x 2x 1 3 2   6 x
Giải: Giải phương trình: 2x 2x 1 3 2   6 x
Lấy logarit theo cơ số 3 cho hai vế ta được: 2 x  log 2  1 log 2 3 3 2x 1
Đưa phương trình về dạng: (x – 1)(2x2 + x – 1 - log 2 ) = 0. 3 1   9  8log 2
Từ đó suy ra nghiệm x = 1; 3 x  4
Đề số255. .Giải bất phương trình log 2 x  log 2 x  3  5(log 2 x  ) 3 2 2 4
Giải: Giải bất phương trình log2 x  log 2 x  3  5(log 2 x  ) 3 2 2 4 x  0 ĐK:  log2 x  log 2 x  3  0 2 2
Bất phương trình đã cho tương đương với log2 x  log 2
x  3  5(log x  ) 3 ) 1 ( 2 2 2 đặt t = log 2 t t   t   t t   t  2 x, BPT (1)  2 3 5( ) 3 ( )( 3 ) 1 5( ) 3 t  1    1 t  1 log x   0  x   t  3   1     2  2  t x  2 3   4 3  log   4 2 (t  )( 1 t  ) 3  ( 5 t  ) 3 8  x  16 1
Vậy BPT đã cho có tập nghiệm là: ( ; 0 ]  ) 16 ; 8 ( 2 Đề số 256
2log (xy  2x y  ) 2  log ( 2 x  2x  ) 1   1 x 2 6
2,Giải hệ phương trình:  y log (y  ) 5  log (x  ) 4   1 x 2 1 y 1 1 4,Giải phương trình: log (x  ) 3  log   . 4 x 18 log 4x 2 2 4 2
2log (xy  2x y  ) 2  log ( 2 x  2x  ) 1  6 Giải  1 x 2 y
2,Giải hệ phương trình:  log (y  ) 5  log (x  ) 4   1 x 2 1 y  4  x  , 1 x  0 §K  y   ; 2 y  1
Đưa phương trình thứ nhất của hệ về dạng : log (2  y)  log   1 x x 2 y 1  2
Đặt t  log (2  y), tìm được T=1 kết hợp với phương trình thứ 2 của hệ, đối chiếu với điều kiện trên, tìm 1x được nghiệm :  ; x y   1 ; 2 1 1
4Giải phương trình: log (x  ) 3  log   . 4 x 18 log 4x 2 2 4 2
ĐK x > 0 và x  1. Đưa phương trình về dạng : log (x  )
3  log x 1  log . 2 2 2 4x
Xét hai khả năng 01, đối chiếu với điều kiện ta tìm được nghiệm của phương trình là x  3   2 3 và x = 3. Đề số 2 1 1
57. Giải phương trình: log (x  ) 3  log (x  ) 1 8  3log (4x) . 2 2 4 4 8 Giải 1 1
Giải phương trình: log (x  ) 3  log (x  ) 1 8  3log (4x) . 2 2 4 4 8 1 1 log (x  ) 3  log (x  ) 1 8  3log (4x) . 2 2 4 4 8 Điều kiện: x  3  
x  1  0  x  . 1 x  0 
Biến đổi theo logarit cơ số 2 thành phương trình 1 loaïi  2 3 1 4 2 3 0 3 2    
x   x     2  xx   log log
x x      x  . x  3 Đề số 258. 2  y  2
1. Giải hệ phương trình sau: 3y  2  x  2  x  2 3x   2  y 2. Giải phương trình: 3 2x 1 3  2x  2 3  2x  3  0 Giải: 2  y  2 3y 
1. Giải hệ phương trình sau: 2  x  2  x  2 3x   2  y 2 2 3
 x y y  2
điều kiện x>0, y>0. Khi đó hệ tương đương  2 2 3
 xy x  2
Trừ vế theo vế hai phương trình ta được: (x-y)(3xy+x+y) = 0  x y thay lại phương trình Giải tìm
được nghiệm của hệ là: (1;1). 2. Giải phương trình: 3 2x 1 3  2x  2 3  2x  3  0
Tập xác định: D = R. Đặt f(x) = 3 3 3
2x 1  2x  2  2x  3 Ta có: 2 2 2 1 3 f ' (x)     ; 0 x   , , 1  (2x  ) 1 (2x  ) 2 3 (2x  ) 3 2 3 2 3 2 2 2
Suy ra hàm số f(x) đồng biến trên tập M=  1   1   3   3 
 ,    ,  1    ,
1      ,  2   2   2   2  Ta thấy f( 1 3
-1)=0  x=-1 là một nghiệm của (1). Ta có: f ( )  ; 3 f ( )  3  2 2
Ta có bảng biến thiên của hàm số f(x): x 3 -∞  -1 1  +∞ 2 2 f’(x)    F(x) +∞ 0 3 -∞ -3
Từ bảng biến thiên ta thấy f(x) = 0  x = -1. Vậy phương trình đã cho có duy nhất một nghiệm x = -1. 3 3  u v 3 u   2x 1 u   v   0
Cách 2: Học sinh có thể đặt  khi đó ta được hệ  2 3
v  2x  3  3 3 v u  2
giải hệ này và tìm được nghiệm.  1 1 2 x x  (1 )  4  y y Đề số 2
59. Giải hệ phương trình: 2 x x 1  . 3    4  x 2 3  y y y Giải  1 1 2 x x  (1 )  4  y y
Giải hệ phương trình:  . 2 x x 1  3    4  x 2 3  y y y   1 1 1    2 1 1 2 a x x x  (1 )  4 x   x   4    2  y §k y  0  y yy y    ®Æt  2 x x 1 1 x 1  x  3 3     4  x x   (  x)  4 b  2 3 3  y y y  y y y  y 2 2 2
a a  2b  4
a a  4  2b
a a  4  2ba  2 Ta ®- îc        3 3 2 2
a  2ab  4
a a(a a  4)  4
a  4a  4  0 b  1 Đề số 260.
2. Giải phương trình : 3
2 3x  2  3 6  5x  8  0 (x  R) 2 2
log (x  y ) 1 log (xy) 2 2
4. Giải hệ phương trình :  (x, y  R) 2 2 x xyy 3  81 Giải 2.Giải phương trình : 3
2 3x  2  3 6  5x  8  0 (x  R) 6 3
2 3x  2  3 6  5x  8  0 , ñieàu kieän : 6  5x  0  x  5 3 t  2 3 8  5t
Ñaët t = 3 3x  2  t3 = 3x – 2  x = vaø 6 – 5x = 3 3 3 8  5t
Phöông trình trôû thaønh : 2t  3  8  0 3 3 8  5t t  4  3  8  2t   3 2 3
15t  4t  32t  40   t = -2. Vaäy x = -2 0 2 2
log (x  y ) 1 log (xy) 2 2
4. Gæai heä phöông trình :  (x, y  R) 2 2 x xyy 3  81 Ñieàu kieän x, y > 0 2 2
log (x  y )  log 2  log (xy)  log (2xy) 2 2 x  y  2xy 2 (x  y)  0 2 2 2 2      2 2 x  xy  y  4 2 2 x  xy  y  4 xy  4 x  y x  2 x  2     hay  xy  4 y  2 y  2 
………………………………………………………………………………………………………………….