






























Preview text:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 0
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 PHẦN I - ĐỀ BÀI
HAI ĐƯỜNG THẲNG CHÉO NHAU VÀ SONG SONG
Dạng 1: Tính diện tích thiết diện, đoạn thẳng dựa vào hai ĐT song song Câu 1.
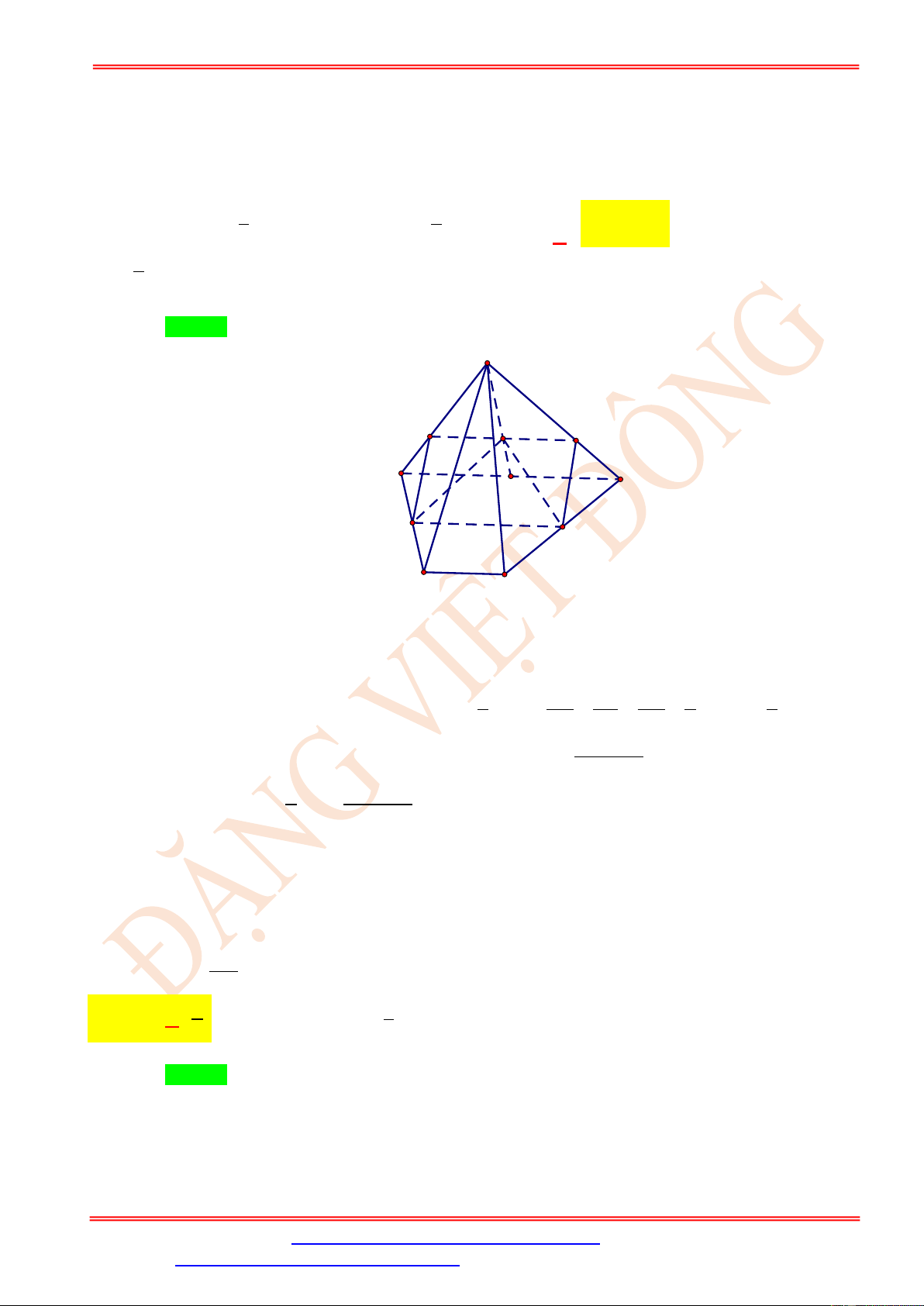
Cho tứ diện ABCD có AB = 6, CD = 8 . Cắt tứ diện bởi một mặt phẳng song song với AB ,
CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng 31 18 24 15 A. . B. . C. . D. . 7 7 7 7 Câu 2.
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a , SA = SD = 3a , SB = SC = 3a 3 . Gọi
M , N lần lượt là trung điểm của các cạnh SA và SD , P là điểm thuộc cạnh AB sao cho
AP = 2a . Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng ( MNP) . 2 9a 139 2 9a 139 2 9a 7 2 9a 139 A. . B. . C. . D. . 4 8 8 16 Câu 3.
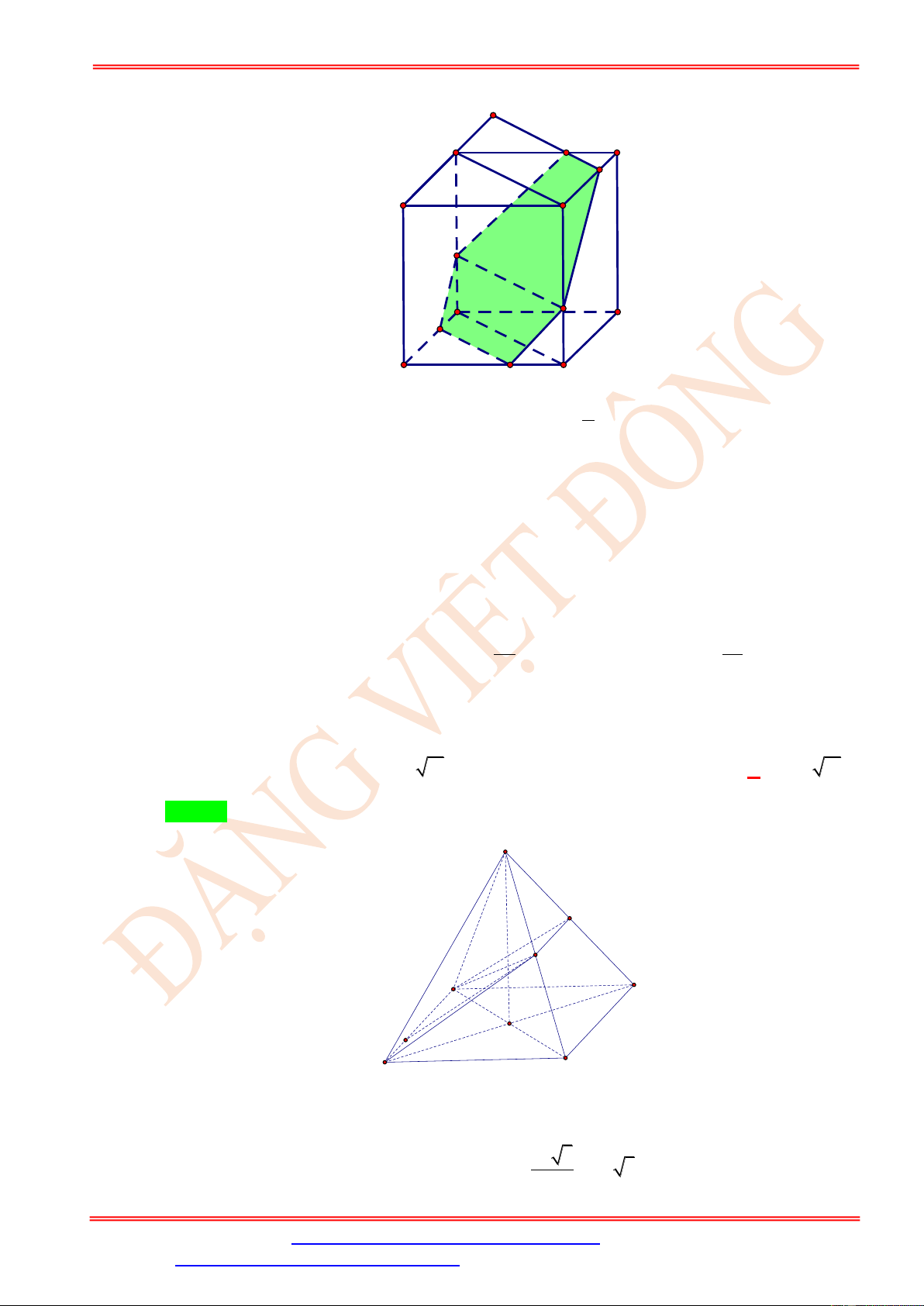
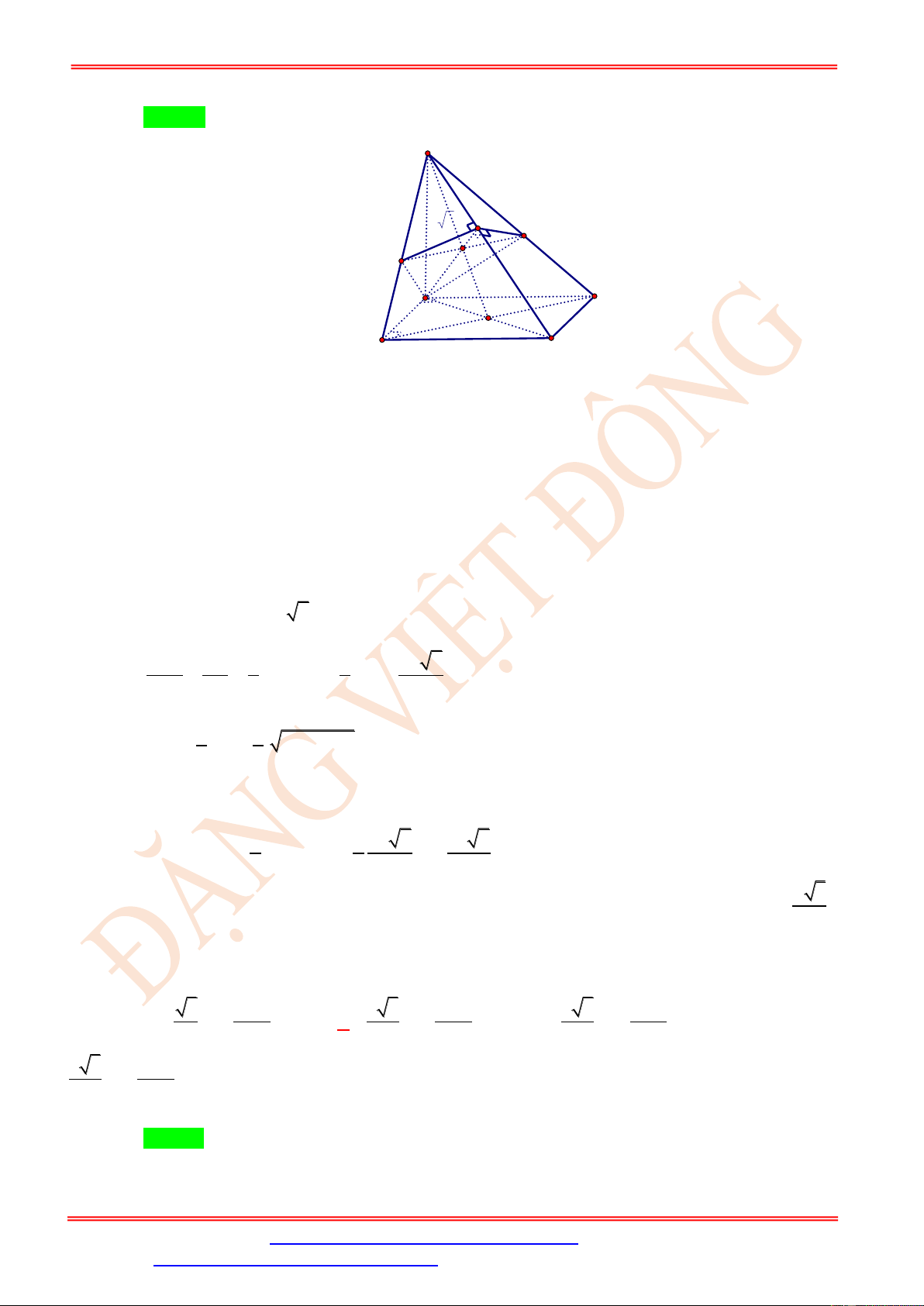
Cho hình lập phương ABC . D A B C D
cạnh a . Các điểm M , N , P theo thứ tự đó thuộc các a
cạnh BB , C D
, DA sao cho BM = C ' N = DP = . Mặt phẳng (MNP) cắt đường thẳng 3
A' B ' tại E. Tính độ dài đoạn thẳng A ' E.
A. A' E = 5a 3.
B. A' E = 3a 4 .
C. A' E = 5a 4 .
D. A ' E = 4a 3. . Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB = 8a ,
SA = SB = SC = SD = 8a . Gọi N là trung điểm cạnh SD . Tính diện tích thiết diện của hình
chóp S.ABCD cắt bởi mặt phẳng ( ABN ) . A. 2 12a . B. 2 6a 11 . C. 2 24a . D. 2 12a 11 . Câu 5.
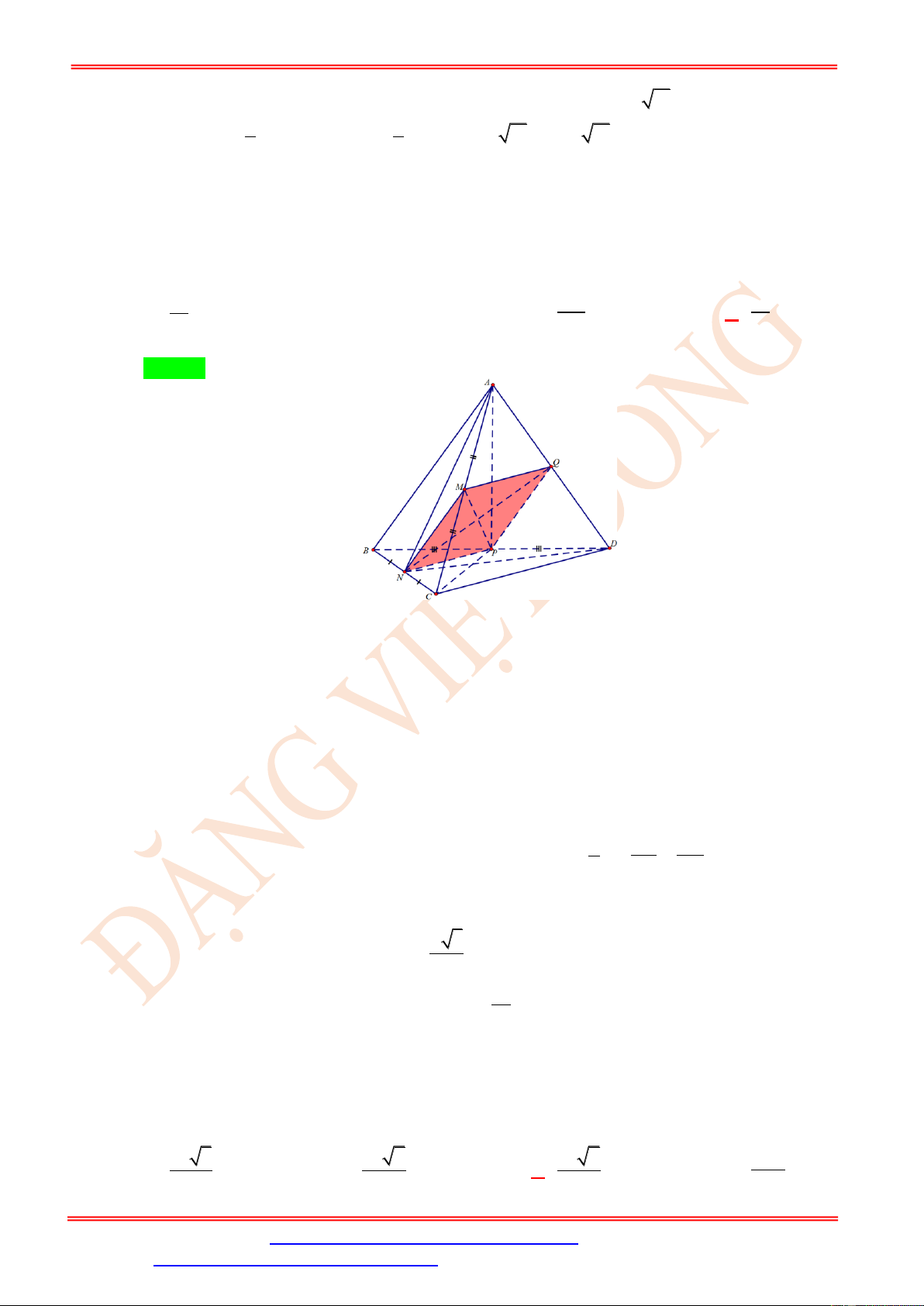
Cho tứ diện ABCD có tất cả các cạnh bằng a . Gọi M, N, P lần lượt là trung điểm của
AC, BC, BD . Gọi tứ giác MNPQ là thiết diện của tứ diện ABCD cắt bởi mặt phẳng ( MNP)
. Tìm diện tích thiết diện MNPQ theo a . 2 2 2 a 3a a A. . B. 2 a . C. . D. . 2 4 4 Câu 6.
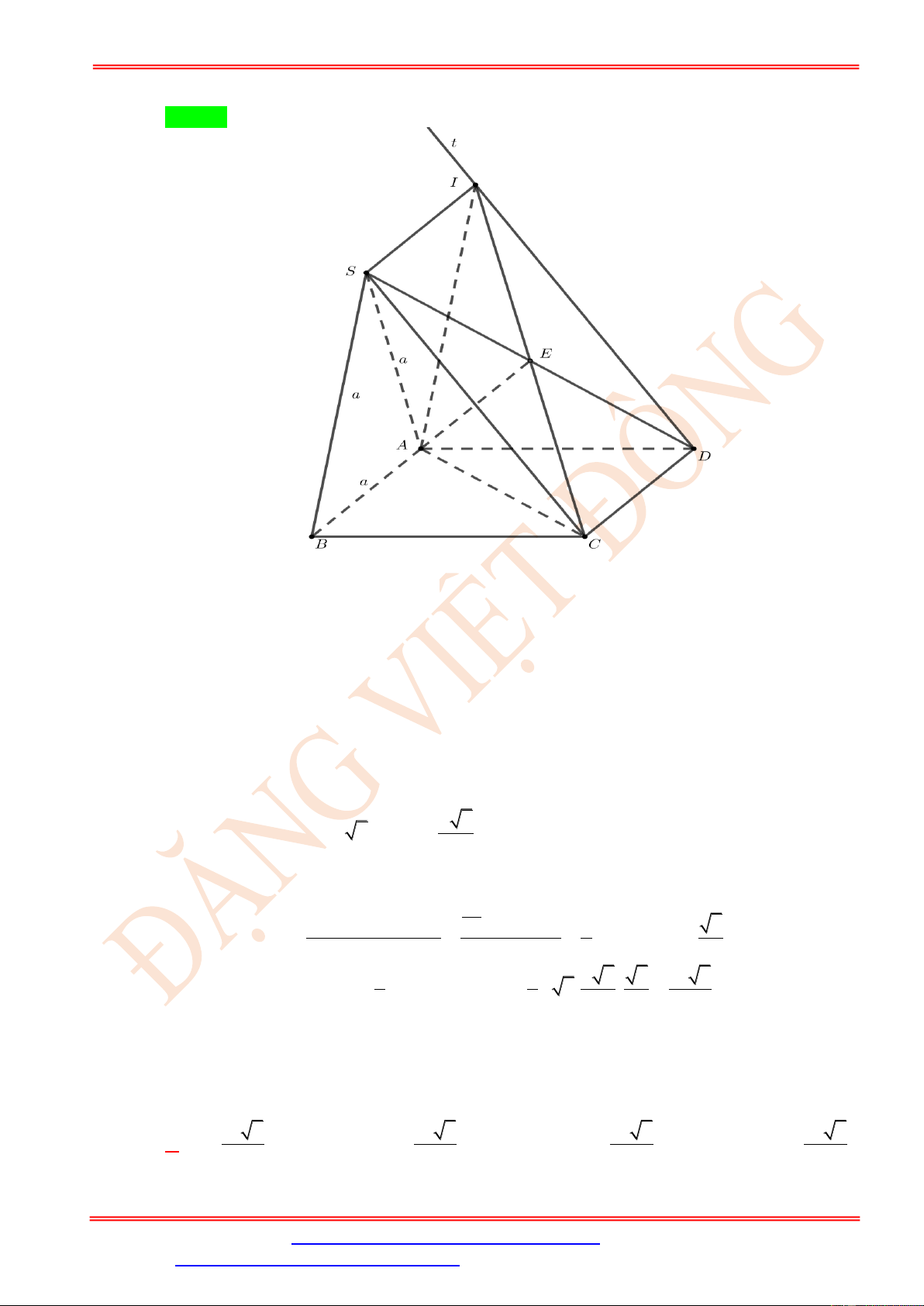
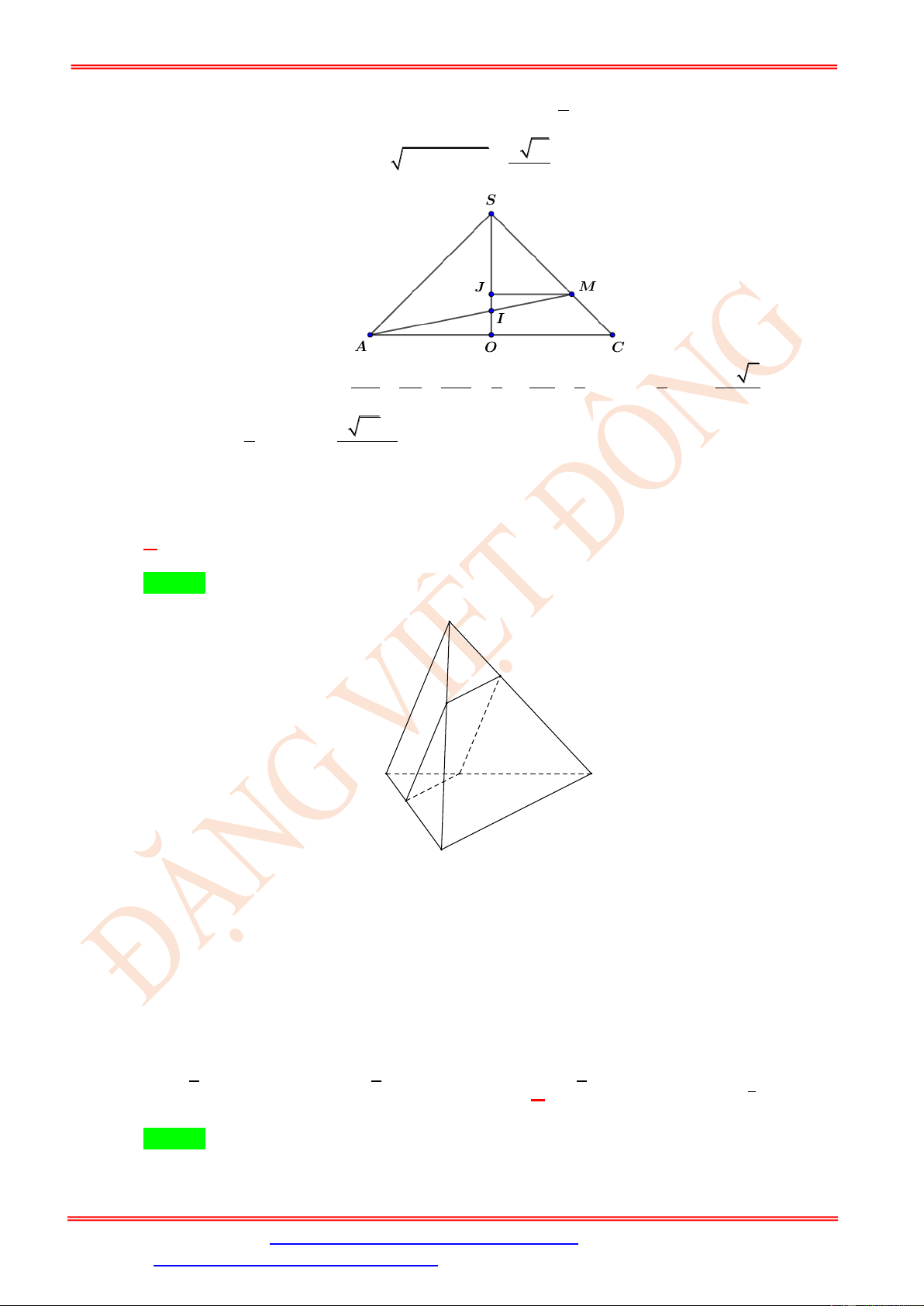
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, biết AB = a , SAD = 90 và tam giác
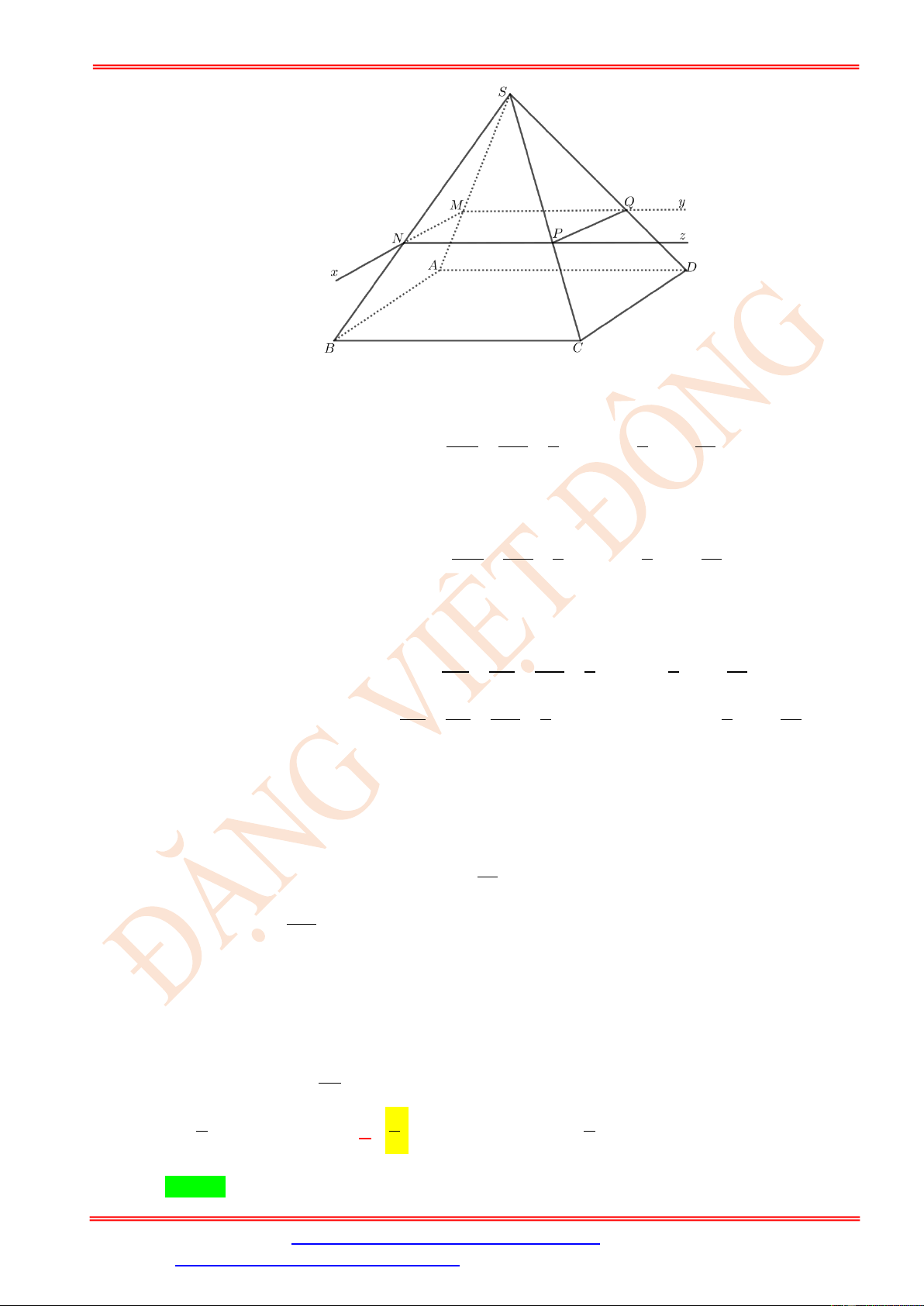
SAB là tam giác đều. Gọi Dt là đường thẳng qua D và song song với SC , I là giao điểm
của Dt với mặt phẳng (SAB) . Thiết diện của hình chóp S.ABCD với mặt phẳng ( AIC) có diện tích là 2 a 5 2 a 2 2 a 7 2 11a A. . B. . C. . D. . 16 4 8 32 Câu 7.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều,
SAD = 90 . Gọi Dx là đường thẳng qua D và song song với SC . Gọi I là giao điểm của
Dx và (SAB) . Tìm thiết diện của hình chóp cắt bởi mặt phẳng của ( AIC ) và tính diện tích
của thiết diện đó 2 a 7 2 a 7 2 a 7 2 a 7 A. S = . B. S = . C. S = . D. S = . 8 4 6 9
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Câu 8.
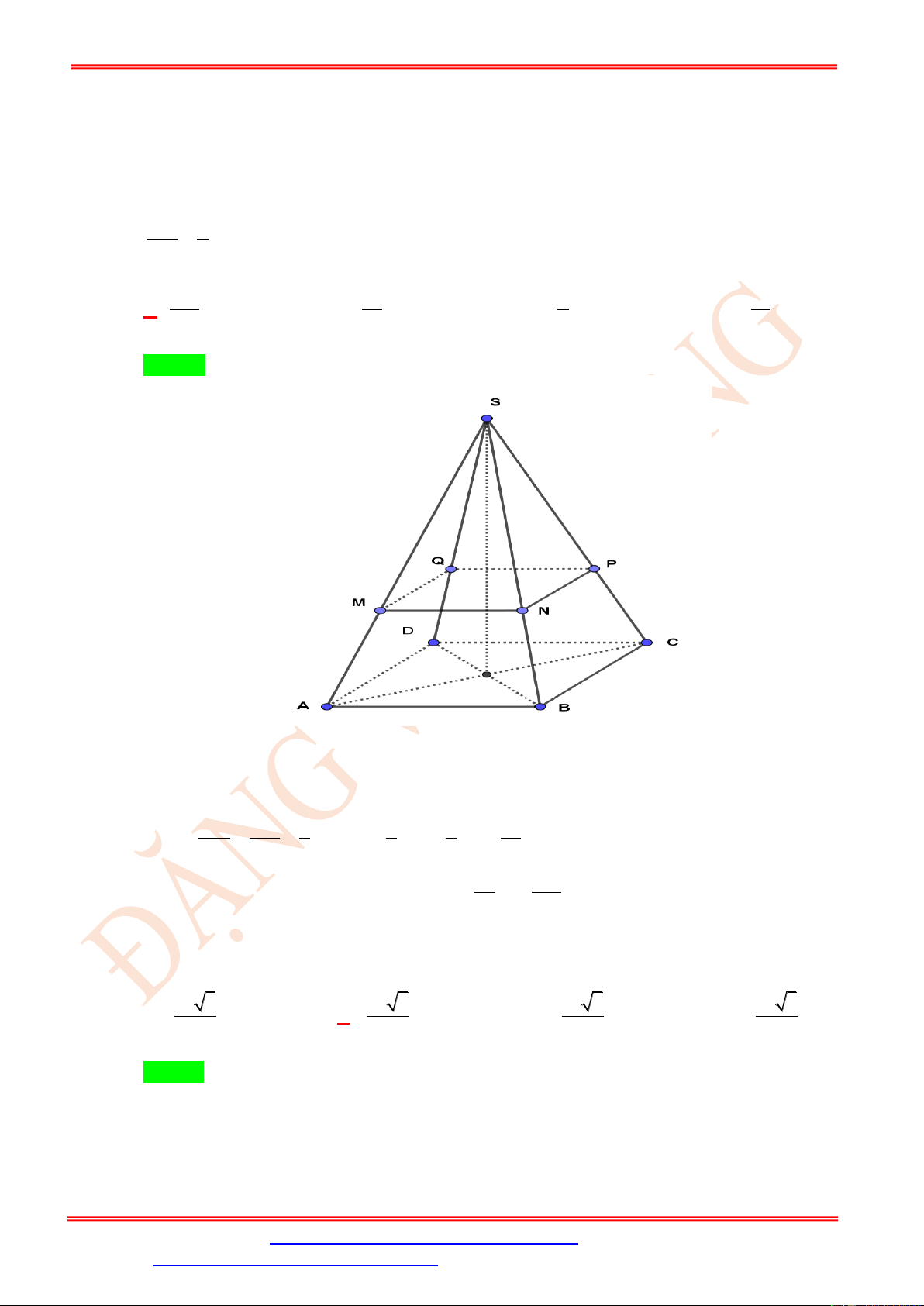
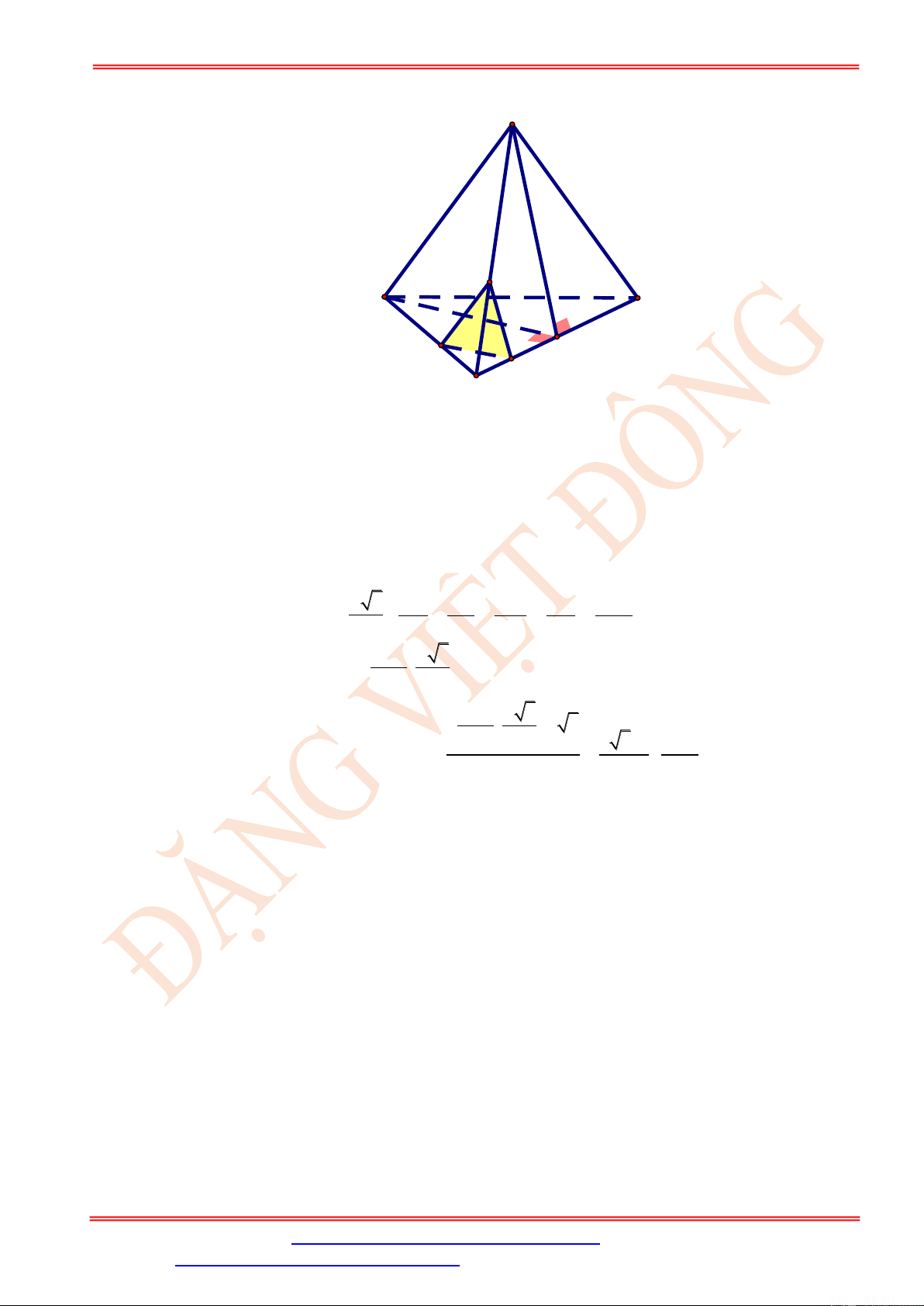
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. M là điểm trên cạnh SA sao cho SM 2
= . Một mặt phẳng ( ) đi qua M song song với AB và AD , cắt hình chóp theo một SA 3
tứ giác có diện tích là 400 20 4 16 A. . B. . C. . D. . 9 3 9 9 Câu 9.
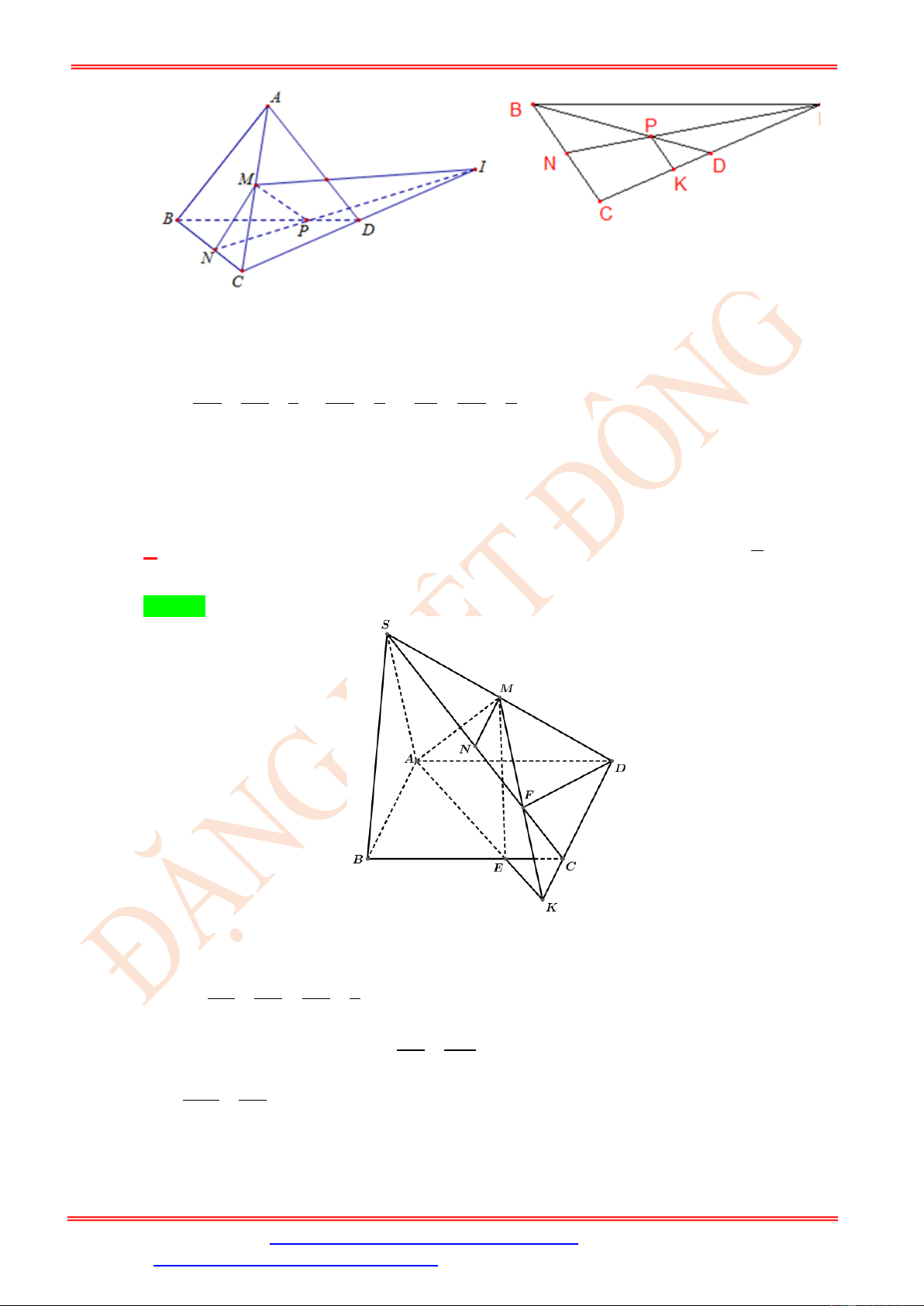
Cho tứ diện ABCD, hai điểm M , N lần lượt là trung điểm của AC, BC . Trên đoạn thẳng
BD lấy điểm P sao cho BP = 2PD . Gọi I là giao điểm của đường thẳng CD và mặt phẳng
(MNP) . Tính tỷ số IP . IN 3 2 1 A. . B. . C. . D. 2 . 2 3 2
Dạng 2: Bài toán tỉ số
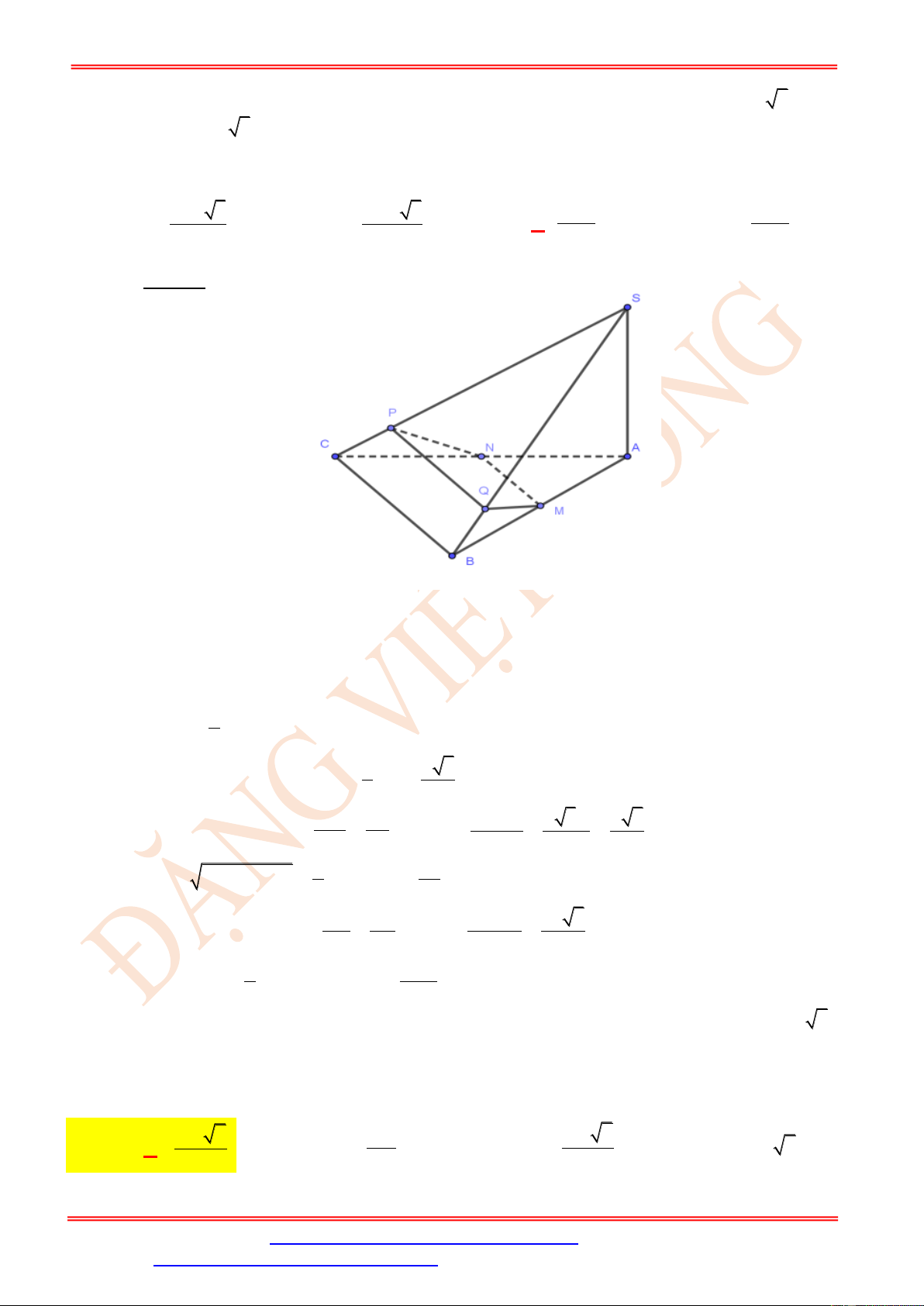
Câu 10. Cho hình chóp S.ABCD có đáy là hình bình hành; M là trung điểm của SD , E thuộc cạnh
BC sao cho BE = 2EC , mặt phẳng ( AME ) cắt SC tại F . Tính tỉ số diện tích 2 tam giác
SFD và FCD. 5 A. 3 . B. 2 . C. 4 . D. . 2
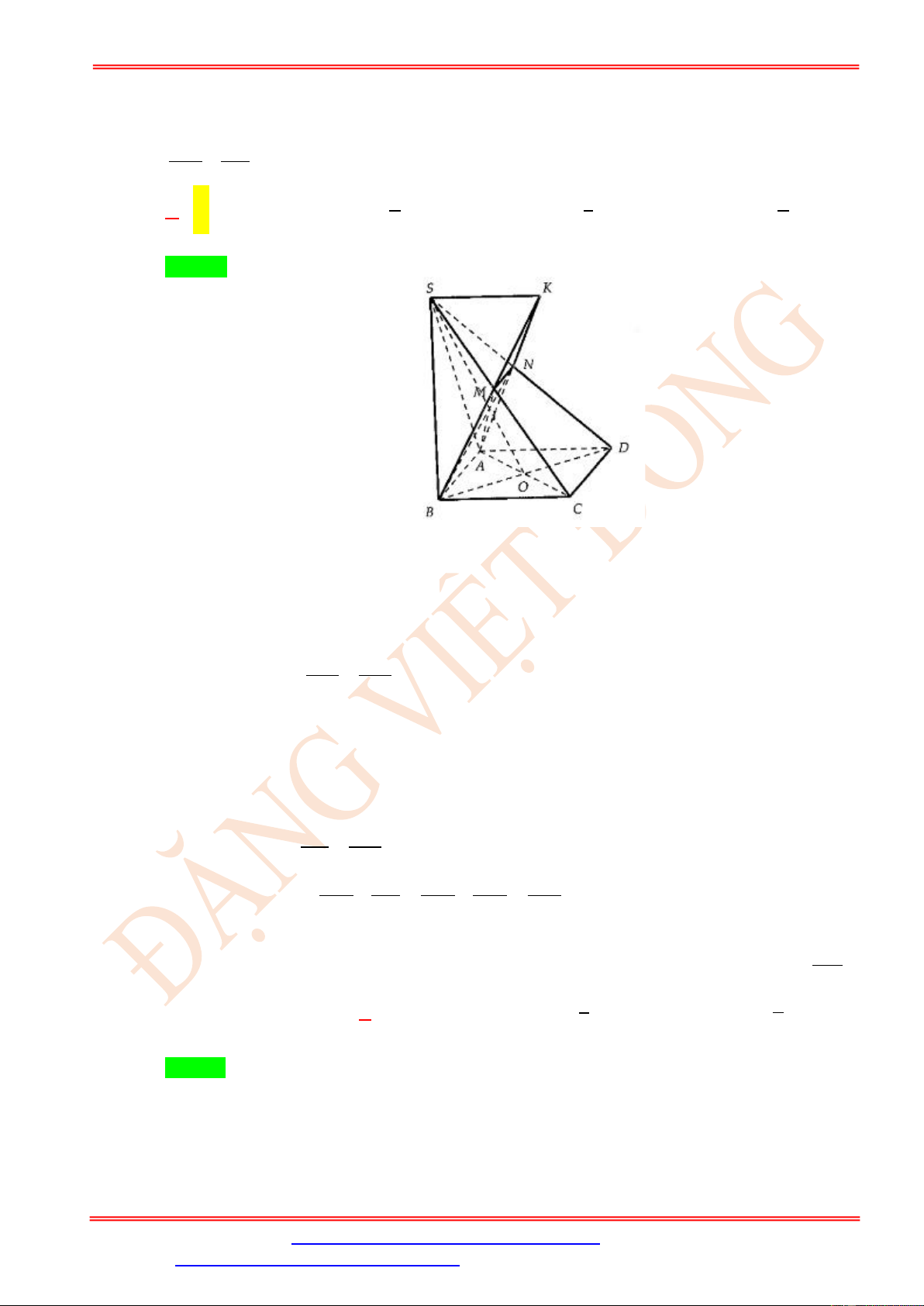
Câu 11. Cho hình chóp S.ABCD với đáy ABCD là hình bình hành tâm O . Mặt phẳng ( ) di động
chứa AB và cắt SC, SD lần lượt tại M , N . Biết K là giao điểm của AN và BM . Tính AB BC − . MN SK 1 1 2 A. 1. B. . C. . D. . 2 3 3 GA
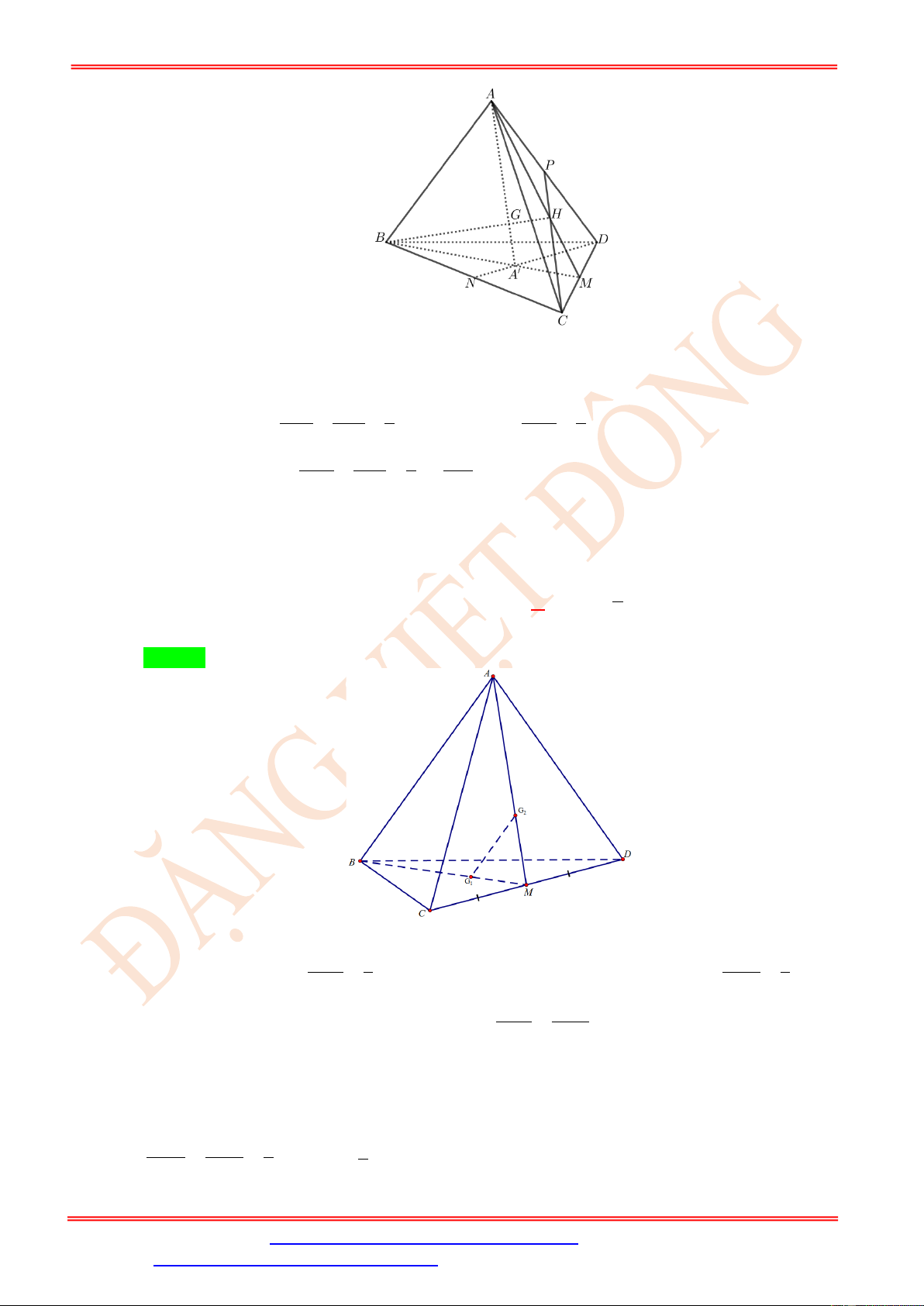
Câu 12. Gọi G là trọng tâm của tứ diện ABCD. Gọi A là trọng tâm của tam giác BCD.Tính GA . 1 1 A. 2 . B. 3 . C. . D. . 3 2
Câu 13. Cho tứ diện ABCD. Gọi G và G lần lượt là trọng tâm của các tam giác BCD và ACD . 1 2
Khẳng định nào sau đây sai?
A. G G // ABD .
B. G G // ABC . 1 2 ( ) 1 2 ( ) 2
C. BG , AG và CD đồng qui. D. G G = AB . 1 2 1 2 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCDlà hình thang ( AB / /CD) . Gọi I , J lần lượt là trung
điểm của các cạnh A ,
D BC và G là trọng tâm tam giác SAB . Biết mặt phẳng (GJI ) cắt SA và
SB lần lượt ở E và F ; EF = IJ . Hỏi khẳng định nào sao đây đúng? 1 3 2
A. AB = CD . AB = CD . AB = 3CD . AB = CD . 3 B. 2 C. D. 3
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác ABC
và M là trung điểm SC . Gọi K là giao điểm của SD với mặt phẳng ( AGM ) . Tính tỷ số KS . KD
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 1 1 A. . B. . C. 2 . D. 3 . 2 3
Câu 16. Cho hình chóp .
S ABCD có đáy ABCD là tứ giác lồi. Gọi N, P lần lượt là trung điểm của SB
và AD . Gọi I là trung điểm của NP và G là giao điểm của SI với mặt phẳng ( ABCD) . Tính tỉ số IS T = . IG 3 3
A. T = 2. B. T = . C. T = .
D. T = 3. 5 4
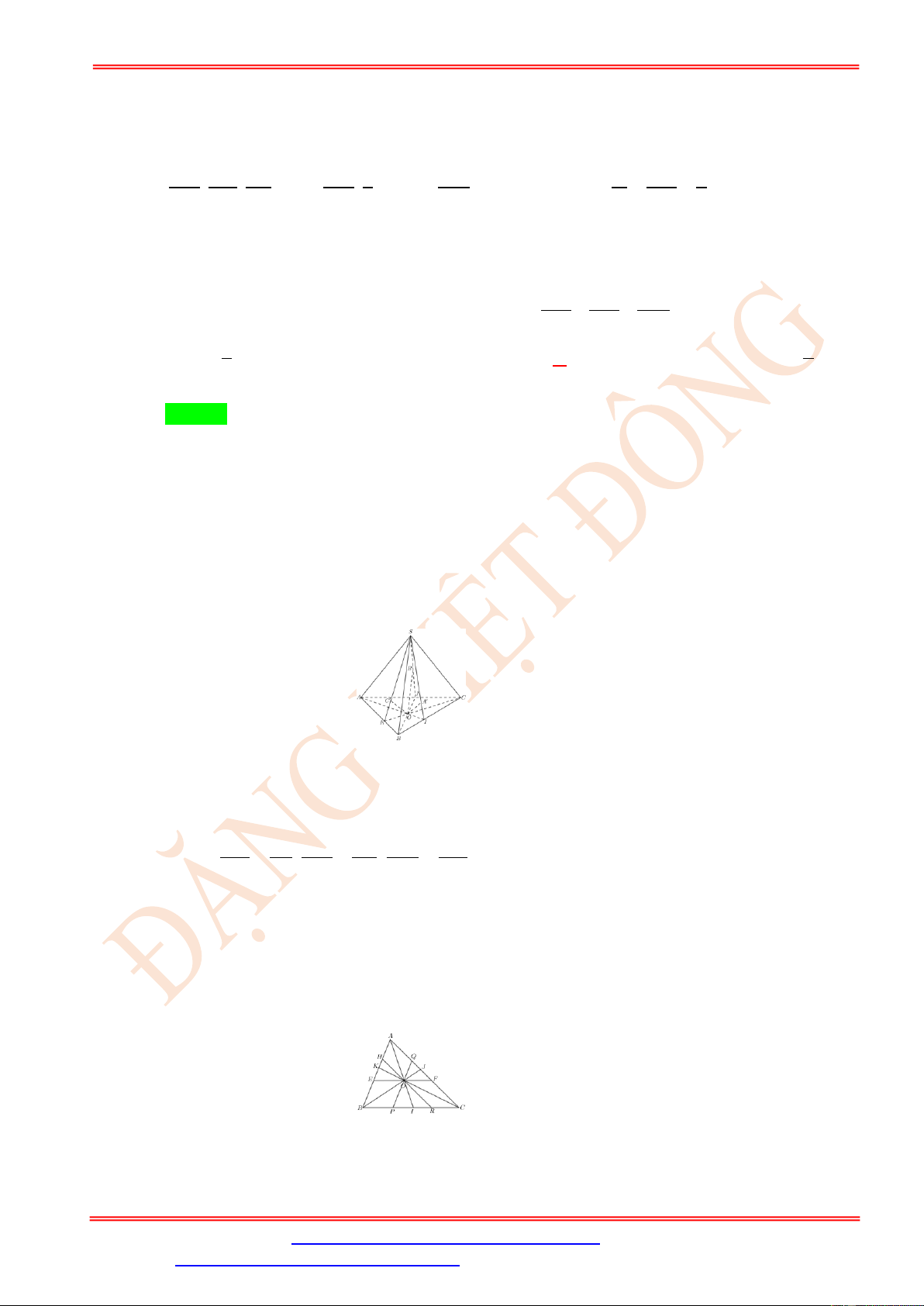
Câu 17. Cho hình chóp SABC . Bên trong tam giác ABC lấy một điểm O bất kỳ. Từ O dựng các đườ (SBC) (SCA)
ng thẳng lần lượt song song với SA , SB , SC và cắt các mặt phẳng , , O A O B OC ( T = + +
SAB ) theo thứ tự lần lượt tại A ,
B , C . Khi đó tổng tỉ số SA SB SC bằng bao nhiêu ? 3 1
A. T = 3. B. T = . C. T =1. D. T = . 4 3
Câu 18. Cho hình lập phương ABC . D A B C D
cạnh a . Các điểm M , N , P theo thứ tự đó thuộc các cạnh a BB, C D
, DA sao cho BM = C N
= DP = . Biết mặt phẳng (MNP) cắt cạnh AB tại 3
điểm I . Tính tỉ số BI . BA 1 2 1 1 A. . B. . C. . D. . 2 3 4 3
Câu 19. Cho tứ diện ABCD. Gọi I , J lần lượt là trung điểm của AC và BC . Trên cạnh BD lấy
điểm K sao cho BK = 2KD. Gọi F là giao điểm của AD với mặt phẳng ( IJK ) . Tính tỉ số FA . FD 7 11 5 A. . B. 2 . C. . D. . 3 5 3
Câu 20. Cho tứ diện 𝐴𝐵𝐶𝐷 có tất cả các cạnh bằng 1. Gọi 𝑀, 𝑁 lần lượt là điểm thuộc cạnh 𝐴𝐷 và 𝐵𝐶 𝑀𝐴 𝑁𝐶 1 sao cho =
= . Độ dài đoạn 𝑀𝑁 thuộc khoảng nào trong các khoảng sau đây? 𝑀𝐷 𝑁𝐵 2 3 1 1 3
A. ( ; 2).
B. (0; ).
C. ( ; 1).
D. (1; ). 2 2 2 2
Câu 21. Cho tứ diện ABCD. Điểm M là trung điểm của cạnh AC , điểm N thuộc cạnh AD sao cho:
AN = 2ND , điểm Q thuộc cạnh BC sao cho BC = 4BQ . Gọi I là giao điểm của đường
thẳng MN và mặt phẳng ( BCD) , J là giao điểm của đường thẳng BD và mặt phẳng (MNQ) . Khi đó JB JQ + bằng JD JI 13 20 3 11 A. . B. . C. . D. . 20 11 5 12
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Hai điểm M , N lần lượt nằm trên các đoạn SM SN m S , O SD sao cho * = = , , m n , ( ,
m n) = 1. Điểm E là trung điểm của SO SD n
BC . Biết thiết diện của hình chóp cắt bởi mp ( MNE ) đi qua trung điểm cạnh SA . Giá trị
m + n bằng
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A. 7 . B. 5 . C. 3 . D. 4 .
Câu 23. Cho hình chóp S.ABC . Bên trong tam giác lấy một điểm O bất kỳ. Từ O dựng các đường
thẳng lần lượt song song với S , A S ,
B SC và cắt các mặt phẳng ( SBC ) ,( SCA) ,(SAB) theo thứ
tự lần lượt tại A , B ,C . Khi đó tổng tỉ số OA OB OC T = + + bằng bao nhiêu? SA SB SC 1 3 A. T = .
B. T = 3. C. T =1. D. T = . 3 4
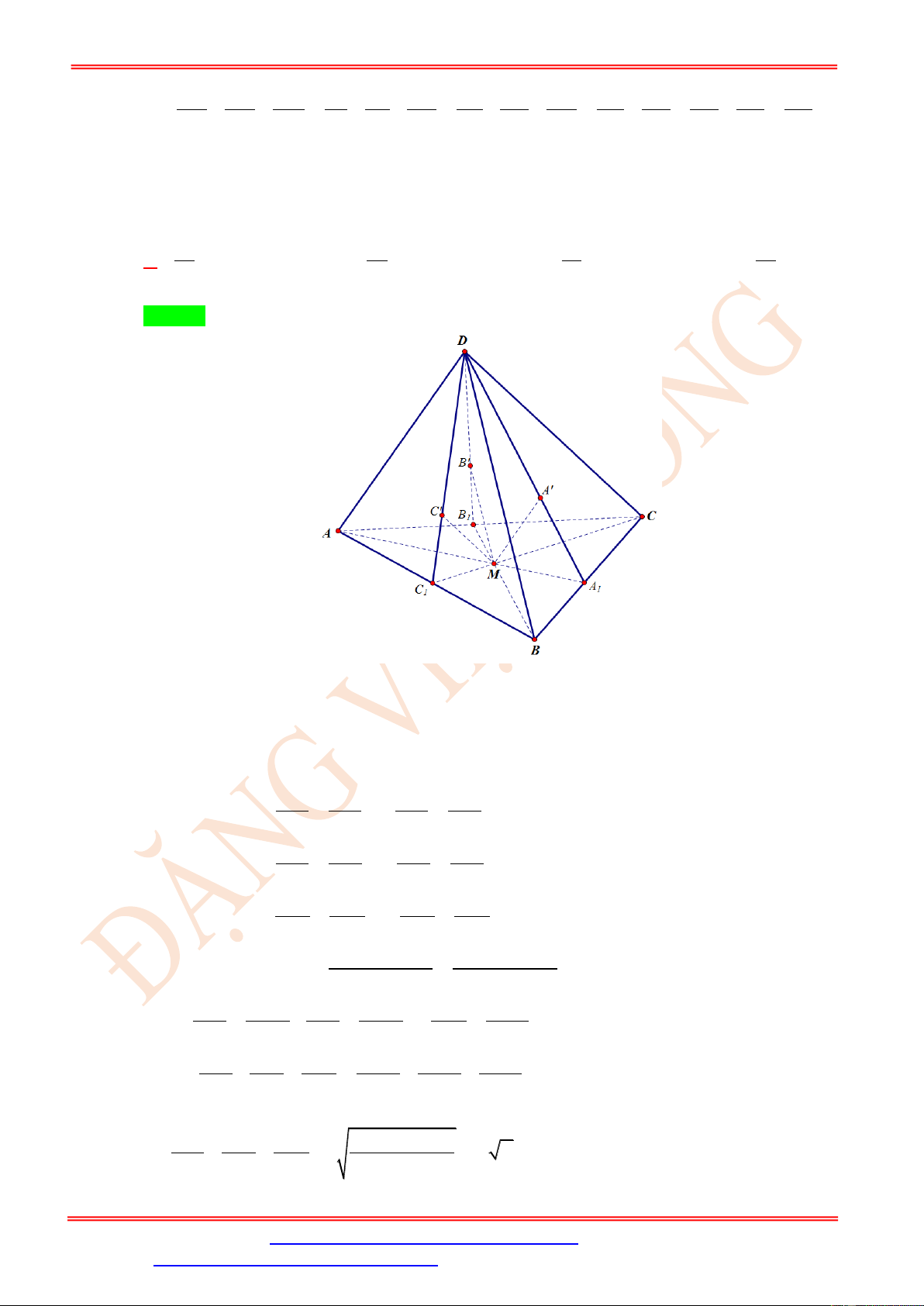
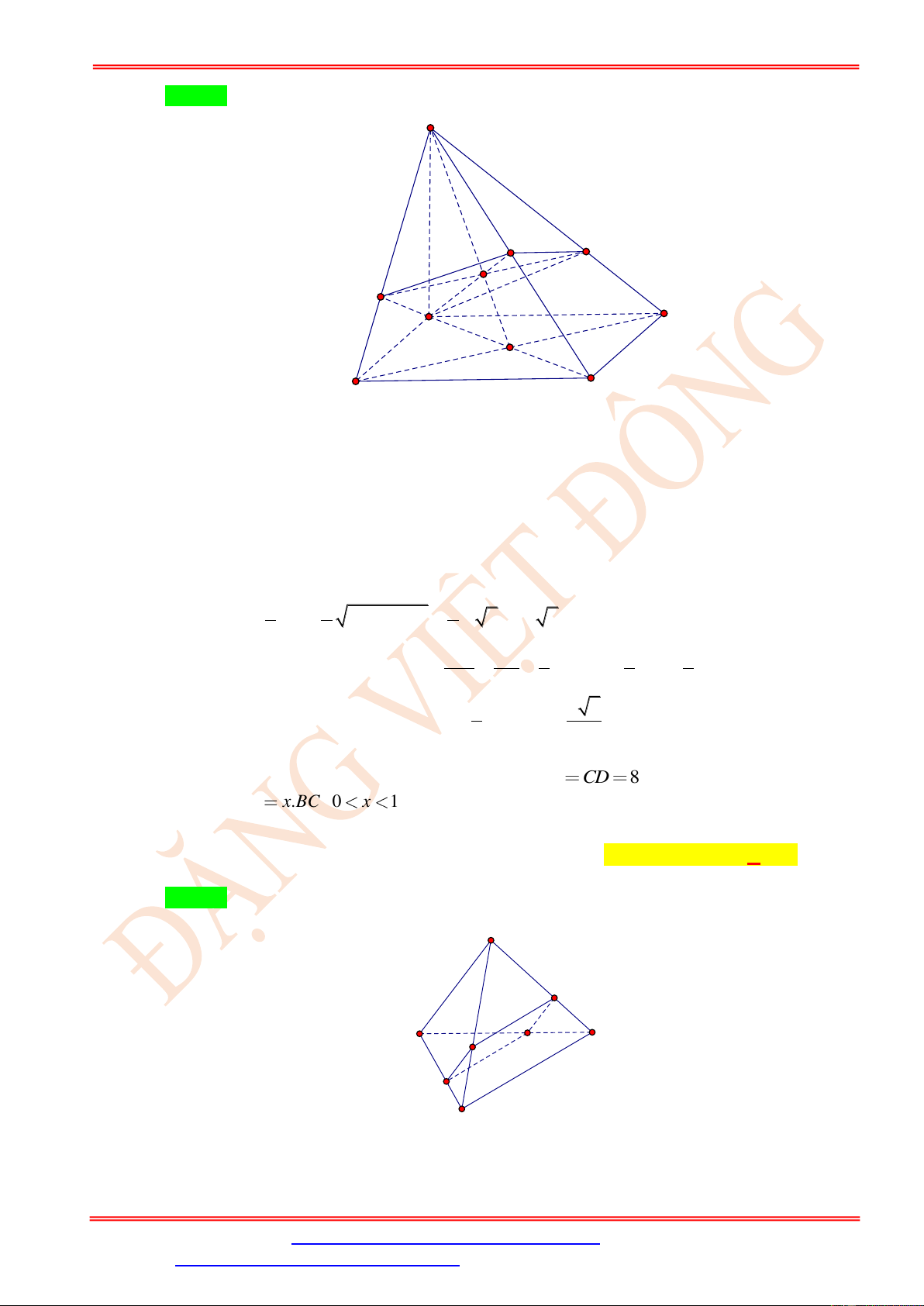
Câu 24. Cho tứ diện ABCDcó AB = CD = 4, BC = AD = 5, AC = BD = 6. M là điểm thay đổi trong
tam giác ABC . Các đường thẳng qua M song song với , AD ,
BD CD tương ứng cắt mặt
phẳng (BCD), ( ACD), ( ABD)tại A , B , C . Giá trị lớn nhất của MA.MB .MC là 40 24 30 20 A. . B. . C. . D. . 9 9 9 9
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
Dạng 1: Tính diện tích thiết diện Câu 25.
Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 0 4, BAC = 30 . Mặt
phẳng song song vơi ( ABC ) cắt đoạn thẳng SA tại M sao cho SM = 2MA. Diện tích thiết
diện của với hình chóp S.ABC bằng. 25 14 16 A. B. . C. . D. 1. 9 9 9
Câu 26. Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh a , SA = SB = SC = 2a . Gọi M là
một điểm trên đoạn thẳng SB mà SM = m (0 m 2a) . Mặt phẳng ( ) qua M , song song
với SA và BC cắt hình chóp theo thiết diện có chu vi là:
A. 4a − 2m . B. 4a .
C. 4a − m .
D. 2a + m .
Câu 27. Bộ c = 1 − , a = 1 − , b = 4 thỏa 2 2 2
A = a + b + c = 18 nên chọn đáp án C Cho hình chóp
S.ABCD có đáy là hình vuông cạnh a , các cạnh bên bằng a 2 . Gọi M là trung điểm của
SD . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng ( ABM ) . 2 3 15a 2 3 5a 2 3 5a 2 15a A. . B. . C. . D. . 16 16 8 16
Câu 28. Cho hình chóp S.ABCD có đáy ABCDlà hình vuông cạnh bằng a , hai tam giác SA , B SAD
vuông cân tại A . Gọi G là trọng tâm tam giác SAB . Gọi ( ) là mặt phẳng đi qua G và song song với S ,
B AD .Thiết diện tạo bởi mp ( ) và hình chóp S.ABCD có diện tích bằng 2 2a 3 2 4a 2 2 4a 2 2 4a 3 A. . B. . C. . D. . 9 3 9 9
Câu 29. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC sao cho
SM = 2MC . Mặt phẳng ( P ) chứa AM và song song với BD. Tính diện tích thiết diện của
hình chóp S.ABCD cắt bởi ( P ) . 2 3a 2 4 26a 2 2 26a 2 2 3a A. . B. . C. . D. . 5 15 15 5
Câu 30. Cho hình chóp S.ABCD có SA vuông góc với mặt đáy, ABCD là hình vuông cạnh a 2 ,
SA = 2a . Gọi M là trung điểm cạnh SC , ( ) là mặt phẳng đi qua A , M và song song với
đường thẳng BD. Tính diện tích thiết diện của hình chóp bị cắt bởi mặt phẳng ( ) . 2 4a 2 4a 2 2 2a 2 A. 2 a 2 . B. . C. . D. . 3 3 3
Câu 31. Cho tứ diện ABCD có AB = a, CD = b . Gọi I , J lần lượt là trung điểm AB và CD , giả sử
AB ⊥ CD . Mặt phẳng ( ) qua M nằm trên đoạn IJ và song song với AB và CD. Tính diện
tích thiết diện của tứ diện ABCD với mặt phẳng ( ) biết IM = 1 IJ . 3 ab 2ab A. ab . B. . C. 2ab . D. . 9 9
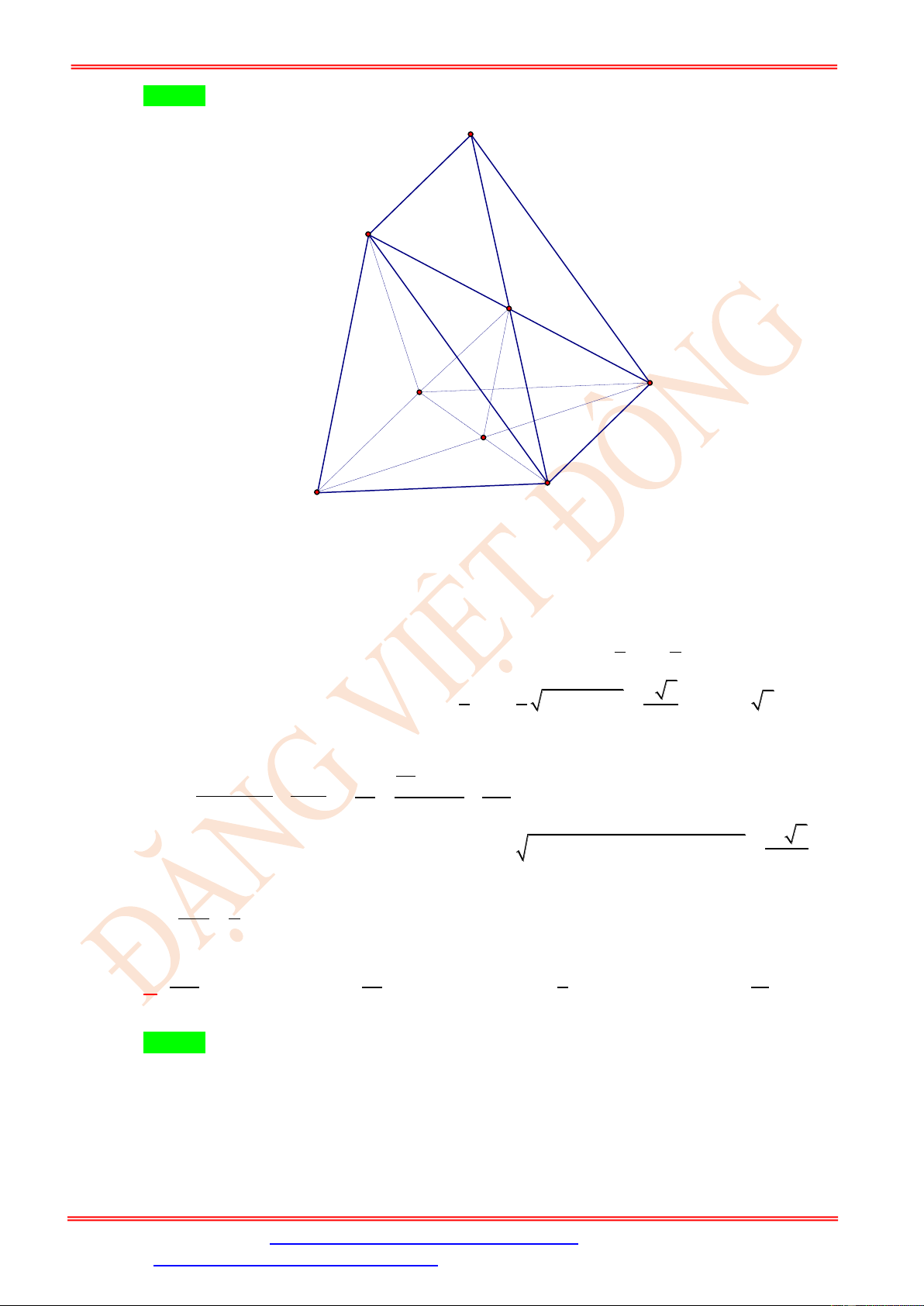
Câu 32. Cho hình tứ diện ABCD có tất cả các cạnh bằng 6a . Gọi M , N lần lượt là trung điểm của C ,
A CB .Gọi P là điểm trên cạnh BD sao cho BP = 2PD . Diện tích S thiết diện của tứ diện
ABCD bị cắt bởi mặt phẳng (MNP) là:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 2 5a 51 2 5a 147 2 5a 51 2 5a 147 A. S = . B. S = . C. S = . D. S = . 2 4 4 2
Câu 33. Cho tứ diện ABCD có tất cả các cạnh bằng a , I là trung điểm của AC , J là một điểm trên
cạnh AD sao cho AJ = 2JD . ( P) là mặt phẳng chứa IJ và song song với AB . Tính diện
tích thiết diện khi cắt tứ diện bởi mặt phẳng ( P) . 2 3a 51 2 3a 31 2 a 31 2 5a 51 A. . B. . C. . D. . 144 144 144 144
Câu 34. Cho tứ diện ABCDcó AB vuông góc với CD và AB = ,
a CD = b . Gọi I , J lần lượt là trung điểm của 1
AB và CD , điểm M thuộc đoạn IJ sao cho IM =
IJ . Gọi ( ) là mặt phẳng qua 3
M , song song với AB và CD . Diện tích thiết diện của tứ diện ABCD cắt bởi mặt phẳng ( ) là 2ab 4ab 2ab 3ab A. . B. . C. . D. . 9 9 3 2
Câu 35. Cho tứ diện ABCDcó AB = a, CD = 3a . Gọi I , J lần lượt là trung điểm AB và CD , giả sử
AB ⊥ CD . Mặt phẳng ( ) qua M nằm trên đoạn IJ và song song với AB và CD. Tính diện
tích thiết diện của tứ diện ABCDvới mặt phẳng ( ) biết IM = 1 IJ . 3 2 3a 2 2a A. 2 2a . B. . C. 2 4a . D. . 2 3
Dạng 2: Bài toán tỉ số
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N , P lần lượt là
trung điểm của AB, AD và SO . Gọi H là giao điểm của SC với mặt phẳng (MNP) . Tính SH . SC 3 2 1 1 A. . B. . C. . D. . 4 3 4 3
Câu 37. Cho tứ diện ABC .
D Gọi G và G lần lượt là trọng tâm các tam giác BCD và AC . D Mệnh 1 2
đề nào sau đây sai? A. G G ABD . B. G G ABC . 1 2 ( ) 1 2 ( ) 2
C. BG , AG và CD đồng qui. D. G G = AB . 1 2 1 2 3
Câu 38. Cho hình hộp 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′. Gọi 𝑀 là trung điểm của 𝐴𝐵. Mặt phẳng (𝑀𝐴′𝐶′) cắt cạnh 𝑀𝑁
𝐵𝐶 của hình hộp 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ tại 𝑁. Tính tỉ số 𝑘 = . 𝐴′𝐶′ 1 1 1 1 A. 𝑘 = . B. 𝑘 = . C. 𝑘 = . D. 𝑘 = . 2 2 2 2
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi ( ) là mặt phẳng đi qua AC
và song song với SB . Mặt phẳng ( ) cắt SD tại E. Chọn khẳng định đúng trong các khẳng định sau 1 1 1 A. SE = ED . B. SE = SD . C. SE = SD .
D. SE = 2SD. 3 2 3
Câu 40. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M , N , P lần lượt là trung
điểm của SB , SD và OC . Gọi giao điểm của (MNP) với SA là K . Tỉ số KS là KA
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 2 1 1 1 A. . B. . C. . D. . 5 3 4 2
Câu 41. Cho tứ diện ABCD . Gọi M ,
lần lượt là trọng tâm các tam giác N
BCD và ACD . Chọn khẳng định sai? 2
A. MN // ( ABD) . B. MN = AB . 3 đồ MN // ABC
C. BM , AN,CD ng quy. D. ( ) .
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của
SB và G là trọng tâm của tam giác SAD . Gọi J là giao điểm của AD và mặt phẳng (OMG)
. Tính tỉ số JA . JD 1 5 A. 2 . B. 1. C. . D. . 2 3
Câu 43. Cho hình bình hành ABCD. Qua A , B , C , D lần lượt vẽ các nửa đường thẳng Ax , By , Cz
, Dt ở cùng phía so với mặt phẳng ( ABCD) , song song với nhau và không nằm trong
( ABCD) . Một mặt phẳng (P) cắt Ax , By , z
C , Dt tương ứng tại A , B, C , D sao cho
AA = 3, BB = 5 , CC = 4 . Tính DD . A. 4 . B. 6 . C. 2 . D. 12 .
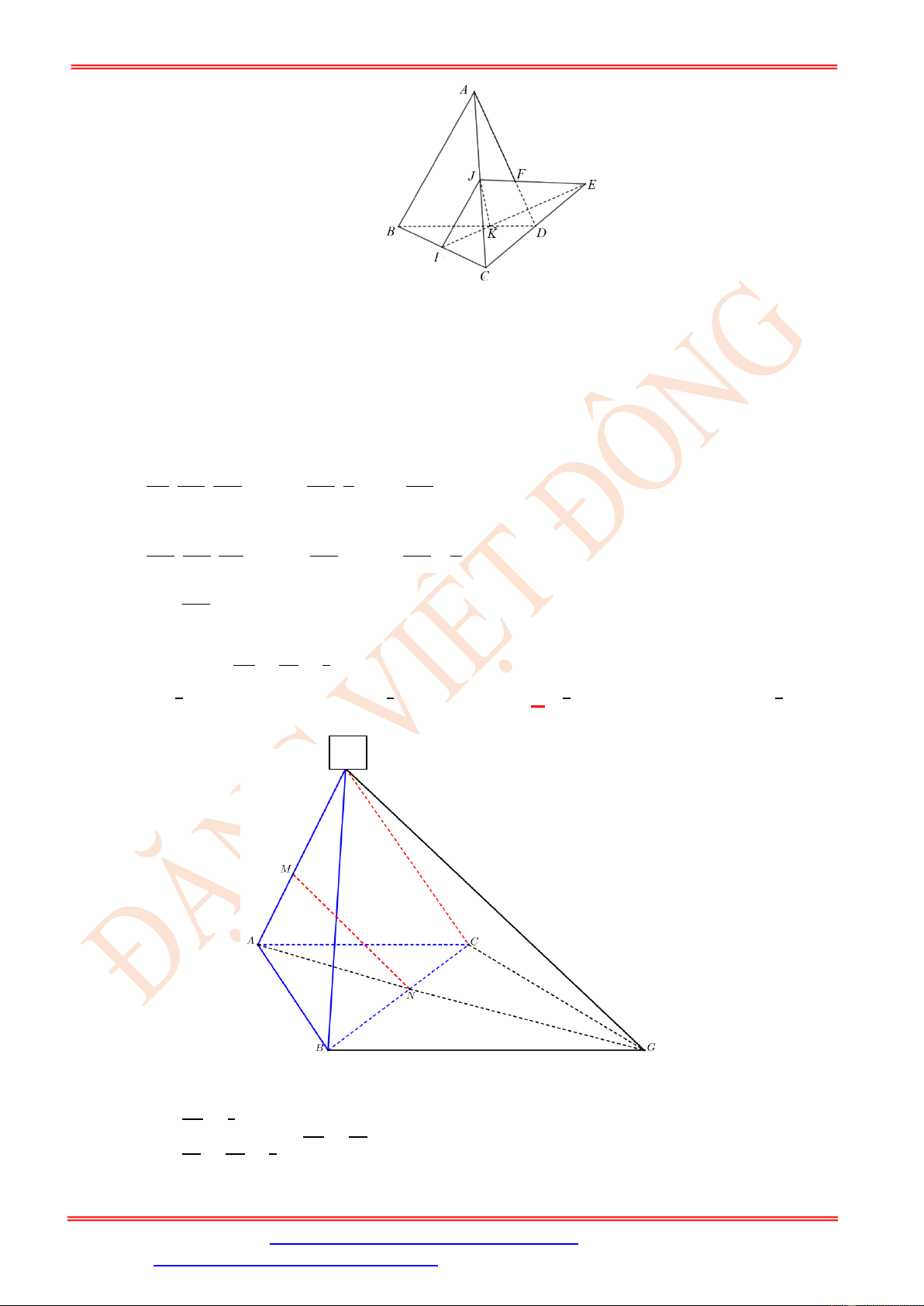
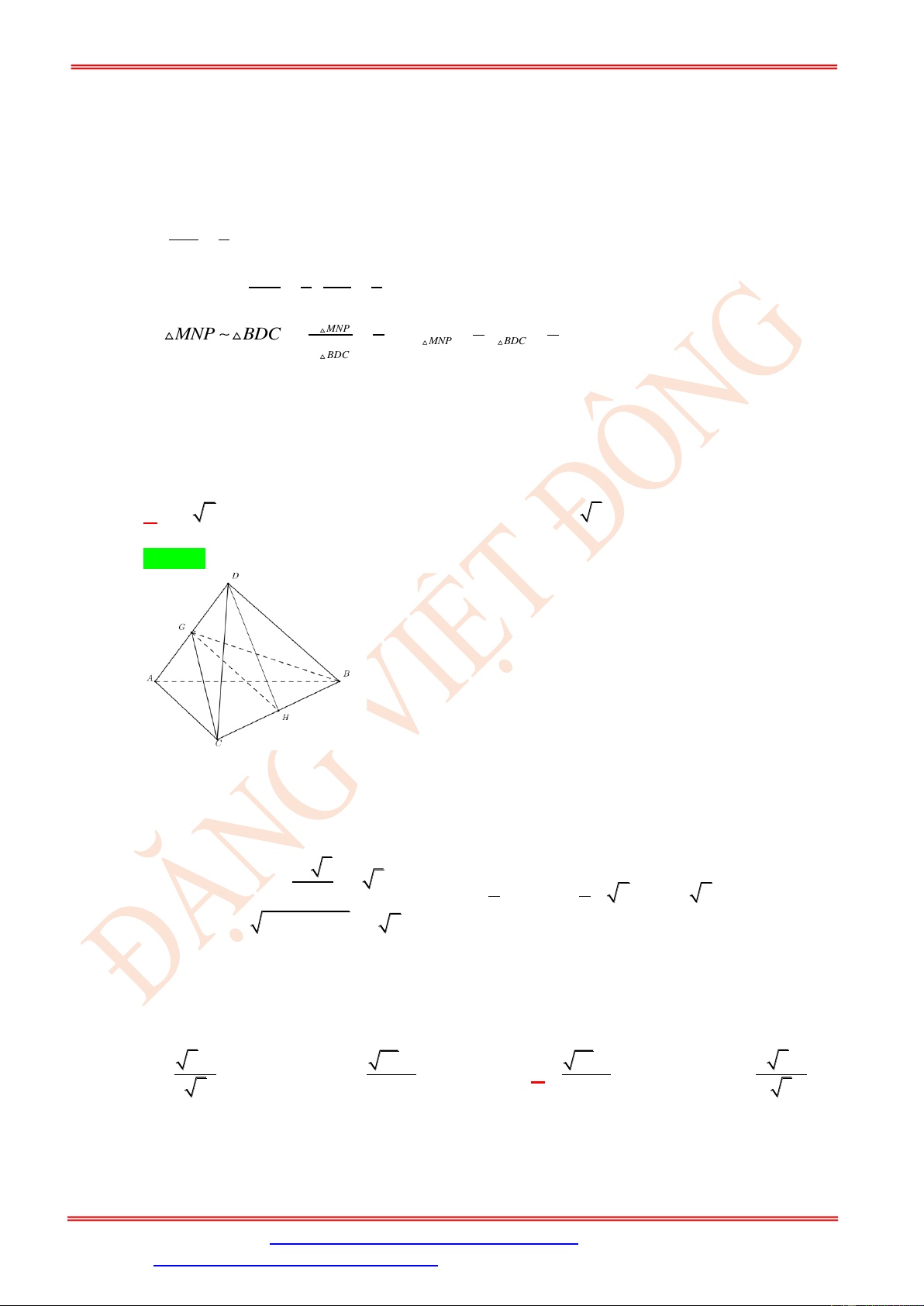
Câu 44. Cho tứ diện ABCDcó tam giác BCD đều cạnh a , tam giác ACD vuông. Gọi I , J lần lượt
là tâm đường tròn nội tiếp các tam giác ABC và ABD. Biết rằng IJ song song với ( BCD) .
Tính diện tích tam giác ACD . 2 a 2 a 3 2 a A. . B. . C. . D. 2 a . 4 4 2
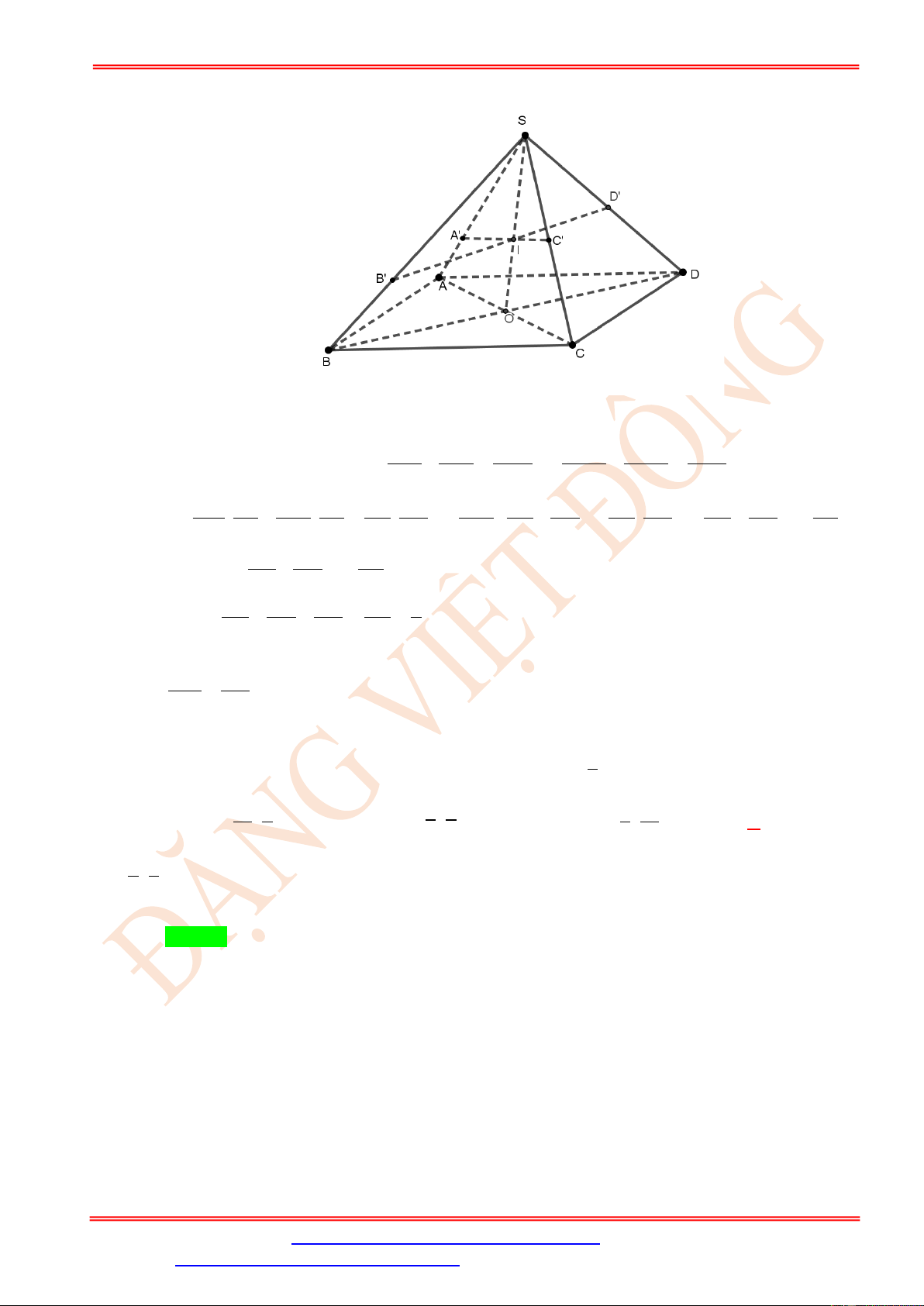
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A là điểm trên SA sao cho 1 A A = A S
. Mặt phẳng ( ) qua A cắt các cạnh SB , 2
SC , SD lần lượt tại B , C , D . Tính SB SD SC
giá trị của biểu thức T = + − SB SD SC . 3 1 1 A. T = . B. T = .
C. T = 2. D. T = . 2 3 2
Câu 46. Cho tứ diện ABCD và M , N lần lượt là các điểm trên hai cạnh A , B CD sao cho AM CN =
= k 0 và ( ) là mặt phẳng qua MN và song song với cạnh BC , gọi P là giao MB ND
điểm của ( ) với cạnh AC . Tìm k biết tỉ số diện tích tam giác MNP và diện tích thiết diện
của tứ diện được cắt bởi mặt phẳng ( ) bằng 1 . 3 3 2 3 4 1 3 2 3 A. k ; . B. k ; . C. k ; . D. k ; . 10 5 5 5 5 10 5 5
Câu 47. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD , N là
trọng tâm tam giác SAB . Đường thẳng MN cắt mặt phẳng (SBC) tại điểm I . Tính tỷ số IN . IM 3 1 1 2 A. . B. . C. . D. . 4 3 2 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 48. Cho t diện ABCD. Gọi M là trung điểm của CD , I là một điểm thuộc cạnh AD sao cho
IA = 3ID ; ( ) là mặt phẳng qua M , ( ) song song với CI và BD ; ( ) cắt AD , AB ,
BC lần lượt tại N, ,
P Q . Gọi R là giao điểm của MP và NQ . Khẳng định nào sau đây sai? RP 7 PN 7 RN 7 PN 7 A. = . B. = . C. = . D. = . RM 4 QM 4 RQ 3 BD 8 2
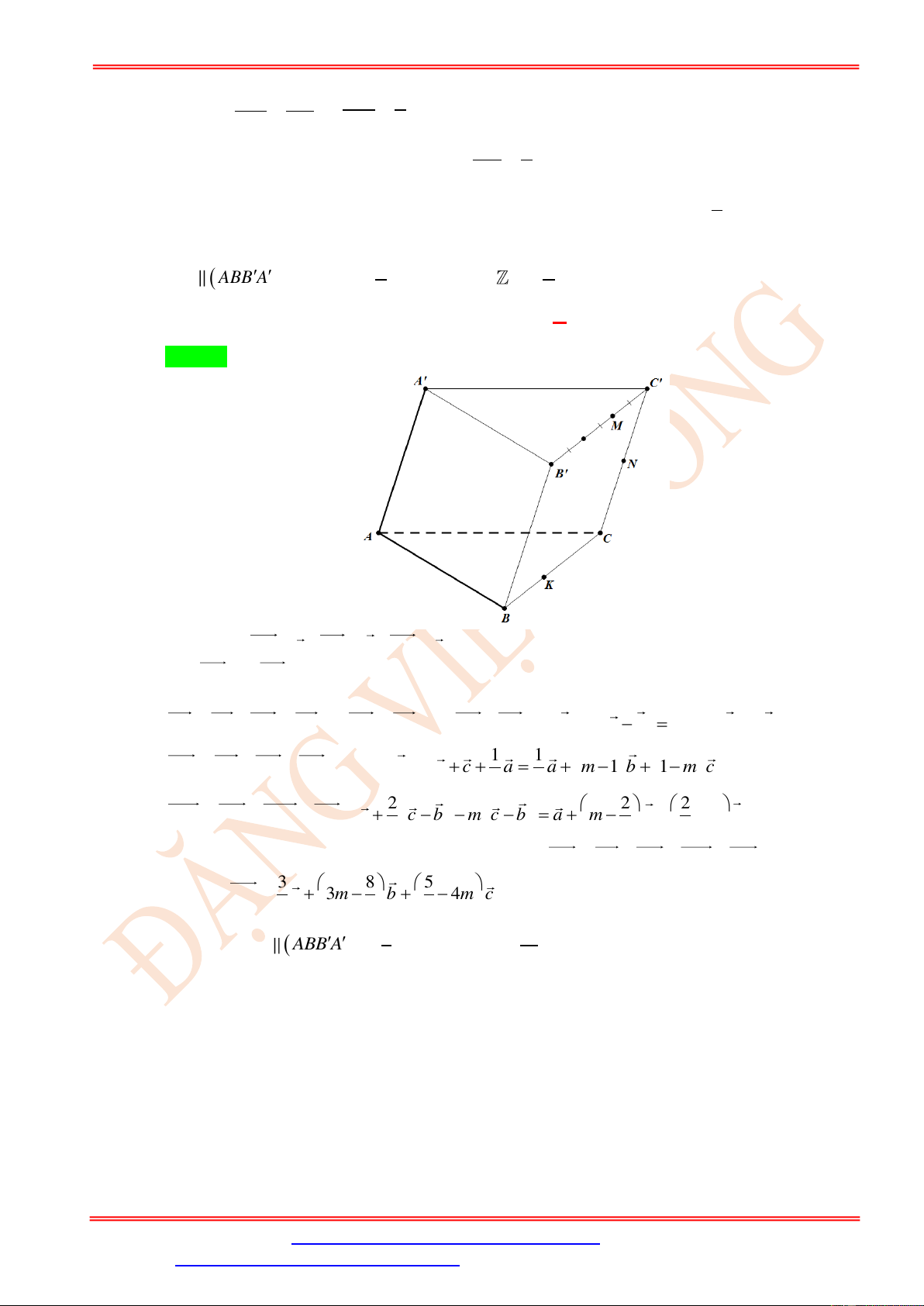
Câu 49. Cho hình lăng trụ AB . C A B C
có M thuộc cạnh B C sao cho B M = B C , N là trung 3
điểm cạnh CC . Gọi G là trọng tâm của tứ diện ANMA và K thuộc cạnh BC sao cho a KG ( ABB A ). Biết a BK = BC với , a b và
là phân số tối giản. Khi đó . a b bằng b b A. 4 . B. 10 . C. 60 . D. 84 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
HAI MẶT PHẲNG SONG SONG
Dạng 1: Tính diện tích thiết diện cắt bởi MP song song với MP khác Câu 50.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho SM 2
= . Một mặt phẳng ( ) đi qua M song song với AB và AD, cắt hình chóp theo một SA 3
tứ giác có diện tích là 400 20 4 16 A. . B. . C. . D. . 9 3 9 9
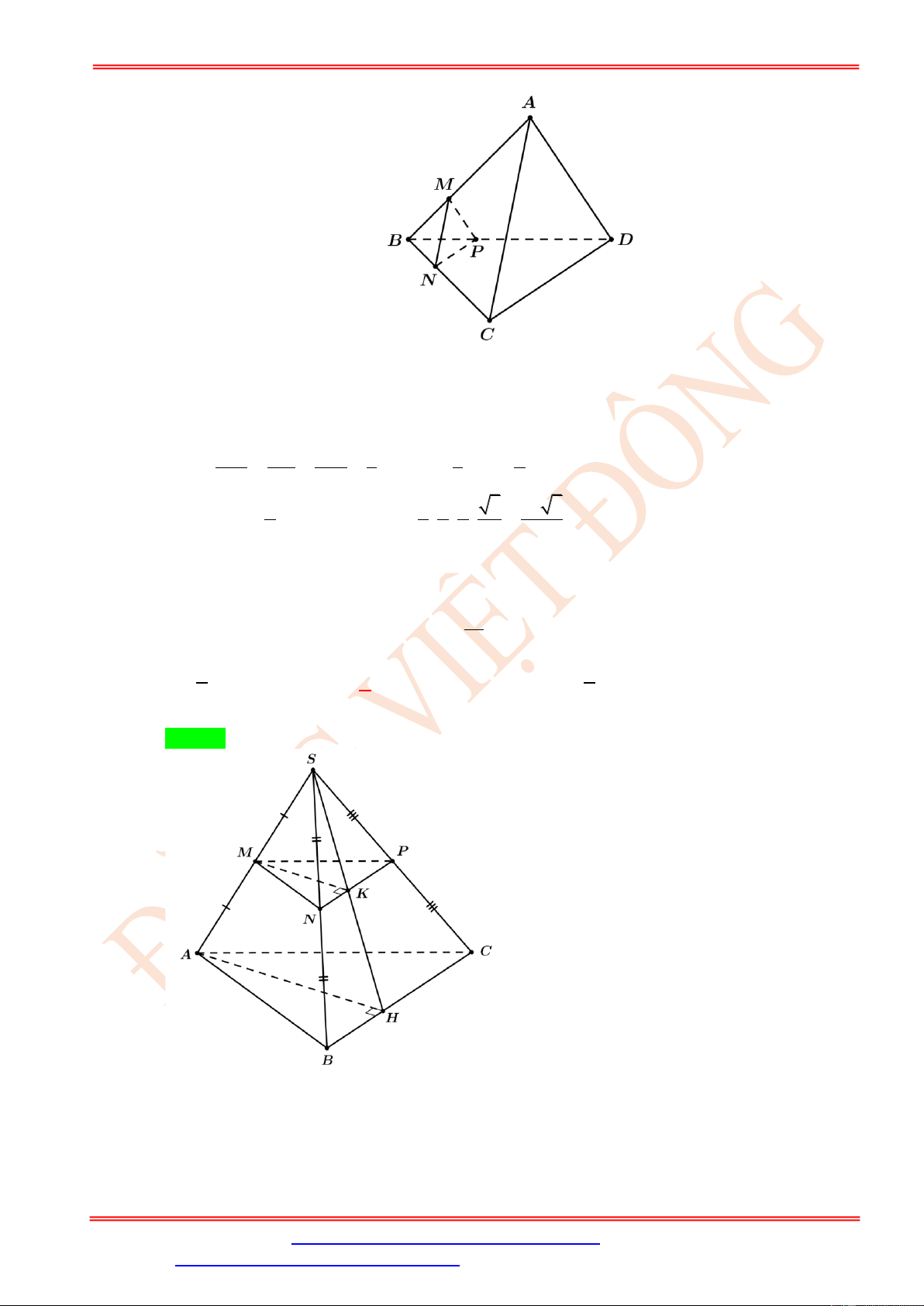
Câu 51. Cho tứ diện đều ABCD có cạnh bằng a , điểm M trên cạnh AB sao cho AM = 2MB . Tính
diện tích thiết diện của hình tứ diện ABCD cắt bởi mặt phẳng qua M và song song với các
đường thẳng AC và CD. 2 a 3 2 a 3 2 a 3 2 a 3 A. . B. . C. . D. . 9 36 4 18
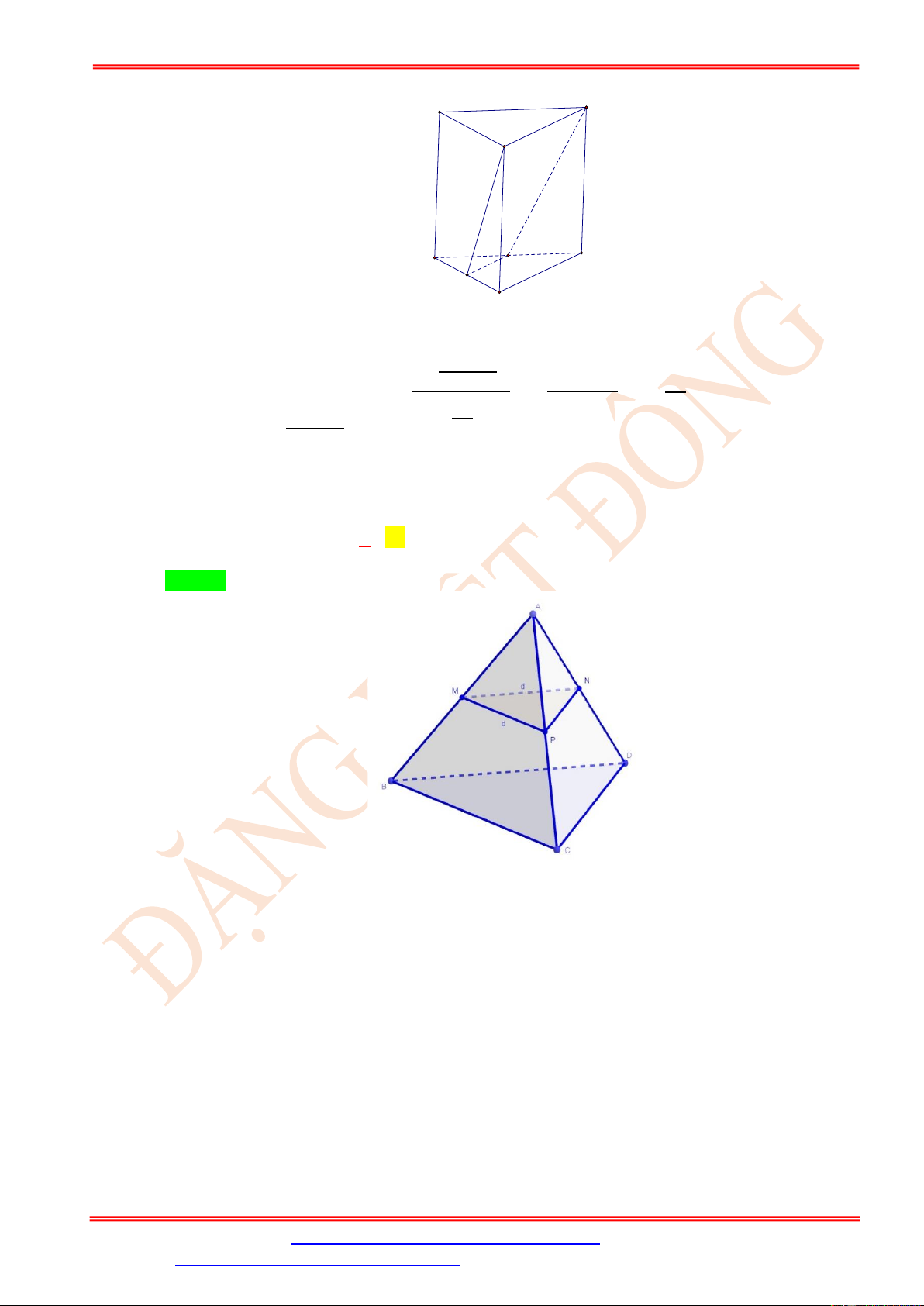
Câu 52. Cho hình chóp S.ABC . Gọi M là trung điểm SA ; ( ) là mặt phẳng qua M và song song
với ( ABC ) . ( ) lần lượt cắt các cạnh SB , SC tại N và P . Gọi S , S lần lượt là diện tích 1 2 S
các tam giác ABC và MNP . Tính 1 . S2 1 1 A. . B. 4 . C. . D. 2 . 4 2
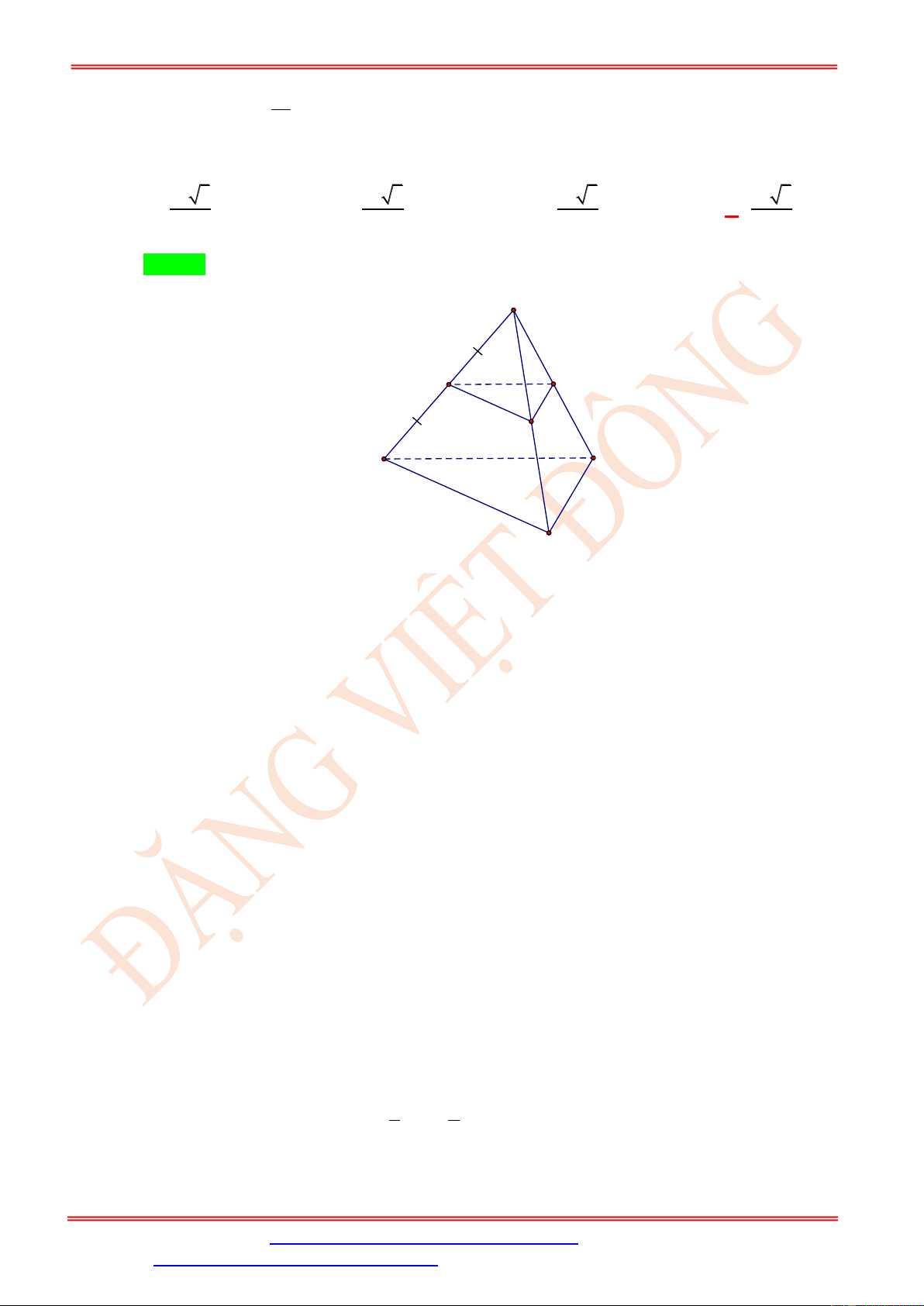
Câu 53. Cho hình chóp ABCD có tất cả các cạnh bằng nhau và bằng x. Gọi I là trung điểm AB, qua I
dựng mp(P) song song với (BCD). Diện tích thiết diện của hình chóp và mp(P) là 2 x 3 2 x 3 2 x 3 2 x 3 A. . B. . C. . D. . 4 8 12 16
Câu 54. Cho tứ diện có các cạnh bằng 4a . Lấy M là điểm trên cạnh AB sao cho AM = a . Tính diện
tích thiết diện của tứ diện ABCD cắt bởi mặt phẳng đi qua M và song song với mặt phẳng ( ACD). 2 9a 3 2 3a 3 2 a 3 A. 2 3a 3 . B. . C. D. . 4 4 4
Câu 55. Cho hình chóp tứ giác S.ABCD có tất cả các cạnh bằng 2a . Gọi M là trung điểm cạnh BC
. Mặt phẳng ( ) qua M và song song với (SB )
D cắt hình chóp theo thiết diện có diện tích bằng 2 a 2 a 2 a 2 a 3 A. . B. . C. . D. . 6 2 3 4
Câu 56. Cho hình chóp S.ABCD có đáy ABCD là hình thang; AB = 2C , D AB
CD . M là trung
điểm của cạnh AD ; mặt phẳng ( ) qua M và song song với mp(SAB) cắt hình chóp
S.ABCD theo một thiết diện là hình (H ) . Biết S = xS
. Giá trị của x là: ( H ) S AB 1 27 1 9 A. . B. . C. . D. . 2 64 4 16
Câu 57. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với cạnh bên BC = 3, hai đáy
AB = 8, CD = 4 . Mặt phẳng ( P ) song song với ( ABCD) và cắt cạnh SA tại M sao cho
SA = 3SM . Diện tích thiết diện của ( P ) và hình chóp S.ABCD bằng bao nhiêu?
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 2 5 7 3 2 5 7 3 A. . B. . C. . D. . 3 9 9 3
Câu 58. Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a , tam giác SAB đều. Gọi
M là điểm trên cạnh AD sao cho AM = x, x (0; a ) . Mặt phẳng ( ) qua M và song song
với (SAB) lần lượt cắt các cạnh C ,
B CS, SD tại N, , P .
Q Khi diện tích tứ giác MNPQ bằng 2 2a
3 thì x bằng bao nhiêu? 9 a 2a a a A. . B. . C. . D. . 2 3 3 4
Câu 59. Cho hình chóp 𝑆. 𝐴𝐵𝐶 có đáy 𝐴𝐵𝐶 là tam giác vuông cân tại 𝐴, 𝐴𝐵 = 𝐴𝐶 = 𝑎; cạnh bên 𝑆𝐴
vuông góc với mặt đáy, 𝑆𝐴 = 𝑎. Gọi 𝑀là trung điểm 𝑆𝐶. Tính diện tích thiết diện của hình
chóp cắt bởi mặt phẳng (𝑃) đi qua 𝑀và vuông góc với 𝐴𝐶. 𝑎2 𝑎2 𝑎2 A. . B. . C. 𝑎2. D. . 2 8 4
Câu 60. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có đáy 𝐴𝐵𝐶𝐷 là hình thang cân với cạnh bên 𝐵𝐶 = 2, hai đáy 𝐴𝐵 =
6, 𝐶𝐷 = 4. Mặt phẳng (𝑃) song song với (𝐴𝐵𝐶𝐷) và cắt cạnh 𝑆𝐴 tại 𝑀 sao cho 𝑆𝐴 = 3 𝑆𝑀.
Diện tích thiết diện của (𝑃) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 bằng bao nhiêu? 5√3 2√3 7√3 A. . B. . C. 2. D. . 9 3 9
Câu 61. Cho hình chóp 𝑆. 𝐴𝐵𝐶 có đáy là tam giác 𝐴𝐵𝐶 thỏa mãn 𝐴𝐵 = 𝐴𝐶 = 4, 𝐵𝐴𝐶 ̂ = 30°. Mặt
phẳng (𝑃) song song với (𝐴𝐵𝐶) cắt đoạn 𝑆𝐴 tại 𝑀 sao cho 𝑆𝑀 = 2𝑀𝐴. Diện tích thiết diện
của (𝑃) và hình chóp 𝑆. 𝐴𝐵𝐶 bằng bao nhiêu? 16 14 25 A. . B. . C. . D. 1. 9 9 9
Câu 62. Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn 0
AB = AC = 4, BAC = 30 . Mặt phẳng
(P) song song với ( ABC) cắt đoạn SA tại M sao cho SM = 2M .
A Diện tích thiết diện của
(P) và hình chóp S.ABC bằng bao nhiêu? 25 14 16 A. . B. 1. C. D. . 9 9 9
Câu 63. Cho tứ diện ABCD , biết tam giác BCD có diện tích bằng 16. Mặt phẳng ( P ) đi qua trung
điểm của AB và song song với mặt phẳng ( BCD) cắt tứ diện theo một thiết diện có diện tích bằng A. 12. B. 4 . C. 8 . D. 16 .
Câu 64. Cho tứ diện đều ABCD có độ dài các cạnh bằng 4. Điểm M là trung điểm của đoạn BC,
điểm E nằm trên đoạn BM sao cho E không trùng B , M . Mặt phẳng ( P) đi qua E và song 4 2
song với mặt phẳng ( AMD) . Diện tích thiết diện của ( P) với tứ diện ABCD bằng . 9
Tính độ dài đoạn BE bằng ? 4 1 2 A. . B. . C. 1. D. . 3 6 3
Câu 65. Cho hình chóp .
S ABCD có SA vuông góc đáy, ABCD là hình vuông cạnh a 2; SA = 2a .
Gọi M là trung điểm của cạnh SC , ( ) là mặt phẳng đi qua ,
A M và song song với đường
thẳng BD . Tính diện tích thiết diện của hình chóp .
S ABCD bị cắt bởi mặt phẳng ( ) . 2 2a 2 2 4a 2 4a 2 A. . B. . C. . D. 2 a 2 . 3 3 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 66. Cho hình lập phương ABC .
D A' B'C ' D' cạnh a . Các điểm M , N , P theo thứ tự đó thuộc các
cạnh BB ', C ' D ', DA a = =
= . Tìm diện tích thiết diện sao cho BM C ' N DP S của hình lập 3
phương khi cắt bởi mặt phẳng (MNP) . 2 17 3a 2 5 3a 2 13 3a 2 11 3a A. S = . B. S = . C. S = . D. S = . 18 18 18 18
Câu 67. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có đáy 𝐴𝐵𝐶𝐷 là hình thang cân với cạnh bên 𝐵𝐶 = √5, hai đáy 𝐴𝐵 =
6, 𝐶𝐷 = 4. Mặt phẳng (𝑃) song song với (𝐴𝐵𝐶𝐷) và cắt cạnh 𝑆𝐴 tại 𝑀 sao cho 𝑆𝐴 = 3 𝑆𝑀.
Diện tích thiết diện của (𝑃) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 bằng bao nhiêu? 5 2√5 2 7√5 A. . B. . C. . D. . 9 3 9 9
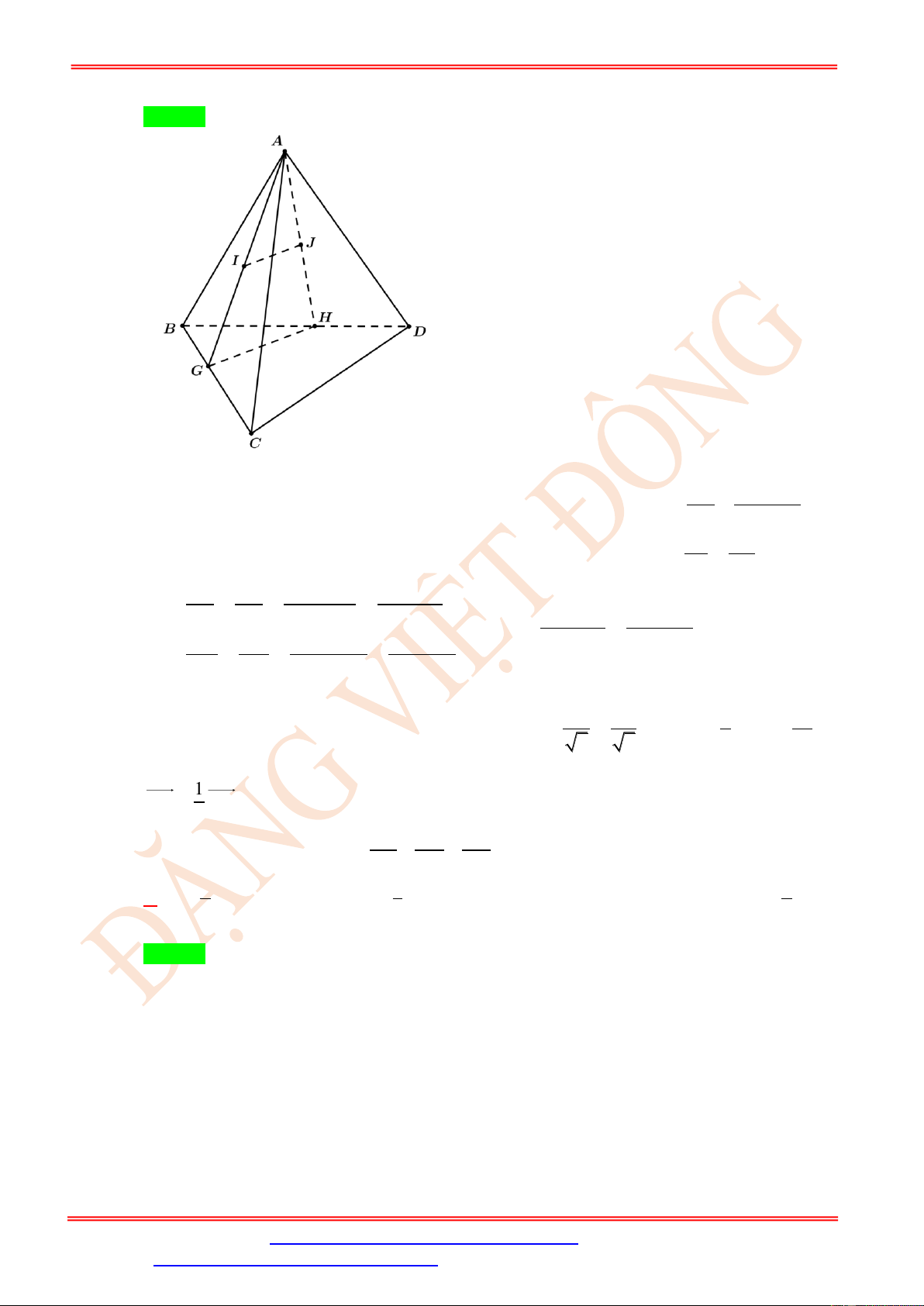
Câu 68. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA = 7a và SA vuông góc với mặt
phẳng đáy. Gọi G , I , J thứ tự là trọng tâm các tam giác SAB , SAD và trung điểm của CD
. Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (GIJ ) bằng 2 93a 2 23a 2 31 33a 2 3 33a A. . B. . C. . D. . 40 60 45 8
Câu 69. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông
tại A , SA = a 3 , SB = 2a . Điểm M nằm trên đoạn AD sao cho AM = 2MD. Gọi ( P ) là
mặt phẳng qua M và song song với (SAB) . Tính diện tích thiết diện của hình chóp cắt bởi
mặt phẳng ( P ) . 2 5a 3 2 5a 3 2 4a 3 2 4a 3 A. . B. . C. . D. . 18 6 9 3
Câu 70. Cho hình hộp ABC . D A B C D
Trên cạnh AB lấy điểm M khác A và B . Gọi ( P) là mặt phẳng
đi qua M và song song với mặt phẳng (ACD )
. Gọi S = S
. Thiết diện tạo bởi mặt phẳng A CD'
(P) và hình hộp có diện tích lớn nhất bằng bao nhiêu theo diện tích tam giác ACD'. S 3S A. . B. S . C. . D. 2S . 2 2
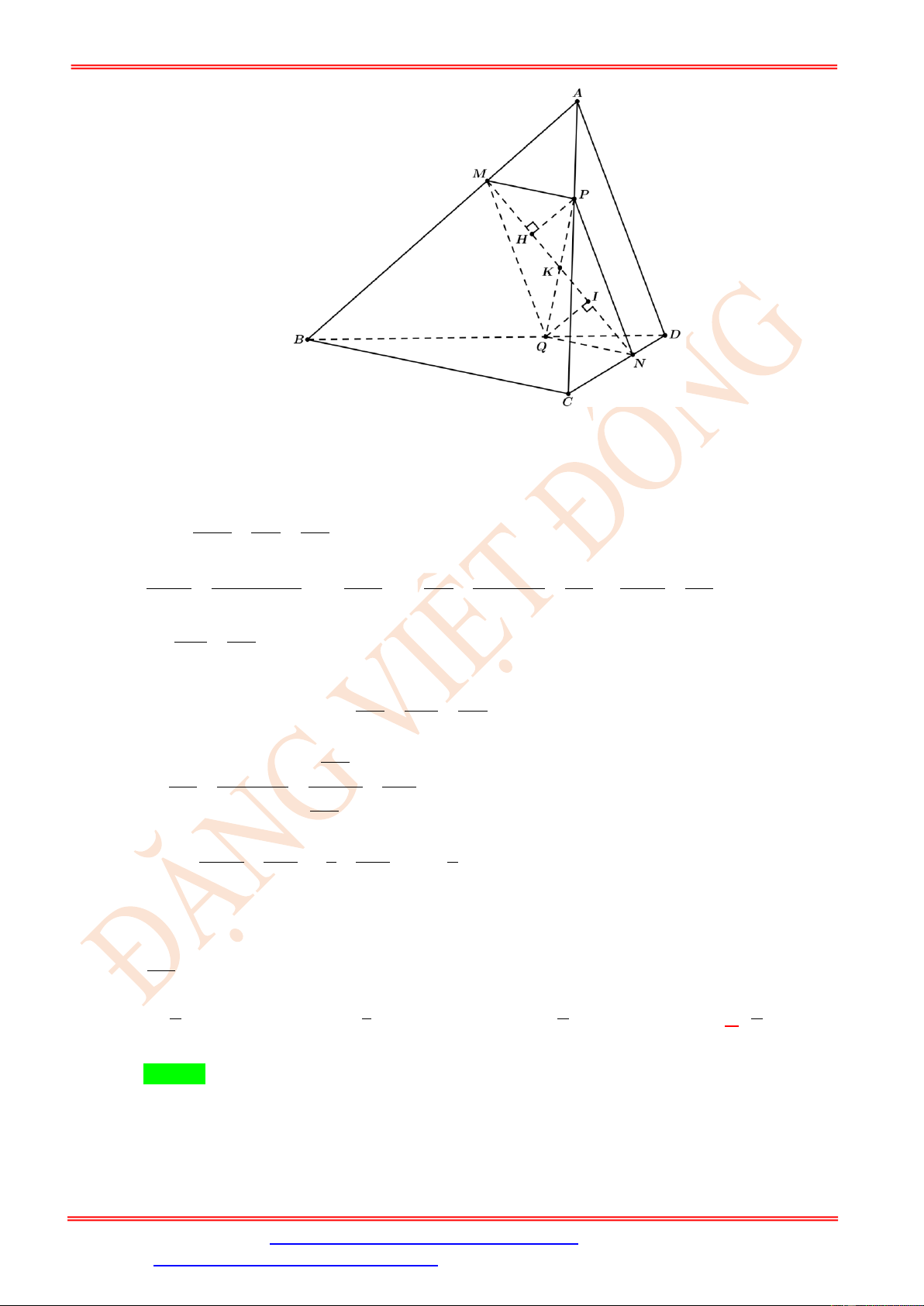
Câu 71. Cho tứ diện ABCD có tất cả các cạnh bằng a . Trên cạnh BC , CD lần lượt lấy M , N sao MC 1 CN 2 cho = ,
= . Trên trung tuyến AH của tam giác ABD lấy điểm P sao cho MB 2 CD 3 PA 4
= . Diện tích thiết diện khi cắt tứ diện ABCD bởi mặt phẳng (MNP) là PH 5 2 5a 11 2 3a 11 2 a 3 2 a 11 A. . B. . C. . D. . 12 12 12 12
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
ĐƯỜNG THẲNG VUÔNG GÓC MẶT PHẲNG
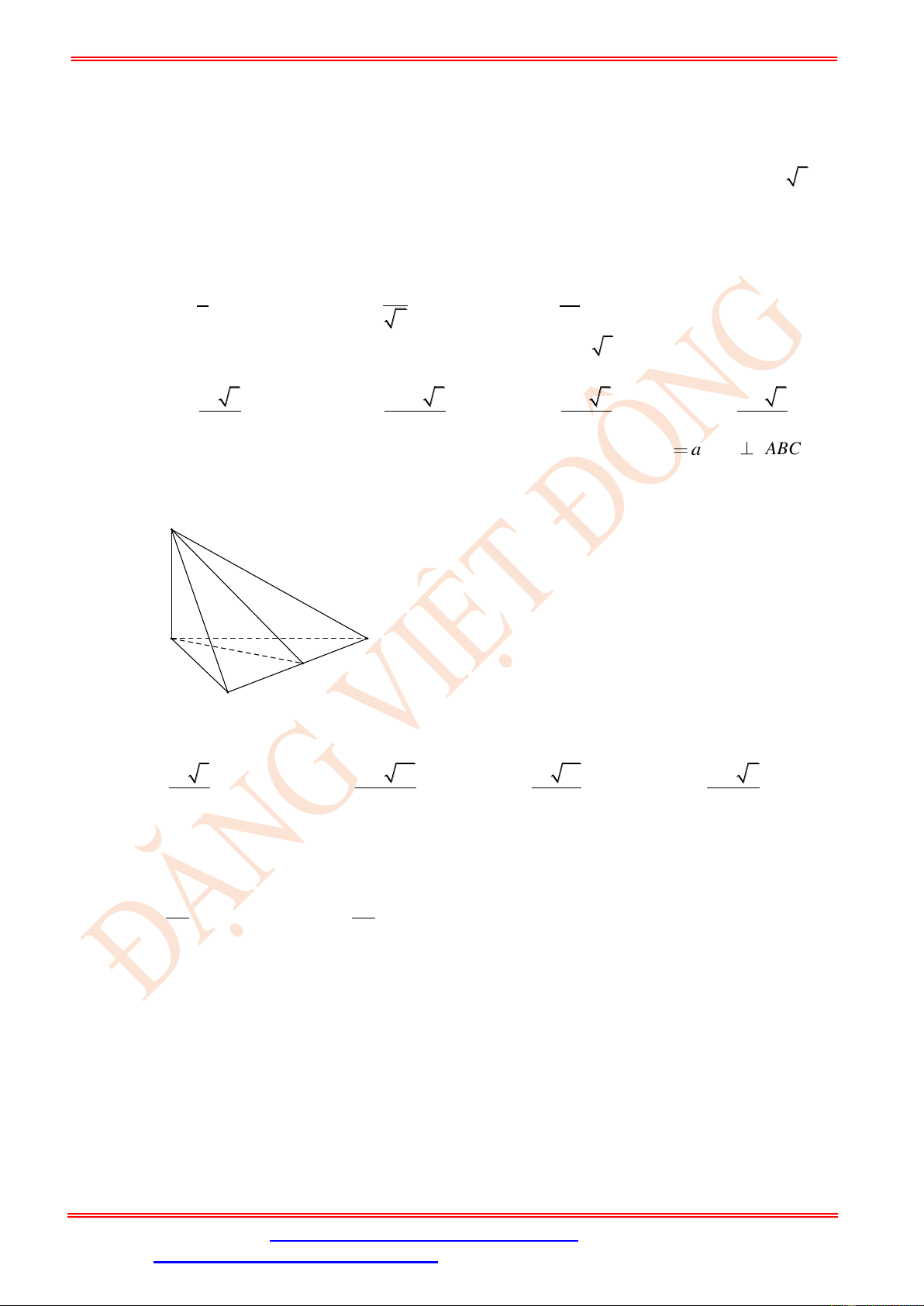
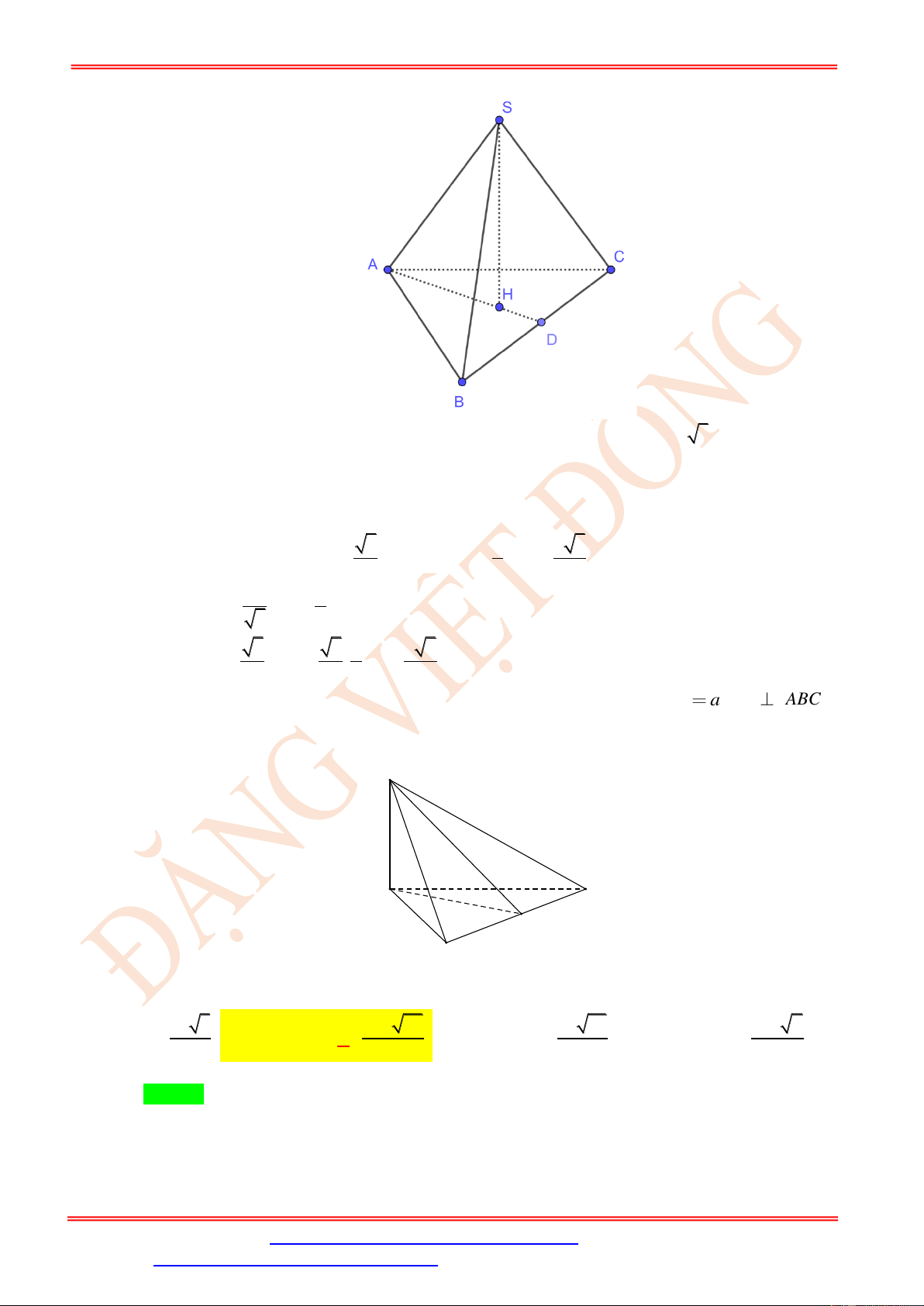
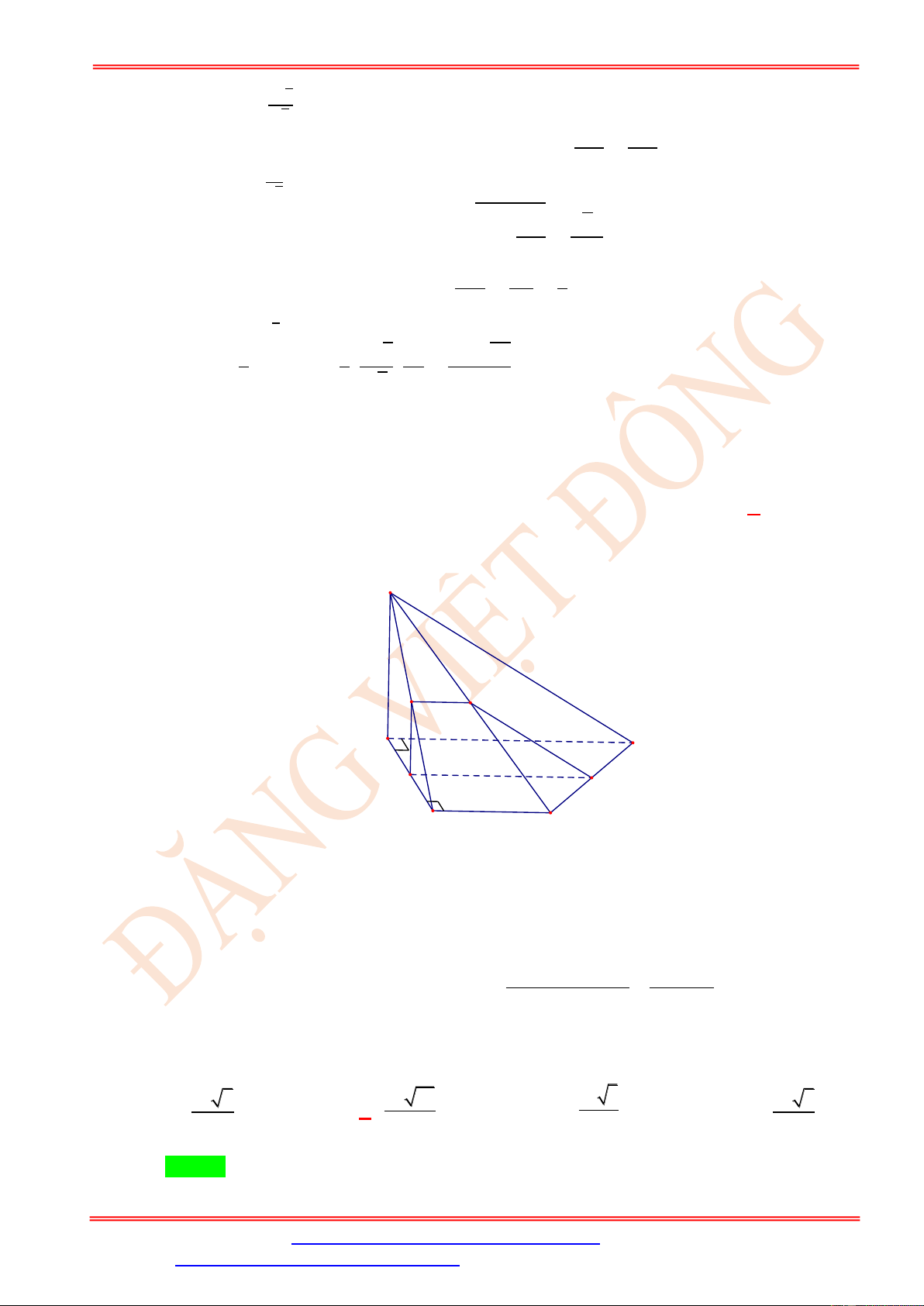
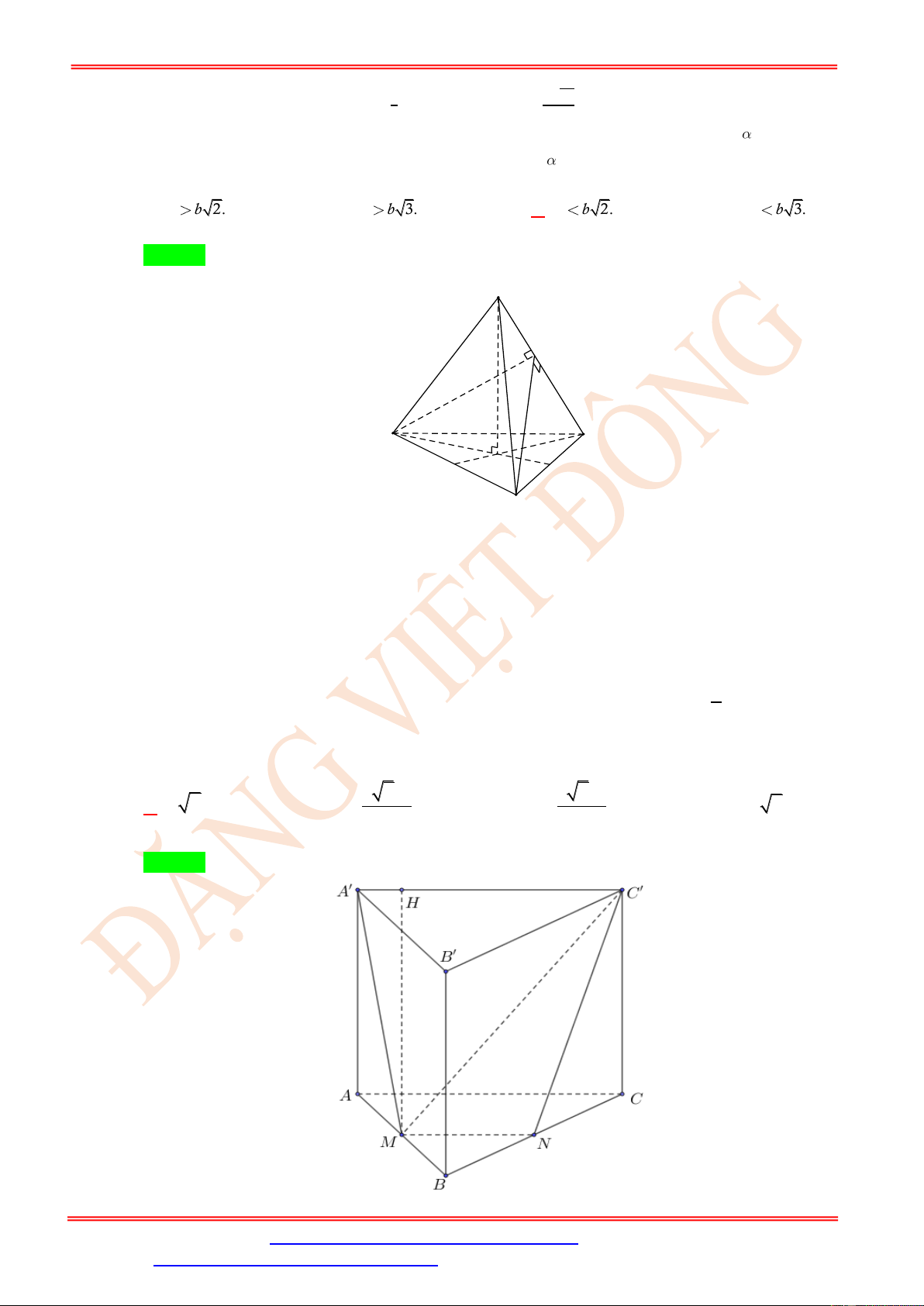
Dạng 1: Thiết diện, tính diện tích thiết diện Câu 72.
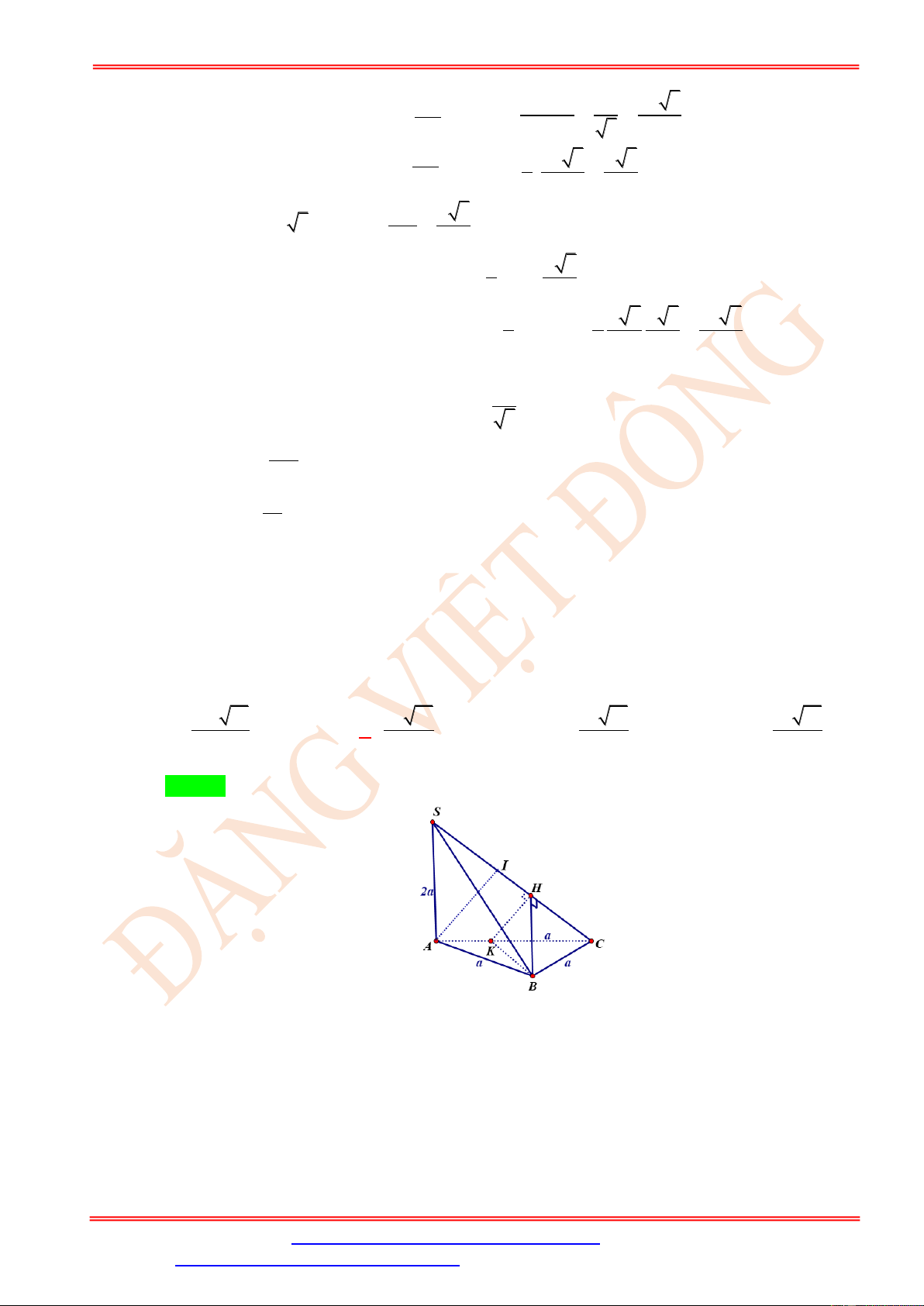
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a, SA = a 3 và
SA ⊥ ( ABC ) . Gọi M là điểm trên cạnh AB và AM = x (0 x a) . Mặt phẳng ( ) đi qua
M và vuông góc với AB . Giả sử thiết diện của hình chóp S.ABC với ( ) là tứ giác MNPQ
. Tìm x để thiết diện MNPQ lớn nhất. a a 3a A. x = . B. x = . C. x = .
D. x = a . 2 2 2
Câu 73. Cho hình chóp tam giác đều, các cạnh bên có độ dài bằng a 3 và tạo với đáy một góc 60 .
Diện tích S của đáy hình chóp là 2 a 3 2 27a 3 2 9a 3 2 3a 3 A. S = . B. S = . C. S = . D. S = . 9 16 16 16
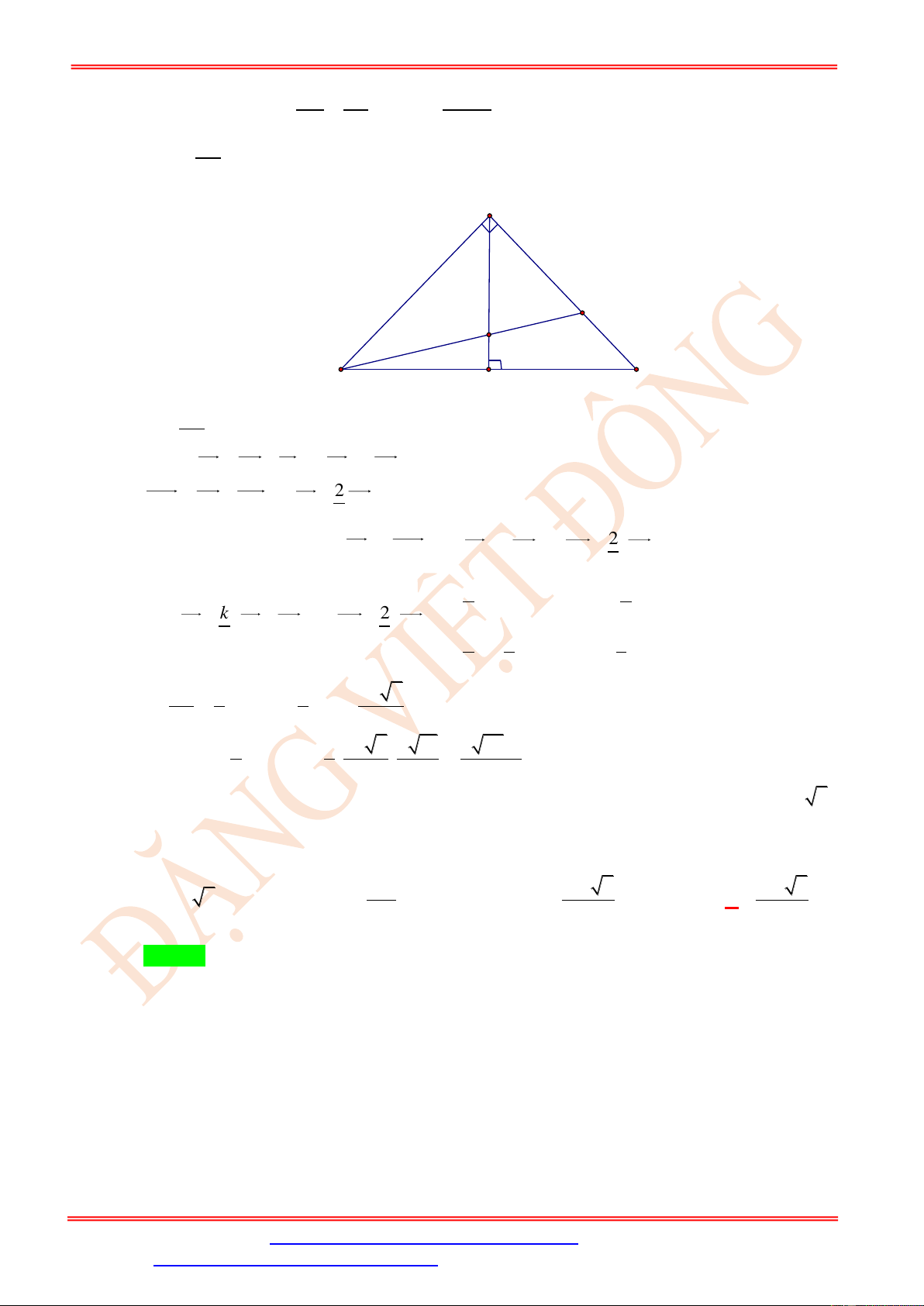
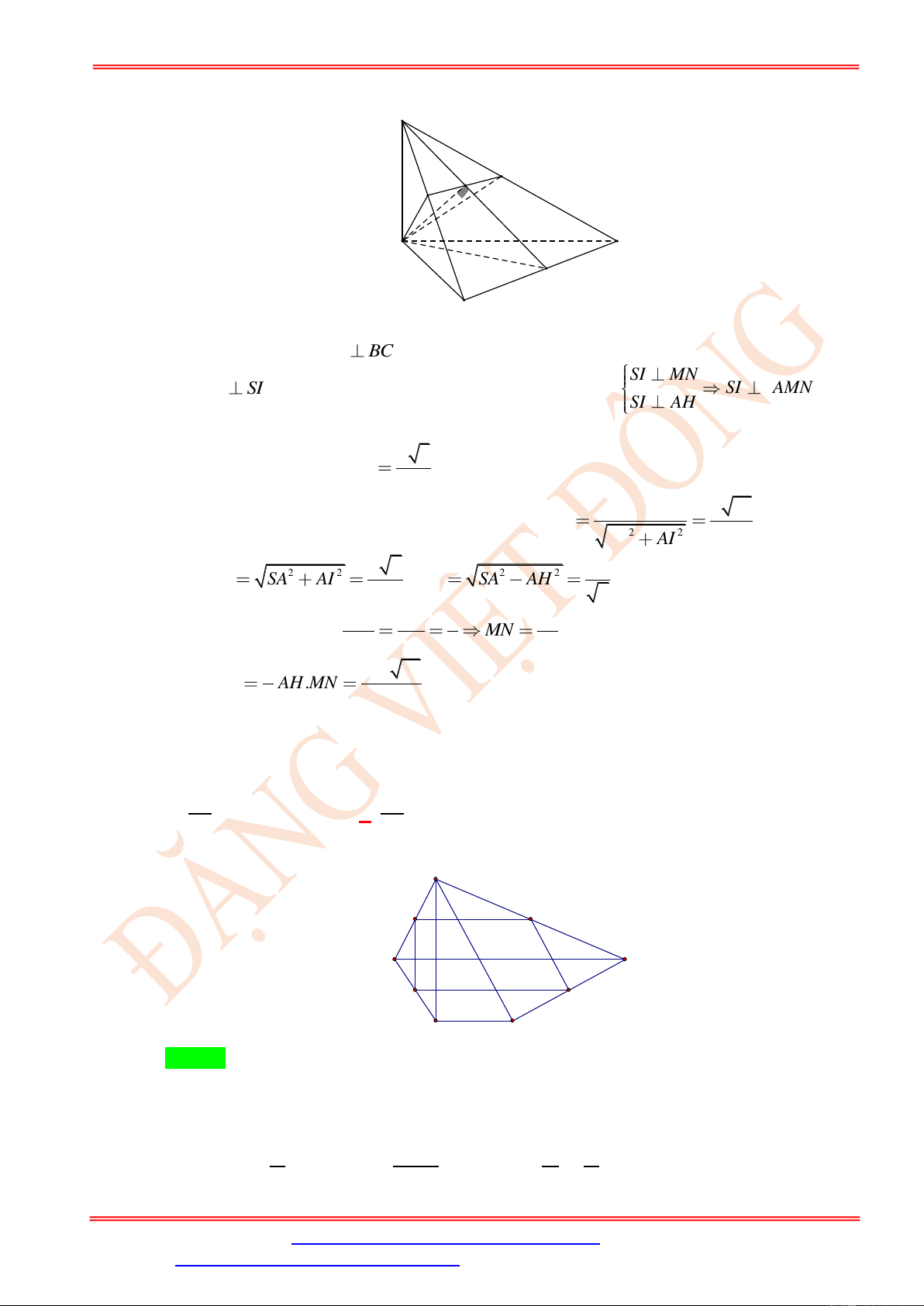
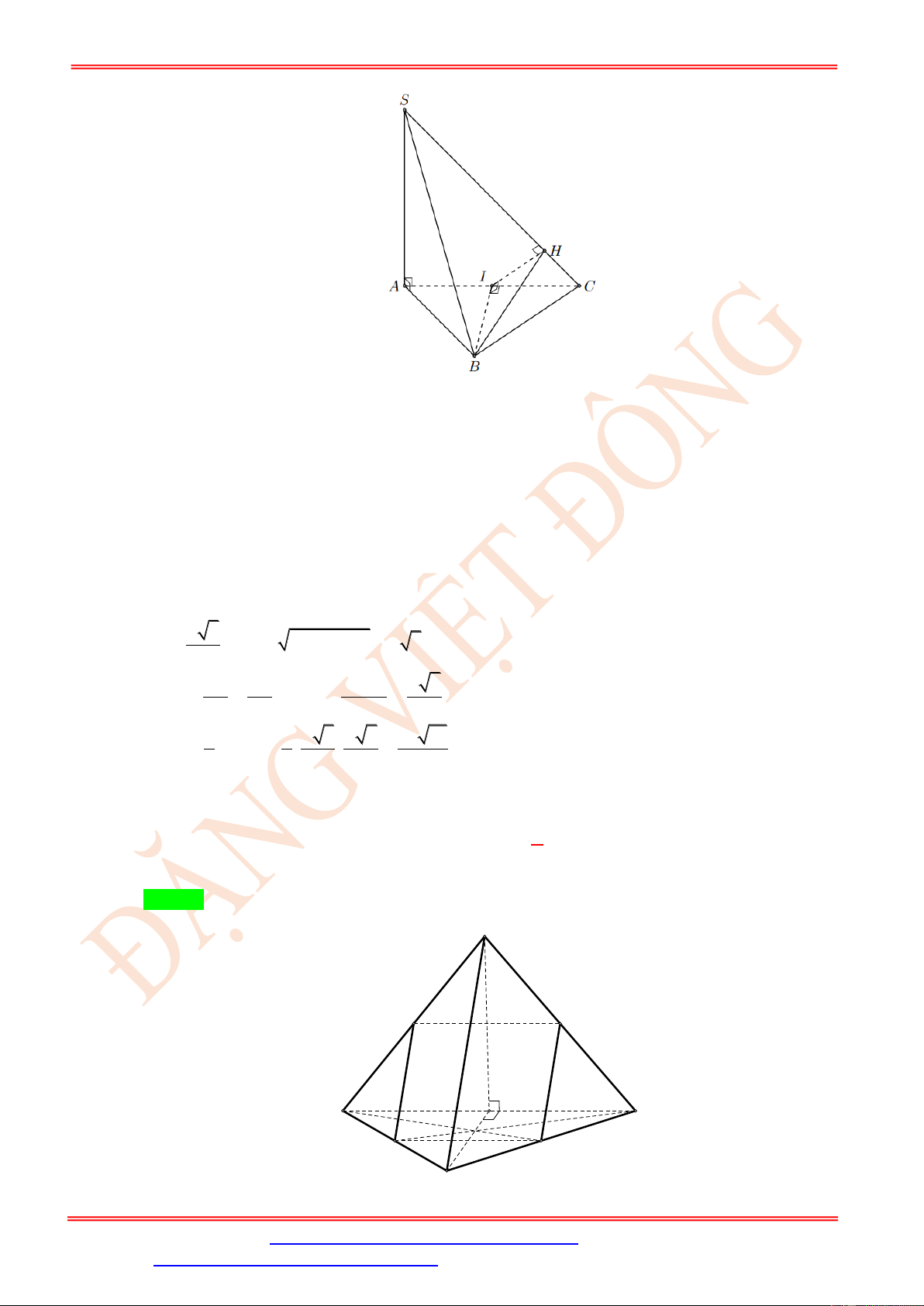
Câu 74. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a , SA a , SA ABC , I
là trung điểm của BC . Gọi P là mặt phẳng qua A và vuông góc với SI . S A C I B
Diện tích thiết diện của mặt phẳng P và hình chóp S.ABC được tính theo a bằng 2 a 3 2 2a 21 2 a 12 2 2a 6 A. . B. . C. . D. . 2 49 7 3
Câu 75. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷có đường cao 𝑆𝐴 = 4𝑎. Biết đáy 𝐴𝐵𝐶𝐷 là hình thang vuông tại 𝐴 và
𝐵 với 𝐴𝐵 = 𝐵𝐶 = 3𝑎, 𝐴𝐷 = 𝑎. Gọi 𝑀 trung điểm cạnh 𝐴𝐵 và (𝛼) là mặt phẳng qua 𝑀 vuông
góc với 𝐴𝐵. Thiết diện của hình chóp 𝑆. 𝐴𝐵𝐶𝐷 cắt bởi mặt phẳng (𝛼) là đa giác có diện tích bằng: 5𝑎2 7𝑎2 A. . B. . C. 7𝑎2. D. 5𝑎2. 2 2
Câu 76. Cho tứ diện đều ABCD . Thiết diện của tứ diện ABCD và mặt phẳng trung trực của cạnh BC là A. hình thang.
B. tam giác vuông.
C. hình bình hành.
D. tam giác cân.
Câu 77. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , SA ⊥ ( ABCD) , SA = AB = a
. Gọi (Q) là mặt phẳng qua SA và vuông góc với (SBD) . Thiết diện của hình chóp S.ABCD cắt bởi (Q) là
A. tam giác vuông.
B. tam giác đều.
C. tam giác vuông cân. D. hình bình hành.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 78. Cho hình vuông ABCDcó cạnh bằng 6 và hình bình hành CDIS không nằm trên cùng một
mặt phẳng. Biết tam giác SAC cân tại S , SB =12. Thiết diện của hình chóp S.ABCD cắt bởi
mặt phẳng ( ACI ) có diện tích bằng A. 36 2 . B. 6 2 . C. 18 2 . D. 8 2 .
Câu 79. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC sao
cho SM = 2MC . Mặt phẳng ( P ) chứa AM và song song với BD . Tính diện tích thiết diện
của hình chóp S.ABCD bởi mặt phẳng ( P) . 2 4 26a 2 3a 2 2 26a 2 2 3a A. . B. . C. . D. . 15 5 15 5
Câu 80. Cho tứ diện 𝐴𝐵𝐶𝐷 có 𝐴𝐵 vuông góc với 𝐶𝐷. Mặt phẳng (𝑃) song song với 𝐴𝐵 và 𝐶𝐷 lần
lượt cắt 𝐵𝐶, 𝐷𝐵, 𝐴𝐷, 𝐴𝐶 tại 𝑀, 𝑁, 𝑃, 𝑄. Tứ giác 𝑀𝑁𝑃𝑄 là hình gì? A. Hình thang.
B. Hình bình hành.
C. Hình chữ nhật.
D. Tứ giác không phải hình thang.
Câu 81. Cho tứ diện 𝐴𝐵𝐶𝐷 trong đó 𝐴𝐵 = 6, 𝐶𝐷 = 3, góc giữa 𝐴𝐵 và 𝐶𝐷 là 60° và điểm 𝑀 trên 𝐵𝐶
sao cho 𝐵𝑀 = 2𝑀𝐶. Mặt phẳng (𝑃) qua 𝑀 song song với 𝐴𝐵 và 𝐶𝐷 cắt 𝐵𝐷, 𝐴𝐷, 𝐴𝐶 lần lượt
tai 𝑀, 𝑁, 𝑄. Diện tích 𝑀𝑁𝑃𝑄 bằng 3 A. 2√2. B. √3. C. 2√3. D. . 2
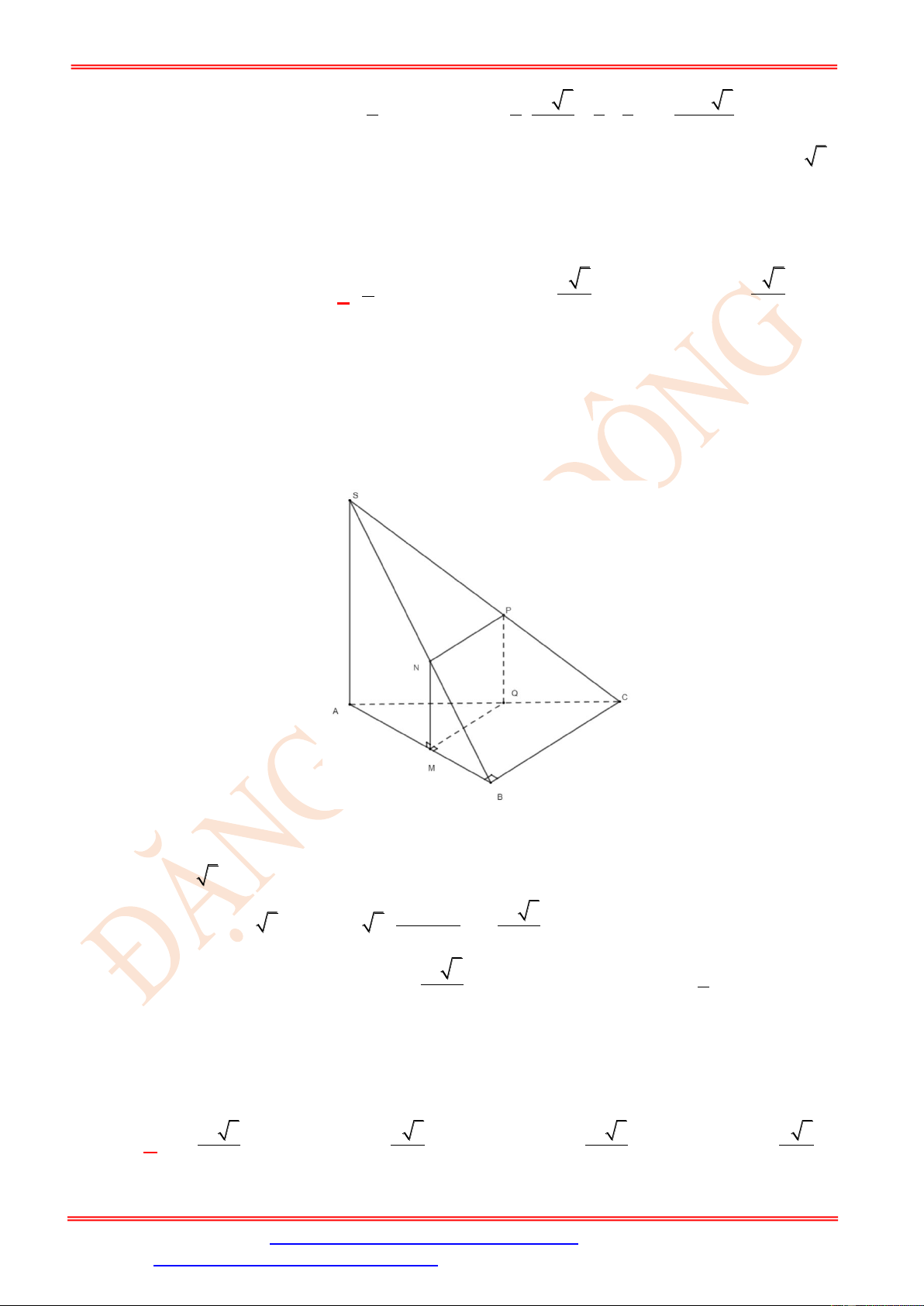
Câu 82. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB = AC = a ; cạnh bên
SA vuông góc với mặt đáy, SA = a . Gọi M là trung điểm của SC . Tính diện tích thiết diện
của hình chóp cắt bởi mặt phẳng ( P ) đi qua M và vuông góc với AC . 2 a 2 a 2 a A. . B. 2 a . C. . D. . 2 8 4
Câu 83. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB = a , BC = a 3 , cạnh
bên SA = a 3 và vuông góc với mặt phẳng ( ABC ) . Mặt phẳng ( P ) đi qua trung điểm M
của AB và vuông góc với SB cắt AC, SC, SB lần lượt tại N, ,
P Q . Diện tích của tứ giác MNPQ bằng: 2 11a 3 2 33a 3 2 33a 2 33a A. . B. . C. . D. . 64 64 64 16
Câu 84. Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCDlà hình vuông cạnh a 2 , SA = 2a
. Gọi M là trung điểm cạnh SC , ( ) là mặt phẳng đi qua ,
A M và song song với đường thẳng
BD . Tính diện tích thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng ( ) . 2 2a 2 2 4a 2 4a 2 A. . B. . C. . D. 2 a 2 . 3 3 3
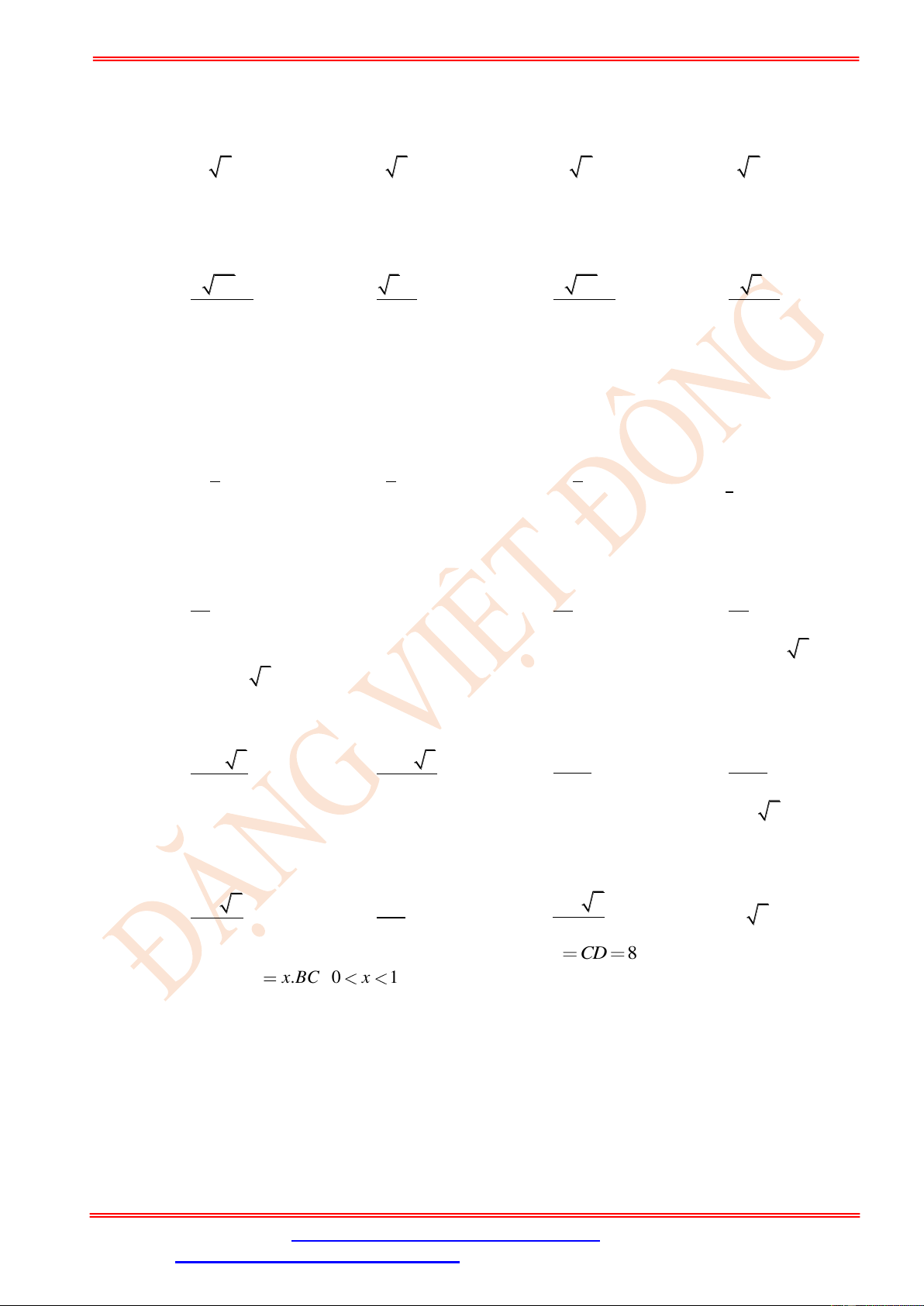
Câu 85. Cho tứ diện ABCD có AB vuông góc với CD , AB CD
8, M là điểm thuộc cạnh BC sao cho MC x.BC 0 x
1 . Mặt phẳng qua M , song song với A ,
B CD và lần lượt cắt D , B A , D AC tại N, ,
P Q . Diện tích lớn nhất của tứ giác MNPQ bằng bao nhiêu? A. 32 . B. 9 . C. 10 . D. 16 .
Câu 86. Trong không gian cho hai tam giác đều 𝐴𝐵𝐶 và 𝐴𝐵𝐶′ có chung cạnh 𝐴𝐵 và nằm trong hai mặt
phẳng khác nhau. Gọi 𝑀, 𝑁, 𝑃, 𝑄 lần lượt là trung điểm của các cạnh 𝐴𝐶, 𝐶𝐵, 𝐵𝐶′ và 𝐶′𝐴. Tứ
giác 𝑀𝑁𝑃𝑄 là hình gì?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình vuông. D. Hình thang.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 87. Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình vuông cạnh a 2; SA = 2 . a
Gọi M là trung điểm của cạnh SC , ( ) là mặt phẳng đi qua A , M và song song với đường
thẳng BD. Tính diện tích thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng ( ) . 2 2a 2 2 4a 2 4a 2 A. B. C. D. 2 a 2 3 3 3 a 3
Câu 88. Cho tứ diện S. ABC có hai mặt ( ABC ) và ( SBC ) là hai tam giác đều cạnh a , SA = . M 2
là điểm trên AB sao cho AM = b (0 b a) . ( P) là mặt phẳng qua M và vuông góc với BC
. Thiết diện của ( P ) và tứ diện S. ABC có diện tích bằng? 2 2 3 3
3 a − b
3 3 a − b 3 3 A.
(a −b)2 . B. C. D.
(a −b)2 16 4 a 16 a 8
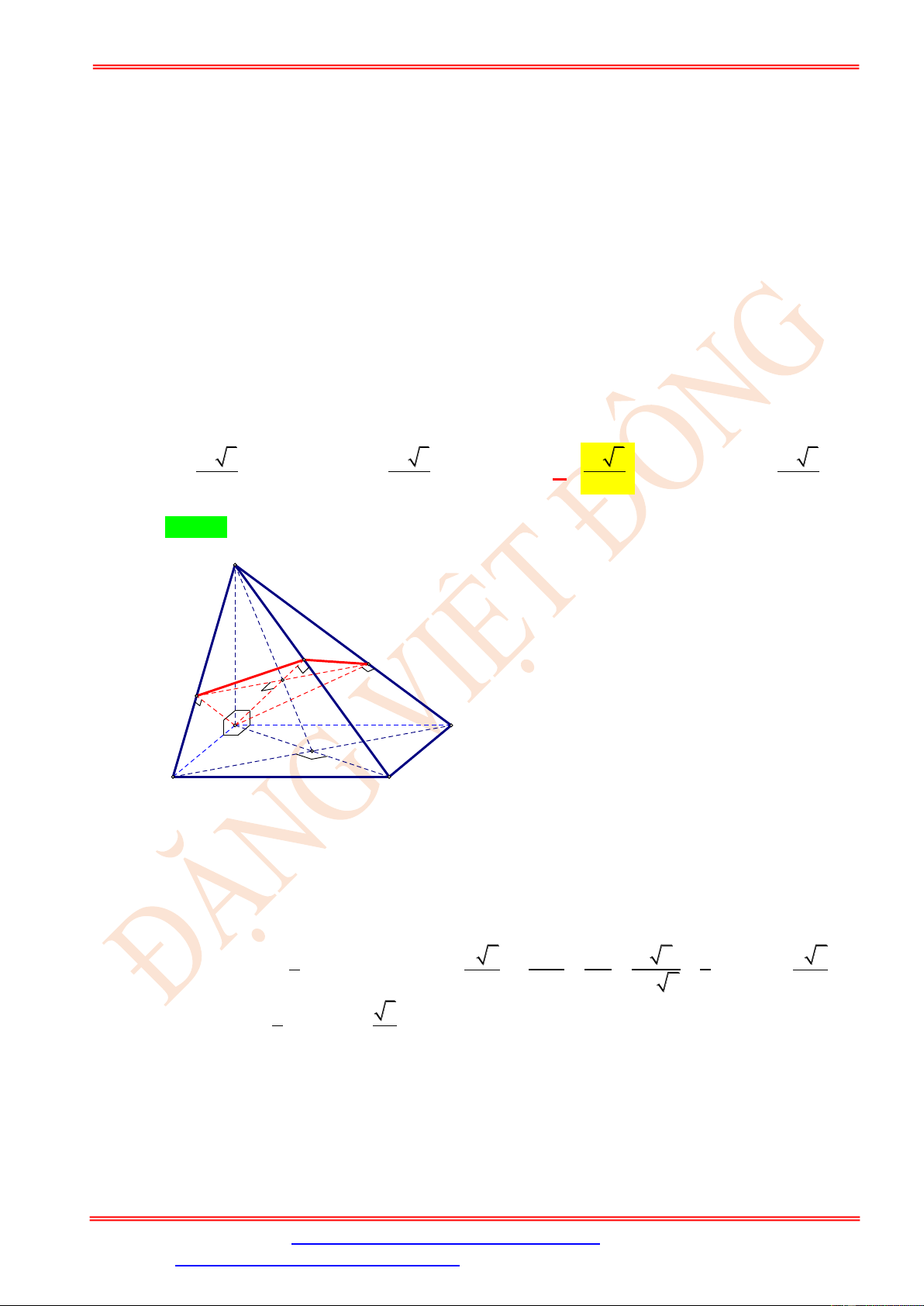
Câu 89. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = a và vuông góc với đáy.
Mặt phẳng ( ) qua A và vuông góc với trung tuyến SI của tam giác SBC . Tính diện tích S
của thiết diện tạo bởi ( ) với hình chóp đã cho. 2 2a 21 2 2a 21 A. S = . B. S = . A MN 49 AMN 7 2 4a 21 2 a 21 C. S = . D. S = . A MN 49 AMN 7
Câu 90. Cho tứ diện ABCD có AB vuông góc với CD , AB 4, CD
6 . M là điểm thuộc cạnh BC sao cho MC
2BM . Mặt phẳng P đi qua M song song với AB và CD . Diện tích thiết diện của
P với tứ diện là 17 16 A. 5. B. 6. C. . . 3 D. 3
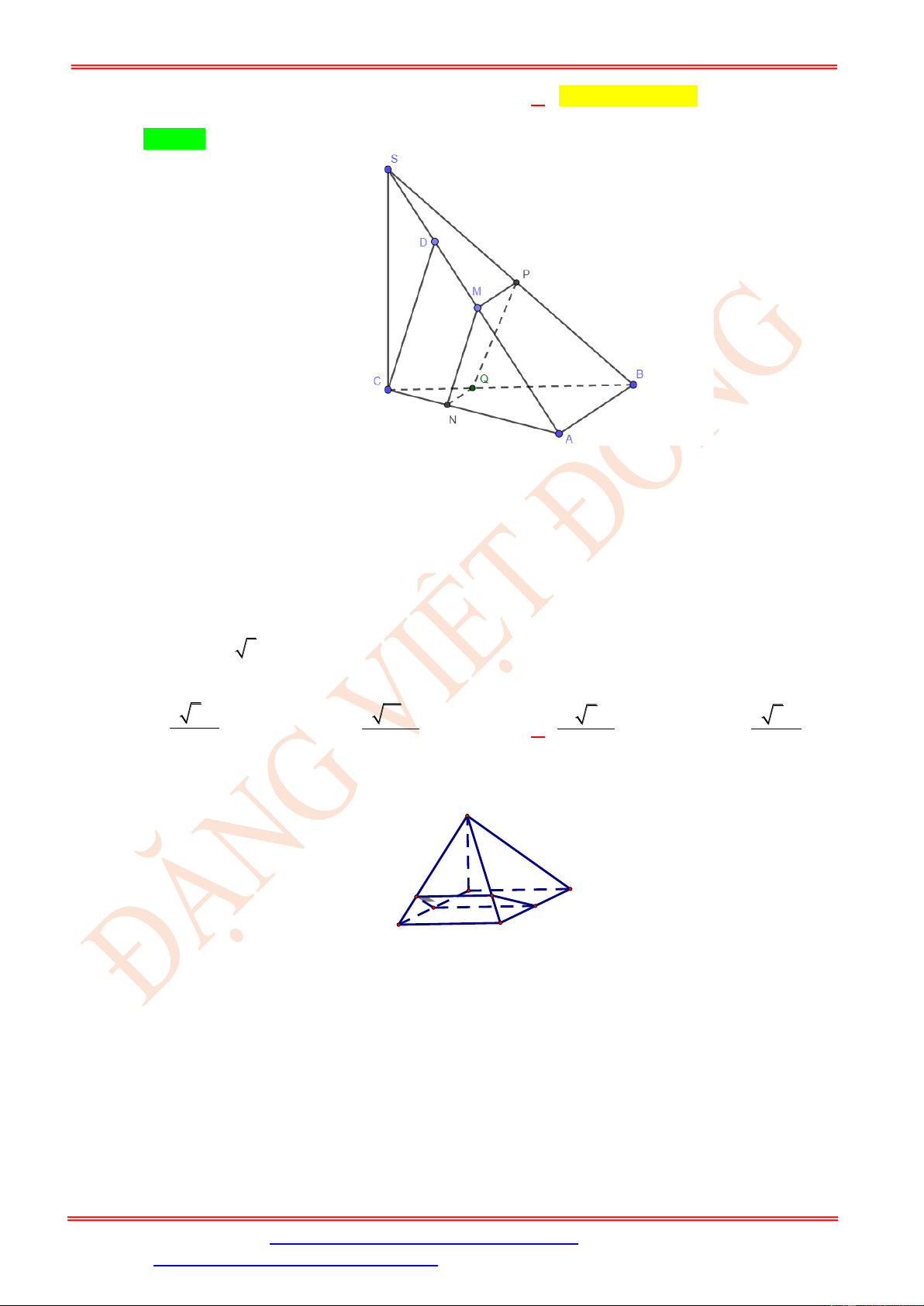
Câu 91. Cho hình chóp 𝑆. 𝐴𝐵𝐶 có đáy 𝐴𝐵𝐶 là tam giác đều cạnh 𝑎, 𝑆𝐴 = 𝑎 và vuông góc với mặt
phẳng đáy. Mặt phẳng (𝛼) qua 𝐴 và vuông góc với trung tuyến 𝑆𝐼 của tam giác 𝑆𝐵𝐶. Tính
diện tích 𝑆 của thiết diện tạo bởi (𝛼) với hình chóp đã cho. 2𝑎2√21 𝟐𝒂𝟐√𝟐𝟏 A. 𝑆Δ𝐴𝑀𝑁 = B. 𝑺 49 𝚫𝑨𝑴𝑵 = 𝟕 𝟒𝒂𝟐√𝟐𝟏 𝑎2√21
C. 𝑺𝚫𝑨𝑴𝑵 = D. 𝑆 𝟒𝟗 Δ𝐴𝑀𝑁 = 7
Câu 92. Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A , đáy lớn AD = 8, đáy nhỏ
BC = 6 , SA vuông góc với đáy, SA = 6 . Gọi M là trung điểm AB , ( P ) là mặt phẳng qua
M và vuông góc với AB . Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( P ) có diện tích bằng A. 20 . B. 16 . C. 30 . D. 15 .
Câu 93. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a SA = 2a và SA vuông góc với
đáy. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua B và vuông góc với SC . 2 2 a 5 2 a 15 a 3 2 a 3 A. . B. . C. . D. . 5 20 20 5
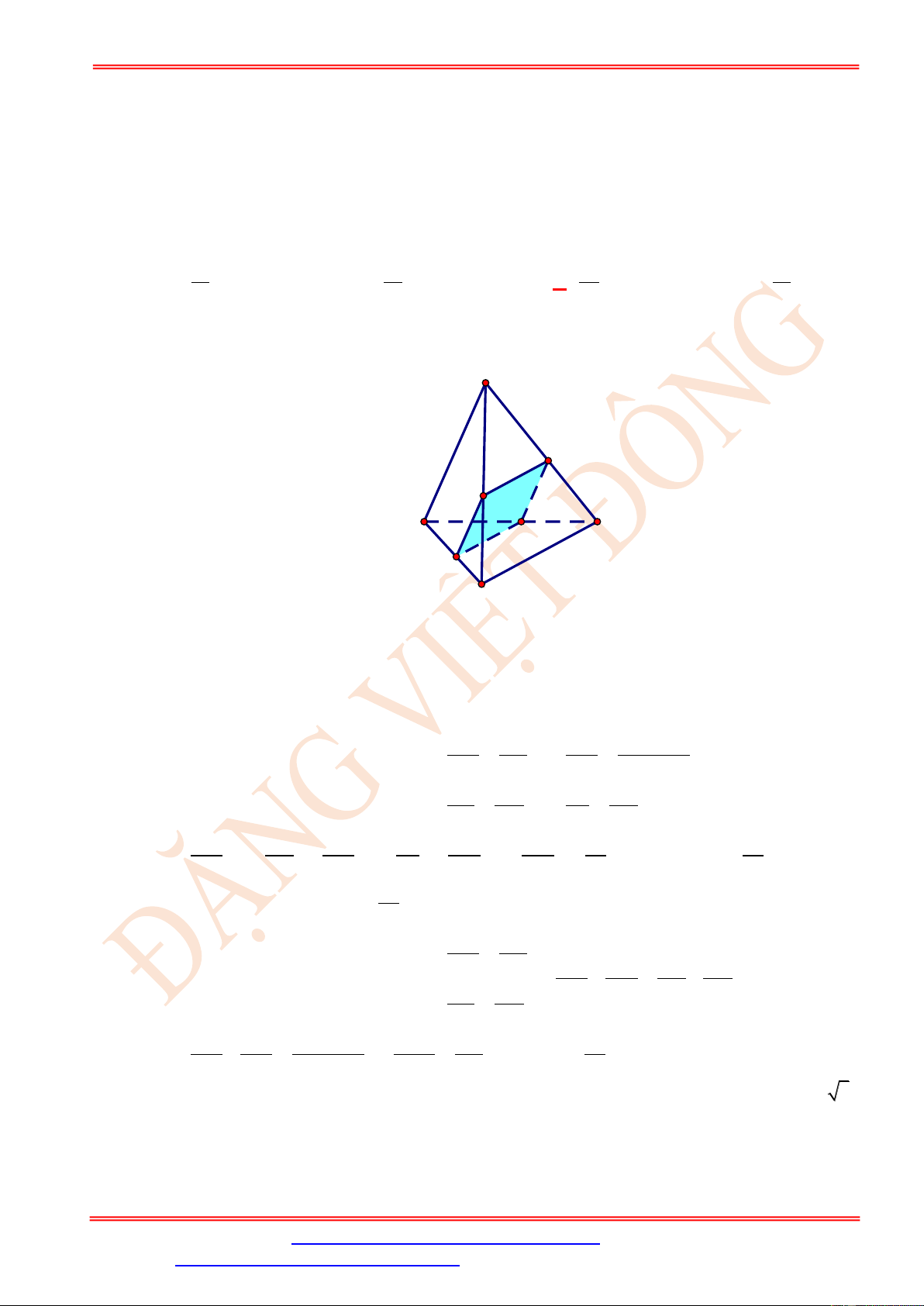
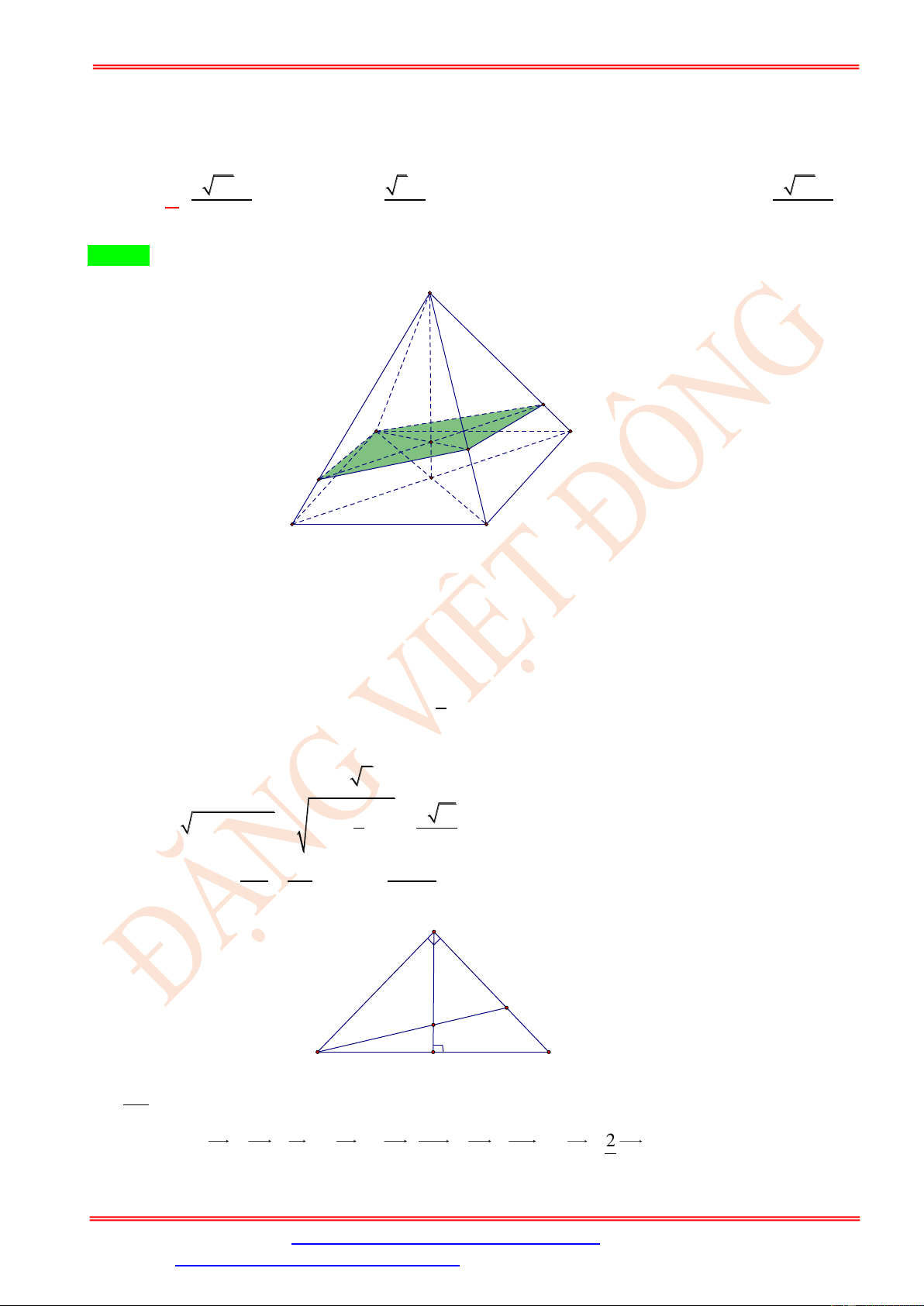
Câu 94. Cho tứ diện đều ABCD , mặt phẳng ( ) qua trung điểm của cạnh AB , song song AC và BD
cắt tứ diện theo thiết diện là
A. Hình tam giác đều.
B. Hình vuông.
C. Hình tam giác vuông cân.
D. Hình thang cân.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 95. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy,
cạnh bên SB tạo với đáy góc 0
45 . Một mặt phẳng ( ) đi qua A và vuông góc với SC cắt hình
chóp S.ABCD theo thiết diện là tứ giác AB C D
có diện tích bằng: 2 a 3 2 a 3 2 a 3 2 a 3 A. . B. . C. . D. . 4 2 6 3
Câu 96. Cho hình chóp S.ABC , đáy ABC là tam giác vuông tại , A AB = , a 0
ABC = 60 , SC = , a
SC ⊥ ( ABC ) . Kẻ CD ⊥ SAtại D . Thiết diện qua M AD và vuông góc với AD là A. Tam giá
B. Hình bình hành.
C. Hình vuông.
D. Hình thang vuông.
Câu 97. Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình vuông cạnh 2a , SA = 2a 3 .
Gọi I là trung điểm của AD , mặt phẳng ( P ) qua I và vuông góc với SD . Tính diện tích
thiết diện của hình chóp cắt bởi mặt phẳng ( P ) . 2 3 5a 2 3 15a 2 15 3a 2 5 3a A. . B. . C. . D. . 16 16 16 16
Câu 98. Cho hình chóp S.ABCD có SA vuông góc với mặt đáy, ABCD là hình vuông cạnh a 2,SA
2a . Gọi M là trung điểm của cạnh SC , là mặt phẳng đi qua , A M và song
song với đường thẳng BD . Tính diện tích thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng . 2 4a 2 4a 2 2 2a 2 A. 2 a 2 . B. . C. . D. . 3 3 3
Câu 99. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AB = a , BC = 2a . Điểm H thuộc cạnh 1 a 6
AC sao cho CH = CA , SH là đường cao hình chóp S.ABC và SH = . 3 3
Gọi I là trung điểm BC . Tính diện tích thiết diện của hình chóp với mặt phẳng đi qua H và
vuông góc với AI . 2 2a 2 2a 2 3a 2 3a A. . B. . C. . D. . 3 6 3 6
Câu 100. Cho tứ diện SABC có ABC
là tam giác đều cạnh a , SA ⊥ (ABC) và S
A= 2a . Gọi ( ) là
mặt phẳng qua B và vuông góc với SC . Tính diện tích thiết diện của tứ diện SABC với ( ) . 2 3a 15 2 a 15 2 a 15 2 a 15 A. . B. . C. . D. . 10 20 5 10
Câu 101. Cho tứ diện 𝐴𝐵𝐶𝐷 có 𝐴𝐵 vuông góc với 𝐶𝐷, 𝐴𝐵 = 𝐶𝐷 = 6. 𝑀 là điểm thuộc cạnh 𝐵𝐶 sao
cho 𝑀𝐶 = 𝑥. 𝐵𝐶(0 < 𝑥 < 1). Mặt phẳng (𝑃) song song với 𝐴𝐵 và 𝐶𝐷 lần lượt cắt
𝐵𝐶, 𝐷𝐵, 𝐴𝐷, 𝐴𝐶 tại 𝑀, 𝑁, 𝑃, 𝑄. Diện tích lớn nhất của tứ giác bằng bao nhiêu? A. 9. B. 11. C. 10. D. 8.
Câu 102. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC sao cho
SM = 2MC . Mặt phẳng ( P ) chứa AM và song song với BD . Tính diện tích thiết diện của
hình chóp S.ABCD cắt bởi ( P ) . 2 2 26a 2 3a 2 4 26a A. . B. . C. 48 . D. . 15 5 15
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 103. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có đáy 𝐴𝐵𝐶𝐷 là hình vuông cạnh bằng 𝑎, hai tam giác 𝑆𝐴𝐵 và 𝑆𝐴𝐷
vuông cân tại 𝐴. Gọi 𝐺 là trọng tâm của tam giác 𝑆𝐴𝐵. Gọi (𝛼) là mặt phẳng đi qua 𝐺 và song
song với 𝑆𝐵 và 𝐴𝐷. Thiết diện tạo bởi mặt phẳng (𝛼) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có diện tích bằng 2𝑎2√3 4𝑎2√2 4𝑎2√2 4𝑎2√3 A. . B. . C. . D. . 9 3 9 9
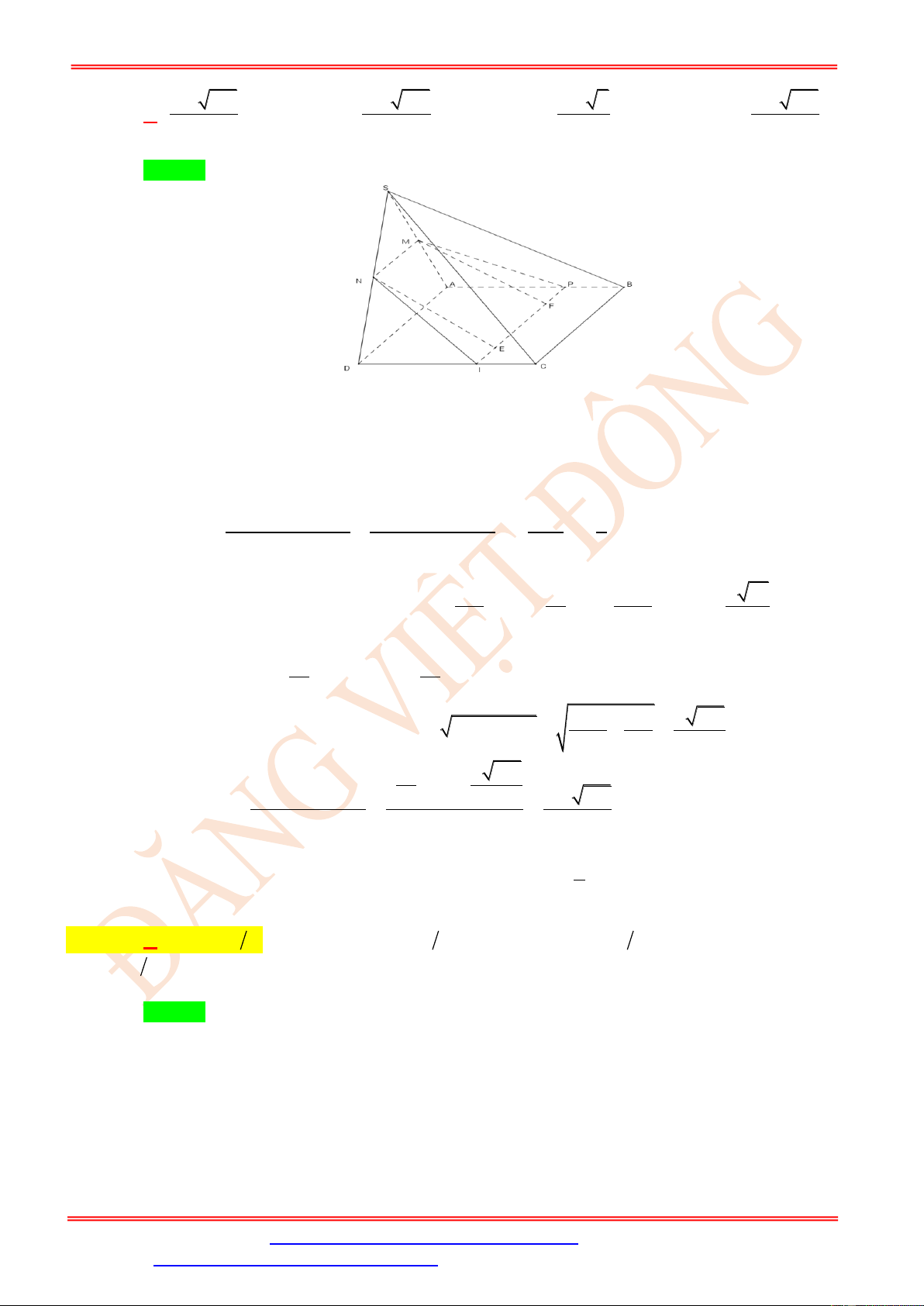
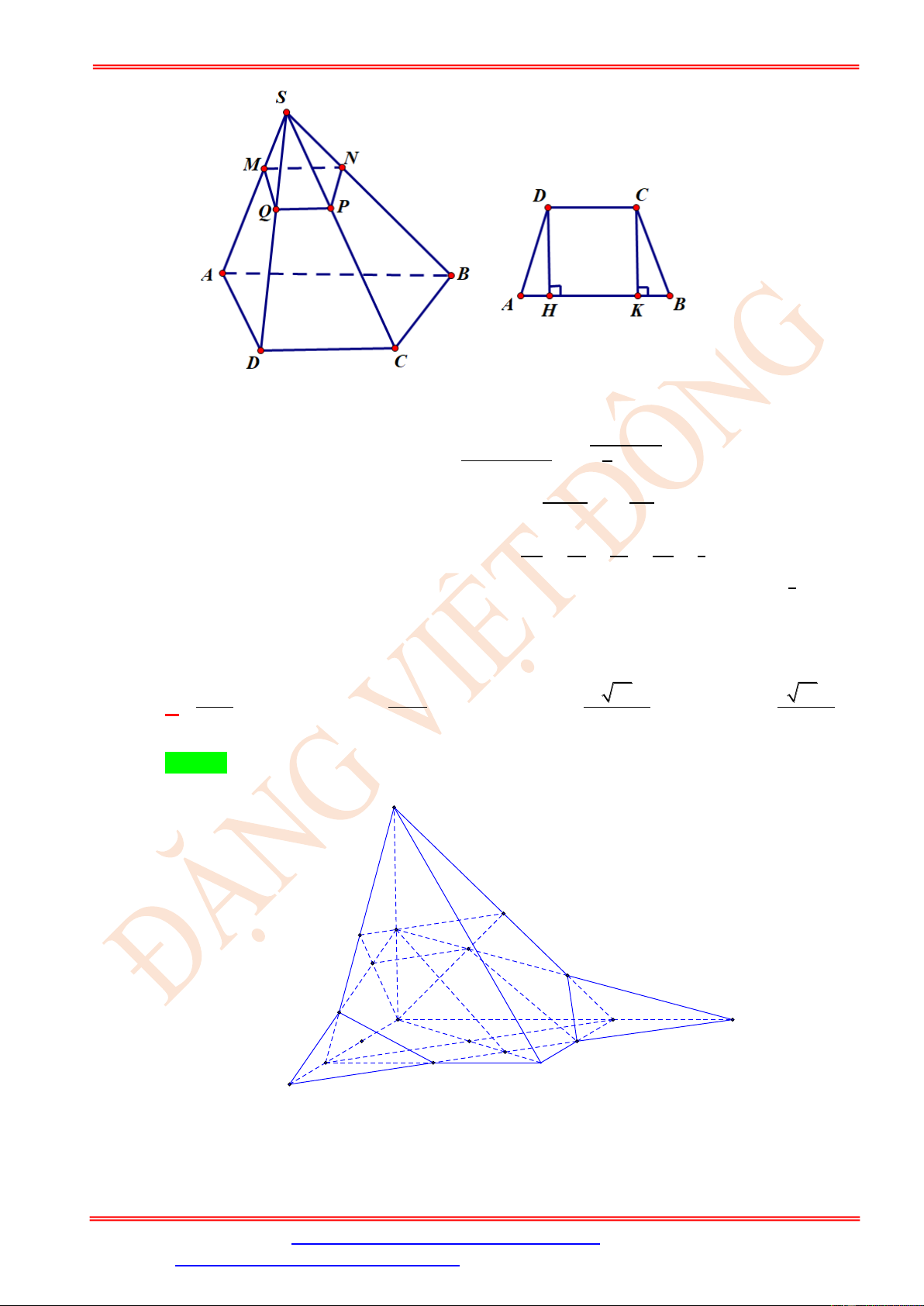
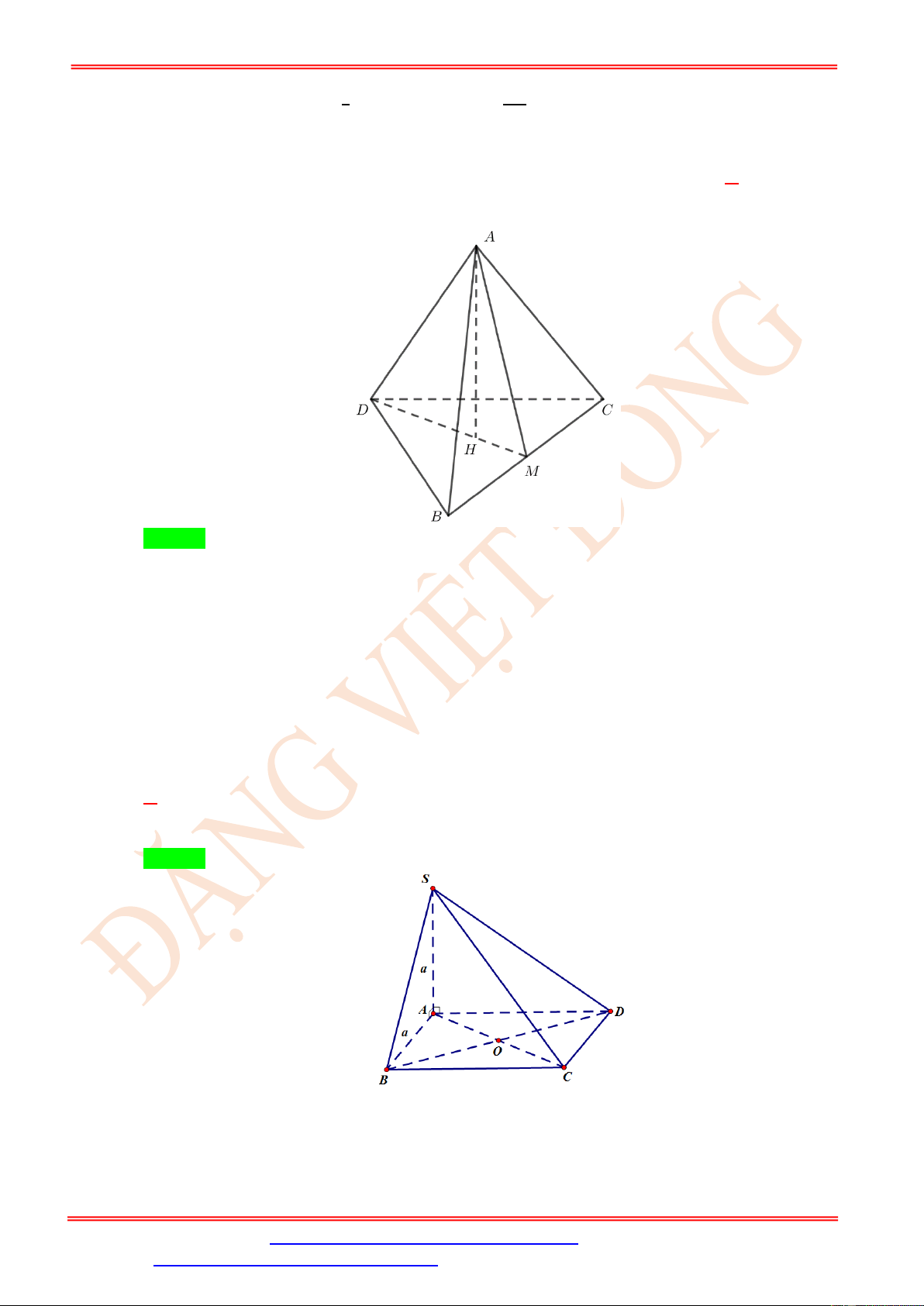
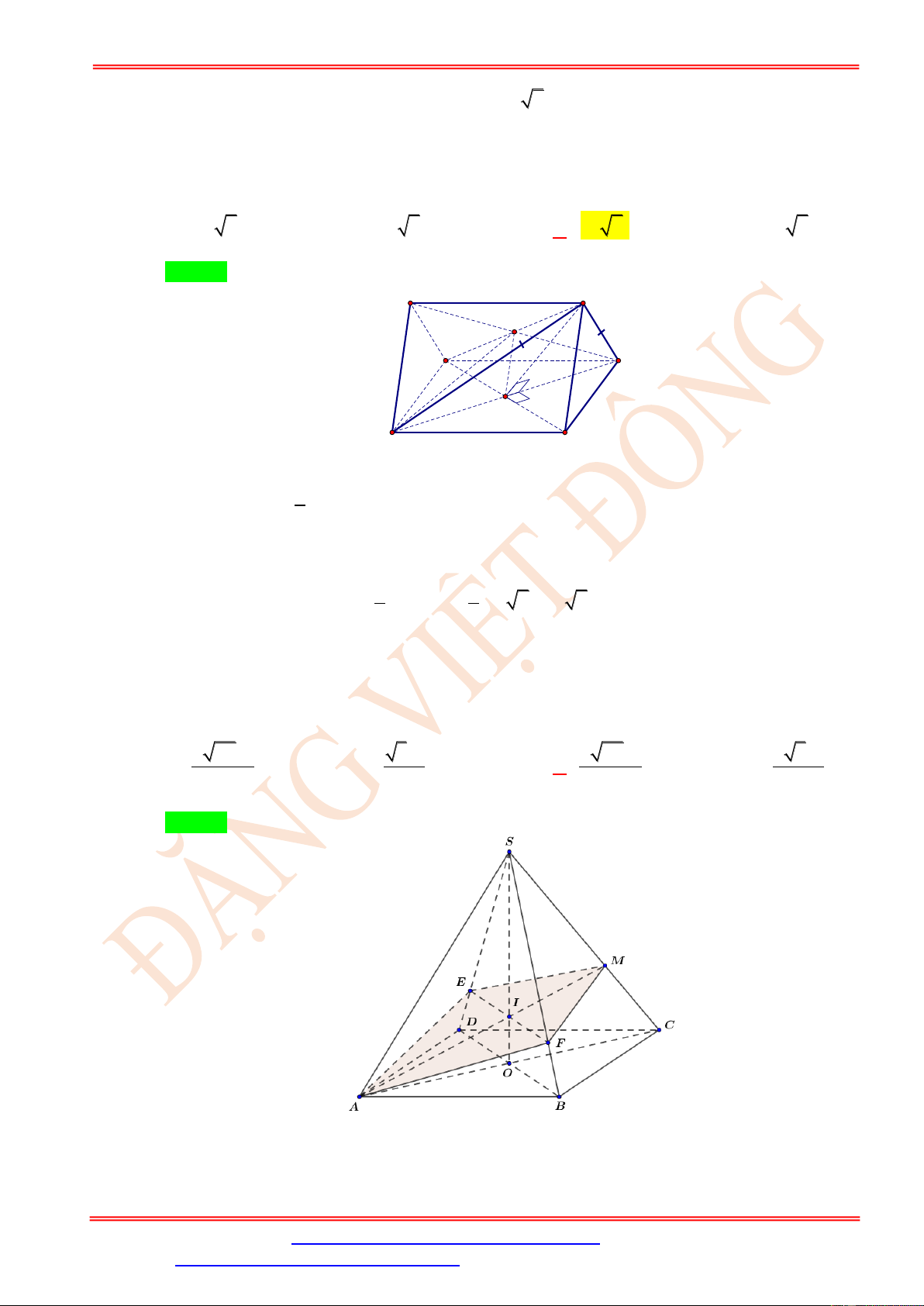
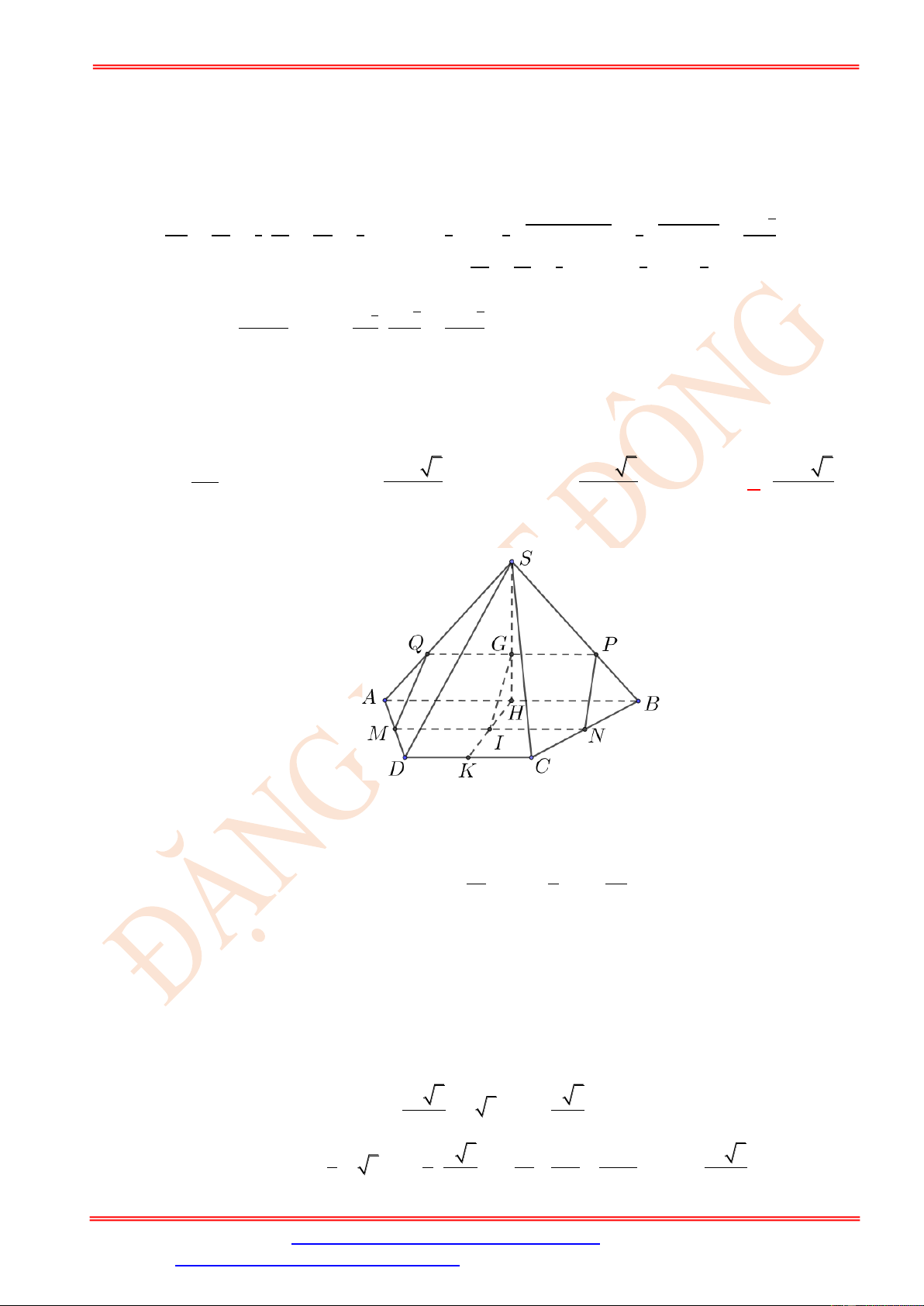
Câu 104. Cho hình chóp S.ABCD có đáy là hình thang cân ABCD ( AB // CD, AB = 2a) ,
BC = CD = DA = a , điểm S cách đều 4 đỉnh , A ,
B C, D đồng thời tam giác SAB đều. Gọi
M , N và G lần lượt là trung điểm của A ,
D CB và trọng tâm tam giác SA .
B Diện tích thiết
diện của hình chóp S.ABCD cắt bởi mp(MNG) bằng 2 9a 2 15a 3 2 15a 3 2 85a 3 A. . B. . C. . D. . 16 12 24 144
Câu 105. Cho tứ diện S.ABC có ABC
vuông cân tại B , AB = a , SA ⊥ ( ABC ) và SA = a 3 . M là
điểm tùy ý trên cạnh AB sao cho AM = x (0 x a) . Mặt phẳng ( ) đi qua M và vuông
góc với AB . Diện tích thiết diện tạo bởi tứ diện S.ABC và mặt phẳng ( ) có giá trị lớn nhất khi x bằng a a 3 a 2 A. a . B. . C. . D. . 2 2 2
Câu 106. Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a , đường cao SO = 2a. Gọi M là điểm
thuộc đường cao AH của tam giác ABC . Xét mặt phẳng ( P) đi qua điểm M và vuông góc
với AH . Đặt AM = x . Tìm x để thiết diện của hình chóp khi cắt bởi mặt phẳng ( P) đạt giá trị lớn nhất. 3a 3 a 3 3a 3 a 3 A. x = . B. x = . C. x = . D. x = . 8 3 4 8
Câu 107. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA ⊥ ( ABCD) và SA = a 2 . Một mặt
phẳng ( ) qua A vuông góc với SC và cắt SC tại C , cắt S ,
B SD lần lượt tại B và D .
Tính diện tích thiết diện của ( ) và hình chóp. 2 a 2 2 2a 2 2 a 2 A. . B. 2 a 2 . C. . D. . 3 3 4 a 3
Câu 108. Cho tứ diện SABC có hai mặt ( ABC ) và ( SBC ) là hai tam giác đều cạnh a , SA = . M 2
là điểm trên cạnh AB sao cho AM = b (0 b a) . ( P ) là mặt phẳng đi qua M và vuông góc
với BC . Thiết diện của ( P ) và tứ diện SABC có diện tích bằng 2 2 2 2 3 a − b 3 3 a − b 3 3 a − b 3 3 a − b A. 2 a . . B. 2 a . . C. 2 a . . D. 2 a . . 4 a 16 a 8 a 4 a
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
HAI MẶT PHẲNG VUÔNG
Dạng 1: Thiết diện, diện tích thiết diện Câu 109.
Cho hình chóp S.ABCD , đáy ABCD là hình vuông, SA ⊥ ( ABCD) . Gọi ( ) là mặt phẳng chứa AB
vuông góc với (SCD) , ( ) cắt hình chóp S.ABCD theo thiết diện là hình gì?
A. Hình bình hành.
B. Hình thang vuông.
C. Hình thang không vuông.
D. Hình chữ nhật.
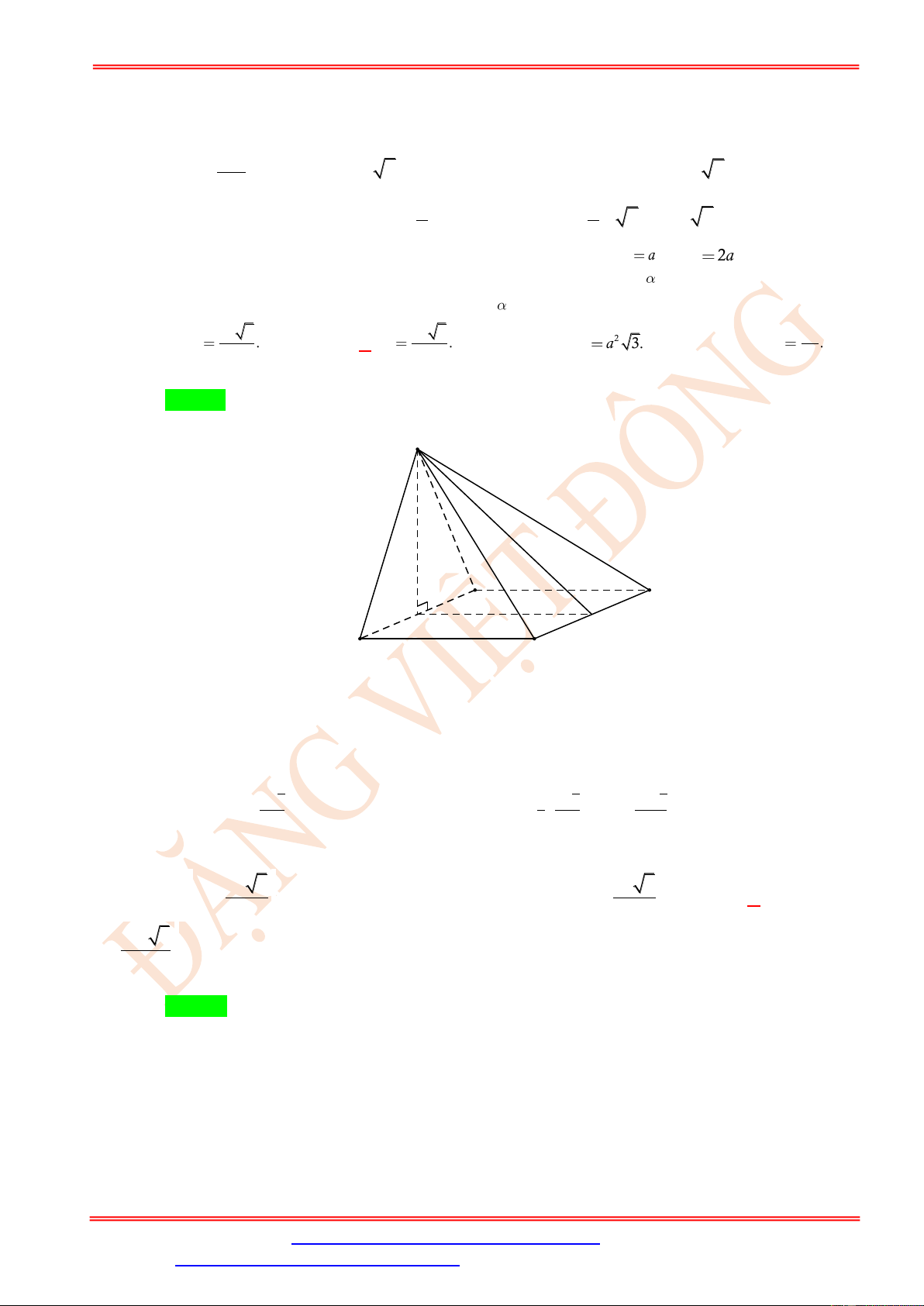
Câu 110. Cho lăng trụ đứng 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′ có đáy 𝐴𝐵𝐶 là tam giác vuông tại 𝐵, 𝐴𝐵 = 2𝑎, 𝐵𝐶 = 4𝑎,
𝐴𝐴′ = 3𝑎. Gọi 𝑀 là trung điểm cạnh 𝐴𝐵. Diện tích của thiết diện của lăng trụ 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′ khi
cắt bởi mặt phẳng (𝑀𝐵′𝐶′) bằng A. 2√10 a2. B. 3√10 a2. C. 4√10 a2. D. 6√10 a2.
Câu 111. Cho tứ diện ABCD , biết tam giác BCD có diện tích bằng 16 . Mặt phẳng ( P ) đi qua trung
điểm của AB và song song mới mặt phẳng ( BCD) cắt tứ diện theo một thiết diện có diện tích bằng A. 12. B. 4 . C. 8 . D. 16 .
Câu 112. Cho tứ diện đều ABCD cạnh a =12 , gọi ( P ) là mặt phẳng qua B và vuông góc với AD .
Thiết diện của ( P ) và hình chóp có diện tích bằng A. 36 2 . B. 40 . C. 36 3 . D. 36 .
Câu 113. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a , điểm M là trung điểm cạnh SC . Mặt
phẳng ( P) chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp S.ABCD
cắt bởi mp ( P) . 2 5a 2 10a 2 10a 2 2 5a A. . B. . C. . D. . 3 3 6 3
Câu 114. Cho hình lăng trụ đều 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′ có cạnh đáy bằng 𝑎, cạnh bên 𝑎√2. Gọi 𝑀 là trung điểm
𝐴𝐵. Tính diện tích thiết diện cắt bởi lăng trụ đã cho bởi mặt phẳng (𝐴′𝐶′𝑀). 7√2 3√35 3√2 9 A. 𝑎2. B. 𝑎2. C. 𝑎2. D. 𝑎2. 16 16 4 8
Câu 115. Cho hình chóp đều S.ABC có cạnh đáy bằng a , cạnh bên bằng b . Mặt phẳng đi qua A và
vuông góc với SC . Tìm hệ thức giữa a và b để
cắt SC tại điểm C S C 1 nằm giữa và . A. a b 2. B. a b 3. C. a b 2. D. a b 3.
Câu 116. Cho lăng trụ đều AB . C A B C
có cạnh đáy bằng 4a , cạnh bên bằng 2a . M là trung điểm của .
AB Cắt hình trụ bởi mặt phẳng ( AC M
). Diện tích của thiết diện là 2 3 7a 2 3 2a A. 2 3 7a . B. . C. . D. 2 6 2a . 4 2
Câu 117. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , BC
2a . Tam giác SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng
đi qua S vuông góc với AB .
Tính diện tích S của thiết diện tạo bởi
với hình chóp đã cho. 2 a 3 2 a 3 2 a A. S . B. S . C. 2 S a 3. S . 4 2 D. 2
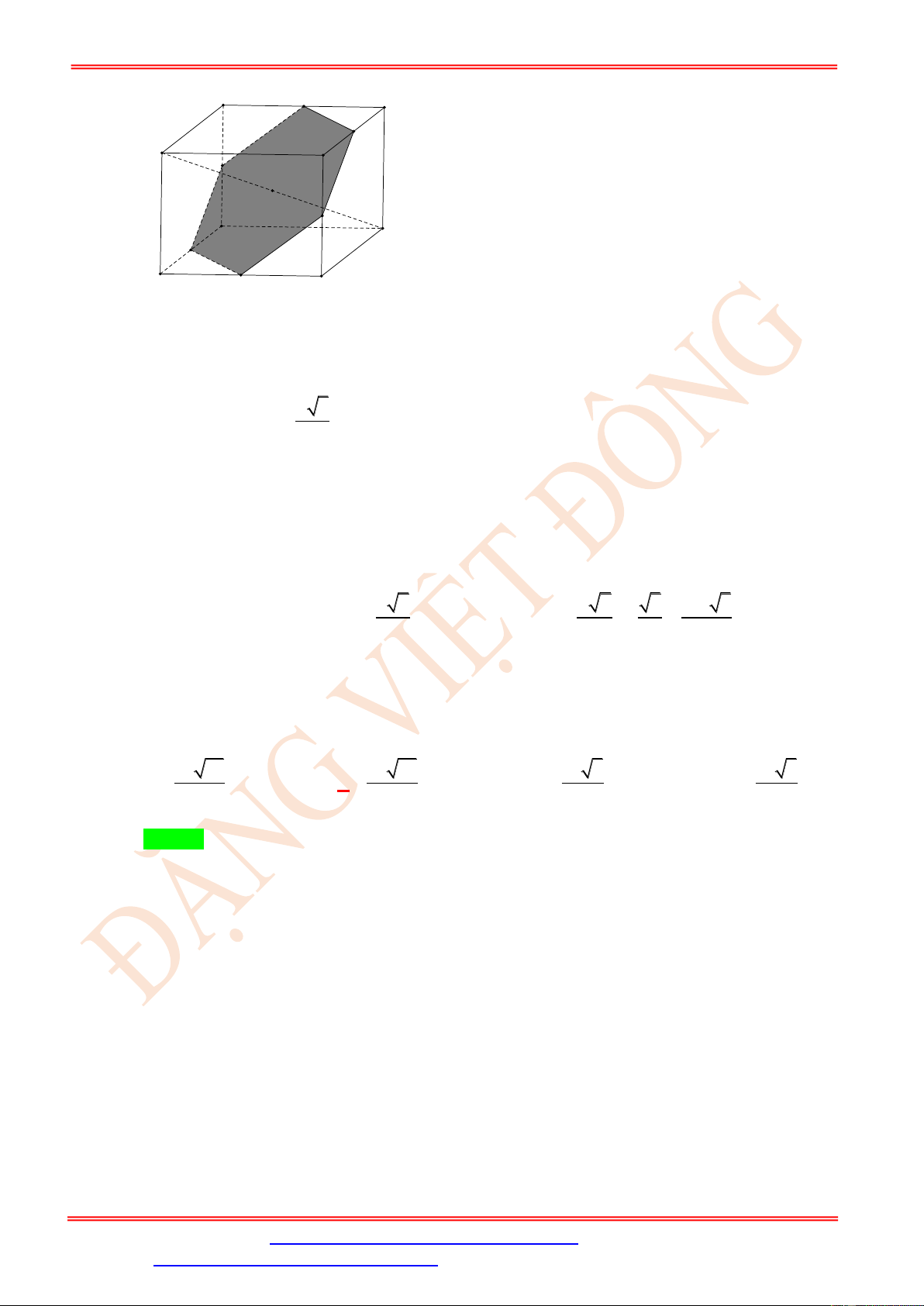
Câu 118. Cho hình lập phương ABC . D A B C D
có cạnh bằng a . Cắt hình lập phương bởi mặt phẳng
trung trực của AC . Diện tích thiết diện là
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 2 a 3 2 a 3 2 3a 3 A. S = . B. 2 S = a . C. S = . D. S = . 2 4 4
Câu 119. Cho hình chóp tam giác đều S.ABC đỉnh S , có độ dài cạnh đáy bằng a . Gọi M và N lần lượt
là các trung điểm của các cạnh SB và SC . Biết mặt phẳng ( AMN ) vuông góc với mặt phẳng
(SBC) . Tính diện tích tam giác AMN theo a . 2 a 10 2 a 10 2 a 5 2 a 5 A. . B. . C. . D. . 24 16 8 4
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
PHẦN II - HƯỚNG DẪN GIẢI
HAI ĐƯỜNG THẲNG CHÉO NHAU VÀ SONG SONG
Dạng 1: Tính diện tích thiết diện, đoạn thẳng dựa vào hai ĐT song song
Câu 1. Cho tứ diện ABCD có AB = 6, CD = 8 . Cắt tứ diện bởi một mặt phẳng song song với
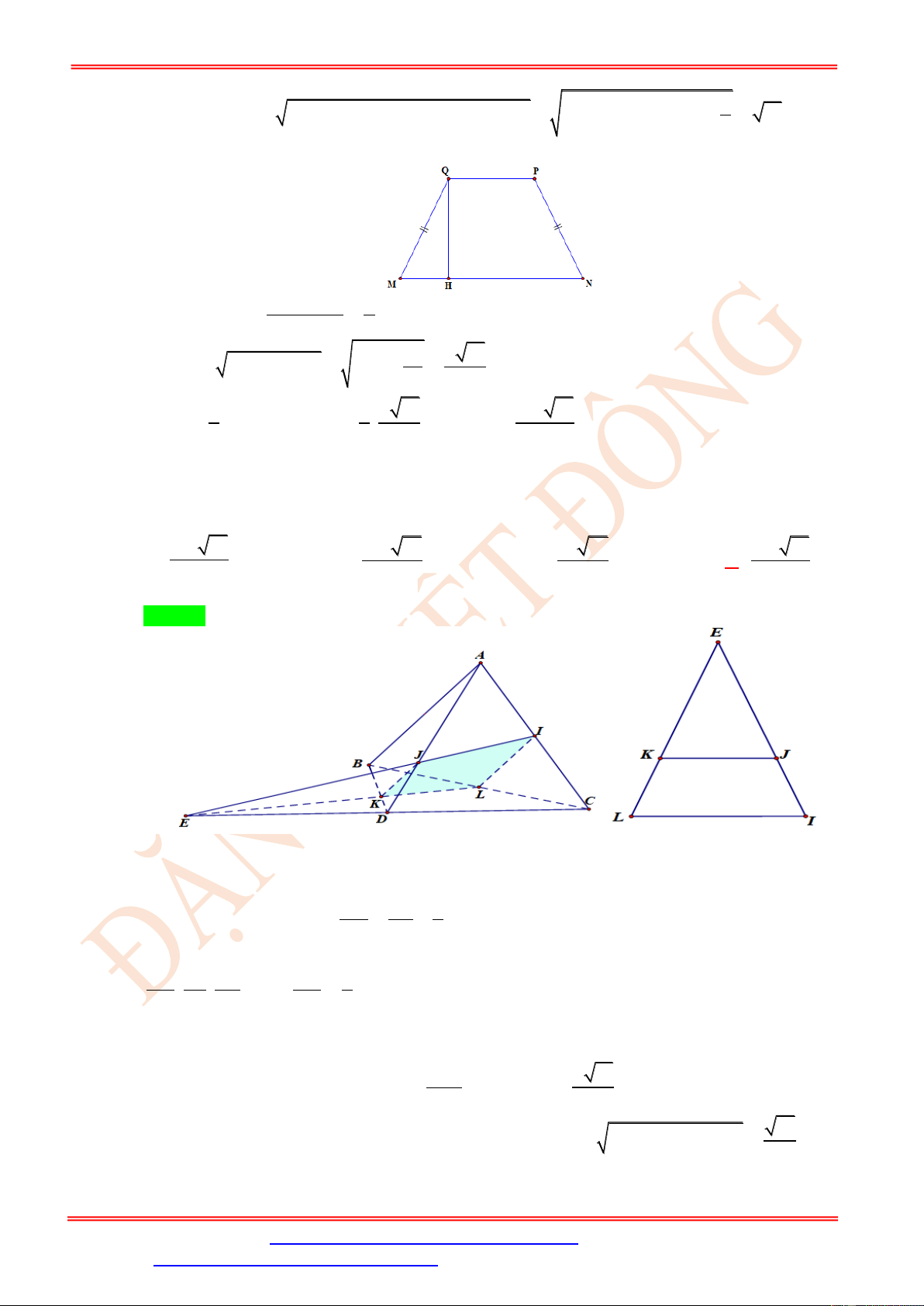
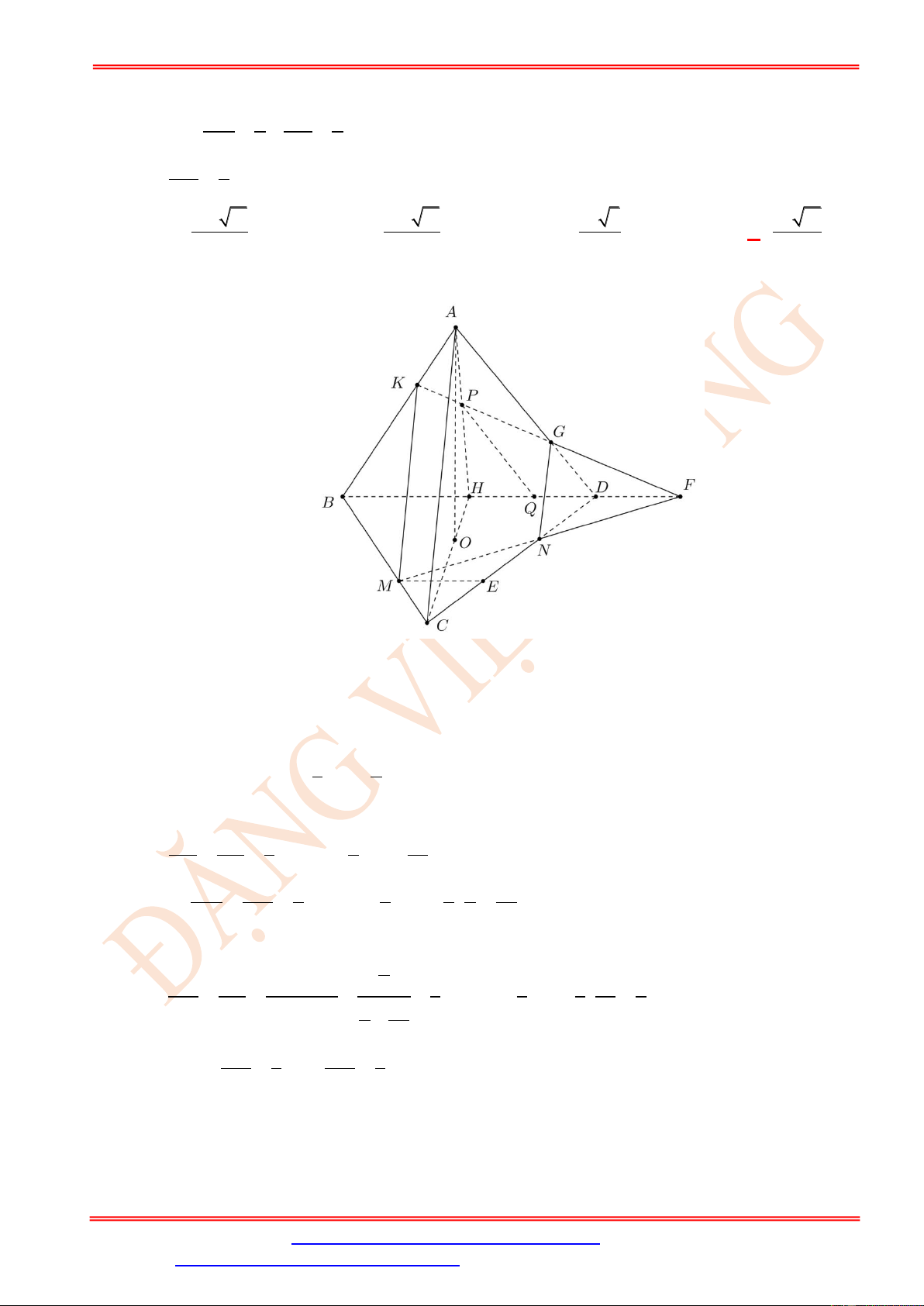
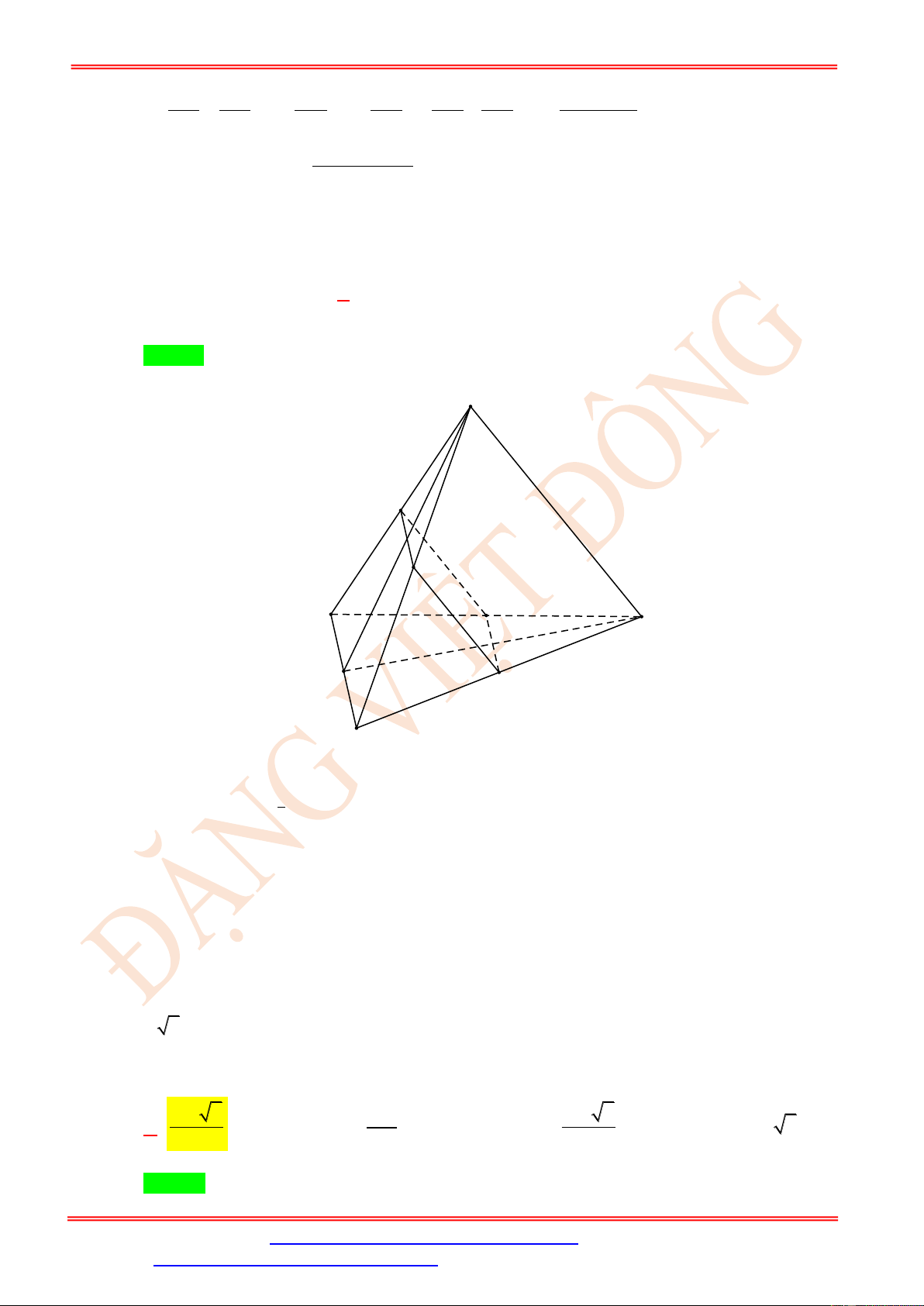
AB , CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng 31 18 24 15 A. . B. . C. . D. . 7 7 7 7 Lời giải Chọn C A I K B D N M C
Giả sử một mặt phẳng song song với AB và CD cắt tứ diện ABCD theo một thiết diện là
MK // AB // IN
hình thoi MNIK như hình vẽ trên. Khi đó ta có: MN // CD // IK . MK = KI MK CK − = MK AC AK = AB AC 6 AC
Cách 1: Theo định lí Ta – lét ta có: KI AK = KI AK = CD AC 8 AC MK AK = MK KI MK MK 1− =1− =1− 7 MK = 24 1 MK = . 6 AC 6 8 6 8 24 7
Vậy hình thoi có cạnh bằng 24 . 7 MK CK = AB AC MK MK CK AK
Cách 2: Theo định lí Ta – lét ta có: + = + KI AK = AB CD AC AC CD AC MK MK AK + KC + = 7MK AC = = 24 1 MK = . 6 8 AC 24 AC 7
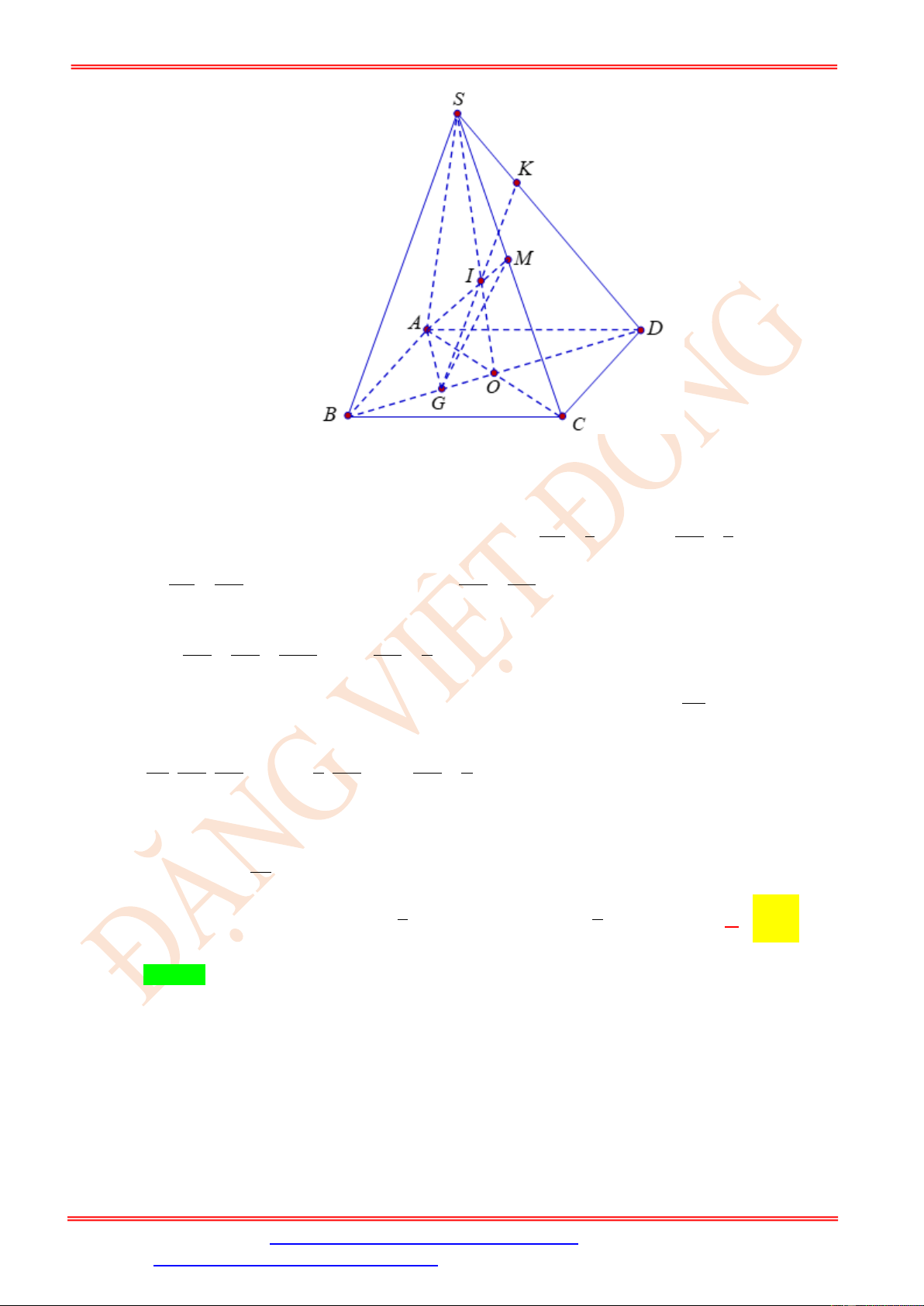
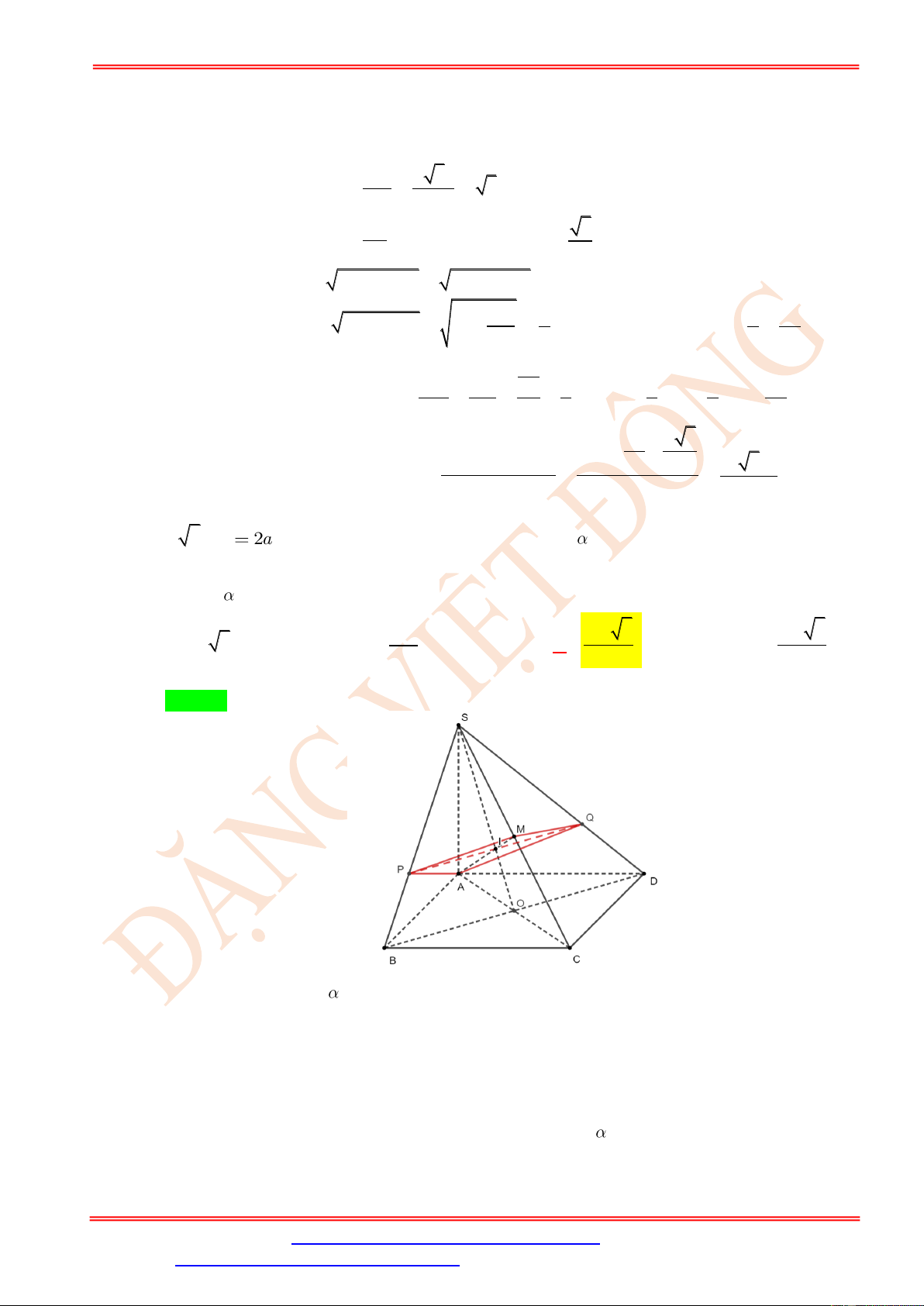
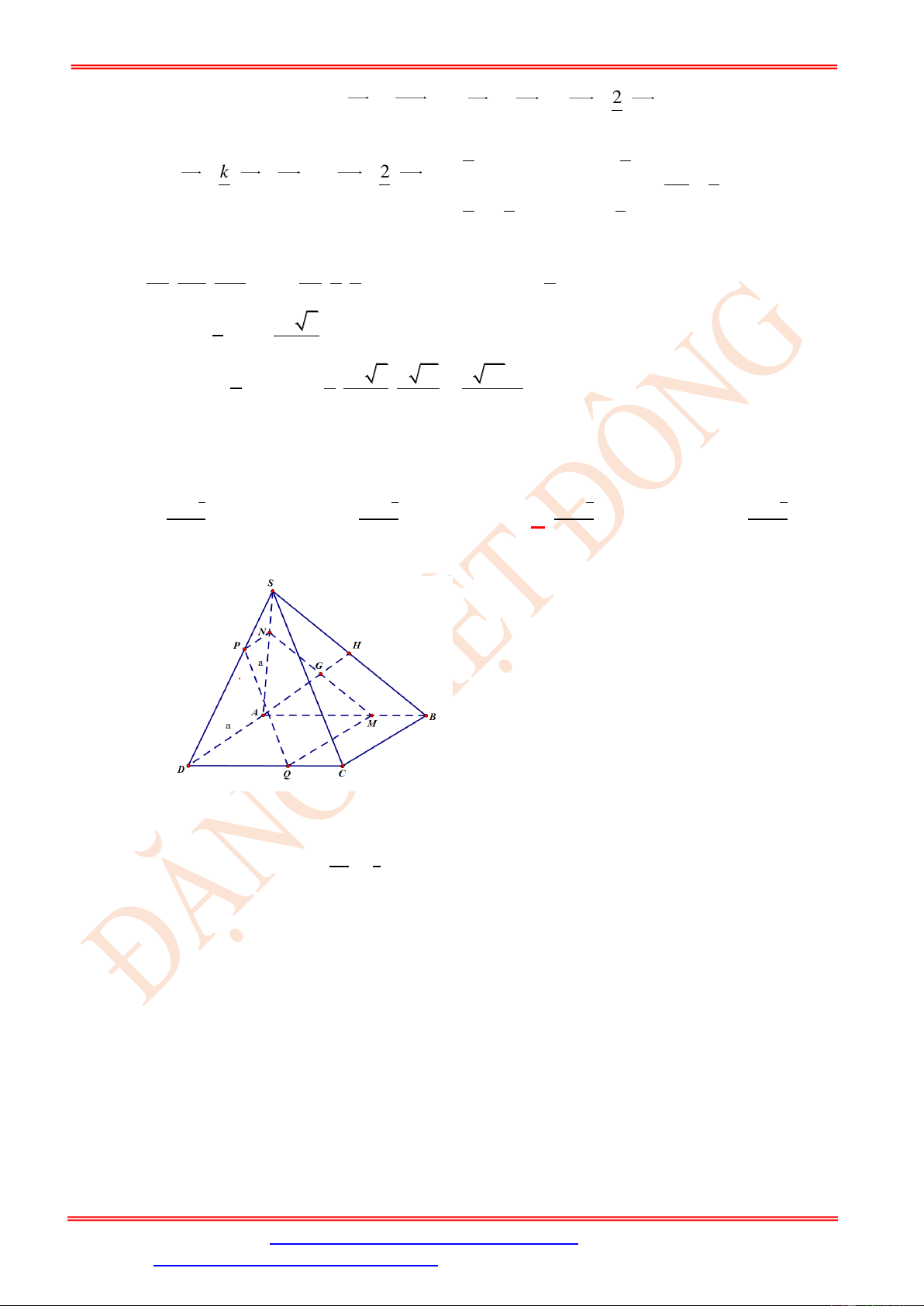
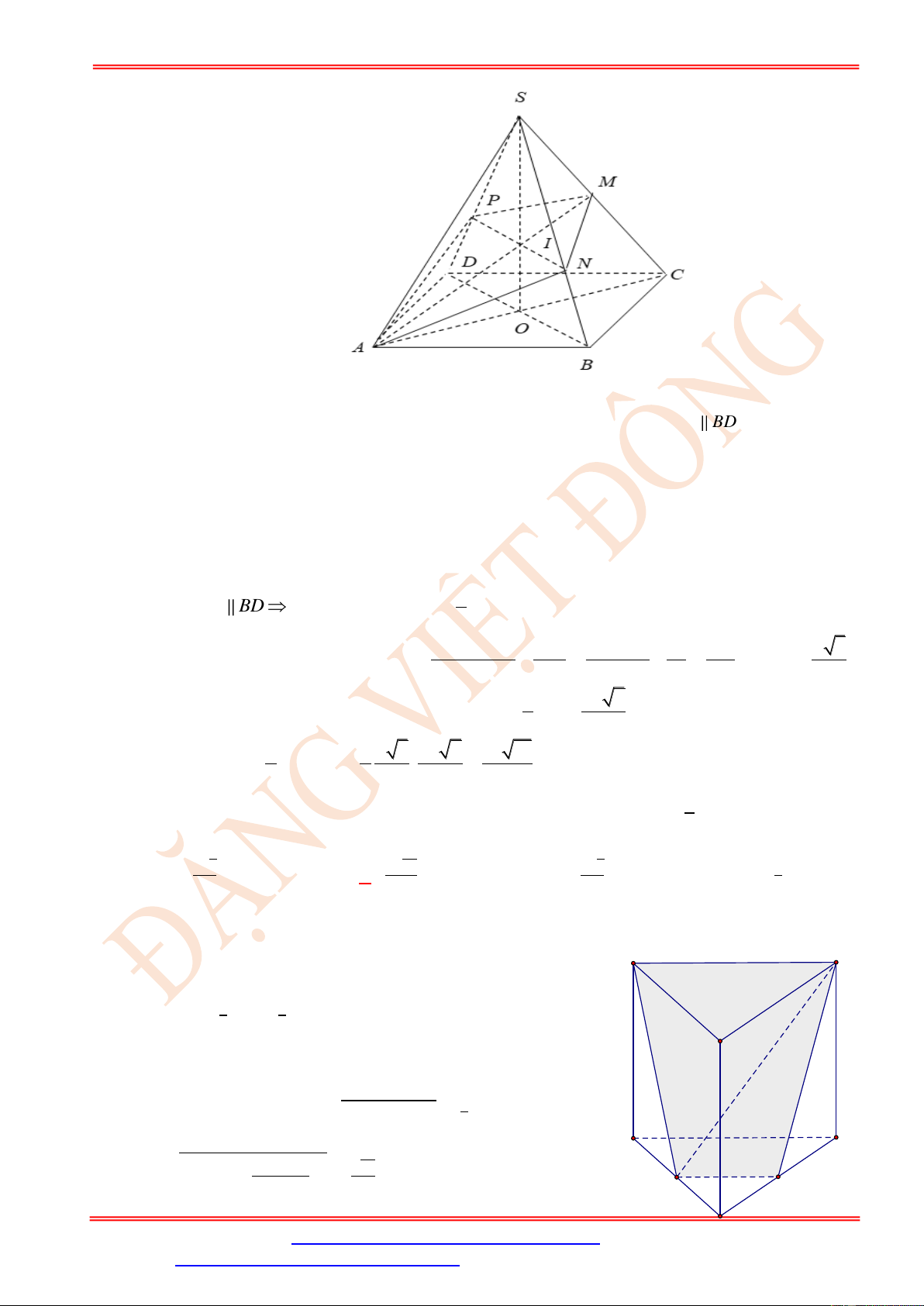
Câu 2. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a , SA = SD = 3a , SB = SC = 3a 3 .
Gọi M , N lần lượt là trung điểm của các cạnh SA và SD , P là điểm thuộc cạnh AB sao
cho AP = 2a . Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng ( MNP) .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
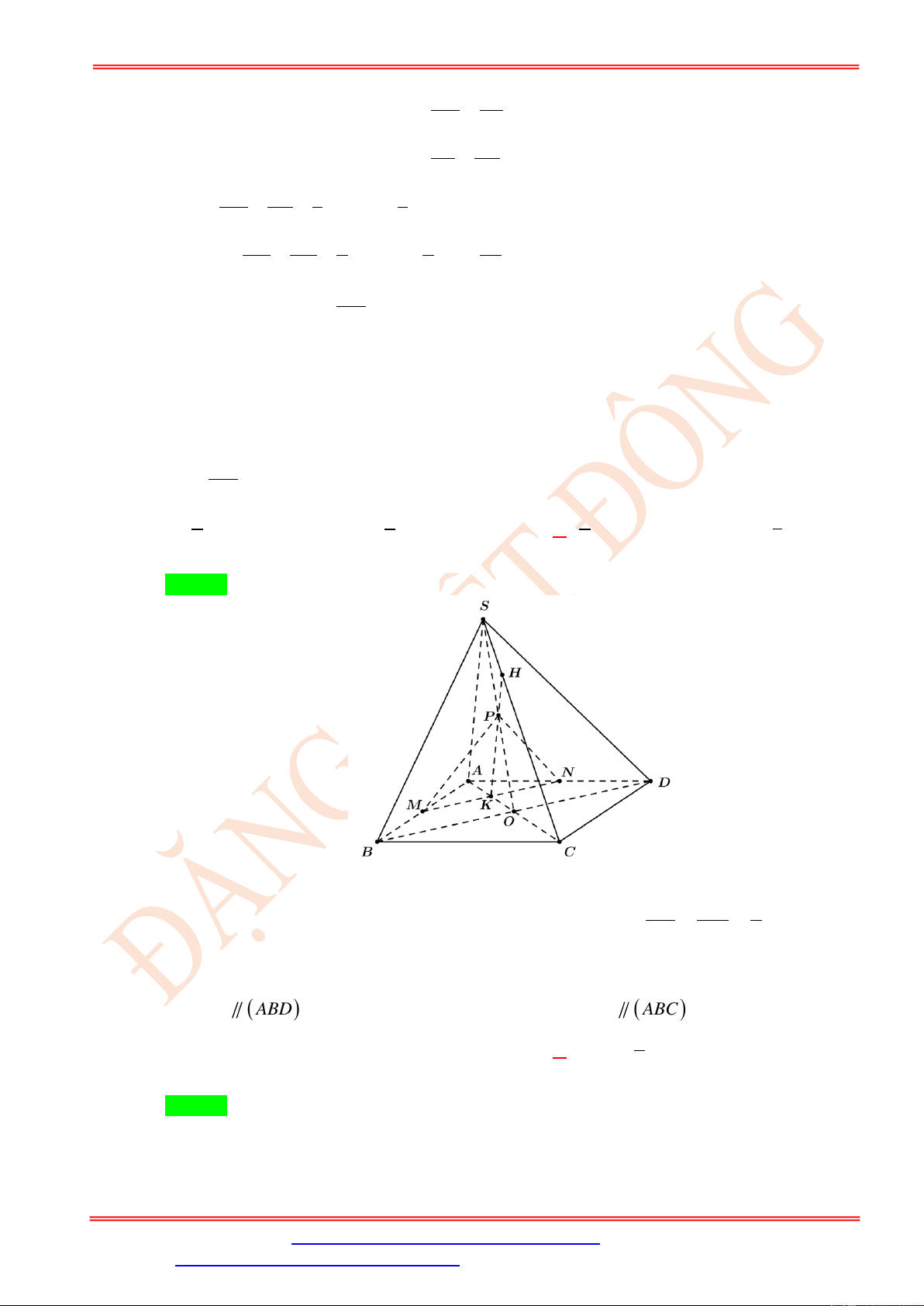
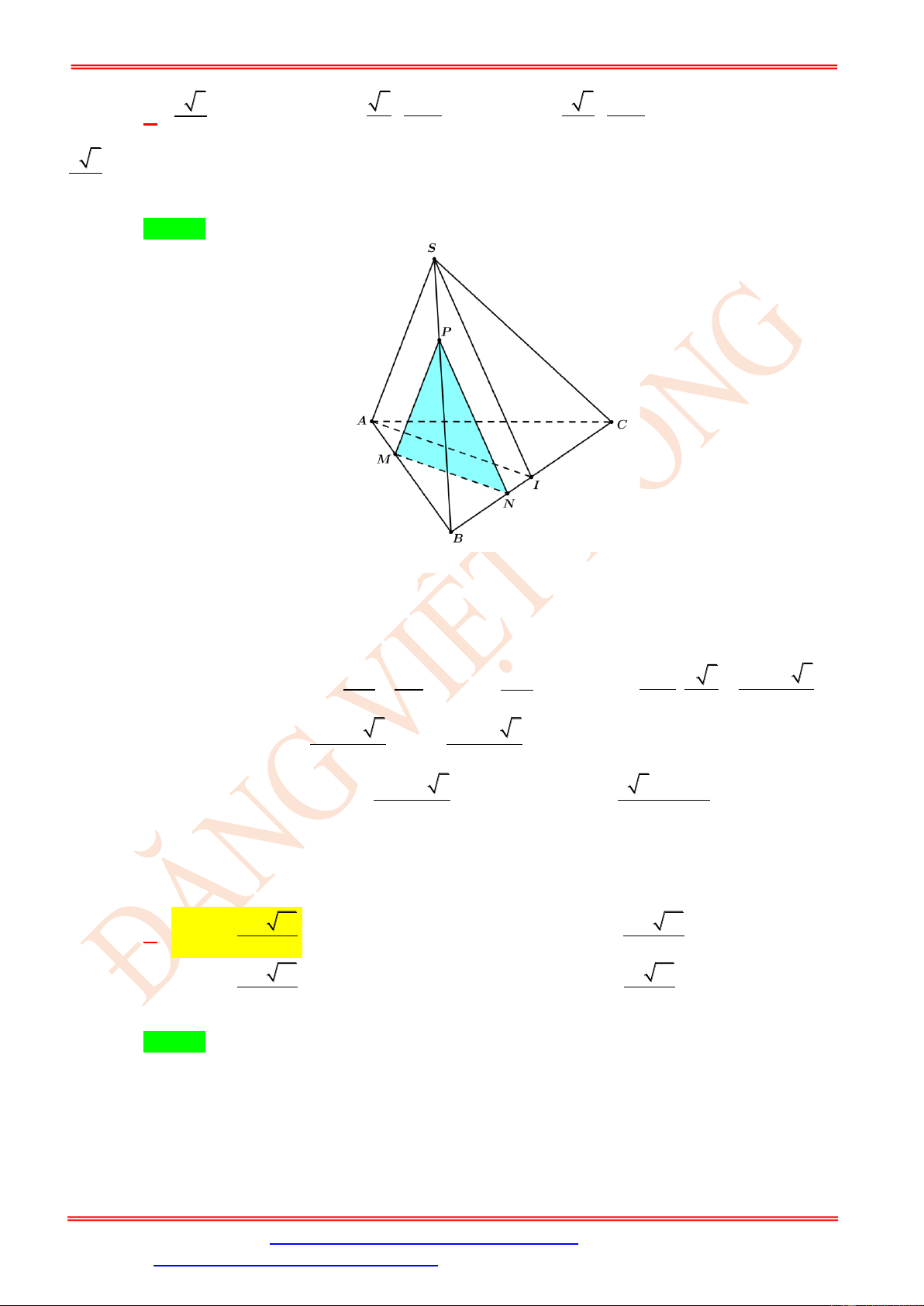
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 2 9a 139 2 9a 139 2 9a 7 2 9a 139 A. . B. . C. . D. . 4 8 8 16 Lời giải Chọn A
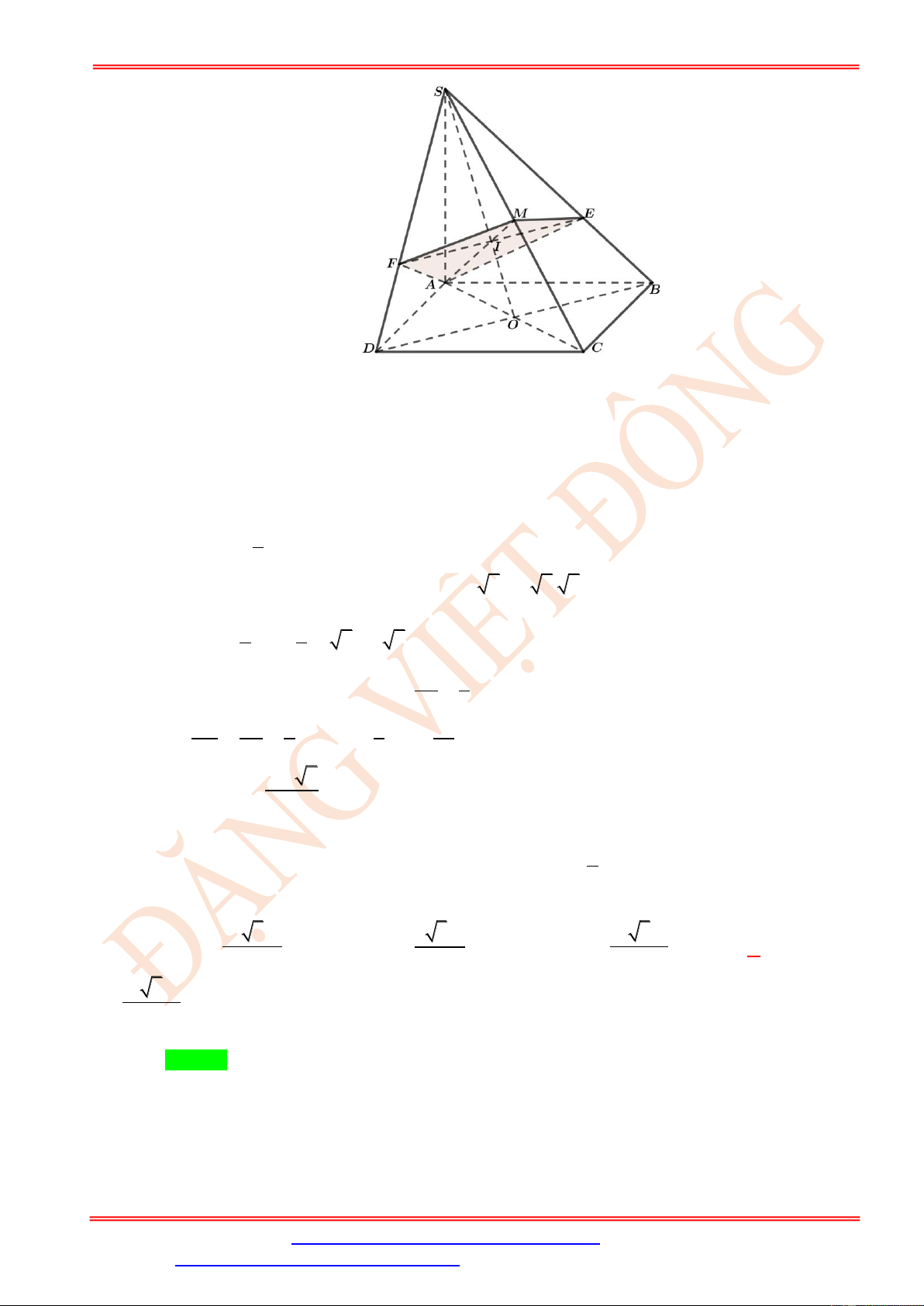
Do MN//AD MN//BC . Vậy ( MNP) cắt mặt phẳng ( ABCD) theo giao tuyến đi qua P ,
song song BC và cắt DC tại điểm I . Thiết diện của khối chóp cắt bởi mặt phẳng ( MNP)
chính là hình thang MNIP . Do N DI = M
AP nên MP = NI . Từ đó suy ra MNIP là hình thang cân.
Trong tam giác SAB , ta có 2 2 2 2 2 2 2
SA + AB − SB
9a + 9a − 27a 9a 1 cos SAB = = = − = − . 2 2.S . A AB 2.3 . a 3a 18a 2
Trong tam giác, MAP , ta có 2 2 9a 3a 37a a 37 2 2 2 2
MP = MA + AP − 2M . A A . P cos MAP = + 4a + 2a = MP = . 4 2 4 2
Từ M kẻ MF ⊥ PI , từ N kẻ NE ⊥ PI . Dễ thấy, tứ giác MNEF là hình chữ nhật và từ đó 3a 3a suy ra MN = EF = PF = EI = . 2 4 2 2 37a 9a a 139
Xét tam giác vuông MFP , ta có 2 2 MF = MP − FP = − = . 4 16 4 3a a 139 ( + MN + IP) 3a 2 .MF 2 4 9a 139 Ta có S = = = . MNIP 2 2 4
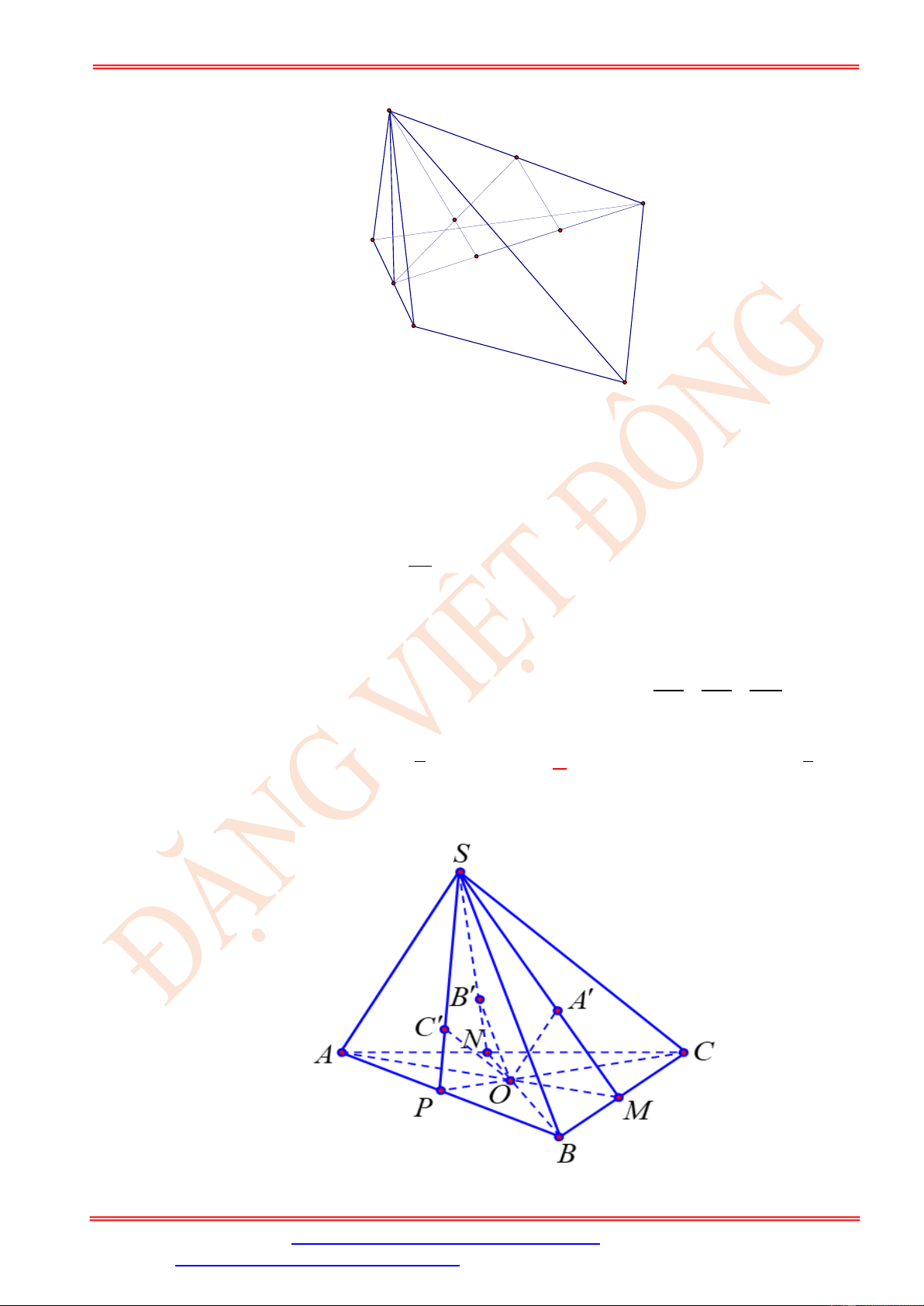
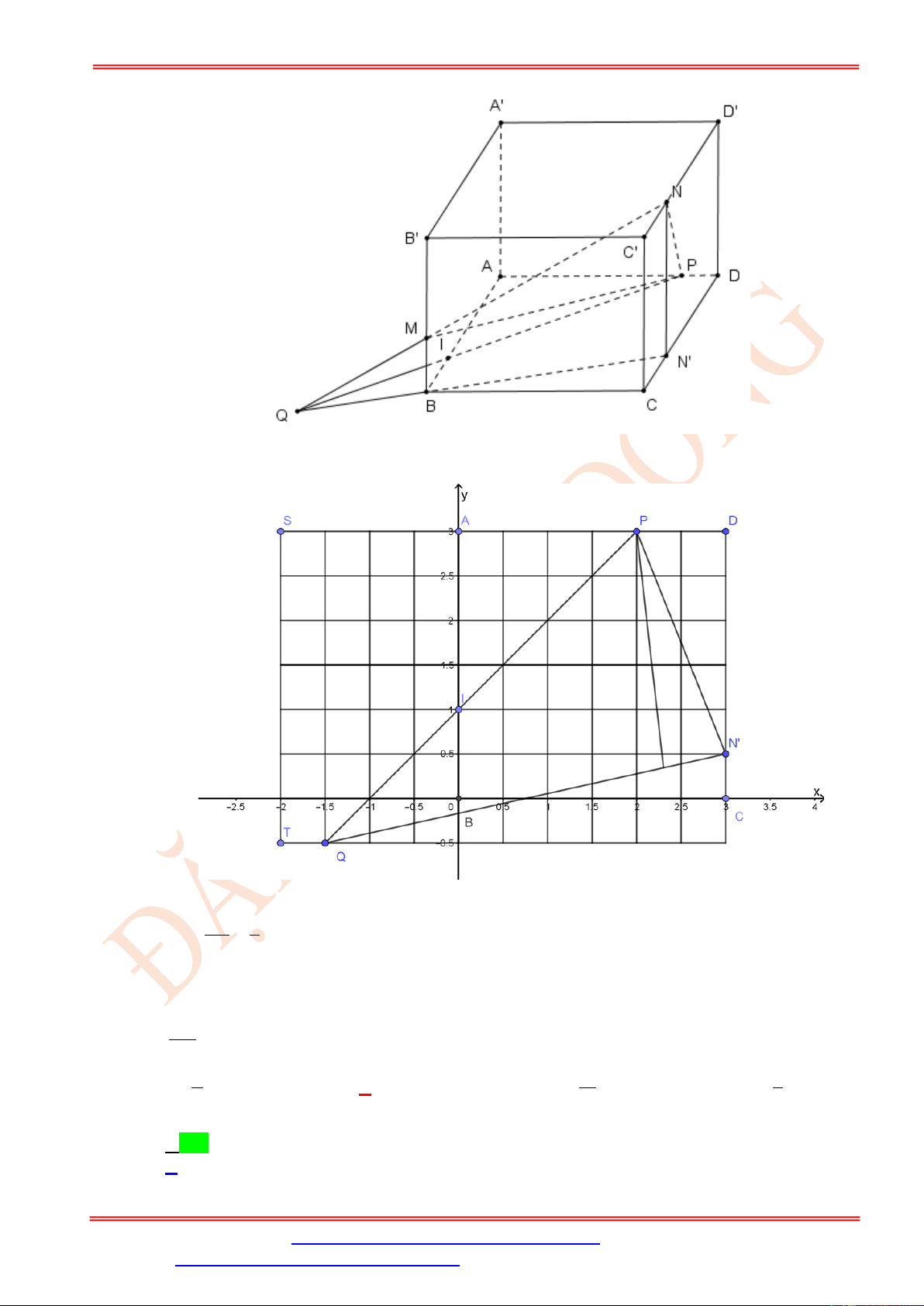
Câu 3. Cho hình lập phương ABC . D A B C D
cạnh a . Các điểm M , N , P theo thứ tự đó thuộc a
các cạnh BB , C D
, DA sao cho BM = C ' N = DP = . Mặt phẳng (MNP) cắt đường 3
thẳng A' B ' tại E. Tính độ dài đoạn thẳng A ' E.
A. A' E = 5a 3.
B. A' E = 3a 4 .
C. A' E = 5a 4 . D.
A ' E = 4a 3. . Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
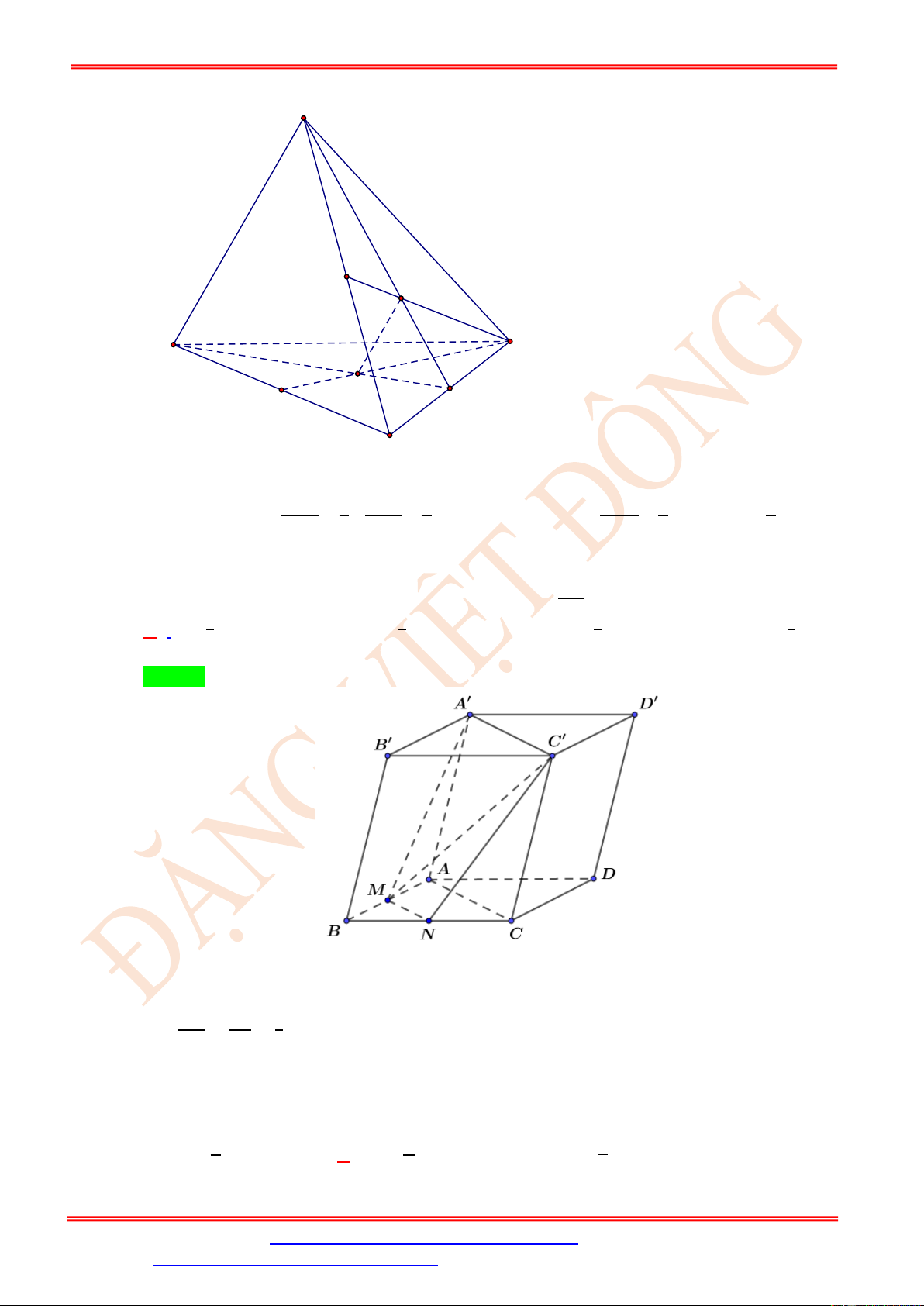
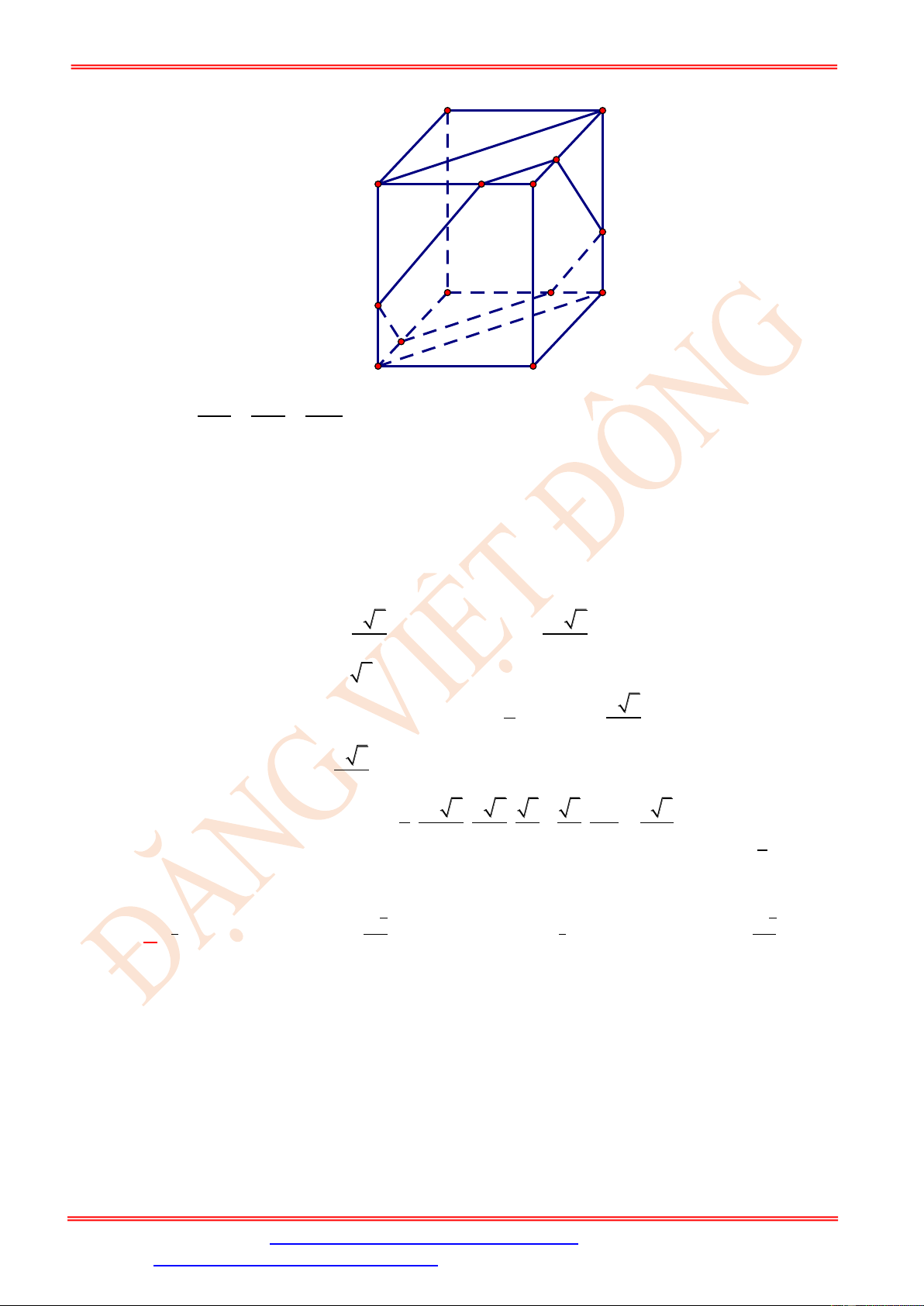
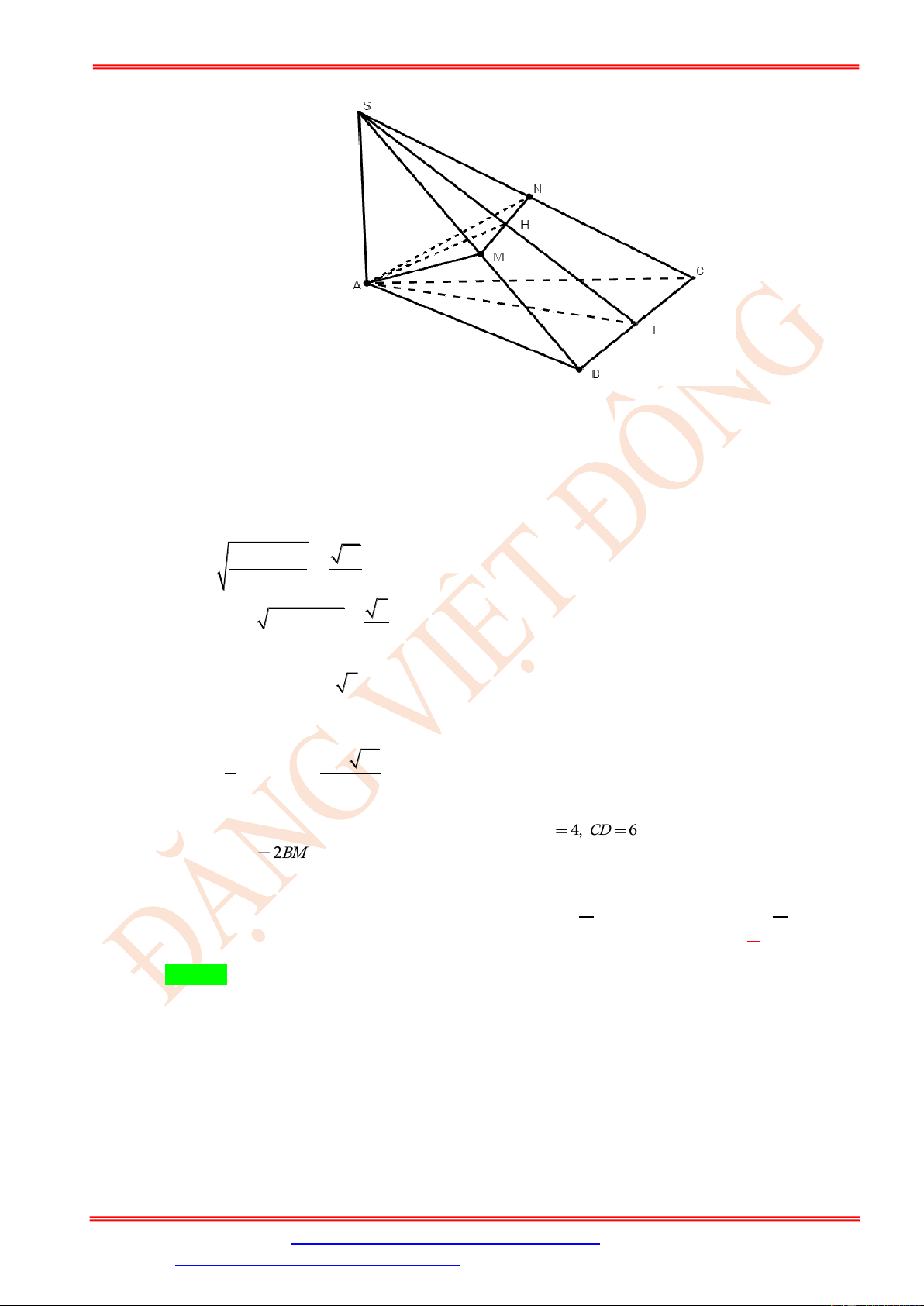
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 E B' C' N D' A' M H C K B A P D a
Lấy H , K thuộc đoạn DD, AB sao cho DH = BK = . 3
Nhận xét KP//BD và MH //BD nên KP// MH , suy ra 4 điểm M, K, , P H đồng phẳng.
Tương tự : MK//AB, DC //A B ; DC //
HN nên MK//HN suy ra 4 điểm M, K, H, N đồng phẳng.
Vậy mặt phẳng ( MNP) chứa các điểm H , K đồng thời mặt phẳng ( MNP) song song với
mặt phẳng ( BDC) . Suy ra mặt phẳng ( MNP) song song với B D .
Xét mặt phẳng ( AB C D
) , qua N kẻ NE//B D cắt A B
tại E là điểm thỏa mãn yêu cầu bài toán. 2a 5a Ta có B E
DN là hình bình hành nên B E = suy ra A E = A B + B E = . 3 3 Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB = 8a ,
SA = SB = SC = SD = 8a . Gọi N là trung điểm cạnh SD . Tính diện tích thiết diện của hình
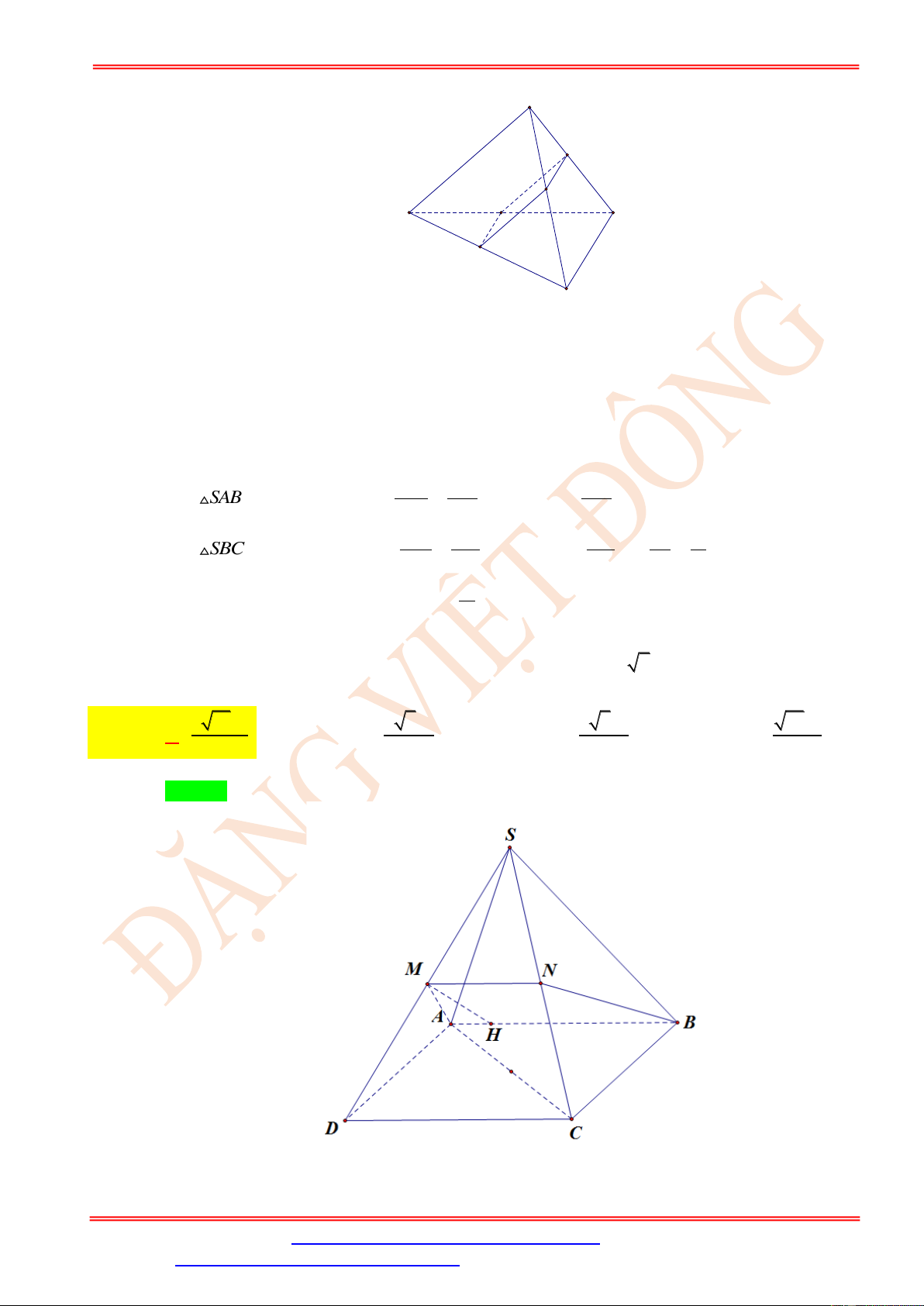
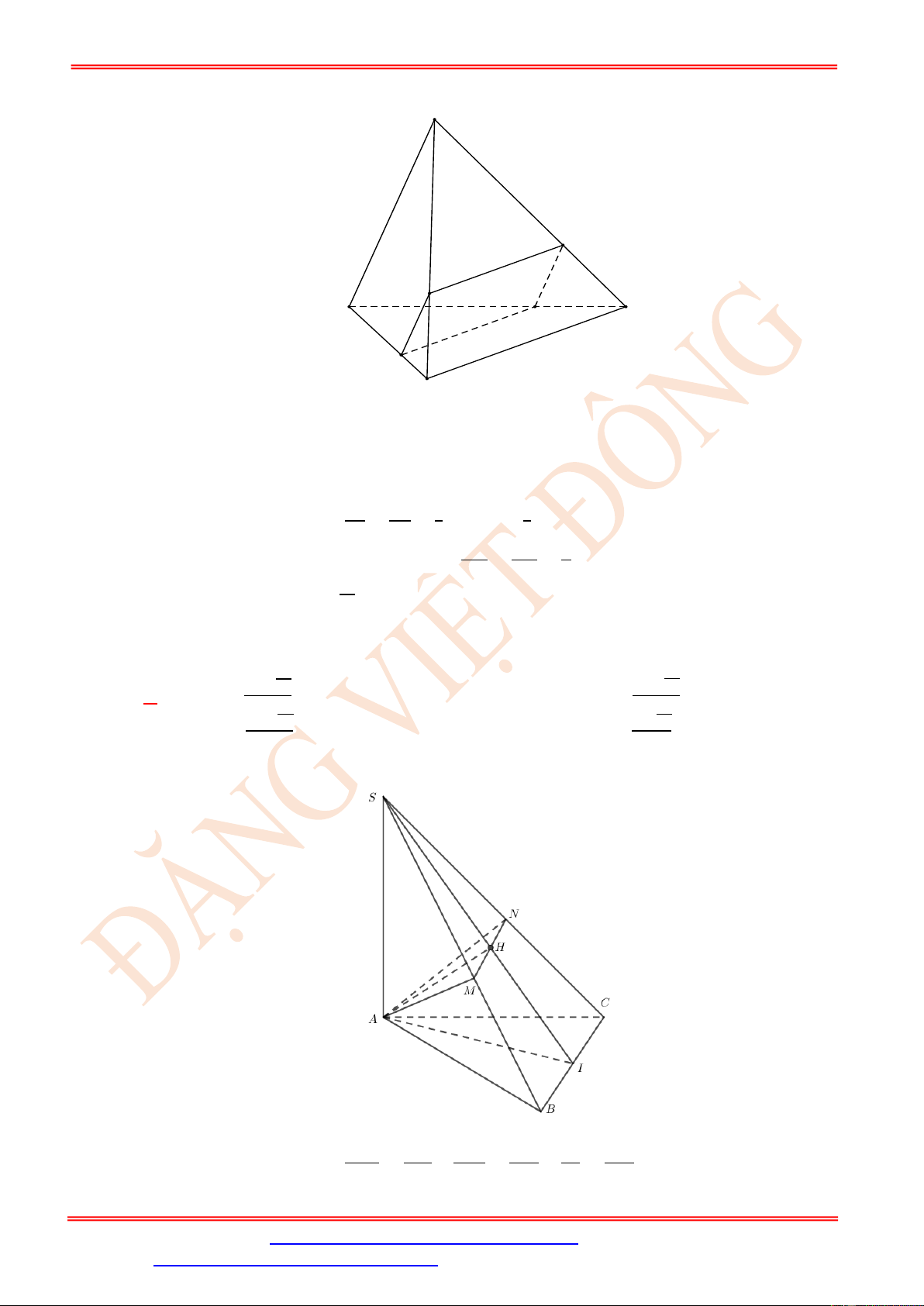
chóp S.ABCD cắt bởi mặt phẳng ( ABN ) . A. 2 12a . B. 2 6a 11 . C. 2 24a . D. 2 12a 11 . Lời giải Chọn D S M N B C I O A D
Mặt phẳng ( ABN ) chứa AB//CD nên cắt mặt phẳng (SCD) theo giao tuyến NM //CD và
M cũng là trung điểm của SC . Suy ra thiết diện cần tìm là hình thang cân ABMN . Hạ a
NI ⊥ AB . Ta có 2 2 2
NI = AN − AI với 8 3 AN = = 4a 3 . 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
2AI = AB − MN = 8a − 4a = 4a AI = 2a . Từ đó suy ra NI = 2a 11 . Vậy 1 1 S = AB + MN NI = (8a + 4a) 2 2a 11 = 12a 11 . ABMN ( ). 2 2
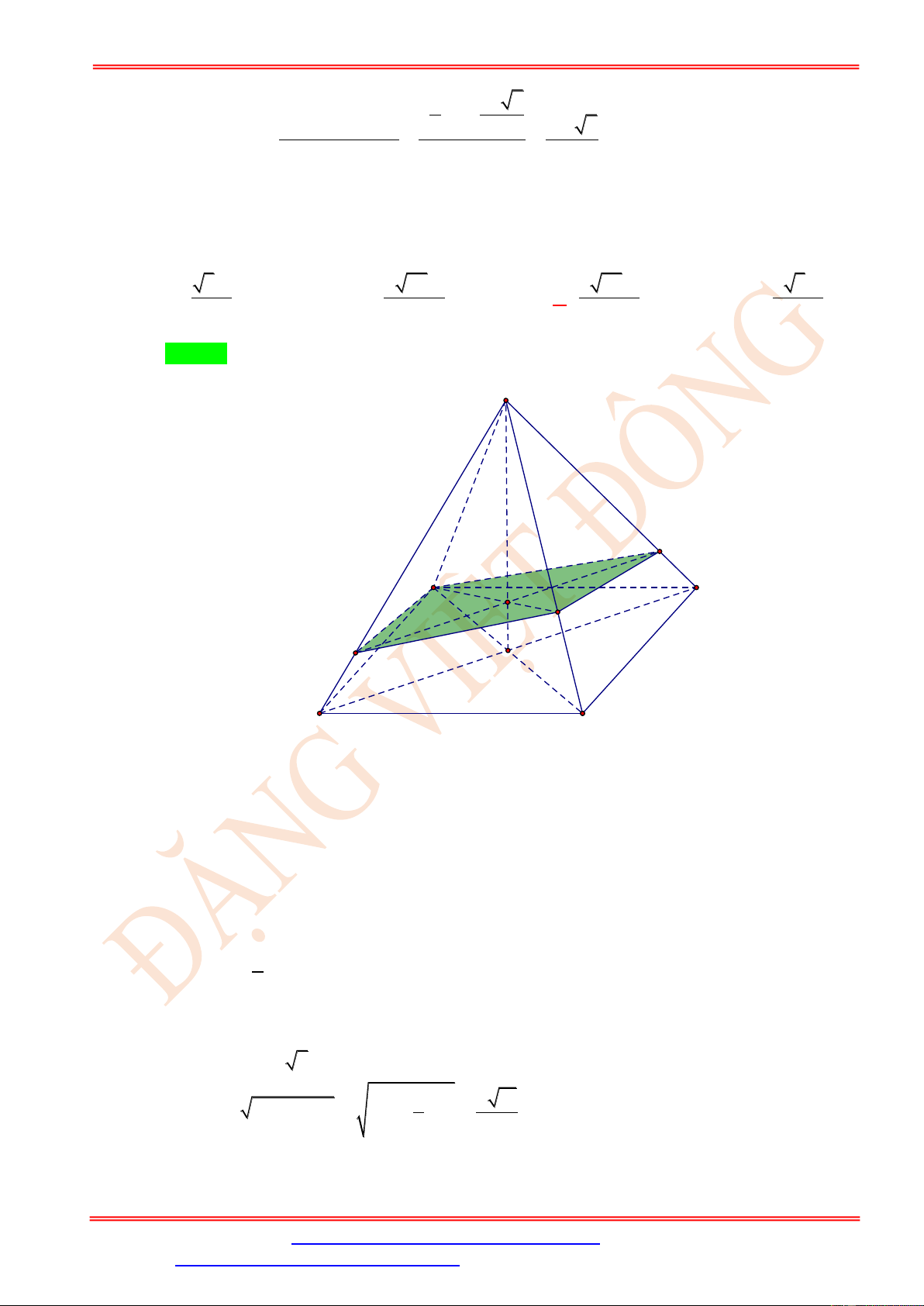
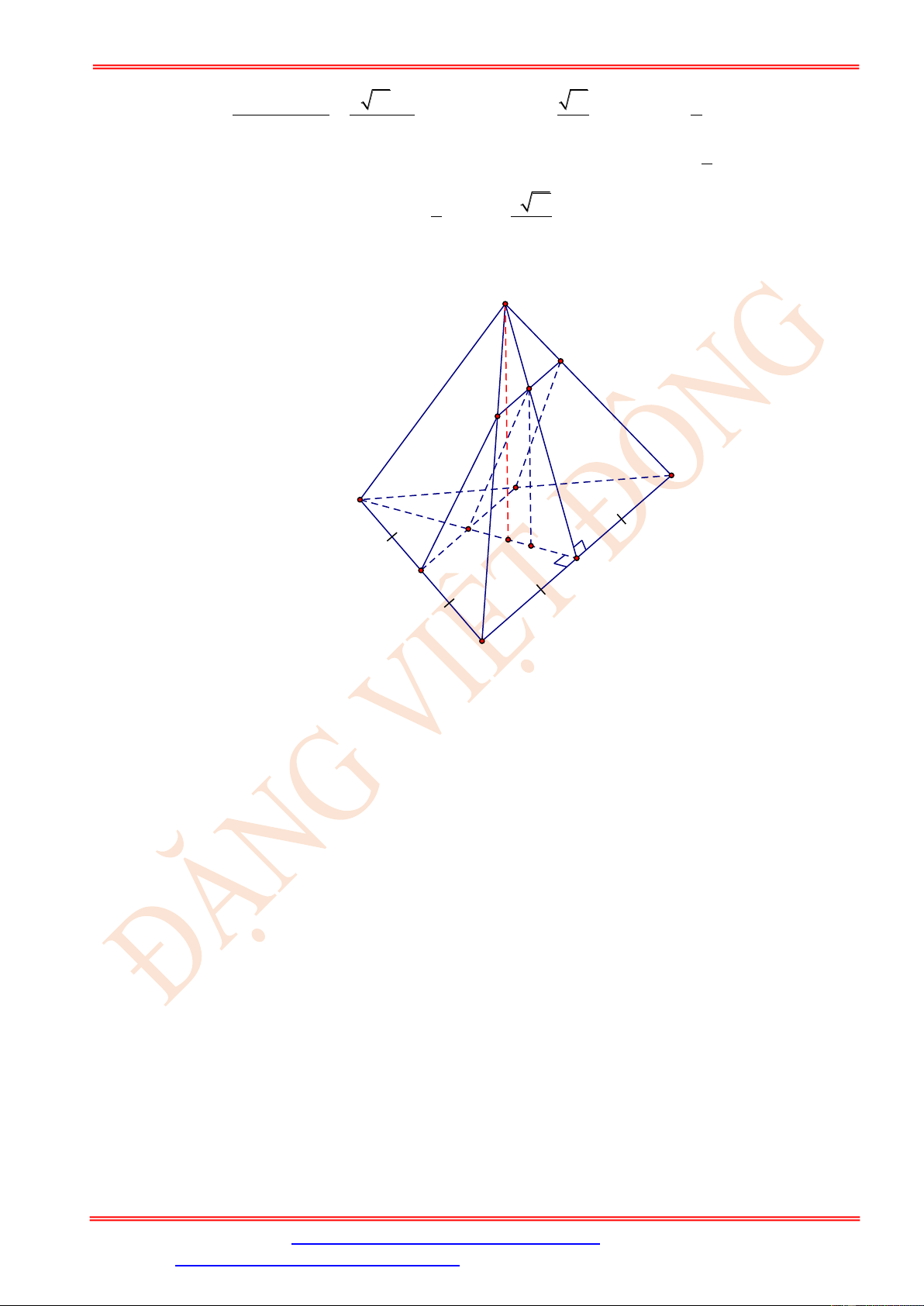
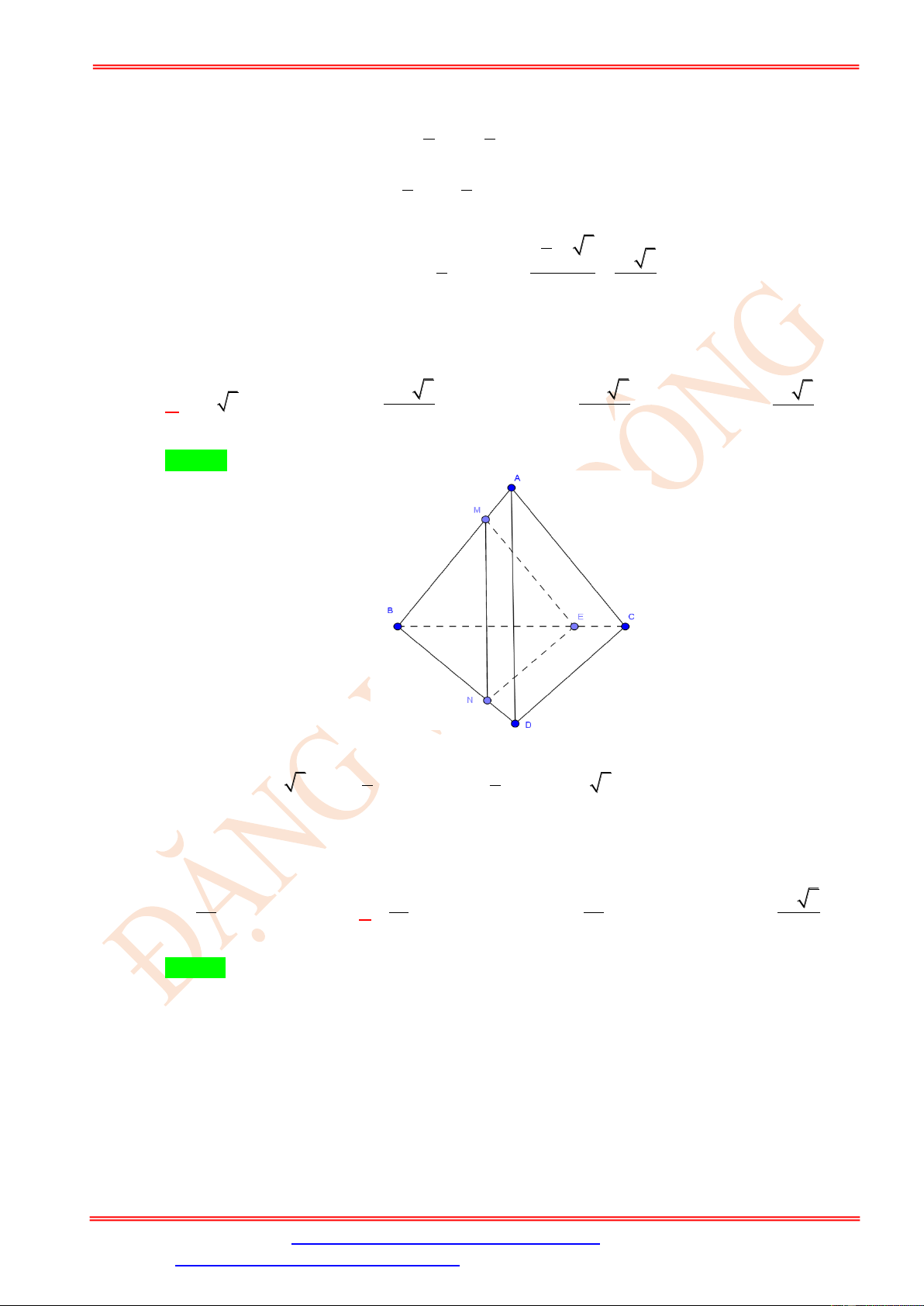
Câu 5. Cho tứ diện ABCD có tất cả các cạnh bằng a . Gọi M , N, P lần lượt là trung điểm của
AC, BC, BD . Gọi tứ giác MNPQ là thiết diện của tứ diện ABCD cắt bởi mặt phẳng
(MNP) . Tìm diện tích thiết diện MNPQ theo a . 2 2 2 a 3a a A. . B. 2 a . C. . D. . 2 4 4 Lời giải Chọn D MN//AB
Ta có MN ,NP lần lượt là đường trung bình của ABC và BCD NP//CD MN //AB AB ( ABD)
(ABD)(MNP) = Px,Px//MN,Px//AB . Trong (ABD), MN (MNP) P ( ABD) (MNP)
Px AD = Q . Trong ABD , vì P là trung điểm của BD và PQ//AB (do Px//AB ) nên Q
là trung điểm của AD do đó PQ là đường trung bình của ABD . Vậy MN //PQ và AB CD
MN = PQ nên MNPQ là hình bình hành. Mà = = a MN NP = = nên MNPQ là 2 2 2 hình thoi. Ta có 3 = = ; = = = = a AC AD a NA ND PA PC
AND = APC (c − c − c) MP = NQ . Vậy 2 2 a
MNPQ là hình vuông. Do đó 2 S = MN = . MNPQ 4
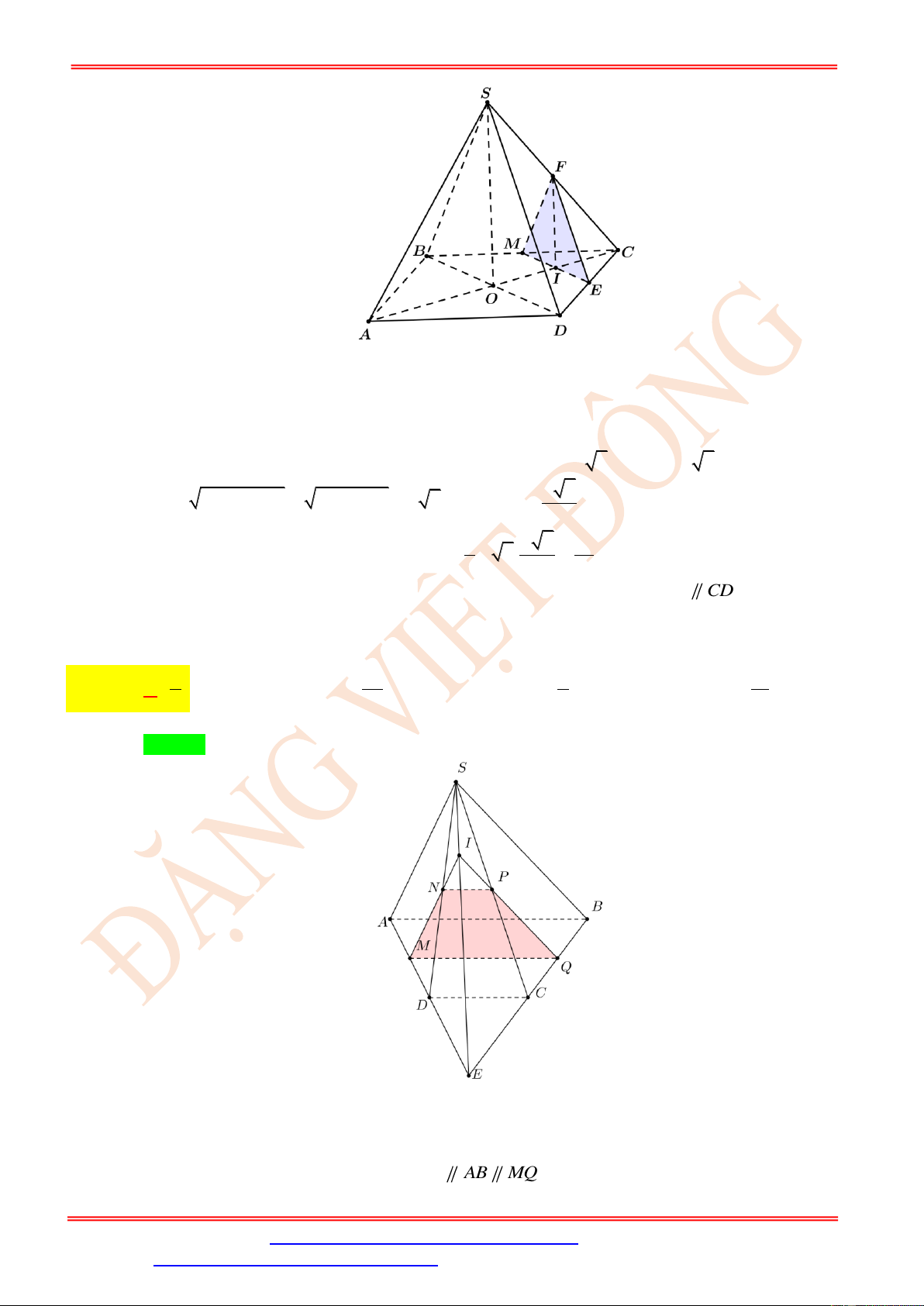
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, biết AB = a , SAD = 90 và tam
giác SAB là tam giác đều. Gọi Dt là đường thẳng qua D và song song với SC , I là giao
điểm của Dt với mặt phẳng (SAB) . Thiết diện của hình chóp S.ABCD với mặt phẳng
( AIC) có diện tích là 2 a 5 2 a 2 2 a 7 2 11a A. . B. . C. . D. . 16 4 8 32
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Lời giải Chọn C
Do Dt / / SC nên hai đường thẳng này cùng nằm trong mặt phẳng ( SCD ) .
Lại có, hai mặt phẳng (SAB) và (SCD) có D là điểm chung, AB / / CD nên giao tuyến của
hai mặt phẳng này là đường thẳng đi qua S và song song với AB .
Mà I là giao điểm của Dt với mặt phẳng ( SAB) nên I thuộc giao tuyến này.
Gọi E là giao điểm của SD và IC . Suy ra thiết diện của hình chóp cắt bởi mặt phẳng
( AIC) là tam giác ACE. DI / / SC
Tứ giác SIDC có:
nên nó là hình bình hành SI = CD SI = AB = a và E là CD / /SI
trung điểm của SD,CI . Mặt khác, a 2
AC = SD = a 2 AE = . 2
Xét tam giác IAC có : 2 CI = ( 2 2 AC + AI ) 2 2 2
− 4AE = 4a CI = 2a CE = a . 2 a 2 2 + − 2 2 2 2a a
AE + AC − CE 3 7 Ta có : 2 cos CAE = = = sin CAE = . 2 2AC.AE 2a 4 4 2
Diện tích thiết diện là 1 1 a 2 7 a 7 : S =
AC.AE.sin CAE = a 2. . = (đvdt). 2 2 2 4 8
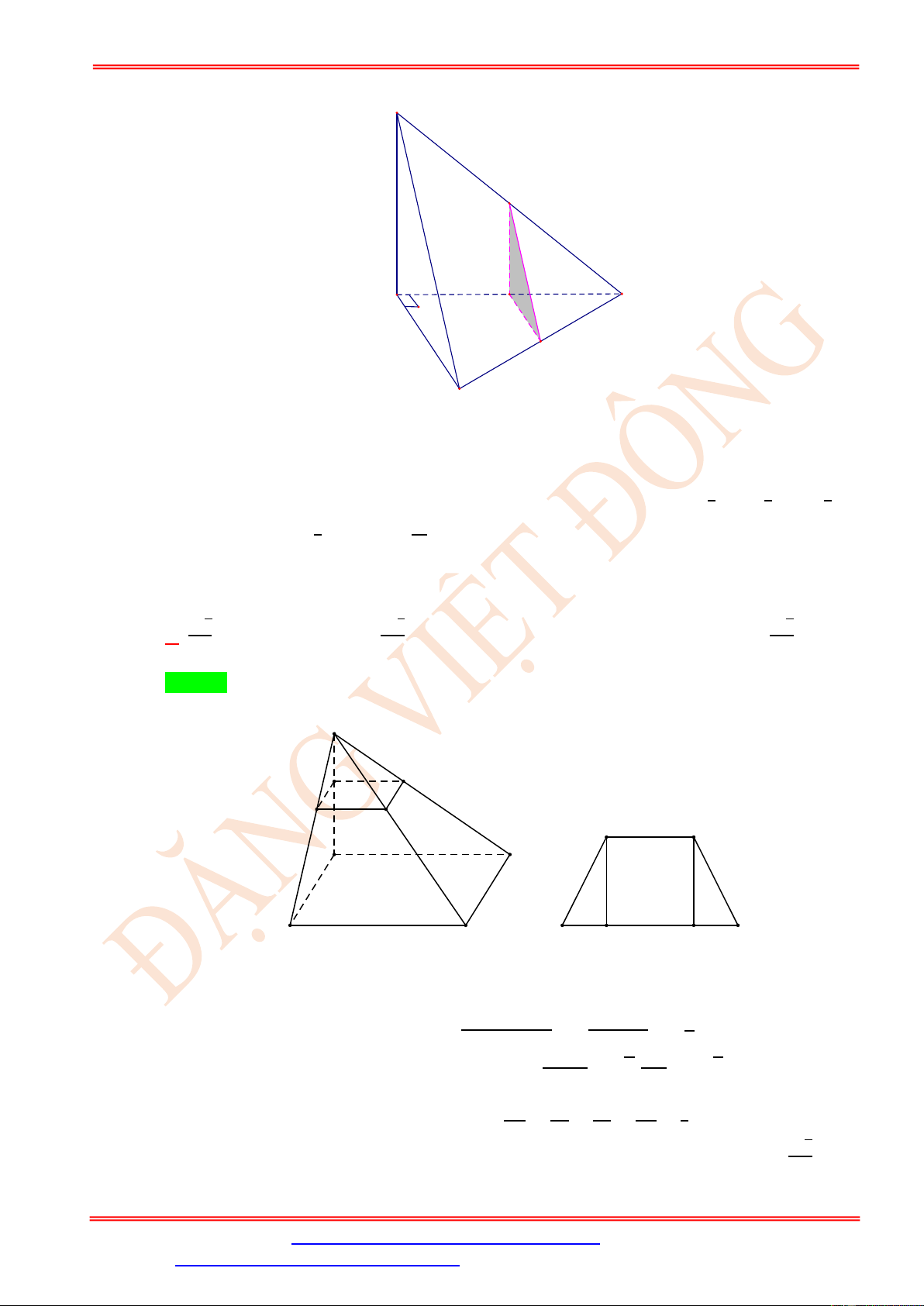
Câu 7. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều,
SAD = 90 . Gọi Dx là đường thẳng qua D và song song với SC . Gọi I là giao điểm của
Dx và (SAB) . Tìm thiết diện của hình chóp cắt bởi mặt phẳng của ( AIC ) và tính diện tích của thiết diện đó 2 a 7 2 a 7 2 a 7 2 a 7 A. S = . B. S = . C. S = . D. S = . 8 4 6 9 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Chọn A I S J A j D O C B
+ Giao tuyến của ( SAB) và ( SCD ) là đường thẳng qua S , song song với AB và CD ,
đường thẳng này cắt Dx tại I thì I = Dx (SAB) .
+ Gọi J là giao điểm của SD và CI , ta có thiết diện là tam giác ACJ . + Dễ thấy 1 a
JO là đường trung bình của tam giác SBD JO = SB = . 2 2 1 1 a 2
+ Tam giác SAD vuông tại A , nên 2 2 AJ = SD = SA + AD = ; AC = a 2 . 2 2 2
+ Xét tam giác ACJ có JO là đường trung tuyến ta có 2 a 2 2 2 2 + JA + JC AC 2 JC 2 2 a 2a JO = − 2 = − JC = a . 2 4 4 2 4
+Áp dụng CT Hê rông, diện tích thiết diện là S = p ( p − AC)( p − JA)( p − JC) 2 a 7 = . 8
Câu 8. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10 . M là điểm trên cạnh SA sao SM 2 cho
= . Một mặt phẳng ( ) đi qua M song song với AB và AD , cắt hình chóp theo SA 3
một tứ giác có diện tích là 400 20 4 16 A. . B. . C. . D. . 9 3 9 9 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 M ( )(SAB) Có: ( ) (SAB) ( =
. Trong mặt phẳng (SAB) gọi N là giao
) AB (SAB) Mx || AB || điểm của MN SM 2 2 20
Mx và SB MN || AB và = = MN = AB = . AB SA 3 3 3 M ( )(SAD) Có: ( ) (SAD) ( =
. Trong mặt phẳng (SAD) gọi Q là giao
) AD (SAD) My || AD || điểm của MQ SM 2 2 20
My và SD MQ || AD và = = MQ = AD = . AD SA 3 3 3 N ( )(SBC) Có: ( ) (SBC) ( =
. Trong mặt phẳng (SBC) gọi P là giao
) BC (SBC) Nz || BC || điểm của NP SN SM 2 2 20
Nz và SC NP || BC và = = = NP = BC = . BC SB SA 3 3 3 SQ SP SM 2 2 20
Ta có: ( ) ( SCD) = PQ . Vì = =
= PQ || CD và PQ = CD = . SD SC SA 3 3 3
Vậy mặt phẳng ( ) cắt các mặt (SAB),(SBC ) , (SCD) ,(SAD) theo các giao tuyến
MN , NP , PQ và QM , do đó thiết diện mà ( ) cắt hình chóp đã cho là tứ giác MNPQ .
Theo cách dựng trên thì ta có tứ giác MNPQ là hình thoi. Mặt khác vì AB ⊥ BC nên MN ⊥ NP .
Vậy MNPQ là hình vuông có cạnh bằng 20 nên diện tích của MNPQ là: 3 400 2 S = MN = . MNPQ 9
Dạng 2: Bài toán tỉ số
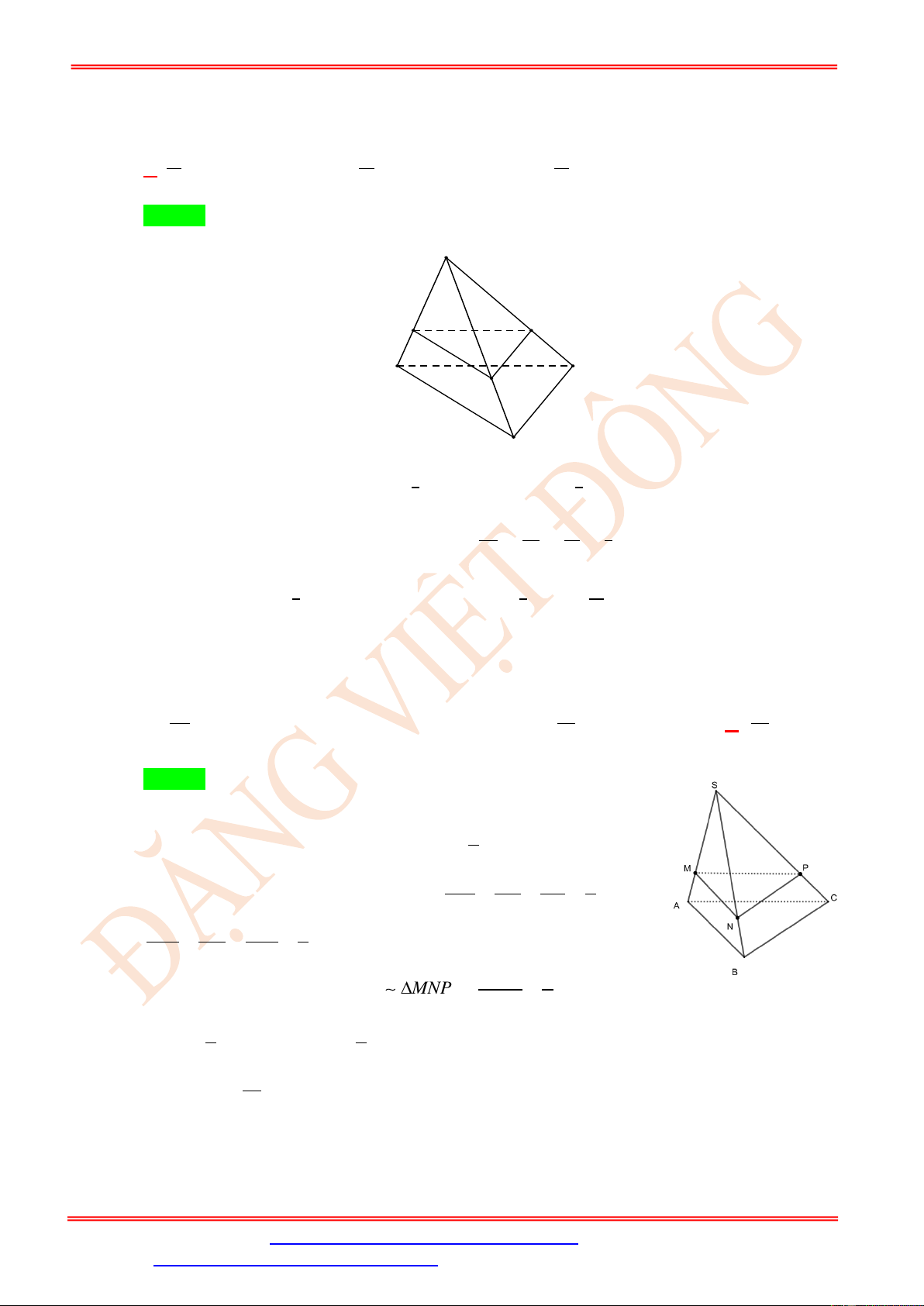
Câu 9. Cho tứ diện ABCD, hai điểm M , N lần lượt là trung điểm của AC, BC . Trên đoạn thẳng
BD lấy điểm P sao cho BP = 2PD . Gọi I là giao điểm của đường thẳng CD và mặt phẳng
(MNP) . Tính tỷ số IP . IN 3 2 1 A. . B. . C. . D. 2 . 2 3 2 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
I NP (MNP)
Gọi I = NP CD. Vì
I = CD (MNP) . I CD
Trong tam giác BCDkẻ PK //NC, K IC . PK DP 1 PK 2 IP PK 2 Ta có = = = = = . BC DB 3 NC 3 IN NC 3
Câu 10. Cho hình chóp S.ABCD có đáy là hình bình hành; M là trung điểm của SD , E thuộc
cạnh BC sao cho BE = 2EC , mặt phẳng ( AME ) cắt SC tại F . Tính tỉ số diện tích 2 tam
giác SFD và FCD. 5 A. 3 . B. 2 . C. 4 . D. . 2 Lời giải Chọn A
Trong mặt phẳng ( ABCD ) gọi K là giao điểm của AE và CD , trong mặt phẳng ( SCD ) ta
có F = MK SC . EC CK CK 1 Khi đó: = = = . EB AB CD 2 CF CK
Gọi N là trung điểm SC , ta có: =
=1 suy ra F là trung điểm NC . FN MN S SF Vậy SFD = = 3. S FC FCD
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 11. Cho hình chóp S.ABCD với đáy ABCD là hình bình hành tâm O . Mặt phẳng ( ) di động
chứa AB và cắt SC, SD lần lượt tại M , N . Biết K là giao điểm của AN và BM . Tính AB BC − . MN SK 1 1 2 A. 1. B. . C. . D. . 2 3 3 Lời giải Chọn A
(α)(SCD) = MN AB (α) . ( ) MN // AB CD SCD AB // CD AB BK
Do MN // AB nên = (1). MN MK
SK = (SAN ) (SBM ) AD (SAN ) . ( )
SK // AD // BC BC SBM AD // BC BC MB
Do SK // BC nên = (2). SK MK AB BC BK MB MK Từ (1) và (2) suy ra − = − = =1. MN SK MK MK MK GA
Câu 12. Gọi G là trọng tâm của tứ diện ABCD . Gọi A là trọng tâm của tam giác BCD.Tính GA . 1 1 A. 2 . B. 3 . C. . D. . 3 2 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi M, N, P lần lượt là trung điểm của C ,
D BC và AD ; H là trọng tâm của tam giác ACD .
Gọi G là giao điểm của AA và BH . Suy ra G là trọng tâm của tứ diện ABCD. MH MA 1 A H 1 Xét M AB ta có = = A H || AB = . MA MB 3 AB 3 A H A G 1 GA Theo Thalets ta có : = = = 3 . AB AG 3 A G
Câu 13. Cho tứ diện ABCD. Gọi G và G lần lượt là trọng tâm của các tam giác BCD và ACD . 1 2
Khẳng định nào sau đây sai?
A. G G // ABD .
B. G G // ABC . 1 2 ( ) 1 2 ( ) 2
C. BG , AG và CD đồng qui. D. G G = AB . 1 2 1 2 3 Lời giải Chọn D
Gọi M là trung điểm của CD. Ta có B,G ,M thẳng hàng và A,G ,M thẳng hàng. 1 2 MG 1 MG 1 Trong ( ABM ) , ta có
1 = ( G là trọng tâm của các tam giác BCD ) và 2 = MB 3 1 MA 3 MG MG
( G là trọng tâm của các tam giác ACD ) nên 1 2 =
G G // AB ( Thalet đảo trong 2 MB MA 1 2 ABM ) G G // ABD 1 2 ( )
nên phương án A và B đúng. Đồng thời theo định lý Thalet ta có G G // ABC 1 2 ( ) G G MG 1 1 1 2 2 =
= G G = AB nên phương án D sai. AB MA 3 1 2 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Rõ ràng BG , AG và CD đồng qui tại M nên phương án C đúng. 1 2
Câu 14. Cho hình chóp S.ABCD có đáy ABCDlà hình thang ( AB / /CD) . Gọi I , J lần lượt là trung
điểm của các cạnh A ,
D BC và G là trọng tâm tam giác SAB . Biết mặt phẳng (GJI ) cắt
SA và SB lần lượt ở E và F ; EF = IJ . Hỏi khẳng định nào sao đây đúng? 1 3
A. AB = CD . AB = CD . AB = 3CD . 3 B. 2 C. D. 2 AB = CD . 3 Lời giải Chọn C S E G F A B H I J D C
Ta có hai mặt phẳng (GJI ) và (SAB) có điểm chung là G.
AB // JI ; AB ( SAB); JI (GJI );(GJI ) ( SAB) = EF
EF // AB và EF đi qua trọng tâm . G EF SF SG
Vì G là trọng tâm tam giác 2 2 2 SAB SG = GH = = = EF = AB . 3 AB SB SH 3 3 AB + CD
Vì JI là đường trung bình hình thang ABCDnên IJ = . 2 2 AB + CD Mà EF = IJ AB = 3 2
4AB = 3AB +3CD AB = 3CD
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác
ABC và M là trung điểm SC . Gọi K là giao điểm của SD với mặt phẳng ( AGM ) . Tính tỷ số KS . KD 1 1 A. . B. . C. 2 . D. 3 . 2 3 Lời giải. Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Cách 1: Gọi O = AC BD , I = AM SO .
Trong mặt phẳng (SBD) , kéo dài GI cắt SD tại K K = SD ( AMG) .
Trong tam giác SAC , có SO, AM là hai đường trung tuyến. Suy ra OI 1 OG
I là trọng tâm tam giác SAC = , ta lại có 1 = . OS 3 OB 3 OI = OG KD GD
GI // SB GK // SB = . OS OB KS GB
Ta có DO = BO = 3GO GD = 4GO , GB = 2GO . Vậy KD GD 4 = = GO = KS 1 2 = . KS GB 2GO D K 2 SI
Cách 2: Trong tam giác SAC , vì I = AM SO nên I là trọng tâm = 2. OI
Áp dụng định lí Mê lê na uýt trong tam giác SOD ta có IS GO KD 1 KD KS 1 . . =1 2. . =1 = . IO GD KS 4 KS KD 2
Câu 16. Cho hình chóp .
S ABCD có đáy ABCD là tứ giác lồi. Gọi N, P lần lượt là trung điểm của
SB và AD . Gọi I là trung điểm của NP và G là giao điểm của SI với mặt phẳng ( ABCD) . Tính tỉ số IS T = . IG 3 3
A. T = 2. B. T = . C. T = .
D. T = 3. 5 4 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S N B I M A G P D C
Gọi M là trung điểm BG, ta có MN là đường trung bình của tam giác SGB MN //IG (1) . SG = 2MN (2)
Mà I là trung điểm PN nên ta có IG là đường trung bình của tam
giác PMN MN = 2IG (3) . Từ (2) và (3) ta có IS SG = 4IG = 3. IG
Câu 17. Cho hình chóp SABC . Bên trong tam giác ABC lấy một điểm O bất kỳ. Từ O dựng các đườ (SBC) (SCA)
ng thẳng lần lượt song song với SA , SB , SC và cắt các mặt phẳng , , O A O B OC ( T = + +
SAB ) theo thứ tự lần lượt tại A ,
B , C . Khi đó tổng tỉ số SA SB SC bằng bao nhiêu ? 3 1
A. T = 3. B. T = . C. T =1. D. T = . 4 3 Lời giải Chọn C
Gọi M , N , P lần lượt là giao điểm của AO , BO , CO với BC , CA , AB .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Từ O dựng các đường thẳng lần lượt song song với SA , SB , SC và cắt các đường thẳng
SM , SN , SP lần lượt tại A , B , C .
Áp dụng định lý Talet trong các tam giác SAM , SBN , SCP ta có: O A O OC = MO B NO PO ; = ; = . SA MA SB NB SC PC O A O B OC Khi đó MO NO PO T = + + = + + SA SB SC MA NB PC
Gọi S , S , S S lần lượt là diện tích các tam giác OBC , OCA , OAB , ABC . Dựng 1 2 3
OH ⊥ BC , AK ⊥ BC nên OH // AK . Khi đó MO OH
áp dụng định lý Talet trong tam giác AKM và tỉ số diện tích ta có 1 = = S . MA AK S Tương tự NO PO : 2 = S và 3 = S . NB S PC S O A O B OC S S S S Vậy 1 2 3 T = + + = + + = =1. SA SB SC S S S S
Cách giải nhanh: Đặc biệt hóa bài toán với O là trọng tâm tam giác ABC sẽ nhanh chóng tìm ra đáp án.
Câu 18. Cho hình lập phương ABC . D A B C D
cạnh a . Các điểm M , N , P theo thứ tự đó thuộc các cạnh a BB, C D
, DA sao cho BM = C N
= DP = . Biết mặt phẳng (MNP) cắt cạnh 3
AB tại điểm I . Tính tỉ số BI . BA 1 2 1 1 A. . B. . C. . D. . 2 3 4 3 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi N là hình chiếu của N trên CD, Q là giao điểm của MN và BN, I là giao điểm
của PQ và AB . I chính là điểm mà ta đề cập.
Đặt ABCD vào (Oxy) như hình vẽ sẽ thấy Q (−1,5;− 0,5), P (2;3) . Tức I (0 ) ;1 . Vậy BI 1 = . BA 3
Câu 19. Cho tứ diện ABCD. Gọi I , J lần lượt là trung điểm của AC và BC . Trên cạnh BD lấy
điểm K sao cho BK = 2KD. Gọi F là giao điểm của AD với mặt phẳng ( IJK ) . Tính tỉ số FA . FD 7 11 5 A. . B. 2 . C. . D. . 3 5 3 Lời giải Chọn B.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
+ Cho AD ( ACD)
Trong mặt phẳng ( BCD) hai đường thẳng IK, CD không song song nên gọi E là giao
điểm của hai đường thẳng IK và CD. Khi đó E ( ACD) .
+ Ta thấy ( ACD) (IJK ) = EJ
+ Trong ( ACD) : EJ AD = F . Khi đó ( IJK ) AD = F .
Xét tam giác BCD, áp dụng định lí Menelaus có : IB EC KD EC 1 EC . . =11. . =1 = 2 IC ED KB ED 2 ED
Xét tam giác ACD , áp dụng định lí Menelaus có : EC FD JA FD FD 1 . . =1 2. .1 = 1 = ED FA JC FA FA 2 Vậy FA = 2 . FD
Câu 20. Cho tứ diện 𝐴𝐵𝐶𝐷 có tất cả các cạnh bằng 1. Gọi 𝑀, 𝑁 lần lượt là điểm thuộc cạnh 𝐴𝐷 và 𝑀𝐴 𝑁𝐶 1 𝐵𝐶 sao cho =
= . Độ dài đoạn 𝑀𝑁 thuộc khoảng nào trong các khoảng sau đây? 𝑀𝐷 𝑁𝐵 2 3 1 1 3 A. ( ; 2). B. (0; ). C. ( ; 1). D. (1; ). 2 2 2 2 Lời giải D Cách 1
Gọi 𝑑 là đường thẳng đi qua 𝐵 và song song với 𝐴𝐶. Trong mặt phẳng (𝐴𝐵𝐶), 𝑑 ∩ 𝐴𝑁 = 𝐺. 𝑀𝐴 1 = 𝑀𝐴 𝑁𝐴 Do {𝑀𝐷 2 ⇒ = ⇒ 𝑁𝐴 𝑁𝐶 1 𝑀𝑁//𝐷𝐺. = = 𝑀𝐷 𝑁𝐺 𝑁𝐺 𝑁𝐵 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 𝐴𝐶 𝑁𝐶 1 Ta có = = ⇒ 𝐵𝐺 = 2. 𝐵𝐺 𝑁𝐵 2
Tam giác 𝐵𝐶𝐺 có 𝐶𝐺2 = 𝐵𝐶2 + 𝐵𝐺2 − 2𝐵𝐶. 𝐵𝐺. 𝑐𝑜𝑠 𝐶𝐵𝐺 ̂ = 1 + 4 − 2 = 3. Ta có 𝐷𝐵 ⃗⃗⃗ . 𝐴𝐶 ⃗⃗⃗ = (𝐴𝐵 ⃗⃗⃗ − 𝐴𝐷 ⃗⃗⃗ ). 𝐴𝐶 ⃗⃗⃗ = 𝐴𝐵 ⃗⃗⃗ . 𝐴𝐶 ⃗⃗⃗ − 𝐴𝐷 ⃗⃗⃗ 𝐴𝐶
⃗⃗⃗ = 0 nên 𝐷𝐵 ⊥ 𝐴𝐶 ⇒ 𝐷𝐵 ⊥ 𝐵𝐺.
Tam giác 𝐷𝐵𝐺 vuông tại 𝐵 ⇒ 𝐷𝐺2 = 𝐷𝐵2 + 𝐵𝐺2 = 1 + 4 = 5 ⇒ 𝐷𝐺 = √5. 𝑀𝐴 1 𝐴𝑀 1 𝑀𝑁 𝐴𝑀 1 1
Tam giác 𝐷𝐴𝐺 có 𝑀𝑁//𝐷𝐺 và = ⇒ = ⇒ =
= ⇒ 𝑀𝑁 = 𝐷𝐺 ⇒ 𝑀𝑁 = 𝑀𝐷 2 𝐴𝐷 3 𝐷𝐺 𝐴𝐷 3 3 √5 1
. Vậy độ dài đoạn 𝑀𝑁 thuộc khoảng ( ; 1). 3 2 Cách 2 𝑀𝐴 1 1 1 1 1
Do 𝑀 thuộc cạnh 𝐴𝐷 và = ⇒ 𝐴𝑀 ⃗⃗⃗ = 𝐴𝐷
⃗⃗⃗ ⇒ 𝐴𝑀2 = 𝐴𝑀 ⃗⃗⃗ 2 = 𝐴𝐷 ⃗⃗⃗ 2 = 𝐴𝐷2 = . 𝑀𝐷 2 3 9 9 9 𝑁𝐶 1 2 2
Do 𝑁 thuộc cạnh 𝐵𝐶 và = ⇒ 𝐵𝑁 ⃗⃗⃗ = 𝐵𝐶 ⃗⃗⃗ ⇒ 𝐴𝑁 ⃗⃗⃗ = 𝐴𝐵 ⃗⃗⃗ + 𝐵𝑁 ⃗⃗⃗ = 𝐴𝐵 ⃗⃗⃗ + 𝐵𝐶 ⃗⃗⃗ = 𝐴𝐵 ⃗⃗⃗ + 𝑁𝐵 2 3 3 2 1 2 1 (𝐴𝐶 ⃗⃗⃗ − 𝐴𝐵 ⃗⃗⃗ ) = 𝐴𝐵 ⃗⃗⃗ + 𝐴𝐶
⃗⃗⃗ ⇒ 𝐴𝑁2 = 𝐴𝑁 ⃗⃗⃗ 2 = ( 𝐴𝐵 ⃗⃗⃗ + 3 3 3 3 2 2 2 2 1 4 4 4 4 7 𝐴𝐶
⃗⃗⃗ ) = AB + AC + A .
B AC = 1 𝐴𝐵2 + 𝐴𝐶2 + 𝐴𝐵 ⃗⃗⃗ . 𝐴𝐶 ⃗⃗⃗ = . 3 9 9 9 9 9 9 9 1 2 1 1 2 1 1 1 Ta có 𝐴𝑁 ⃗⃗⃗ . 𝐴𝑀 ⃗⃗⃗ = ( 𝐴𝐵 ⃗⃗⃗ + 𝐴𝐶 ⃗⃗⃗ ) . 𝐴𝐷 ⃗⃗⃗ = 𝐴𝐵 ⃗⃗⃗ . 𝐴𝐷 ⃗⃗⃗ + 𝐴𝐶 ⃗⃗⃗ . 𝐴𝐷 ⃗⃗⃗ = + = . 3 3 3 9 9 18 9 6 2 7 1 1 𝑀𝑁 ⃗⃗⃗⃗ = 𝐴𝑁 ⃗⃗⃗ − 𝐴𝑀
⃗⃗⃗ ⇒ 𝑀𝑁2 = (𝐴𝑁 ⃗⃗⃗ − 𝐴𝑀
⃗⃗⃗ ) = 𝐴𝑁2 + 𝐴𝑀2 − 2𝐴𝑁 ⃗⃗⃗ . 𝐴𝑀 ⃗⃗⃗ = + − 2. = 9 9 6 5 1
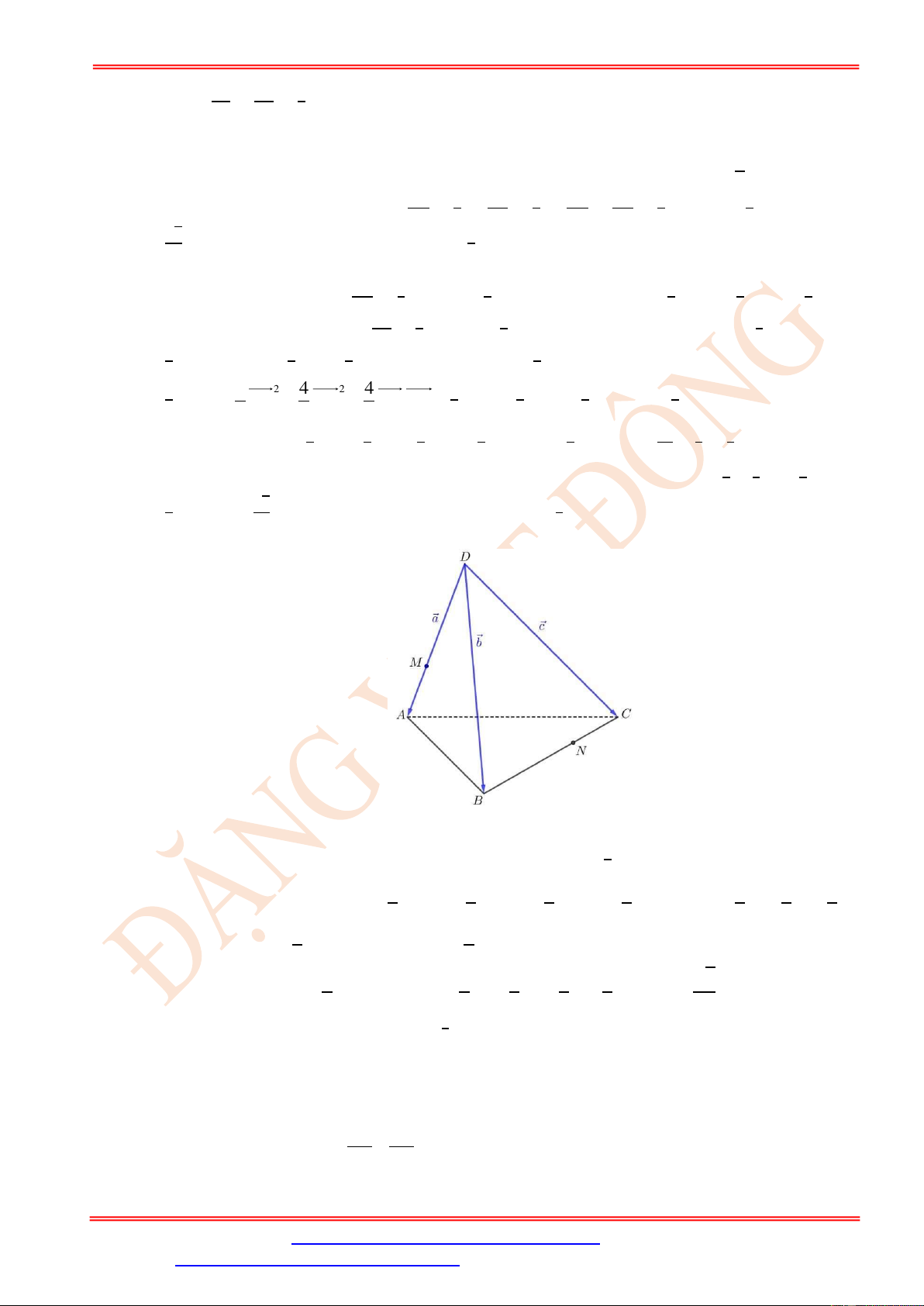
⇒ 𝑀𝑁 = √5. Vậy độ dài đoạn 𝑀𝑁 thuộc khoảng ( ; 1). 9 3 2 Cách 3 𝐷𝐴 ⃗⃗⃗ = 𝑎
|𝑎 | = |𝑏⃗ | = |𝑐 | = 1 Đặt {𝐷𝐵 ⃗⃗⃗ = 𝑏⃗ . Ta có { 1.
𝑎 . 𝑏⃗ = 𝑏⃗ . 𝑐 = 𝑐 . 𝑎 = 1.1. 𝑐𝑜𝑠 6 00 = 𝐷𝐶 ⃗⃗⃗ = 𝑐 2 2 1 2 1 2 1 2 𝑀𝑁 ⃗⃗⃗⃗ = 𝑀𝐷 ⃗⃗⃗ + 𝐷𝐶 ⃗⃗⃗ + 𝐶𝑁
⃗⃗⃗ = − 𝑎 + 𝑐 + 𝐶𝐵
⃗⃗⃗ = − 𝑎 + 𝑐 + (𝑏⃗ − 𝑐 ) = − 𝑎 + 𝑏⃗ + 𝑐 . 3 3 3 3 3 3 3 1 2 1 𝑀𝑁2 =
(−2𝑎 + 𝑏⃗ + 2𝑐 ) = (4𝑎 2 + 𝑏⃗ 2 + 4𝑐 2 − 4𝑎 . 𝑏⃗ + 4𝑏⃗ . 𝑐 − 8𝑐 . 𝑎 ) 9 9 1 1 1 1 5 √5
= (4 + 1 + 4 − 4. + 4. − 8. ) = ⇒ 𝑀𝑁 = . 9 2 2 2 9 3 1
Vậy độ dài đoạn 𝑀𝑁 thuộc khoảng ( ; 1). 2
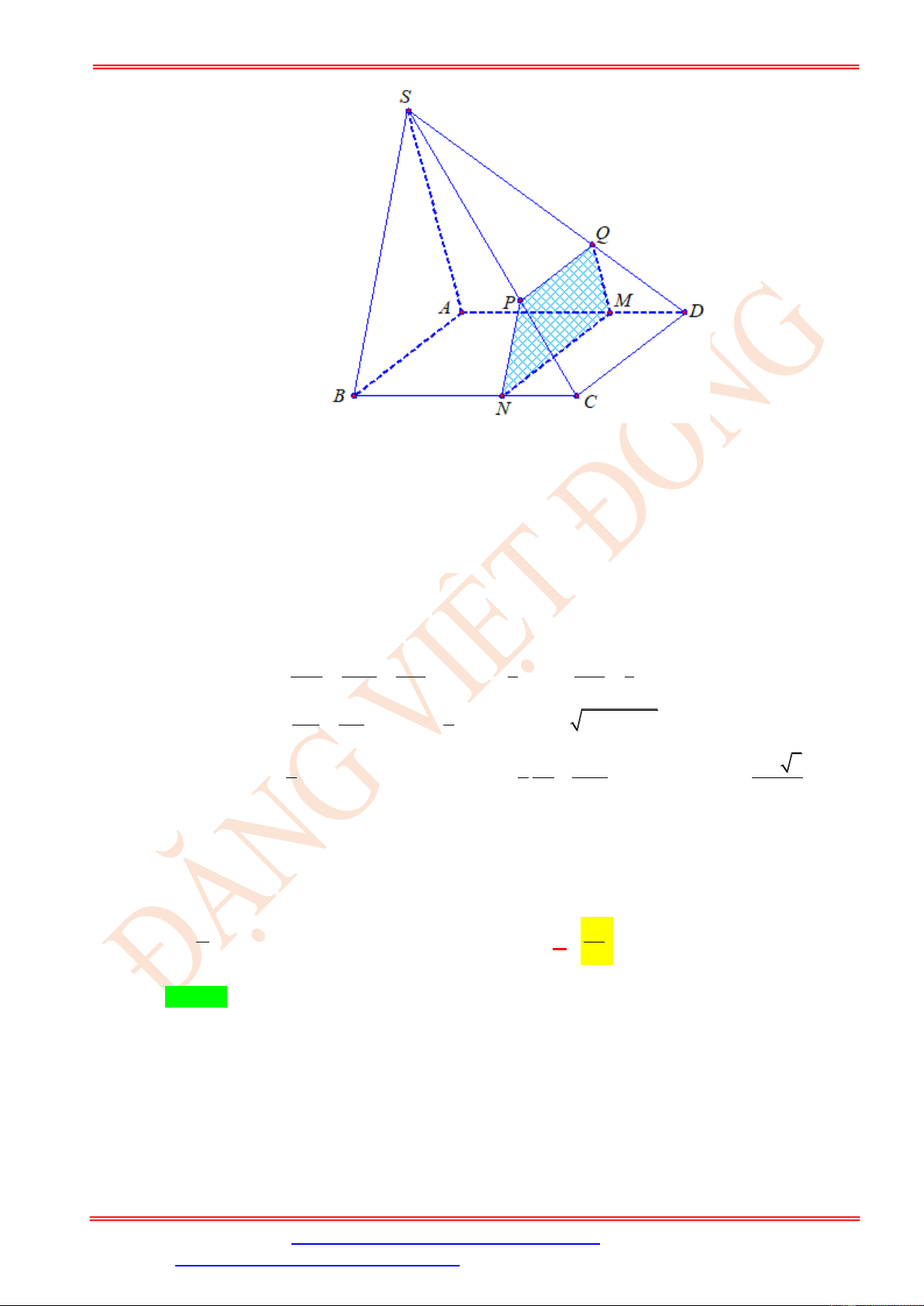
Câu 21. Cho tứ diện ABCD. Điểm M là trung điểm của cạnh AC , điểm N thuộc cạnh AD sao
cho: AN = 2ND , điểm Q thuộc cạnh BC sao cho BC = 4BQ . Gọi I là giao điểm của
đường thẳng MN và mặt phẳng ( BCD) , J là giao điểm của đường thẳng BD và mặt
phẳng (MNQ) . Khi đó JB JQ + bằng JD JI
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 13 20 3 11 A. . B. . C. . D. . 20 11 5 12 Lời giải Chọn D ID CM AN ID 1 +) . . =1 = . IC MA ND IC 2 ID CQ BJ BJ 2 +) . . =1 = . IC BQ JD JD 3 BQ CD IJ IJ JQ 1 +) . . =1 = 4 = . BC DI JQ JQ JI 4 JB JQ 2 1 11 + = + = . JD JI 3 4 12
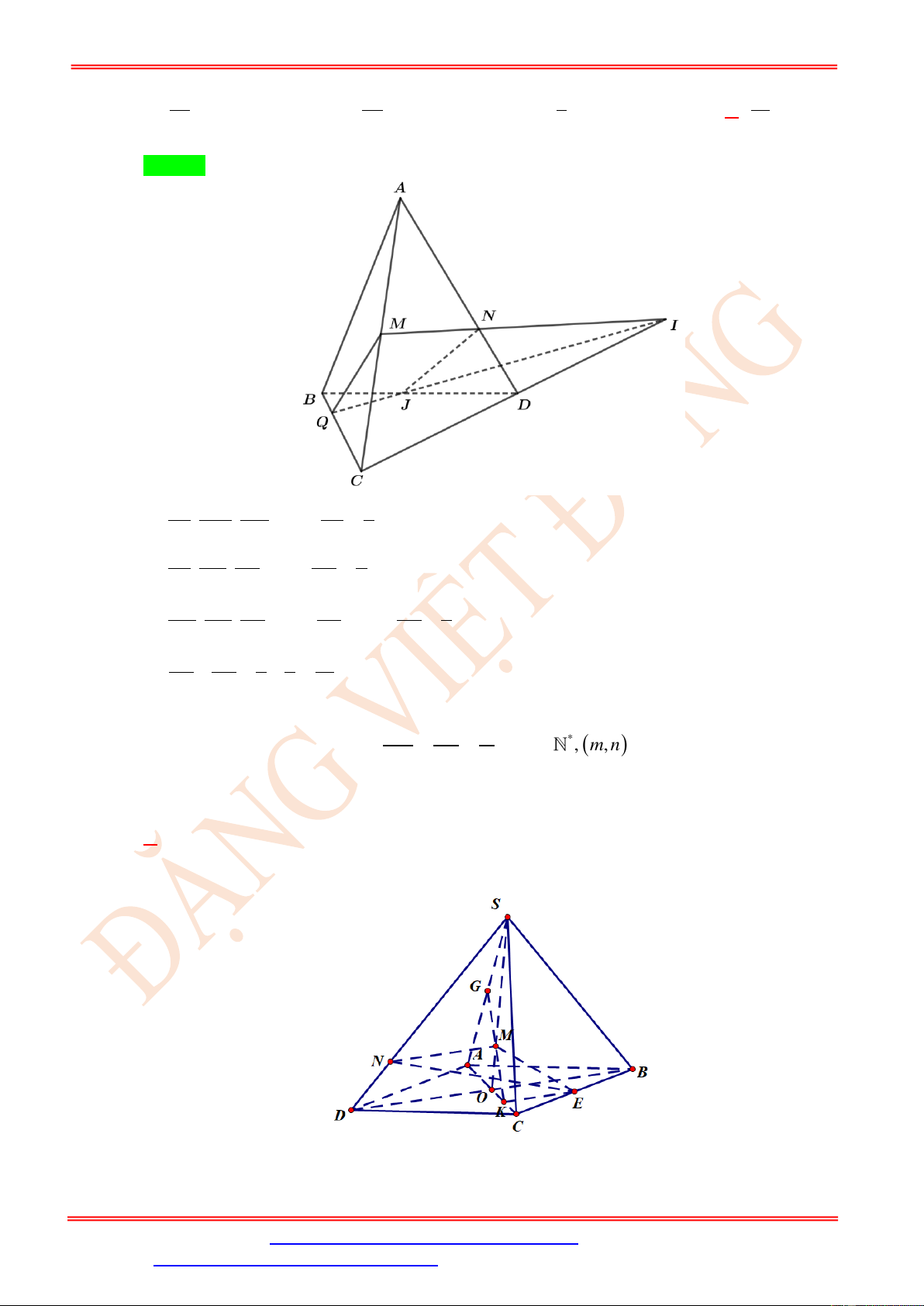
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Hai điểm M , N lần lượt nằm trên các đoạn SM SN m S , O SD sao cho * = = , , m n , ( ,
m n) = 1. Điểm E là trung điểm SO SD n
của BC . Biết thiết diện của hình chóp cắt bởi mp(MNE) đi qua trung điểm cạnh SA. Giá
trị m + n bằng A. 7 . B. 5 . C. 3 . D. 4 . Lời giải Chọn A
Ta có MN // OD nên mặt phẳng ( MNE ) cắt mặt phẳng ( ABCD ) theo giao tuyến đi qua E
và song song với DO , cắt AC tại K .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Vì E là trung điểm của BC nên K là trung điểm của OC .
Gọi G = MK SA thì G = SA (MNE) . Theo giả thiết thì G là trung điểm SA.
Áp dụng định lý Menelaus cho tam giác SAO ta có: MS KO GA MS 1 MS m SM . . =1 . .1 = 1 = 3. Từ đó suy ra 3 = = . MO KA GS MO 3 MO n SO 4 Vậy m+ n = 7.
Câu 23. Cho hình chóp S.ABC . Bên trong tam giác lấy một điểm O bất kỳ. Từ O dựng các đường
thẳng lần lượt song song với S , A S ,
B SC và cắt các mặt phẳng ( SBC ) ,( SCA) ,( SAB) theo
thứ tự lần lượt tại A , B ,C . Khi đó tổng tỉ số OA OB OC T = + + bằng bao nhiêu? SA SB SC 1 3 A. T = .
B. T = 3. C. T =1. D. T = . 3 4 Lời giải Chọn C
(SAO)(SBC) = SI (I = AO BC). Dựng OA song song với SA và cắt SI tại A.
(SBO)(SAC) = SJ (J = BO AC). Dựng OB song song với SB và cắt SJ tại B.
(SCO)(SAB) = SK (K = CO AB) . Dựng OC song song với SC và cắt SK tại C . OA IO OB JO OC KO Ta có: = ; = ; = . SA IA SB JB SC KC
Từ O dựng PQ//A ,
B EF //BC, HR//AC . Khi đó:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 OA OB OC IO JO KO OP OQ OH PQ AQ CQ AQ AC T = + + = + + = + + = + = + = =1 SA SB SC IA JB KC AB AB AC AB AC AC AC AC
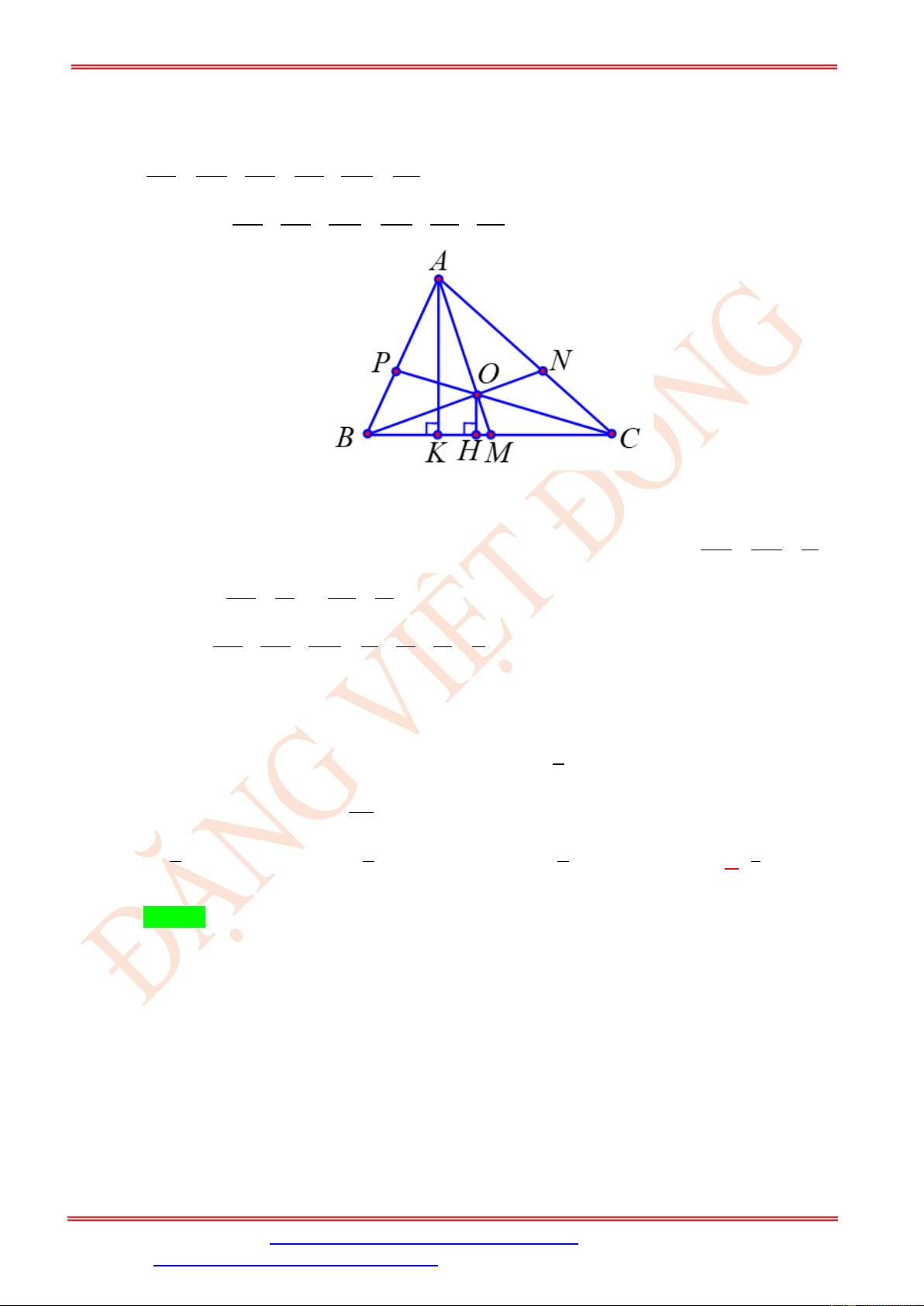
Câu 24. Cho tứ diện ABCDcó AB = CD = 4, BC = AD = 5, AC = BD = 6. M là điểm thay đổi
trong tam giác ABC . Các đường thẳng qua M song song với , AD ,
BD CD tương ứng cắt
mặt phẳng (BCD), ( ACD), ( ABD)tại A , B , C . Giá trị lớn nhất của MA.MB .MC là 40 24 30 20 A. . B. . C. . D. . 9 9 9 9 Lời giải Chọn A
Gọi ( ) là mặt phẳng chứa 2 đường thẳng MA và AD , ( ) là mặt phẳng chứa 2 đường
thẳng MBvà BD, ( ) là mặt phẳng chứa 2 đường thẳng MCvà CD.
Gọi A = BC, B = AC, C = AB . 1 ( ) 1 ( ) 1 ( )
Xét các tam giác A AD, B BD, C CD ta có: 1 1 1 MA MA MA MA
Vì MA / / AD 1 = 1 = (1). AD AA 5 AA 1 1 MB MB MB MB
Vì MB / /BD 1 = 1 = (2). BD BB 6 BB 1 1 MC MC MC MC
Vì MC / /CD 1 = 1 = (3). CD CC 4 CC 1 1
Từ (1), (2) và (3) suy ra MA .MB .MC
MA .MB .MC 1 1 1 = = T . 120
AA .BB .CC 1 1 1 MA S MB S MC S Ta có 1 MBC = , 1 MAC = và 1 M AB = . AA S BB S CC S 1 ABC 1 ABC 1 ABC MA MB MC S S S Suy ra 1 1 1 M BC M AC M AB + + = + + =1 . AA BB CC S S S 1 1 1 A BC A BC A BC
Áp dụng bất đẳng thức AM – GM cho 3 số, ta có: MA MB MC
MA .MB .MC 1 1 1 1 1 1 3 1 = + + 33 = 3. T AA BB CC
AA .BB .CC 1 1 1 1 1 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 1
MA MB MC 3
3 T 1 T . . 1 40
MA .MB .MC . 27 120 27 9
Dấu " = "xảy ra khi và chỉ khi M là trọng tâm của tam giác ABC .
Vậy giá trị lớn nhất của MA.MB .MC bằng 40 . 9
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
Dạng 1: Tính diện tích thiết diện
Câu 25. Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 0 4, BAC = 30 . Mặt
phẳng song song vơi ( ABC ) cắt đoạn thẳng SA tại M sao cho SM = 2MA. Diện tích thiết
diện của với hình chóp S.ABC bằng. 25 14 16 A. B. . C. . D. 1. 9 9 9 Lời giải Chọn C S P M N C A B
Mặt phẳng song song với mp ( ABC ) cắt đoạn thẳng SA tại M sao cho
SM = 2MA, nên cắt SB và SC lần lượt tại N và P sao cho SN = 2NB ;
SP = 2PC .Do đó thiết diện của mp với hình chóp S.ABC là tam giác MNP 2 8 2 8 Ta có MN = AB = ; MP = AC = và 0 NMP = NMP = 30 3 3 3 3 1 1 8 8 16 Diện tích 0 M
NP = .MN.M . P SinNMP = . . .Si 3 n 0 = 2 2 3 3 9
Câu 26. Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh a , SA = SB = SC = 2a . Gọi M là
một điểm trên đoạn thẳng SB mà SM = m (0 m 2a) . Mặt phẳng ( ) qua M , song
song với SA và BC cắt hình chóp theo thiết diện có chu vi là:
A. 4a − 2m . B. 4a .
C. 4a − m .
D. 2a + m . Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S M Q N A B P C
Mặt phẳng ( ) qua M , song song với SA nên ( ) cắt (SAB) theo giao tuyến MN với
MN / / SA và N AB. Tương tự ( ) cắt mp(ABC) theo giao tuyến NP với NP / / BC và
PAC ; ( ) cắt mp(SAC) theo giao tuyến PQ với PQ / / SA và QSC; ( ) cắt
mp (SAB) theo giao tuyến QM . Vậy thiết diện tạo bởi mặt phẳng ( ) và hình chóp . S ABC
là hình bình hành MNPQ . MN BM BM
Xét SAB , vì MN / / SA nên = MN = S . A = 2a − m SA BS SB . MQ SM SM m m
Xét SBC , vì MQ / / BC nên = MQ = BC. = . a = BC SB SB 2a 2 . m
Vậy chu vi thiết diện là 2.(2a − m) + 2. = 4a − m 2 .
Câu 27. Bộ c = 1 − , a = 1 − , b = 4 thỏa 2 2 2
A = a + b + c = 18 nên chọn đáp án C Cho hình chóp
S.ABCD có đáy là hình vuông cạnh a , các cạnh bên bằng a 2 . Gọi M là trung điểm của
SD . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng ( ABM ) . 2 3 15a 2 3 5a 2 3 5a 2 15a A. . B. . C. . D. . 16 16 8 16 Lời giải Chọn A
Gọi là giao tuyến của mặt phẳng ( ABM ) với mặt phẳng (SDC ) .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Ta có AB song song với ( SDC ) nên suy ra AB song song với .
Gọi N là trung điểm SC , ta có N .
Do đó thiết diện là hình thang cân ABNM .
Kẻ MH ⊥ AB tại H , H AB . Do AB = CD và MN CD nên H thuộc đoạn AB .
Áp dụng công thức độ dài đường trung tuyến, ta có 2 2 2 a + 2a 2a AM = − = a . 2 4 a a − − Mặt khác AB MN 2 a a 15 AH = = = nên 2 2 MH = AM − AH = . 2 2 4 4
MH (MN + AB) 2 . 3 15a Suy ra S = = . ABNM 2 16
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , hai tam giác SA ,
B SAD vuông cân tại A . Gọi G là trọng tâm tam giác SAB . Gọi ( ) là mặt phẳng đi qua
G và song song với S ,
B AD .Thiết diện tạo bởi mp ( ) và hình chóp S.ABCD có diện tích bằng 2 2a 3 2 4a 2 2 4a 2 2 4a 3 A. . B. . C. . D. . 9 3 9 9 Lời giải Chọn C
Trong mặt phẳng (SAB) dựng đường thẳng qua G và song song với SB và cắt A , B SA lần
lượt tại M , N .
Trong ( SAD) dựng đường thẳng qua N và song song với AD và cắt SD tại P .
Trong ( ABCD) dựng đường thẳng qua M và song song với AD và cắt CD tại Q .
Khi đó thiết diện tạo bởi mp ( )và hình chóp S.ABCD là tứ giác MNPQ .
Ta có: PN / /MQ / / AD .
BC ⊥ SB (BC ⊥ , SA BC ⊥ AB)
Hơn nữa, MQ / /BC MQ ⊥ MN . MN / /SB
Do đó tứ giác MNPQ là hình thang vuông tại M . 2 2a 2 1 a MN = SB = , NP = AD =
, MQ = AD = a . 3 3 3 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 a 2a 2 ( + NP + MQ) a 2 MN Do đó 3 3 4a 2 S = = = . ABCD 2 2 9
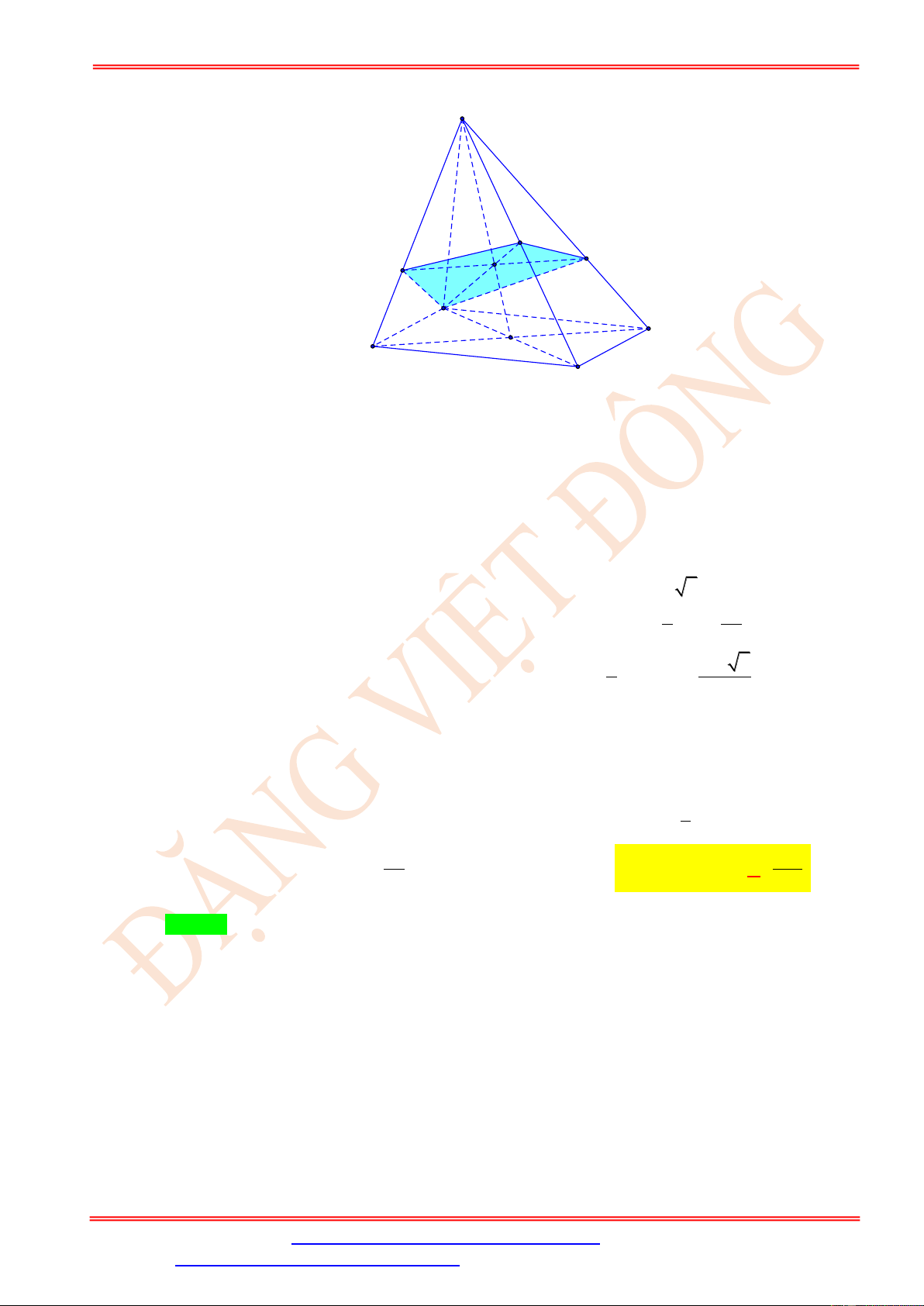
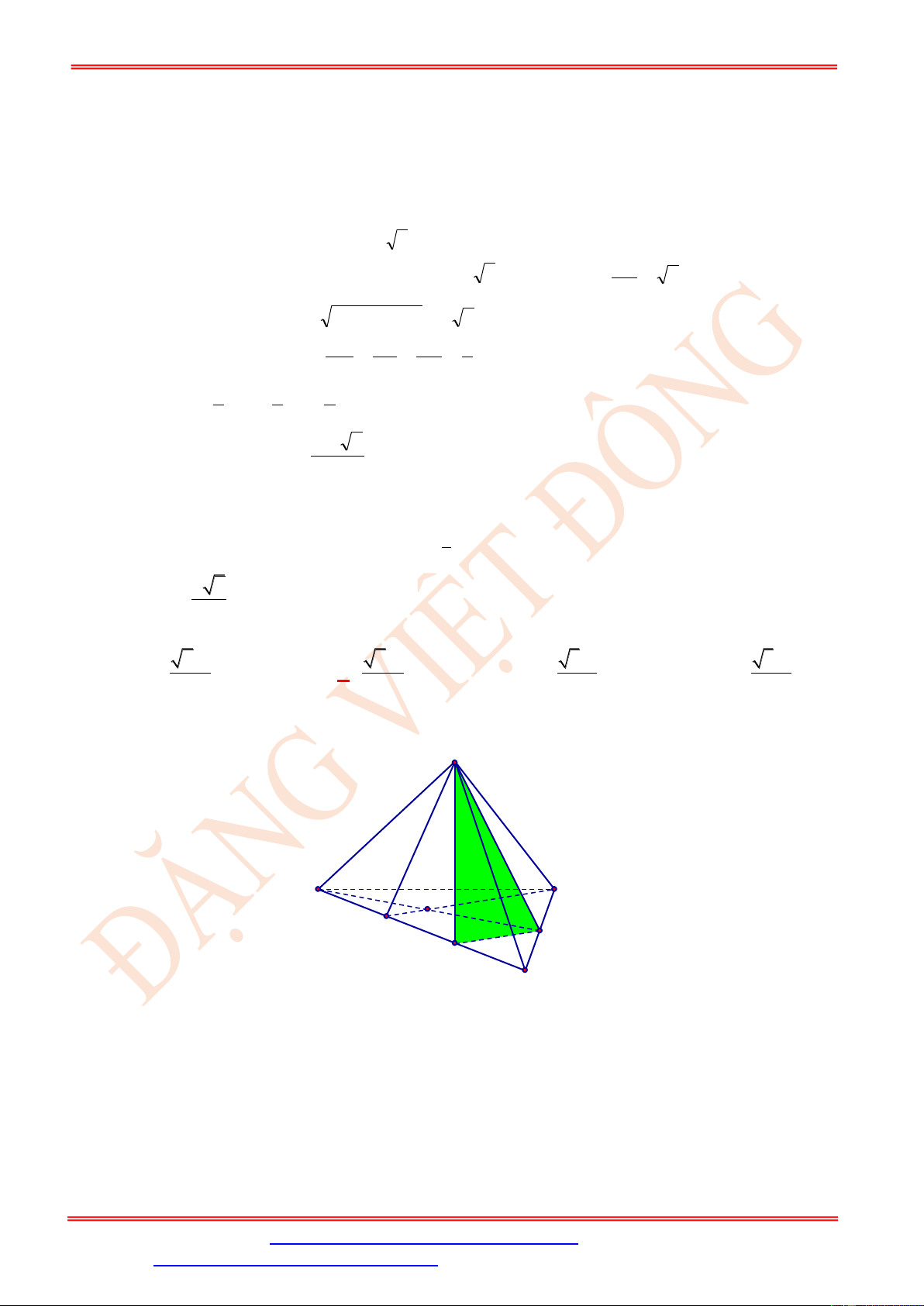
Câu 29. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC sao cho
SM = 2MC . Mặt phẳng ( P ) chứa AM và song song với BD. Tính diện tích thiết diện của
hình chóp S.ABCD cắt bởi ( P ) . 2 3a 2 4 26a 2 2 26a 2 2 3a A. . B. . C. . D. . 5 15 15 5 Lời giải Chọn C S N A B I M P O D C
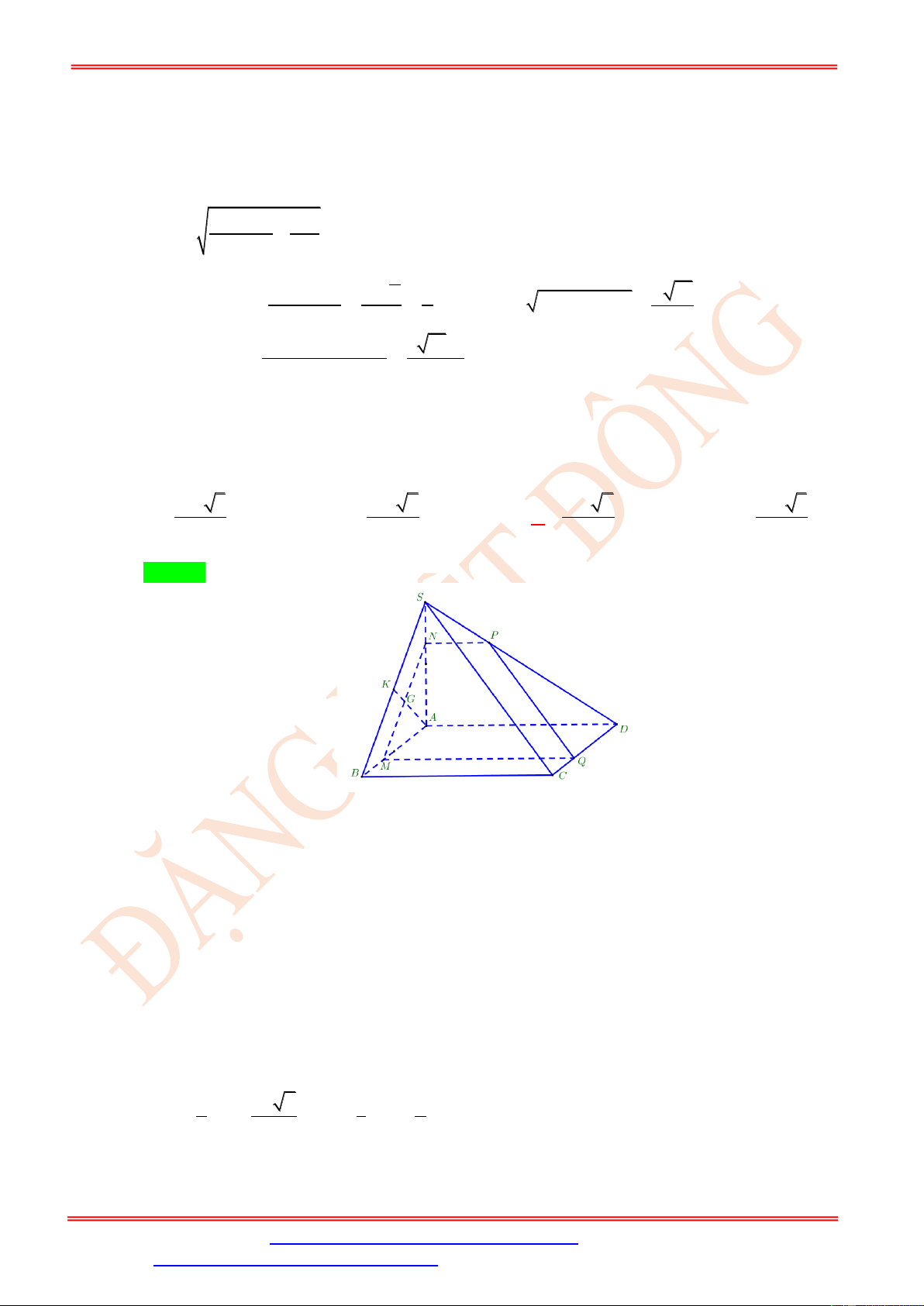
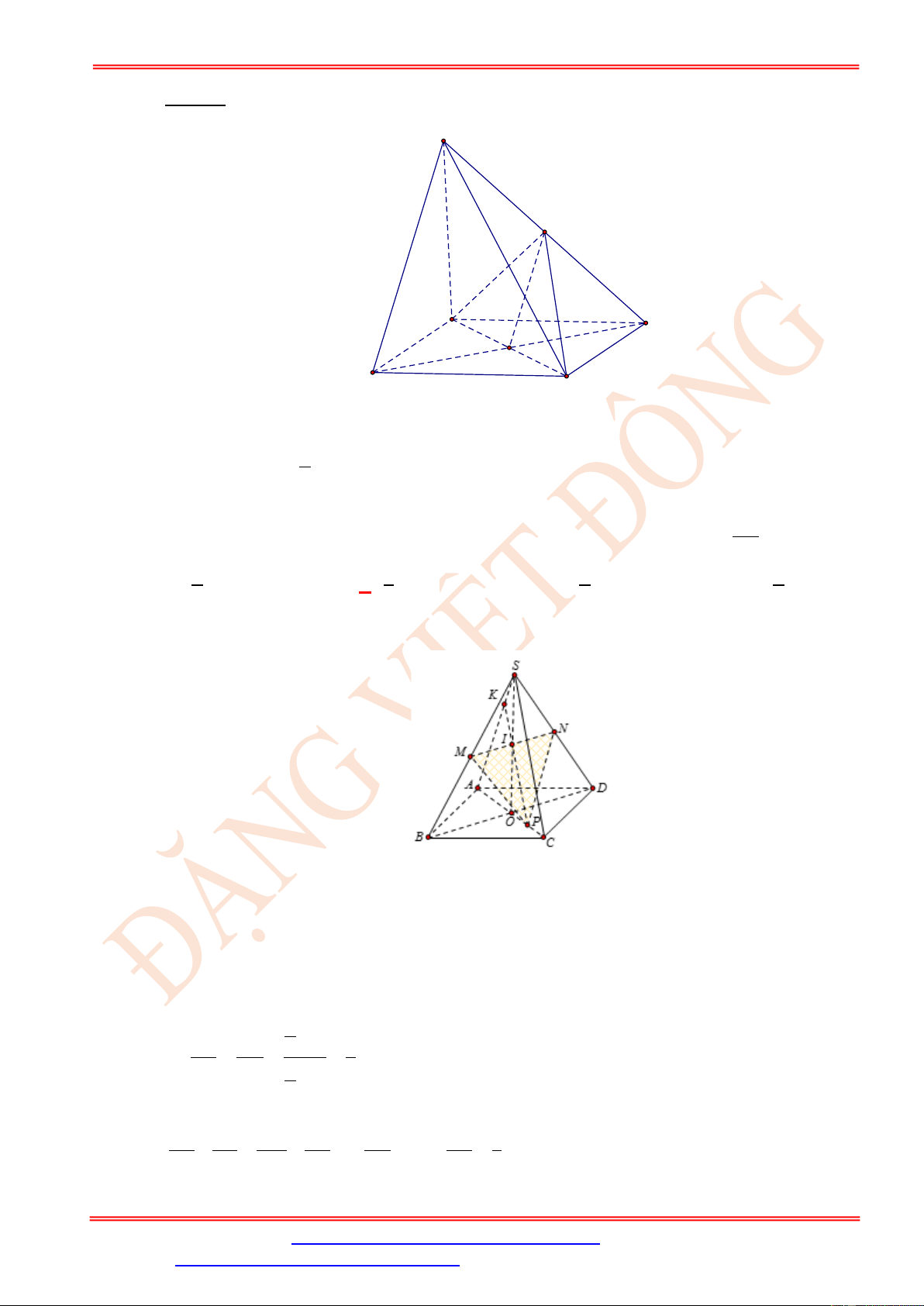
Gọi O = AC BD , I = AM SO .
Trong ( SBD) từ I kẻ đường thẳng song song với BD cắt SB , SD lần lượt tại N , P .
Suy ra thiết diện là tứ giác ANMP . BD ⊥ AC Ta có:
BD ⊥ (SAC) BD ⊥ SO BD ⊥ AM .
Mặt khác: BD / /NP . AM ⊥ NP . 1 S = N . P AM . ANMP 2 + Tính AM :
SA = SC = a Ta có: S
AC vuông cân tại S . AC = a 2 2 a 13 2 2 2 AM = SA + SM 2 = a + a = . 3 3 + Tính AM :
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 NP SI SI BD
Ta có: NP / /BD = . NP = . BD SO SO • SI Tính : SO S M I A C O Gọi SI = k . SO
Ta có: AI = AS + SI = −SA + k SO . AM = AS + 2 SM = −SA + SC . 3
A , I , M thẳng hàng AI = 2
l AM −SA + k SO = l − SA+ lSC 3 1 4 k + l = 1 k = k − 2 5 SA + (SA+SC) 2 = l
− SA+ lSC . 2 3 1 2 3 k − l = 0 = l 2 3 5 SI 4 = 4 a NP = 4 2 BD = . SO 5 5 5 1 2 a a 2 26a S = 1 4 2 13 N . P AM = . . = . ANMP 2 2 5 3 15
Câu 30. Cho hình chóp S.ABCD có SA vuông góc với mặt đáy, ABCD là hình vuông cạnh a 2 ,
SA = 2a . Gọi M là trung điểm cạnh SC , ( ) là mặt phẳng đi qua A , M và song song với
đường thẳng BD. Tính diện tích thiết diện của hình chóp bị cắt bởi mặt phẳng ( ) . 2 4a 2 4a 2 2 2a 2 A. 2 a 2 . B. . C. . D. . 3 3 3 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S M F E I A D O B C
Gọi O = AC BD , I = SO AM . Trong mặt phẳng (SBD) qua I kẻ EF / /BD , khi đó ta
có ( AEMF ) ( ) là mặt phẳng chứa AM và song song với BD. Do đó thiết diện của hình
chóp bị cắt bởi mặt phẳng ( ) là tứ giác AEMF . FE // BD Ta có:
FE ⊥ (SAC) FE ⊥ AM . BD ⊥ (SAC) Mặt khác ta có:
* AC = 2a = SA nên tam giác SAC vuông cân tại A , suy ra AM = a 2 . a
* I là trọng tâm tam giác SAC , mà EF // BD nên tính được 2 4 EF = BD = . 3 3 2 Tứ giác 1 2a 2
AEMF có hai đường chéo FE ⊥ AM nên S = FE.AM = . AEMF 2 3
Câu 31. Cho tứ diện ABCD có AB = a, CD = b . Gọi I , J lần lượt là trung điểm AB và CD , giả
sử AB ⊥ CD . Mặt phẳng ( ) qua M nằm trên đoạn IJ và song song với AB và CD. Tính
diện tích thiết diện của tứ diện ABCD với mặt phẳng ( ) biết IM = 1 IJ . 3 ab 2ab A. ab . B. . C. 2ab . D. . 9 9 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A a G P I F N M L B D H Q E J d C ( ) // CD
Ta có CD ( ICD)
giao tuyến của ( ) với (ICD) là đường thẳng qua M và M ( )(ICD)
song song với CDcắt IC tại L và ID tại N . ( ) // AB AB ( JAB)
giao tuyến của ( ) với (JAB) là đường thẳng qua M và song song M ( )(JAB)
với AB cắt JA tại P và JB tại Q . ( )// AB
Ta có AB ( ABC)
EF// AB (1) L ( )(ABC) ( )// AB
Tương tự AB ( ABD)
HG// AB (2). N ( )(ABD)
Từ (1) và (2) EF// HG// AB (3) ( ) // CD
Ta có CD ( ACD) FG// CD (4) P ( )(ACD) ( ) // CD
Tương tự CD ( BCD) EH// CD (5) Q ( )(BCD)
Từ (4) và (5) FG// EH// CD (6).
Từ (3) và (6), suy ra EFGH là hình bình hành. Mà AB ⊥ CD nên EFGH là hình chữ nhật.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 LN IN
Xét tam giác ICD có: LN// CD = . CD ID IN IM
Xét tam giác ICD có: MN// JD = . ID IJ
Do đó LN = IM = 1 = 1 = b LN CD . CD IJ 3 3 3
Tương tự PQ = JM = 2 = 2 = 2a PQ AB . AB JI 3 3 3 Vậy = Q LN = 2ab S P . . EFGH 9
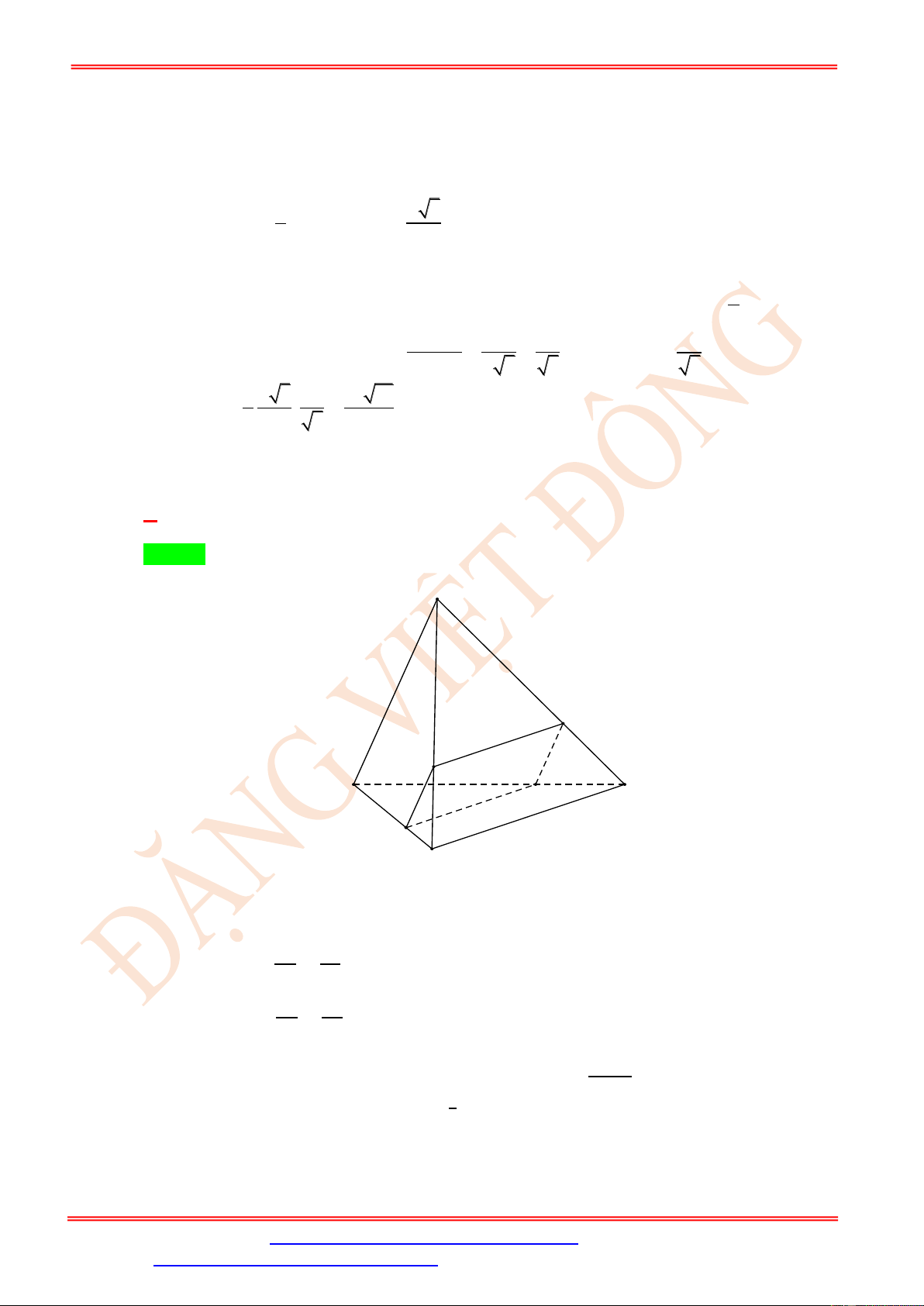
Câu 32. Cho hình tứ diện ABCD có tất cả các cạnh bằng 6a . Gọi M , N lần lượt là trung điểm của C ,
A CB .Gọi P là điểm trên cạnh BD sao cho BP = 2PD . Diện tích S thiết diện của tứ diện
ABCD bị cắt bởi mặt phẳng (MNP) là: 2 5a 51 2 5a 147 2 5a 51 A. S = . B. S = . C. S = . D. 2 4 4 2 5a 147 S = . 2 Lời giải Chọn C 1
M , N lần lượt là trung điểm của C ,
A CB nên MN / / AB và MN = AB = 3a . 2
MN / / AB ( MNP ) / / AB .
Gọi Q = (MNP) AD . Thì PQ = (MNP) ( ABD) PQ / / AB .
MNPQ chính là thiết diện của tứ diện ABCD bị cắt bởi mặt phẳng ( MNP ) .
Trong tam giác ABD, có PQ / / AB và BP = 2PD . Suy ra, PQ DP 1 1 =
= QP = .6a = 2a . AB BD 3 3
Theo giả thiết, ta có A CD và B
CD là các tam giác đều. 1 1 1 AM = AC = .6a =
BC = BN = 3a 2 2 2 2 2 2 Xét A MQ và B
NP có: AQ = AD = .6a = DB = BP = 4a 3 3 3
MAQ = NBP = 60
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 1 Vậy 2 2 2 2 MQ = NP =
AQ + AM − 2.A .
Q AM .cos 60 = 9a +16a − 2.3 .4 a . a = 13a . 2
MNPQ là hình thang cân. Dễ thấy, MN − PQ a MH = = . 2 2 2 a a 51 2 2 2
QH = MQ − MH = 13a − = . 4 2 a a S = QH MN + PQ = a + a = . MNPQ ( ) ( ) 2 1 1 51 5 51 . . 3 2 2 2 2 4
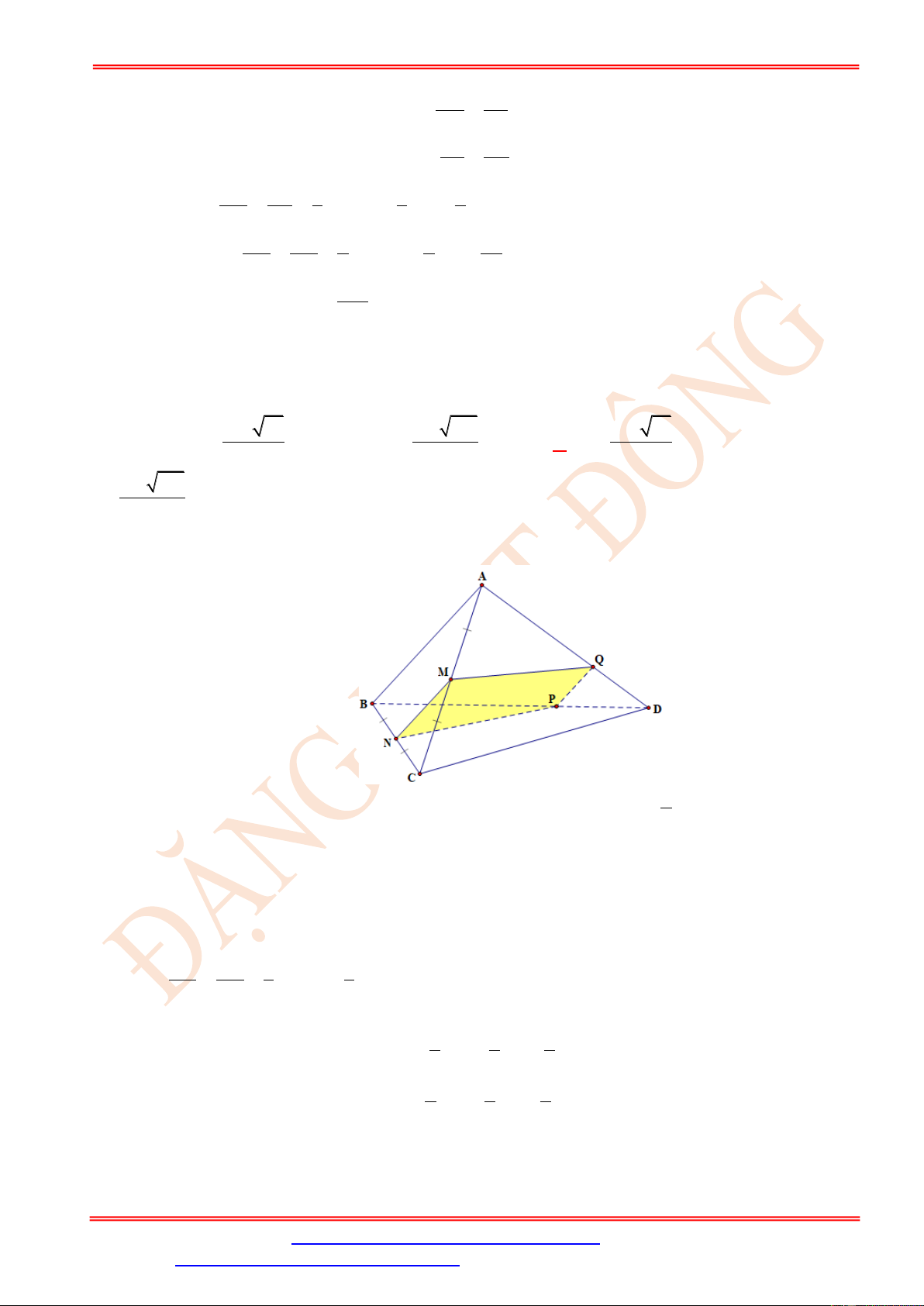
Câu 33. Cho tứ diện ABCD có tất cả các cạnh bằng a , I là trung điểm của AC , J là một điểm
trên cạnh AD sao cho AJ = 2JD . ( P) là mặt phẳng chứa IJ và song song với AB . Tính
diện tích thiết diện khi cắt tứ diện bởi mặt phẳng ( P) . 2 3a 51 2 3a 31 2 a 31 2 5a 51 A. . B. . C. . D. . 144 144 144 144 Lời giải Chọn D
Gọi K = (P) BD , L = (P) BC , E = (P) CD .
Vì ( P) / / AB nên IL / / AB , JK / / AB . Do đó thiết diện là hình thang IJKL và L là trung điểm cạnh KD JD 1 BC , nên ta có = = . KB JA 2
Xét tam giác ACD có I , J , E thẳng hàng. Áp dụng định lí Mê-nê-la-uýt ta có: ED IC JA ED 1 . . = 1
= D là trung điểm EC . EC IA JD EC 2
Dễ thấy hai tam giác ECI và ECL bằng nhau theo trường hợp c-g-c.
Áp dụng định lí cosin cho tam giác ICE ta có: 2 13a a 2 2 2
EI = EC + IC − 2EC.IC.cos 60 = 13 EL = EI = . 4 2 51 Áp dụng công thức Hê 2
-rông cho tam giác ELI ta có: S = p p − x p − y = a ELI ( ) ( ) 2 16
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 + + + Với EI EL IL 2 13 1 13 a p = =
a , x = EI = EL =
a , y = IL = . 2 4 2 2
Hai tam giác ELI và tam giác EKJ đồng dạng với nhau theo tỉ số 2 k = nên 3 2 Do đó: 2 5 51 2 S = S − S = S − S = a . IJKL ELI EKJ ELI 3 ELI 144 Cách giải khác: D M K J B N C H G E F I A (
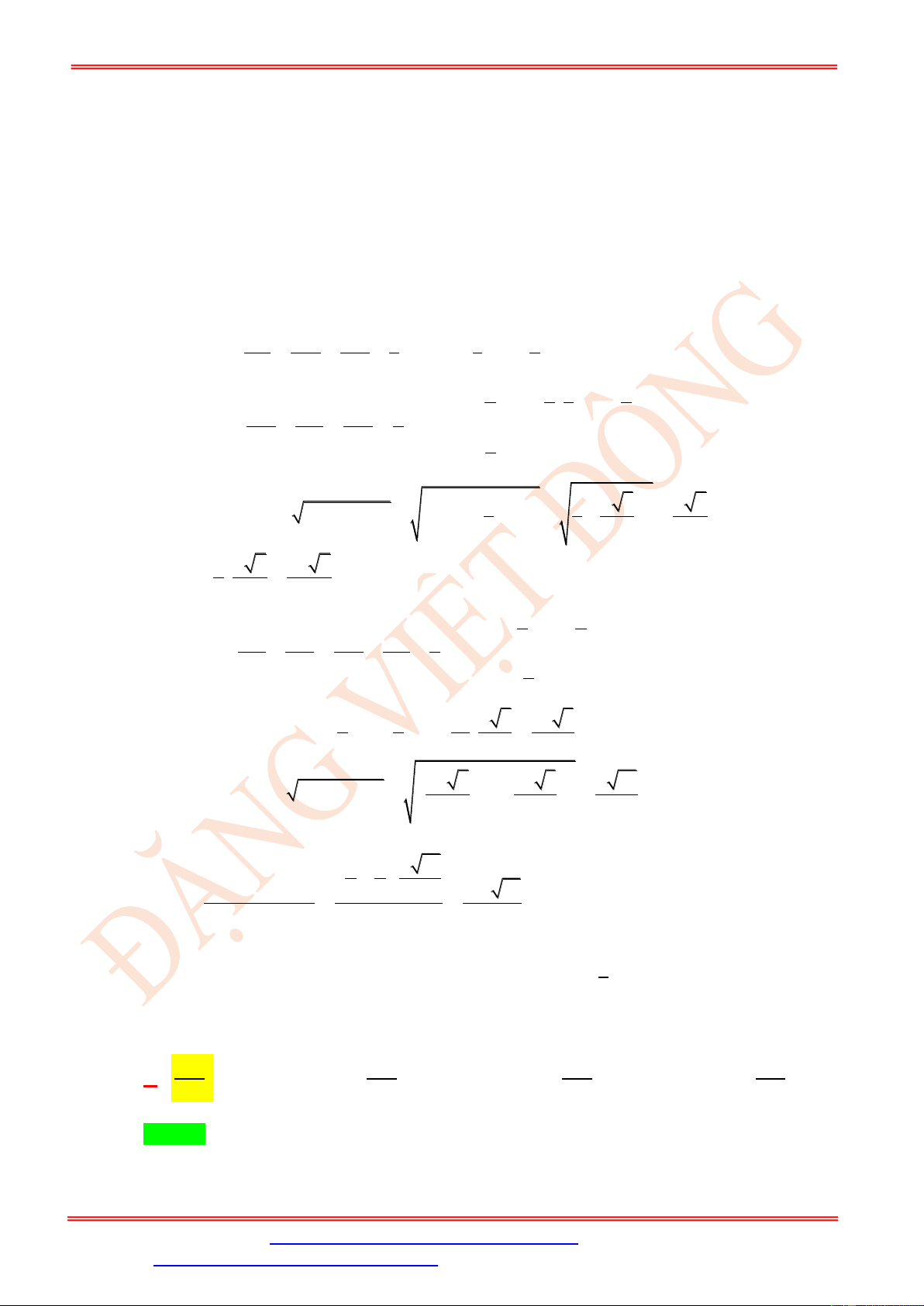
P) ( ABC) = d1
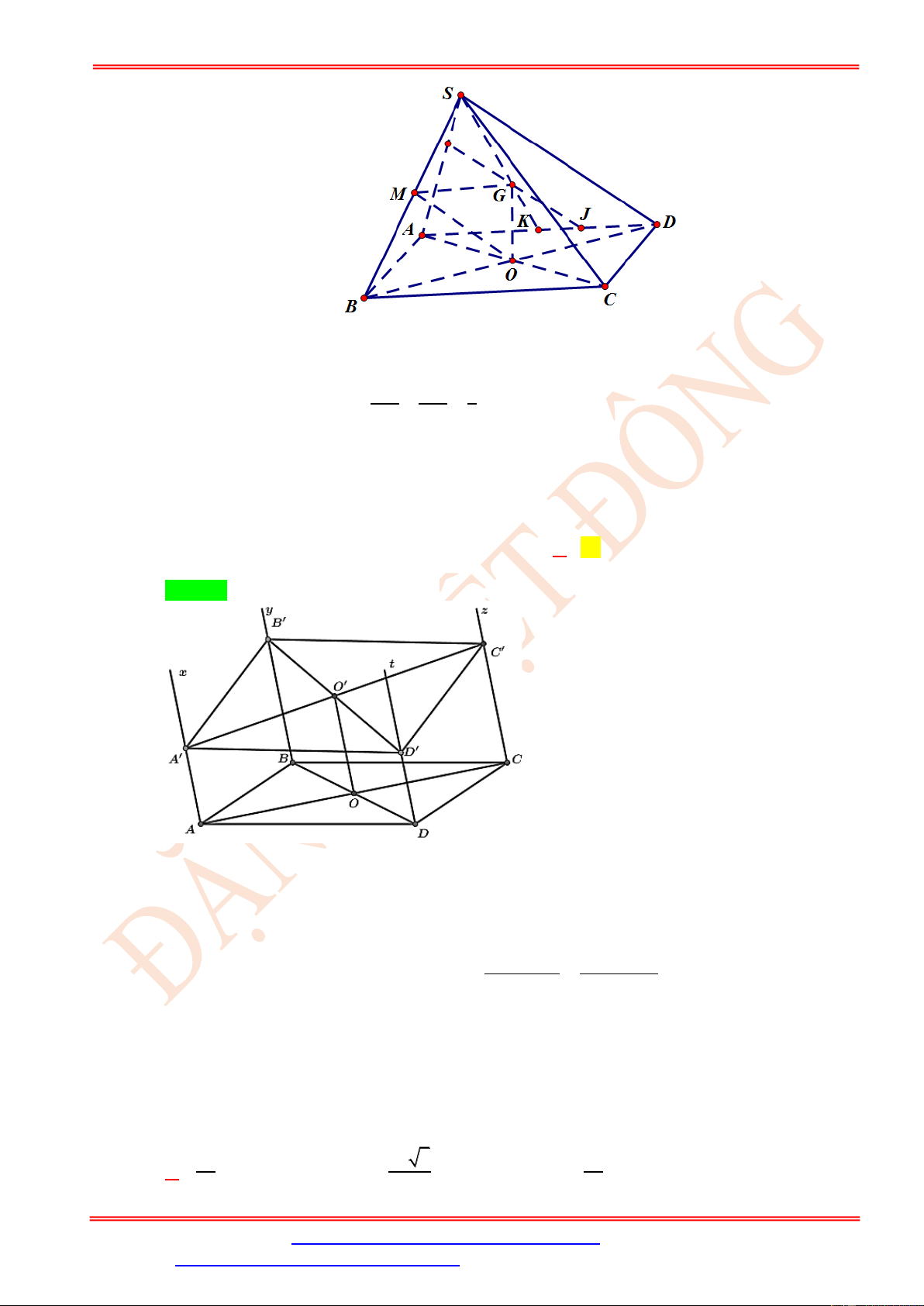
AB ( ABC ); AB // (P) Giao tuyến d qua I và song song với AB 1
I ( P); I ( ABC)
Cách dựng: Trong ( ABC ) : Qua I kẻ đường thẳng d // AB cắt BC tại N 1
(P) ( ABC) = IN (
P) ( ABD) = d2
AB ( ABC ); AB // (P) Giao tuyến d qua J và song song với AB 2
J ( P); J ( ABC)
Cách dựng: Trong ( ABD): Qua J kẻ đường thẳng d // AB cắt BD tại M 2
(P) ( ABD) = JM ( P
) (BCD) = MN Lại có: ( P
) ( ACD) = IJ
Từ đó ta có: Mặt phẳng ( P) cắt tứ diện ABCDtheo thiết diện là hình thang MNIJ DF ⊥ AB
Gọi F là trung điểm của AB
AB ⊥ (CDF ) C F ⊥ AB
Gọi K, H lần lượt là giao điểm của JM với DF và IN với CF
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 IN // AB
Ta có: AB ⊥ (CDF ) IN ⊥ KH KH (CDF )
Chứng minh tương tự: JM ⊥ KH . Từ đó suy ra: KH là đường cao của hình thang MNIJ G CF
Gọi G là trọng tâm ABC DG ⊥ ( ABC)
Trong (CDF ) : Dựng KE // DG ( E CF )
mà DG ⊥ ( ABC ) KE ⊥ ( ABC ) DJ DK JM 1 1 a JM // AB = = = JM = AB = DA DF AB 3 3 3 2 2 1 2 EF = GF = . CF = CF KF EF KE 2 3 3 3 9 KE // DG = = = DF GF DG 3 2 KE = DG 3 2 2 1 8 a 3 a 6 Xét DGF : 2 2 2 DG = DF − GF = DF − CF = . = 3 9 2 3 2 a 6 2a 6 KE = . = 3 3 9 1 a IN = AB = IC NC CH IN 1 2 2 IN // AB = = = = AC BC CF AB 2 1 HF = CF 2 1 2 5 a 3 5a 3
Suy ra: HE = HF − EF = CF − CF = . = 2 9 18 2 36 2 2
2a 6 5a 3 a 51 Xét 2 2 K
HE : KH = KE + HE = + = 9 36 12
Diện tích thiết diện MNIJ là: a a a 51 ( + MJ + IN ) 2 HK 3 2 12 5a 51 S = = = (đvdt) MNIJ 2 2 144
Câu 34. Cho tứ diện ABCDcó AB vuông góc với CD và AB = ,
a CD = b . Gọi I , J lần lượt là trung điểm của 1
AB và CD , điểm M thuộc đoạn IJ sao cho IM =
IJ . Gọi ( ) là mặt phẳng qua 3
M , song song với AB và CD . Diện tích thiết diện của tứ diện ABCD cắt bởi mặt phẳng ( ) là 2ab 4ab 2ab 3ab A. . B. . C. . D. . 9 9 3 2 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Vì ( ) //AB ( ) cắt ( ABJ ) theo giao tuyến qua M và song song với AB .
Gọi NT = ( ) ( ABJ ), N AJ,T BJ .
Mặt khác ( ) //CD ( ) cắt các mặt phẳng ( ACD),(BCD) lần lượt theo các giao
tuyến qua N,T và song song với CD . FH =
( )( ACD),F AC,H AD Gọi . EK =
( )(BCD),E BC,K BD
Suy ra thiết diện là hình bình hành EFHK .
Do AB ⊥ CD EF ⊥ EK nên EFHK là hình chữ nhật. S = EF.EK . EFHK JM MT JT CE EF 2 EF 2a Ta có = = = = = EF = . JI BI JB CB AB 3 AB 3 Tương tự b 2ab EK = . Suy ra S = . 3 EFHK 9
Câu 35. Cho tứ diện ABCDcó AB = a, CD = 3a . Gọi I , J lần lượt là trung điểm AB và CD , giả
sử AB ⊥ CD . Mặt phẳng ( ) qua M nằm trên đoạn IJ và song song với AB và CD. Tính
diện tích thiết diện của tứ diện ABCDvới mặt phẳng ( ) biết IM = 1 IJ . 3 2 3a 2 2a A. 2 2a . B. . C. 2 4a . D. . 2 3 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 ()// CD
Ta có CD ( ICD) M ()(ICD)
giao tuyến của ( ) với (ICD) là đường thẳng qua M và song song với CDcắt ICtại
L và ID tại N . ( )// AB AB ( JAB) M ( )(JAB)
giao tuyến của ( ) với (JAB) là đường thẳng qua M và song song với AB cắt JA tại
P và JB tại Q . ( )// AB
Ta có AB ( ABC)
EF// AB (1). L ( )(ABC) ()// AB
Tương tự AB ( ABD)
HG// AB (2). N ()(ABD)
Từ (1) và (2) EF// HG// AB (3). ()// CD
Ta có CD ( ACD) FG// CD(4). P ( )(ACD) ()// CD
Tương tự CD ( BCD)
EH// CD(5). Q ()(BCD)
Từ (4) và (5) FG// EH// CD(6).
Từ (3) và (6), suy ra EFGH là hình bình hành. Mà AB ⊥ CD nên EFGH là hình chữ nhật.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 LN IN
Xét tam giác ICD có: LN// CD = . CD ID IN IM
Xét tam giác ICD có: MN// JD = . ID IJ
Do đó LN = IM = 1 LN = 1 CD = a. CD IJ 3 3
Tương tự PQ = JM = 2 = 2 = 2a PQ AB . AB JI 3 3 3 2 Vậy = Q LN = 2a S P . . EFGH 3
Dạng 2: Bài toán tỉ số
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N , P lần lượt
là trung điểm của AB, AD và SO . Gọi H là giao điểm của SC với mặt phẳng (MNP) . SH Tính . SC 3 2 1 1 A. . B. . C. . D. . 4 3 4 3 Lời giải Chọn C
Gọi K = AC MN K là trung điểm của AO. SH AK 1
Gọi H = KP SC H = (MNP) SC và KH //SA = = . SC AC 4
Câu 37. Cho tứ diện ABC .
D Gọi G và G lần lượt là trọng tâm các tam giác BCD và AC . D Mệnh 1 2
đề nào sau đây sai? A. G G ABD . B. G G ABC . 1 2 ( ) 1 2 ( ) 2
C. BG , AG và CD đồng qui. D. G G = AB . 1 2 1 2 3 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A G2 B D G1 M C
Gọi M là trung điểm của CD. MG 1 MG 1 G G 1 1 Theo bài ra ta có: 2 = , 1 =
do đó G G // AB và 1 2 = hay G G = AB . 1 2 MA 3 MB 3 AB 3 1 2 3 Vậy D sai.
Câu 38. Cho hình hộp 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′. Gọi 𝑀 là trung điểm của 𝐴𝐵. Mặt phẳng (𝑀𝐴′𝐶′) cắt cạnh 𝑀𝑁
𝐵𝐶 của hình hộp 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ tại 𝑁. Tính tỉ số 𝑘 = . 𝐴′𝐶′ 1 1 1 1 A. 𝑘 = . B. 𝑘 = . C. 𝑘 = . D. 𝑘 = . 2 2 2 2 Lời giải Chọn A
Ta có: 𝐴𝐶 // 𝐴′𝐶′ nên (𝑀𝐴′𝐶′) // AC.
(𝑀𝐴′𝐶′) ∩ (𝐴𝐵𝐶𝐷) = 𝑀𝑁 do đó 𝑀𝑁 // AC ⇒ 𝑁 là trung điểm của 𝐵𝐶.
𝑀𝑁 là đường trung bình của Δ𝐴𝐵𝐶. 𝑀𝑁 𝑀𝑁 1 𝑘 = = = . 𝐴′𝐶′ 𝐴𝐶 2
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi ( ) là mặt phẳng đi qua
AC và song song với SB . Mặt phẳng ( ) cắt SD tại E. Chọn khẳng định đúng trong các khẳng định sau 1 1 1 A. SE = ED . B. SE = SD . C. SE = SD .
D. SE = 2SD. 3 2 3 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 54
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Chọn B S E A D O B C
Gọi E là trung điểm SD . Ta có OE//SB nên ( EAC ) là mặt phẳng chứa AC và song song 1 SB . Suy ra SE = SD . 2
Câu 40. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M , N , P lần lượt là trung
điểm của SB , SD và OC . Gọi giao điểm của (MNP) với SA là K . Tỉ số KS là KA 2 1 1 1 A. . B. . C. . D. . 5 3 4 2 Lời giải Chọn B
Trong mặt phẳng (SBD) , gọi I là giao điểm của MN và SO
Ta có SA ( SAC ) ; ( MNP) ( SAC ) = PI
Trong mặt phẳng (SAC) , PI cắt SA tại K K là giao điểm của SA và (MNP) Mặt khác:
MN là đường trung bình của tam giác SBD nên MN cắt SO tại trung điểm I
PI là đường trung bình của tam giác SOC PI // SC hay PK // SC 1 AC KS PC 1 4 = = = . KA PA 3 3 AC 4
Lưu ý :Giải nhanh bằng trắc nghiệm ta dùng công thức SA SC SB SD + = + SA SK = 1 3 = . SK SC SM SN SK SA 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 55
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 41. Cho tứ diện ABCD. Gọi M ,
lần lượt là trọng tâm các tam giác N
BCD và ACD . Chọn khẳng định sai? 2
A. MN // ( ABD) . B. MN = AB . 3 đồng quy MN // ABC
C. BM , AN,CD . D. ( ) . Lời giải Chọn B
Gọi E là trung điểm cạnh CD . Ta có M ,
lần lượt là trọng tâm các tam giác N BCD và EM EN 1 MN 1 ACD nên: =
= . Suy ra MN // AB và = . Do đó: EB EA 3 AB 3
A đúng vì MN // AB , MN ( ABD) , AB ( ABD ) nên MN // ( ABD) . MN 1 1 B sai vì
= hay MN = AB . AB 3 3
C đúng vì BM , AN,CD đồng quy tại E .
D đúng vì MN // AB , MN ( ABC ) , AB ( ABC ) nên MN // ( ABC ) .
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M là trung điểm của
SB và G là trọng tâm của tam giác SAD . Gọi J là giao điểm của AD và mặt phẳng
(OMG). Tính tỉ số JA . JD 1 5 A. 2 . B. 1. C. . D. . 2 3 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 56
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
+ Mặt phẳng (OMG) cắt mặt phẳng (SAD) theo giả thiết là đường thẳng qua G và song
song với SD . Gọi J = AD Suy ra J = (OMG) AD . KJ KG 1
+ Ta có: GJ / /SD Suy ra: =
= . Vậy JA = 2JD . KD KS 3
Câu 43. Cho hình bình hành ABCD. Qua A , B , C , D lần lượt vẽ các nửa đường thẳng Ax , By ,
Cz , Dt ở cùng phía so với mặt phẳng ( ABCD) , song song với nhau và không nằm trong
( ABCD) . Một mặt phẳng (P) cắt Ax , By , z
C , Dt tương ứng tại A , B , C , D sao cho
AA = 3, BB = 5, CC = 4 . Tính DD . A. 4 . B. 6 . C. 2 . D. 12 . Lời giải Chọn C
Do ( P ) cắt mặt phẳng ( Ax, By ) theo giao tuyến A B
; cắt mặt phẳng (Cz, Dt)theo giao tuyến C D
, mà hai mặt phẳng ( Ax, By) và (Cz, Dt)song song nên A B // C D . Tương tự có A D //B C nên A B C D
là hình bình hành.
Gọi O , O lần lượt là tâm ABCDvà A B C D
. Dễ dàng có OO là đường trung bình của hai AA + CC BB + DD hình thang AA C C và BB D D nên OO = = . 2 2
Từ đó ta có DD = 2.
Câu 44. Cho tứ diện ABCD có tam giác BCD đều cạnh a , tam giác ACD vuông. Gọi I , J lần lượt
là tâm đường tròn nội tiếp các tam giác ABC và ABD. Biết rằng IJ song song với
(BCD) . Tính diện tích tam giác ACD. 2 a 2 a 3 2 a A. . B. . C. . D. 2 a . 4 4 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 57
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Lời giải Chọn A
Ta chứng minh bài toán phụ: Cho tứ diện ABCD , gọi I , J lần lượt là tâm đường tròn nội + tiếp các tam giác BC BA CA
ABC và ABD. Điều kiện cần và đủ để JI || ( BCD) là = . BD BA + DA Thật vậy: Gọi AI JA AI BC = ,
G AJ BD = H . JI || ( BCD) JI || GH = . IG JH BA CA BA + CA BA + CA = = =
BG CG BG + CG BC + + Mà . Như vậy BA CA BA DA = . DA BA BA + DA BA + DA = = = BC BD DH BH DH + BH BD
Áp dụng bài toán trên ta có BC = BD = CD = a BA+ CA = BA+ DA 2 CD a 1 a
CA = DA A
CD vuông cân tại A 2 AC = AD = = S = .AC = . ACD 2 2 2 4
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A là điểm trên SA sao cho 1 A A = A S
. Mặt phẳng ( ) qua A cắt các cạnh SB , 2
SC , SD lần lượt tại B , C , D . SB SD SC
Tính giá trị của biểu thức T = + − SB SD SC . 3 1 1 A. T = . B. T = .
C. T = 2. D. T = . 2 3 2 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 58
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi O là giao của AC và BD . Ta có O là trung điểm của đoạn thẳng AC , BD .
Các đoạn thẳng SO , A C , B D
đồng quy tại I . S S S S S S Ta có: S + S = SA I SC I SA C + = SA I SC I SA C + = S SA' I SC I SA C S S S 2S 2S S SAC SAC SAC SAO SCO SAC SA SI SC SI SA SC SI SA SC SA SC SA SC SO . + . = . + = . + = 2. 2SA SO 2SC SO SA SC 2SO SA SC SA SC SA SC . SI Tương tự SB SD SO : + = 2. SB SD SI SB SD SC SA 3 Suy ra: + − = = SB SD SC SA . 2
Câu 46. Cho tứ diện ABCD và M , N lần lượt là các điểm trên hai cạnh A , B CD sao cho AM CN =
= k 0 và ( ) là mặt phẳng qua MN và song song với cạnh BC , gọi P là MB ND
giao điểm của ( ) với cạnh AC . Tìm k biết tỉ số diện tích tam giác MNP và diện tích
thiết diện của tứ diện được cắt bởi mặt phẳng ( ) bằng 1 . 3 3 2 3 4 1 3 A. k ; . B. k ; . C. k ; . D. 10 5 5 5 5 10 2 3 k ; . 5 5 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 59
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Từ N kẻ đường thẳng song song với BC cắt BD tại Q .
Từ M kẻ đường thẳng song song với BC cắt AC tại P .
Thiết diện là tứ giác MPNQ .
Gọi I, H lần lượt là hình chiếu của ,
Q P trên MN . K = MN PQ . S QI QK Ta có MNQ = = . S PH PK MNP S S + S S + MNPQ MNP MNQ QK PK QK PQ S PK = = 1 MNQ + = 1 MNP + = = = . S S S PK PK PK S PQ MNP MNP MNP MNPQ AM CN Do =
nên theo định lí Thales đảo thì AC, NM , BD lần lượt thuộc ba mặt phẳng MB ND
song song với nhau và đường thẳng PQ cắt ba mặt phẳng này tương ứng tại P, K, Q nên áp
dụng định lí Thales ta được PK AM CN = = = k . KQ MB ND PK PK PK KQ k = = = . PQ PK + KQ PK k +1 +1 KQ S k 1 k 1 Suy ra MNP = = k = S k +1 3 k + . 1 2 MNPQ
Câu 47. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD , N
là trọng tâm tam giác SAB . Đường thẳng MN cắt mặt phẳng (SBC) tại điểm I . Tính tỷ số IN . IM 3 1 1 2 A. . B. . C. . D. . 4 3 2 3 Lời giải. Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 60
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi J; E lần lượt là trung điểm S ; A AB .
Trong mặt phẳng ( BCMJ ) gọi I = MN BC .
•Ta có: IM là đường trung tuyến của tam giác SID .
•Trong tam giác ICD ta có BE song song và bằng 1 CD nên suy ra BE là đường trung 2
bình của tam giác ICD E là trung điểm ID SE là đường trung tuyến của tam giác SID . IN
Ta có: N = IM SE N là trọng tâm tam giác 2 SID = . IM 3
Câu 48. Cho t diện ABCD. Gọi M là trung điểm của CD , I là một điểm thuộc cạnh AD sao cho
IA = 3ID ; ( ) là mặt phẳng qua M , ( ) song song với CI và BD ; ( ) cắt AD , AB ,
BC lần lượt tại N, ,
P Q . Gọi R là giao điểm của MP và NQ . Khẳng định nào sau đây sai? RP 7 PN 7 RN 7 PN 7 A. = . B. = . C. = . D. = . RM 4 QM 4 RQ 3 BD 8 Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 61
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A I P N D B R Q M C L P N R M Q E L
Từ M kẻ MQ//B ,
D Q BC và MN //CI, N AD , khi đó mặt phẳng ( ) cần dựng là mặt phẳng (MQN ) .
Giao tuyến của hai mặt phẳng (MQN ) và ( ABD) là đường thẳng qua N và song song
với BD khi đó AB (MQN ) = AB = P .
Áp dụng định lý Talet vào hai tam giác ABD và CBD ta đượcc: PN AN 7 7 =
= PN = BD (1). D đúng. BD AD 8 8 MQ CM 1 1 =
= MQ = BD(2). BD CD 2 2
Từ (1) và (2) suy ra MQ 4 = B đúng. NP 7
Trong mặt phẳng (MNPQ) gọi L = PQ MN , kẻ ME//QN với E PQ . LE LM LQ MQ 4 Ta có = = = = LQ LN LP NP 7 LE 4 = 3 = QE QL LQ 7 7 PQ 7 Vì = . LQ 4 = 3 = QE 4 PQ QL LP 7 4
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 62
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Mặt khá RP PQ = RP 7 = A đúng. RM QE RM 4
Chứng minh hoàn toàn tương tự ta được RN 7 = C sai. RQ 4 2
Câu 49. Cho hình lăng trụ AB . C A B C
có M thuộc cạnh B C sao cho B M = B C , N là trung 3
điểm cạnh CC . Gọi G là trọng tâm của tứ diện ANMA và K thuộc cạnh BC sao cho a KG ( ABB A ). Biết a BK = BC với , a b và
là phân số tối giản. Khi đó . a b bằng b b A. 4 . B. 10 . C. 60 . D. 84 . Lời giải Chọn C
Giả sử gọi AA = a , AB = b , AC = c .
Đặt BK = mBC . Ta có:
KA = BA − BK = BA − mBC = BA − m ( AC − AB) = b
− − m(c −b ) = (m− ) 1 b − mc .
KN = KA + AC + CN = (m − ) 1 1
1 b − mc + c + a = a + (m − )
1 b + (1− m)c . 2 2 2
KM = BB + B M
− BK = a + (c −b)− m(c −b) 2 2 = a + m − b + − m c . 3 3 3
Do G là trọng tâm của tứ diện ANMA nên ta có 4KG = KA + KN + KM + KA 3 8 5 Suy ra 4KG = a + 3m − b + − 4m c . 2 3 3
Mặt khác KG ( ABB A ) 5 12
− 4m = 0 m = . 3 5 Do đó ab =12.5 = 60.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 63
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
HAI MẶT PHẲNG SONG SONG
Dạng 1: Tính diện tích thiết diện cắt bởi MP song song với MP khác
Câu 50. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho SM 2
= . Một mặt phẳng ( ) đi qua M song song với AB và AD, cắt hình chóp theo SA 3
một tứ giác có diện tích là 400 20 4 16 A. . B. . C. . D. . 9 3 9 9 Lời giải Chọn A
Mặt phẳng ( ) đi qua M song song với AB và AD nên mặt phẳng ( ) song song với mặt
phẳng ( ABCD) . Vậy thiết diện của mặt phẳng ( ) với hình chóp đều S.ABCD là hình vuông MNPQ . MQ SM 2 2 2 20 Ta có: =
= MQ = AD = .10 = . AD SA 3 3 3 3 2 20 400
Diện tích của thiết diện là: 2 S = MQ = = . MNPQ 3 9
Câu 51. Cho tứ diện đều ABCD có cạnh bằng a , điểm M trên cạnh AB sao cho AM = 2MB .
Tính diện tích thiết diện của hình tứ diện ABCD cắt bởi mặt phẳng qua M và song song
với các đường thẳng AC và CD . 2 a 3 2 a 3 2 a 3 2 a 3 A. . B. . C. . D. . 9 36 4 18 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 64
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Vì thiết diện của hình tứ diện ABCD cắt bởi mặt phẳng qua M và song song với các đường
thẳng AC và CD . Nên từ M kẻ đường thẳng song song với AC căt BC tại N. Và từ N
kẻ đường thẳng song song với CD căt BD tại .
P Thiết diện là tam giác MNP .
Mặt khác ( MNP) / / ( ACD) , và A
CD đều. Nên M NP đều. BM BN MN 1 1 a Ta có = =
= MN = .AC = . BA AC AC 3 3 3 2 1 1 a a 3 a 3 Vậy 0 S = .MN.M . P sin 60 = . . . = . M NP 2 2 3 3 2 36
Câu 52. Cho hình chóp S.ABC . Gọi M là trung điểm SA ; ( ) là mặt phẳng qua M và song song
với ( ABC ) . ( ) lần lượt cắt các cạnh SB , SC tại N và P . Gọi S , S lần lượt là diện 1 2 S
tích các tam giác ABC và MNP . Tính 1 . S2 1 1 A. . B. 4 . C. . D. 2 . 4 2 Lời giải Chọn B
Vì ( ) đi qua M và song song với ( ABC ) , cắt SB , SC lần lượt tại N và P nên ta có
MN // AB , NP // BC N , P lần lượt là trung điểm của SB , SC .
Dựng các đường cao AH , MK của ABC và M
NP (xem hình vẽ). Khi đó MK // AH .
Theo tính chất đường trung bình, ta có: BC = 2NP , AH = 2MK
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 65
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S
S = 4S hay 1 = 4 . 1 2 S2
Câu 53. Cho hình chóp ABCD có tất cả các cạnh bằng nhau và bằng x. Gọi I là trung điểm AB, qua I
dựng mp(P) song song với (BCD). Diện tích thiết diện của hình chóp và mp(P) là 2 x 3 2 x 3 2 x 3 2 x 3 A. . B. . C. . D. . 4 8 12 16 Lời giải Chọn D A I E N B D C BC // (P)
Vì ( P) // ( BCD) CD // ( P) BD // (P)
(P) ( ABC) = d1
BC ( ABC ); BC // (P) d // BC . 1
I (P),I ( ABC)
Cách dựng: Trong ( ABC ) : Qua I dựng đường thẳng d song song với BC cắt AC tại N 1
(P) ( ABC) = IN ( ) 1
(P) ( ADC) = d2
DC ( ADC ); DC // (P) d // DC . 2
N (P),N ( ADC)
Cách dựng: Trong ( ADC ) : Qua N dựng đường thẳng d song song với DC cắt AD tại E 2
(P) ( ADC) = NE (2)
Trong ( ABD ) : Nối IE ( P) ( ABD) = IE (3)
Từ (1),(2) và (3) suy ra: mp ( P) cắt hình chóp ABCD theo thiết diện là tam giác INE. Theo cách dựng ta có: AN = NC IN // BC Xét ABC : 1 x IB = IC IN = BC = 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 66
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 AE = ED NE // DC Xét A DC : 1 x AN = NC NE = DC = 2 2 AI = IB 1 x Xét ABD : IE = BD = AE = ED 2 2 2 x 3 2 x 2 x 3 Suy ra: I
NE là tam giác đều cạnh S = = (dvdt) 2 INE 4 16
Câu 54. Cho tứ diện có các cạnh bằng 4a . Lấy M là điểm trên cạnh AB sao cho AM = a . Tính
diện tích thiết diện của tứ diện ABCD cắt bởi mặt phẳng đi qua M và song song với mặt
phẳng ( ACD) . 2 9a 3 2 3a 3 2 a 3 A. 2 3a 3 . B. . C. D. . 4 4 4 Lời giải Chọn A
Ta có thiết diện cần tìm là mặt phẳng (MNE ) . 1 3 Mà 2 S
= 4a 3 , MA = AB 2 S = S = 3a 3 . A CD 4 MNE 4 ACD
Câu 55. Cho hình chóp tứ giác S.ABCD có tất cả các cạnh bằng 2a . Gọi M là trung điểm cạnh
BC . Mặt phẳng ( ) qua M và song song với (SB )
D cắt hình chóp theo thiết diện có diện tích bằng 2 a 2 a 2 a 2 a 3 A. . B. . C. . D. . 6 2 3 4 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 67
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi O = AC BD .
Gọi E là trung điểm của CD, F là trung điểm của SC . Trong mặt phẳng (ABCD) ME
cắt OC tại I . Khi đó ta có ME // BD và MF // SB . Suy ra thiết diện của hình chóp cắt
bởi mặt phẳng ( ) là tam giác MEF có đường cao là FI và cạnh đáy là ME .
Ta có ABCD là hình vuông cạnh cạnh 2a suy ra BD = 2a 2 ME = a 2 . 2 2 2 2 a 2 SO = SD − OD =
4a − 2a = a 2 suy ra FI = . 2 2
Vậy diện tích thiết diện cần tìm là 1 a 2 a S = .a 2. = . M EF 2 2 2
Câu 56. Cho hình chóp S.ABCD có đáy ABCD là hình thang; AB = 2C , D AB
CD . M là trung
điểm của cạnh AD ; mặt phẳng ( ) qua M và song song với mp(SAB) cắt hình chóp
S.ABCD theo một thiết diện là hình (H ) . Biết S = xS
. Giá trị của x là: ( H ) S AB 1 27 1 9 A. . B. . C. . D. . 2 64 4 16 Lời giải Chọn A Gọi N, ,
P Q lần lượt là trung điểm các cạnh S , D SC, BC .
Gọi E = AD BC, I = MN PQ ta có S, I, E thẳng hàng vì cùng thuộc giao tuyến của (SA ) D và (SBC) .
Thiết diện là hình thang MNPQ (vì NP AB MQ ).
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 68
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 NP 1 DC 2 NP 1 1 Ta có S = S − S , mà = , = = S = S MNPQ I MQ I NP DC 2 MQ 3 MQ 3 INP 9 IMQ 1 8 S = S − S = S . MNPQ I MQ 9 IMQ 9 IMQ MI 3
Ta có M là trung điểm AD , D là trung điểm của AE nên = 9 S = S SA 4 IMQ 16 SAB 8 9 1 S = . S = S . MNPQ 9 16 SAB 2 SAB
Câu 57. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với cạnh bên BC = 3, hai
đáy AB = 8, CD = 4 . Mặt phẳng ( P ) song song với ( ABCD) và cắt cạnh SA tại M sao
cho SA = 3SM . Diện tích thiết diện của ( P ) và hình chóp S.ABCD bằng bao nhiêu? 2 5 7 3 2 5 7 3 A. . B. . C. . D. . 3 9 9 3 Lời giải Chọn A
Gọi giao điểm của ( P ) với các cạnh SB, SC và SD là N, ,
P Q ta có tứ giác MNPQ là hình
thang cân với hai đáy là MN và PQ . SM 1 MN NP PQ 1 4 Có = = = = 8
MN = , PQ = , NP = MQ =1. SA 3 AB BC D C 3 3 3 2 2 5 Ta có 2 2 PH = NP − NH = 1− = 3 3 1 S = PH MN + PQ = + = MNPQ ( ) 1 5 8 4 2 5 . . . 2 2 3 3 3 3
Câu 58. Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a , tam giác SAB đều. Gọi
M là điểm trên cạnh AD sao cho AM = x, x (0; a ) . Mặt phẳng ( ) qua M và song song
với ( SAB) lần lượt cắt các cạnh C ,
B CS, SD tại N, , P .
Q Khi diện tích tứ giác MNPQ bằng 2 2a
3 thì x bằng bao nhiêu? 9 a 2a a a A. . B. . C. . D. . 2 3 3 4 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 69
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Chọn C
Kẻ đường thẳng qua M và song song với AB , cắt BC tại N .
Kẻ đường thẳng qua N và song song với SB , cắt SC tại P .
Kẻ đường thẳng qua M và song song với SA , cắt SD tại Q .
Suy ra tứ giác MNPQ là thiết diện của hình chóp S.ABCD cắt bởi ( ) .
( ) (SCD) = PQ
Có (SCD) ( ABCD) = CD
( ABCD) ( ) = MN P , Q C ,
D MN hoặc đôi một song song, hoặc đồng quy.
Mà CD//MN PQ//C .
D ( PQ CD) (1)
Gọi H là hình chiếu vuông góc của S lên ( ABCD ) .
Ta có: SA = SB HA = HB . Suy ra H thuộc đường trung trực đoạn AB .
HC = HD SC = SD SBC = SAD (c − c − c)
PCN = QDM P CN = Q
DM (c − g −c) PN = QM (2)
Từ (1) và (2) ta có tứ giác MNPQ là hình thang cân. PQ SQ AM Ta có: = =
PQ = AM = x. CD SD AD
Gọi E = PN QM E
NM cân tại E. Mà ( , ) = ( , ) = 60o PN NM SB AB E
NM là tam giác đều cạnh a và EPQ
là tam giác đều cạnh x . 2 2 a 3 x 3 S = S − S = − MNPQ E MN E PQ 4 4 2 2 2 2 2a 3 a 3 x 3 2a 3 a Ta có: S = − = x = . MNPQ 9 4 4 9 3
Câu 59. Cho hình chóp 𝑆. 𝐴𝐵𝐶 có đáy 𝐴𝐵𝐶 là tam giác vuông cân tại 𝐴, 𝐴𝐵 = 𝐴𝐶 = 𝑎; cạnh bên
𝑆𝐴 vuông góc với mặt đáy, 𝑆𝐴 = 𝑎. Gọi 𝑀là trung điểm 𝑆𝐶. Tính diện tích thiết diện của
hình chóp cắt bởi mặt phẳng (𝑃) đi qua 𝑀và vuông góc với 𝐴𝐶. 𝑎2 𝑎2 𝑎2 A. . B. . C. 𝑎2. D. . 2 8 4 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 70
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S M A C N P B
Xét trong mặt phẳng (𝑆𝐴𝐶), từ 𝑀 kẻ 𝑀𝑁 ∥ 𝑆𝐴, 𝑁 ∈ 𝐴𝐶 ⇒ 𝑀𝑁 ⊥ 𝐴𝐶(1).
Xét trong mặt phẳng (𝐴𝐵𝐶), từ 𝑁 kẻ 𝑁𝑃 ∥ 𝐴𝐵, 𝑃 ∈ 𝐵𝐶 ⇒ 𝑁𝑃 ⊥ 𝐴𝐶(2).
Từ (1) và (2) suy ra 𝐴𝐶 ⊥ (𝑀𝑁𝑃). Khi đó thiế 1 1 1
t diện cần tìm là tam giác 𝑀𝑁𝑃 vuông tại 𝑁 có 𝑀𝑁 = 𝑁𝑃 = 𝑆𝐴 = 𝐴𝐵 = 𝑎. 2 2 2 Vậy 1 𝑎2
𝑆𝑡𝑑 = 𝑆𝑀𝑁𝑃 = 𝑀𝑁. 𝑁𝑃 = . 2 8
Câu 60. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có đáy 𝐴𝐵𝐶𝐷 là hình thang cân với cạnh bên 𝐵𝐶 = 2, hai đáy
𝐴𝐵 = 6, 𝐶𝐷 = 4. Mặt phẳng (𝑃) song song với (𝐴𝐵𝐶𝐷) và cắt cạnh 𝑆𝐴 tại 𝑀 sao cho
𝑆𝐴 = 3 𝑆𝑀. Diện tích thiết diện của (𝑃) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 bằng bao nhiêu? 5√3 2√3 7√3 A. . B. . C. 2. D. . 9 3 9 Lời giải Chọn A S O P M N D C D C A B A H K B
Gọi 𝐻, 𝐾 lần lượt là hình chiếu vuông góc của 𝐷, 𝐶 trên 𝐴𝐵.
𝐴𝐻 = 𝐵𝐾; 𝐶𝐷 = 𝐻𝐾
𝐴𝐵𝐶𝐷 là hình thang cân ⇒ { ⇒ 𝐵𝐾 = 1.
𝐴𝐻 + 𝐻𝐾 + 𝐵𝐾 = 𝐴𝐵
Tam giác 𝐵𝐶𝐾 vuông tại 𝐾, có 𝐶𝐾 = √𝐵𝐶2 − 𝐵𝐾2 = √22 − 12 = √3. 𝐴𝐵+𝐶𝐷 4+6
Suy ra diện tích hình thang 𝐴𝐵𝐶𝐷 là 𝑆𝐴𝐵𝐶𝐷 = 𝐶𝐾. = √3. = 5√3. 2 2
Gọi 𝑁, 𝑃, 𝑄 lần lượt là giao điểm của (𝑃) và các cạnh 𝑆𝐵, 𝑆𝐶, 𝑆𝐷. 𝑁𝑃 𝑃𝑄 𝑄𝑀 1
Vì (𝑃)//(𝐴𝐵𝐶𝐷) nên theo định lí Talet, ta có 𝑀𝑁 = = = = . 𝐴𝐵 𝐵𝐶 𝐶𝐷 𝐴𝐷 3 Khi đó ( 5 𝑃) √3
cắt hình chóp theo thiết diện 𝑀𝑁𝑃𝑄 có diện tích 𝑆𝑀𝑁𝑃𝑄 = 𝑘2. 𝑆𝐴𝐵𝐶𝐷 = . 9
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 71
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 61. Cho hình chóp 𝑆. 𝐴𝐵𝐶 có đáy là tam giác 𝐴𝐵𝐶 thỏa mãn 𝐴𝐵 = 𝐴𝐶 = 4, 𝐵𝐴𝐶 ̂ = 30°. Mặt
phẳng (𝑃) song song với (𝐴𝐵𝐶) cắt đoạn 𝑆𝐴 tại 𝑀 sao cho 𝑆𝑀 = 2𝑀𝐴. Diện tích thiết diện
của (𝑃) và hình chóp 𝑆. 𝐴𝐵𝐶 bằng bao nhiêu? 16 14 25 A. . B. . C. . D. 1. 9 9 9 Lời giải Chọn A S N M A C P B 1 1
Diện tích tam giác 𝐴𝐵𝐶 là 𝑆𝛥𝐴𝐵𝐶 = . 𝐴𝐵. 𝐴𝐶. sin𝐵𝐴𝐶 ̂ = . 4.4. sin300 = 4. 2 2
Gọi 𝑁, 𝑃 lần lượt là giao điểm của mặt phẳng (𝑃) và các cạnh 𝑆𝐵, 𝑆𝐶. 𝑆𝑁 𝑆𝑃 2
Vì (𝑃)//(𝐴𝐵𝐶) nên theoo định lí Talet, ta có 𝑆𝑀 = = = . 𝑆𝐴 𝑆𝐵 𝑆𝐶 3
Khi đó (𝑃) cắt hình chóp 𝑆. 𝐴𝐵𝐶 theo thiết diện là tam giác 𝑀𝑁𝑃 đồng dạng với tam giác 2 2 2 16
𝐴𝐵𝐶 theo tỉ số 𝑘 = . Vậy 𝑆 ) . 4 = . 3
𝛥𝑀𝑁𝑃 = 𝑘2. 𝑆𝛥𝐴𝐵𝐶 = (3 9
Câu 62. Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn 0
AB = AC = 4, BAC = 30 . Mặt
phẳng ( P) song song với ( ABC ) cắt đoạn SA tại M sao cho SM = 2M .
A Diện tích thiết
diện của (P) và hình chóp S.ABC bằng bao nhiêu? 25 14 16 A. . B. 1. C. D. . 9 9 9 Lời giải Chọn D
(P) song song với ( ABC) cắt đoạn SA tại M và cắt đoạn SB,SC
tại N, P như hình vẽ. 2
SM = 2MA SM = SA 3 Tương tự ta cũng có SM SN SP 2 = = = và SA SB SC 3 MN NP PM 2 = = = (theo Talet) AB BC CA 3 S 9 Suy ra ABC A BC M NP = mà S 4 M NP 1 1 0 S = A . B AC.sinBAC = .4.4.si 3 n 0 = 4 ABC 2 2 Vậy 16 S = M NP 9
Câu 63. Cho tứ diện ABCD, biết tam giác BCD có diện tích bằng 16. Mặt phẳng ( P ) đi qua trung
điểm của AB và song song với mặt phẳng ( BCD) cắt tứ diện theo một thiết diện có diện tích bằng
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 72
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A. 12. B. 4 . C. 8 . D. 16 . Lời giải Chọn B A P N M I D C J B
Gọi M là trung điểm của AB .
Gọi MN = (P) ( ABD) ( N AD), do (P) // (BCD) MN // BD N là trung điểm của AD .
Gọi MP = (P) ( ABC ) ( P AC ), do (P) // (BCD) MP//BC P là trung điểm của AC .
Thiết diện của tứ diện ABCD cắt bởi mặt phẳng ( P) là M NP . Cách 1:
Gọi I, J lần lượt là trung điểm của CD và BD.
Ta chứng minh được M NP = J
DI (c – c – c). 1 1 1 1 1 Ta có S = S
= DI.DJ.sin JDI = . D . B D . C sin BDC = .S = .16 = 4. M NP D IJ 2 4 2 4 DBC 4 Vậy S = 4. MNP Cách 2: 1 Ta có MN = 1 B , D NP = 1 C , D MP = BC M NP và B
CD đồng dạng theo tỉ số 2 2 2 1 k = . 2 2 1 1 S = .S = .16 = 4. MNP 2 BCD 4
Câu 64. Cho tứ diện đều ABCD có độ dài các cạnh bằng 4. Điểm M là trung điểm của đoạn BC,
điểm E nằm trên đoạn BM sao cho E không trùng B , M . Mặt phẳng ( P) đi qua E và
song song với mặt phẳng ( AMD) . Diện tích thiết diện của ( P) với tứ diện ABCD bằng
4 2 . Tính độ dài đoạn BE bằng ? 9 4 1 2 A. . B. . C. 1. D. . 3 6 3 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 73
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 3
Vì tứ diện ABCD là tứ diện đều nên : AM MD 4. 2 3 . 2
Gọi H là trung điểm của AD, khi đó MH là trung tuyến và là đường cao tam giác AMD . 2 2 2 2 MH MD HD 2 3 2 2 2 . 1 1 S MH.AD .2 2.4 4 2 . AMD 2 2
Vì mặt phẳng ( P) đi qua E và song song với mặt phẳng ( AMD) nên :
- ( P ) cắt mặt phẳng ( ABC ) là đường thẳng qua E và song song AM cắt AB tại F .
- ( P ) cắt mặt phẳng ( ABD ) là đường thẳng qua F và song song AD cắt BD tại G .
Vậy thiết diện của tứ diện với mặt phẳng ( P) là tam giác EFG có các cặp cạnh tương ứng
song song với tam giác AMD . BE Đặt x 0 x 1 . BM BE EF FG Khi đó : x . BM AM AD 4 2 S EF FG 1 1 G 9 Mà ta có: EF 2 . x x S AM AD 9 3 AMD 4 2 1 2 Vậy BE BM . 3 3
Câu 65. Cho hình chóp .
S ABCD có SA vuông góc đáy, ABCD là hình vuông cạnh a 2; SA = 2a .
Gọi M là trung điểm của cạnh SC , ( ) là mặt phẳng đi qua ,
A M và song song với đường
thẳng BD . Tính diện tích thiết diện của hình chóp .
S ABCD bị cắt bởi mặt phẳng ( ) . 2 2a 2 2 4a 2 4a 2 A. . B. . C. . D. 2 a 2 . 3 3 3 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 74
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi O = AC BD và I = AM SO. Trong mặt phẳng (SBD) qua I kẻ EF / / BD với E S ,
B F SD , khi đó ( AEMF ) ( ) là mặt phẳng chứa đi qua ,
A M và song song với
BD . Do đó thiết diện của hình chóp .
S ABCD khi cắt bởi ( ) là tứ giác AEMF . Ta có: FE//BD ⊥ (
) FE ⊥ (SAC) FE ⊥ AM BD SAC 1 S = F . E AM AEMF 2
Vì ABCD là hình vuông nên AC = AB 2 = a 2. 2 = 2a = SA , do đó S ACvuông cân tại#A. 1 1
AM = SC = 2a 2 = a 2 2 2 SI 2
Ta có I là trọng tâm S AC nên = SO 3 FE SI 2 = = 2 4a FE = BD = . BD SO 3 3 3 2 2a 2 Vậy S = . AEMF 3
Câu 66. Cho hình lập phương ABC .
D A' B'C ' D' cạnh a . Các điểm M , N , P theo thứ tự đó thuộc a
các cạnh BB ', C ' D ', DA = = = sao cho BM C ' N DP
. Tìm diện tích thiết diện S của 3
hình lập phương khi cắt bởi mặt phẳng (MNP) . 2 17 3a 2 5 3a 2 13 3a A. S = . B. S = . C. S = . D. 18 18 18 2 11 3a S = . 18 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 75
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A' D' N E B' C' F P A M D Q B C BM MB BB Ta có = =
=1, do đó theo định lý ta-let trong không gian thì BC , MN , C N ND C D B D
lần lượt cùng song song với một mặt phẳng. Mà B D // (BC D
) và BC (BC D ) nên
ta có MN // ( BC D
) . Chứng minh tương tự ta có NP// (BC D
) . Do đó (MNP) // (BC D ) .
Qua P , kẻ PQ//B ,
D Q AB . Qua N , kẻ NF //C , D F D D .
Qua M , kẻ ME//BC , E B C .
Khi đó ta có thiết diện tạo bởi mặt phẳng (MNP) với hình lập phương là lục giác MENFPQ . Dễ thấy a 2 2a 2
EN = PF = MQ =
, NF = PQ = ME = và tam giác BC D là tam giác 3 3
đều vì BC = BD = DC = a 2 . Do đó ENF = NFP = FPQ = PQM = QME = MEN = 60 2 a Suy ra: 2 2 2 2
EF = EN + NF − 2.EN.NF.cos 60 = 6 a EF = . 3 3 Tương tự thì a 6 FQ = QE = . 3 2 1 2a 2 a 2 3 3 2a 5 3 Ta có S = 3.S + S = 3. . . . + . 2 = a . MENFPQ ENF EFQ 2 3 3 2 4 3 18
Câu 67. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có đáy 𝐴𝐵𝐶𝐷 là hình thang cân với cạnh bên 𝐵𝐶 = √5, hai đáy
𝐴𝐵 = 6, 𝐶𝐷 = 4. Mặt phẳng (𝑃) song song với (𝐴𝐵𝐶𝐷) và cắt cạnh 𝑆𝐴 tại 𝑀 sao cho 𝑆𝐴 =
3 𝑆𝑀. Diện tích thiết diện của (𝑃) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 bằng bao nhiêu? 5 2√5 2 7√5 A. . B. . C. . D. . 9 3 9 9 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 76
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi 𝐻, 𝐾 lần lượt là hình chiếu vuông góc của 𝐷, 𝐶 trên 𝐴𝐵
𝐴𝐻 = 𝐵𝐾; 𝐶𝐷 = 𝐻𝐾
𝐴𝐵𝐶𝐷 là hình thang cân ⇒ { ⇒ 𝐵𝐾 = 1.
𝐴𝐻 + 𝐻𝐾 + 𝐵𝐾 = 𝐴𝐵 2
Tam giác 𝐵𝐶𝐾 vuông tại 𝐾, có 𝐶𝐾 = √𝐵𝐶2 − 𝐵𝐾2 = √√5 − 12 = 2. 𝐴𝐵+𝐶𝐷 4+6
Suy ra diện tích hình thang 𝐴𝐵𝐶𝐷 là 𝑆𝐴𝐵𝐶𝐷 = 𝐶𝐾. = 2. = 5. 2 2
Gọi 𝑁, 𝑃, 𝑄 lần lượt là giao điểm của (𝑃) và các cạnh 𝑆𝐵, 𝑆𝐶, 𝑆𝐷. 𝑀𝑁 𝑁𝑃 𝑃𝑄 𝑄𝑀 1
Vì (𝑃) // (𝐴𝐵𝐶𝐷) nên theo định lí Talet, ta có = = = = = 𝑘. 𝐴𝐵 𝐵𝐶 𝐶𝐷 𝐴𝐷 3 Khi đó 5
(𝑃) cắt hình chóp theo thiết diện 𝑀𝑁𝑃𝑄 có diện tích 𝑆𝑀𝑁𝑃𝑄 = 𝑘2. 𝑆𝐴𝐵𝐶𝐷 = . 9
Câu 68. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA = 7a và SA vuông góc với mặt
phẳng đáy. Gọi G , I , J thứ tự là trọng tâm các tam giác SAB , SAD và trung điểm của
CD . Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (GIJ ) bằng 2 93a 2 23a 2 31 33a 2 3 33a A. . B. . C. . D. . 40 60 45 8 Lời giải Chọn A S D' M B' N I G L D A F O T J B K C E Ta có GI // B D
nên GI // BD (với B, D lần lượt là trung điểm của SB và SD ).
Suy ra (GIJ ) cắt ( ABCD) theo giao tuyến là đường thẳng d đi qua J và song song với BD .
Trong ( ABCD) có d cắt BC tại K , cắt AD tại F , cắt AB tại E .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 77
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 EB FD 1
Do J là trung điểm của CD nên K là trung điểm của BC và = = . EA FA 3
Trong ( SAB) : đường thẳng EG cắt SA tại M , cắt SB tại L .
Định lí mê nê la uyt cho tam giác LB B A
Bvà cát tuyến G, L, E ta được 2 = . LB 3
Định lí mê nê la uyt cho tam giác MS B A
S và cát tuyến G, L, M ta được 4 = . MA 3 Tương tự ta có DN
FI đi qua M và cắt SD tại N thỏa mãn 1 = . DS 5 Định lí mê nê la uyt MN
cho tam giác MAF và cát tuyến D, N , S ta được 8 = . NF 7
Thiết diện cần tìm là MNJKL . S FN FJ 7 7 Gọi S = S . Ta có FNJ = = S = S . MEF S FM FE 45 FNJ 45 FME Tương tự 7 suy ra S = S . Do đó 31 S = S . ELK 45 MNJKL 45 a 9a Gọi T = AC 3 3 2 KJ AT = AC = . Suy ra 2 2 MT = AM + AT = . 4 4 2 2 2 1 1 9a 3a 2 27a Suy ra S = MT.EF = = . MEF 2 2 2 2 2 8 93
Vậy diện tích thiết diện bằng 2 a . 40
Câu 69. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác vuông
tại A , SA = a 3 , SB = 2a . Điểm M nằm trên đoạn AD sao cho AM = 2MD. Gọi ( P ) là
mặt phẳng qua M và song song với (SAB) . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng ( P ) . 2 5a 3 2 5a 3 2 4a 3 2 4a 3 A. . B. . C. . D. . 18 6 9 3 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 78
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Ta có: ( P ) // (SAB) ( P
) ( ABCD) = MN
và MN // PQ // AB (1)
M AD, M (P) ( P
) (SCD) = PQ ( P ) // (SAB) ( P
) (SAD) = MQ MQ // SA và
M AD, M (P) ( P
) (SBC) = NP NP // SB
Mà tam giác SAB vuông tại A nên SA ⊥ AB MN ⊥ MQ (2)
Từ (1) và (2) suy ra ( P ) cắt hình chóp theo thiết diện là hình thang vuông tại M và Q . Mặt khác MQ DM DQ 1 DQ 1 MQ // SA = = MQ = SA và = . SA DA DS 3 DS 3 PQ SQ 2 PQ // CD = PQ = AB , với 2 2 AB =
SB − SA = a CD SD 3 2 Khi đó 1 1 SA 2AB 5a 3 S = M .
Q PQ + MN S = . + AB S = . MNPQ ( ) 2 MNPQ 2 3 3 MNPQ 18
Câu 70. Cho hình hộp ABC . D A B C D
Trên cạnh AB lấy điểm M khác A và B . Gọi ( P) là mặt
phẳng đi qua M và song song với mặt phẳng (ACD ) . Gọi S = S . Thiết diện tạo bởi A CD'
mặt phẳng ( P) và hình hộp có diện tích lớn nhất bằng bao nhiêu theo diện tích tam giác ACD' . S 3S A. . B. S . C. . D. 2S . 2 2 Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 79
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 I D' Q C' R F A' P D B' C S K O A N E J M B
Trong mp ( ABCD) , qua M vẽ đường thẳng song song với AC cắt DB , BC lần lượt tại E , N . Trong mp ( BD ’ D ’
B ) , qua E vẽ đường thẳng song song với ’
D O ( O = AC BD ) cắt ’ B ’ D tại F . Trong mp ( ’ A ’ B C’ ’
D ) , qua F vẽ đường thẳng song song với AC cắt ’ A ’ D , ’ D ’ C lần lượt tại R , Q . Trong mp ( A ’ A ’
D D ) , qua R vẽ đường thẳng song song với ’ AD cắt ’ AA tại S . Trong mp (CC’ ’
D D ) , qua Q vẽ đường thẳng song song với ’ CD cắt ’ CC tại P .
Thiết diện là lục giác MNPQRS .
Do các mặt đối diên của hình hộp song song nên các cạnh đối của lục giác thiết diên
MNPQRS song song và 3 cặp cạnh đó lần lượt song song với các cạnh tam giác AC ’ D .
Các tam giác JKI , AC ’
D , RQI , JMS , NKP đồng dạng MJ MA NC NK PC PK QD ' QI = = = = = = =
MJ = NK và PK = QI MN MB NB NM PC ' PQ QC ' QP
Các tam giác RQI , JMS , NKP bằng nhau (gọi diện tích của chúng là S và gọi diện tích 1
các tam giác JKI , AC ’
D lần lượt là S , S ). 2
Đặt AM = k; ta có điều kiện 0 k 1và có: AB 2 2 2 S JM AM AM 1 2 = = = = k 2 S = k S . S AC DC AB 1 2 2 2 S JK JM + MK JM MK = = = + = (k + )2 2 1 S = ( 2
k + 2k +1 S . 2 ) S AC AC AC AC
Diện tích thiết diện: S = S − 3S td 2 1 2 1 3 1 3S 1 2
S = 2S(−k + k + ) = 2S − k −
(dấu bằng xảy ra k = ). td 2 4 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 80
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 71. Cho tứ diện ABCD có tất cả các cạnh bằng a . Trên cạnh BC , CD lần lượt lấy M , N sao MC 1 CN 2 cho = ,
= . Trên trung tuyến AH của tam giác ABD lấy điểm P sao cho MB 2 CD 3 PA 4
= . Diện tích thiết diện khi cắt tứ diện ABCD bởi mặt phẳng (MNP) là PH 5 2 5a 11 2 3a 11 2 a 3 2 a 11 A. . B. . C. . D. . 12 12 12 12 Lời giải Chọn D
+) Trong ( BCD) , gọi F = MN BD ;
+) Trong ( ABD ) , gọi G = FP AD và K = FP AB ;
+) Suy ra, thiết diện khi cắt tứ diện ABCD bởi mặt phẳng (MNP) là tứ giác MNGK .
+) Gọi E là trung điểm CN . Dễ thấy: N EM = N DF (g – c – g) 1 a Suy ra FD = ME = BD = . 3 3
+) Trong ( ABD ) , kẻ PQ//AD (Q BD) . Khi đó trong H
AD, theo định Thales ta có: PQ HP 5 5 5a = = PQ = AD = AD HA 9 9 9 DQ AP 4 4 4 a 2a và =
= DQ = DH = = . DH AH 9 9 9 2 9 +) Trong F
QP , theo định Thales ta có: a DG FD FD 3 3 3 5 3 a a = = =
= DG = PQ = = PQ FQ FD + DQ a 2a 5 5 5 9 3 + 3 9 DG 1 DN 1 Suy ra = , mà = (gt) DA 3 DC 3
Nên NG//CA (theo Thales đảo).
+) Xét hai mặt phẳng (MNGK ) và ( ABC ) có điểm chung là M và lần lượt chứa hai đường
thẳng NG//CA (chứng minh trên), nên giao tuyến của hai mặt phẳng này là đường thẳng đi
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 81
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
qua M và song song với NG và CA (giao tuyến đó theo cách dựng bạn đầu thì chính là
MK ). Suy ra MK //NG//CA . Do đó thiết diện MNGK là hình thang. ( ) 1 +) C MN có 2 2 a 2a a 2a a 2 2
MN = CM + CN − 2CM .CN.cos MCN = + − 2 cos60 = 3 3 3 3 3 +) Dễ thấy a A KG = C
MN (c – g – c) KG = MN = . (2) 3 +) Từ ( ) a 2a
1 và (2) suy ra thiết diện cần tìm là hình thang cân có hai đáy NG = , MK = 3 3 và hai cạnh bên a KG = MN =
. Suy ra đường cao của hình thang cân này là: 3 2 2a a 2 − a a 11 3 3 h = − = . 3 2 6 2 +) Vậy 1 2a a a 11 a 11 S = + = . MNGK 2 3 3 6 12
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 82
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
ĐƯỜNG THẲNG VUÔNG GÓC MẶT PHẲNG
Dạng 1: Thiết diện, tính diện tích thiết diện
Câu 72. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a, SA = a 3 và
SA ⊥ ( ABC ) . Gọi M là điểm trên cạnh AB và AM = x (0 x a) . Mặt phẳng ( ) đi qua
M và vuông góc với AB . Giả sử thiết diện của hình chóp S.ABC với ( ) là tứ giác
MNPQ . Tìm x để thiết diện MNPQ lớn nhất. a a 3a A. x = . B. x = . C. x = .
D. x = a . 2 2 2 Lời giải Chọn A S P N A C Q M B
Ta tìm được MNPQ là hình chữ nhật MN MB
(a − x)a 3
MQ = AM = x, = MN = = 3 (a − x) SA AB a 2 a a a S = MN = a − x x = − x − MNPQ ( ) 2 2 3 .MQ 3 3 4 2 4 2 a 3 a max S = khi x = MNPQ 4 2
Câu 73. Cho hình chóp tam giác đều, các cạnh bên có độ dài bằng a 3 và tạo với đáy một góc 60 .
Diện tích S của đáy hình chóp là 2 a 3 2 27a 3 2 9a 3 A. S = . B. S = . C. S = . D. 9 16 16 2 3a 3 S = . 16 Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 83
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Giả sử S.ABC là hình chóp tam giác đều, các cạnh bên có độ dài bằng a 3 và tạo với đáy một góc 60.
Gọi H là hình chiếu vuông góc của S trên mặt phẳng ( ABC ) .
Ta có H là tâm đường tròn ngoại tiếp của tam giác đều ABC và SAH = 60 . Do đó 3 3 3 3 AH = . SA cos 60 = a . Suy ra AD = AH = a . 2 2 4 2 3 Suy ra AB = AD = a . 3 2 Vậy 3 3 9 9 3 2 2 2 S = AB = . .a = a (đvdt). ABC 4 4 4 16
Câu 74. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a , SA a , SA ABC ,
I là trung điểm của BC . Gọi P là mặt phẳng qua A và vuông góc với SI . S A C I B
Diện tích thiết diện của mặt phẳng P và hình chóp S.ABC được tính theo a bằng 2 a 3 2 2a 21 2 a 12 2 2a 6 A. . B. . C. . D. . 2 49 7 3 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 84
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S H N M A C I B
Ta chứng minh được SI BC . SI MN Kẻ AH
SI , Qua H kẻ MN song song với BC . Ta có SI AMN hay SI AH
thiết diện là tam giác AMN . a
Tam giác ABC đều nên 3 AI . 2 S . A AI a 21
AH là đường cao trong tam giác vuông SAI nên AH . 2 2 7 SA AI a 7 2a Ta có 2 2 SI SA AI ; 2 2 SH SA AH . 2 7
Áp dụng định lý Talét: MN SH 4 4a MN . BC SI 7 7 2 Vậy 1 2a 21 S AH .MN . AMN 2 49
Câu 75. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷có đường cao 𝑆𝐴 = 4𝑎. Biết đáy 𝐴𝐵𝐶𝐷 là hình thang vuông tại 𝐴
và 𝐵 với 𝐴𝐵 = 𝐵𝐶 = 3𝑎, 𝐴𝐷 = 𝑎. Gọi 𝑀 trung điểm cạnh 𝐴𝐵 và (𝛼) là mặt phẳng qua 𝑀
vuông góc với 𝐴𝐵. Thiết diện của hình chóp 𝑆. 𝐴𝐵𝐶𝐷 cắt bởi mặt phẳng (𝛼) là đa giác có diện tích bằng: 5𝑎2 7𝑎2 A. . B. . C. 7𝑎2. D. 5𝑎2. 2 2 Lời giải S F E B C M N A D Chọn B 𝑀𝑁 ⊥ 𝐴𝐵
Gọi 𝑁, 𝐹 lần lượt là trung điểm 𝐶𝐷 và 𝑆𝐵 ⇒ {
⇒ (𝑀𝑁𝐹) ⊥ 𝐴𝐵 𝑀𝐹 ⊥ 𝐴𝐵
⇒ (𝑀𝑁𝐹) là mặt phẳng (𝛼)
Từ 𝐹 kẻ 𝐹𝐸||𝑀𝑁 cắt 𝑆𝐶 tại 𝐸 ⇒ thiết diện là hình thang 𝑀𝑁𝐸𝐹 vuông tại 𝑀 và 𝐹 𝑆𝐴 𝐴𝐷+𝐵𝐶 𝐵𝐶 3𝑎 Ta có: 𝑀𝐹 = = 2𝑎, 𝑀𝑁 = = 2𝑎, 𝐸𝐹 = = 2 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 85
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Từ đây ta suy ra 1 7𝑎2
𝑆𝑀𝑁𝐸𝐹 = 𝑀𝐹. (𝑀𝑁 + 𝐸𝐹) = . 2 2
Câu 76. Cho tứ diện đều ABCD . Thiết diện của tứ diện ABCD và mặt phẳng trung trực của cạnh BC là A. hình thang.
B. tam giác vuông.
C. hình bình hành. D. tam giác cân. Lời giải Chọn D
Gọi M là trung điểm của cạnh BC , H là chân đường cao của tứ diện hạ từ A . BC ⊥ DM Ta có
BC ⊥ ( ADM ) . BC ⊥ AH
Suy ra ( ADM ) là mặt phẳng trung trực của cạnh BC .
Thiết diện tạo bởi tứ diện ABCD và ( ADM ) là tam giác ADM cân tại M .
Câu 77. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , SA ⊥ ( ABCD) ,
SA = AB = a . Gọi (Q ) là mặt phẳng qua SA và vuông góc với ( SBD) . Thiết diện của hình
chóp S.ABCD cắt bởi (Q ) là
A. tam giác vuông.
B. tam giác đều.
C. tam giác vuông cân.
D. hình bình hành. Lời giải Chọn A BD ⊥ SA Ta có
BD ⊥ (SAC) . BD ⊥ SC
Do đó (SAC ) ⊥ (SBD) .
Suy ra thiết diện cần tìm la tam giác SAC .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 86
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Tam giác SAC vuông tại A có SA = a, AC = a 2 .
Vậy thiết diện cần tìm là tam giác vuông.
Câu 78. Cho hình vuông ABCDcó cạnh bằng 6 và hình bình hành CDIS không nằm trên cùng một
mặt phẳng. Biết tam giác SAC cân tại S , SB =12. Thiết diện của hình chóp S.ABCD cắt
bởi mặt phẳng ( ACI ) có diện tích bằng A. 36 2 . B. 6 2 . C. 18 2 . D. 8 2 . Lời giải Chọn C I S O' D 12 C 6 O 6 A B
Gọi O , O lần lượt là tâm của hình vuông ABCDvà hình bình hành CDIS . Ta thấy 1 OO ' =
SB = 6 (đường trung bình của SBD ) và mp ( ACI ) cắt hình chóp 2
S.ABCD theo thiết diện là A CO.
Theo giải thiết SAC cân tại S và ABCDlà hình vuông nên AC ⊥ SO và AC ⊥ BD , suy ra 1 1
AC ⊥ OO . Do đó S
= OO .AC = 6.6 2 =18 2 . ACO ' 2 2
Câu 79. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC
sao cho SM = 2MC . Mặt phẳng ( P ) chứa AM và song song với BD . Tính diện tích thiết
diện của hình chóp S.ABCD bởi mặt phẳng ( P) . 2 4 26a 2 3a 2 2 26a 2 2 3a A. . B. . C. . D. . 15 5 15 5 Lời giải Chọn C
Gọi I là giao điểm của AM và SO . Dựng EF đi qua I và song song với BD.
Thiết diện của hình chóp S.ABCD bởi mặt phẳng ( P) là tứ giác AEMF .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 87
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 1
BD ⊥ ( SAC ) BD ⊥ AM EF ⊥ AM . Nên S = AM.EF . AEMF 2 a 13 S
AM vuông tại S , nên 2 2 AM = SA + AM = . 3 Dựng MJ IJ SM 2 SI 4 4 4a 2
MJ / / AC, J SO = = = = EF = BD = AO IO SC 3 SO 5 5 5 2 Vậy 1 2 26a S = AM.EF = . AEMF 2 15
Câu 80. Cho tứ diện 𝐴𝐵𝐶𝐷 có 𝐴𝐵 vuông góc với 𝐶𝐷. Mặt phẳng (𝑃) song song với 𝐴𝐵 và 𝐶𝐷 lần
lượt cắt 𝐵𝐶, 𝐷𝐵, 𝐴𝐷, 𝐴𝐶 tại 𝑀, 𝑁, 𝑃, 𝑄. Tứ giác 𝑀𝑁𝑃𝑄 là hình gì? A. Hình thang. B. Hình bình hành.
C. Hình chữ nhật.
D. Tứ giác không phải hình thang. Lời giải Chọn C A P Q B D N M C (𝑀𝑁𝑃𝑄)//𝐴𝐵 Ta có { ⇒ 𝑀𝑄//𝐴𝐵.
(𝑀𝑁𝑃𝑄) ∩ (𝐴𝐵𝐶) = 𝑀𝑄
Tương tự ta có 𝑀𝑁//𝐶𝐷, 𝑁𝑃//𝐴𝐵, 𝑄𝑃//𝐶D.
Do đó tứ giác 𝑀𝑁𝑃𝑄 là hình bình hành
Lại có 𝑀𝑁 ⊥ 𝑀𝑄(𝑑𝑜 𝐴𝐵 ⊥ 𝐶𝐷 ).
Vậy tứ giác 𝑀𝑁𝑃𝑄 là hình chữ nhật.
Câu 81. Cho tứ diện 𝐴𝐵𝐶𝐷 trong đó 𝐴𝐵 = 6, 𝐶𝐷 = 3, góc giữa 𝐴𝐵 và 𝐶𝐷 là 60° và điểm 𝑀 trên 𝐵𝐶
sao cho 𝐵𝑀 = 2𝑀𝐶. Mặt phẳng (𝑃) qua 𝑀 song song với 𝐴𝐵 và 𝐶𝐷 cắt 𝐵𝐷, 𝐴𝐷, 𝐴𝐶 lần
lượt tai 𝑀, 𝑁, 𝑄. Diện tích 𝑀𝑁𝑃𝑄 bằng 3 A. 2√2. B. √3. C. 2√3. D. . 2 Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 88
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A 6 P Q B D N 3 M C (𝑀𝑁𝑃𝑄)//𝐴𝐵 Ta có { ⇒ 𝑀𝑄//𝐴𝐵.
(𝑀𝑁𝑃𝑄) ∩ (𝐴𝐵𝐶) = 𝑀𝑄
Tương tự ta có 𝑀𝑁//𝐶𝐷, 𝑁𝑃//𝐴𝐵, 𝑄𝑃//𝐶D.
Do đó tứ giác 𝑀𝑁𝑃𝑄 là hình bình hành Ta có (𝐴𝐵; 𝐶𝐷 ̂ ) = (𝑄𝑀; 𝑀𝑃
̂ ) = 600. Suy ra 𝑆𝑀𝑁𝑃𝑄 = 𝑄𝑀. 𝑄𝑁. sin600. 𝐶𝑀 𝑀𝑄 1
Ta có 𝛥𝐶𝑀𝑄 ∽ 𝛥𝐶𝐵𝐴 ⇒ = = ⇒ 𝑀𝑄 = 2. 𝐶𝐵 𝐴𝐵 3 𝐴𝑄 𝑄𝑁 2
𝛥𝐴𝑄𝑁 ∽ 𝛥𝐴𝐶𝐷 ⇒ = = ⇒ 𝑄𝑁 = 2. 𝐴𝐶 𝐶𝐷 3
Vậy 𝑆𝑀𝑁𝑃𝑄 = 𝑄𝑀. 𝑄𝑁. sin600 = 2.2. √3 = 2√3. 2
Câu 82. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB = AC = a ; cạnh bên
SA vuông góc với mặt đáy, SA = a . Gọi M là trung điểm của SC . Tính diện tích thiết diện
của hình chóp cắt bởi mặt phẳng ( P ) đi qua M và vuông góc với AC . 2 a 2 a 2 a A. . B. 2 a . C. . D. . 2 8 4 Lời giải Chọn C
Gọi E , F lần lượt là trung điểm của AC , BC .
Do đó ME // SA , EF // AB (tính chất đường trung bình trong tam giác).
Mà SA ⊥ ( ABC ) (gt) nên ME ⊥ ( ABC ) , suy ra ME ⊥ EF .
Dễ thấy ( MEF ) ( P) , thiết diện là tam giác MEF vuông tại E . 2 1 1 1 1 a
Diện tích thiết diện là S = ME.EF = . S . A AB = . 2 2 2 2 8
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 89
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 83. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB = a , BC = a 3 , cạnh
bên SA = a 3 và vuông góc với mặt phẳng ( ABC ) . Mặt phẳng ( P ) đi qua trung điểm M
của AB và vuông góc với SB cắt AC, SC, SB lần lượt tại N, ,
P Q . Diện tích của tứ giác MNPQ bằng: 2 11a 3 2 33a 3 2 33a 2 33a A. . B. . C. . D. . 64 64 64 16 Lời giải Chọn C
BC ⊥ (SAB) BC ⊥ SB
Do Mặt phẳng ( P ) đi qua trung điểm M của AB và vuông góc với SB cắt AC, SC,SB
lần lượt tại N, ,
P Q nên MN //PQ//BC , do đó tứ giác MNPQ là hình thang vuông tại M , Q . 1 S = MN + PQ MQ MNPQ ( ). 2 1 a 3 + ABC
có MN //BC, MN = BC = ; 2 2 MQ SA S . A MB a 3.a a 3 + M QB ∽ S AB = MQ = = = ; MB SB SB 2 .2 a 4 a 7a 2 2
QB = MB − MQ = SQ = . 4 4 PQ SQ S . Q BC 7a 3
Có: MN //PQ//BC nên = PQ = = . BC SB SB 8 Vậy a S = MN + PQ MQ = . MNPQ ( ) 2 1 33 . 2 64
Câu 84. Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình vuông cạnh a 2 ,
SA = 2a . Gọi M là trung điểm cạnh SC , ( ) là mặt phẳng đi qua ,
A M và song song với
đường thẳng BD. Tính diện tích thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng ( ). 2 2a 2 2 4a 2 4a 2 A. . B. . C. . D. 2 a 2 . 3 3 3 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 90
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Chọn A S M K H I D A O B C
Trong ( ABCD) , gọi O = AC BD .
Trong ( SAC ) , gọi I = SO AM .
Trong ( SBD) kẻ đường thẳng qua I và song song với BDlần lượt cắt SB, SD tại H , K .
Vậy thiết diện của hình chóp cắt bởi mặt phẳng ( ) là tứ giác AMKH . AC ⊥ BD Ta có: ⊥
BD ⊥ AM HK ⊥ AM . SA ⊥ ( ABCD) BD (SAC)
SA ⊥ BD 1 1 1 Ta có 2 2 AM = SC = SA + AC = .2 2a = a 2 . 2 2 2 HK SI 2 2 4
Và I là trọng tâm tam giác SAC nên =
= HK = BD = a . BD SO 3 3 3 Vậy diện tích tứ giác 1 2 2 AHMK là 2 S = AM.HK = a . AHMK 2 3
Câu 85. Cho tứ diện ABCD có AB vuông góc với CD , AB CD
8, M là điểm thuộc cạnh BC sao cho MC x.BC 0 x
1 . Mặt phẳng qua M , song song với A ,
B CD và lần lượt cắt D , B A , D AC tại N, ,
P Q . Diện tích lớn nhất của tứ giác MNPQ bằng bao nhiêu? A. 32 . B. 9 . C. 10 . D. 16 . Lời giải Chọn D A 8 P B D Q N M 8 x C
+) MQ // AB và NP // AB MQ // PN , tương tự PQ// NM (vì cùng //CD ), mà AB ⊥ CD
Tứ giác MNPQ là hình chữ nhật.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 91
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 MQ MC MQ MN MQ + MN +) =
=1− BM =1− MN + =1 =
MQ + MN = 8 . AB BC BC CD AB CD 8 ( + )2 +) S = M . Q MN MQ MN =16 . MNPQ 4
Suy ra diện tích lớn nhất của tứ giác MNPQ bằng 16 .
Câu 86. Trong không gian cho hai tam giác đều 𝐴𝐵𝐶 và 𝐴𝐵𝐶′ có chung cạnh 𝐴𝐵 và nằm trong hai
mặt phẳng khác nhau. Gọi 𝑀, 𝑁, 𝑃, 𝑄 lần lượt là trung điểm của các cạnh 𝐴𝐶, 𝐶𝐵, 𝐵𝐶′ và
𝐶′𝐴. Tứ giác 𝑀𝑁𝑃𝑄 là hình gì?
A. Hình bình hành.
B. Hình chữ nhật.
C. Hình vuông. D. Hình thang. Lời giải Chọn B C' Q P A M C H N B
Vì 𝑀, 𝑁, 𝑃, 𝑄 lần lượt là trung điểm của các cạnh 𝐴𝐶, 𝐶𝐵, 𝐵𝐶′ và 𝐶′𝐴 1 𝑃𝑄 = 𝑀𝑁 = 𝐴𝐵 ⇒ { 2
⇒ 𝑀𝑁𝑃𝑄là hình bình hành. 𝑃𝑄//𝐴𝐵//𝑀𝑁 𝐶𝐻 ⊥ 𝐴𝐵
Gọi 𝐻 là trung điểm của 𝐴𝐵. Vì hai tam giác 𝐴𝐵𝐶 và 𝐴𝐵𝐶′ đều nên { . 𝐶′𝐻 ⊥ 𝐴𝐵
Suy ra 𝐴𝐵 ⊥ (𝐶𝐻𝐶′). Do đó 𝐴𝐵 ⊥ 𝐶𝐶′. 𝑃𝑄//𝐴𝐵
Ta có {𝑃𝑁//𝐶𝐶′ ⇒ 𝑃𝑄 ⊥ 𝑃𝑁. 𝐴𝐵 ⊥ 𝐶𝐶′
Vậy tứ giác 𝑀𝑁𝑃𝑄là hình chữ nhật.
Câu 87. Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình vuông cạnh a 2; SA = 2 .
a Gọi M là trung điểm của cạnh SC , ( ) là mặt phẳng đi qua A , M và song
song với đường thẳng BD. Tính diện tích thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng ( ) . 2 2a 2 2 4a 2 4a 2 A. B. C. D. 2 a 2 3 3 3 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 92
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
+ Xác định mặt phẳng ( )
Gọi O là giao điểm của AC và BD, N là giao điểm của SO và AM .
Trong mặt phẳng (SBD) , qua N kẻ đường thẳng song song với BD, cắt S ,
D SB lần lượt tại I và J .
Ta có, ( ) là mặt phẳng ( AIMJ ) .
Thật vậy, rõ ràng ( AIMJ ) qu ,
A M Mặt khác, BDsong song với IJ (theo cách dựng), nên
BDsong song với ( AIMJ ) .
+ Tính diện tích thiết diện BD ⊥ AC Ta có:
BD ⊥ (SAC) BD ⊥ AM BD ⊥ SA
Mà BD / /IJ nên IJ ⊥ AM. 1 S
= .IJ.AM (Diện tích tứ giác có hai đường chéo vuông góc). AIMJ 2
Ta có: AC = BD = 2 . a
SA vuông góc với đáy nên SA ⊥ AC . Suy ra, 2 2 2 2 SC = SA + AC =
4a + 4a = 2a 2. 1 AM =
SC = a 2 (CT độ dài đường trung tuyến trong tam giác vuông). 2 IJ SN 2 2 2 4a
N là trọng tâm của tam giác SAC . Suy ra, =
= IJ = BD= .2a = . BD SO 3 3 3 3 2 Vậy 1 1 4a 2a 2 S = AM .IJ = . .a 2 = . AIMJ 2 2 3 3 a 3
Câu 88. Cho tứ diện S. ABC có hai mặt ( ABC ) và ( SBC ) là hai tam giác đều cạnh a , SA = . 2
M là điểm trên AB sao cho AM = b (0 b a) . ( P ) là mặt phẳng qua M và vuông góc với
BC . Thiết diện của ( P ) và tứ diện S. ABC có diện tích bằng?
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 93
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 2 2 3 3
3 a − b
3 3 a − b A.
(a −b)2 . B. C. D. 16 4 a 16 a
3 3 (a −b)2 8 Lời giải Chọn A
Gọi I là trung điểm của BC .
Ta có SI ⊥ BC do S
BC đều. Ta có AI ⊥ BC do ABC
đều.Vậy BC ⊥ (SAI ) .
Từ M kẻ MN //AI ( N BC ) và Từ N kẻ NP//SI (P SB) .
Thiết diện cần tìm là M NP . BM MP BM a − b a 3 (a −b) 3 Ta có B MP B AS nên = MP = .AS MP = . = . BA AS BA a 2 2 (a −b) 3 (a −b) 3
Tương tự ta có MN = ; NP = . 2 2 (a −b) 3 (a −b)2 3 3 Vậy M
NP đều có cạnh bằng
. Suy ra diện tích S = . 2 16
Câu 89. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = a và vuông góc với đáy.
Mặt phẳng ( ) qua A và vuông góc với trung tuyến SI của tam giác SBC . Tính diện tích
S của thiết diện tạo bởi ( ) với hình chóp đã cho. 2 2a 21 2 2a 21 A. S = . B. S = . A MN 49 AMN 7 2 4a 21 2 a 21 C. S = . D. S = . A MN 49 AMN 7 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 94
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi H là hình chiếu vuông góc của A lên SI .
Kẻ đường thẳng MN qua H và song song với BC và cắt SB , SC lần lượt tại M , N .
Ta có: SI ⊥ BC SI ⊥ MN và SI ⊥ AH .
SI ⊥ ( AMN ) .
Ta chứng minh được BC ⊥ (SAI ) AH ⊥ BC AH ⊥ MN .
Ta dễ dàng chứng minh được tam giác AMN cân. 2 2 SA .AI 21 AH = = a . 2 2 SA + AI 7 7 Ta có: 2 2 SI = SA + AI = a . 2 2 2
SA = SI.SH SH = a . 7 MN SH 4 Do MN // BC = MN = a . BC SI 7 2 1 2a 21 S = MN.AH = . AMN 2 49
Câu 90. Cho tứ diện ABCD có AB vuông góc với CD , AB 4, CD
6 . M là điểm thuộc cạnh BC sao cho MC
2BM . Mặt phẳng P đi qua M song song với AB và CD . Diện tích thiết diện
của P với tứ diện là 17 16 A. 5. B. 6. C. . . 3 D. 3 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 95
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 A 4 P N B D Q M 6 C (𝑀𝑁𝑃𝑄)//𝐴𝐵 Ta có { ⇒ 𝑀𝑁//𝐴𝐵.
(𝑀𝑁𝑃𝑄) ∩ (𝐴𝐵𝐶) = 𝑀𝑁
Tương tự ta có 𝑀𝑄//𝐶𝐷, 𝑁𝑃//𝐶𝐷, 𝑄𝑃//𝐴𝐵. Do đó tứ giác 𝑀𝑁𝑃𝑄 là hình bình hành Ta có (𝐴𝐵; 𝐶𝐷 ̂ ) = (𝑀𝑁; 𝑀𝑄 ̂ ) = 𝑁𝑀𝑄
̂ = 900 ⇒ tứ giác 𝑀𝑁𝑃𝑄 là hình chữ nhật. 𝐶𝑀 𝑀𝑁 1 4
Lại có 𝛥𝐶𝑀𝑁 ∽ 𝛥𝐶𝐵𝐴 ⇒ = = ⇒ 𝑀𝑁 = ; 𝐶𝐵 𝐴𝐵 3 3 𝐴𝑁 𝑁𝑃 2
𝛥𝐴𝑁𝑃 ∽ 𝛥𝐴𝐶𝐷 ⇒ = = ⇒ 𝑀𝑃 = 4. 𝐴𝐶 𝐶𝐷 3 Vậy 16
𝑆𝑀𝑁𝑃𝑄 = 𝑀𝑁. 𝑁𝑃 = . 3
Câu 91. Cho hình chóp 𝑆. 𝐴𝐵𝐶 có đáy 𝐴𝐵𝐶 là tam giác đều cạnh 𝑎, 𝑆𝐴 = 𝑎 và vuông góc với mặt
phẳng đáy. Mặt phẳng (𝛼) qua 𝐴 và vuông góc với trung tuyến 𝑆𝐼 của tam giác 𝑆𝐵𝐶. Tính
diện tích 𝑆 của thiết diện tạo bởi (𝛼) với hình chóp đã cho. 2𝑎2√21 𝟐𝒂𝟐√𝟐𝟏 A. 𝑆Δ𝐴𝑀𝑁 = B. 𝑺 49 𝚫𝑨𝑴𝑵 = 𝟕 𝟒𝒂𝟐√𝟐𝟏 𝑎2√21
C. 𝑺𝚫𝑨𝑴𝑵 = D. 𝑆 𝟒𝟗 Δ𝐴𝑀𝑁 = 7 Lời giải Chọn A
Tam giác 𝐴𝑀𝑁 cân tại 𝐴 1 1 1 4 1 7 = + = + = 𝐴𝐻2 𝐴𝐼2 𝐴𝑆2 3𝑎2 𝑎2 3𝑎2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 96
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 𝑎√3 Suy ra 𝐴𝐻 = √7 3𝑎2 4𝑎2
𝑆𝐻2 = 𝑆𝐴2 − 𝐴𝐻2 = 𝑎2 − = 7 7 2𝑎 Suy ra 𝑆𝐻 = √7 3𝑎2 √7𝑎 𝑆𝐼 = √𝑎2 + = 4 2 𝑀𝑁 𝑆𝐻 4 = = 𝐵𝐶 𝑆𝐼 7 4 Suy ra 𝑀𝑁 = 𝑎 7 1 1 𝑎√3 4𝑎 2𝑎2√21
𝑆Δ𝐴𝑀𝑁 = 𝐴𝐻. 𝑀𝑁 = . . = 2 2 √7 7 49
Câu 92. Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A , đáy lớn AD = 8, đáy
nhỏ BC = 6, SA vuông góc với đáy, SA = 6 . Gọi M là trung điểm AB , ( P ) là mặt phẳng
qua M và vuông góc với AB . Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( P ) có diện tích bằng A. 20 . B. 16 . C. 30 . D. 15 . Lời giải Chọn D S 6 P Q 8 A D M N B 6 C
Gọi N , P và Q lần lượt là trung điểm của CD, SC và SB .
Ta có: ( P) ( SAB) = MQ , ( P) ( ABCD) = MN , ( P) ( SCD) = NP .
Do đó, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( P ) là tứ giác MNPQ .
Dễ thấy MNPQ là hình thang vuông tại M , Q và MQ = PQ = 3 , MN = 7 . M .
Q (MN + PQ) 3.(7 + 3)
Vậy diện tích hình thang MNPQ là: S = = =15 . MNPQ 2 2
Câu 93. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a SA = 2a và SA vuông góc với
đáy. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua B và vuông góc với SC . 2 2 a 5 2 a 15 a 3 2 a 3 A. . B. . C. . D. . 5 20 20 5 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 97
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi I là trung điểm của AC . Do ABC đều nên BI ⊥ AC .
Mặt khác BI ⊥ SA (do SA ⊥ ( ABC ) và BI ( ABC ) ).
Suy ra BI ⊥ ( SAC ) SC ⊥ BI .
Kẻ IH vuông góc SC tại H .
SC ⊥ (IBH ).
Thiết diện cần tìm là tam giác IBH .
Ta có BI ⊥ ( SAC ) và IH ( SAC ) BI ⊥ IH .
Suy ra tam giác IBH vuông tại I . Ta có: a 3 BI = , 2 2 SC =
SA + AC = a 5 . 2 IH SA IC.SA a 5 sin C = = IH = = . IC SC SC 5 2 1 1 a 3 a 5 a 15 S = I . B IH = . . = . I BH 2 2 2 5 20
Câu 94. Cho tứ diện đều ABCD, mặt phẳng ( ) qua trung điểm của cạnh AB , song song AC và
BD cắt tứ diện theo thiết diện là
A. Hình tam giác đều.
B. Hình vuông.
C. Hình tam giác vuông cân.
D. Hình thang cân. Lời giải Chọn B A E P H B D M N C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 98
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi E , M , N , P , H lần lượt là trung điểm của các cạnh AB , BC , CD , AD và BD. Mặt
phẳng ( ) cắt tứ diện ABCDtheo thiết diện EMNP .
Dễ thấy EM = MN = NP = PE (cùng bằng nữa độ dài cạnh tứ diện), ( ) 1 . AH ⊥ BD Ta có
BD ⊥ ( ACH ) BD ⊥ AC . C H ⊥ BD NP // AC Mà . EP // BD
Suy ra NP ⊥ EP , (2) . Từ ( )
1 và (2) ta có EMNP là hình vuông.
Câu 95. Cho hình chóp S.ABCD có đáy ABCDlà hình vuông cạnh a, cạnh bên SA vuông góc với
đáy, cạnh bên SB tạo với đáy góc 0
45 . Một mặt phẳng ( ) đi qua A và vuông góc với
SC cắt hình chóp S.ABCD theo thiết diện là tứ giác AB C D
có diện tích bằng: 2 a 3 2 a 3 2 a 3 2 a 3 A. . B. . C. . D. . 4 2 6 3 Lời giải Chọn C S C' D' B' I A D O B C
Dễ thấy SBA = 45 . Ta có B D
⊥ SC và BD ⊥ SC và SC không vuông góc với mặt phẳng
(SBD) , suy ra BD/ /B D
. Nên từ I = SO ACnên từ I kẻ B D
/ /BD cắt SB , SD lần
lượt tại B, D . AB ⊥ SC Từ trên suy ra B D
⊥ AC và
AB ⊥ SB . AB ⊥ BC 1 a 6 B D SB a 2 1 a Suy ra S = = = = 2 =
AC .B D . Mà AC = và B D . AB C D 2 3 BD SB 2.a 2 2 2 Vậy 1 3 2 S = = AC .B D a . AB C D 2 6 Câu 96. Cho hình chóp S.ABC , đáy ABC là tam giác vuông tại , A AB = , a 0
ABC = 60 , SC = ,
a SC ⊥ ( ABC ) . Kẻ CD ⊥ SAtại D . Thiết diện qua
M AD và vuông góc với AD là A. Tam giá
B. Hình bình hành.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 99
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
C. Hình vuông.
D. Hình thang vuông. Lời giải Chọn D
Trong mp (SAC) : MN//CD MN ⊥ A . D
Trong mp (SAB) : MP//AB MP ⊥ AD ( MNP) ⊥ AD .
Mặt khác MP//AB MP// ( ABC) (MNP) ( ABC) = QN QN //MP .
Lại có AB ⊥ MN MP ⊥ MN .
Vậy thiết diện cần tìm là hình thang vuông MNQP tại M, N.
Câu 97. Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình vuông cạnh
2a , SA = 2a 3 . Gọi I là trung điểm của AD , mặt phẳng ( P ) qua I và vuông góc với
SD . Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng ( P ) . 2 3 5a 2 3 15a 2 15 3a 2 5 3a A. . B. . C. . D. . 16 16 16 16 Lời giải Chọn C S A H K B I M D C
Kẻ IM //CD với M BC . IM ⊥ SA Ta có
IM ⊥ (SAD) IM ⊥ SD (P) ( ABCD) = IM . IM ⊥ AD
• Kẻ IH ⊥ SD với H SD (P) (SAD) = IH . IM //CD
• Vì IM (P)
(P) (SCD) = HK với HK //IM (//CD) và K SC . CD ( SCD)
• (P) (SBC) = KM .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 100
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Vì IM ⊥ (SAD) nên IM ⊥ IH . Do đó thiết diện của hình chóp cắt bởi mặt phẳng ( P ) là
hình thang IHKM vuông tại I và H .
Ta có IM = AB = 2a . SA a Xét S
AD có: tan SAD = 2 3 = = 3 SDA = 60. AD 2a HI Xét DHI có: sin HDI = HI = I . D sin 60 3 = . a . ID 2 Xét S AD có: 2 2 SD = SA + AD 2 2
= 12a + 4a = 4a . 2 3a a a a Xét DHI có: 2 2 HD = ID − IH 2 = a −
= SH = SD − HD = 4a − 7 = . 4 2 2 2 7a HK SH 7 a
Vì HK //CD nên theo Talet ta có = 2 = = 7 HK = 7 CD = 7 .2a = . CD SD 4a 8 8 8 4 7a a 3 ( 2a + .
IM + HK ).IH 2
Do đó diện tích thiết diện là 4 2 15 3a S = = = . IHKM 2 2 16
Câu 98. Cho hình chóp S.ABCD có SA vuông góc với mặt đáy, ABCD là hình vuông cạnh a 2,SA
2a . Gọi M là trung điểm của cạnh SC , là mặt phẳng đi qua , A M và song
song với đường thẳng BD . Tính diện tích thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng . 2 4a 2 4a 2 2 2a 2 A. 2 a 2 . B. . C. . D. . 3 3 3 Lời giải Chọn C
Xác định mặt phẳng
- Gọi O = AC BD
- Xét mp (SAC) gọi I = SO AM
Xét mp (SBD); do ( )// BD nên qua I kẻ PQ // BD(P SB;Q SB)
Như vậy ( )(SBC) = PM ; ( )(SCD) = QM ; ( )(SAB) = ;
PA ( ) (SAD) = ; QA
Thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng là mp (APMQ )
- Tính diện tích thiết diện tứ giác APMQ
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 101
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 BD ⊥ AC
BD ⊥ (SAC) BD ⊥ SA
BD ⊥ AM (AM (SAC)
PQ ⊥ AM (BD // PQ) S = PQ.AM APMQ
Do ABCDlà hình vuông cạnh a 2 AC = BD = a 2 . SD
SAClà tam giác vuông cân tại A , SD = 2 a 2 ; SM = MC = = 2a 2 2 2
AM ⊥ SC AM = AC − MC = a 2 PQ SP SI 2 Xét SB ; D PQ // BD = =
= ( I là trọng tâm S AC). BD SB SO 3 2 2 4 PQ = BD = a 2 = a . 3 3 3 2 a 4 2 S = PQ.AM = . APMQ 3
Câu 99. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AB = a , BC = 2a . Điểm 1
H thuộc cạnh AC sao cho CH = CA , SH là đường cao hình chóp S.ABC và 3 a 6 SH =
. Gọi I là trung điểm BC . Tính diện tích thiết diện của hình chóp với mặt 3
phẳng đi qua H và vuông góc với AI . 2 2a 2 2a 2 3a 2 3a A. . B. . C. . D. . 3 6 3 6 Lời giải Chọn B S A B P M I N H C
Cách 1: Gọi ( ) là mặt phẳng đi qua H và vuông góc với AI .
Vì SH ⊥ ( ABC ), AI ( ABC ) nên SH ( ) .
Ta có AI = AB = BI = a nên ABI
là tam giác đều. Gọi M là trung điểm AI , ta được BM ⊥ AI ( )
1 . Từ đây suy ra ( ) // BM (vì cùng vuông góc AI ).
Trong ( ABC ) dựng HN // BM với N BC , ta suy ra ( ) ( ABC ) = HN .
Từ đó, thiết diện của mặt phẳng ( ) và hình chóp là S HN .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 102
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 AB AB 2a 2a 3 cos 30 = BP = = = BP cos 30 3 3 Xét ABP vuông có: . AP 1 2a 3 a 3 sin 30 = AP = . = BP 2 3 3 Dễ thấy AC a 3
AC = a 3 CH = =
. Vậy H là trung điểm của CP HN là đường 3 3 trung bình của a C
BP hay N 1 3 I HN = BP = . 2 3 2 1 1 a 6 a 3 a 2
Xét tam giác vuông SHN (H = 90) : S = HS.HN = = . SHN 2 2 3 3 6
Cách 2: Tam giác ABI đều IAH = 30 .
Áp dụng định lí côsin trong a A HI có IH = 3 2 4a 2 AH = 3 2 Vậy a 2 HI = suy ra A
IH vuông đỉnh I hay HI ⊥ AI . 3 2 2 AI = a
Phần tiếp theo giống cách 1.
Câu 100. Cho tứ diện SABC có ABC
là tam giác đều cạnh a , SA ⊥ (ABC) và S
A= 2a . Gọi ( ) là
mặt phẳng qua B và vuông góc với SC . Tính diện tích thiết diện của tứ diện SABC với ( ). 2 3a 15 2 a 15 2 a 15 2 a 15 A. . B. . C. . D. . 10 20 5 10 Lời giải Chọn B
*) Xác định thiết diện:
+) Vì ( ) ⊥ SC nên ( ) cắt mp ( SBC ) theo giao tuyến qua B và vuông góc với SC .
Trong mp (SBC) , kẻ đường thẳng qua B và vuông góc với SC cắt SC tại H .
+) Vì ( ) ⊥ SC nên ( ) cắt mp ( SAC ) theo giao tuyến qua B và vuông góc với
SC .Trong mp ( SAC ) , kẻ đường thẳng qua H và vuông góc với SC cắt AC tại K .
+) Nối B với K ta được thiết diện của ( ) và hình chóp là tam giác BHK . *) Tính diện tích
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 103
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
+) Ta có SC ⊥ ( BHK ) nên SC ⊥ BK . BK ⊥ SC +)
BK ⊥ (SAC) BK ⊥ AC & BK ⊥ HK. Do đó K là trung điểm của AC BK ⊥ SA và B
HK vuông tại K . 1 a 3 +) Ta có S = K . B KH ; KB = ; B KH 2 2
+) Ta có SC = SA + AC = a + ( a)2 2 2 2 2 2
= 5a . Gọi I là hình chiếu của A trên SC . Khi đó 1
AI và HK cùng vuông góc với SC . Vì K là trung điểm của AC nên HK = AI. 2 AS.AC 2 . a a 2a a
+) Ta có AI.SC = A . S AC AI = = = . Suy ra HK = . SC a 5 5 5 2 Vậy 1 a 3 a a 15 S = . = . BHK 2 2 5 20
Câu 101. Cho tứ diện 𝐴𝐵𝐶𝐷 có 𝐴𝐵 vuông góc với 𝐶𝐷, 𝐴𝐵 = 𝐶𝐷 = 6. 𝑀 là điểm thuộc cạnh 𝐵𝐶 sao
cho 𝑀𝐶 = 𝑥. 𝐵𝐶(0 < 𝑥 < 1). Mặt phẳng (𝑃) song song với 𝐴𝐵 và 𝐶𝐷 lần lượt cắt
𝐵𝐶, 𝐷𝐵, 𝐴𝐷, 𝐴𝐶 tại 𝑀, 𝑁, 𝑃, 𝑄. Diện tích lớn nhất của tứ giác bằng bao nhiêu? A. 9. B. 11. C. 10. D. 8. Lời giải Chọn A A 6 P Q B D N 6 M C 𝑀𝑄//𝑁𝑃//𝐴𝐵
Xét tứ giác 𝑀𝑁𝑃𝑄 có {
⇒ 𝑀𝑁𝑃𝑄 là hình bình hành. 𝑀𝑁//𝑃𝑄//𝐶𝐷
Mặt khác, 𝐴𝐵 ⊥ 𝐶𝐷 ⇒ 𝑀𝑄 ⊥ 𝑀𝑁. Do đó, 𝑀𝑁𝑃𝑄 là hình chữ nhật. 𝑀𝑄 𝐶𝑀 Vì 𝑀𝑄//𝐴𝐵 nên =
= 𝑥 ⇒ 𝑀𝑄 = 𝑥. 𝐴𝐵 = 6𝑥. 𝐴𝐵 𝐶𝐵
Theo giả thiết 𝑀𝐶 = 𝑥. 𝐵𝐶 ⇒ 𝐵𝑀 = (1 − 𝑥)𝐵𝐶. 𝑀𝑁 𝐵𝑀 Vì 𝑀𝑁//𝐶𝐷 nên =
= 1 − 𝑥 ⇒ 𝑀𝑁 = (1 − 𝑥). 𝐶𝐷 = 6(1 − 𝑥). 𝐶𝐷 𝐵𝐶
Diên tích hình chữ nhật 𝑀𝑁𝑃𝑄 là 𝑥+1−𝑥 2
𝑆𝑀𝑁𝑃𝑄 = 𝑀𝑁. 𝑀𝑄 = 6(1 − 𝑥). 6𝑥 = 36. 𝑥. (1 − 𝑥) ≤ 36 ( ) = 9. 2 1
Ta có 𝑆𝑀𝑁𝑃𝑄 = 9 khi 𝑥 = 1 − 𝑥 ⇔ 𝑥 = . 2
Vậy diện tích tứ giác 𝑀𝑁𝑃𝑄 lớn nhất bằng 9 khi 𝑀 là trung điểm của 𝐵𝐶.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 104
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Câu 102. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC sao cho
SM = 2MC . Mặt phẳng ( P ) chứa AM và song song với BD . Tính diện tích thiết diện của
hình chóp S.ABCD cắt bởi ( P ) . 2 2 26a 2 3a 2 4 26a A. . B. . C. 48 . D. . 15 5 15 Lời giải Chọn A S N A B I M P O D C
Gọi O = AC BD , I = AM SO .
Trong ( SBD) từ I kẻ đường thẳng song song với BD cắt SB , SD lần lượt tại N , P .
Suy ra thiết diện là tứ giác ANMP . BD ⊥ AC Ta có:
BD ⊥ (SAC) BD ⊥ AM . BD ⊥ SO
Mặt khác: BD / /NP AM ⊥ 1 NP S = N . P AM . ANMP 2
SA = SC = a Ta có: S AC vuông cân tại AC = a 2 2 2 a 13 S 2 2
AM = SA + SM 2 = a + a = . 3 3 NP SI SI BD
Ta có: NP / /BD = . NP = . BD SO SO S M I A C O SI Gọi = k . SO
Cách 1: Ta có: AI = AS + SI = −SA + k SO AM = AS + 2 SM = −SA + SC . 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 105
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
A , I , M thẳng hàng AI = 2
l AM −SA + k SO = l − SA+ lSC 3 1 4 k + l = 1 k = k − 2 5 SI 4 SA + (SA+SC) 2 = l
− SA+ lSC = 2 3 1 2 3 SO 5 k − l = 0 = l 2 3 5 Cách 2: Do A , I , M thẳng hàng nên SI AO MC SI 1 1 4 . . =1 . .
=1 SI = 4IO SI = SO IO AC MS IO 2 2 5 4 a NP = 4 2 BD = . 5 5 1 2 a a 2 26a S = 1 4 2 13 N . P AM = . . = . ANMP 2 2 5 3 15
Câu 103. Cho hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có đáy 𝐴𝐵𝐶𝐷 là hình vuông cạnh bằng 𝑎, hai tam giác 𝑆𝐴𝐵 và
𝑆𝐴𝐷 vuông cân tại 𝐴. Gọi 𝐺 là trọng tâm của tam giác 𝑆𝐴𝐵. Gọi (𝛼) là mặt phẳng đi qua 𝐺
và song song với 𝑆𝐵 và 𝐴𝐷. Thiết diện tạo bởi mặt phẳng (𝛼) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 có diện tích bằng 2𝑎2√3 4𝑎2√2 4𝑎2√2 4𝑎2√3 A. . B. . C. . D. . 9 3 9 9 Lời giải Chọn C
• Ta có: 𝑆𝐴 ⊥ 𝐴𝐷 {
⇒ 𝑆𝐴 ⊥ (𝐴𝐵𝐶𝐷). 𝑆𝐴 ⊥ 𝐴𝐵
• Gọi 𝐻 là trung điểm của 𝑆𝐵. Mà 𝐺 là trọng tâm của tam giác 𝑆𝐴𝐵. Suy ra điể 𝐴𝐺 2 m 𝐺 ∈ 𝐴𝐻 và = . 𝐴𝐻 3
• Xác định thiết diện tạo bởi mặt phẳng (𝛼) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷:
𝐺 ∈ (𝛼) ∩ (𝑆𝐴𝐵) + Ta có: { (𝛼)//𝑆𝐵
⇒ Giao tuyến của hai mặt phẳng (𝑆𝐴𝐵) và (𝛼) là đường thẳng 𝑑1 đi qua điểm 𝐺 và song
song với 𝑆𝐵. Trong mặt phẳng (𝑆𝐴𝐵), gọi 𝑀, 𝑁 lần lượt là giao điểm của 𝑑1với các cạnh 𝐴𝐵, 𝐴𝑆.
𝑁 ∈ (𝛼) ∩ (𝑆𝐴𝐷) + Ta có: { (𝛼)//𝐴𝐷
⇒ Giao tuyến của hai mặt phẳng (𝑆𝐴𝐷) và (𝛼) là đường thẳng 𝑑2 đi qua điểm 𝑁 và song
song với 𝐴𝐷. Trong mặt phẳng (𝑆𝐴𝐷), gọi 𝑃 là giao điểm của 𝑑2với cạnh 𝑆𝐷.
𝑀 ∈ (𝛼) ∩ (𝐴𝐵𝐶𝐷) + Ta có: { (𝛼)//𝐴𝐷
⇒ Giao tuyến của hai mặt phẳng (𝐴𝐵𝐶𝐷) và (𝛼) là đường thẳng 𝑑3 đi qua điểm 𝑀 và song
song với 𝐴𝐷. Trong mặt phẳng (𝐴𝐵𝐶𝐷), gọi 𝑄 là giao điểm của 𝑑3với cạnh 𝐶𝐷.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 106
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Vậy thiết diện tạo bởi mặt phẳng (𝛼) và hình chóp 𝑆. 𝐴𝐵𝐶𝐷 là tứ giác 𝑀𝑁𝑃𝑄. 𝑀𝑄 ⊥ (𝑆𝐴𝐵)
Mặt khác, ta lại có: 𝐴𝐷 ⊥ (𝑆𝐴𝐵) { ⇒ {
⇒ 𝑀𝑄 ⊥ 𝑀𝑁, 𝑃𝑁 ⊥ 𝑀𝑁.
𝑀𝑄 // 𝐴𝐷 // 𝑃𝑁 𝑃𝑁 ⊥ (𝑆𝐴𝐵)
Do đó, tứ giác 𝑀𝑁𝑃𝑄 là hình thang vuông tại 𝑀 và 𝑁.
• Tính diện tích thiết diện.
+ Xét tam giác 𝑆𝐴𝐵 có 𝐺 là trọng tâm của tam giác 𝑆𝐴𝐵 và 𝑀𝑁 // 𝑆𝐵 suy ra: 𝑀𝑁 𝐴𝐺 2 𝑆𝑁 𝐺𝐻 1 2 2 2 2𝑎 = = √2 , =
= ⇒ 𝑀𝑁 = 𝑆𝐵 = √𝑆𝐴2 + 𝐴𝐵2 = √𝑎2 + 𝑎2 = . 𝑆𝐵 𝐴𝐻 3 𝑆𝐴 𝐴𝐻 3 3 3 3 3 𝑃𝑁 𝑆𝑁 1 1 𝑎
+ Xét tam giác 𝑆𝐴𝐷 có 𝑃𝑁//𝐴𝐷 suy ra: = = ⇒ 𝑃𝑁 = 𝐴𝐷 = . 𝐴𝐷 𝑆𝐴 3 3 3
+ Diện hình thang vuông 𝑀𝑁𝑃𝑄 tại 𝑀 và 𝑁là: 𝑎 𝑀𝑄+𝑃𝑁 𝑎+ 2𝑎 4𝑎2 𝑆 3 √2 √3 𝑀𝑁𝑃𝑄 = . 𝑀𝑁 = . = ( đơn vị diện tích). 2 2 3 3
Câu 104. Cho hình chóp S.ABCD có đáy là hình thang cân ABCD ( AB // CD, AB = 2a) ,
BC = CD = DA = a , điểm S cách đều 4 đỉnh , A ,
B C, D đồng thời tam giác SAB đều. Gọi
M , N và G lần lượt là trung điểm của A ,
D CB và trọng tâm tam giác SA .
B Diện tích thiết
diện của hình chóp S.ABCD cắt bởi mp(MNG) bằng 2 9a 2 15a 3 2 15a 3 2 85a 3 A. . B. . C. . D. . 16 12 24 144 Lời giải Chọn D
+) Vì MN // AB nên mp ( MNG) cắt ( SAB) theo giao tuyến qua G song song với AB , cắt S , A SB tại ,
Q P . Thiết diện là tứ giác MNPQ . Mặt khác: MN // PQ nên MNPQ là hình thang. 3a 2 4a
+) Xét hình thang MNPQ , ta có: MN = , PQ = AB = . 2 3 3
Tiếp theo, ta đi dựng và tính đường cao của hình thang.
+) Kẻ SH ⊥ ( ABCD ) . Ta có: SA = SB = SC = SD HA = HB = HC = HD .
Vì tam giác SAB đều nên H là trung điểm của cạnh AB .
Gọi I , K là trung điểm của MN,CD . Khi đó: H , I , K thẳng hàng.
Có MN vuông góc với cả SH, HK nên MN ⊥ GI hay GI là chiều cao của hình thang MNPQ .
Có SH và HK lần lượt là đường cao của hai tam giác đều SAB và HDC với cạnh lần lượt 2a 3 a 3
là 2a và a nên ta được: SH = = a 3, HK =
. Trong tam giác vuông HGI , ta có 2 2 2 2 2 2 2 1 1 a 3 a 3a 25a 5a 3 2 2 2
GI = GH + HI = a 3 + = + = GI = . 3 2 2 3 16 48 12
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 107
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 a a
Vậy diện tích thiết diện bằng GI (MN + PQ) 2 1 1 5 3 3 4 85 3 = + a = . 2 2 12 2 3 144
Câu 105. Cho tứ diện S.ABC có ABC
vuông cân tại B , AB = a , SA ⊥ ( ABC ) và SA = a 3 .
M là điểm tùy ý trên cạnh AB sao cho AM = x (0 x a) . Mặt phẳng ( ) đi qua M và
vuông góc với AB . Diện tích thiết diện tạo bởi tứ diện S.ABC và mặt phẳng ( ) có giá trị
lớn nhất khi x bằng a a 3 a 2 A. a . B. . C. . D. . 2 2 2 Lời giải Chọn B
Dựng thiết diện bằng cách:
Trên mặt phẳng ( ABC ) kẻ MQ song song BC (vớiQ AC ).
Trên mặt phẳng (SAB) kẻ MN song song SA (với N SB ).
Trên mặt phẳng (SAC ) kẻ QP song song SA (với PSC ).
Thiết diện thu được là hình bình hành MNPQ lại có MN ⊥ MQ vì MN / /SA .
Thiết diện thu được là hình chữ nhật MNPQ có MQ = x vuông cân tại (vì AMQ M ).
MN = 3 (a − x) (vì B
MN đồng dạng với BAS ). 2 2
a − x + x a 3 Ta có S
= 3 a − x x = . MNPQ ( ) 3 2 4 2 a 3
Vậy diện tích lớn nhất bằng a S = khi và chỉ khi − = = . MNPQ a x x x 4 2
Câu 106. Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a , đường cao SO = 2a. Gọi M là điểm
thuộc đường cao AH của tam giác ABC . Xét mặt phẳng ( P) đi qua điểm M và vuông góc
với AH . Đặt AM = x . Tìm x để thiết diện của hình chóp khi cắt bởi mặt phẳng ( P) đạt
giá trị lớn nhất. 3a 3 a 3 3a 3 a 3 A. x = . B. x = . C. x = . D. x = . 8 3 4 8 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 108
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Chọn A Trường hợp 1: a 3 x
thì thiết diện nhận được là tam giác cân S B C (hình vẽ) 3 1 1 1 2 1 1 1 2a 2a S
= S H .B C S . O IJ = 2 . a = . S B C 1 1 1 1 1 1 1 2 2 2 3 3 Trường hợp 1: a 3 a 3 x
thì thiết diện nhận được là hình thang cân B C EF (hình 3 2 2 2 vẽ). AM x 2x 3 Ta có 2 B C = BC. = . a = 2 2 AH a 3 3 2 a 3 x − SE JC OM 2 2 3 EF = BC. = BC. = BC. = . a = 2x 3 − 2a SC JC OH a 3 6 a 3 − x HM 2 2 KM = S . O = 2 . a = 6a − 4x 3 2 HO a 3 6 1 x S = B C + EF KM = + x
− a a − x B C EF ( 1 2 3 . 2 3 2 6 4 3 2 2 ) 2 2 2 ( ) 2 2 3 2 3a 8x 3 a a = − 2a
(3a − 2x 3) 4 3 = 2x 3 − a (3a − 2x 3) 2 2 4 2 3 2 = . 3 3 2 3 4 4 3 2
Vậy diện tích thiết diện lớn nhất bằng 3a 3 3a 3 khi 2x 3 −
a = 3a − 2x 3 x = . 4 2 8
Câu 107. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA ⊥ ( ABCD) và SA = a 2 . Một
mặt phẳng ( ) qua A vuông góc với SC và cắt SC tại C , cắt S ,
B SD lần lượt tại B và
D . Tính diện tích thiết diện của ( ) và hình chóp. 2 a 2 2 2a 2 2 a 2 A. . B. 2 a 2 . C. . D. . 3 3 4
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 109
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Lời giải Chọn A S a 2 C' D' B' I D A O B a C
+) Gọi O là tâm của hình vuông ABCD. Trong mặt phẳng (SAC) , kẻ đường thẳng vuông
góc với SC , cắt SC tại C .
+) Gọi I là giao điểm của SO và AC. Từ I , kẻ đường thẳng song song với BD, cắt S ,
B SD lần lượt tại B và D . BD ⊥ AC +) Ta có
BD ⊥ (SAC) BD ⊥ SC BD ⊥ . SA B D
// BD B D ⊥ SC +) SC ⊥ (AB C D
) . Vậy tứ giác AB C D
là thiết diện cần AC ⊥ SC tìm.
+) Vì SA = AC = a 2 nên S
AC là tam giác cân tại A do đó AC là là trung tuyến.
+) I là giao điểm của B D
và SO nên I là trọng tâm S BD. Do đó B D SI 2 2 2a 2 = = B D = BD = . BD SO 3 3 3
+)Tam giác SAC vuông cân tại A , có AC là đường cao nên 1 1 2 2 AC = SC =
. 2a + 2a = a . 2 2 B D // BD +) B D
⊥ (SAC) B D ⊥ AC . BD ⊥ (SAC) 2 Vậy 1 1 2a 2 a 2 S = = = .AC .B D .a . AB C D 2 2 3 3 a 3
Câu 108. Cho tứ diện SABC có hai mặt ( ABC ) và (SBC ) là hai tam giác đều cạnh a , SA = . 2
M là điểm trên cạnh AB sao cho AM = b (0 b a) . ( P ) là mặt phẳng đi qua M và vuông
góc với BC . Thiết diện của ( P ) và tứ diện SABC có diện tích bằng 2 2 2 3 a − b 3 3 a − b 3 3 a − b A. 2 a . . B. 2 a . . C. 2 a . . D. 4 a 16 a 8 a 2 3 3 a − b 2 a . . 4 a Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 110
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S P A C E M N B
Gọi E là trung điểm của BC . AE ⊥ BC Ta có:
BC ⊥ (SAE) . SE ⊥ BC
Kẻ MP//SA (M SB) , NP//SE ( N BE) .
Suy rA. ( MNP) // ( SAE ) (MNP) ⊥ BC .
Khi đó: Thiết diện tạo bởi ( P ) với tứ diện SABC là M NP . a 3 −
Ta có : SA = SE = AE = MP NP MN MB a b , = = = = . 2 SA SE AE AB a a − b a 3
Suy ra : MP = NP = MN = . . a 2 2
a − b a 3 . 3 2 2 a 2 − Do đó diện tích của 3 3a a b M NP : S = = . M NP 4 16 a
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 111
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
HAI MẶT PHẲNG VUÔNG
Dạng 1: Thiết diện, diện tích thiết diện
Câu 109. Cho hình chóp S.ABCD , đáy ABCD là hình vuông, SA ⊥ ( ABCD) . Gọi ( ) là mặt phẳng
chứa AB vuông góc với (SCD) , ( ) cắt hình chóp S.ABCD theo thiết diện là hình gì?
A. Hình bình hành.
B. Hình thang vuông.
C. Hình thang không vuông.
D. Hình chữ nhật. Lời giải Chọn B S K A D H B C (
) ( ABCD) = AB
( ) (SBD) = BH có ( ) cắt hình chóp S. D
ABC theo thiết diện là hình tứ giác (
) (SCD) = HK
( )(SAD) = KA ABHK . Ta lại có: (
ABHK ) ( ABCD) = AB
( ABCD) (S D C ) = D C HK / / AB ThiÕt diÖn là hình thang. ( ABHK
SCD) ( ABHK ) = HK HK / / D C AB / /CD AB ⊥ SA
AB ⊥ (SAD) AB ⊥ AK ThiÕt diÖn ABHK là hình thang vuông. AB ⊥ AD
Vậy ( ) cắt hình chóp S. D
ABC theo thiết diện là hình thang vuông ABHK .
Câu 111. Cho lăng trụ đứng 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′ có đáy 𝐴𝐵𝐶 là tam giác vuông tại 𝐵, 𝐴𝐵 = 2𝑎 , 𝐵𝐶 = 4𝑎,
𝐴𝐴′ = 3𝑎. Gọi 𝑀 là trung điểm cạnh 𝐴𝐵. Diện tích của thiết diện của lăng trụ 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′
khi cắt bởi mặt phẳng (𝑀𝐵′𝐶′) bằng A. 2√10 a2. B. 3√10 a2. C. 4√10 a2. D. 6√10 a2. Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 112
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 C' A' B' A C N M B
Do 𝐵𝐶//𝐵′𝐶′ nên 𝐵𝐶//(𝑀𝐵′𝐶′) ⇒ (𝑀𝐵′𝐶′) ∩ (𝐴𝐵𝐶) = 𝑀𝑁 với 𝑀𝑁//𝐵𝐶 và 𝑁 ∈ 𝐴𝐶.
Dễ thấy thiết diện là hình thang 𝑀𝑁𝐶′𝐵′ vuông tại 𝑀 và 𝐵′. 𝑀𝑁+𝐵′𝐶′
Diện tích thiết diện: 𝑑𝑡(𝑀𝑁𝐶′𝐵′) = . 𝑀𝐵′. 2
𝑀𝑁 = 2𝑎; 𝐵′𝐶′ = 4𝑎 ; 𝑀𝐵′ = √𝑀𝐵2 + 𝐵𝐵′2 = √𝑎2 + 9𝑎2 = 𝑎√10. 𝑀𝑁+𝐵′𝐶′
𝑑𝑡(𝑀𝑁𝐶′𝐵′) =
. 𝑀𝐵′ = 3𝑎2√10. 2
Câu 112. Cho tứ diện ABCD, biết tam giác BCD có diện tích bằng 16 . Mặt phẳng ( P ) đi qua trung
điểm của AB và song song mới mặt phẳng ( BCD) cắt tứ diện theo một thiết diện có diện tích bằng A. 12. B. 4 . C. 8 . D. 16 . Lời giải Chọn B
Gọi M là trung điểm của AB .
Mặt phẳng ( P) đi qua trung điểm M của AB và song song mới mặt phẳng (BCD)
Xét mặt phẳng ( ABC ) có: ( P) / / ( BCD) , BC ( BCD) và điểm M là điểm chung của 2 mặt
phẳng ( P) và ( ABC )
giao tuyến của 2 mặt phẳng ( P) và ( ABC ) là đường thẳng d đi qua điểm M và song song
với đường thẳng BC
d AC =
P MP / /BC
Xét mặt phẳng ( ABD)có: ( P) / / ( BCD) , BD ( BCD) , và điểm M là điểm chung của 2
mặt phẳng ( P) và ( ABD)
giao tuyến của 2 mặt phẳng ( P) và ( ABD)là đường thẳng d đi qua điểm M và song
song với đường thẳng BD
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 113
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
d AD = N MN / /BC
Vậy thiết diện cắt bở mặt phẳng ( P) với hình chóp là mặt phẳng (MNP) .
Xét tam giác ABC có: M là trung điểm của AB và MP / /BC
P là trung điểm của AC
MP là đường trung bình của tam giác ABC MP 1 = BC 2 MN 1 PN 1 CMTT ta có: = , = . BD 2 CD 2 S 1 MNP BDC và MNP = 1 1 S = S = .16 = 4. S 4 MNP 4 BDC 4 BDC
Vậy mặt phẳng ( P) đi qua trung điểm của AB và song song mới mặt phẳng ( BCD) cắt tứ
diện theo một thiết diện có diện tích bằng 4 (đvdt).
Câu 113. Cho tứ diện đều ABCD cạnh a =12 , gọi ( P ) là mặt phẳng qua B và vuông góc với AD .
Thiết diện của ( P ) và hình chóp có diện tích bằng A. 36 2 . B. 40 . C. 36 3 . D. 36 . Lời giải Chọn A
Gọi G là trung điểm AD , H là trung điểm BC . BG ⊥ AD Tam giác AC ,
D ABD là tam giác đều nên
AD ⊥ (BCG) (P). C G ⊥ AD
Vậy thiết diện là B
CG và GH là đường cao trong tam giác GCB . 12 3 BG = CG = = 6 3 1 1 Ta có 2 S
= GH.BC = .6 2.12 = 36 2 . B GC 2 2 2 2 GH
= BG − BH = 6 2
Câu 114. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a , điểm M là trung điểm cạnh SC .
Mặt phẳng ( P) chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp
S.ABCD cắt bởi mp ( P ) . 2 5a 2 10a 2 10a 2 2 5a A. . B. . C. . D. . 3 3 6 3 Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 114
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Gọi O là tâm của hình vuông ABCD. Trong mp (SAC ) , gọi I là giao điểm của AM và
SO . Suy ra I là điểm chung của hai mặt phẳng ( P ) và ( SBD) , mà ( P) BD nên trong mp
(SBD) qua I kẻ giao tuyến PN song song với BD( N SB;PSD ). Thiết diện của hình
chóp S.ABCD cắt bởi ( P ) là tứ giác ANMP .
Do S.ABCD là hình chóp đều nên SO ⊥ ( ABCD) BD ⊥ SO (1)
Mặt kháC. BD ⊥ AC (do đáy ABCD là hình vuông) (2)
Từ (1) và (2) ta có: BD ⊥ ( SAC ) BD ⊥ AM 1
Mà PN BD PN ⊥ AM S = AM .PN ANMP 2 2 2 2 2 2 2 2 AS + AC SC a + 2a a 5a a 5
Trong tam giác SAC ta có: 2 AM = − = − = AM = 2 4 2 4 4 2 2 2a 2
Do I là trọng tâm của tam giác SAC nên PN = BD = 3 3 2 1 1 a 5 2a 2 a 10 Vậy S = AM .PN = . = . ANMP 2 2 2 3 6
Câu 115. Cho hình lăng trụ đều 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′ có cạnh đáy bằng 𝑎, cạnh bên 𝑎√2. Gọi 𝑀 là trung điểm
𝐴𝐵. Tính diện tích thiết diện cắt bởi lăng trụ đã cho bởi mặt phẳng (𝐴′𝐶′𝑀). 7√2 3√35 3√2 9 A. 𝑎2. B. 𝑎2. C. 𝑎2. D. 𝑎2. 16 16 4 8 Lời giải Chọn B
Vì 𝐴𝐵𝐶. 𝐴′𝐵′𝐶′ là lăng trụ đều nên 𝐴𝐴′ ⊥ (𝐴𝐵𝐶) và Δ𝐴𝐵𝐶 A' C' đều cạnh 𝑎.
Gọi 𝑁 là trung điểm BC suy ra 𝑀𝑁//𝐴𝐶//𝐴′𝐶′ và 1 1 𝑀𝑁 = 𝐴𝐶 = 𝑎. 2 2
Vì 𝑀𝑁//𝐴′𝐶′ nên 𝐴′, 𝐶′, 𝑀, 𝑁 đồng phẳng do đó thiết B'
diện cắt bởi lăng trụ đã cho bởi mặt phẳng (𝐴′𝐶′𝑀) là
hình thang cân 𝑁𝑀𝐴′𝐶′. 3
Lại có 𝐶′𝑁 = 𝐴′𝑀 = √𝐴′𝐴2 + 𝐴𝑀2 = 𝑎 nên đường 2
cao của hình thang cân 𝑁𝑀𝐴′𝐶′ là ℎ = A C 2 √ 𝐴′𝐶′−𝑀𝑁 𝐴′𝑀2 − ( ) = √35 𝑎 2 4 M N B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 115
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 Do đó diệ 1 3√35
n tích thiết diện là 𝑆 = (𝐴′𝐶′ + 𝑀𝑁). ℎ = 𝑎2 2 16
Câu 116. Cho hình chóp đều S.ABC có cạnh đáy bằng a , cạnh bên bằng b . Mặt phẳng đi qua A
và vuông góc với SC . Tìm hệ thức giữa a và b để
cắt SC tại điểm C nằm giữa S và 1 C . A. a b 2. B. a b 3. C. a b 2. D. a b 3. Lời giải Chọn C S C1 A C G C' B
Gọi 𝐺 là trọng tâm tam giác 𝐴𝐵𝐶. Do 𝑆. 𝐴𝐵𝐶 là hình chóp đều nên 𝑆𝐺 ⊥ (𝐴𝐵𝐶).
Gọi 𝐶′ là trung điểm 𝐴𝐵. Suy ra 𝐶, 𝐶′, 𝐺 thẳng hàng.
Ta có {𝐴𝐵 ⊥ 𝐶𝐶′ ⇒ 𝐴𝐵 ⊥ (𝑆𝐶𝐶′) ⇒ 𝐴𝐵 ⊥ 𝑆𝐶. (1) 𝑆𝐺 ⊥ 𝐴𝐵
Trong tam giác 𝑆𝐴𝐶, kẻ 𝐴𝐶1 ⊥ 𝑆𝐶. (2)
Từ (1) và (2), suy ra 𝑆𝐶 ⊥ (𝐴𝐵𝐶1).
Suy ra thiết diện cần tìm là tam giác 𝐴𝐵𝐶1 thỏa mãn đi qua 𝐴 và vuông góc với 𝑆𝐶.
Tam giác 𝑆𝐴𝐶 cân tại 𝑆 nên để 𝐶1 nằm giữa 𝑆 và 𝐶 khi và chỉ khi 𝐴𝑆𝐶 ̂ < 900. Suy ra cos𝐴𝑆𝐶
̂ > 0 ⇔ 𝑆𝐴2 + 𝑆𝐶2 − 𝐴𝐶2 > 0 ⇔ 2𝑏2 − 𝑎2 > 0 → 𝑎 < 𝑏√2.
Câu 117. Cho lăng trụ đều AB . C A B C
có cạnh đáy bằng 4a , cạnh bên bằng 2a . M là trung điểm của .
AB Cắt hình trụ bởi mặt phẳng ( AC M
). Diện tích của thiết diện là 2 3 7a 2 3 2a A. 2 3 7a . B. . C. . D. 2 6 2a . 4 2 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 116
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
Ta có M ( ABC ) ( AC M
), AC // A C
( ABC)( A C M
) = Mx // AC . Gọi N là
giao điểm của Mx với BC ( ABC ) ( A C M
) = MN . Thiết diện là hình thang MNC A . AC MN = = 2a , A M
= 2a 2 . Vẽ MH ⊥ A C
(H AC) MH = a 7 . 2
Vậy diện tích thiết diện 1 S = .MH.(MN + 1 A C
) = .a 7.6a 2 = 3 7a . MNC A 2 2
Câu 118. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , BC
2a . Tam giác SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng
đi qua S vuông góc với
AB . Tính diện tích S của thiết diện tạo bởi với hình chóp đã cho. 2 a 3 2 a 3 2 a A. S . B. S . C. 2 S a 3. S . 4 2 D. 2 Lời giải Chọn B S A D H M B C
Gọi 𝐻 là trung điểm 𝐴𝐵 ⇒ 𝑆𝐻 ⊥ 𝐴𝐵. Suy ra: • 𝑆𝐻 ⊂ (𝛼).
• 𝑆𝐻 ⊥ (𝐴𝐵𝐶𝐷)(do (𝑆𝐴𝐵) ⊥ (𝐴𝐵𝐶𝐷) theo giao tuyến)𝐴𝐵.
Kẻ 𝐻𝑀 ⊥ 𝐴𝐵(𝑀 ∈ 𝐶𝐷) ⇒ 𝐻𝑀 ⊂ (𝛼).
Do đó thiết diện là tam giác 𝑆𝐻𝑀 vuông tại 𝐻. 𝑎√3 1 𝑎√3 𝑎2√3 Ta có 𝑆𝐻 =
, 𝐻𝑀 = 𝐵𝐶 = 2𝑎. Vậy 𝑆 . . 2𝑎 = . 2 𝛥𝑆𝐻𝑀 = 2 2 2
Câu 119. Cho hình lập phương ABC . D A B C D
có cạnh bằng a . Cắt hình lập phương bởi mặt phẳng
trung trực của AC . Diện tích thiết diện là 2 a 3 2 a 3 A. S = . B. 2 S = a . C. S = . D. 2 4 2 3a 3 S = . 4 Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 117
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 B C M N D A S O P C' B' R A' Q D' Gọi , O M , N, , P , Q , R S lần lượt là trung điểm của các cạnh AC , BC,C . D DD , AD , A B , BB. a 5
Ta có: MA = MC =
nên M thuộc mặt phẳng trung trực của AC . 2
Tương tự, ta chứng minh được N, , P , Q ,
R S cũng thuộc mặt phẳng trung trực của AC .
Vậy thiết diện của hình lập phương bị cắt bởi mặt phẳng trung trực của AClà đa giác MNPQRS . 2 2
Đây là lục giác đều cạnh bằng a 2 a 2 3 3a 3
nên diện tích S = 6. . = . 2 2 4 4
Câu 120. Cho hình chóp tam giác đều S.ABC đỉnh S , có độ dài cạnh đáy bằng a . Gọi M và N lần
lượt là các trung điểm của các cạnh SB và SC . Biết mặt phẳng ( AMN ) vuông góc với mặt
phẳng (SBC) . Tính diện tích tam giác AMN theo a . 2 a 10 2 a 10 2 a 5 2 a 5 A. . B. . C. . D. . 24 16 8 4 Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 118
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11 S F N M A C O E B
Vì S.ABC là hình chóp tam giác đều nên ABC là tam giác đều và hình chiếu của S trên mặt
phẳng ( ABC ) là tâm O của tam giác đều ABC .
Gọi E là trung điểm của BC , F = MN SE .
MN là đường trung bình tam giác SBC SNEM là hình bình hành
F là trung điểm MN và SE .
Vì AM = AN (hai đường trung tuyến tương ứng của hai tam giác bằng nhau SAB và SAC )
nên tam giác AMN cân tại A , mà AF là đường trung tuyến AF ⊥ MN
AF ⊥ (SBC) (1) (vì ( AMN ) ⊥ (SBC) AF ⊥ SE
Tam giác SAE có AF vừa là trung tuyến vừa là đường cao
SAE là tam giác cân tại A a 3 AS = AE = . 2 2 2
a 3 a 3 a 15
Tam giác SOA vuông tại O , 2 2 SO = SA − AO = − = 2 3 6 2 2
a 15 a 3 a 2
Tam giác SOA vuông tại O , 2 2 SE = SO + EO = + = 6 6 2
Ta có AF.SE = S . O AE (= 2S ) SAE S . O AE a AF = 10 = SE 4 2 1 1 a 10 a a 10 S = AF.MN = . . = AMN 2 2 4 2 16
Câu 121. Bác Bình muốn làm một ngôi nhà mái lá cọ như trong hình với diện tích mặt nền nhà là 2
100 m , mỗi mặt phẳng mái nhà nghiêng so với mặt đất 0 30 , để lợp một 2 m mái nhà cần
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 119
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình học 11
mua 100nghìn đồng lá cọ. Hỏi số tiền bác Bình sử dụng mua lá cọ để lợp tất cả mái nhà gần
nhất với số nào sau đây? .
A. 11,547 triệu đồng.
B. 12,547 triệu đồng.
C. 18,547 triệu đồng.
D. 19,547 triệu đồng. Lời giải Chọn A
Ngôi nhà có hai mái đối xứng nhau và có diện tích bằng nhau, diện tích một nửa mặt nền nhà bằng 2
S = 50 m . Gọi S ' là diện tích một mái, khi đó một mái nhà có hình chiếu vuông
góc là một nửa mặt nền nhà. Ta có S S 100 0 = cos30 2 S ' = =
m . Vậy tổng diện tích S ' 0 cos 30 3 200 mái nhà là 2 m . 3
Số tiền bác Bình cần là 200 .100 11547 nghìn đồng 11,547 triệu đồng. 3
------------- HẾT -------------
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 120
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông





