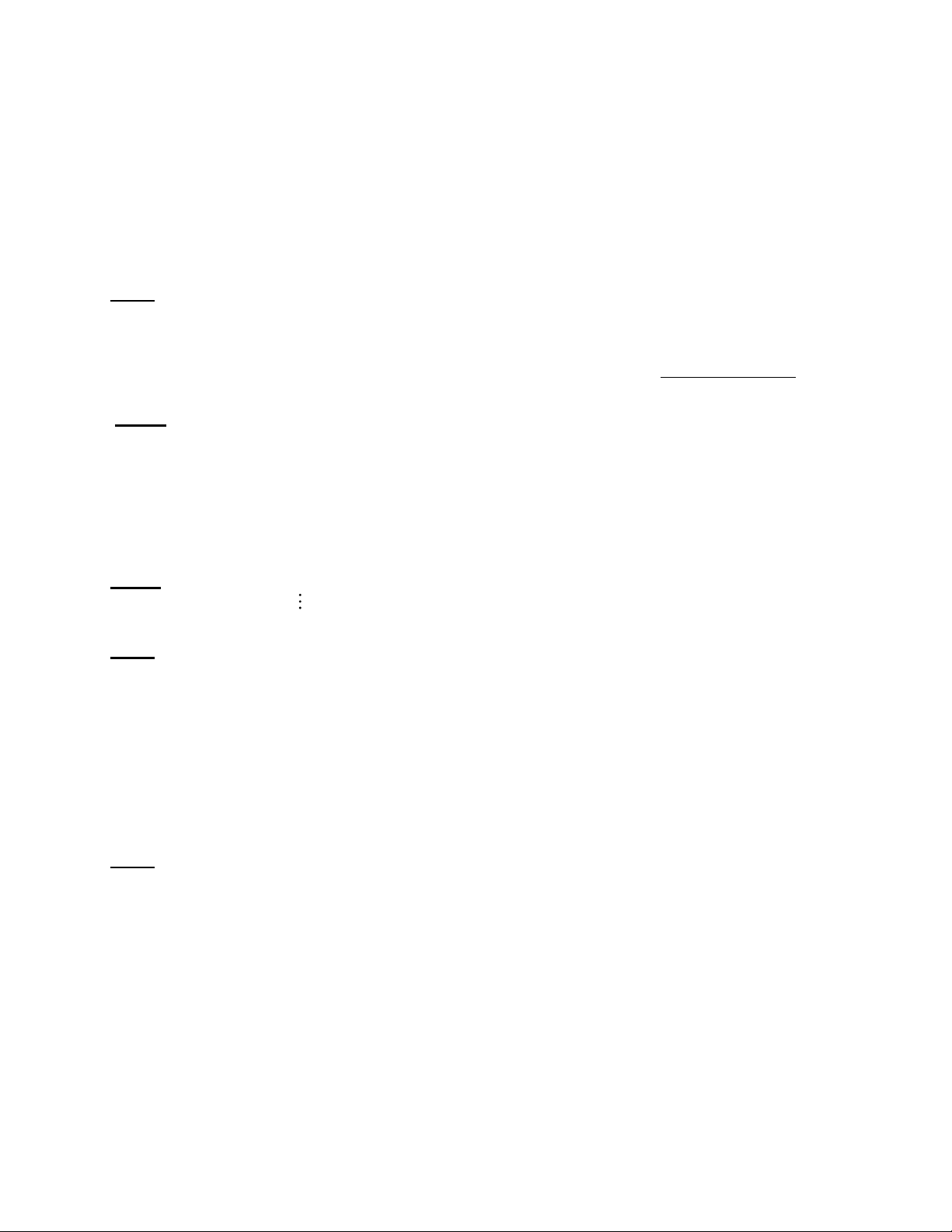
























Preview text:
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG LẦN 1 NĂM HỌC 2021-2022
Môn: TOÁN - Lớp 6
(Thời gian làm bài 120 phút, không kể thời gian giao đề) Bài 1:(3 điểm)
a) Thực hiện phép tính b) Rút gọn biểu thức 19 3 9 4 2 .27 +15.4 .9
23. 53 - 3 {400 -[ 673 - 23. (78 : 76 + 12021)]} A = 9 10 10 6 .2 + 2 Bài 2: (4,0 điểm)
Tìm số tự nhiên x biết:
a) x + (x + 1) + (x + 2) + …+ (x + 99) = 5450. b) 3.(5x - 1) - 2 = 70.
c) 2x + 2x + 1 + 2x + 2 = 960 - 2x + 3
Bài 3: (3 điểm) Chứng tỏ rằng: a) (3100+19990) 2
b) Tổng của 4 số tự nhiên liên tiếp không chia hết cho 4
Bài 4 (6,0 điểm) a) 50 107 và 75 73
b) Tìm số tự nhiên a nhỏ nhất sao cho: a chia cho 2 dư 1, a chia cho 3 dư 1, a chia
cho 5 dư 4, a chia cho 7 dư 3.
c) Cho p là số nguyên tố (p > 3) và 2p + 1 cũng là số nguyên tố. Hỏi 4p + 1 là số
nguyên tố hay hợp số? Vì sao?
Bài 5 (4,0 điểm)
Một nửa số ô vuông của một bàn cờ 8x8 được tô đen như hình vẽ sau. Có tất cả bao
nhiêu hình vuông 2x2, 4x4, 6x6 mà có một nửa số ô vuông được tô đen?
………….. Hết …………
ĐÁP ÁN ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG LẦN 1 NĂM HỌC 2021-2022
Môn: TOÁN - Lớp 6
(Thời gian làm bài 120 phút) Bài Lời giải Điểm Bài 1
a) 23. 53 – 3. {400 -[ 673 - 23 (78 : 76 + 12021)]} (3đ)
= 8.125 – 3.{400-[673-8. ( 49+1)]} 0,5 = 1000 - 3.{ 400-273} 0,5 = 1000 - 381 0,5 = 619 2) 19 3 9 4 19 9 18 8 18 9 2 .27 +15.4 .9 2 .3 + 3.5.2 .3 2 .3 .(2 + 5) 1 A = = = = 9 10 10 9 9 10 6 .2 + 2 2 .3 .2 + ( 2 10 2 .3 ) 19 9 2 .3 .(1+ 6) 2 1,5 Bài 2
a, x + (x + 1) + (x + 2) + …+ (x + 99) = 5450. 0,5đ (4đ)
100x + (1 + 2+ 3+ …+ 99) = 5450
Lí luận tính tổng: 1 + 2+ 3+ …+ 99 = 4950 0,5đ khi đó 100x + 4950 = 5450 100x = 500 0,5đ Vậy x = 5 b,3.(5x - 1) - 2 = 70. 3.(5x - 1) = 70 + 2 0,5đ 3.(5x - 1) = 72 5x - 1 = 72 : 3 5x - 1 = 24 0,5đ 5x = 25 5x = 52 0,5đ Vậy x = 2
c, 2x + 2x + 1 + 2x + 2 = 960 - 2x + 3 2x (1 + 2 + 22 + 23) = 960 2x .15 = 960 0,75đ 2x = 960: 15 2x = 64 2x = 26 0,25đ Vậy x = 6 Bài 3 (3đ) a) Ta có:
3100 = 3.3.3….3 (có 100 thừa số 3)
= (34)25 = 8125 có chữ số tận cùng bằng 1
19990 = 19.19…19 ( có 990 thứa số 19 )
= (192)495 = 361495 ( có chữ số tận cùng bằng 1
Vậy 3100+19990 có chữ số tận cùng bằng 2 nên tổng này chia hết cho 1,5 2
b) Gọi 4 số tự nhiên liên tiếp là : a ; (a +1) ;( a + 2) ;( a + 3 ) ( a N )
Ta có : a + (a+1) + (a+2) + (a+3) = 4a + 6
Vì 4a 4 ; 6 không chia hết 4 nên 4a+ 6 không chia hết 4 1,5 Bài 4 a) Ta thấy: = ( )50 50 50 100 150 107 108 4. 27 = 2 . 3 (1) 0,75 (6đ) = ( )75 75 75 225 150 73 72 8. 9 = 2 . 3 (2) 0,75 Từ (1) và (2) suy ra 50 100 150 225 150 75 107 2 . 3 2 . 3 73 Vậy 50 75 107 73 . 0,5
b) Vì a chia cho 2 dư 1, a chia cho 3 dư 1, a chia cho 5 dư 4, a chia cho 7 dư 3
Nên a −1 2 ; a −1 3 ; a − 4 5 ; a − 3 7 0,5
a +1 2 ; a + 2 3 ; a +1 5 ; a + 4 7
a +11 2 ; a +11 3 ; a +11 5 ; a +11 7 a +11 BC(2;3;5;7) . 0,75
Mà a là số tự nhiên nhỏ nhất a +11 = BCNN (2;3;5;7) . 0,25
Mà các số 2; 3; 5; 7 nguyên tố cùng nhau BCNN (2;3;5;7) = 2.3.5.7 = 210 a +11 = 210. a = 199. 0,75
Vậy số tự nhiên cần tìm là 199. 0,25
c) Vì p là số nguyên tố lớn hơn 3 nên p có dạng 3k + 1 hoặc 3k + 2 (với k N, k >1)
Nếu p = 3k +1 thì 2p + 1 = 2(3k + 1) + 1 = 3(2k + 1)
và lí luận chỉ ra 2p + 1 là hợp số, trái với đề bài 1,5
Do đó p = 3k + 2 khi đó 4p + 1 = 4(3k + 2) + 1 = 3(4k + 3)
và lí luận chỉ ra 4p + 1 là hợp số Kl….. Bài 5
Ta đánh số các dòng từ dưới lên trên là 1, 2 , …, 8 và đánh số các cột 0,25 (4đ)
từ phải sang trái là 1, 2 , …, 8 . 0,5
Hình vuông 2 2 có một nửa số ô vuông được tô màu là các
hình nằm trên các dòng 4 ,
5 hoặc các cột 4 , 5 nên có tất cả 13 hình.
Hình vuông 4 4 có một nửa số ô vuông được tô màu là các 1 hình nằm trên các dòng
3 , 4 , 5 và 6 hoặc các cột 3 , 4 , 5 và 6 nên có tất cả 9 hình. 1
Hình vuông 6 6 có một nửa số ô vuông được tô màu là các hình nằm
trên các dòng 2 , 3 , 4 , 5 , 6 , 7 hoặc các cột 2 , 3 , 4 , 5 , 6 , 7 nên có tất cả 5 hình. 1
Vậy có 13 + 9 + 5 = 27 hình. 0,25
TUYỂN TẬP ĐỀ THI HỌC SINH GIỎI MÔN TOÁN LỚP 6 PHÒNG GD&ĐT
KÌ THI HỌC SINH GIỎI CẤP HUYỆN HUYỆN TƯ NGHĨA Môn thi: Toán 6
Thời gian: 150 phút (không kể thời gian giao đề) ĐỀ SỐ 1 12n +1
Câu 1. (3,0 điểm) Cho A =
. Tìm giá trị của n để: 2n + 3 a) A là một phân số. b) A là một số nguyên Câu 2. (4,0 điểm) − − − − − − a) Không quy đồ 1 1 1 1 1 1 ng hãy tính tổng sau: A = + + + + + 20 30 42 56 72 90 2010 2011 2012 2010 + 2011+ 2012
b) So sánh P và Q, biết: P = + + và Q = 2011 2012 2013 2011+ 2012 + 2013
Câu 3. (3,0 điểm): Tìm x, biết: a) (7x - 11)3 = 25.52 + 200 1 3 b) 3 x + 16 = - 13,25 3 4 Câu 4. (3,0 điể 3
m) Ở lớp 6A, số học sinh giỏi học kỳ I bằng
số còn lại. Cuối năm có 7 2
thêm 4 học sinh đạt loại giỏi nên số học sinh giỏi bằng
số còn lại. Tính số học sinh của lớp 3 6A.
Câu 5. (2,0 điểm) Cho ababab là số có sáu chữ số, chứng tỏ số ababablà bội của 3.
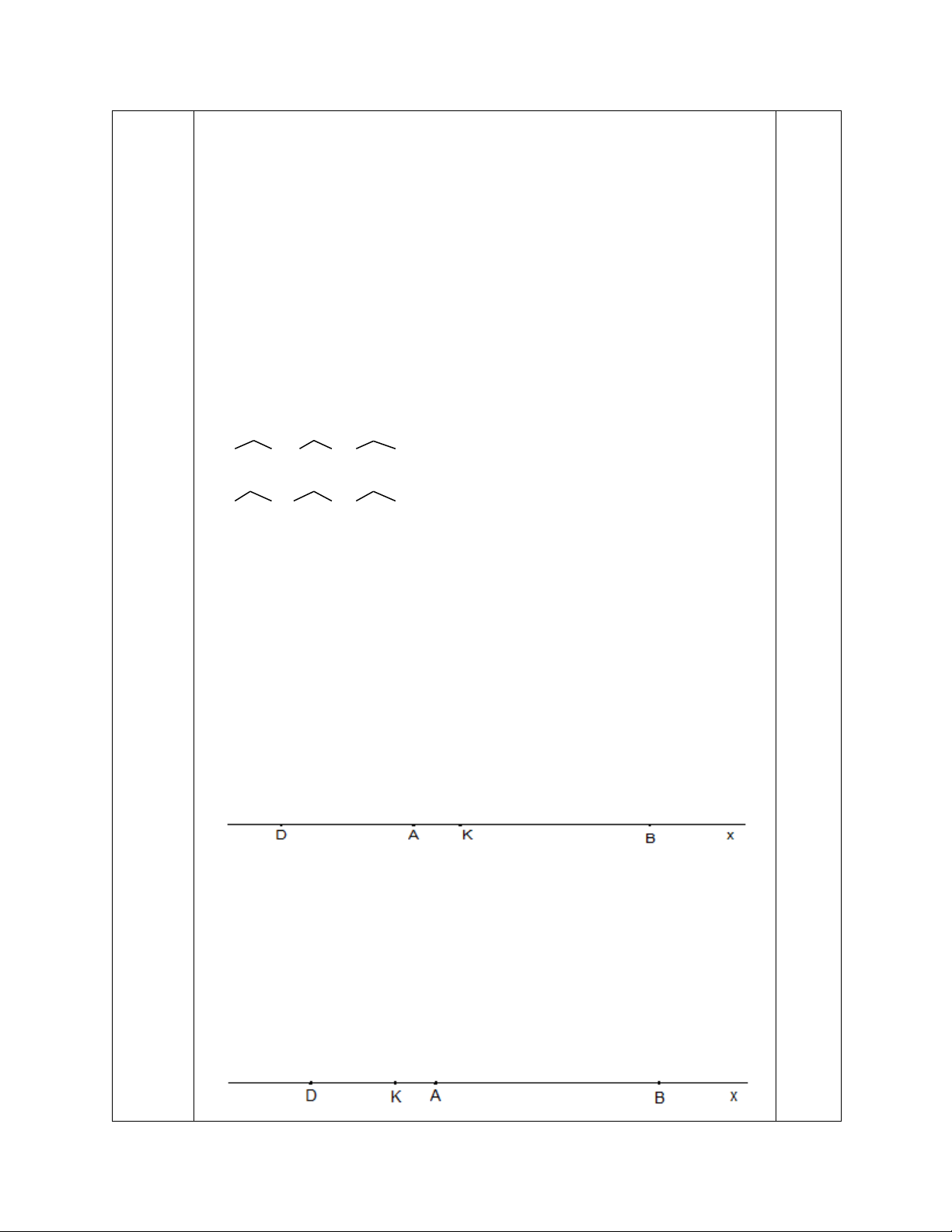
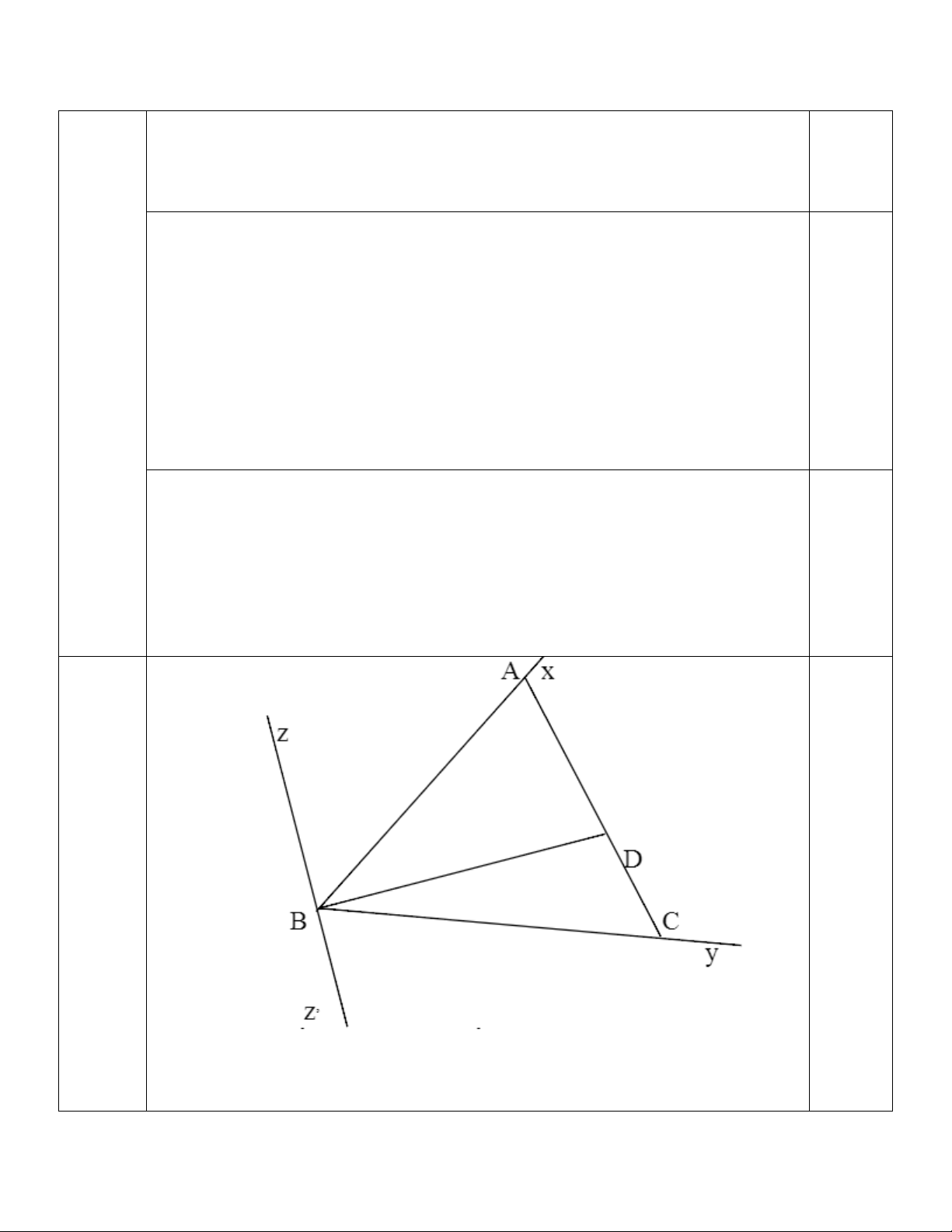
Câu 6. (5,0 điểm) Cho xAy, trên tia Ax lấy điểm B sao cho AB = 5 cm. Trên tia đối của
tia Ax lấy điểm D sao cho AD = 3 cm, C là một điểm trên tia Ay. a) Tính BD.
b) Biết BCD = 850, BCA = 500. Tính ACD
c) Biết AK = 1 cm (K thuộc BD). Tính BK
Đáp án đề thi học sinh giỏi môn Toán lớp 6 Câu Đáp án Điểm 12n +1 a) A =
là phân số khi: 12n + 1Z , 2n + 3Z và 2n + 2n + 3 0,5 3 0 0,5 nZ và n -1,5 Câu 1 12n +1 0,5 (3,0 điể 17 m) b) A = = 6- 2n + 3 2n+3 0,5
A là số nguyên khi 2n + 3Ư(17) 2n + 3 ; 1 17 0,5 n − ; 10 − ; 2 − ; 1 7 0,5 − 1 − 1 − 1 − 1 − 1 − 1 a) Tính A = + + + + + 20 30 42 56 72 90 Câu 2. 1 1 1 1 1 1 = - ( + + + + + ) (4,0 điểm) 4.5 5.6 6.7 7.8 8.9 9.10 0,5 1 1 1 1 1 1 1 1 0,5 = - ( − + − + − + ...+ − ) 4 5 5 6 6 7 9 10 0,5 1 1 = - ( − ) 4 10 − 3 0,5 = 20 b) So sánh P và Q 2010 2011 2012 2010 + 2011+ 2012 0,75 Biết: P = + + và Q = 2011 2012 2013 2011+ 2012 + 2013 0,25 2010 + 2011+ 2012 2010 2011 Q = = + 2011+ 2012 + 2013 2011+ 2012 + 2013 2011+ 2012 + 2013 2012 0,25 + 2011+ 2012 + 2013 2010 2010 Ta có: < 2011+ 2012 + 2013 2011 0,25 2011 2011 < 2011+ 2012 + 2013 2012 2012 2012 < 2011+ 2012 + 2013 2013 0,25 2010 2011 2012 => + + < 2011+ 2012 + 2013 2011+ 2012 + 2013 2011+ 2012 + 2013 2010 2011 2012 + + 2011 2012 2013 0,25 Kết luận: P > Q a) (7x-11)3 = 25.52 + 200 0,25 => (7x -11)3 = 32.25 + 200 0,25 => (7x -11)3 = 800 + 200 0,25 => (7x -11)3 = 1000 = 103 0,25 => 7x - 11 = 10 0,25 => 7x = 21 0,25 => x = 3 1 3 b) 3 x + 16 = - 13,25 3 4 0,5 10 67 -53 => x + = 3 4 4 0,5 10 -53 67 => x = - 3 4 4 Câu 3 0,25 10 => x = -30 (3,0 điểm) 3 0,25 => x = -9 3 0,75
Số học sinh giỏi kỳ I bằng 10 số học sinh cả lớp 2
Số học sinh giỏi cuối bằng 5 số học sinh cả lớp. 0,75 Câu 4 2 3 0,75
(3,0 điểm) 4 học sinh là 5 - 10 số học sinh cả lớp. 1 1
10 số học sinh cả lớp là 4 nên số học sinh cả lớp là 4: 10 = 40 0,75 (học sinh) ababab 0,5
= ab .10000 + ab .100 + ab Câu 5 0,5
(2,0 điểm) = 10101. ab 0,5
Do 10101 chia hết cho 3 nên abababchia hết cho 3 0,5
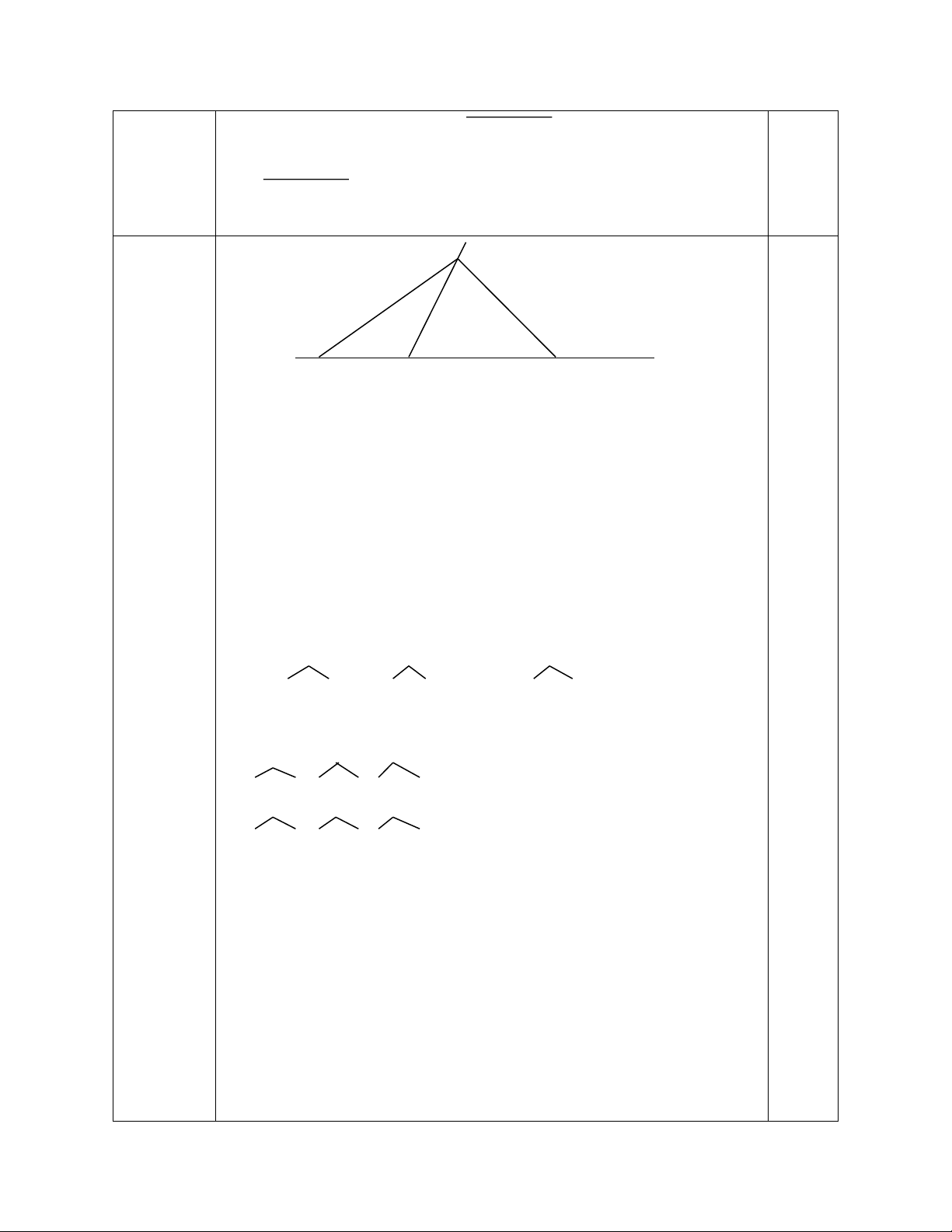
hay ababablà bội của 3. 0,25 y C D A B a) Tính BD
Vì B thuộc tia Ax, D thuộc tia đối của tia Ax 0,25 Câu 6 A nằm giữa D và B
(5,0 điểm) BD = BA + AD = 5 + 3 = 8 (cm) 0,5
b) Biết BCD = 850, BCA = 500. Tính ACD 0,5
Vì A nằm giữa D và B => Tia CA nằm giữa 2 tia CB và CD 0,5 => ACD + ACB = BCD
=> ACD = BCD - ACB = 850 - 500 = 350 0,25
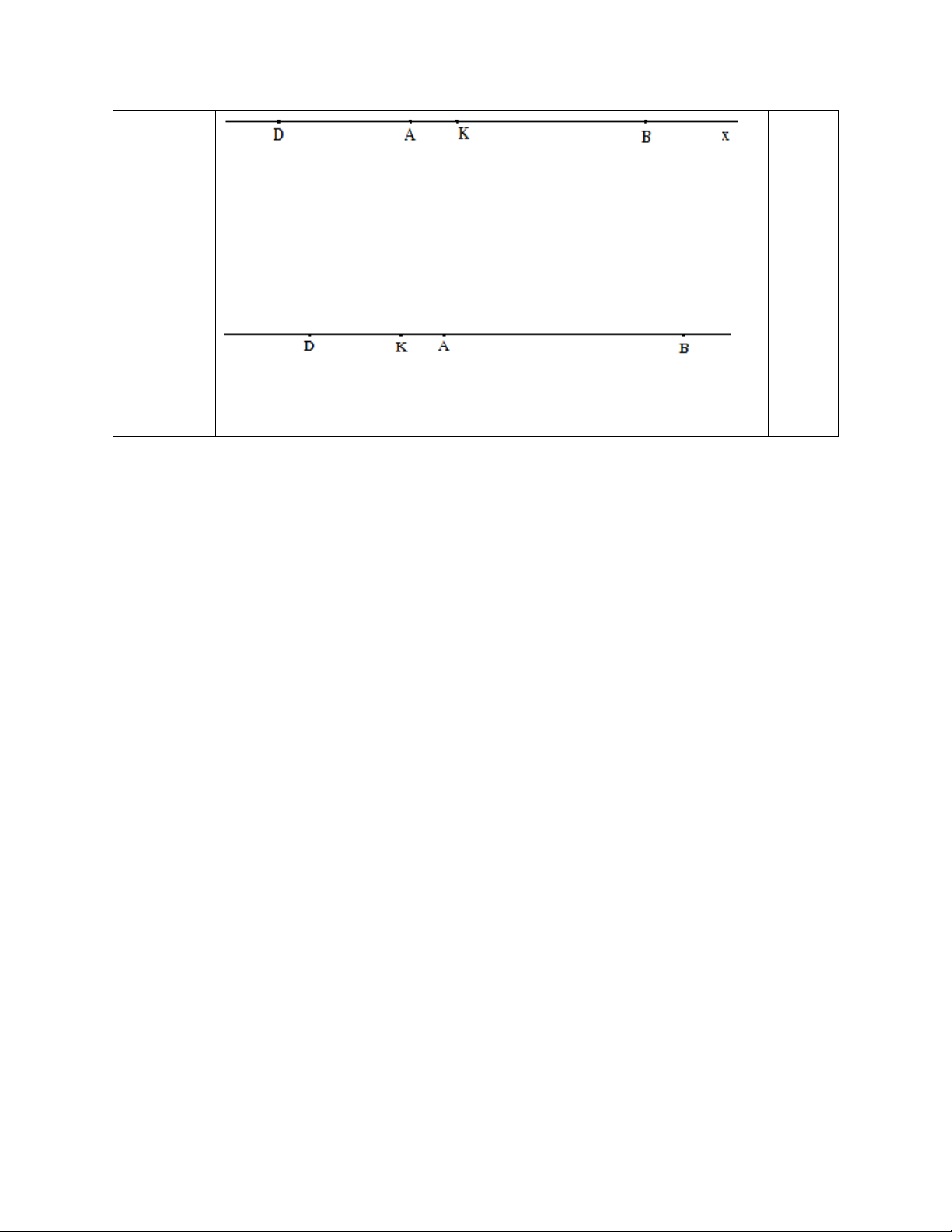
c) Biết AK = 1 cm (K thuộc BD). Tính BK
* Trường hợp 1: K thuộc tia Ax 0,5
- Lập luận chỉ ra được K nằm giữa A và B
- Suy ra: AK + KB = AB KB = AB – AK = 5 – 1 = 4 (cm) 0,25 0,5 0,25 * Trườ 0,25
ng hợp 2: K thuộc tia đối của tia Ax 0,5
- Lập luận chỉ ra được A nằm giữa K và B 0,25
- Suy ra: KB = KA + AB KB = 5 + 1 = 6 (cm) 0,25
* Kết luận: Vậy KB = 4 cm hoặc KB = 6 cm
(Bài thi của thí sinh giải theo cách khác đúng vẫn cho điểm tối đa) ĐỀ SỐ 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA KHẢO SÁT HỌC SINH ĐỘI TUYỂN Năm học 2016 - 2017 TỈNH ĐỒNG THÁP
Môn kiểm tra: TOÁN – LỚP 6 ĐỀ CHÍNH THỨC Ngày kiểm tra: 27/01/2017 (Đề gồm có 01 trang)
Thời gian: 150 phút (không kể thời gian phát đề)
Câu I: (4.0 điểm). Thực hiện phép tính 2 2 9 2 6 2 14 4
5.(2 .3 ) .(2 ) − 2.(2 .3) .3 1) A = 28 18 29 18 5.2 .3 − 7.2 .3 12 12 12 5 5 5 12 − − − 5 + + + 158158158 2) B = 81. 7 289 85 13 169 91 : . 4 4 4 6 6 6 711711711 4 − − − 6 + + + 7 289 85 13 169 91 Câu II: (4.0 điểm) 1) So sánh P và Q 2010 2011 2012 2010 + 2011+ 2012 Biết P = + + và Q = 2011 2012 2013 2011+ 2012 + 2013
2) Tìm hai số tự nhiên a và b, biết: BCNN(a, b) = 420; ƯCLN(a, b) = 21 và a + 21 = b.
Câu III: (4.0 điểm)
1) Chứng minh rằng: Nếu 7x + 4y 37 thì 13x +18y 37 1 3 3 3 3 3 3 2) Cho A = 2 3 4 2012 + + ( ) + ( ) + ( ) +...+ ( ) và B = 2013 ( ) : 2 2 2 2 2 2 2 2 Tính B – A Câu IV. (6.0 điểm)
Cho xÂy, trên tia Ax lấy điểm B sao cho AB = 6 cm. Trên tia đối của tia Ax lấy điểm D sao cho AD = 4 cm. 1) Tính BD.
2) Lấy C là một điểm trên tia Ay. Biết BĈD = 800, BĈA = 450. Tính AĈD
3) Biết AK = 2 cm (K thuộc BD). Tính BK Câu V: (2.0 điểm) x 3 1
1) Tìm các số tự nhiên x, y sao cho: − = 9 y 18 10n − 3
2) Tìm số tự nhiên n để phân số B =
đạt GTLN. Tìm giá trị lớn nhất đó. 4n −10
Đáp án đề thi học sinh giỏi môn Toán lớp 6 Câu Nội dung Điểm 2 2 9 2 6 2 14 4
5.(2 .3 ) .(2 ) − 2.(2 .3) .3 0.5 a) Ta có: A = 28 18 29 18 5.2 .3 − 7.2 .3 18 18 12 28 14 4 5.2 .3 .2 − 2.2 .3 .3 = 0.5 28 18 29 18 5.2 .3 − 7.2 .3 30 18 29 18 5.2 .3 − 2 .3 = 28 18 2 .3 (5 − 7.2) 0.5 29 18 2 .3 (5.2 −1) 2.9 = = = − 2 28 18 2 .3 (5 −14) 9 − 0.5 KL:….. Câu 1 12 12 12 5 5 5 12 − − − 5 + + + 158158158 b) Ta có: 7 289 85 13 169 91 B = 81. : . 4 4 4 6 6 6 711711711 4 − − − 6 + + + 0.5 7 289 85 13 169 91 1 1 1 1 1 1 12 1− − − 5 1+ + + 7 289 85 13 169 91 158.1001001 = 81. : . 1 1 1 1 1 1 711.1001001 4 1− − − 6 1+ + + 7 289 85 13 169 91 0.5 12 5 158 = 81. : . 4 6 711 0.5 18 2 324 = 81. . = = 64,8 5 9 5 KL:…… 0.5 a) Ta có: Câu 2 2010 + 2011+ 2012 2010 2011 1.0 Q = = + + 2011+ 2012 + 2013 2011+ 2012 + 2013 2011+ 2012 + 2013 2012 + 2011+ 2012 + 2013 0.75
Lần lượt so sánh từng phân số của P và Q với các tử là: 2010; 2011;
2012 thấy được các phân thức của P đều lớn hơn các phân thức của Q 0.25 Kết luận: P > Q
b) Từ dữ liệu đề bài cho, ta có:
+ Vì ƯCLN(a, b) = 21, nên tồn tại các số tự nhiên m và n khác 0, sao cho: a = 21m; b = 21n (1) và ƯCLN(m, n) = 1 (2) 0.5
+ Vì BCNN(a, b) = 420, nên theo trên, ta suy ra:
BCNN(21m; 21n) = 420 = 21.20 0.5 BCNN(m; n) = 20 (3)
+ Vì a + 21 = b, nên theo trên, ta suy ra:
21m + 21 = 21n 21.(m + ) 1 = 21n m +1 = n (4)
Trong các trường hợp thoả mãn các điều kiện (2) và (3), thì chỉ có 0.5
Trường hợp: m = 4, n = 5 hoặc m = 2, n = 3 là thoả mãn điều kiện (4).
Vậy với m = 4, n = 5 hoặc m = 2, n = 3 ta được các số phải tìm là: 0.5 a = 21.4 = 84; b = 21.5 = 105
a) Ta có: 5(13x +18y) − 4(7x + 4y) = 65x + 90y − 28x −16y 0.5
= 37x + 74y = 37(x + 2y) 37
Hay 5(13x +18y) − 4(7x + 4 y) 37 (*) 0.5 0.5
Vì 7x + 4 y 37 , mà (4; 37) = 1 nên 4(7x + 4 y) 37
Do đó, từ (*) suy ra: 5(13x +18y) 37 , mà (5; 37) = 1 nên 13x +18y 37 0.5 b) Ta có: 1 3 3 3 3 3 2 3 4 2012 A = + + ( ) + ( ) + ( ) +...+ ( ) (1) 2 2 2 2 2 2 3 3 3 3 3 3 0.5 2 3 4 2013
= A = + ( ) + ( ) + ( ) +...+ ( ) (2) 2 4 2 2 2 2
Lấy (2) – (1), ta được: 0.5 Câu 3 3 3 3 1 3 2013 A − A = ( ) + − − 2 2 4 2 2 2013 1 3 1 3 1 2013 A = ( ) + = A = + 2012 2 2 4 2 2 0.5 2013 2013 3 3 5 Vậy B − A = − + 2014 2012 2 2 2 0.5 Hình vẽ: y C . Câu 4 0.5 D A B x
a) Vì B thuộc tia Ax, D thuộc tia đối của tia Ax A nằm giữa D và B 0.5
BD = BA + AD = 6 + 4 = 10 (cm) 0.5 KL:….. 0.5
b) Vì A nằm giữa D và B => Tia CA nằm giữa 2 tia CB và CD => ACD + ACB = BCD 0.5
=> ACD = BCD – ACB = 800 – 450 = 350 0.5 KL:…. 0.5
c) * Trường hợp 1: K thuộc tia Ax 0.5
- Lập luận chỉ ra được K nằm giữa A và B 0.25 - Suy ra: AK + KB = AB 0.25
KB = AB – AK = 6 – 2 = 4 (cm) 0.25 0.25
* Trường hợp 2: K thuộc tia đối của tia Ax
- Lập luận chỉ ra được A nằm giữa K và B 0.25 - Suy ra: KB = KA + AB 0.25 KB = 6 + 2 = 8 (cm) 0.25
* Kết luận: Vậy KB = 4 cm hoặc KB = 8 cm 0.25 x 3 1 x 1 3 x − a) Từ − = − = 2 1 3 = 9 y 18 9 18 y 18 y 0.25
(2x – 1).y = 54 = 1.54 = 2.27 = 3.18 = 6.9
Vì x là số tự nhiên nên 2x – 1 là ước số lẻ của 54. Ta có bảng sau: 2x – 1 1 3 9 27 0.25 x 1 2 5 14 0.25 y 54 18 6 2 Câu 5 0.25
Vầy (x; y) = (1; 54); (2; 18); (5; 6); (14; 2) 10n − 3 22 b) B = = 2,5 + 0.25 4n − 10 4n −10 22 22 Vì nN nên B = 2,5 + đạt GTLN khi đạt GTLN. 4n −10 4n −10 0.25 22 Mà
đạt GTLN 4n – 10 là số nguyên dương nhỏ nhất. 4n −10 11
- Nếu 4n – 10 = 1 thì n = N (loại) 4 0.25
- Nếu 4n – 10 = 2 thì n = 3. 0.25
Vậy GTLN của B = 13,5 khi n = 3. ĐỀ SỐ 3
PHÒNG GD&ĐT QUỲNH LƯU
ĐỀ THI HSG CẤP TRƯỜNG NĂM HỌC 2015 - 2016 TRƯỜNG THCS QUỲNH GIANG Môn toán lớp 6 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút Câu 1 (2,0 điểm)
a) Tính nhanh: 16 + (27 - 7.6) - (94.7 - 27. 99) 2 2 2 2 b) Tính tổng: A = + + + ....+ . 1 4 . 4 7 10 . 7 97.100
Câu 2 (2,0 điểm) Cho biểu thức: M = 5 + 52 + 53 + … + 580. Chứng tỏ rằng: a) M chia hết cho 6.
b) M không phải là số chính phương. Câu 3 (2,0 điểm) 2n + 5 a) Chứng tỏ rằng:
, (n N ) là phân số tối giản. n + 3 2n + 5
b) Tìm các giá trị nguyên của n để phân số B =
có giá trị là số nguyên. n + 3
Câu 4 (1,0 điểm) Tìm số tự nhiên nhỏ nhất sao cho khi chia số đó cho 3 dư 1; chia cho 4
dư 2; chia cho 5 dư 3; chia cho 6 dư 4 và chia hết cho 11.
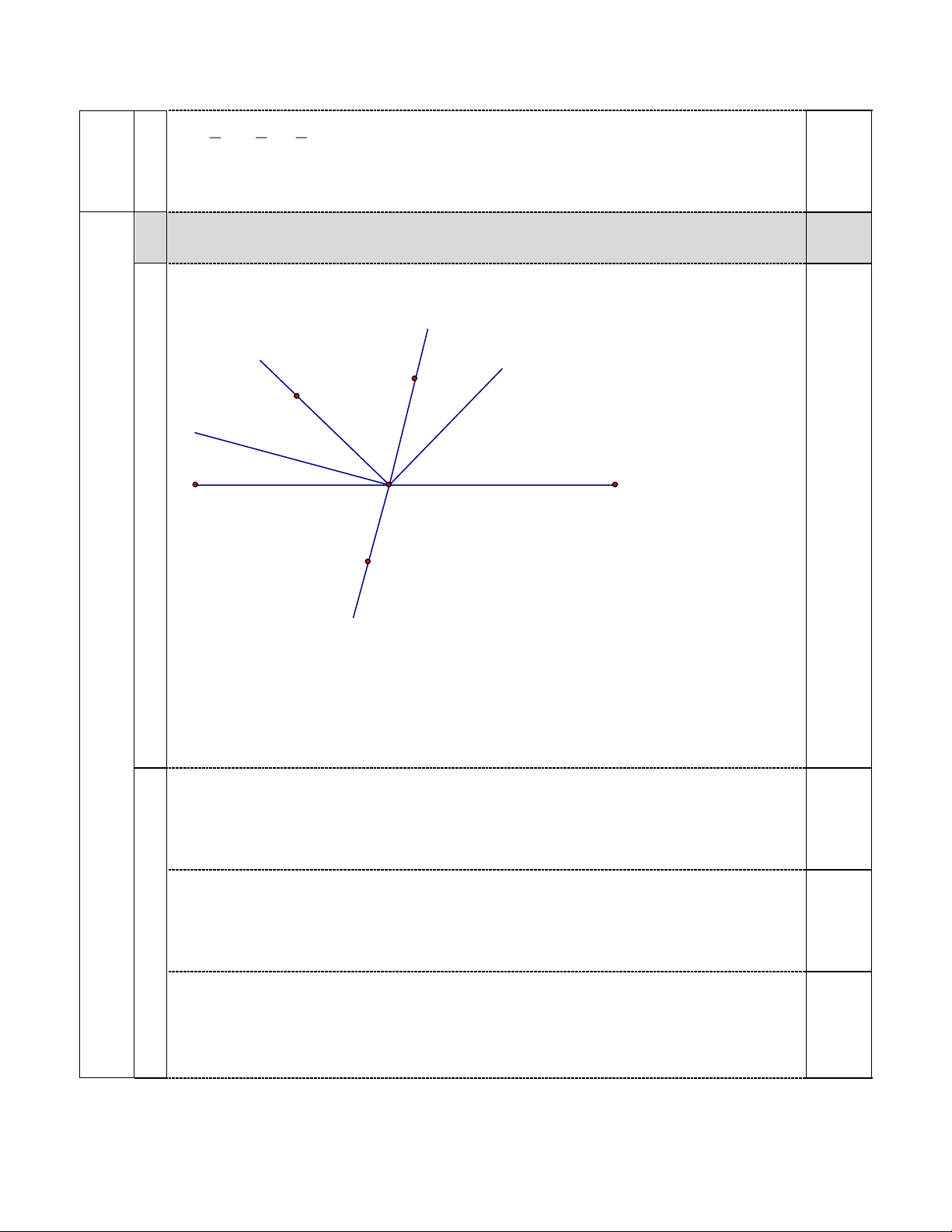
Câu 5 (2,0 điểm) Trên cùng nửa mặt phẳng bờ chứa tia Ox vẽ 3 tia Oy, Oz, Ot sao cho
xOy = 30 ; xOz = 70 ; xOt = 110
a) Tính yOz và zOt
b) Trong 3 tia Oy, Oz, Ot tia nào nằm giữa 2 tia còn lại? Vì sao?
c) Chứng minh: Oz là tia phân giác của góc yOt. 1 1 1 1
Câu 6 (1,0 điểm) Chứng minh rằng: + + +...+ < 1 2 2 2 3 2 4 2 100 ĐÁP ÁN
Câu 1 (Mỗi câu đúng, cho 1,0 điểm)
a) 16 + (27 - 7.6) - (94.7 - 27. 99)
= 16 + 27 - 7.6 - 94.7 + 27.99
= 16 + 27 + 27.99 - 7.6 - 94.7
= 16 + 27(99 + 1) - 7.(6 + 94) = 16 +27.100 - 7. 100
= 16 + 100(27- 7) = 16 + 100.20 = 16 + 2000 = 2016 2 2 2 2 b) A = + + + ....+ . 1 4 . 4 7 10 . 7 97.100 1 1 1 1 2 2 1 1 Ta có = ( − ) = ( − ) . 1 4 3 1 4 4 . 1 3 1 4 Tương tự 2 2 1 1 2 2 1 1 2 2 1 1 : = ( − ); = ( − ) ; ......; = ( − ) 4.7 3 4 7 7.10 3 7 10 97.100 3 99 100 2 1 1 1 1 1 1 1 1 2 1 1 2 99 33 A = ( − + − + − + .....+ − ) = ( − ) = . = 3 1 4 4 7 7 10 99 100 3 1 100 3 100 50
Câu 2 (Mỗi câu đúng, cho 1,0 điểm)
a) Ta có: M = 5 + 52 + 53 + … + 580
= 5 + 52 + 53 + … + 580 = (5 + 52) + (53 + 54) + (55 + 56) +... + (579 + 580)
= (5 + 52) + 52.(5 + 52) + 54(5 + 52) + ... + 578(5 + 52)
= 30 + 30.52 + 30.54 + ... + 30.578 = 30 (1+ 52 + 54 + ... + 578) 30
b) Ta thấy : M = 5 + 52 + 53 + … + 580 chia hết cho số nguyên tố 5.
Mặt khác, do: 52+ 53 + … + 580 chia hết cho 52 (vì tất cả các số hạng đều chia hết cho 52)
M = 5 + 52 + 53 + … + 580 không chia hết cho 52 (do 5 không chia hết cho 52)
M chia hết cho 5 nhưng không chia hết cho 52
M không phải là số chính phương.
(Vì số chính phương chia hết cho số nguyên tố p thì chia hết cho p2).
Câu 3 (Mỗi câu đúng, cho 1,0 điểm) 2n + 5 a). Chứng tỏ rằng:
, (n N ) là phân số tối giản. n + 3
Gọi d là ước chung của n + 3 và 2n + 5 với d N n + 3 d và 2n + 5 d
(n + 3) - (2n + 5) d 2(n + 3) - (2n + 5) d 1 d d = 1 N
ƯC( n + 3 và 2n + 5) = 1 2n + 5
ƯCLN (n + 3 và 2n + 5) = 1
, (n N ) là phân số tối giản. n + 3 2n + 5
b). Tìm các giá trị nguyên của n để phân số B =
có giá trị là số nguyên. n + 3 2n + 5 2(n + 3) −1 1 Ta có: = = 2 - n + 3 n + 3 n + 3 Để 1
B có giá trị nguyên thì nguyên. n + 3 1 Mà nguyên 1 M
(n +3) hay n + 3 là ước của 1. n + 3
Do Ư(1) = 1; Ta tìm được n = {-4 ; - 2} Câu 4: Giải
Gọi số phải tìm là x. Theo bài ra ta có x + 2 chia hết cho 3, 4, 5, 6.
x + 2 là bội chung của 3, 4, 5, 6
Mà BCNN(3; 4; 5; 6) = 60 nên x + 2 = 60.n .
Do đó x = 60.n – 2; (n = 1; 2; 3…..) Mặt khác xM
11 nên lần lượt cho n = 1; 2; 3…. Ta thấy n = 7 thì x = 418 M 11
Vậy số nhỏ nhất phải tìm là 418.
Câu 5 (Vẽ hình đúng, cho 0,5 điểm. Còn lại mỗi ý 0,5 điểm)
a). xOy xOz (300 < 700)
Tia Oy nằm giữa 2 tia Ox và Oz
yOz = 700 - 300 = 400
xOz xOt (700 < 1100)
Tia Oz nằm giữa 2 tia Ox và Ot
zOt = 1100 - 700 = 400
b) xOy xOt (300 < 1100)
Tia Oy nằm giữa 2 tia Ox và Ot t
yOt = 1100 - 300 = 800 z y Theo trên, yOz = 400 300
yOz < yOt (400 < 800) x O
Tia Oz nằm giữa 2 tia Oy và Ot
c). Theo trên: Tia Oz nằm giữa 2 tia Oy và Ot và có: yOz = 400; zOt = 400
Oz là tia phân giác của góc yOt. 1 1 1 1
Câu 6 Chứng minh rằng : + + +...+ < 1 2 2 2 3 2 4 2 100 1 1 1 1 Ta có < = - 2 2 2.1 1 2 1 1 1 1 < = - 2 3 2.3 2 3 .. 1 1 1 1 < = - 2 100 99 1 . 00 99 100 1 1 1 1 1 1 1 1 1 1 + +...+ < - + - + ...+ - = 1- <1 2 2 2 3 2 100 1 2 2 3 99 100 100
Chú ý: Nếu học sinh làm theo cách khác đúng, vẫn cho điểm tối đa. ĐỀ SỐ 4 TRƯỜNG THCS NÔNG
ĐỀ KHẢO SÁT HỌC SINH GIỎI TRANG - T.P VIỆT TRÌ CẤP TRƯỜNG 2014 - 2015 MÔN: TOÁN 6
Thời gian làm bài: 120 phút (không tính thời gian giao đề)
Câu 1 (1,5 điểm): Thực hiện phép tính. 3 3 3 3 3 + − + − 24.47 − 23 a) 7 11 1001 13 A = . 24 + 47 − 23 9 9 9 9 − + − + 9 1001 13 7 11 2 3 2012 1+ 2 + 2 + 2 + ... + 2 b) M = 2014 2 − 2 Câu 2 (2,5 điểm)
a) Cho S = 5 + 52 + 53 + 54 + 55 + 56 +…+ 52012. Chứng tỏ S chia hết cho 65.
b) Tìm số tự nhiên nhỏ nhất sao cho khi chia cho 11 dư 6, chia cho 4 dư 1và chia cho 19 dư 11.
c) Chứng tỏ: A = 10n + 18n - 1 chia hết cho 27 (với n là số tự nhiên) Câu 3 (2,0 điểm)
a) Tìm x, y nguyên biết : 2x (3y – 2) + (3y – 2) = -55 1 1 1 1 1
b) Chứng minh rằng: + + + ...+ 2 2 2 2 4 6 8 (2n) 4
Câu 4 (2,5 điểm): Cho nửa mặt phẳng bờ AB chứa hai tia đối OA và OB.
a) Vẽ tia OC tạo với tia OA một góc bằng ao, vẽ tia OD tạo với tia OCC một góc bằng (a
+ 10)o và với tia OB một góc bằng (a + 20)o Tính ao
b) Tính góc xOy, biết góc AOx bằng 22o và góc BOy bằng 48o
c) Gọi OE là tia đối của tia OD, tính số đo góc kề bù với góc xOD khi góc AOC bằng ao
Câu 5 (1,5 điểm): Cho 2012 2011 2010 2009 A = 10 +10 +10 +10 +8
a) Chứng minh rằng A chia hết cho 24
b) Chứng minh rằng A không phải là số chính phương.
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT
HỌC SINH GIỎI CẤP TRƯỜNG NĂM HỌC 2014 - 2015 Môn: TOÁN 6 Câu Ý Nội dung, đáp án Điểm 1,5 Đặt A=B.C 1 a 24.47 − 23 1128 − 23 1105 0,25 B = = = 24 + 47 − 23 71− 23 48 1 1 1 1 3 1 + − + − 7 11 1001 13 1 C = = 1 1 1 1 3 0,25 9 − + − +1 1001 13 7 11 1105 Suy ra A = 144 0,25 2 3 2012 1+ 2 + 2 + 2 + ... + 2 M = 2014 2 − 2
- Đặt A = 1+2+22+23 + ...+22012 0,25
b - Tính được A = 22013 – 1 - Đặt B = 22014 – 2
- Tính được B = 2.(22013 – 1) 0,25 1 0,25 - Tính được M = 2 2,5
S = 5 + 52 + 53 + 54 + 55 + 56 +…+ 52012. 0,25
S = (5+52+53+54)+55(5+52+53+54)+....+52009(5+52+53+54) 0,25 a Vì (5+52+53+54) =780 65 2 Vậy S chia hết cho 65 0,25
Gọi số cần tìm là a ta có: (a-6) 11 ;(a-1) 4; (a-11) 19. 0,25
b (a-6 +33) 11; (a-1 + 28) 4; (a-11 +38 ) 19. 0,25
(a +27) 11; (a +27) 4; (a +27) 19.
Do a là số tự nhiên nhỏ nhất nên a+27 nhỏ nhất 0,25
Suy ra: a +27 = BCNN (4 ;11 ; 19 ) .
Từ đó tìm được : a = 809 0,25
=10n +18 −1 =10n A n −1− 9n + 27n 0,25
= 99.....9 − 9n + 27n n
= 9.(11.....1− n) + 27n n 0,25
Ta biết số n và số có tổng các chữ số bằng n có cùng số dư khi chia cho 9
do đó 11.....1− n 9 nên 9.(11.....1− )
n 27 . Vậy A 27 0,25 n n 2
Tìm x, y nguyên biết : 2x (3y – 2) + (3y – 2) = -55 =>(3y – 1)(2x + 1) = -55 55 − => 2x +1 = (1) 3y − 2 3 0,25 a
Để x nguyên thì 3y – 2 Ư(-55) = 1;5;11;55; 1 − ; 5 − ; 1 − 1; 5 − 5 0,25
+) 3y – 2 = 1 => 3y = 3 => y = 1, thay vào (1) => x = 28 7
+) 3y – 2 = 5 => 3y = 7 => y = (Loại) 3 13 0,25
+) 3y – 2 = 11 => 3y = 13 => y = (Loại) 3
+) 3y – 2 = 55 => 3y = 57 => y = 19 , thay vào (1) => x = -1 1
+) 3y – 2 = - 1 => 3y = 1 => y = (Loại) 3
+) 3y – 2 = -5 => 3y = -3 => y = -1, thay vào (1) => x = 5
+) 3y – 2 = -11 => 3y = -9 => y = -3 , thay vào (1) => x = 2 −53
+) 3y – 2 = -55 => 3y = -53 => y = (Loại) 3 0,25
Vậy ta có 4 cặp số x, y nguyên thoả mãn là
(x ; y ) = (28 ; 1) , (-1 ; 19) , (5 ; -1), (2 ; -3) 1 1 1 1 1 0,25 b/ Chứng minh rằng : + + + ...+ 2 2 2 2 4 6 8 2n 4 Ta có 1 1 1 1 A = + + + ...+ 2 2 2 2 4 6 8 (2n) 1 1 1 1 A = + + + ...+ b 2 2 2 2 (2.2) (2.3) (2.4) (2.n) 0,25 1 1 1 1 1 1 1 1 1 1 A = + + +...+ + + + 2 2 2 2 4 2 3 4 n
4 1.2 2.3 3.4 (n −1)n 0,25 1 1 1 1 1 1 1 1 1 A − + − + − + ...+ − 4 1 2 2 3 3 4 (n −1) n 1 1 1 A 1− (ĐPCM) 4 n 4 0,25 2,5 Vẽ đúng hình D y C (a+20)o (a+10)o x ao 48o 22o A O B E 4
Cho nửa mặt phẳng bờ AB chứa hai tia đối OA và OB. 0,25
Vẽ tia OC tạo với tia OA một góc bằng ao, vẽ tia OD tạo với tia OCC một
góc bằng (a + 10)o và với tia OB một góc bằng (a + 20)o.Tính ao 0,25
Do OC, OD nằm trên cùng một nửa mặt phẳng bờ AB và
a COD CO (
A a +10 a) . Nên tia OC nằm giữa hai tia OA v à OD 0,25
=> AOC + COD + DOB = AOB
=> ao + (a + 10)o + (a + 20)o = 180o
=> 3.ao + 30o = 180o => ao = 50o 0,25
Tính góc xOy, biết góc AOx bằng 22o và góc BOy bằng 48o
Tia Oy nằm giữa hai tia OA v à OB 0,25 o o o o o
b Ta có : AOy = 180 − BOy = 180 − 48 = 132 AOx = 22
Nên tia Ox nằm giữa hai tia OA và Oy 0,25 => + = = 22o + =132o =
=132o − 22o =110o AOx xOy AOy xOy xOy 0,25
Gọi OE là tia đối của tia OD, tính số đo góc kề bù với góc xOD khi góc AOC bằng ao 0,25
V ì tia OC nằm giữa hai tia OA và OD nên
AOC + COD = AOD = AOD = a + ( o o a +10) o o o o o = + = + = 0,25 c 2a 10 2.50 10 110 Vì AOx (22o 110o AOD
) nên tia Ox nằm giữa hai tia OA và OD => AOx + = = 22o + =110o =
=110o − 22o = 88o xOD AOD xOD xOD 0,25
Vậy số đo góc kề bù với góc xOD có số đo là : 180o – 88o = 92o 1,5
Chứng minh rằng A chia hết cho 24 5 Ta có : a 3 A = ( 2009 2008 2007 2006 + + + )+ = ( 2009 2008 2007 2006 10 10 10 10 10 8 8.125 10 +10 +10 +10 )+8 0,25 A = ( 2009 2008 2007 2006 8. 125 10 +10 +10 +10 )+1 8 (1)
Ta lại có các số : 102012 ; 102011 ; 102010 ; 102009 có tổng tổng các chữ số bằng
1, nên các số 102012 ; 102011 ; 102010 ; 102009 khi chia cho 3 đều có số dư bằng 1 8 chia cho 3 dư 2. 0,25
Vậy A chia cho 3 có số dư là dư của phép chia (1 + 1 + 1 + 1 + 2) chia cho 3
Hay dư của phép chia 6 chia cho 3 (có số dư bằng 0) Vậy A chia hết cho 3
Vì 8 và 3 là hai số nguyên tố cùng nhau nên A chia hết cho 8.3 = 24 0,25
Chứng minh rằng A không phải là số chính phương. 0,25
Ta có các số : 102012 ; 102011 ; 102010 ; 102009 đều có chữ số tận cùng là 0 b Nên 2012 2011 2010 2009 A = 10 +10 +10 +10
+8 có chữ số tận cùng là 8 0,25
Vậy A không phải là số chỉnh phương vì số chính phương là những số có
chữ số tận cùng là 1 ; 4; 5 ; 6 ; 9 0,25
Chú ý: - Mọi cách giải thích khác nếu đúng ghi điểm tối đa.
-----------HẾT-------------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC SINH GIỎI LỚP 6 ĐỀ SỐ 5 HUYỆN HOẰNG HOÁ NĂM HỌC 2014 - 2015 MÔN THI: TOÁN Ngày thi: 18/03/2015
Thời gian: 120 phút (Không kể thời gian giao đề)
(Đề thi này có 05 câu, gồm 01 trang)
Bài 1 (4,5 điểm) Tính giá trị các biểu thức sau: 2 5 1 a. A = 2 + :5 − .( 3 − ) 3 6 18
b. B = 3.{5.[(52 + 23): 11] - 16} + 2015 1 1 1 1 c. C = 1 + 1+ 1+ ... 1+ 1.3 2.4 3.5 2014.2016 Bài 2 (4,0 điểm)
a. Tìm số tự nhiên x biết 8.6 + 288 : (x - 3)2 = 50
b. Tìm các chữ số x; y để A = x183y chia cho 2; 5 và 9 đều dư 1.
c. Chứng tỏ rằng nếu p là số nguyên tố lớn hơn 3 thì p2 - 1 chia hết cho 3. Bài 3 (4,5 điểm) 5
a. Cho biểu thức: B =
(n Z, n 3) n − 3
Tìm tất cả các giá trị nguyên của n để B là số nguyên.
b.Tìm các số nguyên tố x, y sao cho: x2 + 117 = y2 c. Số 100 2
viết trong hệ thập phân có bao nhiêu chữ số . Bài 4 (5,0 điểm)
Cho góc xBy = 550. Trên các tia Bx; By lần lượt lấy các điểm A; C
(A B; C B). Trên đoạn thẳng AC lấy điểm D sao cho ABD = 300
a. Tính độ dài AC, biết AD = 4cm, CD = 3cm.
b. Tính số đo của DBC .
c. Từ B vẽ tia Bz sao cho DBz = 900. Tính số đo ABz . Bài 5 (2,0 điểm)
a. Tìm các chữ số a, b, c khác 0 thỏa mãn: abbc = ab ac 7 2015 94 1 b. Cho 2012 92 A = (7 − 3
) . Chứng minh A là số tự nhiên chia hết cho 5 2
HƯỚNG DẪN CHẤM THI
HỌC SINH GIỎI- MÔN: TOÁN 6 NĂM HỌC 2014 - 2015 Bài
Nội dung cần đạt Điểm 2 5 1 2 1 1 2.2 +1 −1.3 2 1 1,5 đ a. A= 2 + :5 − .( 3 − ) = + − = = = 3 6 18 3 6 2 6 6 3
b. B = 3.{5.[(52 + 23): 11] - 16} + 2015 = 3.{5.[33 : 11] - 16} + 2015 0,5 đ
= 3.{15-16} + 2015 = 3.(-1) + 2015 = 2012 1,0 đ 1 1 1 1 2 2 2 2 2 3 4 2015 0,5đ c. C = 1+ 1+ 1+ ... 1+ = . . ...
1.3 2.4 3.5 2014.2016 1.3 2.4 3.5 2014.2016 (2.3.4...2015).(2.3.4...2015) 1 = (1.2.3...2014).(3.4.5...2016) (4,5 đ) 0,5 đ 2015.2 = 2015 = 2016 1008 0,5 đ x − 3 =12 x =15 1.0 đ
a. Biến đổi được: (x - 3)2 = 144 2 2 =12 = ( 1 − 2) x − 3 = 1 − 2 x = 9 −
Vì x là số tự nhiên nên x = -9 (loại). Vậy x = 15 0.5 đ
b. Do A = x183y chia cho 2 và 5 đều dư 1 nên y = 1. Ta có A = x1831 0,5 đ
Vì A = x1831 chia cho 9 dư 1 x1831 - 1 9 x1830 9 0,5 đ 2
x + 1 + 8 + 3 + 0 9 x + 3 9, mà x là chữ số nên x = 6 (4,0 đ) Vậy x = 6; y = 1 0,5 đ
c. Xét số nguyên tố p khi chia cho 3.Ta có: p = 3k + 1 hoặc p = 3k + 2 ( kN*) 0.25đ
Nếu p = 3k + 1 thì p2 - 1 = (3k + 1)2 -1 = 9k2 + 6k chia hết cho 3 0.25đ
Nếu p = 3k + 2 thì p2 - 1 = (3k + 2)2 -1 = 9k2 + 12k chia hết cho 3 0.25đ
Vậy p2 - 1 chia hết cho 3. 0.25đ 3
a. Để B nhận giá trị nguyên thì n - 3 phải là ước của 5 0,5 đ
(4,5 đ) => n - 3 {-1; 1; -5; 5} => n{ -2 ; 2; 4; 8} 0,75 đ
Đối chiếu đ/k ta được n{ -2 ; 2; 4; 8} 0,25 đ
b. Với x = 2, ta có: 22 + 117 = y2 y2 = 121 y = 11 (là số nguyên tố) 0,5 đ
* Với x > 2, mà x là số nguyên tố nên x lẻ y2 = x2 + 117 là số chẵn => y là số chẵn 0,5 đ
kết hợp với y là số nguyên tố nên y = 2 (loại) 0,25 đ Vậy x = 2; y = 11. 0,25 đ
c. Ta có: 1030 = 100010 và 2100 = 102410. Suy ra : 1030 < 2100 (1) 0,5đ
Lại có: 2100= 231.263.26 = 231.5127.64 và 1031=231.528.53=231.6257.125 0,5đ
Nên: 2100< 1031 (2). Từ (1) và(2) suy ra số 2100 viết trong hệ thập phân có 31 0,5đ chữ số . 0,5 đ 4 (5,0 đ)
a) Vì D thuộc đoạn thẳng AC nên D nằm giữa A và C
=> AC = AD + CD = 4 + 3 = 7 cm 0,5 đ 0,5 đ
b) Chứng minh tia BD nằm giữa hai tia BA và BC ta có đẳng thức: 0,5 đ
ABC = ABD + DBC => DBC = ABC − ABD = 550 – 300 = 250 1,0 đ
c) Xét hai trường hợp:
- Trường hợp 1: Tia Bz và BD nằm về hai phía nửa mặt phẳng có bờ là AB nên 0,5 đ
tia BA nằm giữa hai tia Bz và BD Tính được 0
ABz = 90 − ABD = 0 0 0 90 − 30 = 60 0,5 đ
- Trường hợp 2: Tia Bz, và BD nằm về cùng nửa mặt phẳng có bờ là AB nên tia 0,5 đ
BD nằm giữa hai tia Bz và BA Tính được ,
ABz = 900 + ABD = 0 0 0 90 + 30 = 120 0,5đ
a. Ta có: abbc = ab ac 7 (1) 0,25 đ
100. ab + bc = 7. ab . ac ab (7. ac - 100) = bc bc bc 7. ac - 100 = Vì 0 <
< 10 nên 0 < 7. ac - 100 < 10 ab ab 5 100 110 0,25 đ (2,0 đ) 14 ac 16 100 < 7. ac < 110 . Vậy ac = 15 7 7
thay vào (1) được 1bb5 =1b 15 7 1005 + 110b = 1050 + 105.b 0,25 đ
5b = 45 b =9 Vậy a = 1; b = 9; c = 5 0,25 đ
b) Vì 2012 ; 92 đều là bội của 4 nên 2015 2012 và 94 92 cũng là bội của 4 0,25 đ 2015 = m( * m N ) 96 = n ( * 2012 4. ;92 4. n N ) 2015 94 m n Khi đó 2012 92 4m 4 − = − n = ( 4 ) −( 4 7 3 7 3 7 3 ) = (... ) 1 − (... ) 1 = ...0 0,25 đ 2015 94 2015 94 tức là 2012 92 7
− 3 có tận cùng bằng 0 hay 2012 92 7 − 3 10 0,25 đ 2015 94 2015 94 Dễ thấy 2012 92 7 − 3 > 0 mà 2012 92 7 − 3 10 suy ra 2015 94 1 2012 92 A = (7
− 3 ) = 5.k; k N . Suy ra A là số tự nhiên chia hết cho 5. 2 0,25 đ
Tham khảo đề thi HSG lớp 6:
https://vndoc.com/thi -hoc-sinh-gioi-lop-6




