Tuyển tập hệ phương trình – Mẫn Ngọc Quang

Tài liệu gồm 126 trang hướng dẫn giải chi tiết các bài toán hệ phương trình với đầy đủ các dạng toán thương gặp trong chương trình Toán 10.

Các bài toán được phân dạng dựa theo phương pháp giải, bao gồm 3 dạng sau:
1. Giải hệ phương trình bằng phương pháp hàm số
2. Phương pháp nhân liên hợp
3. Phương pháp đặt ẩn phụ

50 25 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

GIẢI HPT – PHƯƠNG PHÁP HÀM SỐ

Bài 1: Gi

ải hệ phương trình

10 6 5 4

2 2

5 2 1 6

x x y x

x y



  





   





(

,x y  

)

Bài giải:

Điều kiện:

2 1 0

y y

   

- Xét

x=0, từ pt đầu suy ra y=0, thay x=y=0 vào pt thứ hai không thỏa mãn (loại)

- Xét



, chia

2 vế của pt đầu cho



, ta đư

ợc

2 2

y y

x x

æ ö æ ö

  

ç ÷ ç ÷

è ø è ø

(1)

Xét hàm số

 

2 ,f t t

t t

   

. Ta có

 

' 4

5 2 0,f

t t t

   





Vậy hàm số

 

2f t t t 

đồng biến trên



. Do đó (1

)

x y x

   

. Thay và

o pt thứ

2 của hệ ta được:

5 2 1 6

y y

   

(2)

Xét hàm số

( ) 5 2

g y y y

   

  -

Ta có

1 1 1

( ) 0,

2 5 2 1

y y

     -

 

. Vậy g(y) đồng biến trên khoảng

;

æ ö

- 

ç ÷

è ø

Mà g(4)=6 nên (2)

 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Suy ra

y x





  







hoặc

 -









Bài 2: Gi

ải hệ phương trình

 





 





 

3 2

2 2

( 1) 1

3 2 9 3

4 2 1 1 0 2

xy x x y

x y

y x y x x



    -





       





Bài giải:

Biến đổi PT

 

(1) 1 0

y x

x y x

y x





 - - 

 



 



x = y thế vào PT (2) ta được:





 





   

 





   

2 2

3 2 9 3

4 2 1 1 0

2 1 2 1

3 2 ( 3 ) 2 ( 3 ) 3

2 1 3

x x

x x x

x x x x

f x f x

       

   

  -  - 

   -

Xét





( ) 3 2

f t t t

  

có

'( ) 0

, .

f t t 

f là hàm số đồng biến nên:

1 1

2 1 3

5 5

x x x y

 - 

 -   -



y x

 

thế vào

(2)





 





2 2 2 2

3( 1)

2 9 3 4 1 2 1 1 0

x x x x x

   

     

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Vế trái luôn dương, PT vô nghiệm.

Vậy hệ có nghiệm duy nhất:

1 1

; .

5 5

æ ö

- -

ç ÷

è ø

Bài 3: Gi

ải hệ phương trình sau .

 

3 3

3 2

3( ) 6

( 2) 14 1

27 27 20 4

4. 2 1 2

x y x y

y y

x x x y x



    - 





     -





Bài giả

Phương

trình (1) 141563

233

-- yyyxx

   

yyxx -- 2323

Xét hàm số

tttf 3)(



liên t

ục trên R.

Ta có

033)('

 ttf

với

 





hàm số đồng bi

ến trên R.

xyyxyfxfpt

---

22)2()(:

Thế

y = 2-x vào phương trình (2) ta được.

 

141)13(41314420227  xxxxxxxx

Xét hàm số: tttg 4)(

 liên tục trên R.

Ta có

043)('

 ttg



hàm số đồng biến trên R.

Suy ra:

1192727113)1()13(

 xxxxxxxgxg

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI













)(082727

082727

vnxx

xxx

Vậy hệ

phương trình có nghiệm (x;y)=(0;2)

Bài 4: Giải hệ phương trình

 

1 ( 1)(

2) 5 2 2

( 8)( 1)

( 2) 1 3

4 7

x x y x y y

x y

y x

x x



   -     -







- 

 -  -



- 





Bài giả

Điều kiện:

Xét phương trình:

Đặt ta đượ

c phương trình:

Từ phương

trình

ta c

thay vào phương t

rình

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

được

Tiếp tục giải phương trình

Xét hàm số

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Do đó hàm số đồng biến trên

Từ

Giải phương trình

+) Với

Vậy hệ phương t

rình đã cho có nghiệm là:

Bài 5 : G

iải hệ phương trình









 

2 2

2 3

4 1 2 1

( ; )

12 10 2 2 1 2

x x y y

x y

y y x



    









-   





Bài giải:

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Ta có:

2 2

(1) 4 ( 2 ) 4 ( 2 ) (*)

x x y y    -   -

Xét hàm số

đặc trưng

2 2 2

( ) 4 '

( ) 1 0.

4 4 4

t t

t t t

f t t t f t

t t t



 

   

    

  

Suy ra f(t) là hàm số đồng biến trên R. Từ (*) suy ra:

( ) ( 2

) 2

f x f y

x y

 -  

Thay v

ào phương trình (2) ta được:

   

 

32 3

33 3

3 5 2 2

1 2 1 1

2 1 (**)

x x x

x x

   

       

Xét hàm số

( ) 2g t t t 

ta thấy

g(t) đồng biến trên R nên từ (**) suy ra

3 3

1 1

x x





   



 -



. Vậy hệ

có hai nghiệm là

( 1; );

(0;0)

Bài 6: Gi

ải hệ phương trình:

   

 

1 1 1

( , )

2 5 1 2

2 4 2 2

y y y x

x y

x x x x y



    









 -    - 





Bài giải:

Đk:

2 4 2 0

x y

-  

Ta có:

 





1 2 4 2

x y y y

 -  

  thế vào PT (2) ta được

   





1 1 4 2

x x y y

-  - 

  

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

1 1

1 1 (*)

2 2

x x

y y

æ ö

     

ç ÷

è ø

(vì

1 0

y y y y

   



)

Xét hàm

số

 

f t t t

  

trên



 

2 2

' 1 0,

1 1

t t

f t t

t t

 

   

 

 



, do

1 0,t t t t t

      

 

f t



đồng biến

trên



, theo (*

) ta có

 

f f y

æ ö



ç ÷

è ø

2 1x y  

Với

2 1x y 

thay v

ào (1) ta có:





2 2 2

3 5

1 4 1 2

1 2

4 2

y y y y

y y y x

   

      -    

Vậy hệ

có nghiệm

 

5 3

; ;

2 4

x y

æ ö



ç ÷

è ø

Bài 7: Gi

ải hệ phương trình

 

2 2. 2

8 4

2 11 12

7 3 0

x y y x

y x

xy x x y x



-    





 -  -

  - 





Bài giả

Điều kiện

2 , 0

x y

  

Ta có

4 8

2 2. 4( 2)

x y

x y x y

- 

-  - 

. Dấu

“=” xẩy ra khi y=4x–8

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

   

4 8

2 8 8 4

x y

y x y

 

   

. Dấu

“=” xẩy ra khi y=4x–8

Suy ra

 

2 2. 2

8 4

x y y x

y x

-   



. Dấu

“=” xẩy ra khi y=4x–8

Như vậy, pt(1)



y = 4x –

8. Thế vào pt(2) ta có:

 

   

 

   

 

2 2

4 6 11 4

3 7 3 0

4 3 4 3 1 7 3 2 0

3 3

4 3 0 do

4 3 1 7

3 2

1 1

3 4 0

4 3 1 7 3 2

3 0 ( )

1 1

4 (3)

4 3 1 7 3 2

x x x x

x x x x x x

x x x x

x x x

x x x x

x x

x x x x

x x

x x x x

- -    - 

 - -   - -  - -  

- - - -

æ ö

 

 - - - - 



ç ÷

 

   -

 -

 

è ø

 

 - -

- - 

 

   -  -

 



- -  







 



   -  -



1 13 1 13

( ) 3 0

2 2

pt x x x x

 -

  - -     

Đối chiếu điều

kiện ta có

1 13





Hệ có nghiệ

1 13

;2 13 6

æ ö



ç ÷

è ø

+ Xét pt(3)

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

7 1 1

2; 4 3 1 3 10 6

3 6

4 3 1

x x x

 

          

 

  





Xét hàm số

2; : (

) 7 3 2

x g x x x

 ö

   - 



 ø

3 2 7 3

'( ) 1 0

2 7 3 2 7 3

g x

x x

- -

  -   

- -

7 1 1

( ) 3

3 3

7 3 2

x g

x x

æ ö

    

ç ÷

-  -

. Do

đó,

 

 

 

 

1 1 1

3 4

4 3 1 7

3 2x x x x

   

   -

 -

hay pt(

3) vô nghiệm

Vậy, hệ có nghiệm duy nhất

1 13

;2 13 6

æ ö



ç ÷

è ø

Bài 8: Gi

ải hệ phương trình

   

 

3 2 3

2 4 3 1 2 2 3 2 1

2 14 3 2

1 2

x x x x y y

x x y



-  -  - -





  - - 





Bài giả

Ta thấy



không phả

i là nghiệm của hệ, chia cả hai vế của (1) cho

ta được

   

2 3

4 3 1

1 2 2 2 3

y y

x x x

 -  -

 - -

   

1 1

1 1 3 2 3 2 3 2 *

y y y

x x

æ ö æ ö

 -  -  - -  -

ç ÷ ç ÷

è ø è ø

Xét hàm

 

f t t t 

luôn đồng

biến trên



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

   

* 1 3 2

 -  -

Thế

(3) vào (2) ta được

3 3

2 15 1 2

3 2 15 0

x x x x

  - 

  -  - - 

 

3 3

1 1

7 0

2 3

4 2 15

x x



æ ö

ç ÷

 -  

ç ÷

 

-  



ç ÷

è ø





Vậy hệ

đã cho có nghiệm

 

111

; 7; .

x y

æ ö



ç ÷

è ø

Bài 9: Gi

ải hệ phương trình

2 6 1

(1)

9 1 9 0

(2)

x y y

x xy



   -





   





Bài giả

Đk:

6 0

x y

  





 -



+) Nếu

0y 

, để

hệ có nghiệm thì

1 0y 

(1) 2

6 2 5

(1) (

(1) 1

VT x y

VT VP

VP y



  





 



 - 





hệ vô nghiệm

+) Nếu y < 0, từ (2) suy ra x > 0

   

3 3

9 1 9 0

9 9 (3)

x xy y y y

æ ö æ ö

       -  -

ç ÷ ç ÷

è ø è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Xét hàm số

9 2

( ) 9 , 0; '( ) 0 0

f t t t

t f t t



      



3 3 9

(3) ( )f

f y y x

x x

æ ö

 

-   -  

ç ÷

è ø

Thế vào pt(1)

ta có phương trình

2 6 1

y y

   -

(4). H

àm số

( ) 2 6

g y y

  

đồng

biến trên

 

;0-

; hàm số h(y) = 1 – y nghịch biến trên

 

;0-

và phương trình có ngiệm y = –3

nên pt(4) có nghiệm duy nhất y = –3. Vậy, hệ có nghiệm duy nhất (1; –3).

Bài 10: Gi

ải hệ phương trình :

 

2 2

1 2 1 3 1

3 3 7 2

y y x x

xy y

x y y x



-      





   - 





Bài giả

Đk:

1, 0, 3y x y x  

Từ pt (2) ta có :

 

1 2 1 0

y x y x

y x

æ ö

- -  - 



ç ÷

- 

è ø

Suy ra, y = x

+ 1

Thay vào pt (1) ta được

2 2

1 1 7 3

x x x x

 - -   -

Xét hàm số

2 2

( ) 1 1f x x x

x x

   -

- 

Chứng minh hà

m số đồng biến

Ta có nghiệm duy nhất x = 2

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Vậy nghiệm của hệ là (2;3)

Bài 11: Gi

ải hệ phương trình:

 

    

 

3 3 3 1

2 1 1

3 1 1 2

3 1 2 2

x xy x

y x y y

x y y x x x



         





-   - -   -





Bài giả

Pt(1)

  

3 3 1 2

1 1

x x y x

y y

   

  -   

Đặt

 

, 0 ,(

a x

a b

b y













 





trở thành:

2 2

2 0

2 1 0

a b

a b ab

a b





-   -  



  



2 1 0

a b

  

vô nghiệ

m do

, 0

a b



+ Xét a

= b

y x

  

thay v

ào (2) ta được:

    

 

3 3 1 2

x 3 1 2

x x x x x

-   

-   -

    

 

3 3 1 2

x 3 .

1 2

x x x x

 -  

 - 

 

 

3 5( )

3 1 2 1

2x 3 *

x y tm

x x x

  







     - 





(*)

   

1 2 1 2 1 2 1 2

x x x x

 

      -  - 

 

 

 

 

Xét hàm số

   

 

2 2

f t t t

  

0t 

có

 

' 0f t t

  

Suy ra

 

f t

đồng biến mà

 

1 1 1 1f x f x

x x

  - 

  -

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 5

3x 0

x y





   





- 



Vậy hpt c

ó nghiệm:

 

3;5

Bài 12: Gi

ải hệ phương trình:

 

  

 

8 2 1 2 2 1 2 4 1

4 2 2 2

5 12 6 2

x x x y y y

xy y y x y x



- - -  - 







     -



Bài giả

ĐK:

  

2 2 0

y y x











  



. Từ

pt (1)



dể pt có nghiệ

m thì

0y 

 

     

3 2

1 2 2 1

2 2 2 1 4 2 2 1 2 4

x x x y y

 - - -

 -  - 

(*)

Xét hàm số

   

3 2

2 4 0

f t t t t t

 -  

có

   

2 2

3 4 4 2

2 0 0

f t t t

t t t



 -  

 -   

nên f(

luôn đồng biến

Từ pt (*)

 

2 2 1 2

2 1

f x f y

x y

 -  

- 

Thay vào pt ( 2 ) ta được pt

   

2 2 2 3 2

y y y y y

    

Đặt

z y

 

ta được pt

 

 -

  

-  -  









3 3 2 2 2

2 3 2 0

y z loaïi

y z yz y

z y yz z

y z t m

Với y = z

ta được

2 2 1

( / )

y y y x

t m

   

 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 13: Giải hệ phương trình:

   

 

2 2 2 2

3 2 2

2 2

2 1

x x

y x x y

x y

x x y x y

x x



-   -







 -   





 









Bài giả

ĐK:

x y

 

Từ PT(1) tìm được

2 2 2

x x y x

x y

 -  

Thế

vào (2) đưa về pt chỉ có ẩn x

Đưa được về hàm

1 1 2 2

1 1 1 1

x x x x

æ ö

   

  

ç ÷

è ø

Xét hàm

 

f t t t 

đồng bi

ến trên



từ đó được

1 2

1 1

x x

  

giải đư

ợc

   

5 1 5 1

2 2

x L x N

 -

 - 

Nghiệm

5 -1

;  5 - 2

Bài 14: Gi

ải hệ phương trình

  

 

2 2 2 2 3

1 3 2 4

1 1 8 1

2 0

x x y y

x y

x y x



 -    







-  



Bài giả

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

+) Với



thì

   

1 0, 1

VT VP

 

 Hệ phươ

ng trình chỉ có nghiệm (x;y) với



+) vì



nên từ

phương trình (2) của hệ suy ra



Khi đó

 

2 2 2 2

1 1 3 2

2 4 1 1

x x y x

y y

  - 

  -

 

2 2 2 2

1 2 2 4

1 3

x x y y

x y     

Thay

x x y

 -

vào phương trình (3) ta được:

2 2 2 2

1 2 4 1

x x x y

y x y

   



1 1 1

1 2 4 1

y y y

x x x

   

 

+) xét

hàm số:

 

f t t t t  

với

0t 

 

' 1 1 0

f t t

   





với mọi

0t 

 f(t) là hàm đồng bi

ến trên

 



. Mà

 

1 1 1

2 2

f f y y

æ ö

   



ç ÷

è ø

+) Thay



vào phương tr

ình (2) của hệ ta có:

x y

  

Thử lại th

ấy















thỏa mãn

hệ phương trình đã cho.

Kết luận: Hệ phương trình đã cho có nghiệm duy nhất

 

; 4;

x y

æ ö



ç ÷

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 15:

Giải hệ phương trình

   

 

3 2 2

3 4 22

21 2 1 2 1 1

2 11 9 2 2

y y y x x x x

x y

x x y



   -    -







-  







Bài giả

Điều kiện:

 

1/ 2 *

x 

Lấy phư

ơng trình (1) trừ phương trình (2) nhân với 2 ta được:

   

3 2 3 2

3 3 2 1

2 1 4 3 5 3 2 1 2 1

y y y x

x y y y y x x

   

 - -       -

 

3 2

3 3 1 2

2 2 1 2 2 1

y y y y

x x

   

   -  -

   

 

1 2 1 2

1 2 2 1 3

y y x x

    -  -

Xét hàm số:

 

f 2t t t 

với



Ta có

 

f 3 2 0

t t

  

với

 

ft t

  



đồng biến

trên



Do đó:

   

 

3 f 1 f

2 1 1 2 1 2 1 1

y x y x

y x

   -

   -   - -

Thay vào (2)

ta được:

2 2

2 11 9 2

2 1 2 2 2 1 2 11 11

x x x x x

-   -

-  -  - 

 

2 11 11 0

4 2 1 2

11 11 4

x x

x x x



-  







-  - 





 

4 2 3 2

4 8 4 4 121 121 44 44 242x x x x x x

 -    -  -

 

4 3 2 3 2

4 44 1

65 250 125 0 1 4 40 125 125 0

x x x x x

x x x

 -  -

   - -  - 

  

 

1 5 4 2

0 25 0

x x x x

 - - -

 

   

 

   

 

   

 

1 * ,

1 0

5 * ,

5 2

5 / 2

* , **

x tm

x y

x tm

x y

x ktm







  



  



  











Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Vậy tập nghiệm của hệ phương trình đã cho là

     

 

; 1;0

, 5;2

x y 

Bài 16: Giải hệ phương trình:

 

4 2 2 2

3 2 2

3 2

2 5 2 1

x x y y y x y x

x y

y x



 -   



- - -







Bài giả

Điều kiện:

x 

Phương

trình (1)

  

2 2 2

1 0 0

x y x y

x y

 - - 

   

hoặc

1x y 

Trường hợp

x y

 

thế v

ào (2) không thoả mãn.

Trường hợp

1x y 

thế vào (2):

2 3 2 1 0 (3)

y y- - - 

Xét hàm

   

2 3 2 1; ; ; ` 1 0

f t t t

t ma f

æ 

 - - - - 



è 



Suy ra phương

trình (3) có nghiệm duy nhất:

1y 

. Với

1 2 2

y x x     

(thoả đi

ều

kiện)

Vậy nghiệm của hệ phương trình là:

   

2;1 ; 2;1

Bài 17: Giải hệ phương trình:

2 2

2 2 2 2

2 2 2 0

x x x y

y y

x y x y



   

  





 -  -







Bài giả

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Điều kiện:

x y

 -  -

Phương trì

nh thứ hai của hệ tương đương với

2 2 2

x y x y

 -  - 

Thế vào phươn

g trình thứ nhất, ta được

2 2 2

( 2 2 2

) 2 2 2 1

x y x y

x x y y y

 -  -

       

2 2

3 2 2 4 2 2 1x x x y y y        

2 2

( 1) (

1) ( 1) 1 (2 ) 2 2 1

x x x y

y y

   

      

(1)

Xét hàm s

ố

( ) 1f t t t t   

với

 -

Ta có

 

1 1 3

'( ) 2

1 ; ''( ) 2 ; ''( ) 0

2 1

4 1

f t

t f t f t t

    - 

  -



Suy

3 1

'( ) '

4 2

f t f

  

ç ÷

è ø

với mọi

 

1;t

 - 

. Do

đó hàm f(t) đồng biến trên

[ 1; )- 

Suy

ra phương trình (1)

( 1) f(2 y) 1 2 2 1f x x y x y        -

Thế vào pt thứ

hai của hệ, ta

được

 

2 2

2 1 2 2(2 1) 2 0 6 7 1 0

y y y y y y







-  - -

 -   -   







Suy

ra nghiệm (x;y) của hệ là (1;1),

2 1

;

3 6

æ ö

ç ÷

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 18: Giả

i hệ phương trình :









2 2

2 3 3

4 1 2

12 10 2 2

x x y y

y y x



   







-   





Bài giả

Phương trình đầu ên của hệ tương đương với:

   

4 2 4 2x x y y

   -

  -

   

2f x f y

  -

với

 

4y f t t

   

Ta có

   

2 2 2

' 1 0,

4 4

t t

t t t

f t t f t

t t t



 

      

  

là hàm số đồng biết trên R.

Từ đó

   

2 2f x f y

x y

 -  

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Thế

2x y -

vào ph

ương trình sau của hệ phương trình đã cho ta được

   

 





2 3 3

3 3 3

3 5 2 2 1

1 2 1 1

2 1

1 1

x x x

g x g x

   

   

   

  

với

 

2y g t t

  

Ta có

   

' 3 2 0

g t t t

g t

   



là hàm số

đồng biến trên R. Từ đó:

 

3 3

1 1

3 3 0

1 2

0 0

g x g x

x x

x y

  

   

  

 -  





  





Vậy nghi

ệm của hệ phương trình đã cho là:(-1;2),(0;0)

Bài 19: Giả

i hệ phương trình

   

 

2 2 2 1

3 1

5 5 6 2

x x y y

xy x y



 -  



-   -



Bài giả

 Đk

   

 

3 3

, 1 2 1 2 1 3 2 1 3 2 1 3 ;

x x x y y x x y y

  - -    -  -  

ét hàm số

     

3 ' 2

3 , ´ 3

3 0

f t t t

trên co f t t t f t

    

 



đồng

biến tr

ên



,pt(1) trở thành

 

2 1 2 1f y f x y x -   -

;

 Pt(2)

  

5 1 0 5

; 1;

y y x y

y x

  - 

   -  -

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 Với

5 2 1 5

y x

 -  -

 -

vô ng

hiệm

Với

 

1 2 1 1 2 2

2 1 1

y x

x x x

x x





 -  -  -    



-  -



Với

2 2 1 2

x y  

 

nghiệm của hệ

là

 

; 2 2;1

x y   

Bài 20: Giả

i hệ phương trình:

3 2

3 2 3

2 5 3 3 10

6 13 10

x y x y x x y

x x x y y



  - -

-  - - 





-   







Bài giả

Phương trình thứ 2 của hệ được biến đổi thành:

     

2 2 *x x y y

-  -  

Xét h

àm số

 

f t t t 

là hàm số

đồng biến trên R. Ta suy ra (*)

y x

  -

Thế vào ph

ương trình đầu của hệ:

3 3

3 3 5 2

3 10 26

x x x x

 - - 

- - 

   

 

3 2

2 2

3 3 3 1

5 2 3 10 24

3 2 2 2

2 12 12

3 3 3 1

5 2 1 5 2

3 3 3

x x x x x

x x

x x x x x

x x x

  -  - -  - - 





- -



   - - -    - -



   -  -



 



Phương t

rình (1) vô nghiệm vì với

-  

thì

12 0.

x x

- - 

Từ đó suy ra hệ có nghiệm duy nhất



2; 0

x y

 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 21: Giải hệ phương trình

3 2 2 3

3 2

2 2 2 0(

6 5 3 2 3(2)

x xy x

y y x y

y x x y



 - -  - 





    -





Bài giả

3 2 2 3

(1) (

2 ) ( 2 ) ( 2 ) 0

x x y x

y y x y

 -  -

 - 

2 2

( 2 ) (

2 ) ( 2 ) 0

x x y y

x y x y

 -  -

 - 

2 2

( 1)( 2

) 0 2

x y x y

y x

   -

  

( Vì

2 2

1 0, ,

x y x y

   



Thay

vào (2), ta có:

3 2

3 5 3 2 3x x x y    -

3 5 3 5 ( 1) ( 1)

x x x x

       

(*)

Xét hàm s

ố

3 2

( ) , '

( ) 3 1 0,

f t t t

R f t t t R

   

    

. Suy ra hàm s

ố f(t) đồng biến trên

(*)

 

3 5 ( 1)

f x f x

   

3 5 1x x   

3 2

3 4 0

x x

  - 

2 1

x y



  







 -  



Vậy hệ phương trình có hai nghiệm:

æ ö

ç ÷

è ø

;

(-2;-1).

Bài 22: Gi

ải hệ phương trình

3 2 3

3 2 8 2

10 3 12(1)

5 2 8 6 2 (2)

y x x y

y x y xy x



    - 





- -   -





Bài giả

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 2 3

3 2 8 2

10 3 12(1)

5 2 8 6

2 (2)

y x x y

y x y xy x



    - 





- -   -





Điều kiện: x

[-2;2]

Nhậ

n xét y = 0 không thỏa mãn phương trình (2)

(2)

 

2 2

2 3 2 3x x

y y

æ ö æ ö

 -  -

 

ç ÷ ç ÷

è ø è ø

(*)

Xét hàm s

ố

( ) 3f t t t 

trên R



hàm s

ố đồng biến trên R

(*)

 

2 2

2 2f x f x

y y

æ ö

 -  

- 

ç ÷

è ø

hế vào (1)

(1)

3 2 8 2 10 3 12

y x x y xy

     - 

3 2 4 2 2 10 3 6 2

x x x y x x    -  -  -

3 2 6 2

4 4 3 10 0

x x x x

  - -

 -  - 

(**)

Đặt

2 2

2 2 2 10

3 4 4

x x t t

x x

 - - 

  - - -

Phương trì

nh (**) trở thành

3 0

t t





-  







- với t = 0:

; 5

x y 

- với t = 3:

2 2 2 3

x x

 - - 

phương

trình vô nghiệm, vì vế trái

2

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 23: Gi

ải hệ phương trình

2 2 2

4 ( 2)2

3 0

log (

) log .log 0

xy xy

y x y



 -  -





-  



Bài giả

Điều kiện: x > y > 0

Đặt t = xy > 0, phương trính thứ nhất của hệ trở thành

4 ( 2)2

3 0 (2 1)(2 3) 0 2 3 0

t t t t t

t t t t

 -  -

    -    - 

, vì

2 1 0

 

Vì hàm

( ) 2 3

f t t  -

đồng biến trên

R, mà f(1) = 0 nên

2 3 0

 - 

1t 

. Khi đó

ta có

xy = 1, hay



Thế vào pt thứ

hai của hệ ta được:

2 2 2

2 2 2 2

1 1 1

log log

0 log log

x x

x x x

æ ö

-    

ç ÷

è ø

2 2

1 1

log l

1 1

1 1 1

log

x x

x x x

 

- -

 

 





 

    



- 

- -

 



 - 

 

 

Suy

ra hệ của nghiệm là

x 

y 

Bài 24:

Giải hệ phương trình Giải hệ phương trình:

 

2 2

4 4 2 2 0

8 1 2 9 0

x xy y x y

x y



    - 







-  - 







Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài giải:

Xét hệ phương trình:

 

2 2

4 4 2 2 0 1

8 1 2 9

0 2

x xy y x y

x y



    - 





-  - 





Điều kiện

1-2x 0 x

  

. Đặt

t x y 

, phương

trình (1) trở thành:

2 0

t t





 -  



 -



Nếu t =

1 thì

2 1 1 2

x y x y

   -

 

. Thế

vào phương trình (2) ta được phương trình

8 9 0

y y

 - 

Đặt

u y

 

, phương trình

trở thành:

 

4 3 2

8 9 0 1 9

0 1

u u u u

u u u

 -  

-      

. Khi đó

hệ có nghiệm











Nếu t =

-2 thì

2 2 1 2

3 0

x y x y

  - 

-   

. Thế v

ào phương trình (2) ta được phương trình

  

 

8 3 9 0

8 3 3 3 0

8 3 3 0

y y y y y

 -



  -     -   



 -  





Với

 -

thì hệ có ng

hiệm











 -



Xét phương trình

   

8 3 3 0

y y - 



Đặt

3 0

v y

  

, phương

trình (3) trở thành:

6 8 0

v v

-  

Xét hàm số

 

6 8f v v v - 

, ta c

ó:

 

' 3 6

f v v

 -

và

 

' 0 2

f v v

   

Hàm số

 

f v

đạt cực đại

tại

 

2;8 4

-  , đạt cự

c tiểu tại

 

2;8 4

Vì

 

0 8 0

 

và

8 4 2 0- 

nên

 

f v



không có nghiệm



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Vậy hệ phương trình có hai nghiệm là

;









 







 -



Bài 25: Giả

i hệ phương trình

 

4 2

3 2 3

2 4 0

;

3 4

2 4 1

y x y x

x y

x x x y y



- - - - 







    -







Bài giả

Phương trình thứ hai của hệ tương đương với

   

3 3

1 1 2 2x x y y   



(1)

Xét hàm số

 

f t t t 

với



Ta có

   

' 3 , '

f t t t

f t

  

với mọi



. Do đó hàm f(t) đồng biến trên R. Khi đó

phương trình

     

1 1 2 1

2 2 1

f x f y

x y x y

   

    -

Thay vào phương t

rình thứ nhất của hệ ta được

4 3 2

2 3 2 3 0

y y y y

-  - - 

   

2 2

1 5

2 3 0

y y

y y y

y y



- 



 -  - -    



-  -



Suy ra nghiệm (x; y) của hệ là

1 5

æ ö

ç ÷

è ø

và

1 5

æ ö



ç ÷

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 26: Giải hệ phương trình

 

3 2

2 2

4 1 2 3 1

2 4 1 1

x y x y

y x x



  





    





Bài giả

Điều kiện:



 

2 2

1 4 1 2

3 0

PT x x

y y x

 

   

 

 

Khi đó,

   

2 2

2 2 4 1

1 3

PT y y

x x     

Xét hà

 

f t t t

  

trên







Có

   

' 1 0 0

f t t f t

   

 



đồng biế

n trên

 



Khi đó,

     

3 2 2

PT f y f x y x   

Thay v

ào phương trình (1) ta được phương trình:

5 3

x x x x

  

Đặt

t x

 

có hàm s

ố

 

10 6 3

g t t t

  

có

 

9 5 2

' 10 6

3 0

g t t t

   

0t 

Mà

 

1 3 1 1

g t x x   

  

Với

x y

  

. Hệ phươ

ng phương trình có nghiệm duy nhất

 

; 1;

x y

æ ö



ç ÷

è ø

Bài 27: Gi

ải hệ phương trình:

 

3 3 2 2

5 2 10 3

6 0 1

2 4 4 2 2

x y x y

x y

x y x y x y



-  -  -  





  -   - -





Bài giả

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Điều kiện

2; 4

x y

 - 

3 2 3 2

(1) 5

10 6 2 3

( 1) 2(

1) 3( 1) 2 3

x x x y

y y

x x x y

y y

   

  

   

    

Xét hàm

số

3 2 2

( ) 2 3

, '( ) 3 4 3 0

f t t t

t f t t t t R

   

    

Suy ra

( 1) (

) 1

f x f y

y x

   



thay vào pt (2) ta được

Phương trình

3 2

2 3 4 1x x x x

  - 

 - -

 

 

  

3 2 2

2 ( 2)(3

) 2

2 3 3 4

4 ( 1)( 4)

2 3 3

2 (

2)(3 ) 4

( 2)( 2)

2 3 3 ( 2)(3 ) 2

2( 2)

( 2)( 2) 0

2 3 3 ( 2)(3 ) 2

x x

x x x x x x x

x x

x x x

x x x x

x x

x x x

x x x x

 - -

   -

-   - -    -

  - 



- -

   - -

  -   - 

-  

 -  - - 

  -   - 

  

( 2) 2 0

2 3 3 (

2)(3 ) 2

x x x

x x x x

 

 

 - - 

 

 

  -   - 

 

0 (

vi x

  -

2 0

x x





 - - 





 -



Vậy hệ

phương trình có nghiệm:

( ; ) (2;3), ( ; ) ( 1;0)

x y x y

  -

Bài 28:

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Giải hệ phương trì

nh Giải hệ PT

 





 





 

3 2

2 2

, , y

3 2

9 3 4 2 1 1 0

xy x x y x y

y x y x x



    -







       







Bài giả

ĐKXĐ

 

Ta có

 

3 3 3 2 2

1 0

xy x x

y x y x x y y xy x y

   

-  -  -  - 

 

0 1 0

y x

x y x

y x





 -   



 



 

   

 

3x 2 9 3

2 1 3 2 1 2

x x x

   

-    

 

   

 

3 2 9 3

2 1 3 2 1 2

x x x x

   

-   - - 

Xét hàm số

 





2 2

f t t t

  

ta có

 

' 2 2 0

f t t

   





suy ra hàm số

đồng biến

Từ đó suy ra

3 2 1

x x x

 - - 

 -

. Vậy HPT có nghiệm

 

1 1

; ;

5 5

x y

æ ö

 - -

ç ÷

è ø

Với

y  x

1

thay vào PT thứ 2 ta được



1





2  9x

 3







 6





1 x  x

1



 0

. Dễ thấy PT vô nghiệm.

Với

y  x

thay vào PT thứ 2 ta được



2  9x

 3







4x  2





1 x  x

1



 0

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 29: Gi

ải hệ phương trình:

  

 

1 1 2 5 2 2

8 1

2 1 3

4 7

x x y x y y

x y

y x

x x



   -     -





- 

 - 



- 



Bài giả

Điều kiện

1; 2

x y

 - 

Đặt

 

1 ; 2 ,

x a y b

a b

  - 



, từ

(1) ta có:

 

2 2 2 2 2

1 5 2 2 0

a ab a b

b a b ab b a b

  - 

    -  -  - 

  

1 2a 0

a b b

 -  



a b 

(do

, 0 1 2

a 0

a b b

   



)

1 2 3x y y x   -

  

Thế vào (2) ta

được:

  

 

     

2 2

8 4 8 4 1

1 1 3

7 4x 7

1 3

x x x x x

x x

-  -  

   -

 

-  - 

 

 

4 1

4 7

1 3

x x









 





- 



 



8 11;

x y

  

 

   

 

* 1 3 4

1 4x+7

x x x x

     -

   

     

1 3 1 3

2 3 . 2 3 **

x x x x

 





      -  -  

 

   

 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Xét hàm số

   

 

3 3

f t t t

  

với



có

   

' 3 1 0f

t t t

   





nên f(t) đ

ồng

biến trên



Do đó

 

** 1 2

1 2

1 4x 4

f x f x

x x





   -    - 



  - 



 

5 13

5x 3

x T M







  



-  



5 13 11 13

2 2

x y

 

  

Vậy hệ đã cho có nghiệm (x;y) là

 

8;11

và

5 13 11 13

;

2 2

æ ö

 

ç ÷

è ø

Bài 30: Gi

ải hệ phương trình

 

8x 2 2 2x

2 1 2x+1

8x 13 2 82x 29

y y y

y y



 -  - -





- -  -

-  -





Bài giả

Điều kiện:

2 1 0

2 0



 

 -







 

- 









Phương tr

ình

   

 

8 2 2 2 2 2 2 2

x y y y x x x y y



 -  - -    -  -

Xét hàm đặc trưng

   

3 2

,f' 3

1 0

f t t t

t t t

   

 

Hàm số f(t) liên

tục và đồng biến trên R. Suy ra:

2 2

x y

 -

Thế

2x 2

 -

vào phương tr

ình thứ hai ta được:

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

3 2

2x 1 2

x 1 8x 52x 82x 29

-   -

 -

   

 

2x 1 2x 1 2x 1 4x 24x+29

 -   - -

 

2 2

2x 1 2

x+1 4x 24x 29 0 2x 1 2x 1 4x 24x 29 0

 - - 

-   -  -  - 

2 1 0 3

2 1 4 24

29 0

x x y

x x



-   

 







 -  -







Giải phương tr

ình:

2 1 4 24

29 0

x x x

 -  -



Đặt

2 1, 0

2 1

t x t x

   

 -

Ta được phương

trình:

   

2 2 4 2

1 12 1 29 0 14 42 0

t t t t t t

- -  - -   - -  

  

 

1 29

2 3 7

1 29

t loai

t t t t

t loai







 -



 - 

- -  















Với

2 11

t x y

    

Với

1 29 13 29

103 13 29

2 4 2

t x y

  

  

 

Vậy hệ

phương trình đã cho có3cặp nghiệm:

1 3 13 29 103 13 29

;3 ; ;

11 ; ;

2 2 4 2

æ ö

 

æ ö æ ö

ç ÷

ç ÷ ç ÷

ç ÷

è ø è ø

è ø

Bài 31: Gi

ải hệ phương trình

   

 

3 2 3

2 4 3 1 2 2 3 2 1

2 14 3 2

1 2

x x x x y y

x x y



-  -  - -





  - - 





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài giải:

Ta thấy x = 0 không phải là nghiệm của hệ, chia cả hai vế của (1) cho x

ta được

   

2 3

4 3 1

1 2 2 2 3

y y

x x x

 -  -

 - -

   

1 1

1 1 3 2

3 2 3 2 *

y y y

x x

ö æ ö

 -  -  - -  -

ç ÷ ç ÷

è ø è ø

Xét hàm

 

f t t t 

luôn đồ

ng biến trên



   

* 1 3 2

 -  -

Thế (3) vào (2) ta được

3 3

2 15 1 2 3 2 15 0

x x x x

  -    -  - - 

 

3 3

1 1

7 0

2 3

4 2 15

x x



æ ö

ç ÷

 -  

ç ÷

 

- 

 

ç ÷

è ø



Vậy hệ

đã cho có nghiệm

 

111

; 7;

x y

æ ö



ç ÷

è ø

Bài 32: Giải hệ phương trình:

  

2 2 2

2 2 2 4

4 2 12 8 2

y y x x

y x x y

x x y



  - 

 





  - 

 -  -





Bài giả

+ Đk:

x y

 -









+ Từ pt thứ 2 ta có:

  

2 2 2

4 2 12 8 2

y y x y x x y  -   -  -

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

  

2 2 2

8 4 2 1

2 2 0

x y y y

x x y

   -

  -  - 

 

  

2 2 2

2 8 2 4

2 12 2 2 0

x y y y

x x y

   -

  -  - 

 





2 2

2 8 6 2 0

y y x x

  - 

  - - 

2 2

2 8 6

y y

x x y





 



   -



  -





2 0

  

+ Thay v

ào pt 1 ta được:

2 2 2 4

y y x x  - 

 

 

   -

    -   -   

3 3

3 3 3

y 2 y 2

x 4 x y 2 4 y 2 x 4 x

+ Xét hàm

số:

 

f t t

  

t R

. Ta

có:

 

' 1 0, 2

2 4

f t R f f x y x

        - 



+ Vậy ta

sẽ có:

 

2 0

y x



 



 -

 



 

 -



- 







Kl: Nghi

ệm duy nhất của hệ là:

 

: 4; 2

x y

 - -

Bài 33:

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Giải hệ phương trình

Giải hệ phương trình:

    

 

2 1 1

3 8 3

4 1 1



    











- -   





x y x y

x y

x x y

Bài giải:

Điều kiện

 -





 -



      

 

3 2

1 2 1 1 2 1

1 1

 

    

   



 

x x x

x x

y x y y y

x x

 

1 1

æ ö

     

ç ÷

 

è ø

x x

y y

x x

Xét hàm số

 

 f t t t

trên



có

 

' 3 1 0

    

f t t t

suy f(t) đồng biến trên



Nên

 

1 1

æ ö

    

ç ÷

 

è ø

x x

f f y y

x x

. Thay

vào (2) ta được

3x 8 3 4 1- -  x x x

 

2 1 2 1 -   

x x x

6 3 0

3 2 3

2 1 1

5 2 13

2 1 1 3

9 10

3 0

 









- - 

 







  -



  









  -



















- - 





x x

Ta có:

 -



Với

4 3 3

3 2 3



   x y

. Với

5 2 13 41 7

9 72

- 

   -x y

Các nghiệm này đều thỏa mãn điều kiện.

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

KL: Hệ phương trình có hai nghiệm

 

4 3 3

; 3 2 3;

æ ö



 

ç ÷

è ø

x y

 

5 2 13 41 7

; ;

9 72

æ ö

- 

 -

ç ÷

è ø

x y

Bài 34: Giả

i hệ phương trình

 

4 5

1 ln

6 2 1 2 2

x 7



 

- - 



 





    -





y y

x y

y y x

Bài giải:

Xét hệ

 

   

4 5

1 ln 1

2 2

6 2 1 2 2 7 2



 

- - 



 







   - 



y y

x y

x x

y y x x y

(Đ/K:

2 -

)

Ta có:

 

   

2 2

1 1 ln 2

2 2 ln 4 5

    

    

x x x y y

 

2 2

1 ln 1 1

2 ln 2 1 *

    

    x x y y

Xét hàm

 

ln 1 ,

   f t t t t

. Ta có

 

2 2

' 1 0

1 1



     

 

f t t R

t t

, dấu bằng

xảy ra khi và chỉ khi

1 -

Nên f(t) đ

ồng biến trên R theo (*) suy ra

   

1 2 1 2    

 

f x f y x

1  x y

Thay vào (2)

ta được

 

6 1 2 2 2

8 3

-    -

x x x x x

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Xét

1 6 1 2 2 2 3 7 2 8  -      - x x x x x x

nên (3) không có nghiệm trên





;1-

Xét

1x

, khi đó

 

4 2

10 4

6 1 2 2

2 1 1 1

2 2

 

-   

-    

x x

x x x x x

Mà

 

10 4 3

2 8 2 0

2 2

 

 -  

- 

x x

x x x

. Do đó (3)

xảy ra khi và chỉ khi x = 2.

Do đó hệ có nghiệm

   

; y 2;1

x

(thỏa

mãn điều kiện)

Bài 35: Gi

ải hệ phương trình sau trên tập số thực:

 

2 2

3 1 ( 3 3) 6 6 2 2 3 2 1

3 1 6 6 2 1 2

x x x x x x x y y

x x x y



 -  -  - -      





- - -    





Xét hàm số

( ) 1 '

( ) 1 0

2 1

f t t t

f t

   

  



suy ra hàm s

ố đồng biến

Mà

3 3

( 1) (

2) 1 2

f x f y

x y

-   

-  

.Thế vào PT

(2) ta được :

3 1 6 6

x x x x- - -  

Bài giải:

Thế

- x

- 6x  6 

y  2 1- 3 x -1

vào PT(1) ta được :

(x -1)  (x -1)

1 

y  2  y  2 1

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

2 2 2

3 1 6 6

9( 1) 2

6 6 2 6 6

(15 15 2 ) 4 ( 6 6)

( 5)( 1)(4 5) 0

x x x x

x x x x x x

x x x x x

x x x

 -   - 

 -  -

  - 

 - -  - 

 - - - 

Đối chiếu điều

kiện

5 127

4 64

5 62

x y





 







  



Vậy hệ

phương trình có hai nghiệm phân biệt

5 127

;

4 64

æ ö

ç ÷

è ø

và (5;62)

Bài 36: Giải hệ phương trình:

 

1 1

2 5 1

2 2 4 2

y y y x

x y

x x x x y



    









 -    - 





Bài giả

ĐK:

2 1 0

x y

-  

 

2 2

1 2 4 2 2 1 2 3y y y y x      

2 2 2

2 1 1 2

4 2

y y y y

x y

   

  - 





1 2 4 2

y y x y

   

- 

(2) ta có:

 

1 2 5

2 4 2

x x x

x y

-  - 

-  

 

1 2 5

x x x

y y

-  - 

   

 

1 1

2 2

x x

y y

æ ö

   

 

ç ÷

è ø

Ta có:

y y

  

 -

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

1 0 1 0

y y y y

 -  

  

1 1

2 2

x x

y y

æ ö

   

 

ç ÷

è ø

Xét hàm

 

f t t t

  

 

' 1 0

f t t

   



 

f y f

æ ö



ç ÷

è ø

2 1y x  -

thay vào (

2) ta có:

   

2 2

1 4 1 2

2 2 2 2 1 4 5

x x x x x

 -  

 -     -  

   

1 4 1 4

x x

 -  

- - 

Đặt

1x t- 

ta có:

4 4t t  -

 

2 2

4 0

8 12

4 8 16

t TM

t t t





- 







 



  



  - 







Với



3 5 3

2 2 4

x x y

 -     

Vậy

 

5 3

; y ;

2 4

æ ö



ç ÷

è ø

Bài 37:

Giải hệ phương trình

  

 

1 1 2 5 2 2

8 1

2 1 3

4 7

x x y x y y

x y

y x

x x



   -     -







- 

 - 



- 





Bài giả

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Đkxđ:







 -



        

1 1 1 2 2 2 1 2

x x y y x y

    -  - - -  -

Đặt

a,b 0

x a

y b



 







- 





      

2 2

2 1 1

a ab b

a b b b a b a b b

  - 

   -   

  

1 1 0

a b b b

 -  

 

  

2 1 0

a b a b

 -  



2 1 0

a,b 0 a+2b+1>0

a b

a b d









    



Với a = b ta

có:

1 2

x y

  -

3y x  

Thay v

ào (2) ta có:

  

 

8 1 3

1 1 3

4 7

x x

-  

   -

- 

    

 

8 4 1 1

3 4 7

x x x x

x x

 

 -  

  - - 

 

  

 

1 8 4 7

8 4

1 3

x x

 - - 

 -  



 

   

1 2 3

8 4 0

1 3

x x

 





 - 

 

 

 -  - 

 

 

 

 

   

4 1 3 1

2 3

x x x x









 

   

 - 



 



Đặt

a 0

x a

x b



 







- 





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Ta có:

 

   

 

2 2

3 3 3 3

a a b b

   



Xét hàm

 

3 3 t 0

f t t t

    

   

2 2 2 2

f' 2 3

3 2 6 3 3 6 3

t t t t

t t t t t

   

      

 

3 6 3 3

1 0 t 0

t t t

   

   

 f(t) đồng biến

   

a f b

 

2 2

1 2 1 4

4 5 3 0

x x x x

x x x

   -

   -   -  

 

5 13

5 15

x TM

x loai



















Vậy vớ

8 11

x y

  

Với

5 13 11 13

2 2

x y

 

  

Kết luận:

   

5 13 11 1

; 8;11

; ;

2 2

x y

æ ö

 



ç ÷

è ø

Bài 38: Giải hệ phương trình

 

2 2 2

2 2 1 3

9 4 2 6 7

y y x x x

x y R

y x y



 

-  -







-   -





Bài giả

Điều kiện:

3 3

1; ;

2 2

x y

 

  -

 

 

. Ta

có

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

1 2 2 1

2 1 1

y y x x

x x

   -

 -  -

2 2 1 1 1

y y x x x   - -  -

Xét hàm số

 

f t t t 

, ta có

 

' 6 1 0

f t t t

   



suy ra f(t) đồng

biến trên R. Vậy

   

 

1 1 1

f y f

x y x

y x





  - 

 - 



 -



Thế vào (2) ta được:

4 5 2 6 1x x x  - -

 

2 4 5 4

12 2 4 5 1 2 2

PT x x

x x x   - -     -

 

4 5 2 3

4 5 1 2

1 2

x x vn

x loai

x x









  -



 













  -











 -





Với

1 2





 - 



 -





. Vậy hệ có 2 nghiệm

Bài 39: Giả

i hệ phương trình:

4 5 10 6

4 1 2 1

3 1 1

x y y x x

x x x y



  





 - - -

  -





Bài giả

Điều kiện:

1 1, 1x y-   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Nếu x = 0 thay vào hệ phương trình ta được

   

; 0;0

x y 

là một nghiệ

m của hệ phương

trình.

Nếu



, từ

4 5 10 6 5

y y

x y y x

x x x

x x

æ ö

   

  

ç ÷

è ø

Xét

 

f t t t

t R

  

. Ta có

 

' 5 1 0

f t t t

   



, nên f

(t) đồng biến trên R.

Do đó

 

f x f

æ ö



ç ÷

è ø

. Suy r

x y x

  

Thay y = x

vào phương trình

thứ hai ta được

4 1 2 1

3 1 1

x x x x - - -

  -

(*)

Đặt

1 0, 1

u x v x

   

- 

. Ta có

 

2 2

x u v

u v



 -







 



Phương trì

nh (*) trở thành

   

2 2 2 2

3 1

4 2

2 2

u v u v

u v uv

- - - 

 

    

2 2

2 4 2 0

2 2 0

u v u v

v u v u v

  - -

   -  - 

Nếu

2v u

thì

3 9

1 2 1

5 25

x x x y-

    -  

Nếu

v u -

thì

1 2 1

x x-  - 



pt vô nghiệm

Tóm lại phương trình có các nghiệm là

   

3 9

;y 0;0 ; ;

5 25

æ ö

 -

ç ÷

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 40: Giả

i hệ phương trình

 

2 2

4 5 1 4

2 2

4 4 2 1

x y x y x y

x y

y x x x



 - -  - 







-   -







Bài giả

Điều kiện











. Vớ

i điều kiện đó

 

2 2

1 4 20 1

4 2 2

x xy y y

x y

  - -

 - 

 

2 4 16 2

xy xy

x x

   -

. Th

ay vào (1) ta có

   

2 1 2 1

2 2 1 1

x x y y

 -  

  -

Xét hàm số

 

2 1u g t t

   -

với





1;t

 

. Hàm số

này luôn đồng biến.

Vì thế

   

2 1 2 1

2 2 1 1 2 1 1 2

x x y y x

y x y

 -  

  -     - 

Thay vào (2

) ta được

 

1 2 2 2

2 9 8 2

1 2 2 1 1

1 2 2 2 1

x x

x x x

x x



-  - -

-   -

 -  -  



-  -  -





 

2 9 2 2

10 4 2 0

1 2 2 2

2 2 2 1 0

x x



-   





-  - -







- - 



Phương trình bậc hai

 

2 9 2 2

10 4 2 0

x x

-   



có

 

2 2 1  

nên có h

ai nghiệm

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

là

5 2 2





và



. Nghiệm x

bị loại v

2 2 2 1

- - 

Hoàn toàn tương

tự ta có

5 2 2

1 2 2 2

x x x

-  -

 -  

Vậy hệ đã cho có hai nghiệm là

5 2 2 3

2 2

;

2 4

æ ö

- -

ç ÷

è ø

và

5 2 2 3

2 2

;

2 4

æ ö

 

ç ÷

è ø

Bài 41: Giả

i hệ phương trình

 

3 2

2 2

4 2 2 1 3 15 7 2 1

6 2 2 15

4 12

x x y y

y x

y y

x x y x y



- - -    









 -  

-  





   

  

2 2

5 5

1 6 2 11

8 1 2 6 1 2 11 5 5 2 1

2 1 1 6

x x

x x x x x x x x x

x x

- -

-  - 

-   - -  - -  -     - -

 -  -

 

5 0

x A

 - 

với

1 1

2 1 0

1 6 2 1

A x

x x

   -



 -  -

(do

1x 

)

5, 2.

x y

  

Bài 42: Gi

ải hệ phương trình

 

3 2

2 2

4 1 2 3 (1)

2 4 1 1 (

x y x y

y y x x



  







    



Bài giả

Bài giải:

Điều kiện

1 x  6





 f



y 1



 f



2x -1



với





 4t

 3t

. Vì f(t) đồng biến nên

y 1  2x -1  y

 2y  2x - 2

. Thế vào (2):

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Điều kiệ



 

2 2

(1) 4

1 2 3 0

PT x x

y y x

 

   

 

 

Khi đó,

2 2

(2) 2

4 1 1

PT y y

x x

   

 

(3)

Xé thà

 

f t t t

  

trên







Có

 

' 1 0 0

f t t

   



 

f t



đồng bi

ến trên

 



Với

x y

  

. Hệ phương trình có nghiệm duy nhất

 

; 1;

x y

æ ö



ç ÷

è ø

1

Khi đó,

PT (3)  f





 f





 2y  x

Thay vào phương trình (1) ta được phương trình:

 x

 x x  3

Đặt

t  x

> 0 có hàm số





 t

 t

có g'





10t

 6t

 3t

 0 dot  0

Mà





 3 t  1  x  1  x  1

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 43: Giả

i hệ PT

 





 





3 2

2 2

,( , ).

3 2 9 3 4

2 1 1 0

xy x x y x y

x y

y x y x x



    -







       







Bài giải:

ĐKXĐ

 

Ta có

 

3 2 3 2 2

1 0

xy x x y

x y x x y y xy x y

    -

 -  -  - 

 

1 0

y x

x y x y





 - -   



 







   

 





   

 

3 2 9 3 2

1 3 2 1 2

3 2 9 3 2 1 3 2 1 2

x x x x



   -    

    - -  - - 

Xét hàm số





( ) 2 2

f t t t

  

ta có

'( ) 2 2

f t t

    



suy ra hàm

số

đồng biến.

Với

y  x

1

thay vào PT thứ 2 ta được



1





2  9x

 3







 6





1 x  x

1



 0

. Dễ thấy PT vô nghiệm.

Với

y  x

thay vào PT thứ 2 ta được



2  9x

 3







4x  2





1 x  x

1



 0

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Từ đó suy ra

3 2 1 .

x x x

 - - 

 -

Vậy HPT có ng

hiệm

 

1 1

; ; .

5 5

x y

æ ö

 - -

ç ÷

è ø

Bài 44: Gi

ải hệ phương trình:

 

32 5 2 ( 4) 2 2

( 2 1) 2 1 8 13( 2) 82 29

x y y y y x

x y

y x x y x



- -  - - -







- -   - -  -







Bài giả

Đặt đk

, 2

x y

 - 

 

5 2 5

(1) (2 ) 2 ( 4 ) 2 5 2 (2 ) 2 2 2(3)

x x y y y y x x y y   - -  -    -  -

 

3 2

(2 1)

2 1 8 52 82 29

(2 1)

2 1 (2 1)(4 24 29)

(2 1) 2 1 4 24 29 0

2 1 4 24 29 0(4)

x x x x x

x x x x

x x x

-   -  -

 -   - - 

 -  -  - 







 -  - 





Với x=1/2. Ta có y=3

Xét hàm số

f (t)  t

 t, f '(t)  5t

1  0,x  R

, suy ra hàm số f(t) liên tục trên R. Từ (3)

ta có

f (2x)  f ( y - 2)  2x  y - 2

Thay

2x  y -2(x  0)

vào (2) được

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 45: Giải hệ phương trình :











---

---

yxyxyx

2442

0631025

2233

Bài giải:

2 3

(4) ( 2 1

2) (4 24 27) 0 (2 3)(2 9) 0

2 1 2

x x x x

  - - -

   - - - 

 

3/ 2

(2 9) 0(5

)

2 1 2











- 



 



Với x=3/2. Ta có y=11

Xét (5). Đặt

2 1 0 2 1

t x x t

     -

. Thay vao (5) được

3 2

2 10 21 0 (

3)( 7) 0

t t t t t

 - -  

 - - 

. Tìm đượ

1 29





. Từ đó

tìm được

13 29 103

13 29

4 2

x y

 

 

Tất cả vì họ

c sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC TOÁN K

HÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Điều kiện

4y-2;x



   

yyyxxx

32)1(3121

326105)1(

2323





Xét hàm số

Rttttfttttf  0343)(',32)(

223

Suy ra f(x+1) = f(y) => y= x+1 thay và pt (2) ta đuợc

Phương trình :

1432

--- xxxxx

 

  

 

  

 

 

  

 

  

 

022

232332

)2(2

232332

4322

332

2322

44332

223

---

--

-



--

--

--



-

-

--

----

xxx

xxxx

xxx

xxxx

xxxxx

 

  

 

)2(0

232332

-















--

--

xvi

xxxx

xxx







-



--

Vậy hệ pt

có nghiệm (x; y) = (2;3) , (x;y)= (-1; 0)

Bài 46: Giải

hệ phương trình:











--

--

76249

13122

222

yxy

xxxyy

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài giải:

ĐK:



, ta

có:

  

xyxxyyxxxyy ----- 111.2213122

Vì h/s

 

tttf 

đồng biế

n trên R.

Thế vào pt kia ta được pt:

 

15422

154254484

54162

-

-

--

xxxx

xxx

15422 - xx vì



21- x

tmđk.

Bài 47: Gi

ải hệ phương trình:

( 3) 2 (

3 ) 2

9 16 2 2

8 4 2

xy y x x y x y

x y x



-   

 - 





 -   -





( , )

x y

 

Bài giải:

Đk:

0 2

(*)

 





 -



.Vớ

i đk(*) ta có

(1)



( 1) (

3) 2 ( 1) 0

( 3) 2

( 1) (3)

x y y x

y y x x





 

-   -   



 

   





Nội dung

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Với x = 1 thay vào (2) ta được:

2 2 8 1

( )

y y loai

   

Ta có:

 

(3) 2 2 ( )

y y x x

     

(4). Xét hàm số

3 2

( ) '( )

3 1 0;

f t t t

   

   

Hàm số

f(t) là hs đồng biến, do đó:

(4)

( 2) ( ) 2 2

f y f x y x y x

        -

thay vào pt(2) ta được:

4 2 2 2

4 9 16

x x x

-   



2 2 2 2 2

32 8 1

6 2(4 ) 9 8(4 ) 16 2(4 ) ( 8 ) 0

x x x x x

x x

 -  -

  -  - -  

Đặt:

2(4 )

( 0)

t x t

 - 

; PT trở thành:

2 2

4 16 ( 8 ) 0

4 0( )

t t x x

t loai







 -  





 - - 





Hay

0 2

4 2 4 2

2(4 )

2 3 3

x x y







-      









Vậy hệ

pt có nghiệm (x; y) là:

4 2 4 2

;

3 3

æ ö

ç ÷

è ø

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 1: Giả

i hệ phương trình

     

 

1 2 1 1

2 3 6 1 2

2 4 5 3 2

y x y x x

y y

y x y x y x y



- -    - -





-    - - - -





Bài giải chi tiết

Điều kiện:

2 ;4 5 3

x y

x y x y







 - - 



Phương

trình (1) trở thành:

   

 

     

1 1 1 1 1 0

y x y x y

y x y y

 - -  -

-  - - - - 

 

1 1 1 1 0

y x y x y y

 - - -  - - - 

  

1 1

1 1 0

1 1

y x y

x y

x y y

æ ö





 - -

-   

ç ÷



ç ÷

 

-  



è ø

Điều kiện:

1y 

Cách 1: Ph

ân tích thành nhân tử

       

3 2 1 2 1 2 1 1 2 1 0

y y y y y y x

 - - -   - -  

* Với

y  1





 9 - 3x  2 x - 2 - 4x -8

 9 -3x  0  x  3

* Với

x  y 1





 2y

 3y - 2  2 1- y - 1- y  2y

 3y - 2  1- y





Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

2 1 1 2 1

1 0

y y y y y

 - - - 

 - - 

  

2 1 2 1 1

y y y y

 -   -

- 

 

2 1 2 1 0

y VN

y y



-   



  - 



- 



1 5

- 

 

(vì



)

1 5



 

Cách 2: K

hảo sát hàm số

 

3 2 2 1 1

y y y y   - 

Xét hàm số

   

f 2 0

t t t t

  

có

 

f' 4 1 0t t t    

. Do đó f(t) đồng biến trên







Mà

 

f f 1

y y -

nên

1 5

1 1

y y y y y



 -   -  

(vì



)

1 5



 

Sau khi thử l

ại, ta thấy tất cả các nghiệm của phương trình đều thỏa mãn.

Kết luận: Hệ phương trình có nghiệm là:

1 5

;

1 5















 



- 











Bài 2. Giải h

ệ phương trình

   

 

2 2

5 4 4 1

5 4 16 8 16

0 2

y x x

y x y



  -





- -  -  





Bài giải chi tiết

Phương trình (2) tương đương với:

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

    

5 4

2 5 5 4

y x

y x y x

y x

 



 - - 

-  



 -



5 4

y x

 

        

0 4

1 5 4 5

4 4 0 6 5 4

x y

x x x x

x y

  





    -    



 -  



        

4 ; 1 4 5 4 4 0 6 4 0

y x x x x x x

 -  -   -   - 

0 4

4 0

x y

  







  



Kết luận:

Hệ phương trình có nghiệm là:

0 4

; ;

4 0

x x

y y



 

 -

 



  



 







Bài 3. G

iải hệ phương trình

 

3 2 2 2

2 0 1

2 2 0 2

xy x

x x

y x y xy y

 - 





-   - - 





Bài giả

i chi tiết

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

     

 

2 2

2 2 1 2

1 0 2 1 0

x x y y

y x x y x y

 -  

- -   - -  

Bài 4. G

iải hệ phương trình

 

2 2

4 1 0 1

7 2 1 2

x y xy y

y x y x



 -   





 

- -  



 



Bài giải chi tiết

Phương trình (2) tương đương với:

   

 

   

2 2

2 7 2 4 0

15 2 0

y x y y

xy y y x y x y

   

 - - 

-    - - - - 

   

  

3 5 0 3

y x y x y y x

y x







 - - -     -



 



 

0; 1 1

y x

   

(vô lý)

 

1 2

3; 1 2 0

2 5

x y

y x x

x y

   -



 -  - -  



 -  



 

5; 1 9

46 0

y x x x

   

 

(phương trình vô nghiệm)

Kết luận: Hệ phương trình có nghiệm:

1 2

;

2 5

x x

y y

  -

 

 

 -  -

 

Bài 5. G

iải hệ phương trình:

   

 

   

2 2 3

2 2

5x 4 3

2 0 1

2 2

y xy

y x y

xy x y x y



-  -  





   





Bài giải chi tiết

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Phương trình (2) tương đương với:

 

   

 

2 2 2 2 2 2

2 2 2 1 2

xy x y

x y x xy x y

x y





       -  -  



 



* Với

   

2 2 3

1; 1 5

4 3 2 0

xy x y

xy y xy x y

  - 

-  

 

2 2 3

0 vi xy

3 6 3 0

3 0

y loai

x y xy y y x y

x y



 -    -  







x y

   

* Với

 

2 2 2 2 3 2

2; 1 5

4 3 0

x y x y x

y y x y x y

   -

 -   

   

3 2 2 3

4 5 2 0 2

x x y xy

y x y x y

 -  -

   - - 

2 2

5 2

x y

  













 











 













  



 













 









 





 

 









Kết luận

: Hệ phương trình có nghiệm là:

;



 



 





 

 





 





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 6. G

iải hệ phương trình:

 

2 2

2 1 2 2 1 0 1

2 4 3 0

x y x y x y

x y xy x y



 - -  -  -  





 -  - 





Bài giả

i chi tiết

   

1 1 0

2 1 2 2

x y

x y x y

- 

  - 



 -  

 

1 1 0 1

2 1 2 2

x y y x

x y x y

æ ö

 -   

  

ç ÷

 - 

 -

è ø

       

2 1 2 1

4 4 1 0

x x x x

x x

   -

 - -  

2 0 2 3

x x y

 -     

(thỏa mãn)

Kết luận: Hệ phương trình có nghiệm là:











Bài 7. G

iải hệ phương trình:

 

2 2

2 3 2 1 11 2

x x y

x y

y x



- - 







 - - 



Bài giải chi tiết

Điều kiện:

x y

x x y







- - 









Nếu

0 0 0

y x x y

   

- - 

(vô lý). Nên



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Với

   

 

0; 1 0 man

x x y x k

hong thoa

x x













- -    

 

- 















Với

x x y

- - 

, ta có:

 

3 3

2 2

1 1 1

y y

x y x y

x y x x y

 -   -

-  -

- - - -

 

  

2 2

x 1

x y x

x y

x x y

x y y

 - -

- -

  

- - 

- 

 

2 2

1 0

x 1

x y

x y y

æ ö



ç ÷

 - -  

ç ÷

- - 

 - 

è ø

Bài 8. G

iải hệ phương trình:

 

2 2 2 2

2 2x 3

2 2 1

3 4 4 2

x y xy y

x y xy

x y x y

x y



  -    





  -  - 





Bài giả

i chi tiết

Điều kiện:

x y







 -



Phương

trình (1) tương đương với:

     

2 2

1 2 2 3 2 0

x y x xy y x y

 -  -  -  

 

2 2

4 2 3 2

2 2 3 2

xy y x y

x y

x xy y x y

-  - 

 -  

-   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

2 2

2 2 3 2

x y

x xy y x y

 -  

-   

 

2 2

1 0

2 2 3

x y x y

x xy y

x y

æ ö

ç ÷

 -   



ç ÷

-   

è ø

Khi đó:

 

2 2 4 2 2

2 8 16

x x x





  -  

  



 - 



(thỏa

mãn)

Kết luận: Hệ phương trình có nghiệm là:











Bài 9. G

iải hệ phương trình:

 

2 2 2 2

2 1

5 3 2

x y x y

x y



  -







 





Bài giải chi tiết

Điều kiện:

x y

 

Với y =

0 không thỏa mãn hệ phương trình

Với y > 0, ta được:

 

2 2 2 2

1 0

2 2

y y

x y x y

æ ö

  - 

- - 

ç ÷ ç ÷

è ø è ø

2 2 2 2

2 2 2

5 5

4 4

2 2

x y x y

y y x y

- -

  

  - 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

2 2 2 2

5 1 1

2 2

x y

y x y

æ ö

ç ÷

æ ö

 -  

ç ÷

è ø

ç ÷



 - 

è ø

2 2

5 5

4 2

x y x y

   

Khi đó:

 

4 12 9

2 2 3

x x



 - 



   









x y  



(thỏa

mãn)

Kết luận: Hệ phương trình có nghiệm là:















Bài 10.

Giải hệ phương trình:

   

 

3 2 2

1 1 2 4 3

0 1

x x x x y y x y

x x y xy

x xy



-  -  -  -  - 





   



 



Bài giả

i chi tiết

Điều kiện:

1 0

x x y

x x

 -





 - 





  







Phương

trình (2) tương đương với:

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 2 2

x x y xy y y

x xy

   -  -

 

 

  

2 2

3 2 2 3

2 2 2

1 1

x xy y

x y

y y y x

x xy

x x y xy y x x y xy y

  - 

 - 

 

 

       

 

2 2

3 2 2 3

2 2 2

1 0

x xy y

y y

x y

x xy

x x y xy y x x y xy y

 

 



 

 -   

 

 

     

 

 

 

2 2

3 2 2 3

2 2 2

0 1

x xy y

y x

x xy

x x

y xy y x x y xy y

 



    

 

  

    

Thay vào phương trình (1), ta được:

   

1 1 1 1

1 3 0

x x x x

 -  -

-  -  - 

   

 

1 1 1 1

1 2 0

x x x x

 - - -

 - -  - 

 

2 2

1 2 0

1 1 1 1

x x

- -

 -   - 

-  - 

 

1 1

2 1 0

1 1 1 1

æ ö

 -   

ç ÷

-  -



è ø

2 3

x y

   

Sau khi thử

lại ta thấy nghiệm này thỏa mãn đề bài

Kết luận: Hệ phương trình có nghiệm là:











Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 11. G

iải hệ phương trình:

 

   

3 3 3 5

16 2 2

x x y y

y x y xy



-   - -





 -  





Bài giải chi tiết

Điều kiện:











Phương

trình (2) tương đương với:

   

 

2 2

16 2

2 16 2

x y x y

y x y

x y x y

xy y

x y x y

 - - -

  - -

 -  



 - 

 

16 2

x y

x y x y

 

 

 - - 

  

 -



 

Ta có:

 

1 3 3 3

x x y y -  

- -

3 11 11

5 3 3 0

3 3 0

2 4 4

y x x x x

æ ö

 - - 

-     -   

ç ÷

è ø

 

11 7 6 10

9 3 3 16

4 4

x x x



æ ö

   

 -   

ç ÷

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Do đó

 

16 2

x y

xy y

x y

-   



 - 

Thế

vào (1) ta được:

 

2 2

1 2 3 3

5 4 9 2 2 2 2 15

x x x x

x x x    -   -  - -

2 2

9 2 15

2 9 9

x x x x

 - - 

- 

   

2 2

2 9 9 0

6 6

81 2 15 2

9 9

x x

x y

x x x x



-  



   





- -  -







Kết luận

: Hệ phương trình có nghiệm là:











Bài 12. G

iải hệ phương trình:

 

2 2

2 2 4

1 2 1 4

x x y xy x y y

y x x y x



   -

-   





-   

-  -





Điều kiệ

 

2 2

4 1

x y x

y x y



 - - 



 -





-  



ừ (2) ta có:

 

4x 3 1

1 2 0 2 0

x y y x

x x

-  - 

-        

Phương

trình (1) tương đương với:

 

2 2

2 4 2 0

x y x y

xy x y

 -  

 - - - 

     

 

2 2

2 4 4

2 4

x y x

y xy x y

x y

x y xy x y

 -   - - -

  

  

 -

- 

Bài giải chi tiết

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

  

 

2 2

2 4

x y x

y xy

x y

x y xy x y

- - - - 

- -

  

  

 -

- 

 

2 2

1 2

2 0 3

2 4

x y xy

x y

x y xy x y

æ ö

- - 

ç ÷

 - -  

ç ÷

  

 - - 

è ø

Ta có:

      

2 1 1 1

1 1 1 0

x y xy

x y y x y

- -  

-  -    -  

, 1

x y 

 

2 2

1 2

2 4

x y xy

x y xy x y

- - 

  

  

 -

- 

Nên

 

3 2 0

x y

 - - 

. Tha

y vào (2) ta được:

   

2 3 2

3 2 3 4 3 3 4 3 2 3 0 4

x x x x x x x x x x-    -  -  -  - -  - - 

Xét hàm số

 

3 2

3 4 3 2

f x x x

x x x

 -  -

-  - -

với

 



 

 

Có

   

1 1 2 3

' 3 6 4 3

1 1 0

2 2 2 3 2

2 3

x x

f x x x x

x x x x

 - -

 -  -

  -   

 -  -

   

2 3 2 1

0 ;3 2 3 2 3

x x x x

æ ö

 - - 

-       -    -

ç ÷

è ø

Bài 13. G

iải hệ phương trình:

 

2 2

3 3 1 1

2 1

1 3 3 32

24 2

x y x y

x y

y x x



- -

 -   -





    -





Bài giả

i chi tiết

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Điều kiện:

x y

















* Nếu x = 1

thì từ (2) suy ra y =0 thỏa mãn hệ.

* Nếu x > 1 ta có

 

1 3 3 3 2 2 1 0

x y x y x y

 - -  - -  - - 

 

2 1

3 1 0

1 1

x y

x y x y

- 

- -

 - -   

 - - 

 

2 1

1 3 0

1 1

x y

æ ö

 - - -

 

ç ÷

 - -



è ø

1 0

x y

 - - 

(Do

3 3 2 1

1 x y

-  - 

 -

)

Thay v

ào (2) ta được

 

2 2 2

3 3 32 24

x x x

   -

2 2 2 2

2 3 2 3

3 3 32 24

3 3 4 3

8 8 1

x x x x

x x

x x x x x

   

æ ö

  -  -

 - -

ç ÷

è ø

 





 

3 2 2 2 2

3 2

4 3 3 2 3 4

8 4 3

3 2

x x x

x x

x x x

-     

- 

  -

 

 









2 2

3 2

3 3

4 3 0

3 2

x x x

 

  

 

 -   

 

 

 

 

3 2

3 21

4 3 0

x x x



 -

   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

(Do x > 1) suy ra

1 21





Kết luận

: hệ phương trình có nghiệm

   

3 21 1 21

, 1;0

, ;

2 2

x y

æ ö

 



ç ÷

è ø

Bài 14. G

iải hệ phương trình:

     

 

2 2

1 2 1 1 1

3 2 1 2

x y y y x x x y

x x x y x x y



    -    





 -     





Bài giả

i chi tiết

Điều kiện:

3 0

x y

-  

 

2 3 2 1

x x x y

x y

  - 

-  - - 

 

1 1 0 1 0

3 2

x x

x y x

x y

æ ö



 - -    - - 

ç ÷

-  

è ø

Thay v

ào (1) ta được:

   

2 2

1 2 2 1

2 1

x x x x

x x x

 -  

-    -

Đặt

 

, 0

u x x

u v

x x



 - 







  





ta đượ

2 2 2 2

2 2

1 1

1 2

2 2

v u v u

u v u

æ ö æ ö

-  -



  - 

ç ÷ ç ÷

è ø è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

   

1 3 0 1

u v

v u u

v u v x

u v













 -  

 -     -



 











Từ đó ta đư

ợc các nghiệm

   

1 1 7 1

; ; , 1

; 2 , ;

2 2 8 8

x y

æ ö æ ö

 - - -

ç ÷ ç ÷

è ø è ø

Bài 15. Giải hệ phương trình:

 

2 2

4 1 4 1

6 8 1

2 1

2 1 2 1

2 2 1 2

x y x

y x y x y x



-  -  - 









       



Bài giả

i chi tiết

Điều kiện:

x y



     

2 2

2 2 1 2 2 1 2 1 1 0

y y x x y x

  -      -  

   

2 2

4 2

1 2 1 2

1 1

y x y x

y y x x y x

- -

  

   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

2 2

4 2

1 2 1 2

1 1

y x

y y x x y x

 

 -  

 

  

      

 

x y 

Thay v

ào (1) ta có:

2 4 1 6

2 1

x x

-   



Dò nghiệm

ta được x = ½ là nghiệm kép , ta tìm cách đánh giá như sau :

Áp dụng BĐT Cauchy: khi thay x = ½ vào

4 1x -

= 1 ,n

ên ta áp dụng

2 4 1.

1 4 1 1 4 4 6

x x x V

T x

-  - 

   

Ta thay

x = ½ vào

2 1x 

= 4 . nên ta á

p dụng

   

8 8

2 2 1 2

2 2 1 8

2 1 2 1

x x

   



 

       

8 8

4 2 2 2 1 4 2 2 2 2 1 4 2 8 4 6

2 1 2 1

VP x x x x x x

x x

 

 -     -    -    

 

 

 

Dấu

"=" xảy ra khi

1 1

2 2

x y

  

Kết luận

: Vậy hệ có nghiệm

 

1 1

, ;

2 2

x y

æ ö



ç ÷

è ø

Bài 16. Giải hệ phương trình:

 

1 1 1 1

3 2 1

2 1 2

xy x

x y x





-    







 -  





Bài giả

i chi tiết

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Điều kiện:

1 0 0











-   









 -



 

1 1 1 1 1

xy x

 - -  

-  

1 1 2

1 1

  

- 

  

 

1 1

2 0 2 0 2

1 1 2

1 1

xy xy

y x y

æ ö

ç ÷

 -    - 

 

ç ÷

- 

  

ç ÷

è ø

Thay và

o (2) ta được:

1 3 1

x x x

 -  

Áp dụng BĐT Bunhiaiscopki ta có

2 2

1 3 1 1 1

1 1 1 4

1 1 3 4

3 3 3

x x x x x

æ ö æ ö

 -   -   - 

ç ÷ ç ÷

ç ÷

ç ÷ ç ÷

è ø è ø

Suy ra

1 3 2

x x

 - 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Áp dụng BĐT Cauchy cho các số thực dương ta có:

1 1 2

3 3

x x

 



Nên

1 1 3

x x x

   -

Dấu bằng xảy

ra khi

1 3

1 1 1

x x















vô nghiệ

Kết luận: Vậy hệ đã cho vô nghiệm

Bài 17. G

iải hệ phương trình:

 

3 3

2 2

2 2 2 4 2 4 8 4 3 1

2 2 2 2

y x xy x x x

y x y x y x



- - - -  - 







     



Bài giả

i chi tiết

Điều kiện:

4 2 4 0

2 0

2 2 0

xy x

y x

- - 





 





 



  



     

2 2

2 1 2 2

2 1 0

y y x x

y x

  - 

   -  

 

2 2

2 2 1 2

2 1

1 2 2 2

y x y x

y y x x y x

- - - -

  

   

  

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

2 2

1 1

2 2 1 0

1 2 2 2

y x

y y x x y x

æ ö

ç ÷

 - -  

ç ÷

  

   

è ø

2 2 1 0

y x

 - - 

(Do

y x 

)

Thay v

ào (2) ta được

2 3 3

2 2 4 8

4 3

x x x x

-  - 

Áp dụng BĐT

Côsi cho các số dương ta có:

   

3 3 2 3 2

3 2 4 4

2 2 8 4 2 2 4

x x x x

x x x

   

  - 

 -  -  -

   

Dấu bằng xảy

ra khi

4 4

2 2



 -



 



 -





(thoả

mãn)

 

Kết luận

: Vậy hệ có nghiệm duy nhất

æ ö

ç ÷

è ø

Bài 18. G

iải hệ phương trình:

 

3 2

2 2 3

3 3

2 2

2 3 5 5

2 1

3 2

x x y

y x y y

x y x y xy y x y



  -

-  -  - 







  -  



Bài giải chi tiết

   









2 2 2 3

3 3

2 0

x y x x

y x x y xy y

 -  -

 - -  

 





2 2

2 2 4

3 3

2 2 2 3 2 2 3

3 3

x y x y

x x y

x y

x x x y x y

x x x y xy y x y xy y

- 

 -   

 

 - 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 





2 2 2

2 2

4 2

2 2 3

1 0

2 4

x x y

x y

x y xy y

x x y

x x y xy y

 

 



 

 -   

æ ö

 

æ ö

- 

ç ÷ 

 

ç ÷  - 

ç ÷

 

è ø

 

x y

. Thay

vào (2) ta được:

 

3 2

2 3 5 5

2 3

x x

x x x

 -

-  -  - 

Nhẩm x = 3

là nghiệm kép , ta thay x = 3 vào :

2 1

- 

;

 

  

3 2 2

3 5 5 2

3 2 1 7 7

x x x x

x x-  -  - -  

Áp dụng BĐT

Cosi ta có:

   

2 1 2 *

x x

-  - 

Và:

 

3 2 2

2 1

3 5 5 2

3 2 1 **

x x

x x x x x x

 -

-  -  - -  

Cộng vế

theo vế (*) và (**) ta có:

3 2

2 3 5 5

x x

x x x x

 -

-  - 

- 

Dấu bằng xảy

ra khi

1 2

3 2 1

x x

 -



 



-  - 



Nên

 

3 3 3

x y

   

Kết luận

: Vậy hệ có nghiệm duy nhất

 

3;3

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 19. G

iải hệ phương trình:

 

2 1

3 2 2 2 4 2 1 2

y x

x y x

x y x y x



  - 







-    -



Bài giả

i chi tiết

Điều kiện:

2 0

x y







 





- 





 

1 2

y x

x y x y

  - - 

2 0

2 2

y x

x y x y

- 



- -

  



  - 

  -





* Nếu

  

2 2 2 2 0

x y x y x x x y x y

  -     - 

vô nghiệm do

x > 0.

* Nếu

y x

thay vào (2

) ta được:

3 2 2 2

2 1

x x x x

-   

 

2 2 2 1

2 1 2 1 0

x x x x

x x x

 - - 

-   -  

 

2 2

2 1 1 1

1 0 3

x x x x

- -  -  - 

Ta có:

 

2 1 1 0

1 0

x x



- - 



- 





- 



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Với



nên

 

2 1 1

3 1 1

x x y

 















   

 











Kết luận

: Vậy hệ có nghiệm duy nhất

æ ö

ç ÷

è ø

Bài 20. G

iải hệ phương trình:

 

3 3 2

8 3 8 1

4 2 1

x xy

x y

x x y





 - 







     





Bài giả

i chi tiết

Điều kiện:

0, 0,

x y xy

  

 

1 3 1 1 1

1 0 0

4 2

3 1

4 2

xy xy

x xy

y xy

- -

 -  - -    



- 

 

1 1

1 0 1

3 1

4 2

xy xy

y xy

æ ö

ç ÷

 -    

ç ÷



- 

ç ÷

è ø

Thay v

ào (2) được:

 

8 1 3 8

1 4 2 1

x x x

   

 

Áp dụng BĐT Cauchy ta có:

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

 

3 2 2 2

2 8 1 2

2 1 4 2 1 2 1 4 2 1 4 2

x x x x

   -

    -   

6 8 1 2.

3. 8 1 9 8 1 8 10

x x x x

   

   

Suy ra

 

3 2

2 8 1 6 8 1 4 2 8 10 8 4 1

x x x x x

         

 

8 1 3 8 1 4 2 1

x x x

      

Dấu "="

xảy ra khi và chỉ khi

1 1x y  

thử lại thấy thỏa

mãn

Kết luận: Vậy hệ đã cho có nghiệm duy nhất

 

1;1

Bài 21. G

iải hệ phương trình:

 

       

2 2

4 4 2 2

2 9 4 3

x y x x

x y y y x y



-   -   -





- -  -  -





Bài giả

i chi tiết

Điều kiện:

2 2

4 0

x y



-  













 

2 2

1 4 2 4

2 0

x y x x

 -  -

 - - - 

 

   

2 2

4 4

4 2

x y

x y x

-  -

- - -

  

-  -

- 



  

2 2

4 2

x y

x y x

- -  -

- -

  

-  -

- 



 

2 2

2 1

2 0 2 0

4 2

x y

y x y

x y

x y x

æ ö

 -

ç ÷

 - -   

- - 

ç ÷

-  -

 

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Thay vào (2) ta được

   

9 4 6

y y y y

-  - 

Áp dụng BĐT

Bunhiacopxki ta có:

 

      

. 9 4 .

4 9 36 9 4 6

y y y y

y y y y y y y y

-  - 

 - -    -  - 

Dấu bằng xảy

ra khi

4 36 62

9 13 13

y y

y x

y y

   



(thỏa mãn)

ết luận: Vậy hệ đã cho có nghiệm duy nhất

 

62 36

; ;

13 13

x y

æ ö



ç ÷

è ø

Bài 22. Giải hệ phương trình:

 

1 1 1

1 2 4

1 4

x x y y

x x

x y

y x



  -    -





 

  







với



Bài giả

i chi tiết

Điều kiện:

1 0

x x y

x y



  - 



 









 

1 1

1 1 1 0 0

x y y x

x x

y x y x

y x

x x y x

 -  -

   -

-  - -    

 -

  -



 

1 1

1 0 1 0

x y x y

y x

x x y x

æ ö

ç ÷

  -   

 - 

ç ÷

 -

 

- 

è ø

(Do



)

Thay v

ào (2) ta được:

1 5

1 4

y y



- -  



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Ta có:

y y



- - 

với



Thật

vậy:

 

2 2

1 3

1 1 5 2

5 0

2 16

y y y y



æ ö

- - - 

- -  

ç ÷

è ø

Suy ra

 

1 3

y y



-  

Áp dụng BĐT

Cauchy ta có:

 

1 1

1 4

4 1



 



Cộng vế

tương ứng (3), (4) rồi rút gọn ta được:

1 5

1 4

y y



-   



Dấu "="

xảy ra khi

1 0

y x

  

(Thỏa mãn)

ết luận: Vậy hệ có nghiệm duy nhất

 

0;1

Bài 23. G

iải hệ phương trình:

2 2

1 1

x y x y

x xy y

x x y x



  - 

 





-    -





Bài giả

i chi tiết

Điều kiện:

x y







- 





 



Từ (1) ta có:

    

2 2

2 0 2 0

x y x y

x xy y x y x y x y x y

- - - -

    - - - - -  

 

1 2 0

x y x y x

x y

æ ö

 - - -

-   

ç ÷

è ø

(Do

1 2 1 2 0

x y x

x y

- - -  - 

)

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Thay vào (2) ta được:

   

2 2

1 2 1 1

1 2 2 4

x x x x x

-   -

 - -  -  -

   

1 2

2 2 0 2

1 1 2 2

x x x

 

 -  - 

  

 

-  

 

(Do

 

1 2

2 1 1 2

1 1 2 2

x x

 -  

 - -  - 

-  

)

Với

2 2

x y

  

(Thỏa m

ãn)

Kết luận: Vậy hệ có nghiệm duy nhất

   

; 2;2

x y 

Bài 24. G

iải hệ phương trình:

 

2 1 1 2

y x y y

x x y x x y



 -  -

 





 -  -





Bài giả

i chi tiết

Điều kiện:

 

2 1 0

1 0

y x

x y



 - 













- 



- 



(2) tương

đương với

 

xy y x

y x x-  - 

Ta có:

 

2 2

xy x xy x y x

xy y x y

x x x

xy y x y

- - -

- - -   

-  -

Cộng vế

(3) với (4) ta được:

y x x x

xy y x

x x

- - 

-   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

       

2 2

2 2 2 2 2 2

2 4 0

y x x x

x y y x x x x y x x y y x x

 -  -

  -  -   - -    -

Thay v

ào (1) ta được:

2 2 2

1 1 2

x x x x

x x

 -  -

   - 

Áp dụng BĐT

Cauchy ta có:

2 2

1 1

2 2

x x x x

x x

 -  

 -  

2 2

1 1 2

2 2

x x x x

x x

-    -  

-    

Cộng vế

ta được:

2 2

2 1

2 2

x x x x

x x x

 -  

-   

 

 

1 0 1 0

x x y

 -  

  

(thỏa mãn)

Kết luận: Vậy hệ có nghiệm duy nhất

   

, 1;0

x y 

Bài 25. G

iải hệ phương trình:

   

 

2 2 2

2 2 1 1

1 1

2 5 1 21

17 2

x x xy x y x y y y

y x y x x



  -     





-      -





Bài giải chi tiết

Điều kiện:

2 5 0

y x







-  





 -



 

  





2 2

1 1 2 1 0

x y x y

x y

 -  

 - - 

 

2 2

2 1

1 2 1

0 1 0

1 1

x y x

x y x y

x y

x y x y

 - -

æ ö

- - 

ç ÷

   

- -  

ç ÷

   

 - 

è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

1x y  

Thay v

ào (2) ta được

2 2

2 3 21

17 0

x x x x

-   -

- - 

   

2 2

2 3 1 3

2 3 1 21 17 0

x x x x

x x x

 -  -

  -   - - - 

 

1 9

3 2 1 0

3 1 21 17

2 3 1

x x

x x x

æ ö

 -    

ç ÷

-  -

-   

è ø

17 1 1 9

1 0

21 3

3 1 21 17

2 3 1

x x

x x x

   

  

-  -

- 

 

Suy ra phương tr

ình có nghiệm











Kết luận

: Vậy hệ đã cho có các nghiệm

     

, 1;0

, 2;3

x y 

Bài 26. G

iải hệ phương trình:

   

 

2 2

4 8 10 9

6 1 5 1

1 1

1 1 2

x y x y

y x

x y

x x y

x y y



 -    -







- -    -





Bài giả

i chi tiết

Điều kiện:

0 1

1 0

 





-  



Phương trình (2) tương đương với:

2 2

1 1 1 1

x x y y

-   

-  - 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

  

2 2

1 1 1 1

0 0

1 1

x y

x y y x

xy x y

x y y x

x y

y x

x y

y x

- 



æ ö

-   

 - - -

   - 

ç ÷

- 

 

è ø



2 2

0 0

1 1

y x y

x y x y

x y

y x

æ ö

ç ÷

 -

ç ÷

        -

ç ÷

- 

 



-ç ÷



ç ÷

è ø

Thay v

ào (2) ta được:

 

12 19

5 6 1

x x x x

-   -



 

  

 

2 2

12 19 5 0

19 5 0

2 1 3 5

24 25 5 0

12 19 5 6

x x x

x x x x



- -  

 

 

 

- - - 



-   

 



1 1

2 2

25 145 25 145

48 48

x y



 

 -





 



   -





Kết luận

: Vậy hệ đã cho có các nghiệm

 

1 1 25 145

25 145

, ; ; ;

2 48 48

x y

æ ö

 

æ ö

 - -

ç ÷

è ø

Bài 27. G

iải hệ phương trình:

 

     

2 1

1 1 4

xy x y xy x y y

x y xy x x



 - -   





 



   - 

 



Bài giả

i chi tiết

Điều kiện:

, 0

x y



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Nhận thấy

x y

 

không thỏa

mãn (2) nên ta có

x y

 

Phương

trình (1) tương đương với

 

2 0

xy x y xy x y y

 - -  - - 

 

2 2

0 0

2 2

xy x y xy y x y xy y

x y x y

xy x y xy y xy x y xy y

 - - - - - 

- -

     

 

 - -

  - - 

 

0 3

xy y

x y

xy x y xy y

 

- 

 

 -  

 



 - - 

 

 

Ta có phương tr

ình (2) tương đương với

y xy x x

   -



Ta có:

 

  

4 1 2

2 1

2 0

1 1 1

x x x

x x

x x x

  - -



 - -   

  

vớ



Suy ra:

 

2 0 0

xy y

x y

xy x y xy y

- 

-    





 - - 

Nên

 

x y 

thay vào

(2) ta được

 

1 1

1 3 4

1 17 1 17

4 4

x y

x x x

x y



 





 -  

 



  





Kết luận: Vậy hệ đã cho có các nghiệm

   

1 17 1 17

, 1;1

, ;

4 4

x y

æ ö

 



ç ÷

è ø

Bài 28: Gi

ải hệ phương trình:

    

4 4

2 4 1 3 6 1 3 30

x x y x

y y

x x y y y x x



- - - 





- -  -  -    





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài giải chi tiết

Điều kiện:

2 4

1 3

x x y



- - 



 





 



Phương

trình (1) tương đương với:









2 2 2

. 0

x x y x

y x x y x x y y

- - - -

- -  - - - 

 





 

  

2 2

1 1

1 0 0

x x y x

y x y x y

x x y x y x x y y

x x y y

x y x y

- - - - - - 

 - - -

-  - - -    

- - 

- 

 

1 0 1

1 3

2 4

x x

x y

x y x y

x x y y

 

 

- -



 

 - -   

 

 

- - 

-  

 

ç ÷

è ø

 

Thay vào (2) ta được:

  

4 4

2 4 2 4

6 3 30

x x x x

x x x

- -  -

 -   

Áp dụng BĐT

Cauchy ta có:

  

3 3

4 4

2 4

2 4 1

6 3

2 27 27

1 1 1 2

2 1.1.1. 2

4 4

1 1 1 4

4 1.1.1 4

4 4

x x



-  -

-  



  





   -



-  -  



   -

-  -  





Từ các BĐT

trên ta được:

  

4 4

2 4 2 4

6 3 30

x x x x

x x x

- -  -

 -   

Dấu bằng xảy ra khi

3 2

x y

  

Vậy hệ đã cho có nghiệm duy nhất

   

, 3;2

x y 

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bài 29: Giả

i hệ phương trình:

 

3 2 2

2 3 1 4 1 0

2 5 4 1 4

y y x y

x x x x x y x



-       







    

 



Bài giải

chi tiết

Điều kiện:

4 0

x y



 -



  





 



Phương

trình (1) tương đương với:

 

1 4 2 3 0

x y x y x y y

-      -  

 

1 4 2 3 1

2 3 0

x y x y y

x y y

 -   

 -   -   

 

1 1 2 3 0

4 2 3

x y

x y x y y

x y y

- 

 -    -   

   

 

1 1 2 3 0

4 2 3

x y y

x y

æ ö

 -    



ç ÷

  



è ø

1 0 1x y y x -     

Thay và

o (2) ta được:

 

3 2 2

2 5 4 1 2

5x x x x x x

    



 

2 2 2 2 2 2

1 1 1 1 1

2 5 4 2 5 2 5 5 4 0

x x x x x x x x x x

x x x x x

         -   -    

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

1 0

1 3

2 2

1 1

5 4

4 3 2 3

4 4

4 3 2 3

4 4

x y

x x

x x x

x x

x y

x x

x y

 -  







  

 - 



æ ö æ ö



  - -  -    

ç ÷ ç ÷

- -

ç ÷ ç ÷



   -

è ø è ø

 - 







- 



  



Bài 30: Gi

ải hệ phương trình:

    

 

2 2

2 1 2 3 4 0 1

3 3 2 4

2 2 5 5 2 3 2

x y x y x xy y

x x y x y



 - -    





-   -    -





Bài giả

i chi tiết

Điều kiện:

2 2

2 3 4 0

2 2

x xy

x y



  









 





Phương

trình (1) tương đương với:

    

2 2

2 2 3 4

2 0

x y x y

x xy y x y

 -  

 -  

  

 

2 2

2 0

2 3 4 2

x y

x y x y

x xy y x y

 -   

   

   

2 2

2 0 3

2 3 4 2

x y x y

x xy y x y

æ ö

ç ÷

 -   

ç ÷

   

è ø

Từ (2) ta có:

3 3

5 5 2 3

5 2 5 2 0

x y x y x

   

      

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Mà

     

2 2 5 2

2 2 3 2 0 2 0

x y x y

x y x y x y

   

         

Nên

 

3 0

x y x y -  



thay vào

(2) ta được:

7 3 2 5

6 2 3

x x

-   -

Đặt

 

6 2, 3

2 , 0

a x b x

a b

   -



ta đượ

3 2

5 3

7 5 3

1 1

5 3

2 6

b a

x y

a b







 -







   

 

  



- 

æ ö





- 

ç ÷



è ø



(thỏa mãn)

Vậy hệ có nghiệm duy nhất

   

; 1;1

x y 

Bài 31: Gi

ải hệ phương trình:

 

3 2 2 2

2 2 2

2 2 4 2

2 35 38

2 8 8

x x x y

xy x xy x x y

x y

y y y



 

      





 -  -   -





Bài giả

i chi tiết

Điều kiện:















Phương

trình (1) tương đương với:

 





3 2 2 2

2 2 2

2 2 4 2

2 2 2 0

x x x y

xy xy y x xy y x

 

   -

   -  

 

      

3 2 2 2

2 2 2

4 2 2

2 4 2 2

2 2

y x x y x y x y x

x x x y xy xy y x xy y x

- -   - - 

 

   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

  

 

3 2 2 2

2 2 2

4 2

2 4 2

2 2 2

x y x y x

x x x y

xy xy y x xy y x

 



 -    



 

  

      

 

Thay v

ào (2) ta được:

2 35 38

2 8 8 19

x x

 -  -   -

2 2 8 3

5 38 8 19

x x x x

x x x

 -  -

 -   -

 

8 19 2 8

35 38 2 0

x x x x

x x

 - - -

 -  - - 

    

7 17 2 7 17

8 19 2

8 35

38 2

x x x x

x x

x x x

- - -

  

-  -

- 

 -

 

7 17 0

8 19 2

8 35

38 2

x x

x x x

æ ö

 -  

ç ÷

-  -

-   -

è ø

 

(do



)

y 

Vậy hệ

có nghiệm duy nhất

 

17 17

, ;

7 7

x y

æ ö



ç ÷

è ø

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 1 : Giải HPT :

2 4 2 3

2 4 4

( 1) 1 2

( 1)

(3 2) ( 2 )

x y xy y

y xy xy x y

   -





-   



Thế

2 4 4

1 (3 2)

( 2 )

xy xy x

y x y

 - - 

vào PT

(2) ta được

4 2 2

(1 3 4 )

y x y xy

 - 









 









Thấy

0y 

không phả

i nghiệm của hệ

Với

2 4 4 2 2

1 1 2 2 (

1)( 1) 0

xy y y y

y y y y y

    

-  - -   

5 1 2

5 1

1 5 2

1 5

y x





  











  





Với

2 4 4 2

1 2 2 2

1 1 0

3 9 3 3 3 9

y y y y y

xy y y    

-      

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 2: Giải HPT :

 

3 2

3 9 4

2 (1)

2 2

x y xy

y xy



 





 





PT(2) 

 

3 2 3 3 4

( ) 2x y x xy

y xy

 -  



 

2 2 3 3 4

2 2xy x xy y xy

-  



 

2 3 6 2

0 *

x y

x xy

y y

 





-  - 



(*) 

 

3 3 2

3 0

x y xy y

 - - 



4 3 2

4 3 0

xy xy

- - 



x y





 







 -





Với xy=1

 

(1) 

4 2

2 1 0

y y

-  



1y  



1x  

Với

1 1

x =

4 4

 -  -

(1) 

4 2

4 2 1 0

y y

 - 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI



5 1 5 1 1

y = x =

4 2

2 5 1

- -

  





Vậy hệ c

ó nghiệm (x;y) = (0;0),

 

1 5 1

1; 1 , ;

2 5 1

æ ö

ç ÷

  

ç ÷

è ø



Câu 3. Giả

i HPT :

 

4 3 2 2

4 2 2 2

6 12 6

5 1 11 5

x x x y y x

x x y x



- - - 

 





- - - 









   

2 2 2 2

2 2

2 2 2 2

6 1 1

5 1 1

x xy x x y

x x x y



-  - 







-   -



Dễ thấy x=y=0 không phải là nghiệm của hệ.

Ta có:

 

   

2 2

2 2 2 2

1 1

6 (*)

1 1

x y x y

x x

x y y x





 







- -

 





Đặt

(a,b 0)



















Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Hệ trở thành:

2 2

2 2 2 2

a b a b



 





 







4 4 2 2

36 2 5a b ab a

 





Với

1 1 1

2 2

  

(*) 

3 1

2 2

 



1 17

1 5

































Vậy hệ c

ó nghiệm (x;y) =

1 17 1 5

;1 ,

4 2

æ ö æ ö

 

ç ÷ ç ÷

è ø è ø

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 4

Giải

HPT :

2 2 2

(4 4 4

51)( ) 3 0

(2 7)(

) 1 0

x xy y x y

x x y

-  - -

 





- -  



 

2 2 2

3( ) (

) 51 ( ) 3 0

( ) ( )

7 ( ) 1 0

x y x y x y



-   -

-  

 



 





  - - -  





Đặt

x y a

x y b

 





- 



4 2 2 2

2 2

7 1

3 51 3

( 7) 1 0

( 4 1)(

2 2) 0

b b

b a b

b a

a b

b b b b

-  -



 -   





 

 

 -  





-  - 





2 3

3 2 3

2 3

3 2 3

x y

a x y

x y

a x

   

 

 

 

 

 

 -  

 

 

 

 

 

 

 

 -

 

 

 

 

 -  -

 

 

 

Câu 5 : Giải HPT :

3 3

3 5 2 6

2 3 3 8

x y xy

x y

 - 





  



Rút lầ

n lượt

3 3

,x y

theo

ta đượ

c :

3 3 3

3 3

22 21 3 5 8

(22 21 )(

13 12) 1

13 12 2 3

x xy x y

y xy xy xy

y xy x y

x y

 -  

 

  -

-   

 

 -  

 

  

Đoạn giải

PT bậc 3 ẩn

có 2 nghiệ

m rất lẻ không biết có phải do đề không ạ…

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 6:G

iải HPT :

 

2 2

1 1

x y

y x



  







-  -





ĐK:

, 0x y 

   

3 2

1 2 y 3 1

1 2 x 3

x y

-   

   

Ta có hệ

mới:

3 2

3 1

x xy

y x y



 





 







 

x y



 



 

 



 

- 



- 









3 1



















Câu 7 : Gi

ải HPT :

2 2 4

2 2

( )x xy y

x y

x xy y

x y

   -





  -



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Đặt

2 2

4 4

a b

a x y

b x y

a b



 



 







 

 -





 





Thế ta đ

ược :

2 2

4 3 2

3 0 2 3

0 1

4 4

b b

b b b b

b b







- -  

  -   



 -



 









































 -





Câu 8: Giải HPT :

 

2 2

3 1

x y

y x

x y



-  -







 



ĐK:

, 0x y 

PT(1) 

  

x y

x y x

xy y

-   

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Đặt

2 2

y b a

x y a

b a

x y b





- 







 

 









Hệ trở t

hành:

2 2

4 1

b a b a



 



- -











3 3

b a a b

a b



-  













0 1a b b a   



5 1

x y









 

 



 

-  -















Câu 10: Giải HPT :

3 3

2 8

x x y



   - 







  





ĐK:

x 

 0, x+y  3, y  0

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Đặt

a,b

x a

x y b















 - 



Hệ đã cho t

rở thành:

2 2

a b

 





 





 

 





























 

4 10

3 10

4 10

3 10

x y





 -











 

 



 

 







 





 







 -









 

x y

 





 



 

 



 











 







 -







Câu 11:Giải HPT

 

2 2

4 1

5 5 2

x y

x y x

x y



 



- 







  





Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

100

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

ĐK:

2 2

0, x+y 0, xy 0

x y

-   

PT(1) 

  

2 2 2 2 2 2

5 5 4

x y xy x y

x y x y

-    -





5 4

x y y x

y x x y

æ ö

-    - 

ç ÷

è ø

Đặt

y a

x b



 







- 





Hệ

đã cho trở thành:

5 5

5 4

a b

a b ab

 





 























2 2 5

2 2

y x y

x y x



 





 

 



 

- 







- 







    

3 2 0

x y x y x y

- - -  



2 2 3 (

x y



 



 



(*) 

 

























 -

















Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

101

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 12

Giải

HPT :

7 2 5

2 2

x y x y



   





  - 





Đặt

2 2

5 7 2

a x y

x b a

y a b

b x y



 

 -







 

 -

 







Ta có hệ

mới :

2 2 2 2 2

5 5

5 (7 2 ) 10 3(5 ) 8 5 10

a b a b

a b a a b a a a

   

 



 

 - - -  - -  

 

5 77

b a

 









- 















 -











- -













(Bài này k

hông hiểu sao ra lẻ vậy )

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

102

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 13:

2 2

1 1 1

(1 )(1 ) 2

x y y x

x y



-  - 





-  





ĐK:

2 2

1 0, 1 0

x y

-  - 

PT(1) :





  

2 2 2 2 2 2

1 1 1 1 1

x y y x

x x y y

-  - 

 - -  

Dấu “=

” xảy ra 

2 2

1 1

x y

y x



- -



2 2

x y







 



Với

x y

thay vào PT(2) không thỏa mãn.

Với

2 2

x y

 

PT(2) 

2 2

1 0 x 2 1 1 2x y xy y xy xy

-        -









 -



Ta giải được











thỏa mãn hệ.

Câu 13 :

3 2 3 8

8 2 4 2

x y x y



-   -







 - - -

 





Đặt

2 2

3 2

4 2 4

x y a

x y

b a

x y b



- 



 -   - -



 - 





.Ta có h

ệ mới :

Tất cả vì học

sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

103

CÁC EM HỌC TOÁN KHÔ

NG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

10 3

121 4 55

10 3

3 10

10 3

1 2 (10 3 ) 4

2 4 1

121 4 55

a b

b b b

b a

  -

















 -

 







  

 



 

 -

-  - - -

- - - 



























(Lại một bài lẻ

khủng khiếp…)

Câu 14 : Giải HPT

2 2

2 6 1

x x y

x xy y



   





  





Với





 



 -



Với

2 2 2

2 6 (2 6) (2

6) 7 3 18 29 0

x y y y y y y

y y

 - -   - 

      

Câu 15: Giải HPT

 

1 4

1 2

x y x y y

x x y y



   





  - 





Thấy

0y 

không phải là 1 nghi

ệm của phương trình.

PT(1)

 x

 2x  6  y

 2y 1

(3)

Lấy

(3) - (2)  2y

 (x  2)y - 2x -12  0  (y - 2)(2y  x  6)  0

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

104

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Hệ 

 

2 1

x y



æ ö



  



ç ÷

è ø



æ ö





 - 

ç ÷



è ø



Đặ

x y b













 



Hệ đã cho t

rở thành:

 

2 1

a b

 





- 

















x y



 



 





 













 -















Câu 16:Giả

i HPT :

2 2

2 6 1

x x y

x xy y



  - 





  







 

2 2

2 2 5 0

x y x y

y xy



-  - 







  





Đặt

2 2

xy=

x y a

b a

x y b

- 







 



Hệ đã cho t

rở thành:

2 2

2 5 0

3 28

ab a

b a

  





 





3 28

4 4

b b



 -









 



 



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

105

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI



  

2 2

2 3 3 18 29 0

b b b b



 -









- -   





  -













 -







 -









x y

 -  -







 





-  -







  -







Câu 17

Giải

HPT :

2 2

( 1)( 1

)( 2) 6

2 2 3 0

x y x y

y x y

- -  -







 - - - 



3 3 2 2

2 2

( ) 6 (

) 6

36 2 5 0

5 ( ) 2

5 ( ) 6

ab a b ab a b

x a

a b a b

y b

a b a b ab ab a b

   

- 

- - 

  



  

   

- 



  -   



  

2 1 1

1 1 2

2 1 1

b x

a y

a b

b x

a y

   - 

 

 

 

 - 





 

 

 





 

 

 - 

 



 

 

 - 

 

 

 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

106

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 18:

   

2 2

1 1 2 6

2 2 3 0

x y x y

y x y

 - - 

- 





 - - -







Đặt

x a

y b

- 





- 



, hệ đã

cho trở thành:

 

2 2

ab a b

a b

  





 







2 2

( )

a b



 







 





2ab 



 













 -







 -























 -









 -







1 2

1 1

1 2

1 1

1 2

1 1

1 2

 - 







- 





-  -







-  -







- 









- 





-  -









-  -





Câu 19 : Gi

ải HPT :

4 2

2 1

9 3

2(1 ) 2(1 )

x xy

x x

 







 



- -



Dễ thấy

0x 

không ph

ải nghiệm của HPT

1 2

x y

   

. Thế

vào PT2 ta

được :

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

107

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

4 2

9 3(1 2

)

2(1 ) 2(

1 )

x x

 

- -

2 4 2 2

2 2

9 2(1 ) 3

(1 2 )(1 )

(2 2 1)

(2 4 5) 0

x x x x

  -  -

  - - 



3 1

x y



  







- -

  





Câu 20 : Giả

i HPT :

3 3

3 2 3

4 4 8 17

x y x xy x

y x xy x

   





 - -  -



Hệ

2 2

( )( 1) 1

4 ( ) 8 (

1) 17 8

xy x x

x xy x xy x x

  







 -  - 



Đặt

xy x a xy a x

x b

    -





 



Hệ trở thành :

4 8 17 0

a b







 - 



(2 1)(

2 2 8) 0

a a

 -  - 

. Do

1 1

0 1 2

a a b

    

 

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

108

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

xy x





















 



 

 





 -



























Câu 21 : Gi

ải HPT :

4 2 2 2

3 0

3 5 0

x xy x y

x y x y

 -  





 -  



Hệ

2 2 2 2

3 0

( ) 5 0

x y xy

x y x y x

  - 







  - 



Thế

x y x x

  -

vào PT2 ta được

2 2 2 2

2 2

9 6 5 0

x x y x y x y x

 -  - 

2 2

( 5 4) 0

1 1

4 4 0( )

x y y

x y

y x x L

 -  



 





   



    



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

109

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 22 : Gi

ải HPT :

2 2

3 2

x y x

x y



 



 -







 - 





Đặt

2 2

3 2

2 3

x y a

a b

 - 



 

 

 

 



 

- 



giải PT bậc nhất cơ bản

Câu 23 : Giải HPT :

2 2

3 1

( ) 5

x y

y x

x y



-  -







 



PT(1)

3 2

( )( )

x y

x y x y

  - 

. Thế

PT(2) vào PT(1) ta được :

2 2 2

5( ) 6

4 5( ) (6 4 ) ( )

( ) 4 (

) 4 ( )

x y x y

x y x y x y

x y xy

x y xy x y

- - - -

- - 

  

  - -

3 3

5( ) (

) 5 1

x y x y

x y

 -  -

  -  -  -

x y

-  -









 





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

110

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 24 : Gi

ải HPT :

4 4

2 2 3

( ) 3

x x y y

x y

-  -





- 



Đặt :

a b

x y a

x y b a









 







 

-  -











. Đặ

t kì diệu :

3 3 3 3

3 3c a b c

ab c

   

 

.Khi đó :

2 2

4 4 2 2

( )( )( )

2 2

2 2 2

a b a b

y x y x y x y ab

a b a b a c b

x y a b

 

 -

æ ö æ ö

-  -    

 

ç ÷ ç ÷

è ø è ø

 

-  

 -

  -  

2 2 3

(1) ( )

2 2

a b a c b

PT ab c a b a c b

 

æ ö

      

ç ÷

è ø

Ta có hệ mới :

2 2 3

( )

c a b a

c b

ab c b

  







  





2 4 3

2 2

( ) ( 1)( ) 0

c c c

c a a

ac a

a c

a a a





     - -  







Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

111

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Với

a c

3 3

1 1

a c x y

ab c

b x y

 

   

 

 

 

   - 

 

 

Với

1ac 

3 3

1 1 1

3 3

9 9

a x y

b c

x y

 

   

 

 

 

 

  - 

 

Câu 25 : Gi

ải HPT :

2 2

3 3

14 2 2

2 2

xy y

x y

x y x y





 -

 





 -

æ ö

æ ö

 

ç ÷ ç ÷



è ø è ø



Đặt

x y



















3 3

( 9 0; , 0)

a b a b a b

     

2 2

a b x

a b y

 







- 



. Khi

đó

hệ trở thành :

2 2 2 2

2 2

3 3

2( )( ) ( )2

a b a b a b ab

a b

 - 



 







 



3 3

( ) 2( )

14 0

a b a b



 - - 

 



 





 





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

112

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 3

a b

- 







 



8 2 8

1 2

a a x y

x y

   



 

  



 

 - 



 



Câu 26 : Gi

ải HPT :

2 2

1 1 2

29 4

x y



   





 - 





Đặt

a b



















. Hệ

trở thành :

2 2

( 2) 21 1 2

2 2

9 112 128 0

18( )

18(

)

29 4

a b a b

a b

a b a

b b

a b



 -





 -  -   



 

  - - 

  

 

  



 







Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

113

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

... ...; .

b a x y









   

  







Câu 26 : Gi

ải HPT :

2 2 2

2 4 7

2 6 3

x y y xy

  





 





Dễ thấy

0y 

không ph

ải nghiệm của hệ . Khi đó hệ tương đương :

7 4

2 3

2 0

2 3 0

y y



æ ö

-   

- -  



ç ÷



 è ø



 

æ ö æ ö

 

  -



  - 

ç ÷ ç ÷

 

è ø è



è ø è ø



Đặt

3 2 0

( )( 3) 0

3 2 0

x a

a b a b

b a



- 



-  





   - - 

 

  











Với

1 1

0 3 2 0

2 2

a b

a b a

a b

 -  



   

  



 -  



Với

3 3 11

a b a a-   -

 

(Loại

)

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

114

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 27 : Gi

ải HPT :

2 2

3 2 2

3 1

x xy y y

x x y x x

   -





  - 



Dễ thấy

0x 

không ph

ải nghiệm của hệ .

2 2

.(1) (

2) 0 3 1 0

x x xy

 -  

 -  

(3)

Lấy

(3) (

ta được :

2 2

4 3 0

xy y x

y y

- -  

Xét thấ

1x 

không

phải nghiệm của hệ

4 3















Với

0y 

thay vào không thỏa mãn hệ .

Với

4 3



thay vào (2) ta được :

2 2

5 1 5 5

2 2

( 1) 0

5 1 5 5

2 2

x y

x x

x y



- -



 



 -  



- - 

  





Câu 28 : Gi

ải HPT :

2 2

( 3) 2

4 0

( )( 4)

x y x y y

x y x y



  - 

 





-   





(1) ( 1)( 4 ) 0 4

PT x y x y x y x y x y

 -    - -   -   

Thế

x y x y - - -

vào PT(2) ta

được :

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

115

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

2 3

( )( ) 1

(

1) ( ) 1 0

( 1)( )

x y x x

y x y y

x x y x y

x y x y

x y x

x y

-  - - -  

 - -  - - 

-  - 

 - -  

- 

Ta được hệ mới :

x y

x y x

- 



 -







 

 -

  - -





Câu 29 : Gi

ải HPT :

3 2

2 0

3 2 1(

2) 4

x xy y

x xy y x x y

  







   

 





Thế

2x y xy  -

vào PT

(2) ta được :

2 2 2

2 2

2 2 1 2 1 2 4 0

( 1 1)

( 2 1) 0

1 1

2 1

( 1) 1

2 1

2 3

2 1

x y x y x y y x y

x y x y y

x y

x y y

x y

x y y

x y x

x y y

x y xy

- - -      - 

  - 

 -  



 







  





 







  



  -







  



     -

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

116

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Dễ thấy

0x 

không phả

i nghiệm của hệ

1 1

y x

x x

   - 

1 1

5 1 2

5 1

5 1 2

1 5

x y





 -  



 -

   







  





Đối chiếu đ

iều kiện

5 1 2

( ; ) ( 1

;1);( ; )

5 1

x y

 -

  -



Câu 30 : Giải HPT :

2 2

(2 1) (6 ) 2

3 4 7 72

x x y x y x

x xy y



-   - - -





- -  -





, 2 0

x y x

  - 

PT(1)

6 ( ) 6 (

8 4 )

8 4

x y x

-  - -

 

 -

Xét hàm

số

6 6

( ) '( ) 1

f t f t

t t

- -

   - 

suy ra hà

m số nghịch biến

Mà

( ) ( 8 4

) 8 4 8 5

f x y f x

x y x y x

  -  

 -   -

Thế vào PT(2) gi

ải PT bậc 2 cơ bản.

Xét thấy

x  2  2 - x  0  x  y  0  y  -2

không thỏa PT(2)

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

117

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Câu 31 : Gi

ải HPT :

2 2

3 3 2

2 2

2 3

2( ) 6 3( ) 5

x y x

x y

x x y

  





    



Ta có

3 2 2 2

2 .(1

) (2) 2 2 2 3( ) 5 6

x y xy

x x y x

-  - 

   -

(2 2 3

) ( 1)( 5)

y y x x

 - - 

- -

Mà

2 2

3 2 (1 )(3 ) ( 1)( 3)(2 2 3) ( 1)(5 )y x x x x x x y x x x - -  -   -  - -  - -

Với

1 0x y  

Với

5 3 4 7

( 3)(

2 2 3) (5 )

2( 3) 2

x x x

x y

x x y x

x x

-  

 - - 

-     

 

Thế vào PT(1) ta được :

2 2 2 2 2

2 2

4 7

2 3

( 2 )( 3) ( 4 7) 3( 3)

( 1) ( 6 11) 0

1 2

x x

x x x x x x

x x x

x y

 

æ ö

  

ç ÷



è ø

       

    

  -  

Câu 32 : Gi

ải HPT :

3 0

( 3) 1 2 2

x xy x

y x x x y y

   









   





Lấy

2 2

(1) (

2) 2 3 2 2 0

x y x y

-   -

  

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

118

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

2 2

( 2 )(

2 3 ) 0

x y x y

  - 

 

y x

  

Thế vào PT(1) ta được :

3 2

3 3 0 1 3x x x x y      -  

Câu 33

Giải

HPT :

2 2

( )(1

) 5

( 1) 2

x y



  







-  - 



2 2

1 1

( ) ( )

( 1)(

1) 2

1 1

( ) ( )

1 1

( )(

) 2

x y

x y xy

x y



  - 









 - 





  - 









 - 





Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

119

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Đặt

2 2

x a

a b

y b

 













 -







 



 -

 





 

 

 











- 















 -









 -





Xét từ

ng TH giải

,x y

đơn giả

n .

Câu 34: Giả

i HPT :

2 2

( 1) ( 1) 9 0

( 1)( 1) 10 0

x y xy

   





   



1 1

( 2 )(

2 ) 9

1 1

( )(

) 10

x y



   

 -









   -





Đặt

( 2)( 2)

9 3

10 10

x a

a b a b

ab ab

 





 





 -

   -

  -

 

 



  

  



 -  -

 -



 



 

















Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

120

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Do vai trò của

,x y

là như nhau nên ta xét 1 TH của cặp

,a b

rồi hoán đổi lại.

Câu 35 : Gi

ải HPT :

2 2 2

( ) 7 2

1 2

2 7 ( )

2 1 3

x y x y

y xy y

x x x y

y xy x



   

 





   

 -





Ta thấ











thỏa mãn là một

cặp nghiệm của hệ

Xét

2 2

x y

 

Dùng đị

nh thức ta có :

2 2

2 ( )

( )

D x y

D y x y

D x x y



 



 





 -





2 0

x y

x x x

y x



 



   -

  





  -





(Loại

)

Kết hợp

( ; ) (

0;0)

x y 

là nghiệm duy nhất

Câu 36 : Gi

ải HPT :

( ) 2 5

4 3 1

( 2 ) 2

5 6 7 6

x y xy

xy y

x y xy

xy x y



   - 





   

- -





Xét hệ

mới :

2.(1) (2)

3.(1) 2.

(2)







Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

121

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

3 (2 5

) 2 5

( ) 2 5

5 2 15

x y xy

x xy

x y xy y x



- -  -

- 





-   -







3 (2 5

) 2 5

( 3)( 2 5 5) 3( 2 5)

(2 5 2

5)( 2 5 5) 3( 2 5)

( 2 5)

(2 5 5 2 5 3) 0

2 5

2 5 5 2 5 3 0

x y xy x xy

xy x xy xy x xy

x xy xy xy

x xy

xy xy



- -  - - 







- -    - 





  - 

   - 

 -  

   



 





    





Có

2 5 5 2

5 3 0

xy xy

   



2 5

x xy x

   



.Thế vào PT(1) ta được

2 2

5 3( 5

)

2( 5) 1

2 2

x x

- -

  - -



3 2

3 13 15 0

3( )

5 2

x x x

x L

x y

 - -  

 -





  





   -



Câu 37 : Gi

ải HPT :

3 2 2

6 1 0

8 0

y x xy

xy x y x y

  - 







  - 



Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

122

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Lấy

2 2

(1) (

2) ( 1) (3 1)

xy y x

-   -

 -

Lại có

( 1) 2

(3 1)

xy x y

  - 

,( 1)

xy y x

  -

là 2 n

ghiệm của PT

2 2

2(3 1) (3 1) 0 3 1X y X y X y- -  -    -

3 1

1 3 1

xy y

x y y

 -







 -  -



Thấy

0y 

không ph

ải nghiệm của hệ.

Thế

3 1y



vào PT(2)

ta được :

2 3 2

3 1

3 3 3 1

0 1 4

y y y y

y y x

   -

 -    -  

Câu 38 : Gi

ải HPT :

2 2

3 8

3 7

x y





-  







  





Đặt

2 2 2 2

2 2 8 2

( 1) ( 1) 8

2 2 7 2 ( 1) ( 1) 7

x y a b

a a b a b ab a b b a ab

x y b

a b ab b a ab b a a b ab

   

     

 



 

  

- 

       



 

(

0ab 

)

2 2

2 ( 1)

( 1) 8

2 ( 1)

3 ( 1)

2 ( 1)

( 1) 7

a b b a

b a a b

  

   

 

  

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

123

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Mà có

2 2

3 ( 1)

3 ( 1) 15

a b b a

   

2 2

3 5

5 ( 1)

15 3 1 0

3 5

a b ab b b









    -   









Với

3 5 1

1 2 . 2

2 3

b a a a

 

   

  

3 5

x y

 

















Với

3 5 1

1 2 . 2 1

2 3

b a a a a

- 

      

3 5

x y

 















Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

124

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

THẦY QUANG B

ABY

Bài

1 :

2 3 2 2

5 2( 2) 2 2

x x x x

x x

- -  -

 - -

Bài

2 :

3 2

2 5 2(

2) 2 2 7 24 29

x x x x

x x x

-  - -

 -  -

Bài

3 :

2 2

5 2 5 (

1) 3 3 32 114 99(1)

x x x x

x x - - -   

BÀI 2

2 5 6 7

11 4 9

x x x x   

 

, Điều kiện :

 -

Bước 1 , dò n

ghiệm ta được 2 nghiệm : x = 2 , x = -1 .

2 5 6 7 11 4 9

2( 2) 2 5

6 3 7 11 0

1 1

( 2) 2 0

2 5 6 3

11 7

x x x x

x x x x x x

x x

x x x x

     

   

 - - -

 -  -  -  

   

 

 - - - - 

 

  

 

Bước 2 , ta c

hứng minh biểu thức trong ngoặc luôn dương

Ta đặt :

1 1

( ) 2

2 5 6 3

11 7

f x

x x x

 

 - -

 

   

 

 

Chứng minh

( ) 0

f x



, bằ

ng việc sử dụng casio , chức năng Table như sau :

Nhập mode , 7 ,

( )

2 5 6

g x

x x



  

, start

-6/5 , end 5 , step 0,2 thấy g(x) lớn hơn 1,25 , vậy ta tách

biểu thức

5 1

2 5 6x x

  



, còn lại

ta có

3 1

3 11 7

x x

  

Việc còn lại các em biến đổi tương đương thôi .

GIẢI BẤT PHƯƠNG TRÌNH , PHƯƠNG TRÌNH NGHIỆM KÉP

ĐÁNH GIÁ PH

ẦN SAU BẰNG CASIO

Tất cả vì h

ọc sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

125

CÁC EM HỌC

TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Bước

3 : Kết luận

2 2

1 1

( 2) 2 0 2

2 5 6 3 1

1 7

x x x x

 

- - - -   -

- 

 

   

 

 

Nghiệm :

1.25 1

-   -

hoặc



Video hư

ớng dẫn : https://www.youtube.com/watch?v=fGcVf77I-9g

Giải bài 3

: Điều k

iện :

2.5 1







-   -



( ) ( )

'( ) '(

)

f x g x











xét tại

điểm có x = - 2 ta có hệ :

2 1

a b

-  









Vậy ta có

được liên hợp :

2 5 ( 3)

x x

 - 

, làm

hoàn toàn tương tự ta sẽ có :

3 3 (2 1

)

x x

-  

2 2

(1) 5 (

2 5 3) ( 1)( 3 3 2 1) 25( 4 4)

5 1

( 4 4) 25

0 ( 2) . ( ) 0

2 5 3

3 3 2

5 5

( ) 25

2 5 3

3 3 2 1

x x x x x x x x

x x

x x x f x

x x

f x

x x

  - - - - -     

 

   -   

 

 

  

- -

 

 - 

  

- - -

BƯỚC 2

: XỬ LÝ BIỂU THỨC TRONG NGOẶC :

CHÚNG TA GIẢI MỘT BPT CŨNG GIỐNG NHƯ GIẢI MỘT PHƯƠNG TRÌNH , GỒM CÁC BƯỚC SAU :

Bước

1 : Casio ta tìm được nghiệm kép , các em bấm Shift + Cal thì sẽ thầy Eror , nhưng thực tế không

phải là vô nghiệm , các e thử nhật : Mode , 7 , f(x) = VT – VP , Start -2,5 , end -1 , step 0,2 . Các em sẽ thấy x

= -2 thì f(x) = 0 và không đổi dấu , vậy ta sẽ có f(x) = 0 có nghiệm kép

BƯỚC 1: DÒ NGHIỆM : Dùng casio phát hiện ra nghiệm kép (qua chức năng Table ) : x = -2

Tiếp đến chúng ta tạo lien hợp cho các căn :

2x  5  ax  b

: sử dụng điều kiện để 2 đường tiếp xúc :

Tất cả vì

học sinh thân yêu

Facebook cá nhân : https://www.facebook.com/quang.manngoc

126

CÁC EM HỌ

C TOÁN KHÔNG THẤY TIẾN BỘ , THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI

Xét :

5 1

( ) 25

2 5 3

3 3 2 1

x x

f x

x x

 - 

  

- - -

, ta chứ

ng minh nó luôn dương với mọi x thuộc tập

xác định

+)Đầu tiên ta khẳng định rằng :

1x 

thì

( ) 0

f x



, chỗ

này em cứ dung table , mode 7 , star 1 , end 100 ,

step 10 xem , sẽ thầy

+)Xét

2.5 1

-   -

,dung chức năng table ta thấy

5 1

( ) 25 0

2 5 3

3 3

2 1

x x

f x

x x

 -  

  

- -

(bấm mod

e 7 , nhập f(x) , start -2,5 , end -2 , step

0,2)

Chọn riêng hàm

( )

3 3 2 1

g x

x x

 -

- - -

(bấm mod

e 7 , nhập f(x) , start -2,5 , end -2 , step 0,2) thì ta

thấy

( ) 25

g x

 -

, vậ

y ta sẽ có

25 0

2 5 3

x x

 

  

, cá

i này các em dễ chứng minh bằng biến đổi

tương đương .

Vậy trên tập xác định thì

( ) 0

f x



, vậy

(1) (

2) 0 2

x x

   

 -

Đáp sô : x = -2

Bấm Tải xuống để xem toàn bộ.

| 1/126

| | Tải xuống

Preview text:

Tất cả vì học sinh thân yêu
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 1
Tất cả vì học sinh thân yêu
GIẢI HPT – PHƯƠNG PHÁP HÀM SỐ 10 6 5 4
x  2x  y  2x y 
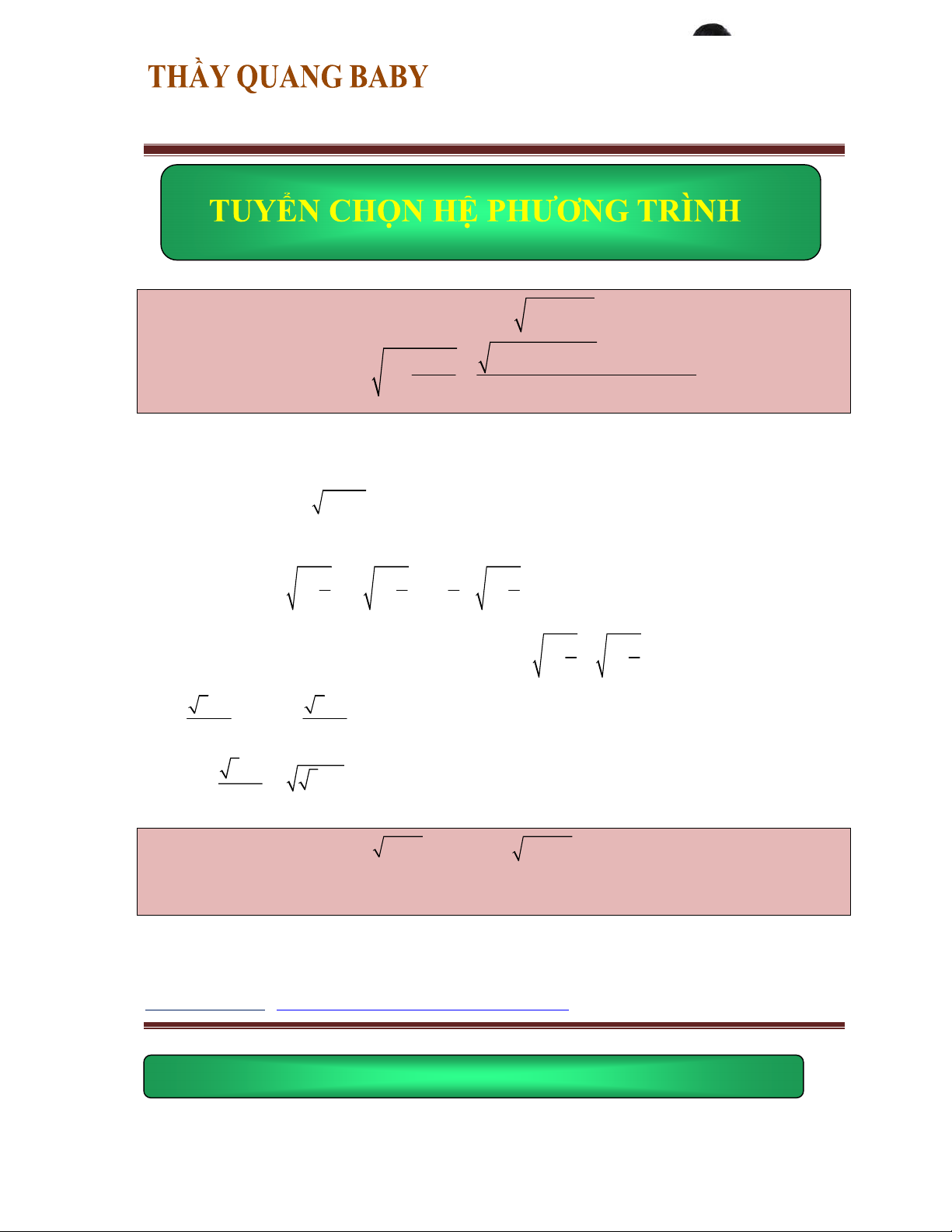
Bài 1: Giải hệ phương trình 
( x, y   ) 2
 x  5  2 y  1  6  Bài giải: 1
Điều kiện: 2 y 1  0  y  - 2
- Xét x=0, từ pt đầu suy ra y=0, thay x=y=0 vào pt thứ hai không thỏa mãn (loại) 5 æ y ö æ y ö -
Xét x  0 , chia 2 vế của pt đầu cho 5 x  0 , ta được 5 x  2x   2 ç ÷ ç ÷ (1) è x ø è x ø
Xét hàm số f t  5
 t  2t, t    . Ta có ' f t  4
 5t  2  0, t    . y
Vậy hàm số f t  5
 t  2t đồng biến trên  . Do đó (1) 2  x 
 y  x . Thay vào pt thứ x 2 của hệ ta được:
y  5  2 y 1  6 (2) 1
Xét hàm số g( y) 
y  5  2 y 1, y   - . 2 1 1 1 æ 1 ö Ta có ' g ( y)    0, y   -
. Vậy g(y) đồng biến trên khoảng - ;  ç ÷ . 2 y  5 2 y 1 2 è 2 ø
Mà g(4)=6 nên (2)  y  4
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 2
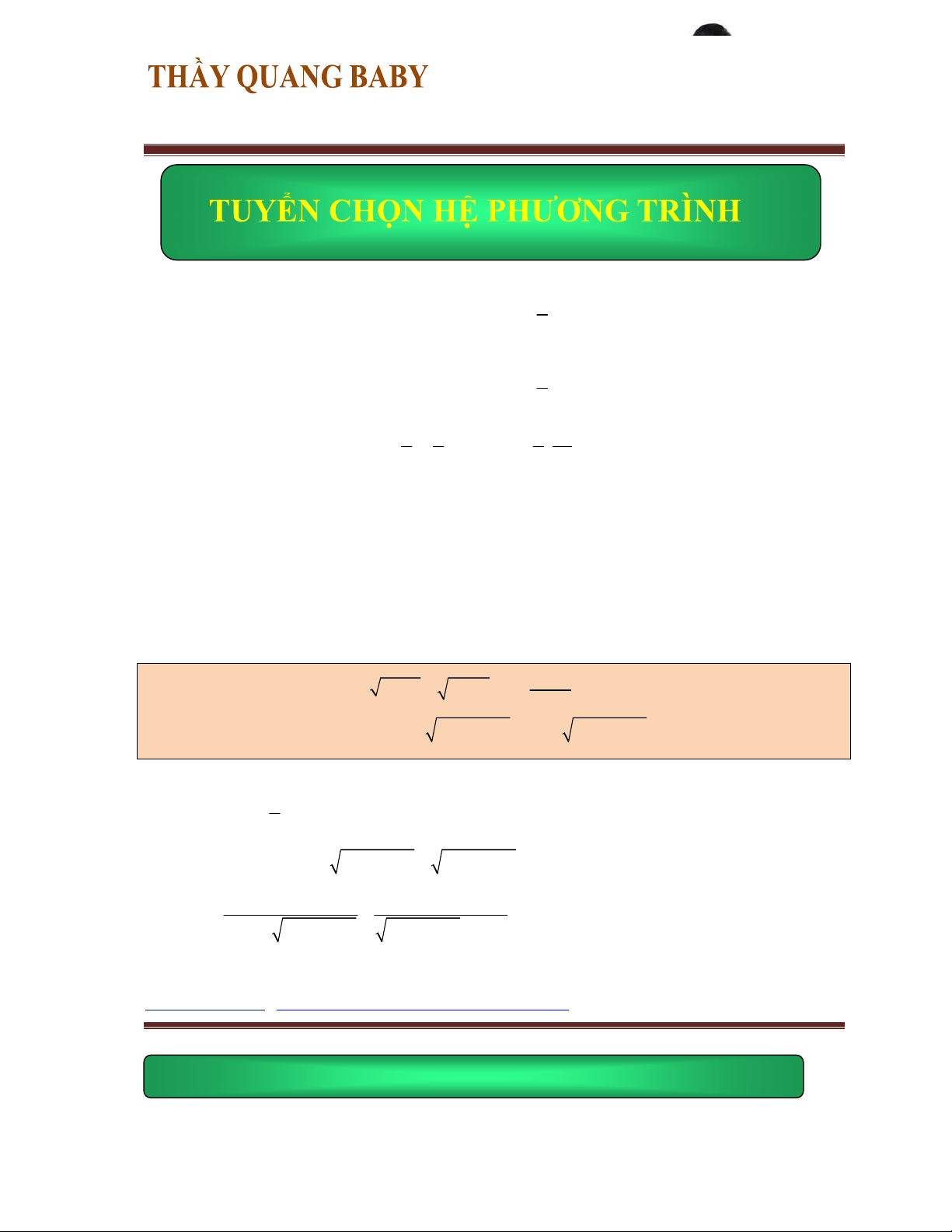
Tất cả vì học sinh thân yêu x  2 x  -2 Suy ra 2
y  x  4   hoặc  y  4  y  4  3 2
xy(x  1)  x  y  x - y   1
Bài 2: Giải hệ phương trình  3y   2
2  9x  3   4y  2 2
1  x  x   1  02  Bài giải:  y  x
Biến đổi PT (1)   x - y 2 x - y   1  0   2 y  x  1 
x = y thế vào PT (2) ta được: 3x 2
2  9x  3  4x  2 2
1  x  x   1  0  2x   1 2x    2 1  3  2 ( 3 - x) 2 2  ( 3 - x)  3 
 f 2x   1  f  3 - x
Xét f t t  2 ( )
t  3  2 có f '(t)  0, t  . 1 1
f là hàm số đồng biến nên: 2x  1  - 3x  x  -  y  - 5 5  2
y  x  1 thế vào (2) 2 x   2  x     2 x    2 3( 1) 2 9 3 4 1 2
1  x  x   1  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 3
Tất cả vì học sinh thân yêu
Vế trái luôn dương, PT vô nghiệm. æ 1 1 ö
Vậy hệ có nghiệm duy nhất: - ;- . ç ÷ è 5 5 ø 3 3
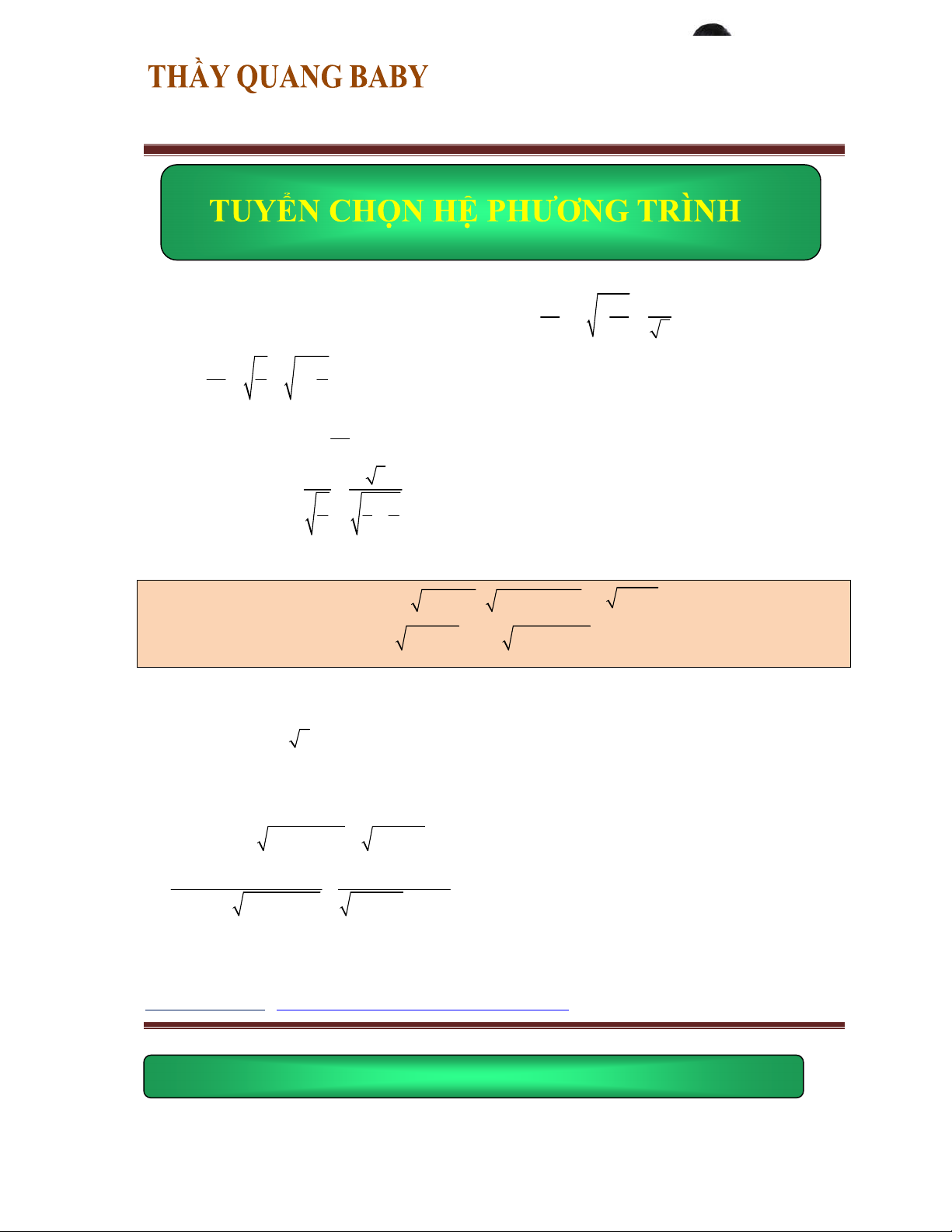
x  y  3(x  y)  6 y( y - 2) 14    1
Bài 3: Giải hệ phương trình sau .  3 2 3
27x  27x  20x  4  4. y  2x -1  2  Bài giải: Phương trình (1) 3  x  3 3
x  - y  6 2 y -15 y  14
 x3  3x  2 - y3   3 2 - y Xét hàm số: f t
( )  t 3  t 3 liên tục trên R.
Ta có f '(t)  3 2
t  3  0 với  t
  R  hàm số đồng biến trên R.
pt : f (x)  f (2 - y)  x  2 - y  y  2 - x
Thế y = 2-x vào phương trình (2) ta được. 3 2
27 x  2x  20x  4  4 1  x  3x  3 3 3 1  4 3 ( x  )
1  x  1  4 x  1 Xét hàm số: g t
( )  t 3  t 4 liên tục trên R.
Ta có g'(t)  3 2
t  4  0  hàm số đồng biến trên R. Suy ra: g 3 ( x  )
1  g(3 x  1)  3x  1 3  x  1  27 3 x  27 2
x  9x  1  x  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 4
Tất cả vì học sinh thân yêu
x  0  y  2  27 3 x  27 2
x  8x  0   2
27x  27x  8  ( 0 vn)
Vậy hệ phương trình có nghiệm (x;y)=(0;2)
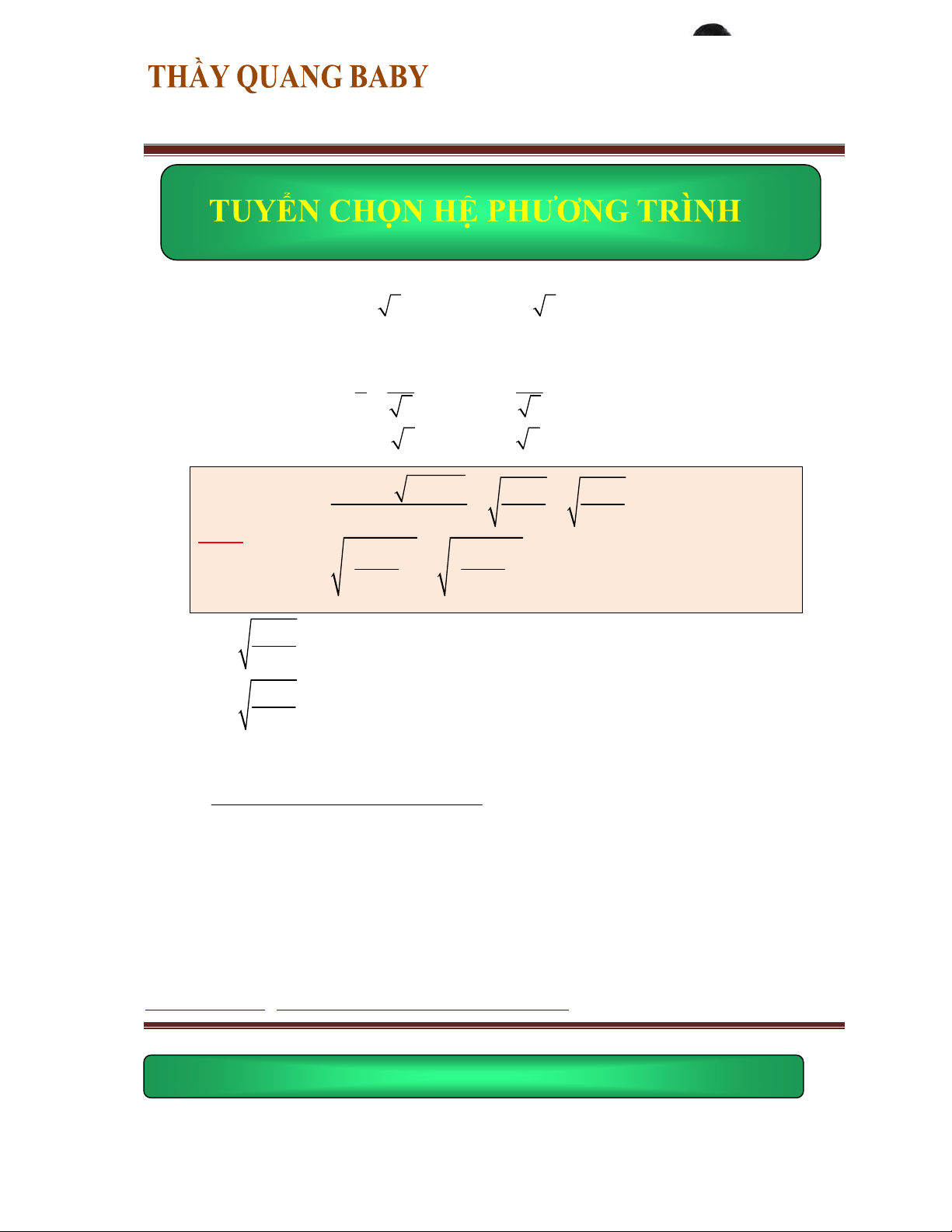
 x 1  (x 1)( y - 2)  x  5  2 y  y - 2 
Bài 4: Giải hệ phương trình  -   x, ( 8)( 1) y x y     ( y - 2) x 1 - 3 2    x - 4x  7 Bài giải: Điều kiện: Xét phương trình: Đặt ta được phương trình: Từ phương trình ta có thay vào phương trình ta
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 5
Tất cả vì học sinh thân yêu được
Tiếp tục giải phương trình Xét hàm số
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 6
Tất cả vì học sinh thân yêu Do đó hàm số đồng biến trên Từ Giải phương trình +) Với +) Với
Vậy hệ phương trình đã cho có nghiệm là:  2
 x  x  4   2 y  y 1  2  1
Bài 5 : Giải hệ phương trình  ( ; x y  ) . 2 3 3 12 
y -10 y  2  2 x 12  Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 7
Tất cả vì học sinh thân yêu Ta có: 2 2 (1)  x  x  4 
(-2 y)  4  (-2 y) (*) . 2 t t  t  4 t  t Xét hàm số đặc trưng 2
f (t)  t  4  t  f '(t)  1    0. 2 2 2 t  4 t  4 t  4
Suy ra f(t) là hàm số đồng biến trên R. Từ (*) suy ra: f (x)  f (-2 y)  x  -2 y .
Thay vào phương trình (2) ta được: 2 3 3
3x  5x  2  2 x 1   x  3 1  2  x   1   3 x   3 3 1  2 x 1 (**) Xét hàm số 3
g(t)  t  2t ta thấy g(t) đồng biến trên R nên từ (**) suy ra x  0 3 3 1 x 1  x 1  
. Vậy hệ có hai nghiệm là ( 1 - ; ); (0;0) . x  -1  2  3  y  2 2
1  y y  1  x    1 
Bài 6: Giải hệ phương trình: 2  (x, y  ) 2
x  x - 2x  5  1 2 2x - 4y  2 2  Bài giải:
Đk: 2x - 4 y  2  0
Ta có:    x - y    y   y2 2 1 2 4 2 1
thế vào PT (2) ta được
 x -    x -   
 y   y2 2 2 1 1 4 2 1
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 8
Tất cả vì học sinh thân yêu 2 x -1 æ x -1 ö 2   1  y  y 1 (*) ç ÷ (vì 2
y 1  y  y  y  0 ) 2 è 2 ø
Xét hàm số f t  2
 t  t 1 trên  2 t t 1  t
f 't   1   0, t    , do 2
t 1  t  t  t  0, t    2 2 t 1 t 1 æ x -1 ö
 f t  đồng biến trên  , theo (*) ta có f  f ç ÷  y è 2 ø
 x  2 y 1
Với x  2 y 1 thay vào (1) ta có:
 y 1 y2 3 5 2 2 2  4 
y 1  y  2 
y 1  2 - y  y   x  4 2 æ 5 3 ö Vậy hệ có nghiệm  ; x y   ; ç ÷ è 2 4 ø
2 x - 2. y  2 
 y  8 x  y  4x
Bài 7: Giải hệ phương trình  .
xy  2x -11  12 - x  y  7 - 3x  0  Bài giải: 7
Điều kiện 2  x  , y  0 3 Ta có 4x - 8  y 2 x - 2. y  4(x - 2) y 
. Dấu “=” xẩy ra khi y=4x–8 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 9
Tất cả vì học sinh thân yêu 4x  y  8
2  y  8 x   y  8 4x 
. Dấu “=” xẩy ra khi y=4x–8 2
Suy ra 2 x - 2. y  2  y  8 x  y  4x . Dấu “=” xẩy ra khi y=4x–8
Như vậy, pt(1)  y = 4x – 8. Thế vào pt(2) ta có: 2
4x - 6x -11 4  3x  7 - 3x  0  4 2
x - x - 3   4  3x - x - 
1   7 - 3x - x  2  0  2 x - x - 3  2 x - x - 3 æ  7  ö 2 
 4 x - x - 3 - -  0 do x  2; ç   ÷
4  3x  x 1 7 - 3x  x - 2 è  3  ø   1 1 2 
 x - x - 3 4 - -  0   
4  3x  x 1
7 - 3x  x - 2  2
x - x - 3  0 ( )    1 1    4 (3)
 4  3x  x 1 7 - 3x  x - 2 1 13 1- 13 + 2 pt( )
  x - x - 3  0  x   x  2 2 1 13
Đối chiếu điều kiện ta có x  2 æ 1 13 ö Hệ có nghiệm ç ; 2 13 - 6 ÷ 2 è ø + Xét pt(3)
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 10
Tất cả vì học sinh thân yêu  7  1 1 x   2; 
4  3x  x  1  3  10  6     3 
4  3x  x 1 6  7 ö Xét hàm số x   2; : g(x)  7 - 3x  x - 2  ÷  3 ø 3 2 7 - 3x - 3  g '(x)  - 1   0 2 7 - 3x 2 7 - 3x æ 7 ö 1 1
 g(x)  g    3 ç ÷ . Do đó, è 3 ø 3 7 - 3x  x - 2  7  1 1 1 x   2;  :  
 3  4 hay pt(3) vô nghiệm 3   
4  3x  x 1 7 - 3x  x - 2 6 æ 1 13 ö
Vậy, hệ có nghiệm duy nhất ç ; 2 13 - 6 ÷ 2 è ø 3 2 3
2x - 4x  3x -1  2x 2 - y 3 - 2y   1 
Bài 8: Giải hệ phương trình  3
 x  2  14 - x 3 - 2 y 1 2  Bài giải:
Ta thấy x  0 không phải là nghiệm của hệ, chia cả hai vế của (1) cho 3 x ta được 4 3 1   1  2 -  -  2 2 - y 3 - 2 y 2 3   x x x 3 æ 1 ö æ 1 ö  1-  1-  ç ÷ ç ÷
3 - 2 y 3 - 2y  3 - 2y * è x ø è x ø Xét hàm   3
f t  t  t luôn đồng biến trên 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 11
Tất cả vì học sinh thân yêu 1
*  1-  3 - 2y 3 x
Thế (3) vào (2) ta được 3 3
x  2  15 - x 1 
x  2 - 3  2 - 15 - x  0 æ ö ç ÷ ç 1 1  ÷  x - 7   0 ç ÷ x  2  3 4 - 2 x 15  ç  x 152 3 3 ÷ ç    ÷ è 0 ø æ 111 ö
Vậy hệ đã cho có nghiệm  ; x y   7; . ç ÷ è 98 ø
2 x  y  6  1- y (1) 
Bài 9: Giải hệ phương trình  2 9 
1 x  xy 9  y  0 (2)  Bài giải:
x  y  6  0 Đk: x  -1 
+) Nếu y  0 , để hệ có nghiệm thì 1  y  0 .
VT (1)  2 x  y  6  2 5  
  VT (1)  VP(1) hệ vô nghiệm.
VP(1)  1 - y  1  
+) Nếu y < 0, từ (2) suy ra x > 0 2 æ 3 ö æ 3 ö
9 1  x  xy 9  y  0  9   ç ÷ ç ÷
- y 9  - y2 2 (3) è x ø è x ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 12
Tất cả vì học sinh thân yêu 2 9  2t Xét hàm số 2
f (t)  t 9  t ,t  0; f '(t)   0 t   0 2 9  t æ 3 ö 3 9 (3)  f  f (- y) 
 - y  x  ç ÷ 2 è x ø x y 9 9
Thế vào pt(1) ta có phương trình 2
 y  6  1- y (4). Hàm số g( y)  2  y  6 đồng 2 y 2 y biến trên - ;
 0 ; hàm số h(y) = 1 – y nghịch biến trên - ;
 0 và phương trình có ngiệm y = –3
nên pt(4) có nghiệm duy nhất y = –3. Vậy, hệ có nghiệm duy nhất (1; –3). 2 2
 y -1  2y 1  x  x  xy  3y   1 
Bài 10: Giải hệ phương trình :  2 2
 x  y  3 
y - 3x  7 2  Bài giải: Đk: 2
y  1, x  0, y  3x æ 1 ö
Từ pt (2) ta có :  y - x -  1 ç
 2 y -1 x ÷  0 ç y 1 x ÷ -  è ø Suy ra, y = x + 1 Thay vào pt (1) ta được 2 2
x  x 1 - x - x 1  7 - 3 Xét hàm số: 2 2 f (x) 
x  x 1 - x - x 1
Chứng minh hàm số đồng biến
Ta có nghiệm duy nhất x = 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 13
Tất cả vì học sinh thân yêu
Vậy nghiệm của hệ là (2;3)
 x  3  xy  x  3y  3  x 1  2 y  y 1  1 
Bài 11: Giải hệ phương trình: x-3   y   1   y -  1  2
x - 2x  3 x 1 - 22  Bài giải: Pt(1) 
x  3   x  3 y  
1  x - 2 y 1  y 1 a  x  3  a  b Đặt 
a,b  0,(1) trở thành: 2 2
a - 2b  ab  a - b  0   b   y 1
a  2b 1  0  
+ a  2b 1  0 vô nghiệm do a, b  0
+ Xét a = b  y  x  2 thay vào (2) ta được:
 x -  x     x   2 3 3
1 x - 2x  3 x 1 - 2 x - 3
  x - 3 x  3   x   1  2
x - 2x  3. x 1 2
x  3  y  5(tm)  
 x  3  x 1  2   x   1  2 x - 2x  3  *  2 2   (*)
 x 1 2  x 1 2 x 1 2    x  1 2       -  -         
Xét hàm số f t   t   2
2 t  2 , t  0 có f 't  0 t   
Suy ra f t  đồng biến mà f  x 1  f  x -  1  x 1  x -1
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 14
Tất cả vì học sinh thân yêu x  1  
 x  3  y  5 2 x - 3x  0 
Vậy hpt có nghiệm: 3;5  x - 
 x - x -   y 2 8 2 1 2 2 1
y - 2 y  4  1
Bài 12: Giải hệ phương trình: 
4xy  2  y  2 y  2x  5y 12x - 62  Bài giải:  1 x   ĐK:  2
. Từ pt (1)  dể pt có nghiệm thì y  0 
 y  2y  2x  0  3 2 PT     x -  -  x -    x -  3 2 1 2 2 1 2 2 2 1 4 2 2
1  y - 2y  4y (*)
Xét hàm số f t 3 2
 t - 2t  4t t  0 có f t  t - t   t  t - 2 2 2 3 4 4 2 2  0 t   0 nên f(t) luôn đồng biến
Từ pt (*)  f 2 2x -1  f y  2 2x -1  y
Thay vào pt ( 2 ) ta được pt 3
y  2 y  2 y  2  3y y  2 
y  -2z loaïi 3 3 2 2 2   Đặt z 
y  2 ta được pt y  2z  3yz  y - zy  yz - 2z   0  y   z t / m
Với y = z ta được y 
y  2  y  2  x  1 (t / m)
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 15
Tất cả vì học sinh thân yêu
xx - y   x  2 x - y 3 2 2 2 2  
Bài 13: Giải hệ phương trình:  x, y   3 2 3 x  2 y   2 x - y  2 2  
 x  y  2 1  x     x 2x 1 Bài giải: ĐK: 2 x  y  0 Từ PT(1) tìm được 2 2 2 x 
x - y  x  x - y
Thế vào (2) đưa về pt chỉ có ẩn x 3 æ 1 ö 1 2 2 Đưa được về hàm 3 ç 1 ÷  1  1  1 ç x ÷ x x x è ø 1 2 Xét hàm   3
f t  t  t đồng biến trên  từ đó được pt 3 1  1 giải được x x 5 1 5 -1 x  -  L, x   N  2 2 æ 5 -1 ö Nghiệm ;  5 - 2 ç ÷ 2 è ø  2 2 
x 1 - 3x y  2   2 4 y 1   2 3 1  8x y   1
Bài 14: Giải hệ phương trình  2
x y - x  2  0 2  Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 16
Tất cả vì học sinh thân yêu
+) Với y  0 thì VT   1  0,VP  
1  0  Hệ phương trình chỉ có nghiệm (x;y) với y  0
+) vì y  0 nên từ phương trình (2) của hệ suy ra x  2 Khi đó:   2 2 2 
x  - x y   x y  2 1 1 3 2 2 4 y 1 -  1 2 2 2 2 
x 1  2  2x y 4 y 1  x y 3 Thay 2
2  x - x y vào phương trình (3) ta được: 2 2 2 2
x 1  x  2x y 4 y 1  2x y 1 1 1 2  1 
 2 y 4 y 1  2 y 2 x x x
+) xét hàm số: f t  2
 t 1 t  t với t  0 2 t f 't  2  1 t 
1  0 với mọi t  0 2 1 t æ 1 ö 1 1
 f(t) là hàm đồng biến trên 0;  . Mà f
 f 2 y 
 2 y  xy  ç ÷ è 2 ø x 2 1 1 +) Thay xy 
vào phương trình (2) của hệ ta có: x  4  y  2 8 x  4  Thử lại thấy 
1 thỏa mãn hệ phương trình đã cho. y    8 æ 1 ö
Kết luận: Hệ phương trình đã cho có nghiệm duy nhất  ; x y   4; ç ÷ è 8 ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 17
Tất cả vì học sinh thân yêu Bài 15: 3 2 2
 y  3y  y  4x - 22x  21   2x   1 2x -1   1
Giải hệ phương trình 
 x, y   2
2x -11x  9  2 y  2  Bài giải:
Điều kiện: x  1/ 2  *
Lấy phương trình (1) trừ phương trình (2) nhân với 2 ta được: 3 2
y  y  y    x   3 2 3 3 2 1
2x -1 - 4 y  y  3y  5 y  3  2x   1 2x -1 3 2
 y  3y  3y 1 2 y  2  2x -1 2 2x -1 3   y  3 1  2  y  
1   2x -1  2 2x -1 3
Xét hàm số: t  3 f
 t  2t với t   Ta có: t  2 f
 3t  2  0 với t
    f t  đồng biến trên 
Do đó: 3  f  y  
1  f  2x -1  y 1  2x -1  y  2x -1 -1 Thay vào (2) ta được: 2 2
2x -11x  9  2 2x -1 - 2  2 2x -1  2x -11x 11 2
2x -11x 11  0 **    2 4 2x -  1   2 2x -11x   11 4    4 2 3 2
4  8x - 4  4x 121x 121- 44x  44x - 242x 4 3 2  x - x  x - x     x -  3 2 4 44 165 250 125 0
1 4x - 40x 125x -125  0
  x -  x -  2 1
5 4x - 20x  25  0 x  1 tm*,*  *  
x  1  y  0
 x  5 tm*,*  * 
 x  5  y  2  
x  5 / 2 ktm   * , ** 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 18
Tất cả vì học sinh thân yêu
Vậy tập nghiệm của hệ phương trình đã cho là  ; x y    1;0,5;2 4 2 2 2 3 2 2
x  x y - y  y  x y  x
Bài 16: Giải hệ phương trình:  x, y   3 2   2 y - 5 - 2x -1  Bài giải: 5 Điều kiện: x  2 Phương trình (1)   2 x - - y  2 2 1
x  y   0  x  y  0 hoặc 2 x  y 1
Trường hợp x  y  0 thế vào (2) không thoả mãn. Trường hợp 2
x  y 1 thế vào (2): 3
2 y - 3 - 2 y -1  0 (3) æ 3 
Xét hàm f t  3
 2t - 3 - 2t -1;t  -; ; ma` f ç   1  0 2  è 
Suy ra phương trình (3) có nghiệm duy nhất: y  1 . Với 2
y  1  x  2  x   2 (thoả điều kiện)
Vậy nghiệm của hệ phương trình là:  2;1;- 2  ;1 2 2  2x  x 
x  2  2 y  y  2 y 1
Bài 17: Giải hệ phương trình:  . 2 2 
x  2 y - 2x  y - 2  0  Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 19
Tất cả vì học sinh thân yêu 1 Điều kiện: x  2 - , y  - 2
Phương trình thứ hai của hệ tương đương với 2
x  -2 y  2x - y  2
Thế vào phương trình thứ nhất, ta được 2 2 2 x  ( 2
- y  2x - y  2)  x  x  2  2 y  y  2 y 1 2 2
 x  3x  2  x  2  4 y  2 y  2 y 1 2 2
 (x 1)  (x 1)  (x 1) 1  (2 y)  2 y  2 y 1 (1) Xét hàm số 2
f (t)  t  t  t 1 với t  1 - . 1 1 3
Ta có f '(t)  2t 1
; f ' (t)  2 -
; f ' (t)  0  t  - 2 t 1 4 t  3 4 1 æ 3 ö 1
Suy ra f '(t)  f '   0 ç ÷ với mọi t  1
- ;  . Do đó hàm f(t) đồng biến trên [-1; ) . è 4 ø 2
Suy ra phương trình (1)  f (x 1)  f(2 y)  x 1  2 y  x  2 y -1.
Thế vào pt thứ hai của hệ, ta  y  1 được 2y 2 2 2 1 2 y 2(2 y 1) y 2 0 6 y 7 y 1 0  -  - -  -   -    1  y   6 æ 2 1 ö
Suy ra nghiệm (x;y) của hệ là (1;1), - ; ç ÷ . è 3 6 ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 20
Tất cả vì học sinh thân yêu  2   x  x  4  2 y  y 1  2
Bài 18: Giải hệ phương trình :  2 3 3 12 
y -10 y  2  2 x 1  Bài giải:
Phương trình đầu ên của hệ tương đương với: x  x   - y2 2 4 2  4  -2 y
 f  x  f  2
- y với y  f t  2
 t  4  t 2 t t  4  t t  t
Ta có f 't   1    0, t
  f t  là hàm số đồng biết trên R. 2 2 2 t  4 t  4 t  4
Từ đó f  x  f  2
- y  x  2 - y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 21
Tất cả vì học sinh thân yêu
Thế x  -2 y vào phương trình sau của hệ phương trình đã cho ta được: 2 3 3
3x  5x  2  2 x 1   x  3 1  2  x   1   3 x   3 3 1  2
x 1 với y  g t  3  t  2t g  x   1  g  3 3 x 1
Ta có g t  2 '
 3t  2  0, t
  g t  là hàm số đồng biến trên R. Từ đó: g  x   1  g  3 3 x 1 3 3  x 1  x 1 2
 3x  3x  0  x  1 -  y  2
 x  0  y  0 
Vậy nghiệm của hệ phương trình đã cho là:(-1;2),(0;0)   2x  2 3
2x -1  y  3y   1
Bài 19: Giải hệ phương trình  2
y - xy  5  5x - 6 y 2  Bài giải: 1  Đk x  ,   1  2x -  1
2x -1  y  3y   2x -13 3 3
 3 2x -1  y  3y; x 2
ét hàm số f t  3 '
 t  t trên  co f t  2 3 , ´
 3t  3  0 t
  f t  đồng
biến trên  ,pt(1) trở thành f  y  f  2x -1  y  2x -1 ; 
Pt(2)   y  5 y - x   1  0  y  5 - ; y  x -1;
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 22
Tất cả vì học sinh thân yêu 
Với y  -5  2x -1  5 - , vô nghiệm x  1
Với y  x -1  2x -1  x -1    x  2  2
2x -1   x - 2 1 
Với x  2  2  y  1 2. nghiệm của hệ là  ;
x y   2  2;1 2  3 2 
 2x  y  5 - 3 - x - y  x - 3x -10 y  6
Bài 20: Giải hệ phương trình:  3 2 3
x - 6x 13x  y  y 10  Bài giải:
Phương trình thứ 2 của hệ được biến đổi thành:
 x - 3   x -  3 2
2  y  y * Xét hàm số   3
f t  t  t là hàm số đồng biến trên R. Ta suy ra (*)  y  x - 2
Thế vào phương trình đầu của hệ: 3 3
3x  3 - 5 - 2x  x - 3x -10x  26   3x 3 -  3  1- 5-2x 3 2
 x -3x -10x  24 x  2 3 x - 2 2 x - 2 2     x - 2 2 x - x -12  2  3 
 x - x -12  1 3x 3 3 1 5 2x     - 1 5- 2x  3x 33 5
Phương trình (1) vô nghiệm vì với -1  x  thì 2 x - x -12  0. 2
Từ đó suy ra hệ có nghiệm duy nhất x  2 x  2; y  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 23
Tất cả vì học sinh thân yêu 3 2 2 3
x  xy - 2x y - 2 y  x - 2 y  0(1) 
Bài 21: Giải hệ phương trình  3 2 3 
6 y  5  x  3x  2 y - 3(2)  Bài giải: 3 2 2 3
(1)  (x - 2x y)  (xy - 2 y )  (x - 2 y)  0 2 2
 x (x - 2 y)  y (x - 2 y)  (x - 2 y)  0 2 2
 (x  y 1)(x - 2 y)  0  2 y  x ( Vì 2 2
x  y 1  0, x  , y  R ). Thay vào (2), ta có: 3 3 2
3x  5  x  3x  2 y - 3 3 3
 3x  5  3x  5  (x 1)  (x 1) (*) 3 2
Xét hàm số f (t)  t  t, R  f '(t)  3t 1  0, t
  R . Suy ra hàm số f(t) đồng biến trên R.  1
x  1  y  3 3 3 2 
(*)  f  3x  5   f (x 1)  3x  5  x 1  x  3x - 4  0  2 .  x  2 -  y  1 -  æ 1 ö
Vậy hệ phương trình có hai nghiệm: 1; ç ÷ ; (-2;-1). è 2 ø 3 
 y 2  x  8 2  x  10 y - 3xy 12(1)
Bài 22: Giải hệ phương trình  3 2 3  5 y
2 - x - 8  6 y  xy 2 - x (2)  Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 24
Tất cả vì học sinh thân yêu 3 
 y 2  x  8 2  x  10 y - 3xy 12(1)  3 2 3  5 y
2 - x - 8  6 y  xy 2 - x (2)  Điều kiện: x [-2;2]
Nhận xét y = 0 không thỏa mãn phương trình (2) 3 3 æ 2 ö æ 2 ö
(2)   2 - x   3 2 - x   3 ç ÷ ç ÷ (*) y y è ø è ø Xét hàm số 3
f (t)  t  3t trên R  hàm số đồng biến trên R æ ö (*)  f  - x  2 2 2  f  2 - x  ç ÷ thế vào (1) y y è ø
(1)  3y 2  x  8 2  x  10 y - 3xy 12  3 2  x  4 2  x 2 - x  10 y - 3x  6 2 - x 2
 3 2  x - 6 2 - x  4 4 - x  3x -10  0 (**) Đặt 2 2
2  x - 2 2 - x  t  t  10 - 3x - 4 4 - x t  0
Phương trình (**) trở thành 2
3t - t  0  t  3  6
- với t = 0: x  ; y  5 5
- với t = 3: 2  x - 2 2 - x  3 phương trình vô nghiệm, vì vế trái  2 .
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 25
Tất cả vì học sinh thân yêu  4xy  ( - 2)2xy xy  xy - 3  0
Bài 23: Giải hệ phương trình  2
log (x - y)  log . x log y  0  2 2 2 Bài giải:
Điều kiện: x > y > 0
Đặt t = xy > 0, phương trính thứ nhất của hệ trở thành
4t  ( - 2)2t  - 3  0  (2t 1)(2t  - 3)  0  2t t t t
 t - 3  0 , vì 2t 1  0 Vì hàm ( )  2t f t
 t - 3 đồng biến trên R, mà f(1) = 0 nên 2t  t - 3  0  t  1 . Khi đó ta có 1 xy = 1, hay y  . x
Thế vào pt thứ hai của hệ ta được: 2 æ 1 ö 1 x -1 2 2 2 log x -  log  0  log  log x 2 ç ÷ 2 2 2 è x ø x x 2 2  x -1  x -1 log  log x  x  2 x 2 2  x x x -1  x       x  2  2 2 2  x -1  x -1 1 x -1  1  log  - log x   2 2 x    x x 1
Suy ra hệ của nghiệm là x  2 , y  2 Bài 24: 2 2
4x  4xy  y  2x  y - 2  0 
Giải hệ phương trình Giải hệ phương trình: 
 x, y   2 8 
1- 2x  y - 9  0 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 26
Tất cả vì học sinh thân yêu Bài giải: 2 2
4x  4xy  y  2x  y - 2  0    1 Xét hệ phương trình:  2
8 1- 2x  y - 9  0  2  1
Điều kiện: 1-2x  0  x 
. Đặt t  2x  y , phương trình (1) trở thành: 2 t  1 2
t  t - 2  0  t  -2 
Nếu t = 1 thì 2x  y  1  1- 2x  y  0 . Thế vào phương trình (2) ta được phương trình 2
8 y  y - 9  0 Đặt u 
y  0 , phương trình trở thành: x  0 4 u  u -   u -  3 2 8 9 0
1 u  u  u  9  0  u  1 . Khi đó hệ có nghiệm y 1 
Nếu t = -2 thì 2x  y  -2  1- 2x  y  3  0 . Thế vào phương trình (2) ta được phương trình  y  3 - 2
8 y  3  y - 9  0  8 y  3   y - 3 y  3  0  8y -3 y 3  0   1 x 
Với y  -3 thì hệ có nghiệm  2  y  3 - 
Xét phương trình 8   y - 3 y  3  0 3 Đặt v 
y  3  0 , phương trình (3) trở thành: 3
v - 6v  8  0
Xét hàm số f v 3
 v - 6v  8 , ta có: f v 2 '
 3v - 6 và f 'v  0  v   2
Hàm số f v đạt cực đại tại - 2;8  4 2  , đạt cực tiểu tại  2;8 - 4 2 
Vì f 0  8  0 và 8 - 4 2  0 nên f v  0 không có nghiệm v  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 27
Tất cả vì học sinh thân yêu  1
x  0 x 
Vậy hệ phương trình có hai nghiệm là  ;  2 y  1   y  -3  4
 y -  x - 2 2 y - x - 4  0 
Bài 25: Giải hệ phương trình   ; x y   3 2
x  3x  4x  2  3 4 y  y -   1  Bài giải: 3 3
Phương trình thứ hai của hệ tương đương với  x  
1  x 1  2 y  2 y (1) Xét hàm số   3
f t  t  t với t  
Ta có f t  2 '
 3t  t, f 't   0 với mọi t   . Do đó hàm f(t) đồng biến trên R. Khi đó phương trình  
1  f  x  
1  f 2y  x 1  2y  x  2 y -1
Thay vào phương trình thứ nhất của hệ ta được 4 3 2
y - 2 y  3y - 2 y - 3  0 2  y - y  1    y - y 2 1 5 2  2 2
y - y  - 3  0   y   2 y - y  -3 2  æ 1- 5 ö æ 1 5 ö
Suy ra nghiệm (x; y) của hệ là ç - 5; ÷ và ç 5; ç ÷ 2 ÷ ç ÷ è ø 2 è ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 28
Tất cả vì học sinh thân yêu 3 x   2 4 y  
1  x 2 y  3   1
Bài 26: Giải hệ phương trình  2 2
2 y  4 y 1  x  x 1 2  Bài giải:
Điều kiện: y  0 PT   2  x  x  2 1 4 y  
1  2 y   3  x  0   Khi đó, PT   2 2
2  2 y  4 y 1  x  x 1 3
Xét hàm f t  2
 t  t 1 trên 0;  t
Có f 't   1  0 t
  0  f t  đồng biến trên 0;  2 t 1
Khi đó, PT 3  f 2y  f  x  2 y  x
Thay vào phương trình (1) ta được phương trình: 5 3
x  x  x x  3 Đặt t 
x  0 có hàm số   10 6 3
g t  t  t  t có g t  9 5 2 '
 10t  6t  3t  0 do t  0 Mà g   1  3  t  1 
x  1  x  1 1 æ 1 ö
Với x  1  y 
. Hệ phương phương trình có nghiệm duy nhất  x; y  1; ç ÷ 2 è 2 ø 3 3 2 2
x - y  5x - 2 y 10x - 3y  6  0    1
Bài 27: Giải hệ phương trình:  3 2
x  2  4 - y  x  y - 4x - 2 y  2  Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 29
Tất cả vì học sinh thân yêu
Điều kiện x  -2; y  4 3 2 3 2
(1)  x  5x  10x  6  y  2 y  3y 3 2 3 2
 (x  1)  2(x  1)  3(x  1)  y  2 y  3y Xét hàm số 3 2 2
f (t)  t  2t  3t, f '(t)  3t  4t  3  0 t   R
Suy ra f (x  1)  f ( y)  y  x  1 thay vào pt (2) ta được Phương trình 3 2
x  2  3 - x  x  x - 4x - 1 2
(x  2)(3 - x) - 2 3 2  
  x  2  3 - x  2
- 3  x  x - 4x - 4 
 (x  1)(x - 4)
x  2  3 - x  3
2(x  2)(3 - x) - 4 2 
 (x  2)(x - x - 2)
 x  2  3- x  3 (x  2)(3- x)  2 2
2(-x  x  2) 2 
- (x  2)(x - x - 2)  0
 x  2  3- x  3 (x  2)(3- x)  2   2 2 (x x 2) x 2   - -    0   x 2 3 x
3 (x 2)(3 x) 2   -   -   
 0 (vi x  -2)  x  2 2
 x - x - 2  0  x  1 - 
Vậy hệ phương trình có nghiệm: ( ; x y)  (2;3), ( ; x y)  (-1;0) Bài 28:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 30
Tất cả vì học sinh thân yêu
xy  x   3 2
1  x  y  x - y 
Giải hệ phương trình Giải hệ PT  x   3y   , , y 2
2  9x  3   4y  2 2
1 x  x     1  0  Bài giải: ĐKXĐ x   
Ta có xy  x   3 3 3 2 2
1  x  y  x - y  x - x y  y - xy  x - y  0  y  x
  x - y 2 x 0 y   1  0   2 y  x 1 
Với y  x2 1 thay vào PT thứ 2 ta được
3 x2 12  9x2  3  4x2  6 1 x  x2 1  0 . Dễ thấy PT vô nghiệm.
Với y  x thay vào PT thứ 2 ta được 3x 2  9x2  3  4x  2 1 x  x2 1  0 
  x    - x   x   2 2 3x 2 9 3 2 1 3 2 1  2  x  
x    - x    - x -   2 2 3 2 9 3 2 1 3 2 1  2 2 t
Xét hàm số f t   t  2t  2  2 ta có f 't 2  t  2  2   0 suy ra hàm số 2 t  2 đồng biến 1 æ 1 1 ö
Từ đó suy ra 3x  2
- x -1  x  - . Vậy HPT có nghiệm  ; x y   - ; - ç ÷ 5 è 5 5 ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 31
Tất cả vì học sinh thân yêu
 x 1   x  
1  y - 2  x  5  2 y  y - 2 
Bài 29: Giải hệ phương trình: x -8 y   1   y - 2 x 1 - 3 2     x - 4x  7 Bài giải:
Điều kiện x  -1; y  2 Đặt x 1  ; a
y - 2  b a,b  2 , từ (1) ta có: 2
a  ab  a -    2 b   2 2 2 1 5 2
2  b  a - b  ab - b  a - b  0
 a - b1 2a  b  0
 a  b (do a, b  0  1 2a  b  0 )  x 1 
y - 2  y  x  3 Thế vào (2) ta được:
 x -8 x  4 x - 8 x  4 x 1 x - 8   x   1  x 1 - 3         2 2 x - 4x  7 x - 4x  7 x 1  3  x  8   x  4 x 1   * 2  
 x - 4x  7 x 1  3
+ x  8  y  11;
+     x    x     x   2 * 1 3 4 1 x - 4x+7  x
 x 2  x     x 2 1 3 1 3 2 3 . 2 3       -  -  *  *        
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 32
Tất cả vì học sinh thân yêu
Xét hàm số f t   t   2
3 t  3 với t  có f t   t  2 ' 3 1  0 t    nên f(t) đồng biến trên  x  2 Do đó * 
*  f  x 1  f  x - 2  x 1  x - 2   2
x 1  x - 4x  4  x  2 5  13    x  T / M  2 x - 5x  3  0 2  5  13 11  13 x   y  2 2 æ 5  13 11 13 ö
Vậy hệ đã cho có nghiệm (x;y) là 8  ;11 và ç ; ÷ ç 2 2 ÷ è ø 3 8
 x  y - 2  y y - 2 - 2x 
Bài 30: Giải hệ phương trình  y-2 -   3 1
2x+1  8x -13 y - 2  82x - 29  Bài giải:  1 2x 1  0 x  - Điều kiện:    2 y - 2  0   y  2  3  Phương trình 3 8x 
y - 2  y y - 2 - 2x  2x  2x   y - 2   y - 2
Xét hàm đặc trưng: f t  3  t  t t 2 , f'
 3t 1  0 t 
Hàm số f(t) liên tục và đồng biến trên R. Suy ra: 2x  y - 2 Thế 2x 
y - 2 vào phương trình thứ hai ta được:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 33
Tất cả vì học sinh thân yêu  -  3 2 2x 1
2x 1  8x - 52x  82x - 29   -     -  2 2x 1 2x 1 2x 1 4x - 24x+29   -  2 -  -     -  2 2x 1 2x+1 4x 24x 29 0 2x 1
2x 1 - 4x  24x - 29  0  1
2x -1  0  x   y  3   2  2
 2x 1 - 4x  24x - 29  0  Giải phương trình: 2
2x 1 - 4x  24x - 29  0 Đặt 2 t 
2x 1, t  0  2x  t -1 2
Ta được phương trình: t -  2 t -    2t -  4 2 1 12
1 - 29  0  t -14t - t  42  0 t  2 t  3 - loai  
 t - t   2 t - t -  1- 29 2 3 7  0  t  loai  2  1 29 t   2 3
Với t  2  x   y  11 2 1 29 13  29 103 13 29 Với t   x   y  2 4 2 æ 1 ö æ 3 æ ö 13 29 103 1  3 29 ö
Vậy hệ phương trình đã cho có3cặp nghiệm: ;3 ; ;11 ; ç ÷ ç ÷ ç ; ÷ 2 2 ç 4 2 ÷ è ø è ø è ø 3 2 3
2x - 4x  3x -1  2x 2 - y 3- 2y   1 
Bài 31: Giải hệ phương trình  3
 x  2  14 - x 3 - 2 y 1 2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 34
Tất cả vì học sinh thân yêu Bài giải:
Ta thấy x = 0 không phải là nghiệm của hệ, chia cả hai vế của (1) cho x3 ta được 4 3 1   1  2 -  -  2 2 - y 3 - 2 y 2 3   x x x 3 æ 1 ö æ 1 ö  1-  1-  ç ÷ ç ÷
3 - 2 y 3 - 2y  3 - 2 y * è x ø è x ø Xét hàm   3
f t  t  t luôn đồng biến trên  1
*  1-  3 - 2y 3 x
Thế (3) vào (2) ta được 3 3
x  2  15 - x 1 
x  2 - 3  2 - 15 - x  0 æ ö ç ÷ ç 1 1  ÷  x - 7   0 ç x 2 3 ÷   4 - 2 x 15  ç  x 152 3 3 ÷ ç    ÷ è 0 ø æ 111 ö
Vậy hệ đã cho có nghiệm  ; x y  7; ç ÷ è 98 ø 3  3 2 y  2  y - 2  x  4  x 
Bài 32: Giải hệ phương trình: 
  y  4 2x 12 2
- 8  x  y -  2 x  2 2 x - y  Bài giải:  y  2 - + Đk:  2 x  y  + Từ pt thứ 2 ta có:
 y   y   2
-  x  y -  2 x   2 4 2 12 8 2 x - y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 35
Tất cả vì học sinh thân yêu 2
 x   y -  y   y   -  2 x   2 8 4 2 12 2 x - y  0   2 x   y -
 y   y   -  2 x   2 2 8 2 4 2 12 2 2 x - y  0   y  -
y     x  - x - y 2 2 2 2 2 8 6 2  0
 2 y  8  y  6     y  -2 2 2  x  2  x - y   y  2  0 + Thay vào pt 1 ta được: 3 3 2 y  2  y - 2  x  4  x 3    - 
3     -    -  3 3 3 3 y 2 y 2 x 4 x y 2 4 y 2 x  4  x + Xét hàm số: 3 f
 t  t  4 t  R . Ta có: t 2 3t f '  1  0, t   R  f  f x  y -  x t   3 2 3      y-2 3  2 t  4 3  y  2  0   x  - 4 + Vậy ta sẽ có:    TM  3  y - 2  x  y  2 -  
Kl: Nghiệm duy nhất của hệ là:  x y   3 : - 4; 2 -  Bài 33:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 36
Tất cả vì học sinh thân yêu  x 2 x 
  y  2  x   1  y    1
Giải hệ phương trình Giải hệ phương trình: x 1 
 x, y   2 3
 x -8x - 3  4x   1 y 1  Bài giải: x  1 -
Điều kiện  y  -1  3 2 3
x  x  x
x  x  x   1   1 
  y  2  x   1  y   1 
  y  2 y 1 x 1  x   1 x 1 3 æ x ö x    ç ÷  y  3 1  y 1 è x 1 ø x 1
Xét hàm số f t  3
 t  t trên  có f t  2 '
 3t 1  0t   suy f(t) đồng biến trên  . æ x ö x Nên f  ç ÷
f  y 1  
y 1 . Thay vào (2) ta được è x 1 ø x 1 2
3x - 8x - 3  4x x 1
  x -    x  x  2 2 2 1 2 1 x  1  2 x - 6x - 3  0   x  3  2 3
2 x 1  x -1      1   5 - 2 13 2 x 1  1- 3  x x    x  3    9 2  9
 x -10x - 3  0  2 x Ta có: y  -1 x 1 4  3 3 5 - 2 13 41  7 13
Với x  3  2 3  y  . Với x   y  - 2 9 72
Các nghiệm này đều thỏa mãn điều kiện.
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 37
Tất cả vì học sinh thân yêu æ 4  3 3 ö
KL: Hệ phương trình có hai nghiệm  ;
x y   ç 3  2 3; ÷ ç 2 ÷ è ø æ 5 - 2 13 41 7 13 ö &  ; x y  ç ; - ÷ ç 9 72 ÷ è ø 2  y  4 y  5 x - y -1  ln 
Bài 34: Giải hệ phương trình 2 x  2x  2 
6 y  2 y   2 3 1
x  2  2x - y  7  Bài giải: 2  y  4 y  5 x - y -1  ln    1 Xét hệ 2 x  2x  2  (Đ/K: x  2 - )
6 y  2 y   2 3 1
x  2  2x - y  7 2 
Ta có:    x    2
x  x    y    2 1 1 ln 2 2
2 ln y  4 y  5  x  
x 2    y    y  2 1 ln 1 1 2 ln 2   1 * 2t 1 t2
Xét hàm f t   t   2 ln t  
1 , t  R . Ta có f 't   1 
 0t  R , dấu bằng 2 2 1 t 1 t
xảy ra khi và chỉ khi t  1 -
Nên f(t) đồng biến trên R theo (*) suy ra f  x  
1  f  y  2  x 1  y  2  x  y 1 Thay vào (2) ta được 3 2
6 x -1  2x x  2  2x - x  8 3
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 38
Tất cả vì học sinh thân yêu Xét 3 2
x  1  6 x -1  2x x  2  2 3  7  2x - x  8 nên (3) không có nghiệm trên   ;1 - 4  x  2 x 10x  4 3   2
Xét x  1 , khi đó 6 x -1  2x x  2  2 x -  1 1  1  x  2 2 2 x 10x  4 3 2 Mà 2
 2x - x  8 
 x - 2  0. Do đó (3) xảy ra khi và chỉ khi x = 2. 2 2
Do đó hệ có nghiệm  ; x y  2 
;1 (thỏa mãn điều kiện)
Bài 35: Giải hệ phương trình sau trên tập số thực: 2 2  3 x  3 x -1 
x(x - 3x  3) - x - 6x  6  2 y  2  y  3  2    1  2 3 3 
x -1 - x - 6x  6  y  2   1 2  Bài giải:
Thế - x2 - 6x  6  3 y  2  1 - 3 x -1 vào PT(1) ta được :
(x -1)  (x -1)3  1  3 y  2  y  2  1 2 3t Xét hàm số 3
f (t)  t  t  1  f '(t)  1 
 0 suy ra hàm số đồng biến 3 2 t  1 Mà 3 3
f (x -1)  f ( y  2)  x -1 
y  2 .Thế vào PT(2) ta được : 2 3 x -1 -
x - 6x  6  x
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 39
Tất cả vì học sinh thân yêu 2
 3 x -1  x  x - 6x  6 2 2
 9(x -1)  2x - 6x  6  2x x - 6x  6 2 2 2 2
 (15x -15 - 2x )  4x (x - 6x  6)
 (x - 5)(x -1)(4x - 5)  0  5 127 - x   y  Đối chiếu điều kiện   4 64
x  5 y  62  æ 5 127 ö
Vậy hệ phương trình có hai nghiệm phân biệt ; - ç ÷ và (5;62) è 4 64 ø  3  y  2 2
1  y y 1  x  
Bài 36: Giải hệ phương trình: 2 
 x, y    2
x  x - 2x  5  1 2 2x - 4 y  2  Bài giải:
ĐK: x - 2 y 1  0   2 2
1  2 y  4 y  2  2 y y 1  2x  3 2 2 2
 y  2 y y 1  y 1  2x - 4 y  2
  y  y  2 2 1
 2x - 4 y  2  x -  2
1  x - 2x  5 (2) ta có:
2x - 4 y  2  2 2  x -  x - x  2 x -1 æ x -1 ö  y  y 1   2 2 1 2 5 2    2 y  y 1   1 ç ÷ 2 2 è 2 ø 1 Ta có: 2 y 1  y  2 y 1 - y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 40
Tất cả vì học sinh thân yêu 2 x -1 æ x -1 2 2 ö
y 1 - y  0 
y 1  y  0 2  y  y 1   1 ç ÷ 2 è 2 ø
Xét hàm f t  2
 t  t 1 t
f 't   1  0 t  2 t 1 æ x -1 ö
f  y  f ç
÷  2 y  x -1 thay vào (2) ta có: è 2 ø
x   x - 2    x - x  
 x   x - 2 1 4 1 2 2 2 2 2 1  4  5   x - 2 1  4   x -  1 - 4  0
Đặt x -1  t ta có: 2
t  4  4 - t t   4 4 - t  0 t  4        3 2 2
t  4  t - 8t 16 8t  12 t    TM    2 3 3 5 3 Với t   x -1   x   y  2 2 2 4 æ 5 3 ö Vậy  ; x y  ; ç ÷ è 2 4 ø
 x 1   x  
1  y - 2  x  5  2 y  y - 2 
Bài 37: Giải hệ phương trình   -    x, 8 1 y x y    y - 2 x 1 - 3 2     x - 4x  7 Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 41
Tất cả vì học sinh thân yêu  y  2 Đkxđ: x  1 -    1 
x 1   x  
1  y - 2  2 y - 2 -  x -  1  y - 2  x 1  a  Đặt  a,b  0  y - 2  b  2 2
a  ab  2b - a  b  1 b  b - ab  a  b 1 b
 a - b1 b  b  
1  0  a - ba  2b   1  0 a  b
 a  2b 1 0 do a,b  0  a+2b+1>0 
Với a = b ta có: x 1  y - 2  y  x  3 Thay vào (2) ta có:
 x - 8 x 1 3  x 1 x 1-3  x- x   x  x -  2 8 4 1
1 3  x - 4x  7 2    x - 4x  7  
 x   x -  2 1
8 x - 4x  7 
 x    x - 2 1 2  3 
  x - 8 x  4 
 x 8 x 4     -  -  0 x 1  3  x 1 3       x  8
 x 4 x 1 3 x 1x 22 3      -       x 1  a Đặt  a  0 x - 2  b 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 42
Tất cả vì học sinh thân yêu Ta có:  2
a  a    b   2 3 3 3 b  3
Xét hàm f t    2
t  3t  3 t   0
t  t t   2 2 2 2 f' 2
3  t  3  2t  6t  t  3  3t  6t  3
 t  t   t  2 2 3 6 3 3 1  0 t  0
 f(t) đồng biến  f a  f b 2 2 
x 1  x - 2  x 1  x - 4x  4  x - 5x  3  0  5  13 x   TM  2   5- 15  x  loai  2
Vậy với x  8  y  11 5  13 11  13 Với x   y  2 2 æ 5  13 11 13 ö Kết luận:  ; x y   8;  11 ;ç ; ÷ ç 2 2 ÷ è ø 3
2 y  y  2x 1- x  3 1 - x 
Bài 38: Giải hệ phương trình   , x y  R 2 2 2
 9 - 4 y  2x  6 y - 7  Bài giải:  3 3 
Điều kiện: x  1; y  - ;  . Ta có 2 2   
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 43
Tất cả vì học sinh thân yêu   3
1  2 y  y  2 1 - x  2x 1 - x  1 - x 3
 2 y  y  2 1 - x 1 - x  1 - x
Xét hàm số f t  3
 2t  t , ta có f t  2 '
 6t  1  0 t
  R suy ra f(t) đồng biến trên R. Vậy  y  0  
1  f  y  f  1- x   y  1- x   2 y  1 - x  Thế vào (2) ta được: 2
4x  5  2x - 6x - 1 PT  x   x - x -   x 
 2   x - 2 2 2 4 5 4 12 2 4 5 1 2 2  1 x    x   x - vn 2 4 5 2 3   
 x 1 2 loai
 4x  5  1 - 2x   x  1- 2  4  y  2
Với x  1 - 2   . Vậy hệ có 2 nghiệm 4  y  - 2  4 5 10 6
x y  y  x  x 
Bài 39: Giải hệ phương trình: 4 1 x - 2 1- x -3x 1 1- y  Bài giải:
Điều kiện: -1  x  1, y  1
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 44
Tất cả vì học sinh thân yêu
Nếu x = 0 thay vào hệ phương trình ta được  ;
x y  0;0 là một nghiệm của hệ phương trình. 5 æ y ö y Nếu x  0 , từ 4 5 10 6 5
x y  y  x  x    x  x ç ÷ è x ø x Xét f t  5
 t  t,t  R . Ta có f t  4 '
 5t  1  0, t
  R , nên f(t) đồng biến trên R. æ y ö y
Do đó f  x  f ç ÷ . Suy ra 2
 x  y  x è x ø x
Thay y = x2 vào phương trình thứ hai ta được 2
4 1  x - 2 1 - x - 3x  1  1 - x (*)  1 x   2 2 u - v 
Đặt u  1  x  0, v  1 - x  0 . Ta có  2 2 2 u   v  2  3 1
Phương trình (*) trở thành 4u - 2v -  2 2
u - v    2 2
u  v   uv 2 2 2
 u  v -  2 2
4 u - v  2v  0  2u - vu  v - 2  0 3 9
Nếu v  2u thì 1 - x  2 1  x  x  -  y  5 25
Nếu v  2 - u thì 1 - x  2 - 1  x  pt vô nghiệm æ 3 9 ö
Tóm lại phương trình có các nghiệm là  x; y  0;0; - ; ç ÷ è 5 25 ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 45
Tất cả vì học sinh thân yêu 2 x  y   x -  2 4
5 -1  4 y - x  2 2 y
Bài 40: Giải hệ phương trình   , x y  
4 y  x - 4  x  2 x -1  Bài giải: x  1 Điều kiện  . Với điều kiện đó y  0    2 2
1  x  4xy - 20 y - 1  4 y - x  2 2 y
2  4xy  16xy  2 x -1 - x . Thay vào (1) ta có x 
x -   y  2 2 2 1 2 1  2 2y   1 -1
Xét hàm số u  g t  2
 t  2 t -1 với t 1; . Hàm số này luôn đồng biến. 2 Vì thế 2
x  2 x -1  2y   1  2 2y  
1 -1  x  2 y  1  x -1  2 y Thay vào (2) ta được
 x -1  2x - 2 2 -1
2x - 9x  8  2 x -1  2 x - 2   x -1  2 2 2 1  
 x -1  - 2x  2 2 -1  2 2x - 
9  2 2x 10  4 2  0 x -1  2x - 2 2 -1    2x - 2 2 -1  0  Phương trình bậc hai 2
2x - 9  2 2x 10  4 2  0 có     2 2 2 1 nên có hai nghiệm
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 46
Tất cả vì học sinh thân yêu 5  2 2 là x 
và x  2 . Nghiệm x 2x - 2 2 -1  0 1 2 bị loại vì 2 2 2 5 - 2 2
Hoàn toàn tương tự ta có x - 1  - 2x  2 2 -1  x  2 æ 5 - 2 2 3 - 2 2 ö æ 5  2 2 3  2 2 ö
Vậy hệ đã cho có hai nghiệm là ç ; ÷ và ç ; ç ÷ 2 4 ÷ ç ÷ è ø 2 4 è ø 4 3 2
2x 2x - 1 - y - 3y   15y  7  2x 1  
Bài 41: Giải hệ phương trình  y y  2 2 2 
 6 - x  2x  2 y - 15x  4 y  12   2 Bài giải:
Điều kiện: 1  x  6 1  f  y 1  f  2x -1 với f t  4t3  3t . Vì f(t) đồng biến nên y  1 
2x - 1  y2  2 y  2x - 2 . Thế vào (2): x - 5 5 - x 2
x -1  6 - x  2x -11x  8   x -1 - 2   6 - x -  2
1  2x -11x  5  
  x - 52x -  1 2  x -1 1  6 - x 1 1
  x - 5 A  0 với A  2x  1 -
 0 (do x  1 )  x  5, y  2. 1  6 - x 2  x -1 3 x   2 4 y  
1  x 2 y  3 (1)
Bài 42: Giải hệ phương trình  2 2
2 y  4 y  1  x  x  1 (2)  Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 47
Tất cả vì học sinh thân yêu
Điều kiện: y  0 2 PT  x  x  2 (1) 4 y  
1  2 y   3  x  0   Khi đó, 2 2
PT (2)  2 y  4 y  1  x  x  1 (3)
Xé thàm f t  2
 t  t  1 trên0;  t
Có f 't   1   0 t
  0  f t  đồng biến trên 0;  t2  1
Khi đó, PT (3)  f 2 y  f  x  2 y  x
Thay vào phương trình (1) ta được phương trình: x5  x3  x x  3 Đặt t 
x > 0 có hàm số g t   t10  t6  t3 có g't   10t9  6t5  3t2  0 dot  0
Mà g 1  3 t  1  x  1  x  1 1 æ 1 ö
Với x  1  y 
. Hệ phương trình có nghiệm duy nhất  ; x y   1; ç ÷ 2 è 2 ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 48
Tất cả vì học sinh thân yêu
xy  x   3 2
1  x  y  x - y 
Bài 43: Giải hệ PT  x y   3y   , ( , ). 2
2  9x  3   4y  2 2
1 x  x   1  0  Bài giải: ĐKXĐ x   . 
Ta có xy  x   3 2 3 2 2
1  x  y  x - y  x - x y  y - xy  x - y  0  y  x
  x - y 2 x - y   1  0   2 y  x 1 
Với y  x2 1 thay vào PT thứ 2 ta được
3 x2 12  9x2  3  4x2  6 1 x  x2 1  0 . Dễ thấy PT vô nghiệm.
Với y  x thay vào PT thứ 2 ta được 3x 2  9x2  3  4x  2 1 x  x2 1  0
 3x 2  9x  3  -2x   1 3  2x    2 2 1  2
 3x 2  9x  3  -2x -  1 3   2 - x -   2 2 1  2 2 t
Xét hàm số f t  t  2 ( ) t  2  2 ta có 2
f '(t)  t  2  2   0 suy ra hàm số 2 t  2 đồng biến.
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 49
Tất cả vì học sinh thân yêu 1 æ 1 1 ö
Từ đó suy ra 3x  2
- x -1  x  - . Vậy HPT có nghiệm  ; x y   - ; - . ç ÷ 5 è 5 5 ø 5 3
 2x - 5 y - 2  y( y - 4) y - 2 - 2x 
Bài 44: Giải hệ phương trình:   , x y   . 3 ( 
y - 2 -1) 2x 1  8x -13( y - 2)  82x - 29  Bài giải: 1
Đặt đk x  - , y  2 2 +)  x
 x  y - y y -  y -  x
 x   y - 5 5 2 5 (1) (2 ) 2 ( 4 ) 2 5 2 (2 ) 2 2  y - 2(3)
Xét hàm số f (t)  t5  t, f '(t)  5t 4 1  0,x  R , suy ra hàm số f(t) liên tục trên R. Từ (3)
ta có f (2x)  f ( y - 2)  2x  y - 2 Thay 2x 
y - 2(x  0) vào (2) được 3 2
(2x -1) 2x 1  8x - 52x  82x - 29 2
 (2x -1) 2x 1  (2x -1)(4x - 24x  29)  (2x -1)  2
2x 1 - 4x  24x - 29  0  1 x   2  2
 2x 1 - 4x  24x - 29  0(4)  Với x=1/2. Ta có y=3
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 50
Tất cả vì học sinh thân yêu 2x - 3 2
(4)  ( 2x 1 - 2) - (4x - 24x  27)  0 
- (2x - 3)(2x - 9)  0 2x 1  2 x  3 / 2   1  (2x - 9)  0(5)  2x 1  2 Với x=3/2. Ta có y=11 Xét (5). Đặt 2 t 
2x 1  0  2x  t -1. Thay vao (5) được 1 29 3 2
t  2t -10 - 21  0  (t  3)(t - t - 7)  0 . Tìm được t  . Từ đó tìm được 2 13  29 103 13 29 x  , y  4 2 3 3 2 2 
x - y  5x - 2 y  10x - 3y  6  0
Bài 45: Giải hệ phương trình :  3 2
 x  2  4 - y  x  y - 4x - 2 y Bài giải:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 51
Tất cả vì học sinh thân yêu
Điều kiện x  -2; y  4 ) 1 (
 x3  5x2  10x  6  y 3  2 y 2  3y  x   1 3   2 x   1 2  ( 3 x  )
1  y3  2 y 2  3y Xét hàm số f t
( )  t 3  t 2 2  t 3 , f ' t ( )  t 3 2  t 4  3  0 t   R
Suy ra f(x+1) = f(y) => y= x+1 thay và pt (2) ta đuợc
Phương trình : x  2  3 3 2
- x  x  x - 4x -1 x x    - - x  2  3 - x  3 2 2  23  2
- 3  x  x - 4 x - 4   x   1  2 x - 4 x  2  3 - x  3 2 
 x  23 - x - 4 2    x  x - x - x  2  3 - x  3 2 ( 2)
x  23 - x  2   2( 2 - x  x  2) 2   - x  x - x -  x  2  3 - x  3 2 2
x  23 - x  2    0     2 x - x - 2 2  x  2      x  2  3 - x  3 0
x  23 - x  2  0 (vi x  -2 )  x  2  2
x - x - 2  0  x  -1
Vậy hệ pt có nghiệm (x; y) = (2;3) , (x;y)= (-1; 0) 3 
2y  y  2x 1- x  3 1- x
Bài 46: Giải hệ phương trình:  2 2 2
 9 - 4 y  2x  6 y - 7
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 52
Tất cả vì học sinh thân yêu Bài giải: ĐK: x  1 , ta có:  3
2 y3  y  2x 1 - x  3 1 - x  2 y3  y  2 
. 1 - x   1- x  y  1- x
Vì h/s f t  t 3 2
 t đồng biến trên R.
Thế vào pt kia ta được pt: 2
2x - 6x -1  4x  5 2
 4x - 8x  4  4x  5  2 4x  5 1
 2x - 2   4x  5  2 2 1
 2 - 2x  4x  5 1 vì x  1  x  1- 2 tmđk. 5
(xy - 3) y  2  x  x  (y - 3x) y  2 
Bài 47: Giải hệ phương trình: 
(x, y  ) 2
 9x 16 - 2 2 y  8  4 2 - x  Bài giải: 0  x  2 Đk:  (*) .Với đk(*) ta có y  2 -   x  1
(1)  (x -1) ( y  3) y  2 - (x 1) x   0    
( y  3) y  2  (x 1) x (3)  Nội dung
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 53
Tất cả vì học sinh thân yêu 31
Với x = 1 thay vào (2) ta được: 2 2 y  8  1  y  - (loai) 8 Ta có:   y  3 3 (3) 2 
y  2  ( x )  x (4). Xét hàm số 3 2
f (t)  t  t  f '(t)  3t 1  0; t
  Hàm số f(t) là hs đồng biến, do đó:
(4)  f ( y  2)  f ( x)  y  2 
x  y  x - 2 thay vào pt(2) ta được: 2
4 2 - x  2 2x  4  9x 16 2 2 2 2 2
 32 - 8x 16 2(4 - x )  9x  8(4 - x ) 16 2(4 - x ) - (x  8x)  0  x t   Đặt: 2 t  2(4 - x )
(t  0) ; PT trở thành: 2 2 2
4t 16t - (x  8x)  0   x
t  - - 4  0(loai)  2 0  x  2 x  4 2 4 2 - 6 Hay 2 2(4 - x )    32  x   y  2 2 x  3 3   9 æ 4 2 4 2 - 6 ö
Vậy hệ pt có nghiệm (x; y) là: ç ; ÷ ç 3 3 ÷ è ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 54
Tất cả vì học sinh thân yêu 
 1- y x - y  x  2   x - y -   1 y   1
Bài 1: Giải hệ phương trình  2
2 y - 3x  6 y 1  2 x - 2 y - 4x - 5y - 3 2  Bài giải chi tiết x  y  0
Điều kiện: x  2y;4x -5y -3  0 
Phương trình (1) trở thành:  
1  1- y x - y    x - y -  1   y - 
1 -  x - y -  1 y  0
 1- y x - y - 
1   x - y -  1 1- y   0 æ 1 1 ö  y  1
 1- y x - y -  1 ç  ÷  0   ç x - y 1 y 1 ÷ x  y 1 è ø  * Với y  1
2  9 - 3x  2 x - 2 - 4x -8
 9 - 3x  0  x  3
* Với x  y 1
2  2y2  3y - 2  2 1- y - 1- y  2y2  3y - 2  1- y 3
Điều kiện: y  1
Cách 1: Phân tích thành nhân tử
3  21- y - 2y 1- y  2y   1
1- y - y 2x   1  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 55
Tất cả vì học sinh thân yêu
 2 1- y  1- y - y  2y  
1  1- y - y  0
 2 1- y  2y  
1  1- y - y  0
2 1- y  2 y 1  0VN  2    1- y  y  1- y  y  1 -  5 1 5  y 
(vì y  0 )  x  4 2
Cách 2: Khảo sát hàm số
   y  y   - y 2 2 3 2 2 1  1- y Xét hàm số t  2 f
 2t  t t  0 có f't   4t 1  t
  0 . Do đó f(t) đồng biến trên 0;  1 -  5 1 5
Mà f  y  f  1- y  nên 2
y  1- y  y  1- y  y 
(vì y  0 )  x  4 2
Sau khi thử lại, ta thấy tất cả các nghiệm của phương trình đều thỏa mãn.  1 5 x  x 3    2
Kết luận: Hệ phương trình có nghiệm là:  ;  y  1   1 -  5 y    2 2  y  
5x  44 - x  1
Bài 2. Giải hệ phương trình  2 2
y - 5x - 4xy 16x - 8 y 16  0  2  Bài giải chi tiết
Phương trình (2) tương đương với:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 56
Tất cả vì học sinh thân yêu
 y  5x  4
2   y - 5x - 5 y  x - 4  0  y  4- x  * y  5x  4
 x  0  y  4   1
5x 42 5x 4 x 4 0 6x 5x 4      -     4
 x  -  y  0  5 2
* y  4 - x; 
1   x - 4  5x  4 x - 4  0  6x  x - 4  0
x  0  y  4
*  x  4  y  0   4
x  0 x  4 x  -
Kết luận: Hệ phương trình có nghiệm là:  ;  ;  5 y  4 y  0    y  0 
xy  x - 2  0    1
Bài 3. Giải hệ phương trình  3 2 2 2
2x - x y  x  y - 2xy - y  0  2  Bài giải chi tiết
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 57
Tất cả vì học sinh thân yêu   2
 x  x - y    y  y - x -     2 2 2 1 2 1 0
x - y 2x - y   1  0 2 2
x  y - xy  4 y 1  0   1 
Bài 4. Giải hệ phương trình  y 7 x y2 - -  2  2 x    1 2    Bài giải chi tiết
Phương trình (2) tương đương với:   y   x y2   y xy y y 
 x y  x y2 2 2 7 2 4 0 15 2   - -  -    - - - -  0      y  0 
 y  x - y - 3 x - y  5  0  y  x - 3 
 y  x  5  * y    2
0; 1  x 1  0 (vô lý)
 x  1  y  2 -
* y  x - 3;  2
1  x - x - 2  0  x  2 -  y  -5  * y  x    2
5; 1  x  9x  46  0 (phương trình vô nghiệm) x  1 x  2 -
Kết luận: Hệ phương trình có nghiệm:  ;  y  2 - y  5 -   2 2 3 5
 x y - 4xy  3y - 2  x  y  0  1 
Bài 5. Giải hệ phương trình: xy 
x  y   2  x  y2 2 2 2  Bài giải chi tiết
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 58
Tất cả vì học sinh thân yêu
Phương trình (2) tương đương với: xy  1 2  xy  2 2
x  y   2   2 2
x  y   2x   xy -  1  2 2
x  y - 2  0   2 2 x  y  2  * Với xy    2 2 3
1; 1  5x y - 4xy  3y - 2xy  x  y  0 2
 y  0 loai vi xy=1 2 2 3  
 3x y - 6xy  3y  0  3y  x - y  0  
 x  y  1 x  y  * Với 2 2 x  y    2 2 3
 x y - xy  y -  2 2 2; 1 5 4 3
x  y  x  y  0
 -x  x y - xy  y 
  x - y2 3 2 2 3 4 5 2 0
 x - 2y  0 x  1  2  2x  2 y  1     2 2 x  y
x  y  2    2       x   2 x 2 y    5   y  2  5     2 2 x  y  1   2  y  2    5  2 x     5 x  1
Kết luận: Hệ phương trình có nghiệm là:  ;  y  1  2  y  2   5
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 59
Tất cả vì học sinh thân yêu
 2x  y -1 - x  2y - 2  x - y 1  0    1
Bài 6. Giải hệ phương trình:  2 2
x  y - 2xy  4x - 3y  0  2  Bài giải chi tiết x - y 1   1 
  x - y   1  0
2x  y -1  x  2 y - 2 æ 1 ö
  x - y   1 ç
1÷  0  y  x 1 ç 2x y 1 x 2 y 2 ÷  -   - è ø
   x   x  2 2 2
1 - 2x  x  
1 - 4x - 4  x   1  0
 x - 2  0  x  2  y  3 (thỏa mãn) x  2
Kết luận: Hệ phương trình có nghiệm là:  y  3   y 2
x - x - y    1 
Bài 7. Giải hệ phương trình: 3 x - y  2 2 2
x  y  - 3 2x -1  112  Bài giải chi tiết  x  y  Điều kiện: 2
x - x - y  0  1 x   2 y Nếu 2 y  0   0 
x - x - y  0 (vô lý). Nên y  0 3 x - y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 60
Tất cả vì học sinh thân yêu  y  0  y  0  Với 2
x - x - y  0;  1    
 x  0 khong thoa man 2 2    x - x  0   x 1  Với 2
x - x - y  0 , ta có: y y   3 3 1  x - y   x - y -1  -1 2 2 x - x - y x - x - y x - y -1
 x  y x - y -  1    0  x - y2 2 3 3  x - y 1
x - x - y 1 æ ö 1 x  y  x y  1 ç ÷  - -   0 ç  ÷ x - y 2 2 3 3  x - y 1
x - x - y 1 è ø 2 2 2 2
x  y  2 2x - 3xy  2y  x  y  2xy    1
Bài 8. Giải hệ phương trình:   x  y 
x - y  3x - 4 y  42  Bài giải chi tiết x  y
Điều kiện: x  -y 
Phương trình (1) tương đương với:
    x - y2 2 2 1
 2 2x - 3xy  2 y -  x  y  0
4 2x - 3xy  2 y - x  y 2    2 2 2
  x - y   0 2 2
2 2x - 3xy  2 y  x  y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 61
Tất cả vì học sinh thân yêu 2 7  x - y2
  x - y   0 2 2
2 2x - 3xy  2 y  x  y æ 7 ö
  x - y2 ç1
÷  0  x  y 2 2 ç 2 2x 3xy 2 y x y ÷ -    è ø Khi đó: x  4
2  2x  4 - x  
 x  2  y  2 (thỏa mãn) 2
2x  x - 8x 16  x  2
Kết luận: Hệ phương trình có nghiệm là:  y  2  2 2 2 2
 x  y  x - y  2y    1
Bài 9. Giải hệ phương trình: 
 x  y 5  32  Bài giải chi tiết
Điều kiện: x  y  0
Với y = 0 không thỏa mãn hệ phương trình Với y > 0, ta được: æ 3y ö æ y   2 2 2 2 ö 1  x  y -  x - y -  0 ç ÷ ç ÷ è 2 ø è 2 ø 2 5 2 2 5 2 x - y x - y 4 4    0 2 2 3 2 2 y x  y  y x - y  2 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 62
Tất cả vì học sinh thân yêu æ ö 5 ç ö 1 1 ÷ æ 2 2  x - y   0 ç ÷ ç ÷ è 4 3 y ø 2 2 2 2 ç x  y  y x - y  ÷ è 2 2 ø 5 5 2 2  x  y  x  y 4 2 Khi đó: 2
x  4x -12x  9  
2  x  2x  3   3 x    2 2
 x  1  y  (thỏa mãn) 5 x  1 
Kết luận: Hệ phương trình có nghiệm là:  2 y    5   x -  2 1
x 1 - x  x - y 
y - 2  4x - 3y  0   1 
Bài 10. Giải hệ phương trình: 2  y 3 2 2
3 x  x  y  xy   2 x  xy 1  Bài giải chi tiết x  1 -  2
x  x - y  0
Điều kiện: x  xy 1 0   y  2 
Phương trình (2) tương đương với:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 63
Tất cả vì học sinh thân yêu 2 y 3 2 2
3 x  x  y  xy - y  - y x  xy 1  2 2
x  xy  y  x - y   1 y  y  
1  y - x   1  
3  x  x  y  xy2 3 2 2 3 2 2 2 3 x  xy 1
 y x  x  y  xy  y    2 2
x  xy  y  y  y    1  
 x - y   1   0   3
  x  x  y  xy2 3 2 2 3 2 2 2 3 x  xy 1
 y x  x  y  xy  y     2 2
x  xy  y  y  y   1 Do 
 0  y  x 1
3  x  x  y  xy2 3 2 2 3 2 2 2 3 x  xy 1
 y x  x  y  xy  y
Thay vào phương trình (1), ta được:     x -  2 1 1
x 1 - x -1  x -1  x - 3  0 2 
x -1  x -1 -  1   x -1 - 
1   x - 2  0 x - 2 x - 2 2  x -1    x - 2  0 x -1 1 x -1 1 2 æ x 1 1 ö -   x - 2ç  1÷  0 ç x 1 1 x 1 1 ÷ -  -  è ø
 x  2  y  3
Sau khi thử lại ta thấy nghiệm này thỏa mãn đề bài x  2
Kết luận: Hệ phương trình có nghiệm là:  y  3 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 64
Tất cả vì học sinh thân yêu
x - 3 x  3  3 y - 5 - y   1 
Bài 11. Giải hệ phương trình:  2
 x 16 y - x  y  2 xy 2  Bài giải chi tiết x  0
Điều kiện:  y  5 
Phương trình (2) tương đương với: 2 2
x 16 y - x - y 2 y x - y 2  
2  x 16 y - x - y  2 xy - y     2
x 16 y - x  y xy  y  x 16 2 y  -
  x - y  -   0 2
 x 16 y - x  y xy  y    Ta có:  
1  x - 3 x  3  3 y - 5 - y 2 æ 3 ö 11 11  y - 5 -
 x - 3 x  3 
 0  x - 3 x  3   0 ç ÷ è 2 ø 4 4 2 æ 11 ö 7  6 10  x   9 ç ÷  x  3  3 -  x   16 è 4 ø 4
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 65
Tất cả vì học sinh thân yêu x -16 2 y Do đó -
 0  x  y 2
x 16 y - x  y xy  y Thế vào (1) ta được:
   x   x   x -  2  x   2 1 2 3 3 5 4
9 2x - 2  2 x - 2x -15  2 2
 9 x - 2x -15  2x - 9x  9 2
2x - 9x  9  0   
 x  6  y  6 81 
x - 2x -15  2x -9x  92 2 2  x  6
Kết luận: Hệ phương trình có nghiệm là:  y  6  2 2
 x  2  x  y - xy 
 x - y  2  y  4
Bài 12. Giải hệ phương trình:  2
 1- y  x  2  x  y -  1  4x - 3  Bài giải chi tiết 2 2
x  y - xy  x - y  0 
Điều kiện: x  2 -  4 -  y  1  3 Từ (2) ta có: 2
4x - 3  x 1- y  1- y  x  2  0  x   x  2  0 4
Phương trình (1) tương đương với: 2 2 x  2 -
y  4  x  y - xy  x - y - 2  0
 x  2 -  y  4 2 2
x  y - xy  x - y - 4    0 2 2 x  2  y  4
x  y - xy  x - y  2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 66
Tất cả vì học sinh thân yêu x - y - 2
 x - y - 2 x - y - xy  2    0 2 2 x  2  y  4
x  y - xy  x - y  2 æ 1 x y xy 2 ö - - 
  x - y - 2ç  ÷  03 2 2 ç x  2  y  4
x  y - xy  x - y  2 ÷ è ø 3
Ta có: x - y - xy  2  x 1- y  1- y 1   x  
1 1- y 1  0 do x  , y  1 4 1
x - y - xy  2    0 2 2 x  2  y  4
x  y - xy  x - y  2
Nên 3  x - y - 2  0 . Thay vào (2) ta được: 2 - x 
 x  x  x -  3 2 3 2
3  4x - 3  x - 3x  4x - 3 - x  2 - 3 - x  0 4  3 
Xét hàm số f  x 3 2
 x - 3x  4x - 3 - x  2 - 3 - x với x  ;3  4    1 1 x  2 - 3 - x
Có f ' x  3x - 6x  4 -   3 x - 2 2 1 1  0 2 x  2 2 3 - x 2 x  2 3 - x æ 3 ö
Do  x  2 - 3 - x  2x -1  0 x  
;3  x  2  3 - x 
x  2  3 - x ç ÷ è 4 ø 3
 x - 3y -1 x -1  y  2 x - y   1 
Bài 13. Giải hệ phương trình: y 2 1  3 2 2
x  3  32x - 242  Bài giải chi tiết
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 67
Tất cả vì học sinh thân yêu x  1 
Điều kiện:  y  0 x  y 
* Nếu x = 1 thì từ (2) suy ra y =0 thỏa mãn hệ.
* Nếu x > 1 ta có  
1  3x - 3y - 3  2 - 2 x - y  x -1 - y  0
2 1- x  y x -1- y
 3 x - y -  1    0 1 x - y x -1  y æ 2 1 ö
  x - y -  1 ç 3 -  ÷  0 ç 1 x y x 1 y ÷  - -  è ø 2
 x - y -1  0 (Do 3 -  3 - 2  1) 1 x - y
Thay vào (2) ta được  2 x   2 2 3
x  3  32x - 24 2 2 2 2 x  3 x  3 32 24 x  3 x  3 æ 4 3 ö   -  - 8  8 - -1 2 3 2 ç 3 ÷ x x x x x 3 è x x ø  3 2
x - 4x  3 2 2 2
x  3  2x x  3  4x  8 3 2 x - 4x  3   -  3 2  3 3 2 x x x x   x  3  x  3x  8  3 2  2 2 2
  x - 4x  3   0      3  2  3 3 2 x x x x    3  21 3 2
 x - 4x  3  0  x  2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 68
Tất cả vì học sinh thân yêu 1 21
(Do x > 1) suy ra y  2 æ 3  21 1 21 ö
Kết luận: hệ phương trình có nghiệm  x, y  1;0,ç ; ÷ ç 2 2 ÷ è ø   x    2 1
y  y  2   y -  2 1
x  x 1  x  y   1
Bài 14. Giải hệ phương trình:  2  x  x 2
x - y  3  2x  x  y 12  Bài giải chi tiết
Điều kiện: x - y  3  0     2 2
x  x x - y  3 - 2  x - y -1  0 2 æ x x ö 
  x - y -  1 ç
1÷  0  x - y -1  0 ç x y 3 2 ÷ -   è ø
Thay vào (1) ta được:  x   2
x - x    x -  2 1 2 2
x  x 1  2x -1 2 u    x - x  2 2 2 2 2 æ v - u 1 ö æ v - u 1 ö Đặt 2 2 
u,v  0 ta được 1 u  - 2  v - u ç ÷ ç ÷ 2 v  x  x 1 2 2  è ø è ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 69
Tất cả vì học sinh thân yêu  1 x   2 u  v 
 v - u u  v  
1 u  v - 3  0   x  1 -   u  v  3   7 x   8 æ 1 1 ö æ 7 1 - ö
Từ đó ta được các nghiệm  ; x y   ; - , ç ÷  1 - ; -2, ; ç ÷ è 2 2 ø è 8 8 ø  8
4x -1  4 y -1  6 -  8x   1 
Bài 15. Giải hệ phương trình: 2x 1  2 2
2y 1 x  2y 1  x  2 y  2x 12  Bài giải chi tiết 1
Điều kiện: x, y  4
    y   2 2 2 2
1 - 2 y  2x 1  x  2 y 1 -  x   1  0 4  y - x 2 y - x    0 2 2 y 1 y  2x 1
x  2 y 1  x 1
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 70
Tất cả vì học sinh thân yêu  4 2 
  y - x     0 2 2  y 1 y  2x 1
x  2 y 1  x 1    x  y Thay vào (1) ta có: 8
2 4x -1  6  8x  2x 1
Dò nghiệm ta được x = ½ là nghiệm kép , ta tìm cách đánh giá như sau :
Áp dụng BĐT Cauchy: khi thay x = ½ vào 4x -1 = 1 ,nên ta áp dụng
2 4x -1.1  4x -11  4x  VT  4x  6 8 8 8 Ta thay x = ½ vào
= 4 . nên ta áp dụng 22x   1   2 22x   1  8 2x  1 2x 1 2x 1  8  8
VP  4x - 2  22x   1 
 4x - 2  2 22x   1
 4x - 2  8  4x  6  VT  Dấu  2x 1   2x 1 1 1 "=" xảy ra khi x   y  2 2 æ 1 1 ö
Kết luận: Vậy hệ có nghiệm  x, y  ; ç ÷ è 2 2 ø  y  2 xy -1  x 1  1    1 y 
Bài 16. Giải hệ phương trình:   3 2 1 2 y  1-   2  x y 3x  Bài giải chi tiết
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 71
Tất cả vì học sinh thân yêu  y  0 xy 1   3 Điều kiện: 1  -  0  x  0 x  x  0 x  -1  2   1  xy -1 -1 x 1 - 1  0 y 2 x - xy - 2 y    0 xy -1 1 2
x 1  1 y æ ö ç ÷ 1 1  xy 2ç ÷  - 
 0  xy - 2  0  xy  2 ç xy 1 1 2 ÷ -  ç
y x 1  y 1 ÷ y è ø 1 3 1 Thay vào (2) ta được:  1-  x  x x 3x
Áp dụng BĐT Bunhiaiscopki ta có 2 2 æ 1 3 ö æ 1 1 1 ö æ 1 1 1 ö 4 ç  1- ÷  ç1  3 - ÷  4  -  ç ÷ ç x x ÷ ç x 3 x ÷ è x 3 x ø 3 è ø è ø 1 3 2 Suy ra  1-  x x 3
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 72
Tất cả vì học sinh thân yêu 1 1 2
Áp dụng BĐT Cauchy cho các số thực dương ta có: x   2 x  3x 3x 3 1 1 3 Nên x    1- 3x x x  1 x   3x  
Dấu bằng xảy ra khi  1 3 vô nghiệm.   1 1 1  -   x 3 x
Kết luận: Vậy hệ đã cho vô nghiệm 
 2y - 2y - 2x   3 3
4xy - 2x - 4  8 x - 4  3x   1
Bài 17. Giải hệ phương trình:  2 2
 y  x  2 y  x  y  2x  2 2  Bài giải chi tiết
4xy - 2x - 4  0  3
 y  x  4 Điều kiện:  2 x  2 y  0   2
y  2x  2  0 
    y   2 2 2 1 -
y  2x  2  x  2 y -  x   1  0 2 y - 2x -1 2 y - 2x -1    0  y   2 2 1  y  2x  2
x  2 y  x 1
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 73
Tất cả vì học sinh thân yêu æ 1 1 ö
 2 y - 2x -  1 ç  ÷  0 ç  y  2 2 1 y 2x 2 x 2 y x 1 ÷        è ø
 2 y - 2x -1  0 (Do 3 y  x  4 ) Thay vào (2) ta được 2 3 3
2x 2x - 4  8 x - 4  3x
Áp dụng BĐT Côsi cho các số dương ta có: 3 x     3
x -   x    2 x -  3 2 3 2 4 4 2
2   8 x - 4  2x 2x - 4     3  4  x - 4 5 Dấu bằng xảy ra khi 
 x  2 (thoả mãn)  y  2 2  x - 2  2 æ 5 ö
Kết luận: Vậy hệ có nghiệm duy nhất 2; ç ÷ è 2 ø 2 
x  x  2 y - 2 3 2
y - 2  3x - 5 y  5 y - 2     1
Bài 18. Giải hệ phương trình: 2   2 2 3 2 3 3 3x  y 
x y - xy  y  x y 2  Bài giải chi tiết
    x - y   2 x - x y    2 2 3 3 3 2
x - x y - xy  y   0
x  x - y
 x - y 2 2 2 x  y 
  x - y    0
x  x x y  x y
x  x x y - xy  y   x y - xy  y 2 2 2 4 2 3 3 2 2 2 3 2 2 3 3 3
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 74
Tất cả vì học sinh thân yêu      2 2 2 x x y  
  x - y 1      0 2 2  æ 3 ö 2 2 3 æ 3 x y 3 x y xy y ö -  3   ç x  ÷  x y ç x  ÷ 
x y - xy  y  ç 2 ÷ 4 ç ÷  2 4 2 3 2 2 3 3  2 4 è ø   è ø  2 x  3x - 2
x  y . Thay vào (2) ta được: 3 2
x - 2  3x - 5x  5x - 2  3 2
Nhẩm x = 3 là nghiệm kép , ta thay x = 3 vào : x - 2  1; 3 2
x - x  x -   x -  2 3 5 5 2 3 2 x - x   1  77 x -1
Áp dụng BĐT Cosi ta có: x - 2  1 x - 2  * 2 2 x  2x -1 Và: 3 2
3x - 5x  5x - 2  3x - 2 2 x - x   1  ** 2 2 x  3x - 2
Cộng vế theo vế (*) và (**) ta có: 3 2
x - 2  3x - 5x  5x - 2  2 1   x - 2 Dấu bằng xảy ra khi   x  3 2
3x - 2  x - x 1 
Nên 3  x  3  y  3
Kết luận: Vậy hệ có nghiệm duy nhất 3;3
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 75
Tất cả vì học sinh thân yêu  2 y - x
x  y  2x - y    1 
Bài 19. Giải hệ phương trình: 2x   2
3x - 2 y  2  2 x  4 y 2x -1 2  Bài giải chi tiết  1 x   2 
Điều kiện: x  y  0 2x - y  0   2 y - x   1 
x  y - 2x - y  2x - - 2 y - x  0 2 y x 2 y x    
x  y  2x - y 2x
 x  y  2x - y  2x 
* Nếu x  y  2x - y  2x  x  2  x  y2x - y  0 vô nghiệm do x > 0.
* Nếu 2 y  x thay vào (2) ta được: 2
3x - x  2  2 x  2x 2x -1  x  x - x -  2 2 2 2
1  x - 2x 1 x - 2 x 1  0  x  x - - 2 2   x - 2 2 1 1 1   x -  1  0 3 x   2x -1 - 2 1  0  2 Ta có:  x -   1  0  x - 2 1  0 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 76
Tất cả vì học sinh thân yêu x  0  2x -1 1  1  1 Với x 
nên 3  x  1
 x  1  y   2 2  x 1    æ 1 ö
Kết luận: Vậy hệ có nghiệm duy nhất 1; ç ÷ è 2 ø  3 2  y  x  xy -  
Bài 20. Giải hệ phương trình: 4 2 y   x 
 y 8  3 8x 1  4  2x  y  2 3 3 2 1  Bài giải chi tiết 3
Điều kiện: x  0, y  0, xy  4 1 3 1 xy -1 xy -1   1  x -  xy - -  0    0 y 4 2 y  xy   1 3 1 xy -  4 2 æ ö ç 1 1 ÷   xy -  1 ç  ÷  0  xy  1 ç y  xy   1 3 1 ÷ xy -  ç ÷ è 4 2 ø Thay vào (2) được: x  
x     x  2 3 8 1 3 8 1 4 2 1
Áp dụng BĐT Cauchy ta có:
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 77
Tất cả vì học sinh thân yêu 3 x    x   2 x - x   2 2 2 8 1 2 2 1 4 2
1  2x 1 4x - 2x 1  4x  2
6 8x 1  2.3. 8x 1  9  8x 1  8x 10 Suy ra x  
x   x   x     x  2 3 2 2 8 1 6 8 1 4 2 8 10 8 4 1  x  
x     x  2 3 8 1 3 8 1 4 2 1
Dấu "=" xảy ra khi và chỉ khi x  1  y  1 thử lại thấy thỏa mãn
Kết luận: Vậy hệ đã cho có nghiệm duy nhất 1  ;1 2 2
 x - y  4  x - 4  2 x  y - 2    1
Bài 21. Giải hệ phương trình: 
  x - 2 9 - y  y 4 - y  3 x - y 2  Bài giải chi tiết 2 2
x - y  4  0 
Điều kiện: x  4  y  2    2 2 1 
x - y  4 - 2 x  x - 4 - y - 2  0  2 2
x - y  4 - 4x
 x - 4 -  y - 2    0 2 2
x - y  4  2 x x - 4  y - 2
 x - y - 2 x  y - 2 x - y - 2    0 2 2
x - y  4  2 x x - 4  y - 2 æ x y 2 1 ö  -
  x - y - 2ç 
÷  0  x - y - 2  0 2 2 ç
x - y  4  2 x x 4 y 2 ÷ -  - è ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 78
Tất cả vì học sinh thân yêu Thay vào (2) ta được
y 9 - y  y 4 - y  6
Áp dụng BĐT Bunhiacopxki ta có:
 y - y  - y y 2 . 9 4 .
  y  4 - y9 - y  y  36  y 9 - y  y 4 - y  6 y 4 - y 36 62 Dấu bằng xảy ra khi   y   x  (thỏa mãn) 9 - y y 13 13 æ 62 36 ö
Kết luận: Vậy hệ đã cho có nghiệm duy nhất  ; x y   ; ç ÷ è 13 13 ø 2
 x  x  y -1  y  x  1- x   1 
Bài 22. Giải hệ phương trình:  1 x  2 y  4 với x  0 2 y  x    2 y 1 4  Bài giải chi tiết 2
x  x  y -1  0  Điều kiện: 2 x  y  0  y  0  x  y -1 y  x -1   2 1 
x  x  y -1 - x 
y - 1- x  0    0 2
x  x  y -1  x y  1- x æ 1 1 ö
  x  y -  1 ç 
÷  0  x  y -1  0 (Do x  0 ) 2 ç
x  x  y -1  x y 1 x ÷  - è ø 1 y  5 Thay vào (2) ta được: 2 y - y -1   y 1 4
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 79
Tất cả vì học sinh thân yêu y 1 Ta có: 2 y - y -1  với y  0 2 2 2 æ y 1 ö 3 2 Thật vậy:  2 y - y -  1 -  ç ÷  y -  1  2
5y - 2 y  5  0 è 2 ø 16 y 1 Suy ra 2 y - y 1  3 2 y 1 1
Áp dụng BĐT Cauchy ta có:   14 4 y 1 1 y  5
Cộng vế tương ứng (3), (4) rồi rút gọn ta được: 2 y - y 1   y 1 4
Dấu "=" xảy ra khi y  1  x  0 (Thỏa mãn)
Kết luận: Vậy hệ có nghiệm duy nhất 0  ;1 2 2
2x  y  x - y  x  xy  y 
Bài 23. Giải hệ phương trình:  2
 x -1  x  y  x -1  Bài giải chi tiết x  1 
Điều kiện: x - y  0 x  y  0  Từ (1) ta có: 2 2
x - y - x - y - 2x  xy  y  0   x - y - x - y -  x - y2x  y  0 æ 1 ö 1
  x - yç1-
- 2x - y ÷  0  x  y (Do 1-
- 2x - y  1- 2x  0 ) ç x y ÷ - è ø x - y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 80
Tất cả vì học sinh thân yêu Thay vào (2) ta được: 2 x - 
x  x -   x - -    x -  2 1 2 1 1 1 2 2  x - 4  1 2    x - 2 
-  x  2  0  x  2    x -1 1 2x  2  1 2 (Do 
-  x  2  11- x - 2  -x  0 ) x -1 1 2x  2
Với x  2  y  2 (Thỏa mãn)
Kết luận: Vậy hệ có nghiệm duy nhất  ; x y  2;2
 y  2x -1  1- y  y  2 
Bài 24. Giải hệ phương trình:  x x  y  x -  2 1  x - y  Bài giải chi tiết
 y  2x -1  0  y 1  
Điều kiện: x  0  yx -  1  0  2 x - y  0  (2) tương đương với 2
xy - y  x - y  x x 3 2 2 xy - x xy - x y - x Ta có: 2
xy - y - x - y    4 2
xy - y  x - y x x x 2 y - x
x - x  y
Cộng vế (3) với (4) ta được: 2 xy - y  x x   x x
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 81
Tất cả vì học sinh thân yêu 
y  x - x  x - x  y  y  x - x   x - x  y2   x - x - y2 2 2 2 2 2 2 2 4
 0  y  x - x Thay vào (1) ta được: 2 2 2
x  x -1  -x  x 1  x - x  2
Áp dụng BĐT Cauchy ta có: 2 2 x  x -11 x  x 2 x  x -1   2 2 2 2
-x  x 11 -x  x  2 2
-x  x 1   2 2 2 2 x  x -x  x  2 Cộng vế ta được: 2 x - x  2    x 1 2 2   x - 2 1
 0  x  1  y  0 (thỏa mãn)
Kết luận: Vậy hệ có nghiệm duy nhất  x, y  1;0 2 2
 x x  xy  x - y  x   y   2 2 2 1  y y 1 1   1
Bài 25. Giải hệ phương trình: 
 2 y - x  5  y 1  x  21x -17 2  Bài giải chi tiết x  1 
Điều kiện: 2 y - x  5  0  y  -1 
    x - y   2
x  y    2 1 1 2 x - y -  1  0  2
2 x  y  2 x - y -  2 2 1 x y 1 æ x y ö - -     0   2 1 2 x - y -  1 ç  ÷  0 2 2 x y 1 x - y 1 ç x y 1 x - y 1 ÷     è ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 82
Tất cả vì học sinh thân yêu 2  x  y 1 Thay vào (2) ta được 2 2
2x - x  3  x - x - 21x -17  0 2 
x - x  -  x   2 2 3
1  x - 3x  2  3x -  1 - 21x -17  0 æ ö   1 9 2
x - 3x  2ç1  ÷  0 2 è
2x - x  3  x 1
3x -1 21x -17 ø 17 1 1 9 Do x   x   1   0 2 21 3
2x - x  3  x 1 3x -1 21x -17 x  1
Suy ra phương trình có nghiệm x  2 
Kết luận: Vậy hệ đã cho có các nghiệm  ,
x y  1;0,2;3 2 2
4x  8y -10x  9y  y 6 x   1 - 5   1  
Bài 26. Giải hệ phương trình: 2  x 1 1 x  y  1- x -  x  1 2 y     1  - 2  x y y  Bài giải chi tiết 0  x  1 Điều kiện:  1 -  x  0  2 2 1- x x 1 y 1 1 y
Phương trình (2) tương đương với: -  -  - 2 2 x x y y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 83
Tất cả vì học sinh thân yêu x  y
 x - y x  y 2 2 2 2 æ 1- x 1 y ö æ y 1 x 1 ö xy x y  ç - - ÷ - ç  ÷  0  -  0 2 2 ç ÷ ç ÷ 2 2 x y y x 1- x 1 y è ø y 1 x 1 è ø  -  2 2 x y y x æ ö ç ÷ x  y 1 x - y ç ÷  
 0  x  y  0  x  - y ç 2 2 xy 1 x 1 y ÷ -  y 1 x 1 ç  -  ÷ 2 2 ç x y y x ÷ è ø Thay vào (2) ta được: 2
12x -19x  5  -x 6 x   1 -x  2
12x -19x  5  0 -x    2
12x -19x  5  0      2
 12x -19x  52 2
 x 6x  6   2x -  1 3x - 5 2
24x - 25x  5  0    1 1 x   y  -  2 2    25  145 25  145 x   y  -  48 48 æ 1 1 æ ö 25  145 25  145 ö
Kết luận: Vậy hệ đã cho có các nghiệm  x, y  ; - ; ç ÷ ç ; - ÷ 2 2 ç 48 48 ÷ è ø è ø
 xy  x - y 
 xy - 2  x  y  y  1
Bài 27. Giải hệ phương trình: x 1y xy  x1-x  4 2    Bài giải chi tiết
Điều kiện: x, y  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 84
Tất cả vì học sinh thân yêu
Nhận thấy x  y  0 không thỏa mãn (2) nên ta có x  y  0
Phương trình (1) tương đương với xy   x - y xy - 2  x - y - y  0
xy   x - y xy -  2 2 - y -
 x - y xy - 2  y x y  x - y    0    0   -  - 2 x  y    -  - 2 x  y xy x y xy y xy x y xy  y    xy - 2  y 1    x - y   0 3      -  - 2 x  y xy x y xy  y    4
Ta có phương trình (2) tương đương với 2 y  xy   x - x x 1 4 4   x   1  2 x - x - 2 x  2 x -1 2    2 Ta có:
 x - x - 2    0 với x  0 x 1 x 1 x 1 xy - 2  y 1
Suy ra: xy - 2  y  0    0   -  - 2 x  y xy x y xy  y
x  1  y  1
Nên 3  x  y thay vào (2) ta được  x  1  2 3x x  4   -   1 17 1 17 x   y   4 4 æ 1 17 1 17 ö
Kết luận: Vậy hệ đã cho có các nghiệm  x, y  1;  1 , ç ; ÷ ç 4 4 ÷ è ø 2  3
x - x - y. x - y  y 
Bài 28: Giải hệ phương trình:  4
  x - 2 4 - x 
y -1  3 - y  6  y   3 4 4 1 3x  x  30 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 85
Tất cả vì học sinh thân yêu Bài giải chi tiết 2
x - x - y  0 
Điều kiện: 2  x  4 1   y  3 
Phương trình (1) tương đương với:  2 2 x - x - y
x - y - x - x - y    2 3 .
x - x - y - y  0 2
x - x - y x - y -1
x - y -1 x  y 2 
x - x - y  x - y -  1   2 3
x - x - y - y       0    0  x - y2 2 3 3  x - y 1
x - x - y  y    2  x - x - y x  y  x y  1    - - 
 0  x  y 1 2 2  æ 1 ö 3 x x y y  - -  3  x - y   ç ÷   è 2 ø 4 
Thay vào (2) ta được: 4  x - 24 - x 4 4 3
 x - 2  4 - x  6x 3x  x  30  x - 2  4 - x 4
  x - 2 4 - x   1 2   3 3
6x 3x  2 27x  x  27 
Áp dụng BĐT Cauchy ta có:  111 x - 2 x 1 4 4
 x - 2  1.1.1. x - 2    4 4  111 4 - x 7 - x 4 4
4 - x  1.1.1 4 - x     4 4
Từ các BĐT trên ta được: 4  x - 24 - x 4 4 3
 x - 2  4 - x  6x 3x  x  30
Dấu bằng xảy ra khi x  3  y  2
Vậy hệ đã cho có nghiệm duy nhất  x, y  3;2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 86
Tất cả vì học sinh thân yêu 
 x - y 2y  3  
1  x  y  4 1  0 
Bài 29: Giải hệ phương trình:  1 3 2
2x  5x  4x 1  x  x  y  4 2 x   x Bài giải chi tiết  3 y  -  2 
Điều kiện: x  y  4  0  1 2 x   0  x
Phương trình (1) tương đương với: x - y 1
x  y  4   x - y 2y  3  0
 x - y 1 x  y  4 - 2 y  3   x - y   1 2 y  3  0 x - y 1
 x - y 1
  x - y   1 2 y  3  0
x  y  4  2 y  3 æ 1 ö
  x - y   1 ç1  2 y  3 ÷  0 ç x y 4 2 y 3 ÷     è ø
 x - y 1  0  y  x 1 1 Thay vào (2) ta được: 3 2
2x  5x  4x 1  x 2x  5 2 x  x 1 1 1 1 1 2  2x 
 5x  4  2x  5 2 2 2 2 2 x   x  - 2x x   x - 5 x   5x  4  0 x x x x x
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 87
Tất cả vì học sinh thân yêu
x  -1  y  0  1 3  1 x   y  2 2 x  - x  1   2 2 æ 1 ö æ 1 ö 2 2 x  ç x 
- x ÷ - 5ç x  - x ÷  4  0     4 - - 3 2 3 2 ç x ÷ ç x ÷  1 x   y  - è ø è ø 2  x  - x  4  4 4  x  4 -  3 2 3 2 x   y   4 4   x  2 y 
 x - y -  2 2
1  2x  3xy  4 y  0   1
Bài 30: Giải hệ phương trình:  3 3 
3x - 2  4 2x  y - 2  5 x  5y  2 - 3 2  Bài giải chi tiết 2 2
2x  3xy  4 y  0   2
Điều kiện: x  3 
2x  y  2 
Phương trình (1) tương đương với:
 x  y x - y 2 2 2
 2x  3xy  4 y -  x  2 y  0
x  x - y
  x - y x  2 y   0 2 2
2x  3xy  4 y  x  2 y æ x ö
  x - yç x  2 y  ÷  03 2 2 ç 2x 3xy 4 y x 2 y ÷     è ø 3 Từ (2) ta có: 3 3
5 x  5 y  2  3 
x  5 y  2 
 x  5 y  2  0 5
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 88
Tất cả vì học sinh thân yêu
Mà 2x  y  2   x  5y  2  2x  y  2  3 x  2y  0  x  2 y  0
Nên 3  x - y  0  x  y thay vào (2) ta được: 3
7 3x - 2  5 6x  2 - 3 Đặt 3
a  6x  2, b  3x - 2 a,b  0 ta được:  5a - 3 b  7b 5a 3   -  7 a  2     
 x  1  y  1 (thỏa mãn) 2 3 2 a - 2b  6  æ 5a - 3 ö b  1 3 a - 2 - 6  0  ç ÷   è 7 ø
Vậy hệ có nghiệm duy nhất  ; x y  1;  1 3 2 2 2 2 2 2
2 2x  4x  x y  2xy  2x  xy  2x  4  x  2 y  
Bài 31: Giải hệ phương trình:  x - 2 35 38   x - 2  8 -   8y -19 2  y y y  Bài giải chi tiết x  2  Điều kiện:  19 y    8
Phương trình (1) tương đương với: 3 2 2 2 2  x x x y xy  xy y     -      2 2 2 2 4 2 2
2x  xy - y x  2   0 4
-  y - x x  y x  2 2
-  y - x y  x   0 3 2 2 2 2 2 2
2x  4x  x y  2xy  xy  2 y
2x  xy  y x  2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 89
Tất cả vì học sinh thân yêu  4 x 2 2  
  x - y x  y  
  0  x  y 3 2 2 2 2 2 2
 2x  4x  x y  2xy  xy  2 y
2x  xy  y x  2    x - 2 35 38 Thay vào (2) ta được:  x - 2  8 -   8x -19 2 2 x x 2
 x - 2  x x - 2  8x - 35x  38  x 8x -19  x  x - - x -  2 8 19
2  8x - 35x  38 -  x - 2  0 x 7x -17
 x - 27x -17    0 2 8x -19  x - 2
8x - 35x  38  x - 2 æ x x - 2 ö  7x -17ç  ÷  0 2 8x -19  x - 2 è
8x - 35x  38  x - 2 ø 17 17  x 
(do x  2 )  y  7 7 æ 17 17 ö
Vậy hệ có nghiệm duy nhất  x, y  ; ç ÷ è 7 7 ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 90
Tất cả vì học sinh thân yêu 2 4 2 3
(x  1) y  1  2xy ( y -1)
Câu 1 : Giải HPT :  2 4 4
xy (3xy - 2)  xy (x  2 y)  1  Thế 2 4 4
1  xy (3xy - 2) - xy (x  2 y) vào PT (2) ta được : 4 2 2
y (1  3x y - 4xy)  0   y  0   xy  1   1 xy   3
Thấy y  0 không phải nghiệm của hệ Với 2 4 4 2 2
xy  1 y  y  1  2 y - 2 y  ( y - y -1)( y  y  1)  0  5  1 2 y   x   2 5  1    1- 5 2  y   x   2 1 - 5 2 4 4 2 1 y 2 y 2 y y y 2 y Với 4 xy    y  1  -     1  0 y  3 9 3 3 3 9 3
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 91
Tất cả vì học sinh thân yêu 3 2
x  y  2xy (1) 
Câu 2: Giải HPT :  3 9 4
x  y  2xy  2  PT(2)  3 x  y  2 3 3
x - xy  y  4 ( )  2xy  2 xy  2 3 3
x - xy  y  4 2  2xy x  y  0   2 3 6 2
x - xy  y - y  0 * 
(*)   x  y 2 3 3 2 - 3xy - y  0  4 3 2
4xy - 3xy - y  0  x  y  0   xy  1   1 xy  -  4 1
Với xy=1  x  y (1)  4 2
y - 2 y  1  0  y  1   x  1  1 1 Với xy  -  x = - 4 4 y (1)  4 2
4 y  2 y -1  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 92
Tất cả vì học sinh thân yêu 5 -1 5 -1 1  2 y   y =   x =  4 2 2 5 -1 æ 1 5 1 ö -
Vậy hệ có nghiệm (x;y) = (0;0),  1  ;  1 , ç  ; ÷ ç 2 2 5 1 ÷ - è ø 4 6x -  3 x - x 2
y -  y 12 2 x  6  0 
Câu 3. Giải HPT : 5
 x -  x - 2 4 2 2 2
1 y -11x  5  0  6   x - 2 2 2 1  xy  2 x -  2 1  x y   5   x - 2 1
 x   x - 2 2 2 2 2 1 y 
Dễ thấy x=y=0 không phải là nghiệm của hệ.  x - 2 2 2 1 x -1 1 6   (*) 2 2  x y x y Ta có:    x - 2 1 x - 2 2 2 1 1 5    2 2 2 2 x y y x  2  x -1  a   x Đặt  (a,b  0) 1   b  y 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 93
Tất cả vì học sinh thân yêu 2 2 
6a b  a  b Hệ trở thành:  2 2 2 2 5
 a b  a  b  1  4 4 2 2
36a b  2ab  5a b  ab  2 2 1 x -1 1 Với ab    2 xy 2  1  17 x  3 y 1  y 1   4 (*)        2 2 y y  2   1  5 x    2 æ 1 17 ö æ 1 5 ö
Vậy hệ có nghiệm (x;y) = ç ;1÷, ç ;2 ÷ 4 2 è ø è ø
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 94
Tất cả vì học sinh thân yêu 2 2 2
(4x - 4xy  4 y - 51)(x - y)  3  0
Câu 4 : Giải HPT : (2x - 7)(x - y) 1 0  2 2 2
3(x - y)  (x  y) - 51 (x - y)  3  0  
 (x  y)(x - y)-7 
(x - y) 1 0  Đặt 2  b -  7b -1
x  y  a 4 2 2 2 3
 b  a b - 51b  3  0 a       b
x - y  b 
(a  b - 7)  1  0  2 2
(b - 4b 1)(2b - b  2)  0       x  y  3 b 2 3    a  3 
x - y  2  3         - x  y  3 b 2 3      a 3   
x - y  2 - 3  3 3
3x  5 y - 2xy  6
Câu 5 : Giải HPT :  3 3
2x  3y  3xy  8  Rút lần lượt 3 3
x , y theo xy ta được : 3 3 3
x  22 - 21xy
3x  5 y  8 3 3 
 x y  (22 - 21xy)(13xy -12)  xy  1   3 3 3 y  13xy - 12 2x  3y  5  
 x  y  1
Đoạn giải PT bậc 3 ẩn xy có 2 nghiệm rất lẻ không biết có phải do đề không ạ…
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 95
Tất cả vì học sinh thân yêu  1 1   2   2 2
x  y    1  x 2 y Câu 6:Giải HPT : 1 1 2 2  -  y - x 2  x 2 y  ĐK: x, y  0   1 - 2 3 2  y  3x y  1   1  2 3 2  x  3xy  2 3 2 
x  3xy  2 Ta có hệ mới:  3 2
 y  3x y  1    x  y  3 3  3  x  y  3     
 x - y3  1 x - y  1   3  3  1 x    2   3  3 -1 y    2 2 2 4
x  xy  y  (x - y)
Câu 7 : Giải HPT :  2 2
x - xy  y  x - y 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 96
Tất cả vì học sinh thân yêu 2 2 3a b 4   b a x y     4 4 Đặt    2 2
b  x - y  a 3b    b   4 4 b  0 2 2 b 9b  Thế ta được : 4 3 2 b - - 3b 
 0  b  2b - 3b  0  b  1 4 4  b  3 -   b   0 a  0    b   1    a  1   b   1   a  1 -   3 1 2 2 x - y  -   1  Câu 8: Giải HPT : 2 y x  
 x  y3  5  ĐK: x, y  0 x - y 1
PT(1)   x - y x  y   xy 2 y
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 97
Tất cả vì học sinh thân yêu
2 y  b - a
x - y  a  Đặt 2 2    b - a
x  y  b  xy    4  4a 1 ab    Hệ trở thành: 2 2  b - a b - a 3 b  5  3 3 b 
 a - a b  5a  b    3
a b  b  0  a  1 - 3 b   5  3  5 -1 x  3 x y 5      2     3 x - y  1 -   5  1 y    2  1 x  
x  y - 3  3   y
Câu 10: Giải HPT :  1
2x  y   8  y  1
ĐK: x  y  0, x+y  3, y  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 98
Tất cả vì học sinh thân yêu  1 x   a  Đặt y  a,b  0
 x  y - 3  b  a  1    1 a  b  3 b  2  
Hệ đã cho trở thành:   2 2 a  b  5   a  2  2  b  1   x  4 - 10 1  x  1    y  3  10    1  y     x  4  10 x  y  7    y  3 - 10  x  3  1  x   4 y  1    2 y     x  5 x  y  4    y  1 -   x 5y   4 1 2 2  
 x - y x  y  Câu 11:Giải HPT  2 2 x - 5 y 5  x  y   5 2  xy 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 99
Tất cả vì học sinh thân yêu ĐK: 2 2
x - y  0, x+y  0, xy  0 PT(1)  2 2 2 2
x - y  xy  x y   2 x - y 2 5 5 4 x  y  x 5 y æ y öæ x ö  -
 y  5x  4 x -  y ç ÷ç ÷ y x è x ø y è ø  x y   a   y
a  5b  5 Đặt 
Hệ đã cho trở thành:  y 
a  5b  4ab  x -  b   x  5  x 5 a  y    2   2  y 2 
2 y  2x  5 y       1 2 y 1 
2x - 2 y  x b   x  -    2   x 2
 3 x - y - 2 x - y x  y  0 x  1   1  3  y  x  y    2   2 (*)    3
2x  2 y  3 (*)  x  -  2  y  3 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 100
Tất cả vì học sinh thân yêu
 7x  y  2x  y  5 
Câu 12 : Giải HPT : 
 2x  y  x - y  2  2 2
a  2x  y  5
 x  b - a Đặt    2 2 b   7x  y
5 y  7a - 2b   Ta có hệ mới : a  b  5 a  b  5    2 2 2 2 2 2
5a  b - a - (7a - 2b )  10
3(5 - a) - 8a  5a  10    b   5 - a   5 -  77  a    2  
(Bài này không hiểu sao ra lẻ vậy ) b   5 - a   5 - - 77  a    2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 101
Tất cả vì học sinh thân yêu 2 2 
x 1 - y  y 1 - x  1 Câu 13: 
(1 - x)(1  y)  2  ĐK: 2 2
1 - x  0, 1 - y  0 PT(1) :  2 2 x - y  y - x    2 2 x  - x  2 2 1 1 1
1 - y  y  1 2 2 x y  x  y Dấu “=” xảy ra    2 2  1 - y 1 - x 2 2 x  y  1 
Với x  y thay vào PT(2) không thỏa mãn. Với 2 2 x  y  1 PT(2)  2 2
x - y  xy 1  0  x y  2xy  1  1 - 2xy xy  0 x  0   Ta giải được  thỏa mãn hệ. xy  4 -  y  1 
 3x - 2 y  3 8  x - y  10  Câu 13 : 
 8  x - y - 2 4 - 2x  y  1 
 3x - 2 y  a  Đặt 2 2 
 4 - 2x  y  b - a - 4 .Ta có hệ mới :
 8  x - y  b 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 102
Tất cả vì học sinh thân yêu
a  10 - 3b   121  4 55  b 
a  3b  10 a 10 3b   -     33      2 2 2 2 b
 - 2 b - a - 4  1 b 
 -1  2 b - (10 - 3b) - 4 a  10 - 3b    121 - 4 55  b    33
(Lại một bài lẻ khủng khiếp…) 2 
 x  2x  6  y  1
Câu 14 : Giải HPT :  2 2
x  xy  y  7 
PT(1)  x2  2x  6  y2  2 y 1 (3)
Lấy (3) - (2)  2 y2  (x  2) y - 2x - 12  0  ( y - 2)(2 y  x  6)  0  x  1
Với y  2  x  3 -  Với 2 2 2 x  2
- y - 6  (2 y  6) - (2 y  6) y  y  7  3y 18y  29  0 y  2
x  1  y  x  y  4 y 
Câu 15: Giải HPT  2x   
1  x  y - 2  y 
Thấy y  0 không phải là 1 nghiệm của phương trình.
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 103
Tất cả vì học sinh thân yêu 2
æ x 1ö  x  y  4 ç ÷ 2  x  1 y è ø   a Hệ   Đặt  y 2 æ  x  1ö  ç
÷ x  y - 2  1
x  y  b   y è  ø a  b  4 a  1 2 x  1  y
Hệ đã cho trở thành:     
a b - 2  1  b  3  x  y  3  x  1  y  2    x  2 -   y  5  2 
 x  2x  6 - y  1
Câu 16:Giải HPT :  2 2
x  xy  y  7  2 2
x - y  2x - 2 y  5  0  2 2
x - y  a b - a   Đặt   xy=  x  y  2  7  xy
x  y  b 4    5 a  -
ab  2a  5  0   b  2
Hệ đã cho trở thành:    2 2 3b  a  28  25 2 3  b   28 2   b  4b  4
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 104
Tất cả vì học sinh thân yêu a  1 -
x - y  1 -  5   a  -  b  3   x  y  3    b  2       2  a  5 - x - y  5 -
b - 2b - 3 2
3b  18b  29  0     b  1 - 
 x  y  1 - 
(x - 1)( y -1)(x  y - 2)  6
Câu 17 : Giải HPT :  2 2
x  y - 2x - 2 y - 3  0  3 3 2 2 x -1  a
ab(a  b)  6
ab(a  b)  6 36 
- 2a b - 5a b  0        2 2 2 y -1  b a  b  5
(a  b) - 2ab  5
ab(a  b)  6      b   2 x -1  1   ab  2 a  1 y -1  2         a b 3   b  1     x -1  2      a  2   y -1  1 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 105
Tất cả vì học sinh thân yêu   x -   1  y - 
1  x  y - 2  6 Câu 18:  2 2
x  y - 2x - 2 y - 3  0  x - 1  a ab 
a  b  6 Đặt 
, hệ đã cho trở thành:  y - 1  b  2 2 a  b  5  a  2 x -1  2   b  1   y -1  1   a  2 - x -1  2 -  36   2 (a  b)    b  1 -   y -1  1 -   2 2 
a b  ab  2     2 2  a  1 x -1  1 a  b  5       b  2   y -1  2    a  1 - x -1  1 -    b  2 -   y -1  2 -  2
2x  xy  1  Câu 19 : Giải HPT : 2  9x 3xy  1   4 2 2(1 - x) 2(1 - x)  2 1 - 2x
Dễ thấy x  0 không phải nghiệm của HPT  x  0  y  . Thế vào PT2 ta x được :
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 106
Tất cả vì học sinh thân yêu 2 2 9x 3(1 - 2x )  1  4 2 2(1 - x) 2(1 - x) 2 4 2 2
 9x  2(1 - x)  3(1 - 2x )(1 - x) 2 2
 (2x  2x -1)(2x - 4x  5)  0  3 -1 x   y  2  2   - 3 -1 x   y  2   2 3 3
x y  x  xy  x  1
Câu 20 : Giải HPT :  3 2 3
4x y  4x - 8xy - 17x  -8  2
(xy  x)(x  1)  1 Hệ   2 2
4x(xy  x) - 8xy(x  1) -17x  -8 
xy  x  a  xy  a - x Đặt  2 x  1  b  ab  1 Hệ trở thành :  2
4a  8b -17  0  1 1 2
 (2a -1)(2a  2 - 8)  0 . Do 0  a   1  a   b  2 b 2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 107
Tất cả vì học sinh thân yêu x  1   1 -  1  y  xy x     2   2   2 x  1 - x 1     3 - y    2 2
x  xy - 3x  y  0
Câu 21 : Giải HPT :  4 2 2 2
x  3x y - 5x  y  0  2
x  y  xy - 3x  0 Hệ   2 2 2 2
(x  y)  x y - 5x  0  Thế 2
x  y  3x - xy vào PT2 ta được 2 2 2 2 2 2
9x  x y - 6x y  x y - 5x  0 2 2
 x ( y - 5 y  4)  0
x  0  y  0 
 y  1  x  1  2
 y  4  x  x  4  0(L) 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 108
Tất cả vì học sinh thân yêu  3 2 y   1 2 2   x  y -1 x
Câu 22 : Giải HPT :  2x 2 2 x  y -  4  y  2 2
x  y -1  a  3 2     1 Đặt  x  a b
 giải PT bậc nhất cơ bản  b  y a - 2b  3    3 1 2 2 x - y  -  Câu 23 : Giải HPT : 2 y x  3
(x  y)  5  3x - 2 y
PT(1)  (x  y)(x - y) 
. Thế PT(2) vào PT(1) ta được : 2xy 5(x - y) 6x - 4 y
5(x - y) - (6x - 4 y) -(x  y)    2 2 2 (x  y) 4xy
(x  y) - 4xy (x - y) 3 3
 5(x - y)  -(x  y)  5
-  x - y  1 - x - y  1 -    3 x  y  5 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 109
Tất cả vì học sinh thân yêu 4 4
x - 2x  y - y
Câu 24 : Giải HPT :  2 2 3 (x - y )  3   a  b x 
x  y  a   2 Đặt :    . Đặt kì diệu :
x - y  b a - b   y    2 3 3 3 3
c  3  a b  3  c  ab  c .Khi đó : 2 2 æ a  b ö æ a - b  4 4 2 2 ö
x - y  (x - y)(x  y)(x  y )  ab   ç ÷ ç ÷  è 2 ø è 2 ø   3 a - b a  3b a  c b
 2x - y  a  b -   2 2 2 2 2 3 æ a  b ö a  c b 2 2 3
 PT (1)  ab 
 c(a  b )  a  c b ç ÷ è 2 ø 2 2 2 3
c(a  b )  a  c b  Ta có hệ mới :  c
ab  c  b    a 2 4 3 c c c ac  1 2  c(a  )  a   (ac -1)(a - )  0  2 2  a a a a  c 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 110
Tất cả vì học sinh thân yêu 3 3  a  c  3  x  y  3
Với a  c :    
ab  c  b  1  x - y  1   1 1  1 a   x  y    Với ac  1 : 3 3  c 3   3   2 3  3 b  c  9 x - y  9   2 2
 2xy  y x - y x  y x - y     14 2 2
Câu 25 : Giải HPT :  3 3
 æ x  y ö æ x - y ö   9  ç ÷ ç ÷  è 2 ø è 2 ø
 x  y  a   2 2 2
a  b  x Đặt 3 3 
(a  b  9  a  b  0;a,b  0)   . Khi đó 2 2  x - y
a - b  y   b   2 hệ trở thành : 2 2 2 2 2 2
 2(a  b )(a - b )  (a - b )2ab   a  b  14 3 3 a  b  9  3 3
(a  b) 2(a - b ) -14  0      3 3 a  b  9 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 111
Tất cả vì học sinh thân yêu 3 3 a - b  7 3 a  8 a  2 x  y  8         3 3 a  b  9 3  b  1 b  1 x - y  2   
 x 1  y 1  2 
Câu 26 : Giải HPT :  72xy 2 2 3
 29 x - y  4  x - y   a  b x    2 Đặt  . Hệ trở thành : a - b  y    2  2 a  b a - b 2 2  8  1   1  2 (  2) -  2  a  b a b - a   2 2   3   2 2   9
 b -112b -128  0 18(a - b ) 2 2 3 18(a - b )    29 ab  4 3  29 ab  4 a  2  b b   
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 112
Tất cả vì học sinh thân yêu  b  4  4 -   b 
 a  ...  x  ...; y  ...  3  8 - b   3 2 2 2
x y  2 y  4  7xy
Câu 26 : Giải HPT :  2 2 2
x  2 y  6 y  3xy 
Dễ thấy y  0 không phải nghiệm của hệ . Khi đó hệ tương đương : 2 7x 4   2 æ 2 ö 3x x -  2   0  - x -  2  0 2  y y ç ÷ y y  è ø   2  2 æ x ö æ 2 ö  æ  x ö æ 2  2  3 - x  0 ö ç ÷ ç ÷  2  3 - x  0  y y ç  ÷ ç ÷ è  ø è ø y y è  ø è ø  2 - x  a 2   y
a - 3b  2  0 Đặt   
 (a  b)(a - b - 3)  0 2 x
b  3a  2  0   b   y  a  1 -  b  1 Với 2
a  b  0  a  3a  2  0  a  2 -  b  2  Với 2
a - b  3  a - 3a 11  0 (Loại)
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 113
Tất cả vì học sinh thân yêu 2 2
x  xy  y  3y -1
Câu 27 : Giải HPT :  3 2 2
x  x y  x - x  1 
Dễ thấy x  0 không phải nghiệm của hệ . 2 2  .(
x 1) - (2)  0  x  xy - 3xy 1  0 (3) Lấy (3) - (1) ta được : 2 2
xy - y - 4xy  3y  0  y  0
Xét thấy x  1 không phải nghiệm của hệ   4x - 3  y   x -1
Với y  0 thay vào không thỏa mãn hệ . 4x - 3 Với y  thay vào (2) ta được : x -1  5 -1 5 - 5 x   y   2 2 2 2
(x  x -1)  0   - 5 -1 5  5 x   y    2 2 
(x  y  3) x - y  2 y  4  0
Câu 28 : Giải HPT :  2 2
(x - y)(x  4)  y  1 
PT (1)  ( x - y 1)(x  y  4 - x - y )  0 
x - y  x  y  4 Thế 4 
x - y - x - y vào PT(2) ta được :
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 114
Tất cả vì học sinh thân yêu 2 2
(x - y)(x 
x - y - x - y)  y  1 2 3
 x (x - y -1)  ( x - y ) -1  0 x - y  x - y  1 2
 (x - y -1)(x  )  0 x - y  1 x - y  1  x  1 - Ta được hệ mới :    x  y  x - y - 4 y  2 -   2
x  2xy  y  0 
Câu 29 : Giải HPT :  3 2
x  3xy  2 y  1(x  x y  2)  4  Thế 2 x  y  2
- xy vào PT(2) ta được : 2 2 2 2
- x y - x - y  2x y  1  2 y  1 x y  2 - 4  0 2 2 2
 (x y  1 -1)  ( x y  2 - y  1)  0 x y 1  1    2  x y  2  y  1  2
x ( y  1)  1   2
x y  2  y  1  2 2
x y  2  3 - x   2
x y  2  y  1  2
 x  y  2  xy  1 -
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 115
Tất cả vì học sinh thân yêu 1 - 1
Dễ thấy x  0 không phải nghiệm của hệ 2  y   x -  2 x x  x  1 -  y  1   5  1 2 -  x   y   2 5  1   5 -1 2 x   y   2 1 - 5 5  1 2 -
Đối chiếu điều kiện  ( ; x y)  ( 1 - ;1);( ; ) 2 5  1 
(2x -1) x  y  (6 - x - y) 2 - x
Câu 30 : Giải HPT :  2 2 3
 x - 4xy - 7 y  72 -  Xét thấy x  2  2 - x  0 
x  y  0  y  -2 không thỏa PT(2)
 x  y , 2 - x  0 6 - (x  y) 6 - (8 - 4x) PT(1)   x  y 8 - 4x 2 6 - t -6
Xét hàm số f (t)   f '(t) 
-1  0 suy ra hàm số nghịch biến 2 t t
Mà f ( x  y )  f ( 8 - 4x )  x  y  8 - 4x  y  8 - 5x
Thế vào PT(2) giải PT bậc 2 cơ bản.
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 116
Tất cả vì học sinh thân yêu 2 2
x  y  2x  3
Câu 31 : Giải HPT :  3 3 2 2 2
2(x  y )  6x  3(x  y )  5  Ta có 3 2 2 2 2 2 .
x (1) - (2)  2 y - 2xy  2x  3(x  y )  5 - 6x 2
 y (2 y - 2x - 3)  (x -1)(x - 5) Mà 2 2
y  3 - x - 2x  (1 - x)(3  x)  (x -1)(x  3)(2 y - 2x - 3)  (x -1)(5 - x)
Với x  1  y  0 2 5 - x 3 x  4x  7
Với (x  3)(2 y - 2x - 3)  (5 - x)  y   x   2(x  3) 2 x  3
Thế vào PT(1) ta được : 2 2
æ x  4x  7 ö 2 x  2x   3 ç ÷ x  3 è ø 2 2 2 2 2
 (x  2x)(x  3)  (x  4x  7)  3(x  3) 2 2
 (x  1) (x  6x  11)  0  x  1 -  y  2 2
x  xy  x  3  0 
Câu 32 : Giải HPT :  2
 y(x  3)  x  1  2 x y  2 y  Lấy 2 2
(1) - (2)  x  2 - 3y  2 x y  2 y  0
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 117
Tất cả vì học sinh thân yêu 2 2  ( x  2 -
y )( x  2  3 y )  0 2
 y  x  2
Thế vào PT(1) ta được : 3 2
x  x  3x  3  0  x  1 -  y  3  1 2 2 (x  y )(1  )  5  2 2 Câu 33 : Giải HPT : x y  2 2 2
(xy -1)  x - y  2   1 1 2 2
(x  )  ( y - )  5   x y  2 2
(x 1)(y -1)  2xy   1 1 2 2
(x  )  ( y - )  5   x y   1 1
(x  )( y - )  2  x y 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 118
Tất cả vì học sinh thân yêu  b   2 a 1    b   2  1 - x   a  2 2   x a  b  5  a  1 -  Đặt     1  ab  2 b     1 y -  b  y     a  2    b   1 -   a  2 - 
Xét từng TH giải x, y đơn giản . 2 2
(x  1) ( y  1)  9xy  0
Câu 34: Giải HPT :  2 2
(x  1)( y  1)  10xy  0   1 1
(x  2  )( y  2  )  9 -   x y   1 1
(x  )(y  )  1 - 0  x y   b   2  1 x   a    x
(a  2)(b  2)  9 - a  b  3 - a  5 -   Đặt       1 ab 10 ab 10   -  -    b   5 y   b -  y     a  2 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 119
Tất cả vì học sinh thân yêu
Do vai trò của x, y là như nhau nên ta xét 1 TH của cặp ,
a b rồi hoán đổi lại. 2 2 2
(x  y) x  7  y 2y 1  xy  2y 
Câu 35 : Giải HPT :  2 2 2
2x x  7  (x  y) 2 y  1  3xy - x  x  0 Ta thấy 
thỏa mãn là một cặp nghiệm của hệ y  0  Xét 2 2 x  y  0 Dùng định thức ta có : 2 2
D  x  y  2 2
D  2 y(x  y ) x  2 2
D  -x(x  y ) y   Dx x   2 y   D    x  2
- x  x  y  0 (Loại) Dy  y   -x   D Kết hợp  ( ;
x y)  (0;0) là nghiệm duy nhất
(x  y) 2xy  5  4xy - 3y 1 
Câu 36 : Giải HPT : 
(x  2 y) 2xy  5  6xy  x - 7 y - 6  2.(1) - (2)
Xét hệ mới : 3.(1) - 2.(2) 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 120
Tất cả vì học sinh thân yêu
x - y - 3  (2xy - 5) - x 2xy  5  
(x - y) 2xy  5  5 y - 2x  15 
x - y - 3  (2xy - 5) - x 2xy  5   
(x - y - 3)( 2xy  5  5)  3(x - 2xy  5) 
 (2xy  5 - x 2xy  5)( 2xy  5  5)  3(x - 2xy  5)
 (x - 2xy  5)(2xy  5  5 2xy  5  3)  0
x  2xy  5  
2xy  5  5 2xy  5  3  0 
Có 2xy  5  5 2xy  5  3  0 2 x - 5
 x  2xy  5  xy 
.Thế vào PT(1) ta được 2 2 2 x - 5 3(x - 5) 2 2 x   2(x - 5) -  1 2 2x 3 2
 x - 3x -13x  15  0  x  -3(L) 
 x  5  y  2 
 x  1  y  2 -  2
 y  x  xy - 6 y  1  0
Câu 37 : Giải HPT :  3 2 2
xy  x y  x - 8 y  0 
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 121
Tất cả vì học sinh thân yêu Lấy 2 2
(1) - (2)  xy( y  x -1)  (3y -1) Lại có 2
xy  (x  y -1)  2(3y -1) 2
 xy,( y  x -1) là 2 nghiệm của PT 2 2
X - 2(3y -1) X  (3y -1)  0  X  3y -1 xy  3y -1   2
x  y -1  3y -1 
Thấy y  0 không phải nghiệm của hệ. 3y -1 Thế x  vào PT(2) ta được : y 3y -1 2 3 2
 y  3y  y - 3y  3y -1  0  y  1 -  x  4 y  3x  y 3x - y   8 2 2   x - y
Câu 38 : Giải HPT :  3x - y 3  x  y   7 2 2  x - y  Đặt 2 2 2 2
x  y  a
2b a  a b  2a  b  8ab
2a(b  1)  b(a  1)  8ab      2 2 2 2
x - y  b 
2a b  ab  2b  a  7ab
2b(a  1)  a(b  1)  7ab   ( ab  0 ) 2 2
2a(b  1)  b(a  1) 8 2 2  
 2a(b  1)  3b(a  1) 2 2
2b(a  1)  a(b  1) 7
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 122
Tất cả vì học sinh thân yêu Mà có 2 2
3a(b 1)  3b(a 1)  15ab  3  5 b   2 2 2
 5a(b  1)  15ab  b - 3b  1  0   3- 5 b    2 2 3  5 b  1 Với 2 b   a  1  2 . a
 2a  a  1 2 3b x  y  1    3  5 x - y    2 2 3 - 5 b  1 Với 2 b   a  1  2 . a
 2a  a  1 2 3b x  y  1    3 - 5 x - y    2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 123
Tất cả vì học sinh thân yêu
GIẢI BẤT PHƯƠNG TRÌNH , PHƯƠNG TRÌNH NGHIỆM KÉP
ĐÁNH GIÁ PHẦN SAU BẰNG CASIO THẦY QUANG BABY Bài 1 : 2
2x - 3x - 2  x 2x - 5  2( x - 2) 2x - 2 Bài 2 : 3 2
x 2x - 5  2(x - 2) 2x - 2  x - 7 x  24x - 29 Bài 3 : 2 2
5x 2x  5 - (x - 1) 3x - 3  32x  114x  99(1) 6 BÀI 2 : 2
2x  5x  6  7x 11  4x  9 , Điều kiện : x  - 5
Bước 1 , dò nghiệm ta được 2 nghiệm : x = 2 , x = -1 . 2
2x  5x  6  7x 11  4x  9 2
 2(x - x - 2) -  x  2 - 5x  6  -  x  3 - 7x 11  0      1 1 2 
 (x - x - 2) 2 - -  0   
x  2  5x  6
x  3  11x  7 
Bước 2 , ta chứng minh biểu thức trong ngoặc luôn dương  1 1 
Ta đặt : f (x)  2 - -   
x  2  5x  6
x  3  11x  7 
Chứng minh f (x)  0 , bằng việc sử dụng casio , chức năng Table như sau : 1
Nhập mode , 7 , g(x) 
, start -6/5 , end 5 , step 0,2 thấy g(x) lớn hơn 1,25 , vậy ta tách
x  2  5x  6 5 1 3 1 biểu thức -  0, còn lại ta có - 4
x  2  5x  6 4
x  3  11x  7
Việc còn lại các em biến đổi tương đương thôi .
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 124
Tất cả vì học sinh thân yêu  1 1 
Bước 3 : Kết luận : 2 2 (x - x - 2) 2 - -
 0  x - x - 2  0   
x  2  5x  6
x  3  11x  7  Nghiệm : 1 - .25  x  1 - hoặc x  2
Video hướng dẫn : https://www.youtube.com/watch?v=fGcVf77I-9g x  1
Giải bài 3 : Điều kiện :  2 - .5  x  1 - 
CHÚNG TA GIẢI MỘT BPT CŨNG GIỐNG NHƯ GIẢI MỘT PHƯƠNG TRÌNH , GỒM CÁC BƯỚC SAU :
Bước 1 : Casio ta tìm được nghiệm kép , các em bấm Shift + Cal thì sẽ thầy Eror , nhưng thực tế không
phải là vô nghiệm , các e thử nhật : Mode , 7 , f(x) = VT – VP , Start -2,5 , end -1 , step 0,2 . Các em sẽ thấy x
= -2 thì f(x) = 0 và không đổi dấu , vậy ta sẽ có f(x) = 0 có nghiệm kép
BƯỚC 1: DÒ NGHIỆM : Dùng casio phát hiện ra nghiệm kép (qua chức năng Table ) : x = -2
Tiếp đến chúng ta tạo lien hợp cho các căn : 2x  5  ax  b : sử dụng điều kiện để 2 đường tiếp xúc :
 f (x)  g(x)  2 - a  b  1 
xét tại điểm có x = - 2 ta có hệ : 
f '(x)  g '(x)  a  1 
Vậy ta có được liên hợp : 2x  5 - (x  3) , làm hoàn toàn tương tự ta sẽ có : 2
3x - 3  (2x  1) 2 2
(1)  5x( 2x  5 - x - 3) - (x -1)( 3x - 3  2x 1)  25(x  4x  4)  5x x -1  2 2
 (x  4x  4) -
 25  0  (x  2) . f (x)  0   2
2x  5  x  3  3x - 3 - 2x -1  5x 5x f (x)  -  25 2
2x  5  x  3 3x - 3 - 2x -1
BƯỚC 2 : XỬ LÝ BIỂU THỨC TRONG NGOẶC :
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 125
Tất cả vì học sinh thân yêu 5x x -1 Xét : f (x)  -
 25 , ta chứng minh nó luôn dương với mọi x thuộc tập 2
2x  5  x  3 3x - 3 - 2x -1 xác định
+)Đầu tiên ta khẳng định rằng : x  1thì f (x)  0 , chỗ này em cứ dung table , mode 7 , star 1 , end 100 , step 10 xem , sẽ thầy +)Xét 2 - .5  x  1 - ,dung chức năng table ta thấy 5x x -1 f (x)  -
 25  0 (bấm mode 7 , nhập f(x) , start -2,5 , end -2 , step 2
2x  5  x  3 3x - 3 - 2x -1 0,2) x -1
Chọn riêng hàm g(x)  -
(bấm mode 7 , nhập f(x) , start -2,5 , end -2 , step 0,2) thì ta 2 3x - 3 - 2x -1 5x
thấy g(x)  -25 , vậy ta sẽ có
 25  0 , cái này các em dễ chứng minh bằng biến đổi
2x  5  x  3 tương đương .
Vậy trên tập xác định thì f (x)  0 , vậy 2
(1)  (x  2)  0  x  -2 Đáp sô : x = -2
Facebook cá nhân : https://www.facebook.com/quang.manngoc
CÁC EM HỌC TOÁN KHÔNG THẤY TIẾN BỘ ,
THẦY QUANG SẼ GIÚP CÁC EM THAY ĐỔI 126

Tuyển tập hệ phương trình – Mẫn Ngọc Quang

Thông tin :

Tài liệu liên quan:

Chuyên đề một số phương pháp đếm trong các bài toán tổ hợp

Các dạng toán vectơ Toán 10 thường gặp

Các dạng toán mệnh đề và tập hợp Toán 10 thường gặp

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Hoàng Văn Thụ – Hà Nội

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Xuân Đỉnh – Hà Nội