Thông tin
Quiz

Tuyển tập phiếu ôn tập thi THPT Quốc gia 2017 môn Toán – Lê Bá Bảo

Tài liệu tuyển tập các phiếu ôn tập chuẩn bị cho kỳ thi THPT Quốc gia 2017 môn Toán, mỗi phiếu có 20 câu hỏi trắc nghiệm, có phân tích và giải chi tiết. Mời mọi người đón xem

Chủ đề:

Tài liệu ôn thi THPTQG môn Toán 257 tài liệu

Môn:

Toán 1.9 K tài liệu

Thông tin:

29 trang 1 năm trước

Tác giả:

Nguyễn Vân

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tuyển tập phiếu ôn tập thi THPT Quốc gia 2017 môn Toán – Lê Bá Bảo

60 30 lượt tải Tải xuống

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU TỔNG ÔN SỐ 01

Tổng ôn tập:

NéI DUNG VËN DôNG

¤N THI THPT QuèC GIA

M¤N TO¸N

Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế

SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế

Nội dung đề bài, đáp án chúng tôi trích từ các đề thi thử của các trường trên toàn quốc, nguồn tài

nguyên Page Toán Học Bắc Trung Nam, Page CLB Giáo viên trẻ TP Huế và các tư liệu tham khảo của quý

thầy cô đăng trên internet! Xin chân thành cảm ơn!

Câu 1: Cho hàm số

 

y f x

liên tục trên



và có đồ thị như

hình bên. Tìm số điểm cực trị của hàm số.

A. 4. B. 5.

C. 6. D. 7.

-2

-1

Câu 2: Cho hàm số

 

0y ax bx c a   

có bảng biến thiên dưới đây:



1















Giá trị

,,a b c

tương ứng là:

1; 4; 1.a b c   

1; 2; 1.a b c    

1; 2; 1.a b c   

1; 4; 1.a b c    

Câu 3: Một tấm kẽm hình vuông

ABCD

có cạnh bằng

 

30 .cm

Người ta gập tấm kẽm theo hai cạnh

và

cho đến khi

và

trùng nhau như hình vẽ bên

để được một hình lăng trụ hai đáy. Tìm

để thể tích

khối lăng trụ lớn nhất.

 

5.x cm

 

9.x cm

 

8.x cm

 

10 .x cm

Câu 4: Cho hàm số

 

3 2 3 2

   





   

   

có đồ thị

 

. Trong các khẳng định sau,

khẳng định nào đúng?

 

đồng biến trên



. B. Đường thẳng

1y 

là tiệm cận ngang của

 

C. Đồ thị

 

tiếp xúc với trục

. D. Đồ thị

 

đi qua các điểm

 

0;2 , 2;







Câu 5: Bác An đầu tư 67 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất 5,99% mỗi

quý. Hỏi sau 2 năm rút tiền lãi thì bác An thu được bao nhiêu tiền lãi? (giả sử rằng lãi suất hàng

quý không đổi)

A. 39,707 triệu đồng. B. 24,699 triệu đồng.

C. 58,004 triệu đồng. D. 9,2 triệu đồng.

Câu 6: Tìm tất cả các giá trị thực của tham số m để phương trình

 

9 1 .3 0

mm   

có 2 nghiệm

thực phân biệt

;xx

sao cho

4.xx

9; 9mm  

. B.

9; .

mm

mm  

Câu 7: Tìm hàm số

 

,Fx

biết rằng

 

   

2 2 1





 

2 2 1

F x C

  



 

2 1 2

F x C

  



 

2 1 2

F x C

  



 

2 1 2





Câu 8: Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng

16m

và độ dài trục bé

bằng

10m

. Ông muốn trồng hoa trên một dải đất rộng

và nhận trục bé của elip làm trục đối

xứng (như hình vẽ). Biết kinh phí để trồng hoa là

100.000

đồng/

. Hỏi ông An cần bao nhiêu

tiền để trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn).

7.862.000

đồng.

7.653.000

đồng.

7.128.000

đồng.

7.826.000

đồng

Câu 9: Biết

 

sin

cos2

ln ; ; 0

x a b a b b



   







. Giá trị

ab

bằng

10.

12.

Câu 10: Có bao nhiêu số phức

thỏa mãn điều kiện

z z z

Câu 11: Điều kiện để số phức

có điểm biểu diễn thuộc

phần tô đậm (kể cả bờ) trong hình vẽ bên là

có phần ảo không nhỏ hơn phần thực.

có phần thực không nhỏ hơn phần ảo và có

môđun không lớn hơn

có phần thực không nhỏ hơn phần ảo.

có môđun không lớn hơn

-4

-3

-2

-1

Câu 12: Cho số phức

thỏa mãn

1z 

. Tìm giá trị lớn nhất của biểu thức

1 3 1 .P z z   

3 15

2 20.

Câu 13: Các khối đa diện đều loại

 

;pq

được sắp xếp theo thứ tự tăng dần của số mặt là:

         

3;3 , 3;4 , 3;5 , 4;3 , 5;3

. B.

         

3;3 , 4;3 , 3;4 , 5;3 , 3;5

         

3;3 , 3;4 , 4;3 , 3;5 , 5;3

. D.

         

3;3 , 4;3 , 3;4 , 3;5 , 5;3

Câu 14: Cho hình chóp

.S ABCD

, có đáy là hình bình hành. Gọi

là trọng tâm tam giác

SBD

Mặt phẳng

 

chứa

và song song với

, cắt

,,SB SC SD

lần lượt tại

', ', 'B C D

. Tìm tỉ số

thể tích giữa khối

. ' ' 'S AB C D

và khối

..S ABCD

k 

Câu 15: Cho tam giác đều

ABC

cạnh

và hình vuông

MNPQ

nội tiếp trong tam giác

ABC

thuộc

,AB

thuộc

,AC

thuộc

).BC

Gọi

là phần mặt phẳng chứa các điểm thuộc tam

giác

ABC

nhưng không chứa các điểm thuộc hình vuông

.MNPQ

Tính thể tích của vật thể tròn

xoay khi quay

quanh trục là đường thẳng qua

vuông góc với

.BC

810 467 3





. B.

4 3 3





. C.

4 3 3



. D.

54 31 3





Câu 16: Cho hình chóp

.S ABC

có

vuông góc với đáy, tam giác

ABC

có

2; 2AB AC

và



120BAC 

. Biết góc giữa

 

SBC

và

 

ABC

bằng



với

tan 2.





Tính bán kính mặt cầu ngoại

tiếp hình chóp

..S ABC

Câu 17: Để chuẩn bị cho Tết Nguyên Đán 2017, ban dự án đường hoa Nguyễn Huệ, quận 1,

Thành phố Hồ Chí Minh dự định xây dựng một khối cầu có bán kính bằng

để trưng bày hoa

tươi xung quanh, để tiết kiệm diện tích Ban quản lý xây một hình trụ nội tiếp mặt cầu. Tính bán

kính của hình trụ sao cho khối trụ có thể tích lớn nhất.

r 

. B.

32 3





. C.

r 

. D.

r 

Câu 18: Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

  



  









. Đường thẳng

đi

qua

 

0;1; 1A 

cắt và vuông góc với đường thẳng



. Phương trình nào sau đây là phương trình

của đường thẳng

















  



. B.

















  



. C.



















. D.



  

















Câu 19: Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

đi qua điểm

 

1;2;3M

và cắt ba

tia

lần lượt tại

sao cho thể tích tứ diện

OABC

nhỏ nhất. Viết phương trình mặt

phẳng

 

123



. B.

369



. C.

369



. D.

123



Câu 20: Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 4 7 1 36S x y z     

và

mặt phẳng

 

: 3 0P x y z m   

. Tìm

để mặt phẳng

 

cắt

 

theo giao tuyến là một đường

tròn có bán kính lớn nhất.

20m 

. B.

6m 

. C.

36m 

. D.

20m 

------- HẾT -------

Cố gắng lên các em! Thầy rất mệt và các em còn.. mệt hơn!

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU TỔNG ÔN SỐ 01

Tổng ôn tập:

NéI DUNG VËN DôNG

¤N THI THPT QuèC GIA

M¤N TO¸N

BẢNG ĐÁP ÁN

Câu

Đáp án

Câu

Đáp án

ĐÁP ÁN CHI TIẾT

Câu 1: Dựa vào đồ thị đồng thời áp dụng định nghĩa và quy tắc 1 ta suy ra hàm số đã cho có 7

điểm cực trị



Chọn đáp án D.

Câu 2: Kiểm tra đồ thị hàm số có 3 điểm cực trị

     

0;1 ; 1;2 ; 1;2



Chọn đáp án C.

Câu 3: Ta có:

, 30 2 15.

DHF

DF CH x FH x p



     

Thể tích khối lăng trụ như hình vẽ là:

   

. 30 15 15 15 15 30 2

FDH

V S EF x x x     

   

30 15 15 2 15 ; ;15

x x x



   





Xét hàm số

     

15 2 15 ; ;15 .

f x x x x



   





Ta có:

         

' 2 15 2 15 2 15 2 15 3 30f x x x x x x         

;

 

' 0 .











Bảng biến thiên:

Dựa vào BBT,

 

;15

max 125fx









khi

10.x 

Do đó thể tích khối lăng trụ như hình vẽ lớn nhất

khi

 

10 .x cm

Khi đó

 

max

750 3 .V cm



Chọn đáp án D.

Câu 4:

(A):

   

0 2 1

ff  

nên

 

không đồng biến trên



. Khẳng định (A) sai.

(B):

   

lim , lim

f x f x

 

   

nên

 

không có TCN. Khẳng định (B) sai.

(C):

 

0,f x x  

nên

 

không tiếp xúc với trục

. Khẳng định (C) sai.

(D):

   

0 2, 2

ff

nên

 

đi qua

 

0;2 , 2;







. Khẳng định (D) đúng.



Chọn đáp án D.

Câu 5:

Áp dụng công thức lãi kép, số tiền thu được (cả vốn lẫn lãi) là:

(1 )

T A r

với tiền gửi

67A 

triệu đồng, lãi suất

0,0599r 

2.4 8N 

kỳ.

Ta được:

106,707T 

triệu đồng⟹ Số tiền lãi bằng:

39,707TA

triệu đồng.



Chọn đáp án A.

Câu 6: Ta có: PT

       

9 3 .3 0 3 3 1 3 1 0 3 1 . 3 0

x x x x x x x x

m m m m             

3 1 0



  











. Với

1 2 2

0 4 2 .

x x x









      











Chọn đáp án C.

Câu 7: Ta có:

 

       

d d d

2 2 2 2

3 2 3 2

2 2 1 2 2 1

F x x x x

x x x x





   



   



  

       

3 2 2 2 1 2 1 .

2 1 2

x x x x C



        







Chọn đáp án B.

Câu 8: Giả sử elip có phương trình



. Từ giả thiết ta có

2 16 8aa  

và

2 10 5bb  

Vậy phương trình của elip là

 

64 25

y y E



  



  









. Khi đó diện tích dải vườn được

giới hạn bởi các đường

   

; ; 4; 4E E x x  

và diện tích của dải vườn là

2 64 64

S x x x x



   



. Tính tích phân này bằng phép đổi biến

8sinxt

, ta

được











. Khi đó số tiền là

80 .100000 7652891,82 7.653.000





  









Chọn đáp án B.

Câu 9: Ta có:

   

 

sin d sin

d d sin

sin sin sin

4 4 4

0 0 0

1 2 1 2

cos2 1 1 1 1

1 2 ln2 ln 2.

1 2 2 1 2 2 1 2 2 2

I x x x

x x x

  







      

  

  

0; 2.ab  

. Vậy

4.ab



Chọn đáp án A.

Câu 10:

Đặt

 

,z a bi a b  

, ta có:

2 2 2 2

2 2 2 2 2

a b a b a

z z z a b abi a b a bi

ab b



   



         









0 1 1



   







  

  







  





1 1 1 1

2 2 2 2

z z i z i         

. Vậy có 3 số phức thỏa mãn.



Chọn đáp án A.

Câu 11: Gọi

 

; ;z x yi x y   

. Điểm

 

;M x y

biểu diễn

trên mặt phẳng tọa độ.

Từ hình vẽ ta có:

















Chọn đáp án B.

Câu 12: Gọi

 

;;z x yi x y   

. Ta có:

2 2 2 2

1 1 1 1;1 .z x y y x x         



Ta có:

       

1 3 1 1 3 1 2 1 3 2 1P z z x y x y x x             

Xét hàm số

     

2 1 3 2 1 ; 1;1 .f x x x x     



Hàm số liên tục trên

1;1 



và với

 

1;1x

ta có:

 

   

 

1 3 4

0 1;1 .

2 1 2 1

f x x



       



Ta có:

   

max

1 2; 1 6; 2 20 2 20.

f f f P



      







Chọn đáp án D.

Câu 13: Sắp xếp theo thứ tự tăng dần số mặt của các khối đa diện đều là: Khối tứ diện

 

3;3

, khối

lập phương

 

4;3

, khối tám mặt đều

 

3;4

, khối mười hai mặt đều

 

5;3

và khối hai mươi mặt

đều

 

3;5



Chọn đáp án B.

Câu 14: Gọi

là tâm hình hình hành

ABCD

là trọng tâm

SBD

nên



là

trọng tâm

'SAC C

là trung điểm

.SC

+ Qua

dựng

 

' '/ / ' , 'B D BD B SB D SD  

thiết diện cần tìm là tứ giác

' ' '.AB C D

là

trung điểm

' ' ' ' ' ' '

AB C AD C AB C D

B D S S S



  

Suy ra:

. ' ' ' . ' '

' ' 1

. . .

S AB C D S AB C

S ABCD S ABC

SA SB SC

V V SA SB SC

  



Chọn đáp án C.

Câu 15: Thể tích của vật thể tròn xoay khi quay

quanh trục là đường thẳng

bằng hiệu thể

tích khối nón khi quay tam giác

ABC

và thể tích khối trụ khi quay hình vuông

MNPQ

quanh trục

là đường thẳng

. Gọi độ dài cạnh hình vuông là

Khi đó:

MN AN CN NP

BC AC CA AH

    

1 2 3 3

x     

1 1 3 810 467 3

. . .

3 2 2 2 24

  

    

   

   

   



Chọn đáp án A.

Câu 16: Gọi

là trung điểm của cạnh

 

BC AM

BC BC SAM BC SM

BC SA



    







Suy ra

   

 



;.SBC ABC SMA

Theo giả thiết:

tan .tan

SA AM



  



.cos .tan 2.AB BAM





Ta có:



222

2 . .cos 12BC AB AC AB AC BAC   

3.BC a

Xét



: 2 2 :

sin

ABC R R

BAC



   

bán kính

đường tròn ngoại tiếp

.ABC

Vậy bán kính mặt cầu là

 

' 5.

RR  



Chọn đáp án A.

Câu 17: Ta có :

. . 4

V r h R h h



  



    





Xét hàm số

 

( ) 4 ( ) 4 , 0;2

V h h V h h R





      

( ) 0

V h h



  

Bảng biến thiên :

()Vh







()Vh

32 3



Từ bảng biến thiên, suy ra

max

32 3





khi và chỉ khi

h 

r



Chọn đáp án C.

Câu 18: Ta có:

(1;1; 1)u







; Gọi

(1 ;2 ;1 )M d M t t t     

 

1 ;1 ;2AM t t t    



 

. 0 1 1 2 0u AM u AM t t t t



          

   

Đường thẳng

có vec tơ chỉ phương

 

1;1;2AM 



và đi qua

 

0;1; 1A 

: 1 .

d y t









  







  





Chọn đáp án B.

Câu 19: Gọi

 

;0;0Aa

;

 

0;0;Bb

;

 

0;0;Cc

 

; ; 0a b c 

. Mặt phẳng

 

có phương trình đoạn chắn

a b c

  

. Vì

   

1;2;3MP

nên

1 2 3

a b c

  

Áp dụng bất đẳng thức Cauchy cho

số dương

;

và

ta được

1 2 3 6 6

1 3 1 27. 162abc

a b c abc abc

       

. Do đó,

OABC

V abc

Dấu

""

xảy ra

1 2 3 1

a b c





     









. Vậy

 

369

P 



Chọn đáp án B.

Câu 20: Mặt cầu

tâm

 

4;7; 1I 

bán kính

6R 

. Mặt phẳng

 

cắt

 

theo giao tuyến là một

đường tròn có bán kính lớn nhất khi mặt mặt

 

đi qua tâm

của mặt cầu, khi đó đường tròn

giao tuyến còn gọi là đường tròn xích đạo. Khi đó

 

4;7; 1IS



20.m 



Chọn đáp án A.

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU TỔNG ÔN SỐ 02

Tổng ôn tập:

NéI DUNG VËN DôNG

¤N THI THPT QuèC GIA

M¤N TO¸N

Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế

SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế

Nội dung đề bài, đáp án chúng tôi trích từ các đề thi thử của các trường trên toàn quốc,

nguồn tài nguyên Page Toán Học Bắc Trung Nam, Page CLB Giáo viên trẻ TP Huế và các tư liệu

tham khảo của quý thầy cô đăng trên internet! Xin chân thành cảm ơn!

Câu 1: Cho hàm số

 

0; ; ;

bx c

y a a b c



  





có

dạng đồ thị như hình vẽ bên. Khẳng định nào sau

đây đúng?

0, 0, 0.a b c  

0, 0, 0.a b c  

0, 0, 0.a b c  

0, 0, 0.a b c  

Câu 2: Cho hàm số

 

y f x

liên tục trên

0; 3



và có bảng biến thiên:





2

5

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số

 

y f x

trên

0; 3



lần lượt là

và

2

và

5

và

Câu 3: Gia đình chú Luân có một vườn thanh long khá lớn và dự định mở rộng thêm quy mô, qua

một năm thu hoạch, chú Luân thấy rằng trên

50 m

diện tích trồng thanh long có

cây thanh long

thì trung bình mỗi cây có thu hoạch là

 

900 30f x x

(kg). Số cây mà ông Hùng cần trồng trên

50 m

là bao nhiêu để thu hoạch được khối lượng thanh long lớn nhất?

cây. B.

cây. C.

cây. D.

cây.

Câu 4: Tìm giá trị nhỏ nhất của biểu thức

 

log 6 log









với

là các số thực thay

đổi và thỏa mãn

1.ba

. B.

. C.

. D.

Câu 5: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức

   

0 .2 ,

s t s

trong đó

 

là số lượng vi khuẩn A lúc ban đầu,

 

là số lượng vi khuẩn A có sau

t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu,

số lượng vi khuẩn A là 10 triệu con?

A. 48 phút. B. 19 phút. C. 7 phút. D. 12 phút.

Câu 6: Cho biết phương trình

 

log 5.2 24 2 log 4



  

có hai nghiệm

và

. Tính tổng

2 1 2 1

4 4 .





97S 

. B.

20,5S 

. C.

68S 

. D.

24,25S 

Câu 7: Cho hàm số

 

liên tục và có đạo hàm trên



. Mệnh đề nào sau đây đúng?

     

d .

f x x f b f a













   

d .f x x f x







 

   

d ;.f x x f x C C



  





     

d .

f x x f b f a







Câu 8: Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu

 

98 / .ms

Gia

tốc trọng trường là

 

9,8 / .ms

Tính quãng đường viên đạn đi được từ lúc bắn lên cho đến khi

chạm đất.

 

490 .m

 

978 .m

 

985 .m

 

980 .m

Câu 9: Cho hình thang cong

 

giới hạn bởi các đường

ye

0y 

0x 

ln4x 

. Đường thẳng

; (0 ln4)x k k  

chia

 

thành hai

hình phẳng là

và

như hình vẽ bên. Quay

,SS

quanh trục

được các khối tròn xoay có thể tích lần lượt là

và

Với giá trị nào của

thì

2?VV

1 32

ln .

k 

ln11.

k 

1 11

ln .

k 

ln .

k 

Câu 10: Có bao nhiêu số phức

thỏa







và







ln4

Câu 11: Cho số phức

thỏa mãn đồng thời hai điều kiện

2zm

và

 

1 1 2,i z i   

với

là tham số thực. Tìm tập hợp tất cả các giá trị

để tồn tại hai số phức thỏa mãn các điều kiện trên.

 

2 2; 2 2 .

2 2; 2 2 .









 

2 2; 2 2 \ 0 .







 

 

2 2; 2 2 \ 0 .

Câu 12: Cho số phức

thỏa mãn

13z i z i   

. Tính môđun lớn nhất của số phức

; 0.z



Câu 13: Trong các hình đa diện dưới đây, hình nào không tồn tại mặt cầu ngoại tiếp?

hình 4

hình 3

hình 2

hình 1

A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.

Câu 14: Cho hình bình hành

ABCD

có



; 3 ; 45AD a AB a BAD  

(như hình bên). Tính thể tích

khối tròn xoay nhận được khi quay hình bình hành

ABCD

quanh trục

.AB

5.Va





6.Va













Câu 15: Cho hình hộp chữ nhật

.ABCD A B C D

   

có thể tích bằng

và

là trọng tâm của tam

giác

BCD



. Tính thể tích

của khối chóp

. '.G ABC

V 

. B.

V 

. C.

V 

. D.

V 

Câu 16: Một cái phễu có dạng hình nón.

Người ta đổ một lượng nước vào phễu sao

cho chiều cao của lượng nước trong phễu

bằng

chiều cao của phễu. Hỏi nếu bịt kín

miệng phễu rồi lộn ngược phễu lên thì chiều

cao của nước gần bằng giá trị nào sau đây?

Biết rằng chiều cao của phễu là 15cm.

A. 0,188 (cm). B. 0,216

(cm).

C. 0,3 (cm). D. 0,5 (cm).

Câu 17: Một khúc gỗ có dạng với độ dài các

cạnh được cho như hình vẽ bên. Tính thể tích

khối đa diện tương ứng.

 

2960

V cm

 

2560 .V cm

 

2960 .V cm

 

2590 .V cm

3 cm

40 cm

7 cm

5 cm

Câu 18: Trong không gian với hệ tọa độ

,Oxyz

gọi

1 2 3

,,M M M

lần lượt là điểm đối xứng của

 

1; 2; 3M 

qua các mặt phẳng

     

,,Oxy Oxz Oyz

. Phương trình mp

 

1 2 3

M M M

là

6 2 3 6 0.x y z   

6 2 3 6 0.xyz   

6 3 2 6 0.x y z   

6 3 2 6 0.x y z   

Câu 19: Trong không gian với hệ tọa độ

Oxyz

, cho 3 điểm

     

;0;0 , 0; ;0 , 0;0;A a B b C c

,,a b c

là

những số thực dương thay đổi thỏa

2 2 2

3a b c  

. Tìm giá trị nhỏ nhất khoảng cách từ gốc tọa độ

đến mặt phẳng

 

.ABC

. B.

. C.

. D.

Câu 20: Trong không gian với hệ tọa độ

,Oxyz

cho hai mặt phẳng

 

: 2 2 1 0P x y z   

và

 

: 2 2 3 0Q x y z   

và đường thẳng

4 1 1



  



Có bao nhiêu mặt cầu có tâm nằm trên

đường thẳng



, đồng thời tiếp xúc với hai mặt phẳng

 

và

 

. B.

. C.

. D.Vô số.

------- HẾT -------

Cố gắng lên các em! Mọi việc rồi sẽ tốt đẹp thôi!

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU TỔNG ÔN SỐ 02

Tổng ôn tập:

NéI DUNG VËN DôNG

¤N THI THPT QuèC GIA

M¤N TO¸N

BẢNG ĐÁP ÁN

Câu

Đáp án

Câu

Đáp án

ĐÁP ÁN CHI TIẾT

Câu 1: Đồ thị hàm số có dạng như hình vẽ, có tiệm cận đứng

0;xa

tiệm cận ngang

0yb

Mặt khác

 

0; 0

C Oy



   





và

0 0.ac  



Chọn đáp án D.

Câu 2: Sử dụng phép biến đổi đồ thị từ đồ thị

 

y f x

suy ra đồ thị

 

y f x

trên

0; 3



ta có kết

quả

 

0;3

min 0fx







và

 

0;3

max 5.fx









Chọn đáp án A.

Câu 3: Sau một năm, trên

50 m

diện tích trồng, chú Luân thu hoạch được

 

900 30 .x x kg

Xét hàm số

   

( ) 900 30 , 0;g x xf x x x x    

( ) 900 60 ( ) 0 15g x x g x x



      

Bảng biến thiên :



()gx







()gx

6750

Từ bảng biến thiên, suy ra

max

( ) 6750gx 

khi và chỉ khi

15x 



Chọn đáp án B.

Câu 4: Ta có

 

2log 6 log .









Đặt



. Vậy

b a x

và

Suy ra:

   

 

2log 6 log 4 log log 6 log

a x a a x

P a x a x xa





    







     

2 2 2

4 2 log 6 log log 4 2 log 6 1 .

log

a x x a

x x a x



       





Đặt

 

log log 1 0 4 2 6 1 .

t x P t



       





Xét hàm số

   

4 2 6 1 ,f t t



   





với

 

0;t  

có

     

 

12 1

8 2 12 1 . 8 2 .

f t t t



  



      





Ta có:

 

   

 

2 2 3 1

2 4 3 3 0

t t t



 

  



  





  

   





 

       

 

1 2 6 6 3 0

2 1 6 1 6 1 3 1 0

t t t t

t t t t t t t



 



 



   



    

       





Từ đó suy ra

   

1 60f t f

, nên

60P 

. Dấu

""

xảy ra

log 1

x

nên

xa

hay

a b a

  



Chọn đáp án D.

Câu 5: Ta có:

   

3 0 .2ss

 

0 78125;

s  

   

0 .2

s t s

 

2 128 7.

    



Chọn đáp án C.

Câu 6: Ta có:

 

log 5.2 24 2 log 4



  

 

log 5.2 24 log 4 2



   

5.2 24







2 5.2 6 0

   

log 3















Khi đó:

1 2 2

2 1 2 1 2.log 3 1

2.1 1

4 4 4 4 24,25

  



    



Chọn đáp án D.

Câu 7: Ta có:

 

d 0

f x x













vì

 

f x x



là hằng số



A sai.

     

d ;f x x f x C C



   





B sai.

 

df x x F x C f x



   



C sai.

       

d .

f x x f x f b f a



  





Chọn đáp án D.

Câu 8: Gọi

 

là vận tốc của viên đạn. Ta có

   

' 9,8.v t a t  

Suy ra

 

9,8 .v t t C  

Vì

 

0 98v 

nên

98.C 

Vậy

 

9,8 98.v t t  

Gọi

là thời điểm viên đạn đạt độ cao lớn nhất. Tại đó viên đạn có vận tốc bằng 0. Vậy

 

0vT 

. Suy ra

9,8

T 

(

). Vậy quãng đường

mà viên đạn đi được là

   

2 2 9,8 98 980 .L S t t m    





Chọn đáp án D.

Câu 9: Ta có:

 

2 2 2

V e x





   







và

 

ln4

V e x



  



   







Theo giả thiết:

2 2 8 11 2 ln11 ln11.

2 2 2 2

V V e k k

  





          







Chọn đáp án B.

Câu 10: Ta có :

4 2 3 3

z i z

z i z i z

















  

  



  

      

   

  

   



















Vậy có 1 số phức thỏa điều kiện đề bài.



Chọn đáp án A.

Câu 11: Gọi

là điểm biểu diễn

trên mặt phẳng tọa độ.

Từ điều kiện:

   

2 2 4z m x m y x m y M          

thuộc đường tròn

 

có tâm

 

;0 ,Im

bán kính

2.R 

Từ điều kiện:

   

1 1 2 1 2

i z i i z



       



2. 2 1z i z i     

 

11x y M    

thuộc đường tròn

 

có tâm

 

0;1 ,I

bán kính

1.R 

Để tồn tại hai số số phức thỏa mãn các điều kiện đề bài khi chỉ khi tồn tại hai điểm

, điều này

xãy ra khi và chi khi

 

và

 

cắt nhau tại hai điểm phân

biệt

1 2 1 2 1 2 1 2

1 3.R R I I R R I I       

Ta có:

 

 

2 2 2

1 2 1 2

;1 1 1 1 3 0 8 2 2; 2 2 \ 0 .I I m I I m m m m              





Chọn đáp án D.

Câu 12: Gọi

 

;;z x yi x y  

có điểm

 

;M x y

biểu diễn

trên mặt phẳng tọa độ.

Từ giả thiết

     

2 2 2

1 3 1 1 3 2 4 7 0z i z i x y x y x y              

suy ra

: 2 4 7 0.M x y   

Với

là gốc tọa độ, ra có:

 

min

7 5 1 2 5

;

10 7

max

z d O



     



khi

10 5

zi

Câu 13: Hình 3 là lăng trụ đứng với đáy là hình thang vuông với hai đáy có độ dài khác nhau nên

đáy không tồn tại đường tròn ngoại tiếp. Vậy hình 3 không tồn tại mặt cầu ngoại tiếp.



Chọn đáp án C.

Câu 14:Gọi

là hình chiếu vuông góc của

lên

cạnh

AB 

2.DH a

Khối tròn xoay nhận được khi quanh hình bình

hành

ABCD

quanh trục

có thể tích đúng bằng

thể tích khối trụ có đường sinh

và bán kính đáy

(hai hình nón bù trừ nhau).

Vậy

..V HK DH DC DH





 

3 . 2 6 .a a a







Chọn đáp án B.

Câu 15:

Gọi

là trung điểm của



theo tính chất trọng

tâm của

ta có

GM CM

. . .

1 1 1 1 1

. . . .

3 3 3 3 2

G ABC C ABC A BCC

V V V AB CB CC

  



   

1 1 1

. . .

18 18 18

ABCD A B C D

AB BC CC V

   



  



Chọn đáp án D.

Cách khác: (Phương pháp tọa độ)

Gọi

       

0;0;0 , 1;0;0 , 0;1;0 , ' 0;0;1 .A B Ox D Oy A Oz  

Xác định tọa độ

, viết phương trình

   

 

. ' '

' ; ' .

G ABC ABC

ABC V d G ABC S





 

1 1 1

; ' . , ' .

3 2 18

d G ABC AB AC







 

Câu 16: Tính thể tích của phần hình nón không chứa nước, từ đó suy ra chiều cao

, chiều cao của

nước bằng chiều cao phễu trừ đi

'.h

Công thức thể tích khối nón:





Gọi bán kính đáy phễu là

, chiều cao phễu là

 

15h cm

, do chiều cao nước trong phễu

ban đầu bằng

nên bán kính đáy hình nón tạo bởi lượng nước là

. Thể tích phễu và thể tích

nước lần lượt là

 

2 2 3

.15 5

V R R cm





và

 

1 15 5

3 3 3 27

V R cm











. Suy ra thể tích

phần khối nón không chứa nước là

 

2 2 2 3

5 130

27 27

V V V R R R cm

  

    

 



Gọi

và

là chiều cao và bán kính đáy của khối nón không chứa nước, ta có

 

' ' '

h r h h

h R V

   

Từ (1) và (2) suy ra

 

' 5 26 15 5 26 0,188 .h h cm    



Chọn đáp án A.

Câu 17: Ta có diện tích đáy bằng:

 

5 3 7

7 74





. Vậy

 

40.74 2960 .V cm



Chọn đáp án C.

Câu 18: Ta có:

     

1 2 3

1; 2;3 ; 1; 2; 3 ; 1;2; 3M M M    

. Suy ra:

 

0; 4; 6MM   



 

2;0; 6MM 



và

   

1 2 1 3

, 24; 12;8 6; 3; 2

M M M M



   



 

 

1 2 3

M M M

qua

 

1; 2; 3M 

và nhận

 

6; 3;2n 



làm vectơ pháp tuyến, có phương trình:

6 3 2 6 0.x y z   



Chọn đáp án C.

Câu 19: Ta có:

 

: 1 0.

ABC bcx acy abz abc

a b c

       

Lúc đó:

 

2 2 2

2 2 2 2 2 2 2

2 2 2 2 2 2

1 1 1

;

3 9 3

a b c abc

d O ABC a b c a b c

b c a c a b

abc

      



max

d



Chọn đáp án A.

Câu 20:

Để ý rằng

   

//PQ

. Đường thẳng



có 1 vectơ chỉ phương là

 

4;1;1u







và

 

0;1;0 .A

Ta có:

 

/ / .



















Mặt khác:

 

;

;;

;

d A P

d A P d A Q

d A Q



















Vậy



song song và cách đều hai mặt phẳng

 

và

 

Q 

có vô số mặt cầu có tâm nằm trên



đồng thời tiếp xúc với hai mặt phẳng

 

và

 



Chọn đáp án D.

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU TỔNG ÔN SỐ 03

Tổng ôn tập:

NéI DUNG VËN DôNG

¤N THI THPT QuèC GIA

M¤N TO¸N

Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế

SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế

Nội dung đề bài, đáp án chúng tôi trích từ các đề thi thử của các trường trên toàn quốc, nguồn tài

nguyên từ sách ôn thi TNTHPT 2016 (Thầy Đoàn Quỳnh chủ biên), Page Toán Học Bắc Trung Nam, Page

CLB Giáo viên trẻ TP Huế và các tư liệu tham khảo của quý thầy cô đăng trên internet! Xin chân thành cảm

ơn!

Câu 1: Cho hàm số

 

0y ax bx c a   

có đồ thị như hình

vẽ bên. Mệnh đề nào dưới đây đúng?

0, 0, 0.a b c  

0, 0, 0.a b c  

0, 0, 0.a b c  

0, 0, 0.a b c  

Câu 2: Kí hiệu

 

là đồ thị của hàm số







Với mỗi điểm

 

;M x y

thuộc

 

xét điểm

 

2; 1 .M x y





Trong các hàm số sau, tìm hàm số có đồ thị tạo bởi các điểm



đó.















Câu 3: Tìm hàm số dạng

(

, , ,y ax bx cx d a b c d   

là các hằng số,

0)a 

sao cho

 

là hàm

số lẻ, đồ thị của nó tiếp xúc với đường thẳng

9 16yx

tại điểm

 

2; 2 .A

 

5.f x x x  

 

2 7 .f x x x

 

2 9 .f x x x  

 

3.f x x x

Câu 4: Kí hiệu

,Mm

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

6 2cos4

sin2 .





Tính

.Mm

Câu 5: Đường cong trong hình bên là đồ thị của một

hàm số trong bốn hàm số được liệt kê ở bốn phương án

A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

(C)

-3

-1

y 

2 1.

y 

log 1.yx

Câu 6: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức

 

Q t Q e











với t là khoảng thời gian tính bằng giờ và

là dung lượng nạp tối đa (pin

đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0%) thì sau

bao lâu sẽ nạp được

90%

(kết quả làm tròn đến hàng phần trăm)?

1,54 .th

1,2 .th

1.th

1,34 .th

Câu 7: Cho hàm số

 

cos .

G x t t



Đạo hàm của

 

là

 

2 cos .G x x x





 

2 cos .G x x x





 

cos .G x x x





 

2 sin .G x x x





Câu 8: Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt

đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển

động theo phương thẳng đứng với vận tốc tuân theo quy luật

 

10v t t t

, trong đó

(phút) là

thời gian tính từ lúc bắt đầu chuyển động,

 

được tính theo đơn vị mét/phút (

/mp

). Nếu như

vậy thì khi bắt đầu tiếp đất vận tốc

của khí cầu là

 

/5v m p

. B.

 

/7v m p

. C.

 

/9v m p

. D.

 

/3v m p

Câu 9: Cho hình phẳng

 

giới hạn bởi các đường

yx

và

.yx

Tính thể tích khối tròn xoay

tạo ra khi

 

quay quanh

.Ox

 

đvttd

.x x x







 

đvttd

.x x x







 

đvttd

.x x x







 

đvttd

.x x x







Câu 10: Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình

16 0.z 

16.

32.

Câu 11: Biết tập hợp tất cả các điểm biểu diễn số

phức

là đường tròn cho bởi hình vẽ bên. Hỏi tập

hợp tất cả các điểm biểu diễn số phức

34zi

được thể hiện bởi đường tròn trong hình vẽ nào

trong bốn hình vẽ dưới đây?

-4

-3

-2

-1

-4

-3

-2

-1

-4

-3

-2

-1

-4

-3

-2

-1

-4

-3

-2

-1

Câu 12: Cho số phức

thỏa mãn

13z i z i   

. Tính môđun nhỏ nhất của

.zi

Câu 13: Tính diện tích tất cả các mặt của hình đa diện đều loại

 

3; 5

có cạnh bằng

2.a

4 3 .Sa

16 3 .Sa

8 3 .Sa

6 3 .Sa

Câu 14: Cho hình lăng trụ

.ABC A B C

  

có thể tích là

là điểm trên cạnh



sao cho

3.MA AM





 

Tính thể tích khối

..M BCC B



Câu 15: Cho hai đường tròn

 

tâm

, bán kính bằng

 

tâm

, bán kính bằng

lần

lượt nằm trên hai mặt phẳng

   

,PP

sao cho

   

//PP

và

 

1 2 1 1 2

; 3.O O P O O

Tính diện

tích mặt cầu qua hai đường tròn đó,

24 .



20 .



16 .



12 .



Câu 16: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh bằng



1, 60 .BAD 

Biết hai mặt

phẳng

 

SDC

và

 

SAD

cùng vuông góc với mặt phẳng

 

,ABCD

góc giữa

và mặt đáy bằng

45 .

Tính diện tích mặt cầu ngoại tiếp tứ diện

..S BCD



Câu 17: Một người kĩ sư muốn thiết kế một bồn chứa

xăng với thể tích

cho trước, hình dạng như hình vẽ bên,

các kích thước

,rh

thay đổi. Tính nguyên liệu ít nhất để

làm bồn xăng (tính theo

48 .V



36 .V



16 .V



52 .V



Câu 18: Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

1; 2;3 , 1; 4; 2 , 0;1; 3 .A B C

Tính

diện tích đường tròn ngoại tiếp tam giác

.ABC





. B.













Câu 19: Trong không gian với hệ tọa độ

Oxyz

, cho bốn đường thẳng

1 2 2

: ; : ;

1 1 2 1 1 3

x z x z



  

   

  

: ; : .

1 1 2 1 1 2

x z x z





   



Có bao nhiêu

đường thẳng cắt cả bốn đường thẳng đã cho?

. D. vô số.

Câu 20: Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

     

: 1 1 4S x y z    

và

đường thẳng

: 3 .

  













Hỏi có bao nhiêu mặt phẳng

 



chứa



và

 



tiếp xúc với mặt cầu

 

D. vô số.

------- HẾT -------

Cố gắng lên các em! Tất cả rồi sẽ tốt đẹp thôi!

Page: CLB GIÁO VIÊN TRẺ TP HUẾ

PHIẾU TỔNG ÔN SỐ 03

Tổng ôn tập:

NéI DUNG VËN DôNG

¤N THI THPT QuèC GIA

M¤N TO¸N

BẢNG ĐÁP ÁN

Câu

Đáp án

Câu

Đáp án

ĐÁP ÁN CHI TIẾT

Câu 1: Dựa vào đồ thị suy ra hệ số

0a 



loại phương án C. Hàm số có 1 điểm cực trị

0ab

00ab  

. Mặt khác:

   

0;0 0.C Oy O c   



Chọn đáp án D.

Câu 2: Ta có:

   

 

2 2 1

; 2; 1 1 .

x x x x

M x y x y y



     







   

       









   







Vậy

 

:.M C y







Chọn đáp án C.

Câu 3: Do

 

là hàm lẻ trên



nên dễ suy ra

0.bd

Từ đó, do

 

22f 

và

 

2 9 1; 3.f a c



    

Vậy

 

3.f x x x



Chọn đáp án D.

Câu 4: Biến đổi

6 2 cos4

sin2 sin2 2 sin 2 .

y x x x



    

Đặt

sin 2 1;1 , .t x t x     





Ta có hàm số

   

2 , 1;1 1 0 1

g t t t t f t t



          





là nghiệm duy nhất, nên

trong

 

1;1

thì

 

0ft





vô nghiệm. Do

   

1 0, 1 2ff  

nên

2, 0 2.M m M m    



Chọn đáp án B.

Câu 5:

Đồ thị

 

qua

   

1; 3 , 1; 3AB

, cắt

tại điểm

 

0; 2 .



Chọn đáp án C.

Câu 6: Pin nạp được

90%

tức là

0 0 0

0,9 0,9 1 1 0,9

Q Q Q Q e e





      





 

0,1 ln0,1 ln0,1 1,54 .



       



Chọn đáp án A.

Câu 7: Đặt

   

 

   

 

cos cos cos 0 .2

t t F t F t t t t F x F G x F x x

  

       



2 .cos 2 cos 2 cosx x x x x x  



Chọn đáp án B.

Câu 8: Gọi thời điểm khí cầu bắt đầu chuyển động là

0t 

, thời điểm khinh khí cầu bắt đầu tiếp

đất là

. Quãng đường khí cầu đi được từ thời điểm

0t 

đến thời điểm khinh khí cầu bắt đầu

tiếp đất là

là

 

10 5 162

t t t t   



4,93 10,93 9t t t      

. Do

 

0 0 10v t t   

nên chọn

9t 

. Vậy khi bắt đầu tiếp đất vận tốc

của khí cầu là

   

9 10.9 9 9v m p  



Chọn đáp án C.

Câu 9: Xét phương trình hoành độ giao điểm











Suy ra

 

d d d

1 1 1

2 4 4

0 0 0

.V x x x x x x x x x

  

     

  



Chọn đáp án D.

Câu 10:

Ta có:

  

4 2 2

1 2 3 4

16 0 4 4 0 2 2 2 2 .

z z z z z z i z i





                









2 2 2 2

1 2 3 4

16.z z z z    



Chọn đáp án B.

Câu 11: Dựa vào hình vẽ, tập hợp tất cả các điểm

 

;M x y

biểu diễn số phức

trên mặt phẳng tọa

độ là đường tròn có phương trình:

   

2 2 4xy   

Ta có:

   

3 4 3 4z i x y i     

có điểm

 

3; 4M x y





biểu diễn trên mặt phẳng tọa độ.

Ta biểu diễn:

       

2 2 4 3 1 4 2 4x y x y

   

          

   

     

: 1 2 4.M C x y



     

Với phương trình như vậy, ta thấy đáp án B thỏa mãn.



Chọn đáp án B.

Câu 12: Gọi

 

;;z x yi x y  

có điểm

 

;M x y

biểu diễn

trên mặt phẳng tọa độ.

Từ giả thiết

13z i z i   

suy ra

: 2 4 7 0.M x y   

Ta có:

 

1z i x y i   

có điểm

 

;1M x y





biểu diễn

trên mặt phẳng tọa độ.

Ta có:

 

2 4 7 0 2 4 1 3 0 : 2 4 3 0.x y x y M x y



            

Vậy

 

min

z i d O





    



khi

10 5

zi



Chọn đáp án D.

Câu 13: Đa diện đều loại

 

4; 3

là bát diện đều. Diện tích mỗi mặt bằng

 

a

Vậy diện tích tất cả các mặt của hình đa diện đều bằng

8 3 .a



Chọn đap an B.

Câu 14: Do

. . ' '

/ / .

M BCC B A BCC B

MA BC V V





Ta có:

 

. . .

1 1 2

; . .

3 3 3

A A B C A B C A BCC B A A B C

V d A A B C S V V V V V

          



  

     



Chọn đáp án C.

Câu 15: Đặt

 

03IO x x  

   

2 2 2 2 2 2

2 2 2 2

3 4 4 3

x IB O B R R x

x IA O A R R x



      







        





 

2 2 2

4 3 1 2 5.x x x R IO BO          

Vậy

4 20 .SR







Chọn đáp án B.

Câu 16: Ta có:

   

 

SDC ABCD

SD ABCD

SAD ABCD

















 



;SC ABCD SCD

Mặt khác:

ABD

cân tại

và



60BAD ABD  

đều

BCD

đều.

Gọi

là trọng tâm

BCD

và

là giao điểm hai

đường như hình vẽ.

R SI SK KI   

Vậy mặt cầu có diện tích







Chọn đáp án D.

Câu 17: Để ý rằng

h V r h r h









     

Vậy diện tích cần có để tạo ra bồn đựng xăng là

4 2 .

r V r

S r rh





  

Ta có:







   

Lập bảng biến thiên

min

36 .SV





Nhận xét: Có thể thấy ngay nguyên liệu "ít tốn kém" nhất khi

0.h 

Nhưng thầy vẫn luôn nhắc chúng ta

phải biết thành lập hàm số để khảo sát, đề phòng các dạng câu hỏi không cho test đáp án!



Chọn đáp án B.

Câu 18: Ta có:

     

2;2; 1 ; 1; 1;0 ; 1; 3;1 .AB AC BC       

  

Kiểm tra được:

.0AB AC 

 

và

,,A B C

không thẳng hàng

ABC

vuông tại

Vậy tâm đường tròn ngoại tiếp

ABC

là trung điểm cạnh

và bán kính

R 

Vậy diện tích hình tròn cần tìm là







Chọn đáp án B.

Câu 19: Kiểm tra được

//dd

Mặt phẳng

 



chứa

,dd

có phương trình:

1 0.xyz   

Ta có:

       

1;0;0 ; 2;1; 2d A d B



    

và

,dd

không thuộc

 



Kiểm tra:

 

1;1; 2AB 



cùng phương với vectơ chỉ phương của

và

.Ad

Vậy không tồn tại đường thẳng nào cắt cả bốn đường thẳng đã cho.



Chọn đáp án A.

Câu 20: Mặt cầu

 

có tâm

 

1;1; 0 ,I

bán kính

2.R 

Đường thẳng



qua

 

1; 3;0A

và có một

vectơ chỉ phương là

 

1;0;3 .u







Ta có:

 

0; 2; 0IA 



và

2IA

IA u























là một tiếp tuyến của mặt cầu

 

Vậy tồn tại duy nhất một

mặt phẳng

 



chứa



và

 



tiếp xúc với mặt cầu

 

(mặt phẳng

 



qua

 

1; 3;0A

và có một

vectơ pháp tuyến là





Chọn đáp án B.

Bấm Tải xuống để xem toàn bộ.

| 1/29

| | Tải xuống

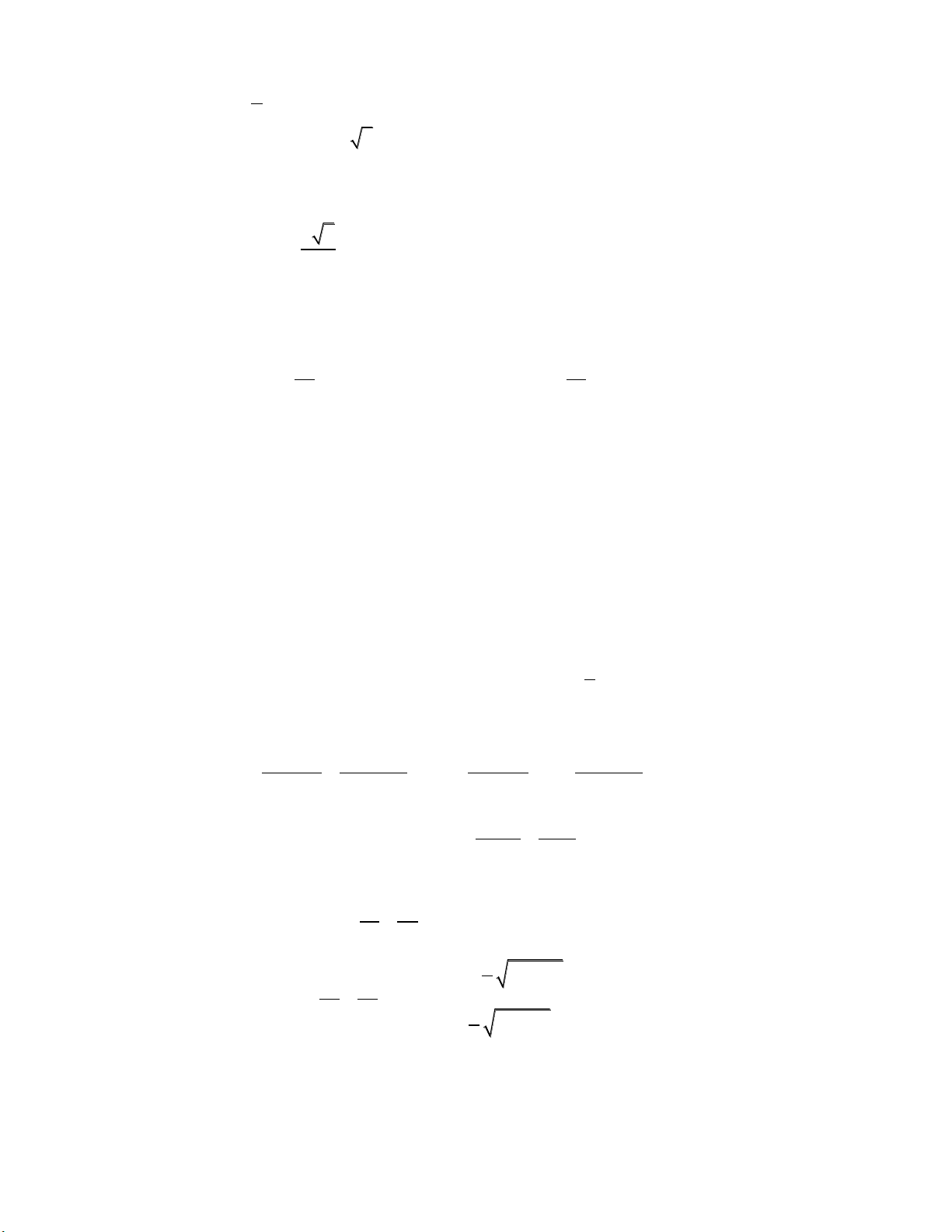
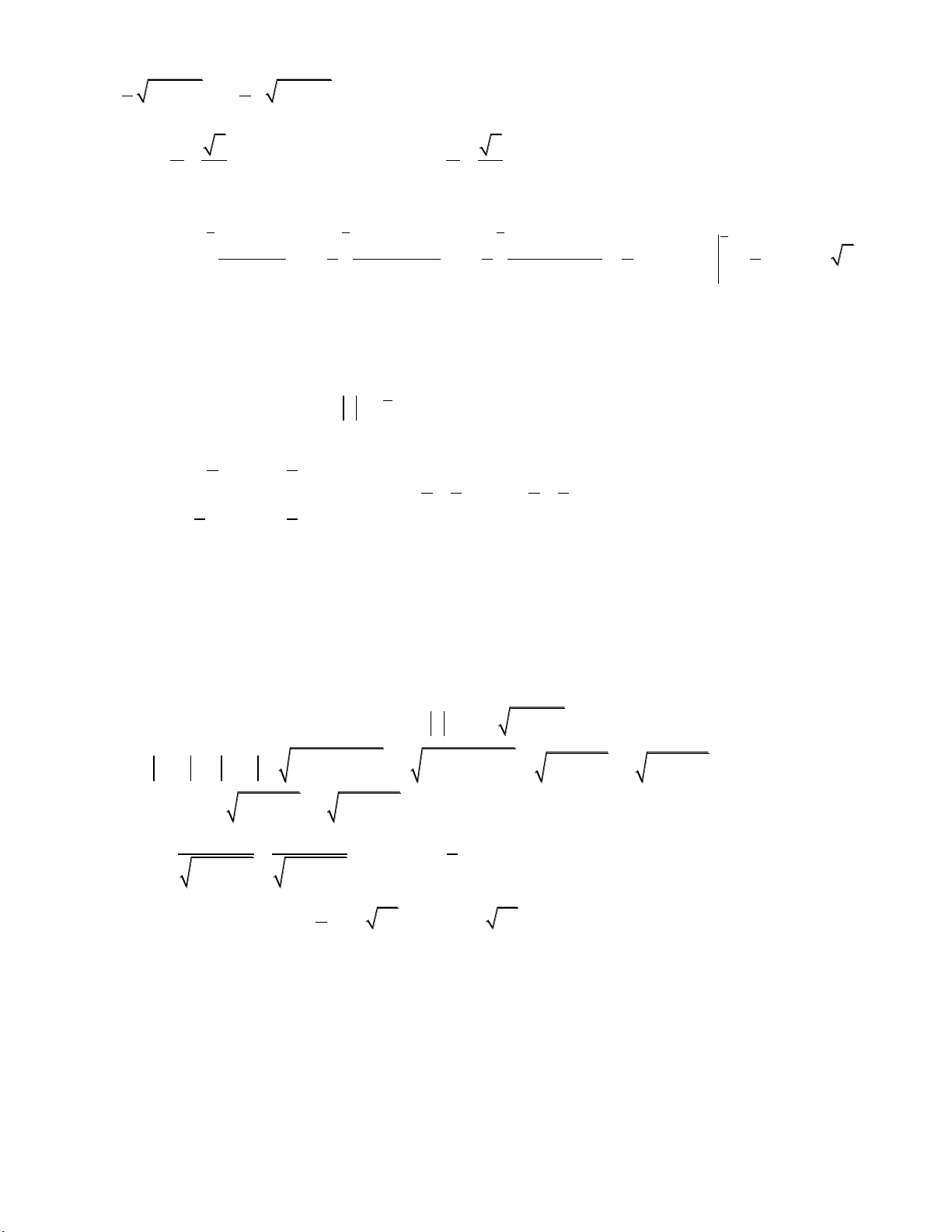
Preview text:

Page: CLB GIÁO VIÊN TRẺ TP HUẾ Tổng ôn tập: NéI DUNG VËN DôNG ¤N THI THPT QuèC GIA
PHIẾU TỔNG ÔN SỐ 01 M¤N TO¸N
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Nội dung đề bài, đáp án chúng tôi trích từ các đề thi thử của các trường trên toàn quốc, nguồn tài
nguyên Page Toán Học Bắc Trung Nam, Page CLB Giáo viên trẻ TP Huế và các tư liệu tham khảo của quý
thầy cô đăng trên internet! Xin chân thành cảm ơn!
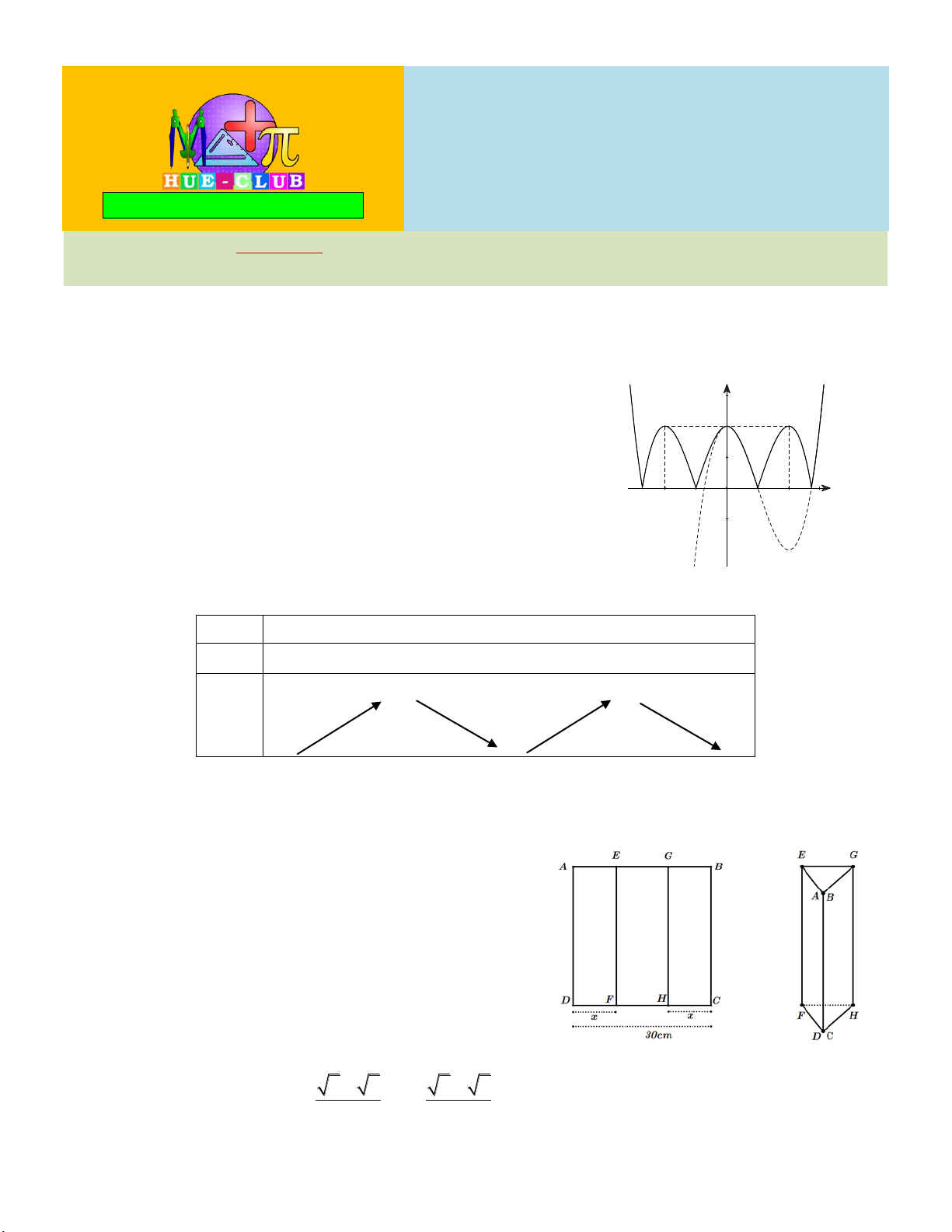
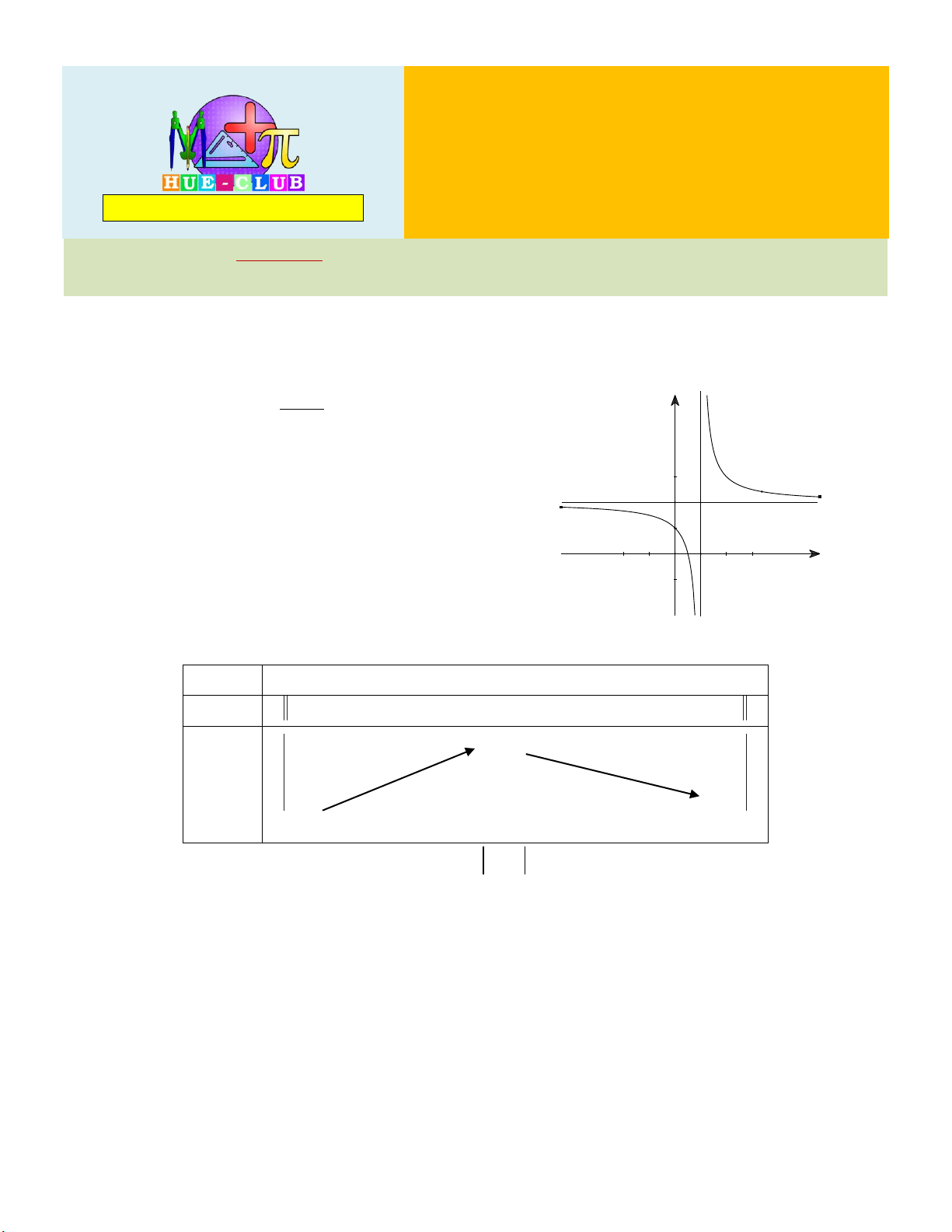
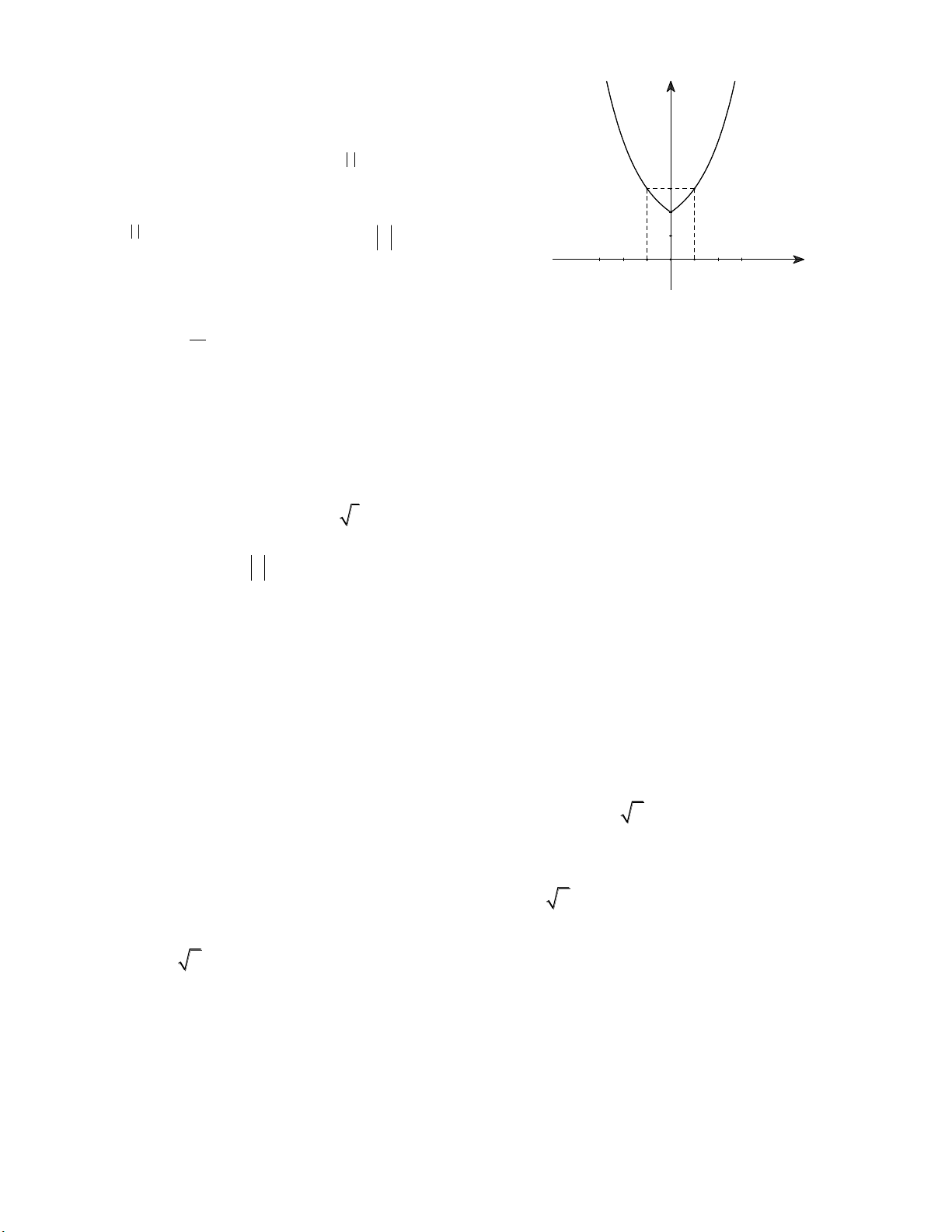
Câu 1: Cho hàm số y  f x liên tục trên  và có đồ thị như y
hình bên. Tìm số điểm cực trị của hàm số. 2 A. 4. B. 5. 1 C. 6. D. 7. -2 -1 O 1 2 x Câu 2: Cho hàm số 4 2
y  ax  bx  c a  0 có bảng biến thiên dưới đây: x  1  0 1  y  0  0  0  2 2 y  1 
Giá trị a, b, c tương ứng là:
A. a  1; b  4  ; c  1.
B. a  1; b  2  ; c  1  . C. a  1
 ; b  2; c  1. D. a  1  ; b  4  ; c  1.
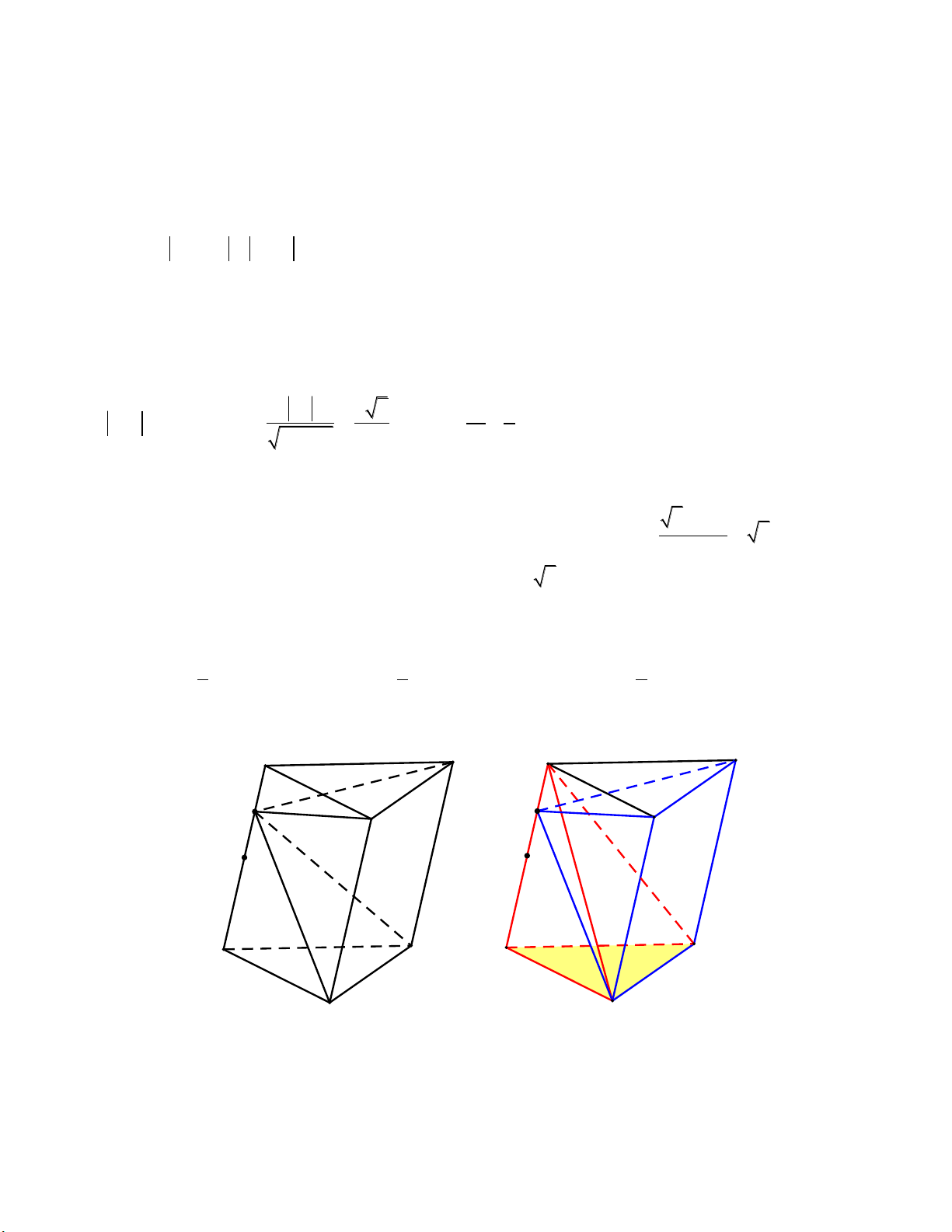
Câu 3: Một tấm kẽm hình vuông ABCD có cạnh bằng
30 cm. Người ta gập tấm kẽm theo hai cạnh EF và
GH cho đến khi AD và BC trùng nhau như hình vẽ bên
để được một hình lăng trụ hai đáy. Tìm x để thể tích
khối lăng trụ lớn nhất.
A. x  5 cm.
B. x  9 cm.
C. x  8 cm.
D. x  10 cm. x x      
Câu 4: Cho hàm số f x 3 2 3 2       
có đồ thị C . Trong các khẳng định sau, 3   3      khẳng định nào đúng?
A. f x đồng biến trên  .
B. Đường thẳng y  1 là tiệm cận ngang của C .  
C. Đồ thị C tiếp xúc với trục Ox .
D. Đồ thị C đi qua các điểm A  10 0; 2 , B 2;  .  9 
Câu 5: Bác An đầu tư 67 triệu đồng vào một công ty theo thể thức lãi kép với lãi suất 5,99% mỗi
quý. Hỏi sau 2 năm rút tiền lãi thì bác An thu được bao nhiêu tiền lãi? (giả sử rằng lãi suất hàng quý không đổi) A. 39,707 triệu đồng. B. 24,699 triệu đồng. C. 58,004 triệu đồng. D. 9,2 triệu đồng.
Câu 6: Tìm tất cả các giá trị thực của tham số m để phương trình 9x     1 .3x m
 m  0 có 2 nghiệm
thực phân biệt x ; x sao cho 2 2 x  x  4. 1 2 1 2 2 1 1
A. m  9; m  9  . B.
C. m  9; m  .
D. m  3; m   . 3 9 3 3 2
Câu 7: Tìm hàm số F x , biết rằng F 'x    x  2 . 2 2x12 A. F x 3 1    C. B. F x 1 3    C. x  2 2x  1 2x  1 x  2 C C. F x 2 3    C. D. F x 1   . 2x  1 x  2 2x  1 x  2
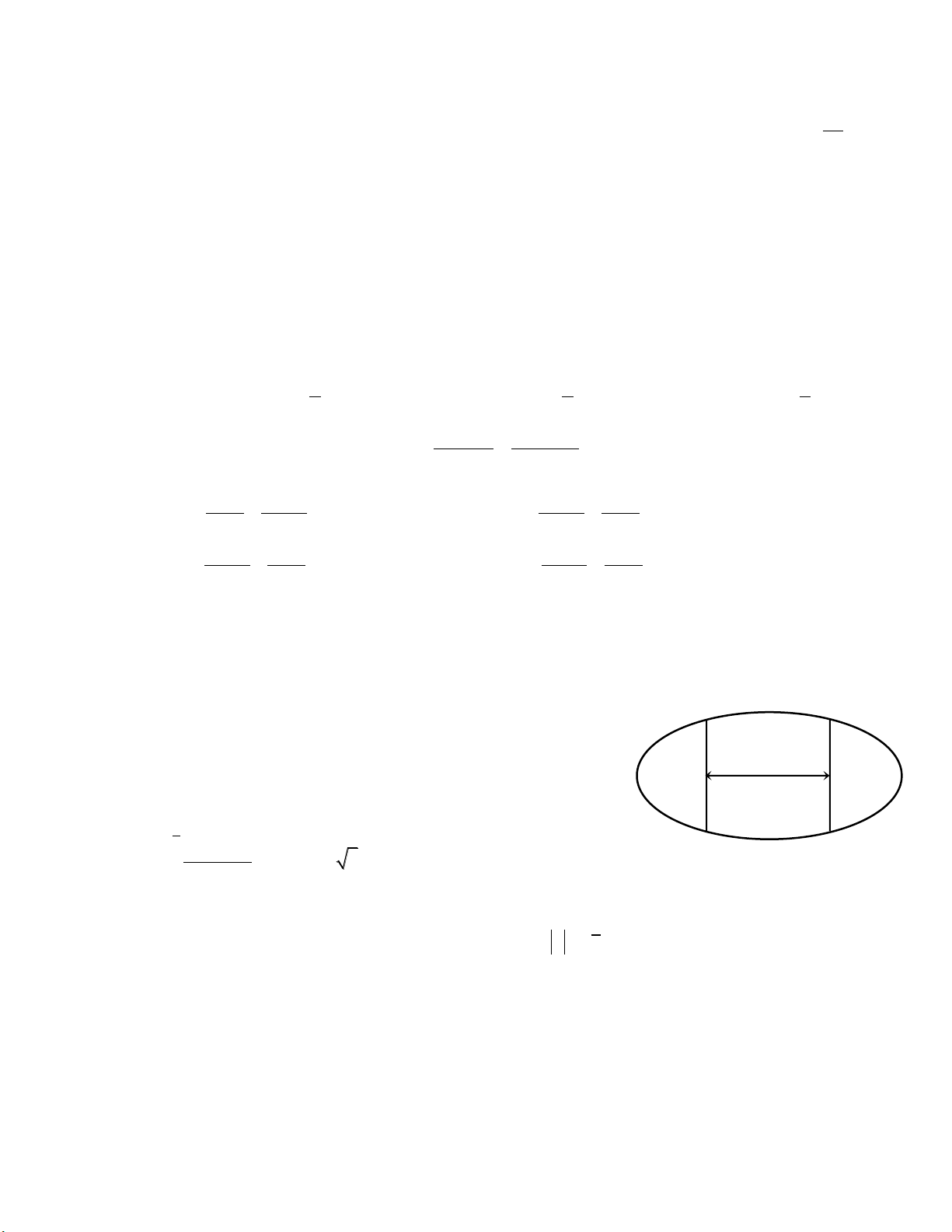
Câu 8: Ông An có một mảnh vườn hình elip có độ dài trục lớn bằng 16m và độ dài trục bé
bằng 10m . Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối
xứng (như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/ 2
1m . Hỏi ông An cần bao nhiêu
tiền để trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn). A. 7.862.000 đồng. B. 7.653.000 đồng. 8m C. 7.128.000 đồng. D. 7.826.000 đồng  4 cos 2x Câu 9: Biết
dx  a  ln b 
a; b; b  0. Giá trị 2 2 a  b bằng 1  sin2x 0 A. 4. B. 10. C. 12. D. 6. 2
Câu 10: Có bao nhiêu số phức z thỏa mãn điều kiện 2
z  z  z ? A. 3. B. 4. C. 2. D. 1.
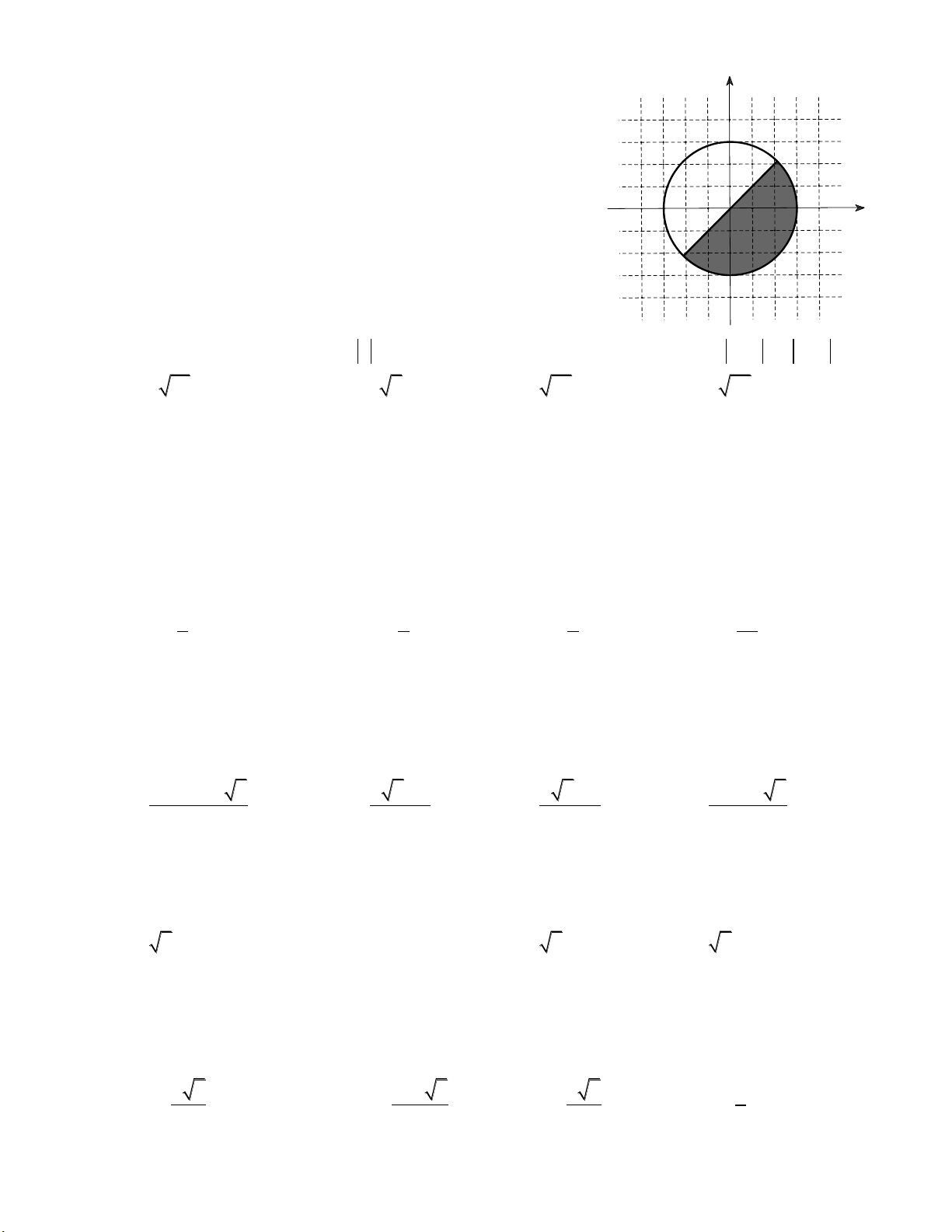
Câu 11: Điều kiện để số phức z có điểm biểu diễn thuộc y
phần tô đậm (kể cả bờ) trong hình vẽ bên là
A. z có phần ảo không nhỏ hơn phần thực. 3
B. z có phần thực không nhỏ hơn phần ảo và có 2 môđun không lớn hơn 3. 1 x
C. z có phần thực không nhỏ hơn phần ảo. -3 -1 O 1 2 3 -1
D. z có môđun không lớn hơn 3. -2 -3 -4
Câu 12: Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  1 z  3 1 z . A. 3 15 B. 6 5 C. 20 D. 2 20.
Câu 13: Các khối đa diện đều loại p; 
q được sắp xếp theo thứ tự tăng dần của số mặt là: A. 3;  3 , 3;  4 , 3;  5 , 4;  3 , 5;  3 . B. 3;  3 , 4;  3 , 3;  4 , 5;  3 , 3;  5 . C. 3;  3 , 3;  4 , 4;  3 , 3;  5 , 5;  3 . D. 3;  3 , 4;  3 , 3;  4 , 3;  5 , 5;  3 .
Câu 14: Cho hình chóp .
S ABCD, có đáy là hình bình hành. Gọi G là trọng tâm tam giác SBD .
Mặt phẳng P chứa AG và song song với BD , cắt S ,
B SC, SD lần lượt tại B', C', D' . Tìm tỉ số thể tích giữa khối .
S AB'C ' D' và khối . S ABC . D 1 2 1 8 A. k  . B. k  . C. k  . D. k  . 9 9 3 27
Câu 15: Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC (M
thuộc AB, N thuộc AC, P , Q thuộc BC). Gọi S là phần mặt phẳng chứa các điểm thuộc tam
giác ABC nhưng không chứa các điểm thuộc hình vuông MNP .
Q Tính thể tích của vật thể tròn
xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC. 810  467 3 4 3  3 4 3  3 54  31 3 A.  . B.  . C. . D.  . 24 96 96 12
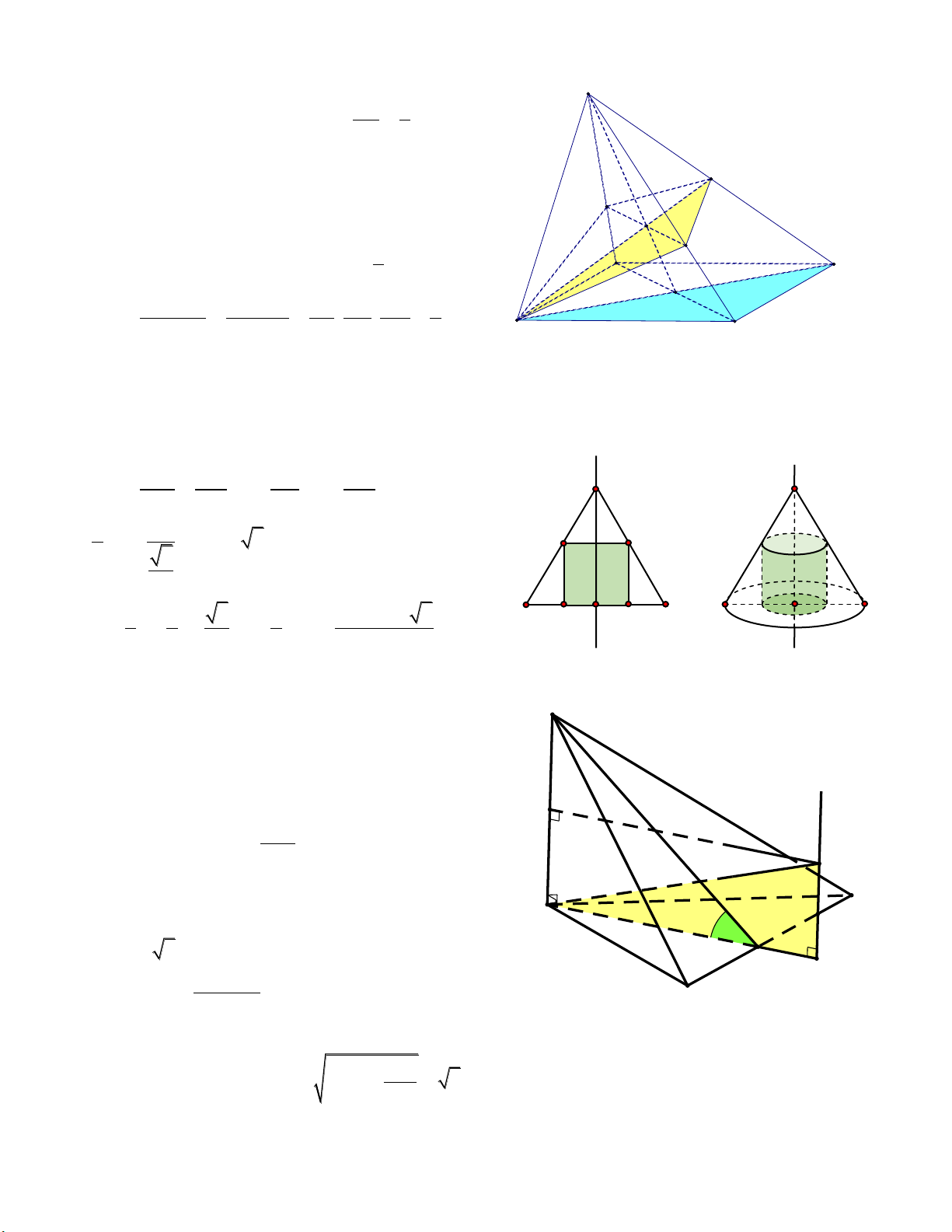
Câu 16: Cho hình chóp .
S ABC có SA vuông góc với đáy, tam giác ABC có AB  2; AC  2 và  0
BAC  120 . Biết góc giữa SBC và  ABC bằng  với tan  2. Tính bán kính mặt cầu ngoại tiếp hình chóp . S AB . C A. 5. B. 2. C. 3. D. 2.
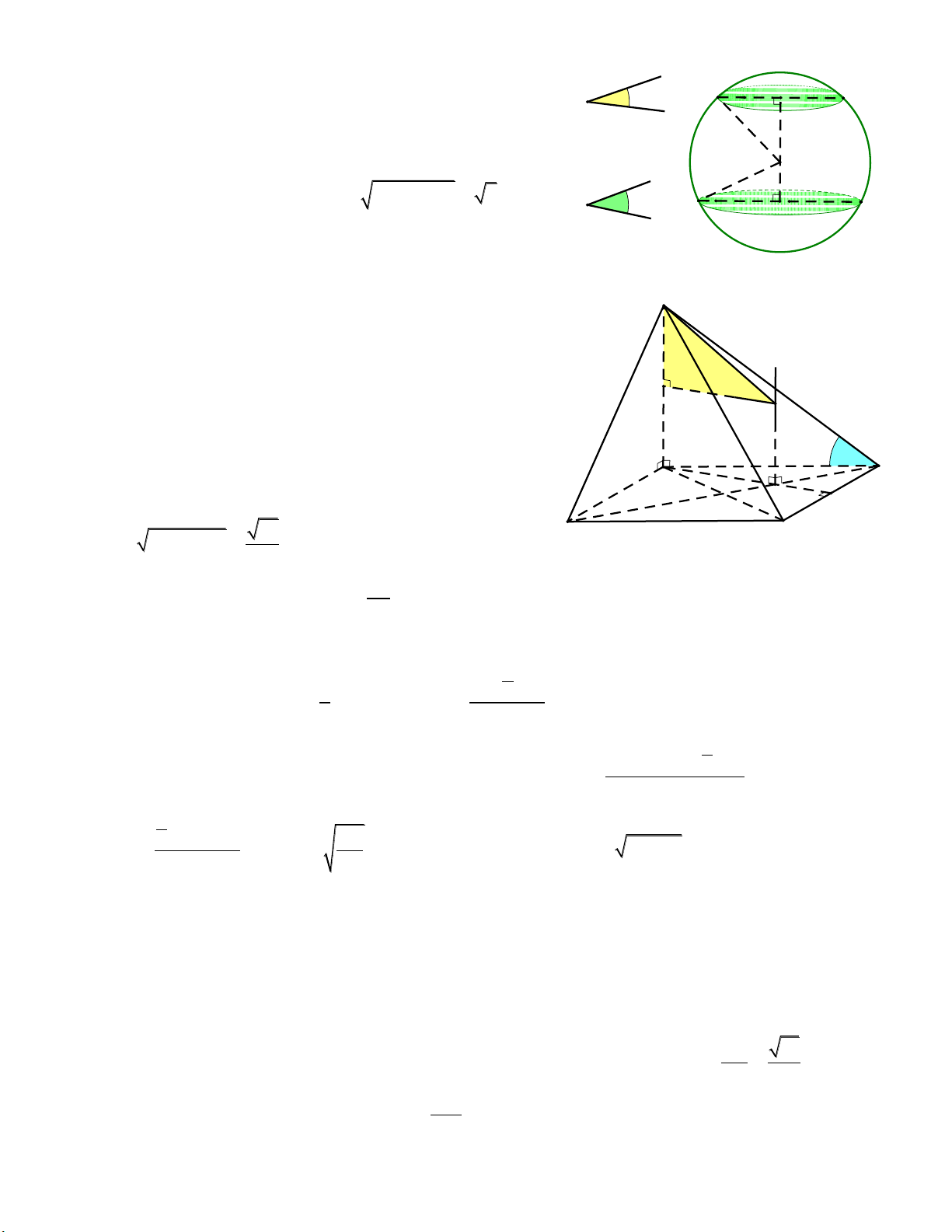
Câu 17: Để chuẩn bị cho Tết Nguyên Đán 2017, ban dự án đường hoa Nguyễn Huệ, quận 1,
Thành phố Hồ Chí Minh dự định xây dựng một khối cầu có bán kính bằng 2 m để trưng bày hoa
tươi xung quanh, để tiết kiệm diện tích Ban quản lý xây một hình trụ nội tiếp mặt cầu. Tính bán
kính của hình trụ sao cho khối trụ có thể tích lớn nhất. 4 3 32 3 2 6 8 A. r  . B. r  . C. r  . D. r  . 3 9 3 3 x  1 t 
Câu 18: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  : y  2  t . Đường thẳng d đi z  1t  qua A0;1;  
1 cắt và vuông góc với đường thẳng  . Phương trình nào sau đây là phương trình
của đường thẳng d ? x  5t x  t x  5
x  5  5t    
A. y  1 5t .
B. y  1 t .
C. y  5  t .
D. y  6  5t .     z  1   8t  z  1   2t 
z  10  t 
z  9  8t 
Câu 19: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P đi qua điểm M 1;2;3  và cắt ba
tia Ox , Oy , Oz lần lượt tại A , B , C sao cho thể tích tứ diện OABC nhỏ nhất. Viết phương trình mặt phẳng P. x y z x y z x y z x y z A.    1. B.    1. C.    0 . D.    0 . 1 2 3 3 6 9 3 6 9 1 2 3 2 2 2
Câu 20: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S : x  4  y  7  z   1  36 và
mặt phẳng P : 3x  y  z  m  0 . Tìm m để mặt phẳng P cắt S theo giao tuyến là một đường
tròn có bán kính lớn nhất. A. m  20  . B. m  6 . C. m  36 . D. m  20 . ------- HẾT -------
Cố gắng lên các em! Thầy rất mệt và các em còn.. mệt hơn!
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Tổng ôn tập: NéI DUNG VËN DôNG ¤N THI THPT QuèC GIA
PHIẾU TỔNG ÔN SỐ 01 M¤N TO¸N BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án D C D D A C B B A A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án B D B C A A C B B A ĐÁP ÁN CHI TIẾT
Câu 1: Dựa vào đồ thị đồng thời áp dụng định nghĩa và quy tắc 1 ta suy ra hàm số đã cho có 7 điểm cực trị
Chọn đáp án D.
Câu 2: Kiểm tra đồ thị hàm số có 3 điểm cực trị 0;  1 ; 1; 2;  1  ; 2
Chọn đáp án C.
Câu 3: Ta có: DF  CH  x, FH  30  2x  p  15. DHF 
Thể tích khối lăng trụ như hình vẽ là: V  S
.EF  30 1515  x15  x15  30  2x FDH     
 x2  x   15 30 15 15 2 15 ; x  ;15  2  2  15 
Xét hàm số f x  15  x 2x 15; x ;15.  2    2 x
Ta có: f 'x  2
 15 x2x 15 215 x  2
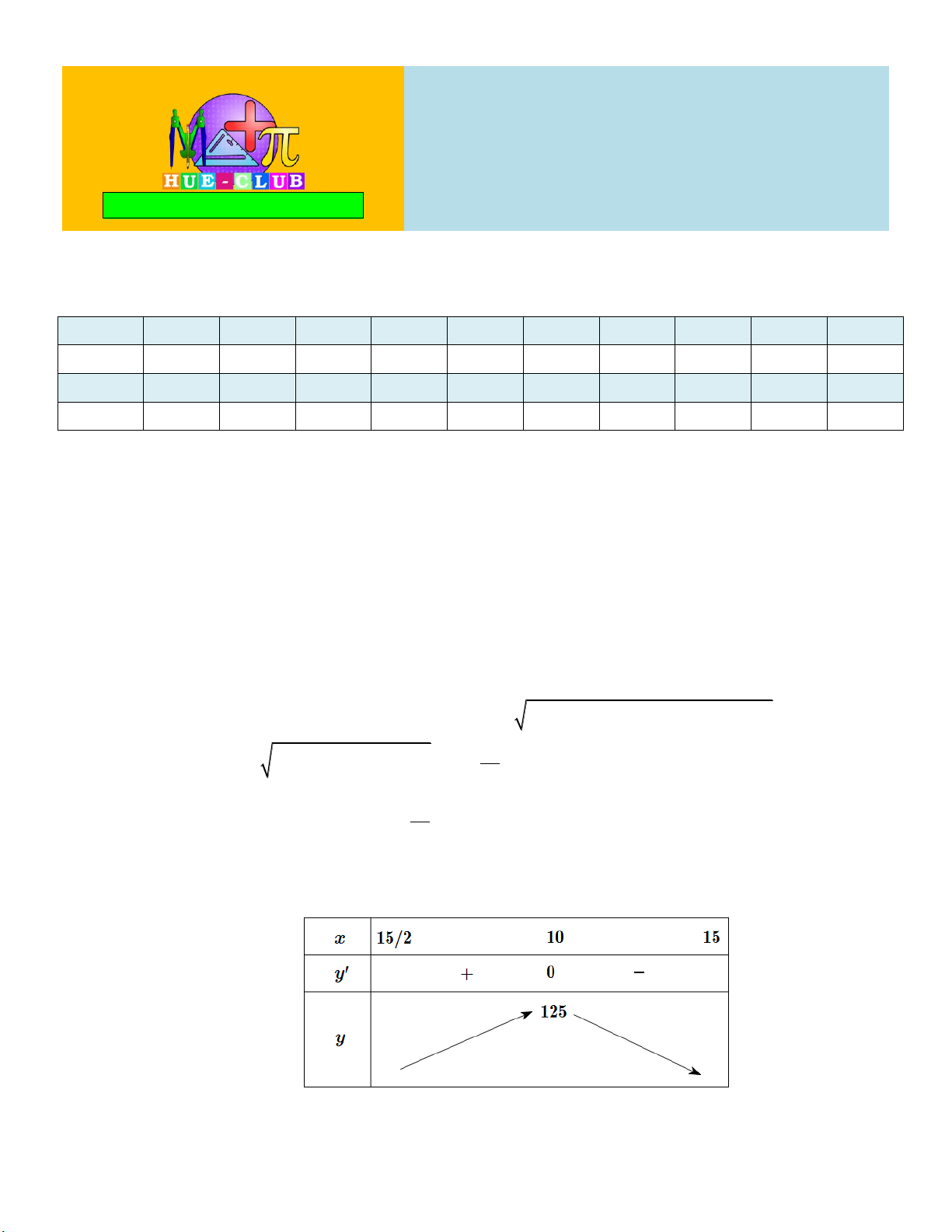
 15 x3x  30; f x 10 '  0   . x   15 Bảng biến thiên:
Dựa vào BBT, max f x  125 khi x  10. Do đó thể tích khối lăng trụ như hình vẽ lớn nhất  15   ;15  2 
khi x  10 cm. Khi đó V  750 3  3 cm . max 
Chọn đáp án D. Câu 4:
(A): f     f   2 3 0 2 1 
nên f x không đồng biến trên  . Khẳng định (A) sai. 3
(B): lim f x  , lim f x   nên C không có TCN. Khẳng định (B) sai. x x
(C): f x  0, x
  nên C không tiếp xúc với trục Ox . Khẳng định (C) sai.   (D): f    f   10 0 2, 2 
nên C đi qua A  10 0; 2 , B 2;
 . Khẳng định (D) đúng. 9  9 
Chọn đáp án D. Câu 5:
Áp dụng công thức lãi kép, số tiền thu được (cả vốn lẫn lãi) là:  (1 )N T A r
với tiền gửi A  67 triệu đồng, lãi suất r  0,0599, N  2.4  8 kỳ.
Ta được: T  106,707 triệu đồng⟹ Số tiền lãi bằng: T  A  39,707 triệu đồng.
Chọn đáp án A.
Câu 6: Ta có: PT  9x  3x  .3x 
 0  3x 3x   1 
3x  10 3x  1.3x m m m  m  0 2   m  3  9
3x  1  x  0 1    . Với 2
x  0  x  4  x  2   .    1 3x  m 1 2 2 2 m  3   9
Chọn đáp án C.   3 2 3 2
Câu 7: Ta có: F x            x x x x 2 2x  d 1     x2 d 2x1 d 2 2 2 2 2  2  1 3
 3x 2 dx 22x  1 d 2x   1    . C 2x  1 x  2
Chọn đáp án B. 2 2 x y
Câu 8: Giả sử elip có phương trình 
 1 . Từ giả thiết ta có 2a  16  a  8 và 2b  10  b  5 2 2 a b  5 2    2 2 y 64 y  E1 x y
Vậy phương trình của elip là 8   1  
. Khi đó diện tích dải vườn được 64 25  5 2 y 
64  y E1   8
giới hạn bởi các đường E ; E ; x  4;
 x  4 và diện tích của dải vườn là 1   2 4 4 5 2 5 S  2 64  x d 2 x  64  x dx  
. Tính tích phân này bằng phép đổi biến x  8sint , ta  8 2 4 0   3    3  được S  80  
 . Khi đó số tiền làT  80 
.100000  7652891,82  7.653.000 .  6 4   6 4 
Chọn đáp án B.      4 4 cos 2x 1 1 sin2x 4 d 1 1sin2x 4 1 1
Câu 9: Ta có: I  dx  dx     
1sin2x  ln2  ln 2. 1 sin2x 2 1  sin2x 2 1  sin2x 2 2 0 0 0 0
 a  0; b  2. . Vậy 2 2 a  b  4.
Chọn đáp án A. Câu 10: 2 2 2 2  2
a  b  a  b  a
Đặt z  a  bi a,b , ta có: 2 2 2 2 2
z  z  z  a  b  2abi  a  b  a  bi  
2ab  b  1  1       0 a a a    2  2  1 1 1 1     
 z  0  z    i  z    i . Vậy có 3 số phức thỏa mãn. b   0 1 1  2 2 2 2 b   b    2  2
 Chọn đáp án A.
Câu 11: Gọi z  x  yi ;x; y  . Điểm M x; y biểu diễn z trên mặt phẳng tọa độ. 2 2
x  y  9 Từ hình vẽ ta có:  . y  x
 Chọn đáp án B.
Câu 12: Gọi z  x  yi; x; y  . Ta có: 2 2 2 2
z  1  x  y  1  y  1 x  x   1  ;1.   2 2
Ta có: P   z 
 z    x 2  y   x 2 1 3 1 1 3 1
 y  21 x  3 21 x .
Xét hàm số f x  21 x  3 21 x; x  1  ;1. 
 Hàm số liên tục trên  1  ;1   và với x 1  ;1 1 3 4
ta có: f x  
 0  x    1  ;    x  x 1 . 5 2 1 2 1  4  Ta có: f   1  2; f   1  6; f   2 20  P    2 20. max  5 
 Chọn đáp án D.
Câu 13: Sắp xếp theo thứ tự tăng dần số mặt của các khối đa diện đều là: Khối tứ diện 3;  3 , khối lập phương 4; 
3 , khối tám mặt đều 3; 
4 , khối mười hai mặt đều 5;  3 và khối hai mươi mặt đều 3;  5 .
Chọn đáp án B.
Câu 14: Gọi O là tâm hình hình hành ABCD . S SG 2
Do G là trọng tâm S  BD nên   G là SO 3 trọng tâm S
 AC  C' là trung điểm SC. C'
+ Qua G dựng B' D'/ /BD B'SB, D'SD  D' G
thiết diện cần tìm là tứ giác AB'C' D'. Do G là B' 1 trung điểm D
B' D'  S  S  S . C A  B'C' A  D'C' AB'C' D' 2 V 2V SA SB' SC ' 1 O
Suy ra: S.AB'C'D' S.AB'C'   . .  . A V 2V SA SB SC 3 B S.ABCD S.ABC
 Chọn đáp án C.
Câu 15: Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng AH bằng hiệu thể
tích khối nón khi quay tam giác ABC và thể tích khối trụ khi quay hình vuông MNPQ quanh trục
là đường thẳng AH . Gọi độ dài cạnh hình vuông là x . MN AN CN NP Khi đó:   1  1 A A BC AC CA AH x x   1  x  2 3  3 M N 1 3 2 2 2 1  1  3  x  810  467 3  V  .  .    .x   . B Q H P C B C 3  2  2  2  24
Chọn đáp án A.
Câu 16: Gọi M là trung điểm của cạnh S BC  AM BC  
 BC  SAM  BC  SM. BC   SA
Suy ra  SBC ABC  ;  SM . A K SA Theo giả thiết: tan   SA  A . M tan AM I  R  A . B cos BA . M tan  2. A C 2 2 2 
Ta có: BC  AB  AC  2A . B A .
C cos BAC  12 α  BC  a 3. M R' O BC Xét A  BC :       2R R 2 : bán kính B sin BAC
đường tròn ngoại tiếp A  B . C SA
Vậy bán kính mặt cầu là R  R  2 2 '   5. 4
 Chọn đáp án A. 2 3  h  h Câu 17: Ta có : 2 2
V   r h   . R 
.h  4 h   4  4 3 2 h 3 h
Xét hàm số V (h)  4 h 
 V (h)  4 
, h 0; 2R  4 3 V (
 h)  0  h  4 4 3 Bảng biến thiên : 4 3 h 0 2R 3 V (  h)  0  32 3 V (h) 9 32 3 4 3
Từ bảng biến thiên, suy ra V 
khi và chỉ khi h  2 6  r  . max 9 3 3
Chọn đáp án C.  
Câu 18: Ta có: u  (1;1; 1
 ) ; Gọi M  d  (
M 1 t; 2  t;1 t)  AM  1 t;1 t; 2  t     
u  AM  u.AM  0  1 t  1 t  2 t  t  0     x t 
Đường thẳng d có vec tơ chỉ phương AM  1;1; 2 và đi qua A0;1;  
1  d : y  1 t . z  1   2t 
Chọn đáp án B.
Câu 19: Gọi A ;
a 0; 0 ; B0; 0; b ; C 0; 0; c  ; a ;
b c  0 . Mặt phẳng P có phương trình đoạn chắn x y z    1 2 3
1 . Vì M 1; 2; 3P nên    1. a b c a b c 1 2 3
Áp dụng bất đẳng thức Cauchy cho 3 số dương ; và ta được a b c 1 2 3 6 6 1 3 1     3  1  27.
 abc  162 . Do đó, V  abc  27 . a b c abc abc OABC 6 a  3 1 2 3 1  x y z Dấu "  " xảy ra 
    b  6 . Vậy P :    1. a b c 3  3 6 9 c  9 
Chọn đáp án B.
Câu 20: Mặt cầu S tâm I 4;7;  
1 bán kính R  6 . Mặt phẳng P cắt S theo giao tuyến là một
đường tròn có bán kính lớn nhất khi mặt mặt  
P đi qua tâm I của mặt cầu, khi đó đường tròn
giao tuyến còn gọi là đường tròn xích đạo. Khi đó I 4;7;  
1 S  m  20. 
Chọn đáp án A.
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Tổng ôn tập: NéI DUNG VËN DôNG ¤N THI THPT QuèC GIA
PHIẾU TỔNG ÔN SỐ 02 M¤N TO¸N
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Nội dung đề bài, đáp án chúng tôi trích từ các đề thi thử của các trường trên toàn quốc,
nguồn tài nguyên Page Toán Học Bắc Trung Nam, Page CLB Giáo viên trẻ TP Huế và các tư liệu
tham khảo của quý thầy cô đăng trên internet! Xin chân thành cảm ơn! bx  c y
Câu 1: Cho hàm số y  a  0; ; a ;
b c   có x  a
dạng đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0. O x
D. a  0, b  0, c  0.
Câu 2: Cho hàm số y  f x liên tục trên 0; 3 
 và có bảng biến thiên: x 0 1 3 y '  0  1 y 2  5 
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  f x trên 0; 3   lần lượt là A. 0 và 5. B. 2  và 5. C. 5  và 1. D. 1 và 5.
Câu 3: Gia đình chú Luân có một vườn thanh long khá lớn và dự định mở rộng thêm quy mô, qua
một năm thu hoạch, chú Luân thấy rằng trên 2
50 m diện tích trồng thanh long có x cây thanh long
thì trung bình mỗi cây có thu hoạch là f x  900  30x (kg). Số cây mà ông Hùng cần trồng trên 2
50 m là bao nhiêu để thu hoạch được khối lượng thanh long lớn nhất? A. 12 cây. B. 15 cây. C. 20 cây. D. 30 cây. 2   2 b
Câu 4: Tìm giá trị nhỏ nhất của biểu thức P   2 log b   6log
 với a , b là các số thực thay a  b a   a 
đổi và thỏa mãn b  a  1. A. 30 . B. 40 . C. 50 . D. 60 .
Câu 5: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức    0.2t s t s
, trong đó s0 là số lượng vi khuẩn A lúc ban đầu, st là số lượng vi khuẩn A có sau
t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu,
số lượng vi khuẩn A là 10 triệu con? A. 48 phút. B. 19 phút. C. 7 phút. D. 12 phút.
Câu 6: Cho biết phương trình log  x2 5.2
 24  2x  log 4 có hai nghiệm x và x . Tính tổng 2  1 1 2 2 2x 1  2x 1  1 2 S  4  4 . A. S  97 . B. S  20,5 . C. S  68 . D.S  24,25 .
Câu 7: Cho hàm số f x liên tục và có đạo hàm trên  . Mệnh đề nào sau đây đúng?  b   A.  f
 xdx  f b f a.   B. f 
 xdx  f x.  a   b
C.  f xdx  f x C; C   . D. f 
 xdx  f b f a. a
Câu 8: Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu 98 m / s. Gia tốc trọng trường là  2
9,8 m / s . Tính quãng đường viên đạn đi được từ lúc bắn lên cho đến khi y chạm đất. A. 490 m. B. 978 m. C. 985 m. D. 980 m.
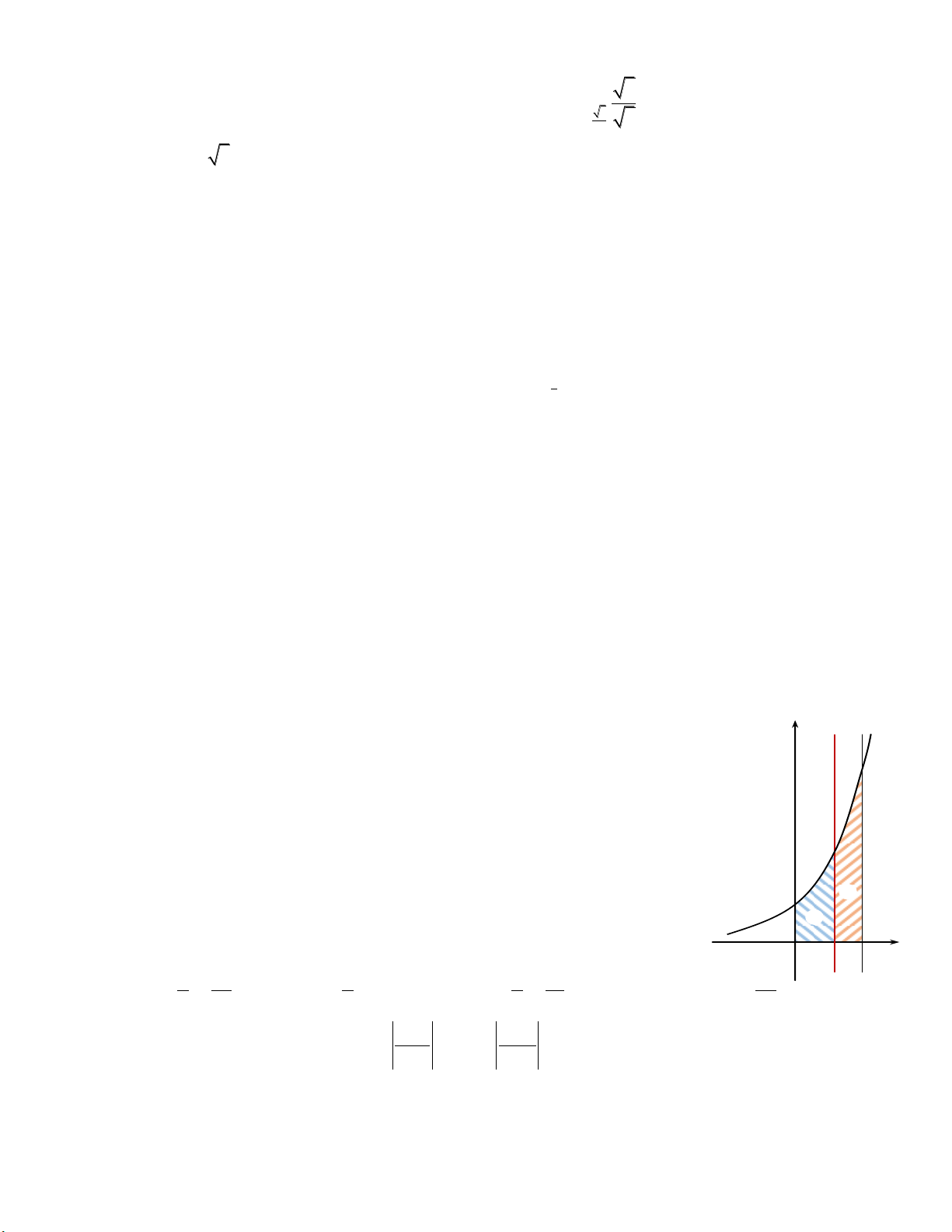
Câu 9: Cho hình thang cong H  giới hạn bởi các đường x
y  e , y  0 ,
x  0 , x  ln 4 . Đường thẳng x  k; (0  k  ln 4) chia H  thành hai
hình phẳng là S và S như hình vẽ bên. Quay S , S quanh trục Ox 1 2 1 2 S2
được các khối tròn xoay có thể tích lần lượt là V và V . 1 2 S1 x
Với giá trị nào của k thì V  2V ? 1 2 O k ln 4 1 32 1 1 11 32 A. k  ln . B. k  ln11. C. k  ln . D. k  ln . 2 3 2 2 3 3 z  1 z  i
Câu 10: Có bao nhiêu số phức z thỏa  1  i  và 1? z 2  z A. 1. B. 2. C. 3. D. 4.
Câu 11: Cho số phức z thỏa mãn đồng thời hai điều kiện z  m  2 và 1 i z  1 i  2, với m
là tham số thực. Tìm tập hợp tất cả các giá trị m để tồn tại hai số phức thỏa mãn các điều kiện trên. A.  2  2; 2 2 . B.  2  2; 2 2.    C. 2  2; 2 2 
 \ 0. D.  2 2;2 2 \ 0. 1
Câu 12: Cho số phức z thỏa mãn z  1 i  z  3i . Tính môđun lớn nhất của số phức ; z  0. z 7 5 2 5 4 5 9 5 A. . B. . C. . D. . 10 7 7 10
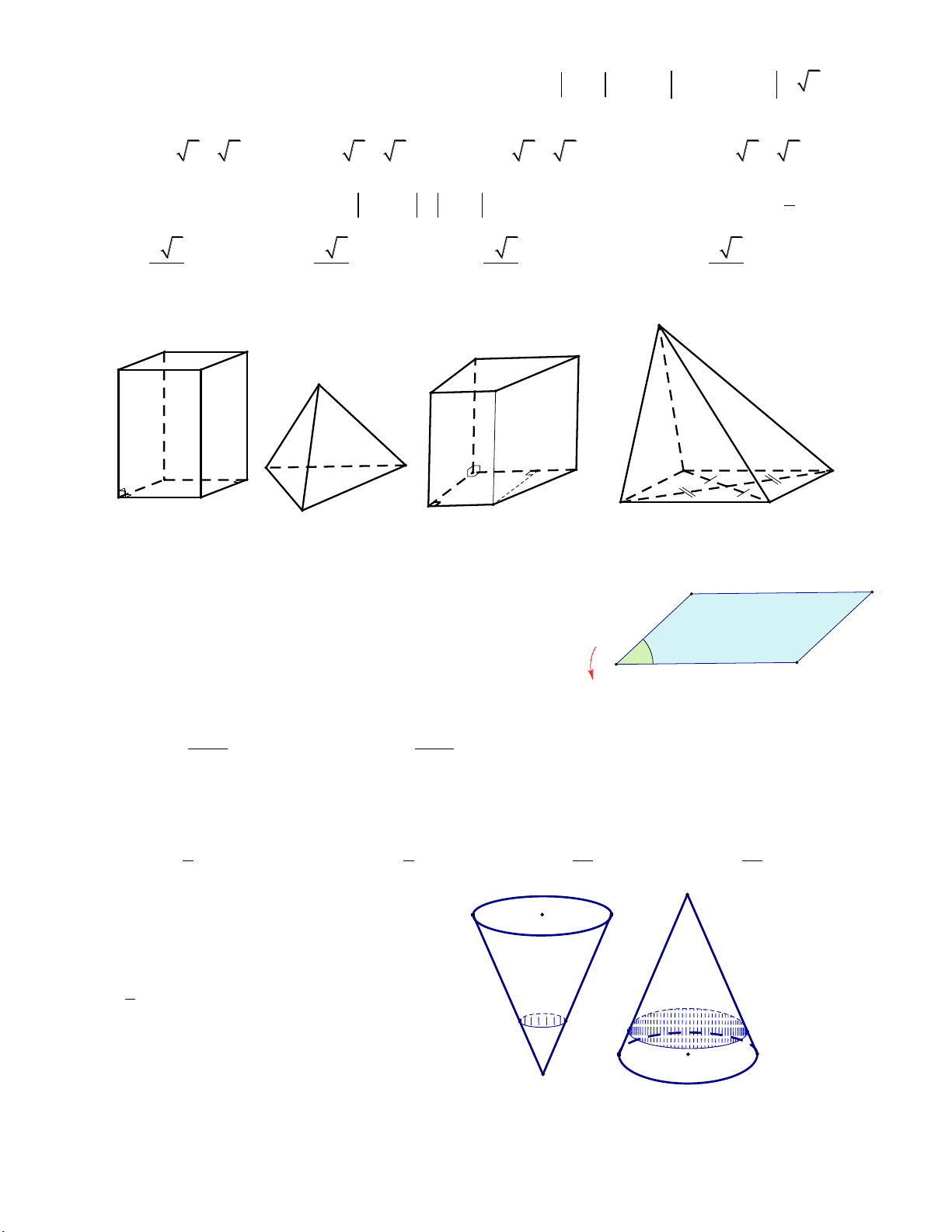
Câu 13: Trong các hình đa diện dưới đây, hình nào không tồn tại mặt cầu ngoại tiếp? hình 1 hình 2 hình 3 hình 4 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Câu 14: Cho hình bình hành ABCD có D C 
AD  a AB  a 0 ;
3 ; BAD  45 (như hình bên). Tính thể tích 2a
V khối tròn xoay nhận được khi quay hình bình hành 450 ABCD quanh trục . AB A B 3a A. 3 V  5 a . B. 3 V  6 a . 3 9 a 3 5 a C. V  . D. V  . 2 2
Câu 15: Cho hình hộp chữ nhật ABC . D A B  C  D
  có thể tích bằng 1 và G là trọng tâm của tam
giác BCD. Tính thể tích V của khối chóp . G ABC'. 1 1 1 1 A. V  . B. V  . C. V  . D. V  . 3 6 12 18
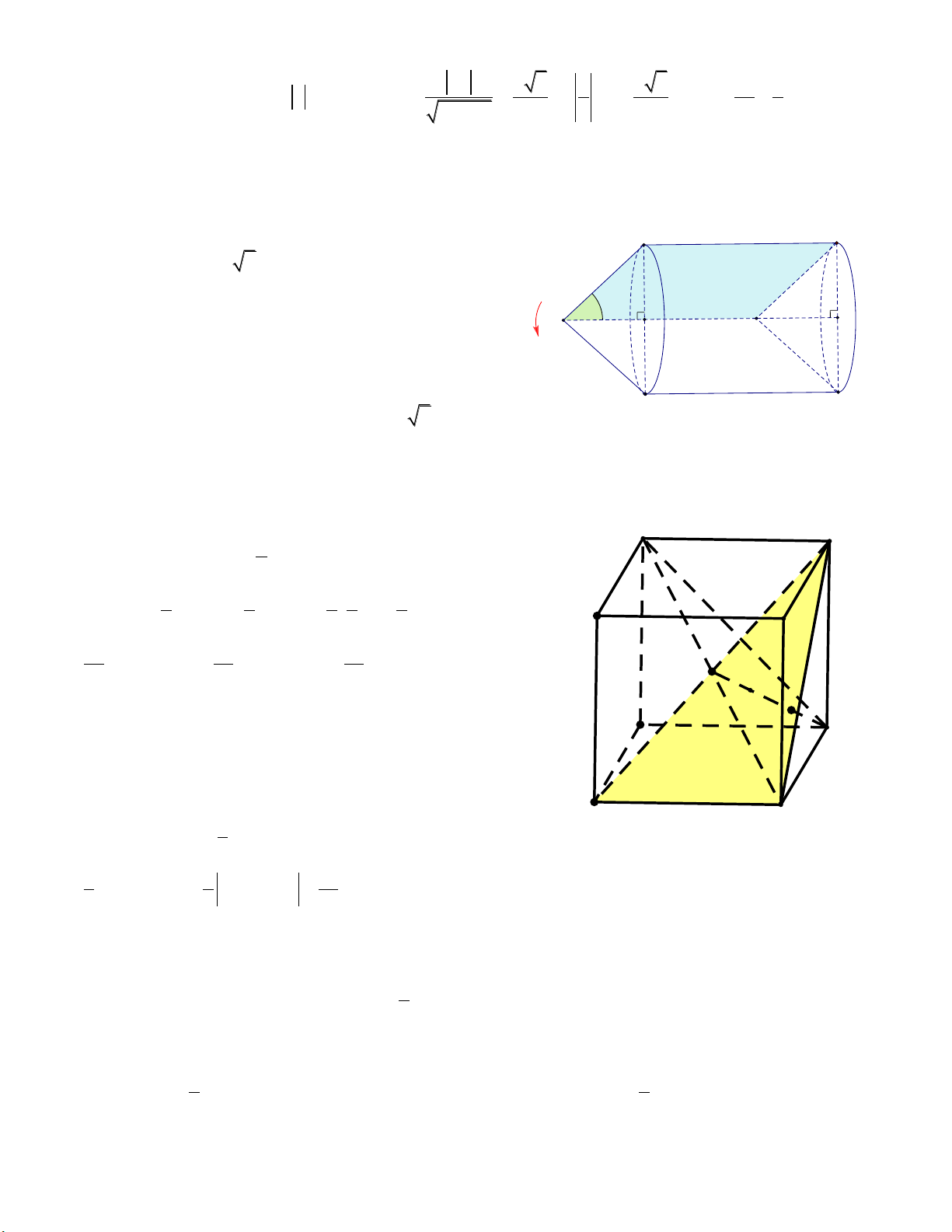
Câu 16: Một cái phễu có dạng hình nón.
Người ta đổ một lượng nước vào phễu sao
cho chiều cao của lượng nước trong phễu 1 bằng
chiều cao của phễu. Hỏi nếu bịt kín 3
miệng phễu rồi lộn ngược phễu lên thì chiều
cao của nước gần bằng giá trị nào sau đây?
Biết rằng chiều cao của phễu là 15cm. A. 0,188 (cm). B. 0,216 (cm). C. 0,3 (cm). D. 0,5 (cm).
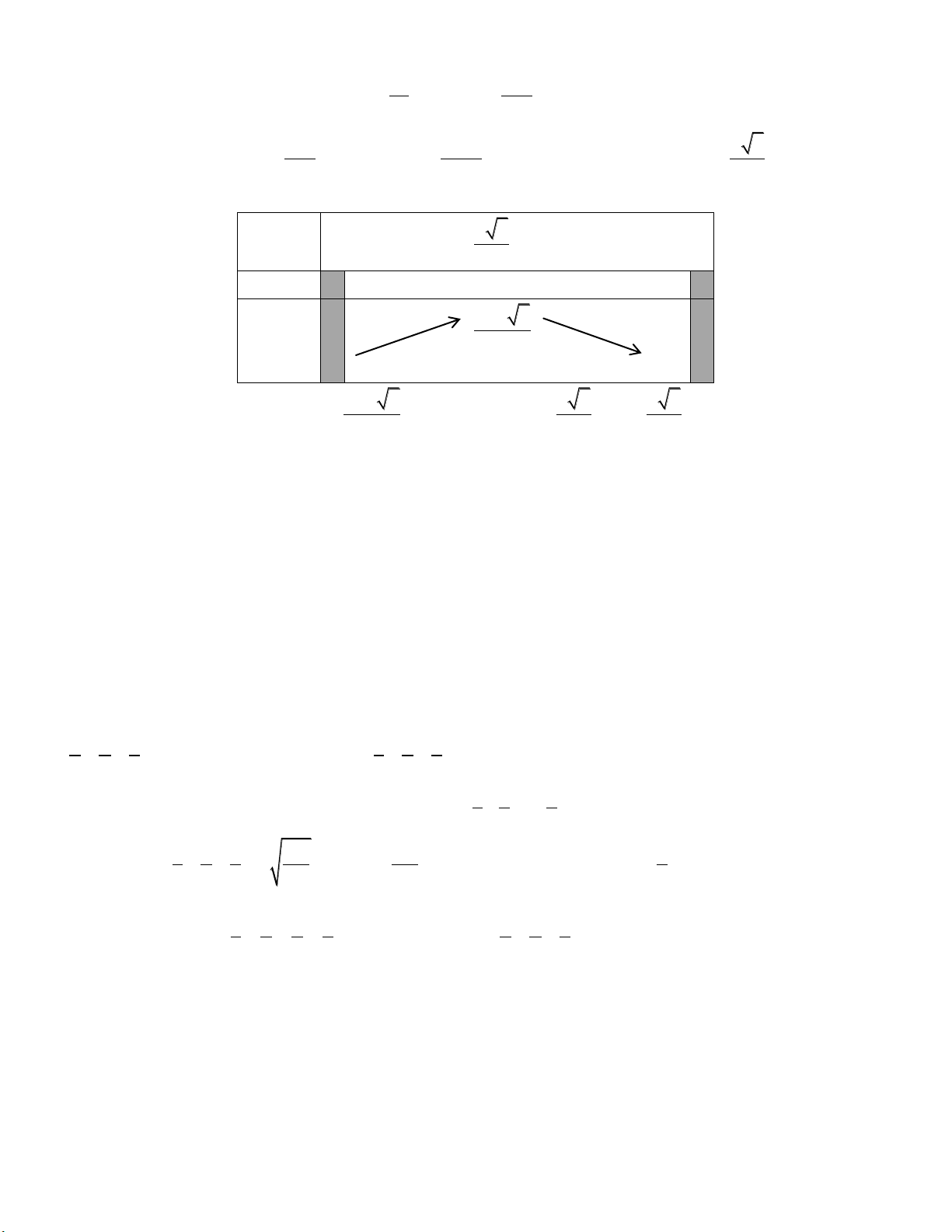
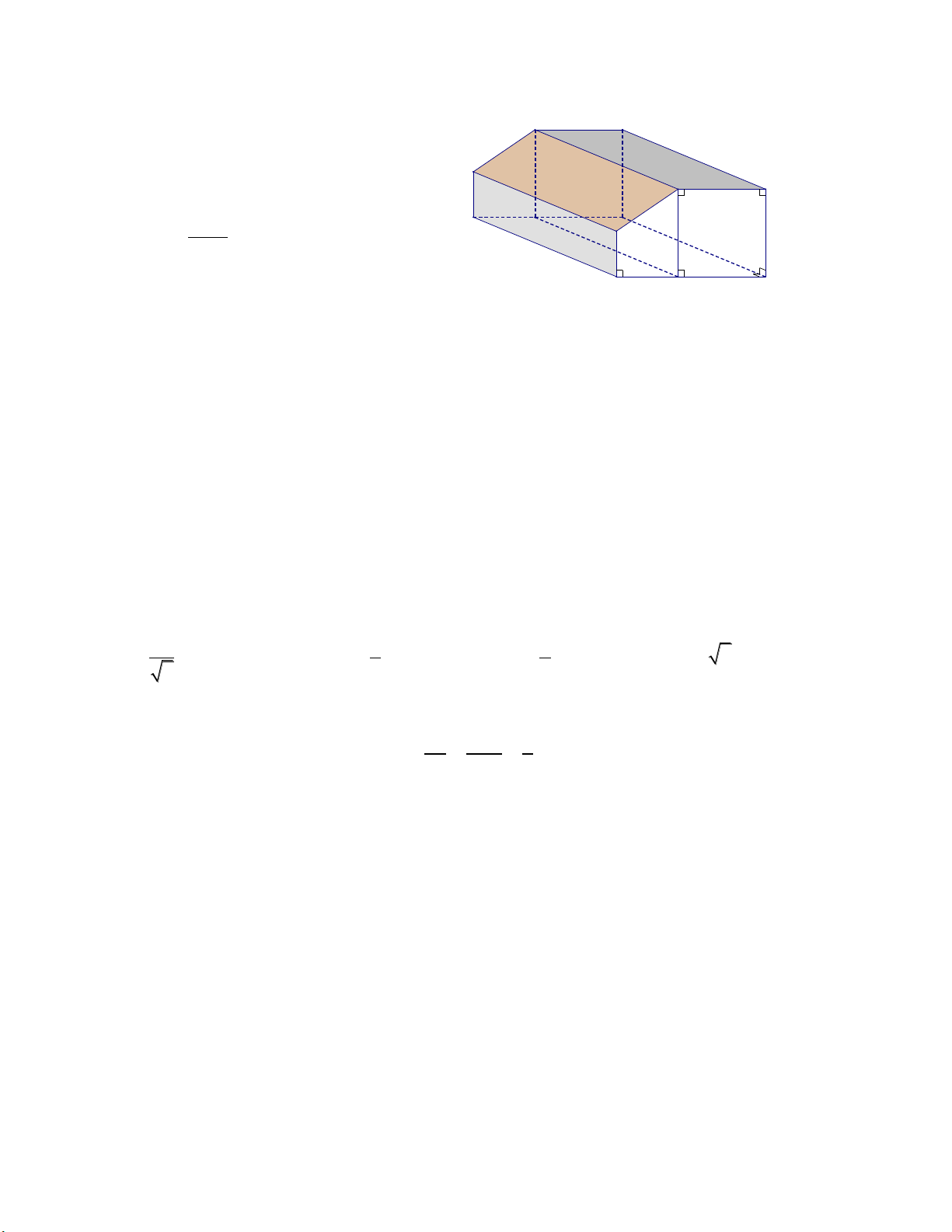
Câu 17: Một khúc gỗ có dạng với độ dài các 40 cm
cạnh được cho như hình vẽ bên. Tính thể tích
V khối đa diện tương ứng. 2960 A. V   3 cm . B. 7 cm 3 3 cm V   3 2560 cm . 5 cm 7 cm C. V   3 2960 cm . D. V   3 2590 cm .
Câu 18: Trong không gian với hệ tọa độ Oxyz, gọi M , M , M lần lượt là điểm đối xứng của 1 2 3 M  1  ; 2; 
3 qua các mặt phẳng Oxy , Oxz , Oyz . Phương trình mp M M M là 1 2 3 
A. 6x  2y  3z  6  0.
B. 6x  2y  3z  6  0.
C. 6x  3y  2z  6  0.
D. 6x  3y  2z  6  0.
Câu 19: Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A ;
a 0; 0, B0; ;
b 0, C 0;0; c , a,b,c là
những số thực dương thay đổi thỏa 2 2 2
a  b  c  3 . Tìm giá trị nhỏ nhất khoảng cách từ gốc tọa độ
O đến mặt phẳng  ABC. 1 1 1 A. . B. . C. . D. 3 . 3 3 9
Câu 20: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng P : x  2y  2z 1  0 và  x y  1 z
Q : x  2y  2z  3  0 và đường thẳng  : 
 . Có bao nhiêu mặt cầu có tâm nằm trên 4  1 1
đường thẳng  , đồng thời tiếp xúc với hai mặt phẳng P và Q? A. 0 . B. 1 . C. 2 . D.Vô số. ------- HẾT -------
Cố gắng lên các em! Mọi việc rồi sẽ tốt đẹp thôi!
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Tổng ôn tập: NéI DUNG VËN DôNG ¤N THI THPT QuèC GIA
PHIẾU TỔNG ÔN SỐ 02 M¤N TO¸N BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án D A B D C D D D B A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D B C B D A C C A D ĐÁP ÁN CHI TIẾT
Câu 1: Đồ thị hàm số có dạng như hình vẽ, có tiệm cận đứng x  a  0; tiệm cận ngang y  b  0 .  c  c
Mặt khác C Oy  0;    
0 và a  0  c  0.  a  a
Chọn đáp án D.
Câu 2: Sử dụng phép biến đổi đồ thị từ đồ thị y  f x suy ra đồ thị y  f x trên 0; 3   ta có kết
quả min f x  0 và max f x  5. 0;3   0;3  
Chọn đáp án A.
Câu 3: Sau một năm, trên 2
50 m diện tích trồng, chú Luân thu hoạch được 2
900x  30x kg.
Xét hàm số g x  xf x 2 ( )
 900x  30x , x0;  g ( )
x  900  60x  g (  )
x  0  x  15 . Bảng biến thiên : x 0 15  g (  x)  0  6750 ( g x)
Từ bảng biến thiên, suy ra ( g ) x
 6750 khi và chỉ khi x  15 . max
Chọn đáp án B. 2   2 2 b b a
Câu 4: Ta có P  2 log b  6log  . Đặt x    1. Vậy 2 b  a x và a b  a  2 2 a a 2  a  2 2 2   2 2 a x Suy ra: P    2ax       2 2 log 6 log
4 log a  log x  6 log xa  a x a a  x    a  2      x  x  a   x     a 2  x x 2  a 2 1 4 2 log 6 log log 4 2 log 6 1 .  log x a  2 2 2  1  2  1 
Đặt t  log x  log 1  0  P  4t  2  6 1 
 . Xét hàm số f t  4t  2  6 1   , với a a  t   t   1  1  12 t  1
t 0;  có f t  8t  2  12 1 .  8t  2      . 2 3  t  t t t    0; t    0; t  0; Ta có:       f   t 3  0 2t 
t 2  3t   4 3 1
2t  4t  3t  3  0 t  0;   t    0;      t  1. 3 2t  t   2
1  6t t  
1  6t t   1  3t 1   0 t  1   3 2
2t  6t  6t  3  0
Từ đó suy ra f t  f  
1  60 , nên P  60 . Dấu "  " xảy ra  log x  1 nên x  a hay a b 3
 a  b  a . 2 a
Chọn đáp án D. s 3 s t t  
Câu 5: Ta có: s   s  3 3 0 .2  s0     78125;  0 .2t s t s  2 
 128  t  7. 3     2 s0
Chọn đáp án C. Câu 6: Ta có: log  x2 5.2
 24  2x  log 4  log  x2 5.2
 24  log 4  2x 2  2  1 2 2 x2 5.2  24 2x  2 x  1 2   2 x 2 2 x 5.2x    6  0     . 4 2x  3 x  log 3 2 Khi đó: 2x 1  2x 1  2.1 1  2.log 3 1  1 2 2 S  4  4  4  4  24,25.
Chọn đáp án D.  b   b
Câu 7: Ta có:  f
 xdx  0  
vì f xdx  là hằng số  A sai.  a  a
f xdx  f x C; C      B sai.  
 f xdx FxC  f x  C sai. b b f 
 xdx  f x  f b f a. a a
Chọn đáp án D.
Câu 8: Gọi v t là vận tốc của viên đạn. Ta có v't  at  9
 ,8. Suy ra vt  9  ,8t  . C Vì
v0  98 nên C  98. Vậy vt  9  ,8t  98.
Gọi T là thời điểm viên đạn đạt độ cao lớn nhất. Tại đó viên đạn có vận tốc bằng 0. Vậy 98
vT  0 . Suy ra T 
 10 ( s ). Vậy quãng đường L mà viên đạn đi được là 9,8 10
L  2S  2  9
 ,8t  98dt  980 m. 0
Chọn đáp án D. k ln 4 k 2x 2k ln 4 2x 2k 2     2  e   e Câu 9: Ta có: x e e V   e x        và x V   e x       8  . 2   d 1   d  2  2 2  2  2 0 0 k k 2k 2k e   e  k 1 Theo giả thiết: 2 V  2V    28 
  e  11  2k  ln11  k  ln11. 1 2 2 2  2  2
Chọn đáp án B.  z 1  3   1    i  z    1 x z  i  z x  y  2 3 3 Câu 10: Ta có :       
 z    .i  z  i
 z  i  2  z  
4x  2y  3  3 2 2  1 y   2   z  2
Vậy có 1 số phức thỏa điều kiện đề bài.
 Chọn đáp án A.
Câu 11: Gọi M là điểm biểu diễn z trên mặt phẳng tọa độ. 2 2
Từ điều kiện: z  m   x  m 2
 y   x  m 2 2 2
 y  4  M thuộc đường tròn C có tâm 1  I ;
m 0 , bán kính R  2. 1   1  i
Từ điều kiện:   i z   i     i 1 1 1 2 1 z   2  z  i   z  i  1 2. 2 1 i
 x  y  2 2
1  1  M thuộc đường tròn C có tâm I 0;1 , bán kính R  1. 2   2  2
Để tồn tại hai số số phức thỏa mãn các điều kiện đề bài khi chỉ khi tồn tại hai điểm M , điều này xãy ra khi và chi khi
C và C cắt nhau tại hai điểm phân 2  1 
biệt  R  R  I I  R  R  1  I I  3. 1 2 1 2 1 2 1 2 
Ta có: I I   ; m  2 2 2
1  I I  m  1  1  m  1  3  0  m  8  m 2  2; 2 2 \ 0 . 1 2 1 2    
 Chọn đáp án D.
Câu 12: Gọi z  x  yi; x; y  có điểm M x; y biểu diễn z trên mặt phẳng tọa độ. 2 2 2 Từ giả thiết
z   i  z  i  x     y   2 1 3 1 1
 x y 3  2x  4y 7  0 suy ra
M  : 2x  4y  7  0. 7  7 5 1 2 5 7 7
Với O là gốc tọa độ, ra có: z
 dO;     khi z   i. min 2 2  10 z 7 2 4 10 5 max
Câu 13: Hình 3 là lăng trụ đứng với đáy là hình thang vuông với hai đáy có độ dài khác nhau nên
đáy không tồn tại đường tròn ngoại tiếp. Vậy hình 3 không tồn tại mặt cầu ngoại tiếp.
Chọn đáp án C.
Câu 14:Gọi H là hình chiếu vuông góc của D lên D C
cạnh AB  DH  a 2. 2a
Khối tròn xoay nhận được khi quanh hình bình 450
hành ABCD quanh trục AB có thể tích đúng bằng K A H B 3a
thể tích khối trụ có đường sinh DC và bán kính đáy
DH (hai hình nón bù trừ nhau). Vậy 2 2 V  H .
K  DH  D .
C  DH  a  a 2 3 3 . 2  6a .
 Chọn đáp án B. Câu 15:
Gọi M là trung điểm của BD theo tính chất trọng D' C' 1
tâm của G ta có GM  CM 3 1 1 1 1 1  V      V  V  . .A . B C . B CC G.ABC C.ABC A. 3 3 BCC 3 3 2 A' B' 1 1 1  A . B BC.CC  V      . ABCD. 18 18 A B C D 18 M G
Chọn đáp án D. D
Cách khác: (Phương pháp tọa độ) C
Gọi A0;0;0, B1;0;0Ox, D0;1;0Oy, A'0;0;1O . z Xác định tọa độ G , viết phương trình  A B ABC  1 '  V
 d G; ABC' .S G.ABC'    ABC' 3 1  
 dG ABC  1 1 ;
' . AB, AC'  . 3 2   18
Câu 16: Tính thể tích của phần hình nón không chứa nước, từ đó suy ra chiều cao h' , chiều cao của
nước bằng chiều cao phễu trừ đi h'. 1
Công thức thể tích khối nón: V   R2.h 3
Gọi bán kính đáy phễu là R , chiều cao phễu là h  15cm , do chiều cao nước trong phễu 1 1
ban đầu bằng h nên bán kính đáy hình nón tạo bởi lượng nước là R . Thể tích phễu và thể tích 3 3 2 1 1  R  15 5 nước lần lượt là 2 2
V   R .15  5 R  3 cm  và 2 V     .   R  3
cm . Suy ra thể tích 1  3 3  3  3 27 5 130 V 26
phần khối nón không chứa nước là 2 2 2
V  V  V  5 R   R   R  3 cm 2     1 . 2 1  27 27 V 27
Gọi h' và r là chiều cao và bán kính đáy của khối nón không chứa nước, ta có 3 3 h' r V h' h' 2     2 . Từ (1) và (2) suy ra 3 3
h'  5 26  h  15  5 26  0,188 cm . 1   3 3   h R V h 15
Chọn đáp án A. 5 3  7 2  
Câu 17: Ta có diện tích đáy bằng: 7   74  2
cm  . Vậy V    3 40.74 2960 cm . 2
Chọn đáp án C.  Câu 18: Ta có: M  1  ; 2; 3; M  1  ; 2  ; 3  ; M 1;2; 3
 . Suy ra: M M  0; 4;  6  , 1 2   1 2 3   
  1 M M  2; 0; 6
 và M M , M M   24; 1  2;8  6; 3  ; 2 1 2 1 3     1 3     4 
Mp M M M qua M 1
 ; 2; 3 và nhận n  6; 3
 ; 2 làm vectơ pháp tuyến, có phương trình: 1   1 2 3 
6x  3y  2z  6  0.
Chọn đáp án C. x y z
Câu 19: Ta có:  ABC :    1  bcx  acy  abz  abc  0. a b c 2 2 2 a b c abc 1 1 1 1 Lúc đó: 2 d  ; O  ABC 3 2 2 2    a b c   2 2 2
a  b  c   d  . 2 2 2 2 2 2  3
b c  a c  a b max 3 abc 3 9 3 3
Chọn đáp án A. Câu 20: 
Để ý rằng P / /Q . Đường thẳng  có 1 vectơ chỉ phương là u   
 4;1; 1 và A0;1;0.   d
 A;P 1  u    n  Ta có:  P    Mặt khác: 3 
 dA;P  dA;Q . A   P / / P.
dA Q 1 ;   3
Vậy  song song và cách đều hai mặt phẳng P và Q  có vô số mặt cầu có tâm nằm trên  ,
đồng thời tiếp xúc với hai mặt phẳng P và Q.
Chọn đáp án D.
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Tổng ôn tập: NéI DUNG VËN DôNG ¤N THI THPT QuèC GIA
PHIẾU TỔNG ÔN SỐ 03 M¤N TO¸N
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế
Nội dung đề bài, đáp án chúng tôi trích từ các đề thi thử của các trường trên toàn quốc, nguồn tài
nguyên từ sách ôn thi TNTHPT 2016 (Thầy Đoàn Quỳnh chủ biên), Page Toán Học Bắc Trung Nam, Page
CLB Giáo viên trẻ TP Huế và các tư liệu tham khảo của quý thầy cô đăng trên internet! Xin chân thành cảm ơn! Câu 1: Cho hàm số 4 2
y  ax  bx  c a  0 có đồ thị như hình y
vẽ bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0. x O
D. a  0, b  0, c  0. x  1
Câu 2: Kí hiệu C là đồ thị của hàm số y 
. Với mỗi điểm M x; y thuộc C , xét điểm x  2
Mx  2; y  
1 . Trong các hàm số sau, tìm hàm số có đồ thị tạo bởi các điểm M đó. x  2 2 3 x A. y  . B. y  . C. y  . D. y  . x  1 x  2 x x  2
Câu 3: Tìm hàm số dạng 3 2
y  ax  bx  cx  d (a, b, c, d là các hằng số, a  0) sao cho f x là hàm
số lẻ, đồ thị của nó tiếp xúc với đường thẳng y  9x 16 tại điểm A2; 2. A. f x 3  x  5 . x B. f x 3  2x 7 .
x C. f x 3  2  x  9 .
x D. f x 3  x  3 . x
Câu 4: Kí hiệu M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 6  2 cos 4x y  sin 2x  . Tính M  . m 2 A. 4. B. 2. C. 1. D. 5.
Câu 5: Đường cong trong hình bên là đồ thị của một y (C)
hàm số trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 2x y  . B. 2 x y  . -3 2 C. 2 x y   1.
D. y  log x  1. 1 2 -1 O 1 x
Câu 6: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức    Qt 3t 2
 Q 1 e  , với t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin 0   0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0%) thì sau
bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)? A. t  1,54 . h B. t  1,2 . h C. t  1 . h D. t  1,34 . h 2 x
Câu 7: Cho hàm số G x  cos tdt. 
Đạo hàm của G x là 0
A. Gx  2xcos x .
B. Gx  2xcos . x
C. Gx  xcos . x
D. Gx  2xsin . x
Câu 8: Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt
đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển
động theo phương thẳng đứng với vận tốc tuân theo quy luật vt 2
 10t t , trong đó t (phút) là
thời gian tính từ lúc bắt đầu chuyển động, v t được tính theo đơn vị mét/phút ( m/p ). Nếu như
vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là
A. v  5m/p .
B. v  7 m/p .
C. v  9m/p .
D. v  3m/p .
Câu 9: Cho hình phẳng H  giới hạn bởi các đường 2
y  x và y  x. Tính thể tích khối tròn xoay
tạo ra khi H  quay quanh . Ox 1 1 A.   4
x  xdx đvtt. B.   2
x  x dx đvtt. 0 0 1 1 C.   2
x  x dx đvtt. D.   4
x  x dx đvtt. 0 0
Câu 10: Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình 4 z 16  0. A. 8. B. 16. C. 4. D. 32.
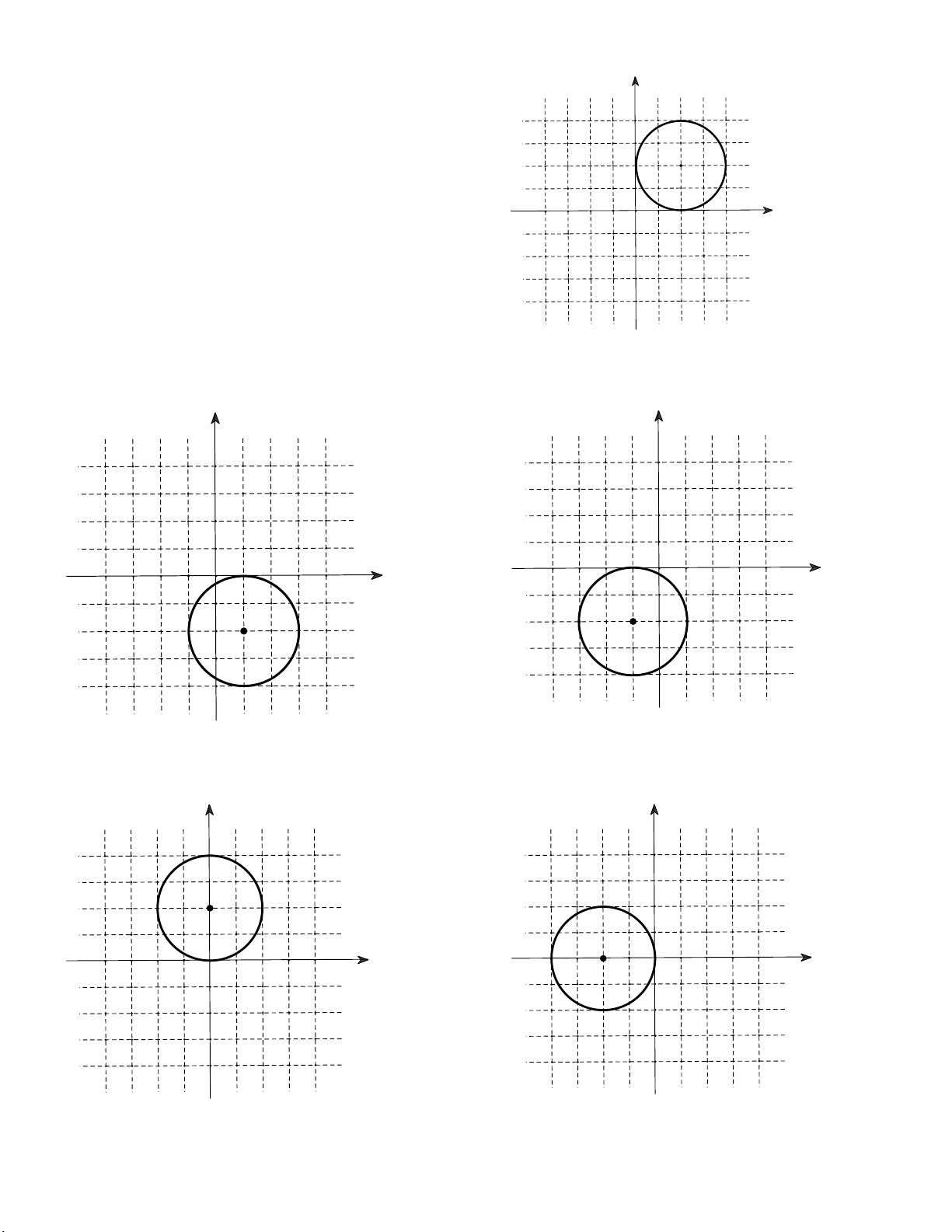
Câu 11: Biết tập hợp tất cả các điểm biểu diễn số y
phức z là đường tròn cho bởi hình vẽ bên. Hỏi tập
hợp tất cả các điểm biểu diễn số phức z  3  4i 3
được thể hiện bởi đường tròn trong hình vẽ nào 2 1
trong bốn hình vẽ dưới đây? x -3 -2 -1 O 1 2 3 -1 -2 -3 -4 A. B. y y 2 2 1 1 x 1 -2 -1 O O -3 2 x 3 1 2 3 -3 -2 -1 -1 -1 -2 -2 -3 -3 -4 -4 C. D. y y 2 2 1 1 x O x O -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -2 -2 -3 -3 -4 -4
Câu 12: Cho số phức z thỏa mãn z  1 i  z  3i . Tính môđun nhỏ nhất của z  . i 3 5 7 5 4 5 3 5 A. . B. . C. . D. . 5 10 5 10
Câu 13: Tính diện tích tất cả các mặt của hình đa diện đều loại 3;  5 có cạnh bằng 2 . a A. 2 S  4 3a . B. 2 S  16 3a . C. 2 S  8 3a . D. 2 S  6 3a .
Câu 14: Cho hình lăng trụ AB . C A B  C
  có thể tích là V , M là điểm trên cạnh AA sao cho   MA  3A .
M Tính thể tích khối . M BCC B  . V V 2V 3V A. . B. . C. . D. . 2 3 3 4
Câu 15: Cho hai đường tròn C tâm O , bán kính bằng 1 , C tâm O , bán kính bằng 2 lần 2  1  1 2
lượt nằm trên hai mặt phẳng P  , P sao cho P / / P và O O  P ; O O  3. Tính diện 1 2  1 1   2 1  2 1 2
tích mặt cầu qua hai đường tròn đó, A. 24 . B. 20 . C. 16 . D. 12 . 
Câu 16: Cho hình chóp .
S ABCD có đáy ABCD là hình thoi cạnh bằng 0
1, BAD  60 . Biết hai mặt
phẳng SDC và SAD cùng vuông góc với mặt phẳng  ABCD , góc giữa SC và mặt đáy bằng 0
45 . Tính diện tích mặt cầu ngoại tiếp tứ diện . S BC . D 7 7 7 A. 7 . B. . C. . D. . 2 4 3
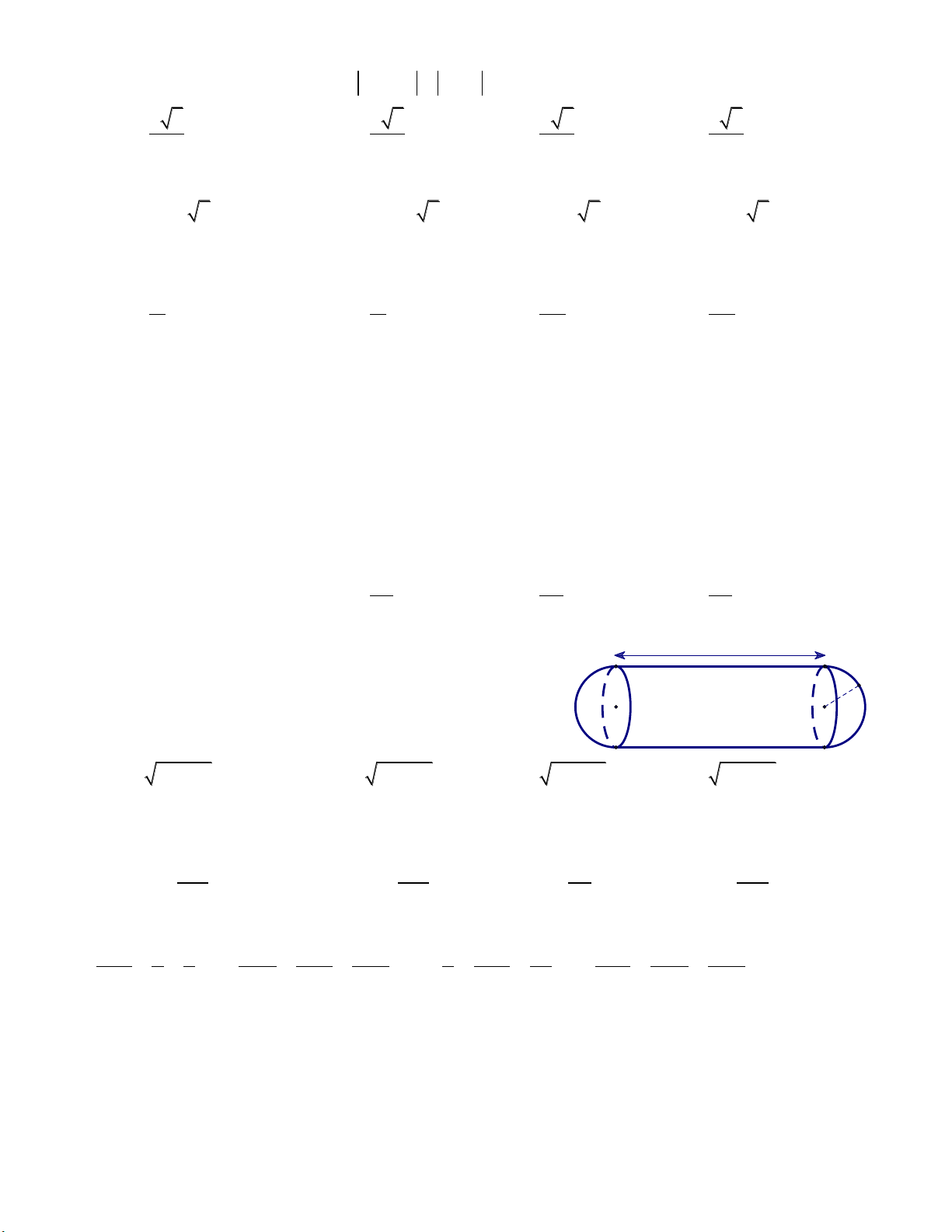
Câu 17: Một người kĩ sư muốn thiết kế một bồn chứa h
xăng với thể tích V cho trước, hình dạng như hình vẽ bên,
các kích thước r, h thay đổi. Tính nguyên liệu ít nhất để r
làm bồn xăng (tính theo V ). A. 3 2 48 V . B. 3 2 36 V . C. 3 2 16 V . D. 3 2 52 V .
Câu 18: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1; 2; 3 , B 1
 ; 4; 2, C0;1;3. Tính
diện tích đường tròn ngoại tiếp tam giác AB . C 11 11 7 21 A. S  . . B. S  . C. S  . D. S  . 2 4 4 4 Câu 19: Trong không gian với hệ tọa độ Oxyz , cho bốn đường thẳng x  1 y z x  2 y  1 z  2 x y  1 z x  1 y  2 z  2 d :   ; d :   ; d :   ; d :   . Có bao nhiêu 1 2 1  1 2 1  1  3 3 3 1 1 2  1 1 2 
đường thẳng cắt cả bốn đường thẳng đã cho? A. 0. B. 1. C. 2. . D. vô số. 2 2
Câu 20: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S x    y   2 : 1 1  z  4 và x  1 t 
đường thẳng  : y  3
. Hỏi có bao nhiêu mặt phẳng   chứa  và   tiếp xúc với mặt cầu z  3t  S? A. 0. B. 1. C. 2. D. vô số. ------- HẾT -------
Cố gắng lên các em! Tất cả rồi sẽ tốt đẹp thôi!
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Tổng ôn tập: NéI DUNG VËN DôNG ¤N THI THPT QuèC GIA
PHIẾU TỔNG ÔN SỐ 03 M¤N TO¸N BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án D C D B C A B C D B Câu 11 12 13 14 15 16 17 18 19 20 Đáp án B D B C B D B B A B ĐÁP ÁN CHI TIẾT
Câu 1: Dựa vào đồ thị suy ra hệ số a  0  loại phương án C. Hàm số có 1 điểm cực trị  ab  0 ,
do a  0  b  0 . Mặt khác: C Oy  O0;0  c  0.
Chọn đáp án D.
x  x  2  x  x  2  2 x  2  1 3
Câu 2: Ta có: Mx ; y  x  2; y     1     y x    
y  y  1    1 x  1 . 1 2  2 x  x  2
Vậy MC 3 : y  . x
Chọn đáp án C.
Câu 3: Do f x là hàm lẻ trên  nên dễ suy ra b  d  0. Từ đó, do f 2  2 và
f 2  9  a  1; c  3
 . Vậy f x 3  x  3 . x
Chọn đáp án D. 6  2cos 4x Câu 4: Biến đổi 2 y  sin 2x 
 sin2x  2 sin 2 . x 2
Đặt t  sin 2x  t   1  ;1 , x   .    t
Ta có hàm số g t 2
 t  2 t , t  1  ;1  f    t 1
 0  t  1 là nghiệm duy nhất, nên 2 2  t trong  1  ; 
1 thì f t  0 vô nghiệm. Do f   1  0, f  
1  2 nên M  2, m  0  M  m  2.
Chọn đáp án B. Câu 5:
Đồ thị C qua A1; 3 , B 1
 ; 3, cắt Oy tại điểm 0;2.
Chọn đáp án C. 3  t 3  t  
Câu 6: Pin nạp được 90% tức là 2 2
Q  0,9Q  0,9Q  Q 1 e   1 e  0,9 0 0 0   3  t 3  t 2 2  e  0,1 
 ln0,1  t   ln0,1  1,54 h. 2 3
Chọn đáp án A. 2 x
Câu 7: Đặt cos tdt  F 
t  Ft  cos t  cos tdt  F 
 2xF0Gx  F 2x.2x 0 2  2 .
x cos x  2x cos x  2x cos x .
Chọn đáp án B.
Câu 8: Gọi thời điểm khí cầu bắt đầu chuyển động là t  0 , thời điểm khinh khí cầu bắt đầu tiếp
đất là t . Quãng đường khí cầu đi được từ thời điểm t  0 đến thời điểm khinh khí cầu bắt đầu 1 t1 3 t
tiếp đất là t là  2 10t  t d 2 1 t  5t   162  t  4
 ,93 t  10,93 t  9 . Do vt  0  0  t  10 1 1 3 0
nên chọn t  9 . Vậy khi bắt đầu tiếp đất vận tốc v của khí cầu là v  2
9  10.9  9  9m/p
Chọn đáp án C. x  0
Câu 9: Xét phương trình hoành độ giao điểm 2 x  x   . x   1 1 1 1 2 2
Suy ra V     2
x    x d 4
x   x  xdx     4 x  x d . x 0 0 0
Chọn đáp án D. Câu 10: z  4
Ta có: z  16  0  z  4z  4 2 4 2 2  0  
 z  2  z  2
  z  2i  z  2i. 2 1 2 3 4 z  4  2 2 2 2
 z  z  z  z  16. 1 2 3 4
 Chọn đáp án B.
Câu 11: Dựa vào hình vẽ, tập hợp tất cả các điểm M x; y biểu diễn số phức z trên mặt phẳng tọa 2 2
độ là đường tròn có phương trình: x  2  y  2  4 .
Ta có: z  3  4i  x  3  y  4i có điểm Mx  3; y  4 biểu diễn trên mặt phẳng tọa độ. 2 2 2 2
Ta biểu diễn: x  2  y  2  4    x  3  1   y4  2  4 
 MC x  2 y  2 : 1 2  4.
Với phương trình như vậy, ta thấy đáp án B thỏa mãn.
 Chọn đáp án B.
Câu 12: Gọi z  x  yi; x; y  có điểm M x; y biểu diễn z trên mặt phẳng tọa độ.
Từ giả thiết z  1 i  z  3i suy ra M  : 2x  4y  7  0.
Ta có: z  i  x  y  
1 i có điểm Mx; y  
1 biểu diễn z trên mặt phẳng tọa độ.
Ta có: 2x  4y  7  0  2x  4y  
1  3  0  M 
 : 2x  4y  3  0. 3  3 5 3 8 Vậy z  i
 dO;   , khi z   . i min 2 2  10 2 4 10 5
 Chọn đáp án D. 3 2a2
Câu 13: Đa diện đều loại 4; 
3 là bát diện đều. Diện tích mỗi mặt bằng 2  3a . 4
Vậy diện tích tất cả các mặt của hình đa diện đều bằng 2 8 3a .
Chọn đáp án B.
Câu 14: Do MA / /BC  V    V . M.BCC B A.BCC'B' 1 1 2 Ta có: V             d ; A A B C .S    V V   V V    V . A.A B C    ABC A.BCC B A. 3 3 A B C 3
Chọn đáp án C. C C A A M M B B A' C' A' C' B' B'
Câu 15: Đặt IO  x 0  x  3 1   A O2 P1 2 2 2 2 2 2
x  IB O B  R 1  R  1 x  1  R   3  x 
2  IA O A  R 4  R  43x2 2 2 2 2 2 I R  4  3 x2 2 2 2
 1 x  x  2  R  IO  BO  5. 1 1 P2 B O1 Vậy 2
S  4 R  20. 
Chọn đáp án B. SDC   ABCD S Câu 16: Ta có:    SAD  
ABCD SD ABCD   R
SC  ABCD  ;  SCD . K  Mặt khác: A
 BD cân tại A và 0 BAD  60  A  BD I đều  B  CD đều. 450 D
Gọi G là trọng tâm B
 CD và I là giao điểm hai C đường như hình vẽ. G O M A B 2 2 21
R  SI  SK  KI  . 6 
Vậy mặt cầu có diện tích 2 7 S  4 R  . 3
Chọn đáp án D. 4 3 V   r 4
Câu 17: Để ý rằng 3 2 3
h  0  V   r  h r  h  . 2 3 r 3 8 3
4 r  2V   r
Vậy diện tích cần có để tạo ra bồn đựng xăng là 2 3
S  4 r  2 rh  . r 8 3 r  2V 3V Ta có: 3  3 S   0  r  . Lập bảng biến thiên 3 2  S  36V . 2 r 4 min
Nhận xét: Có thể thấy ngay nguyên liệu "ít tốn kém" nhất khi h  0. Nhưng thầy vẫn luôn nhắc chúng ta
phải biết thành lập hàm số để khảo sát, đề phòng các dạng câu hỏi không cho test đáp án!
Chọn đáp án B.   
Câu 18: Ta có: AB   2  ;2;   1 ; AC   1  ; 1
 ;0; BC  1; 3  ;  1 .  
Kiểm tra được: A .
B AC  0 và A, B, C không thẳng hàng  A  BC vuông tại . A BC 11
Vậy tâm đường tròn ngoại tiếp A
 BC là trung điểm cạnh BC và bán kính R   . 2 2 
Vậy diện tích hình tròn cần tìm là 2 11 S   R  . 4
Chọn đáp án B.
Câu 19: Kiểm tra được d / /d Mặt phẳng   chứa d , d có phương trình: x  y  z 1  0. 3 4 3 4
Ta có: d    A1;0;0; d    B 2;1; 2
 và d , d không thuộc  . 1 2     1 2 
Kiểm tra: AB  1;1; 2
  cùng phương với vectơ chỉ phương của d và Ad . 3 3
Vậy không tồn tại đường thẳng nào cắt cả bốn đường thẳng đã cho.
Chọn đáp án A. d1 d2 d3 A B d4 α
Câu 20: Mặt cầu S có tâm I 1;1; 0 , bán kính R  2. Đường thẳng  qua A1; 3; 0 và có một 
vectơ chỉ phương là u     1;0;3.  IA   2 Ta có: IA  0; 2;
 0 và     là một tiếp tuyến của mặt cầu S. Vậy tồn tại duy nhất một
IA  u
mặt phẳng   chứa  và   tiếp xúc với mặt cầu S (mặt phẳng   qua A1; 3; 0 và có một 
vectơ pháp tuyến là IA ).
Chọn đáp án B.