Ứng dụng lý thuyết trò chơi để phân tích các chiến lược kinh doanh của công ty cổ phần hàng không Vietjet trên thị trường hàng không ở Việt Nam giai đoạn từ 2020-nay | Bài thảo luận kinh tế vi mô

TRƯỜNG ĐẠI HỌC THƯƠNG MẠI KHOA KINH TẾ BÀI THẢO LUẬN MÔN: KINH TẾ VI MÔ 2
Đề tài: Ứng dụng lý thuyết trò chơi để phân tích các chiến lược
kinh doanh của công ty cổ phần hàng không Vietjet trên thị trường
hàng không ở Việt Nam giai đoạn từ 2020-nay
GIẢNG VIÊN HƯỚNG DẪN: Th.S Ninh Thị Hoàng Lan NHÓM: 03
LỚP HỌC PHẦN: 2324MIEC0311 MỤC LỤC
LỜI MỞ ĐẦU ........................................................................................................................................ 4
CHƯƠNG 1: CƠ SỞ LÍ LUẬN CƠ BẢN VỀ ĐỘC QUYỀN NHÓM VÀ LÍ THUYẾT TRÒ CHƠI 5
1.1. Độc quyền nhóm ..................................................................................................................... 5
1.1.1. Khái niệm về thị trường độc quyền nhóm ............................................................................... 5
1.1.2. Các đặc trưng cơ bản của thị trường độc quyền nhóm............................................................ 5
1.1.3. Nguyên tắc xác định trạng thái cân bằng trên thị trường độc quyền nhóm ............................. 6
1.1.4 Các mô hình độc quyền nhóm .................................................................................................. 8
1.2 Lý thuyết trò chơi ...................................................................................................................... 13
1.2.1. Một số khái niệm cơ bản về lý thuyết trò chơi ....................................................................... 13
1.2.2. Xác định cân bằng Nash trong trò chơi đồng thời ................................................................. 16
1.2.3. Xác định cân bằng Nash trong trò chơi tuần tự ..................................................................... 20
CHƯƠNG 2: PHÂN TÍCH CHIẾN LƯỢC KINH DOANH CỦA CÔNG TY CỔ PHẦN HÀNG
KHÔNG VIETJET TRÊN THỊ TRƯỜNG HÀNG KHÔNG TẠI VIỆT NAM GIAI ĐOẠN 2020-
NAY ...................................................................................................................................................... 23
2.1. Tổng quan về thị trường hàng không tại Việt Nam ................................................................. 23
2.2 Tổng quan về doanh nghiệp Cổ phần hàng không Vietjet ........................................................ 30
2.2.1 Lịch sử hình thành và phát triển của Công ty Cổ phần hàng không Vietjet .............................. 30
2.2.2 Thực trạng kinh doanh của Công ty Cổ phần hàng không Vietjet giai đoạn 2020-nay ............. 31
2.3 Chiến lược cạnh tranh của Vietjet giai đoạn 2020-nay ............................................................. 36
2.3.1 Những nhân tố ảnh hưởng đến chiến lược cạnh tranh của Vietjet ......................................... 36
2.3.2 Sự lựa chọn chiến lược cạnh tranh của vietjet giai đoạn 2020-2023 ....................................... 40
2.4. Phân tích chiến lược cạnh tranh của Vietjet dưới góc độ lý thuyết trò chơi....................... 43
2.4.1 Chiến lược truyền thông của Vietjet Air .......................................................................... 43
2.4.2 Chiến lược giá của Vietjet Air trong dịp Tết Nguyên đán 2023 ........................................ 44
2.5. Đánh giá các ưu điểm và hạn chế trong chiến lược cạnh tranh của Công ty Cổ phần hàng
không Vietjet .................................................................................................................................... 46
2.5.1. Ưu điểm ......................................................................................................................... 46
2.5.2. Hạn chế và nguyên nhân ................................................................................................. 48
CHƯƠNG 3: MỘT SỐ GIẢI PHÁP NHẰM HOÀN THIỆN CHIẾN LƯỢC CẠNH TRANH CỦA
CÔNG TY CỔ PHẦN HÀNG KHÔNG VIETJET TRÊN THỊ TRƯỜNG HÀNG KHÔNG Ở VIỆT
NAM TRONG THỜI GIAN TỚI ........................................................................................................ 50
3.1. Xu hướng thị trường hàng không ở Việt Nam giai đoạn 2023-2025 và mục tiêu phát triển của
Công ty Cổ phần hàng không Vietjet .............................................................................................. 50
3.1.1. Xu hướng thị trường hàng không ở Việt Nam giai đoạn 2023-2025 ...................................... 50 2
3.1.2. Mục tiêu phát triển của công ty cổ phần hàng không Vietjet từ nay đến 2025 ...................... 52
3.2 Một số giải pháp nhằm hoàn thiện chiến lược cạnh tranh của Công ty Cổ phần hàng không
Vietjet thời gian tới .......................................................................................................................... 53
3.3. Một số kiến nghị ........................................................................................................................ 54
KẾT LUẬN .......................................................................................................................................... 56
TÀI LIỆU THAM KHẢO ................................................................................................................... 57 3 LỜI MỞ ĐẦU
Kinh tế học vi mô phần hai là môn học cơ sở trong các chương trình đào tạo khối
ngành kinh tế ở bậc đại học với vấn đề nghiên cứu chính nhất là cách khai thác và sử dụng
một cách hiệu quả các nguồn lực khan hiếm của các tác nhân trong nền kinh tế. Với vấn đề
nghiên cứu đó, kinh tế học vi mô phần hai đóng vai trò thiết thực đối với sinh viên, tạo điều
kiện để sinh viên có thể hiểu rõ hơn cách vận hành của nền kinh tế cũng như cung cấp
những kiến thức nền cơ bản nhất cho các môn học chuyên ngành sau này. Trong môn học,
việc nghiên cứu về các doanh nghiệp trên thị trường độc quyền nhóm, cách thức và chiến
lược cạnh tranh của các doanh nghiệp đó là một trong các vấn đề thứ yếu mà sinh viên cần
phải tìm hiểu và nắm rõ. Đặt trong thực trạng nước ta hiện nay, khi mà nền kinh tế đang
dần chuyển biến tích cực sau một thời gian dài diễn ra đại dịch, khi mà mọi hoạt động kinh
tế, xã hội đều bị trì trệ thì nhóm nghiên cứu nhận thấy việc đưa ra các chiến lược cạnh tranh
của các doanh nghiệp trên thị trường độc quyền nhóm sẽ có tác động to lớn tới thị trường
độc quyền nói riêng, các thị trường khác nói chung. Tiêu biểu trong đó là nhóm thị trường
hàng không, nơi mà sức mạnh độc quyền của các hãng hàng không là vô cùng đáng kể. Do
vậy, nhóm nghiên cứu đã quyết định ứng dụng lý thuyết trò chơi để phân tích chiến lược
cạnh tranh của Công ty Cổ phần hàng không Vietjet trong ngành hàng Việt Nam với mục
đích sau cùng là nắm rõ được lý thuyết cũng như biết cách áp dụng lý thuyết vào thực tế một cách hiệu quả. 4
CHƯƠNG 1: CƠ SỞ LÍ LUẬN CƠ BẢN VỀ ĐỘC QUYỀN NHÓM VÀ LÍ THUYẾT TRÒ CHƠI 1.1. Độc quyền nhóm
Độc quyền được giải thích là “ đặc quyền chiếm giữ một mình”. Khi một cá nhân,
tổ chức nắm giữ, cung cấp một sản phẩm, dịch vụ nào đó mà duy nhất một mình họ có,
mới được cung cấp thì có thể gọi những cá nhân, tổ chức này đang độc quyền nắm giữ
sản phẩm hoặc độc quyền cung cấp dịch vụ.
Cấu trúc thị trường là một thuật ngữ mô tả hành vi của người bán và người mua
trong thị trường. Các nhà kinh tế căn cứ vào mức độ cạnh tranh hay mức độ độc quyền và
chia ra các cấu trúc thị trường như sau: cạnh tranh hoàn hảo, độc quyền thuần túy, cạnh
tranh độc quyền và cuối cùng là độc quyền nhóm.
Sau đây chúng ta sẽ cùng tìm hiểu kĩ hơn về một cấu trúc thị trường. Cụ thể là thị
trường độc quyền nhóm. Đã có rất nhiều định nghĩa về thị trường độc quyền nhóm ra đời,
trong các tài liệu khác nhau, tuy có ít nhiều sự khác biệt về một vài khía cạnh nhưng nhìn
chung đều chỉ ra được bản chất của thị trường này.
1.1.1. Khái niệm về thị trường độc quyền nhóm
Độc quyền nhóm là hình thái thị trường mà trong đó thị trường có một số doanh
nghiệp cùng tham gia hợp tác sản xuất kinh doanh một hoặc một số loại hàng hóa , mà sản
lượng của họ chiếm toàn bộ hoặc là phần chủ yếu sản lượng của phần kinh tế.
Độc quyền nhóm được hiểu cơ bản là một cấu trúc thị trường mà trong đó có một
lượng nhỏ các công ty mà không công ty nào trong số đó có thể loại bỏ ảnh hưởng đáng kể
đến công ty khác. tỉ lệ tập trung đo lường thị phần của các công ty lớn. Hãng cạnh tranh
độc quyền sẽ tối đa hóa lợi nhuận hoặc tối thiểu hóa thua lỗ trong ngắn hạn bằng cách sản
xuất ở mức sản lượng có doanh thu cận biên bằng chi phí cận biên.
Một số ví dụ về thị trường độc quyền nhóm: Chế tạo sắt, thép, than, tivi...
1.1.2. Các đặc trưng cơ bản của thị trường độc quyền nhóm
Số lượng người bán ít nhưng có nhiều người mua
Số lượng người bán trong nhóm thường khá ít. Khoảng từ hai công ty trở lên. Không
có giới hạn chính xác cho số lượng doanh nghiệp trong một nhóm độc quyền, những con 5
số này phải đủ thấp để các hành động của một công ty có thể gây ảnh hưởng đáng kể lên các công ty khác.
Hàng hóa của doanh nghiệp đưa ra thị trường có thể giống nhau hoặc khác nhau
Trên thị trường độc quyền nhóm (bán độc quyền), sản phẩm có thể là đồng nhất
(thép, nhôm, xi măng, dầu…) hay phân biệt (ngành sản xuất ô-tô, thiết bị điện, máy tính…)
và các sản phẩm có khả năng thay thế lẫn nhau.
Tính phụ thuộc lẫn nhau giữa các doanh nghiệp là rất lớn
Đây chính là đặc điểm nổi bật nhất của hình thái độc quyền nhóm, nghĩa là khi một
doanh nghiệp trong nhóm nếu thay đổi giá cả, sản lượng, quảng cáo… thì nó sẽ ảnh hưởng
đến toàn bộ những doanh nghiệp còn lại trong nhóm, lúc này bắt buộc các doanh nghiệp
này phải phản ứng để bảo vệ thị phần của mình trên thị trường Vì vậy, mỗi doanh nghiệp
khi xây dựng các đối sách của mình đều phải chú ý đến hành vi của các đối thủ.
Việc gia nhập vào thị trường là rất khó khăn
Giấy phép của chính phủ, bằng sáng chế, bản quyền, quyền sở hữu tài nguyên và
chi phí đầu tư khổng lồ là một số rào cản để gia nhập thị trường độc quyền. Các công ty
khác khó có thể tham gia vào mô hình thị trường này khi đã có một nhà cung cấp kiểm soát
việc sản xuất và phân phối một sản phẩm hoặc dịch vụ độc quyền cụ thể. Một khi chính
phủ xác định rằng các sản phẩm hoặc dịch vụ do một công ty độc quyền cung cấp là cần
thiết vì lợi ích công cộng: công ty năng lượng, viễn thông,... thì những công ty đó không
được tự ý rút khỏi thị trường.
1.1.3. Nguyên tắc xác định trạng thái cân bằng trên thị trường độc quyền nhóm
Thế cân bằng trong thị trường độc quyền nhóm
Cân bằng Nash là một khái niệm trong lý thuyết trò chơi trong đó kết quả tối ưu của
một trò chơi là nơi không có động cơ để đi chệch khỏi chiến lược ban đầu. Cụ thể hơn, cân
bằng Nash là một khái niệm của lý thuyết trò chơi trong đó kết quả tối ưu của một trò chơi
là kết quả mà người chơi không có động cơ để đi chệch khỏi chiến lược đã chọn của họ sau
khi cân nhắc lựa chọn của đối thủ.
Cân bằng Nash là một cân bằng không hợp tác - mỗi doanh nghiệp ra quyết định
sao cho thu được lợi nhuận cao nhất, khi biết hành động của các doanh nghiệp đối thủ. Khi 6
không hợp tác hành động, lẽ ra lợi nhuận của mỗi doanh nghiệp thu được cao hơn lợi nhuận
thu được trong cạnh tranh hoàn hảo, nhưng lại thấp hơn lợi nhuận thu được nếu các doanh nghiệp cấu kết nhau.
Trong thị trường độc quyền nhóm, trạng thái cân bằng Nash là trạng thái cân bằng
được xác định bởi đặc điểm là không ai trong số các nhà độc quyền có thể tăng lợi nhuận
của mình bằng cách đơn phương thay đổi chiến lược giá.
Nguyên tắc xác định cân bằng Nash trên thị trường độc quyền nhóm
Cân bằng Nash là một định lý ra quyết định trong lý thuyết trò chơi nói rằng một
người chơi có thể đạt được kết quả mong muốn bằng cách không đi chệch khỏi chiến lược
ban đầu của họ. Ở trạng thái cân bằng Nash, mỗi người chơi được cho là biết các chiến
lược cân bằng của những người chơi khác và không người chơi nào có được lợi ích bằng
cách chỉ thay đổi chiến lược của riêng họ.
Nếu mỗi người chơi đã chọn một chiến lược – một kế hoạch hành động dựa trên
những gì đã xảy ra cho đến nay trong trò chơi – và không người chơi nào có thể tăng lợi
nhuận dự kiến của họ bằng cách thay đổi chiến lược của họ trong khi những người chơi
khác giữ nguyên của họ, thì tập hợp các lựa chọn chiến lược hiện tại tạo thành cân bằng Nash.
Ở trạng thái cân bằng Nash, chiến lược của mỗi người chơi là tối ưu khi xem xét
các quyết định của những người chơi khác. Mọi người chơi đều chiến thắng bởi vì mọi
người đều đạt được kết quả mà họ mong muốn. Nhưng điểm cân bằng Nash không phải
lúc nào cũng có nghĩa là chiến lược tối ưu nhất được chọn. => KẾT LUẬN:
Cân bằng Nash rất quan trọng bởi vì nó giúp người chơi xác định mức thưởng tốt nhất
trong một tình huống không chỉ dựa trên quyết định của họ mà còn dựa trên quyết định của
các bên khác có liên quan. Cân bằng Nash có thể được sử dụng trong nhiều khía cạnh của
cuộc sống, từ chiến lược kinh doanh đến việc bán nhà cho đến chiến tranh và khoa học xã
hội. Không có một công thức cụ thể nào để tính điểm cân bằng Nash, nhưng thay vào đó,
nó có thể được xác định bằng cách mô hình hóa các tình huống khác nhau trong một trò 7
chơi nhất định để xác định lợi nhuận của từng chiến lược và chiến lược nào sẽ là chiến lược tối ưu để lựa chọn
Cân bằng Nash được ứng dụng phổ biến trong thị trường độc quyền nhóm. Trong kinh
doanh, cân bằng Nash có lợi cho việc mô hình hóa các hành vi cạnh tranh giữa các tác nhân
kinh tế trong doanh nghiệp. Các doanh nghiệp thường có một số lựa chọn chiến lược ảnh
hưởng đến khả năng hiện thực khóa lợi ích kinh tế của họ.
1.1.4 Các mô hình độc quyền nhóm Mô hình Cournot
Là mô hình độc quyền nhóm do Augustin Cournot đưa ra vào năm 1838, trong đó
mô hình Cournot nói về các doanh nghiệp độc quyền nhóm hoạt động độc lập với nhau,
cùng sản xuất và lựa chọn sản phẩm bán đồng thời. Sản phẩm của thị trường độc quyền
nhóm là đông nhất (giống nhau).Sản lượng của thị trường là tổng sản lượng của các doanh
nghiệp cộng lại. Bản chất của mô hình Cournot là mỗi hãng coi sản lượng của hãng đối thủ
là cố định và từ đó đưa ra mức sản lượng của mình.
Hình 1.1.4a: Lựa chọn sản lượng tối ưu của hãng 1 theo sản lượng của hãng 2
Giả sử có 2 hãng: hãng 1 và hãng 2 và 2 hãng đều biết về đường cầu thị trường. Hãng 1
sản xuất bao nhiêu đơn vị sẽ phụ thuộc vào hãng 1 dự đoán hãng 2 sản xuất bao nhiêu.
Chi phí cận biên của hãng 1 MC1 cố định. 8
Nếu hãng 1 dự báo hãng 2 không sản xuất Q2 =0 thì khi đó, đường cầu hãng 1 sẽ là
D1(0) và doanh thu cận biên của hãng là MR1(0). Để tối đa hóa lợi nhuận thì hãng 1 sẽ
sản xuất sản lượng Q1=50.
Nếu hãng 1 dự báo hãng 2 sản xuất Q2=50 thì khi đó, đường cầu hãng 1 sẽ là
D1(50), doanh thu cận biên của hãng là MR1(50). Để tối đa hóa lợi nhuận thì hãng 1 sẽ
sản xuất sản lượng Q1=25.
Nếu hãng 1 dự báo hãng 2 sản xuất Q2=75 thì khi đó, đường cầu của hãng 1 sẽ là
D1(75), doanh thu cận biên của hãng là MR1(75). Để tối đa hóa lợi nhuận thì hãng 1 sẽ
sản xuất sản lượng Q1=12,5.
=> Kết luận: Ta có đồ thị như hình 1.1.4a
Thứ nhất, sản lượng tối đa hóa lợi nhuận của một hãng phụ thuộc vào lượng sản phẩm
của các hãng khác quyết định sản xuất.
Thứ hai, phản ứng chỉ ra mối quan hệ giữa mức sản lượng tối đa hóa lợi nhuận của một
hãng với mức sản lượng mà hãng nghĩ ra các hãng khác định sản xuất.
Đường phản ứng là đường thể hiện mối quan hệ giữa mức sản lượng tối đa hóa lợi nhuận
của một hãng với mức sản lượng mà hãng nghĩ rằng các hãng khác định sản xuất.
Thế cân bằng Cournot xảy ra khi mỗi hãng dự báo đúng mức sản lượng của các hãng đối
thủ và xác định mức sản lượng của mình theo mức dự báo đó. Cân bằng xảy ra tại điểm
giao nhau giữa hai đường phản ứng. Cân bằng Cournot chính là cân bằng Nash khi mỗi
hãng sản xuất ở mức sản lượng làm hãng tối đa hóa lợi nhuận giả định hãng biết các hãng
đối thủ sản xuất bao nhiêu. 9
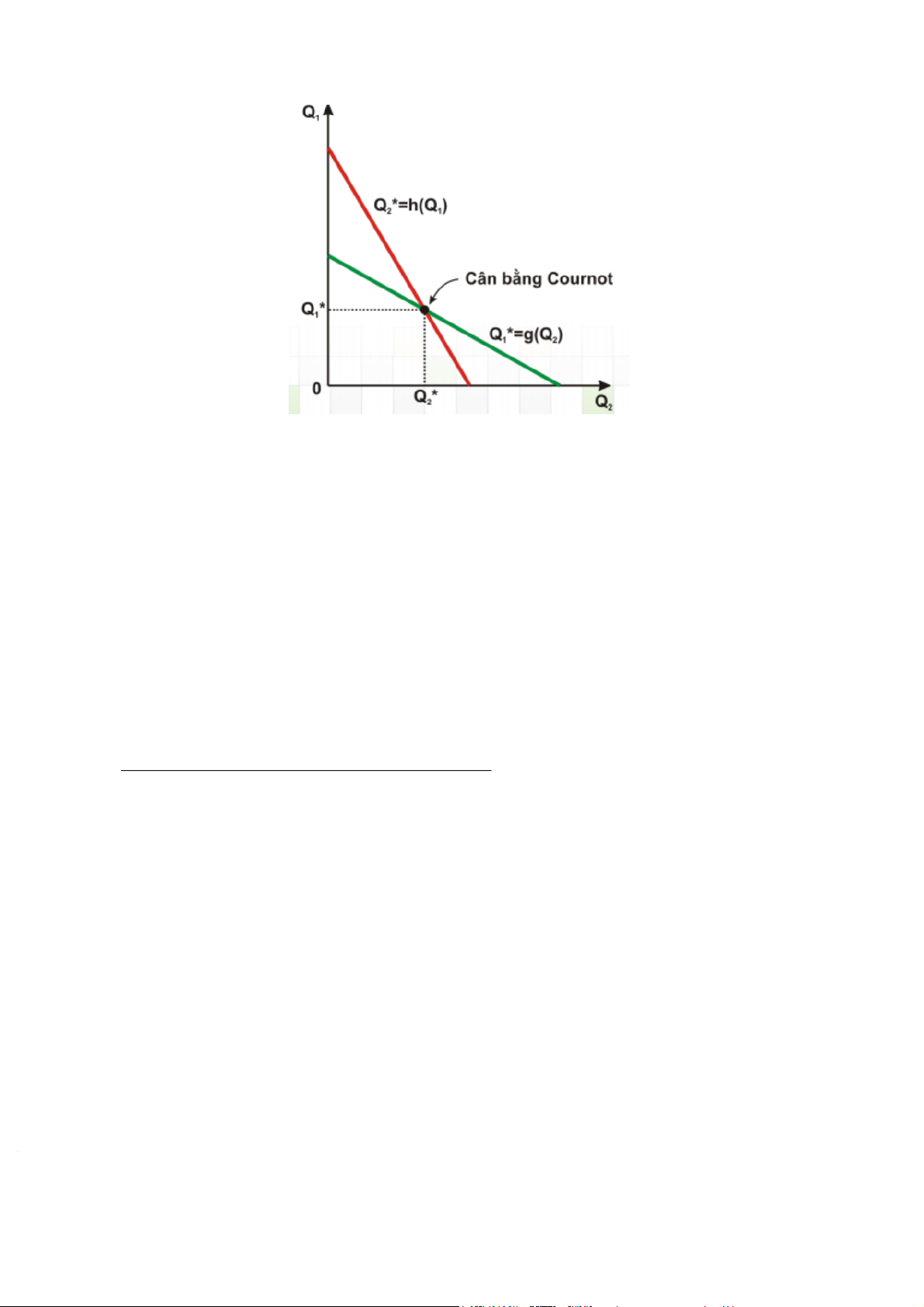
Hình 1.1.4b: Cân bằng Cournot
Giả sử có 2 hãng trên thị trường: hãng 1 và hãng 2. Đường phản ứng của hãng 1 là
Q1*=g(Q2) và đường phản ứng của hãng 2 là Q2*=g(Q1). Cân bằng Cournot sẽ xảy ra tại
điểm giao của 2 đường phản ứng. Nếu thị trường rơi vào một điểm khác điểm cân bằng
Cournot thì ít nhất 1 hãng sẽ thay đổi quyết định của mình. Trong trường hợp 2 doanh
nghiệp cấu kết với nhau, cả hai hãng sản xuất ít hơn, giá bán cao hớn, lợi nhuận cao hơn
với thế cân bằng Cournot được gọi là đường đồng hợp (đường đồng hợp là tập hợp các tổ
hợp sản lượng của doanh nghiệp để tối đa hóa lợi nhuận chung) Nhưng trong thực tế, khó
chỉ một lần doanh nghiệp chọn đúng sản lượng ở thế cân bằng Cournot, mà phải trải qua
tham dò, điều chỉnh mới có thể đạt được.
Mô hình Stackelberg (lợi thế của người đi trước)
Quyết đinh tuần tự: một hãng ra quyết định sản lượng trước, hãng kia căn cứ vào quyết
định của hãng trước để ra quyết định sản lượng của mình.
- Hai hãng 1 và hãng 2 cùng quyết định lựa chọn sản lượng để sản xuất các sản phẩm đồng
nhất. Hai hãng hoạt động độc lập và thông tin thị trường là hoàn hảo.
- Hãng 1 chiếm ưu thế (hãng đi đầu), hãng 2 sẽ quan sát hãng 1 và quyết định sản phẩm sản xuất ra.
- Các hãng này phải đối mặt với hàm cầu ngược sau P= a-bQ, trong đó Q=Q1+Q2.
- Hàm lợi nhuận của mỗi hãng là 10
Π1 =PQ1 - cQ1 = (a-bQ1 - bQ2)Q1 - cQ1
Π2 =PQ2 - cQ2 = (a-bQ2 - bQ1)Q2 - cQ2
Áp dụng hàm lợi nhuận tối đa đối với hãng 2: ∂Π2 ∂Q2 = a-bQ1-2bQ1-C=0
Giải phương trình, sản lượng của hãng 2 là: Q2= (a−bQ1−c) 2𝑏
Thay thế Q2 vào trong phương trình lợi nhuận của hãng 1, ta được: Π1 =aQ1/2 -bQ12/2- cQ1/2
Áp dụng điều kiện tối đa hóa lợi nhuận cho hãng 1: ∂ΠQ1 = 𝑎2 - 2bQ21 - 𝑐 2
Giải phương trình, xác định được mức sản lượng tối ưu đối với hãng 1: Q1= (a−c) 2𝑏
=>Mức sản lượng tối đa với hãng 2: Q2= 𝑎−𝑐 4𝑏
Qua đó cho ta thấy hãng 1 thông báo trước sản lượng của mình (lợi thế của người đi trước),
nó sẽ sản xuất lượng sản phẩm cao hơn và lợi nhận cao hơn so với hãng 2 Mô hình Bertrand
Là mô hình của các hãng độc quyền nhóm cạnh tranh về giá. Có ba trường hợp :
TH1: Sản phẩm đồng nhất
Khi các hãng giả định rằng giá của hãng khác là cố định, mỗi hãng sẽ cố gắng đặt giá thấp
hơn so với giá đối thủ đặt một chút ít (để có được toàn bộ thị trường)
Cân bằng của thị trường đạt được khi cả hai hãng đều đặt giá bằng chi phí biên
P = MC = c. Khi đó, cả hai hãng đều thu được lợi nhuận kinh tế bằng 0.
TH2: Sản phẩm khác biệt - quyết định đồng thời
- Đường phản ứng của hãng 1 là: P1= 𝑎+𝑏𝑃2+𝑐 2
- Đường phản ứng của hãng 2 là: P2= 𝑎+𝑏𝑃1+𝑐 2 11
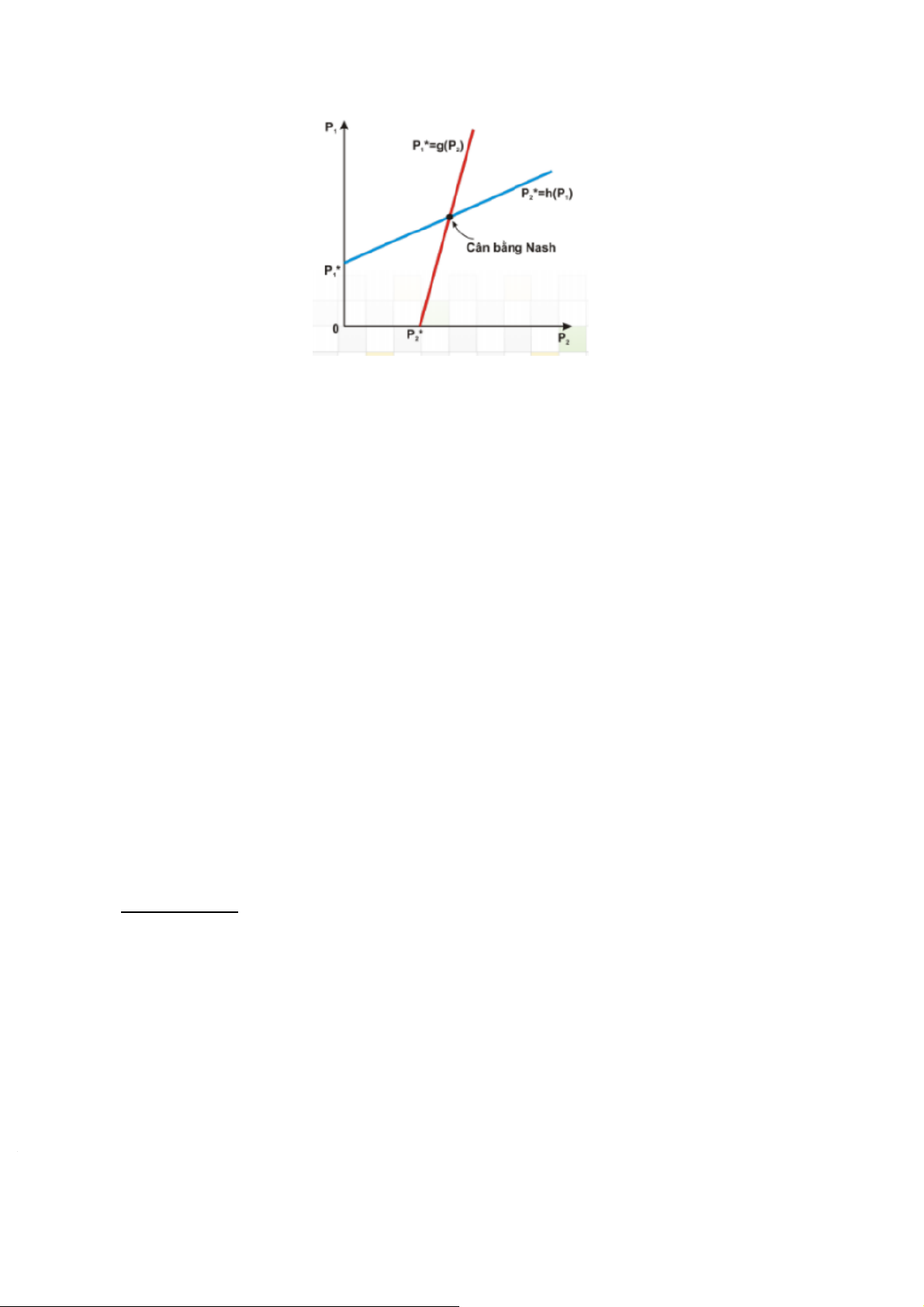
Hình 1.1.4c: Đồ thị xác định cân bằng Bertrand
Cân bằng đạt được tại điểm hai đường phản ứng cắt nhau. Tại điểm cân bằng thì cho biết
cả 2 hãng đều dự báo đúng và giúp hãng tối đa hóa lợi nhuận. Nếu thị trường rơi vào một
điểm thuộc đường phản ứng của hãng 2 và khác điểm cân bằng thì khi đó, hãng 2 sẽ tối đa
hóa lợi nhuận còn hãng 1 không có lợi nhuận tối đa. Ngược lại, nếu thị trường rơi vào điểm
thuộc đường phản ứng của hãng 1 và khác điểm cân bằng thì hãng 1 sẽ tối đa hóa lợi nhuận
và hãng 2 không có lợi nhuận tối đa.
TH3: Sản phẩm khác biệt- một hãng quyết định trước hãng kia theo sau
Giả sử có một thị trường với hai hãng cạnh tranh về giá cả. Mức giá của hai hãng tương
ứng là P1 và P2. Phương trình đường cầu cho mỗi hãng là: Q1 = a - P1 + bP2
Q2 = a - P2 + bP1 với b ≥ 0
Chi phí cận biên của mỗi hãng là cố định và đều bằng c.
Hãng 1 quyết định về giá trước, sau đó hãng 2 căn cứ vào mức giá của hãng 1 để đưa ra
quyết định về giá cho hãng.
=>Làm tương tự đối như đối với mô hình Stackelberg. Đường cầu gãy
Mô hình đường cầu gãy nhằm giải thích tính cứng nhắc của giá cả trong thị trường
độc quyền nhóm do giá trên thị trường độc quyền nhóm ít biến động (Hình 1.4). Trên các
thị trường khác (không còn là thị trường độc quyền) khi hãng đối mặt với sự thay đổi
trong chi phí sản xuất hãng sẽ thay đổi giá và số lượng đáp ứng lượng thay đổi đó. 12
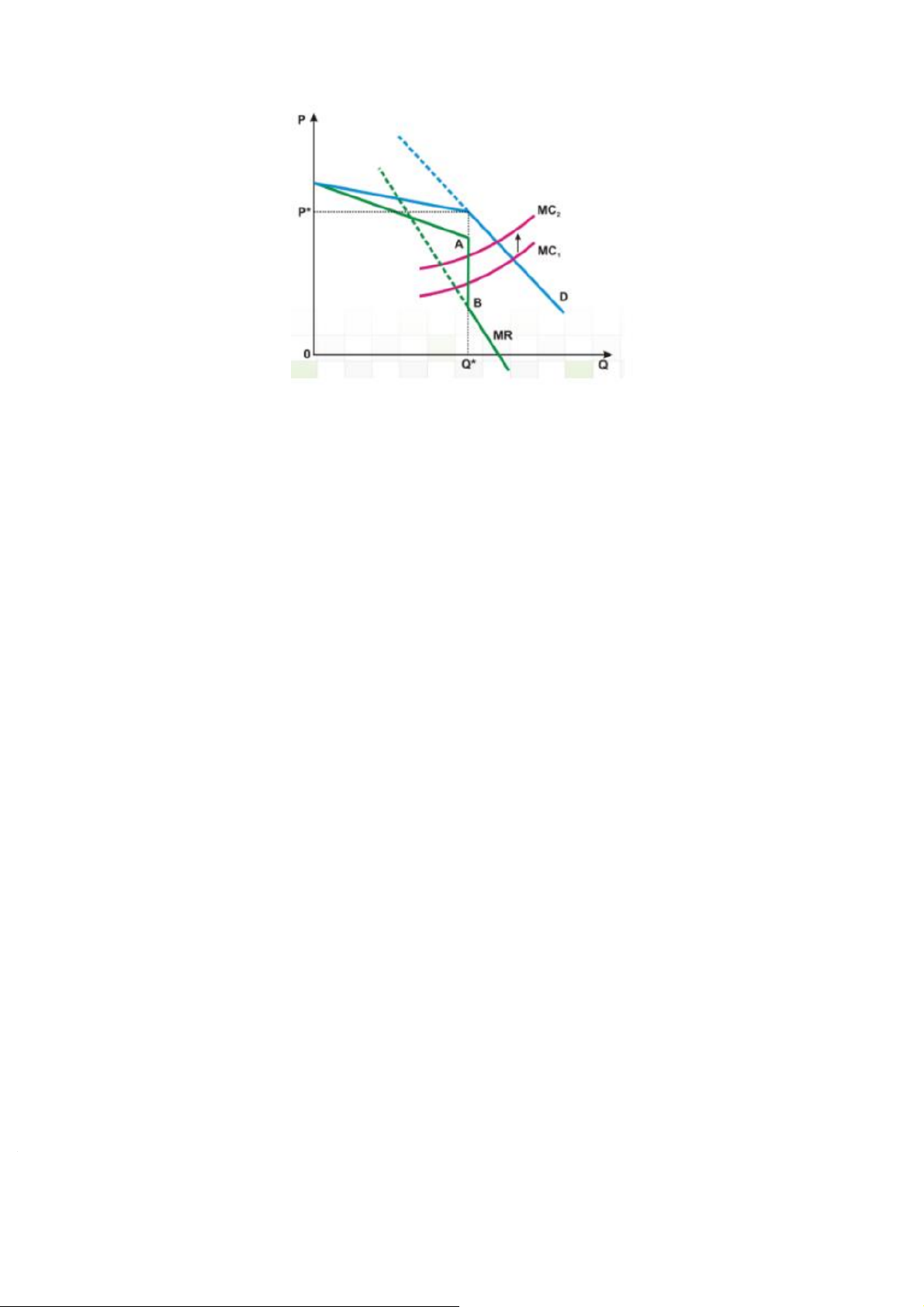
Hình 1.1.4d: Mô hình đường cầu gãy
Giả sử ban đầu hãng đặt mức giá là P*. Nếu hãng giảm giá, hãng lo sợ các hãng khác
cũng sẽ giảm giá; khi đó, hãng có thể tăng sản lượng nhưng không tăng nhiều. Kết quả là
với P

hãng lo sợ các hãng khác không tăng giá theo; khi đó, sản lượng của hãng sẽ giảm mạnh.
Kết quả là với P>P*, hãng sẽ đối mặt với đường cầu co dãn hơn (thoải hơn).Vì thế,
đường cầu của doanh nghiệp độc quyền nhóm là đường cầu gãy tại mức giá hiện hành
P*, đường doanh thu biên tương ứng không liên tục tại sản lượng Q*. Do đó nếu chi phí
biên tăng từ MC1 lên MC2 (hoặc giảm từ MC2 xuống MC1) trong khoảng (A,B) thì doanh
nghiệp vẫn sản xuất ở sản lượng như cũ Q*(MC2 = MR) với giá bán ra vẫn không đổi
P*.Nhược điểm của mô hình đường cầu gãy là không giải thích được sự hình thành mức giá thị trường P*.
=> Ngày nay các doanh nghiệp luôn né tránh cuộc cạnh tranh bằng giá cả, vì hậu quả của
nó là các bên đều bị thiệt hại, nhưng để tồn tại và phát triển, các doanh nghiệp luôn nỗ
lực tìm kiếm những hình thức cạnh tranh phi giá cả, an toàn và hữu hiệu hơn. 1.2 Lý thuyết trò chơi
1.2.1. Một số khái niệm cơ bản về lý thuyết trò chơi
1.2.1.1 Lý thuyết trò chơi 13
Lý thuyết trò chơi là một nhánh của toán học ứng dụng sử dụng các mô hình để nghiên
cứu các tình huống chiến thuật và những người tham gia cố gắng để tối đa kết quả thu được
của mình có tính đến hành động và phản ứng của các đối thủ khác.
Trò chơi là một tình huống mà trong đó người chơi (người tham gia) đưa ra quyết định
chiến lược có tính đến hành động và phản ứng của đối thủ. Trong đó:
+ Người chơi: là những người tham gia và hành động của hộ có tác động đến kết quả của bạn.
+ Chiến lược: là nguyên tắc hoặc kế hoạch hành động trong khi tiến hành trò chơi.
+ Kết cục: giá trị tương ứng với một kết quả có thể xảy ra và phản ánh lợi ích thu
được của mỗi người chơi.
Trò chơi đồng thời: các đối thủ ra quyết định khi không biết đến quyết định của đối phương.
Trò chơi tuần tự: một người chơi ra quyết định trước, người chơi tiếp theo ra quyết định
căn cứ vào quyết định của người đi trước.
Trò chơi hợp tác: là trò chơi mà trong đó những người chơi có thể đàm phán những cam
kết ràng buộc lẫn nhau cho phép họ cùng lập các kế hoạch chiến lược chung.
Trò chơi bất hợp tác: các bên tham gia không thể đàm phán và thực thi có hiệu lực các cam kết ràng buộc. Các giả định:
+ Người chơi là những người có lý trí: mục đích của những người chơi đều là tối đa hóa
kết cục bản thân họ, những người chơi đều là những người có tính toán hoàn hảo.
+ Hiểu biết chung: mỗi người đều biết về nguyên tác của trò chơi, mỗi người chơi đều biết
rằng người khác cũng biết nguyên tắc cảu trò chơi, mỗi người chơi đều biết người chơi
khác là người có lý trí.
Cân bằng Nash:là hợp các chiến lược (hoặc hành động) mà người chơi có thể làm điều tốt
nhất cho mình, khi cho trước dự đoán đúng hành động của đối thủ.
1.2.1.2 Chiến lược cạnh tranh
Các chiến lược có ảnh hưởng chi phối: 14
Chiến lược ưu thế: là một chiến lược hoặc hành động mang lại kết cục tốt nhất dù
cho các đối thủ quyết định làm gì đi chăng nữa. (tôi đang làm những gì tốt nhất có thể được
cho tôi, bất kể bạn có thể làm gì đi nữa. Bạn đang làm điều tốt nhất có thể cho bạn, bất kể tôi làm gì đi nữa).
Nguyên tắc ra quyết định khi có chiến lược ưu thế:
+ Nếu bạn có chiến lược ưu thế, hãy sử dụng nó.
+ Dự đoán rằng đối thủ của bạn cũng sử dụng chiến lược ưu thế của họ nếu như họ
cũng có chiến lược ưu thế.
Chiến lược bị lấn át: là một chiến lược luôn có chiến lược khác tốt hơn nó.
Nguyên tắc ra quyết định khi có chiến lược bị lấn át:
+ Loại bỏ chiến lược bị lấn át.
+ Làm giảm kích thước của ma trận lợi ích.
+ Lặp lại bước trên cho đến khi không còn chiến lược bị lấn át.
+ Xác định điểm cân bằng.
Ví dụ: Nếu có hai hãng chạy đều có chiến lược ưu thế và chiến lược bị lấn át:
Nếu hãng A chạy quảng cáo thì lợi nhuận của hãng A là 90 mà hãng B không chạy quảng
cáo thì lợi nhuận của hãng B là 10 ngược lại.Nếu cả hai hãng đều quảng cáo thì lợi nhuận
của 2 hãng là 50.Nếu cả hai hãng đều không chạy quảng cáo thì lợi nhuận của 2 hãng là 70.Ta có mô hình như sau: Hãng B Quảng cáo Không quảng cáo Hãng A Quảng cáo (50;50) (90,10) Không quảng cáo (10;90) (70,70)
- Nếu hãng A không chọn quảng cáo thì hãng B chọn quảng cáo.
- Nếu hãng A chọn quảng cáo thì hãng B cũng chọn quảng cáo.
- Nếu hãng B chọn quảng cáo thì hãng A chọn quảng cáo.
- Nếu hãng B chọn không quảng cáo thì hãng A chọn quảng cáo.
=> Như vậy, hãng B sẽ chọn quảng cáo bất kể khi hãng A quyết định gì và hãng A cũng sẽ
chọn quảng cáo bất kể khi hãng B chọn gì. Do vậy, cả 2 hãng đều có chiến lược ưu thế là 15
quảng cáo và chiến lược lấn át là không quảng cáo. Cân bằng Nash xảy ra khi cả 2 hãng
đều quyết định chọn quảng cáo. Khi ở cân bằng này, lựa chọn của 2 hãng có tính ổn định
về mặt chiến lược và 2 hãng không có ý định thay đổi quyết định của mình. Ta có thể thấy
khi 2 hãng lựa chọn không quảng cáo thì sẽ có lợi nhuận lớn hơn nhưng cân bằng Nash
không xảy ra ở ô 2 hãng lựa chọn không quảng cáo tại ở đó không có tính ổn định về mặt
chiến lược, hãng A hoặc B có thể sẽ thay đổi quyết định, chiếm lĩnh thị trường; từ đó sẽ có
lợi nhuận cao hơn, hãng còn lại sẽ bị thiệt và cũng sẽ thay đổi quyết định của mình.
Chiến lược Maximin(cực tiểu cực đại): Đối với mỗi chiến lược, xác định kết cục thấp
nhất. Trong đó chiến lược thấp nhất này, lựa chọn kết cục có giá trị cao nhất . Chiến lược
Maximin là chiến lược thận trọng, nhưng không tối thiểu hóa lợi nhuận (nó có thể là cân
bằng Nash hoặc không).Ví dụ: Hãng 2 Không đầu tư Đầu tư Hãng 1 Không đầu tư (0;0) (-10,10) Đầu tư (-100;0) (20,10)
- Nếu hãng 1 không đầu tư, kết cục xấu sẽ là -10.
- Nếu hãng 1 đầu tư, kết cục xấu sẽ là -100.
=> Khi đầu tư hãng 1 sẽ lo sợ hãng 2 sẽ chọn không đầu tư và như thế, hãng 1 nhận kết cục
xấu nhất. Do đó, theo chiến lược Maximin, hãng 1 quyết định không đầu tư dù chưa đạt
đến mục tiêu tối đa hóa lợi nhuận.
1.2.2. Xác định cân bằng Nash trong trò chơi đồng thời
Người chơi có chiến lược ưu thế Bảng Ma trận lợi ích: HÃNG B Không quảng cáo Quảng cáo 16 HÃNG A Không quảng cáo 50,50 20,60 Quảng cáo 60,20 30,30
Phản ứng tốt nhất của hãng A: Nếu B không quảng cáo là Quảng cáo, nếu B Quảng cáo
cũng là Quảng cáo. Vậy nên hãng A sẽ quảng cáo bất kể hãng B có quảng cáo hay không
nên hãng B cũng phải quảng cáo để nhận mức lợi nhuận là 30 thay vì có mức lợi nhuận
20 nếu không quảng cáo. Như vậy, chiến lược ưu thế của hãng A là Quảng cáo. Cân bằng
Nash xảy ra khi cả 2 hãng đều quyết định lựa chọn thực hiện quảng cáo. Khi ở cân bằng
này, lựa chọn của 2 hãng có tính ổn định về mặt chiến lược và 2 hãng không có ý định
thay đổi quyết định của mình.
Người chơi có chiến lược bị lấn át
Trong một số trò chơi, các đối thủ có thể nhận thấy rằng một hoặc một vài chiến
lược của mình luôn luôn đem lại các kết cục kém hơn các chiến lược khác. Các chiến lược
kém hơn này được gọi là các chiến lược bị lấn át, còn các chiến lược tốt hơn kia được gọi
là chiến lược lấn át. Trong các tình huống như vậy, lợi ích của người chơi sẽ không
bị tổn hại nếu người đó loại bỏ các chiến lược bị lấn át. Cách giải một trò chơi trên cơ
sở loại bỏ các chiến lược bị lấn át có thể thấy rõ trong một trò chơi nổi tiếng có tên là
Nghịch cảnh của Người tù (Prisoner`s Dilemma), lần đầu tiên được nhà kinh tế học A.
Tucker mô phỏng vào những năm 1940. Trò chơi tình thế lưỡng nan của Người tù
mô phỏng một tình huống sau: có 2 người cùng nhau phạm tội và bị công an bắt. Tuy
nhiên, do không có đầy đủ các chứng cứ, tòa án chỉ có thể buộc tội mỗi người 1 năm tù
giam. Mặc dù vậy, phía công an cho rằng, mức độ phạm tội của họ nghiêm trọng hơn
nhiều. Để khai thác các đối tượng phạm tội nói trên, công an tách 2 nghi can sang 2 phòng
riêng biệt để hỏi cung. Điều kiện đặt ra là: nếu 2 người cùng không khai nhận, mỗi người
sẽ bị kết án 1 năm tù. Nếu 2 người cùng khai nhận, mỗi người sẽ bị kết án 3 năm tù.
Tuy nhiên, nếu chỉ một người khai nhận, người đó sẽ được tha bổng, còn người kia sẽ
bị kết án 5 năm tù. Tình huống trên(còn được gọi là thế lưỡng nan của người tù) có thể
được mô phỏng dưới dạng ma trận như sau: 17 NGHI CAN 2 Khai Không khai NGHI CAN 1 Khai (-3;-3) (0;-5) Không khai (-5;0) (-1;-1)
Trong tình huống trên, do cả 2 nghi can đều là những người duy lý và chỉ quan tâm đến
lợi ích của bản thân mình, nên họ sẽ suy luận như sau: nếu người kia chọn
phương án “khai”, thì tốt nhất là mình cũng nên chọn phương án “khai” và bị kết án 3 năm
tù (-3), bởi nếu chọn phương án “không khai”, mình sẽ bị kết án 5 năm tù (-5). Nếu người
kia chọn phương án “không khai”, thì tốt nhất mình cũng nên chọn phương án
“khai”, bởi như thế mình sẽ được tha bổng (0), trong khi việc chọn phương án “không
khai” sẽ dẫn đến hậu quả là bị kết án 3 năm tù (-3).
=> Như vậy, với cả 2 nghi can ở trên, chiến lược “khai” luôn luôn tốt hơn chiến lược
“không khai” hay nói cách khác là chiến lược “không khai” luôn bị chiến lược “khai” lấn
át, vì nó luôn đem lại lợi ích nhỏ hơn, bất chấp người kia chọn chiến lược nào đi chăng
nữa. Kết quả là sẽ không ai chọn chiến lược “bị lấn át”. Kết cục của trò chơi là cả 2 nghi
can đều chọn chiến lược “khai” và bị kết án 3 năm tù. Kết cục này, rõ ràng là tồi hơn so
với kết cục cả 2 người đều không khai nhận tội lỗi của mình cũng như của đồng phạm.
Trò chơi tình thế lưỡng nan của người tù cho thấy, việc mọi người theo đuổi lợi ích của
mình không phải lúc nào cũng đem lại kết cục tốt cho bản thân, cũng như cho cả cộng
đồng (ở đây cộng đồng chỉ giới hạn trong 2 người phạm tội). Nó cũng cho thấy rằng,
các lợi ích tập thể, nếu không hài hòa với lợi ích cá nhân, sẽ không có được sự bền vững.
Loại bỏ các chiến lược bị lấn át là một trong những cách giải trò chơi rất đơn giản và lô-
gíc. Tuy nhiên, trên thực tế, không phải lúc nào trong trò chơi cũng có những chiến lược
bị lấn át như vậy (điều này phụ thuộc vào cấu trúc ma trận lợi ích của trò chơi).
Người chơi đều không có chiến lược ưu thế hay chiến lược bị lấn át 18
Trong ma trận lợi ích được trình bày tại bảng , các đối thủ A và B đều không có các chiến
lược nào ưu thế hay bị lấn át bởi chiến lược khác. Nếu đối thủ A chọn chiến lược a1, thì
chiến lược tốt nhất cho đối thủ B là chiến lược b2 (mang lại lợi ích là 4 và lớn hơn lợi ích
là 3 khi sử dụng chiến lược b1). Ngược lại, nếu đối thủ A chọn chiến lược a2, thì chiến
lược tốt nhất của B là b1 (vì 8>7). Đối với đối thủ A cũng vậy. Nếu B chọn chiến lược b1,
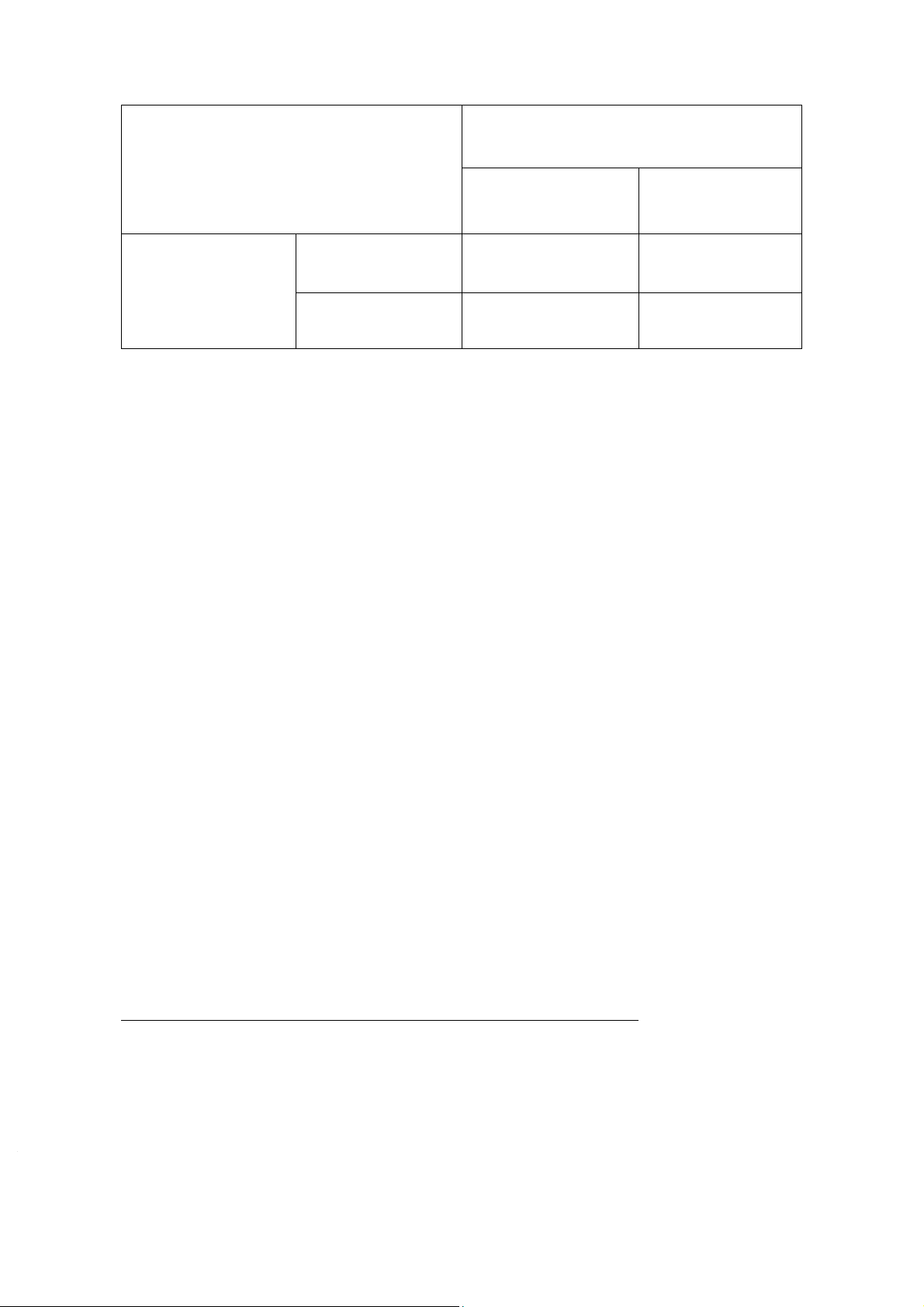
thì a2 là chiến lược tốt nhất đối với A. Nhưng nếu B chọn b2, thì a1 mới là chiến lược tốt nhất. ĐỐI THỦ B Chiến lược b1 Chiến lược b2 ĐỐI THỦ A Chiến lược a1 (1;3) (7;4) Chiến lược a2 (7;8) (6;7)
Câu hỏi đặt ra là các đối thủ A và B sẽ chọn chiến lược nào, khi không biết được chiến
lược của người kia ? Hay nói cách khác, đâu là kết cục của trò chơi.
Cân bằng Nash xảy ra tại lát cắt chiến lược (a2; b1) chính là kết cục của trò chơi. Tại
điểm cân bằng này, không đối thủ nào muốn đơn phương thay đổi chiến lược một khi đã
biết được chiến lược của người kia.Tại lát cắt chiến lược (a2, b1), đối thủ A nhận được
lợi ích là 7 và đối thủ B nhận được lợi ích là 8. Nếu A chuyển sang áp dụng chiến lược
a1, trong khi B vẫn giữ nguyên chiến lược b1, lợi ích của A sẽ chỉ còn 1 (nhỏ hơn 7).
Tương tự, nếu A vẫn giữ chiến lược a2 mà B chuyển sang chiến lược b2, lợi ích của B sẽ
bị giảm từ 8 xuống còn 7.
=> Như vậy là tại điểm cân bằng Nash (cặp chiến lược a2, b1), tốt nhất là cả 2 đối thủ
đều nên giữ nguyên lựa chọn chiến lược của mình. Nói cách khác, cân bằng Nash, một
khi đã đạt được, thì sẽ có được sự ổn định. Thuộc tính ổn định của cân bằng Nash cũng
là thuộc tính của các điểm cân bằng trong kinh tế học mà chúng ta thường gặp. Nhờ
thuộc tính này, khái niệm cân bằng Nash có thể giúp giải thích được nhiều hiện tượng 19
kinh tế - xã hội tồn tại trên thực tế, chẳng hạn như tại sao các cải cải cách kinh tế, chính
trị lại khó thực hiện. Khi một trạng thái kinh tế xã hội nào đó đã đạt được cân bằng
Nash, thì sẽ không dễ bị thay đổi.
1.2.3. Xác định cân bằng Nash trong trò chơi tuần tự
Phần lớn các trò chơi thường gặp trong cuộc sống lại là các trò chơi với những bước đi
tuần tự, trong đó một đối thủ đi trước và đối thủ còn lại, tùy thuộc vào sự lựa chọn của
đối thủ kia, sẽ chọn bước đi của mình.Để tìm lời giải cho những trò chơi với các bước đi
tuần tự, người ta có thể áp dụng phương pháp suy luận ngược. Phương pháp suy luận
ngược sẽ được làm rõ trong ví dụ sau:
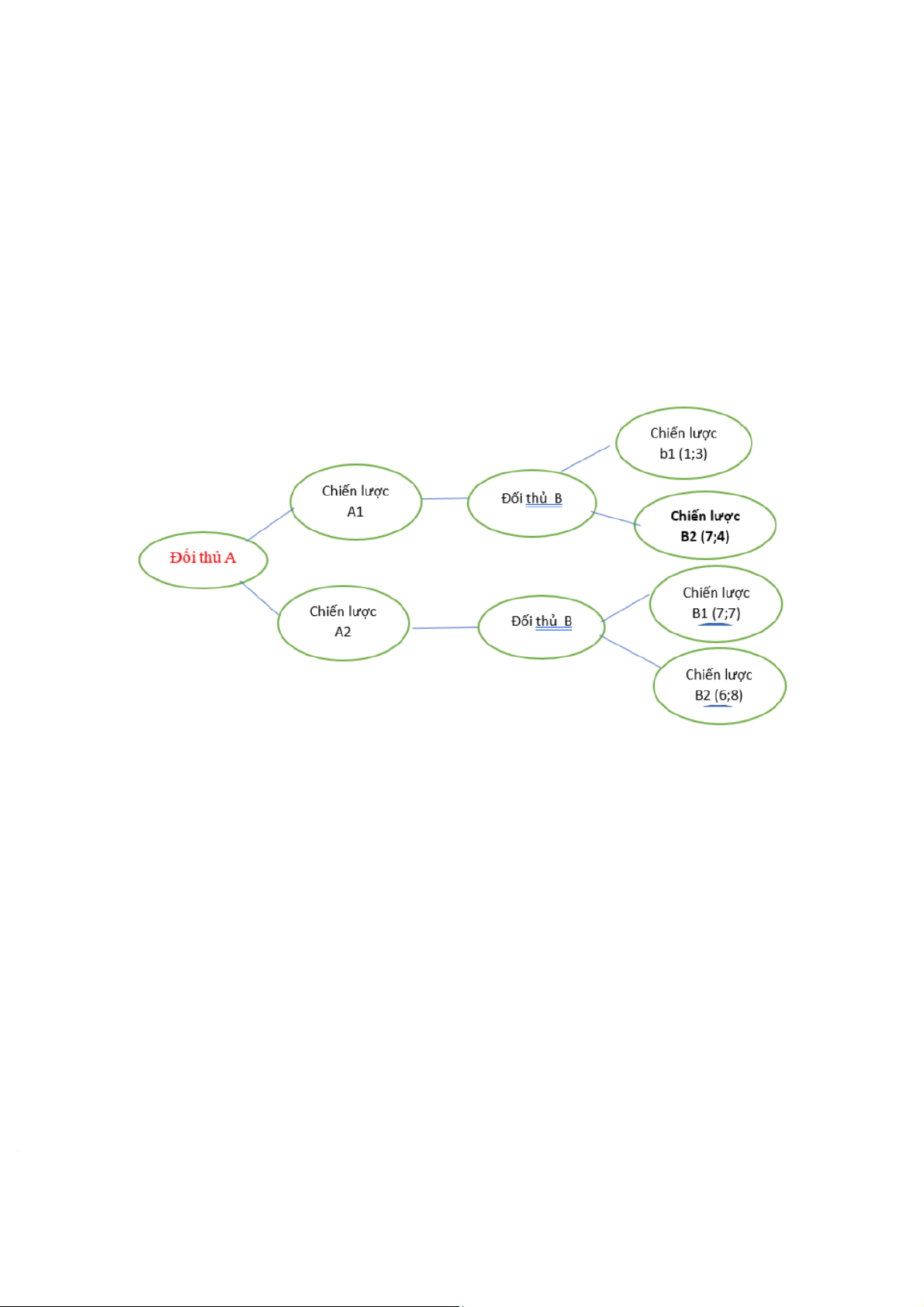
Trong trò chơi được trình bày ở sơ đồ trên , đối thủ A là người lựa chọn chiến lược
trước. Đối thủ B, tùy thuộc vào lựa chọn của đối thủ A, sẽ chọn bước đi của mình. Câu
hỏi đặt ra là đối thủ A sẽ chọn bước đi nào? Để xác định bước đi của mình, đối thủ A sẽ suy luận ngược như sau:
- Nếu A chọn chiến lược a1, B sẽ chọn chiến lược b2, vì chiến lược này sẽ đem lại
cho B lợi ích là 4, trong khi việc chọn chiến lược b1 chỉ đem lại lợi ích là 3. Nếu
B chọn chiến lược b2 và A chọn chiến lược a1, lợi ích của A sẽ là 7. 20