Ứng dụng phương pháp hàm số giải phương trình mũ và logarit

Tài liệu gồm 35 trang được biên soạn bởi tập thể quý thầy, cô giáo nhóm Nhóm Word Và Biên Soạn Tài Liệu Môn Toán THPT, hướng dẫn ứng dụng phương pháp hàm số giải phương trình mũ và logarit

106 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

35 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 696
KIẾN THỨC CẦN NHỚ:
1. Định lý: Nếu hàm số
y f x
đồng biến (hoặc luôn nghịch biến) và liên tục trên
;a b
thì
*
; ; :u v a b f u f v u v
.
* Phương trình
f x k
k const
có nhiều nhất 1 nghiệm trên khoảng
;a b
.
2. Định lý: Nếu hàm số
y f x
đồng biến (hoặc nghịch biến) và liên tục trên
;a b
, đồng thời
lim . lim ( ) 0
x a x b
f x f x
thì phương trình
f x k k const
có duy nhất nghiệm trên
;a b
.
3. Tính chất của logarit:
1.1. So sánh hai logarit cũng cơ số:
Cho số dương
1a
và các số dương
,b c
.
Khi
1a
thì log log
a a
b c b c .
Khi 0 1a thì
log log
a a
b c b c
.
1.2. Hệ quả:
Cho số dương
1a
và các số dương
,b c
.
Khi
1a
thì log 0 1
a
b b .
Khi 0 1a thì
log 0 1
a
b b
.
log log
a a
b c b c .
2. Logarit của một tích:
Cho 3 số dương
1 2
, ,a b b
với 1a , ta có
1 2 1 2
log ( . ) log log
a a a
b b b b
3. Logarit của một thương:
Cho 3 số dương
1 2
, ,a b b
với 1a , ta có
1
1 2
2
log log log
a a a
b
b b
b
Đặc biệt: với
, 0, 1a b a
1
log log
a a
b
b
.
4. Logarit của lũy thừa:
Cho
, 0, 1a b a
, với mọi
, ta có
log log
a a
b b
.
Đặc biệt:
1
log log
n
a a
b b
n
(
n
nguyên dương).
5. Công thức đổi cơ số:
Cho 3 số dương
, ,a b c
với
1, 1a c
, ta có
log
log
log
c
a
c
b
b
a
.
Đặc biệt:
1
log
log
a
c
c
a
và
1
log log
a
a
b b
với
0
.
ỨNG DỤNG PHƯƠNG PHÁP HÀM SỐ GIẢI PHƯƠNG TRÌNH MŨ VÀ LOGARIT
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 697
BÀI TẬP MẪU
Có bao nhiêu cặp số nguyên
;
x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9 ?
y
x x y
A.
. B.
6
. C.
. D.
4
.
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Ứng dụng tính đơn điệu của hàm số để giải phương trình mũ, logarit.
Phương pháp
Tìm hàm đặc trưng của bài toán, đưa phương trình về dạng
f u f v
.
2. HƯỚNG GIẢI:
B1: Đưa phương trình đã cho về dạng
f u f v
.
B2: Xét hàm số
y f t
trên miền
D
.
* Tính
y
và xét dấu
y
.
* Kết luận tính đơn điệu của hàm số
y f t
trên
D
.
B3: Tìm mối liên hệ giữa
;
x y
rồi tìm các cặp số
;
x y
rồi kết luận.
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn D
ĐK:
1
x
.
Ta có
3
log 3 3 2 9
y
x x y
3
log 3 3
2 1
3
3log 3 3 3 3 2 1 3 (*)
x
y
x y
Xét hàm số
3 3
t
f t t
trên
, vì
3 3 .ln 3 0, 0
t
f t t
nên hàm số
f t
đồng biến trên
.
Từ đó
*
3
log 3 3 2 1
f x f y
3
log 3 3 2 1
x y
.
Mặt khác
3 3 3
0 2020 log 3 3 1;log 6063 2 1 1;log 6063
x x y
3
1 2 1 log 6063
0 3
y
y
y Z
. Vậy có
4
cặp
;
x y
thỏa mãn.
Bài tập tương tự và phát triển:
Câu 47.1: Có bao nhiêu giá trị nguyên của tham số
2019; 2019
m
để phương trình
2 1 2 1
2019 0
1 2
x
x mx m
x x
có đúng 3 nghiệm thực phân biệt ?
A.
4038
. B.
2019
. C.
2017
. D.
4039
.
Lời giải
Chọn C
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 698
TXĐ:
\ 1; 2 . D
Ta có
2 1 2 1
2019 0
1 2
2 1 ( 2) 1
2019 0
1 2
2 1 1
2019 . (*)
1 2
x
x
x
x mx m
x x
x m x
x x
x
m
x x
Đặt
2 1 1
( ) 2019 .
1 2
x
x
f x
x x
Khi đó
2 2
3 1
'( ) 2019 ln 2019 0 .
( 1) ( 2)
x
f x x D
x x
Ta có bảng biến thiên
Dựa vào bảng biến thiên, để phương trình
(*)
có 3 nghiệm thực phân biệt thì
2 2. m m
Mà
2019; 2019 m
và
m
nên có
2017
giá trị
m
thỏa mãn.
Câu 47.2: Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020y
và
3
2 1
log 1 2 ?
x
x
y
y
A. 2019. B.
11
. C. 2020 . D.
4
.
Lời giải
Chọn B
Từ giả thiết ta có:
0
2 1
0 2 1 0
0
x
x
y
x
y
y
Ta có: PT
3 3
log 2 1 2 1 log (*)
x x
y y
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 699
Xét hàm số
3
log
f t t t
trên
0;

Khi đó
1
1 0
ln 3
f t
t
do đó hàm số
3
log
f t t t
đồng biến trên
0;

(*) có dạng
2 1 2 1
x x
f f y y
Vì
2
0 2020 0 2 1 2020 1 2 2021 0 log 2021
x x
y x
2
0 log 2021
0;1;2;3;4;5;6;7;8;9;10
x
x
x
. Vậy có
11
cặp
;
x y
thỏa mãn.
Câu 47.3: Có bao nhiêu giá trị nguyên của tham số
m
để tồn tại cặp số
;
x y
thỏa mãn
3 5 3 1
e e 1 2 2
x y x y
x y
, đồng thời thỏa mãn
2 2
3 3
log 3 2 1 6 log 9 0
x y m x m
?
A.
6
. B.
5
. C.
8
. D.
7
.
Lời giải
Chọn B
Ta có
3 5 3 1
e e 1 2 2
x y x y
x y
3 5 3 1
e 3 5 e 3 1
x y x y
x y x y
(1)
Xét hàm số
e
t
f t t
trên
. Ta có
e 1 0
t
f t
nên hàm số đồng biến trên
.
Khi đó (1)
3 5 3 1
f x y f x y
3 5 3 1
x y x y
2 1 2
y x
.
Thế vào phương trình còn lại ta được
2 2
3 3
log 6 log 9 0
x m x m
(2)
Đặt
3
log
t x
. Số nghiệm của phương trình (2) chính là số nghiệm của phương trình
2 2
6 9 0
t m t m
(3)
Phương trình (3) có nghiệm khi
0
2
3 12 0
m m
0 4
m
.
Do đó có
5
số nguyên
m
thỏa mãn.
Câu 47.4: Có bao nhiêu số nguyên của
m
để phương trình
2
2 2
log 2 2log 4 2 1
x m x x x m có
hai nghiệm thực phân biệt ?
A.
2
. B.
3
. C.
1
. D.
4
Lời giải
Chọn C
Điều kiện
0
2
x
m
x
2
2 2
log 2 2log 4 2 1
x m x x x m
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 700
2
2 2
2 2
2 2
log 2 2log 2 2 1
log 2 2 2 1 log
x m x x x m
x m x m x x
2 2
2 2
log 2 2 2 2 logx m x m x x (1)
Xét
2
log , 0 f u u u u
1
' 1 0
ln 2
f u
u
, do đó hàm số đồng biến trên (0; ) .
Khi đó (1)
2 2 2
2 2 2 2 4 2f x m f x x m x x x m
Xét hàm số
2
4 , 0g x x x x
Phương trình có 2 nghiệm dương khi 4 2 0 2 0 m m suy ra có 1 giá trị nguyên.
Câu 47.5: Biết
1
x ,
2
x là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
2
4
x x a b
với
a
,
b
là hai số nguyên dương. Tính
a b
.
A. 13 a b . B. 11 a b . C. 16 a b . D. 14 a b .
Lời giải
Chọn D
Điều kiện:
1
0,
2
x x
.
Ta có:
2
2 2 2
7 7 7
4 4 1
log 4 1 6 log 4 4 1 4 4 1 log 2 2
2
x x
x x x x x x x x
x
.
Xét hàm số
7
log f t t t có
1
1 0
ln7
f t
t
0 t
nên là hàm số đồng biến trên
0;
.
Do đó ta có
2 2
3 5
4 4 1 2 4 6 1 0
4
x x x x x x
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 701
Khi đó
1 2
3 5 3 5 1
2 2 9 5
4 4 4
x x hoặc
1 2
3 5 3 5 1
2 2 9 5
4 4 4
x x .
Vậy
1 2
3 5 3 5
;
4 4
x x . Do đó
9; 5
a b và
9 5 14
a b
.
Câu 47.6: Biết phương trình
5 3
2 1 1
log 2log
2
2
x x
x
x
có một nghiệm dạng
2
x a b
trong
đó
,
a b
là các số nguyên. Tính
2
a b
.
A.
3
. B.
8
. C.
4
. D.
5
.
Lời giải
Chọn B
Ta có
5 3 5 3
2 1 1 2 1 1
log 2log log 2log 1 .
2
2 2
x x x x
x x
x x
ĐKXĐ:
1
x
.
5 3 5 3
1 log 2 1 2log 2 log 2log 1 (*)
x x x x
Xét hàm số
5 3
log 2log 1
f t t t
, với
1
t
.
1 2
0
.ln 5 1 ln 3
f t
t t
với mọi
1
t
, suy ra
f t
đồng biến trên khoảng
1;
.
Từ (*) ta có
2 1
f x f x
nên suy ra
2
2 1 2 1 0 1 2
x x x x x
(do
1
x
).
Suy ra
3 2 2 3; 2 2 8
x a b a b .
Câu 47.7: Tìm tổng tất cả các giá trị nguyên của
m
để phương trình
3
3 3 3 2 3
3 9 24 .3 3 1
x m x x x
x x x m có 3 nghiệm phân biệt.
A.
45
. B.
34
. C.
27
. D.
38
.
Lời giải
Chọn C
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 702
3
3
3
3 3 3 2 3
3
3 3 3
3
3 3 3
3 9 24 .3 3 1
3 3 27 3 .3 3 1
3 3 3 27 3 3 1
x m x x x
x m x x x
m x x
x x x m
x m x
x m x
3 3 3 3
1 3 27 27. 3 3 3
b a b a
b a b a
Đặt
3
3 ; 3a x b m x , phương trình (1) trở thành
3 3 3 3
3 27 27. 3 3 3
b a b a
b a b a .
Xét hàm số
3 2
3 ' 3 .ln 3 3 0,
t t
f t t f t t t
3
3
3 2
(1) 3 3
3 3 9 24 27
f a f b a b x m x
m x x x x x
3 2 2
9 24 27 ' 3 18x 24
' 0 2 4
g x x x x g x x
g x x x
Đồ thị:
Dựa vào đồ thị ta thấy điều kiện để phương trình có 3 nghiệm phân biệt là 7 11m hay
8;9;10m .
Câu 47.8: Tìm các giá trị
m
để phương trình
sin 5 cos 5
sin 5 cos 10
3 log 5
x x m
x x
m có nghiệm.
A. 6 6 m . B.
5 5 m
. C.5 6 5 6 m . D. 6 5 m .
Lời giải
Chọn C
Ta có
sin 5 cos 5
sin 5 cos 10
sin 5 cos 10
5
3 log 5
ln 5
3
3
ln sin 5 cos 10
x x m
x x
x x
m
m
m
x x
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 703
5
sin 5cos 10
3 .ln sin 5 cos 10 3 .ln 5
m
x x
x x m
(1)
Xét
ln .3 , 5
t
f t t t
, vì
1
3 ln 3 ln 3 0, 5
t t
f t t t
t
nên hàm số
f t
đồng
biến trên
(5; )

.
Khi đó
(1) sin 5 cos 10 5
f x x f m
sin 5 cos 10 5
sin 5 cos 5
x x m
x x m
Mà
6 sin 5 cos 6
x x nên để phương trình có nghiệm ta phải có
5 6 5 6.
m
Câu 47.9: Số nghiệm thực của phương trình
6
6 3log 5 1 2 1
x
x x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Điều kiện:
1
5
x
.
PT:
6
log 5 1
6 6
6 3 3log 5 1 5 1 6 3 6 3log 5 1 (1)
x
x x
x x x x x
.
Xét hàm số
6 3
t
f t t
, vì
6 .ln 6 3 0,
t
f t t
nên
f t
đồng biến trên
.
Khi đó
1
6 6 6
log 5 1 log 5 1 log 5 1 0
f x f x x x x x
Xét hàm số
6
log 5 1
h x x x
trên
1
;
5

, ta có
5
1
5 1 ln 6
h x
x
2
25 1
0,
5
5 1 ln 6
h x x
x
và
1
5
lim ; lim 1
x
x
h x h x


Bảng biến thiên:
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 704
Từ BBT suy ra phương trình
0h x
có nhiều nhất 2 nghiệm thuộc khoảng
1
;
5

Mà
0 0, 1 0h h
.
Vậy phương trình đã cho có đúng hai nghiệm
0, 1x x
.
Câu 47.10: Tính tổng S tất cả các nghiệm của phương trình
1
5 3
ln 5 5.3 30 10 0
6 2
x x
x x
x
x
.
A. 1S . B. 2S . C. 1S . D. 3S .
Lời giải
Chọn A
Điều kiện
1
.
3
x
Phương trình tương đương
ln 5 3 ln 6 2 5 5 3 5 6 2 0
x x x x
x x
ln 5 3 5 5 3 ln 6 2 5 6 2
x x x x
x x
(1).
Xét hàm số
ln 5 , 0f t t t t
. Có
1
' 5 0f t
t
,
0t
nên
f t
đồng biến trên
0;
.
Từ
1
suy ra
5 3 6 2
x x
f f x 5 3 6 2
x x
x 5 3 6 2 0
x x
x
Xét
5 3 6 2
x x
g x x
,
' 5 ln5 3 ln3 6
x x
g x
2 2
'' 5 ln 5 3 ln 3 0
x x
g x ,
1
3
x .
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 705
Nên
' 0g x
có không quá 1 nghiệm suy ra
0g x
có không quá 2 nghiệm trên
1
;
3

. Mà
0 1 0g g
. Vậy phương trình có tập nghiệm là
0,1 . Do đó 1.S
Câu 47.11: Số nghiệm của phương trình
2
1 2
80
ln 2.3 2 80 ln 3
3
x
x
x
x
là
A.
2
. B.
3
. C. 1. D. 0.
Lời giải
Chọn C
PT
2 2 1 1
ln 80 2 80 ln 3 2.3 (1)
x x
x x
Xét hàm số
ln 2 , 0f t t t t
; Ta có:
1
2 0, 0f t t
t
Hàm số
f t
đồng biến
trên
0;
.
Từ (1) suy ra
2 1 2 1 2 1 1 2
80 3 80 3 80 9 9 80 0
x x x x
f x f x x x
Xét hàm số
1 2
9 80
x
g x x
trên . Ta có:
1
2
1
2.9 ln3 2
4.9 ln 3 2
x
x
g x x
g x
2 2
0 9 0 9
0 log 2ln 3 1 ( ) log 2ln 3 1 3,7 0g x x x g x g
lim ; lim ( )
x x
g x g x
 
 
Bảng biến thiên:
Dựa vào bảng biến thiên ta có
' 0,g x x
hàm số
g x
đồng biến trên
phương trình
0g x
có nhiều nhất một nghiệm.
Mà
1 0g
Do đó phương trình đã cho có duy nhất 1 nghiệm .
Câu 47.12: Cho phương trình
2
2 log
x
m x m
với m là tham số. Có bao nhiêu giá trị nguyên của
18;18m
để phương trình đã cho có hai nghiệm?
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 706
A. 20. B. 17 . C. 9 . D.
21
.
Lời giải
Chọn B
Điều kiện x m
PT
5
log ( )
2 2
2 log 2 2 log ( ) (1)
x mx x
x x m x m x x m
Xét hàm số
2 ,
t
f t t t
; Ta có:
2 ln 2 1 0,
t
f t t
Hàm số
f t
đồng
biến trên
.
Từ (1) suy ra
2 2
log ( ) log ( )f x f x m x x m 2 2
x x
x m m x
Xét hàm số
2
x
g x x
trên
;m 
. Ta có:
' 1 2 ln 2
x
g x
;
2 2
' 0 2 ln2 1 log log
x
g x x e
2 2 2 2 2
log log log log logg e e e
lim 2 ; lim ( )
m
x
x m
g x m g x


Bảng biến thiên:
Do đó. Phương trình đã cho có 2 nghiệm
2 2 2 2 2 2
2 log log log log log log 0,91
m
m m e e m e e
Vì
18;18
m
m
nên
17; 16; 15;....; 1 m
Vậy có 17 giá trị của m .
Câu 47.13: Cho phương trình
3 2 3 2
3 1 3 1 2
3 2
81 3
3 2
1
2 .log 3 1 2 2 .log 0
3 1 2
m m x x
x x
m m
Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có
6
nghiệm hoặc
7
nghiệm
hoặc 8 nghiệm phân biệt . Tính tổng bình phương tất cả các phần tử của tập
S
.
A. 20. B. 19. C. 14 . D. 28 .
Lời giải
Chọn A
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 707
Ta có
3 2 3 2
3 1 3 1 2
3 2
81 3
3 2
1
2 .log 3 1 2 2 .log 0
3 1 2
m m x x
x x
m m
3 2 3 2
3 1 2 3 1 2
3 2 3 2
3 3
2 .log 3 1 2 2 .log 3 1 2
x x m m
x x m m
.
Xét hàm số
3
2 .log
t
f t t
với 2t ; Ta có
3
1
2 ln 2.log 2 . 0 2
ln3
t t
f t t t
t
.
Suy ra hàm số
f t
đồng biến trên
2;
.
Do đó phương trình tương đương với
3 2 3 2
3 1 3 1 1m m x x
.
Vẽ đồ thị hàm số
3 2
3 1g x x x
từ đó suy ra đồ thị
g x
và đồ thị của
g x
như hình
vẽ.
Từ đồ thị suy ra
1
có
6, 7,8
nghiệm
0 3g m
.
Từ đồ thị suy ra các giá trị nguyên của
m
là
3, 1,0,1,3
.
Vậy 20S .
Câu 47.14: Cho phương trình
2
2
2 2
2 log 2 4 log 2 2
x a
x
x x a
. Gọi S là tập hợp các giá trị
a thuộc đoạn
0;2020
và chia hết cho 3 để phương trình có hai nghiệm. Hãy tính tổng các
phần tử của S .
A. 0. B. 2041210 . C. 680403. D. 680430 .
Lời giải
Chọn C
Phương trình tương đương
2
2
2
2 2
2 log 2 2 log 2 2
x a
x
x x a
2
2
2
2 2
4.2 log 2 4.2 log 2 2
x a
x
x x a
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 708
2
2 2
2 2
2 2
2 log 2 2 log 2 2
x a
x
x x a
(*)
Xét hàm số
2 log , 2
t
f t t t
. Có
2
2
' 2 ln 2.log 0, 2
ln 2
t
t
f t t t
t
, nên
f t
đồng
biến
2;
.
Khi đó (*)
2
2
2 2 2
2 2; 2 | | 2 2
f x f x a
x x a
2
2
x x a
(1)
2
2
2 2
2
2 2 0 (2)
2 2 2 0 (3)
x x a
x x a
x x a x x a
Phương trình (2)
2
1 2
a
, phương trình (3) có
(3)
1 2
a
.
Vì
(3)
2
2 0
nên ít nhất một trong hai phương trình (2), (3) luôn có hai nghiệm phân
biệt. Để phương trình (1) có hai nghiệm phân biệt, ta xét các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt:
2
1
0 1 2 0
2
a a
. Khi đó
(3)
0
nên (3) vô
nghiệm. Trường hợp này thỏa mãn điều kiện bài toán.
* TH1: (3) có hai nghiệm phân biệt:
(3)
1
0 1 2 0
2
a a
. Khi đó
(2)
0
nên (2) vô
nghiệm. Trường hợp này cũng thỏa mãn điều kiện bài toán.
Do đó phương trình đã cho có 2 nghiệm khi và chỉ khi
1 1
; ;
2 2
a

Vì
0;2020
a và chia hết cho 3 nên
3;6;9;12;...,2019
a S
Tổng các phần tử của
S
là:
3 6 9 ... 2019 3.1 3.2 3.3 ... 3.673
673.674
3 1 2 3 ... 673 3. 680403
2
BỔ SUNG CÁCH 2:
Xét phương trình
2
2
x x a
*
Vẽ đồ thị hàm số
2
1 ; 2 2
y x y x a trên cùng một hệ trục tọa độ ta được:
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 709
Xét 2 vị trí nhánh trái và phải của đồ thị hàm số
2
tiếp xúc với
1
khi đó dễ dàng tìm được
1 1
;
2 2
a a
ứng với đồ thị
2 ; 3 (hình vẽ).
Từ đồ thị nhận xét :
Phương trình
* đã cho có 2 nghiệm khi và chỉ khi
1 1
; ;
2 2
a
 
Vì
0;2020a
và chia hết cho 3 nên
3;6;9;12;...,2019a S
Tổng các phần tử của S là: 3 6 9 ... 2019 3.1 3.2 3.3 ... 3.673
673.674
3 1 2 3 ... 673 3. 680403
2
Câu 47.15: Có bao nhiêu giá trị thực của tham số a để phương trình
2
2 2
1
2
2
4 log 2 3 2 log 2 2 0
x a
x x
x x x a
có 3 nghiệm thực phân biệt ?
A. 0. B. 2 . C. 1. D. 3.
Lời giải
Chọn D
PT đã cho tương đương với
1 1
2
2
2
2
2
2
2
1 1
log 2 3 log 2 2 0
2
2
x a
x x
x x x a
.
2
2
2
2
2 2
2
2
2
2 1 2
2 2
2 2
2 3 2
2 2
2 1
log 2 3 log 2 2
2
2
2 log 2 3 2 log 2 2
2 log 2 3 2 log 2 2 (1)
x a
x x
x a
x x
x a
x x
x x x a
x x x a
x x x a
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 710
Xét hàm số
2
2 .log , 2
t
f t t t
; Ta có:
2
2 ln 0, 2
ln 2
t
t
f t t t
t
Hàm số
f t
đồng biến trên
2;

.
Từ (1) suy ra
2 2
2 3 2 2 2 3 2 2
f x x f x a x x x a
2
2 1 2
x x x a
(*)
2
2
2 2
2 1 2
4 2 1 0 (2)
2 1 2 2 1 (3)
x x x a
x x a
x x x a x a
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):
2
(3)
3
0
3 2 0
1
2
2 1 0 1
2
0
2
a
a
a
a
a
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):
2
(3)
3
0
3 2 0
3
2
2 1 0 1
2
0
2
a
a
a
a
a
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung:
Điều này xảy ra khi hệ
2
2
4 2 1 0
2 1
x x a
x a
có nghiệm
2
2
4 2 1 0 1
1 1
2 1
x x a x a x
a a
x a
Khi
1
a
ta có:
2
trở thành
2
1
4 3 0
3
x
x x
x
3
trở thành
2
1
1
1
x
x
x
Khi đó: PT đã cho có 3 nghiệm.
Vậy
1 3
;1;
2 2
a
.
BỔ SUNG CÁCH 2:
Xét phương trình
2
2 1 2
x x x a
*
Vẽ đồ thị hàm số
2
2 1 1 ; 2 2
y x x y x a trên cùng một hệ trục tọa độ ta được:
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 711
Nhận xét
*
có 3 nghiệm phân biệt
nh¸nh bªn tr¸i cña (2) tiÕp xóc víi (1)
nh¸nh bªn ph¶i cña (2) tiÕp xóc víi (1)
(1) vµ (2) cïng trïng cùc trÞ t¹i 1
2
2
1
2
2 1 2
3
2 1 2
2
1
1
cã nghiÖm kÐp
cã nghiÖm kÐp
a
x x a x
x x x a a
a
a
Vậy có
3
giá trị của
a
thỏa mãn bài toán.
Câu 47.16: Tìm tổng tất cả các giá trị của tham số a để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x a
x x
x a
có đúng ba nghiệm phân biệt.
A.
2
. B.
3
. C. 1. D. 0.
Lời giải
Chọn B
PT đã cho tương đương với
2
2 3 2 2
2
ln 2 2
3
ln 2 3
x x x a
x a
x x
2
2 2
2 3 2
3 .ln 2 3 3 .ln 2 2 (1)
x a
x x
x x x a .
Xét hàm số
3 .ln , 2
t
f t t t
; Ta có:
3
3 ln 3.ln 0, 2
t
t
f t t t
t
Hàm số
f t
đồng biến trên
2;
.
Từ (1) suy ra
2 2
2 3 2 2 2 3 2 2f x x f x a x x x a
2
2 1 2x x x a
(*)
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 712
2
2
2 2
2 1 2
4 2 1 0 (2)
2 1 2 2 1 (3)
x x x a
x x a
x x x a x a
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):
2
(3)
3
0
3 2 0
1
2
2 1 0 1
2
0
2
a
a
a
a
a
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):
2
(3)
3
0
3 2 0
3
2
2 1 0 1
2
0
2
a
a
a
a
a
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung:
Điều này xảy ra khi hệ
2
2
4 2 1 0
2 1
x x a
x a
có nghiệm
2
2
4 2 1 0 1
1 1
2 1
x x a x a x
a a
x a
Khi
1
a
ta có:
2
trở thành
2
1
4 3 0
3
x
x x
x
3
trở thành
2
1
1
1
x
x
x
Khi đó: PT đã cho có 3 nghiệm.
Vậy
1 3
;1;
2 2
a
.
Câu 47.17: Tìm số giá trị nguyên của
m
thuộc
20;20
để phương trình
2 2 2
2
log ( 4) (2 9) 1 (1 2 ) 4
x m x x m x m x
có nghiệm.
A. 12. B. 23. C. 25. D. 10.
Lời giải
Chọn B
Điều kiện xác định:
2 2
4 0
x m x x
.
2 2 2
2
log 4 2 9 1 1 2 4
x m x x m x m x
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 713
2 2 2
2
log 4 2 9 1 4 2 4
x x x m mx x x m x
2 2
2
2
4
log 2 9 1 4 2 4
4
x
m mx x x m x
x x
2
2 2
2
2
4 4
log 2 9 1 4 2 4
4
x m x mx
mx x x m x
x x
2 2 2 2
2 2
log 4 4 8 2 4 2 1 log 4 4
x m x mx x m x mx x x x x
2 2 2 2
2 2
log 8 2 4 2 8 2 4 2 log 4 4 1
x m x mx x m x mx x x x x
Xét hàm số
2
log
f t t t
,
0;

t .
1
1 0, 0;
ln 2
f t t
t
nên hàm số đồng biến trên
0;

.
Khi đó
1
2 2
8 2 4 2 4
x m x mx x x
2 2
2 4 4 8
m x x x x x
2
8
2 1
4
x
m
x x
2
8 4
2 1
4
x x x
m
2
2 1 2 4
m x x x
2 2
1 2
4
2
m
x x x
.
Xét hàm số
2 2
( ) 4
g x x x x
với
;

x
.
Ta có
2
2
2
4
( ) 0,
4
x x
g x x
x
.
2
lim lim 4
 
x x
g x x x x
2
4
lim
4

x
x
x x
2
4
lim 2
4
1 1

x
x
;
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 714
2
2
4
lim lim 1 1
 

x x
g x x
x
.
Ta có bảng biến thiên của ( )g x
Để phương trình có nghiệm thì
1 2 5
2
2 2
m
m
.
Do
m
nguyên thuộc
20;20
nên số giá trị
m
là 23.
Câu 47.18: Cho
,x y
là hai số thực dương thỏa mãn
2 2 2
2 2 2 2
4 9.3 4 9 .7 .
x y x y y x
Giá trị nhỏ nhất
của biểu thức
2 18x y
P
x
là
A. 9. B.
3 2
.
2
C. 1 9 2. D. 17.
Lời giải
Chọn A
Ta có
2 2 2 2 2 2
2 2 2 2 2 2 2( 2 ) 2 2
4 9.3 4 9 .7 4 3 4 3 .7
x y x y y x x y x y y x
2 2
2 2
2 2 2( 2 )
2 2 2( 2 )
4 3 4 3
(*).
7 7
x y x y
x y x y
Xét hàm số
4 3
( )
7
t
t
f t trên
.
Ta có
1 3
( ) 4.
7 7
t t
f t
nghịch biến trên
.
2 2 2 2 2 2
(*) 2 2 2( 2 ) 2 2 2( 2 ) 2 2 2 2.
f x y f x y x y x y x y y x
Từ đó
2
16 16 16
1 2 . 1 9.
x x
P x x P
x x x
Dấu
" "
xảy ra khi và chỉ khi
4.x
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 715
Câu 47.19: Cho các số dương
,
x y
thỏa mãn
5
1
log 3 2 4
2 3
x y
x y
x y
. Giá trị nhỏ nhất của biểu
thức
4 9
6 2
A x y
x y
bằng
A.
31 6
.
4
B.
11 3.
C.
27 2
.
2
D.
19.
Lời giải
Chọn D
ĐK:
1
0
2 3
1
, 0
x y
x y
x y
x y
Ta có:
5
5 5
5 5
1
log 3 2 4
2 3
log 1 1 5 1 log 2 3 2 3
log 5 1 5 1 log 2 3 2 3 *
x y
x y
x y
x y x y x y x y
x y x y x y x y
Xét hàm số
5
( ) log
f t t t
trên
0;
, vì
1
( ) 1 0, 0;
ln5
f t t
t
nên hàm số
( )
f t
đồng biến trên
0; .
* 5 1 2 3 3 2 5
x y x y x y
Mặt khác, ta có
4 9 4 9
6 2 9 4 3 2 2.6 2.6 5 19
A x y x y x y
x y x y
.
Dấu “ = ” xảy ra
4
9
2
9
3
4
3
2
3 2 5
x
x
x
y
y
y
x y
(thỏa mãn điều kiện).
Vậy GTNN của
A
là 19.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 716
Câu 47.20: Cho hai số thực
,
x y
lớn hơn 1 và thỏa mãn
.( ) .( ) .
y x
x x e y y e
y e x e
Tìm giá trị nhỏ nhất của
biểu thức
log log .
x y
P xy x
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Lời giải
Chọn C
Với
, 1
x y
, ta có
.( ) .( )
ln .( ) ln .( )
ln ln
ln ln
(1).
y x
y x
x x e y y e
x x e y y e
y x
y x
y e x e
y e x e
x y xe y x ye
y e x e
y y x x
Xét hàm số
( ) 1 ln
t t
g t te e t
trên
1; ,

có
1
( ) 0, 1.
t
g t te t
t
Hàm số
( )
g t
đồng biến trên
1;

nên
( ) (1) 1 0, 1.
g t g t
Xét hàm số
ln
( )
t
t e
f t
t t
trên
1;

, có
2
( )
'( ) 0, 1,
g t
f t t
t
nên
( )
f t
đồng biến trên
(1; ).
Với
, 1
x y
thì
(1) ( ) ( ) .
f y f x y x
Đặt
log .
x
u y
Do
1
y x
nên
1.
u
Ta có
1 1
( ) .
2
u
P h u
u
Nhận thấy
2
2
2
'( )
2
u
h u
u
,
nên
'( ) 0
h u khi
2,
u
'( ) 0
h u khi
1 2,
u
'( ) 0
h u khi
2.
u
Dẫn tới
1 2 2
( ) 2 , 1,
2
P h u h u đẳng thức xảy ra khi
2.
u
Vậy
1 2 2
min ,
2
P đạt được khi
2
y x
và
1.
x
Câu 47.21: Cho hai số thực
,
x y
thỏa mãn
0 , 1
x y
trong đó
,
x y
không đồng thời bằng 0 hoặc 1 và
3
log 1 . 1 2 0
1
x y
x y
xy
. Tìm giá trị nhỏ nhất của
P
với
2
P x y
A.
2
. B.
1
. C.
1
2
. D.
0
.
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 717
Chọn B
Từ điều kiện đề bài và
0;1 0
1
x y
xy
xy
0;1 0
x y xy
khi đó
3 3 3
log 1 . 1 2 0 log log 1 1 1
1
x y
x y x y x y xy xy
xy
Xét hàm số
3
log 0
f t t t t có
1
1 0 0
.ln 3
f t t
t
f t
là hàm số đồng biến trên khoảng
0;
.
Vậy phương trình
1 1
1 1 2
1 1
x x
x y xy y P x
x x
Xét hàm số
1
( ) 2
1
x
f x x
x
với
0; 1
x
có
2
2
( ) 2
1
f x
x
cho
0
( ) 0
2
x
f x
x
0;1
0 1; 1 2 min ( ) 1
f f f x
chọn B
Câu 47.22: Xét các số thực dương
x
,
y
thỏa mãn
1 2
ln 3 1
x
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
1 1
P
x
xy
.
A.
min
8
P
. B.
min
4
P
. C.
min
2
P
. D.
min
16
P
.
Lời giải
Chọn A
Điều kiện
1
0
2
x
.
Từ giả thiết
1 2
ln 3 1
x
x y
x y
ln 1 2 1 2 ln
x x x y x y
1
Xét hàm số
ln
f t t t
trên

0;
có
1
f t
t
,
0
t
do đó hàm
f t
đơn điệu.
Vậy
1 1 2 3 1
x x y x y
2
Có
1 1 1 2 1 2
1 2
P
x x x y x x
xy
Đặt
1 2
1 2
g x
x x
, ta có
2 2
1 4
1 2
g x
x
x
suy ra
1
0
4
g x x
.
Do đó
1
0;
2
min 8
g x
. Vậy
min
8
P
.
Bổ sung: có thể đánh giá
1 1 1 2 1 2 4 1
1
1 2 8
2
P
x x x y x x
xy
x x
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 718
Câu 47.23: Cho hai số thực ,x y không âm thỏa mãn
2
2
2 1
2 1 log
1
y
x x y
x
. Giá trị nhỏ nhất của
biểu thức
2 1 2
4 2 1
x
P e x y
là
A.
1
2
. B.
1
. C.
1
2
. D.
1
.
Lời giải
Chọn A
2
2
2 1
2 1 log
1
y
x x y
x
2 2
2 2
2 1 log 2 1 log 2 1 2 1x x y y
.
Xét hàm số
2
log , 0f t t t t
;
1
1 0, 0
.ln 2
f t t
t
Suy ra
2
2 1 2 1x y
2
2 2 1 1y x
.
2 1 2
4 2 1
x
P e x y
2
2 1 2
4 2 1 1 1
x
e x x
2 1 2
2 4
x
e x x g x
.
2 1
2 4 4
x
g x e x
là hàm số đồng biến trên nửa khoảng
0;
nên
0g x
có tối đa 1
nghiệm, nhẩm được nghiệm
1
2
x
nên nghiệm đó là duy nhất.
Vậy
1
min
2
P
tại
1
2
x
.
Câu 47.24: Cho hai số thực dương
x
, y thay đổi thỏa mãn đẳng thức
2
2 1 2
1 .2 .2 .
xy x y
xy x y
Tìm giá trị nhỏ nhất
min
y của y .
A.
min
3y . B.
min
2y . C.
min
1y . D.
min
3y
.
Lời giải
Chọn B
Ta có
2
2 1 2
1 2 2
xy x y
xy x y
2
2 1 2 1
2 1 1 2 2 1
xy x y
xy x y
Xét hàm
1 .2
t
f t t
với 1t .
Khi đó
2 1 .2 .ln2 0
t t
f t t
với
1t
.
Từ
2
1 2 1 1xy x y
2
2
2 1
x
y
x
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 719
2
2
2 2 4
0
2 1
x x
y
x
2
2 2 4 0
x x
2
1
x
x
Loại
1
x
vì điều kiện của
t
nên
2 2
f
.
Câu 47.25: Cho
,
, 1
x y
x y
sao cho
3 3
ln 2 ln 3 19 6 ( 2 )
x
x y xy x y
y
. Tìm giá trị nhỏ nhất
m
của biểu thức
1
3
T x
x y
.
A.
1 3
m
. B.
2
m
. C.
5
4
m
. D.
1
m
.
Lời giải
Chọn C
Ta có
3 3
3 3
ln 2 ln3 19 6 ( 2 ) ln 2 2 ln 3 3 1
x
x y xy x y y x y x y y
y
Xét hàm số
3
ln
f t t t
với
0
t
có
2
1
3 0 0
f t t t f t
t
đồng biến
Vậy
1
1 2 3
4
y x y x y T x
x
Áp dụng bất đẳng thức AM-GM
1 3 1 3 1 3 1 3 1 5
2 .
4 4 4 4 4 4 4 4 2 4 2 4
x x x x x
T x
x x x
Dấu bằng xảy ra khi
1
x y
Câu 47.26: Cho
;
x y
là các số thực dương thỏa mãn điều kiện
4 4
3 5
5 1 3 4
3 5
xy
x y x y
xy
x y x
. Tìm giá trị nhỏ nhất của biểu thức
P x y
.
A.
3
. B.
5 2 5
. C.
3 2 5
. D.
1 5
.
Lời giải
Chọn B
Ta có
4 4
3 5
5 1 3 4
3 5
xy
x y x y
xy
x y x
4 4 1 1
5 3 4 5 3 1 1
x y x y xy xy
x y xy
.
Xét hàm số
5 3
t t
f t t
trên
.
Vì
5 .ln5 3 .ln 3 1 0;
t t
f t x
nên hàm số
f t
đồng biến trên
2
.
Từ
1
và
2
ta có
4 1 3
x y xy
. Dễ thấy
4
x
không thỏa mãn
3
.
Với
4
x
,
1
3
4
x
y
x
kết hợp điều kiện
0
y
suy ra
4
x
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 720
Do đó
1
4
x
P x y x
x
.
Xét hàm số
1
4
x
g x x
x
trên
4; .
Ta có
2
5
1 0
4
g x
x
4 5
4 5
x
x
.
x
4
4 5

g x
–
0
g x

5 2 5

Dựa vào bảng biến thiên ta có
min
4;
min 5 2 5P g x

.
Câu 47.27: Cho
x
, y là các số thực dương thỏa mãn
2 2
3 5
5 1 3 ( 2)
3 5
xy
x y x y
xy
x y x
. Tìm giá
trị nhỏ nhất của biểu thức T x y .
A.
min
2 3 2 T . B.
min
3 2 3 T . C.
min
1 5 T . D.
min
5 3 2 T .
Lời giải
Chọn B
Theo đề ra ta có
2 2
2 1
2 1
3 5
5 1 3 ( 2)
3 5
1 1
5 2 5 1
3 3
xy
x y x y
xy
x y xy
x y xy
x y x
x y xy
Xét
1
5
3
t
t
f t t
.
5 ln 5 3 ln 3 1 0
t t
f t
1
2 1
2
x
x y xy y
x
.Do
1
0, 0 0 2
2
x
y x x
x
Ta có:
2
1 1
2 2
x x x
T x y x
x x
2
2
2 3 2;
4 1
0
2
2 3 2;
x
x x
T
x
x


Bảng biến thiên
Chỉnh lại bbt cho em,chỉ xét với
2x
nhé,kết quả không thay đổi.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 721
Từ bảng biến thiên ta thấy
min
3 2 3 T tại 2 3 x .
Câu 47.28: Xét các số thực dương ,x y thỏa mãn
3
3
log 3 1
1
x y
xy y x
xy
. Tìm giá trị nhỏ nhất của
biểu thức
1
A x
y
.
A.
min
14
3
A . B.
min
14
3
A . C.
min
6A
. D.
min
6A
.
Lời giải
Chọn D
Điều kiện:
3 0x y
.
3 3 3
3
log 3 1 log 3 log 1 3 1
1
x y
xy y x x y xy xy y x
xy
3 3
log 3 3 log 1 1 1x y x y xy xy .
Xét hàm
3
log , 0f t t t t .
1
1 0, 0
.ln3
f t t
t
.
Suy ra hàm số
f t đồng biến trên
0; nên
1
1 3 1
3
x
x y xy y
x
.
1 3
1
x
A x x
y x
.
Đặt
3
1
x
A A x x
x
2
4
1 0 3
1
A x x
x
do
, 0x y
.
Câu 47.29: Cho
, 0x y
thỏa
2
2 2
2
4 2
2019 0
2
x y x y
x
. Tìm giá trị nhỏ nhất
min
P của
2 4P y x
.
A. 2018 . B. 2019 . C.
1
2
. D.
2
.
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 722
Chọn D
Ta có:
2 2
2 2 2 4 4 2 4 2
2 2
4 2 4 2
2019 0 2019
2 2
x y x x x yx y x y
x x
2
2
2 2 2 4 2
2019 . 2 2019 . 4 2 *
x x y
x x y
.
Đặt
2
2
, 0
4 2
u x
u v
v x y
Khi đó:
2 2
* 2019 . 2019 .
u v
u v
f u f v
với
2
2019 . ,( 0)
t
f t t t
2 2
' 2019 .2 ln 2019. 2019 0, 0
t t
f t t t
Do đó:
f u f v u v
2
2
2 4 2 2.
x x y y x
2
2
2 4 2 4 4 2 1 2 2
P y x x x x
.
Vậy
min
2 1
P x
.
Câu 47.30: Cho
2
số thực dương
,
x y
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
. Giá trị nhỏ
nhất của biểu thức
2
P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3
P
. D.
min
3 6 2
P
.
Lời giải
Chọn D
Ta có
1
3
log 1 1 9 1 1
y
x y x y
3 3
1 log 1 log 1 1 1 9
y x y x y
.
3 3
1 log 1 log 1 1 9
y x y x
3 3
9
log 1 1 log 1
1
x x y
y
3 3
9 9
log 1 1 2 2 log
1 1
x x
y y
.
Xét hàm số
3
log 2
f t t t
với
0
t
có
1
1 0
ln 3
f t
t
với mọi
0
t
nên hàm số
f t
luôn đồng biến và liên tục trên

0;
.
Từ đó suy ra
9
1
1
x
y
8
9
1
1 1
y
x
y y
, do
0
x
nên
0; 8
y .
Vậy
8
9 9
2 2 2 1 2 1 3 3 6 2
1 1 1
y
P x y y y y
y y y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 723
Vậy
min
3 6 2
P
khi
9 3
2 1 1
1
2
y y
y
.
Câu 47.31: Xét các số thực dương
,
x y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Lời giải
Chọn B
3 3 3
1
log 3 3 4 log 1 log 3 3 3 4
3
y
xy x y y x xy xy x y
x xy
3 3
log 3 1 3 1 log 3 3
y y x xy x xy
Xét hàm
3
log , 0
f t t t t
có
1
' 1 0, 0
ln 3
f t t
t
. Suy ra hàm số đồng biến trên
0;

. Suy ra
3 3
log 3 1 3 1 log 3 3
y y x xy x xy
3 1 3
y x xy
3 1 3 1
1 3 1 3
y y
x x y y
y y
4 3 4
3
. Vậy
min
4 3 4
3
P
.
Câu 47.32: Xét các số thực dương
,
x y
thỏa mãn
2 2
3
log 3 3 .
2
x y
x x y y xy
x y xy
Tìm
giá trị lớn nhất
max
P
của biểu thức
3 2 1
.
6
x y
P
x y
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn C
Ta có:
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
2 2 2 2
3 3
log 3 3 log 2 2
x y x y x y xy x y xy
.
Xét hàm số
3
log
f t t t
,
0
t
có
1
1 0, 0
ln 3
f t t
t
. Vậy hàm số
f t
luôn
đồng biến và liên tục trên khoảng
0;

.
Do đó:
2 2 2 2
3 2 3 2
f x y f x y xy x y x y xy
1
Từ
1
2
3 2
xy x y x y
.
Ta có
2
1
1
2
x y
x x xy xy x y xy xy
Đẳng thức xảy ra khi và chỉ khi
1
x y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 724
Do đó từ
1
, suy ra:
2
2
1
3 2
4
x y
x x y x y .
Đặt
t x y
,
0
t
.
Suy ra:
2
2
2
1
2 1 3 2
2 1
3 22 3
4
6 6 4 6
t
t t t
x y x
t t
P f t
x y t t
.
Ta có:
2
2
3 36 135
0 3
4 6
t t
f t t
t
(nhận)
Bảng biến thiên
Dựa vào BBT, ta có
0;
max max 3 1

P f t f khi và chỉ khi
1 2
3 1
x y x
x y y
.
Câu 47.33: Xét các số thực dương
x
,
y
thỏa mãn
2
2 1
2
2
2018
1
x y
x y
x
. Tìm giá trị nhỏ nhất
min
P
của
2 3
P y x
.
A.
min
1
2
P
. B.
min
7
8
P
. C.
min
3
4
P
. D.
min
5
6
P
.
Lời giải
Chọn B
Cách 1: Ta có
2
2 1
2
2
2018
1
x y
x y
x
2
2018
2
2
2 1 log
1
x y
x y
x
2 2
2018 2018
2 1 2 2 log 2 log 1
x x y x y x
2 2
2018 2018
2 1 log 1 2 2 log 2
x x x y x y
Có dạng
2
1 2
f x f x y
với
2018
2 log
f t t t
,
0
t
.
Xét hàm số
2018
2 log
f t t t
,
0
t
, ta có
1
2 0
.ln 2018
f t
t
0
t
nên hàm số
f t
đồng biến trên khoảng
0;
. Khi đó
2
1 2
f x f x y
2
1 2
x x y
2
1
y x
.
Ta có
2 2
2 3 2 1 3 2 3 2
P y x x x x x
.

3
0
t
f t
f t
0
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 725
Bảng biến thiên
x
3
4
P

7
8

Vậy
min
7
8
P khi
3
4
x .
Câu 47.34: Cho
2
số thực dương ,x y thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
. Giá trị nhỏ
nhất của biểu thức 2P x y là
A.
min
11
2
P . B.
min
27
5
P . C.
min
5 6 3P . D.
min
3 6 2P .
Lời giải
Chọn D
Ta có
1
3
log 1 1 9 1 1
y
x y x y
3 3
1 log 1 log 1 1 1 9y x y x y
.
3 3
1 log 1 log 1 1 9y x y x
3 3
9
log 1 1 log 1
1
x x y
y
3 3
9 9
log 1 1 2 2 log
1 1
x x
y y
(*).
Xét hàm số
3
log 2f t t t với
0t
có
1
1 0
ln 3
f t
t
với mọi
0t
nên hàm số
f t
luôn đồng biến và liên tục trên
0; .
Từ (*) suy ra
9
1
1
x
y
9 8
1
1 1
y
x
y y
, do
0x
nên
0;8y .
Vậy
8 9 9
2 2 2 1 2 1 3 3 6 2
1 1 1
y
P x y y y y
y y y
.
Vậy
min
3 6 2P khi
9 3
2 1 1
1
2
y y
y
.
Câu 47.35: Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x . Giá trị nhỏ nhất
của biểu thức
6 8
3 2P x y
x y
bằng
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 726
A.
59
3
. B.
19
. C.
53
3
. D.
8 6 2
.
Lời giải
Chọn B
Điều kiện:
0
0 6
x
y
.
Từ giả thiết ta có:
2 2
2 2 2 2
log log 6 6 log log 6 6
x x x y y x x x x y x y
(*)
Xét hàm số
2
log
f t t t
với
0
t
, Ta có
1
' 1 0, 0
ln 2
f t t
t
nên hàm số
2
log
f t t t
đồng biến trên khoảng
0;

.
Do đó
2 2
* 6 6 6 6 **
f x f x y x x y x y x y
( do
0
x
)
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức
**
, ta có:
6 8 3 3 6 8 3 3 6 8
3 2 .6 2 . 2 . 19
2 2 2 2 2 2
x y x y
P x y x y
x y x y x y
.
Đẳng thức xảy ra khi và chỉ khi
6
2
3 6
4
2
8
2
x y
x
x
y
x
y
y
. Vậy giá trị nhỏ nhất của
P
bằng 19.
Câu 47.36: Cho
,
x y
là các số dương thỏa mãn
2 2
2 2
2
2 2
5
log 1 10 9 0
10
x y
x xy y
x xy y
. Gọi
,m
M
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
2 2
2
9
x xy y
P
xy y
. Tính
10
T M m
.
A.
60
T
. B.
94
T
. C.
104
T
. D.
50
T
.
Lời giải
Chọn B
2 2
2 2
2
2 2
5
log 1 10 9 0
10
x y
x xy y
x xy y
2 2 2 2 2 2 2 2
2 2 2
log 5 log 10 log 2 2 5 10 0
x y x xy y x y x xy y
2 2 2 2 2 2 2 2
2 2
log 2 10 2 5 log 10 10
x y x y x xy y x xy y
2 2 2 2
2 10 10
x y x xy y
vi)
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 727
2 2
10 9 0
x xy y
2
10 9 0
x x
y y
1 9
x
y
2 2
2
9
x xy y
P
xy y
2
9
1
x x
y y
x
y
Đặt
x
t
y
, điều kiện :
1 9
t
2
9
1
t t
f t
t
;
2
2
2 8
1
t t
f t
t
;
4
0
2
t
f t
t
11
1
2
f
;
2 5
f
;
99
9
10
f
Nên
99
10
M
,
5
m
. Vậy
10 94
T M m
.
Câu 47.37: Vậy
min
6
A
.Cho các số thực dương
x
và
y
thỏa mãn
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
.
Tìm giá trị nhỏ nhất của biểu thức
2 18
x y
P
x
.
A.
9
P
. B.
3 2
2
P
.
C.
1 9 2
P
. D. Hàm số không có giá trị nhỏ nhất.
Lời giải
Chọn A
Từ giả thiết ta đặt
2
2
t x y
,
t
.
Phương trình
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
trở thành
49 7
4 9.3 4 9 . 4 7 49 9 9. 49 0
7 3
t
t t t t
t
.
Nhận thấy
2
t
là nghiệm phương trình.
Ta chứng minh
2
t
là nghiệm duy nhất của phương trình.
Xét
2
t
:
7 49
t
và
7
9. 49
3
t
nên vế trái phương trình luôn dương, nên phương trình vô
nghiệm.
Xét
2
t
:
7 49
t
và
7
9. 49
3
t
nên vế trái phương trình luôn âm, nên phương trình vô
nghiệm.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 728
Vậy
2
2 2
t x y
2
2
2
x
y
thay vào
2
2 18 16
x y x x
P
x x
16 16
1 2 . 1 9
x x
x x
. Dấu bằng đạt được khi
16
4
x x
x
.
Câu 47.38: Cho
,
x y
là các số thực lớn hơn
1
sao cho
y x
e e
x x y y
y e x e
. Tìm giá trị nhỏ nhất của
biểu thức:
log log
x y
P xy x
.
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Lời giải
Chọn C
Cách 1.
Ta có:
ln ln
y x y x
e e e e
x x y y x x y y
y e x e y e x e
ln ln
ln ln
y x
x y
x y
x y xe y x ye
x e y e
(*) (vì
ln
x
y e x
có
1
' 0; 1
x
y e x
x
nên
1 0
y y e
)
Xét hàm số:
ln
t
t
f t
t e
trên
1;
ta có
2
ln 1
'
ln
t t
t
t e te
f t
t e
. Với hàm số
ln 1
t t
g t t e te
có
1
' ln 1 ' 0, 1
t t t
g t t e te te t
t
Nên
1 1 ' 0; 1
g t g f t t
y f t
là hàm nghịch biến trên
1;

nên với (*)
1
f x f y y x
Khi đó
1 1 1 1 1 1 1 2 2
log log log 2 log .
2 2 log 2 2 log 2
x y x x
x x
P xy x y y
y y
Dấu “=” xảy ra khi:
2
2
1 1
log log 2
2 log
x x
x
y y y x
y
Vậy:
min
1 2 2
2
P
.
Câu 47.39: Tính giá trị của biểu thức
2 2
1
P x y xy
biết rằng
2
2
1
1
2
4 log 14 2 1
x
x
y y
với
0
x
và
13
1
2
y
.
A.
4
P
. B.
2
P
. C.
1
P
. D.
3
P
.
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 729
Chọn B
Xét
2
2
1
1
2
4 log 14 2 1
x
x
y y
.
Ta có
2
2
2
2
1
1
2 . 1
1
4 4 4
x
x
x
x
, dấu bằng xảy ra khi và chỉ khi
1
x
, .
Mặt khác
3
14 2 1 14 3 1 1
y y y y
.
Đặt
1
t y
ta có
30
0
2
t
. Xét hàm số
3
3 14
f t t t
. Ta tìm GTLN – GTNN của
hàm số trên đoạn
30
0;
2
được
30
0;
2
30
min
2
f t f
56 9 30
4
;
30
0;
2
max 1 16
f t f
.
Suy ra
2 2
log 14 2 1 log 16 4
y y
, .
Từ và suy ra ta có
1
1 1
x
t y
1
0
x
y
. Thay vào
2
P
.
Câu 47.40: Cho hai số thực
x
,
y
thỏa mãn
1
0
2
x
,
1
0
2
y
và
log 11 2 2 4 1
x y y x
. Xét
biểu thức
2
16 2 3 2 5
P yx x y y
. Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn
nhất của
P
. Khi đó giá trị của
4
T m M
bằng bao nhiêu?
A.
16
. B.
18
. C.
17
. D.
19
.
Lời giải
Chọn A
Ta có
log 11 2 2 4 1
x y y x
2 2 log 11 2 1 0
x y x y
Đặt 2
t x y
,
0 11
t
. Phương trình trở thành:
2 log 11 1 0
t t
.
1
Xét hàm số
2 log 11 1
f t t t
trên khoảng
0;11
.
Có
1
2 0
11
y
t
,
0;11
t . Do đó hàm số
f t
luôn đồng biến.
Dễ thấy
1
có nghiệm
1
t
. Do đó
1
t
là nghiệm duy nhất của
1
.
Suy ra 2 1
x y
. Khi đó
2
1
16 1 3 2 5
4
y
P y y y y
3 2
4 5 2 3
y y y
.
Xét hàm số
3 2
4 5 2 3
g y y y y
trên
1
0;
2
, có
2
12 10 2 0
g y y y
,
1
2
y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 730
Do đó,
1
0;
2
min 0 3
g y g
,
1
0;
2
max 1 4
g y g
.
Suy ra
3
m
,
4
m
.
Vậy
4.3 4 16
T
.
| 1/35
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
ỨNG DỤNG PHƯƠNG PHÁP HÀM SỐ GIẢI PHƯƠNG TRÌNH MŨ VÀ LOGARIT
KIẾN THỨC CẦN NHỚ:
1. Định lý: Nếu hàm số y f x đồng biến (hoặc luôn nghịch biến) và liên tục trên  ; a b thì *  ; u v  ;
a b : f u  f v  u v .
* Phương trình f x  k k const  có nhiều nhất 1 nghiệm trên khoảng  ; a b .
2. Định lý: Nếu hàm số y f x đồng biến (hoặc nghịch biến) và liên tục trên  ; a b , đồng thời
lim f x. lim f (x)  0 thì phương trình f x  k k const có duy nhất nghiệm trên  ; a b . x ax b  
3. Tính chất của logarit:
1.1. So sánh hai logarit cũng cơ số: 1.2. Hệ quả:
Cho số dương a  1 và các số dương , b c .
Cho số dương a  1 và các số dương , b c .
 Khi a  1 thì log b  log c b c .
 Khi a 1 thì log b  0  b 1. a a a
 Khi 0  a  1 thì log b  log c b c .
 Khi 0  a  1 thì log b  0  b  1. a a a
 log b  log c b c . a a
2. Logarit của một tích:
3. Logarit của một thương:
Cho 3 số dương a, b , b với a  1, ta có
Cho 3 số dương a, b , b với a  1, ta có 1 2 1 2
log (b .b )  log b  log b b a 1 2 a 1 a 2 1 log
 log b  log b a a 1 a 2 b2 1 Đặc biệt: với ,
a b  0, a  1 log   log b . a a b
4. Logarit của lũy thừa:
5. Công thức đổi cơ số: Cho ,
a b  0, a  1, với mọi , ta có Cho 3 số dương a, ,
b c với a  1, c  1 , ta có
log b log b . log b a a log c b  . a log a c 1
Đặc biệt: log n b
log b ( n nguyên dương). a a n 1 1
Đặc biệt: log c  và log  với  b log b a log a a a c  0 . Trang 696
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 BÀI TẬP MẪU
Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  x  2020 và log 3  3   2  9y x x y ? 3   A. 2019 . B. 6 . C. 2020 . D. 4 .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Ứng dụng tính đơn điệu của hàm số để giải phương trình mũ, logarit. Phương pháp
Tìm hàm đặc trưng của bài toán, đưa phương trình về dạng f u   f v . 2. HƯỚNG GIẢI:
B1: Đưa phương trình đã cho về dạng f u   f v .
B2: Xét hàm số y f t  trên miền D .
* Tính y và xét dấu y .
* Kết luận tính đơn điệu của hàm số y f t  trên D .
B3: Tìm mối liên hệ giữa ;
x y rồi tìm các cặp số  ;
x y  rồi kết luận.
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn D ĐK: x  1  . Ta có log 3  3   2  9y x x y 3   3log 3x 3 log3 3x3 3 32y  2 y 1 1 3        (*) 3 Xét hàm số    3  3t f t t
trên  , vì     3  3t f t
.ln 3  0, t  0 nên hàm số f t  đồng biến trên  . Từ đó  
*  f log 3x  3  f 2y 1  log 3x  3  2 y 1. 3   3    
Mặt khác 0  x  2020  log 3x  3  1  ; log
6063   2 y  1 1  ; log 6063  3    3    3   1 
  2 y  1  log 6063 3   
 0  y  3 . Vậy có 4 cặp  x; y  thỏa mãn.  y Z
Bài tập tương tự và phát triển:
Câu 47.1: Có bao nhiêu giá trị nguyên của tham số m  2019; 2019 để phương trình x mx m x 2 1  2 1 2019  
 0 có đúng 3 nghiệm thực phân biệt ? x 1 x  2 A. 4038 . B. 2019 . C. 2017 . D. 4039 . Lời giải Chọn C Trang 697
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
TXĐ: D   \ 1;  2 . Ta có x mx m x 2 1  2 1 2019    0 x 1 x  2 x m x x 2 1 (  2) 1  2019    0 x 1 x  2 x x 2 1 1  2019     . m (*) x 1 x  2 x x 2 1 1
Đặt f (x)  2019   . Khi đó x 1 x  2 x 3 1
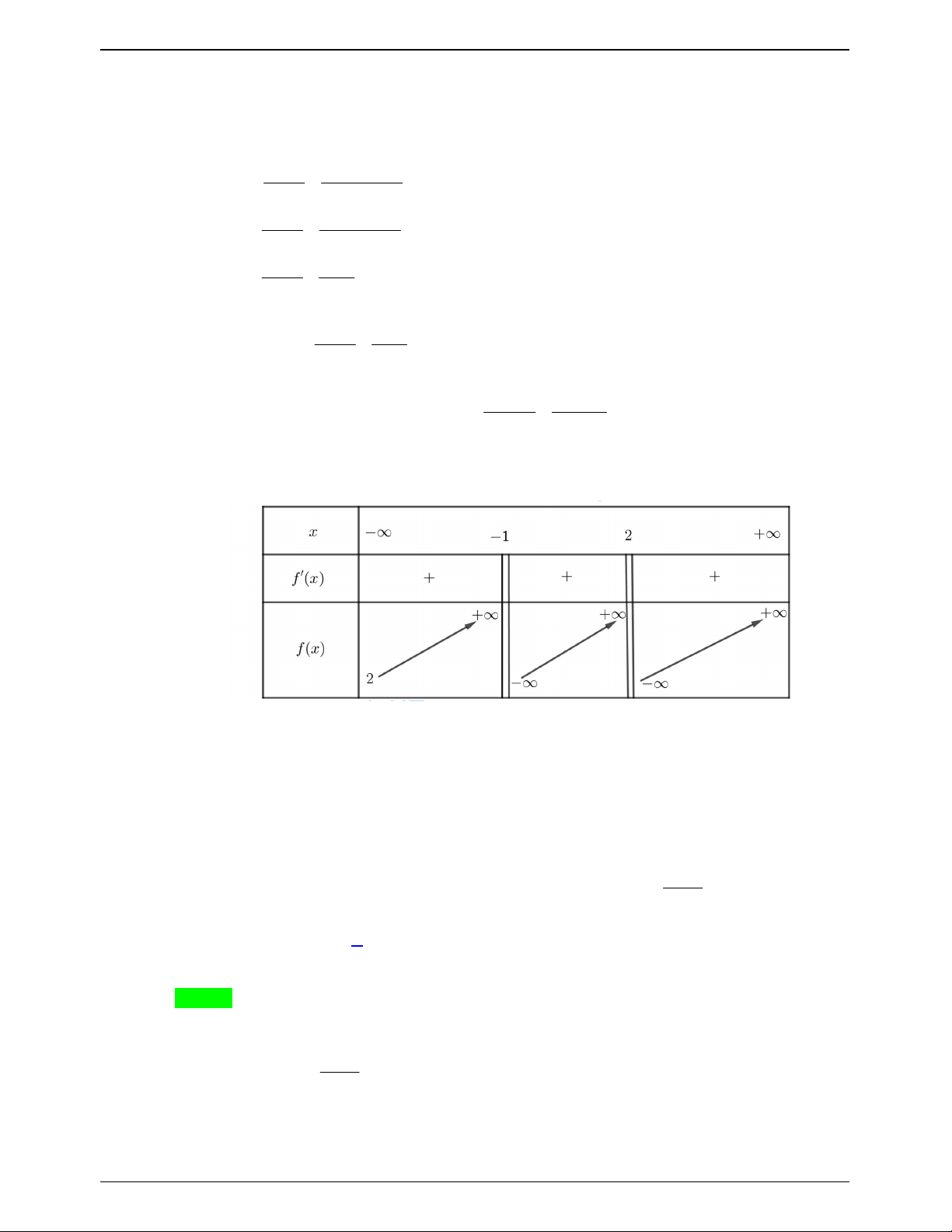
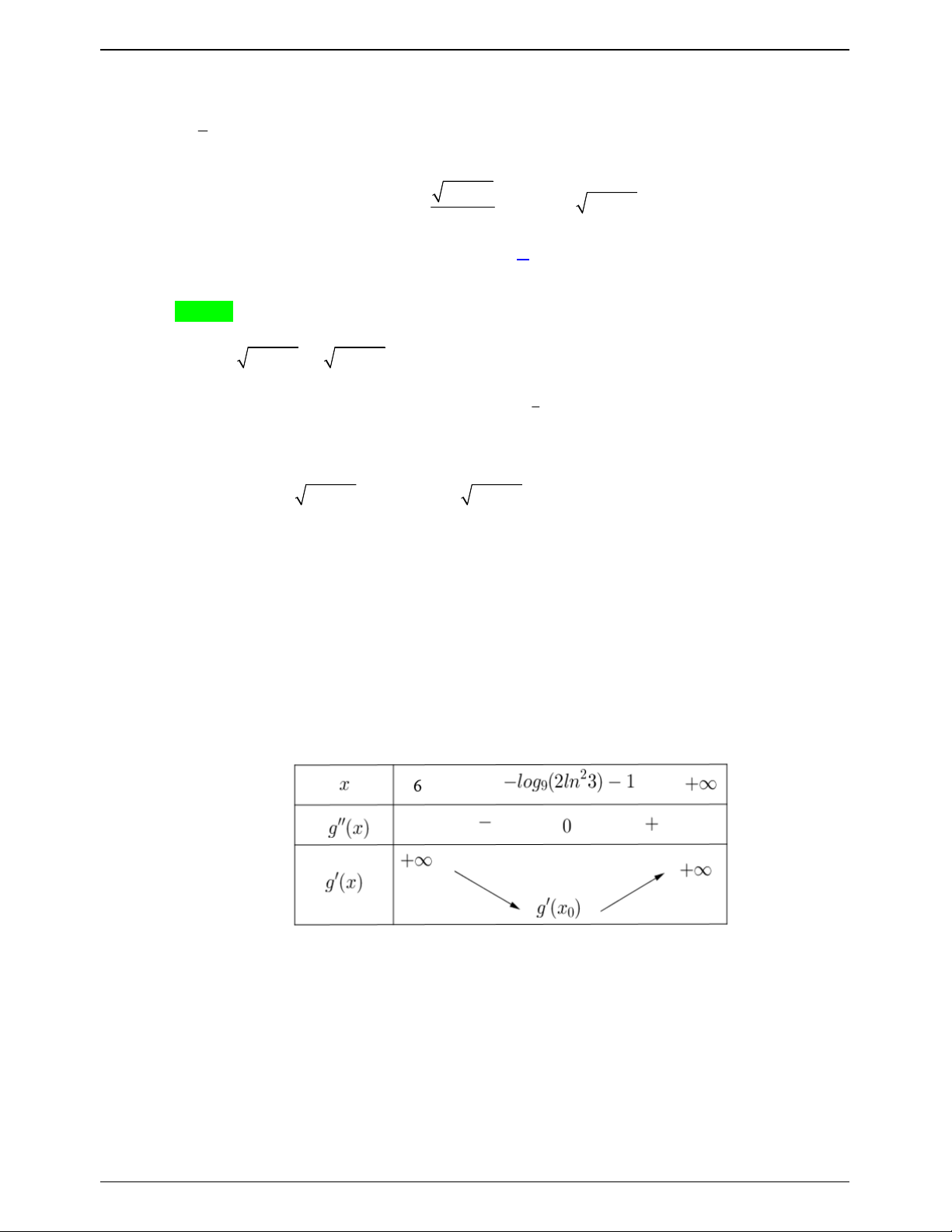
f '(x)  2019 ln 2019    0 x  . D 2 2 (x 1) ( x  2) Ta có bảng biến thiên
Dựa vào bảng biến thiên, để phương trình (*) có 3 nghiệm thực phân biệt thì
m  2  m  2  .
Mà m 2019; 2019 và m   nên có 2017 giá trị m thỏa mãn.  2x 1
Câu 47.2: Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  y  2020 và log  1 2x y ? 3   y   A. 2019 . B. 11. C. 2020 . D. 4 . Lời giải Chọn B y  0   2x 1 Từ giả thiết ta có: x
 0  2  1  x  0  yy  0  Ta có: PT  log
2x 1  2x 1  log y y (*) 3   3 Trang 698
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Xét hàm số f t   log t t trên 0;  3 1
Khi đó f t  
 1  0 do đó hàm số f t   log t t đồng biến trên 0;  t ln 3 3 (*) có dạng 2x   1      2x f f y y 1 Vì 0 
 2020  0  2x 1  2020  1  2x y
 2021  0  x  log 2021 2    0  x  log 2021 2   
x 0;1; 2;3; 4;5; 6; 7;8;9;1 
0 . Vậy có 11 cặp  x; y thỏa mãn. x   
Câu 47.3: Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số  ; x y thỏa mãn 3x5 y x3 y 1 e e  
 1 2x  2 y , đồng thời thỏa mãn 2
log 3x  2y   1  m  6 2
log x m  9  0 3 3 ? A. 6 . B. 5 . C. 8 . D. 7 . Lời giải Chọn B Ta có 3x5 y x3 y 1 e e  
 1 2x  2 y 3x5 yx yx3 y 1 e 3 5 e     
  x  3y   1 (1) Xét hàm số    et f t
t trên  . Ta có    et f t
1  0 nên hàm số đồng biến trên  .
Khi đó (1)  f 3x  5y  f x  3y  
1  3x  5 y x  3 y 1  2 y  1  2 x .
Thế vào phương trình còn lại ta được 2
log x  m  6 2
log x m  9  0 (2) 3 3
Đặt t  log x . Số nghiệm của phương trình (2) chính là số nghiệm của phương trình 3 2
t  m   2
6 t m  9  0 (3)
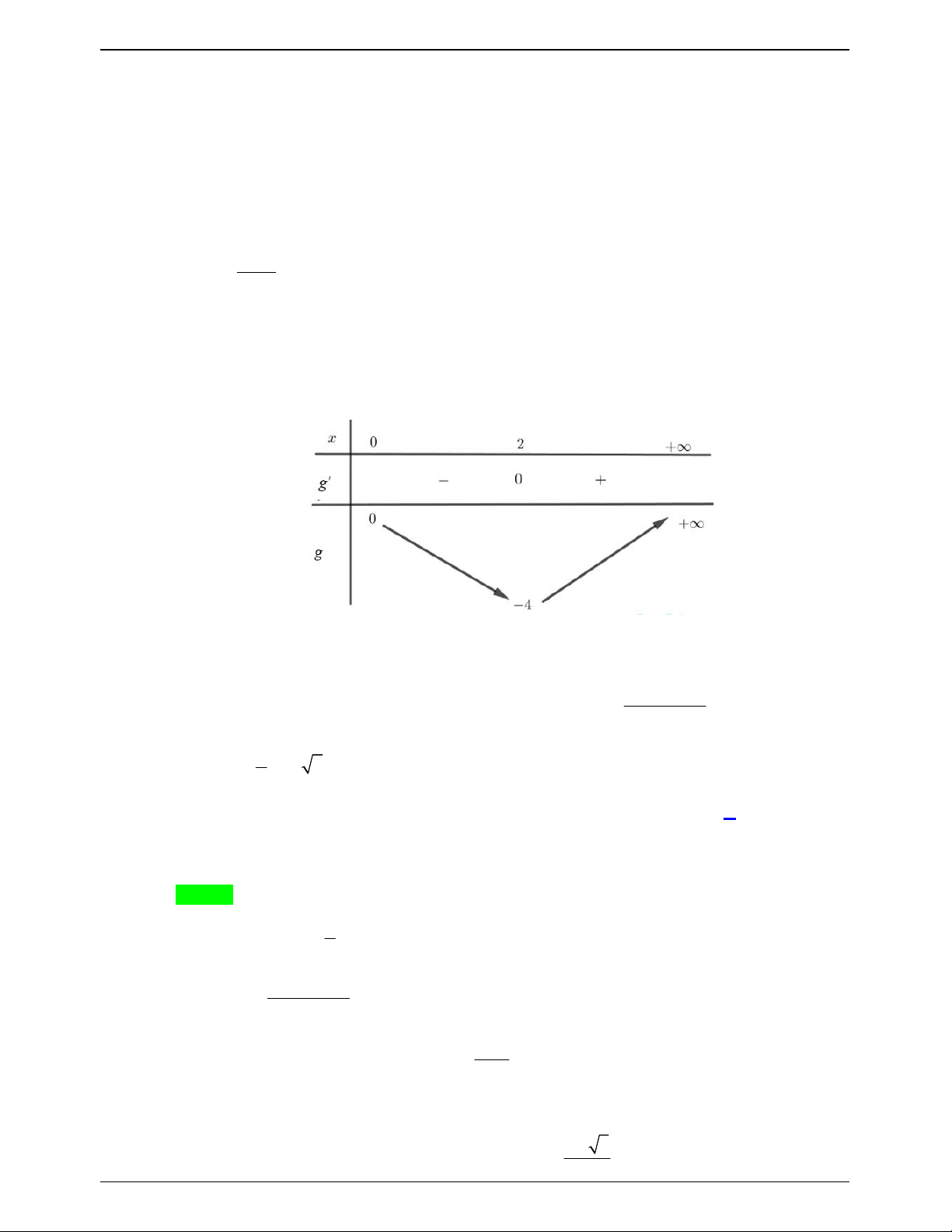
Phương trình (3) có nghiệm khi   0  2
3m  12m  0  0  m  4 .
Do đó có 5 số nguyên m thỏa mãn.
Câu 47.4: Có bao nhiêu số nguyên của m để phương trình log 2x m 2
 2 log x x  4 x  2m 1 có 2 2
hai nghiệm thực phân biệt ? A. 2 . B. 3 . C. 1. D. 4 Lời giải Chọn C x  0  Điều kiện  m x     2
log 2x m 2
 2 log x x  4 x  2m 1 2 2 Trang 699
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
 log 2x m 2
 2 log x x  2 x  2m 1 2 2  
 log 2x m  2 x  2m 2 2
1  log x x 2 2
 log 2 2x m  2 x  2m 2 2  log x x (1) 2 2
Xét f u   log u u, u  0 2   1 f 'u 
1  0 , do đó hàm số đồng biến trên (0; ) . u ln 2
Khi đó (1)  f   x m  f  2
x    x m 2 2 2 2 2 2
x x  4x  2m
Xét hàm số g x 2
x  4x,  x  0
Phương trình có 2 nghiệm dương khi 4  2m  0  2  m  0 suy ra có 1 giá trị nguyên. 2
 4x  4x 1 
Câu 47.5: Biết x , x là hai nghiệm của phương trình 2 log
 4x 1  6x và 1 2 7   2  x  1 x  2x
a b với a , b là hai số nguyên dương. Tính a b . 1 2   4
A. a b  13 .
B. a b  11.
C. a b  16 .
D. a b  14 . Lời giải Chọn D 1
Điều kiện: x  0, x  . 2 2
 4x  4x 1  Ta có: 2 log
 4x  1  6x  log    2
4x  4x 1 2
 4x  4x 1  log 2x  2x . 7 7 7   2  x  1
Xét hàm số f t   log t t có f t 
1  0 t  0 nên là hàm số đồng biến trên 7 t ln 7 0; . 3  5 Do đó ta có 2 2
4x  4x 1  2x  4x  6x 1  0  x  . 4 Trang 700
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Khi đó 3  5 3  5 1 3  5 3  5 1 x  2x   2 
9  5 hoặc x  2x   2  9  5 . 1 2   1 2   4 4 4 4 4 4 3  5 3  5 Vậy x  ; x
. Do đó a  9;b  5 và a b  9  5  14 . 1 2 4 4 2 x 1  x 1 
Câu 47.6: Biết phương trình log  2 log  
có một nghiệm dạng x a b 2 trong 5 3   x 2 2   x  đó ,
a b là các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5 . Lời giải Chọn B 2 x 1  x 1  2 x 1  x 1  Ta có log  2 log     log  2 log 1 . 5 3 5 3      x 2 2   x x  2 x  ĐKXĐ: x  1 .  
1  log 2 x 1  2log 2 x  log x  2log x 1 (*) 5   3 5 3  
Xét hàm số f t   log t  2 log t 1 , với t  1. 5 3   1 2
f t   
 0 với mọi t  1, suy ra f t  đồng biến trên khoảng 1;  . t.ln 5 t   1 ln 3
Từ (*) ta có f 2 x  
1  f x nên suy ra
x   x   x 2 2 1  2 x 1  0  x  1 2 (do x  1).
Suy ra x  3  2 2  a  3;b  2  2a b  8 . Câu 47.7: Tìm tổng tất cả các giá trị nguyên của m để phương trình 3
x3 m 3 x   3 2     x3 3 9 24 .3  3x x x x m
1 có 3 nghiệm phân biệt. A. 45 . B. 34 . C. 27 . D. 38 . Lời giải Chọn C Trang 701
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 3 x3 m3 3 x   3 2
x  9x  24x mx 3 .3   3x 1 3
3x  mx x 33 3 3 x3 27 m 3x       .3  3x 1   3
 3 mx   x  33 3 3 3
m  3x  27  3  3 x   1   b 3 3 a b 3 a 3
1  3  27  b a  27.  3  3  b  3  a Đặt 3 a  3  ;
x b m  3x , phương trình (1) trở thành b 3 3 a b 3 a 3
3  27  b a  27.  3  3  b  3  a .
Xét hàm số f t t 3 
t f t t 2 3 '
 3 .ln 3  3t  0, t  
(1)  f a  f b 3
a b  3  x m  3x
m  3  x3 3 2
 3x   x  9x  24x  27 g x 3 2
 x x x   g x 2 9 24 27 '  3  x 18 x 24
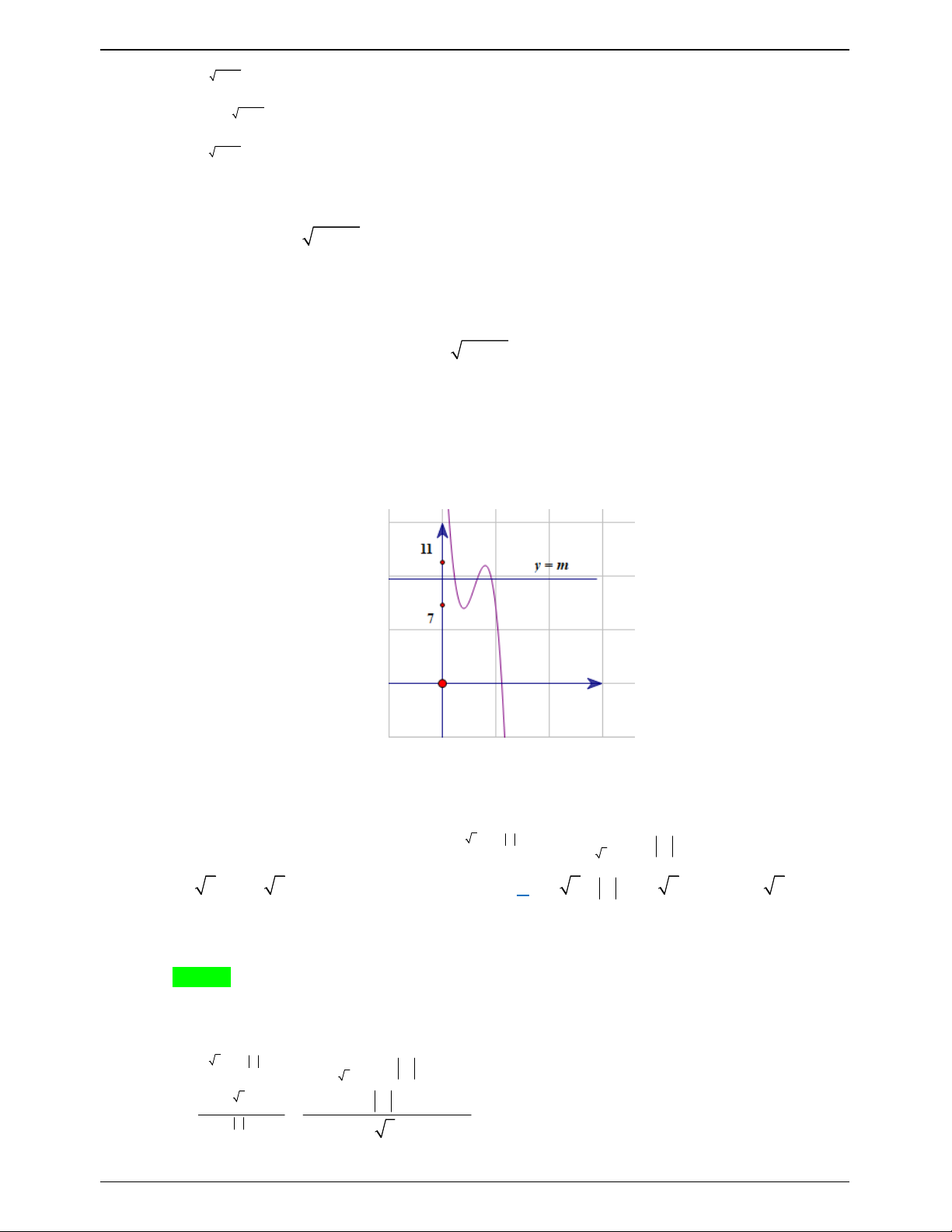
g ' x  0  x  2  x  4 Đồ thị:
Dựa vào đồ thị ta thấy điều kiện để phương trình có 3 nghiệm phân biệt là 7  m  11 hay m 8;9;1  0 .
Câu 47.8: Tìm các giá trị m để phương trình sin x 5 cos xm 5 3  log m  5 có nghiệm.
sin x  5 cos x 1  0  
A. 6  m  6 .
B. 5  m  5 .
C. 5  6  m  5  6 .
D.  6  m  5 . Lời giải Chọn C Ta có
sin x 5 cos xm 5 3  log m  5
sin x 5 cos x 1  0  
sin x 5 cos x10 3 ln  m  5   m 5 3
ln sin x  5 cos x 10 Trang 702
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
sin x 5 cos x 10 3  
.ln sin x  5 cos x 10 m 5  3 .ln  m  5 (1) 1 Xét
   ln  .3t f t t
, t  5 , vì     3t  ln  3t f t t
ln 3  0,t  5 nên hàm số f t  đồng t biến trên (5; ) . Khi đó
(1)  f sin x  5 cos x 10  f m  5
 sin x  5 cos x 10  m  5
 sin x  5 cos x  5  m
Mà  6  sin x  5 cos x  6 nên để phương trình có nghiệm ta phải có 5  6  m  5  6.
Câu 47.9: Số nghiệm thực của phương trình 6x  3log
5x 1  2x 1 là 6   A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B 1
Điều kiện: x   . 5
PT:  6x  3x  3log 5x   x log6 5x  1
1  5x  1  6  3x  6  3log 5x 1 (1) . 6 6   Xét hàm số    6t f t
 3t , vì    6t f t .ln 6  3  0, t
   nên f t đồng biến trên  . Khi đó  
1  f x  f log 5x 1  x  log 5x 1  log 5x 1  x  0 6   6   6    1 
Xét hàm số h x  log 5x 1  x trên  ;  , ta có 6      5  5 h x  1 5x   1 ln 6 25 1
h  x    0, x
   và lim h x   ;
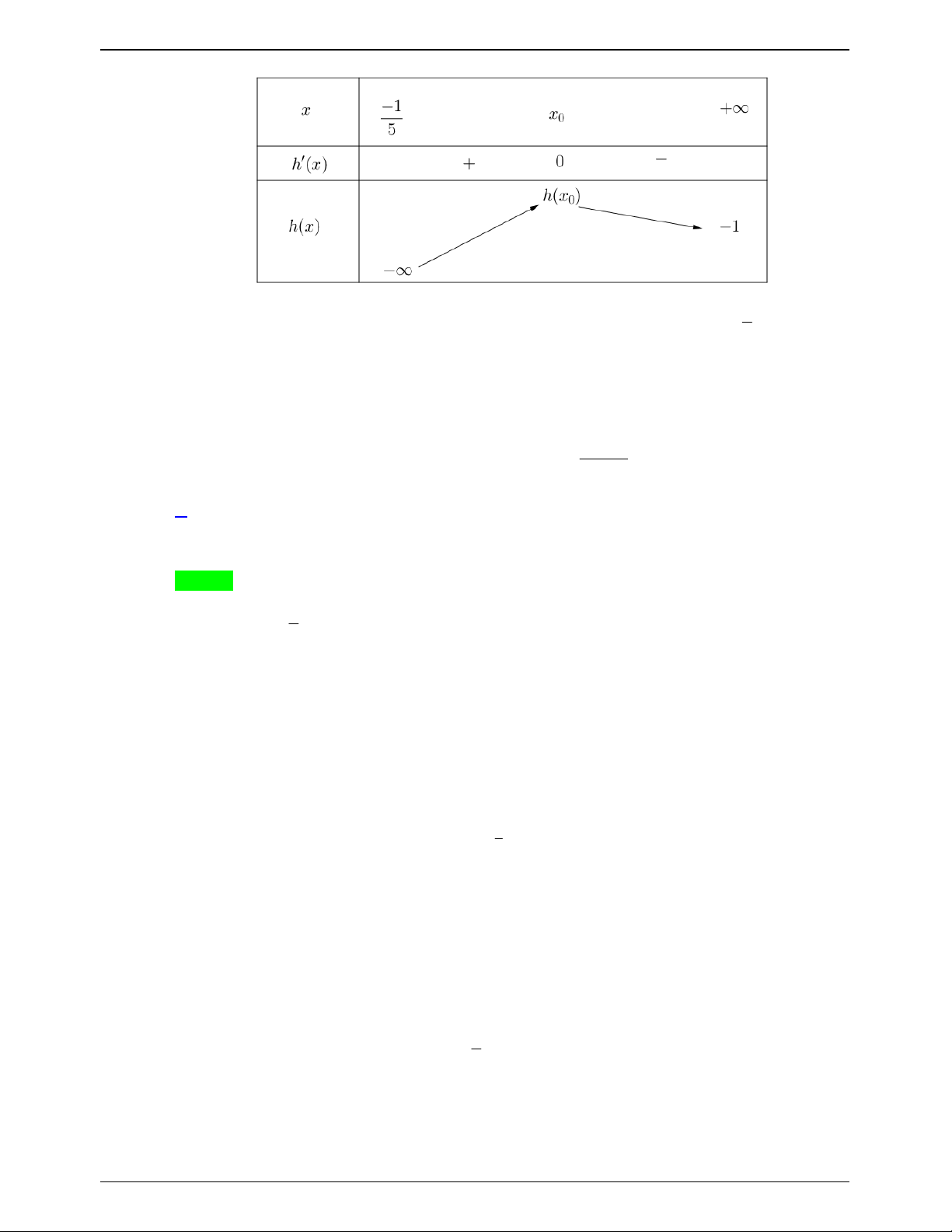
 lim h x  1 5x  2 1 ln 6 5  1 x   x     5  Bảng biến thiên: Trang 703
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  1 
Từ BBT suy ra phương trình h x  0 có nhiều nhất 2 nghiệm thuộc khoảng  ;     5 
Mà h 0  0, h  1  0 .
Vậy phương trình đã cho có đúng hai nghiệm x  0, x  1 .
 5x  3x Câu 47.10:
Tính tổng S tất cả các nghiệm của phương trình x 1 ln
 5   5.3x  30x 10  0   . 6x  2   A. S 1 . B. S  2 . C. S  1  . D. S  3. Lời giải Chọn A 1
Điều kiện x   . 3
Phương trình tương đương
ln 5x  3x   ln 6  2  55x  3x x
 56x  2  0
 ln 5x  3x   55x  3x   ln 6x  2  56x  2 (1). 1
Xét hàm số f t   ln t  5t,t  0 . Có f 't    5  0 ,  t  0 nên f t đồng biến trên t 0;   . Từ  
1 suy ra 5x  3x f
  f 6x  2  5x  3x  6x  2  5x  3x  6x  2  0
Xét    5x  3x g x
 6x  2 , '  5x ln 5 3x g x   ln 3  6 1   x  2 x g x    2 ' 5 ln 5 3 ln 3  0 , x    . 3 Trang 704
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Nên g ' x  0 có không quá 1 nghiệm suy ra g x  0 có không quá 2 nghiệm trên  1   ;  
 . Mà g 0  g  
1  0 . Vậy phương trình có tập nghiệm là 0,  1 . Do đó S  1.  3  2 x  80 Câu 47.11:
Số nghiệm của phương trình x 1  2 ln  2.3
 2 x  80  ln 3 là 3x A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn C PT 2 2 x 1  x 1 ln x 80 2 x 80 ln 3 2.3        (1) 1
Xét hàm số f t   ln t  2t, t
  0 ; Ta có: f t    2  0, t
  0  Hàm số f t  đồng biến t trên 0; . Từ (1) suy ra f  2 x
  f x 1 2 x 1  2 x 1  x 1  2 80 3  x  80  3  x  80  9  9  x  80  0
Xét hàm số g xx 1  2  9
x  80 trên  . Ta có: g xx 1  2.9  ln 3  2x
g  x  4.9x ln 32 1  2
g  x  0  x x  log  2
2 ln 3 1 g (x )  glog  2 2 ln 3 1  3, 7  0 0 9 0 9  
lim g x   ;  lim g (  x)   x x Bảng biến thiên:
Dựa vào bảng biến thiên ta có g ' x  0, x
    hàm số g x đồng biến trên  
phương trình g x  0 có nhiều nhất một nghiệm. Mà g   1  0
Do đó phương trình đã cho có duy nhất 1 nghiệm . Câu 47.12:
Cho phương trình 2x m  log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 2   m  1
 8;18 để phương trình đã cho có hai nghiệm? Trang 705
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 A. 20 . B. 17 . C. 9 . D. 21 . Lời giải Chọn B
Điều kiện x m
PT  2x x x m  log  x mx l 5 og ( xm)  2  x  2  log (x  ) m (1) 2 2 Xét hàm số    2t f tt, t
   ; Ta có:    2t f t ln 2 1  0, t
    Hàm số f t  đồng biến trên  .
Từ (1) suy ra f x  f log (x m)  x  log (x m)    2x    2x x m m x 2  2
Xét hàm số     2x g x x trên  ;
m  . Ta có: '  1 2x g x   ln 2 ; '   0  2x g x
ln 2  1  x  log log e g log log e  log log e  log e 2  2  2  2  2  2  2
lim g x  m  2m; lim g(x)   xmx Bảng biến thiên:
Do đó. Phương trình đã cho có 2 nghiệm  2m m
m  log log e  log e m  log log e  log e  0  , 91 2  2  2 2  2  2 m    Vì  nên m  1  7; 1  6; 1  5;....;   1 m   18;18 
Vậy có 17 giá trị của m . Câu 47.13: Cho phương trình   3 2  m m
x x   2 .log  x 3x 1 2 3 2 3 1 3 1 2 1 3 2 2 .log        0 81 3 3 2
m  3m 1  2   
Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có 6 nghiệm hoặc 7 nghiệm
hoặc 8 nghiệm phân biệt . Tính tổng bình phương tất cả các phần tử của tập S . A. 20 . B. 19 . C. 14 . D. 28 . Lời giải Chọn A Trang 706
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020   3 2 3 2  m 3m 1   x 3 x 1  2 1 Ta có 2 .log  3 2 x 3x 1 2 2 .log        0 81  3 3 2
m  3m 1  2    3 2 x x   m m    2
.log  x 3x 1  2 3 2 3 1 2 3 1 2 3 2  2 .log  3 2
m  3m 1  2 . 3 3  t t 1 Xét hàm số    2t f t
.log t với t  2; Ta có f t  2 ln 2.log t  2 .  0 t   2 . 3 3 t ln 3
Suy ra hàm số f t  đồng biến trên 2; .
Do đó phương trình tương đương với 3 2 3 2
m  3m 1  x  3x 1   1 .
Vẽ đồ thị hàm số g x 3 2
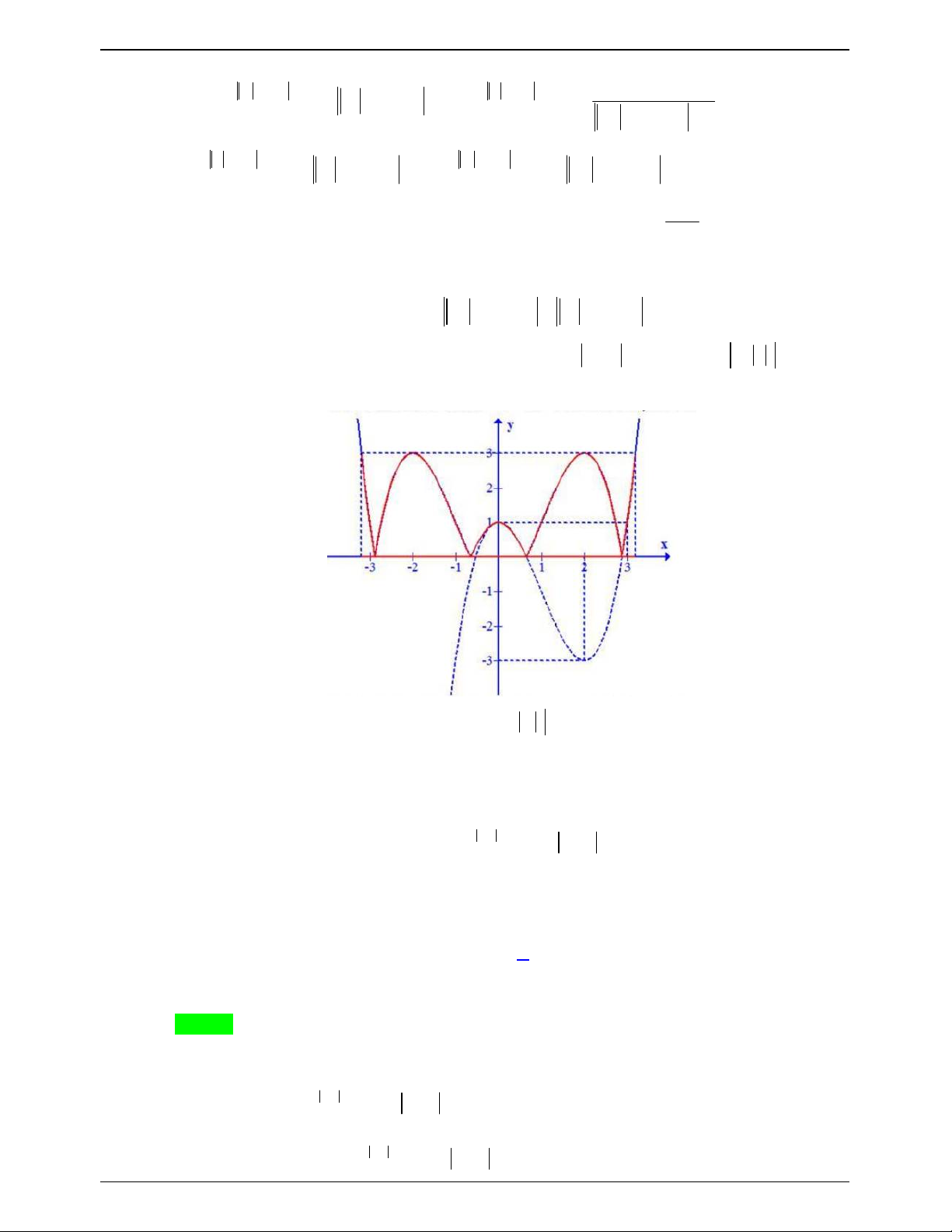
x  3x 1 từ đó suy ra đồ thị g x và đồ thị của g x  như hình vẽ.
Từ đồ thị suy ra  
1 có 6, 7, 8 nghiệm  0  g m   3 .
Từ đồ thị suy ra các giá trị nguyên của m là 3, 1, 0,1, 3 . Vậy S  20 . 2 Câu 47.14:
Cho phương trình 2x log  2
x  2  4 xa log
2 x a  2 2  2   
 . Gọi S là tập hợp các giá trị
a thuộc đoạn 0;2020 và chia hết cho 3 để phương trình có hai nghiệm. Hãy tính tổng các phần tử của S . A. 0 . B. 2041210 . C. 680403 . D. 680430 . Lời giải Chọn C
Phương trình tương đương 2 2x log  2
x  2  2 xa log
2 x a  2 2  2 2     2  4.2x log  2
x  2  4.2 xa log
2 x a  2 2  2 2     Trang 707
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 x 2  2 log  2
x  2  2 xa  log
2 x a  2 2  2 2 2     (*) t 2t Xét hàm số    2t f t
log t, t  2 . Có f 't   2 ln 2.log t   0, t
  2 , nên f t  đồng 2 t ln 2 biến 2;   .  f   2
x  2  f 2 x a  2 Khi đó (*)    2
x  2 x a (1) 2
x  2  2; 2 | x a | 2  2  2
x  2 x a 2
x  2x  2a  0 (2)     2
x  2 x a 2
x  2x  2a  0 (3)  
Phương trình (2)   1 2a , phương trình (3) có   1 2a . 2 (3)
Vì     2  0 nên ít nhất một trong hai phương trình (2), (3) luôn có hai nghiệm phân 2 (3)
biệt. Để phương trình (1) có hai nghiệm phân biệt, ta xét các trường hợp sau: 1
* TH1: (2) có hai nghiệm phân biệt:  
 0  1 2a  0  a  
. Khi đó   0 nên (3) vô 2 2 (3)
nghiệm. Trường hợp này thỏa mãn điều kiện bài toán. 1
* TH1: (3) có hai nghiệm phân biệt:   0  1 2a  0  a
. Khi đó   0 nên (2) vô (3) 2 (2)
nghiệm. Trường hợp này cũng thỏa mãn điều kiện bài toán.  1   1 
Do đó phương trình đã cho có 2 nghiệm khi và chỉ khi a  ;   ;       2   2 
Vì a 0; 2020 và chia hết cho 3 nên a S  3;6;9;12;..., 201  9
Tổng các phần tử của S là: 3 6  9  ...  2019  3.1 3.2  3.3...  3.673 673.674
 31 2  3  ...  673  3.  680403 2 BỔ SUNG CÁCH 2: Xét phương trình 2
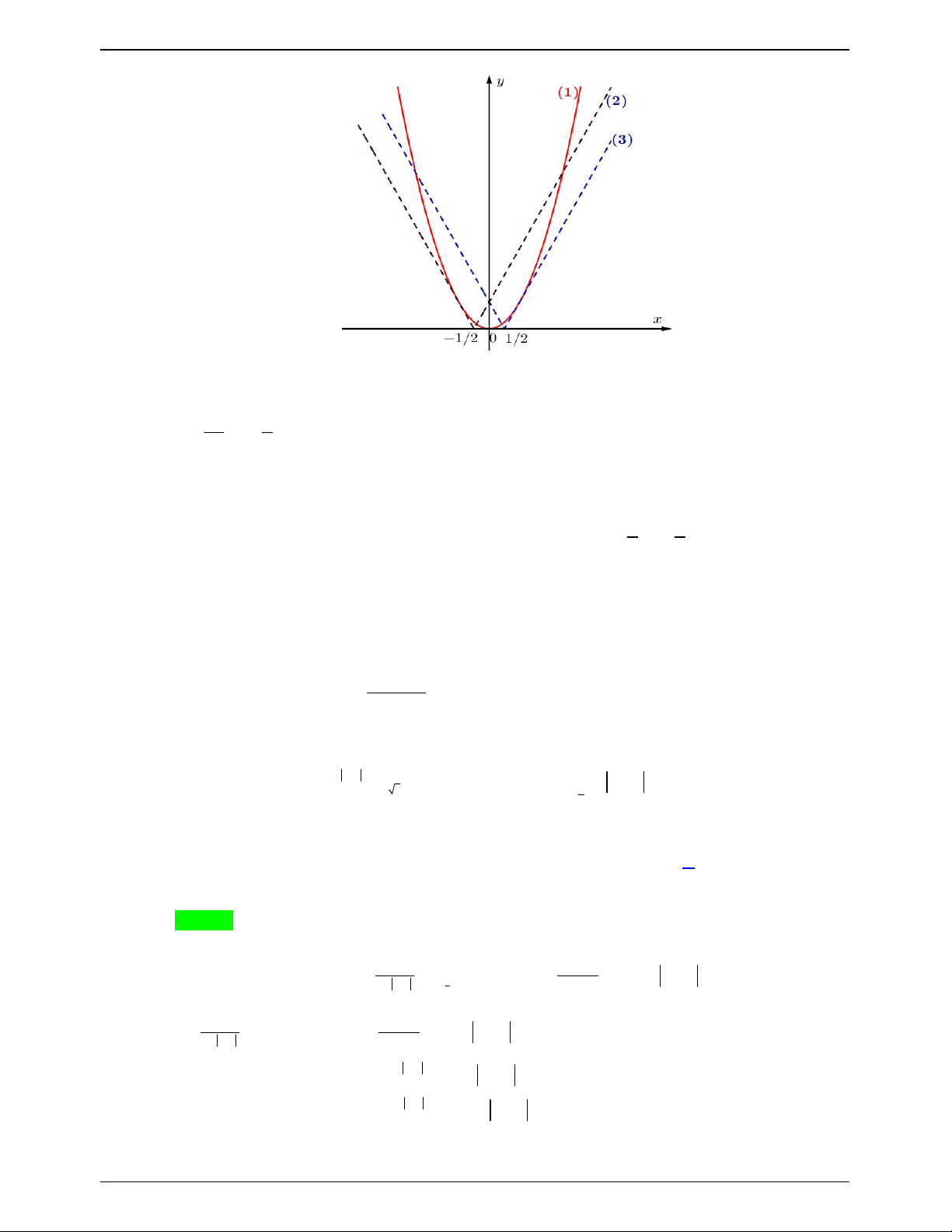
x  2 x a * Vẽ đồ thị hàm số 2 y x
1; y  2 x a 2 trên cùng một hệ trục tọa độ ta được: Trang 708
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Xét 2 vị trí nhánh trái và phải của đồ thị hàm số 2 tiếp xúc với 1 khi đó dễ dàng tìm được 1  1 a  ; a
ứng với đồ thị 2; 3 (hình vẽ). 2 2
Từ đồ thị nhận xét :  1   1 
Phương trình * đã cho có 2 nghiệm khi và chỉ khi a   ;    ;       2   2  Vì a 0;202 
0 và chia hết cho 3 nên a S  3;6;9;12;..., 201  9
Tổng các phần tử của S là: 3  6  9  ...  2019  3.1 3.2  3.3 ...  3.673 673.674
 31 2  3  ...  673  3.  680403 2 Câu 47.15:
Có bao nhiêu giá trị thực của tham số a để phương trình 4 xa log   2  3 2 2  x 2  2 x x x log
2 x a  2  0 1 2   2
có 3 nghiệm thực phân biệt ? A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn D 1 1
PT đã cho tương đương với 2 log
x  2x  3  log    .  2 x a 2 0 1 2 xa   2 1 x 2x 2   2 2 2 2 2  log x x   x a xa  1 2 2 3 log 2 2 2  2 2 2   x 2 2 2 x 2 x 2 x 1  2  log  2
x  2x  3  2 xa log 2 x a  2 2  2 2   2 x 2 x3  2 log  2
x  2x  3  2 xa  log 2 x a  2 (1) 2  2 2 2   Trang 709
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 t 2t Xét hàm số    2t f t .log t, t
  2 ; Ta có: f t  2 ln t   0, t
  2  Hàm số f t 2 t ln 2
đồng biến trên 2; . Từ (1) suy ra f  2
x x    f x a   2 2 3 2
2  x  2x  3  2 x a  2 2
x  2x  1  2 x a (*) 2
x  2x 1  2  x a 2
x  4x  2a 1  0 (2)     2
x  2x 1  2  x a  2 x  2a 1 (3)  
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):  3   0 a         2 3 2a 0  2 1       a    0 2a 1  0 1 2  (3)   a    2
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):  3   0 a         2 3 2a 0  2 3       a    0 2a 1  0 1 2  (3)   a    2
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung: 2 
x  4x  2a 1  0
Điều này xảy ra khi hệ  có nghiệm 2 x  2a 1  2 
x  4x  2a  1  0 x ax  1      2 x  2a 1 a  1 a  1    x  1 
Khi a  1 ta có: 2 trở thành 2
x  4x  3  0  x  3   x  1 3 trở thành 2
x  1  x  1 
Khi đó: PT đã cho có 3 nghiệm.  1 3 
Vậy a   ;1;  .  2 2  BỔ SUNG CÁCH 2: Xét phương trình 2
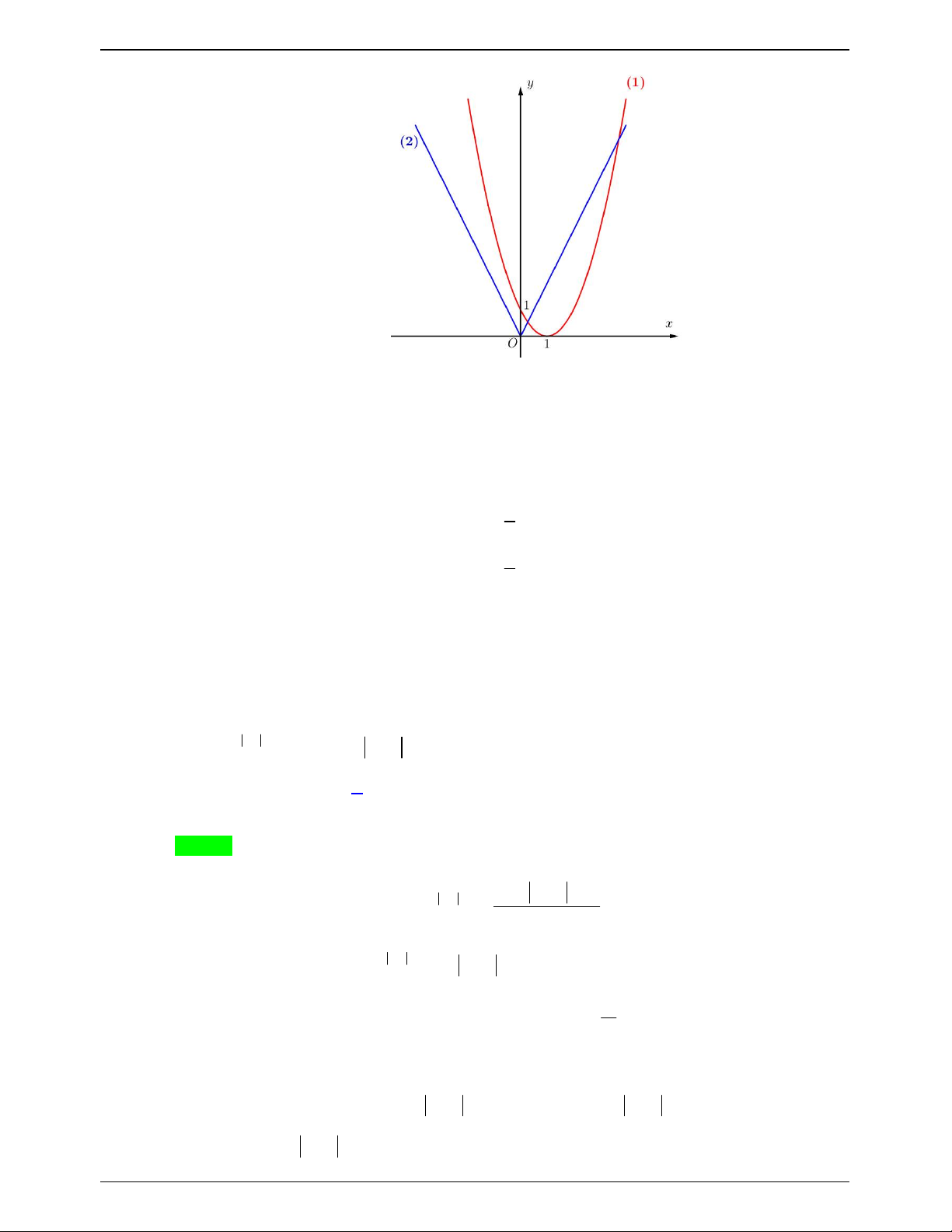
x  2 x 1  2 x a * Vẽ đồ thị hàm số 2
y x  2x 1  
1 ; y  2 x a 2 trên cùng một hệ trục tọa độ ta được: Trang 710
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
nh¸nh bªn tr¸i cña (2) tiÕp xóc víi (1) Nhận xét  
* có 3 nghiệm phân biệt  nh¸nh bªn ph¶i cña (2) tiÕp xóc víi (1) 
(1) vµ (2) cïng trïng cùc trÞ t¹i 1   1 a  2 
x  2x 1  2a x cã nghiÖm kÐp 2   3 2 x 2x 1
2  x a cã nghiÖm kÐp        a   2 a 1   a  1  
Vậy có 3 giá trị của a thỏa mãn bài toán. Câu 47.16: Tìm tổng tất cả các giá trị của tham số a để phương trình 2 x 2 x 1  2 3 xa  log
2 x a  2 có đúng ba nghiệm phân biệt. 2 x 2 x3   A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn B 2
ln 2 x a  2
x 2 x32 xa 2  
PT đã cho tương đương với 3
 ln 2x 2x3 2 x 2 x3   2 3
.ln x  2x  3 2 xa 2  3
.ln 2 x a  2 (1) . t 3t Xét hàm số    3t f t .ln t, t
  2 ; Ta có: f t  3 ln 3.ln t   0, t
  2  Hàm số f t t
đồng biến trên 2;  . Từ (1) suy ra f  2
x x    f x a   2 2 3 2
2  x  2 x  3  2 x a  2 2
x  2x 1  2 x a (*) Trang 711
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2
x  2x 1  2  x a 2
x  4x  2a 1  0 (2)     2
x  2x 1  2  x a  2 x  2a 1 (3)  
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):  3   0 a         2 3 2a 0  2 1       a    0 2a 1  0 1 2  (3)   a    2
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):  3   0 a         2 3 2a 0  2 3       a    0 2a 1  0 1 2  (3)   a    2
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung: 2 
x  4x  2a 1  0
Điều này xảy ra khi hệ  có nghiệm 2 x  2a 1  2 
x  4x  2a  1  0 x ax  1      2 x  2a 1 a  1 a  1    x  1 
Khi a  1 ta có: 2 trở thành 2
x  4x  3  0  x  3   x  1 3 trở thành 2
x  1  x  1 
Khi đó: PT đã cho có 3 nghiệm. 1 3 
Vậy a   ;1; .  2 2  Câu 47.17:
Tìm số giá trị nguyên của m thuộc 20; 20 để phương trình 2 2 2
log (x m x x  4)  (2m  9)x 1 (1 2 ) m
x  4 có nghiệm. 2 A. 12. B. 23. C. 25. D. 10. Lời giải Chọn B Điều kiện xác định: 2 2
x m x x  4  0 . log  2 2
x m x x  4   2m 9 x 1 1 2m 2 x  4 2 Trang 712
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  log x 2
x  4  x m 2 2
 2mx  9x 1
x  4  2m x  4 2  4x  2 2  log 
m   2mx  9x 1 x  4  2m x  4 2 2  x  4  x  2  4x m x 4     mx 2 2  log 
  2mx  9x 1 x  4  2m x  4 2  2 x 4     x   log  2
4x m x  4  mx   2
8x  2m x  4  2mx1 log  2
x  4  x   2 x  4  x 2 2   log  2
8x  2m x  4  2mx   2
8x  2m x  4  2mx  log  2
x  4  x   2 x  4  x 1 2 2   
Xét hàm số f t   log t t , t  0;  . 2 1 f t 
1  0, t  0;  nên hàm số đồng biến trên 0; . t ln 2 Khi đó   1 2 2
 8x  2m x  4  2mx x  4  xm  2
x   x   2 2 4
x  4  x 8x 8x  2m  1 2 x  4  x x  2 8 x  4  x  2m  1  4
m   x  2 2 1 2 x  4  x 1 2m 2 2
x x  4  x  . 2 Xét hàm số 2 2
g (x)  x x  4  x với x  ;   .
x 4  x2 2 Ta có g (  x)   0, x   . 2 x  4  4  4 g x x x x  lim x   lim  2  ; x x   2 lim lim 4          x 2 
x  4  x x 4  1 1 2 x Trang 713
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020   4  lim g x 2  lim x  1  1   . 2 x x     x 
Ta có bảng biến thiên của g(x) 1 2m 5
Để phương trình có nghiệm thì  2   m  . 2 2
Do m nguyên thuộc  2
 0 ; 20 nên số giá trị m là 23. 2 2 2 Câu 47.18: Cho ,
x y là hai số thực dương thỏa mãn x 2  y   x 2 
y  2yx 2 4 9.3 4 9 .7 . Giá trị nhỏ nhất x  2 y 18
của biểu thức P  là x 3  2 A. 9. B. . C. 1 9 2. D. 17. 2 Lời giải Chọn A 2 2 2 2 2 2 Ta có x 2 y
x 2 y  2yx 2 x 2 y2 2( x 2 y ) 2 y x  2 4 9.3 4 9 .7 4 3 4 3         .7   2 2 x 2 y2 2( x 2 y ) 4  3 4  3   (*). 2 2 x 2 y 2 2( x 2 y ) 7 7 t t 4  3t  1   3 
Xét hàm số f (t) 
trên . Ta có f (t)  4.   
  nghịch biến trên . 7t  7   7   f  2 x y   2 2 2 2 2 (*) 2
2  f 2(x  2 y)  x  2y  2  2(x  2y)  x  2 y  2  2 y x  2.   2 x x 16 16 16 Từ đó P   x  1  2 . x 1  P  9. x x x
Dấu "  " xảy ra khi và chỉ khi x  4. Trang 714
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
x y 1  Câu 47.19: Cho các số dương , x y thỏa mãn log
 3x  2 y  4 . Giá trị nhỏ nhất của biểu 5   2x  3  y  4 9
thức A  6x  2 y   bằng x y 31 6 27 2 A. . B. 11 3. C. . D. 19. 4 2 Lời giải Chọn D
x y 1  0  ĐK: 2x  3  y
x y  1 x, y  0  Ta có:
x y 1 log
 3x  2 y  4 5   2x  3  y
 log x y 1 1  5 x y 1  log 2x  3y  2x  3y 5      5  
 log 5 x y 1   5 x y 1  log
2x  3y  2x  3 y * 5     5       1
Xét hàm số f (t)  log
t t trên 0;   , vì f (  t)  1  0, t
 0;  nên hàm số 5   t ln 5
f (t) đồng biến trên 0;  .
*  5 x y  
1  2x  3y  3x  2 y  5 Mặt khác, ta có 4 9  4   9 
A  6x  2 y    9x   4 y     
 3x  2 y   2.6  2.6  5  19 . x yx y    4 9x   x  2  x  9    3
Dấu “ = ” xảy ra  4y   
(thỏa mãn điều kiện). y 3   y  3
x  2 y  5   2  
Vậy GTNN của A là 19. Trang 715
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 y x Câu 47.20:
Cho hai số thực x, y lớn hơn 1 và thỏa mãn x.( x )e y .( y )e y e x e
. Tìm giá trị nhỏ nhất của biểu thức P  log xy  log . x x y 2 1 2 2 1 2 A. . B. 2 2 . C. . D. . 2 2 2 Lời giải Chọn C Với , x y  1, ta có y x x y .( x
e )e y x .( y e )e y x  ln  x y .( x
e )e   ln  y x .( y e )e   x ln y y
xe y ln x x ye ln y y e ln x x e     (1). y y x x t 1
Xét hàm số ( )  t t g t te
e 1 ln t trên 1; , có g (
t)  te   0, t   1. t
Hàm số g(t) đồng biến trên 1;  nên g(t)  g(1) 1  0,t 1. ln t t e g(t)
Xét hàm số f (t)  
trên 1;  , có f '(t) 
 0,t  1, nên f (t) đồng biến trên t t 2 t (1;  )
 . Với x, y  1 thì (1)  f ( y)  f (x)  y  . x 1 u 1 2 u  2 Đặt u  log .
y Do y x  1 nên u  1. Ta có P h(u) 
 . Nhận thấy h '(u)  , x 2 u 2 2u
nên h '(u)  0 khi u  2, h '(u)  0 khi 1  u  2, h '(u)  0 khi u  2. Dẫn tới
P h u h   1 2 2 ( ) 2 
,u  1, đẳng thức xảy ra khi u  2. 2 1 2 2 Vậy min P  , đạt được khi 2 y x và x  1. 2 Câu 47.21:
Cho hai số thực x, y thỏa mãn 0  x, y  1 trong đó x, y không đồng thời bằng 0 hoặc 1 và  x y  log  x 1 . y 1
2 0 . Tìm giá trị nhỏ nhất của P với P  2x y 3          1  xy  1 A. 2 . B. 1 . C. . D. 0 . 2 Lời giải Trang 716
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn B x y
Từ điều kiện đề bài và
 0; 1  xy  0  x y  0;1  xy  0 khi đó 1  xyx y  log  x 1 . y 1 2 0 log x y x y log 1 xy 1 xy 1 3
         3         3            1   xy  1
Xét hàm số f t  log t t t  0 có f t   1  0 t  0 3  t.ln 3
f t  là hàm số đồng biến trên khoảng 0;  . 1 x 1 x Vậy phương trình 1  
x y  1  xy y   P  2x  1  x 1  x 1  x 2 x  0
Xét hàm số f (x)  2x
với x  0; 1 có f (x)  2 
cho f (x)  0   x  1    2 x  1 x    2
f 0  1; f  
1  2  min f (x)  1  chọn B 0;    1  1  2x Câu 47.22:
Xét các số thực dương x , y thỏa mãn ln  3x y   
1. Tìm giá trị nhỏ nhất P x  min  y  1 1 của P   . x xy A. P  8 . B. P  4 . C. P  2 . D. P  16 . min min min min Lời giải Chọn A 1
Điều kiện 0  x  . 2  1  2x  Từ giả thiết ln  3x y   
1  ln 1  2x  1 2x  ln x y  x y 1 x   y  1
Xét hàm số f t   ln t t trên 0;   có f t    1  0 , t  0 do đó hàm f t đơn điệu. t
Vậy 1  1  2x x y  3x y  1 2 1 1 1 2 1 2 Có P       x xy x x y x 1  2x 1 2 1 4 1
Đặt g x  
, ta có g x   
suy ra gx  0  x  . x 1  2x 2 x  2 1 2x 4
Do đó min g x  8 . Vậy P  8 . min  1   0 ;   2  1 1 1 2 1 2 4 1
Bổ sung: có thể đánh giá P         x xy x x y x 1  2x 1 8 x   x 2 Trang 717
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 y 1 Câu 47.23:
Cho hai số thực x, y không âm thỏa mãn 2
x  2x y 1  log
. Giá trị nhỏ nhất của 2 x 1 biểu thức 2x 1  2 P e
 4x  2y 1 là 1 1 A.  . B. 1. C. . D. 1. 2 2 Lời giải Chọn A 2 y 1 2 2 2
x  2x y 1  log  2  x   1  log 2 x  1  log
2 y  1  2 y  1 . 2     2     2 x 1 1
Xét hàm số f t   t  log t , t  0 ; f t   1   0, t  0 2   t.ln 2 Suy ra  x  2 2
1  2y 1  y   x  2 2 2 1 1. 2x 1  2 P e
 4x  2y 1 x e  
x   x  2 2 1 2 4 2 1 11 2x 1  2  e
 2x  4x g x . g x 2 x 1 2e   
 4x  4 là hàm số đồng biến trên nửa khoảng 0; nên g x  0 có tối đa 1 1
nghiệm, nhẩm được nghiệm x
nên nghiệm đó là duy nhất. 2 1 1 Vậy min P   tại x  . 2 2 Câu 47.24:
Cho hai số thực dương x , y thay đổi thỏa mãn đẳng thức    xy     2 2 1 2 1 .2 .2x y xy x y .
Tìm giá trị nhỏ nhất y của y . min A. y  3 . B. y  2 . C. y  1. D. y  3 . min min min min Lời giải Chọn B 2 Ta có 
  xy     2 2 1 2 1 2 2x y xy x yxy  2xy 1  2 x
yx y 1 2 1 1 2 2         1 Xét hàm       1 .2t f t t với t  1.
Khi đó    2t     1 .2t f t t
.ln 2  0 với t  1. 2 x  2 Từ   2
1  2xy 1  x y 1  y  2x 1 Trang 718
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 2x  2x  4 x  2 y   0 2
 2x  2x  4  0   2x  2 1 x  1  Loại x  1
 vì điều kiện của t nên f 2  2 . x, y     x    Câu 47.25: Cho          sao cho 3 3 ln 2 x ln 3 19 y 6xy(x 2 y)  
. Tìm giá trị nhỏ nhất m x, y 1   y  1
của biểu thức T x  . x  3y 5
A. m  1 3 . B. m  2. C. m  . D. m 1. 4 Lời giải Chọn C Ta có  x       x  
y xy x y
y x y x3   y y3 3 3 ln 2 ln 3 19 6 ( 2 ) ln 2 2 ln 3 3   1     y  1
Xét hàm số f t  t 3 ln
t với t  0 có f t 2
 3t  0 t  0  f tđồng biến t Vậy   1
1  2 y x  3y x y T x  4x
Áp dụng bất đẳng thức AM-GM 1 3x x 1 3x x 1 3x 1 3 1 5 T x       2 . 
    Dấu bằng xảy ra khi 4x 4 4 4x 4 4 4x 4 2 4 2 4
x y 1 Câu 47.26: Cho x; y là các số thực dương thỏa mãn điều kiện  y 3 5xy x 4 x 4 5   x 1
 3  y yx 4. Tìm giá trị nhỏ nhất của biểu thức P x y . 3xy 5 A. 3. B. 5  2 5 . C. 3 2 5 . D. 1 5 . Lời giải Chọn B xy 3 5xy Ta có 4 x 4 5   x 1
3  y yx 4 3xy 5  x4yx4 y xy 1  1 5 3   4  5 3 xy x yxy   1  1 . Xét hàm số   5t 3 t f t     t trên  . Vì
  5t.ln 5 3 t f t    
.ln 3 1 0; x   nên hàm số f t đồng biến trên  2 . Từ  
1 và 2 ta có x  4 y xy   1 
3 . Dễ thấy x  4 không thỏa mãn 3. x  Với x  4 ,   1 3  y
kết hợp điều kiện y  0 suy ra x  4 . x  4 Trang 719
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x 1
Do đó P x y x  . x  4 x
Xét hàm số g x 1  x  trên 4;   . x  4  5 x  4  5 
Ta có gx 1  0  .   x  42 x  4 5  x 4 4  5  g x – 0   
g x 5  2 5
Dựa vào bảng biến thiên ta có P
 min g x  5  2 5 . min   4;   xy xy 3 5 Câu 47.27:
Cho x , y là các số thực dương thỏa mãn 2  x2 5   x 1   3
y y(x  2) . Tìm giá 3xy 5
trị nhỏ nhất của biểu thức T x y . A. T  2  3 2 . B. T  3  2 3 . C. T  1 5 . D. T  5  3 2 . min min min min Lời giải Chọn B Theo đề ra ta có xy xy 3 5 2  x2 5   x  1   3
y y(x  2) 3xy 5 xy 1 xy  1 2 1  5 
x  2 y  5   xy 1 x2 y xy 1 3 3  t 1
Xét f t   5   t . 
   5t ln 5  3  t f t ln 3 1  0 3t x 1 x 1
x  2 y xy 1  y
.Do y  0, x  0   0  x  2 x  2 x  2 2 x 1 x x 1
Ta có: T x y x   x  2 x  2 2  x  2  3 x x  2; 4 1     T    0    x  22
x  2  3  2;   Bảng biến thiên
Chỉnh lại bbt cho em,chỉ xét với x  2 nhé,kết quả không thay đổi. Trang 720
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Từ bảng biến thiên ta thấy T
 3  2 3 tại x  2  3 . min x  3 y Câu 47.28:
Xét các số thực dương x, y thỏa mãn log
xy  3 y x 1 . Tìm giá trị nhỏ nhất của 3 xy 1 1
biểu thức A x  . y 14 14 A. A  . B. A   . C. A  6  . D. A  6 . min 3 min 3 min min Lời giải Chọn D
Điều kiện: x  3 y  0 . x  3 y log
xy  3 y x  1  log
x  3 y  log
xy  1  xy  3 y x  1 3 3   3   xy 1  log
x  3 y x  3y  log
xy 1  xy 1 1 . 3     3    
Xét hàm f t   log t t, t  0 . 3 1
f  t   1  0, t   0 . t.ln 3 x 1
Suy ra hàm số f t  đồng biến trên 0;   nên  
1  x  3y xy 1  y  . x  3 1 x  3 A x   x  . y x 1 x  3 4
Đặt A A x  x
A  x  1
 0  x  3 do x, y  0 . x 1  x  2 1  2 2 x y2 4x y  2 Câu 47.29: Cho , x y  0 thỏa 2019 
 0 . Tìm giá trị nhỏ nhất P của  min x  22
P  2y 4x . 1 A. 2018 . B. 2019 . C. . D. 2 . 2 Lời giải Trang 721
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn D
 2xy  4x y  2  2 2 2
2 x 4 x  4  
2 4 xy  2 4x y  2 Ta có: 2019   0  2019  x  22 x  22 x 2    2019 .x  22 2 2  2 4 x y 2  2019
.4 x y  2  * . u  x   2 2 Đặt  u,v   0 v
  4xy 2  Khi đó:   2u 2 *  2019 .  2019 v u
.v f u  f v với   2  2019 t f t .t, (t  0)    2t 2 '
 2019 .2 ln 2019.  2019 t f t t  0, t  0
Do đó: f u  f v  u v  x  2 2 2
 4x y  2  y x  2.
P y x x x   x  2 2 2 4 2 4 4 2 1  2  2 . Vậy P  2  x 1. min y1 Câu 47.30:
Cho 2 số thực dương x, y thỏa mãn log  x 1 y 1 9
x 1 y 1 . Giá trị nhỏ 3              
nhất của biểu thức P x  2y là 11 27 A. P  . B. P  . C. P  5  6 3 . D. P  3  6 2 . min 2 min 5 min min Lời giải Chọn D y1
Ta có log  x 1 y 1 9 x 1 y 1 3              
 y  1 log x 1 log y 1 x 1 y 1 9 . 3     3 
          
  y  1 log x 1 log y 1 x 1 9 3     3          9  log x 1 x 1 log y 1 3        3    y  1 9 9  log x 1 x 1 2 2 log . 3          y  3 1 y  1 1
Xét hàm số f t  log t t  2 với t  0 có f t 
 1  0 với mọi t  0 nên hàm số 3 t ln 3
f t luôn đồng biến và liên tục trên 0;  . 9 9 8  y
Từ đó suy ra x  1   x   1 
, do x  0 nên y  0; 8 . y  1 y  1 y  1 8  y 9 9
Vậy P x  2y
 2y  2y  1 
 2  y  1   3  3  6 2 . y  1 y  1 y  1 Trang 722
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 9 3 Vậy P
 3  6 2 khi 2  y  1   y   1 . min y  1 2 1 y Câu 47.31:
Xét các số thực dương x, y thỏa mãn log
 3xy x  3y  4 . Tìm giá trị nhỏ nhất 3 x  3xy P
của P x y . min 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9 Lời giải Chọn B 1 y log
 3xy x  3y  4  log 1 y  log
x  3xy  3xy x  3y  4 3 3   3   x  3xy
 log 3 1 y  3 1 y  log
x  3xy x  3xy 3     3     1
Xét hàm f t   log t t, t  0 có f 't   1  0, t
  0 . Suy ra hàm số đồng biến trên 3 t ln 3
0; . Suy ra  log 3 1 y  3 1 y  log x  3xy x  3xy  31 y  x  3xy 3     3     31 y 31 y 4 3  4 4 3  4  x
x y y   . Vậy P  . 1 3y 1 3y 3 min 3 x y Câu 47.32:
Xét các số thực dương x, y thỏa mãn log
x x  3  y y  3  x . y Tìm 3 2 2    
x y xy  2 3x  2 y 1
giá trị lớn nhất P
của biểu thức P  . max x y  6 A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn C Ta có: x y log
x x  3  y y  3  xy 3 2 2
x y xy  2  log
3 x y   3 x y  log  2 2
x y xy  2 2 2
x y xy  2 . 3 3 1
Xét hàm số f t   log t t , t  0 có f t  
1  0, t  0 . Vậy hàm số f t  luôn 3 t ln 3
đồng biến và liên tục trên khoảng 0;  .
Do đó: f   x y  f  2 2
x y xy     x y 2 2 3 2 3
x y xy  2   1 Từ   2
1  xy   x y  3 x y  2 . 2
x y  1 
Ta có x x xy xy x y   1  xy     xy  2 
Đẳng thức xảy ra khi và chỉ khi x y 1. Trang 723
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
x y  2 1 2 Do đó từ   1 , suy ra: x
  x y   3 x y  2 . 4
Đặt t x y , t  0 . t  2 1 2 2 x y 2t 1
t  3t  2 2 1 x 3
t  22t  3 Suy ra: 4 P   
f t  . x y  6 t  6 4t  6 2
3t  36t 135
Ta có: f  t 
 0  t  3 (nhận) 4 t  62 Bảng biến thiên t 0 3  f t   0  f t  x y 1 x  2
Dựa vào BBT, ta có max P  max f t   f 3  1 khi và chỉ khi    . 0; x y  3 y  1    2 2 x y  1 2x y Câu 47.33:
Xét các số thực dương x , y thỏa mãn 2018 
. Tìm giá trị nhỏ nhất P của  min x  2 1
P  2 y  3x . 1 7 3 5 A. P  . B. P  . C. P  . D. P  . min 2 min 8 min 4 min 6 Lời giải Chọn B  2 2 x y  1 2x y 2x y Cách 1: Ta có 2018   2  2 x y   1  log  2018 2 x  2 1  x   1  2  x  2
1  2 2x y  log
2x y  log x  2 1 2018 2018  2  x  2 1  log  x  2 1
 2 2x y  log 2x y 2018   2018   2 Có dạng f   x  1  
f 2x y với f t   2t  log t ,  t   0 .   2018 1
Xét hàm số f t   2t  log t ,  t
  0 , ta có f t   2   0  t   0 nên hàm số 2018 t.ln 2018 2
f t  đồng biến trên khoảng 0;   . Khi đó f   x  1  
f 2x y   x  2 1  2x y   2
y x 1.
Ta có P y x   2 x   2 2 3 2
1  3x  2x  3x  2 . Trang 724
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Bảng biến thiên 3 x   4  7  P 8 7 3 Vậy P  khi x  . min 8 4 y 1  Câu 47.34:
Cho 2 số thực dương x, y thỏa mãn log  x  1 y 1   9  x 1 y 1 3         . Giá trị nhỏ
nhất của biểu thức P x  2 y là 11 27 A. P. B. P. C. P  5   6 3 . D. P  3   6 2 . min 2 min 5 min min Lời giải Chọn D y 1  Ta có log  x  1 y 1   9  x 1 y 1 3           y   1 log x 1  log
y 1   x 1 y 1  9  3   3       .   y   1 log x 1  log
y 1  x 1  9  3   3    9  log
x 1  x 1   log y 1 3   3   y 1 9 9  log
x 1  x 1 2   2  log (*). 3   3 y 1 y 1 1
Xét hàm số f t   log t t  2 với t  0 có f t  
 1  0 với mọi t  0 nên hàm số f t  3 t ln 3
luôn đồng biến và liên tục trên 0;  . 9 9 8  y
Từ (*) suy ra x 1   x  1 
, do x  0 nên y  0;8 . y 1 y 1 y 1 8  y 9 9
Vậy P x  2 y
 2 y  2 y 1  2  y   1   3  3  6 2 . y 1 y 1 y 1 9 3 Vậy P  3
  6 2 khi 2  y   1   y  1. min y 1 2 Câu 47.35:
Cho hai số thực dương x, y thỏa mãn log x x x y  log
6  y  6x . Giá trị nhỏ nhất 2   2   6 8
của biểu thức P  3x  2 y   bằng x y Trang 725
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 59 53 A. . B. 19 . C. . D. 8  6 2 . 3 3 Lời giải Chọn Bx  0 Điều kiện:  . 0  y  6  Từ giả thiết ta có:
log x x x y  log 6  y  2 2
 6x  log x x  log x 6  y   x 6  y 2 2 2 2       (*) 1
Xét hàm số f t   log t t với t  0 , Ta có f 't   1  0, t   0 nên hàm số 2 t ln 2
f t   log t t đồng biến trên khoảng 0;  . 2
Do đó    f  2
x   f x  y 2 * 6
  x x 6  y  x  6  y x y  6**   ( do x  0 )
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức *  * , ta có: 6 8 3  3x 6   y 8  3 3x 6 y 8
P  3x  2 y   
x y      .6  2 .  2 .  19     . x y 2  2 x  2 y 2 2 x 2 y    x y  6  3x 6 x  2
Đẳng thức xảy ra khi và chỉ khi    
. Vậy giá trị nhỏ nhất của P bằng 19. 2 x y  4    y 8   2 y  2 2 x  5 y Câu 47.36:
Cho x, y là các số dương thỏa mãn 2 2 log
 1  x  10 xy  9 y  0 . Gọi M ,m 2 2 2
x  10 xy y 2 2
x xy  9 y
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P
. Tính T  10 M m . 2 xy y A. T  60 . B. T  94 . C. T  104 . D. T  50 . Lời giải Chọn B 2 2 x  5 y 2 2 log
 1  x  10 xy  9 y  0 2 2 2
x  10 xy y  log  2 2
x  5 y   log  2 2
x 10 xy y   log 2  2 2 2
x  5 y    2 2
x 10xy y  0 2 2 2   log  2 2
2x 10 y   2 2 2
x  5 y   log  2 2
x 10xy y    2 2
x 10xy y 2 2  2 2 2 2
 2x  10 y x  10xy y vi) Trang 726
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2  x   x  2 2 x
x 10xy  9 y  0   10  9  0      1   9 y y     y 2  x x   9 2 2  
x xy  9 y y y P     2 xy y x  1 y x Đặt t
, điều kiện : 1  t  9 y 2 t t  9 2 t  2t  8 t  4 f t 
; f t  
; f t   0   t  1 t  2 1 t  2  11 99 f 1 
; f 2  5 ; f 9  2 10 99 Nên M
, m  5 . Vậy T  10 M m  94 . 10 2 2 2 Câu 47.37: Vậy A
 6 .Cho các số thực dương x và y thỏa mãn x 2 y    x 2 y   2yx 2 4 9.3 4 9 .7 . min x  2 y 18
Tìm giá trị nhỏ nhất của biểu thức P  . x 3  2 A. P  9 . B. P  . 2
C. P  1 9 2 .
D. Hàm số không có giá trị nhỏ nhất. Lời giải Chọn A Từ giả thiết ta đặt 2
t x  2 y , t   . 2 2 2 Phương trình x 2 y    x 2 y   2yx 2 4 9.3 4 9 .7 trở thành t   tt  49               . ttt 7 4 9.3 4 9 . 4 7 49 9 9. 49 0 7   3   
Nhận thấy t  2 là nghiệm phương trình.
Ta chứng minh t  2 là nghiệm duy nhất của phương trình. t  7  
Xét t  2 : 7t  49 và 9.  49  
nên vế trái phương trình luôn dương, nên phương trình vô  3  nghiệm. t  7  
Xét t  2 : 7t  49 và 9.  49  
nên vế trái phương trình luôn âm, nên phương trình vô  3  nghiệm. Trang 727
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 x  2 2 x  2 y 18 x x 16 Vậy 2
t x  2 y  2  y  thay vào P   2 x x 16 16 16  x  1  2 . x
1  9 . Dấu bằng đạt được khi x   x  4 . x x x y x e e Câu 47.38:
Cho x, y là các số thực lớn hơn 1 sao cho x x y   y y e x
e  . Tìm giá trị nhỏ nhất của
biểu thức: P  log xy  log x . x y 2 1  2 2 1  2 A. . B. 2 2 . C. . D. . 2 2 2 Lời giải Chọn C Cách 1. y x y x e e e e
Ta có: x x y y
ln  x x   ln  y y y e x e y e x e              x yx ln y
y xe y ln x x ye   (*) (vì x
y e  ln x có ln x x e ln y y e x 1 y '  e
 0;x  1 nên y y   1  e  0 ) x t ln t t e 1 tte
Xét hàm số: f t  
trên 1;  ta có f 't   . Với hàm số ln t t e ln t t e 2    ln t  1 t g t t ete có     t t     1 ' ln 1 ' t g t t e te
  te  0,t  1 t
Nên g t   g  
1  1  f 't   0; t   1
y f t  là hàm nghịch biến trên 1;  nên với (*) f x  f y  y x  1 1 1 1 1 1 1 1 2 2 Khi đó P  log xy  log x   log y    2 log . yx y 2 2 x log y 2 2 x log y 2 x x 1 1
Dấu “=” xảy ra khi: log y   y   y x x logx 2 2 2 2 log y x 1  2 2 Vậy: P  . min 2 2 1 x  1  Câu 47.39:
Tính giá trị của biểu thức 2 2
P x y xy 1 biết rằng 2 4 x  log 1  4  y  2 y  1 2     13
với x  0 và 1  y  . 2 A. P  4 . B. P  2 . C. P  1 . D. P  3 . Lời giải Trang 728
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn B 2 1 x  1  Xét 2 4 x  log 1  4  y  2 y  1 . 2     2 1 2 1 x  1  2 x . 1  2 2 Ta có 4 x  4 x
 4 , dấu bằng xảy ra khi và chỉ khi x  1 , . Mặt khác
  y   y   
y    y  3 14 2 1 14 3 1 1 . 30 Đặt t
y 1 ta có 0  t
. Xét hàm số f t  3  t
  3t 14 . Ta tìm GTLN – GTNN của 2  30   30  56  9 30 hàm số trên đoạn 0; 
 được min f t   f   
; max f t   f   1  16 . 2      30  2 4  30  0;     0;   2    2    Suy ra log 1  4  y  2
y 1  log 16  4 , . 2   2   x  1  x  1 Từ và suy ra ta có    . Thay vào P  2 . t   y 1  1  y  0  1 1 Câu 47.40:
Cho hai số thực x , y thỏa mãn 0  x  , 0  y
và log 11 2x y  2y  4x 1. Xét 2 2 biểu thức 2
P  16 yx  2x 3y  2  y  5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn
nhất của P . Khi đó giá trị của T  4m M  bằng bao nhiêu? A. 16 . B. 18 . C. 17 . D. 19 . Lời giải Chọn A Ta có
log 11 2x y  2y  4x 1  22x y  log 11 2x y  1  0
Đặt t  2x y , 0  t  11 . Phương trình trở thành: 2t  log 11 t  1  0 .   1
Xét hàm số f t   2t  log 11 t  1 trên khoảng 0;1  1 . 1 Có y  2   0 , t   0;1 
1 . Do đó hàm số f t  luôn đồng biến. 11 t Dễ thấy  
1 có nghiệm t  1. Do đó t  1 là nghiệm duy nhất của   1 .   y2 1
Suy ra 2x  1 y . Khi đó P  16 y
 1 y3y  2  y  5 3 2
 4 y  5 y  2 y  3 . 4  1 
Xét hàm số g y 3 2
 4 y  5 y  2 y  3 trên 0;  , có 2     1  g y 2
 12 y 10 y  2  0 , y   0;  . 2    Trang 729
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Do đó, min g y   g 0  3 , max g y  g   1  4 .  1   1  0;  0; 2       2
Suy ra m  3 , m  4 .
Vậy T  4.3  4  16 . Trang 730