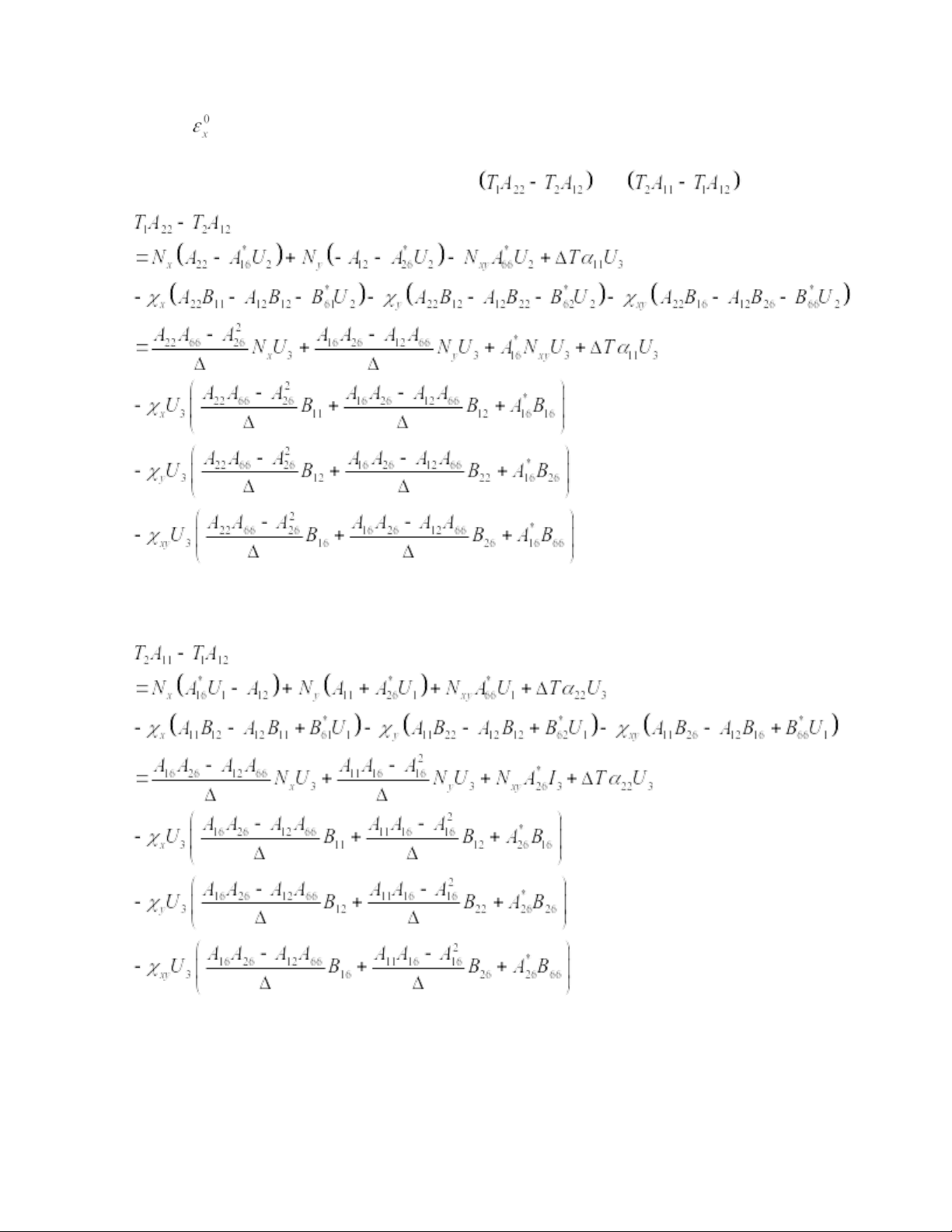




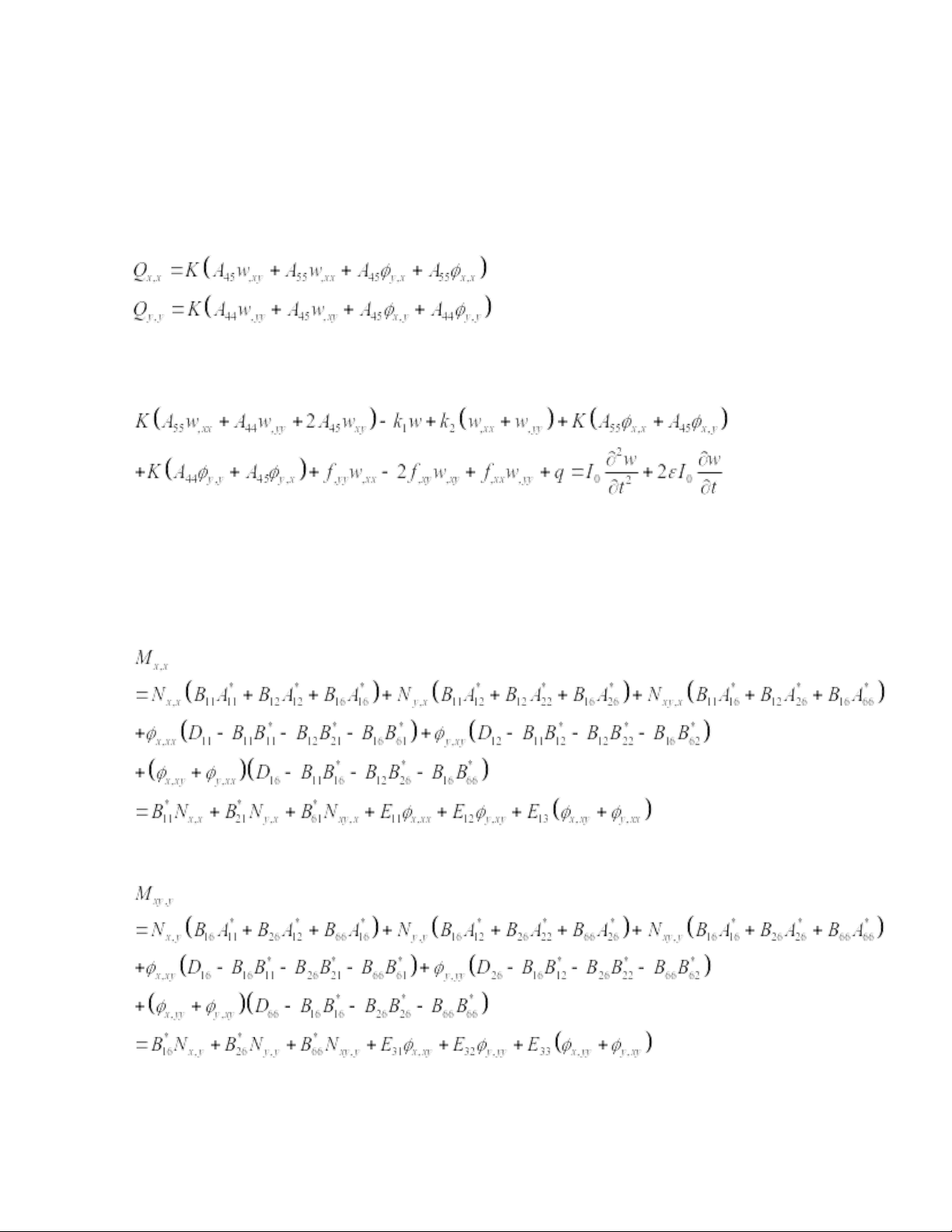


Preview text:
lOMoAR cPSD| 59735516
Sử dụng lý thuyết biến dạng trượt bậc nhất, các mối quan hệ biến dạng – chuyển vị có tính
đến các thuật ngữ phi tuyến Von Karman như sau: (1) với (2)
Định luật Hooke cho vật liệu composite ba pha nhiều lớp tại lớp thứ k như sau: (3) Với lOMoAR cPSD| 59735516 (4) với (5)
và α là góc hợp bởi phương của sợi và trục Ox.
I. Tiến độ tuần 1: Tính các thành phần nội lực, mô-men, lực cắt
Các thành phần nội lực, momen cho vât liệu có N lớp được xác định như sau: (6)
Thay (1) vào (3) xong thay (3) vào (6) ta được các thành phần nội lực, momen cụ thể như sau, với K = 5/6 và : * Ni (7.1) lOMoAR cPSD| 59735516 * Mi (7.2) * Qx , Qy (7.3) lOMoAR cPSD| 59735516 Trong đó: (8) trong đó: (9)
Tổng hợp (7.1),(7.2),(7.3) ta được: (7)
II. Tiến độ tuần 2: Tính ra được hệ phương trình (19) pdf huybich2014 lOMoAR cPSD| 59735516
1. Từ phương trình nội lực Ni tính 3 thành phần biến dạng tại mặt giữa tấm a) Tính
_ Lấy A16Nx – A11Nxy ta được: (10.1)
_ Lấy A16Ny – A12Nxy ta được: (10.2) Đặt: (11)
_ Lấy phương trình (10.2) nhân với U1 trừ cho phương trình (10.1) nhân với U2 ta được: (10.3)
Xét A12U1 – A11U2 ta được: (10.4)
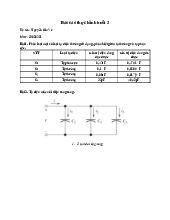
_ Thay (10.4) vào phương trình (10.3) và chia cả 2 vế cho A16 ta được như sau: lOMoAR cPSD| 59735516 Ta được như sau: (10.5) Trong đó: (12.1) b) Tính , _ Ta có: (10.6)
Thay (10.5) vào (10.6) ta được dạng , như sau: (10.7) Trong đó: (10.8) lOMoAR cPSD| 59735516 _ Tính :
Từ (10.8) kết hợp (11) và (12.1), tính cụm và ta được: (10.9) (10.10)
Thay (10.9) và (10.10) vào (10.7) ta được: lOMoAR cPSD| 59735516 (10.11) Trong đó: (12.2) c) Tổng hợp lại
Kết hợp các kết quả (10.5), (10.11) và (12.1),(12.2): ta tính được các biến dạng tại mặt giữa , , như sau: (10) Trong đó (12) lOMoAR cPSD| 59735516
2. Hệ phương trình chuyển động
a) Biến đổi ra được 3 pt (18a-18c) pdf huybich2014
Hệ phương trình chuyển động của tấm FGM tương đối dày sử dụng lý thuyết biến
dạng trượt bậc nhất với giá trị được cho bởi: (13a) (13b) (13c) (13d) (13e) trong đó:
q là áp lực ngoài phân bố đều, biến đổi điều hòa theo thời gian
Để giải ta dùng phương pháp hàm ứng suất với cách chọn: Ta có: (15) lOMoAR cPSD| 59735516 (14) (16)
Thay (16) vào (13a) và (13b) ta được:
(17) Thay (15) và (17) vào 3 phương trình (13c-13e) ta được: (18a) (18b) (18c)
b) Xử lí nốt để ra được 3 phương trình (19) pdf huybich2014
Thay (2), (10) và (15) vào 5 phương trình tính mô-men Mx , My , Mxy và lực cắt Qx ,
Qy của (7) rồi thay các kết quả thu được vào (18a-18c) ta được như sau: lOMoAR cPSD| 59735516 (19a) (19b) (19c) Trong đó: (20) lOMoAR cPSD| 59735516
Cụ thể tính toán như sau: * Với (18a): Tính Qx,x và Qy,y ta có: (18.1)
Thay (18.1) vào (18a) ta thu được: * Với (18b): Tính Mx,x và Mxy,y ta có:
Thay (2) ,(10) vào (7), kết hợp sử dụng (12) ta được: (18.2) (18.3) lOMoAR cPSD| 59735516 trong đó: (20.1)
Thay (15) và (18.2), (18.3) vào (18b) ta thu được: * Với (18c): Tính My,y và Mxy,x ta có:
Thay (2) ,(10) vào (7), kết hợp sử dụng (12) và (20.1) ta được: (18.4) (18.5) trong đó: lOMoAR cPSD| 59735516 (20.2)
Thay (15) và (18.4), (18.5) vào (18c) ta thu được: