Vật lý nguyên tử | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội
Vật lý nguyên tử | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 24 trang giúp bạn tham khảo ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem.
Preview text:
Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn ViÖn VËt lý kü thuËt
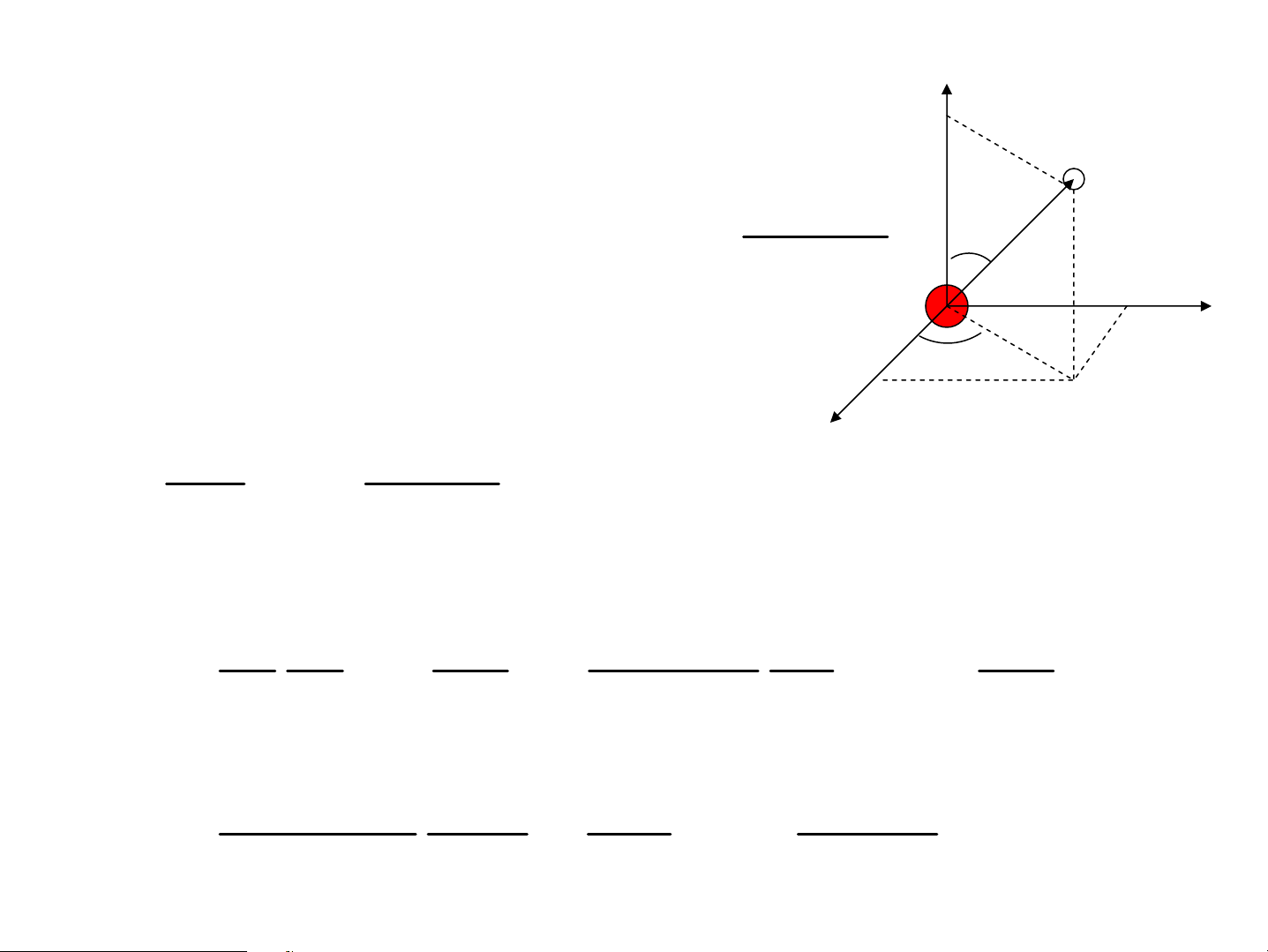
Tr−êng §H B¸ch khoa Hμ néi Ch−¬ng 7 VËt lý nguyªn tö 1. Nguyªn tö hydro z ChuyÓn ®éng cña ®iÖn tö e 2 - trong nguyªn tö hydro Ze r = − θ U 4πε r 1.1 Ph−¬ng tr×nh 0 0 + y ϕ Schrodinger x 2m Ze2 ψ = ψ(r, , θ ϕ) Δψ + (E + )ψ = 0 2 4πε r h 0 x=r.sinθcosϕ y=r.sinθsinϕ z=rcosθ 1 ∂ ψ ∂ ∂ ψ ∂ 2 1 (r ) + (sin θ ) + r2 r ∂ r ∂ r2 sin θ θ ∂ θ ∂ 1 2 ∂ ψ 2m Ze2 + (E + )ψ = 0 r2 sin2 2 2 θ ϕ ∂ h 4πε r 0 ψ = R(r)Y( , θ ϕ) 1 d 2 dR 2 2 (r ) + 2mr ( + Ze E ) = λ R dr dr 2 h 4πε r 0 1 ∂ ∂Y 1 ∂2 (sin θ ) + Y = −λ Y sin θ θ ∂ θ ∂ 2 Y sin θ ϕ ∂ 2 R = R (r) Y = Y (θ, ϕ ) λ = ( nl lm l l + 1) ψ = R (r)Y ( , θ ϕ) nlm nl lm
n= 1, 2, 3, ...Sè l−îng tö chÝnh
l = 0, 1, 2, ...n-1 Sè l−îng tö quÜ ®¹o m = , 0 ± , 1 ± ,..., 2 ±l Sè l−îng tö tõ Zr 1 Z − − 3/ 2 a 2 R 0 = = π , 1 0 2( ) e 0 Y ,0 (4 ) a0 Rh 4 m e E = − e 15 1 − R = = , 3 10 . 27 s n 2 n 2 4 4π(4πε ) 0 h H»ng sè Ritbe 1.2 C¸c kÕt luËn:
a. N¨ng l−îng gi¸n ®o¹n: L−îng tö ho¸ b. N¨ng l−îng Ion ho¸ E=0-E =Rh=2,185.10-18J=13,5eV 1 c. Tr¹ng th¸i l−îng tö: ψ (r, , θ ϕ) = R (r).Y ( , θ ϕ) l Tr¹ng th¸i n,l,m nl lm n, , m. n=1 c¬ së, 0 s l n>=2 møc suy biÕn n2 1 p ∑ n−1 2 d (2l + ) 1 = 2 n 3 f l=0
d. MËt ®é x¸c suÊt t×m h¹t
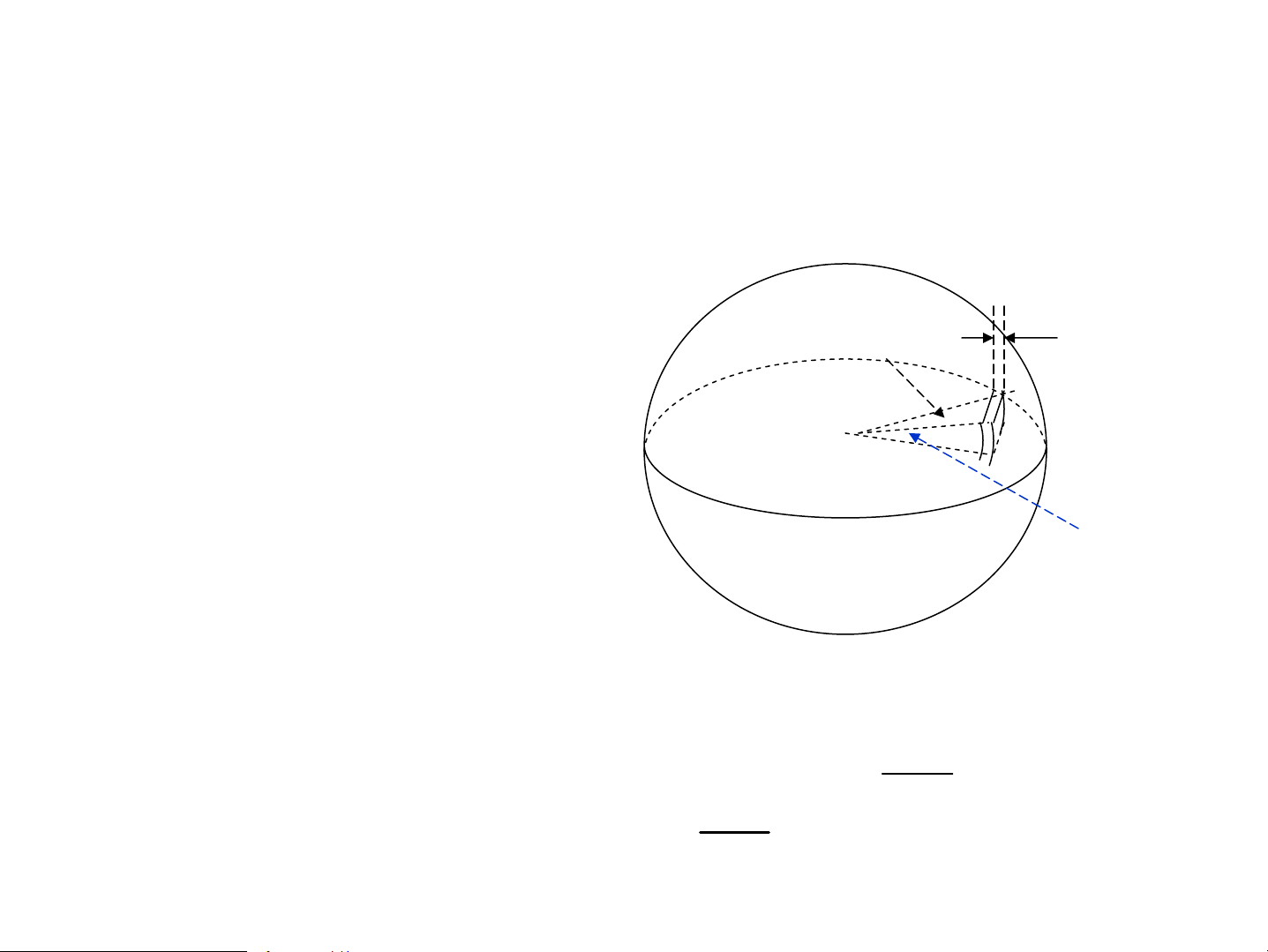
X¸c suÊt t×m h¹t theo thÓ tÝch:
∫|ψ |2 dv = ∫|ψ (r,θ,ϕ) |2 r2 sinθdrdθdϕ nlm X¸c suÊt t×m h¹t theo dϕ dr b¸n kÝnh: . ∫ R2 (r)r2dr nl dθ
MËt ®é x¸c suÊt theo b¸n kÝnh 2Zr − 2 2 Z 3 a0 ρ = R ,10.r = ( 4 ) e .r2 , 1 0 a0 2Zr dρ − ρ (r) , 1 0 Z = , 1 0 ( 4 )3e a Zr 0 (1 .2r - ) = 0 dr a0 a0
§èi víi H, Z=1 cã r=0 vμ r=a . 0 r e. Gi¶i thÝch quang phæ H a =0,53.10-10m 0 Cùc tÝm B¸n kÝnh Bohr 1 1 υ = R( − Liman ) 1 1 12 n2 υ = R( − Perfund ) 52 n2 ∞ 1 1 υ = R( − Bracket ) ngo¹i! 42 n2 n=6 O 1 1 n=5 υ = R( − Pasen ) N n=4 32 n2 Hång M n=3 1 1 υ = − L n=2 R( Banme ) 22 n2 K n=1 ¸nh s¸ng nhÝn thÊy 2. Nguyªn tö kim lo¹i kiÒm
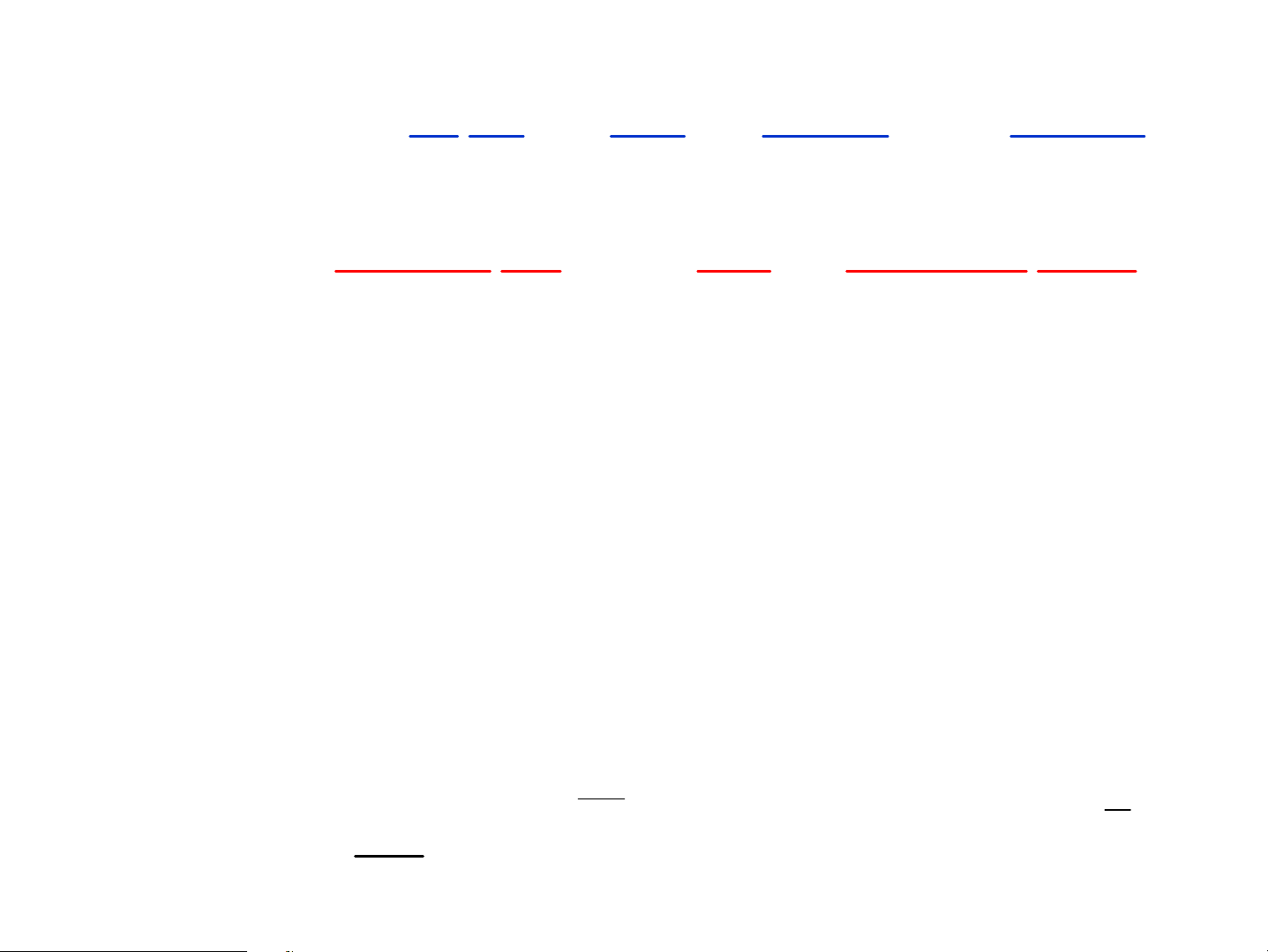
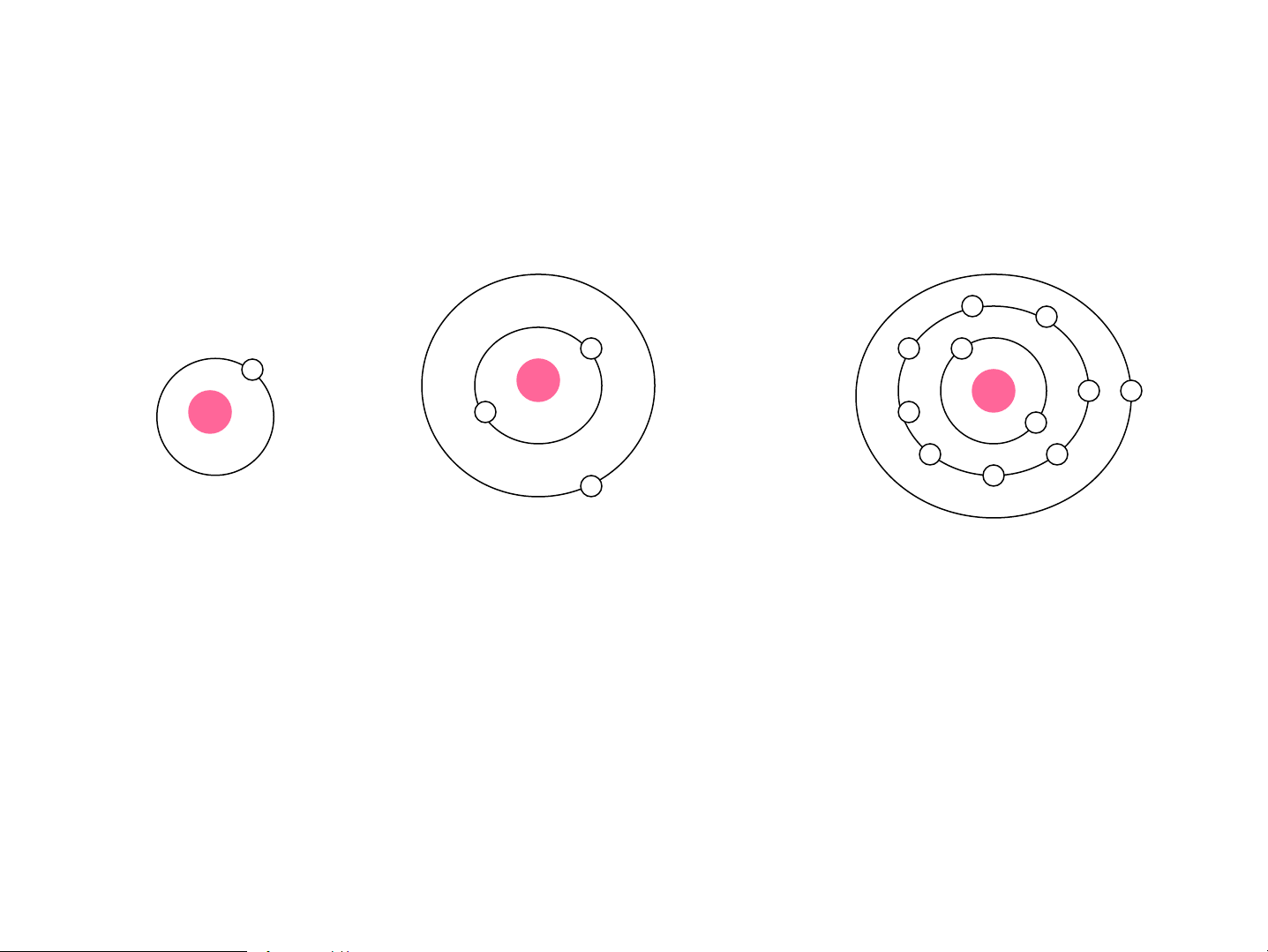
2.1. N¨ng l−îng cña ®iÖn tö ho¸ trÞ trong nguyªn tö kim lo¹i kiÒm - - - - - - + + - - + - - - - - - - H Li Na
§iÖn tö ho¸ trÞ t−¬ng t¸c víi h¹t nh©n vμ c¸c
®iÖn líp trong (víi lâi nguyªn tö)
N¨ng l−îng tÝnh t−¬ng tù nh− cña H vμ thªm phÇn bæ chÝnh Δl Rh W = − nl 2 (n + Δ ) l
Δ phô thuéc vμo sè l−îng tö l vμ nguyªn tè l Z Nguyªn tè Δ Δ Δ Δ s p d f 3 Li -0,412 -0,041 -0,002 0
11 Na -1,373 -0,883 -0,010 -0,001 37 Rb -3,195 -2,711 -1,233 -0,012 3D n=3 3P 3S 2P n=2 2S n=1 1S
2.2. Tr¹ng th¸i vμ møc n¨ng l−îng bÞ t¸ch n Tr¹ng th¸i l Møc n¨ng l−îng Líp 1 0 1s 1S K 2 0 2s 2S L 1 2p 2P 3 0 3s 3S M 1 3p 3P 2 3d 3D
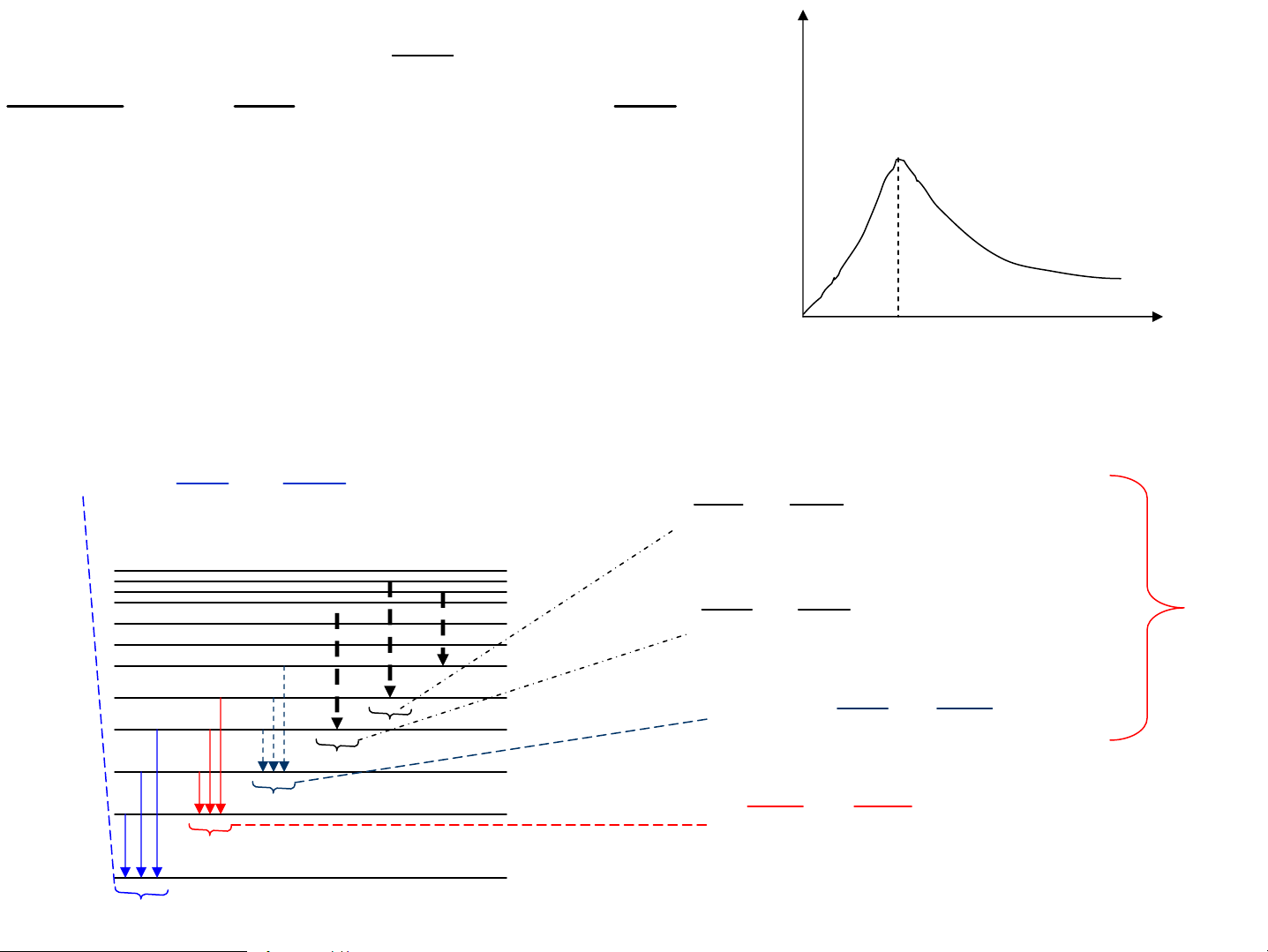
2.3. Quang phæ cña kim lo¹i kiÒm
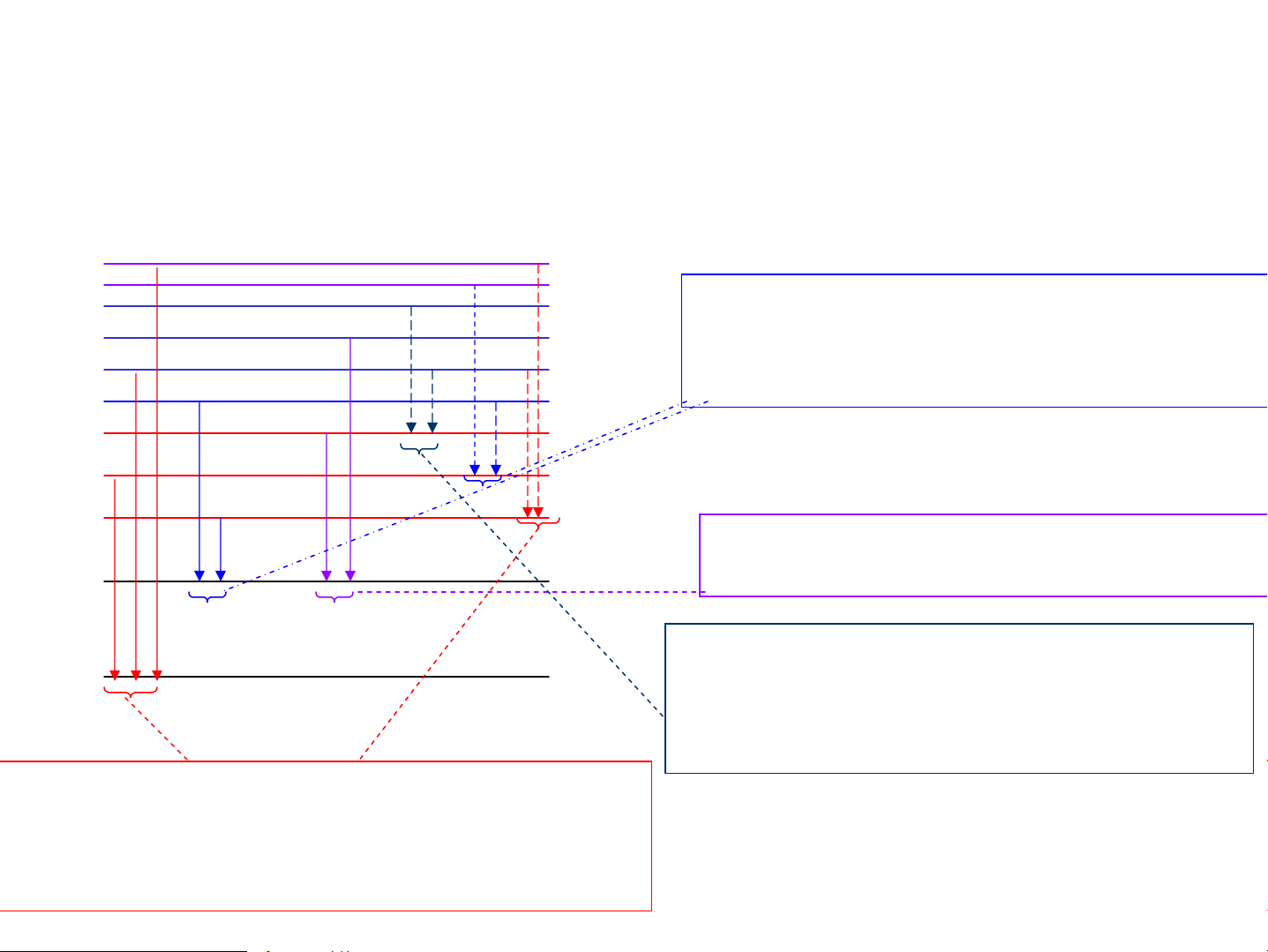
Khi ph¸t x¹ photon: §iÖn tö chuyÓn tõ møc cao xuèng thÊp h¬n Vμ Δl = ±1 5P 5S 4F 4D D·y phô II: hν = 2P- nS Li 4P hν = 3P-nS Na 4S 3D 3P Na 3S D·y Phô I: hν = 2P- nD 2P Li 2S D·y C¬ b¶n: hν = 3D-nF hν = 3D-nP D·y chÝnh: hν = 2S- nP Li S, P, D...møc n¨ng hν = 3S- nP Na l−îng
2.4. M«men ®éng l−îng vμ m«men
tõ cña ®iÖn tö chuyÓn ®éng quanh h¹t nh©n
M«men ®éng l−îng/orbital: QuÜ ®¹o kh«ng x¸c
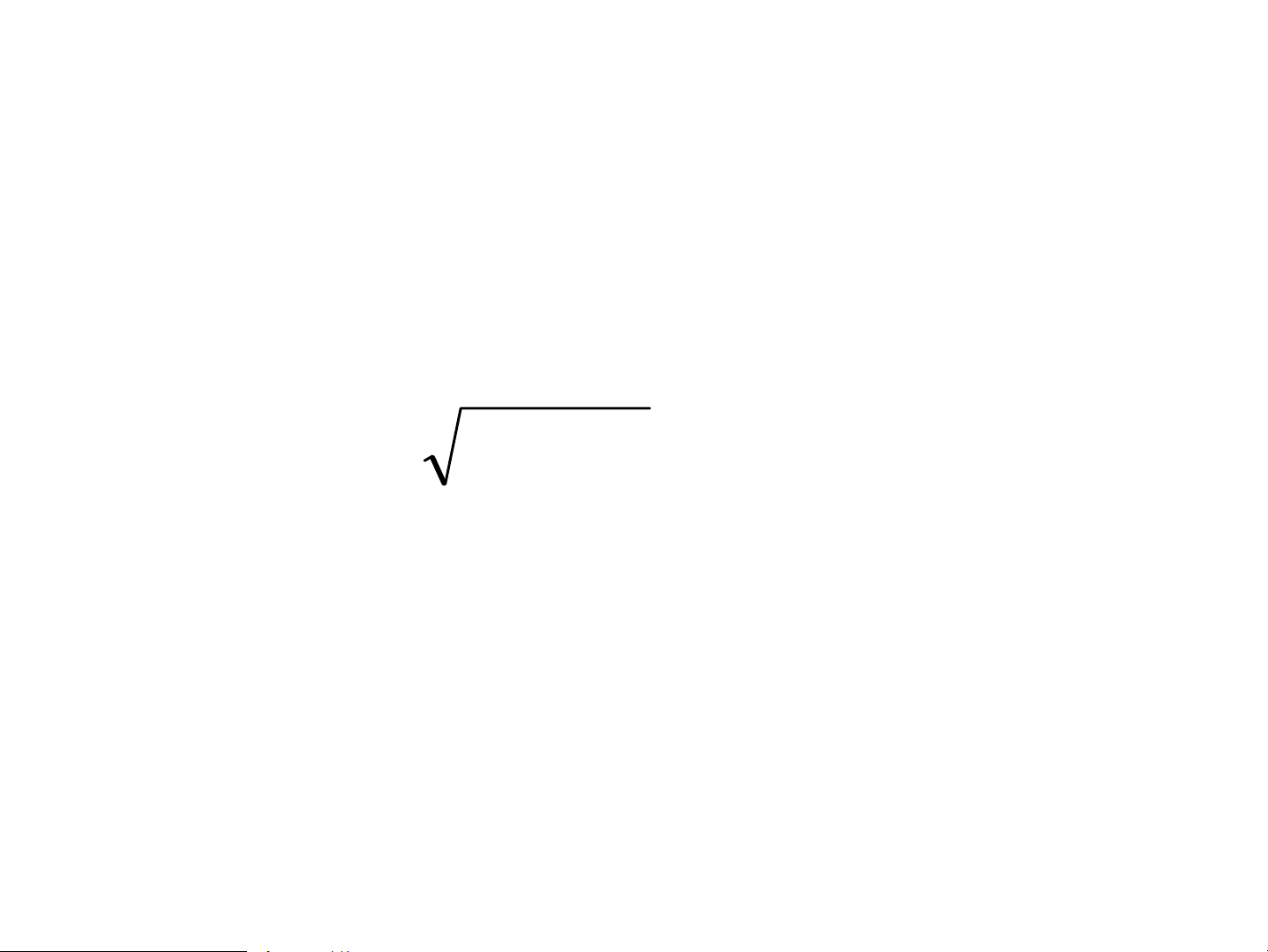
®Þnh -> vÐc t¬ m«men kh«ng x¸c ®Þnh. Gi¸ trÞ x¸c ®Þnh: L = l(l + ) 1 h .
l = 0, 1, 2, ..., n-1 Sè l−îng tö quÜ ®¹o
H×nh chiÕu lªn ph−¬ng bÊt kú: L = ± z h . m m=0, ±1, ±2.. l
M«men ®éng l−îng vμ h×nh chiÕu cña nã ®Òu bÞ l−îng tö ho¸
M«men tõ: §iÖn tö quay quanh h¹t nh©n g©y ra
dßng ®iÖn ng−îc chiÒu víi chiÒu quay
-> m«men tõ ng−îc chiÒu víi m«men ®éng r r l−îng e μ = − L 2me
H×nh chiÕu cña m«men tõ lªn z: e μ = − e = −m h = −mμ z Lz 2m B 2m e e eh −24 2 Magneton Bohr: μ = = , 9 26.10 Am B 2me
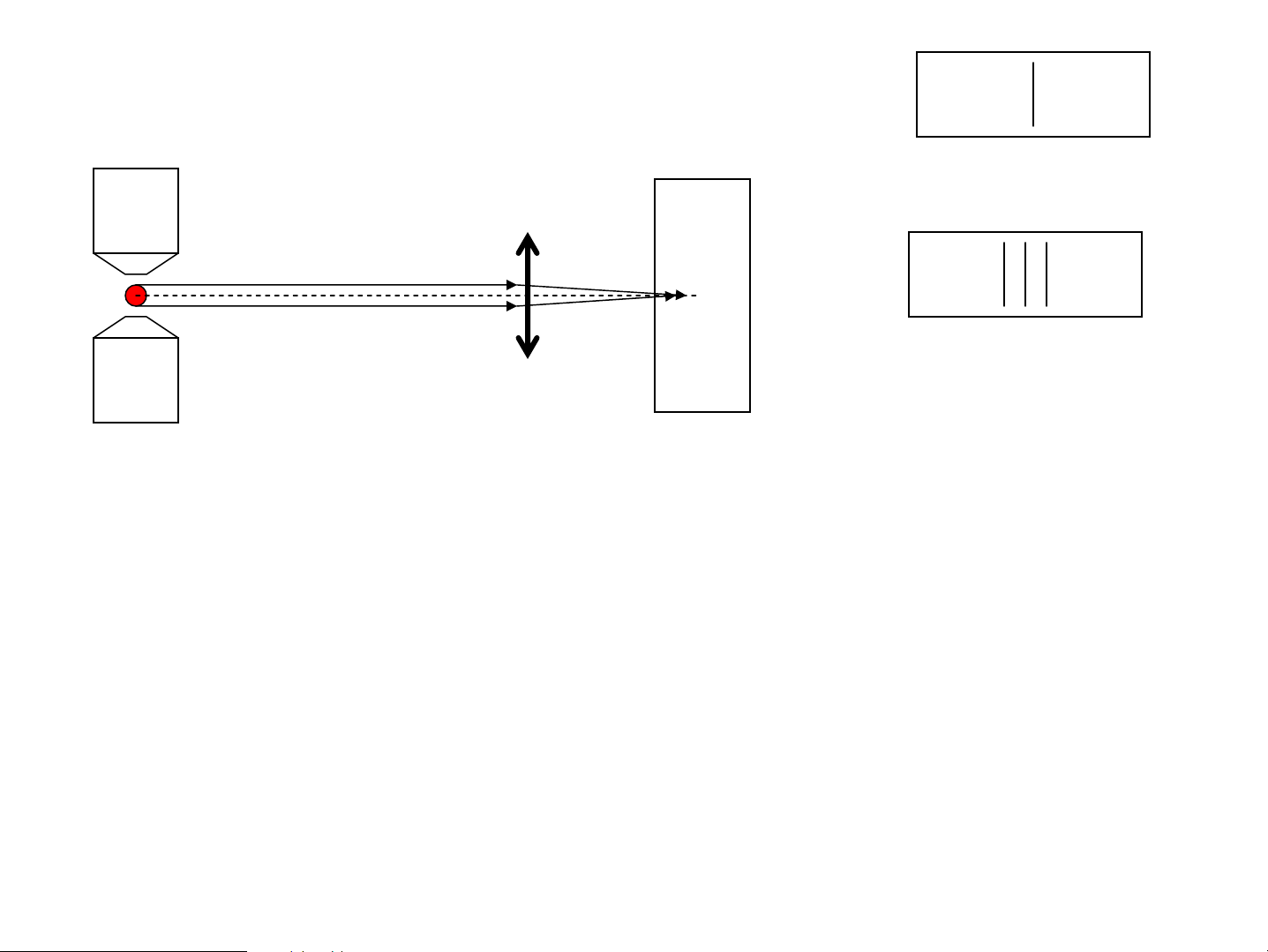
-> H×nh chiÕu cña m«men tõ lªn z ®−îc l−îng tö ho¸ 2.5. HiÖn t−îng Diman/Zeeman: B=0 ->1 v¹ch H Nam ch©m ®iÖn B≠0-> 3 v¹ch Phim ghi QP
N¨ng l−îng t−¬ng t¸c gi÷a m«men tõ cña ®iÖn tö
víi tõ tr−êng cña nam ch©m: r r ΔW = . μ − B ΔW = μ − B = mμ B z B
Møc n¨ng l−îng cña ®iÖn tö W′ = W + mμ B B
Bøc x¹ khi tõ møc W’ xuèng møc W’ cã: 2 1 , W' − W' W − W Δmμ B 2 1 2 1 B υ = = + h h h μ B B υ + Δm=0, ±1 nªn cã h υ' = υ 3 v¹ch øng víi μ B B υ − h 3. Spin cña ®iÖn tö
Nhê cã thiÕt bÞ quang phæ tinh vi ph¸t hiÖn cÊu
tróc béi phæ: c¸c v¹ch sÝt nhau: Cña Na 28,90 vμ 28,96pm
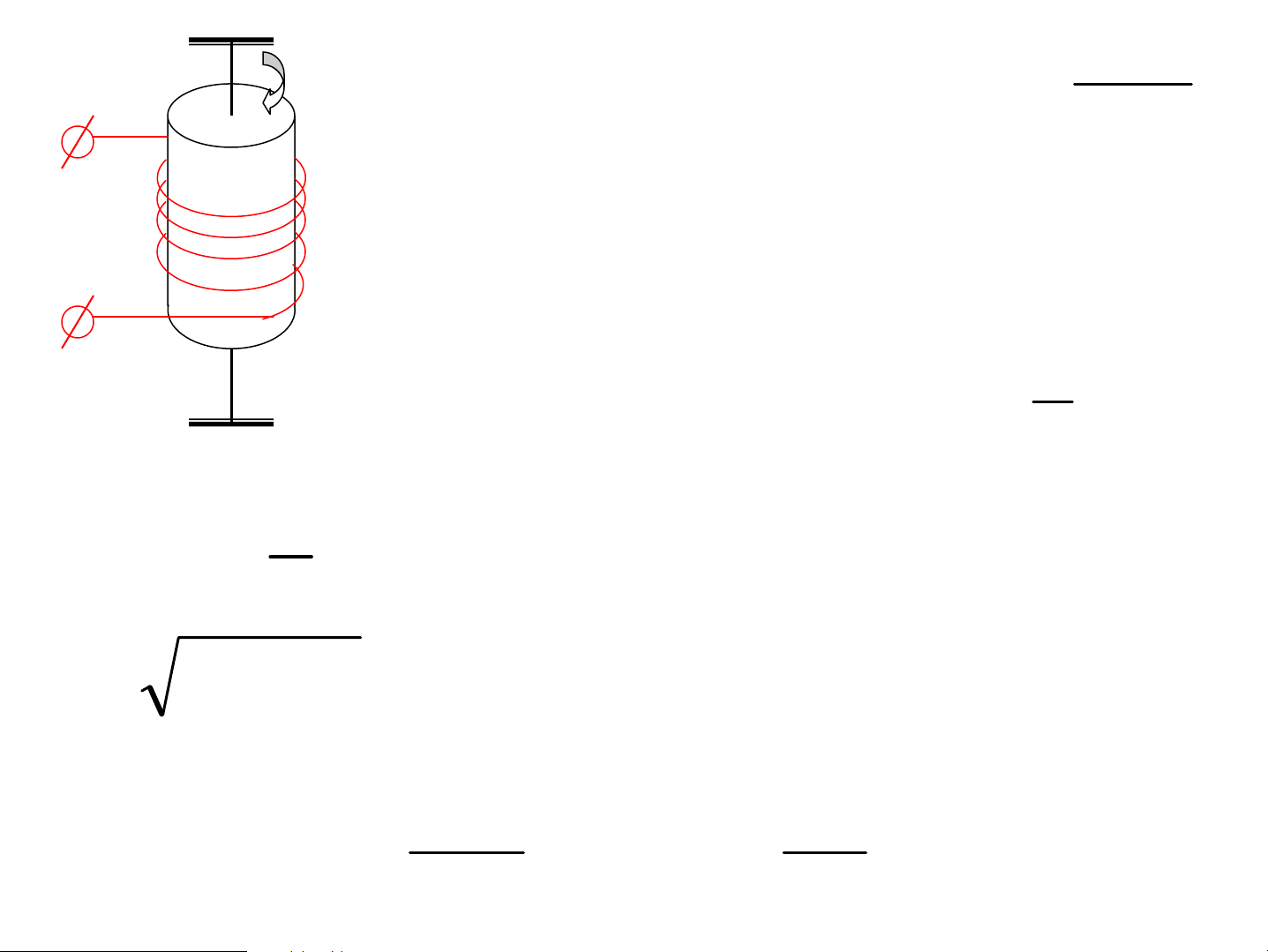
ThÝ nghiÖm cña Anhxtanh-§¬g¸t μ e §o ®−îc tû sè = − L me r Kh«ng ®óng víi hÖ sè e L − tõ c¬ lý thuyÕt 2me μr
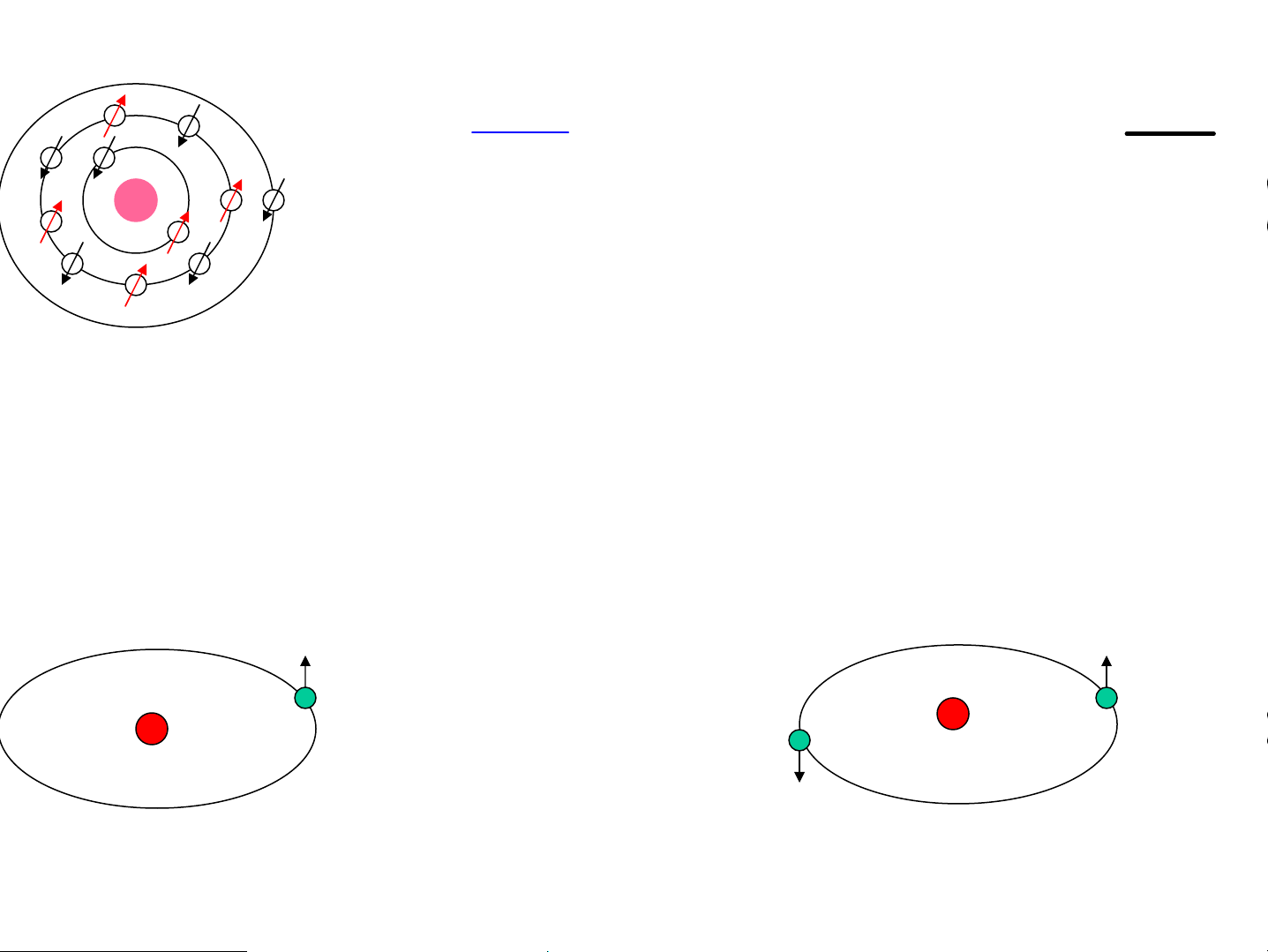
Gi¶i thÝch: Do vËn ®éng néi t¹i, r ®iÖn tö cã m«men spin S H×nh chiÕu lªn S h = ± = m . z h trôc z lμ: 2 s 1
Sè l−îng tö h×nh chiÕu spin m = ± s 2 S = s(s + ) 1 h . s-Sè l−îng tö spin M«men tõ riªng §óng kÕt eh r e r μ = ±μ = qu¶ thùc m ⇒ μ = − S sz B 2m s m nghiÖm e e
M«men tõ orbital: M«men tõ riªng r e r r e r - - μ = − L (spin): L μ = − S s - - 2me me + - - - -
• Các điện tử có spin với số lượng tử - - -
spin m ↑ hoặc m ↓ các momen spin Na s s
tạo ra các momen từ spin riªng.
• Momen từ orbital g©y ra m«men c¶m øng
trong tõ tr−êng ®ãng gãp vμo tÝnh nghÞch tõ, cßn
momen tõ spin ®ãng gãp vμo tÝnh thuËn tõ m ↑ m ↑ - s + - s + => HÖ sè tõ - m ↓ s H c¬ lμ e/m . He e LÎ ®iÖn tö: thuËn tõ
Ch½n sè ®iÖn tö: nghÞch tõ
4. Tr¹ng th¸i vμ n¨ng l−îng ®iÖn tö trong nguyªn tö
Do t−¬ng t¸c gi÷a m«men tõ riªng vμ m«men tõ
quü ®¹o vμ gi÷a c¸c m«men tõ riªng cña c¸c
®iÖn tö trong nguyªn tö, nªn: r r r
§iÖn tö cã m«men toμn phÇn: J = L + S Gi¸ trÞ cña J lμ J = ( j j + ) 1 h . 1
j lμ sè l−îng tö m«men toμn phÇn j = l ± 2
Tr¹ng th¸i l−îng tö cña ®iÖn tö trong nguyªn tö
gåm 4 sè l−îng tö: n, , m vμ m l s
=> n¨ng l−îng toμn phÇn cña ®iÖn tö phô thuéc vμo 3 sè l−îng tö l n, vμ j l = 0 chØ cã 1 møc; 1 1
l > 0 t¸ch thμnh 2 møc øng víi l − 2 v μ l + 2
=>CÊu tróc tÕ vi cña møc;
KÝ hiÖu n2X sè 2 chØ møc kÐp: j
n =1, 2, 3, ... Sè l−îng tö chÝnh X=S, P, D, F, ...øng víi l = , 1 , 0 ,... 3 , 2 1 j = l ± 2 n 1 2
Sè tr¹ng th¸i trong líp n lμ ∑ − 2(2l + ) 1 = 2n l=0
Tr¹ng th¸i ®tö ho¸ trÞ trong H vμ klo¹i kiÒm: n j tr¹ng th¸i Møc l ®tö ho¸ trÞ n¨ng l−îng 1 0 1/2 1s 12S 1/2 1/2 2 0 1/2 2s 22S 1/2 1/2 1 1/2 2p 22P 1/2 1/2 3/2 2p 22P 3/2 3/2 3 0 1/2 3s 32S 1/2 1/2 1 1/2 3p 32P 1/2 1/2 3/2 3p 32P 3/2 3/2 2 3/2 3d 32D 3/2 3/2 5/2 3d 32D 5/2 5/2