Viết phương trình đường thẳng đi qua 2 điểm
1. Phương trình tổng quát của đường thẳng
Phần mềm thiết kế đường thẳng 3D
Đường thẳng Δ có phương trình tổng quát là: ax+by+c=0;(a2+b2≠0) nhận
n→=(a;b) làm vectơ pháp tuyến.
2. Phương trình tham số của đường thẳng
- Phương trình tham số của đường thẳng đi qua điểm A(x0,y0) nhận
u→(a,b) làm vecto chỉ phương, Ta có:
B(x,y)∈d⇔AB→=tu→⇔{x−x0=aty−y0=bt
⇔{x=x0+aty=y0+bt;(a2+b2≠0,t∈R)
- Đường thẳng d đi qua điểm A(x0,y0), nhận u→(a,b) là vecto chỉ
phương, phương trình chính tắc của đường thẳng là x−x0a=y−y0b với (a,b≠0)
3. Cách viết phương trình đường thẳng đi qua hai điểm
a. Sử dụng định nghĩa
Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B. Phương pháp: Bước 1: Tính:
AB→=(c−a;d−b) (vectơ chỉ phương của đường thẳng d)
Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: n→=(b−d;c−a)
Bước 3: Phương trình đường thẳng d:
(b−d)(x−a)+(c−a)(y−b)=0
b. Sử dụng phương trình tổng quát
Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B. Phương pháp:
Bước 1: Gọi phương trình tổng quát của đường thẳng d là y = mx + n (*)
Bước 2: Thay tọa độ A, B vào phương trình tổng quát ta thu được hệ phương trình ẩn m, n {b=am+nd=cm+n⇒(m;n)=(?;?)
Thay m, n vừa tìm được vào phương trình (*) ta suy ra phương trình cần tìm.
4. Bài tập ví dụ minh họa
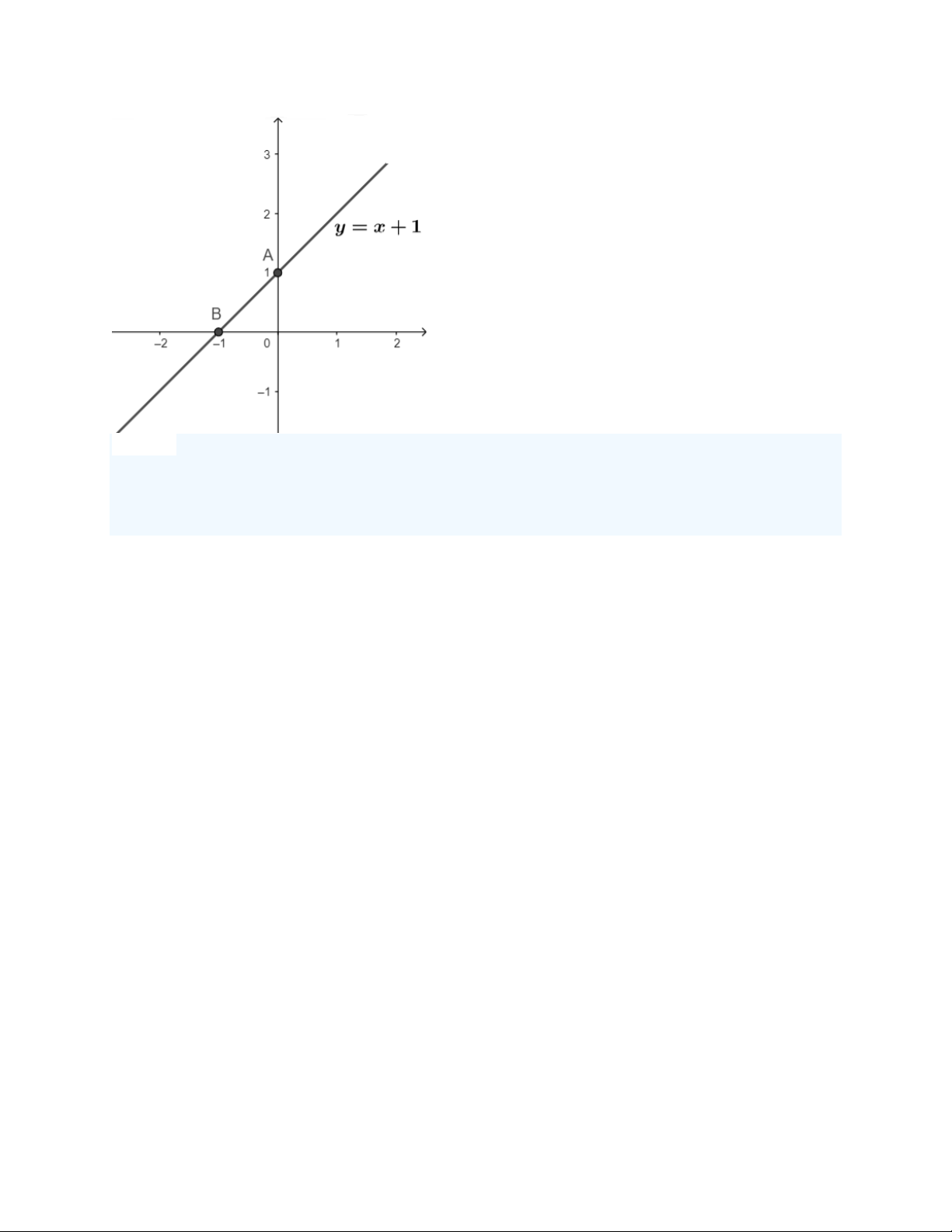
Ví dụ 1: Viết phương trình đường thẳng tham số, phương trình tổng quát đi qua 2 điểm
A (1;2) và B (2;3). Vẽ đường thẳng vừa tìm được trên hệ tọa độ Oxy. Hướng dẫn giải
Cách 1: Sử dụng định nghĩa
Cách 2: Sử dụng phương trình tổng quát AB→=(1,1) AB→=(1,1) Phương trình tham Phương trình tham số: x−11=y−21 số: x−11=y−21
Gọi phương trình tổng quát là: n→=(−1,1) y = ax + b Phương trình tổng quát:
Do PTĐT đi qua 2 điểm A, B nên ta có:
−1.(x−1)+1.(y−2)=0⇒y=x+1 {2=a.1+b3=a.2+b⇒(a;b)=(1;1)
Vậy PT tổng quát cần tìm là: y=x+1
Ví dụ 2: Viết phương trình đường thẳng y = ax + b biết
a) Đi qua 2 điểm A(-3,2), B (5,-4). Tính diện tích tam giác được tạo bởi đường thẳng và 2 trục tọa độ.
b) Đi qua A (3,1) song song với đường thẳng y = -2x + m -1 Hướng dẫn giải
a. Gọi phương trình tổng quát là: y = ax + b
Do PTĐT đi qua 2 điểm A, B nên ta có:
{2=−3a+b−4=5a+b⇒(a;b)=(−34;−14)
Vậy PT tổng quát cần tìm là: y=−34x−14
Giao điểm của đường thẳng với trục Ox là: y=0⇒x=−13⇒A(−13;0)
⇒OA→=(−13;0)⇒|OA→|=13
Giao điểm của đường thẳng với trục Oy là: x=0⇒y=−14⇒B(0;−14)
⇒OB→=(0;−14)⇒|OB→|=14 ⇒SOAB=12.OA.OB=12.13.14=124
b. Gọi phương trình tổng quát là: y = ax + b
Do đường thẳng song song với y = -2x + m -1 ⇒ a = -2
Phương trình đường thẳng trở thành y = -2x + b
Mà đường thẳng qua điểm A(3; 1) ⇒ 1 = 3.(-2) + b ⇒ b = 7
Vậy phương trình tổng quát là: y = -2x + 7
Ví dụ 3: Tìm m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2x3 + 3(m
- 1)x2 + 6(m - 2)x - 1 song song với đường thẳng y = -4x + 1. Lời giải
Ta có y' = 6x2 + 6(m - 1)x + 6(m - 2)
Hàm số có cực trị ⇔ y' = 0 có 2 nghiệm phân biệt
⇔ Δ' > 0 ⇔ 9(m - 1)2 - 36(m - 2) > 0 ⇔ 9(m - 3)2 > 0 ⇔ m ≠ 3
Thực hiện phép chia y cho y' ta có phương trình đường thẳng đi qua 2 điểm cực trị là:
d: y = (-m2 + 6m - 9)x - m2 + 3m - 3
Khi đó d song song với đường thẳng y = -4x + 1