Which of the following factors reflect pure market risk for a givencorporation?

1.
Which of the following factors reflect pure market risk for a given corporation?
a) Increased short-term interest rates.
b) Fire in the corporate warehouse. c) Increased insurance costs. d) Death of the CEO. e) Increased labor costs. 2.
When adding real estate to an asset allocation program that currently
includes only stocks, bonds, and cash, which of the properties of real estate
returns affect portfolio risk? Explain. a) Standard deviation. b) Expected return.
c) Correlation with returns of the other asset classes.
Answer: After real estate is added to the portfolio, there are four asset classes
in the portfolio: stocks, bonds, cash, and real estate. Portfolio variance now
includes a variance term for real estate returns and a covariance term for real
estate returns with returns for each of the other three asset classes. Therefore,
portfolio risk is affected by the variance (or standard deviation) of real estate
returns and the correlation between real estate returns and returns for each of the other asset classes. 3.
Which of the following statements about the minimum variance portfolio of all risky securities
are valid? (Assume short sales are allowed.) Explain.
a) Its variance must be lower than those of all other securities or portfolios.
b) Its expected return can be lower than the risk-free rate.
c) It may be the optimal risky portfolio.
d) It must include all individual securities.
Answer: Its variance must be lower than those of all other securities or
portfolios. (a) is valid because it provides the definition of the minimum variance portfolio.
The following data apply to Problems 4 through 10: (Page 223) 4.
What are the investment proportions in the minimum-variance portfolio
of the two risky funds, and what is the expected value and standard deviation of its rate of return?
The parameters of the opportunity set are:
E(rS) = 20%, E(rB) = 12%, σS = 30%, σB = 15%, ρ = 0.10
From the standard deviations and the correlation coefficient we generate
the covariance [note that Cov(r , ) = S rB
 x σS x σB ]: Cov(rS ,rB ) = 45
The minimum-variance portfolio is computed as follows: wMin(S) = = = 0.1739
wMin(B) = 1 - 0.1739 = 0.8261
The minimum variance portfolio mean and standard deviation are:
E(rMin) = (0.1739 × 20%) + (0.8261 × 12%) = 13.39% σMin =
= [(0.17392 x 900) + (0.82612 x 225) + (2 x 0.1739 x 0.8261 x 45)]1/2 = 13.92% 5.
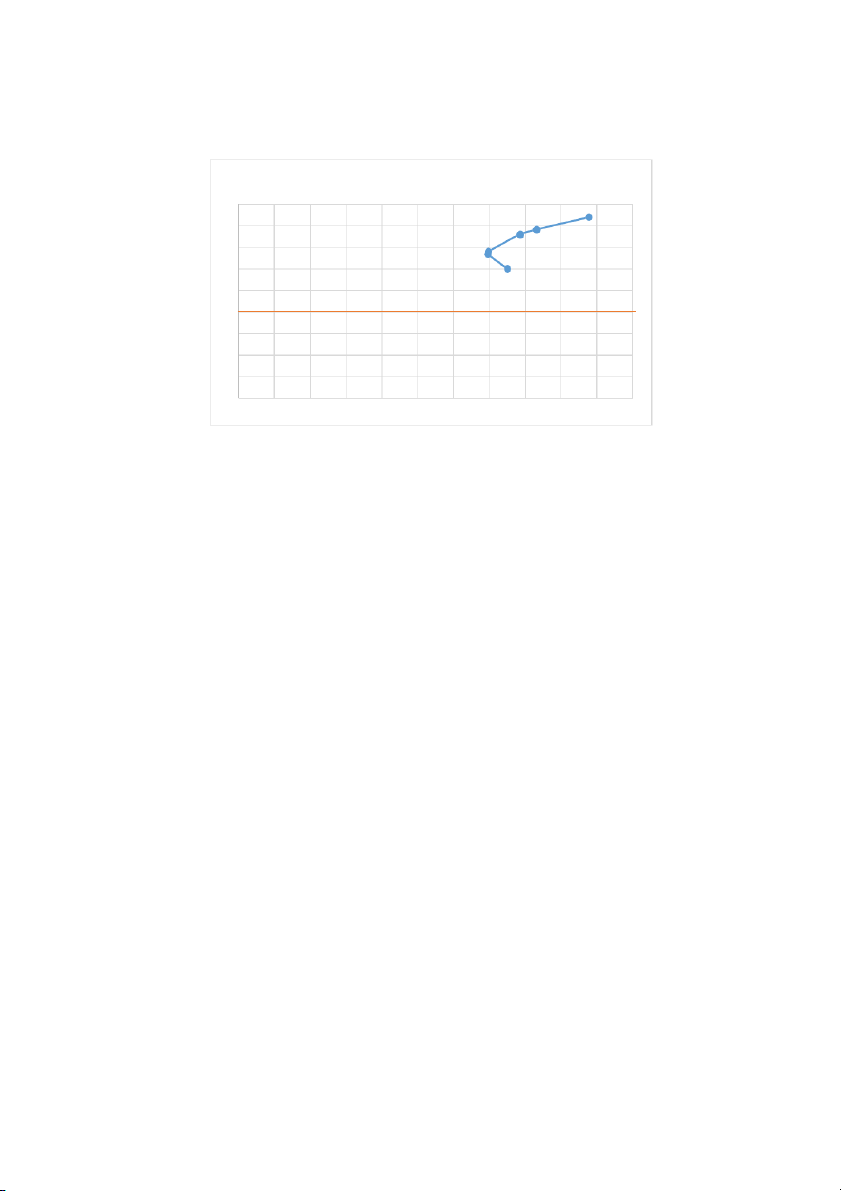
Tabulate and draw the investment opportunity set of the two risky funds.
Use investment proportions for the stock fund of zero to 100% in increments of 20%. Proporti Proporti Expect Standar on in on in ed d Stock Bond Return Deviati Fund (%) Fund (%) (%) on(% ) 0.00 100.00 12 15 17.39 82.61 13.3912 13.91746 Min. var. portfolio 20.00 80.00 13.6 13.94274 40.00 60.00 15.2 15.7035 45.6423 54.3577 15.65138 16.6223 Tangency portfolio 60.00 40.00 16.8 19.53458 80.00 20.00 18.4 24.48265 100.00 0.00 20 30
(Note that I have added two extra portfolios in the table above to set
apart the minimum variance portfolio and the tangency portfolio. I used
Excel to calculate the exact value. In an exam environment only
approximate values would suffice.) Graph shown below. Expected Return 18 16 14 12 10 8 6 4 2 0 0 2 4 6 8 10 12 14 16 18 20 22 6.
Draw a tangent from the risk-free rate to the opportunity set. What does
your graph show for the expected return and standard deviation of the optimal portfolio?
The above graph indicates that the optimal portfolio is the tangency
portfolio with expected return approximately 15.6% and standard deviation
approximately 16.5%. (Note that this problem is for your understanding. If
such question appears in the exam, then it would be designed such that the
answer would be more discernible.) 7.
Solve numerically for the proportions of each asset and for the expected
return and standard deviation of the optimal risky portfolio ws = = wB = 1- 0.4516 = 0.5484
The proportion of the optimal risky portfolio invested in the stock fund is given by:
E(rP) = (0.4516 × 20%) + (0.5484 × 12) = 15.61%
σp = [(0.45162 × 900) + (0.54842 × 225) + (2 x 0.4516 × 0.5484 x 45)]1/2 = 16.54% 8.
What is the reward-to-volatility ratio of the best feasible CAL?
The reward-to-volatility ratio of the optimal CAL is: = = 0.46 9.
You require that your portfolio yield an expected return of 14%, and that
it be efficient, on the best feasible CAL.
a. What is the standard deviation of your portfolio?
b. What is the proportion invested in the T-bill fund and each of the two risky funds? Answer: a.
If you require that your portfolio yield an expected return of 14%, then
you can find the corresponding standard deviation from the optimal CAL. The equation for this CAL is:
E(rc ) = rf + = 0.08 + 0.4601σc
If E(rC) is equal to 14%, then the standard deviation of the portfolio is 13.04%. b.
To find the proportion invested in the T-bill fund, remember that the mean
of the complete portfolio (i.e., 14%) is an average of the T-bill rate and the
optimal combination of stocks and bonds (P). Let y be the proportion invested
in the portfolio P. The mean of any portfolio along the optimal CAL is: E(r y
c ) = (1- ) × rf + y × E(rp ) = r +
f y × [E(r ) - ] = 8 + p rf y × (15.61 - 8)
Setting E(rC) = 14% we find: y = 0.7884 and (1 − y) = 0.2116 (the proportion invested in the T-bill fund).
To find the proportions invested in each of the funds, multiply 0.7884 times the
respective proportions of stocks and bonds in the optimal risky portfolio:
Proportion of stocks in complete portfolio = 0.7884 × 0.4516 = 0.3560
Proportion of bonds in complete portfolio = 0.7884 × 0.5484 = 0.4324 10.
If you were to use only the two risky funds, and still require an expected
return of 14%, what would be the investment proportions of your portfolio?
Compare its standard deviation to that of the optimized portfolio in Problem 9. What do you conclude?
Using only the stock and bond funds to achieve a portfolio expected return of
14%, we must find the appropriate proportion in the stock fund (w ) S and the
appropriate proportion in the bond fund (wB = 1 − w ) as follows: S
14% = 20% × w + 12% × (1 − S w ) = 12% + 8% × S wS  w = S 0.25
So the proportions are 25% invested in the stock fund and 75% in the
bond fund. The standard deviation of this portfolio will be:
σP = [(0.252 × 900) + (0.752 × 225) + (2 × 0.25 × 0.75 × 45)]1/2 = 14.13%
This is considerably greater than the standard deviation of 13.04% achieved
using T-bills and the optimal portfolio. 11.
Stocks offer an expected rate of return of 18%, with a standard deviation
of 22%. Gold offers an expected return of 10% with a standard deviation of 30%.
a. In light of the apparent inferiority of gold with respect to both mean return
and volatility, would anyone hold gold? If so, demonstrate graphically why one would do so.
b. Given the data above, reanswer (a) with the additional assumption that the
correlation coef- ficient between gold and stocks equals 1. Draw a graph
illustrating why one would or would not hold gold in one’s portfolio. Could this
set of assumptions for expected returns, standard deviations, and correlation
represent an equilibrium for the security market? Answer: a.
Even though it seems that gold is dominated by stocks, gold might still be
an attractive asset to hold as a part of a portfolio. If the correlation between gold
and stocks is sufficiently low, gold will be held as a component in a portfolio,
specifically, the optimal tangency portfolio. b.
If gold had a correlation coefficient with stocks of +1, it would not be
held. The set of risk/return combinations of stocks and gold would plot as a
straight line with a negative slope (see the following graph). The graph shows
that in this case, any portfolio that contains any gold is dominated by the stock-
only portfolio. Therefore, no one will hold gold. Stated differently, the CAL for
the portfolio with stock only is steeper than any other CAL passing through all
other possible portfolios on the portfolio frontier. (Of course, this situation
could not persist. If no one desired gold, its price would fall and its expected
rate of return would increase until it became an attractive enough asset to hold).
The graph shows that in this case, any portfolio that contains any
gold is dominated by the stock-only portfolio. Therefore, no one will hold gold.
Stated differently, the CAL for the portfolio with stock only is steeper than any
other CAL passing through all other possible portfolios on the portfolio frontier.
(Of course, this situation could not persist. If no one desired gold, its price
would fall and its expected rate of return would increase until it became an
attractive enough asset to hold.) 12.
Suppose that there are many stocks in the security market and that the
characteristics of Stocks A and B are given as follows: Stock Expected Return Standard Deviation A 10% 5% B 15 10 Correlation –1
Suppose that it is possible to borrow at the risk-free rate, rf. What must be the
value of the riskfree rate? (Hint: Think about constructing a risk-free portfolio
from stocks A and B.) Answer:
Since Stocks A and B are perfectly negatively correlated, a risk-free portfolio
can be constructed and its rate of return in equilibrium will be the risk-free rate.
To find the proportions of this portfolio (wA invested in Stock A and wB = 1 -
wA in Stock B), set the standard deviation equal to zero.
With perfect negative correlation, the portfolio standard deviation reduces to: σp = | wAσA - wBσB| => 0 = | 5wA - 10 (1-wA) | => wA =0.6667
The expected rate of return on this risk-free portfolio is:
E(R) = 0.6667 x 10% + (0.3333 x 15%) ≈ 11.67%.
=>To avoid arbitrage, the risk-free rate must also be 11.67%. 13.
Assume that expected returns and standard deviations for all securities
(including the risk-free rate for borrowing and lending) are known. In this
case all investors will have the same optimal risky portfolio. (True or false?)
Assume that expected returns and standard deviations for all securities
(including the risk-free rate for borrowing and lending) are known. In this case
all investors will have the same optimal risky portfolio. (True or false?)
Answer: False. If the borrowing and lending rates aren’t identical, then
depending on the tastes of the individuals (that is, the shape of their indifference
curves), borrowers and lenders could have different optimal risky portfolios.
The portfolio standard deviation equals the weighted average of the component-
asset standard deviations only in the special case that all assets are perfectly positively correlated. 14.
The standard deviation of the portfolio is always equal to the weighted
average of the standard deviations of the assets in the portfolio. (True or false?)
Answer: False. Only in the special case that all assets are perfectly
positively correlated, will the portfolio standard deviation reduce the weighted
average of the component-asset standard deviations. Otherwise, as the formula
for portfolio standard deviations show, the portfolio standard deviations. The
portfolio variance will be a weighted sum of the elements in the covariance
matrix, with the products of the portfolio proportions as weights. 15.
Suppose you have a project that has a .7 chance of doubling your
investment in a year and a .3 chance of halving your investment in a year. What
is the standard deviation of the rate of return on this investment? Answer: Probability Rate of return 0.7 100% 0.3 -50%
Mean = (0.7 x 100%) + (0.3 x (-50%)) = 0.55 = 55%
Variance = [0.7 x (100-55)2] + [0.3 x (-50-55)2] = 4725 Standard deviation = 68.738% 16.
Suppose that you have $1 million and the following two opportunities
from which to construct a portfolio:
a. Risk-free asset earning 12% per year.
b. Risky asset with expected return 30% per year and standard deviation of 40%.
If you construct a portfolio with a standard deviation of 30%, what is its expected rate of return? Answer:
y = σc/σP = 0.30/0.40 = 0.75
E(rC) = rF + y[E(rP) – rf] = 0.12 + 0.75[0.30 – 0.12] = 25.50%
The following data are for Problems 17 through 19: The correlation
coefficients between pairs of stocks are as follows: Corr(A,B) = .85;
Corr(A,C) = .60; Corr(A,D) = .45. Each stock has an expected return of 8%
and a standard deviation of 20%. 17.
If your entire portfolio is now composed of stock A and you can add some of only one stock to
your portfolio, would you choose (explain your choice): a. B. b. C. c. D. d. Need more data.
Answer: Choose C. D because it has the lowest correlation of 0.45 which
in turn lower the risk by the largest amount. 18.
Would the answer to Problem 17 change for more risk-averse or risk- tolerant investors? Explain.
Answer: No, it wouldn’t change because it isn’t a factor when deciding
between risk-averse or risk-tolerant investor. This is because the lower the risk
better no matter what level of risk you are on. 19.
Suppose that in addition to investing in one more stock you can invest in
T-bills as well. Would you change your answers to Problems 17 and 18 if the T- bill rate is 8%?
Answer: No, neither part would change because the T-Bills rate would
stay stagnant at 8% since both stocks have the same expected returns but
different SDs. Meaning that the most profitable porfolio would be one that has
the least amount of deviation. Also, a portfolio is dependent on someone’s risk profile.