Chương 3 lý thuyết mẫu môn Lý thuyết xác suất và thống kê toán | Học viện Tài chính

Chương 3 LÝ THUYẾT MẪU 1
Bài 1. Một số tham số đặc trưng của mẫu
Bài 2. Ước lượng điểm một số tham số lý thuyết
Bài 3. Ước lượng khoảng một số tham số lý thuyết
BÀI 1. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 2
I. Đám đông (tổng thể) và mẫu
II. Biểu diễn số liệu mẫu
III. Một số tham số đặc trưng của mẫu I. ĐÁM ĐÔNG VÀ MẪU 3
 Tập hợp tất cả các vật thể ban đầu mà ta muốn
nghiên cứu được gọi là đám đông hay tổng thể nghiên cứu.
 Số phần tử của đám đông được gọi là kích thước
đám đông, thường ký hiệu là N.
 Tập hợp các vật thể lấy ra từ đám đông để nghiên
cứu được gọi là mẫu.
 Số phần tử của mẫu được gọi là kích thước mẫu, thường ký hiệu là n.
II. BIỂU DIỄN SỐ LIỆU MẪU 4  Dãy thống kê
 Đa giác tần số - Đa giác tần suất
 Biểu đồ hình chữ nhật  Biểu đồ hình quạt
II. BIỂU DIỄN SỐ LIỆU MẪU 5
 Dãy thống kê dạng điểm cho dưới dạng tần số: X x x … x … x 1 2 i k m m m … m … m 1 2 i k Ở đó:
➢ X là dấu hiệu ta cần nghiên cứu.
➢ x , x , ..., x là các giá trị của X trong mẫu với số lần 1 2 k
xuất hiện tương ứng là m , m ,…, m . 1 2 k
Chú ý: m + m +…+m = n, n là kích thước mẫu. 1 2 k
II. BIỂU DIỄN SỐ LIỆU MẪU 6
 Dãy thống kê dạng điểm cho dưới dạng tần suất: X x x … x … x 1 2 i k f f f … f … f 1 2 i k m Ở đó: i f = ,i = 1, k i n Chú ý: f + f +…+ f = 1. 1 2 k
II. BIỂU DIỄN SỐ LIỆU MẪU 7
 Dãy thống kê dạng khoảng cho dưới dạng tần số: X
[a ; a ) [a ; a ) … [a ; a ) … [a ; a ) 0 1 1 2 i-1 i k-1 k m m m … m … m 1 2 i k
Ở đó: m là số giá trị thuộc [a ; a ), i = 1,2,…,k. i i-1 i
II. BIỂU DIỄN SỐ LIỆU MẪU 8
 Dãy thống kê dạng khoảng cho dưới dạng tần suất: X [a ; a ) [a ; a ) … [a ; a ) … [a ; a ) 0 1 1 2 i-1 i k-1 k f f f … f … f 1 2 i k
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 9  Trung bình mẫu  Phương sai mẫu
 Phương sai mẫu điều chỉnh
 Độ lệch tiêu chuẩn mẫu - Độ lệch tiêu chuẩn mẫu điều chỉnh  Tần suất mẫu
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 10
 Giả sử cần nghiên cứu dấu hiệu X của một đám
đông. Ta có X là một đại lượng ngẫu nhiên.
 Từ đám đông ta lấy ra một mẫu kích thước n. Gọi
X là giá trị quan sát lần thứ i về đại lượng ngẫu i
nhiên X, ( i = 1, n ). Nếu mẫu chưa chọn cụ thể thì
mỗi X sẽ là một ĐLNN  (X , X , …, X ) gọi là i 1 2 n mẫu ngẫu nhiên.
 Khi đã lấy mẫu cụ thể thì X nhận giá trị cụ thể là x . i i
Khi đó (x , x , …, x ) được gọi là mẫu cụ thể. 1 2 n
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 11
 Trung bình mẫu của X được kí hiệu và xác định như sau: n 1 X = Xi n i 1 =
X đặc trưng cho giá trị trung bình của X trong mẫu.
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 12
➢ Với mẫu cụ thể (x , x , …, x ) thì X nhận giá trị cụ 1 2 n thể: n 1 x = xi n i 1 =
➢ Nếu ta có dãy thống kê dạng điểm thì: k k 1 x = m x =f x i i i i n i 1 = i 1 =
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 13
 Phương sai mẫu của X được kí hiệu và xác định như sau: ( ) n 1 S X = (X −X)2 = X −(X)2 2 2 i n i 1 = 2
S (X) đặc trưng cho độ phân tán các giá trị của X
trong mẫu so với trung bình mẫu.
 Độ lệch tiêu chuẩn mẫu 2 S = S
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 14 2
➢ Với mẫu cụ thể (x , x , …, x ) thì S nhận giá trị cụ 1 2 n thể: n 1 = ( − ) n 2 1 s x x = x −(x)2 2 2 i i n = n i 1 i 1 =
➢ Nếu ta có dãy thống kê dạng điểm thì ta có: k 1 =  ( − ) k 2 1 s m x x = m x −(x)2 2 2 i i i i n = n i 1 i 1 = k = f (x − x) k 2 = f x −(x)2 2 i i i i i 1 = i 1 =
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 15
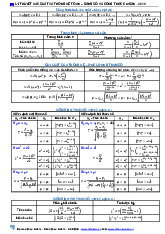
 Ví dụ 1: Cho dãy thống kê: X 18,5 19,2 20,7 21,3 m 6 8 9 3
Hãy tính trung bình mẫu, phương sai mẫu và độ lệch tiêu chuẩn mẫu của X.
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 16
 Phương sai mẫu điều chỉnh của X được kí hiệu và xác định như sau: 2 n 2 S = S n −1
 Độ lệch tiêu chuẩn mẫu điều chỉnh 2 S = S
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 17
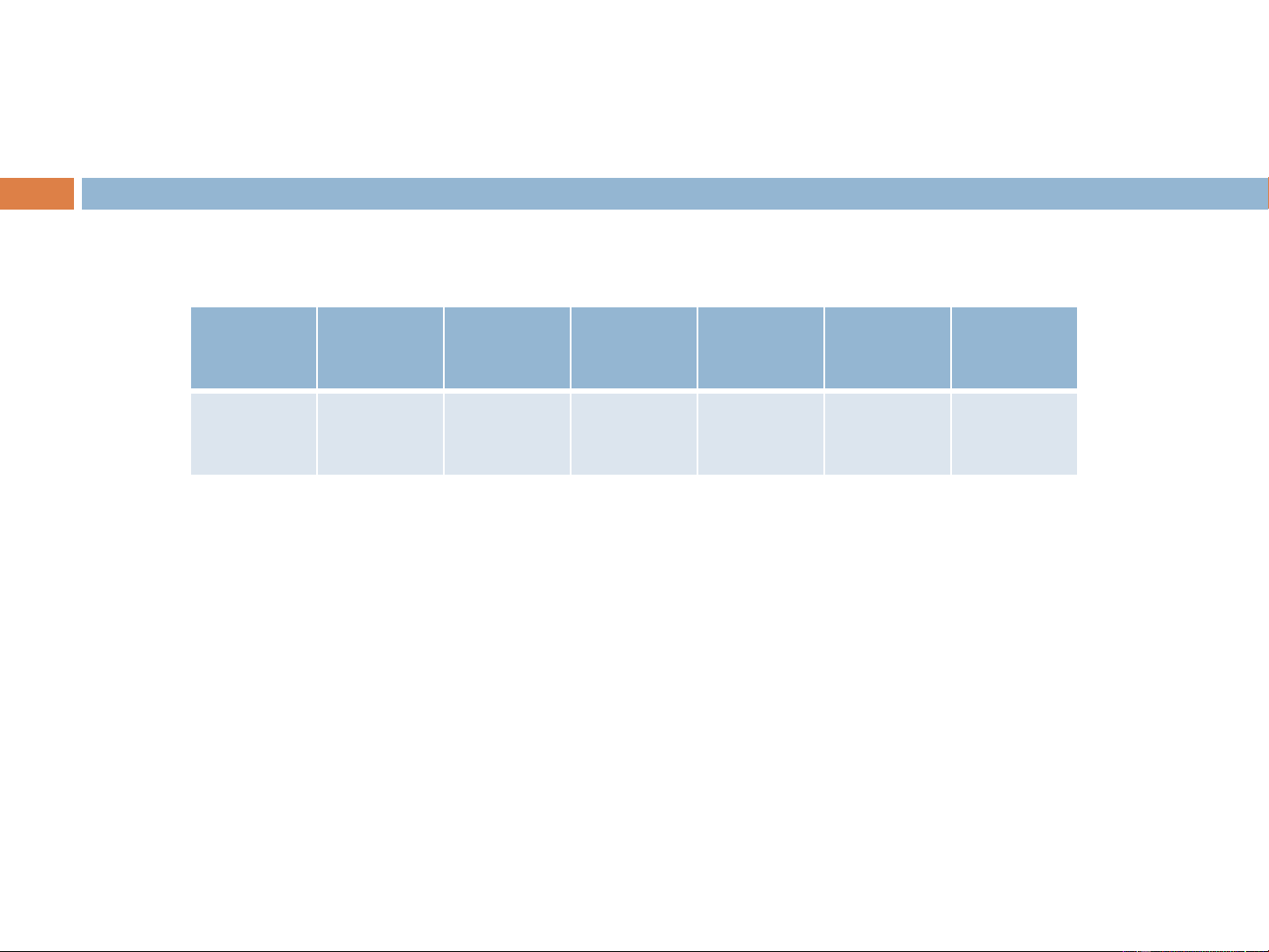
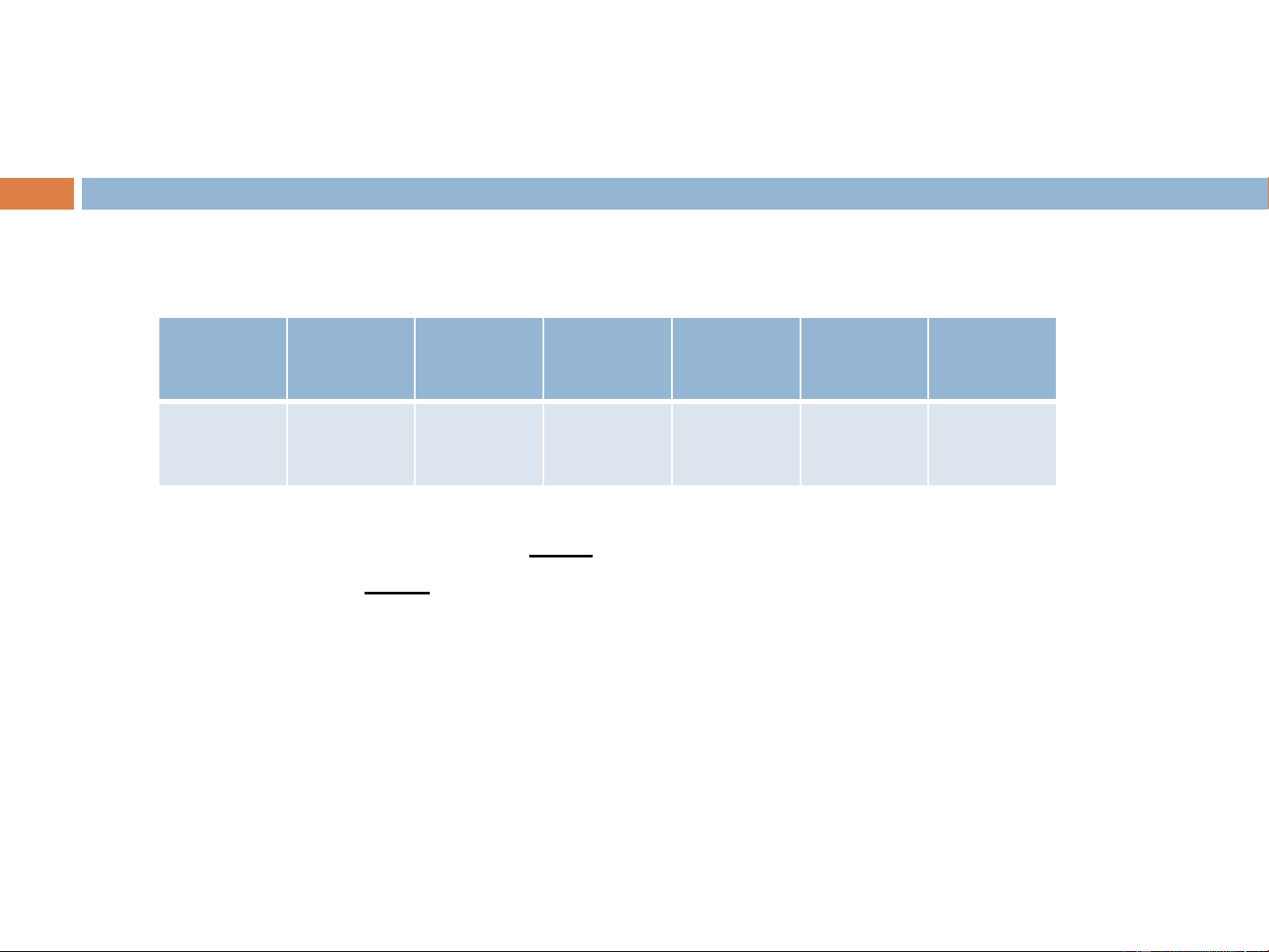
 Ví dụ 2: Điều tra chiều cao X (đơn vị tính: cm) của
một số học sinh của một trường phổ thông ta được dãy thống kê: X 155 160 163 164 165 168 170 m 5 8 10 12 7 6 6 Hãy tính x, s
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 18
 Giả sử đám đông có N phần tử, trong đó có M phần tử M mang đặc tính A thì p = là tử lệ phần tử mang đặc N tính A trong đám đông.
 Chọn ngẫu nhiên mẫu kích thước n, gọi X là số
phần tử mang đặc tính A trong mẫu thì X = là tỷ lệ f
phần tử mang đặc tính A trong mẫu. n
f được gọi là tần suất mẫu
III. MỘT SỐ THAM SỐ ĐẶC TRƯNG CỦA MẪU 19
➢ Với mẫu cụ thể thì f nhận giá trị cụ thể kí hiệu là f . 0
 Ví dụ 3: Xét Ví dụ 2, hãy tính tỉ lệ học sinh có
chiều cao không dưới 165 cm trong mẫu.
BÀI 2. ƯỚC LƯỢNG ĐIỂM MỘT SỐ THAM SỐ LÝ THUYẾT 20
1. Một số loại ước lượng điểm
2. Các kết quả ước lượng điểm