


Preview text:
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 1 TOÁN LỚP 12 ĐỀ SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. Câu 1: Cho hàm 2
y = x − 6x + 5 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (6;+∞).
B. Hàm số đồng biến trên khoảng (2;+∞).
C. Hàm số đồng biến trên khoảng ( ; −∞ 3).
D. Hàm số nghịch biến trên khoảng (6;+∞).
Câu 2: Hàm số y = log ( 2
x − 3x + 2 nghịch biến trên khoảng nào dưới đây? 2 ) A. . B. (1;2) . C. ( ) ;1 −∞ . D. ( 2;+∞) .
Câu 3: Hàm số y = log ( 2 −x + 4x 0,5
) có số điểm cực trị là? A. 1. B. 0 . C. 2 . D. 3. 2 x − 3x + 5
Câu 4: Hàm số y =
nghịch biến trên các khoảng nào? x +1 A. ( 4; − 2) . B. ( ; −∞ 2 − ). C. ( ; −∞ − ) 1 và ( 1; − +∞) . D. ( 4; − − ) 1 .
Câu 5: Giá trị lớn nhất của hàm số 3 2
y = x − 3x + 3 trên khoảng ( 1;
− 3) đạt được tại x = x . Giá trị x là 0 0 A. 1. B. 2. C. 0 . D. 3. 2
Câu 6: Tiệm cận đứng của đồ thị hàm số 2x − 3x −1 y = là x − 2 A. x = 2 − . B. x = 2 . C. y = 2 . D. 1 y = − . 2 Câu 7: Cho hàm số 1 y = 2x −1+
. Tiệm cận xiên của đồ thị hàm số đã cho là x − 2 A. x = 2 .
B. y = x − 2.
C. y = x −1.
D. y = 2x −1
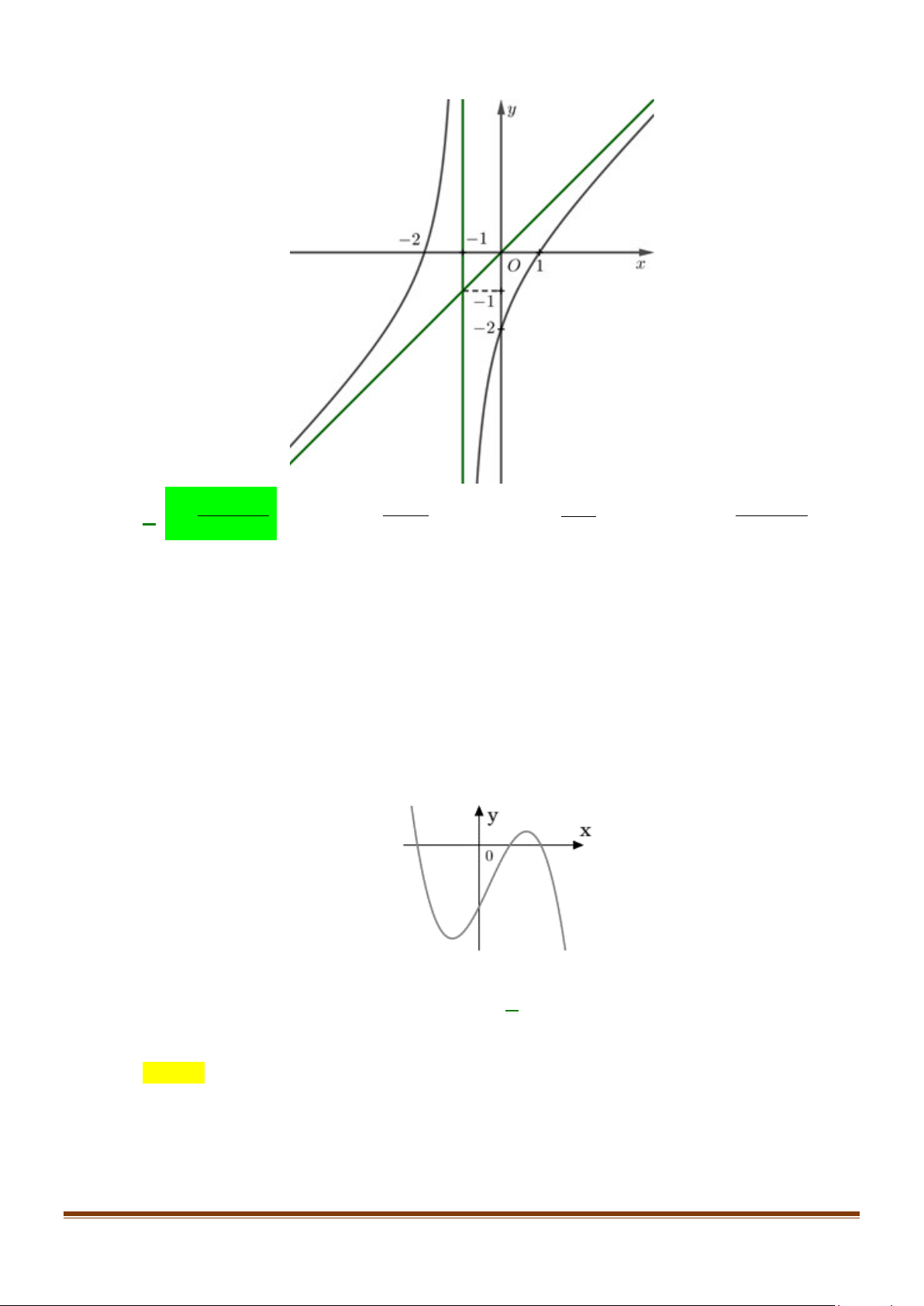
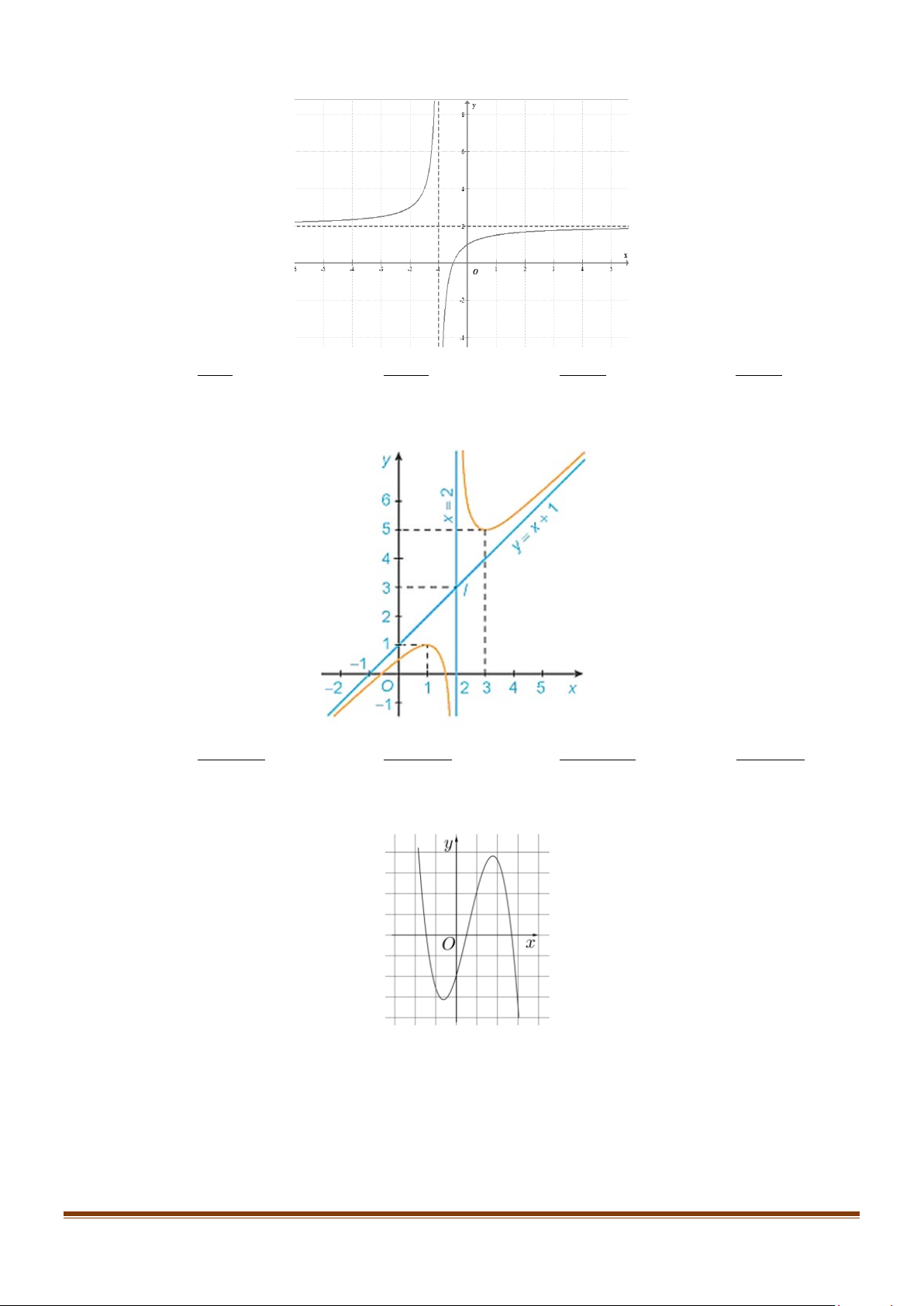
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x −1. B. 4 2
y = x − 2x −1. C. 3 2
y = x − 3x −1. D. 3 2
y = −x + 3x −1.
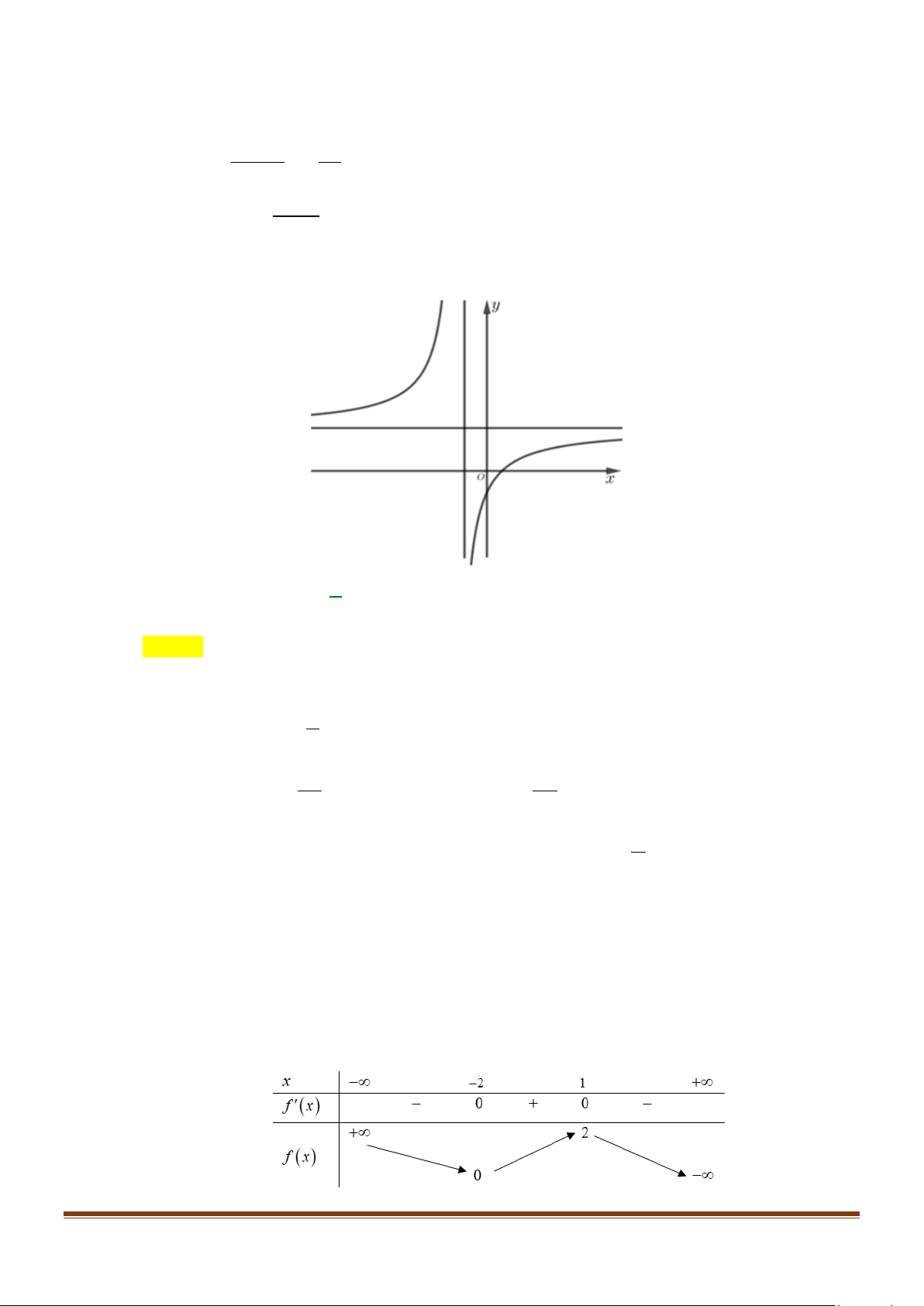
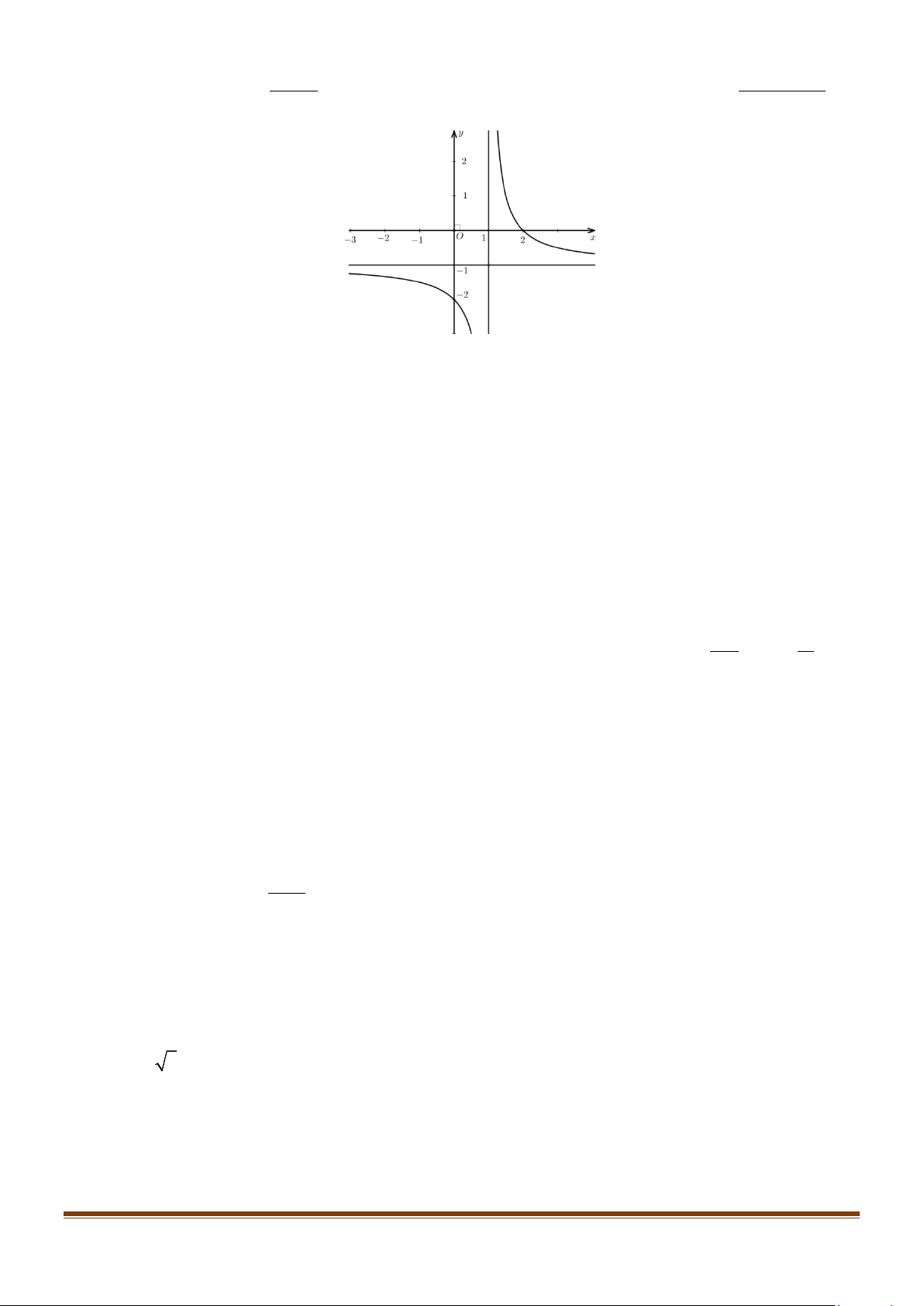
Câu 9: Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 2x −1 y + = B. x 1 y = C. 4 2
y = x + x +1 D. 3
y = x − 3x −1 x −1 x −1 Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
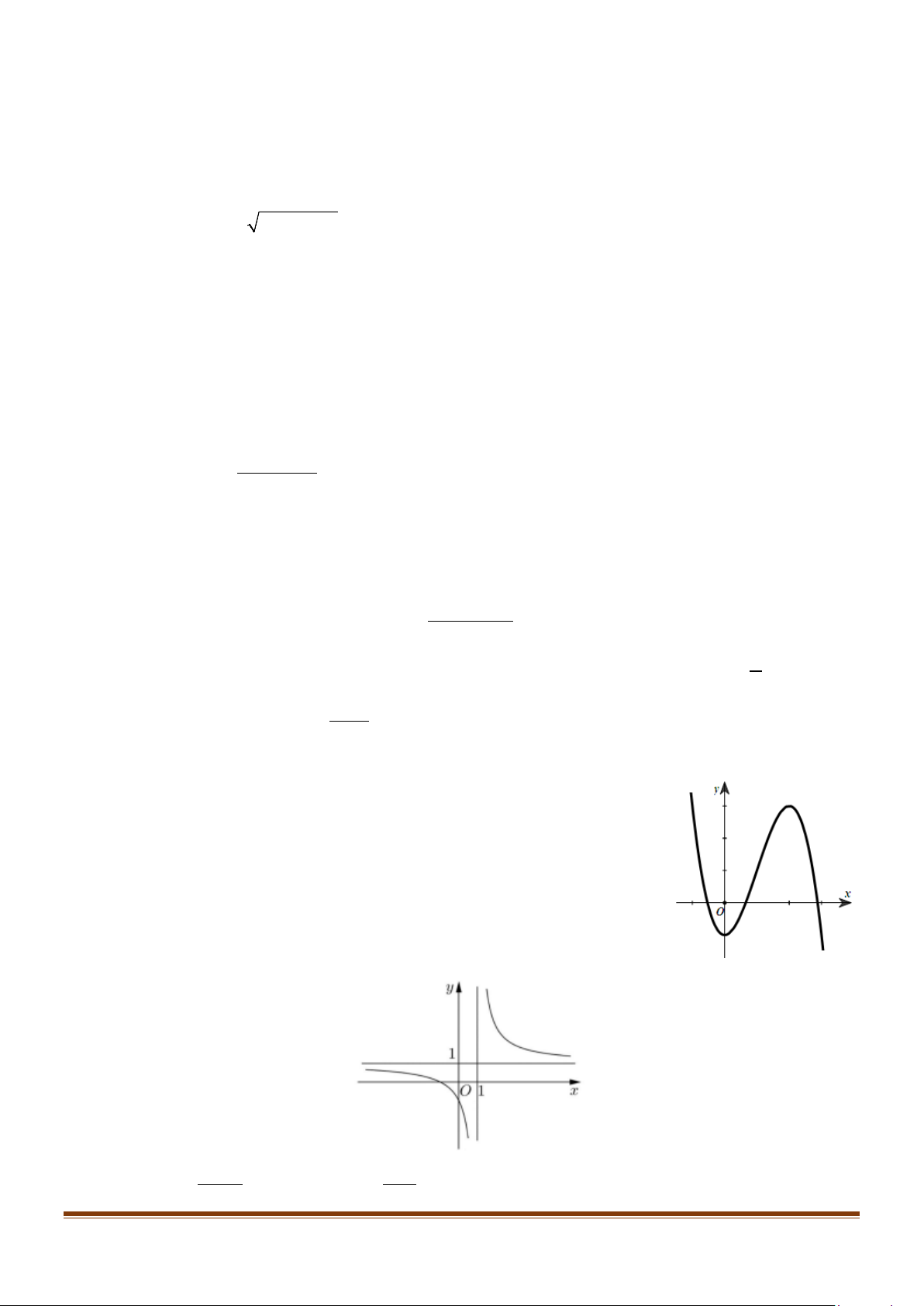
Câu 10: Đường cong dưới đây là đồ thị hàm số nào? 2 x + x − 2 2 x − x 2 x + x − 2 A. y = . B. y = . C. x −1 y = . D. y = . x +1 x +1 x +1 x − 2 Câu 11: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A. a < 0,b < 0,c < 0,d < 0
B. a < 0,b > 0,c > 0,d > 0
C. a < 0,b > 0,c < 0,d > 0
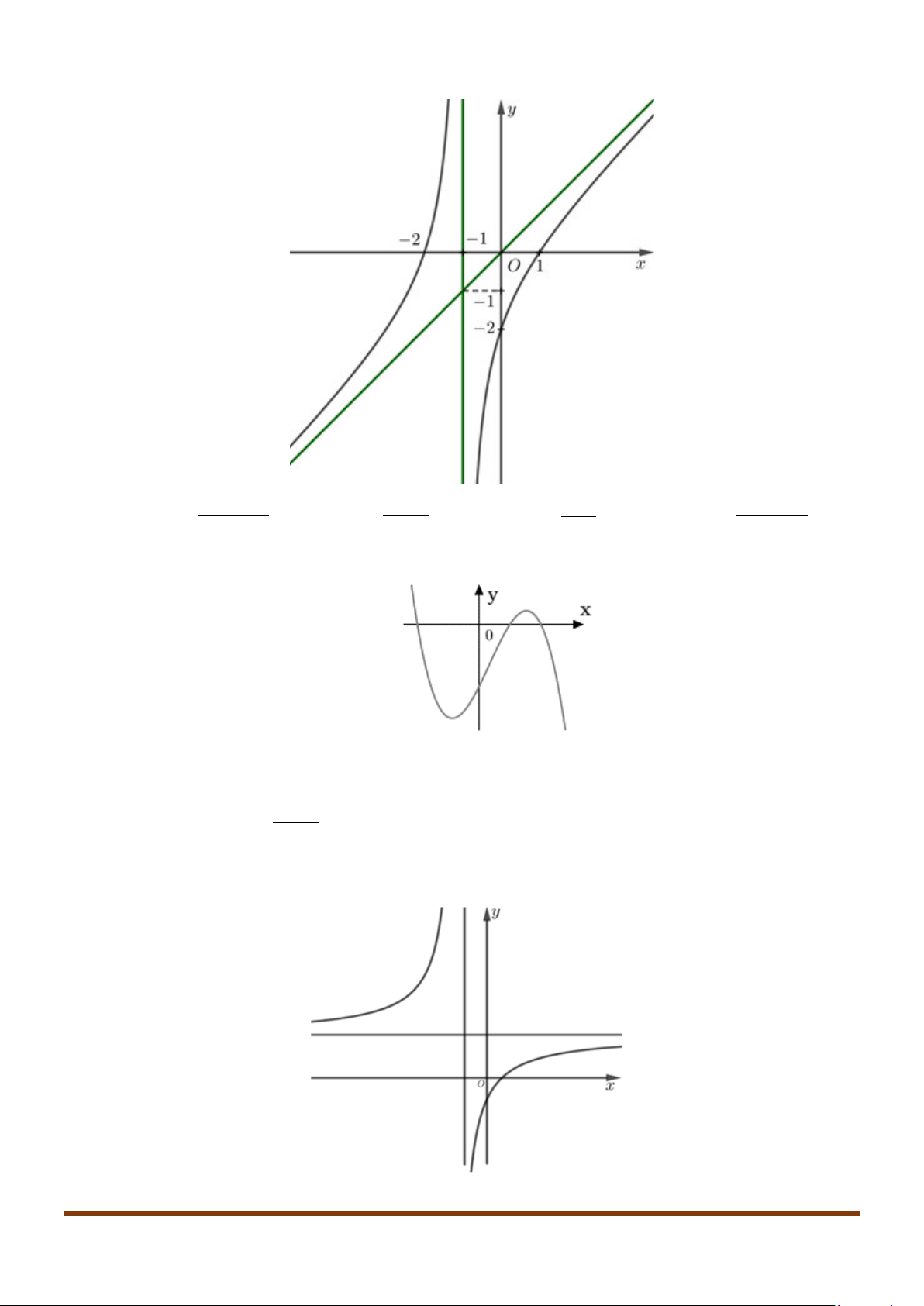
D. a < 0,b > 0,c > 0,d < 0 + Câu 12: Cho hàm số ax b y =
có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi cx + d
trong các số b,c,d có tất cả bao nhiêu số dương? A. 1. B. 2 . C. 0 . D. 3. Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
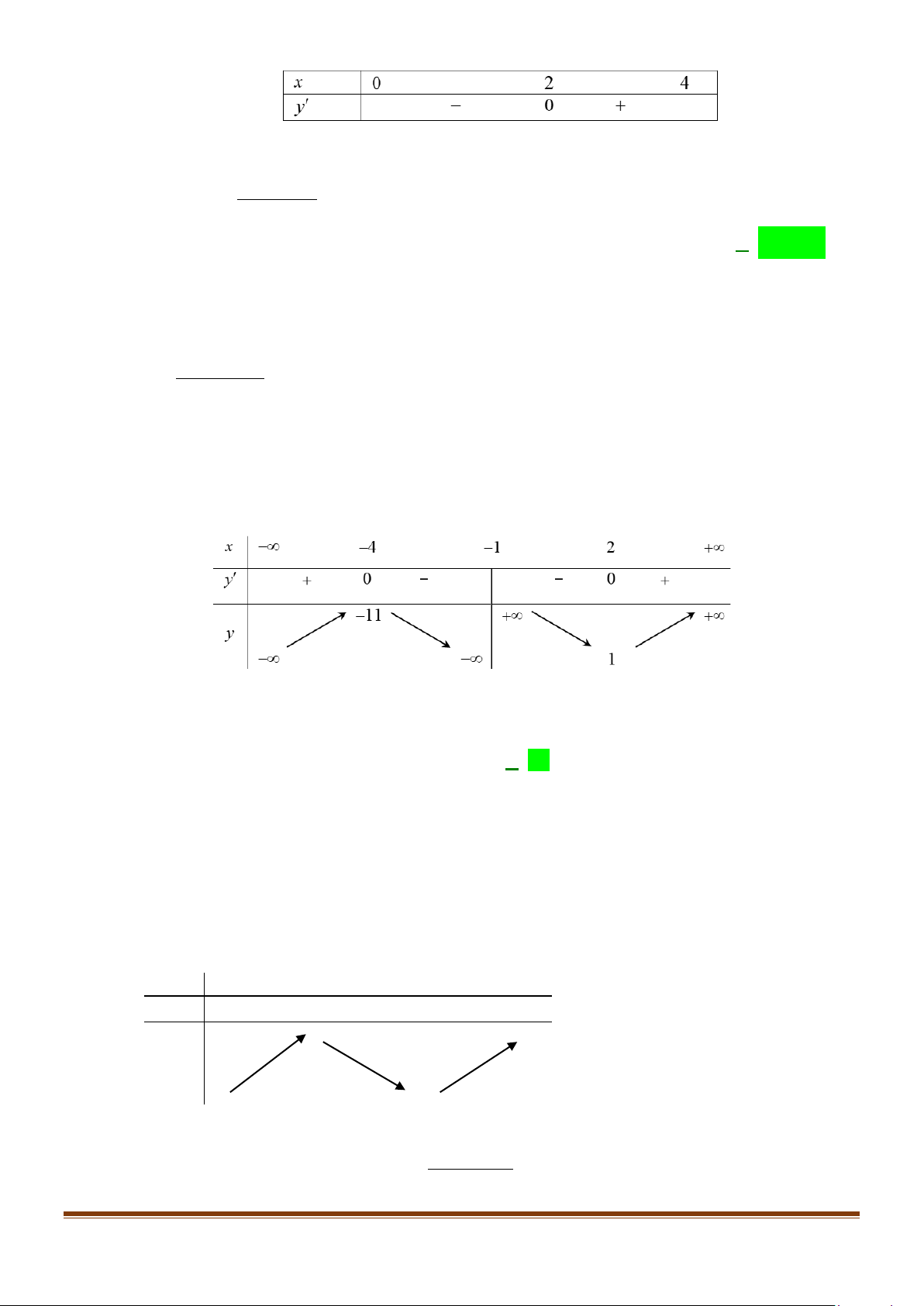
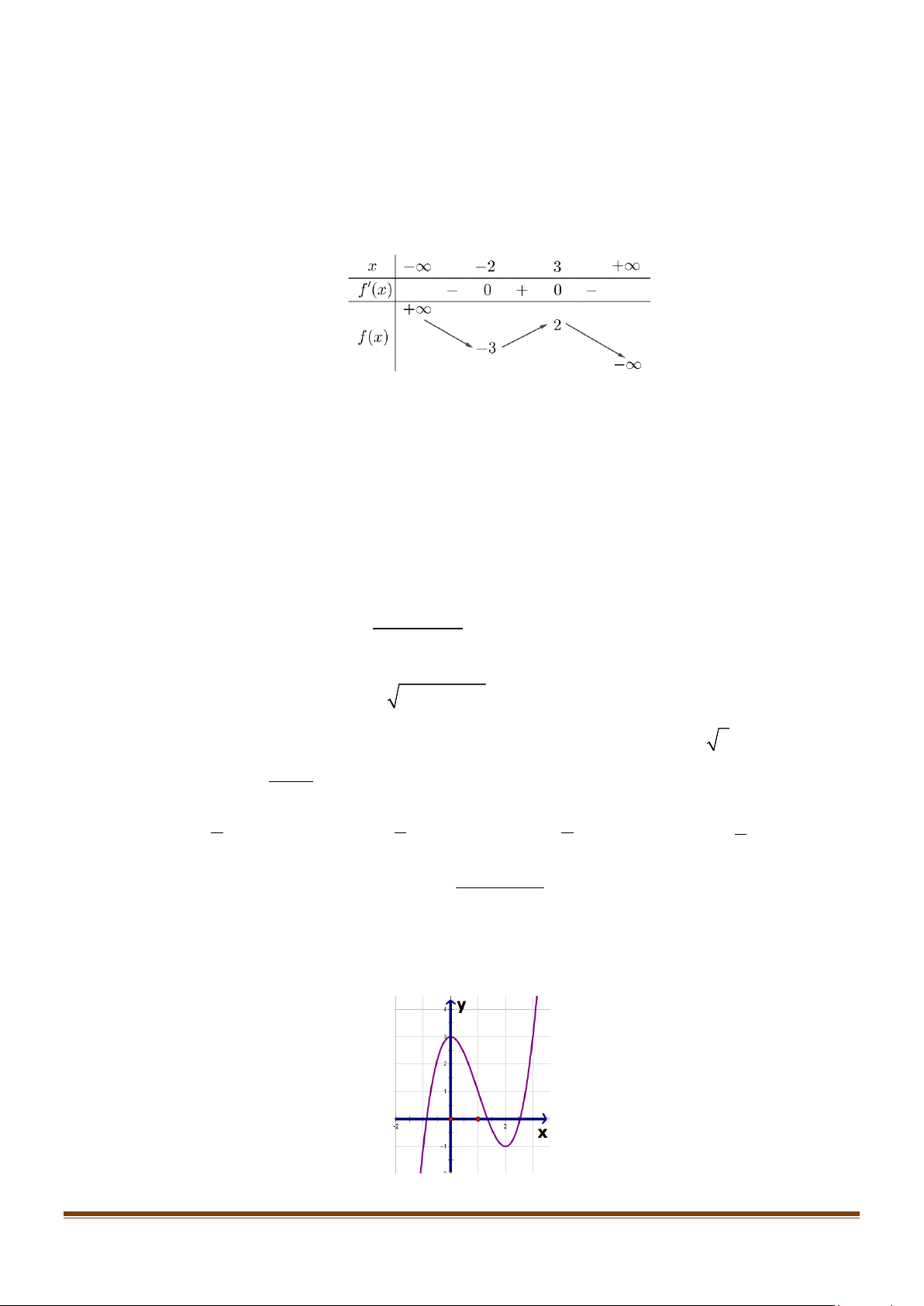
Câu 1: Cho hàm số f (x) 3 2
= ax + bx + cx + d (a ≠ 0) có bảng biến thiên như sau:
a) Hàm số f (x) đồng biến trên khoảng (0;2) .
b) Hàm số f (x) nghịch biến trên khoảng (2;+∞) .
c) Hàm số f (x) đồng biến trên khoảng ( 2; − ) 1 .
d) Hàm số y = f (2x − )
1 nghịch biến trên khoảng 1 ; −∞ − . 2
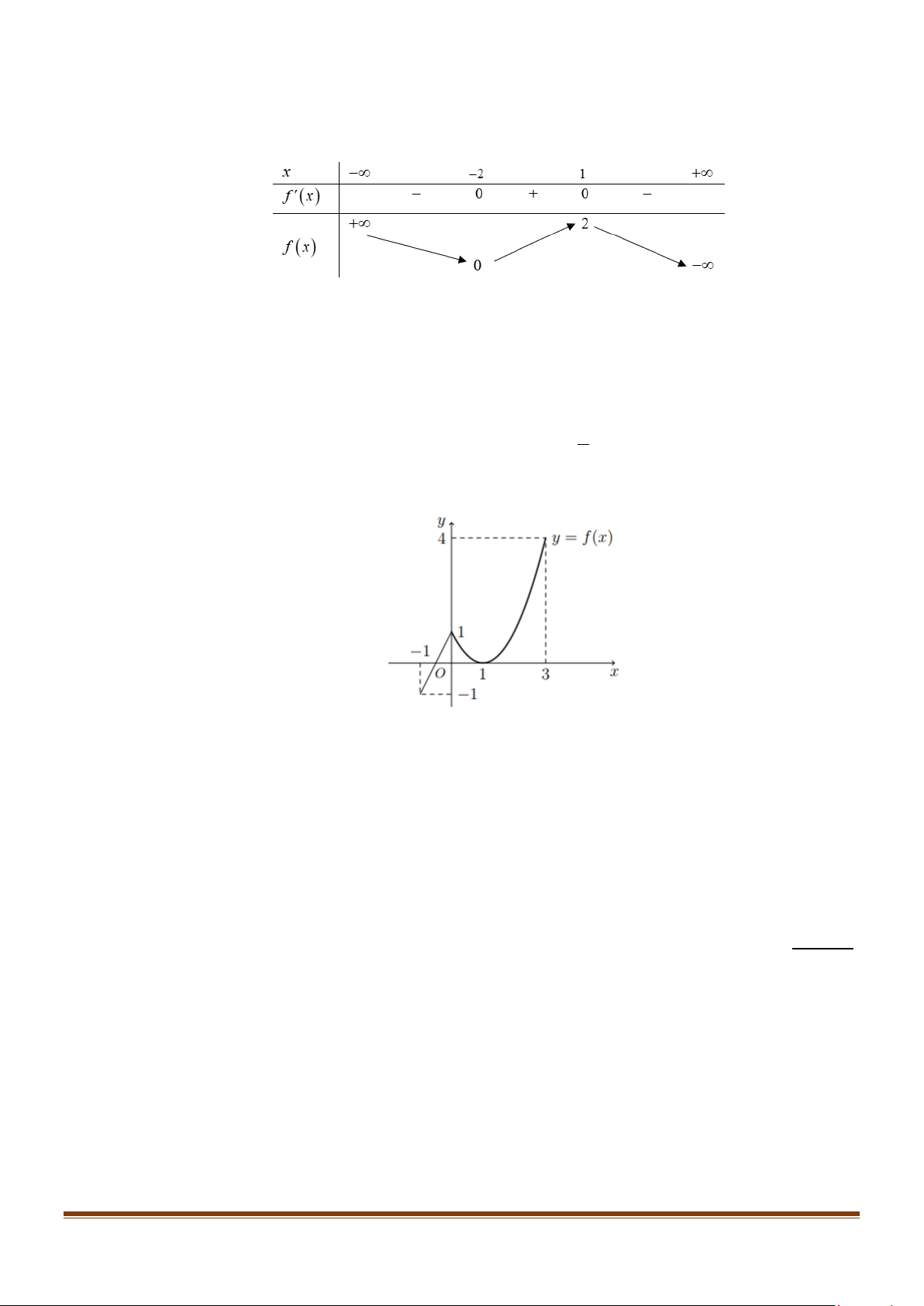
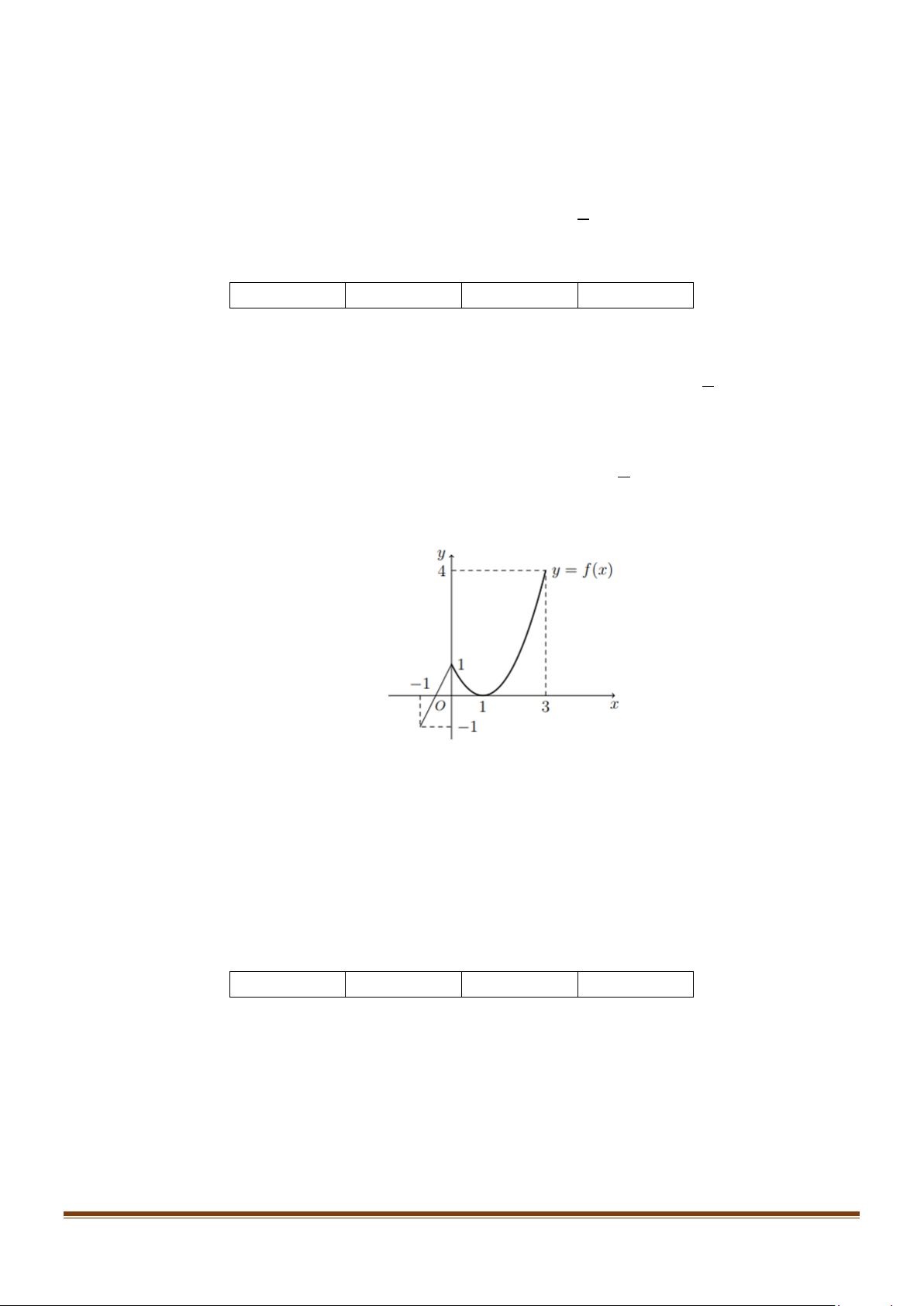
Câu 2: Cho hàm số y f x liên tục trên [ 1; − ]
3 và có đồ thị như hình vẽ bên.
a) Giá trị nhỏ nhất của hàm số y = f (x) trên [ 1; − ]3 là 1 − .
b) Giá trị lớn nhất của hàm số y = f (x) trên [ 1; − 3) là 4.
c) Gọi M ,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f (x) trên [ 1; − ] 3
thì M − m = 5 .
d) Hàm số g (x) = f (x −3) đạt giá trị nhỏ nhất trên [2;6] là 1 − . +
Câu 3: Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f (t) 26t 10 = t + 5
( f (t) được tính bằng nghìn người). Xem y = f (t) là một hàm số xác định trên nửa khoảng [0;+ ∞) .
a) Dân số của thị trấn đó vào năm 2025 là 34 nghìn người.
b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng.
c) Đồ thị hàm số y = f (t) có đường tiệm cận ngang là y = 26 .
d) Dân số của thị trấn đó không thể vượt quá 26 nghìn người. Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Câu 4: Một cơ sở đóng giầy sản xuất mỗi ngày được x đôi giầy. 1≤ x ≤ 20. Tổng chi phí sản xuất x
đôi giầy là C (x) 3 2
= x − 6x −88x + 592 . Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá
200 nghìn đồng /một đôi. Gọi T (x) là số tiền bán được và L(x) là lợi nhuận thu được sau khi
bán hết x đôi giầy.
a) Giả sử trong một ngày nào đó cơ sở sản xuất được 10 đôi giầy thì lợi nhuận thu được là 1888.
b) Giả sử trong một ngày nào đó cơ sở lợi nhuận thu được là 1584 khi đó cơ sở phải sản xuất được 9 đôi giầy.
c) Cơ sở này sản xuất được 12 đôi giầy thì lợi nhuận thu được là nhiều nhất.
d) Lợi nhuận tối đa thu được trong một ngày là 1980 nghìn đồng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hàm số y = f (x) liên tục trên và có đạo hàm f ′(x) = (x − )
1 (x −3)(x −5). Hàm số = ( ) = ( 2 y g x
f x ) có bao nhiêu điểm cực trị?
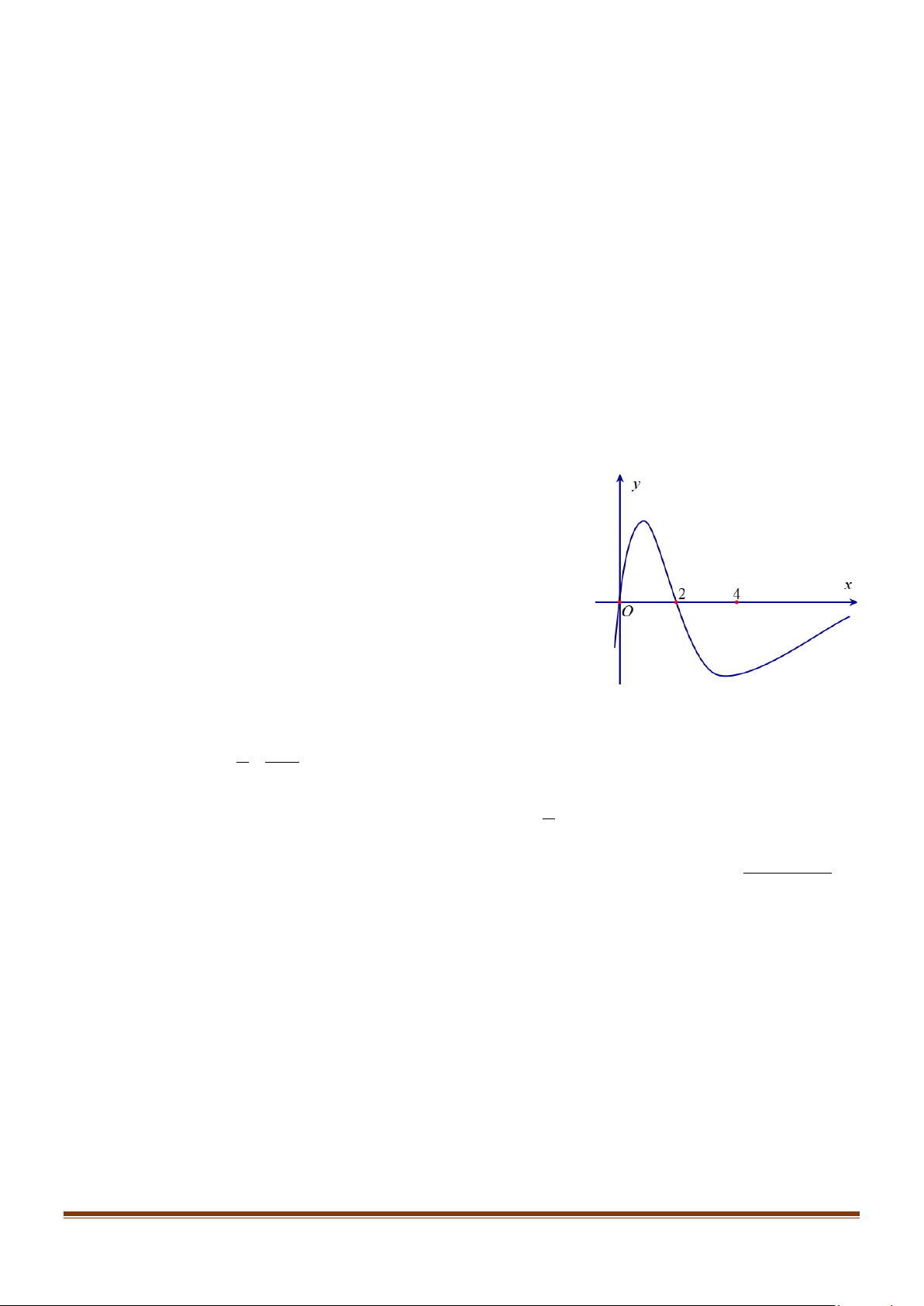
Câu 2: Cho hàm số có f (x) có đạo hàm là hàm f '(x) . Đồ thị
hàm số f '(x) như hình vẽ bên. Biết rằng
f (0) − f (2) = f (4) − f (3). Giả sử giá trị nhỏ nhất m và
giá trị lớn nhất M của f (x) trên đoạn [0;4] đạt được lần
lượt tại x và x . Tìm x và x . 0 1 0 1
Câu 3: Số lượng sản phẩm bán được của một cửa hàng quần áo trong t được cho bởi công thức: S (t) 2 8 200 = −
với t ≥ 1. Xem y = S (t) là một hàm số xác định trên nửa khoảng [1;+∞) 3 2 t +
, biết rằng tiệm cận ngang của đồ thị hàm số có dạng a *
,a,b∈ N ,(a,b) =1. Tính P = a − 2b b 2 2x − 3x + 3
Câu 4: Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số hàm số y = có x +1
dạng y = ax + b . Khi đó a + b bằng
Câu 5: Một khách sạn có 60 phòng. Chủ khách sạn nhận thấy nếu cho thuê mỗi phòng với giá 500.000
đồng/ ngày thì tất cả các phòng đều được thuê hết và cứ tăng giá thêm 50.000 đồng một phòng
thì có thêm 2 phòng trống. Hỏi chủ khách sạn nên cho thuê mỗi phòng với giá bao nhiêu tiền một
ngày để tổng doanh thu một ngày là lớn nhất?
Câu 6: Một công ty sản xuất những chiếc xô bằng nhôm hình trụ không có nắp đủ chứa được10 lít nước.
Hỏi bán kính đáy của chiếc xô bằng bao nhiêu để cửa hàng tốn ít nguyên vật liệu nhất. (kết quả
làm tròn đến hàng phần mười)
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. Câu 1: Cho hàm 2
y = x − 6x + 5 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (6;+∞).
B. Hàm số đồng biến trên khoảng (2;+∞).
C. Hàm số đồng biến trên khoảng ( ; −∞ 3).
D. Hàm số nghịch biến trên khoảng (6;+∞). Lời giải
Tập xác định: D = ( ; −∞ ] 1 ∪[5;+∞) . − Ta có x 3 y′ = > 0 , x ∀ ∈(6;+∞) . 2 x − 6x + 5
Vậy hàm số đồng biến trên khoảng (6;+∞).
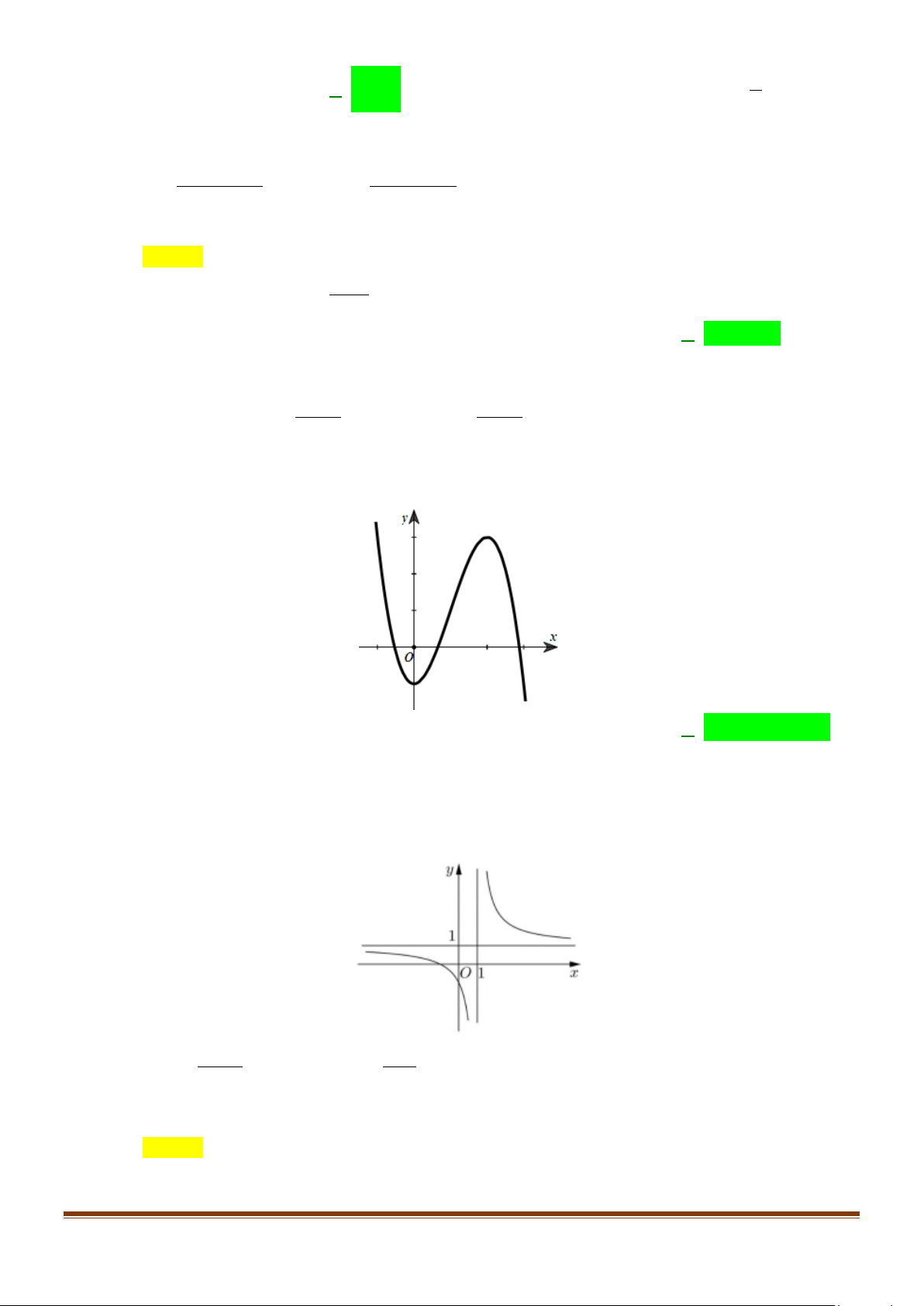
Câu 2: Hàm số y = log ( 2
x − 3x + 2 nghịch biến trên khoảng nào dưới đây? 2 ) A. . B. (1;2) . C. ( ) ;1 −∞ . D. ( 2;+∞) . Lời giải
Tập xác định D = ( ; −∞ ) 1 ∪(2;+∞). ( 2x 3x 2)′ − + Ta có 2x − 3 y′ = ( = 2
x − 3x + 2)ln 2 ( 2
x − 3x + 2)ln 2 2x − 3 2x − 3 < 0 y′ < 0 ⇔ ( < 0 ⇔ ⇔ x <1 2
x − 3x + 2)ln 2 x ∈ D
Vậy hàm số nghịch biến trên khoảng ( ) ;1 −∞ .
Câu 3: Hàm số y = log ( 2 −x + 4x 0,5
) có số điểm cực trị là? A. 1. B. 0 . C. 2 . D. 3. Lời giải Điều kiện 2
−x + 4x > 0 ⇔ 0 < x < 4 . Suy ra TXĐ: D = (0;4). Ta có 2 − x + 4 y′ = ( . 2 −x + 4x)ln 0,5
Với điều kiện trên, ta có 2 − x + 4 y′ = 0 ⇔ ( = 0 ⇔ 2
− x + 4 = 0 ⇔ x = 2 2 −x + 4x)ln 0,5 Bảng xét dấu y′ Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Dựa theo bảng xét dấu, hàm số đạt cực tiểu tại x = 2 . Vậy hàm số có 1 cực trị. 2 x − 3x + 5
Câu 4: Hàm số y =
nghịch biến trên các khoảng nào? x +1 A. ( 4; − 2) . B. ( ; −∞ 2 − ). C. ( ; −∞ − ) 1 và ( 1; − +∞) . D. ( 4; − − ) 1 . Lời giải TXĐ: D = \ {− } 1 . 2 + − Ta có. x 2x 8 y′ = ,∀x ∈ ( D . x + )2 1 x = 4 − Khi đó y′ = 0 2
⇒ x + 2x − 8 = 0 ⇒ . x = 2 Bảng biến thiên:
Vậy hàm số nghịch biến trên khoảng ( 4; − − ) 1 .
Câu 5: Giá trị lớn nhất của hàm số 3 2
y = x − 3x + 3 trên khoảng ( 1;
− 3) đạt được tại x = x . Giá trị x là 0 0 A. 1. B. 2. C. 0 . D. 3. Lời giải +) Ta có 2
y′ = 3x − 6x x = 0 2
y′ = 0 ⇔ 3x − 6x = 0 ⇔ x = 2
+) Ta có bảng biến thiên của hàm số 3 2
y = x − 3x + 3 trên khoảng ( 1; − 3) x 1 − 0 2 3 y ' + 0 − 0 + 0 3 3 y 1 − 1 −
Vậy giá trị lớn nhất của hàm số đã cho trên khoảng ( 1;
− 3) bằng 3đạt được tại x = 0 . 2
Câu 6: Tiệm cận đứng của đồ thị hàm số 2x − 3x −1 y = là x − 2 Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12 A. x = 2 − . B. x = 2 . C. y = 2 . D. 1 y = − . 2 Lời giải 2 2x − 3x −1 2 lim − − = +∞ và 2x 3x 1 lim
= −∞ nên x = 2 là tiệm cận đứng của đồ thị hàm số x 2+ → x − 2 x 2− → x − 2 đã cho. Chọn B Câu 7: Cho hàm số 1 y = 2x −1+
. Tiệm cận xiên của đồ thị hàm số đã cho là x − 2 A. x = 2 .
B. y = x − 2.
C. y = x −1.
D. y = 2x −1 Lời giải Ta có 1 1 lim 2x −1+ − (2x −1) = lim =
0 nên đường thẳng y = 2x −1 là tiệm cận x→±∞ 2x −1 x→±∞ 2x −1
xiên của đồ thị hàm số đã cho.
Câu 8: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x −1. B. 4 2
y = x − 2x −1. C. 3 2
y = x − 3x −1. D. 3 2
y = −x + 3x −1. Lời giải
Dựa vào đồ thị có dạng đồ thị của hàm số bậc 3 có hệ số a < 0 nên đáp án D đúng.
Câu 9: Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 2x −1 y + = B. x 1 y = C. 4 2
y = x + x +1 D. 3
y = x − 3x −1 x −1 x −1 Lời giải Chọn B
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng và ngang x =1; y =1 Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Câu 10: Đường cong dưới đây là đồ thị hàm số nào? 2 x + x − 2 2 x − x 2 x + x − 2 A. y = . B. y = . C. x −1 y = . D. y = . x +1 x +1 x +1 x − 2 Lời giải
Loại đáp án C vì đồ thị đã cho không phải dạng đồ thị của hàm số.
Loại đáp án D vì tiệm cận đứng của đồ thị này là x = 2 còn tiệm cận đứng của đồ thị đã cho là x = 1. −
Loại đáp án B vì đồ thị cắt trục hoành tại điểm có hoành độ x = 0 và x =1 còn đồ thị đã cho
cắt trục hoành tại điểm có hoành độ x = 2 − và x =1.
Đáp án A là đáp án đúng. Câu 11: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A. a < 0,b < 0,c < 0,d < 0
B. a < 0,b > 0,c > 0,d > 0
C. a < 0,b > 0,c < 0,d > 0
D. a < 0,b > 0,c > 0,d < 0 Lời giải Chọn D
- Dựa vào hình dáng của đồ thị suy ra hệ số a < 0 .
- Đồ thị cắt trục Oy tại điểm có tung độ âm nên d < 0 . Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương trình 2
y′ = 3ax + 2bx + c = 0 có 2 nghiệm x , x < ⇒ > 1 2 trái dấu kéo theo 3 . a c 0 c 0 . x + x b - Mặt khác 1 2 = − > 0 ⇒ b > 0. 2 3a + Câu 12: Cho hàm số ax b y =
có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi cx + d
trong các số b,c,d có tất cả bao nhiêu số dương? A. 1. B. 2 . C. 0 . D. 3. Lời giải Chọn B
Nhìn vào đồ thị ta thấy a
• tiệm cận ngang y = nằm trên trục hoành nên c > 0 c − − • tiệm cận đứng d x =
nằm bên trái trục tung nên d < 0. Suy ra d > 0 c c
• giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên b < 0. d Suy ra b < 0
Vậy c > 0,d > 0
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số f (x) 3 2
= ax + bx + cx + d (a ≠ 0) có bảng biến thiên như sau: Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
a) Hàm số f (x) đồng biến trên khoảng (0;2) .
b) Hàm số f (x) nghịch biến trên khoảng (2;+∞) .
c) Hàm số f (x) đồng biến trên khoảng ( 2; − ) 1 .
d) Hàm số y = f (2x − )
1 nghịch biến trên khoảng 1 ; −∞ − . 2 Lời giải a) Sai b) Đúng c) Đúng d) Đúng
d) Đúng. Xét hàm số y = f (2x − )
1 có y′ = 2 f ′(2x − ) 1 1 2x −1≤ 2 − x ≤ −
Hàm số nghịch biến khi y′ ≤ 0 ⇔ 2 f ′(2x − ) 1 ≤ 0 ⇔ ⇔ 2 . 2x −1 ≥1 x ≥1
Vậy hàm số y = f (2x − )
1 nghịch biến trên các khoảng 1 ; −∞ − và (1;+∞). 2
Câu 2: Cho hàm số y f x liên tục trên [ 1; − ]
3 và có đồ thị như hình vẽ bên.
a) Giá trị nhỏ nhất của hàm số y = f (x) trên [ 1; − ]3 là 1 − .
b) Giá trị lớn nhất của hàm số y = f (x) trên [ 1; − 3) là 4.
c) Gọi M ,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f (x) trên [ 1; − ] 3
thì M − m = 5 .
d) Hàm số g (x) = f (x −3) đạt giá trị nhỏ nhất trên [2;6] là 1 − . Lời giải a) Đúng b) Sai c) Đúng d) Đúng
a) Giá trị nhỏ nhất của hàm số y = f (x) trên [ 1; − ]3 là -1.
b) Hàm số y = f (x) trên [ 1;
− 3) không có giá trị lớn nhất. c) Trên [ 1; − ] 3 M = 4,m = 1
− thì M − m = 5 .
d) Đặt t = x − 3 vì x∈[2;6] ⇒ t ∈[ 1; − ] 3 Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Xét hàm số y = f (t) với t ∈[ 1; − ] 3
Dựa vào đồ thị ta có giá trị nhỏ nhất của hàm số y = f (t) trên [ 1; − ] 3 là 1 − . +
Câu 3: Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f (t) 26t 10 = t + 5
( f (t) được tính bằng nghìn người). Xem y = f (t) là một hàm số xác định trên nửa khoảng [0;+ ∞) .
a) Dân số của thị trấn đó vào năm 2025 là 34 nghìn người.
b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng.
c) Đồ thị hàm số y = f (t) có đường tiệm cận ngang là y = 26 .
d) Dân số của thị trấn đó không thể vượt quá 26 nghìn người. Lời giải a) Sai b) Sai c) Đúng d) Đúng
a) Dân số của thị trấn đó vào năm 2025 là f ( ) 26⋅55 +10 55 =
= 24 nghìn người. Suy ra a) sai. 55 + 5
b) Đạo hàm của hàm số f ′(t) 120 = > 0 5 t
∀ ≠ − luôn nhận giá trị dương trên khoảng. 2 ( ) (t +5) Suy ra b) sai. c) Ta có: f (t) 26t +10 lim = lim
= 26 . Do đó đồ thị hàm số f (t) có đường tiệm cận ngang là t→+∞ t→+∞ t + 5
y = 26 . Suy ra c) đúng.
d) Ta có f (t) 26t +10 26t +130 = <
= 26 . Vì vậy dân số của thị trấn đó không thể vượt quá 26 t + 5 t + 5
nghìn người. Suy ra d) đúng.
Câu 4: Một cơ sở đóng giầy sản xuất mỗi ngày được x đôi giầy. 1≤ x ≤ 20. Tổng chi phí sản xuất x
đôi giầy là C (x) 3 2
= x − 6x −88x + 592 . Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá
200 nghìn đồng /một đôi. Gọi T (x) là số tiền bán được và L(x) là lợi nhuận thu được sau khi
bán hết x đôi giầy.
a) Giả sử trong một ngày nào đó cơ sở sản xuất được 10 đôi giầy thì lợi nhuận thu được là 1888.
b) Giả sử trong một ngày nào đó cơ sở lợi nhuận thu được là 1584 khi đó cơ sở phải sản xuất được 9 đôi giầy.
c) Cơ sở này sản xuất được 12 đôi giầy thì lợi nhuận thu được là nhiều nhất.
d) Lợi nhuận tối đa thu được trong một ngày là 1980 nghìn đồng. Lời giải a) Đúng b) Sai c) Đúng d) Sai
a) Lợi nhuận thu được là L(x) = T (x) −C (x) 3 2
= −x + 6x + 288x − 592 . Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Một ngày nào đó cơ sở sản xuất được 10 đôi giầy thì lợi nhuận thu được là: L( ) 3 2 10 = 10 −
+ 6.10 + 288.10 − 592 =1888 . Chọn đúng.
b) Lợi nhuận thu được là 1584, khi đó ta có 3 2
1584 = −x + 6x + 288x − 592 x = 1 − + 273 3 2
⇔ x − 6x − 288x + 2176 = 0 ⇔ x = 1 − − 273 . x = 8 Chọn sai.
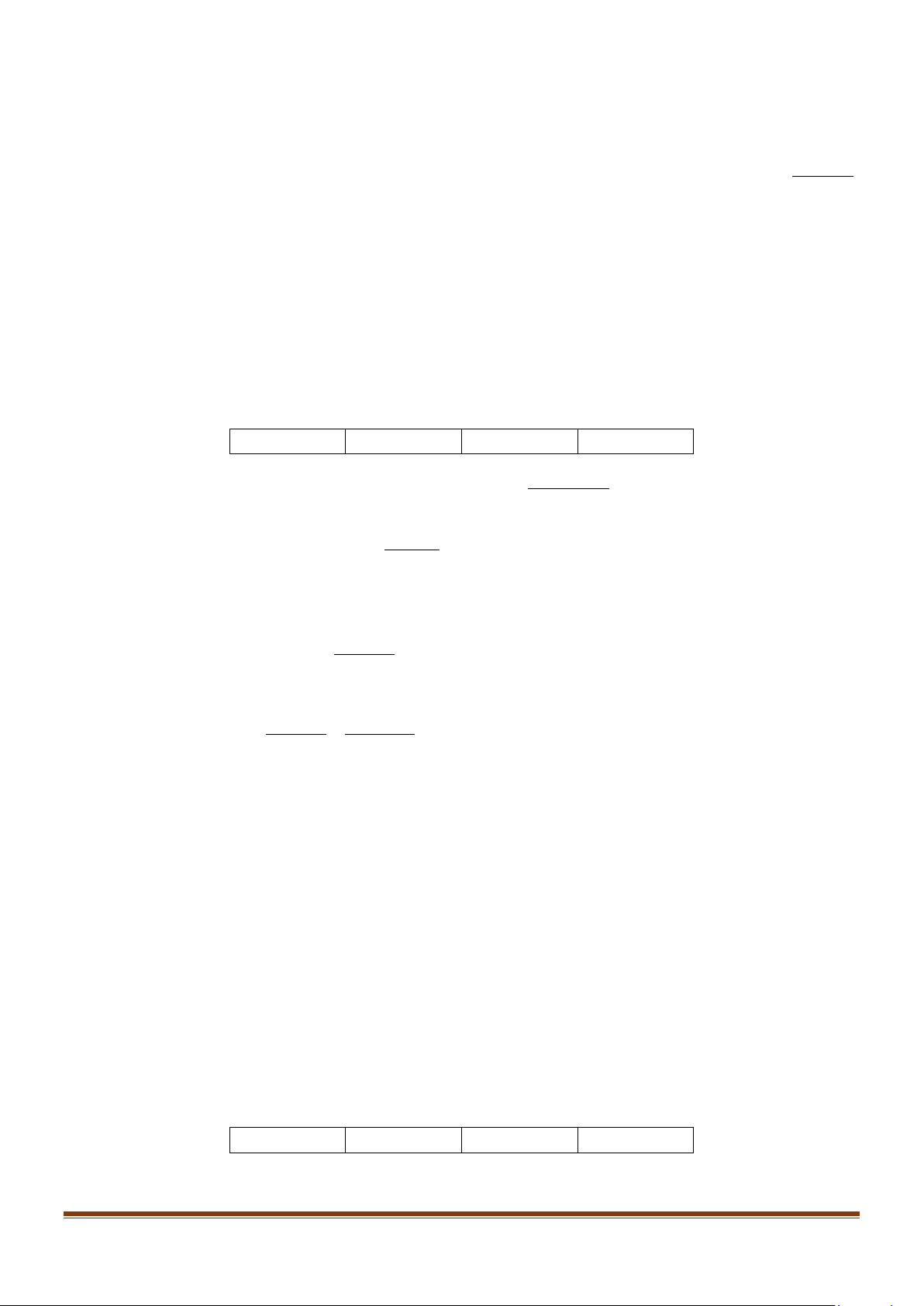
c) Xét hàm số L(x) 3 2
= −x + 6x + 288x − 592 với 1≤ x ≤ 20. L′(x) 2 = 3
− x +12x + 288 = L′(x) x 12 2 = 0 ⇔ 3
− x +12x + 288 = 0 ⇔ x = 8( − l) Bảng biến thiên
Vậy cơ sở sản xuất được 12 đôi giầy thì lợi nhuận đạt cao nhất. Chọn đúng.
d) Khi đó lợi nhuận tối đa đạt được trong một ngày là 1980. Chọn sai.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hàm số y = f (x) liên tục trên và có đạo hàm f ′(x) = (x − )
1 (x −3)(x −5). Hàm số = ( ) = ( 2 y g x
f x ) có bao nhiêu điểm cực trị? Lời giải Trả lời : 7 Xét hàm số = ( ) = ( 2 y g x f x ).
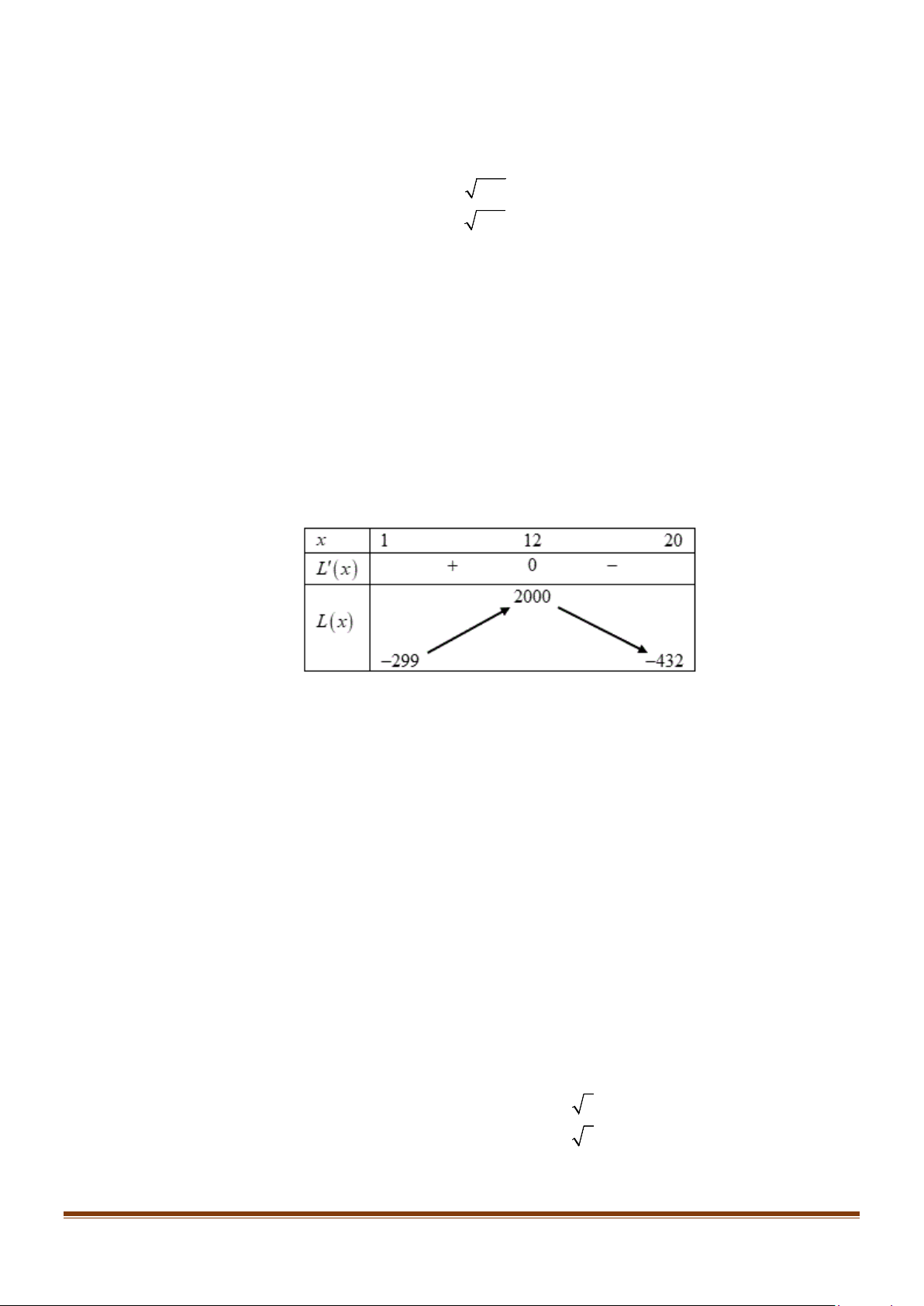
Có g′(x) = x f ′( 2 x ) = x( 2 x − )( 2 x − )( 2 2 . 2 1 3 x − 5). x = 0 x 0 = x = 1 ± Ta có g (x) 0 ′ = ⇔ . ( ⇔ 2 x
)1( 2x 3)( 2x 5) 0 − − − = x = ± 3 x = ± 5
Ta có bảng xét dấu của g′(x) như sau: Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Dựa vào BXD ta thấy g′(x) đổi dấu 7 lần, vậy hàm số y = g (x) có 7 điểm cực trị.
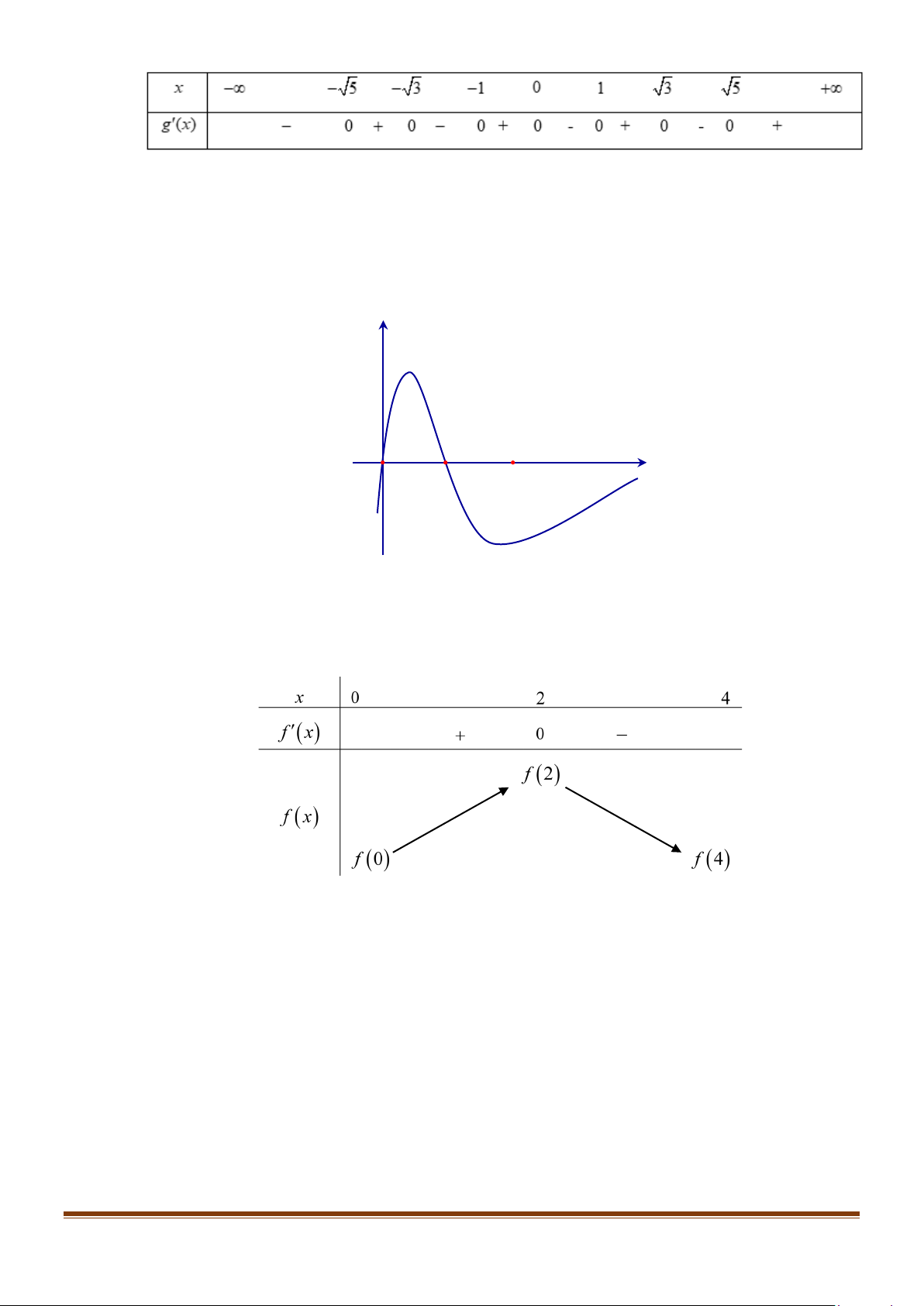
Câu 2: Cho hàm số có f (x) có đạo hàm là hàm f '(x) . Đồ thị hàm số f '(x) như hình vẽ bên. Biết
rằng f (0) − f (2) = f (4) − f (3). Giả sử giá trị nhỏ nhất m và giá trị lớn nhất M của f (x) trên
đoạn [0;4] đạt được lần lượt tại x và x . Tìm x và x . 0 1 0 1 y 2 4 x O Lời giải Trả lời : 6.
Dựa vào đồ thị của hàm f '(x) ta có bảng biến thiên.
Vậy giá trị lớn nhất M = f (2) ⇒ x = 2. 1
Hàm số nghịch biến trên khoảng (2;4)nên f (2) > f (3) ⇒ f (2) − f (3) > 0 .
Theo giả thuyết: f (0) − f (2) = f (4) − f (3)
⇔ f (0) − f (4) = f (2) − f (3) > 0 ⇒ f (0) > f (4)
Suy ra giá trị nhỏ nhất m = f (4) ⇒ x = 4 . 0
Vậy x = 4; x = 2 , ta có x + x = 6 0 1 0 1 Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Câu 3: Số lượng sản phẩm bán được của một cửa hàng quần áo trong t được cho bởi công thức: S (t) 2 8 200 = −
với t ≥ 1. Xem y = S (t) là một hàm số xác định trên nửa khoảng [1;+∞) 3 2 t +
, biết rằng tiệm cận ngang của đồ thị hàm số có dạng a *
,a,b∈ N ,(a,b) =1. Tính P = a − 2b b Lời giải Trả lời : 394 Ta có: S (t) 2 8 2 400 lim = lim 200 − = 200. =
⇒ a = 400;b = 3 x→+∞ x→+∞ 3 2 + t 3 3
Vậy P = a − 2b = 400 − 6 = 394 2 2x − 3x + 3
Câu 4: Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số hàm số y = có x +1
dạng y = ax + b . Khi đó a + b bằng Lời giải Trả lời : 1
Ta có D = \{− } 1 . 2 2x + 4x − 6 y′ = . (x + )2 1
x =1 ⇒ y =1⇒ A(1; ) 1 y′ = 0 ⇔ . x = 3 − ⇒ y = 15 − ⇒ B ( 3 − ; 15 − ) AB( 4 − ; 1 − 6) = 4
− (1;4) . Khi đó, một vecto pháp tuyến của đường thẳng AB là n = (4;− ) 1 .
Phương trình đường thẳng AB có dạng: 4(x − ) 1 −1( y − )
1 = 0 ⇔ y = 4x − 3.
Do đó a = 4; b = 3
− . Vậy a + b = 4 + ( 3 − ) =1.
Câu 5: Một khách sạn có 60 phòng. Chủ khách sạn nhận thấy nếu cho thuê mỗi phòng với giá 500.000
đồng/ ngày thì tất cả các phòng đều được thuê hết và cứ tăng giá thêm 50.000 đồng một phòng
thì có thêm 2 phòng trống. Hỏi chủ khách sạn nên cho thuê mỗi phòng với giá bao nhiêu tiền một
ngày để tổng doanh thu một ngày là lớn nhất? Lời giải Trả lời : 1000
Gọi giá tiền mà chủ khách sạn cho thuê một phòng là x . (500 ≤ x )
Vì cứ tăng giá thêm 50.000 đồng một phòng thì có thêm 2 phòng trống nên số phòng được thuê là: x − 500 60 − .2 = 80 x − . 50 25 2
Khi đó tổng doanh thu tương ứng trong 1 ngày là: 80 x − = 80 x x x − . 25 25 Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12 2 Đặt ( ) = 80 x f x x − . Ta có: 25 2 '( ) = 80 x f x − = 0 ⇔ x =1000 . 25
Vì f (x) là tam thức bậc hai có hệ số cao nhất âm nên f (x) đạt giá trị lớn nhất tại x =1000 .
Vậy để tổng doanh thu là lớn nhất thì chủ khách sạn nên cho thuê phòng với giá 1000 một ngày.
Câu 6: Một công ty sản xuất những chiếc xô bằng nhôm hình trụ không có nắp đủ chứa được10 lít nước.
Hỏi bán kính đáy của chiếc xô bằng bao nhiêu để cửa hàng tốn ít nguyên vật liệu nhất. (kết quả
làm tròn đến hàng phần mười) Lời giải Trả lời : 14,7 Ta có: 3 10l =10000cm . Gọi V
x ( x > 0 ) là bán kính của chiếc xô. Khi đó 2
V = π x h ⇒ h = . 2 π x
Diện tích phần tôn làm chiếc xô là: 2 2 V 2 10000 2 20000
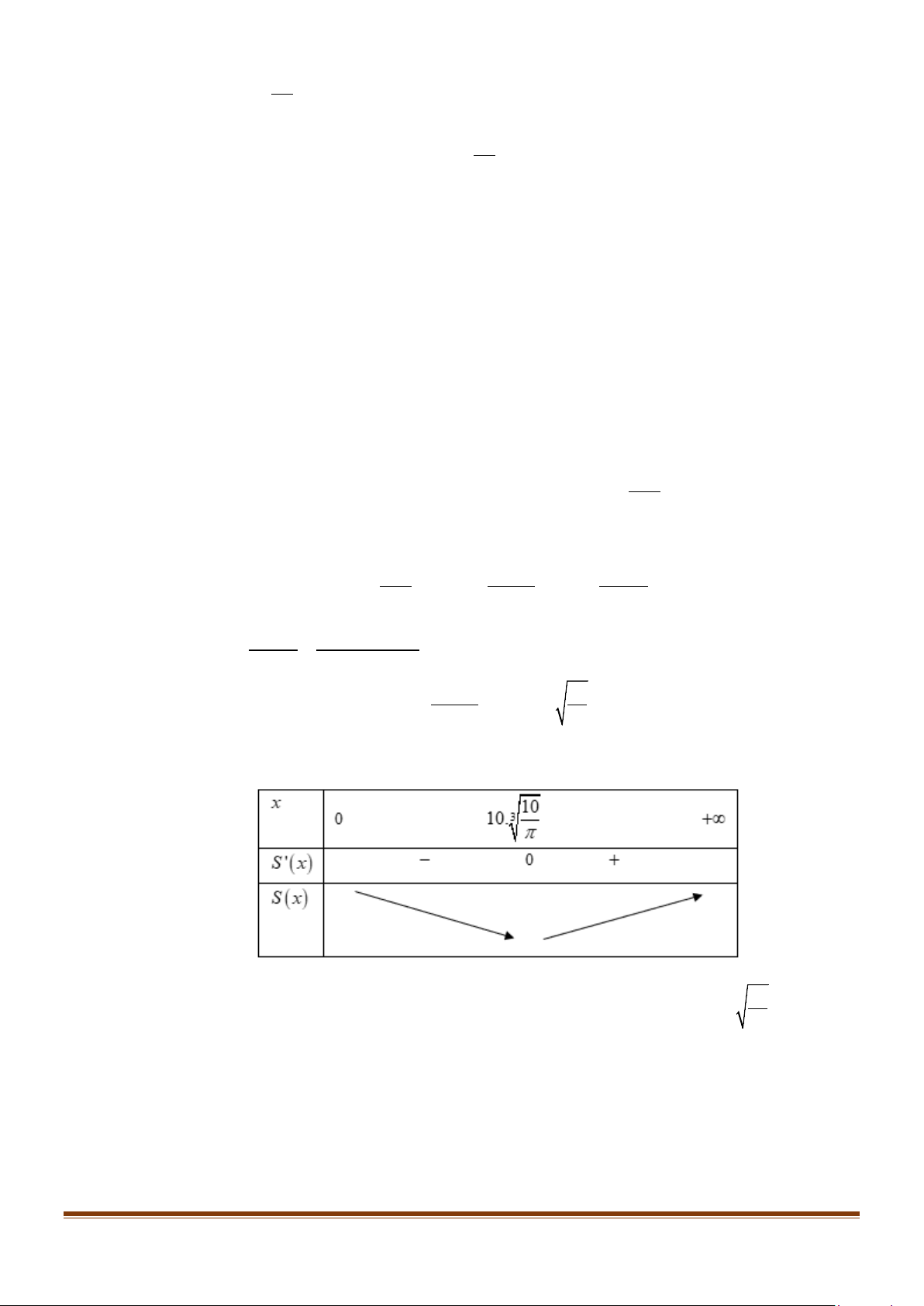
S(x) = π x + 2π xh = π x + 2π x = π x + 2 = π x + 2 π x x x 3 20000 2π − 20000 '( ) = 2 x S x π x − = . 2 2 x x 3 3 10000 10 = ⇔ π − = ⇔ = ⇔ = 3 S '(x) 0 2 x 20000 0 x x 10. π π Bảng biến thiên:
Ta thấy diện tích phần nhôm làm chiếc xô nhỏ nhất khi bán kính đáy xô là 10 = 3 x 10 ≈ 14,7(cm) π
---------- HẾT ---------- Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KÌ 1 TOÁN LỚP 12 ĐỀ SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Cho hàm số f (x) có bảng biến thiên như sau.
Giá trị cực tiểu của hàm số đã cho bằng A. 3. B. 3 − . C. 2 − . D. 2 .
Câu 2: Cho hàm số y = f (x) có đạo hàm y = f ′(x) = x(x − 2), x
∀ ∈ . Hàm số y = f (x) nghịch biến
trên khoảng nào dưới đây? A. (0;2) . B. (0;+∞). C. ( ;0 −∞ ). D. (2;+∞) .
Câu 3: Cho hàm số f (x) có đạo hàm f ′(x) = x(x + )2 (x − )3 1
2 ,∀x∈ . Số điểm cực trị của hàm số là A. 1. B. 2 . C. 3. D. 0 . 2
Câu 4: Điểm cực tiểu của hàm số −x + 2x −1 y = là x + 2 A. x =1. B. x = 5 − . C. x = 2 . D. x = 5.
Câu 5: Giá trị nhỏ nhất của hàm số y = x2 − x 2 + 4 trên khoảng ( 1; − 5) là A. 0 . B. 2. C. 3 . D. 3 . Câu 6: Cho hàm số x +1 y =
. Tiệm cận đứng của đồ thị hàm số là: 2x −1 1 1 1 A. y = − .
B. x = − . C. y = . D. 1 x = . 2 2 2 2 2
Câu 7: Số đường tiệm cận của đồ thị hàm số 2x − 3x − 2 y = là 2 x − 4 A. 0. B. 2. C. 1. D. 0.
Câu 8: Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số dưới đây. Hỏi hàm số đó là hàm số nào? A. 3 2
y = −x − 3x + 3. B. 3
y = x − 3x + 3. C. 3 2
y = −x + 3x + 3. D. 3 2
y = x − 3x + 3. Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Câu 9: Hình vẽ bên dưới là đồ thị của hàm số nào? A. x −1 y x + x − x + = . B. 2 1 y = . C. 2 3 y = . D. 2 5 y = . x +1 x +1 x +1 x +1
Câu 10: Đường cong trong hình bên là đồ thị của hàm số nào? 2 2 2 2 A. x − x −1 y − − − − − + = . B. x x 1 y = . C. x 2x 1 y = . D. x x 1 y = . x + 2 x − 2 x − 2 x − 2 Câu 11: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. a < 0, b > 0, 0, c > d < 0 B. a < 0, b < 0, 0, c > d < 0. C. a > 0, b < 0, c < 0, d > 0 D. a < 0, b > 0, 0, c < d < 0. Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12 + − + Câu 12: Cho hàm số ax b y =
có đồ thị như hình dưới đây. Tính giá trị biểu thức a 2b 3d T = . cx + d c
A. T = 6 .
B. T = 0 . C. T = 8 − .
D. T = 2.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Câu 1: Cho hàm số ( ) 3 2 1 7 − − − = = x x x y f x
. Các mệnh đề sau đúng hay sai?
a) Tập xác định của hàm số là D = . b) ( ) ( ) 3 2 2 − − 1 3 2 1 .7 − ′ = − − x x x f x x x .ln 7 .
c) Hàm số y = f (x) đạt cực đại tại x =1.
d) Hàm số = ( x
y f e ) đạt cực tiểu tại x = 0 . 4 t
Câu 2: Thể tích nước của một bể bơi sau t phút bơm tính theo công thức V (t) 1 3 = 30t − với 100 4
(0 ≤ t ≤ 90) . Tốc độ bơm nước tại thời điểm t được tính bở công thức f (t) = V'(t).
a) Thể tích nước của bể bơi sau 20 phút bơm là 2000.
b) Tốc độ bơm nước tại thời điểm t là f (t) 2 3 = 90t − t .
c) Tốc độ bơm giảm từ phút thứ 70 đến phút thứ 90.
d) Tốc độ bơm lớn nhất tại thời điểm t = 60. x + Câu 3: Cho hàm số 2 y =
có đồ thị là (C). x − 2
a) Đồ thị (C) có đường tiệm cận đứng x = 2 .
b) Đồ thị (C) nhận điểm I (1; )
1 làm tâm đối xứng.
c) Đường thẳng đường thẳng d : y = x −1 cắt đồ thị (C) tại 2 điểm phân biệt có độ dài bằng 4 5.
d) Gọi M là điểm bất kì thuộc đồ thị (C). Khi đó tổng khoảng cách từ điểm M đến hai
đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất bằng 4. Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Câu 4: Chi phí nhiên liệu của một chiếc tầu chạy trên sông được chia làm hai phần. Phần thứ nhất không
phụ thuộc vào vận tốc và bằng 480 nghìn đồng trên 1 giờ. Phần thứ hai tỉ lệ thuận với lập phương
của vận tốc, khi v =10 thì phần thứ hai bằng 30 nghìn đồng/giờ. Xét tính đúng sai của các mệnh đề sau:
a) Khi vận tốc v =10 thì chi phí nguyên liệu cho phần thứ nhất trên 1 km đường sông là 48000 đồng.
b) Hàm số xác định tổng chi phí nguyên liệu trên 1 km đường sông với vận tốc x(km / h) là 480 3 f (x) = + 0,03x . x
c) Khi vận tốc v = 30 thì tổng chi phí nguyên liệu trên 1 km đường sông là 43000 đồng.
d) Vận tốc của tàu để tổng chi phí nguyên liệu trên 1 km đường sông nhỏ nhất là v = 20 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 2 2
x + x + m − 6
Câu 1: Cho hàm số y =
. Tìm số giá trị nguyên của tham số m để hàm số đơn điệu trên x + 2 mỗi khoảng xác định.
Câu 2: Tìm giá trị nhỏ nhất cả hàm số f (x) 4 17 = x + 4x +
(kết quả làm tròn đến hàng phần trăm) 4
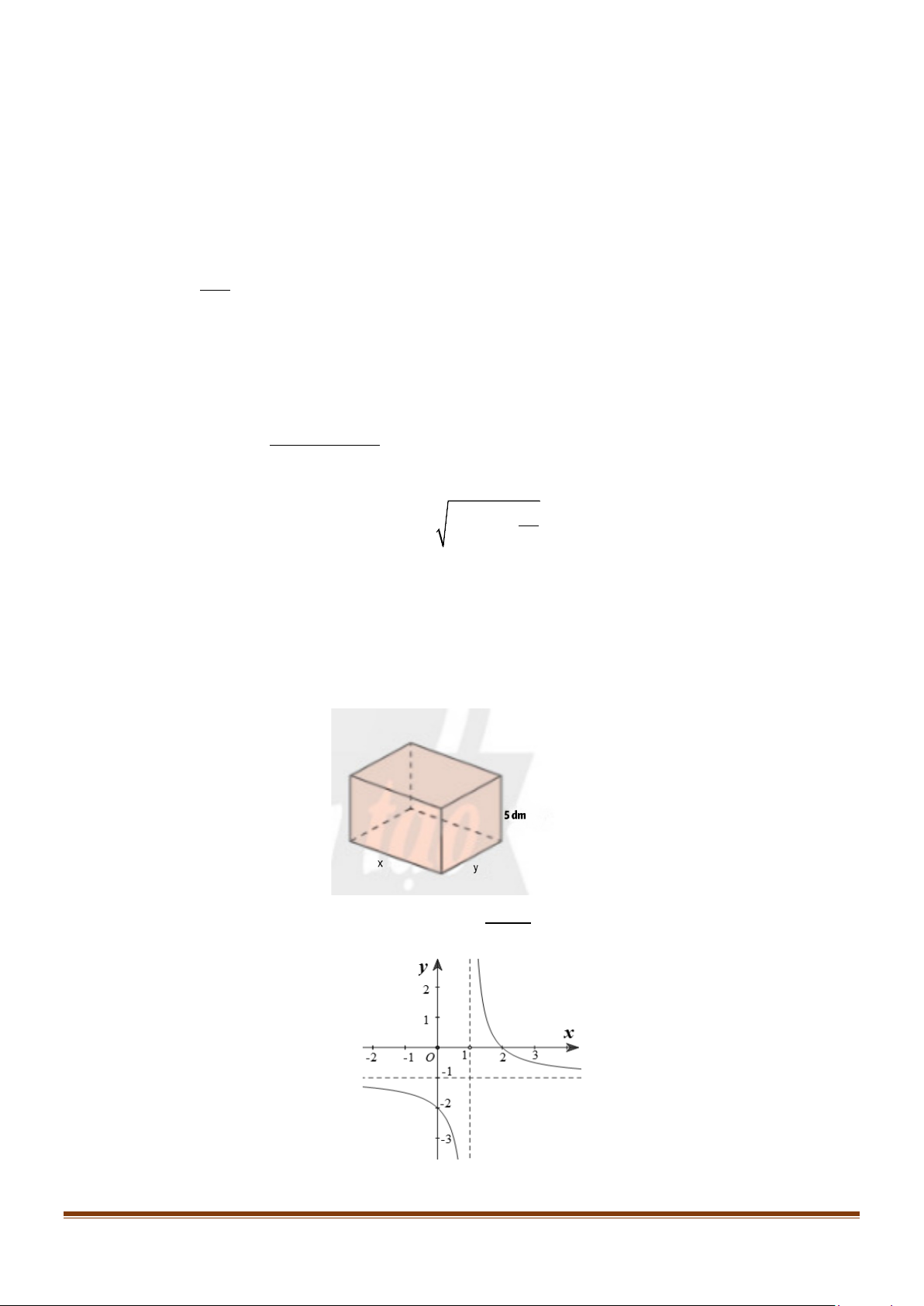
Câu 3: Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp có thể tích bằng 3
1m . Chiều cao của bể là 5dm , các kích thước khác là x(m), y(m) với x > 0
và y > 0. Diện tích toàn phần của bể là hàm số S (x) trên khoảng (0;+∞). Đường tiệm cận
xiên của đồ thị hàm số S (x) là đường thẳng y = ax + b . Tính giá trị của biểu thức 2 2
P = a + b . +
Câu 4: Đồ thị trong hình bên dưới là của hàm số ax b y = . x + c
Khi đó tổng a + b + c bằng Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GK1 TOÁN 12
Câu 5: Một rạp chiếu phim có sức chứa 800 người, trung bình mỗi ngày rạp có khoảng 360 khách với
giá mỗi vé là 100.000đ. Nếu giá mỗi vé giảm 10.000đ thì mỗi ngày rạp có thêm 60 khách đến
xem. Hỏi cần giảm giá vé đến bao nhiêu nghìn đồng để doanh thu của rạp là lớn nhất.
Câu 6: Giả sử một công ty du lịch bán tour với giá là x /khách thì doanh thu sẽ được biểu diễn qua hàm số 2 f (x) = 200 −
x + 550x . Công ty phải bán giá tour cho một khách là bao nhiêu để doanh thu từ
tua xuyên Việt là lớn nhất. (kết quả làm tròn đến hàng phần trăm)
---------- HẾT ---------- Page 5
Sưu tầm và biên soạn




