10 Đề Kiểm Tra Cuối Học Kỳ 1 Toán 9 Cánh Diều 2025-2026 Có Đáp Án
Hòa 200g dung dịch NaCl loại I với 300g dung dịch NaCl loại II được một dung dịch NaCl có nồng độ 27%.Tính nồng độ phần trăm của mỗi dung dịch loại I và loại II,biết rằng nồng độ phần trăm dung dịch loại II ít hơn hồng độ phần trăm dung dịch lạo I là 5%. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề HK1 Toán 9 442 tài liệu
Môn: Toán 9 2.6 K tài liệu
Tác giả:
Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 9 CÁNH DIỀU
A. PHẦN TRẮC NGHIỆM: (2,0 điểm) (Viết phương án đúng(A, B, C hoặc D) vào bài thi)
Câu 1: (NB) Với hai số thực a, b, ta có 𝑎𝑏 > 0 khi A. a,b cùng dấu
B. a, b trái dấu C. a dương, b âm D. a âm, b dương.
Câu 2: (TH) Hãy chọn câu đúng. Nếu a b thì
A. −3a −3b B. 3 − a 3 − b
C. −3a −3b
D. −3b −3a
Câu 3: (NB) Bất phương trình nào dưới đây là bất phương trình bậc nhất một ẩn? 1 1 A. −1 0 . B. x + 2 0 . C. 2 x 0 .
D. 0.x + 3 0 . x 3
Câu 4: (TH) Nghiệm của bất phương trình 2 + x 10 là
A. x 5 .
B. x 12 .
C. x 8 . D. x 5 .
Câu 5: (NB) Hãy chọn câu sai :
A. Căn bậc hai của số thực a không âm là số x sao cho 2 x = a
B. Mỗi số thực dương a có đúng hai căn bậc hai, là hai số đối nhau, số dương kí hiệu là a , số âm kí hiệu là − a
C. Căn bậc hai của một số âm là một số âm.
D. Căn bậc hai của số 0 bằng 0, kí hiệu 0 = 0.
Câu 6 (NB) . Căn bậc hai số học của số a không âm là :
A. số có bình phương bằng a B. − a C. a D. a
Câu 7 (TH). Căn bậc ba của −125 là : A. 5 B. 5 − C. 5 D. −25
Câu 8 (NB) Cho a, b R. Trong các khẳng định sau khẳng định nào đúng: a a
A. a. b = ab B. =
(với a 0; b > 0) b b
C. a + b = a + b (với a, b 0) D. A, B, C đều đúng.
Câu 9 (NB) : Tâm đối xứng của đường tròn là A. Tâm của đường tròn
B. Điểm thuộc đường kính của đường tròn
C. Điểm nằm trên đường tròn
D. Điểm nằm trong đường tròn.
Câu 10 (NB) Hình nào dưới đây biểu diễn góc nội tiếp? A. Hình a. B. Hình b. C. Hình c. D. Hình d.
Câu 11 (NB). Công thức tính độ dài cung tròn 0 n , bán kính R là Trang 1 2 2 Rn R n Rn R n A. l = . B. l = . C. l = . Dl = . 360 180 180 360
Câu 12. ( T H ) Cho đường tròn (0; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4
cm. Kết luận nào sau đây đúng về vi trí giữa đường tròn (O) và đường thẳng a ?
A. (O) và a cắt nhau tại hai điểm. B. (O) và a tiếp xúc.
C. (O) và a không có điểm chung. D. (O) và a có duy nhất điểm chung.
B. PHẦN TỰ LUẬN: (7,0 điểm)
Câu 13. (1,0 điểm). Giải phương trình và bất phương trình sau :
a) (3𝑥 − 4)(9𝑥 + 18) = 0 b) 8−3x − x < 5 2
Câu 14. (1 điểm) : Rút gọn các biểu thức sau 1 x - 1 1 - x
a) A = 5 + 20 + 45 . b) B = x - : +
với x 0, x 1. x x x + x
Câu 15. (1 điểm): Hòa 200g dung dịch NaCl loại I với 300g dung dịch NaCl loại II được một dung dịch
NaCl có nồng độ 27%.Tính nồng độ phần trăm của mỗi dung dịch loại I và loại II,biết rằng nồng độ phần
trăm dung dịch loại II ít hơn hồng độ phần trăm dung dịch lạo I là 5%.
Câu 16 : (3,0 điểm).
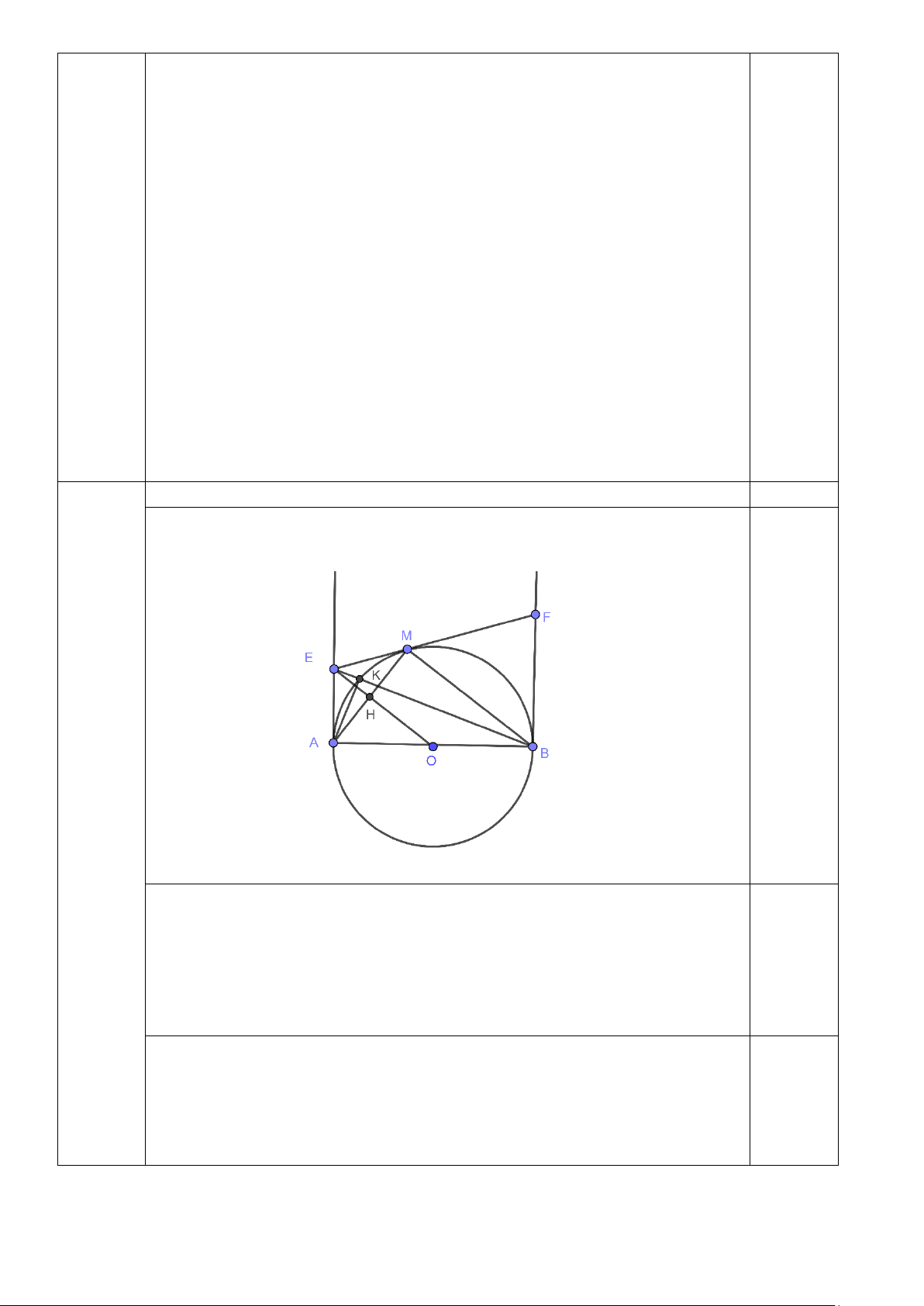
1. Cho nửa đường tròn (O), đường kính AB. Từ A và B kẻ hai tiếp tuyến Ax và By. Qua điểm M thuộc nửa
đường tròn này, kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax và By lần lượt ở E và F.
a) Chứng minh tam giác AMB vuông và AM vuông góc EO
b) Gọi H là giao điểm của EO và AM, K là giao điểm của EB và (O). Chứng minh EK.EB = EH . EO
2. Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng
1,2m, chiểu dài 1,8m và hai đầu là hai nửa hình tròn có đường kính là chiều rộng của hình chữ nhật (như
hình vẽ).Tính số tiền bác Long phải trả để làm được mặt bàn đó, biết giá gia công mỗi mét vuông mặt bàn
là 100 000 đồng. (làm tròn kết quả đến hàng nghìn của đồng). Câu 17. (1,0 điểm).
a) Để lập đội tuyển năng khiếu về bóng rổ của trường THCS Nguyễn Hiền, thầy Nam đưa ra quy định
tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 15 quả bóng vào rổ, quả bóng vào rổ được cộng 2
điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào
đội tuyển. Hỏi một học sinh muốn được chọn vào đội tuyển thì phải ném ít nhất bao nhiêu quả vào rổ?
b) Cho a, b, c là ba số thực dương thỏa mãn điều kiện a + b + c = 1. ab bc ca 3 Chứng minh rằng: + + . c + ab a + bc b + ca 2 ĐÁP ÁN
I. ĐÁP ÁN 12 CÂU TRẮC NGHIỆM
Mỗi câu đúng được 0,25 điểm
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu Câu Câu 10 11 12 A B B C C C B B A B C A II. TÓM TẮT LỜI GIẢI:
Câu 1: Mức độ nhận biết, đáp án A
Câu 2: Mức độ thông hiểu, đáp án B
Vì a > b nên – 3a < -3b do – 3 < 0
Câu 3: Mức độ nhận biết, đáp án B
Câu 4: Mức độ thông hiểu, đáp án C 2 + 𝑥 ≤ 10 Trang 2 𝑥 ≤ 8
Câu 5: Mức độ nhận biết, đáp án C
Số âm không có căn bậc hai
Câu 6: Mức độ nhận biết, đáp án C
Câu 7: Mức độ thông hiểu, đáp án B
Câu 8: Mức độ nhận biết, đáp án B
Câu 9: Mức độ nhận biết, đáp án A
Câu 10: Mức độ nhận biết, đáp án B
Câu 11: Mức độ nhận biết, đáp án C
Câu 12: Mức độ thông hiểu, đáp án A
Khoảng cách từ tâm O đến đường thẳng a là h = 4cm < R = 6cm
(O) và a cắt nhau tại hai điểm
B. PHẦN TỰ LUẬN: (8,0 điểm) Câu Đáp án Điểm B. PHẦN TỰ LUẬN 8 đ a) (0,5 điểm) (3𝑥 − 4)(9𝑥 + 18) = 0 Câu 13
=> 3x - 4 = 0 hoặc 9x + 18 = 0 0,25 đ
Giải pt x = 4 ; x = - 2 0,25 đ 3 b) (0,5 điểm) 8 − 3x − x < 5 2 0,25 8 − 3𝑥 − 2𝑥 < 10 −𝟓𝒙 < 𝟐 0,25 −2 𝑥 > 5
a) (0,5 điểm) 0,25 A = 5 + 20 + 45 0,25 = √5 + 2√5 + 3√5 Câu 14 = 6√5 b) (0,5 điểm) x − 1 (√x − 1)(√x + 1) 1 − √x 0,25 B = : ( + ) √x √x(√x + 1) √x(√x + 1) 2 x−1 ( = . √x(√x+1) = √x+1) 0,25 √x 𝑥−√𝑥 √𝑥 Câu 15 (1 đ) Trang 3
Gọi nồng độ phần trăm của dung dịch NaCl loại (I) là x% (x >0) 0,25đ
Gọi nồng độ phần trăm của dung dịch NaCl loại (II) là y% (y >0)
Vì nồng độ phần trăm dung dịch NaCl loại II ít hơn nồng độ phần trăm dung
dịch loại I là 5% nên ta có PT x% - y% = 5% 0,25đ x – y = 5 (1)
Khối lượng chất tan có trong dung dịch NaCl loại (I) là 200.x% = 2x(g)
Khối lượng chất tan có trong dung dịch NaCl loại (II) là 300.y% = 3y(g)
Khối lượng chất tan có trong dung dịch NaCl 27% là (200 + 300).27% = 135(g) Ta có PT : 0,25đ 2x + 3y = 135 (2) 𝑥 − 𝑦 = 5
Từ (1) và (2) ta có hệ PT : { 2𝑥 + 3𝑦 = 135
Giải hpt => x = 30 ; y = 25
Vậy nồng độ phần trăm của dung dịch NaCl loại (I) là 30%
nồng độ phần trăm của dung dịch NaCl loại (I) là 25% 0,25đ 3,0đ 1(2 điểm) Hình vẽ (đúng) cho ý 0,5 Câu 16 (3đ) a) 1 điểm AMB
̂ = 900 (góc nội tiếp chắn nửa đường tròn) 0,5
=> Tam giác AMB vuông tại M
Ta có EA = EM (TC 2 tiếp tuyến cắt nhau) OA = OM
=>EO là đường trung trực của AM => EO vuông góc AM 0,5 b) 0,75
Chứng minh tam giác AEO đồng dạng HEA => EA2 =EH.EO
Chứng minh tam giác AEB đồng dạng KEA => EA2 =EK.EB 0,25 Do đó EH.EO = EK.EB 0,25 Trang 4 4.2( 1 điểm)
Diện tích mặt bàn là 1,8.1,2+ 3,14.0,62=3,2904 (cm2) 0,5
Số tiền bác Long phải tra là:
3,2904 . 100 000 = 329 040 (đồng) ≈ 329 000 (đ) 0,5 Câu 5 a) 0,5 đ (1 đ)
Gọi số bóng ít nhất được ném vào rổ là x (x∈ 𝑁∗)
Số quả bóng ném ra ngoài là 15 – x
Tổng số điểm khi ném 15 quả bóng: 2x – (15 – x) = 3x – 15 0,25
Theo bài ra để học sinh muốn được chọn vào đội tuyển thì 3x-15 ≥ 15 0,25 x ≥ 10
Vậy học sinh đó phải ném ít nhất 10 quả bóng vảo rổ b) 0,5 đ
Ta có: a + b + c = c = (a + b + c) 2 1
.c = ac + bc + c 0,25 2
c + ab = ac + bc + c + ab = a(c + b) + c(b + c) = (c + a)(c + b)
a + bc = (a + b)(a + c) Tương tự ta có : 0,25
b + ca = (b + c)(b + a) a b + ab ab
c + a c + b = c + ab
(c + a)(c + b) 2 b c + 0,25 bc bc
a + b a + c = a + bc
(a + b)(a + c) 2 c a 0,25 + ca ca
b + c b + a = b + ca
(b + c)(b + a) 2 a b b c c a
a + c c + b b + a + + + + + + + + + + + + + + + + 3 c a c b a b a c b c b a a c c b b a P = = 2 2 2 1
Dấu “=” xảy ra a = b = c = 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I ĐỀ 2 MÔN: TOÁN 9 CÁNH DIỀU
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
Câu 1: Phương trinh ẩn x: (𝑎 − 1)𝑥 + 3 = 0 có nghiệm duy nhất khi: A. 𝑎 = 1 B. 𝑎 > 1 C. 𝑎 < 1 D. 𝑎 ≠ 1
Câu 2: Nghiệm của bất phương trình 4𝑥 + 1 > 0 là: Trang 5 1 − 1 − A. x 0 B. x 1 C. x D. x 4 4
Câu 3: Điều kiện xác định của biểu thức √2𝑥 − 4 là: A. x 2 B. x 2 C. x 2 D. 𝑥 ≥ 0
Câu 4: Gía trị của 𝑥 để 3√𝑥 = 12 là: A. 2 B. 4 C. −4 D. 16
Câu 5: Biết đồ thị hàm số 𝑦 = 𝑎x + b (với 𝑎 ≠ 0) đi qua điểm 𝐴(2; 3) và điểm 𝐵(−1; 0), khi đó giá trị của hệ số 𝑎 là: A. 1 B. 0 C. 2 D. 3
Câu 6: Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴, khi đó giá trị lượng giác sin𝐴𝐵𝐶 là AB AB AC BC A. sin ABC = B. sin ABC = C. sin ABC = D. sin ABC = AC BC BC AB
Câu 7: Hình tròn có đường kinh bằng 24 cm có diện tích là: A. 144𝜋cm2 B. 576𝜋cm2 C. 24𝜋cm2 D. 48𝜋cm2
Câu 8: Cho hai đường tròn (O; 3cm) và (O’; 1,5cm), biết OO’ = 5cm. Vị trí tương đối của hai đường tròn trên là: A. Cắt nhau B. Ngoài nhau
C. Đự𝑛𝑔 𝑛ℎ𝑎𝑢 D. Tiếp xúc ngoài
II. PHÀN TỰ LUẬN (8,0 điểm) 2 x x
3x + 3 x − 7
Câu 1: (1,5 điểm) Cho P = + + +1
(với 𝑥 ≥ 0, 𝑥 ≠ 9 ). x + 3 x − 3 9 x x +1 −
1.1: (1,0 điểm) Rút gọn biểu thức P.
1.2: (0,5 điểm) Tìm các giá trị của 𝑥 để 𝑃 < 0. 3x − y = 4
Câu 2: (1,0 điểm) Giải hệ phương trình x + 2y = 1 − 5
Câu 3: (2,0 điểm)
3.1: (1,0 điểm) Giải bất phương trình 5x − (2x − 3) < 4(x − 2)
3.2: (1,0 điểm) Cho hai số a, b sao cho 𝑎 ≥ 𝑏 .Chứng minh 1 − 4𝑎 ≤ 1 − 4𝑏 . C
Câu 4: (1,5 điểm) Từ đỉnh của tòa nhà AB cao 75m người ta quan sát đỉnh C của
ngọn núi với phương nhìn AC tạo với phương nằm ngang một góc 56o . Hỏi ngọn
núi đó cao bao nhiêu so với mặt đất biết rằng khoảng cách từ chân tòa nhà đến chân núi bằng 124m. 56o A 75m 124m B D
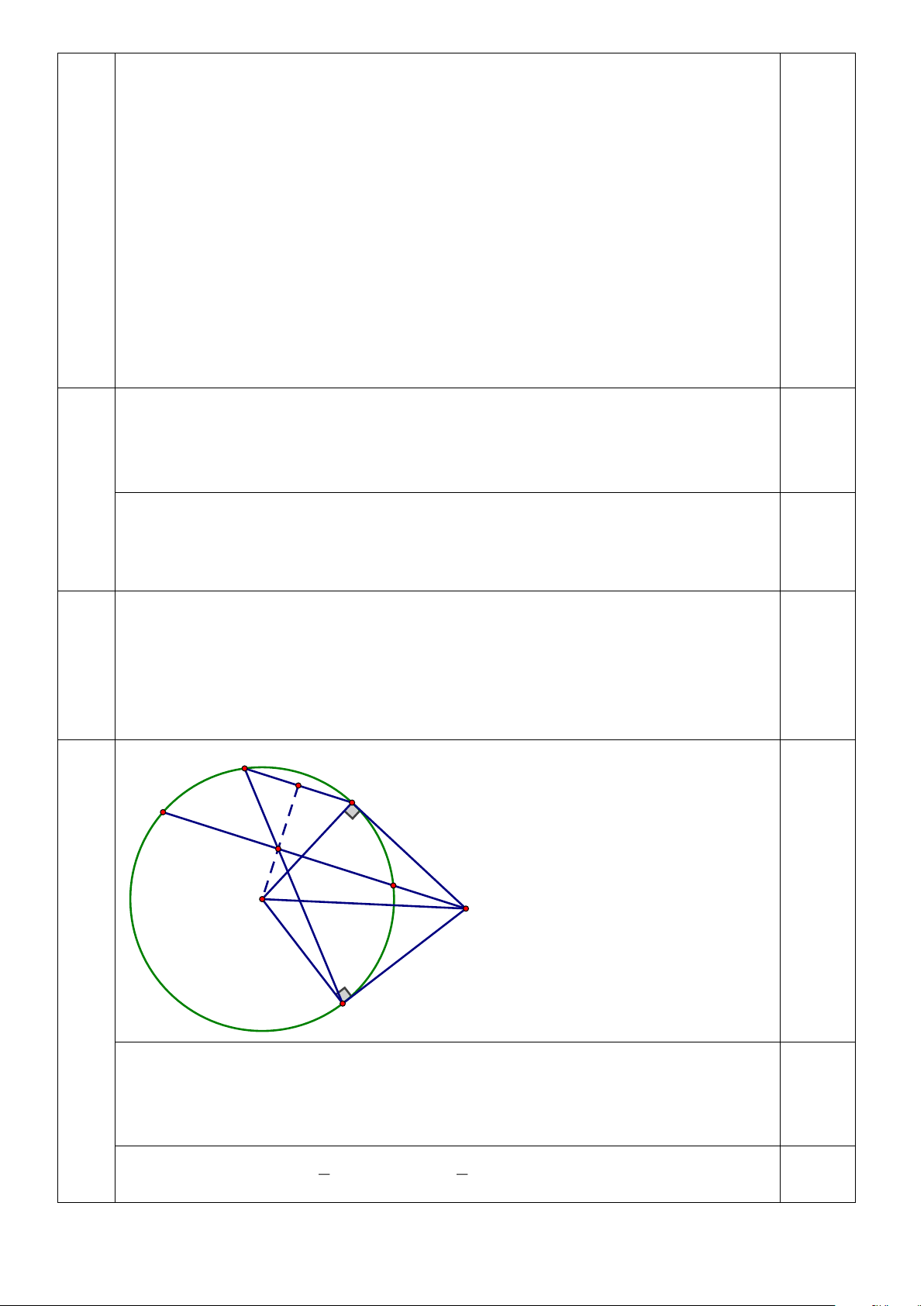
Câu 5: (2 điểm) Qua điểm M nằm ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA, Trang 6
MB (A, B là các tiếp điểm) và cát tuyến MPQ (MP < MQ). Gọi I là trung điểm của dây PQ, E là giao điểm
thứ hai của đường thẳng BI và đường tròn (O).
5.1: (1,0 điểm) Chứng minh các điểm O, I, A, M, B cùng thuộc một đường tròn..
5.2: (1,0 điểm) Chứng minh BOM = BE . A HẾT.
ĐÁP ÁN VÀ THANG ĐIỂM
(Đáp án này gồm 03 trang)
I. PHẦN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 Đáp án D C D D A C A B II. PHÀN TỰ LUẬN Câu Nội dung Điểm 1
1.1. Điều kiện x 0, x 9 (2,0 2 x x
3x + 3 x − 7 đ) P = + + +1 0,25đ x + 3 x − 3 9 x x +1 − 2 x x 3x + 3
x − 7 + x +1 P = + − x 3
x 3 ( x 3)( x 3) x 1 + − + − + 0,25đ
2 x( x − 3) + x( x + 3) − (3x + 3) 2 x − 6 P =
( x + 3)( x − 3) x +1 0,25đ 3 − x − 3 2( x − 3)
P = ( x +3)( x −3) x +1 0,25đ 3( x +1) 2( x − 3)
P = − ( x +3)( x −3) x +1 6 P = − x +3 6 0,5đ 1.2. P = − <0 vô lí x + 3 Trang 7 2 3x − y = 4 (1,0 .
a x+2y = −15 0,25đ đ) 6x − 2y = 8 0,25đ
x + 2y = −15 7x = 7 − 0,25đ
x + 2y = −15 x = 1 − 0,25đ 1 − + 2y = −15 x = 1 − y = 7 −
3.1. 5x − (2x − 3) < 4(x − 2) 3 5x – 2x + 3 < 4x – 8 0,5đ (2,0 x > 11 0,5đ đ) 3.2. 𝑎 ≥ 𝑏 −4𝑎 ≤ −4𝑏 0,5đ 1 − 4𝑎 ≤ 1 − 4𝑏 0,5đ
Gọi H là chân đường vuông góc hạ từ A xuống CD. Tứ giác AHDB là hình chữ nhật 4
suy ra AH = 124m, HD = AB = 75m. 0,5đ
(1,5 Tam giác ACH vuông tại H có = .tan = 124.tan56o CH AH CAH 183,84m 0,5đ đ)
Do đó chiều cao của ngọn núi là CD = CH+HD 258,84 . m 0,5đ E 5 (2,0 K A Q đ) I P O M B
5.1: Chứng minh OI vuông góc MQ 0,5đ
Gọi T là trung điểm OM. Tam giác OIM, OAM, OBM vuông có T là trung điểm cạnh 0,25đ
huyền OM nên TO = TI = TA = TM = TB nên các điểm O, I, A, M, B cùng thuộc 0,25đ đường tròn tâm T 1 1 0,5đ
5.2: Chứng minh BOM = BOA BOM = d s A .
B (Góc ở tâm có số đo bằng số đo 2 2 Trang 8 của cung bị chắn). 1 0,5đ Trong (O) ta có BEA = d s A .
B (góc nội tiếp có số đo bằng nửa số đo cung bị chắn). 2
Do đó BEA = BOM. ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I MÔN: TOÁN 9 CÁNH DIỀU
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
I. TRẮC NGHIỆM (3,0 điểm): Khoanh tròn vào đáp án đúng nhất
Câu 1. Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn? x + y =1 x + 2y = 3 −x + y =1 x − y = 2 2
A. y + z = 3;
− B. x − y = 1
− ; C. 2y =1; D. 0x +0y = 0.
Câu 2. Trong các hệ hai phương trình bậc nhất hai ẩn sau, hệ phương trình nào nhận cặp số (- 1;- 2) là nghiệm?
ìï 12x - 3y = - 6
ìï 0,2x - 3y = 0, 7 ìï - x + y = 1 ìï x + 3y = 2 A. ï ï ï ï í B. C. D. ï í í í - 5x = 5. ï
ï - x - 0, 8y = 2. ï 3x + y = - 2.
ï 31x + 5y = -1. î ïî ïî ïî
Câu 3. Cho tam giác ABC vuông tại A. Đặt BC = , a AC = ,
b AB = c . Trong các khẳng định dưới đây,
khẳng định nào SAI: c
A. b = a. sin B . B. b = c t
× an B . C. c = a. cosC . D. cot B = . b
Câu 4. Phương trình (2x +10)( x − 4) = 0 có nghiệm là :
A. x = -5; x = 4 B. x = - 5; x = -4 C. x = 5; x = -4 D. x = 5; x = - 4
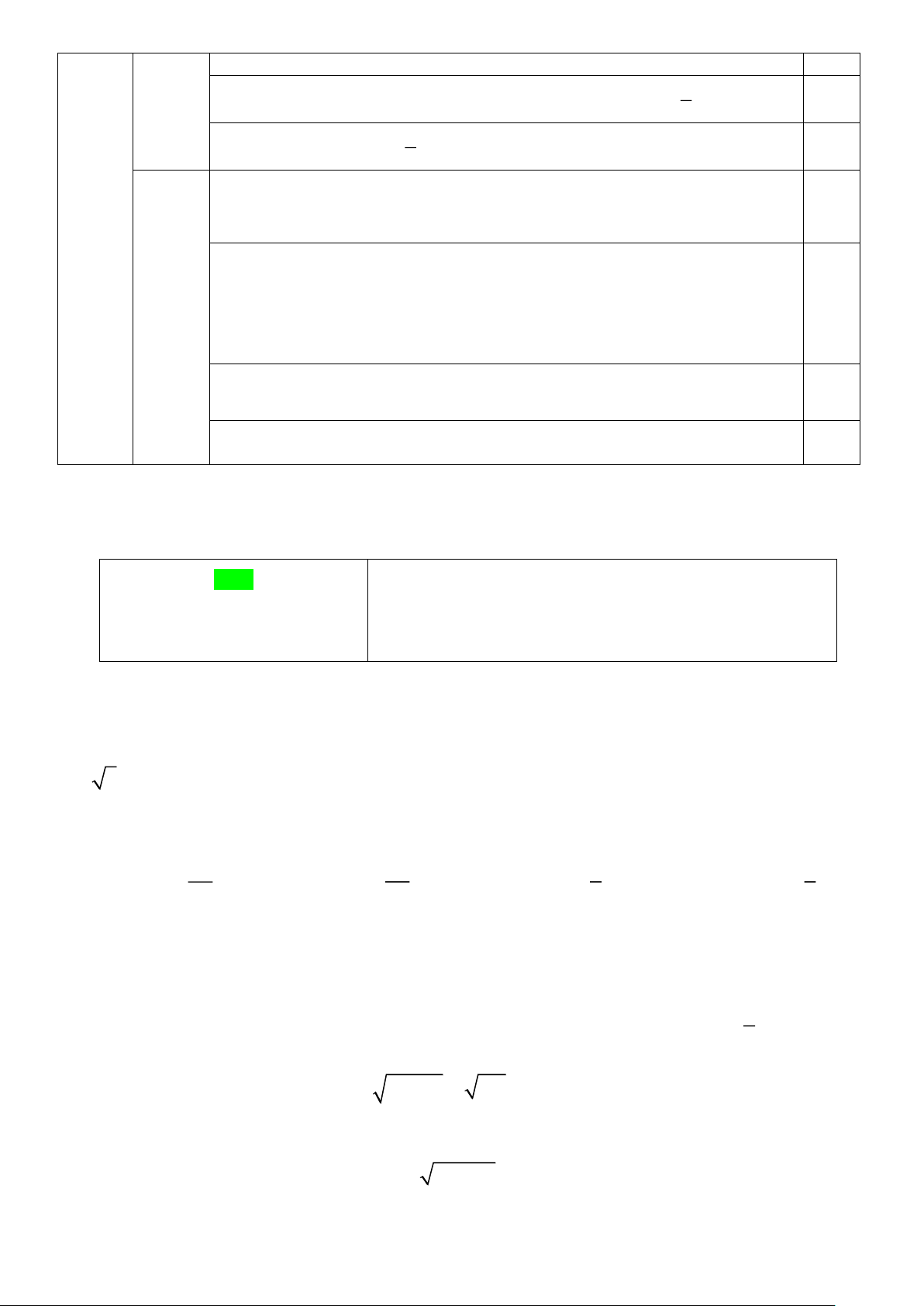
Câu 5. Tính giá trị biểu thức B = √ 3 (−13)3 + √
3 263; ta được kết quả A. 39 B. 13 C. 26 D. -39
Câu 6. Biểu thức 15 − 3x có điều kiện xác định là
A, x 5. B. x 5. C. x 5. D. x 5.
Câu 7. Cho a > b. thì
A. a - 2 < b – 2 B. 3.a < 3.b C. -5a > -5b D. a + 3 > b – 2
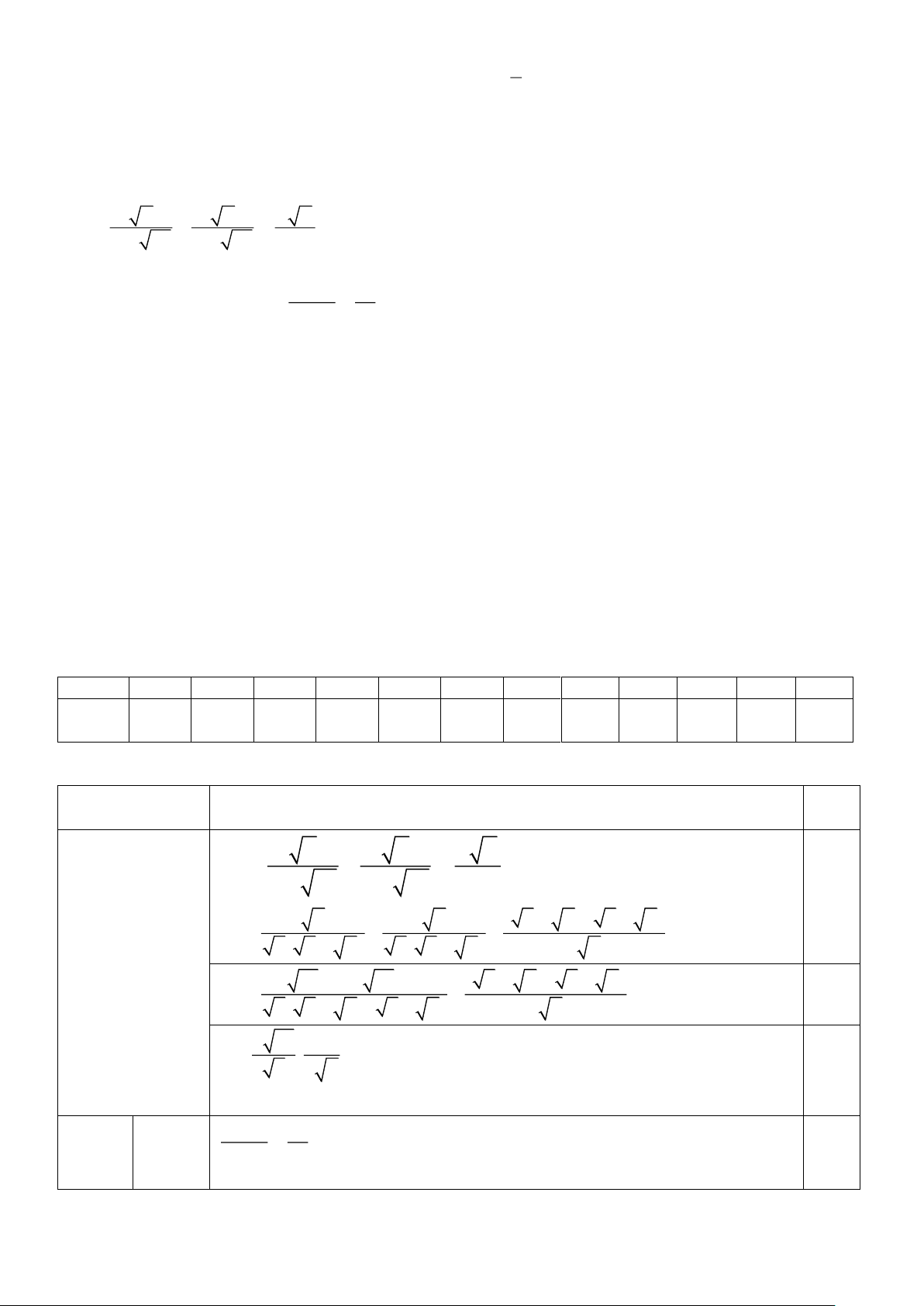
Câu 8. Một tòa tháp có bóng trên mặt đất dài 15 m, biết rằng góc tạo bởi tia nắng
mặt trời với mặt đất là 55° (xem hình vẽ). Tính chiều cao của tòa tháp (làm tròn
đến chữ số thập phân thứ hai của mét).
A. 8,6 m B. 21,42 m C. 12,29m D. 10,5 m
Câu 9. Cho tam giác A BC vuông tại A . Ta có sin B bằng AB A C AB AC A. . B. . C. . D. . AC A B BC BC 8
Câu 10. Giá trị của bằng: 25 2 2 4 2 4 2 2 A. − . B. C. . D. 5 5 5 5
Câu 11. Trong các bất phương trình sau, bất phương trình bậc nhất một ẩn là: Trang 9 A. x-1 > 3x2+1 B. 3x -1> 0 1 D. 0x - 5<0 C. x − 0 x
Câu 12. Góc nội tiếp chắn nửa đường tròn có số đo bằng A. 0 120 . B. 0 60 . C. 0 90 . D. 0 45 .
II. TỰ LUẬN (7,0 điểm).
Câu 13. (1,5 điểm). Rút gọn biểu thức sau: y y 2 y A = + :
; x 0, y 0, x y
x + xy x − xy x − y
Câu 14 (1,5 điểm). Giải các phương trình, hệ phương trình sau: 4x − 3 29 1) Giải phương trình: = x − 5 3 x - y = 3 −
2) Giải hệ phương trình: 5 x + 3y = 1
Câu 15. (1,5 điểm). Giải bài toán bằng cách lập phương trình, hệ phương trình.
Hai bạn Hoa và Hồng đến một hiệu sách để mua bút và vở. Bạn Hoa mua 10 chiếc bút và 20 quyển vở với
tổng số tiền là 230 nghìn đồng. Bạn Hồng mua 5 chiếc bút và 15 quyển vở với tổng số tiền là 165 nghìn
đồng. Tính giá bán của mỗi chiếc bút và của mỗi quyển vở, biết rằng hai bạn Hoa và Hồng mua cùng loại bút và vở.
Câu 16. (2,5 điểm). Cho đường tròn (O, R), dây AB khác đường kính. Kẻ OH vuông góc với AB tại H.
a) Tính diện tích tam giác AOB, nếu biết R = 13cm, OH = 5cm ;
b) Đường thẳng OH cắt tiếp tuyến tại A của đường tròn ở điểm M. Chứng minh: MB là tiếp tuyến của đường tròn (O);
D. ĐÁP ÁN – BIỂU ĐIỂM ĐỀ KIỂM TRA HỌC KÌ I
LỚP 9- NĂM HỌC 2024 – 2025
I. TRẮC NGHIỆM (3,0 điểm)
Phần 1(1,5 điểm). Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp C D C B A C D B D D B C án Đáp án: 21,42 m
II. TỰ LUẬN (7 điểm) Câu Đáp án Biểu điểm y y 2 y 0,5 A = + :
; x 0, y 0, x y
x + xy x − xy x − y Câu 11. y y
( x + y ).( x − y) A = + .
(1,5 điểm) x( x y ) x( x y ) + − 2 y
xy − y + xy + y
( x + y).( x − y) 0,5 A = . x( x y ).( x y ) + − 2 y 2 xy 1 0,5 A = . =1 x 2 y
Vậy A = 1 với x 0, y 0, x y 4x − 3 29 0,25 = x − 5 3
Điều kiện xác định x 5 Trang 10
(4x − 3)3 = 29(x − 5) 0,25 1
12x − 9 = 29x −145
(0,75đ) 12x − 29x = −145+ 9 0,25 −17x = −136 Câu 136 12. (1,5 x = 17
điểm). 136
Vậy phương trình đã cho có nghiệm là: x = 17 x - y = 3 − 0,25 5 x + 3y = 1
Rút x từ phương trình thứ nhất ta được: x = y – 3 (3), Thay vào phương trình 2 2 ta được
(0,75đ) 5 (y – 3) + 3y = 1 5y - 15 +3y = 1 8y = 16 y = 2
Thay y = 2 vào phương trình (3) ta có x = 2-3 = -1 0,25 0,25
Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y) =(-1; 2)
Gọi x (nghìn đồng), y (nghìn đồng) lần lượt là giá của mỗi chiếc bút và mỗi 0,25
quyển vở. (x > 0; y > 0)
Vì Hoa mua 10 chiếc bút và 20 quyển vở với tổng số tiền là 230 nghìn đồng 0,25 Câu 13.
nên ta có phương trình: 10x + 20y = 230 (1)
(1,5 điểm).
Vì Bình mua 5 chiếc bút và 15 quyển vở với tổng số tiền là 165 nghìn đồng 0.25
nên ta có phương trình: 5x + 15y = 165 (2) 1
0x + 20y = 230 0,25
Từ (1) và (2) ta có hệ
5x +15y =165.
Giải hệ này ta được nghiệm ( ; x y) = (3;10). 0,25
Vậy giá mỗi chiếc bút là 3 nghìn đồng, giá mỗi quyển vở là 10 nghìn đồng 0,25 Câu a 0,25 A 14 (1, 5đ) (2,5) O H M Q P C B N
a). Ta có OH ⊥ AB tại H AOH vuông tại H
AO2 = OH2 + HA2 (định lí Pitago) 0,25
Thay số ta được 132 = 52 + HA2 HA = 12cm
Xét đường tròn (O); AB là dây cung, OH ⊥ AB tại H (gt) H là trung
điểm của AB (Quan hệ vuông góc giữa đường kính và dây cung) 0, 5 Trang 11 AB = 2AH = 24cm 0.25 1
AOB có OH là đường cao (vì OH ⊥ AB tại H) SAOB = OH . AB 2 1
Thay số ta được SAOB = .5.24 = 60cm2 2 0,25
2b (1, b, Có OA = OB OAB cân tại O 0,25 đ)
lại có OH là đường cao (cmt) OH là đường phân giác (....) AOH = BOH AOM = BOM Xét AOM và BOM có 0,5 OA = OB AOM = BOM OM chung
AOM = BOM (c.g.c) OAM = OBM
Có MA là tiếp tuyến của đường tròn (O) MA ⊥ AO 0 OAM = 90 0,25 Do đó 0 OBM = 90 MB ⊥ BO
Xét đường tròn (O) có : MB ⊥ BO (cmt); BO là bán kính 0,25
MB là tiếp tuyến của đường tròn (O)
* Chú ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa. ĐỀ 4
ĐỀ ÔN TẬP CUỐI HỌC KỲ I MÔN: TOÁN 9 CÁNH DIỀU
I. TRẮC NGHIỆM (3,0 điểm)
Câu 1. (NB) Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn? A. 3x − y = 0 B. 0x + 3y = 5 C. 3x + 2 y = 8
D. 0x − 0 y = 10
Câu 2. (NB) Phương trình: (9 − x)(3x + 8) = 0 có nghiệm là: 8 − 8 − 8 8 A. x = 9; − y =
B. x = 9; y =
C. x = 9; y = D. x = 9; − y = 3 3 3 3
Câu 3. (TH) Cho tam giác ABC vuông tại A . Đặt BC = , a AC = ,
b AB = c . Trong các khẳng định
dưới đây, khẳng định nào sai? A. 2 2 2
a = b + c B. b = a c × os B C. c = a s × in C c D. cot B = b
Câu 4. (TH) Tính giá trị biểu thức: 2 3 3 B = ( 2
− 1) + 13 ; ta được kết quả là: A. 8 B. 8 − C. −34 D. 34
Câu 5. (TH) Điều kiện xác định của biểu thức 12 − 3x là: Trang 12 A. x 4 B. x 4 C. x 4 D. x 4
Câu 6. (NB). Cặp số (1;−1) là nghiệm của hệ phương trình nào sau đây? 2 − x + 7 y =12 3 x − 2y = 4 − 2x + 5y = 3 − 3x − y =17 A. B. C. D. 5 x − y = 3 −x + 2y = 8 3 x − y = 4 x + 4y = −3 0 cot 32
Câu 7. (TH) Giá trị của biểu thức: 2 0 2 0 0 0
C = sin 25 + sin 65 − tan35 + cot 55 − là: 0 tan58 A. 0 B. 1 C. - 1 D. 2
Câu 8: (TH) Cho Cho a > b. Khẳng định nào sau đây sai?
A. a + 1 b + 1
B. −7a −7b C. 3a 3b
D. 2a + 2 2b + 1
Câu 9: (NB) Góc ở tâm của đường tròn (O) là A. AmB . B. AnB . C. AOB . D. AB .
Câu 10. (NB) Bất phương trình nào là bất phương trình bậc nhất một ẩn A. 0x – 3 0 B. 2x + 5 0 C. 2 x +1 0 D. 3x + 2 1 −
Câu 11. (NB) Cho hai đường tròn tiếp xúc ngoài (O; R) và (O ;r ) với R r và OO = d . Khi đó:
A. d = R + r .
B. d R + r .
C. R − r d R + r . D. d R + r .
Câu 12. (TH) Nghiệm của bất phương trình: −3x + 9 0 là: A. x 3 B. x −3 C. x 3 D. x −3
II. TỰ LUẬN (7,0 điểm).
Câu 13. (1,0 điểm). Rút gọn biểu thức sau: a 2 1 B = + +
với a 0 , a 4 . a − 4 2 − a a + 2 a) Rút gọn B .
b) Tìm giá trị nguyên của a để B nhận giá trị nguyên.
Câu 14. (1,5 điểm). Giải các phương trình, hệ phương trình sau: Trang 13 2x x −14 x − 2 1) Giải phương trình: − = x − 7 x( x − 7) x 4x + 3y = 7 −
2) Giải hệ phương trình: 2x − 5y =16
Câu 15. (1,0 điểm). Giải bài toán bằng cách lập phương trình, hệ phương trình.
Một người mua một cái bàn là và một cái quạt điện với tổng số tiền theo giá niêm yết là 750 nghìn đồng.
Khi trả tiền người đó được khuyến mại 10% đối với bàn là và 20% đối với quạt điện so với giá niêm yết.
Vì vậy người đó phải trả tổng cộng 625 nghìn đồng. Tính giá tiền bàn là và quạt điện theo giá niêm yết.
Câu 16. (3,0 điểm).
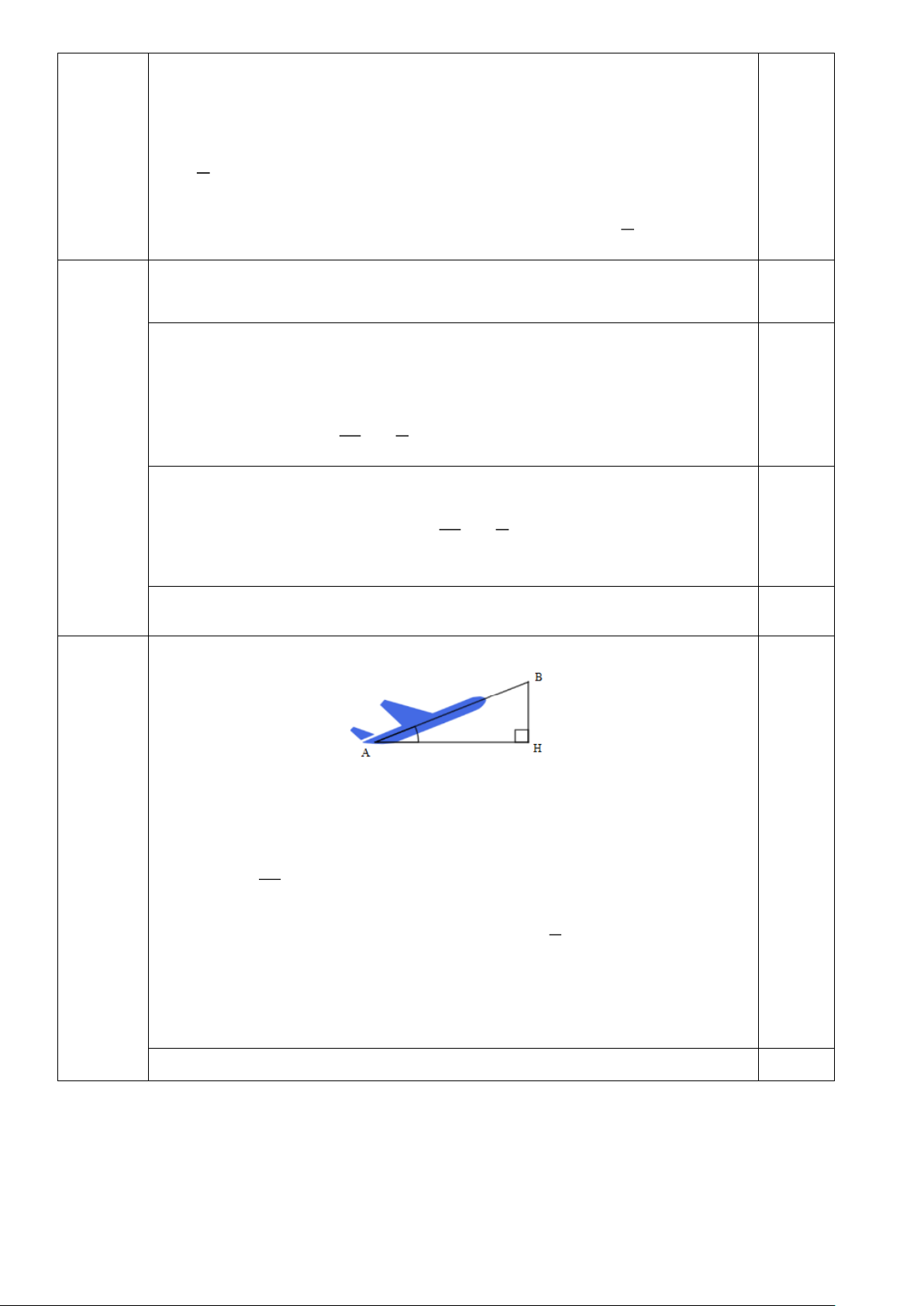
1) Một chiếc máy bay bay lên với vận tốc 450km / h . Đường bay lên tạo với phương nằm ngang một góc o
34 . Hỏi sau 3 phút máy bay ở độ cao bao nhiêu ki – lô – mét so với mặt đất? (kết quả làm tròn đến chữ số
thập phân thứ hai)
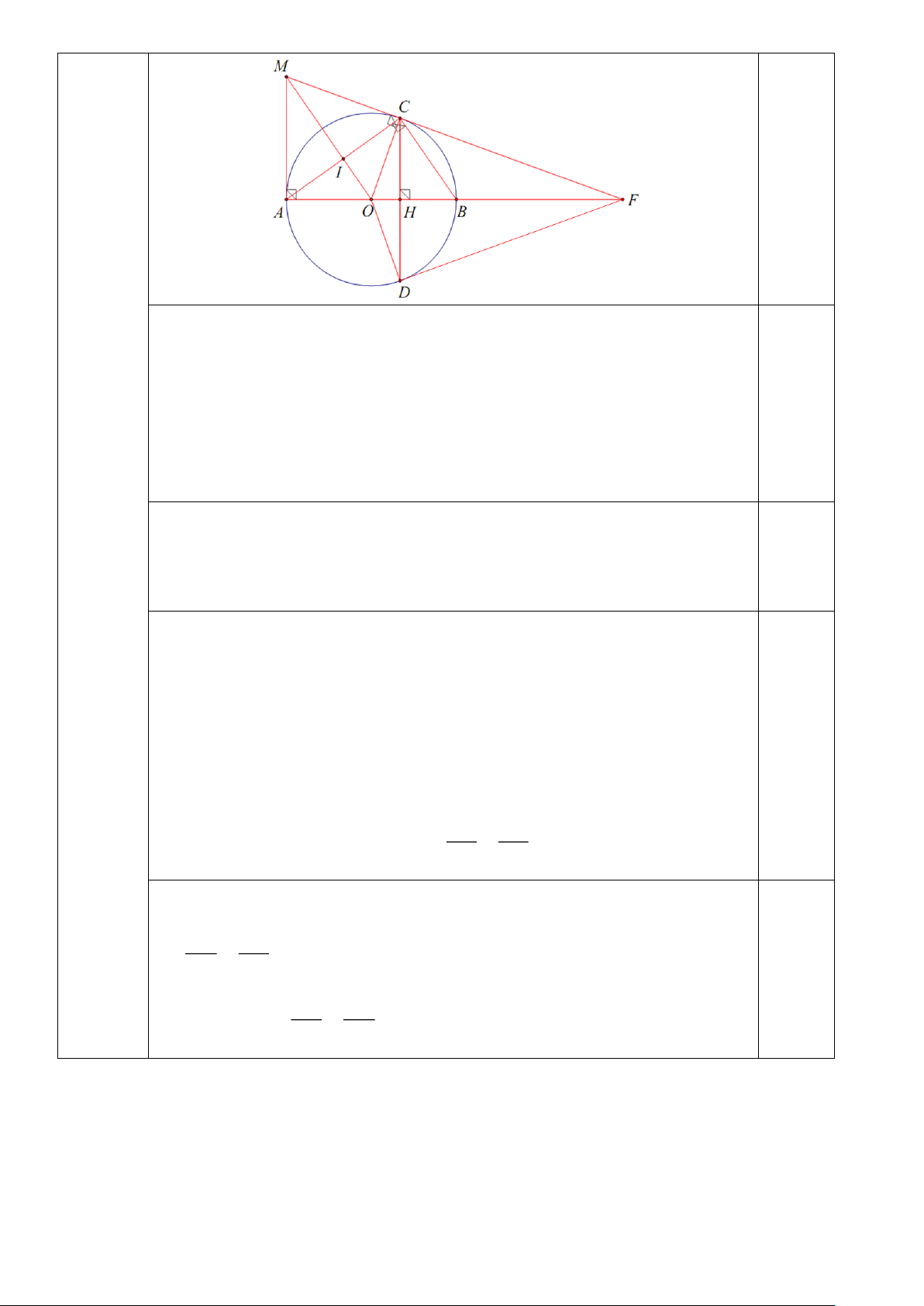
2) Cho đường tròn (O; R) , đường kính AB . Lấy điểm C thuộc (O; R) sao cho AC BC . Kẻ đường
cao CH của ABC (H AB) kéo dài CH cắt (O; R) tại điểm D (D C) . Tiếp tuyến tại điểm A
và tiếp tuyến tại điểm C của đường tròn (O; R) cắt nhau tại điểm M . Gọi I là giao điểm của OM và
AC . Hai đường thẳng MC và AB cắt nhau tại F .
a) Chứng minh DF là tiếp tuyến của (O; R) .
b) Chứng minh: AF.BH = BF.AH .
Câu 17. (0,5 điểm).
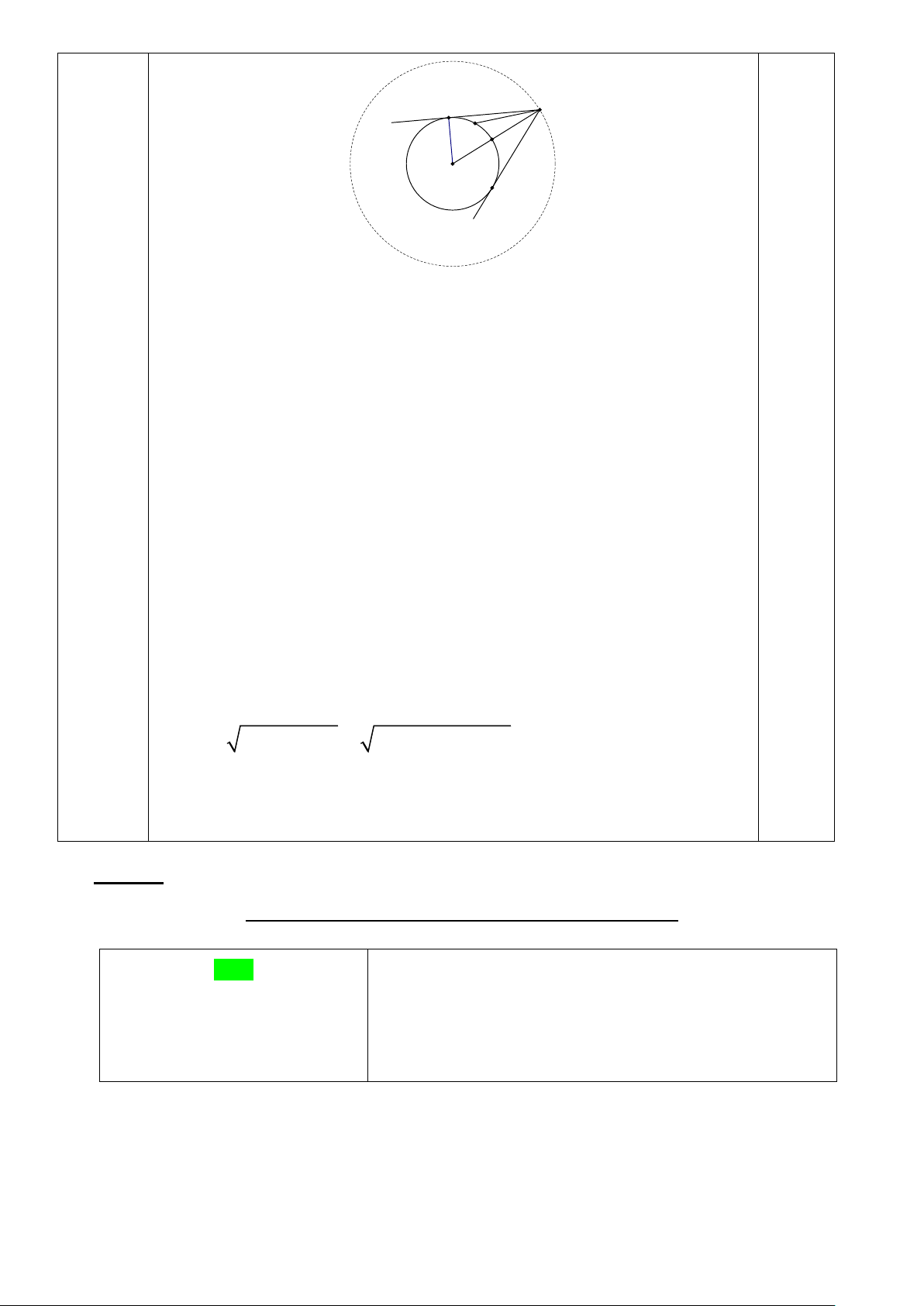
Một vệ tinh nhân tạo địa tĩnh chuyển động theo một quỹ đạo tròn
cách bề mặt Trái Đất một khoảng 35786 , tâm quỹ đạo của vệ tinh
trùng với tâm O Trái Đất. Vệ tinh phát tín hiệu vô tuyến theo một
đường thẳng đến một vị trí trên bề mặt Trái Đất. Hỏi vị trí xa nhất trên
bề mặt Trái Đất có thể nhận tín hiệu từ vệ tinh này ở cách vệ tinh một
khoảng là bao nhiêu km (ghi kết quả gần đúng chính xác đến hàng đơn
vị). Biết rằng Trái Đất được xem như một hình cầu có bán kính khoảng 6400km .
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HKI MÔN TOÁN 9
NĂM HỌC 2024 – 2025
I. Trắc nghiệm (3,0 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án D B B D C C A B C B A C
II. Tự luận (7,0 điểm) Câu Nội Dung Điểm a) Rút gọn B . 0,25 Trang 14 a 2 1 13 B = + + (1,0 a − 4 2 − a a + 2 điểm) a 2 1 = ( − + a + 2)( a − 2) a − 2 a + 2
a − 2( a + 2) + ( a − 2) = ( a + 2)( a − 2)
a − 2 a − 4 + a − 2 −6 6 0,25 = ( = =
(với a 0 , a 4 ). a + 2)( a − 2) a − 4 4 − a 6
b) Ta có: Vì a Z nên để B Z
Z 6 (4 − a) 4 − a (4 − a) 1 , 2, 3,
6 a 5; 3; 6; 2; 7; 1; − 2; 1 0 0, 25
Đối chiếu điều kiện ta có a 5;3;6;2;7;1;1 0 0,25
Vậy a 5;3;6;2;7;1;1
0 thì B nhận giá trị nguyên. x x −14 x − 2 a) − =
(ĐK: x 0, x 7 ). x − 7 x( x − 7) 0,75 14 x (1,5 2 x x −14
(x − 2)(x − 7) điểm) − = x(x − 7) x( x − 7) x(x − 7) 2 2 x x −14
x − 7x − 2x +14 − = x(x − 7) x( x − 7) x(x − 7) 2 2
x − x +14 = x − 7x − 2x +14 8x = 0 x = 0(KTM )
Vậy phương trình đã cho vô nghiệm.
4x + 3y = −7 ( ) 1 0,75 b)
2x − 5y =16 ( 2)
Nhân cả hai về của phương trình (2) với 2, phương trình (1) giữ nguyên ta được: 4x + 3y = 7 −
4x −10y = 32
Trừ từng vế của 2 phương trình trên cho nhau được: 13y = 3 − 9 y = 3 − Trang 15
Thay y = −3 vào phương trình (1) được: 4x − 9 = −7 4x = 2 1 x = 2 1
Vậy hệ phương trình đã cho có nghiệm duy nhất là: ( , x y) = ; 3 − 2
Gọi x, y (nghìn đồng) lần lượt là giá niêm yết của bàn là và quạt điện. 0,25 15 x y (1,0 ĐK: , 0 điểm)
Tổng số tiền của bàn là và quạt điện theo giá niêm yết là 750 nghìn nên ta có 0,25 x + y = 750 ( ) 1
Do bàn là được khuyến mại 10% và quạt là 20% nên phải trả 625 nghìn, ta 9 1 có phương trình x + y = 625 (2) 10 4 x + y = 750 0,25 x = 250 Từ ( ) 1 , (
2) ta có hệ phương trình 9 4 (thỏa x + y = 625 y = 500 10 5 mãn)
Vậy theo giá niêm yết thì bàn là giá 250 nghìn và quạt điện giá 500 nghìn 0,25 đồng. 16 1) 1,0 (3 điểm)
Gọi AB là quãng đường máy bay bay được.
BH là độ cao của máy bay so với mặt đất sau khi bay được 3 phút. Đường bay
lên tạo với phương nằm ngang góc: 0 BAH = 34 1 Đổi 3 phút = giờ. 20 1
Quãng đường máy bay bay được sau 3 phút là: 450. = 22,5( ) km 2
Xét tam giác ABH vuông tại H có: 0 BH = A .
B sin BAH = 22,5.sin 34 12,58(km) .
Vậy sau khi bay được 3 phút máy bay ở độ cao cách mặt đất khoảng 12,58 km. 2) 0,5 Trang 16 0,5
a) Xét OCD có: OC = OD = R nên OCD cân tại O .
Mà OH là đường cao của OCD nên OH là đường phân giác của OCD · · COF = DOF
Chứng minh được: C OF = D OF( . c g.c) · · COF = DOF (tương ứng) Mà · 0
OCF = 90 (do OC ⊥ MF ) · 0 ODF = 90 Do · 0
ODF = 90 OD ⊥ DF tại D . 0,5
Xét (O; R) có: OD ⊥ DF tại D và D ( ; O R)
Suy ra: DF là tiếp tuyến của (O; R) tại D (đpcm). 0,25 b) Ta có: · 0 · BCF = 90 − OCB (1) Lại có: · 0 · BCH = 90 − OBC (2)
Chứng minh OBC cân tại O · · OCB = OBC (3)
Từ (1),(2) và (3) suy ra: · · BCF = BCH BH CH
CB là tia phân giác của · HCF = (*) BF CF 0,25
Chứng minh được CA là phân giác ngoài của HCF tại đỉnh C AH CH = (**) AF CF BH AH Từ (*) và (**) =
AF.BH = BF.AH (đpcm). BF AF Trang 17 17 0,5 (0,5 điểm) A C B E O D
Gọi A là vị trí của vệ tinh địa tĩnh, O là tâm trái đất, B là điểm trên mặt đất
có thể nhận tín hiệu từ vệ tinh A (như hình vẽ).
Khi đó, B di chuyển trên cung nhỏ CD của (O) (với AC, AD là các tiếp
tuyến kẻ từ A ).
Ta có: vị trí xa nhất trên trái đất có thể nhận được tín hiệu từ vệ tinh là điểm B
sao cho AB lớn nhất
Mà AB lớn nhất khi B trùng với C hoặc D , khi đó: m (
ax AB)= AC = AD
Do AC là tiếp tuyến (O) nên AC ⊥ CO tại C suy ra ACO vuông tại C
Gọi E là giao điểm của AO và (O) , ta có AE = 35786 km ;
OE = 6400 km OA = OE + EA = 35786 + 6400 = 42186 km
Áp dụng định lí Pitago trong ACO vuông tại C , ta được: 2 2 2 2 2
CA = OA − CO = 42186 − 6400 41698 km
Vậy vị trí xa nhất trên bề mặt trái đất có thể nhận được tín hiệu từ vệ tinh là
điểm cách vệ tinh khoảng 41698 km
Ghi chú: - Mọi cách giải khác nếu đúng và lý luận phù hợp ghi điểm tối đa.
- Điểm bài thi làm tròn đến chứ số thập phân thứ nhất. ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I MÔN: TOÁN 9 CÁNH DIỀU
A. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1.(NB) Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Trang 18
A. xy + x = 3. B. 2x – y = 0. C. x2 + 2y = 1. D. x + 3 = 0.
Câu 2.(NB) Phương trình bậc nhất hai ẩn 3x - 2y = 4 có một nghiệm là :
A. ( 0; -1). B. (0;1). C. (2; 1). D.(2; -1).
Câu 3. (NB) Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn x, y ? x + y = 1 x + y = 1 x + 2y = 0 x + y = 1 A. . B. . C. 2 . D. . 2 x + y = 3. x + 2 y = 3. x + = 3y. x − 2y = 3. y
Câu 4.(NB) Căn bậc hai số học của 9 là: A. 81. B. 9. C. 3. D. 3 và -3.
Câu 5. (NB) Căn bậc ba của - 27 là: A. 3. B. -3. C. 27. D. -27.
Câu 6. (NB) Trong các biểu thức sau biểu thức nào không phải là căn thức bậc hai? A. x +1 . B. 5 . C. 2 x −1 . D. x+1 .
Câu 7. (NB) Cho tam giác ABC vuông tại A có B = A AB AC A. sin = . B. sin = . AC AB AC AB α C. sin = . D. sin = . B C BC BC
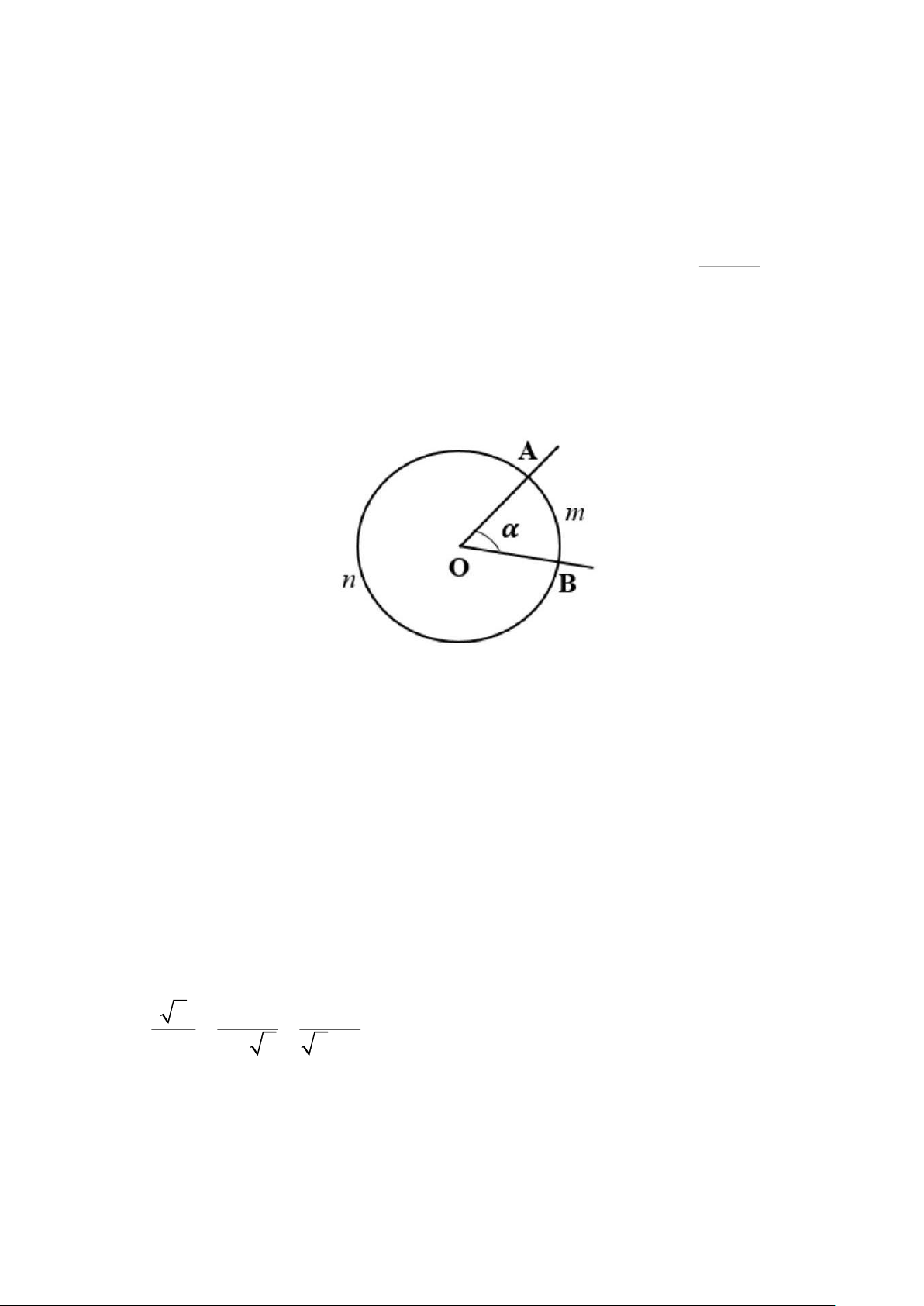
Câu 8. (NB) Trong hình 1, ta có cosα bằng 4 3 3 4 A. . B. . C. . D. . 3 4 5 5
Câu 9. (NB). Trong hình 1, ta có tanα bằng 4 3 3 4 A. . B. . C. . D. . 3 4 5 5
Câu 10. (NB) Đường tròn có bao nhiêu tâm đối xứng? A. 1 B. 2 C. 0 D. Vô số
Câu 11. (NB) Trong đường tròn (O), AOB là A. góc nội tiếp. B. góc ở tâm. C. góc tù. O D. góc vuông. B A
Câu 12. (NB) Trong đường tròn (O), BAC là Trang 19 A. góc nội tiếp. A B. góc ở tâm. C. góc tù. D. góc vuông. O B C m
B. PHẦN TỰ LUẬN (7,0 điểm)
Câu 13. TH (1,0 điểm) Cho a b ; Chứng minh 2a + 5 2b + 5 .
Câu 14. VD (1,0 điểm) Giải bất phương trình sau: a) 2x − 5 3 ;
b) 3x + 2 5x − 8 . Câu 15. (1,0 điểm) 75 a) Tính ; 3
b) Tính (gần đúng) các tỉ số lượng giác sau (làm tròn đến hàng phần trăm): Sin 350; cos 480.
Câu 16. VD (1,0 điểm)
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và
N. Chứng minh rằng MN < BC.
Câu 17. TH (1,0 điểm)
Cho tam giác ABC vuông tại A, AB = 3cm; BC = 5cm. Đường thẳng AB có tiếp xúc với đường tròn (C; 4cm) hay không? Vì sao?
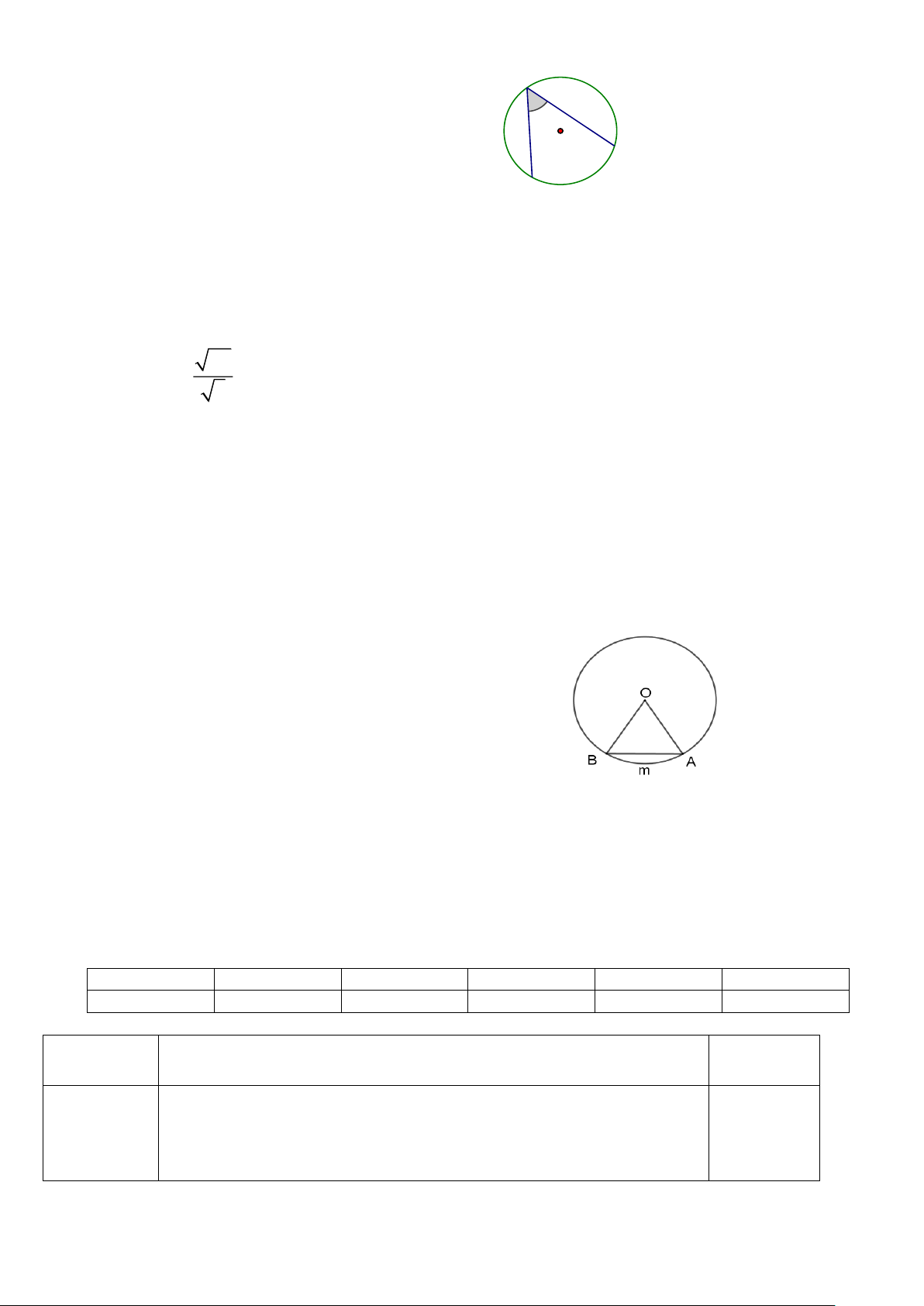
Câu 18. TH (1,0 điểm)
Cho hình bên, biết cung AmB có số đo là o 60 . a) Tính số đo AOB
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB và tính số đo góc đó.
Câu 19. (VDC) (1,0 điểm) Lúc 7 giờ một người đi xe máy khởi hành từ A với vận tốc 40 km/h. Sau đó,
lúc 8 giờ 30 phút, một người khác cũng đi xe máy từ A đuổi theo với vận tốc 60 km/h. Hỏi hai người gặp nhau lúc mấy giờ ? ----- HẾT ----- V. ĐÁP ÁN
A. PHẦN TRẮC NGHIỆM (3,0 điểm) 1D 2C 3D 4B 5B 6D 7C 8C 9A 10A 11B 12A
B. PHẦN TỰ LUẬN (7,0 điểm) Câu Nội dung Điểm a b 13
Ta có: 2a 2b 0,5 (1 điểm)
2a + 5 2b + 5 0,5 Trang 20