













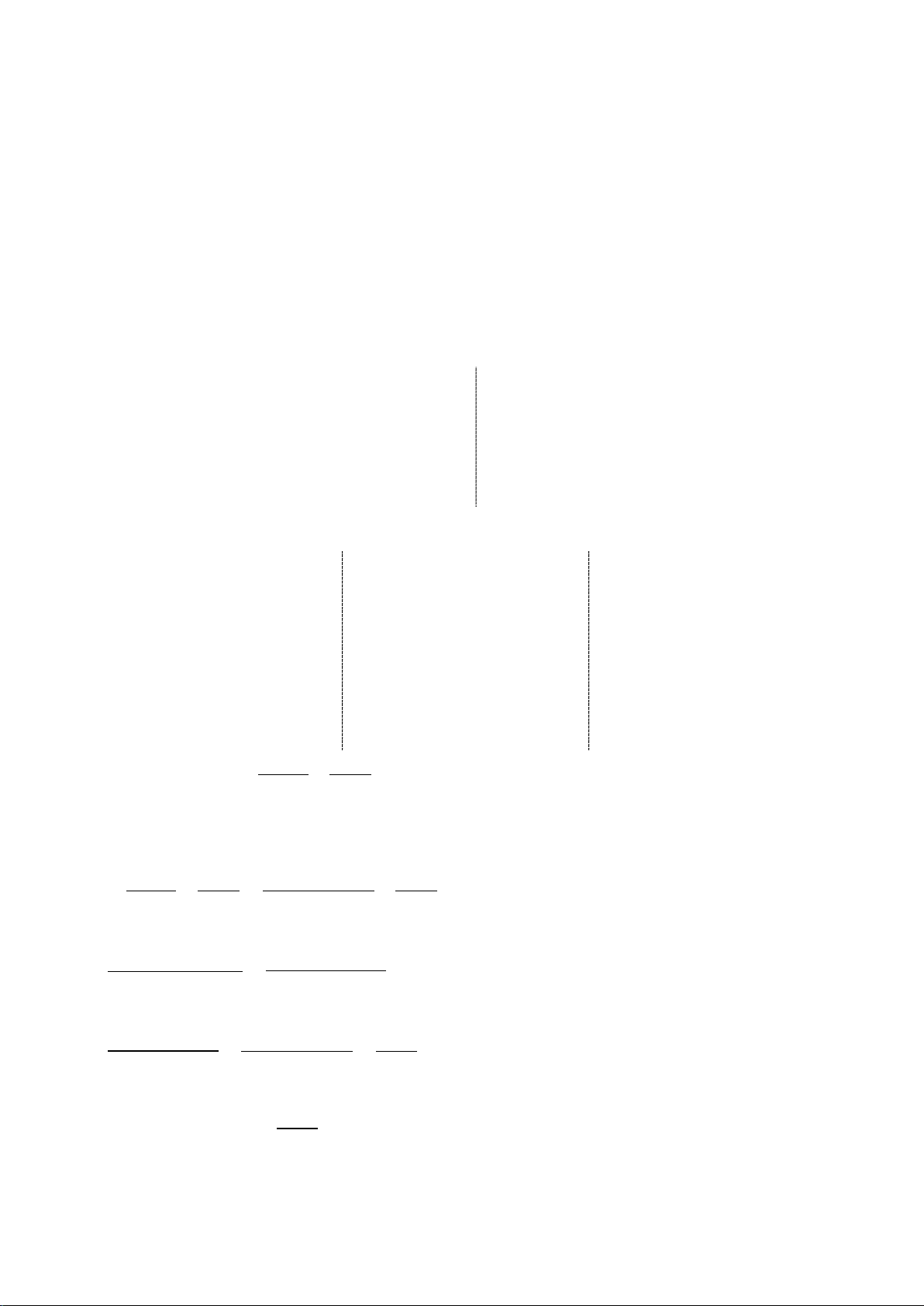















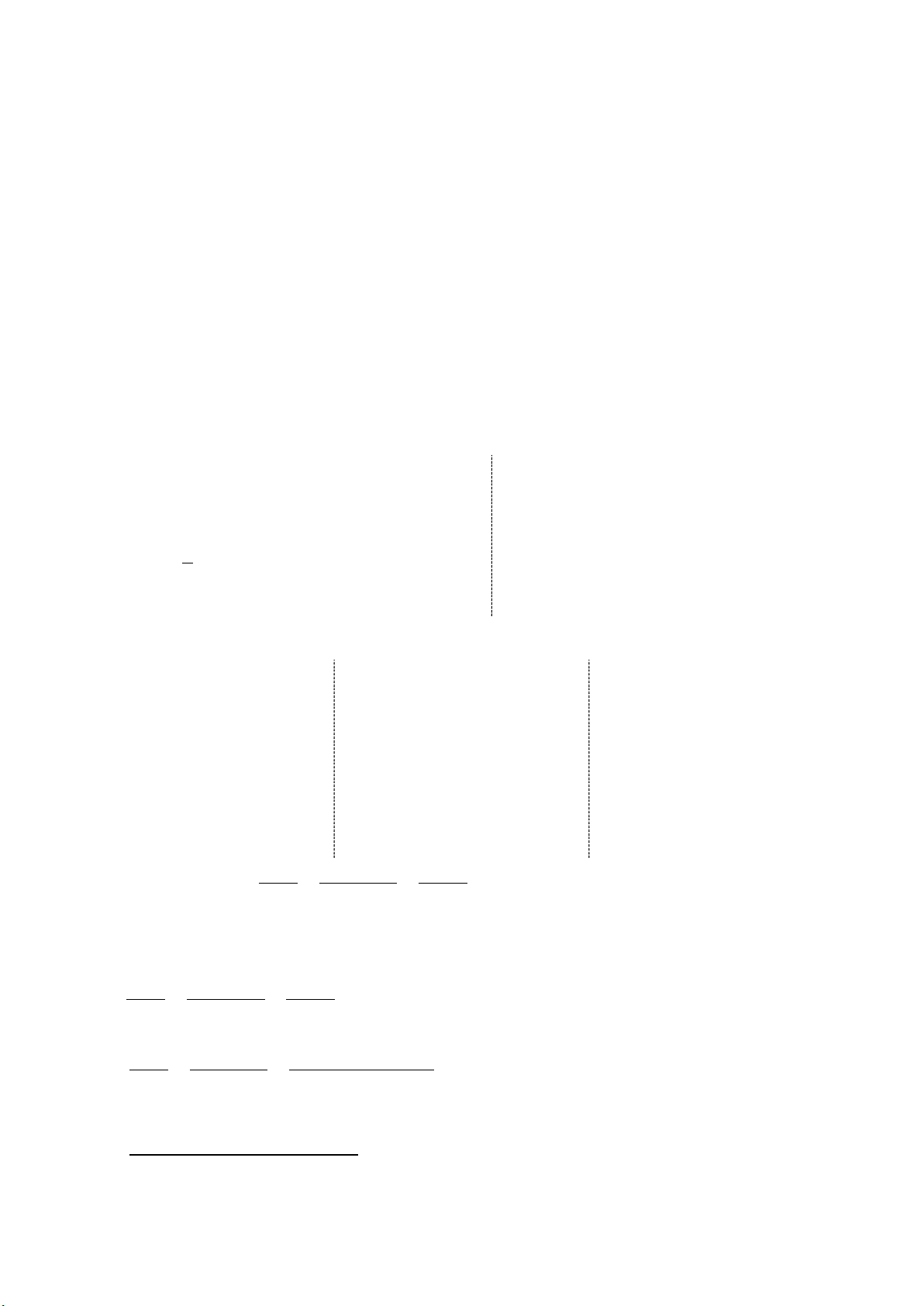

























































Preview text:
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 01
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 1 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (0,5đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 2 1 2 1 1
đa thức thành nhân tử (0,5đ) (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 20%
trực quan tứ giác đều (0,5đ) (0,5đ) (1,0đ) Định lí 1 1 Định lí Pythagore 4 Pythagore. (0,25đ) (0,5đ) 15% Tứ giác Tứ giác 1 1 (0,25đ) (0,5đ)
Tổng: Số câu 8 1 4 6 5 1 25 Điểm (2,0đ) (0,5đ) (1,0đ) (3,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 25% 40% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 1TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 2TN 1TN, 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, 2TL thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TN 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TN 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT101
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức? 2 A. 1 x z + y ; B. − ; C. ( − ) 2 2 x y ; D. xyz . x 5
Câu 2. Đa thức nào sau đây không phải là đa thức bậc 4? A. 2 4xy z ; B. 4 5 x − 3 ; C. 2 xy + xyzt ; D. 4 1 3 x − xy z . 2 Câu 3. Cho đa thức 1 2 1 2 2 3 2
A = − xy + x y + xy − x .
y Giá trị của A tại x = 2; − y = 3 là 3 2 4 A. 15 A = − ; B. A = 12 − ; C. A = 15 − ; D. A = 14. 13
Câu 4. Khẳng định nào sau đây là đúng? A. (x − y)( 2 2
x + xy + y ) 3 2 2 4 = x + (2y)3; B. (x − y)( 2 2
x + xy + y ) 3 2 2 4 = x − (4y)3; C. (x − y)( 2 2
x + xy + y ) 3 2 2 4 = x + (4y)3; D. (x − y)( 2 2
x + xy + y ) 3 2 2 4 = x − (2y)3.
Câu 5. Điền vào chỗ trống sau: (x + )2 2 2 = x + + 4 A. 2x ; B. 4x ; C. 2 ; D. 4 .
Câu 6. Kết quả phân tích đa thức 2 2
6x y − 12xy là
A. 6xy (x − 2y) ;
B. 6xy (x − y) ;
C. 6xy (x + 2y) ;
D. 6xy (x + y) .
Câu 7. Phân thức A xác định khi nào? B A. B < 0; B. B = 0 ; C. B ≠ 0 ; D. B > 0 .
Câu 8. Ta không nên quy đồng cho bài toán nào dưới đây? A. 1 x − ; B. 2 3 1 1 − ; C. 1 x − ; D. + . x − 1 1 − x x − y x + y x + y 2 a − 1 a − 1
Câu 9. Hình chóp tứ giác đều có mặt bên là hình gì? A. Tam giác cân; B. Tam giác đều; C. Hình chữ nhật; D. Hình vuông.
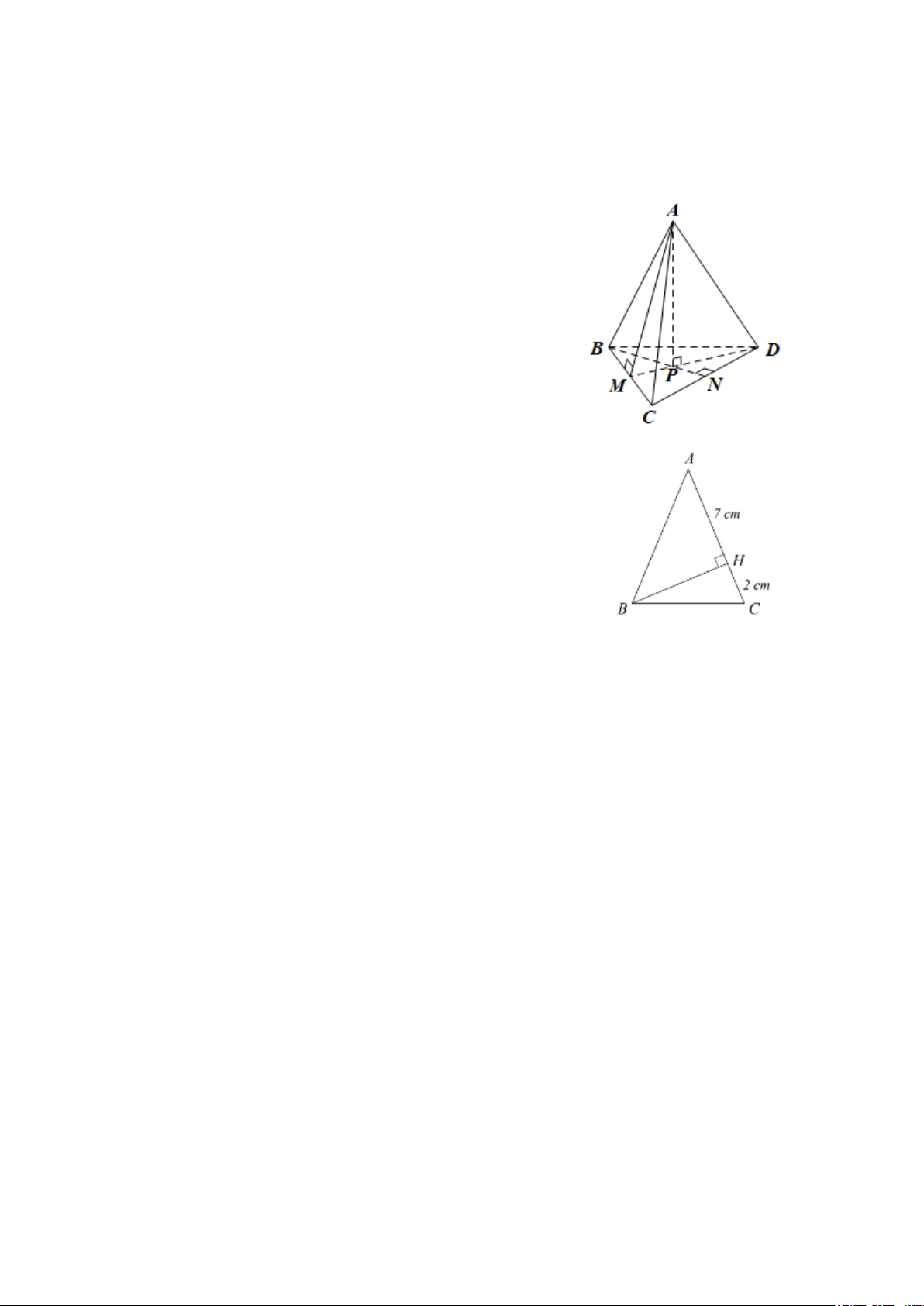
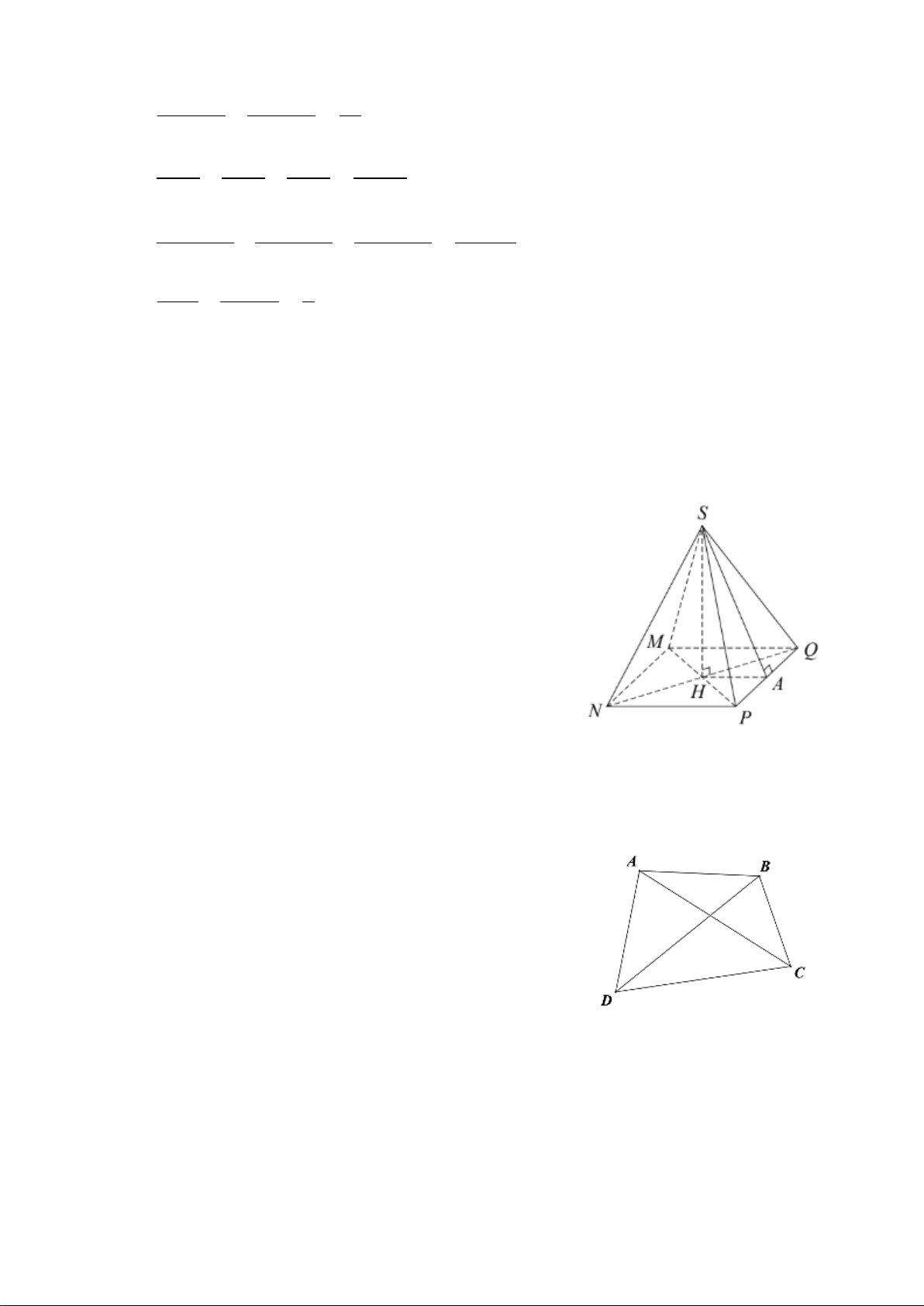
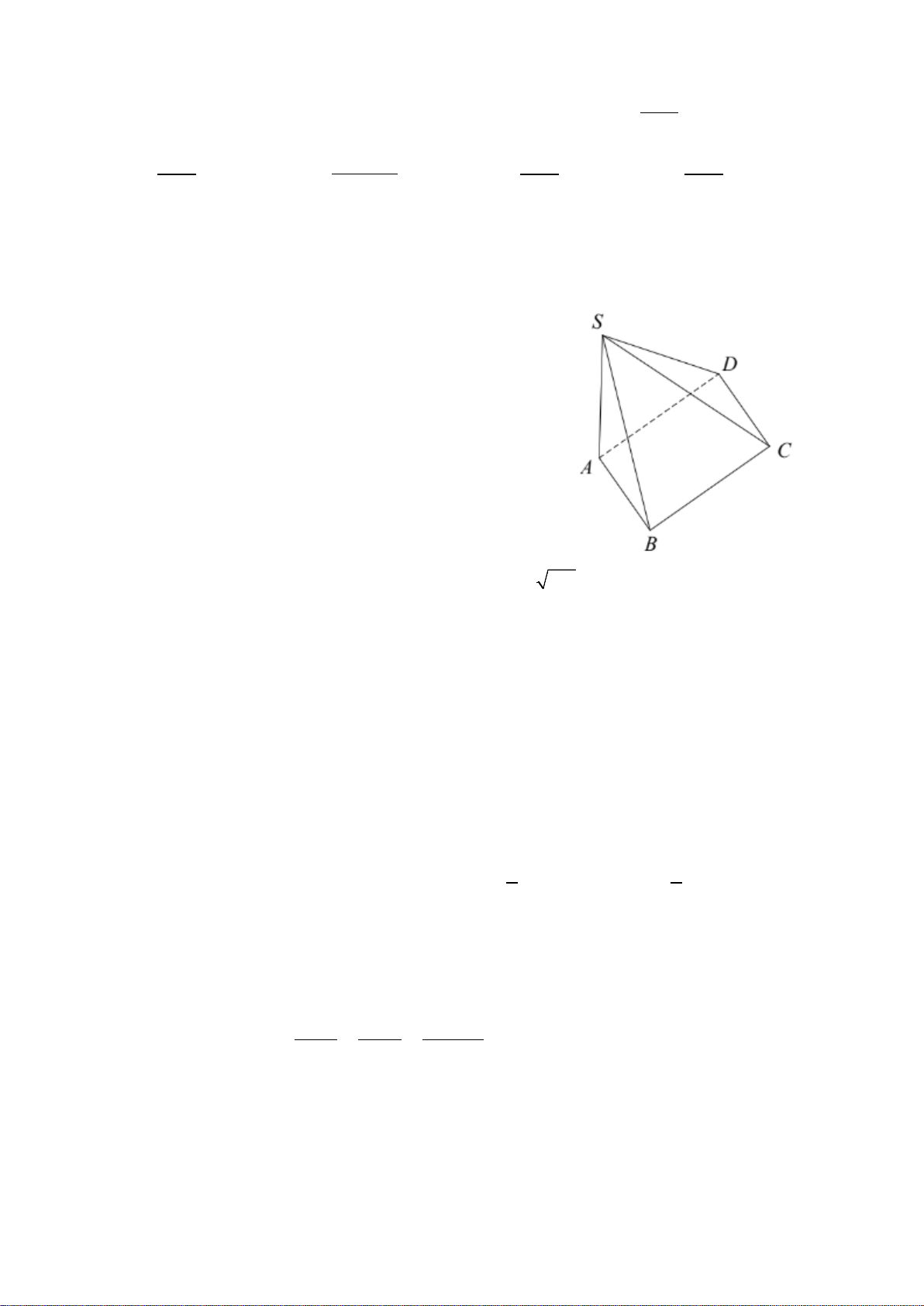
Câu 10. Cho hình chóp tam giác đều . A BCD như hình vẽ
bên. Đoạn thẳng nào sau đây là trung đoạn của hình chóp? A. AC ; B. AM ; C. BN ; D. AP .
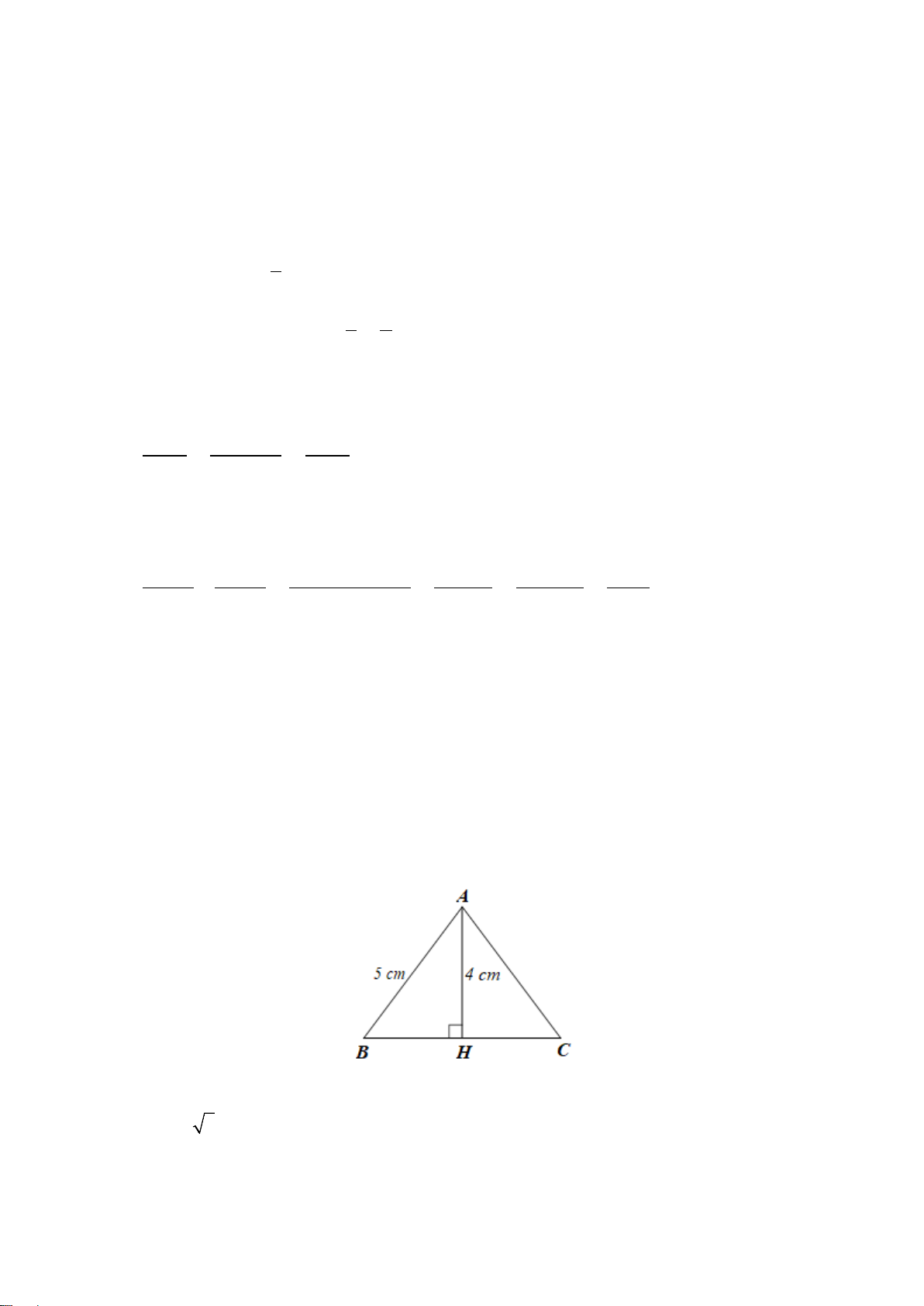
Câu 11. Độ dài cạnh BC trong A
∆ BC cân tại A ở hình vẽ bên là A. 4 cm ; B. 5 cm ; C. 6 cm; D. 7 cm .
Câu 12. Tổng số đo các góc trong tứ giác bằng A. 90° ; B. 120° ; C. 180° ; D. 360° .
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thu gọn biểu thức: a) ( 13 15 10 14
− x y + x y ) ( 10 14 12 6 : 3 − x y ); b) (x − y)( 2
x − x + y) 3 2 2 − x + x . y
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 2
xy + y – x – y; b) (x y − )2 2 2 8 − 1; c) 2 x – 7x – 8. 2
Bài 3. (1,5 điểm) Cho biểu thức x x 2 A = − − . 2
x − 4 x − 2 x + 2
a) Viết điều kiện xác định của biểu thức . A
b) Rút gọn biểu thức A .
c) Tìm giá trị của x để A = 2.
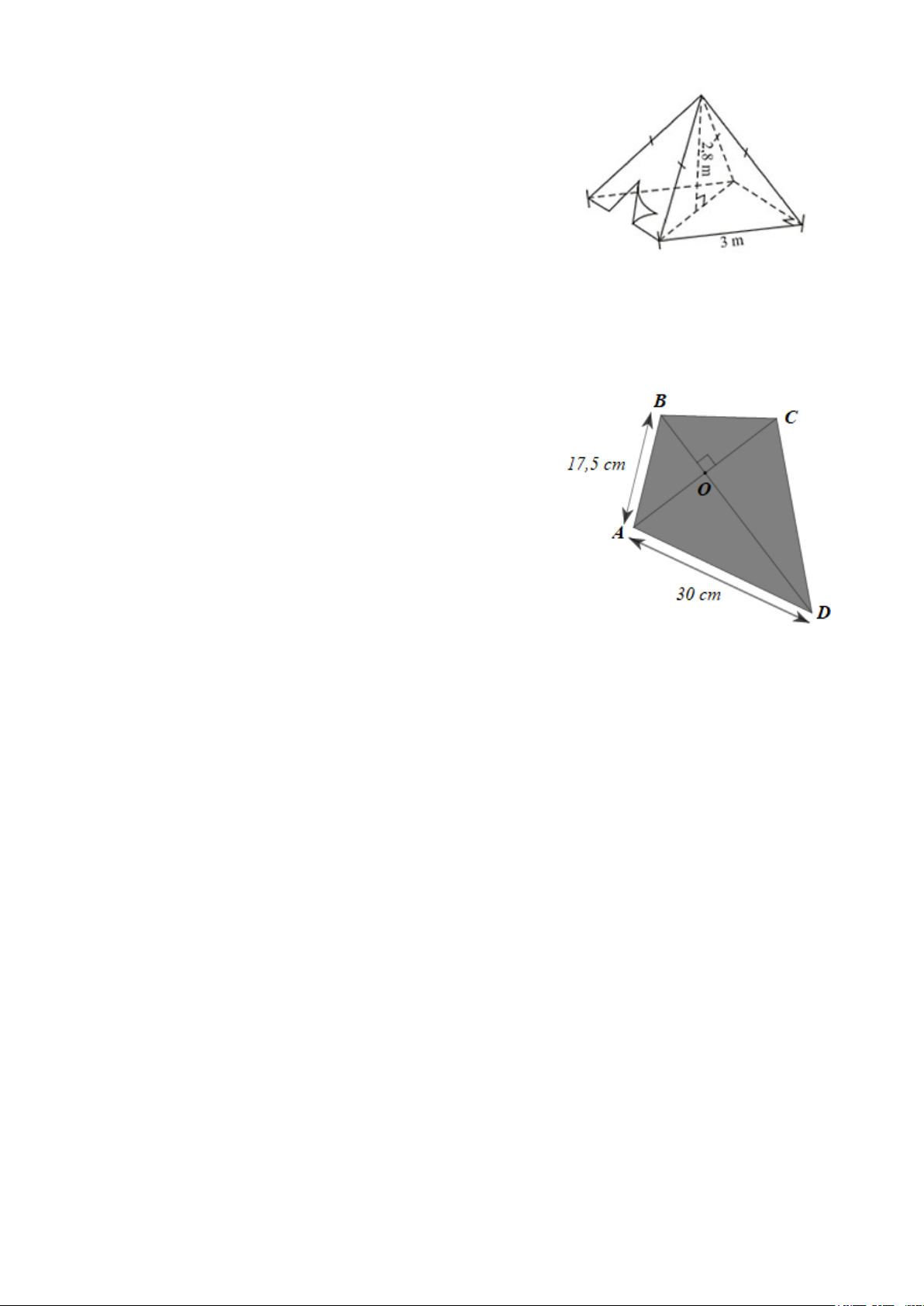
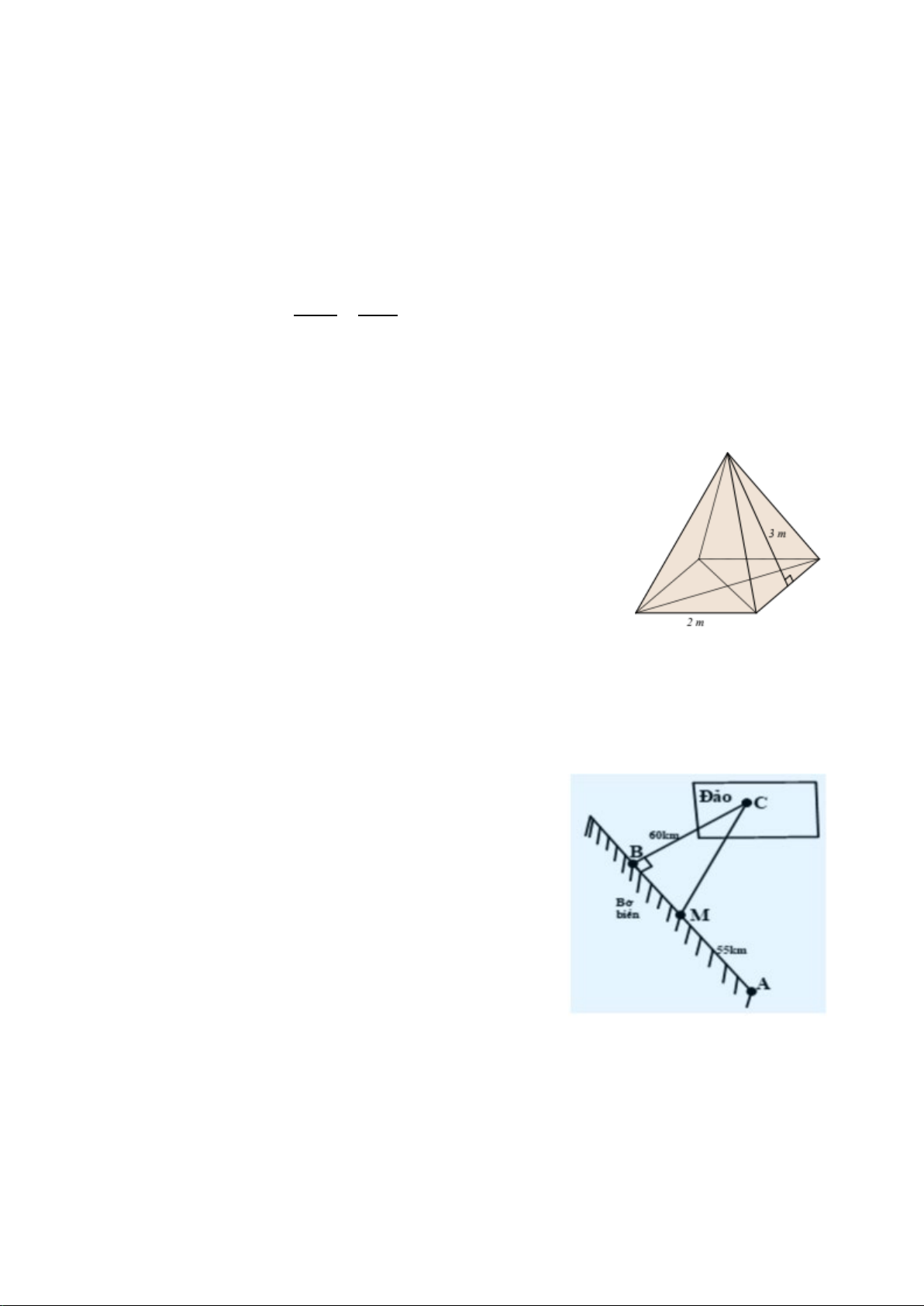
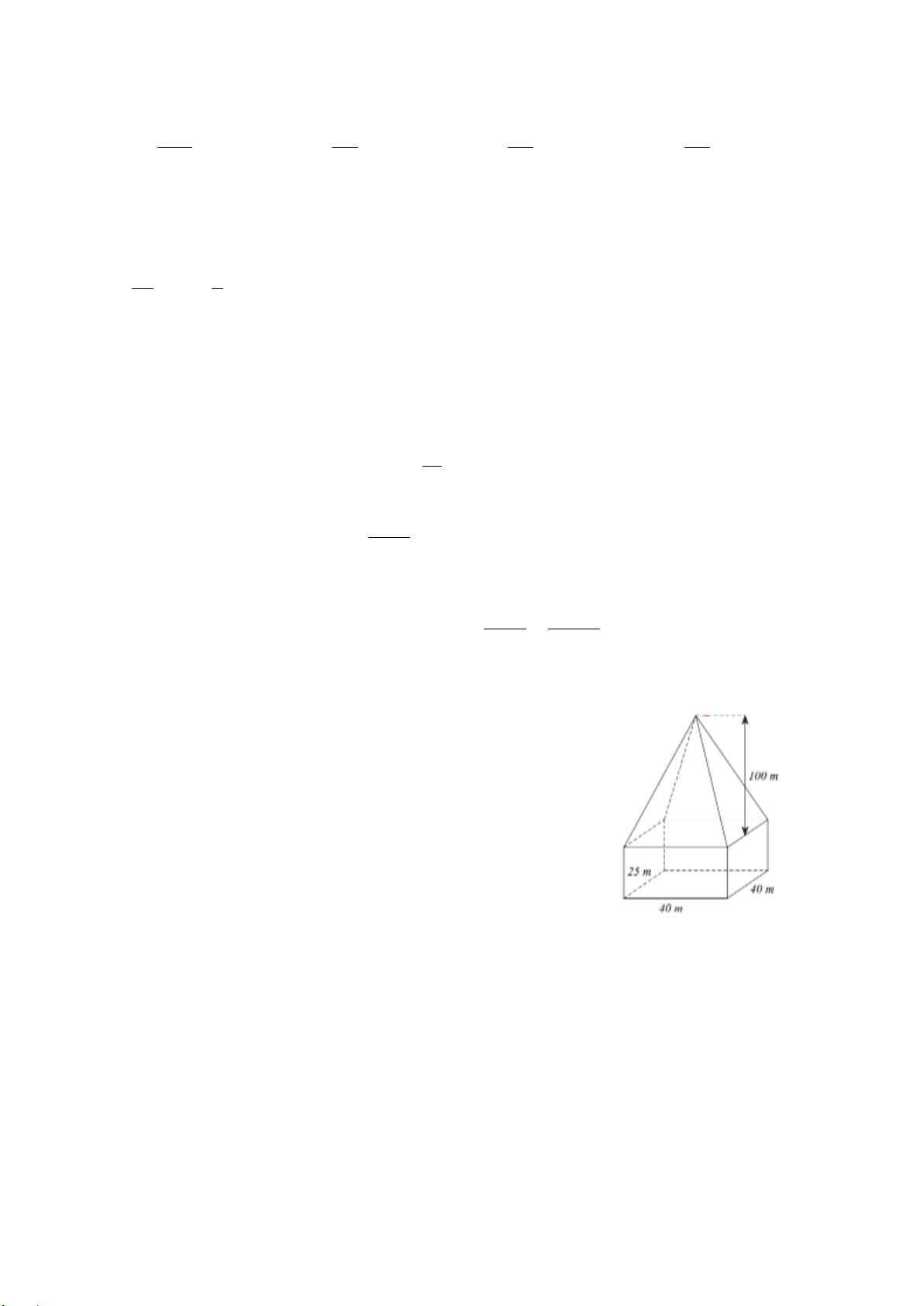
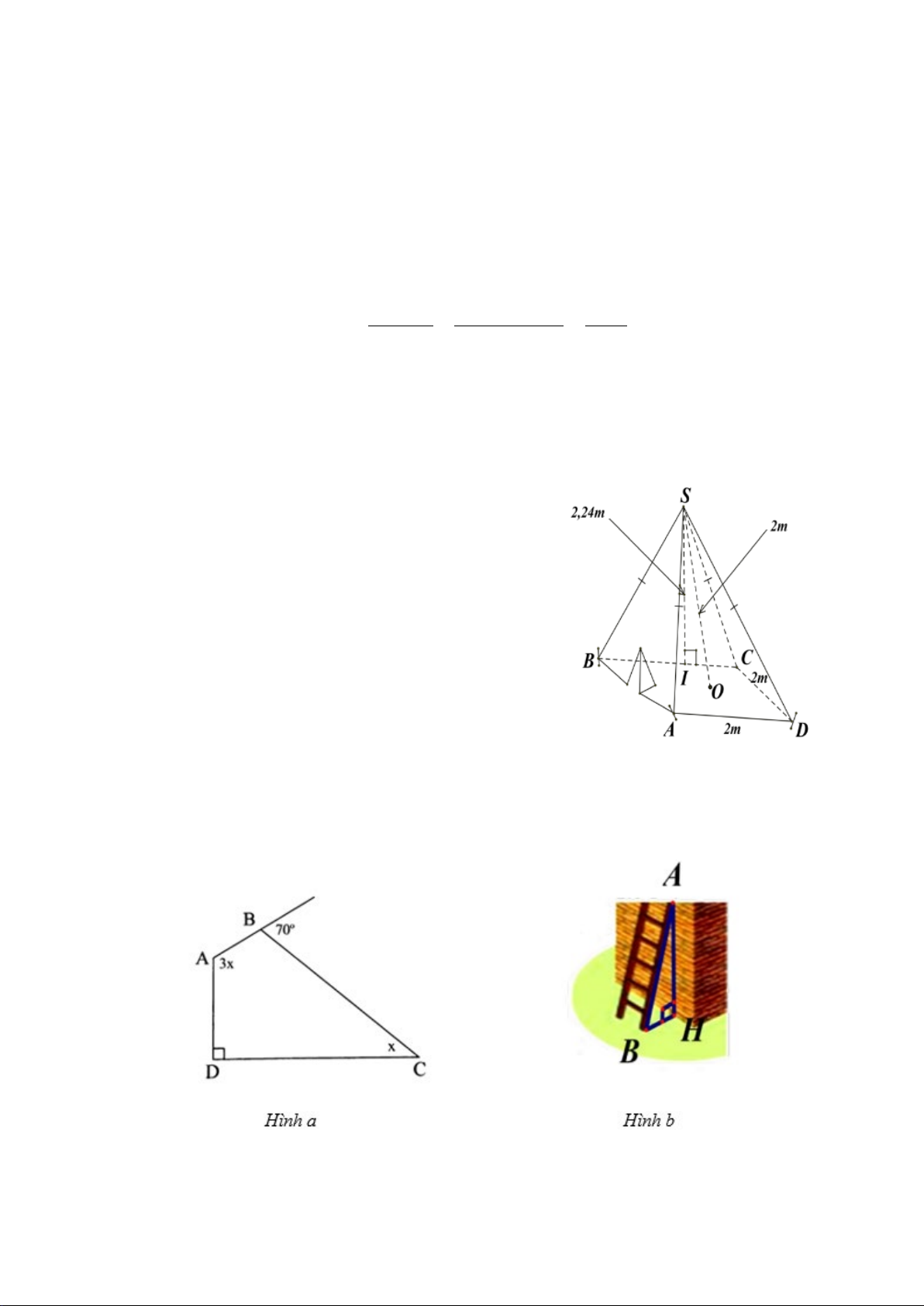
Bài 4. (1,5 điểm) Một chiếc lều có dạng hình chóp tứ giác đều
ở trại hè của học sinh có kích thước như hình bên.
a) Tính thể tích không khí bên trong chiếc lều.
b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho
chiếc lều (coi các mép nối không đáng kể). Biết chiều cao
của mặt bên xuất phát từ đỉnh của chiếc lều là 3,18 m và
giá vải là 15 000 đồng/m2. Ngoài ra, nếu mua vải với hóa
đơn trên 20 m2 thì được giảm giá 5% trên tổng hóa đơn.
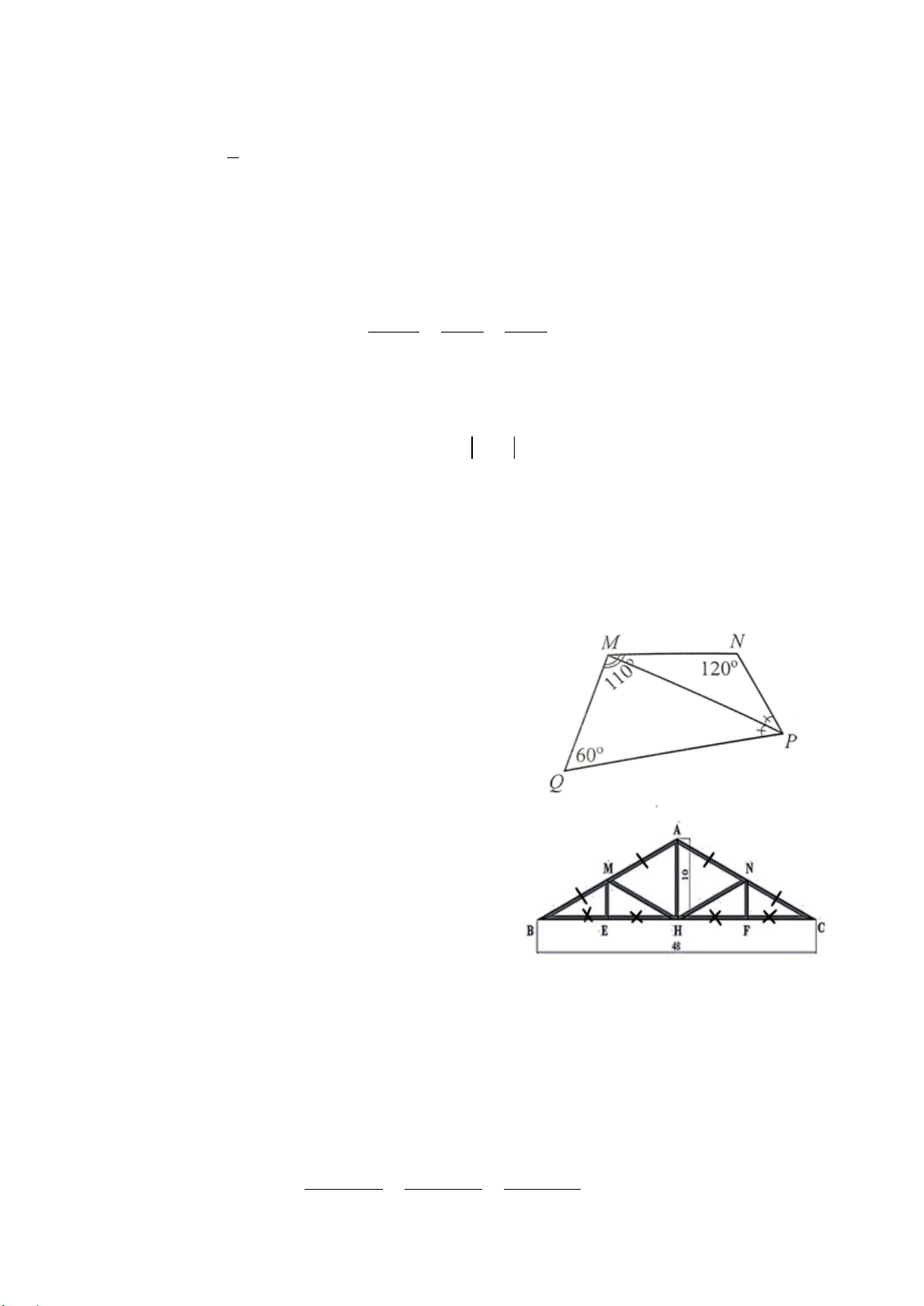
Bài 5. (1,0 điểm) Một chiếc diều được mô tả như hình vẽ bên.
a) Tính số đo góc D ở đuôi chiếc diều biết các góc ở đỉnh = = A B C = 102 .°
b) Tính độ dài khung gỗ đường chéo BD biết
OD = 26,7 cm (làm tròn kết quả đến hàng phần mười).
Bài 6. (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức 2
M = x − x( y + ) 2 2 1 + 3y + 2025. -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT101
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B D C D B A C A A B C D
Hướng dẫn giải phần trắc nghiệm Câu 1. Đáp án đúng là: B 2 Biểu thức x z 1 2 −
= − x z là đơn thức. 5 5 Câu 2. Đáp án đúng là: D Đa thức 4 1 3
x − xy z có bậc là 5. 2 Câu 3. Đáp án đúng là: C Ta có: 1 2 1 2 2 3 2
A = − xy + x y + xy − x y 3 2 4 1 2 2 1 2 3 2 xy xy x y x y = − + + − 3 2 4 2 2 1 2 = xy − x y . 3 4 Thay x = 2
− và y = 3 vào biểu thức A ta được: 2 A = ⋅ (− ) 2 1 2 ⋅ 3 − ⋅ ( 2 − )2 ⋅ 3 = 12 − − 3 = 15. − 3 4 Câu 4. Đáp án đúng là: D
Ta có: (x − y)( 2 2
x + xy + y ) 3 2 2 4 = x − (2y)3 . Câu 5. Đáp án đúng là: B Ta có: (x + )2 2
2 = x + 4x + 4 . Câu 6. Đáp án đúng là: A Ta có: 2 2
6x y − 12xy = 6xy(x − 2y). Câu 7. Đáp án đúng là: C
Phân thức A xác định khi B ≠ 0 . B Câu 8. Đáp án đúng là: A + Ta có: 1 x 1 x x 1 − = + =
. Do đó ta không cần quy đồng mẫu cho phép cộng x − 1 1 − x x − 1 x − 1 x − 1 phân thức này. Câu 9. Đáp án đúng là: A
Các mặt bên của hình chóp tứ giác đều là hình tam giác cân. Câu 10. Đáp án đúng là: B
Trung đoạn của hình chóp .
A BCD là đoạn thẳng AM . Câu 11. Đáp án đúng là: C
Tam giác ABC cân tại A nên AB = AC = AH + HC = 7 + 2 = 9 cm Xét A
∆ BH vuông tại H có: 2 2 2 2 2
CH = AB − AH = 9 − 7 = 32 (định lí Pythagore) Xét B
∆ CH vuông tại H có: 2 2 2 2
BC = BH + CH = 32 + 2 = 36 (định lí Pythagore) Suy ra BC = 36 = 6 cm. Câu 12. Đáp án đúng là: D
Tổng số đo các góc trong tứ giác bằng 360 .°
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) a) ( 13 15 10 14
− x y + x y ) ( 10 14 12 6 : 3 − x y ) b) (x − y)( 2
x − x + y) 3 2 2 − x + x y = ( 13 15 − x y ) ( 10 14 − x y ) + ( 10 14 x y ) ( 10 14 12 : 3 6 : 3 − x y ) = x( 2
x − x + y) − y( 2
x − x + y) 3 2 2 2 − x + x y 3 = 4x y − 2. 3 2 2 2 3 2
= x − 2x + xy − x y + 2xy − y − x + x y 2 2 = 2
− x + 3xy − y . Bài 2. (1,5 điểm) a) 2
xy + y – x – y b) (x y − )2 2 2 8 − 1 c) 2 x – 7x – 8 = ( 2
xy + y ) – (x + y) 2
= x − x + 8x − 8 = ( 2 2 x y − − )( 2 2 8 1 x y − 8 + )
1 = x(x − )1 + 8(x − )1
= y (x + y) – (x + y) = ( 2 2 x y − )( 2 2 9 x y − 7) = (x − ) 1 (x + 8).
= (x + y)( y − ) 1 .
= (xy − )(xy + )( 2 2 3 3 x y − 7). 2
Bài 3. (1,5 điểm) 2x x 2 A = − − . 2
x − 4 x − 2 x + 2
a) Điều kiện xác định của biểu thức A là: 2
x − 4 ≠ 0; x − 2 ≠ 0; x + 2 ≠ 0 Mà 2
x − 4 = (x − 2)(x + 2)
Vậy điều kiện xác định của biểu thức A là x − 2 ≠ 0 và x + 2 ≠ 0 hay x ≠ 2. ±
b) Với điều kiện xác định x ≠ 2 ± ta có: 2 2x x 2 A = − − 2
x − 4 x − 2 x + 2 2 2x x(x + 2) 2(x − 2) = ( − −
x − 2)(x + 2) (x − 2)(x + 2) (x + 2)(x − 2) 2 2
2x − x − 2x − 2x + 4 2 − + = x 4x 4 ( = x − 2)(x + 2) (x − 2)(x + 2) (x − )2 2 − = x 2 ( = . x − 2)(x + 2) x + 2 c) Với − x ≠ 2,
± để A = 2 thì x 2 = 2 x + 2
Suy ra x − 2 = 2(x + 2)
Do đó x − 2 = 2x + 4 Hay x = 6
− (thỏa mãn điều kiện) Vậy x = 6. − Bài 4. (1,5 điểm)
a) Diện tích đáy hình vuông của chiếc lều là: 2 S = = đáy ( 2 3 9 m )
Thể tích không khí bên trong chiếc lều là: 1 1
V = S h = ⋅ ⋅ = . đáy 9 2,8 8,4 ( 3 m ) 3 3
Chú ý: Có thể không cần bước tính diện tích đáy.
b) Diện tích xung quanh của chiếc lều là: 1 1
S = ⋅ C ⋅ d = ⋅ ⋅ ⋅ = xq 4 3 3,18 19,08 ( 2 m ) 2 2
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
S = 9 + 19,08 = 28,08 (m2).
Do 28,08 > 20 nên số tiền mua vải được giảm giá 5% trên tổng hóa đơn.
Vậy số tiền mua vải là: 28,08 ⋅ 15 000 ⋅ (100% − 5%) = 400 140 (đồng). Bài 5. (1,0 điểm)
a) Số đo góc D ở đuôi chiếc diều là: = ° − + + D 360
(A B C ) = 360° − (102° +102° +102°) = 54 .° b) Xét OA ∆
D vuông tại O , theo định lí Pythagore ta có: 2 2 2 2 2
OA = AD − OD = 30 − 26,7 = 187,11 Xét OA ∆
B vuông tại O, theo định lí Pythagore ta có: 2 2 2 2
OB = AB − OA = 17,5 − 187,11 = 119,14
Do đó OB = 119,14 ≈ 10,9 (cm).
Suy ra BD = OB + OD = 10,9 + 26,7 = 37,6 (cm). Bài 6. (0,5 điểm) Ta có: 2
M = x − x( y + ) 2 2 1 + 3y + 2025 2
= x − x( y + ) + ( y + )2 − ( 2 y + y + ) 2 2 1 1 2 1 + 3y + 2025 2
= x − x( y + ) + ( y + )2 2 2 1
1 + 2y − 2y + 2024 2
= x − x( y + ) + ( y + )2 2 1 1 2 1
1 + 2 y − y + + 2024 − 4 2 2
= (x − y − )2 1 4047 1 + 2 y − + . 2 2
Nhận xét: với mọi x, y ta có:
• (x − y − )2 1 ≥ 0; 2 • 1 2 y − ≥ 0 2 2
Do đó M = (x − y − )2 1 4047 4047 1 + 2 y − + ≥ 2 2 2 (
x − y − )2 1 = 0
x − y − 1 = 0 3 x =
Dấu “=” xảy ra khi và chỉ khi 2 2 1 hay 1 nên 2 y − = 0 y − = 0 1 = 2 2 y 2
Vậy giá trị nhỏ nhất của biểu thức M là 4047 khi 3 x = và 1 y = . 2 2 2 -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 02
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 1 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (0,5đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 2 1 2 1 1
đa thức thành nhân tử (0,5đ) (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 20%
trực quan tứ giác đều (0,5đ) (0,5đ) (1,0đ) Định lí 1 1 Định lí Pythagore 4 Pythagore. (0,25đ) (0,5đ) 15% Tứ giác Tứ giác 1 1 (0,25đ) (0,5đ)
Tổng: Số câu 8 1 4 6 5 1 25 Điểm (2,0đ) (0,5đ) (1,0đ) (3,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 25% 40% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 1TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 2TN 1TN, 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, 2TL thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TN 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TN 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT102
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Biểu thức nào sau đây là đơn thức? A. ( + ) 3 1 x x ; B. x + 2y ;
C. (xy + z)t ; D. 2 5 3xy z .
Câu 2. Bậc của đa thức 8 2 7 5
M = x + x y − y + x là A. 1; B. 5; C. 8 ; D. 9.
Câu 3. Giá trị của đa thức 2 2 2 2 2x y −
+ 3xy − 2yx − 2y x + 3 tại 2 1 x = ; y = là 3 2 A. 17 − ; B. 17 ; C. 19 − ; D. 19 . 6 6 6 6
Câu 4. Đẳng thức nào sau đây là hằng đẳng thức? A. 2 2
x − x = −x + x ; B. x(x − ) 2 1 = x − x ; C. ( − )2 = ( − )2 a b b a ;
D. a − 2 = 2 − a .
Câu 5. Điền vào chỗ trống sau: 2 x −
= (x − 4)(x + 4) A. 2 ; B. 4 ; C. 8 ; D. 16. Câu 6. Biết 3 x + 125 = .
A B và A là đa thức có bậc bằng 1. Khi đó biểu thức B là A. 2 x − 5x + 25 ; B. 2 x + 5x + 25 ; C. 2
x − 10x + 25 ; D. 2 x + 10x + 25.
Câu 7. Phân thức A C = ( , A B ≠ 0) khi B D A. AB = CD ; B. AD = BC ; C. A C = ; D. A B = . D B D C
Câu 8. Kết quả nào sau đây là sai? 2 2
A. 4x − 5z 4x + 5z 8x + = ; 3xy 3xy 3y B. x + 3 x x − 3 −x + 6 + − = ; x − y y − x x − y x − y 2 2 2 2
C. 3a − 5ab 2a − 4b 7ab − 3b 5a + 7b + + = ; 2 2 2 2 2 2 a − b b − a a − b a + b D. 3 x − 6 2 − = . 2
x + 3 x + 3x x
Câu 9. Hình chóp tam giác đều không có đặc điểm nào sau đây?
A. Có các cạnh bên bằng nhau;
B. Có đáy là hình vuông;
C. Có các mặt bên là các tam giác cân;
D. Có chân đường vuông góc của đỉnh là tâm đường tròn ngoại tiếp tam giác đáy.
Câu 10. Cho hình vẽ bên, trung đoạn của hình chóp tứ giác S.MNPQ là A. SH ; B. SA ; C. HA ;
D. NQ hoặc MP .
Câu 11. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau? A. 15 cm; 8 cm; 18 cm ; B. 21 dm; 20 dm; 29 dm ; C. 5 m; 6 m; 8 m ; D. 2 cm; 3 cm; 4 cm .
Câu 12. Cho hình vẽ bên.
Khẳng định nào sau đây là khẳng định sai?
A. Hai đỉnh kề với đỉnh A là B và D ;
B. Hai đỉnh đối nhau là A và C; B và D ;
C. Tứ giác ABCD có 2 đường chéo;
D. Các cạnh của tứ giác là AB, BC, CD, ,
DA AC, BD .
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thu gọn biểu thức: a) ( 4 2 2 5
x − x y + x y) ( 2 4 8 12 : 4 − x ); b) 2 x ( 2
x − y ) − xy( − xy) 3 1 − x .
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 2
10x (2x − y) + 6xy( y − 2x); b) 2 2
x − 2x + 1 − y ; c) 2 x − 8x + 12 .
Bài 3. (1,5 điểm) Cho biểu thức x + 15 2 A = + với x ≠ 3 ± . 2 x − 9 x + 3
a) Rút gọn biểu thức A . b) Tìm x để −
A có giá trị bằng 1 . 2
c) Tìm số tự nhiên x để A có giá trị nguyên.
Bài 4. (1,5 điểm) Kim tự tháp là một công trình kiến trúc tuyệt đẹp bằng kính tọa lạc ngay lối vào của
bảo tàng Louvre, Pari. Kim tự tháp có dạng là hình chóp tứ giác đều với chiều cao 21 m và độ dài
cạnh đáy là 34 m. Các mặt bên của kim tự tháp là các tam giác đều (xem hình ảnh minh họa bên).
a) Tính thể tích của kim tự tháp Louvre.
b) Hỏi nếu sử dụng loại gạch hình vuông có cạnh là 60 cm để lót sàn thì cần bao nhiêu viên gạch?
Biết diện tích của các đường rãnh giữa các viên gạch lót sàn là 156 m2.
Bài 5. (1,0 điểm)
a) Cho tứ giác ABCD có = ° = ° − C 60 , D 80 , A
B = 10 .° Tính số đo của A .
b) Tính chiều dài đường trượt AC trong hình
vẽ bên (kết quả làm tròn hàng phần mười).
Bài 6. (0,5 điểm) Cho các số x, y thỏa mãn đẳng thức: 2 2
5x + 5y + 8xy − 2x + 2y + 2 = 0. Tính giá
trị của biểu thức M = (x + y)2023 + (x − )2024 + ( y + )2025 2 1 .
-----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT102
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án D D B C D A B C B B B D
Hướng dẫn giải phần trắc nghiệm Câu 1.
Đáp án đúng là: D Biểu thức 2 5
3xy z là đơn thức. Câu 2.
Đáp án đúng là: D Bậc của đa thức 8 2 7 5
M = x + x y − y + x là 9. Câu 3.
Đáp án đúng là: B Thu gọn đa thức: 2 2 2 2
2x y + 3xy − 2yx − 2y x + 3 = ( 2 2 x y − x y) + ( 2 2 2 2
3xy − 2xy ) + 3 2 = xy + 3 Thay 2 − 1 x =
; y = vào đa thức đã 2 xy + 3 ta được: 3 2 2 2 − 1 2 − 1 17 ⋅ + 3 = ⋅ + 3 = . 3 2 3 4 6 Câu 4.
Đáp án đúng là: C
Ta có: (a − b)2 2 2
= a + 2ab + b = (b − a)2
Vậy đẳng thức ( − )2 = ( − )2 a b
b a là hằng đẳng thức. Câu 5.
Đáp án đúng là: D Ta có: 2
x − 16 = (x − 4)(x + 4) . Vậy điền số 16. Câu 6. Đáp án đúng là: A Ta có: 3 x + = (x + )( 2 125
5 x − 5x + 25) . Vậy đa thức B là 2 x − 5x + 25. Câu 7. Đáp án đúng là: B Phân thức A C = ( ,
A B ≠ 0) khi AD = BC . B D Câu 8. Đáp án đúng là: C Ta có: 2 2 2 2 2
• 4x − 5z 4x + 5z
4x − 5z + 4x + 5z 8x 8x + = = = ; 3xy 3xy 3xy 3xy 3y • x + 3 x x − 3
x + 3 − x − x + 3 −x + 6 + − = = ; x − y y − x x − y x − y x − y 2 2 2 2 2 2 2 2
• 3a − 5ab 2a − 4b 7ab − 3b
3a − 5ab − 2a + 4b + 7ab − 3b + + = 2 2 2 2 2 2 2 2 a − b b − a a − b a − b
a + 2ab + b (a + b)2 2 2 a + b = = = ; 2 2 a − b
(a − b)(a + b) a − b 3 x − 6 3x − x + 6 2x + 6 2(x + 3) • 2 − = = = = . 2
x + 3 x + 3x x(x + 3) x(x + 3) x(x + 3) x
Do đó phương án C là khẳng định sai. Câu 9. Đáp án đúng là: B
Hình chóp tam giác đều có đáy là hình tam giác đều. Do đó khẳng định B là sai. Câu 10. Đáp án đúng là: B
Trung đoạn của hình chóp tứ giác S.MNPQ là đoạn thẳng SA . Câu 11. Đáp án đúng là: B Ta có: 2 29 = 841 và 2 2 20 + 21 = 400 + 441 = 841. Do đó 2 2 2
20 + 21 = 29 nên bộ ba độ dài 21 dm; 20 dm; 29 dm là độ dài ba cạnh của tam giác vuông. Câu 12. Đáp án đúng là: D
AC và BD không phải cạnh mà là đường chéo của tứ giác.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) a) ( 4 2 2 5
x − x y + x y) ( 2 4 8 12 : 4 − x ) b) 2 x ( 2
x − y ) − xy( − xy) 3 1 − x 4 = x ( 2 − x ) 2 2 − x y ( 2 − x ) 5 + x y ( 2 4 : 4 8 : 4 12 : 4 − x ) 3 2 2 2 2 3
= x − x y − xy + x y − x 2 2 3 = −x .
= −x + 2y − 3x . y y
Bài 2. (1,5 điểm) a) 2
10x (2x − y) + 6xy( y − 2x) b) 2 2
x − 2x + 1 − y c) 2 x − 8x + 12 2 2
= 10x (2x − y) − 6xy(2x − y) = ( 2 x − x + ) 2 2 1 − y
= x − 2x − 6x + 12 = ( 2
x − 2x) − (6x − 12) = ( x − y)( 2 2 10x − 6xy) = (x − )2 2 1 − y
= x(x − 2) − 6(x − 2)
= 2x(2x − y)(5x − 3y).
= (x − 1 − y)(x − 1 + y).
= (x − 2)(x − 6).
Bài 3. (1,5 điểm) x + 15 2 A = + 2 x − 9 x + 3 a) Với x ≠ 3 ± ta có: x + 15 2 x + 15 2 A = + = + 2 x − 9 x + 3
(x + 3)(x − 3) x + 3
x + 15 + 2(x − 3)
x + 15 + 2x − 6 = ( = x + 3)(x − 3) (x + 3)(x − 3) 3x + 9 3(x + 3) = 3 ( = =
x + 3)(x − 3) (x + 3)(x − 3) x − 3 Vậy với x ≠ 3 ± thì 3 A = . x − 3 b) Với x ≠ 3 ± , để 1 A − − = thì ta có: 3 1 = 2 x − 3 2 Suy ra −x + 3 = 6 Do đó x = 3 − (không thỏa mãn)
Vậy không có giá trị nào của x để 1 A − = . 2 c) Với x ≠ 3
± , để A nguyên thì 3 ∈ , tức x − 3 ∈Ư(3) x − 3 Mà Ư(3) = { 1; ± ± } 3 , ta có bảng sau: x − 3 3 − 1 − 1 3 x 0 2 4 6
Các giá trị x tìm được ở trên đều thỏa mãn điều kiện x ≠ 3
± và x là số tự nhiên. Vậy x ∈ {0;2;4; } 6 .
Bài 4. (1,5 điểm)
a) Diện tích sàn của tự kim tháp là: 2 S = = (m2). đáy 34 1156
Thể tích của kim tự tháp là: 1 1 V = S h = ⋅ ⋅ = (m3). đáy 1156 21 8 092 3 3
b) Diện tích một viên gạch hình vuông là: 2 2 2 S = = = gach 6 36 cm 0,36 m
Diện tích sàn cần lát của kim tự tháp là: 1156 − 156 = 1 000 (m2).
Số viên gạch hình vuông cần dùng là: 1 000 ≈ 2 778 (viên). 0,36
Bài 5. (1,0 điểm) a) Ta có: + = ° − + A B 360
(C D ) = 360° − (60° + 80°) = 220° Mà − A
B = 10° nên ta có 220 10 A ° + ° = = 115°. 2
b) Áp dụng định lí Pythagore trong tam giác AHB vuông tại H ta có: 2 2 2
AB = AH + HB Suy ra 2 2 2 2 2
HB = AB − AH = 5 − 3 = 25 − 9 = 16
Do đó HB = 16 = 4 cm, nên CH = BC − HB = 10 − 4 = 6 cm.
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H ta có: 2 2 2 2 2
AC = AH + HC = 3 + 6 = 9 + 36 = 45
Suy ra AC = 45 ≈ 6,7 m.
Vậy chiều dài đường trượt AC là 6,7 m.
Bài 6. (0,5 điểm) Ta có: 2 2
5x + 5y + 8xy − 2x + 2y + 2 = 0 ( 2 2
x + xy + y ) + ( 2
x − x + ) + ( 2 4 8 4 2 1 y + 2y + ) 1 = 0
( x + y)2 + (x − )2 + ( y + )2 2 2 1 1 = 0 (*)
Với mọi x, y ta có: ( x + y)2 ≥ (x − )2 ≥ ( y + )2 2 2 0; 1 0; 1 ≥ 0 (
2x + 2y)2 = 0
Do đó (*) xảy ra khi và chỉ khi ( x − )2 1 = 0 ( y + )2 1 = 0 2x + 2y = 0 x + y = 0 Hay x − 1 = 0 , tức x = 1 y + 1 = 0 y = 1 −
Khi đó M = (x + y)2023 + (x − )2024 + ( y + )2025 2023 2 1 = 0 + (1 − 2)2024 + ( 1 − + )2025 1 = 1. -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 03
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 1 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (0,5đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 2 1 2 1 1
đa thức thành nhân tử (0,5đ) (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 20%
trực quan tứ giác đều (0,5đ) (0,5đ) (1,0đ) Định lí 1 1 Định lí Pythagore 4 Pythagore. (0,25đ) (0,5đ) 15% Tứ giác Tứ giác 1 1 (0,25đ) (0,5đ)
Tổng: Số câu 8 1 4 6 5 1 25 Điểm (2,0đ) (0,5đ) (1,0đ) (3,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 25% 40% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 1TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 2TN 1TN, 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, 2TL thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TN 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TN 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT103
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Biểu thức nào sau đây là đa thức? A. x + 2y ; B. 1 x + ; C. 2 2
−x + y − 3y ; D. 1 2 + y . 3 y x 2x
Câu 2. Cặp đơn thức nào dưới đây là hai đơn thức đồng dạng? A. 4 4 12x y và 4 6 12x y ; B. 4 4 12 − x y và 6 6 12x y ; C. 6 4 12x y và 6 4 2 − x y ; D. 4 6 12x y và 6 6 12x y . Câu 3. Đa thức 3 2 4 3
7x y z − 2x y chia hết cho đơn thức nào dưới đây? A. 4 3x ; B. 4 3 − x ; C. 3 2 − x y ; D. 3 2xy .
Câu 4. Kết quả của phép nhân ( 2 x − 2x + ) 1 (x − ) 1 là A. 3 2
x − 3x + 3x − 1; B. 3 2
x + 3x + 3x − 1; C. 3 2
x − 3x + 3x + 1; D. 3 2
x + 3x + 3x + 1.
Câu 5. Kết quả của biểu thức (x + )2 2 − 4(x + 2) + 4 là A. 2 x + 16; B. 2 x + 8x + 16 ; C. 2 x − 4x ; D. 2 x . Câu 6. Đa thức 2 2 2 2
14x y − 21xy + 28x y được phân tích thành
A. 7xy(2x − 3y + 4xy) ;
B. xy(14x − 21y + 28xy) ; C. 2
7x y(2 − 3y + 4xy); D. 2
7xy (2x − 3y + 4x) .
Câu 7. Biểu thức nào sau đây không phải là phân thức đại số? A. 1 ; B. x ; C. 0 ; D. x . x x 0
Câu 8. Phân thức nào sau đây không phải là phân thức đối của phân thức 1 − x ? x −(1 − x) A. x + 1; B. ; C. 1 − x − − ; D. x 1 . x x x x
Câu 9. Đặc điểm nào sau đây là sai đối với hình chóp tam giác đều S.ABC ?
A. Đáy ABC là tam giác đều;
B. SA = SB = SC ;
C. Tam giác SBC là tam giác đều; D. SA ∆ B = SB ∆ C = SC ∆ A .
Câu 10. Diện tích xung quanh của hình chóp S.ABCD
(hình bên) gồm diện tích những mặt nào?
A. Mặt SBC, ABCD, SAB ;
B. Mặt SAB, SBC, SCD, SDA;
C. Mặt SAB, SAD, SBC, ABCD ; D. Mặt ABCD .
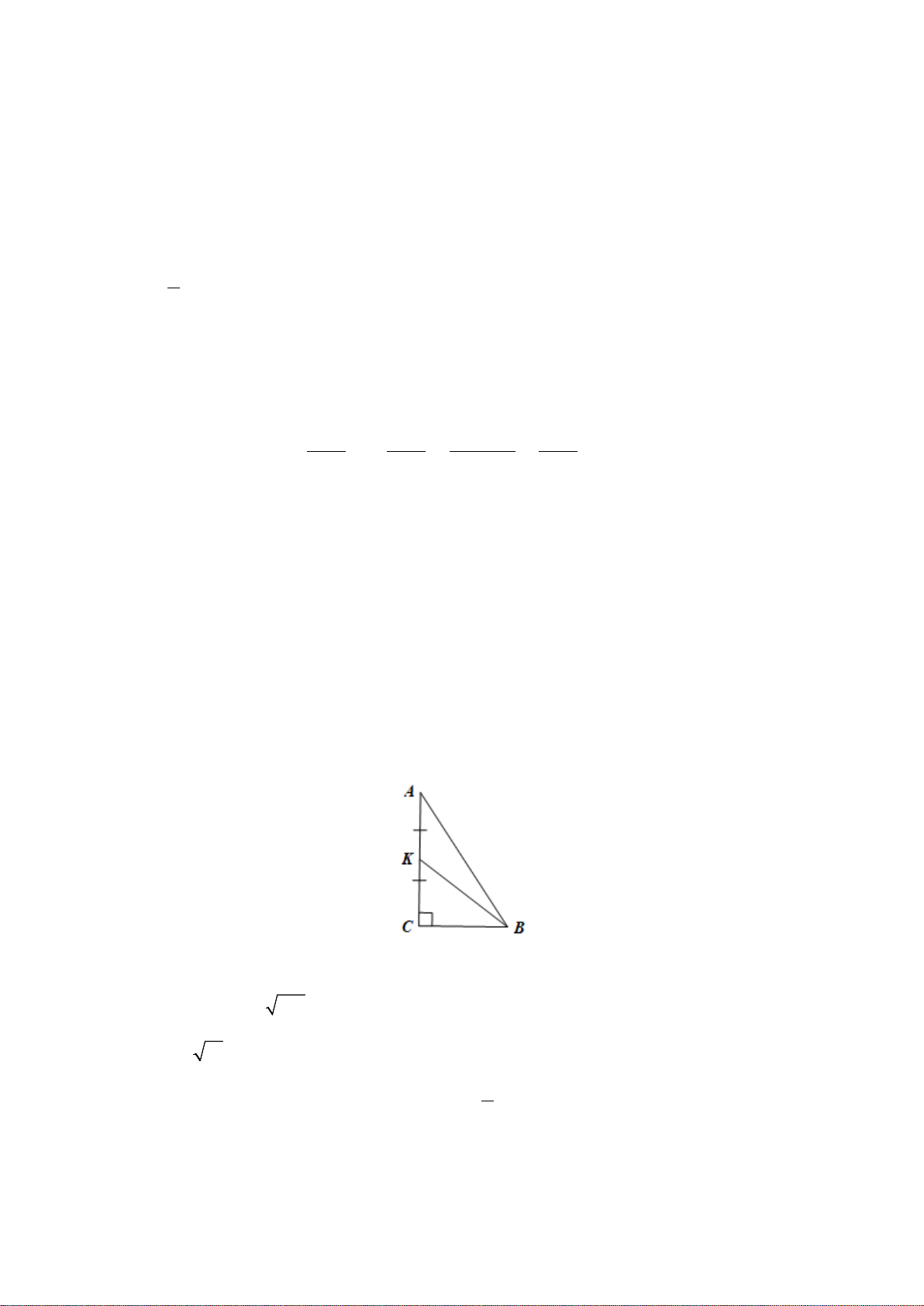
Câu 11. Cho tam giác ABC vuông có cạnh huyền AB = 117 cm, BC = 6 cm. Gọi K là trung
điểm của đoạn thẳng AC . Độ dài BK là A. 3 cm ; B. 4,5 cm ; C. 7,5 cm ; D. 10 cm .
Câu 12. Cho tứ giác ABCD . Khẳng định nào sau đây là sai?
A. AB và BC là hai cạnh kề nhau;
B. BC và AD là hai cạnh đối nhau;
C. A và B là hai góc đối nhau;
D. AC và BD là hai đường chéo.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thu gọn biểu thức: a) ( 2 3 3 2 2
− x y + x y − xy ) 2 9 6 4 : 3xy ; b) 1 xy( 5 3 x y ) 2 1 4 3 x y x y − − − . 2 4
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử:
a) 3x(3 − x) − 6(x − 3) ; b) (x + )2 2 2 1 − 4x ; c) 6 3 2
x + x − x − 1. 2
Bài 3. (1,5 điểm) Cho x + 1 x − 1 x + 4x A = + + với x ≠ 2. ± 2 x − 2 x + 2 4 − x a) Rút gọn biểu thức . A
b) Tính giá trị của A khi x = 4.
c) Tìm giá trị nguyên của x để A nhận giá trị nguyên dương.
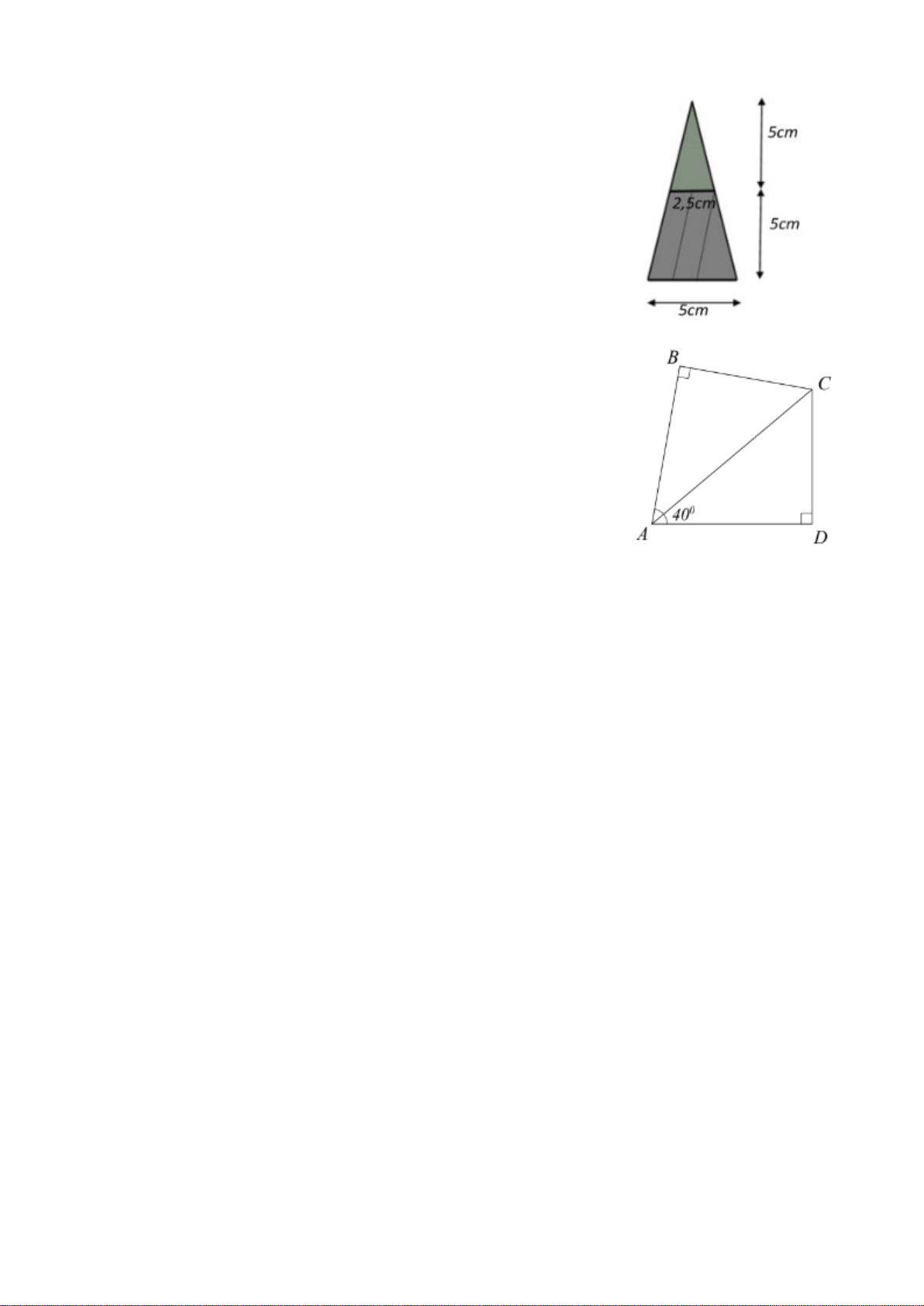
Bài 4. (1,5 điểm) Hình ảnh bên là ảnh của một lọ nước hoa hình kim
tự tháp. Khi đậy nắp, lọ có dạng hình chóp tứ giác đều (tính cả thân lọ
và nắp lọ) trong đó nắp lọ cũng là hình chóp tứ giác đều có chiều cao
5 cm, cạnh đáy 2,5 cm. Chiều cao thân lọ và cạnh đáy lọ đều bằng
chiều cao của nắp lọ. Bỏ qua độ dày của vỏ.
a) Tính thể tích của lọ nước hoa hình kim tự tháp đó.
b) Tính dung tích của lọ nước hoa đó ra đơn vị mi – li – lít (làm tròn
kết quả đến hàng đơn vị).
Bài 5. (1,0 điểm) Một hồ bơi có dạng tứ giác ABCD được mô tả như
hình vẽ bên. Biết AC là tia phân giác BAD và DAC = 40° . a) Tính BC . D
b) Biết AB = 7,66 m và BC = 6,43 m. Một vận động viên bơi lội
muốn bơi từ A đến C trong 20 giây thì cần bơi với vận tốc là bao
nhiêu (làm tròn kết quả đến hàng phần mười)?
Bài 6. (0,5 điểm) Cho x, y thỏa mãn 2 2
x + 2xy + 6x + 6y + 2y + 8 = 0. Tìm giá trị lớn nhất và nhỏ
nhất của biểu thức P = x + y + 2024. -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT103
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A C C A D A D A C B C C
Hướng dẫn giải phần trắc nghiệm Câu 1.
Đáp án đúng là: A
Biểu thức x + 2y 1
= (x + 2y) là đa thức. 3 3 Câu 2.
Đáp án đúng là: C Hai đơn thức 6 4 12x y và 6 4 2
− x y là hai đơn thức đồng dạng vì cùng có hệ số khác 0 và cùng phần biến 6 4 x y . Câu 3.
Đáp án đúng là: C Đa thức 3 2 4 3
7x y z − 2x y chia hết cho 3 2 − x y . Hạng tử 3 2
7x y z không chia hết cho đơn thức 4 3x , 4 3 − x và 3
2xy nên đa thức 3 2 4 3
7x y z − 2x y cũng không chia hết cho 4 3x , 4 3 − x và 3 2xy . Câu 4.
Đáp án đúng là: A Ta có: ( 2
x − x + )(x − ) = (x − )2 (x − ) = (x − )3 3 2 2 1 1 1 1
1 = x − 3x + 3x − 1. Câu 5. Đáp án đúng là: D
Ta có: (x + )2 − (x + ) + = (x + − )2 2 2 4 2 4 2 2 = x . Câu 6.
Đáp án đúng là: A Ta có: 2 2 2 2
14x y − 21xy + 28x y = 7xy(2x − 3y + 4xy) . Câu 7.
Đáp án đúng là: D
Biểu thức x không phải là phân thức đại số. 0 Câu 8.
Đáp án đúng là: A 1 − x −(1 − x)
Phân thức đối của phân thức 1 − x là x − 1 − = = x x x x Vậy phương án A là sai. Câu 9. Đáp án đúng là: C
Hình chóp tam giác đều S.ABC có mặt bên là các tam giác cân nên S
∆ BC là tam giác cân. Câu 10. Đáp án đúng là: B
Diện tích xung quanh của hình chóp S.ABCD gồm diện tích những mặt SAB, SBC, SCD, SD . A Câu 11. Đáp án đúng là: C Xét A
∆ BC vuông tại C , theo định lí Pythagore ta có:
AC = AB − BC = ( )2 2 2 2 2 117 − 6 = 81 Suy ra AC = 81 = 9 cm
Do K là trung điểm của đoạn thẳng AC nên 1
CK = AC = 4,5 cm 2 Xét B
∆ CK vuông tại C , theo định lí Pythagore ta có: 2 2 2 2 2
BK = BC + CK = 6 + 4,5 = 56,25
Suy ra BK = 56,25 = 7,5 cm . Câu 12. Đáp án đúng là: C
Tứ giác ABCD có các cặp góc đối nhau là A và C ; B và D .
Do đó phương án C là khẳng định sai.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) a) ( 2 3 3 2 2
− x y + x y − xy ) 2 9 6 4 : 3xy b) 1 xy( 5 3 x y ) 2 1 4 3 x y x y − − − 2 4 2 3 2 3 2 2 2 2 = 9
− x y : 3xy + 6x y : 3xy − 4xy : 3xy 1 5 1 3 2 1 4 2 3
= xy ⋅ x − xy ⋅ y − x y ⋅ x + x y ⋅ y 2 4 = 3
− xy + 2x − . 2 2 4 3 1 6 1 4 1 6 2 4
= x y − xy − x y + x y 2 2 4 1 6 1 6 1 4 2 4 =
x y − x y − xy + x y 2 4 2 1 6 1 4 2 4
= x y − xy + x y 4 2
Bài 2. (1,5 điểm)
a) 3x(3 − x) − 6(x − 3) b) (x + )2 2 2 1 − 4x c) 6 3 2
x + x − x − 1
= 3x(3 − x) + 6(3 − x) = ( 6 3 x + x ) − ( 2 x + ) 1 = ( 2 x + )2 1 − (2x)2
= (3 − x)(3x + 6) 3 = x ( 2 x + ) − ( 2 1 x + ) 1 = ( 2 x + − x)( 2 1 2 x + 1 + 2x)
= 3(3 − x)(x + 2). = ( 2 x + )( 3 1 x − ) 1
= (x − )2 (x + )2 1 1 . = ( 2 x + )(x − )( 2 1 1 x + x + ) 1 . 2
Bài 3. (1,5 điểm) x + 1 x − 1 x + 4x A = + + với x ≠ 2. ± 2 x − 2 x + 2 4 − x a) Với x ≠ 2 ± , ta có: 2 x + 1 x − 1 x + 4x A = + + 2 x − 2 x + 2 4 − x 2 x + 1 x − 1 x + 4x = + − x − 2
x + 2 (x − 2)(x + 2)
(x + )(x + ) (x − )(x − ) 2 1 2 1 2 x + 4x = ( + −
x − 2)(x + 2) (x − 2)(x + 2) (x − 2)(x + 2) 2 2 2
x + 3x + 2 + x − 3x + 2 − x − 4x = ( x − 2)(x + 2) x − 4x + 4 (x − )2 2 2 x − 2 = ( = = . x − 2)(x + 2)
(x − 2)(x + 2) x + 2 Vậy với x ≠ 2 ± ta có x − 2 A = . x + 2
b) Thay x = 4 (thỏa mãn) vào biểu thức A ta có: 4 2 2 1 A − = = = . 4 + 2 6 3 c) Với x ≠ 2 ± và x ∈ − + − ta có: x 2 x 2 4 4 A = = = 1 − x + 2 x + 2 x + 2
Để A nhận giá trị nguyên thì x + 2 ∈Ư(4) = { 1 ± ; 2 ± ;± } 4 Ta có bảng sau: x + 2 1 − 1 2 − 2 4 − 4 x 2 3 − 0 6 − (x 1 − 4 − ≠ 2 ± và (không
(thỏa mãn) (thỏa mãn) (thỏa mãn) (thỏa mãn) (thỏa mãn) x ∈ ) thỏa mãn) x − 2 A = x 3 − + 2 1 − 5 3 2 (A nguyên (không (không (thỏa mãn) (thỏa mãn) (thỏa mãn) thỏa mãn) thỏa mãn) dương) Vậy x ∈ { 3 − ; 4 − ;− } 6 .
Bài 4. (1,5 điểm)
a) Thể tích của lọ nước hoa hình kim tự tháp là: 1 2 250 V = ⋅ 5 ⋅ 10 = ( 3 cm . 1 ) 3 3
b) Thể tích của nắp lọ nước hoa là: 1 2 125 V = ⋅ 2,5 ⋅ 5 = ( 3 cm . 1 ) 3 12
Dung tích của lọ nước hoa đó là: 250 125 3 − ≈ 73 cm = 73 ml . 3 12
Bài 5. (1,0 điểm)
a) Do AC là tia phân giác
BAD nên ta có =
BAD 2DAC = 2 ⋅ 40° = 80°
Xét tứ giác ABCD có: + + + BAD B BCD D = 360° Suy ra = ° − + + BCD 360
(BAD B D ) = 360° − (80° − 90° − 90°) = 100°. b) Xét A
∆ BC vuông tại B , theo định lí Pythagore ta có: 2 2 2 2 2
AC = AB + BC = 7,66 + 6,43 = 100,0205
Suy ra AC = 100,0205 ≈ 10,0 m.
Khi đó vận động viên cần bơi với vận tốc là 10,0 = 0,5 (m/s). 20
Bài 6. (0,5 điểm) Ta có: 2 2
x + 2xy + 6x + 6y + 2y + 8 = 0 ( 2 2
x + xy + y ) + (x + y) 2 2 6 + 9 + y − 1 = 0
(x + y)2 + (x + y) 2 6 + 9 − 1 = −y (x + y + )2 2 3 − 1 = −y
(x + y + − )(x + y + + ) 2 3 1 3 1 = −y
(x + y + )(x + y + ) 2 2 4 = −y (x + y + − )(x + y + − ) 2 2024 2022 2024 2020 = −y (P − )(P − ) 2 2022 2020 = −y (P − )(P − ) 2 2022 2020 = −y Mà 2 y ≥ 0 nên 2
−y ≤ 0 với mọi y
Do đó (P − 2022)(P − 2020) ≤ 0 (*)
Lại có (P − 2020) − 2 < P − 2020 hay P − 2022 < P − 2020
Suy ra (*) xảy ra khi P − 2022 ≤ 0 ≤ P − 2020
Nên 2020 ≤ P ≤ 2022 x + y + 2 = 0 x = 2 −
Vậy GTLN của P bằng 2022 khi , tức ; 2 − y = 0 y = 0 x + y + 4 = 0 x = 4 −
GTNN của P bằng 2020 khi , tức . 2 − y = 0 y = 0 -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 04
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 1 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (0,5đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 2 1 2 1 1
đa thức thành nhân tử (0,5đ) (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 20%
trực quan tứ giác đều (0,5đ) (0,5đ) (1,0đ) Định lí 1 1 Định lí Pythagore 4 Pythagore. (0,25đ) (0,5đ) 15% Tứ giác Tứ giác 1 1 (0,25đ) (0,5đ)
Tổng: Số câu 8 1 4 6 5 1 25 Điểm (2,0đ) (0,5đ) (1,0đ) (3,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 25% 40% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 1TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 2TN 1TN, 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, 2TL thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TN 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TN 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT104
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Đa thức nào sau đây chưa thu gọn? A. 2
4x + x − y ; B. 4 4
x y + x − 2yx ; + C. 3 2 2 −x y + y ; D. x 2y . 5 5
Câu 2. Tích của hai đơn thức 1 3
xy và x(− y) 2
8 xz có phần hệ số là 2 A. 1 ; B. 8 − ; C. 4 − ; D. 7 . 2 Câu 3. Biết 2 2 2
M + 5x − 2xy = 6x + 10xy − y . Đa thức M là A. 2 2
M = x + 12xy − y ; B. 2 2
M = x − 12xy − y ; C. 2 2
M = x − 12xy + y ; D. 2 2
M = −x − 12xy + y .
Câu 4. Các đơn thức điền vào ô trống trong khai triển (a + )3 2 2 2
= a + 9a b + 27ab + lần lượt là A. 3b và 3 3b ; B. b và 3 3b ; C. 3b và 3 27b ; D. 3b và 2 9b .
Câu 5. Kết quả của biểu thức (x − )2 − (x + )2 5 5 là A. 20 − x B. 50 C. 20x ; D. 2 2x + 50 .
Câu 6. Phân tích đa thức 3 2
x − 2x + x thành nhân tử ta được A. x(x − )2 1 ; B. 2 x (x − ) 1 ; C. x( 2 x − ) 1 ; D. x(x + )2 1 .
Câu 7. Đâu là tính chất đúng của phân thức đại số? ⋅ ⋅ A. A A M = (B,M ≠ 0); B. A A M = (B,M ≠ 0); B B ⋅ M B B ⋅ C. A A = (B,M ≠ 0); D. A A M =
(B,M ≠ 0, N ≠ M ) . B B ⋅ M B B ⋅ N
Câu 8. Thực hiện phép tính x − 1 1 − y + ta được kết quả là x − y y − x A. − + + − 0 ; B. x y 2 ; C. x y 2 ; D. 1. x − y x − y
Câu 9. Hình chóp tứ giác đều có bao nhiêu đường trung đoạn? A. 1; B. 2 ; C. 3; D. 4 .
Câu 10. Hình chóp tam giác đều và hình chóp tứ giác đều có chung đặc điểm nào sau đây?
A. Đáy là tam giác đều; B. Đáy là hình vuông;
C. Các cạnh bên bằng nhau;
D. Mặt bên là các tam giác đều.
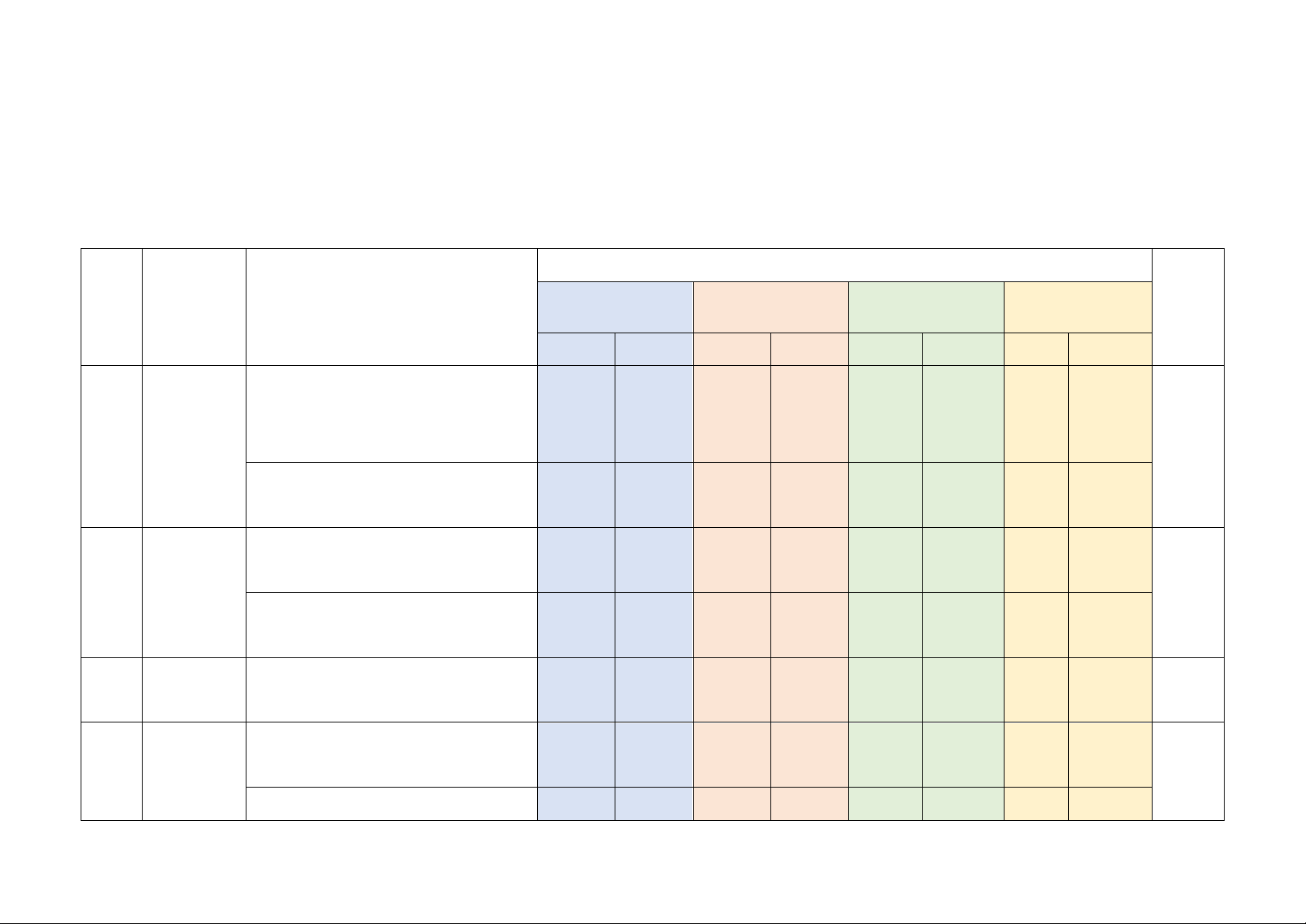
Câu 11. Cho tam giác ABC có đường cao AH. Biết AC = 15 cm, AH = 12 cm, BH = 9 cm. Hỏi
tam giác ABC là tam giác gì?
A. Tam giác vuông; B. Tam giác cân; C. Tam giác đều; D. Tam giác tù.
Câu 12. Các góc của tứ giác có thể là A. 4 góc nhọn; B. 4 góc tù;
C. 2 góc vuông, 1 góc nhọn và 1 góc tù;
D. 1 góc vuông và 3 góc nhọn.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thu gọn biểu thức: a) ( 4 3 2 3 4 4 x y − x y − x y ) 2 3 30 25 3 : 5x y ; b) 3 4 x y ( 2 3 x − y ) 3 3 − x y ( 4 4 2 2 x − y ).
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 2
5x (x − y) − 15xy( y − x) ;
b) (x + y)2 − 6(x + y) + 9 ; c) 2 x − 5x + 6 .
Bài 3. (1,5 điểm) Cho 1 x 2x + 1 P = + + với x ≠ 1. 2 3
x − 1 x + x + 1 1 − x a) Rút gọn biểu thức . P
b) Tính giá trị của biểu thức P tại x = 2.
c) Chứng minh P > 0 với x > 0, x ≠ 1.
Bài 4. (1,5 điểm) Vẽ, cắt và gấp mảnh bìa như đã chỉ ra ở hình bên dưới để được hình chóp tứ giác đều.
a) Trong hình vẽ trên có bao nhiêu tam giác cân bằng nhau?
b) Tính diện tích tất cả các mặt của hình chóp tứ giác đều này. Biết độ dài trung đoạn của
hình chóp tứ giác đều là 9,68 cm.
Bài 5. (1,0 điểm)
a) Tìm x trong hình vẽ bên.
b) Một công ty muốn làm một đường ống dẫn từ nhà
máy C trên bờ đến một điểm B trên đất liền. Điểm
A đảo cách bờ biển ở điểm B là 9 km. Giá để xây
dựng đường ống từ nhà máy trên biển điểm B đến
diểm C trên bờ là 5 000 USD / km. Khoảng cách từ
A đến C là 12 km. Em hãy tính chi phí làm đường
ống từ điểm B tới điểm C của công ty trên bằng tiền
VNĐ. Biết 1 USD = 23 150 VNĐ tại thời điểm đó.
Bài 6. (0,5 điểm) Cho x, y, z là ba số thỏa mãn điều kiện: 2 2 2
4x + 2y + 2z − 4xy − 4xz + 2yz − 6y − 10z + 34 = 0.
Tính giá trị của biểu thức S = (x − )2023 + ( y − )2025 + (z − )2027 4 4 4 . -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT104
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B C A C A A A C D C B C
Hướng dẫn giải phần trắc nghiệm Câu 1.
Đáp án đúng là: B Ta có: 4 4 4 4 4
x y + x − 2yx = x y − 2x y + x = −x y + x Vậy đa thức 4 4
x y + x − 2yx là đa thức chưa thu gọn. Câu 2.
Đáp án đúng là: C Ta có: 1 3 xy ⋅ x( 8 − y) 2 3 4 2 xz = 4
− x y z , đa thức này có phần hệ số là 4 − . 2 Câu 3.
Đáp án đúng là: A Ta có: 2 2 2
M + 5x − 2xy = 6x + 10xy − y Suy ra 2 2 2
M = 6x + 10xy − y − 5x + 2xy Do đó 2 2
M = x + 12xy − y . Câu 4.
Đáp án đúng là: C
Ta có: (a + b )3 2 2 2 3 3
= a + 9a b + 27ab + 27b . Câu 5. Đáp án đúng là: A
Ta có: (x − )2 − (x + )2 5
5 = (x − 5 + x + 5)(x − 5 − x − 5) = 2x ⋅ ( 10 − ) = 20 − x . Câu 6.
Đáp án đúng là: A Ta có: 3 2
x − x + x = x( 2 2 x − 2x + ) 1 = x(x − )2 1 . Câu 7. Đáp án đúng là: A ⋅
Với B, M ≠ 0 ta có: A A M = . B B ⋅ M Câu 8. Đáp án đúng là: C
Ta có: x − 1 1 − y x − 1 1 − y
x − 1 − 1 + y x + y − 2 + = − = = . x − y y − x x − y x − y x − y x − y Câu 9. Đáp án đúng là: D
Hình chóp tứ giác đều có 4 mặt bên nên có 4 đường trung đoạn. Câu 10. Đáp án đúng là: C
Hình chóp tam giác đều có đáy là tam giác đều, hình chóp tứ giác đều có đáy là hình vuông.
Hình chóp tam giác đều và hình chóp tứ giác đều có mặt bên là tam giác cân.
Hình chóp tam giác đều và hình chóp tứ giác đều có các cạnh bên bằng nhau.
Câu 11. Cho tam giác ABC có đường cao AH. Biết AC = 15 cm, AH = 12 cm, BH = 9 cm. Hỏi
tam giác ABC là tam giác gì? A. Tam giác cân;
B. Tam giác vuông; C. Tam giác cân; D. Tam giác tù.
Đáp án đúng là: B Xét A
∆ HC vuông tại H , theo định lí Pythagore ta có 2 2 2 2 2
CH = AC − AH = 15 − 12 = 81 Do đó CH = 81 = 9 cm
Suy ra BH = CH = 9 cm hay H là trung điểm của BC
Tam giác ABC có đường cao AH đồng thời là đường trung tuyến nên A
∆ BC cân tại A . Câu 12. Đáp án đúng là: C
Giả sử có một tứ giác có 4 góc nhọn có số đo nhỏ hơn 90° , khi đó tổng số đo các góc của tứ giác nhỏ
hơn 4 ⋅ 90° = 360°, điều này mâu thuẫn với định lí tổng số đo các góc của tứ giác bằng 360° . Như
vậy, không tồn tại tứ giá có 4 góc nhọn.
Tương tự như vậy, cũng không tồn tại tứ giác có 4 góc tù.
Giả sử có một tứ giác có 1 góc vuông, 3 góc nhọn, khi đó tổng số đo các góc của tứ giác cũng nhỏ
hơn 90° + 3 ⋅ 90° = 360°. Vậy không tồn tại tứ giác như vậy. Ta chọn phương án C.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) a) ( 4 3 2 3 4 4 x y − x y − x y ) 2 3 30 25 3 : 5x y b) 3 4 x y ( 2 3 x − y ) 3 3 − x y ( 4 4 2 2 x − y ) 4 3 2 3 2 3 2 3 4 4 2 3
= 30x y : 5x y − 25x y : 5x y − 3x y : 5x y 3 4 2 3 4 3 3 3 4 3 3 4
= x y ⋅ x − x y ⋅ 2y − 2x y ⋅ x + 2x y ⋅ y 5 4 3 7 7 3 3 7 2 3 2
= 6x − 5 − x . y
= x y − 2x y − 2x y + 2x y 5 5 4 7 3
= x y − 2x y .
Bài 2. (1,5 điểm) a) 2
5x (x − y) − 15xy( y − x)
b) (x + y)2 − 6(x + y) + 9 c) 2 x − 5x + 6 2 2
= 5x (x − y) + 15xy(x − y)
= x − 2x − 3x + 6 = (x + y − )2 3 . = ( 2
x − 2x) − (3x − 6) = (x − y)( 2 5x + 15xy)
= x(x − 2) − 3(x − 2)
= 5x(x − y)(x + 3y).
= (x − 2)(x − 3) .
Bài 3. (1,5 điểm) 1 x 2x + 1 P = + + 2 3
x − 1 x + x + 1 1 − x
a) Với x ≠ 1 ta có: 1 x 2x + 1 P = + + 2 3
x − 1 x + x + 1 1 − x 1 x 2x + 1 = + − 2
x − 1 x + x + 1 (x − ) 1 ( 2 x + x + ) 1 2
x + x + 1 + x(x − ) 1 − 2x − 1 = ( x − ) 1 ( 2 x + x + ) 1 2 2
x + x + 1 + x − x − 2x − 1 = ( x − ) 1 ( 2 x + x + ) 1 2 2x − 2x 2x(x − ) 1 = ( = x − ) 1 ( 2 x + x + ) 1 (x − ) 1 ( 2 x + x + ) 1 2x = . 2 x + x + 1
b) Với x = 2 (thỏa mãn) thay vào biểu thức P ta được: 2 2 4 P ⋅ = = . 2 2 + 2 + 1 7
c) Với x > 0, x ≠ 1 ta có: ⦁ 2x > 0; 2 ⦁ 2 2 1 3 1 3
x + x + 1 = x + x + + = x + + > 0. 4 4 2 4 Do đó 2x P = > 0 . 2 1 3 x + + 2 4
Bài 4. (1,5 điểm)
a) Trong hình vẽ bên dưới có 4 tam giác cân bằng nhau.
b) Diện tích xung quanh của hình chóp tứ giác đều là: 1 1 S = C d = = . xq . . .(5.4).9,68 96,8 ( 2 cm ) 2 2
Diện tích tất cả các mặt của hình chóp tứ giác đều là: 2 + = ( 2 96,8 5 121,8 cm ).
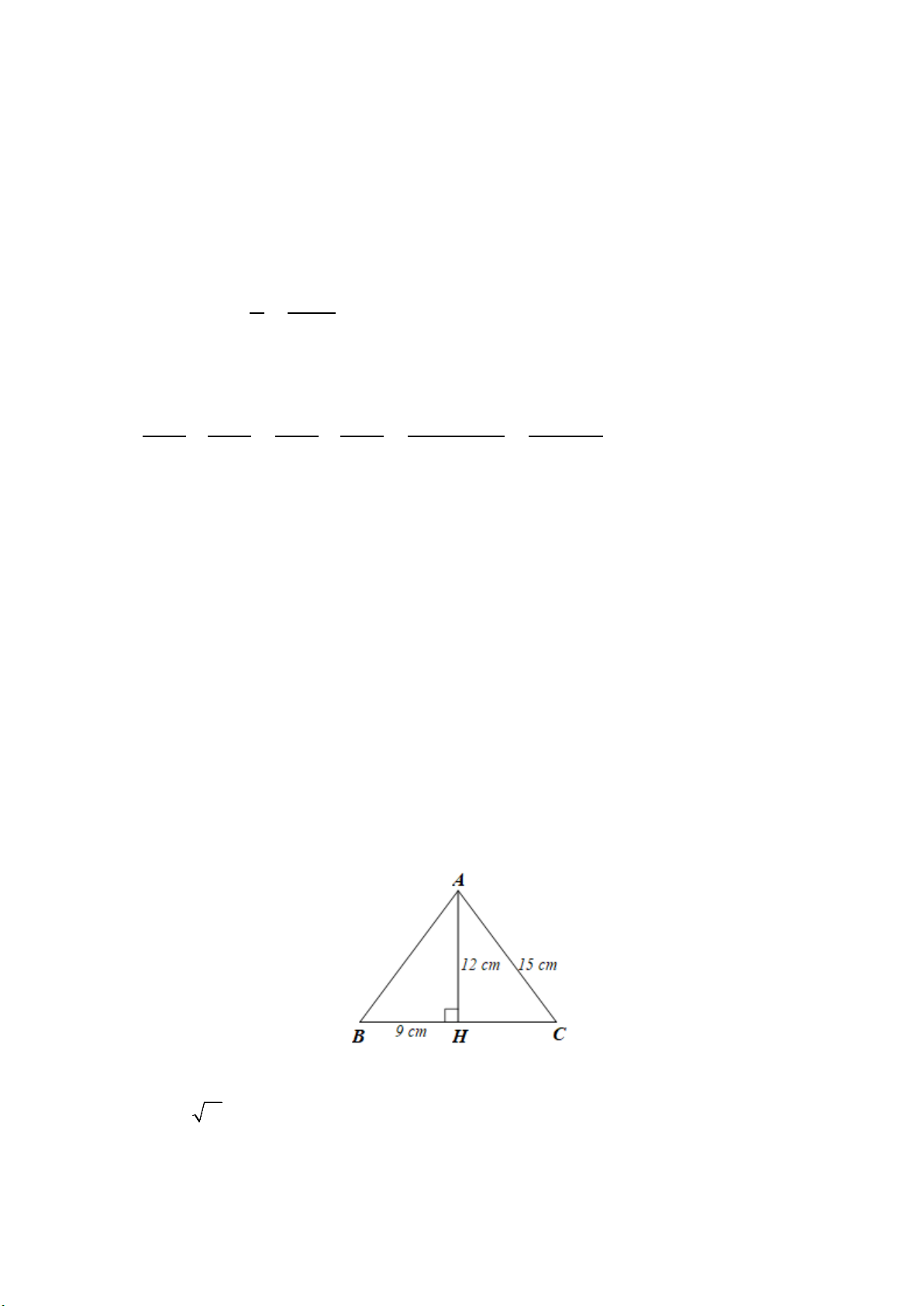
Bài 5. (1,0 điểm)
a) Vì góc ngoài tại K có số đo là 100° nên
IKL = 180° − 100° = 80°.
Góc ngoài tại L có số đo là 60° nên
KLR = 180° − 60° = 120°.
Ta có tổng các góc trong tứ giác là 360° nên + + + IKL KLR R I = 360°
Suy ra 80° + 120° + 90° + x = 360° Do đó x = 70°.
b) Áp dụng định lý Pythagore vào tam giác vuông ABC vuông tại B ta có: 2 2 2
AC = AB + BC Suy ra 2 2 2 2
BC = AC − AB = 12 − 9 = 63 (km).
Chi phí làm đường ống từ B tới điểm C của công ty trên bằng tiền VNĐ là:
63 ⋅5 000⋅23 150 ≈ 918 737 142,8 (VNĐ).
Bài 6. (0,5 điểm) Ta có: 2 2 2
4x + 2y + 2z − 4xy − 4xz + 2yz − 6y − 10z + 34 = 0 2
x − x( y + z) + ( 2 2
y + yz + z ) 2 4 4 2
+ z − 6y − 10z + 34 = 0 2
x − x( y + z) + ( y + z)2 + ( 2y − y + ) + ( 2 4 4 6 9
z − 10z + 25) = 0
( x − y − z)2 + ( y − )2 + (z − )2 2 3 5 = 0 (*)
Với mọi x, y, z ta có: ( x − y − z)2 ≥ ( y − )2 ≥ (z − )2 2 0, 3 0, 5 ≥ 0 (
2x − y − z)2 = 0
Do đó (*) xảy ra khi và chỉ khi ( y − 3)2 = 0 ( z − 5)2 = 0
2x − y − z = 0 x = 4 Hay y − 3 = 0 , tức là y = 3 z − 5 = 0 z = 5
Khi đó S = ( − )2023 + ( − )2025 + ( − )2027 4 4 3 4 5 4 = 0 − 1 + 1 = 0. -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 05
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 1 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (0,5đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 2 1 2 1 1
đa thức thành nhân tử (0,5đ) (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 20%
trực quan tứ giác đều (0,5đ) (0,5đ) (1,0đ) Định lí 1 1 Định lí Pythagore 4 Pythagore. (0,25đ) (0,5đ) 15% Tứ giác Tứ giác 1 1 (0,25đ) (0,5đ)
Tổng: Số câu 8 1 4 6 5 1 25 Điểm (2,0đ) (0,5đ) (1,0đ) (3,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 25% 40% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 1TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 2TN 1TN, 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, 2TL thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TN 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TN 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT105
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Trong các biểu thức sau, biểu thức nào không là đơn thức? A. (x + ) 1 y ; B. 2 1 2x − y ; C. 2 x zt ; D. 0 . 2
Câu 2. Đơn thức nào sau đây đồng dạng với đơn thức 2 3 − x y ? A. 1 xyx ; B. 2 3x yz ; C. 2 xy ; D. 2 3 − x z . 2
Câu 3. Giá trị của biểu thức 1 2 2 2 S = 6
− xy x yz + 2zxy x khi x = 2
− , y = 1, z = 1 − là 2 A. S = 8; B. S = 8 − ; C. S = 4 − ; D. S = 4 . Câu 4. Đa thức 2 4
− x + 12x − 9 được viết thành
A. (2x − 3)(2x + 3) ; B. −( x − )2 2 3 ; C. ( − )2 3 2x ; D. −( x + )2 2 3 .
Câu 5. Biểu thức (x − y)( 2 2 2
x + 2xy + 4y ) là dạng phân tích nhân tử của đa thức A. (x − y)3 2 ; B. (x + y)3 2 ; C. 3 3 x − 8y ; D. 3 3 x + 8y .
Câu 6. Tổng các trị của x thỏa mãn 3x(x − 2) − x + 2 = 0 là A. 7 − ; B. 5 − ; C. 5 ; D. 7 . 3 3 3 3
Câu 7. Phân thức 1 − x bằng với phân thức nào sau đây? y − x A. x − 1 ; B. 1 − x ; C. x − 1 ; D. y − x . y − x x − y x − y 1 − x
Câu 8. Kết quả của phép tính 5x + 7 2x − 5 − là 3xy 3xy A. 3x + 2 ; B. 3x − 2 ; C. x − 4 ; D. x + 4 . 3xy 3xy xy xy
Câu 9. Hình chóp tam giác đều có bao nhiêu mặt? A. 3; B. 4 ; C. 5; D. 6 .
Câu 10. Hình chóp tam giác đều và hình chóp tứ giác đều không có chung đặc điểm nào sau đây?
A. Các cạnh đáy bằng nhau;
B. Mặt đáy là hình vuông;
C. Các cạnh bên bằng nhau;
D. Mặt bên là các tam giác cân.
Câu 11. Cho tam giác ABC cân tại A có đường cao AH. Cho AH = 4 cm, AB = 5 cm. Chu vi tam giác ABC bằng A. 12 cm ; B. 15 cm ; C. 16 cm ; D. 18 cm .
Câu 12. Khẳng định nào sau đây là đúng?
A. Tứ giác có 4 đường chéo;
B. Tổng các góc của một tứ giác bằng 180°;
C. Tồn tại một tứ giác có 1 góc tù và 3 góc vuông;
D. Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Thu gọn biểu thức: a) 3 3 3 1 2 2 x y : x y − ; b) ( 2 3 4 4 x y − x y ) 2 x y − ( 2 − x y)( 2 9 15 : 3 1 3 y − ) 1 . 4 2
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) x(x + ) 2 2
2 + x (−x − 2) ; b) 6 x − 1; c) 2 2x − 3x + 1. 2
Bài 3. (1,5 điểm) Cho biểu thức 4 + A 2 2x 4x = và B = + với x ≠ 1. 2 x + x + 1 3 1 − x x − 1
a) Tính giá trị của biểu thức A khi x = 2. −
b) Tìm biểu thức C biết A = B + C .
c) Chứng minh giá trị của biểu thức C luôn nhận giá trị dương với mọi x ≠ 0, x ≠ 1.
Bài 4. (1,5 điểm) Một khối rubik có dạng hình chóp tam giác đều (các mặt khối rubic là các tam giác
đều bằng nhau), có chu vi đáy bằng 234 mm, đường cao của mặt
bên hình chóp là 67,5 mm .
a) Tính diện tích xung quanh, diện tích toàn phần (tổng diện
tích các mặt) của khối rubik đó.
b) Biết chiều cao của khối rubik là 63,7 mm. Tính thể tích của khối rubik đó.
Bài 5. (1,0 điểm)
a) Cho tứ giác ABCD , biết rằng A B C D = = = . Tính B . 1 2 3 4
b) Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo
của màn hình điện thoại, biết 1 inch ≈ 2,54 cm, điện thoại có chiều rộng là 7 cm; chiều dài là
15,5 cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị)
Bài 6. (0,5 điểm) Cho các số x, y thỏa mãn 2 2
2x + 10y − 6xy − 6x − 2y + 10 = 0. Tính giá trị của (x + y − )2024 2024 4 − y biểu thức A = . x -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT105
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A A B B C D C D B B C D
Hướng dẫn giải phần trắc nghiệm Câu 1.
Đáp án đúng là: A Biểu thức (x + )
1 y không là đơn thức. Câu 2.
Đáp án đúng là: A Ta có: 1 1 2
xyx = x y , đơn thức này đồng dạng với đơn thức 2 3 − x y . 2 2 Câu 3.
Đáp án đúng là: B Ta có: 1 2 2 2 3 2 3 2 3 2 S = 6
− xy x yz + 2zxy x = 3
− x y z + 2x y z = −x y z 2 Thay x = 2
− , y = 1, z = 1 − vào biểu thức 3 2 −x y z ta được: S = −(− )3 2 2 ⋅ 1 ⋅ (− ) 1 = 8. − Câu 4. Đáp án đúng là: B Ta có: 2
− x + x − = −( 2 4 12 9
4x − 12x + 9) = −(2x − 3)2 . Câu 5. Đáp án đúng là: C
Ta có: (x − y)( 2 2
x + xy + y ) 3 = x − ( y)3 3 3 2 2 4 2 = x − 8y . Câu 6.
Đáp án đúng là: D
Ta có: 3x(x − 2) − x + 2 = 0
3x(x − 2) − (x − 2) = 0
(x − 2)(3x − )1 = 0
x − 2 = 0 hoặc 3x − 1 = 0 x = 2 hoặc 1 x = . 3
Vậy tổng các giá trị của x là: 1 7 2 + = . 3 3 Câu 7. Đáp án đúng là: C 1 − x −(x − ) 1 Ta có: x − 1 = = . y − x −(x − y) x − y Câu 8. Đáp án đúng là: D 5x + 7 2x − 5
5x + 7 − 2x + 5 3x + 12 3(x + 4) Ta có: x + 4 − = = = = . 3xy 3xy 3xy 3xy 3xy xy Câu 9. Đáp án đúng là: B
Hình chóp tam giác đều có 4 mặt. Câu 10.
Đáp án đúng là: B
Hình chóp tam giác đều có mặt đáy là tam giác đều, hình chóp tứ giác đều có mặt đáy là hình vuông. Câu 11. Đáp án đúng là: C Xét A
∆ BH vuông tại H , theo định lí Pythagore ta có: 2 2 2 2 2
BH = AB − AH = 5 − 4 = 9 Do đó BH = 9 = 3 cm.
Do tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến
Do đó BH = CH nên BC = 2BH = 2 ⋅ 3 = 6 cm. Mà A
∆ BC cân tại A nên AC = AB = 5 cm
Vậy chu vi tam giác ABC bằng 5 + 5 + 6 = 16 cm. Câu 12. Đáp án đúng là: D
Tứ giác có 2 đường chéo, tổng các góc bằng 360 .°
Giả sử có tứ giác có 1 góc tù và 3 góc vuông khi đó tổng số đo các góc của tứ giác này là lớn hơn
90° + 3 ⋅ 90° = 360°, điều này mâu thuẫn với định lí tổng các góc của một tứ giác.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) 2 3 4 4 2 2 2 a) 3 3 3 1 2 2 x y :
b) (9x y − 15x y ) : 3x y − (1 − 3x y)( y − ) 1 x y − 4 2 2 3 2 4 4 2 = x y x y − x y x y − ( 2 y − ) 2 + x y ( 2 9 : 3 15 : 3 1 3 y − ) 1 3 1 = : − ⋅ ( 3 2 x : x ) ⋅ ( 3 2 y : y ) 4 2 2 2 3 2 2 3 2
= 3y − 5x y − y + 1 + 3x y − 3x y 3 2 2 3 2 = − x . y
= 2y − 2x y + 1 − 3x . y 2
Bài 2. (1,5 điểm) a) x(x + ) 2 2
2 + x (−x − 2) b) 6 x − 1 c) 2 2x − 3x + 1 2 = x(x + ) 2 2 2 − x (x + 2) = (x )2 3 2 − 1
= 2x − 2x − x + 1 = ( 2
2x − 2x) − (x − ) 1 = (x + )( 2 2 2x − x ). = ( 3 x − )( 3 1 x + ) 1 = 2x(x − ) 1 − (x − ) 1 = (x − )( 2
x + x + )(x + )( 2 1 1 1 x − x + ) 1 . = (x − ) 1 (2x − ) 1 . 2
Bài 3. (1,5 điểm) 4 + A 2 2x 4x = và B = +
với x ≠ 0, x ≠ 1. 2 x + x + 1 3 1 − x x − 1 a) Thay x = 2
− (thỏa mãn) vào biểu thức A ta được: 4 4 4 A = = = . ( 2 − )2 + ( 2 − ) + 1 4 − 2 + 1 3
b) Ta có A = B + C nên C = A − B 2 4 2 2x + 4x C = − + 2 3 x x 1 1 x x 1 + + − − 2 4 2 2x + 4x = − − 2 3
x + x + 1 1 − x x − 1 2 4 2 2x + 4x = + − 2
x + x + 1 x − 1 (x − ) 1 ( 2 x + x + ) 1 4(x − ) 1 + 2( 2 x + x + ) 1 − ( 2 2x + 4x) = ( x − ) 1 ( 2 x + x + ) 1 2 2
4x − 4 + 2x + 2x + 2 − 2x − 4x = ( x − ) 1 ( 2 x + x + ) 1 2x − 2 = ( x − ) 1 ( 2 x + x + ) 1 2(x − ) 1 = 2 ( = x − ) 1 ( 2 x + x + ) 1 2 x + x + 1
Vậy với x ≠ 1 ta có 2 C = . 2 x + x + 1
c) Với x ≠ 1 ta có 2 2 2 C = = = 2 2 x + x + 1 2 1 1 3 1 3 x + 2. . x + + 2 4 4 x + + 2 4 2 2 Mà 1 x 2 + ≥ 1 3 0 nên x + + > 0 , do đó C =
> 0 với mọi x ≠ 1. 2 2 4 2 1 3 x + + 2 4
Bài 4. (1,5 điểm)
a) Đường cao mặt bên hình chóp chính là trung đoạn d = 67,5 mm
Diện tích xung quanh của khối rubik đó là: 1 1 S = C d = = xq . . .234.67,5 7897,5 ( 2 cm ). 2 2
Đáy là tam giác đều có cạnh là 234 : 3 = 78 cm;
Chiều cao của tam giác đáy là 67,5 cm.
Diện tích toàn phần của khối rubik đó là: 1 S = + = tp 7897,5 78.67,5 10530 ( 2 cm ) 2
b) Thể tích của khối rubik đó là: 1 1 V . .78.67,5 = .63,7 = 55896,75 ( 2 cm ). 3 2
Bài 5. (1,0 điểm)
a) Xét tứ giác ABCD có + + + A B C D = 360°
Áp dụng tính chất dãy tỉ số bằng nhau + + + A B C D A B C D 360° = = = = = = 36 .° 1 2 3 4 1 + 2 + 3 + 4 10 Vậy
B = 36° ⋅ 2 = 72 .°
b) Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: 2 2 2
BC = AC + AB
Suy ra BC = AC + AB = ( )2 2 2 2 15,5 + 7 ≈17 (cm).
Vì 1 inch ≈ 2,54 cm nên chiếc điện thoại theo hình vẽ có : 17 ≈ 7 inch. 2,54
Bài 6. (0,5 điểm) Ta có: 2 2
2x + 10y − 6xy − 6x − 2y + 10 = 0 ( 2 2
x − xy + y ) + ( 2
x − x + ) + ( 2 6 9 6 9 y − 2y + ) 1 = 0
(x − y)2 + (x − )2 + ( y − )2 3 3 1 = 0 (*)
Với mọi x, y ta có: (x − y)2 ≥ (x − )2 ≥ ( y − )2 3 0, 3 0, 1 ≥ 0 (
x − 3y)2 = 0
Do đó (*) xảy ra khi và chỉ khi ( x − 3)2 = 0 ( y − )2 1 = 0 x − 3y = 0 x = 3
Hay x − 3 = 0 , tức là y = 1 y − 1 = 0 (x + y − )2024 2024 − y ( + − )2024 2024 4 3 1 4 − 1 Khi đó 0 − 1 1 A = = = = − . x 3 3 3 -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 06
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 2 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (1,0đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 1 2 1 1
đa thức thành nhân tử (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 15%
trực quan tứ giác đều (0,5đ) (0,5đ) (0,5đ) Định lí 1 Định lí Pythagore 4 Pythagore. (1,0đ) 20% Tứ giác Tứ giác 1 (1,0đ)
Tổng: Số câu 6 1 2 7 5 1 22 Điểm (1,5đ) (0,5đ) (0,5đ) (4,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 20% 45% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 2TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 1TN 2TL 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT201
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Biểu thức nào sau đây là đơn thức thu gọn? A. 2 5 − xy ; B. xyz + xz ; C. ( 2 2 2 x + y ); D. 3 − x4yxz .
Câu 2. Có bao nhiêu nhóm đơn thức đồng dạng với nhau trong các đơn thức sau: 2 3 2 2 2 3 3 1 2
− x y; − xy ; 5x y; 6xy ;2x y; ; x y ? 3 4 2 A. 2; B. 3; C. 4; D. 5.
Câu 3. Cho biểu thức 3 3 A = 2
− y + 2x + 8y − 35 − x . Giá trị của biểu thức A tại x = 3, y = 4 − là A. 32 − ; B. 28 − ; C. 16; D. 86 .
Câu 4. Hằng đẳng thức ( A − B)2 2 2
= A − 2AB + B có tên là
A. bình phương của một tổng;
B. bình phương của một hiệu; C. tổng hai bình phương; D. hiệu hai bình phương.
Câu 5. Khẳng định nào sau đây là đúng?
Với đa thức B khác 0 ta có A. A −A − − = ; B. A A = ; C. A A = ; D. A A = − . B −B B −B B B B −B 3
Câu 6. Kết quả của phép tính x − x là 2 x − 1 A. −x ; B. x ; C. 2 − x ; D. 2x .
Câu 7. Hình chóp tứ giác đều có đáy là A. hình thoi; B. hình vuông; C. tam giác đều; D. tam giác.
Câu 8. Thể tích của hình chóp tam giác đều bằng
A. diện tích đáy nhân với chiều cao;
B. 1 diện tích đáy nhân với chiều cao; 3
C. 1 chiều cao nhân với diện tích đáy;
D. 3 diện tích đáy nhân với chiều cao. 2 2
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Thu gọn biểu thức: a) 3 24xy : (6xy);
b) x(x − y) − y( 2 y − x); c) ( 2 2 2
6x y − 9xy ) : (3xy) − (x + 3)(2y − ) 1 .
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 3 2 3x + 6x y; b) 2 9
− + 6x − x ; c) 2 2
2x + 3xy − 5y . Bài 3. +
(1,5 điểm) Cho x x 1 A = + . x + 2 x
a) Tìm điều kiện xác định của biểu thức . A
b) Rút gọn biểu thức A .
c) Tìm giá trị của x để A = 2.
Bài 4. (1,0 điểm) Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp
tứ giác đều với độ dài cạnh đáy là 2 m, trung đoạn của hình chóp là 3
m. Bác Khôi muốn sơn tất cả các mặt của hộp gỗ. Cứ mỗi mét vuông
sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi cần phải
trả chi phí là bao nhiêu?
Bài 5. (2,0 điểm)
a) Cho tứ giác MNPQ có = N M +10 ,° = P N +10 ,° =
Q P +10 .° Tính số đo của M của tứ giác MNPQ .
b) Một công ty muốn xây dựng một đường ống dẫn dầu từ
điểm A trên bờ biển đến một điểm C trên một hòn đảo
như hình vẽ. Giá để xây dựng đường ống trên bờ là 40 000
USD mỗi km và 130 000 USD mỗi km để xây dưới nước.
Hỏi công ty nên xây đường ống theo phương án nào để tiết
kiệm chi phí nhất? Biết rằng công ty đưa ra ba phương án:
Phương án 1: Xây đường ống từ điểm A trên bờ đến
điểm C trên đảo.
Phương án 2: Xây đường ống từ điểm A đến điểm M trên bờ biển, rồi xây đường ống từ điểm
M đến điểm C trên hòn đảo.
Phương án 3: Xây đường ống từ điểm A đến điểm B trên bờ biển, rồi xây đường ống từ điểm
B đến điểm C trên hòn đảo. Biết BC = 60 km, AB =100 km, AM = 55 km.
Bài 6. (0,5 điểm) Tìm giá trị lớn nhất của biểu thức 2 2
A = 5 − 2x − 4y + 4xy − 8x − 12 . y -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT201
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 Đáp án A B A B A B B B
Hướng dẫn giải phần trắc nghiệm Câu 1. Đáp án đúng là: A Biểu thức 2 5
− xy là đơn thức thu gọn;
Biểu thức xyz + xz và ( 2 2
2 x + y ) là đa thức. Biểu thức 3
− z4yxz là đơn thức chưa thu gọn. Câu 2. Đáp án đúng là: B
Có ba nhóm đơn thức đồng dạng trong cac đơn thức đã cho gồm: Nhóm thứ nhất: 2 3 3 − x y; 2x y 3 Nhóm thứ hai: 2 1 2 5x y; x y 2 Nhóm thứ ba: 2 2 −xy ; 6xy . Câu 3. Đáp án đúng là: A Ta có: 3 3 3 A = 2
− y + 2x + 8y − 35 − x = x + 6y − 35
Thay x = 3, y = 4
− vào biểu thức A thu gọn ở trên ta được: 3 A = 3 + 6.( 4
− ) − 35 = 9 − 24 − 35 = 32 − . Câu 4. Đáp án đúng là: B
Hằng đẳng thức ( A − B)2 2 2
= A − 2AB + B có tên là bình phương của một hiệu. Câu 5. Đáp án đúng là: A Với đa thức −
B khác 0 ta có A A = . B −B Câu 6. Đáp án đúng là: B x x x − x x( 2 3 3 x − ) 1 Ta có: − = = = x . 2 2 2 2 x − 1 x − 1 x − 1 x − 1 Câu 7. Đáp án đúng là: B
Hình chóp tứ giác đều có đáy là hình vuông. Câu 8. Đáp án đúng là: B
Thể tích của hình chóp tam giác đều bằng 1 diện tích đáy nhân với chiều cao. 3
PHẦN II. TỰ LUẬN (8,0 điểm) Bài 1. (1,5 điểm) a) 3 24xy : (6xy) b) ( − ) − ( 2 x x y y y − x) c) ( 2 2 2
6x y − 9xy ) : (3xy) − (x + 3)(2y − ) 1 2 = 4y . 2 3
= x − xy − y + xy
= 2xy − 3y − (2xy − x + 6y − 3) 2 3 = x − y .
= 2xy − 3y − 2xy + x − 6y + 3 = 9 − y + x + 3. Bài 2. (1,5 điểm) a) 3 2 3x + 6x y b) 2 9 − + 6x − x c) 2 2
2x + 3xy − 5y 2
= 3x (x + 2y). = −( 2 9 − 6x + x ) 2 2
= 2x − 2xy + 5xy − 5y = −( − x)2 3 . = ( 2 x − xy) + ( 2 2 2 5xy − 5y )
= 2x(x − y) + 5y(x − y)
= (x − y)(2x + 5y) . Bài 3. + (1,5 điểm) x x 1 A = + x + 2 x
a) Điều kiện xác định của biểu thức A là x + 2 ≠ 0 và x ≠ 0 , tức là x ≠ 2 − và x ≠ 0. b) Với x ≠ 2
− và x ≠ 0 , ta có: x x + 1 A = + x + 2 x 2 x + (x + ) 1 (x + 2) = x(x + 2) 2 2
x + x + 2x + x + 2 = x(x + 2) 2 2x + 3x + 2 = . x(x + 2) 2 c) Với + + x 2x 3x 2 ≠ 2
− và x ≠ 0 , để A = 2 thì = x(x + ) 2 2 Suy ra 2 2
2x + 3x + 2 = 2x + 4x
x = 2 (thỏa mãn điều kiện) Vậy x = 2 . Bài 4. (1,0 điểm)
Diện tích mặt đáy của khối gỗ là: 2 2 = 4 (m2).
Diện tích xung quanh của khối gỗ là: 1 .(4.2).3 = 12 (m2). 2
Diện tích cần sơn là: 4 + 12 = 16 (m2).
Chi phí bác Khôi cần phải trả là: 16.30 000 = 480 000 (đồng).
Bài 5. (2,0 điểm)
a) Ta có + + + M N P Q = 360° . Thay = N
M + 10° , = + ° = P N 10
M + 20°, = + ° = Q P 10
M + 30° vào biểu thức trên, ta được
+ + ° + + ° + M M 10 M 20 M + 30° = 360° 4M + 60° = 360° M = 75° Vậy M = 75°.
b) Độ dài đoạn BM là: BM = AB − AM =100 − 5 = 45 km Xét MB ∆
C vuông tại B , áp dụng định lý Pythagore ta có: 2 2 2 2
CM = BC + BM = 60 + 45 = 5 625 = 75 km.
Xét tam giác ABC vuông tại B , áp dụng định lý Pythagore ta có: 2 2 2 2
AC = BC + AB = 60 +100 = 13 600 ≈116,62 km .
Tổng số tiền xây dựng theo phương án 1:
T =130 000⋅116,62 =15 160 474,93 (USD) 1
Tổng số tiền xây dựng theo phương án 2:
T = 40 000⋅55 +130 000⋅75 =11 950 000 (USD) 2
Tổng số tiền xây dựng theo phương án 3:
T = 40 000⋅100 +130 000⋅60 =11 800 000 (USD) 3
Do T > T > T nên phương án 3 là phương án xây dựng đường ống mà tiết kiệm chi phí nhất. 1 2 3 Bài 6. (0,5 điểm) Ta có: 2 2
A = 5 − 2x − 4y + 4xy − 8x − 12y Suy ra 2 2 −A = 5
− + 2x + 4y − 4xy + 8x + 12y 2
= x − x( y − ) 2 2 4
2 + 4y + 12y − 5 2
= x − x( y − ) + ( y − )2 2 2 2 2
2 + 4y + 12y − 5 − 2( y − 2)2 = x − ( y − ) 2 2 2
2 + 2y + 20y − 13
= (x − y + )2 + ( y − )2 2 2 2 5 − 63
Do đó A = − (x − y + )2 − ( y − )2 2 2 2 5 + 63
Nhận xét: − (x − y + )2 ≤ − ( y − )2 2 2 0, 2 5 ≤ 0
Khi đó A = − (x − y + )2 − ( y − )2 2 2 2 5 + 63 ≤ 63 2
− (x − y + 2)2 = 0
x − y + 2 = 0 x = 3
Dấu “=” xảy ra khi và chỉ khi , tức là hay 2 − − = = ( y − 5)2 = 0 y 5 0 y 5
Vậy giá trị lớn nhất của A là 63 khi ( ; x y) = (3;5). -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 07
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 2 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (1,0đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 1 2 1 1
đa thức thành nhân tử (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 15%
trực quan tứ giác đều (0,5đ) (0,5đ) (0,5đ) Định lí 1 Định lí Pythagore 4 Pythagore. (1,0đ) 20% Tứ giác Tứ giác 1 (1,0đ)
Tổng: Số câu 6 1 2 7 5 1 22 Điểm (1,5đ) (0,5đ) (0,5đ) (4,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 20% 45% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 2TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 1TN 2TL 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT202
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Bậc của đa thức 3 5 2 5
x y − 9x + 7y là A. 7 ; B. 8 ; C. 9; D. 15.
Câu 2. Có bao nhiêu nhóm đơn thức đồng dạng với nhau trong các đơn thức sau: 2 2 2
2xy; 9y ; 2y; 5xy; 4xy ; y ? A. 1; B. 2; C. 3; D. 4.
Câu 3. Giá trị của biểu thức 3 2 3 2
A = x − 5y + 2x + 4y + 10 tại x = 1; − y = 2 là A. 3 − ; B. 3; C. 9; D. 11.
Câu 4. Hằng đẳng thức 2 2
A − B = ( A − B)( A + B) có tên là
A. bình phương của một tổng;
B. bình phương của một hiệu; C. tổng hai bình phương; D. hiệu hai bình phương. Câu 5. − −
Phân thức x y bằng với phân thức nào sau đây? 3 − + − + A. x y ; B. x y ; C. x y ; D. x y . 3 − 3 3 3 −
Câu 6. Kết quả của phép tính 3x − 1 1 − là 2xy y A. x − 1 ; B. x + 1; C. x + 1 ; D. −x + 1 . 2xy 2xy 2 − xy 2xy
Câu 7. Hình nào sau đây là hình chóp tứ giác đều?
A. Hình có đáy là tứ giác;
B. Hình có đáy là hình vuông;
C. Hình có đáy là hình vuông và tất cả các cạnh bên bằng nhau;
D. Hình có đáy là tam giác đều và có một cặp cạnh bên vuông góc với nhau.
Câu 8. Một hình chóp tam giác đều có chiều cao ,
h thể tích V. Diện tích đáy S là A. h S = ; B. V S = ; C. 3V S = ; D. 3h S = . V h h V
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Thu gọn biểu thức: a) 9 5 x y ( 4 4 65 : 13 − x y );
b) x(x − y) + y(x + y); c) ( 3 2 2
12x y − 12x y ) : 3xy − (x − ) 1 (x + xy) .
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử:
a) 5( y − 3) − x(3 − y) ; b) 6 9 x + y ; c) ( + )2 − ( + )2 2 3 x x y
y x y + x y − x .
Bài 3. (1,5 điểm) Cho biểu thức 2 A = . 2 x − 1
a) Tìm điều kiện xác định của biểu thức A .
b) Tìm giá trị của biểu thức A khi x = 2. − 2
c) Tìm biểu thức C sao cho A + C = B biết 6 2x B = − . 2 x − 3 1 − x
Bài 4. (3,0 điểm)
1. Cho tứ giác ABCD biết A = 75° , B = 90°, C =120° . Tính
số đo các góc ngoài tại đỉnh D của tứ giác ABC . D
2. Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì
nhận thấy các cạnh đều có cùng độ dài là 20 cm.
a) Tính độ dài trung đoạn của hình chóp.
b) Tính diện tích xung quanh của chiếc đèn.
c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ
đáy của đèn cách mặt trền là 1 m là tốt nhất. Vậy bạn Nam cần
đưa đoạn dây điện từ đầu đèn (vị trí )
A tới mặt trần là bao nhiêu
(làm tròn kết quả đến hàng phần mười)?
Bài 5. (0,5 điểm) Tìm giá trị lớn nhất của biểu thức 2 2
A = −x + 2xy − 4y + 2x + 10y − 3. -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT202
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 Đáp án B B B D D A C C
Hướng dẫn giải phần trắc nghiệm Câu 1. Đáp án đúng là: B Bậc của 3 5
x y là 8; bậc của 2 9
− x là 2; bậc của 5 7y là 5.
Vậy bậc của đa thức đã cho là 8. Câu 2. Đáp án đúng là: B
Có hai nhóm đơn thức đồng dạng trong các đơn thức đã cho gồm:
Nhóm thứ nhất: 2xy; 5x . y Nhóm thứ hai: 2 2 9y ; y . Câu 3. Đáp án đúng là: B Ta có: 3 2 3 2 3 2
A = x − 5y + 2x + 4y + 10 = 3x − y + 10 Thay x = 1;
− y = 2 vào biểu thức A thu gọn ở trên ta được: A = (− )3 2 3. 1 − 2 + 10 = 3 − − 4 + 10 = 3. Câu 4. Đáp án đúng là: D Hằng đẳng thức 2 2
A − B = ( A − B)( A + B) có tên là hiệu hai bình phương. Câu 5. Đáp án đúng là: D −x − y −(−x − y) Ta có: x + y = = . 3 3 − 3 − Câu 6. Đáp án đúng là: A Ta có: 3x − 1 1 3x − 1 2x 3x − 1 − 2x x − 1 − = − = = . 2xy y 2xy 2xy 2xy 2xy Câu 7. Đáp án đúng là: C
Hình có đáy là hình vuông và tất cả các cạnh bên bằng nhau là hình chóp tứ giác đều. Câu 8. Đáp án đúng là: C
Ta có thể tích của hình chóp tam giác đều là 1 V = Sh 3 Suy ra 3V S = . h
PHẦN II. TỰ LUẬN (8,0 điểm) Bài 1. (1,5 điểm) a) 9 5 x y ( 4 4 65 : 13
− x y ) b) x(x − y) + y(x + y) c) ( 3 2 2
12x y − 12x y ) : 3xy − (x − ) 1 (x + xy) 5 = 5 − x y . 2 2
= x − xy + xy + y 2
= x − xy − ( 2 2 4 4
x + x y − x − xy) 2 2 = x + y . 2 2 2
= 4x − 4xy − x − x y + x + xy 2 2
= 3x − 3xy − x y + x . Bài 2. (1,5 điểm)
a) 5( y − 3) − x(3 − y) c) ( + )2 − ( + )2 2 3 x x y
y x y + x y − x
= 5( y − 3) + x( y − 3) = ( + )2 ( − ) 2 x y
x y − x (x − y)
= ( y − 3)(5 + x). = ( − ) ( + )2 2 x y x y − x b) 6 9 x + y
= (x − y)(x + y − x)(x + y + x) = ( )3 + ( )3 2 3 x y
= (x − y) ⋅ y ⋅ (2x + y) . = ( 2 3 + )( 4 2 3 6 x y
x − x y + y ). Bài 3. (1,5 điểm)
a) Điều kiện xác định của biểu thức A là 2 x − 1 ≠ 0 hay 2
x ≠ 1, tức x ≠ 1 và x ≠ 1. − b) Thay x = 2
− (thỏa mãn) vào biểu thức A ta được: 2 2 2 A = = = . ( 2 − )2 − 1 4 − 1 3
c) Ta có: A + C = . B 2 Suy ra 6 2x 2
C = B − A = − − 2 2 x − 3 1 − x x − 1 2 6 2x 2 C = + − 2 2
x − 3 x − 1 x − 1 2 6 2x − 2 = + 2 x − 3 x − 1 6 2( 2 x − ) 1 6 2 = + = + 2 x − 3 x − 1 x − 3 1 6 2x − 6 = + 2x = . x − 3 x − 3 x − 3 Bài 4. (3,0 điểm)
1. Xét tứ giác ABCD , ta có + + + A B C D = 360° Do đó ° + ° + ° + 75 90 120 D = 360° Hay ° + 285 D = 360° Suy ra
D = 360° − 285° = 75°
Khi đó góc ngoài tại đỉnh D của tứ giác là 180° − 75° = 105 .° 2.
a) Chiếc đèn được mô phỏng thành hình chóp tam giác đều . A BCD
như hình vẽ. Gọi AH là trung đoạn kẻ từ đỉnh A của hình chóp.
Theo bài ta có: AB = AC = AD = 20 cm
BC = CD = DB = 20 cm. A
∆ CD đều nên AH vừa là đường cao vừa là đường trung tuyến. Do đó 1
DH = CH = CD = 10 cm. 2 Xét A
∆ HC vuông tại H , theo định lí Pythagore ta có: 2 2 2 2 2
AH = AC − CH = 20 − 10 = 300 Suy ra AH = = = ( )2 300 100.3 10 3 = 10 3 cm.
b) Chu vi đáy của hình chóp là: C = 3BD = 3.20 = 60 cm.
Diện tích xung quanh của chiếc đèn là: 1 1 S = C AH = = cm2. xq . .60.10 3 300 3 2 2 c) Vì A ∆ DC và B
∆ DC đều là các tam giác đều có cạnh 20 cm nên hai đường cao AH và BH của hai tam giác bằng nhau.
Vì O là trọng tâm B ∆ DC nên 1 10 3 OH = BH = cm. 3 3 A
∆ OH vuông tại O , theo định lí Pythagore ta có: 2 2 2 2 10 3 300 800
AO = AH − OH = 300 − = 300 − = 3 9 3 Suy ra 800 AO = ≈ 16,3 cm. 3
Khi đó bạn Nam cần đưa dây diện từ đầu đèn tới trần nhà khoảng là 100 − 16,3 = 83,7 cm. Bài 5. (0,5 điểm) Ta có: 2 2
A = −x + 2xy − 4y + 2x + 10y − 3. Suy ra 2 2
−A = x − 2xy + 4y − 2x − 10y + 3 2
= x − x( y + ) + ( y + )2 2 2 1
1 + 4y − 10y + 3 − ( y + )2 1 2
= x − x( y + ) + ( y + )2 2 2 1
1 + 3y − 12y + 2 = x − ( y + ) 2 + ( 2 1
3 y − 4y + 4) − 10
= (x − y − )2 + ( y − )2 1 3 2 − 10
Do đó A = −(x − y − )2 − ( y − )2 1 3 2 + 10
Nhận xét: −(x − y − )2 ≤ − ( y − )2 1 0; 3
2 ≤ 0 với mọi x, y
Suy ra A = −(x − y − )2 − ( y − )2 1 3 2 + 10 ≤ 10
−(x − y − )2 1 = 0
x − y − 1 = 0 x = 3
Dấu “=” xảy ra khi và chỉ khi , tức là , hay 3 − ( y − 2)2 = 0 y − 2 = 0 y = 2
Vậy giá trị lớn nhất của biểu thức A là 10 khi ( ; x y) = (3;2) . -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 08
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 2 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (1,0đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 1 2 1 1
đa thức thành nhân tử (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 15%
trực quan tứ giác đều (0,5đ) (0,5đ) (0,5đ) Định lí 1 Định lí Pythagore 4 Pythagore. (1,0đ) 20% Tứ giác Tứ giác 1 (1,0đ)
Tổng: Số câu 6 1 2 7 5 1 22 Điểm (1,5đ) (0,5đ) (0,5đ) (4,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 20% 45% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 2TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 1TN 2TL 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT203
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Bậc của đa thức 2 5 2 4 6
x y − x y + y + 1 là A. 4 ; B. 5; C. 6 ; D. 7 .
Câu 2. Cặp đơn thức nào sau đây không đồng dạng? A. 3 7x y và 1 3 x y ; B. 1 − (xy)2 2 x và 2 3 32x y ; 15 8 C. 2 2 5x y và 2 2 2 − x y ; D. 2 ax y và 2
2bx y (a,b là các hằng số khác 0).
Câu 3. Giá trị của biểu thức 4 2
A = x + 4x y − 6z tại x = 4, y = 5, − z = 2 − là A. 76 − ; B. 52 − ; C. 25 − ; D. 37 . Câu 4. Cho 3 2
x + 12x + 48x + 64 = (x + a)3 . Giá trị của a là A. 64 − ; B. 64; C. 4 − ; D. 4.
Câu 5. Quy đồng mẫu thức hai phân thức 2 và 3 ta được mẫu thức chung là 2 x y 2 xy A. 2 x y ; B. 2 xy ; C. 2 2 x y ; D. 3 3 x y .
Câu 6. Phân thức x − 1 là kết quả của phép tính nào dưới đây? x + 1 A. x 2 − ; B. 2x 2 − ; x + 1 x + 1 x + 1 x + 1 C. −x 1 x 1 − − ; D. − . x + 1 x + 1 x + 1 −(x + ) 1
Câu 7. Hình nào sau đây là hình chóp tam giác đều?
A. Hình có đáy là tam giác;
B. Hình có đáy là tam giác đều;
C. Hình có đáy là tam giác đều và tất cả các cạnh đều vuông góc với mặt đáy;
D. Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.
Câu 8. Một hình chóp tứ giác đều có diện tích xung quanh S và chiều cao h . Khi đó nửa chu vi xq đáy là 2S S S A. xq ; B. xq ; C. xq ; D. 2h . h h 2h Sxq
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Thu gọn biểu thức: a) 27 3 5 9 2 x yz : xz ; 15 5
b) 3x(x − y) − y( y − 3x) ; c) (x − y)( 2 2 x + y ) − ( 4 4
x y − xy ) : xy .
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 3 2 2x − 6x ; b) 2 1 2 9x − y ; c) 2 2 3
x y + 5xy + 6y . 16
Bài 3. (1,5 điểm) Cho biểu thức x − 2 A = . x + 2
a) Tìm điều kiện xác định của biểu thức . A
b) Tìm biểu thức C sao cho C = A − B với x 9x + 2 B = + (x ≠ 2 ± ). 2 x − 2 4 − x
c) Tính giá trị của biểu thức C khi 3x(2x + ) 1 − 6(2x + ) 1 = 0.
Bài 4. (1,0 điểm) Một khối bê tông có dạng như hình vẽ bên.
Phần đáy của bê tông có dạng hình hộp chữ nhật, đáy là hình
vuông có cạnh 40 cm, chiều cao 25 m. Phần trên của khối bê tông
có dạng hình chóp tứ giác đều, chiều cao 100 cm. Tính thể tích
của khối bê tông đó (làm tròn kết quả đến hàng đơn vị).
Bài 5. (2,0 điểm)
a) Cho tứ giác ABCD, trong đó có + A
B = 140° . Tính tổng số đo góc ngoài tại đỉnh C và D của tứ giác.
b) Khi xây móng nhà, để kiểm tra xem 2 phần
móng có vuông góc với nhau hay không, người thợ xây
thường lấy AB = 3 cm, AC = 4 cm (A là
điểm chung của hai phần móng nhà hay còn gọi
là góc nhà), rồi đo đoạn BC nếu BC = 5 cm
thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?
Bài 6. (0,5 điểm) Chứng minh rằng với mọi a,b,c ta luôn có:
(a + b + c)3 3 3 3
= a + b + c + 3(a + b)(b + c)(c + a). -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT203
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 Đáp án D B B D C D D B
Hướng dẫn giải phần trắc nghiệm Câu 1. Đáp án đúng là: D Ta có 2 5
x y có bậc là 7; 2 4 x y có bậc là 6; 6
y có bậc là 6; 1 có bậc là 0.
Vậy đa thức đã cho có bậc là 7. Câu 2. Đáp án đúng là: B 1 − (xy)2 2 1 4 2
x = − x y không đồng dạng với đơn thức 2 3 32x y . 8 8 Câu 3. Đáp án đúng là: B
Thay x = 4, y = 5, − z = 2
− vào biểu thức A ta được: 4 2 A = 4 + 4.4 .( 5 − ) − 6.( 2 − ) = 256 − 320 + 12 = 52 − . Câu 4. Đáp án đúng là: D Ta có: 3 2
x + 12x + 48x + 64 = (x + 4)3. Vậy a = 4. Câu 5. Đáp án đúng là: C
Mẫu thức chung của hai phân thức 2 và 3 là 2 2 x y . 2 x y 2 xy Câu 6. Đáp án đúng là: D Ta có: • x 2 x − 2 − = . Do đó A sai. x + 1 x + 1 x + 1 • 2x 2 2x − 2 − = . Do đó B sai. x + 1 x + 1 x + 1 −x 1 −x − 1 −(x + ) 1 • − = = = 1 − . Do đó C sai. x + 1 x + 1 x + 1 x + 1 • x 1 − x 1 − x − 1 − = + = . Do đó D đúng. x + 1 −(x + ) 1 x + 1 x + 1 x + 1 Câu 7. Đáp án đúng là: D
Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau là hình chóp tam giác đều. Câu 8. Đáp án đúng là: B
Ta có diện tích xung quanh của hình chóp tứ giác đều là 1
S = Ch = ph xq 2 S
Trong đó p là nửa chu vi đáy. Do đó xq p = . h
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) 2 2 4 4 a) 27 3 5 9 2
x yz : xz b) 3x(x − y) − y ( y − 3x)
c) (x − y)(x + y ) − (x y − xy ) : xy 15 5 2 2
= 3x − 3xy − y + 3xy 3 2 = + − ( 2 3 + ) − ( 3 3 x xy x y y x − y ) 2 2 = x yz . 2 2 = 3x − y . 3 2 2 3 3 3
= x + xy − x y − y − x + y 2 2 = xy − x y . Bài 2. (1,5 điểm) a) 3 2 2x − 6x b) 2 1 2 9x − y c) 2 2 3
x y + 5xy + 6y 2 = 2x (x − 3). 16 = y ( 2 2
x + 5xy + 6y ) 2 ( x)2 1 3 y = − 4 = y ( 2 2
x + 2xy + 3xy + 6y ) 1 1 3x y = y x
( x + 2y) + 3y ( x + 2y) 3x y = − + . 4 4
= y (x + 2y)(x + 3y) . Bài 3. (1,5 điểm)
a) Điều kiện xác định của biểu thức A là x + 2 ≠ 0 hay x ≠ 2. − b) Với x ≠ 2
± , ta có: C = A − B Suy ra x − 2 x 9x + 2 C = − + 2 x 2 x 2 4 x + − − x − 2 x 9x + 2 C = − − 2 x + 2 x − 2 4 − x x − 2 x 9x + 2 = − + 2 x + 2 x − 2 x − 4 (x − )2
2 − x(x + 2) + 9x + 2 = ( x + 2)(x − 2) 2 2
x − 4x + 4 − x − 2x + 9x + 2 = ( x + 2)(x − 2) 3x + 6 = ( x + 2)(x − 2) 3(x + 2) 3 = ( = . x + 2)(x − 2) x − 2
c) Ta có: 3x(2x + ) 1 − 6(2x + ) 1 = 0
(2x + )1(3x − 6) = 0
2x + 1 = 0 hoặc 3x − 6 = 0 1
x = − (thỏa mãn) hoặc x = 2 (không thỏa mãn). 2 Thay 1
x = − vào biểu thức 3 C = ta được: 2 x − 2 3 3 6 C − = = = . 1 5 5 − − 2 − 2 2 Bài 4. (1,0 điểm)
Thể tích phần trên khối bê tông có dạng hình chóp tứ giác đều là: 1 2 160 000 V = .40 .100 = (m3). 1 3 3
Thể tích phần dưới đáy khối bê tông có dạng hình hộp chữ nhật là:
V = 40.40.25 = 40 000 (m3). 2
Thể tích khối bê tông là: 160 000 280 000
V = V + V = + 40 000 = (m3) ≈ 93 333 (m3). 1 2 3 3 Bài 5. (2,0 điểm)
a) Xét tứ giác ABCD có + + + A B C D = 360° Suy ra + = ° − + C D 360 (A B ) Hay + C
D = 360° − 140° = 220°
Do đó tổng số đo góc ngoài tại đỉnh C và D là: ° − (180 C ) + ° −
(180 D ) = ° − + 360
(C D ) = 360° − 220° = 140 .° b) Xét A ∆ BC có: 2 2 BC = 5 = 25 và 2 2 2 2
AB + AC = 3 + 4 = 25 Do đó 2 2 2
BC = AB + AC
Theo định lí Pythagore đảo, ta có tam giác ABC vuông tại A .
Vậy hai phần móng đó vuông góc với nhau. Bài 6. (0,5 điểm)
Ta có: (a + b + c)3 = (a + b)3 + (a + b)2 c + (a + b) 2 3 3 3 c + c 3 2 2 3
= a + a b + ab + b + (a + b)2 c + (a + b) 2 3 3 3 3 3 c + c 3 3 3
= a + b + c + ab(a + b) + (a + b)2 c + (a + b) 2 3 3 3 c 3 3 3
= a + b + c + (a + b) ab + (a + b) 2 3 3 3 c + 3c 3 3 3
= a + b + c + (a + b)( 2 3
ab + ac + bc + c ) 3 3 3
= a + b + c + 3(a + b) a(b + c) + c(b + c) 3 3 3
= a + b + c + 3(a + b)(b + c)(a + c) . -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 09
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 2 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (1,0đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 1 2 1 1
đa thức thành nhân tử (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 15%
trực quan tứ giác đều (0,5đ) (0,5đ) (0,5đ) Định lí 1 Định lí Pythagore 4 Pythagore. (1,0đ) 20% Tứ giác Tứ giác 1 (1,0đ)
Tổng: Số câu 6 1 2 7 5 1 22 Điểm (1,5đ) (0,5đ) (0,5đ) (4,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 20% 45% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 2TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 1TN 2TL 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT204
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm. 1 Câu 1. Đơn thức 2 3 − x y ( 3 5 −
x y)ax (a là hằng số) có hệ số và bậc lần lượt là 5 A. a và 6 ; B. 1 và 10; C. a và 10; D. 1 và 6.
Câu 2. Cặp đơn thức nào sau đây là đồng dạng với nhau? A. 1 2 x y và 2 2xy ; B. 2 4 −x y và 2 4 2x y ; 2
C. 6yt và 26y ; D. mxy và 2 nxy (với ,
m n là hằng số khác 0).
Câu 3. Giá trị của biểu thức 5 2
A = x y + 7x y + 9 tại x = 1, − y = 2 là A. 21; B. 25; C. 7 − ; D. 3 − .
Câu 4. Chọn đẳng thức sai trong các đẳng thức sau đây: A. (a + b)3 3 2 2 3
= a + 3a b + 3ab + b ; B. (−a − b)3 3 2 2 3
= −a − 3a b − 3ab − b ; C. (−a + b)3 3 2 2 3
= −a − 3a b + 3ab + b ; D. (a − b)3 3 2 2 3
= a − 3a b + 3ab − b .
Câu 5. Phân thức nào sau đây bằng với phân thức y (với giả thiết các phân thức đều có nghĩa)? 3x 2 3 2 2 3 3y A. y ; B. y ; C. y ; D. . 2 9xy 2 9xy 9xy 2 9xy
Câu 6. Kết quả của phép tính a − 2 2 − b − là a − b b − a A. 1 − ; B. 1; C. a − b ;
D. a + b − 4 . b − a a − b
Câu 7. Tổng số cạnh bên và cạnh đáy của một hình chóp tam giác đều là A. 4; B. 6; C. 8; D. 10.
Câu 8. Diện tích xung quanh của hình chóp tứ giác đều bằng bao nhiêu lần diện tích một mặt bên? A. 2; B. 3; C. 4; D. 5.
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Thu gọn biểu thức: a) 2 5 − x y z ( 3 3 : 15xy ); b) 2
x ( x + y) − y( 2 3 2 2 4x − y);
c) (x + y)(x − y) − ( 4 2 3 x y − x y ) 2 3 2 6 : x y .
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 4 2 3 −x y + xy ; b) 2 2
y − x + 6x − 9 ; c) 3
x + 27 + (x + 3)(x − 9). 1 1 1
Bài 3. (1,5 điểm) Cho biểu thức A = + + . x(x + ) 1
(x + )1(x + 2) x + 2
a) Tìm điều kiện xác định của biểu thức . A
b) Rút gọn biểu thức A .
c) Tính giá trị của biểu thức A biết x thỏa mãn (x − 2024)(x + ) 1 = 0.
Bài 4. (1,0 điểm) Một chiếc lều ở một trại hè của học sinh
tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích
thước như hình vẽ bên.
a) Thể tích không khí bên trong lều là bao nhiêu (làm tròn
kết quả đến chữ số thập phân thứ hai)?
b) Xác định số vải bạt cần thiết để dựng lều (không tính
đến đường viền, nếp gấp, ...) là bao nhiêu (làm tròn kết
quả đến chữ số thập phân thứ hai)? Biết độ dài trung đoạn
của lều trại là 2, 24 cm.
Bài 5. (2,0 điểm)
a) Tìm số đo x trong hình a.
b) Một chiếc thang có chiều dài AB = 3,7 m đặt cách một bức tường khoảng cách BH = 1,2 m.
Hỏi khoảng cách đặt thang cách chân tường là BH có “an toàn” không? Biết rằng khoảng cách
“an toàn” khi 2,0 AH < < 2, 2 (xem hình b). BH
Bài 6. (0,5 điểm) Cho ba số thực a,b,c khác 0 thỏa mãn 3 3 3
a + b + c = 3 .
abc Tính giá trị của biểu a b c thức A = 1 + 1 + 1 + . b c a -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT204
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 Đáp án C B A C C B B C
Hướng dẫn giải phần trắc nghiệm Câu 1. Đáp án đúng là: C 1 1 Ta có: 2 3 − x y ( 3 5
− x y)ax = − .( 5 − ). . a ( 2 3
x .x .x).( 3y.y) 6 4 = ax y 5 5
Do đó đơn thức trên có hệ số bằng ; a bậc là 10. Câu 2. Đáp án đúng là: B Ta có 2 4
−x y đồng dạng với đơn thức 2 4 2x y . Câu 3. Đáp án đúng là: A Thay x = 1,
− y = 2 vào biểu thức A ta được: A = (− )5 + (− )2 1 .2 7. 1 .2 + 9 = 2 − + 14 + 9 = 21. Câu 4. Đáp án đúng là: C
Ta có: (−a + b)3 = (b − a)3 3 2 2 3 3 2 2 3
= b − 3b a + 3ba − a = −a + 3a b − 3ab + b . Câu 5. Đáp án đúng là: C 2 y 3 .yy 3y Ta có: = = .
3x 3 .y3x 9xy Câu 6. Đáp án đúng là: B
Ta có: a − 2 2 − b a − 2 2 − b
a − 2 + 2 − b a − b − = + = = = 1. a − b b − a a − b a − b a − b a − b Câu 7. Đáp án đúng là: B
Số cạnh bên của hình chóp tam giác đều là 3.
Số cạnh đáy của hình chóp tam giác đều là 3.
Tổng số cạnh bên và cạnh đáy của hình chóp tứ giác đều là: 3 + 3 = 6. Câu 8. Đáp án đúng là: C
Hình chóp tứ giác đều có 4 mặt bên đều là các tam giác cân bằng nhau. Do đó diện tích xung quanh
của hình chóp tứ giác đều bằng 4 lần diện tích một mặt bên.
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) a) 2 5 − x y z ( 3 3 : 15xy ) 1 − 2 4 2 3 2 = xy z .
c) (x + 3y)(x − 2y) − (x y − 6x y ) : x y 5 2 2
= x − xy + xy − y − ( 2 2 2 3 6 x − 6y ) b) 2
x ( x + y) − y( 2 3 2 2 4x − y) 2 2 2 2 3 2 2 2
= 6x + 3x y − 8x y + 2y
= x + xy − 6y − x + 6y = xy . 3 2 2
= 6x − 5x y + 2y .
Bài 2. (1,5 điểm) a) 4 2 3 −x y + xy b) 2 2
y − x + 6x − 9 c) 3
x + 27 + (x + 3)(x − 9) 2 = −xy ( 3 x − y). 2 = y − ( 2 x − 6x + 9) = ( x + )( 2
3 x − 3x + 9) + (x + 3)(x − 9) 2
= y − ( x − 3)2 = (x + )( 2
3 x − 3x + 9 + x − 9)
= ( y − x + 3)( y + x − 3) . = (x + )( 2 3 x − 2x)
= (x + 3) x(x − 2) . 1 1 1
Bài 3. (1,5 điểm) A = + + . x(x + ) 1
(x + )1(x + 2) x + 2
a) Điều kiện xác định của biểu thức A là: x ≠ 0, x + 1 ≠ 0, x + 2 ≠ 0 hay x ≠ 0, x ≠ 1 − , x ≠ 2 − .
b) Với x ≠ 0, x ≠ 1 − , x ≠ 2 − ta có: 1 1 1 A = + + x(x + ) 1
(x + )1(x + 2) x + 2
x + 2 + x + x + 1 = x(x + ) 1 (x + 2) 3x + 3 = x(x + ) 1 (x + 2) 3(x + ) 1 = x(x + ) 1 (x + 2) 3 = . x(x + 2)
c) Ta có: (x − 2024)(x + ) 1 = 0
Suy ra x − 2024 = 0 (do x + 1 ≠ 0)
Do đó x = 2024 (thỏa mãn điều kiện) 3 3 3
Thay x = 2024 vào biểu thức A ta được: A = ( + ) = = . 2024. 2024 2 2024.2026 4 100 624 Bài 4. (1,0 điểm)
a) Thể tích không khí bên trong lều chính là thể tích hình chóp tứ giác đều: 1 1 2 8 V = Sh = .2 .2 = ≈ 2,67 (m3). 3 3 3
b) Số mét vải bạt cần thiết để dựng lều chính là diện tích xung quanh hình chóp tứ giác đều và bằng: 1 1 S = Cd = ≈ (m2). xq (2.4).2,24 8,96 2 2 Bài 5. (2,0 điểm)
a) Góc ngoài tại đỉnh B có số đo bằng 70° nên góc trong tại đỉnh B có số đo bằng 180° − 70° = 110°
Xét tứ giác ABCD, ta có: + + + A B C D = 360°
Do đó 3x + 110° + x + 90° = 360°
Suy ra 4x = 160° nên x = 40° Vậy x = 40° .
b) Áp dụng định lí Pytthagore vào tam giác ABH vuông tại H ta có: 2 2 2
AB = AH + BH Suy ra 2 2 2
AH = AB − BH Do đó 2 2 2 2
AH = AB − BH = 3,7 −1,2 = 3,5( m) AH 3,5 Ta có = ≈ 2,9 BH 1,2
Mà 2,9 > 2,2 nên khoảng cách đặt thang cách chân tường là không an toàn. Bài 6. (0,5 điểm) Ta có: 3 3 3
a + b + c − 3abc
= (a + b)3 − ab(a + b) 3 3 + c − 3abc = (a + b)3 3
+ c − 3ab(a + b) − 3abc = (a + b)3 3
+ c − 3ab(a + b + c)
= (a + b + c)(a + b)2 − (a + b) 2
c + c − 3ab(a + b + c) = ( + + )( 2 2 2
a b c a + b + c − ab − bc − ca) Suy ra 3 3 3
a + b + c = 3abc hay 3 3 3
a + b + c − 3abc = 0
Nên a + b + c = 0 hoặc 2 2 2
a + b + c − ab − bc − ca = 0 (*) Mặt khác ( 2 2 2
2 a + b + c − ab − bc − ca) 2 2 2
= 2a + 2b + 2c − 2ab − 2bc − 2ca
= ( − )2 + ( − )2 + ( − )2 a b b c c a Do đó 2 2 2 1
a + b + c − ab − bc − ca = (a − b)2 + (b − c)2 + (c − a)2 ≥ 0 với mọi a,b,c 2 (
a − b)2 = 0 a − b = 0 Nên để (*) xảy ra thì (
b − c)2 = 0 , hay b
− c = 0 tức a = b = c . (
c − a)2 = 0 c − a = 0
⦁ Trường hợp 1: a + b + c = 0
Suy ra a + b = − ; c b + c = − ;
a c + a = b − a b
c a + b b + c c + a −c −a b −
Khi đó A = 1 + 1 + 1 + = . . = . . = 1. − b c a b c a b c a a b c
⦁ Trường hợp 2: a = b = c thì ta được A = 1 + 1 + 1 + = 2.2.2 = 8 . b c a -----HẾT-----
BỘ SÁCH: CÁNH DIỀU
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8 ĐỀ SỐ 10
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % Chủ đề điểm TN TL TN TL TN TL TN TL
Đa thức nhiều biến. Các phép toán 2 1 2 1
cộng, trừ, nhân, chia các đa thức Đa thức (0,5đ) (0,25đ) (1,0đ) (0,5đ) 1 nhiều biến 45%
nhiều biến Hằng đẳng thức đáng nhớ. Phân tích 1 2 1 1
đa thức thành nhân tử (0,25đ) (1,0đ) (0,5đ) (0,5đ)
Phân thức đại số. Tính chất cơ bản 1 1
Phân thức của phân thức đại số. (0,25đ) (0,5đ) 2 20% đại số
Các phép toán cộng, trừ các phân 1 1 1 thức đại số (0,25đ) (0,5đ) (0,5đ)
Hình học Hình chóp tam giác đều, hình chóp 2 1 1 3 15%
trực quan tứ giác đều (0,5đ) (0,5đ) (0,5đ) Định lí 1 Định lí Pythagore 4 Pythagore. (1,0đ) 20% Tứ giác Tứ giác 1 (1,0đ)
Tổng: Số câu 6 1 2 7 5 1 22 Điểm (1,5đ) (0,5đ) (0,5đ) (4,0đ) (3,0đ) (0,5đ) (10đ) Tỉ lệ 20% 45% 30% 5% 100% Tỉ lệ chung 65% 35% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1
Số câu hỏi theo mức độ Chương/
Mức độ kiến thức, kĩ năng cần kiểm tra, STT
Nội dung kiến thức Nhận Thông Vận Vận dụng Chủ đề đánh giá biết hiểu dụng cao 1 Đa thức
Đa thức nhiều biến. Nhận biết: 2TN 1TN, 1TL
nhiều biến Các phép toán cộng, – Nhận biết được đơn thức, đa thức nhiều biến, 2TL
trừ, nhân, chia các đa đơn thức và đa thức thu gọn. thức nhiều biến
– Nhận biết hệ số, phần biến, bậc của đơn thức và bậc của đa thức.
– Nhận biết các đơn thức đồng dạng. Thông hiểu:
– Tính được giá trị của đa thức khi biết giá trị của các biến.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức
và phép chia hết một đơn thức cho một đơn thức. Vận dụng:
– Thực hiện được các phép tính: phép cộng, phép
trừ, phép nhân các đa thức nhiều biến trong
những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho
một đơn thức trong những trường hợp đơn giản.
Hằng đẳng thức đáng Nhận biết: 1TN 2TL 1TL 1TL
nhớ. Phân tích đa thức – Nhận biết được các khái niệm: đồng nhất thức, thành nhân tử hằng đẳng thức.
– Nhận biết được các hằng đẳng thức: bình
phương của tổng và hiệu; hiệu hai bình phương;
lập phương của tổng và hiệu; tổng và hiệu hai lập phương).
– Nhận biết phân tích đa thức thành nhân tử. Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương
của tổng và hiệu; hiệu hai bình phương; lập
phương của tổng và hiệu; tổng và hiệu hai lập phương.
– Mô tả ba cách phân tích đa thức thành nhân tử:
đặt nhân tử chung; nhóm các hạng tử; sử dụng hằng đẳng thức. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích
đa thức thành nhân tử ở dạng: vận dụng trực tiếp
hằng đẳng thức; vận dụng hằng đẳng thức thông
qua nhóm hạng tử và đặt nhân tử chung.
– Vận dụng phân tích đa thức thành nhân tử để
giải bài toán tìm x, rút gọn biểu thức.
Vận dụng cao:
– Vận dụng hằng đẳng thức, phân tích đa thức
thành nhân tử để chứng minh đẳng thức, bất đẳng thức.
– Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức nhiều biến. 2 Phân thức
Phân thức đại số. Tính Nhận biết: 1TN, đại số
chất cơ bản của phân – Nhận biết được các khái niệm cơ bản về phân 1TL thức đại số.
thức đại số: định nghĩa; điều kiện xác định; giá
trị của phân thức đại số; hai phân thức bằng nhau. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để
xét sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép toán cộng, Thông hiểu: 1TN, 1TL
trừ các phân thức đại – Thực hiện được các phép tính: phép cộng, phép 1TL số
trừ đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết
hợp, quy tắc dấu ngoặc trong tính toán với phân thức đại số. 3 Hình học
Hình chóp tam giác Nhận biết: 2TN 1TL 1TL
trực quan đều, hình chóp tứ giác – Nhận biết đỉnh, mặt đáy, mặt bên, cạnh bên của đều
hình chóp tam giác đều và hình chóp tứ giác đều. Thông hiểu:
– Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) và tạo
lập được hình chóp tam giác đều và hình chóp tứ giác đều.
– Tính được diện tích xung quanh, thể tích của
một hình chóp tam giác đều và hình chóp tứ giác đều. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc tính thể tích, diện tích xung quanh của
hình chóp tam giác đều và hình chóp tứ giác đều
(ví dụ: tính thể tích hoặc diện tích xung quanh
của một số đồ vật quen thuộc có dạng hình chóp
tam giác đều và hình chóp tứ giác đều, ...). 4 Định lí Định lí Pythagore Thông hiểu: 1TL Pythagore.
– Giải thích được định lí Pythagore. Tứ giác
– Tính được độ dài cạnh trong tam giác vuông
bằng cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn
với việc vận dụng định lí Pythagore (ví dụ: tính
khoảng cách giữa hai vị trí). Tứ giác Nhận biết: 1TL
– Nhận biết được tứ giác, tứ giác lồi. Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng o 360 .
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 8 MÃ ĐỀ MT205
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức bậc 5? A. 5 x y + 1; B. 2 3 x + y ; C. 2 5 x y ; D. 2 xy zx .
Câu 2. Cho các đơn thức 3 A = 4x y( 5 − xy) 4 2 3 6 , B = 17
− x y , C = x y . Các đơn thức nào sau đây 5 đồng dạng với nhau?
A. Đơn thức A và đơn thức C ;
B. Đơn thức B và đơn thức C ;
C. Đơn thức A và đơn thức B ; D. Cả ba đơn thức ,
A B,C đồng dạng với nhau.
Câu 3. Giá trị của biểu thức 1 2 2 2 2 1 2
A = xy + x y + xy + xy − x y tại 1 x = và y = 1 − là 2 3 3 2 A. 1 ; B. 4 ; C. 1 ; D. 7 . 6 3 3 6
Câu 4. Đơn thức điền vào ô trống trong đẳng thức (x − )3 3 2 = x − + 12x − 8 là A. 2 6 − x ; B. 2 2 − x ; C. 2 2x ; D. 2 6x . Câu 5. −
Với điều kiện nào của x x thì phân thức 3 xác định? 6x + 24 A. x ≠ 2 ; B. x ≠ 3; C. x ≠ 4 − ; D. x ≠ 4 . Câu 6. +
Kết quả của phép tính 2x 1 5 + là x − 3 3 − x + − + A. 2x 4 ; B. 2x 4 ; C. 2x + 4 ; D. 2x 6 . x − 3 x − 3 (x − 3)2 x − 3
Câu 7. Hình chóp tứ giác đều có cạnh đáy là 1 cm. Khi đó chu vi đáy của hình chóp này là A. 3 cm; B. 4 cm; C. 5 cm; D. 6 cm.
Câu 8. Hình chóp tam giác đều có một mặt bên là tam giác đều có diện tích bằng a , khi đó diện tích
tất cả các mặt của hình chóp tam giác đều đó là A. 3a ; B. 4a ; C. 5a ; D. 6a .
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Thu gọn biểu thức: a) ( 6 2 − x y ) ( 3 2 4 : 0, − 1x y ) ; b) ( 2 xy + ) 5 5 2 : ; 2 c) y( 2 3 y − x ) + ( 2 x + y)( 2 3 3 xy − y ) .
Bài 2. (1,5 điểm) Phân tích đa thức thành nhân tử: a) 2 18x − 20xy ; b) 2 2
8xy − 2x − 8y ; c) 2 2
3x + 5x − 3y − 5y . Bài 3. −
(1,5 điểm) Cho biểu thức 5x 2 3 x A = − + . 2
x − 4 x + 2 x − 2
a) Tìm điều kiện xác định của biểu thức . A b) Rút gọn biểu thức . A
c) Tính giá trị của biểu thức A với x thỏa mãn x + 3 = 5.
Bài 4. (1,0 điểm) Từ một khúc gỗ hình lập phương cạnh 30 cm. Người ta cắt đi một phần gỗ để được
phần còn lại là một hình chóp tứ giác đều có đáy là hình vuông cạnh 30 cm và chiều cao của hình
chóp cũng bằng 30 cm. Tính thể tích của phần gỗ bị cắt đi.
Bài 5. (2,0 điểm)
a) Cho tứ giác NMPQ có PM là tia phân giác của NPQ , = ° = ° QMN 110 , N
120 ,Q = 60°. Tính số đo của MPQ và Q . MP
b) Trên hình là một khung mái nhà tam giác cân tại ,
A được làm từ các thanh thép bằng cách hàn chúng lại với nhau. Biết độ dài cạnh
AH = 10 dm ( AH ⊥ BC)
, độ dài cạnh BC = 48
dm. Để hoàn thành khung mái nhà này người thợ cắt
các đoạn thẳng A ;
B AC; ME; MH; NH; NF. Hãy tính độ dài các đoạn thẳng trên để giúp chú
thợ hàn cắt chuẩn kích thước. Biết rằng 4 điểm M; N; E; F lần lượt là trung điểm của các đoạn thẳng A ; B AC; ;
HB HC và ME // AH // NF.
Bài 6. (0,5 điểm) Cho các số thực a,b,c thỏa mãn ab + bc + ca = 2025 . Chứng minh rằng 2 2 2 a − bc b − ca c − ab + + = 0 . 2 2 2
a + 2025 b + 2025 c + 2025 -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – TOÁN 8
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 1 MÃ ĐỀ MT205
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 Đáp án D C A A C B B B
Hướng dẫn giải phần trắc nghiệm Câu 1. Đáp án đúng là: D Ta có: 2 2 2
xy zx = x y z là đơn thức bậc 5. Câu 2. Đáp án đúng là: C Ta có: 3
A = x y (− xy) 4 2 4 5 = 20
− x y nên suy ra A và B là hai đơn thức đồng dạng, nhưng không
đồng dạng với đơn thức C. Câu 3. Đáp án đúng là: A Ta có: 1 2 2 2 2 1 2 A xy xy x y x y = + + − + xy 2 3 3 3 2 1 2
= xy + x y + xy 2 3 Thay 1 x = và y = 1 − vào biểu thức 3 2 1 2
A = xy + x y + xy ta được: 2 2 3 2 3 1 A ( )2 1 1 = − + (− ) 1 + (− ) 3 1 1 1 . . 1 . . 1 . 1 = − − = . 2 2 3 2 2 4 12 2 6 Câu 4. Đáp án đúng là: A Ta có: (x − )3 3 2 2 3 3 2
2 = x − 3.x .2 + 3. .2 x
− 2 = x − 6x + 12x − 8. Vậy ta điền đơn thức 2 6
− x vào ô trống. Câu 5. Đáp án đúng là: C −
Phân thức x 3 xác định khi và chỉ khi 6x + 24 ≠ 0 tức là x ≠ 4 − . 6x + 24 Câu 6. Đáp án đúng là: B + + + − − Ta có: 2x 1 5 2x 1 5 2x 1 5 2x 4 + = − = = . x − 3 3 − x x − 3 x − 3 x − 3 x − 3 Câu 7. Đáp án đúng là: B
Đáy của hình chóp tứ giác đều là hình vuông
Do đó chu vi đáy của hình chóp tứ giác đều là 4.1 = 4 cm. Câu 8. Đáp án đúng là: B
Hình chóp tam giác đều có mặt bên là tam giác đều nên tất cả các mặt là tam giác đều bằng nhau nên có diện tích bằng nhau.
Do đó diện tích tất cả 4 mặt của hình chóp tam giác đều đó là 4a (đvdt).
PHẦN II. TỰ LUẬN (8,0 điểm) Bài 1. (1,5 điểm) a) ( 6 2 − x y ) ( 3 2 4 : 0, − 1x y ) 3 = 40x . c) y( 2 3 y − x ) + ( 2 x + y)( 2 3 3 xy − y ) 3 3 3 2 2 2 3 b) ( 2 xy + ) 5 5 2 :
= 3y − x y + x y − x y + 3xy − 3y 2 2 2 2
= −x y + 3xy . 2 4 = 2xy + . 5 Bài 2. (1,5 điểm) a) 2 18x − 20xy b) 2 2
8xy − 2x − 8y c) 2 2
3x + 5x − 3y − 5y
= 2x(9x − 10y) . = − ( 2 2
2 x − 4xy + 4y ) = ( 2 2
3x − 3y ) + (5x − 5y) = − (x − y)2 2 2 . = ( 2 2
3 x − y ) + 5(x − y)
= 3(x − y)(x + y) + 5(x − y)
= (x − y)(3x + 3y + 5) . Bài 3. − (1,5 điểm) 5x 2 3 x A = − + . 2
x − 4 x + 2 x − 2
a) Điều kiện xác định của biểu thức A là 2
x − 4 ≠ 0 , x + 2 ≠ 0 và x − 2 ≠ 0. Tức là x ≠ 2. ± b) Với x ≠ 2, ± ta có: 5x − 2 3 x A = − + 2
x − 4 x + 2 x − 2
5x − 2 − 3(x − 2) + x(x + 2) = ( x + 2)(x − 2) 2
5x − 2 − 3x + 6 + x + 2x = ( x + 2)(x − 2) 2 x + 4x + 4 = ( x + 2)(x − 2) (x + )2 2 x + 2 = ( = . x + 2)(x − 2) x − 2 c) Ta có: x + 3 = 5
x + 3 = 5 hoặc x + 3 = 5 −
x = 2 (không thỏa mãn) hoặc x = 8 − (thỏa mãn) + Thay x = 8 − vào biểu thức x 2 A = ta được: x − 2 8 2 6 3 A − + − = = = . 8 − − 2 10 − 5 Bài 4. (1,0 điểm)
Thể tích khúc gỗ hình lập phương là: 3 30 = 27 000 (cm3).
Thể tích của phần gỗ còn lại hình chóp tứ giác đều là: 1 2 .30 .30 = 9 000 (cm3). 3
Thể tích của khối gỗ bị cắt đi là: 27 000 − 9 000 = 18 000 (cm3). Bài 5. (2,0 điểm)
a) Trong tứ giác MNPQ , ta có: + + + Q QMN N NPQ = 360° Suy ra = ° − + + NPQ 360
(QMN N Q) = 360° − (110° +120° + 60°) = 70°.
Do PM là tia phân giác của góc NPQ nên ta có: NPQ 70 NPM MPQ ° = = = = 35° . 2 2
Trong tam giác MPQ , ta có: + + Q QMP MPQ = 180° Suy ra = ° − + QMP 180
(MPQ Q) = 180° − (35° + 06°) = 85°. Vậy = NPM MPQ = 35°, QMP = 85° .
b) Vì H là trung điểm BC nên 1 1
BH = CH = BC = .48 = 24 dm. 2 2
Áp dụng định lý Pythagore trong tam giác ABH vuông tại H ta có: 2 2 2 2 2
AB = AH + BH =10 + 24 = 676
Do đó AB = 676 = 26 dm nên AB = AC = 26 dm (Vì tam giác ABC là tam giác cân tại ). A
E là trung điểm BH nên 24 BE = EH = =12 dm; 2
F là trung điểm HC nên 24 HF = FC = =12 dm ; 2
M là trung điểm AB nên 26 AM = MB = =13 dm ; 2
N là trung điểm AC nên 26 AN = AC = =13 dm ; 2
Áp dụng định lý Pythagore vào tam giác MBE vuông tại E ta có: 2 2 2 2
ME = MB − BE = 13 −12 = 5 dm
Áp dụng định lý Pythagore vào tam giác NFC vuông tại F ta có 2 2 2 2
NF = NC − FC = 13 −12 = 5 dm ;
Áp dụng định lý Pythagore vào tam giác MEH vuông tại E ta có 2 2 2 2
MH = ME + EH = 5 +12 =13 dm ;
Áp dụng định lý Pythagore vào tam giác NHF vuông tại F ta có 2 2 2 2
NH = NF + HF = 5 +12 =13 dm ;
Vậy AB = AC = 26 dm ; ME = NF = 5 dm ; MH = NH =13 dm. Bài 6. (0,5 điểm) Ta có: 2 2
a + 2025 = a + ab + bc + ca = (a + b)(c + a) 2 2
Khi đó a − bc a − bc = . 2 a + 2025
(a + b)(c + a) 2 2 2 2
Tương tự ta cũng có: b − ca b − ca = ; c − ab c − ab = 2 b + 2025
(a + b)(b + c) 2c + 2025 (b + c)(c + a) 2 2 2 Suy ra a − bc b − ca c − ab P = + + 2 2 2
a + 2025 b + 2025 c + 2025 2 2 2 a − bc b − ca c − ab = ( + +
a + b)(c + a) (b + c)(a + b) (c + a)(b + c)
( 2 − )( + ) + ( 2 − )( + ) + ( 2 a bc b c b ca c a
c − ab)(a + b) = (
a + b)(b + c)(c + a) 2 2 2 2 2 2 2 2 2 2 2 2
a b + a c − b c − bc + b c + b a − c a − ca + c a + c b − a b − ab = ( = .
a + b)(b + c)(c + a) 0 -----HẾT-----
Document Outline
- 1. Đề thi số 1 - CD - Toán 8 - Giữa HK1
- 2. Đề thi số 2 - CD - Toán 8 - Giữa HK1
- 3. Đề thi số 3 - CD - Toán 8 - Giữa HK1
- 4. Đề thi số 4 - CD - Toán 8 - Giữa HK1
- 5. Đề thi số 5 - CD - Toán 8 - Giữa HK1
- 6. Đề thi số 6 - CD - Toán 8 - Giữa HK1
- 7. Đề thi số 7 - CD - Toán 8 - Giữa HK1
- 8. Đề thi số 8 - CD - Toán 8 - Giữa HK1
- 9. Đề thi số 9 - CD - Toán 8 - Giữa HK1
- 10. Đề thi số 10 - CD - Toán 8 - Giữa HK1




