







Preview text:
ĐỀ ÔN TẬP CUỐI HỌC KỲ I ĐỀ 1 NĂM HỌC 2024-2025 MÔN: TOÁN 8 KẾT NỐI TRI THỨC
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Trong các đơn thức 2 2 2 2
M = 2xyz ; N = 4
− y z; P = −xz ; Q = 5yz , đơn thức
đồng dạng với đơn thức 2 − yz là A. M. B. N. C. . P D. . Q
Câu 2. Bậc của đơn thức x y( y )2 2 3 2 2 là A. 5. B. 7. C. 8. D. 9.
Câu 3. Trong các đẳng thức dưới đây, đẳng thức nào là đẳng thức sai?
A. ( x + y)2 = ( x + y)( x + y). B. 2 2
x − y = ( x + y)( x − y).
C. (−x − y)2 = (−x)2 − 2(−x) 2 y + y .
D. ( x − y)( x − y) 2 2 = y − x .
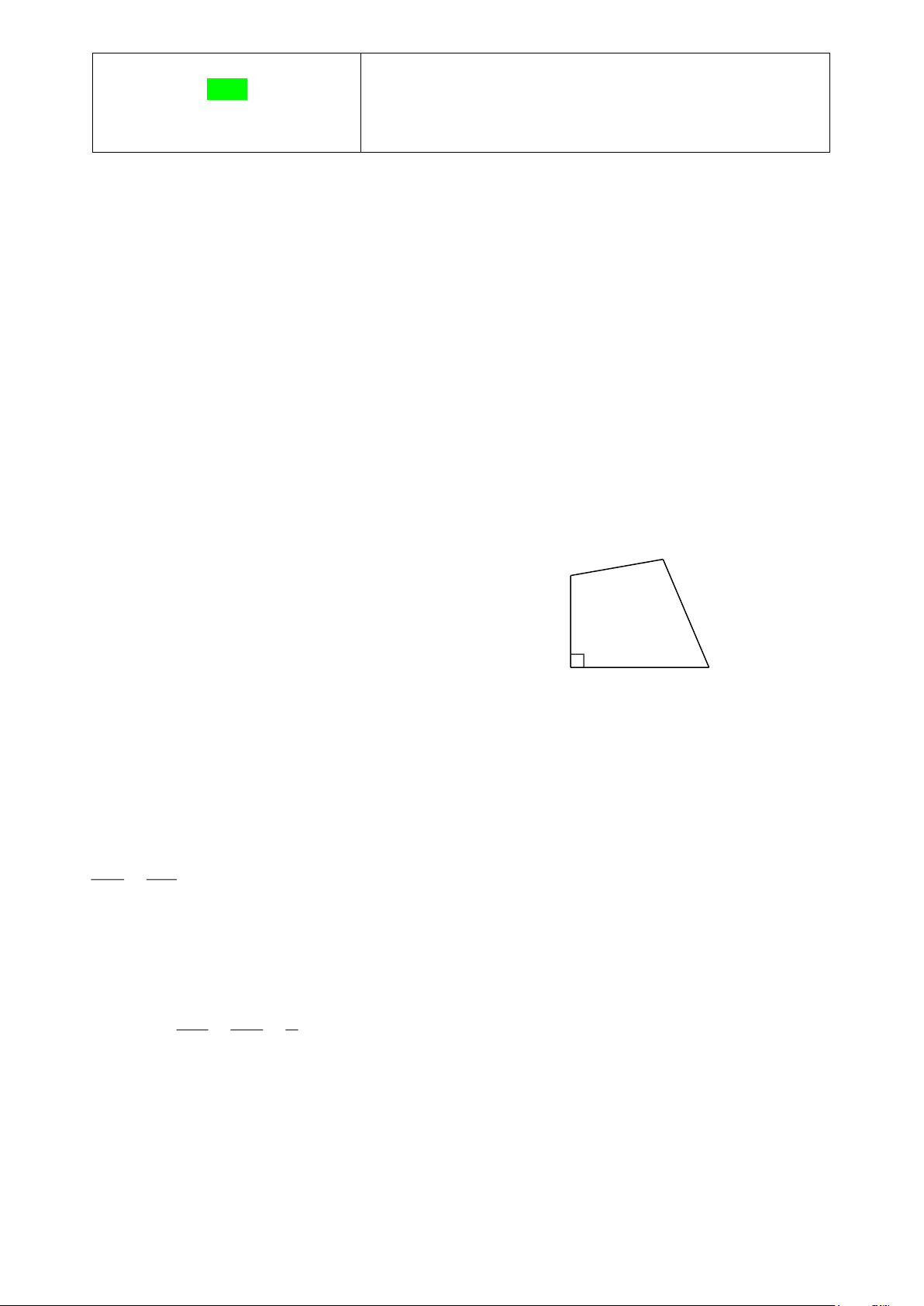
Câu 4. Số đo x trong hình vẽ bên là A A. 83 . B. 93 . D x C. 103 . D. 113 . 100° 67° C B
Câu 5. Chọn nhận định sai.
Tứ giác nào có hai đường chéo bằng nhau? A. Hình thoi. B. Hình vuông. C. Hình chữ nhật. D. Hình thang cân. Câu 6. Cho ABC
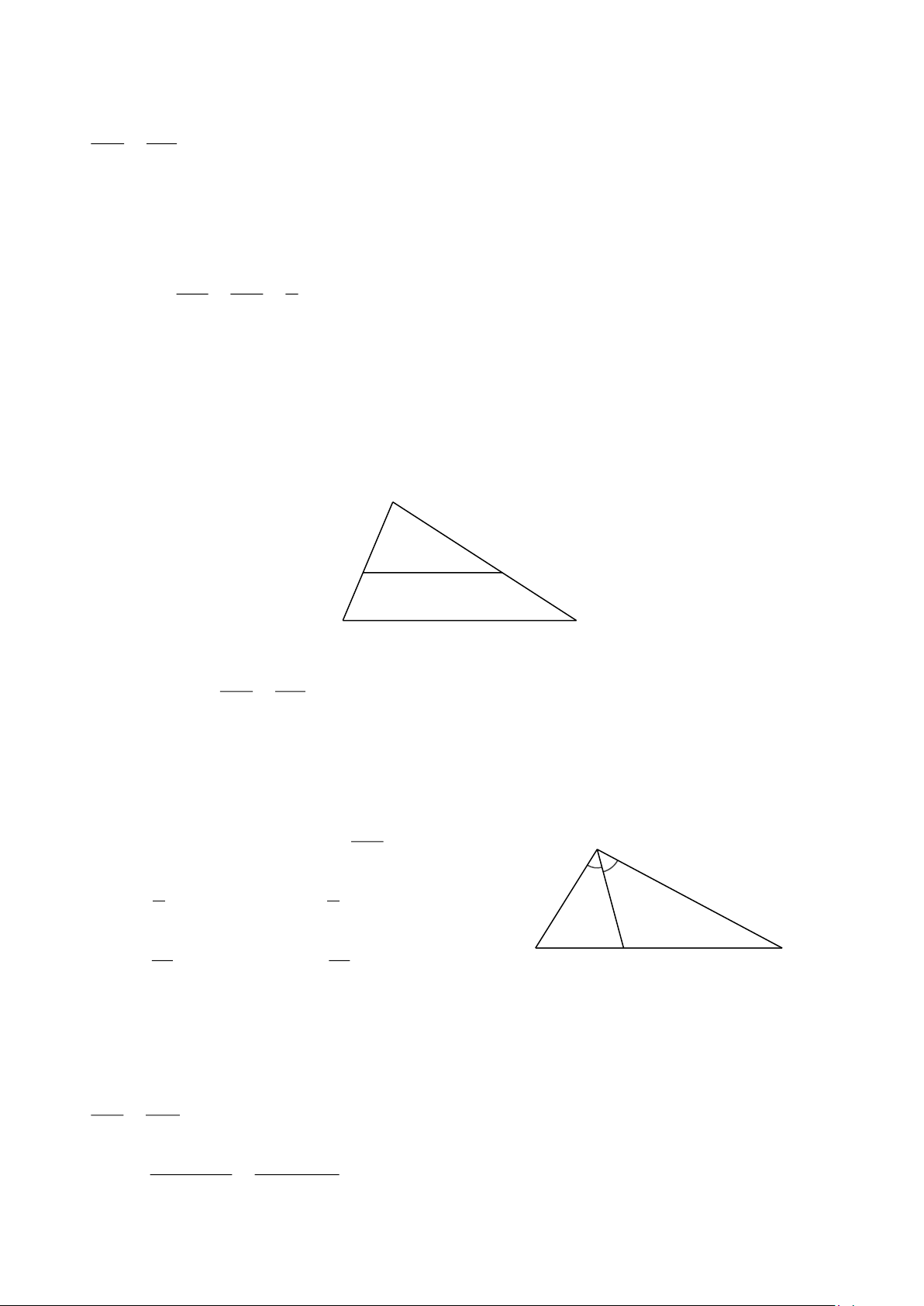
có D, E lần lượt là hai điểm nằm trên AB và BC sao cho AD CE = . AB CB Cho các khẳng định sau:
(I) DE là đường trung bình của . ABC (II) DE // AC. BD DE 1 (III) = = . BA AC 2
Khẳng định nào sau đây là đúng? A. Chỉ có (I) đúng; B. Chỉ có (II) đúng;
C. Chỉ có (I) và (III) đúng;
D. Cả (I), (II) và (III) đều đúng. BD
Câu 7. Cho hình vẽ bên. Tỉ số bằng A BC 5 9 A. . B. . 9 cm 5 cm 9 5 5 9 C. . D. . B D C 14 14
Câu 8. Trong các dãy dữ liệu sau đây, dữ liệu nào là dữ liệu liên tục?
A. Dữ liệu về danh sách các bạn học sinh tham dự hội khỏe Phù Đổng của thành phố.
B. Dữ liệu về đánh giá hiệu quả của chuyến đi dã ngoại cho học sinh khối 8.
C. Dữ liệu về chiều cao của học sinh lớp 8A.
D. Dữ liệu về danh sách học sinh đến trường bằng xe bus.
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,0 điểm) Cho hai đa thức: A = ( 2 xy − x + ) 2 4
2 xy và B = ( 3 4 4 3 2 3
15x y − 20x y +10x y ):5x . y
a) Tìm đa thức C biết A = B − . C
b) Tính giá trị của đa thức C khi x = 2; − y =1.
Bài 2. (1,0 điểm) Phân tích các đa thức sau thành nhân tử: a) 3 2 2
3x + 6x y + 3xy ; b) 2 x − 7x + 6.
Bài 3. (1,0 điểm) Tìm x, biết: a) 3 2
x − 3x + 3x −126 = 0; b) 16 8 8
x + 2x − x = 2.
Bài 4. (3,0 điểm) Cho ΔABC vuông tại A ( AB AC ) có AM là đường trung tuyến.
Gọi D, E lần lượt là hình chiếu của M trên cạnh A , B A . C
a) Giải thích tại sao tứ giác ADME là hình chữ nhật, từ đó suy ra AE = DM.
b) Kẻ đường cao AH của Δ .
ABC Chứng minh tứ giác DHME là hình thang cân.
c) Lấy điểm N sao cho M là trung điểm của .
NE Kẻ EK vuông góc với . BC
Chứng minh AK ⊥ KN.
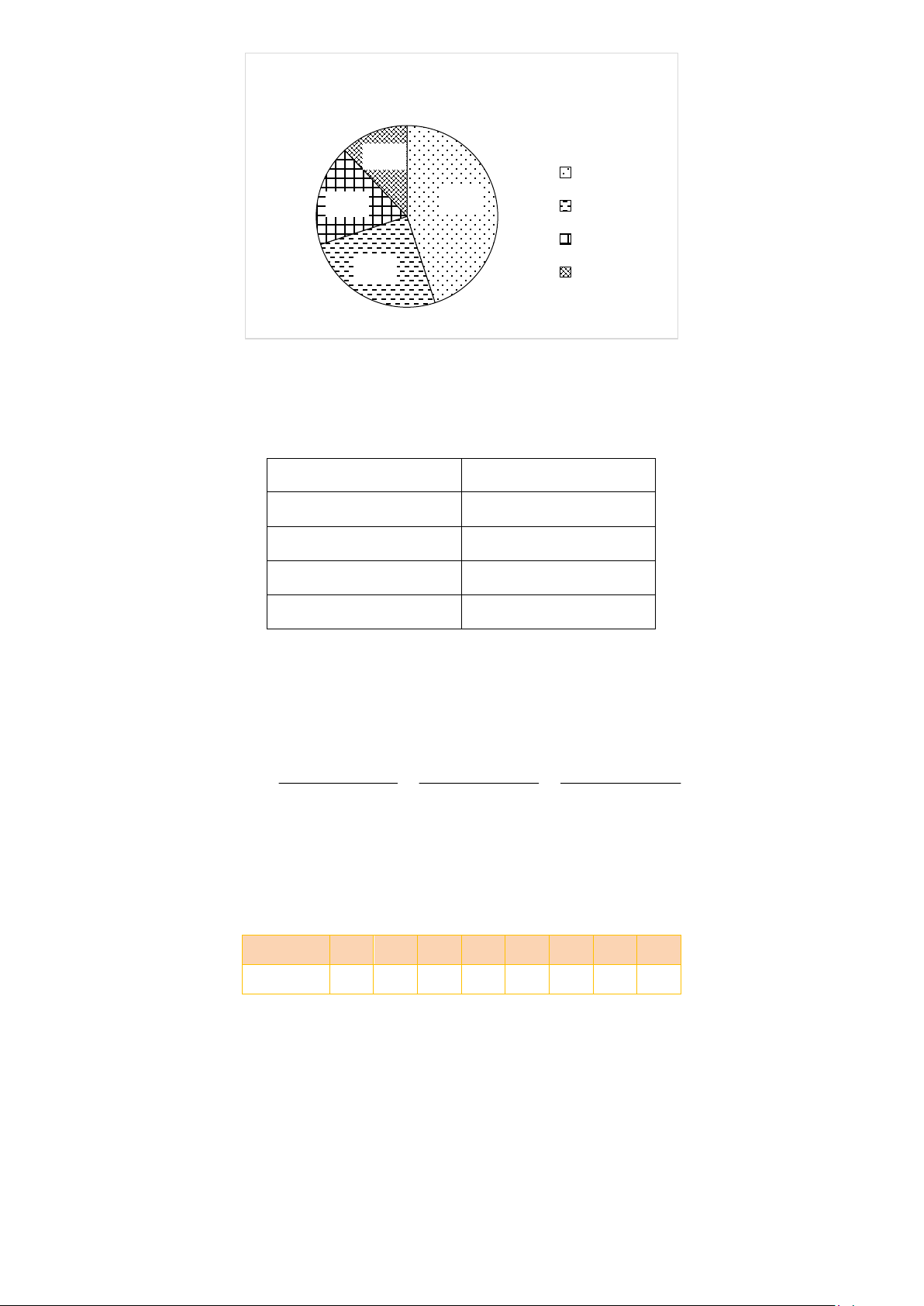
Bài 5. (1,5 điểm) Tỉ lệ phần trăm kết quả phỏng vấn 1 000 khách hàng về sự lựa chọn
món ăn của một cửa hàng được thể hiện trong biểu đồ sau:
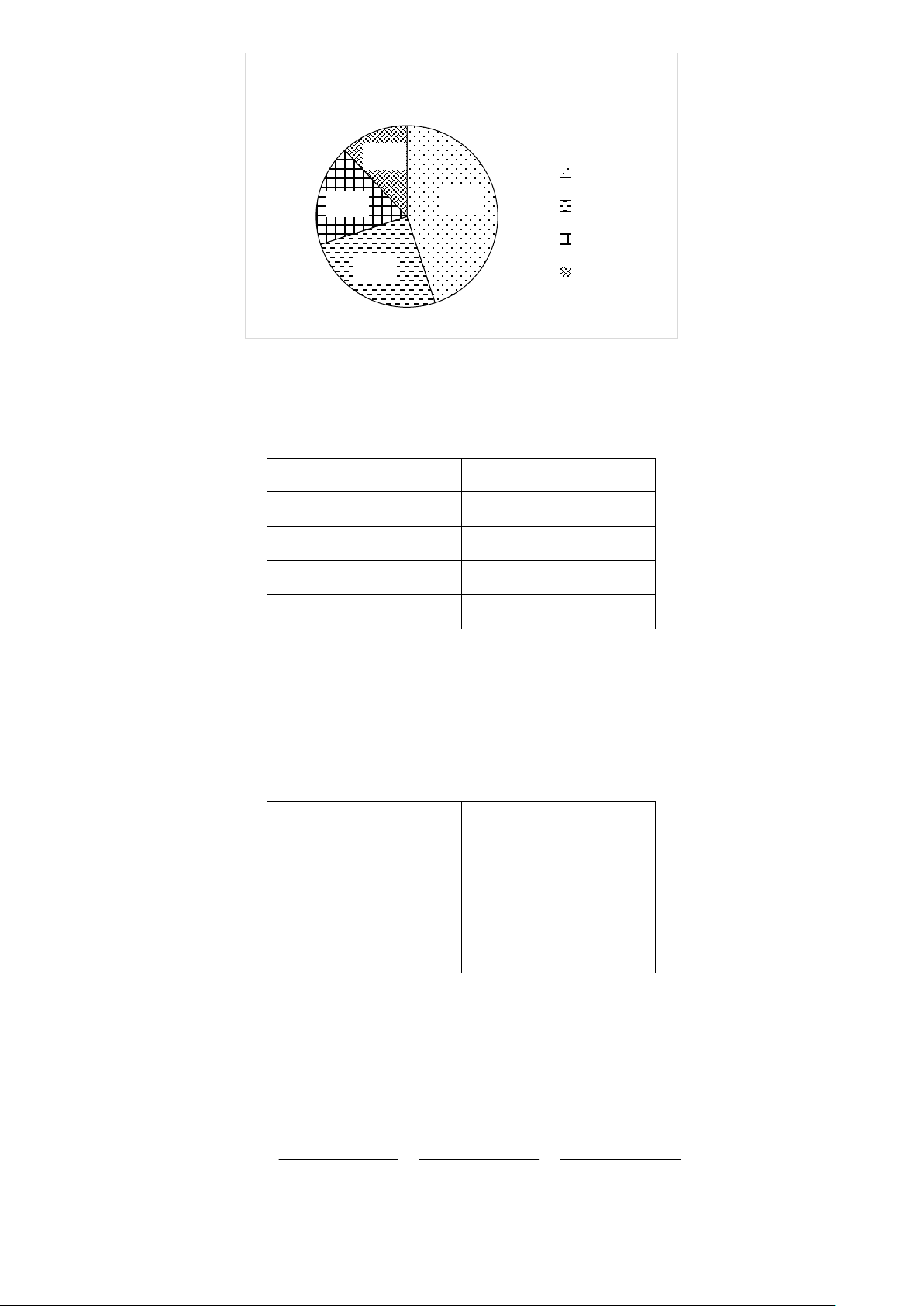
Tỉ lệ phần trăm món ăn được chọn của một cửa hàng 12% Phở 45% 18% Bún bò Bánh mì 25% Gỏi cuốn
a) Cửa hàng đã thu thập dữ liệu được biểu diễn trong biểu đồ trên bằng phương
pháp nào? Đây là phương pháp thu thập trực tiếp hay gián tiếp?
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau: Món ăn Tỉ lệ phần trăm Phở ? Bún bò ? Bánh mì ? Gỏi cuốn ?
c) Nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì cửa hàng nên
ưu tiên chọn món nào? Tại sao?
Bài 6. (0,5 điểm) Cho ba số thực a, b, c khác 2 và thỏa mãn a + b + c = 6. Tính giá trị của biểu thức: (a − )2 (b − )2 (c − )2 2 2 2 M = ( + +
b − )(c − ) (a − )(c − ) (a − )(b − ). 2 2 2 2 2 2
−−−−−HẾT−−−−−
ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1 – TOÁN 8
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8
Đáp án D D D C A B C C
Hướng dẫn giải phần trắc nghiệm
Câu 1. Trong các đơn thức 2 2 2 2
M = 2xyz ; N = 4
− y z; P = −xz ; Q = 5yz , đơn thức
đồng dạng với đơn thức 2 − yz là A. M. B. N. C. . P D. . Q Hướng dẫn giải Đáp án đúng là: D
Đơn thức đồng dạng với đơn thức 2 − yz là 2
Q = 5yz (vì hai đơn thức này đều có hệ số
khác 0 và có cùng phần biến là 2 yz ).
Câu 2. Bậc của đơn thức x y( y )2 2 3 2 2 là A. 5. B. 7. C. 8. D. 9. Hướng dẫn giải Đáp án đúng là: D
Ta có x y( y )2 2 3 2 6 2 7 2 2
= 2x y 4y = 8x y .
Đơn thức trên có bậc là 2 + 7 = 9.
Vậy đơn thức x y( y )2 2 3 2 2 có bậc là 9.
Câu 3. Trong các đẳng thức dưới đây, đẳng thức nào là đẳng thức sai?
A. ( x + y)2 = ( x + y)( x + y). B. 2 2
x − y = ( x + y)( x − y).
C. (−x − y)2 = (−x)2 − 2(−x) 2 y + y .
D. ( x − y)( x − y) 2 2 = y − x . Hướng dẫn giải Đáp án đúng là: D
Đẳng thức sai là ( − )( − ) 2 2
x y x y = y − x vì ( x − y)( x − y) = ( x − y)2 .
Câu 4. Số đo x trong hình vẽ bên là A A. 83 . B. 93 . D x C. 103 . D. 113 . 100° 67° C B Hướng dẫn giải Đáp án đúng là: C
Xét tứ giác ABCD có
A + B + C + D = 360 (tổng các góc của một tứ giác)
x + 67 + 90 +100 = 360 x + 257 = 360 x = 360 − 257 x =103 . Vậy x =103 . Ta chọn phương án C.
Câu 5. Chọn nhận định sai.
Tứ giác nào có hai đường chéo bằng nhau? A. Hình thoi. B. Hình vuông. C. Hình chữ nhật. D. Hình thang cân. Hướng dẫn giải Đáp án đúng là: A
Hình thang cân, hình chữ nhật và hình vuông có hai đường chéo bằng nhau.
Hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường.
Vậy ta chọn phương án A. Câu 6. Cho ABC
có D, E lần lượt là hai điểm nằm trên AB và BC sao cho AD CE = . AB CB Cho các khẳng định sau:
(I) DE là đường trung bình của . ABC (II) DE // AC. BD DE 1 (III) = = . BA AC 2
Khẳng định nào sau đây là đúng? A. Chỉ có (I) đúng; B. Chỉ có (II) đúng;
C. Chỉ có (I) và (III) đúng;
D. Cả (I), (II) và (III) đều đúng. Hướng dẫn giải Đáp án đúng là: B B D E A C AD CE Xét ABC có =
nên DE // AC (định lí Thalès đảo). Do đó (II) đúng. AB CB
Do D, E lần lượt không phải trung điểm của AB và BC nên DE không là đường trung bình của . ABC
Do đó (I) sai, nên (III) cũng sai.
Vậy chỉ có (II) đúng. Ta chọn phương án B. BD
Câu 7. Cho hình vẽ bên. Tỉ số bằng A BC 5 9 A. . B. . 9 cm 5 cm 9 5 5 9 C. . D. . B D C 14 14 Hướng dẫn giải Đáp án đúng là: C Xét ABC
có AD là đường phân giác của góc BAC (do BAD = CAD), nên AB DB =
(tính chất đường phân giác). AC DC AB BD Do đó =
(tính chất tỉ lệ thức) AB + AC BD + DC BD 5 5 Suy ra = = . BC 5 + 9 14
Câu 8. Trong các dãy dữ liệu sau đây, dữ liệu nào là dữ liệu liên tục?
A. Dữ liệu về danh sách các bạn học sinh tham dự hội khỏe Phù Đổng của thành phố.
B. Dữ liệu về đánh giá hiệu quả của chuyến đi dã ngoại cho học sinh khối 8.
C. Dữ liệu về chiều cao của học sinh lớp 8A.
D. Dữ liệu về danh sách học sinh đến trường bằng xe bus. Hướng dẫn giải Đáp án đúng là: C
Dữ liệu về chiều cao của học sinh lớp 8A là dữ liệu liên tục.
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,0 điểm) Cho hai đa thức: A = ( 2 xy − x + ) 2 4
2 xy và B = ( 3 4 4 3 2 3
15x y − 20x y +10x y ):5x . y
a) Tìm đa thức C biết A = B − . C
b) Tính giá trị của đa thức C khi x = 2; − y =1. Hướng dẫn giải a) Ta có: A = ( 2 xy − x + ) 2 2 2 2 2 2 3 3 2 2 4
2 xy = xy xy − 4x xy + 2 xy = x y − 4x y + 2xy . B = ( 3 4 4 3 2 3
15x y − 20x y +10x y ):5xy 3 4 = x y ( xy) 4 3 − x y ( xy) 2 3 15 : 5 20 : 5 +10x y : (5xy) 2 3 3 2 2
= 3x y − 4x y + 2xy .
Mà A = B − C, suy ra C = B − A Do đó 2 3 3 2 2
C = x y − x y + xy − ( 2 3 3 2 2 3 4 2
x y − 4x y + 2xy ) 2 3 3 2 2 2 3 3 2 2
= 3x y − 4x y + 2xy − x y + 4x y − 2xy = ( 2 3 2 3
x y − x y ) + ( 3 2 3 2
− x y + x y ) + ( 2 2 3 4 4 2xy − 2xy ) 2 3 = 2x y . Vậy 2 3 C = 2x y . b) Thay x = 2;
− y =1 vào biểu thức 2 3
C = 2x y đã được thu gọn ở câu a, ta được: C = (− )2 3 2 2 1 = 2 4 = 8.
Vậy C = 8 khi x = 2; − y =1.
Bài 2. (1,0 điểm) Phân tích các đa thức sau thành nhân tử: a) 3 2 2
3x + 6x y + 3xy ; b) 2 x − 7x + 6. Hướng dẫn giải a) 3 2 2
3x + 6x y + 3xy b) 2 x − 7x + 6 = x( 2 2
3 x + 2xy + y ) 2
= x − x − 6x + 6
= x(x + y)2 3 . = x(x − ) 1 − 6( x − ) 1 = (x − ) 1 ( x − 6).
Bài 3. (1,0 điểm) Tìm x, biết: a) 3 2
x − 3x + 3x −126 = 0; b) 16 8 8
x + 2x − x = 2. Hướng dẫn giải a) 3 2
x − 3x + 3x −126 = 0 b) 16 8 8
x + 2x − x = 2 3 2
x − 3x + 3x −1−125 = 0 16 8 8
x + 2x − x − 2 = 0 (x − )3 1 =125 ( 16 8 x + x ) − ( 8 2 x + 2) = 0 (x − )3 3 1 = 5 8 x ( 8 x + ) − ( 8 2 x + 2) = 0 Suy ra x −1= 5 ( 8x + )( 8 2 x − ) 1 = 0 x = 6
( 8x + )( 4x + )( 4 2 1 x − ) 1 = 0 Vậy x = 6.
( 8x + )( 4x + )( 2x + )( 2 2 1 1 x − ) 1 = 0
( 8x + )( 4x + )( 2 2 1 x + ) 1 ( x + ) 1 ( x − ) 1 = 0
Suy ra x +1= 0 hoặc x −1= 0 (Vì 8 4 2
x + 2 0, x +1 0, x +1 0 với mọi x) Do đó x = 1 − hoặc x =1. Vậy x 1 − ; 1 .
Bài 4. (3,0 điểm) Cho ΔABC vuông tại A ( AB AC ) có AM là đường trung tuyến.
Gọi D, E lần lượt là hình chiếu của M trên cạnh A , B A . C
a) Giải thích tại sao tứ giác ADME là hình chữ nhật, từ đó suy ra AE = DM.
b) Kẻ đường cao AH của Δ .
ABC Chứng minh tứ giác DHME là hình thang cân.
c) Lấy điểm N sao cho M là trung điểm của .
NE Kẻ EK vuông góc với . BC
Chứng minh AK ⊥ KN. Hướng dẫn giải B N H M D I K A E C
a) Xét tứ giác ADME có:
AEM = 90 (do ME ⊥ AC);
EAD = 90 (do ABC vuông tại ); A
ADM = 90 (do MD ⊥ AB)
Suy ra tứ giác ADME là hình chữ nhật (dấu hiệu nhận biết).
Do đó AE = DM (tính chất hình chữ nhật). (1) b) ⦁ Xét ABC
có M là trung điểm của BC và MD // AC (cùng vuông góc với AB)
Nên D là trung điểm của . AB
Chứng minh tương tự ta cũng có E là trung điểm của . AC
Khi đó DE là đường trung bình của . ABC
Do đó DE // BC (tính chất đường trung bình), hay DE // HM.
Tứ giác DHME có DE // HM nên DHME là hình thang. ⦁ Xét A
HC vuông tại H có HE là đường trung tuyến ứng với cạnh huyền AC nên 1
HE = AC (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) 2 1
Mà E là trung điểm của AC nên AE = AC. Do đó HE = AE (2). 2
Từ (1) và (2) suy ra DM = H . E
Hình thang DHME có DM = HE nên là hình thang cân.
c) Vì ADME là hình chữ nhật nên AD = ME (tính chất hình chữ nhật). Lại có ,
D M lần lượt là trung điểm của A ,
B NE nên AB = 2AD và NE = 2M . E Do đó AB = N . E
Tứ giác ABNE có AB = NE (chứng minh trên) và AB // NE (cùng vuông góc với
AC) nên là hình bình hành.
Lại có BAE = 90 nên hình bình hành ABNE là hình chữ nhật.
Khi đó hai đường chéo AN, BE bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Gọi I là giao điểm của AN, BE thì I là trung điểm của AN, B . E Xét B
KE vuông tại K có KI là đường trung tuyến ứng với cạnh huyền BE nên 1
KI = BE (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) 2 1
Mà AN = BE nên KI = AN. 2 1 Xét A
KN có KI là đường trung tuyến ứng với cạnh AN và KI = AN. 2 Do đó A
KN vuông tại K nên AK ⊥ KN tại K.
Bài 5. (1,5 điểm) Tỉ lệ phần trăm kết quả phỏng vấn 1 000 khách hàng về sự lựa chọn
món ăn của một cửa hàng được thể hiện trong biểu đồ sau:
Tỉ lệ phần trăm món ăn được chọn của một cửa hàng 12% Phở 45% 18% Bún bò Bánh mì 25% Gỏi cuốn
a) Cửa hàng đã thu thập dữ liệu được biểu diễn trong biểu đồ trên bằng phương
pháp nào? Đây là phương pháp thu thập trực tiếp hay gián tiếp?
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau: Món ăn Tỉ lệ phần trăm Phở ? Bún bò ? Bánh mì ? Gỏi cuốn ?
c) Nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì cửa hàng nên
ưu tiên chọn món nào? Tại sao? Hướng dẫn giải
a) Cửa hàng đã thu thập dữ liệu được biểu diễn trong biểu đồ trên bằng phương pháp
phỏng vấn 1 000 khách hàng. Đây là phương pháp thu thập trực tiếp.
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau: Món ăn Tỉ lệ phần trăm Phở 45% Bún bò 25% Bánh mì 18% Gỏi cuốn 12%
c) Nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì cửa hàng nên ưu
tiên chọn món Phở. Vì đây là món ăn được khách hàng lựa chọn nhiều nhất (chiếm 45%).
Bài 6. (0,5 điểm) Cho ba số thực a, b, c khác 2 và thỏa mãn a + b + c = 6. Tính giá trị của biểu thức: (a − )2 (b − )2 (c − )2 2 2 2 M = ( + +
b − )(c − ) (a − )(c − ) (a − )(b − ). 2 2 2 2 2 2 Hướng dẫn giải (a − )2 (b − )2 (c − )2 2 2 2 Ta có: M = ( + +
b − 2)(c − 2) (a − 2)(c − 2) (a − 2)(b − 2)
(a − )3 + (b − )3 + (c − )3 2 2 2 = (
a − 2)(b − 2)(c − 2) Đặt a − 2 = ; x b − 2 = ; y c − 2 = . z 3 3 3 x + y + z Khi đó M = . xyz
Mặt khác, từ a + b + c = 6 suy ra (a − 2) + (b − 2) + (c − 2) = 0
Hay x + y + z = 0
Suy ra x + y = −z ( + )3 = (− )3 x y z 3 3
x + y + xy( x + y) 3 3 = −z 3 3
x + y + xy(−z) 3 3 = −z 3 3 3
x + y + z = 3xyz 3 3 3 x + y + z 3xyz Do đó M = = = 3. xyz xyz Vậy M = 3.
−−−−−HẾT−−−−−
ĐỀ ÔN TẬP CUỐI HỌC KỲ I Thuvienhoclieu.Com NĂM HỌC 2024-2025 ĐỀ 2 MÔN: TOÁN 8 KẾT NỐI TRI THỨC
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Kết quả của phép cộng hai đơn thức 2 2xy z và 2 −x yz là A. Một đơn thức.
B. Một đa thức nhưng không phải đơn thức. C. Một số. D. Không xác định. Câu 2. Đa thức 2 2
3xyz − 5x y − 6xyz + 4x yz có bậc là A. 1. B. 2. C. 3. D. 4.
Câu 3. Trong các đẳng thức dưới đây, đẳng thức nào là đẳng thức đúng? A. ( A + B)2 2 2
= A + 2AB + B . B. ( A + B)2 2 2
= A + AB + B . C. ( A + B)2 2 2 = A + B . D. ( A + B)2 2 2
= A − 2AB + B .
Câu 4. Một hình thang vuông có một góc bằng 75 ,
góc còn lại không vuông của
hình thang đó có số đo là A. 25 . B. 75 . C. 105 . D. 125 .
Câu 5. Trong các hình sau, các hình nào có hai đường chéo vuông góc với nhau?
A. Hình chữ nhật, hình bình hành, hình thoi.
B. Hình bình hành, hình vuông, hình chữ nhật.
C. Hình thoi, hình vuông.
D. Hình thang cân, hình chữ nhật.
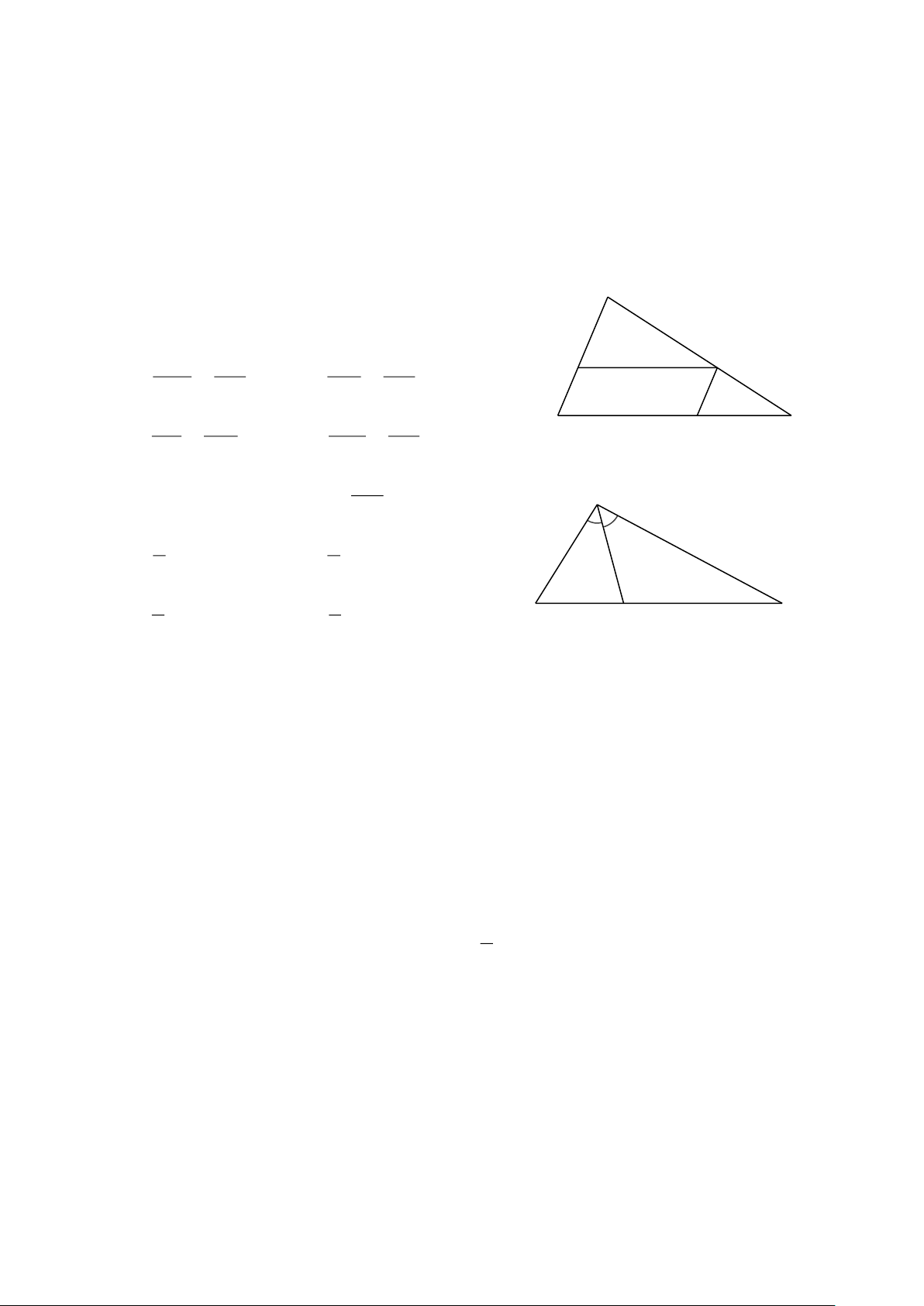
Câu 6. Cho hình vẽ bên, biết MN // BC, NP// AB. A
Khẳng định nào sau đây là sai? AM AB AN BP N A. = . B. = . M MN BC AC BC CP CN MN NP C. = . D. = . B P C BP AN BC AB AC
Câu 7. Cho hình vẽ bên. Tỉ số bằng A CD 5 4 A. . B. . 5 cm 4 5 4 5 C. . D. . B 4 cm D C 9 9
Câu 8. Trong các trường hợp sau, trường hợp nào là thu thập dữ liệu gián tiếp?
A. Phỏng vấn các bạn học sinh về tình hình bạo lực học đường.
B. Lập phiếu hỏi về các món ăn mà các bạn học sinh trong lớp yêu thích.
C. Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam.
D. Làm thí nghiệm để xác định tính chất hóa học của oxygen.
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,0 điểm) Cho hai đa thức: A = xy( 2 2 2 xy − 3x y + ) 1 và B = ( 4 5 5 4 3 3 x y − x y + x y ) 2 2 12 36 6 : 6x y .
a) Tìm đa thức M biết A = M + . B 1
b) Tính giá trị của đa thức M khi x = − ; y = 3. 4
Bài 2. (1,0 điểm) Phân tích các đa thức sau thành nhân tử: a) 2
25x ( x − 3y) −15(3y − x); b) 4 2 x − 5x + 4.
Bài 3. (1,0 điểm) Tìm x, biết: a) ( x + )( 2 x − x + ) 3 1
1 − x + 2x = 0; b) ( − x)( 2 x + x + ) 2 + x ( x − ) 2 3 5 3 2 3 3 5 3 5 = 15 − x + 9x .
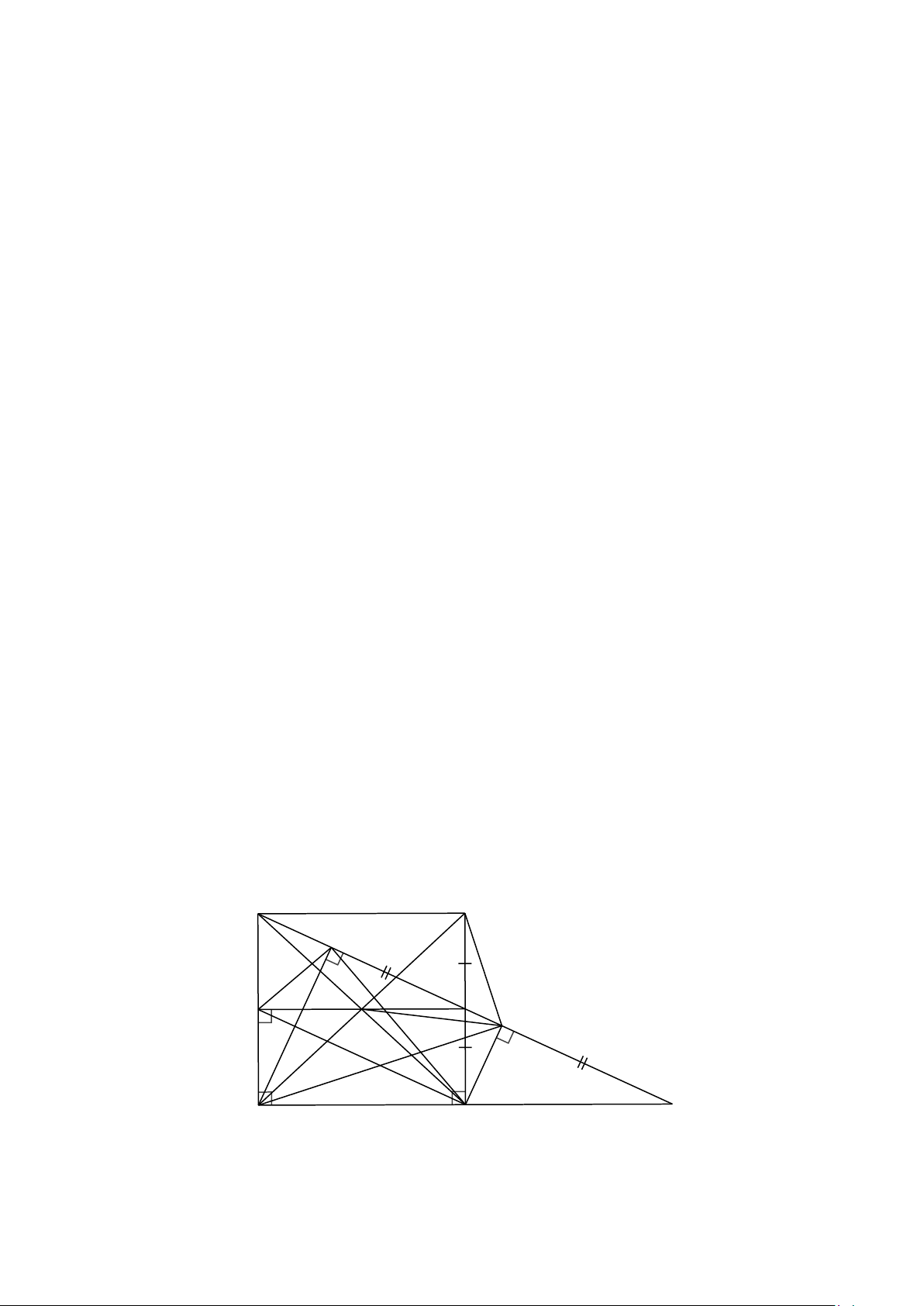
Bài 4. (3,0 điểm) Cho ABC
nhọn ( AB AC ). Các đường cao BF và CE cắt nhau
tại H. Gọi M là trung điểm của .
BC Trên tia đối của tia MH lấy điểm K sao cho MH = MK.
a) Giải thích tại sao tứ giác BHCK là hình bình hành, từ đó suy ra BK ⊥ A . B
b) Kẻ HG ⊥ BC tại .
G Trên tia đối của tia GH lấy điểm I sao cho G là trung
điểm của HI. Chứng minh tứ giác BIKC là hình thang cân.
c) Kẻ CQ ⊥ BK tại .
Q Chứng minh EFQ là tam giác vuông.
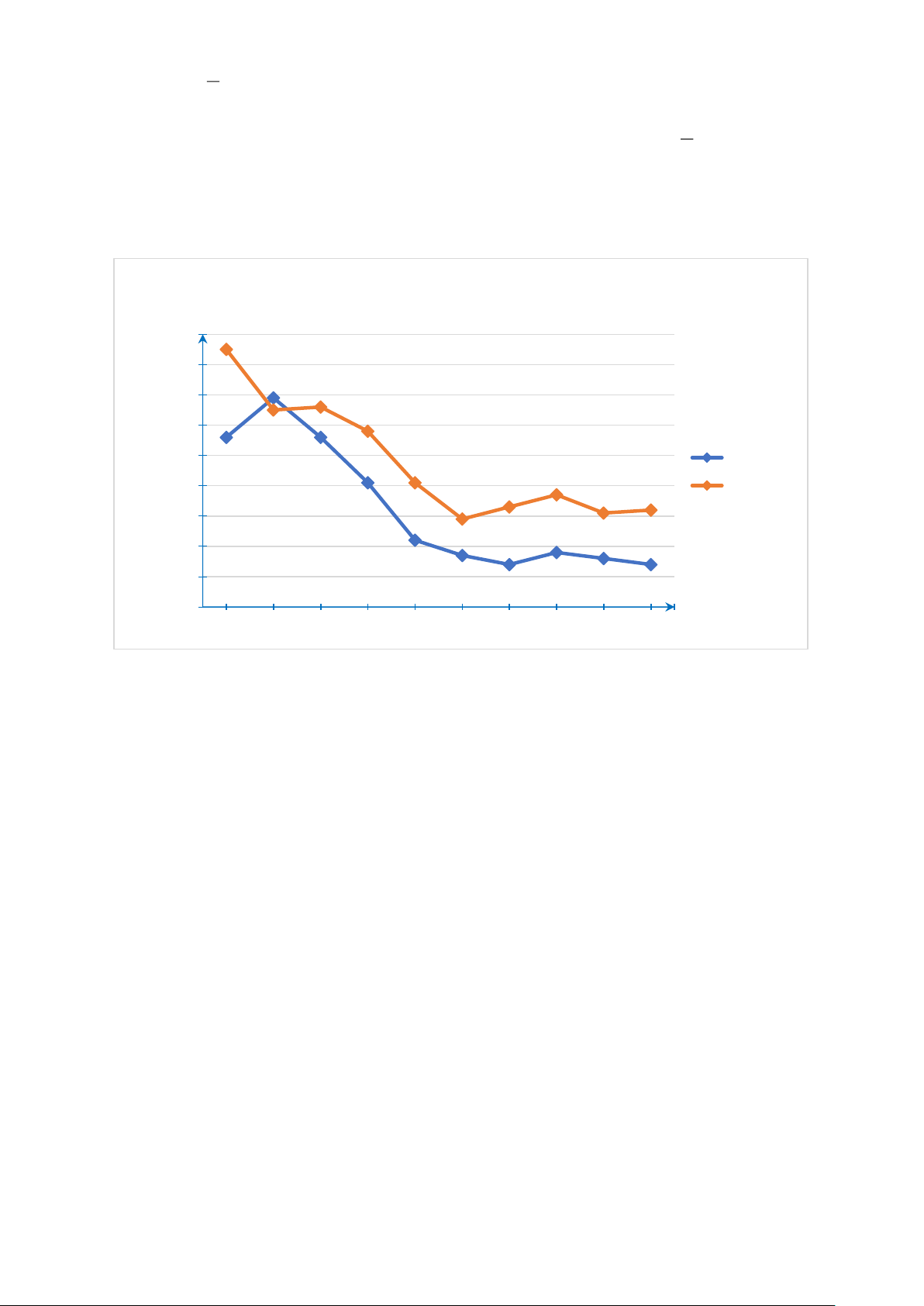
Bài 5. (1,5 điểm) Biểu đồ dưới đây biểu diễn xếp hạng thế giới của đội tuyển bóng đá
nam Việt Nam và Thái Lan vào tháng 10 trong 10 năm từ năm 2014 đến năm 2023.
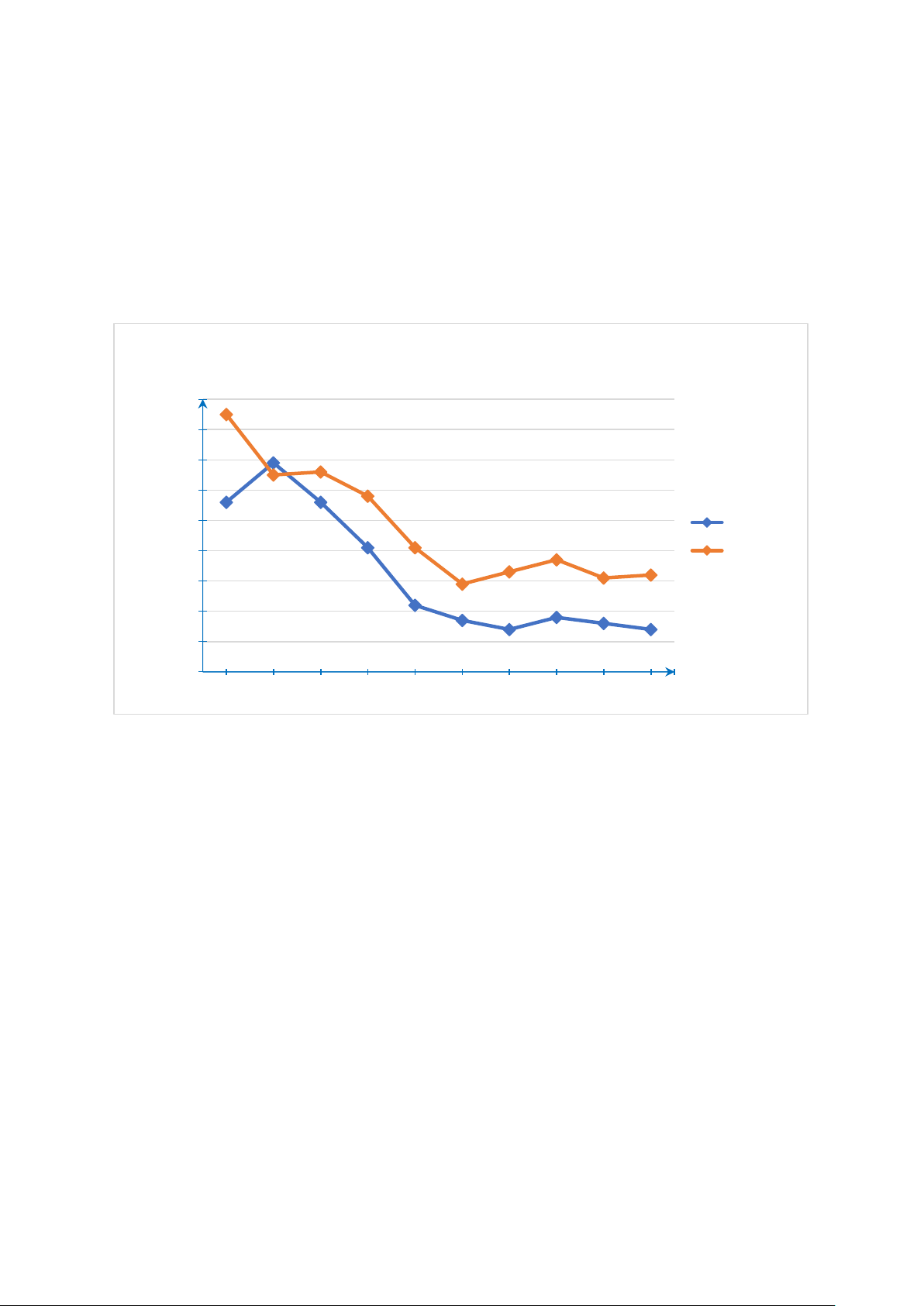
Xếp hạng FIFA của bóng đá Việt Nam và Thái Lan trong 10 năm Hạng165 170 160 145 146 150 138 149 140 130 136 136 121 Việt Nam 117 120 113 111 112 Thái Lan 121 109 110 100 102 90 97 98 94 96 94 80 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 Năm
Hình a. Theo Liên đoàn bóng đá thế giới (FIFA)
a) Dãy số liệu về xếp hạng thế giới của bóng đá nam Việt Nam là dãy số liệu rời
rạc hay liên tục? Chỉ ra những năm đội tuyển bóng đá nam Thái Lan có xếp
hạng cao hơn đội tuyển bóng đá nam Việt Nam.
b) Trong 10 năm, thứ hạng cao nhất của đội tuyển Việt Nam là bao nhiêu, đạt được vào năm nào?
c) Cho biểu đồ dưới đây:
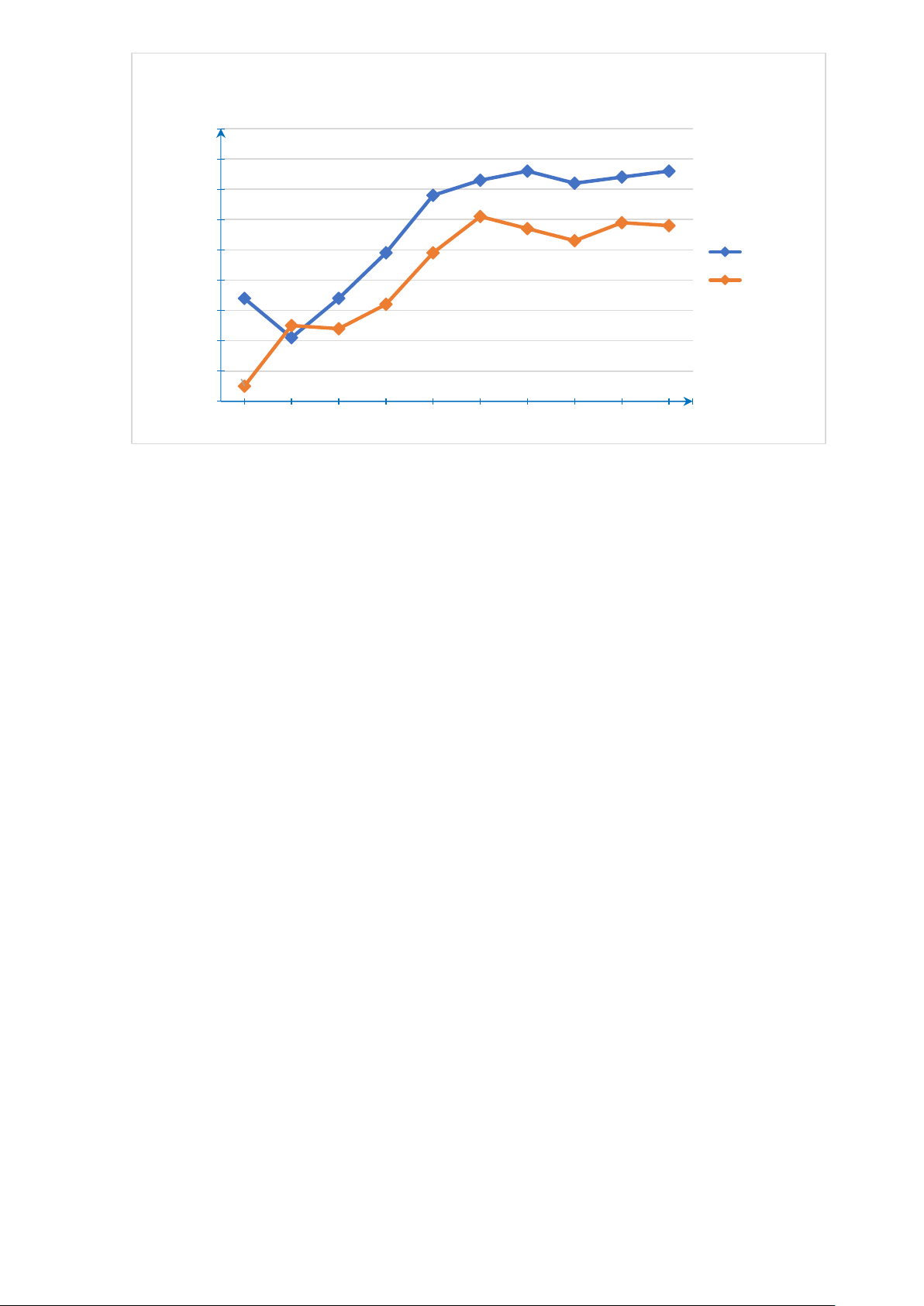
Xếp hạng FIFA của bóng đá Việt Nam và Thái Lan trong 10 năm Hạng 80 94 90 97 98 96 94 102 100 110 121 109 120 113 111 112 Việt Nam 117 130 136 136 121 Thái Lan 140 149 138 150 145 146 160 165 170 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 Năm
Hình b. Theo Liên đoàn bóng đá thế giới (FIFA)
Dữ liệu được biểu diễn trên biểu đồ So sánh sự khác nhau trong việc biểu diễn
các trục ở Hình a, Hình b. Biểu diễn ở Hình b có ưu điểm gì trong việc nhận ra xu thế của thứ hạng?
Bài 6. (0,5 điểm) Cho a, b, c là các số hữu tỉ thỏa mãn điều kiện ab + bc + ca =1.
Chứng minh rằng biểu thức M = ( 2 a + )( 2 b + )( 2 1 1 c + )
1 là bình phương của một số hữu tỉ.
−−−−−HẾT−−−−−
ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1 – TOÁN 8
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8
Đáp án A D A C C D A C
Hướng dẫn giải phần trắc nghiệm
Câu 1. Kết quả của phép cộng hai đơn thức 2 2xy z và 2 −x yz là A. Một đơn thức.
B. Một đa thức nhưng không phải đơn thức. C. Một số. D. Không xác định. Hướng dẫn giải Đáp án đúng là: A
Phép cộng của hai đơn thức 2 2xy z và 2 −x yz là 2 xy z + ( 2 −x yz) 2 2 = xy z.
Kết quả nhận được là 2
xy z, đây một đơn thức. Câu 2. Đa thức 2 2
3xyz − 5x y − 6xyz + 4x yz có bậc là A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải Đáp án đúng là: D Ta có 2 2
xyz − x y − xyz + x yz = ( xyz − xyz) 2 2 3 5 6 4 3 6
− 5x y + 4x yz 2 2 = 3
− xyz − 5x y + 4x yz Vì các đơn thức 3 − xyz và 2
−5x y đều có bậc là 3; đơn thức 2
4x yz có bậc là 4. Nên đa thức 2 2 3
− xyz − 5x y + 4x yz có bậc là 4. Vậy đa thức 2 2
3xyz − 5x y − 6xyz + 4x yz có bậc là 4.
Câu 3. Trong các đẳng thức dưới đây, đẳng thức nào là đẳng thức đúng? A. ( A + B)2 2 2
= A + 2AB + B . B. ( A + B)2 2 2
= A + AB + B . C. ( A + B)2 2 2 = A + B . D. ( A + B)2 2 2
= A − 2AB + B . Hướng dẫn giải Đáp án đúng là: A
Đẳng thức đúng là ( A + B)2 2 2
= A + 2AB + B . Đây là hẳng đẳng thức bình phương của một tổng.
Câu 4. Một hình thang vuông có một góc bằng 75 ,
góc còn lại không vuông của
hình thang đó có số đo là A. 25 . B. 75 . C. 105 . D. 125 . Hướng dẫn giải Đáp án đúng là: C
Do hình thang đã cho là hình thang vuông nên nó có hai góc vuông. Gọi số đo góc
còn lại của hình vuông là . x
Mà tổng các góc của một tứ giác bằng 360 nên ta có:
75 + 90 + 90 + x = 360
Suy ra x = 360 − (75 + 90 + 90) = 360 − 255 =105.
Vậy góc còn lại không vuông của hình thang đó có số đo là 105 .
Câu 5. Trong các hình sau, các hình nào có hai đường chéo vuông góc với nhau?
A. Hình chữ nhật, hình bình hành, hình thoi.
B. Hình bình hành, hình vuông, hình chữ nhật.
C. Hình thoi, hình vuông.
D. Hình thang cân, hình chữ nhật. Hướng dẫn giải Đáp án đúng là: C
Hình thoi và hình vuông có hai đường chéo vuông góc với nhau.
Câu 6. Cho hình vẽ bên, biết MN // BC, NP // AB. A
Khẳng định nào sau đây là sai? AM AB AN BP A. = . B. = . MN BC AC BC N M CP CN MN NP C. = . D. = . BP AN BC AB B P C Hướng dẫn giải Đáp án đúng là: D Xét ABC
với MN // BC, ta có: AM MN AN AM AB ⦁ = =
(hệ quả của định lí Thalès). Suy ra = . Do đó A là AB BC AC MN BC khẳng định đúng. Xét ABC
với NP // AB, ta có: AN BP ⦁ =
(hệ quả của định lí Thalès). Do đó B là khẳng định đúng. AC BC CP CN ⦁ =
(định lí Thalès). Do đó C là khẳng định đúng. BP AN CN NP ⦁ =
(hệ quả của định lí Thalès). AC AB AN CN
Ta có AN CN nên . AC AC MN AN CN NP MN NP Mà = và = nên
. Do đó D là khẳng định sai. BC AC AC AB BC AB
Vậy ta chọn phương án D. AC
Câu 7. Cho hình vẽ bên. Tỉ số bằng A CD 5 4 A. . B. . 5 cm 4 5 4 5 C. . D. . B 4 cm D C 9 9 Hướng dẫn giải Đáp án đúng là: A Xét ABC
có AD là đường phân giác của góc BAC (do BAD = CAD), nên AB DB =
(tính chất đường phân giác). AC DC AB AC Suy ra =
(tính chất tỉ lệ thức) DB DC AC 5 Do đó = . CD 4
Câu 8. Trong các trường hợp sau, trường hợp nào là thu thập dữ liệu gián tiếp?
A. Phỏng vấn các bạn học sinh về tình hình bạo lực học đường.
B. Lập phiếu hỏi về các món ăn mà các bạn học sinh trong lớp yêu thích.
C. Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam.
D. Làm thí nghiệm để xác định tính chất hóa học của oxygen. Hướng dẫn giải Đáp án đúng là: C
Trường hợp tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam là
phương pháp thu thập gián tiếp.
PHẦN II. TỰ LUẬN (8,0 điểm)
Bài 1. (1,0 điểm) Cho hai đa thức: A = xy( 2 2 2 xy − 3x y + ) 1 và B = ( 4 5 5 4 3 3 x y − x y + x y ) 2 2 12 36 6 : 6x y .
a) Tìm đa thức M biết A = M + . B 1
b) Tính giá trị của đa thức M khi x = − ; y = 3. 4 Hướng dẫn giải a) Ta có A = xy( 2 2 xy − x y + ) 2 2 2 3 3 2 2 3
1 = 2xy xy − 2xy 3x y + 2xy 1 = 2x y − 6x y + 2x . y B = ( 4 5 5 4 3 3 x y − x y + x y ) 2 2 12 36 6 : 6x y 4 5 = x y ( 2 2 x y ) 5 4 − x y ( 2 2 x y ) 3 3 + x y ( 2 2 12 : 6 36 : 6 6 : 6x y ) 2 3 3 2
= 2x y − 6x y + xy Mà A = M + . B
Suy ra M = A − B 2 3 3 2
M = x y − x y + xy − ( 2 3 3 2 2 6 2
2x y − 6x y + xy) 2 3 3 2 2 3 3 2
= 2x y − 6x y + 2xy − 2x y + 6x y − xy = ( 2 3 2 3
x y − x y ) + ( 3 2 3 2 2 2 6
− x y + 6x y ) + (2xy − xy) = . xy Vậy M = x . y 1
b) Thay x = − ; y = 3 vào M = xy đã thu gọn ở câu a, ta được: 4 1 3 M = − 3 = − . 4 4 3 1
Vậy M = − khi x = − ; y = 3. 4 4
Bài 2. (1,0 điểm) Phân tích các đa thức sau thành nhân tử: a) 2
25x ( x − 3y) −15(3y − x); b) 4 2 x − 5x + 4. Hướng dẫn giải a) 2
25x ( x − 3y) −15(3y − x) b) 4 2 x − 5x + 4 4 2 2 2
= 25x (x − 3y) +15(x − 3y)
= x − x − 4x + 4 2 = x ( 2 x − ) − ( 2 1 4 x − ) = ( 1 x − y)( 2 3 25x +15) = ( 2 x − )( 2 4 x − ) = ( 1 x − y)( 2 5 3 5x + 3).
= (x − 2)(x + 2)(x − ) 1 ( x + ) 1 .
Bài 3. (1,0 điểm) Tìm x, biết: a) ( x + )( 2 x − x + ) 3 1
1 − x + 2x = 0; b) ( − x)( 2 x + x + ) 2 + x ( x − ) 2 3 5 3 2 3 3 5 3 5 = 15 − x + 9x . Hướng dẫn giải a) ( x + )( 2 x − x + ) 3 1
1 − x + 2x = 0 3 3
x +1− x + 2x = 0 ( 3 3
x − x ) +1+ 2x = 0 2x +1= 0 2x = 1 − 1 x = − . 2 1 Vậy x = − . 2 b) ( − x)( 2 x + x + ) 2 + x ( x − ) 2 3 5 3 2 3 3 5 3 5 = 15 − x + 9x
( − x)( 2x + x + ) 2 − x ( − x) 2 5 3 2 3 3 5 5 3 = 3
− x (5 − 3x)
( − x)( 2x + x + ) 2 − x ( − x) 2 5 3 2 3 3 5
5 3 + 3x (5 − 3x) = 0 ( − x)( 2 2 2 5 3
2x + 3x + 3 − 5x + 3x ) = 0
(5 − 3x)(3x + 3) = 0
Suy ra 5 − 3x = 0 hoặc 3x + 3 = 0
3x = 5 hoặc 3x = 3 − 5
x = hoặc x = 1 − 3 5 Vậy x ; 1 − . 3
Bài 4. (3,0 điểm) Cho ABC
nhọn ( AB AC ). Các đường cao BF và CE cắt nhau
tại H. Gọi M là trung điểm của .
BC Trên tia đối của tia MH lấy điểm K sao cho MH = MK.
a) Giải thích tại sao tứ giác BHCK là hình bình hành, từ đó suy ra BK ⊥ A . B
b) Kẻ HG ⊥ BC tại .
G Trên tia đối của tia GH lấy điểm I sao cho G là trung
điểm của HI. Chứng minh tứ giác BIKC là hình thang cân.
c) Kẻ CQ ⊥ BK tại .
Q Chứng minh EFQ là tam giác vuông. Hướng dẫn giải A F H E B G M C I K Q
a) Xét tứ giác BHCK có M là trung điểm của hai đường chéo BC và HK (do MH = MK)
Suy ra tứ giác BHCK là hình bình hành (dấu hiệu nhận biết).
Do đó BK //CH (tính chất hình bình hành).
Mà CE ⊥ AB hay CH ⊥ AB nên BK ⊥ AB tại . B b) ⦁ Xét I
HK có M là trung điểm của HK (do MH = MK) và G là trung điểm của HI
Nên GM là đường trung bình của I HK
Suy ra GM // IK Mà ,
G M BC nên BC // IK
Tứ giác BIKC có BC // IK nên là hình thang.
⦁ Ta có HG ⊥ BC hay BC ⊥ HI tại trung điểm G của HI
Nên BC là đường trung trực của HI
Suy ra BH = BI (tính chất đường trung trực của đoạn thẳng) B
IH có BH = BI nên B
HI tại cân H B
HI tại cân H có BC là đường trung trực của HI nên đồng thời là đường phân
giác của góc HBI, hay IBC = HBC (1)
Tứ giác BHCK là hình bình hành nên BH // KC
Suy ra BCK = HBC (hai góc so le trong) (2)
Từ (1) và (2) suy ra BCK = IBC (= HBC).
Hình thang BIKC có BCK = IBC nên BIKC là hình thang cân. c) ⦁ Xét BFC
vuông tại F có FM là đường trung tuyến ứng với cạnh huyền BC 1
nên FM = BC (tính chất đường trung tuyến ứng với cạnh huyền của tam giác 2 vuông). Xét BEC
vuông tại E có EM là đường trung tuyến ứng với cạnh huyền BC nên 1
EM = BC (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông). 2 1
Suy ra FM = EM = BC 2
⦁ Xét tứ giác BECQ có:
BEC = 90 (do CE ⊥ AB);
EBQ = 90 (do BK ⊥ A ); B
BQC = 90 (do CQ ⊥ BK)
Suy ra tứ giác BECQ là hình chữ nhật (dấu hiệu nhận biết).
Khi đó hai đường chéo BC và EQ của hình chữ nhật BECQ cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC nên M cũng là trung điểm của EQ 1
⦁ Ta có FM = EM (chứng minh trên) và ME = MQ = EQ (do M là trung điểm của 2 EQ) 1 Suy ra FM = E . Q 2 1 Xét EFQ
có đường trung tuyến FM ứng với cạnh EQ và FM = E . Q 2 Do đó EFQ
là tam giác vuông tại F.
Bài 5. (1,5 điểm) Biểu đồ dưới đây biểu diễn xếp hạng thế giới của đội tuyển bóng đá
nam Việt Nam và Thái Lan vào tháng 10 trong 10 năm từ năm 2014 đến năm 2023.
Xếp hạng FIFA của bóng đá Việt Nam và Thái Lan trong 10 năm Hạng165 170 160 145 146 150 138 149 140 130 136 136 121 Việt Nam 117 120 113 111 112 Thái Lan 121 109 110 100 102 90 97 98 94 96 94 80 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 Năm
Hình a. Theo Liên đoàn bóng đá thế giới (FIFA)
a) Dãy số liệu về xếp hạng thế giới của bóng đá nam Việt Nam là dãy số liệu rời
rạc hay liên tục? Chỉ ra những năm đội tuyển bóng đá nam Thái Lan có xếp
hạng cao hơn đội tuyển bóng đá nam Việt Nam.
b) Trong 10 năm, thứ hạng cao nhất của đội tuyển Việt Nam là bao nhiêu, đạt được vào năm nào?
c) Cho biểu đồ dưới đây:




