10 Đề Thi Chọn HSG Môn Toán 8 Cấp Huyện Có Lời Giải Chi Tiết
Cho hình bình hành ABCDcó đường chéo AClớn hơn đường chéo BD. Gọi E, F lần lượt là hình chiếu của B và D xuống đường thẳng AC. Gọi H và K lần lượt là hình chiếu của C xuống đường thẳng AB và AD. Tứ giác BEDF là hình gì? Vì sao? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 8 467 tài liệu
Môn: Toán 8 2 K tài liệu
Tác giả:
Preview text:
ĐỀ THI HỌC SINH GIỎI TOÁN 8 Câu 1. (4,0 điểm)
Phân tích các đa thức sau thành nhân tử: 2
a)3x − 7x + 2 b) a( 2 x + ) − x( 2 1 a + ) 1 Câu 2. (5,0 điểm) 2 2 2 + x 4x
2 − x x − 3x Cho biểu thức : A = − − : 2 2 3
2 − x x − 4 2 + x 2x − x
a) Tìm ĐKXĐ rồi rút gọn biểu thức A
b) Tìm giá trị của x để A 0
c) Tính giá trị của A trong trường hợp x − 7 = 4 Câu 3. (5,0 điểm)
a) Tìm x, y, z thỏa mãn phương trình sau: 2 2 2
9x + y + 2z −18x + 4z − 6y + 20 = 0 x y z 2 2 2 + + = x y z 1 a b c + + =1 2 2 2 b) Cho a b c và +
+ = 0.Chứng minh rằng: a b c x y z Câu 4. (6,0 điểm)
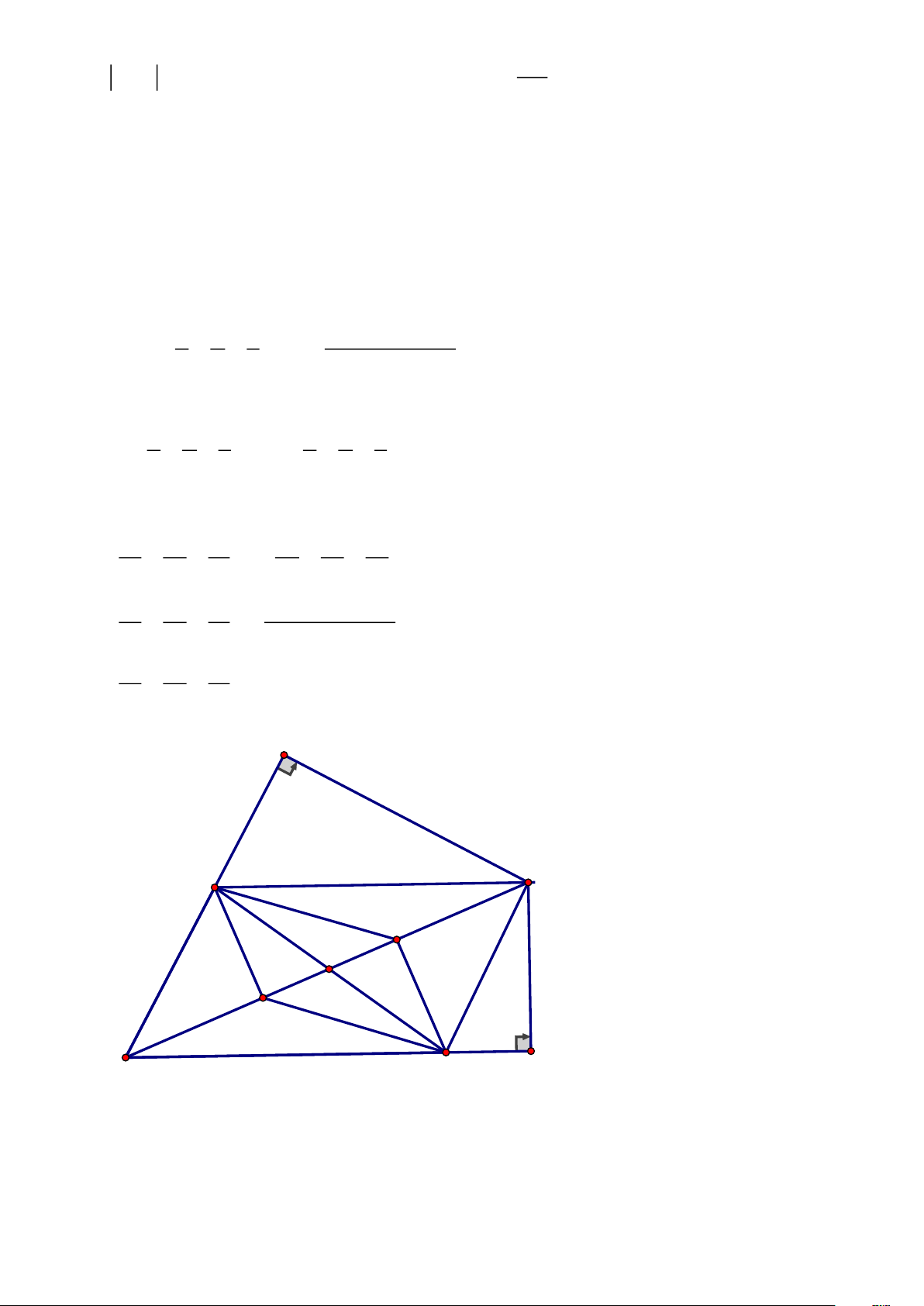
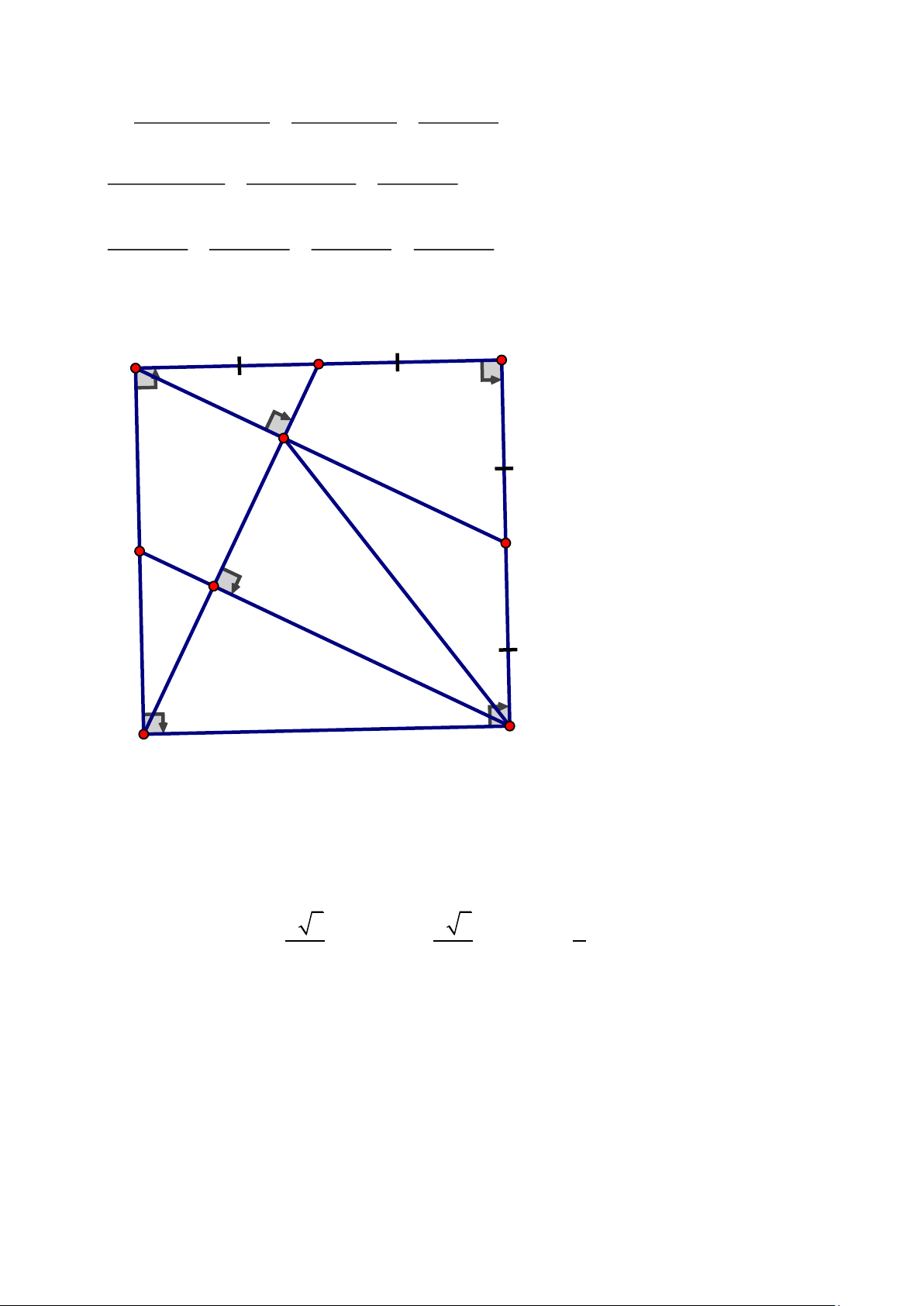
Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo .
BD Gọi E, F lần lượt
là hình chiếu của B và D xuống đường thẳng AC. Gọi H và K lần lượt là hình chiếu của C xuống đường thẳng AB và AD
a) Tứ giác BEDF là hình gì ? Vì sao ?
b) Chứng minh rằng : CH.CD = C . B CK 2 c) Chứng minh rằng: . AB AH + . AD AK = AC ĐÁP ÁN Câu 1. 2 2
a)3x − 7x + 2 = 3x − 6x − x + 2
= 3x(x − 2) − (x − 2) = (3x − ) 1 ( x − 2) b)a( 2 x + ) 1 − x( 2 a + ) 2 2
1 = ax + a − a x − x
= ax(x − a) − (x − a) = (x − a)(ax − ) 1 Câu 2.
ĐKXĐ: x 0; 2 ; 3 2 2 2 + x 4x
2 − x x − 3x
(2 + x)2 + 4x −(2 − x)2 2 2 x (2 − x) a)A = − − : = . 2 2 3
2 − x x − 4 2 + x 2x − x (2 − x)(2 + x) x(x − 3) 2 4x + 8x x(2 − x)
4x(x + 2) x(2 − x) 2 4x = ( = = − x)( + x). 2 2 x − 3
(2 − x)(2 + x)(x −3) x −3 2 4x b) A 0
0 x − 3 0 x 3(tmdk) x − 3
Vậy x 3 thì A 0 Trang 1 x − 7 = 4 x =11(tm) 121
c) x − 7 = 4 A = khi x = 11 x 7 4 − = − x = 3(ktm) 2 Câu 3. 2 2 2
a) 9x + y + 2z −18x + 4z − 6 y + 20 = 0 ( 2
9x −18x + 9) + ( 2
y − 6y + 9) + 2( 2 z + 2z + ) 1 = 0 9(x − )2
1 + ( y − 3)2 + 2( z + )2 1 = 0(*)
Do ( x − )2 ( y − )2 ( z + )2 1 0; 3 0; 1 0
Nên : x = 1; y = 3; z = −1 a b c
ayz + bxz + cxy + + = 0 = 0 b) Từ x y z xyz
ayz + bxz + cxy = 0 2 x y z x y z Ta có: + + =1 + + =1 a b c a b c 2 2 2 x y z xy xz yz + + + 2 + + =1 2 2 2 a b c ab ac bc 2 2 2 x y z
cxy + bxz + ayz + + + 2 =1 2 2 2 a b c abc 2 2 2 x y z + + =1(dfcm) 2 2 2 a b c Câu 4. H B C F O E A D K ⊥ ⊥ a) Ta có BE
AC(gt); DF AC(gt) BE / /DF Chứng minh BE O = D FO(g. .
c g) BE = DF
Suy ra tứ giác BEDF là hình bình hành
b) Ta có : ABC = ADC HBC = KDC Trang 2 CH CK Chứng minh C BH C
DK(g.g) =
CH.CD = CK.CB CB CD ( AF AK AFD AKC g.g ) = A .
D AK = AF.AC c) Chứng minh AD AC CF AH Chứng minh C FD A
HC(g.g) = CD AC CF AH Mà CD = AB = A .
B AH = CF.AC AB AC
Suy ra AB AH + AB AH = CF AC + AF AC = (CF + AF ) 2 . . . . .AC = AC
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN Môn: Toán lớp 8
Thời gian làm bài : 150 phút Câu 1. (2,0 điểm) 3 3 3
x − y − z − 3xyz
Rút gọn biểu thức B = (
x + y)2 + ( y − z)2 + ( x + z)2 Câu 2. (4,0 điểm)
a) Tìm số dư trong phép chia đa thức ( x + )
1 ( x + 3)( x + 5)( x + 7) + 9 cho 2 x + 8x +12. 3 2 2
b) Tìm mọi số nguyên x sao cho x − 2x + 7x − 7 chia hết cho x + 3 Câu 3. (4,0 điểm)
Giải các phương trình: 3 3 1 3 x + 3 + x − 4 + (1− x)3 = 0 a) 4 4 3 − x 3 − x x x + = 2 b) x +1 x +1 Câu 4. (4,0 điểm)
Tìm giá trị nhỏ nhất của các biểu thức:
A = 3x +1 + x + 2 − 4x + 3 a) 2 14x − 8x + 9 B = 2 b) 3x + 6x + 9 Câu 5. (4,0 điểm)
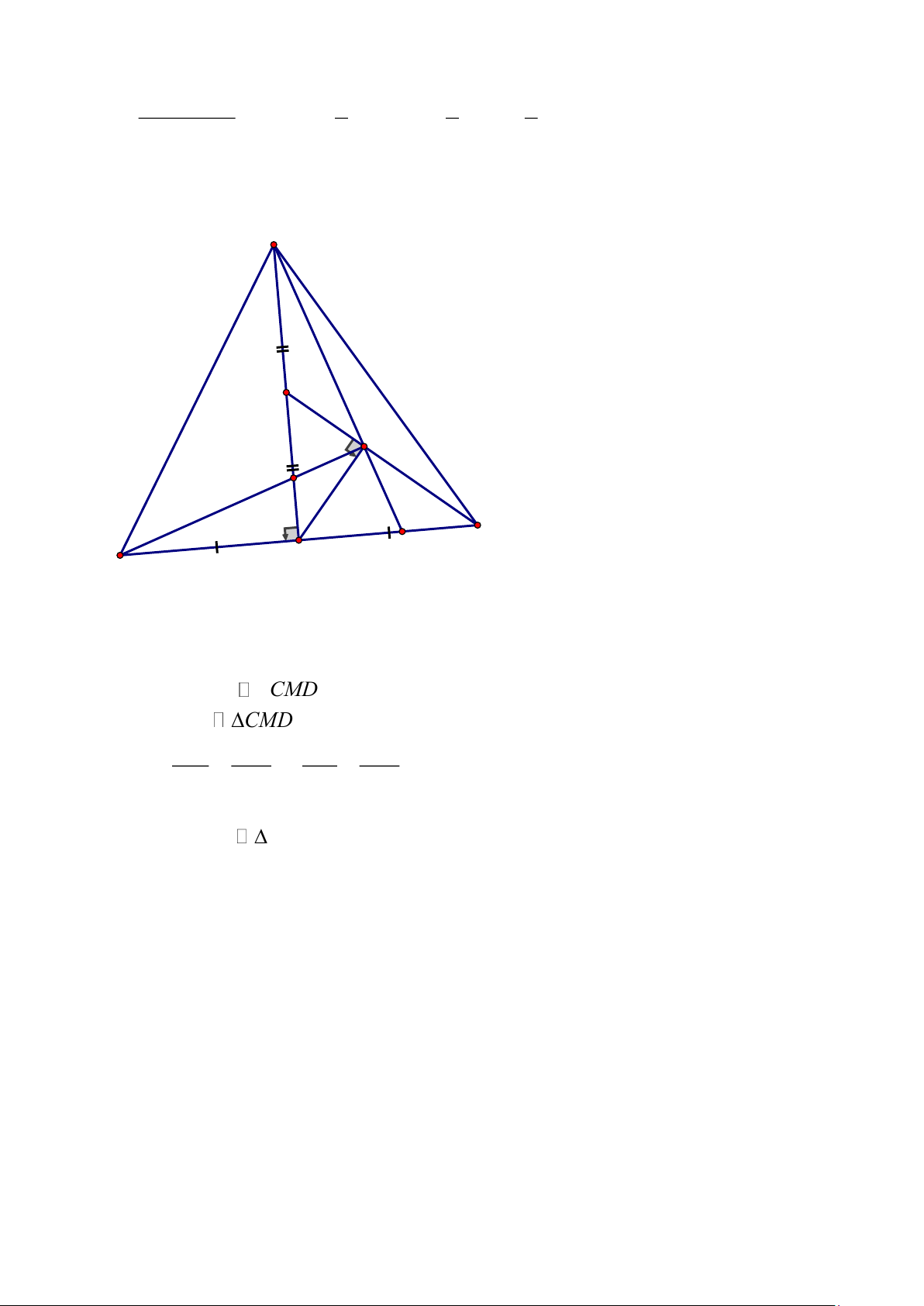
Cho tam giác ABC cân tại A. M , D tương ứng là trung điểm của BC, AM. H là hình chiếu
của M trên CD. AH cắt BC tại N, BH cắt AM tại E. Chứng minh rằng a) MHD C MD
b) E là trực tâm ABN Câu 6. (2,0 điểm)
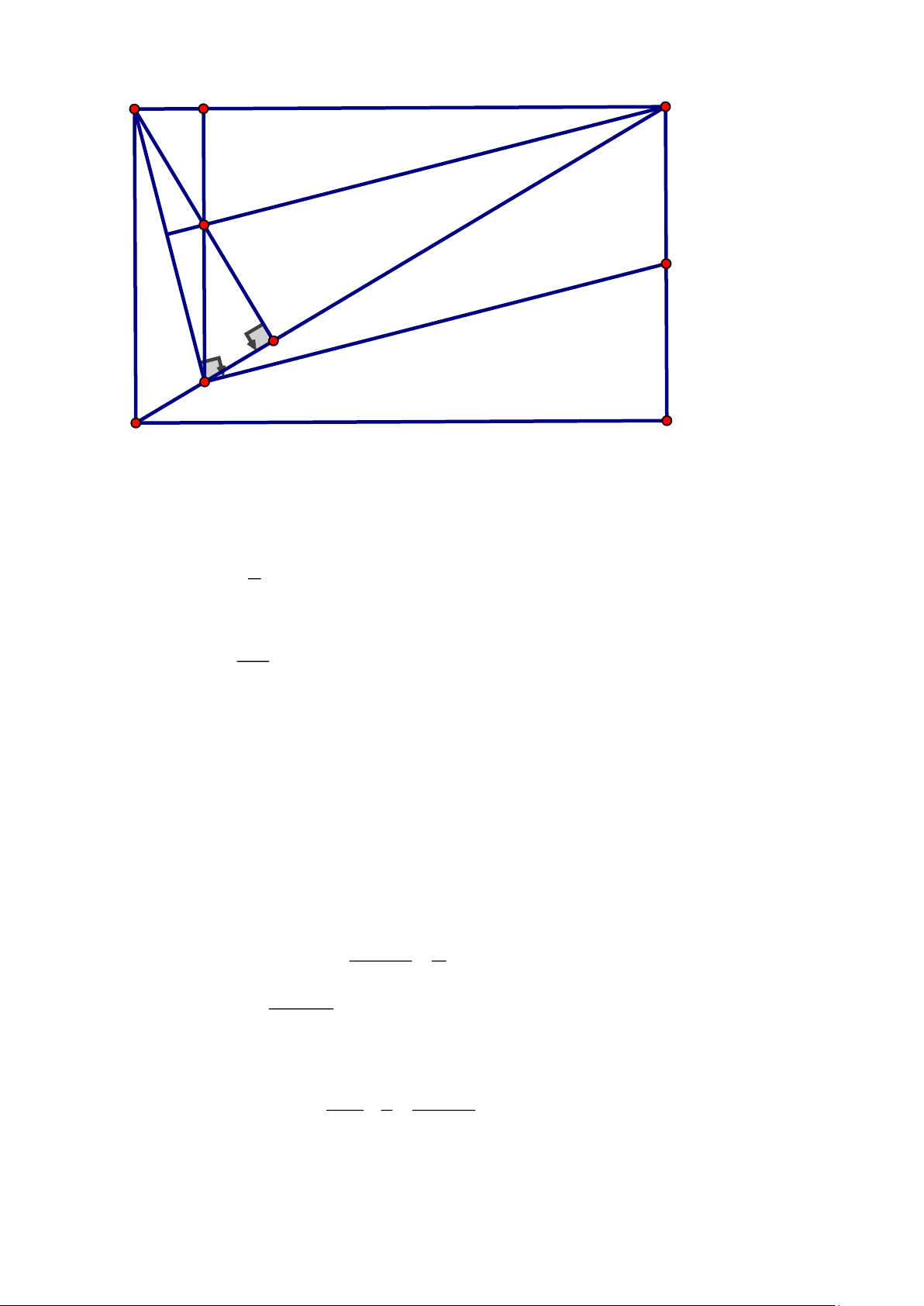
Cho hình chữ nhật ABC .
D Gọi M là trung điểm của cạnh CD và N là một điểm trên
đường chéo AC sao cho 0
BNM = 90 .Gọi F là điểm đối xứng của A qua N. Chứng minh rằng FB ⊥ AC. ĐÁP ÁN Trang 3 Câu 1. Ta có:
x − y − z − 3xyz = ( x − y)3 3 3 3
+ 3xy(x − y) 3 − z − 3xyz
= (x − y − z)3 + 3(x − y) z(x − y − z) + 3xy(x − y − z)
= (x − y − z)(x − y − z)2 + 3xz − 3yz + 3xy
= (x − y − z)( 2 2 2
x + y + z − 2xy − 2xz + 2yz + 3xz − 3yz + 3xy)
= (x − y − z)( 2 2 2
x + y + z + xy − yz + xz)
*)( x + y)2 + ( y − z)2 + ( x + z)2 2 2 2 2 2 2
= x + 2xy + y + y − 2yz + z + x + 2xz + z 2 = 2(x + 2 2
y + z + xy − yz + xz)
(x − y − z)( 2 2 2
x + y + z + xy − yz + xz) x − y − z Vậy B = = 2( 2 2 2
x + y + z + xy − yz + xz) 2 Câu 2.
f ( x) = (x + )
1 ( x + 3)(x + 5)(x + 7) + 9 a) Đặt
Ta có: A = ( x + )
1 ( x + 7)( x + 3)( x + 5) + 9 = ( 2 x + 8x + 7)( 2 x + 8x +15) + 9 = ( 2
x + 8x + 7)( 2x + 8x +12) + 3 + 9 = ( 2 x + 8x + 7)( 2
x + 8x +12) + 3( 2 x + 8x + 7) + 9 = ( 2 x + 8x + 7)( 2
x + 8x +12) + 3( 2
x + 8x +12) + 9 −15 = ( 2 x + 8x +12)( 2
x + 8x +10) − 6
Vậy số dư trong phép chia f ( x) cho 2 x + 8x +12 là 6 − 3 2 2
b) Thực hiện phép chia đa thức B = x − 2x + 7x − 7 cho C = x + 3, ta được: Đa thức
thương: x − 2; đa thức dư: 4x −1 Suy ra : 3 2
x − x + x − = ( 2 2 7 7
x + 3)(x − 2) + 4x −1 Do đó B ( 2
x + ) ( x − ) ( 2 3 4 1 3x + 3) (1) Vì 4x 1 vs 4x 1 − nên: ( ) 1 (4x − ) 1 (4x + ) 2 1 x + 3 ( 2 16x − ) 1 ( 2 x + 3) 16( 2 x + 3) 2 + 49 (x + 3) 2 49 (x + 3) Vì 2
x + 3 3nên xảy ra một tong hai trường hợp sau: 2
•x + 3 = 49, không có giá trị nào thỏa mãn x = 2(tm) 2 2
•x + 3 = 7 x = 4 x = −2(ktm) Vậy x = 2 Trang 4 Câu 3. 1 3
a = x + 3;b = x − 4 a + b = x −11− x = −(a + b) a) Đặt 4 4
Ta có (pt đề) a + b − (a + b)3 3 3 = 0 3 3 3 3
a + b − a − b − 3ab(a + b) = 0
−3ab(a + b) = 0 1 x + 3= 0 x = 12 4 − a = 0 3 16 b = 0
x − 4 = 0 x = 4 3 a + b = 0 x −1= 0 x =1 16 Vậy S = 1 − 2; ;1 3 b) ĐKXĐ: x −1 2 2 3 − x 3 − x
3x − x x + x − 3 − x x x + = 2 . = 2 x +1 x +1 x +1 x +1 ( 2 3x − x )( 2 x + 3) = (x + ) 2 2 1 3 4 2 2
3x + 9x − x − 3x = 2x + 4x + 2 4 3 2
x − 3x + 5x − 5x + 2 = 0 (x − )2 1 .( 2 x − x + 2) = 0 x −1 = 0 x =1(tm) 2
x − x + 2 = 0 VN Vậy S = 1 Câu 4.
a) Áp dụng tính chất a a,dấu " = " xảy ra a 0, ta có:
A = 3x +1 + x + 2 − 4x + 3 3x +1+ x − 2 − 4x + 3 = 6 A 6 1 −
Dấu “=” xảy ra 3x + 1 0 và x + 2 0 x và x − 1 2 x − 3 3 1 −
Vậy min A = 6 x 3 2
2 14x − 8x + 9 2 B − = − 2 b) Ta có 3 3x + 6x + 9 3 ( 2
14x − 8x + 9) − 2( 2 x + 2x + 3) 2 12x −12x + 3 (2x − )2 1 = = = 3( 2 x + 2x + 3) 3( 2
x + 2x + 3) (x + )2 1 + 2 Trang 5
Với mọi x, ta có: ( x − )2 ( x + )2 3 2 1 0, 1 + 2 2 0 (2x − )2 1 2 2 1 − = ( x + ) 0 B 0 B x 2 1 + 2 3 3 2 Câu 5. A D H E C N M B
a) Vì M là trung điểm của BC nên AM là đường trung tuyến của ABC
Mà ABC cân tại A (gt) nên AM là đường cao của ABC
Xét MHD và CMD có: 0
MHD = CMD = 90 ;MDH = CDM M HD CM D( g.g ) b) MHD C MD (câu a) HD HM HD HM = = (Vi MD = A , D CM = BM ) MD CM AD BM Mặt khác ta có: 0
ADH = 90 + DMH = BMH Suy ra H DA H MB( . c g.c) Do đó: 0
AHD = BHM AHB = DHM = 90 BH ⊥ AN
Kết hợp với AM ⊥ BC E là trực tâm ABN. Câu 6. Trang 6 B E C I M F N A D
Gọi I là trung điểm của BF, đường thẳng NI cắt BC tại E
Ta có: F đối xứng với A qua N (gt) N là trung điểm của AF
Mà I là trung điểm của BF nên NI là đường trung bình ABF 1
NI / / AB, NI = AB 2 Mặt khác AB / / ;
CD AB = CD (ABCD là hình chữ nhật và M là trung điểm của CD) CD
AB ⊥ BC;CM =
suy ra NI ⊥ BC; NI / /CM và NI = CM 2
Tứ giác CINM là hình bình hành CI / /MN Mà MN ⊥ BN ( 0
BNM = 90 ) CK ⊥ BN tại K
Do đó I là trực tâm BCN BF ⊥ AC.
ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN MÔN: TOÁN LỚP 8
Bài 1. Phân tích đa thức thành nhân tử 2 2
a) x − y − 5x + 5y 2
b) 2x − 5x − 7 2 4x −16 A
Bài 2. Tìm đa thức A, biết rằng = 2 x + 2 x +
Bài 3. Cho phân thức 5x 5 2 2x + 2x
a) Tìm điều kiện của x để giá trị của phân thức được xác định
b) Tìm giá trị của x để giá trị của phân thức bằng 1 x + 2 1 2
Bài 4. a) Giải phương trình : − = x − 2 x x (x − 2)
b) Giải bất phương trình : ( x − )( x + ) (x + )2 3 3 2 + 3
Bài 5. Giải bài toán sau bằng cách lập phương trình
Một tổ sản xuất lập kế hoạch sản xuất, mỗi ngày sản xuất được 50 sản phẩm. Khi thực Trang 7
hiện, mỗi ngày tổ đó sản xuất được 57 sản phẩm. Do đó đã hoàn thành trước kế hoạch 1 ngày và
còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch tổ phải sản xuất bao nhiêu sản phẩm và thực hiện trong bao nhiêu ngày
Bài 6. Cho ABC vuông tại A, có AB = 15 c , m AC = 20 c .
m Kẻ đường cao AH và trung tuyến AM
a) Chứng minh ABC HBA b) Tính BC; AH; BH; CH
c) Tính diện tích AHM
ĐÁP ÁN ĐỀ THI HSG TOÁN 8 CẤP HUYỆN Bài 1. 2 2
a) x − y − 5x + 5y = ( 2 2
x − y ) − 5(x − y)
= (x + y)(x − y) − 5(x − y) = (x − y)(x + y − 5) 2 2
b) 2x − 5x − 7 = 2x + 2x − 7x − 7 = ( 2
2x + 2x) − (7x + 7) = 2x(x + ) 1 − 7( x + ) 1 = ( x + ) 1 (2x − 7) Bài 2. A = x ( 2
4x −16) x(2x − 4)(2x + 4) 4x(x − 2)(x + 2) = = = 4x −8 2 x + 2x x(x + 2) x(x + 2) Bài 3. 2
a) 2x + 2x = 2x(x +1) 0
2x 0 va x +1 0 x 0 à v x 1 − b) Rút gọn 5x + 5 5(x +1) 5 = = 2 2x + 2x 2x(x +1) 2x 5 5
= 1 5 = 2x x = (t / m) 2x 2 5 x = 2
Bài 4. a) Điều kiện xác định x 0; x 2
x(x + 2) − (x − 2) 2 2 =
x + 2x − x + 2 = 2 x(x − 2) x(x − 2)
x = 0(loai)vs x = 1 − Vậy S = − 1
b) ( x − )( x + ) (x + )2 3 3 2 + 3 2 2
x − 9 x + 4x + 7 2 2
x − x − 4x 7 + 9 −4x 16 x −4
Vậy nghiệm của phương trình là x −4 Bài 5.
- Gọi số ngày tổ dự đinh sản xuất là : x ngày ( x *, x 1)
- Vậy số ngày tổ đã thực hiện x −1 (ngày)
- Số sản phẩm làm theo kế hoạch là : 50x (sản phẩm)
- Số sản phẩm thực hiện là : 57.(x −1) (sản phẩm)
Theo đề bài ta có phương trình : 57(x −1) − 50x = 13
57x − 57 − 50x =13 7x = 70 x =10 (thỏa mãn)
Vậy số ngày dự định sản xuất là 10 ngày Trang 8
Số sản phẩm phải làm theo kế hoạch là : 50.10 = 500 (sản phẩm) Bài 6 A C B H M
a) Xét ABC và HBA có: 0
A = H = 90 ; B chung AB C H
BA(g.g)
b) Áp dụng định lý Pytago trong tam giác vuông ABC có 2 2 2 2
BC = AB + AC = 15 + 20 = 625 = 25(c ) m Vì AB AC BC A BC H BA nên 15 20 25 = = hay = = HB HA BA HB HA 15 20.15 15.15 AH = =12(c ) m ; BH = = 9(c )
m ; HC = BC − BH = 25 − 9 = 16(c ) m 25 25 BC 25
c) HM = BM − BH = − BH = − 9 = 3,5(cm) 2 2 1 1 2 S
= AH.HM = .12.3,5 = 21(cm ) AHM 2 2
ĐỀ THI KSCL HỌC SINH GIỎI MÔN: TOÁN 8 Bài 1. (2 điểm)
a) Phân tích đa thức sau thành nhân tử: x (x − )2 3 2 7 − 36x
b) Dựa vào kết quả trên hãy chứng minh :
A = n (n − )2 3 2
7 − 36n chia hết cho 210 với mọi số tự nhiên n Bài 2. (2 điểm) 3 2 1− x 1− x Cho biểu thức A = − x : x −1;1 2 3 ( ) 1− x
1− x − x + x a) Rút gọn biểu thức A 2
b) Tính giá trị của biểu thức A tại x = 1 − 3
c) Tìm giá trị của x để A 0
Bài 3. (1 điểm) Cho ba số a,b,c thỏa mãn abc = 2004 2004a b c Tính M = + +
ab + 2004a + 2004 bc + b + 2004 ac + c +1 Trang 9
Bài 4. (4 điểm) Cho hình vuông ABCD có cạnh bằng 4 .
cm Gọi M , N lần lượt là trung điểm của
AB, BC.Gọi P là giao điểm của AN với DM
a) Chứng minh APM là tam giác vuông
b) Tính diện tích của tam giác APM
c) Chứng minh tam giác CPD là tam giác cân Bài 5. (1 điểm)
Tìm các giá trị x, y nguyên dương sao cho 2 2
x = y + 2y +13 ĐÁP ÁN Bài 1.
a)x (x 7)2 36x x (x 7x)2 3 2 3 36 − − = − − = x( 3
x − 7x − 6)( 3
x − 7x + 6) = x( 3
x − x − 6x − 6)( 3
x − x − 6x + 6) ...... = x(x + ) 1 ( x − )
1 ( x − 3)( x + 2)( x − 2)( x + 3) b) Theo phần a ta có:
A = n (n − )2 3 2
7 − 36n = (n − 3)(n − 2)(n − ) 1 n(n + )
1 (n + 2)(n + 3)
Đây là tích của 7 số nguyên liên tiếp nên có một bộ của 2, 1 bội của 3, 1 bội của 5, 1 bội của 7
Mà (2,3,5,7) =1nên A (2.3.5.7) A 210 Bài 2.
a) Với x 1 thì 3 2
1− x − x + x (1− x)(1+ x) A = : 1− x (1+ x)( 2
1− x + x ) − x(1+ x) (1− x)( 2
1+ x + x − x) (1− x)(1+ x) = : 1− x (1+ x)( 2 1− 2x + x ) = ( 2 + x ) 1 1 : = ( 2 1+ x )(1− x) 1− x 2 2 x = 1 − A =10 b) Tại 3 27
c) Với x 1thì A ( 2 0
1+ x )(1− x) 0 1− x 0 x 1 Trang 10 Bài 3
Thay 2004 = abc vào M ta có: 2 a bc b c M = + + 2
ab + a bc + abc bc + b + abc ac + c +1 2 a bc b c = + +
ab(1+ ac + c) b(c +1+ ac) ac + c +1 ac 1 c ac + c +1 = + + = =1
1+ ac + c c +1+ ac
ac + c +1 1+ ac + c Bài 4. M A B 1 1 P I N H 1 D C = = a) Chứng minh ADM BAN(cgc) A D 1 1 Mà 0
D + M = 90 ( ADM vuông tại A) 1 1 Do đó: 0 0
A + M = 90 APM = 90 .Hay APM vuông tại P 1 1 4 5 2 5 4 2 AP = (c ) m , AM = c , m S = (cm ) APM b) Tính được 5 5 5
c) Gọi I là trung điểm của AD. Nối C với I; CI cắt DM tại H
Chứng minh tứ giác AICN là hình bình hành
AN / /CI mà AN ⊥ DM CI ⊥ DM
Hay CH là đường cao trong C PD(1)
Vận dụng định lý về đường trung bình trong ADP chứng minh được H là trung điểm DP suy ra
CH là trung tuyến trong C PD(2)
Từ (1) và (2) suy ra CPD cân tại C Bài 5.
Biến đổi đẳng thức đã cho về dạng ( x + y + )
1 ( x − y − ) 1 = 12 Trang 11
Lập luận để có x + y +1 x − y −1và x + y +1; x − y −1là các ước dương của 12 từ đó có các trường hợp x + y +1 12 6 4 x − y −1 1 2 3 x 13 4 7 2 2 y 9 1 1 − 2 2
Mà x, y nguyên dương nên ( ; x y) = (4; ) 1 ĐỀ BÀI
Câu 1. ( 5 điểm) Tìm số tự nhiên n để: 3 2
a) A = n − n + n −1 là số nguyên tố 4 3 2
n + 3n + 2n + 6n − 2 b) B =
có giá trị là một số nguyên 2 n + 2 5
c) D = n − n + 2 là số chính phương.
Câu 2. (5 điểm) Chứng minh rằng: a b c + + =1
a) ab + a +1 bc + b +1 ac + c +1 biết abc = 1
b) Với a + b + c = 0 thì a + b + c = (ab + bc + ca)2 4 4 4 2 2 2 2 a b c c b a + + + + 2 2 2 c) b c a b a c
Câu 3. (5 điểm) Giải các phương trình sau: x − 214 x −132 x − 54 + + = 6 a) 86 84 82 x( x − )2 2 8 1 .(4x − ) 1 = 9 b) 2 2 − + − − = c) x y
2x 4y 10 0 với x, y nguyên dương.
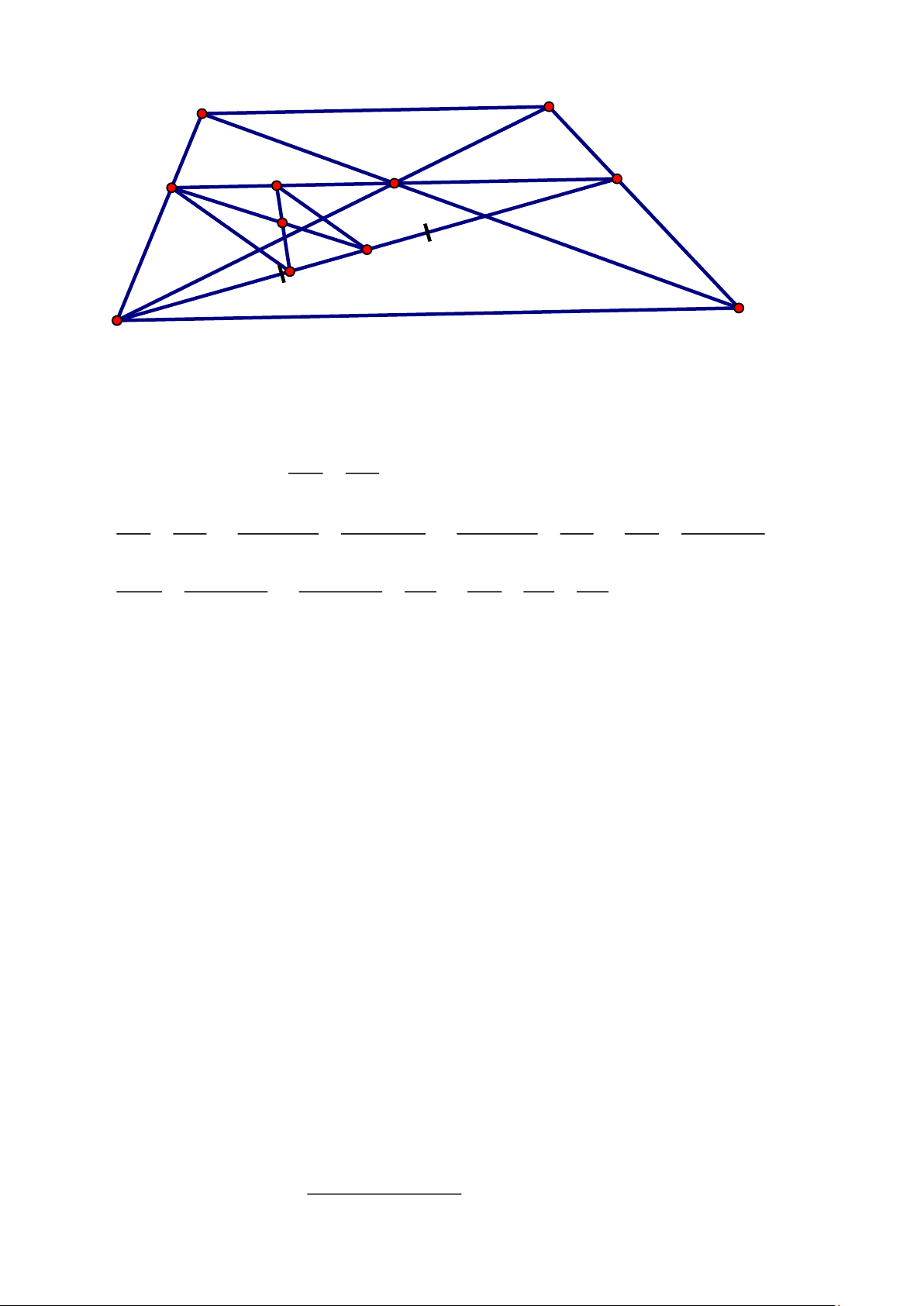
Câu 4. (5 diểm) Cho hình thang ABCD( AB / /CD) , O là giao điểm hai đường chéo. Qua O kẻ
đường thẳng song song với AB cắt DAtại E, cắt BC tại F
a) Chứng minh : Diện tích tam giác AOD bằng diện tích tam giác BOC 1 1 2 + = b) Chứng minh: AB CD EF
c) Gọi K là điểm bất kỳ thuộc OE.Nêu cách dựng đường thẳng đi qua K và chia đôi diện Trang 12 tích tam giác DEF ĐÁP ÁN Câu 1. 3 2
A = n − n + n − = ( 2 1 n + ) 1 (n − ) 1 a)
Để A là nguyên tố thì n −1 = 1 n = 2 . Khi đó A = 5 2 2
B = n + 3n − 2 b) n + 2
B có giá trị nguyên 2 2 n + 2 2 n + 2 =1 2 n = −1(ktm) 2
n + 2 là ước tự nhiên của 2 2 n + 2 = 2 n = 0 (tm)
Vậy với n = 0 thì B có giá trị nguyên. c) 5
D = n − n + 2 = n( 4 n − ) 1 + 2 = n(n + ) 1 (n − ) 1 ( 2 n + ) 1 + 2 = n(n − ) 1 (n + ) 1 ( 2
n − 4) + 5 + 2 = n(n − ) 1 (n + )
1 (n − 2)(n + 2) + 5n(n − ) 1 (n + ) 1 + 2 Mà n(n − ) 1 (n + )
1 (n − 2)(n + 2) 5(tích 5 số tự nhiên liên tiếp) Và 5n(n − ) 1 (n + )
1 5. Vậy D chia 5 dư 2
Do đó D có tận cùng là 2 hoặc 7 nên D không phải là số chính phương.
Vậy không có giá trị nào của n để D là số chính phương. Câu 2. a) a b c ac abc c + + = + + 2
ab + a +1 bc + b +1 ac + c +1 abc + ac + c
abc + abc + ac ac + c +1 ac abc c abc + ac +1 = + + = =1 1+ ac + c c +1+ ac
ac + c +1 abc + ac +1 b) 2 2 2
a + b + c = 0 a + b + c + 2(ab + ac + bc) = 0 2 2 2
a + b + c = −2(ab + ac + bc) (1) 4 4 4
a + b + c + 2( 2 2 2 2 2 2
a b + a c + b c ) = 4( 2 2 2 2 2 2
a b + a c + b c ) + 8abc(a + b + c)
(Vì a + b + c = 0 )
(ab + ac + bc) = ( 2 2 2 2 2 2 2
2 a b + a c + b c ) (2)
Từ (1) và (2) a + b + c = (ab + ac + bc)2 4 4 4 2 2 2 + =
c) Áp dụng bất đẳng thức x y
2xy . Dấu bằng xảy ra khi x y 2 2 a b a b a + 2. . = 2. 2 2 b c b c c 2 2 a c a c c + 2. . = 2. 2 2 b a b a b 2 2 c b c b b + 2. . = 2. 2 2 a c a c a
Cộng từng vế ba bất đẳng thức trên ta có: Trang 13 2 2 2 2 2 2 a b c a c b a b c a c b 2 + + 2 + + + + + + 2 2 2 2 2 2 b c a c b a b c a c b a
Dấu " = " xảy ra khi a = b = c Câu 3. a) x − 214 x −132 x − 54 + + = 6 86 84 82 x − 214 x −132 x − 54 −1 + − 2 + − 3 = 0 86 84 82 x − 300 x − 300 x − 300 + + = 0 86 84 82 ( x − ) 1 1 1 300 + +
= 0 x − 300 = 0 x = 300 86 84 82 Vậy S = 300 b) 2x(8x − )2 1 .(4x − ) 1 = 9 ( 2 64x −16x + ) 1 ( 2
8x − 2x) = 9 ( 2 64x −16x + ) 1 ( 2 64x −16x) = 72 Đặt 2 1
64x −16x + = k 2 Ta có: (k + )(k − ) 2 0,5
0,5 = 72 k = 72,25 k = 8 ,5 1 x = 2
Với k = 8,5 ta có phương trình : 2
64x −16x − 8 = 0 (2x − ) 1 (4x + ) 1 = 0 1 − x = 4 Với k = 8
− ,5 ta có phương trình: x −
x + = ( x − )2 2 64 16 9 0 8 1 + 8 = 0 (vô nghiệm) 1 1 Vậy S = ;− 2 4 2 2
x − y + x − y − = ( 2
x + x + ) − ( 2 2 4 10 0 2 1
y + 4 y + 4) − 7 = 0 c)
(x + )2 − ( y + )2 1
2 = 7 ( x − y − )
1 ( x + y + 3) = 7
Vì x, y nguyên dương nên x + y + 3 x − y −1 x = 3
x + y + 3 = 7 và x − y −1 =1 y =1
Phương trình có nghiệm dương duy nhất ( ; x y) = (3; ) 1 Câu 4. Trang 14 A B K F E I O M N D C
a) Vì AB / /CD S = S
(cùng đáy và cùng đường cao) DAB CBA S − S = S − S hay S = S DAB AOB CBA AOB AOD BOC EO AO EO / /DC = . b) Vì DC
AC Mặt khác AB / /DC AB AO AB AO AB AO EO AB = = = = DC OC AB + BC AO + OC AB + BC AC DC AB + DC EF AB AB + DC 2 1 1 2 = = + = 2DC AB + DC . AB DC EF DC AB EF
c) Dựng trung tuyến EM , dựng EN / /MK ( N DF )
Kẻ đường thẳng KN là đường phải dựng. Chứng minh: S = S (1) EDM EFM
Gọi giao điểm của EM và KN là I thì S = S (2 IKE IMN )
Từ (1) và (2) suy ra S = S DEKN KFN
ĐỀ THI HỌC SINH GIỎI HUYỆN MÔN TOÁN 8
Bài 1 (3 điểm) Chứng minh rằng: 5 11 a) 8 + 2 chia hết cho 17 19 19 b) 19 + 69 chia hết cho 44 Bài 2. (3 điểm) 2 x + x − 6 3 2
a) Rút gọn biểu thức : x − 4x −18x + 9 Trang 15 1 1 1 + + = yz xz xy 0( , x y, z 0). + + 2 2 2 b) Cho x y z Tính x y z Bài 3. (3 điểm)
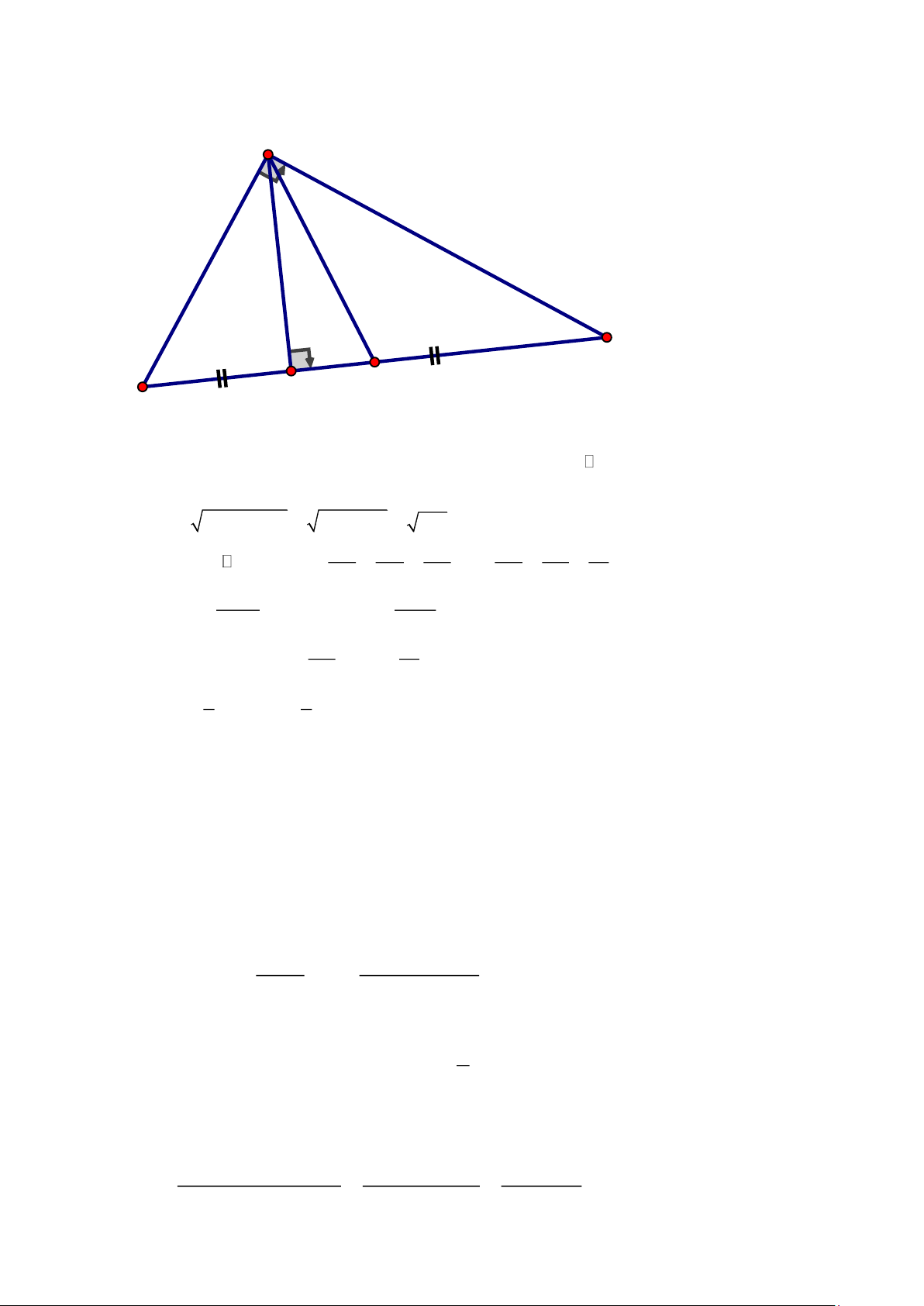
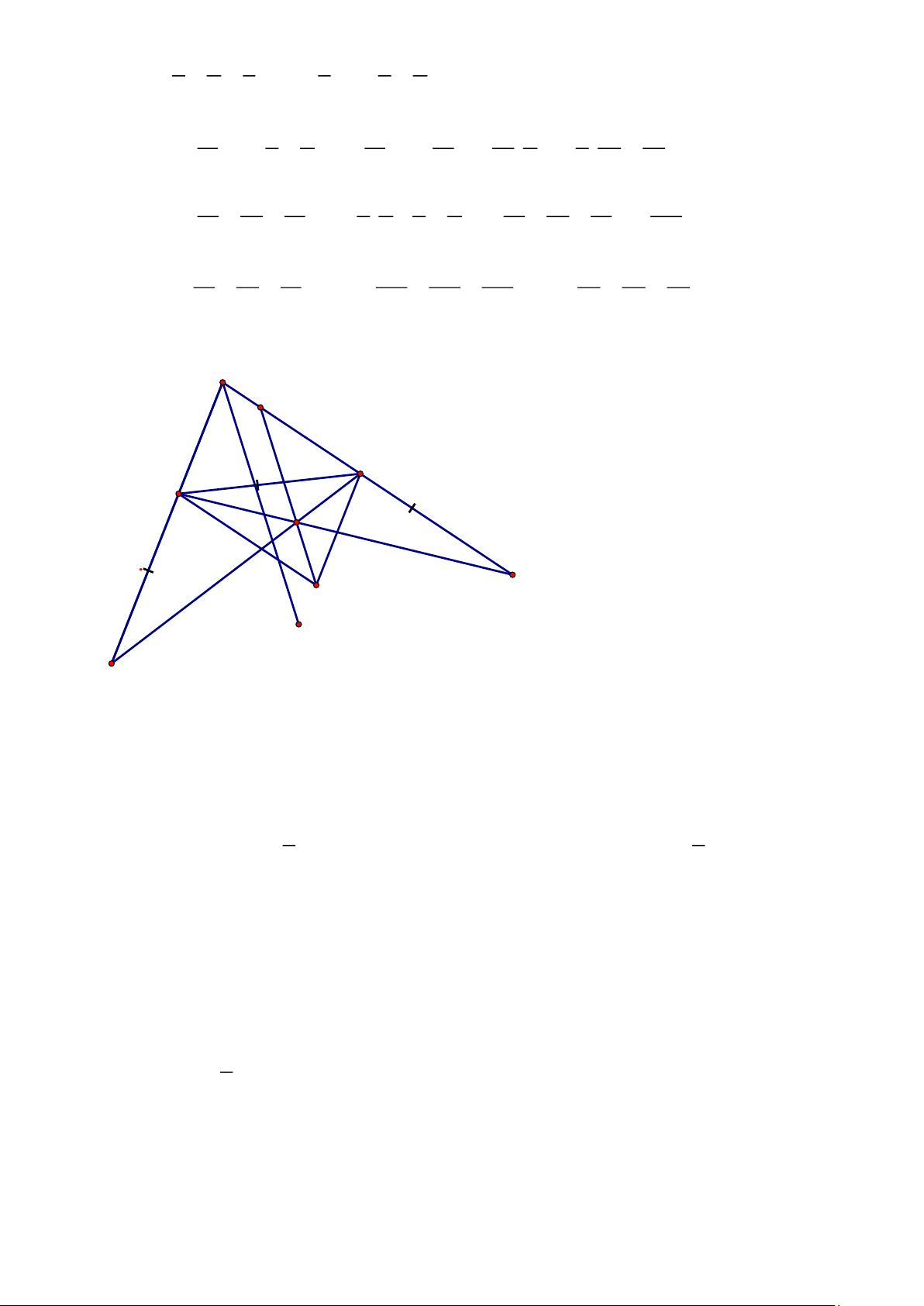
Cho tam giác ABC.Lấy các điểm D, E theo thứ tự thuộc tia đối của các tia B , A CA sao cho
BD = CE = BC.Gọi O là giao điểm của BE và CD. Qua O vẽ đường thẳng song song với tia
phân giác của góc A, đường thẳng này cắt AC ở K. Chứng minh rằng AB = CK Bài 4. (1 điểm)
Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức sau (nếu có): 2
M = 4x + 4x + 5 ĐÁP ÁN Bài 1. + = ( )5 5 11 3 11 15 11 11 + = + = ( 4 + ) 11 8 2 2 2 2 2 2 . 2 1 = 2 .17 a) Ta có:
Rõ ràng kết quả trên chia hết cho 17
b) Áp dụng hằng đẳng thức n n a b
(a b)( n 1− n−2 n−3 2 n−2 n 1 a a b a b ..... ab b − + = + − + − − + )với mọi n lẻ Ta có: 19 19 + = ( + )( 18 17 18 19 69
19 69 19 −19 .69 + ...... + 69 ) = ( 18 17 18
88. 19 −19 .69 + ..... + 69 ) chia hết cho 44 Bài 2. a) Ta có: 2 2
*)x + x − 6 = x + 3x − 2x − 6 = x( x + 3) − 2( x + 3) = ( x − 2)(x + 3) 3 2 3 2 2
*)x − 4x −18x + 9 = x + 3x − 7x − 21x + 3x + 9 2
= x (x + 3) − 7x(x + 3) + 3(x + 3) = (x + 3)( 2 x − 7x + 3) 2 x + x − 6 (x + 3)(x − 2) x − 2 2 = =
x −1; x − 7x + 3 0 3 2
x − 4x −18x + 9 ( x + 3)( 2 x − 7x + 3) 2 ( ) x − 7x + 3 Trang 16 1 1 1 1 1 1 + + = 0 = − + x y z z x y 3 1 1 1 1 1 1 1 1 1 1 = − + = − + 3. . + 3. . + 3 3 3 2 2 3 z x y z x x y x y y 1 1 1 1 1 1 1 1 1 1 1 + + = −3. . . + + + = 3. 3 3 3 3 3 3 x y z x y x y x y z xyz b) Vì 1 1 1 xyz xyz xyz yz zx xy Do đó: xyz + + = 3 + + = 3 + + = 3 3 3 3 3 3 3 2 2 2 x y z x y z x y z Bài 3. A K 2 1 C 1 B 1 O E M D
Vẽ hình bình hành ABMC ta có: AB = CM
Để chứng minh AB = KC ta cần chứng minh KC = CM .
Thật vậy, xét tam giác BCE có BC = CE ( gt) CBE
cân tại C B = E 1
Vì góc C là góc ngoài của tam giác BCE 1 1 1
C = B + E B = C mà AC / /BM (ta vẽ) C = CBM B = CBM nên BO là tia 1 1 1 1 2 1 1 2
phân giác của CBM .Hoàn toàn tương tự ta có CD là tia phân giác của BCM . Trong tam giác
BCM, OB, CO, MO đồng quy tại O
MO là tia phân giác của CMB
Mà BAC, BMC là hai góc đối của hình bình hành BMCA MO / / với tia phân giác của góc A
theo giả thiết tia phân giác của góc A còn song song với OK
K,O,M thẳng hàng 1
Ta lại có: M = BMC(cmt); A = M M = A mà A = K (2 góc đồng vị) 1 1 2 2 2 1
K = M CKM
cân tại C CK = CM . 1 1
Kết hợp AB = CM AB = CK (dfcm) Bài 4.
Ta có M = x + x + = ( x + x + ) + = ( x + )2 2 2 4 4 5 4 4 1 4 2 1 + 4 Trang 17
Vì ( x + )2 ( x + )2 2 1 0 2
1 + 4 4 M 4 1
Vậy Min = 4 x = − M 2
ĐỀ KHẢO SÁT HỌC SINH GIỎI
MÔN : Toán 8. Thời gian làm bài: 120 phút x 3 − 3x x + 4
Câu 1. (2 điểm) Cho biểu thức A = − + 2 3
x +1 x − x +1 x +1
a) Rút gọn biểu thức A
b) Chứng minh rằng giá trị của A luôn dương với mọi x −1 Câu 2. (3 điểm)
a) Chứng minh rằng: Với mọi x
thì giá trị của đa thức :
M = ( x + 2)( x + 4)( x + 6)( x + 8) +16 là bình phương của một số hữu tỉ
x +1 = x( x + ) 1 b) Giải phương trình :
Câu 3. (1,5 điểm) Đa thức P(x) bậc 4 có hệ số bậc cao nhất là 1. Biết P(1) = 0;
P(3) = 0; P(5) = 0 .
Hãy tính giá trị của biểu thức Q = P( 2 − ) + 7P(6)
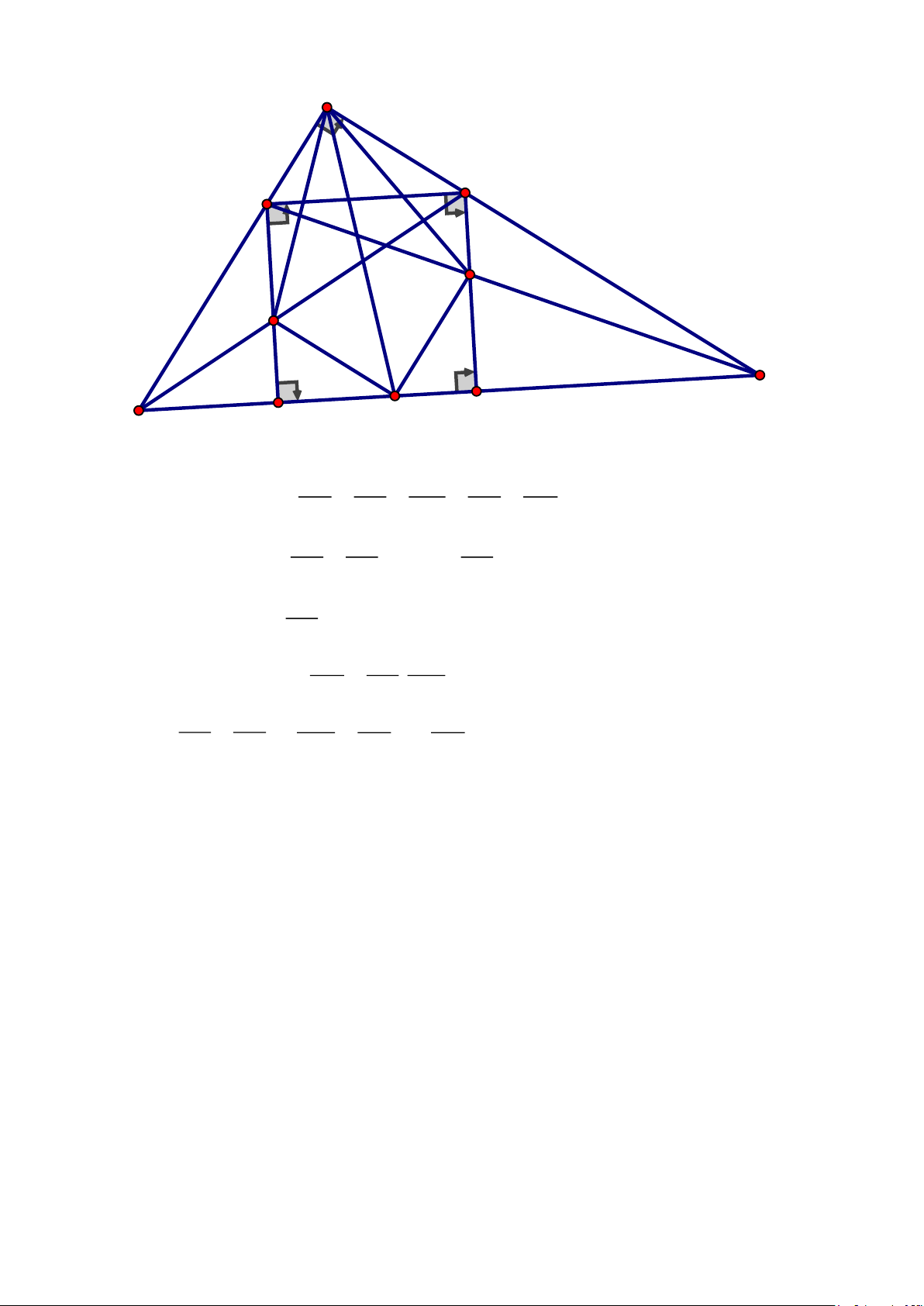
Câu 4. (2,5 điểm) Cho tam giác ABC vuông tại A, đường phân giác AD. Vẽ hình vuông
MNPQ có M thuộc cạnh AB, N thuộc cạnh AC, P và Q thuộc cạnh BC. Gọi E và F lần lượt là
giao điểm của BN và MQ; CM và NP. Chứng minh rằng
a) DE song song với AC
b) DE = DF; AE = AF
Câu 5. (1 điểm) Chứng minh bất đẳng thức: a b c 3 + +
với a b c 0
a + b b + c c + a 2 Trang 18 ĐÁP ÁN Câu 1. a) x 3 − 3x x + 4 x( 2 x − x + ) 1 − ( x + )
1 (3 − 3x) + x + 4 A = − + = 2 3
x +1 x − x +1 x +1 (x + ) 1 ( 2 x − x + ) 1
x + 2x + 2x +1 (x + ) 1 ( 2 3 2 x + x + ) 2 1 x + x +1 = ( = = x + ) 1 ( 2 x − x + ) 1 (x + ) 1 ( 2 x − x + ) 2 1 x − x +1 2 1 3 x + + 2 x x 1 + + 2 4
b) Với mọi x −1thì A = = 2 2 x − x +1 1 3 x − + 2 4 2 2 1 3 1 3 Vì x + + 0; x − + 0, x
−1 A 0, x −1 2 4 2 4 Câu 2. M = ( 2 x + x + )( 2 10
16 x +10x + 24) +16 a) Ta có: Đặt 2
a = x +10x +16
Suy ra M = a(a + ) + = a + a + = (a + )2 2 8 16 8 16 4
Vậy M = (x + x + )2 2 10 20 (dpc ) m
b / x +1 = x( x + ) 1 x(x + )
1 − x +1 = 0 x . x +1 − x +1 = 0 x +1 .( x − ) 1 = 0 x +1 = 0 x +1 = 0 x =1 x −1 = 0 x = 1 x = 1 − Câu 3.
Ta có: P(x) (x −1),( x − 3),( x − 5)
Nên P( x)có dạng P( x) = ( x − )
1 ( x − 3)( x − 5)( x + a) Khi đó: P( 2 − ) + 7.P(6) = ( 3 − ).( 5 − ).( 7 − ).( 2
− + a) + 7.5.3.1.(6 + a)
= −105.(−2 + a) +105.(6 + a)
=105.(2 − a + 6 + a) = 840 Câu 4. Trang 19 A N M F E 1 2 C B P Q D BE BQ BQ AB BD a) Chứng minh được = = = =
DE / /NC hay DE / /AC EN QP MQ AC DC DE BD BD DE / / AC = DE = .CN (1) b) Do CN BC BC CD Tương tự: DF = .BM (2) BC DE BD CN Từ (1) và (2) suy ra = . DF CD BM BD AB CN AC DE Mà = và = nên =1 DE = DF CD AC BM AB DF
Ta có: D = DAC = DAB = D A DE = A
DF AE = AF 1 2 Trang 20