10 Đề Toán Tuyển Sinh 10 Không Chuyên 2026 Có Đáp Án Và Lời Giải-Tập 5
Hai ô tô khởi hành cùng một lúc từ Ađến B. Vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô tô thứ hai là 10 km/h nên ô tô thứ nhất đến B trước ô tô thứ hai 1/2 giờ. Tính vận tốc mỗi ô tô biết quãng đường AB dài 150 km. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 289 tài liệu
Môn: Toán 9 3.1 K tài liệu
Tác giả:
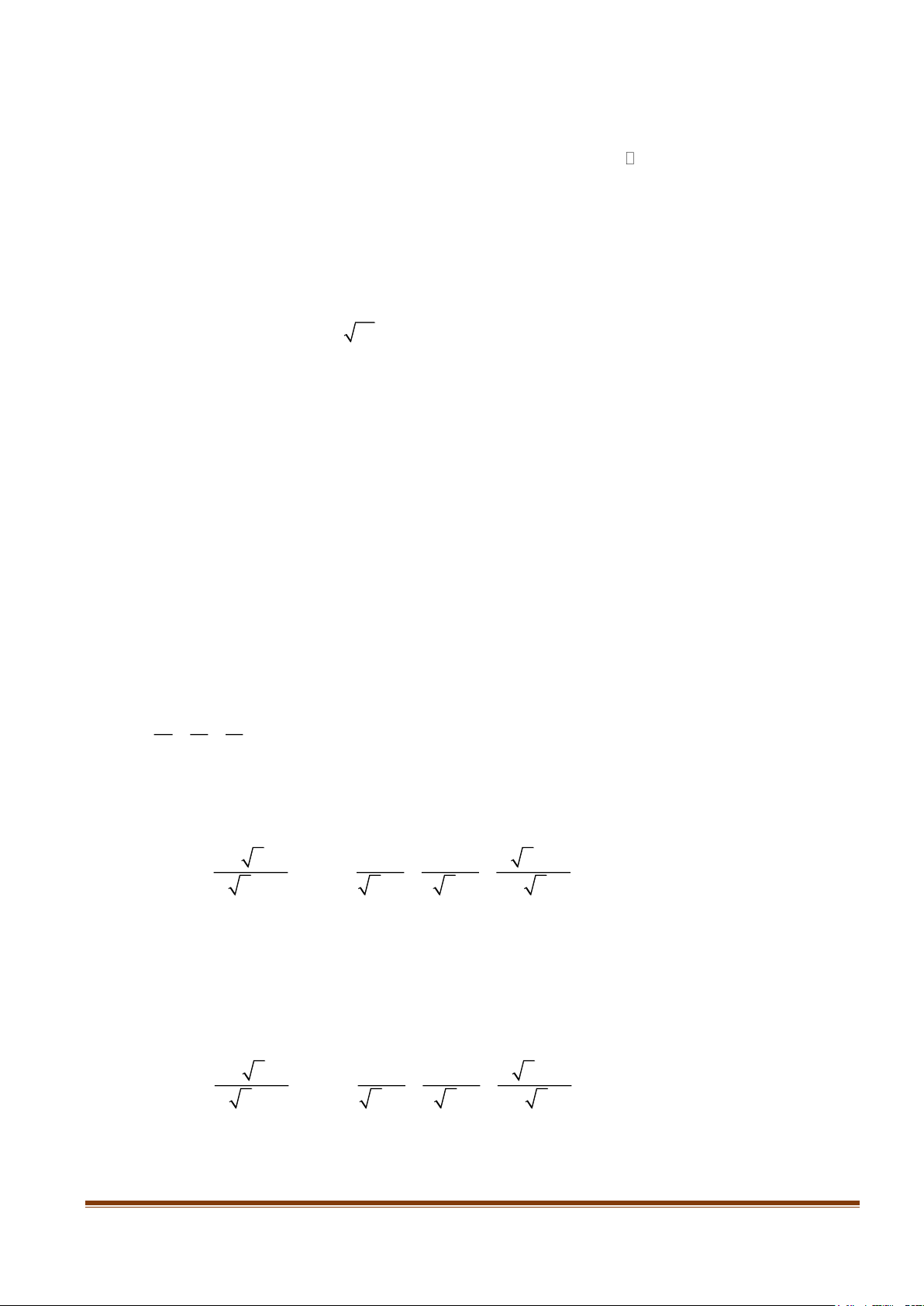
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH KỲ THI TUYỂN SINH VÀO LỚP 10
Môn thi: TOÁN ( không chuyên)
Thời gian làm bài: 120 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề có 01 trang, thí sinh không phải chép đề vào giấy thi) Câu 1: (1,0 điểm)
Tính giá trị biểu thức T = 4 + 25 − 9 Câu 2: (1,0 điểm)
Tìm mđể đồ thị hàm số y = m+ 2 (2 1)x đi qua điểm ( A 1;5) . Câu 3: (1,0 điểm) Giải phương trình 2
x − x − 6 = 0. Câu 4: (1,0 điểm)
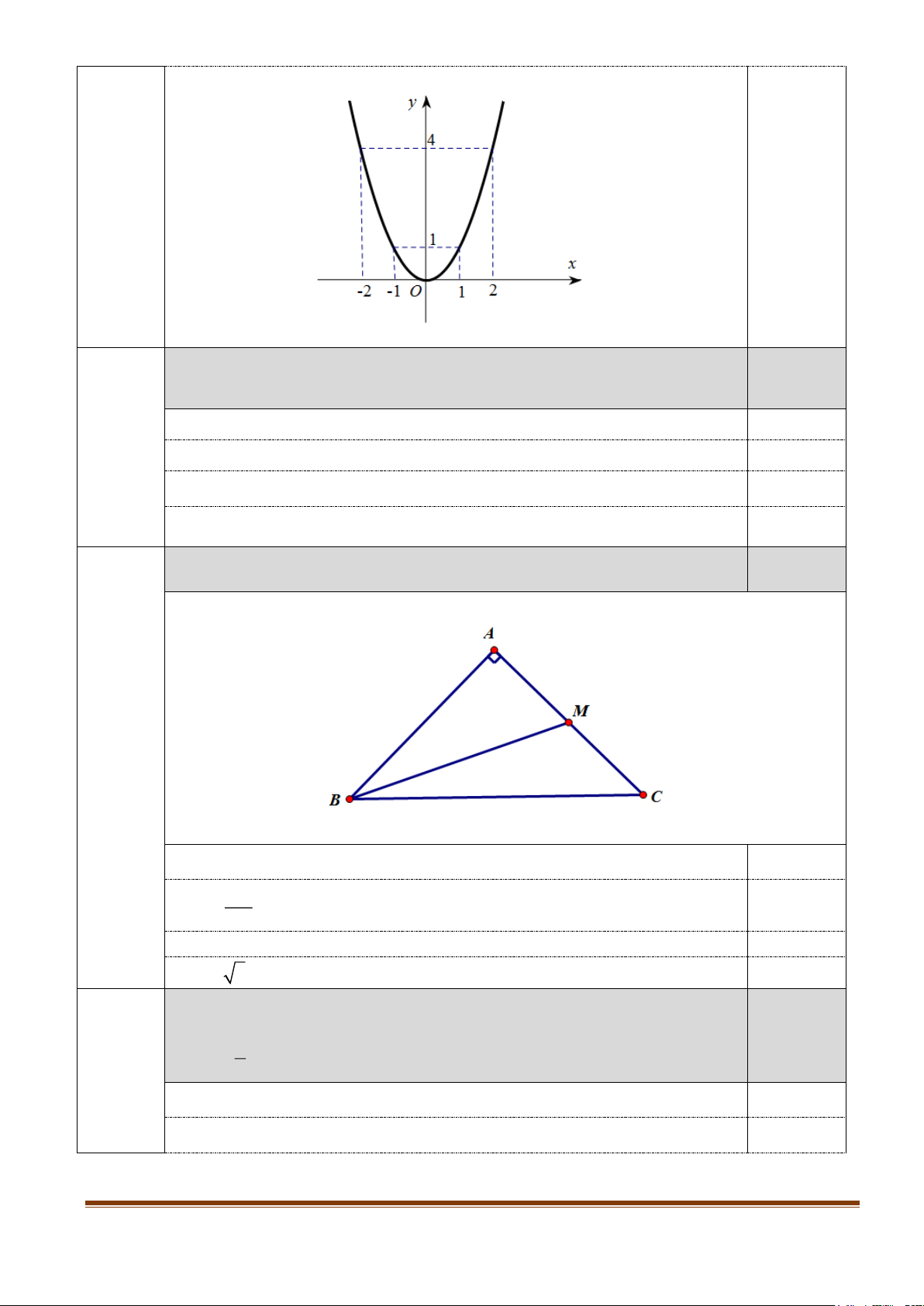
Vẽ đồ thị của hàm số = 2 y x . Câu 5: (1,0 điểm)
Tìm tọa độ giao điểm của đường thẳng d : y = 2x +1và đường thẳng d : y = x + 3. 1 2 Câu 6: (1,0 điểm)
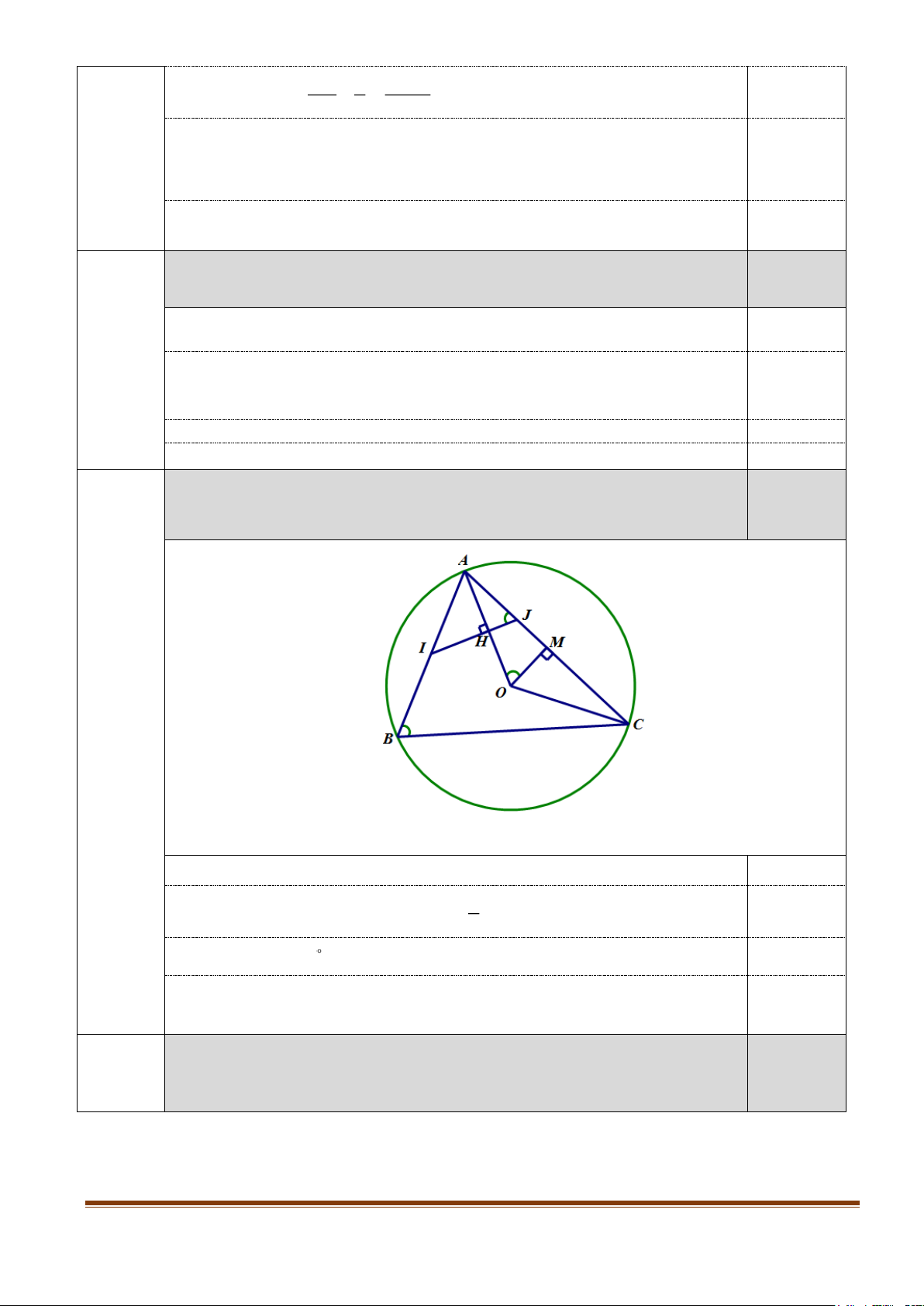
Cho tam giác ABC vuông cân tại A có đường trung tuyến BM ( M thuộc cạnh AC ). Biết
AB = 2a . Tính theo a độ dài AC , AM và BM . Câu 7: (1,0 điểm)
Hai ô tô khởi hành cùng một lúc từ A đến B . Vận tốc của ô tô thứ nhất lớn hơn vận tốc của ô 1
tô thứ hai là 10 km/h nên ô tô thứ nhất đến B trước ô tô thứ hai giờ. Tính vận tốc mỗi ô tô biết 2
quãng đường AB dài 150 km. Câu 8: (1,0 điểm)
Tìm các giá trị nguyên của m để phương trình 2
x − 4x + m+1= 0 có hai nghiệm phân biệt x1 và x thỏa 3 x + 3 x 100 2 1 2 Câu 9: (1,0 điểm)
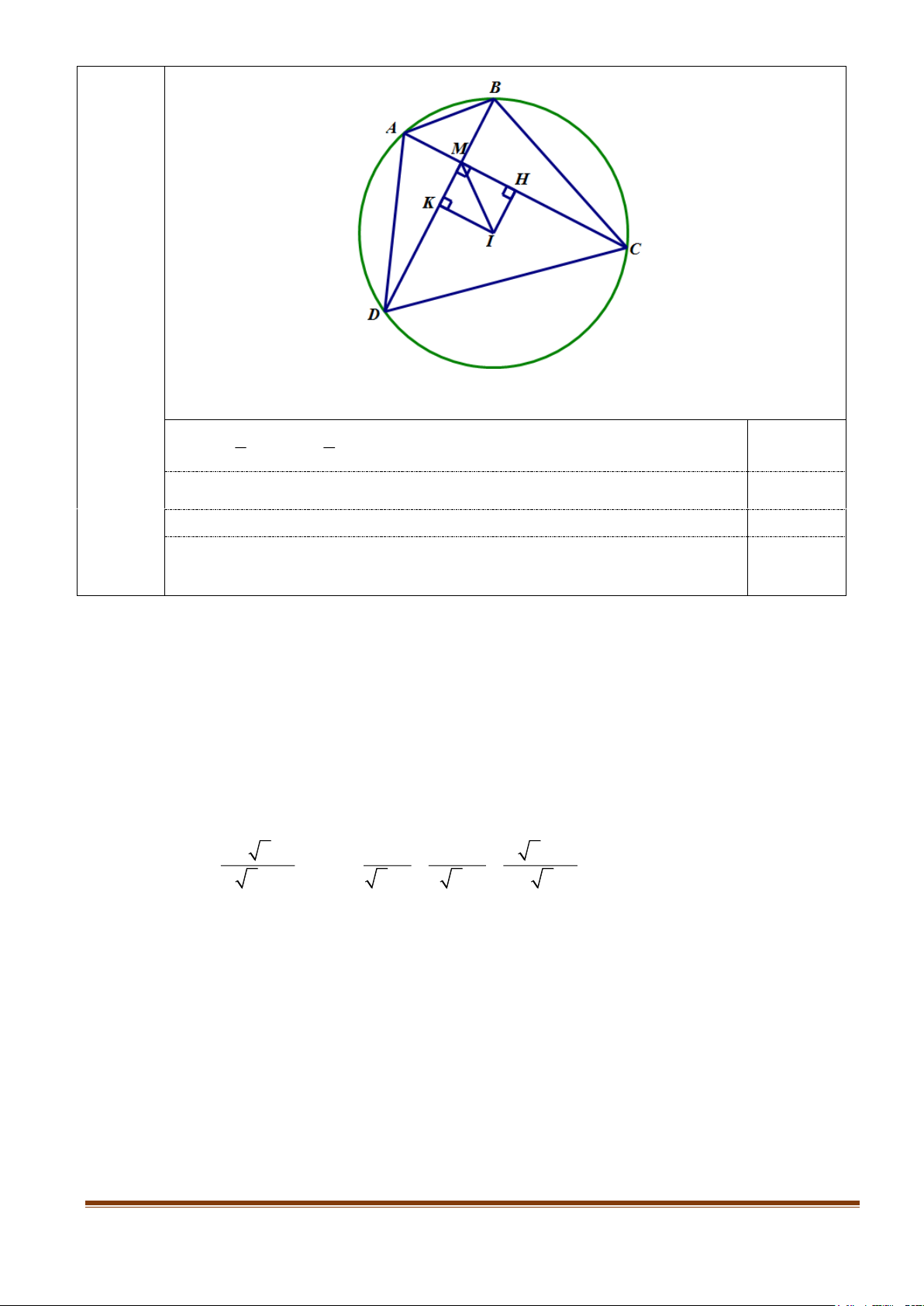
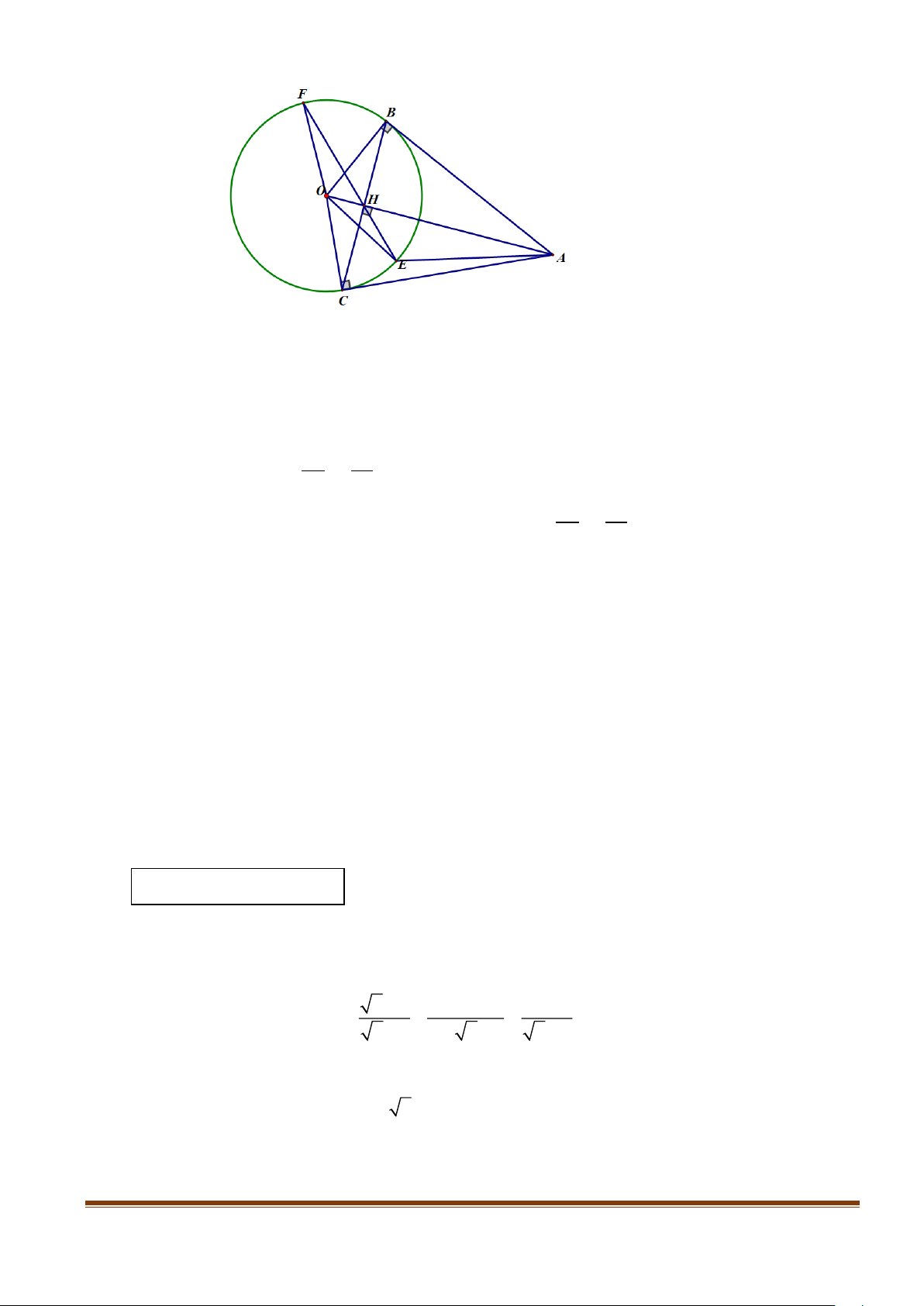
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O . Gọi I là trung điểm AB .
Đường thẳng qua I vuông góc AO và cắt AC tại J . Chứng minh: B,C, J và I cùng thuộc một đường tròn. Câu 10: (1,0 điểm)
Cho đường tròn (C) có tâm I và có bán kính R = 2a . Xét điểm M thay đổi sao cho IM = a .
Hai dây AC, BD đi qua M và vuông góc với nhau. ( ,
A B,C, D thuộc (C) ). Tìm giá trị lớn nhất của
diện tích tứ giác ABCD . ---Hết---
Họ và tên thí sinh:...................................................................................Số báo danh:............................
Chữ kí của giám thị 1:.............................................Chữ kí của giám thị 2:............................................. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
KỲ THI TUYỂN SINH VÀO LỚP 10
HƯỚNG DẪN CHẤM THI
Môn thi: TOÁN ( không chuyên)
(Bản hướng dẫn này có 04 trang)
A. Hướng dẫn chung
1. Nếu thí sinh làm bài theo cách riêng nhưng đáp ứng được yêu cầu cơ bản như trong
hướng dẫn chấm thi vẫn cho điểm đúng như hướng dẫn chấm qui định.
2. Việc chi tiết hóa điểm số (nếu có) so với biểu điểm phải bảo đảm không sai lệch với
hướng dẫn chấm, thống nhất trong toàn tổ và được lãnh đạo Hội đồng chấm thi phê duyệt.
3. Sau khi cộng điểm toàn bài được làm tròn đến 0,25 điểm.
B. Đáp án và thang điểm Câu
Nội dung cần đạt Điểm
Tính giá trị biểu thức T = 4 + 25 − 9 1,0 điểm • 4 = 2 0,25 1 • 25 = 5 0,25 • 9 = 3 0,25 Vậy T = 4 0,25
Tìm mđể đồ thị hàm số y = m+ 2 (2 1)x đi qua điểm ( A 1;5) . 1,0 điểm A(1; )
5 thuộc đồ thị hàm số y = ( m+ ) 2 2
1 x suy ra 5 = 2m+1 0,25 2 2m = 4 0,25 m = 2 0,25
Vậy m = 2 là giá trị cần tìm. 0,25 Giải phương trình 2
x − x − 6 = 0. 1,0 điểm 2 = b − 4ac 0,25 3 = 25 0,25
Vậy phương trình đã cho có hai nghiệm là x = −2 0,25 x = 3 0,25
Vẽ đồ thị của hàm số = 2 y x . 1,0 điểm
Bảng sau cho một số giá trị tương ứng của x và y x −2 −1 0 1 2 4 2 y = x 4 1 0 1 4 0,5
(nếu đúng 3 cặp ( ;
x y) thì được 0,25 điểm) Vẽ đồ thị: 0,5 Trang 2
(nếu vẽ qua đúng 3 điểm thì được 0,25 điểm)
Tìm tọa độ giao điểm của đường thẳng d : y = 2x +1và đường thẳng 1 1,0 điểm
d : y = x + 3. 2
Phương trình hoành độ giao điểm của d và d là 2x +1= x + 3 0,25 1 2 5 x = 2 0,25
Với x = 2 tìm được y = 5 0,25
Vậy tọa độ giao điểm của d và d là (2; ) 5 . 1 2 0,25
Cho tam giác ABC vuông cân tại A có đường trung tuyến BM ( M thuộc 1,0 điểm
cạnh AC ). Biết AB = 2a . Tính theo a độ dài AC , AM và BM . 6
AC = AB = 2a 0,25 AC AM = = a 0,25 2 2 2 2
BM = AB + AM 0,25 BM = 5a 0,25
Hai ô tô khởi hành cùng một lúc từ A đến B . Vận tốc của ô tô thứ nhất lớn
hơn vận tốc của ô tô thứ hai là 10 km/h nên ô tô thứ nhất đến B trước ô tô 1 1,0 điểm
thứ hai giờ. Tính vận tốc mỗi ô tô biết quãng đường AB dài 150 km. 7 2
Gọi x(km/h) là vận tốc ô tô thứ nhất. Điều kiện x 10 0,25
Khi đó vận tốc ô tô thứ hai là x −10(km/h) 0,25 Trang 3 150 1 150 Từ giả thiết ta có + = x 2 x −10 x = 60 2
x −10x − 3000 = 0 x = 50 − 0,25
Do x 10 nên nhận x = 60.
Vậy vận tốc của ô tô thứ nhất là 60km/h và vận tốc của ô tô thứ hai là 0,25 50 km/h
Tìm các giá trị nguyên của m để phương trình 2
x − 4x + m+1= 0 có hai 1,0 điểm
nghiệm phân biệt x và x thỏa 3 x + 3 x 100 1 2 1 2
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi
0 m 3 0,25 8
x + x = 4; x .x = m+1. 1 2 1 2 0,25
Ta có x + x 100 (x + x )3 3 3
− 3x x x + x 100 m 4 − 1 2 1 2 1 2 ( 1 2 )
Kết hợp với điều kiện m 3 ta được −4 m 3 0,25
Vậy các giá trị nguyên của m cần tìm là 3 − ; 2 − ;−1;0;1;2 0,25
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O . Gọi I là
trung điểm AB . Đường thẳng qua I vuông góc AO và cắt AC tại J . 1,0 điểm
Chứng minh: B,C, J và I cùng thuộc một đường tròn. 9
Gọi M là trung điểm AC ; H là giao điểm của IJ và AO
Ta có AOC = 2ABC ( góc ở tâm và góc chắn cung) 0,25 1
Tam giác OAC cân tại O nên AOM = AOC ABC = AOM ( ) 1 0,25 2
Mặt khác AJI = 90 − OAM = AOM (2) 0,25 Từ ( )
1 và (2) suy ra IBC = AJI . Vậy bốn điểm ,
B C,J và I cùng thuộc 0,25 một đường tròn.
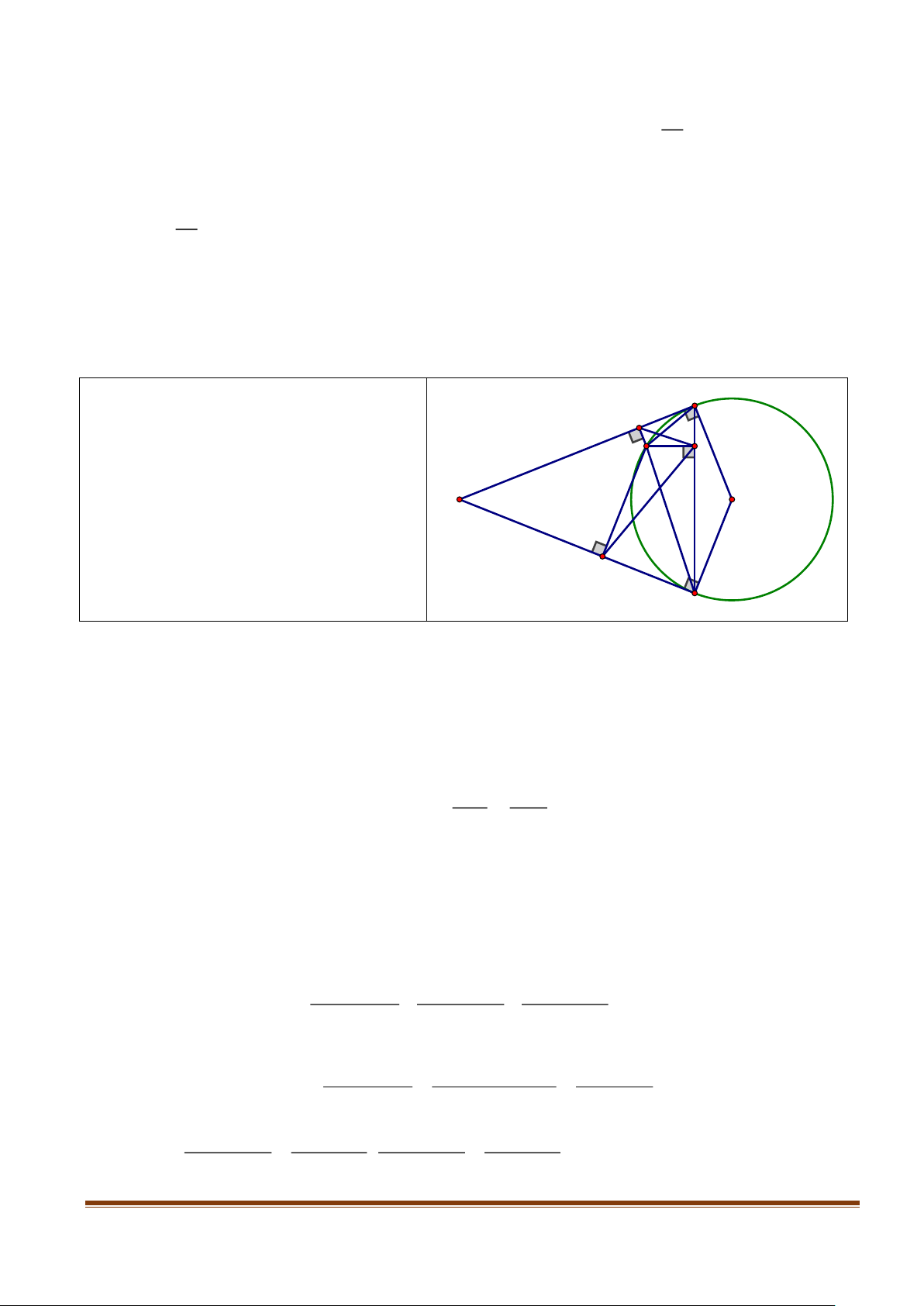
Cho đường tròn (C) có tâm I và có bán kính R = 2a . Xét điểm M thay 10
đổi sao cho IM = a . Hai dây AC, BD đi qua M và vuông góc với nhau. 1,0 điểm ( ,
A B,C, D thuộc (C) ). Tìm giá trị lớn nhất của diện tích tứ giác ABCD . Trang 4
Đặt H,K lần lượt là trung điểm của AC và BD , S
là diện tích tứ giác ABCD . ABCD 1 1 S = A . C BD AC + BD . 0,25 ABCD ( 2 2 ) 2 4 2 2 AC + BD = ( 2 2 AH + BK ) = ( 2 2 2 2 4
4 R − IH + R − IK ). 0,25 Do 2 2 2
IH + IK = IM nên 2 2 2
AC + BD = 28a . 0,25 2 S
= 7a khi AC = BD . ABCD 0,25
Vậy giá trị lớn nhất của diện tích tứ giác ABCD là 2 7a . ---Hết---
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2019-2020 THÁI BÌNH Môn: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài 120 phút (không kể thời gian giao đề)
Câu 1. (2,0 điểm) x + x +1 1 x + 2 x +1 Cho A = và B = − −
với x 0 , x 1. x +1
x −1 x x −1 x + x +1
a).Tính giá trị của biếu thức A khi x = 2 .
b).Rút gọn biểu thức B .
c).Tìm x sao cho C = − .
A B nhận giá trị là số nguyên.
Câu 2. (2,0 điểm) 4x + y = 3
a).Giải hệ phương trình
(không sử dụng máy tính cầm tay). 2x − y =1
b).Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài mảnh vườn hơn
chiều rộng mảnh vườn là 5 m . Tính chiều rộng mảnh vườn. Trang 5
Câu 3. (2,0 điểm)
Cho hàm số y = (m − 4) x + m + 4 ( m là tham số)
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên .
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol (P) 2
: y = x tại hai điểm phân biệt. Gọi x , x là hoành độ các giao điểm, tìm m sao cho 1 2
x x −1 + x x −1 = 18 . 1 ( 1 ) 2 ( 2 )
c).Gọi đồ thị hàm số đã cho là đường thẳng (d ) . Chứng minh khoảng cách từ điểm O (0;0)
đến (d ) không lớn hơn 65 .
Câu 4. (3,5 điểm)
Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD vuông góc với AB tại H ( H
nằm giữa A và O , H khác A và O ). Lấy điểm G thuộc CH ( G khác C và H ), tia
AG cắt đường tròn tại E khác A .
a).Chứng minh tứ giác BEGH là tứ giác nội tiếp.
b).Gọi K là giao điểm của hai đường thẳng BE và CD . Chứng minh: KC.KD = KE.KB .
c).Đoạn thẳng AK cắt đường tròn O tại F khác A . Chứng minh G là tâm đường tròn
nội tiếp tam giác HEF .
d).Gọi M , N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng
minh HE + HF = MN .
Câu 5. Cho a , b , c là các số thực dương thỏa mãn a + b + c + ab + bc + ac = 6 . Chứng minh rằng: 3 3 3
a + b + c 3. b c a Hướng dẫn giải
Câu 1. (2,0 điểm) x + x +1 1 x + 2 x +1 Cho A = và B = − −
với x 0 , x 1. x +1
x −1 x x −1 x + x +1
a).Tính giá trị của biếu thức A khi x = 2 .
b).Rút gọn biểu thức B .
c).Tìm x sao cho C = − .
A B nhận giá trị là số nguyên. Lời giải x + x +1 1 x + 2 x +1 Cho A = và B = − −
với x 0 , x 1. x +1
x −1 x x −1 x + x +1
a).Tính giá trị của biếu thức A khi x = 2 . Trang 6 x x 1 ( x − ) 1 (x + x + + + )1 3 x −1 Có A = = = x +1 x −1 x −1
Khi x = 2 A = 2 2 −1.
b).Rút gọn biểu thức B .
c).Tìm x sao cho C = − .
A B nhận giá trị là số nguyên. 1 x + 2 x +1 Có B = − −
x −1 x x −1 x + x +1
x + x +1− ( x + 2) − ( x + ) 1 ( x − ) 1 −x + x − x B = ( = = x − ) 1 (x + x + ) 1
( x − )1(x+ x + )1 x+ x +1 3 x −1 − x x 1 Có C = − . A B = − . = =1− x 1 x x 1 − + + x +1 x +1
Có x +1 1, x 0 , x 1.
C nhận giá trị là số nguyên x +1 = 1 x = 0 (nhận).
Câu 2. (2,0 điểm) 4x + y = 3
a).Giải hệ phương trình
(không sử dụng máy tính cầm tay). 2x − y =1
b).Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài mảnh vườn hơn
chiều rộng mảnh vườn là 5 m . Tính chiều rộng mảnh vườn. Lời giải 4x + y = 3
a).Giải hệ phương trình
(không sử dụng máy tính cầm tay). 2x − y =1 2 = 4x + y = 3 6x = 4 x Có 3 . 2x − y =1 2x − y = 1 1 y = 3 2 1 Vậy nghiệm của hệ là ; 3 3
b).Một mảnh vườn hình chữ nhật có diện tích 2
150 m . Biết rằng, chiều dài mảnh vườn hơn
chiều rộng mảnh vườn là 5 m . Tính chiều rộng mảnh vườn.
Gọi x , y lần lượt là chiều dài, chiều rộng của mảnh vườn, điều kiện x 0 y 0 , x y . Trang 7 x − y = 5 x = y + 5 Có xy = 150 y (y + ) 5 = 150 ( ) 1 ( ) y = 10 (nhaän) 2
1 y + 5y −150 = 0 . y = −15 (loaïi)
Vậy chiều rộng mảnh vườn là 10(m)
Câu 3. (2,0 điểm)
Cho hàm số y = (m − 4) x + m + 4 ( m là tham số)
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên .
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol (P) 2
: y = x tại hai điểm phân biệt. Gọi x , x là hoành độ các giao điểm, tìm m sao cho 1 2
x x −1 + x x −1 = 18 . 1 ( 1 ) 2 ( 2 )
c).Gọi đồ thị hàm số đã cho là đường thẳng (d ) . Chứng minh khoảng cách từ điểm O (0;0)
đến (d ) không lớn hơn 65 . Lời giải
a).Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên .
y = (m − 4) x + m + 4 đồng biến trên m− 4 0 m 4 .
Vậy m 4 thì hàm số đồng biến trên .
b).Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol (P) 2
: y = x tại hai điểm phân biệt. Gọi x , x là hoành độ các giao điểm, tìm m sao cho 1 2
x x −1 + x x −1 = 18 . 1 ( 1 ) 2 ( 2 )
(d): y = (m − 4) x + m + 4 , (P) 2
: y = x .
Phương trình hoành độ giao điểm của (d) , (P) : 2
x = (m− 4) x + m+ 4 2
x − (m− 4) x −(m+ 4) = 0 ( ) 1 , Có a = 1 0 2 2
Có = (m− ) + (m+ ) 2 4 4
4 = m − 4m+ 32 = (m− 2) + 28 0, m a 0 Do có 0, m
Suy ra (d) cắt luôn cắt (P) tại hai điểm phân biệt .
Có x x −1 + x x −1 = 18 2 2
x + x − x + x −18 = 0 1 2 ( 1 2) 1 ( 1 ) 2 ( 2 ) Trang 8
x + x = m− 4 (
x + x )2 − 2x x − x + x −18= 0, mà 1 2 1 2 1 2 ( 1 2) x x = − m+ 4 1 2 ( ) m= 5 (m− )2
4 + 2(m+ 4) − (m− 4) −18 = 0 2
m − 7m+10 = 0 (m− ) 5 (m− 2) = 0 . m= 2
Vậy m = 5, m = 2 thỏa yêu cầu bài
c).Gọi đồ thị hàm số đã cho là đường thẳng (d ) . Chứng minh khoảng cách từ điểm
O (0;0) đến (d ) không lớn hơn 65 . ( m+ 4
d ) : y = (m − 4) x + m + 4 cắt trục Ox ,Oy lần lượt ở A − ;0
và B(0;m+ 4) . m− 4
*Trường hơp 1: Xét m− 4 = 0 m = 4 , thì (d) :y = 8, (d) song song trục Ox , (d) cắt trục Oy tại B(0; ) 8
Có khoảng cách từ O đến đường thẳng (d) là OB = 8
Gọi H là hình chiếu của O lên đường thẳng (d) .
OAB vuông tại O có OH ⊥ AB , Có OH.AB = O . AOB 2 1 1 1 (m−4)2 1 (m−4) +1 = + = + = 2 2 2 OH OA OB ( 2 m+ 4)2 (m+ 4)2 (m+ 4) (m+ 4)2 2 OH = ( m− 4)2 +1 (m+4)2 Giả sử OH 65 2 OH 65 65 2 m + m+ ( 2 8
16 65 m − 8m+1 ) 7 (m−4)2 +1 2
64m − 528m+1089 0 ( )2 2
8m − 2.16.8m+ 33 0 ( m− )2 8 33 0 (sai) Vậy OH 65 .
Câu 4. (3,5 điểm)
Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD vuông góc với AB tại H ( H
nằm giữa A và O , H khác A và O ). Lấy điểm G thuộc CH ( G khác C và H ), tia
AG cắt đường tròn tại E khác A .
a).Chứng minh tứ giác BEGH là tứ giác nội tiếp.
b).Gọi K là giao điểm của hai đường thẳng BE và CD . Chứng minh: KC.KD = KE.KB . Trang 9
c).Đoạn thẳng AK cắt đường tròn O tại F khác A . Chứng minh G là tâm đường tròn nội tiếp tam giác HEF .
d).Gọi M , N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF . Chứng
minh HE + HF = MN . K N E C F T M G O A B H Q D Lời giải
a).Chứng minh tứ giác BEGH là tứ giác nội tiếp.
Có BHG = BEG = 90 BHG + BEG = 180 .
Tứ giác BEGH nội tiếp đường tròn đường kính BG .
b).Gọi K là giao điểm của hai đường thẳng BE và CD . Chứng minh: KC.KD = KE.KB . KE KC
Có KEC = KDB , EKC = DKB (góc chung) KEC ∽ K DB = KD KB
KC.KD = KE.KB
c).Đoạn thẳng AK cắt đường tròn O tại F khác A . Chứng minh G là tâm đường tròn
nội tiếp tam giác HEF .
KAB có ba đường cao AE , BF , KH đồng qui tại G . Suy ra G là trực tâm của KAB .
Có GHE = GBE = 1 sñGE (trong đường tròn BEGH ) 2
Có GBE = GAF = 1 sñEF (trong đường tròn (O) ) 2 Trang 10
Có GAF = GHF = 1 sñEG (tứ giác AFGH nội tiếp đường tròn đường kính AG ) 2
Suy ra GHE = GHF HG là tia phân giác của EHF .
Tương tự EG là tia phân giác của FEG .
EHF có hai tia phân giác HG và EG cắt nhau tại G . Suy ra G là tâm đường tròn nội tiếp EHF .
d).Gọi M , N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF .
Chứng minh HE + HF = MN .
Gọi Q là giao điểm của tia EH và đường tròn (O) .
Có EOB = 2EFB = sñEB , 2EFB = EFO (do FG là tia phân giác của EFH )
EOB = EFH Tứ giác EFHO nội tiếp đường tròn.
FOH = FEH = 1 sñEQ = 1 FOQ FOH = 1 FOQ. 2 2 2
OH là tia phân giác của FOQ
OFH,OQH có OH chung, OF = OQ , FOH = QOH
OFH = OQH HF = HQ
Do đó HE + HF = HE + HQ = EQ .
Có AMN = MNT = NTA =
90 . Suy ra AMNT là hình chữ nhật, nên AT = MN .
Suy ra AQ = FA = ET AE // QT , mà AETQ nội tiếp đường tròn (O) .
AETQ là hình thang cân EQ = AT = MN
Vậy HE + HF = MN .
Câu 5. Cho a , b , c là các số thực dương thỏa mãn a + b + c + ab + bc + ac = 6 . Chứng minh rằng: 3 3 3
a + b + c 3. b c a Lời giải 3 3 3 a b c Đặt P = + + . b c a
Có a , b , c là các số thực dương, theo bất đẳng thức AM-GM có: Trang 11 3 a + ab 2 2a b 3 b 3 3 3 a b c + bc 2 2b . P = + + ( 2 a + 2 b + 2 2
c )−(ab+ bc+ ac) , mà c b c a 3 c + ac 2 2c a
a + b + c + ab + bc + ac = 6 . P ( 2 a + 2 b + 2 2
c ) + (a+ b+ c) − 6 .
Có (a− b)2 + (b− c)2 + (a− c)2 0 ( 2 a + 2 b + 2 2
c ) 2(ab+ bc+ ca) ( + + ) ( + + )2 2 2 2 3 a b c a b c . 2 2
Suy ra P (a+ b+ c) + (a+ b+ c) − 6. 3 Có 2 2 2
ab + bc + ca a + b + c ( + + ) ( + + )2 3 ab bc ac a b c . 1
Do đó 6 = a + b + c + ab + bc + ac a + b + c + (a + b + c)2 3 1
(a+ b+ c)2 + (a+ b+ c)− 6 0. (a+ b+ c) 3, (a+ b+ c)2 9. 3 2
Suy ra P .9+ 3− 6 = 3. Dấu đẳng thức xảy ra khi a = b = c . 3 3 3 3 a b c Vậy + + 3. b c a
UBND TỈNH THÁI NGUYÊN
THI TUYỂN SINH VÀO LỚP 10 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO Năm học 2019 – 2020 MÔN: TOÁN
Thời gian làm bài 120 phút không kể thời gian giao đề
( Đề thi gồm 01 trang, 10 câu, mỗi câu 01 điểm )
Câu 1. Chứng minh A = 2
A = 2 5 + 6 − ( 5 −1) + 2018 là một số nguyên
Câu 2. Rút gọn biểu thức a −1 b − 2 b +1 P = với a < 1 và b > 1 2
b −1 a − 2a +1
Câu 3. Tìm các giá trị của m 1 để hàm số y = (2m – 1) x2 đạt giá trị lớn nhất bằng 0 2 tại x = 0. Trang 12
Câu 4. Cho hàm số y = ax + b với a 0. Xác định các hệ số a, b biết đồ thị hàm số
song song với đường thẳng y = 2x + 2019 và cắt trục tung tại điểm có tung độ là 2020.
Câu 5. Một địa phương cấy 10ha giống lúa loại I và 8ha giống lúa loại II. Sau một mùa
vụ, địa phương đó thu hoạch và tính toán sản lượng thấy:
+ Tổng sản lượng của hai giống lúa thu về là 139 tấn;
+ Sản lượng thu về từ 4ha giống lúa loại I nhiều hơn sản lượng thu về từ 3ha giống lúa loại II là 6 tấn.
Hãy tính năng suất lúa trung bình ( đơn vị: tấn/ ha) của mỗi loại giống lúa.
Câu 6. Cho phương trình
x2 – 4x + m – 1 = 0. Tìm m để phương trình có hai nghiệm x 2 2
1, x2 thỏa mãn x1 + x2 -10x1x2 = 2020.
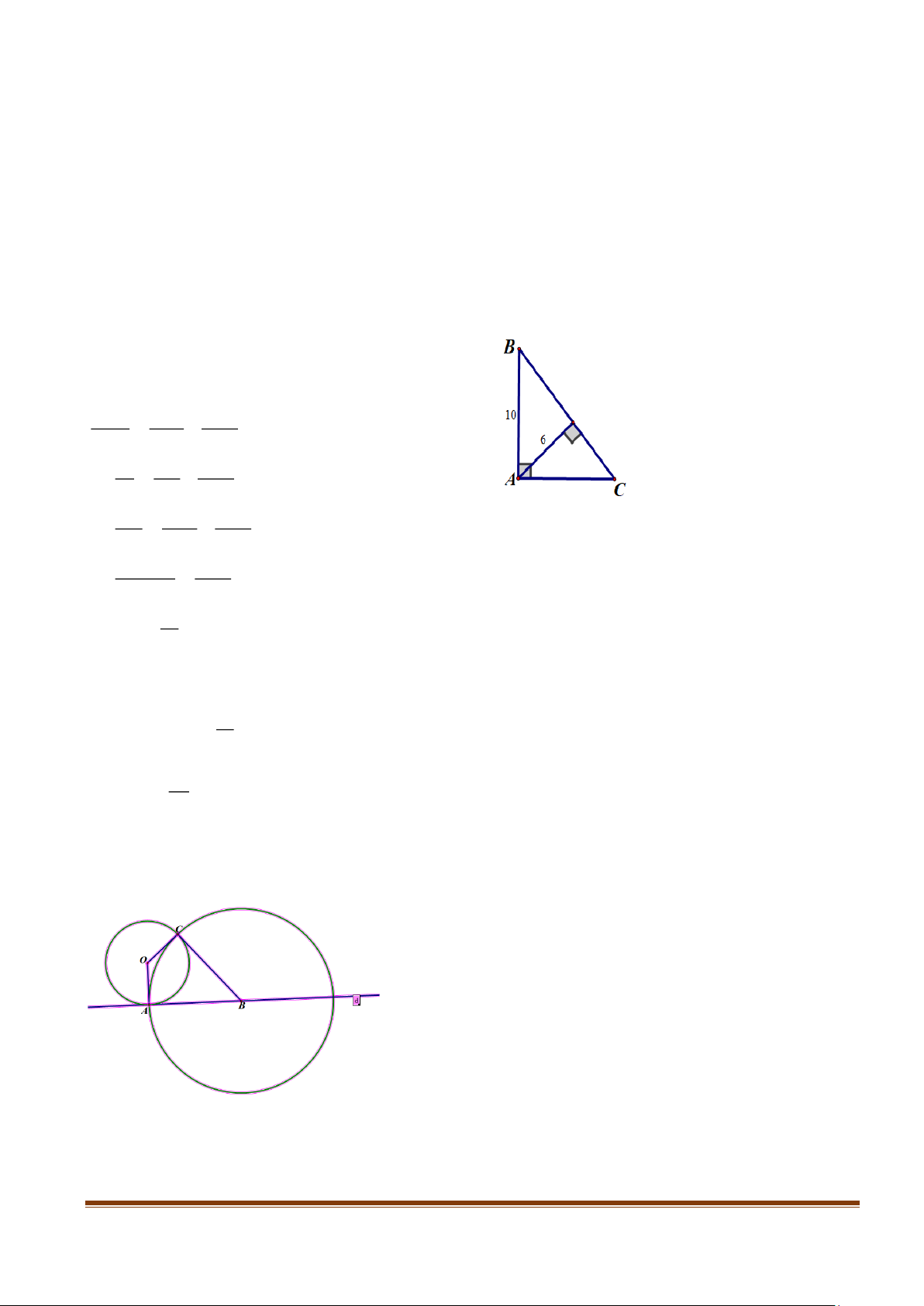
Câu 7. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, AH = 6cm,
Tính độ dài các cạnh AC, BC của tam giác ABC.
Câu 8. Cho đường tròn (O). Đường thẳng d tiếp xúc với đường tròn ( O) tại A. Trên d
lấy một điểm B( B khác A), vẽ đường tròn (B, BA) cắt đường tròn ( O) tại điểm C ( C
khác A). Chứng minh BClà tiếp tuyến của (O).
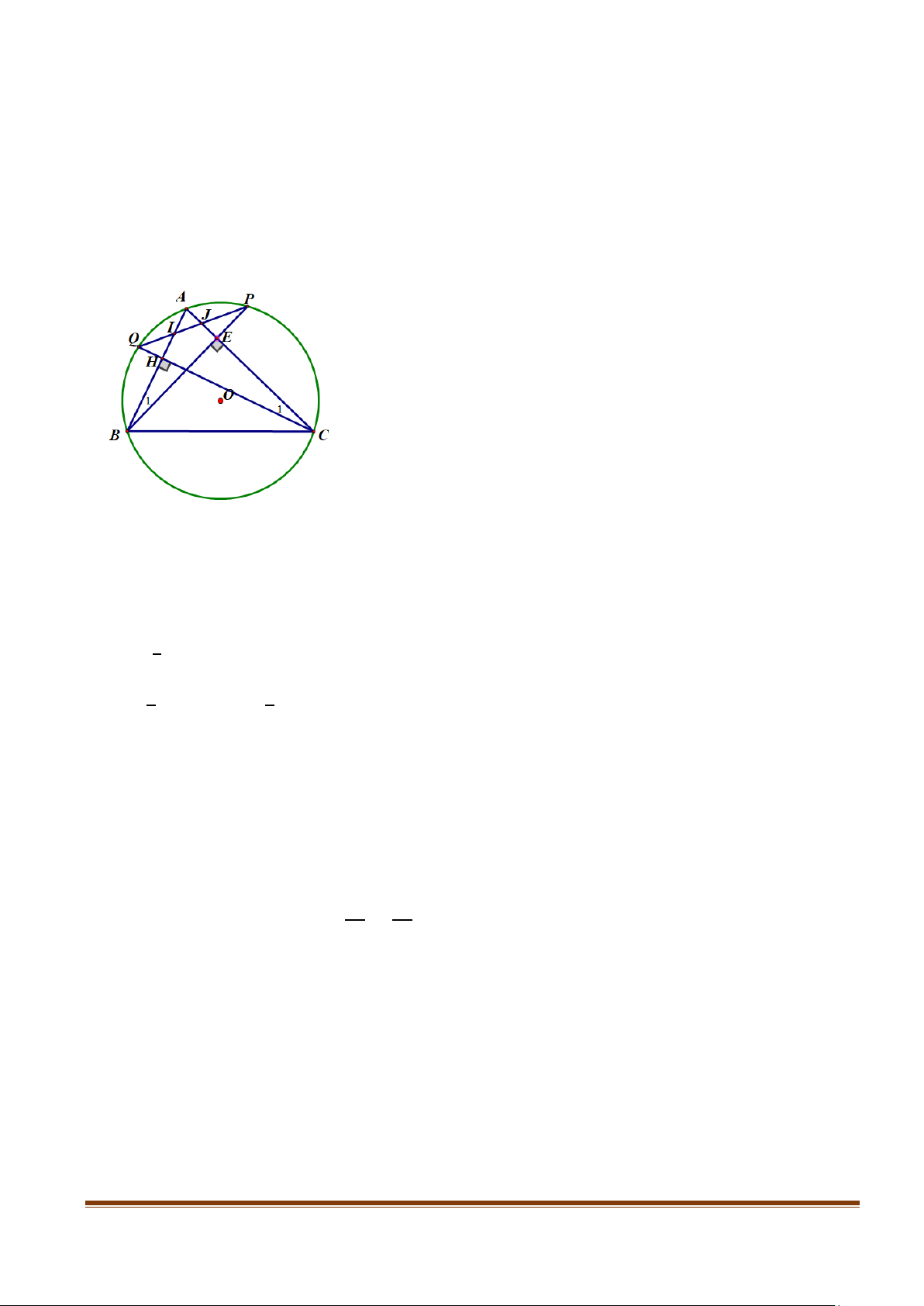
Câu 9. Cho tam giác ABC( AB< AC) có ba góc nhọn nội tiếp đường tròn (O). Lấy các
điểm P, Q lần lượt thuộc các cung nhỏ AC, AB sao cho BP vuông góc với AC, CQ
vuông góc với AB. Gọi I, J lần lượt là giao điểm của PQ với AB và AC. Chứng minh IJ.AC = AI.CB.
Câu 10. Từ điểm A nằm ngoài đường tròn ( O) kẻ các tiếp tuyến AB, AC đến đường
tròn ( B, C là tiếp điểm ). Gọi H là giao điểm của OA và BC. a. Chứng minh OB2 = OH. OA
b. EF là một dây cung của (O) đi qua H sao cho A, E, F không thẳng hàng. Chứng
minh bốn điểm A, E, O, F nằm trên cùng một đường tròn. ----Hết--- ĐÁP ÁN Câu 1. Chứng minh 2 22 A = =( 25 5 + +) 1 6 − − (( 5 5 − − 1 1 ) ) ++22001188 = 5 +1− 5 +1+ 2018 = 2020
Vậy A là một số nguyên Câu 2. Trang 13 a −1 b − 2 b +1 P = 2
b −1 a − 2a +1 ( b a − − )2 1 1
= b −1 (a− )2 1 b −1 a −1 = . b −1 a −1 a −1 b −1 = . b −1 1− a = −1 ( do a < 1 và b > 1)
Câu 3. Hàm số y = (2m – 1) x2 đạt giá trị lớn nhất tại x = 0.
Khi 2m – 1 < 0 ↔ m < 1 2
Câu 4. ( d): y = ax + b ( a 0) song song với (∆): y = 2x + 2019 → a = 2 (1) b 2019
+ (d) cắt Oy tại điểm có tung độ 2020 → b = 2020 (2)
Từ (1), (2) ta có: y = 2x + 2020 Câu 5.
Gọi năng suất lúa trung bình của loại I là x ( 0 < x < 139)
Gọi năng suất lúa trung bình của loại II là y (0 < y < 139)
Theo bài ra ta có hệ phương trình 10𝑥 + 8𝑦 = 139 𝑥 = 7,5 { ↔ { 4𝑥 − 3𝑦 = 6 𝑦 = 8
Vậy năng suất lúa trung bình của loại I là: 7,5 (tấn / ha)
Vậy năng suất lúa trung bình của loại II là: 8 (tấn / ha)
Câu 6. Cho phương trình
x2 – 4x + m – 1 = 0. Tìm m để phương trình có hai nghiệm x 2 2
1, x2 thỏa mãn x1 + x2 -10x1x2 = 2020. ∆’ = 4-m-1 = 3-m
+ PT có 2 nghiệm ↔ ∆’ ≥ 0 ↔ 3-m ≥ 0 ↔ m ≤ 3 + Theo viet 𝑥 { 1 + 𝑥2 = 4 (1) 𝑥1𝑥2 = 𝑚 + 1 Mà: x 2 2 1 + x2 -10x1x2 = 2020 Trang 14
↔ (x1 + x2 )2 - 12 x1x2 -2020 = 0 (2)
Thế (1) vào (2) ↔ 16 - 12(m+1) – 2020 = 0 ↔ -12m - 2016 = 0 ↔ m = -168 ( t/m) Câu 7. Ta có: 1 1 1 = + 2 2 2 AH AB AC 1 1 1 = + 2 2 2 6 10 AC 1 1 1 = + 2 36 100 AC 64 1 = 2 36.100 AC 15 AC = (cm) 2 Ta có: AH.BC = AB.AC 6.BC = 10.15 2 BC = 25 (cm) 2 Câu 8.
Theo bài ra ta có AB là tiếp tuyến của đường tròn (O) → AB ⊥ OA (1)
Xét hai tam giác ∆OAB và ∆OCB có: Trang 15 OA = OC
BA = BC → ∆OAB = ∆OCB ( c.c.c) (2) OB chung
Từ (1), (2) suy ra 𝑂𝐴𝐵 ̂ = 𝑂𝐶𝐵 ̂ (=900) hay 𝑂𝐶𝐵 ̂ =900 nên BC ⊥ OC
Vậy BClà tiếp tuyến của (O) Câu 9.
Tứ giác HECB nội tiếp đường tròn ( vì 2 đỉnh liên tiếp nhìn 1 cạnh cố định dưới góc vuông) → 𝐵1 ̂ = 𝐶1
̂ ( Nội tiếp chắn cung HE) → AP = AQ 𝐴𝐶𝐵 ̂ = 1 AB 2 𝐴𝐼𝑃
̂ = 1( AP + BQ ) = 1 AB (vì AP = AQ ) 2 2 → 𝐴𝐶𝐵 ̂ = 𝐴𝐼𝑃 ̂
Xét tam giác ∆AIJ và ∆ ACB Có 𝐴̂ chung 𝐴𝐶𝐵 ̂ = 𝐴𝐼𝑃 ̂ (cmt)
Vậy ∆AIJ và ∆ ACB (g.g) 𝐼𝐽
→ 𝐴𝐼 = → IJ.AC = AI.CB 𝐴𝐶 𝐶𝐵 Câu 10. Trang 16 a. Xét tam giác ∆OBA và ∆OHB có: 𝑂̂ chung 𝐻 ̂ = 𝐵̂ = 900 → ∆OBA 𝑂𝐵 𝑂𝐴 ~ ∆OHB → = → OB2 = OH. OA 𝑂𝐻 𝑂𝐵
b. theo cmt: OB2 = OH. OA → OE2 = OH. OA → 𝑂𝐸 𝑂𝐴 = lại có: 𝐻𝑂𝐸 ̂ = 𝐴𝑂𝐸 ̂ 𝑂𝐻 𝑂𝐸
→∆OEH ~ ∆OAE →𝑂𝐴𝐸 ̂ = 𝑂𝐸𝐹 ̂ ( 1)
Vì ∆OEF cân nên: 𝑂𝐹𝐸 ̂ = 𝑂𝐸𝐹 ̂ (2)
Từ (1), (2) suy ra: 𝑂𝐴𝐸 ̂ = 𝑂𝐹𝐸
̂ ( hai đỉnh liên tiếp bằng nhau cùng nhìn dưới
cạnh cố định OE) → Tứ giác OEAF nội tiếp đường tròn
Vậy bốn điểm A, E, O, F nằm trên cùng một đường tròn
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀOLỚP 10 THPT THANH HÓA NĂM HỌC 2019 - 2020
------------------------- Môn Toán : Lớp 10 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút) --------------------------- + Bài 1. (2 điểm) x 2 5 1 Cho biểu thức: A = − −
với x 0; x 4.
x + 3 x + x − 6 x − 2
1. Rút gọn A
2. Tìm giá trị của cảu A khi x = 6 + 4 2 Bài 2. (2 điểm) Trang 17
1. Cho đường thẳng (d ) : y = ax+b . Tìm a, b để đường thẳng (d) song song với đường
thẳng (d ') : y = 5x+6 và đi qua điểm A(2;3) 3 x + 2y =11
2. Giải hệ phương trình x + 2y = 5 Bài 3: ( 2 điểm) 1. Giải phương trình 2
x − 4x + 3 = 0 2. Cho phương trình: 2 x − 2(m− )
1 x + 2m− 5 = 0 với m là tham số.Chứng minh rằng
phương trình luôn có hai nghiệm phân biệt x1, x2 với mọi m. Tìm m để các nghiệm đó thỏa mãn hệ thức ( 2
x − 2mx − x + 2m− 3 x 2mx x 2m 3 19. 1 1 2 )( 2 − − + − 2 2 1 )=
Bài 4. (3,0 điểm) Từ một điểm A nằm ngoài đường tròn tâm O bán kính R, kẻ các tiếp tuyến
AB, AC với đường tròn ( B, C là các tiếp điểm). Trê cung nhỏ BC lấy một điểm M bất kỳ khác
B và C. Gọi I,K,P lần lượt là hình chiếu vuông góc của M trên các đường thẳng AB, AC, BC
1) Chứng minh AIMK là tứ giác nội tiếp;
2) Chứng minh MPK = MBC
3) Xác định vị trí điểm M trên cung nhỏ BC để tích MI .MK.MP đạt giá trị nhỏ nhât..
Bài 5. (1,0 điểm) Cho các số thực a, b, c thỏa mãn abc = 1, Chứng minh rằng: ab + bc + ca 1 4 a + 4 b + 4 ab b + 4 c + 4 bc c + 4 a + ca ------Hết------- Lời giải Câu I.
1. Rút gọn biểu thức A với với x 0; x 4. x + 2 5 1 A = − −
x + 3 ( x + 3)( x − 2) x − 2
x − 4 − 5 − ( x + 3) = ( x + 3)( x − 2) x − x −12 = ( x + 3)( x − 2) x − 4 = x − 2 Trang 18
2. Tìm giá trị của cảu A khi x = 6 + 4 2 x = + = ( + )2 6 4 2 2 2 tmđk (2+ 2)−4 2− 2
x = 2 + 2 thay vào A ta đc: A = ( = = − 2 + 2 ) 1 2 − 2 2
Vậy với x = 6 + 4 2 thì A = 1− 2 Bài 2. (2 điểm)
1. Cho đường thẳng (d ) : y = ax+b . Tìm a, b để đường thẳng (d) song song với đường
thẳng (d ') : y = 5x+6 và đi qua điểm A(2;3) a = 5
Vì (d ) / / (d ') nên b 6
Vì (d) đi qua A(2;3) nên ta có: 3 = 5.2+b b = 7 −
Vậy a = 5;b = −7 ta có (d ) : y = 5x − 7 3 x + 2y =11
2. Giải hệ phương trình x + 2y = 5 3 x + 2y =11 x = 3 2x = 6 y =1 Bài 3: ( 2 điểm) 1. Giải phương trình 2
x − 4x + 3 = 0
PT có : a + b + c = 1− 4 + 3 = 0 nên PT có hai nghiệm: x = 1; x = 3 1 2
2. Ta có: = (m− )2 − m+ = m − m+ = (m− )2 2 ' 1 2 5 4 6
2 + 2 0 m nên phương
trình luôn có hai nghiệm phân biệt x1, x2 với mọi m Có : 2 x − 2(m− )
1 x + 2m− 5 = 0 2
x − 2mx + 2m− 3 = 2 − 2x
Vì x1, x2 là các nghiệm của PT (1) nên ta có: 2
x − 2mx + 2m− 3 = 2 − 2x ; 2
x − 2mx + 2m− 3 = 2 − 2x thay vào (*) ta đc: 1 1 1 2 2 2 ( 2
x − 2mx − x + 2m− 3 x 2mx x 2m 3 19 1 1 2 )( 2 − − + − 2 2 1 )=
(2− 2x − x )(2− 2x − x ) =19 1 2 2 1 2(x + x 6 x x x x 15 1 2 )2 − ( + 1 2 ) + = 1 2
x + x = 2 m 1 1 2 ( − ) Theo Vi-et có thay vào ta đc: x x = 2m− 5 1 2 Trang 19 m= 0 (m− )2 8 1 −12(m− ) 1 + 2m− 5 = 15 2
8m − 26m= 0 m = 13 4 m= 0 Vây: m = 13 4
Bài 4. (3,0 điểm) Từ một điểm A nằm ngoài đường tròn tâm O bán kính R, kẻ các tiếp tuyến
AB, AC với đường tròn ( B, C là các tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ
khác B và C. Gọi I,K,P lần lượt là hình chiếu vuông góc của M trên các đường thẳng AB, AC, BC
1. Chứng minh AIMK là tứ giác nội B tiếp; I Có: = = 90o AIM AKM nên tứ giác M P AIMK nội tiếp.
2. Chứng minh MPK = MBC . A O
TT câu a ta cm đc tứ giác KCPM nội tiếp.
Suy ra: MCK = MPK ( hai góc nt cùng K chắn cung MK) (1) C
Mà MCK = PBM ( góc tạo bởi tia tiếp tuyến và dây và góc nt cùng chắn cung MC của (O)) (2)
Từ (1) và (2) suy ra MPK = MBP hay MPK = MBC
1) Xác định vị trí điểm M trên cung nhỏ BC để tích MI .MK.MPđạt giá trị nhỏ nhât.. IM MP
Chứng minh được IMP ∽ PMK nên: = MP MK MI MK = 2
MP MI MK MP = 3 . . . MP
Để MI .MK.MPlớn nhất khi chỉ khi MP lớn nhất, nên M là điểm chính giữa cung nhỏ BC
Bài 5. (1,0 điểm) Cho các số thực a, b, c thỏa mãn abc = 1, Chứng minh rằng: ab + bc + ca 1 4 a + 4 b + 4 ab b + 4 c + 4 bc c + 4 a + ca ab ab 1 Ta có: 4 + 4 ( 2 + 2 a b ab a b ) 4 4 a b ab ab( 2 a + 2 b ) = + + + 2 ab a + 2 b +1 bc 1 ca 1 Tương tự có: ; 4 b + 4 c + 2 bc b + 2 c +1 4 c + 4 a + 2 ca c + 2 a +1 Trang 20