10 Đề Trắc Nghiệm Ôn Tập Chương Khối Đa Diện Hình 12 Có Đáp Án

10 đề trắc nghiệm ôn tập chương Khối Đa Diện Tích 12 được biên soạn dưới dạng file PDF gồm 26 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

98 49 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

26 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 1
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1:Khi hp ch nhtcó 3 cnh xut phát t mnh l dài
,,abc
.
Th tích
V
ca khi hp ch nht.
A.
.V abc
B.
1
.
3
V abc
C.
1
.
6
V abc
D.
4
.
3
V abc
Câu 2: Tìm s cnh ít nht cn có 5 mt.
A.6 cnh. B.7 cnh. C. 8 cnh. D. 9 cnh
Câu 3: Trong mt khn, m đúng ?
A.Hai cnh bt kì có ít nht mm chung. B.Hai mt bt kì có ít nht mm chung.
C.Mnh chung ca ít nht 3 mt. D.Hai mt bt kì có ít nht mt cnh chung.
Câu 4:
A.
B.
C.
D.
Câu 5:Các khu mà mnh cnh chung ca ba mt thì s nh
Đ
và s
cnh
C
ca các khu kin nào?
A.
B.
C.
2.ĐC
D.
.ĐC
Câu 6:Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
,a
5SA a
và vuông góc
vi mt phi
H
m ca
, SB K
là hình chiu vuông góc ca
A
lên
.SD
Tính
th tích
V
ca khi chóp
..S AHK
A.
3
55
.
24
Va
B.
3
55
.
48
Va
C.
3
55
.
36
Va
D.
3
55
.
72
Va
Câu 7: 


.S ABCD

2,a

SA

CD

3.a



V
c

..S ABCD
A.
3
3
.
3
a
V
B.
3
4 3 .Va
C.
3
3.Va
D.
3
43
.
3
a
V
Câu 8: 


.S ABC

ABC

,C
5 , .AB a AC a

3SA a
. 


V
c

..S ABC
A.
3
.Va
B.
3
5
.
2
Va
C.
3
2.Va
D.
3
3.Va
Câu 9:
ABCD
, tam giác
ABC

C
, tam giác
DAB

2AB a
.

ABC
và
DAB
. 
V

.ABCD
A.
3
3.Va
B.
3
3
.
3
a
V
C.
3
2 3.Va
D.
3
3
.
9
a
V
Trang2
Câu 10:  u
ABC A B C
có
AB a
ng thng
'AB
to vi mt
phng
BCC B
mt góc 30
0
. Tính th tích
V
ca kh 
A.
3
3
.
4
a
V
B.
3
.
4
a
V
C.
3
6
.
4
a
V
D.
3
6
.
12
a
V
Câu 11:  tam giác
' ' '
.ABC ABC

ABC
u cnh
,a
hình chiu
cm
'A
trên mt phng
ABC
trùng vm ca cnh
.BC
Bit
'CC
to vi mt
phng
ABC
mt góc 45
0
. Tính th tích
V
ca khn
' ' '
..ABC ABC
A.
3
3
.
8
a
V
B.
3
3
.
8
a
V
C.
3
3
.
6
a
V
D.
3
.
4
a
V
Câu 12: Cho hình chóp tam giác
.S ABC
 
ABC
vuông ti
A
,
AB a
,
3AC a
. Tam
giác
SBC
u và nm trong mt phng vuông góc v tích
V
ca khi

A.
3
3
.
2
a
V
B.
3
3
.
2
a
V
C.
3
.
2
a
V
D.
3
2
.
3
a
V
Câu 13: 
.S ABCD
có
,AB a
3SA a

SD

( ).SAC
A.
30
arccos .
12
B.
30
arccos .
6
C.
5
arccos .
6
D.
6
arccos .
6
Câu 14: 
.S ABCD

,a
3SA a
.
M


.BC

ABCD

SBC

A.
5
arctan .
2
B.
2
arctan .
2
C.
arctan 5.
D.
arctan 10.
Câu 15: Cho t din
ABCD
có
14, 6AD BC
. Gi
,MN
lm ca các cnh
,AC BD
và
8MN
. Gi
là góc ging thng
BC
và
MN
. Tính
sin
.
A.
22
3
B.
3
2
C.
1
2
D.
2
4
Câu 16: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
a
và cnh bên
SA
vuông
góc vi mi
E
m ca cnh
.CD
Bit th tích khi chóp
.S ABCD
bng
3
3
a
.
Tính khong cách
h
t m
A
n mt phng
.SBE
A.
3
.
3
a
h
B.
2
.
3
a
h
C.
.
3
a
h
D.
2
.
3
a
h
Câu 17: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
a
,
SA
vuông góc vi mt
phng
,ABCD
góc ging thng
SC
và mt phng
ABCD
bng 45
0
. Tính khong cách
d
ging thng
, .SB AC
Trang3
A.
.
5
a
d
B.
2
.
5
a
d
C.
3
.
5
a
d
D.
2
.
7
a
d
Câu 18: Cho hình chóp
.S ABC
có
0 0 0
60 , 90 , 120 , .ASB CSB ASC SA SB SC a
Tính
khong cách
d
t m
A
n mt phng
.SBC
A.
2 6.da
B.
2.da
C.
2
.
2
a
d
D.
6
.
3
a
d
Câu 19:
.S ABC

2
3a
và
3
6a
. 

h
.
A.
2a 3.h
B.
3.ha
C.
6 3.ha
D.
23
.
3
a
h
Câu 20: Cho hình chóp tam giác
.S ABC

ABC
u cnh
, 2a SA a
và
.SA ABC
Gi
M
và
N
lt là hình chiu vuông góc ca
A
ng thng
SB
và
.SC
Tính
3
50 3V
a
, vi
V
là th tích khi chóp
..A BCNM
A.9. B. 10. C. 11. D. 12.
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
C
C
A
A
D
D
A
B
C
A
C
B
D
B
D
B
C
C
A
ĐỀ 2
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1:  u
. ' ' 'ABC A B C
có
AB a
ng thng
'AB
to vt góc
60
. Gi
,MN
lm cnh
AC
và
''BC
 n thng
MN
theo
a
.
A.
13
6
a
MN
. B.
13
3
a
MN
. C.
13
2
a
MN
. D.
13
4
a
MN
.
Câu 2: Tính th tích khu có cng
a
và cnh bên to vi m
30
.
A.
3
3
4
a
. B.
2
3
36
a
. C.
3
3
36
a
. D.
3
3
12
a
.
Câu 3: Cho hình h ng
. ' ' ' 'ABCD A B C D
  ABCD là hình thoi cnh
a
và có góc
60BAD 
. Tính khong cách ging thng DC và mt phng
' ' AA B B
.
A.
2a
. B.
3
2
a
. C.
a
. D.
3a
.
Câu 4: Khi lnh bng
a
thì th tích là công thc nào?
Trang4
A.
2
a
. B.
4
a
. C.
3
a
. D.
3
1
3
a
.
Câu 5: Cho khi chóp
.D ABC

ABC
u cnh
a
,
2DA a
và
DA
vuông góc
vi
,MN
lt là hình chiu vuông góc ca
A
ng thng
DB
và
DC
.
Tính th tích khi chóp
.A BCMN
theo
a
.
A.
3
33
50
a
V
. B.
3
33
25
a
V
. C.
3
3
6
a
V
. D.
3
3
25
a
V
.
Câu 6: Cho hình chóp t u
.S ABCD
có cng
a
, tâm O. Gi M và N lt
m ca SA và BC. Bit rng góc gia MN và
ABCD
bng
60
 n MN.
A.
10
2
a
. B.
5
2
a
. C.
2
2
a
. D.
3
2
a
.
Câu 7:     u
.ABC A B C
có c  ng
a
,
AC
hp vi mt phng
ABB A

mt góc
30
. Tính th tích ca kh
.ABC A B C
tính theo
a
.
A.
3
15
.
8
a
B.
3
15
.
12
a
C.
3
6
.
4
a
D.
3
3
.
4
a
Câu 8: Cho hình chóp S.ABCD ABCD là hình vuông tâm O cnh
a
, cnh SA vuông góc vi
mng thng SC và mt phng
ABCD
là
45
, gi G là trng tâm tam giác
SCD. Tính khong cách h ging thng chéo nhau OG và AD.
A.
5
2
a
h
. B.
3
2
a
h
. C.
2
3
a
h
. D.
5
3
a
h
.
Câu 9: i hai mnh?
A.30. B.20. C.16. D.12.
Câu 10: Cho hình chóp
.S ABC
u cnh
a
. Hình chiu ca S trên
ABC
thuc cnh AB sao cho
2HB AH
, bit mt bên
SAC
hp vt góc
60
. Tính th tích
khi chóp
.S ABC
.
A.
3
3
.
36
a
B.
3
3
.
24
a
C.
3
3
.
12
a
D.
3
3
.
8
a
Câu 11:   nào?
A. có tt c các cnh bng nhau.
B. u và các cnh bên bng nhau.
C. u và cnh bên vuông góc v
D. u.
Câu 12: Cho hình chóp
.S ABC

ABC
là tam giác vuông ti
B
. Bit
SAB
u
và nm trong mt phng vuông góc vi mt phng
ABC
. Tính th tích khi chóp
.S ABC
bit
AB a
,
3AC a
.
A.
3
4
a
B.
3
6
4
a
C.
3
2
6
a
D.
3
6
12
a
Trang5
Câu 13: u S.ABC có cng
a
. Góc gia mt bên vi m
bng
60
. Tính khong cách t m A n mt phng
SBC
.
Câu 14: Hình lt phi xng?
A.8 B.9 C.6 D.7
Câu 15: M 
A.S cnh ca mn luôn nh c bng s nh cn y.
B.S cnh ca mn luôn bng s nh cn y.
C.S cnh ca mn luôn nh  nh cn y.
D.S cnh ca mn luôn nh  nh cn y.
Câu 16: Cho hình chóp
.S ABCD
nh
3a
. Tam giác
SBC
vuông ti S và
nm trong mt phng vuông góc vi mng thng
SD
to vi mt phng
SBC
mt góc
60
. Tính góc gia
SBD
và
ABCD
.
A.
90
. B.
60
. C.
30
. D.
45
.
Câu 17: Cho hình chóp S.ABC ABC là tam giác vuông cân ti B,
AB a
. Hai mt phng
SAB
và
SAC
cùng vuông góc vi mng cách t A n mt phng
SBC
là
2
2
a
.
Tính góc
to bng thng SB và AC.
A.
45

. B.
90

.
C.
30

. D.
60

.
Câu 18: Cho hình hp
.'ABCD A B C D
ABCD là hình thoi cnh
3a
,
3BD a
. Hình
chiu vuông góc ca B lên mt phng
' ' ' 'A B C D
m ca
''AC
. Bit rng côsin ca
góc to bi hai mt phng
ABCD
và
''CDD C
bng
21
7
. Tính th tích khi hp
.'ABCD A B C D
.
A.
3
9
4
a
. B.
3
5
4
a
. C.
3
11
4
a
. D.
3
7
4
a
.
Câu 19: Cho khi chóp
.S ABCD
nh
a
,
SA a
và vuông góc vi
M m ca SD. Tính th tích khi t din MACD.
A.
3
1
2
a
. B.
3
12
a
. C.
3
4
a
. D.
3
36
a
.
Câu 20: Cho hình chóp
.S ABCD
có
SA ABCD

ABCD
là hình ch nht. Tính th tích
.S ABCD
, bit
AB a
,
2AD a
,
3SA a
.
A.
3
2a
. B.
3
6a
. C.
3
a
. D.
3
3
a
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
Trang6
B
C
D
ĐỀ 3
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1: Mnh ca bát dinh chung ca bao nhiêu cnh ?
A.3. B.5. C.8. D.4.
Câu 2:i xng?
A. T diu.B. Bát diu. C. Hình l D.  lu.
Câu 3: Khu có 12 mt thì có bao nhiêu cnh?
A.24. B.12. C.30. D.60.
Câu 4: Gi
1
;VV
lt là th tích ca khi l
. ' ' ' 'ABCD A B C D
và ca khi t din
'.A ABD
H th
A.
1
6.VV
B.
1
4.VV
C.
1
3.VV
D.
1
2.VV
Câu 5: S cnh ca mt hình hp ch nht bng ?
A.
16
cnh. B.
6
cnh. C.
12
cnh. D.
8
cnh.
Câu 6:     ng
. ' ' ' 'ABCD A B C D
     nht vi
3, 2AB a BC a
và
' 4 .A C a
Tính th tích
V
ca kh
. ' ' ' 'ABCD A B C D
.
A.
3
2 69
.
3
Va
B.
3
2 3 .Va
C.
3
2 69 .Va
D.
3
6 3 .Va
Câu 7: Cho hình chóp
. , , S ABC M N
lm
SB
và
.SC
Tính th tích
V
ca khi
chóp
..S AMN
Bit th tích ca khi chóp
.S ABC
bng
3
.a
A.
3
.
2
a
V
B.
3
.
8
a
V
C.
3
.
4
a
V
D.
3
3
.
2
a
V
Câu 8: Tng din tích các mt ca khi lng
2
216 cm
. Tính th tích
V
ca khi lp

A.
3
36 .V cm
B.
3
216 .V cm
C.
3
72 .V cm
D.
3
144 .V cm
Câu 9:Cho t din
ABCD
có th tích bng 12 và
G
là trng tâm ca tam giác
.BCD
Tính th tích
V
ca khi chóp
.AGBC
A.
3.V
B.
4.V
C.
6.V
D.
5.V
Trang7
Câu 10:Cho khn
S ABCDA B C D
có cnh
   AA BB CC DD
bng 4 và cùng vuông
góc vi
,ABCD
t giác
ABCD
là hình ch nht,
12, 8.AB BC
Khong cách t
S
ti
ABCD
bng
8.
Th tích
V
ca khn
S ABCD A B C D
A.
640.V
B.
1152.V
C.
768.V
D.
740.V
Câu 11 :Cho hình chóp
.S ABC

ABC
là tam giác vuông cân ti
,A
2BC a
,
SA
vuông
góc vi mt ph
ABC
. Tính th tích
V
ca khi chóp
.S ABC
bit
SC
to vi mt phng
SAB
mt góc
30 .
o
A.
3
6
.
9
a
V
B.
3
6
.
3
a
V
C.
3
26
.
3
a
V
D.
3
6
.
6
a
V
Câu 12:  tam giác
. ' ' 'ABC A B C

ABC
là tam giác vuông cân ti
,A
cnh
2 2.AC
Bit
'AC
to vi mt phng
ABC
mt góc 60
0
và
' 4.AC
Tính th tích
V
ca
khn
. ' '.ABC B C
A.
8
.
3
V
B.
8 3.V
C.
83
.
3
V
D.
16 3
.
3
V
Câu 13:Cho hình chóp
.S ABCD

ABCD
là hình thoi cnh bng
2 3,a
góc
BAD
bng
120
0
. Hai mt phng
SAB
và
SAD
cùng vuông góc va mt phng
SBC
và
ABCD
bng 45
0
. Tính khong cách
h
t m
A
n mt phng
.SBC
A.
2 2.ha
B.
22
.
3
a
h
C.
32
.
2
a
h
D.
3.ha
Câu 14: Cho hình chóp
.S ABCD

ABCD
là hình thoi cnh
a
,
( ).SA ABCD
Gi
M
là
m
.BC
Bit
120 , 45 .BAD SMA
Khong cách
d
t m
D
n mt phng
.SBC
A.
6
.
6
a
d
B.
6
.
3
a
d
C.
6
.
5
a
d
D.
6
.
4
a
d
Câu 15: Cho hình chóp
.S ABCD
 nht. Hình chiu ca
S
lên
ABCD
là trung
m
H
ca
,AB
tam giác
SAB
vuông cân ti
.S
Bit
, 3 .SH a CH a
Tính khong cách
d
ging thng
SD
và
.CH
A.
4 82
.
41
a
d
B.
82
.
22
a
d
C.
4 82
.
21
a
d
D.
66
.
11
a
d
Câu 16: 
.S ABC

.a

G

.ABC


S
A
B
A'
B'
C
C'
D
D'
Trang8
A.
5
cos .
5
B.
3
cos .
3
C.
5
cos .
10
D.
3
cos .
2
Câu 17: Cho hình chóp
.S ABC

ABC
là tam giác vuông cân vi
,BA BC a SA a
và
vuông góc vi mt ph
gia hai mt phng
SAC
và
.SBC
A.
2
cos .
2
B.
2
cos .
3
C.
1
cos .
2
D.
3
cos .
2
Câu 18: Cho hình chóp tam giác
.S ABC
u cnh
2,a
có
SA
vuông góc vi
,ABC
tam giác
SBC
cân ti
.S
 th tích ca khi chóp
.S ABC
là
3
3
3
a
thì góc
gia hai
mt phng
SBC
và
.ABC
A.
0
60 .
B.
0
30 .
C.
0
45 .
D.
0
90 .
Câu 19:  t giác
ABCD A B C D

ABCD
là hình vuông cnh
a
và th
tích bng
3
3.a
Tính chiu cao
h
c 
A.
.ha
B.
9.ha
C.
3.ha
D.
.
3
a
h
Câu 20:Mt khi chóp tam giác có ba góc phng vuông tnh, có th tích
V
và hai cnh bên
bng
,ab
. Tính cnh bên th ba
x
ca kh
A.
3
.
V
x
ab
B.
4
.
V
x
ab
C.
5
.
V
x
ab
D.
6
.
V
x
ab
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D
A
C
A
D
D
C
B
B
A
B
D
C
D
D
B
A
B
C
D
ĐỀ 4
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1:n trong hình v bên có bao nhiêu mt ?
A. 8. B. 11.
C. 12. D. 10.
Câu 2: Ch có 5 loi kh :
A.
3 ;3 , 4 ;3 , 3 ;4 , 5 ;3 , 5 ;6 .
B.
3 ;3 , 4 ;3 , 3 ;4 , 5 ;3 , 3 ;6 .
C.
3 ;3 , 4 ;5 , 3 ;4 , 5 ;3 , 3 ;5 .
D.
3 ;3 , 4 ;3 , 3 ;4 , 5 ;3 , 3 ;5 .
Câu 3: Cho mn . Tìm khnh sai trong các khnh sau:
A.Mi cnh là cnh chung ca ít nht ba mt
B.Mnh chung ca ít nht ba mt
Trang9
C.Mi mt có ít nht ba cnh
D.Mnh chung ca ít nht ba cnh
Câu 4: 

sai?
A.





.
B.









.
C.
 










 .
D.

c gii h









.
Câu 5: Khu loi {4; 3} là:
A.Khu 4 cnh, 3 mt.
B.Khn có 3 cnh và 4 mt.
C.Khu có 6 mt, 12 cnh.
D.Khn có 12 cng chéo.
Câu 6: Cho hình chóp tam giác
.S ABC

ABC
là tam giác vuông cân ti
B
vi
AC a
.
Bit cnh bên
SA
vuông góc vi mt ph
SB
hp vi mt góc
0
60 .
Tính th
tích
V
ca khi chóp
..S ABC
A.
3
6
.
24
a
V
B.
3
6
.
8
a
V
C.
3
3
.
3
a
V
D.
3
3.Va
Câu 7:Cho t din
ABCD
có th tích bng
V
và
G
là trng tâm ca tam giác
,BCD
M
là trung
m
.CD
Tính th tích ca khi chóp
..AGMC
A.
.
18
V
B.
.
9
V
C.
.
6
V
D.
.
3
V
Câu 8: Cho hình chóp
.S ABC

ABC
u cnh
.A
Bit
()SA ABC
và
3.SA a
Tính th tích
V
ca khi chóp
..S ABC
A.
3
.
4
a
V
B.
3
.
2
a
V
C.
3
3
.
4
a
V
D.
3
3
.
3
a
V
Câu 9: 
ABC A B C
u cnh
.a
Hình chiu vuông góc ca
m
A
lên mt phng
ABC
trùng vi trng tâm tam giác
.ABC
Bit khong cách gia hai
ng thng
AA
và
BC
bng
3
.
4
a
Tính th tích
V
ca kh
ABC A B C
A.
3
3
.
3
a
V
B.
3
3
.
24
a
V
C.
3
3
.
12
a
V
D.
3
3
.
6
a
V
Câu 10: Cho hình chóp
.S ABC

ABC
cân ti
A
, và
5, 6AB AC BC
,
các mt u hp v
0
45
và hình chiu ca
S
trên mt phng
()ABC
nm trong
ABC
 tích khi chóp
..S ABC
A.
4.V
B.
6.V
C.
8.V
D.
12.V
Câu 11:  ng
. ' ' 'ABC A B C
i
, 2,A BC a
' 3 .A B a
Tính th tích
V
ca kh
. ' ' '.ABC A B C
A.
3
2
.
3
a
V
B.
3
2.Va
C.
3
2
.
4
a
V
D.
3
2
.
2
a
V
Trang10
Câu 12: Cho hình chóp
.S ABCD
 
ABCD
là hình thoi cnh
a
, góc
0
60BAD
,
SA ABCD
,
SA a
. Gi
'C
m ca
,SC
mt phng
P

'AC
và song song
,BD
ct các cnh
,SB SD
lt ti
'B
và
D
Th tích khi chóp
' ' '.SAB C D
A.
3
3
.
6
a
V
B.
3
3
.
18
a
V
C.
3
3
3
a
V
. D.
3
3
.
12
a
V
Câu 13: Cho hình chóp
.S ABCD

SAB
u và nm trong mt phng
vuông góc vt
2 , 3 .AC a BD a
Tính khong cách
d
ging thng
AD
và
.SC
A.
3 208
.
2 217
a
d
B.
208
.
3 217
a
d
C.
208
.
217
da
D.
208
.
2 217
a
d
Câu 14: u
.S ABC
có th tích bng
3
3
24
a
, có cng
.a
ng
cách
d
t m
A
n mt phng
.SBC
A.
3
.
2
a
d
B.
2
.
2
a
d
C.
3.da
D.
3
.
4
a
d
Câu 15: 
.ABC A B C

ABC
u
,AB a
Hình chiu vuông góc
ca
A
trên
ABC
nm trùng vm
.BC
Tính theo
a
khong cách
d
t m
A
n
mt phng
.A BC
A.
2
.
3
a
d
B.
25
.
5
a
d
C.
3
.
2
a
d
D.
5.da
Câu 16 : Cho hình chóp
.S ABCD
nh
,a
( ), .SA ABCD SA x
Tìm
x
theo
a
 góc gia
()SBA
và
()SCD
bng
0
60 .
A.
2
2
a
B.
3
3
a
C.
2.a
D.
3.a
Câu 17 : Cho hình chóp
.S ABCD
nh
,a SA a
và
( ).SA ABCD
Tính
tan ,
vi
là góc gia
SC
và
( ).SAB
A.
tan 2.
B.
2
tan
2

C.
tan 3.
D.
tan 1.
Câu 18: Cho hình l
ABCDA B C D
. Góc
ging thng
BA
và
.CD
A.
90 .

B.
60 .

C.
30 .

D.
45 .

Câu 19: Khu
.S ABCD
có tt c các cu bng
.a
 ng cao
h
ca
kh
A.
3.ha
B.
2
.
2
a
h
C.
3
.
2
a
h
D.
.ha
Câu 20: 
. ' ' 'ABC A B C

ABC
là tam giác vuông cân có
.CA CB a
Gi
Trang11
G
là trng tâm tam giác
.ABC
Bit th tích ca khi chóp
. ' ' 'G A B C
bng
3
.
3
a
Tính chiu cao
h
c 
A.
.
2
a
h
B.
.ha
C.
3
.
2
a
h
D.
2.ha
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
D
D
A
C
A
A
C
A
C
D
B
B
A
D
C
B
B
D
B
D
ĐỀ 5
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1: ?
A. 3 . B. ) ).
C. ) ). D. ) ).
Câu 2:
Cho ba m: (I): Khu loi {4; 3} là khi l
(II): Khu loi {3; 5} là khu;
(III): Khu loi {3; 4} là khi mu.
Số mệnh đề đúng trong 3 mệnh đề trên là:
A. 3. B. 0. C. 2. D. 1.
Câu 3: Trong các m sau, m  ?
A. Khi hai mu có 36 cnh. B. Khi lnh.
C. Khi bát dinh. D. Khnh.
Câu 4: 

.S ABCD

.O

SO





?
A.
, SI


..S ABCD
B.
O


..S ABCD
C.
, SO


..S ABCD
D.
I


..S ABCD
Câu 5: Cho khi chóp
.S ABCD

ABCD
là hình bình hành. Xét các m:
(I) Khi chóp
.S ABCD
có th phân chia thành hai khi chóp
.S ABC
và
.S ADC
(II) Khi chóp
.S ABCD
có có th phân chia thành hai khi chóp
.S ABC
và
.S ABD
M 
Trang12
A. C u sai. B. 
C. C  D. 
Câu 6:Hình chóp
.S ABCD

ABCD
là hình vuông cnh
, a SA
vuông góc vi mt phng

.SA a
 tích
V
ca khi t din
..S BCD
A.
3
.
3
a
V
B.
3
.
8
a
V
C.
3
.
4
a
V
D.
3
.
6
a
V
Câu 7: Khi chóp
.S ABCD

ABCD
là hình vuông cnh
.a
Bit
SA
vuông góc vi mt

2.SB a
Gi
,MN
lm
,.SB BC
Tính th tích
V
ca khi chóp
..ASCNM
A.
3
3
.
12
a
V
B.
3
3
.
16
a
V
C.
3
3
.
8
a
V
D.
3
3
.
24
a
V
Câu 8: Cho kh ng
. ' ' 'D'ABCD A B C
có th tích là
3
36 .m
Gi
M
m tùy ý trên
mt phng
.ABCD
Tính th tích
V
ca khi chóp
. ' ' ' 'M A B C D
.
A.
3
12 .Vm
B.
3
24 .Vm
C.
3
36 .Vm
D.
3
6.Vm
Câu 9: Khi hng
ABCD A B C D
nh
,a
0
60BAD
,
3.AA a
Th
tích
V
ca khi hng.
A.
3
3
.
2
a
V
B.
3
3
.
8
a
V
C.
3
3
.
4
a
V
D.
3
3
.
2
a
V
Câu 10: Cho hình chóp t giác
.S ABCD

ABCD
là hình vuông cnh a, cnh bên
SA
vuông
góc vi mt pha
SC
và (
ABCD
) bng 45
0
. Th tích
V
ca khi chóp
..S ABCD
A.
3
2
.
6
a
V
B.
3
2
.
4
a
V
C.
3
2.Va
D.
3
2
.
3
a
V
Câu 11:  ng tam giác
' ' 'ABC A B C

ABC
là tam giác vuông cân ti
B
vi
,BA BC a
bit
'AB
hp vi mt phng
ABC
mt góc
0
60 .
Th tích
V
ca khi  
cho.
A.
3
3
.
2
a
V
B.
3
3
.
4
a
V
C.
3
3
.
6
a
V
D.
3
3.Va
Câu 12: Cho hình chóp tam giác
.S ABC

ABC
là tam giác vuông cân ti
B
vi
AC a
. Bit cnh bên
SA
vuông góc vi mt ph
SB
hp vi mt góc
0
60 .
Tính th
tích
V
ca khi chóp
..S ABC
A.
3
6
.
24
a
V
B.
3
6
.
8
a
V
C.
3
3
.
3
a
V
D.
3
3.Va
Câu 13 :Cho hình chóp
.S ABCD

ABCD
là hình vuông tâm
O
cnh
a
,
SO
vuông góc vi
mt phng
ABCD
và
SO a
. Khong cách
d
gia
SC
và
.AB
A.
5
.
5
a
d
B.
25
.
5
a
d
C.
3
.
15
a
d
D.
23
.
15
a
d
Trang13
Câu 14: Cho hình chóp
.S ABC

ABC
u cnh
,a
cnh bên
SA
vuông góc
vi mt ph
6
.
2
SA
a
ng cách
d
t m
A
n mt phng
.SBC
A.
2
.
3
a
d
B.
2
.
2
a
d
C.
.da
D.
.
2
a
d
Câu 15: 



.S ABC

a

3
.
3
a
SO


d

m
O

.SAB
A.
6
.
3
a
d
B.
15
.
15
a
d
C.
2.da
D.
15.da
Câu 16 : Cho hình chóp
.S ABCD
i
,AB
và
( ).SA ABCD
Bit
, 2 .SA AB BC a AD a
Tính
tan ,
vi
là góc gia
()SCD
và
( ).ABCD
A.
tan 2.
B.
1
tan
2

C.
tan 2.
D.
2
tan
2

Câu 17 : Cho hình chóp
.S ABCD
nh
,a SA a
và
( ).SA ABCD
Tính
tan ,
vi
là góc gia
SC
và
( ).SAB
A.
tan 2.
B.
2
tan
2

C.
tan 3.
D.
tan 1.
Câu 18: Cho hình chóp
.S ABCD
có tt c các cu bng
.a
Gi
,IJ
lm
ca
AB
và
.SB
S a góc ging thng
IJ
và
SB
bng:
A.
90 .
o
B.
60 .
o
C.
30 .
o
D.
45 .
o
Câu 19: Cho bit th tích ca khi chóp
. S ABCD
bng
3
8
3
a
, din tích hình vuông
ABCD
bng
2
2.a
Chiu cao
h
c
A.
2.ha
B.
8.ha
C.
2
.
3
a
h
D.
8
.
3
a
h
Câu 20: K
V

S
thì 
x
nó
A.
.
V
x
S
B.
3
.
V
x
S
C.
.
2
V
x
S
D.
.
V
x
S
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
C
B
D
B
D
C
A
A
D
A
A
B
B
B
D
B
B
A
D
ĐỀ 6
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Trang14
Câu 1: Cho hình chóp
.S ABCD
nh a,
17
D
2
a
S
hình chiu vuông góc
H ca S lên mm cn
AB
.Gm ca
AD
. Tính khong
cách ging SD và HK theo a
A.
3a
5
B.
3
7
a
C.
21
5
a
D.
3
5
a
Câu 2:     ng
.'ABCD A B C D
 
ABCD
là hình vuông. Bit cnh bên
bng chéo
' 5 .BD a
Tính th tích kh này là:
A.
3
8a
B.
3
a
C.
3
27a
D.
3
18a
Câu 3: Cho t din
ABCD
có
2.AB CD a
Gi
,MN
lm ca
BC
và
.AD
Bit
2.MN a
Góc
ging thng
AB
và
CD
bng
A.
0
60
B.

0
90
C.
0
30
D.

0
45
Câu 4: Cho hình chóp
.S ABCD

ABCD
là hình ch nht, cnh
, 2 ,AB a AD a
cnh bên
SA
vuông góc vi mt ph
.ABCD
Khong cách
h
ging thng
SA và BD
bng
A.
5
5
h a
B.
2h a
C.
ha
D.
25
5
ha
Câu 5: Cho kh ng
.ABC ABC
u cnh a, góc ging
60
0
. Chiu cao ca kh ng
.ABC A B C
theo a bng:
A.
3a
B.
2a
C.a D.
5a
Câu 6: Cho hình chóp

ABCD
là hình vuông cnh
,a
mt phng
SAB
vuông
góc vi mt ph 
()ABCD
, tam giác
SAB
u. Gi góc gia hai mt phng
SCD
và
SAB
là

bng
A.
3
2
B.
3
3
2
C.
3
2
a
D.
2
3
a
Câu 7: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh a, bit
()SA ABCD
và SA =
3a
. Góc ging thng SB và mt phng
(S )AD
bng :
A.60
0
B.45
0
C.30
0
D.90
0
Câu 8: Khi l cnh bng:
A.8 B.12 C.6 D.10
Câu 9:  dài cnh ca hình l
2 cm
thì th tích ca khi la

3
.cm
Cnh ca hình l
A.5 B.3 C.4 D.2
Trang15
Câu 10:    ng
.ABC ABC
      i A, AC=a,
·
0
60ACB
.
a mo vi mt pht góc
0
30
. Tính th tích
ca khtr theo a
A.
3
6a
B.
3
26
3
a
C.
3
46
3
a
D.
3
6
3
a
Câu 11: 
.ABC A B C
i A, bit AB=2a .
Hình chiu vuông góc cng
()ABC
m ca BC. Co vi mt phng

()ABC
mt góc 30
o
.Tính th tích kh này
A.
3
3
3
a
B.
3
3
16
a
C.
3
26
3
a
D.
3
6
16
a
Câu 12: Chn khnh sai. Trong mt khn:
A.Mi mt có ít nht ba cnh
B.Mnh chung ca ít nht 3 mt
C.Mi cnh ca mt khnh chung ct
D.Hai mt bt k luôn có ít nht mm chung
Câu 13: S nh cu là
A.20 B.16 C.12 D.3
Câu 14: Chohìnhchóp
.SABCD

ABCD
là hình ch nht, có AB =
2a
, BC = 2a. SA vuông
góc v   a mt bên
(S )BC
và m  ng 60
0
. Tính theo a th tích khi chóp
.SABCD
.
A.
3
43
3
a
B.
3
23
3
a
C.
3
43
9
a
D.
3
3
3
a
Câu 15:  dài tt c các cnh ca mt khi hp ch nht lên gp ba ln thì th tích khi
hng s
A.n B.n C.n D.n
Câu 16: Cho khi chóp t u
.S ABCD
có cng
a
.Góc hp bi cnh bên và mt
ng
0
60
.Tính chiu cao SH:
A.
26
3
a
B.
6
3
a
C.
6
4
a
D.
6
2
a
Câu 17:Cho hình chóp
.S ABCD
có
ABCD
là hình ch nht,
SAB unm trong mt phng
vuông góc vi (ABCD) bit
23SC a
, SC to vi hp vi (
ABCD
) mt góc 30
o
.Tính th tích
hình chóp
..S ABCD
A.
3
26
3
a
B.
3
3
a
C.
3
46
3
a
D.
3
a
Câu 18: Cho hình chóp
.S ABC
i B vi AC = a bit SA
vuông góc vp vt góc 60
o
. Tính th tích hình chóp
A.
3
6
8
a
B.
3
6
48
a
C.
3
6
24
a
D.
3
3
24
a
Trang16
Câu 19: Cho hình chóp
.S ABC
i A, mt bên SBC là tam giác
u cnh a và mt phng (SBC) vuông góc vi mt phng cách t n mt
phng
(S )AB
tính theo a là:
A.
21
3
a
h
B.
21
21
a
h
C.
21
7
a
h
D.
7
21
a
V
Câu 20: u
.S ABC
có cng 3a. Góc gia mt bên và m
bng 45
0
. Tính theo a th tích khi chóp
.SABC
.
A.
3
27
8
a
B.
3
9
8
a
C.
3
3
8
a
D.
3
9
4
a
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 7
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1:  ng i A, góc
·
0
30BCA
, AB =a.
Khong cách t n mt ph
A.
3
2
a
B.
3
2
a
C.
a3
D.
3
6
a
Câu 2: Cho khi chóp SABCD  
ABCD
là hình thoi cnh a và góc nhn A bng 60
o
và
()SA ABCD
.Bit rng khong cách t A n cnh SC bằng.Tính th tích khi chóp
.SABCD
A.
3
2
12
a
B.
3
3a
C.
3
3
6
a
D.
3
2
4
a
Câu 3: Cho bit th tích ca khi chóp
bng
3
8
,
3
a
din tích hình vuông
ABCD
bng
2
2a
.Chiu cao ca hình chóp bng
A.
2a
B.
8a
C.
8
3
a
D.
2
3
a
Trang17
Câu 4: Cho hình chóp
.S ABC

ABC
là tam giác vuông ti B,
,SA ABC
góc gia mt
bên
SBC
và mt ph
()ABC
bng
0
60
,
3BC a
,
2AC a
, gi G là trng tâm tam
giác SAB. Khong cách t m G n mt phng (SBC) bng
A.
3
3
a
B.
3
6
a
C.
2
4
a
D.
6
4
a
h
Câu 5: Cho hình chóp

ABCD
là hình ch nht,
2,AB a AD a
, mt phng
SAD
vuông góc vi mt ph
()ABCD
, tam giác
SAD
u. Gi góc gia hai mt phng
SAD
và
SBC
là

bng
A.
23
3
B.
3
2
C.
3
2
a
D.
43
3
Câu 6: Cho hình chóp
.SABCD
 
ABCD
là hình vuông cnh a, bit
()SA ABCD
và
3SA a
. Góc ging thng
SB
và
CD
bng :
A.
0
60
B.
0
45
C.
0
30
D.
0
90
Câu 7: Cho khi chóp
.SABC
trên cnh SC lm N sao cho
2
SN
NC
. 
1
V
,
2
V



.
.ABC. T s
1
2
V
V
là:
A.
2
3
B.
3
4
C.
1
2
D.
5
7
Câu 8: Ch có 5 loi kh :
A.{3; 3}, {4; 3}, {3; 4}, {5; 3}, {3; 5} B.{3; 3}, {4; 3}, {3; 4}, {5; 3},
5
C.{3; 3}, {4; 5}, {3; 4}, {5; 3}, {3; 5} D.{3; 3}, {4; 3}, {3; 4}, {5; 3}, {3; 6}
Câu 9: S nh ca mt hình bát diu là:
A.10 B.6 C.8 D.12
Câu 10:
Cho hình hng
. ' ' ' 'ABCD A B C D

ABCD
là hình thoi cnh
a
, góc
·
0
60BAD
,
'BD AC
 tích ca khi h
A.
3
2
2
a
B.
3
5
2
a
C.
3
3
8
a
D.
3
6
2
a
Câu 11: u S.ABC có cng
2a
. Góc gia cnh bên và m
bng 30
0
. Tính theo a th tích khi chóp S.ABC.
A.
3
6
36
a
B.
3
2
6
a
C.
3
6
6
a
D.
3
6
18
a
Câu 12: Cho khi chóp t nh a và có chiu cao h, th tích khi chóp
bng
A.
2
ah
B.
2
1
3
ah
C.
ah
D.
1
3
ah
Trang18
Câu 13: Mnh chung ít nht :
A.Hai mt B.Bn mt C.Ba mt D.t
Câu 14: Cho hình chóp t giác
.S ABCD

ABCD
là hình ch nht
,3AB a AD a
,
()SA ABCD
và góc ging thng
SC
và mt ph
()ABCD
bng
60
o
. Th tích
V
ca
khi chóp
.S ABCD
bng
A.
3
V a
B.
3
3V a
C.
3
2V a
D.
3
2
3
V
a
Câu 15:  dài cnh ca hình l
2 cm
thì th tích ca khi la

3
98 .cm
Cnh ca hình l
A.5 B.3 C.4 D.2
Câu 16: Cho hình chóp
.S ABC

ABC
vuông ti
,B
·
0
30ACB
,
,AB a
22,aSC
SA
vuông góc vi mt ph
.ABC
Góc
ging thng
SC
vi mt ph
ABC
bng
A.
0
90
B.

0
45
C.
0
30
D.

0
60
.
Câu 17:  tam giác
. ' ' 'ABC A B C

ABC
u cnh
.a
Hình chiu
vuông góc cm
'A
xung mt ph
ABC
trùng vi tâm
O
ng tròn ngoi tip ca
tam giác
,ABC
bit
'AA
hp vi mt ph
ABC
mt góc
0
60 .
Th tích
V
ca kh
tr
. ' ' 'ABC A B C
bng
A.
3
3
4
a
V
B.
3
5
4
a
V
C.
3
6
4
a
V
D.
3
2
4
a
V
Câu 18: Cho ng
.ABC A B C
u cnh
2
3
a
. Góc gia cnh
CB
và m
0
. Tính theo a th tích kh
.ABC A B C
.
A.
3
2
27
a
B.
3
2
3
a
C.
3
2
9
a
D.
3
2
54
a
Câu 19: Cho hình chóp
.S ABCD

ABCD
là hình vuông tâm
,O
cnh
,a
cnh bên
SA
vuông
góc vi mt ph
()ABCD
và
.SA a
Khong cách
h
ging thng
AC
và
SB
bng
A.
3
2
h
a
B.
23ha
C.
3
3
h
a
D.
3 ha
Câu 20: Cho hình chóp
.S ABC
i B, AC=2a ,
·
0
60ACB
, Hình
chiu vuông góc H cnh S trên mt phm ca AC và
2SH a
. Th tích
ca khi chóp
.SABC
theo a là :
A.
3
3
3
a
B.
3
6
3
a
C.
3
6
6
a
D.
3
6
12
a
----------- HT ----------
Trang19
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 8
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1: Cho hình chóp
.S ABC
u cnh
2a
và th tích bng
3
.a
Tính chiu cao h
ca hình 
A.
3
.
2
a
h
B.
3.ha
C.
3
.
3
a
h
D.
3
.
6
a
h
Câu 2: i xng ?
A.Hình t diu. B. u.
C.Hình bát din u. D.Hình l
Câu 3: Tìm s cnh ci hai mu.
A.20. B.12. C.30. D.16.
Câu 4: Cho t din
ABCD
có th tích bng 12 và G là trng tâm ca tam giác
.BCD
Tính th tích V
ca khi chóp
..AGBC
A.
6.V
B.
4.V
C.
5.V
D.
3.V
Câu 5: Cho khi chóp
.SABCD
 nht,
, 3,AB a AD a SA
vuông góc v
mt phng
()SBC
to vt góc
0
60 .
Tính th tích V ca kh
A.
3
3.Va
B.
3
3
.
3
a
V
C.
3
.
3
a
V
D.
3
.Va
Câu 6: Cho hình chóp
.SABCD
nh
,a SA
vuông góc vi mSD to
vi mt phng
()SAB
mt góc bng
0
30
. Tính th tích V ca khi chóp
..SABCD
A.
3
6
.
3
a
V
B.
3
6
.
18
a
V
C.
D.
3
3.Va
Câu 7: Mt phng
()AB C

chia kh
.ABC ABC
thành các khn nào ?
A.Mt khi chóp tam giác và mt khi chóp t giác.
B.Hai khi chóp tam giác.
C.Mt khi chóp tam giác và mt kh
D.Hai khi chóp t giác.
Câu 8:  u có bao nhiêu mt phi xng ?
A.4 mt phng. B.1 mt phng. C.3 mt phng. D.2 mt phng.
Câu 9:    u S.ABCD     nh a và bit th tích khi chóp là
3
6
6
Va
. Tìm
là góc to bi cnh bên và m
A.
0
30 .
B.
0
60 .
C.
0
45 .
D.
0
90 .
Trang20
Câu 10: Hình hp ch nht khác nhau có bao nhiêu mt phi xng ?
A.4 mt phng. B.6 mt phng. C.3 mt phng. D.9 mt phng.
Câu 11: Cho hình chóp
.,S ABCD

ABCD
là hình vuông cnh a và có tâm là O.
SA
vuông góc
vi mt ph
SB
to vt góc
0
45 .
Khong cách h t O n
( ).SBC
A.
2
.
4
a
h
B.
2
.
2
a
h
C.
2
.
3
a
h
D.
2
.
8
a
h
Câu 12: Cho khi chóp
.SABC
có
SA
vuông góc v
4, 6, 10SA AB BC
và
8CA
. Tính
th tích V ca kh
A.
192.V
B.
40.V
C.
24.V
D.
32.V
Câu 13:     ng
.ABC ABC
 
ABC
là tam giác cân vi
0
, 120AB AC a BAC
, mt phng
()ABC

to vt góc
0
60 .
Tính th tích V ca kh
tr 
A.
3
9
.
8
a
V
B.
3
3
.
4
a
V
C.
3
.
8
a
V
D.
3
3
.
8
a
V
Câu 14: u S.ABCD nh a và cnh bên to vt góc
60
o
. Tính th tích V ca kh
A.
3
6
.
3
Va
B.
3
6
.
4
Va
C.
3
6
.
6
Va
D.
3
6
.
2
Va
Câu 15: Cho hình chóp S.ABCD nh a, SA vuông góc vSC t
mt góc bng . Tính khong cách h t m D n mt phng
SBC
tính theo
.a
A.
3
.
3
a
h
B.
6
.
6
a
h
C.
3
.
6
a
h
D.
6
.
3
a
h
Câu 16: Cho hình chóp
.S ABC
có mt bên
SBC
u cnh
a
, cnh bên SA vuông góc
vi mt ph
0
120BAC
 n thng
.AB
A.
3
.
3
a
AB
B.
.
2
a
AB
C.
D.
3
.
2
a
AB
Câu 17: Cho hình t diu cnh bng 2. Tìm chiu cao h ca khi t di
A.
2 3.h
B.
26
.
3
h
C.
2 6.h
D.
6.h
Câu 18: Tính th tích V ca khi l
/ / / /
.ABCD A B C D
, bit
/
3.AC a
A.
3
36
.
4
Va
B.
3
1
.
3
Va
C.
3
.Va
D.
3
3 3 .Va
Câu 19: Cho hình chóp
.S ABC

ABC
u cnh
.a
Bit SA vuông góc vi mt
ph tích ca khi chóp
.S ABC
là
3
3
24
a
V
. Tìm
là góc hp gia hai mt phng
(ABC) và (SBC).
A.
0
45 .
B.
0
30 .
C.
0
90 .
D.
0
60 .
0
45
Trang21
Câu 20: Cho hình chóp
SABCD.
ABCD là hình vuông cnh a, cnh bên SA vuông góc vi
mt pht th tích ca khi chóp
SABCD.
theo a là
3
3
3
Va
. Góc
ging thng
SD và mt phng (SAB ?
A.
0
90 .
B.
0
60 .
C.
0
45 .
D.
0
30 .
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 9
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1: Cho hình chóp u S.ABCD nh
a
và cnh bên bng
2.a
Gi
là góc
hp bi cnh bên và mt ph
.
A.
0
60 .
B.
0
135 .
C.
0
30 .
D.
0
90 .
Câu 2: Cho khi chóp
.SABC
có
SA
vuông góc v
4, 6, 10SA AB BC
và
8CA
. Tính th
tích V ca kh
A.
40.V
B.
32.V
C.
24.V
D.
192.V
Câu 3: Cho t din
ABCD
có th tích bng 18 và G là trng tâm ca tam giác
.BCD
Tính th tích V
ca khi chóp
..AGBC
A.
5.V
B.
6.V
C.
3.V
D.
4.V
Câu 4:  ABC là tam giác vuông cân ti B,
2AC a
. Hình
chiu vuông góc ca
/
A
trên mt phng (ABCm ca cnh ACng thng
/
AB
to
vi mt phng (ABC) mt góc
0
45
. Tính th tích V ca kh 
A.
3
1
.
2
Va
B.
3
.Va
C.
3
2 2 .Va
D.
3
2.Va
Câu 5: Hình lt phi xng ?
A.7 mt phng. B.3 mt phng. C.9 mt phng. D.6 mt phng.
Câu 6: M 
A.Lp ghép hai khi hp s c mt khn li.
B.Khi t din là khn li.
C.Khi hp là kha din li.
D.Kh tam giác là khn li.
Câu 7: Cho hình chóp
.SABCD
nh
3
,
SA
vuông góc vi m
5.SA
Tính th tích V ca khi chóp
..SABCD
A.
5.V
B.
5
.
3
V
C.
15.V
D.
45.V
. ' ' 'ABC A B C
Trang22
Câu 8: Mt phng
()ABC
chia kh
.ABC ABC
thành các khn nào ?
A.Mt khi chóp tam giác và mt khi chóp t giác.
B.Hai khi chóp tam giác.
C.Mt khi chóp tam giác và mt kh
D.Hai khi chóp t giác.
Câu 9: i xng ?
A.Hình bát diu. B.Hình l
C. u. D.Hình t diu.
Câu 10: Cho hình chóp
SABCD.
ABCD là hình vuông cnh a, cnh bên SA vuông góc vi
mt ph
6
.
2
a
SA
Gi
là góc hp bi hai mt phng
()SBC
và
( ).ABCD
Tìm
.
A.
0
90 .
B.
0
60 .
C.
0
30 .
D.
0
45 .
Câu 11: 
. ' ' 'ABC A B C
 dài c u bng 2a  ABC là tam giác
vuông ti A,
AB a AC a,3
và hình chiu vuông góc cnh
A'
trên mt phng
ABC
là trung
m ca cnh BC. Tính th tích V ca khi chóp
'.A ABC
c tính theo
.a
A.
3
1
.
6
Va
B.
3
1
.
2
Va
C.
3
1
.
3
Va
D.
3
1
.
4
Va
Câu 12: Hình bát diu có bao nhiêu mt phi xng ?
A.6 mt phng. B.3 mt phng. C.9 mt phng. D.5 mt phng.
Câu 13:    u S.ABCD      nh
a
và bit
0
3
60 , .
2
a
BAD SA SB SD
Gi
là góc gia hai mt phng
()SBD
và
( ).ABCD
Tìm
tan .
A.
tan 3.
B.
2
tan .
3
C.
tan 5.
D.
1
tan .
5
Câu 14:     ng
.ABC ABC
 
ABC
   u cnh bng 4 và bit
5.CC
Tính th tích V ca kh 
A.
4 3.V
B.
16
.
3
V
C.
20 3
.
3
V
D.
20 3.V
Câu 15:  u
.ABC A B C
có
AB a
, góc gia hai mt phng
()A BC
và
()ABC
bng
0
60 .
Gi G là trng tâm ca tam giác
.A BC
Tính khong cách d t m G n mt
phng
( ).ABC
A.
.
4
a
d
B.
.da
C.
.
3
a
d
D.
.
2
a
d
Câu 16: Cho hình chóp S.ABCD nh a, SA vuông góc vSC t
mt góc bng . Tính khong cách d t m B n mt phng
SCD
tính theo
.a
A.
3
.
3
a
d
B.
6
.
6
a
d
C.
3
.
6
a
d
D.
6
.
3
a
d
Câu 17: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
a
, cnh bên SA vuông góc vi
mt ph
.SA a
. Tính khong cách d ging thng chéo nhau
SC
và
.BD
0
45
Trang23
A.
3
.
3
a
d
B.
5
.
5
a
d
C.
7
.
7
a
d
D.
6
.
6
a
d
Câu 18: 
.ABC A B C
có
BB a
và góc gia
BB
vi mt phng
0
60 .
Tính khong cách d gia hai m cho.
A.
2
.
3
a
d
B.
.
3
a
d
C.
3
.
2
a
d
D.
2
.
2
a
d
Câu 19: Tính th tích V ca khi t diu cnh bng
.a
A.
3
2
.
12
a
V
B.
3
6
.
3
a
V
C.
3
.
12
a
V
D.
3
3
.
3
a
V
Câu 20: Cho hình chóp
.S ABC
u có chiu cao bng
3a
và th tích khi chóp
.S ABC
bng
3
.a
 dài cx ca tam giác
.ABC
A.
2.xa
B.
.
3
a
x
C.
2.xa
D.
3.xa
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 10
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN
HÌNH HỌC 12
Câu 1: Khi hp ch nhc lt là
, , a b c
thì th tích bng công thc nào?
A.
abc
. B.
1
2
abc
. C.
1
3
abc
. D.
3
a
.
Câu 2: Cho khi chóp
.S ABC
     i
B
. Cnh SA vuông góc v 
60ACB 
,
BC a
,
3SA a
. Gi M m
SB
. Tính th tích khi
MABC
.
A.
3
a
. B.
3
6
a
. C.
3
36
a
. D.
3
4
a
.
Câu 3:  u cnh
a
. Hình chiu vuông góc ca
A
lên mt phng (ABC) trùng vm ca AB. Góc gia cnh bên và mng
60
. Gi
,MN
lm cnh
AC
,
''BC
 dn
MN
.
A.
3
2
a
. B.
5
2
a
. C.
7
2
a
. D.
2
2
a
.
Câu 4:  ng
. ' ' 'ABC A B C
i B,
2AC a
, góc
gia
AB
ng
60
. Tính th tích ca kh
. ' ' 'ABC A B C
.
. ' ' 'ABC A B C
Trang24
A.
3
3
2
a
. B.
3
3a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 5:    
. ' ' 'ABC A B C
có
10
'
4
a
AA
,
2AC a
,
BC a
,
135ACB 
.
Hình chiu vuông góc ca
'C
lên mt phng
ABC
trùng vm M ca
AB
. Tính th
tích ca kh
. ' ' 'ABC A B C
.
A.
3
3
8
a
. B.
3
7
8
a
. C.
3
6
8
a
. D.
3
5
8
a
.
Câu 6: Cho hình chóp
.S ABC

ABC
là tam giác vuông ti C,
3,AC a BC a
, các
cu bng nhau, góc gia
SC
và mng
60
. Gi M m cnh
SC
, tính
 n
BM
.
A.
3
2
a
. B.
6
2
a
. C.
2a
. D.
3
2
a
.
Câu 7: Cho hình chóp
.S ABCD

ABCD
là hình thoi. Mt bên
SAB
là tam giác vuông cân
ti
S
và nm trong mt phng vuông góc vi mt phng
ABCD
. Tính th tích khi chóp
.S ABCD
bit
BD a
,
3AC a
.
A.
3
3
a
B.
3
3
4
a
C.
3
3
12
a
D.
3
a
.
Câu 8: Cho hình chóp S.ABCD ABCD là hình thoi tâm O cnh a, góc
120BAD 
. Các mt
phng
SAB
và
SAD
cùng vuông góc vi mi M m SD, th tích khi chóp
S.ABCD là
3
3
3
a
. Hãy tính khong cách h t M ti mt phng
SBC
theo
a
.
A.
228
19
a
h
. B.
228
38
a
h
. C.
25
5
a
h
. D.
25
19
a
h
.
Câu 9: i hai mu có bao nhiêu cnh?
A.20 B.12. C.30. D.16.
Câu 10: Hình t diu có bao nhiêu mt phi xng?
A.6. B.10. C.4. D.8.
Câu 11: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
a
, mt bên
SAB
là tam giác
u và nm trong mt phng vuông góc vi mt phng cách h t m A n mt
phng
SCD
.
A.
3
4
a
h
. B.
3
7
a
h
. C.
21
7
a
h
. D.
ha
.
Câu 12: Cho hình chóp
.S ABCD
nh 2
a
, SAD là tam giác cân ti S và nm
trong mt phng vuông góc va mt bên (SBC) và mng
0
60
. Tính th tích
khi chóp
.S ABCD
.
Trang25
A.
3
6 3.a
B.
3
4 15
.
5
a
C.
3
2 15
.
5
a
D.
3
83
.
3
a
Câu 13:  nào?
A.Hình chóp có tt c các cnh bên, cu bng nhau.
B.u và cnh bên vuông góc v
C.Hình chóp có cng cao trùng v
D.u và tt c các cnh bên bng nhau.
Câu 14:  u
. ' ' 'ABC A B C
có cnh bên
2a
, góc to bi
'AB
và mt

60
. Gi m
BC
.Tính cosin góc to bng thng
'AC
và
AM
.
A.
2
4
. B.
3
2
. C.
3
6
. D.
3
4
.
Câu 15:  ng
. ' ' 'ABC A B C
có mu, cnh
'3A A a
. Bit
góc gia
'A BC
ng
45
. Tính khong chéo nhau
'AB
và
'CC
theo
a
.
A.
a
. B.
3a
. C.
33
3
a
. D.
33
2
a
.
Câu 16: Cho hình chóp S.ABC u cnh a, hai mt phng
SAB
và
SAC
cùng
vuông góc vi m
3SA a
. Tính côsin ca góc gia hai mt phng
SAB
và
SBC
.
A.
5
cos
2
. B.
5
cos
5
. C.
7
cos
7
. D.
3
cos
3
.
Câu 17: Cho hình chóp
.S ABC
có
SA ABC
, 
ABC
 u. Tính th tích khi
chóp
.S ABC
, bit
AB a
,
SA a
.
A.
3
3
12
a
. B.
3
a
. C.
3
3
a
D.
3
3
4
a
.
Câu 18: M 
A.S cnh ca mn luôn l mt cn y.
B.S cnh ca mn luôn bng s mt cn y.
C.S cnh ca mn luôn nh c bng s mt cn y.
D.S cnh ca mn luôn nh  mt cn y.
Câu 19: Cho hình chóp S.ABC ABC là tam giác vuông ti B, , SC hp vi
 , SA vuông góc vm I thuc cnh SC sao cho . Tính th tích ca khi
chóp
IABC
.
A.
10 3
3
. B.
53
3
. C.
43
. D.
33
.
Câu 20: Tính th tích khi chóp t u có cng
a
và mt bên to vi m
60
.
A.
3
3
2
a
. B.
3
3
3
a
. C.
3
3
12
a
. D.
3
3
6
a
.
M
3, 5AB AC
60
2SI IC
Trang26
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 1
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN HÌNH HỌC 12
Câu 1:Khối hộp chữ nhậtcó 3 cạnh xuất phát từ một đỉnh lần lượt có độ dài a, , b c .
Thể tích V của khối hộp chữ nhật. 1 1 4
A.V ab . c B.V ab . c C.V ab . c D.V ab . c 3 6 3
Câu 2: Tìm số cạnh ít nhất của hình đa diện có 5 mặt. A.6 cạnh. B.7 cạnh. C. 8 cạnh. D. 9 cạnh
Câu 3: Trong một khối đa diện, mệnh đề nào sau đây đúng ?
A.Hai cạnh bất kì có ít nhất một điểm chung. B.Hai mặt bất kì có ít nhất một điểm chung.
C.Mỗi đỉnh là đỉnh chung của ít nhất 3 mặt. D.Hai mặt bất kì có ít nhất một cạnh chung.
Câu 4:Trong các phát biểu sau, phát biểu nào đúng ?
A.Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
B.Hình lăng trụ đều là hình lăng trụ có tất cả các cạnh bằng nhau.
C.Hình lăng trụ đều là hình lăng trụ có đáy là đa giác đều và các cạnh bên bằng nhau.
D.Hình lăng trụ đều là hình lăng trụ có tất cả các mặt là đa giác đều.
Câu 5:Các khối đa diện đều mà mỗi đỉnh của nó đều là đỉnh chung của ba mặt thì số đỉnh Đ và số
cạnh C của các khối đa diện đó luôn thỏa mãn điều kiện nào?
A. 3Đ  2C. B. 3C  2 . Đ
C. Đ C  2.
D. Đ C.
Câu 6:Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA a 5 và vuông góc
với mặt phẳng đáy. Gọi H là trung điểm của S ,
B K là hình chiếu vuông góc của A lên . SD Tính
thể tích V của khối chóp S.AHK. 5 5 5 5 5 5 5 5 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 24 48 36 72
Câu 7: Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng
SA và CD bằng 3 .
a Thể tích V của khối chóp S.ABC . D 3 3a 3 4 3a A.V  . B. 3 V  4 3a . C. 3 V  3a . D.V  . 3 3
Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AB  5a, AC  . a Cạnh
SA  3a và vuông góc với mặt phẳng đáy. Thể tích V của khối chóp S.ABC. 5 A. 3 V a . B. 3 V a . C. 3 V  2a . D. 3 V  3a . 2
Câu 9:Cho khối tứ diện ABCD , tam giác ABC vuông cân tại C , tam giác DAB đều, AB  2a .
Mặt phẳng  ABC  và  DAB vuông góc với nhau. Tính thể tích V của khối tứ diện ABC . D 3 a 3 3 a 3 A. 3 V a 3. B. V  . C. 3 V  2a 3. D. V  . 3 9 Trang1
Câu 10: Cho hình lăng trụ tam giác đều AB . C ’ A ’ B ’
C có AB a , đường thẳng AB' tạo với mặt phẳng  BCC’ ’
B  một góc 300. Tính thể tích V của khối lăng trụ đã cho. 3 3a 3 a 3 a 6 3 a 6 A.V  . B.V  . C.V  . D.V  . 4 4 4 12
Câu 11: Cho hình lăng trụ tam giác ' ' ' AB .
C A B C có đáy ABC là tam giác đều cạnh a, hình chiếu
của điểm A' trên mặt phẳng  ABC  trùng với trung điểm của cạnh BC. Biết CC ' tạo với mặt
phẳng  ABC  một góc 450. Tính thể tích V của khối đa diện ' ' ' AB . C A B C . 3 3a 3 3a 3 3a 3 a A.V  . B.V  . C.V  . D.V  . 8 8 6 4
Câu 12: Cho hình chóp tam giác S.ABC , có đáy ABC vuông tại A, AB a , AC a 3 . Tam
giác SBC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khi đó thể tích V của khối chóp đã cho. 3 3a 3 3a 3 a 3 2a A.V  . B.V  . C.V  . D.V  . 2 2 2 3
Câu 13: Cho hình chóp tứ giác đều S.ABCD có AB  ,
a SA a 3 . Góc giữa đường thẳng SD
với mặt phẳng (SAC). 30 30 5 6 A. arccos . B. arccos . C. arccos . D. arccos . 12 6 6 6
Câu 14: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, SA a 3 . M là trung điểm
của cạnh BC. Góc giữa hai mặt phẳng  ABCD với SBC  bằng: 5 2 A. arctan . B. arctan . C. arctan 5. D. arctan 10. 2 2
Câu 15: Cho tứ diện ABCD có AD  14, BC  6. Gọi M , N lần lượt là trung điểm của các cạnh
AC, BD và MN  8 . Gọi  là góc giữa hai đường thẳng BC và MN . Tính sin . 2 2 3 1 2 A. B. C. D. 3 2 2 4
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông 3 a
góc với mặt đáy. Gọi E là trung điểm của cạnh .
CD Biết thể tích khối chóp S.ABCD bằng . 3
Tính khoảng cách h từ điểm A đến mặt phẳng  SBE . a 3 a 2 a 2a A. h  . B. h  . C. h  . D. h  . 3 3 3 3
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt
phẳng  ABCD, góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 450. Tính khoảng cách d
giữa 2 đường thẳng S , B A . C Trang2 a a 2 a 3 a 2 A. d  . B. d  . C. d  . D. d  . 5 5 5 7
Câu 18: Cho hình chóp S.ABC có  0  0  0
ASB  60 ,CSB  90 , ASC 120 , SA SB SC  . a Tính
khoảng cách d từ điểm A đến mặt phẳng  SBC . a 2 a 6
A. d  2a 6.
B. d a 2. C. d  . D. d  . 2 3
Câu 19:Cho khối chóp S.ABC có diện tích mặt đáy và thể tích lần lượt là 2 a 3 và 3 6a . Tính độ
dài đường cao h của hình chóp đã cho. 2a 3
A. h  2a 3.
B. h a 3.
C. h  6a 3. D. h  . 3
Câu 20: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh ,
a SA  2a và
SA   ABC .Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB 50V 3 và SC. Tính
, với V là thể tích khối chóp . A BCNM . 3 a A.9. B. 10. C. 11. D. 12. ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A C C A A D D A B C A C B D B D B C C A ĐỀ 2
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
Câu 1: Cho hình lăng trụ đều AB .
C A' B'C ' có AB a và đường thẳng A' B tạo với đáy một góc
60 . Gọi M , N lần lượt là trung điểm cạnh AC và B'C ' . Tính độ dài đoạn thẳng MN theo a . a 13 a 13 a 13 a 13 A. MN  . B. MN  . C. MN  . D. MN  . 6 3 2 4
Câu 2: Tính thể tích khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với mặt đáy góc 30 . 3 a 3 2 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 36 36 12
Câu 3: Cho hình hộp đứng ABC .
D A' B 'C ' D' có đáy ABCD là hình thoi cạnh a và có góc 
BAD  60. Tính khoảng cách giữa đường thẳng DC và mặt phẳng  AA'B'B . 3 A. 2a . B. a . C. a . D. a 3 . 2
Câu 4: Khối lập phương có cạnh bằng a thì thể tích là công thức nào? Trang3 1 A. 2 a . B. 4 a . C. 3 a . D. 3 a . 3
Câu 5: Cho khối chóp .
D ABC có đáy ABC là tam giác đều cạnh a , DA  2a và DA vuông góc
với đáy. Gọi M , N lần lượt là hình chiếu vuông góc của Alên trên các đường thẳng DB và DC .
Tính thể tích khối chóp . A BCMN theo a . 3 3a 3 3 3a 3 3 a 3 3 a 3 A.V . B.V . C.V . D.V . 50 25 6 25
Câu 6: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
a , tâm O. Gọi M và N lần lượt
là trung điểm của SA và BC. Biết rằng góc giữa MN và  ABCD bằng 60 , tính độ dài đoạn MN. a 10 a 5 a 2 a 3 A. . B. . C. . D. . 2 2 2 2
Câu 7: Cho hình lăng trụ đều ABC.AB C
  có cạnh đáy bằng a , AC hợp với mặt phẳng  ABB A
  một góc 30 . Tính thể tích của khối lăng trụ ABC.AB C   tính theo a . 3 a 15 3 a 15 3 a 6 3 3a A. . B. . C. . D. . 8 12 4 4
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a , cạnh SA vuông góc với
mặt đáy. Góc giữa đường thẳng SC và mặt phẳng  ABCD là 45 , gọi G là trọng tâm tam giác
SCD. Tính khoảng cách h giữa hai đường thẳng chéo nhau OG và AD. a 5 a 3 a 2 a 5 A. h  . B. h  . C. h  . D. h  . 2 2 3 3
Câu 9: Hình mười hai mặt đều có bao nhiêu đỉnh? A.30. B.20. C.16. D.12.
Câu 10: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Hình chiếu của S trên  ABC
thuộc cạnh AB sao cho HB  2AH , biết mặt bên  SAC  hợp với đáy một góc 60 . Tính thể tích
khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 36 24 12 8
Câu 11: Hình lăng trụ đều là hình như thế nào?
A.Lăng trụ có tất cả các cạnh bằng nhau.
B.Lăng trụ có đáy là tam giác đều và các cạnh bên bằng nhau.
C.Lăng trụ có đáy là tam giác đều và cạnh bên vuông góc với đáy.
D.Lăng trụ đứng có đáy là đa giác đều.
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B . Biết S
AB là tam giác đều
và nằm trong mặt phẳng vuông góc với mặt phẳng  ABC  . Tính thể tích khối chóp S.ABC biết
AB a , AC a 3 . 3 a 3 a 6 3 a 2 3 a 6 A.B.C.D.  4 4 6 12 Trang4
Câu 13: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a . Góc giữa mặt bên với mặt đáy
bằng 60 . Tính khoảng cách từ điểm A đến mặt phẳng  SBC  .
Câu 14: Hình lập phương có bao nhiêu mặt phẳng đối xứng? A.8 B.9 C.6 D.7
Câu 15: Mệnh đề nào sau đây đúng?
A.Số cạnh của một hình đa diện luôn nhỏ hơn hoặc bằng số đỉnh của hình đa diện ấy.
B.Số cạnh của một hình đa diện luôn bằng số đỉnh của hình đa diện ấy.
C.Số cạnh của một hình đa diện luôn nhỏ hơn số đỉnh của hình đa diện ấy.
D.Số cạnh của một hình đa diện luôn nhỏ hơn số đỉnh của hình đa diện ấy.
Câu 16: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3 . Tam giác SBC vuông tại S và
nằm trong mặt phẳng vuông góc với mặt đáy, đường thẳng SD tạo với mặt phẳng  SBC  một góc
60 . Tính góc giữa SBD và  ABCD. A. 90 . B. 60 . C. 30 . D. 45 .
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB a . Hai mặt phẳng  a 2
SAB  và  SAC  cùng vuông góc với mặt đáy, khoảng cách từ A đến mặt phẳng  SBC  là . 2
Tính góc  tạo bởi hai đường thẳng SB và AC. A.  45 . B.  90 .       C. 30 . D. 60 .
Câu 18: Cho hình hộp AB . CD A BCD
 ' có đáy ABCD là hình thoi cạnh a 3 , BD  3a . Hình
chiếu vuông góc của B lên mặt phẳng  A'B'C 'D' là trung điểm của A'C ' . Biết rằng côsin của 21
góc tạo bởi hai mặt phẳng  ABCD và CDD'C ' bằng
. Tính thể tích khối hộp 7 AB . CD A BCD  '. 3 9a 3 5a 3 11a 3 7a A. . B. . C. . D. . 4 4 4 4
Câu 19: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA a và vuông góc với đáy, gọi
M là trung điểm của SD. Tính thể tích khối tứ diện MACD. 1 3 a 3 a 3 a A. 3 a . B. . C. . D. . 2 12 4 36
Câu 20: Cho hình chóp S.ABCD có SA   ABCD, đáy ABCD là hình chữ nhật. Tính thể tích
S.ABCD , biết AB a , AD  2a , SA  3a . 3 a A. 3 2a . B. 3 6a . C. 3 a . D.  3 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A Trang5 B C D ĐỀ 3
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
Câu 1: Mỗi đỉnh của bát diện đều là đỉnh chung của bao nhiêu cạnh ? A.3. B.5. C.8. D.4.
Câu 2:Hình đa diện nào dưới đây không có tâm đối xứng?
A. Tứ diện đều.B. Bát diện đều.
C. Hình lập phương. D. Lăng trụ lục giác đều.
Câu 3: Khối đa diện đều có 12 mặt thì có bao nhiêu cạnh? A.24. B.12. C.30. D.60.
Câu 4: Gọi V ; V lần lượt là thể tích của khối lập phương ABC .
D A' B'C ' D' và của khối tứ diện 1 A' AB .
D Hệ thức nào sau đây là đúng ?
A.V  6V .
B.V  4V .
C.V  3V .
D.V  2V . 1 1 1 1
Câu 5: Số cạnh của một hình hộp chữ nhật bằng ? A.16 cạnh.
B. 6 cạnh. C.12 cạnh. D. 8 cạnh.
Câu 6: Cho hình lăng trụ đứng ABC .
D A' B'C ' D' có đáy là hình chữ nhật với
AB a 3, BC  2a và A'C  4 .
a Tính thể tích V của khối lăng trụ ABC .
D A' B'C ' D' . 2 69 A. 3 V a . B. 3 V  2 3 a . C. 3 V  2 69 a . D. 3 V  6 3 a . 3
Câu 7: Cho hình chóp S.ABC, M , N lần lượt là trung điểm SB và SC. Tính thể tích V của khối
chóp S.AMN. Biết thể tích của khối chóp S.ABC bằng 3 a . 3 a 3 a 3 a 3 a 3 A.V  . B.V  . C.V  . D.V  . 2 8 4 2
Câu 8: Tổng diện tích các mặt của khối lập phương bằng 2
216 cm . Tính thể tích V của khối lập phương ? A. 3 V  36 cm . B. 3 V  216 cm . C. 3 V  72 cm . D. 3 V  144 cm .
Câu 9:Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BC . D Tính thể tích V của khối chóp . A GBC
A. V  3. B. V  4. C. V  6. D. V  5. Trang6
Câu 10:Cho khối đa diện S.ABCD ’ A ’ B ’ C ’
D có cạnh A ’ A , B ’ B ,C ’ C , D ’
D bằng 4 và cùng vuông
góc với  ABCD, tứ giác ABCD là hình chữ nhật, AB 12, BC  8. Khoảng cách từ S tới
ABCD bằng 8. Thể tích V của khối đa diện S.ABCD ’ A ’ B ’ C ’. D ? S
A.V  640.
B.V  1152. D C
C.V  768. A B C'
D.V  740. D' A' B'
Câu 11 :Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A BC  2a , SA vuông
góc với mặt phẳng đáy  ABC  . Tính thể tích V của khối chóp S.ABC biết SC tạo với mặt phẳng
SAB một góc 30 .o 3 a 6 3 a 6 3 2a 6 3 a 6 A.V  . B.V  . C.V  . D.V  . 9 3 3 6
Câu 12: Cho hình lăng trụ tam giác AB .
C A' B'C ' có đáy ABC là tam giác vuông cân tại , A cạnh
AC  2 2. Biết AC ' tạo với mặt phẳng  ABC  một góc 600 và AC '  4. Tính thể tích V của khối đa diện AB . C B 'C '. 8 8 3 16 3 A.V  . B.V  8 3. C.V  . D.V  . 3 3 3
Câu 13:Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 2a 3, góc BAD bằng
1200. Hai mặt phẳng  SAB  và  SAD cùng vuông góc với đáy. Góc gữa mặt phẳng  SBC  và
ABCD bằng 450 . Tính khoảng cách h từ điểm A đến mặt phẳng SBC. 2a 2 3a 2
A. h  2a 2.B. h  .C. h
. D. h a 3. 3 2
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , SA  ( ABCD). Gọi M là trung điể  
m BC.Biết BAD  120 ,  SMA  45 .
 Khoảng cách d từ điểm D đến mặt phẳng SBC . a 6 a 6 a 6 a 6 A. d  . B. d  . C. d  . D. d  . 6 3 5 4
Câu 15: Cho hình chóp S.ABCD có đáy là hình chữ nhật. Hình chiếu của S lên  ABCD là trung điểm H của ,
AB tam giác SAB vuông cân tại S. Biết SH  , a CH  3 .
a Tính khoảng cách d
giữa hai đường thẳng SD và CH. 4a 82 a 82 4a 82 a 66 A. d  . B. d  . C. d  . D. d  . 41 22 21 11
Câu 16: Cho hình chóp tam giác đều S.ABC có cạnh bằng .
a Gọi G là trọng tâm tam giác ABC.
Tính cosin của góc  tạo bởi cạnh bên và mặt phẳng đáy. Trang7 5 3 5 3 A. cos  .B. cos  . C. cos  .D. cos  . 5 3 10 2
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân với BA BC  , a SA a và
vuông góc với mặt phẳng đáy. Tính côsin góc  giữa hai mặt phẳng  SAC  và  SBC . 2 2 1 3 A. cos  . B. cos  . C. cos  . D. cos  . 2 3 2 2
Câu 18: Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh 2a, có SA vuông góc với  3 a 3
ABC , tam giác SBC cân tại S. Để thể tích của khối chóp S.ABC là thì góc  giữa hai 3
mặt phẳng  SBC  và  ABC . A. 0   60 . B. 0   30 . C. 0   45 . D. 0   90 .
Câu 19: Cho hình lăng trụ tứ giác ABC . D ’ A ’ B ’ C ’
D có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
3a . Tính chiều cao h của hình lăng trụ đã cho. a A. h  . a B. h  9 . a C. h  3 . a D. h  . 3
Câu 20:Một khối chóp tam giác có ba góc phẳng vuông tại đỉnh, có thể tích V và hai cạnh bên
bằng a,b . Tính cạnh bên thứ ba x của khối chóp đã cho. 3V 4V 5V 6V A. x  . B. x  . C. x  . D. x  . ab ab ab ab ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 D A C A D D C B B A B D C D D B A B C D ĐỀ 4
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
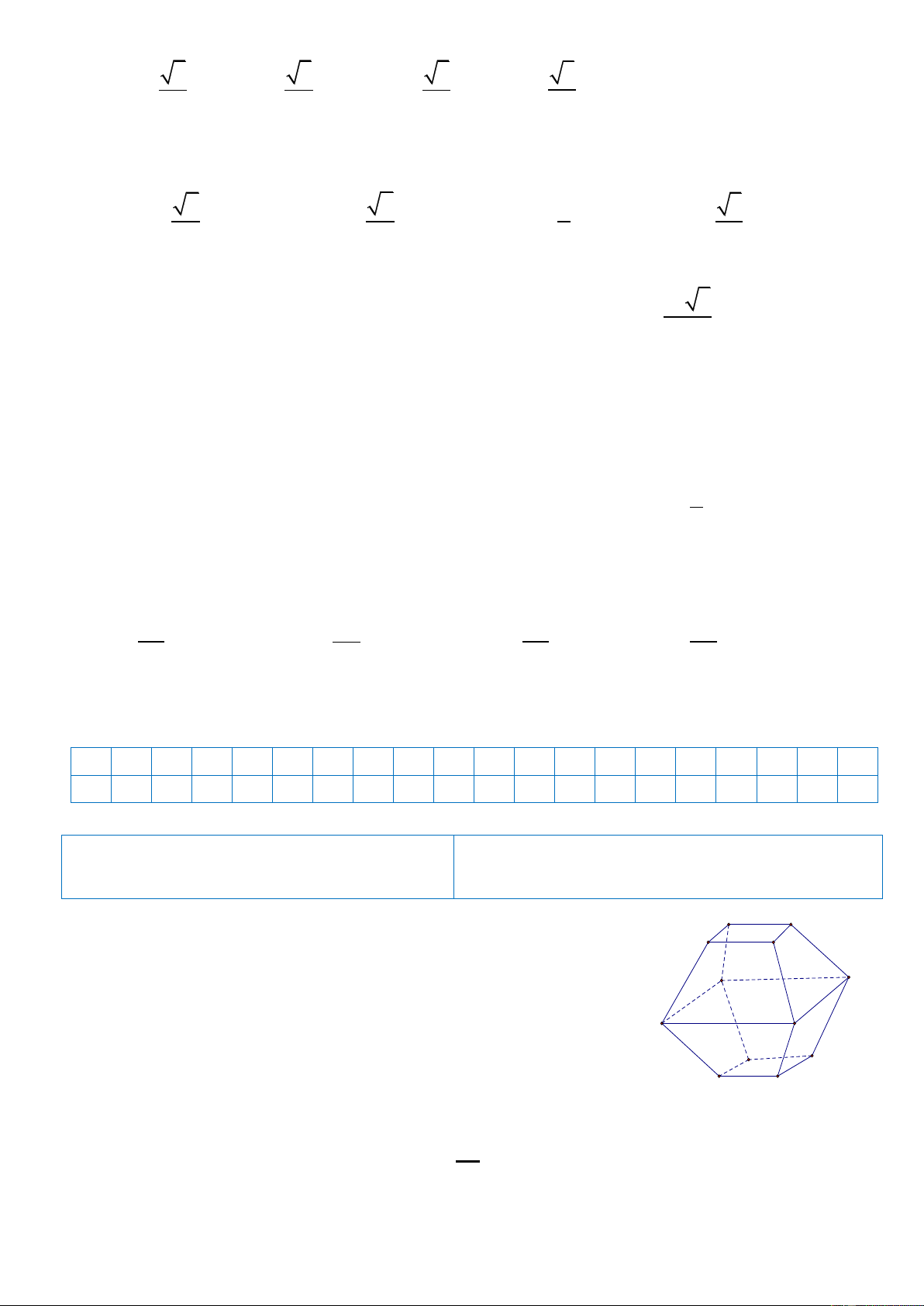
Câu 1:Hình đa diện trong hình vẽ bên có bao nhiêu mặt ? A. 8. B. 11. C. 12. D. 10.
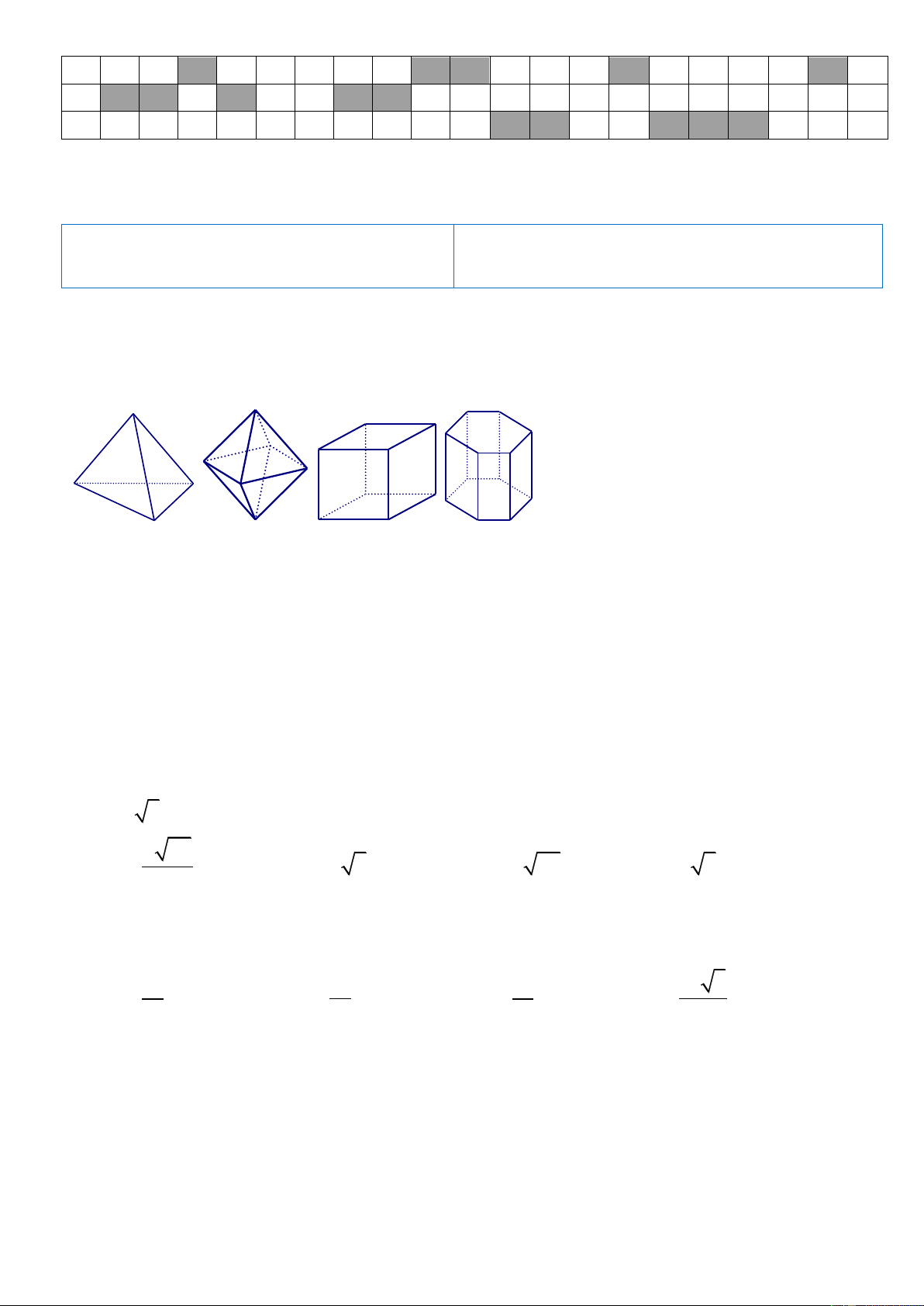
Câu 2: Chỉ có 5 loại khối đa diện đều . Đó là : A.3 ;  3 , 4 ;  3 , 3 ;  4 , 5 ;  3 , 5 ;  6 . B.3 ;  3 , 4 ;  3 , 3 ;  4 , 5 ;  3 , 3 ;  6 . C.3 ;  3 , 4 ;  5 , 3 ;  4 , 5 ;  3 , 3 ;  5 . D.3 ;  3 , 4 ;  3 , 3 ;  4 , 5 ;  3 , 3 ;  5 .
Câu 3: Cho một hình đa diện . Tìm khẳng định sai trong các khẳng định sau:
A.Mỗi cạnh là cạnh chung của ít nhất ba mặt
B.Mỗi đỉnh là đỉnh chung của ít nhất ba mặt Trang8
C.Mỗi mặt có ít nhất ba cạnh
D.Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh
Câu 4: Mê ̣nh đề nào sau đây sai?
A.Khối chóp và khối lăng tru ̣ là các khối đa diê ̣n.
B.Mỗi ca ̣nh của hình đa diê ̣n đều là ca ̣nh chung của đúng hai đa giác .
C.Hai hình đa diê ̣n go ̣i là bằng nhau nếu có mô ̣t phép biến hình biến hình này thành hình kia .
D.Khối đa diê ̣n là phần không gian được giới hạn bởi mô ̣t hình đa diê ̣n và kể cả hình đa diê ̣n đó.
Câu 5: Khối đa diện đều loại {4; 3} là:
A.Khối đa diện đều 4 cạnh, 3 mặt.
B.Khối đa diện có 3 cạnh và 4 mặt.
C.Khối đa diện đều có 6 mặt, 12 cạnh và 8 đỉnh.
D.Khối đa diện có 12 cạnh, 12 đỉnh và 6 đường chéo.
Câu 6: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B với AC a .
Biết cạnh bên SA vuông góc với mặt phẳng đáy và SB hợp với mặt đáy một góc 0 60 . Tính thể
tích V của khối chóp S.ABC. 3 a 6 3 a 6 3 a 3 A.V  . B.V  . C.V  . D. 3 V a 3. 24 8 3
Câu 7:Cho tứ diện ABCD có thể tích bằng V và G là trọng tâm của tam giác BC , D M là trung điểm .
CD Tính thể tích của khối chóp . A GMC. V V V V A. .B. . C. . D. . 18 9 6 3
Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh .
A Biết SA  ( ABC) và
SA a 3. Tính thể tích V của khối chóp S.AB . C 3 a 3 a 3 3a 3 a 3 A.V  . B.V  . C.V  . D.V  . 4 2 4 3
Câu 9: Cho hình lăng trụ AB . C ’ A ’ B ’
C có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của điểm ’
A lên mặt phẳng  ABC  trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai a 3 đường thẳng ’
AA và BC bằng
. Tính thể tích V của khối lăng trụ AB . C ’ A ’ B ’. C 4 3 a 3 3 a 3 3 a 3 3 a 3 A.V  . B.V  . C.V  . D.V  . 3 24 12 6
Câu 10: Cho hình chóp S.ABC có đáy là tam giác ABC
cân tại A, và AB AC  5, BC  6 ,
các mặt bên đều hợp với đáy góc 0
45 và hình chiếu của S trên mặt phẳng ( ABC) nằm trong ABC
. Khi đó thể tích khối chóp S.ABC.
A.V  4.
B.V  6.
C.V  8.
D.V  12.
Câu 11: Cho lăng trụ đứng AB .
C A' B'C ' có đáy là tam giác vuông cân tại , A BC a 2, A' B  3 .
a Tính thể tích V của khối lăng trụ AB .
C A' B 'C '. 3 a 2 3 a 2 3 a 2 A.V  . B. 3 V a 2.C.V  . D.V  . 3 4 2 Trang9
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc 0 BAD  60 ,
SA   ABCD , SA a . Gọi C ' là trung điểm của SC, mặt phẳng  P  đi qua AC ' và song song ,
BD cắt các cạnh S ,
B SD lần lượt tại B'và ’.
D Thể tích khối chóp SAB 'C ' D'. 3 a 3 3 a 3 3 a 3 3 a 3 A.V  . B.V  . C.V . D.V  . 6 18 3 12
Câu 13: Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng
vuông góc với đáy. Biết AC  2a, BD  3 .
a Tính khoảng cách d giữa hai đường thẳng AD và SC. 3a 208 a 208 208 a 208 A. d  . B. d  .
C. d a . D. d  . 2 217 3 217 217 2 217 3 a 3
Câu 14: Cho hình chóp đều S.ABC có thể tích bằng , có cạnh đáy bằng . a Khi đó khoảng 24
cách d từ điểm A đến mặt phẳng  SBC . a 3 a 2 3a A. d  . B. d  .
C. d a 3. D. d  . 2 2 4
Câu 15: Hình lăng trụ ABC.AB C
  có đáy ABC là tam giác đều AB  ,
a Hình chiếu vuông góc
của A trên  ABC  nằm trùng với trung điểm BC. Tính theo a khoảng cách d từ điểm A đến
mặt phẳng  ABC . 2a 2a 5 a 3 A. d  . B. d  . C. d  .
D. d a 5. 3 5 2
Câu 16 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA  ( ABCD), SA  . x Tìm x
theo a để góc giữa ( )
SBA và (SCD) bằng 0 60 . a 2 a 3 A. B. C. a 2. D. a 3. 2 3
Câu 17 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA a và SA  ( ABCD). Tính
tan, với  là góc giữa SC và (SAB). 2 A. tan  2. B. tan   C. tan  3. D. tan 1. 2
Câu 18: Cho hình lập phương ABCDAB C
 D. Góc  giữa hai đường thẳng BA và . CD A.  90 .  B.  60 .  C.  30 .  D.  45 . 
Câu 19: Khối chóp đều S.ABCD có tất cả các cạnh đều bằng .
a Khi đó độ dài đường cao h của khối chóp đã cho. a 2 a 3 A. h  3 . a B. h  . C. h  . D. h  . a 2 2
Câu 20: Cho hình lăng trụ AB .
C A' B'C ' có đáy ABC là tam giác vuông cân có CA CB  . a Gọi Trang10 3 a
G là trọng tâm tam giác ABC. Biết thể tích của khối chóp .
G A' B'C ' bằng . Tính chiều cao h 3
của hình lăng trụ đã cho. a 3a A. h  . B. h  . a C. h  . D. h  2 . a 2 2 ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 D D A C A A C A C D B B A D C B B D B D ĐỀ 5
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
Câu 1: Các hình nào dưới đây không phải là khối đa diện ? A. Cả 3 hình trên.
B. Hình a) và Hình b).
C. Hình b) và Hình c).
D. Hình a) và Hình c).
Câu 2: Cho ba mệnh đề: (I): Khối đa diện đều loại {4; 3} là khối lập phương;
(II): Khối đa diện đều loại {3; 5} là khối hai mươi mặt đều;
(III): Khối đa diện đều loại {3; 4} là khối mười mặt đều.
Số mệnh đề đúng trong 3 mệnh đề trên là: A. 3. B. 0. C. 2. D. 1.
Câu 3: Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Khối mười hai mặt đều có 36 cạnh. B. Khối lập phương có 12 cạnh.
C. Khối bát diện đều có 8 đỉnh.
D. Khối hai mươi mặt đều có 20 đỉnh.
Câu 4: Cho khối chóp S.ABCD có đáy là hình vuông tâm .
O Gọi I là trung điểm của SO Khẳng
đi ̣nh nào sau đây đúng?
A. S, I là các điểm ngoài của khối chóp S.ABC . D
B. O là điểm trong của khối chóp S.ABC . D
C. S, O là các điểm ngoài của khối chóp S.ABC . D
D. I là điểm trong của khối chóp S.ABC . D
Câu 5: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Xét các mệnh đề:
(I) Khối chóp S.ABCD có thể phân chia thành hai khối chóp S.ABC và S.ADC
(II) Khối chóp S.ABCD có có thể phân chia thành hai khối chóp S.ABC và S.ABD Mệnh đề nào đúng? Trang11
A. Cả (I) và (II) đều sai. B. (I) đúng, (II) sai.
C. Cả (I) và (II) đều đúng.
D. (I) sai, (II) đúng.
Câu 6:Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA vuông góc với mặt phẳng đáy, SA  .
a Tính thể tích V của khối tứ diện S.BC . D 3 a 3 a 3 a 3 a A.V  . B.V  . C.V  . D.V  . 3 8 4 6
Câu 7: Khối chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Biết SA vuông góc với mặt đáy, SB  2 .
a Gọi M , N lần lượt là trung điểm S , B B .
C Tính thể tích V của khối chóp . A SCNM . 3 a 3 3 a 3 3 a 3 3 a 3 A.V  . B.V  . C.V  . D.V  . 12 16 8 24
Câu 8: Cho khối lăng trụ đứng ABC .
D A' B'C 'D' có thể tích là 3
36m . Gọi M là điểm tùy ý trên mặt phẳng ABC .
D Tính thể tích V của khối chóp M .A' B 'C ' D'. A. 3
V  12m . B. 3
V  24m . C. 3
V  36m . D. 3
V  6m .
Câu 9: Khối hộp đứng ABC . D ’ A ’ B ’ C ’
D đáy là hình thoi cạnh a, 0
BAD  60 , A ’
A a 3. Thể
tíchV của khối hộp đứng. 3 3a 3 a 3 3 3a 3 a 3 A.V  . B.V  . C.V  . D.V  . 2 8 4 2
Câu 10: Cho hình chóp tứ giác S.ABCD , đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông
góc với mặt phẳng đáy và góc giữa SC và ( ABCD ) bằng 450. Thể tích V của khối chóp S.ABC . D 3 a 2 3 a 2 3 a 2 A.V  . B.V  . C. 3 V a 2. D.V  . 6 4 3
Câu 11: Cho lăng trụ đứng tam giác ABC A' B'C ' có đáy ABC là tam giác vuông cân tại B với BA BC  ,
a biết A' B hợp với mặt phẳng  ABC  một góc 0
60 . Thể tích V của khối lăng trụ đã cho. 3 a 3 3 a 3 3 a 3 A.V  . B.V  . C.V  . D. 3 V a 3. 2 4 6
Câu 12: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B với AC a
. Biết cạnh bên SA vuông góc với mặt phẳng đáy và SB hợp với mặt đáy một góc 0 60 . Tính thể
tích V của khối chóp S.ABC. 3 a 6 3 a 6 3 a 3 A.V  . B.V  . C.V  . D. 3 V a 3. 24 8 3
Câu 13 :Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a , SO vuông góc với
mặt phẳng  ABCD và SO a . Khoảng cách d giữa SC và . AB a 5 2a 5 a 3 2a 3 A. d  . B. d  . C. d  . D. d  . 5 5 15 15 Trang12
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc a 6
với mặt phẳng đáy và SA
. Khi đó khoảng cách d từ điểm A đến mặt phẳng  SBC . 2 a 2 a 2 a A. d  . B. d  . C. d  . a D. d  . 3 2 2 a 3
Câu 15: Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a và đường cao SO  . Khoảng 3
cách d từ điểm O đến mặt phẳng SAB. a 6 a 15 A. d  . B. d  .
C. d a 2.
D. d a 15. 3 15
Câu 16 : Cho hình chóp S.ABCD có đáy là hình thang vuông tại ,
A B và SA  ( ABCD). Biết
SA AB BC  , a AD  2 .
a Tính tan, với  là góc giữa (SCD) và ( ABCD). 1 2
A. tan  2. B. tan   C. tan  2. D. tan   2 2
Câu 17 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA a và SA  ( ABCD). Tính
tan, với  là góc giữa SC và (SAB). 2 A. tan  2. B. tan   C. tan  3. D. tan 1. 2
Câu 18: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng .
a Gọi I , J lần lượt là trung điểm của AB và .
SB Số đo của góc giữa hai đường thẳng IJ và SB bằng: A. 90 . o B. 60 . o C. 30 . o D. 45 . o 3 a 8
Câu 19: Cho biết thể tích của khối chóp S. ABCD bằng
, diện tích hình vuông ABCD 3 bằng 2
2a . Chiều cao h của hình chóp đã cho. a 2 a 8
A. h a 2.
B. h a 8. C. h  . D. h  . 3 3
Câu 20: Khối lăng trụ đứng có thể tích V và diện tích đáy bằng S thì độ dài cạnh bên x của nó V 3V V V A. x  . B. x  . C. x  . D. x  . S S 2S S ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A C B D B D C A A D A A B B B D B B A D ĐỀ 6
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12 Trang13 a 17
Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, D S  hình chiếu vuông góc 2
H của S lên mặt (ABCD) là trung điểm của đoạn A B .Gọi K là trung điểm của A D . Tính khoảng
cách giữa hai đường SD và HK theo a 3a a 3 a 21 3a A. B. C. D. 5 7 5 5
Câu 2: Cho hình lăng trụ đứng ABC . D AB CD
 ' có đáy ABCD là hình vuông. Biết cạnh bên
bằng 4a và đường chéo BD'  5 .
a Tính thể tích khối lăng trụ này là: A. 3 8a B. 3 a C. 3 27a D. 3 18a
Câu 3: Cho tứ diện ABCD có AB CD  2 .
a Gọi M , N lần lượt là trung điểm của BC và . AD
Biết MN a 2. Góc  giữa hai đường thẳng AB và CD bằng A. 0   60 B.   0 90 C. 0   30 D.   0 45
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh AB  , a AD  2 , a cạnh bên
SA vuông góc với mặt phẳng đáy  ABCD. Khoảng cách h giữa hai đường thẳng S A và BD bằng 2 5
A. h  5 a
B. h  2a
C. h a D. h a 5 5
Câu 5: Cho khối lăng trụ đứng AB . C A B
C . Tam giác ABC đều cạnh a, góc giữa CB’ và đáy bằng
600 . Chiều cao của khối lăng trụ đứng ABC.AB C   theo a bằng: A. a 3 B. a 2 C.a D. a 5
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt phẳng  SAB vuông
góc với mặt phẳng đáy ( ABCD) , tam giác SAB đều. Gọi góc giữa hai mặt phẳng  SCD và
SAB là . Khi đó tan bằng 3 2 3 3 2 A. B. C. a D. a 2 3 2 3
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, biết SA  ( ABCD) và SA =
a 3. Góc giữa đường thẳng SB và mặt phẳng (S AD) bằng : A.600 B.450 C.300 D.900
Câu 8: Khối lập phương có số cạnh bằng: A.8 B.12 C.6 D.10
Câu 9: Khi độ dài cạnh của hình lập phương tăng thêm 2 cm thì thể tích của khối lập phương của nó tăng thêm 152 3
cm . Cạnh của hình lập phương đã cho là A.5 B.3 C.4 D.2 Trang14 ·
Câu 10: Cho lăng trụ đứng AB . C A B
C có đáy là tam giác vuông tại A, AC=a, 0 ACB  60 .
Đường chéo BC’ của mặt bên (BCC’B’) tạo với mặt phẳng (AA’C’C) một góc 0 30 . Tính thể tích
của khối lăng trụ theo a 3 3 2a 6 4a 6 3 a 6 A. 3 a 6 B. C. D. 3 3 3
Câu 11: Cho hình lăng trụ ABC.AB C
  có đáy ABC là tam giác vuông cân tại A, biết AB=2a .
Hình chiếu vuông góc của A’ xuống (ABC) là trung điểm của BC. Cạnh A’B tạo với mặt phẳng
đáy ( ABC) một góc 30o.Tính thể tích khối lăng trụ này 3 a 3 3 3 2a 6 3a 3 a 6 A. 3 B. C. 3 D. 16 16
Câu 12: Chọn khẳng định sai. Trong một khối đa diện:
A.Mỗi mặt có ít nhất ba cạnh
B.Mỗi đỉnh là đỉnh chung của ít nhất 3 mặt
C.Mỗi cạnh của một khối đa diện cũng là cạnh chung của đúng 2 mặt
D.Hai mặt bất kỳ luôn có ít nhất một điểm chung
Câu 13: Số đỉnh của hình hai mươi mặt đều là A.20 B.16 C.12 D.3
Câu 14: Chohìnhchóp .
S ABCD có đáy ABCD là hình chữ nhật, có AB = a 2 , BC = 2a. SA vuông
góc với đáy. Góc giữa mặt bên (S BC) và mặt đáy bằng 600. Tính theo a thể tích khối chóp . S ABCD . 3 4a 3 3 3 3 2a 3 4a 3 a 3 A. B. C. D. 3 3 9 3
Câu 15: Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp ba lần thì thể tích khối hộp tương ứng sẽ A.tăng 27 lần B.tăng 6 lần C.tăng 9 lần D.tăng 3 lần
Câu 16: Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a .Góc hợp bởi cạnh bên và mặt đáy bằng 0 60 .Tính chiều cao SH: 2a 6 a 6 a 6 a 6 A. B. C. 3 3 4 D. 2
Câu 17:Cho hình chóp S.ABCD có ABCD là hình chữ nhật,  SAB đềunằm trong mặt phẳng
vuông góc với (ABCD) biết SC  2a 3 , SC tạo với hợp với ( ABCD ) một góc 30o .Tính thể tích
hình chóp S.ABC . D 3 2a 6 3 a 3 4a 6 A. B. C. D. 3 a 3 3 3
Câu 18: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA
vuông góc với đáy ABC và SB hợp với đáy một góc 60o. Tính thể tích hình chóp 3 a 6 3 a 6 3 a 6 3 a 3 A. B. C. D. 8 48 24 24 Trang15
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác
đều cạnh a và mặt phẳng (SBC) vuông góc với mặt phẳng đáy. Khoảng cách từ điểm C đến mặt
phẳng (S AB) tính theo a là: a 21 a a 21 a A. h B. h  21 C. h D.V  7 3 21 7 21
Câu 20: Chohìnhchóp tam giác đều S.ABC có cạnh đáy bằng 3a. Góc giữa mặt bên và mặt đáy
bằng 450. Tính theo a thể tích khối chóp . S ABC . 3 27a 3 3 9a 3a 3 9a A. B. C. D. 8 8 8 4 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 7
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12 ·
Câu 1: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A, góc 0 BCA  30 , AB =a.
Khoảng cách từ C đến mặt phẳng (ABB’A’) là: a 3 a 3 a 3 B. C. a 3 D. A. 2 2 6
Câu 2: Cho khối chóp SABCD có đáy ABCD là hình thoi cạnh a và góc nhọn A bằng 60o và
SA  ( ABCD) .Biết rằng khoảng cách từ A đến cạnh SC bằng.Tính thể tích khối chóp . S ABCD 3 a 2 3 a 3 3 a 2 A. B. 3 a 3 C. D. 12 6 4 3 a 8
Câu 3: Cho biết thể tích của khối chóp S.ABCD bằng
, diện tích hình vuông ABCD bằng 3 2
2a .Chiều cao của hình chóp bằng a 8 a 2 A. a 2 B. a 8 C. D. 3 3 Trang16
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA   ABC , góc giữa mặt
bên  SBC  và mặt phẳng đáy ( ABC) bằng 0
60 , BC a 3 , AC  2a , gọi G là trọng tâm tam
giác SAB. Khoảng cách từ điểm G đến mặt phẳng (SBC) bằng a 3 a 3 a 2 a A. B. C. D. h  6 3 6 4 4
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  2a, AD a , mặt phẳng
SAD vuông góc với mặt phẳng đáy (ABCD), tam giác SAD đều. Gọi góc giữa hai mặt phẳng
SAD và SBC là . Khi đó tan bằng 2 3 3 3 4 3 A. B. C. a D. 3 2 2 3
Câu 6: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a, biết SA  ( ABCD) và
SA a 3 . Góc giữa hai đường thẳng SBvà CD bằng : A. 0 60 B. 0 45 C. 0 30 D. 0 90 SN
Câu 7: Cho khối chóp .
S ABC trên cạnh SC lấy điểm N sao cho
 2 . Gọi V , V lần lượt là thể NC 1 2 V
tích của hai khối chóp S.ABN và S.ABC. Tỷ số 1 là: V2 2 3 1 5 A. B. C. D. 3 4 2 7
Câu 8: Chỉ có 5 loại khối đa diện đều. Đó là :
A.{3; 3}, {4; 3}, {3; 4}, {5; 3}, {3; 5}
B.{3; 3}, {4; 3}, {3; 4}, {5; 3},   5
C.{3; 3}, {4; 5}, {3; 4}, {5; 3}, {3; 5}
D.{3; 3}, {4; 3}, {3; 4}, {5; 3}, {3; 6}
Câu 9: Số đỉnh của một hình bát diện đều là: A.10 B.6 C.8 D.12
Câu 10: Cho hình hộp đứng ABC . D '
A B'C' D' có đáy ABCD là hình thoi cạnh a , góc · 0 BAD  60 ,
BD'  AC. Khi đó thể tích của khối hộp đã cho là: 3 a 5 3 a 2 3 a 3 3 a 6 A. B. 2 C. D. 2 8 2
Câu 11: Chohìnhchóp tam giác đều S.ABC có cạnh đáy bằng a 2 . Góc giữa cạnh bên và mặt đáy
bằng 300. Tính theo a thể tích khối chóp S.ABC. 3 a 6 3 a 2 3 a 6 3 a 6 A. B. C. D. 36 6 6 18
Câu 12: Cho khối chóp tứ giác có đáy là hình vuông cạnh a và có chiều cao h, thể tích khối chóp bằng 1 1 A. 2 a h B. 2 a h C. ah D. ah 3 3 Trang17
Câu 13: Mỗi đỉnh hình đa diện là đỉnh chung ít nhất : A.Hai mặt B.Bốn mặt C.Ba mặt D.Năm mặt
Câu 14: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật AB a, AD a 3 ,
SA  ( ABCD) và góc giữa đường thẳng SC và mặt phẳng đáy ( ABCD) bằng 60o . Thể tích V của
khối chóp S.ABCD bằng 3 a 2 A. 3 V a B. 3 V  3a C. 3 V  2a D.V  3
Câu 15: Khi độ dài cạnh của hình lập phương tăng thêm 2 cm thì thể tích của khối lập phương của nó tăng thêm 3
98 cm . Cạnh của hình lập phương đã cho là A.5 B.3 C.4 D.2
Câu 16: Cho hình chóp S.ABC có đáy ABC vuông tại , B · 0
ACB  30 , AB  ,
a SC  2a 2, SA
vuông góc với mặt phẳng đáy  ABC . Góc  giữa đường thẳng SC với mặt phẳng đáy  ABC bằng A. 0   90 B.   0 45 C. 0   30 D.   0 60 .
Câu 17: Cho hình lăng trụ tam giác AB .
C A' B'C ' có đáy ABC là tam giác đều cạnh . a Hình chiếu
vuông góc của điểm A' xuống mặt phẳng đáy  ABC  trùng với tâm O đường tròn ngoại tiếp của
tam giác ABC, biết AA' hợp với mặt phẳng đáy  ABC  một góc 0
60 . Thể tích V của khối lăng trụ AB .
C A' B'C ' bằng 3 a 3 3 a 5 3 a 6 3 a 2 A.V B.V C.V D.V  4 4 4 4 a 2
Câu 18: Cholăng trụ đứng ABC.AB C
  có đáy ABC là tam giác đều cạnh . Góc giữa cạnh 3 C B
 và mặt đáy là 300. Tính theo a thể tích khối lăng trụ ABC.AB C   . 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 27 3 9 54
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm ,
O cạnh a, cạnh bên SA vuông
góc với mặt phẳng đáy ( ABCD) và SA  .
a Khoảng cách h giữa hai đường thẳng AC và SB bằng a a A. h  3
B. h  2a 3 C. h  3
D. h a 3 2 3 ·
Câu 20: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, AC=2a , ACB  0 60 , Hình
chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của AC và SH a 2 . Thể tích của khối chóp . S ABC theo a là : 3 a 3 3 3 a 6 a 6 3 a 6 A. B. C. D. 3 3 6 12 ----------- HẾT ---------- Trang18 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 8
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
Câu 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. a 3 a 3 a 3 A. h  .
B. h a 3. C. h  . D. h  . 2 3 6
Câu 2: Hình đa diện nào dưới đây không có tâm đối xứng ?
A.Hình tứ diện đều.
B.Hình lăng trụ tam giác đều.
C.Hình bát diện đều.
D.Hình lập phương.
Câu 3: Tìm số cạnh của hình mười hai mặt đều. A.20. B.12. C.30. D.16.
Câu 4: Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BC .
D Tính thể tích V của khối chóp . AGB . C A.V  6. B.V  4. C.V  5. D.V  3.
Câu 5: Cho khối chóp .
S ABCD có đáy là hình chữ nhật, AB  ,
a AD a 3,SA vuông góc với đáy và
mặt phẳng (SBC) tạo với đáy một góc 0
60 . Tính thể tích V của khối chóp đã cho. 3 3 3 A. 3 V  3a . B.a V . C.a V . D. 3 V a . 3 3
Câu 6: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh ,
a SA vuông góc với mặt đáy, SD tạo
với mặt phẳng (SA ) B một góc bằng 0
30 . Tính thể tích V của khối chóp . S ABCD. 3 6a 3 6a 3 3a A.V  . B.V  . C.V  . D. 3 V  3a . 3 18 3
Câu 7: Mặt phẳng (AB C
 ) chia khối lăng trụ AB . C ABC
  thành các khối đa diện nào ?
A.Một khối chóp tam giác và một khối chóp tứ giác.
B.Hai khối chóp tam giác.
C.Một khối chóp tam giác và một khối chóp ngũ giác.
D.Hai khối chóp tứ giác.
Câu 8: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ? A.4 mặt phẳng. B.1 mặt phẳng. C.3 mặt phẳng. D.2 mặt phẳng.
Câu 9: Cho hình chóp đều S.ABCD đáy là hình vuông cạnh a và biết thể tích khối chóp là V  6 3
a . Tìm  là góc tạo bởi cạnh bên và mặt đáy. 6 A.  0 30 . B.  0 60 . C.  0 45 . D.  0 90 . Trang19
Câu 10: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ? A.4 mặt phẳng. B.6 mặt phẳng. C.3 mặt phẳng. D.9 mặt phẳng.
Câu 11: Cho hình chóp S.ABC ,
D có đáy ABCD là hình vuông cạnh a và có tâm là O. SA vuông góc
với mặt phẳng đáy; SB tạo với đáy một góc 0
45 . Khoảng cách h từ O đến (SBC). a 2 a 2 a 2 a 2 A. h  . B. h  . C. h  . D. h  . 4 2 3 8
Câu 12: Cho khối chóp .
S ABC có SA vuông góc với đáy, SA  4, AB  6,BC  10 và CA  8. Tính
thể tích V của khối chóp đã cho. A.V 192. B.V  40. C.V  24. D.V  32.
Câu 13: Cho hình lăng trụ đứng AB . C ABC
  có đáy ABC là tam giác cân với  0 AB AC  ,
a BAC  120 , mặt phẳng (AB C
 ) tạo với đáy một góc 0
60 . Tính thể tích V của khối lăng trụ đã cho. 3 9a 3 3a 3 a 3 3a A.V  . B.V  . C.V  . D.V  . 8 4 8 8
Câu 14: Cho hình chóp đều S.ABCD đáy là hình vuông cạnh a và cạnh bên tạo với đáy một góc
60o. Tính thể tích V của khối hình chóp đã cho. 6 6 6 6 A.V  3 a . B.V  3 a . C.V  3 a . D.V  3 a . 3 4 6 2
Câu 15: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SC tạo đáy một góc bằng 0
45 . Tính khoảng cách h từ điểm D đến mặt phẳng SBC tính theo . a a a a a 6 A. h  3 . B. h  6 . C. h  3 . D. h  . 3 6 6 3
Câu 16: Cho hình chóp S.ABC có mặt bên SBC  là tam giác đều cạnh a , cạnh bên SA vuông góc
với mặt phẳng đáy và  0
BAC  120 . Độ dài đoạn thẳng . AB a 3 a a 3 A. AB  . B. AB  .
C. AB a 3. D. AB  . 3 2 2
Câu 17: Cho hình tứ diện đều cạnh bằng 2. Tìm chiều cao h của khối tứ diện đó. 2 6 A. h  2 3. B. h  . C. h  2 6. D. h  6. 3
Câu 18: Tính thể tích V của khối lập phương / / / / ABC . D A B C D , biết / AC a 3. 3 6 1 A.V  3 a . B.V  3 a . C.V  3 a . D. 3 V  3 3a . 4 3
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh .
a Biết SA vuông góc với mặt 3 a 3
phẳng đáy và thể tích của khối chóp S.ABC là V
. Tìm  là góc hợp giữa hai mặt phẳng 24
(ABC) và (SBC). A. 0   45 . B. 0   30 . C. 0   90 . D. 0   60 . Trang20
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với 3
mặt phẳng đáy. Biết thể tích của khối chóp S.ABCD theo a là V  3
a . Góc  giữa đường thẳng 3
SD và mặt phẳng (SAB) là bao nhiêu độ ? A.  0 90 . B.  0 60 . C.  0 45 . D.  0 30 . ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 9
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
Câu 1: Cho hình chóp đều S.ABCD đáy là hình vuông cạnh a và cạnh bên bằng a 2.Gọi  là góc
hợp bởi cạnh bên và mặt phẳng đáy. Tìm . A. 0   60 . B. 0  135 . C. 0   30 . D. 0   90 .
Câu 2: Cho khối chóp .
S ABC có SA vuông góc với đáy, SA  4, AB  6,BC  10 và CA  8. Tính thể
tích V của khối chóp đã cho. A.V  40. B.V  32. C.V  24. D.V 192.
Câu 3: Cho tứ diện ABCD có thể tích bằng 18 và G là trọng tâm của tam giác BC .
D Tính thể tích V của khối chóp . AGB . C A.V  5. B.V  6. C.V  3. D.V  4.
Câu 4: Cho hình lăng trụ AB .
C A' B'C ' có đáy ABC là tam giác vuông cân tại B, AC  2a . Hình chiếu vuông góc của /
A trên mặt phẳng (ABC) là trung điểm của cạnh AC, đường thẳng / A B tạo
với mặt phẳng (ABC) một góc 0
45 . Tính thể tích V của khối lăng trụ đã cho. 1 A.V  3 a . B. 3 V a . C.V  3 2 2a . D.V  3 2a . 2
Câu 5: Hình lập phương có bao nhiêu mặt phẳng đối xứng ? A.7 mặt phẳng. B.3 mặt phẳng. C.9 mặt phẳng. D.6 mặt phẳng.
Câu 6: Mệnh đề nào dưới đây sai?
A.Lắp ghép hai khối hộp sẽ được một khối đa diện lồi.
B.Khối tứ diện là khối đa diện lồi.
C.Khối hợp là khối đa diện lồi.
D.Khối lăng trụ tam giác là khối đa diện lồi.
Câu 7: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh 3, SA vuông góc với mặt đáy và SA  5.
Tính thể tích V của khối chóp . S ABCD. 5 A.V  5. B.V  . C.V  15. D.V  45. 3 Trang21
Câu 8: Mặt phẳng ( 
A BC) chia khối lăng trụ AB . C ABC
  thành các khối đa diện nào ?
A.Một khối chóp tam giác và một khối chóp tứ giác.
B.Hai khối chóp tam giác.
C.Một khối chóp tam giác và một khối chóp ngũ giác.
D.Hai khối chóp tứ giác.
Câu 9: Hình đa diện nào dưới đây không có trục đối xứng ?
A.Hình bát diện đều.
B.Hình lập phương.
C.Hình lăng trụ tam giác đều.
D.Hình tứ diện đều.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với a mặt phẳng đáy và 6 SA
. Gọi  là góc hợp bởi hai mặt phẳng (SBC) và ( ABCD). Tìm . 2 A.  0 90 . B.  0 60 . C.  0 30 . D.  0 45 .
Câu 11: Cho hình lăng trụ AB . C ' A ' B '
Ccó độ dài cạnh bên đều bằng 2a, đáy ABC là tam giác
vuông tại A, AB a, AC a 3 và hình chiếu vuông góc của đỉnh A' trên mặt phẳng  ABC là trung
điểm của cạnh BC. Tính thể tích V của khối chóp A'.ABC được tính theo . a 1 1 1 1 A.V  3 a . B.V  3 a . C. 3 V a . D.V  3 a . 6 2 3 4
Câu 12: Hình bát diện đều có bao nhiêu mặt phẳng đối xứng ? A.6 mặt phẳng. B.3 mặt phẳng. C.9 mặt phẳng. D.5 mặt phẳng.
Câu 13: Cho hình chóp đều S.ABCD có đáy là hình thoi cạnh a và biết  a 3 0
BAD  60 , SA SB SD
. Gọi  là góc giữa hai mặt phẳng (SBD) và ( ABCD). Tìm tan. 2 2 1 A. tan  3. B. tan  . C. tan  5. D. tan   . 3 5
Câu 14: Cho hình lăng trụ đứng AB . C ABC
  có đáy ABC là tam giác đều cạnh bằng 4 và biết
CC  5. Tính thể tích V của khối lăng trụ đã cho. 16 20 3 A.V  4 3. B.V  . C.V  . D.V  20 3. 3 3
Câu 15: Cho hình lăng trụ tam giác đều AB . C A BC
  có AB a , góc giữa hai mặt phẳng (A BC) và ( ABC) bằng 0
60 . Gọi G là trọng tâm của tam giác A B  .
C Tính khoảng cách d từ điểm G đến mặt phẳng ( ABC). a a a A. d  . B. d  . a C. d  . D. d  . 4 3 2
Câu 16: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SC tạo đáy một góc bằng 0
45 . Tính khoảng cách d từ điểm B đến mặt phẳng SCD tính theo . a a 3 a 6 a 3 6 A. d  . B. d  . C. d  . D.a d . 3 6 6 3
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt phẳng đáy và SA  .
a . Tính khoảng cách d giữa hai đường thẳng chéo nhau SC và . BD Trang22 a 3 a 5 a 7 a 6 A. d  . B. d  . C. d  . D. d  . 3 5 7 6
Câu 18: Cho hình lăng trụ AB . C A BC
  có BB  a và góc giữa BB với mặt phẳng đáy bằng 0 60 .
Tính khoảng cách d giữa hai mặt đáy của lăng trụ đã cho. a 2 a a 3 a 2 A. d  . B. d  . C. d  . D. d  . 3 3 2 2
Câu 19: Tính thể tích V của khối tứ diện đều cạnh bằng . a 3 a 2 3 a 6 3 a 3 a 3 A.V  . B.V  . C.V  . D.V  . 12 3 12 3
Câu 20: Cho hình chóp S.ABC có đáy là tam giác đều có chiều cao bằng a 3 và thể tích khối chóp S.ABC bằng 3
a . Tìm độ dài cạnh đáy x của tam giác . ABC a A. x  2 . a B. x  . C. x  2 . a D. x  3 . a 3 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 10
ĐỀ ÔN TẬP CHƯƠNG KHỐI ĐA DIỆN Thuvienhoclieu.Com HÌNH HỌC 12
Câu 1: Khối hộp chữ nhật có ba kích thước lần lượt là , a ,
b c thì thể tích bằng công thức nào? 1 1 A. abc . B. abc . C. abc . D. 3 a . 2 3
Câu 2: Cho khối chóp S.ABC có đáy là tam giác vuông tại B . Cạnh SA vuông góc với đáy, 
ACB  60, BC a , SA a 3 . Gọi M là trung điểm SB . Tính thể tích khối MABC . 3 a 3 a 3 a A. 3 a . B. . C. . D. . 6 36 4
Câu 3: Cho hình lăng trụ ABC.A'B 'C ' có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A
lên mặt phẳng (ABC) trùng với trung điểm của AB. Góc giữa cạnh bên và mặt đáy bằng 60 . Gọi
M , N lần lượt là trung điểm cạnh AC , B'C ' . Tính độ dại đoạn MN . a 3 a 5 a 7 a 2 A. . B. . C. . D. . 2 2 2 2
Câu 4: Cho hình lăng trụ đứng AB .
C A' B'C ' có đáy là tam giác vuông cân tại B, AC a 2 , góc
giữa AB và đáy bằng 60 . Tính thể tích của khối lăng trụ AB .
C A' B'C ' . Trang23 3 3a 3 3a 3 3a A. . B. 3 3a . C. . D. . 2 6 3 a 10 
Câu 5: Cho hình lăng trụ AB .
C A' B'C ' có A' A
, AC a 2 , BC a , ACB  135 . 4
Hình chiếu vuông góc của C ' lên mặt phẳng  ABC  trùng với trung điểm M của A B . Tính thể
tích của khối lăng trụ AB .
C A' B'C ' . 3 a 3 3 a 7 3 a 6 3 a 5 A. . B. . C. . D. . 8 8 8 8
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AC a 3, BC a , các
cạnh bên đều bằng nhau, góc giữa SC và mặt đáy bằng 60 . Gọi M là trung điểm cạnh SC , tính
độ dài đoạn BM . a 3 a 6 3a A. . B. . C. 2a . D. . 2 2 2
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên  SAB  là tam giác vuông cân
tại S và nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD. Tính thể tích khối chóp
S.ABCD biết BD a , AC a 3 . 3 a 3 a 3 3 a 3 A.B.C.D. 3 a . 3 4 12 
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, góc BAD  120 . Các mặt
phẳng  SAB  và SAD cùng vuông góc với mặt đáy. Gọi M là trung điểm SD, thể tích khối chóp 3 a 3 S.ABCD là
. Hãy tính khoảng cách h từ M tới mặt phẳng  SBC  theo a . 3 a 228 a 228 2a 5 2a 5 A. h  . B. h  . C. h  . D. h  . 19 38 5 19
Câu 9: Hình mười hai mặt đều có bao nhiêu cạnh? A.20 B.12. C.30. D.16.
Câu 10: Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng? A.6. B.10. C.4. D.8.
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm A đến mặt phẳng SCD. a 3 a 3 a 21 A. h  . B. h  . C. h  .
D. h a . 4 7 7
Câu 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 a , SAD là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy. Góc giữa mặt bên (SBC) và mặt đáy bằng 0 60 . Tính thể tích
khối chóp S.ABCD . Trang24 3 4a 15 3 2a 15 3 8a 3 A. 3 6a 3. B. . C. . D. . 5 5 3
Câu 13: Hình chóp đều là hình như thế nào?
A.Hình chóp có tất cả các cạnh bên, cạnh đáy đều bằng nhau.
B.Hình chóp có đáy là đa giác giác đều và cạnh bên vuông góc với đáy.
C.Hình chóp có cạnh đáy bằng nhau và chân đường cao trùng với tâm đáy.
D.Hình chóp có đáy là đa giác đều và tất cả các cạnh bên bằng nhau.
Câu 14: Cho hình lăng trụ tam giác đều AB .
C A' B'C ' có cạnh bên 2a , góc tạo bởi A' B và mặt
đáy là 60 . Gọi M là trung điểm BC .Tính cosin góc tạo bởi 2 đường thẳng A'C và AM . 2 3 3 3 A. . B. . C. . D. . 4 2 6 4
Câu 15: Cho hình lăng trụ đứng AB .
C A' B'C ' có mặt đáy là tam giác đều, cạnh A' A  3a . Biết
góc giữa  A' BC  và đáy bằng 45 . Tính khoảng cách hai đường chéo nhau A'B và C 'C theo a . 3a 3 3a 3 A. a . B. 3a . C. . D. . 3 2
Câu 16: Cho hình chóp S.ABC có đáy tam giác đều cạnh a, hai mặt phẳng  SAB  và  SAC  cùng
vuông góc với mặt đáy và SA a 3 . Tính côsin của góc  giữa hai mặt phẳng  SAB  và  SBC  . 5 5 7 3 A. cos  . B. cos  . C. cos  . D. cos  . 2 5 7 3
Câu 17: Cho hình chóp S.ABC có SA   ABC  , đáy ABC là tam giác đều. Tính thể tích khối
chóp S.ABC , biết AB a , SA a . 3 a 3 3 a 3 a 3 A. . B. 3 a . C. D. . 12 3 4
Câu 18: Mệnh đề nào sau đây đúng?
A.Số cạnh của một hình đa diện luôn lớn hơn số mặt của hình đa diện ấy.
B.Số cạnh của một hình đa diện luôn bằng số mặt của hình đa diện ấy.
C.Số cạnh của một hình đa diện luôn nhỏ hơn hoặc bằng số mặt của hình đa diện ấy.
D.Số cạnh của một hình đa diện luôn nhỏ hơn số mặt của hình đa diện ấy.
Câu 19: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  3, AC  5 , SC hợp với
đáy 60 , SA vuông góc với đáy. Điểm I thuộc cạnh SC sao cho SI  2IC . Tính thể tích của khối chóp IA BC . 10 3 5 3 A. . B. . C. 4 3 . D. 3 3 . 3 3
Câu 20: Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng a và mặt bên tạo với mặt đáy góc 60 . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 3 12 6 Trang25 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D Trang26