Chuyên Đề Thể Tích Khối Đa Diện Có Yếu Tố Góc Ôn Thi Tốt Nghiệp THPT Có Đáp Án Và Lời Giải

Chuyên đề thể tích khối đa diện có yếu tố gốc ôn thi tốt nghiệp THPT được biên soạn dưới dạng file PDF gồm 62 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

141 71 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

62 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
CHUYÊN ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN CÓ YẾU TỐ GÓC
I. KIẾN THỨC CẦN NHỚ:
1. Góc giữa đƣờng thẳng và mặt phẳng
Định nghĩa:
Nếu
0
( ; ) 90d P d P
Nếu
; ; 'd P d P d d AIH
với
'd
là hình chiu ca d lên
P
Chú ý:
00
0 ; 90dP
2. Góc giữa hai mặt phẳng
Định nghĩa:
Cách 1: hai ng thng
a
,
b
lt vuông góc vi hai mt phng
P
và
Q
.
a hai mt phng
P
và
Q
chính là góc ging thng a và b
Cách 2: Ta thc hic
c 1: Tìm giao tuyn d ca hai mt phng (P) và (Q).
c 2: Tìm 1 điểm I thuc d sao cho trong mp (P) ta d c mng th
I và vuông góc vng thc mng th
góc vng thng d.
a hai mp(P) và mp(Q) chính bng góc gia a và b
5. Thể tích khối đa diện
a. Công thức tính thể tích khối chóp
  
Chú ý:  và , , thuộc , , ta có
P
d'
d
A
H
I
c
a
b
d
b
a
I
1
.
3
V S h=
S
h
.S ABC
'A
'B
'C
SA
SB
SC
Trang2
.
b. Công thức thể tích khối lăng trụ:
.V Bh
(
B
là di
h
là chiu cao)
XÁC ĐỊNH CHIỀU CAO THƢỜNG GẶP
a)Hnh chp c một cnh bên vuông gc với
đa
y: 










.
Ví dụ: 
.S ABC


SA
vuông góc vi mt
phc
()SA ABC^


.SA
b)Hnh chp c 1 mă
t bên vuông go
c vơ
i mă
t
đa
y: 











.
Ví dụ: 
.S ABCD

()SAB



t ph

()ABCD

SH

.SABD
c)Hnh chp c 2 mă
t bên vuông go
c vơ
i mặt
đa
y: 







t ph
.
Ví dụ: 
.S ABCD

()SAB

()SAD




()ABCD

cao c
.SA
d) Hnh chp đu:








i v
giác thì tâm là trng tâm G cu.
Ví dụ: u
.S ABCD










ABCD

.SO
XÁC ĐỊNH DIỆN TÍCH ĐÁY HAY GẶP
1. 


vuông.
S= n
2 .
Pitago:
2 2 2
AB AC AC+=
2. 


u.
S= ()
2
.
3
4
h= ().
3
2
. ' ' '
.
' ' '
..
S A B C
S ABC
V
SA SB SC
V SA SB SC
=
D
B
C
A
S
H
A
C
B
S
D
B
C
A
S
O
D
B
C
A
S
Trang3
3. 

:
. S= ()
2
. Pitago:
2 2 2
AB AD BD+=
.
.
2
4. 

 nht:
. S= dài x rng.
5. 

:
.
1
..
2
S AC BD=
. S= 2.S
ABC
=2.S
ADC
6. 

:
. S= na chin+bé)
.
( )
1
.
2
S AH AB CD=+
II. CÁC DẠNG BÀI TẬP TƢƠNG TỰ
Th tích khn
Góc ging thng và mt phng
Góc gia hai mt phng
Công thc t s th tích
Khong cách t m ti mt phng
Khong cách ging thng chéo nhau
BÀI TẬP MẪU
(ĐỀ MINH HỌA-BDG 2020-2021)Cho hình chóp
.S ABC

ABC
u cnh
a
, cnh
bên
SA
vuông góc va
SA
và mt phng
SBC
bng
45
( tham kho hình bên). Th tích
ca khi chóp
.S ABC
bng:
A.
3
8
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
4
a
.
ng dn gii
1. DẠNG TOÁN:ng toán tính th tích bit chiu cao khn bit góc gia mt bên và mt

2. HƢỚNG GIẢI:
B1: Tính di
B2:tính th tích kh
.V S h
Từ đ, ta c thể giải bài toán cụ thể nhƣ sau:
Lờigiải
Trang4
ChọnA
Gi
M
m
BC
thì
AM BC
và
SA BC
nên
BC SAM
.
T  thy góc cn tìm là
45ASM
.

SAM
vuông cân ti
A
và
3
2
a
SA AM
.
Suy ra
23
.
1 3 3
..
3 2 4 8
S ABC
a a a
V 
Bài t và phát trin:
Mức độ 1
Câu 1. Cho hình chóp có din tích m
2
3a
và chiu cao bng
2a
. Th tích ca khi chóp bng
A.
3
6a
. B.
3
2a
. C.
3
3a
. D.
3
a
.
Lờigiải
ChọnB
Ta có
23
11
. 3 .2 2
33
đ
V S h a a a
.
Câu 2. Th tích
V
ca khi chóp có chiu cao bng
h
và ding
3B
là
A.
3V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Lời giải
Chọn D
Ta có
1
.3 .
3
V B h Bh
.
Câu 3.  dài các cnh ca mt khi chóp lên
2
ln thì th tích ca kh
thà nào?
A. 
4
ln.. B.
8
ln.. C.
2
ln. D.i.
Lời giải
Chọn B
Th tích khi chóp là:
1
.
3
V B h
.
 dài c
2
ln thì din tích m
2
24
ln.
C
2
ln thì chiu cao c
2
ln.
V dài các cnh ca mt khi chóp lên
2
ln thì th tích ca kh
8
ln.
Câu 4. Công thc tính th tích ca khi chóp có di
B
và chiu cao
h
là
A.
4
3
V Bh
. B.
1
3
V Bh
. C.
V Bh
. D.
1
2
V Bh
.
Lời giải
Chọn B
Công thc tính th tích ca khi chóp có di
B
và chiu cao
h
là
1
3
V Bh
.
Câu 5. Khi chóp
.S ABCD
có
A
,
B
,
C
,
D
c nh và
S
chng thng song song vi
AC
.
 tích khi chóp
.S ABCD
s:
A.Gim phân na.. B.. C.p bn. D.Gi nguyên..
Lời giải.
Chọn D
Gi
ng thng qua
S
và song song
AC
.
Ta có:
1
.
3
V B h
+
song song
AC
nên
ABCD
,,d S ABCD d ABCD h
i.
Trang5
+
A
,
B
,
C
,
D
c nh nên din tích t giác
ABCD
i.
Vì vy th tích khi chóp
.S ABCD
s gi nguyên.
Câu 6. Cho khi chóp
H
có th tích là
3
2a
nh
2a
 dài chiu cao khi
chóp
H
bng.
A.
3a
. B.
a
. C.
4a
. D.
2a
.
Lời giải
Chọn A
3
23
2
1 1 6
. ( 2 ) 2 3
3 3 2
a
V B h a a h a
a
.
Câu 7. Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
a
và th tích bng
3
a
.Tính chiu
cao
h
c
A.
.ha
. B.
2.ha
. C.
3.ha
. D.
3.ha
.
Lời giải
ChọnC
Ta có:
3
2
1 3 3
. 3 .
3
Va
V S h h a
Sa
.
Câu 8. Cho hình chóp
.S ABC
u cnh
2a
và th tích bng
3
3a
. Tính chiu cao
h
c
A.
3
3
a
h
. B.
3
2
a
h
. C.
3ha
. D.
3
6
a
h
.
Lời giải
ChọnC
u nên
2
2
23
3
4

ABC
a
Sa
.
Mà
3
2
1 3 3
.3
3
3
ABC
ABC
Va
V S h h a
S
a
.
Câu 9. N dài chiu cao ca kh
5
ln, dii thì th tích ca
khi chóp s 
A.
5
ln. B.
20
ln. C.
15
ln. D.
10
ln.
Lờigiải
ChọnA
Th tích khi chóp s 
5
ln.
Câu 10. Cho hình chóp
.S ABC
u cnh
a
và chiu cao
4a
. Tính th tích ca hình

A.
3
23
3
a
V
. B.
3
43
3
a
V
. C.
3
3
3
a
V
. D.
3
3
4
a
V
.
Lời giải
ChọnC
u nên
2
3
4
ABC
a
S
.
Mà
23
1 1 3 3
. . .4
3 3 4 3
ABC
aa
V S h a
.
Câu 11. Cho hình chóp tam giác
.S ABC

ABC
là tam giác vuông ti
A
,
AB a
,
2AC a
, cnh
bên
SA
vuông góc vi m
SA a
. Tính th tích ca khi chóp
.S ABC
.
A.
3
Va
. B.
3
2
a
V
. C.
3
3
a
V
. D.
3
4
a
V
.
Lờigiải
V
Trang6
ChọnB
Di
2
1
.2
2
ABC
B S a a a
Chiu cao:
ha
3
2
' ' '
11
..
3 3 3
ABCA B C
a
V B h a a
Câu 12. Cho hình chóp tam giác
.S ABC

ABC
u cnh , cnh bên
SA
vuông góc
vi m
SA a
. Tính th tích ca khi chóp
.S ABC
.
A.
3
2
3
a
V
B.
3
3
12
a
V
C.
3
3
3
a
V
D.
3
3
4
a
V
.
Lờigiải
Chọn B
Di
2
3
4
ABC
a
BS
Chiu cao:
ha
23
' ' '
1 1 3 3
..
3 3 4 12
ABCA B C
aa
V B h a
Câu 13. 
.S ABC
có
SA

ABC

ABC

A
,
2BC a

SB
và
ABC
là
30

.S ABC
.
A.
3
6
9
a
. B.
3
6
3
a
. C.
3
3
3
a
. D.
3
2
4
a
.
Lời giải
Chọn A
a
V
Trang7
Ta có
AB
là hình chiu ca
SB
lên
ABC
suy ra góc gia
SB
và
ABC
là góc
30SBA 
.
Tam giác
ABC
vuông cân ti
A
,
2BC a
2AB AC a
.
Xét
SAB
vuông ti
A
có
36
.tan30 2.
33
a
SA AB a
.
Ta có
22
1
2
ABC
S AB a
. Vy
3
2
.
1 1 6 6
. . . .
3 3 3 9
S ABC ABC
aa
V SAS a 
.
Câu 14. Cho khi chóp
.S ABCD

ABCD
là hình ch nht,
AB a
,
3AD a
,
SA
vuông góc
vi mt pht phng
SBC
to vt góc
o
60
. Tính th tích
V
ca khi
chóp
.S ABCD
.
A.
3
3Va
. B.
3
3
3
a
V
. C.
3
Va
. D.
3
3
a
V
.
Lời giải
Chọn C
Ta có
2
. . 3 3
ABCD
S AB AD a a a
.
D thy
o
; 60BC AB BC SB SBA
.
Xét tam giác vuông
1SAB A v
có:
oo
tan60 tan60 3
SA
SA AB a
AB
Vy
23
.
11
. 3. 3
33
S ABCD ABCD
V S SA a a a
.
Câu 15. Cho hình chóp
.S ABC
có
SA a
và vuông góc v
ABC
. Bit rng tam giác
ABC
u
và mt phng
SBC
hp v
ABC
mt góc
30
. Tính th tích
V
ca khichóp
.S ABC
.
A.
3
3
3
a
V
. B.
3
2
3
a
V
. C.
3
3
12
a
V
. D.
3
3
a
V
.
Lời giải:
30
°
A
C
B
S
60
a
a
3
D
A
B
C
S
Trang8
Chọn A
Gi
I
m
,BC
ta có
30SIA 
Xét tam giác
SIA
vuông ti
A
ta có
3SA a AI a
Ta có
3
2.
2
AI AB AB a
Din tích
22
3
3
4
ABC
S AB a
Th tích
3
13
..
33
ABC
a
V SAS
Câu 16. 
.S ABC
có
SA

ABC

ABC

A
,
2BC a

SB
và
ABC
là
30

.S ABC
.
A.
3
6
9
a
. B.
3
6
3
a
. C.
3
3
3
a
. D.
3
2
4
a
.
Lời giải:
Chọn A
AB
là hình chiu ca
SB
lên
ABC
suy ra góc gia
SB
và
ABC
là góc
30SBA 
.
Tam giác
ABC
vuông cân ti
A
,
2BC a
2AB AC a
.
36
.tan30 2.
33
a
SA AB a
.
22
1
2
ABC
S AB a
.
3
2
.
1 1 6 6
. . . .
3 3 3 9
S ABC ABC
aa
V SAS a 
.
Câu 17. Cho hình chóp
.S ABC

ABC

2a
, tam giác
SAB


.S ABC
.
30
°
A
C
B
S
Trang9
A.
3
2
a
V
. B.
3
Va
. C.
3
3
2
a
V
. D.
3
3Va
.
Lời giải:
Chọn B

H

AB
.
SAB ABC
SAB ABC AB
SH ABC
SH AB
SH SAB


3
3
2
AB
SH a
,
2
2
3
3
4
ABC
AB
Sa
.
3
.
1
.
3
S ABC ABC
V SH S a
.
Câu 18. Cho hình chóp
.S ABCD

ABCD
là hình ch nht. Tam giác
SAB
u và nm trong mt
phng vuông góc vi mt ph
ABCD
. Bit
23SD a
và góc to bng thng
SC
và mt phng
ABCD
bng
0
30
. Tính th tích
V
ca khichóp
.S ABCD
.
A.
3
23
7
a
V
. B.
3
3
13
a
V
. C.
3
3
4
a
V
D.
3
46
3
a
V
Lời giải
ChọnD.
Ta có
23SC SD a
,
0
.sin 2 3.sin30 3SI SC SCI a a
,
0
.cos 2 3.cos30 3CI SC SCI a a
.
3
2
2
AB
SI AB a
.
2
2 2 2
3 2 2BC CI BI a a a
T 
2
. 2 .2 2 4 2
ABCD
S AB BC a a a
Vy
3
2
.
1 1 4 6
. . .4 2. 3
3 3 3
S ABCD ABCD
a
V S SI a a
.
Trang10
Câu 19. Cho hình chóp
.S ABCD
 
A
và
B
,
AB BC a
,
2AD a
.

S

ABCD

AB

5SC a
.
Tính theo
a

V

.S ABCD
.
A.
3
5
4
a
V
B.
3
15
3
a
V
. C.
3
15
4
a
V
. D.
3
25
3
a
V
.
Lời giải
Chọn C.

M

AB
. Ta có:
22
5
2
a
MC BC MB
suy ra
15
2
a
SM
.
Nên
3
.
2
1 15 15
.
3 2 2 4
S ABCD
a a a
aa
V

.
Câu 20. Cho khi chóp u
.S ABC
có cng
a
và cnh bên bng
2a
. Tính th tích
V
ca khi chóp
.S ABC
A.
3
13
12
a
V
. B.
3
11
12
a
V
. C.
3
11
6
a
V
. D.
3
11
4
a
V
.
Lời giải
Chọn B.
u nên gi
I
m cnh
BC

AI
ng cao ca tam
nh lý Pitago ta có
2
2
3
42
aa
AI a
, và
2 2 3 3
3 3.2 3
aa
AO AI
.
Trong tam giác
SOA
vuông ti
O
ta có
2
2
11
4
3
3
aa
SO a
Vy th tích khi chóp
.S ABC
là
3
1 1 3 11 11
..
3 2 2 12
3
a a a
Va
.
Mức độ 2
Câu 1. Cho khi chóp
.S ABCD
nh
a
,
SA
vuông góc v
SC
to vi
mt phng
SAB
mt góc
0
30 .
Tính th tích
V
ca kh
A.
3
2
3
a
V
. B.
3
6
3
a
V
. C.
3
2
3
a
V
. D.
3
2Va
.
M
A
D
B
C
S
O
I
A
C
B
S
Trang11
Lờigiải
ChọnA
Ta có
0
; ; 30CB SAB SC SAB SC SB CSB


Suy ra
0
.cot30 3;SB BC a
22
2SA SB AB a
Th tích khi chóp :
3
12
.
33
ABCD
a
V S SA
.
Câu 2. Cho hình chóp
.S ABCD
c 
ABCD
là hình ch nht
AB a
,
2BC a
,
2SA a
,
SA
vuông góc vi mt phng
ABCD
. Tính th tích khi chóp
.S ABCD
tính theo
a
.
A.
3
8
3
a
B.
3
4
3
a
C.
3
6
3
a
D.
3
4a
Lời giải
Chọn B
Ta có
.
ABCD
S AB CD
2
2a
.
Th tích khi chóp
.S ABCD
là
.
1
.
3
S ABCD ABCD
V SA S
3
2
14
2 .2
33
a
aa
.
Câu 3. Cho hình chóp
.S ABC

ABC
vuông ti
C
,
5AB a
,
AC a
. Cnh bên
3SA a
và vuông góc vi mt phng
ABC
. Tính th tích khi chóp
.S ABC
.
A.
3
5
.
2
a
B.
3
.a
C.
3
3.a
D.
3
2.a
Lời giải
Chọn B.
Vì tam giác
ABC
vuông ti
C
nên
2 2 2 2
5 2 .BC AB AC a a a
2
11
. . .2 .
22
ABC
S AC BC a a a
23
.
11
. .3 .
33
S ABC ABC
V SA S a a a
 .
Câu 4. Cho hình chóp
.S ABCD

ABCD
là hình ch nht,
AB a
,
2BC a
ng thng
SA
vuông góc vi mt phng
ABCD
và
3SA a
. Th tích ca khi chóp
.S ABCD
bng
A.
3
2a
. B.
3
3a
. C.
3
6a
. D.
3
a
.
Trang12
Lời giải
Chọn A
Áp dng công thc tính th tích khi chóp ta có
.
1
. .2 .3
3
S ABCD
V a a a
3
2a
.
Câu 5. Cho hình chóp
.S ABC
có cnh bên
SA
vuông góc vi mt ph
ABC
. Bit
SA a
,
tam giác
ABC
là tam giác vuông cân ti
A
,
2AB a
. Tính theo
a
th tích
V
ca khi chóp
.S ABC
.
A.
3
2
a
V
B.
3
2Va
C.
3
6
a
V
D.
3
2
3
a
V
Lời giải
Chọn D
Ta có:
1
..
3
ABC
V SA S

11
. . .
32
SA AB AC
2
1
. . 2
6
aa
3
2
3
a
(dvtt).
Câu 6. Cho khi chóp tam giác
.S ABC
có
SA ABC
, tam giác
ABC
 dài
3
cnh là
5AB a
;
8BC a
;
7AC a
, góc gia
SB
và
ABC
là
45
. Tính th tích khi chóp
.S ABC
.
A.
3
50 3a
. B.
3
50 3
3
a
. C.
3
50
3
a
. D.
3
50 7
3
a
.
Lời giải
Chọn B
2a
a
3a
C
B
A
D
S
A
C
B
S
Trang13
Ta có na chu vi
ABC
là
10
2
AB AC BC
pa


.
Din tích
ABC
là
2
10 .5 .3 .2 10 3
ABC
S a a a a a

.
SA ABC
nên
SAB
vuông, cân ti
A
nên
5SA AB
.
Th tích khi chóp
.S ABC
là
.
1
.
3
S ABC ABC
V SA S
2
1
5 .10 3
3
aa
3
50 3
3
a
.
Câu 7. Cho hình chóp
.S ABC
có mt phng
SAC
vuông góc vi mt phng
ABC
,
SAB
là tam
u cnh
3a
,
3BC a
ng thng
SC
to vi mt phng
ABC
góc
60
. Th tích
ca khi chóp
.S ABC
bng
A.
3
3
3
a
. B.
3
6
2
a
. C.
3
6
6
a
. D.
3
26a
.
Lờigiải
ChọnC
Ta thy tam giác
ABC
cân ti
B
, gi
H
m ca
AB
suy ra
.BH AC
Do
SAC ABC
nên
BH SAC
.
Ta li có
BA BC BS
nên
B
thuc trng tròn ngoi tip tam giác
ABC
H
là tâm
ng tròn ngoi tip tam giác
SAC
SA SC
.
Do
AC
là hình chiu ca
SC
lên mt phng
ABC
0
60SCA
.
Ta có
0
.cot 60SC SA a
,
0
2
sin 60
SA
AC a
HC a
22
2BH BC HC a
.
.S ABC
V
1
.
3
SAC
BH S
1
..
6
BH SA SC
3
6
6
a
.
Câu 8. Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh
2a
, cnh
SB
vuông góc v
và mt phng
SAD
to vt góc
60
. Tính th tích khi chóp
.S ABCD
.
A.
3
33
4
a
V
. B.
3
33
8
a
V
. C.
3
83
3
a
V
. D.
3
43
3
a
V
.
Lời giải
Chọn C
60
o
A
C
B
S
H
Trang14
Ta có:
SB ABCD
SB AD
AD ABCD

mà
AD AB AD SA
.
,
,
SAD ABCD AD
AB AD AB ABCD
SA AD SA SAD


; ; 60SAD ABCD SA AB SAB
Ta có:
.tan60 2 3SB BD a

. Vy
3
2
1 1 8 3
. 2 3.4
3 3 3
ABCD
a
V SB S a a
.
Câu 9. 


.S ABCD

ABCD
 nh
a
, hai mt phng
SAB
và
SAD
cùng vuông góc vi mt phng
ABCD
;  ng thng
SC
 t phng
ABCD

60
. Tính theo
a
th 

.S ABCD
.
A.
3
3a
. B.
3
6
9
a
. C.
3
6
3
a
. D.
3
32a
.
Lờigiải
ChọnC
Ta có
SAB ABCD
SAD ABCD SA ABCD
SAB SAD SA

AC
là hình chiu vuông góc ca
SC
lên mt phng
ABCD
, 60SC ABCD SCA
Tam giác
SAC
vuông ti
A
có
.tan60 6SA AC a
.

3
2
1 1 6
. . . 6.
3 3 3
SABCD ABCD
a
V SAS a a
.
Câu 10. Cho hình chóp
.S ABCD

ABCD
là hình ch nht vi
AB a
,
3BC a
. Cnh bên
SA
vuông góc vng thng
SC
to vi mt phng
SAB
mt góc
30
. Tính th
Trang15
tích
V
ca khi chóp
.S ABCD
theo
a
.
A.
3
26
3
a
V
. B.
3
2
3
a
V
. C.
3
3Va
. D.
3
3
3
a
V
.
Lời giải
Chọn A
Ta có:
BC SA
BC SAB
BC AB

SB
là hình chiu ca
SC
lên mt phng
SAB
.
, , 30SC SAB SC SB CSB
.
Xét tam giác
SBC
vuông ti
B
có
tan30 3
BC
SB a
SB
.
Xét tam giác
SAB
vuông ti
A
có
22
22SA SB AB a
.
Mà
2
.3
ABCD
S AB BC a
.
Vy
3
1 2 6
.
33
ABCD
a
V S SA
.
Câu 11. Cho hình chóp  u
.S ABCD
có cng
a
và cnh bên to vi mt ph
mt góc
0
60
. Tính th tích
V
ca khi chóp
.S ABCD
.
A.
3
6
2
a
V
. B.
3
6
3
a
V
. C.
3
3
2
a
V
. D.
3
6
6
a
V
Lời giải
Chọn.D.
Ta có:
2
ABCD
Sa
.
Chiu cao
SO
:
0
26
.tan .tan60
22
aa
SO OB SBO
.
Vy
3
2
.
1 1 6 6
. . . .
3 3 2 6
S ABCD ABCD
aa
V S SO a
.
Câu 12. Cho hình chóp t giác u
.S ABCD
có cng
a
và mt bên to vi mt ph
mt góc
0
60
. Tính th tích
V
ca khi chóp
.S ABCD
.
Trang16
A.
3
6
2
a
V
. B.
3
6
3
a
V
. C.
3
3
2
a
V
. D.
3
6
6
a
V
Lời giải
ChọnD.
Ta có:
2
ABCD
Sa
.
Gi
M
m
BC
, góc gia mt bên
()SBC
và
()ABCD
là
SMO
Ta có
1
.
22
a
OM AB
Chiu cao
SO
:
0
3
.tan .tan60
22
aa
SO OB SBO
.
Vy
3
2
.
1 1 3 3
. . . .
3 3 2 6
S ABCD ABCD
aa
V S SO a
.
Câu 13.  
ABC.A B C
¢ ¢ ¢
i
A
,
2AB AC a
,
120CAB
, góc
gia
( )
A BC
¢
và
( )
ABC
là
45°
. Tính th  
A.
3
6
2
a
V
. B.
3
3
3
a
V
. C.
3
3
2
a
V
. D.
3
3Va
Lời giải
ChọnD.
Gi
M
m ca
BC
. Ta có
AM BC^
và
·
CAM 60=°
( do
ABCD
cân ti
A
)
c góc gia
( )
A BC
¢
và
( )
ABC
là
·
A MA 45
¢
=°
Ta có
·
ABC
1
S AB.AC.sinBAC
2
D
=
( )
2
1
. 2a sin120
2
=°
2
a3=
và
·
AM AC cosMAC=
2a.cos60=°
a=
;
·
AA AM.tan A MA a
¢¢
==
Vy
3
ABC
ABC.A B C
V AA .S a 3
¢ ¢ ¢
D
¢
==
 th tích).
Câu 14. Cho hình chóp tam giác u có cng
a
và cnh bên t
0
60
. Th tích ca
khng:
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
36
a
. D.
3
3
18
a
.
Lời giải
Trang17
Chọn A
Ta có:
2
3
4
ABC
a
S
. Gi
O
là trng tâm ca tam giác
ABC
, suy ra
SO ABC
.
Ta có
AO
là hình chiu ca
SA
lên mt phng
ABC
.
Suy ra
0
, , 60SA ABC SA AO SAO
. Xét tam giác
SAO
vuông ti
O
, ta có:
0
2 2 3
tan .tan .tan60 . . . 3
3 3 2
SO
SAO SO AO SAO AM a a
AO
.
Vy
23
.
1 1 3 3
. . .
3 3 4 12
S ABC ABC
aa
V S SO a
.
Câu 15.   u
.ABC ABC
. Mt phng
()A BC
¢
to vi mt phng
()ABC
mt góc
30°
và tam giác
A BC
¢
có din tích bng
2
8a
. Tính th tích kh
.ABC ABC
.
A.
3
2
12
a
V
. B.
3
83Va
. C.
3
8
6
a
V
. D.
3
2
4
a
V
.
Lời giải
Chọn B.
K ng cao
AM
ca tam giác
ABC

M
m ca
()BC BC A AM
¢
Þ^
Tam giác
'
A AM
vuông ti
A
nên góc
'A MA
là góc nhn.
Góc gia hai mt phng
( ' )A BC
và
()ABC
bng góc gia
AM
¢
và
AM
và bng góc
·
A MA
¢
,
bng
30°
Tam giác
ABC
là hình chiu vuông góc ca tam giác
A BC
¢
trên
()ABC
Suy ra
2
'
. os30 4 3
o
ABC A BC
S S c a==
.
t
0AB x=>
. Diu
ABC
theo
x
là
2
3
4
ABC
x
S =
.
Vy có
2
2
33
4 3 4 2 3
42
xx
a x a AM a= Û = Þ = =
60
M
O
A
C
B
S
Trang18
Tam giác
A MA
¢
vuông ti
A
,
1
.tan30 2 3. 2
3
o
AA AM a a
¢
= = =
.
Th tích c
.ABC A B C
là
23
. 2 .4 3 8 3
ABC
V AA S a a a
¢
= = =
.
Câu 16. Cho hình hp  nht
.ABCD A B C D
nh bên bng
4a
ng
chéo
5a
.Tính th tích hình hp ch nht này.
A.
3
3Va
. B.
3
9Va
. C.
3
Va
. D.
3
6Va
.
Lời giải
Chọn B.
2 2 2 2
' ' 9 3BD BD DD a BD a
ABCD là hình vuông
3
2
a
AB
ABCD
BS
2
9
4
a
Vy
3
. . ' 9
ABCD
V B h S AA a
Câu 17. Cho hình chóp
.S ABC

ABC
vuông ti
B
,
AB a
,
2AC a
. Hình chiu
vuông góc ca
S
lên
ABC
m
M
ca
AC
. Góc gia
SB
ng
60
. Th
tích
.S ABC
là bao nhiêu?
A.
3
3
2
a
. B.
3
2
a
. C.
3
4
a
. D.
3
2
12
a
.
Lời giải
Chọn B.
Din tích ABC :
2
13
.
22
ABC
S AB BC a

00
* 60 .tan60 3SBM SM MB a
Th tíchS.ABC :
3
.
1
.
32
S ABC ABC
a
V SM S

.
Câu 18. Cho hìnhchóp
.S ABCD

ABCD
là hình ch nht vi
2AB a
,
AD a
. Hình chiu ca
S
lên mt phng
ABCD
m
H
ca cnh
AB
ng thng
SC
to vt
góc
0
45
. Tính th tích
V
ca khi chóp
.S ABCD
.
5a
4a
D'
C'
B'
A'
D
C
B
A
Trang19
A.
3
22
3
a
V
. B.
3
3
a
V
. C.
3
2
3
a
V
. D.
3
3
2
a
V
Lời giải
ChọnA.
Ta có
2
2 . 2
ABCD
S a a a
.
Do
SC
to vt góc
0
45
nên
SH HC
.
Mà
2 2 2 2
2HC BH BC a a a
. Vy
3
2
1 1 2 2
. . .2 . 2
3 3 3
ABCD ABCD
a
V S SH a a
.
Câu 19. Cho khi chóp
.S ABCD

ABCD
là hình vuông cnh
2a
,
SAD
cân ti
S
và nm trong
mt phng vuông góc va
SBC
và mng
o
60
. Tính th tích
.S ABCD
bng:
A.
3
23
3
a
. B.
3
83
3
a
. C.
3
43
3
a
. D.
3
23a
.
Lời giải
Chọn B
Gi
H
m
AD
.
Ta có:
SAD ABCD
SAD ABCD AD SH ABCD
SH AD
.
ABCD
là hình vuông cnh
2a
nên
22
4
ABCD
S AB a
.
Tam giác
SBC
cân ti
S
SM BC
, mà
HM BC
góc gia mt phng
SBC
và mt
phng
ABCD
là góc ging thng
HM
,
SM
chính là góc
SMH
. Theo bài ra có
o
60SMH
.
o
2 .tan60 2 3SH a a
.
Vy th tích
.S ABCD
:
3
2
1 1 8 3
. .2 3.4
3 3 3
SABCD ABCD
a
V SH S a a
.
Câu 20. u
.S ABC
có cng
3a
, cnh bên bng
2a
. Tính th tích
Trang20
V
ca khi chóp
.S ABC
.
A.
3
3
4
a
V
. B.
3
33
2
a
V
. C.
3
33
4
a
V
. D.
3
3
4
a
V
.
Lời giải
Chọn D
Di
2
2
. 3 3
33
44
ABC
a
a
BS
;
3
33
AB a
AH a
Chiu cao:
2 2 2 2
43h SH SA AH a a a
23
.
1 1 3 3 3
. . 3
3 3 4 4
S ABC
aa
V B h a
Mức độ 3
Câu 1. Cho hình chóp
.S ABCD
nh
a
,
SA ABCD
,
SA a
. Gi
G
là trng
tâm tam giác
SCD
. Tính th tích khi chóp
.G ABCD
.
A.
3
1
6
a
. B.
3
1
12
a
. C.
3
2
17
a
. D.
3
1
9
a
.
Lời giải
Chọn D
Gi
,MN
lm ca
CD
và
SD
.
G
N
M
C
A
D
B
S
Trang21
Ta có
,
1
3
,
d G ABCD
GM
SM
d S ABCD

.
Ta có
3
.
1 1 1
, . . .
3 3 3 9
G ABCD ABCD ABCD
a
V d G ABCD S SA S
.
Câu 2. Cho hình chóp
.S ABC

ABC
vuông ti
B
,
AB a
,
2BC a
. Tam giác
SAB
cân ti
S
và nm trong mt phng vuông góc v i
G
là trng tâm tam giác
ABC
, mt phng
SAG
to vt góc
60
. Th tích khi t din
ACGS
bng
A.
3
6
36
a
V
B.
3
6
18
a
V
C.
3
3
27
a
V
D.
3
6
12
a
V
Lời giải
Chọn A
Ta có:
2
1
..
2
ABC
S AB BC a

2
1
33
ACG ABC
a
SS

.
Gi
H
m ca
AB
SH ABC
.
Gi
N
m ca
BC
,
I
m ca
AN
và
K
m ca
AI
.
Ta có
AB BN a
BI AN
HK AN
.
Do
AG SHK
nên góc gia
SAG

60SKH 
.
Ta có:
12
22
a
BI AN
12
24
a
HK BI
,
6
.tan60
4
a
SH SK
.
Vy
.ACGS S ACG
V V V
3
16
..
3 36
ACG
a
SH S

.
Câu 3. Cho hình chóp
.S ABC
có tam giác
ABC
vuông cân ti
B
,
2, AC a
mt phng
SAC
vuông góc vi m 
ABC
. Các mt bên
SAB
,
SBC
to vi m  ng
nhau và bng
60
. Tính theo
a
th tích
V
ca khi chóp
.S ABC
.
A.
3
3
2
a
V
B.
3
3
4
a
V
C.
3
3
6
a
V
D.
3
3
12
a
V
Lời giải
Chọn D
K
I
G
N
H
A
C
B
S
Trang22
Ta có:
SAC ABC
và
SAC ABC AC
.
Trong mt phng
SAC
, k
SH AC
thì
SH ABC
.
Gi
I
,
K
lt là hình chiu vuông góc ca
H
lên cnh
AB
và
AC
thì
,SAB ABC SIH
và
,SAC ABC SKH
.
Mà
60SIH SKH
nên
HI HK
t giác
BIHK
là hình vuông
H
m
cnh
AC
.
 giác
BIHK
là hình vuông cnh
2
a
và
3
.tan60
2
a
SH HI
.
Vy
1
.
3
SABC ABC
V S SH
2
3
2
1 3 3
..
3 2 4 12
SABC
a
aa
V
.
Câu 4. Hình chóp
.S ABCD

ABCD
là hình vuông cnh
,a
SAB
là tam giác cân ti
S
và nm
trong mt phng vuông góc v
ABCD
. Bit côsin ca góc to bi mt phng
SCD
và
ABCD
bng
2 17
17
. Th tích
V
ca khi chóp
.S ABCD
là
A.
3
13
6
a
V
. B.
3
17
6
a
V
. C.
3
17
2
a
V
. D.
3
13
2
a
V
.
Lờigiải
ChọnA
Gi
H
m
AB
SH ABCD
,
K
m
CD
CD SK
Ta có
,SCD ABCD
,SK HK SKH
.
cos
HK
SKH
SK
17
2
a
SK
13
2
a
SH
Trang23
Vy
1
..
3
ABCD
V SH S
2
1 13
..
32
a
a
3
13
6
a
.
Câu 5. Cho hình chóp
.S ABCD
v
ABCD
là hình thang vuông ti
A
và
D
 ca hình
thang là
CD
, cnh bên
15SC a
. Tam giác
SAD
u cnh
2a
và nm trong mt
phng vuông góc vi
H
m cnh
AD
, khong cách t
B
ti
mt phng
SHC
bng
26a
. Tính th tích
V
ca khi chóp
.S ABCD
?
A.
3
86Va
. B.
3
12 6Va
. C.
3
46Va
. D.
3
24 6Va
.
Lời giải
ChọnC
,
SAD ABCD AD
SH ABCD
SH AD SH SAD



Ta có
22
3SH SD DH a
,
2 2 2 2
15 3 2 3HC SC SH a a a
.
2 2 2 2
12 11CD HC HD a a a
.
Ta có
BF BC
BF SHC
BF SH

nên
, 2 6d B SHC BF a
.
2
11
. .2 3 .2 6 6 2
22
HBC
S BF HC a a a
t
AB x
nên
1
..
22
AHB
a
S AH AB x
;
2
1 11
.
22
CDH
a
S DH DC
1
11
2
ABCD
S CD AB AD a x a
.
AHB ABCD CDH BHC
S S S S
2
2
11
. 11 6 2 12 2 11
22
aa
x a x a a x a
.
2
11 12 2 11 12 2
ABCD
S a a a a
.
Vy
23
.
11
. . 3.12 2 4 6
33
S ABCD ABCD
V SH S a a a
.
Câu 6. Cho hình chóp
.S ABCD
 
ABCD
là hình thang vuông ti
A
và
D
; bit
2 , .AB AD a CD a
Góc gia hai mt phng
SBC
và
ABCD
bng
0
60 .
Gi
I
là
m ca
AD
, bit hai mt phng
SBI
và
SCI
cùng vuông góc vi mt phng
ABCD
. Tính th tích ca khi chóp
.S ABCD
.
A.
3
35
8
a
. B.
3
3 15
5
a
. C.
3
35
5
a
. D.
3
3 15
8
a
.
Lời giải
Chọn B
A
B
D
C
S
F
H
Trang24
.
c c thì do hai mt phng và cùng vuông góc vi
nên nên
SI
ng cao ca
.S ABCD
.
K ti
K
c . Ta v hình phng
ca m ta chc
CD
ng tng bình ca tam giác
.ABM
 . Ta có
.
 . .
Câu 7. Cho hình chóp
.S ABCD

ABCD
là hình vuông tâm
O
, mt bên
SAB
là tam giác
vuông cân ti
S
và nm trong mt phng vuông góc v  t th tích ca khi chóp
.S OCD
bng
3
3
a
. Tính khong cách
h
t
A
n mt phng
SBD
?
A.
26
3
a
h
. B.
3
3
a
h
. C.
23
3
a
h
. D.
23ha
.
Lời giải
Chọn A
.
Gi
x
 dài
AB
,k
SF AB
ti
F
, ta có
3
23
.OCD .ABCD
1 1 1
.SF 2 2
2 4 12 24 3
SS
xa
SF V V AB x x a
.
SBI
SCI
ABCD
SI ABCD
IK BC
; 60SKI SBC ABCD
M AD BC
22
4 ; 2 4 2 5; 3AM a BM a a a IM a
KMI AMB
33
.2
2 5 5
IM IK a a
IK a
BM AB
a
3 3 3
.tan60 . 3
55
aa
SI IK
3
1 3 3 1 3 15
. . 2 .2
3 2 5
5
aa
V a a a
Trang25
Do
F
m ca
AB
nên khong cách
h
t
A
n mt phng
SBD
gp
2
ln khong
cách
d
t
F
n mt phng
SBD
mà
sin 45
22
o
FB x
EF a
.
Tính
d
: k
;FE DB
FH SE
, ta chc
SH SBD
,
2 2 2 2 2 2
1 1 1 1 1 3 6
2 2 3
a
FH d
FH FE FS a a a
, vy
26
2.
3
a
hd
.
Câu 8. Cho hình chóp
.S ABCD

ABCD
là hình thang vuông ti
A
và
B
,
1
2
BC AD a
.
Tam giác
SAB
u và nm trong mt phng vuông góc va
SC
và mt phng
ABCD
bng
sao cho
15
tan
5
. Tính th tích khi chóp
.S ACD
theo
a
.
A.
3
.
2
S ACD
a
V
. B.
3
.
3
S ACD
a
V
. C.
3
.
2
6
S ACD
a
V
. D.
3
.
3
6
S ACD
a
V
.
Lời giải
Chọn D
Gi
H
m
AB
, t gi thit ta có:
SH ABCD
,
·
,SC ABCD SCH

.
t
AB x
, ta có:
2
2 2 2
4
x
HC BH BC a
,
2
2
15
.tan .
45
x
SH HC a
.
Mt khác
3
2
x
SH
. Vy ta có:
2
2
15 3
.
4 5 2
xx
a
xa
.
2
.
3
22
ABCD
AD BC AB
a
S

;
2
2
3
ACD ABCD
S S a
;
3
.
13
.
36
S ACD ACD
a
V SH S
.
Câu 9. 


.S ABCD
 ;
;2AB a AD a
. 

SAB


S
 . 
SC

ABCD

45
. 
M

SD
. 
a

d



M

SAC
.
A.
1513
89
a
d
. B.
2 1315
89
a
d
. C.
1315
89
a
d
. D.
2 1513
89
a
d
.
Lời giải
Chọn A
Trang26

H

AB
SH ABCD
.

BCH


B
, :
2
2
17
4
42
aa
CH a
.

SHC


H
, :
17 34
;
22
aa
SH SC
.

SAH


H
, :
22
17 3 2
4 4 2
aa
SA a
.

ABC


B
, :
22
45AC a a a
.
2
89
4
SAC
Sa
.

:
3
.
1 17
..
33
S ABCD ABCD
a
V V SH S
;
3
.
1 17
26
S ACD
a
VV
.
3
..
1 17
2 12
S ACM S ACD
a
VV
. 
2
.
1 89
. . .
3 12
S MAC SAC
V d S a d
1513
89
a
d
.
Câu 10. Cho hình chóp
.S ABCD

ABCD
là hình ch nht, tam giác
SAD
vuông ti
S
và nm
trong mt phng vuông góc vt
AB a
,
2SA SD
. Mt phng
SBC
to vi
t góc
o
60
. Th tích khi chóp
.S ABCD
là
A.
3
3
2
a
B.
3
5
2
a
C.
3
5a
D.
3
15
2
a
Lời giải
Chọn B
Gi
H
là hình chiu ca
S
lên cnh
AD
,
I
là hình chiu ca
H
lên cnh
BC
, ta có
SH ABCD
và
BC SHI
;SBC ABCD
SIH
o
60
. Suy ra
3SH a
.
Trong tam giác vuông
SAD
t
22SA SD x
nên t
.SA SD
SH
AD
ta có
2
3
5
x
a
.

15
2
a
x
. Suy ra
5AD x
53
2
a
.
a
I
B
C
A
D
S
H
Trang27
Th tích khi chóp
.S ABCD
là
1 5 3
. . 3
32
a
V a a
3
5
2
a
.
Câu 11. Cho hình chóp
.S ABCD

ABCD
là hình ch nht, mt bên
SAD
là tam giác vuông ti
S
. Hình chiu vuông góc ca
S
trên mt ph   m
H
thuc cnh
AD
sao cho
3HA HD=
. Bit rng
23SA a=
và
SC
to vt góc bng
30°
. Tính theo
a
th tích
V
ca khi chóp
.S ABCD
.
A.
3
86Va=
. B.
3
86
3
a
V =
. C.
3
82Va=
. D.
3
86
9
a
V =
.
Lời giải
Chọn B
22
. 3 3SH HD HA HD SH HD= = Þ =
Có:
22
tan 3
3 2 4
3
tan
SH
SDH
SA SA
DH
SD a DA SD SA a
SA
SD
SDH
SD
ì
ï
ï
==
ï
ï
ï
Þ = Þ = = Þ = + =
í
ï
ï
=
ï
ï
ï
î
.
1
4
DH DA a==
.
Tam giác
SHC
có
tan tan30 3
tan30
SH SH SH
SCH HC a
HC HC
= Þ ° = Þ = =
°
.
Tam giác
DHC
có
22
22DC DH HC a= + =
Vy
3
.
1 1 8 6
. . . 3 .4 .2 2
3 3 3
S ABCD
a
V SH AD DC a a a= = =
.
Câu 12. Cho hình chóp
.S ABC
u cnh
2a
,
90SAB SCB
. Gi
M
là trung
m ca
SA
. Bit khong cách t
A
n
MBC
bng
6
21
a
. Th tích ca kh
bng
A.
3
8 39
3
a
. B.
3
10 3
9
a
. C.
3
4 13
3
a
. D.
3
23a
.
Lời giải
Chọn A
Trang28
Trong mp
ABC
m
D
sao cho t giác
ABCD
vuông ti
A
và
C

AB AD
AB SD
AB SA

;
CB CD
CB SD
CB SC

Vy
SD ABCD
.
1
.
3
S ABC ABC
V SD S

Có tam giác
ABC
u cnh
2a
2
3
ABC
Sa


Gi
I
m
AC
vì tam giác
ABC
u,
ABCD
ni ting kính
BD
I BD AC BD
Gi
G
là trng tâm tam giác
ABC
và
N
m
BC
Vì tam giác
ABC
u 
D thy là hình thoi
Xét hình chóp  là hình thang vuông ti C, N.
Khong cách t n mt phng bng vì .
Trong mp gi
Trong mp k tia gi
Gi K là hình chiu ca G trên mt phng

Trong mp k ta có
M
G
B
I
D
A
C
S
N
SD
AN BC
// AN CD
// CG BD
AGCD
2 2 3 2 3
2
3 3 2 3
a
CD AG AN a
1
.S ANCD
ANCD
A
MNC
6
21
a
MNC MBC
S
F
P
M
E
D
A
C
N
H
ABCD
E CN AD
SAD
//At SD
P EM At
CMB
//AP SD AP CN
APN CN
AN CN


APN
AH PN
6
,
21
a
AH d A MCN
Trang29
Mà tam giác u cnh
T
D thy
Xét tam giác có nên (theo )
Xét tam giác có nên
T và ta có
Vy .
Câu 13. Cho hình chóp bit rng , , và .
Th tích khi chóp là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có , suy ra tam giác u .
Li có , suy ra tam giác vuông cân ti .
Mt khác, , , áp dnh lí cosin cho tam giác c:
.
Xét tam giác có suy ra tam giác vuông ti .
Vy din tích tam giác là: .
Gi m ca cnh suy ra ng tròn ngoi tip tam giác .
Mà .
Xét tam giác vuông vuông ti có .
Vy th tích khi chóp là: .
Câu 14. Cho hình chóp có . Các mt bên to v
. Tính th tích khi chóp . Bit hình chiu vuông góc ca trên thuc min
trong ca tam giác .
A. . B. . C. . D. .
Lời giải
ABC
2a
3AN a
2 2 2
1 1 1
AH AP AN

2 2 2 2
1 21 1 1
36 3 4AP a a a
2AP a
APM SFM
2SF AP a
2
EAN
//CD AN
2
3
ED CD
EA AN

1
EAP
//FD PA
FD ED
PA EA
24
33
FD a
FD
PA
3
2
3
10
3
a
SD SF FD
3
2
.
1 1 10 10 3
. . . 3
3 3 3 9
S ABC ABC
aa
V SD S a
.S ABC
SA SB SC a
120ASB 
60BSC 
90ASC 
.S ABC
3
2
12
a
3
2
6
a
3
3
4
a
3
3
8
a
SB SC a
60BSC 
BSC
BC a
SA SC a
90ASC 
ASC
S
2AC a
SA SB a
120ASB 
ASB
2 2 2 2
2 . . 3 3AB SA SB SASBcosASB a AB a
ABC
2 2 2 2 2 2
23BC AC a a a AB
ABC
C
ABC
2
12
.
22
ABC
a
S AC BC

O
AB
O
ABC
SA SB SC
SO ABC
ASO
O
2
2 2 2
3
22
aa
SO SA AO a




.S ABC
23
.
1 1 2 2
. . . .
3 3 2 2 12
S ABC ABC
a a a
V S SO
.S ABC
7,AB cm
8,BC cm
9AC cm
30
.S ABC
S
ABC
ABC
3
20 3
3
cm
3
20 3 cm
3
63 3
2
cm
3
72 3 cm
Trang30
Chọn A
Ta có .
Din tích tam giác là
Gi là hình chiu vuông góc ca trên .
Gi là hình chiu vuông góc ca trên , .
Theo bài ra ta có .
Ta có vì
,
chung,
.
Suy ra .
Vy ng tròn ni tip tam giác .
 .
.
Th tích khi chóp là .
Câu 15. Cho hình chóp có , , , . Tính th
tích khi chóp
A. . B. . C. . D. .
Lời giải
Chọn C
12
2
AB BC AC
p cm


ABC
2
12 5S p p AB p AC p BC cm
H
S
ABC
,K
,N
M
H
,AB
BC
CA
30SKH SNH SMH
SKH SNH SMH
90SHK SHN SHM
SH
30SKH SNH SMH
KH NH MH
H
ABC
5
ABC
S
KH NH MH cm
p
15
tan30
3
SH HK cm
.S ABC
3
1 1 15 20 3
. .12 5.
3 3 3 3
ABC
V SH S cm
.S ABC
4AB AC==
2BC =
43SA =
30SAB SAC==º
..S ABC
.
8
S ABC
V =
.
6
S ABC
V =
.
4
S ABC
V =
.
12
S ABC
V =
Trang31
Gi m ca cnh . Vì cân ti (do ) nên .
; .
nên . Gi là hình chiu vuông góc cm trên
mt phng suy ra .
Áp dnh lí cosin cho , ta có: .
vuông ti nên .
Áp dnh lí cosin cho , ta có .
.
.
Vy .
Cách 2:
Áp dnh lí cosin cho , ta có
.
S dng công thc
.
Câu 16. Cho hình chóp  là hình thoi cnh , , gm
và . Hình chiu vuông góc ca S lên mt phng là sao cho là trung
m ca . Góc gia và bng . Tính th tích ca khi chóp .
A. . B. . C. . D. .
Lời giải
M
BC
ABCD
A
4AB AC==
AM BC^
22
15AM AC MC= - =
1
. 15
2
ABC
S AM BC
D
==
( )
SAB SAC c g cD = D - -
SB SC=
H
S
( )
ABC
H AMÎ
SABD
2 2 2
2 . .cos30 16 4SB SA AB SA AB SB= + - ° = Þ =
SMBD
M
22
15SM SB MB= - =
SAMD
2 2 2
3
cos
2. . 5
SM AM SA
SMA
SM AM
+-
= = -
2
4
sin 1 cos
5
SMA SMAÞ = - =
4 4 15
.sin 15.
55
SH SM SMAÞ = = =
.
1 1 4 15
. . 15. 4
3 3 5
S ABC ABC
V S SH
D
= = =
ABCD
2 2 2
7
cos
2 . 8
AB AC BC
A
AB AC
+-
==
2 2 2
1 cos cos cos 2cos cos cos
6
abc
V
= - - - +
2
22
. . 7 7
1 cos 30 cos 30 2cos30 .cos30 . 4
6 8 8
AB AC SA
V
æö
÷
ç
Þ = - °- °- + ° ° =
÷
ç
÷
ç
èø
.S ABCD
ABCD
x
60BAD =°
AC
BD
()ABCD
H
H
BI
SC
()ABCD
45°
V
.S ABCD
3
39
12
x
V =
3
39
36
x
V =
3
39
24
x
V =
3
39
48
x
V =
Trang32
Chọn C
Tam giác u cnh
Áp dnh lí cosin cho tam giác
Xét tam giác vuông ti :
Do tam giác vuông ti , có nên tam giác vuông cân
ti . Suy ra:
Vy th tích khi chóp :
Câu 17. Cho hình chóp  u cnh , khong cách t m n mt
phng là , khong cách gia và là . Bit hình chiu ca lên mt
phng nm trong tam giác , tính th tích khi chóp .
A. . B. . C. . D. .
Lời giải
Chọn D
Dng hình bình hành . Gi là hình chiu vuông góc ca lên mt phng .
Dng thng  , vuông góc vi và ct lt ti .
 .
Trong , dng và .
Ta có và nên .
Vì vy .
ABD
x
Þ
4
x
BD x IH= Þ =
22
3
: 2 . . os120 3
2
x
ABC AC x x x xc x IC= + - ° = Þ =
IHC
I
22
22
3 13
16 4 4
x x x
HC IH IC= + = + =
SHC
H
( )
( )
, 45SCH SC ABCD= = °
SHC
H
13
4
x
HC SH==
.S ABCD
3
.
1 1 1 13 39
. . . . . 3. .
3 2 6 4 24
S ABCD
xx
V AC BD SH x x= = =
.S ABC
ABC
a
A
()SBC
15
5
a
SA
BC
15
5
a
S
()ABC
ABC
.S ABC
3
4
a
3
3
8
a
3
8
a
3
3
4
a
ABCD
O
S
()ABCD
d
O
BC
,BC AD
,HM
, ( )AD BC SHM^
SHMD
()HK SM K SM^Î
()MN SH N SH^Î
MN SH^
MN BC^
()MN SBC^
15
( ,( )) ( ,( ))
5
a
MN d M SBC d A SBC= = =
Trang33
Do nên . Suy ra .
Do ng cao nên cân ti . Suy ra m ca .
Ta có (do u, cnh bng ). Suy ra
.
ng dng và , ta có
.
Vy th tích khi chóp là .
Câu 18.     ng   là tam giác vuông cân ti , cnh
. Góc gia mt phng và mt phng bng . Tính th tích
khn .
A. B. C. D.
Hƣớng dẫn giải
Chọn D
Gi m , ta có và (trung tuyn trong
tam giác vuông bng na cnh huyn).
K mà suy ra
Vy góc gia mt phng và mt phng là .
Ta có ;
Mt khác .
Câu 19. Cho hình chóp có là hình thoi cnh và . Bit rng ,
và . là trng tâm tam giác . Tính th tích ca t din
( )
//BC SAD
( , ) ( ,( )) ( ,( ))d BC SA d BC SAD d H SAD HK= = =
15
5
a
HK =
SHMD
MN HK=
S
O
MH
3
( , ) ( , )
2
a
MH d AD BC d A BC= = =
ABCD
a
3
4
a
MO =
MKH
MOS
22
3 15
.3
45
2
3 15
25
aa
KH MK MO KH a
SO
SO MO MK
aa
´
= Þ = = =
æ ö æ ö
÷÷
çç
÷÷
-
çç
÷÷
çç
÷÷
çç
è ø è ø
.S ABC
23
1 1 3 3
332 48
ABC
a a a
V SO S
D
= ´ = ´ ´ =
.ABC AB C
ABC
A
6BC a
AB C
BCC B

60
ABCAC
3
3
3
a
3
33
2
a
3
3
2
a
3
3a
I
a
6
C'
B'
A'
C
B
A
a
6
2
a
6
H
I
B'
B
C'
C
A
a
I
BC
AI BC
AI BB C C
AI CC


6
2
a
AI
IH BC
AI B C
AH B C
AB C
BCC B

60AHI 
2
tan60 2
AI a
IH 
22
CH CI IH a
CIH CB B

IH CH
B B CB

.
3
IH CB
BB a
CH
3
1 1 6
. . . . 3. 6 3
3 3 2
AB CA C ABB C C BCC B
a
V V AI S a a a
.S ABCD
ABCD
a
60ABC
SA SC
SB SD
SAB SBC
G
SAD
V
Trang34
.
A. B. C. D.
Hƣớng dẫn giải
Chn B
Ta có .
* Tính ?
Gi , do .
K , do nên .
Suy ra .
Do và là trung tuyn nên tam giác vuông cân ti .
 và .
Mà tam giác vuông ti ng cao nên .
Vy .
* Tính ?
Gi m ca thì .
Gi m ca thì .
Suy ra .
Vy .
Câu 20. Cho hình chóp  là hình vuông cnh , và vuông góc vi
i m , m thuc cnh sao cho . Tính th tích
ca khi t din .
GSAC
3
2
96
a
V
3
2
48
a
V
3
2
24
a
V
3
2
12
a
V
1
,.
3
GSAC SAC
V d G SAC S
SAC
S
O AC BD
SA SC SO AC
SO ABCD
SB SD SO BD

OH SB
AC SBD
SB AHC
, , 90SAB SBC AH CH AHC
OH AC
OH
AHC
H
1
22
a
OH AC
3
2
a
OB
SOB
O
OH
2 2 2
1 1 1 6
4
a
SO
OH OS OB
2
1 1 6 6
. . . .
2 2 4 8
SAC
aa
S SO AC a
,d E SAC
E
AD
,2
3
,
d G SAC SG
SE
d E SAC

F
OA
EF SAC
13
,
24
a
d E SAC EF OD
2 2 3 3
, , .
3 3 4 6
aa
d G SAC d E SAC
23
.
1 1 3 6 2
, . . .
3 3 6 8 48
G SAC SAC
a a a
V d G SAC S
.S ABCD
ABCD
a
SA a
SA
M
SB
N
SD
2SN ND
V
ACMN
Trang35
A. . B. . C. . D.
Hƣớng dẫn giải
Chọn D
Cách1. Ta có
Suy ra .
Mt khác
Vy .
Cách2. Gi m ca và .
Ta có . Vì nên .

.
Câu 21.   ng, góc bng . Góc gia
ng thng và mt phng bng . Tính th  
A. . B. . C. . D. .
Lời giải
Chọn B.
3
1
36
Va
3
1
6
Va
3
1
8
Va
3
1
12
Va
3
.
1
.
33
S ABCD ABCD
a
V SA S
3
2
1 1 1 1
. . .
3 3 3 2 18
NDAC DAC
a
V NH S a a



3
2
1 1 1
. . .
3 3 2 2 12
MABC ABC
aa
V MK S a



3
1
,.
3 18
SMN
a
d A SMN S
3
1 1 2 1
. . . .
3 3 3 2 2 18
NSAM SAM
aa
V NL S a a



3
.
11
, . , .
3 3 18
C SMN SMN SMN
a
V d C SMN S d A SMN S

.ACMN S ABCD NSAM NADC MABC SCMN
V V V V V V
33333
3
1
3 18 18 12 18 12
aaaaa
a
O
AC
BD
3
.
1
.
33
S ABCD ABCD
a
V SA S
//OM SD
//SD AMC
; ; ;d N AMC d D AMC d B AMC
3
. . . . .
1
4 12
ACMN N MAC D MAC B MAC M BAC S ABCD
a
V V V V V V
.ABC A B C
,2AC a BC a==
·
ACB
120
o
AC
¢
()ABB A
¢¢
30
o
3
13
12
a
V
3
105
14
a
V
3
104
6
a
V
3
105
4
a
V
Trang36
K   ng nên 
.
Góc gia và bng góc và bng (tam giác vuông ti nên
góc nhn)
Xét tam giác , áp dnh lý cosin cho cnh có:
.
.
Mt khác

Xét tam giác vuông ti nên
Xét tam giác vuông ti nên
Th tích c là .
Câu 22. Cho hình chóp  là tam giác vuông ti .Bit vuông góc vi mt phng
, . Mt mt phng qua vuông góc ti và ct
ti . Tính th tích khi chóp theo .
A. . B. . C. . D. .
Lời giải
Chọn B.
Ta có , suy ra
Vì vuông cân ti nên m ca
.Ta có:
C K A B
¢ ¢ ¢
^
.ABC A B C
C K AA
¢¢
^
()C K ABB A
¢ ¢ ¢
^
AC
¢
()ABB A
¢¢
·
C AK
¢
30°
C AK
¢
K
'C AK
ABC
AB
2 2 2 2 2 2
2. . .cos120 7 7
o
AB AC BC AB AC a A B a
¢¢
= + - = Þ =
2
1 1 3
. .sin .2 .sin120
2 2 2
o
ABC
ABC
a
S S CACB ACB a a
¢ ¢ ¢
= = = =
11
. . 7
22
ABC
S C K A B C K a
¢ ¢ ¢
¢ ¢ ¢ ¢
==
2
1 3 3
.7
22
7
aa
C K a C K
¢¢
= Û =
'AKC
K
3
.cot30 . 3
7
o
a
AK C K C K
¢¢
= = =
''A C K
K
2
2 2 2
22
32
7
7
5
7
aa
A K A C KC a
a
AA AK A K
¢ ¢ ¢ ¢
= - = - =
¢¢
Þ = - =
.ABC A B C
23
5 3 105
..
2 14
7
ABC
a a a
V AA S
¢
= = =
.S ABC
ABC
B
SA
ABC
, 3,AB a BC a SA a
A
SC
H
SB
K
.S AHK
a
3
.AHK
3
20
S
a
V
3
.
3
30
S AHK
a
V
3
.
3
60
S AHK
a
V
3
.
3
90
S AHK
a
V
AK SC AK
AK BC BC SAB


AK SBC AK SB
SAB
A
K
SB
A
B
C
S
K
H
Trang37
. Ta có

, li có
Vy .
Câu 23. Cho hình chóp  nh . Hình chiu
vuông góc ca lên mt phng m ca . Mt phng hp vi
mt pht góc bng . Tính th tích khi chóp .
A. B. C. D.
Lời giải
Chọn D.
Góc gia   .
có .

Câu 24. Cho hình chóp  là tam giác vuông cân ti , có ; Mt bên
vuông góc vt bên còn lu to vi mt góc 45
0
. Tính th tích khi
chóp .
A. . B. . C. . D. .
Lời giải
Chọn A
.
.
..
. . 2
S AHK
S ABC
V
SASK SH SH
V SASB SC SC

22
2AC AB BC a
22
5SC AC SA a
2
22
.SC 1
5
SH SH SA
SC SC SC
.
.
1
2 10
S AHK
S ABC
V
SH
V SC
3
.
1 1 3
. . .
3 2 6
S ABC
a
V SA AB BC
3
.
3
60
S AHK
a
V
.S ABC
ABC
,A AB AC a
S
ABC
H
BC
SAB
60
.S ABC
3
2
.
12
a
V
3
3
.
4
a
V
3
3
.
6
a
V
3
3
.
12
a
V
SAB
SKH
60SKH
23
.
3 3 3 3
.
4 2 8
ABC A B C
a a a
V

0
3
.tan60
2
a
SH KH
3
13
. . ... .
3 12
ABC
a
V SH S
.S ABC
ABC
B
BC a
SAC
SABC
3
12
a
3
a
3
6
a
3
24
a
S
B
C
A
K
H
Trang38
Gi là hình chiu vuông góc ca lên cnh nên .
Gi , lt là hình chiu vuông góc ca lên cnh và o bi
hai mt phng , to vt là , cùng bng .
Hai tam giác , có , , nên hai tam
giác bng nhau hay . Mà là tam giác vuông cân nên m ca .
Ta có: . Vy .
Câu 25. Cho hình chóp  là hình ch nht, mt bên u cnh
và nm trong mt phng vuông góc vi mt phng . Góc gia mt phng
và mt phng là . Th tích ca khi chóp là:
A. . B. . C. . D. .
Lời giải
Chọn A
+) Gi lm ca (vì u).
Gi m ca (vì và vuông góc vi nhau).
Suy ra
+) Tam giác cân ti , mà góc gia mt phng và
mt phng là góc ging thng chính là góc . Theo bài ra
có .
+) Vì u cnh nên ta có .
. Vy th tích ca ca khi chóp là
.
Câu 26. Cho hình chóp  là tam giác vuông ti , , . Hình
chiu cm trên mt phng trùng vm cn thng . Bit rng
góc gia mt phng và mt phng bng . Th tích ca khi chóp là
A. . B. . C. . D. .
Lời giải
Chọn D
H
S
AC
SH ABC
E
F
H
AB
AC
SAB
SAC
SEH
SFH
45
SEH
SFH
90SHE SHF
chungSH
45HSE HSF
HE HF
ABC
H
AC
22
BC a
SH HE
23
.
11
. . .
3 3 2 2 12
S ABC ABC
a a a
V S SH
.S ABCD
ABCD
SAD
2a
ABCD
SBC
ABCD
0
30
.S ABCD
3
23
3
a
3
3
2
a
3
43
3
a
3
23a
30
°
M
H
A
D
B
C
S
H
AD
SH AD
SAD
M
BC
HM SH
SAD
ABCD
SH ABCD
SBC
S
SM BC
HM BC
SBC
ABCD
,HM SM
SMH
0
30SMH
SAD
2a
3SH a
0
3
tan30
a
HM a
2
.2
ABCD
S AB AD a
.S ABCD
3
2
1 1 2 3
. . . 3.2
3 3 3
ABCD ABCD
a
V SH S a a
.S ABC
ABC
A
2AB a
5AC a
S
ABC
BC
SAB
ASC
60
.S ABC
3
56
12
a
3
5 10
12
a
3
210
24
a
3
30
12
a
Trang39
, k và ,
suy ra .
t c và .
Vy ,
Tam giác vuông ti có
Vy .
Câu 27. Cho hình chóp có , , và , , .
 là
A. . B. . C. . D. .
Lời giải
Chọn B
Ly m ca và ly sao cho . Ta có nên
hình chiu vuông góc ca lên trùng vi tâm cng tròn ngoi tip tam giác
.
Ta có: vì tam giác u (cân ti và có mt góc bng )
vì là cnh huyn ca tam giác vuông có cnh góc vuông bng 1.
()SAB SAC SA
BE SA
GH BE
, , 60SAC SAB GH SAC HGI
SH h
2
2
7
4
a
SA h
2
2
5
4
a
SP h
2
2
2
2
5
2.
2
4
2
7
4
SAB
a
ah
S
BE
BE HG
SA
a
h
2
2
2
.
.
2
2
a
h
SH HM
HI
SM
a
h

GIH
I
2
2
24
42
22
22
25
2
.
.
3 7 15 2 3
24
2
sin60 . 0
2 4 8 4
7
42
aa
a
h
h
IH a a a
h h h
HG
aa
hh

3
1 30
..
6 12
SABC
a
V AB AC SH
.S ABC
60ASB 
90ASC 
120CSB 
1SA
2SB
3SC
.S ABC
2
4
2
2
2
2
6
M
SB
N SC
1SN
1SA SM SN
S
AMN
O
AMN
1AM
SAM
S
60
2AN
SAN
S
A
B
C
M
N
O
Trang40
D c tam giác vuông ti nên có
Suy ra
Suy ra
Áp dng công thc t s th tích ta có suy ra
Câu 28.  có và  , 
và .  và  và . 
 .
A. . B. . C. . D. .
Lời giải
Chọn D
 
Ta có:
 .
Câu 29. Cho hình chóp tam giác có   m ,  m trên sao cho
m trên sao cho . Kí hiu , lt là th tích khi chóp
và . Tính t s .
A. . B. . C. . D. .
Lời giải.
Chọn A
22
2 . .cos120 3MN SM SN SM SN
AMN
A
2
2
AMN
S
. . 2. 3 3
4. 2
2
4.
2
AMN
AM AN MN
OA
S
22
31
1
42
SO SA AO
.
1 1 2 2
..
3 2 2 12
S AMN
V 
.
.
1 1 1
1 2 3
S AMN
S ABC
V
V
..
2
6.
2
S ABC S AMN
VV
ABCD
2AB CD a
2AC a
M
N
AB
CD
MN a
MN
AB
CD
ABCD
3
6
2
a
3
6
3
a
3
3
2
a
3
3
3
a
ABCD
22
AE AC DE a
22
3BC AB AE a
3
1 1 3
. . . 3
3 3 3
ABCD
a
V V a a a
.S ABC
M
SB
N
SC
S2N NC
SA
2PA PS
1
V
2
V
BMNP
.S ABC
1
2
V
V
1
2
1
9
V
V
1
2
3
4
V
V
1
2
2
3
V
V
1
2
1
3
V
V
Trang41
Ta có ;
Suy ra ; .
Câu 30. Cho hình chóp  Gi m i xng vi qua
Mt phng chia khi chóp thành hai phn có th tích lt là vi
Tính t s
A. . B. . C. . D.
Lời giải
ChọnA
Gi lt là chiu cao và dia khi chóp 
Ni ct ti , ct ti Tam giác có ln
m ca và suy ra là trng tâm tam giác T giác là
hình bình hành nên m
Ta có
.
.
1
,.
3
1
,.
3
BMP
N BMP
C SAB
SAB
d N SAB S
V
V
d C SAB S
,
2
3
,
d N SAB
NS
CS
d C SAB

.
.
1 1 1 2 1 1
. . .
2 2 3 3 6 9
N BMP
SBM BPS SAB
C SAB
V
S S S
V
..S ABCD
N
,SB
M
B
.A
MNC
.S ABCD
12
,VV
12
.VV
1
2
.
V
V
1
2
5
.
7
V
V
1
2
5
.
11
V
V
1
2
5
.
9
V
V
1
2
5
.
13
V
V
,hS
.S ABCD
.
1
..
3
S ABCD
V S h
MN
SA
E
MC
AD
.F
SBM
,AN
BM
SB
E
.SBM
ACDM
F
.MC
..
.
BNC AEF ABCEN E ACF
V V V
.
..
.
2 1 1 1
.
3 2 3 3
S ENC
S ENC S ABC
S ABC
V
SE SN
VV
V SA SB

. . .
2 2 1 1
.
3 3 2 3
ABCEN S ABC S ABCD S ABCD
V V V V




F
E
M
N
S
A
C
B
D
Trang42

Suy ra
Mức độ 4
Câu 1. Cho hình chóp  u cnh , bit khong cách t n
là , t n là , t n là và hình chiu vuông góc ca
xum trong tam giác . Tính th tích khi chóp .
A. B. C. D.
Lời giải
ChọnB
Gi lt là hình chiu ca lên các cnh .
t .
Ta có
c
Ta có
Vy .
Câu 2. Cho hình chóp  là hình vuông cnh . Tam giác vuông ti
và nm trong mt phng vuông góc vi là góc to bng thng và mt
phng , vi . Tìm giá tr ln nht ca th tích khi chóp .
A. B. C. D.
Lời giải
Chọn C
..
1 1 1 1 1
. , . . .
3 3 4 3 12
E ACF ACF S ABCD
V S d E ACF S h V


. . . . . 1
1 1 5
.
3 12 12
BNC AEF ABCEN E ACF S ABCD S ABCD S ABCD
V V V V V V V
1
2.
2
75
.
12 7
S ABCD
V
VV
V
.S ABC
ABC
1
A
SBC
6
4
B
SCA
15
10
C
SAB
30
20
S
ABC
.S ABC
V
1
36
1
48
1
12
1
24
,,M N P
H
,,AC BC AB
.
1 3 3
..
3 4 12
S ABC
h
SH h V h
.
26
3 30
2 : 10
2 20
;
SAB S ABC
SAB
SV
h
AP S h
AB
d C SAB
2,HM h HN h
22
3PH SP SH h
1
2
ABC HAB HAC HBC
S S S S HP HM HN
33
3
4 12
hh
.
3 3 1
.
12 12 48
S ABC
V 
.S ABCD
ABCD
2a
SAB
S
SD
SBC
45

.S ABCD
3
4a
3
8
3
a
3
4
3
a
3
2
3
a
Trang43
Gi nh th a hình bình hành .
 mà (vì , ) nên là hình chiu vuông góc
ca lên .
Góc gia và là  .
t , .
Gi là hình chiu ca lên  ta có .
 t giá tr ln nht khi ln nht. Vì tam giác vuông ti nên
T  khi .
Suy ra .
Câu 3. Xét t din có các cnh và , i. Giá tr ln
nht ca th tích t din bng
A. . B. . C. . D. .
Lời giải
Chọn B
Gi , lm và .
Theo gi thit ta có: và là các tam giác cân có m ca nên
và . Và có cân ti.
H
D'
D
B
C
A
S
D
SADD
DD SA
//
SA SBC
SA SB
SA BC
D
D
SBC
SD
SBC
DSD SDA

.tan 2 .tanSA AD a


tan x
0;1x
H
S
AB
2
.
11
. . 4 .
33
S ABC ABC
V S SH a SH
DD
.S ABCD
V
SH
SAB
S
.SA SB
SH
AB
22
.SA AB SA
AB
2 2 2
2 4 4
2
ax a a x
a
2
21ax x
22
1
2
2
xx
aa


maxSH a
2
tan
2
23
.
14
max . .4
33
S ABCD
V a a a
ABCD
2AC CD DB BA
AD
BC
ABCD
16 3
9
32 3
27
16 3
27
32 3
9
N
M
A
B
C
D
M
N
AD
BC
ABD
ACD
M
AD
BM AD
CM AD
AD BMC
BM CM
MBC
Trang44
Trong tam giác có vng cao va là trung tuyn nên
.
n tích tam giác là:
Th tích t din là: .
t , ta có:
.
Ta có: .
 . Du bng xy ra khi .
Ta li có:
.
Du bng xy ra khi .
Vy giá tr ln nht ca th tích t din là: tnh
.
Câu 4. u có cng . Gi lm
ca Tính th tích khi chóp . Bit mt phng vuông góc vi mt
phng .
A. . B. . C. . D. .
Lời giải
Chọn B
m nên
.
SE va là trung tuyn vng cao nên cân ti
MBC
MN
2
22
4
BC
MN MB
22
22
44
AD BC
MN AB
22
4
4
AD BC
MN
MBC
1
.
2
MBC
S MN BC
22
1
.4
24
AD BC
BC

ABCD
1
..
3
ABCD MBC
V AD S
22
1
. . . 4
34
AD BC
BC AD

AD x
BC y
22
1
. . . 4
34
ABCD
xy
V x y

22
2x y xy
22
42
x y xy

22
42
x y xy
1
. . . 4
32
ABCD
xy
V x y
2
2
8
6
ABCD
V xy xy
xy
2
8xy xy
4. . . 8
22
xy xy
xy
3
8
22
4.
3
xy xy
xy





3
4.8
27
8
2
xy
xy
16
3
xy
4
3
xy
ABCD
3
m
2
ax
4.8
6 27
ABCD
V
32 3
27
.S ABC
3a
,MN
,SB BC
.ABCNM
AMN
SBC
3
15
32
a
3
3 15
32
a
3
3 15
16
a
3
3 15
48
a
E
BC
,CB AE CB SH
CB SAE CB SE
SBC
S
Trang45
m ca vi .
Gi thit
và nên cân ti
.
.
Vy .
Câu 5. Cho hình chóp có , và khong cách t
n mt phng bng . Tính th tích khi .
A. . B. . C. . D. .
Lời giải
Chọn B
H ti có
.
Ch có .
Hai tam giác vuông và bng nhau suy ra .
Gi m ca suy ra t giác là hình thoi và .
Gi là tâm hình thoi có
.
.
H ti ta có ti suy ra .
F
MN
SE
1
,
2
SF MN SF SE
SF MN
AMN SBC
SF AMN
AMN SBC MN


SE AF
1
2
SF SE
SAE
3
2
a
A AE AS
22
2 2 3 5
.
3 3 2 2
aa
AH AE a SH SA AH 
3
2
.
1 1 3 5 15
. . 3 .
3 3 4 2 8
S ABC ABC
aa
V S SH a
3
.
.
.
1 15
.
4 32
S AMN
S AMN
S ABC
V
SM SN a
V
V SB SC

3
..
3 15
32
S ABC S AMN
a
V V V
.S ABC
0
, 120AB BC a ABC
0
90SAB SCB
B
SAC
2 21
21
a
.S ABC
3
5
10
a
V =
3
15
10
a
V =
3
15
5
a
V =
3
5
2
a
V =
a
a
I
E
D
I
D
S
E
B
C
B
A
S
K
SE ABC
E
0
90
AB SE
AB SAE AB AE BAE
AB SA
0
90BCE
BCE
BAE
0
60CBE ABE
D
BE
ABCD
BD DE a
I
ABCD
1 1 2 21 2 21
, , , 3.
3 3 21 7
aa
BI EI d B SAC d E SAC d E SAC
CA BD
CA SEI SAC SEI
CA SE
EK SI
K
EK SAC
K
2 21
,
7
a
d E SAC EK EK
Trang46
Tam giác vuông ti ng cao có
.
Vy .
Câu 6. Cho khi chóp i , , , .
Gi là góc gia hai mt phng và . Khi thì th tích kh
cho bng
A. . B. . C. . D. .
Lời giải
Chọn D
K suy ra và .
 .
Ch ta có suy ra t giác ni ting kính
 bng .
D thy nên u.
cân ti có suy ra .
 .
D thy nên .
Trong mt phng k .
Trong mt phng k .
Xét hai tam giác vuông và có , (vì )
suy ra mà và nm gia và nên .
T  và .
 .
t
Xét có .
Xét vuông ti có
.
SBE
E
EK
2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 7 4 5 6 5
12 9 36 5
a
SE
EK EI SE SE EK EI a a a
3
02
1 1 1 1 3 6 5 15
. . .sin120 . . .
3 3 2 6 2 5 10
SABC ABC
aa
V S SE BABC SE a



.S ABC
A
AB a
120BAC 
90SBA SCA
SAB
SAC
3
cos
4
3
3a
3
a
3
3
4
a
3
4
a
,SH ABC H ABC
SH AB
SH AC
SH AB
AB SBH AB BH
SB AB
AC CH
ABHC
AH
BHC
60
AHB AHC HB HC
HBC
ABC
A
, 120AB a BAC
22
3BC a
2 2 2 2
3HB HC BC a
SHB SHC SB SC
SAB SAC
SAB
,BK SA K SA
SAC
11
,CK SA K SA
KAB
1
K AC
AB AC
1
BAK CAK
SAB SAC
11
KAB K AC AK AK
K
1
K
S
A
1
KK
CK SA
BK CK
cos cos BKC
2 2 2
3
2 . 4
BK CK BC
BK CK


22
2
23
1
4
2
BK BC
BK

, 0 .SH x x
SHB
2 2 2 2 2
3SB SH HB a x
SAB
B
2 2 2
1 1 1
BK BA BS

2 2 2 2
1 1 1
3BK a a x
2 2 2
2
22
3
4
a a x
BK
ax

Trang47
Thay vào ta có .
Vy th tích khi chóp là .
Câu 7. Cho t diu có cnh bng , và lng trên hai cnh
( và không trùng vi ) sao cho mt phng luôn vuông góc vi mt
phng . Gi lt là th tích ln nht và nh nht ca t din . Tính
tích .
A. . B. . C. . D. .
Lời giải
Chọn C
K (vì ). Suy ra là trng tâm ca tam giác
u .
y và  ng tâm ca tam giác .
t , ( , )
+ .
+ (*)
+ (**)
 (***)
Mt khác t (*) và (**) suy ra , ( , ).
1
2 2 2
2
22
2 2 2
22
23
3
3
4
4
23
4
a a x
a
ax
a a x
ax
3xa
.S ABC
3
2
1 1 1 1
. . . . .sin . 3. . sin120
3 2 3 2 4
a
SH AB AC BAC a a
ABCD
1
M
N
,AB AC
M
N
A
DMN
ABC
12
,VV
ADMN
12
.VV
12
2
.
27
VV
12
2
.
24
VV
12
1
.
324
VV
12
8
.
9
VV
DH MN
DH ABC
DMN ABC
H
ABC
M
N
MN
ABC
,AM x AN y
01x
01y
2 2 2
12
1
33
DH DA AH
2
3
DH
13
. .sin
24
AMN
S AM AN MAN xy

AMN AMH ANH
S S S

1
. .sin30
2
AH x y
3
12
xy
1
.
3
ADMN AMN
V DH S
1 3 2 2
3 4 12
3
xy xy





3x y xy
01x
01y
Trang48
t u kin: .
 là nghim c , .
Ta tìm  có nghim phân bit thuc hoc có nghim kép thuc
Ta có không phi là nghim ca nên .
t , . Ta có: .
Bng bin thiên ca
Da vào BBT, có nghim phân bit thuc hoc có nghim kép thuc
(thu kin) hay .
Kt hp (***) ta có , .
Câu 8. Cho khi t diu cnh bng Gi lt là trng tâm ca ba tam
giác Tính th tích ca khi chóp
A. . B. . C. . D. .
Lời giải
Chọn C
3xy t x y t
2
0 3 2
9 4 0
t
tt


2
0
3
4
9
0
t
t
t

42
93
t
,xy
2
3 0 1X tX t
42
93
t
42
;
93



t
1
2
0;1
0;1
1
3
X
1
2
1
31
X
t
X

2
31
X
gX
X
0;1X
2
2
32
0
31
XX
gX
X

0
2
3
X
X
gX
1
2
0;1
0;1
41
92
t
41
92
xy
22
27 24
ADMN
V
1
2
24
V
2
2
27
V
12
1
.
324
VV
ABCD
2.cm
,,M N P
, , .ABC ABD ACD
V
.AMNP
3
2
162
V cm
3
22
81
V cm
3
42
81
V cm
3
2
144
V cm
Trang49
Tam giác u
.
Mà
Li có: .
Câu 9. Cho hình chóp có , , . Hình chiu vuông góc ca
xung mt phng nm bên trong tam giác . Các mt phng , ,
u to vt góc . Gi , , ng phân giác ca tam giác
vi , , . Th tích gn vi s 
A. B. C. D.
Lời giải
ChọnD
P
N
M
H
K
F
E
A
B
C
D
BCD
23
3
3
DE DH
22
26
3
AH AD DH
EF
, D,BC
1 1 1 1 3
. . . .
2 2 2 2 4
K
E FK
S d FK d BC
EF
1 1 2 6 3 2
. . .
3 3 3 4 6
SKFE K
V AH S
2
3
AM AN AP
AE AK AF
8 8 4 2
..
27 27 81
AMNP
AMNP AEKF
AEKF
V
AM AN AP
VV
V AE AK AF
.S ABC
5 cmAB
6 cmBC
7 cmCA
S
ABC
ABC
SAB
SBC
SCA
60
AD
BE
CF
ABC
D BC
E AC
F AB
.S DEF
3
2,9 cm
3
4,1 cm
3
3,7 cm
3
3,4 cm
60
°
H
F
E
D
I
C
B
A
S
Trang50
Vì các mt phng , , u to vt góc và hình chiu vuông
góc ca xung mt phng nm bên trong tam giác nên ta có hình chiu ca
chính là tâm cng tròn ni tip tam giác .
Gi là na chu vi tam giác thì .
Ta có : và .
Suy ra chiu cao ca hình chóp là :
Vì là phân giác ca góc nên ta có : .
 : , .
 : .
 : , .

, vi , ,
.
Suy ra
Câu 10. Trong tt c các khi chóp t u ngoi tip mt cu bán kính bng , th tích ca khi
chóp có th tích nh nht.
A. . B. . C. . D. .
Lời giải
Chọn D
SAB
SBC
SCA
60
S
ABC
ABC
S
I
ABC
p
ABC
9
2
AB BC CA
p


66
ABC
S p p AB p BC p AC
26
3
S
r
p

.tan60 2 2hr
F
E
D
C
B
A
I
BE
B
EA BA
EC BC
FA CA
FB CB
DB AB
DC AC
.
AEF
ABC
S
AE AF
S AC AB
.
AB AC
AB BC AC BC

.
CED
ABC
S
CA CB
S CA AB CB AB

.
BFD
ABC
S
BC BA
S BC CA BA CA

1
DEF ABC
ab bc ac
SS
a c b c b a c a a b c b




BC a
AC b
AB c
2
.
ABC
abc
S
a b b c c a
210 6
143
.
1 210 6
. .2 2
3 143
S DEF
V
33
280 3
cm 3,4 cm
143

a
V
3
8
3
a
V
3
10
3
a
V
3
2Va
3
32
3
a
V
Trang51
Gi s ta có: ;
Xét ta có:
Th tích khi chóp là:
Xét hàm s
; (do )
Bng bin thiên
Vy giá tr nh nht ca th tích là: .
Câu 11. Cho hình chóp   là hình bình hành tha mãn ,
. Bit tam giác cân ti , tam giác vuông ti và khong cách t n
mt phng bng . Th tích ca khng
A. . B. . C. . D. .
Lời giải
Chọn A
SO x
SI x a
2
22
2 SE x a a x ax
SEI SON∽
SE IE
SO NO
2
.
2
IE SO ax
NO
SE
x ax
2
22
2
1 2 4
.
3 3 2
2




ax a x
Vx
xa
x ax
2
2
x
fx
xa
02ax
2
2
4
2
x ax
fx
xa
0
fx
4xa
02ax
3
32
3
a
V
.S ABCD
ABCD
,3AB a AC a
2aBC
SBC
S
SCD
C
D
()SBC
3
3
a
3
2a
35
3
35
a
3
33
a
3
5
a
Trang52
Nhn thy tam giác vuông ti ( do ).
Gi i xng ca qua ta có t giác là hình ch nht, và tam giác
u cnh .
Hay
Gi m cn , ta có: .
Trong k vuông góc vi ti  .
Ta có ( Do ) Suy ra .
Xét tam giác có va là trung tuyn vng cao nên tam giác cân ti .
Xét hình chóp u , các cnh bên .
Nên gi ta có .
Tam giác vuông ti nên .
Tam giác vuông ti nên .
.
Câu 12. Cho hình chóp u có cnh bng . Bit rng các mt bên ca
hình chóp có din tích bng nhau và mt trong các cnh bên bng . Tính th tích nh nht
ca khi chóp .
A. . B. . C. . D. .
Lời giải
Chọn C
ABC
A
2 2 2
AB AC BC
E
B
A
DEAC
EBC
2a
1
( ) ( ,( )) ( ,( )) ( ,( ))
2
AD SBC d D SBC d A SBC d E SBC
2a 3
( ,( )) 2.d( ,( ))
3
d E SBC D SBC
I
BC
, ( )BC EI BC SI BC SEI
()mp SEI
EH
SI
H
23
( ,( ))
3
a
d E SBC EH
D ( )C SAC
D , DC SC C AC
()AB SAC
ESB
SA
ESB
S
.S EBC
EBC
SE SB SC
F EI CA
()SF EBC
EHI
H
23
2
3
sin
3
3
a
HE
I
EI
a
SIF
F
2
2
2
1 sin 1 2a
3
.tan . 3.
33
2 15
1 sin
1 ( )
3
I
SF FI I EI a
I
3
. D D
1 1 1 2 2a
. . . . . 3
3 3 3
15 3 5
S ABC ABC
a
V SF S SF ABCA a a
.S ABC
ABC
a
3a
.S ABC
3
2
6
a
3
2
2
a
3
6
12
a
3
6
4
a
Trang53
Gi là hình chiu ca trên mt ph ; lt là hình chiu ca
trên .
Vì din tích các mt bên ca hình chóp bng nhau nên ta có
và vì tam giác u nên ta có .
TH1: nu nm trong tam giác ng tròn ni tiu .
 và
.
TH2: Nu nm ngoài tam giác . Không mt tính tng quát gi s nm khác phía
vi so vng thng
 n có . Vì tam giác u nên ng
tròn bàng tip góc và ,
. Vì th cnh không th bng
.
Vy .
Câu 13. Cho hình chóp i , , .
H
S
ABC
,,M N K
S
,,AB BC CA
1 1 1
. . .
2 2 2
SM AB SN BC SK CA
ABC
SM SN SK
HM HN HK
H
ABC
H
ABC
23
33
a
AH AN
3SA SB SC a
2
2 2 2
3 2 6
3
93
aa
SH SA AH a
23
.
1 1 3 2 6 2
. . .
3 3 4 3 6
S ABC ABC
a a a
V S SH
H
ABC
H
A
BC
HM HN HK
ABC
H
A
3
2
a
AM AB BN
1
:
60 2 2
BN a
HB a
cos
33
: 30 : 3
22
a
AH AM cos a
SA
3a
3SB SC a
2 2 2 2
32SH SB BH a a a
23
.
1 1 3 6
. . . 2
3 3 4 12
S ABC ABC
aa
V S SH a
3 3 3
min
2 6 6
min ,
6 12 12
a a a
V






.S ABC
A
AB a
120 ,BAC 
90SBA SCA
Trang54
Gi là góc gia và tha mãn , khong cách t n m
 . Th tích ca khi chóp bng
A. . B. . C. . D. .
Lời giải.
Chọn C
Gi là hình chiu vuông góc ca  t .
Ta có .   .
Tam giác cân ti và và u
cnh .
Tam giác vuông ti
K ti .
Gi , xét vuông ti và
m ca .
Theo gi thit
. So sánh vu kin suy ra .
Vy .
Câu 14. Cho t din có ; . Bit góc gia
hai mt phng bng . Th tích ca t din bng
A. . B. . C. . D. .
Lời giải.
Chọn D
SB
SAC
3
sin
8
S
2a
.S ABC
3
3
4
a
3
3
6
a
3
3
12
a
3
3
24
a
K
C
A
I
B
D
S
D
S
ABC
02SD x x a
AC SC
AC SDC AC DC
AC SD
AB DB
ABC
A
120CAB 
3BC a
60DBC DCB DBC
3a
SDC
D
22
3SC a x SB
DK SC
K DK SAC
22
.3
,
3
xa
d D SAC DK
ax
I BD AC
DIC
C
60BDC 
23
DC
DI a
cosBDC
B
DI
1
,,
2
d B SAC d D SAC
,
,( sin
d B SAC
SB SAC
SB

22
33
8
23
xa
ax

22
3 4 0x a ax
2
4 3 0
xx
aa



3
xa
xa
xa
3
.
13
..
3 12
S ABC ABC
a
V S SD

ABCD
90DAB CBDº
; 5; 135AB a AC a ABC
,ABD BCD
30
ABCD
3
23
a
3
2
a
3
32
a
3
6
a
Trang55
Dng .
Ta có  .
Tam giác có , vuông cân ti .
Áp dnh lý cosin, ta có .
Vy .
Dng và .
Suy ra và tam giác vuông ti .
t  , .
Suy ra .Vy .
Câu 15. Cho hình chóp        i , ,
và khong cách t m n bng . Din tích ca mt cu
ngoi tip hình chóp bng
A. . B. . C. . D. .
Lời giải.
Chọn D
Gi là hình chiu ca lên .
Ta có: .
 .
Và vuông cân ti nên là hình vuông. Gi , là tâm hình
vuông.
Dng mng thng qua vuông góc vi , dng mt phng trung trc ca
m ct ti là tâm mt cu ngoi tip.
a
a
5
A
B
C
H
D
E
F
DH ABC
BA DA
BA AH
BA DH

BC DB
BC BH
BC DH

AHB
AB a
o
45ABH
HAB
A
AH AB a
2BC a
2
1 1 2
. . .sin . . 2.
2 2 2 2
ABC
a
S BABC CBA a a
HE DA
HF DB
HE DAB
HF DBC
,,DBA DBC HE HF EHF
HEF
E
DH x
22
ax
HE
ax
22
2
2
xa
HF
ax
22
22
32
cos
4
22
HE x a
EHF x a
HF
xa
3
1
..
36
ABCD ABC
a
V DH S

.S ABC
B
3AB BC a
90SAB SCB
A
SBC
2a
.S ABC
2
2 a
2
8 a
2
16 a
2
12 a
H
S
ABC
BC SC
HC BC
SH BC

AH AB
ABC
B
ABCH
O AC BH
O
d
O
ABCH
SA
J
d
II
Trang56
Ta hoàn toàn có m , hay .
Bán kính mt cu ngoi tip:
Do .
( là hình chiu ca lên và ).
. Tam giác vuông ti .
Tam giác vuông ti .
.
Câu 16.  u có c ; bit khong cách ging thng
và bng . Th tích ca kh tính theo bng:
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có
t .
Tam giác cân ti , .
Din tích tam giác là
Th 
Li có .
 .
.
Câu 17.  ng  là tam giác cân ti , cnh và góc
.  khong cách ging thng và bng .Th tích ca khi
 tính theo bng:
//IJ SA IJ AB I
SB
I d SC
22
.
3
;
22
S ABC
a
r AI IJ JA IJ

// , ,AH SBC d A SBC d H SBC HK
K
H
SC
BC SHC HK SBC
2HK a
SHC
H
6SH a
SHA
H
3SA a
22
.
3
3 4 12
22
S ABC mc
SA a
JA r AI a S r a

.ABC A B C
a
AB
AC
¢
15
5
a
.ABC A B C
a
3
33
8
a
3
3
2
a
3
3
8
a
3
3
4
a
,
,,
15
/ / / /
5
AB A C
AB A B C B A B C
a
AB A B AB A B C d d d
0AA x

CA B

C
22
CA CB a x

CA B

2 2 2
2 2 2 2
1 1 3 4 1
. . . 3 4
2 4 2 2 4
CA B
a a x
S a a x a a a x

2
3
.1
4
a
Vx
22
.
,
1 15 1
3 3. . . . 3 4
3 5 4
B A B C A B C
B A B C
a
V V d S a a x

2
2 2 2 2
3 15 1
. . . 3 4 5 3 15. 3 4 3
4 5 4
aa
x a a x x a x x a
23
33
.
44
aa
Vx
. ' ' 'ABC A B C
ABC
C
AB a=
30BAC 
AB
CB
¢
2
a
.ABC A B C
a
Trang57
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
t .
c .
Din tích tam giác là .
Tam giác cân ti , .
Din tích tam giác cân là
Th tr là
Li có
 .
Câu 18. Cho hình  tr u , có cng . Khong cách t m n mt
phng bng . Th tích ca kh tính theo bng:
A. . B. . C. . D. .
Lời giải
Chọn A
3
83
a
3
3
2
a
3
23
3
a
3
43
3
a
,
,,
/ / / /
2
AB B C
AB A B C B A B C
a
AB A B AB A B C d d d
0AA x

3
a
AC BC
ABC
2
1
. . .sin120
2
43
o
ABC
a
S AC CB
CA B

C
2 2 2
2
3
3
3
a a x
CA CB x

CA B

2 2 2 2 2
1 1 3 12
. . . .
2 2 2 3 4 4
23
CA B
a a x a a a x
S A B CH



2
..
43
ABC
a
V AA S x

22
.
,
1 12
3 3. . . .
3 2 4
23
B A B C A B C
B A B C
a a a x
V V d S

2 2 2 3
12
. . .
2 4 2
4 3 2 3 8 3
a a a a x a a
x x V
. ' ' 'ABC A B C
a
A
()A BC
¢
2
a
.ABC A B C
a
3
32
16
a
3
52
16
a
3
2
16
a
3
52
8
a
Trang58
Gi là trung m ca , là hình chiu vuông góc ca trên .
Chc khong cách t n là .
t .
Xét tam giác vuông ti :
Ta có ng cao: .
Th  là .
Câu 19.   là hình thoi cnh , tâm và . Góc
gia cnh bên và mng nh m , , . Tính theo
th tích kh 
A. . B. . C. . D. .
Lời giải
Chọn C
Hình thoi cnh , nên góc , suy ra tam giác u cnh
.
Din tích  là .
Gi là trng tâm tam giác . Ta có .
Tính c .
Góc gia và mng góc và bng .
Ta có .
H
BC
I
A
AH
A
( ' )A BC
2
a
AI
0AA x

A AH
A
AI
2 2 2 2 2 2
1 1 1 1 4 4 3
3
22
a
x
AI AA AH x a a
23
3 3 3 2
..
4 16
22
ABC
a a a
V x S
. ' ' ' 'ABCD A B C D
ABCD
a
O
·
0
120ABC =
'AA
0
60
'A
A
B
D
a
3
3
2
a
V =
=
3
3
6
a
V
3
3
2
a
V =
3
3Va=
ABCD
a
·
120ABC =°
60BAD 
ABD
a
ABCD
22
33
2. 2.
42
ABD
aa
SS
H
ABD
A H ABCD
33
,
23
aa
AO AH
'AA
A AH
60°
3
.tan60 . 3
3
a
A H AH a
Trang59
Th tích  tr .
Câu 20. Cho hình chóp u cnh , Các mt bên ca hình chóp cùng to vi
mt góc và hình chiu ca trên mt ph  .
Tính th tích khi chóp .
A. . B. . C. . D. .
Lời giải
Chọn A
Gi là hình chiu ca trên mt phng .
Gi hình chiu ca lên các cnh lt là .
D dàng có c góc gia các mt bên v .
Vy ta có ba tam giác vuông cân bng nhau , suy ra .
là tâm ng tròn bàng tip . Do u, không mt tính tng quát, ta coi
ng tròn báng tip góc .
Gi là bán kính ng tròn bàng tip góc thì
Vy .
Câu 21. Cho  chóp ng cao , tam giác vuông có , góc
. Gi là hình chiu ca trên . Gi i xng ca qua mt
phng . Tính th tích khi chóp .
A. . B. . C. . D. .
Lời giải
Chọn A
23
33
..
22
aa
V A H S a
.S ABC
a
45
S
ABC
.S ABC
3
8
a
V
3
4
a
V
3
6
a
V
3
24
a
V
H
S
ABC
H
,,AB BC CA
,,P Q R
45SPH SQH SRH
,,SHP SHQ SHR
HP HQ HR
H
ABC
ABC
H
A
a
r
A
3
2
a
Sa
r
pa

3
2
a
a
SH r
23
.
1 1 3 3
.
3 3 2 4 8
S ABC ABC
a a a
V SH S
.S ABC
2SA a
ABC
C
2AB a
30CAB 
H
A
SC
B
B
SAC
.H AB B
3
23
7
a
3
23
7
a
3
63
7
a
3
3
7
a
Trang60
Ta có , . Ta có:
; ;
Câu 22. Cho hình chóp t u có cng , cnh bên hp vt góc .
Gi i xng ca qua , m .Mt phng chia khi
chóp thành hai phn. T s th tích gia hai phn (phn ln trên phn bé) bng:
A. . B. . C. . D. .
Lời giải
Chọn A
Gi là th tích khi chóp
V
1
là th tích khi chóp và là th tích ca khi chóp còn l
ct ti  là trung m ca .
ct ti là trng tâm ca
Ta có
Mt khác
Mà
Suy ra .
BC a
3AC a
2 2 2 2 2 2
1 1 1 1 1 7
4 3 12AH SA AC a a a
23
7
a
AH
22
3
7
a
HC AC AH
2
1 3 3
.
27
HAC
a
S AH HC
23
1 1 3 3 3
..
3 3 7 7
HABC HAC
aa
V S BC a
3
'
23
2
7
HAB B HABC
a
VV
.S ABCD
a
0
60
M
C
D
N
SC
BMN
.S ABCD
7
5
1
7
7
3
6
5
V
.S ABCD
.PDQ BCN
2
V
12
V V V
MB
AD
P
P
AD
MN
SD
Q
Q
SMC
.
.
1 1 2 1
. . . .
2 2 3 6
M PDQ
M BCN
V
MP MD MQ
V MB MC MN
. . 1 1 .
5
6
M BCN M PDQ M BCN
V V V V V
1
, ( ;( )) ( ;( ))
2
MBC ABCD
S S d S ABCD d S ABCD

. . . 1 2 2 1
1 5 7
: 7:5
2 2 12 12
M BCN N MBC S ABCD
V
V V V V V V V V V
Trang61
Câu 23. Cho t din , và m thuc và sao cho , ,
là mt phng qua và song song vi . Kí hiu và là các khn
c khi chia khi t din bi mt phng  chm ,
chm ; và lt là th tích ca và . Tính t s .
A. . B. . C. . D. .
Lời giải.
ChọnA
Kí hiu là th tích khi t din .
Gi , lt là giao m ca vng thng , .
Ta có . Khi chia khi bi   c hai khi chóp và
.
Ta có .
.
.Suy ra .
.
.
Câu 24. Cho hình chóp      vuông cân ti
Góc gia và mt phng là tha mãn Gi là
trng tâm tam giác m . Th tích là
A. . B. . C. . D. .
Lời giải
Chọn C
.S ABC
M
N
SA
SB
2MA SM
2SN NB
MN
SC
1
H
2
H
.S ABC
1
H
S
2
H
A
1
V
2
V
1
H
2
H
1
2
V
V
4
5
5
4
3
4
4
3
V
.S ABC
P
Q
BC
AC
// //NP MQ SC
1
H
QNC
.N SMQC
.N QPC
.
.
,
.
,
N SMQC SMQC
B ASC SAC
d N SAC
VS
VS
d B SAC
,
2
3
,
d N SAC
NS
BS
d B SAC

2
45
99
AMQ SMQC
ASC ASC
SS
AM
S AS S



.
.
2 5 10
.
3 9 27
N SMQC
B ASC
V
V

.
.
,
1 1 2 2
. . . . .
3 3 3 27
,
N QPC QPC
S ABC ABC
d N QPC
VS
NB CQ CP
V S SB CA CB
d S ABC
..
1 1 1
. . 1 2 2
10 2 4 4 4
27 27 9 9 5
N SMQC N QPC
B ASC S ABC
VV
V V V
V V V V V V
.S ABC
ABC
,,B AB BC a
0
90 .SAB SCB
SB
()ABC
tan 2.
G
,ABC M
SA
SMGB
3
3
a
3
15
a
3
18
a
3
6
a
Trang62
Lm sao cho là hình vuông
Ta có 
Ta có
Ta có
Vy
Câu 25.  có th tích . Gi m ; m nm trên
cnh sao cho ; m . Hãy tính theo th tích khi t din
:
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có:
Li có
.
D
ABCD
,BC CD BC SC BC SD
.AB SD
.
1 1 1
.
2 6 12
SMGB SABG SABC S ABCD
V V V V
3
2
.
1 1 2
. .2 .
3 3 3
S ABCD ABCD
a
V SD S a a
3
.
18
SMGB
a
V
.ABC A B C
V
M
AC
N
BC
2CN NB
K
AB
V
CMNK
11
36
V
2
15
V
5
18
V
12
V
; ; ;d C MNK d C AB C d B AB C

MNK AB C AMK MNC B NK
S S S S S

. . .
AB C AB C AB C AB C
AM AK CM CN B N B K
S S S S
AC AB AC CB B C AB

1 1 1 2 1 1 1
. . .
2 2 2 3 3 2 4
AB C AB C AB C AB C AB C
S S S S S
1 1 1 1 1 1
; . ; . .
3 3 4 4 4 3 12
C MNK MNK AB C B ABC
V
V d C MNK S d B AB C S V V


| 1/62
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN CÓ YẾU TỐ GÓC
I. KIẾN THỨC CẦN NHỚ:
1. Góc giữa đƣờng thẳng và mặt phẳng
Định nghĩa:
Nếu d   P  d P 0 ( ; )  90 A d d' I H (P)   
Nếu d  P  d;P  d;d '   AIH với d 'là hình chiếu của d lên P 0  Chú ý:
 d P 0 0 ;  90
2. Góc giữa hai mặt phẳng Định nghĩa:
Cách 1: Dùng định nghĩa: Tìm hai đường thẳng a , b lần lượt vuông góc với hai mặt phẳng  P và Q .
Khi đó, góc giữa hai mặt phẳng P và Q chính là góc giữa hai đường thẳng a và b b a    c
Cách 2: Ta thực hiện theo 2 bước
Bước 1: Tìm giao tuyến d của hai mặt phẳng (P) và (Q).
Bước 2: Tìm 1 điểm I thuộc d sao cho trong mp (P) ta dễ dàng tìm được một đường thẳng a đi qua
I và vuông góc với đường thẳng d và trong mp(Q) ta tìm được một đường thẳng b cũng đi qua I và vuông
góc với đường thẳng d.
Khi đó: Góc giữa hai mp(P) và mp(Q) chính bằng góc giữa a và b b a d I
5. Thể tích khối đa diện
a. Công thức tính thể tích khối chóp 1 V = S.h 3
Trong đó: S là diện tích đáy, h là chiều cao khối chóp.
Chú ý: Cho khối chóp S.ABC và A ' , B ' , C ' là các điểm tùy ý lần lượt thuộc SA , SB , SC ta có Trang1 V
SA ' SB ' SC '
S . A ' B 'C ' = . . . V SA SB SC S . ABC
b. Công thức thể tích khối lăng trụ: V  .
B h ( B là diện tích đáy, h là chiều cao)
XÁC ĐỊNH CHIỀU CAO THƢỜNG GẶP
a)Hình chóp có một cạnh bên vuông góc với
Ví dụ: Hình chóp S .A BC có S
đáy: Chiều cao của hình chóp là đô ̣ dài ca ̣nh bên cạnh bên SA vuông góc với mặt vuông góc với đáy.
phẳng đáy, tức SA ^ (A B C ) thì
chiều cao của hình chóp là SA. A C B
b)Hình chóp có 1 mă ̣t bên vuông góc với mă ̣t
Ví dụ: Hình chóp S .A BCD S
đáy: Chiều cao của hình chóp là chiều cao của
có mặt bên (SA B ) vuông góc
tam giác chứa trong mă ̣t bên vuông góc với đáy.
với mặt phẳng đáy (A BCD)
thì chiều cao của hình chóp là A
SH là chiều cao của D SA B . D H B C
c)Hình chóp có 2 mă ̣t bên vuông góc với mặt
Ví dụ: Hình chóp S .A BCD S
đáy: Chiều cao của hình chóp là giao tuyến của
có hai mặt bên (SA B ) và
hai mă ̣t bên cùng vuông góc với mặt phẳng đáy.
(SA D) cùng vuông góc với
mă ̣t đáy (A BCD) thì chiều D A
cao của hình chóp là SA. B C
d) Hình chóp đều:
Ví dụ: Hình chóp đều S
Chiều cao của hình chóp là đoa ̣n thẳng nối đỉnh
S .A BCD có tâm đa giác
và tâm của đáy. Đối với hình chóp đều đáy là tam đáy là giao điểm của hai
giác thì tâm là trọng tâm G của tam giác đều.
đường chéo hình vuông
A B CD thì có đường cao là A D SO. O B C
XÁC ĐỊNH DIỆN TÍCH ĐÁY HAY GẶP
1. Diê ̣n tích tam giác vuông.
S= nửa tích 2 cạnh góc vuông.  2 2 2
Pitago: A B + A C = A C
2. Diê ̣n tích tam giác đều.  3 S= (cạnh)2. 4  3 h= (cạnh). 2 Trang2
3. Diê ̣n tích hình vuông: . S= (cạnh)2 . Pitago: 2 2 2
A B + A D = BD
.Đường chéo hình vuông bằng ca ̣nh. 2
4. Diê ̣n tích hình chữ nhật: . S= dài x rộng.
5. Diê ̣n tích hình thoi: 1 . S = .A C .BD 2 . S= 2.SABC=2.SADC
6. Diê ̣n tích hình thang:
. S= nửa chiều cao x (đáy lớn+bé) 1 .S =
A H .(A B + CD ) 2
II. CÁC DẠNG BÀI TẬP TƢƠNG TỰ
 Thể tích khối đa diện
 Góc giữa đường thẳng và mặt phẳng
 Góc giữa hai mặt phẳng
 Công thức tỉ số thể tích
 Khoảng cách từ 1 điểm tới mặt phẳng
 Khoảng cách giữa hai đường thẳng chéo nhau BÀI TẬP MẪU
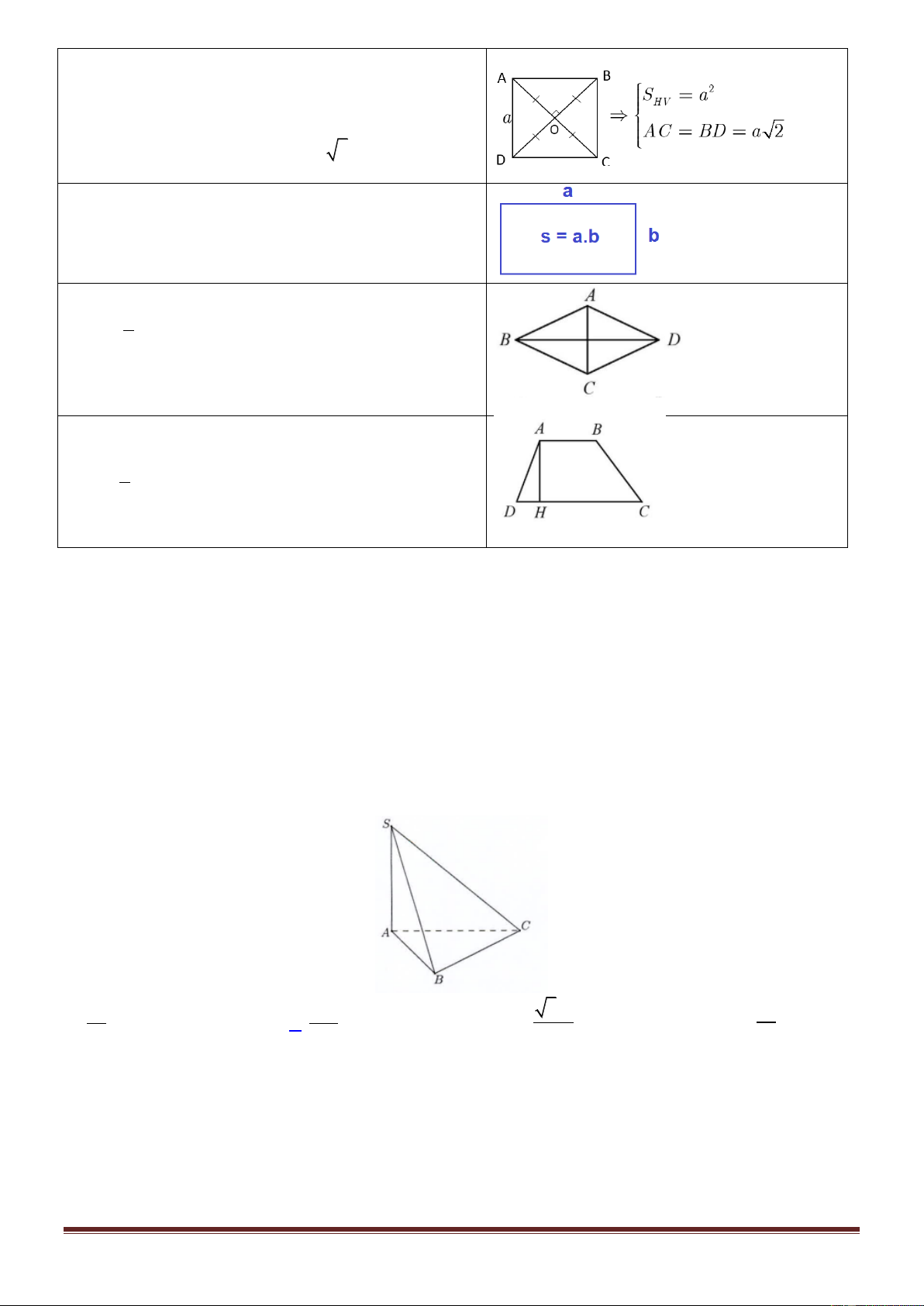
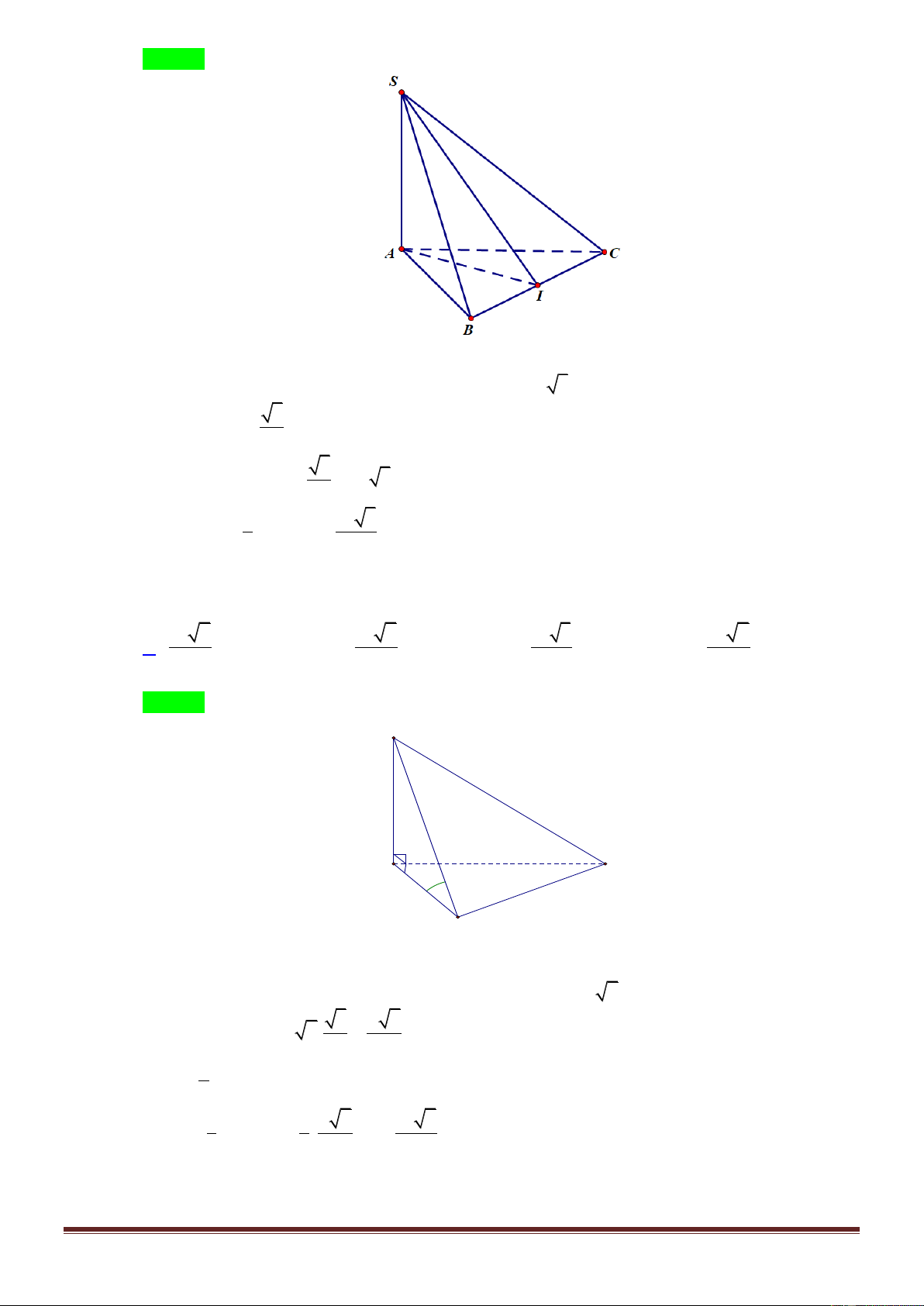
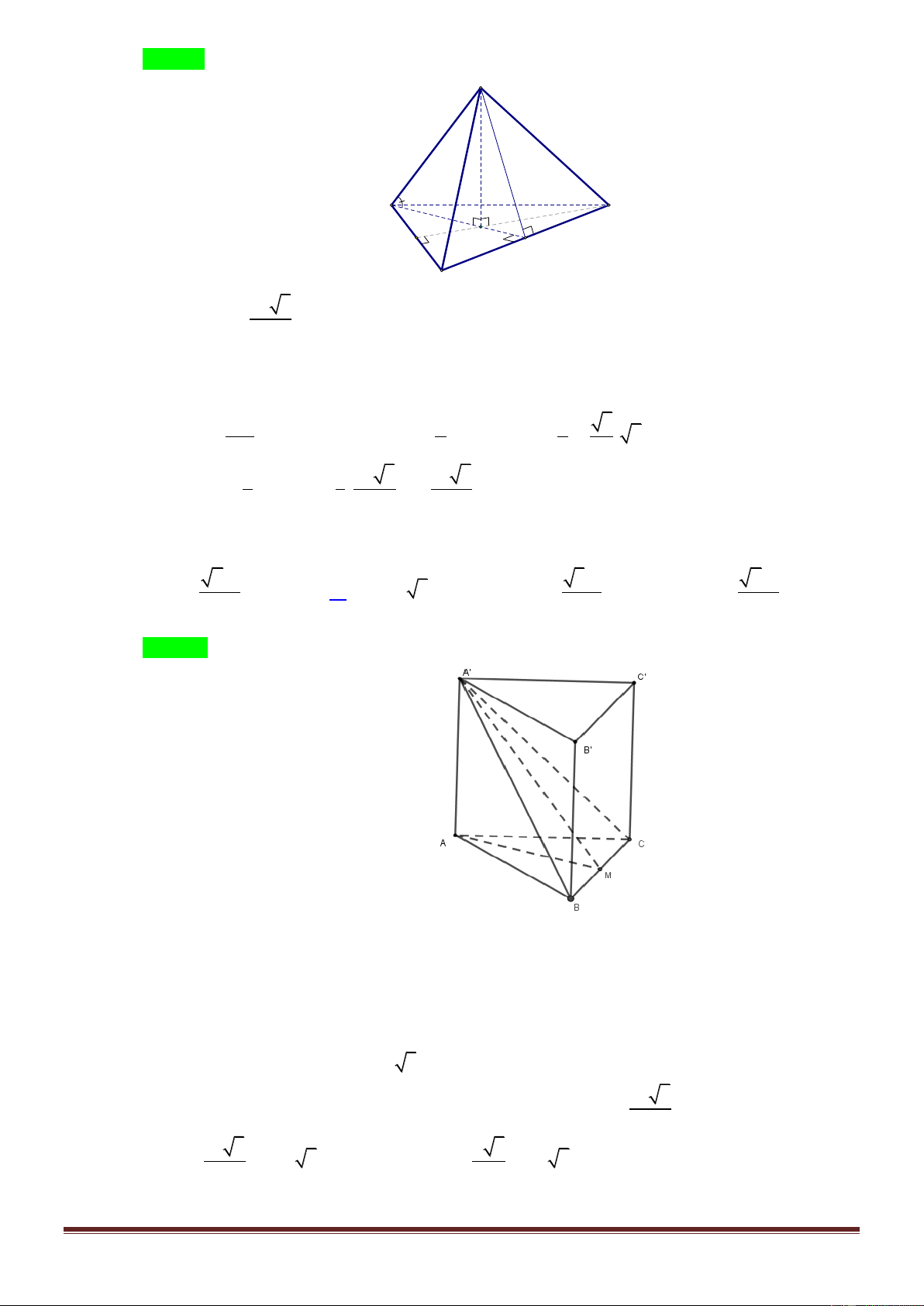
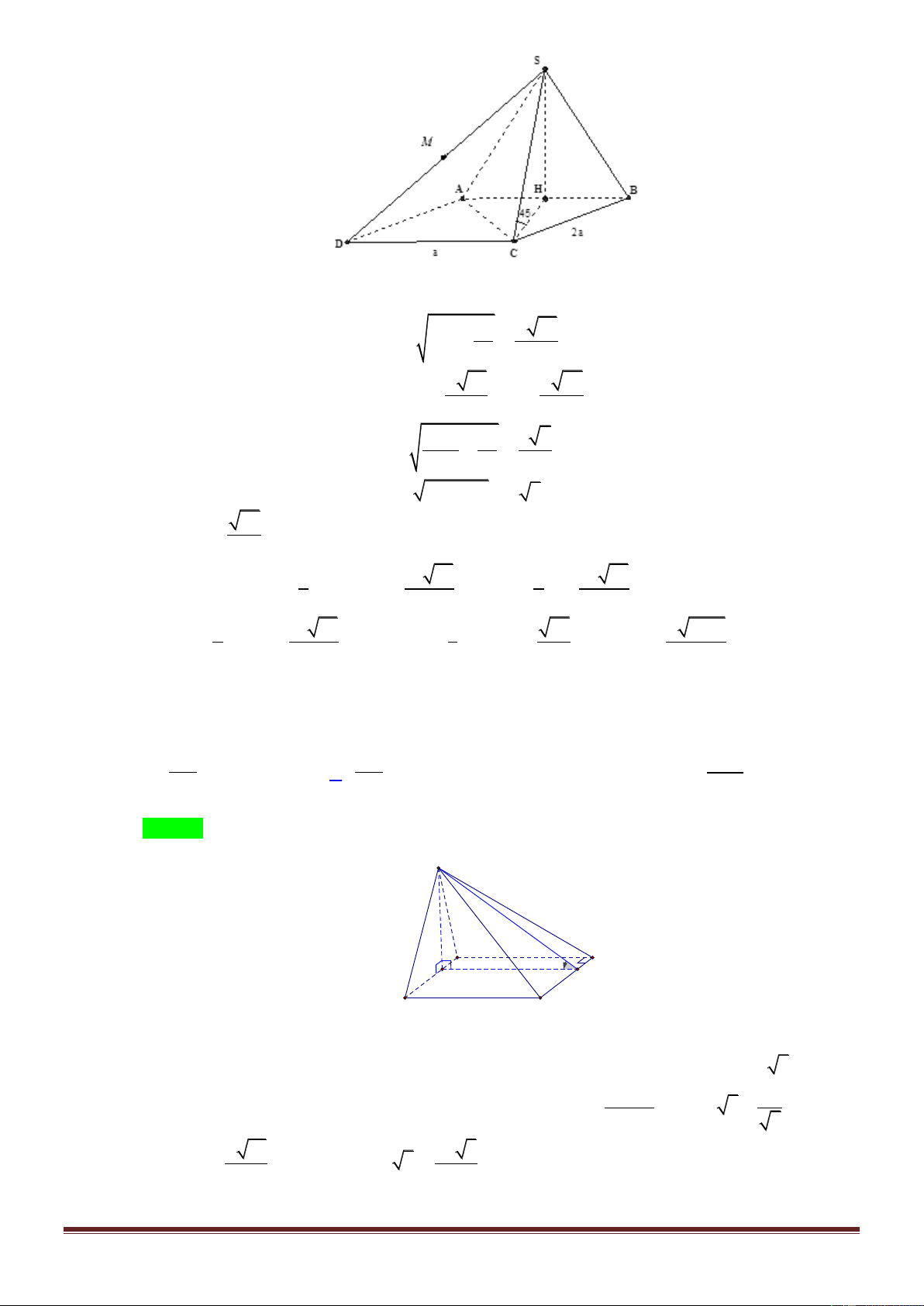
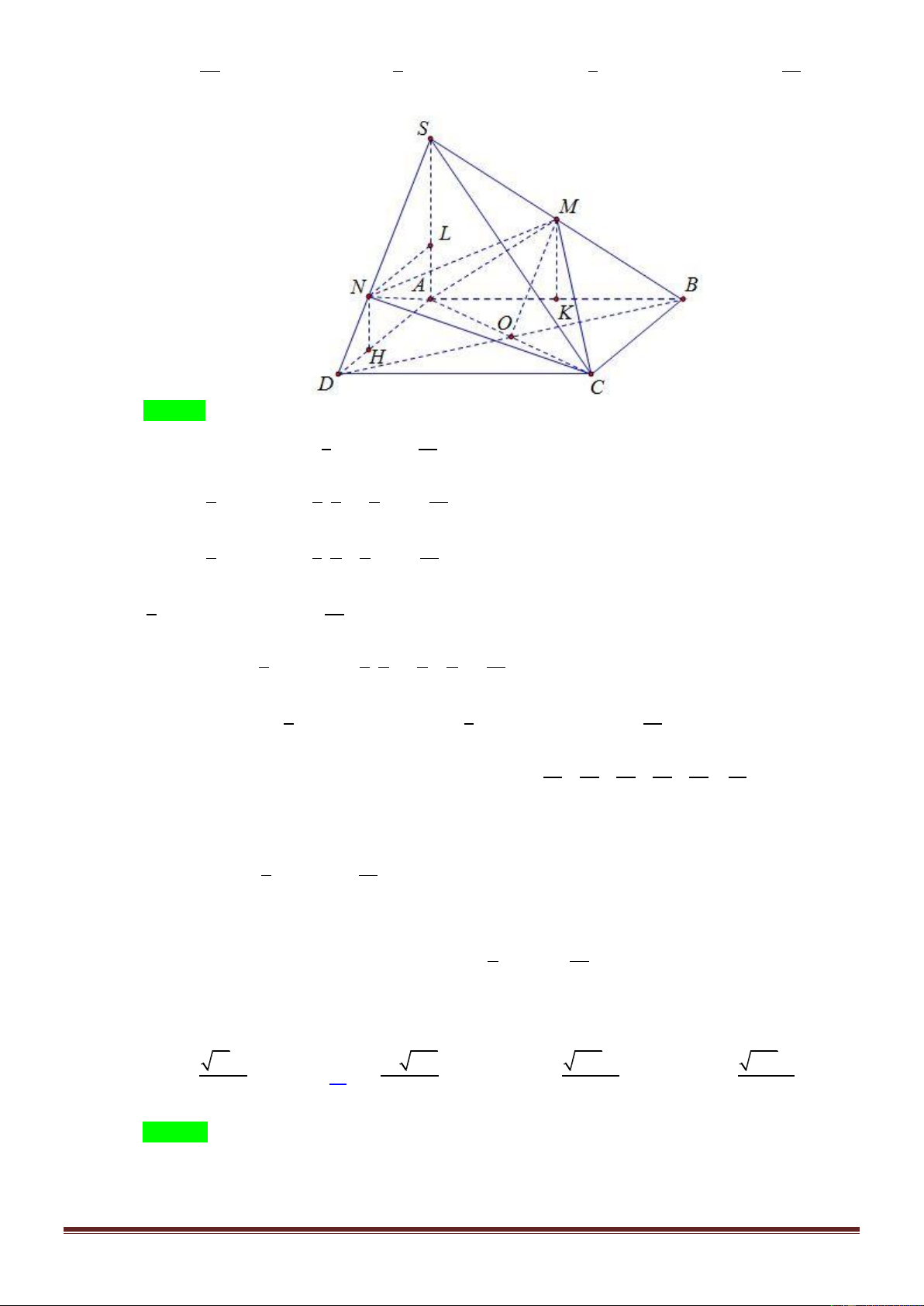
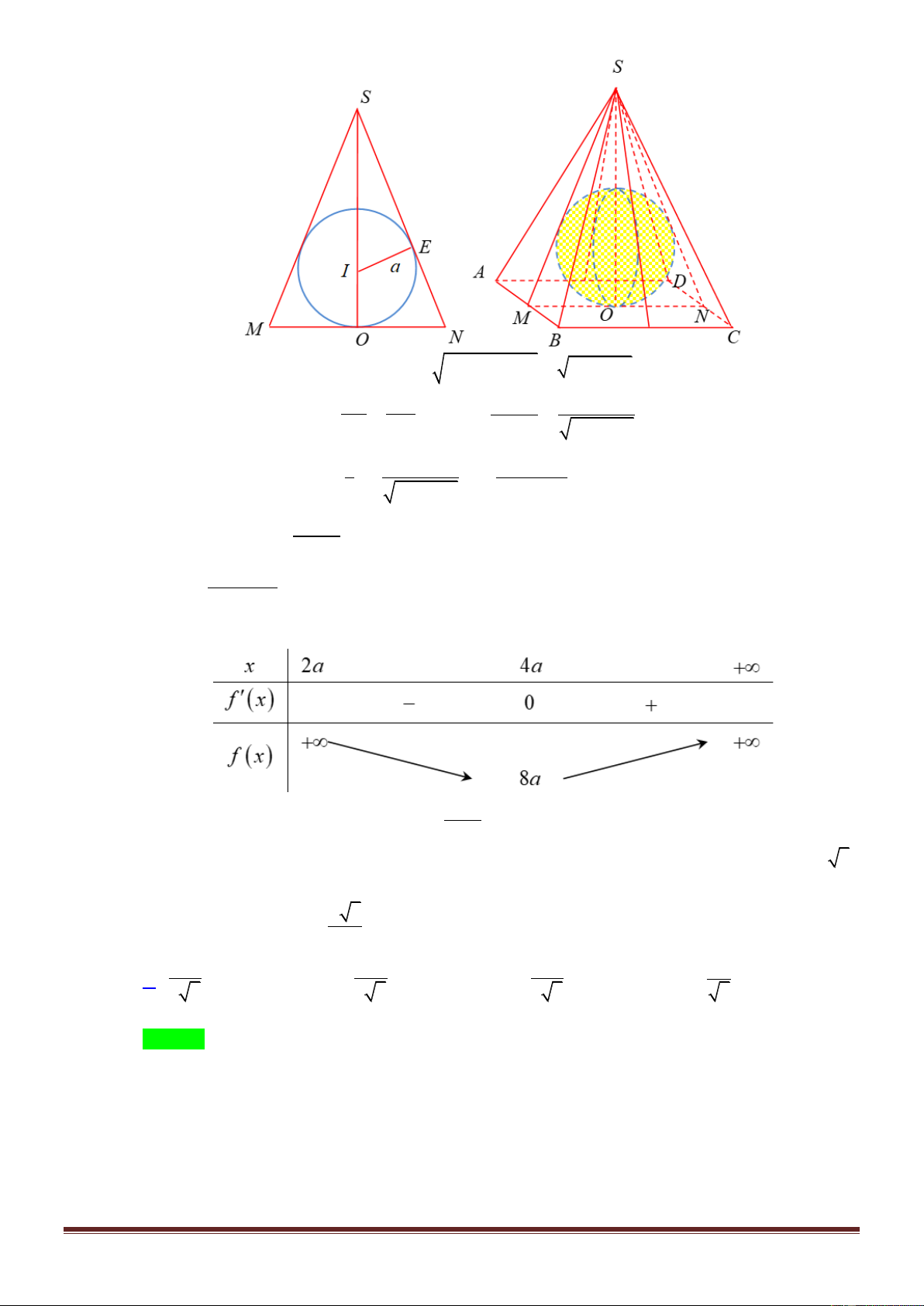
(ĐỀ MINH HỌA-BDG 2020-2021)Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh
bên SA vuông góc với đáy, góc giữa SA và mặt phẳng SBC  bằng 45( tham khảo hình bên). Thể tích
của khối chóp S.ABC bằng: 3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 8 12 4
Phân tích hướng dẫn giải
1. DẠNG TOÁN:Đây là dạng toán tính thể tích biết chiều cao khối đa diện biết góc giữa mặt bên và mặt đáy. 2. HƢỚNG GIẢI:
B1: Tính diện tích đáy
B2:tính thể tích khối lăng trụ V S.h
Từ đó, ta có thể giải bài toán cụ thể nhƣ sau: Lờigiải Trang3 ChọnA
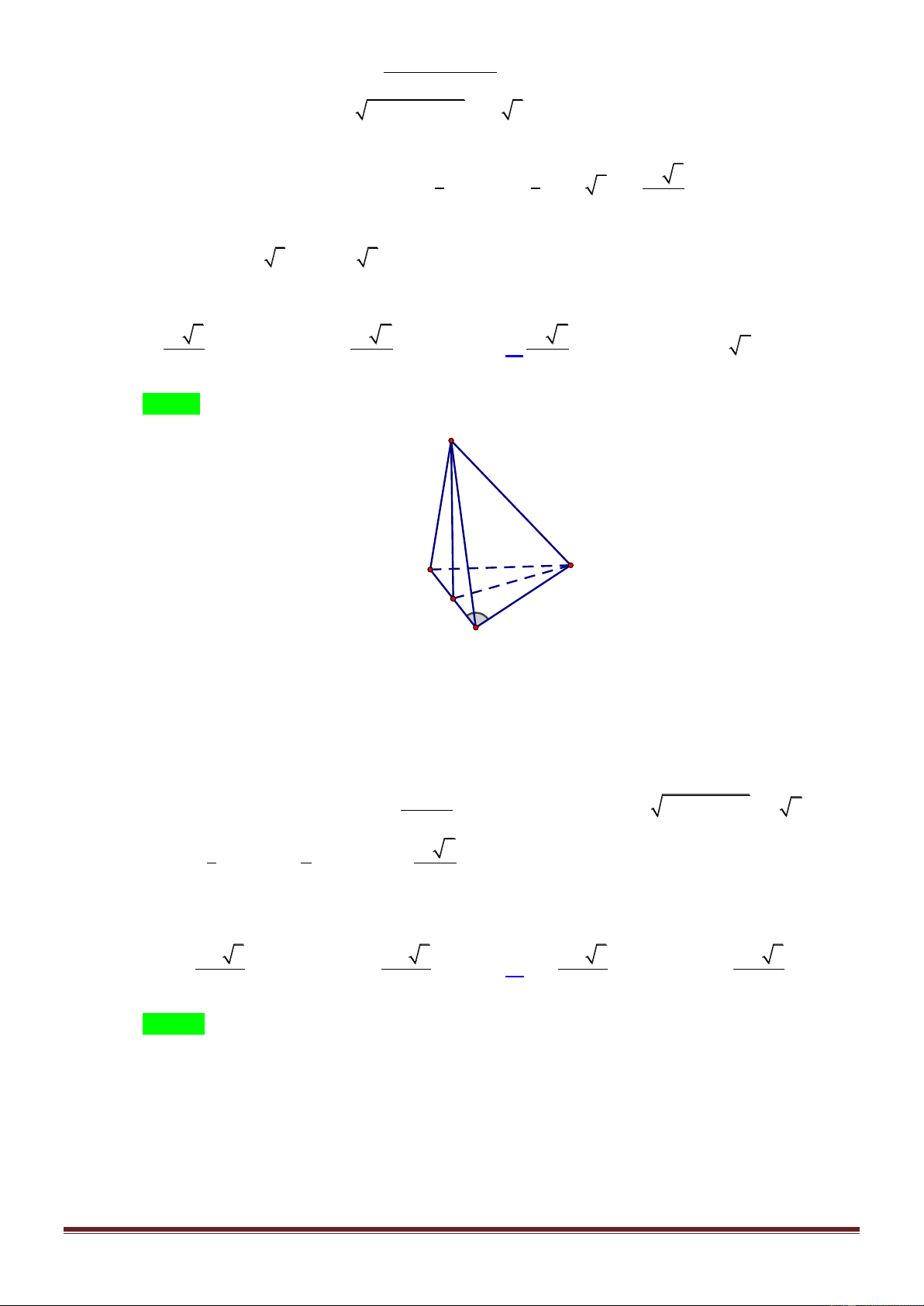
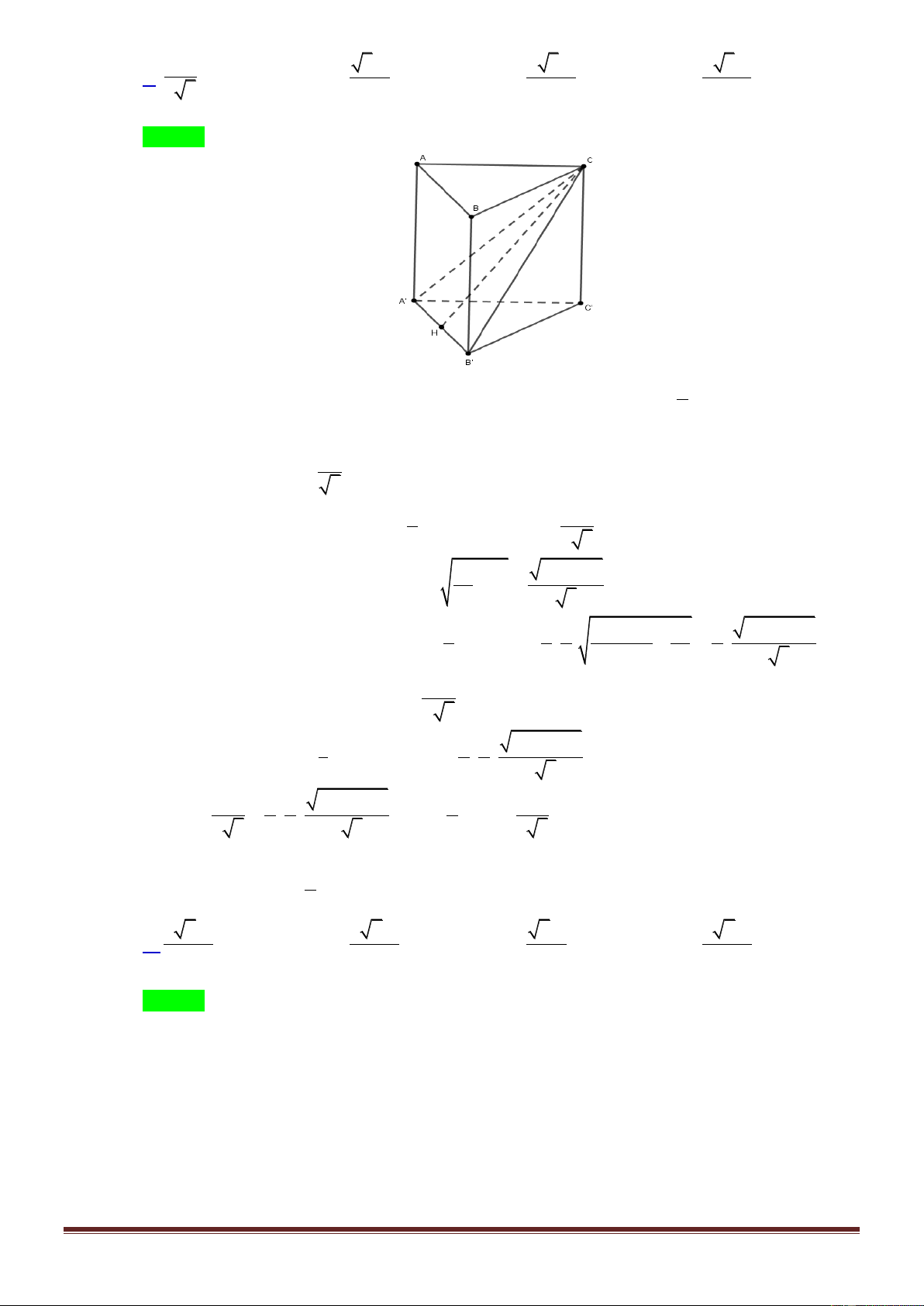
Gọi M là trung điểm BC thì AM BC và SA BC nên BC  SAM  .
Từ đây dễ thấy góc cần tìm là 
  ASM  45 . Do đó tam giác a 3
SAM vuông cân tại A và SA AM  . 2 2 3 1 a 3 a 3 a Suy ra V  . .  S.ABC 3 2 4 8
Bài tập tương tự và phát triển: Mức độ 1 Câu 1.
Cho hình chóp có diện tích mặt đáy là 2
3a và chiều cao bằng 2a . Thể tích của khối chóp bằng A. 3 6a . B. 3 2a . C. 3 3a . D. 3 a . Lờigiải ChọnB 1 1 Ta có 2 3 V S .h  3a .2a  2 đ a . 3 3 Câu 2.
Thể tích V của khối chóp có chiều cao bằng h và diện tích đáy bằng 3B là 1 1
A. V  3Bh . B. V Bh . C. V Bh .
D. V Bh . 3 6 Lời giải Chọn D 1 Ta có V  .3 . B h Bh . 3 Câu 3.
Khi tăng độ dài các cạnh của một khối chóp lên 2 lần thì thể tích của khối chóp thay đổi như thà nào? A. Tăng 4 lần.. B.Tăng 8 lần.. C.Tăng 2 lần. D.Không thay đổi. Lời giải Chọn B 1
Thể tích khối chóp là: V  . B h . 3
Độ dài cạnh đáy tăng lên 2 lần thì diện tích mặt đáy tăng 2 2  4 lần.
Cạnh bên tăng lên 2 lần thì chiều cao của hình chóp tăng lên 2 lần.
Vậy khi tăng độ dài các cạnh của một khối chóp lên 2 lần thì thể tích của khối chóp tăng lên 8 lần. Câu 4.
Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h là 4 1 1 A. V Bh . B. V Bh .
C. V Bh . D. V Bh . 3 3 2 Lời giải Chọn B 1
Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h là V Bh . 3 Câu 5.
Khối chóp S.ABCD có A , B , C , D cố định và S chạy trên đường thẳng song song với AC .
Khi đó thể tích khối chóp S.ABCD sẽ: A.Giảm phân nửa.. B.Tăng gấp đôi.. C.Tăng gấp bốn. D.Giữ nguyên.. Lời giải. Chọn D
Gọi  là đường thẳng qua S và song song AC . 1 Ta có: V  . B h 3
+  song song AC nên   ABCD  d S, ABCD  d  ,
  ABCD  h không đổi. Trang4
+ A , B , C , D cố định nên diện tích tứ giác ABCD cũng không đổi.
Vì vậy thể tích khối chóp S.ABCD sẽ giữ nguyên. Câu 6.
Cho khối chóp  H  có thể tích là 3
2a , đáy là hình vuông cạnh a 2 . Độ dài chiều cao khối
chóp  H  bằng. A. 3a . B. a . C. 4a . D. 2a . Lời giải Chọn A 3 1 1 6a 2 3 V  . B h
( 2a)  2a h   3a . 2 3 3 2a Câu 7.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và thể tích bằng 3 a .Tính chiều
cao h của hình chóp đã cho. A. h  . a . B. h  2 . a . C. h  3 . a . D. h  3 . a . Lời giải ChọnC 3 1 3V 3a Ta có:V
S.h h    3 . a . 2 3 S a Câu 8.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
3a . Tính chiều cao h của hình chóp đã cho. 3a 3a 3a A. h  . B. h  .
C. h  3a . D. h  . 3 2 6 Lời giải ChọnC 2a2 3
Do đáy là tam giác đều nên 2 S   a 3  . ABC 4 3 1 3V 3a Mà V S .h h    3  a . ABC 2 3 Sa ABC 3 Câu 9.
Nếu độ dài chiều cao của khối chóp tăng lên 5 lần, diện tích đáy không đổi thì thể tích của khối chóp sẽ tăng lên A. 5 lần. B. 20 lần. C.15 lần. D.10 lần. Lờigiải ChọnA
Thể tích khối chóp sẽ tăng lên 5 lần.
Câu 10. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và chiều cao 4a . Tính thể tích của hình chóp đã cho. 3 2a 3 3 4a 3 3 a 3 3 a 3 A.V  . B.V  . C.V  . D.V  . 3 3 3 4 Lời giải ChọnC 2 Do đáy là tam giác đề a 3 u nên S  . ABC  4 2 3 1 1 a 3 a 3 Mà V S .h  . .4a   . 3 ABC 3 4 3
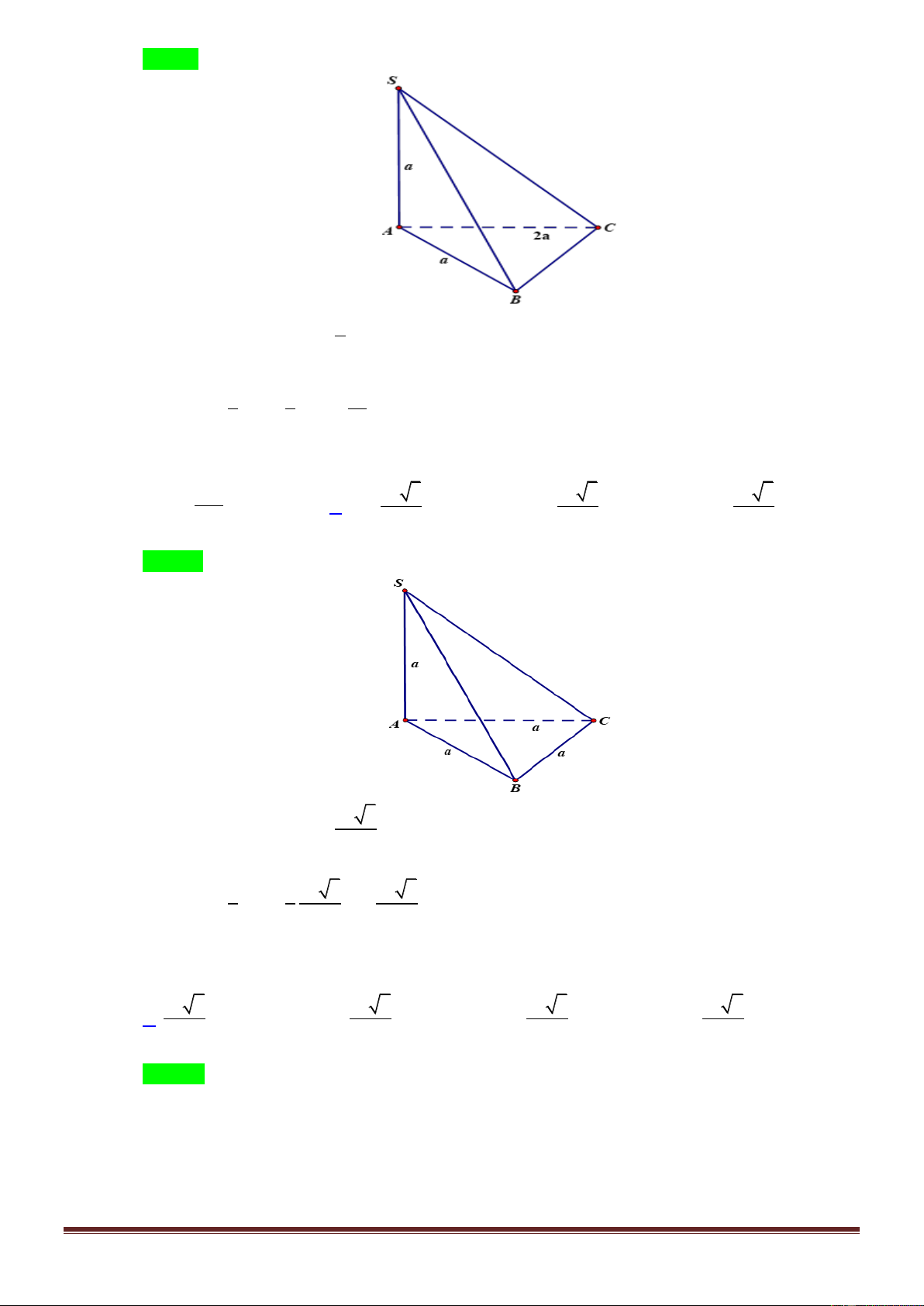
Câu 11. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A , AB a , AC  2a , cạnh
bên SA vuông góc với mặt đáy và SA a . Tính thể tích V của khối chóp S.ABC . 3 a 3 a 3 a A. 3 V a . B.V  . C.V  . D.V  . 2 3 4 Lờigiải Trang5 ChọnB 1 Diện tích đáy 2 B S  .2 a a a ABC 2
Chiều cao: h a 3 1 1 a 2 V  . B h a .a
ABCA' B 'C ' 3 3 3
Câu 12. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc
với mặt đáy và SA a . Tính thể tích V của khối chóp S.ABC . 3 2a 3 a 3 3 a 3 3 a 3 A.V B.V C.V D.V  . 3 12 3 4 Lờigiải Chọn B 2 a 3
Diện tích đáy B SABC 4
Chiều cao: h a 2 3 1 1 a 3 a 3 V  . B h  .a
ABCA' B 'C ' 3 3 4 12
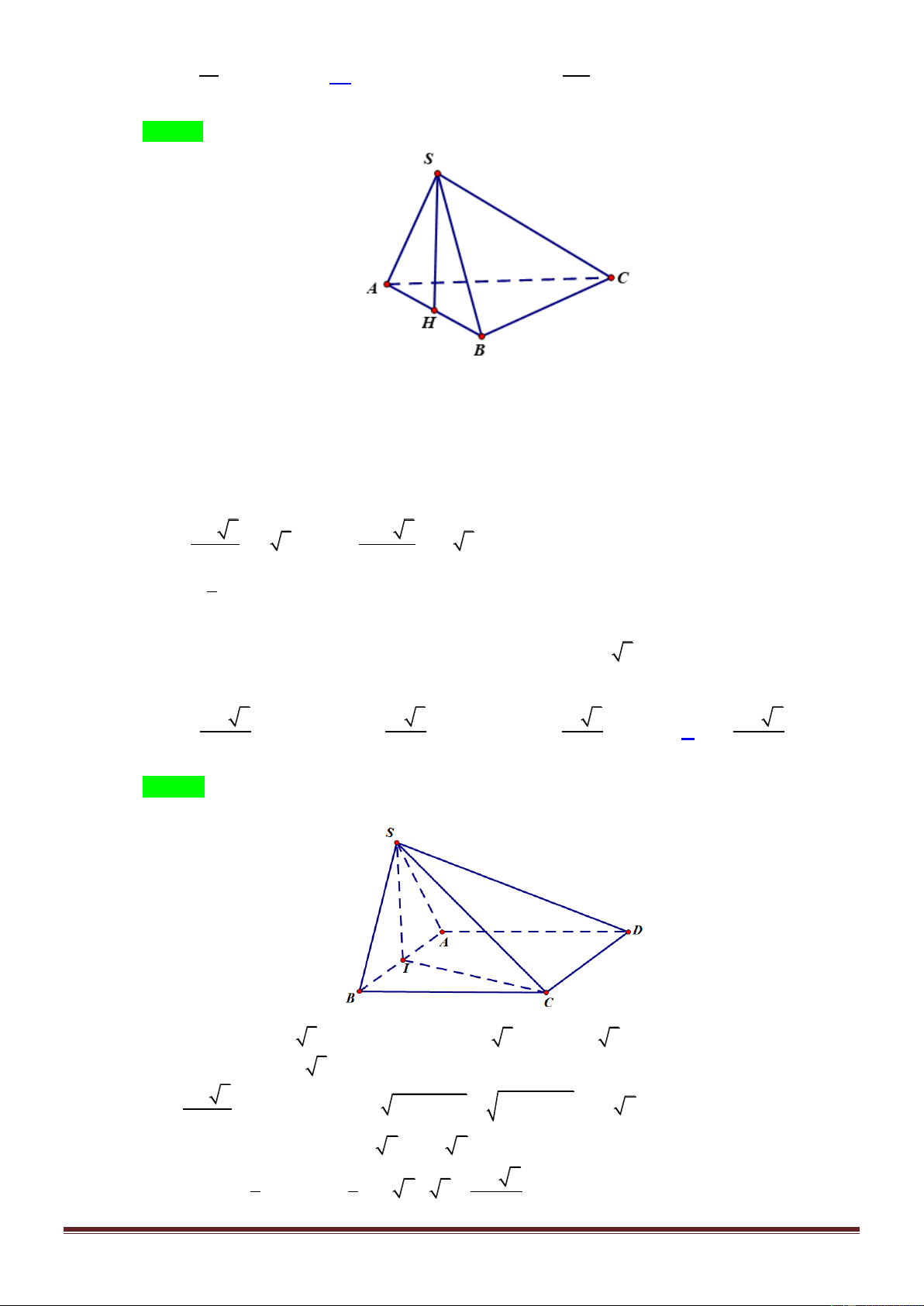
Câu 13. Cho khối chóp S.ABC có SA vuông góc với  ABC  , đáy ABC là tam giác vuông cân tại A ,
BC  2a , góc giữa SB và  ABC  là 30 . Tính thể tích khối chóp S.ABC . 3 a 6 3 a 6 3 a 3 3 a 2 A. . B. . C. . D. . 9 3 3 4 Lời giải Chọn A Trang6 S A C 30° B
Ta có AB là hình chiếu của SB lên  ABC  suy ra góc giữa SB và  ABC  là góc  SBA  30 .
Tam giác ABC vuông cân tại A , BC  2a AB AC a 2 . 3 a 6 Xét S
AB vuông tại A có SA A .
B tan 30  a 2.  . 3 3 1 3 1 1 a 6 a 6 Ta có 2 2 S
AB a . Vậy 2 V  .S . A S  . .a  . ABC 2 S.ABC 3 ABC 3 3 9
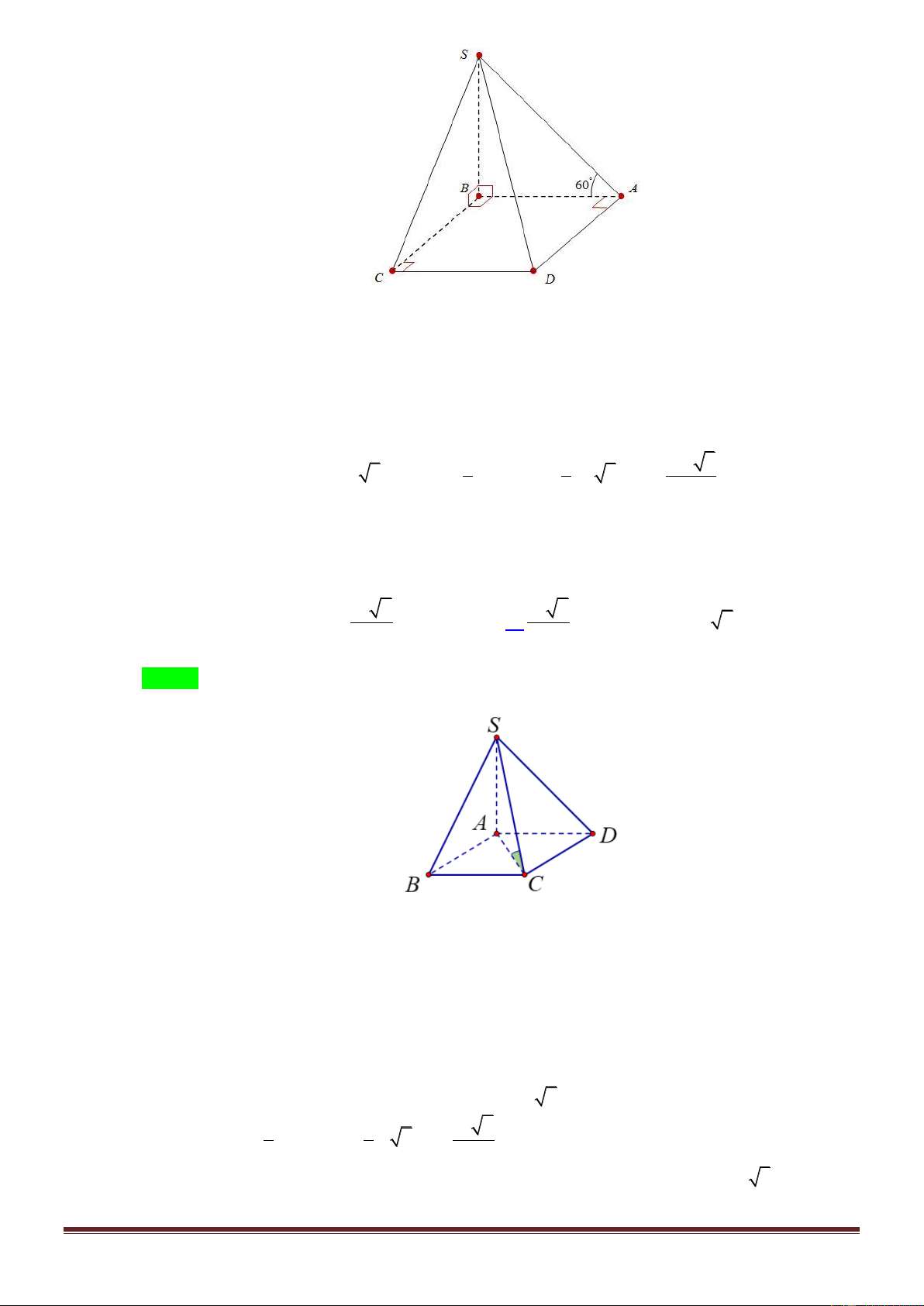
Câu 14. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a , AD a 3 , SA vuông góc
với mặt phẳng đáy và mặt phẳng SBC  tạo với đáy một góc o
60 . Tính thể tích V của khối chóp S.ABCD . 3 3a 3 a A. 3 V  3a . B. V  . C. 3 V a . D. V  . 3 3 Lời giải Chọn C S a 60 B A a 3 D C Ta có 2 SA . B AD  . a a 3  3a . ABCD Dễ thấy  o
BC AB;BC SB SBA  60 . SA Xét tam giác vuông 
SAB A 1v có: o o tan 60 
SA AB tan 60  a 3 AB 1 1 Vậy 2 3 VS .SA a 3.a 3  a . S . ABCD 3 ABCD 3
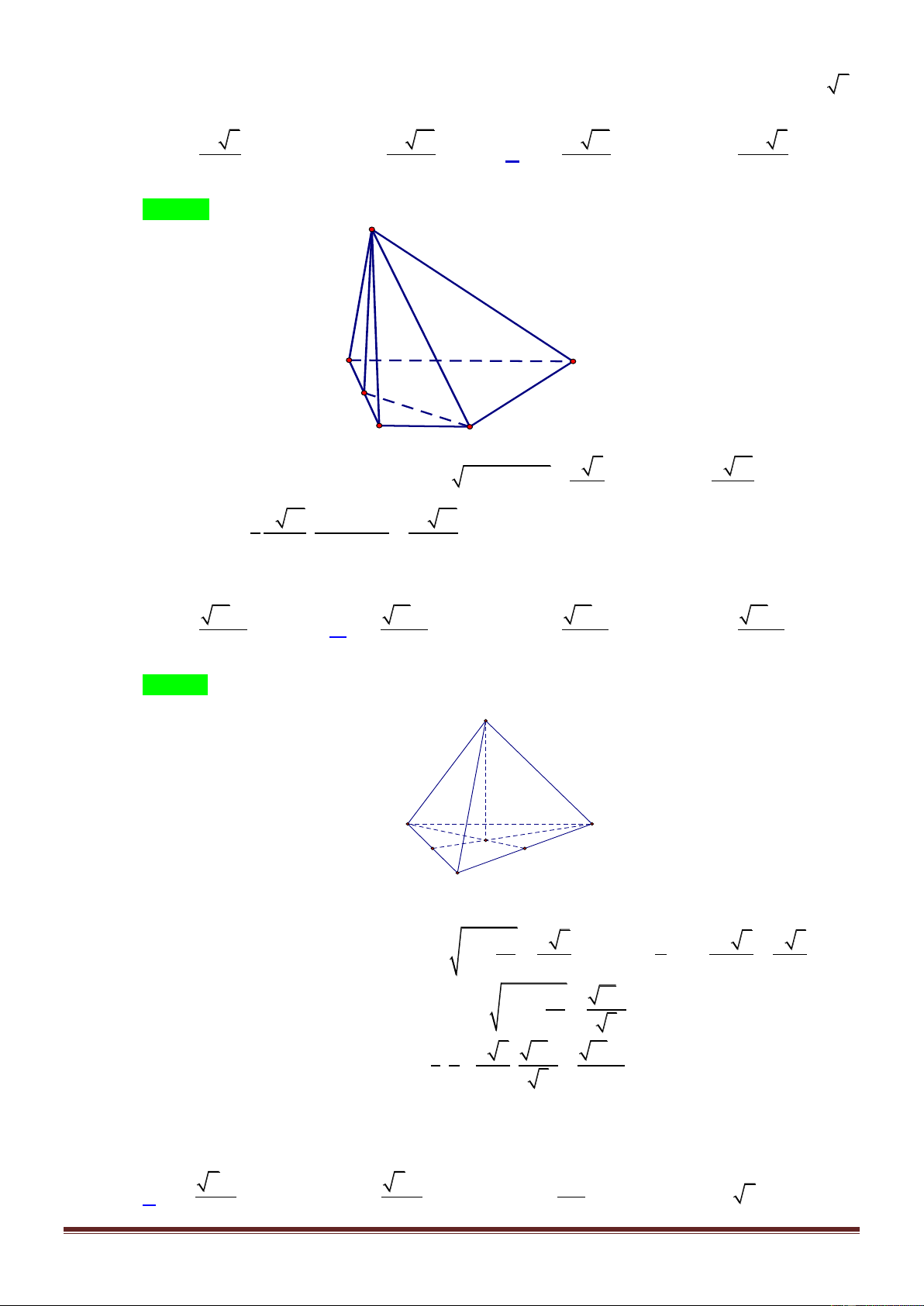
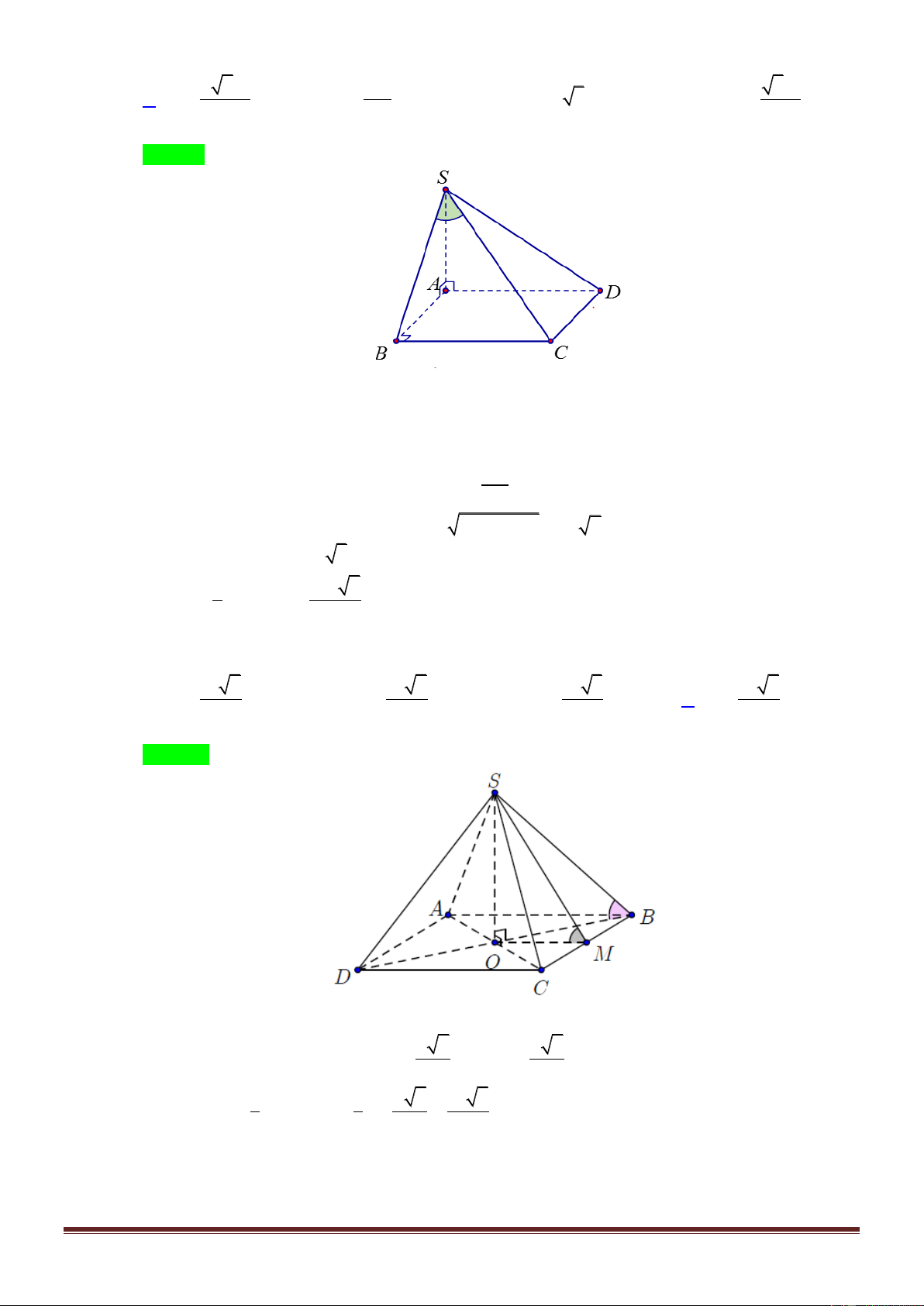
Câu 15. Cho hình chóp S.ABC có SA a và vuông góc với đáy ABC . Biết rằng tam giác ABC đều
và mặt phẳng SBC  hợp với đáy  ABC  một góc 30 . Tính thể tích V của khốichóp S.ABC . 3 a 3 3 2a 3 a 3 3 a A. V  . B. V  . C. V  . D. V  . 3 3 12 3 Lời giải: Trang7 Chọn A
Gọi I là trung điểm BC, ta có  SIA  30
Xét tam giác SIA vuông tại A ta có SA a AI a 3 3 Ta có AI ABAB  2 . a 2 3 Diện tích 2 2 SABa 3 ABC 4 3 1 a 3
Thể tích V  .S . A S  3 ABC 3
Câu 16. Cho khối chóp S.ABC có SA vuông góc với  ABC  , đáy ABC là tam giác vuông cân tại A ,
BC  2a , góc giữa SB và  ABC  là 30 . Tính thể tích khối chóp S.ABC . 3 a 6 3 a 6 3 a 3 3 a 2 A. . B. . C. . D. . 9 3 3 4 Lời giải: Chọn A S A C 30° B
AB là hình chiếu của SB lên  ABC  suy ra góc giữa SB và  ABC  là góc  SBA  30 .
Tam giác ABC vuông cân tại A , BC  2a AB AC a 2 . 3 a 6 SA A .
B tan 30  a 2.  . 3 3 1 2 2 SAB a . ABC 2 3 1 1 a 6 a 6 2 V  .S . A S  . .a  . S.ABC 3 ABC 3 3 9
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , tam giác SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC . Trang8 3 a 3 3a A. V  . B. 3 V a . C. V  . D. 3 V  3a . 2 2 Lời giải: Chọn B
Gọi H là trung điểm của AB .
SAB   ABC   
SAB   ABC   AB SH  ABCSH AB   SH  SAB  AB 3 2 AB 3 SH   a 3 , 2 S   a 3 . 2 ABC 4 1 3 VSH.Sa . S . ABC 3 ABC
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy  ABCD . Biết SD  2a 3 và góc tạo bởi đường thẳng
SC và mặt phẳng  ABCD bằng 0
30 . Tính thể tích V của khốichóp S.ABCD . 3 2a 3 3 a 3 3 a 3 3 4a 6 A. V  . B. V  . C. V D.V  7 13 4 3 Lời giải ChọnD. …
Ta có SC SD  2a 3 ,  0 SI S .
C sin SCI  2a 3.sin 30  a 3 ,  0 CI S .
C cosSCI  2a 3.cos30  3a . AB 3 SI
AB  2a . BC CI BI   a2 2 2 2 3  a  2a 2 2 Từ đó: 2 SA . B BC  2 .
a 2a 2  4a 2 ABCD 3 1 1 4a 6 Vậy 2 V  .S .SI  .4a 2.a 3  . S.ABCD 3 ABCD 3 3 Trang9
Câu 19. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AB BC a , AD  2a .
Hình chiếu của S lên mặt phẳng  ABCD trùng với trung điểm cạnh AB . Biết rằng SC a 5 .
Tính theo a thể tích V của khối chóp S.ABCD . 3 a 5 3 a 15 3 a 15 3 2a 5 A. V B. V  . C. V  . D. V  . 4 3 4 3 Lời giải Chọn C. S A D M B C Gọi a 5 a 15
M là trung điểm AB . Ta có: 2 2 MC BC MB  suy ra SM  . 2 2
1 a 15 a  2a 3 a a 15 Nên V  .  . S.ABCD 3 2 2 4
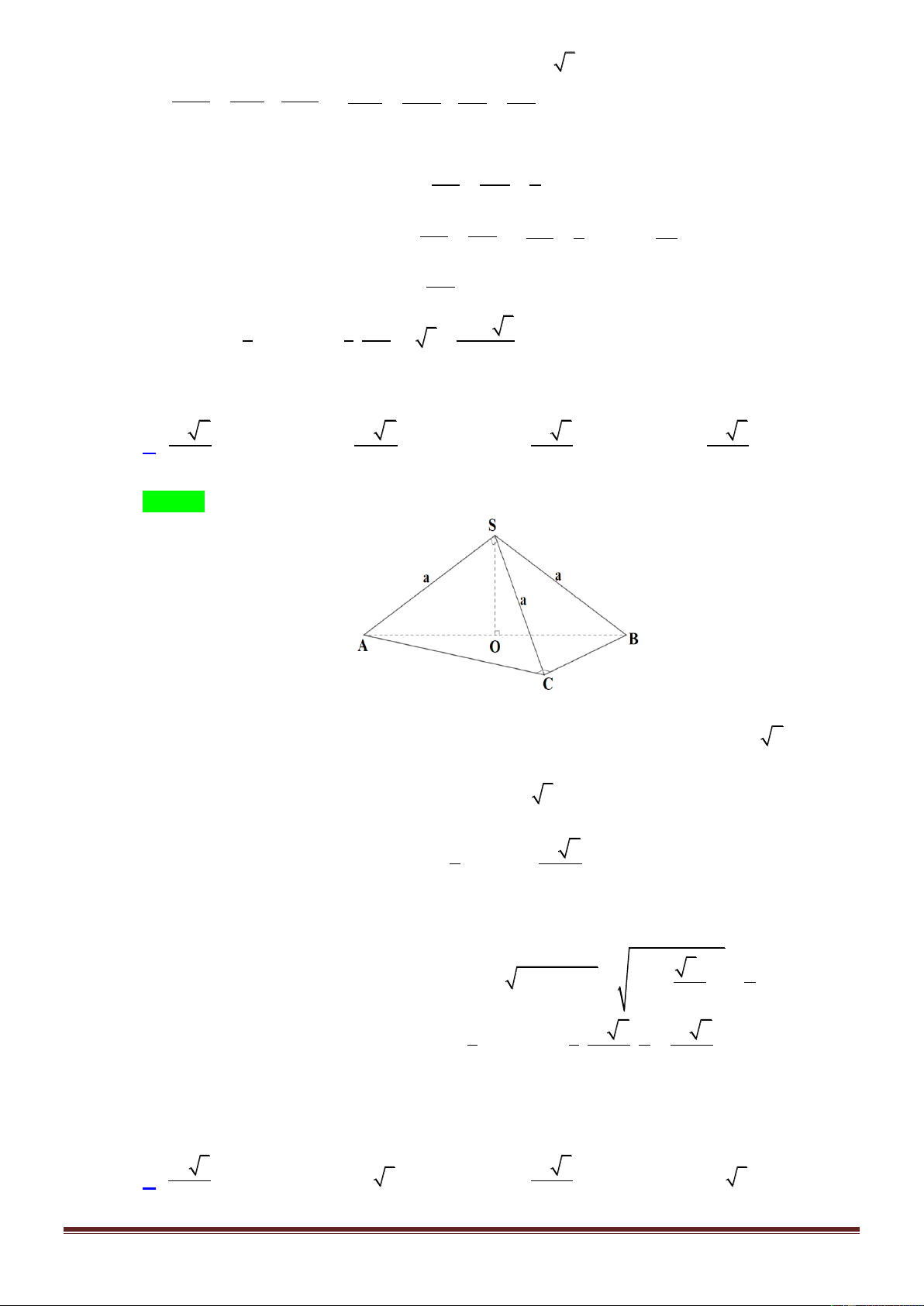
Câu 20. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a . Tính thể tích
V của khối chóp S.ABC 3 13a 3 11a 3 11a 3 11a A. V  . B.V  . C. V  . D. V  . 12 12 6 4 Lời giải Chọn B. S A C O I B
Do đáy là tam giác đều nên gọi I là trung điểm cạnh BC , khi đó AI là đường cao của tam 2 giác đáy. Theo đị a a 3 2 2a 3 a 3 nh lý Pitago ta có 2 AI a   , và AO AI   . 4 2 3 3.2 3 2 a 11a
Trong tam giác SOA vuông tại O ta có 2 SO  4a   3 3 3 1 1 a 3 11a 11a
Vậy thể tích khối chóp S.ABC là V  . a .  . 3 2 2 3 12  Mức độ 2 Câu 1.
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và SC tạo với
mặt phẳng  SAB một góc 0
30 . Tính thể tích V của khối chóp đã cho. 3 2a 3 6a 3 2a A.V  . B.V  . C.V  . D. 3 V  2a . 3 3 3 Trang10 Lờigiải ChọnA
Ta có CB  SAB  SC  SAB   SC SB  0 ; ;  CSB  30 Suy ra 0 SB B .
C cot 30  a 3; 2 2
SA SB AB a 2 3 1 2a
Thể tích khối chóp : V S .SA  . 3 ABCD 3 Câu 2. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật AB a , BC  2a , SA  2a , SA
vuông góc với mặt phẳng  ABCD. Tính thể tích khối chóp .
S ABCD tính theo a . 3 8a 3 4a 3 6a A. B. C. D. 3 4a 3 3 3 Lời giải Chọn B Ta có SA . B CD 2  2a . ABCD 1 3 1 4a Thể tích khối chóp . S ABCD là V  . SA S 2  2 .2 a a  . S . ABCD 3 ABCD 3 3 Câu 3.
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C , AB a 5 , AC a . Cạnh bên
SA  3a và vuông góc với mặt phẳng  ABC  . Tính thể tích khối chóp S.ABC . 3 a 5 A. . B. 3 a . C. 3 3a . D. 3 2a . 2 Lời giải Chọn B.
Vì tam giác ABC vuông tại C nên 2 2 2 2 BC
AB AC  5a a  2 . a 1 1 2 SA . C BC  . .
a 2a a . ABC 2 2 1 1 2 3 V  . SA S  .3 .
a a a (đvtt). . S . ABC 3 ABC 3 Câu 4.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a , BC  2a , đường thẳng SA
vuông góc với mặt phẳng  ABCD và SA  3a . Thể tích của khối chóp S.ABCD bằng A. 3 2a . B. 3 3a . C. 3 6a . D. 3 a . Trang11 Lời giải Chọn A S 3a D A a 2a B C 1
Áp dụng công thức tính thể tích khối chóp ta có V  3 . .2 a .3 a a  2a . S . ABCD 3 Câu 5.
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy  ABC  . Biết SA a ,
tam giác ABC là tam giác vuông cân tại A , AB  2a . Tính theo a thể tích V của khối chóp S.ABC . 3 a 3 a 3 2a A. V B. 3 V  2a C. V D. V  2 6 3 Lời giải S A C B Chọn D 1 1 2
Ta có: V  .S . A S  1 1  3   S . A .A . B AC . . a 2a2 a (dvtt). 3 ABC 3 2 6 3 Câu 6.
Cho khối chóp tam giác S.ABC có SA   ABC , tam giác ABC có độ dài 3 cạnh là AB  5a
; BC  8a ; AC  7a , góc giữa SB và  ABC là 45. Tính thể tích khối chóp S.ABC . 50 3 50 50 7 A. 3 50 3a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 Lời giải Chọn B Trang12
AB AC BC Ta có nửa chu vi ABC  là p   10a . 2 Diện tích ABC  là 2 S  10 . a 5 . a 3 .
a 2a  10 3a . ABC
SA   ABC nên S
AB vuông, cân tại A nên SA AB  5. 1 1 50 3
Thể tích khối chóp S.ABC là VS . A S 2  5a.10 3a 3  a . S . ABC  3 ABC 3 3 Câu 7.
Cho hình chóp S.ABC có mặt phẳng SAC  vuông góc với mặt phẳng  ABC  , SAB là tam
giác đều cạnh a 3 , BC a 3 đường thẳng SC tạo với mặt phẳng  ABC góc 60. Thể tích
của khối chóp S.ABC bằng 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. 3 2a 6 . 3 2 6 Lờigiải ChọnC B A S 60o H C
Ta thấy tam giác ABC cân tại B , gọi H là trung điểm của AB suy ra BH A . C
Do SAC    ABC  nên BH  SAC  .
Ta lại có BA BC BS nên B thuộc trục đường tròn ngoại tiếp tam giác ABC H là tâm
đường tròn ngoại tiếp tam giác SAC SA SC .
Do AC là hình chiếu của SC lên mặt phẳng  ABC    0 SCA  60 . SA Ta có 0 SC S .
A cot 60  a , AC
 2a HC a 2 2
BH BC HC a 2 . 0 sin 60 1 3 a 6 V  1 BH .SBH. . SA SC  . S . ABC 3 SAC 6 6 Câu 8.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh SB vuông góc với đáy
và mặt phẳng SAD tạo với đáy một góc 60 . Tính thể tích khối chóp S.ABCD . 3 3a 3 3 3a 3 3 8a 3 3 4a 3 A.V  . B.V  . C.V  . D.V  . 4 8 3 3 Lời giải Chọn C Trang13
SB   ABCD  Ta có:
mà AD AB AD SA .  
  SB AD AD ABCD 
SADABCD  AD 
AB AD, AB   ABCD  SAD  ABCD SA AB  ; ; SAB 60    
SA AD, SA  SAD  3  1 1 8a 3
Ta có: SB B .
D tan 60  2a 3 . Vậy 2 V SB.S  2a 3.4a  . 3 ABCD 3 3 Câu 9.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông c ạnh a , hai mặt phẳng SAB và
SAD cùng vuông góc với mặt phẳng ABCD ; góc giữa đư ờng thẳng SC và mặt phẳng
ABCD bằng 60. Tính theo a thể tích khối chóp S.ABCD . 3 a 6 3 a 6 A. 3 3a . B. . C. . D. 3 3 2a . 9 3 Lờigiải ChọnC
SAB   ABCD  Ta có 
SAD   ABCD
SA   ABCD   SAB
SAD  SA
AC là hình chiếu vuông góc của SC lên mặt phẳng  ABCD  SC    ABCD  ,  SCA  60
Tam giác SAC vuông tại A có SA AC.tan 60  a 6 . 3 Khi đó 1 1 a 6 2 V  .S . A S  .a 6.a  . SABCD 3 ABCD 3 3
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , BC a 3 . Cạnh bên
SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng SAB một góc 30 . Tính thể Trang14
tích V của khối chóp S.ABCD theo a . 3 2 6a 3 2a 3 3a A. V  . B. V  . C. 3 V  3a . D. V  . 3 3 3 Lời giải Chọn A BC SA Ta có: 
BC  SAB  SB là hình chiếu của SC lên mặt phẳng SAB. BC AB  
SC SAB   SC SB  , ,  CSB  30 . BC
Xét tam giác SBC vuông tại B có tan 30   SB  3a . SB
Xét tam giác SAB vuông tại A có 2 2
SA SB AB  2a 2 . Mà 2 SA . B BC a 3 . ABCD 3 1 2a 6 Vậy V S .SA  . 3 ABCD 3
Câu 11. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABCD . 3 a 6 3 a 6 3 a 3 3 a 6 A. V  . B. V  . C. V  . D. V  2 3 2 6 Lời giải Chọn.D. Ta có: 2 Sa . ABCD a 2 a 6 Chiều cao SO :  0 SO O . B tan SBO  .tan 60  . 2 2 3 1 1 a 6 a 6 Vậy 2 V  .S .SO  .a .  . S.ABCD 3 ABCD 3 2 6
Câu 12. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và mặt bên tạo với mặt phẳng đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABCD . Trang15 3 a 6 3 a 6 3 a 3 3 a 6 A. V  . B. V  . C. V  . D. V  2 3 2 6 Lời giải ChọnD. Ta có: 2 Sa . ABCD
Gọi M là trung điểm BC , góc giữa mặt bên (SBC ) và ( ABCD) là  SMO 1 a Ta có OM AB  . 2 2 a a 3 Chiều cao SO :  0 SO O . B tan SBO  .tan 60  . 2 2 3 1 1 a 3 a 3 Vậy 2 V  .S .SO  .a .  . S.ABCD 3 ABCD 3 2 6
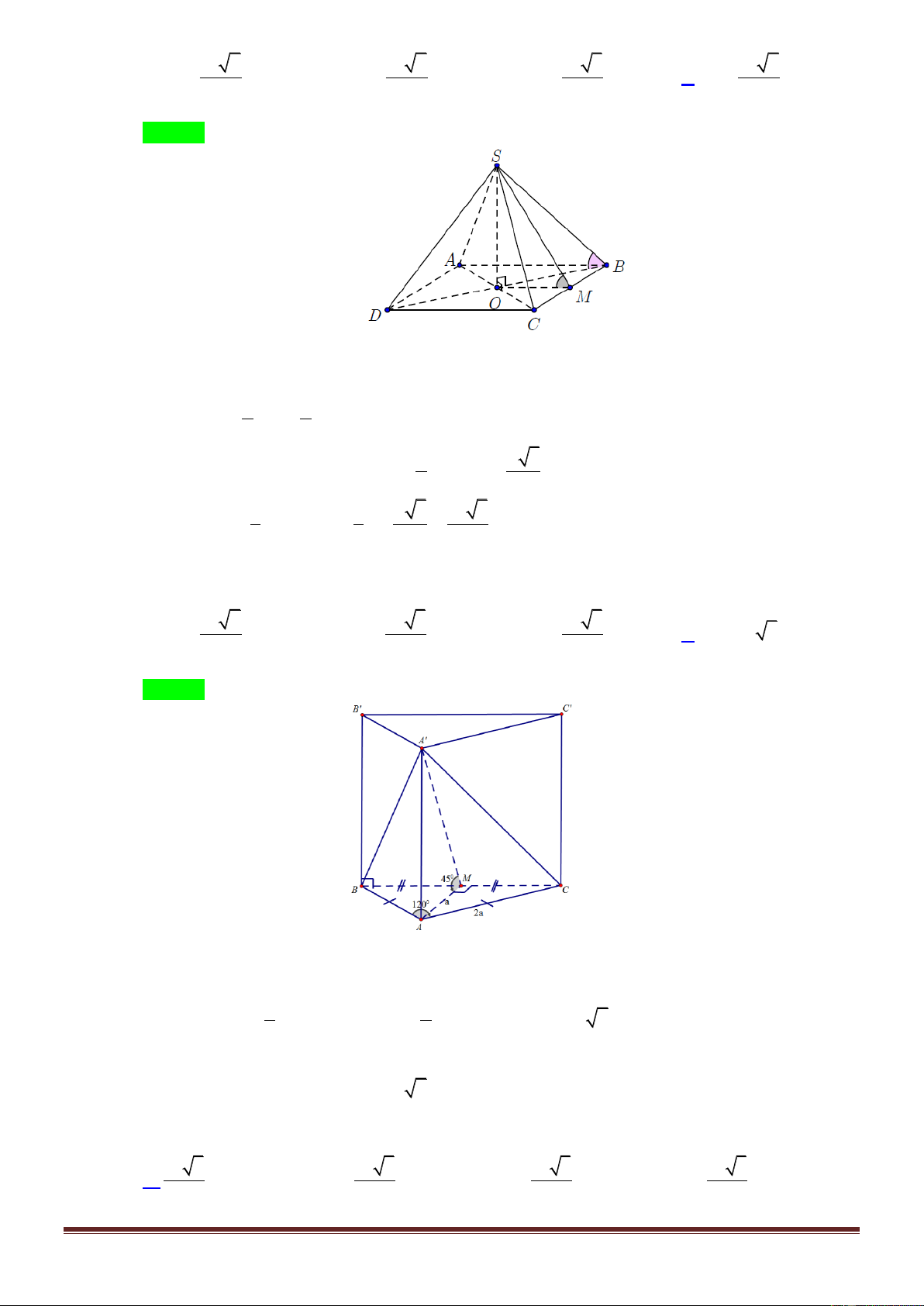
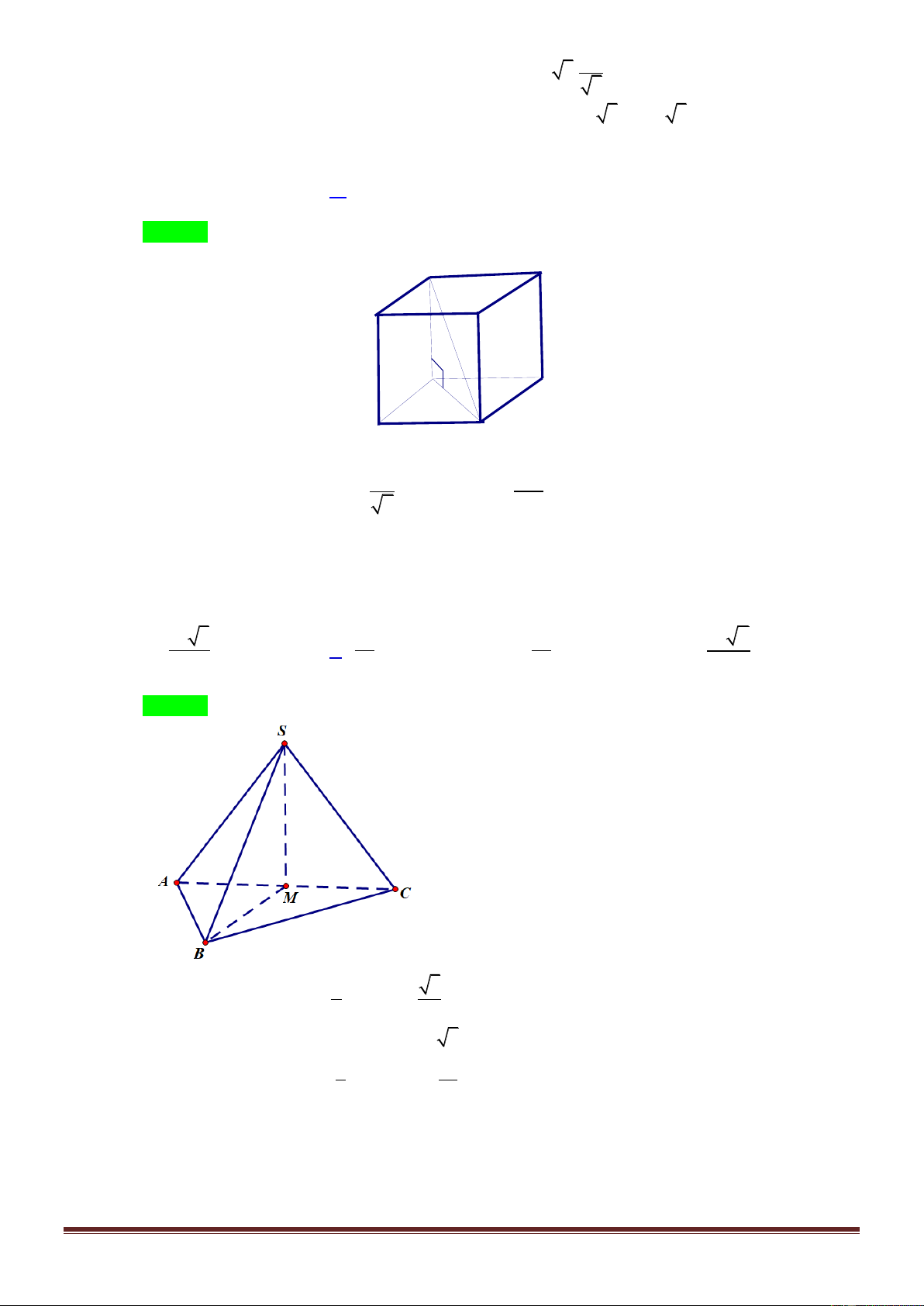
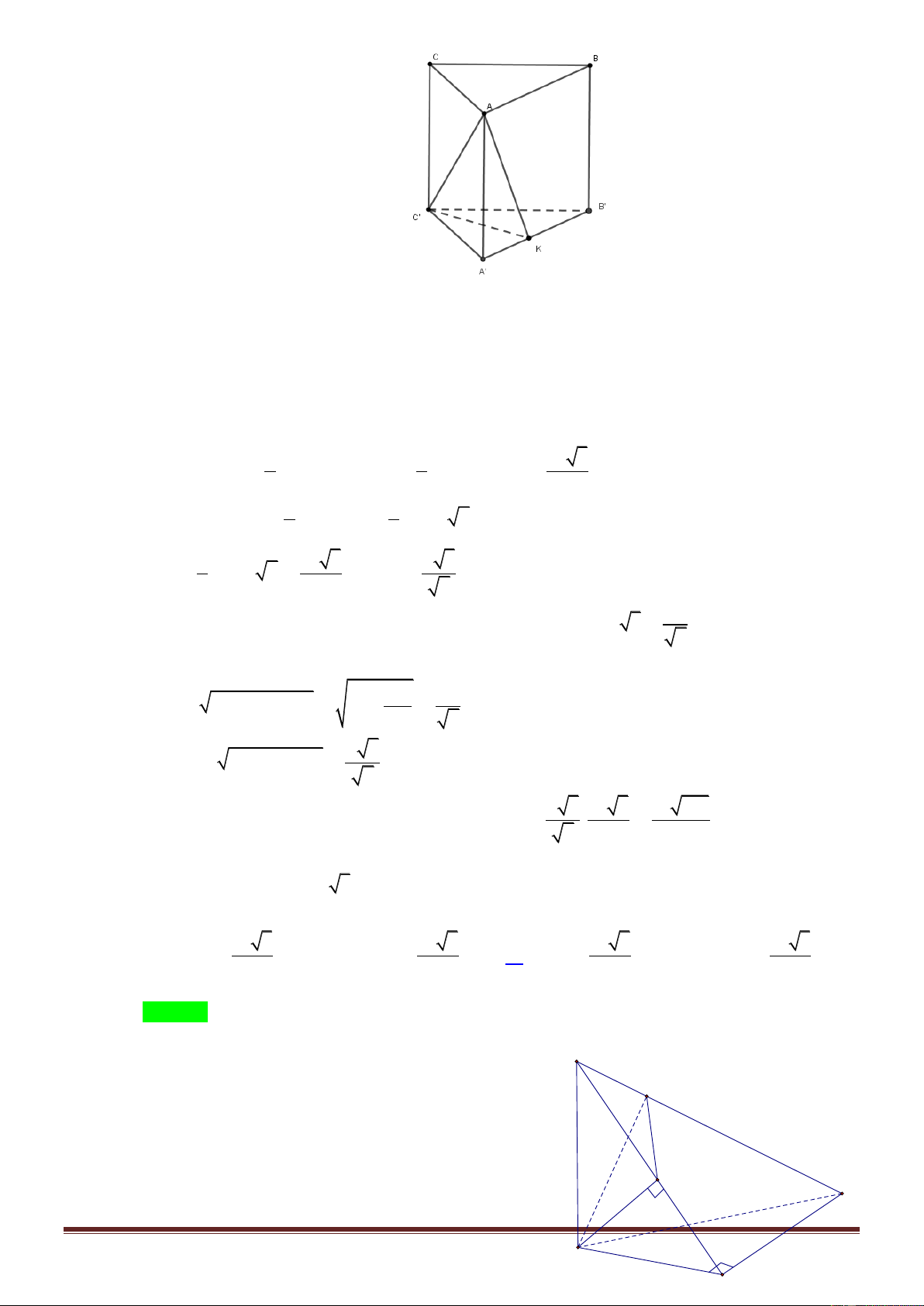
Câu 13. Cho lăng trụ đứng ABC.A B ¢ C
¢ ¢có đáy là tam giác cân tại 
A , AB AC  2a ,  CAB  120 , góc giữa (A BC ¢
) và (ABC) là 45° . Tính thể tích lăng trụ đã cho. 3 a 6 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. 3 V a 3 2 3 2 Lời giải ChọnD. ·
Gọi M là trung điểm của BC . Ta có AM ^ BC và CAM = 60° ( do DABC cân tại A ) Ta xác định đượ · c góc giữa (A BC ¢
) và (ABC) là A M ¢ A = 45° 1 1 Ta có · S = ° 2 D ABC = AB.AC.sinBAC (
. 2a)2 sin 120 = a 3 và 2 2 · ·
AM = AC cos MAC = 2a.cos60° = a ; AA¢= AM .tan A M ¢ A= a Vậy 3 V = AA .S ¢ = a
3 (đơn vị thể tích). ABC .A B ¢ C ¢ ¢ D ABC
Câu 14. Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo đáy góc 0 60 . Thể tích của
khối chóp đó bằng: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 6 36 18 Lời giải Trang16 Chọn A S 60 A C O M B 2 a 3 Ta có: S
. Gọi O là trọng tâm của tam giác ABC , suy ra SO   ABC . ABC 4
Ta có AO là hình chiếu của SA lên mặt phẳng  ABC  .
Suy ra SA ABC  SA AO  0 , ,
SAO  60 . Xét tam giác SAO vuông tại O , ta có:  SO  2 2 3 0 tan SAO   SO A . O tan SAO AM .tan 60  . . a . 3  a . AO 3 3 2 2 3 1 1 a 3 a 3 Vậy VS .SO  . .a  . S.ABC 3 ABC 3 4 12
Câu 15. Cho hình lăng trụ đều AB . C A BC
  . Mặt phẳng (A B
¢ C) tạo với mặt phẳng (ABC) một góc 30° và tam giác A B
¢ C có diện tích bằng 2
8a . Tính thể tích khối lăng trụ AB . C A BC   . 3 2a 3 8a 3 2a A. V  . B. 3 V  8a 3 . C. V  . D. V  . 12 6 4 Lời giải Chọn B.
Kẻ đường cao AM của tam giác ABC . Khi đó M là trung điểm của BC Þ BC ^ (A A ¢ M ) Tam giác '
A AM vuông tại A nên góc A ' MA là góc nhọn. ·
Góc giữa hai mặt phẳng ( A ' BC) và ( ABC) bằng góc giữa A M
¢ và AM và bằng góc A MA ¢ , bằng 30°
Tam giác ABC là hình chiếu vuông góc của tam giác A B
¢ C trên (ABC) Suy ra o 2 S = S . o c s30 = 4a 3 . ABC A' BC 2 Đặ x 3
t AB = x > 0 . Diện tích tam giác đều ABC theo x là S = . ABC 4 2 x 3 x 3 Vậy có 2
= 4a 3 Û x = 4a Þ AM = = 2a 3 4 2 Trang17 o 1 Tam giác A M
¢ Avuông tại A , AA¢= AM.tan30 = 2a 3. = 2a . 3
Thể tích của lăng trụ AB . C A BC   là 2 3 V = AA .S ¢ = 2 . a 4a 3 = 8a 3 . ABC
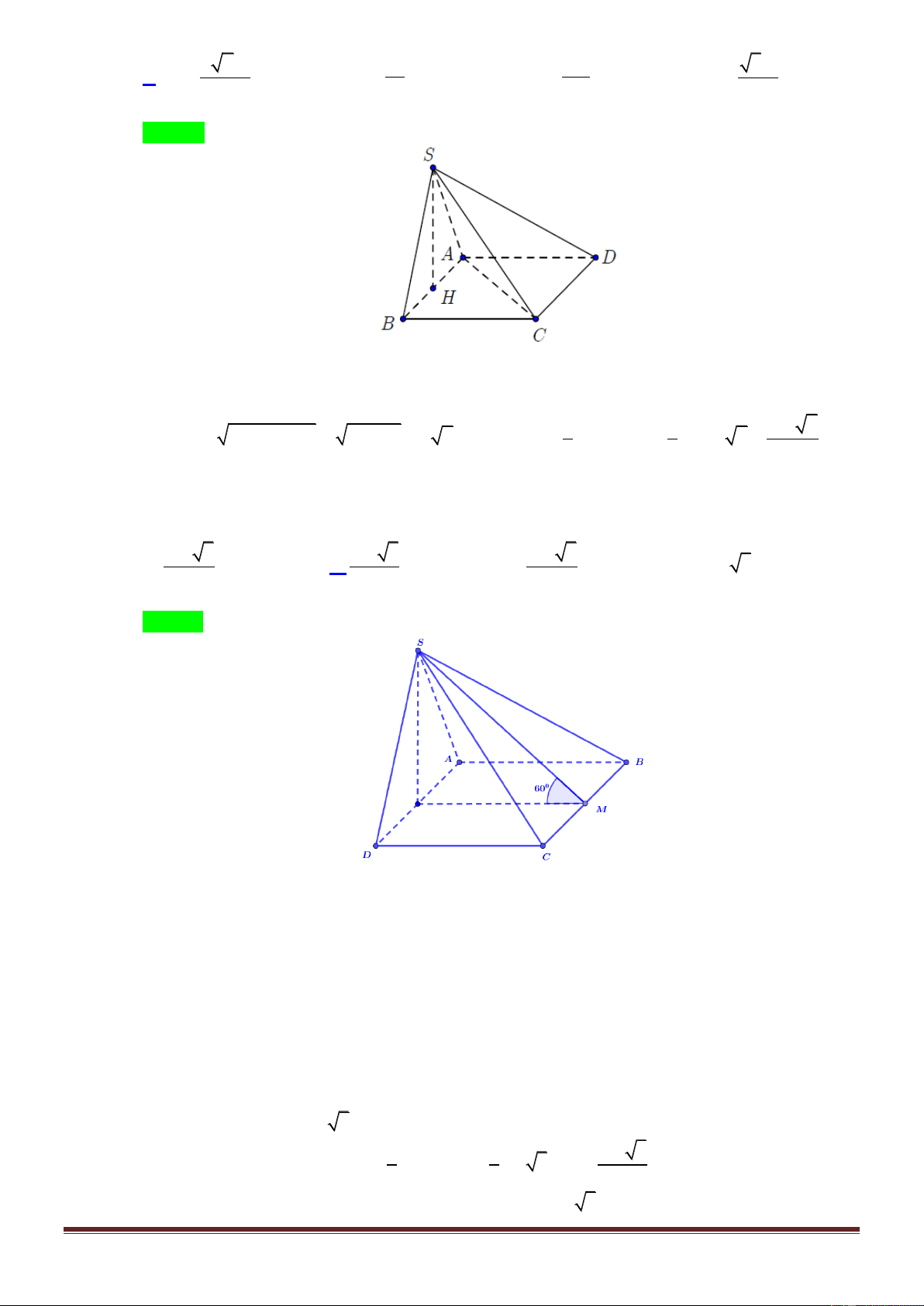
Câu 16. Cho hình hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông, cạnh bên bằng 4a và đường
chéo 5a .Tính thể tích hình hộp chữ nhật này. A. 3 V  3a . B. 3 V  9a . C. 3 V a . D. 3 V  6a . Lời giải Chọn B. C' D' A' B' 4a 5a D C A B 2 2 2 2
BD BD '  DD '  9a BD  3a 3a 2 9a
ABCD là hình vuông  AB   B SABCD 2 4 Vậy 3 V  . B h S .AA'  9a ABCD
Câu 17. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B , AB a , AC  2a . Hình chiếu
vuông góc của S lên  ABC  là trung điểm M của AC . Góc giữa SB và đáy bằng 60 . Thể
tích S.ABC là bao nhiêu? 3 a 3 3 a 3 a 3 a 2 A. . B. . C. . D. . 2 2 4 12 Lời giải Chọn B. 1 3 Diện tích ABC : 2 SA . B BC a ABC  2 2  0 0
* SBM  60  SM M .
B tan 60  a 3 3 1 a Thể tíchS.ABC : VSM.S  . S .ABC  3 ABC 2
Câu 18. Cho hìnhchóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a , AD a . Hình chiếu của
S lên mặt phẳng  ABCD là trung điểm H của cạnh AB , đường thẳng SC tạo với đáy một góc 0
45 . Tính thể tích V của khối chóp S.ABCD . Trang18 3 2 2a 3 a 3 2a 3 3a A. V  . B. V  . C. V  . D. V  3 3 3 2 Lời giải ChọnA. Ta có 2 S  2 . a a  2a . ABCD
Do SC tạo với đáy một góc 0
45 nên SH HC . 3 1 1 2a 2 Mà 2 2 2 2 HC BH BC
a a a 2 . Vậy 2 V  .S
.SH  .2a .a 2  . ABCD 3 ABCD 3 3
Câu 19. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , S
AD cân tại S và nằm trong
mặt phẳng vuông góc với đáy. Góc giữa SBC  và mặt đáy bằng o
60 . Tính thể tích S.ABCD bằng: 3 2a 3 3 8a 3 3 4a 3 A. . B. . C. . D. 3 2a 3 . 3 3 3 Lời giải Chọn B
Gọi H là trung điểm AD . 
SAD   ABCD  Ta có: 
SAD  ABCD  AD SH   ABCD . SH AD
ABCD là hình vuông cạnh 2a nên 2 2 SAB  4a . ABCD
Tam giác SBC cân tại S SM BC , mà HM BC  góc giữa mặt phẳng SBC  và mặt
phẳng  ABCD là góc giữa hai đường thẳng HM , SM chính là góc  SMH . Theo bài ra có  o SMH  60 . o  SH  2 .
a tan 60  2a 3 . 3 1 1 8a 3
Vậy thể tích S.ABCD : 2 VSH.S  .2a 3.4a  . SABCD 3 ABCD 3 3
Câu 20. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 , cạnh bên bằng 2a . Tính thể tích Trang19
V của khối chóp S.ABC . 3 a 3 3 3a 3 3 3a 3 3 3a A.V  . B.V  . C.V  . D.V  . 4 2 4 4 Lời giải Chọn D a 2 2 . 3 3 3a 3
Diện tích đáy B S   ; ABC 4 4 AB a 3 AH    a 3 3 Chiều cao: 2 2 2 2
h SH SA AH  4a a a 3 2 3 1 1 3a 3 3a V  . B h  .a 3  S.ABC 3 3 4 4  Mức độ 3 Câu 1.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA   ABCD , SA a . Gọi G là trọng
tâm tam giác SCD . Tính thể tích khối chóp . G ABCD . 1 1 2 1 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 6 12 17 9 Lời giải Chọn D S N G D A M B C
Gọi M , N lần lượt là trung điểm của CD và SD . Trang20 1 GM
d G, ABCD Ta có   . 3 SM
d S, ABCD 1 1 1 a Ta có Vd G ABCD SSA S  . G ABCD  ,  3 . . . . 3 ABCD 3 3 ABCD 9 Câu 2.
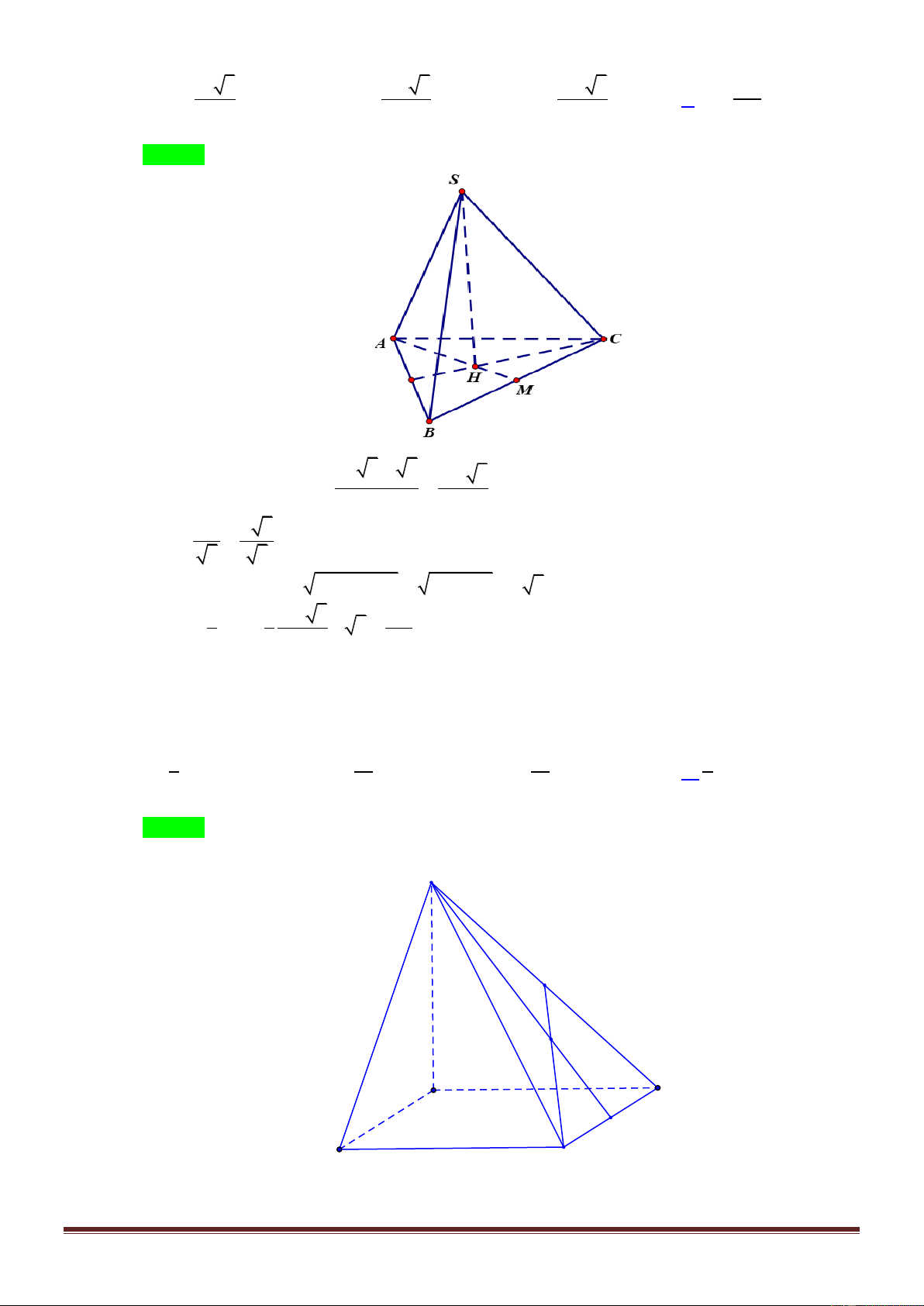
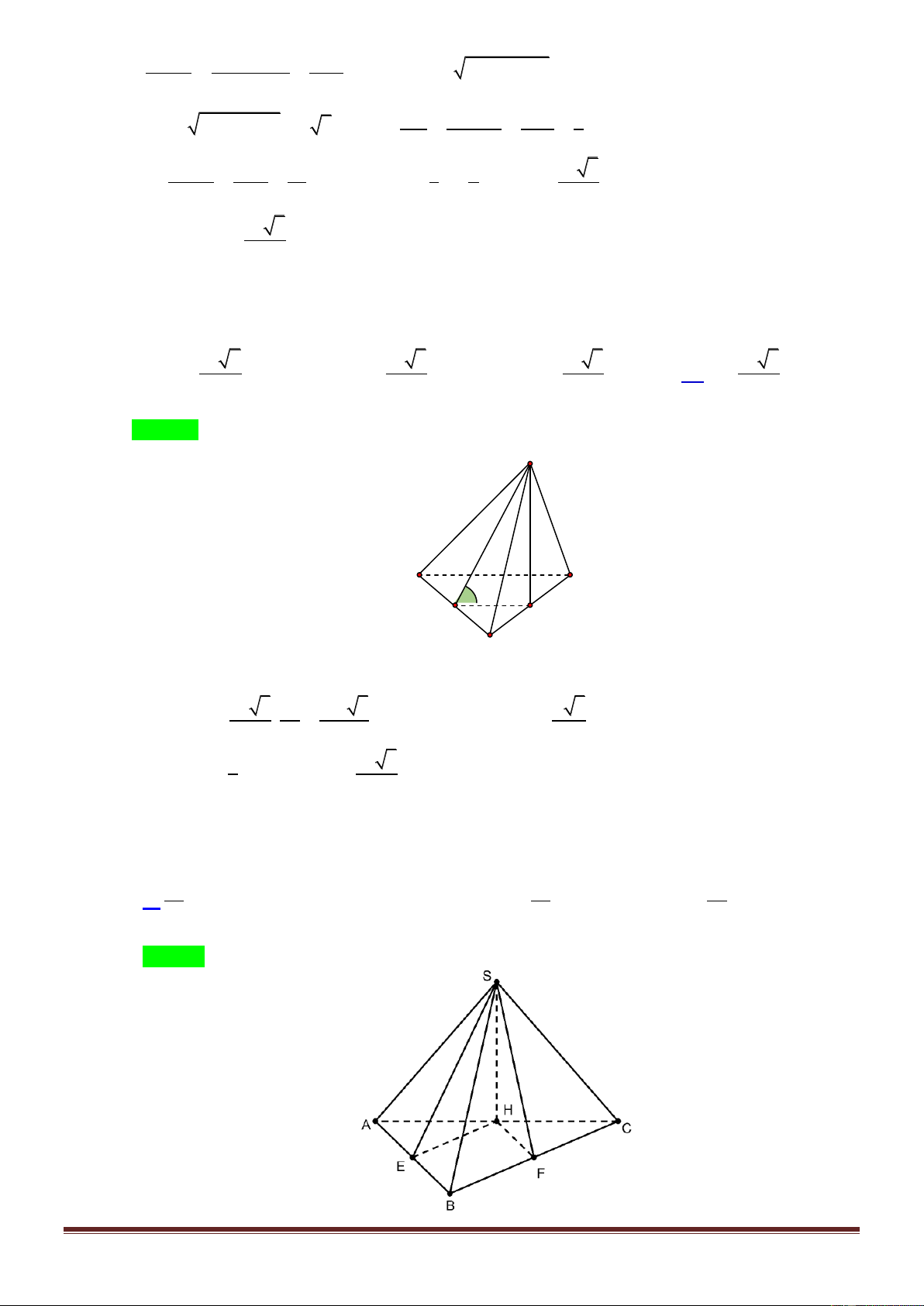
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B , AB a , BC  2a . Tam giác
SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi G là trọng tâm tam giác
ABC , mặt phẳng SAG tạo với đáy một góc 60 . Thể tích khối tứ diện ACGS bằng 3 a 6 3 a 6 3 a 3 3 a 6 A. V B. V C. V D. V  36 18 27 12 Lời giải Chọn A S K A I C G H N B 1 2 1 a Ta có: 2 S  .A . B BC a     S S . ABC   2 ACG 3 ABC 3
Gọi H là trung điểm của AB SH   ABC  .
Gọi N là trung điểm của BC , I là trung điểm của AN và K là trung điểm của AI .
Ta có AB BN a BI AN HK AN .
Do AG  SHK  nên góc giữa SAG và đáy là  SKH  60 . 1 a 2 a a 6 Ta có: BI AN  1 2
HK BI
, SH SK.tan 60  . 2 2 2 4 4 3 1 a 6 Vậy V VV  .SH.S  . ACGS S .ACG  3 ACG 36 Câu 3.
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B , AC a 2, mặt phẳng SAC
vuông góc với mặt đáy  ABC  . Các mặt bên SAB , SBC  tạo với mặt đáy các góc bằng
nhau và bằng 60 . Tính theo a thể tích V của khối chóp S.ABC . 3 3a 3 3a 3 3a 3 3a A. V B. V C. V D. V  2 4 6 12 Lời giải Chọn D Trang21
Ta có: SAC    ABC  và SAC  ABC  AC .
Trong mặt phẳng SAC  , kẻ SH AC thì SH   ABC  .
Gọi I , K lần lượt là hình chiếu vuông góc của H lên cạnh AB và AC thì   
SAB  ABC   ,
SIH và SAC ABC  ,  SKH . Mà  
SIH SKH  60 nên HI HK  tứ giác BIHK là hình vuông  H là trung điểm cạnh AC . Khi đó tứ a a 3
giác BIHK là hình vuông cạnh
và SH HI.tan 60  . 2 2 a a 2 1 3 2 1 3 a 3 Vậy VS .SH V  . .  . SABC 3 ABC SABC 3 2 4 12 Câu 4.
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác cân tại S và nằm
trong mặt phẳng vuông góc với đáy  ABCD . Biết côsin của góc tạo bởi mặt phẳng SCD và  2 17 ABCD bằng
. Thể tích V của khối chóp S.ABCD là 17 3 a 13 3 a 17 3 a 17 3 a 13 A.V  . B.V  . C.V  . D.V  . 6 6 2 2 Lờigiải ChọnA
Gọi H là trung điểm AB SH   ABCD , K là trung điểm CD CD SK   HK a a
Ta có SCD, ABCD  SK HK   ,  SKH .  cos SKH  17  SK  13  SH SK 2 2 Trang22 1 1 a 13 3 a 13
Vậy V  .SH .S 2  . .a . 3 ABCD 3 2 6 Câu 5.
Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D , đáy nhỏ của hình
thang là CD , cạnh bên SC a 15 . Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt
phẳng vuông góc với đáy hình chóp. Gọi H là trung điểm cạnh AD , khoảng cách từ B tới
mặt phẳng SHC  bằng 2 6a . Tính thể tích V của khối chóp S.ABCD ? A. 3 V  8 6a . B. 3 V  12 6a . C. 3 V  4 6a . D. 3 V  24 6a . Lời giải ChọnC S A B H D C F   SAD
  ABCD  AD
SH   ABCD
SH AD, SH   SAD Ta có 2 2
SH SD DH a 3 , 2 2 2 2
HC SC SH  15a  3a  2 3a . 2 2 2 2 CD
HC HD  12a a a 11 . BF BC Ta có 
BF  SHC nên d B,SHC  BF  2 6a . BF SH 1 1 2 S
BF.HC  .2 3 .2 a 6a  6 2a HBC 2 2 1 a 2 Đặ 1 a 11
t AB x nên S
AH.AB  .x ; SDH.DC AHB 2 2 CDH 2 2 1 S
CD AB AD ax a . ABCD    11  2 2 a a 11 SSSS
 .x  a 11 x 2 a
 6 2a x  12 2  11a . AHB ABCD CDH BHC 2 2 S  a    a 2 11 12 2 11 a  12 2a . ABCD 1 1 Vậy 2 3 VSH.S
 .a 3.12 2a  4 6a . S . ABCD 3 ABCD 3 Câu 6.
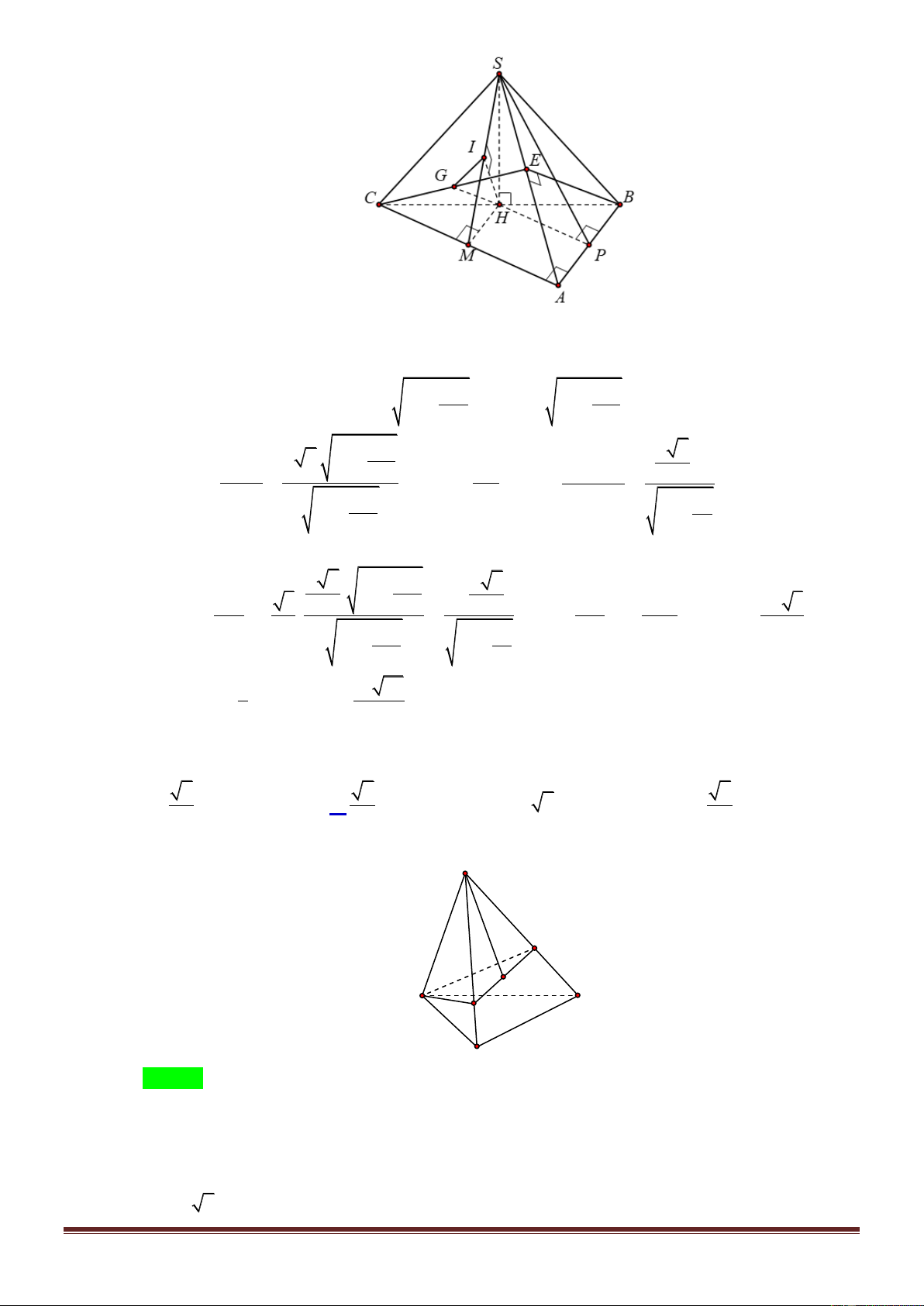
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D ; biết
AB AD  2 , a CD  .
a Góc giữa hai mặt phẳng SBC  và  ABCD bằng 0 60 . Gọi I là
trung điểm của AD , biết hai mặt phẳng SBI  và SCI  cùng vuông góc với mặt phẳng
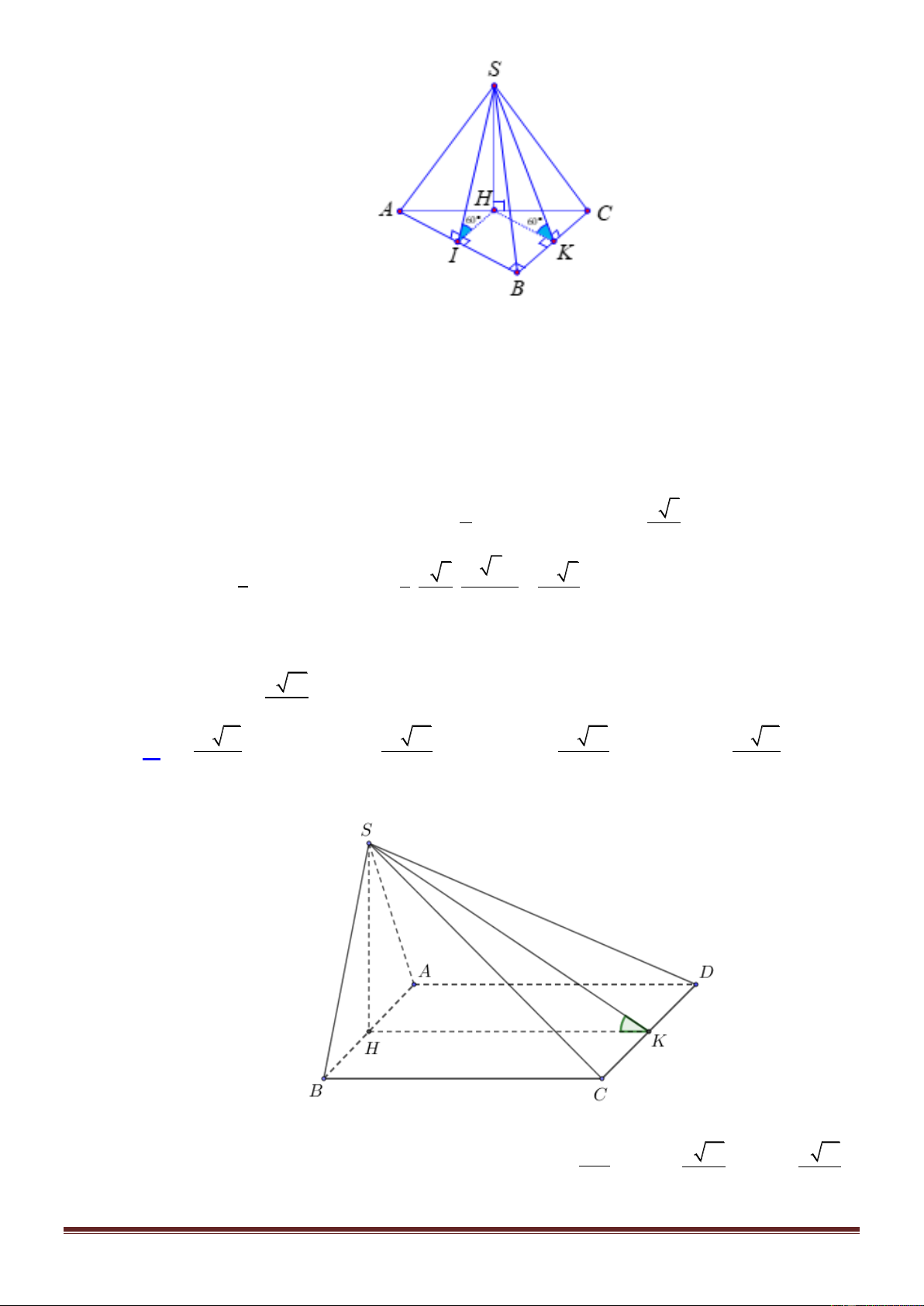
ABCD . Tính thể tích của khối chóp S.ABCD . 3 3 5a 3 3 15a 3 3 5a 3 3 15a A. . B. . C. . D. . 8 5 5 8 Lời giải Chọn B Trang23 .
Như đã nhắc ở Câu trước thì do hai mặt phẳng SBI và SCI cùng vuông góc với ABCD
nên SI   ABCD nên SI là đường cao của S.ABCD .  Kẻ IK BC
tại K . Khi đó ta chứng minh được SKI   SBC; ABCD  6  0 . Ta vẽ hình phẳng
của mặt đáy. Ta có M AD BC ta chứng minh được CD là đường tủng bình của tam giác 2 2
ABM. Khi đó AM  4a; BM  2a  4a  2a 5; IM  3a . Ta có KMI  AMB
IM IK   3a a  3a IK .2 . BM AB 2a 5 5 3 Khi đó 1 3a 3 1 3a 15 SI IK   3a  3a 3 .tan 60 . 3 . V  .
. a  2a.2a  . 5 5 3 5 2 5 Câu 7.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , mặt bên SAB là tam giác
vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của khối chóp 3 a S.OCD bằng
. Tính khoảng cách h từ A đến mặt phẳng SBD ? 3 2 6a a 3 2 3a A. h  . B. h  . C. h  .
D. h  2 3a . 3 3 3 Lời giải Chọn A .
Gọi x là độ dài AB ,kẻ SF AB tại F , ta có 3 x 1 1 1 a 2 3 SF   VVAB .SF  x
x  2 2a . S .OCD S .ABCD 2 4 12 24 3 Trang24
Do F là trung điểm của AB nên khoảng cách h từ A đến mặt phẳng SBD gấp 2 lần khoảng FB x
cách d từ F đến mặt phẳng SBD mà EF    a . sin 45o 2 2
Tính d : kẽ FE DB; FH SE , ta chứng minh được SH  SBD , 1 1 1 1 1 3 a 6       2 6a FH
d , vậy h  2d  . 2 2 2 2 2 2 FH FE FS a 2a 2a 3 3 . 1 Câu 8.
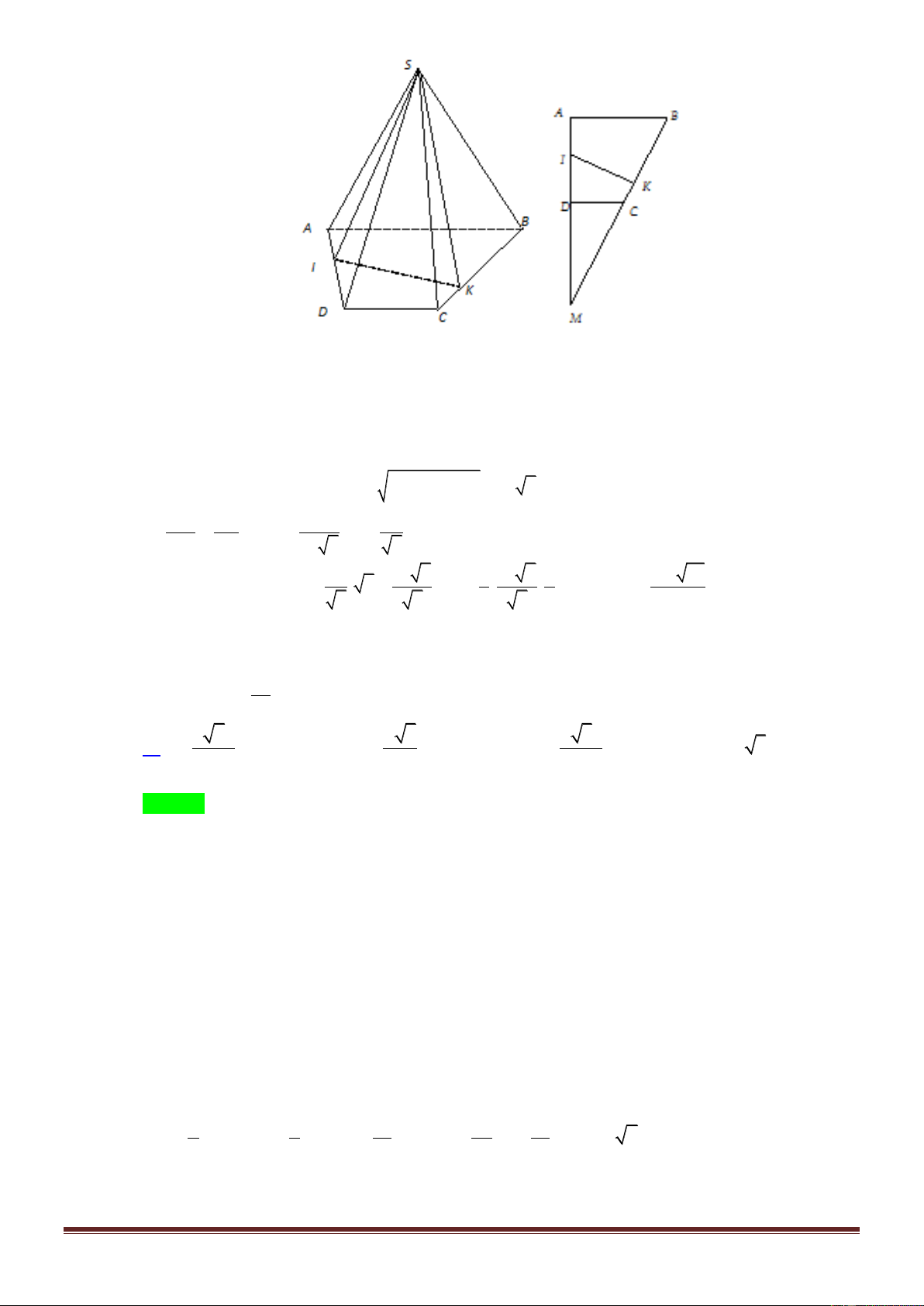
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , BC AD a . 2
Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, góc giữa SC và mặt phẳng  15
ABCD bằng  sao cho tan 
. Tính thể tích khối chóp S.ACD theo a . 5 3 a 3 a 3 a 2 3 a 3 A. V  . B. V  . C. V  . D. V  . S . ACD 2 S . ACD 3 S.ACD 6 S.ACD 6 Lời giải Chọn D
Gọi H là trung điểm AB , từ giả thiết ta có: SH   ABCD , SC ABCD · ,  SCH   . 2 2 Đặ x x 15
t AB x , ta có: 2 2 2 HC BH BC   a , 2 SH H . C tan   a . . 4 4 5 x 3 2 x 15 x 3 Mặt khác SH  . Vậy ta có: 2  a .   x a . 2 4 5 2  AD BC 2 .AB 3a 2 3 1 a 3 S   ; 2 SSa ; VSH.S  . ABCD 2 2 ACD 3 ABCD S.ACD 3 ACD 6 Câu 9. Cho hình chóp .
S ABCD có đáy là hình chữ nhật ; AB a; AD  2a . Tam giác SAB cân ta ̣i S
và nằm trong mặt phẳng vuông góc với đáy . Góc giữa đường thẳng SC và mp  ABCD bằng
45 . Gọi M là trung điểm của SD . Tính theo a khoảng cách d từ điểm M đến SAC . a 1513 2a 1315 a 1315 2a 1513 A. d  . B. d  . C. d  . D. d  . 89 89 89 89 Lời giải Chọn A Trang25
Gọi H là trung điểm đoạn AB SH   ABCD. 2 Xét a a 17
BCH vuông ta ̣i B , có: 2 CH  4a   . 4 2 Xét a 17 a 34
SHC vuông cân ta ̣i H , có: SH  ; SC  . 2 2 2 2 Xét 17a a 3 2
SAH vuông ta ̣i H , có: SA    a . 4 4 2
Xét  ABC vuông ta ̣i B , có: 2 2 AC
a  4a a 5 . 89 2  Sa .  SAC 4 3 3 Ta co 1 a 17 1 a 17 ́: V
V  .SH.S  ; VV  . S. ABCD 3 ABCD 3 S. ACD 2 6 3 1 a 17 1 89 a VV  . Mà 2 V  .d.Sa .d  1513 d  . S. ACM S.  2 ACD 12 S.MAC 3 SAC 12 89
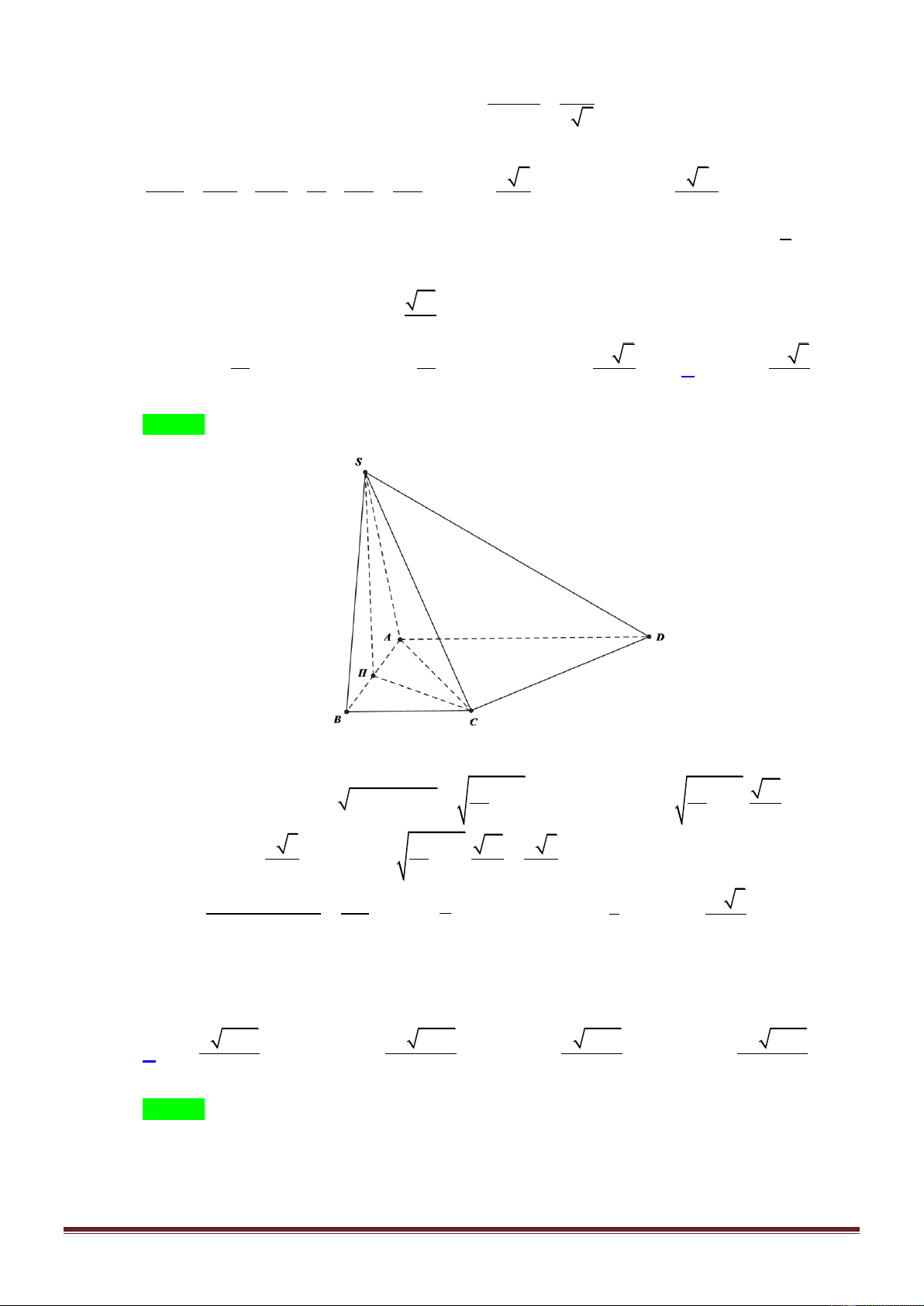
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tam giác SAD vuông tại S và nằm
trong mặt phẳng vuông góc với đáy. Cho biết AB a , SA  2SD . Mặt phẳng SBC  tạo với đáy một góc o
60 . Thể tích khối chóp S.ABCD là 3 3a 3 5a 3 15a A. B. C. 3 5a D. 2 2 2 Lời giải Chọn B S D C H I A a B
Gọi H là hình chiếu của S lên cạnh AD , I là hình chiếu của H lên cạnh BC , ta có
SH   ABCD và BC  SHI   SBC; ABCD   SIH o
 60 . Suy ra SH a 3 . S . A SD 2x
Trong tam giác vuông SAD đặt SA  2SD  2x nên từ SH  ta có a 3  . AD 5 Do đó a 15 a x  . Suy ra AD  5 3 x 5  . 2 2 Trang26 1 5a 3 3 5a
Thể tích khối chóp S.ABCD là V  . a .a 3  . 3 2 2
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại
S . Hình chiếu vuông góc của S trên mặt phẳng đáy là điểm H thuộc cạnh AD sao cho
HA = 3HD . Biết rằng SA = 2a 3 và SC tạo với đáy một góc bằng 30° . Tính theo a thể tích
V của khối chóp S.ABCD . 3 8 6a 3 8 6a A. 3
V = 8 6a . B. V = . C. 3
V = 8 2a . D. V = . 3 9 Lời giải Chọn B 2 2 SH = H .
D HA = 3HD Þ SH = 3HD ìï  SH ï tan SDH = = 3 ïï DH SA SA Có: 2 2 í Þ = 3 Þ SD =
= 2a Þ DA = SD + SA = 4a . ïï  SA SD 3 ï tan SDH = ïïî SD 1 DH = DA = a . 4 SH SH SH Tam giác SHC có  tan SCH = Þ tan 30° = Þ HC = = 3a . HC HC tan 30° Tam giác DHC có 2 2 DC =
DH + HC = 2 2a 3 1 1 8 6a Vậy V =
SH .AD.DC =
. 3a.4a.2 2a = . S.ABCD 3 3 3
Câu 12. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a ,  
SAB SCB  90 . Gọi M là trung điể 6a
m của SA . Biết khoảng cách từ A đến  MBC  bằng
. Thể tích của khối chóp đã cho 21 bằng 3 8a 39 3 10a 3 3 4a 13 A. . B. . C. . D. 3 2a 3 . 3 9 3 Lời giải Chọn A Trang27 S M D A I C G N B
Trong mp  ABC  xác định điểm D sao cho tứ giác ABCD vuông tại A và C AB AD CB CD Khi đó ta có: 
AB SD ;   CB SD AB SA CB SC 1
Vậy SD   ABCD   VSD .S S .ABC  3 ABC
Có tam giác ABC là tam giác đều cạnh 2a 2  Sa 3 ABC  Ta đi tìm SD
Gọi I là trung điểm AC
vì tam giác ABC đều, ABCD nội tiếp đường tròn đường kính BD I BD AC BD
Gọi G là trọng tâm tam giác ABC và N là trung điểm BC
Vì tam giác ABC đều  AN BC AN // CD , tương tự CG // BD 2 2 3 2 3a
Dễ thấy AGCD là hình thoi  CD AG AN  2a    1 3 3 2 3
Xét hình chóp S.ANCD có đáy ANCD là hình thang vuông tại C, N. 6a
Khoảng cách từ A đến mặt phẳng  MNC  bằng
vì MNC   MBC  . 21 S P M F H E A D C N
Trong mp  ABCD gọi  
E CN AD
Trong mp  SAD kẻ tia At / /SD gọi  
P EM At
Gọi K là hình chiếu của G trên mặt phẳng CMB
AP / /SD AP CN Khi đó ta có 
  APN   CN AN CN a
Trong mp  APN  kẻ AH PN ta có AH d A MCN  6 ,  21 Trang28
Mà tam giác ABC là tam giác đều cạnh 2a AN a 3 1 1 1 1 21 1 1 Từ        AP  2a 2 2 2 AH AP AN 2 2 2 2 AP 36a 3a 4a Dễ thấy APM S
FM SF AP  2a 2 ED CD 2
Xét tam giác EAN có CD / / AN nên   (theo   1 ) EA AN 3 FD ED FD a
Xét tam giác EAP có FD / /PA nên  2 4    FD  3 PA EA PA 3 3 10a
Từ 2 và 3 ta có SD SF FD  3 3 1 1 10a 10a 3 Vậy 2 VSD.S  . .a 3  . S.ABC  3 ABC 3 3 9
Câu 13. Cho hình chóp S.ABC biết rằng SA SB SC a ,  ASB  120 ,  BSC  60 và  ASC  90 .
Thể tích khối chóp S.ABC là 3 a 2 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 12 6 4 8 Lời giải Chọn A
Ta có SB SC a , 
BSC  60 suy ra tam giác BSC đều  BC a .
Lại có SA SC a , 
ASC  90 suy ra tam giác ASC vuông cân tại S AC a 2 .
Mặt khác, SA SB a , 
ASB  120 , áp dụng định lí cosin cho tam giác ASB , ta được: 2 2 2  2
AB SA SB  2S . A S .
B cos ASB  3a AB a 3 .
Xét tam giác ABC có 2 2 2 2 2 2
BC AC a  2a  3a AB suy ra tam giác ABC vuông tại C . 2 1 a 2
Vậy diện tích tam giác ABC là: SAC.BC  . ABC  2 2
Gọi O là trung điểm của cạnh AB suy ra O là tâm đường tròn ngoại tiếp tam giác ABC .
Mà SA SB SC SO   ABC  . 2  3a a
Xét tam giác vuông ASO vuông tại O có 2 2 2
SO SA AO a     .   2 2   2 3 1 1 a 2 a a 2
Vậy thể tích khối chóp S.ABC là: V  .S .SO  . .  . S.ABC  3 ABC 3 2 2 12
Câu 14. Cho hình chóp S.ABC có AB  7cm, BC  8cm, AC  9cm . Các mặt bên tạo với đáy góc 30
. Tính thể tích khối chóp S.ABC . Biết hình chiếu vuông góc của S trên  ABC  thuộc miền
trong của tam giác ABC . 20 3 63 3 A.  3 cm  . B.  3 20 3 cm  . C.  3 cm  . D.  3 72 3 cm  . 3 2 Lời giải Trang29 Chọn A
AB BC AC Ta có p   12cm . 2
Diện tích tam giác ABC là S
p p AB p AC  p BC    2 12 5 cm
Gọi H là hình chiếu vuông góc của S trên  ABC  .
Gọi K , N , M là hình chiếu vuông góc của H trên AB, BC , CA .   
Theo bài ra ta có SKH SNH SMH  30 . Ta có SKH SNH SMH vì   
SHK SHN SHM  90 , SH chung,   
SKH SNH SMH  30 .
Suy ra KH NH MH .
Vậy H là tâm đường tròn nội tiếp tam giác ABC . S Khi đó ABC KH NH MH      5 cm . p 15
SH HK tan 30  cm . 3 1 1 15 20 3
Thể tích khối chóp S.ABC là V SH.S  .12 5.  cm ABC   3 . 3 3 3 3
Câu 15. Cho hình chóp S. ABC có AB = AC = 4 , BC = 2 , SA = 4 3 ,  
SAB = SAC = 30º . Tính thể
tích khối chóp S. ABC. A. V = 8 . B. V = 6 . C. V = 4 . D. V = 12 . S. ABC S. ABC S. ABC S. ABC Lời giải Chọn C Trang30
Gọi M là trung điểm của cạnh BC . Vì DABC cân tại A (do AB = AC = 4 ) nên AM ^ BC . 2 2 1 AM = AC - MC = 15 ; S = AM .BC = 15 D ABC . 2
DSAB = DSAC (c - g - c) nên SB = SC . Gọi H là hình chiếu vuông góc của điểm S trên
mặt phẳng (ABC) suy ra H Î AM .
Áp dụng định lí cosin cho DSAB , ta có: 2 2 2
SB = SA + AB - 2 . SA .
AB cos 30° = 16 Þ SB = 4 .
DSMB vuông tại M nên 2 2 SM = SB - MB = 15 . 2 2 2
SM + AM - SA 3
Áp dụng định lí cosin cho DSAM , ta có  cos SMA = = - . 2.SM .AM 5  4 2 
Þ sin SMA = 1- cos SMA = . 5  4 4 15
Þ SH = SM.sin SMA = 15. = . 5 5 1 1 4 15 Vậy V = S .SH = . 15. = 4 . S . ABC 3 DABC 3 5 Cách 2:
Áp dụng định lí cosin cho DABC , ta có 2 2 2
AB + AC - BC 7 cos A = = . 2 . AB AC 8 abc Sử dụng công thức 2 2 2 V =
1- cos  - cos  - cos  + 2 cos cos  cos  6 2 A . B AC.SA 7 æ ö 7 2 2 Þ V = 1- cos 30°- cos 30°- ç ÷ ç ÷ + 2cos30 . ° cos30 . ° = 4 . 6 çè8÷ø 8 
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh x , BAD = 60° , gọi I là giao điểm
AC và BD . Hình chiếu vuông góc của S lên mặt phẳng ( ABCD) là H sao cho H là trung
điểm của BI . Góc giữa SC và (ABCD) bằng 45°. Tính thể tích V của khối chóp S.ABCD . 3 39x 3 39x 3 39x 3 39x A. V = . B. V = . C. V = . D. V = . 12 36 24 48 Lời giải Trang31 Chọn C x
Tam giác ABD đều cạnh x Þ BD = x Þ IH = 4 x 3
Áp dụng định lí cosin cho tam giác 2 2 ABC : AC = x + x - 2 . x . x o
c s120° = x 3 Þ IC = 2 2 2 x 3x x 13
Xét tam giác IHC vuông tại I : 2 2 HC = IH + IC = + = 16 4 4
Do tam giác SHC vuông tại H
, có SCH = (SC,(ABCD))= 45° nên tam giác SHC vuông cân x 13
tại H . Suy ra: HC = SH = 4 3 1 1 1 x 13 x 39
Vậy thể tích khối chóp S.ABCD : V = . .A . C B . D SH = .x 3. . x = S.ABCD 3 2 6 4 24
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , khoảng cách từ điểm A đến mặt a 15 a 15 phẳng (SBC ) là
, khoảng cách giữa SA và BC là
. Biết hình chiếu của S lên mặt 5 5
phẳng ( ABC) nằm trong tam giác ABC , tính thể tích khối chóp S.ABC . 3 a 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 4 8 8 4 Lời giải Chọn D
Dựng hình bình hành ABCD . Gọi O là hình chiếu vuông góc của S lên mặt phẳng ( ABCD) .
Dựng đường thẳng d đi qua O , vuông góc với BC và cắt BC, AD lần lượt tại H , M .
Khi đó AD, BC ^ (SHM ) .
Trong DSHM , dựng HK ^ SM (K Î SM ) và MN ^ SH (N Î SH ) .
Ta có MN ^ SH và MN ^ BC nên MN ^ (SBC) . a 15
Vì vậy MN = d (M , (SBC)) = d ( , A (SBC)) = . 5 Trang32 a 15
Do BC / / (SAD) nên d (BC, )
SA = d (BC, (SA )
D ) = d( H , (SA )
D ) = HK . Suy ra HK = . 5
Do DSHM có hai đường cao MN = HK nên cân tại S . Suy ra O là trung điểm của MH . a 3
Ta có MH = d( A , D BC) = d( , A BC) =
(do DABC đều, cạnh bằng a ). Suy ra 2 a 3 MO = . 4
Xét hai tam giác đồng dạng MKH và MOS , ta có a 3 a 15 ´ KH MK M . O KH a 3 4 5 = Þ SO = = = . 2 2 SO MO MK 2 a æ 3ö a æ 15ö ç ÷ ç ÷ ç ÷ - ç ÷ ç ÷ ç ÷ ç ÷ è 2 ø çè 5 ÷ø 2 3 1 1 a 3 a 3 a
Vậy thể tích khối chóp S.ABC là V = SO´ S = ´ ´ = . 3 DABC 3 2 4 8
Câu 18. Cho hình lăng trụ đứng AB . C AB C
  có đáy ABC là tam giác vuông cân tại A , cạnh
BC a 6 . Góc giữa mặt phẳng  AB C
  và mặt phẳng BCC B
  bằng 60 . Tính thể tích khối đa diện AB C
AC. 3 a 3 3 3 3a 3 a 3 3 A. B. C. D. a 3 3 2 2 Hƣớng dẫn giải Chọn D A A' B' a 6 C' 2 B B' I B A a 6 I a H a 6 C C C' AI BC a 6
Gọi I là trung điểm BC , ta có 
AI  BB CC   và AI  (trung tuyến trong AI CC 2
tam giác vuông bằng nửa cạnh huyền). Kẻ IH B C
 mà AI B C
 suy ra AH B C  
Vậy góc giữa mặt phẳng  AB C
  và mặt phẳng BCC B
  là AHI  60 . AI a 2 Ta có IH   ; 2 2
CH CI IH a tan 60 2 IH.CB Mặt khác CIH IH CH CB B     BB   a 3 . B BCB CH 1 1 a 6 3 V        V   .AI.S   . .a 3.a 6 a 3 AB CA C ABB C C 3 BCC B 3 2  
Câu 19. Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a và ABC  60 . Biết rằng SA SC ,
SB SD và  SAB   SBC . G là trọng tâm tam giác  SAD . Tính thể tích V của tứ diện Trang33 GSAC . 3 a 2 3 a 2 3 a 2 3 a 2 A. V B. V C. V D. V 96 48 24 12 Hƣớng dẫn giải Chọn B 1 Ta có V
d G,SAC .S GSAC SAC . 3 * Tính S SAC ?
SA SC SO AC
Gọi O AC BD , do 
SO   ABCD .
SB SD SO BD
Kẻ OH SB , do AC   SBD nên SB   AHC  .
Suy ra  SAB   SBC    AH CH   , ,  AHC  90 .
Do OH AC và OH là trung tuyến nên tam giác AHC vuông cân tại H . 1 a Khi đó a OH AC  3 và OB  . 2 2 2 1 1 1 a 6
Mà tam giác SOB vuông tại O có đường cao OH nên    SO  . 2 2 2 OH OS OB 4 2 1 1 a 6 a 6 Vậy S  .S . O AC  . .a  . SAC 2 2 4 8
* Tính d E,SAC  ?
d G,SAC  SG 2
Gọi E là trung điểm của AD thì   .
d E, SAC  SE 3 a
Gọi F là trung điểm của OA thì EF   SAC   d E SAC  1 3 ,
EF OD  . 2 4 2 2 a 3 a 3
Suy ra d G, SAC  
d E,SAC   .  . 3 3 4 6 1 1 a 3 a 6 2a Vậy V
d G,SAC 2 3 .S  . .  . G.SAC  3 SAC 3 6 8 48
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA a và SA vuông góc với
đáy. Gọi M là trung điểm SB , N là điểm thuộc cạnh SD sao cho SN  2ND . Tính thể tích
V của khối tứ diện ACMN . Trang34 1 1 1 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a 36 6 8 12 Hƣớng dẫn giải Chọn D 3 1 a Cách1. Ta có V  . SA SS . ABCD ABCD 3 3 3 1 1 1  1  a 2 VNH.S  . . a aNDAC DAC   3 3 3  2  18 3 1 1 a  1  a 2 VMK.S  . . aMABC ABC   3 3 2  2  12
A SMN 3 1 a d , .SSMN 3 18 3 1 1 2  1 a a Suy ra VN . L S  . . a . aNSAM SAM   . 3 3 3  2 2  18 1 1 a Mặt khác Vd C SMN Sd A SMN SC SMN  , . SMN  ,  3 . . SMN 3 3 18 3 3 3 3 3 a a a a a 1 3 Vậy VVVVVV       a ACMN S .ABCD NSAM NADC MABC SCMN . 3 18 18 12 18 12
Cách2. Gọi O là giao điểm của AC và BD . 3 1 a Ta có V  . SA SOM //SD SD//  AMC S . ABCD ABCD . Vì nên . 3 3
Do đó d N; AMC  d  ;
D AMC  d  ; B AMC 3 1 aVVVVVVACMN N .MAC D.MAC B.MAC M .BAC S. ABCD . 4 12 ·
Câu 21. Cho lăng trụ AB . C A BC
  là lăng trụ đứng, AC = a,BC = 2a góc ACB bằng 120o . Góc giữa đường thẳng AC
¢ và mặt phẳng (ABB A ¢ )
¢ bằng 30o . Tính thể tích lăng trụ đã cho. 3 13a 3 a 105 3 104a 3 105a A. V  . B.V  . C. V  . D. V  . 12 14 6 4 Lời giải Chọn B. Trang35 Kẻ C K ¢ ^ A B ¢ . Vì lăng ¢ trụ AB . C A BC
  là lăng trụ đứng nên C K ¢ ^ AA . Do đó ¢ C K ¢ ^ (ABB A ¢ ) ¢ . Góc giữa AC ¢ và (ABB A ¢ ) ¢ · bằng góc C A
¢ K và bằng 30° (tam giác C A
¢ K vuông tại K nên
góc C ' AK nhọn)
Xét tam giác ABC , áp dụng định lý cosin cho cạnh AB có: 2 2 2 o 2 2 2
AB = AC + BC - 2. .
AB AC.cos120 = 7a Þ A B ¢ ¢ = 7a . 2 1 1 a o 3 S S C . A C . B sin ACB . a 2 . a sin120 ¢ ¢ ¢ = = = = . A B C ABC 2 2 2 1 1 Mặt khác S = C K ¢ .A B ¢ ¢= C K ¢ .a 7 ¢ ¢ ¢ A B C 2 2 2 Do đó 1 a 3 a 3 C K ¢ .a 7 = Û C K ¢ = 2 2 7 a o 3
Xét tam giác AKC ' vuông tại K nên AK = C K ¢ .cot30 = C K ¢ . 3 = 7
Xét tam giác A'C ' K vuông tại K nên 2 3a 2a 2 2 2 A K ¢ = A C
¢ ¢ - KC¢ = a - = 7 7 a 5 2 2 Þ AA¢= AK - A K ¢ = 7 2 3 a 5 a 3 a 105
Thể tích của lăng trụ AB . C A BC
  là V = AA .S ¢ = . = . ABC 7 2 14
Câu 22. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B .Biết SA vuông góc với mặt phẳng
ABC , AB  ,aBC a 3,SA a . Một mặt phẳng  qua A vuông góc SC tại H và cắt
SB tại K . Tính thể tích khối chóp S.AHK theo a . 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C.V  . D. V  . S .AHK 20 S .AHK 30 S .AHK 60 S .AHK 90 Lời giải Chọn B.
AK SC AK    Ta có  , suy ra SAK BC
BC  SAB H
AK  SBC  AK SB Vì S
AB vuông cân tại A nên K là trung điểm của SB .Ta có: K C Trang36 A B V S . A SK.SH SH S. AHK   . Ta có 2 2 AC
AB BC  2a V S . A S . B SC 2SC S.ABC 2 2 2 SH SH.SC SA 1 SC
AC SA a 5 , khi đó    2 2 SC SC SC 5 V SH 1 3 1 1 a 3 S.AHK    , lại có VS . A .A . B BC V 2SC 10 S. ABC 3 2 6 S. ABC 3 a 3 Vậy V  . S .AHK 60
Câu 23. Cho hình chóp S.ABC có đáy là ABC tam giác vuông cân đỉnh ,
A AB AC a . Hình chiếu
vuông góc của S lên mặt phẳng  ABC  là trung điểm H của BC . Mặt phẳng SAB hợp với
mặt phẳng đáy một góc bằng 60 . Tính thể tích khối chóp S.ABC . 3 a 2 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 12 4 6 12 Lời giải Chọn D. S A B K H C
Góc giữa mặt phẳng SAB và mặt phẳng đáy là góc  SKH   SKH  60 . 2 3 a 3 3a 3a 3 a 3 V   0      . có SH KH.tan 60 . ABC. A B C 4 2 8 2 3 1 a 3
Do đó V  .SH.S  ...  . 3 ABC 12
Câu 24. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , có BC a ; Mặt bên SAC
vuông góc với đáy, các mặt bên còn lại đều tạo với mặt đáy một góc 450. Tính thể tích khối chóp SABC . 3 a 3 a 3 a A. . B. 3 a . C. . D. . 12 6 24 Lời giải Chọn A Trang37
Gọi H là hình chiếu vuông góc của S lên cạnh AC nên SH   ABC  .
Gọi E , F lần lượt là hình chiếu vuông góc của H lên cạnh AB và AC . Khi đó, góc tạo bởi
hai mặt phẳng SAB , SAC  tạo với đáy lần lượt là  SEH , 
SFH cùng bằng 45. Hai tam giác SEH , SFH có  
SHE SHF  90 , SH chung ,  
HSE HSF  45 nên hai tam
giác bằng nhau hay HE HF . Mà ABC
là tam giác vuông cân nên H là trung điểm của AC . BC a 2 3 1 1 a a a
Ta có: SH HE   . Vậy VS .SH  . .  . 2 2 S . ABC 3 ABC 3 2 2 12
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh
2a và nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD . Góc giữa mặt phẳng SBC
và mặt phẳng  ABCD là 0
30 . Thể tích của khối chóp S.ABCD là: 3 2a 3 3 a 3 3 4a 3 A. . B. . C. . D. 3 2a 3 . 3 2 3 Lời giải Chọn A S A B 30° H M D C
+) Gọi H lần lượt là trung điểm của AD SH AD (vì SAD đều).
Gọi M là trung điểm của BC HM SH (vì SAD và  ABCD vuông góc với nhau).
Suy ra SH   ABCD
+) Tam giác SBC cân tại S SM BC , mà HM BC  góc giữa mặt phẳng SBC  và
mặt phẳng  ABCD là góc giữa hai đường thẳng HM , SM chính là góc SMH . Theo bài ra có 0 SMH  30 . a 3
+) Vì SAD là tam giác đều cạnh 2a nên ta có SH a 3  HM   a . 0 tan 30 2 SA .
B AD  2a . Vậy thể tích của của khối chóp S.ABCD là ABCD 3 1 1 2a 3 2 V  .SH.S  .a 3.2a  . ABCD 3 ABCD 3 3
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB a 2 , AC a 5 . Hình
chiếu của điểm S trên mặt phẳng  ABC  trùng với trung điểm của đoạn thẳng BC . Biết rằng
góc giữa mặt phẳng SAB và mặt phẳng  ASC bằng 60. Thể tích của khối chóp S.ABC là 3 5a 6 3 5a 10 3 a 210 3 a 30 A. . B. . C. . D. . 12 12 24 12 Lời giải Chọn D Trang38
(SAB)  SAC  SA , kẻ BE SA và GH BE ,
suy ra SAC SAB  GH SAC  , ,  HGI  60. 2 2 Đặ 7a 5a
t SH h , ta tính được 2 SA h  và 2 SP h  . 4 4 2 5a 2 a 2 a 2. h  .h 2S BE SH.HM SAB 4 Vậy BE    HG  , 2 HI   2 SA 2 7a 2 SM 2 a h  2 h  4 2
Tam giác GIH vuông tại I có 2 a 2 5a 2 a 2 . h  . h 2 4 IH 3 2 4 7a 15a 2a 3 2 4 2 sin 60   .   h h   0  h  2 2 HG 2 4 8 4 7a a 2 2 h h  4 2 3 1 a 30 Vậy VA . B AC.SH  . SABC 6 12
Câu 27. Cho hình chóp S.ABC có  ASB  60 ,  ASC  90 , 
CSB  120 và SA 1, SB  2 , SC  3 .
Khi đó thể tích khối chóp S.ABC là 2 2 2 A. . B. . C. 2 . D. . 4 2 6 Lời giải S N O A C M B Chọn B
Lấy M là trung điểm của SB và lấy N SC sao cho SN 1 . Ta có SA SM SN 1 nên
hình chiếu vuông góc của S lên  AMN  trùng với tâm O của đường tròn ngoại tiếp tam giác AMN .
Ta có: AM  1 vì tam giác SAM đều (cân tại S và có một góc bằng 60 ) AN
2 vì là cạnh huyền của tam giác vuông SAN có cạnh góc vuông bằng 1. Trang39 2 2 MN
SM SN  2SM .SN.cos120  3 2
Dễ đánh giá được tam giác AMN vuông tại A nên có SAMN 2 AM .AN.MN 2. 3 3 OA    4.SAMN 2 2 4. 2 3 1 Suy ra 2 2 SO
SA AO  1  4 2 1 1 2 2 Suy ra V  . .  S . AMN 3 2 2 12 V 1 1 1 2
Áp dụng công thức tỉ số thể tích ta có S.AMN    suy ra V  6.VV 1 2 3 S . ABC S .AMN 2 S . ABC
Câu 28. Cho tứ diện ABCD có AB CD  2a và AC a 2 . Gọi M , N lần lượt là trung điểm của
AB và CD . Biết MN a và MN là đoạn vuông góc chung của AB và CD . Tính thể tích tứ diện ABCD . 3 a 6 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 2 3 2 3 Lời giải Chọn D
Dựng hình hộp chữ nhật chứa tứ diện ABCD như hình vẽ. Ta có: 2 2 AE
AC DE a 2 2 BC
AB AE a 3 3 1 1 a 3 Vậy VV  . . a . a a 3  . ABCD 3 3 3
Câu 29. Cho hình chóp tam giác S.ABC có M là trung điểm SB , N là điểm trên SC sao cho S
N  2NC , là điểm trên SA sao cho PA  2PS . Kí hiệu V , V lần lượt là thể tích khối chóp 1 2 V
BMNP và S.ABC . Tính tỉ số 1 . V2 V 1 V 3 V 2 V 1 A. 1  . B. 1  . C. 1  . D. 1  . V 9 V 4 V 3 V 3 2 2 2 2 Lời giải. Chọn A Trang40
1 d N,SAB.SBMP V Ta có N.BMP 3  ; V 1 C.SAB
d C,SAB.S 3 SAB
d N,SAB NS 2 1 1 1 V 2 1 1 Suy ra   ; N . SS  . . BMP S   .  .
d C,SAB CS 3 SBM 2 BPS 2 3 SAB V 3 6 9 C.SAB
Câu 30. Cho hình chóp đều S.ABC .
D Gọi N là trung điểm SB, M là điểm đối xứng với B qua . A
Mặt phẳng  MNC  chia khối chóp S.ABCD thành hai phần có thể tích lần lượt là V , V với 1 2 V
V V . Tính tỉ số 1 . 1 2 V2 V 5 V 5 V 5 V 5 A. 1  .. B. 1  . . C. 1  . . D. 1  . V 7 V 11 V 9 V 13 2 2 2 2 Lời giải ChọnA S N E M B F A D C
Gọi h, S lần lượt là chiều cao và diện tích đáy của khối chóp S.ABCD . Khi đó 1 VS. . h MN SA E MC AD F. SBM , A N S . ABCD Nối cắt tại , cắt tại Tam giác có lần 3
lượt là trung điểm của BM và SB suy ra E là trọng tâm tam giác SBM. Tứ giác ACDM là
hình bình hành nên F là trung điểm . MC Ta có VVV . BNC. AEF ABCEN E.ACF V SE SN 2 1 1 1  S.ENC  .     V   V S.ENC S. V SA SB 3 2 3 3 ABC S. ABC 2 2  1  1  V   VVV .   ABCEN S .ABC S .ABCD S . 3 3  2  3 ABCD Trang41 1 1 1 1 1 VS
.d E, ACF   . S. h V . E. ACF ACF    S . ABCD 3 3 4 3 12 1 1 5 Do đó VVVVVVV . BNC. AEF ABCEN E. ACF S . ABCD S . ABCD S . ABCD 1 3 12 12 7 V 5 Suy ra 1 V V    . 2 S. 12 ABCD V 7 2  Mức độ 4 Câu 1.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 1, biết khoảng cách từ A đến SBC  6 15 30 là
, từ B đến  SCA là
, từ C đến  SAB là
và hình chiếu vuông góc của S 4 10 20
xuống đáy nằm trong tam giác ABC . Tính thể tích khối chóp V . S .ABC 1 1 1 1 A. B. C. D. 36 48 12 24 Lời giải ChọnB
Gọi M , N , P lần lượt là hình chiếu của H lên các cạnh AC, BC, AB . Đặ 1 3 h 3
t SH h V  . . h  . S.ABC 3 4 12 2S 6V h 3 30 Ta có SAB S. AP   2 ABC S   :  h 10 SAB AB
d C;SAB 2 20
Tương tự, tính được HM  2h, HN h 2 2
PH SP SH  3h 1 Ta có SSSSHP HM  3 3 HN  3h   h ABC HAB HAC HBC   2 4 12 3 3 1 Vậy V  .  . S.ABC 12 12 48 Câu 2.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a . Tam giác SAB vuông tại S
và nằm trong mặt phẳng vuông góc với đáy. Gọi  là góc tạo bởi đường thẳng SD và mặt
phẳng SBC  , với   45 . Tìm giá trị lớn nhất của thể tích khối chóp S.ABCD . 3 8a 3 4a 3 2a A. 3 4a B. C. D. 3 3 3 Lời giải Chọn C Trang42 S D' D A H B C
Gọi D là đỉnh thứ tư của hình bình hành SADD . Khi đó DDS
// A mà SA  SBC (vì SA SB , SA BC ) nên D là hình chiếu vuông góc
của D lên SBC  .
Góc giữa SD và SBC  là  
  DSD  SDA, do đó SA A . D tan  2 . a tan .
Đặt tan  x , x 0  ;1 . 1 1
Gọi H là hình chiếu của S lên AB , theo đề ta có 2 V  .S .SH  4a .SH S . ABCD ABCD . 3 3 Do đó V
đạt giá trị lớn nhất khi SH lớn nhất. Vì tam giác SAB vuông tại S nên S . ABCD . SA SB 2 2 . SA AB SA 2 2 2
2ax 4a  4a x 2 2 x 1 x SH    2
 2ax 1 x  2aa AB AB 2a 2 Từ đó max SH  2 a khi tan  . 2 1 4 Suy ra 2 3 maxV  . .4 a a a S . ABCD . 3 3 Câu 3.
Xét tứ diện ABCD có các cạnh AC CD DB BA  2 và AD , BC thay đổi. Giá trị lớn
nhất của thể tích tứ diện ABCD bằng 16 3 32 3 16 3 32 3 A. . B. . C. . D. . 9 27 27 9 Lời giải Chọn B A M B D N C
Gọi M , N lần lượt là trung điểm AD và BC .
Theo giả thiết ta có: ABD và ACD là các tam giác cân có M là trung điểm của AD nên
BM AD và CM AD AD   BMC  . Và có BM CM MBC cân tại. Trang43 2 BC Trong tam giác M
BC có MN vừa là đường cao vừa là trung tuyến nên 2 2 MN MB  4 2 2 AD BC 2 2 AD BC 2 2
MN AB    MN  4  . 4 4 4 2 2  Khi đó diệ 1 AD BC n tích tam giác M  1 BC là: SMN.BC  . BC 4  MBC 2 2 4 1 2 2 1 AD BC
Thể tích tứ diện ABCD là: V  . . AD S  .B . C A . D 4  ABCD MBC . 3 3 4 2 2  Đặ 1 x y
t AD x , BC y ta có: V  . . x . y 4  ABCD . 3 4 2 2 x y xy 2 2 x y xy 2 2
Ta có: x y  2xy       . 4 2 4 2 1 xy 2 2 Do đó: V  . . x . y 4   Vxyxy x y ABCD   8  ABCD . Dấu bằng xảy ra khi . 3 2 6 3  xy xy    8  xyxy xy   3 4.8
xy2 8  xy  4. . .8  xy 2 2  Ta lại có: 4.   . 2 2 3   27   xy Dấu bằng xảy ra khi  8  16 xy xy  4  x y  . 2 3 3 3 2 4.8
Vậy giá trị lớn nhất của thể tích tứ diện ABCD là: tập xác định maxVABCD 6 27 32 3  . 27 Câu 4.
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 . Gọi M , N lần lượt là trung điểm
của SB, BC Tính thể tích khối chóp .
A BCNM . Biết mặt phẳng  AMN  vuông góc với mặt phẳng SBC . 3 a 15 3 3a 15 3 3a 15 3 3a 15 A. . B. . C. . D. . 32 32 16 48 Lời giải Chọn B
E là trung điểm BC nên CB AE,CB SH 
CB  SAE  CB SE .
SE vừa là trung tuyến vừa là đường cao nên S
BC cân tại S Trang44 1
F là giao điểm của MN với SE 
SF MN,SF SE . 2   AMN    SBCSF MN Giả thiết  
SF   AMN    AMN
SBC  MNa SE  1 AF và SF SE nên S  3
AE cân tại A AE AS  2 2 2 2 3a a 5 2 2 AH AE  .  a 
SH SA AH  3 3 2 2 1 1 3 a 5 a 15 VS .SH  . a 3 .  S. ABC ABC   3 2 . 3 3 4 2 8 3 V SM SN 1 a 15 S . AMN  .   V   . S . V SB SC 4 AMN 32 S . ABC 3 3a 15 Vậy V VV  . S. ABC S. AMN 32 Câu 5.
Cho hình chóp S.ABC có  0
AB BC a, ABC    0
120 , SAB SCB  90 và khoảng cách từ B đế 2a 21
n mặt phẳng SAC  bằng
. Tính thể tích khối S.ABC . 21 3 a 5 3 a 15 3 a 15 3 a 5 A. V = . B. V = . C. V = . D. V = . 10 10 5 2 Lời giải Chọn B S S K E D A I a a E B C B D I
Hạ SE   ABC  tại E có AB SE
  AB  SAE  0
AB AE BAE  90 . AB SA  0
Chứng minh tương tự có BCE  90 .   0
Hai tam giác vuông BCE và BAE bằng nhau suy ra CBE ABE  60 .
Gọi D là trung điểm của BE suy ra tứ giác ABCD là hình thoi và BD DE a .
Gọi I là tâm hình thoi ABCD có 1 BI
EI d B SAC 1
d E SAC  d E SAC 2a 21 2a 21 , , ,  3.  . 3 3 21 7 CA BD
  CA  SEI   SAC  SEI  . CA SE a
Hạ EK SI tại K ta có EK  SAC tại K suy ra d E SAC 2 21 ,
EK EK  . 7 Trang45
Tam giác SBE vuông tại E đường cao EK có 1 1 1 1 1 1 7 4 5 6a 5          SE  . 2 2 2 2 2 2 2 2 2 EK EI SE SE EK EI 12a 9a 36a 5 3 1 1  1  1 3 6a 5 a 15 Vậy 0 2 VS .SE B . A B . C sin120 .SE a . .  . SABC    3 ABC 3  2  6 2 5 10 Câu 6.
Cho khối chóp S.ABC có đáy là tam giác cân tại A , AB a ,  BAC  120 ,  
SBA SCA  90 . 3
Gọi  là góc giữa hai mặt phẳng  SAB và SAC  . Khi cos 
thì thể tích khối chóp đã 4 cho bằng 3 3 3a 3 a A. 3a 3 . B. a . C. . D. . 4 4 Lời giải Chọn D
Kẻ SH   ABC , H   ABC  suy ra SH AB và SH AC . SH AB Khi đó ta có 
AB  SBH   AB BH . SB AB
Chứng minh tương tự ta có AC CH suy ra tứ giác ABHC nội tiếp đường tròn đường kính
AH . Do đó góc BHC bằng 60 . Dễ thấy AHB A
HC HB HC nên HBC đều. ABC  cân tại A
có AB a, BAC  120 2 2
suy ra BC  3a . Do đó 2 2 2 2
HB HC BC  3a . Dễ thấy SHB S
HC SB SC nên SAB SAC .
Trong mặt phẳng  SAB kẻ BK S ,
A K SA .
Trong mặt phẳng SAC  kẻ CK S , A K SA 1  1  .
Xét hai tam giác vuông KAB và KAC    BAK CAK    1 có AB AC , (vì SAB SAC ) 1 suy ra KAB K
AC AK AK K K A K K 1 1 mà
và 1 nằm giữa S và nên 1 .
Từ đó ta có CK SA và BK CK . 2 2 2
BK CK BC 3 2 2 2BK BC 3 Do đó  cos  cos BKC       1 . 2BK.CK 4 2 2BK 4 Đặt SH  ,
x x  0. Xét S  2 2 2 2 2
HB có SB SH HB  3a x . 1 1 1 1 1 1 Xét S
AB vuông tại B có      2 2 2 BK BA BS 2 2 2 2 BK a 3a x 2 a  2 2 3a x 2   BK  . 2 2 4a x Trang46 2 2a  2 2 3a x  2  3a 2 2  3 4a x Thay vào   1 ta có   x a 3 . 2 2a  2 2 3a x  4 2 2 4a x 3 1 1  1 1 a 2
Vậy thể tích khối chóp S.ABC là .SH. .A .
B AC.sin BAC  .a 3. . a sin120  . 3 2 3 2 4 Câu 7.
Cho tứ diện đều ABCD có cạnh bằng 1, M và N lần lượt là hai điểm di động trên hai cạnh
AB, AC ( M và N không trùng với A ) sao cho mặt phẳng  DMN  luôn vuông góc với mặt
phẳng  ABC  . Gọi V , V lần lượt là thể tích lớn nhất và nhỏ nhất của tứ diện ADMN . Tính 1 2
tích V .V . 1 2 2 2 1 8
A. V .V  .
B. V .V  .
C.V .V  .
D. V .V  . 1 2 27 1 2 1 2 1 2 24 324 9 Lời giải Chọn C
Kẻ DH MN DH   ABC  (vì DMN    ABC ). Suy ra H là trọng tâm của tam giác đều ABC .
Như vậy M và N là hai điểm di động nhưng MN luôn đi qua trọng tâm của tam giác ABC .
Đặt AM x, AN y , ( 0  x 1, 0  y  1 ) 1 2 + 2 2 2
DH DA AH  1  2  DH  . 3 3 3 1 3 +  S
AM.AN.sin MAN xy (*) AMN 2 4 1 3 + SSS
AH.x y.sin 30 
x y (**) AMN AMH ANH 2 12   Do đó 1 V  1 3 2 2 DH .S   xy   xy (***) ADMN    3 AMN 3 4 3 12  
Mặt khác từ (*) và (**) suy ra x y  3xy , ( 0  x 1, 0  y  1 ). Trang47  2 0  t    3 0  3t  2  Đặ 4 2
t xy t x y  3t . Điều kiện:    4   t  . 2 9
t  4t  0 t   9 3 9  t  0
Khi đó x, y là nghiệm của phương trình 2
X  3tX t  4 2 0   1 ,  t  . 9 3 4 2 Ta tìm t  ; để  
1 có 2 nghiệm phân biệt thuộc 0; 
1 hoặc có nghiệm kép thuộc 0;  1   9 3 1 X Ta có X
không phải là nghiệm của   1 nên   2 1  t  . 3 3X 1 X  0 2  Đặ X 3X 2X  t g X  2  , X 0; 
1 . Ta có: g X    0  2 . 3X 1   3X  2 1 X   3
Bảng biến thiên của g X  Dựa vào BBT,  
1 có 2 nghiệm phân biệt thuộc 0; 
1 hoặc có nghiệm kép thuộc 0;  1 4 1   t  4 1 (thỏa điều kiện) hay  xy  . 9 2 9 2 2 2 2 2 1 Kết hợp (***) ta có  V  V  , V   V .V  . 1 2 27 ADMN 24 1 24 2 27 324 Câu 8.
Cho khối tứ diện đều ABCD cạnh bằng 2 .
cm Gọi M , N , P lần lượt là trọng tâm của ba tam giác ABC, ABD, .
ACD Tính thể tích V của khối chóp AMN . P 2 2 2 4 2 2 A. 3 V cm . B. 3 V cm . C. 3 V cm . D. 3 V cm . 162 81 81 144 Lời giải Chọn C Trang48 A N M P B K D H E F C 2 3
Tam giác BCD đều  DE  3  DH  3 2 6 2 2 AH AD DH  3 1 1 1 1 3 S  .d .FK  . d . BC   EFKE,FK D,BC 2 2 2 2 4 1 1 2 6 3 2 VAH.S  . .   . SKFE EF 3 K 3 3 4 6 AM AN AP 2 Mà    AE AK AF 3 V AM AN AP 8 8 4 2 Lại có: AMNP  . .  VV  . V AE AK AF 27 AMNP 27 AEKF 81 AEKF Câu 9.
Cho hình chóp S.ABC có AB  5 cm , BC  6 cm , CA  7 cm . Hình chiếu vuông góc của S
xuống mặt phẳng  ABC  nằm bên trong tam giác ABC . Các mặt phẳng  SAB ,  SBC  ,
SCA đều tạo với đáy một góc 60 . Gọi AD , BE , CF là các đường phân giác của tam giác
ABC với DBC , E AC , F AB . Thể tích S.DEF gần với số nào sau đây? A. 3 2,9 cm B. 3 4,1 cm C. 3 3,7 cm D. 3 3,4 cm Lời giải ChọnD S E A C 60° I F D H B Trang49
Vì các mặt phẳng  SAB , SBC  ,  SCA đều tạo với đáy một góc 60 và hình chiếu vuông
góc của S xuống mặt phẳng  ABC  nằm bên trong tam giác ABC nên ta có hình chiếu của S
chính là tâm I của đường tròn nội tiếp tam giác ABC .
AB BC CA
Gọi p là nửa chu vi tam giác ABC thì p   9 . 2 S Ta có : S
pp AB p BC p AC  2 6 6 6 r   ABC và . p 3
Suy ra chiều cao của hình chóp là : h  . r tan 60  2 2 A E F I C B D EA BA
Vì BE là phân giác của góc B nên ta có :  . EC BC FA CA Tương tự :  DB AB ,  . FB CB DC AC S AE AF AB AC Khi đó : AEF  .  . . S AC AB
AB BC AC BC ABC S CA CB S BC BA Tương tự : CED  . , BFD  . . S
CA AB CB AB S
BC CA BA CA ABC ABC Do đó,  ab bc acSS 1    , với BC a , AC b , DEF ABC
a cb c b ac a a bc b          AB c 2abc  210 6 .SABC .
a bb cc a 143 1 210 6 280 3 Suy ra V  . .2 2   3 cm   3, 4  3 cm  S.DEF 3 143 143
Câu 10. Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng a , thể tích V của khối
chóp có thể tích nhỏ nhất. 3 8 3 10 3 32 A. a V . B. a V . C. 3 V  2a . D.a V . 3 3 3 Lời giải Chọn D Trang50
Giả sử SO x ta có: SI x a ; SE   x a2 2 2
a x  2ax SE IE I . E SO ax
Xét SEI ∽SON ta có:   NO   SO NO 2 SE x  2ax 2 2 2 1  2ax  4a x
Thể tích khối chóp là: V  . x    2 3   3  x 2 2 a x axx
Xét hàm số f x 2 
0  2a xx  2a   2 x  4  ax f x
; f  x  0  x  4a (do 0  2a x ) x  2a2 Bảng biến thiên 3 32
Vậy giá trị nhỏ nhất của thể tích là:  a V . 3
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thỏa mãn AB  , a AC a 3 ,
BC  2a . Biết tam giác SBC cân tại S , tam giác SCD vuông tại C và khoảng cách từ D đến a 3
mặt phẳng (SBC ) bằng
. Thể tích của khối chóp đã cho bằng 3 3 2a 3 a 3 a 3 a A. . B. . C. . D. . 3 5 3 5 3 3 5 Lời giải Chọn A Trang51
Nhận thấy tam giác ABC vuông tại A ( do 2 2 2
AB  AC BC ).
Gọi E là điểm đối xứng của B qua A ta có tứ giác DE AC
là hình chữ nhật, và tam giác EBC
là tam giác đều cạnh 2a . 1
AD  (SBC)  d (D, (SBC))  d ( , A (SBC)) 
d (E, (SBC)) 2 2a 3
Hay d (E, (SBC))  2.d( , D (SBC))  3
Gọi I là trung điểm của đoạn BC , ta có: BC EI , BC SI BC  (SEI ) . 2a 3
Trong mp(SEI ) kẻ EH vuông góc với SI tại H . Khi đó: d (E, (SBC))  EH  . 3
Ta có CD  (SAC) ( Do CD  SC, CD  AC ) Suy ra AB  (SAC) . Xét tam giác E
SB có SA vừa là trung tuyến vừa là đường cao nên tam giác E
SB cân tại S .
Xét hình chóp S.EBC có đáy là tam giác đều EBC , các cạnh bên SE SB SC .
Nên gọi F EI CA ta có SF  (EBC) . 2a 3 HE 2
Tam giác EHI vuông tại H nên  3 sin I    . EI a 3 3 2 1 sin I 1 2a Tam giác 
SIF vuông tại F nên 3
SF FI.tan I EI.  a 3.  . 2 3  3 2 15 1 sin I 2 1 ( ) 3 3 1 1 1 2a 2a VSF.SSF.A . B CA  . . a a 3  . S . AB D C AB D 3 C 3 3 15 3 5
Câu 12. Cho hình chóp S.ABC , đáy là tam giác đều ABC có cạnh bằng a . Biết rằng các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng a 3 . Tính thể tích nhỏ nhất
của khối chóp S.ABC . 3 a 2 3 a 2 3 a 6 3 a 6 A. . B. . C. . D. . 6 2 12 4 Lời giải Chọn C Trang52
Gọi H là hình chiếu của S trên mặt phẳng đáy  ABC  ; M , N , K lần lượt là hình chiếu của S
trên AB, BC, CA . 1 1 1
Vì diện tích các mặt bên của hình chóp bằng nhau nên ta có SM .AB SN.BC SK.CA 2 2 2
và vì tam giác ABC đều nên ta có SM SN SK HM HN HK .
TH1: nếu H nằm trong tam giác ABC H là tâm đường tròn nội tiếp tam giác đều ABC . Khi đó ta có 2 a 3 AH AN
và SA SB SC a 3 3 3 2  3a 2a 6 2 2 2
SH SA AH  3a   9 3 2 3  1 1 a 3 2a 6 a 2 VS .SH  . .  . S. ABC 3 ABC 3 4 3 6
TH2: Nếu H nằm ngoài tam giác ABC . Không mất tính tổng quát giả sử H nằm khác phía
với A so với đường thẳng BC
Tương tự như trên ta vẫn có HM HN HK . Vì tam giác ABC đều nên H là tâm đường 3a BN a
tròn bàng tiếp góc A và AM AB BN   1 HB   :  a , 2 cos60 2 2 3a 3
AH AM : cos30  :
a 3 . Vì thế cạnh SA không thể bằng a 3  SB SC a 3 2 2 2 3  1 1 a 3 a 6 2 2 2 2 SH
SB BH  3a a a 2  VS .SH  . .a 2  . S. ABC 3 ABC 3 4 12 3 3 3
a 2 a 6  a 6 Vậy V  min  ,   . min  6 12   12 
Câu 13. Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB  
a , BAC  120 ,   
SBA SCA  90 . Trang53 3
Gọi  là góc giữa SB và SAC  thỏa mãn sin 
, khoảng cách từ S đến mặt đáy nhỏ 8
hơn 2a . Thể tích của khối chóp S.ABC bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 4 6 12 24 Lời giải. Chọn C S K C D A B I
Gọi D là hình chiếu vuông góc của S lên đáy  ABC  , đặt SD x 0  x  2a  . AC SC Ta có 
AC  SDC  AC DC . Tương tự ta cũng có AB DB . AC SD
Tam giác ABC cân tại A và 
CAB  120  BC a 3 và  
DBC DCB  60  DBC đều cạnh a 3 .
Tam giác SDC vuông tại D 2 2
SC  3a x SB . x a 3
Kẻ DK SC tại K DK  SAC   d  ,
D SAC   DK  . 2 2 3a x
Gọi I BD AC , xét D
IC vuông tại C và  BDC  60 DC  1 DI   a
B là trung điểm của DI d B,SAC  d D,SAC  .  2 3 cosBDC 2
d B, SAC   3 xa 3
Theo giả thiết   SB,(SAC    sin    SB 8 2 2 2 3a x  2  x xx a 2 2
x  3a  4ax  0   4  3  0    
. So sánh với điều kiện suy ra x a .  a ax  3a 3 1 a 3 Vậy V  .S .SD  . S.ABC  3 ABC 12
Câu 14. Cho tứ diện ABCD có  
DAB CBD  90º ;  AB  ;
a AC a 5; ABC  135 . Biết góc giữa
hai mặt phẳng  ABD,  BCD bằng 30 . Thể tích của tứ diện ABCD bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 3 2 3 2 6 Lời giải. Chọn D Trang54 D E F C H a 5 A a B
Dựng DH   ABC . BA DABC DB Ta có 
BA AH . Tương tự   BC BH . BA DHBC DH
Tam giác AHB có AB a ,  o ABH  45  H
AB vuông cân tại A AH AB a .
Áp dụng định lý cosin, ta có BC a 2 . 2 1 1 2 a Vậy  S  .B . A B . C sin CBA  . . a a 2.   . ABC 2 2 2 2 HE DA Dựng 
HE  DAB và HF  DBC . HF DB  
Suy ra DBA DBC  HE HF   , ,
EHF và tam giác HEF vuông tại E . ax xa 2
Đặt DH x , khi đó HE  , HF  . 2 2 a x 2 2 2a x 2 2  HE 3 x  2a 3 1 a Suy ra cos EHF   
x a .Vậy V  .DH.S  .  2 2 HF 4 ABCD ABC 2x  2a 3 6
Câu 15. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB BC a 3 ,  
SAB SCB  90 và khoảng cách từ điểm A đến SBC  bằng a 2 . Diện tích của mặt cầu
ngoại tiếp hình chóp S.ABC bằng A. 2 2 a . B. 2 8 a . C. 2 16 a . D. 2 12 a . Lời giải. Chọn D
Gọi H là hình chiếu của S lên  ABC  . BC SC Ta có:   HC BC . SH BC
Tương tự AH AB . Và ABC
vuông cân tại B nên ABCH là hình vuông. Gọi O AC BH , O là tâm hình vuông.
Dựng một đường thẳng d qua O vuông góc với  ABCH  , dựng mặt phẳng trung trực của SA
qua trung điểm J cắt d tại I I là tâm mặt cầu ngoại tiếp. Trang55
Ta hoàn toàn có IJ SA IJ // AB I là trung điểm SB , hay I d SC .  a 3
Bán kính mặt cầu ngoại tiếp: 2 2 r
AI IJ JA ; IJ   S. ABC 2 2
Do AH // SBC d  ,
A SBC   d H,SBC   HK .
( K là hình chiếu của H lên SC và BC  SHC HK  SBC  ).
HK a 2 . Tam giác SHC vuông tại H SH a 6 .
Tam giác SHA vuông tại H SA  3a . SA 3a 2 2 JA    r
AI a 3  S  4 r  12 a . . 2 2 S ABC mc
Câu 16. Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy a ; biết khoảng cách giữa hai đường thẳng a AB và A C ¢ 15 bằng
. Thể tích của khối lăng trụ AB . C A BC
  tính theo a bằng: 5 3 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 8 2 8 4 Lời giải Chọn D a 15
Ta có AB / / A B
   AB / /  A BC    ddd   AB,A C
AB,A BC
B,A BC 5
Đặt AA  x  0 . Tam giác CA B   cân tại C , 2 2
CA  CB  a x . 2 2 2 1 a 1 3a  4x 1
Diện tích tam giác CA B   là 2 2 2 2 S         . . a a x . a a 3a 4x CA B 2 4 2 2 4 2 a 3
Thể tích lăng trụ V  . x   1 4 1 a 15 1 Lại có 2 2 V  3V      3. d .S     . . a 3a 4x . B.A B C
B,A B C 3 A B C 5 4 2 a 3 a 15 1 Do đó 2 2 2 2 . x  . .
a 3a  4x  5x 3  15. 3a  4x x a 3 . 4 5 4 2 3 a 3 3a V  . x  . 4 4
Câu 17. Cho hình lăng trụ đứng AB .
C A' B 'C ' , đáy ABC là tam giác cân tại C , cạnh AB = a và góc  a
BAC  30 . Biết khoảng cách giữa hai đường thẳng AB và CB
¢ bằng .Thể tích của khối 2 lăng trụ AB . C A BC
  tính theo a bằng: Trang56 3 a 3 3a 3 2 3a 3 4 3a A. . B. . C. . D. . 8 3 2 3 3 Lời giải Chọn A a
Ta có AB / / A B
   AB / /  A BC    ddd   . AB,B C
AB,AB C
B,AB C 2
Đặt AA  x  0 . Tính đượ a c AC BC  . 3 2 1 a
Diện tích tam giác ABC là S  .AC. . CB sin120o ABC . 2 4 3 2 2 2 a a  3x Tam giác CA B   cân tại C , 2
CA  CB   x  . 3 3 2 2 2 2 2 1 1 a a  3x a a a 12x
Diện tích tam giác cân CA B   là S         A B .CH . . . CA B 2 2 2 3 4 4 2 3 2 a
Thể tích lăng trụ là V AA .S  . x ABC 4 3 2 2 1 a a a 12x
Lại có V  3V     3. d .S     . . B.A B C
B,A B C 3 A B C 2 4 2 3 2 2 2 3 a a a a 12x a a Do đó . x  . .
x  V  . 4 3 2 4 2 3 2 8 3
Câu 18. Cho hình lăng trụ đều AB .
C A' B 'C ' , có cạnh đáy bằng a . Khoảng cách từ điểm A đến mặt a phẳng ( A B
¢ C) bằng . Thể tích của khối lăng trụ AB . C A BC
  tính theo a bằng: 2 3 3 2a 3 5 2a 3 2a 3 5 2a A. . B. . C. . D. . 16 16 16 8 Lời giải Chọn A Trang57
Gọi H là trung điểm của BC , I là hình chiếu vuông góc của A trên AH . a
Chứng minh được khoảng cách từ A đến ( A ' BC) là AI  . 2
Đặt AA  x  0 .
Xét tam giác AAH vuông tại A : 1 1 1 1 4 4 a 3
Ta có AI là đường cao:       x  . 2 2 2 2 2 2 AI AAAH x 3a a 2 2 2 3 a 3 a 3 3 2a
Thể tích lăng trụ là V  . x S  .  . ABC 2 2 4 16
Câu 19. Cho lăng trụ · ABC .
D A ' B 'C ' D ' có đáy ABCD là hình thoi cạnh a , tâm O và 0 ABC = 120 . Góc
giữa cạnh bên AA ' và mặt đáy bằng 0
60 . Đỉnh A ' cách đều các điểm A , B , D . Tính theo a
thể tích khối lăng trụ đã cho. 3 3 3a a 3 3 a 3 A.V = . B.V = . C.V = . D. 3 V = a 3 . 2 6 2 Lời giải Chọn C
Hình thoi ABCD cạnh · 
a , ABC = 120° nên góc BAD  60 , suy ra tam giác ABD đều cạnh a . 2 2 a 3 a 3
Diện tích đáy ABCD là S  2.S  2.  . ABD 4 2
Gọi H là trọng tâm tam giác ABD . Ta có A H    ABCD . a 3 a 3 Tính được AO  , AH  . 2 3
Góc giữa AA ' và mặt đáy bằng góc AAH và bằng 60° . a 3 Ta có A H
  AH.tan 60  . 3  a . 3 Trang58 2 3 a 3 a 3
Thể tích lăng trụ V A H  .S  . a  . 2 2
Câu 20. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , Các mặt bên của hình chóp cùng tạo với
mặt đáy một góc 45 và hình chiếu của S trên mặt phẳng đáy năm fngoài tam giác ABC .
Tính thể tích khối chóp S.ABC . 3 a 3 a 3 a 3 a A. V  . B.V  . C.V  . D.V  . 8 4 6 24 Lời giải Chọn A
Gọi H là hình chiếu của S trên mặt phẳng  ABC  .
Gọi hình chiếu của H lên các cạnh AB, BC,CA lần lượt là P,Q, R .
Dễ dàng có được góc giữa các mặt bên với đáy chính là các góc   
SPH SQH SRH  45 .
Vậy ta có ba tam giác vuông cân bằng nhau SHP, SHQ, SHR , suy ra HP HQ HR .
H là tâm đường tròn bàng tiếp ABC  . Do ABC
đều, không mất tính tổng quát, ta coi H
là tâm đường tròn báng tiếp góc A . S a 3
Gọi r là bán kính đường tròn bàng tiếp góc A thì r   a a p a 2 a 3  SH r a 2 2 3 1 1 a 3 a 3 a Vậy VSH.S   . S.ABC 3 ABC 3 2 4 8
Câu 21. Cho khối chóp S.ABC có đường cao SA  2a , tam giác ABC vuông ở C có AB  2a , góc 
CAB  30 . Gọi H là hình chiếu của A trên SC . Gọi B là điểm đối xứng của B qua mặt
phẳng  SAC  . Tính thể tích khối chóp H.AB B  . 3 2a 3 3 2a 3 3 6a 3 3 a 3 A. . B. . C. . D. . 7 7 7 7 Lời giải Chọn A Trang59 1 1 1 1 1 7
Ta có BC a , AC a 3 . Ta có:      2 2 2 2 2 2 AH SA AC 4a 3a 12a 2 3a 2  3a 1 3 3a AH  ; 2 2 HC AC AH  ; SAH.HC HAC 7 7 2 7 2 3 1 1 3 3a a 3 3 2a 3 VS .BC  .a  V  2VHABC 3 HAC 3 7 7 HAB ' B HABC 7
Câu 22. Cho hình chóp tứ giá đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc 0 60 .
Gọi M là điểm đối xứng của C qua D , N là trung điểm SC .Mặt phẳng  BMN  chia khối
chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng: 7 1 7 6 A. . B. . C. . D. . 5 7 3 5 Lời giải Chọn A
Gọi V là thể tích khối chóp S.ABCD V  
1 là thể tích khối chóp PD .
Q BCN và V là thể tích của khối chóp còn lại, khi đó V V V 2 1 2
MB cắt AD tại P → P là trung điểm của AD .
MN cắt SD tại Q → Q là trọng tâm của SMC VM PDQ MP MD MQ 1 1 2 1 Ta có .  . .  . .  V MB MC MN 2 2 3 6 M .BCN 5 Mặt khácVV
V V V M .BCN M .PDQ 1 1 M .BCN 6 1 Mà SS
, d (S; ( ABCD)) 
d (S; ( ABCD)) MBC ABCD 2 1 V 5 7 Suy ra VVV   V V V
V V :V  7 : 5 M .BCN N .MBC S . ABCD 1 2 2 1 . 2 2 12 12 Trang60
Câu 23. Cho tứ diện S.ABC , M và N là các điểm thuộc SA và SB sao cho MA  2SM , SN  2NB ,
 là mặt phẳng qua MN và song song với SC . Kí hiệu HH2 1  và là các khối đa diện
có được khi chia khối tứ diện S.ABC bởi mặt phẳng   , trong đó H S H2  1  chứa điểm , V
chứa điểm A ; V và V lần lượt là thể tích của  HH 1 2  1  và . Tính tỉ số . 1 2 V2 4 5 3 4 A. . B. . C. . D. . 5 4 4 3 Lời giải. ChọnA
Kí hiệu V là thể tích khối tứ diện S.ABC .
Gọi P , Q lần lượt là giao điểm của   với các đường thẳng BC , AC .
Ta có NP//MQ//SC . Khi chia khối  HQNCN.SMQC 1  bởi
, ta được hai khối chóp và N.QPC . V d N, SAC S N .SMQC    SMQC Ta có  . . V d B, SAC S B. ASC    SAC
d N,SAC  NS 2   .
d B,SAC  BS 3 2 SAM S V AMQ 4 SMQC 5  N SMQC 2 5 10      .Suy ra .  .  . SAS  9 S 9 V 3 9 27 ASC ASC B.ASC V d N , QPC S N .QPC  
 QPC NB CQ CP 1 1 2 2  .  . .  . .  . V d S, ABC S SB CA CB 3 3 3 27 S . ABC    ABC V V V N .SMQC N .QPC 10 2 4 V 4 V 4 1 1 1          . V V V 27 27 9 V V 9 V 5 B.ASC S .ABC 1 2 2
Câu 24. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB BC a,   0
SAB SCB  90 . Góc giữa SB và mặt phẳng ( ABC) là  thỏa mãn tan  2. Gọi G là
trọng tâm tam giác ABC, M là trung điểm SA . Thể tích SMGB là 3 3 a a 3 a 3 a A. . B. . C. . D. . 3 15 18 6 Lời giải Chọn C Trang61
 Lấy điểm D sao cho ABCD là hình vuông
 Ta có BC CD, BC SC BC SD , tương tự AB S . D 1 1 1  Ta có VVVV . SMGB SABG SABC S . ABCD 2 6 12 3  1 1 2a Ta có 2 V  . SD S  .2 . a a S . ABCD 3 ABCD 3 3 3  a Vậy V  . SMGB 18
Câu 25. Cho hình lăng trụ AB . C A BC
  có thể tích V . Gọi M là trung điểm AC ; N là điểm nằm trên cạnh B C
 sao cho CN  2NB ; K là trung điểm AB . Hãy tính theo V thể tích khối tứ diện C MNK : 11V 2V 5V V A. . B. . C. . D. . 36 15 18 12 Lời giải Chọn D
Ta có: d C;MNK   d C; AB C
   d B;AB C   Lại có SS       S S S     MNK AB C AMK MNC B NK AM AK CM CN B NB K   S      . S  . S  . S  AB C AB C AB C AB C AC ABAC CBB CAB 1 1 1 2 1 1 1  S       . S  . S  . S  S  AB C 2 2 AB C 2 3 AB C 3 2 AB C 4 AB C  1 V V         d C MNK S d B AB C S    V V C MNK    1 MNK    1 1 1 1 ; . ; . . . 3 3 4 AB C 4 B ABC 4 3 12 Trang62