10 Đề Tuyển Sinh 10 Môn Toán Không Chuyên 2026 Có Đáp Án Và Lời Giải-Tập 1
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán kính 3 km) và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đường đi nào để đến vị trí tai nạn nhanh hơn nên đội cứu hộ quyết định điều hai xe cứu thương cùng xuất phát ở trạm đến vị trí tai nạn. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 289 tài liệu
Môn: Toán 9 3.1 K tài liệu
Tác giả:
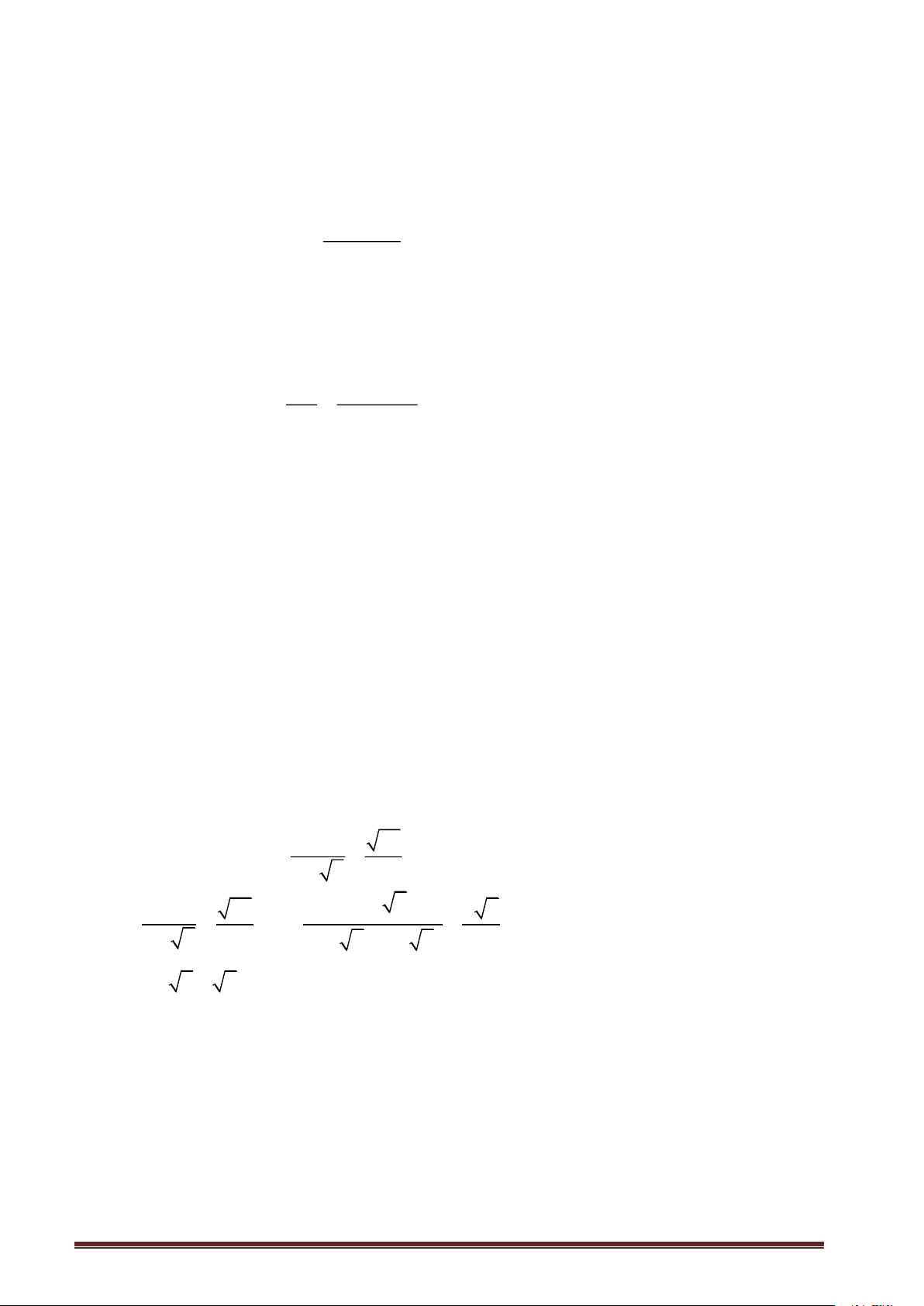
Preview text:
SỞ GIÁO DUC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT
TỈNH BÀ RỊA – VŨNG TÀU
ĐỀ CHÍNH THỨC Thời gian làm bài : 120 phút (Đề thi gồm 2 trang) Bài 1 (3.5 điểm).
a) giải phương trình: 2
x − 3x + 2 = 0 x + 3y = 3
b) giải hệ phương trình: 4x − 3y = 1 − 8 2 28
c) Rút gọn biểu thức: A = + − 2 3 + 7 2 2
d) giải phương trình: (x − x) + (x − )2 2 2 1 −13 = 0 Bài 2 (1.5 điểm). Cho Parabol (P): 2 y = 2
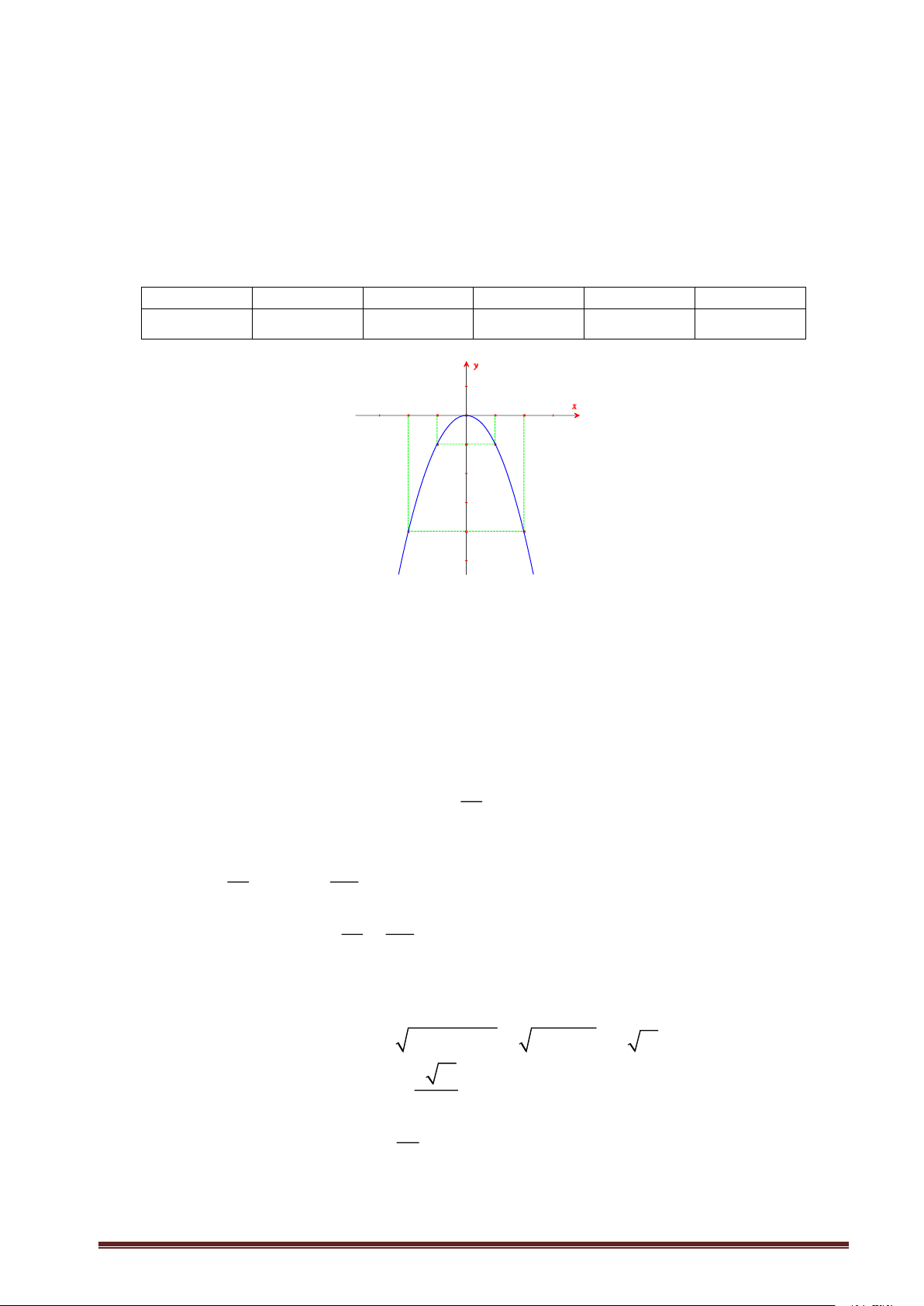
− x và đường thẳng (d): y = x − m (với m là tham số). a) Vẽ parabol (P).
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành
độ x , x thỏa mãn điều kiện x + x = x . x 1 2 1 2 1 2 Bài 3 (1.0 điểm).
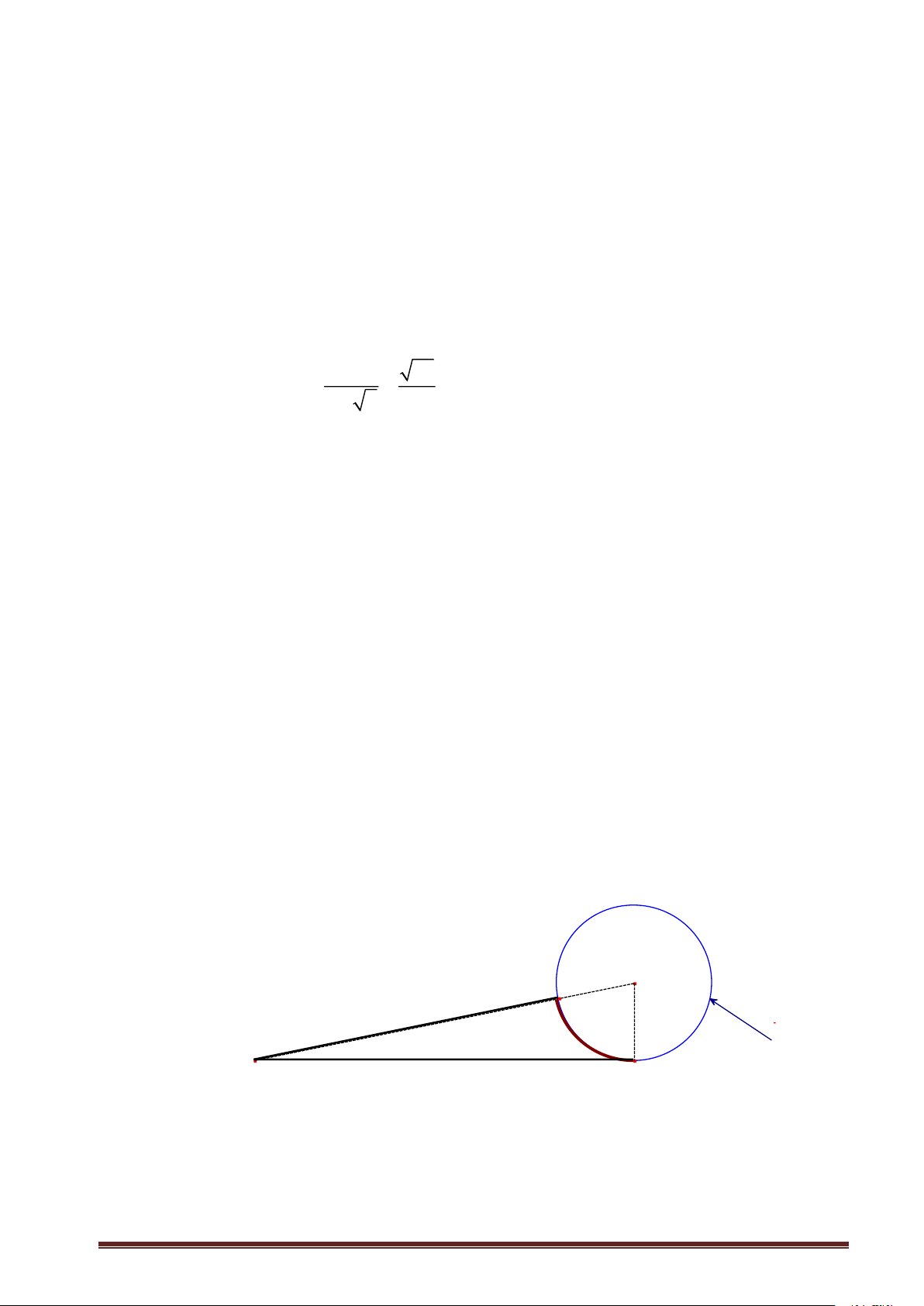
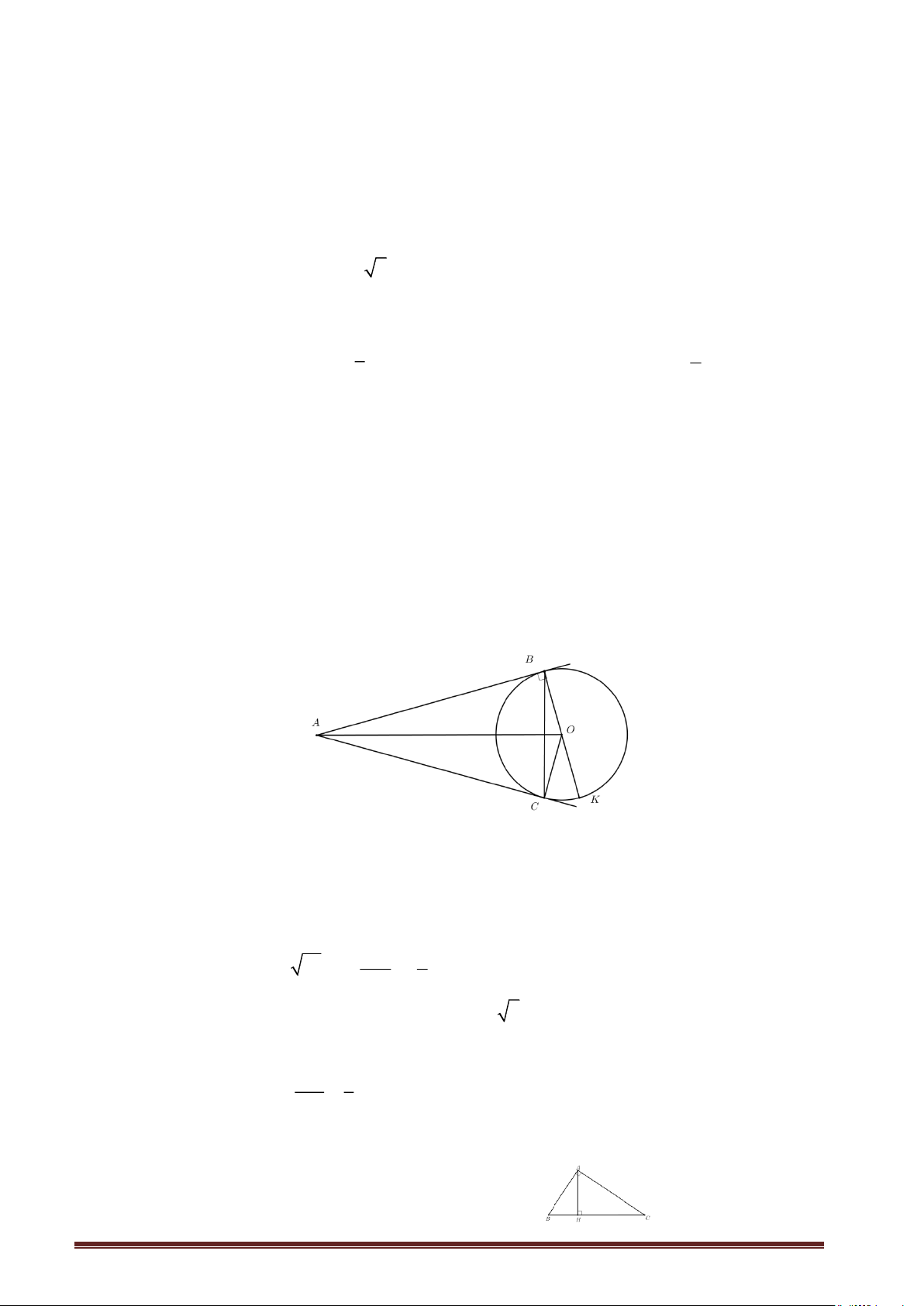
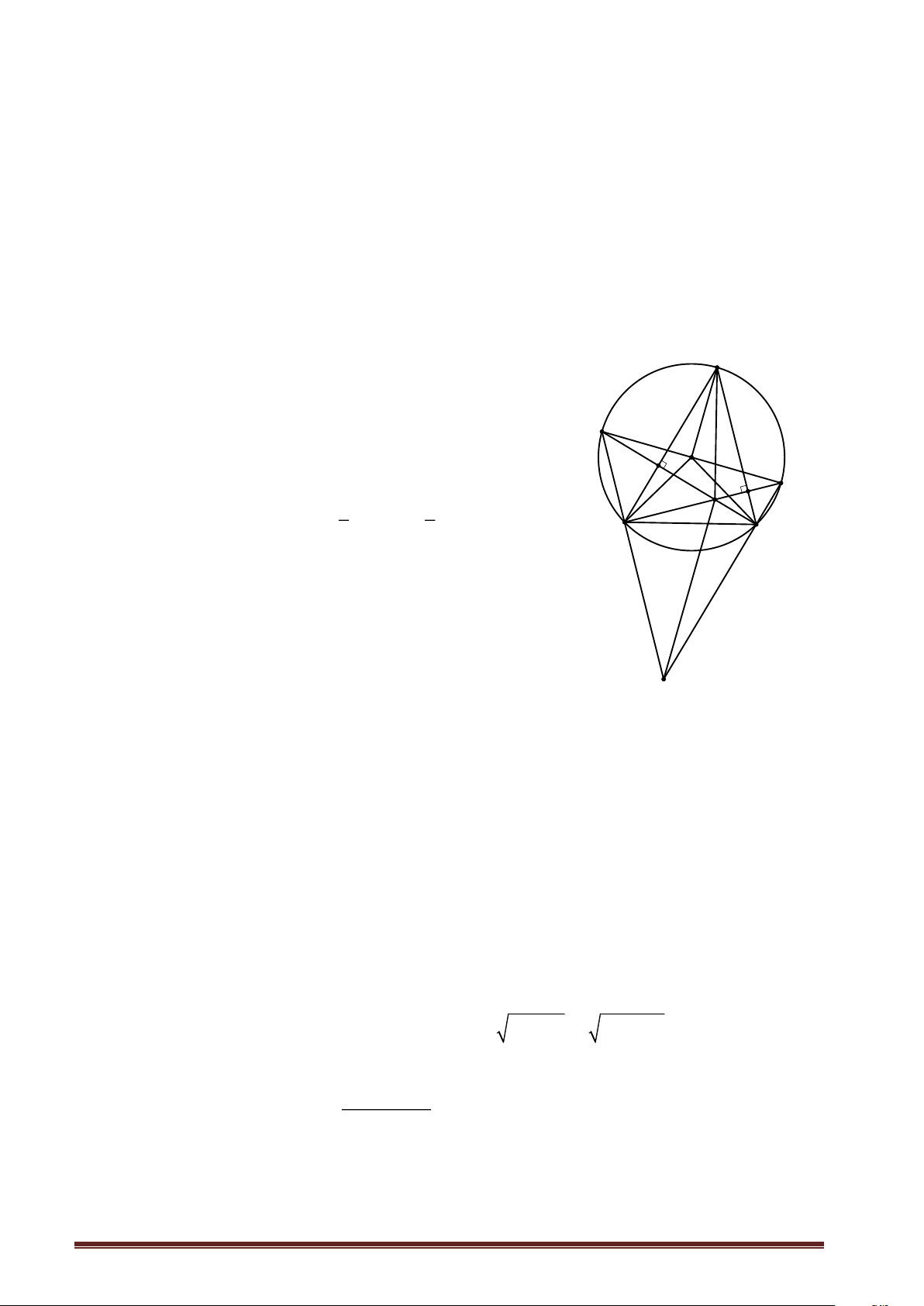
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán
kính 3 km) và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đường đi nào để đến vị
trí tai nạn nhanh hơn nên đội cứu hộ quyết định điều hai xe cứu thương cùng xuất phát ở trạm đến
vị trí tai nạn theo hai cách sau:
Xe thứ nhât : đi theo đường thẳng từ A đến B, do đường xấu nên vận tốc trung bình của xe là 40 km/h.
Xe thứ hai: đi theo đường thẳng từ A đến C với vận tốc trung bình 60 km/h, rồi đi từ C đến B
theo đường cung nhỏ CB ở chân núi với vận tốc trung bình 30 km/h ( 3 điểm A, O, C thẳng hàng và
C ở chân núi). Biết đoạn đường AC dài 27 km và 0 ABO = 90 .
a) Tính độ dài quãng đường xe thứ nhất đi từ A đến B.
b) Nếu hai xe cứu thương xuất phát cùng một lúc tại A thì xe nào thì xe nào đến vị trí tai nạn trước ? O C A Chân núi B Trang 1 Bài 4 (3.5 điểm).
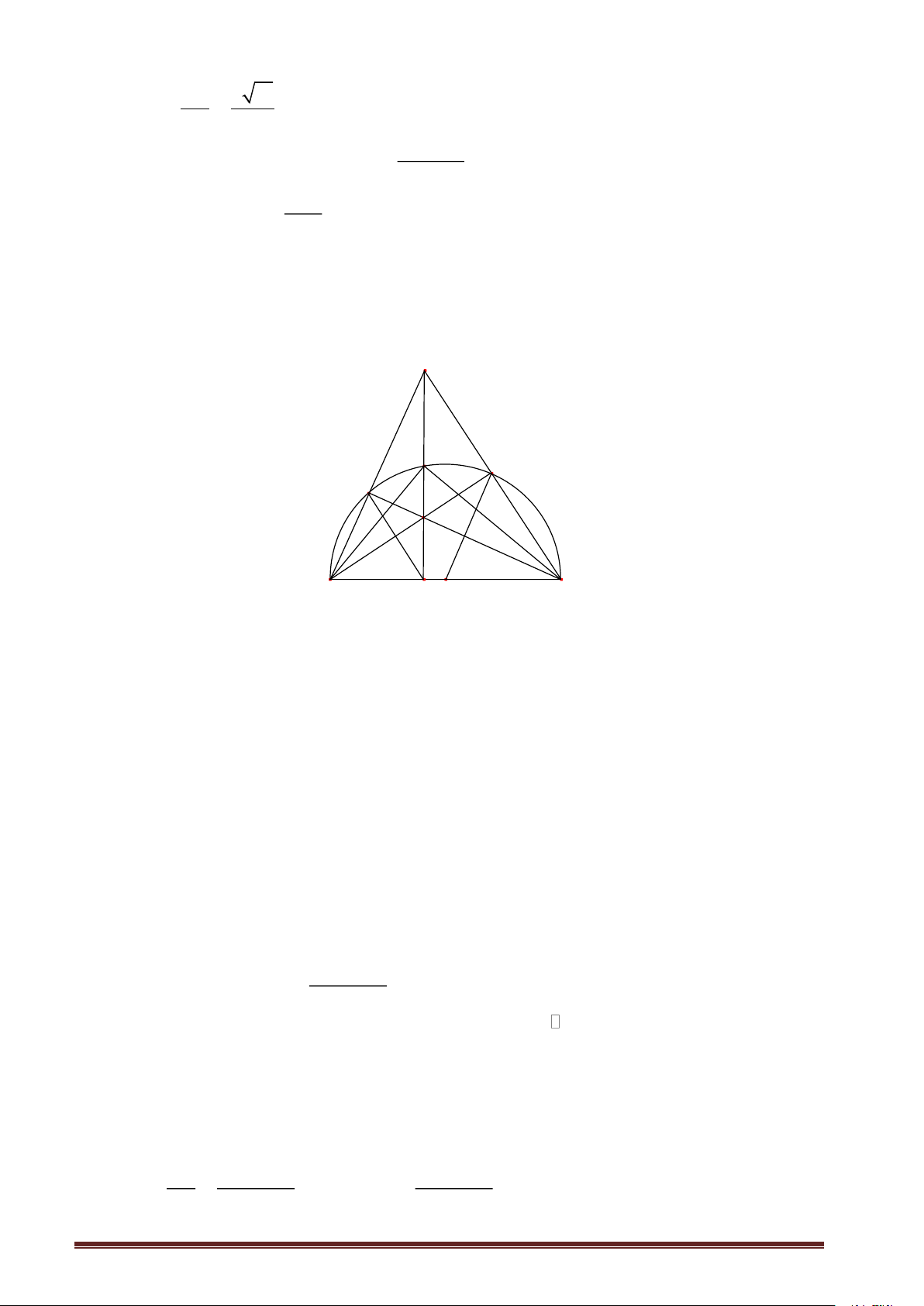
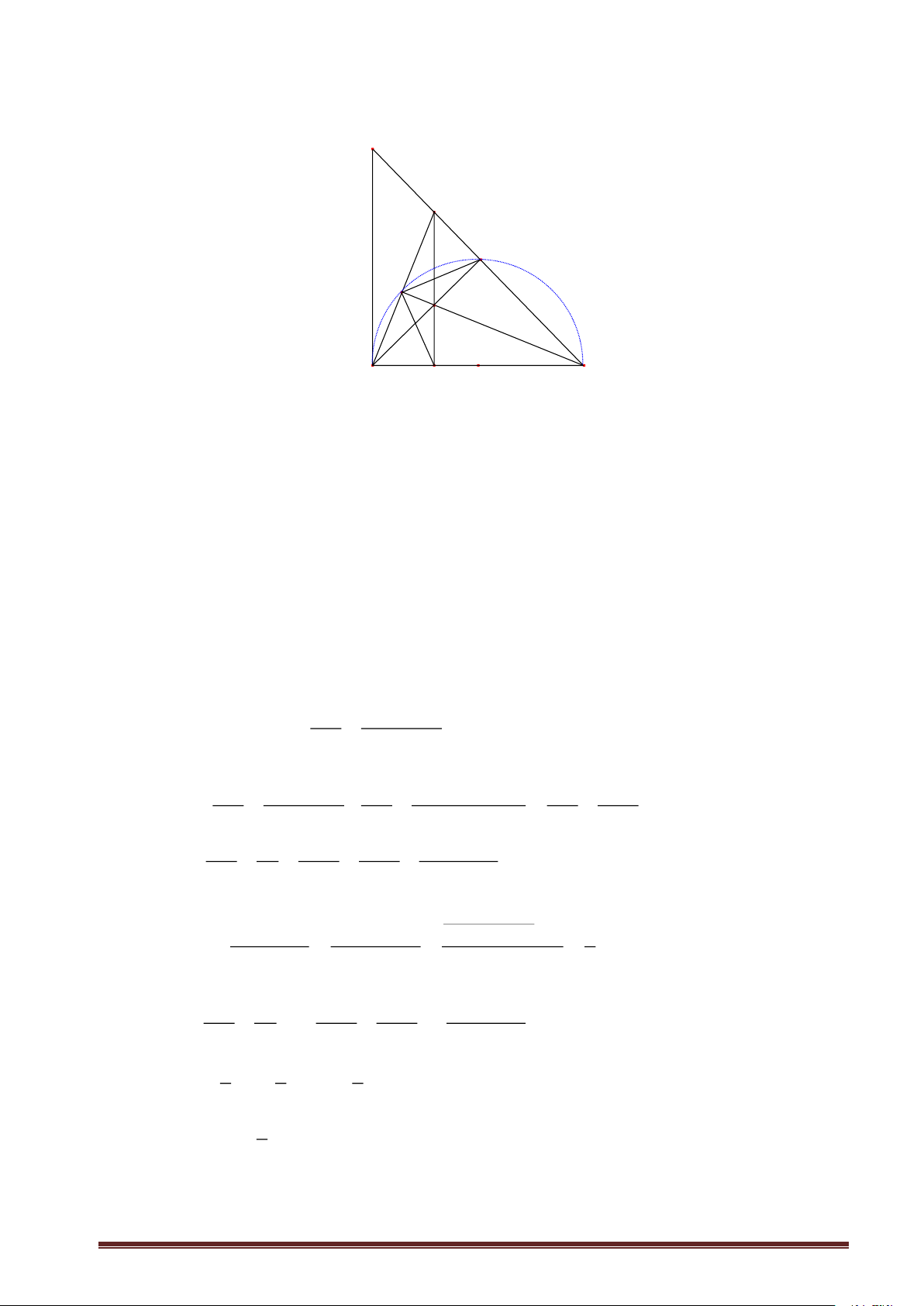
Cho nửa đường tròn tâm O đường kính AB và E là điểm tùy ý trên nửa đường tròn đó (E khác
A, B). Lêy1 điểm H thuộc đoạn EB (H khác E, B). Tia AH cắt nửa đường tròn tại điểm thứ hai là F.
Kéo dài tia AE và tia BF cắt nhau tại I. Đường thẳng IH cắt nửa đường tròn tại P và cắt AB tại K.
a) Chứng minh tứ giác IEHF nội tiếp được đường tròn.
b) chứng minh AIH = ABE PK + BK
c) Chứng minh: cos ABP = PA + PB
d) Gọi S là giao điểm của tia BF và tiếp tuyến tại A của nửa đường tròn (O). Khi tứ giác AHIS
nội tiếp được đường tròn , chứng minh EF vuông góc với EK. Bài 5 (0.5 điểm).
Cho các số thực dương x, y thỏa mãn x + y 3 . Tìm giá trị nhỏ nhất của biểu thức 1 5 P = + 5xy x + 2y + 5
----------------------------HẾT ----------------------------
HƯỚNG DẪN VÀ ĐÁP ÁN Bài 1 (3.5 điểm).
a) giải phương trình: 2
x − 3x + 2 = 0
có a + b + c = 1− 3 + 2 = 0 nên pt có 2 nghiệm phân biệt x = 1 , x = 2 1 2 x + 3y = 3
b) giải hệ phương trình: 4x − 3y = 1 − 8 x + 3y = 3 5 x = 1 − 5 x = 3 − x = 3 − 4x − 3y = 1 − 8 x + 3y = 3 3 − + 3y = 3 y = 2 x = 3 −
Vậy hệ pt có 1 nghiệm duy nhất : y = 2 2 28
c) Rút gọn biểu thức: A = + − 2 3 + 7 2 2.(3− 7 2 28 ) 2 7 A = + − 2 = + − 2 3 + 7 2 (3+ 7)(3− 7) 2
A = 3 − 7 + 7 − 2 = 1 2
d) giải phương trình: (x − x) + (x − )2 2 2 1 −13 = 0
(x −2x)2 +(x− )2 2 1 −13 = 0 (x − 2x)2 2 + ( 2 x − 2x + ) 1 −13 = 0 t = 3 Đặt 2
t = x − 2x , khi đó ta có 2
t + t −12 = 0 t = 4 − Trang 2 x = 1 − * Với t = 3 2 2
x − 2x = 3 x − 2x − 3 = 0 x = 3 * Với t = 2 2 4
− x − 2x = 4
− x − 2x + 4 = 0 (pt vô nghiệm)
Vậy pt đã cho có hai nghiệm: x = 1 − , x = 3 Bài 2 (1.5 điểm). a) vẽ Parabol (P): 2 y = 2 − x Bảng giá trị: x −2 −1 0 1 2 2 y = 2 − x −8 −2 0 −2 −8 1 -2 -1 O 2 1 -2 -8
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành
độ x , x thỏa mãn điều kiện x + x = x . x 1 2 1 2 1 2
Phương trình hoành độ giao điểm của (P) và (d) là: 2 2
− x = x − m 2
2x + x − m = 0 = 1+ 8m 1 −
Để (d) cắt (P) tại hai điểm phân biệt m 8
- Vì x , x là hai nghiệm của pt hoành độ giao điểm, nên ta có: 1 2 1 − −m x + x = ; x .x = 1 2 1 2 2 2− −m
Khi đó : x + x = 1 x .x = m =1 (Thỏa ĐK) 1 2 1 2 2 2 Bài 3 (1.0 điểm).
a) OA = AC + R = 27 + 3 = 30 km
Xét ABO vuông tại B, có: 2 2 2 2
AB = OA − OB = 30 − 3 = 9 11 km 9 11
b) t/gian xe thứ nhất đi từ A đến B là: 0.75 (giờ) 40 27
t/gian xe thứ hai đi từ A đến C là: = 0.45 (giờ) 60
Xét ABO vuông tại B, có: Trang 3 AB 9 11 0 tan O = = O 84.3 OB 3 3. . 84,3
Độ dài đoạn đường từ C đến B là l = 4,41 km CB 180 4,41
T/gian đi từ C đến B là : 0,15 giờ 30
Suy ra thời gian xe thứ hai đi từ A đến B là : 0,45 + 0,15 = 0,6 giờ
Vậy xe thứ hai đến điểm tai nạn trước xe thứ nhất. Bài 4 (3.5 điểm). I P F E H A K O B
a) Chứng minh tứ giác IEHF nội tiếp được đường tròn. Ta có: 0
AEB = 90 (góc nội tiếp chắn nửa đường tròn) 0
HEI = 90 (kề bù với AEB ) T. tự, ta có: 0 HFI = 90
Suy ra: HEI + HFI 0 = 90 + 0 90 0 = 180
tứ giác IEHF nội tiếp được đường tròn (tổng hai góc đối nhau bằng 0 180 )
b) chứng minh AIH = ABE
Ta có: AIH = AFE (cùng chắn cung EH)
Mà: ABE = AFE (cùng chắn cung AE)
Suy ra: AIH = ABE PK + BK
c) Chứng minh: cos ABP = PA + PB
ta có: AF ⊥ BI , BE ⊥ AI nên suy ra H là trực tâm của IAB
IH ⊥ AB PK ⊥ AB
Tam giác ABP vuông tại P có PK là đường cao nên ta có: BP.PA = AB.PK và 2 BP = . AB BK Suy ra: BP.PA + 2 BP = . AB BK + AB.PK B .(
P PA + BP) = A .( B PK + BK ) BP PK + BK PK + BK = cos ABP = AB PA + BP PA + BP Trang 4
d) Gọi S là giao điểm của tia BF và tiếp tuyến tại A của nửa đường tròn (O). Khi tứ giác AHIS nội
tiếp được đường tròn , chứng minh EF vuông góc với EK. S I F E H A B K O
Ta có: SA // IH (cùng vuông góc với AB)
Tứ giác AHIS là hình thang.
Mà tứ giác AHIS nội tiếp được đường tròn (gt)
Suy ra: AHIS là hình thang cân. ASF vuông cân tại F AFB vuông cân tại F Ta lại có: 0
FEB = FAB = BEK = 45 0
FEK = 2.FEB = 90 EF ⊥ EK Bài 5 (0.5 điểm).
Cho các số thực dương x, y thỏa mãn x + y 3 . Tìm giá trị nhỏ nhất của biểu thức 1 5 P = + 5xy x + 2y + 5 1 5 1 5 1 5 P = + = + + 5xy
x + 2y + 5 5xy (x + y) + y + 5 5xy y + 8 1 xy 5
y + 8 xy + y + 8 P + + + − 5xy 20 y + 8 20 20 (x + y + )2 1 +8 xy + y + 8 y(x +1) + 8 3 Ta lại có: 4 = 20 20 20 5 Khi đó: 1 xy 5
y + 8 xy + y + 8 P + + + −
5xy 20 y + 8 20 20 1 3 3
P +1− P 5 5 5 3 x =1 Vậy P = Min 5 y = 2 Trang 5
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG BẮC GIANG NĂM HỌC 2019 - 2020 MÔN THI: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 02/6/2019
Thời gian làm bài 120 phút, không kể thời gian giao đề
(Đề thi gồm 02 trang) Mã đề 101
PHẦN I. TRẮC NGHIỆM (3,0 điểm)
Câu 1: Giá trị của tham số m để đường thẳng y = mx +1 song song với đường thẳng y = 2x − 3 là A. m = −3. B. m = −1. C. m = 1. D. m = 2.
Câu 2: Tổng hai nghiệm của phương trình 2
x − 4x + 3 = 0 bằng A. 4. − B. 4. C. 3. D. 3. −
Câu 3: Giá trị nào của x dưới đây là nghiệm của phương trình 2
x + x − 2 = 0 ? A. x = 4. B. x = 3. C. x = 2. D. x = 1.
Câu 4: Đường thẳng y = 4x − 5 có hệ số góc bằng A. −5. B. 4. C. −4. D. 5.
Câu 5: Cho biết x = 1là một nghiệm của phương trình 2
x + bx + c = 0 . Khi đó ta có
A. b + c = 1.
B. b + c = 2.
C. b + c = 1. −
D. b + c = 0.
Câu 6: Tất cả các giá trị của x để biểu thức x − 3 có nghĩa là A. x 3. B. x 3. C. x 3. D. x 3.
Câu 7: Cho tam giác ABC có AB = 3c , m AC = 4c ,
m BC = 5cm . Phát biểu nào dưới đây đúng?
A. Tam giác ABC vuông.
B. Tam giác ABC đều.
C. Tam giác ABC vuông cân.
D. Tam giác ABC cân.
Câu 8: Giá trị của tham số m để đường thẳng y = (2m + )
1 x + 3 đi qua điểm A( 1 − ;0) là A. m = −2. B. m = 1. C. m = −1. D. m = 2.
Câu 9: Căn bậc hai số học của 144 là A. 13. B. −12. C. 12 và −12. D. 12.
Câu 10: Với x 2 thì biểu thức 2
(2 − x) + x − 3 có giá trị bằng A. −1. B. 2x − 5. C. 5 − 2 . x D. 1. 3 + 3
Câu 11: Giá trị của biểu thức bằng 3 +1 1 1 A. 3. B. C. D. 3. 3 3 x − y = 1
Câu 12: Hệ phương trình
có nghiệm là ( x ; y . Giá trị của biểu thức x + y bằng 0 0 ) x + 2y = 7 0 0 A. 1. B. −2. C. 5. D. 4.
Câu 13: Cho tam giác ABC vuông tại A , có BC = 4c ,
m AC = 2cm . Tính sin ABC. 3 1 1 3 A. B. C. D. 2 2 3 3
Câu 14: Tam giác ABC cân tại B có =120o ABC
, AB =12cm và nội tiếp đường tròn (O). Bán kính
của đường tròn (O) bằng A. 10 . cm B. 9 . cm C. 8 . cm D. 12 . cm
Câu 15: Biết rằng đường thẳng y = 2x + 3 cắt parabol 2
y = x tại hai điểm. Tọa độ của các giao điểm là A. (1; ) 1 và ( 3 − ;9). B. (1; ) 1 và (3;9). C. (−1; ) 1 và (3;9). D. (−1; ) 1 và ( 3 − ;9). Trang 6
Câu 16: Cho hàm số y = f (x) = ( 4
1+ m ) x +1, với m là tham số. Khẳng định nào sau đây đúng? A. f ( ) 1 f (2).
B. f (4) f (2).
C. f (2) f (3). D. f (− ) 1 f (0). x + y = 3
Câu 17: Hệ phương trình
có nghiệm ( x ; y thỏa mãn x = 2y . Khi đó giá trị của m 0 0 ) mx − y = 3 0 0 là A. m = 3. B. m = 2. C. m = 5. D. m = 4.
Câu 18: Tìm tham số m để phương trình 2
x + x + m +1 = 0 có hai nghiệm x , x thỏa mãn 1 2 2 2 x + x = 5. 1 2 A. m = 3. − B. m = 1. C. m = 2. D. m = 0.
Câu 19: Cho tam giác ABC vuông tại A , có AC = 20c .
m Đường tròn đường kính AB cắt BC tại M (
M không trùng với B ), tiếp tuyến tại M của đường tròn đường kính AB cắt AC tại I. Độ dài đoạn AI bằng A. 6 . cm B. 9cm C. 10 . cm D. 12 . cm
Câu 20: Cho đường tròn (O; R) và dây cung AB thỏa mãn 90 .o AOB =
Độ dài cung nhỏ AB bằng R R 3 R A. B. . R C. D. 2 4 2
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 1 (2,0 điểm). x − y = 2
a) Giải hệ phương trình 3 x + 2y =11
2(x −2 x + )1 2 x −1 x
b) Rút gọn biểu thức A = − :
với x 0; x 4 . x − 4 x + 2 x − 2
Câu 2 (1,0 điểm). Cho phương trình 2 x − (m + )
1 x + m − 4 = 0 ( ) 1 , m là tham số.
a) Giải phương trình (1) khi m = 1.
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x , x 1 2 thỏa mãn
( 2x −mx +m)( 2x −mx +m = 2. 1 1 2 2 )
Câu 3 (1,5 điểm). Đầu năm học, Hội khuyến học của một tỉnh tặng cho trường A tổng số 245 quyển 1 2
sách gồm sách Toán và sách Ngữ văn. Nhà trường đã dùng số sách Toán và số sách Ngữ văn đó 2 3
để phát cho các bạn học sinh có hoàn cảnh khó khăn. Biết rằng mỗi bạn nhận được một quyển sách
Toán và một quyển sách Ngữ văn. Hỏi Hội khuyến học tỉnh đã tặng cho trường A mỗi loại sách bao nhiêu quyển?
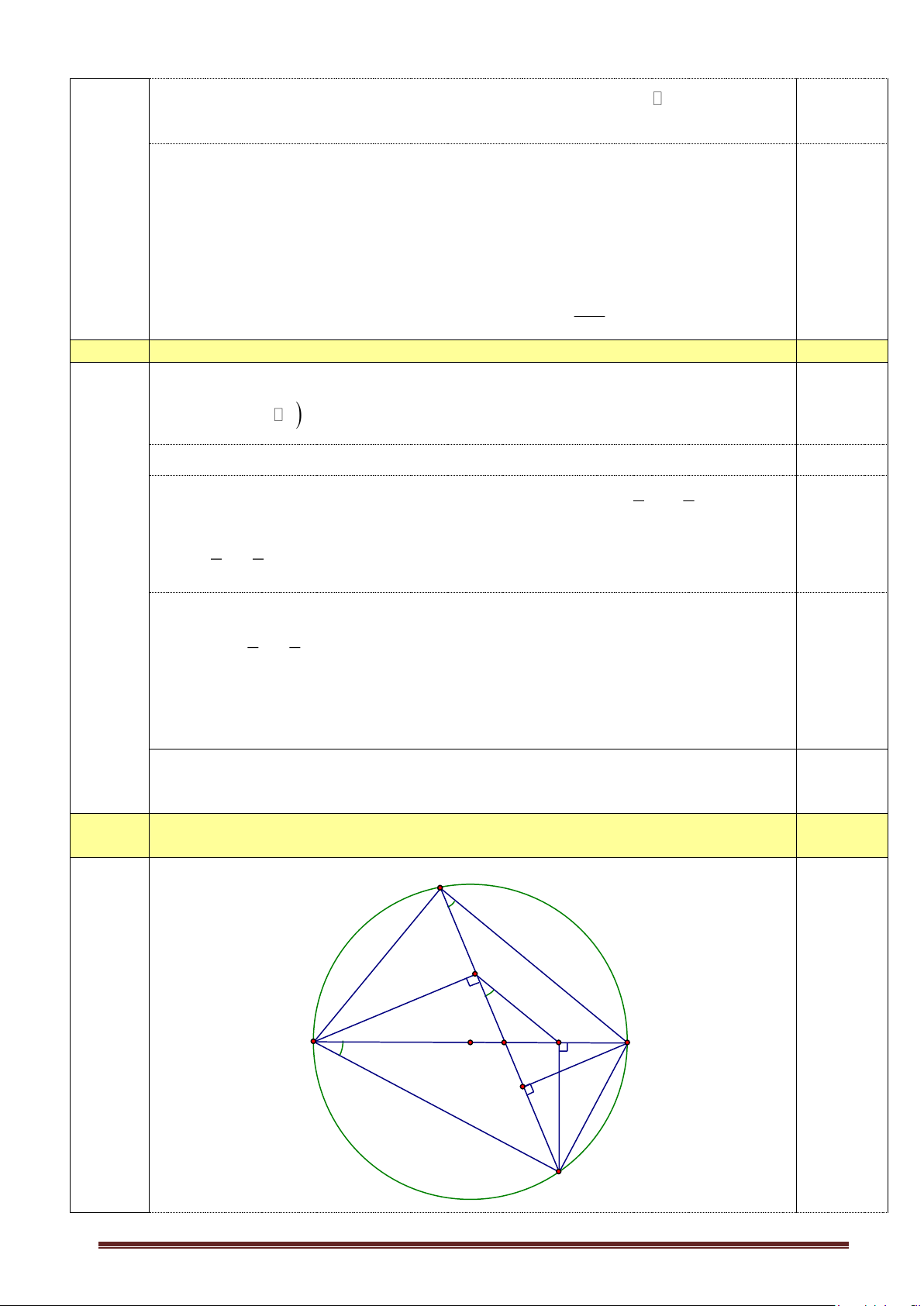
Câu 4 (2,0 điểm). Cho tam giác ABC nội tiếp đường tròn (O) đường kính AC (BA BC ) . Trên
đoạn thẳng OC lấy điểm I bất kỳ (I C ). Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là .
D Kẻ CH vuông góc với BD (H BD), DK vuông góc với AC (K AC).
a) Chứng minh rằng tứ giác DHKC là tứ giác nội tiếp.
b) Cho độ dài đoạn thẳng AC là 4 cm và 60o ABD =
. Tính diện tích tam giác AC . D
c) Đường thẳng đi qua K song song với BC cắt đường thẳng BD tại E. Chứng minh rằng khi
I thay đổi trên đoạn thẳng OC (I C ) thì điểm E luôn thuộc một đường tròn cố định. Trang 7
Câu 5 (0,5 điểm). Cho x, y là các số thực thỏa mãn điều kiện 2 2
x + y = 1. Tìm giá trị nhỏ nhất của biểu
thức P = (3− x)(3− y).
-------------------------------Hết--------------------------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ............................................. Số báo
danh:...........................................................
Cán bộ coi thi 1 (Họ tên và ký):
.........................................................................................................
Cán bộ coi thi 2 (Họ tên và ký):
.........................................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM BÀI THI TUYỂN SINH LỚP 10 BẮC GIANG
TRUNG HỌC PHỔ THÔNG NGÀY THI: 02/06/2019
MÔN THI:TOÁN- PHẦN TỰ LUẬN
HDC ĐỀ CHÍNH THỨC
Bản hướng dẫn chấm có 04trang Câu
Hướng dẫn, tóm tắt lời giải Điểm Câu 1 (2,0điểm) x − y = 2 x = 2 + y Ta có 0,5 3 x + 2y =11 3
(2 + y) + 2y =11 a) 5 y = 5 0,25 (1,0 x = 2 + y điểm) x = 3 . y =1 0,25
Vậy hệ phương trình có nghiệm ( ; x y) = (3;1) .
Với x 0; x 4 , ta có − − x − x + (2 x )1( x 2 2 4 2 ) x A = 0,25 ( −
x + 2)( x − 2) ( x + 2)( x − 2) : x − 2 b) 2x − 4 x + 2 2x − 5 x + 2 x = − : (1,0 0,25
( x + 2)( x − 2) ( x + 2)( x − 2) x − 2 điểm) x x = ( 0,25
x + 2)( x − 2): x − 2 1 = 1 . Kết luận A = 0,25 x + 2 x + 2 Câu 2 (1,0điểm) a)
Với m = 1, phương trình (1) trở thành 2
x − 2x − 3 = 0. (0,5 0,25 điểm)
Giải ra được x = −1, x = 3. 0,25 Trang 8 = (m + )2
1 − (m − ) = m − m + = (m − )2 2 4 4 2 17 1 +16 0, m . 0,25
Kết luận phương trình luôn có hai nghiệm x , x với mọi m. 1 2 2 x − (m + ) 2
1 x + m − 4 = 0 x − mx + m = x + 4. 1 1 1 1 1 b) Tương tự 2
x − mx + m = x + 4. 2 2 2 (0,5
( 2x −mx +m)( 2x −mx +m = 2 1 1 2 2 ) điểm) 0,25
(x + 4 x + 4 = 2 x x + 4 x + x +16 = 2 * . 1 )( 2 ) 1 2 ( 1 2 ) ( )
Áp dụng định lí Viet, ta có: ( ) ( −
m − ) + (m + ) 14 * 4 4
1 +16 = 2 5m +14 = 0 m = Kết luận. 5 Câu 3 (1,5điểm)
Gọi số sách Toán và sách Ngữ văn Hội khuyến học trao cho trường A lần lượt là x, y 0,25 (quyển), ( * x, y ).
Vì tổng số sách nhận được là 245 nên x + y = 245 ( ) 1 0,5 1 2
Số sách Toán và Ngữ văn đã dùng để phát cho học sinh lần lượt là x và y (quyển) 2 3 0,25 1 2
Ta có: x = y (2) (1,5 2 3 điểm) x + y = 245 Đưa ra hệ 1 2 . x = y 2 3 0,25 x =140
Giải hệ được nghiệm y =105
Kết luận: Hội khuyến học trao cho trường 140 quyển sách Toán và 105 quyển sách 0,25 Ngữ văn Câu 4 (2,0điểm) B E K A C O I H a) (1,0 điểm) D Trang 9 + Chỉ ra được 0 DHC = 90 ; 0,25 + Chỉ ra được 0 AKC = 90 0,25
Nên H và K cùng thuộc đường tròn đường kính CD 0,25
+ Vậy tứ giác DHKC nội tiếp được trong một đường tròn. 0,25 b) Chỉ ra được 0 ACD = 60 ; 0 ADC = 90 0,25 (0,5 điểm)
Tính được CD = 2c ;
m AD = 2 3 cm và diện tích tam giác ACD bằng 2 2 3 cm . 0,25
Vì EK / /BC nên DEK = DBC. c)
Vì ABCD nội tiếp nên DBC = DAC. Suy ra DEK = DAK. 0,25 (0,5
Từ đó tứ giác AEKD nội tiếp và thu được = =90o =90 .o AED AKD AEB điểm)
Kết luận khi I thay đổi trên đoạn OC thì điểm E luôn thuộc đường tròn đường kính . AB 0,25 cố định. Câu 5 (0,5điểm) ( − + + =
− x)( − y) = − (x + y) 18 6( x y) 2xy P 3 3 9 3 + xy = 2 17 + ( 2 2
x + y ) − 6(x + y) + 2xy 8 + (x + y)2 − 6(x + y) + 9 = = 0,25 2 2 (x + y −3)2 = + 4. 2 (0,5 Từ 2 2
x + y = 1 chỉ ra được(x + y)2 2 − 2 x + y 2; điểm)
Suy ra − 2 − 3 x + y − 3 2 − 3 0. (x + y − ) ( − )2 2 2 3 3 19 − 6 2 P = + 4 + 4 = 0,25 2 2 2 19 − 6 2 2
Vậy giá trị nhỏ nhất của P là khi x = y = 2 2
(Chú ý: Nếu học sinh dò đúng đáp án nhưng không lập luận đúng thì không cho điểm). Tổng 7,0 điểm Lưu ý khi chấm bài:
- Trên đây chỉ là sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ, hợp
logic. Nếu học sinh trình bày cách làm đúng khác thì cho điểm các phần theo thang điểm tương ứng.
- Với Câu1 ý a nếu học sinh dùng MTCT bấm và cho được kết quả đúng thì cho 0,75 điểm
- Với Câu4, nếu học sinh không vẽ hình thì không chấm.
- Điểm toàn bài không được làm tròn.
----------------*^*^*---------------- Trang 10
SỞ GIÁO DỤC, KHOA HỌC VÀ
KỲ THI TUYỂN SINH LỚP 10 THPT CÔNG NGHỆ NĂM HỌC 2019 – 2020
Môn thi: TOÁN (Không chuyên) ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
(Đề thi có 01 trang) Ngày thi: 07/6/2019 .
Câu 1: (4,0 điểm) Rút gọn biểu thức: a) A = 45 − 2 20 − b) B = − ( − )2 3 5 27 3 12 . 3 − 5 Câu 2: (4,0 điểm) 2x − y = 4
a) Giải hệ phương trình x + y = 5 b) Cho hàm số 2
y = 3x có đồ thị (P) và đường thẳng (d ) : y = 2x +1. Tìm tọa độ gia0
điểm của (P) và (d ) bằng phép tính. Câu 3: (6,0 điểm) Cho phương trình: 2
x − 2mx − 4m − 5 ( ) 1 (m là tham số). a) Giải phương trình ( ) 1 khi m = −2 .
b) Chứng minh phương trình ( )
1 luôn có nghiệm với mọi giá trị của m.
c) Gọi x ; x là hai nghiệm của phương trình ( ) 1 . Tìm m để: 1 2 1 33 2
x − m −1 x + x − 2m + = 762019. 1 ( ) 1 2 2 2 Câu 4: (6,0 điểm)
Trên nửa đường tròn đường kính AB, lấy hai điểm I, Q sao cho I thuộc cung AQ. Gọi C
là giao điểm hai tia AI và BQ; H là giao điểm hai dây AQ và BI.
a) Chứng minh tứ giác CIHQ nội tiếp.
b) Chứng minh: CI.AI = HI.BI .
c) Biết AB = 2R . Tính giá trị biểu thức: M = AI.AC + . BQ BC theo R.
-----------Hết----------- Trang 11 HƯỚNG DẪN GIẢI.
Câu 1: (4,0 điểm) Rút gọn biểu thức: a) A = 45 − 2 20 − b) B = − ( − )2 3 5 27 3 12 3 − 5 Giải: a) 2 2
A = 45 − 2 20 = 3 .5 − 2 2 .5 = 3 5 − 2.2 5 = − 5 − − b) B = − ( − )2 3 5 27 3 5 3 3 3 12 = − 3− 12 3 − 5 3 − 5 3( 5 − 3) = − (−3+ 12) (do 2 3 12 3 12 ) 3 − 5 = 3 − + 3− 12 = − 12 = 2 − 3 . Câu 2: (4,0 điểm) 2x − y = 4
a) Giải hệ phương trình x + y = 5 b) Cho hàm số 2
y = 3x có đồ thị (P) và đường thẳng (d ) : y = 2x +1. Tìm tọa độ giao
điểm của (P) và (d ) bằng phép tính. Giải: 2x − y = 4 3 x = 9 x = 3 a) x + y = 5 y = 5 − x y = 2
Vậy hệ phương trình có nghiệm là: ( ; x y) = (3;2)
b) Phương trình hoành độ giao điểm: 2 2
3x = 2x +1 3x − 2x −1 = 0 (*)
Phương trình (*) có hệ số: a = 3; b = 2 − ; c = 1
− a + b + c = 0 − c 1
Phương trình (*) có hai nghiệm: x =1; x = = 1 2 a 3 - Với 2
x = 1 y = 3.1 = 3 A 1;3 1 ( ) 2 1 − 1 − 1 1 − 1 - Với x = y = 3. = B ; 2 3 3 3 3 3 1 − 1
Vậy tọa độ giao điểm của (P) và (d ) là A(1;3) và B ; . 3 3 Câu 3: (6,0 điểm) Cho phương trình: 2
x − 2mx − 4m − 5 ( ) 1 (m là tham số). a) Giải phương trình ( ) 1 khi m = −2 .
b) Chứng minh phương trình ( )
1 luôn có nghiệm với mọi giá trị của m.
c) Gọi x ; x là hai nghiệm của phương trình ( ) 1 . Tìm m để: 1 2 1 33 2
x − m −1 x + x − 2m + = 762019 1 ( ) 1 2 2 2 Giải: Trang 12
a) Thay m = −2 vào phương trình ( ) 1 ta có: x = 3 − 2
x + 4x + 3 = 0 x (x + 3) + (x + 3) = 0 (x + 3)(x + ) 1 = 0 x = 1 −
Vậy với m = −2 thì phương trình có tập nghiệm S = 3 − ; − 1
b) Ta có: = m − (− m − ) = (m + )2 ' 2 4 5 2 +1 0, m Do đó phương trình ( )
1 luôn có hai nghiệm với mọi giá trị của m. c) Do phương trình ( )
1 luôn có hai nghiệm với mọi giá trị của m, gọi x ; x là hai 1 2
nghiệm của phương trình ( ) 1
x + x = 2m
Áp dụng định lí Vi-ét ta có: 1 2 x x = 4 − m − 5 1 2 1 33 Ta có: 2
x − m −1 x + x − 2m + = 762019 1 ( ) 1 2 2 2 2
x − 2(m − )
1 x + 2x − 4m + 33 = 1524038 1 1 2 2
x − 2mx − 4m − 5 + 2 x + x = 1524000 1 ( 1 2 ) 1
2(x + x =1524000 (do x là nghiệm của ( ) 1 nên 2
x − 2mx − 4m − 5 = 0 ) 1 2 ) 1 1 1
2.2m = 1524000 m = 381000
Vậy m = 381000 thỏa mãn yêu cầu bài toán. Câu 4: (6,0 điểm)
Trên nửa đường tròn đường kính AB, lấy hai điểm I, Q sao cho I thuộc cung AQ. Gọi C
là giao điểm hai tia AI và BQ; H là giao điểm hai dây AQ và BI.
a) Chứng minh tứ giác CIHQ nội tiếp.
b) Chứng minh: CI.AI = HI.BI .
c) Biết AB = 2R . Tính giá trị biểu thức: M = AI.AC + . BQ BC theo R. Giải: C Q I H A O B a) Ta có: 0
AIB = AQB = 90 (góc nội tiếp chắn nửa đường tròn) 0
CIH = CQH = 90 Xét tứ giác CIHQ có 0 0 0
CIH + CQH = 90 + 90 = 180
tứ giác CIHQ nội tiếp
b) Xét AHI và BCI có: 0
AIH = BIC = 90 AH I ∽ BC
I ( g.g ) IAH = IBC AI HI =
CI.AI = HI.BI BI CI Trang 13
c) Ta có: M = AI.AC + B .
Q BC = AC ( AC − IC ) + BQ (BQ + QC ) 2 2
= AC − AC.IC + BQ + . BQ QC 2 2 2
= AQ + QC − AC.IC + BQ + . BQ QC = ( 2 2
AQ + BQ ) + QC (QC + BQ) − AC.IC 2
= AB + QC.BC − AC.IC
Tứ giác AIBQ nội tiếp (O) CIQ = CBA (cùng phụ với AIQ )
Xét CIQ và CBA có:
ACB chung C IQ∽ C
BA (g.g ) CIQ = CBA IC QC =
QC.BC = AC.IC BC AC
QC.BC − AC.IC = 0
Suy ra: M = AB = ( R)2 2 2 2 = 4R
-----------Hết-----------
ĐỀ TUYỂN SINH VÀO 10 BẮC NINH NĂM HỌC 2019-2020
I. TRẮC NGHIỆM (3,0 điểm) Chọn phương án trả lời đúng trong các câu sau: 4
Câu 1: Khi x = 7 biểu thức có giá trị là x + 2 - 1 1 4 4 A. . B. . C. . D. 2 . 2 8 3
Câu 2: Trong các hàm số sau, hàm số nào đồng biến trên ?
A.y = 1 - x .
B.y = 2x - 3 .
C.y = (1- 2)x . D.y = - 2x + 6.
Câu 3: Số nghiệm của phương trình 4 2
x - 3x + 2 = 0 là A.1 . B. 2 . C. 3 . D. 4 . Câu 4: Cho hàm số 2
y = ax (a ¹ 0). Điểm M (1;2) thuộc đồ thị hàm số khi 1 A.a = 2 . B.a = . C.a = - 2 . D. 1 a = . 2 4
Câu 5: Từ điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến A B,A C tới đường tròn (
B,C là các tiếp điểm). Kẻ đường kính BK . Biết ·
BA C = 30o ,số đocủa cung nhỏ CK là A. 30° . B. 60° . C.120° . D.150° .
Câu 6: Cho tam giác A BC vuông tại A . Gọi H là chân đường cao hạ từ đỉnh A xuống cạnh HB 1
BC . Biết A H = 12cm , =
. Độ dài đoạn BC là HC 3
A. 6cm . B. 8cm .
C. 4 3cm . D.12cm .
II. TỰ LUẬN (7,0 điểm) Trang 14
( x + )2 + ( x - )2 1 1 3 x + 1
Câu 7: Cho biểu thức A = x ³ ( - với 0 , x ¹ 1 . x - )( x + ) x - 1 1 1
a) Rút gọn biểu thức A.
b) Tìm x là số chính phương để 2019A là số nguyên.
Câu 8: An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấynhiều hơn16 bài.
Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160 . Hỏi An được
bao nhiêu bài điểm 9 và bao nhiêu bài điểm 10 ?
Câu 9: Cho đường tròn (O), hai điểm A,B nằm trên (O) sao cho ·
A OB = 90º . Điểm C nằm
trên cung lớn A B sao cho A C > BC và tam giác A BC có ba góc đều nhọn. Các
đường cao A I , BK của tam giác A BC cắt nhau tại điểm H . BK cắt (O) tại điểmN
(khác điểm B ); A I cắt (O) tại điểmM (khác điểmA ); NA cắt MB tại điểmD . Chứng minh rằng:
a) Tứ giác CIHK nội tiếp một đường tròn.
b) MN là đường kính của đường tròn (O).
c) OC song song với DH .
Câu 10: a) Cho phương trình 2
x - 2mx - 2m - 1 = 0 ( )
1 với m là tham số. Tìm m để phương trình ( )
1 có hai nghiệm phân biệt x , x sao cho x + x +
3 + x x = 2m + 1. 1 2 1 2 1 2
b) Cho hai số thực không âm a,b thỏa mãn 2 2
a + b = 2 . Tìm giá trị lớn nhất, giá trị nhỏ 3 3 a + b + 4
nhất của biểu thức M = . ab + 1 == ==== Hết ====== LỜI GIẢI
I. TRẮC NGHIỆM (3,0 điểm) Chọn phương án trả lời đúng trong các câu sau: 4
Câu 1: Khi x = 7 biểu thức có giá trị là x + 2 - 1 1 4 4 A. . B. . C. . D. 2 . 2 8 3 Lời giải Chọn: D 4
Thay x = 7 (thỏa mãn) vào biểu thức
ta tính được biểu thức có giá trị bằng x + 2 −1 4 4 = = 2 . 7 + 2 −1 3 −1
Câu 2: Trong các hàm số sau, hàm số nào đồng biến trên ? A.y = 1 - x . B.y = 2x - 3 .
C.y = (1- 2)x . D.y = - 2x + 6. Lời giải Chọn: B
Hàm số y = 2x − 3 đồng biến trên . Trang 15
Câu 3: Số nghiệm của phương trình 4 2
x - 3x + 2 = 0 là A.1 . B. 2 . C. 3 . D. 4 . Lời giải Chọn: D Đặt 2
t = x (t 0) . Khi đó phương trình tương đương 2
t − 3t + 2 = 0 .
Ta thấy 1- 3 + 2 = 0 . Nên phương trình có hai nghiệm t = 1 (thỏa mãn); t = 2 (thỏa mãn). 2 x =1 x = 1 Khi đó 2 x = 2 x = 2 Câu 4: Cho hàm số 2
y = ax (a ¹ 0). Điểm M (1;2) thuộc đồ thị hàm số khi 1 A.a = 2 . B.a = . C.a = - 2 . D. 1 a = . 2 4 Lời giải
Chọn A .
Vì M (1;2) thuộc đồ thị hàm số 2
y = ax (a 0) nên ta có 2 2 = .1 a
a = 2 (thỏa mãn).
Câu 5: Từ điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến A B,A C tới đường tròn (
B,C là các tiếp điểm). Kẻ đường kính BK . Biết ·
BA C = 30o , số đo của cung nhỏ CK là A. 30° . B. 60° . C.120° . D.150° . Lời giải Chọn: A.
Từ giả thiết ta suy ra tứ giác
nội tiếp nên BAC = COK = 30 , mà COK = sđ CK nên
Số đo cung nhỏ CK là 30 .
Câu 6: Cho tam giác A BC vuông tại A . Gọi H là chân đường cao hạ từ đỉnh A xuống cạnh HB 1
BC . Biết A H = 12cm , =
. Độ dài đoạn BC là HC 3 A. 6 cm . B. 8 cm . C. 4 3 cm . D.12 cm . Lời giải Chọn: B HB 1 Theo đề bài ta có:
= HC = 3HB . Áp HC 3
dụng hệ thức lượng trong tam giác ABC vuông
tại A có đường cao AH ta có 2
AH = BH.HC 12 = BH.3BH 2
BH = 4 BH = 2 Trang 16
HC = 3.HB = 3.2 = 6
BC = HB + HC = 2 + 6 = 8 (cm)
II. TỰ LUẬN (7,0 điểm)
( x + )2 + ( x - )2 1 1 3 x + 1
Câu 7: Cho biểu thức A = x ³ ( - với 0 , x ¹ 1 . x - )( x + ) x - 1 1 1
a) Rút gọn biểu thức A .
b) Tìm x là số chính phương để 2019A là số nguyên. Lời giải
( x + )2 + ( x - )2 1 1 - 3 x - 1
x + 2 x + 1 + x - 2 x + 1 - 3 x - 1 a) A = = x - 1 x - 1 2x - 2 x - x + 1 ( x - )1(2 x x x - - + )1 2 3 1 2 x - 1 = = = = . x - 1 x - 1 ( x - )1( x + )1 x + 1 2019(2 x + 2 - 3) 6057 2019A = = 4038 - . x + 1 x + 1 b)
2019A là số nguyên khi và chỉ khi x + 1 là ước nguyên dương của 6057 gồm: 1; 3;9;673, 2019;6057 .
+) x + 1 = 1 Û x = 0 , thỏa mãn.
+) x + 1 = 3 Û x = 4 , thỏa mãn.
+) x + 1 = 9 Û x = 64 , thỏa mãn.
+) x + 1 = 673 Û x = 451584 , thỏa mãn.
+) x + 1 = 2019 Û x = 4072324 , thỏa mãn.
+) x + 1 = 6057 Û x = 36675136 , thỏa mãn.
Câu 8: An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấynhiều hơn16 bài.
Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160 . Hỏi An được
bao nhiêu bài điểm 9 và bao nhiêu bài điểm 10 ? Lời giải
Gọi số bài điểm 9 và điểm 10 của An đạt được lần lượt là x, y (bài)(x,y Î ¥ ).
Theo giả thiết x + y > 16 .
Vì tổng số điểm của tất cả các bài kiểm tra đó là 160 nên 9x + 10y = 160 . Ta có = x + y ³ (x + y) 160 160 9 10 9 Þ x + y £ . 9 160
Do x + y Î ¥ và 16 < x + y £
nên x + y = 17 . 9 ìï x + y = 17 ìï x = 17- y ìï x = 10 Ta có hệ ï ï ï í Û í Û í (thỏa mãn).
ï 9x + 10y = 160 ï 9 ïî
ï (17 - y )+ 10y = 160 ï y = 7 ï ï î î
Vậy An được 10 bài điểm 9 và 7 bài điểm 10 . Trang 17
Câu 9: Cho đường tròn (O), hai điểm A,B nằm trên (O) sao cho ·
A OB = 90º . Điểm C nằm
trên cung lớn A B sao cho A C > BC và tam giác A BC có ba góc đều nhọn. Các
đường cao A I , BK của tam giác A BC cắt nhau tại điểm H . BK cắt (O) tại điểmN
(khác điểm B ); A I cắt (O) tại điểmM (khác điểmA ); NA cắt MB tại điểmD . Chứng minh rằng:
a) Tứ giác CIHK nội tiếp một đường tròn.
b) MN là đường kính của đường tròn (O).
c) OC song song với DH . Lời giải a)Ta có C ìï HK ^ KC ï · · í
Þ HKC + HIC = 90º + 90º = 180º ï HI ^ IC ïî N . O
Do đó,CIHK là tứ giác nội tiếp. K
b) Do tứ giác CIHK nội tiếp nên M I · · 1 ¼ 1 ¼ H
45º = ICK = BHI = sđBM + sđA N . 2 2 A B
sđBM + sđA N = 90 . ¼ » ¼ ¼
Suy ra, sđMN = sđA B + (sđBM + sđA N ) hay = 90° + 90° = 180º
MN là đường kính của (O). D
c) Do MN là đường kính của (O) nên MA ^ DN ,NB ^ DM . Do đó, H là trực tâm
tam giác DMN hay DH ^ MN .
Do I , K cùng nhìn A B dưới góc 90º nên tứ giác A BIK nội tiếp. Suy ra, · · ¼ »
CA I = CBK Þ sđCM = sđCN Þ C là điểm chính giữa của cung
MN Þ CO ^ MN .
Vì A C > BC nên D A BC không cân tại C do đó C ,O, H không thẳng hàng. Từ đó
suy ra CO / / DH .
Câu 10: a) Cho phương trình 2
x - 2mx - 2m - 1 = 0 ( )
1 với m là tham số. Tìm m để phương trình ( )
1 có hai nghiệm phân biệt x , x sao cho x + x +
3 + x x = 2m + 1. 1 2 1 2 1 2
b) Cho hai số thực không âm a,b thỏa mãn 2 2
a + b = 2 . Tìm giá trị lớn nhất, giá trị nhỏ 3 3 a + b + 4
nhất của biểu thức M = . ab + 1 Lời giải
a) D¢= m + m + = (m + )2 2 2 1 1 . Trang 18 Phương trình ( )
1 có hai nghiệm phân biệt khi và chỉ khi D ¢> 0 Û m ¹ - 1.
Áp dụng ĐL Vi-ét ta có x + x = 2m;x .x = - 2m - 1 . 1 2 1 2
Ta có 2m + 2 - 2m = 2m + 1 ( ĐK 0 £ m £ 1 (*)) 2m - 1 2m - 1 Û
2m - 1 + 2 - 2m - 1 - (2m - ) 1 = 0 Û - - (2m - ) 1 = 0 2m + 1 2 - 2m + 1 é 1 m ê = æ ö (t / m ( ) * ) Û ( ê m - ) 1 1 ç ÷ 2 2 1 ç - - 1÷= 0 Û ê ç ÷ ç ÷ è + - + ø ê 1 1 2m 1 2 2m 1 - - 1 = 0 ê (2) êë 2m + 1 2 - 2m + 1 1
Vì 2m + 1 ³ 1, " m thỏa mãn 0 £ m £ 1 Þ
£ 1 . Do đó, V T (2)< 0 = VP (2) hay (2) 2m + 1 vô nghiệm. 1
Vậy giá trị cần tìm là m = . 2 b) Ta có 3 3 a + b + = ( 3 3 4 a + b + )
1 + 3 ³ 3ab + 3 . Dấu bằng xảy ra khi và chỉ khi a = b = 1. 3 3 3(ab a b + + + ) 1 4
Vì ab + 1 > 0 nên M = ³ = 3 . ab + 1 ab + 1
Do đó, giá trị nhỏ nhất của biểu thức M là 3 đạt được khi a = b = 1. +) Vì 2 2 a + b = 2 nên Suy ra 3 3 a + b + ( 2 2 4
2 a + b ) + 4 = 2 2 + 4 . 1 3 3 a + b + 4 Mặt khác
1 do ab +11. Suy ra M = 2 2 + 4. ab +1 ab +1
Dấu bằng xảy ra khi và chỉ khi 2 2 ìï a + b = 2 ï í
Û (a;b) = (0; 2)Ú(a;b)= ( 2;0). ï ab = 0 ïî
Giá trị lớn nhất của biểu thức M là 4 + 2 2 đạt được khi
(a;b)= (0; 2)Ú(a;b)= ( 2;0)
---------------Hết--------------- Trang 19
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 BẾN TRE
TRUNG HỌC PHỔ THÔNG CÔNG LẬP NĂM HỌC 2019-2020 ĐỀ CHÍNH THỨC Môn: TOÁN (chung)
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm)
a) Rút gọn biểu thức: A = 27 − 12 7x − 3y = 5
b) Giải hệ phương trình: x + 3y = 3
Câu 2. (2.0 điểm)
a) Trong mặt phẳng tọa độ (Oxy) , cho parabol (P) 2 : y = 2
− x . Vẽ (P).
b) Tìm m để đường thẳng y = (5m − 2) x + 2019 song song với đường thẳng y = x + 3 .
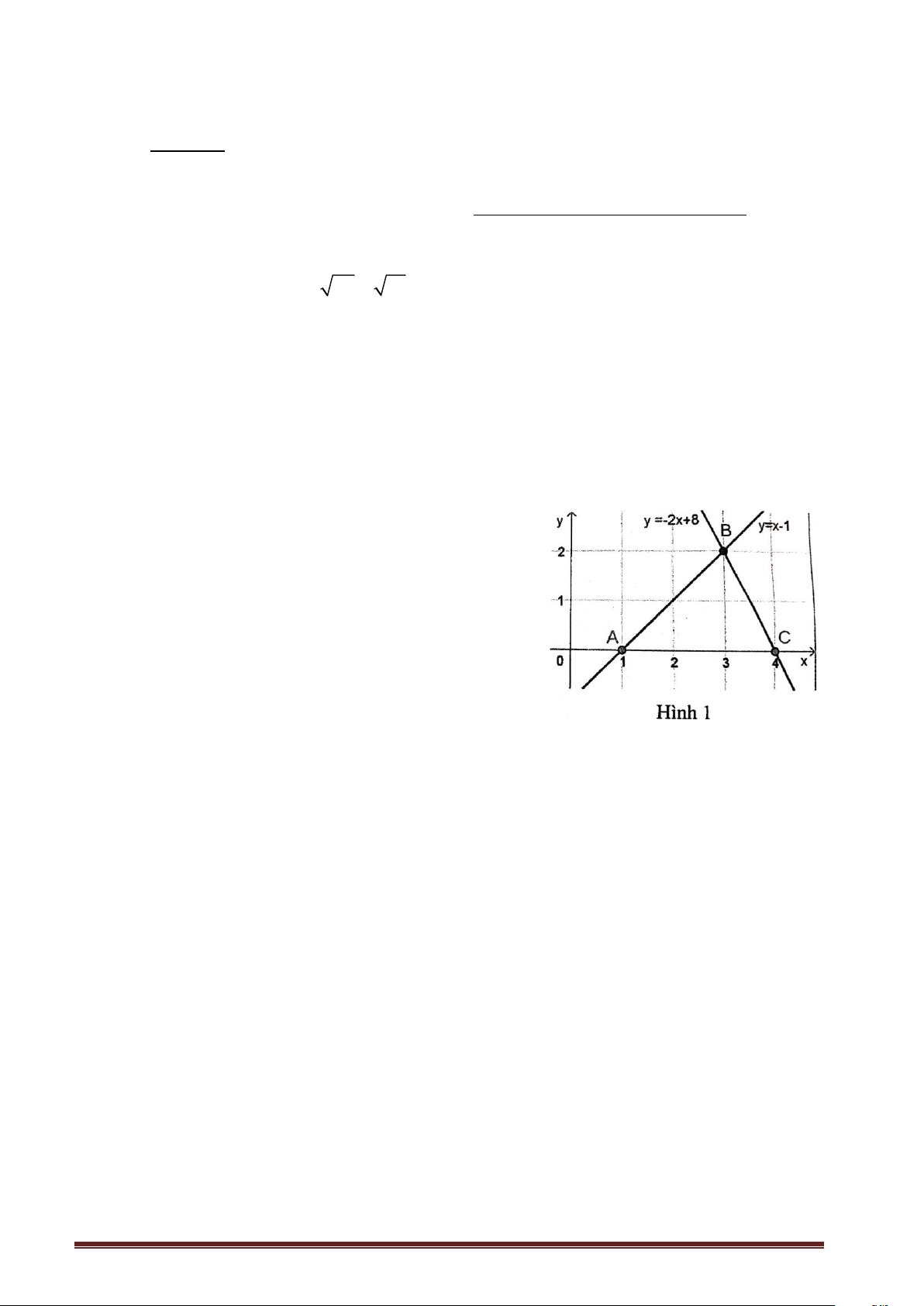
c) Hai đường thẳng y = x −1 và y = −2x + 8 cắt nhau
tại điểm B và lần lượt cắt trục Ox tại điểm A, C (hình 1).
Xác định tọa độ các điểm A, B, C và tính diện tích tam giác ABC.
Câu 3. (1,5 điểm) a) Giải phương trình: 2
x + 2x − 3 = 0
b) Tìm m để phương trình: 2 x − (m + ) 2 2
1 x + m + 3m − 7 = 0 vô nghiệm.
Câu 4. (1,5 điểm)
Cho tam giác ABC vuông tại ,
A đường cao AH. Biết AB = 3c , m AC = 4c . m Tính đọ dài
đường cao AH , tính cos ACB và chu vi tam giác ABH .
Câu 5. (1,5 điểm)
a) Sau Kỳ thi tuyển sinh vào lớp 10 năm học 2019-2020, học sinh hai lớp 9A và 9B tặng lại
thư viện trường 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo. Trong đó, mỗi học
sinh lớp 9A tặng 6 quyển sách giáo khoa và 3 quyển sách tham khảo; mỗi học sinh lớp 9B tặng 5
quyển sách giáo khoa và 4 quyển sách tham khảo. Biết số sách giáo khoa nhiều hơn số sách tham
khảo là 166 quyển. Tính số học sinh của mỗi lớp.
b) Một bồn chứa xăng đặt trên xe gồm hai nửa hình cầu có đường kính là 2, 2m và một hình
trụ có chiều dài 3,5m (hình 2). Tính thể tích của bồn chứa xăng (kết quả làm tròn đến chữ số thập
phân thứ hai sau dấu phẩy). Trang 20