10 Đề Tuyển Sinh Toán 10 Chuyên 2025-2026 Có Lời Giải Chi Tiết
Hai ngọn nến hình trụ có chiều cao và đường kính khác nhau được đặt thẳng đứng trên mặt bàn. Ngọn nến thứ nhất cháy hết trong 6 giờ, ngọn nến thứ hai cháy hết trong 8 giờ. Hai ngọn nến được thắp sáng cùng lúc, sau 3 giờ chúng có cùng chiều cao. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 216 tài liệu
Môn: Toán 9 2.9 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TỈNH AN GIANG
Môn thi: TOÁN - CHUYÊN
ĐỀ THI C HÍNH THỨC
Thời gian làm bài: 150 phút
(Không kể thời gian phát đề) Bài 1. (3,0 điểm)
a) Rút gọn A = 419 − 40 19 + 419 + 40 19 . b) Giải phương trình 2
2x + (2 3 + 3) x + 3 3 = 0.
c) Biết nghiệm của phương trình 2
2x + (2 3 + 3) x + 3 3 = 0 là nghiệm của phương trình 4 2
4x + bx + c = 0 . Tìm các số b, c . Bài 2. (2,0 điểm)
a) Vẽ đồ thị (P) của hàm số 2 y = −x .
b) Viết phương trình đường thẳng (d ) đi qua điểm A(0; )
1 và tiếp xúc với (P) . Bài 3. (1,0 điểm)
Cho hai số a,b phân biệt thỏa mãn 2 2
a − 2021a = b − 2021b = c , với c là một số thực dương. 1 1 2021 Chứng minh rằng: + + = 0 . a b c Bài 4. (2,0 điểm)
Cho tam giác ABC ( AB AC ) nội tiếp trong đường tròn (O) đường kính AC . Gọi I là một
điểm thuộc đoạn OC ( I khác O và C ). Qua I kẻ đường vuông góc với AC cắt BC tại E và AB
kéo dài tại D . Gọi K là điểm đối xứng của C qua điểm I .
a) Chứng minh rằng các tứ giác BDCI và AKED nội tiếp.
b) Chứng minh IC.IA = IE.ID . Bài 5. (1,0 điểm)
Cho tam giác ABC đều có diện tích 2
36 cm . Gọi M , N , P là ba
điểm lần lượt nằm trên ba cạnh
AB, BC,CA sao cho
MN ⊥ BC; NP ⊥ AC; PM ⊥ AB . Chứng tỏ rằng tam giác MNP đều
và tính diện tích tam giác MNP . Bài 6. (1,0 điểm)
Hai ngọn nến hình trụ có chiều cao và đường kính khác nhau được
đặt thẳng đứng trên mặt bàn. Ngọn nến thứ nhất cháy hết trong 6 giờ,
ngọn nến thứ hai cháy hết trong 8 giờ. Hai ngọn nến được thắp sáng cùng
lúc, sau 3 giờ chúng có cùng chiều cao.
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
b) Biết tổng chiều cao của hai ngọn nến là 63 cm. Tính chiều cao của mỗi ngọn nến.
= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = = Hướng dẫn giải: Bài 1. (3,0 điểm)
a) Rút gọn A = 419 − 40 19 + 419 + 40 19 . b) Giải phương trình 2
2x + (2 3 + 3) x + 3 3 = 0. Trang 1
c) Biết nghiệm của phương trình 2
2x + (2 3 + 3) x + 3 3 = 0 là nghiệm của phương trình 4 2
4x + bx + c = 0 . Tìm các số b,c . Lời giải a) Rút gọn
A = 419 − 40 19 + 419 + 40 19 = − + + + + = ( − )2 + ( + )2 400 2.20. 19 19 400 2.20. 19 19 20 19 20 19
= 20 − 19 + 20 + 19 = 20 − 19 + 20 + 19 = 40 . Vậy A = 40 . b) Giải phương trình 2
2x + (2 3 + 3) x + 3 3 = 0. = ( + )2 − = + + − = + − = ( − )2 2 3 3
4.2.3 3 12 9 12 3 24 3 12 9 12 3 2 3 3 0
phương trình có hai nghiệm phân biệt. −(2 3 +3)+(2 3 −3) 3 − −(2 3 +3)−(2 3 −3) x = = ; x = = − 3 . 1 2.2 2 2 2.2 3 −
Vậy phương trình có tập nghiệm là S = − 3; . 2
c) Biết nghiệm của phương trình 2
2x + (2 3 + 3) x + 3 3 = 0 là nghiệm của phương trình 4 2
4x + bx + c = 0 . Tìm các số b,c . 3 − Xét phương trình 4 2
4x + bx + c = 0 , có hai nghiệm là − 3; nên ta có: 2 4
(− 3)4 + b(− 3)2 + c = 0 4.9 + .3 b + c = 0 3 b + c = 3 − 6 4 2 81 9 3 3 − − 4. + . b + c = 0 9 + + = b + 4c = 8 − 1 4 b c 0 16 4 2 2 c = 27 9 b + 3c = 108 − c = 27 36 − − c . 9 b + 4c = 81 − b = b = 21 − 3
Vậy b = −21;c = 27 là các giá trị cần tìm. Bài 2. (2,0 điểm)
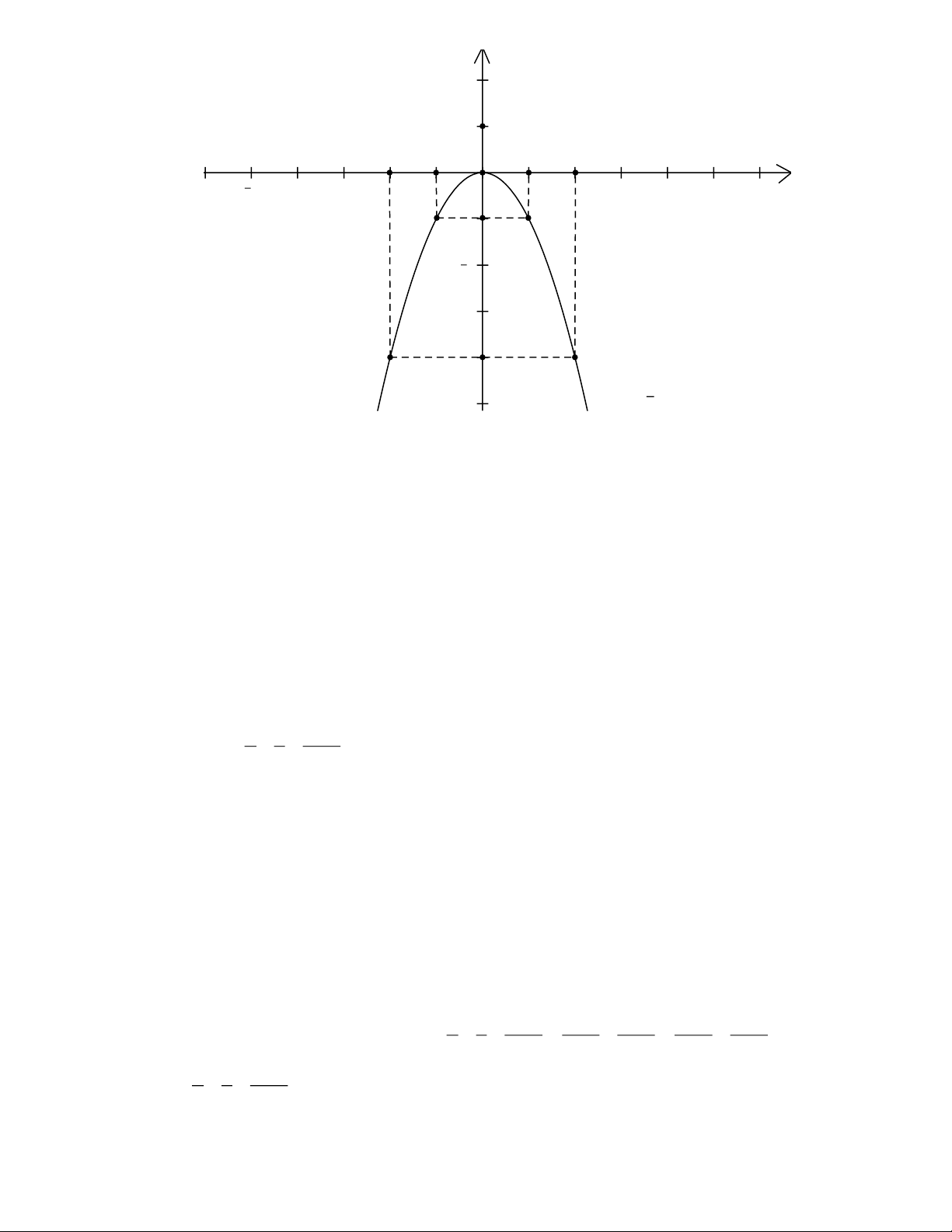
a) Vẽ đồ thị (P) của hàm số 2 y = −x .
b) Viết phương trình đường thẳng (d ) đi qua điểm A(0; )
1 và tiếp xúc với (P) . Lời giải a) Vẽ đồ thị hàm số 2
y = −x (P) , ta có bảng sau: x -2 -1 0 1 2 2 y = x -4 -1 0 -1 -1 Vậy đồ thị hàm số 2
y = x (P) là Pa-ra-bol đi qua ( 2 − ; 4 − ),( 1 − ;− ) 1 ,(0 : 0),(1;− ) 1 ,(2; 4 − ) và
nhận Oy làm trục đối xứng. Trang 2 y 2 1 x 5 -2 -1 O 1 2 5 -1 2 4 f x ( ) = x2
b) Viết phương trình đường thẳng (d ) đi qua điểm A(0; )
1 và tiếp xúc với (P) .
Giả sử phương trình đường thẳng (d ) có dạng y = ax + b .
(d ) đi qua A(0; ) 1 nên ta có 1 = .0
a + b b = 1 (d ) có dạng y = ax +1.
Xét phương trình hoành độ giao điểm của (d ) và (P) : 2 2
−x = ax +1 x + ax +1 = 0 (1). Để (d) và (P) tiếp xúc nhau thì (1) có nghiệm kép 2 2
= 0 a − 4.1.1 = 0 a = 4 a = 2 .
Vậy ta có hai đường thẳng (d ) thỏa mãn là y = 2x +1 và y = 2 − x +1. Bài 3. (1,0 điểm)
Cho hai số a,b phân biệt thỏa mãn 2 2
a − 2021a = b − 2021b = c , với c là một số thực dương. 1 1 2021 Chứng minh rằng: + + = 0 . a b c Lời giải Theo bài ra ta có 2 2
a − 2021a = b − 2021b 2 2
a − b − 2021a + 2021b = 0
(a − b)(a + b − ) 2021 = 0
a = b(ktm) . a + b = 2021
Với a = b loại do a,b phân biệt. Với 2 a + b = b = − a ab =
a − a = − ( 2 2021 2021 2021
a − 2021a) = −c .
1 1 2021 a + b 2021 2021 2021
Thay a + b = 2021; ab = −c vào ta được + + = + = + = 0 . a b c ab c −c c 1 1 2021 Vậy + + = 0 . a b c Bài 4. (2,0 điểm) Trang 3
Cho tam giác ABC ( AB AC ) nội tiếp trong đường tròn (O) đường kính AC . Gọi I là một
điểm thuộc đoạn OC ( I khác O và C ). Qua I kẻ đường vuông góc với AC cắt BC tại E và AB
kéo dài tại D . Gọi K là điểm đối xứng của C qua điểm I .
a) Chứng minh rằng các tứ giác BDCI và AKED nội tiếp.
b) Chứng minh IC.IA = IE.ID . Lời giải D B E A K O C I
a) Chứng minh rằng các tứ giác BDCI và AKED nội tiếp.
Ta có ABC = 90 (góc nội tiếp chắn nửa đường tròn) DBC = 90 (kề bù với ABC = 90 );
DIC = 90 ( DI ⊥ AC ) tứ giác BDCI nội tiếp đường tròn đường kính CD .
ECI = EDB (hai góc nội tiếp cùng chắn BI ).
Lại có K là điểm đối xứng của C qua điểm I nên I là trung điểm của CK EKC có EI
vừa là trung tuyến, vừa là đường cao nên cân tại E EKI = ECI EKI = EDB (= ECI ) tứ giác
AKED có góc ngoài đỉnh K bằng góc trong đỉnh D nên là tứ giác nội tiếp.
b) Chứng minh IC.IA = IE.ID .
Xét IDA và ICE có:
IDA = ICE (hai góc nội tiếp cùng chắn BI );
AID = EIC (= 90 , DI ⊥ AC) ” ( ID IC IDA ICE g.g ) =
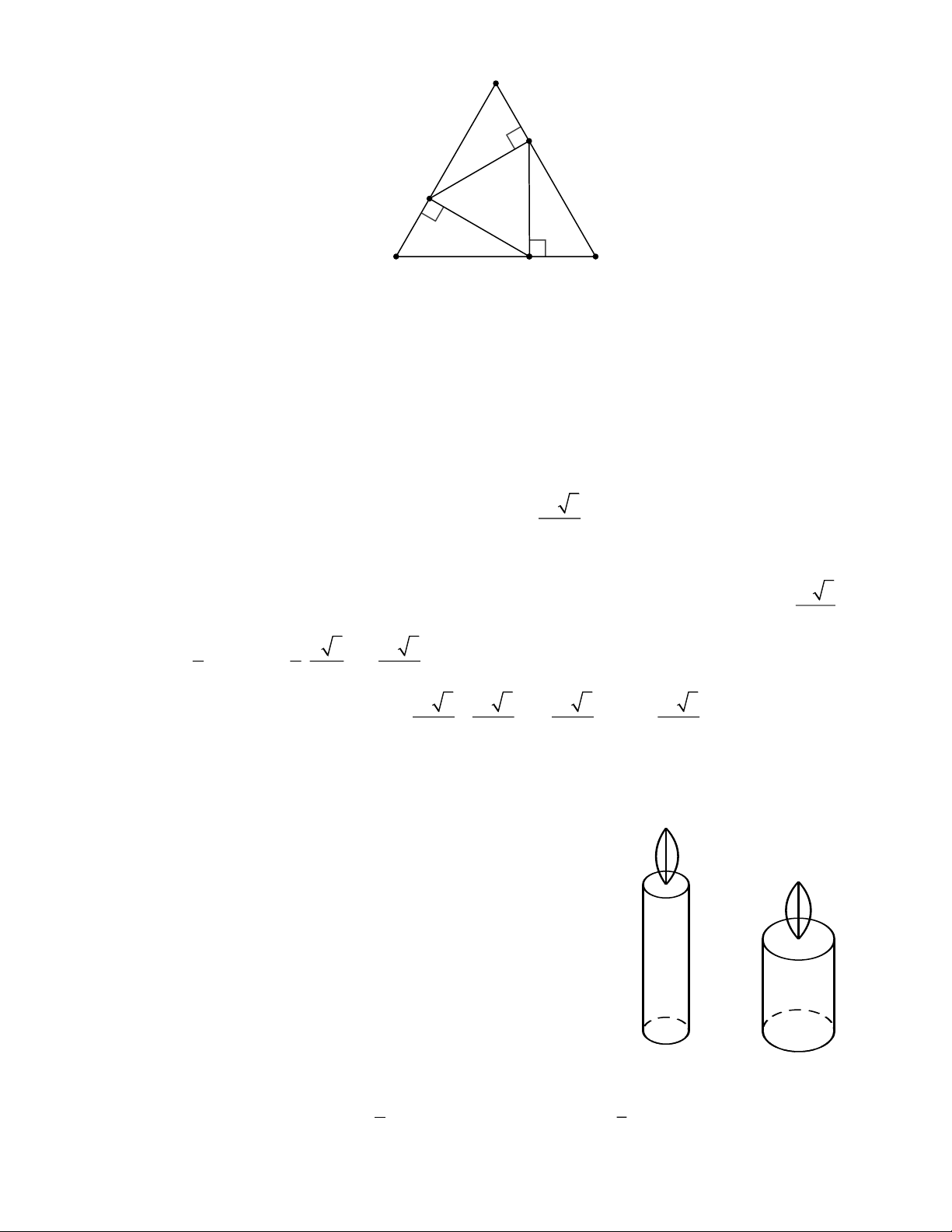
IC.IA = IE.ID . IA IE Bài 5. (1,0 điểm)
Cho tam giác ABC đều có diện tích 2
36 cm . Gọi M , N , P là ba điểm lần lượt nằm trên ba cạnh
AB, BC,CA sao cho MN ⊥ BC; NP ⊥ AC; PM ⊥ AB . Chứng tỏ rằng tam giác MNP đều và tính
diện tích tam giác MNP . Lời giải Trang 4 C N P A B M
Trong MNB vuông tại M , ta có MBN + MNB = 90 ; mà PN ⊥ BC (GT )
MNB + MNP = 90 MNP = MBN = 60(= 90− MNB) ;
Trong AMP vuông tại P , ta có
AMP + PAM = 90 ; mà NM ⊥ AB (GT )
AMP + PMN = 90 PMN = PAM = 60(= 90− AMP);
MNP có MNP = PMN = 60 nên là tam giác đều. 2 x 3
Đặt MN = NP = PN = x vì MNP đều nên S = . MNP 4
Mặt khác BMN = CNP = APM (cạnh huyền – góc nhọn) S = S = S . BMN CNP APM x. 3
Trong tam giác BMN vuông tạ M ta có BM = MN.tan B = . x cot 60 = 3 2 1 1 x 3 x 3 S = BM.MN = . .x = . BMN 2 2 3 6 2 2 2 2 x 3 x 3 x 3 x 3 S = 3.S + S 36 = 3. + 3 = 36 =12 cm . ABC BMN MNP ( 2) 6 4 4 4 Vậy 2 S = 12 cm . MNP Bài 6. (1,0 điểm)
Hai ngọn nến hình trụ có chiều cao và đường kính khác nhau
được đặt thẳng đứng trên mặt bàn. Ngọn nến thứ nhất cháy hết trong 6
giờ, ngọn nến thứ hai cháy hết trong 8 giờ. Hai ngọn nến được thắp sáng
cùng lúc, sau 3 giờ chúng có cùng chiều cao.
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
b) Biết tổng chiều cao của hai ngọn nến là 63 cm. Tính chiều cao của mỗi ngọn nến. Lời giải
a) Tìm tỉ lệ chiều cao lúc đầu của hai ngọn nến.
Gọi chiều cao ngọn nến thứ nhất là a cm, chiều cao ngọn nến thứ
hai là b cm, ( a,b 0 ).
Giả sử tốc độ tiêu hao khi cháy của hai ngọn nến là không đổi. 1 1
Mỗi giờ cây nến thứ nhất giảm chiều cao, cây nến thứ hai giảm chiều cao. 6 8 Trang 5 1 1
Sau 3 giờ cây nến thứ nhất còn 1− 3. = chiều cao. 6 2 1
Chiều cao của cây nến thứ nhất còn lại là a . 2 1 5
Sau 3 giờ cây nến thứ hai còn 1− 3. = chiều cao. 8 8 5
Chiều cao của cây nến thứ hai còn lại là b . 8
Vì sau 3 giờ chiều cao của hai cây nến bằng nhau nên 1 5 a 5 a = b = . 2 8 b 4 5
Vậy tỉ lệ chiều cao ban đầu của ngọn nến thứ nhất so với ngọn nến thứ hai là . 4
b) Biết tổng chiều cao của hai ngọn nến là 63 cm. Tính chiều cao của mỗi ngọn nến.
Tổng chiều cao ngọn nến là 63 cm a + b = 63 .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: a 5 a b a + b 63 = = = = = 7 . b 4 5 4 5 + 4 9 a b Vì
= 7 a = 7.5 = 35(cm); = 7 b = 7.4 = 28(cm) . 5 4
Vậy ban đầu ngọn nến thứ nhất cao 35 cm, ngọn nến thứ hao cao 28 cm.
= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =
TUYỂN SINH LỚP 10 THPT CHUYEN LÊ QUÝ ĐÔN TỈNH BÀ RỊA VŨNG TÀU
ĐỀ THI MÔN : TOÁN (Chuyên) Năm học: 2021-2022 Câu 1 (3,0 điếm). − + − a) Rút gon biểu thức x x 1 x 1 x 2 P = −
với x 0, x 1, x 4 .
1+ x + x x 1
x − x − 2 −
b) Giadi phương trình 5x − (x + 4) 2x +1 + 4 = 0. 2 2
2x + y + 3xy + 4x + 3y + 2 = 0
c) Giai hế phương trinh . 2
x − y + 3 + x + y +1 = 2 Câu 2 (2, 0 điểm). a) Cho hai da thức 3 2
P(x) = x + ax + bx + c và 2
Q(x) = 3x + 2ax + b(a, ,
b c ) . Biết rằng
P(x) có ba nghiệm phân biệt. Chưng minh Q(x) có hai nghiềm phân biệt.
b) Tìm tất cả các cặp số nguyên ( ;
x y) thơa mần phương trình 2 2 2
(xy −1) = x + y .
Câu 3 (1, 0 điểm). Xét các số thực a,b,c không âm, thòa măn 2 2 2
a + b + c = 1. Tìm giá trị
lớn nhất và giá trị nhỏ nhất của biểu thức a b c S = + + .
1+ bc 1+ ac 1+ ab Trang 6
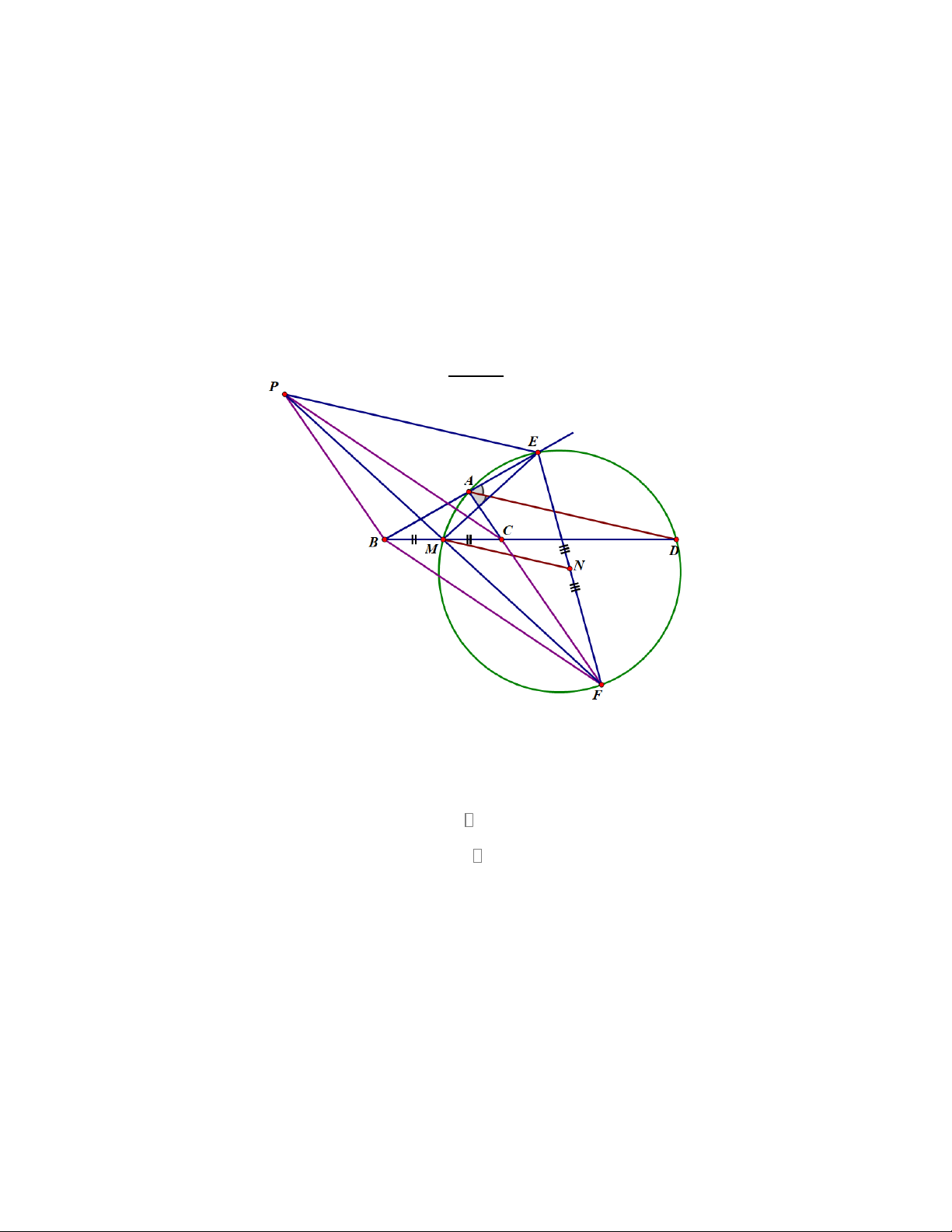
Câu 4 (3, 0 điểm). Cho tam giác ABC nhọn ( AB AC ). Một đường trơn đi qua B,C và
khỏng đi qua A cat các cạnh AB, AC lần lượt tại E, F (E khác B; F khác C ); BF cảt
CE tại D . Gọi P là trung điểm của BC và K là điềm đối xứng với D qua P .
a) Chứng minh tam giác KBC đồng dạng với tam giác DFE và AE DE = . AC CK
b) Gọi M , N lần lượt là hình chiếu vuông góc của D trên AB, AC . Chửng minh MN
vuông góc với AK và 2 2 2 2
MA + NK = NA + MK .
c) Gọi I, J lần lựt là trung điềm AD và MN , Chứng minh ba điếm I, J , P thẳng hàng.
d) Đường thẳng IJ cát đường tròn ngoại tiếp tam giác IMN tại T ( T khade l ). Chưng
minh AD là tićp tuyến của đường tròn ngoại tiếp tam giác DTJ .
Câu 5: (1 điểm) Cho tam giác ABC và điểm O thay đổi trong tam giác.Tia Ox song song với AB
cắt BC tại D , tia Oy song song vói BC cắt AC tai E , tia Oz song song vói AC cắt AB 2 2 2 AB BC AC tạ
F . Tìm giá trị nhỏ nhất của biểu thức S = + + OD OE OF HƯỚNG DẪN Câu 1 (3.0 điêm). − + −
a) Rút gọn biểu thức sau x x 1 x 1 x 2 P = − với
1+ x + x x 1
x − x − 2 −
x 0, x 1, x 4
b) Giải phương trình 5x − (x + 4) 2x +1 + 4 = 0 . 2 2
2x + y + 3xy + 4x + 3y + 2 = 0
c) Giải hệ phương trình . 2
x − y + 3 + x + y +1 = 2 3 ( x) −1 x +1 x − 2 P = −
1+ x + x ( x +1)( x −1) ( x +1)( x − 2) 1 1 = ( x −1) − x −1 x +1 2 = ( x −1) ( x −1)( x +1) 2 = x +1 Điều kiện: 1
x − . Đặi t = 2x +1(t 0) . Ta có phương trình 3 2 t
− + 5t − 7t + 3 = 0 2 t = (t −1)( 1 2 t
− + 4t − 3) = 0 (nhận). t = 3
* Vơi t = 1 2x +1 = 1 x = 0 (thỏa).
* Với t = 3 2x +1 = 3 x = 4 (thỏa). Trang 7 2 2
2x + y + 3xy + 4x + 3y + 2 = 0 (1)
2x − y+3+ x+ y+1=2 (2) 2
x − y + 3 0 Điềù kiện: x + y +1 0 (1): 2 2
y + (3x + 3) y + 2x + 4x + 2 = 0 y = 2 − x 2
= (x +1) nên (1) y y = −x
* TH1: y = −x −1 thay vào (2) ta có phương trình
x = 0 y = 1 − 2
x + x + 4 = 2 (nhận) x = 1 − y = 0 * TH2: y = 2
− x − 2 thay vào (2) ta có phương trình 2 2
x + 2x + 5 + −x −1 = 2 (x +1) + 4 + −(x +1) = 2 Ta có 2
(x +1) + 4 + −(x +1) 2 , với mọi giá trị của x −1 Dấu bằng xảy ra khi
x = −1 y = 0 (nhận) Vậy hệ phương trình có các nghiệm là (0; 1 − ),( 1 − ;0) . Câu 2 (2, 0 điểm). a) Cho hai đa thức 3 2
P(x) = x + ax + bx + c và 2
Q(x) = 3x + 2ax + b(a, ,
b c ) . Biết rằng
P(x) có ba nghiệm phân biệt. Chứng minh Q(x) có hai nghiệm phân biệt.
b) Tìm tất cả các cặp số nguyên ( ;
x y) ihỏa mãn phương trình 2 2 2
(xy −1) = x + y
a) Gọi x , x , x là ba nghiệm phân biệt của P(x) , ta có P(x) = (x − x x − x x − x 1 ) ( 2 ) ( 3 ) 1 2 3 3
= x − (x + x + x ) 2
x + x x + x x + x x x − x x x 1 2 3 ( 1 2 1 3 2 3) 1 2 3
Đồng nhất hệ số của P(x) ta có: 2
= a − 3b = (x + x + x )2 − (
3 x x + x x + x x ) Q 1 2 3 1 2 1 3 2 3 1
= (x − x )2 + (x − x )2 + (x − x )2 1 2 2 1 3 0 2 3
Vậy Q(x có hai nghiệm phân biệt
Lưu y: hs sử dụng Viet vẫn cho điểm tối đa b/ 2 2 2 2 2
Ta có: (xy-1)2=x2+y2 (xy) − 2xy +1 = x + y (x + y) − (xy) = 1
x + y − xy =1 ) 1 (
x + y + xy = 1
(x + y − xy)(x + y + xy) = 1
x + y − xy = − 1 ( ) 2
x + y + xy = −1
Giải hệ (1) ta được cặp nghiệm (0;1),(1;0)
Giải hệ (2) ta được cặp nghiệm (0;-1),(-1;0) Câu 3: Trang 8 1 ( + bc)2 = 1+ 2 2 2 2 2 2
bc + b c = a + b + c + 2bc + 2 2 2 b c 2 2 2 2 2 2 1
= a + (b + c) + b c a + (b + c) (a + b + c)2 2 Ta có : 1 a c 1+ bc
(a + b + c) 2 ...tuongtu 2 1+ bc a + b + c S a b c 2( + + ) = 2
a + b + c a + b + c a + b + c
Khi a=b= 2 ,c = 0 thì S = 2 . Vậy giá trị lớn nhất của S là 2 . 2 Theo BĐT AM-GM: 2 2 2 2 2 2 2 2 2 a +1 b + c (a + )( 1 2 + b + c )
1 a +1+ 2 + b + c 2 a 1 ( + bc) 1 ( + ) = ( ) 2 2 4 4 2 Từ đó : a 2 b 2 c 2 2 2 2 a . Tuong tu b ;
c S a + b + c =1 Khi a =1;b = c = 0 thì S =1 . 1+ bc 1+ ac 1+ ab
Vậy giá trị nhỏ nhất của S là 1. Câu 4:(3 điểm) Chưa vẽ hình
Tứ giác BCFE nội tiếp nên ta có: DEF = DBC ; DFE = DCB
Mặt khác: BDCK là hình bình hành nên BCK = DBC ; CBK = DCB DFE = C K B KBC D FE(gg)
Do đó : DEF = BCK ; DE EF FE AE KBC D FE = (1); A EF A CB = (2) CK BC BC AC Từ (1) và AE DE (2) = AC CK
Gọi Q là giao điểm của MN và AK . Ta có: AEC = ABK (đồng vi) và
ABK = ABD + DBK = ACE + DCK = ACK
(Do ABD = ACE; DBK = DCK) Xét DE AE
AED và ACK có: AED = ACK, = A ED A
CK(c − g − c) CK AC
KAC = DAE hay QAC = DAM
b) Có AMD + AND = 180 AMDN nội tiếp DNM = DAM = QAN .
Mà DNM + MNA = 90 QAN + MNA = 90 AQN = 90 AK ⊥ MN Do đó: 2 2 2 2 2 2
MA + NK = QM + QA + QN + QK 2 2 2 2 2 2
= QN + QA + QM + QK = NA + MK Trang 9 Ta có 1 MI =
AD = NI I thuộc đường trung trực của MN (3) 2
c) Ta có IP là đường trung bình của tam giác ADK IP / / AK IP ⊥ MN (4)
Từ (3) và (4) suy ra IP là đường trung trực của MN I, J , P thẳng hàng. Từ (3) và Ta
có IMN cân tại I, IJ ⊥ MN nên IT là đường kính của đường tròn ngoại tiếp 2 I
MN INT = 90 IJ.IT = IN Mà 2
IN = ID IJ.IT = ID I DJ I
TD( g − g) IDJ = ITD
ID là tiếp tuyến của đường tròn ngoại tiếp DTJ .
Câu 5(1,0 điểm). Cho tam giác ABC và điểm O thay đổi trong tam giác. Tia Ox song
song với AB cắt BC tại D , tia Oy song song với BC cắt AC tại E , tia Oz song song 2 2 2 AB BC AC với
AC cắt AB tại F . Tìm giá trị nhỏ nhất của biểu thức S = + + OD OE OF
Kẻ DM / / OF(M AB), EN / /OD(N BC), FP / /OE(P AC) Ta có: OD EN NC OE DN = = (1); = (2); OF MD BD = = (3) AB AB BC BC BC AC AC BC Từ OD OE OF NC DN BD (1),(2),(3) + + = + + =1 AB BC AC BC BC BC
Theo bất đẳng thức AM-GM: OD OE OF OD OE OF AB BC AC 3 1 = + + 3 27 AB BC AC AB BC AC OD OE OF 2 2 2 2 AB BC AC AB BC AC 3 S = + + 3 = 27 OD OE OF OD OE OF
Đẳng thức xảy ra khi O là trọng tâm ABC . Vậy giá trị nhỏ nhất của S là 27 .
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 BẾN TRE
TRUNG HỌC PHỔ THÔNG CÔNG LẬP
NĂM HỌC 2021 – 2022 ĐỀ CHÍNH THỨC Môn: TOÁN (chuyên)
Thời gian: 150 phút (không kể phát đề) Câu 1. (2,0 điểm)
a) Tìm tất cả các giá trị của tham số m để hàm số y = (6 − 7m) x + 2 nghịch biến trên . b) Cho Parabol ( P) 2
: y = 2x và đường thẳng (d ) : y = −x + 6 . Biết (d ) cắt ( P) tại hai
điểm phân biệt A( x ; y , B( x ; y với x x . Tính 4x + y . 2 2 ) 1 1 ) 1 2 2 1
c) Rút gọn biểu thức A = ( x − − )2
2 1 + 4x + 4 x − 2 − 7 (với x 2 ). Câu 2. (1,0 điểm) Cho phương trình: 2
x − (m + 3) x + 4m − 4 = 0 (1), với m là tham số. Tìm m để phương trình (1)
có hai nghiệm phân biệt x x
x + x + x x = 20 1 ; 2 thỏa . 1 2 1 2 Câu 3. (3,0 điểm)
a) Giải phương trình nghiệm nguyên: 2 2 2
x y − xy + 2x −1 = y − xy − 2y . Trang 10 2
y − 2xy − 2 = 0
b) Giải hệ phương trình: 2 2
4x − y + y − 2x + 2 = 0.
c) Giải phương trình: ( x + )( x + − x + ) 2 3 2 5 2
2 + 2x + 9x +10 = 1. Câu 4. (1,0 điểm)
Cho ba số thực dương x , y z thỏa 3 xy + xz = 2 . Chứng minh rằng:
4yz 5xz 7xy + + 8 . x y z Câu 5. (2,0 điểm)
Cho tam giác ABC vuông tại A với ( AB AC ), có đường cao AH . Biết BC = 1dm và 12 AH = dm . 25
a) Tính độ dài hai cạnh AB và AC
b) Kẻ HD ⊥ AB ; HE ⊥ AC (với D AB , E AC ). Gọi I là trung điểm của BC . Chứng
minh IA ⊥ DE . Câu 6. (1,0 điểm)
Cho tam giác ABC có đường phân giác ngoài của góc A cắt đường thẳng BC tại điểm D . Gọi
M là trung điểm của BC . Đường tròn ngoại tiếp ADM cắt các đường thẳng AB , AC lần lượt tại
E và F (với E , F khác A ). Gọi N là trung điểm của EF . Chứng minh rằng MN // AD .
LỜI GIẢI CHI TIẾT Câu 1. (2,0 điểm)
a) Tìm tất cả các giá trị của tham số m để hàm số y = (6 − 7m) x + 2 nghịch biến trên . b) Cho Parabol ( P) 2
: y = 2x và đường thẳng (d ) : y = −x + 6 . Biết (d ) cắt ( P) tại hai
điểm phân biệt A( x ; y , B( x ; y với x x . Tính 4x + y . 2 2 ) 1 1 ) 1 2 2 1
c) Rút gọn biểu thức A = ( x − − )2
2 1 + 4x + 4 x − 2 − 7 (với x 2 ). Lời giải 6
a) Hàm số y = (6 − 7m) x + 2 nghịch biến trên
6 − 7m 0 m . 7 6
Vậy m thì hàm số đã cho nghịch biến trên . 7
b) Xét phương trình hoành độ giao điểm của ( P) và (d ) , ta có: 2 2
2x = −x + 6 2x + x − 6 = 0 Có: = (− )2 1 + 4.2.6 = 49 0
Vậy phương trình có 2 nghiệm phân biệt: 1 − − 49 1 − + 49 3 x = = 2 − và x = = 1 2.2 2 2.2 2
Với x = −2 , ta có y = 8 , suy ra A(−2;8). 1 1 3 9 3 9
Với x = , ta có y = , suy ra B ; . 2 2 2 2 2 2 Khi đó, ta có: Trang 11 3
4x + y = 4. + 8 = 4 1 . 2 1 2
Vậy 4x + y = 14 . 2 1 c)
A = ( x − 2 − )2
1 + 4x + 4 x − 2 − 7
= x − 2 − 2 x − 2 +1+ (2 x − 2)2 + 2.2 x − 2 +1
= x −1− 2 x − 2 + (2 x − 2 + )2 1
= x −1− 2 x − 2 + 2 x − 2 +1
= x −1− 2 x − 2 + 2 x − 2 +1 (do 2 x − 2+1 0) = x Vậy A = x . Câu 2. (1,0 điểm) Cho phương trình: 2
x − (m + 3) x + 4m − 4 = 0 (1), với m là tham số. Tìm m để phương trình (1)
có hai nghiệm phân biệt x x
x + x + x x = 20 1 ; 2 thỏa . 1 2 1 2 Lời giải 2 2
Ta có: = (m + 3) − (4m − 4) 2 2 4
= m + 6m + 9 −16m +16 = m −10m + 25 = (m − 5)
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi (m − )2 0
5 0 m − 5 0 m 5
Vậy với m 5 thì phương trình (1) có hai nghiệm phân biệt. x 0
Theo đề bài ta có: x + x + x x = 20 (2), với điều kiện 1 1 2 1 2 x 0 2
Do đó, phương trình (1) có hai nghiệm phân biệt thỏa mãn x 0 và x 0 , nghĩa là 1 2 m 5 m 5 m 5
m + 3 0 m 3 − (*) m 1 4m − 4 0 m 1
x + x = m + 3
Áp dụng định lý Vi-et, ta có: 1 2 x x = 4m − 4 1 2 Ta có:
( x + x )2 = x + x + 2 x x 1 2 1 2 1 2
= m + 3 + 2 4m − 4
= m + 3 + 4 m −1
= m −1+ 4 m −1+ 4 = ( m −1+ 2)2 Từ đó, ta suy ra
x + x = m −1+ 2
do m −1+ 2 0, m 1 1 2 ( )
Từ phương trình (2), ta được Trang 12
x + x + x x = 20 m −1+ 2 + 4m − 4 = 0
2 m −1 = 22 − 4m (3) 1 2 1 2 11
Giải phương trình (3) với điều kiện: 22 − 4m 0 m (**) 2
(3) m −1 = (22 − 4m)2 2
m −1 = 484 −176m +16m 2
16m −177m + 485 = 0 (4) Ta có: = ( 177 − )2 − 4.16.485 = 289 0
Vậy phương trình (4) có 2 nghiệm phân biệt: 177 − 289 177 + 289 97 m = = 5 và m = = 2.16 2.16 16
So với điều kiện (*) và (**) thì m .
Vậy không tồn tại giá trị của m thỏa mãn yêu cầu bài toán. Câu 3. (3,0 điểm)
a) Giải phương trình nghiệm nguyên: 2 2 2
x y − xy + 2x −1 = y − xy − 2y . 2
y − 2xy − 2 = 0
b) Giải hệ phương trình: 2 2
4x − y + y − 2x + 2 = 0.
c) Giải phương trình: ( x + )( x + − x + ) 2 3 2 5 2
2 + 2x + 9x +10 = 1. Lời giải a) Ta có: 2 2 2
x y − xy + 2x −1 = y − xy − 2y 2 2 2
x y − xy + 2x −1− y + xy + 2y = 0 ( 2 2 x y + xy ) − ( 2
xy + y ) + 2( x + y) = 1
xy(x + y) − y(x + y) + 2(x + y) = 1
(x + y)(xy − y + 2) = 1 ( ) 1
Vì đây là phương trình nghiệm nguyên nên ta có: x + y = 1 (*) − + = ( ) xy y 2 1 1 x + y = −1 ( **)
xy − y + 2 = −1 x =1− y = − = − ( ) x 1 y x 1 y x = 0; y =1 * ( y = 1− y ) 1 2 y − y +1 = 0 −y +1 = 0 x = 2; y = 1 − y = 1 − x = 1 − − y x = 1 − − y x = 1 − − y x = 2 − ; y = 1 ( * * ) ( y = 1 − − y ) 1 2 y − y + 3 = 0
−y − 2y + 3 = 0 x = 2; y = 3 − y = 3 − Trang 13
Vậy tập nghiệm của hệ phương trình là: S = ( 0; )1,(2;− )1,( 2 − ; ) 1 ,(2; 3 − ). b) Ta có: 2 2
y − 2xy − 2 = 0
y − 2xy = 2 2 2
4x − y + y − 2x + 2 = 0 ( 2 2 4x − y
)+ ( y − 2x)+ ( 2y − 2xy) = 0 2
y − 2xy = 2
(2x− y
)(2x + y) − (2x − y) − y(2x − y) = 0 2
y − 2xy = 2 ( 2x − y
)2x + y −1− y = 0 2
y − 2xy = 2
(2x− y )(2x − ) 1 = 0 2 y − 2xy = 2
2x − y = 0 2x −1 = 0 Mặt khác, 2
y − 2xy = 2 y ( y − 2x) = 2, nghĩa là y − 2x 0 .
Do đó, từ hệ phương trình ban đầu đề cho, ta giải hệ phương trình sau: 1 1 x = 2 y − 2xy = 2 x = 2 2 − = y = 1 2x 1 0 − 2
y − y − 2 = 0 y = 2 1 1
Vậy hệ có tập nghiệm là S = ; 1 − , ;2 2 2
c) Giải phương trình (*): ( x + )( x + − x + ) 2 3 2 5 2
2 + 2x + 9x +10 = 1. 5 − 2x + 5 0 x 2
Điều kiện xác định: x + 2 0 x 2 − x 2 − . 2
2x + 9x +10 0 5 − x x 2 − 2
a = 2x + 5 (a ) 1 Ta đặt b = x + 2 (b 0) 2 2
a − 2b = (2x + 5) − 2(x + 2) =1 Ta thấy 2 2
a − b = (2x + 5) − ( x + 2) = x − 3
ab = (2x + 5)( x + 2) 2 = 2x + 9x +10
Phương trình (*) trở thành: Trang 14 ( 2 2
a − b )(a − 2b) 2 2
+ ab = a − 2b ( 2 2
a − b )(a − 2b) − ( 2 2 a − b ) + ( 2 b + ab) = 0 ( 2 2
a − b )(a − 2b − ) 1 + ( 2 b + ab) = 0
(a − b)(a + b)(a − 2b − )
1 + b(a + b) = 0
(a + b)(a − b)(a − 2b − ) 1 + b = 0 a + b = 0 ( ) 1
(a−b)(a−2b− )1+b =0 (2)
Vì a + b 1 nên ta chỉ giải phương trình (2)
(a − b)(a − 2b − )
1 + b = 0 (a − b)(a − b − )
1 − b(a − b) + b = 0
(a − b)(a − b − )
1 − b(a − b − ) 1 = 0 ( − − =
a − b − )(a − b) a b 1 0 1
2 = 0 a−2b = 0
TH1: Với a − 2b = 0 , ta có
a − 2b = 0 2x + 5 − 2 x + 2 = 0
2x + 5 = 2 x + 2
x + = ( x + ) 3 2 5 4 2 x = − 2 3
So với điều kiện thì x = − (Nhận). 2
TH2: Với a − b −1 = 0 , ta có
a − b −1 = 0 2x + 5 − x + 2 −1 = 0
2x + 5 = x + 2 +1
2x + 5 = x + 3 + 2 x + 2
x + 2 − 2 x + 2 = 0
x + 2( x + 2 − 2) = 0 x + 2 = 0 x + 2 = 0 x = 2 − x = 2 − x + 2 − 2 = 0 x + 2 = 2 x + 2 = 4 x = 2
So với điều kiện thì x = 2 (Nhận) và x = −2 (Nhận). 3
Vậy tập nghiệm của phương trình là S = 2 − ;− ; 2 . 2 Câu 4. (1,0 điểm)
Cho ba số thực dương x , y z thỏa 3 xy + xz = 2 . Chứng minh rằng:
4yz 5xz 7xy + + 8 . x y z Lời giải
4yz 5xz 7xy Ta đặt M = + + , ta có x y z Trang 15
4yz 5xz 7xy M = + + x y z yz yz xz xz xy xy = + 3 + + 4 + 3 + 4 x x y y z z yz xz yz xy xz xy = + + 3 + + 4 + x y x z y z
Áp dụng bất đẳng thức Cauchy, ta được yz xz yz xy xz xy M 2 . + 3.2 . + 4.2 . x y x z y z
2z + 6y + 8x
(2z + 2x) + (6y + 6x)
Tiếp tục áp dụng bất đẳng thức Cauchy, ta được
M 2.2 xz + 6.2 xy
4( xz + 3 xy) = 4.2 = 8
x = y = z 1
Dấu “ = ” xảy ra khi và chỉ khi
x = y = z = .
xz + 3 xy = 2 2 1
Vậy khi x = y = z = thì M 8 (đpcm). 2 Câu 5. (2,0 điểm)
Cho tam giác ABC vuông tại A với ( AB AC ), có đường cao AH . Biết BC = 1dm và 12 AH = dm . 25
a) Tính độ dài hai cạnh AB và AC
b) Kẻ HD ⊥ AB ; HE ⊥ AC (với D AB , E AC ). Gọi I là trung điểm của BC . Chứng
minh IA ⊥ DE . Lời giải
a) Tính độ dài hai cạnh AB và AC
Áp dụng hệ thức lượng và định lý Pytago cho ABC vuông tại A , ta có: Trang 16 2 2 2 2 2
AB + AC = BC =1 AB + AC = 1 12 2 2 144 A .
B AC = AH.BC = AB .AC = 25 625 Khi đó, 2 AB và 2
AC là các nghiệm dương của phương trình.
Áp dụng hệ quả của định lý Vi-et, ta được 2 144 X −1X + = 0 6 5 2 Ta có: 2 144 49 = 1 − 4.1. =
0 nên phương trình trên có 2 nghiệm phân biệt: 625 6 5 2 49 49 1− 1+ 625 9 625 16 X = = và X = = 1 2.1 25 2 2 25
Theo giả thiết, AB AC , nên ta được: 2 16 4 AB = X = AB = 1 2 2 25 5
AB AC 9 3 2 AC = X = AC = 2 25 5 4 3
Vậy AB = dm và AC = dm . 5 5
b) Chứng minh IA ⊥ DE .
Gọi F là giao điểm của AI và DE . HEA = 90 (HE ⊥ AC )
Xét tứ giác EHDA , ta có: HDA = 90 (HD ⊥ AB) DAE = 90 ( ABC vuoâng taïi A )
Tứ giác EHDA là hình chữ nhật (tứ giác có 3 góc vuông)
Tứ giác EHDA là tứ giác nội tiếp.
ADE = AHE (hai góc nội tiếp cùng chắn cung AE )
Mà AHE = ECH (cùng phụ với CHE )
ADE = ECH ADE = ACB (1)
Xét ABC vuông tại A có I là trung điểm của BC 1
IA = IB = BC (định lý đường trung tuyến trong tam giác vuông) 2 I
AB cân tại I IAB = IBA (2)
Từ (1) và (2), ta suy ra: ADE IAB ACB IBA ACB ABC 90 + = + = + =
( ABC vuông tại A )
Áp dụng định lý tổng 3 góc trong ADF , ta có: Trang 17
FAD + FDA + AFD = 180 AFD = 180 − (FAD + FDA)
AFD = 180 − (IAB + ACB)
AFD = 180 − (ABC + ACB)
AFD = 180 − 90 = 90 (ABC vuoâng taïi A)
Do đó, IA ⊥ DE (đpcm) Câu 6. (1,0 điểm)
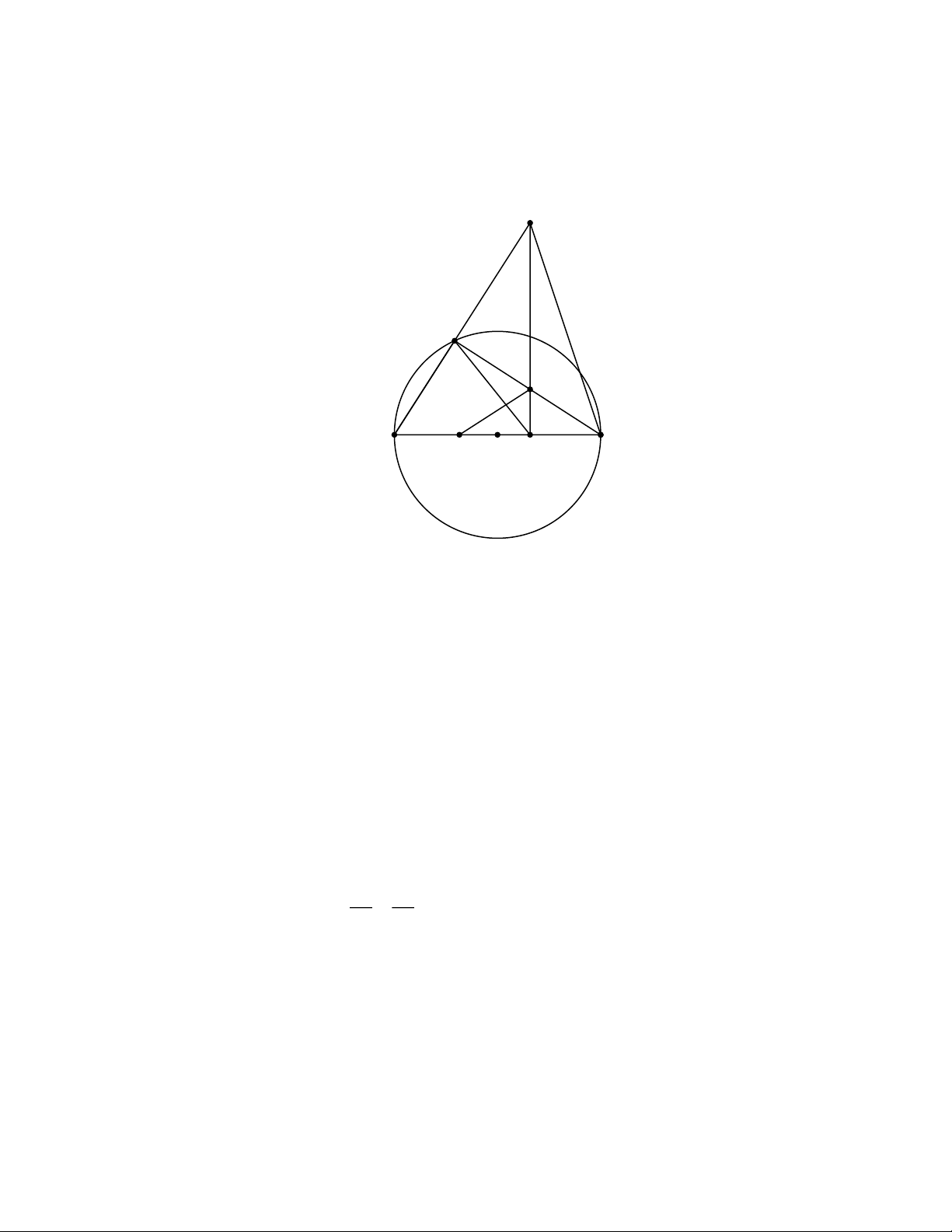
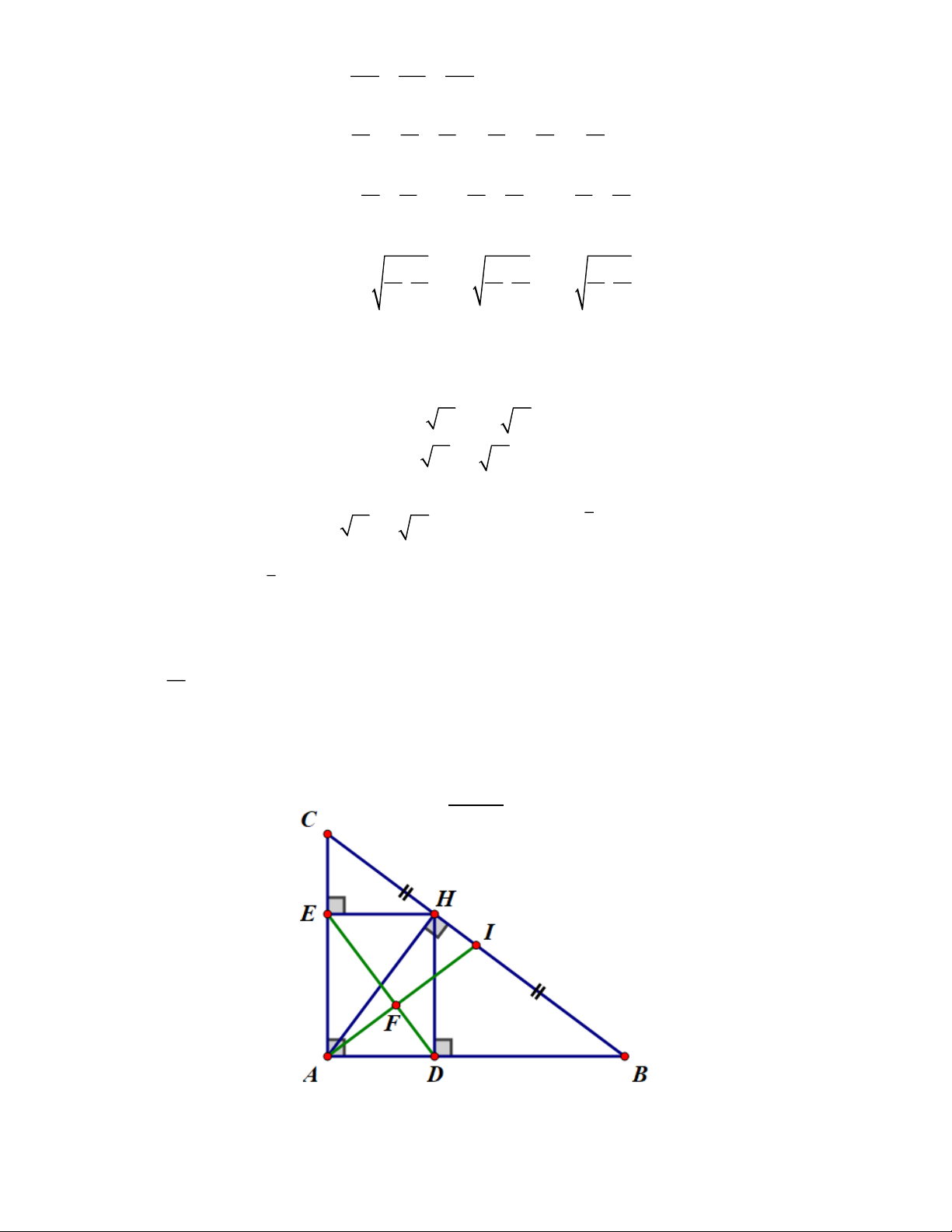
Cho tam giác ABC có đường phân giác ngoài của góc A cắt đường thẳng BC tại điểm D . Gọi
M là trung điểm của BC . Đường tròn ngoại tiếp ADM cắt các đường thẳng AB , AC lần lượt tại
E và F (với E , F khác A ). Gọi N là trung điểm của EF . Chứng minh rằng MN // AD . Lời giải
Dựng hình bình hành BPCF .
Hai đường chéo BC và PF cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC (gt) M cũng là trung điểm của PF .
Xét PEF , ta có N là trung điểm của EF (gt), M là trung điểm của PF (cmt)
MN là đường trung bình của PEF MN EP (1)
Ta có: MPB = MFA (cặp góc so le trong của PB FA , PBFC là hình bình hành)
Mà MDA = MEA = MFA (các góc nội tiếp cùng chắn cung AM )
MEA = MPB , nghĩa là MEB = MPB
Xét tứ giác BMEP , ta có MEB = MPB (cmt)
Tứ giác BMEP nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau)
BEP = BMP (hai góc nội tiếp cùng chắn cung BP )
Mà BMP = FMD (đối đỉnh)
Mặt khác FMD = FAD (hai góc nội tiếp cùng chắn cung FD )
BEP = FAD , nghĩa là AEP = FAD (2)
Ta có: AD là phân giác ngoài của BAC (gt) Trang 18 Mà BAC CAE 180 + = (kề bù)
AD là phân giác của CAE FAD = EAD (3)
Từ (2) và (3), ta suy ra AEP = EAD
Mà 2 góc nằm ở vị trí so le trong nên EP AD (4)
Từ (1) và (4), ta suy ra MN AD (đpcm)
SỞ GIÁO DỤC – ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021- 2022 BÌNH ĐỊNH
Đề chính thức Môn thi: Toán
Ngày thi: 11/6/2021 Thời gian làm bài: 120’
Bài 1: (2 điểm). x 1 1 2 1.Cho biểu thức P = − : +
Với x>0;x 1 x −1 x +1 x +1 x −1
a) Rút gọn biểu thức P −
b) Tìm giá trị của P khi x = 4 2 3 x + 2y = 6
2. Giải hệ phương trình: 2x + 3y = 7 Bài 2: (2 điểm)
1. Cho phương trình x2-(m+3)x-2m2+3m=0 (m là tham số). Hãy tìm giá trị của m để x=3 là nghiệm của
PT và xác định nghiệm còn lại của PT ( nếu có)
2. Cho Parabol (P): y=x2 và đường thẳng (d) : y= (2m+1)x-2m (m là tham số). Tìm m để đường thẳng (d)
cắt (P) tại hai điểm phân biệt A (x , y ; B (x , y sao cho: y 2 2 ) 1 1 ) 1+y2 - x1 x2=1
Bài 3: (2,0 điểm)
Một xe máy khởi hành tại địa điểm A đi đến địa điểm B cách A 160 km, sau đó 1 giờ, một ô tô đi từ
B đên A. Hai xe gặp nhau tại địa điểm C cách B 72 km. Biết vận tốc ô tô lớn hơn vận tốc xe máy 20km/h. Tính vận tốc mỗi xe.
Bài 4: (4,0 điểm) Cho tam giác ABC có 0
ACB 90 nội tiếp trong đường tròn tâm O. Gọi M là trung điểm của BC,
đường thảng OM cắt cung nhỏ BC tại D, cắt cung lớn BC tại E. Gọi F là chân đường vuông góc hạ từ E
xuống AB; H là chân đường vuông góc hạ từ B xuống AE
a) Chứng minh tứ giác BEHF nội tiếp.
b) Chứng minh MF ⊥ AE
c) Đường thẳng MF cắt AC tại Q. Đường thẳng EC cắt AD, AB lần lượt tại I và K. Chứng minh EC EK 0 EQA = 90 & = IC IK
Bài 5 (1,0 điểm). 1 1 1 1
Cho a,b, c là các số dương thỏa: + +
= 2.CMR : abc .
1+ a 1+ b 1+ c 8
HƯỚNG DẪN GIẢI Bài 1: 1.
a) Rút gọn biểu thức P : ĐK: x 0; x 1 Trang 19 x 1 1 2 x + x − x +1 x −1+ 2 x +1 x −1 x +1 P = − : + = = = x −1 x +1 x +1 − ( x − )1( x + ) : 1 ( x − ) 1 ( x + ) . x 1 1 x −1 x +1 x +1 x +1 Vậy P =
với x 0; x 1 x +1
b) Tìm giá trị của P khi x = 4 − 2 3 :
với x 0; x 1, ta có: x = − = ( − )2 4 2 3 3 1 = 3 −1 = 3 −1 x +1 4 − 2 3 +1 5 − 2 3 5 3 − 6 P = = = = x +1 3 −1+1 3 3 Vậy ………. x + 2y = 6 x = −4 2. ....
Vậy HPT có nghiệm duy nhất 2x + 3y = 7 y = 5
Bài 2: (2điểm)
1. Cho phương trình x2-(m+3)x-2m2+3m=0 (m là tham số). Hãy tìm giá trị của m để x=3 là nghiệm của
PT và xác định nghiệm còn lại của PT ( nếu có).
Vì x=3 là nghiệm của PT, nên: 2 − (m + ) 2 2 3
3 .3 − 2m + 3m = 0 2m = 0 m = 0 b
Khi đó theo hệ thức Vi-et, ta có: x + x = −
= m + 3 = 0 + 3 = 3 x = 3 − x = 3 − 3 = 0 1 2 2 1 a Vậy……….
2. Cho Parabol (P): y=x2 và đường thẳng (d) : y= (2m+1)x-2m (m là tham số). Tìm m để đường thẳng (d)
cắt (P) tại hai điểm phân biệt A (x , y ; B(x , y sao cho: y 2 2 ) 1 1 ) 1+y2 - x1 x2=1:
Hoành độ giao điểm của (d) và (P) là nghiệm của pt:
x2=(2m+1)x-2m x2- (2m+1)x+2m=0 (1) = (2m + ) 2 1 −
m = + m + m − m = m − m + = ( m − − )2 2 2 4.1.2 1 4 4 8 4 4 1 2 1 0
(d) cắt (P) tại hai điểm phân biệt A (x , y ; B(x , y PT (1) có 2 nghiệm phân biệt x 2 2 ) 1 1 ) 1 x2
( m − )2 1 0 2
1 0 2m −1 0 m 2 b
x + x = − = 2m +1 1 2 a
Theo hệ thức Vi- ét, ta có: mà y= x2, nên: c
x .x = = 2m 1 2 a 2 2 2 2
y + y − x x = 1 x + x − x x = 1 x + x
− 3x x = 1 2m +1 − 2 3. m = 1 1 2 1 2 1 2 1 2 ( 1 2) 1 2 ( ) m = 0 (TM ) 2 4m 2m 0 2m(2m 1) 0 − = − = 1 m = (KTM ) 2
Vậy m=0 thỏa mãn yêu cầu .
Bài 3: (2,0 điểm) 160 km Trang 20 A B C 72 km