20 Đề Thi Tuyển Sinh 10 Môn Toán Các Tỉnh Thành 2025-2026 Có Lời Giải Chi Tiết-Bộ 3
Vào tháng 5 năm 2021, chỉ sau 26 giờ phát hành sản phẩm âm nhạc MV “Trốn tìm” của rapper Đen Vâu đã chính thức dành Top 1 trending của YoutubeViệt Nam. Giả sử trong tất cả những người đã xem MV, có 60% số người đã xem 2 lượt và những người còn lại mới xem 1 lượt.Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 289 tài liệu
Môn: Toán 9 3.1 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NGHỆ AN Môn thi: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề
ĐỀ THI CHÍNH THỨC Câu 1. (2,5 điểm)
a) Tính A = 64 + 16 − 2 36
b) Xác định các hệ số a,b của đường thẳng y = ax + b, biết đường thẳng này đi qua điểm
M (1;9)và song song với đường thẳng y = 3x 1 2
x + x x 0
c) Rút gọn biểu thức P = − .
x 1+ x 1− x x 1 Câu 2. (2,0 điểm) a) Giải phương trình 2
2x − 5x + 2 = 0 b) Cho phương trình 2
x −12x + 4 = 0 có hai nghiệm dương phân biệt x ; x .Không giải 1 2 2 2 x + x
phương trình, hãy tính giá trị của biểu thức 1 2 T = x + x 1 2
Câu 3. (1,5 điểm) Vào tháng 5 năm 2021, chỉ sau 26 giờ phát hành sản phẩm âm nhạc MV
“Trốn tìm” của rapper Đen Vâu đã chính thức dành Top 1 trending của Youtube Việt Nam.
Giả sử trong tất cả những người đã xem MV, có 60% số người đã xem 2 lượt và những
người còn lại mới xem 1 lượt. Hỏi đến thời điểm nói trên có bao nhiêu người đã xem MV,
biết tổng số lượt xem là 6,4 triệu lượt ?
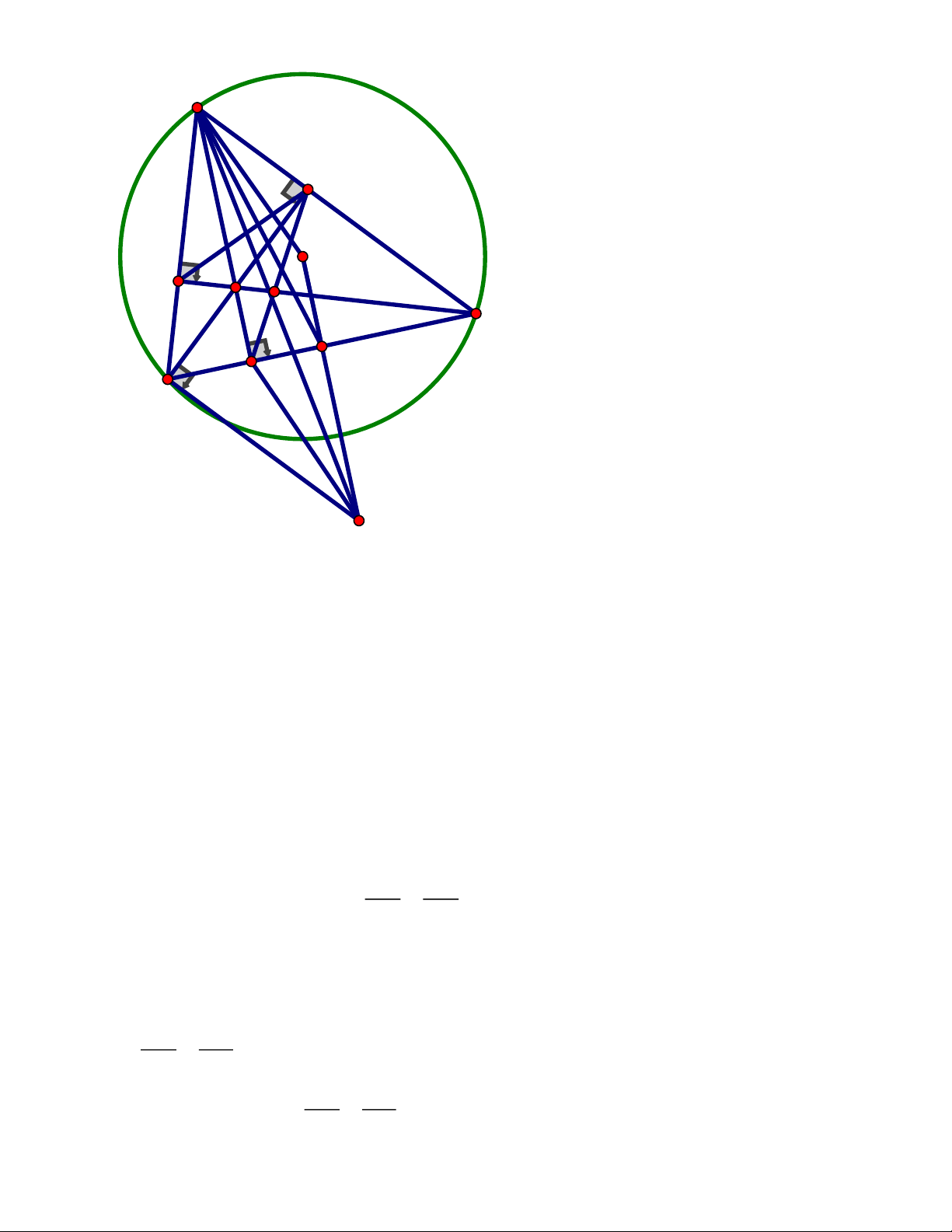
Câu 4. (3,0 điểm) Cho tam giác nhọn ABC ( AB AC) nội tiếp đường tròn tâm O, các
đường cao AD, BE,CF (D BC,E AC,F AB) cắt nhau tại H
a) Chứng minh BCEF là tứ giác nội tiếp
b) Gọi N là giao điểm của CF và DE. Chứng minh DN.EF = HF.CN
c) Gọi M là trung điểm của BC, tiếp tuyến tại B của đường tròn (O)cắt đường thẳng OM tại .
P Chứng minh OAM = DAP
x − 3y + 2 xy = 4 ( x − y)
Câu 5. (1,0 điểm) Giải hệ phương trình x, y ( x + ) 1
(y + xy − x + x) ( ) 2 = 4 ĐÁP ÁN Trang 1 Câu 1.
a) Tính A = 64 + 16 − 2 36 Ta có :
A = 64 + 16 − 2 36 = 8 + 4 − 2.6 = 0 Vậy A = 0
b) Xác định các hệ số a,b của đường thẳng y = ax + b, biết đường thẳng này đi qua
điểm M (1;9)và song song với đường thẳng y = 3x
Ta có : M (1;9)thuộc đường thẳng có phương trình y = ax + b nên ta có :a + b = 9( ) 1 a = 3
Đường thẳng y = ax + b song song với đường thẳng y = 3x nên b 0
Thay a = 3 vào (1) ta được b = 6(tm)
Vậy a = 3,b = 6 1 2
x + x x 0 P = − . + −
c) Rút gọn biểu thức x 1 x 1 x x 1
Với x 0; x 1 x ( x x x x x + + + − )1 1 2 1 2 P = − . = x + x − x x.(1+ x ) . 1 1 1− x 1− x = =1 1− x
Vậy P = 1với x 0, x 1 Câu 2.
a) Giải phương trình 2
2x − 5x + 2 = 0 Ta có : 2
= 5 − 4.2.2 = 9 0 nên phương trình có hai nghiệm phân biệt b − + 5 + 9 x = = = 2 1 2a 2.2 b − − 5 − 9 1 x = = = 2 2a 2.2 2 Trang 2 1
Vậy tập nghiệm của phương trình là S = 2; 2
b) Cho phương trình 2
x −12x + 4 = 0 có hai nghiệm dương phân biệt x ; x .Không 1 2 2 2 x + x
giải phương trình, hãy tính giá trị của biểu thức 1 2 T = x + x 1 2 Vì phương trình 2
x −12x + 4 = 0 có hai nghiệm dương phân biệt x ; x nên theo định lý Vi-et 1 2 x + x =12 ta có : 1 2 . Ta có : x x = 4 1 2 2 2
x + x = ( x + x ) 2
− 2x x =12 − 2.4 =136 1 2 1 2 1 2 (
x + x )2 = x + x + 2 x x =12 + 2 4 =16 x + x = 4 1 2 1 2 1 2 1 2 2 2 x + x 136 Vậy 1 2 T = = = 34 x + x 4 1 2
Câu 3. Vào tháng 5 năm 2021, chỉ sau 26 giờ phát hành sản phẩm âm nhạc MV “Trốn
tìm” của rapper Đen Vâu đã chính thức dành Top 1 trending của Youtube Việt Nam.
Giả sử trong tất cả những người đã xem MV, có 60% số người đã xem 2 lượt và
những người còn lại mới xem 1 lượt. Hỏi đến thời điểm nói trên có bao nhiêu người đã
xem MV, biết tổng số lượt xem là 6,4 triệu lượt ?
Gọi x là số người đã xem MV ( triệu người) ( x *)
Khi đó số người đã xem hai lượt là 60%x = 0,6x (người) và số người chỉ xem 1 lượt là
40%x = 0,4x(người)
Vì tổng số lượt xem là 6,4 triệu nên ta có phương trình 0,6 .2 x + 0,4 .1
x =1,6x = 6,4 x = 4
Vậy có 4 triệu người xem MV. Câu 4. Trang 3 A E O H F N C M D B P
a) Chứng minh BCEF là tứ giác nội tiếp
Ta có : BEC = BFC = 90 (do BE ⊥ AC,CF ⊥ AB)
BCEF là tứ giác nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau)
b) Gọi N là giao điểm của CF và DE . Chứng minh rằng DN.EF = HF.CN Ta có : CD H = CE
H = 90(gt) CD H + CE
H =180 nên CHDE là tứ giác nội tiếp
(tứ giác có tổng hai đối bằng 180 ) D CN = N
EH (hai góc nội tiếp cùng chắn cung DH )
Xét tam giác DCN và tam giác HEN có : D CN = N
EH (cmt); D NC = H
NE (đối đỉnh) DN HN D CN ∽ H
EN(g.g) =
(hai cặp cạnh tương ứng tỉ lệ) (1) NC EN
Ta có BCEF là tứ giác nội tiếp (cmt) nên DCN = HEF (2 góc nội tiếp cùng chắn cung BF ) mà D CN = N
EH (cmt) nên NEH = HEF
Hay EH là tia phân giác của NEF HN HF =
(tính chất đường phân giác) (2) EN EF DN HF Từ ( ) 1 và (2)ta được =
DN.EF = HF.CN (dfc ) m NC EF Trang 4
c) Gọi M là trung điểm của BC, tiếp tuyến tại B của đường tròn (O)cắt đường
thẳng OM tại .
P Chứng minh OAM = DAP
Ta có M là trung điểm của BC nên OM ⊥ BC (quan hệ vuông góc giữa đường kính và dây
cung), mà BC ⊥ AD( gt) nên OM / / AD OP / / AD
DAP = APO (so le trong) (3)
Mặt khác ta có : PB là tiếp tuyến của (O)tại B nên OB ⊥ BP O BP = 90
Áp dụng hệ thức lượng trong tam giác OPB vuông tại B có BM là đường cao Ta có : 2
OB = OM .OP OM OA Mà 2 2 2
OA = OB OA = OM.OP = OA OP OM OA
Xét OAM và OPA ta có : AOP chung; = (cmt) OA OP O AM ∽ O ( PA .
c g.c) O AM = O
PA (hai góc tương ứng) (4) Từ (3),(4) O AM = D AP Câu 5.
x − 3y + 2 xy = 4 ( x − y)
Giải hệ phương trình : x, y ( x + ) 1
(y + xy − x + x) ( ) 2 = 4
x − 3y + 2 xy = 4 ( x − y)( )1 ( x + ) 1 ( 2
y + xy − x + x) = 4(2)
ĐKXĐ: x, y 0
( )1 x − xy + 3 xy − 3y = 4( x − y)
x ( x − y ) + 3 y ( x − y ) = 4( x − y )
( x − y )( x + 3 y ) = 4( x − y )
( x − y )( x + 3 y − 4) = 0 x = y
x +3 y =4 Trang 5
TH1: x = y x = .
y Thay vào (2) ta có : (x + ) 1 ( 2
x + x − x + x) = 4 (x + ) 1 ( 2 3x − x ) = 4 3 2
x − 2x − 3x + 4 = 0 (x − ) 1 ( 2
x − x − 4) = 0 x =1 = y 1+ 17 x =
= y(do x, y 0) 2 x + 3 y = 4 TH2: ( x + ) 1 ( 2
y + xy − x + x) = 4 4 − a
a + b = 4 b =
Đặt x = a, y = b(a,b 0) 3 ( 2 a + )1( 2 4 2
b + ab − a + a ) = 4(*) 4 − a Thế b = vào (*) ta được 3 ( − − a + ) 2 2 4 a 4 a 4 2 1 + . a − a + a = 4 3 3 ( + ) 2 2 4 2 − + + − − + 2 16 8a a 12a 3a 9a 9a a 1 . = 4 9 ( 2 a + ) 1 .( 4 2 9
− a + 7a + 4a +16) = 32 4 4 3 2
9a + 2a − 4a − 23a − 4a + 20 = 0 (a − )2 1 ( 4 3 2
9a +18a + 29a + 36a + 20) = 0 = ( − x = x = a 1 do a 0) 4 1 1 1 b = =1 3
y =1 y =1 + +
Vậy nghiệm của hệ phương trình là ( x y) ( ) 1 17 1 17 ; 1;1 ; ; 2 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT TỈNH NINH BÌNH
NĂM HỌC 2021 – 2022
Bài thi môn: TOÁN – Ngày thi: 09/06/2021 Trang 6
ĐỀ THI CHÍNH THỨC
Thời gian làm bài : 120 phút Câu 1. (2,0 điểm)
1) Hàm số y = 2x − 3 là hàm số đồng biến hay nghịch biến trên ? Vì sao ?
2) Rút gọn biểu thức A = 18 − 2 50 + 3 8 x − y =1
3) Giải hệ phương trình : 2x + y = 5 Câu 2. (2,5 điểm) Cho phương trình 2
x − mx + m −1 = 0 ( )
1 với m là tham số a) Giải phương trình ( ) 1 với m = 3
b) Chứng minh rằng phương trình ( )
1 luôn có nghiệm với mọi m
c) Gọi x ; x là hai nghiệm của phương trình ( )
1 .Tìm giá trị của m để biểu thức 1 2 2 2
P = x + x đạt giá trị nhỏ nhất 1 2
Câu 3.(1,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một người đi xe đạp từ A đến B cách nhau 24 .
km Khi đi từ B trở về , A người đó tăng
vận tốc thêm 4km / ,
h vì vậy thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của
người đi xe đạp khi đi từ A đến . B Câu 4. (3,5 điểm)
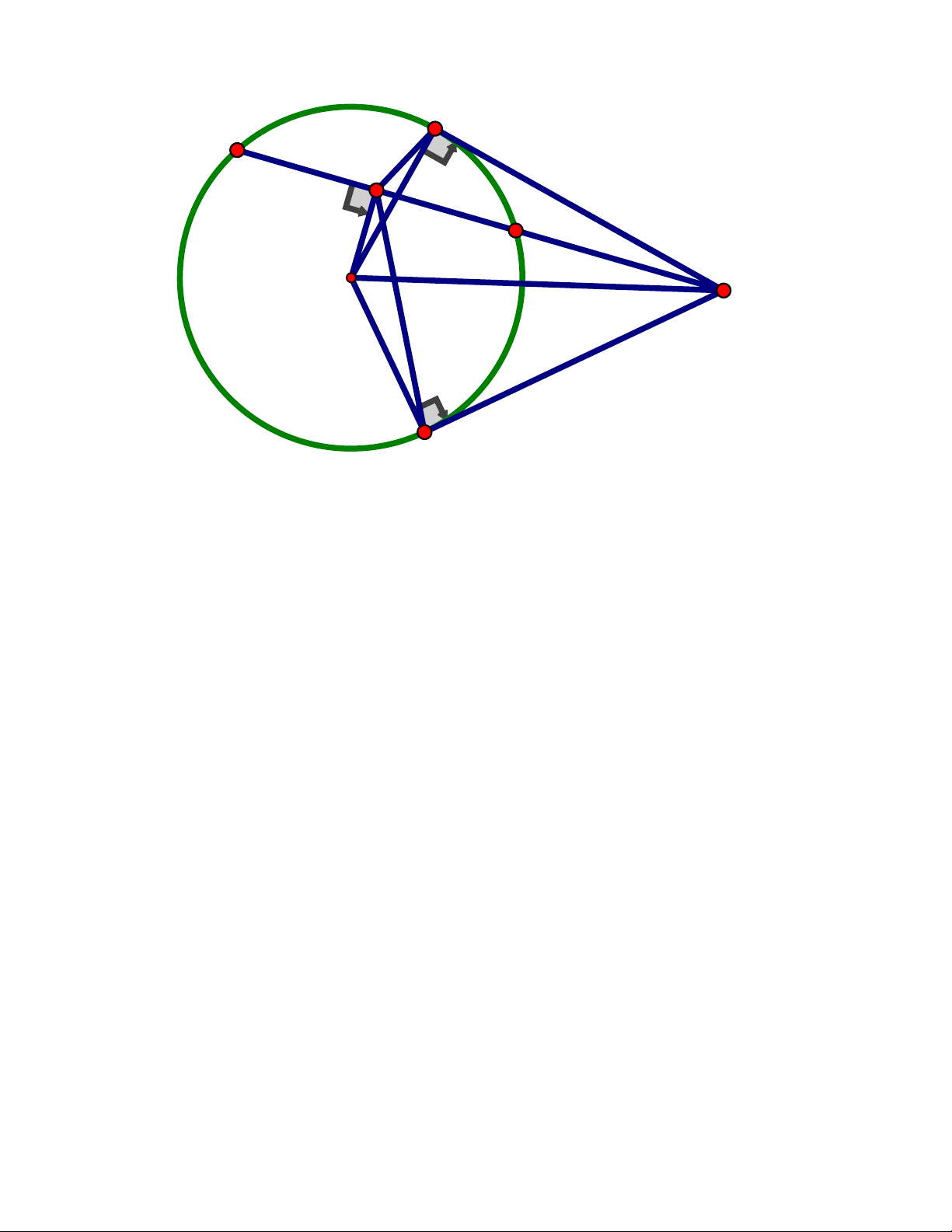
1. Cho đường tròn tâm O và điểm A nằm bên ngoài đường tròn. Từ A vẽ các tiếp tuyến
AB, AC với đường tròn (B,C là các tiếp điểm)
a) Chứng minh tứ giác ABOC là tứ giác nội tiếp
b) Vẽ cát tuyến ADE không đi qua tâm O của đường tròn (D nằm giữa A và E)
Gọi M là trung điểm của DE. Chứng minh MA là tia phân giác của góc BMC
2. Một dụng cụ đựng chất lỏng có dạng hình trụ với chiều cao bằng 3dm và bán kính đáy bằng 2 .
dm Dụng cụ này đưng được bao nhiêu lít chất lỏng (Bỏ qua độ dày của
thành và đáy dụng cụ, lấy 3,14) Câu 5. (1,0 điểm)
1) Tìm tất cả các cặp số nguyên ( ;
x y)thỏa mãn phương trình 2 2
x + 2y + 2xy =1
2) Cho a,b là hai số thực dương thỏa mãn điều kiện 2 2
a + b = 2ab 1 1 1 Chứng minh rằng : + 4 4 4 2 2 2 2
a + b + 2ab
a + b + 2a b 2 Trang 7
ĐÁP ÁN ĐỀ THI VÀO 10 TỈNH NINH BÌNH MÔN TOÁN 2021 Câu 1.
1) Hàm số y = 2x − 3 là hàm số đồng biến hay nghịch biến ? Vì sao ?
Hàm số y = 2x − 3 có a = 2 0 nên hàm số y = 2x − 3 đồng biến trên
2) Rút gọn biểu thức A = 18 − 2 50 + 3 8
A = 18 − 2 50 + 3 8 = 9.2 − 2 25.2 + 3 4.2
= 3 2 − 2.5 2 + 3.2 2 = 3 2 −10 2 + 6 2 = − 2 Vậy A = − 2 x − y =1
3) Giải hệ phương trình : 2x + y = 5 x − y =1 3 x = 6 x = 2 Ta có : 2x + y = 5 y = x −1 y =1
Vậy hệ phương trình có nghiệm ( ; x y) = (2; ) 1 Câu 2. Cho phương trình 2
x − mx + m −1 = 0 ( )
1 (m là tham số)
1) Giải phương trình ( )
1 khi m = 3 Với m = 3 thì ( ) 1 trở thành 2
x − 3x + 2 = 0 x =1 1
Ta có a + b + c = 1− 3 + 2 = 0 nên phương trình có hai nghiệm c x = = 2 2 a
Vậy tập nghiệm phương trình là S = 1; 2
2) Chứng minh rằng phương trình (1) luôn có nghiệm với moi m Phương trình ( )
1 có : = m − (m − ) = m − m + = (m − )2 2 2 4 1 4 4
2 0 (với mọi m)
Suy ra phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
3) Gọi x ; x là hai nghiệm của phương trình ( )
1 . Tìm giá trị của m để 2 2
P = x + x đạt 1 2 1 2 giá trị nhỏ nhất
Theo câu 2) phương trình luôn có hai nghiệm x ; x với mọi m 1 2
x + x = m
Áp dụng hệ thức Vi − et ta có : 1 2 . Khi đó ta có : x x = m −1 1 2 Trang 8
P = x + x = (x + x )2 − 2x x = m − 2(m − ) 1 = (m − )2 2 2 2 1 +1 1 2 1 2 1 2 Nhận thấy (m − )2
1 0 (với mọi m) (m − )2
1 +11(với mọi m)
Vậy P =1 m = 1 min Vậy m = 1
Câu 3. Một người đi xe đạp từ A đến B cách nhau 24 .
km Khi đi từ B trở về , A người đó
tăng vận tốc thêm 4km / ,
h vì vậy thời gian về ít hơn thời gian đi là 30 phút. Tính vận
tốc của người đi xe đạp khi đi từ A đến . B
Gọi vận tốc của người đi xe đạp từ A đến B là x(km / h)( x 0) Do khi đi từ B trở về ,
A người đó tăng vận tốc lên 4km / h nên vận tốc của người đó khi về
là x + 4(km / h) 24
Thời gian người đi xe đạp từ A tới B là (h) x 24
Thời gian người đi xe đạp từ B về A là : (h) x + 4 1
Vì thời gian về ít hơn thời gian đi là 30 phút = h nên ta có phương trình 2 24 24 1
24( x + 4) − 24x 1 96 1 − = = = x x + 4 2 x( x + 4) 2 x( x + 4) 2 x(x + 4) 2
=192 x + 4x −192 = 0 Ta có : 2 2
' = 2 +192 =196 =14 0 nên phương trình có hai nghiệm phân biệt :
x = −2 +14 =12(tm)
x = −2 −14 = −16(ktm)
Vậy vận tốc người đi xe đạp từ A đến B là 12km / h Câu 4. 1) Trang 9 B E M D O A C
a) Chứng minh tứ giác ABOC là tứ giác nội tiếp
Vì AB, AC là các tiếp tuyến của (O)lần lượt tại , A B nên OB
⊥ AB OBA = 90 (định nghĩa) OC
⊥ AC OCA = 90
Xét tứ giác ABOC có OBA + OC
A = 90 + 90 =180
Vậy ABOC là tứ giác nôi tiếp (dấu hiệu nhận biết)
b) Vẽ cát tuyến ADE không đi qua tâm O của đường tròn (D nằm giữa A và E).
Gọi M là trung điểm của DE. Chứng minh MA là tia phân giác của góc BMC
Vì M là trung điểm của DE nên OM ⊥ DE (quan hệ vuông góc giữa đường kính và dây
cung) OMA = 90
Xét tứ giác OMAC có OMA + OCA = 90 + 90 = 180 nên OMAC là tứ giác nội tiếp
5điểm O, B, ,
A C,M cùng thuộc một đường tròn
Ta có AMC = AOC (2 góc nội tiếp cùng chắn cung AC)
AMB = AOB (2 góc nội tiếp cùng chắn cung AB)
Mà AOC = AOB (tính chất hai tiếp tuyến cắt nhau) AM C = AMB
Vậy MA là tia phân giác của BMC
2) Một dụng cụ đựng chất lỏng có dạng hình trụ với chiều cao bằng 3dm và bán kính đáy bằng 2 .
dm Dụng cụ này đưng được bao nhiêu lít chất lỏng (Bỏ qua độ
dày của thành và đáy dụng cụ, lấy 3,14) Trang 10
Thể tích của dụng cụ đựng chất lỏng là 2 2 3
V = r h = .2 .3 =12 37,68(dm ) Đổi 3
37,68dm = 37,68l
Vậy dụng cụ này đựng được 37,68 lít Câu 5.
1) Tìm tất cả các cặp số nguyên ( ;
x y)thỏa mãn phương trình 2 2
x + 2y + 2xy =1 Ta có :
x + y + xy = x + xy + y + y = (x + y)2 2 2 2 2 2 2 2 2 1 2 1 + y =1
Do x, y nguyên nên ( x + y)2 2
, y nguyên. Mặt khác ( x + y)2 2
0, y 0nên ta có : y = 0 ( x + y) 2 =1 x = 1 2 y = 0 x =1 ( x + y)2 = y = 1 0 − 2 x = −1 y =1 y =1 Vậy cặp nghiệm ( ;
x y)thỏa mãn phương trình là ( 1;0);( 1 − ;0);( 1 − ; ) 1 ;(1;− ) 1
2) Cho a,b là hai số thực dương thỏa mãn điều kiện 2 2
a + b = 2ab 1 1 1 Chứng minh rằng : + 4 4 4 2 2 2 2
a + b + 2ab
a + b + 2a b 2 a = x Đặt
(x, y 0) x + y = 2xy . Khi đó ta cần chứng minh : 2 b = y 1 1 1 + 4 2 2 2 4 2
x + y + 2xy
x + y + 2x y 2 4 2 2
x + y 2x y Có
(bất đẳng thức Cô – si ) 2 4 2
x + y 2xy Trang 11 1 1 1 = 4 2 2 2 2
x + y + 2xy 2x y + 2xy
2xy (x + y) 1 1 1 = 2 4 2 2 2
x + y + 2x y 2xy + 2x y
2xy (x + y) 1 1 1 1 1 + + = 4 2 2 2 4 2
x + y + 2xy
x + y + 2x y
2xy (x + y) 2xy(x + y) xy(x + y) 1 1 Ta sẽ chứng minh . Ta có :
xy(x + y) 2 1 1 x + y + + + =
xy( x + y) xy( x y) 2
(x y) 2(dox y 2xy) 2 2
(x + y)2 4 x + y 2 2 x + y
Thật vậy, x + y = xy (x + y)2 2
4(x + y) x + y 4(do x + y 0) 2
Vậy ta có điều phải chứng minh
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT NINH THUẬN NĂM HỌC 2020-2021
Khóa ngày : 05/06/2021
(Đề chính thức) Môn thi: TOÁN
Thời gian làm bài : 120 phút
(Không kể thời gian giao đề) ĐỀ
(Đề thi này gồm 01 trang)
Bài 1. (2,0 điểm) Giải các phương trình, hệ phương trình sau : ) 1 3 x + y = 4
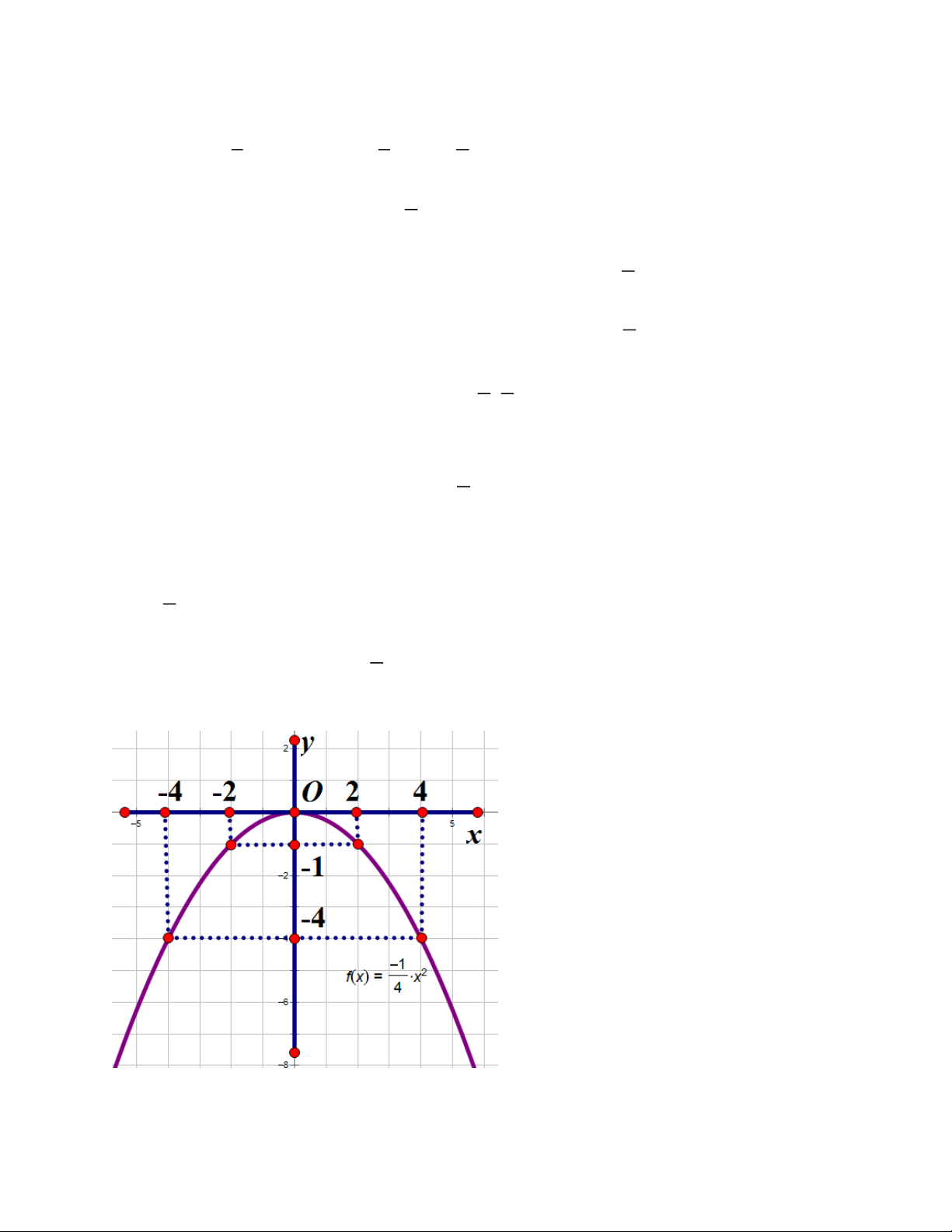
1 2x −1 = x − 2) 3 7x − 5y = 9 − Bài 2. (2,0 điểm) 1
1) Vẽ đồ thị (P) của hàm số 2 y = − x 4 Trang 12
2) Tìm điều kiện của m để đường thẳng (d ) : y = −x + m cắt (P) tại hai điểm phân biệt
có hoành độ trái dấu .
Bài 3. (2,0 điểm) Bạn Hoàng làm việc tại nhà hàng nọ, bạn ấy được trả 800.000 đồng cho
40 giờ làm việc tại quán trong một tuần. Mỗi giờ làm thêm trong tuần bạn được trả bằng
150% số tiền mà mỗi giờ bạn ấy được trả trong 40 giờ đầu. Nếu trong tuần đó, bạn Hoàng
được trả 920000đồng thì bạn ấy đã phải làm thêm bao nhiêu giờ ?
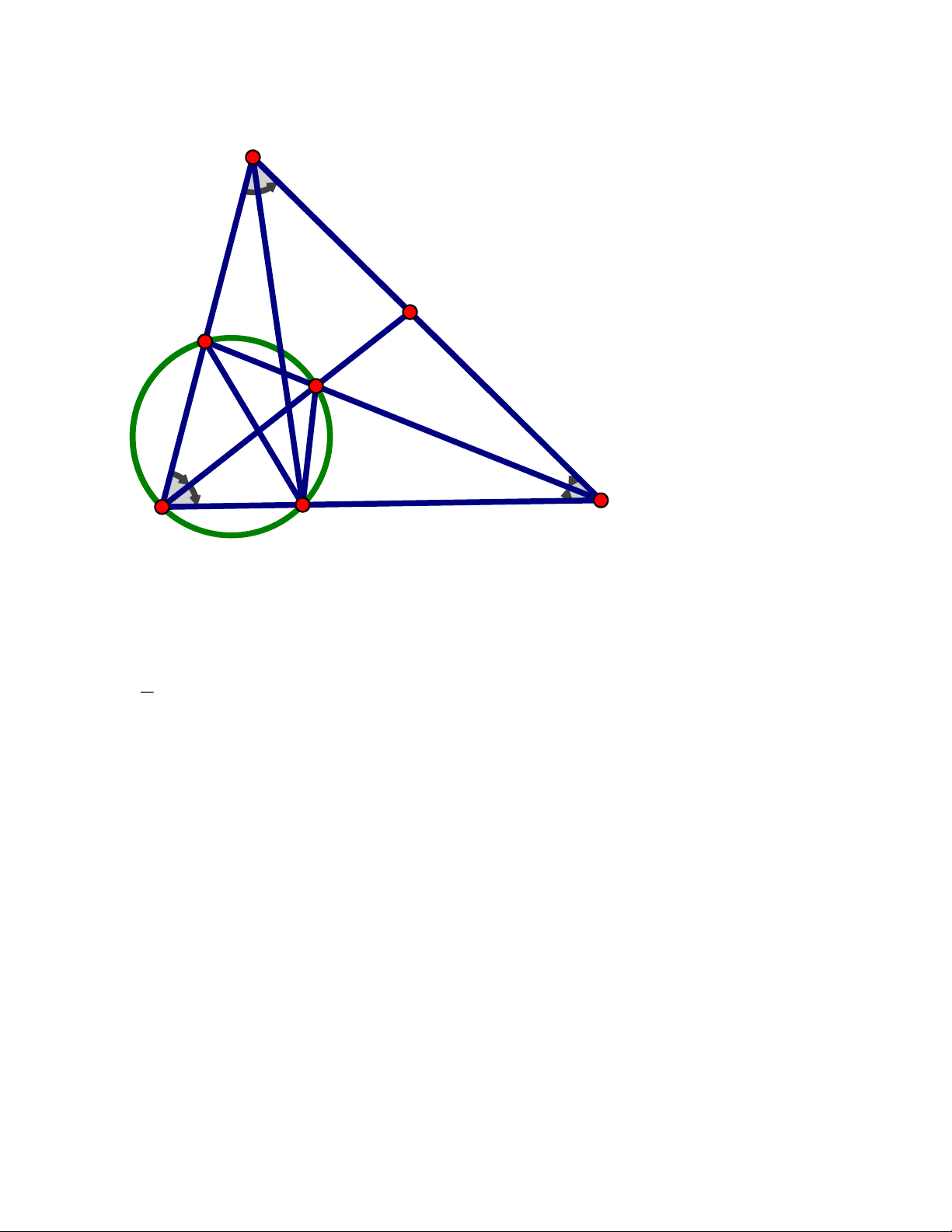
Bài 4. (4,0 điểm) Cho tam giác ABC có các góc A BC, A
CB nhọn và BAC = 60 . Các
đường phân giác trong BE,CF của tam giác ABC cắt nhau tại I
1) Chứng minh tứ giác AEIF nội tiếp
2) Gọi K là giao điểm thứ hai (K khác B) của đường thẳng BC với đường tròn ngoại
tiếp tam giác BFI.Chứng minh rằng tam giác AFK cân tại F Trang 13 ĐÁP ÁN
Bài 1. Giải các phương trình, hệ phương trình 1 1 2
1)2x −1 = x − 2x − x =1− x = 3 3 3 2
Vậy phương trình có nghiệm x = 3 1 = 3 + = 4 15 + 5 = 20 22 =11 x x y x y x 2 2) 7x − 5y = 9 − 7x − 5y = 9 − y = 4 − 3x 5 y = 2
Vậy hệ phương trình có nghiệm ( x y) 1 5 ; = ; 2 2 Bài 2. 1
1) Vẽ đồ thị (P) của hàm số 2
y = − x 4 Ta có bảng giá trị x 4 − 2 − 0 2 4 1 2 y = − x 4 − 1 − 0 1 − 4 − 4 1
Vậy đồ thị hàm số (P) 2
: y = − x là đường cong đi qua các điểm 4 ( 4 − ; 4 − ),( 2 − ;− ) 1 ,(0;0),(2;− ) 1 ,(4; 4 − )
2) Tìm điêu kiện của m để đường thẳng (d ) : y = −x + m cắt (P) tại hai điểm phân
biệt có hoành độ trái dấu Trang 14
Phương trình hoành độ giao điểm của (d ) và (P) : 1 2 2
− x = −x + m x − 4x + 4m = 0( ) * 4
(d )cắt (P)tại hai điểm phân biệt có hoành độ trái dấu (*)có hai nghiệm trái dấu
1.4m 0 m 0
Vậy m 0 thỏa mãn bài toán.
Bài 3. Bạn Hoàng làm việc tại nhà hàng nọ, bạn ấy được trả 800.000 đồng cho 40 giờ
làm việc tại quán trong một tuần. Mỗi giờ làm thêm trong tuần bạn được trả bằng
150% số tiền mà mỗi giờ bạn ấy được trả trong 40 giờ đầu. Nếu trong tuần đó, bạn
Hoàng được trả 920000đồng thì bạn ấy đã phải làm thêm bao nhiêu giờ ?
Gọi số giờ bạn Hoàng đã làm thêm trong tuần là x (giờ), ĐK: x 0
Bạn Hoàng được trả 800 nghìn đồng cho 40 giờ làm việc trong tuần nên mỗi giờ làm việc 800
trong tuần bạn Hoàng nhận được = 20 (nghìn đồng) 40
Vì mỗi giờ làm thêm trong tuần Hoàng được trả bằng 150% số tiền mà mỗi giờ bạn ấy được
trả trong 40 giờ đầu tiên nên mỗi giờ làm thêm Hoàng nhận được 20.150% = 30 (nghìn đồng)
Suy ra tổng số tiền Hoàng nhận được (tính cả làm thêm) trong mỗi tuần là 800 + 30x (nghìn đồng)
Vì trong tuần đó , bạn Hoàng được trả 920000đồng nên ta có phương trình :
800 + 3x = 920 3x =120 x = 40
Vậy Hoàng đã làm thêm 40 giờ. Trang 15 Bài 4. A 60° E F I 1 1 2 2 B K C
1) Chứng minh tứ giác AEIF nội tiếp
Ta có : BAC = 60 ABC + BC
A =120 (tổng 3 góc trong tam giác bằng 180 ) 1 ( A BC + B
CA) = 60 B + C = 60 2 2 2 B
IC =180 − ( B + C
=120 (tổng 3 góc trong tam giác) 2 2 )
FIE = BIC =120(hai góc đối đỉnh)
Xét tứ giác AEIF ta có :BAC + EIF = 60 +120 = 180
AEIF là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng 180 )
2) Gọi K là giao điểm thứ hai (K khác B) của đường thẳng BC với đường tròn
ngoại tiếp tam giác BFI.Chứng minh rằng tam giác AFK cân tại F
Ta có : Tứ giác BFIK nội tiếp FKB = FIB (hai góc nội tiếp cùng chắn cung BF ) F KB = F
IB =180 − E IB = 60 F AC = F KB = 60
AFKC là tứ giác nội tiếp (tứ giác có hai đỉnh kề 1 cạnh nhìn cạnh đối diện dưới các góc bằng nhau)
FAK = FCK (hai góc nội tiếp cùng chắn cung FK) Và FKA = FC
A (hai góc nội tiếp cùng chắn cung AF) Trang 16 Mà FC A = FC
K (CF là phân giác ) KCA F AK = F
KA(= FCA) AKF cân tại F (dfcm)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT PHÚ THỌ
NĂM HỌC 2021 – 2022 MÔN TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài : 120 phút (không kể giao đề) Đề thi có 02 trang
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Điều kiện xác định của biểu thức x − 5 là : . A x 5 . B x 5 C.x 5 . D x 5
Câu 2. Với giá trị nào của m thì hai đường thẳng y =12x + 5 − m và y = 3x + m + 3cắt nhau
tại 1 điểm trên trục tung .5 A . B − 3 C.1 .4 D
Câu 3. Hàm số y = (m + 2) x + 4đồng biến trên khi : . A m 2 − . B m 2 − C.m 2 − . D m 2 − x + 3y =10
Câu 4. Nghiệm của hệ phương trình là :
2x − y = −1 . A (3; ) 1 . B (1;3) C.( 1 − ; 3 − ) . D ( 3 − ;− ) 1
Câu 5.Với giá trị nào của m thì đồ thị hàm số y = (m − ) 2
2 x đi qua điểm A(1;2)? .0 A .2 B C.4 . D − 2
Câu 6. Phương trình 2
x − 2x + m = 0 có hai nghiệm phân biệt khi . A m 1 . B m =1 C.m 1 . D m 1
Câu 7.Phương trình nào sau đây vô nghiệm ? 2 2 2 2 . A x + x +1 = 0 .
B x − 4x + 4 = 0 C.x + x −1 = 0 .
D x + 5x + 6 = 0
Câu 8.Cho ABC vuông tại ,
A đường cao AH.Biết AC = 5(cm), HC = 4(cm).Khi đó độ dài cạnh BC là : 25 25 5 . A 9cm . B cm C. cm . D cm 4 16 4
Câu 9.Cho đường tròn tâm O, bán kính R =13c ,
m dây cung AB = 24 . cm Khoảng cách từ
tâm O đến dây AB là : .3 A cm .4 B cm C.5cm .6 D cm
Câu 10. Cho tứ giác MNPQ nội tiếp trong một đường tròn. Biết MNP = 60 ,
PMQ = 40. Số đo MPQ bằng (tham khảo hình vẽ bên) Trang 17 N 60° M 40° P Q .10 A .20 B C.40 .50 D
PHẦN II. TỰ LUẬN (7,5 điểm) 7 − x + 6
x x 0
Câu 1. (1,5 điểm) Cho biểu thức A = + x − 4
x − 2 x 4
a) Tính giá trị biểu thức A khi x = 16
b) Rút gọn biểu thức A Câu 2. (2,0 điểm)
1. Cho đường thẳng (d ) : y = 2mx + 2m − 3 và parabol (P) 2 : y = x
a) Tìm m để đường thẳng (d ) đi qua A(1;5)
b) Tìm m để đường thẳng (d ) tiếp xúc với Parabol (P)
2x − y = m −1
2. Cho hệ phương trình ( m là tham số) 3
x + y = 4m +1
a) Giải hệ phương trình với m = 2
b) Tìm m để hệ phương trình có nghiệm duy nhất ( ; x y)thỏa mãn 2 2x − 3y = 2
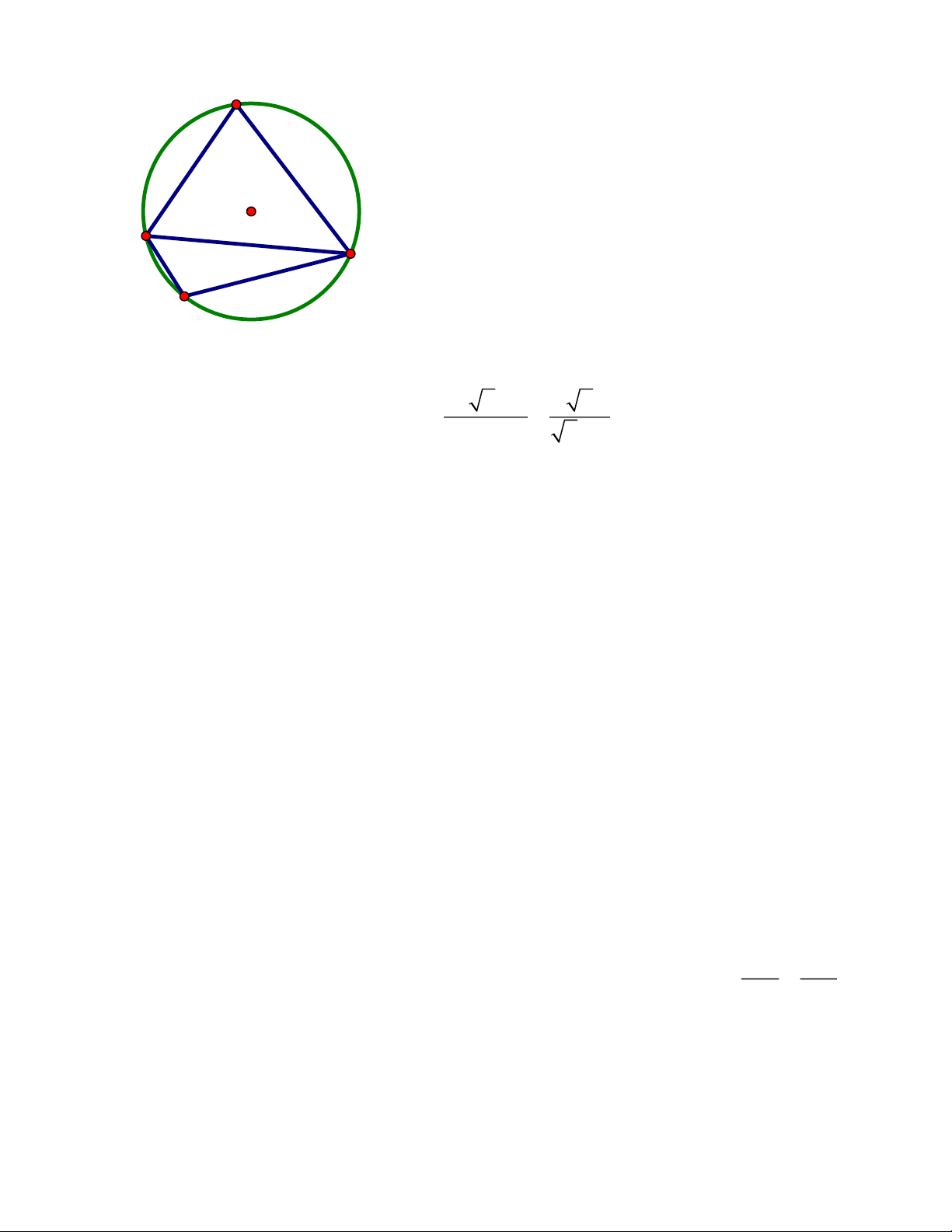
Câu 3. (3,0 điểm) Cho đường tròn (O)đường kính .
AB Trên tia đối của tia BA lấy điểm C
(C không trùng với B).Kẻ tiếp tuyến CD với đường tròn (O),Dlà tiếp điểm. Tiếp tuyến tại
A của đường tròn (O)cắt đường thẳng CD tại E
a) Chứng minh tứ giác AODE nội tiếp
b) Gọi H là giao điểm của AD và OE, K là giao điểm của BE với đường tròn (O)( N
không trùng với B).Chứng minh EHK = KBA EA MO
c) Đường thẳng vuông góc với AB tại O cắt CE tại M. Chứng minh − =1 EM MC
Câu 4. (1,0 điểm) Cho a,b,c là các số dương thỏa mãn 2 2 2
a + b + c = 1. Tìm giá trị
lớn nhất của biểu thức A = (1+ 2a)(1+ 2bc)
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 NĂM 2021 MÔN TOÁN TỈNH PHÚ THỌ Trang 18 I.TRẮC NGHỆM 1A 2C 3D 4B 5C 6D 7A 8B 9C 10B II.TỰ LUẬN Câu 1.
a) Tính giá trị biểu thức A khi x = 16 7 − 16 + 6 16 22 − 1
x =16(tmdk) A = + = + 2 = 16 − 4 16 − 2 12 6 1
Vậy khi x = 16 thì A = 6
b) Rút gọn biểu thức A
Điều kiện : x 0, x 4 7 − x + 6 + x − x + x ( x +2 7 6 ) A = + = x − 4 x − 2 ( x −2)( x +2) 7 −
x + 6 + x + 2 x x − 5 x + 6 = ( = x − 2)( x + 2) ( x −2)( x +2) x. x − x − x +
( x −3)−2( x −3 3 2 6 ) = ( = x − 2)( x + 2) ( x −2)( x +2)
( x −2)( x −3) x −3 = ( = x − 2)( x + 2) x + 2 x − 3 Vậy A = x + 2 Câu 2.
1) Cho đường thẳng (d ) : y = 2mx + 2m − 3 và parabol (P) 2 : y = x
a) Tìm m để đường thẳng (d ) đi qua A(1;5)
Đường thẳng (d ) đi qua A(1;5) 5 = 2 .1
m +1m − 3 4m = 8 m = 2
Vậy m = 2 thì đường thẳng (d ) đi qua A(1;5)
b) Tìm m để đường thẳng (d ) tiếp xúc với parabol (P)
Xét phương trình hoành độ giao điểm của (d ) và (P) ta có : 2 2
x = 2mx + 2m − 3 x − 2mx − 2m + 3 = 0( ) 1
Đường thẳng (d ) tiếp xúc với parabol (P) phương trình (1) có nghiệm kép Trang 19 2
= m − (− m + ) 2 ' 0 2
3 = 0 m + 2m − 3 = 0 ( = m − )(m + ) m 1 1 3 = 0 m = 3 −
Vậy m = 1hoặc m = −3 thì đường thẳng (d ) tiếp xúc với parabol (P)
2x − y = m −1
2) Cho hệ phương trình
(mlà tham số) 3
x + y = 4m +1
a) Giải hệ phương trình với m = 2
Với m = 2 ta có hệ phương trình : 2x − y =1 5 x =10 x = 2 3 x + y = 9 y = 2x −1 y = 3
b) Tìm m để hệ phương trình có nghiệm duy nhất ( ;
x y)thỏa mãn 2
2x − 3y = 2
2x − y = m − ( 1 ) 1 3
x + y = 4m + ( 1 2)
Cộng vế theo vế của phương trình (1) và (2) ta được : 5x = 5m x = m ( )
1 y = 2x − m +1 y = 2m − m +1 y = m +1
Hệ phương trình đã cho luôn có nghiệm duy nhất ( ; x y) = ( ; m m + ) 1 Theo đề bài ta có : 2 2x − 3y = 2 2 m − (m + ) 2 2 2 3
1 = 2 2m − 3m − 3 − 2 = 0 2m − 3m − 5 = 0
Phương trình có a − b + c = 2 − ( 3 − ) − 5 = 0 c 5
Phương trình có hai nghiệm phân biệt m = 1, − m = − = 1 2 a 2 5 Vậy với m = 1,
− m = thỏa mãn bài toán 2 Trang 20