20 Đề Thi Tuyển Sinh 10 Môn Toán Toàn Quốc 2025-2026 Có Lời Giải Chi Tiết-Bộ 1
Một bức tường được xây bằng các viên gạch hình chữ nhật bằng nhau và được bố trí như hình vẽ bên. Phần sơ màu (gạch chéo) là phần ngoài của một hình tam giác có cạnh đáy 10 dmvà chiều cao 6 dm. Tính diện tích phần tô đậm. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 289 tài liệu
Môn: Toán 9 3.1 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT AN GIANG Môn thi: TOÁN
Thời gian làm bài : 120 phút ĐỀ CHÍNH THỨC
(Đề thi gồm có 01 trang)
Câu 1. (3,0 điểm) Giải các phương trình và hệ phương trình sau đây : a)( 2 + ) 1 x − 2 = 2 4 2
b)x + x − 6 = 0 2x + y =11
c)x− y = 4 Câu 2. (2,0 điểm) Cho hai hàm số 2
y = x có đồ thị là Parabol (P) và y = x + 2 có đồ thị là đường thẳng (d )
a) Vẽ đồ thị (P) và (d ) trên cùng một hệ trục tọa độ
b) Bằng phép tính, tìm tọa độ giao điểm (P) và (d ) Câu 3. (2,0 điểm)
Cho phương trình bậc hai 2 x − (m − ) 2 2
1 x + m − 3m − 4 = 0(m là tham số, x là ẩn số)
a) Tìm m để phương trình có hai nghiệm phân biệt x , x 1 2 b) Đặt 2 2
A = x + x − x x .Tính A theo m và tìm m để A = 18 1 2 1 2 Câu 4. (2,0 điểm) Cho 4 điểm ,
A B,C, D theo thứ tự lần lượt nằm trên nửa đường tròn đường kính .
AD Gọi E là giao điểm của AC và .
BD Kẻ EF vuông góc với AD (F AD)
a) Chứng minh tứ giác ABEF nội tiếp
b) Chứng minh BD là tia phân giác của CBF Câu 5. (1,0 điểm)
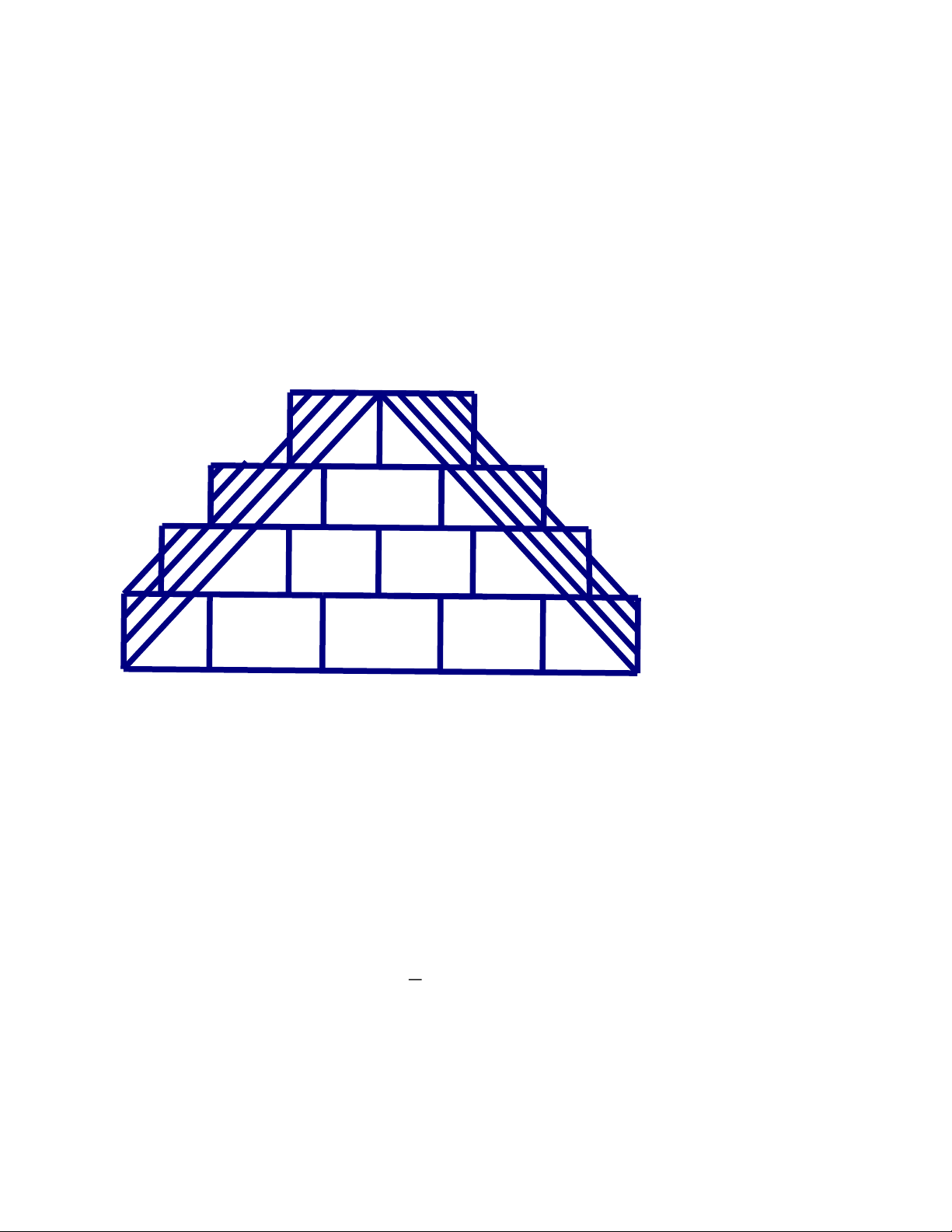
Một bức tường được xây bằng các viên gạch hình chữ nhật bằng nhau và được bố
trí như hình vẽ bên. Phần sơ màu (gạch chéo) là phần ngoài của một hình tam giác có
cạnh đáy 10dm và chiều cao 6 .
dm Tính diện tích phần tô đậm Trang 1 ĐÁP ÁN
Câu 1. Giải các phương trình và hệ phương trình sau a)( 2 + )
1 x − 2 = 2 ( 2 + ) 1 x = 2 + 2 2 + 2 x = = 2 2 +1 4 2
b)x + x − 6 = 0 Đặt 2
x = t (t 0). Nên phương trình thành : 2 2
t + t − 6 = 0 t + 3t − 2t − 6 = 0 t (t + 3) − 2(t + 3) = 0 ( = − t + )(t − ) t 3(ktm) 3 2 = 0 2
t = 2 x = 2 x = 2
Vậy phương trình có tập nghiệm S = 2 2x + y =11 3 x =15 x = 3 c) x − y = 4 y = x − 4 y =1
Vậy hệ phương trình đã cho có nghiệm duy nhất (5; ) 1 Câu 2.
a) Học sinh tự vẽ đồ thị (P),(d )
b) Ta có phương trình hoành độ giao điểm (P) và (d ) : 2 2 2
x = x + 2 x − x − 2 = 0 x − 2x + x − 2 = 0 ( = = x − )( x + ) x 2 y 4 2
1 = 0 x = 1− y =1
Vậy đường thẳng (d ) cắt (P) tại hai điểm phân biệt ( 1 − ; ) 1 ,(2;4) Câu 3. a) 2 x − (m − ) 2 2
1 x + m − 3m − 4 = 0(*)
Phương trình (*) có hai nghiệm phân biệt x , x ' 0 1 2 Trang 2 (m − )2 1 − ( 2
m − 3m − 4) 0 2 2
m − 2m +1− m + 3m + 4 0 m 5 −
Vậy với m −5 thì phương trình đã cho có hai nghiệm phân biệt x ; x 1 2
b) Với m −5 thì phương trình đã cho có hai nghiệm phân biệt x ; x . Theo hệ thức 1 2 Vi – et ta có :
x + x = 2 m −1 = 2m − 2 1 2 ( ) 2
x x = m − 3m − 4 1 2 Theo đề bài ta có :
A = x + x − x x = ( x + x )2 − 2x x − x x = (x + x )2 2 2 − 3x x 1 2 1 2 1 2 1 2 1 2 1 2 1 2 = 4(m − )2 1 − 3( 2
m − 3m − 4) = 4( 2 m − 2m + ) 2
1 − 3m + 9m +12 2 2 2
= 4m − 8m + 4 − 3m + 9m +12 = m + m +16 2
A =18 m + m +16 =18 m =1 2
m + m − 2 = 0 (m − )
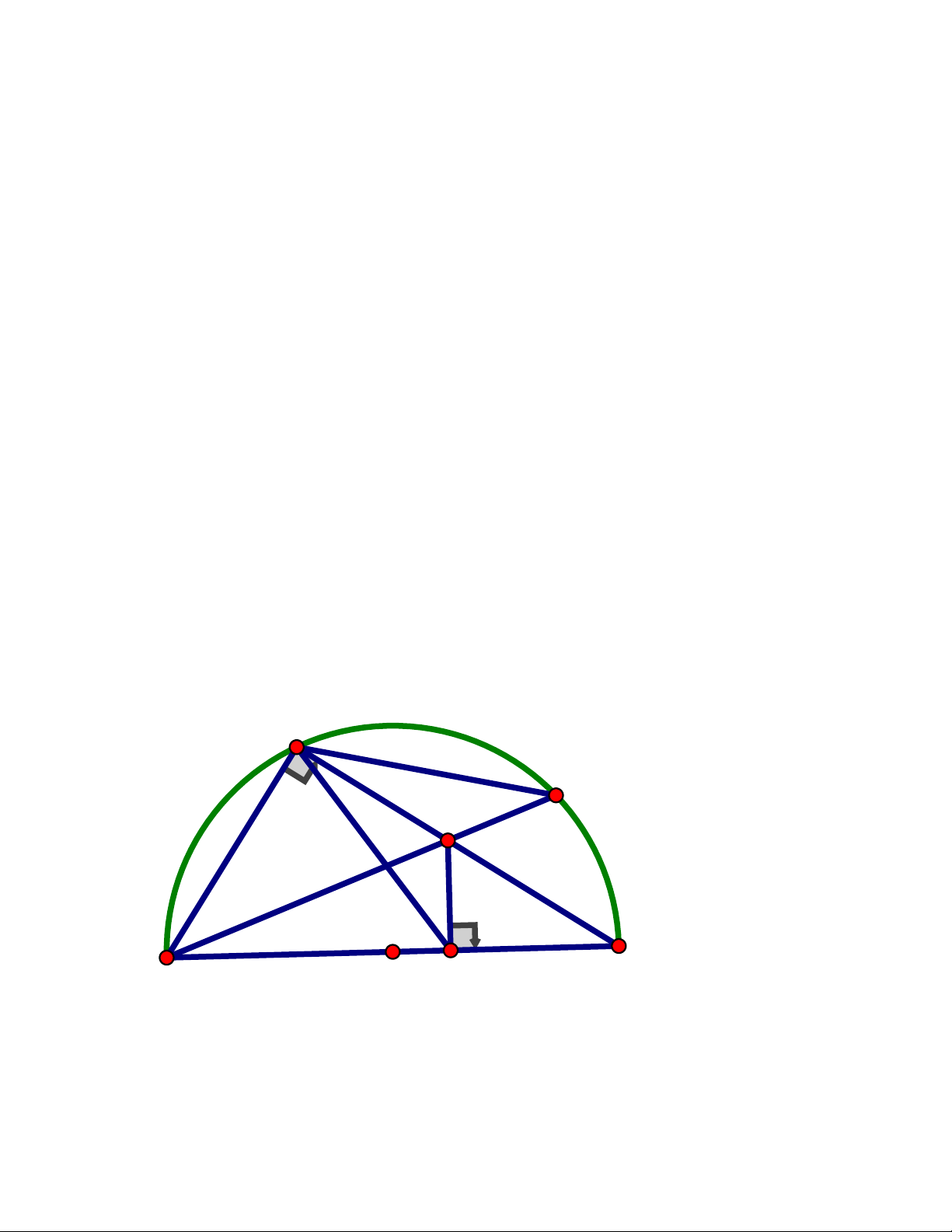
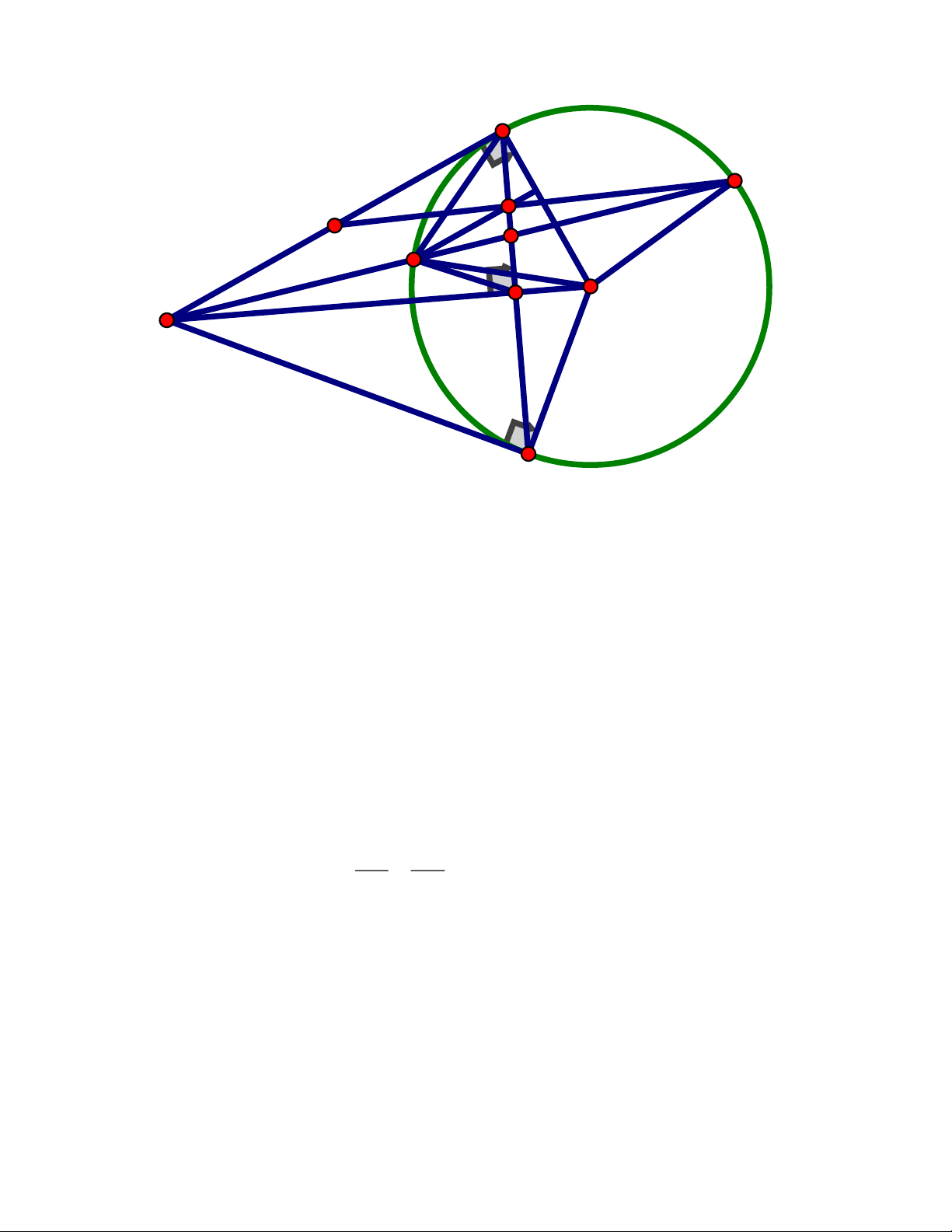
1 (m + 2) = 0 m= 2− Vậy m 2 − ; 1 thỏa mãn bài toán Câu 4. B C E A F D O
a) Chứng minh tứ giác ABEF nội tiếp
Ta có ABD là góc nội tiếp chắn nửa đường tròn đường kính AD Trang 3 A
BD = 90 hay A BE = 90
Xét tứ giác ABEF có ABE + AFE = 90 + 90 =180
ABEF là tứ giác nội tiếp (tứ giác có tổng 2 góc đối diện bằng 180 )
b) Chứng minh BD là tia phân giác CBF
Vì ABEF là tứ giác nội tiếp (cmt) FBE = FAE (hai góc nội tiếp cùng chắn cung
EF ) hay CAD = FBD
Lại có : CBD = CAD (hai góc nội tiếp cùng chắn cung CD) CB D = F BD(= CA
D) BD là phân giác của FBC Câu 5.
Chiều rộng của một viên gạch là : 6 : 4 =1,5(dm)
Chiều dài của một viên gạch : 10 : 5 = 2(dm)
Diện tích của một viên gạch: 2 1,5.2 = 3(dm )
Tổng số viên gạch để xây bức tường là : 2 + 3 + 4 + 5 = 14(viên)
Diện tích của bức tường là : 2 3.14 = 42(dm ) 1
Diện tích tam giác trong hình là : .6.10 = 30( 2 dm ) 2
Diện tích phần son màu là : 2 42 − 30 =12(dm )
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN LÊ QUÝ ĐÔN Trang 4
TỈNH BÀ RỊA – VŨNG TÀU
NĂM HỌC 2021 – 2022
ĐỀ THI MÔN: TOÁN (chung)
ĐỀ THI CHÍNH THỨC
Thời gian làm bài : 120 phút, không kể giao đề Ngày thi: 04/06/2021 Câu 1. (2,5 điểm) a) Giải phương trình: 2
x + 6x − 7 = 0 x − y = 5
b) Giải hệ phương trình : 2x + y = 4
c) Rút gọn biểu thức M = 20 − 45 + 5
Câu 2. (2,0 điểm) Cho parabol (P) 2
: y = x và đường thẳng (d ) : y = x − m + 3(m là tham số) a) Vẽ parabol (P)
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d ) cắt parabol (P) tại hai
điểm phân biệt A( x ; y ,B x ; y thỏa mãn y + y =1 1 1 ) ( 2 2) 1 2 Câu 3. (1,5 điểm)
a) Theo kế hoạch, một đội xe phải chở 150 tấn hàng từ một khu công nghiệp thuộc
huyện Châu Đức đến cảng Cái Mép – Thị Vải. Khi thực hiện thì trong đội có 5 xe
phải đi làm việc khác, nên mỗi xe còn lại của đội phải chở thêm 5 tấn hàng. Tính
số xe lúc đầu của đội (biết khối lượng trên mỗi xe chở là như nhau) b) Giải phương trình ( 2 x − x + )( 2 3
1 x − 3x + 2) = 2
Câu 4. (3,5 điểm) Cho đường tròn (O)và điểm A nằm bên ngoài đường tròn. Kẻ các
tiếp tuyến AB, AC của đường tròn (O)(B,C là các tiếp điểm). Một đường thẳng đi qua
A cắt đường tròn (O)tại hai điểm phân biệt D, K (D nằm giữa ,
A K và B, D nằm cùng
phía đối với đường thẳng ).
OA Gọi H là giao điểm của AO và BC
a) Chứng minh ABOC là tứ giác nội tiếp b) Chứng minh 2 A . D AK = AB và 2 .
AD AK + OH.OA = OA
c) Chứng minh AOD = ODH
d) Đường thẳng qua D và vuông góc với OB cắt BC tại M .Gọi P là trung điểm của .
AB Chứng minh ba điểm K, M , P thẳng hàng
Câu 5. (0,5 điểm) Với x, y là các số thực dương, tìm giá trị lớn nhất của biểu thức 1 1 1 1
S = 2( x + y) + − + 3 3 2 2 x + y
y + x x y
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 THPT CHUYÊN
MÔN TOÁN – VŨNG TÀU 2021 Trang 5 Câu 1.
a) Giải phương trình 2
x + 6x − 7 = 0
Ta có : a + b + c = 1+ 6 − 7 = 0 nên phương trình có 2 nghiệm phân biệt x =1 1 c x = = −7 2 a
Vậy tập nghiệm của phương trình là S = 7 − ; 1 x − y = 5
b) Giải hệ phương trình 2x + y = 4 x − y = 5 3 x = 9 x = 3 Ta có: 2x + y = 4 y = x − 5 y = −2
Vậy hệ có nghiệm duy nhất (3;−2)
c) Rút gọn biểu thức M = 20 − 45 + 5
M = 20 − 45 + 5 = 2 5 − 3 5 + 5 = 0 Vậy M = 0
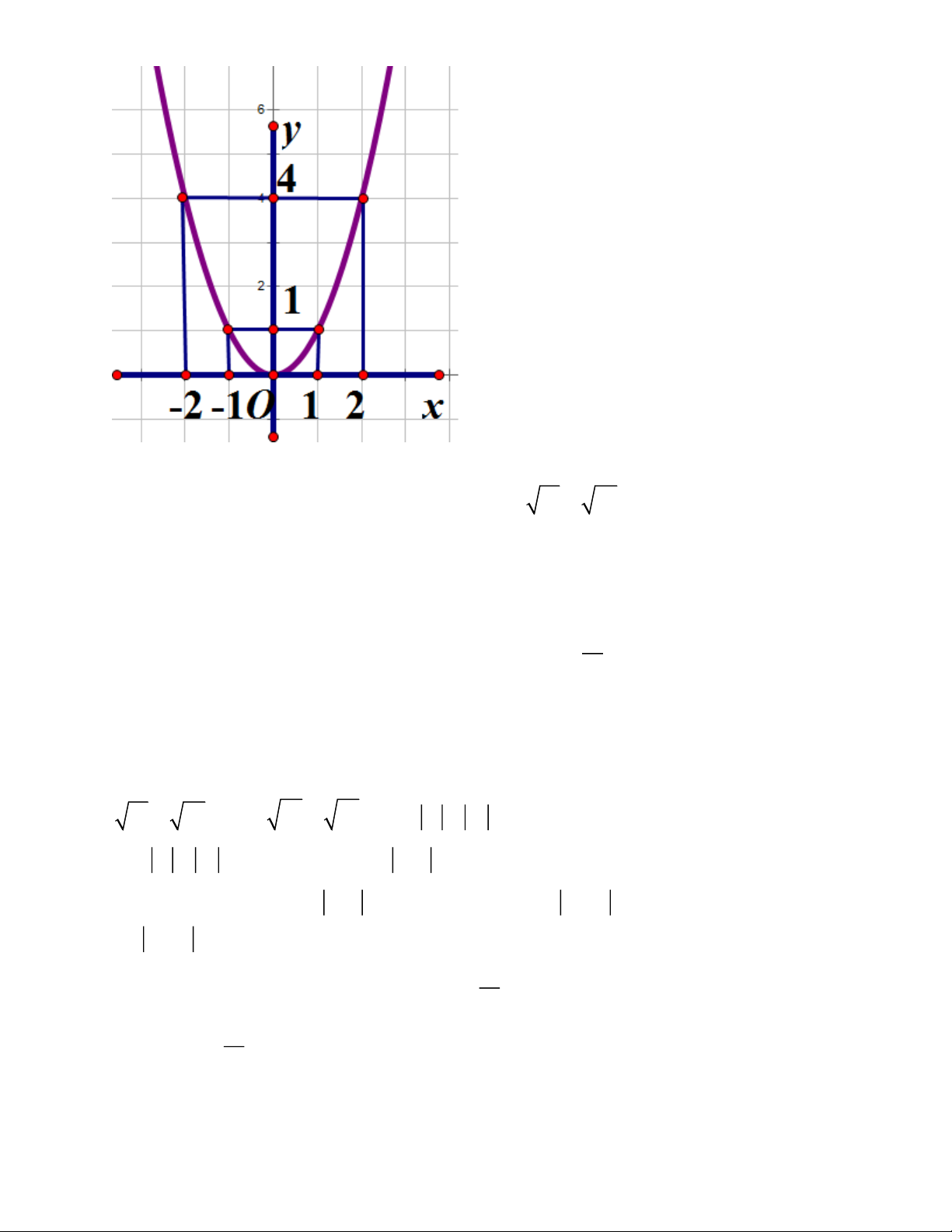
Câu 2. Cho parabol (P) 2
: y = x và đường thẳng (d ) : y = x − m + 3(với m là tham số) a) Vẽ Parabol (P) Parabol (P) 2
: y = x có bề lõm hướng lên và nhận Oy làm trục đối xứng
Ta có bảng giá trị sau : x 2 − 1 − 0 1 2 2 y = x 4 1 0 1 4 Đồ thi Parabol (P) 2 : y = x Trang 6
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d ) cắt (P) tại hai điểm
phân biệt A( x ; y ,B x ; y thỏa mãn y + y =1 1 1 ) ( 2 2) 1 2
Xét phương trình hoành độ giao điểm giữa (P) và (d) ta được : 2 2
x = x − m + 3 x − x + m − 3 = 0( ) 1
Để (P) cắt (d ) tại hai điểm phân biệt ( )
1 có hai nghiệm phân biệt
− (m − ) 13 0 1 4
3 0 1− 4m +12 0 m (*) 4 x + x =1
Khi đó, áp dụng hệ thức Vi-et ta có : 1 2 . x x = m − 3 1 2 Ta có ,
A B (P)nên A( 2
x ; x ),B( 2
x ; x . Khi đó ta có : 1 1 2 2 ) 2 2
y + y = 1 x + x = 1 x + x = 1 1 2 1 2 1 2 ( x + x )2 2 2
=1 x + x + 2 x x =1 1 2 1 2 1 2
(x + x )2 − 2x x + 2 x x =11− 2 m − 3 + 2 m − 3 =1 1 2 1 2 1 2 ( )
m − 3 = m − 3 m − 3 0 m 3 13
Kết hợp với điều kiện (*) ta được 3 m 4 13 Vậy 3 m
thỏa mãn yêu cầu bài toán. 4 Câu 3. Trang 7
a) Theo kế hoạch, một đội xe phải chở 150 tấn hàng từ một khu công nghiệp thuộc huyện
Châu Đức đến cảng Cái Mép – Thị Vải. Khi thực hiện thì trong đội có 5 xe phải đi làm việc
khác, nên mỗi xe còn lại của đội phải chở thêm 5 tấn hàng. Tính số xe lúc đầu của đội (biết
khối lượng trên mỗi xe chở là như nhau)
Gọi số xe lúc đầu của đội là x( x 5, x )(xe) 150
Số hàng mà mỗi xe phải chở là (tấn hàng) x
Số xe thực tế tham gia chở hàng là x − 5 (xe) 150
Số hàng thực tế mà mỗi xe phải chở là : (tấn hàng) x − 5
Do thực tế mỗi xe phải chở thêm 5 tấn hàng nên ta có phương trình : 150 150 −
= 5 150x −150x + 750 = 5x(x − 5) x − 5 x 2 2
5x − 25x − 750 = 0 x − 5x −150 = 0 = ( 5 − )2 − 4.1.( 15
− 0) = 625 0 = 25
Nên phương trình có hai nghiệm phân biệt: 5 + 25 x = =15(tm) 1 2 5 − 25 x = = −10(ktm) 2 2
Vậy số xe tham gia chở hàng lúc đầu của đội là 15 xe
b) Giải phương trình : ( 2 x − x + )( 2 3
1 x − 3x + 2) = 2
( 2x −3x + )1( 2x −3x + 2) = 2 ( 2x −3x + )1( 2x −3x +1+ )1= 2
(x − 3x + )2 2 1 + ( 2 x − 3x + ) 1 − 2 = 0 Đặt 2
t = x − 3x +1khi đó phương trình trở thành : 2 t + t − 2 = 0 t =1 1
Ta có: a + b + c = 1+1− 2 = 0 nên phương trình có 2 nghiệm c t = = 2 − 2 a x = 0 Với 2 2
t = 1 x − 3x +1 = 1 x − 3x = 0 x = 3 Với 2 t = 2
− x − 3x + 3 = 0, = 3 − 0 VN
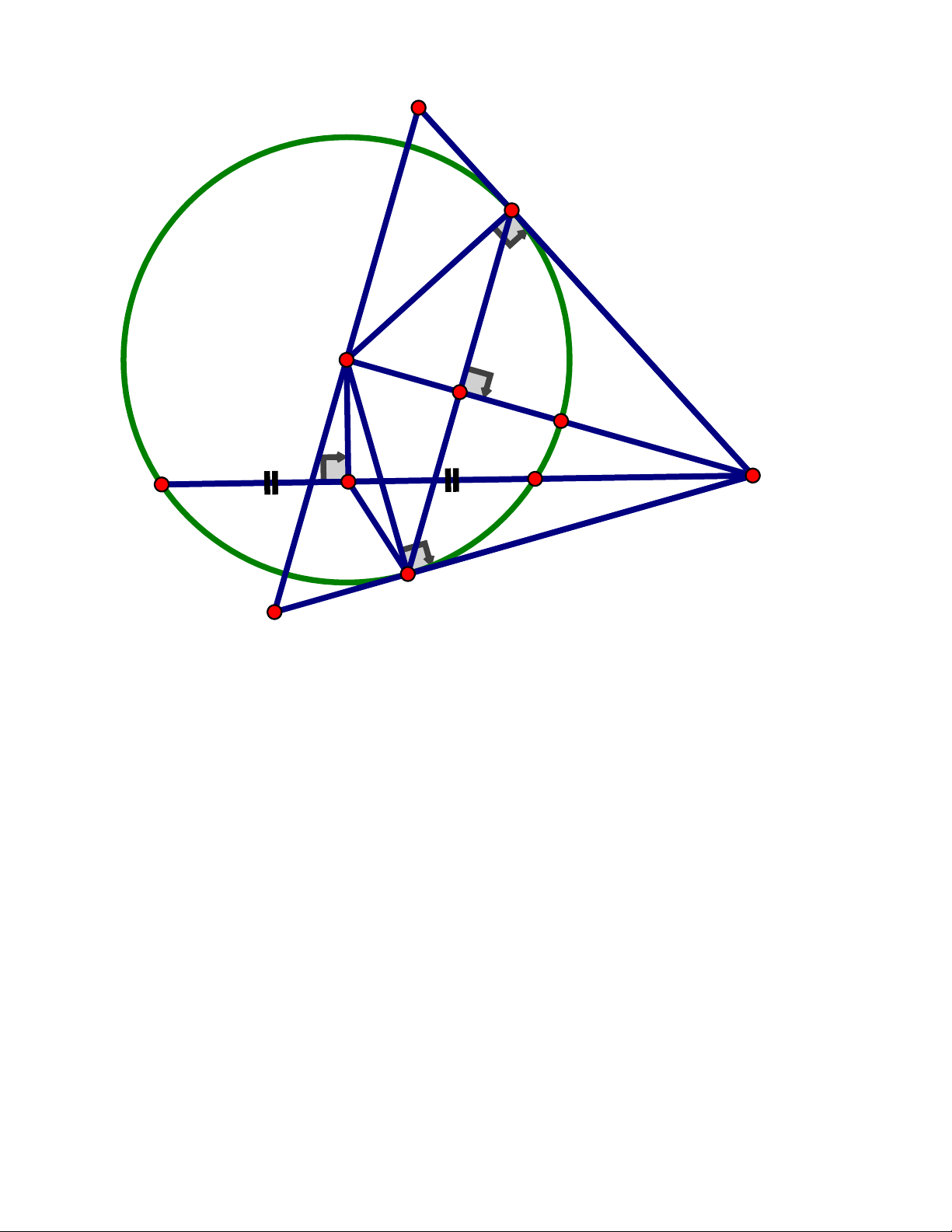
Vậy tập nghiệm của phương trình S = 0; 3 Câu 4. Trang 8 B K P M D J H O A C
a) Chứng minh ABOC là tứ giác nội tiếp AB ⊥ OB
Ta có : AB, AC là các tiếp tuyến của đường tròn (O)nên AC ⊥ OC
ABO = ACO = 90
ABO + ACO =180 ABOC là tứ giác nội tiếp (đpcm) b) Chứng minh 2 A .
D AK = AB và 2 .
AD AK + OH.OA = OA
Ta có ABD = BKD (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BD)
Xét ABD và AKB ta có : BA K chung, AB D = BKD (cmt) AD AB A BD ∽ A
KB(g.g) =
(2 cặp cạnh tương ứng tỉ lệ) AB AK 2 A . D AK = AB ( ) 1
Ta có: OB = OC (= R) nên O thuộc trung trực của BC
AB = AC (tính chất 2 tiếp tuyến cắt nhau) nên A thuộc trung trực của BC
OAlà trung trực của BC OA ⊥ BC tại H
Áp dụng hệ thức lượng trong tam giác vuông AOB vuông tại B, đường cao BH ta có : 2 OB = OH.OA (2) 2 2 2 OA = OB + AB Trang 9 Từ (1) và (2) ta có: 2 2 2 A .
D AK + OH.OA = AB + OB = OA (dfcm)
c) Chứng minh OAD = ODH OH OD Ta có : 2
OB = OH.O ( A cmt) . Mà 2
OB = OD OD = OH.OA = OD OA OH OD
Xét OHD và ODA ta có :DOA chung, = (cmt) OD OA O HD ∽ O D ( A .
c g.c) O AD = O
DH (2 góc tương ứng ) (đpcm)
d) Đường thẳng qua D và vuông góc với OB cắt BC tại M .Gọi P là trung điểm của .
AB Chứng minh ba điểm K, M , P thẳng hàng
Gọi J là giao điểm của AK và BC
Gọi P là giao điểm của KM và .
AB Ta sẽ chứng minh P là trung điểm của AB
Kẻ ON ⊥ DK ( N DK ) N là trung điểm của DK
Lại có ANO = 90nên N thuộc đường tròn đường kính OA hay O, N, B, , A C cùng
thuộc một đường tròn.
Xét tam giác ABJ và ANB ta có : BAN chung, A BJ = B
NA(= ACB)(các góc nội tiếp chắn các cung bằng nhau) ∽ ( AJ AB ABJ ANB g.g ) = (cặp cạnh tương ứng) 2
AB = AJ.AN AB AN AB AD Tương tự ta có : 2 A BD ∽ A
KB(g.g) =
AB = AK.AD AK AB AN AK AK − AN KN DN
AJ.AN = AK.AD = = = = AD AJ AJ − AD DJ EJ AK AJ
(Vì N là trung điểm của DK) = DN EJ AB AJ =
DM ⊥ OB(gt) Ta lại có : / / DM DJ DM AB (Định lý Ta – let)
AB ⊥ OB(gt) AP AK = DM DK AP AK 1 AJ 1 AB AB = = . = . AP = DM 2DN 2 EJ 2 DM 2
Vậy P là trung điểm của AB(dfcm)
Câu 5. Với x, y là các số thực dương, tìm giá trị lớn nhất của biểu thức 1 1 1 1
S = 2( x + y) + − + 3 3 2 2 x + y
y + x x y Trang 10
Theo BĐT cộng mẫu Schwwarz 2
(x + y)2 ( y + x)2 1 1 S = . + − + 2 2 2 2 x + y x + y y + x x y 2 2 3 2 2 x y y x 1 1 S . + + + − + 3 2 2 2
x + y x y y x x y 2 1 1 1 1 S . + + x + y − + 2 2
x + y x y x y 2 2 1 1 1 1 S + 2 − − S 2 − − 2 2 2 xy x y x y Vậy S
= 2 x = y =1 max
SỞ GIÁO DỤC, KHOA HỌC
KỲ THI TUYỂN SINH LỚP 10 THPT
VÀ CÔNG NGHỆ BẠC LIÊU
NĂM HỌC 2021 – 2022
Môn thi: Toán (không chuyên) ĐỀ CHÍNH THỨC Ngày thi: 23/06/2021
(Đề thi có 01 trang)
Thời gian : 120 phút (không kể giao đề) Câu 1. (4,0 điểm)
a) Rút gọn biểu thức A = 28 + 63 − 2 7 x y + y x 1 b) Chứng minh rằng :
= x − y với x 0, y 0và x y xy x − y Câu 2. (4,0 điểm) x − 2y = 5
a) Giải hệ phương trình 2x − y = 7 1 1 b) Cho hàm số 2
y = − x có đồ thị (P) và đường thẳng d : y = x − 2. Vẽ đồ thị 4 2
(P)và tìm tọa độ giao điểm của (P)với đường thẳng d bằng phép tính Câu 3. (6,0 điểm) Cho phương trình 2
x − (m + 2) x + m +1= 0( ) 1 ( m là tham số) Trang 11
a) Giải phương trình khi m = −3
b) Chứng minh phương trình (1) luôn có nghiệm với mọi số thực m
c) Tìm m để phương trình ( )
1 có hai nghiệm phân biệt x , x là độ dài hai cạnh góc 1 2
vuông của một tam giác vuông có độ dài đường cao kẻ từ đỉnh góc vuông xuống 2 cạnh huyền là h = 5 Câu 4. (6,0 điểm)
Cho đường tròn (O;R)và đường thẳng d không qua O cắt đường tròn (O)tại hai điểm , A .
B Trên tia đối của tia ,
BA lấy một điểm M , qua M kẻ hai tiếp tuyến MC và
MD với đường tròn (O)(C,D là các tiếp điểm). Gọi H là trung điểm của AB
a) Chứng minh rằng tứ giác OMCH nội tiếp được trong một đường tròn
b) OM cắt đường tròn (O)tại I và cắt CD tại K. Chứng minh 2
OK.OM = R
c) Đường thẳng qua O vuông góc với OM cắt các tia MC, MD lần lượt tại P và . Q
Tính độ dài OM theo R sao cho diện tích tam giác MPQ nhỏ nhất Trang 12
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 NĂM 2021 MÔN TOÁN TỈNH BẠC LIÊU Câu 1.
a) Rút gọn biểu thức A = 28 + 63 − 2 7 Ta có :
A = 28 + 63 − 2 7 = 4.7 + 9.7 − 2 7 = 2 7 + 3 7 − 2 7 = 3 7 Vậy A = 3 7 x y + y x 1 b) Chứng minh rằng :
= x − y với x 0, y 0và x y xy x − y
Với x 0, y 0và x y ta có : xy. + 1
( x + y) ( x − y x y y x ) VT = : = . xy x − y xy 1
= ( x + y )( x − y ) = x − y =VP(dfcm) Câu 2. x − 2y = 5
a) Giải hệ phương trình 2x − y = 7 x − 2y = 5 x − 2y = 5 3 − x = 9 − x = 3 2x − y = 7
−4x + 2y = −14 y = 2x − 7 y = −1
Vậy hệ có nghiệm duy nhất ( ; x y) = (3;− ) 1 1 1 b) Cho hàm số 2
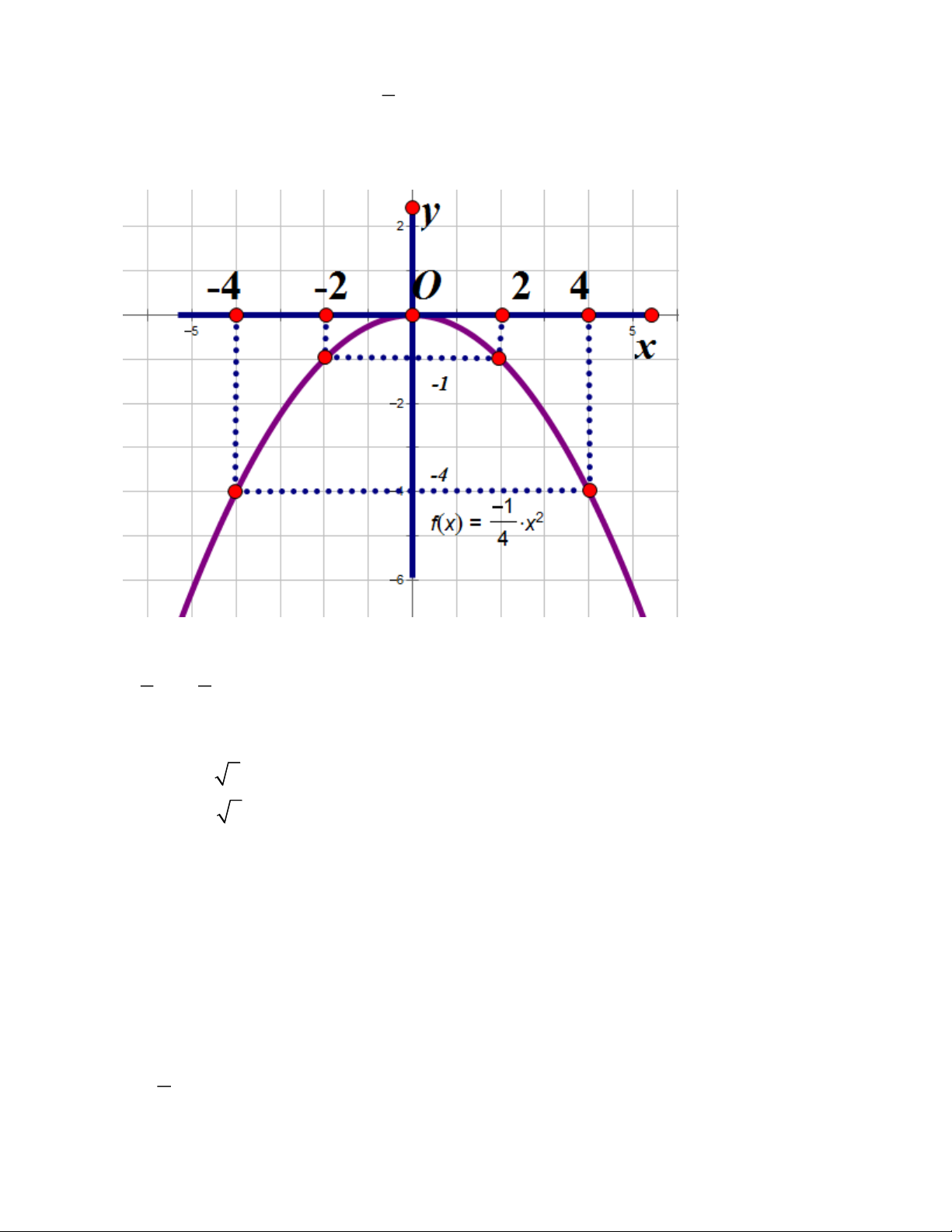
y = − x có đồ thị (P) và đường thẳng d : y = x − 2. Vẽ đồ 4 2
thị (P) và tìm tọa độ giao điểm của (P) với đường thẳng d bằng phép tính 1 Vẽ đồ thị hàm số 2 y = − x 4 Ta có bảng giá trị x 4 − 2 − 0 2 4 1 2 y = − x 4 − 1 − 0 1 − 4 − 4 Trang 13 1
Vậy đồ thị hàm số (P) 2
: y = − x là đường cong đi qua các điểm ( 4 − ; 4 − ); 4 ( 2 − ;− ) 1 ;(0;0);(2;− ) 1 ;(4; 4 − ) Đồ thị hàm số
Phương trình hoành độ giao điểm của d và (P) là : 1 2 1 2
− x = x − 2 x + 2x − 8 = 0 4 2
Phương trình có = (− )2 '
1 + 8 = 9 0 Phương trình có hai nghiệm phân biệt x = 1
− + 9 = 2 y = −1 1 x = 1 − − 9 = 4 − y = −4 2
Vậy đường thẳng (d ) cắt (P) tại hai điểm phân biệt (2;− ) 1 và ( 4 − ; 4 − )
Câu 3. Cho phương trình 2
x − (m + 2) x + m +1= 0( )
1 ( m là tham số)
a) Giải phương trình khi m = −3
Khi m = −3 phương trình (1) trở thành 2 x + x − 2 = 0
Vì a + b + c = 1+1− 2 = 0 nên phương trình có hai nghiệm phân biệt x =1 c . x = = 2 − a Trang 14
Vậy khi m = −3 thì phương trình có tập nghiệm S = 1;− 2
b) Chứng minh phương trình (1) luôn có nghiệm với mọi số thực m Ta có : hệ số của 2
x là 1 0 nên phương trình (1) là phương trình bậc hai một ẩn
Lại có = (m + )2 − (m + ) 2 2 2 4
1 = m + 4m + 4 − 4m − 4 = m 0 (với mọi m)
Do đó phương trình (1) luôn có nghiệm với mọi số thực m
c) Tìm m để phương trình ( )
1 có hai nghiệm phân biệt x , x là độ dài hai cạnh 1 2
góc vuông của một tam giác vuông có độ dài đường cao kẻ từ đỉnh góc vuông 2
xuống cạnh huyền là h = 5
Phương trình (1) có = (m + )2 − (m + ) 2 2 2 4
1 = m + 4m + 4 − 4m − 4 = m
Để phương trình (1) có hai nghiệm phân biệt x , x thì 0 m 0 1 2 b − x + x = = m + 2 1 2
Khi đó, áp dụng định lý Viet ta có : a c x x = = m +1 1 2 a
Do hai nghiệm phân biệt x , x là độ dài hai cạnh góc vuông nên ta có x , x 0 suy ra : 1 2 1 2 x + x 0 m + 2 0 1 2 m −1 x x 0 m +1 0 1 2
Vì x , x là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao kẻ 1 2 2
từ đỉnh góc vuông xuống cạnh huyền h =
nên áp dụng hệ thức lượng trong tam giác 5 vuông ta có : 1 1 1 x + x 5 x + x − 2x x 5 1 2 ( )2 2 2 1 2 1 2 + = = = 2 2 2 2 2 2 2 x x 2 x x 4 x x 4 1 2 1 2 1 2 5
4.(m + 2)2 − 2(m + ) 1 = 5(m + )2 2 2
1 4m + 8m + 8 = 5m +10m + 5 2
m + 2m − 3 = 0
Ta có : a + b + c =1+ 2 + ( 3
− ) = 0 nên phương trình (*) có hai nghiệm phân biệt m =1(tm) 1 c m = = 3 − (ktm) 2 a
Vậy m = 1là giá trị cần tìm. Câu 4. Trang 15 Q D O I K A H B M C P
a) Chứng minh rằng tứ giác OMCH nội tiếp được trong một đường tròn
Vì H là trung điểm của AB( gt) OH ⊥ AB (quan hệ vuông góc giữa đường kính và
dây cung) OHM = 90
Xét tứ giác OMCH có OHM = OCM = 90 OMCH là tứ giác nội tiếp (Tứ giác có
2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau) b)
OM cắt đường tròn (O)tại I và cắt CD tại K. Chứng minh 2
OK.OM = R
Vì MC = MD (tính chất hai tiếp tuyến cắt nhau) M thuộc trung trực của CD
OC = OD(= R)nên O thuộc trung trực của CD OM là trung trực của CD
OM ⊥ CD tại K
Xét tam giác OMD vuông tại D có đường cao DK ta có : 2 2
OD = OK.OM = R (hệ thức lượng trong tam giác vuông) Trang 16 c)
Đường thẳng qua O vuông góc với OM cắt các tia MC, MD lần lượt tại P và .
Q Tính độ dài OM theo R sao cho diện tích tam giác MPQ nhỏ nhất
Ta có : MO là phân giác của PMQ (tính chất 2 tiếp tuyến cắt nhau)
MO là đường cao của P
MQ(doPQ ⊥ OM (gt)) M
PQ cân tại M (tam giác có đường cao đồng thời là đường phân giác)
MO đồng thời là trung tuyến của MPQ O là trung điểm của PQ 1 1
OP = PQ . Ta có : S = .M .
O PQ = OM.OP 2 M PQ 2
Áp dụng hệ thức lượng trong tam giác OMP vuông tại O có đường cao OC ta có : 1 1 1 1 + = = 2 2 2 2 OM OP OC R 1 1
Áp dụng BĐT Cô-si cho hai số dương và ta có : 2 OM 2 OP 1 1 2 2 1 2 2 + = S 2R 2 2 2 OM OP OM . MPQ OP S R S M PQ MPQ O M = OP O M = OP Dấu " = " xảy ra 2 1 = O M = R 2 2 2 OM R Vậy S
đạt giá trị nhỏ nhất bằng 2
2R khiOM = R 2 MPQ
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 BẮC CẠN
NĂM HỌC 2021 – 2022 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài : 120 phút không kể giao đề
(Đề thi gồm có 01 trang)
Câu 1. (1,5 điểm) Rút gọn các biểu thức sau :
a)A = 3 2 − 32 + 50 1 x 1 x 0 b)B = − : x − 2 x − 4 x + 2 x 4 Câu 2. (2, 5 điểm)
a) Giải các phương trình sau: 4 2 1)2x − 4 = 0
2)x − x −12 = 0 2x + y = 3
b) Giải hệ phương trình x − 2y = 4 Trang 17
c) Một người đi xe máy từ huyện Ngân Sơn đến huyện Chợ Mới cách nhau 100 . km
Khi về người đó tăng vận tốc thêm 10km / h so với lúc đi ,do đó thời gian về ít hơn
thời gian đi là 30 phút. Tính vận tốc đi của xe máy Câu 3. (1,5 điểm)
a) Vẽ đồ thị các hàm số 2
y = 2x và y = −x + 2 trên cùng mặt phẳng tọa độ Oxy
b) Tìm a,b để đường thẳng (d ') : y = ax + b đi qua điểm M (1;2) và song song với
đường thẳng (d ) : y = −x + 2
Câu 4. (1,5 điểm) Cho phương trình 2 x − (m + ) 2 2
1 x + m + 4 = 0( ) 1 (m là tham số) a) Giải phương trình ( ) 1 với m = 2
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x , x thỏa mãn 1 2 2 x + 2(m + ) 2 1 x 2m + 20 1 2
Câu 5. (3,0 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các
đường cao AD, BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm .
A Gọi I là giao
điểm của hai đường thẳng HK và BC . Chứng minh I là trung điểm của đoạn thẳng BC AH BH CH c) Tính + + AD BE CF
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 MÔN TOÁN – TỈNH BẮC CẠN 2021
Câu 1. Rút gọn các biểu thức sau :
a)A = 3 2 − 32 + 50 = 3 2 − 4 2 + 5 2 = 4 2 Vậy A = 4 2 1 x 1 b) B = − : x − 2 x − 4 x + 2
Với x 0, x 4 ta có : 1 x 1 x + 2 − x x + 2 2 B = − : = = x − 2 x − x + 2
( x −2)( x +2). 4 1 x − 2 2 Vậy B =
, với x 0, x 4 x − 2 Câu 2.
a) Giải các phương trình sau : Trang 18
1)2x − 4 = 0 2x = 4 x = 2
Vậy phương trình có nghiệm x = 2 2) Đặt 2
t = x (t 0), khi đó phương trình trở thành : 2
t − t −12 = 0
Ta có : = (− )2 − (− ) 2 1
4. 12 = 49 = 7 0 nên phương trình có hai nghiệm phân biệt: 1+ 7 t = = 4(tm) 2 1− 7 t = = −3(ktm) 2 x = 2 Với 2
t = 4 x = 4 x = −2
Vậy tập nghiệm của phương trình là S = 2 − ; 2 2x + y = 3
b) Giải hệ phương trình x − 2y = 4 2x + y = 3 4x + 2y = 6 5 x =10 x = 2 Ta có : x − 2y = 4 x − 2y = 4 y = 3 − 2x y = 1 −
Vậy hệ phương trình đã cho có nghiệm duy nhất ( ; x y) = (2;− ) 1
c) Một người đi xe máy từ huyện Ngân Sơn đến huyện Chợ Mới cách nhau 100 .
km Khi về người đó tăng vận tốc thêm 10km / h so với lúc đi ,do đó thời
gian về ít hơn thời gian đi là 30 phút. Tính vận tốc đi của xe máy
Gọi vận tốc lúc đi của xe máy là x(km / h)( x 0) 100 Lúc đi, xe máy đi hết (giờ) x
Vận tốc lúc về của xe máy : x +10(km / h) 100 Lúc về, xe máy đi hết (giờ) x +10 1
Do lúc về xe máy tăng tốc nên thời gian về ít hơn thời gian đi là 30 phút = h nên ta có 2 phương trình : Trang 19 100 100 1 −
= 2(100x +1000 −100x) = x(x +10) x x +10 2 2
x +10x − 2000 = 0 2
=10 + 4.2000 = 8100 0 = 90 −10 + 90 x = = 40(tm) 1 2 10 − − 90 x = = −50(ktm) 2 2
Vậy vận tốc của xe máy là 40km / h Câu 3.
a) Vẽ đồ thị các hàm số 2
y = 2x và đường thẳng y = −x + 2 trên cùng mặt phẳng
tọa độ Oxy
+) Đồ thị hàm số 2 y = 2x Đồ thị hàm số 2
y = 2x có hệ số a = 2 0 nên có bề lõm hướng lên, đồng biến khi x 0,
nghịch biến khi x 0 và nhận Oy làm trục đối xứng
Ta có bảng giá trị sau : x −2 1 − 0 1 2 2 y = 2x 8 2 0 2 8 2
y = 2x là đường cong đi qua các điểm ( 2 − ;8),( 1 − ;2),(0;0),(1;2),(2;8)
+)Đường thẳng y = −x + 2 Ta có bảng giá trị: x 0 2 y = −x + 2 2 0
y = −x + 2là đường thẳng đi qua các điểm (0;2);(2;0) Trang 20