20 Đề Thi Tuyển Sinh 10 Môn Toán Trên Cả Nước 2025-2026 Có Lời Giải Chi Tiết-Bộ 2
Một lọ thủy tinh hình trụ có đường kính đáy bằng 15cm (độ dày của thành lọ và đáy lọ không đáng kể) chứa nước. Người ta thả chìm hoàn toàn 10 viên bi dạng khối cầu và cùng đường kính bằng 4cmvào lọ, biết nước trong lọ không tràn ra ngoài. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 289 tài liệu
Môn: Toán 9 3.1 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 GIA LAI
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG
Môn: Toán (không chuyên) ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian phát đề)
(Đề thi có 01 trang) Câu 1. (2,0 điểm) a) Giải phương trình : 2
x − 6x + 8 = 0 b) Cho phương trình 2
x − 2mx + 2m − 2 = 0,với m là tham số. Tìm giá trị của
phương trình đã cho có hai nghiệm x ; x thỏa mãn x + 3x = 6 1 2 1 2 Câu 2.(2,0 điểm)
a) Cho hàm số y = ax + .
b Xác định hệ số a,b biết đồ thị của hàm số đã cho là một
đường thẳng song song với đường thẳng y = 3x và đi qua điểm M (5; ) 1
b) Trong mặt phẳng tọa độ cho đường thẳng (d ) : y = 2x + m và parabol (P) 2
: y = −x .Tìm m để (d ) và (P) có một điểm chung. Câu 3.(2,0 điểm) x −1
x +1 1 x 0
a) Rút gọn biểu thức M = − . x +1 x −1 x x 1 b) Giải phương trình : 3 2 3 4 2 2
12 x −1 − 6 x − 2x +1 + x − 9 = 0 Câu 4.(2,0 điểm)
a) Một hình chữ nhật có chu vi bằng 68 .
cm Nếu tăng chiều rộng 6cm và giảm chiều
dài 10cm thì được hình vuông có cùng diện tích với hình chữ nhật ban đầu. Tìm
kích thước của hình chữ nhật ban đầu.
b) Một lọ thủy tinh hình trụ có đường kính đáy bằng 15cm (độ dày của thành lọ và
đáy lọ không đáng kể) chứa nước. Người ta thả chìm hoàn toàn 10 viên bi dạng
khối cầu và cùng đường kính bằng 4cm vào lọ, biết nước trong lọ không tràn ra
ngoài. Tính chiều cao của lượng nước dâng lên so với mực nước ban đầu (kết quả
lấy đến một chữ số sau dấu phẩy) Câu 5.
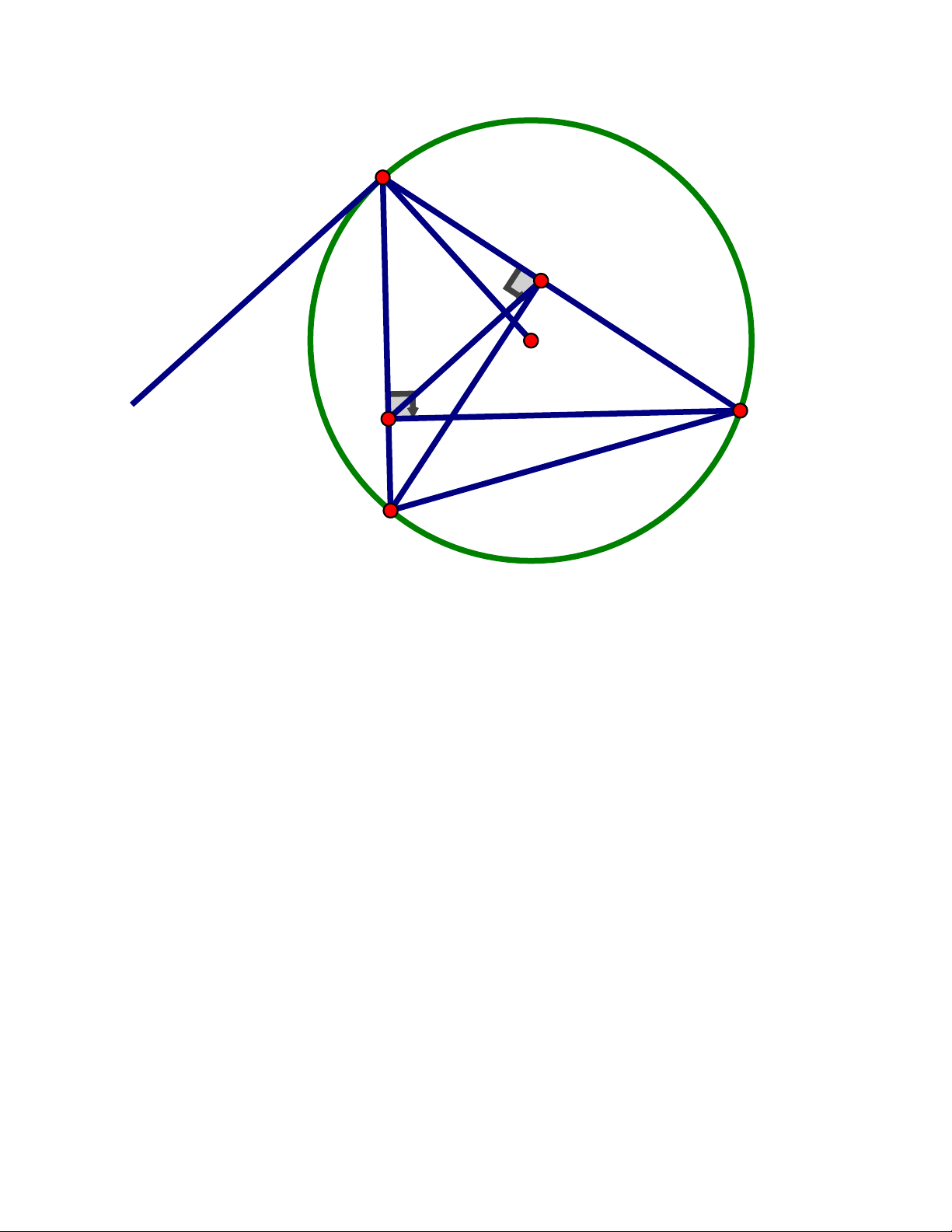
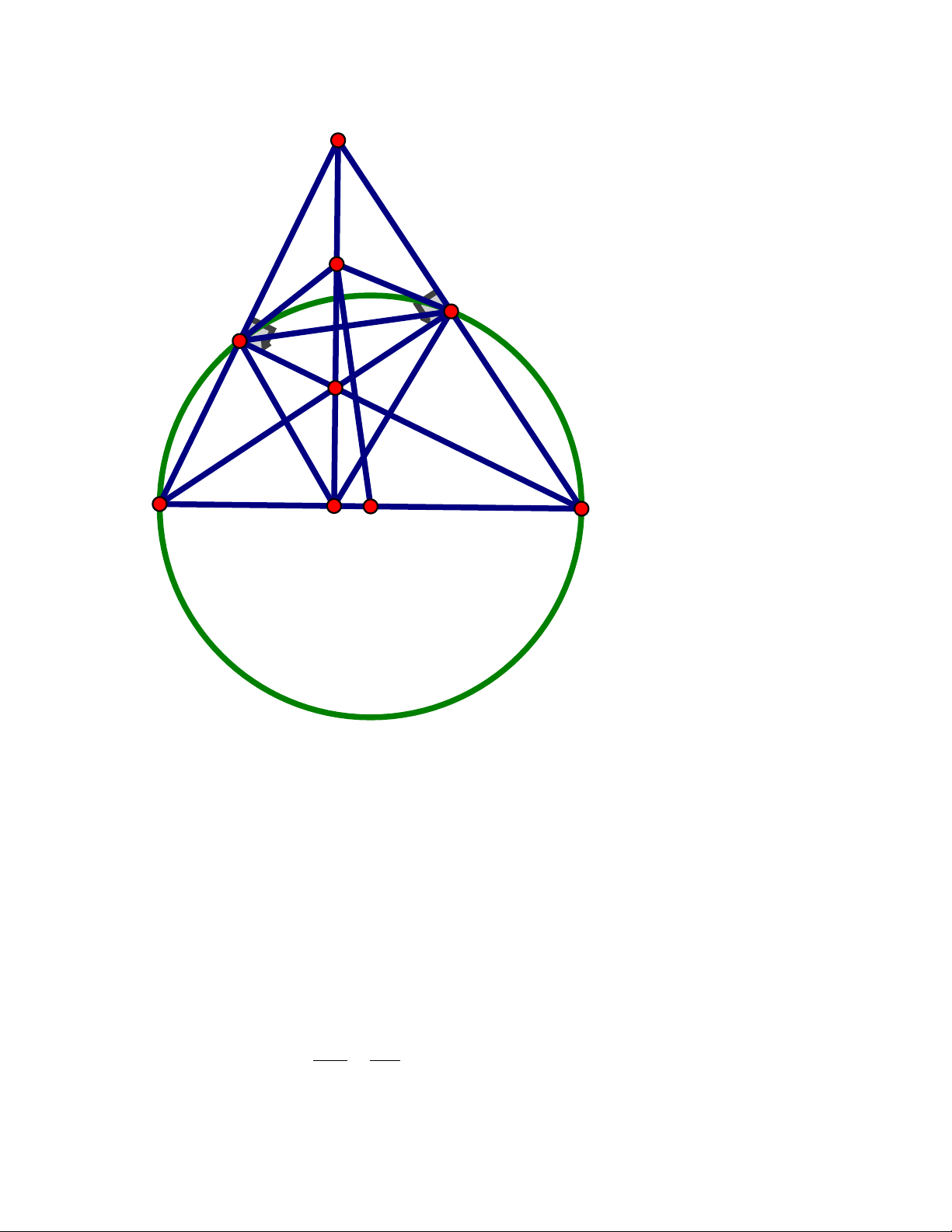
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O, hai đường cao BE,CF cắt
nhau tại H (E AC, F AB)
a) Chứng minh tứ giác AEHF nội tiếp một đường tròn
b) Chứng minh EF vuông góc OA Trang 1
ĐÁP ÁN VÀO 10 TỈNH GIA LAI Câu 1.
a) Giải phương trình : 2
x − 6x + 8 = 0 2 2
x − 6x + 8 = 0 x − 4x − 2x + 8 = 0 =
x(x − ) − (x − ) = (x − )(x − ) x 2 4 2 4 0 2 4 = 0 x = 4 Vậy S = 2; 4
b) Cho phương trình 2
x − 2mx + 2m − 2 = 0,với m là tham số. Tìm giá trị của
phương trình đã cho có hai nghiệm x ; x thỏa mãn x + 3x = 6 1 2 1 2 2
x − 2mx + 2m − 2 = 0 ( ) 1
= (−m)2 − ( m − ) = m − m + = (m − )2 2 ' 2 2 2 2
1 +1 0 (với mọi m)
' 0 phương trình ( )
1 luôn có hai nghiệm phân biệt với mọi m
x + x = 2m 1 2
Áp dụng định lý Vi – et và đề ta có : x x = 2m − 2 1 2 x + 3x = 6 1 2
x + x = 2m x = 3m − 3 Từ (1), (3) 1 2 1 x + 3x = 6 x = 3 − m 1 2 2
Thay vào (2) (3m − 3)(3 − m) = 2m − 2 2 2 3
− m +12m − 9 = 2m − 2 3m −10m + 7 = 0 10 + 16 7 m = = = (− ) 1 2 6 3 10 − 4.3.7 = 16 10 − 16 m = =1 2 6 7
Vậy m ;1thì thỏa đề 3 Câu 2. Trang 2
a) Cho hàm số y = ax + .
b Xác định hệ số a,b biết đồ thị của hàm số đã cho là
một đường thẳng song song với đường thẳng y = 3x và đi qua điểm M (5; ) 1 a = 3
Vì (d ) : y = ax + b song song với đường thẳng y = 3x b 0
(d): y = 3x + b qua M (5; )
1 1 = 3.5 + b b = 14 − (tm)
Vậy a = 3,b = 1 − 4
b) Trong mặt phẳng tọa độ cho đường thẳng (d ) : y = 2x + m và parabol (P) 2
: y = −x .Tìm m để (d ) và (P) có một điểm chung.
Ta có phương trình hoành độ giao điểm của (P) và (d ) : 2 2
−x = 2x + m x + 2x + m = 0(*) 2
' =1 − m =1− m
Để (d ) và (P) có một điểm chung thì (*) có một nghiệm duy nhất
' = 0 1− m = 0 m =1 Câu 3. x −1
x +1 1 x 0
a) Rút gọn biểu thức M = − . x +1 x −1 x x 1 − +
( x − )2 −( x x x + )2 1 1 1 1 1 1 M = − . = x + x − x
( x + )( x − ) . 1 1 1 1 x
( x −1− x − )1( x −1+ x + )1 1 2.2 − x 4 − = . = = x −1 x (x − ) 1 x x −1 4 −
Vậy khi x 0, x 1thì M = x −1
b) Giải phương trình : 3 2 3 4 2 2
12 x −1 − 6 x − 2x +1 + x − 9 = 0 3 2 3 4 2 2
12 x −1 − 6 x − 2x +1 + x − 9 = 0 3 3
12 x −1 − 6 (x − )2 2 2 2
1 + x −1− 8 = 0 Đặt 3 2
t = x −1, phương trình thành: Trang 3 2 3 3 2
12t − 6t + t − 8 = 0 t − 6t +12t − 8 = 0 (t − 2)3 3 2
= 0 t = 2 x −1 = 2 2 2
x −1 = 8 x = 9 x = 3 Câu 4.
a) Một hình chữ nhật có chu vi bằng 68 .
cm Nếu tăng chiều rộng 6cm và giảm
chiều dài 10cm thì được hình vuông có cùng diện tích với hình chữ nhật ban
đầu. Tìm kích thước của hình chữ nhật ban đầu.
Gọi x(cm)là chiều dài (6 x 34) Chiều rộng ban đầu : 34 − x
Diện tích ban đầu : x(34 − x)
Nếu tăng chiều rộng 6cm và giảm chiều dài 10cm thì diện tích không đổi nên ta có phương trình :
(x −10)(34 − x + 6) = x(34 − x) 2 2
−x + 50x − 400 = −x + 34x 16x = 400 x = 25 Vậy ban dầu,
Chiều dài : 25cm, chiều rộng 34 − 25 = 9m
b) Một lọ thủy tinh hình trụ có đường kính đáy bằng 15cm (độ dày của thành lọ
và đáy lọ không đáng kể) chứa nước. Người ta thả chìm hoàn toàn 10 viên bi
dạng khối cầu và cùng đường kính bằng 4cm vào lọ, biết nước trong lọ
không tràn ra ngoài. Tính chiều cao của lượng nước dâng lên so với mực
nước ban đầu (kết quả lấy đến một chữ số sau dấu phẩy) 15 225 Bán kính đáy R =
= 7,5cm Diện tích đáy : S = 2 4 3 3 10.4 R 10.4.2 320
Diện tích 10 khối cầu : V = = = ( 3 cm ) 3 3 3 320 225
Chiều cao dâng lên : h = : 1,9(cm) 3 4 Trang 4 Câu 5. A E x F O C B
a) Chứng minh tứ giác AEHF nội tiếp một đường tròn
ABC có CF, BE là hai đường cao AFH = AEH = 90
Suy ra tứ giác AEHF có AEH + AFH = 90 + 90 =180
AEHF là tứ giác nội tiếp
b) Chứng minh EF vuông góc OA
Kẻ tiếp tuyến Ax Ta có : BC A = BAx
(cùng chắn cung AB) ( ) 1
Tứ giác BFEC có BFC = BEC = 90 nên E, F là hai đỉnh liên tiếp cùng nhìn BC
dưới 1 góc 90 BFEC là tứ giác nội tiếp
BCA = EFA(góc trong và góc ngoài tại đỉnh đối diện ) (2)
Từ (1), (2) EFA = BAx mà 2 góc ở vị trí so le trong EF / / Ax
Mà OA ⊥ Ax (tính chất tiếp tuyến) EF ⊥ OA
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 HÀ GIANG
TRƯỜNG THPT CHUYÊN, NĂM HỌC 2021 -2022 Ngày thi: 09/6/2021 ĐỀ CHÍNH THỨC
ĐỀ THI MÔN: TOÁN HỌC (chung) Trang 5
Thời gian làm bài : 120 phút Câu 1. (2,0 điểm) 1 1 x +1 Cho biểu thức A = + : x − x
x −1 ( x − )2 1
a) Rút gọn biểu thức A
b) Tìm các giá trị của x để biểu thức A 0 Câu 2. (1,5 điểm) Cho (P) 2
: y = x và đường thẳng (d ) y = ( 2 m − ) 2 :
4 x + m − 3 (m là tham số)
a) Tìm tọa độ giao điểm của parabol (P) với đường thẳng d khi m = 0
b) Tìm các giá trị của tham số m để đường thẳng (d ) y = ( 2 m − ) 2 :
4 x + m − 3 luôn
cắt (P) tại hai điểm phân biệt
Câu 3. (2,0 điểm) Hai phân xưởng của một nhà máy theo kế hoạch phải làm tổng cộng
300 sản phẩm. Nhưng khi thực hiện thì phân xưởng 1 vượt mức 10% so với kế hoạch,
phân xưởng II vượt mức 20% so với kế hoạch. Do đó cả hai phân xưởng đã làm được
340 sản phẩm. Tính số sản phẩm mỗi phân xưởng phải làm theo kế hoạch. Câu 4. (3,5 điểm)
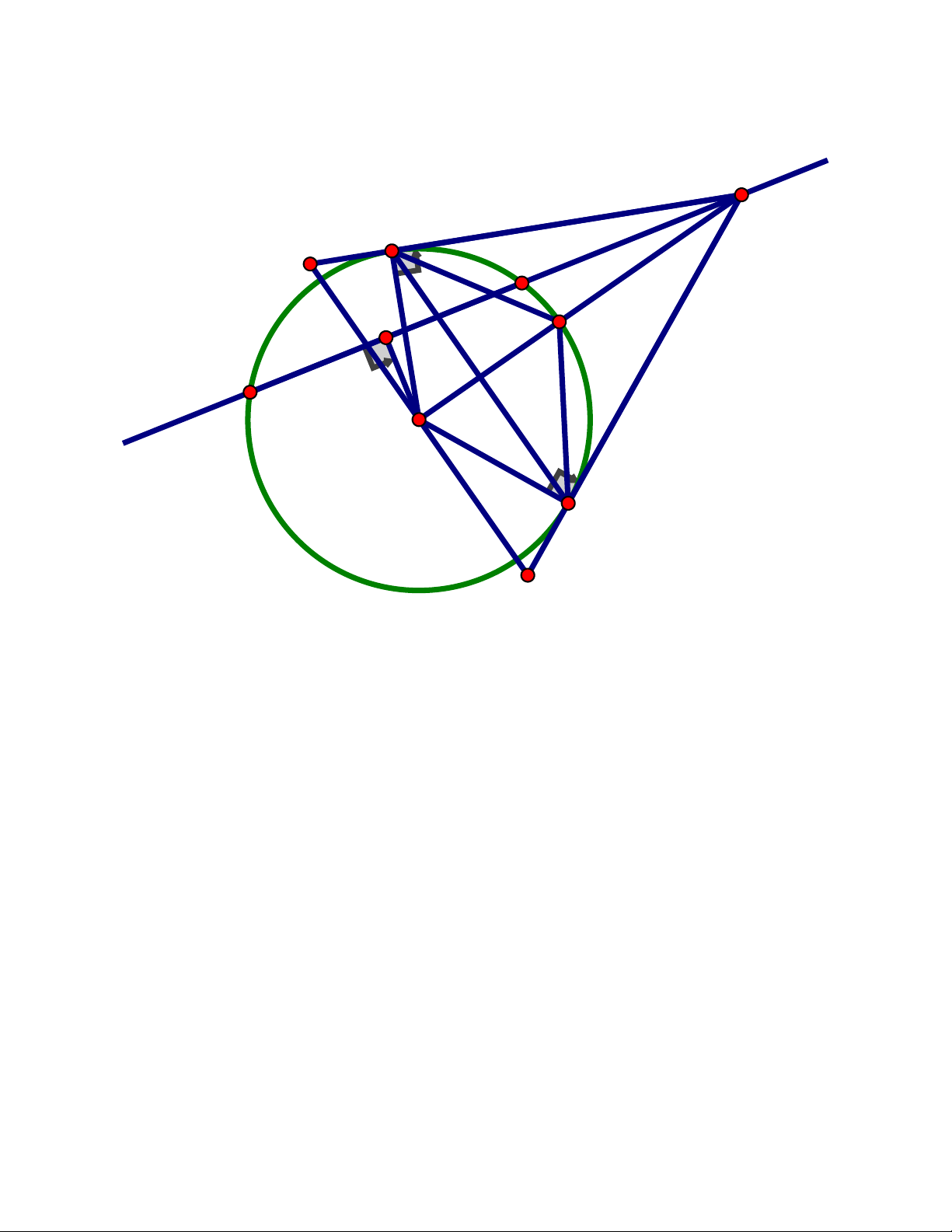
Cho đường tròn (O;R)và đường thẳng d không qua O cắt đường tròn tại hai điểm , A .
B Lấy một điểm M trên tia đối của tia ,
BA kẻ hai tiếp tuyến MC,MD với
đường tròn (C, D là các tiếp điểm). Gọi H là trung điểm của AB
a) Chứng minh rằng các điểm M , D,O, H cùng nằm trên một đường tròn
b) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MCD
c) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD theo thứ tự tại P và .
Q Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất
Câu 5. (1,0 điểm) Cho các số thực dương x, y, z thỏa mãn 2 2 2
x + y + z = 3xyz 2 2 2 x y z 3 Chứng minh rằng : + + 4 4 4 x + zy y + xz z + xy 2
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 THPT HÀ GIANG NĂM 2021 MÔN TOÁN CHUNG Câu 1.
a) Rút gọn biểu thức A Trang 6 x 0 x − x 0 x 0 ĐKXĐ: x 1 0 − x 1 ( x − )2 1 0 1 1 x +1 A = + : x − x
x −1 ( x − )2 1 ( x x − + )2 1 1 x −1 = = x ( x − ). 1 x +1 x x −1
Vậy với x 0, x 1ta có : A = x
b) Tìm các giá trị của x để biểu thức A 0
Điều kiện : x 0, x 1 x −1 A 0
0 x −1 0 (do x 0) x
x 1 x 1
Kết hợp với điều kiện ta được x 1thỏa mãn
Vậy x 1thì A 0 Câu 2.
a) Tìm tọa độ giao điểm của parabol (P) với đường thẳng d khi m = 0
Xét phương trình hoành độ giao điểm của d và (P) : 2 x = ( 2 m − ) 2 2
x + m − x − ( 2 m − ) 2 4 3
4 x − m + 3 = 0( ) 1
Thay m = 0vào phương trình trên ta được phương trình: 2 x + 4x + 3 = 0
Ta có ' = 4 − 3 = 1 0 nên phương trình có hai nghiệm phân biệt : x = 2 − + 1 = 1 − , x = 2 − − 1 = 3 − 1 2 x = 1 − y =1; x = 3 − y = 9 1 1 2 2
Vậy khi m = 0thì (d ) cắt (P) tại hai điểm ( 1 − ; ) 1 ,( 3 − ;9)
b) Tìm các giá trị của tham số m để đường thẳng (d ) y = ( 2 m − ) 2 : 4 x + m − 3
luôn cắt (P) tại hai điểm phân biệt
Xét phương trình hoành độ giao điểm của (d ),(P) là : Trang 7 2 x − ( 2 m − ) 2
4 x − m + 3 = 0( ) 1
Đường thẳng d luôn cắt (P) tại hai điểm phân biệt ( )
1 có hai nghiệm phân biệt
0 (m − 4)2 2 − 4( 2 −m + 3) 0 4 2 2 4 2
m − 8m +16 + 4m −12 0 m − 4m + 4 0 (m − 2)2 2 2
0 m − 2 0 m 2
Vậy với m 2 thì (d ) cắt (P) tại hai điểm phân biệt
Câu 3. Hai phân xưởng của một nhà máy theo kế hoạch phải làm tổng cộng 300
sản phẩm. Nhưng khi thực hiện thì phân xưởng 1 vượt mức 10% so với kế hoạch,
phân xưởng II vượt mức 20% so với kế hoạch. Do đó cả hai phân xưởng đã làm
được 340 sản phẩm. Tính số sản phẩm mỗi phân xưởng phải làm theo kế hoạch.
Gọi số sản phẩm phân xưởng I phải làm theo kế hoạch là x (sản phẩm) ( x *)
số sản phẩm phân xưởng II làm theo kế hoạch là 300 − x (sản phẩm)
Vì khi thực hiện thì phân xưởng I vượt mức 10% so với kế hoạch nên số sản phẩm phân
xưởng I làm được là : x + .10 x
% = x + 0,1x = 1,1x (sản phẩm)
Phân xưởng II vượt mức 20% so với kế hoạch nên số sản phẩm phân xưởng II làm
được là : 300 − x + (300 − x).20% = (300 − x).1,2 (sản phẩm)
Tổng số sản phẩm cả hai phân xưởng làm được là 340 sản phẩm nên ta có phương trình
: 1,1x + (300 − x).1,2 = 340 x = 200(tm)
Vậy phân xưởng I cần làm 200 sản phẩm và phân xưởng II cần làm 300 − 200 =100 sản phẩm Trang 8 Câu 4. d M P C B H I A O D Q
a) Chứng minh rằng các điểm M , D, H ,O cùng nằm trên một đường tròn
Do H là trung điểm của AB nên OH ⊥ AB (tính chất đường kính – dây cung)
Xét tứ giác MDOH có: MHO + MDO = 90 + 90 = 180
Tứ giác MDOH nội tiếp (dấu hiệu nhận biết)
Vậy các điểm M , D,O, H cùng nằm trên một đường tròn
b) Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội
tiếp tam giác MCD
Do MC, MD là hai tiếp tuyến của (O)nên MO là phân giác của C
MD hay MI là phân giác của C MD( ) 1
OI là phân giác của COD hay C OI = DO
I CI = DI I CM = I CD
Suy ra CI là phân giác của M CD(2) Từ ( )
1 ,(2) I là giao điểm của các đường phân giác của MCD
I là tâm đường tròn nội tiếp tam giác MCD(dfcm)
c) Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD theo thứ tự tại P và .
Q Tìm vị trí của điểm M trên d sao cho diện tích tam giác MQP bé nhất Trang 9 1 1 Ta có : S = M . O PQ = M .
O 2.OP = M . O OP MPQ 2 2 MO CO Mà M CO ∽ M
OP(g.g) = M . O OP = M . P CO MP OP S = M .
P CO = (MC + CP).CO 2 MC.CP.CO MPQ
Dấu " = " xảy ra MC = CP MOP vuông cân PMO
= 45 CMD = 90
MCOD là hình vuông cạnh R MO = R 2
Vậy diện tích tam giác MQP bé nhất khi MO = R 2 Câu 5.
Cho các số thực dương x, y, z thỏa mãn 2 2 2
x + y + z = 3xyz 2 2 2 x y z 3 Chứng minh rằng + + 4 4 4 x + yz y + xz z + xy 2
Áp dụng bất đẳng thức Cô-si cho hai số 4
x và yz ta có : 4 4 2
x + yz 2 x zy = 2x yz 4 2
y + xz 2y xz Tương tự : 4 2
z + xy 2z xy 2 2 2 2 2 2 x y z x y z + + + + 4 4 4 2 2 2 x + yz y + xz z + xy 2x yz 2 y xz 2z xy 2 2 2 x y z 1 1 1 1 + + + + 4 4 4 x yz y xz z xy 2 yz xz xy + + + 2 2 2 x y z 1 x + y + z + + . 4 4 4 x + yz y + xz z + xy 2 xyz
Sử dụng bất đẳng thức phụ : (a + b + c)2 ( 2 2 2
3 a + b + c )(sử dụng phép biến đổi tương đương để chứng minh) Trang 10
( x + y + z)2 3(x+ y + z)
(x + y + z)2 3.( 2 2 2
x + y + z ) = 9xyz
x + y + z 3 xyz ( x + y + z )2 3.3 xyz = 9 xyz 4
x + y + z 3 xyz 2 2 2 4 x y z 1 3 xyz 3 1 + + . = . 4 4 4 4 x + yz y + xz z + xy 2 xyz 2 xyz
Ta sẽ chứng minh 4 xyz 1
Áp dụng bất đẳng thức Cô – si cho 3 số 2 2 2
x , y , z ta được :
x + y + z 3 ( xyz)2 3xyz 3 ( xyz)2 2 2 2 3 3 3 4
xyz 1(do xyz 0) xyz 1 xyz 1 2 2 2 4 x y z 1 3 xyz 3 1 3 + + . = . 4 4 4 4 x + yz y + xz z + xy 2 xyz 2 xyz 2
Dấu " = " xảy ra khi x = y = z = 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN HÀ NAM
Năm học 2021 – 2022
Môn : Toán (Đề chung) ĐỀ CHÍNH THỨC
Thời gian làm bài : 120 phút không kể giao đề Câu 1. (2,0 điểm)
1) Rút gọn biểu thức A = 20 − 45 + 6 + 2 5 1 1
x +1 x 0
2) Cho biểu thức B = + : x − x
x −1 ( x − )2 x 1 1 1
Rút gọn biểu thức B và tìm tất cả các giá trị nguyên của x sao cho B 2 Câu 2. (2,0 điểm) 1) Giải phương trình : 2
x − 6x + 5 = 0
2(x + 2) = 3( y − ) 1
2) Giải hệ phương trình 3 x + y = 6 Câu 3. (1,5 diểm) Trang 11
Trong mặt phẳng tọa độ Oxy,cho parabol (P) có phương trình 2
y = x và đường
thẳng (d ) có phương trình y = mx + 5(m là tham số)
1) Trên parabol (P), tìm các điểm có tung độ bằng 2
2) Chứng minh rằng đường thẳng (d ) luôn cắt parabol (P)tại hai điểm phân biệt ,
A B . Gọi x , x lần lượt là hoành độ của , A .
B Tìm các giá trị của m để 1 2 x − x = 6 1 2 Câu 4. (4,0 điểm)
Cho nửa đường tròn (O) có đường kính AB = 2 .
R Lấy hai điểm phân biệt C và D
trên nửa đường tròn (O)sao cho C thuộc cung AD(C, D không trùng với , A B). Gọi H
là giao điểm của AD và BC, E là giao điểm của AC và BD
1) Chứng minh tứ giác CEDH nội tiếp
2) Chứng minh CE.CA = CH.CB
3) Gọi F là giao điểm của EH và .
AB Chứng minh H là tâm đường tròn nội tiếp tam giác CDF
4) Khi C, D thay đổi trên nửa đường tròn (O)sao cho CD = R 3.Chứng minh trung
điểm I của EH thuộc một đường tròn cố định. Câu 5. (0,5 điểm)
Cho a,b,c là các số thực dương thỏa mãn 6a + 3b + 2c = abc 1 2 3
Tìm giá trị lớn nhất của biểu thức Q = + + 2 2 2 a +1 b + 4 c + 9
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 THPT MÔN TOÁN HÀ NAM Câu 1.
1) Rút gọn biểu thức A = 20 − 45 + 6 + 2 5 Ta có : A = − + + = − + ( + )2 20 45 6 2 5 2 5 3 5 5 1 = − 5 + 5 +1 =1 Vậy A = 1 1 1
x +1 x 0
2) Cho biểu thức B = + : x − x
x −1 ( x − )2 x 1 1 1 1
x +1 x 0 B = + : x − x
x −1 ( x − )2 x 1 1 ( x x − + )2 1 1 x −1 = = x ( x − ). 1 x +1 x Trang 12 x −1 Vậy B = x 1 Ta có B = 2 x −1 1
= 2 x − 2 = x x = 2 x = 4(tm) x 2 1
Vậy x = 4thì B = 2 Câu 2.
1) Giải phương trình 2
x − 6x + 5 = 0 Phương trình 2
x − 6x + 5 = 0 có dạng a + b + c = 1− 6 + 5 = 0
Vậy phương trình có tập nghiệm S = 1; 5
2(x + 2) = 3( y − ) 1
2) Giải hệ phương trình 3 x + y = 6
2(x + 2) = 3( y − ) 1
2x + 4 = 3y − 3 2x − 3y = 7 − 3 x + y = 6 3 x + y = 6 9
x + 3y =18 11 x =11 x =1 y = 6 − 3x y = 3
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (1;3) Câu 3.
1) Trên parabol (P), tìm các điểm có tung độ bằng 2
Gọi M ( x ;2 là điểm thuộc (P) và có tung độ bằng 2 0 ) M 2;2 x = 2 1 2 0 ( ) Khi đó ta có : x 2 = 0 x 2 = − − 0 M 2;2 2 ( )
Vậy trên (P) có hai điểm có tung độ bằng −2 là M 2;2 và M − 2;2 2 ( ) 1 ( )
2) Chứng minh rằng đường thẳng (d ) luôn cắt parabol (P) tại hai điểm phân biệt , A .
B Gọi x ; x lần lượt là hoành độ của ,
A B . Tìm các giá trị của m để 1 2
x − x = 6 1 2
Phương trình hoành độ giao điểm của (d ) và (P) là : 2 2
x = mx + 5 x − mx − 5 = 0(*)
(d )cắt (P)tại hai điểm phân biệt ,
A B (*)có hai nghiệm phân biệt Trang 13 2
0 m + 5 0 (với mọi m) (d )luôn cắt (P) tại hai điểm phân biệt , A B với mọi m
Gọi x ; x lần lượt là hoành độ của ,
A B x , x là hai nghiệm của phương trình (*) 1 2 1 2
x + x = m
Áp dụng hệ thức Vi – et ta có : 1 2
. Theo đề bài, ta có x − x = 6 x x = −5 1 2 1 2
(x − x )2 = 36 (x + x )2 − 4x x = 36 1 2 1 2 1 2 m = 4 2 m − 4.( 5 − ) 2
= 36 m =16 m= 4−
Vậy m = 4 thỏa mãn bài toán Trang 14 Câu 4. E I D C H A F O B
1) Chứng minh tứ giác CEDH nội tiếp
Vì C, D đường tròn đường kính AB do đó ACB = ADB = 90 . Do đó
ECH = EDH = 90
Vậy tứ giác CEDH nội tiếp đường tròn đường kính EH
2) Chứng minh CE.CA = CH.CB
Từ ý 1) ta nhận xét AD, BC thứ tự là các đường cao từ ,
A B của tam giác EAB,nên H là trực tâm tam giác .
EAB Vì vậy, EH ⊥ AB hay EFB = 90 .
Ta có ECB = EFB = 90 tứ giác ECFB nội tiếp đường tròn đường kính EB
Như vậy CEF = CBF hay CEH = CBA
Xét hai tam giác CEH và CBAđều vuông tại C và có CEH = CBA CE CB C EH ∽ C BA =
CE.CA = CH.CB CH CA
3) Gọi F là giao điểm của EH và .
AB Chứng minh H là tâm đường tròn nội tiếp
tam giác CDF Trang 15
Theo ý 1) ta có tứ giác CEDH nội tiếp, nên H CD = H EC = FEB . Lại có tứ giác
ECFB nội tiếp (cmt), do đó FEB = FC B = H CF
Kết hợp 2 điều trên, ta có : HCD = HCF , hay CH là phân giác của FC . D
Chứng minh tương tự, DH là phân giác CDF, do đó H là tâm đường tròn nội tiếp tam giác CDF
4) Khi C, D thay đổi trên nửa đường tròn (O)sao cho CD = R 3.Chứng minh
trung điểm I của EH thuộc một đường tròn cố định.
Ta có tam giác ECH vuông tại C, có CI là đường trung tuyến nên IC = IH = IE.Do đó
tam giác CIH cân tại I, suy ra I CH = I HC
Vì C thuộc đường tròn đường kính AB tâm O nên ta cũng có OC = OA = OB = R
Suy ra OCB cân tại O nên OCB = OBC . Lại có: I CO = I CH + H CO = I HC + C BO = FH B + H BF = 90
Suy ra tam giác ICO vuông tại C
Tương tự tam giác EDH vuông tại D, có trung tuyến DI nên ID = IE = IH
Do đó IC = ID và vì C, D cùng thuộc đường tròn đường kính AB tâm O
OC = OD = R
Nên IO là trung trực của CD, do đó IO cắt CD tại Q là trung điểm của CD, và IO ⊥ CD R 3
Vì CD = R 3 nên CQ =
. Áp dụng định lý Pytago cho tam giác CQO vuông tại Q 2 2 R R ta có : 2 2 2 3
OQ = CO − CQ = R − = 4 2
Ta có ICO vuông tại C , đường cao CQ , áp dụng hệ thức lượng , ta có : 2 2 2 OC R OC = O . Q OI OI = = = 2R OQ R / 2
Vậy I luôn thuộc đường tròn tâm O, bán kính 2R cố định Câu 5. 6 3 2
Giả thiết của bài toán được viết lại thành + + =1. bc ca ab 1 2 3
Đặt a = ,b = ,c = , khi đó ta được xy + yz + zx =1 x y z x y z
Biểu thức B được viết lại thành B = + + 2 2 2 x +1 y +1 z +1
Để ý đến giả thiết xy + yz + zx =1ta có : 2 2
x +1 = x + xy + yz + zx = ( x + y)( z + x) Trang 16 x x Khi đó ta được : =
. Hoàn toàn tương tự ta được : 2 x +1
(x + y)(x + z) x y z Q = + +
(x + y)(x + z)
(x + y)( y + z)
(z + x)( y + z)
Áp dụng bất đẳng thức Cô – si ta được: x 1 x x + (
x + y)( z + x) 2 x + y z + x y 1 y y + (
x + y)( z + x) 2 x + y y + z z 1 z z + (
x + z)( y + z) 2 z + x y + z
Cộng vế theo vế các bất đẳng thức trên ta được : x y z 3 Q = + +
(x + y)(x + z)
(x + y)( y + z)
(z + x)( y + z) 2 3
Vậy Max Q = a = 3,b = 2 3,c = 3 3 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT HÀ NAM
Năm học 2021 – 2022 Môn Toán ĐỀ CHÍNH THỨC
Thời gian làm bài : 120 phút Câu I. (2,0 điểm) 1. Giải phương trình : 2 x + 7x +10 = 0
2(x − 3) = y −1
2. Giải hệ phương trình : 3 x + 4y =13 Câu II. (2,0 điểm) 1 1 1 x 0
1. Cho biểu thức A = + +
2 x − 2 2 x + 2
x −1 x 1
a) Rút gọn biểu thức A
b) Tìm các số nguyên x để A đạt giá trị nguyên
2. Một mảnh vườn hình chữ nhật ban đầu có diện tích bằng 2
680m , nếu tăng chiều
dài thêm 6m và giảm chiều rộng đi 3m thì diện tích mảnh vườn không thay đổi.
Tính chu vi mảnh vườn ban đầu. Câu III. (1,5 điểm)
Trong mặt phẳng tọa độ Oxy,cho parabol (P) có phương trình 2
y = x và đường
thẳng (d ) có phương trình y = (m − ) 2 2
1 x + m + 2m(m là tham số) Trang 17
1. Tìm tọa độ các điểm thuộc parabol (P) có tung độ bằng 9
2. Chứng minh đường thẳng (d ) luôn cắt parabol (P) tại hai điểm phân biệt , A . B
Gọi y , y lần lượt là tung độ của hai điểm , A .
B Tìm tất cả các giá trị của m để 1 2 y + y = 4 1 2 Câu IV. (4,0 điểm)
Cho tam giác ABC có ba góc nhọn. Đường tròn (O) đường kính BC cắt các cạnh
AB, AC lần lượt tại các điểm E, F (E B,F C) . Gọi H là giao điểm của BF và CE
1. Chứng minh tứ giác AEHF nội tiếp
2. Chứng minh AF.AC = . AB AE
3. Gọi K là trung điểm của đoạn thẳng AH.Chứng minh EBF = EFK
4. Từ điểm A kẻ các tiếp tuyến AM , AN của đường tròn (O) ( M , N là các tiếp
điểm). Chứng minh ba điểm M , H , N thẳng hàng. Câu V. (0,5 điểm)
Cho a,b,c là ba số dương thỏa mãn a + b + c = 3.Chứng minh rằng : 3a + bc 3b + ac 3c + ab + + 2
a + 3a + bc
b + 3b + ac
c + 3c + ab Trang 18
ĐÁP ÁN ĐỀ THI VÀO LỚP 10 MÔN TOÁN – TỈNH HÀ NAM 2021 Câu I. 1.
Giải phương trình : 2
x + 7x +10 = 0 Ta có 2 2
= 7 − 4.10 = 9 = 3 0nên phương trình đã cho có hai nghiệm phân biệt −7 + 3 x = = −2 1 2 −7 − 3 x = = −5 2 2
Vậy phương trình đã cho có tập nghiệm S = 5 − ;− 2
2(x − 3) = y −1
2. Giải hệ phương trình : 3 x + 4y =13 Ta có :
2(x − 3) = y −1 2x − y = 5 8
x − 4y = 20 3 x + 4y =13 3 x + 4y =13 3 x + 4y =13 11 x = 33 x = 3 y = 2x − 5 y =1
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (3; ) 1 Câu II. 1 1 1 x 0
1. Cho biểu thức A = + + 2 x − 2 2 x + 2
x −1 x 1
a) Rút gọn biểu thức A
Với x 0, x 1ta có : 1 1 1 x 0 A = + +
2 x − 2 2 x + 2
x −1 x 1 2( x x x x + + + − + + )1 1 1 2 2 2 1 = = = = 2( x − ) 1 ( x + ) 1 2( x − ) 1 ( x + ) 1 2( x − ) 1 ( x + ) 1 x −1 1
Vậy với x 0, x 1thì A = x −1
b) Tìm các số nguyên x để A đạt giá trị nguyên Trang 19 1 Để A thì
mà x nên x −1U ( ) 1 = 1 − ; 1 x −1 t 1
h : x −1 =1 x = 2 x = 4(tm) th2 : x −1 = 1
− x = 0 x = 0(tm)
Vậy để A thì x 0; 4
2. Một mảnh vườn hình chữ nhật ban đầu có diện tích bằng 2 680m , nếu
tăng chiều dài thêm 6m và giảm chiều rộng đi 3m thì diện tích mảnh vườn
không thay đổi. Tính chu vi mảnh vườn ban đầu.
Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là x, y(m)DK : x, y 0
Vì diện tích mảnh vườn là 2
680m nên ta có phương trình xy = 680( ) 1
Khi tăng chiều dài thêm 6m và giảm chiều rộng đi 3m thì diện tích chiều dài mới của
mảnh vườn là x + 6(m) và chiều rộng mới của mảnh vườn y − 3(m)
Vì diện tích mảnh vườn lúc sau không đổi nên ta có phương trình :
(x + 6)( y −3) = 680(2) xy = 680
Từ (1) và (2) ta có hệ phương trình : ( x + 6 )( y − 3) = 680 xy = 680 xy = 680
xy − 3x + 6y −18 = 680
680 − 3x + 6y −18 = 680 xy = 680 xy = 680 xy = 680 3
x − 6y +18 = 0
x − 2y = −6 x = 2y − 6 ( 2y − 6) 2 y = 680
2y − 6y − 680 = 0( ) 1 x = 2y − 6 x = 2y − 6 (2) ( ) 2
1 y − 3y − 340 = 0 = (−3)2 2 + 4.340 =1369 = 37 0 3 + 37 y =
= 20 x = 2.20 − 6 = 34(tm) 1 2 3 − 37 y = = −17(ktm) 2 2 Trang 20