23 kỹ thuật sử dụng máy tính cầm tay Casio – Vinacal giải nhanh Toán 12 – Nguyễn Chiến

23 kỹ thuật sử dụng máy tính cầm tay Casio – Vinacal giải nhanh Toán 12 – Nguyễn Chiến được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

46 23 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Page | 1

MÁY TÍNH

CASIO - VINACAL

 



1. 

 màu trắng  

trực tiếp.

 màu vàng 

sau phím SHIFT.

 màu đỏ thì 

phím ALPHA.

2. 

 ALPHA 

+  gán mt s vào ô nh A gõ:

S CN GÁN → q → J (STO) → z [A]

+  truy xut s trong ô nh A gõ: Qz





 C

.....



.....

3. 



 

log 5 7



x 2





 

log 5 7X

CALC.

.

Nguyễn Chiến. 0973514674

Page | 2

  

=

log 5 7

x

4. tìm 

BSHIFT + CALC 

 

2 4.2 2 4 0



   

x x x x x



 :

2 4.2 2 4 0



   

X X X X X

     

SHIFT + CALC

Máy hói Solve for X cò nghïa là

bän muốn bắt đầu dñ nghiệm

với giá trð của X bắt đầu từ số

nào? chî cần nhập 1 giá trð bất

kì thóa mãn điều kiện xác đðnh

là được. Chẳng hän ta chọn số 0

rồi bấm nút =

 

X0

ta chia

(X - 





XA



SHIFT + CALC cho ta



X 1

. 

!  cho

X-1



= máy báo  do

     



0, x 1

Page | 3

5. – MODE 7



 hình dung hình dáng 



ng giá tr: w7

 

fX ?

Nhp hàm cn lp bng giá tr n

ab;





Start? Nhp giá tr bu a

End? Nhp giá tr kt thúc b

Step? Nhc nhy k:





min

tùy vào giá tr cn

ab;





ng là 0,1 hoc 0,5; 1.

Nhng giác, siêu vit cho Step nh:













TALBE: qwR51 

 

Ví dụ:  tìm nghim c

x x x

3 1 1   



MODE 7 TABLE.

 

 

X X 3X X 1 1    f

 =



    





1

 =

     



=

 



0,5.

=

Nguyễn Chiến. 0973514674

Page | 4

 

 Từ bâng giá trð này ta thấy

phương trình cò nghiệm

x 0

và

hàm số đồng biến trên





 



. Do

đò,

0x 

chính là nghiệm duy nhất

của phương trình. Qua cách nhẩm

nghiệm này ta biết được

 

f x x x x

3 1 1    

là hàm số

đồng biến trên





1; 

6. 

+  qy 



 



Vi dụ: Tính đäo hàm

 

f x x x

7

täi

2x

Nhp qy

 





bm=



 

2 39



  f

+ Tính tích phân :  y 

 

và các



Ví dụ: Tính tích phân

 

x x dx

32



Nhp y

 

X X dx

32



. bm =



 

x x dx

3 2 4.



7. Các MODE tính toán



Tên MODE

Thao tác

Tính toán chung

COMP

MODE 1



CMPLX

MODE 2

 

, 



EQN

MODE 5

Page | 5

eo 

TABLE

MODE 7



SHIFT 9 1 = =

 

Kĩ thuật 1: Tính 



* Tp 1 : qy

* T

 

'' lim









   

y x y x

' 0, 000001 '

0, 000001





* 

 

 



Quy trình bấm máy tính đạo hàm cấp 1:

Bước 1:  qy

Bước 2:  thức

 



và ấn =.

Quy trình bấm máy tính đạo hàm cấp 2:

Bước 1: 



Bước 2: 



0,000001xx

Bước 3: 

Ans PreAns

ấn =.

Ví dụ 1: 

 











1

là

2.

Lời giâi



 





 













Phép tính

Quy trình bm máy

Màn hình hin th













qyaQ)+2R

sQ)d+3$$

$1=

Nguyễn Chiến. 0973514674

Page | 6

Vậy

 

0,125









   









Chọn C.

Ví dụ 2: 



y x x

 





    

19.

25.

48.

Lời giâi

Phép tính

Quy trình bm máy

Màn hình hin th

Ti

2





2



qyQ)^4$

psQ)$$2=



2 0,000001x





2 0,000001



!!+0.000

001=

Tính

 

   

' 2 0.000001 ' 2

'' 2

0.000001





nh

Ans PreAns

aMpQMR0.

000001=

Vậy

 



2 48y



Chọn D.

Ví dụ 3: 





 

1 2 1 ln2





 





1 2 1 ln2

 

1 2 1 ln2





 

1 2 1 ln2





Lời giâi

Ta c

x 0,5





0,5X

. 

dx X

0,5











Page | 7

Phép tính

Quy trình bm máy

Màn hình hin th



  





0,5

dx X

qyaQ)+1R

4^Q)$$$0

.5=

t qu

va tìm

c vào

bin A

qJz

Ly A tr t qu tính giá tr các biu thc  u ra 0

thì ch



pa1p2(Q)

+1)h2)R2^

2Q)r0.5=

S

8,562.10 0





. Nếu chưa ra kết quâ là 0 thì thay các đáp án cñn

läi bao giờ ra 0 thì chọn



Chọn A.

Ví dụ 4: 

sin

y e x







F y y'' 2 '





2Fy

Fy

Fy

2Fy

Lời giâi

Phép tính

Quy trình bm máy

Màn hình hin th

Tính

 

y ' 2 0,001

qw4qyQK

^pQ)$jQ)

)$2+0.000

001=qJz

t qu

va tìm

c vào

bin A

qJz

Tính

 

y' 0

E!!ooooo

oooo=qJx

Nguyễn Chiến. 0973514674

Page | 8

t qu

va tìm

c vào

bin B

qJx

Thay vào công thc

 

   

f x x f x

f x C

  





aQzpQxR0

.000001=

qJc

Tính

'' 2 ' 2 0.2461... 2F y y C B y       



Chọn A.

Kĩ thuật 2: MTCT trong bài toán





+ Cách 1 : 





h

+ Cách 2:         

  

   

 

m f x



 

m f x

. Tìm

Min Max,



 



+ Cách 3:         



.

Ví dụ 1:  m 

mx m

2







m21  

m21  

m01

D. 

Page | 9

Lời giâi



 

Dm\



d mX m

dx X m













Gán

X 0

, không gán

Y 0

vì

xm

nên

XY



X, Y 

Gán

Y 2



0



Gán

Y 2



0



Gán

Y 1



Ví dụ 2: 



tan 2

tan



























m 2

12m

m 2

Lời giâi



xttan 





 

f x xtan

Phép tính

Quy trình bm máy

Màn hình hin th

u

kin cho

 

tanf x x

qw4w7lQ

))==0=qK

P4=(qKP4

)P19=



x0 tan 1



 

t 0;1

. 





2







 

0;1

Nguyễn Chiến. 0973514674

Page | 10

Tính :

   

 

t m t

t m t m

  







 

' 0 0 2



    



(1)



 

t m m t m0 0;1     

(2)

















Chọn A.

Kĩ thuật 3: Tìm    và bài toán 

  .

Phương pháp : 





thì

 

'' 0















. 

thì

 

'' 0















Qy



   

f x f x

' : ''



  1:        

  

 

y x mx m x m

3 2 2 2

3 3 1 3 5     



x 1











m 2

1m 

m 0

Lời giâi

Cách 1: i

m 0



x 1

hay không ?

Phép tính

Quy trình bm máy

Màn hình hin th

Ti

x 1

qyQ)^3$p

3Q)+5$1=

Ti

x 1 0,1

!!p0.1=

Ti

x 1 0,1

!!oooo+0

.1=



y '



x 1

0m





A D sai

Page | 11



m 2

Phép tính

Quy trình bm máy

Màn hình hin th

Ti

x 1

qyQ)^3$p

6Q)d+9Q)

p7$1=

Ti

x 1 0,1

!!p0.1=

Ti

x 1 0,1

!!oooo+0

.1=



y '





hàm  



1x 



Chọn B.

Cách 2: 

   

' : ''f x f x

   

 

2 2 2 2

X 1

X YX Y : X YX Y

3 6 3 1 3 6 3 1



      

-  X = 1 

- 



+ Khi

0m

k

x 1

có là ci hay không ?

Phép tính

Quy trình bm máy

Màn hình hin th

Ti

0m

Thay

XY1; 0

3Q)dp6Qn

nQ)+3(Qn

dp1)Qyqy

3Q)dp6Qn

Q)+3(Qnd

p1)$1r1=

Tìm



!!p0.1=

Tìm



Khi

0m

thì

   

ff1 0, 1 6 0

 

  

x 1

là cc tiu loại A,D

Nguyễn Chiến. 0973514674

Page | 12

+ Khi

m 2

k

x 1

có là cc i hay không ?

Ti

2m

Thay

XY1; 2

Phép tính

Quy trình bm máy

Màn hình hin th

Tìm



===2=

Tìm



Khi

2m

thì

   

ff1 0, 1 6 0

 

   

1x

là cc i

 án B. Ta khi

m 1

+ Khi

m 1

k

1x

có là cc i hay không

Ti

m 1

Thay

1; 1XY

Phép tính

Quy trình bm máy

Màn hình hin th

Tìm



====1=

Tìm



Khi

m 1

thì

   

ff1 3 0, 1 0

 

   

1x

không phi là cc tr



Chọn B.

Ví dụ 2: 

y x x

4  

   

Lời giâi

Tính

y x x x' 3 2

















. Dùng MODE 7 vi thit lp

sao cho

chy qua 3 giá tr này ta s khc s i du

ca

y '

Page | 13

Quy trình bm máy

Màn hình hin th

w73Q)qcQ)$p2

Q)=po=p2=2=1

P3=



 

fx'





Chọn C.

Kĩ thuật 4: 





Phương trình đường thẳng đi qua hai điểm cực trð của đồ thð hàm

số

y ax bx cx d

   

có däng :

 

g x y

 





+ Bước 1: Bm w2  chuyn ch  máy tính sang môi

ng s phc.

+ Bước 2: Nhp vào máy tính biu thc:

 





hoc

 

   

 

f x m f x m

f x m

, . ,

 





+ Bước 3: Bm =  u thc.

+ Bước 4: Bm r vi

xi

 s ph làm xut hin

ta bm b)

+ Bước 5: Nhn kt qu dng

Mi N

n tìm

có dng:

y Mx N.

Ví dụ: 



y x x

2 3 1   

là

yx1.

yx1.

yx1.  

yx1.  

Nguyễn Chiến. 0973514674

Page | 14

Lời giâi

Phép tính

Quy trình bm máy

Màn hình hin th

S phc

Nhp vào

máy tính

biu thc

p2Q)qd+

3Q)d+1+(p

Q)d+Q))(

p2Q)+1)

Thay

xi

rb=

K

i 1



yx1  

Chọn B.

Kĩ thuật 5: Tm .

Phương pháp:  r 

  1:            

x x x

2 1 3

   

















3x 













x 3

Lời giâi

ng thng



là tim c ng c  th hàm s u

kin cn :

là nghim cu s bng 0

Nên ta ch qng thng

x 3

và

x 2

Phép tính

Quy trình bm máy

Màn hình hin th

Vi

3x

a2Q)p1ps

Q)d+Q)+3

RQ)dp5Q)

+6r3+0.00

00000001=

Page | 15

Vi

x 2

r2+0.0000

000001=

+ Vi

x 3

xét

x x x

2 1 3

lim



   

  



x 3

là mt tim

cng

+ Vi

x 2

xét

2 1 3

lim

x x x



   

  



Kt qu không ra vô

cùng

x 2

không là mt tim cng



Chọn B.

Ví dụ 2: 





x mx







?

m 1

1m













11m  

Lời giâi







ti



1m 











2 1 0xx  

có



x 1

Tính

lim





  





A sai

Phép tính

Quy trình bm máy

Màn hình hin th

Vi

1m

a5Q)p3RQ

)dp2Q)+1

r1+0Ooo1

0^p6)=



m 0











10





 khi

m 0



Chọn D.

Ví dụ 3: 











?

m 0

B. Không có

 mãn

m 0

0m 

Nguyễn Chiến. 0973514674

Page | 16

Lời giâi

+ A 

m 0



m 2,15

Tính

lim

2.15 1







Phép tính

Quy trình bm máy

Màn hình hin th

Vi

m 2,15

aQ)+1Rsp2

.15Q)d+1

r10^9)=



lim

2.15 1







 



 

2.15 1







không



+ B 

m 0

Tính

 

lim lim 1

 







Phép tính

Quy trình bm máy

Màn hình hin th

Vi

m 0

Q)+1r10^

9)=



 

xlim 1



   



 

yx1

     

ngang

+ D 

m 2.15

Phép tính

Quy trình bm máy

Màn hình hin th

Vi

m 2.15

 x

aQ)+1Rs2.

15Q)d+1r

10^9)=

lim 0.6819943402

2.15 1









Phép tính

Quy trình bm máy

Màn hình hin th

Page | 17

Vi

m 2.15

x

rp10^9)=

lim 0.6819943402

2.15 1





  



.         

ngang

y 0.6819943402



Chọn D.

Kĩ thuật 6: 

– nh nht ca hàm s trên on

ab;





. S

TABLE

 :

1. Nhấn w7

 

fX

 

3. Step ? a

4. End ? b

5. Step?  





;ab



là max min.

*Chú ý:



Start

End

Step (có





x x xsin ,cos , tan ...



Radian: qw4











2;4





là

A. 6 B.

2

3

Lời giâi

Phép tính

Quy trình bm máy

Màn hình hin th

 







w7aQ)d+

3RQ)+1==

Nguyễn Chiến. 0973514674

Page | 18

 

b qua

Bm =

Star ? 2 End ?

4 Step ? 0,2.

kéo xung

để tìm GTNN.

2=4=0.2=

RRRR

Quan sát bảng giá trị tìm kết quả nào gần với đáp án để kết luận



Chọn A.

Kĩ thuật 7: 

– nh nht ca hàm s . SSOLVE









 

y f x

t

 

0f x M

 

f x m 0

- 

SOLVE  



- .

Ví dụ: Tìm giá trị lớn nhất của hàm số

y x x x

2 4 1   

trên đoạn

1;3







max

max 2

max 7

max 4

Lời giải

Các kết quả xếp theo thứ tự

     

247

. Do vậy ta giải phương

trình

x x x

2 4 1

   

Phép tính

Quy trình bm máy

Màn hình hin th

 



Q)qdp2Q)

dp4Q)+1pa

67R27=

Page | 19

Cho

X 2 1;3







=qr2=

c nghim

x 3,33333 1;3







nên loại A.

+ Tiếp theo thay đáp án

max 2

, giải phương trình :

x x x

2 4 1 2    

Phép tính

Quy trình bm máy

Màn hình hin th

 

FX 2

!oooooooo

Cho

X 2 1;3







=qr2=

c nghim

x 2 1;3







nên



Chọn B.



 

2FX



* Chú ý: SOLVE 

TABLE 

.

Kĩ thuật 8: 

 .

 

:.d y kx m

+ 

 

k y x





q y 

 



= k.

+ ! 

 

   

f X x X f X





r 





phím = 

Nguyễn Chiến. 0973514674

Page | 20

Ví dụ 1: 



 













1.



 



là





  

  

Lời giâi

Phép tính

Quy trình bm máy

Màn hình hin th

dx X













qya2Q)+1

RQ)p1$$p

 ! 

 

d X X

dx X X

2 1 2 1















 r với

X 1

 = 

=!(pQ))+a2Q)

+1RQ)p1=

 

là:

  



Chọn B.

Ví dụ 2: 

 

C y x x

: 3 2  





y x y x9 18; 9 22.   

y x y x9 14; 9 18.   

y x y x9 18; 9 22.   

y x y x9 14; 9 18.   

 

2

 

 

X X X

9 3 2   

r 

X 2



 =     

14

d y x

: 9 14.  

Page | 21

 

2

 

 

X X X

9 3 2   

r 

X 2

  =     

d y x

18 : 9 18.  



Chọn B.

Ví dụ 3:     

 

C y x x

: 4 3 1   

  

 

A 1;2



y x y x9 7; 2.     

y x y x9 11; 2.     

y x y9 11; 2.   

y x y9 7; 2.   

 Cho

 

bằng kết quâ các đáp án, từ đò ta thu được các

phương trình.

 Sử dụng chức năng giâi phương trình bậc ba của máy tính bó

túi bằng cách bấm tổ hợp phím w 5 4 và

nhập hệ số

phương trình.

Thông thường máy tính cho số nghiệm thực nhó hơn số bậc của

phương trình là 1 thì ta chọn đáp án đò.

+ Đầu tiên thử với đáp án A, ta cho:

x x x x x

4 3 1 9 7 4 12 6 0.          

Máy tính cho 3 nghiệm



Loäi A.

 Thử với đáp án B, ta cho:

x x x x x

4 3 1 2 4 4 1 0.          

Máy tính cho 3 nghiệm



Loäi B.

 Thử với đáp án B, ta cho:

x x x x x

4 3 1 9 11 4 12 10 0.          

Máy tính hiển thð 1 nghiệm thực và 2 nghiệm phức (phương

trình cò số nghiệm thực là một nhó hơn bậc của phương trình

là 2)



Loäi C.

Thử với đáp án :

x x x x x

4 3 1 9 7 4 12 8 0          

máy tính hiển thị 2 nghiệm

x 1;

x 2

(nhận).

x x x x

4 3 1 2 4 3 1 0        

máy tính hiển thị 2 nghiệm

  

(nhận).



Chọn D.

Nguyễn Chiến. 0973514674

Page | 22

Kĩ thuật 9:  .





 MODE 5 

nh SOLVE

 





y x mx

16  



m 12

m 12

m 0

m 0





y x mx

16  





16 0x mx  



+ 

m 14



Quy trình

bm máy

w541=0=14=16====

Màn hình

hin th



;





 



A

+ 

m 14



Quy trình

bm máy

w541=0=4o14

=16====

Page | 23

Màn hình

hin th





B C



m 1



m 1





Chọn B.

Ví dụ 2: 



 

x x m

log log 2  



m1    

m1    

m0    

m0    





   

x x f x

log log 2  

 

m f x

  

  m thì

    

 

hay

   

f m fmin max





ODE 7 



là Start 2 End 10 Step

0.5



   

f X X X

log log 2  

Quy trình bm máy

Màn hình hin th

w7i2$Q)$pi2$

Q)p2==2=10=0.



 



 

f 10 0.3219

A và

B 



 





 



 



 

fx 0





Nguyễn Chiến. 0973514674

Page | 24

Quy trình bm máy

Màn hình hin th

i2$Q)$pi2$Q)

p2qr3=

Máy vô = 

 

0fx

m 0



Chọn D.

Ví dụ 3:      

  

x x x

m5.16 2.81 .36

?

m 0











C 

D 

Lời giâi

Ta có

x x x

m5.16 2.81 .36

5.16 2.81





t

 

5.16 2.81





. Khi u

 

f x m



 

y f x



9

End

Step



 

5.16 2.81





Quy trình bm máy

Màn hình hin th

w7a5O16^Q)$p

2O81^Q)R36^Q

)==p9=10=1=

Quan sát bng giá tr ta thy

 

luôn gim hay hàm s

 

y f x

luôn nghch bin. u này có nghng thng

ym

luôn

c th hàm s

 

y f x

tm



Chọn C.

Page | 25

Kĩ thuật 10: Tìm 



+Bước 1:  





0

+Bước 2:         



Ví dụ 1:  

x x x x x x x x x

2 4 6 2 4 4 6 6 2

log log log log log log log log log  

:

 

2;4;6

 

1;12

 

1;48

Lời giâi





X X X X

2 4 6 2 4 4 6 6 2

log X log X log log X log log X log log X log  

Quy trình bm máy

Màn hình hin th

i2$Q)$i4$Q)$

i6$Q)$pi2$Q)

$i4$Q)$pi4$Q

)$i6$Q)$pi6$

Q)$i2$Q)

Vì nên CALC X=1

Quy trình bm máy

Màn hình hin th

r1=



hay không

r12=









Nguyễn Chiến. 0973514674

Page | 26

r48=





Chọn D.

Ví dụ 2: 

9 3.3 2 0  



 

xx



23A x x

là

4 log 2

3log 2

2log 3

Lời giâi

* Cách 1 : SHIFT SLOVE + CALC

Quy trình bm máy

Màn hình hin th

9^Q)$p3O3^Q)

$+2=





ò 

 



qr1=





qJz

C



2



Eqrp2=

       

A0 

nên

x x A

0;

ta có

Page | 27

x x A

1 2 3

2 3 2.0 3. 1.8927 3log 2    



Chọn C.

* Cách 2 

N



Quy trình bm máy

Màn hình hin th

9^Q)$p3O3^Q)

$+2=qr1=qJz

Quay  



Eqrp1=

Ta có

2 3 1.8927 3log 2AB  



Chọn C.

Kĩ thuật 11: - logarit.



+ Bước 1: Chuyển phương trình về däng Vế trái = 0

+ Bước 2: Sử dụng chức năng MODE 7 để xét lập bâng giá trð

của vế trái .

+ Bước 3: Quan sát và đánh giá :

- Nếu

 

F 0





thì



là 1 nghiệm

- Nếu

   

F a F b.0

thì phương trình cò 1 nghiệm thuộc

 

ab;

 

x x x

6.4 12.6 6.9 0  

là

A. 3 B. 1 C. 2 D. 0

Lời giâi

 MODE 7 

Quy trình bm máy

Màn hình hin th

w76O4^Q)$p12

O6^Q)$+6O9^

Nguyễn Chiến. 0973514674

Page | 28



là : Start

9

End

Step

==p9=10=1=



0x 

thì

 

00F 



x 0





 



làm cho

 

FX 0

    

 

  

x 0

là 



Chọn B.

       

sin

tan













 

0;2







là

Lời giâi



sin

tan 0

















Step





Quy trình bm máy

Màn hình hin th

qw4w7QK^jQ)

paQKR4$)$plQ

))==0=2qK=2q

KP19=



   

ff0.6613 . 0.992 0





 

0.6613;0.992

   

ff1.3227 . 1.6634 0





 

1.3227;1.6534

Page | 29

   

ff3.6376 . 3.9683 0





 

3.6376;3.9683

   

ff4.6297 . 4.9604 0





 

4.6297;4.9604

   



Chọn D.

Kĩ thuật 12: - logarit.

  1: CALC

+Bước 1: 

             



0



0

+ Bước 2: 

 toán .

*Chú ý:



 

;ab

   

 

;ab



 

ab;

và

 

cd,



   

a b c d,,

thì

 

cd,

.



+ Bước 1: 

             



0



0

+ Bước 2: 





: ng trình

log log 0















 

;2  

 

4; 

   

2;1 1;4

   

; 2 4;     

Lời giâi

Cách 1 : CALC



Quy trình bm máy

Màn hình hin th

ia1R2$$i3$a2

Q)+1RQ)p1

Nguyễn Chiến. 0973514674

Page | 30

A



2 0.1X   



rp2p0.1=





10X 

rp10^5)=

 mãn, A 

B thì ta

 B   A  B   A



B   



Chọn D.

Cách 2: MODE 7 

Quy trình bm máy

Màn hình hin th

w7ia1R2$$i3$

a2Q)+1RQ)p1



2;4;1





sao cho



Start

4

End 5 Step 0.5

==p4=5=0.5=

          

 

;2  

và

 

4; 

l  



Chọn D.

Kĩ thuật 13: Tính giá  - logarit.



Page | 31

+ Bước 1 : 



+ Bước 2 : 

A B C,,

  

+ Bước 3 : 

Ví dụ 1: Cho

a b c

27 8 2

log 5; log 7; log 3  

. Tính

log 35

theo a, b, c ?

b ac



b ac



b ac



b ac



Lời giâi

log 5

qJz 

log 7

qJx    

log 3

qJc (Gán gi  

log 35

qJpj   



B AC









Qjpa3Qx+2QzQcRQc+2=



0,21





B AC







Qjpa3Qx+3QzQcRQc+2=

Đáp án bằng 0



Chọn B.

Ví dụ 2: Cho

 

x y x y

9 12 16

log log log  



là





Lời giâi



9 12

log log

log

12

. Thay 

 

9 16

log logx x y



 

log

9 16

log log 12 0  



 

log

9 16

log log 12 0  

 SOLVE

Quy trình bm máy

Màn hình hin th

i9$Q)$pi16$Q

)+12^i9$Q)$$

$qr1=

Nguyễn Chiến. 0973514674

Page | 32



qJz

Tính được giá trị

log

12

12^i9$Qz=





qJx

Tỉ số



aQzRQx=



0,6180339887







Chọn B .

Kĩ thuật 14:  



Phương pháp:

Phần nguyên của một số: số N được gọi là phần nguyên của một

số A nếu

N A N 1  

. Kí hiệu







Phím Int: Q+ Phần nguyên của một số.

Số chữ số của một số nguyên dương:

Alog 1







: ?

2003 2500

11 9

693 600

23 25

445 523

29 31

445 523

29 31

Bài giâi

Quy trình bm máy

Màn hình hin th



2003

và

2500



Page | 33

Q+2003g11))

+1=

Q+2500g9))+1=



2500



2003

nên

2500 2003

9 11



A sai



693

và

600



Q+693g23))+1=

Q+600g25))+1=



693



600

nên

693 600

23 25



B sai

 

445

và

523

:

Q+693g23))+1=

Q+600g25))+1=



445

n

523

nên

445 523

29 31



Chọn C.

Ví dụ 2: 





phân và







mn

là

Lời giâi



30 30

2 10 log2  

Nguyễn Chiến. 0973514674

Page | 34



   

k 1







Quy trình bm máy

Màn hình hin th

Q+30g2))+1=







30 900 2 log 900

h   





là

h 1







Quy trình bm máy

Màn hình hin th

Q+i2$900$)+



  

mn10 10 20    



Chọn B.

Ví dụ 3 : 



21



          

  

phân?

1243

1234

2452

2467





có d

21

. 

21





21

  

trong





 

2 13

2 10 2 log 2  

 



phân là

k 1







Quy trình bm máy

Màn hình hin th

Q+2^13$g2))

+1=



Chọn D.

Page | 35

Kĩ thuật 15: Tính nguyên hàm



 

 



   

 

f A F x







.

Ví dụ: 

 

1 ln







1 ln





1 ln





1 ln





1 ln





Lời giâi



 

1 ln





   



 3X



Quy trình bm máy

Màn hình hin th

ap2RQ)(1+hQ)

))dr3=

qJz

K



  









1 lnX

Quy trình bm máy

Màn hình hin th

pqya1+hQ))R1

phQ))$$3=



B



  









1 lnX

Nguyễn Chiến. 0973514674

Page | 36



Quy trình bm máy

Màn hình hin th

!!!!!!!!o+

E!!!op=





Chọn B.

Kĩ thuật 16: 



+  y

Ví dụ 1: Tích phân

 

x x dx

3 1 2







Lời giâi

n

 

x x dx

3 1 2



Chú ý: G qc

Quy trình bm máy

Màn hình hin th

y(qc3Q)p1$p2

qcQ)$)R0E1

= 

phân là

I 0,016666589

qJz

Page | 37







Chọn A.

Ví dụ 2:       

 

y x y x xln 1 , ln2. , 2   





ln 16. 2 1 3 ln 3 1  





ln2. 2 1 3ln 3 1

   

16 4

ln 2 ln 2 1

27 3



16 4

ln ln2 1

27 3



Lời giâi



x 2

.  SHIFT SOLVE 



 

xxln 1 ln2. 0   

Quy trình bm máy

Màn hình hin th

hQ)+1)ph2sQ)

$)qr=



x 1

. 

xx1; 2



 

yxln 1

yxln2.



xx1; 2

là

 

S x x dx

ln 1 ln2.  



Quy trình bm máy

Màn hình hin th

yqchQ)+1)ph2

)OsQ)R1E2=

 

các  

Quy trình bm máy

Màn hình hin th

qJz

Nguyễn Chiến. 0973514674

Page | 38

Thay 

Qzp(hqs16$(

s2$+1)p3h3)+

1)=



Qzp(pa4R3$h2

)(s2$+1)+3h3)

p1)=





Chọn B .

Ví dụ 3: Cho

:

y x y x xsin ; 0; 0;



   

. Khi

quay quanh



    



Lời giâi



yxsin



y 0



x 0













V x dx

sin 0







Quy trình bm máy

Màn hình hin th

qw4qKyqcjQ)

)R0EaqKR2=







Chọn B

Ví dụ 4 : 

a b c

ln2 ln 3 ln 5  







a b c,,



Tính

S a b c  

S 6

S 2

S 2

S 0

Lời giâi

Page | 39

Tính tích phân





 n

Quy trình bm máy

Màn hình hin th

ya1RQ)d+Q)R3

E4=

qJz

Khi đó

 

a b c a b c A

A a b c A e

ln2 ln 3 ln5 ln 2 .3 .5 2 .3 .5

       

QK^Qz=

Ta có:

a b c

a b c S

4 1 1

16 2.2.2.2

2 .3 .5 2 .3 .5 4; 1; 1 2

15 3.5



          



Chọn B.

Ví dụ 5 : Cho

 

I x dx a b c

ln 1 ln 3 ln2    



 

a b c Z,, 





23a b c

Lời giâi



 

I x dx

ln 1





Quy trình bm máy

Màn hình hin th

yhQ)+1)R1E2=

qJz



a b c A a b c A a b

a b c A e e e e

ln 3 ln2 ln(3 .2 . ) ln 3 .2 . 3 .2        



3 .2



 

3 .2

Nguyễn Chiến. 0973514674

Page | 40

Quy trình bm máy

Màn hình hin th

w7aQK^QzRQK

^Q)==p9=10=



 



. 

1Xc  

thì

ab 32

3 .2 6.75 3 .2



  

ab3; 2   



a b c2 3 3 4 3 2     



Chọn C.

Kĩ thuật 17: 





+ w2 (CMPLX).

+ La s phc là qc

+ 

là q22

+ q21

1: arg: 

z a bi

2: Conjg: 

z a bi





: 

z a bi





agrment

a bi

:   

z a bi

     



Ví dụ 1: Tìm số phức liên hợp của số phức

z i i(3 1)

zi3

zi3  

zi3

zi3  

Lời giải

 w2  q22.



 

ii31

 =.

Quy trình bm máy

Màn hình hin th

Page | 41

w2q22b(3b+1)=

zi3  



Chọn D.

Ví dụ 2: Ta s phc tha mãn

 

i z i i1 3 3 7 2   

z 1

 4z

 2z



Lời giâi

z 

7 2 3







Quy trình bm máy

Màn hình hin th

w2qca7bp2p3b

R1p3b=



 2z



Chọn C.

Ví dụ 3: 



z 1

  

1 





1

Lời giâi

t s phc

z a bi

thì

z a b

1  

Chn

a 0.5

0.5 1  

. S dng ch 

tìm

 này vào

Quy trình bm máy

Màn hình hin th

w1s0.5d+Q)d$

p1qr0.5=

qJx

Tr li ch   tính giá tr

1 

Nguyễn Chiến. 0973514674

Page | 42

Quy trình bm máy

Màn hình hin th

w2a1R1p(0.5+

Qxb)=

Vy phn thc ca

là



Chọn A.

Kĩ thuật 18:  

Phương pháp

Cách 1: w2. Bình 



Cách 2: w2.

+ z Ans

+ :

sqcM$$qz21M)a2

+ Nh= z.



Cách 3: w1.

+ q+ Pol( 

=q).

+qp 

XRec ,









= 

Ví dụ : 

   

i z i i1 2 4 2 2 9    

i22

i12

i12

i12

Lời giải

 w2 thu 

Page | 43

Quy trình bm máy

Màn hình hin th

Ca4bp2p(2b+9)

R1p2b=

z 

zi34  

Cách 1:  

Cách 2: Bật chế độ w2.

Quy trình bm máy

Màn hình hin th

sqcM$$qzaq21

M)R2=

Vậy số phức cò một căn bậc hai là

zi12



Chọn B.

Cách 3: w1.



 

Pol 3, 4

 = t





XRec , Y : 2

 =

Quy trình bm máy

Màn hình hin th

q+p3q)p4)=

qpsQ)$q)QnP2

Vậy số phức cò một căn bậc hai là

12zi



Chọn B.

Kĩ thuật 19: C 

Phương pháp:

Bật chế độ w2. Nhập số phức vào màn hình rồi ấn q23

được





. Trong đó r là môđun,



là góc lượng giác.

Ngược lại, bấm





rồi bấm q24.

Ví dụ: Cho 

13zi

. Tìm góc z?



Lời giâi

 w2 

q23  qw4

Quy trình bm máy

Màn hình hin th

Nguyễn Chiến. 0973514674

Page | 44

w21+s3$bq23=

qw4



Chọn C.

Kĩ thuật 20: 





t

z x yi

, biu din s phc theo yêu c bài, t 

và thu v mt h thc mi :

+ Nu h thc có dng

Ax By C 0  

thì tp hm là

ng thng

+ Nu h thc có dng

   

x a y b R

   

thì tp hp

ng tròn tâm

 

I a b;

bán kính

+ Nu h thc có dng

1

thì tp hm có dng

mt Elip

+ Nu h thc có dng

1

thì tp hm là mt

Hyperbol

+ Nu h thc có dng

y Ax Bx C

  

thì tp hm là

mt Parabol

+ m i din thuc qu tích cho  i th

 bài, nu th

Đường thẳng thay 2 điểm, đường cong thay 3 điểm.

Ví dụ 1: 



 

i z i13  







M N P Q, , ,

A

B

C

D

Lời giâi

Page | 45

S d tìm

Quy trình bm máy

Màn hình hin th

w2a3pbR1+b=

zi12  

m biu din

trong h trc thc o có t

 

1; 2

m có tho âm s nm  góc ph IV



m phi tìm là



Chọn B.

Ví dụ 2 : 



z i z i22   

xy4 2 1 0  

xy4 2 1 0  

xy4 2 1 0  

xy4 6 1 0  

Lời giâi

Gi s phc

có dng

z a bi

. Ta him

biu din s

phc

thì

có t

 

M a b;

Gi s A 

thung thng

xy4 2 1 0  

thì

ab4 2 1 0  

Chn

a 1

thì



zi1 2.5  

. S phc

tha mãn

z i z i22   

thì

z i z i2 2 0    

Quy trình bm máy

Màn hình hin th

qc1+2.5bp2pb

$pqc1p2.5b+2

Ta thy ra mt kt qu khác 0 Loi A.

 v B chn

a 1

thì

b 1.5

và

zi1 1.5

Quy trình bm máy

Màn hình hin th

qc1+1.5bp2pb

$pqc1p1.5b+2

Nguyễn Chiến. 0973514674

Page | 46

Kt qu ra 0 vy

z i z i2 2 0    



Chọn B.

Ví dụ 3: 



z 4

 



 

w i z i34  



bán kính



r 4

r 5

r 20

r 22

Lời giâi

 tìm ng tròn ta cn m biu din ca

, vì

s sinh

u tiên ta s chn 3 giá tr i din ca

tha mãn

z 4

+ Chn

zi40

(tha mãn

z 4

). Tính

  

w i i i

3 4 4 0   

Quy trình bm máy

Màn hình hin th

(3+4b)O4+b=

m biu din ca

là

 

M 12;17

+ Chn

zi4

(tha mãn

z 4

). Tính

  

w i i i

3 4 4  

Quy trình bm máy

Màn hình hin th

(3+4b)O4b+b=

m biu din ca

là

 

N 16;13

Chn

zi4

(tha mãn

z 4

). Tính

  

w i i i

3 4 4   

Quy trình bm máy

Màn hình hin th

(3+4b)(p4b)

+b=

m biu din ca

là

 

P 16; 11

Vm

M N P,,

thung tròn biu din s phc

Page | 47

ng tròn này s có dng tng quát

x y ax by c

0    

 tìm

a b c,,

ta s dng máy tính Casio vi ch

Quy trình bm máy

Màn hình hin th

w5212=17=1=p

12dp17d=p16=

13=1=p16dp13

d=16=p11=1=p

16dp11d==

Png tròn :

 

x y y x y

2 2 2 2

2 399 0 1 20       

ng tròn tp hm biu din s phc

là 20



Chọn C.

Kĩ thuật 21: . K

 CALC và CALC: 100+ 0,01i

Phương pháp

 

 

c).

+ 

z z z; ; ...



XY100; 0,01

  

Ví dụ 1: 

 

z i z i

5 8 0    



z i z i3 ; 3    

z i z i1 3 ; 1 3    

z i z i3 2 ; 2   

z i z i1 ; 1    

Quy trình bm máy

Màn hình hin th

Nguyễn Chiến. 0973514674

Page | 48

w2Q)dp(5pb)Q

)+8pbr3+b=



13zi

p1+3b=



32zi

r3p2b=



zi2

r2+b=



Chọn C.

Ví dụ 2 : 



10  







Lời giâi

Tính nghim cc hai

10  

bng chc



Quy trình bm máy

Màn hình hin th

w531=p1=1==





và



 



Page | 49

Quy trình bm máy

Màn hình hin th

w2qca1R2$+as

3R2$b$+qca1R

2$pas3R2$b=

2  



Chọn B .

Ví dụ 3: 

   

i z i z i1 2 11    

. Tính

Lời giâi

Nh vi

z X Yi z X Yi;   

CALC

XY100; 0,01

Quy trình bm máy

Màn hình hin th

w2(1+b)(Q)+Q

nb)+(2pb)(Q)

pQnb)r100=0.

01=

Ta có kt qu v trái

299,98 0,01 i

Phân tích

xy299,98 300 0,02 3 2   

và

i yi0,01 

ng nht v trái và v phi cho phn thc và phn o bng nhau

x y x

z i z

3 2 11 3

3 10



  



     



   







Chọn C.

Cách 2 : Xem công thc gii nhanh s phc. Cho s phc z tha

mãn:

az bz c

thì :

ca cb









Chọn C .

Kĩ thuật 22:  



Phương pháp

  = 

Ans

Nguyễn Chiến. 0973514674

Page | 50

+ 

 

f '



Ans

= 



+ -et:

. 

Ví dụ: 

 

z i z i

2 3 4 18 0    

. Tính giá



2

34.

54.

27.



=



 

f '



Ans

= 

.

Quy trình bm máy

Màn hình hin th

w21=paMd+(2+

3b)Mp4+18bR2M

+2+3b

Page | 51

= 

2 4 .zi





2 4 .

Tìm n . Theo vi-et



:

Quy trình bm máy

Màn hình hin th

ap4+18bR2p4b=

Vậy



2 4 ;zi

4  

2 54  



Chọn C.

Kĩ thuật 23: 



+ Lng vecto MODE 8

+ Nhp thông s vecto MODE 8 1 1

+ ng ca 2 vecto : vectoA SHIFT 5 7 vectoB

+ ng ca hai vecto : vectoA vectoB

+ Lnh giá tr tuyi SHIFT HYP

L ln mt vecto SHIFT HYP

* Chức năng w8 (VECTOR).



N1 

1 Oxyz.

Ví dụ

     

  

1;2;3 , 3;2;1 ; 4;5;6a b c

Nguyễn Chiến. 0973514674

Page | 52



 

a 1;2;3

thì  1=2=3=.



w8213=2=1=

Tính tích có hướng của vecto A và B bấm như sau:

Cq53q54=

Tính tích vô hướng của hai vecto A và B bấm như sau:

Cq53q57q54=

Để tính tích hỗn tạp của ba vecto thì sẽ nhập thêm dữ liệu cho

vectoC.

Cq51314=5=6=

C(q53Oq54)q57q55=

Để tính độ dài vecto A, bấm qcq53=

Ví dụ 1: 

Oxyz

cho

 

A 1;2;0

 

B 3; 1;1

 

C 1;1;1

 

 giác

ABC

S 3

S 2



Lời giâi

Nhp 2 vecto

AB AC,

vào máy tính Casio

Page | 53

Quy trình bm máy

Màn hình hin th

w8112=p3=1=w

8210=p1=1=

Diện tích tam giác

ABC

S AB AC







Quy trình bm máy

Màn hình hin th

Wqcq53Oq54

)P2=

ABC

S 1.732050808... 3  



Chọn A.

Ví dụ 2 : Cho

 

A 2; 1;6

 

B 3; 1; 4  

 

C 5; 1;0

 

D 1;2;1

. 



ABCD



Lời giâi

Th tích t din

ABCD

V AB AC AD

;







Quy trình bm máy

Màn hình hin th

w811p5=0=p10

=w8213=0=p6=

w831p1=3=p5=

Wqcq53q57(q

54Oq55))P6=

V AB AC AD

; 30



  





Chọn A.

Ví dụ 3. 

x y z3 1 3

2 1 1

  

  





 

P x y z: 2 5 0   

Nguyễn Chiến. 0973514674

Page | 54

Lời giâi

ng thng



có vecto ch 

 

u 2;1;1

và mt phng

 

có

vecto pháp tuyn

 

n 1;2; 1

Gi



là góc gia gi

un,

. Ta có

 

cos





Quy trình bm máy

Màn hình hin th

w8112=1=1=w8

211=2=p1=Wqc

q53q57q54)P(

qcq53)Oqcq5

4))=

qjM)=

Gi



là góc ging thng



và mt phng

 

sin cos 0.5



  







Chọn A.

Ví dụ 4: 

Oxyz



x y z

1 2 2

  







 

M 2;1; 1



Lời giâi

Khong cách t

n

tính theo công thc :

 

MN u

d M d

;







Nhp hai vecto

MN u,

vào máy tính.

Quy trình bm máy

Màn hình hin th

Page | 55

w8111p(p2)=2

p1=p2pp1=w82

11=2=p2=

Tính

 

MN u

d M d

;







Quy trình bm máy

Màn hình hin th

Wqcq53Oq54)P

qcq54)=

 

d M d

; 2.357022604

  



Chọn D.

Ví dụ 5 : hai :

x y z

1 2 3

1 1 1

  





và

d y t

' : 1 2

















Lời giâi

 

Md1; 2;3

và

có vecto ch 

 

u 1;1; 1

 

Md' 0;1;6 '

và

có vecto ch 

 

u ' 1;2;3

Ta có

 

1;3;3

. Hai ng thng trên chéo nhau



Khong cách cn tìm là

 

MM u u

d d d

' , '











Quy trình bm máy

Màn hình hin th

Nguyễn Chiến. 0973514674

Page | 56

w811p1=3=3=w

8211=1=p1=w8

311=2=3=Wqcq

53q57(q54q55

))Pqcq54q55

 

MM u u

d d d

' , '

; ' 2,160246899...





  







Chọn D.

Bấm Tải xuống để xem toàn bộ.

| 1/56

| | Tải xuống

Preview text:

KỸ THUẬT SỬ DỤNG MÁY TÍNH
CẦM TAY CASIO - VINACAL
I. MỘT SỐ CHỨC NĂNG CHÍNH MÁY TÍNH CẦM
TAY PHỤC VỤ KÌ THI THPTQG
1. Những quy ước mặc định
+ Các phím chą màu trắng thì çn trực tiếp.
+ Các phím chą màu vàng thì çn sau phím SHIFT.
+ Các phím chą màu đỏ thì çn sau phím ALPHA.
2. Bấm các kí tự biến số
Bçm phím ALPHA kết hợp vĉi phím chăa các biến.
+ Để gán mût sø vào ô nhĉ A gõ:
SỐ CẦN GÁN → q → J (STO) → z [A]
+ Để truy xuçt sø trong ô nhĉ A gõ: Qz
Biến số A Biến số B Biến số C ..... Biến số M .....
3. Công cụ CALC để thay số
Phím CALC cò tác dĀng thay sø vào mût biểu thăc.
Ví dụ: Tính giá trð cþa biểu thăc 2 log x2 5
 7 täi x  2 ta thĆc hiện 3
các bāĉc theo thă tĆ sau:
Bước 1: Nhêp biểu thăc 2 2 log 5X  7 3
Bước 2: Bçm CALC. Máy hói X? Ta nhêp 2. Page 1 |
Bước 3: Nhên kết quâ bçm dçu = 2 2 9 log 5x  7  3 4
4. Công cụ SOLVE đề tìm nghiệm
Bçm tù hợp phím SHIFT + CALC nhêp giá trð biến muøn tìm
Ví dụ: Để tìm nghiệm cþa phāćng trình: 2 2 x x x x 2 2  4.2  2 x  4  0
ta thĆc hiện theo các bāĉc sau:
Bước 1: Nhêp vào máy : 2 2 X  X X X 2 2  4.2  2 X  4  0
Bước 2: Bçm tù hợp phím SHIFT + CALC
Máy hói Solve for X cò nghïa là
bän muốn bắt đầu dñ nghiệm
với giá trð của X bắt đầu từ số
nào? chî cần nhập 1 giá trð bất
kì thóa mãn điều kiện xác đðnh
là được. Chẳng hän ta chọn số 0 rồi bấm nút =
Bước 3: Nhên nghiệm: X  0
Để tìm nghiệm tiếp theo ta chia
biểu thăc cho (X - nghiệm
trāĉc), nếu nghiệm lẻ thì lāu
biến A, chia cho X  A tiếp tĀc
bçm SHIFT + CALC cho ta
đāợc 1 nghiệm X  1. Nhçn nýt
! sau đò chia cho X-1 nhçn
dçu = máy báo Can’t Sole do
vêy phāćng trình chî cò hai
nghiệm x  0,x  1 1 2
Nguyễn Chiến. 0973514674 Page 2 |
5. Công cụ TABLE – MODE 7
Table là cöng cĀ quan trõng để lêp bâng giá trð . TĂ bâng
giá trð ta hình dung hình dáng cć bân cþa hàm sø và nghiệm cþa đa thăc.
Tính năng bâng giá trị: w7
f X   ? Nhêp hàm cæn lêp bâng giá trð trên đoän a  ;b  
Start? Nhêp giá trð bít đæu a
End? Nhêp giá trð kết thúc b Step? Nhêp bāĉc nhây k: b  a k  min 25
tùy vào giá trð cþa đoän a  ;b 
 , thöng thāĈng là 0,1 hoðc 0,5; 1.
Nhąng bài cho hàm lāợng giác, siêu việt cho Step nhó: b  b  b  a  a a k ; k  ; k  10 19 25
Kéo dài bâng TALBE: qwR51 để bó đi g x
Ví dụ: Để tìm nghiệm cþa phāćng trình: x3  x 4 3  x  1  1
ta thĆc hiện theo các bāĉc sau:
Düng tù hợp phím MODE 7 để vào TABLE.
Bước 1: Nhêp vào máy tính f   3 4 X  X  3X  X 1 1 Sau đò bçm = Bước 2:
Màn hình hiển thð Start? Nhêp 1  . Bçm = 
Màn hình hiển thð End?  Nhêp 3. Bçm = 
Màn hình hiển thð Step? 0,5. Bçm = Page 3 |
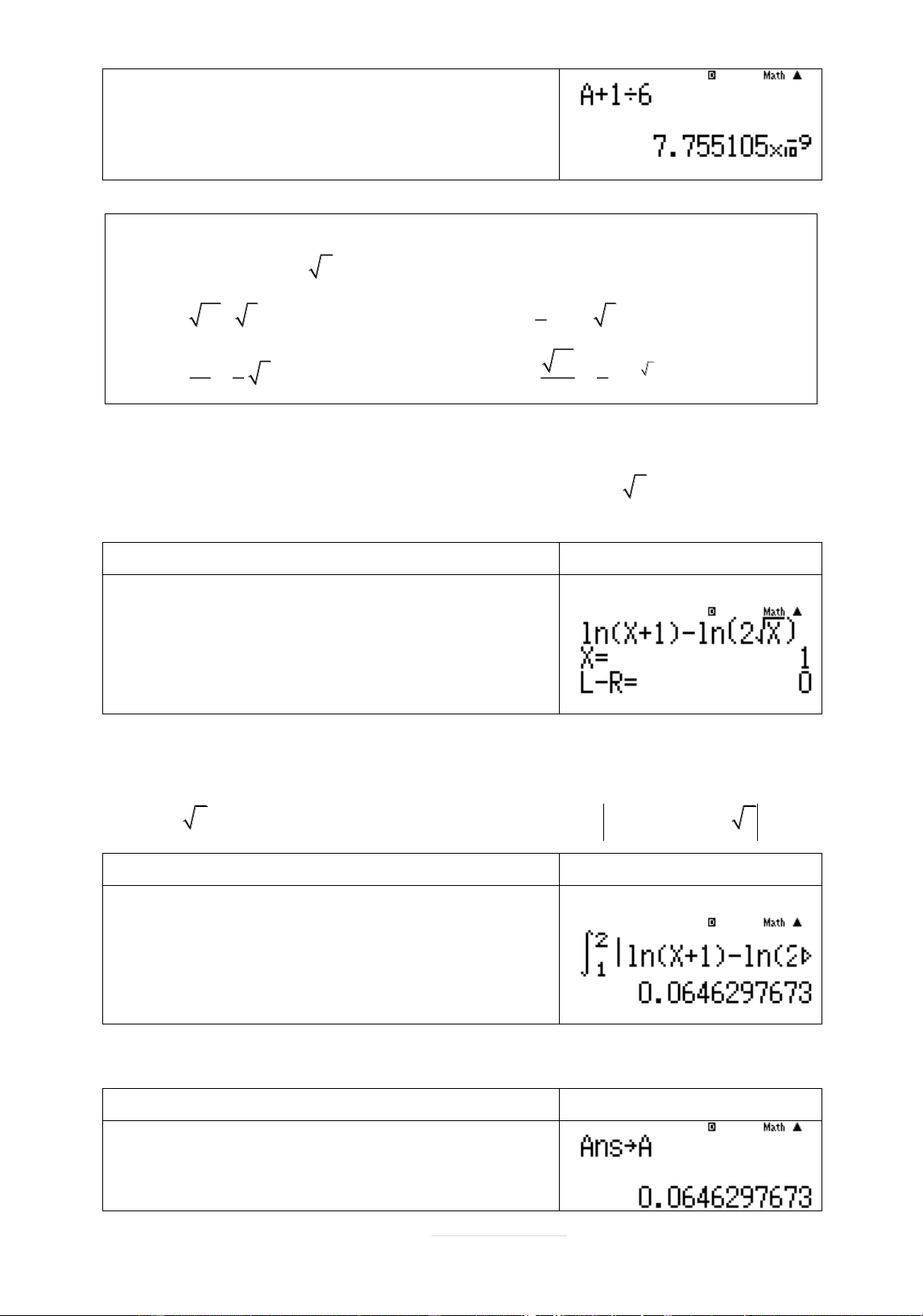
Bước 3: Nhên bâng giá trð 
Từ bâng giá trð này ta thấy
phương trình cò nghiệm x  0 và
hàm số đồng biến trên  1  ;  . Do
đò, x  0 chính là nghiệm duy nhất
của phương trình. Qua cách nhẩm nghiệm này ta biết được
f x   x3  x 4
3  x  1  1 là hàm số
đồng biến trên  1  ;. 6.
Tính đạo hàm tích phân
+ Tính đạo hàm tại 1 điểm: Nhêp tù hợp phím qy sau đò
nhêp hàm f x täi điểm cæn tính
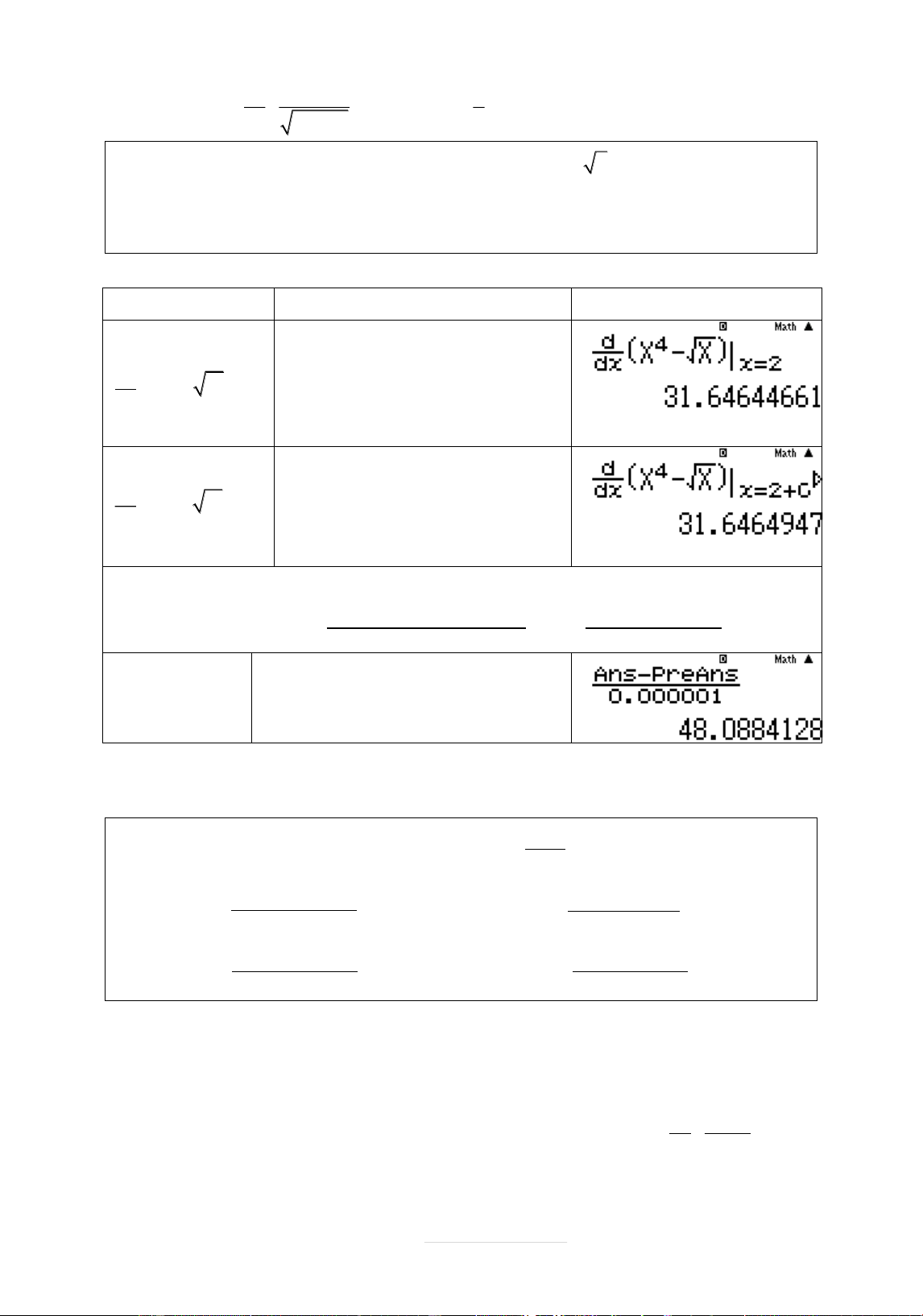
Vi dụ: Tính đäo hàm f x  x4  x 7 täi x  2  Nhêp qy
d X4  7X bçm= x dx 1  Vêy f  2    3  9
+ Tính tích phân : Nhêp phím y sau đò nhêp hàm f x và các cên tích phån 2
Ví dụ: Tính tích phân  x2 3  x 2 dx 0 2
Nhêp y  X2 3  X 2 dx . bçm = 0 2 Vêy  x2 3  x 2 dx  4. 0 7. Các MODE tính toán Chức năng MODE Tên MODE Thao tác Tính toán chung COMP MODE 1 Tính toán vĉi sø phăc CMPLX MODE 2 Giâi phāćng trình bêc 2,
bêc 3, hệ phāćng trình bêc EQN MODE 5 nhçt 2, 3 èn
Nguyễn Chiến. 0973514674 Page 4 |
Lêp bâng sø theo biểu thăc TABLE MODE 7
Xòa các MODE đã cài đðt SHIFT 9 1 = =
II. MỘT SỐ KĨ THUẬT SỬ DỤNG MÁY TÍNH
Kĩ thuật 1: Tính đạo hàm bằng máy tính Phương pháp:
* Tính đạo hàm cấp 1 : qy
* Tính đạo hàm cấp 2 :
y ' x  0,00000  1  y ' x 0 0    ' ''  lim  0  y y x x  0 x  0, 000001
* Dự đoán công thức đạo hàm bậc n :
+ Bāĉc 1 : Tính đäo hàm cçp 1, đäo hàm cçp 2, đäo hàm cçp 3
+ Bāĉc 2 : Tìm quy luêt về dçu, về hệ sø, về sø biến, về sø mÿ r÷i
rýt ra cöng thăc tùng quát.
Quy trình bấm máy tính đạo hàm cấp 1: Bước 1: Ấn qy Bước 2: Nhêp biểu d thức f X và ấn =. X x dx 0
Quy trình bấm máy tính đạo hàm cấp 2:
Bước 1: Tính đäo hàm cçp 1 täi điểm x  x0
Bước 2: Tính đäo hàm cçp 1 täi điểm x  x 0,000001 0
Bước 3: Nhêp vào máy tính Ans - PreAns ấn =. X
Ví dụ 1: Hệ sø gòc tiếp tuyến cþa đ÷ thð hàm sø C x  y  2 : täi 2 x  3
điểm cò hoành đû x  1 là 0 A. 1 B. 7 . C. 1 . D. 2.  4 2 8 Lời giâi Hệ sø gòc tiếp tuyến
d  X  2 
k  y Nhêp vào máy tính     1 dx  
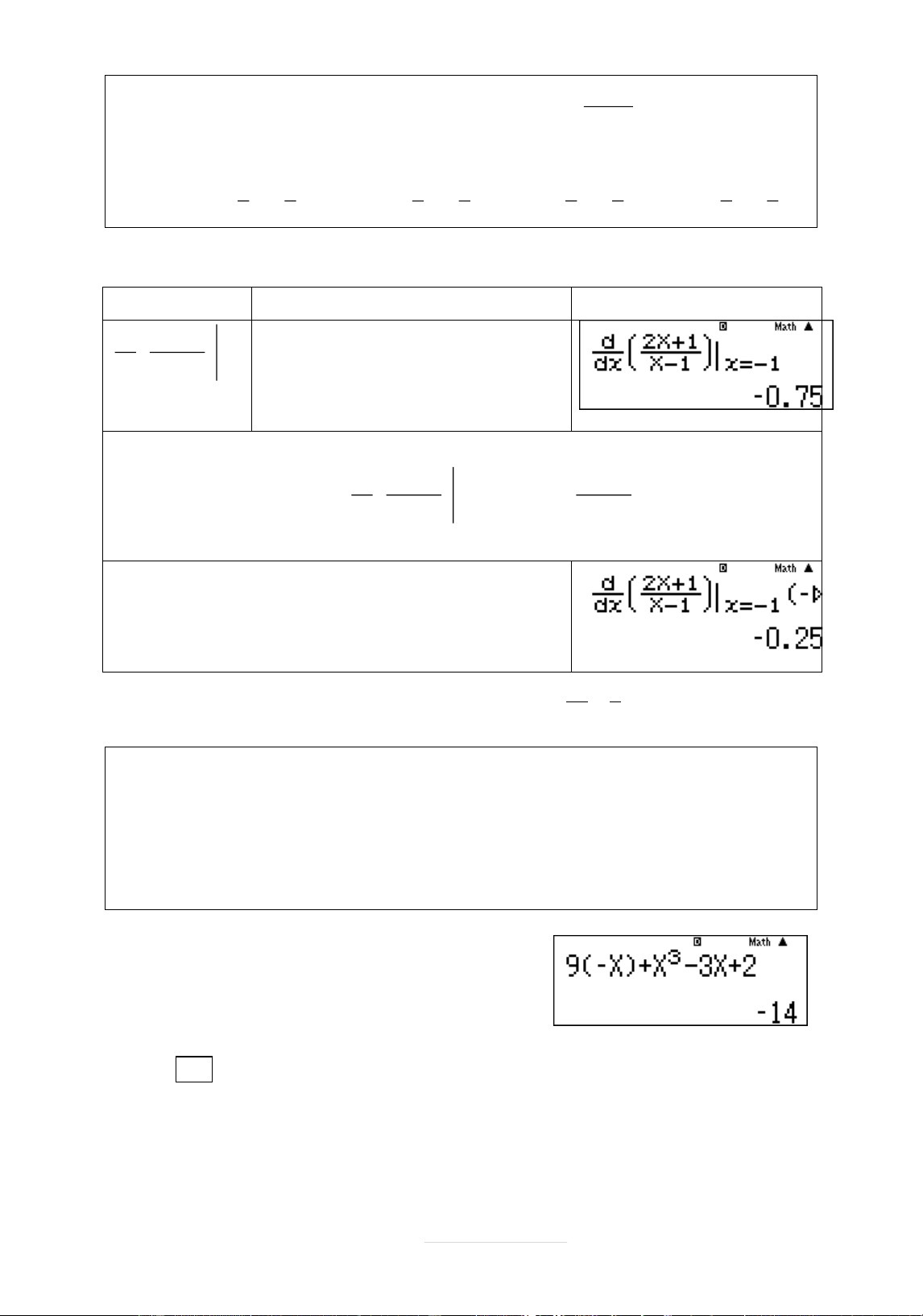
 X2  3 X 1 Phép tính Quy trình bçm máy Màn hình hiển thð  d X   qyaQ)+2R  2   sQ)d+3$$ 2 
dx  X  3 X1 $1= Page 5 | Vậy
d  X  2  1
k  y      0,125   Chọn C. 1 dx    X2 8  3 X 1
Ví dụ 2: Đäo hàm cçp 2 cþa hàm sø  4 y
x  x täi điểm cò hoành
đû x  2 gæn sø giá trð nào nhçt trong các giá trð sau: 0 A. 7. B. 19. C. 25. D. 48. Lời giâi Phép tính Quy trình bçm máy Màn hình hiển thð Täix  2 qyQ)^4$ 0 psQ)$$2=
d X4  X  dx X 2 x  2  0,000001 !!+0.000 0 d  001= X 4  X  dx X 2  0,000001   Tính ' 2 0.000001 ' 2 -
y '' 2 y   y    nhĈ Ans PreAns 0.000001 X aMpQMR0. 000001=
Vậy y2  48  Chọn D.
Ví dụ 3: Tính đäo hàm cþa hàm sø x  1 y  x 4 1  2 x   1 ln 2 A. 1  2 x  1 ln 2 y '  B.   y'  2x 2 2 2 x 1  2 x   1 ln 2 C. 1 2 x 1 ln 2 y '  D.   y '  x2 2 2 2x Lời giâi
Ta chõn tính đäo hàm täi điểm bçt kì ví dĀ chõn x  0,5 r÷i tính đäo hàm cþa hàm sø täi
d  X  1 
X  0,5 . Nhêp vào máy tính   dx X 4  X0,5
Nguyễn Chiến. 0973514674 Page 6 | Phép tính Quy trình bçm máy Màn hình hiển thð
d  X  1  qyaQ)+1R   dx  4X  4^Q)$$$0 X0,5 .5= Lāu kết quâ qJz vĂa tìm đāợc vào biến A
Lçy A trĂ đi kết quâ tính giá trð các biểu thăc Ċ các đáp án nếu ra 0 thì chõn đáp án đò. đáp án A pa1p2(Q) +1)h2)R2^ 2Q)r0.5= Sø 12 8,562.10 
 0 . Nếu chưa ra kết quâ là 0 thì thay các đáp án cñn
läi bao giờ ra 0 thì chọn  Chọn A.
Ví dụ 4: Cho hàm sø x
y  e sin x , đðt F  y '' y 2 ' khîng đðnh nào
sau đåy là khîng đðnh đýng ?
A. F  2y
B. F  y
C. F  y 
D. F  2y Lời giâi Phép tính Quy trình bçm máy Màn hình hiển thð Tính qw4qyQK y ' 2  0,00  1 ^pQ)$jQ) )$2+0.000 001=qJz Lāu kết quâ qJz vĂa tìm đāợc vào biến A Tính y'0 E!!ooooo oooo=qJx Page 7 | Lāu kết quâ qJx vĂa tìm đāợc vào biến B
f ' x  x   f ' x
Thay vào công thăc f ''x   0   0   0 C x  0 aQzpQxR0 .000001= qJc
Tính F  y' 2y'  C  2B  0  .2461...  2
 y  Chọn A.
Kĩ thuật 2: Kĩ thuật giâi nhanh bằng MTCT trong bài toán
đồng biến, nghịch biến. Phương pháp:
+ Cách 1 : SĄ dĀng chăc nëng lêp bâng giá trð MODE 7 cþa
máy tính Casio . Quan sát bâng kết quâ nhên đāợc, khoâng nào
làm cho hàm sø luön tëng thì là khoâng đ÷ng biến, khoâng nào
làm cho hàm sø luön giâm là khoâng nghðch biến.
+ Cách 2: Tính đäo hàm, thiết lêp bçt phāćng trình đäo
hàm, cö lêp m và đāa về däng m  f x hoðc m  f x . Tìm
Min,Max cþa hàm f  x r÷i kết luên.
+ Cách 3: Tính đäo hàm, thiết lêp bçt phāćng trình đäo
hàm. SĄ dĀng tính nëng giâi bçt phāćng trình INEQ cþa máy
tính Casio (đøi vĉi bçt phāćng trình bêc hai, bêc ba).
Ví dụ 1: Vĉi giá trð nào cþa tham sø m thì hàm sø mx  m  2 y  x  m
nghðch biến trên tĂng khoâng xác đðnh? A. 2   m  1 B. 2   m  1 C. 0  m  1 D. Đáp án khác
Nguyễn Chiến. 0973514674 Page 8 | Lời giâi
Têp xác đðnh D  \  m .
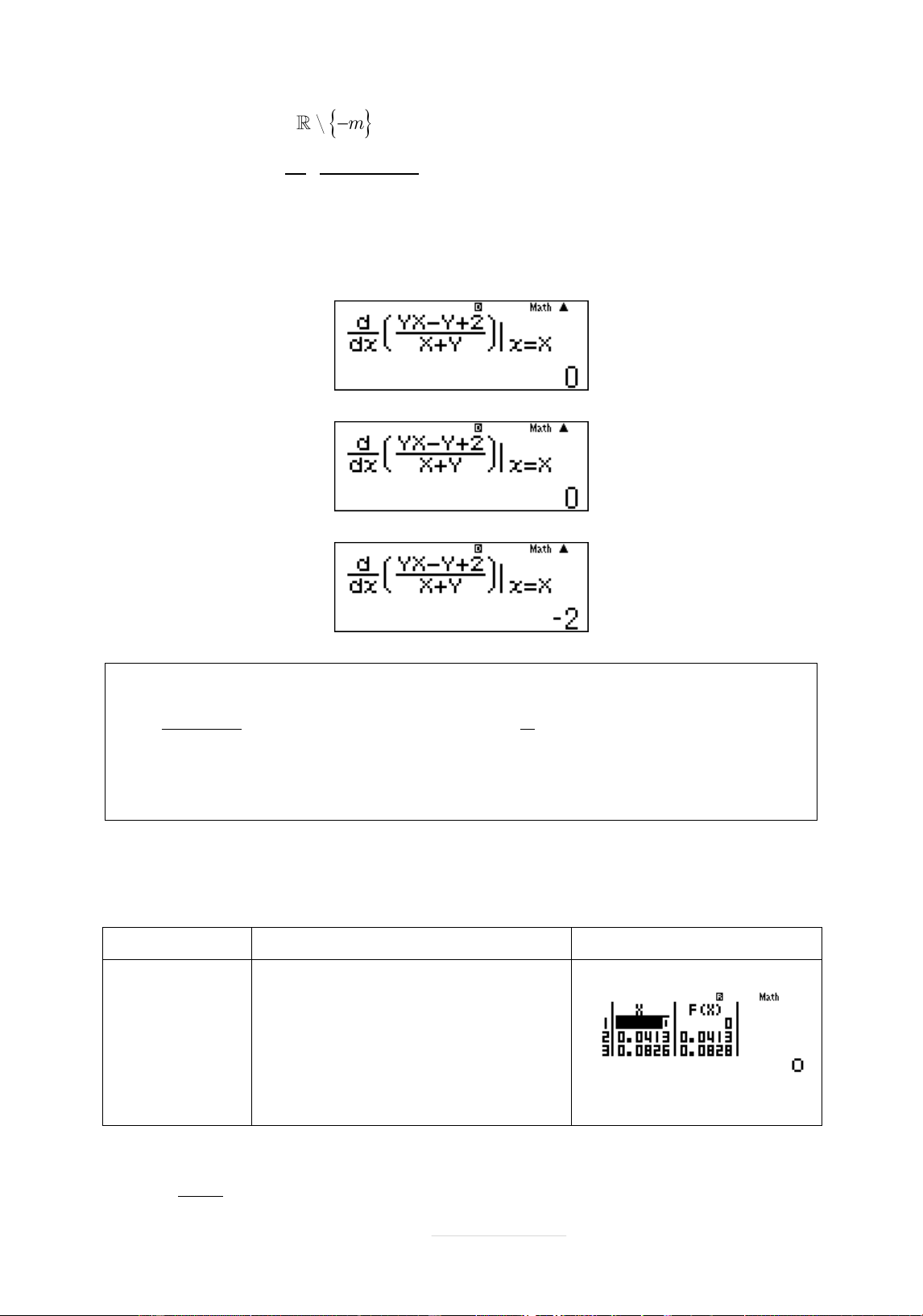
Nhêp biểu thăc d  mX  m  2    dx X  m  x  X
Gán X  0, không gán Y  0 vì x  m  nên X  Y  (hoðc nhąng giá
trð X, Y tāćng ăng). Gán Y  2
 , đāợc kết quâ  0 , Loäi B. Gán Y  2
 , đāợc kết quâ  0 . Loäi C. Gán Y  1
 , đāợc kết quâ. Vêy đáp án A.
Ví dụ 2: Tìm tçt câ các giá trð thĆc cþa tham sø m sao cho hàm sø tan x  2    y 
đ÷ng biến trên khoâng 0;  ? tan x  m 4   A. m  0  B. m  2 C.1 m  2 D. m  2 1  m   2 Lời giâi
Đðt tanx  t . Đùi biến thì phâi tìm miền giá trð cþa biến mĉi. Để
làm điều này ta sĄ dĀng chăc nëng MODE 7 cho hàm f x  tanx Phép tính Quy trình bçm máy Màn hình hiển thð Tìm điều kiện cho qw4w7lQ ))==0=qK
f  x  tan x P4=(qKP4 )P19=
Ta thçy 0  tanx  1 vêy t  0; 1. Bài toán trĊ thành tìm m để hàm sø t  2 y 
đ÷ng biến trên khoâng 0;1 t  m Page 9 |
t m  t  2 Tính : 2  m 2  m y '   y '  0   0  m  2 (1)  2 2 2 t  m  t m t m
Kết hợp điều kiện xác đðnh t  m  0  m  t  m  0; 1 (2) 
TĂ (1) và (2) ta đāợc m  0   Chọn A. 1  m  2 
Kĩ thuật 3: Tìm cực trị của hàm số và bài toán tìm tham số
để hàm số đạt cực trị tại điểm cho trước.
Phương pháp : DĆa vào 2 quy tíc tìm cĆc tri.
Đøi vĉi däng toán tìm m để hàm sø bêc 3 đät cĆc trð täi x0
f 'x  0
f 'x  0 0  0 
CĆc đäi täi x thì 
. CĆc tiểu täi x thì  0 f ' 0  f '  x  0 0   x  0 0 
SĄ dĀng chăc nëng tính liên tiếp giá trð biểu thăc “ Dçu :”Qy
Tính đāợc f 'x  : f ''x tĂ đò chõn đāợc đáp án 0 0 
Ví dụ 1: Tìm tçt các các giá trð thĆc cþa m để hàm sø
y  x 3  mx2  m2  x  m2 3 3 1 3
 5 đät cĆc đäi täi x  1 A. m  0  B. m  2 C. m 1 D. m  0 m   2 Lời giâi
Cách 1: Kiểm tra khi m  0 thì hàm sø cò đät cĆc đäi täi x  1 hay không ? Phép tính Quy trình bçm máy Màn hình hiển thð Täi x  1 qyQ)^3$p 3Q)+5$1= Täi x  1  0,1 !!p0.1=
Täi x  1  0,1 !!oooo+0 .1=
Vêy y ' đùi dçu tĂ åm sang dāćng qua giá trð x  1  m  0 loäi
 Đáp án A hoðc D sai
Nguyễn Chiến. 0973514674 Page 10 |
Tāćng tĆ kiểm tra khi m  2 Phép tính Quy trình bçm máy Màn hình hiển thð Täi x  1 qyQ)^3$p 6Q)d+9Q) p7$1= Täi x  1  0,1 !!p0.1=
Täi x  1  0,1 !!oooo+0 .1=
Ta thçy y ' đùi dçu tĂ dāćng sang åm  hàm sø đät cĆc đäi
täi x 1  Chọn B.
Cách 2: SĄ dĀng chăc nëng tính liên tiếp giá trð biểu thăc: d
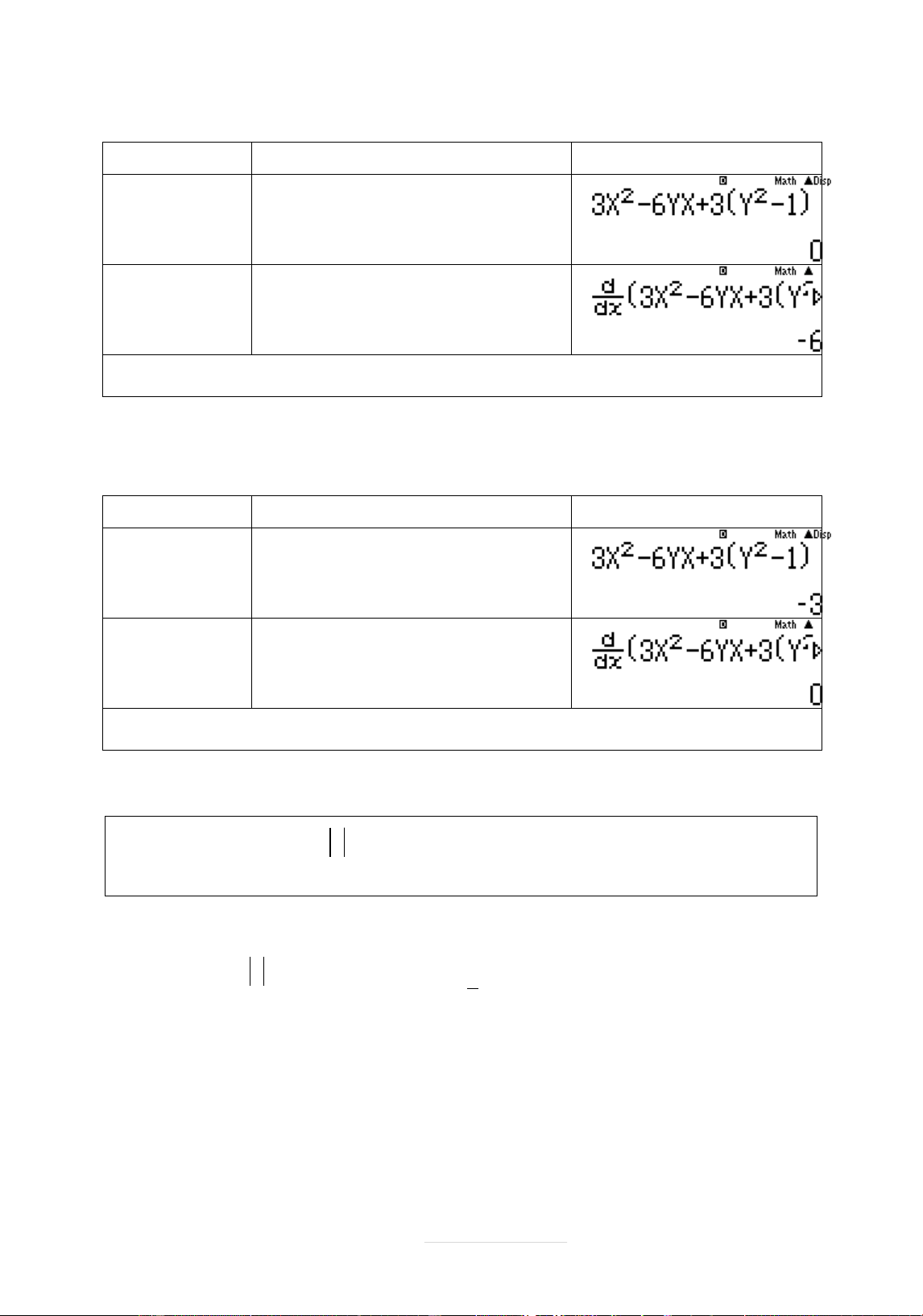
f ' x : f ' x 2  X 3  Y 6 X  3  2 Y   1 :  2X 3  Y 6 X  3  2 Y   1 0   0 dx X  1
- Nhêp giá trð X = 1 và Y là giá trð cþa m Ċ múi đáp án
- Nếu biểu thăc thă nhçt bìng khöng và biểu thăc thă hai nhên giá trð åm thì chõn.
+ Khi m  0 kiểm tra  x  1 có là cĆc đäi hay không ? Phép tính Quy trình bçm máy Màn hình hiển thð Täi 3Q)dp6Qn m  0 Thay nQ)+3(Qn dp1)Qyqy X  1Y ;  0 3Q)dp6Qn Q)+3(Qnd p1)$1r1= 0= Tìm f  !!p0.1= Tìm f  =
Khi m  0 thì f  1  0,f  1  6  0  x  1là cĆc tiểu loại A,D Page 11 |
+ Kiểm tra khi m  2 kiểm tra  x  1 có là cĆc đäi hay không ?
Täi m  2 Thay X  1Y ;  2 Phép tính Quy trình bçm máy Màn hình hiển thð Tìm f  ===2= Tìm f  =
Khi m  2 thì f  1  0,f  1  6
  0  x 1 là cĆc đäi
Chõn đáp án B. Ta cò thể thĄ thêm trāĈng hợp khi m  1
+ Khi m  1 kiểm tra  x 1 có là cĆc đäi hay không
Täi m  1 Thay X 1;Y 1 Phép tính Quy trình bçm máy Màn hình hiển thð Tìm f  ====1= Tìm f  =
Khi m  1 thì f  1  3
  0, f   
1  0  x 1 không phâi là cĆc trð  Chọn B.
Ví dụ 2: Hàm sø 3
y  x  x2  4 cò tçt câ bao nhiêu điểm cĆc trð? A. 2 B. 1 C. 3 D. 0 Lời giâi x   0 Tính y '  x 3 x  x 2 y ' 0   
2 . Dùng MODE 7 vĉi thiết lêp x     3
sao cho x chäy qua 3 giá trð này ta sẽ khâo sát đāợc sĆ đùi dçu cþa y '
Nguyễn Chiến. 0973514674 Page 12 | Quy trình bçm máy Màn hình hiển thð w73Q)qcQ)$p2 Q)=po=p2=2=1 P3=
Ta thçy f 'x đùi dçu 3 læn Chọn C.
Kĩ thuật 4: Viết phương trình đường thẳng đi qua hai điểm
cực trị của đồ thị hàm số bậc ba Phương pháp:
Phương trình đường thẳng đi qua hai điểm cực trð của đồ thð hàm số .  y ax3 bx2  
 cx  d có däng :   y y
g x  y  y3
+ Bước 1: Bçm w2 để chuyển chế đû máy tính sang môi trāĈng sø phăc.
+ Bước 2: Nhêp vào máy tính biểu thăc: y y . 
f  x,m f .  x,m y 
hoðc f x,m      y 3 
3f x,m
+ Bước 3: Bçm = để lāu biểu thăc.
+ Bước 4: Bçm r vĉi x  i (đćn vð sø phăc, để làm xuçt hiện i ta bçm b)
+ Bước 5: Nhên kết quâ däng Mi  N  phāćng trình cæn tìm
có däng: y  Mx  N.
Ví dụ: Phāćng trình đāĈng thîng đi qua hai điểm cĆc trð cþa đ÷
thð hàm sø y   x3  x2 2 3  1 là
A. y  x  1.
B. y  x  1.
C. y  x   1.
D. y  x   1. Page 13 | Lời giâi Phép tính Quy trình bçm máy Màn hình hiển thð Sø phăc w2 Nhêp vào p2Q)qd+ máy tính 3Q)d+1+(p biểu thăc Q)d+Q))( p2Q)+1) Thay x  i rb=
Kết quâ däng i  1  phāćng trình cæn tìm: y  x  1  Chọn B.
Kĩ thuật 5: Tìm tiệm cận.
Phương pháp: Ứng dĀng kï thuêt düng r tính giĉi hän
Ví dụ 1: Tìm tçt câ các tiệm cên đăng cþa đ÷ thð hàm sø x
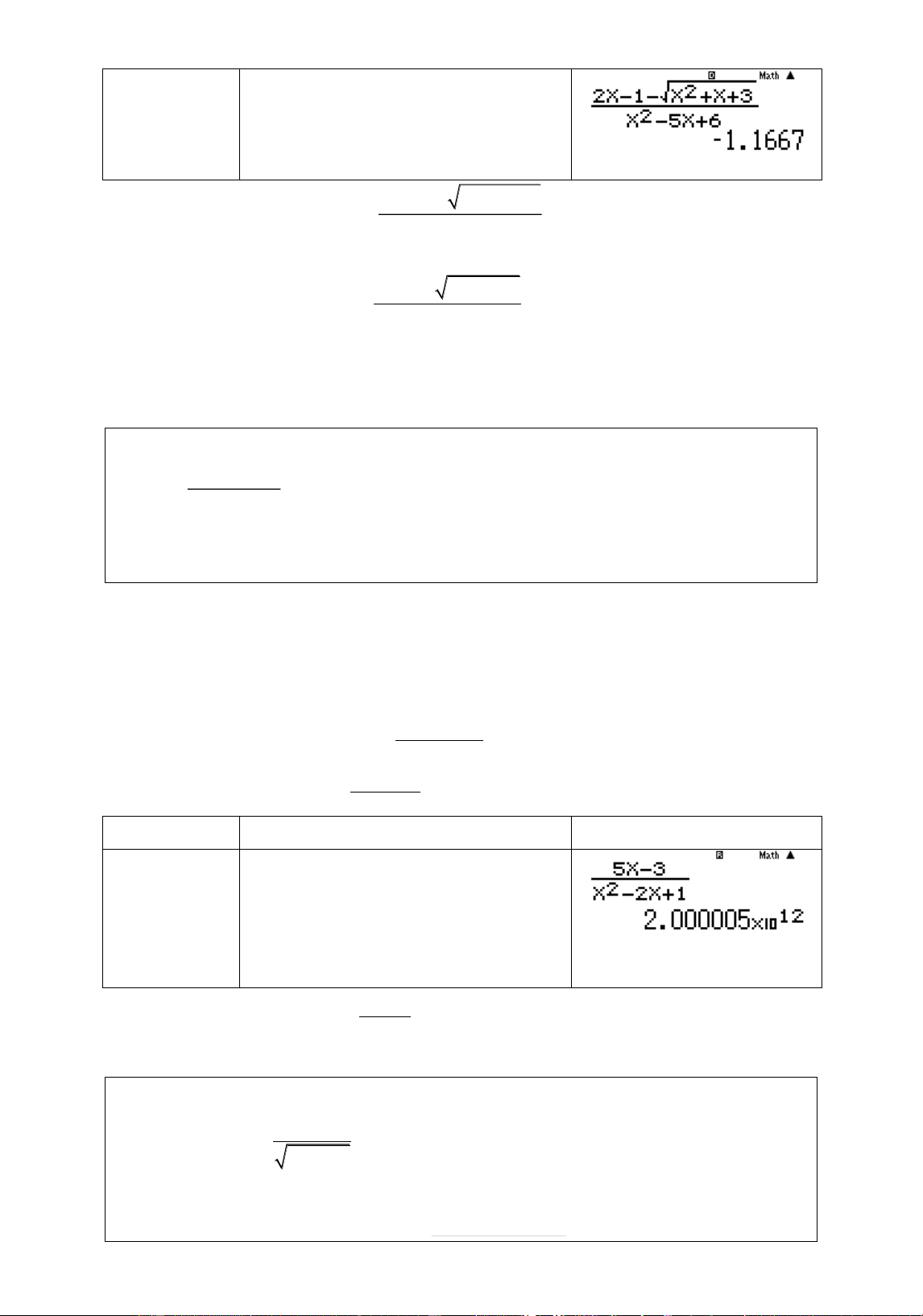
2  1  x2  x  3 y  x2  x 5  6   A. x  3   3  B. x  3  C. x  D. x  3 x  2   x  2  Lời giâi
ĐāĈng thîng x  x là tiệm cên đăng cþa đ÷ thð hàm sø thì điều 0
kiện cæn : x là nghiệm cþa phāćng trình méu sø bìng 0 0
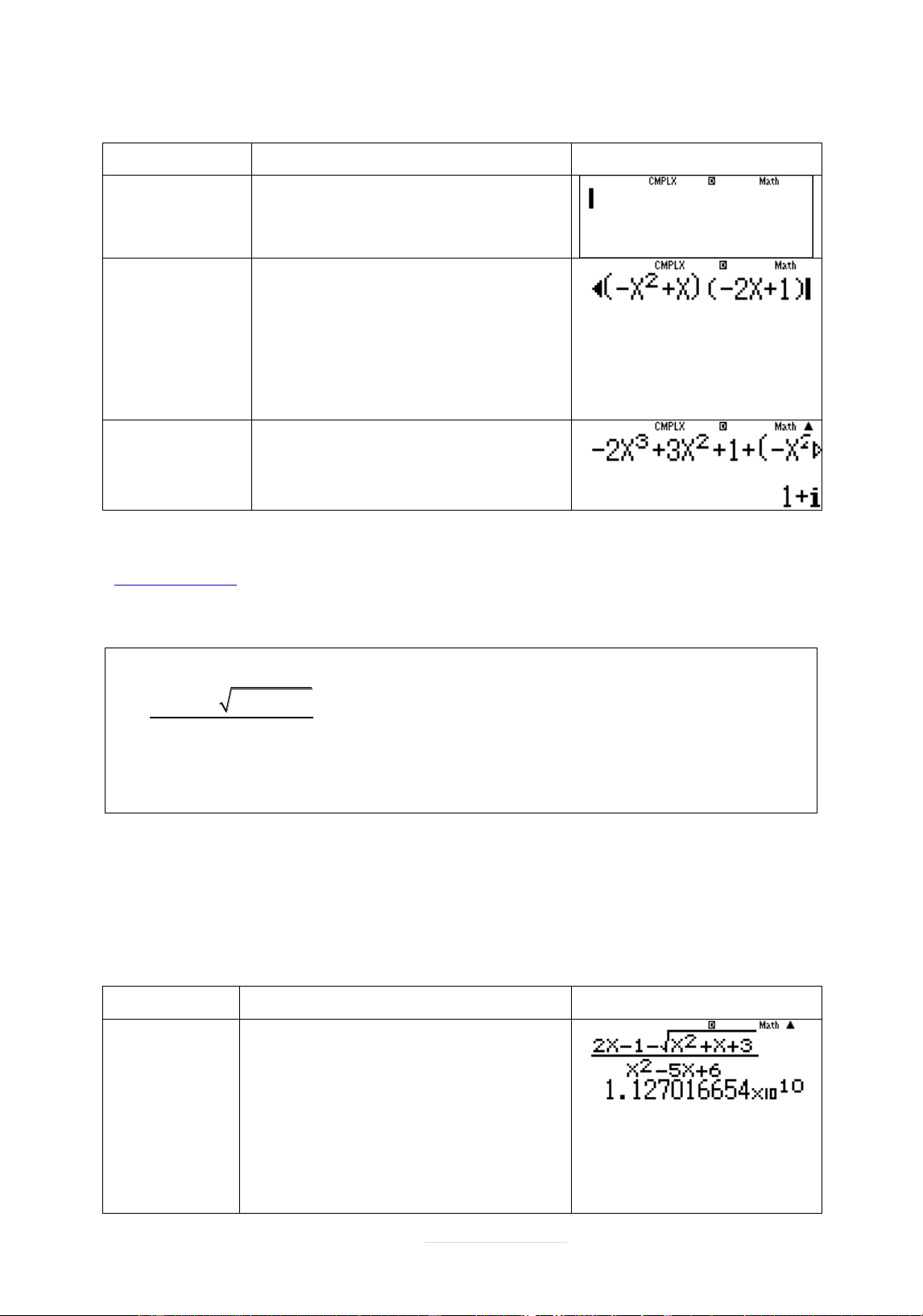
Nên ta chî quan tåm đến hai đāĈng thîng x  3 và x  2 Phép tính Quy trình bçm máy Màn hình hiển thð Vĉi x  3 a2Q)p1ps Q)d+Q)+3 RQ)dp5Q) +6r3+0.00 00000001=
Nguyễn Chiến. 0973514674 Page 14 | Vĉi x  2 r2+0.0000 000001= 2 + Vĉi x
2  1  x  x  3 x  3 xét lim
    x  3 là mût tiệm x   x2 3  x 5  6 cên đăng + Vĉi     x  2 xét 2 2x 1 x x 3 lim
   Kết quâ không ra vô 2 x2 x  5x  6
cùng x  2 không là mût tiệm cên đăng  Chọn B.
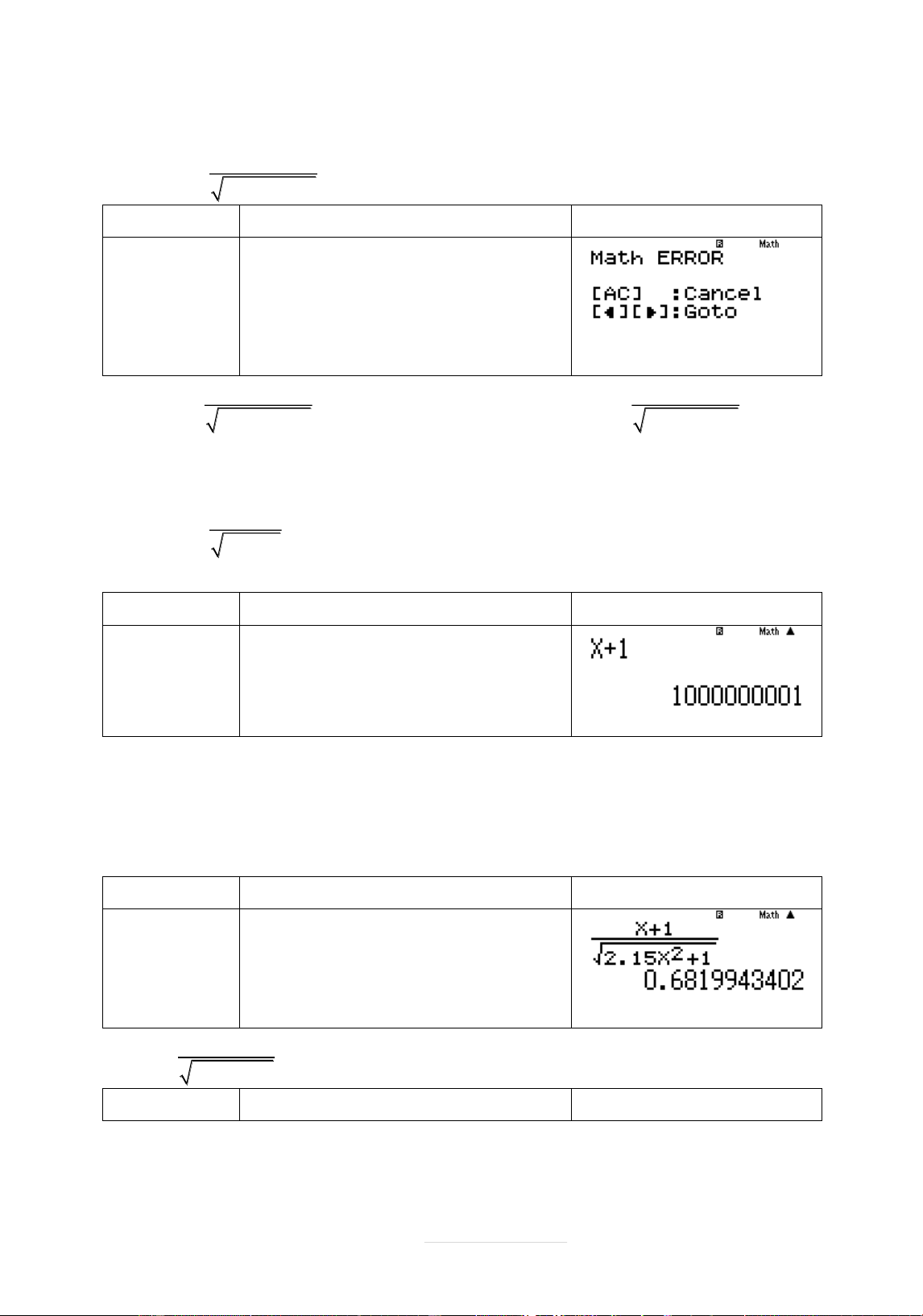
Ví dụ 2: Tìm tçt các các giá trð cþa tham sø m sao cho đ÷ thð hàm sø 5x  3 y 
khöng cò tiệm cên đăng? 2 x  2mx 1  A.  1  m  1 B. m  1 C. m  D. 1   m 1 m  1  Lời giâi
Để đ÷ thð hàm sø khöng cò tiệm cên đăng thì phāćng trình méu
sø bìng 0 khöng cò nghiệm hoðc cò nghiệm nhāng giĉi hän hàm
sø khi x tiến tĉi nghiệm khöng ra vö cüng. Vĉi 5  3 m  1 . Hàm sø x  y  . Phāćng trình 2
x  2x 1  0 có x2  x 2  1 nghiệm  x  1 Tính 5x 3 lim
    Đáp sø A sai 2 x 1  x  x 1 Phép tính Quy trình bçm máy Màn hình hiển thð Vĉi m  1  a5Q)p3RQ )dp2Q)+1 r1+0Ooo1 0^p6)= Vĉi 5  3 m  0 hàm sø x  y 
. Phāćng trình x2  1  0 vö nghiệm x2  1
 Đ÷ thð hàm sø khöng cò tiệm cên đăng khi m  0  Chọn D.
Ví dụ 3: Tìm tçt câ các giá trð thĆc cþa tham sø m sao cho đ÷ thð cþa hàm sø x  1 y  cò hai tiệm cên ngang? mx2  1 A. m  0
B. Không có m thóa mãn C. m  0 D. m  0 Page 15 | Lời giâi
+ ThĄ đáp án A ta chõn 1 giá trð m  0 , ta chõn m  2  ,15 . Tính x  1 lim x  2  .1 x2 5  1 Phép tính Quy trình bçm máy Màn hình hiển thð Vĉi aQ)+1Rsp2 m  2  ,15 .15Q)d+1 r10^9)= Vêy x  1  1 lim khöng t÷n täi  hàm sø x y  không x  2  .1 x2 5  1 2  .1 x2 5  1 thể cò 2 tiệm cên ngang
+ ThĄ đáp án B ta chõn gán giá trð m  0 . Tính x  1 lim  lim x   1 x  x x2 0  1  Phép tính Quy trình bçm máy Màn hình hiển thð Vĉi m  0 Q)+1r10^ 9)=
Vêy lim x  1     hàm sø y  x  1 khöng thể cò 2 tiệm cên x  ngang
+ ThĄ đáp án D ta chõn gán giá trð m  2.15 . Phép tính Quy trình bçm máy Màn hình hiển thð Vĉi aQ)+1Rs2. m  2.15 15Q)d+1r x   10^9)= x  1  lim  0.6819943402 x  2.1 x2 5  1 Phép tính Quy trình bçm máy Màn hình hiển thð
Nguyễn Chiến. 0973514674 Page 16 | Vĉi rp10^9)= m  2.15 x   x  1  lim  0
 .6819943402 . Vêy đ÷ thð hàm sø cò 2 tiệm cên x  2.1 x2 5  1 ngang y  0
 .6819943402  Chọn D.
Kĩ thuật 6: Kĩ thuật giâi nhanh bài bài toán tìm giá trị lớn
nhất – nhỏ nhất của hàm số trên đoạn a  ;b 
 . Sử dụng tính
năng bâng giá trị TABLE Phương pháp : 1. Nhấn w7
2. f X  Nhêp hàm sø vào.
3. Step ? Nhêp giá trð a
4. End ? Nhêp giá trð b
5. Step? Nhêp giá trð: 0,1; 0,2; 0,5 hoðc 1 tüy vào đoän a;b  
Quan sát bâng giá trð máy tính hiển thð, giá trð lĉn nhçt xuçt hiện
là max , giá trð nhó nhçt xuçt hiện là min. *Chú ý:
Ta thiết lêp miền giá trð cþa biến x Start a End b Step (có
thể làm trñn để Step đẹp)
Hàm sø chăa sinx,cosx,tanx... ta chuyển máy tính về chế đû Radian: qw4 2
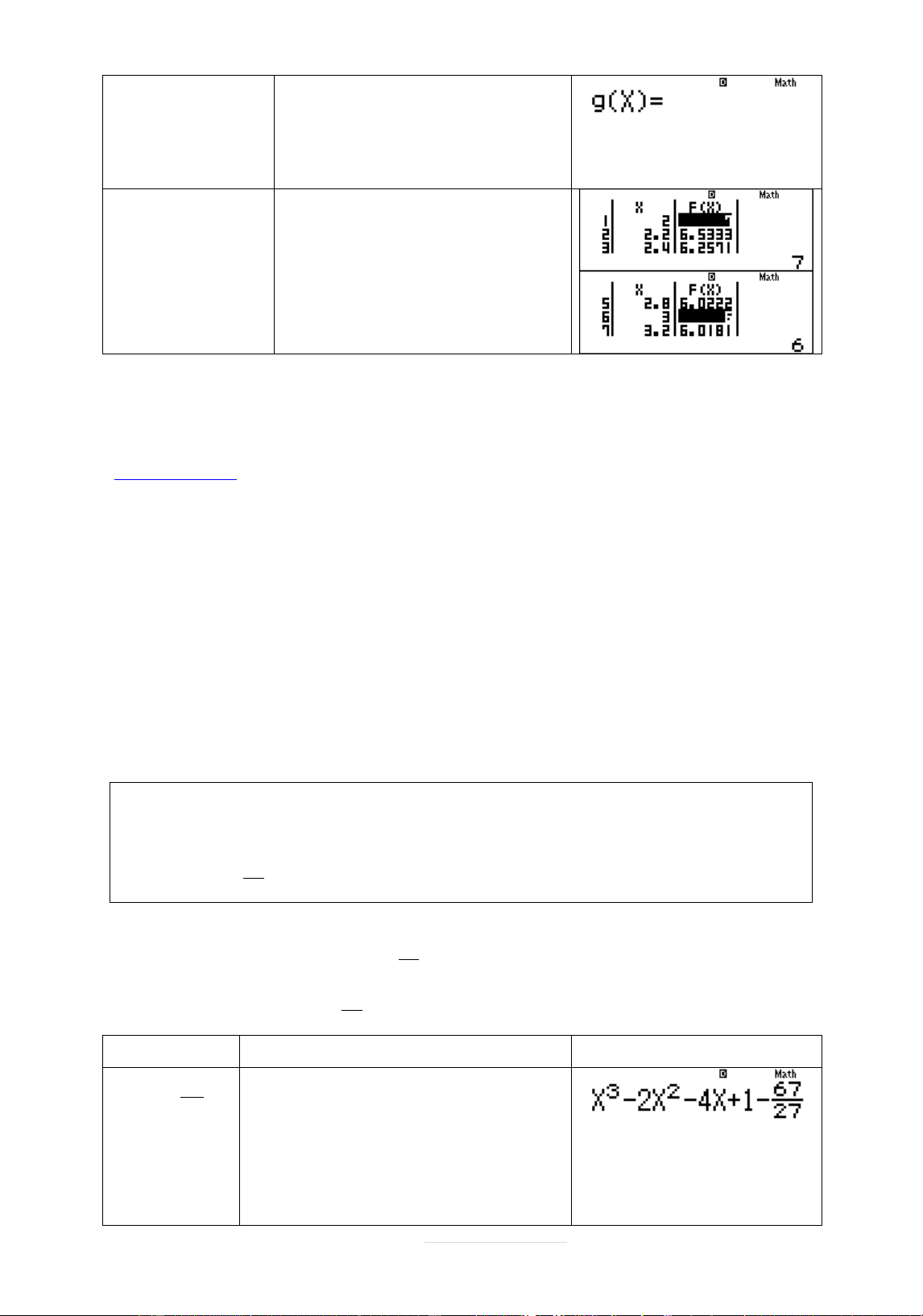
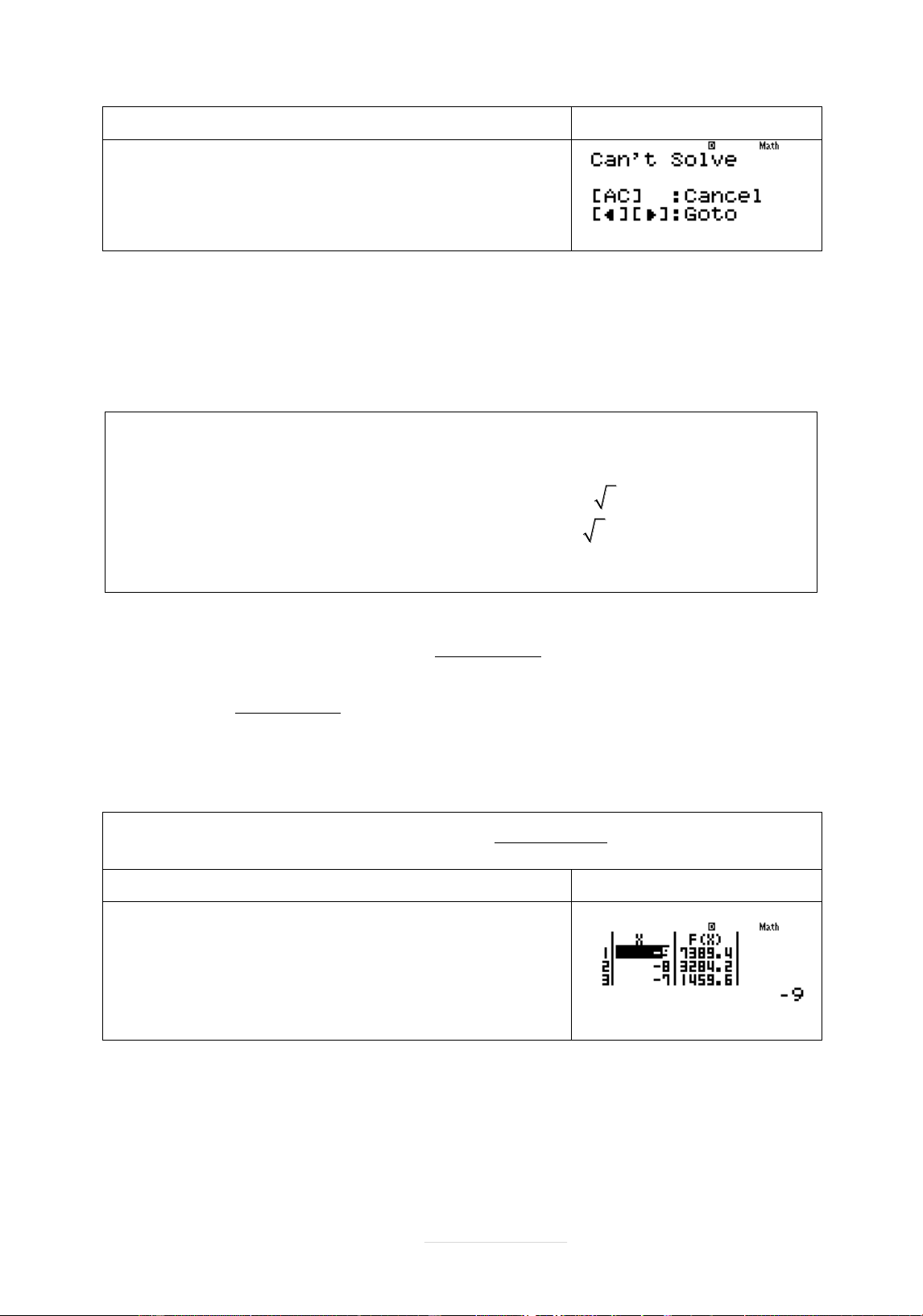
Ví dụ 1: Giá trð nhó nhçt cþa hàm sø x  3 y  trên đoän 2  ;4 x  1   là A. 6 B. 2  C. 3  D. 193 Lời giâi Phép tính Quy trình bçm máy Màn hình hiển thð   X2  3 F X  X 1 w7aQ)d+ 3RQ)+1== Page 17 |
g X  bó qua Bçm = Star ? 2 End ? 4 Step 2=4=0.2= ? 0,2. RRRR kéo xuøng để tìm GTNN.
Quan sát bảng giá trị tìm kết quả nào gần với đáp án để kết luận  Chọn A.
Kĩ thuật 7: Kĩ thuật giâi nhanh bài bài toán tìm giá trị lớn
nhất – nhỏ nhất của hàm số . Sử dụng tính năng SOLVE Phương pháp :
Để tìm giá trð lĉn nhçtM , giá trð nhó nhçt m cþa hàm sø
y  f x  ta giâi phāćng trình f x  M  0 , f x   m  0
- Tìm GTLN ta thay các đáp án tĂ lĉn đến nhó sau đò sĄ
dĀng SOLVE để tìm nghiệm , nếu nghiệm thuûc đoän, khoâng đã cho ta chõn luön.
- Tìm GTNN thì thay đáp án tĂ nhó đến lĉn.
Ví dụ: Tìm giá trị lớn nhất của hàm số y  x3  x2 2  x 4  1 trên đoạn 1  ;3   A.  67 max B. max  2  C. max  7  D. max  4  27 Lời giải
Các kết quả xếp theo thứ tự 67  2  4  7 . Do vậy ta giải phương 27 67
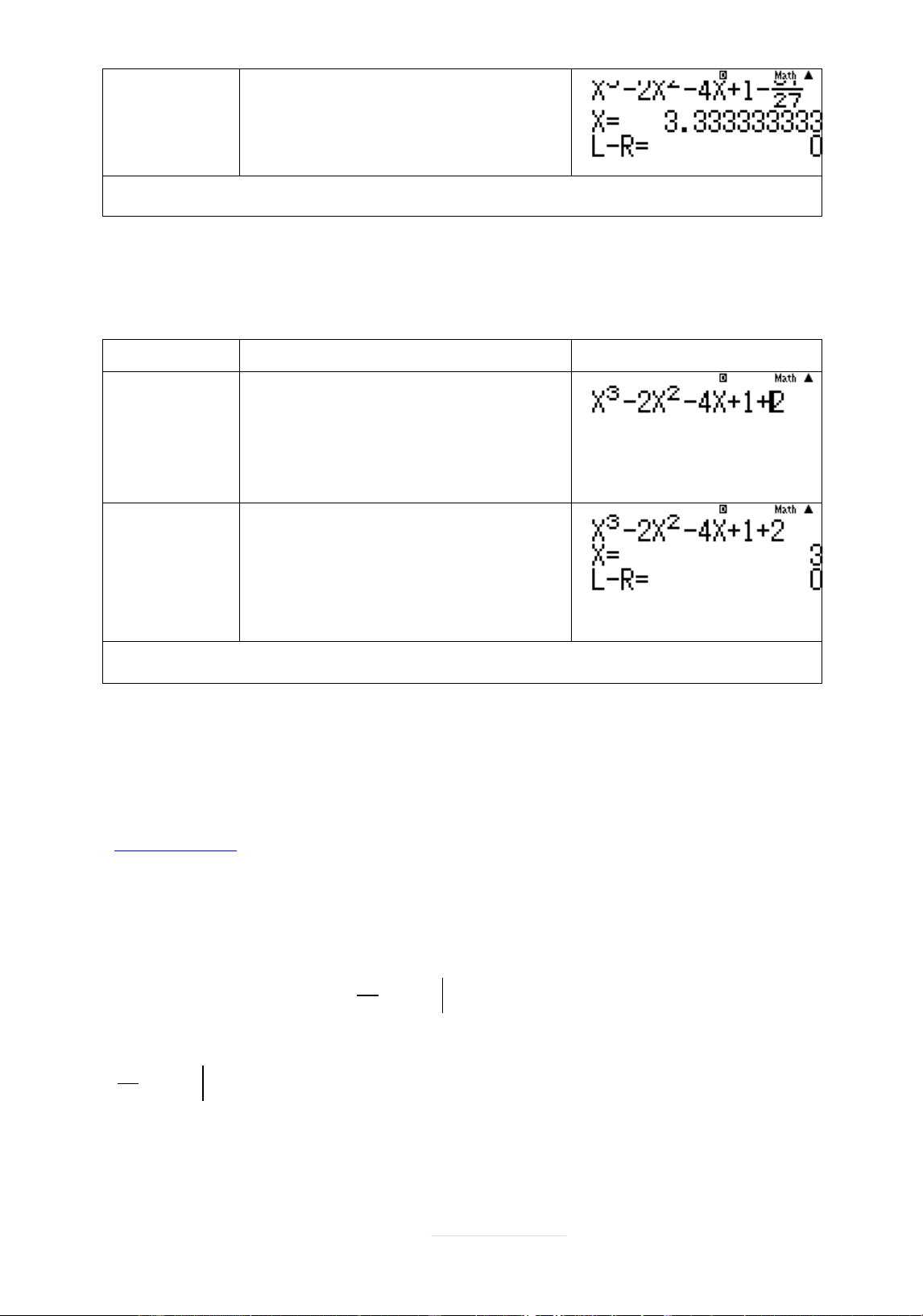
trình x 3  x2 2  x 4  1  trước 27 Phép tính Quy trình bçm máy Màn hình hiển thð F X  67 27 Q)qdp2Q) dp4Q)+1pa 67R27=
Nguyễn Chiến. 0973514674 Page 18 | Cho X  2  1  ;3 =qr2=  
Ta đāợc nghiệmx  3,33333  1  ;3   nên loại A.
+ Tiếp theo thay đáp án max  2  , giải phương trình : x3  x2 2  x 4  1  2  Phép tính Quy trình bçm máy Màn hình hiển thð F X   2  !oooooooo +2 Cho =qr2= X  2  1  ;3  
Ta đāợc nghiệmx  2  1  ;3 
 nên  Chọn B.
Khöng thĄ các đáp án cñn läi nąa vì FX  2 đã là lĉn nhçt
* Chú ý: Kï thuêt SOLVE tuy tiến hành låu hćn nhāng mänh
hćn, đâm bâo chíc chín hćn TABLE nhiều đðc biệt vĉi các bän
cñn thiếu kï nëng phån tích bâng giá trð.
Kĩ thuật 8: Kĩ thuật lập phương trình tiếp tuyến của đồ thị hàm số .
Phương pháp : Phāćng trình tiếp cò däng d : y  kx . m
+ Đæu tiên tìm hệ sø gòc tiếp tuyến k  yx . 0 
Bçm q y và nhêp d f X
, sau đò bçm = ta đāợc k. dx x x  0
+ Tiếp theo: Bçm phím ! để sĄa läi thành
d f X x  X
   f X , sau đò bçm phím r vĉi X  x và bçm dx x x  0 0 phím = ta đāợc m. Page 19 |
Ví dụ 1: Cho điểm 2  1
M thuûc đ÷ thð   x C : y  và cò hoành đû x  1 bìng 1.
 Phāćng trình tiếp tuyến cþa đ÷ thð C  täi điểm M là A. 3 1 3 1 3 1 3 1
y  x  .
B. y  x  . C. y   x  . D. y   x  . 4 4 4 4 4 4 4 4 Lời giâi Phép tính Quy trình bçm máy Màn hình hiển thð d  X 2  1   dx X  1   qya2Q)+1 x 1  RQ)p1$$p 1=
Bçm phím ! để sĄa läi thành: d  X 2  1     X 2  1 x X  dx X  1 X  1   x 1 
sau đò bçm phím r với X  1
 và bçm phím = ta đāợc kết quâ =!(pQ))+a2Q) +1RQ)p1=
Vêy phāćng trình tiếp tuyến täi 3 1 M là: x y     Chọn B. 4 4
Ví dụ 2: Phāćng trình tiếp tuyến cþa đ÷ thð C  y  x3 :  x 3  2 cò hệ sø gòc bìng 9 là
A. y  x
9  18; y  x 9  22.
B. y  x
9  14; y  x 9  18.
C. y  x
9  18; y  x 9  22.
D. y  x
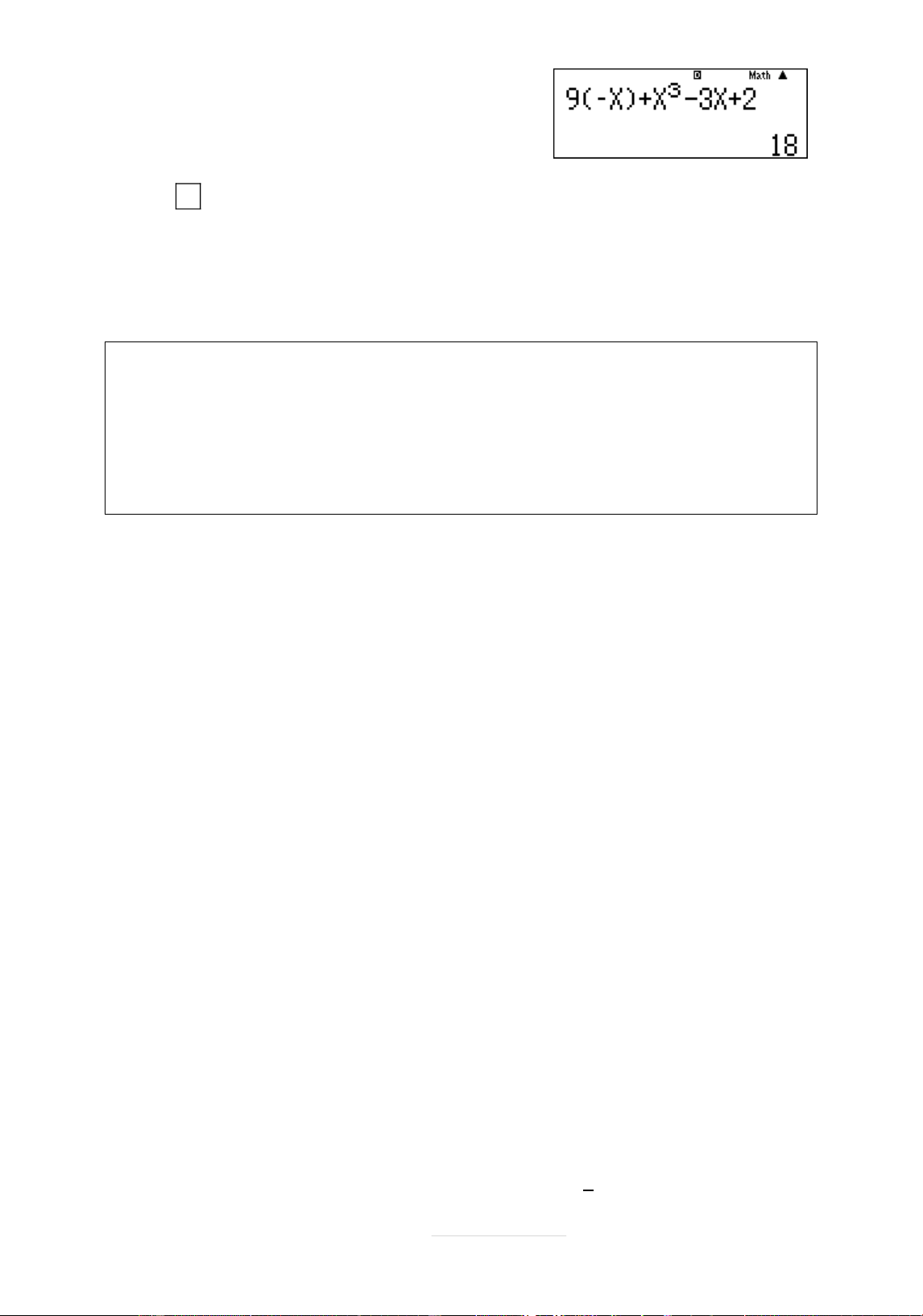
9  14; y  x 9  18.  Vĉi x  2 ta nhêp 0  X    X3 9  X
3  2 r vĉi X  2 r÷i
bçm = ta đāợc kết quâ là 14 
 d : y  x 9  14. 1
Nguyễn Chiến. 0973514674 Page 20 |  Vĉi x  2  ta nhêp 0  X    X3 9  X 3  2 r vĉi X  2 
r÷i bçm = ta đāợc kết quâ là
18  d : y  x 9  18. 2  Chọn B.
Ví dụ 3: Tiếp tuyến cþa đ÷ thð C  y   x3 : 4  x 3  1 đi qua điểm A 1
 ;2 cò phāćng trình là
A. y   x 9  7; y  x   2.
B. y   x
9  11; y  x   2.
C. y   x 9  11; y  2.
D. y   x 9  7; y  2.
 Cho f x bằng kết quâ các đáp án, từ đò ta thu được các phương trình.
 Sử dụng chức năng giâi phương trình bậc ba của máy tính bó
túi bằng cách bấm tổ hợp phím w 5 4 và nhập hệ số phương trình.
Thông thường máy tính cho số nghiệm thực nhó hơn số bậc của
phương trình là 1 thì ta chọn đáp án đò.
+ Đầu tiên thử với đáp án A, ta cho:
 x3  x    x    x3 4 3 1 9 7 4  1 x 2  6  0.
Máy tính cho 3 nghiệm  Loäi A.
 Thử với đáp án B, ta cho:  x3  x   x     x3 4 3 1 2 4  x 4  1  0.
Máy tính cho 3 nghiệm  Loäi B.
 Thử với đáp án B, ta cho:
 x3  x    x    x3 4 3 1 9 11 4  1 x 2  10  0.
Máy tính hiển thð 1 nghiệm thực và 2 nghiệm phức (phương
trình cò số nghiệm thực là một nhó hơn bậc của phương trình là 2) Loäi C. 3 3
+ Thử với đáp án :  x 4  x 3  1   x 9  7   x 4  1 x 2  8  0
máy tính hiển thị 2 nghiệm x  1
 ; x  2 (nhận). 3 3  x 4  x 3  1  2   x 4  x 3  1  0 1
máy tính hiển thị 2 nghiệm x  1
 ; x  (nhận). 2  Chọn D. Page 21 |
Kĩ thuật 9: Kĩ thuật giâi bài toán tương giao đồ thị hàm số. Phương pháp :
Để tìm nghiệm cþa phāćng trình hoành đû giao điểm ta düng chăc
nëng lêp bâng giá trð MODE 7, giâi phāćng trình MODE 5 hoðc lệnh SOLVE
Ví dụ 1: Tìm tçt câ các giá trð thĆc cþa tham sø m sao cho đ÷ thð
hàm sø y  x3  mx  16 cít trĀc hoành täi 3 điểm phån biệt A. m  12 B. m  12  C. m  0 D. m  0 Lời giâi
Để đ÷ thð hàm sø y  x3  mx  16 cít trĀc hoành täi 3 điểm phån biệt thì phāćng trình 3
x  mx 16  0 (1) cò 3 nghiệm phån biệt
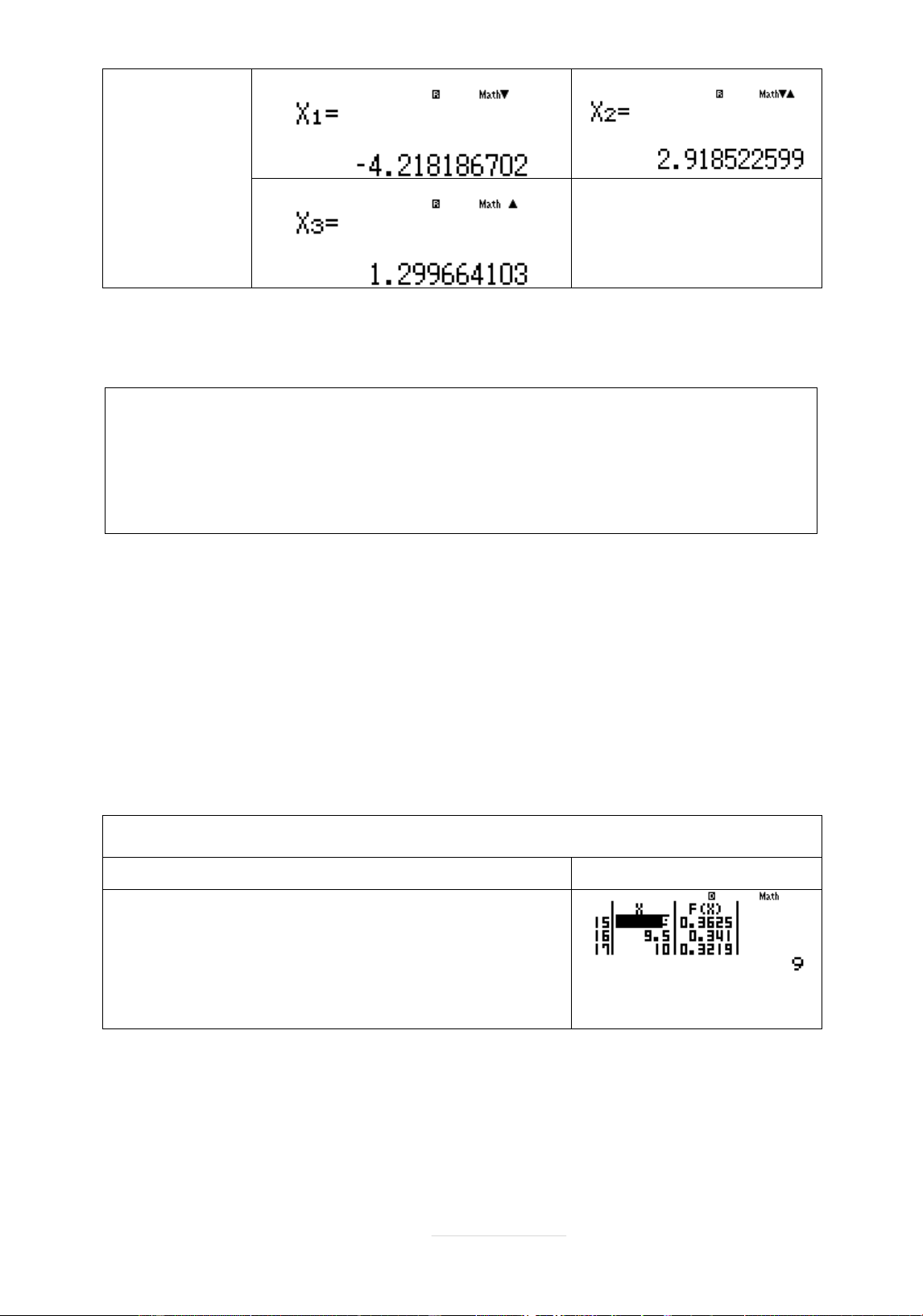
+ Vĉi m  14 sĄ dĀng lệnh giâi phāćng trình bêc 3 MODE 5 Quy trình w541=0=14=16==== bçm máy Màn hình hiển thð
Ta thçy nghiệm x ;x là nghiệm phăc  khöng đþ 3 nghiệm thĆc 2 3  Loäi A + Vĉi m  14
 sĄ dĀng lệnh giâi phāćng trình bêc 3 MODE 5 Quy trình w541=0=4o14 bçm máy =16====
Nguyễn Chiến. 0973514674 Page 22 | Màn hình hiển thð
Ta thçy ra 3 nghiệm thĆc  Đáp án đýng cò thể là B hoðc C
ThĄ thêm mût giá trð m  1
 nąa thì thçy m  1  khöng thóa  Chọn B.
Ví dụ 2: Tìm têp hợp tçt các các giá trð cþa m để phāćng trình
log x  log x  2  m cò nghiệm : 2 2
A. 1  m   
B. 1  m   
C. 0  m   
D. 0  m    Lời giâi
Đðt log x  log x  2  f x  m  f x (1). Để phāćng trình 2 2 
(1) cò nghiệm thì m thuûc miền giá trð cþa f x hay
f min  m  f max
Tĉi đåy bài toán tìm tham sø m đāợc quy về bài toán tìm
min, max cþa mût hàm sø. Ta sĄ dĀng chăc nëng MODE 7 vĉi
miền giá trð cþa x là Start 2 End 10 Step0.5
Nhêp hàm f X  log X  log X  2 2 2  Quy trình bçm máy Màn hình hiển thð w7i2$Q)$pi2$ Q)p2==2=10=0. 5=
Quan sát bâng giá trð F X ta thçy f 10  0.3219 vêy đáp sø A và
B sai. Đ÷ng thĈi khi x càng tëng vêy thì F X càng giâm. Vêy
cåu hói đðt ra là F X cò giâm đāợc về 0 hay khöng? Nếu F X
giâm đāợc về 0 cò nghïa là phāćng trình f x  0 cò nghiệm. Để
kiểm tra dĆ đoán này ta sĄ dĀng chăc nëng dñ nghiệm SOLVE Page 23 | Quy trình bçm máy Màn hình hiển thð i2$Q)$pi2$Q) p2qr3=
Máy phāćng trình này vô nghiệm. Vêy dçu = khöng xây ra
 f x  0  m  0  Chọn D.
Ví dụ 3: Têp giá trð cþa tham sø m để phāćng trình x x x
5.16  2.81  m.36 cò đýng 1 nghiệm?  A.   2 m  0 B. m m   2  C. Vĉi mõi m
D. Khöng t÷n täi m Lời giâi x x Ta có 5.16  2.81 x x x
5.16  2.81  m.36  m  x 36 Đðt 5.16  2.81 f x  x x 
. Khi đò phāćng trình ban đæu  f x  m x 36
SĄ dĀng MODE 7 để khâo sát sĆ biến thiên cþa đ÷ thð hàm sø
y  f x  vĉi thiết lêp Start 9  End 10 Step 1 Nhêp hàm 5.16  2.81 f X  X X  X 36 Quy trình bçm máy Màn hình hiển thð w7a5O16^Q)$p 2O81^Q)R36^Q )==p9=10=1=
Quan sát bâng giá trð ta thçy f x luôn giâm hay hàm søy  f x
luôn nghðch biến. Điều này có nghïa là đāĈng thîng y  m luôn
cít đ÷ thð hàm sø y  f x täi 1 điểm  Chọn C.
Nguyễn Chiến. 0973514674 Page 24 |
Kĩ thuật 10: Tìm nghiệm của phương trình. Phương pháp :
+Bước 1: Chuyển PT về däng Vế trái = 0 . Vêy nghiệm cþa PT
sẽ là giá trð cþa x làm cho vế trái  0
+Bước 2: SĄ dĀng chăc nëng CALC hoðc MODE 7 hoðc
SHIFT SOLVE để kiểm tra xem nghiệm . Ví dụ 1: Phāćng trình
log x log x log x  log x log x  log x log x  log x log x 2 4 6 2 4 4 6 6 2 cò têp nghiệm là : A.  1 B. 2;4;  6 C. 1;1  2 D. 1;4  8 Lời giâi
Nhêp vế trái vào máy tính
Nhêp log Xlog Xlog X  log Xlog X  log Xlog X  log Xlog X 2 4 6 2 4 4 6 6 2 Quy trình bçm máy Màn hình hiển thð i2$Q)$i4$Q)$ i6$Q)$pi2$Q) $i4$Q)$pi4$Q )$i6$Q)$pi6$ Q)$i2$Q)
Vì giá trð 1 xuçt hiện nhiều nhçt nên CALC X=1 Quy trình bçm máy Màn hình hiển thð r1= Vêy 1 là nghiệm.
Ta tiếp tĀc kiểm tra giá trð 12 cò phâi là nghiệm hay không r12=
Đåy là mût kết quâ khác 0 vêy 12 khöng phâi là nghiệm  Loäi C
Tiếp tĀc kiểm tra giá trð 48 cò phâi là nghiệm khöng Page 25 | r48=
Vêy 48 là nghiệm Chọn D.
Ví dụ 2: Phāćng trình x x
9  3.3  2  0 cò hai nghiệm x ,x x  x . 1 2  1 2
Giá trð A  2x 3x là 1 2 A. 4log 2 B. 1 C. 3log 2 D. 2log 3 3 3 2 Lời giâi
* Cách 1 : SHIFT SLOVE + CALC Quy trình bçm máy Màn hình hiển thð 9^Q)$p3O3^Q) $+2=
Vì chāa biết 2 đáp án , mà 2 đáp án vai trñ khöng bình đîng trong
quan hệ Ċ đáp án. Nên ta phâi sĄ dĀng dñ câ 2 nghiệm vĉi chăc
nëng SHIFT SOLVE Ċ măc đû khò hćn . Đæu tiên ta dò nghiệm
trong khoâng dāćng, ví dĀ chõn X gæn vĉi 1 qr1=
Lāu nghiệm này vào giá trð A ta đāợc 1 nghiệm. qJz Chõn X gæn 2
 . Gõi là phāćng trình và dñ nghiệm Eqrp2=
Ta đāợc 1 nghiệm nąa là 0. Vì 0  A nên x  0;x  A ta có 1 2
Nguyễn Chiến. 0973514674 Page 26 | x 2  x 3  2.0  3 A
.  1.8927  3 log 2  Chọn C. 1 2 3
* Cách 2 : CASIO 2 LẦN SHIFT SOLVE
Nhêp vế trái vào máy tính Casio. Nhçn nýt để lāu vế trái läi r÷i
SHIFT SOLVE tìm nghiệm thă nhçt và lāu vào A Quy trình bçm máy Màn hình hiển thð 9^Q)$p3O3^Q) $+2=qr1=qJz
Quay läi vế trái. SHIFT SOLVE mût læn nąa để tìm nghiệm thă hai và lāu vào B Eqrp1=
Ta có 2A3B 1.8927  3log 2  Chọn C. 3
Kĩ thuật 11: Tìm số nghiệm của phương trình mũ - logarit. Phương pháp :
+ Bước 1: Chuyển phương trình về däng Vế trái = 0
+ Bước 2: Sử dụng chức năng MODE 7 để xét lập bâng giá trð của vế trái .
+ Bước 3: Quan sát và đánh giá :
- Nếu F   0 thì  là 1 nghiệm
- Nếu F a F
. b  0 thì phương trình cò 1 nghiệm thuộc a;b
Ví dụ 1: Sø nghiệm cþa phāćng trình x x x
6.4  12.6  6.9  0 là A. 3 B. 1 C. 2 D. 0 Lời giâi
SĄ dĀng MODE 7 nhêp hàm Quy trình bçm máy Màn hình hiển thð w76O4^Q)$p12 O6^Q)$+6O9^ Q) Page 27 |
Thiết lêp miền giá trð cþa X là : Start 9  End 10 Step 1 ==p9=10=1=
Ta thçy khi x  0 thì F 0  0 vêy x  0 là nghiệm.
Tiếp tĀc quan sát bâng giá trð F X nhāng khöng cò giá trð nào
làm cho F X  0 hoðc khoâng nào làm cho F X  đùi dçu nên
x  0 là nghiệm duy nhçt  Chọn B.   
Ví dụ 2: Sø nghiệm cþa phāćng trình sinx  e 4 
  tan x trên đoän 0;2    là A. 1 B. 2 C. 3 D. 4 Lời giâi   
Chuyển phāćng trình về däng : sinx  e 4    tan x  0
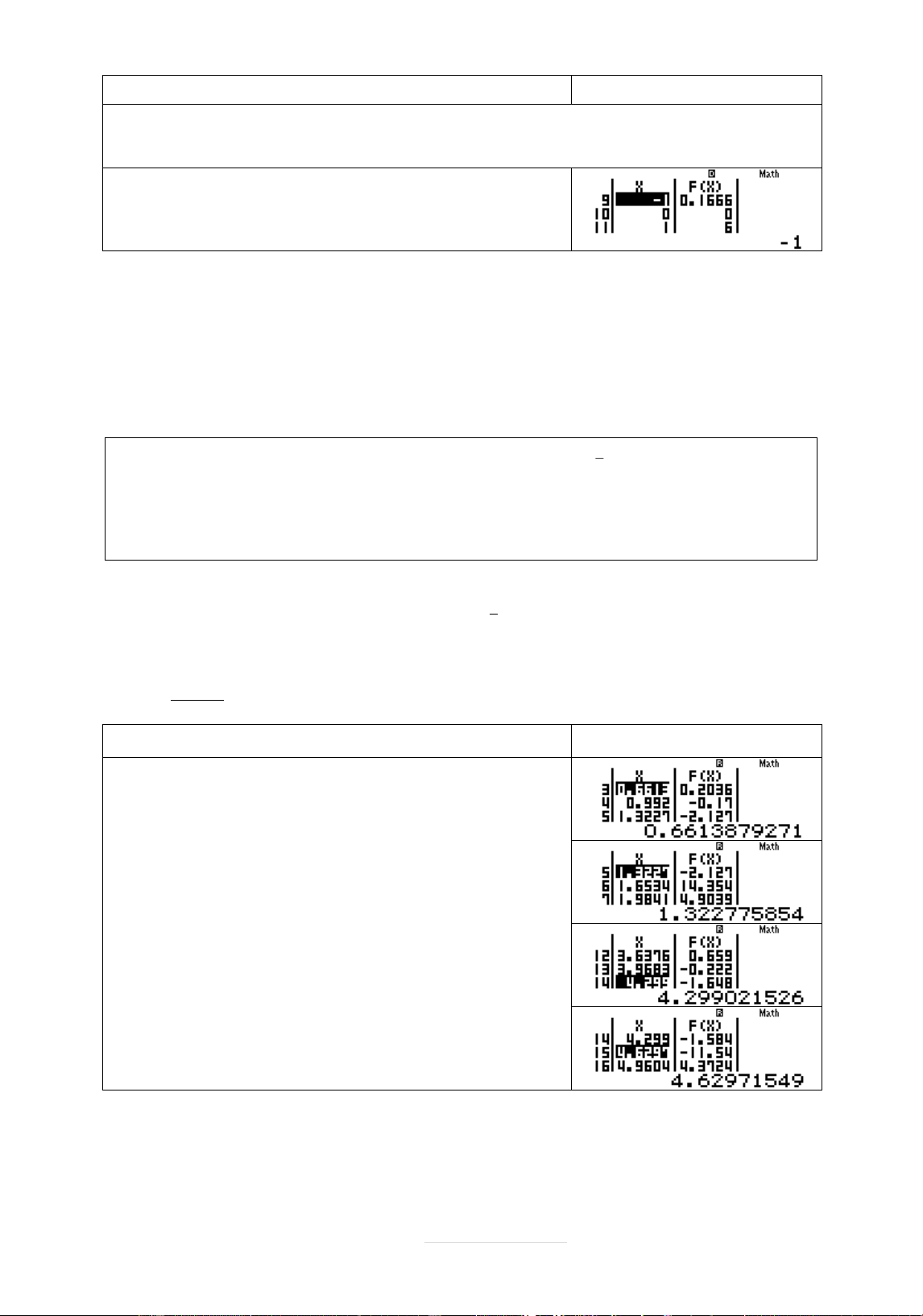
SĄ dĀng chăc nëng MODE 7 vĉi thiết lêp Start 0 End 2 Step 2  0 19 Quy trình bçm máy Màn hình hiển thð qw4w7QK^jQ) paQKR4$)$plQ ))==0=2qK=2q KP19=
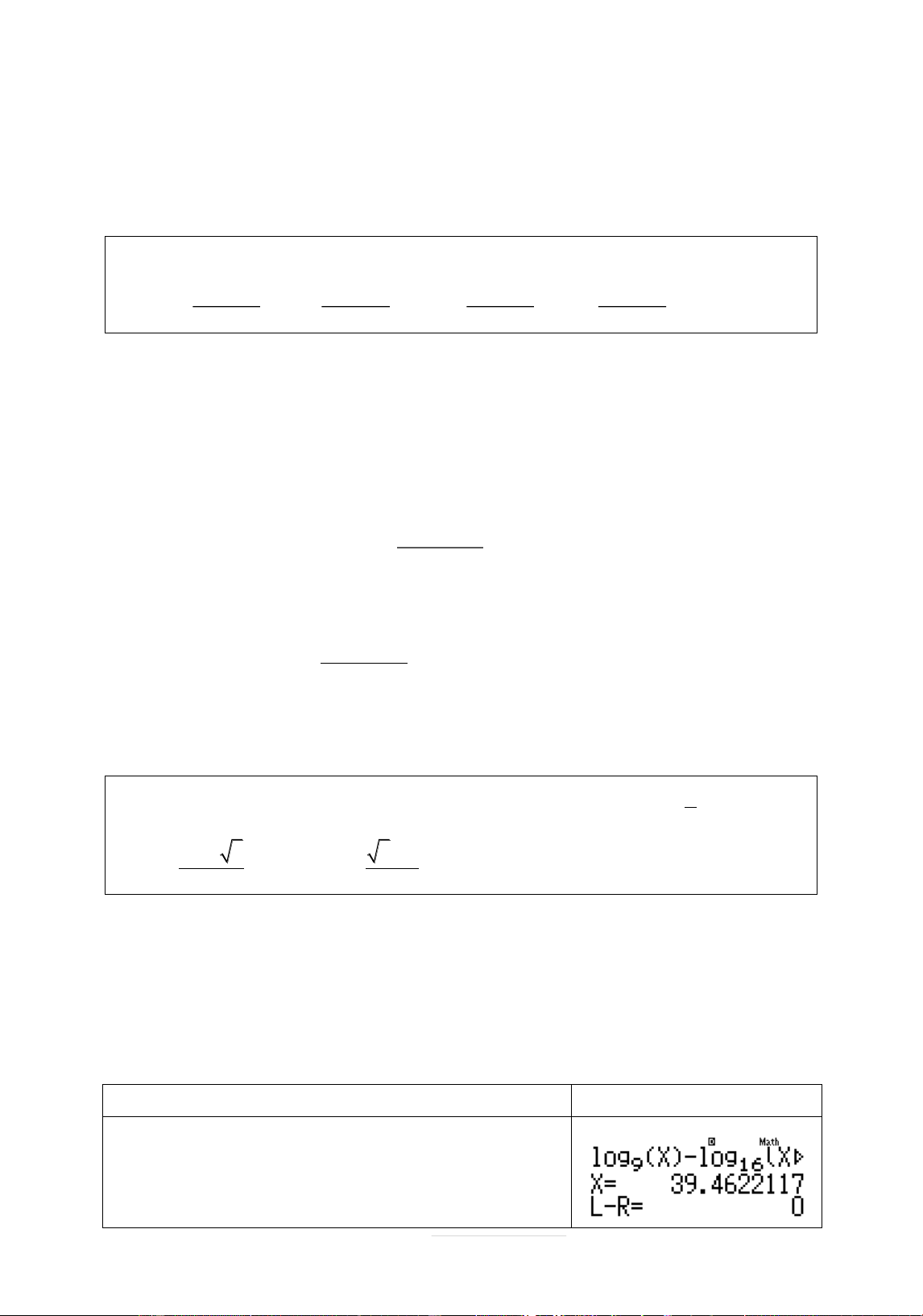
Quan sát bâng giá trð ta thçy 3 khoâng đùi dçu nhā trên :
f 0.6613 f. 0.992  0  cò nghiệm thuûc khoâng 0.6613;0.992
f 1.3227 f. 1.6634  0  cò nghiệm thuûc khoâng 1.3227;1.6534
Nguyễn Chiến. 0973514674 Page 28 |
f 3.6376 f. 3.9683  0  cò nghiệm thuûc khoâng 3.6376;3.9683
f 4.6297 f. 4.9604  0  cò nghiệm thuûc khoâng 4.6297;4.9604
Vêy phāćng trình ban đæu cò 4 nghiệm  Chọn D.
Kĩ thuật 12: Tìm nghiệm bất phương trình mũ - logarit. Phương pháp 1: CALC
+Bước 1: Chuyển bài toán bçt phāćng trình về bài toán xét
dçu bìng cách chuyển hết các sø häng về vế trái. Khi đò bçt
phāćng trình sẽ cò däng Vế trái  0 hoðc Vế trái  0
+ Bước 2: SĄ dĀng chăc nëng CALC để xét dçu các khoâng
nghiệm tĂ đò rýt ra đáp sø đýng nhçt cþa bài toán . *Chú ý:
Nếu bçt phāćng trình cò nghiệm têp nghiệm là khoâng
 ;ab thì bçt phāćng trình đýng vĉi mõi giá trð thuûc khoâng  ;ab
Nếu khoâng a;b và c,d cüng thóa mãn mà a,b  c,d
thì c,d là đáp án chính xác.
Phương pháp 2: MODE 7
+ Bước 1: Chuyển bài toán bçt phāćng trình về bài toán xét
dçu bìng cách chuyển hết các sø häng về vế trái. Khi đò bçt
phāćng trình sẽ cò däng Vế trái  0 hoðc Vế trái  0
+ Bước 2: SĄ dĀng chăc nëng lêp bâng giá trð MODE 7 cþa
máy tính Casio để xét dçu các khoâng nghiệm tĂ đò rýt ra đáp sø
đýng nhçt cþa bài toán .
Ví dụ: Bçt phāćng trình  x 2  1  log log
  0 cò têp nghiệm là : 1 3 x  1 2   A.  ;  2   B. 4;  C.  2  ;  1  1;4 D.  ;  2    4;  Lời giâi Cách 1 : CALC
Nhêp vế trái vào máy tính Quy trình bçm máy Màn hình hiển thð ia1R2$$i3$a2 Q)+1RQ)p1 Page 29 |
Kiểm tra tính Đýng Sai cþa đáp án A
CALC vĉi giá trð cên trên X  2   0.1 ta đāợc rp2p0.1=
Đåy là 1 giá trð dāćng vêy cên trên thóa mãn
CALC vĉi giá trð cên dāĉi 5 X  10  rp10^5)=
Đåy là 1 giá trð dāćng vêy cên dāĉi thóa mãn, đáp án A đýng
Tāćng tĆ nhā vêy ta kiểm tra tính Đýng Sai cþa đáp án B thì ta
thçy B cÿng đýng A đýng B đýng vêy A B là đýng nhçt  Chọn D.
Cách 2: MODE 7 nhêp vế trái vào máy tính Casio Quy trình bçm máy Màn hình hiển thð w7ia1R2$$i3$ a2Q)+1RQ)p1
Quan sát các cên cþa đáp sø là 2
 ;4;1 nên ta phâi thiết lêp miền
giá trð cþa X sao cho X chäy qua các giá trð này . Ta thiết lêp Start 4  End 5 Step 0.5 ==p4=5=0.5=
Quan sát bâng giá trð ta thçy rô ràng hai khoâng  ;  2   và
4;  làm cho dçu cþa vế trái dāćng Chọn D.
Kĩ thuật 13: Tính giá trị biểu thức mũ - logarit. Phương pháp
Nguyễn Chiến. 0973514674 Page 30 |
+ Bước 1 : DĆa vào hệ thăc điều kiện buûc cþa đề bài chõn giá trð thích hợp cho biến
+ Bước 2 : Tính các giá trð liên quan đến biến r÷i gín vào A,B C ,
nếu các giá trð tính đāợc lẻ
+ Bước 3 : Quan sát 4 đáp án và chõn chính xác
Ví dụ 1: Cho a  log 5;b  log 7;c  log 3 . Tính log 35 theo a, b, c ? 27 8 2 12 A. b 3  ac 2 B. b 3  ac 3 C. b 3  ac 2 D. b 3  ac 3 c  2 c  2 c  3 c  1 Lời giâi log 5 27
qJz (Gán giá trð này cho A) log 7
qJx (Gán giá trð này cho B) 8 log 3
qJc (Gán giá trð này cho C) 2
log 35 qJpj (Gán giá trð này cho D) 12 Và nhêp vào màn hình B 3  A 2 C D  çn “=”. C  2 Qjpa3Qx+2QzQcRQc+2= Đáp án bìng 0,21, loäi A Nhêp biểu thăc B 3  A 3 C D  C  2 Qjpa3Qx+3QzQcRQc+2= Đáp án bằng 0  Chọn B.
Ví dụ 2: Cho log x  log y  log x  y Giá trð cþa tî sø x là 9 12 16  y A. 1   5 B. 5  1 C. 1 D. 2 2 2 Lời giâi
TĂ đîng thăc log x  log y log x  y 9  12 . Thay vào hệ thăc 9 12 log x log x  log
x  y ta đāợc : log x  log  12  0 9 16 x 9  9 16  
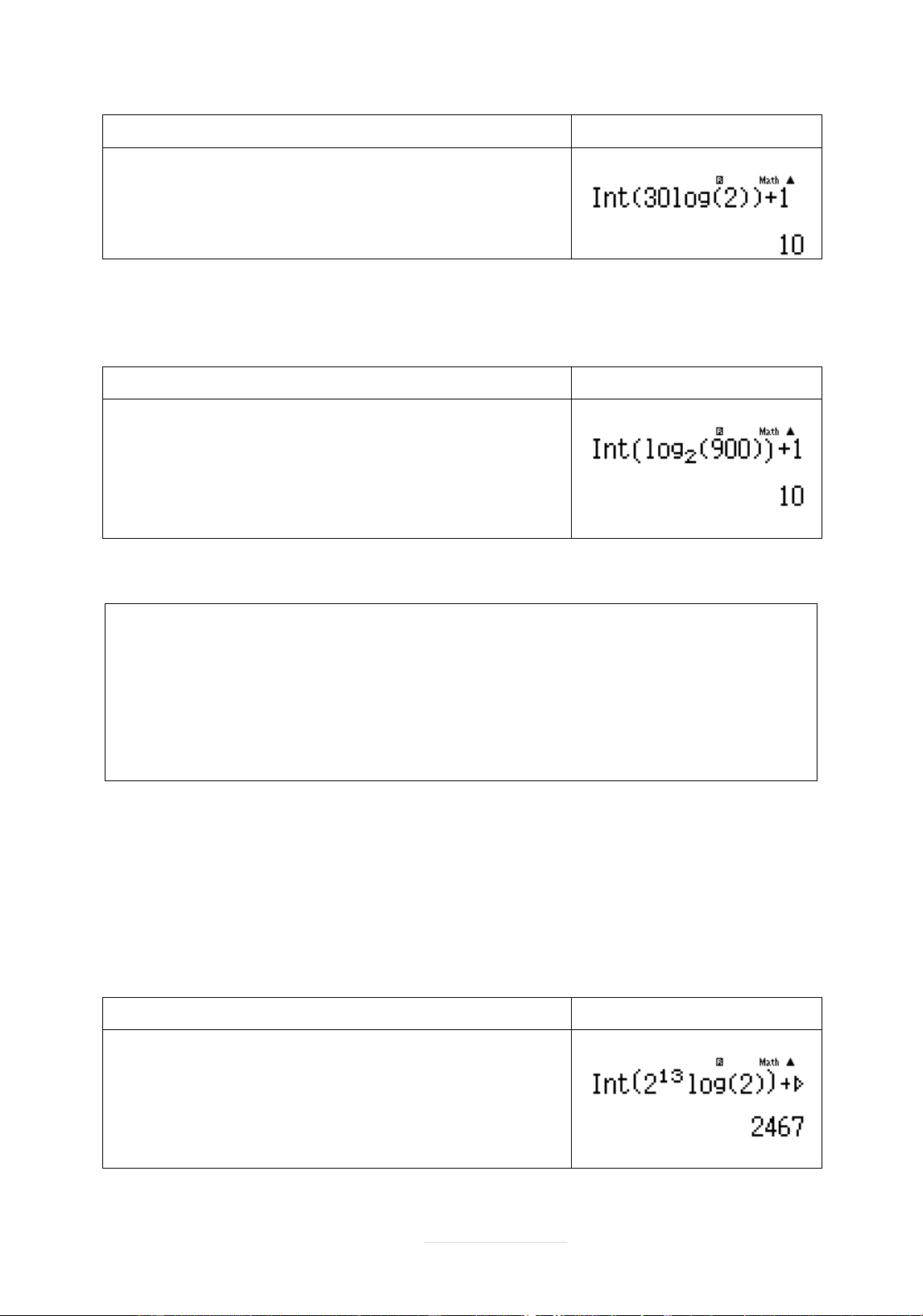
Ta cò thể dñ đāợc nghiệm phāćng trình log  log  12  0 9 16  log x x x 9  bìng chăc nëng SOLVE Quy trình bçm máy Màn hình hiển thð i9$Q)$pi16$Q )+12^i9$Q)$$ $qr1= Page 31 |
Lāu nghiệm này vào giá trð A qJz Tính được giá trị log x y 9  12 12^i9$Qz=
Lāu giá trð y này vào biến B qJx Tỉ số x A  y B aQzRQx= Ta thçy 5 1 0, 6180339887   Chọn B . 2
Kĩ thuật 14: So sánh lũy thừa các số, tìm số chữ số của một lũy thừa Phương pháp:
Phần nguyên của một số: số N được gọi là phần nguyên của một
số A nếu N  A  N  1. Kí hiệu N  A     .
Phím Int: Q+ Phần nguyên của một số.
Số chữ số của một số nguyên dương: logA  1   .
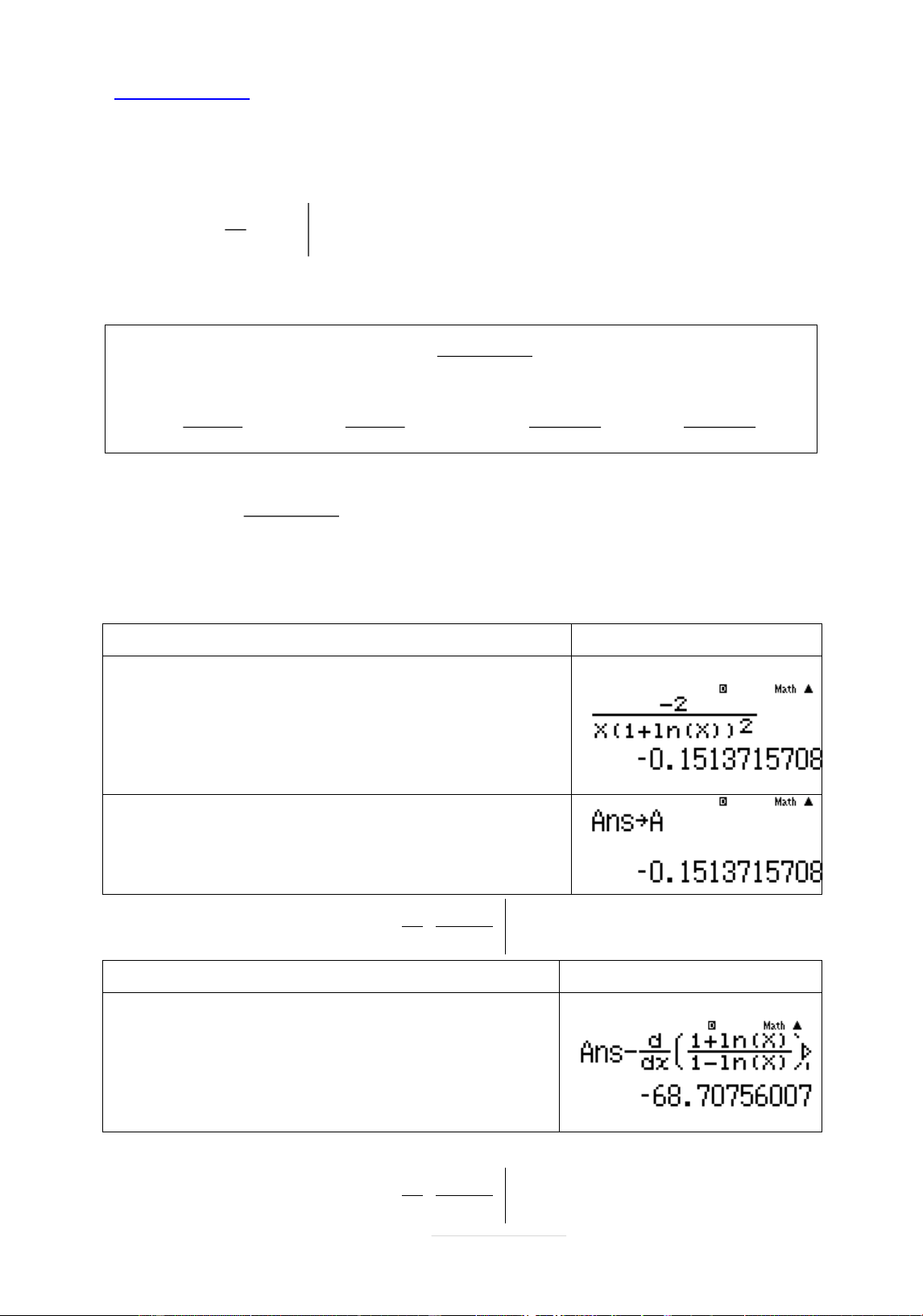
Ví dụ 1: So sánh nào sau đåy là đýng? A. 2003 2500 11  9 B. 693 600 23  25 C. 445 523 29  31 D. 445 523 29  31 Bài giâi Quy trình bçm máy Màn hình hiển thð Sø chą sø cþa 2003 11 và 2500 9
trong hệ thêp phån læn lāợt là :
Nguyễn Chiến. 0973514674 Page 32 | Q+2003g11)) +1= Q+2500g9))+1= Sø chą sø cþa 2500 9
nhiều hćn sø chą sø cþa 2003 11 nên 2500 2003 9  11  A sai Sø chą sø cþa 693 23 và 600
25 trong hệ thêp phån læn lāợt là : Q+693g23))+1= Q+600g25))+1= Sø chą sø cþa 693 23
nhiều hćn sø chą sø cþa 600 25 nên 693 600 23  25  B sai  Sø chą sø cþa 445 29 và 523
31 trong hệ thêp phån læn lāợt là: Q+693g23))+1= Q+600g25))+1= Sø chą sø cþa 445 29
nhó hćn sø chą sø cþa 523 31 nên 445 523 29  31  Chọn C.
Ví dụ 2: Gõi m là sø chą sø cæn düng khi viết sø 30 2 trong hệ thêp
phân và n là sø chą sø cæn düng khi viết sø 2 30 trong hệ nhð phån.
Ta cò tùng m  n là A. 18 B. 20 C. 19 D. 21 Lời giâi Đðt 30 k   k 30 2 10  log2 . Page 33 | Sø chą sø cþa 30 2
trong hệ thêp phån là k    1   Quy trình bçm máy Màn hình hiển thð Q+30g2))+1= Vêy sø chą sø cþa 30
2 trong hệ thêp phån là 10 Đðt 2
30  900  2h  h  log 900 . Sø chą sø cþa 2 30 trong hệ nhð phån 2 là h    1   Quy trình bçm máy Màn hình hiển thð Q+i2$900$)+ 1= Vêy sø chą sø cþa 2
30 trong hệ nhð phån là 10  m  n  10  10  20  Chọn B.
Ví dụ 3 : Nhà toán hõc Pháp Pierre de Fermat là ngāĈi đæu tiên
đāa ra khái niệm sø Fecmat n F 2
 2  1 là mût sø nghuyên tø vĉi n n
là sø dāćng khöng åm. Hãy tìm sø chą sø cþa F trong hệ nhð 13 phân? A.1243 B. 1234 C. 2452 D. 2467 Lời giâi Sø F có däng 132 2  1 . Ta thçy sø 13 2 2  1 khöng thể tên cüng 13
là 9 nên sø chą sø cþa 132 2
1 cÿng chính là sø chą sø cþa 13 2 2 trong hệ thêp phån. Đðt 132 k   k 13 2 10
 2 log 2 . Sø chą sø cþa 132 2 trong hệ thêp phân là k    1   Quy trình bçm máy Màn hình hiển thð Q+2^13$g2)) +1=  Chọn D.
Nguyễn Chiến. 0973514674 Page 34 |
Kĩ thuật 15: Tính nguyên hàm Phương pháp:
+ Tính giá trð hàm sø täi 1 điểm thuûc têp xác đðnh
+ Tính đäo hàm các đáp án täi điểm đò Lçy   d f A 
F x CALC giá trð bçt kì thuûc têp xác đðnh. Nếu dx x A
đáp án nào bìng 0 thì chõn đáp án đò.
Ví dụ: Tìm nguyên hàm cþa 2  dx  ? 2
x 1  lnx  1  ln x 1  ln x 1   lnx 1  ln x A.  C B.  C C.  C D.  C 1  ln x 1  ln x 1  ln x 1   lnx Lời giâi Tính giá trð 2 
täi điểm bçt kì thuûc têp xác đðnh ví dĀ 2
x 1  lnx 
chõn X  3 và lāu thành biến A Quy trình bçm máy Màn hình hiển thð ap2RQ)(1+hQ) ))dr3= qJz Kiểm tra đáp án A. Lçy d  1 lnX  A   
dx  1 lnX  X3 Quy trình bçm máy Màn hình hiển thð pqya1+hQ))R1 phQ))$$3=
Kết quâ khác 0 nên loäi đáp án A Kiểm tra đáp án B. Lçy d  1 lnX  A   
dx  1 lnX  X3 Page 35 |
Bçm nýt quay läi để sĄa biểu thăc trong đäo hàm Quy trình bçm máy Màn hình hiển thð !!!!!!!!o+ E!!!op=
Kết quâ bìng 0  Chọn B.
Kĩ thuật 16: Tính tích phân và các ứng dụng tích phân Phương pháp:
+ Để tính giá trð 1 tích phån xác đðnh ta sĄ dĀng lệnh y 1
Ví dụ 1: Tích phân  x3 1  2 x dx bìng 0 7 11 A.  1 B. C. D. 0 6 6 6 Lời giâi 1
Nhêp tích phån  x3 1  2 x dx 0
Chú ý: Giá trð tuyệt đøi qc Quy trình bçm máy Màn hình hiển thð y(qc3Q)p1$p2 qcQ)$)R0E1
Nhçn nýt = ta sẽ nhên đāợc giá trð tích phân là I  0  ,016666589 Lāu vào biến A qJz
Nguyễn Chiến. 0973514674 Page 36 |
Sau đò trĂ đi các đáp án
Kết quâ bìng 0 Chọn A.
Ví dụ 2: Tính diện tích hình phîng giĉi hän bĊi đ÷ thð hàm sø
y  ln x  
1 ,y  ln2. x,x  2 ? A. 3 4 ln 16. 2   1  3 ln 3  1
B.  ln2. 2  1  3ln3 1 3 3 C. 16 4 16 4 ln  2 ln 2  1 D. 2 ln  ln2  1 27 3 27 3 Lời giâi
Cên đæu tiên là x  2 . Düng chăc nëng SHIFT SOLVE giâi
phāćng trình hoành đû giao điểm  lnx  1  ln2. x  0 Quy trình bçm máy Màn hình hiển thð hQ)+1)ph2sQ) $)qr=
Ta đāợc nghiệm x  1. Vêy ta tìm đāợc hai cên x  1;x  2
Diện tích hình phîng giĉi hän bĊi hai hàm sø y  lnx  1 , 2
y  ln 2. x và hai đāĈng thîng x  1;x  2 là S  ln
 x  1  ln2. x dx 1 Quy trình bçm máy Màn hình hiển thð yqchQ)+1)ph2 )OsQ)R1E2=
Lāu kết quâ vĂa tìm đāợc vào biến A sau đò trĂ đi các kết quâ Ċ
các đáp án kết quâ nào bìng 0 thì chõn. Quy trình bçm máy Màn hình hiển thð qJz Page 37 | Thay đáp án A Qzp(hqs16$( s2$+1)p3h3)+ 1)=
Kết quâ khác 0 nên loäi A, tiếp theo thay đáp án B Qzp(pa4R3$h2 )(s2$+1)+3h3) p1)=
Kết quâ bìng 0  Chọn B .
Ví dụ 3: Cho D là miền hình phîng giĉi hän bĊi : 
y  sin x ;y  0;x  0;x 
. Khi D quay quanh Ox täo thành mût khøi 2
trñn xoay. Thể tích cþa khøi trñn xoay thu đāợc là A.1 B. C. 2 D. 2 Lời giâi
Hàm thă nhçt : y  sinx , hàm thă hai : y  0 Cên thă nhçt : 
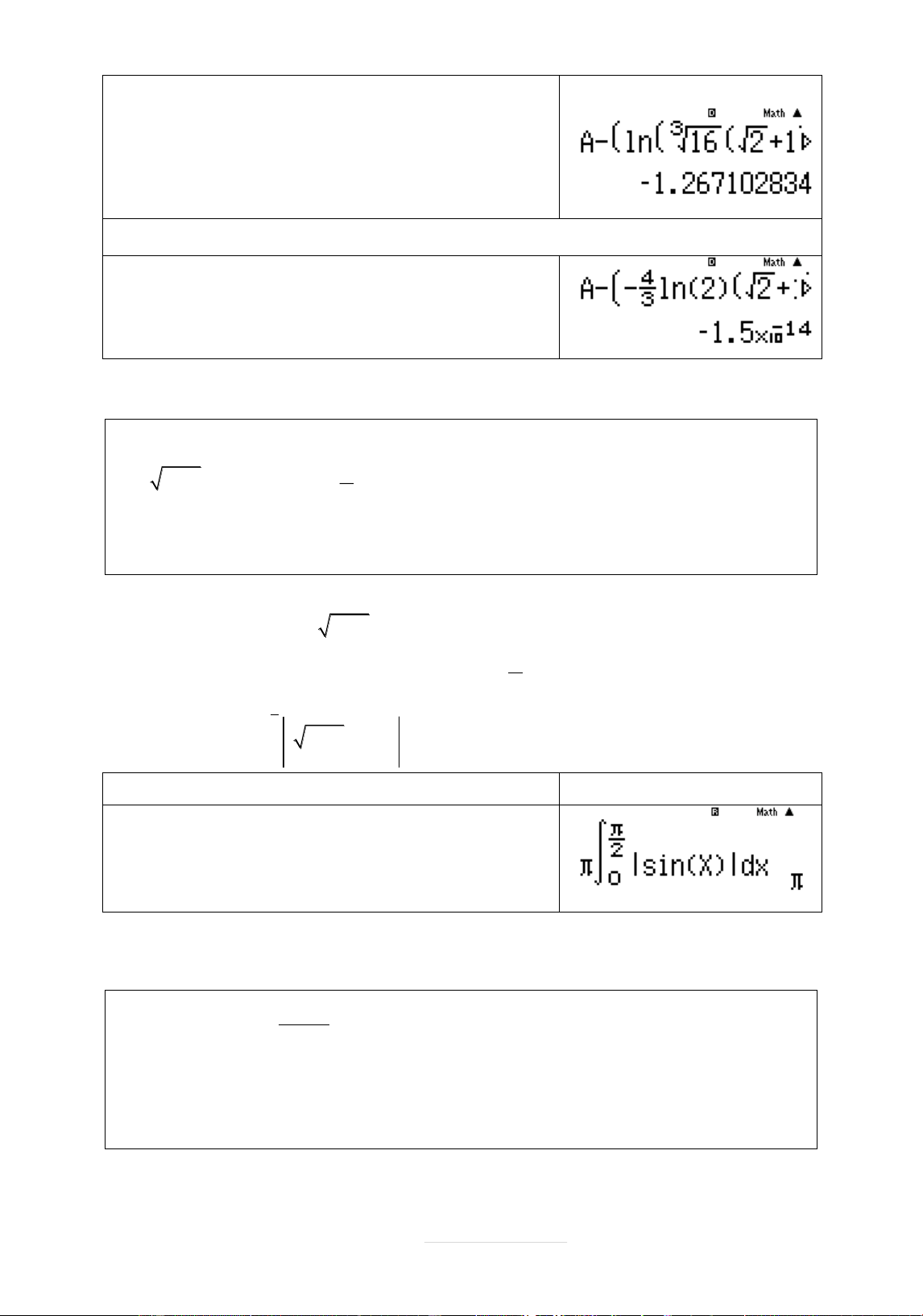
x  0 , cên thă hai : x  2  2 Thể tích 2
V     sinx  2  0 dx 0 Quy trình bçm máy Màn hình hiển thð qw4qKyqcjQ) )R0EaqKR2=
V    Chọn B 4
Ví dụ 4 : Biết dx
 a ln2  b ln 3  c ln 5 
vĉi a,b,c là các sø nguyên. x2  x 3
Tính S  a b  c A. S  6 B. S  2 C.S  2  D. S  0 Lời giâi
Nguyễn Chiến. 0973514674 Page 38 | 4 Tính tích phân dx 
và lāu vào biến A x2  x 3 Quy trình bçm máy Màn hình hiển thð ya1RQ)d+Q)R3 E4= qJz
Khi đó  ln2  ln 3  ln 5   ln  16 a b c 2 .3 .5  a b c A A a b c A
 2 .3 .5  e  15 QK^Qz= 16 2.2.2.2 Ta có: 4 1  1  a b c 
 2 .3 .5  2 .3 .5  a  4;b  1  ;c  1   S  2 15 3.5  Chọn B. 2
Ví dụ 5 : Cho I  ln
 x  1dx  a ln3 b ln2 c a,b,c Z . Tính giá trð 1
cþa biểu thăc a  2b 3c ? A. 0 B. 1 C. 2 D. 3 Lời giâi 2
Tính giá trð tích phån I  ln
 x  1dx r÷i lāu vào biến A 1 Quy trình bçm máy Màn hình hiển thð yhQ)+1)R1E2= qJz A Khi đò e a b c A a b c A a b
a ln 3  b ln 2  c  A  ln(3 .2 e
. )  lne  3 .2 e
.  e  3 .2  c e
Để tính đāợc a b
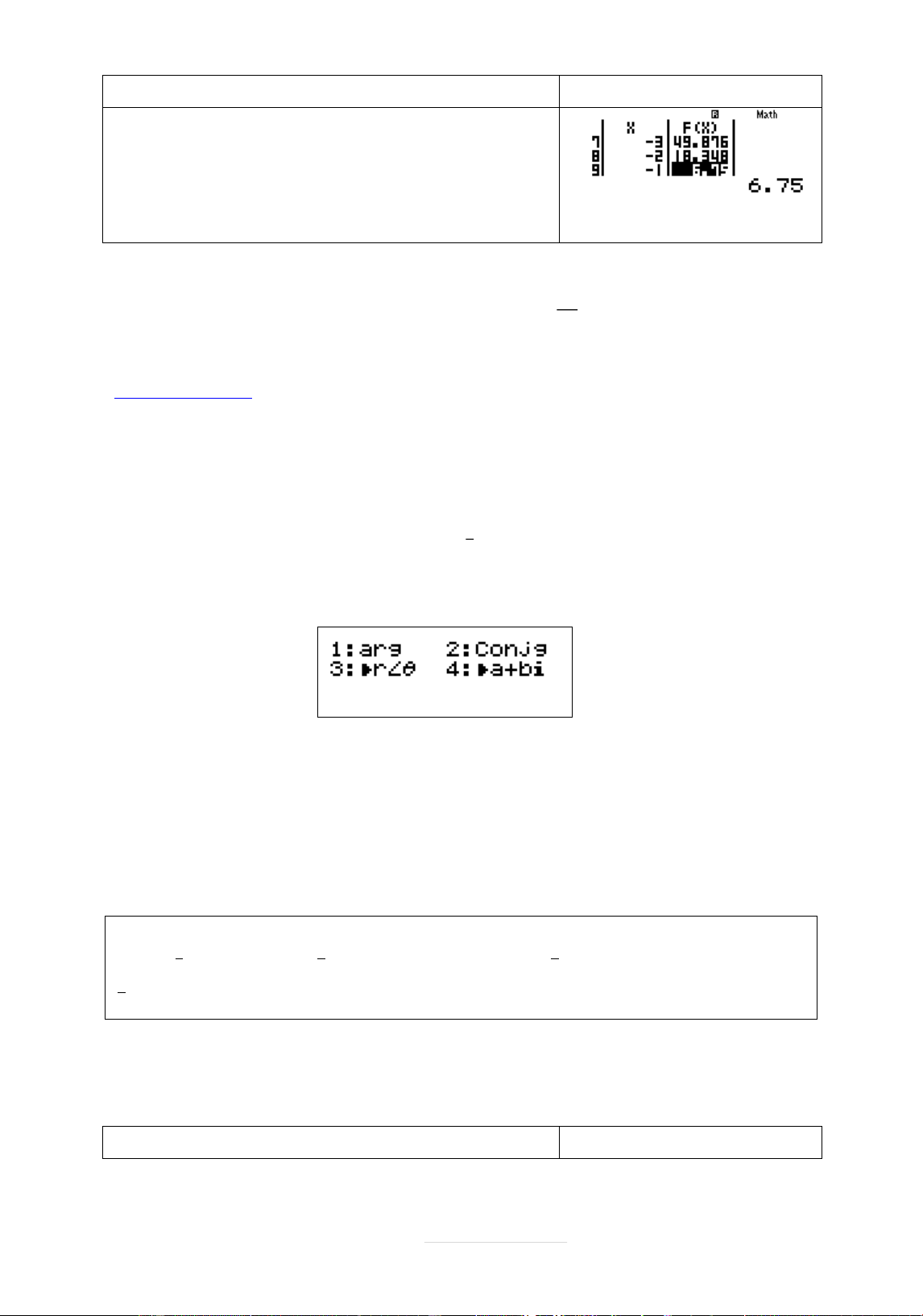
3 .2 ta sĄ dĀng chăc nëng MODE 7 vĉi hàm f X  A e a b  3 .2  ce Page 39 | Quy trình bçm máy Màn hình hiển thð w7aQK^QzRQK ^Q)==p9=10= 1=
Quan sát màn hình xem giá trð nào cþa f X  là sø hąu tî thì nhên. Dễ thçy vĉi 27 X  c  1  thì a b 3 2 3 .2 6.75 3 .2   
 a  3;b  2  4 Vêy a  b 2  c
3  3  4  3  2  Chọn C.
Kĩ thuật 17: Tìm phần thực, phần âo, Môđun, Argument, số phức liên hợp Phương pháp:
+ Để xĄ lý sø phăc ta sĄ dĀng tù hợp phím w2 (CMPLX).
+ Lệnh tính Möđun cþa sø phăc là qc
+ Lệnh tính sø phăc liên hợp z là q22
+ Lệnh tính Acgument cþa sø phăc là q21
1: arg: Mût Argument cþa sø phăc z  a bi .
2: Conjg: Sø phăc liên hợp cþa sø phăc z  a bi . 3: r 
 : Chuyển sø phăc z  a  bi thành Möđun  agrment
4: a bi : Chuyển về däng z  a bi (thāĈng áp dĀng cho nhąng
mön khác và chuyển tĂ däng lāợng giác sang däng đäi sø).
Ví dụ 1: Tìm số phức liên hợp của số phức z  i( i3  1)
A. z  3  i B. z  3   i
C. z  3  i D. z  3   i Lời giải Bçm w2 và çn q22.
Nhêp nhā sau: conjgi  i3  1 và çn =. Quy trình bçm máy Màn hình hiển thð
Nguyễn Chiến. 0973514674 Page 40 | w2q22b(3b+1)=
 z  3  i  Chọn D.
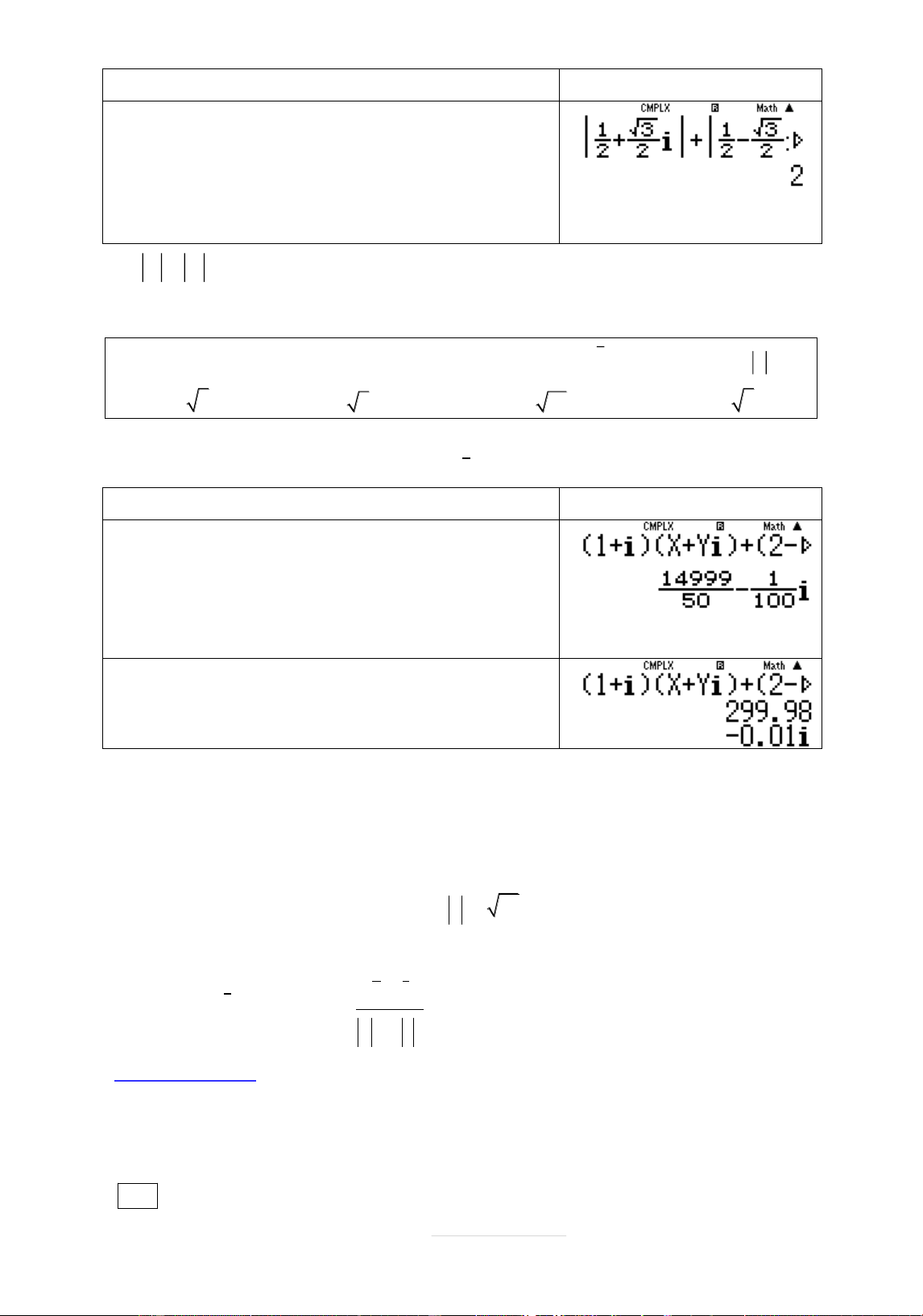
Ví dụ 2: Tìm möđun cþa sø phăc thóa mãn 1  i3z  i3  i7  2 A. 5 z  1 B. z  4 C. z  2 D. z  3 Lời giâi Chuyển z về däng i 7  2  i 3 z  1  i 3 Quy trình bçm máy Màn hình hiển thð w2qca7bp2p3b R1p3b=
Vêy z  2 Chọn C.
Ví dụ 3: Nếu sø phăc 1
z thóa mãn z  1 thì phæn thĆc cþa 1  z bìng A. 1 B. 1  C.2 D. 1  2 2 Lời giâi
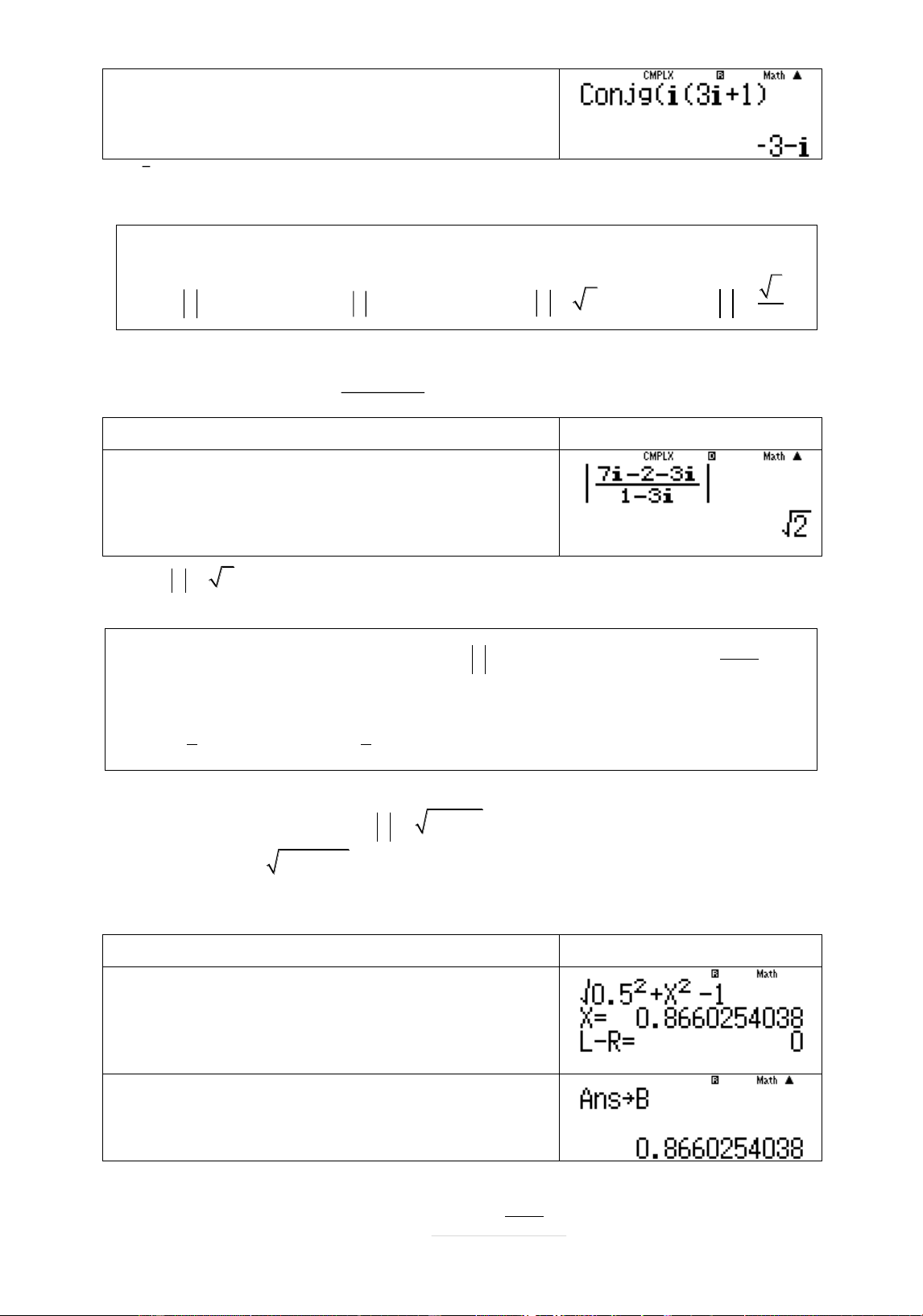
Đðt sø phăc z  a bi thì z  a2  b2  1 Chõn a  0.5 2   b2 0.5
 1 . SĄ dĀng chăc nëng SHIFT SOLVE để
tìm b và lāu giá trð này vào B Quy trình bçm máy Màn hình hiển thð w1s0.5d+Q)d$ p1qr0.5= qJx
TrĊ läi chế đû CMPLX để tính giá trð 1 : 1  z Page 41 | Quy trình bçm máy Màn hình hiển thð w2a1R1p(0.5+ Qxb)=
Vêy phæn thĆc cþa z là 1  Chọn A. 2
Kĩ thuật 18: Tìm căn bậc hai số phức Phương pháp
Cách 1: Để máy Ċ chế đû w2. Bình phāćng các đáp án xem
đáp án nào trüng vĉi sø phăc đề cho.
Cách 2: Để máy Ċ chế đû w2.
+ Nhêp sø phăc z bìng để lāu vào Ans + Viết lên màn hình: sqcM$$qz21M)a2
+ Nhçn = đāợc mût trong hai cën bêc hai cþa sø phăc z.
cën bêc hai cñn läi ta đâo dçu câ phæn thĆc và phæn âo.
Cách 3: Để chế đû w1.
+ Ấn q+ sẽ xuçt hiện và nhêp Pol( phæn thĆc, phæn âo)
và sau đò çn =. Lāu ý dçu “,” là q).
+Ấn tiếp qp sẽ xuçt hiện và nhêp  Y 
Rec  X,  sau đò çn 2  
= thì đāợc læn lāợt phæn thĆc, phæn âo cþa cën bêc hai sø phăc.
Ví dụ : Tìm mût cën bêc hai cþa sø phăc 1  i2z  i4  2   i2  9. A. 2  i 2 B. 1  i 2 C. 1  i 2 D. 1   i 2 Lời giải
Để chế đû w2 thu gõn sø phăc
Nguyễn Chiến. 0973514674 Page 42 | Quy trình bçm máy Màn hình hiển thð Ca4bp2p(2b+9) R1p2b=
Sau đò rýt gõn z về däng tøi giân z  3   i 4 .
Cách 1: Bình phāćng các đáp án ta đāợc đáp án B.
Cách 2: Bật chế độ w2. Quy trình bçm máy Màn hình hiển thð sqcM$$qzaq21 M)R2=
Vậy số phức cò một căn bậc hai là z  1  i 2  Chọn B.
Cách 3: Bêt läi chế đû w1. Bçm Pol  3  , 4
 bçm = tiếp tĀc bçm Rec X,Y : 2 bçm = Quy trình bçm máy Màn hình hiển thð q+p3q)p4)= qpsQ)$q)QnP2 )=
Vậy số phức cò một căn bậc hai là z  12i Chọn B.
Kĩ thuật 19: Chuyển số phức về dạng lượng giác Phương pháp:
Bật chế độ w2. Nhập số phức vào màn hình rồi ấn q23 được r 
 . Trong đó r là môđun,  là góc lượng giác.
Ngược lại, bấm r   rồi bấm q24.
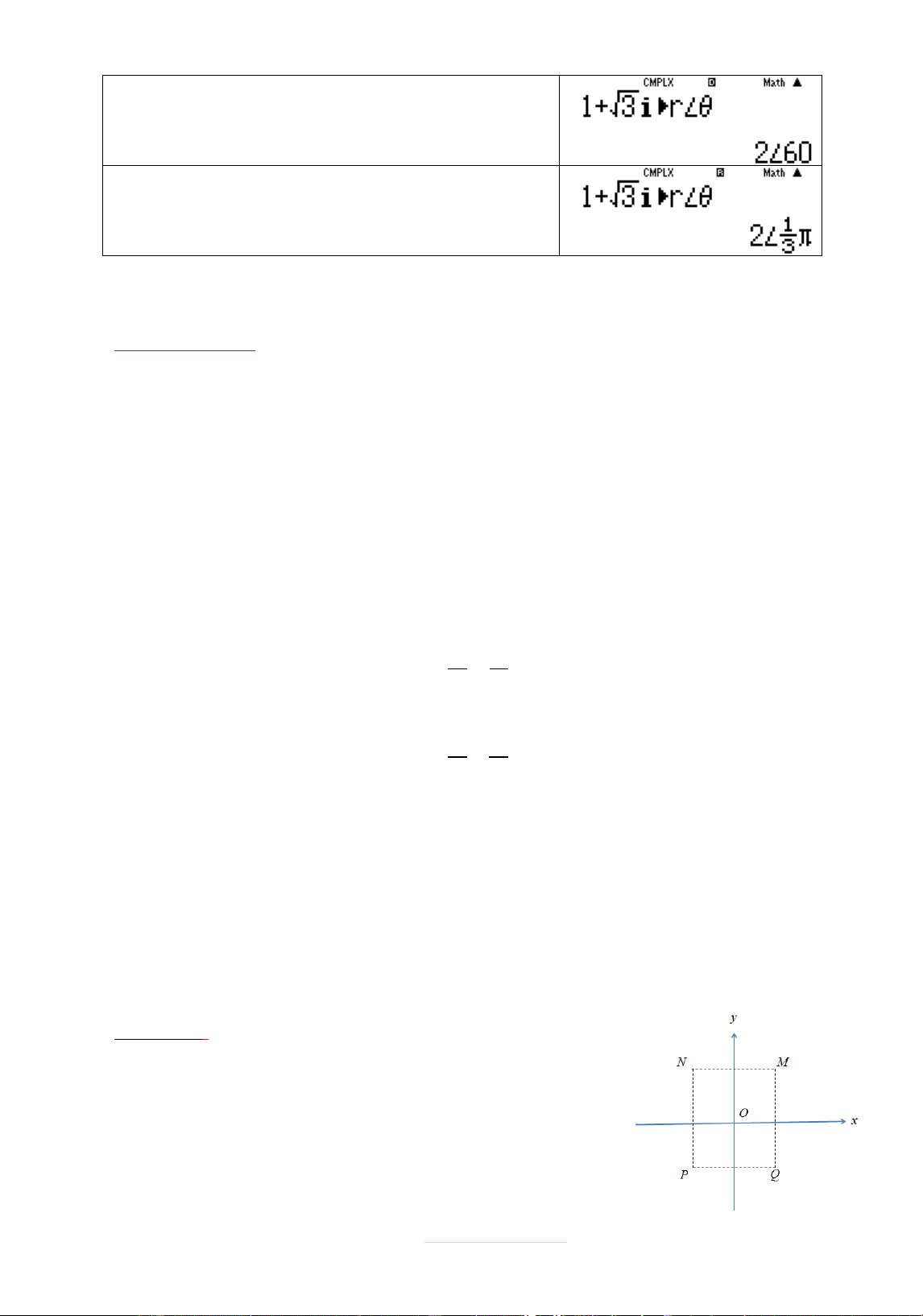
Ví dụ: Cho sø phăc z  1 3i . Tìm góc lāợng giác cþa sø phăc z? A.  B.  C.  D.  6 2 3 4 Lời giâi
Bêt chế đû w2 sau đò nhêp sø phăc vào màn hình và bçm
q23 để chuyển sang Radian bçm qw4 Quy trình bçm máy Màn hình hiển thð Page 43 | w21+s3$bq23= qw4  Chọn C.
Kĩ thuật 20: Biểu diễn hình học của số phức. Tìm quỹ tích
điểm biểu diễn số phức Phương pháp
Đðt z  x  yi , biểu diễn sø phăc theo yêu cæu đề bài, tĂ đò khĄ i
và thu về mût hệ thăc mĉi :
+ Nếu hệ thăc có däng Ax  By C  0 thì têp hợp điểm là đāĈng thîng
+ Nếu hệ thăc có däng  2 2 x a  y b R2     thì têp hợp
điểm là đāĈng tròn tâm I a;b bán kính R 2 2
+ Nếu hệ thăc có däng x y 
 1 thì têp hợp điểm có däng a2 b2 mût Elip 2 2
+ Nếu hệ thăc có däng x y 
 1 thì têp hợp điểm là mût a2 b2 Hyperbol
+ Nếu hệ thăc có däng y Ax2 
 Bx C thì têp hợp điểm là mût Parabol
+ Tìm điểm đäi diện thuûc quỹ tích cho Ċ đáp án r÷i thế
ngāợc vào đề bài, nếu thóa mãn thì là đýng
Đường thẳng thay 2 điểm, đường cong thay 3 điểm.
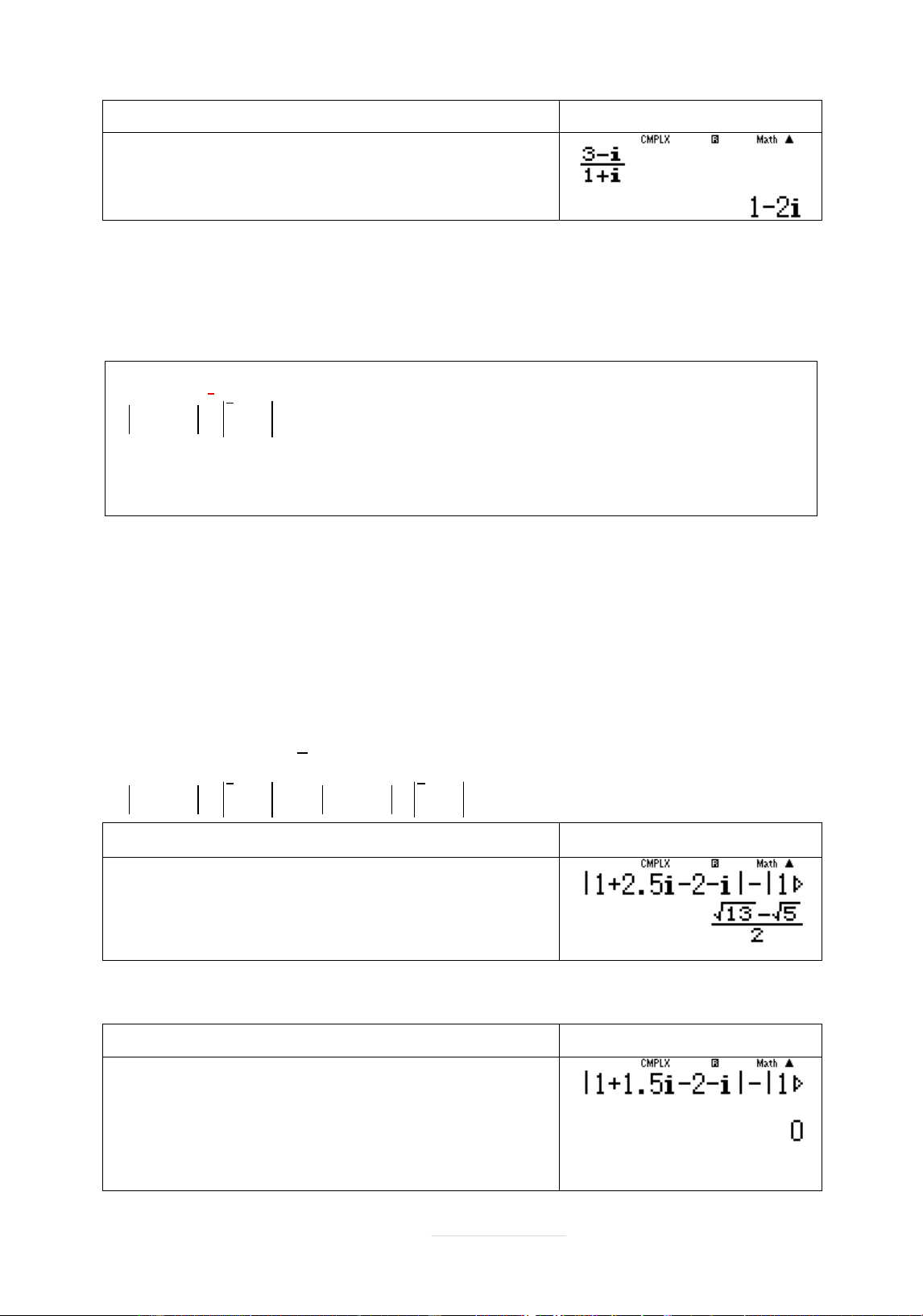
Ví dụ 1: Cho sø phăc z thóa mãn 1  iz  3  i
Hói điểm biểu diễn sø phăc z là điểm nào
trong các điểm M,N,P Q , A.điểm P B.điểm Q C.điểm M D.điểm N Lời giâi
Nguyễn Chiến. 0973514674 Page 44 |
SĄ dĀng máy tính Casio trong möi trāĈng CMPLX để tìm z Quy trình bçm máy Màn hình hiển thð w2a3pbR1+b=
 z  1  i
2 và điểm biểu diễn z trong hệ trĀc thĆc âo có tõa đû 1; 2
  Điểm có thĆc dāćng và âo âm sẽ nìm Ċ góc phæn tā thă IV
 Điểm phâi tìm là Q  Chọn B.
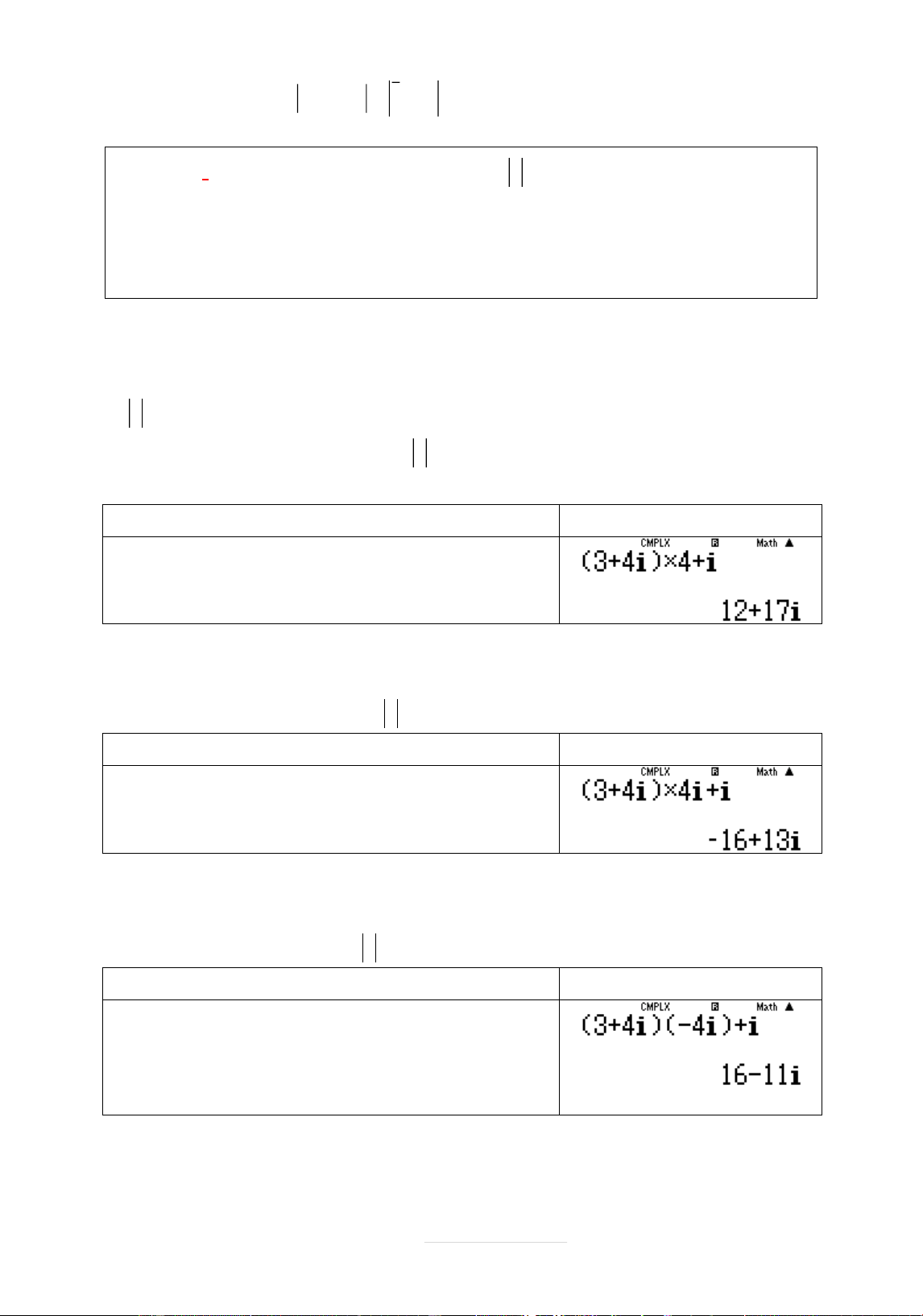
Ví dụ 2 : Têp hợp các điểm biểu diễn sø phăc z thóa mãn
z  2  i  z  i 2 A. x 4  y 2  1  0 B. x 4  y 2  1  0 C. x 4  y 2  1  0 D. x 4  y 6  1  0 Lời giâi
Gõi sø phăc z có däng z  a bi . Ta hiểu : điểm M biểu diễn sø
phăc z thì M có tõa đû M a;b .
Giâ sĄ đáp án A đýng thì M thuûc đāĈng thîng x 4  y 2  1  0 thì a 4  b 2  1  0 Chõn 5
a  1 thì b 
 z  1  2. i
5 . Sø phăc z thóa mãn 2
z  2  i  z  i
2 thì z  2  i  z  i 2  0 Quy trình bçm máy Màn hình hiển thð qc1+2.5bp2pb $pqc1p2.5b+2 b=
Ta thçy ra mût kết quâ khác 0 Loäi A.
Tāćng tĆ vĉi đáp sø B chõn a  1 thì b  1.5 và z  1  1. i 5 Quy trình bçm máy Màn hình hiển thð qc1+1.5bp2pb $pqc1p1.5b+2 b= Page 45 |
Kết quâ ra 0 vêy z  2  i  z  i
2  0  Chọn B.
Ví dụ 3: Cho các sø phăc z thóa mãn z  4 . Biết rìng têp hợp các
điểm biểu diễn các sø phăc w  3  i4z  i là mût đāĈng trñn. Tính
bán kính r cþa đāĈng trñn đò. A.r  4 B.r  5
C.r  20D.r  22 Lời giâi
Để tìm 1 đāĈng tròn ta cæn 3 điểm biểu diễn cþa w , vì z sẽ sinh
ra w nên đæu tiên ta sẽ chõn 3 giá trð đäi diện cþa z thóa mãn z  4
+ Chõn z  4  i
0 (thóa mãn z  4 ). Tính w  3  i 4 4  i 0   i 1 Quy trình bçm máy Màn hình hiển thð (3+4b)O4+b=
Ta cò điểm biểu diễn cþa z là M 12;17 1 + Chõn z  i
4 (thóa mãn z  4 ). Tính w  3  i 4  i 4   i 2 Quy trình bçm máy Màn hình hiển thð (3+4b)O4b+b=
Ta cò điểm biểu diễn cþa z là N  1  6;13 2
Chõn z   i
4 (thóa mãn z  4 ). Tính w  3  i 4  i 4   i 3 Quy trình bçm máy Màn hình hiển thð (3+4b)(p4b) +b=
Ta cò điểm biểu diễn cþa z là P 16; 1   1 3
Vêy ta cò 3 điểm M,N,P thuûc đāĈng tròn biểu diễn sø phăc w
Nguyễn Chiến. 0973514674 Page 46 |
ĐāĈng tròn này sẽ có däng tùng quát x2  y2  ax by  c  0 . Để tìm
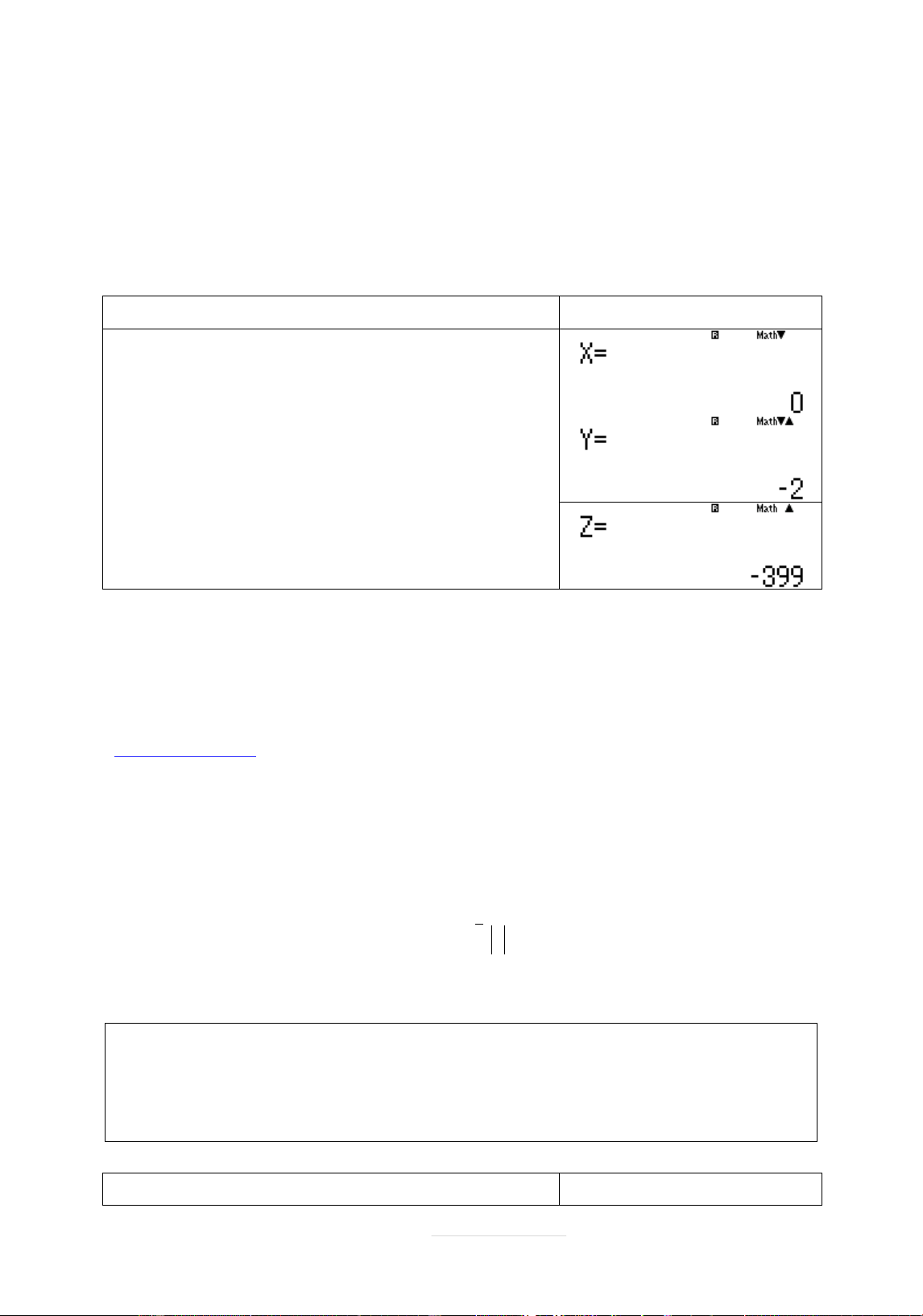
a,b,c ta sĄ dĀng máy tính Casio vĉi chăc nëng MODE 5 3 Quy trình bçm máy Màn hình hiển thð w5212=17=1=p 12dp17d=p16= 13=1=p16dp13 d=16=p11=1=p 16dp11d== Phāćng trình đāĈng tròn 2
: x2  y2  y 
  x2  y   2 2 399 0 1  20
Bán kính đāĈng tròn têp hợp điểm biểu diễn sø phăc w là 20  Chọn C.
Kĩ thuật 21: Tìm số phức, giâi phương trình số phức. Kĩ
thuật CALC và CALC: 100+ 0,01i Phương pháp
+ Nếu phāćng trình cho sïn nghiệm thì thay tĂng đáp án
+ Nếu phāćng trình bêc 2,3 chî chăa z vĉi hệ sø thĆc, ta giâi
nhā phāćng trình sø thĆc (nhên câ nghiệm phăc).
+ Nếu phāćng trình chăa câ z;z; z ...düng kï thuêt CALC vĉi X  100 Y ;
 0,01 sau đò phån tích kết quâ.
Ví dụ 1: Phāćng trìnhz2  5  iz  8  i  0 cò nghiệm là:
A. z  3  i;z  3   i
B. z  1  i 3 ;z  1   i 3
C. z  3  i 2 ;z  2  i
D. z  1  i;z  1   i Quy trình bçm máy Màn hình hiển thð Page 47 | w2Q)dp(5pb)Q )+8pbr3+b=
Kết quâ khác 0 loäi A, tiếp theo nhìn sang đáp án B thay z  13i p1+3b=
Kết quâ khác 0 loäi B, thay đáp án C thay z  32i r3p2b=
Kết quâ bìng 0 thay tiếp z  2  i r2+b=  Chọn C.
Ví dụ 2 : Gõi z ,z là hai nghiệm phăc cþa phāćng trình 1 2
z2  z  1  0 . Giá trð cþa z  z bìng 1 2 A.0 B.1 C. 2 D.4 Lời giâi
Tính nghiệm cþa phāćng trình bêc hai z2  z  1  0 bìng chăc nëng MODE 5 3 Quy trình bçm máy Màn hình hiển thð w531=p1=1== Vêy ta đāợc hai nghiệm 1 3 1 3 z   i và z   i . Tính tùng 1 2 2 2 2 2
Möđun cþa hai sø phăc trên ta läi düng chăc nëng SHIFT HYP
Nguyễn Chiến. 0973514674 Page 48 | Quy trình bçm máy Màn hình hiển thð w2qca1R2$+as 3R2$b$+qca1R 2$pas3R2$b=
 z  z  2  Chọn B . 1 2
Ví dụ 3: Cho sø phăc thóa mãn: 1  iz  2  iz  11  i . Tính z ? A. 2 B. 5 C. 10 D.2 2 Lời giâi
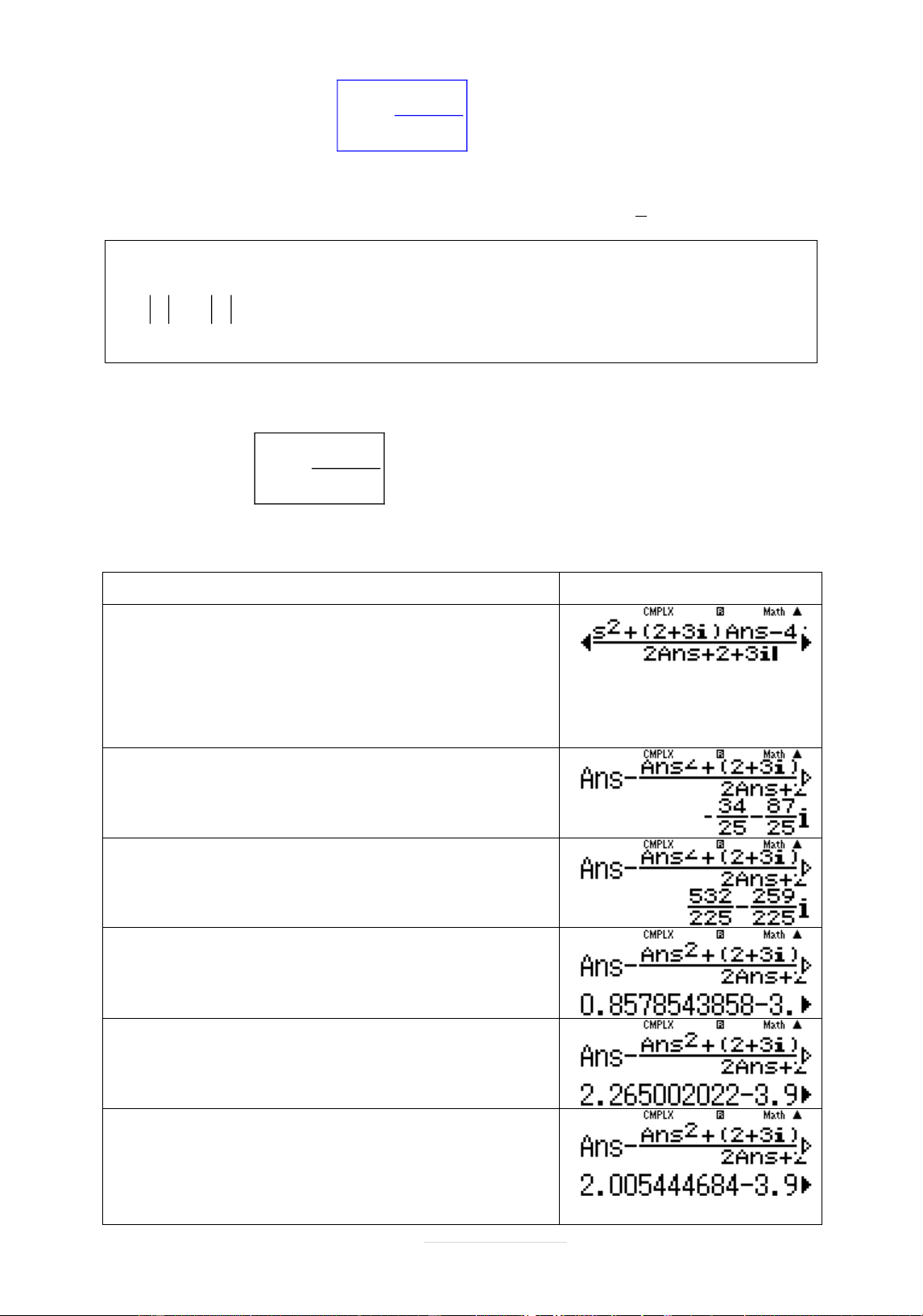
Nhêp phāćng trình vĉi z  X Yi;z  X Yi CALC X  100Y ;  0,01 Quy trình bçm máy Màn hình hiển thð w2(1+b)(Q)+Q nb)+(2pb)(Q) pQnb)r100=0. 01= n
Ta có kết quâ vế trái 299,980,01i
Phân tích 299,98  300  0,02  x 3  y 2 và 0, 0 i 1  yi
Đ÷ng nhçt vế trái và vế phâi cho phæn thĆc và phæn âo bìng nhau  x 3  y 2  11 x   3   
 z  3  i  z  10  Chọn C. y  1  y  1   
Cách 2 : Xem công thăc giâi nhanh sø phăc. Cho sø phăc z thóa mãn: 
az  bz  c thì : ca cb z   Chọn C . 2 2 a  b
Kĩ thuật 22: Giâi phương trình số phức dùng phương pháp lặp New tơn Phương pháp
+ Nhêp 1 sø bçt kì sau đò bçm = máy tính cho kết quâ đò là Ans Page 49 | f Ans
+ Sau đò nhêp Ans 
bçm dçu = liên tiếp cho đến f ' Ans
khi kết quâ khöng thay đùi ta đāợc 1 nghiệm.
+ Tìm nghiệm cñn läi ta dĆa vào Vi-et: c x x .  1 2 a
Ví dụ: Cho sø phăc z thóa mãn :z2  2  i3z  4  1 i8  0 . Tính giá trð 2 2 z  2 z 1 2 ? A. 8. B. 34. C. 54. D. 27. Lời giâi
Nhêp 1 sø bçt kì ví dĀ nhêp 1 = f Ans Sau đò nhêp Ans 
bçm dçu = liên tiếp đến khi kết quâ f ' Ans
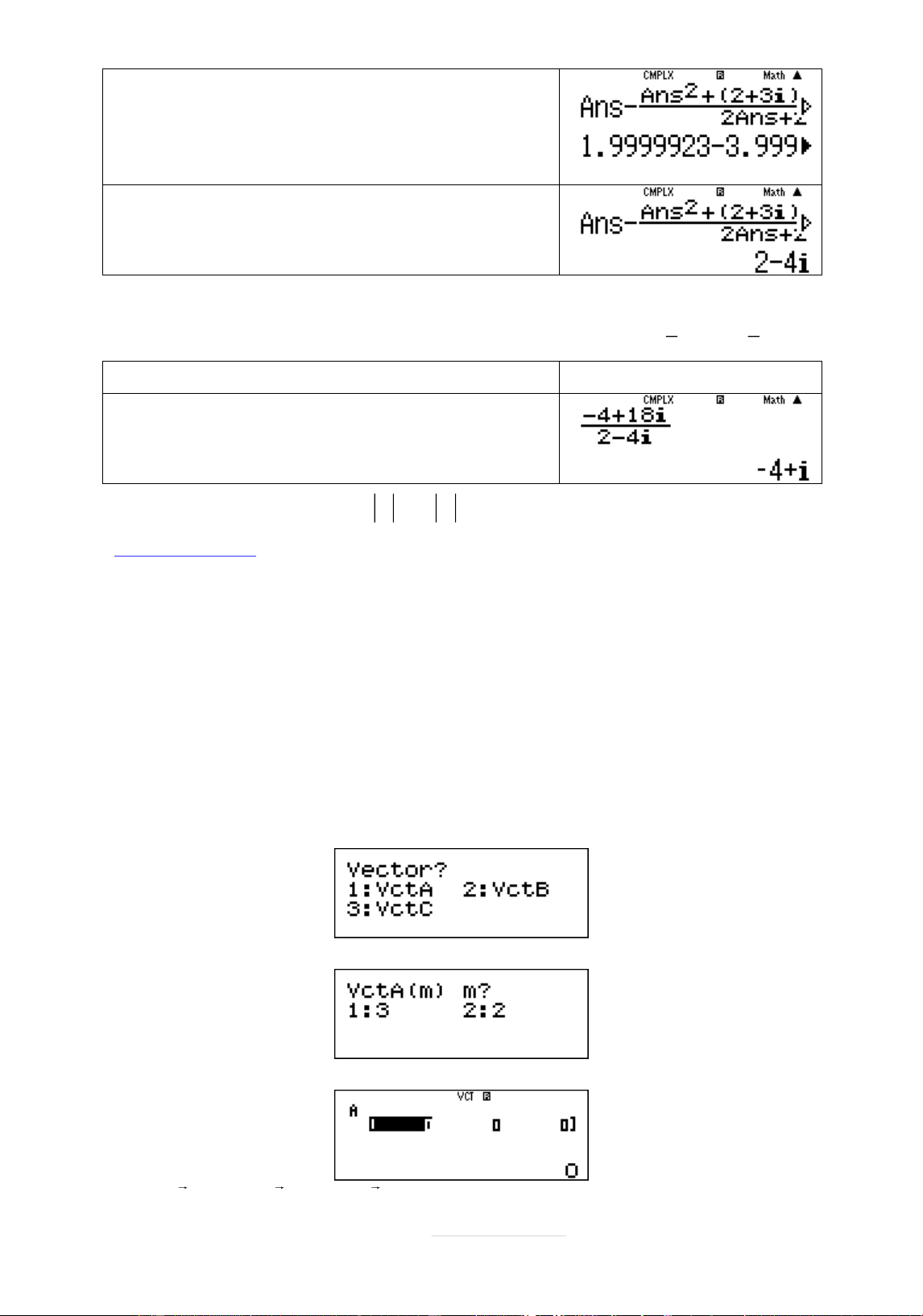
khöng thay đùi sẽ tìm đāợc nghiệm. Quy trình bçm máy Màn hình hiển thð w21=paMd+(2+ 3b)Mp4+18bR2M +2+3b = = = = =
Nguyễn Chiến. 0973514674 Page 50 | = =
Bçm = liên tiếp vén đāợc kết quâ z  24 .i Vêy phāćng trình cò
nghiệm z  2  i 4 .  c  z  : z 1
Tìm nghiệm thă 2. Theo vi-et c z z 1 2 a 2 a 1 Quy trình bçm máy Màn hình hiển thð ap4+18bR2p4b= 2 2
Vậy z  2  4i; z  4
  i  z  2 z
 54  Chọn C. 1 2 1 2
Kĩ thuật 23: Tính tích vô hướng có hướng véc tơ Phương pháp
+ Lệnh đëng nhêp möi trāĈng vecto MODE 8
+ Nhêp thông sø vecto MODE 8 1 1
+ Tính tích vö hāĉng cþa 2 vecto : vectoA SHIFT 5 7 vectoB
+ Tính tích cò hāĉng cþa hai vecto : vectoA vectoB
+ Lệnh giá trð tuyệt đøi SHIFT HYP
Lệnh tính đû lĉn mût vecto SHIFT HYP
* Chức năng w8 (VECTOR).
Khi đò màn hình máy tính sẽ xuçt hiện nhā sau:
Nhêp dą liệu cho tĂng vectć: Chõn 1 để nhêp cho Vectć A.
Chõn 1 để chõn hệ trĀc tõa đû Oxyz.
Ví dụ a  1; 2; 3,b  3; 2;  1 ; c  4; 5; 6 Page 51 |
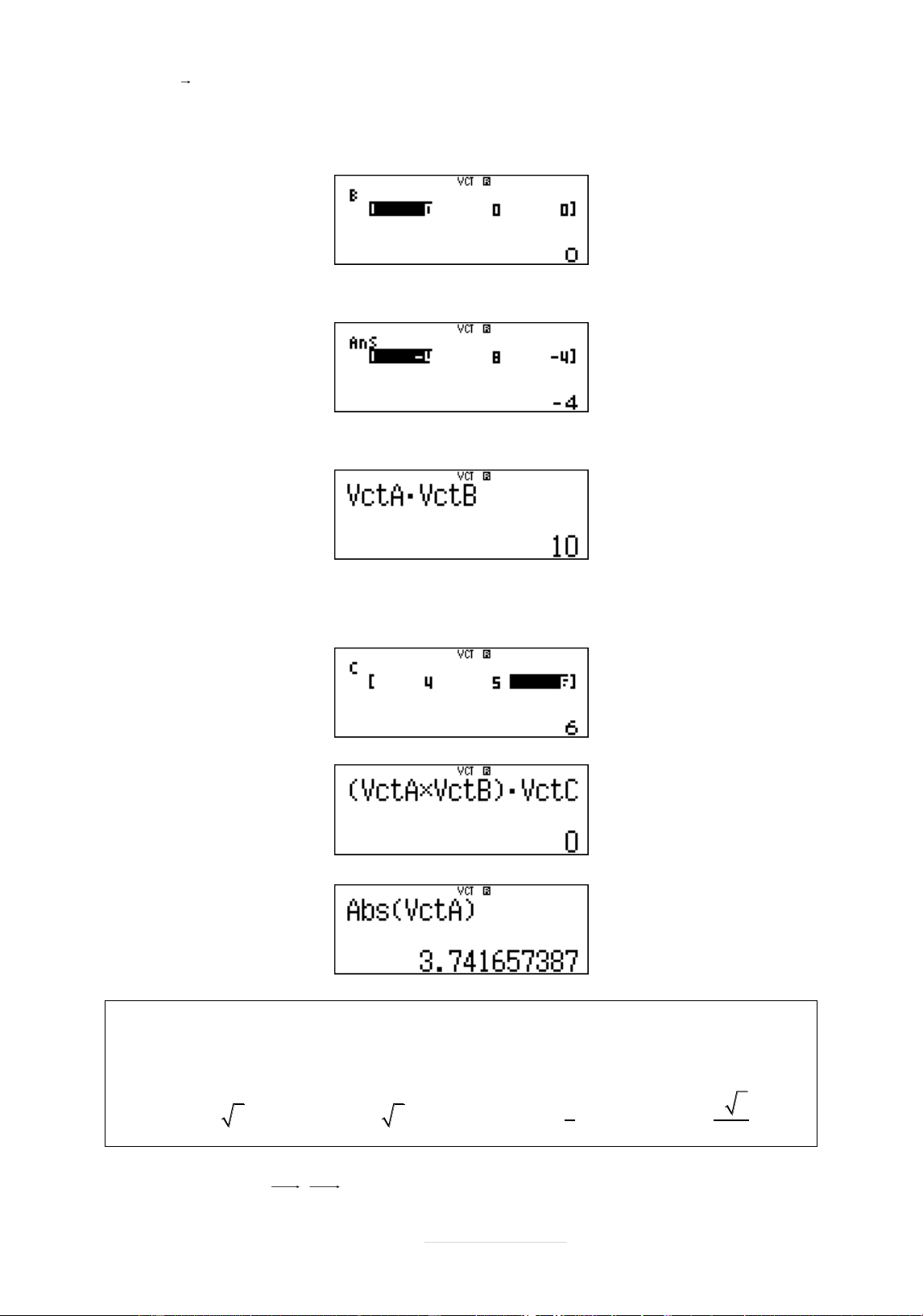
Nhêp a  1;2;3 thì bçm 1=2=3=.
Để nhêp tiếp dą liệu cho vectoB thì bçm w8213=2=1=
Tính tích có hướng của vecto A và B bấm như sau: Cq53q54=
Tính tích vô hướng của hai vecto A và B bấm như sau: Cq53q57q54=
Để tính tích hỗn tạp của ba vecto thì sẽ nhập thêm dữ liệu cho vectoC. Cq51314=5=6= C(q53Oq54)q57q55=
Để tính độ dài vecto A, bấm qcq53=
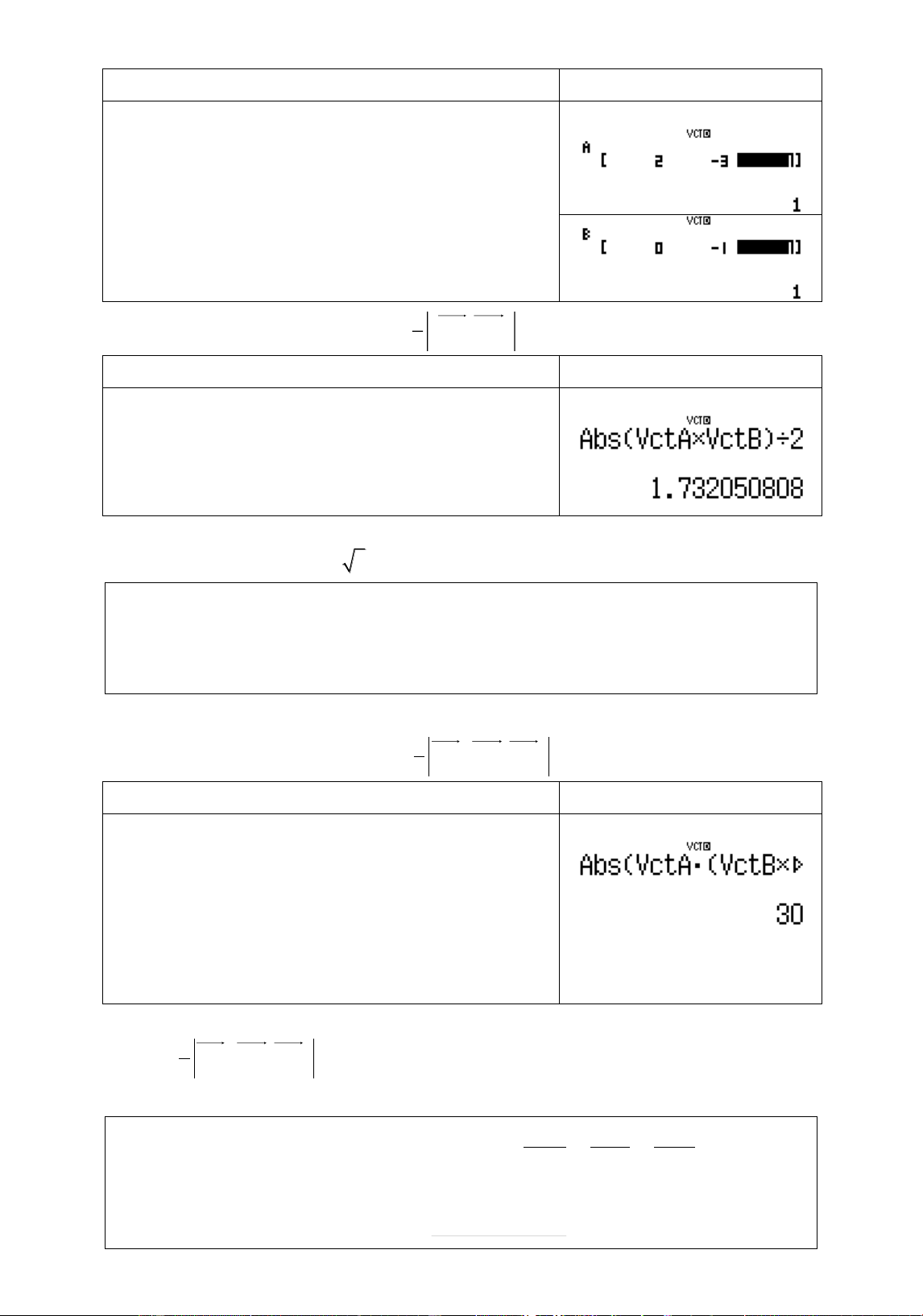
Ví dụ 1: Trong khöng gian vĉi hệ tõa đû Oxyz cho A1;2;0 , B 3; 1  ;  1 , C 1;1; 
1 . Tính diện tích S cþa tam giác ABC ? A. 1 4 3 S  3 B.S  2 C.S  D. S  1 2 3 Lời giâi
Nhêp 2 vecto AB,AC vào máy tính Casio
Nguyễn Chiến. 0973514674 Page 52 | Quy trình bçm máy Màn hình hiển thð w8112=p3=1=w 8210=p1=1= 1
Diện tích tam giác ABC :S A  B,AC   ABC 2   Quy trình bçm máy Màn hình hiển thð Wqcq53Oq54 )P2=  S
 1.732050808...  3  Chọn A. ABC
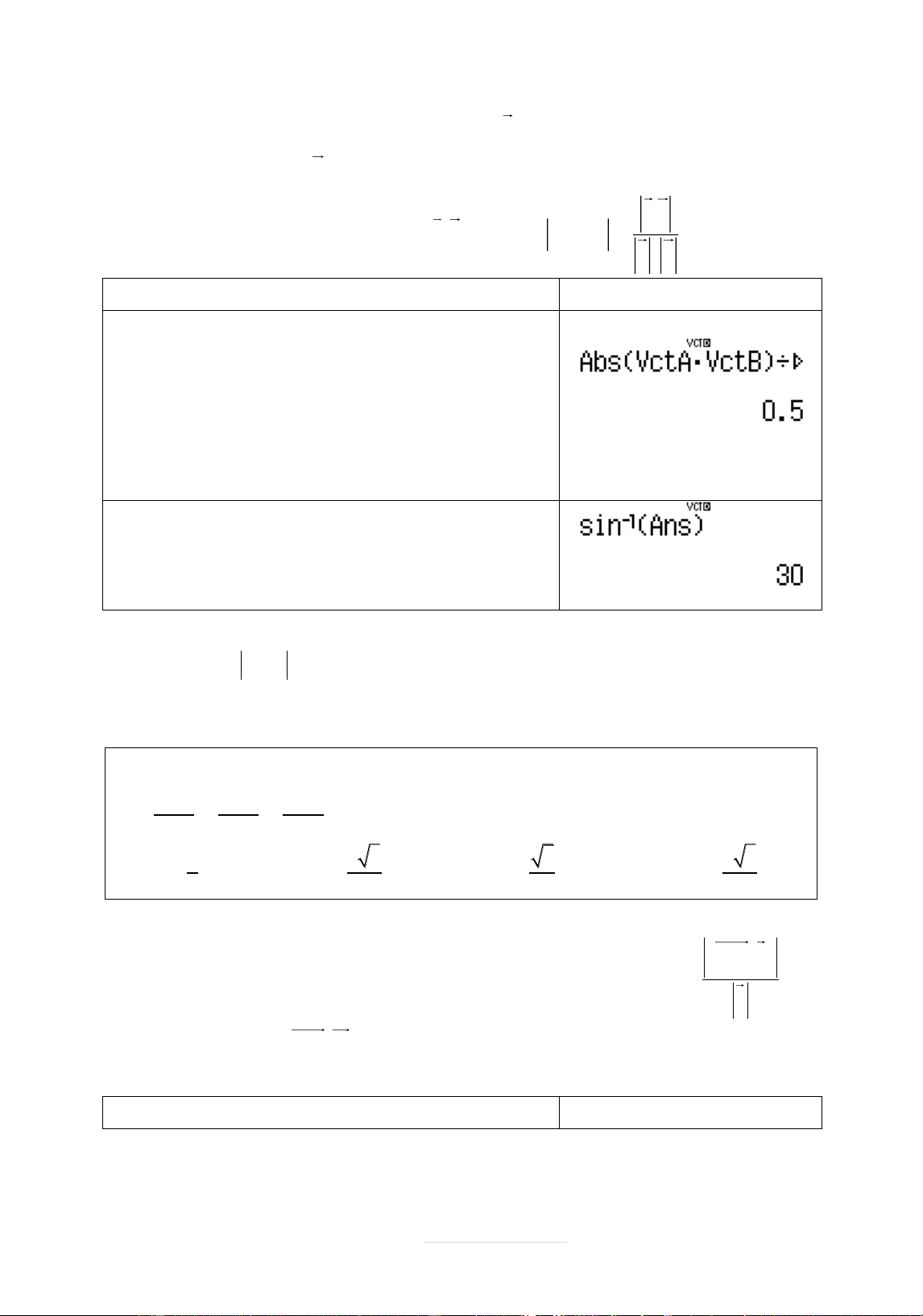
Ví dụ 2 : Cho A2; 1  ;6, B  3  ; 1  ; 4  , C 5; 1
 ;0, D 1;2;  1 . Thể tích tă diện ABCD bìng A. 30 B. 40 C. 50 D.60 Lời giâi Thể tích tă diện 1 ABCD : V AB A  C;AD  6   Quy trình bçm máy Màn hình hiển thð w811p5=0=p10 =w8213=0=p6= w831p1=3=p5= Wqcq53q57(q 54Oq55))P6= 1 V AB A  C;AD  
 30  Chọn A. 6  
Ví dụ 3. Tính gòc giąa đāĈng thîng x  3 y  1 z  3  :   và mðt 2 1 1
phîng P : x  y 2  z  5  0 A. 0 30 B. 0 45 C. 0 60 D. 0 90 Page 53 | Lời giâi
ĐāĈng thîng  có vecto chî phāćng u 2;1; 1 và mðt phîng P có
vecto pháp tuyến n 1;2; 1   .
Gõi  là góc giąa giąa 2 vectć u,n . Ta có cos  u n  u .n Quy trình bçm máy Màn hình hiển thð w8112=1=1=w8 211=2=p1=Wqc q53q57q54)P( qcq53)Oqcq5 4))= qjM)=
Gõi  là góc giąa đāĈng thîng  và mðt phîng
P  sin  cos  0.5 0
   30  Chọn A.
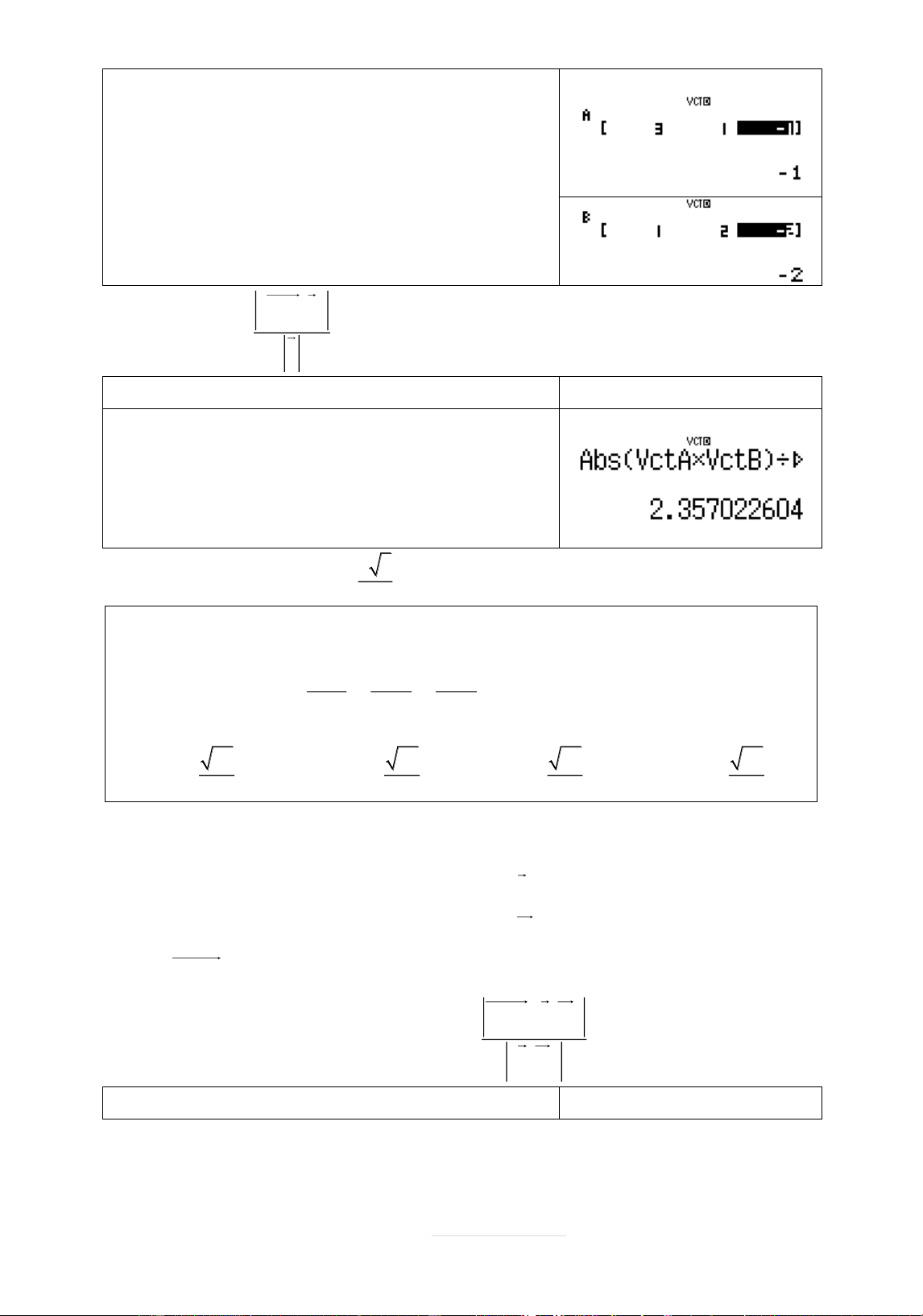
Ví dụ 4: Trong khöng gian vĉi hệ tõa đû Oxyz , cho đāĈng thîng x  1 y  2 z  2 d :  
. Tính khoâng cách tĂ điểm M  2  ;1;   1 tĉi d 1 2 2  A. 5 B. 5 2 C. 2 D. 5 2 3 2 3 3 Lời giâi M  N,u Khoâng cách tĂ  
M đến d tính theo công thăc : d M;d   u
Nhêp hai vecto MN,u vào máy tính. d Quy trình bçm máy Màn hình hiển thð
Nguyễn Chiến. 0973514674 Page 54 | w8111p(p2)=2 p1=p2pp1=w82 11=2=p2= M  N,u Tính  
d M;d   u Quy trình bçm máy Màn hình hiển thð Wqcq53Oq54)P qcq54)= 5 2
 d M;d   2.357022604   Chọn D. 3
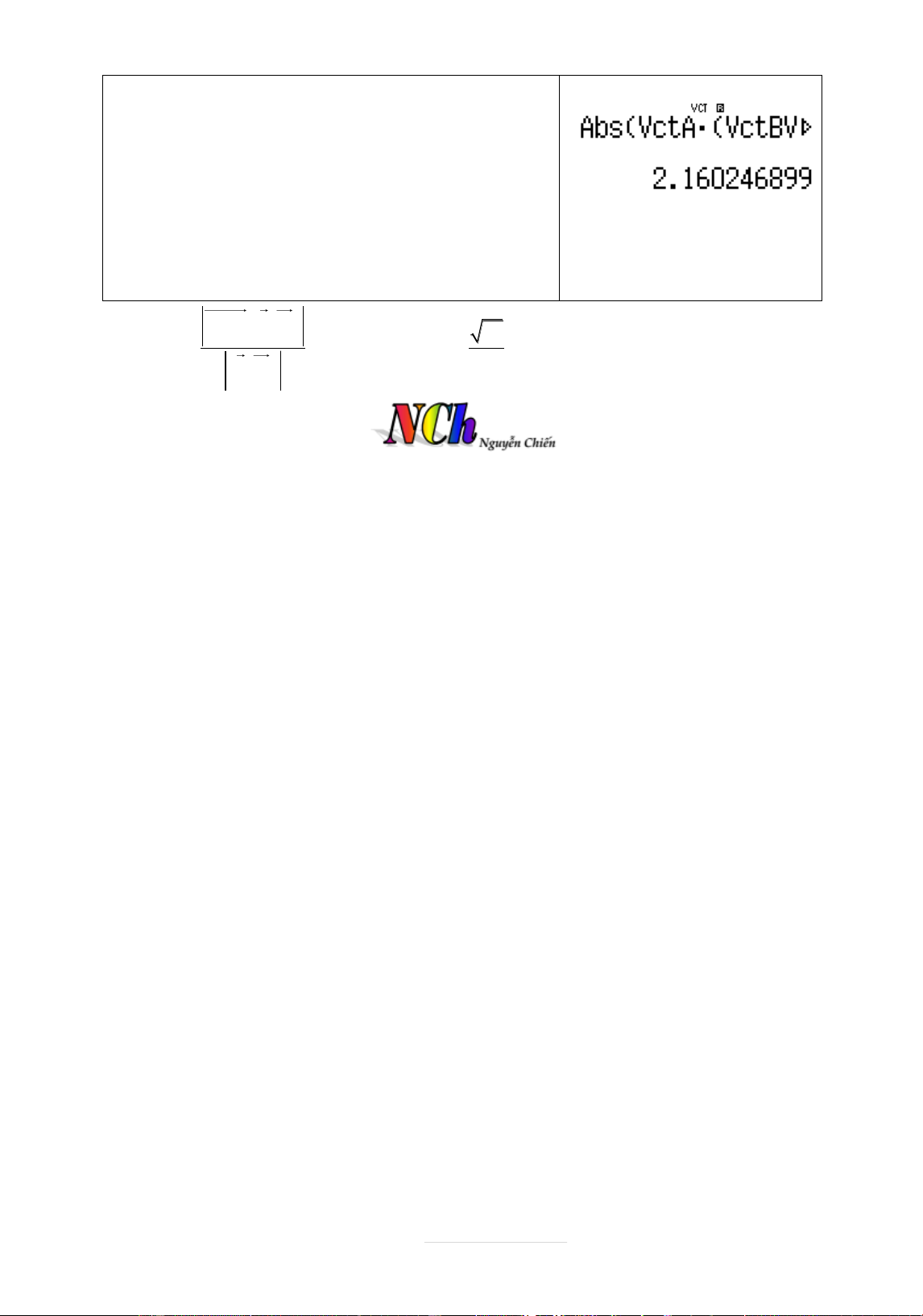
Ví dụ 5 : Tính khoâng cách giąa hai đāĈng thîng: x   t x  1 y  2 z  3  d :   và d ' : y   1  t 2 1 1 1  z   6  t3  A. 42 B. 46 C. 46 D. 42 9 9 3 3 Lời giâi M 1; 2
 ;3 d và d có vecto chî phāćng ud 1;1;  1  .
M '0;1;6 d ' và d 'có vecto chî phāćng u '1;2;3 Ta cóM M  1
 ;3;3 . Hai đāĈng thîng trên chéo nhau 1 2   MM ' u  ,u '
 Khoâng cách cæn tìm là  
d d;d '  u  ,u '   Quy trình bçm máy Màn hình hiển thð Page 55 | w811p1=3=3=w 8211=1=p1=w8 311=2=3=Wqcq 53q57(q54q55 ))Pqcq54q55 )= MM ' u  ,u '   42
d d;d '   2,160246899...   Chọn D. u  u  3 , '  
Nguyễn Chiến. 0973514674 Page 56 |

23 kỹ thuật sử dụng máy tính cầm tay Casio – Vinacal giải nhanh Toán 12 – Nguyễn Chiến

Thông tin :

Tài liệu liên quan:

Hình nón là gì? Công thức tính diện tích xung quanh hình nón | Toán 12

Đề tham khảo kỳ thi tốt nghiệp THPT từ năm 2025 môn Toán

Đề thi thử TN THPT 2025 lần 1 môn Toán trường THPT Lương Tài 2 – Bắc Ninh

Lời giải chi tiết đề tham khảo kỳ thi tốt nghiệp THPT môn Toán từ năm 2025

Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Bắc Giang