25 Đề Kiểm Tra Học Kỳ 1 Toán 8 Cánh Diều 2025-2026 Có Đáp Án
Một giỏ hoa gỗ mini có dạng hình chóp tam giác đều (như hình bên) có độ dài cạnh đáy là 10cm và độ dài trung đoạn bằng 20cm. Tính diện tích xung quanh giỏ hoa gỗ mini đó. Cho hình bình hành ABCD có AB = AC. Gọi I là trung điểm của BC, E là điểm đối xứng của A qua I. Tài liệu giúp bạn tham khảo, ôn tập và đtạ kết quả cao. Mời đọc đón xem!
Chủ đề: Đề HK1 Toán 8 244 tài liệu
Môn: Toán 8 2.2 K tài liệu
Tác giả:
Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8 CÁNH DIỀU
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào các chữ cái trước câu trả lời em chọn đúng.
Câu 1. Biểu thức nào sau đây không phải là phân thức đại số? 5 − x + 7 x − 4 A. . B. . C. . D. 2 x −14 . x 6 0 3 − x
Câu 2. Phân thức bằng với phân thức là: x − 2 3 − x x + 2 x − 3 x − 3 A. − . B. . C. . D. . x − 2 3 − x 2 − x x − 2 Câu 3. Biểu thức 2 2
x + 2xy + y bằng A. 2 2 x + y . B. 2 2 x − y . C. ( − )2 x y . D. ( + )2 x y .
Câu 4. Đơn thức nào sau đây đồng dạng với đơn thức 2 −3x y ? 1 A. xyz ; B. 2 3x y ; C. 2 xy ; D. 2 −3x z . 2 2x −1
Câu 5. Phân thức đối của là: 5 − x 2x −1 − (2x − ) 1 1− 2x 1− 2x A. B. C. D. − 5 − x x − 5 5 − x 5 − x
Câu 6. Trong mặt phẳng tọa độ Oxy cho điểm B như hình vẽ.
Tọa độ của điểm B là. A. (-2;4) B. (4; -2) C. (-3; 2) D. (3; 3) x −1
Câu 7. Phân thức nghịch đảo của phân thức là: x − 2 x − 2 x +1 A. B. x −1 2 − x 2 − x 2 − x C. D. x +1 1− x
Câu 8. Hình chóp tam giác đều có mặt bên là hình gì? A. Tam giác đều. B. Tam giác cân. C. Tam giác vuông. D. Tam giác vuông cân.
Câu 9. Hai đường chéo của hình chữ nhật có tính chất nào sau đây? A. vuông góc với nhau B. bằng nhau
C. cắt nhau tại trung điểm mỗi đường
D. bằng nhau và cắt nhau tại trung điểm mỗi đường
Câu 10. Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
A. Tứ giác có 4 cạnh bằng nhau
B. Tứ giác có hai đường chéo vuông góc
C. Tứ giác có hai đường chéo bằng nhau
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường. P Trang 1 M N
Câu 11. Nếu tam giác MNP vuông tại M thì: A. NM2 = MP2 + NP2 B. NP = MP + NM C. PM2 = NP2 + NM2 D. NP2 = MP2 + NM2
Câu 12. Cho hàm số f(x) = -2x2 + 1. Tính f(-1) A. f(-1) = 1; B. f(-1) = -1; C. f(-1) = 3; D. f(-1) = -3.
PHẦN II. TỰ LUẬN: (7,0 điểm)
Bài 1:(1,0 điểm) Thực hiện phép tính, thu gọn rồi tính giá trị của biểu thức A = 2
(x − y) − x(x − 2 y) tại x = 2023 và y = −1 2 x - 9
Bài 2: (0,75 điểm) Cho phân thức 2x - 6
a) Viết điều kiện xác định của phân thức? b) Rút gọn phân thức .
Bài 3: (1,75 điểm) Thực hiện phép tính: 2 2 2 2 2x − 7 3 − x x − 25 5x − x a) + b) : (x 0; x 5) 2
x − 2x x (x − 2) x x
Bài 4: (1,5 điểm) Giá bán 1kg bưởi da xanh loại I là 25000 đồng
a/ Viết công thức biểu thị số tiền y (đồng) thu được khi bán x (kg) bưởi da xanh loại I. Hỏi y có
phải là hàm số bậc nhất của x hay không?
b/ Tính số tiền thu được khi bán 18 kg bưởi da xanh loại I.
Bài 5: (2 điểm) Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AB, K là điểm đối xứng với H qua điểm I.
a) Tứ giác AHBK là hình gì? Vì sao?
b) Tam giác ABC có thêm điều kiện gì thì tứ giác AHBK là hình vuông?
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HKI MÔN TOÁN 8
PHẦN I. TRẮC NGHIỆM: (3,0 điểm)
Mỗi câu khoanh đúng ghi 0,25 điểm x 12 câu = 3,0 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 ĐA C C D B C A A B D A D B
PHẦN II. TỰ LUẬN: (7,0 điểm) Đáp án Điểm A = 2
(x − y) − x(x − 2 y) = 2 2 2
x − 2xy + y − x + 2xy 0,25đ Bài 1: = y2 0,25đ (1,0 điểm)
Thế x = 2023 và y = -1 vào biểu thức ta được: A = (-1)2 = 1 0,25đ A = 48 0,25đ Bài 2:
a) Điều kiện xác định của phân thức là 2x − 6 0 x 3 0,25đ (0,75 2 x - 9 (x - 3)(x + 3) x + 3 = đểm) b) = 0,5đ 2x - 6 2(x - 3) 2 Bài 3: 2 2 2x − 7 3 − x 2 2 2x −7 3 − x a) + = + 0,25đ (1,75 2
x − 2x x (x − 2) x(x − 2) x(x −2) Trang 2 đểm) 2 x − 4 = 0,25đ x(x − 2)
(x − 2)(x + 2) x + 2 = = 0,25đ x(x − 2) x x 0; x 5 2 2 x − 25 5x − x 2 x − 25 x 0,25đ : = . x x 2 x 5x − x (x − 5)(x + 5) x = . b) x x(5 − 0,25đ x) (x − 5)(x + 5) x = . x −x(x − 0,25đ 5) −(x + 5) = 0,25đ x
Công thức biểu thị số tiền y (đồng) thu được khi bán x (kg) bưởi da xanh loại 0,5đ Bài 3: a) I là: y = 25000.x (1,5
y là hàm số bậc nhất của x 0,5đ đểm)
Số tiền thu được khi bán 18kg bưởi da xanh loại I là: b) 0,5đ 25000. 18 = 450000 (đồng) HS vẽ đúng hình K A 0,25đ I B H C Xét tứ giác AHBK có: 0,25đ
IA = IB (gt), IH = IK (K đối xứng với H qua I) a)
=> Tứ giác AHBK là hình bình hành (1) 0,25đ Mà 0 AHB = 90 (gt) (2) 0,25đ
Từ (1) và (2) suy ra tứ giác AHBK là hình chữ nhật
Hình chữ nhật AHBK trở thành hình vuông
AB là đường phân giác của KAH 0,25đ 0 KAH 90 => 0 KAB = BAH = = = 45 2 2 m) b)
Trong tam giác cân ABC có AH là đường cao ứng với cạnh đáy nên nó cũng iể
là đường phân giác => 0 BAH = HAC = 45 0,25đ 2,0 đ Xét tam giác ABC có: 0 0 0
BAC = BAH + HAC = 45 + 45 = 90 0,25đ
Tam giác ABC vuông tại A ài 3: ( 0,25đ B
Vậy tam giác ABC vuông cân tại A thì tứ giác AHBK là hình vuông
Ghi chú: - Mọi cách giải khác nếu đúng và lý luận phù hợp ghi điểm tối đa.
- Điểm bài thi làm tròn đến chứ số thập phân thứ nhất. Trang 3 ĐỀ 2
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8 CÁNH DIỀU
A.TRẮC NGHIỆM KHÁCH QUAN: ( 3 điểm )
Câu 1: Viết đa thức x2 + 6x + 9 dưới dạng bình phương của một tổng ta được kết quả nào sau đây? A. (x + 3)2 B. (x + 5)2 C. (x + 9)2 D. (x + 4)2 2 3
Câu 2: : Biểu thức A = + xác định khi: x + 3 x +1
A. x −3, x −1
B. x −3, x 1
C. x 3, x −1
D. x 3, x 1 2 x − 4
Câu 3: Rút gọn phân thức
(với 𝑥 ≠ −2), ta được: x + 2 A. x +2 B. x – 2 C. x D. – 2
Câu 4: Tam giác ABC vuông tại A có BC= 10 cm, AC= 8 cm. Độ dài đoạn AB là: A. 3 cm B. 9 cm C . 6 cm D. 12 cm
Câu 5: Tổng số đo các góc trong một tứ giác bằng: A. 1800 B. 900 C. 7200 D. 3600.
Câu 6: Trong các tính chất sau, tính chất nào không phải là tính chất của hình chữ nhật?
A. Các cặp cạnh đối song song và bằng nhau.
B. Hai đường chéo bằng nhau.
C. Hai đường chéo cắt nhau tại trung điểm mỗi đường.
D. Hai đường chéo vuông góc.
B. TỰ LUẬN: ( 7 điểm )
Câu 7:(1,5 điểm)
a) Vẽ đồ thị của các hàm số sau: y = x 2 + 1 Trang 4
b) Một giỏ hoa gỗ mini có dạng hình chóp tam giác đều
(như hình bên) có độ dài cạnh đáy là 10cm và độ dài trung đoạn bằng 20cm.
Tính diện tích xung quanh giỏ hoa gỗ mini đó.
Câu 8: (2,5 điểm) Cho biểu thức: A = 𝑥 2𝑥 3𝑥2+9 + − (với 𝑥 ≠ ±3) 𝑥+3 𝑥−3 𝑥2−9
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A tại x = -1002
c) Tìm các giá trị nguyên của x để biểu thức A có giá trị nguyên. Câu 9: (2,5đ)
Cho hình bình hành ABCD có AB = AC. Gọi I là trung điểm của BC, E là điểm đối xứng của A qua I.
a) Chứng minh ABEC là hình thoi. b) Tính số đo góc DAE.
c) Tìm điều kiện của tam giác ADE để tứ giác ABEC trở thành hình vuông. Câu 10: (0,5đ)
Tìm giá trị nhỏ nhất của biểu thức 2
M = x − x ( y + ) 2 2 1 + 3y + 2025.
................................................ Hết .............................................................
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CHẤT LƯỢNG CUỐI HỌC KÌ I MÔN: TOÁN LỚP 8
I. TRẮC NGHIỆM: ( 3 điểm ) ( Mỗi câu đúng được 0,5 điểm ) 1 2 3 4 5 6 A A B C D D
II. TỰ LUẬN (7 điểm) Trang 5 Câu Hướng dẫn giải Điểm Câu 7 1,5đ
Xét hàm số 𝑦 = 2𝑥 + 1 −1 x 0 2 y 1 0 0,5đ
Vậy đồ thị của hàm số 𝑦 = 2𝑥 + 1 là đường thẳng đi qua hai điểm A(0;1); B (−1;0) 2 a y O 0,25đ x
Diện tích xung quanh giỏ hoa gỗ mini là : b 1 1 0,75đ
S = .C.d = . = cm xq (3.10) 2 .20 300( ) 2 2 Câu 8 2,5 đ A = 𝑥 2𝑥 3𝑥2+9 + − (với 𝑥 ≠ ±3) 𝑥+3 𝑥−3 𝑥2−9 a = 𝑥 2𝑥 3𝑥2+9
𝑥(𝑥−3)+2𝑥(𝑥+3)−3𝑥2−9 + − = 0,5đ 𝑥+3 𝑥−3 (𝑥−3)(𝑥+3) (𝑥−3)(𝑥+3) 0,5đ
= 𝑥2−3𝑥+2𝑥2+6𝑥−3𝑥2−9 = 3𝑥−9 = 3(𝑥−3) = 3 (𝑥−3)(𝑥+3) (𝑥−3)(𝑥+3) (𝑥−3)(𝑥+3) 𝑥+3 Trang 6
Thay x = -1002( thỏa mãn điều kiện) vào A ta có A = 3 0,5đ −1002+3 b A = 3 −999 A = 1 − 333
Vậy với x = -1002 thì biểu thức A có giá trị là: 1 − 333 0,25đ
Để 𝐴 ∈ ℤ thì 3 ∈ ℤ ⇒ 𝑥 + 3 ∈Ư(3) = 1; 3 𝑥+3 x+3 -3 -1 1 3 0,5đ c x -6 -4 -2 0
Vậy 𝑥 ∈ {−6; −4; −2; 0} thì 𝐴 ∈ ℤ 0,25 đ Câu 9 2,5đ A B Vẽ hình đúng 0,5đ I E D C
Ta có AE, BC cắt nhau tại trung điểm I của mỗi đường nên ABEC là a 0,5 đ hình bình hành
và AB = AC nên ABEC là hình thoi 0,25 đ
Ta có ABEC là hình thoi nên 𝐴𝐸 ⊥ 𝐵𝐶 (1)
Mà ABCD là hình bình hành nên BC // AD (2) 0,5đ b
Từ (1) và (2) suy ra 𝐴𝐸 ⊥ 𝐴𝐷 ⇒ 𝐷𝐴𝐸 ̂ = 90° 0,25đ c
Để hình thoi ACEB là hình vuông thì 𝐴𝐸 = 𝐵𝐶 0,5đ
Có 𝐵𝐶 = 𝐴𝐷 ⇒ 𝐴𝐸 = 𝐴𝐷 ⇒ ADE vuông cân tại A Trang 7 Câu10 0,5đ Ta có: 2
M = x − x ( y + ) 2 2 1 + 3y + 2025
= x − x( y + ) + ( y + )2 2 − ( 2 y + y + ) 2 2 1 1 2 1 + 3y + 2025
= x − x( y + ) + ( y + )2 2 2 2 1
1 + 2y − 2y + 2024 0,25 đ
= x − 2x( y + ) 1 + ( y + )2 1 1 2 2
1 + 2 y − y + + 2024 − 4 2 2 ( = x − y − )2 1 4047 1 + 2 y − + . 2 2
Nhận xét: với mọi x, y ta có: 2 1
( x − y − )2 1 0; 2 y − 0 2 2
Do đó M = (x − y − )2 1 4047 4047 1 + 2 y − + 2 2 2 ( x − y − )2 1 = 0
x − y − 1 = 0
Dấu “=” xảy ra khi và chỉ khi 2 1 hay 1 2 y − = 0 y − = 0 2 2 3 x = nên 2 1 y = 2 4047 3 1
Vậy giá trị nhỏ nhất của biểu thức M là khi x = và y = . 2 2 2 0,25đ ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8 CÁNH DIỀU
I.Trắc nghiệm: (3đ) Khoanh tròn chữ cái đứng trước câu trả lời đúng.
Câu 1: Đâu không phải đơn thức? Trang 8 3 A. 5x – 2 B. – 3 C. 2 x y D. x 2
Câu 2: Chọn câu đúng.
A. (A + B)2= A2– 2AB + B2 B. (A + B)2= A2+ B2
C. (A + B)2= A2+ AB + B2. D. (A + B)2= A2+ 2AB + B2 A Câu 3: Phân thức xác định khi: B
A. B = 0 B. B 0 C. A = 0 D. A 0 A C
Câu 4: Với B 0 và D 0, hai phân thức = khi : B D
A. A.C = B.D B. A.B = C.D C. A.D = B.C D. A.D B.C 3
Câu 5 : Phân thức nghịch đảo của phân thức là : x +1 x +1 3 − 3 − 3 − A.
3 B. x +1 C. x −1 D. −x −1 5 7
Câu 6 : Mẫu thức chung của các phân thức , là : 3
2(x − 3) (x − 3)
A. (x - 3)3 B. x – 3 C. 2(x - 3) D. 2(x - 3)3 2 x 4
Câu 7: Kết quả của phép tính − là: x + 2 x + 2 A. x +2 B. x - 2 C. 2x D. x
Câu 8: Cho hàm số y = f(x) = -2x + 1. Chọn câu trả lời đúng:
A. f(0) = -1 B. f(0) = 0 C. f(0) = 1 D. f(0) = 3
Câu 9: Cho tam giác ABC vuông tại A khi đó: A. 2 2 2
BC = AB + AC B. 2 2 2
BC = AB − AC C. 2 2 2
AC = AB + BC D. 2 2 2
AB = AC + BC
Câu 10: Điền cụm từ thích hợp vào chổ trống: “ Tứ giác có hai đường chéo ... thì tứ giác
đó là hình bình hành “ A. Bằng nhau B. Song song
C. Cắt nhau D. Cắt nhau tại trung điểm của mỗi đường
Câu 11: Tam giác vuông có độ dài hai cạnh góc vuông là 3cm và 4cm thì độ dài đường
trung tuyến ứng với cạnh huyền là: A. 6cm B. 2,5cm C. 8cm D. 3,5 cm Trang 9
Câu 12: Hình vuông là tứ giác có:
A. Có bốn cạnh bằng nhau B.Có bốn góc bằng nhau
C. Có 4 góc vuông và bốn cạnh bằng nhau D. Cả A, B, C đều sai
II. Tự luận: (7đ)
Bài 1. Rút gọn rồi tính giá trị của biểu thức : (1đ) P = 2 2 2 2 2
(5x − 2xy + y ) − (x + y ) − (4x − 5xy +1) tại x = -1, y = 1.
Bài 2. Rút gọn phân thức : (1đ) 4 5 15x y x − xy a) b) 3 6 9x y 2 3xy − 3xy
Bài 3. Tìm điều kiện của x để các phân thức sau được xác định: (1đ) x 2 − a) b) 2x + 2 2 x − 4 Bài 4. Tính: (1đ) 3x 6 4x +12 3(x + 3) a) + b) : x + 2 x + 2 2 (x + 4) x + 4
Bài 5. (1đ) Một nhóm học sinh tổ chức cắm trại hè. Nhóm này dựng trại có dạng hình
chóp tứ giác đều S.ABCD. Biết AB = 6m. SA = 5m. Tuy nhiên do thời tiết không
thuận lợi nên nhóm này quyết định hạ thấp trại xuống bớt sao cho SA = 4m. Tính diện
tích xung quanh phần phải cắt bỏ của lều trại đó.(làm tròn đến chữ số thập phân thứ hai).
Bài 6. (2đ) Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh huyền BC. Kẻ MD
vuông góc với AB tại D, ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật
b) Gọi I là trung điểm của DE. Chứng minh ba điểm A, I, M thẳng hàng. ĐÁP ÁN I.
TRẮC NGHIỆM : (3đ) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A D B C A D B C A D B C Trang 10 II. TỰ LUẬN : (7đ) Bài
Bài giải chi tiết Thang điểm P = 2 2 2 2 2
(5x − 2xy + y ) − (x + y ) − (4x − 5xy +1) = 2 2 2 2 2
5x − 2xy + y − x − y − 4x + 5xy −1 Bài 1: (0,5đ) (1đ) = 3xy −1
Thay x = -1, y = 1 vào P ta có : (0,5đ) P = 3.(-1).1 - 1 = -4 4 5 15x y 5x (0,5đ) Bài 2 : a . = 3 6 9x y 3y (1đ) x − xy x(1− y) 1 b. = = (0,5đ) 2 3xy − 3xy 3xy(1− y) 3y
a. Phân thức xác định khi : Bài 3:
2x + 2 0 x −1 (0,5đ) (1đ)
b. Phân thức xác định khi : x 2 2
x − 4 0 (x − 2)(x + 2) 0 (0,5đ) x 2 − 3x 6 + + + 3x 6 3(x 2) = = 3 (0,5đ)
a. x + 2 x + 2 = x + 2 x + 2 Bài 4: (1đ) 4x +12 3(x + 3) : 2 b. (x + 4) x + 4 = 4(x + 3) x + 4 4 (0,5đ) . = 2 (x + 4) 3(x + 3) 3(x + 4)
Độ dài trung đoạn của hình chóp lúc đầu: (0,25đ) 2 2 5 − 3 = 4m
Diện tích xung quanh của hình chóp lúc đầu 1 : 2
S = 6.4.4 = 48(m ) 2 Bài 5 (1đ)
Độ dài trung đoạn của hình chóp sau khi cắt (0,25đ) bớt 1m : 2 2 4 − 3 = 2,64(m)
Diện tích xung quanh của hình chóp lúc sau 1
: S = .6.4.(2,64) = 31,68 2 (m ) 2
Diện tích xung quanh phần phải cắt bỏ là: 48 (0,25đ) – 31,68 = 16,32( 2 m ) (0,25đ) (0,5đ) a. HS vẽ hình đúng Trang 11 Bài 6 (0,5đ) (2đ) Xét tứ giác ADME ta có: 0
A = D = E = 90 (gt) (0,5đ)
Tứ giác ADME là hình chữ nhật. (0,5đ)
b. Vì I là trung điểm của DE
I cũng là trung điểm của AM (đ/l) Hay A, I, M thẳng hàng. ĐỀ 4
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8 CÁNH DIỀU
I.Trắc nghiệm: (3đ) Khoanh tròn chữ cái đứng trước câu trả lời đúng.
Câu 1: Đâu không phải đơn thức? 3 A. 2
x y B. – 3 C. x + 1 D. x 2
Câu 2: Chọn câu đúng.
A. (A + B)2= A2 + 2AB + B2 B. (A + B)2= A2+ B2
C. (A + B)2= A2+ AB + B2. D. (A + B)2= A2 - 2AB + B2 A Câu 3: Phân thức xác định khi: B
A. B = 0 B. A 0 C. A = 0 D. B 0 A C
Câu 4: Với B 0 và D 0, hai phân thức = khi : B D
A. A.C = B.D B. A.D = B.C C. A.B = C.D D. A.D B.C 3
Câu 5 : Phân thức nghịch đảo của phân thức là : x +1 3 − 3 − x +1 3 −
A. x −1 B. x +1 C. 3 D. −x −1 5 7
Câu 6 : Mẫu thức chung của các phân thức , là : 3
2(x − 3) (x − 3)
A. 2(x - 3)3 B. x – 3 C. 2(x - 3) D. (x - 3)3 Trang 12 2 x 4
Câu 7: Kết quả của phép tính − là: x + 2 x + 2 A. x +2 B. x C. 2x D. x -2
Câu 8: Cho hàm số y = f(x) = -2x + 1. Chọn câu trả lời đúng:
A. f(0) = -1 B. f(0) = 1 C. f(0) = 0 D. f(0) = 3
Câu 9: Cho tam giác ABC vuông tại A khi đó: A. 2 2 2
AC = AB + BC B. 2 2 2
BC = AB − AC C. 2 2 2
BC = AB + AC D. 2 2 2
AB = AC + BC
Câu 10: Điền cụm từ thích hợp vào chổ trống: “ Tứ giác có hai đường chéo ... thì tứ giác
đó là hình bình hành “
A. Cắt nhau tại trung điểm của mỗi đường B. Song song C. Cắt nhau D. Bằng nhau
Câu 11: Tam giác vuông có độ dài hai cạnh góc vuông là 3cm và 4cm thì độ dài đường
trung tuyến ứng với cạnh huyền là: A. 6cm B. 3,5cm C. 8cm D. 2,5 cm
Câu 12: Hình vuông là tứ giác có:
A. Có bốn cạnh bằng nhau B. Có 4 góc vuông và bốn cạnh bằng nhau
C. Có bốn góc bằng nhau D. Cả A, B, C đều sai
II. Tự luận: (7đ)
Bài 1. Rút gọn rồi tính giá trị của biểu thức : (1đ) Q = 2 2 2 2 2
(5x − 2xy + y ) − (x + y ) − (4x − 5xy +1) tại x = -1, y = -1.
Bài 2. Rút gọn phân thức : (1đ) 3 4 20x y x + xy a) b) 2 6 15x y 2 5xy + 5xy
Bài 3. Tìm điều kiện của x để các phân thức sau được xác định: (1đ) −x 3 a) b) 2x − 2 2 x − 9 Bài 4. Tính: (1đ) 2 x 4 3x + 6 2x − 4 a) − b) . x + 2 x + 2 4x − 8 x + 2 Trang 13
Bài 5. (1đ) Một nhóm học sinh tổ chức cắm trại hè. Nhóm này dựng trại có dạng hình
chóp tứ giác đều S.ABCD. Biết AB = 6m. SA = 5m. Tuy nhiên do thời tiết không
thuận lợi nên nhóm này quyết định hạ thấp trại xuống bớt sao cho SA = 4m. Tính diện
tích xung quanh phần phải cắt bỏ của lều trại đó.(làm tròn đến chữ số thập phân thứ hai).
Bài 6. (2đ) Cho tam giác MNP vuông tại M. Lấy điểm I thuộc cạnh huyền NP. Kẻ IH
vuông góc với MN tại H, IK vuông góc với MP tại K.
a) Chứng minh tứ giác MHIK là hình chữ nhật
b) Gọi O là trung điểm của HK. Chứng minh ba điểm M, O, I thẳng hàng. ĐÁP ÁN I.
TRẮC NGHIỆM : (3đ) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C A D B C A D B C A D B II. TỰ LUẬN : (7đ) Bài
Bài giải chi tiết Thang điểm P = 2 2 2 2 2
(5x − 2xy + y ) − (x + y ) − (4x − 5xy +1) = 2 2 2 2 2
5x − 2xy + y − x − y − 4x + 5xy −1 Bài 1: (0,5đ) (1đ) = 3xy −1
Thay x = -1, y = -1 vào P ta có : (0,5đ) P = 3.(-1).(-1) - 1 = 2 3 4 20x y 4x (0,5đ) Bài 2 : a . = 2 6 15x y 2 3y (1đ) x + xy x(1+ y) 1 b. = = (0,5đ) 2 5xy + 5xy 5xy(1+ y) 5y
a. Phân thức xác định khi : Bài 3:
2x − 2 0 x 1 (0,5đ) (1đ)
b. Phân thức xác định khi : x 3 2
x − 9 0 (x − 3)(x + 3) 0 (0,5đ) x 3 − 2 x 4 (x − 2)(x + 2) a. − = = x − 2 (0,5đ) x + 2 x + 2 x + 2 Bài 4: (1đ) 3x + 6 2x − 4
3(x + 2) 2(x − 2) 3 b. . = . = (0,5đ) 4x − 8 x + 2 4(x − 2) x + 2 2 Trang 14
Độ dài trung đoạn của hình chóp lúc đầu: (0,25đ) 2 2 5 − 3 = 4m
Diện tích xung quanh của hình chóp lúc đầu 1 (0,25đ) : 2
S = 6.4.4 = 48(m ) 2 Bài 5 (1đ)
Độ dài trung đoạn của hình chóp sau khi cắt bớt 1m : 2 2 4 − 3 = 2,64(m)
Diện tích xung quanh của hình chóp lúc sau 1 (0,25đ)
: S = .6.4.(2,64) = 31,68 2 (m ) 2 (0,25đ)
Diện tích xung quanh phần phải cắt bỏ là: 48 – 31,68 = 16,32( 2 m ) (0,5đ) a. HS vẽ hình đúng Bài 6 (0,5đ) (2đ) Xét tứ giác MHIK ta có: 0
M = H = K = 90 (gt) (0,5đ)
Tứ giác MHIK là hình chữ nhật. (0,5đ)
b. Vì O là trung điểm của HK
O cũng là trung điểm của MI (đ/l) Hay M, O, I thẳng hàng. ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8 CÁNH DIỀU
A. TRẮC NGHIỆM (1,0 điểm)
Học sinh ghi lại chữ cái đứng trước câu trả lời đúng trong các Câu 1 – 4 vào bài thi x + 5
Câu 1. Điều kiện để giá trị của phân thức xác định là: (x - 2)(x + 3) A. x 5 −
B. x 2
C. x 2 và x −3
D. x −3
Câu 2. Giá trị của biểu thức: 3 2
x - 3x + 3x - 1 tại x = 101 bằng: Trang 15 A. 10000 B. 1001 C. 1000000 D. 300
Câu 3. Kết quả rút gọn biểu thức 2 2 2 2
(x − 2y)(x + 2xy + 4y ) − (x + 2y)(x − 2xy + 4y ) là: A. 3 −16y B. 3 4 − y C. 3 16y D. 3 −12y
Câu 4. Cho các khẳng định sau:
1. Hình bình hành có hai đường chéo bằng nhau.
2. Hình thang có hai cạnh bên bằng nhau là hình thang cân.
3. Trong hình chữ nhật, giao của hai đường chéo cách đều bốn đỉnh của hình chữ nhật.
4. Hình bình hành có hai cạnh kề bằng nhau là hình chữ nhật.
Số các khẳng định đúng là A. 0 B. 1 C. 2 D. 3
B. TỰ LUẬN (9,0 ĐIỂM)
Bài 1. (1,5 điểm) Phân tích đa thức thành nhân tử: 2 2 2
a) 2xy - 4xy + 2x
b) 4x − 9 + y − 4xy c) 2
x + 9x + 20
Bài 2. (1,5 điểm) Tìm x, biết:
a) 6x(x − 3) + 4(3 − x) = 0 2
b) (x − 3)(x + 3x + 9) − x(x − 1)(x + 1) = 14 2 x + x + 1 3 + = 2 c) 2 3 x + x + 1 2x - 1 x 3 6x - 4
Bài 3. (2,0 điểm) Cho hai biểu thức A = và B = + -
với x ¹ ± 1. x - 1 2 x - 1 x + 1 x - 1
a) Tính giá trị của A khi x = 4.
b) Rút gọn B.
c) Đặt P = A B, tìm tất cả các giá trị nguyên âm của x để P nhận giá trị là số nguyên. Bài 4. (3,5 điểm)
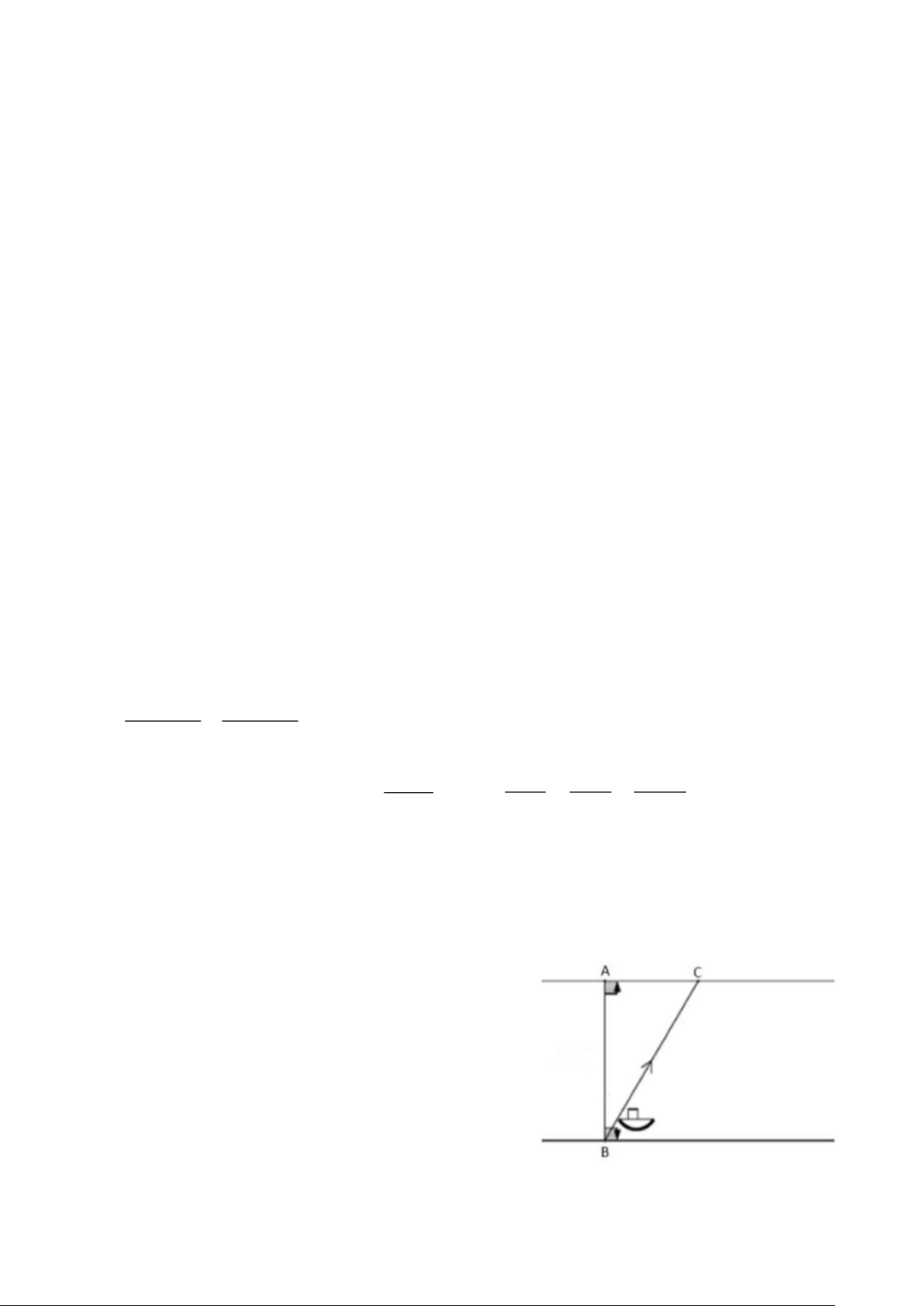
1) Một chiếc xuồng máy qua sông từ vị trí B hướng tới
vị trí A. Tuy nhiên do nước chảy nên khi qua tới bờ,
thuyền tới vị trí C cách A một khoảng là 22 m. Trong
suốt quá trình qua sông, vận tốc chuyển động của
xuồng là v = 2 m/s. Biết độ dài quãng đường xuồng
đi được cho bởi hàm số s = vt, với t là thời gian.
Tính độ rộng của sông biết rằng để đi từ B tới C thì
xuồng mất khoảng thời gian là 61 giây.
2) Cho tam giác A BC cân tại A, đường cao A H . Gọi N là điểm đối xứng của A qua H . Trang 16
a) Tứ giác A BNC là hình gì? Vì sao?
b) Gọi F là trung điểm của A C , I là trung điểm của A H . Lấy M đối xứng với H qua F.
Chứng minh A HCM là hình chữ nhật. Từ đó suy ra I là trung điểm của BM .
c) Kẻ HK vuông góc với BN (K BN ). Gọi O là trung điểm HK . Chứng minh ON vuông
góc với CK . Bài 5. (0,5 điểm) 2 2
a) Cho các số thực dương x, y thỏa mãn x y và 3x + 2y = 5xy. Tính giá trị của biểu thức y + 2x S = . y − 2x 2 2
b) Cho các số thực x, y thỏa mãn điều kiện 2x + xy + 3y = 41. Tìm giá trị lớn nhất của biểu thức 2 2
M = 7x − 13xy + y . Trang 17 ĐÁP ÁN
A. TRẮC NGHIỆM (1,0 điểm) Câu 1 2 3 4 Đáp án C C A B
B. TỰ LUẬN (9,0 điểm)
Bài 1. (1,5 điểm) Phân tích đa thức thành nhân tử: 2 2
a) 2xy - 4xy + 2x
= 2x(y − 1) 0,5 điểm 2 2
b) 4x − 9 + y − 4xy
= (2x − y − 3)(2x − y + 3) 0,5 điểm c) 2 x + 9x + 20
= (x + 4)(x + 5) 0,5 điểm
Bài 2. (1,5 điểm) Tìm x, biết: 2
a) 6x(x − 3) + 4(3 − x) = 0 x 3; 0,5 điểm 3 2
b) (x − 3)(x + 3x + 9) − x(x − 1)(x + 1) = 14 x = 41 0,5 điểm 2 x + x + 1 3 + = 2 c) 2 3 x + x + 1 x 1;− 3 0,5 điểm 2x - 1 x 3 6x - 4
Bài 3. (2,0 điểm) Cho hai biểu thức A = và B = + -
với x ¹ ± 1. x - 1 2 x - 1 x + 1 x - 1 7
a) Tính giá trị của A khi x = 4. A = 0,5 điểm 3 x − 1
b) Rút gọn B. B = 0,5 điểm x + 1
c) Đặt P = A B, tìm tất cả các giá trị nguyên âm của x để P nhận giá trị là số nguyên. x 2;0; 2 − ; − 4 0,5 điểm Bài 4. (3,5 điểm)
1) Một chiếc xuồng máy qua sông từ vị trí B hướng tới
vị trí A. Tuy nhiên do nước chảy nên khi qua tới bờ,
thuyền tới vị trí C cách A một khoảng là 22 m. Trong
suốt quá trình qua sông, vận tốc chuyển động của
xuồng là v = 2 m/s. Biết độ dài quãng đường xuồng
đi được cho bởi hàm số s = vt, với t là thời gian.
Tính độ rộng của sông biết rằng để đi từ B tới C thì
xuồng mất khoảng thời gian là 61 giây. Giải. Trang 18 AC = 2 61 = 122 m 0,25 điểm AB2 = AC2 – AC2 2 2
122 − 22 = 14400 AB = 120 m 0,25 điểm
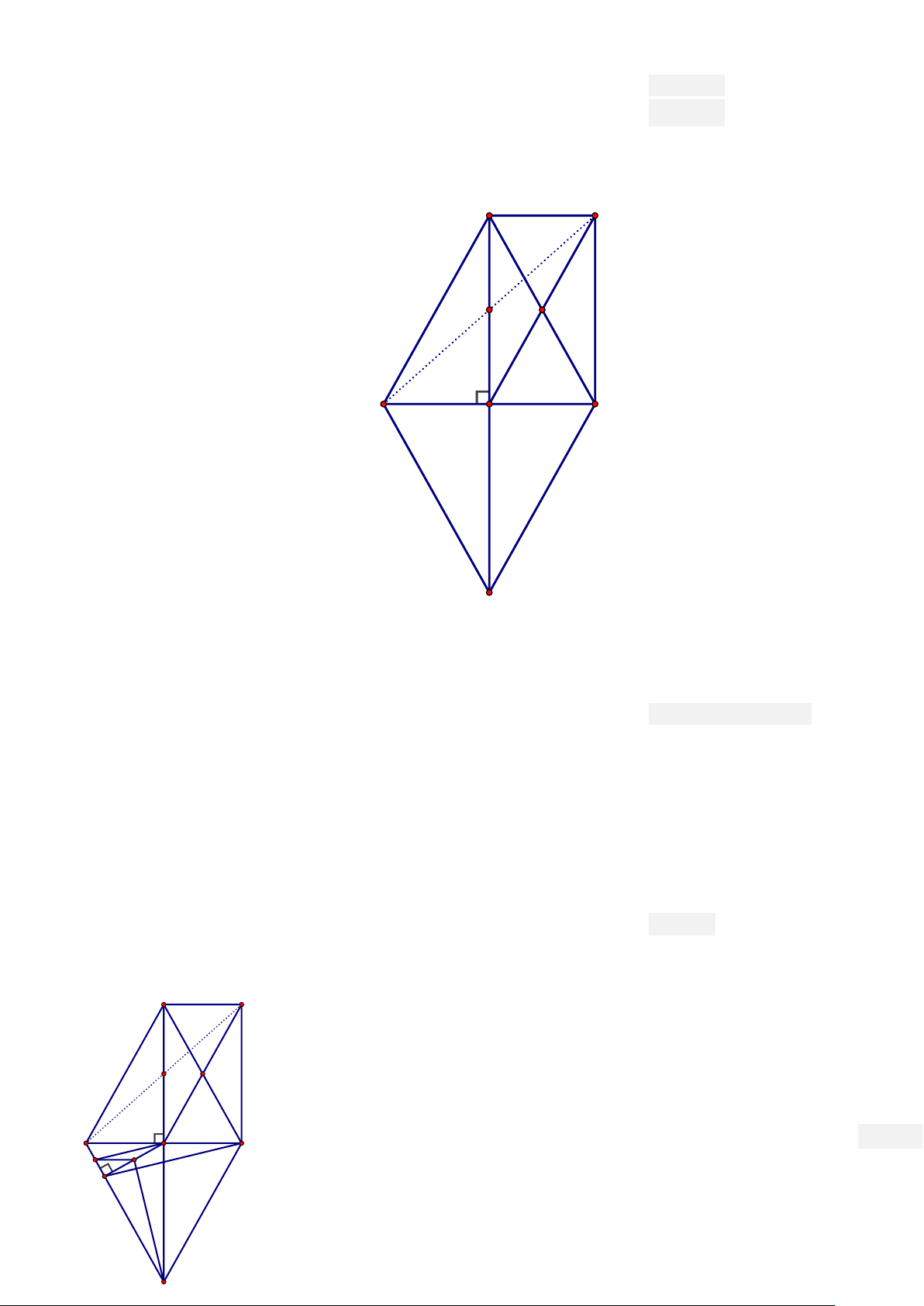
2) Cho tam giác A BC cân tại A, đường cao A H . Gọi N là điểm đối xứng của A qua H . A M I F B H C N
a) Tứ giác A BNC là hình gì? Vì sao?
Hình thoi (hai đường chéo vuông góc tại trung điểm mỗi đường)
1,5 điểm (0,5 đ hình)
b) Gọi F là trung điểm của A C , I là trung điểm của A H . Lấy M đối xứng với H qua F.
Chứng minh A HCM là hình chữ nhật. Từ đó suy ra I là trung điểm của BM .
Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Suy ra A M ||= HC A M ||= BH
A BHM là hình bình hành
I là trung điểm BM 1,0 điểm c)
Kẻ HK vuông góc với BN (K BN ). Gọi O là trung điểm A M
HK . Chứng minh ON vuông góc với CK .
Gọi E là trung điểm BK thì I F
OE || BH OE ⊥ NH O là trực tâm tam giác HEN NO ⊥ HE H
Chỉ ra HE || CK ON ⊥ CK . 0,5 điểm B C E O K Bài 5. (0,5 điểm) Trang 19 N 2 2
a) Cho các số thực dương x, y thỏa mãn x y và 3x + 2y = 5xy. Tính giá trị của biểu thức y + 2x S = . y − 2x 2 2 2 2
3x + 2y = 5xy 3x − 5xy + 2y = 0 (x − y)(3x − 2y) = 0 3
Do x y y = x S = 7. − 0,25 điểm 2 2 2
b) Cho các số thực x, y thỏa mãn điều kiện 2x + xy + 3y = 41. Tìm giá trị lớn nhất của biểu thức 2 2
M = 7x − 13xy + y . 2 2 2 2 2 M
7x − 13xy + y
9x − 12xy + 4y (3x − 2y) + 1 = + 1 = = 0 2 2 2 2 41
2x + xy + 3y
2x + xy + 3y 41 M 41 − M = 41 − min 2 2 2
x + xy + 3y = 41 x = 2;y = 3 Dấu " = " xảy ra khi 0,25 điểm 3x = 2y
x = −2;y = −3 ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8 CÁNH DIỀU
I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm).
Tô kín vòng tròn tương ứng với chữ cái đứng trước câu trả lời đúng (mỗi câu trả lời đúng được 0,25 điểm)
Câu 1. Chọn phát biểu đúng.
A. Hình bình hành có một góc vuông là hình vuông.
B. Hình thoi có hai đường chéo bằng nhau là hình vuông.
C. Hình bình hành có hai đường chéo bằng nhau là hình vuông.
D. Tứ giác có hai đường chéo bằng nhau là hình vuông.
Câu 2. Hãy chọn câu trả lời đúng. Hình bình hành A BCD là hình chữ nhật khi:
A. A B = BC .
B. A C = BD .
C. BC = CD .
D. A C ^ BD .
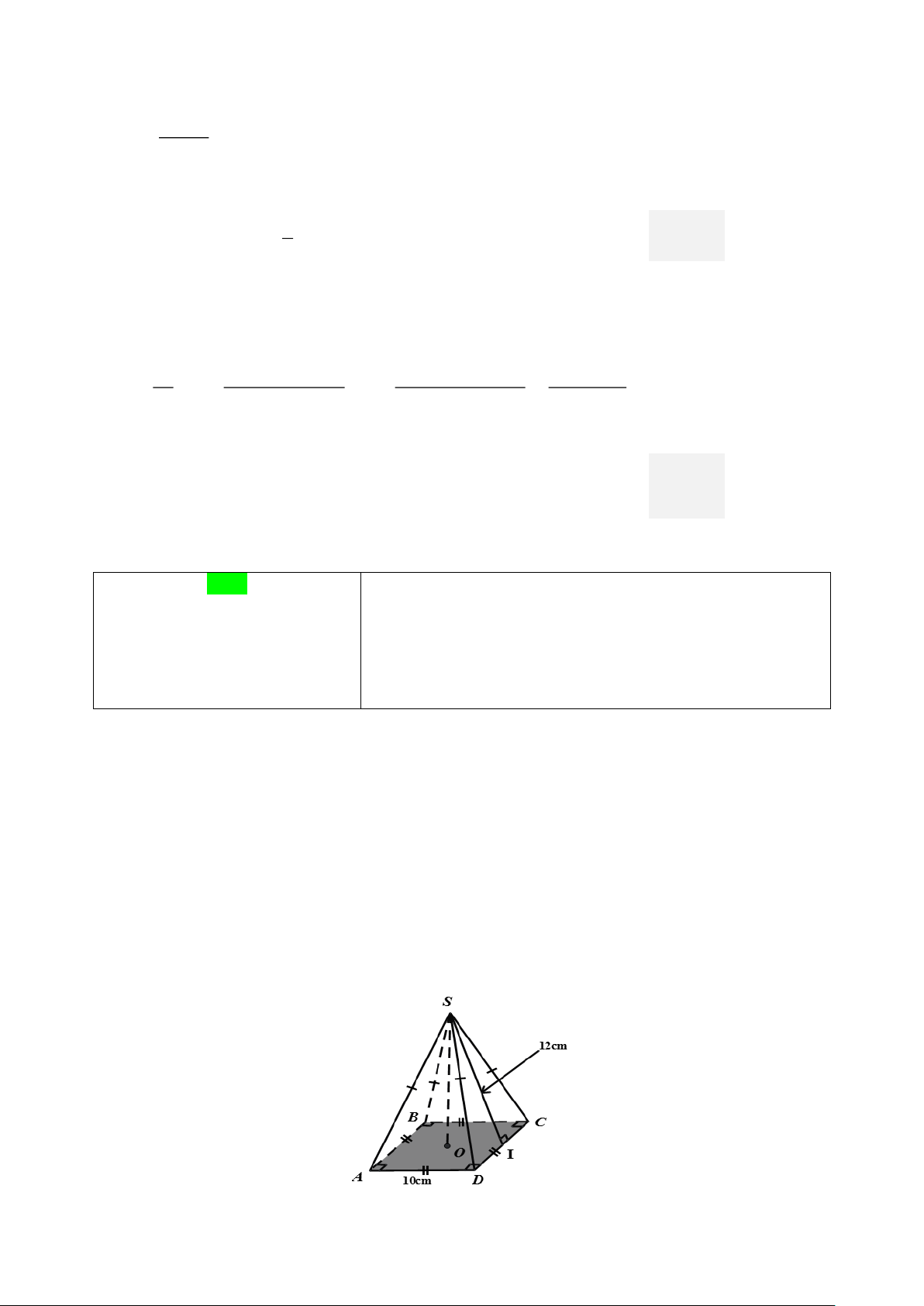
Câu 3. Cho hình chóp tứ giác đều S.ABCD với kích thước (Như hình vẽ dưới). Diện tích xung quanh của
hình chóp tam giác đều S.ABCD là A. 2 240cm . B. 2 204cm . C. 2 420cm . D. 2 402cm . Trang 20