Hướng dẫn ôn tập học phần 4 môn Toán lớp 9 năm học 2025-2026

HƯỚNG DẪN ÔN TẬP HỌC PHẦN 4 MÔN: TOÁN LỚP 9 NĂM HỌC: 2025-2026
Họ và tên: ...........................................................................Lớp:..............................
Phạm vi kiểm tra: MẠCH SỐ HỌC, ĐẠI SỐ Chương Nội dung + Dãy số
Chương 9: Dãy số, căn thức và tập + Số hữu tỉ và số vô tỉ hợp
+ Căn thức có giá trị vô tỉ + Tập hợp
Chương 10: Đường thẳng và + Đồ thị tuyến tính phương trình bậc hai
+ Biểu thức và phương trình bậc hai
Kiểm tra: dự kiến 28/01/2026. Thời gian: 45 phút (kiểm tra trong tiết Toán của TKB)
MỘT SỐ BÀI TẬP TỰ LUYỆN
MTC 9.a: HS viết tiếp một dãy số hoặc mẫu sắp xếp cho trước dựa trên quy luật truy hồi.
MTC 9.b: HS tìm được quy tắc số hạng thứ n của dãy số.
MTC 9.c: Sử dụng quy luật số hạng thứ n của dãy số để tìm một số hạng chưa biết trong dãy.
Câu 1.1 Với mỗi dãy số sau đây, hãy:
i. Viết ba số hạng tiếp theo
ii.Tìm hạng tử thứ n
iii. Tìm hạng tử thứ 150
a) 1, 6, 11, 16, … b) 20, 14, 8, 2, …
Câu 1.2 Với mỗi dãy số sau đây, hãy:
i. Viết ba số hạng tiếp theo
ii.Tìm hạng tử thứ n
iii. Tìm hạng tử thứ 100
a) 5; 7; 10; 14; … b) 2; 9; 28; 65; 126; … Câu 2.1 Câu 2.2
Câu 3. Cho dãy số với số hạng tổng quát là Un = 2(n – 3)
a) Viết 6 số hạng đầu tiên của dãy
b) Tìm hạng tử thứ 93 của dãy
c) Hạng tử nào của dãy bằng 86?
MTC 9.e: Biểu diễn số thập phân vô hạn tuần hoàn dưới dạng phân số
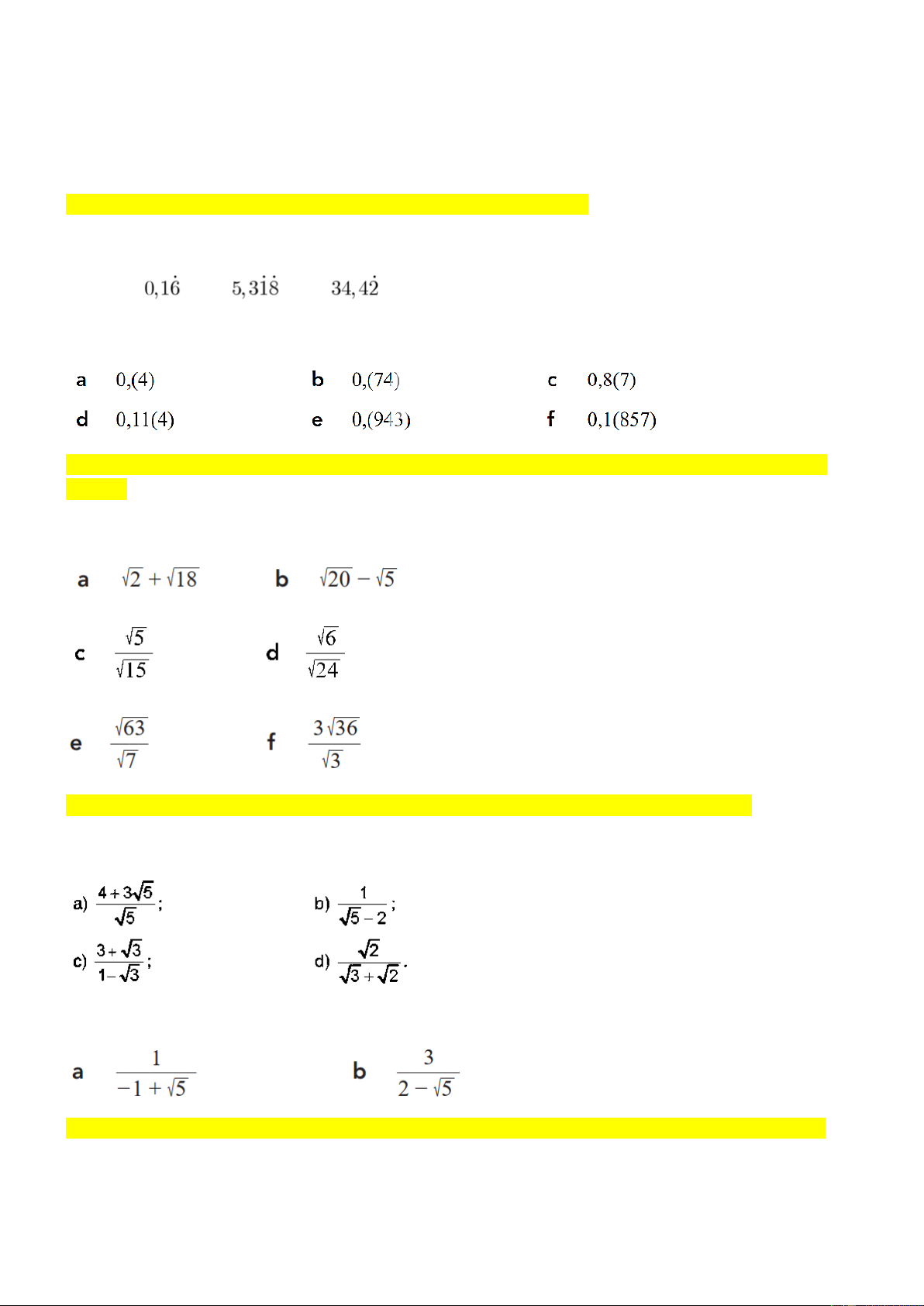
Câu 4. 1 Viết các số sau dưới dạng phân số tối giản:
Câu 4.2 Viết các số sau dưới dạng phân số tối giản:
MTC 9.f: Thực hiện được phép cộng, trừ, nhân, chia các căn thức có giá trị vô tỉ và viết đáp án ở dạng tối giản. Câu 5. Rút gọn
MTC 9.g: Thực hiện được phép trục căn thức ở mẫu thức và viết kết quả dưới dạng tối giản.
Câu 6.1 Thực hiện trục căn thức ở mẫu:
Câu 6.2 Thực hiện trục căn thức ở mẫu:
MTC 9.h: Sử dụng các quy tắc tính toán với căn thức có giá trị vô tỉ để giải quyết các bài toán thực tế. Câu 7.
MTC 9.i: Mô tả, biểu diễn tập hợp bằng ngôn ngữ, kí hiệu Toán học và biểu đồ Venn. Câu 8.
MTC 9.j: Biểu diễn mối quan hệ giữa các tập hợp bằng kí hiệu Toán học và biểu đồ Venn.
Câu 9.1. Cho không gian mẫu  = 1;2;3;4;5;6;7;8;9;10;11;1 
2 và hai tập hợp A = 2;4;6;8;1  0 và B = 4;5;6;7;8;  9 .
a) Tìm A  B b) A  B
c) Tìm A ' B
d) Hoàn thiện biểu đồ Venn sau để biểu thị không gian mẫu  , tập hợp A và tập hợp B bằng cách viết
các phần tử vào đúng vị trí.
Câu 9.2. Cho không gian mẫu  = 1;2;3;4;5;6;7;8;9;10;11;1  2 và hai tập hợp
A = 1;3;4;6;8;10;1  2 và
B = {x : x là số lẻ, x  10}
a) Tìm A  B
b) n ( A  B)
c) Tìm A ' B
d) Hoàn thiện biểu đồ Venn sau để biểu thị không gian mẫu  , tập hợp A và tập hợp B bằng cách viết
các phần tử vào đúng vị trí.
MTC 9.k: Nhận biết được khái niệm về căn thức bậc hai của một biểu thức đại số.
MTC 9.l: Thực hiện được một số phép biến đổi đơn giản về căn thức bậc hai của biểu thức đại số (căn
thức bậc hai của một bình phương, căn thức bậc hai của một tích, căn thức bậc hai của một thương).
Câu 10. Thực hiện phép tính:  1 
a) 2 32 − 3 50 + 6 72 . b) 12 + 4 27 − 75 : 3   .  2   16 27 4  c)  6  − +10  : 0,01  . d) + − ( − )2 2 7 4 7 2 . 9  3 25  
MTC 10.a: HS vẽ được một đường thẳng từ phương trình của nó bằng cách lập bảng giá trị và vẽ các
điểm trên mặt phẳng tọa độ.
Câu 11. Vẽ đồ thị các hàm số tuyến tính sau:
a) y = x − 3
b) y = −x − 2
c) y = 2x − 3 d) y = 3 − x +1
a) y = x − 3
b) y = −x − 2 x −2 e) y = +1 f) y = x − 2 2 3
g) 2x − y = 5
h) 4x + y = 7
MTC 10.b: HS xác định được hệ số góc và tung độ gốc của một đường thẳng thông qua đồ thị cho trước
trên mặt phẳng tọa độ và qua phương trình đường thẳng.
Câu 12.1. Xác định hệ số góc và tung độ gốc của các đường thẳng sau: −2 1 a) y = 5x – 1 b) y = x c) y = x + 3 5 12 4 d) y = −3𝑥 −
e) 4y + 7 = 2x f) 5x + 4y = 1 7
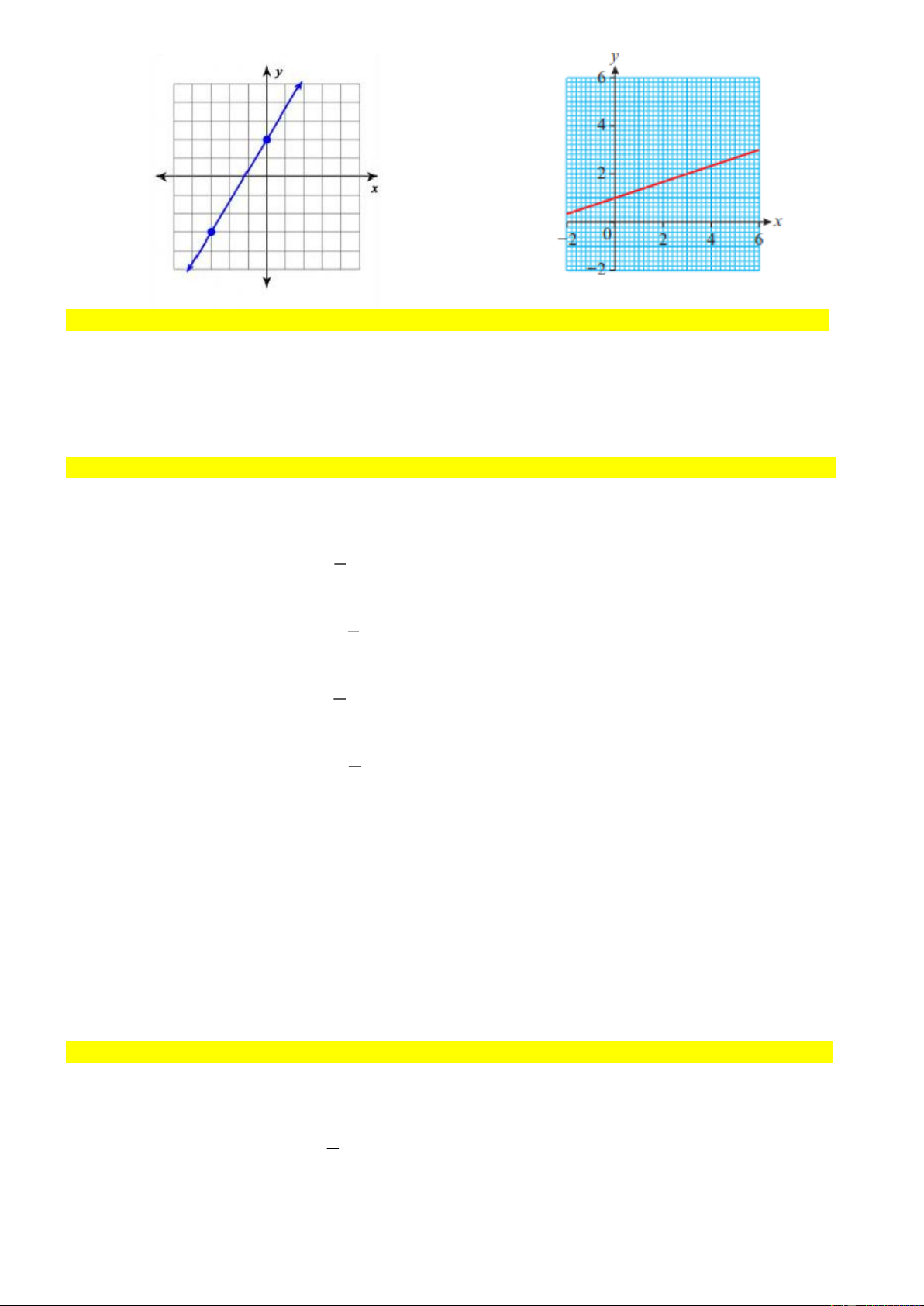
Câu 12.2. Xác định hệ số góc và tung độ gốc của các đường thẳng sau: a) b) c) d)
MTC 10.c: HS tìm được hệ số góc của đường thẳng khi biết tọa độ hai điểm nằm trên đường thẳng đó.
Câu 13. Tìm hệ số góc của đường thẳng đi qua các cặp điểm sau: a) (1;6) ; (3;8) b) ( 2 − ;5) ; (5;7) c) (4; 3 − ) ; (2;4) d) (7; 2 − ) ; (0; 3 − )
MTC 10.d: Tìm hệ số góc và phương trình của đường thẳng vuông góc với một đường thẳng cho trước.
Câu 14.1. Viết phương trình đường thẳng trong các trường hợp sau: 1
a) Vuông góc với đường thẳng y =
x + 5 và đi qua điểm (1;4) 2 1
b) Vuông góc với đường thẳng y = −
x − 2 và đi qua điểm ( 2 − ;3) 3 2
c) Vuông góc với đường thẳng y =
x − 1 và đi qua điểm (2;7) 3 4
d) Vuông góc với đường thẳng y = −
x + 2 và đi qua điểm (8; 2 − ) 5
Câu 14.2. Viết phương trình đường thẳng trong các trường hợp sau:
a) Vuông góc với đường thẳng 2x − y − 3 = 0 và đi qua điểm (3; 3 − )
b) Vuông góc với đường thẳng x + y − 2 = 0 và đi qua điểm (5; )1 −
c) Vuông góc với đường thẳng x − 5y −15 = 0 và đi qua điểm (1;3)
d) Vuông góc với đường thẳng 3x + 4y − 7 = 0 và đi qua điểm ( 1 − ;5)
MTC 10.e: Tìm hệ số góc và phương trình của đường thẳng song song với một đường thẳng cho trước.
Câu 15.1. Viết phương trình đường thẳng trong các trường hợp sau: 2
a) song song với đường thẳng y =
x + 4 và đi qua điểm (3; ) 1 3
b) song song với đường thẳng y = 3
− x − 4 và cắt trục tung tại điểm là 3
c) song song với đường thẳng y = 3
− x − 7 và đi qua gốc toạ độ. 1
d) song song với đường thẳng y = −
x − 2 và đi qua điểm ( 6 − ;4) 3
Câu 15.2. Viết phương trình đường thẳng trong các trường hợp sau:
a) song song với đường thẳng 5x − y −1 = 0 và cắt trục tung tại điểm là 1
b) song song với đường thẳng x + 2y −1 = 0 và đi qua điểm (3; ) 1
c) song song với đường thẳng x − 4y + 8 = 0 và đi qua điểm (0;4)
d) song song với đường thẳng 2x − 6y + 1 = 0 và đi qua điểm (3;2)
MTC 10.f: HS tìm được tọa độ trung điểm các đoạn thẳng khi biết tọa độ hai điểm đầu mút.
MTC 10.g: HS tính được độ dài đoạn thẳng khi biết tọa độ hai điểm đầu mút.
Câu 16.1. Tìm toạ độ trung điểm và độ dài của các đoạn thẳng sau khi biết toạ độ hai đầu mút. a) A(2; 8 − ) ; B(4;10)
b) C (3;7) ; D( 1 − ;3) c) E ( 1 − ;5) ; F( 5 − ;8) d) G (3; 5 − ) ; (4; 2 − )
Câu 16.2. Hai điểm (x;y) và (-x; -y) được vẽ trên mặt phẳng toạ độ Descartes. Tìm khoảng cách
giữa hai điểm này theo các giá trị đại số.
MTC 10.h: Áp dụng 3 hằng đẳng thức cơ bản và tìm nhân tử chung để phân tích được các biểu thức bậc
hai và bậc ba đơn giản thành nhân tử.
Câu 17. Phân tích các đa thức sau thành nhân tử 4 a) 9𝑥2 −
b) (𝑥 − 2)2 − (4 + 3𝑥)2
c) 4𝑏2𝑐2 − (𝑏2 + 𝑐2)2 81 d) 12𝑥 − 9𝑥2 − 4
e) 𝑥2 + 4𝑥 − 𝑦2 − 4𝑦
f) 3𝑥2 + 6𝑥𝑦 + 3𝑦2 − 3𝑧2 g) 2𝑥2 + 3𝑥 + 1 h) 5𝑦2 − 8𝑦 + 3 i) 12𝑥2 − 𝑥 − 6
MTC 10.i: Giải được các phương trình bậc hai có hệ số của x^2 là 1.
Câu 18. Giải các phương trình sau a) 𝑥2 + 2𝑥 − 5 = 0 b) 𝑥2 + 4𝑥 − 3 = 0 c) 𝑥2 + 3𝑥 = 8 d) 𝑥2 + 8𝑥 = −6 e) −𝑥2 + 3𝑥 + 40 f) 𝑥2 − 7𝑥 − 8 = 0
g) −60 − 17𝑥 = −𝑥2 14 h) 𝑥 + 5 = 𝑥2+4𝑥−12 𝑥 i) = −2 3𝑥−6 2 1 1 j) − =
k) 𝑥3 − 7𝑥2 + 10𝑥 = 0 𝑥2−1 𝑥+1 𝑥−1
MTC 10.j: HS có thể khai triển tích của các biểu thức đại số có ⩾ 2 bộ dấu ngoặc.
Câu 19. Khai triển tích các biểu thức sau a) (3 + 7𝑦)(7𝑦 − 3) b) (2𝑥 + 3)(5 − 𝑥)
c) (𝑥 + 3)(𝑥2 + 2𝑥 + 5)
d) (𝑥 − 1)(𝑥 + 2)(𝑥 − 4) e) (𝑥 − 1)(𝑥 − 2)2 f) 3(𝑥 − 4)3
MTC 10.k: Vẽ phác thảo được đồ thị các hàm số bậc nhất.
Câu 20. Vẽ đồ thị các hàm số bậc nhất sau a) 𝑦 = 𝑥 + 5 b) 𝑦 = −2𝑥 − 1 c) 𝑥 = 4 d) 𝑦 = −2 1 e) 𝑦 = −2𝑥 − f) 0 = 𝑥 − 2𝑦 − 1 2 1 g) 𝑥 + 𝑦 = − h) 𝑦 = 7 − 2𝑥 i) 4 = 2𝑥 − 5𝑦 2