

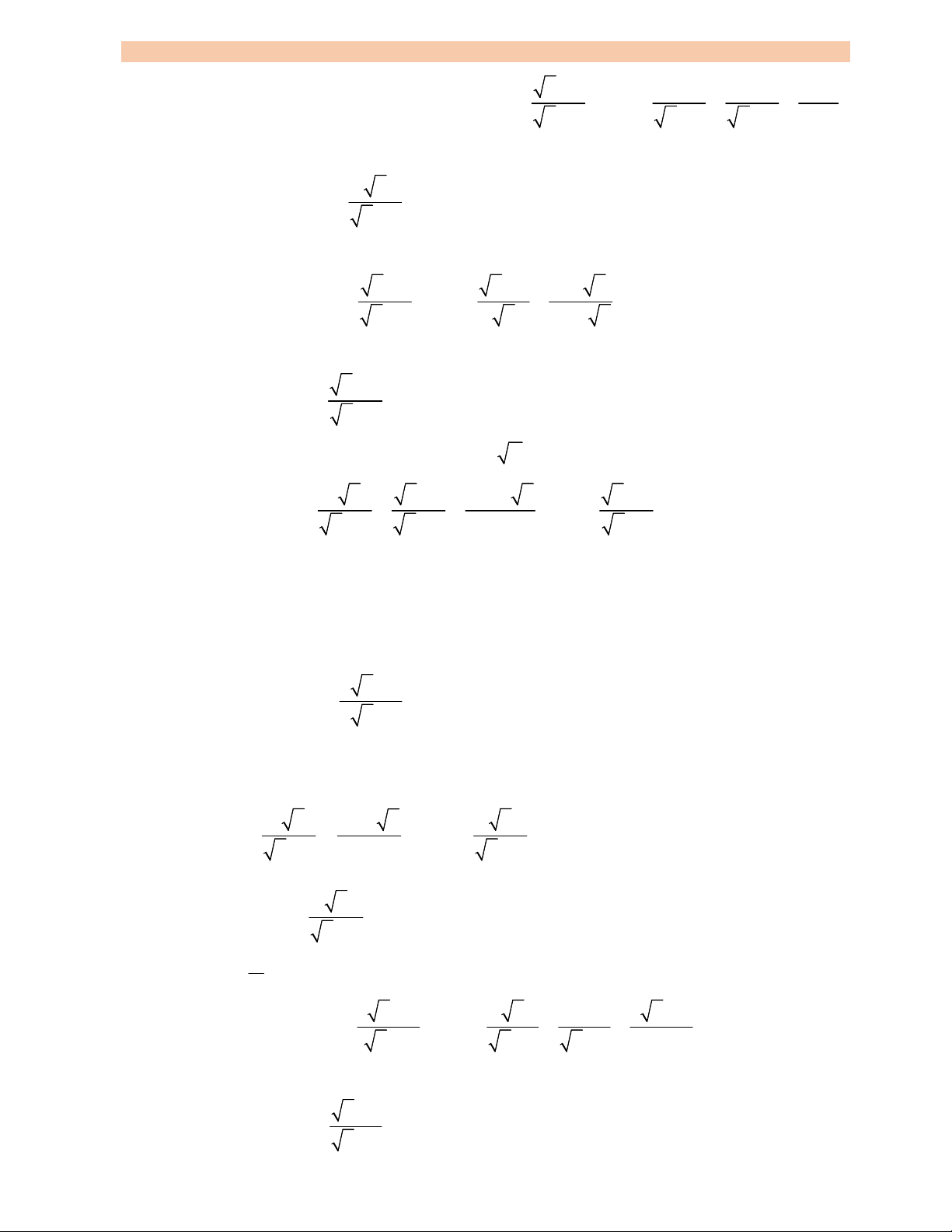




Preview text:
TRƯỜNG THCS NGHĨA TÂN - PHƯỜNG NGHĨA ĐÔ
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ 1 MÔN TOÁN 9 Năm học: 2025 - 2026 A. GIỚI HẠN KIỂM TRA
Đại số: Hết chương III
Hình học: Hết bài độ dài cung tròn, diện tích hình quạt, hình viên phân B. BÀI TẬP THAM KHẢO
NỘI DUNG 1: GIẢI PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH
Bài 1. Giải các phương trình sau:
1) 32x - 1 - 54x - 2 0 x 5x 15x x 2) - - - 5 3 6 12 4 2
3) x 2x 1 4x 1 4) x x 2 2 2 5 4 x 5) 2 2x 5x 1 0 6) 2 5x x 2 0 1 1 1 80 75 7) 8) 1 x x 9 20 x 5 x 4 4 11 1 1 1 9) 10) . x x 2 15 x x 10 12
Bài 2. Giải các hệ phương trình sau: x 2y 5 0,2x 0,3y 0,5 x 1 y 1) 1 2 x 2) 4y 10 3x 4y 2 3) 3 2 x 3 y 1 2 2 3 (
x 1) 2(y 2) 5
x 1y 1 xy 1 4) 2 x 4 y 1 3(x 1) (y 2) 5) 6) 1 x 3 y 3 xy 3 x 4 2y 4
Bài 3. Giải các bất phương trình sau 1) -4x 15 24 - 7x x 3 5x 1 1 2x 1 x 2x 1 2) 3) 2 4 3 3 6 2 x 1 1 2x 1 2 6) x 32x 1 4) 5) 2 0 3x 2 3 x 2 2x 2x 2x 7) 0 8) 1 9) 1 2 x 1 2 x 1 2 x 1
NỘI DUNG 2: GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
HỆ PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH
Bài 4. Một dây chuyền có kế hoạch sản xuất 480 chi tiết máy cùng loại trong một số ngày quy định.
Thực tế, mỗi ngày dây chuyền đã sản xuất nhiều hơn 8 chi tiết máy so với số chi tiết máy dự định
làm trong một ngày theo kế hoạch. Vì vậy, dây chuyền đã hoàn thành công việc sớm hơn kế hoạch
2 ngày. Hỏi theo kế hoạch, mỗi ngày dây chuyền phải sản xuất bao nhiêu chi tiết máy? (Giả định
rằng số chi tiết máy dây chuyền làm trong mỗi ngày là bằng nhau).
Bài 5. Khi Nam trúng tuyển vào trường THPT, bố Nam dự định mua cho Nam một chiếc xe đạp
điện và một bộ máy tính tổng cộng hết 20 000 000 đồng. Tuy nhiên bố Nam mua đúng vào
đợt khuyến mại nên số tiền dùng để mua xe đạp điện và máy tính rẻ hơn so với giá niêm yết
là 3 600 000 đồng. Biết rằng một chiếc xe đạp điện được giảm 20% so với giá niêm yết,
một bộ máy tính được giảm 15% so với giá niêm yết. Hãy tính giá niêm yết của chiếc xe
đạp điện và bộ máy tính?
Bài 6. Một đội xe tải dự định chở 280 tấn đá đến điểm tập kết để đưa ra xây dựng các đảo chìm ở
quần đảo Hoàng Sa - Việt Nam. Sau khi tính toán, đội cần chở thêm 6 tấn. Vì vậy đội đã bổ sung
thêm 1 xe, nên mỗi xe chở ít hơn dự định ban đầu 2 tấn. Biết tất cả các xe đều chở khối lượng đá
như nhau. Tính số xe dự định ban đầu.
Bài 7. Một mảnh vườn hình chữ nhật có chu vi 100 m . Nếu tăng chiều rộng thêm 3m và giảm
chiều dài đi 4m thì diện tích mảnh vườn giảm 2
2 m . Tính diện tích của mảnh vườn ban đầu.
Bài 8. Một khúc sông từ A đến B dài 45 km. Một cano đi xuôi dòng từ A đến B rồi ngược dòng
từ B về A hết tất cả 6 giờ 15 phút. Biết vận tốc của dòng nước là 3 km / h . Tính vận tốc của cano khi nước yên lặng.
Bài 9. Cạnh huyền của một tam giác vuông bằng 13cm. Nếu tăng độ dài cạnh góc vuông thứ nhất
1cm và giảm độ dài cạnh góc vuông thứ hai 2cm thì diện tích không đổi. Tìm độ dài hai cạnh góc vuông ban đầu.
Bài 10. Đến kỷ niệm ngày Quốc tế Phụ nữ Việt Nam 20 10 , một cửa hàng hoa ở chợ Quảng Bá
đã nhập 500 giỏ hoa hồng từ Đà Lạt về để bán. Các giỏ hoa hồng được chuyển về đến cửa hàng vào
sáng ngày 19 / 10 / 2025. Cửa hàng treo giá niêm yết bán một giỏ hoa hồng tăng 25% so với giá
lúc nhập về. Đến hết ngày 20 / 10 / 2025, cửa hàng bán được 400 giỏ hoa hồng. Đến ngày
21 / 10 / 2025, cửa hàng treo bảng giá mới (giảm 50% so với giá lúc nhập về) và đã bán hết số giỏ
hoa hồng còn lại. Hỏi giá một giỏ hoa hồng lúc cửa hàng nhập về là bao nhiêu? Biết cửa hàng khi
bán hết 500 giỏ hoa hồng thì lãi được 10 000000 đồng.
Bài 11. Trên địa bàn thành phố X có 1850 học sinh lớp 9 đăng kí dự thi tuyển sinh vào lớp 10
của hai trường THPT A và B, kết quả có 680 học sinh trúng tuyển. Biết tỉ lệ trúng tuyển của trường
A là 30% và trường B là 80%. Hỏi mỗi trường có bao nhiêu có bao nhiêu học sinh lớp 9 đăng kí dự thi vào lớp 10 .
Bài 12. Bạn Nam mua hai hộp bánh ở siêu thị và phải trả tổng cộng 480 000 đồng, trong đó đã tính
cả 40 000 đồng thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với hộp bánh thứ
nhất là 10%, thuế VAT đối với hộp bánh thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam
phải trả mỗi hộp bánh là bao nhiêu tiền?
Bài 13. Nhà cô An vừa thu hoạch vườn bưởi được 2 380 quả. Cô phân làm hai loại bưởi và bán với
giá20000 đồng một quả bưởi loại I , 15 000 đồng một quả bưởi loại II . Sau khi bán hết toàn bộ
số bưởi đã thu hoạch, cô tính ra còn thiếu 400 000 đồng nữa thì được tròn 40 triệu đồng. Tính số
bưởi loại I, loại II mà nhà cô An thu hoạch được.
Bài 14. Hiện tại gia đình bác Phương có số tiền tiết kiệm là 250 triệu đồng. Sau thời điểm đó, mỗi
tháng gia đình bác Phương đều tiết kiệm được 25 triệu đồng. Gia đình bác Phương dự định mua
một chiếc ô tô với giá tối thiểu là 650 triệu đồng. Hỏi sau ít nhất bao nhiêu tháng gia đình bác
Phương có thể mua được chiếc ô tô đó bằng số tiền tiết kiệm được?
Bài 15. Một ngân hàng đang áp dụng lãi suất tiết kiệm kì hạn 12 tháng là 4,7%/năm (lãi tính vào
cuối năm). Chị Minh dự kiến gửi một khoản tiền vào ngân hàng này và cần số tiền lãi sau một năm
ít nhất là 50 triệu đồng để chi tiêu. Hỏi số tiền chị Minh cần gửi tiết kiệm ít nhất là bao nhiêu (làm
tròn đến triệu đồng)?
Bài 16. Một hãng taxi có giá mở cửa là 15 nghìn đồng và giá 12 nghìn đồng cho mỗi kilomet tiếp
theo. Hỏi với 200 nghìn đồng thì hành khách có thể di chuyển được tối đa bao nhiêu kilomet ? (làm
tròn đến hàng đơn vị)
NỘI DUNG 3: BÀI TOÁN RÚT GỌN x 2 1 1 x
Bài 17. Với x 0,x 4,x 9 , cho hai biểu thức: A và B x 3 x 2 x 2 4 x
1) Tính giá trị của biểu thức A khi x 16 x 2) Chứng minh B . x 2 3) Với P . AB . Tìm x để P 0. x 1 x 1 2 x
Bài 18. Cho hai biểu thức: P và Q với điều kiện x 0 x 2 x x 2 x
1) Tính giá trị của biểu thức P khi x 25 . x 4 2) Chứng minh Q . x 2
3) Đặt A P :Q . Tìm giá trị nhỏ nhất của A . 2 x x 1 3 11 x x 3 Bài 19. Cho biểu thức A = và B = (x 0,x 9 ) x 3 x 3 9 x x 1
1) Tính giá trị của B tại x 25 2) Rút gọn biểu thức A
3) Tìm số nguyên x để M AB nhận giá trị nguyên
4) Tìm giá trị nhỏ nhất của biểu thức M. 7 x 2 Bài 20. Cho 2 biểu thức A =
và B . Với x 0,x 9 2 x 1 1) Rút gọn B 2) Tìm x để A B
3) Tìm x để B nhận giá trị là số nguyên dương 2 x x 9 x x Bài 21. Cho A = - và B =
với x 0;x 9;x 25 x 3 x 9 x 5
1) Tính giá trị của B tại x 4 x 2) Chứng minh A x 3 A
3) Đặt P . So sánh P với 1 B 2 x 4 x 3 6 x 4
Bài 22. Cho hai biểu thức: A và B với x 0,x 1. x 1 x 1 x 1 x 1
1) Tính giá trị của A khi x 9 ; x 2) Chứng minh B 1 ; x 1 3) ĐặtP .
AB , tìm số nguyên x để P 1 0. 2 x 1 x 3 6 x 4
Bài 23. Cho hai biểu thức A = và B , với x ≥ 0; x ≠ 1 x 1 x 1 x 1 x 1
1) Tính giá trị của biểu thức A khi x = 25.
2) Rút gọn biểu thức B.
3) Đặt P = A.B. Tìm x để x x 4 2 2 x 2.P . x 3 1 x 2 x
Bài 24. Cho hai biểu thức A và B với x 0,x 1. x 1 x 1 x 1 1 x 1) Rút gọn biểu thức B
2) Cho biểu thức P = B:A. Tìm x để P < 0. 1
3) Tìm giá trị nhỏ nhất của với x > 1. P x 3 x x 3 2 x 12
Bài 25. Cho biểu thức A và B x 0;x 9 x 2 x 3 3 x 9 x
1) Tính giá trị của A tại x 16.
2) Rút gọn biểu thức B . 3) Cho P .
AB . Tìm giá trị nhỏ nhất của P.
NỘI DUNG 4: HÌNH HỌC THỰC TẾ
Bài 26. Một chiếc bánh Pizza size L có đường kính 30 cm được
chia đều thành 8 phần bằng nhau. Tính diện tích của một phần
bánh pizza đó? Lấy 3,14 , kết quả làm tròn đến chữ số thập phân thứ hai
Bài 27. Để giữ cho những chiếc thớt gỗ không bị nứt hay cong vênh
khi sử dụng người ta thường làm một chiếc đai kim loại bao quanh chiếc
thớt. Tính độ dài thanh kim loại cần dùng để bao quanh một chiếc thớt gỗ
hình tròn có đường kính 35 cm (Coi độ dài mối ghép không đáng kể, lấy
3,14 , kết quả làm tròn đến hàng phần mười)
Bài 28. Một đĩa CD như hình dưới đây có dạng hình vành khuyên giới hạn
bởi hai đường tròn có bán kính lần lượt là 1,5 cm và 6 cm . Hình vành
khuyên đó có diện tích bằng bao nhiêu 2
cm (Lấy 3,14 , kết quả làm tròn đến hàng đơn vị)
Bài 29. Một con lắc di chuyển từ A đến vị trí B (Hình vẽ). Tính độ dài
quãng đường AB mà con lắc đó đã di chuyển, biết rằng dợi dây OA có
độ dài l 2 cm và tia OA tạo với phương thẳng đứng góc 15 . Lấy
3,14 , kết quả làm tròn đến chữ số thập phân thứ nhất.
Bài 30. Bà Hoà muốn làm một chiếc quạt giấy mà khi mở rộng hết cỡ
thì số đo góc chỗ tay cầm là 150, chiều dài mỗi nan tre tính từ chỗ
gắn đinh nẹp (để cố định các nan tre lại) đến rìa ngoài quạt là 25 cm ,
khoảng cách từ rìa giấy bên trong đến đinh nẹp là 4 cm (chỗ cầm
tay, không bọc giấy). Tính diện tích giấy để làm quạt (giấy dán cả hai
mặt, diện tích phần mép dán không đáng kể) ( kết quả tính theo đơn
vị cm , làm tròn kết quả đến hàng phần trăm, lấy 3,14 )
NỘI DUNG 5: HÌNH HỌC TỔNG HỢP
Bài 31. Cho O; R và điểm A nằm ngoài đường tròn. Vẽ các tiếp tuyến AB; AC với O ( B; C là hai tiếp điểm.
a) Chứng minh rằng AO BC
b) H là giao điểm của AO và BC. Chứng minh rằng: 2 4OH.HA AB
c) M và N lần lượt là trung điểm của AB; AC. Trên cung nhỏ BC lấy điểm D sao cho tiếp
tuyến tại D của O cắt tia MN tại I. T là hình chiếu của D trên OI . Chứng minh rằng
OH.OA OT.OI và IA ID.
Bài 32. Cho nửa đường tròn O;R có đường kínhAB . Lấy điểm C trên nửa đường tròn (O ) sao
cho AC BC . Kẻ OH AC tại H. Tia OH cắt tiếp tuyến Ax của nửa đường tròn tại D. a) Chứng minh hệ thức 2 OH.OD R
b) Gọi E là giao của BD với nửa đường tròn Chứng minh: 4 điểm , A D,E,H cùng thuộc một
đường tròn và DC là tiếp tuyến của O
c) Gọi M là trung điểm của DH, I là giao của AM với nửa đường tròn. Chứng minh 3 điểm B,H,I thẳng hàng.
Bài 33. Cho điểm S nằm ngoài đường tròn O;R. Qua S kẻ các tiếp tuyến SC,SD với đường
tròn (C và D là tiếp điểm). Gọi I là giao điểm của CD vàSO .
a) Chứng minh bốn điểm S,C, ,
O D cùng nằm trên một đường tròn.
b) CHứng minh SO là trung trực của đoạn thẳngCD . tính độ dài OI nếuR 3cm,OS 5cm .
c) Kẻ đường kính CK của đường tròn O;R. Chứng minh DK song song với SO .
d) Vẽ tia Sx nằm giữa hai tia SC vàSO . Tia Sx cắt đường tròn O;R tại hai điểm A và B (A
nằm giữa S vàB ). Gọi H là trung điểmAB . Tiếp tuyến tại B của đường tròn O;R cắt tia OH
tạiQ . Chứng minh ba điểm Q,C,D thẳng hàng.
Bài 34. Từ điểm M bên ngoài đường tròn O;R, vẽ hai tiếp tuyến MA, MB (A, B là các tiếp
điểm). Gọi H là giao điểm của MO và AB . 1) Chứng minh OM AB .
2) Kẻ đường kính BC của đường tròn O . Gọi I là trung điểm của AC . Chứng minh tứ giác OIAH là hình chữ nhật.
3) Tiếp tuyến tại C của đường tròn O cắt tia BA tại D ; tia DI cắt đoạn OC tại K ; tia DO cắt BD CD
đoạn AC ở E . Chứng minh và BOD = EIK . BO CI
Bài 35. Cho O đường kính AB, C là điểm bất kì trên nửa đường tròn sao cho CB C , A K là
trung điểm BC. Tiếp tuyến tại B cắt OK tại D .
a) Chứng minh DB DC và DC là tiếp tuyến của O
b) CH là đường cao của tam giác ABC. Chứng minh C nằm trên đường tròn ngoại tiếp tam giác OHK
c) Gọi I là trung điểm CH, tiếp tuyến tại A của O cắt BI tại E. Chứng minh , D E, C thẳng hàng
Bài 36. Cho ABC nội tiếp đường tròn O đường kính BC. Vẽ dây cung AD của O vuông
góc với đường kính BC tại H. Gọi M là trung điểm cạnh OC và I là trung điểm cạnh AC. Từ
M vẽ đường thẳng vuông góc với OC , đường thẳng này cắt tia OI tại N. Trên tia ON lấy điểm
S sao cho N là trung điểm của OS.
a) Chứng minh ABC vuông tại A và HA HD. b) Chứng minh MN S
C và SC là tiếp tuyến của O.
c) Gọi K là trung điểm cạnh HC, vẽ đường tròn đường kính AH cắt cạnh AK tại F. Chứng minh BH.HC AF.AK.
d) Trên tia đối tia BA lấy điểm E sao cho B là trung điểm cạnh AE. Chứng minh E, H, F thẳng hàng.
Bài 37. Cho nửa đường tròn O;R có đường kính AB . Tia Ax là tiếp tuyến tại A của nửa đường
tròn O (tia Ax thuộc nửa mặt phẳng bờ AB chứa nửa đường tròn tâm O ). Lấy điểm M trên tia
Ax và kẻ tiếp tuyến MC với nửa đường tròn O (C là tiếp điểm).
a) Chứng minh: Bốn điểm ,
A M,C,O cùng thuộc một đường tròn.
b) Đường thẳng AC cắt tiếp tuyến tại B của nửa đường tròn O tại điểm D . Chứng minh: đường
thẳng OM là đường trung trực của đoạn thẳng AC và 2 AM.BD 2R .
c) Chứng minh: BM vuông góc OD .
NỘI DUNG 6: MỘT SỐ BÀI TOÁN NÂNG CAO
Bài 38. Một nhà đầu tư có số vốn 2 tỉ đồng để phân bổ vào hai quỹ đầu tư: Quỹ cổ phiếu A và
quỹ trái phiếu B . Quỹ cổ phiếu A có tỷ suất sinh lời 14% /năm, quỹ trái phiếu B có tỷ suất sinh
lời 6% / năm. Theo quy định của các quỹ thì nhà đầu tư phải đầu tư ít nhất 400 triệu đồng vào
quỹ trái phiếu B và không được đầu tư quá 1,2 tỉ đồng vào quỹ cổ phiếu . A
Hãy xác định cách phân bổ vốn vào hai quỹ nói trên để nhà đầu tư có thể đạt lợi nhuận tối đa mỗi
năm và tính lợi nhuận đó.
Bài 39. Một cửa hàng bán 3 loại trái cây: táo, cam và quýt. Mỗi ngày, số lượng hộp quả táo, hộp quả cam
và hộp quả quýt nhập về được ký hiệu lần lượt là x,y,z (x, ,
y z là các số tự nhiên). Cửa hàng có các thông
tin và điều kiện như sau:
1. Chi phí nhập mỗi hộp quả táo là 100 000đồng, mỗi hộp quả cam là 200 000 đồng và mỗi hộp quả quýt là 100 000đồng.
2. Tổng chi phí nhập không được vượt quá 1000 000 đồng.
3. Cửa hàng phải nhập đủ cả 3 loại trái cây.
4. Cửa hàng cần nhập ít nhất 3 hộp quả táo và cam cộng lại.
Lợi nhuận (lãi) thu về từ việc bán mỗi loại trái cây là: 200 000 đồng cho mỗi hộp quả táo, 300 000 đồng
cho mỗi hộp quả cam và 100 000 đồng cho mỗi hộp quả quýt.
Giả định rằng tất cả số trái cây nhập về đều được bán hết trong ngày, hãy chỉ ra phương án nhập hàng giúp
người bán hàng có được lợi nhuận cao nhất.
Bài 40. Trong một xưởng cơ khí đang có sẵn những thanh thép dài 7,4m . Một công trình xây dựng
đang cần có 1000 đoạn thép dài 0,7m và 2 000 đoạn thép dài 0,5m (cùng kích cỡ với thanh thép
7,4 m ). Em hãy tìm xem cần dùng bao nhiêu thanh thép 7,4m để thỏa mãn yêu cầu trên với chi phí tiết kiệm nhất.
Bài 41. Thầy Khánh có hai cô bạn gái, mỗi cô thích ăn một
loại rau khác nhau nên thầy dự định làm một hàng rào hình
chữ E dọc theo con sông (như hình vẽ bên) để quây một
khu đất thành hai phần hình chữ nhật bằng nhau, mỗi phần
trồng một loại rau mà hai cô bạn thầy thích. Chi phí tính
theo độ dài hàng rào là 500 nghìn đồng mỗi mét chiều dài
đối với mặt hàng rào AB (mặt hàng rào song song bờ sông) và 400 nghìn đồng mỗi mét chiều dài
đối với ba mặt hàng rào AD, BE, CG (ba mặt hàng rào song song và bằng nhau). Tìm diện tích lớn
nhất của cả khu đất mà thầy Khánh có thể quây hàng rào với tổng chi phí tối đa là 12 triệu đồng.
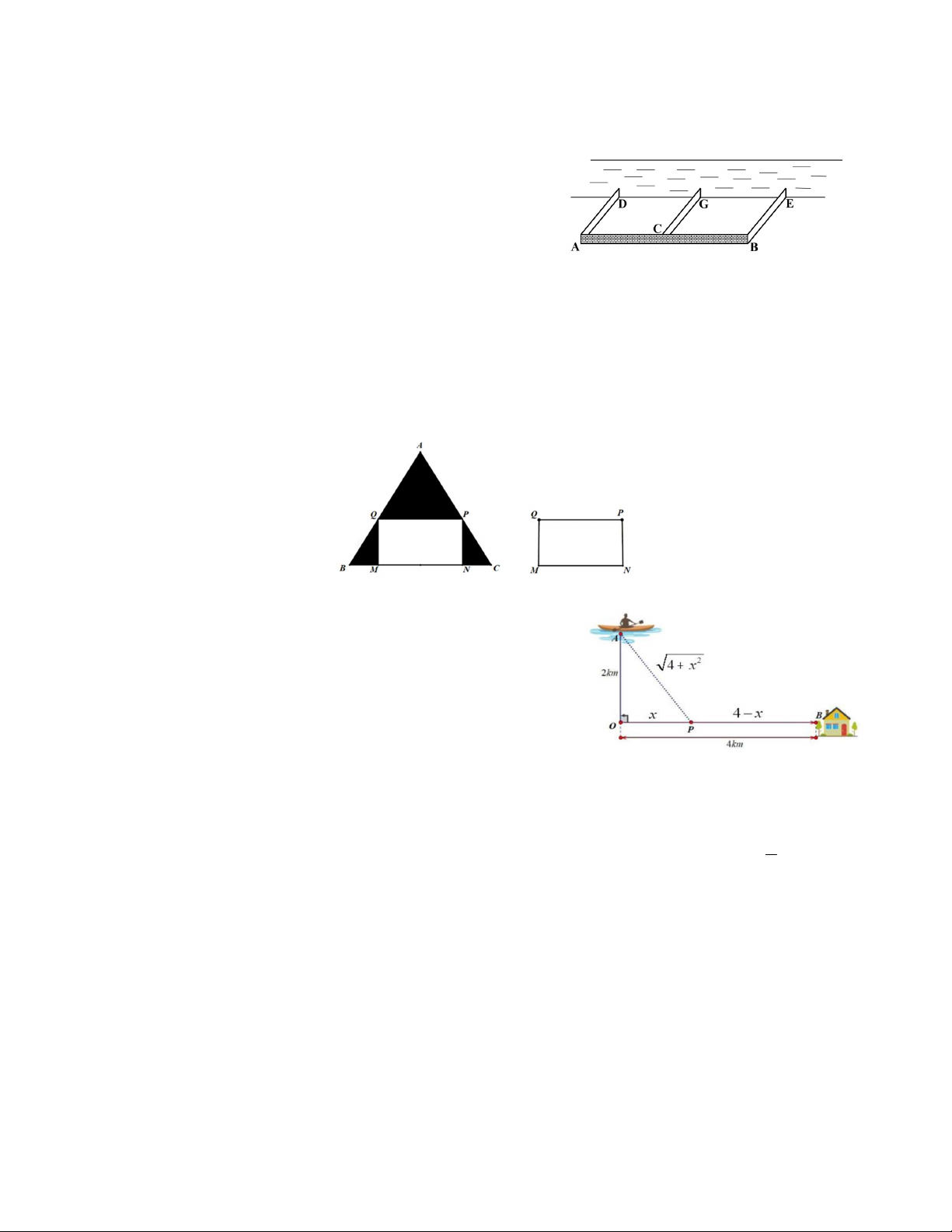
Bài 42. Cho một tấm nhôm hình tam giác đều có cạnh bằng 20(cm). Người ta cắt ở ba góc của tấm
nhôm đó ba tam giác như hình vẽ dưới đây để được hình chữ nhật MNPQ . Tìm độ dài đoạn MB
để hình chữ nhật MNPQ có diện tích lớn nhất.
Bài 43. Bác Nam đang trên chiếc thuyền đánh cá tại vị trí
A cách bờ biển 2 km và chèo thuyền về nhà ở địa điểm B
trên bờ sông. Để về nhà với thời gian ngắn nhất bác dự định
chèo thuyền vào bờ ở một vị trí P nằm giữa O,B và tiếp
tục chạy bộ theo một đường thẳng để về nhà tại địa điểm
B cách vị trí O trên bờ gần với thuyền nhất là 4 km (hình
vẽ). Biết rằng thuyền di chuyển với vận tốc 6 km/h (bỏ
qua sức gió và vận tốc của dòng nước) và bác Nam chạy bộ
trên bờ với vận tốc 10 km/h . Tìm vị trí điểm P để khoảng thời gian bác Nam đi từ vị trí A về đến
nhà (điểm B ) là ngắn nhất? Khi đó thời gian ngắn nhất là bao nhiêu phút? 8
Bài 44. Người ta làm một chiếc hòm bằng tôn có dạng hình hộp chữ nhật thể tích là 3 m có cả 3
nắp. Biết đáy hòm có chiều dài bằng hai lần chiều rộng. Để tốn ít vật liệu nhất (coi mối ghép và độ
dày tấm tôn không đáng kể) thì chiều dài mặt đáy của chiếc hòm có độ dài bằng bao nhiêu? PHẦN II. ĐỀ THAM KHẢO
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2024-2025 MÔN: TOÁN - LỚP 9 Ngày kiểm tra: 26/12/2024
Thời gian làm bài: 90 phút 5 x 6 x 3
Câu 1. (2,5 điểm) Cho hai biểu thức A và B x x 3 x 3 x 9 x 3 với x 0,x 9 .
a) Tính giá trị của biểu thức A khi x 4 . x 3 b) Chứng minh B . x 3 B 16 c) Đặt P . Tìm x để P x . A 5
Câu 2. (2,0 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Bác Hà muốn mua một chiếc áo sơ mi và một chiếc quần âu. Tổng số tiền theo giá niêm
yết của chiếc áo sơ mi và chiếc quần âu đó là 700 nghìn đồng. Bác Hà mua vào dịp “Tuần
lễ người Việt Nam ưu tiên dùng hàng Việt Nam” nên so với giá niêm yết, áo sơ mi được
giảm 15% và quần âu được giảm 18%. Do đó tổng số tiền bác Hà phải trả là 583 nghìn
đồng. Hỏi giá niêm yết của mỗi mặt hàng trên là bao nhiêu? Câu 3. (1,5 điểm) 2
x y 3x y 4
a) Giải hệ phương trình: . x y 2x y 5 b) Giải phương trình: 2
x x 3 43 x 0.
c) Giải bất phương trình: x x x 2 4 3 1 3 2 5 11. Câu 4. (3,5 điểm)
1) Bậc thềm của tòa nhà cao 0,5 m so với mặt đất. Để hỗ trợ
người khuyết tật đi lại, người ta thiết kế lối đi dành cho xe lăn
là một dốc nghiêng với khoảng cách từ chân dốc đến đỉnh dốc
là 6 m. Hỏi đường lên dốc tạo với phương nằm ngang một góc
bao nhiêu độ? (Số đo góc làm tròn đến độ)
2) Cho đường tròn O;R và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AB với
đường tròn O (B là tiếp điểm). Kẻ đường kính BC của đường tròn O , đoạn thẳng
AC cắt đường tròn O tại điểm thứ hai D . Kẻ OH CD H CD.
a) Chứng minh bốn điểm A, B , O , H cùng thuộc một đường tròn. b) Chứng minh O HC đồng dạng với A BC và 2 CH.CA 2R .
c) Gọi N là giao điểm của BH và DO . Kẻ AK BH (K K BH , AK cắt
BD tại I . Chứng minh các điểm C , N , I thẳng hàng.
Câu 5. (0,5 điểm) Một khách sạn có 100 phòng cùng giá tiền cho thuê. Qua khảo sát người ta thấy
rằng: nếu ban đầu mỗi phòng khách sạn cho thuê với giá 480 nghìn đồng trong một ngày
thì luôn kín các phòng, tuy nhiên khi tăng giá phòng thêm x% (x 0) so với mức giá ban 4x
đầu thì số lượng phòng cho thuê giảm đi
% phòng. Hỏi khách sạn phải niêm yết giá 5
tiền thuê phòng mỗi ngày là bao nhiêu để khách sạn đạt doanh thu một ngày cao nhất? ---HẾT---



