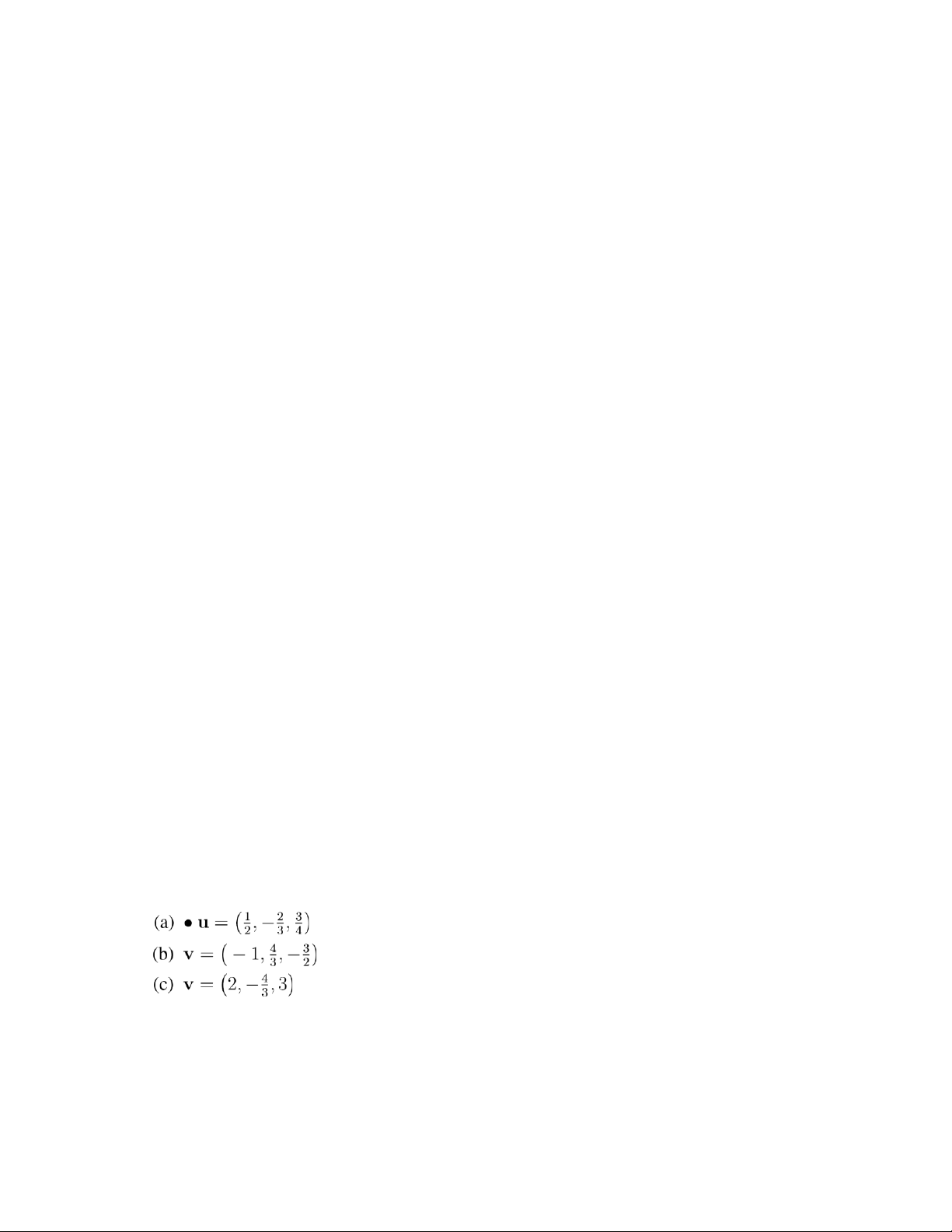



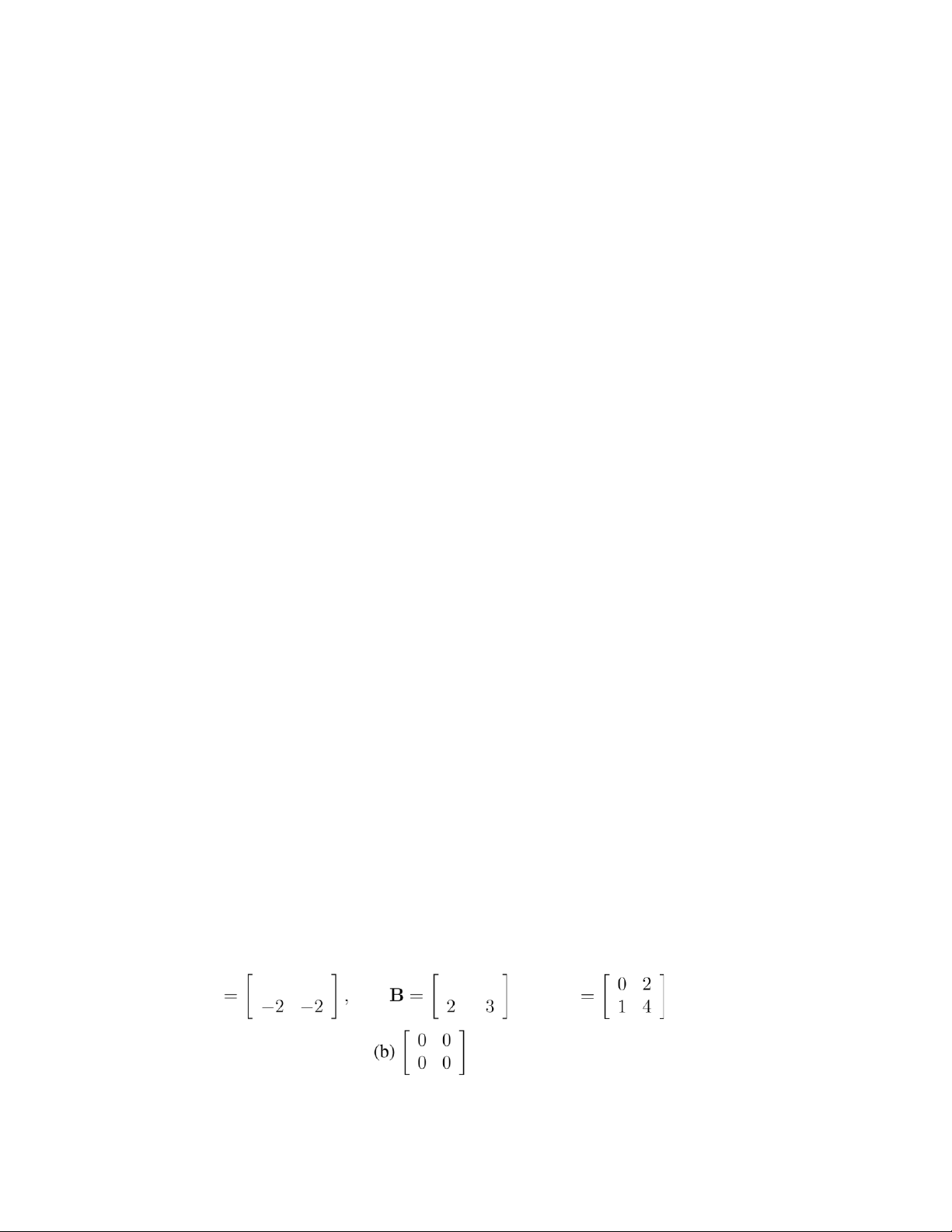







Preview text:
APPLIED LINEAR ALGEBRA EXERCISES FOR CHAPTER 2:
A. Non-assessed Exercises (corrected in class): 0.1.2(a), 0.1.4, 0.2.5(a), 0.2.4, 0.2.8, 0.2.10, 0.2.13(a), 0.2.14(b),
0.2.16(a), 0.2.17(b), 0.2.18(a), 0.3.4(b), 0.3.6, 0.3.7, 0.3.8(a), 0.3.9(c),
0.3.10, 0.3.12, 0.3.17, 0.3.20, 0.3.23, 0.3.25, 0.3.27(a), (c), 0.3.28.
B. Assessed Assignments (to be submitted):
0.1.2(b), (c), 0.1.3, 0.1.5, 0.1.8, 0.2.1, 0.2.3, 0.2.5(a), (b), (d), 0.2.7, 0.2.9, 0.2.11,
0.2.13(b), (c), 0.2.14(a), (c), 0.2.16(b), (c), 0.2.17(a),
(c), 0.2.18(b)–(e), 0.3.1, 0.3.2, 0.3.3, 0.3.4(a), (c), (d)? 0.3.5, 0.3.8(b), 0.3.9(a), (b), (d)?
0.3.11, 0.3.13, 0.3.14, 0.3.18, 0.3.21, 0.3.22,
0.3.24, 0.3.26, 0.3.27(b), (d), 0.3.29, 0.3.30. 0.1 EUCLIDEAN n-SPACE 0.1.1 Vectors in n-Space
Exercise 0.1.1. Let u = (−3,1,2), v = (4,0,−8), and w = (6,−1,−4). Find the
components of the following vectors. (a) 6u + 2v.
(b) −3(v− 8w).
(c) (2u− 7w) − (8v + u).
Exercise 0.1.2. Determine whether each vector is a scalar multiple of x = (6,−4,9). . . .
Exercise 0.1.3. Let u = (1,−1,0,1) and v = (0,2,3,−1). Solve for w if
(a) 3w = u− 2v; 1
(b) 21w = 2u + 3v;
(c) w + 3v = −2u.
Exercise 0.1.4. • Show that there do not exist scalars c1,c2, and c3 such that c1(1,0,1,0)
+ c2(1,0,−2,1) + c3(2,0,1,2) = (1,−2,2,3).
Exercise 0.1.5. Write the third column of each matrix as a linear combination of the
first two columns, if possible. A , B .
Exercise 0.1.6. If x0 and v are vectors in Rn, and if v is nonzero, then the equation
x = x0 + tv (0.1.1)
defines the line through x0 that is parallel to v. In the special case where x0 = 0, the line
is said to pass through the origin. If x0 = (x0,1,x0,2,...,x0,n) and v = (v1,v2,...,vn), then
Equation (0.1.1) can be written in terms of the components as
x1 = x0,1+tv1,
x2 = x021+tv2,...,xn = x0,n+tvn, −∞ < t < ∞, (0.1.2)
which are called parametric equations of the line.
(a) Find a vector equation and parametric equations of the line in R3 that passes
through the origin and is parallel to the vector v = (−3,0,1).
(b) Find a vector equation and parametric equations of the line in R3 that passes
through the point (−9,3,4) and is parallel to the vector v = (−1,6,0).
Exercise 0.1.7. Use the given equation of a line to find a point on the line and a vector parallel to the line. 2
(a) (x,y,z) = (4t,7,4 + 3t).
(b) x = (1 − t)(4,6) + t(−2,0). 0.1.2
Norm, Dot Product, and Distance in Rn
Exercise 0.1.8. Evaluate the given expression with u = (−2,−1,4,5), v = (3,1,−5,7), and
w = (−6,2,1,1).
(a) ∥3u− 5v + w∥; (b) ∥u∥ + ∥− 2v∥ + ∥− 3w∥; . 0.2 VECTOR SPACES 0.2.1 Real Vector Spaces
Exercise 0.2.1. Let V be the set of all ordered pairs of real numbers, and consider the
following addition and scalar multiplication operations on u = (u1,u2) and v = (v1,v2):
u + v = (u1 + v1,u2 + v2),
ku = (0,ku2).
(a) Compute u + v and ku for u = (−1,2), v = (3,4), and k = 3.
(b) Show that Axioms 7, 8, and 9 hold.
(c) Show that Axiom 10 fails and hence that V is not a vector space under the given operations.
Exercise 0.2.2. Let V be the set of all ordered pairs of real numbers, and consider the
following addition and scalar multiplication operations on u = (u1,u2) and v = (v1,v2):
u + v = (u1 + v1 + 1,u2 + v2 + 1), ku = (ku1,ku2).
(a) Compute u + v and ku for u = (0,4), v = (1,−3), and k = 2.
(b) Show that u + (0,0) ̸= u for all u∈ V .
(c) Show that u + (−1,−1) = (−1,−1) + u = u for all u∈ V .
(d) Show that Axiom 5 holds by producing an ordered pair −u such that u + (−u) =
(−1,−1) for u = (u1,u2).
(e) Find two vector space axioms that fail to hold. 3
Exercise 0.2.3. Let n be positive interger. Show that the set Mn,n of all n × n matrices
with the usual operations of addition and scalar multiplication is a vector space. 0.2.2 Subspaces
Exercise 0.2.4. • Let V be any vector space. Show that W = {0} is a subspace of V . We
call W the zero subspace of V .
Exercise 0.2.5. Determine which of the following are subspaces of R3.
(a) All vectors of the form (a,1,1).
(b) All vectors of the form (a,b,c), where b = a + c.
(c) All vectors of the form (a,b,c), where b = a + c + 1.
(d) All vectors of the form (a,b,0).
Exercise 0.2.6. Let W be the set
. Show that W is a subspace of R3.
Exercise 0.2.7. Show that the set of symmetric n × n matrices is a subspace of Mn,n.
(Mn,n is the space of all square matrices of order n.) Similarly, the sets of upper
triangular matrices, lower triangular matrices, and diagonal matrices are subspaces of Mn,n.
Exercise 0.2.8. • Show that if W1,W2,...,Wr are subspaces of a vector space V , then the
intersection of these subspaces is also a subspace of V .
Exercise 0.2.9. Let W be the set of all 3 × 2 matrices of the form
Show that W is a subspace of V = M3,2. 4
Exercise 0.2.10. • Let W be the set of all matrices in Mn,n with determinants equal to 1.
Is W a subspace of Mn,n?
Exercise 0.2.11. Determine whether the given subset of Mn,n is a subspace of Mn,n with
the standard operations. Justify your answer.
(a) The set of all n × n matrices A that commute with a given matrix B, that is, AB = BA.
(b) The set of all n × n singular matrices.
(c) The set of all n × n invertible matrices.
Exercise 0.2.12. Let W be the set of all functions that are differentiable on [−1,1]. Show
that W is a subspace of C[−1,1].
Exercise 0.2.13. Express the following vectors as linear combinations of u = (2,1,4), v
= (1,−1,3), and w = (3,2,5).
(a) • (−9,−7,−15) (b) (6,11,6) (c) (0,0,0).
Exercise 0.2.14. Express v as linear combinations of u1, u2, and u3 if possible..
(a) v = (−1,7,2), u1 = (1,3,5), u2 = (2,−1,3), u3 = (−3,2,−4).
(b) •v = (0,5,3,0), u1 = (1,1,2,2), u2 = (2,3,5,6), u3 = (−3,1,−4,2).
(c) v = (7,2,5,−3), u1 = (2,1,1,2), u2 = (−3,3,4,−5), u3 = (−6,3,1,2).
Exercise 0.2.15. Let v be a nonzero vector in Rn. Show that span{v} is the set of all
scalar multiples of v, that is span{v} = {tv : t ∈R}. Thus span{v} the line through the
origin determined by v (see Exercise 0.1.6).
Exercise 0.2.16. Which of the following are linear combinations of 4 0 1 −1 A, C? 5 .
Exercise 0.2.17. Suppose that v1 = (2,1,0,3), v2 = (3,−1,5,2), and v3 = (−1,0,2,1). Which
of the following vectors are in span{v1,v2,v3}?
(a) (2,3,−7,3)
(b) • (0,0,0,0)
(c) (1,1,1,1)
(d) (−4,6,−13,4).
Exercise 0.2.18. Let f(x) = cos2 x and g = sin2 x be function in C[0,2π]. Which of the
following lie in the space spanned by f and g? (a) • cos2x (b) 3 + x2 (c) 1 (d) sinx (e) 0. 0.3 BASIS AND DIMENSION 0.3.1 Linear Independence
Exercise 0.3.1. Show that the set of standard unit vectors e1 = (1,0,0,...,0), e2 =
(0,1,0,...,0),..., en = (0,0,0,...,1) is a linearly independent set in Rn.
Exercise 0.3.2. • Let Pn denote the set of all real polynomials of degree n or less. Show that the polynomials 1, x, x2,..., xn
form a linearly independent set in Pn.
Exercise 0.3.3. In each part, determine whether the vectors are linearly independent or are linearly dependent in P2.
(a) 2 − x + 4x2,
3 + 6x + 2x2, 2 + 10x − 4x2.
(b) 1 + 3x + 3x2, x + 4x2,
5 + 6x + 3x2, 7 + 2x − x2.
Exercise 0.3.4. Determine which of the following sets of vectors in C[0,2π] are 6 linearly dependent.
(a) 6, 3sin2x, 2cos2x;
(b) • x, cosx;
(c) 1, sinx, sin2x;
(d) (3 − x)2, x2 − 6x, 5.
Exercise 0.3.5. Determine whether the matrices A , B , C
are linearly independent or dependent in M3,3.
Exercise 0.3.6. • Determine all values of k for which the following matrices are linearly independent in M2,2. A , B , C .
Exercise 0.3.7. For which real values of a do the following vectors form a linearly dependent set in R3?
v1 = (a,−1,−1), v2 = (−1,a,−1), v3 = (−1,−1,a).
Exercise 0.3.8. (a) • Show that is linearly dependent in R3. (b) Show that is linearly dependent in R4.
Exercise 0.3.9. Determine whether the given set S spans R3. . . . .
Exercise 0.3.10. • Prove that if S = {v1,v2,...,vr} is a linearly independent set of vectors,
then so is every nonempty subset of S. 7
0.3.2 Coordinates, Basis, and Dimension
Exercise 0.3.11. Show that the following set of vectors forms a basis for R3. .
Exercise 0.3.12. • Show that the following polynomials form a basis for P2 (see Exercise 0.3.2). x2 + 1, x2 − 1, 2x − 1.
Exercise 0.3.13. Show that the following polynomials form a basis for P3. .
Exercise 0.3.14. Show that the following matrices form a basis for M2,2. A .
Exercise 0.3.15. Show that the following matrices do not form a basis for M2,2. A .
Exercise 0.3.16. Let V be the subspace of C[0,2π] spanned by f1 = cos2 x, f2 = sin2 x, f3 = cos2x.
(a) Show that S = {f1,f2,f3} is not a basis for V .
(b) Find a basis for V .
In Exercises 0.3.17–0.3.18, first show that the set is a basis
for M2,2, then express A as a linear combination of the vectors in S. Exercise 0.3.17. • 8 A , A . Exercise 0.3.18. A , A .
0.3.3 Nullspace, Row Space, and Column Space of a Matrix Let A be
an m × n matrix.
(i) The row space of A is the subspace of Rn spanned by the row vectors of A.
(ii) The column space of A is the subspace of Rm spanned by the column vectors of A.
(iii) The set of all solutions of the homogeneous system of linear equationsAx = 0 is
a subspace of Rn called the nullspace of A and is denoted by N(A). So, : Ax .
Exercise 0.3.19. Find the nullspaces of the following matrices. A , B , C .
In Exercises 0.3.20–0.3.21, use the fact that matrices A and B are row-equivalent.
(a) Find the rank and the dimension of the nullspace of A. 9
(b) Find a basis for the nullspace of A.
(c) Find a basis for the row space of A.
(d) Find a basis for the column space of A.
(e) Determine whether the rows of A are linearly independent.
(f) Let the columns of A be denoted by a1, a2, a3, a4, and a5. Determine whether
each set is linearly independent.
(i) {a1,a2,a3};
(ii) {a1,a2,a4};
(ii) {a1,a2,a5}. Exercise 0.3.20. • A . Exercise 0.3.21. A .
In Exercises 0.3.22–0.3.24, find (a) a basis for the row space and (b) the rank of the
given matrix by reducing it to row echelon form. Exercise 0.3.22. A Exercise 0.3.23. • 10 A . Exercise 0.3.24. A
In Exercises 0.3.25–0.3.26, find (a) a basis for the column space and (b) the rank of the given matrix. Exercise 0.3.25. A . Exercise 0.3.26. A.
Exercise 0.3.27. Find a basis for the subspace of R4 spanned by S. . . . .
In Exercises 0.3.28–0.3.30, find (a) a basis for and (b) the dimension of the solution
space of the homogeneous system of linear equations. Exercise 0.3.28. • 11
3x1 + 3x2 + 15x3 + 11x4 = 0 x1 − 3x2 + x3 + x4 = 0
2x1 + 3x2 + 11x3 + 8x4 = 0. Exercise 0.3.29.
2x1 + 2x2 + 4x3 − 2x4 = 0 x1 + 2x2 + x3 + 2x4 = 0
−x1 + x2 + 4x3 − 2x4 = 0. Exercise 0.3.30.
x1 + 3x2 + 2x3 + 22x4 + 13x5 = 0 x1 + x3 − 2x4 + x5 = 0
3x1 + 6x2 + 5x3 + 42x4 + 27x5 = 0. 12




