Assignment Presentation 9 môn Kinh tế vi mô | Trường Đại học Kinh Tế Quốc Dân

Assignment Presentation 9 Problem 1 :
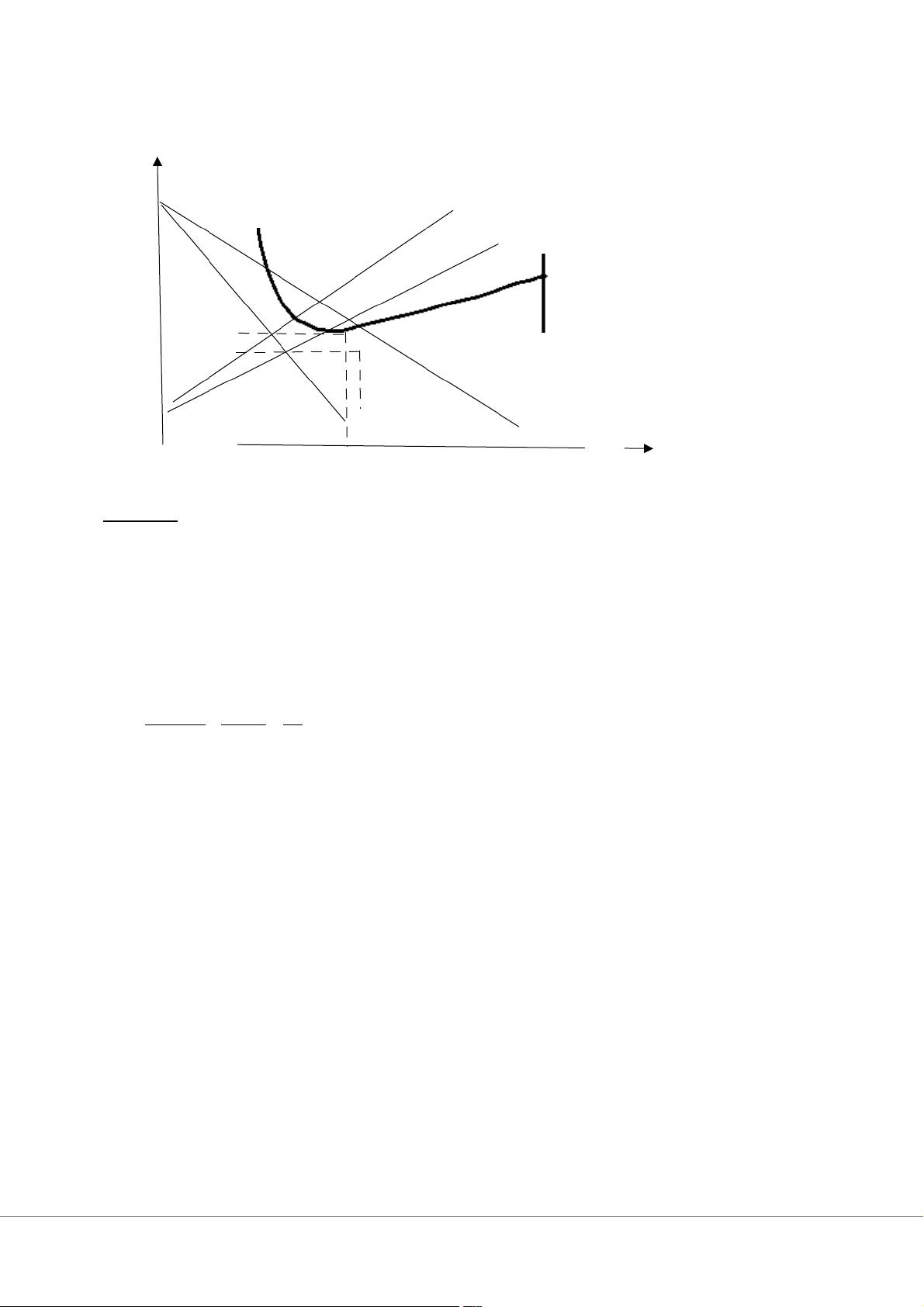
a. Complete the table: Q P TR MR TC ATC MC 0 8.5 0 - 5 - - 1 8.0 8.0 8 9 9 4 2 7.5 15 7 11.5 5.75 2.5 3 7.0 21 6 12.5 4.167 1 4 6.5 26 5 13.5 3.375 1 5 6.0 30 4 14.0 2.8 0.5 6 5.5 33 3 16.0 2.67 2 7 5.0 35 2 20.0 2.86 4 8 4.5 36 1 25.0 3.125 5 9 4.0 36 0 32.0 3.56 7 10 3.5 35 -1 40.0 4 8
b. What quantity will the monopolist produce?
The monopolist will produce quantity to maximize profit.
To maximize profit, we have : MR=MC Q¿=6 According to the table =>
c. What price will the monopolist charge? Q¿=6=¿P¿=5.5 ($)
d. What will the profit be at this price?
Q¿ (P¿−AT C¿ ) Profit = = 6. (5.5-2.67) = 16.98 ($)
Problem 2: A firm has demand function of P=100-Q ($) and total cost function of TC=500+ 4Q+Q2 ($).
a. Is this firm a perfect competitive firm? Why?
This firm isn’t a perfect competitive. Because , if the firm is a perfect competitive, D is perfect elastic.
But D in this situation is P= 100 – Q => Slope down D.
b. What is price and quantity to maximize total revenue ? What is that maximum total revenue ? )
100 Q−Q2=− (Q2−100 Q+2500 +2500=−(Q−50 ) TR= P.Q = 2+2500 ≤2500
=> TRmax = 2500 When Q = 10 and P = 50
c. What is price and optimal quantity to maximize profit? What is that maximum total profit ? MC = TC’ = 2Q + 4
D: P= 100 – Q => MR= 100 – 2Q
To maximize profit, we have : MR = MC 100 – 2Q = 2Q +4  Q= 24 => P= 76  TC Q=500+4Q+ Q Q2 =500 24 +4.24+ 2 ATC = = 48.83 24
 Profit = Q.(P-ATC)= 24.(76 - 48.83) = 652.08 ($)
d. Assume government imposes a tax of 8 $ per unit of good sold, what is price and optimal quantity
that gives the firm maximum profit? What is this maximum profit?
Before government imposes a tax: TC=500+4Q+Q2
After government imposes a tax : TC1=500+4Q+Q2+8Q=500+12Q+Q2  MC1= 2Q + 12 To maximize profit: MR = MC 100 – 2Q = 2Q + 12  Q = 22  P = 78  TC
Q=Q2+12Q 500 + ATC = 22=56.72
 Profit = Q. ( P – ATC) = 22.(78 – 56.72 ) = 468.16 ($)
e. Asume government imposes a fixed tax of 100 $, what is price and optimal quantity that gives the firm maximum profit?
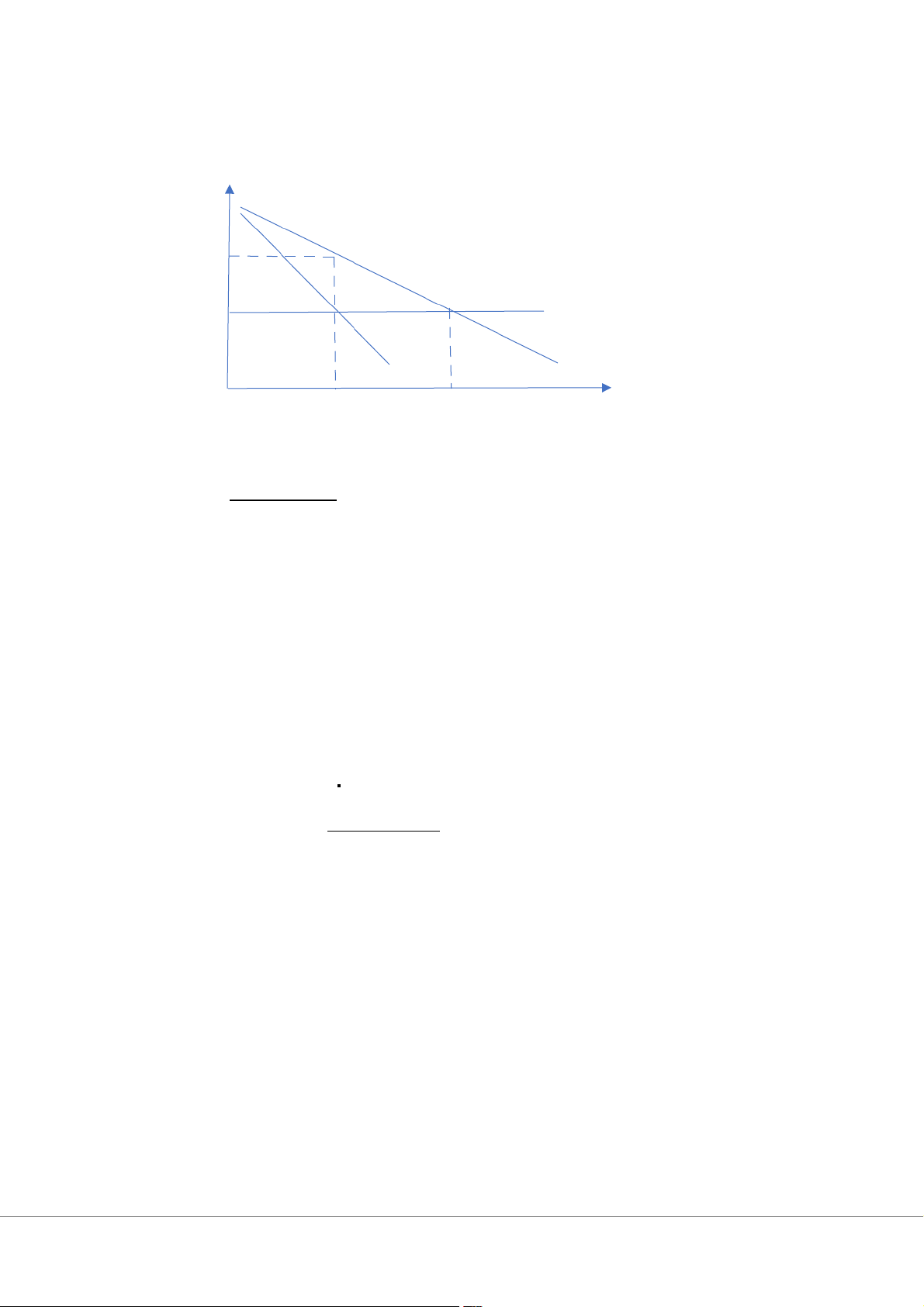
Government imposes a fixed tax of 100$ : TC2= 500 100 600 +4Q+Q2+ = +4Q+Q2 => MC2= 2Q+4 To maximize profit: MR=MC 100 – 2Q = 2Q +4  Q= 24 => P= 76  P MC1 ATC 78 76 D MR Q 22 24
Problem 3: A monopoly has a demand function of P=15-Q ($) and total cost function of TC= 7Q ($)
a. What is price and optimal quantity that gives the firm maximum profit?
Using Lerner indicator (L) to identify market power of this firm? MR = 15 – 2Q MC = TC’ = 7
To maximize profit, we have: 15 – 2Q = 7 Q = 4  P = 11  P−M P C =11 7 − 11=4 L = 11  Market power high.
b. What is price and optimal quantity for society (for perfect competitive market)? Identify dead-weight
loss (DL) created by this firm?
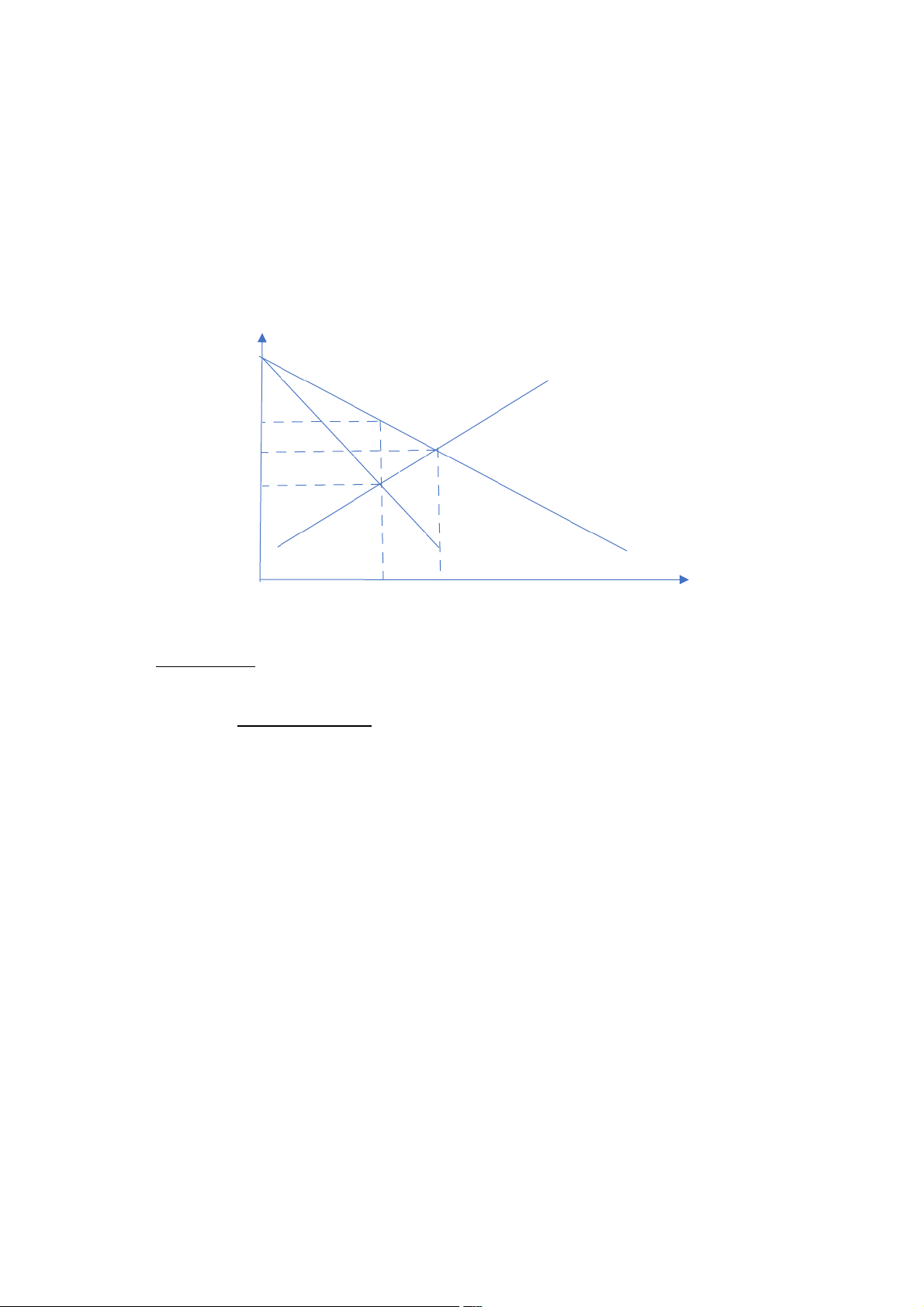
To maximize profit in perfect competitive market, we have : MC = P 7 = 15 – Q  Q  =8 => P=7 A 11 B MC 7 E MR D 4 8 (11 7 − ). (8−4 ) DWL= S AEB= = 8 2
Problem 4: A monopolist has demand function of P= 100-Q and cost functions of AVC= Q+4; FC=200
a. What is optimal output level that maximizes profit? What is that maximum profit?
AVC = Q +4 => VC = Q2+4Q=¿TC=Q2+4Q+200 => MC = 2Q +4 MR= 100 -2Q To maximize profit: MR = MC 100 -2Q =2Q +4  Q = 24  P =76  242 4.24 200 + +
Profit = Q.(P-ATC)= 24.( 76 – ) = 952.08 24
b. What is consumer surplus (CS) and deadweight loss (DL) created by this firm?
If the firm is perfect competitive: P = MC 100 – Q = 2Q +4  Q= 32; P=68  MC 76 A 68 B 52 E MR D 24 32 (100 76 − ).24 CS = 2=288 (76 52 − ). (32 24 − ) DWL = S AEB = 2=96
c. Assume this firm applies perfect price discrimination, what is quantity and variable profit of the firm?
If this firm applies perfect price discrimination, expand output to Q=32 => The firm increase profit by
taking more CS and DWL => Profit = 952.08 + 288 +96 = 1,336.08