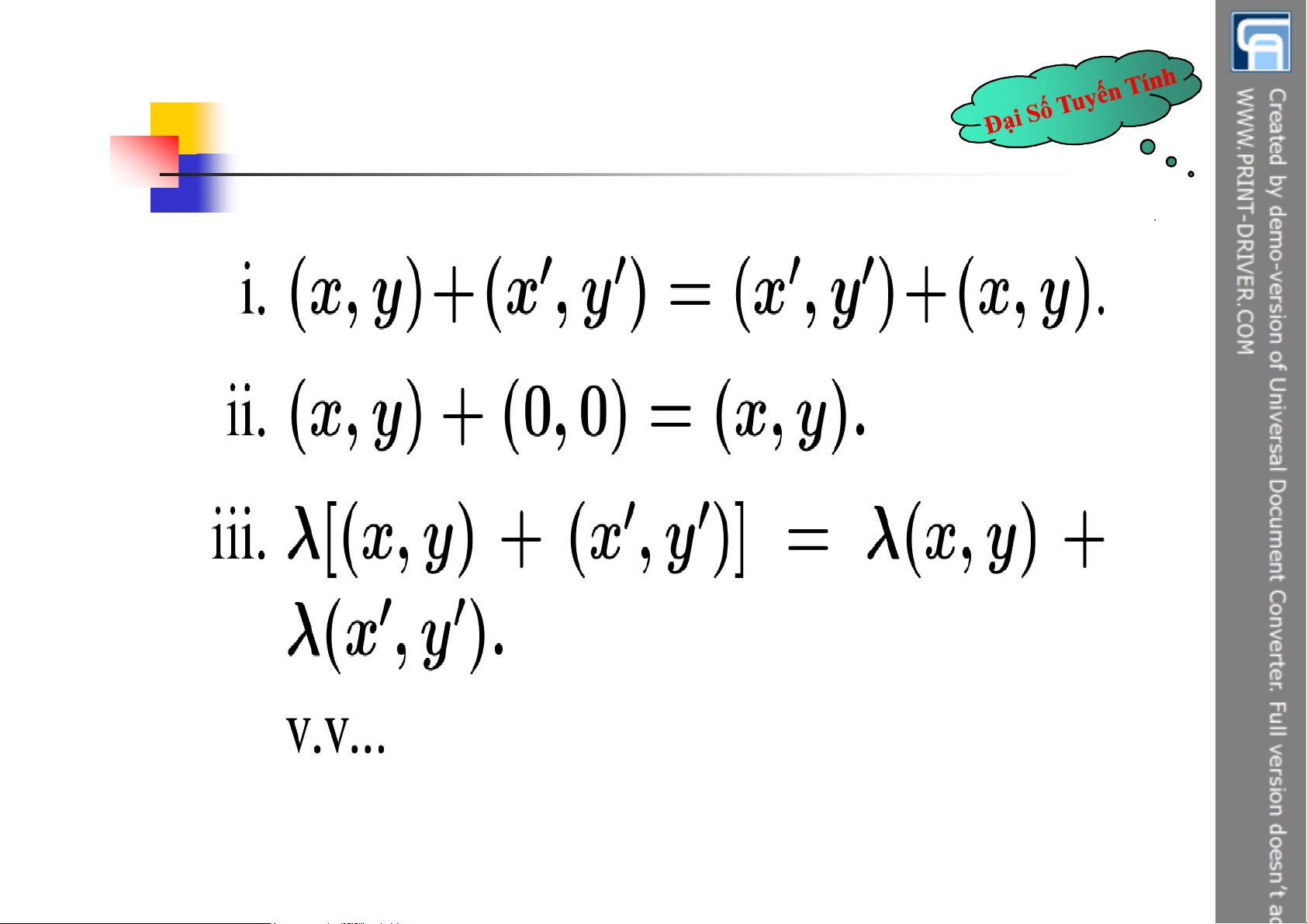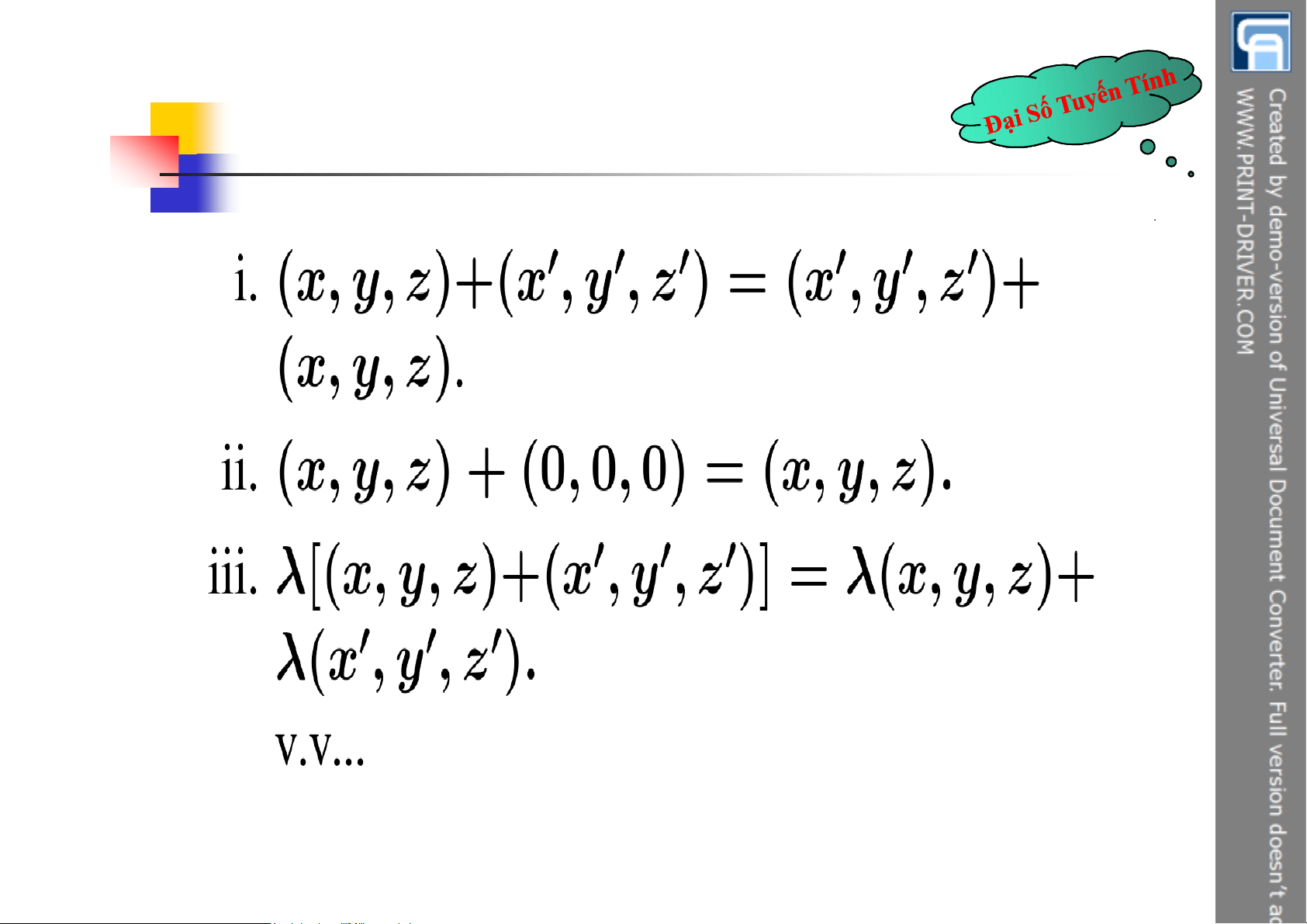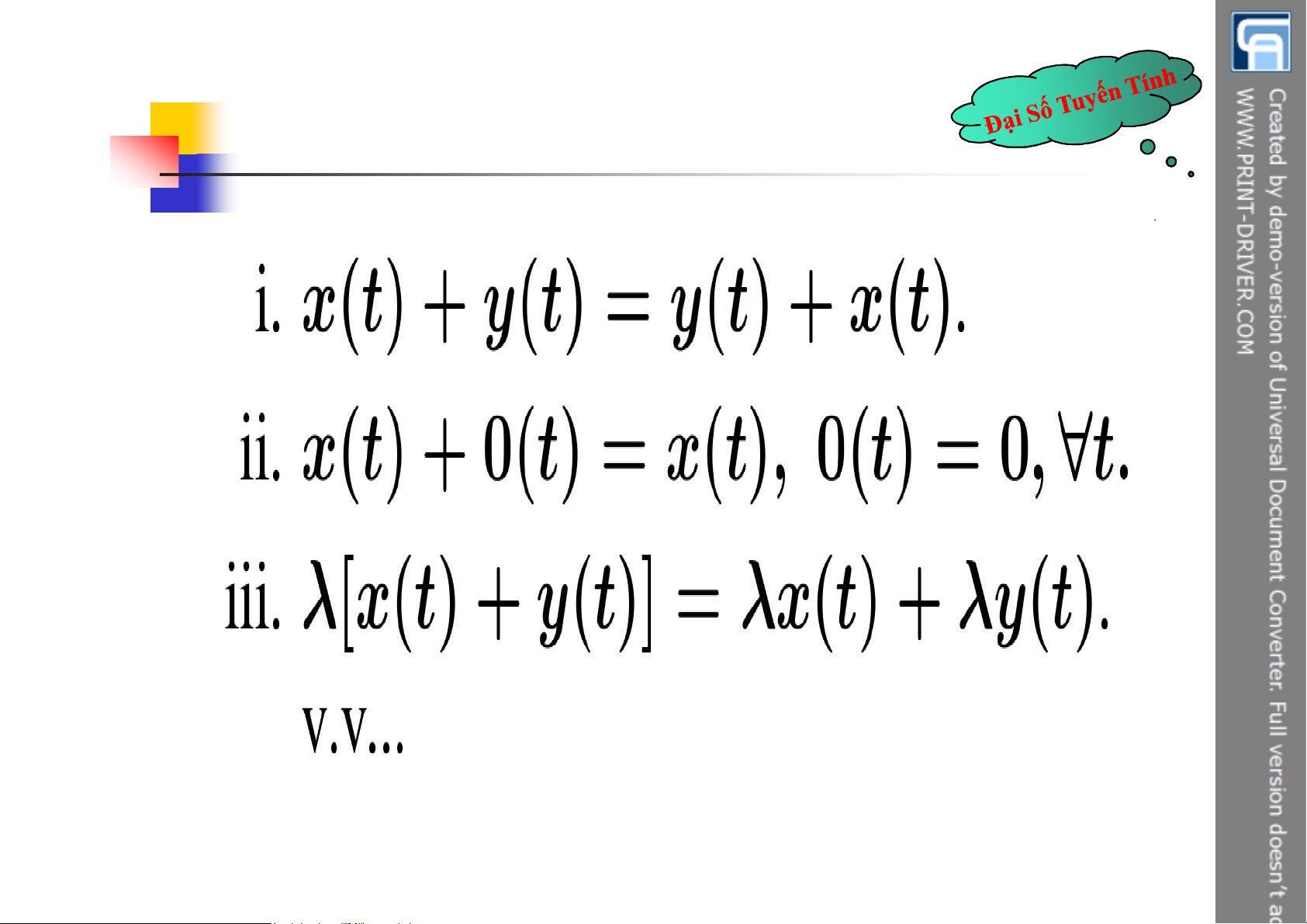Bài 1: Không gian vector | Bài giảng môn Đại số các nhóm ngành chuẩn | Đại học Bách khoa hà nội
Để chứng minh một tập con W của không gian vecto V là không gian con của V ta cần chỉ ra. Tài liệu trắc nghiệm môn Đại số các nhóm ngành chuẩn giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Đại số các nhóm ngành chuẩn (THH)
Trường: Đại học Bách Khoa Hà Nội
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
CHƯƠNG 3 1 §1: Không gian vector
Cơ cấu tổ chức của trường đại học Hiệu trưởng Trưởng Trưởng Trưởng Trưởng phòng phòng phòng phòng nghiên cứu Đào tạo hành chính Tài vụ Khoa học
§1 : Không gian vector
Cơ cấu tổ chức của công ty Giám đốc Trưởng Trưởng Trưởng Trưởng phòng phòng phòng phòng kinh doanh hành chính tài vụ kế hoạch
§1 : Không gian vector
§ 1: Không gian vector
§ 1 : Không gian vector
§ 1 : Không gian vector
§ 1 : Không gian vector
§ 1 : Không gian vector
§ 1 : Không gian vector
§ 1 : Không gian vector
§ 1 : Không gian vector 1.1. Khái niệm. 1.1.1. Định nghĩa.
Cho tập V khác rỗng và một trường số K, cùng hai phép toán:
- phép cộng: "" : V V V
(u,v ) u v
- Phép nhân với vô hướng
" ." : K V V
(k ,v ) kv
§ 1 : Không gian vector
Bộ ba (V;+;.) gọi là một không gian vecto
(KGVT) trên K hay một K-không gian vecto
nếu thỏa mãn 8 tiên đề:
§1: Không gian vector
§1: Không gian vector 1.1.2. Ví dụ
VD1: Tập các số thực R là một R - không gian vecto với - véc tơ không là số 0
- vecto đối của u là số đối (-u)
§1: Không gian vector VD2.
§1: Không gian vector VD3.
§1: Không gian vector Tổng quát n
(x ;x ;...;x )|x ,i , 1 n 1 2 n i với hai phép toán:
"" : (x ; x ; ...; x ) ( y ; y ; ...; y ) 1 2 n 1 2 n
( x y ; x y ; ...; x y ) 1 1 2 2 n n
" ." : k( x ; x ; ...; x ) (kx ; kx ; ...; kx ) 1 2 n 1 2 n
là một R-kgvt với vecto không θ=(0;0;…;0) và
vecto đối của v= (x , x ,…, x ) là 1 2 n (-v)=(-x ,- x ,…, -x ) 1 2 n
§1: Không gian vector VD4.
§1: Không gian vector VD5