Bài 3: Các Mức Độ Thống Kê Mô Tả và Phân Tích Dữ Liệu môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 3
CÁC MỨC ĐỘ THỐNG KÊ MÔ TẢ 1
CÁC MỨC ĐỘ CỦA HIỆN TƯỢNG
1. Số tuyệt đối và số tương đối trong thống kê 2. Các mức độ trung tâm
3. Các mức độ biến thiên
4. Hình dáng phân phối của dãy số 5. Hiệp phương sai 6. Hệ số tương quan 2 1 2025-05-12 1.1. SỐ TUYỆT ĐỐI
Số tuyệt đối trong thống kê biểu hiện quy mô, khối lượng của hiện
tượng nghiên cứu trong điều kiện thời gian và địa điểm cụ thể Đặc điểm
Bao hàm nội dung KT – XH
Không phải là số tùy ý
Đơn vị tính: cái, con, chiếc, người,… kg, tấn, tạ,… m, m2, m3…
Ghép: tấn – km, lượt – khách,… Ý nghĩa:
Là sự thật khách quan về quy mô, khối lượng của hiện tượng
Căn cứ để phân tích và tính toán các mức độ khác 3
CÁC LOẠI SỐ TUYỆT ĐỐI
Căn cứ vào đặc điểm tồn tại về quy mô của hiện tượng qua thời gian:
Số tuyệt đối thời kỳ Đặc điểm:
+ Có sự tích lũy về lượng
+ Khoảng thời gian nhất định mang tính quy ước
VD: Tổng sản lượng gạo của địa phương A năm 2008 là 350 tấn.
Số tuyệt đối thời điểm Đặc điểm:
+ Không có sự tích lũy về lượng
+ Thường dùng để nghiên cứu biến động của hiện tượn g qua thời gian
VD: Số lao động của Xí nghiệp X ngày 1/3/2008 là 200 người 4 2 2025-05-12 1.2. SỐ TƯƠNG ĐỐI
Số tương đối trong thống kê biểu hiện mối quan hệ so sánh giữa
hai mức độ của hiện tượng nghiên cứu Đặc điểm:
Không trực tiếp có được qua điều tra
Mỗi số tương đối đều có gốc so sánh
Đơn vị tính: lần, %, %o,…
Ghép: km/h, người/km2, trđ/ng… Ý nghĩa:
Biểu hiện mối quan hệ so sánh
Sử dụng trong trường hợp giữ bí mật số tuyệt đối 5
CÁC LOẠI SỐ TƯƠNG ĐỐI 6 3 2025-05-12
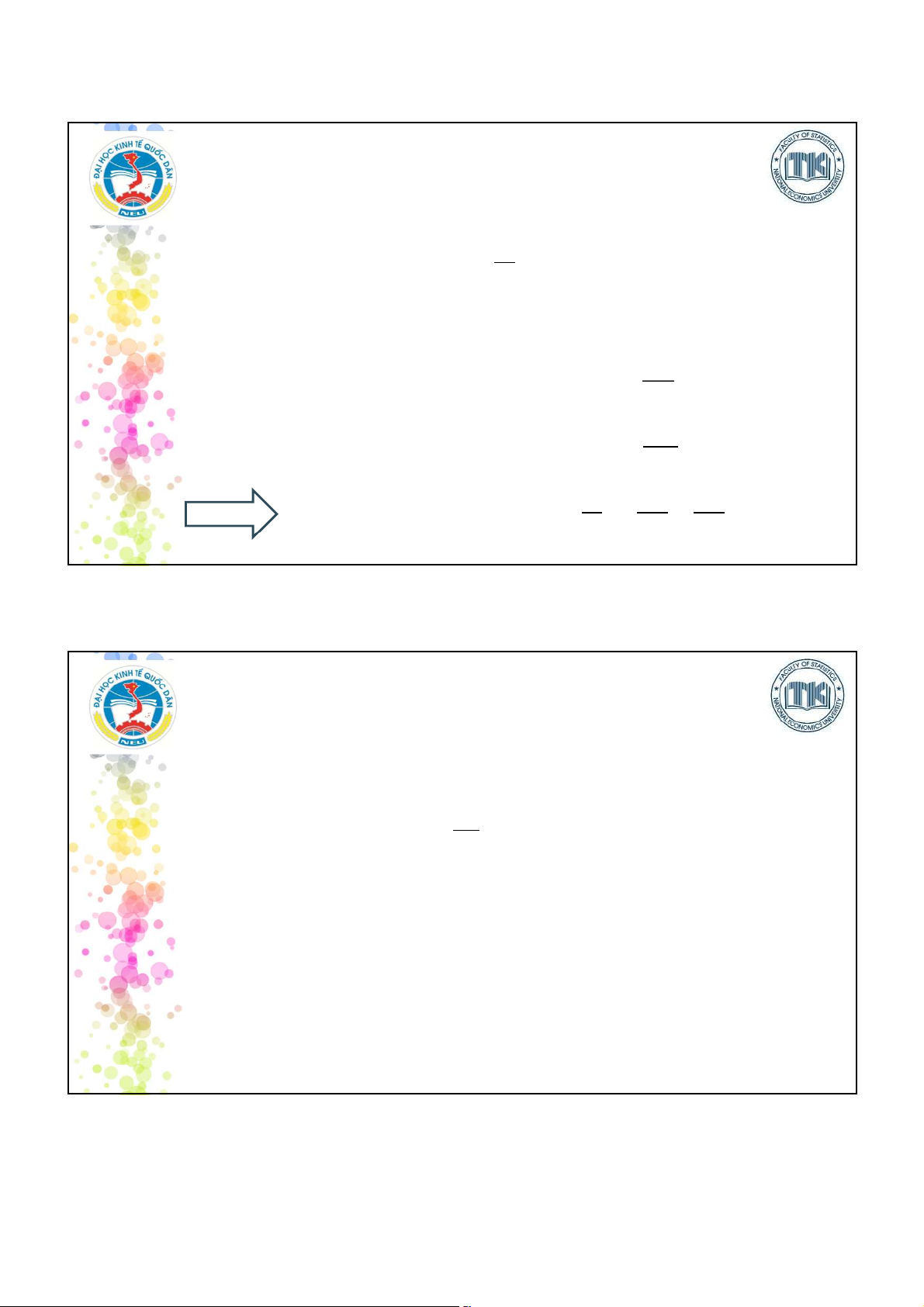
CÁC LOẠI SỐ TƯƠNG ĐỐI
Số tương đối động thái (tốc độ phát triển): t = y y(100)
Số tương đối kế hoạch: K=y
Số tương đối nhiệm vụ kế hoạch: y(100) K=y
Số tương đối thực hiện kế hoạch: y (100) t 𝑦 ykh y  K  hay = x  n  K T 𝑦 y ykh 7
CÁC LOẠI SỐ TƯƠNG ĐỐI
•Số tương đối kết cấu: Phản ánh tỷ trọng của từng bộ phận cấu thành trong một tổng thể. = y d   Σy (100) 
•Số tương đối không gian: so sánh
˗hai hiện tượng cùng loại nhưng khác nhau về không gian
˗hai mức độ giữa hai bộ phận trong một tổng thể
•Số tương đối cường độ: so sánh chỉ tiêu của hai hiện tượng khác nhau nhưng có quan hệ với nhau. 8 4 2025-05-12
VẬN DỤNG CHUNG SỐ TUYỆT ĐỐI VÀ SỐ TƯƠNG ĐỐI
•Phân tích lý luận KTXH, đặc điểm của hiện tượng nghiên cứu để rút ra kết luận
•Vận dụng kết hợp số tương đối với số tuyệt đối
Số tương đối được tính ra từ số tuyệt đối
Mỗi số tương đối với gốc so sánh khác nhau sẽ có ý nghĩa khác nhau
Ý nghĩa của số tương đối còn phụ thuộc trị số tuyệt đối mà nó phản ánh 9 2. Các mức độ trung tâm Số trung bình ( 𝑥) Số Trung vị (Me) Mốt (M0) 10 5 2025-05-12
2.1. SỐ TRUNG BÌNH - 𝒙 (0)
Số trung bình là mức độ đại biểu cho toàn bộ các lượng biến theo một
biến nào đó của tổng thể bao gồm những đơn vị cùng loại Đặc điểm: San bằng
Dữ liệu sử dụng thang đo khoảng, tỷ lệ
Tất cả các giá trị trong tổng thể đều tham gia vào công thức tính
Chỉ tính được một giá trị trung bình
Tổng chênh lệch của các giá trị so với trung bình cộng bằng 0
Chịu ảnh hưởng của lượng biến đột xuất 11
2.1. SỐ TRUNG BÌNH - 𝒙 (1) Ý nghĩa:
Biểu hiện mức độ đại biểu
So sánh hiện tượng không cùng quy mô
Nghiên cứu qua thời gian Xu hướng phát triển của hiện tượng
Lập kế hoạch và phân tích thống kê 12 6 2025-05-12
2.1. Số trung bình- 𝒙 (2) Trung bình cộng Trung bình nhân 13
2.1. Số trung bình/ số trung bình - 𝒙 (3) Số trung bình cộng Công thức tổng quát
𝑆ố 𝑏ì𝑛ℎ 𝑞𝑢â𝑛 𝑐ộ𝑛𝑔 = 𝑇ổ𝑛𝑔 𝑙ượ𝑛𝑔 𝑏𝑖ế𝑛 𝑐ủ𝑎 𝑏𝑖ế𝑛
𝑇ổ𝑛𝑔 𝑠ố đơ𝑛 𝑣ị 𝑐ủ𝑎 𝑡ổ𝑛𝑔 𝑡ℎể Trong đó:
Tổng lượng biến của biến: tổng giá trị lượng biến của tất cả các đơn vị
trong tổng thể (∑𝑀𝑖=∑𝑥𝑖𝑓𝑖)
Tổng số đơn vị của tổng thể (∑ 𝑓𝑖) 14 7 2025-05-12
2.1. Số trung bình/ số trung bình - 𝒙 (4) Số trung bình cộng
Số trung bình cộng giản đơn Áp dụng khi:
- Tính từ tài liệu ban đầu chưa phân tổ
- Tài liệu phân tổ nhưng có f bằng nhau hoặc bằng 1 i
𝑥 = 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥 =∑𝑥 𝑖 𝑛 𝑛 15
2.1. Số trung bình/ số trung bình - 𝒙 (5) Số trung bình cộng
Số trung bình cộng gia quyền Áp dụng khi:
- Tính từ tài liệu về xi và fi (tài liệu phân tổ) - Các f không bằng nhau i
𝑥 = 𝑥1𝑓1 + 𝑥2𝑓2 + 𝑥3𝑓3 + ⋯+ 𝑥𝑓 =∑𝑥 𝑖𝑓𝑖
𝑓1 + 𝑓2 + 𝑓3 + ⋯+ 𝑓 ∑𝑓 𝑖
Trong đó: fi là quyền số 16 8 2025-05-12
2.1. Số trung bình/ số trung bình - 𝒙 (6) Số trung bình cộng
Số trung bình cộng gia quyền Chú ý
Nếu có tần suất di, có thể sử dụng để thay thế cho fi như sau: x  i x i d (di tính bằng lần)  hay i x i d  x (di tính bằng %) 100 17
2.2.1. Số trung bình/ số trung bình - 𝒙 (7) Số trung bình cộng Số trung bình điều hòa Áp dụng khi:
- Tính từ tài liệu về xi và Mi (tài liệu phân tổ)
Trường hợp 1: trung bình điều hòa gia quyền
Giá trị các M không bằng nhau i
𝑥 = 𝑀1 + 𝑀2 + 𝑀3+ ⋯+ 𝑀 =∑𝑀 𝑖 𝑀1 +𝑀 +𝑀 + ⋯+ 𝑀 ∑𝑀 𝑥 2 3 𝑛 𝑖 1 𝑥2 𝑥3 𝑥𝑛 𝑥𝑖 Trong đó: M là quyền số i 18 9 2025-05-12
2.1. Số trung bình/ số trung bình - 𝒙 (8) Số trung bình cộng Số trung bình điều hòa Áp dụng khi:
- Tính từ tài liệu về x và M (tài liệu phân tổ) i i
Trường hợp 2: trung bình điều hòa giản đơn
-Giá trị các M bằng nhau i 𝑥 = 𝑛. 𝑀 =𝑛 𝑀1 +1 +1 + ⋯ + 1 ∑1 𝑥1 𝑥2 𝑥3 𝑥𝑛 𝑥𝑖 19
2.1. Số trung bình/ số trung bình - 𝒙 (9) Số trung bình nhân
Điều kiện vận dụng: các lượng biến có quan hệ tích
(Thường để tính các tốc độ phát triển trung bình)
trung bình nhân giản đơn: vận dụng khi các tần số f bằng nhau i n ni x 1 x x x  nnx 1 . 2..    i
trung bình nhân gia quyền: vận dụng khi các tần số f khác nhau i  ∑ 𝑥 = ∑ 𝑥   
1  𝑥2 .. . 𝑥𝑛  =  𝑥  20 10 2025-05-12 2.2. Số trung vị - Me (1)
Số trung vị là lượng biến của đơn vị đứng ở vị trí chính giữa chia dãy số thành 2 phần bằng nhau Cách xác định
Đối với dãy số không có khoảng cách tổ
Nếu số đơn vị của tổng thể là lẻ (∑𝑓 𝑖 = 2𝑚 + 1)→ 𝑀𝑒 = 𝑥 
Nếu số đơn vị của tổng thể là chẵn (∑𝑓 𝑖 = 2𝑚)→ 𝑀𝑒 =  
Đối với dãy số có khoảng cách tổ
Bước 1: Xác định tổ chứa Me (sử dụng Si)
Bước 2: Tính trị số gần đúng của Me ∑𝑓𝑖 𝑀𝑒 = 𝑥 2 − 𝑆   + ℎ 𝑓𝑀𝑒 21 2.2. Số trung vị - Me (2) Đặc điểm
•Không chịu ảnh hưởng của lượng biến đột xuất
•Dữ liệu sử dụng thang đo thứ bậc, khoảng, tỷ lệ Tác dụng
•Biểu hiện mức độ đại biểu của hiện tượng
•Là một trong những tham số nêu lên đặc trưng phân phối của dãy số
•Vận dụng trong các công tác kỹ thuật, phục vụ công cộng ở nơi thuận tiện
∑|𝑥𝑖 −𝑀𝑒| = 𝑚𝑖𝑛 hay
∑|𝑥𝑖 −𝑀𝑒|𝑓𝑖 = 𝑚𝑖𝑛 22 11 2025-05-12 2.3. Mốt - M (1) 0
Mốt là biểu hiện của biến được gặp nhiều nhất trong tổng thể Cách xác định
Đối với dãy số không có khoảng cách tổ M0= ximà có fimax
Đối với dãy số có khoảng cách tổ
Bước 1: Xác định tổ chứa M0(sử dụng fihay 𝑚𝑖= ) 
Bước 2: Tính trị số gần đúng của M0
Công thức tính trong trường hợp dãy số có khoảng cách tổ bằng nhau f  M f M 1 M  o o x min h f f f o f 1 o o M M     ( 1M0 M ) ( M M ) o o o 23 2.3. Mốt - M0 (2) Đặc điểm
Dữ liệu sử dụng tất cả các loại thang đo
Không bị ảnh hưởng của giá trị đột xuất (ngoại lai)
Một số trường hợp không có mốt hoặc có nhiều mốt Tác dụng của Mốt
•Biểu hiện mức độ đại biểu của hiện tượng
•Không chịu ảnh hưởng của lượng biến đột xuất
•Là một trong những tham số nêu lên đặc trưng phân phối của dãy số
•Vận dụng trong các bài toán lý thuyết phục vụ đám đông Nhược điểm
•Có thể có trường hợp dãy số không có Mốt hoặc dãy số có nhiều Mốt 24 12 2025-05-12
SO SÁNH TRUNG BÌNH, TRUNG VỊ, MỐT Phân phối chuẩn Phân phối Phân phối lệch trái lệch phải fi fi fi xixixi < Me < Mo Mo < Me < x x 25
3. CÁC MỨC ĐỘ BIẾN THIÊN (PHÂN TÁN) Khoảng biến thiên Khoảng tứ phân vị Phương sai Độ lệch chuẩn Hệ số biến thiên 26 13 2025-05-12
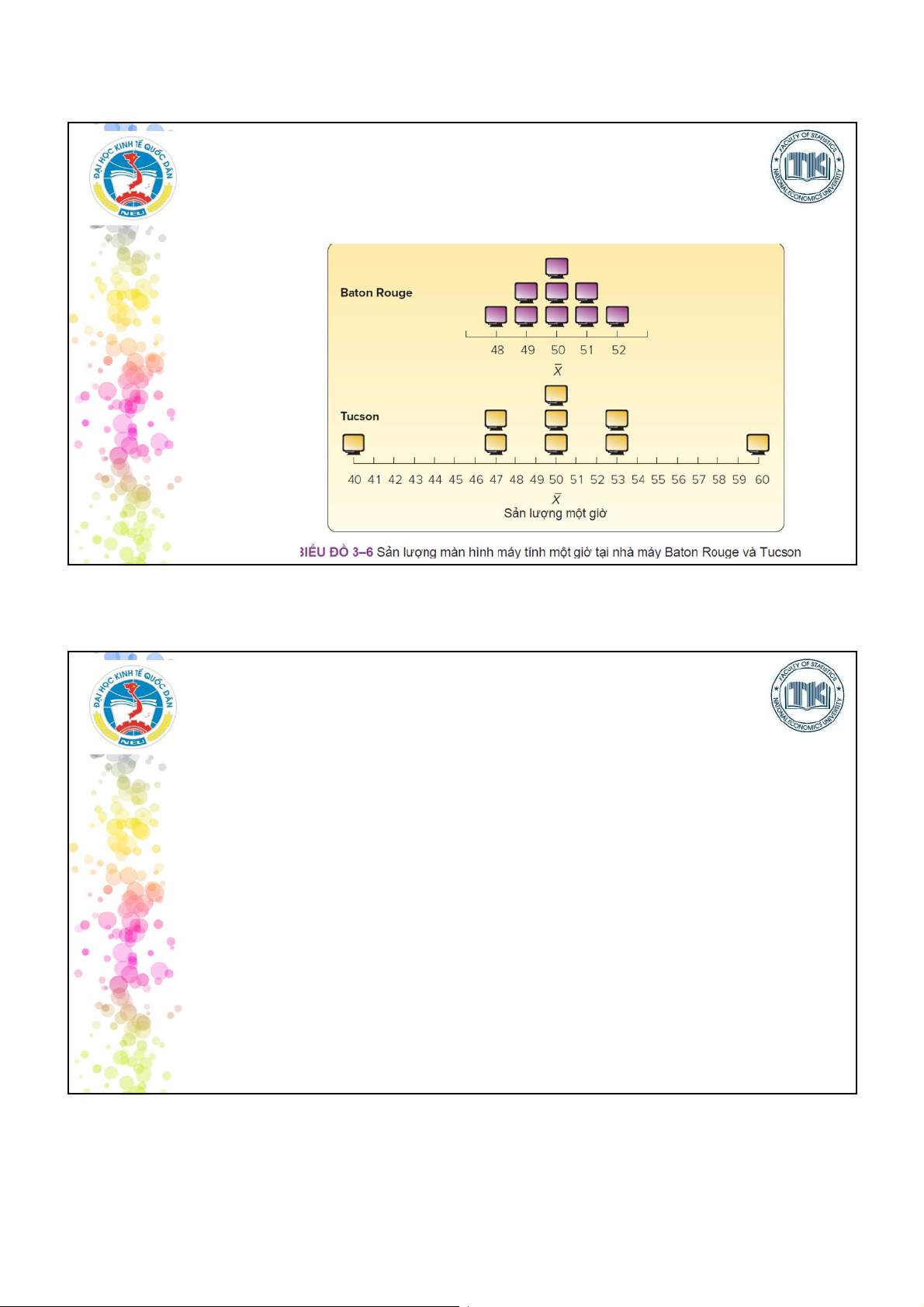
Tại sao phải đo độ biến thiên
Ví dụ: Trang 70, dữ liệu ghi lại việc sản xuất trong 9 giờ của 2 nhà máy 27 3.1. KHOẢNG BIẾN THIÊN
Là chênh lệch giữa lượng biến lớn nhất và lượng biến
nhỏ nhất của biến nghiên cứu R=x -x max min
Ưu điểm: Dễ tính toán
Hạn chế: Chỉ tính đến lượng biến đầu và cuối sẽ rất
không chính xác nếu có lượng biến đột xuất, dẫn đến làm
sai bản chất của hiện tượng. 28 14 2025-05-12 3.2. Khoảng tứ phân vị
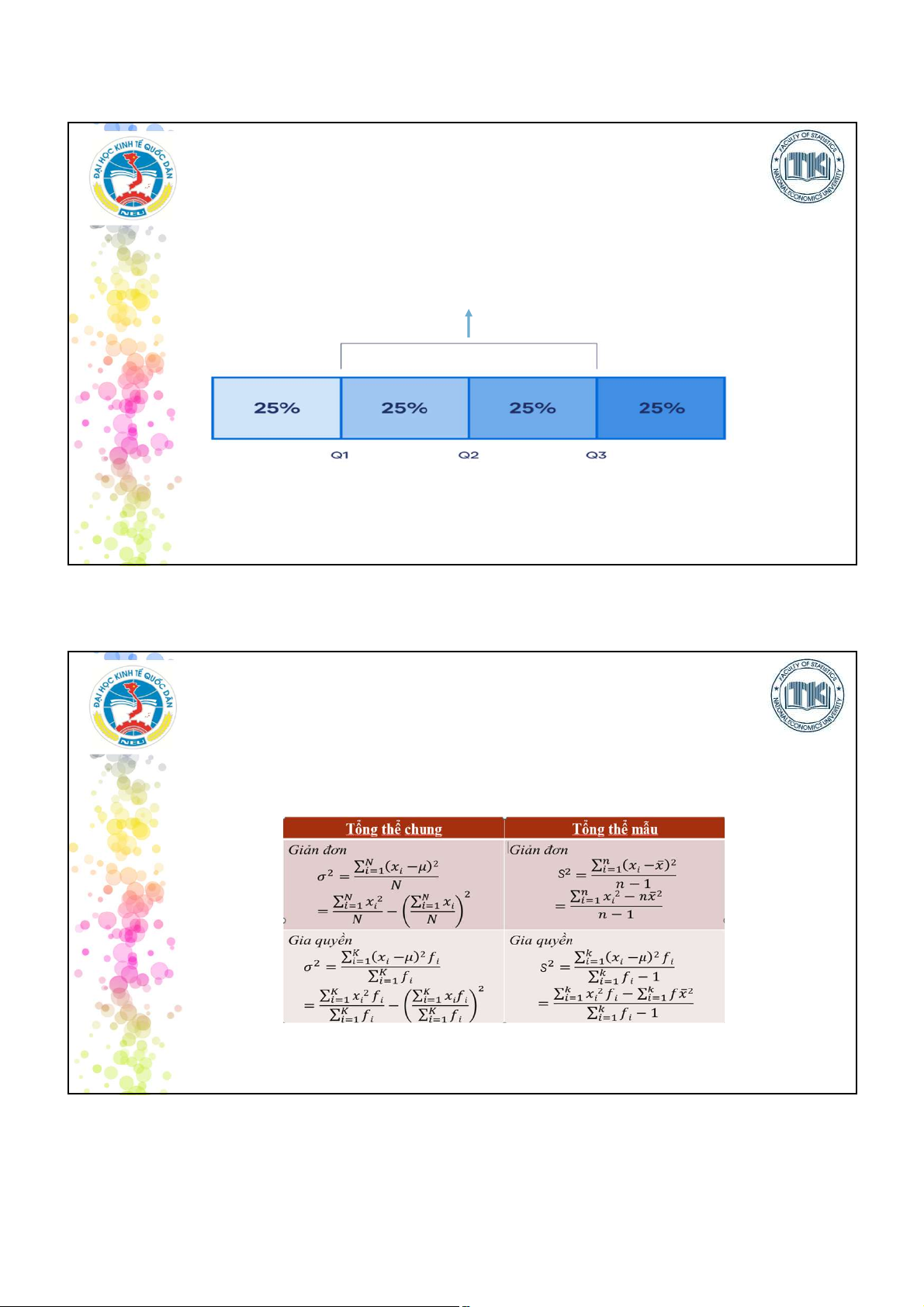
Tứ phân vị: Các giá trị chia tập hợp dữ liệu (đã được sắp xếp từ nhỏ
đến lớn) thành 4 phần bằng nhau.
Thập phân vị: Các giá trị chia tập hợp dữ liệu (đã được sắp xếp từ
nhỏ đến lớn) thành 10 phần bằng nhau.
Bách phân vị: Các giá trị chia tập hợp dữ liệu (đã được sắp xếp từ
nhỏ đến lớn) thành 100 phần bằng nhau. 29 3.2. Khoảng tứ phân vị
Cách xác định bách phân vị: L= (n + 1) p
Xác định vị trí của phân vị thứ p: 100
Tính giá trị của phân vị thứ p dựa vào vị trí 30 15 2025-05-12 3.2. CÁC PHÂN VỊ
Là chênh lệch giữa giá trị tứ phân vị thứ ba và tứ phân vị thứ nhất. IQR = Q3 – Q1 31
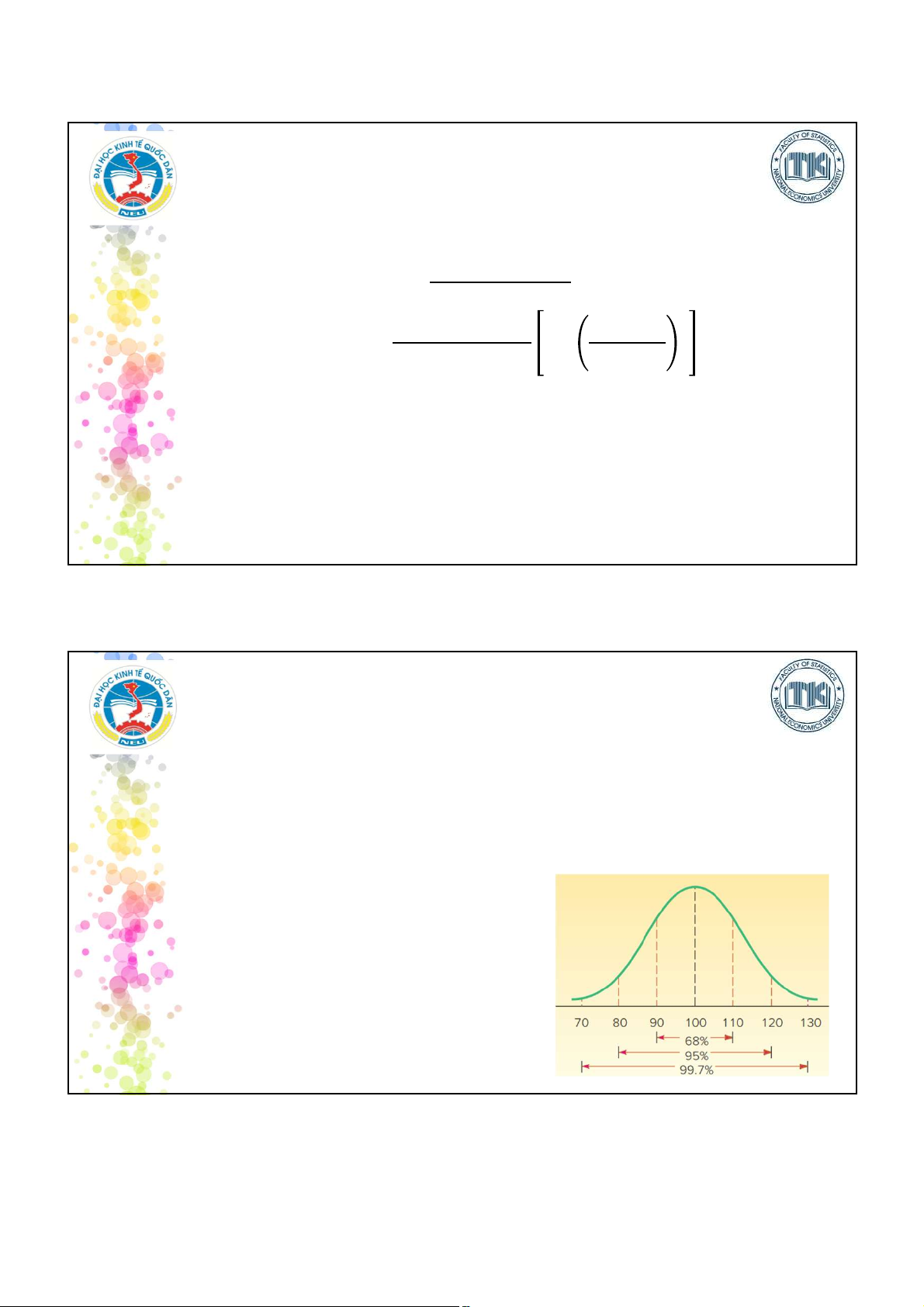
3.3. PHƯƠNG SAI (𝝈𝟐 hoặc S2)
Phương sai là trung bình cộng của tổng bình phương các độ lệch
giữa các lượng biến với số trung bình của các lượng biến đó Công thức tính
Hạn chế: Vì là bình phương của các độ lệch nên giá trị bị khuyếch
đại và không có đơn vị tính phù hợp 32 16 2025-05-12
3.4. Độ lệch chuẩn (𝝈 hoặc S)
Là căn bậc 2 của phương sai
Độ lệch chuẩn của tổng thể: σ = σ
Độ lệch chuẩn của mẫu: S = S
Phản ánh lượng biến của biến biến thiên xoay quanh giá trị trung bình bao nhiêu đơn vị
Lưu ý: cả 4 chỉ tiêu nói trên đều chỉ được sử dụng để so sánh độ biến
thiên giữa các hiện tượng cùng loại và có số trung bình bằng nhau 33
3.5. Hệ số biến thiên (V)
Được sử dụng để so sánh độ biến thiên giữa các hiện tượng cùng
loại và có số trung bình khác nhau và so sánh độ biến thiên giữa các
hiện tượng khác loại (so sánh độ biến thiên giữa NSLĐ và tiền
lương của người công nhân) 𝑉 = 𝑆 Công thức tính 𝑥100(%)
Lưu ý: Hệ số biến thiên được tính bằng đơn vị % có ý nghĩa gì? Hệ
số biến thiên chỉ ra lượng biến của biến biến thiên xoay quanh giá trị trung bình bao nhiêu %. 34 17 2025-05-12
4. HÌNH DẠNG PHÂN PHỐI CỦA DÃY SỐ
•Biểu đồ hộp ria mèo (boxplot) biểu diễn 5 mức độ thống
kê mô tả: giá trị lớn nhất (max), giá trị nhỏ nhất (min), tứ
phân vị thứ nhất (Q1), tứ phân vị thứ ba (Q3) và trung vị (Q2) 35
4. HÌNH DẠNG PHÂN PHỐI CỦA DÃY SỐ
•Xác định lượng biến đột xuất
có giá trị chênh lệch khá nhiều so với mức độ của các quan sát
khác. Giá trị lớn hơn Q3+1.5*IQR hoặc nhỏ hơn Q1-1.5*IQR là lượng biến đột xuất. 36 18 2025-05-12
4. HÌNH DẠNG PHÂN PHỐI CỦA DÃY SỐ
•Hệ số Skewness: là thước đo độ đối xứng của phân phối sk = 3(x − Median) Pearson: 𝑠
sk = (𝑛 − 1𝑛)(𝑛 − 2) (𝑥 − x)  Phần mềm: 𝑠 Đặc điểm Khoảng giá trị [-3, 3]
Sk < 0 -> dãy số phân phối lệch trái
Sk > 0 -> dãy số phân phối lệch phải 37
4. HÌNH DẠNG PHÂN PHỐI CỦA DÃY SỐ
•Quy tắc 3 sigma: Đối với phân phối chuẩn:
Khoảng 68.26% các quan sát nằm trong phạm vi (+) và (-) 1 lần độ lệch chuẩn so với trung bình
Khoảng 95.44% các quan sát nằm trong phạm vi (+) và (-) 2 lần độ lệch chuẩn so với trung bình
Khoảng 99.74% các quan sát nằm trong
khoảng (+) và (-) 3 lần độ lệch chuẩn so với trung bình 38 19 2025-05-12 THỰC HÀNH SPSS
•Chọn Analyze > Descriptive Statistics > Frequencies…
Đưa các biến cần tính toán sang ô Variable(s) Chọn Statistics…
Chọn các thống kê cần tính toán 39 5. HIỆP PHƯƠNG SAI
Dùng để mô tả mối liên hệ giữa 2 biến
Phản ánh chiều hướng của mối liên hệ Công thức:
COV x, y = ∑x− x 𝑦− y  Tổng thể: N
Cov x, y = ∑x− x 𝑦− y Mẫu: n − 1 40 20