Bài 3 Tóm tắt dữ liệu bằng tham số đặc trưng / Các mức độ thống kê mô tả môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Tóm tắt Bài 3
•Sốtuyệtđối, sốtương đối
TÓM TẮT DỮ LIỆU BẰNG THAM •Các mứcđộ trung tâm SỐ ĐẶC TRƯNG /
•Các mứcđộ đođộ phân tán (biến thiên)
•Kết hợp các mứcđộ trung tâm và độ phân tán
CÁC MỨC ĐỘ THỐNG KÊ MÔ TẢ
•Các mứcđộ thống kê mô tảphản ánh mối liên hệ
•Thực hành với phần mềm thống kê 0 1 0 1 Sốtuyệtđối •VD:
SỐ TUYỆT ĐỐI VÀ SỐ TƯƠNG ĐỐI
–Giá trịgia tăng của doanh nghiệp năm 2024: 205 triệuđồng
–Quy mô của lớp học vào lúc 8:00am: 52
•Khái niệm: Sốtuyệtđối trong thống kê biểu hiện
quy mô, khối lượng của hiện tượng nghiên cứu
trong điều kiệnthời gian và địađiểmcụthể. 23 2 3
Các loại sốtuyệtđối (1)
Các loại sốtuyệtđối (2)
•Sốtuyệtđối thời kỳ:
•Sốtuyệtđối thờiđiểm:
Khái niệm: biểu hiệnquy mô, khối lượng của
Khái niệm: biểu hiệnquy mô, khối lượng của
hiện tượng trong mộtđộ dài thời gian nhấtđịnh
hiện tượng vào một thờiđiểm nhấtđịnh Đặ Đặcđiểm cđiểm
–Không có sựtích luỹvềmặt lượng
–Có sựtích luỹvềmặt lượng
–Không thểcộng các giá trịlại với nhau
–Có thểcộng các giá trịlại với nhau VD: Ví dụ
–Quy mô của lớp học vào lúc …: 52
–Giá trịgia tăng của doanh nghiệp giai đoạn 2022-2023: 400 triệuđồng 4 5 4 5 1
Đặcđiểm và đơn vịtính Sốtương đối
•Bao hàm một nội dung kinh tế xã hộicụ thể
•Khái niệm: Sốtương đối trong thống kê biểu
trong điều kiện thời gian và địa điểm nhất định.
hiện quan hệso sánh giữahai mứcđộ của hiện •Phải qua đ tượng.
iều tra thực tếvà tổng hợpmới xác định được. •VD: •Đơn vị tính:
- Tốcđộ phát triển doanh thu của công ty X năm 2016 là 118%
-Đơn vịhiện vật: cái, con, chiếc, m, kg,…
-Đơn vịgiá trị: VND, USD,…
-Đơn vịkép: kwh, ngày-người,… 6 7 6 7
Các loại sốtương đối (1)
Các loại sốtương đối (2) y ố ương đối kết cấ 1 • S t u:
•Sốtương đốiđộng thái (tốcđộ phát triển) t y0 y d  BP •
Sốtương đối kếhoạch: yTT y kKn
- Sốtương đối nhiệm vụkếhoạch
• Sốtương đối không gian: 0 y y
- Số tương thực hiện kế hoạch k1  yA I Ty (A/B)  K yB y y y 1 K 1
- Mối quan hệ:  t  k k hay n T  x y y y 0 0 K 8 9 8 9
Đặcđiểm và đơn vịtính
Các loại sốtương đối (3)
•Không thu được qua điều tra thống kê mà phải •
Sốtương đối cường độ: so sánh chỉtiêu của
thực hiện thông qua quan hệso sánh.
hai hiện tượng khác nhau nhưng có mối liên hệ.
•Mỗi sốtương đốiđều phải có gốc dùng để so sánh. •
VD: mậtđộ dân số(nghìn người/km2) •Đơn vị tính:
- So sánh hai mứcđộ cùng loại: lần, %
- So sánh hai mứcđộ khác loại có mối liên hệ: đơn vị kép: người/km2 10 11 10 11 2
Điều kiện vận dụng sốtuyệtđối và sốtương đối
Điều kiện vận dụng sốtuyệtđối và sốtương đối
•Xem xét đặcđiểmcủa hiện tượng nghiên cứuđể
rút ra kết luận cho đúng
•Cần vận dụng kết hợpsốtương đối với sốtuyệt đối •Q: Tại sao? 12 13
Nguồn: dữliệu từILO, APO 12 13 Các mứcđộ trung tâm
•Các mứcđộ trung tâm cho chúng ta biết vị
trí trung tâm của một dãy sốphân phối Trung bình cộng
•Ba tham sốhay được sửdụng: - Trung bình/mean - Trung vị/Median - Mốt/Mode 14 15 14 15
Tính trung bình cộng từdữliệu thô
Tính trung bình từbảng TSPP giảnđơn N  Xi
•Trung bình của tổng thể: 1 i   Công thức: N k n  x f x i i •Trung bình của mẫu: i  i 1 x  i 1 xn  k  fi i1
Trong đó: X x – giá trịcủa mỗi quan sát i, i
N, n– tổng sốđơn vịtổng thểvà mẫu
trong đó: x – giá trịlượng biến của tổthứ i i
f – tần sốcủa tổthứ i i 16 17 16 17 3
Trung bình từdãy sốphân phối có KCT Ví dụ
Quay trởlại ví dụvềbảng lương ở bài 2
•Sửdụng công thức tương tựdãy sốkhông có khoảng cách tổ Lương (xi ) (fi) fix i k f x  ≤$60 $50 4 200 i i i  1 k x > $60 – ≤$80 $70 6 420 k   fi ix i  2165 86.6 f 1  i > $80 – ≤$90 $85 6 510 x k 25 i  1 > $90 – ≤$120 $105 6 630  fi i 1
nhưng: x – trịsốgiữa của tổthứi > $120 $135 3 405 i
f – tần sốcủa tổthứi Total 25 2165 i 18 19 18 19
Ưu nhượcđiểm của sốtrung bình cộng Mean is sensitive to outliers •Ưuđiểm:
–Dễhiểu và dễtính toán
–Tất cảcác giá trịtrong dãy sốđền tham gia vào
tính toán => trung bình đại diện cho cảdãy số •Nhượcđiểm
–Bịảnh hưởng bởi các giá trịngoại lai –Ví dụ:
43; 38; 37; : : : ; 27; 34 => x 33.5 Có giá trịngoại lai
43; 38; 37; : : : ; 27; 1934 => x 71.5 20 21 20 21
Điều kiện vận dụng sốtrung bình
 Sốtrung bình chỉnên tính từtổng thểđồng Trung bình nhân chất.
 Sốtrung bình cầnđược vận dụng kết hợp với
dãy sốphân phối. 22 23 22 23 4
Phương pháp tính và điều kiện vận dụng Ví Dụ •
Điều kiện vận dụng: Trung bình nhân được tính khi
•Trung bình nhân giảnđơn: có tốcđộ phát triển về
các lượng biến có quan hệtích số.
doanh thu của một DN nhưsau: 
VD: tốcđộ phát triển - Năm 2015 so với 2014: 116% - Năm 2016 so với 2015: 111%
Sốtrung bình nhân giảnđơn - Năm 2017 so với 2016: 112% n 1 2
x  nn x  x  ... x  n  x (1)
•Tính tốcđộ phát triển trung bình vềdoanh thu của i i 1  DN trong giai đoạn trên.
Sốtrung bình nhân gia quyền 𝑡  1.16 ∗1.11 ∗1.12 1.12 ℎ𝑎𝑦 112%  n 1 2  finf f f  x x x ... x  ii f x (2) 1 2 n  fi
•Trung bình nhân gia quyền: i1 24 25 24 25 Trung vị
•Trung vịlà giá trịlượng biến củađơn vịnằmở Trung vị
vịtrí chính giữa trong dãy sốlượng biến, nó
chia dãy sốra làm 2 phần có sốlượng đơn vị bằng nhau
•3 trường hợp có thểxảy ra
–Tính trung vịtừdữliệu thô
–Tính trung vịtừdãy sốphân tổkhông có khoảng cách tổ
–Tính trung vịtừdãy sốphân tổcó khoảng cách tổ 26 27 26 27 Trung vịtừdữliệu thô
Trung vịtừdữliệu thô (cont.)
•Nếu tổng sốđơn vịlà lẻ:
•Các bước tính trung vị: t h ịtrí chính giữ ( n 1 )
1. Sắp xếp lại dãy sốtheo thứtựtăng/giảm –Đơn vịnằmở v a là: 2
dần của giá trịlượng biến
M e d ia n x  ( 1) th n
2. Dựa vào tổng sốđơn vịcủa dãy sốđểxác 2
•Nếu tổng sốđơn vịlà chẵn:
định đơn vịnằmở vịtrí chính giữa
–Sẽcó 2 đơn vịnằmở vịtrí chính giữa và trung
3. Trung vịchính là giá trịlượng biến của vịlà:
đơn vịnằmở vịtrí chính giữa M ed ia n (  x x th th ) / 2  n  n      1 2 2   29 28 28 29 5 Ví dụvềtính trung vị
Trung vịtừdãy sốphân phối
•VD3. Tính trung vịtừdãy sốsau
•VD1. Dữliệu thô: 11, 11, 13, 14, 17 => Tính trung vị X Tần số 8 3
•VD2. Dữliệu thô : 11, 11, 13, 14, 16, 17 => 12 7 Tính trung vị 16 12 17 8 19 5 30 31 30 31
Trung vịtừdãy sốphân phối
Ưu nhượcđiểm của trung vị
•VD4: Tính trung vịtừdãy sốsau •Ưuđiểm: x i Tần số Tần sốtích lũy
–Dễhiểu và dễtính toán 0-0.99 1 1 1.00-1.99 4 5
–Không bịảnh hưởng bởi các giá trịngoại 2.00-2.99 8 13
lai => vì vậy có thểsửdụng khi sốtrung 3.00-3.99 6 19 bình không đại diện 4.00-4.99 3 22 5.00-5.99 1 23 •Nhượcđiểm  f S
–Chỉlà giá trịcủa 1 hoặc 2 quan sát nên ( 1)  (min) 2Me M x h f
nhiều khi không thểhiện tốt vai trò đại e Me Me Me 32 33 diện 32 33 Mốt
•Mốt là giá trịlượng biếnđược gặp nhiều nhất Mốt trong dãy sốlượng biến •Các bước tìm mốt
1. Lập bảng tần sốphân phối
2. Xác định giá trịthường xuyên xảy ra nhất 34 35 34 35 6 Ví dụ Hai mốt hoặc nhiều mốt •Quay trởlại VD3. X Tần số 8 3 12 7 16 12 17 8 19 5 Bimodal (two modes) Multimodal (several modes) 36 37 36 37
Tính mốt từdãy sốphân phối có khoảng
Vịtrí của các mức độ trung tâm trong cách tổ
dãy sốphân phối
•Xác định tổchứa mốt
•Sửdụng biểuđồ tần sốphân phối Lệch trái
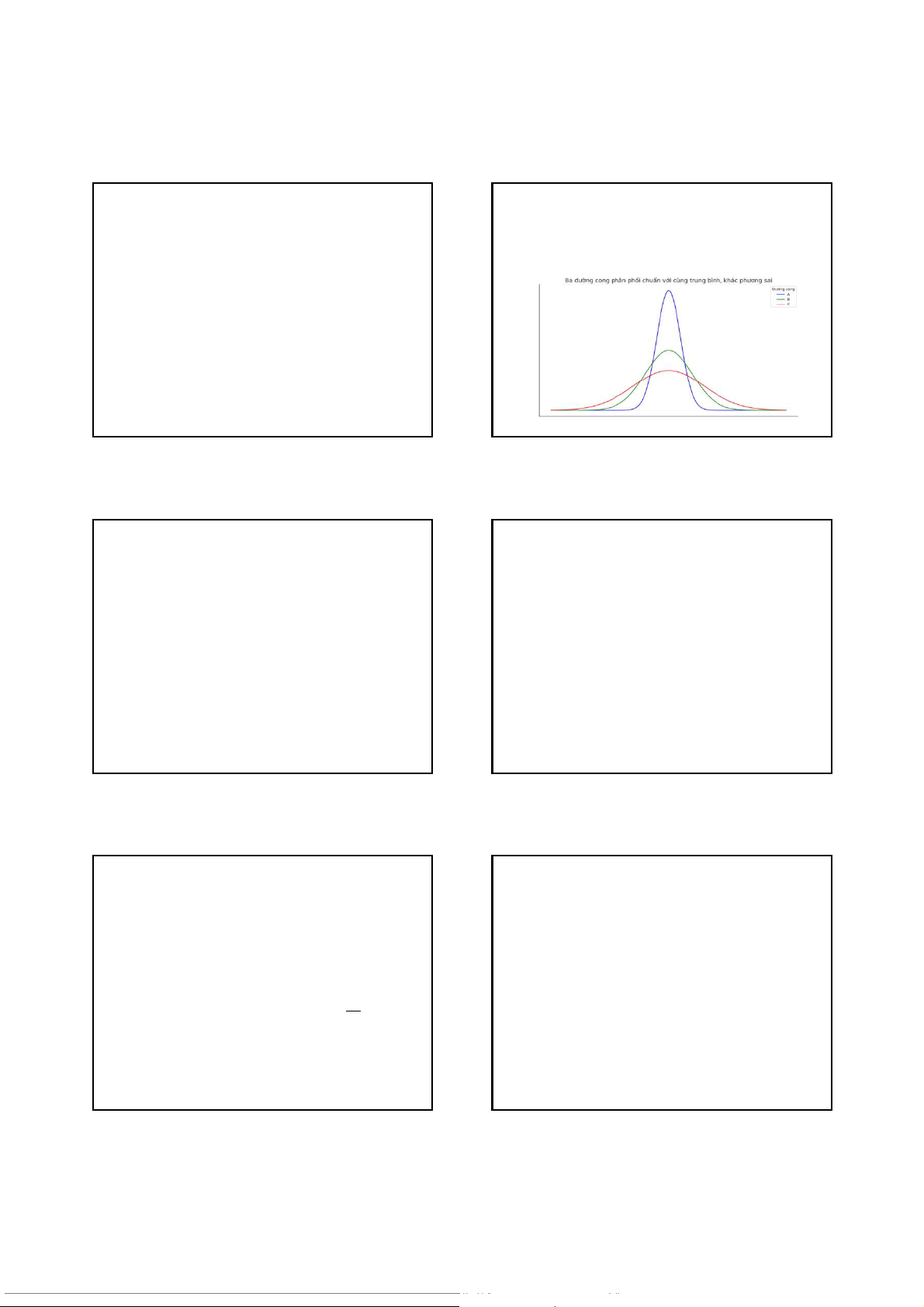
Phân phối chuẩn
Lệch phải 38 38 39
Tham sốtrung tâm nào là tốt nhất?
Các mứcđộ đođộ phân tán
•Trung bình nhìn chung hay được sửdụng nhất
 Các mứcđộ đođộ phân tán (còn gọi là các mứcđộ
nhưng lại có nhượcđiểm là nhạy cảm với các giá trị
biến thiên) cho biết các giá trịkhác phân bốxung đột xuất (ngoại lai)
quanh giá trịtrung tâm nhưthếnào
•Nếu phân phối bịlệch (trái hoặc phải) => nên sử dụng trung vị
 Các mứcđộ đođộ phân tán
•Mốt hay sửdụng cho biếnđịnh tính
• Khoảng biến thiên, khoảng tứphân vị
• Phương sai và độ lệch chuẩn 40 41 40 41 7
Tại sao cần các mứcđộ đođộ phân tán?
Tại sao cần các mứcđộ đođộ phân tán?
TB của dãy sốphân phối nào có tính đại biểu cao hơn? A? B? C?
•Các mứcđộ trung tâm mới phản ánh một phần dãy số
phân phối => Cần thêm thông tin để đánh giá mứcđộ
đại biểu của giá trịtrung tâm •VD: có hai dãy sốsau
–Dãy số1: 100, 40, 40, 35, 35 => TB: 50
–Dãy số2: 70, 55, 50, 40, 35 => TB: 50
TB của dãy sốnào có tính đại biểu cao hơn 42 43 42 43 Khoảng biến thiên
Tại sao cần các mứcđộ đođộ phân tán?
•KBT là chênh lệch giữa giá trịlượng biến cao nhất
Cần phải biếtđộ phân tán xung quanh giá trịtrung
và thấp nhất => Cần sắp xếp lại dữliệu trước khi
tâm để đánh giá mứcđộ đại biểu của các giá trịtrung tính KBT
tâm và có một cái nhìn tổng quan vềhiện tượng
•Công thức: KBT = maximum - minimum •Ưuđiểm: dễtính. •Nhượcđiểm:
–Chỉtính đến 2 giá trịở hai đầu mút
–Bịảnh hưởng bởi các giá trịngoại lai
–Khó tính toán cho dãy sốphân tổcó khoảng cách tổ 44 45 44 45 Phân vị Tứphân vị
•Phân vị: phân vịthứp
th là đơn vịnằmở vịtrí sao
•Tứphân vị: được xác định bởi các giá trịlượng
cho có p% các đơn vịtrong dãy sốlượng biến nằm
biến của các đơn vịchia dãy sốra làm 4 phần bằng
ở bên trái p và (100-p)% các đơn vịtrong dãy số nhau nằmở bên phải p
–Q : giá trịlượng biến củađơn vịnằmở vịtrí thứ25% 1
•Công thức tính phân vị:
trong dãy số(tức là có 25% sốđơn vịtrong dãy sốcó giá
trịlượng biến < Q 1
- Xác định vịtrí của phân vị: 𝐿 󰇛𝑛1󰇜   –  Q : trung vị 2
- Sửdụng nguyên tắc tính Me để tính phân vị
–Q - giá trịlượng biến củađơn vịnằmở vịtrí thứ75% 3
trong dãy số(tức là có 75% sốđơn vịtrong dãy sốcó giá
trịlượng biến < Q 3 46 47 46 47 8 Khoảng tứphân vị
Ví dụtính khoảng tứphân vị
•Tìm tứphân vịtừdãy sốsau: •Khoảng tứphân vị= Q – Q 3 1 11 12 14 15 15 16 18 18 20 22 
•Độ lệch tứphân vị= Q Q 3 1 2 •Khoảng tứphân vị: Q – Q =? 3 1
•Ưuđiểm của tứphân vị: ít bịảnh hưởng bởi các giá trịngoại Q  Q lai hơn KBT
•Độ lệch tứphân vị: 3 1 = ? 2
•Nhượcđiểm: chỉtính đến 50% dãy số 48 49 48 49 Phương sai
Phương sai: công thức rút gọn 2 
•Phương sai của tổng thể: 2( )  Xi   N •Phương sai mẫu
•VD: Phương sai tổng thể 2 ∑󰇛x 2( ) x  x   μ󰇜 
• Phương sai mẫu tính từdữliệu thô: sn  σ Nx  μ  1 2 2( )  x  x f
• Phương sai mẫu tính từdãy sốphân tổ sf  1
•Ưuđiểm: Tính đến tất cảcác giá trịtrong dãy số
•Nhượcđiểm: giá trịbịkhuếch đại và không có đơn vịtính 50 51 50 51 Độ lệch chuẩn (  )
Ứng dụng của S.D: lĩnh vực tài chính
•Độ lệch chuẩn (S.D) là căn bậc 2 của phương sai
•Độ lệch chuẩn của tổng thể
•Phương sai (hoặc S.D) thường được sửdụng để 2   
đánh giá rủi ro trong đầu tưtài chính.
•Phương sai càng lớnđộ rủi ro càng lớn
•Độ lệch chuẩn của mẫu 2 s  s •Ưuđiểm:
• Khắc phụcđược nhượcđiểm của phương sai
• Là tham sốhay được sửdụng nhấtđể đođộ phân tán
(giá trịcàng lớnđộ phân tán của dãy sốcàng cao) 52 52 53 9
VD: hai khoảnđầu tưtrong vòng 10 năm (1)
VD: hai khoảnđầu tưtrong vòng 10 năm (2) •Tỷsuất lợi nhuận
 Phụthuộc vào mứcđộ chấp nhận rủi ro của bạn:
Khoản A: rủi ro cao hơn nhưng tỷsuất sinh lời A 8.3
-6.2 20.9 -2.7 33.6 42.9 24.4 5.2 3.1 30.5 cũng cao hơn.
B 12.1 -2.8 6.4 12.2 27.8 25.3 18.2 10.7 -1.3 11.4 x  A 16% 2 2 s  A 280.34(%)
•Bạnđầu tưvào đâu? A? B? 54 55
1. Xác định giá trịngoại lai: Quy tắc 3 
Xác định giá trịđột xuất hoặc ngoại lai
•Áp dụng với mộtphân phối chuẩn hoặc xấp xỉ chuẩn:
–68.26% giá trịrơi vào khoảng lượng biến: (x  1  )s ( x 1 s )
–95.45% giá trịrơi vào khoảng lượng biến: (x 2 ) s ( x s 2 )
–99.73% giá trịrơi vào khoảng lượng biến : (x 3 )s ( x s3 )
–Giá trịnằm ngoài khoảng 3s được coi là đột xuất hay ngoại lai 56 57 56 57
2. Tính hệsốbiến thiên (V) Hệsốbiến thiên (cont.)
•Khi hai dãy sốphân phối có trung bình khác nhau, chúng ta
tính V để so sánh độ phân tán của hai dãy sốđó. •Công thức: s
•Dãy sốnào có V lớn hơn thì dãy sốđó có độ phân tán lớn V = hơn x VD: có 2 dãy số •V
= 0.417 và V =0.408 => A có độ phân tán A B A B lớn hơn B TB 120 125 S.D 50 51
Dãy sốnào có độ phân tán lớn hơn 58 59 58 59 10
3. Tính hệsốđo hình dạng của phân phối(K)
Hệsốđo hình dạng của phân phối (VD)
•Có sốliệu về2 dãy sốnhưsau:
•Sửdụng công thức của Pearson. K = 3 x (TB-Me)/S.D 1: 2: Tuổi của sv Lương
•Nếu K càng lớn, phân phối càng lệch TB 22.4839 294.3
•Nếu K>0 => phân phối lệch phải (positive skew) Me 21 292.5
•Nếu K<0 => phân phối lệch trái (negative skew) S.D 6.3756 125.93 •
Tính K và mô tảhình dạng phân phối của 2 dãy sốnày 60 61 60 61
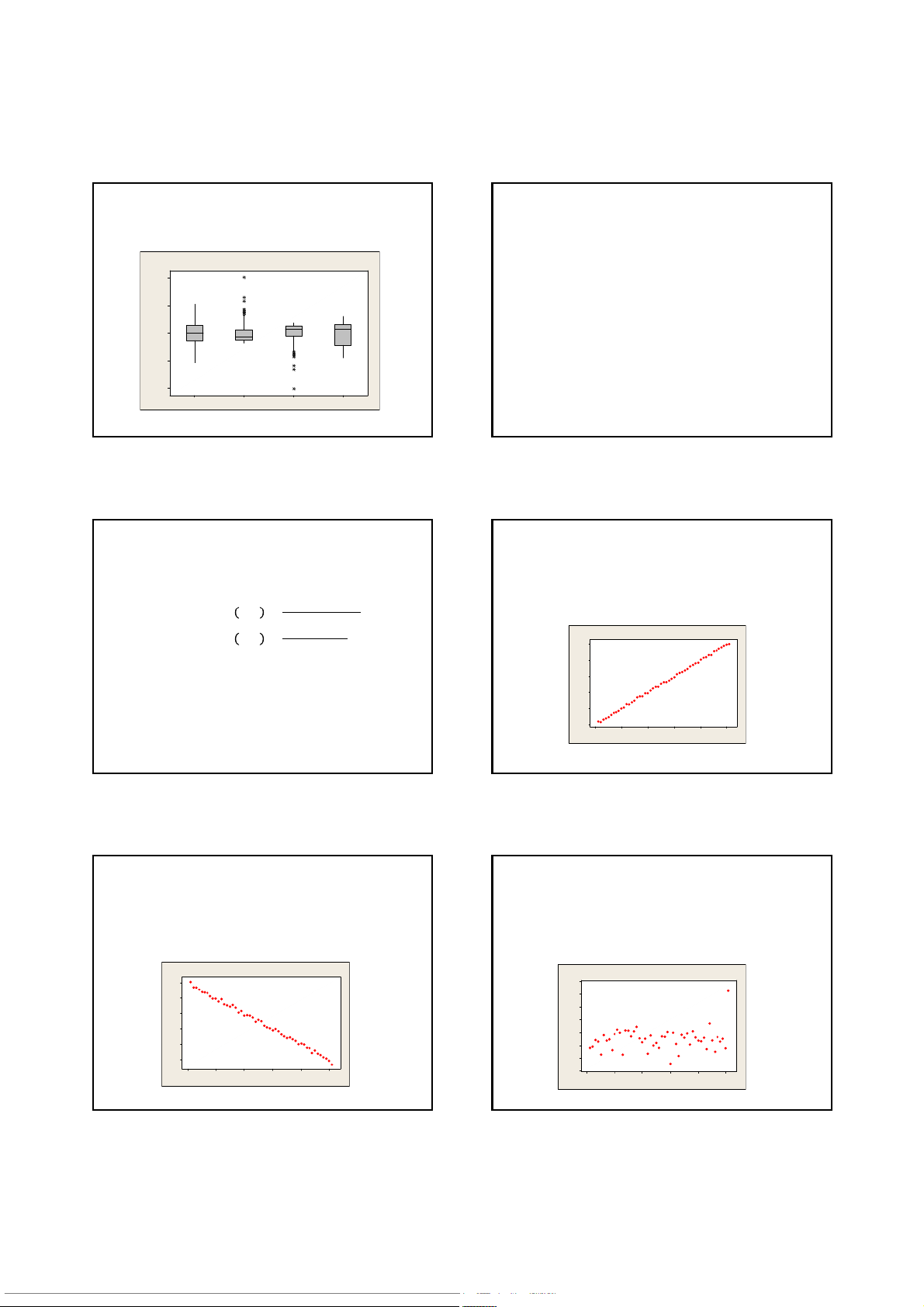
Hệsốđo hình dạng của phân phối (VD) Boxplot
Boxplot dướiđây phản ánh phân phối chiều cao của sinh viên Boxplot of Height 200 Frequency Frequency 190 whisker 180 upper quartile 0 50 100 150 200 0 2 4 6 8 10 Height 170 20 40 60 80 100 200 300 400 500 600 age wages box median 160 lower quartile Lệch phảiXấp xỉchuẩn 150 whisker 62 63 62 63 Boxplot Boxplots
•Cần biết trung vịvà tứphân vịđểtạo boxplot
•Khoảng tứphân vị(IQR) = Q -Q 3 1
•Râu: chiều dài bằng 1.5*IQR; kéo từhộpđếnđiểm dữliệu xa nhất
•Điểm dữliệu nằm giữa 1.5 và 3*IQR đượcđánh dấuogọi
là ngoại biên (outliers)/ lượng biếnđột xuất
•Các điểm dữliệu nằm từ3*IQR đượcđánh dấu bởi dấu *
là lượng biến cực kỳđột xuất 64 65 64 65 11 Hình dạng củaBoxplots
Các mứcđộ thống kê mô tảphản ánh mối liên hệ
Boxplot of Symmetric, Positive skew, Negative skew, Bimodal •Hiệp phương sai 5.0 •Hệsốtương quan 2.5 0.0 Data -2.5 -5.0 Symmetric Positive skew Negative skew Bimodal 66 66 67 Hiệp phương sai
Giá trị của hiệp phương sai (1)
•Hiệp phương sai (Covariance) tính cho hai biến định lượng:
•Nếu cov>0, thì khi X tăng => Y tăng; và khi X giảm
=> Y giảm. Đây là mối liên hệ tương quan thuận - Tổng thể: ∑󰇛 Cov X, Y 
󰇜󰇛 󰇜  - Mẫu: ∑󰇛
Scatterplot of Positive vs X values Cov X, Y   󰇜󰇛󰇜  100 Ưuđiểm: 80
–Cho biết hai biến có tương quan tuyến tính với nhau hay 60 không Positive 40
–Cho biết chiều hướng của mối liên hệ 20 Nhượcđiểm: 0 0 10 20 30 40 50
–Không cho biết cường độ của mối liên hệ X values 68 69
Giá trị của hiệp phương sai (2)
Giá trị của hiệp phương sai (3)
•Nếu cov<0, thì khi X tăng => Y giảm và ngược lại.
•Nếu cov=0, thì khi X thay đổi, Y không thay đổi 
Đây là mối liên hệ tương quan nghịch.
Hai biến không có mối liên hệ tương quan tuyến tính
Scatterplot of Negative vs X values
Scatterplot of Zero vs X values 50 1.0 0.5 40 0.0 30 -0.5 Nega 20 tive Zero -1.0 10 -1.5 0 -2.0 -2.5 0 10 20 30 40 50 X values 0 10 20 30 40 50 X values 70 71 12 Hệsốtương quan
•Hệsốtương quan (Correlation Coefficient) Hướng dẫn sửdụng SPSS - Tổng thể:  , ρ 
 Thực hành với bộdữliệu gss.sav - Mẫu:  , R   Ưuđiểm:
–Cho biết hai biến có tương quan tuyến tính với nhau hay không
–Cho biết chiều hướng của mối liên hệ: R dương (thuận), R âm (nghịch)
–Cho biết cường độ của mối liên hệ: R →0, mối liên hệ
càng lỏng lẻo; R →-1 hoặc +1, mối liên hệcàng chặt chẽ 73 72 73 13