Bài 4: Phân Tích Hồi Quy và Tương Quan Trong Kinh Tế môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 4: Phân tích hồi quy và tương quan
BÀI 4: PHÂN TÍCH HỒI QUY VÀ TƯƠNG QUAN Nội dung Mục tiêu
 Nhiệm vụ của phân tích hồi quy và
 Cung cấp phương pháp phân tích th ng kê ố tương quan.
nghiên cứu mối liên hệ nhân quả giữa các
 Một số mô hình hồi quy và cách xác
hiện tượng kinh tế – xã h i. ộ
định các tham số của mô hình.
Thời lượng học
Hướng dẫn học  7 tiết 
Đọc bài giảng và thảo luận.
 Trả lời câu hỏi ôn tập, câu hỏi trắc nghiệm và làm bài tập. v1.0 69
Bài 4: Phân tích hồi quy và tương quan
TÌNH HUỐNG DẪN NHẬP
Tên tình huống: Phân tích thị trường xe máy
Giả sử bạn đang nghiên cứu về vấn đề mua bán xe máy
Honda Wave đã qua sử dụng. Bạn nhận thấy giá bán c a ủ
chiếc xe do rất nhiều nhân tố quyết định. Đó có thể là số
năm sử dụng xe, màu sắc, đối tượng mua, đối tượng bán,
thậm chí cả nhu cầu mua, nhu cầu bán cũng có ảnh hưởng
đến giá cả của nó... Bạn thực hiện một điều tra thống kê trên
11 chiếc xe để tìm hiểu mối liên hệ giữa các nhân tố ảnh
hưởng và giá bán của nó. Số liệu cho thấy, dường như đúng
là có mối liên hệ giữa các nhân tố nêu trên với giá của chiếc
xe. Nhưng bạn lại không biết biểu diễn mối liên hệ ó nh đ ư thế nào. Câu hỏi
Bài học này sẽ giúp bạn cách thức xây dựng mối liên hệ ụ
ph thuộc qua lại giữa các hiện tượng
kinh tế – xã hội, đồng thời cũng sẽ hướng dẫn bạn cách đánh giá mức độ chặt chẽ của mối liên hệ ó nh đ ư thế nào? 70 v1.0
Bài 4: Phân tích hồi quy và tương quan
4.1. Nhiệm vụ của phân tích hồi quy và tương quan
4.1.1. Mối liên hệ giữa các hiện tượng kinh tế xã hội
Các hiện tượng kinh tế – xã hội tồn tại trong mối liên hệ phụ thuộc lẫn nhau. Các mối
liên hệ này có thể diễn ra theo thời gian hay không gian nhất định. Các mối liên hệ
diễn ra theo thời gian nghĩa là sự tác động qua lại và sự phụ thu c ộ vào nhau c a các ủ
hiện tượng khi chúng ở các giai o
đ ạn và quá trình của sự phát triển. Các mối liên hệ
diễn ra theo không gian nghĩa là sự tác động qua lại và sự phụ thuộc vào nhau của các
hiện tượng khi chúng ở cùng một thời gian. Thậm chí ngay trong cùng một hiện tượng
nghiên cứu bao gồm nhiều tiêu thức khác nhau, thì những tiêu thức này cũng có mối
liên hệ qua lại nhất định. Tuỳ theo mức độ chặt chẽ, mà người ta chia mối liên hệ
thành các loại dưới ây. đ
4.1.1.1. Liên hệ hàm số
 Khái niệm: Liên hệ hàm số là mối liên hệ hoàn
toàn chặt chẽ. Sự thay đổi của hiện tượng này có
tác dụng quyết định đến sự thay đổi của hiện tượng
liên quan theo một tỷ lệ xác định.
Liên hệ hàm số được viết dưới dạng: y = f(x), có
nghĩa là cứ mỗi giá trị của x thì theo một hàm nào
đó có một giá trị của y tươ ứ ng ng.
Mối liên hệ này thường có trong tự nhiên. Ví dụ
trong vật lý: S = v  t...
 Đặc điểm: Liên hệ hàm số không những được biểu hiện ở tổng thể mà còn được
biểu hiện trên từng đơn vị cá biệt.
4.1.1.2. Liên hệ tương quan
 Khái niệm: Liên hệ tương quan là mối liên hệ không hoàn toàn chặt chẽ. Sự thay
đổi của hiện tượng này có thể làm hiện tượng liên quan thay đổi theo nhưng không
có ảnh hưởng hoàn toàn quyết định.
Mối liên hệ này rất phổ biến và thường gặp trong các hiện tượng kinh tế – xã hội.
 Đặc điểm: Liên hệ tương quan không được biểu hiện trên từng đơn vị cá biệt mà
phải thông qua hiện tượng s l ố ớn (là tổng thể).
Ví dụ: Mối liên hệ giữa tuổi nghề và NSLĐ. Tuổi nghề có tác ng độ đến NSLĐ
nhưng NSLĐ không chỉ chịu ảnh hưởng của tuổi nghề mà còn chịu ảnh hưởng c a ủ
các nhân tố khác. Mặt khác, nếu nghiên cứu riêng lẻ từng đơn vị cá biệt, có những
đơn vị, tuổi nghề hoàn toàn không ảnh hưởng tới NSLĐ. Vì vậ để y, có thể nêu lên
được mối liên hệ tương quan cần phải nghiên cứu hiện tượng s l ố ớn.
4.1.2. Nhiệm vụ của phân tích hồi quy và tương quan
Phương pháp phân tích hồi quy và tương quan giải quyết hai nhiệm vụ ch y ủ ếu sau:
4.1.2.1. Xác định mô hình hồi quy phản ánh mối liên hệ
Nhiệm vụ đầu tiên của phân tích hồi quy tương quan là xây dựng mô hình (hay
phương trình) hồi quy và xác định tính chất (thuận – nghịch) c ng nh ũ ư hình thức của
mối liên hệ (loại mô hình). v1.0 71
Bài 4: Phân tích hồi quy và tương quan
Để giải quyết nhiệm vụ này, cầ ả
n ph i thực hiện 4 bước sau:
 Bước 1: Giải thích sự tồn tại thực tế và bản chất của mối liên hệ bằng phân tích lý
luận. Tuỳ theo mục đích nghiên cứu cụ thể mà xác định trong mối liên hệ đó, âu đ
là nguyên nhân, đâu là kết quả.
Ví dụ: Tuổi nghề có ảnh hưởng tới NSLĐ. Như vậy, tuổi nghề là nguyên nhân có ảnh hưởng đến NSLĐ.
Nhưng nếu xét trong mối liên hệ với khối lượng sản phẩm sản xuất và giá thành
đơn vị, ta thấy: NSLĐ tăng dẫn tới khối lượng sản phẩm sản xuất tă đ ng. Khi ó,
NSLĐ lại là nguyên nhân, khối lượng sản phẩm là kết quả. Khi khối lượng sản
phẩm sản xuất tăng thì giá thành giảm. Khối lượng sản phẩm sản xuất lại đóng vai
trò là nguyên nhân, giá thành là kết quả.
Ví dụ: Mối liên hệ giữa chi phí quảng cáo và
doanh thu. Khi nghiên cứu các nhân tố tác động
đến doanh thu thì chi phí quảng cáo là một nguyên
nhân. Nhưng khi nghiên cứu nhân tố tác động đến
chi phí quảng cáo thì doanh thu cũng lại là một
nguyên nhân. Trong trường hợp này phải chú ý đến
mục đích nghiên cứu là gì để xác định đâu là tiêu
thức nguyên nhân, đâu là tiêu thức kết quả.
Trong mối liên hệ này, có thể có nhiều nguyên
nhân nhưng chỉ có một kết quả.
 Bước 2: Thăm dò mối liên hệ bằng các phương pháp th ng kê: ph ố ương pháp đồ
thị, phân tổ, số bình quân, phương pháp quan sát 2 dãy số song song…
 Bước 3: Lập phương trình hồi quy biểu hiện mối liên hệ.
Ví dụ: Các phương trình y = a + bx; y = a + bx + cx2…
 Bước 4: Tính toán các tham số và giải thích ý nghĩa của chúng.
4.1.2.2. Đánh giá mức độ chặt chẽ của mối liên hệ tương quan
Sau khi đã xây dựng được phương trình hồi quy biểu diễn mối liên hệ giữa các hiện
tượng kinh tế – xã hội, nhiệm vụ thứ hai của phân tích hồi quy tương quan là đánh giá
mức độ chặt chẽ của mối liên hệ tương quan và sự phù hợp của mô hình thông qua hệ
số tương quan (tuyến tính) và tỷ số tương quan (phi tuyến tính).
4.1.3. Ý nghĩa của phân tích hồi quy và tương quan
Phân tích hồi quy và tương quan là phương pháp thường được sử d ng ụ để nghiên cứu
mối liên hệ tương quan giữa các hiện tượng kinh tế – xã hội. Bên cạnh đó, nó còn
được sử dụng nhiều trong nghiên cứu thống kê, như phân tích dãy số thời gian, dự đoán thống kê...
Trong phần tiếp theo, bài giảng sẽ đi vào trình bày cách thức xây dựng và phân tích
một mô hình hồi quy thể hiện mối liên hệ giữa một tiêu thức nguyên nhân và một tiêu thức kết quả.
4.2. Hồi quy và tương quan giữa hai tiêu thức số lượng
Trước hết là dạng mô hình đơn giản nhất, mô hình hồi quy tuyến tính. 72 v1.0
Bài 4: Phân tích hồi quy và tương quan
4.2.1. Mô hình hồi quy tuyến tính giữa hai tiêu thức số lượng
4.2.1.1. Mô hình hồi quy
Trước khi đi vào xây dựng mô hình hồi quy, chúng ta hãy xem xét một số khái niệm có liên quan.
 Một số khái niệm liên quan
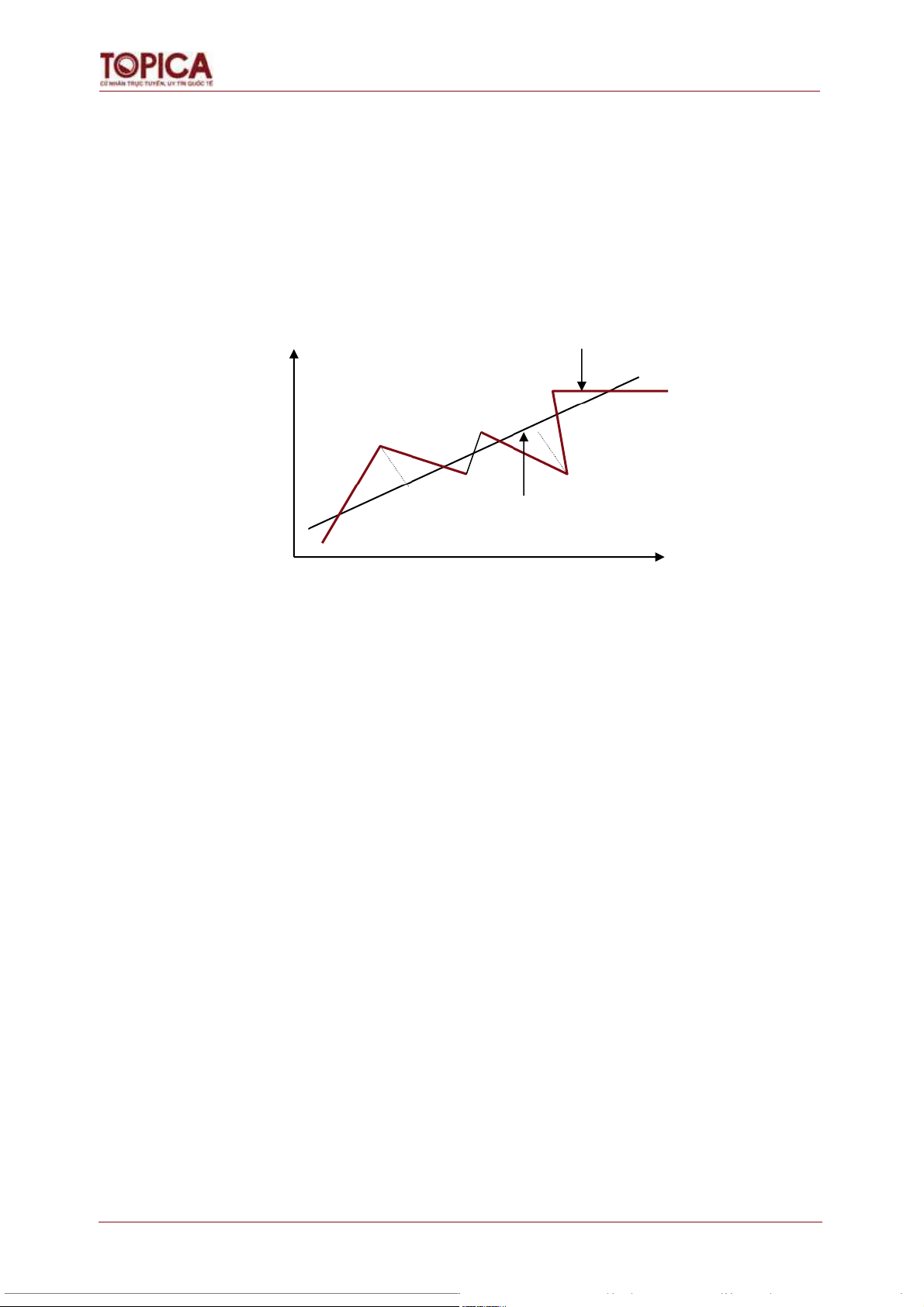
o Đường hồi quy thực nghiệm: là đườ đượ ng
c hình thành bởi các tài liệu thực tế.
o Đường hồi quy lý thuyết: là đường điều chỉnh bù trừ các chênh lệch ngẫu nhiên
vạch ra xu hướng cơ bản của hiện tượng. Đường hồi quy thực nghiệm Đường hồi quy lý thuyết
o Mô hình hồi quy là mô hình xác định vị trí của đườ ồ
ng h i quy lý thuyết sao cho
mô tả gần đúng nhất mối liên hệ thực tế.
 Xây dựng mô hình hồi quy tuyến tính đơn
o Mô hình hồi quy tuyến tính biểu diễn mối liên hệ giữa 2 tiêu thức số lượng có dạng: ˆy = b0 + b1x x Trong đó:  x: Trị s c
ố ủa tiêu thức gây ảnh hưởng (nguyên nhân) (biến độc lập).
 x ˆy : Trị số điều chỉnh của tiêu thức chịu ảnh hưởng (kết quả) (biến ph ụ
thuộc) theo quan hệ với x.  b0: Hệ s
ố tự do (hệ số chặn), là điểm xuất phát của đường hồi quy lý thuyết,
nêu lên ảnh hưởng của các nhân tố khác (tiêu thức nguyên nhân khác) ngoài x tới sự biến ng c độ ủa y.  b1: Hệ s h
ố ồi quy (hệ số góc, độ dốc), phản ánh ảnh hưởng trực tiếp của tiêu
thức nguyên nhân x đến tiêu thức kết quả y. Mỗi khi x tăng lên 1 đơn vị thì
y sẽ thay đổi trung bình b1 đơn vị.
b1 nói lên chiều hướng của mối liên hệ: b1 > 0: Mối liên hệ thuận; b1 < 0: Mối liên hệ nghịch.
o Cách xác định tham số:
b0, b1 phải được xác định sao cho đường hồi quy lý thuyết mô tả gần đúng nhất
mối liên hệ thực tế. Trên hình vẽ, khoảng cách từ điểm thực tế đến điểm thu c ộ
đường hồi quy lý thuyết nh nh ỏ ất sẽ là tốt nhất.
Sử dụng phương pháp bình phương nh nh ỏ
ất (OLS – Ordinary Least Square)
với nội dung: tổng bình phương các độ lệch giữa giá trị thực tế và giá trị lý thuyết của biế ụ
n ph thuộc (tiêu thức kết quả) là nhỏ nhất. v1.0 73
Bài 4: Phân tích hồi quy và tương quan 2 S  (y ˆy ) min  ix Hay 2 S    (y b b x) min  i 0 1
Để thỏa mãn điều kiện trên, cần tính đạo hàm riêng theo 2 tham số cần tìm. Từ ó, b đ
0 và b1 phải thỏa mãn hệ phương trình:  y nb b x  0 1 
 Hệ phương trình chuẩn 2 xy b x b x  0 1 
Từ hệ phương trình trên, sau khi biến đổi, b0 và b1 có thể được tính đơn giản hơn theo công thức: b xy xy  12 x b0 = y – b1x x  y  Trong đó: x i in yn 2 xy  2 x  x x (x)  xy n 2 2 2      x n n   Chú ý:
Nên sử dụng công thức rút gọn ở trên để tính b0 và b1 chứ không nên giải hệ phương trình chuẩn.
Ví dụ: Có tài liệu về 11 xe máy Honda Wave đã qua sử d ng nh ụ ư sau: Stt
Số năm sử dụng Giá bán
(triệu đồng) y xy x2 y2 (năm) x 1 5 72,25 8,5 25,0 42,5 2 4 106,09 10,3 16,0 41,2 3 6 49,00 7,0 36,0 42,0 4 5 67,24 8,2 25,0 41,0 5 5 79,21 8,9 25,0 44,5 6 5 96,04 9,8 25,0 49,0 7 6 43,56 6,6 36,0 39,6 8 6 90,25 9,5 36,0 57,0 9 2 285,61 16,9 4,0 33,8 10 7 49,00 7,0 49,0 49,0 11 7 23,04 4,8 49,0 33,6 Tổng 58 97,5 473,2 326,0 961,29 Trung bình 5,273 8,864 43,018 29,636 87,390
Yêu cầu: Lập mô hình hồi quy tuyến tính biểu diễn mối liên hệ giữa số năm
sử dụng xe và giá bán của xe.
Hướng dẫn: Ở đ đ ây chúng ta ứ
ang nghiên c u các nhân tố ả
nh hưởng đến giá bán xe máy
nên số năm sử dụng sẽ là tiêu thức nguyên nhân x, còn giá bán sẽ là tiêu thức kết quả y. 74 v1.0
Bài 4: Phân tích hồi quy và tương quan
Mô hình hồi quy có dạng: ˆ x y = b0 + b1x
Xác định các tham số: 2 2 2 2  xx  (x  ) 29,  636 5  , 273 1,831 b xy xy  = 43,018 5, 273 8,864 2,03
< 0  mối liên hệ nghịch 12 1,831 x
b0 = y – b1x= 8,864 – (–2,03  5,273) = 19,57
Vậy phương trình hồi quy tuyến tính biểu diễn mối liên hệ giữa số năm sử
dụng và giá bán có dạng: ˆy = 19,57 – 2,03x x Trong đó:
b0 = 19,57 nêu lên ảnh hưởng của các nhân tố khác ngoài số năm sử dụng tới
sự thay đổi của giá bán.
b1 = – 2,03 nêu lên ảnh hưởng trực tiếp của số năm sử dụng tới sự thay đổi của
giá bán. Khi số năm sử dụng tăng thêm 1 năm thì giá bán của chiếc xe sẽ giảm
đi trung bình 2,03 triệu đồng.
Cách kiểm tra kết quả:
 x tăng từ 2 đến 7 năm làm y giảm từ 16,9 xuống còn 4,8 triệu đồng; vậy x
tăng làm y giảm, ta có mối liên hệ nghịch, tức b1 < 0.
 Thay bất kỳ giá trị nào của x vào phương trình hồi quy phải ra giá trị x ˆy≈ yx. Lưu ý:
 Từ phương trình hồi quy trên, nếu ta có một giá trị của x, thay vào phương
trình ta sẽ tính được giá trị của y tương ứng và ngược lại.
 Trong trường hợp trên, khi x = 0, xˆy = b0 = 19,57 (triệu đồng), đây chính là
mức giá của 1 chiếc xe Honda Wave mới.
Sau khi đã xây dựng xong mô hình hồi quy phản ánh mối liên hệ giữa các hiện tượng
kinh tế – xã hội, nhiệm vụ tiếp theo của phân tích hồi quy và tương quan là phải đánh
giá được trình độ chặt chẽ của mối liên hệ đó cũng như sự phù hợp của mô hình đã có.
4.2.1.2. Hệ số tương quan
 Khái niệm: Hệ số tương quan là chỉ tiêu đánh giá mức độ chặt chẽ của mối liên hệ
tương quan tuyến tính đơn.
 Tác dụng:
o Xác định cường độ của mối liên hệ từ đó chọn ra nguyên nhân chủ yếu hoặc
thứ yếu đối với hiện tượng nghiên cứu.
o Xác định chiều hướng cụ thể của mối liên hệ (thuận – nghịch).
o Hệ số tương quan còn dùng trong nhiều trường hợp dự đoán thống kê và tính sai số của dự đoán.
 Công thức tính: xy x  y x r b  1   x y y v1.0 75
Bài 4: Phân tích hồi quy và tương quan
Như vậy, dấu của hệ s
ố tương quan r phụ thuộc vào dấu c a h ủ ệ s b ố 1 vì phương sai luôn mang dấu dương.
Các tính chất của hệ số tương quan: Miền xác định: –1 ≤ r ≤ 1.
o r > 0: Mối liên hệ tương quan tuyến tính thuận.
o r < 0: Mối liên hệ tương quan tuyến tính nghịch.
o r = ± 1: Mối liên hệ hàm số hoàn toàn chặt chẽ.
o r = 0: Không có mối liên hệ tương quan tuyến tính giữa x và y.
o r càng gần 1: Mối liên hệ càng chặt chẽ (cường m độ ối liên hệ).
o r  0,9: Mối liên hệ rất chặt chẽ.
o 0,7  r  0,9: Mối liên hệ tương đối chặt chẽ.
o 0,5  r  0,7: Mối liên hệ bình thường (trong dự đoán thường không sử dụng r
này đối với tiêu thức số lượng nhưng với tiêu thức thuộc tính thì vẫn sử dụng).
o r < 0,5 : Mối liên hệ hết sức lỏng lẻo.
Vận dụng vào ví dụ trên, ta có: 2 2 2 2  y  yy y  87,390  8,864 2,97  353 , 1 = – 0,925 r = (–2,03)  97 , 2
Kết luận: Mối liên hệ giữa số năm sử dụng và giá bán xe Honda Wave cũ là mối liên
hệ tương quan tuyến tính nghịch và rất chặt chẽ.
4.2.1.3. Hệ số xác định
Khái niệm: Hệ số xác định dùng để đánh giá sự phù hợp của mô hình, nó cho biết tỷ
lệ % thay đổi của y được giải thích bởi mô hình.
Ở ví dụ trên, ta có: r2 = (– 0,925)2 = 0,8556.
Như vậy, 85,56% sự thay đổi của giá bán xe máy Honda Wave cũ được giải thích bởi
mô hình đã nói ở trên trong mối quan hệ với số năm sử d ng. ụ
Điều đó nói lên rằng,
số năm sử dụng là hoàn toàn hữu ích khi dự đoán mức giá bán của một chiếc xe cũ.
4.2.1.4. Kiểm định các tham số của phương trình hồi quy tuyến tính đơn
 Trong mối liên hệ tương quan giữa x và y, cứ mỗi giá trị của x ta có thể thu được
nhiều giá trị của y. Khi đó, chúng ta phải có một số giả định sau:
o Đường hồi quy tổng thể chung: với phương trình tuyến tính x y ˆ= 0 + 1x, thì
mỗi giá trị của x sẽ có nhiều giá trị tương ứng của y, khi đó số bình quân của các
giá trị này sẽ nằm trên một đường thẳng. Đường thẳng đ ọ
ó g i là đường hồi quy
tổng thể chung và phương trình của nó là phương trình hồi quy tổng thể chung.
o Độ lệch tiêu chuẩn: độ lệch tiêu chuẩn
 của tổng thể chung gồm các giá trị y
tương ứng với một giá trị cụ thể của x là như nhau, bất kể x là bao nhiêu.
o Phân phối chuẩn: với một giá trị của x, tổng thể chung gồm các giá trị y tương
ứng có phân phối chuẩn. 76 v1.0
Bài 4: Phân tích hồi quy và tương quan
Nói cách khác, các giả định trên cho rằng, nếu có các tham số không đổi là 0, 1
và  thì với mỗi giá trị của x, tổng thể chung gồm các giá trị của y tương ứng sẽ
có phân phối chuẩn với số bình quân là 0 + 1x và độ lệch tiêu chuẩn .
 Kiểm định hệ số hồi quy của phương trình tuyến tính đơn: Bài toán đặt ra như sau:
Giả sử, phương trình hồi quy tuyến tính đơn x y
ˆ= 0+ 1x, biểu diễn mối liên hệ
phụ thuộc giữa tiêu thức nguyên nhân x và tiêu thức kết quả y. Từ phương trình
đó, chúng ta cho rằng có thể dùng x để dự đoán giá trị của y. Nhưng có thật sự là như vậy hay không?
Chúng ta đã biết, trong mô hình hồi quy, hệ s
ố hồi quy thể hiện mối liên hệ giữa x
và y, nó cho biết ảnh hưởng trực tiếp của nguyên nhân x đến kết quả y. Chính vì
vậy, để trả lời câu hỏi trên, người ta thực hiện kiểm định hệ s ố hồi quy của phương trình tuyến tính đơn.
Trình tự thực hiện kiểm định như sau:
o Bước 1: Phát biểu giả thiết không và giả thiết đối của nó.
Giả thiết không là: H0: 1 = 0 (x không có mối liên hệ với y)
Giả thiết đối là: H1: 1 ≠ 0 (có mối liên hệ tuyến tính giữa x và y)
o Bước 2: Xác định mức ý nghĩa α (với 1 – α là hệ số tin cậy).
o Bước 3: Chọn tiêu chuẩn kiểm định và tính giá trị của tiêu chuẩn kiểm định từ mẫu quan sát.
Trên thực tế, các giá trị 0, 1 và  là không biết nhưng chúng ta có thể ước lượng
được qua một mẫu cụ thể.
Giả sử rằng với một mẫu cụ thể, chúng ta xác định được phương trình hồi quy mẫu với hệ s h
ố ồi quy là b1, b1 có phân phối chuẩn với số bình quân   và độ lệch 1 b 1  tiêu chuẩn S  1 b2
. Khi đó, biến ngẫu nhiên chuẩn hoá z cũng có phân (x x) i phối chuẩn. b  1 1 zS b1
Nhưng trong phương trình trên, chúng ta chưa biết  , nên có thể dùng sai số tiêu 2 (y  ˆy )
 của mẫu để thay thế. Khi đó, biến ngẫu nhiên kết quả chuẩn i x Sn 2  e
có phân phối t-student với bậc tự do df = n – 2. b   1 1 tS e 2 (x x)   i
Với giả thiết không H0: 1 = 0, tiêu chuẩn kiểm định là: b1 tS e 2 (x x)   i v1.0 77
Bài 4: Phân tích hồi quy và tương quan
o Bước 4: Xác định miền bác bỏ và kết luận có bác bỏ giả thiết không hay không.
Giá trị tới hạn là  tα/2, với bậc tự do là n – 2. Tra bảng t để xác định giá trị tới hạn đó.
Nếu giá trị tuyệt đối của t tính được mà lớn hơn giá trị tới hạn t tra bảng thì bác b ỏ
giả thiết H0. Ngược lại, thì chưa có cơ sở để bác bỏ giả thiết H0. Ví dụ:
Với số liệu ở ví dụ trên, giả sử có cơ sở cho rằng s
ố năm sử dụng không có ảnh
hưởng đến mức giá bán của chiếc xe Honda Wave cũ. Khi đó, ta sẽ thực hiện kiểm định giả thiết sau:
Giả thiết không là: H0: 1 = 0 (số năm sử dụng không có mối liên hệ với mức giá bán).
Giả thiết đối là: H1: 1 ≠ 0 (có mối liên hệ tuyến tính giữa s n ố ăm sử dụng và mức giá bán).
Chúng ta thực hiện kiểm định giả thiết trên với mức ý nghĩa  = 0,05.
Giá trị tới hạn là  tα/2 =  t0,025, với bậc tự do là n – 2 = 11 – 2 = 9.
Tra bảng ta tính được giá trị tới hạn ± t0,025 =  2,262.
Từ mẫu đã cho, tính tiêu chuẩn kiểm định t: b2,03  1  t  7, 25 S 1, 2577 e 2 (x x)  20,182  i Trong đó: Stt
Số năm sử dụng Giá bán
(triệu đồng) y y 2
(x - x) ˆ2 (y -y ) (năm) x ˆ x i i x 0,846 0 ,075 1 5 9 ,42 8 ,5 1,323 1 ,621 2 1 4 1 ,4 1 5 0 ,3 0,152 0 ,529 3 6 7 ,39 7 ,0 1,488 0 ,075 4 5 9 ,42 8 ,2 0,270 0 ,075 5 5 9 ,42 8 ,9 0,144 0 ,075 6 5 9 ,42 9 ,8 0,624 0 ,529 7 6 7 ,39 6 ,6 4,452 0 ,529 8 6 7 ,39 9 ,5 1,93 1 2 0 ,713 9 1 2 5 ,5 1 1 6 ,9 2,69 2 0 ,91 80 3 7 5,3 7 6 ,0 0,31 2 4 ,91 81 3 7 5,3 4 6 ,8 14,236 20,182 Tổng 5 8 97,5 Trung bình 5,273 8,864 2 (y ˆy ) 14, 236  ix S   1, 2577 e n  2  11 2
Vậy ta có t> ± t0,025, bác bỏ giả thiết H0.
Kết luận: Với mẫu đã cho, ở mức ý nghĩa 5%, có thể kết luận rằng: s ố năm sử
dụng xe máy Honda Wave có ảnh hưởng tới giá bán của chiếc xe đó. 78 v1.0
Bài 4: Phân tích hồi quy và tương quan
 Kiểm định hệ số tương quan của phương trình tuyến tính đơn
Tương tự với bài toán trên, giả sử với hai biến x và y, chúng ta nhận thấy chúng có
mối liên hệ tuyến tính với nhau. Tuy nhiên, có cơ sở để giả định rằng không có
mối liên hệ tương quan tuyến tính đó trong tổng thể chung.
Khi đó chúng ta thực hiện kiểm định hệ số tương quan tuyến tính của cả tổng thể
chung . Giả thiết cần kiểm định:  = 0 (không có mối liên hệ tương quan tuyến tính giữa x và y).
Để kiểm định giả thiết này, lấy mẫu n từ tổng thể chung, khi đó xác định được hệ số tương quan mẫu r.
Tiêu chuẩn kiểm định được chọn là thống kê: r t 
có phân phối t – student với bậc tự do n – 2. 2 1 r n 2 
Với mức ý nghĩa α cho trước, tuỳ thuộc vào dạng của giả thiết đối mà miền bác bỏ
được xây dựng như sau:
H0: = 0 nếu t > tα, bác bỏ giả thiết H0 (kiểm định phải) H1: > 0
H0: = 0 nếu t> tα, bác bỏ giả thiết H0 (kiểm định trái) H1: < 0
H0: = 0 nếu t> tα/2, bác bỏ giả thiết H0 (kiểm định hai phía) H1: ≠ 0
Ví dụ: Với số liệu ở ví dụ trên, có cơ sở cho rằng giữa s ố năm sử dụng và giá
bán xe Honda Wave cũ không có mối liên hệ tương quan tuyến tính với nhau. Với  là hệ s
ố tương quan tuyến tính của tổng thể chung, ta thực hiện kiểm định giả thiết sau: H0: = 0 (s n
ố ăm sử dụng và giá bán không có mối liên hệ tuyến tính)
H1:  < 0 (số năm sử dụng và giá bán có mối liên hệ tương quan tuyến tính nghịch)
Với mức ý nghĩa α = 0,05, giá trị tới hạn t = 1,833 khi bậc tự do n – 2 = 9.
Từ mẫu đã cho, tính tiêu chuẩn kiểm định t: r 0,925  t  7,  303   2 2  1  r 1 ( 0,925) n  2  11 2
Ta thấy t> tα = 1,833, bác bỏ giả thiết H0.
Với mẫu đã cho, ở mức ý nghĩa 5%, có thể kết luận rằng s n
ố ăm sử dụng xe và giá
bán của chiếc xe Honda Wave có mối liên hệ tương quan tuyến tính với nhau, và
đây là mối liên hệ nghịch.
Tuy nhiên, trên thực tế, không phải mối liên hệ nào cũng là mối liên hệ tương quan
tuyến tính. Vì vậy, chúng ta nghiên cứu trường hợp tiếp theo (mô hình hồi quy phi
tuyến tính), mối liên hệ này thường gặp nhiều hơn trong thực tế. v1.0 79
Bài 4: Phân tích hồi quy và tương quan
4.2.2. Mô hình hồi quy phi tuyến giữa hai tiêu thức số lượng
4.2.2.1. Một số dạng mô hình hồi quy phi tuyến thường gặp
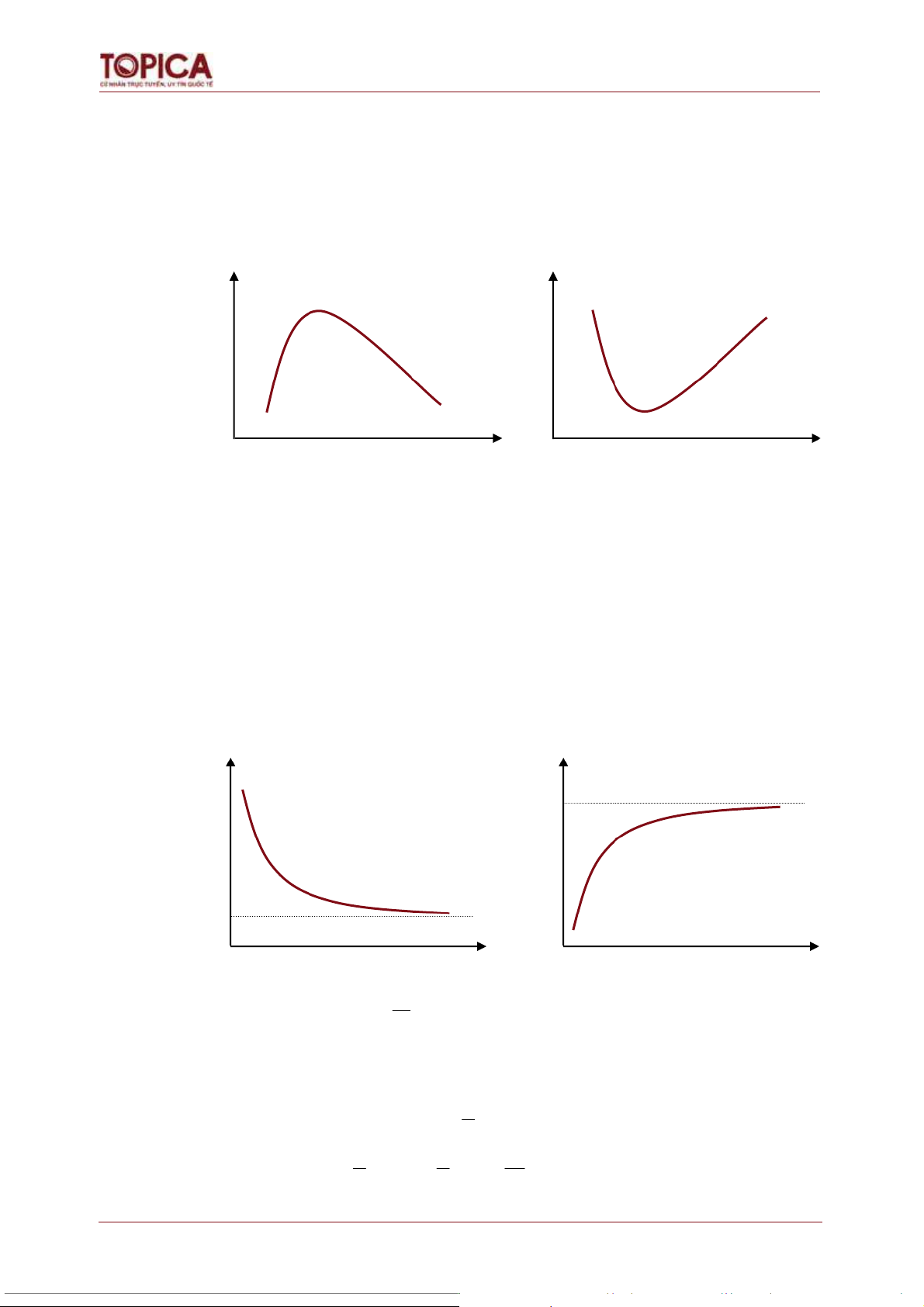
 Phương trình parabol (bậc 2)
o Vận dụng khi tiêu thức nguyên nhân tăng hay giảm với 1 lượng đều nhau thì tiêu
thức kết quả biến động với 1 lượng không đều nhau (nhanh hơn hoặc chậm hơn).
Ví dụ: Chi phí quảng cáo và doanh thu. o Mô hình hồi quy: 2 ˆy  b   b x b x x 0 1 2
b0, b1, b2 là các tham số của mô hình hồi quy, được xác định bằng phương pháp
bình phương nhỏ nhất và phải thỏa mãn hệ phương trình: 2  y b n b x b x    01 2   2 3  xy b x b x b x  0 1 2  2 2 3 4  x y b x b x b x  0 1 2  Phương trình hypebol
o Vận dụng khi tiêu thức nguyên nhân tăng thì tiêu thức kết quả giảm với tốc độ không đều nhau. o Mô hình hồi quy: b1 ˆy b x x 0
b0, b1 là tham số của mô hình hồi quy, được xác định bằng phương pháp bình phương nh nh ỏ
ất và phải thỏa mãn hệ phương trình:  1 y b n b x  0 1   1 1 1  y b b  0 1 2  x x x 80 v1.0
Bài 4: Phân tích hồi quy và tương quan  Phương trình hàm mũ
o Vận dụng khi trị số của tiêu thức kết quả thay i theo c đổ ấp số nhân. o Mô hình hồi quy: x ˆy  b b x 0 1 hay: lny = lnb0 + x  lnb1
lnb0, lnb1 phải thỏa mãn hệ phương trình:  ln y n  ln b ln b x  0 1  2 x ln y ln b x ln b x   0 1
4.2.2.2. Tỷ số tương quan
 Khái niệm: Tỷ s t
ố ương quan là chỉ tiêu ánh giá trình đ
độ chặt chẽ của mối liên hệ tương quan phi tuyến.
 Công thức:   2 y y ˆ i x  1      2 y y i
 Tính chất:
o Tỷ số tương quan nằm trong khoảng [0,1].
o η = 0: Không có mối liên hệ tương quan phi tuyến.
o η = 1: Mối liên hệ tương quan phi tuyến hoàn toàn chặt chẽ.
o η càng gần 1: Mối liên hệ càng chặt chẽ. Nhận xét
η luôn > 0 do đó tỷ số tương quan chỉ có thể đánh giá trình độ chặt chẽ của mối liên hệ
chứ không nói được chiều hướng của mối liên hệ.
η có thể dùng cho cả phi tuyến và tuyến tính (khi r  0). v1.0 81
Bài 4: Phân tích hồi quy và tương quan
TÓM LƯỢC CUỐI BÀI
 Các hiện tượng kinh tế – xã hội luôn tồn tại trong một mối liên hệ ràng buộc lẫn nhau.
Tuỳ theo mức độ chặt chẽ của mối liên hệ mà có thể phân ra thành hai loại: liên hệ hàm số và liên hệ tương quan.  Phân tích h i quy và t ồ
ương quan thực chất là phương pháp phân tích mối liên hệ phụ thuộc
với hai nhiệm vụ chủ yếu: xây dựng phương trình h i quy bi ồ
ểu diễn mối liên hệ và đánh giá
mức độ chặt chẽ của mối liên hệ.
 Với mối liên hệ đơn giả ấ
n nh t giữa hai tiêu thức số lượng, tuỳ theo việc thăm dò dạng của
mô hình hồi quy mà ta có thể xây dựng phương trình tuyến tính hoặc phi tuyến. Các hệ s ố
của mô hình hồi quy được xác định theo phương pháp bình phương nh nh ỏ ất. Hệ s ố tương quan và tỷ s
ố tương quan được sử d ng ụ
để đánh giá mức độ chặt chẽ của mối liên hệ tương
quan giữa hai tiêu thức số lượng. 82 v1.0
Bài 4: Phân tích hồi quy và tương quan
CÂU HỎI ÔN TẬP
1. Thế nào là liên hệ hàm số và liên hệ tương quan?
2. Nêu nhiệm vụ của phân tích hồi quy và tương quan. 3. Nêu ý nghĩa c a h ủ ệ s ố tự do và hệ s
ố hồi quy trong mô hình hồi quy tuyến tính giữa hai tiêu thức số lượng.
4. Trình bày tác dụng và tính chất của hệ s t ố ương quan.
5. Trình bày tác dụng và tính chất của tỷ s t ố ương quan. v1.0 83
Bài 4: Phân tích hồi quy và tương quan BÀI TẬP
1. Có tài liệu về chi tiêu cho nghiên cứu và phát triển (R&D) và lợi nhuận thu được hàng năm
của một doanh nghiệp như sau: Năm
Chi cho R&D (tỷ đồng)
Lợi nhuận hàng năm (tỷ đồng) 2003 2 20 2004 3 25 2005 5 34 2006 4 30 2007 11 40 2008 5 31
a) Hãy xác định trong hai chỉ tiêu trên, đâu là tiêu thức nguyên nhân, đâu là tiêu thức kết quả. Giải thích.
b) Trình bày bằng đồ thị mối liên hệ giữa chi cho R&D và lợi nhuận hàng năm của doanh
nghiệp trên và cho nhận xét.
c) Xây dựng phương trình hồi quy tuyến tính đơn biểu diễn mối liên hệ giữa chi cho R&D
và lợi nhuận hàng năm của doanh nghiệp trên. Giải thích ý nghĩa của các tham số.
d) Đánh giá trình độ chặt chẽ của mối liên hệ.
2. Một nhà kinh tế đang quan tâm đến mối quan hệ giữa thu nhập khả dụng và chi cho lương
thực thực phẩm hàng năm của các hộ gia đình ở nông thôn nước ta. Để nghiên cứu ông ta
tiến hành hỏi ngẫu nhiên 8 h gia ộ
đình có cùng quy mô hộ (cha, mẹ và 2 con) và có mức thu
nhập trung bình. Kết quả như sau:
Thu nhập khả dụng
Chi cho lương thực thực phẩm
(triệu đồng)
(triệu đồng) 30 5,5 36 6,0 27 4,2 20 4,0 16 3,7 24 2,6 19 3,9 25 4,3
a) Vẽ đồ thị biểu diễn mối liên hệ giữa thu nhập khả dụng và chi cho lương thực thực phẩm của các hộ trên.
b) Xác định phương trình hồi quy biểu diễn mỗi liên hệ đó. Giải thích ý nghĩa của các tham số. c) Sử ụ
d ng phương trình hồi quy để dự đoán chi cho lương thực thực phẩm hàng năm của hộ
gia đình có mức thu nhập khả dụng là 25 triệu ng. đồ 84 v1.0
Bài 4: Phân tích hồi quy và tương quan
3. Có kết quả điều tra một mẫu gồm 8 sinh viên về thời gian tự học trong hai tuần và điểm kiểm
tra môn học đó sau hai tuần như sau:
Thời gian tự học (giờ)
Điểm kiểm tra 10 9,2 15 8,1 12 8,4 20 7,4 8 8,5 16 8,0 14 8,4 22 8,0
a) Xây dựng phương trình hồi quy tuyến tính đơn biểu diễn mối liên hệ giữa thời gian tự h c ọ
và điểm kiểm tra của các sinh viên trong mẫu nói trên. Giải thích ý nghĩa của các tham số.
b) Đánh giá trình độ chặt chẽ của mối liên hệ trên.
c) Hãy cho biết phương trình vừa xây dựng được có phù hợp để giải thích mối liên hệ giữa hai biến trên không?
4. Có tài liệu về chiều cao và cân nặng của 11 phụ nữ trong độ tuổi 18 – 24 được lựa chọn ngẫu nhiêu như sau:
Cân nặng (kg)
Chiều cao (cm) 65 175 67 133 71 185 71 163 66 126 75 198 67 153 70 163 71 159 69 151 69 155
a) Khi chiều cao tăng thêm 1 cm thì cân nặng thay đổi như thế nào.
b) Đánh giá trình độ chặt chẽ giữa cân nặng và chiều cao của nhóm người trên.
5. Có số liệu về giá trị sản xuất và lượ ệ
ng nhiên li u tiêu thụ ở các phân xưởng của một nhà máy như sau: Phân xưởng
Giá trị sản xuất
Nhiên liệu tiêu thụ
(triệu đồng)
(triệu đồng) A 520 23 B 595 20 C 945 25 D 640 19 E 500 10 G 720 18 v1.0 85
Bài 4: Phân tích hồi quy và tương quan
a) Xây dựng phương trình hồi quy tuyến tính đơn biểu diễn ảnh hưởng của giá trị sản xuất
tới lượng nhiên liệu tiêu thụ. Giải thích ý nghĩa các tham số. b) Liệu có đầy
đủ bằng chứng để kết luận rằng hệ s
ố hồi quy trong phương trình nói trên là
khác 0 và vì vậy có thể sử dụng giá trị sản xuất để dự đoán lượng nhiêu liệu tiêu th hay ụ
không? Hãy thực hiện kiểm định giả thiết cần thiết với mức ý nghĩa 5%.
6. Công ty Coca Cola đang nghiên cứu ảnh hưởng của chiến dịch quảng cáo gần nhất. Họ tiến
hành phỏng vấn ngẫu nhiên 10 người để biết xem những người này đã đọc hay xem quảng cáo
của hãng bao nhiêu lần và số lon Coca Cola mà họ đã mua trong tuần qua. Kết quả như sau:
Số lần xem hay đọc quảng cáo
Số lon đã mua 4 12 9 14 3 7 0 6 1 3 6 5 2 5 5 10
a) Hãy xây dựng phương trình hồi quy tuyến tính đơn biểu diễn mối liên hệ giữa hai biến trên.
b) Đánh giá trình độ chặt chẽ của mối liên hệ.
c) Với kết quả điều tra ở trên, có thể kết luận rằng số quảng cáo ã
đ đọc hay xem có mối liên
hệ tương quan tuyến tính thuận với số lon Coca Cola đã mua hay không? Hãy thực hiện
kiểm định giả thiết với mức ý nghĩa 0,05.
7. Có số liệu về độ tuổi và nhịp tim của một mẫu gồm 10 người được chọ ẫ n ng u nhiên như sau: Tuổi
Nhịp tim (lần) 30 186 38 183 41 171 38 177 29 191 39 177 46 175 41 176 42 171 24 196
a) Giữa hai biến trên liệu có mối liên hệ với nhau không? Nếu có, hãy xác định đâu là
nguyên nhân, đâu là kết quả.
b) Khi tăng thêm 1 tuổi thì nhịp tim sẽ thay đổi thế nào?
c) Có thể dùng tuổi để dự đoán nhịp tim của m t ng ộ
ười hay không? Với mức ý nghĩa 0,05, hãy giải thích tại sao? 86 v1.0
Bài 4: Phân tích hồi quy và tương quan
8. Một nghiên cứu của cơ quan giao thông ở Atlanta về ảnh hưởng của giá vé xe buýt đến số
lượng hành khách thu được kết quả như sau: Giá vé (Cents)
Số hành khách trên 100 dặm 15 440 20 430 25 430 30 370 35 360 40 340 45 350 50 350
a) Vẽ đồ thị biểu diễn mối liên hệ trên.
b) Xây dựng phương trình hồi quy biểu diễn mối liên hệ trên.
c) Với mức ý nghĩa 5%, có thể kết luận rằng, giữa giá vé xe buýt và số lượng hành khách có
mối liên hệ tương quan tuyến tính âm hay không?
9. Để dự đoán về những chi phí quản lý phải trả dựa trên s ố lượng sả ẩ n ph m sản xuất ra, một
nhà quản lý đã thu thập thông tin ở các đơn vị khác nhau và thu được kết quả sau:
Chi phí quản lý phải trả (triệu đồng)
Số lượng sản phẩm 191 40 170 42 272 53 155 35 280 56 173 39 234 48 116 30 153 37 178 40
a) Xây dựng phương trình hồi quy biểu diễn mối liên hệ trên.
b) Dự đoán chi phí quản lý phải trả khi có 50 sản phẩm được sả ấ n xu t ra.
c) Tính sai số tiêu chuẩn của mô hình dự đ oán trên.
10. Liệu có phải có điểm cao khi học thì ra trường sẽ có việc làm với mức lương cao hơn? Một
sinh viên thống kê doanh nghiệ đ p ã thực hiệ đ
n iều tra ngẫu nhiên một mẫu gồm một số người v1.0 87
Bài 4: Phân tích hồi quy và tương quan
bạn mới tốt nghiệp của anh ta về mức lương khởi điểm và điểm trung bình khi học đại học
của họ. Kết quả như sau:
Mức lương khởi điểm (triệu đồng)
Điểm trung bình học đại học 3,1 7,0 2,5 6,0 2,5 6,5 1,9 5,0 2,2 6,0 2,8 6,5 1,6 5,5 2,2 5,5
a) Vẽ đường hồi quy thực nghiệm và đường hồi quy lý thuyết biểu diễn mố ệ i liên h trên.
b) Đánh giá trình độ chặt chẽ của mối liên hệ trên.
c) Dự đoán mức lương khởi điểm cho sinh viên có điểm trung bình khi học đại học là 8,0.
d) Tính sai số tiêu chuẩn của mô hình dự đoán trên. 88 v1.0