Bài 4: Tổng Quan Về Xác Suất & Định Lý Giới Hạn Trung Tâm môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

Bài 4 TỔNG QUAN VỀ XÁC SUẤT
VÀ ĐỊNH LÝ GIỚI HẠN TRUNG TÂM 1 NỘI DUNG CHÍNH 4.1 4.2 Tổng Định lý quan về giới hạn xác suất trung tâm 2 1 2025-05-12
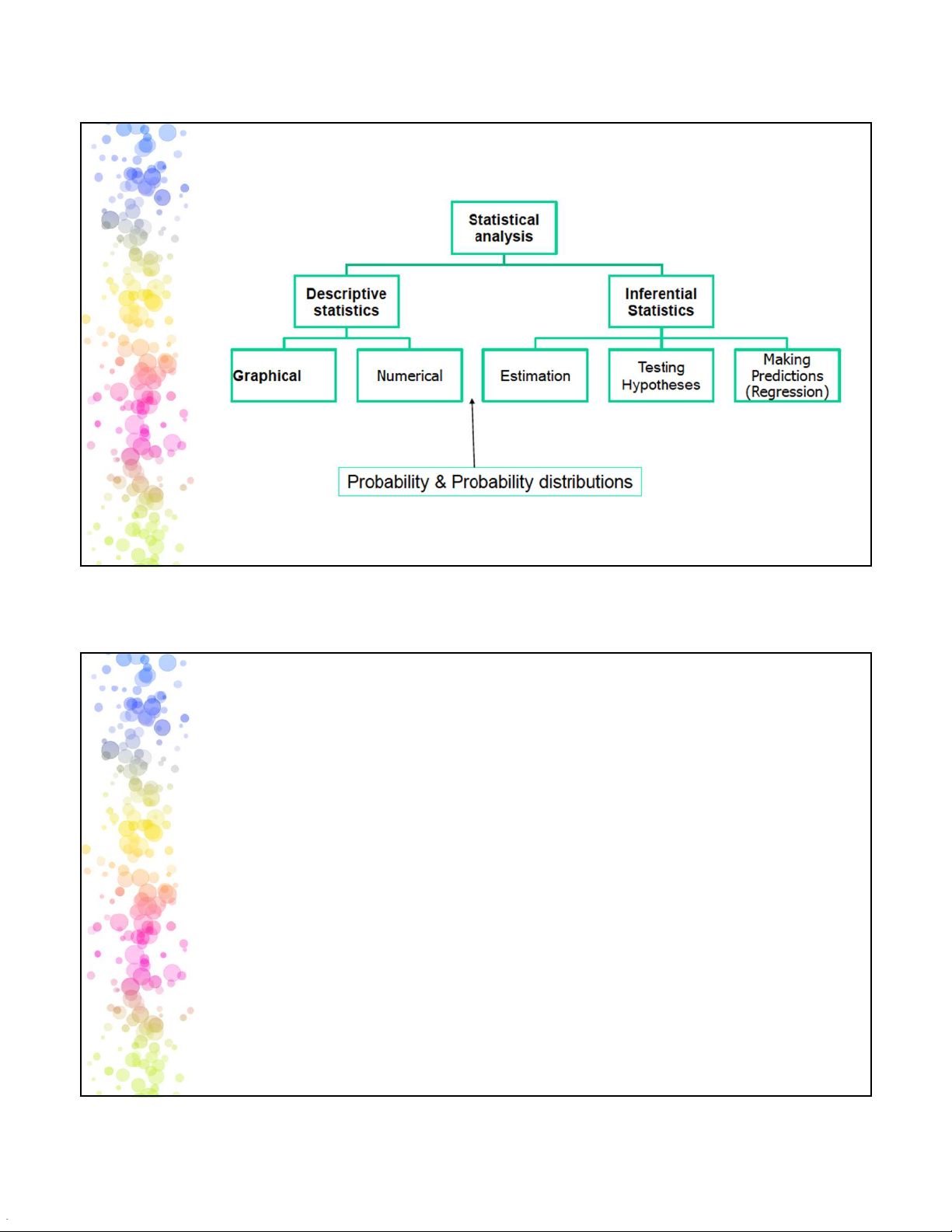
4.1. Tổng quan về xác suất 4.1.1
Khái niệm về xác suất và biến ngẫu nhiên 4.1.2
Phân phối xác suất của biến ngẫu nhiên liên tục 3 Xác suất là gì
Xác suất là khả năng tương đối một biến cố có thể xảy ra
•Giá trị nằm trong khoảng [0, 1]
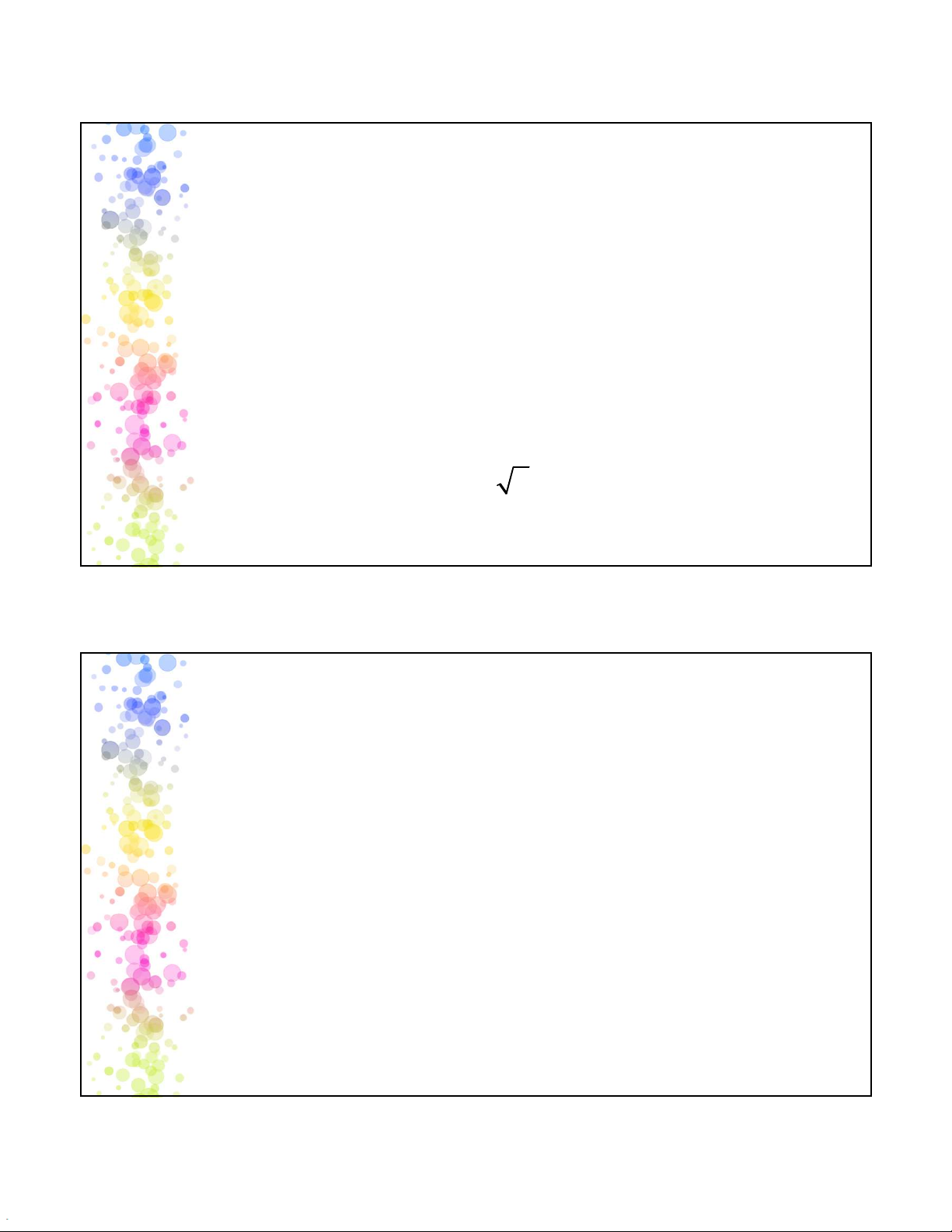
•Công thức tính: 𝑃𝐴 =
ố ườ ợ ậ ợ
ổ ố ườ ợ
VD: Trong 1 ngày, một siêu thị có 100 khách hàng, trong đó có 30 người mua
sản phẩm A. Tính xác suất một khách được chọn ngẫu nhiên mua sản phẩm A 𝑃𝐴 = 30 100 = 0.3 hay 30% 4 2 2025-05-12
Tại sao chúng ta cần học xác suất và phân phối xác suất? 5
Biến ngẫu nhiên và Xác suất
• X là biến ngẫu nhiên nếu giá trị của X=x là hoàn toàn ngẫu nhiên.
• Xác suất để X nhận giá trị xlà p(x)=P(X=x).
• Nếu một biến ngẫu X nhận giá trị x , khi đó i 1. 0  p  x x i  1 for all i 2. 1 p x   i  i x 6 3 2025-05-12 PHÂN PHỐI CHUẨN
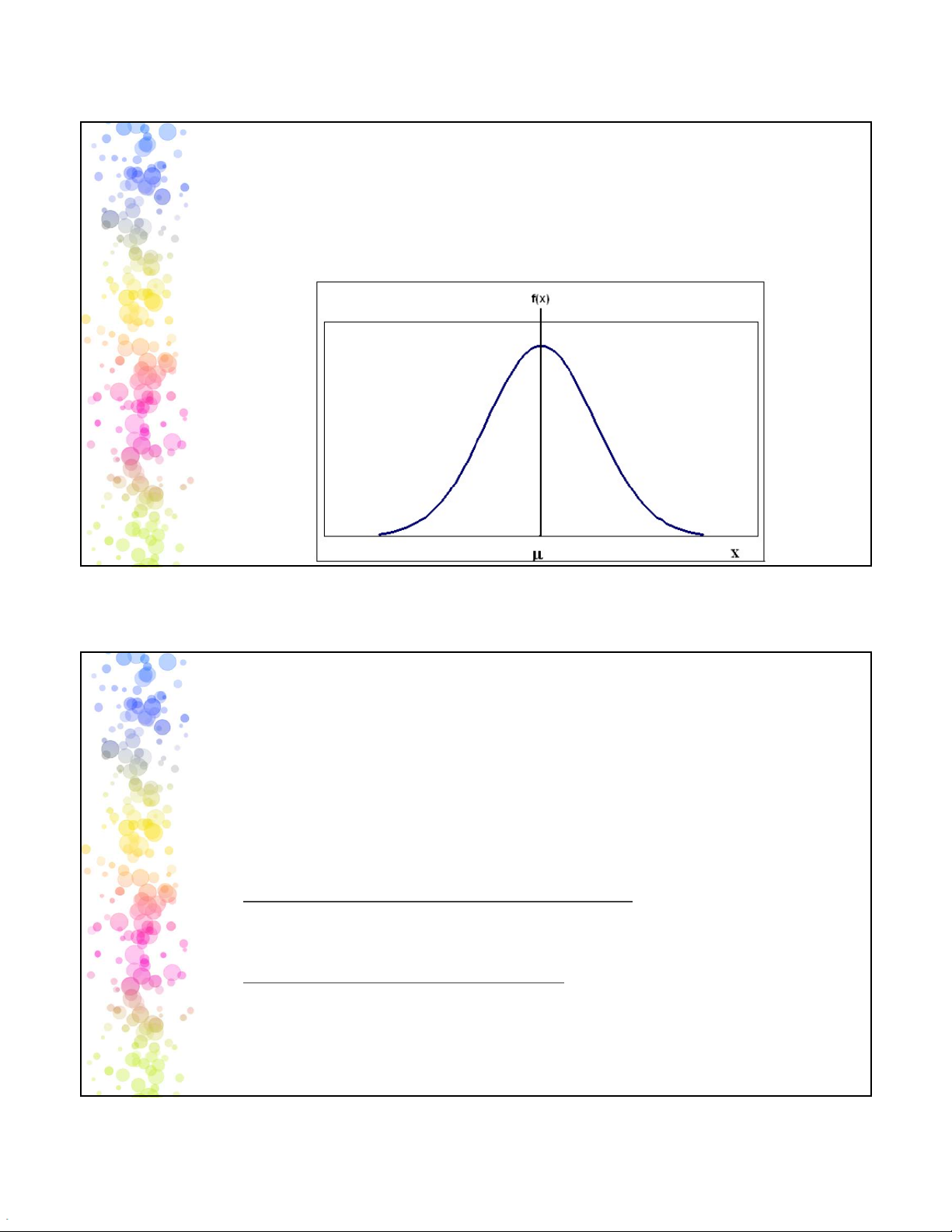
• Dạng hình chuông, đối xứng qua giá trị trung
tâm µ, có đỉnh tại x=µ
• đồ thị tiệm cận 0 khi x→±∞. 7 TÍNH CHẤT 1. E(X) = µ; V(X) = σ².
2. Diện tích dưới đường cong = 1 3. Kí hiệu: X~N(µ, σ²).
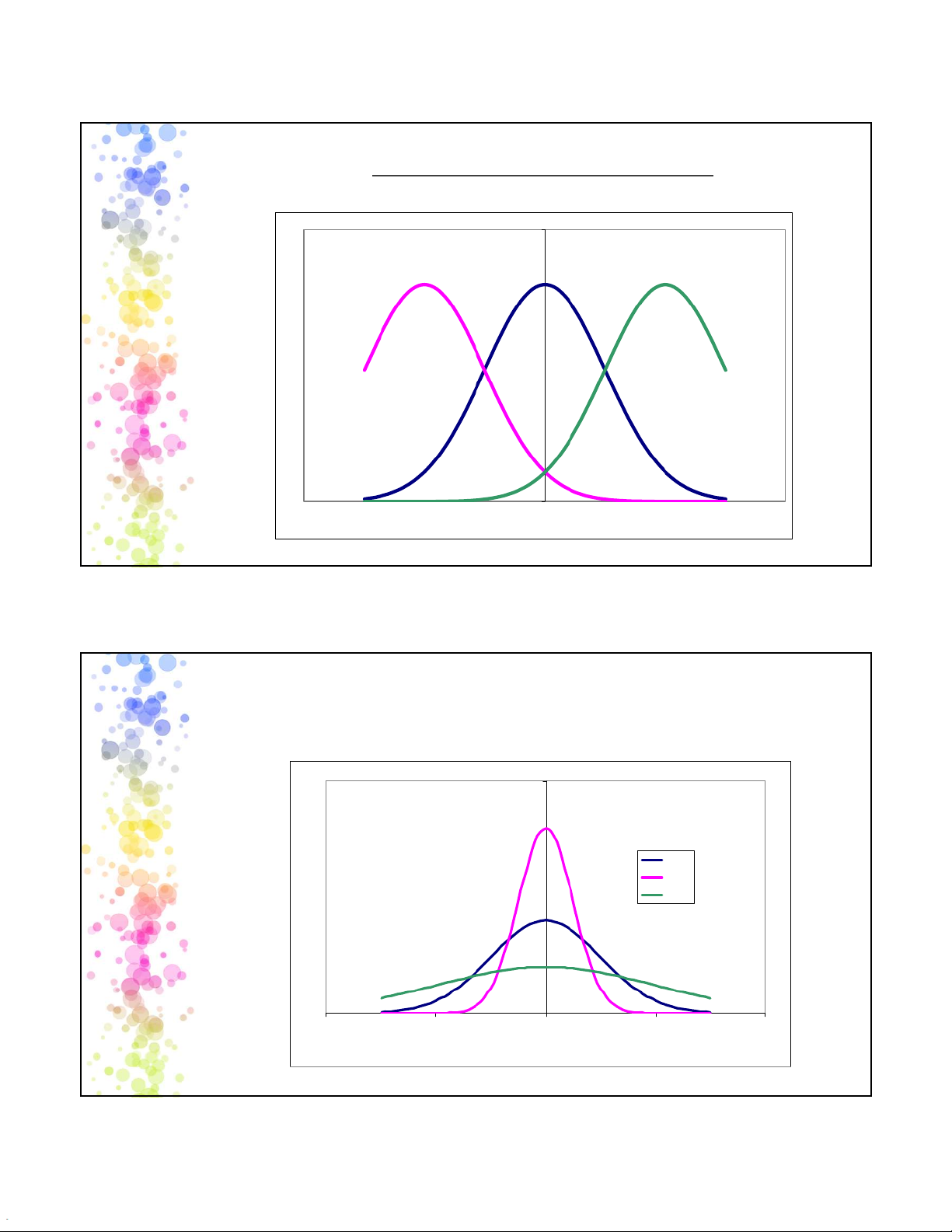
4. Giá trị trung bình khác nhau – vị trí thay đổi dọc theo trục x
5. Phương sai khác nhau – đồ thị nhọn hoặc thoải 8 4 2025-05-12 Giá trị TB khác nhau 0.5 f(x) 0 x 9 Phương sai khác nhau 1 σ=1 σ=0.5 σ=2 f(x) 0 -4 -2 0 2 4 x 10 5 2025-05-12 Tính xác suất từ PPC •
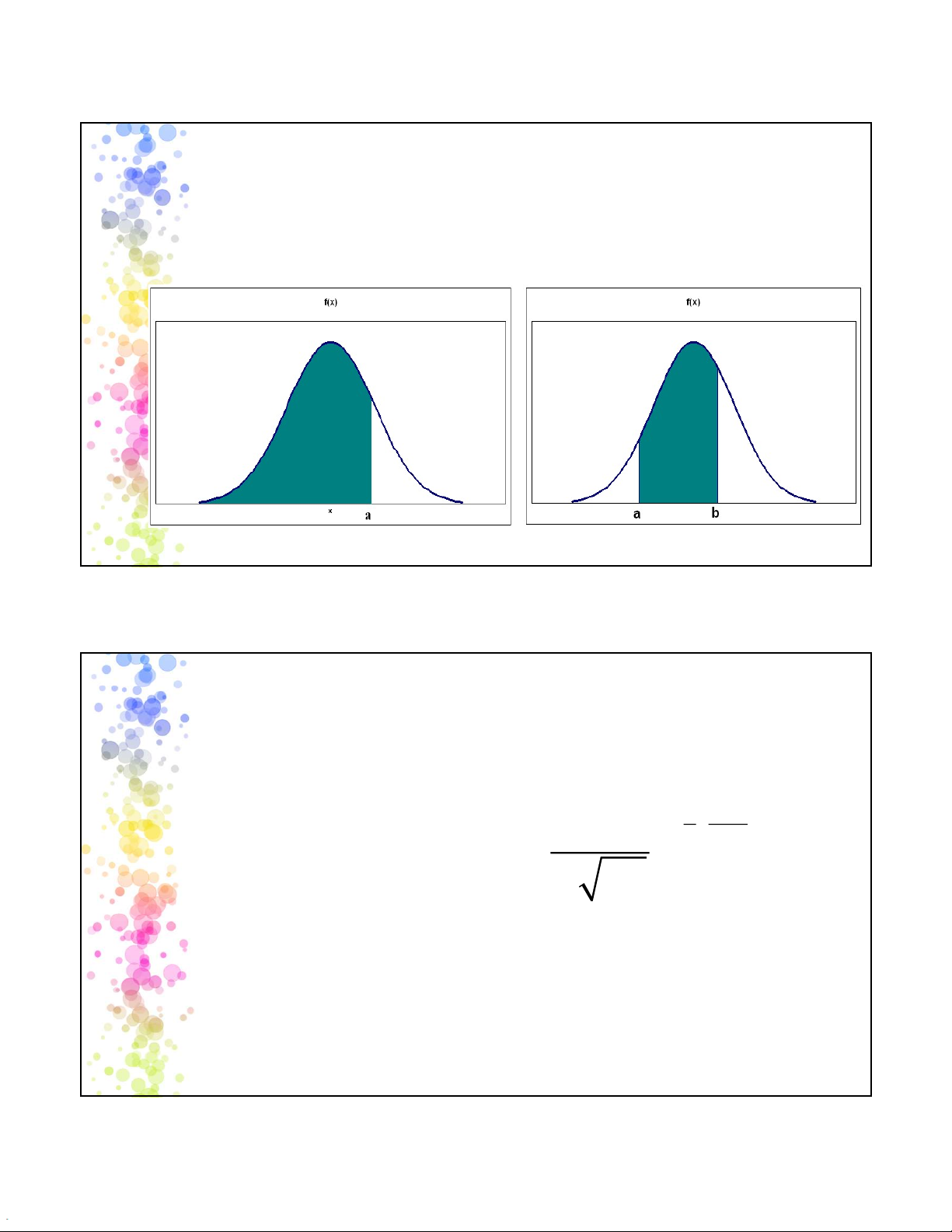
Tính P(X• Hoặc tính P(a11
Có nghĩa là cần tính diện tích dưới đường cong
• Toán học, cần lấy tích phân : 2 b b -1 æç x ö -m dx 1 2è s ø÷ DT = f x ò   e dx ò . a s 2p a • Không dễ! 12 6 2025-05-12 Chuẩn hóa (1)
• Là quá trình chuyển một biến phân phối chuẩn về phân phối chuẩn hóa
• Nếu X~N(μ,σ²), sử dụng công thức dưới đây để chuẩn hóa: X - m Z N  ~ (0,1) s
Sử dụng bảng Z để tra X/S 13 Quy tắc tính xác suất • Quy tắc đối xứng P(Z<-a) = P(Z>a)
P(Z>a) = 1 – P(Z• P(a14 7 2025-05-12 Quy tắc 3 sigma
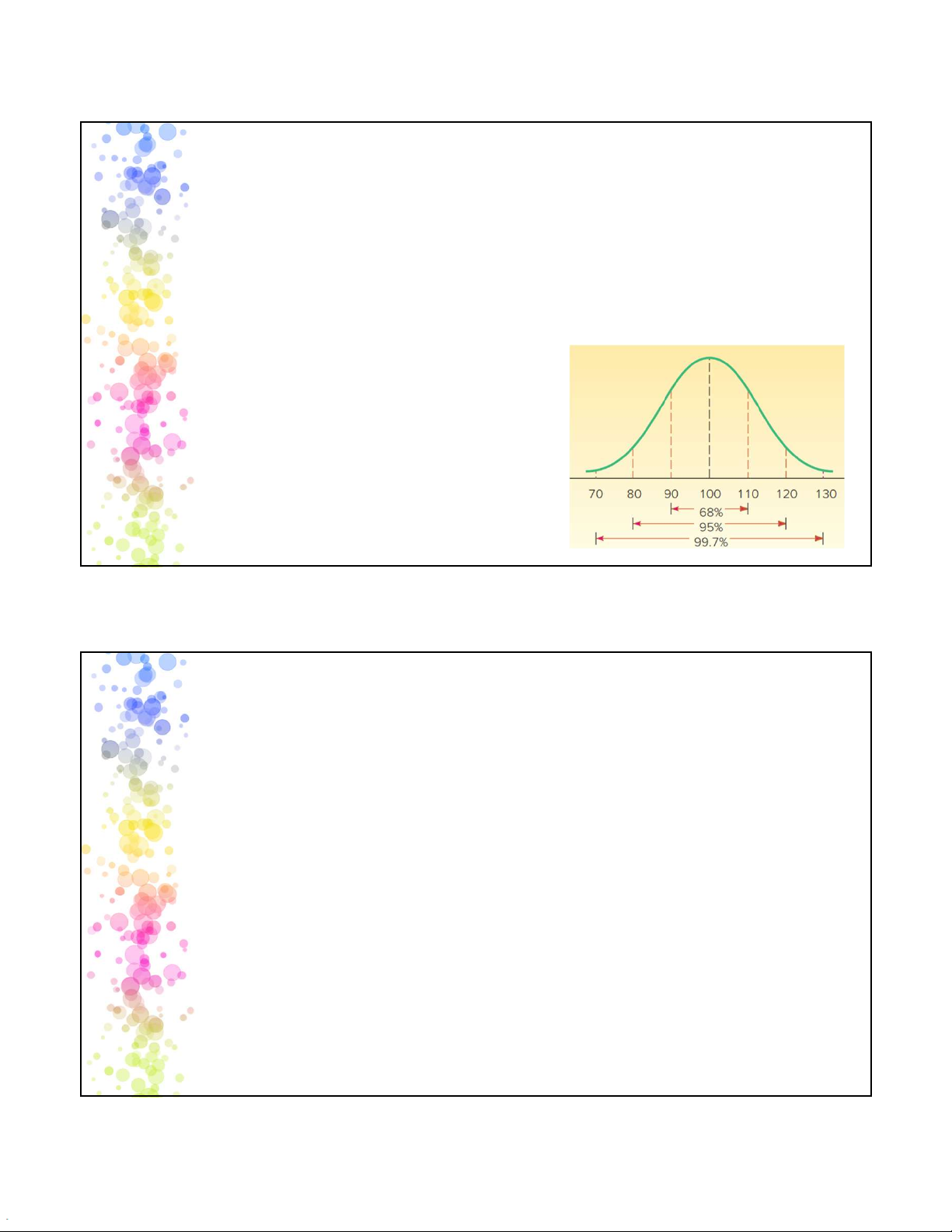
Đối với phân phối chuẩn:
Khoảng 68.26% các quan sát nằm trong phạm vi (+) và (-) 1 lần độ lệch chuẩn so với trung bình
Khoảng 95.44% các quan sát nằm trong phạm vi (+) và (-) 2 lần độ lệch chuẩn so với trung bình
Khoảng 99.74% các quan sát nằm trong
khoảng (+) và (-) 3 lần độ lệch chuẩn so với trung bình 15 Bài tập áp dụng
Tính xác suất dựa vào Quy tắc 3 Sigma: Bài 9, 10, 11, 12 (trang 219) Tính Z và xác suất:
Bài 13, 14, 15, 16 (trang 223) Bài 17 – 22 (trang 225) Bài 23 – 30 (trang 228) 16 8 2025-05-12
4.2. ĐỊNH LÝ GIỚI HẠN TRUNG TÂM Phân phối của mẫu
Phân phối của trung bình mẫu
Định lý giới hạn trung tâm 17 PHÂN PHỐI CỦA MẪU
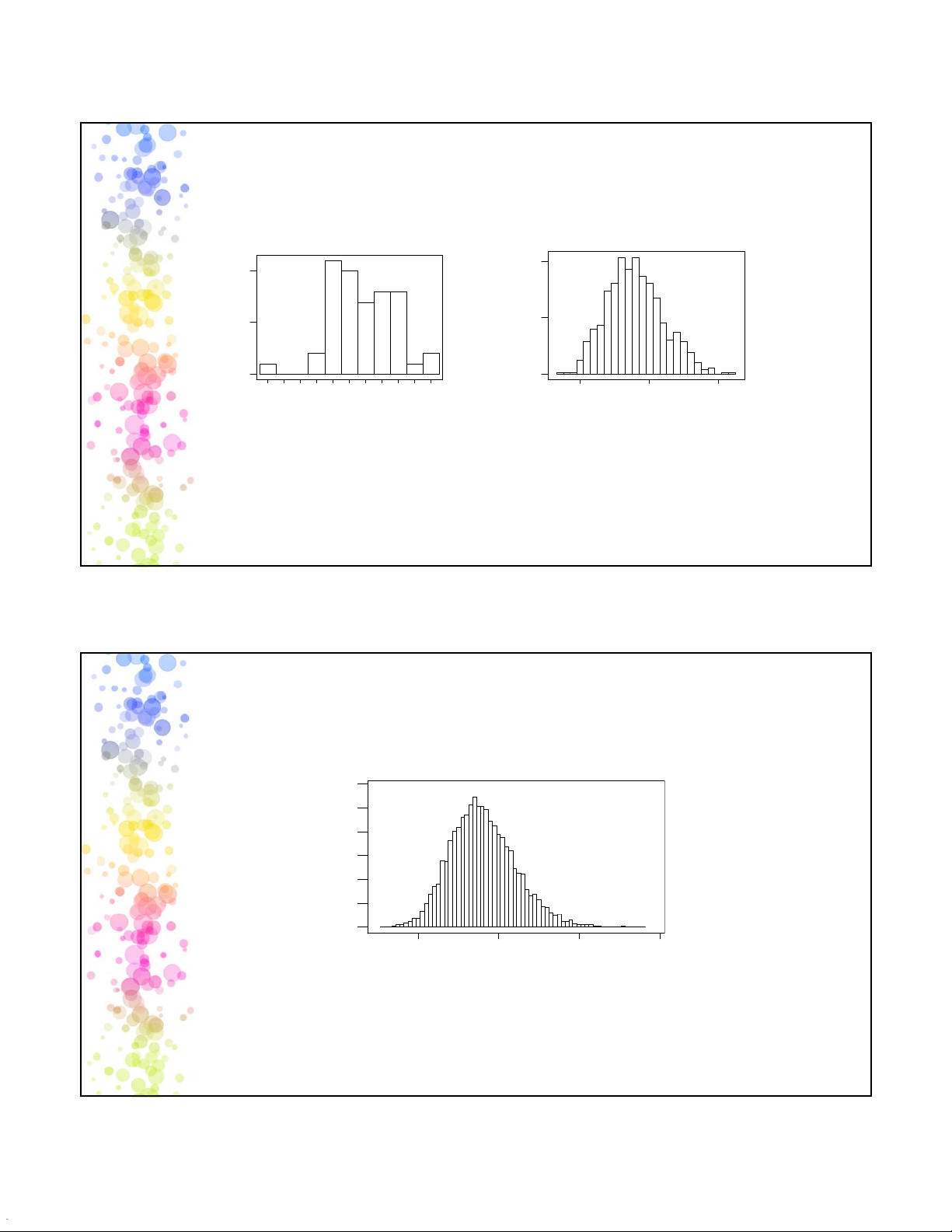
• Lấy một mẫu gồm 50 quan sát (obs) từ dữ liệu thống kê về
thời gian giao Pizza, có đồ thị và thống kê mô tả cho dưới đây 10 5 Frequency 0 10 12 14 16 18 20 22 24 26 Pizza time Variable N Mean Median SD
Pizza time 50 17.256 17.041 3.743 18 9 2025-05-12
Một mẫu 50 obs khác; 1000 obs cũng từ tổng thể trên 100 10 5 50 Frequency Frequency 0 0 6 8 10 12 14 16 18 20 22 24 26 10 20 30 Pizza time Pizza time Variable N Mean Median SD
Pizza time 50 17.585 17.374 3.872
Pizza time 1000 17.934 17.627 4.009 19
Tăng cỡ mẫu lên đến 10,000 obs từ tổng thể đó 600 500 400 300 Fr 2 eq0 u0 ency 100 0 10 20 30 40 Pizza time Variable N Mean Median SD
Pizza time 10000 18.046 17.744 4.006
Khi cỡ mẫu tăng lên (đặc biệt tăng đến vô hạn và tiệm cận với quy mô
của tổng thể), phân phối của mẫu sẽ tiệm cận về phân phối chuẩn. 20 10 2025-05-12
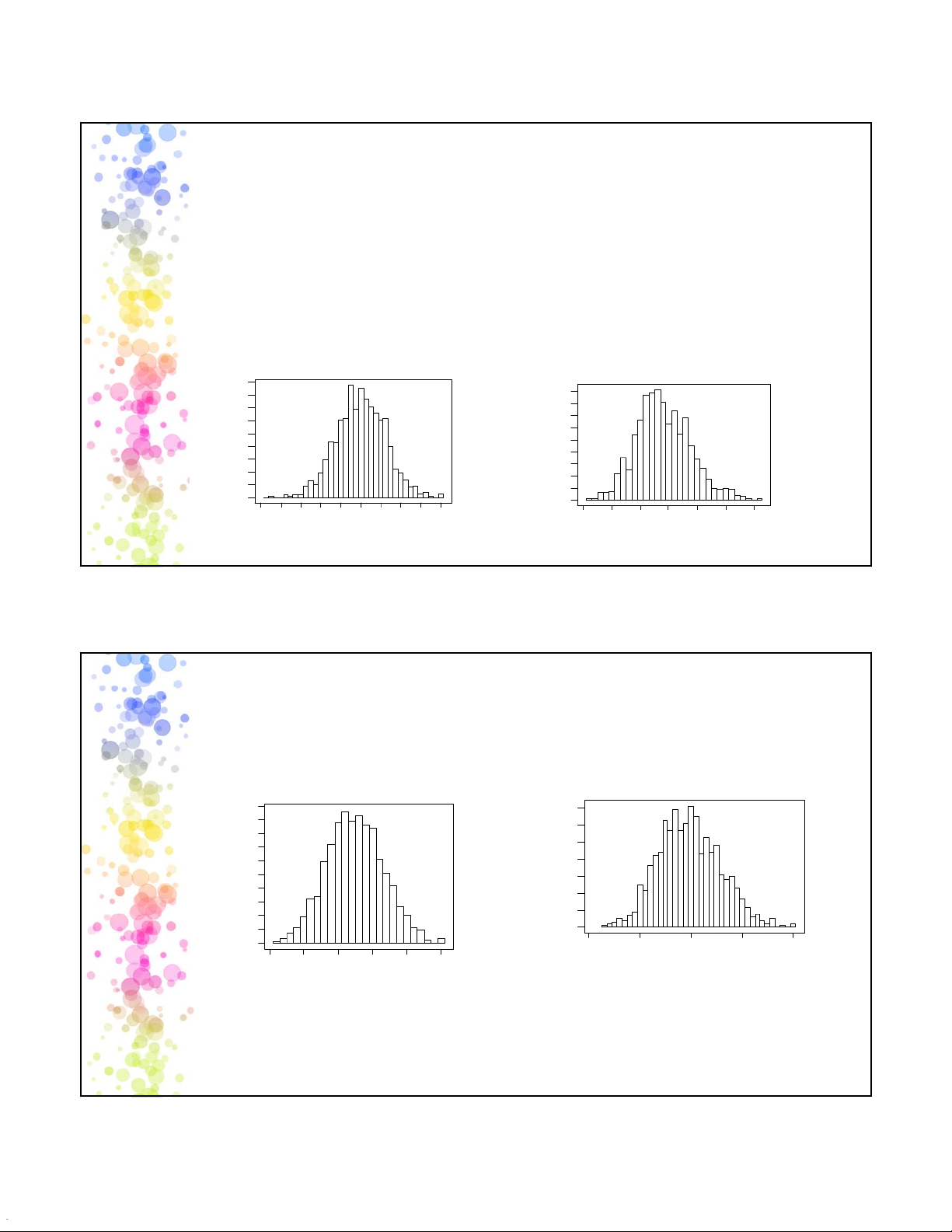
PHÂN PHỐI CỦA CÁC TRUNG BÌNH MẪU
• Lấy 1000 mẫu khác nhau, mỗi mẫu gồm 10 quan sát. Tính
trung bình và độ lệch chuẩn của mỗi mẫu rồi biểu diễn ở đồ thị dưới đây. Thống kê N Mean SD Trung bình chung các mẫu 1000 18.007 1.231 S.D chung các mẫu 1000 3.8183 0.9505 90 80 90 70 80 70 60 60 50 50 40 40 30 Frequency Fr30 equency 20 20 10 10 0 0 13 14 15 16 17 18 19 20 21 22 1 2 3 4 5 6 7 average stdev 21 Tăng cỡ mẫu
• Lấy 1000 mẫu khác với cỡ mẫu 25 100 70 90 60 80 70 50 60 40 50 30 40 Frequency Fre 20 30 quency 10 20 10 0 0 2 3 4 5 6 15.5 16.5 17.5 18.5 19.5 20.5 stdev average Thống kê N Mean SD TB chung các mẫu 1000 17.991 0.814 S.D chung các mẫu 1000 3.964 0.605 22 11 2025-05-12 NHẬN XÉT
• Bất kể biến ngẫu nhiên ban đầu có dạng phân
phối như thế nào, khi cỡ mẫu tăng lên phân
phối của các trung bình mẫu tiệm cận về phân phối chuẩn. Và
• Bất kể biến ngẫu nhiên ban đầu có dạng phân
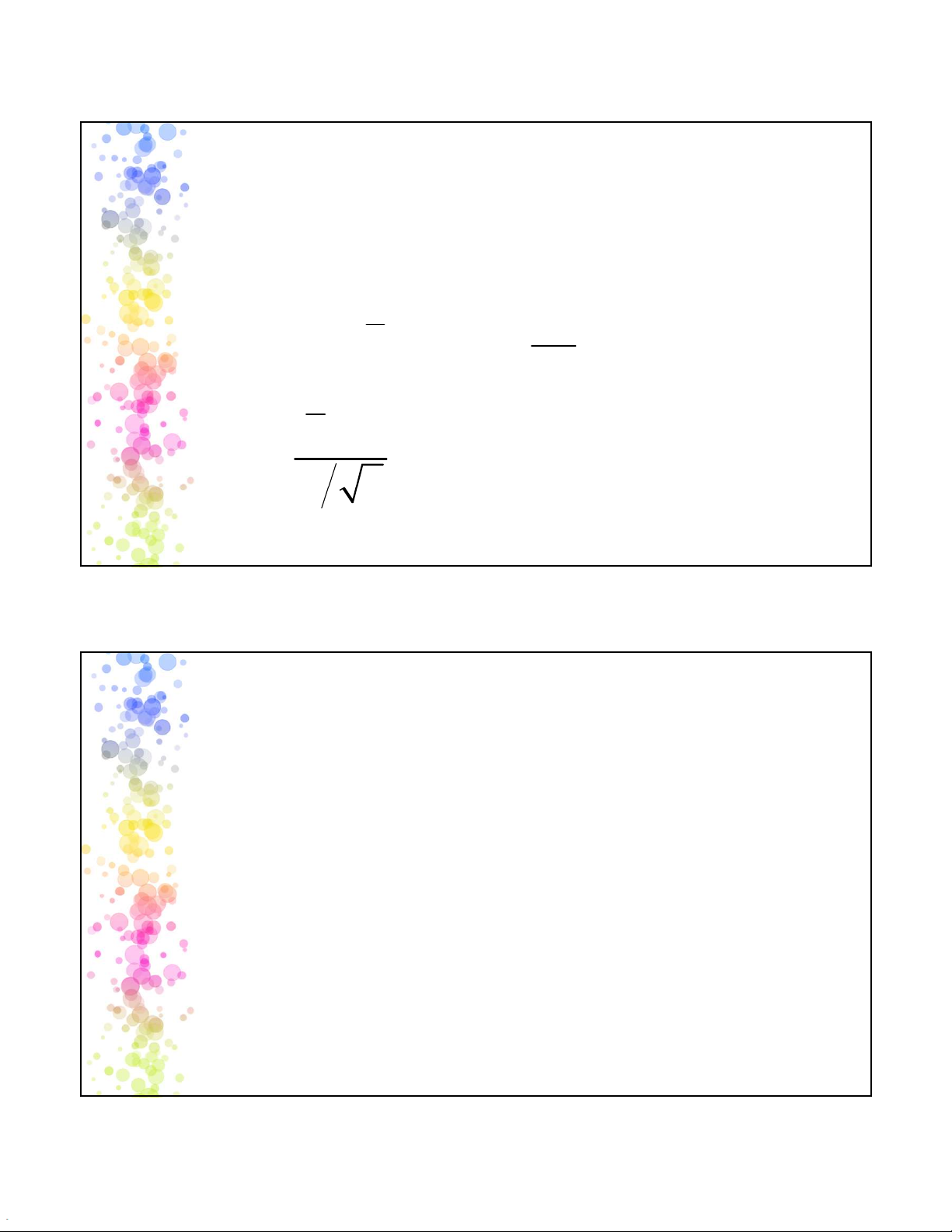
phối như thế nào, với một cỡ mẫu n, độ lệch
chuẩn của các trung bình mẫu (sai số bình quân
chọn mẫu) bằng s / n , kí hiệu là SE (Standard error of the mean). 23 Ý NGHĨA
Bất kể tổng thể có phân phối thế nào (chuẩn hay
không chuẩn), khi cỡ mẫu đủ lớn phân phối của
các trung bình mẫu sẽ tuân theo quy luật phân
phối chuẩn và chúng ta có thể sử dụng thống kê Z
để tính xác suất cho bất kỳ giá trị trung bình nào 24 12 2025-05-12
Định lý giới hạn trung tâm
• Nếu Xlà một biến ngẫu nhiên có giá trị trung
bình là µ và phương sai là σ², thì 2 æ ö s X N ç ÷ nm, è ø XZ N - m  ~ n   0,1 as  .  s n 25
Cỡ mẫu như thế nào là đủ lớn?
• Nếu tổng thể có phân phối chuẩn, quy mô mẫu có thể nhận bất kỳ giá trị nào.
• Nếu không biết hình dạng phân phối của tổng thể, quy mô mẫu
rất quan trọng. Phân phối của các trung bình mẫu sẽ tiệm cận về
phân phối chuẩn khi cỡ mẫu tăng lên vô hạn. Trên thực tế, phân
phối của các trung bình mẫu sẽ gần giống với phân phối chuẩn
khi cỡ mẫu ít nhất là 30 đơn vị.
• Xác định cỡ mẫu đề cập ở bài 5. 26 13 2025-05-12 Thank you! 27 14