Bài 5: Ước Lượng Và Kiểm Định Giả Thuyết Thống Kê môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

2025-05-12 BÀI 5 ƯỚC LƯỢNG VÀ
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 1 NỘI DUNG CHÍNH 1. Những vấn đề chung
2. Ước lượng kết quả Điều tra chọn mẫu
3. Kiểm định giả thuyết thống kê 2 1 2025-05-12
1. NHỮNG VẤN ĐỀ CHUNG (1) Điều tra chọn mẫu
- Là một loại điều tra không toàn bộ
- Chọn ra từ tổng thể chung một số đơn vị theo những nguyên tắc nhất định
- Kết quả của ĐTCM được sử dụng để tính toán và suy rộng cho
kết quả của tổng thể chung 3
1. NHỮNG VẤN ĐỀ CHUNG (2) Ưu điểm
Tiết kiệm chi phí, nhân lực, thời gian
Mở rộng nội dung điều tra
Tài liệu có độ chính xác cao Tổ chức đơn giản Hạn chế
Không cho biết thông tin đầy đủ về tổng thể Sai số khi suy rộng
Kết quả điều tra không thể tiến hành phân tổ theo mọi phạm vi nghiên cứu 4 2 2025-05-12
1. NHỮNG VẤN ĐỀ CHUNG (3)
Trường hợp vận dụng
Thay thế cho điều tra toàn bộ
Kết hợp với điều tra toàn bộ
Kiểm định giả thuyết thống kê 5
1. NHỮNG VẤN ĐỀ CHUNG (4) Chỉ tiêu Tổng thể chung Tổng thể mẫu Quy mô N n Tham số ’  Số bình quân 𝜇 𝑥 Tỷ lệ theo một p f hoặc 𝜋 tiêu thức S2 𝜎 Phương sai f(1 – f) p(1 – p) hoặc 𝜋(1-𝜋) 6 3
1. NHỮNG VẤN ĐỀ CHUNG (5)
Công thức tính Phương sai
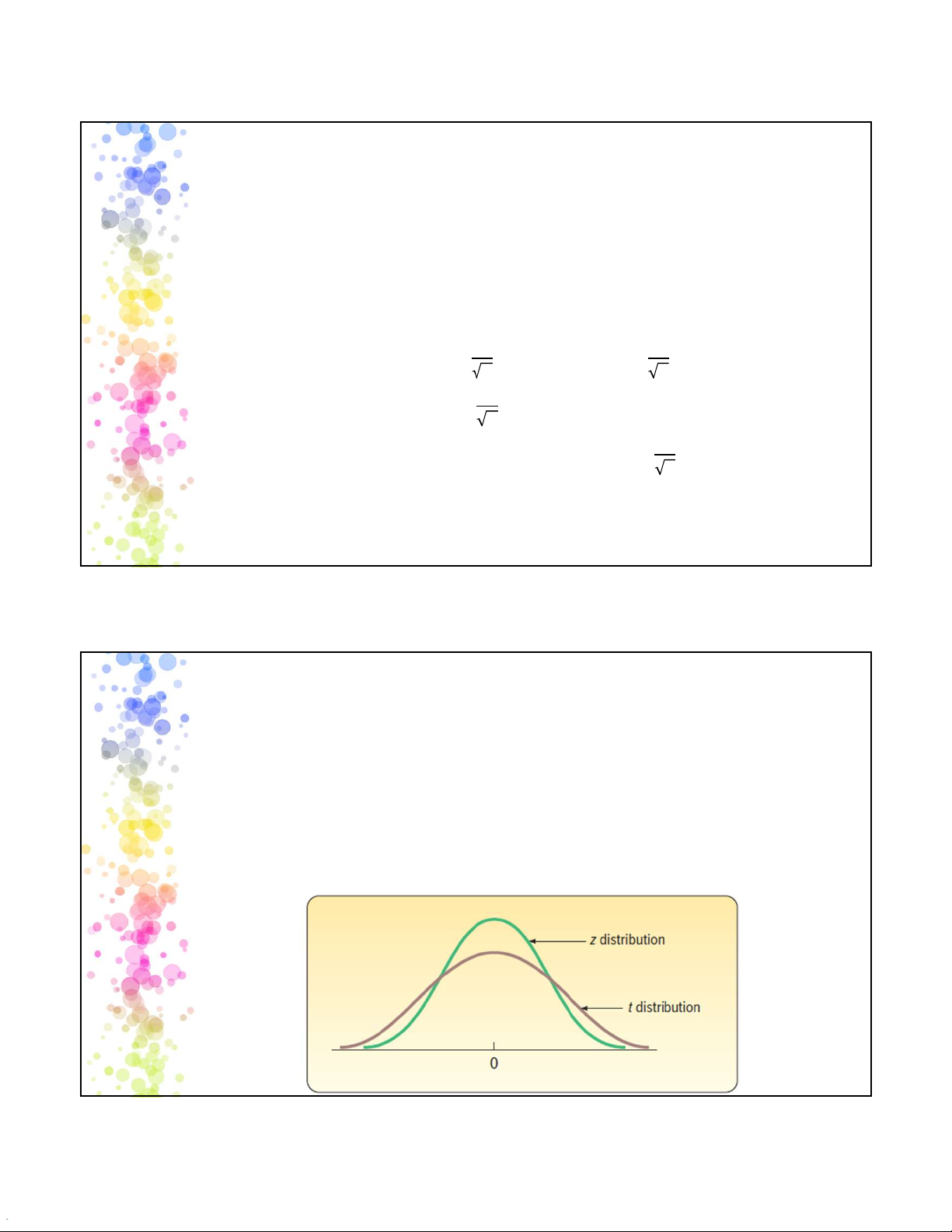
trong trường hợp Ước lượng số bình quân Trường hợp Tổng thể chung Tổng thể mẫu =∑𝑥 =∑𝑥 𝑁−∑𝑥−𝜇 − 𝑥 𝜎  𝑆   =∑𝑥 𝑁  =∑𝑥  𝑛 − 1 Giản đơn 𝜎   𝑆 − 𝑛𝑥    =∑  𝑥  =∑𝑥  𝑁 𝑛 − 1 𝜎 − 𝜇 𝑓  𝑆 − 𝑥 𝑓     =∑𝑥 ∑ − 𝑓 ∑𝑥    =∑𝑥 ∑𝑓 − 1   Gia quyền 𝑓 𝑓 −∑𝑓 𝜎   𝑆 𝑓 𝑥      ∑𝑓   ∑𝑓     ∑𝑓 − 1    𝑓 = 𝑁 𝑓 = 𝑛 Lưu ý:   𝑖 = 1, 𝐾 𝑖 = 1, 𝑘 7
1. NHỮNG VẤN ĐỀ CHUNG (8) Phương pháp chọn mẫu Phương pháp chọn Phương pháp chọn Hoàn lại Không hoàn lại
• Quy mô tổng thể chung không • Quy mô tổng = t 𝑁h!ể chung giảm
thay đổi trong quá trình chọn mẫu
dần trong quá trình chọn mẫu
• Số mẫu có thể thiết lập:
• Số mẫu có thể thiết lập: 𝑘 = 𝐶 k = Nn  𝑛! (𝑁 − 𝑛)!  8 4 2025-05-12 NỘI DUNG CHÍNH
1. Những vấn đề chung về Điều tra chọn mẫu
2. Cơ sở ước lượng và kiểm định
3. Ước lượng kết quả Điều tra chọn mẫu
4. Kiểm định giả thuyết thống kê 9
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA
ƯỚC LƯỢNG BẰNG KHOẢNG TIN CẬY là khoảng giá trị
được xác định từ thống kê mẫu mà với xác suất cụ thể, tham số của
tổng thể sẽ thuộc khoảng đó. 10 5 2025-05-12
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA Công thức tổng quát 𝜃 = 𝜃′ ± 𝜀
𝜃Tham số của tổng thể chung (parameters) 𝜃’ Thống kê mẫu (statistics)
𝜀Phạm vi sai số chọn mẫu 11
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA
Nguyên nhân sai số trong ĐTCM
•Vi phạm nguyên tắc chọn mẫu
•Số lượng đơn vị mẫu không đủ lớn
•Kết cấu tổng thể mẫu khác với kết cấu tổng thể chung
•Sai số do đăng ký, ghi chép 12 6 2025-05-12
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA 𝒏𝟐
- Theo định lý giới hạn trung tâm: X ~ N(𝝁, 𝝈𝟐), thì 𝒙 ~ 𝑵 𝝁, 𝝈
Thống kê 𝑍 =  / ~ N(0, 1) P  Z    9 , 1 6  9 , 1  6 9 , 0 5 13
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA
Ước lượng số bình quân Với mức ý nghĩa 
(1 - ) là xác suất hay trình độ tin cậy
Khi biết phương sai Tổng thể chung (hoặc chưa biết phương sai tổng
thể chung và mẫu lớn - n≥ 30) Hai phía
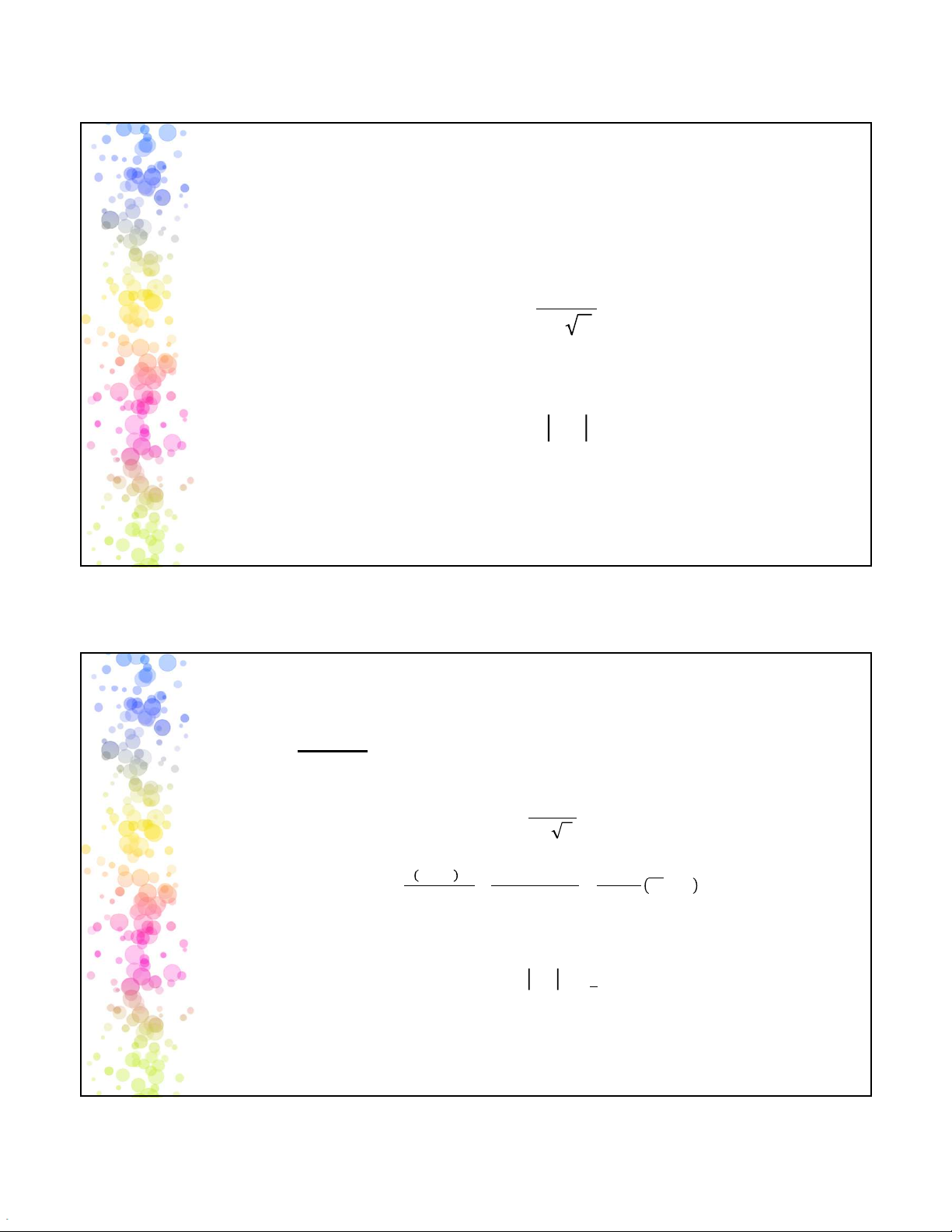
𝑥 − 𝑧/ ≤ 𝜇 ≤ 𝑥 + 𝑧/   Vế phải
𝑥 − 𝑧 ≤ 𝜇 ≤ ∞ Vế trái
−∞ ≤ 𝜇 ≤ 𝑥 + 𝑧 
Với 𝑧là hệ số tin cậy (giá trị tới hạn mức của phân phối chuẩn hóa) 14 7 2025-05-12
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA
Ước lượng số bình quân Với mức ý nghĩa 
(1 - ) là xác suất hay trình độ tin cậy
Khi chưa biết phương sai Tổng thể chung và mẫu nhỏ Hai phía 𝑥 − 𝑡    
/ ≤ 𝜇 ≤ 𝑥 + 𝑡/  Vế phải 𝑥 − 𝑡    ≤ 𝜇 ≤ ∞ Vế trái
−∞ ≤ 𝜇 ≤ 𝑥 + 𝑡    
Với 𝑡là hệ số tin cậy (giá trị tới hạn mức của phân phối Student với n-1 bậc tự do) 15
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA
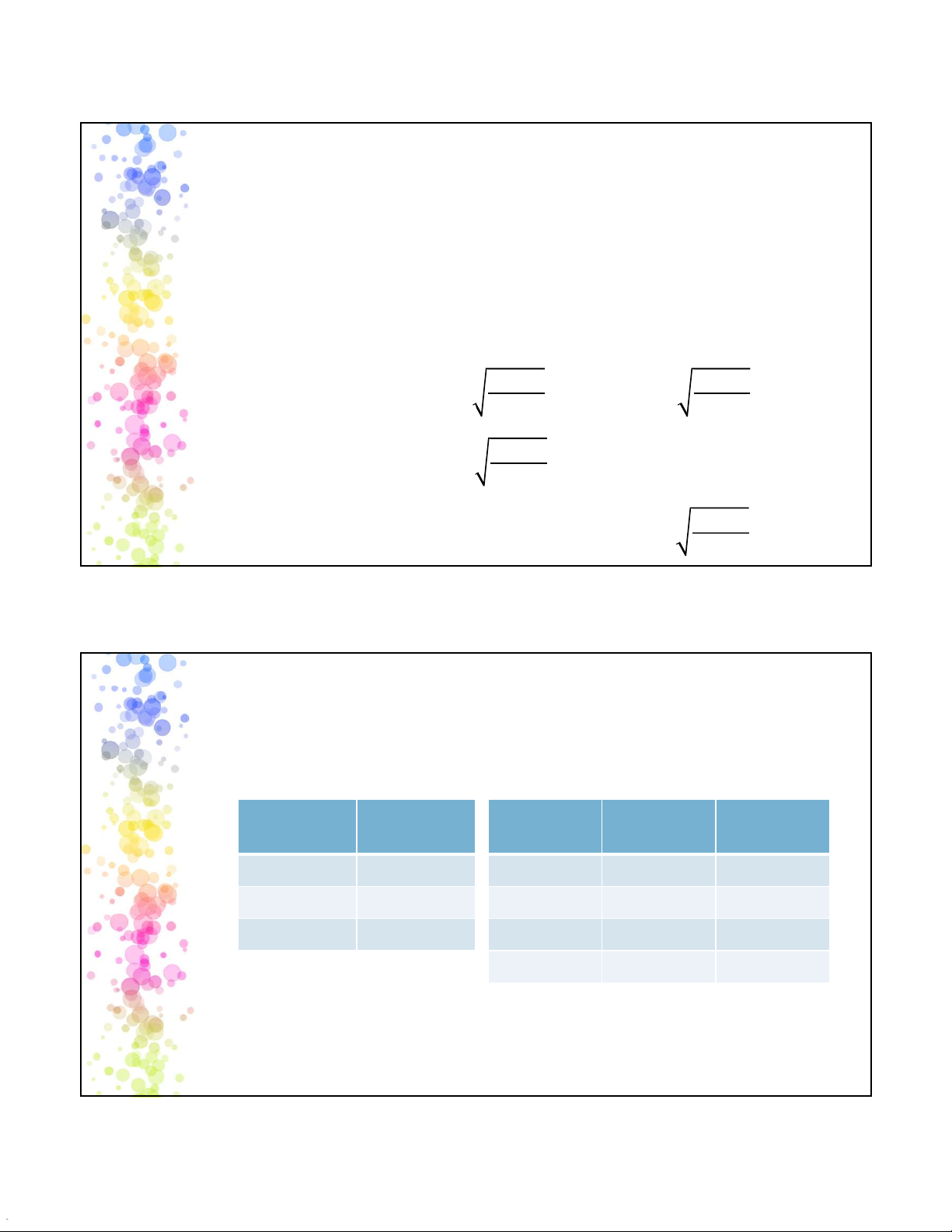
Tính chất của phân phối t: - Là phân phối liên tục -
Có dạng hình chuông và đối xứng -
Phân phối trải rộng hơn so với phân phối chuẩn hóa -
Có nhiều phân phối t có trung bình bằng 0 nhưng độ lệch chuẩn khác nhau (phụ thuộc vào n). 16 8 2025-05-12
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA Ước lượng số tỷ lệ Với mức ý nghĩa 
Với độ tin cậy (1 – α)
cỡ mẫu đủ lớn [ n 𝜋 ≥ 5 và n(1- 𝜋) ≥ 5 ] Hai phía
𝜋 − 𝑧/ ()≤ 𝑝 ≤π+𝑧/ ()  Vế phải
𝜇 − 𝑧()≤ 𝑝 ≤ ∞ Vế trái
−∞ ≤ 𝑝 ≤ 𝜋 + 𝑧 ()   17
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA (6)
Một số giá trị đặc biệt của phân phối chuẩn hóa 𝒁 Xác suất / Xác suất Mức ý 𝒁/ tin cậy tin cậy nghĩa 1 0.6828 0.900 0.100 1.645 2 0.9544 0.950 0.050 1.960 3 0.9973 0.975 0.025 2.326 0.990 0.010 2.576
𝜎 , 𝜎 được gọi là Sai số bình quân chọn mẫu 18 9 2025-05-12
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA (7)
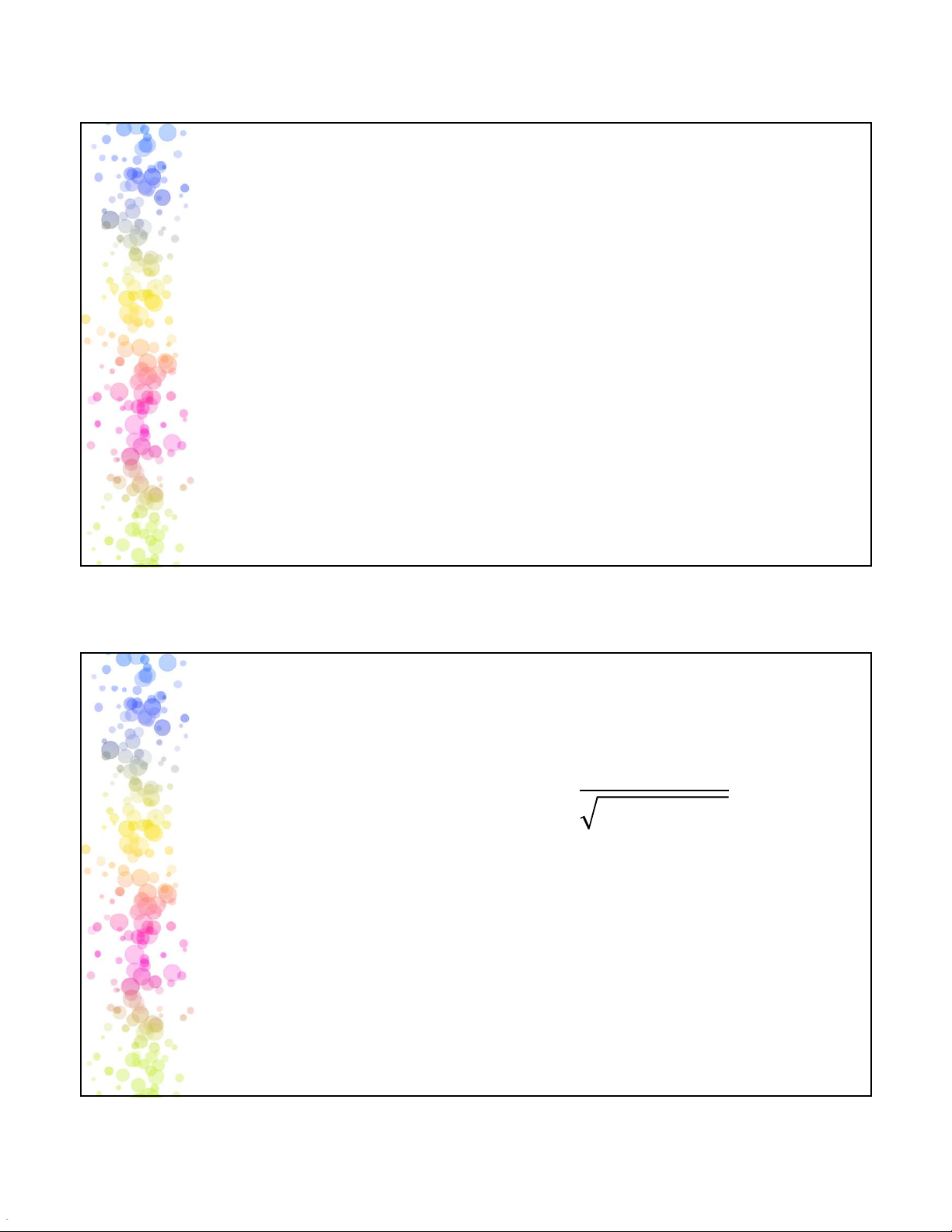
Sai số bình quân chọn mẫu Cách chọn Hoàn lại Không hoàn lại – tổng thể vô hạn – tổng thể hữu hạn Suy rộng (chọn nhiều lần) (chọn một lần) =𝜎  =𝜎  𝑛(𝑁 − 𝑛 Số bình 𝜎 𝑛 𝜎 𝑁 − 1) quân =𝑆  =𝑆  𝑛(𝑁 − 𝑛 𝜎 𝜎 𝑁 − 1) 𝑛  Tỷ lệ =𝑓(1 − 𝑓)
=𝑓 1 − 𝑓𝑛(𝑁 − 𝑛 𝜎 𝜎 𝑁 − 1) 𝑛  19
3. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA (7)
Xác định số đơn vị mẫu điều tra Yêu cầu: + Sai số nhỏ nhất + Chi phí thấp nhất Cách xác định Cách chọn Công thức Suy rộng 𝑛 = 𝑧/𝜎 Bình quân 𝜀
𝑛 = 𝑧 𝑝(1 − 𝑝) Tỷ lệ / 𝜀 20 10 2025-05-12
2. ƯỚC LƯỢNG KẾT QUẢ ĐIỀU TRA (7)
Xác định số đơn vị mẫu điều tra
Các nhân tố tác động tới kích thước mẫu điều tra + Hệ số tin cậy (z)
+ Phương sai của TTC (2)
+ Phạm vi SSCM cho phép ()
Một số phương pháp xác định phương sai TTC 2
+ Lấy 2 lớn nhất trong các lần điều tra trước hoặc p gần 0.5 nhất
+ Lấy phương sai của các cuộc điều tra khác có tính chất tương tự
+ Điều tra thí điểm để xác định phương sai
+ Ước lượng phương sai nhờ khoảng biến thiên R x  max x min    6 6
Lưu ý: khi mẫu đủ lớn (n > 30) thì có thể coi 𝜎  = 𝑆 21 NỘI DUNG CHÍNH 1. Những vấn đề chung
2. Ước lượng kết quả Điều tra chọn mẫu
3. Kiểm định giả thuyết thống kê 22 11 2025-05-12
3. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
3.1. Một số vấn đề chung
Giả thuyết thống kê là giả thuyết về một tham số của tổng thể chung
Kiểm định giả thuyết là quy trình dựa trên dữ liệu mẫu và lý thuyết xác
suất để xác định giả thuyết đưa ra có hợp lý không
Bước 1 Bước 2 Bước 3 Bước 4 Bước 5 Bước 6 Nêu giả Lựa chọn tiêu Xác định quy thuyết không Lựa chọn chuẩn kiểm tắc ra quyết Ra quyết định Nêu kết luận và giả thuyết mức ý nghĩa định định đối 23
Bước 1. Nêu giả thuyết không và giả thuyết đối
H0: là tuyên bố về giá trị của tham số tổng thể nhằm mục đích kiểm định
H1(hoặc Ha): là tuyên bố được chấp nhận nếu H0sai.
Chú ý: Giả thuyết đối (bao gồm các trường hợp còn lại mà không được đề cập tới trong H0) 24 12 2025-05-12
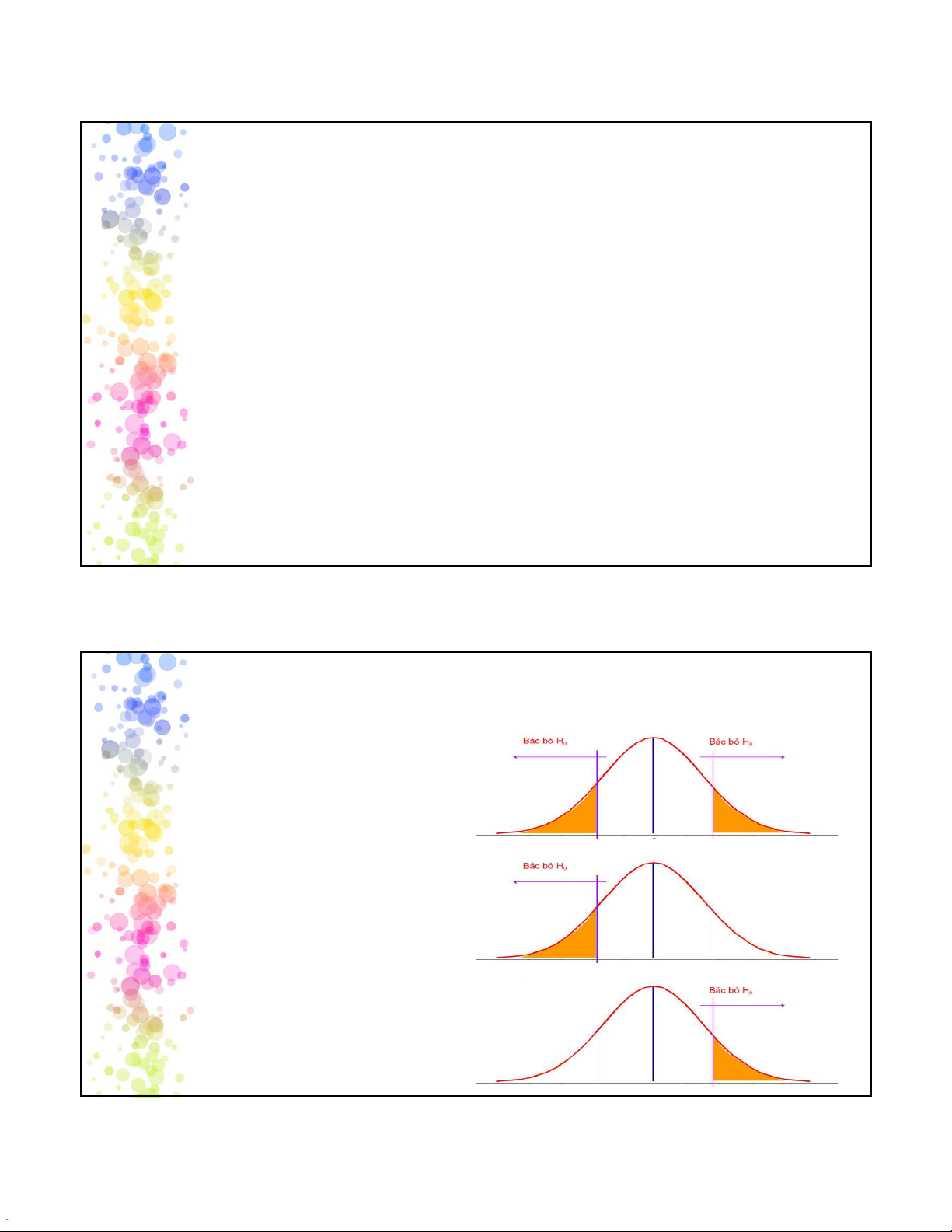
Bước 2. lựa chọn mức ý nghĩa
Sai lầm và mức ý nghĩa trong kiểm định Kết luận Chấp nhận H Bác bỏ H 0 0 Thực tế H Kết luận đúng Sai lầm loại I 0 đúng Mức ý nghĩa  H sai Sai lầm loại II Kết luận đúng 0 25
Bước 2. lựa chọn mức ý nghĩa
Xác định xác suất mắc sai lầm loại II (Ví dụ trang 338) 26 13 2025-05-12
Bước 3. Lựa chọn tiêu chuẩn Tiêu chuẩn kiểm định
Là quy luật phân phối xác suất được sử dụng để kiểm định giả thuyết
Lưu ý: trong tập hợp các kiểm định thống kê có cùng
mức ý nghĩa , kiểm định nào có xác suất mắc sai lầm
loại II nhỏ nhất được xem là tốt nhất. 27
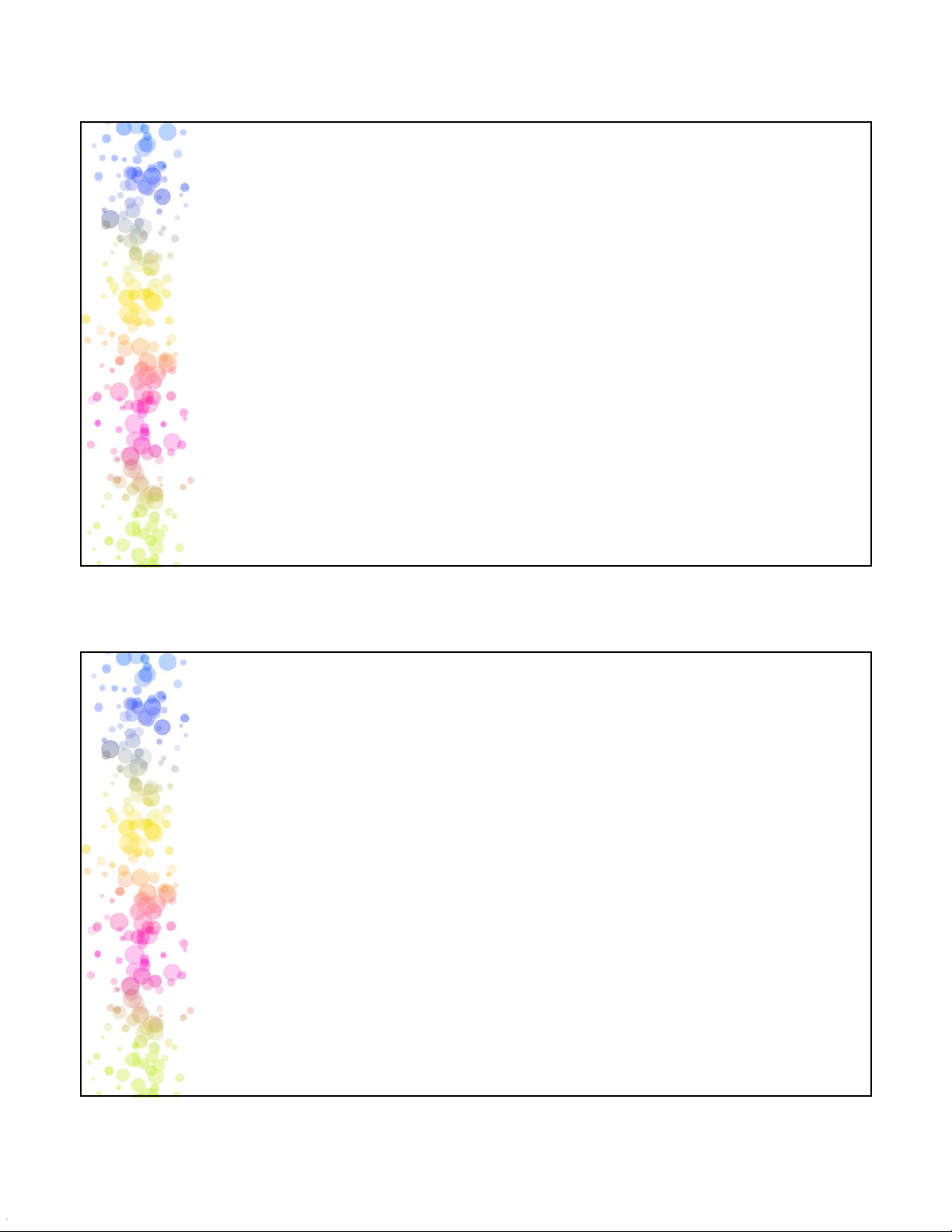
Bước 4. Xác định quy tắc ra quyết định Kiểm định hai phía H0:𝜇 = 𝜇  H1: 𝜇 ≠ 𝜇 Kiểm định phía trái H0:𝜇 ≥ 𝜇  H1: 𝜇 < 𝜇 Kiểm định phía phải H0:𝜇 ≤ 𝜇  H1: 𝜇 > 𝜇 28 14 2025-05-12
Bước 5 & 6. Ra quyết định và kết luận
Quy tắc kiểm định giả thuyết thống kê
- Nếu giá trị tiêu chuẩn kiểm định thuộc miền bác bỏ
(𝑊)Có cơ sở để bác bỏ H 0
- Nếu giá trị tiêu chuẩn kiểm định không thuộc miền
bác bỏ (𝑊)Chưa đủ cơ sở để bác bỏ H 0 29
Bước 5 & 6. Ra quyết định và kết luận
Phương pháp tiếp cận P-value trong kiểm định giả thuyết thống kê
P-value là xác suất lớn nhất có thể bác bỏ giả thuyết H0
Nếu P-value <   Có cơ sở để bác bỏ giả thuyết H 0
Nếu P-value ≥   Chưa đủ cơ sở để bác bỏ giả thuyết H 0 30 15 2025-05-12
Bước 5 & 6. Ra quyết định và kết luận
Quy tắc ra quyết định dựa vào Khoảng tin cậy
Bác bỏ giả thuyết H khi  không thuộc khoảng tin 0 0
cậy (1 - ) của ước lượng giá trị trung bình 31
3.2. Kiểm định giá trị trung bình của 1 tổng thể
•Giả sử biến ngẫu nhiên 𝑋~𝑁(𝜇, 𝜎)
•Chưa biết 𝜇nhưng có cơ sở để giả định nó bằng 𝜇 (H : 𝜇 = 𝜇) 0
•Để kiểm định giả thuyết trên, lấy mẫu ngẫu nhiên n đơn
vị điều tra, từ đó tính toán các thống kê mẫu
•Tính toán tiêu chuẩn kiểm định 32 16 2025-05-12
3. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
Trường hợp đã biết phương sai của tổng thể Tiêu chuẩn kiểm định 𝑍 = 𝑥 − 𝜇 𝜎/ 𝑛
Nếu H đúng Thống kê Z sẽ tuân theo quy luật phân phối chuẩn hóa 0 Miền bác bỏ W - Kiểm định 2 phía: 𝑍 > 𝑧/ - Kiểm định phía phải: 𝑍 > 𝑧 - Kiểm định phía trái: 𝑍 < −𝑧 33
3. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ
Trường hợp chưa biết phương sai của tổng thể chung Tiêu chuẩn kiểm định 𝑇 = 𝑥 − 𝜇 𝑆/ 𝑛 Trong đó: =∑𝑥 − 1 =∑𝑥  − 1 =∑𝑓 𝑆  − 𝑥 𝑓
 𝑓 −∑𝑓  𝑥  ∑𝑓 − 1 𝑥  − 𝒙𝟐  ∑𝑓  ∑𝑓
Nếu H đúng Thống kê T sẽ tuân theo quy luật phân phối Student với bậc tự do là (n-1) 0 Miền bác bỏ W - Kiểm định 2 phía:
𝑇 > 𝑡,()  - Kiểm định phía phải:
𝑇 > 𝑡,() - Kiểm định phía trái:
𝑇 < −𝑡,() 34 17 2025-05-12
3.2. Kiểm định tỷ lệ của 1 tổng thể
•Tỷ lệ của tổng thể là p
•Chưa biết 𝑝nhưng có cơ sở để giả định nó bằng 𝑝 (H0: 𝑝 = 𝑝)
•Để kiểm định giả thuyết trên, lấy mẫu ngẫu nhiên n đơn
vị điều tra, từ đó tính toán các thống kê mẫu
•Tính toán tiêu chuẩn kiểm định 35
3.2. Kiểm định tỷ lệ của 1 tổng thể
Khi n đủ lớn (n.𝜋5 và n(1- 𝜋) 5) Tiêu chuẩn kiểm định 𝑍 = (𝜋 − 𝑝) 𝜋(1 − 𝜋)/𝑛
Nếu H đúng, Thống kê Z tuân theo quy luật phân phối chuẩn hóa 0 Miền bác bỏ W - Hai phía: Z  qs > z /2 - Vế phải: Z > z qs  - Vế trái: Z < -z qs  36 18 2025-05-12 ỨNG DỤNG SPSS
TRONG ƯỚC LƯỢNG VÀ KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 37 Ước lượng thống kê
Chọn Analyze > Descriptive Statistics > Explore …
Đưa các biến cần tính toán các tha m số sang Dependent List
Muốn phân tích theo biến nào đó th
ì đưa sang biến sang Factor List
Trong mục Display chọn Statistics hoặc Both 38 38 19 2025-05-12
Kiểm định giả thiết về giá trị trung bình của một tổng thể
Analyze > Compare Means > One-Sample T Test…
Đưa các biến cần kiểm định giá trị tru ng bình vào Test Variable(s)
Nhập giá trị cần kiểm định trung bình vào Test Value Nhấn Options... 39 39
Kiểm định giả thiết về giá trị trung bình của một tổng thể
Analyze > Compare Means > One-Sample T Test…
Nhập độ tin cậy của kiểm định vào Confidence Interval
Chỉ kiểm định đối với các quan sát có ý
nghĩa của biến chọn Exclude cases analysis by analysis
Chỉ kiểm định đối với các quan sát có đầy
đủ trong các biến chọn Exclude cases listwise (n như nhau) 40 40 20