Bài 6: Phân Tích Hồi Quy - Tương Quan môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Tóm tắt Baì 6
•Mối liên hệgiữa các hiện tượng
PHÂN TÍCH HỒI QUY-TƯƠNG QUAN •Phân tích tương quan •Phân tích hồi quy đơn •Phân tích hồi quy bội
•Thực hành với phần mềm thống kê 2 1 2
Mối liên hệgiữa các hiện tượng
Có mối liên hệgiữa mức lương và điểm thi kinh tế- xã hội
đầu vào Đại học không?
•Mẫu: 1,532 sv tốt nghiệp từNEU sau hai năm;
•Điểm thi đầu vào từ17,5 đến 29,5
•Mức lương từ1đến 35 tr đồng/tháng.
Source: fb Nguyễn Việt Cường 3 4 3 4
Liên hệhàm sốvà liên hệtương quan (1)
Liên hệhàm sốvà liên hệtương quan (2)
Liên hệtương quan: là mối liên hệkhông hoàn toàn
chặt chẽ. Sựthay đổi của hiện tượng này có thểlàm
Liên hệhàm số:
hiện tượng liên quan thay đổi theo nhưng không có
là mối liên hệhoàn toàn chặt chẽ. Sựthay đổi của
ảnh hưởng hoàn toàn quyếtđịnh (<100%).
hiện tượng này có tác dụng quyếtđịnh đến sựthay Ví dụ:
đổi của hiện tượng liên quan (100%) theo một tỷlệ xác định. –Chiều cao và tuổi
–Sốgiờtựhọc và điểm
Đặcđiểm: liên hệhàm sốkhông những được biểu
–Doanh thu và chi phí quảng cáo
hiệnởtổng thểmà còn được biểu hiện trên từng đơn
–Hai cổphiếu liên hệvới nhau nhưthếnào vịcá biệt
Đặcđiểm: liên hệtương quan không được biểu hiện
trên từng đơn vịcá biệt mà phải thông qua hiện tượng sốlớn. 5 6 1 Mục đích
•Chỉnghiên cứu mối liên hệgiữa hai biến
Phân tích tương quan (Correlation) 7 7 8 Công cụ
1. Hiệp phương sai (nhắc lại) •Biếnđịnh tính
•Cho phép đánh giá chiều hướng của mối liên hệ
- Bảng dữliệu chéo (đã họcở bài 2)
tương quan tuyến tính giữa hai biếnđịnh lượng X
- Kiểmđịnh Khi bình phương (không đề cậpở khóa học này) và Y.
- Hệsốtương quan hạng (không đề cậpở khóa học này) •Công thức: n •Biếnđịnh lượng ( X X  )(Y ) Y  ii
- Hiệp phương sai (đã họcở bài 3) i 1 cov(X , ) Y   n 1
- Hệsốtương quan (đã họcở bài 3) 1 n 
-Đồ thịphân tán (đồ thịcác chấmđiểm / Scatterplot)  X Y nXY  n 1 i i  i1
•Đánh giá mứcđộ: KHÓ 9 10
2. Hệsốtương quan Pearson (nhắc lại)
Giảthiết của hệsốtương quan Pearson
•Cho phép đánh giá được cả mức độ và chiều
hướng của mối liên hệ tương quan tuyến tính. •Liên hệ tuyến tính.
•Công thức tính cho tổng thể và mẫu: •Phân phối chuẩn •Phương sai đồng nhất COV( X, ) Y cov( , X )   , Y rs s X Y X Y 11 12 2
Giá trị của hệ số tương quan 3. Đồ thịphân tán
Cho phép đánh giá dạng, chiều hướng, và mứcđộ của mối liên hệtương quan.
•Nếu r=-1, liên hệhàm sốvà là mối liên hệnghịch
Ví dụ:Đồ thịphân tán mô tảmối liên hệgiữa thời gian
•Nếu r=+1, liên hệhàm sốvà là mối liên hệthuận
sống tại thành phốvà tình cảm yêu mếnđối với thành
•Nếu r => +/- 1, mối liên hệtương quan càng chặt chẽ
phốđó => Mối liên hệtuyến tính
•Nếu r=0 => không có mối liên hệtương quan TUYẾN TÍNH
S c a tt e r p l o t o f A t t i tu d e T o w a r ds C i t y v s D u r a t i o n o f R e s id e n c e 1 1 1 0 9 8 7 6 5 4 At titude Towards City 3 2 0 5 1 0 1 5 2 0
D ur a t io n o f R e s id e nc e 14 13 14 Các dạng liên hệ
Liên hệ tương quan thuận
Liên hệ tương quan nghịch
Phân tích hồi quy (Regression)
Liên hệ phi tuyến tính
Không có mối liên hệ 15 16 15 16
Ý nghĩa của phân tích hồi quy
Nguyên lý của phân tích hồi quy
•Đánh giá tác động của một hay nhiều biến
•Nêu giảthuyết kiểmđịnh: Căn cứvào mục tiêu
độc lập (X) đến một biến phụthuộc (Y)
nghiên cứu, lý thuyết vềkinh tếvà kinh doanh,
quan sát thực tế=> đưa ra các giảthuyết vềmối
Kiểmđịnh các giảthuyết vềmối quan hệphụ liên hệ thuộc giữa các biến
Lưu ý: Mọi mô hình hồi quy phảiđược xây dựng từ cơsởlý thuyết
Thực hiện dựđoán giá trịcủa biến phụthuộc khi biết biếnđộc lập •Thiết lập mô hình •Ước lượng tham số
•Đánh giá và kiểmđịnh mô hình •Diễn giải kết quả Dựđoán Ra quyếtđịnh
TS. Trần Thị Bích - Khoa Thống kê 17
TS. Trần Thị Bích - Khoa Thống kê 18 17 18 3 Các dạng liên hệ I. Hồi quy đơn
•Liên hệtuyến tính và phi tuyến tính
•Phân tích mối liên hệgiữa 2 biếnđịnh lượng:
•Liên hệtuyến tính giữa 2 biến và liên hệtuyến tính
–Một biến phụthuộc Y là biếnđịnh lượng giữa nhiều biến.
–Một biếnđộc lập X cũng là biếnđịnh lượng
Hồi quy cho phép phân tích mối liên hệnày:
Chủyếu xét dạng liên hệtuyến tính - Phân tích hồi quy đơn - Phân tích hồi quy bội 19 20 19 20
Các bước trong phân tích hồi quy
Hồi quy tuyến tính đơn: khái niệm
1. Xác định bản chất của mối liên hệ.
2. Biểu diễn mối liên hệbằng đồ thị
•Một biến độc lập
3. Xây dựng mô hình hồi quy biểu diễn mối liên hệ •Có nquan sát
4. Ước lượng và giải thích ý nghĩa của các tham số •X
= giá trị của biến độc lập của quan sát thứ ith i của mô hình
•Y = giá trị của biến phụ thuộc của quan sát thứ i ith 5. Kiểmđịnh mô hình •s
= S.D của biến độc lập (tính trên mẫu) x
6. Đánh giá sựphù hợp của mô hình hồi quy •s
= S.D của biến phụ thuộc (tính trên mẫu) y
7. Suy diễn và dựđoán thống kê
•giá trị trung bình của biến phụ thuộc Y •g X
iá trị trung bình của biến độc lập 21 22 21 22
Bước 1: Phân tích bản chất của mối liên hệ Ví dụ 1
•Biến nào tác động đến biến nào? thay đổi của biến
•Phân tích mối liên hệgiữa thời gian sống tại thành
độc lập (X) sẽdẫnđến sựthay đổi của biến phụ
phốvà tình cảm yêu mếnđối với TP đó. thuộc (Y) ra sao?
Tình cảm của bạnđối với thành phốmà bạnđang sống, đo
Có chiều tác động ngược lại không?
theo thang điểm từ1-11 (1=không thích tí nào, 11= rất thích). -
VD: thay đổi chi phí quảng cáo sẽdẫnđến thay đổi về
doanh sốbán? Có chiều ngược lại không?
Muốn tìm hiểu xem thời gian bạn sống ở thành phố(tính
bằng năm) ảnh hưởng thếnào đến tình cảm của bạn.
Hai biến có thực sựcó mối liên hệkhông? (lý
Sốliệu: thu thập trên mẫu 12 người. thuyết và thực nghiệm) -
VD: mối liên hệgiữa doanh sốbán kính râm và doanh sốbán kem. 23 24 23 24 4 Dữ liệu
Bước 2: Vẽđồthịphân tán STT Thời gian sống ở Chất lượng Tình cảm đối thành phố CSHT với thành phố
•Ví dụ – Tình cảm đối với thành phố và thời gian sống 1 10 3 6 2 12 11 9 3 12 4 8
Scatterplot of Attitude Towards City vs Duration of Residence 11 4 4 1 3 10 5 12 11 10 9 6 6 1 4 8 7 7 8 7 5 6 8 2 4 2 5 Attitude Towards City 9 18 8 11 4 3 10 9 10 9 2 11 17 8 10 0 5 10 15 20 Duration of Residence 12 2 5 2 25 26 25 26
Mô hình hóa liên hệtương quan bằng liên hệhàm số
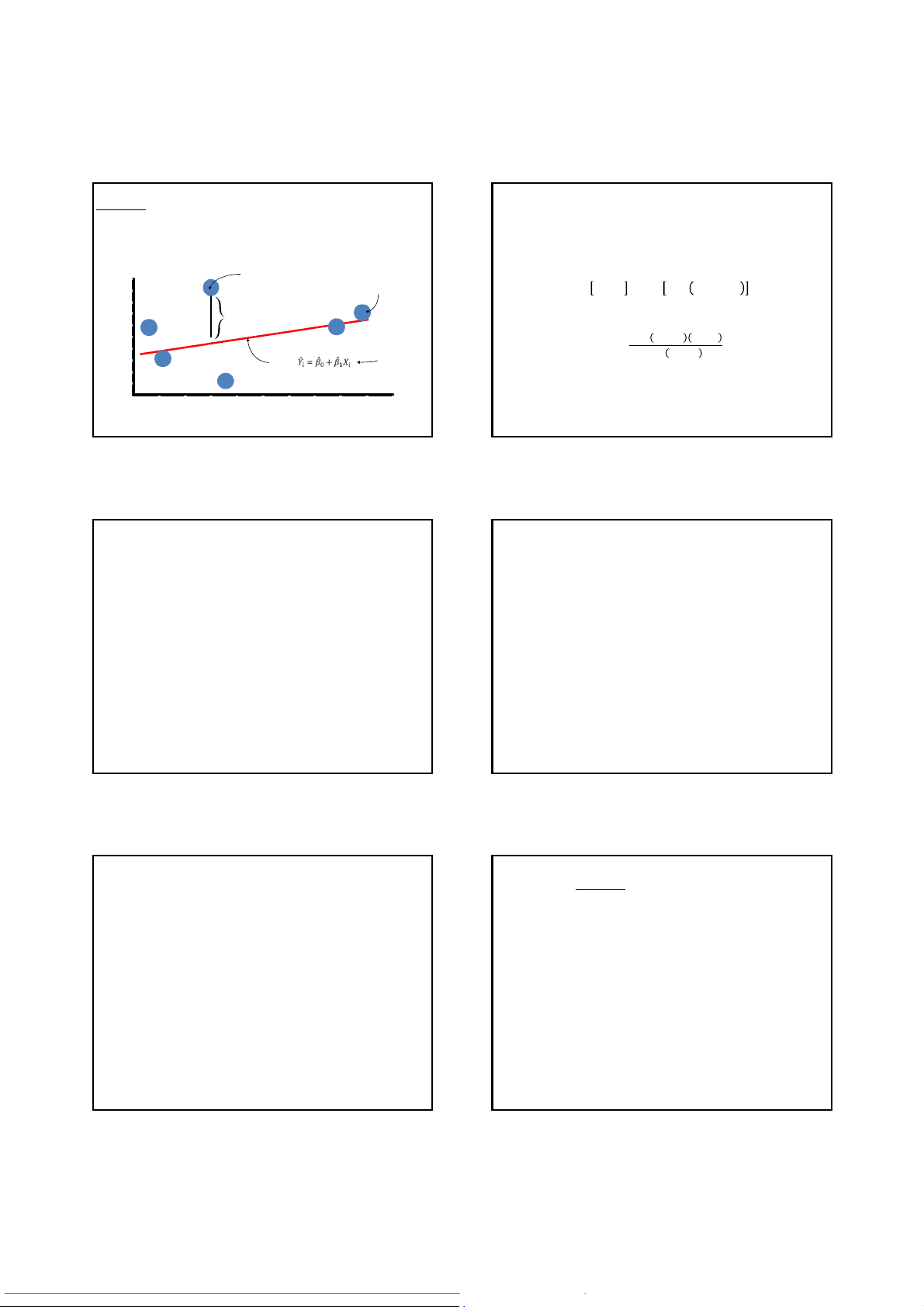
Đường hồi quy và sai sốcủa mô hình
•Tìm mộtđường hồi quy phản ánh mối liên hệgiữa thời gian sống
tại TP và tình cảm yêu mếnđối với thành phố.
•Đường thẳng liên kết mối liên hệgiữa thời gian
sống ở thành phốvà tình cảmđối với thành phố
=> Mỗi giá trịcủaXcho 1 giá trịduy nhấtcủaY
•Trên thực tế, mỗi giá củaXcho nhiều giá trịcủa
Y. Điều này là do có sai sốhay ‘nhiễu’
•Sai sốhay ‘nhiễu’phản ánh chênh lệch giữa giá
trịthực tếcủa y và giá trịtính toán được dựa vào
phương trình hồi quy. Vềmặt thống kê, sai sốđại
biểu cho việcđưa thiếu các biến vào mô hình và sai sốdo ghi chép 27 28 27 28
Bước 3: Xây dựng mô hình hồi quy
Đường hồi quy tốt nhất
•VD vềmối liên hệgiữa thời gian sống tại TP và tình cảm yêu
•Việc đặt đường thẳng xuyên qua các chấm điểm
mếnđối với thành phố.
tương đương với việc xây dựng mô hình hồi quy dưới đây: Hệ số tự do Sai số mô hình Y X      i 0 1 i i Hệ số góc
Hệ số tự do và hệ số góc được ước lượng bằng
phương pháp bình phương nhỏ nhất (OLS). 29 30 29 30 5
Bước 4: Ước lượng MHHQ - Phương pháp OLS OLS: vềmặt toán học 2  Muốn:  i min Y
Cần tìm 𝛽󰆹 và 𝛽󰆹 sao cho
Y     X  Giá trị    i 0 1 i i quan sát
𝑢  𝑌  𝑌  𝑌   𝛽󰆹 𝛽󰆹𝑋  𝑚𝑖𝑛     i = sai số Kết quả: ∑𝑋 𝑋𝑌 𝑌 𝛽󰆹    PTHQ  ∑𝑋 𝑋    mẫu
𝛽󰆹 𝑌𝛽󰆹 𝑋   X 31 32 31 32 Áp dụng cho ví dụ 1 Lưu ý vềphương pháp OLS •Hệ số góc = 16.333/27.697
 Hệsốcủa phương trình hồi mẫuđược giải hoàn = 0.5897 toàn bằng toán học
•Hệ số tự do = 6.5833-0.5897*9.333
 Hai biến không có ý nghĩa vềmặt kinh tếvẫn =1.0796 cho ra PTHQ tốt. •Phương trình hồi quy:
 Các sai sốKHÔNG quan sát được nên có thể
tìm được rất nhiều giá trịcho beta để phương ˆ1.0796 0.5897 *  Y X trình thỏa mãn. i i  Giảthiết của OLS 33 34 33 34 Giảthiết của OLS
Bước 4: Giải thích kết quả •= 0.ˆ5
 897 nêu ảnh hưởng trực tiếp của thời gian 1
sống tại thành phốđối với tình cảm yêu mến thành phố.
 Các sai sốtuân theo quy luật phân phối chuẩn
Nếu thời gian sống ở thành phốtăng thêm 1 năm thì
 Các sai sốcó kỳvọng bằng 0 và phương sai không đổi
tình cảm yêu mếnđối với thành phốsẽtăng trung bình
 Các sai sốđộc lập với nhau là 0.5897 điểm
 Các biếnđộc lập là ngoại sinh. Tức là: Cov (X , )  0  •= 1.07 ˆ
 96 (là giá trịcủa Y tại X=0) nêu ảnh hưởng 0
của các nhân tốkhác ngoài thời gian sống tại thành phố
đến tình cảm yêu mếnđối với thành phố.
•Lưu ý: trong một sốtrường hợp kˆ  hông giải thích 0
được khi X=0. Khi đó chúng ta không giải thích ý nghĩa của hệsốnày 35 36 35 36 6 Bước 5: Kiểmđịnh Áp dụng cho ví dụ 1 •Phươngtr  ình hồi quy ˆ1.0796 0.5897 * •H =0 i Y iX 0:β1
tính được trên cơsởsốliệu của mẫu • H 1:β1 ≠0
•Cần kiểmđịnh xem liệu có tồn tại mối liên hệtương quan
• Tiêu chuẩn kiểm định:
tuyến tính cho toàn bộtổng thểkhông ˆ0.5897 0 8.412  1 1 ts  0.0701 ˆ1 
•Do đó chúng ta bác bỏ giả thiết H 0 vì t>2.2281 với mức ý
nghĩa 5% (bậc tự do df=10)
•Hoặc từ SPSS, p_value=0.000 nên bác bỏ H và kết luận có 0
tồn tại mối liên hệ tương quan tuyến tính giữa thời gian sống
tại thành phố và tình cảm yêu mến thành phố 37 38
Bước 6: Đánh giá sựphù hợp của mô hình hồi quy 1. Hệsốxác định
•Nhằmđánh giá khảnăng dựđoán của mô hình hồi quy
•Hệsốnày đượcđo bởi tỉlệgiữa phần biến thiên được giải
thích bởi X và biến thiên toàn bộY => đánh giá mứcđộ chặt
•Cần sửdụng hai tham số:
chẽvà sựphù hợp của MH
–Hệsốxác định: đánh giá sựphù hợp của mô hình hồi quy. Hệ
•Dao động trong mẫu của biến phụthuộc Y (Total sum of
sốxác định càng gần 100%, sựphù hợp của MH càng lớn và Squares):
giá trịdựđoán càng chính xác. •𝑆𝑆𝑇  ∑𝑌    𝑌 
–Sai sốchuẩn củaước lượng (Sxy hoặc Se): Sai sốchuẩn của
•Tổng bình phương các phần dư(Sum of Squares of Errors)
ước lượng đánh giá độ phân tán của các giá trịquan sát của Y
xung quanh đường hồi quy tại một giá trịcụthểcủa X. Se •𝑆𝑆𝐸  ∑𝑌  𝑌  
càng nhỏ,đường hồi quy càng gần với dữliệu và MHHQ có
•Biến thiên của hồi quy (Sum of Squares of Regression)
thểsửdụng để dựđoán. •𝑆𝑆𝑅  ∑𝑌  𝑌   
•SST=SSE+SSR =>SSR=SST-SSE 39 40 39 40
Hệsốxác định: minh họa
Hệsốxác định: công thức •𝑅
   1   
•Có thểđược tính theo công thức khác: 2      2 n X Y X Y r   
 n  X     2 2 2 2 X * n Y Y       41 42 41 42 7 Áp dụng cho ví dụ 1 Hệ số tương quan r 2 •𝑅 𝑅  = 87.6% •𝑅𝛽 󰆹
•Có nghĩa là có đến 87.6% sự thay đổi của Yđược 
giải thích bởi sự thay đổi của X 43 44 43 44
2. Sai sốchuẩn củaước lượng
Sai sốchuẩn củaước lượng: minh họa
•S  hoặc S được tính theo công thức dướiđây: S S  MSE
Với MSE là Mean of Sum of Squares of Errors và được tính nhưsau: MSE SSE n2 46 45 46
Khoảng tin cậy của hệsốhồi quy
Bước 7: Suy diễn và dựđoán thống kê
•KTC 2 phía cho hệsốhồi quy
•Bài toán 1: Xây dựng khoảng tin cậy 𝛽󰆹 𝑡
𝑆𝑒 𝛽󰆹 𝛽 𝛽󰆹 𝑡 𝑆𝑒 𝛽󰆹        (KTC) cho hệsốhồi quy , ,
•Diễn giải: Vớiđộ tin cậy là 1 , khi biếnXtăng 1
•Bài toán 2: Dựđoán giá trịcủa Y
đơn vịthì trung bình Y tăng trong khoảng này
•KTC để ước lượng GTLN cho hệsốhồi quy
∞;𝛽󰆹 𝑡, 𝑆𝑒 𝛽󰆹
•KTC để ước lượng GTNN cho hệsốhồi quy 𝛽󰆹 𝑡 𝑆𝑒 𝛽󰆹  ,  ; ∞
TS. Trần Thị Bích - Khoa Thống kê 47 48 47 48 8 Dựđoán giá trịcủa Y
Lưu ý: Chỉthực hiện nội suy. Tức là dựđoán giá trịcủa
Y tại các giá trịX nằm trong phạm vi dữliệu mẫuđã j Áp dụng vào ví dụ1
cho. Điều này là do mối liên hệgiữa X và Y với các giá
trịX nằm ngoài khoảng giá trịđã cho có thểcó dạng khác.
•Dựđoán điểm: thay giá trịX vào PTHQ mẫu •Dựđoán khoảng:
- Khoảng giá trịcá biệt của Y tại một giá trịcủa X
- Khoảng giá trịtrung bình của Y tại một giá trịcủa X
TS. Trần Thị Bích - Khoa Thống kê 49 50 49 50
Dựđoán giá trịcá biệt của Y tại một
Dựđoán giá trịTB của Y tại một giá giá trịcụthểcủa X trịcụthểcủa X
•Dựđoán giá trịcủa Y cho một quan sát nhận một giá trị
•Dựđoán giá trịcủa Y cho tất cảcác quan sát nhận một giá cụthểcủaX: X X trịcụthểcủa X: X X j 0 j 0 𝑌 𝑡
𝑆 𝑌𝑌  𝑡 𝑆    𝑌 𝑆𝑒 𝑌 𝑆𝑒󰇛𝑌 ,   ,   𝑡 
 𝑌  𝑌 𝑡 󰇜 , , 𝑆
𝑆𝐸  𝑆𝑒󰇛𝑌  󰇜 𝑛󰇛𝑋 𝑋󰇜   𝑆𝑒 𝑌 𝑆𝐸  1   𝑛1𝑆𝑒󰇛𝑋󰇜
•SE: Sai sốchuẩn của UL; n: cỡmẫu, X ạ 0 là giá trịcủa X t i
đó dựđoán giá trịTB của Y 51 52 51 52 II. Hồi quy bội •Dữliệu: –Một biến phụthuộc
Thực hành với phần mềm thống kê
–Hai hoặc nhiều biếnđộc lập
•Ví dụ:Thu nhập phụthuộc vào trình độ học vấn,
thâm niên công tác, giới tính, ....
•Lưu ý khi phân tích hồi quy bội: sốlượng biến phải ít hơn sốquan sát
•Nguyên lý phân tích tương tựhồi quy đơn
TS. Trần Thị Bích - Khoa Thống kê 53 54 53 54 9
Tại sao phải sửdụng mô hình hồi quy bội?
Mô hình hồi quy bội – dạng tổng quát •Mô hình:
Y    X  X   X u 0 1 1 2 2  k k
•đượcước lượng bởi:
•Mô hình hồi quy đơn thường vi phạm giảthiết Cov (X , ) 0  ˆk k ˆ ˆ  ˆ ˆ Y     X  X  X 0 1 1 2 2
 Các ưu việt khác của mô hình hồi quy bội
–Cung cấp thêm thông tin nên làm gia tăng chất lượng dựbáo
•Tương tựnhưhồi quy đơn, phương trình hồi quy được
–So sánh tác động của các yếu tố
ước lượng bằng phương pháp bình phương nhỏnhất
–Cho phép sửdụng dạng hàm phong phú hơn
•là hệsốhồi quy bội hay hệsốhồi quy riêng phần thể
hiện tác động của biến X
lên giá trịtrung bình của Y k
trong điều kiện các biến X khác trong mô hình không thay đổi 55 56 55 56 Ví dụ2 Mô hình hồi quy bội
•Tình cảm yêu mếnđối với thành phốgiờ
được giải thích bởi hai nhân tố:
•Y= tình cảm yêu mếnđối với TP - Thời gian sống tại TP •X = Thời gian sống tại TP 1
- Chất lượng cơsởhạtầng •X
= Chất lượng cơsởhạtầng 2 Y      X  X  0 1 1 2 2 57 58 57 58 Ước lượng bằng SPSS
Giải thích hệsốhồi quy bội
Attitude Towards City = 0.337 + 0.481 Duration of Residence
+ 0.289 quality of infrastructure
•Giải thích ý nghĩa của từng hệsốhồi quy bội (hay hệ Coefficientsa sốgóc). Unstandardized Standardized
•Lưu ý tác động của một biếnXtới Y phải dựa trên cơ Coefficients Coefficients B Std. Error Model Beta t Sig.
sởcác yếu tốcòn lại không thay đổi. 1 (Constant) .337 .567 .595 .567 •Áp dụng vào VD 2 duration .481 .059 .764 8.160 .000 quality .289 .086 .314 3.353 .008
a. Dependent Variable: attitude 59 60 59 60 10 Hệsốhồi quy chuẩn hóa
Đánh giá sựphù hợp của mô hình
Hệsốhồi quy chuẩn hóa: dùng để xác định vai trò tác
•Đánh giá độ phù hợp của mô hình
động của các biếnđộc lập tới biến phụthuộc trong mô hình hồi quy.
•Hệsốxác định: giống hồi quy đơn ỉ S
•Hệsốxác định hiệu ch nh Betab  S
R21(1R2)n1 Trong đó: n k
∑󰇛 󰇜   S∑󰇛  󰇜 S  62 61 62 Kiểmđịnh mô hình
1. Kiểmđịnh ý nghĩa thống kê của toàn bộMH
•Kiểmđịnh ý nghĩa thống kê của mô hình:
•H : β = β = β =…= β =0 0 1 2 3 k
1. Kiểmđịnh ý nghĩa thống kê của toàn bộmô hình
•H A: Có ít nhất MỘT hệsốgóc khác 0
2. Kiểmđịnh ý nghĩa thống kê của từng hệsốgóc •Sửdụng thống kê:
(tương tựnhưhồi quy đơn) 𝑆𝑆 Ú 𝑅 𝑘 𝑘 Ú1𝑅  𝑘 Ú 
Kiểmđịnh sựphù hợp của mô hình 𝐹 MSR MSE  𝑆𝑆 𝐸 𝑛
1𝑅 󰇜󰇛Ú𝑛𝑘1
•Nếu 𝐹𝐹 , , bác bỏH 0 . Tức là có một hoặc nhiều
hệsốgóc khác 0 => cần kiểmđịnh bước 2 để xem hệ
sốgóc nào có ý nghĩa thống kê 63 64 63 64
2. Kiểmđịnh ý nghĩa thống kê của từng hệsốgóc
Xây dựng KTC cho hệsốhồi quy bội •H : β =0 0 j
•KTC 2 phía cho hệsốhồi quy của biếnX j •H : β ≠0 A j
𝑡𝛽 󰆹 𝛽𝛽 󰆹   
•Tiêu chuẩn kiểmđịnh: 𝑆𝑒󰇛𝛽󰆹 𝑆𝑒󰇛𝛽󰆹  𝛽󰆹 𝑡  
,𝑆𝑒 𝛽󰆹 𝛽 𝛽󰆹 𝑡 ,𝑆𝑒 𝛽 󰆹
•Nguyên tắc ra quyếtđịnh: so với phân phối t với
•Diễn giải: Vớiđộ tin cậy là 1 , k  hi biếnX tăng 1
bậc tựdo (n-k-1) j
đơn vịvà trong điều kiện các yếu tốkhác không đổi •NếuH
bịbác bỏ=> hệsốgóc của biến thứj th 0
thì trung bình Y thay đổi trong khoảng này
khác 0. Có nghĩa là khi xem xét cảcác biến khác,
biếnđộc lập thứj th vẫn có mối liên hệtuyến tính
với biến phụthuộc và mối liên hệnày là có ý nghĩa thống kê. 65 66 65 66 11
Xây dựng KTC cho hệsốhồi quy bội
•KTC 2 phía cho hệsốhồi quy của biếnX j
𝛽󰆹 𝑡 ,𝑆𝑒 𝛽󰆹 𝛽 𝛽󰆹 𝑡 ,𝑆𝑒 𝛽󰆹
•Diễn giải: Vớiđộ tin cậy là 1 , khi biếnX tăng 1 j
đơn vịvà trong điều kiện các yếu tốkhác không đổi
thì trung bình Y thay đổi trong khoảng này 67 67 12